8 класс. Алгебра. Рациональные уравнения. Иррациональные уравнения. — Иррациональные уравнения.

Комментарии преподавателя

В ходе этого занятия мы узнаем об уравнениях, в которых переменная стоит под знаком квадратного или другого корня, такие уравнения называются иррациональными. Мы приведём пример иррациональных уравнений, а также научимся их правильно решать.

Тема: Квад­рат­ные урав­не­ния

Урок: Ир­ра­ци­о­наль­ные урав­не­ния

Для на­ча­ла нам необ­хо­ди­мо по­нять, что же такое ир­ра­ци­о­наль­ное урав­не­ние. Ир­ра­ци­о­наль­ны­ми на­зы­ва­ют­ся такие урав­не­ния, в ко­то­рых пе­ре­мен­ная стоит под зна­ком корня. При­ве­дём при­ме­ры ир­ра­ци­о­наль­ных урав­не­ний:

Те­перь решим вы­ше­при­ве­ден­ные урав­не­ния.

Нам необ­хо­ди­мо воз­ве­сти обе части урав­не­ния в квад­рат, чтобы из­ба­вить­ся от знака корня.

Таким об­ра­зом мы видим, что, решая ир­ра­ци­о­наль­ные урав­не­ния, нам необ­хо­ди­мо все­гда де­лать про­вер­ку по­лу­чен­ных кор­ней. Для того чтобы по­нять, по­че­му это про­ис­хо­дит, да­вай­те решим ещё один при­мер.

Ре­ша­ем по уже из­вест­ной нам схеме и воз­во­дим обе части в квад­рат.

Не за­бы­ва­ем, что мы ре­ши­ли квад­рат­ное урав­не­ние и нашли его корни, а не корни ис­ход­но­го ир­ра­ци­о­наль­но­го урав­не­ния. Чтобы про­ве­рить, под­хо­дят ли они нам, де­ла­ем про­вер­ку.

Про­вер­ка:

Мы видим, что ра­вен­ство по­лу­чи­лось невер­ное, зна­чит,  – не ко­рень ис­ход­но­го ир­ра­ци­о­наль­но­го урав­не­ния.

Видим, что ра­вен­ство по­лу­чи­лось вер­ное, по­это­му  – ко­рень ис­ход­но­го урав­не­ния.

Ответ: 

Те­перь вер­нём­ся к на­ше­му во­про­су, по­че­му же необ­хо­ди­мо про­ве­рять корни.

Для этого рас­смот­рим один не боль­шой, но на­гляд­ный при­мер:

Од­на­ко если мы обе части воз­ве­дём в квад­рат, то по­лу­чим:

Т. е. мы из невер­но­го нера­вен­ства по­лу­чи­ли вер­ное: если после воз­ве­де­ния в квад­рат числа равны, это не зна­чит, что ис­ход­ные числа тоже равны (имен­но по­это­му корни урав­не­ний необ­хо­ди­мо про­ве­рять).

Рас­смот­рим необ­хо­ди­мость про­вер­ки кор­ней с дру­гой сто­ро­ны:

Пусть мы имеем ир­ра­ци­о­наль­ное урав­не­ние, где . Ре­ша­ем его так же, как и преды­ду­щие при­ме­ры, т. е. воз­во­дим обе части в квад­рат . Далее пред­по­ло­жим, что мы ре­ши­ли это урав­не­ние и по­лу­чи­ли корни.

От­ку­да же бе­рут­ся по­сто­рон­ние корни?  

По­лу­чен­ное урав­не­ние будет пра­виль­ным тогда и толь­ко тогда, когда хотя бы одна из

ско­бок равна 0, т. е. => . По­смот­рим на всё ре­ше­ние: нам необ­хо­ди­мо было ре­шить ис­ход­ное урав­не­ние , мы его ре­ши­ли и нашли, что , од­на­ко вме­сте с этим мы также по­лу­чи­ли ре­ше­ние , ко­то­рое не яв­ля­ет­ся ре­ше­ни­ем, имен­но по­это­му при ре­ше­нии ир­ра­ци­о­наль­ных урав­не­ний мы де­ла­ем про­вер­ку, чтобы по­нять какой из кор­ней яв­ля­ет­ся непо­сред­ствен­но ре­ше­ни­ем на­ше­го ис­ход­но­го урав­не­ния. Таким об­ра­зом мы можем сде­лать сле­ду­ю­щий вывод: из ра­вен­ства квад­ра­тов не сле­ду­ет ра­вен­ство ар­гу­мен­тов, од­на­ко из ра­вен­ства ар­гу­мен­тов сле­ду­ет ра­вен­ство квад­ра­тов.

 => 

Про­вер­ка

Мы знаем, что квад­рат­ный ко­рень – ве­ли­чи­на неот­ри­ца­тель­ная, по­это­му не будем вы­чис­лять зна­че­ние под его зна­ком, а про­сто ска­жем, что . Тогда, по опре­де­ле­нию квад­рат­но­го корня, также такое нера­вен­ство долж­но вы­пол­нять­ся  . Те­перь под­ста­вим по­лу­чен­ное нами пер­вое зна­че­ние :  – это нера­вен­ство невер­но, по­это­му можем сразу ска­зать, что  не яв­ля­ет­ся кор­нем ис­ход­но­го ир­ра­ци­о­наль­но­го урав­не­ния.

Сде­ла­ем ана­ло­гич­но со вто­рым кор­нем:  :  невер­ное нера­вен­ство, по­это­му ко­рень  также не яв­ля­ет­ся кор­нем ис­ход­но­го ир­ра­ци­о­наль­но­го квад­рат­но­го урав­не­ния.

Таким об­ра­зом по­лу­ча­ет­ся, что в дан­ном урав­не­нии нет кор­ней.

Ответ: кор­ней нет.

Глав­ная осо­бен­ность ре­ше­ния ир­ра­ци­о­наль­ных урав­не­ний: если мы воз­во­дим ир­ра­ци­о­наль­ное урав­не­ние в квад­рат, то  после на­хож­де­ния кор­ней вто­рич­но­го урав­не­ния мы обя­за­ны про­ве­рить, яв­ля­ют­ся ли эти корни кор­ня­ми ис­ход­но­го ир­ра­ци­о­наль­но­го урав­не­ния.

Итак, мы с вами на дан­ном уроке по­зна­ко­ми­лись с ир­ра­ци­о­наль­ны­ми квад­рат­ны­ми урав­не­ни­я­ми, по­зна­ко­ми­лись со спо­со­ба­ми ре­ше­ния про­стей­ших ир­ра­ци­о­наль­ных квад­рат­ных урав­не­ний. Вы­учи­ли, что неко­то­рые корни при ре­ше­нии могут ока­зать­ся невер­ны­ми, а для того чтобы из­бе­жать непра­виль­но­го от­ве­та, нам необ­хо­ди­мо все­гда после пол­но­го ре­ше­ния урав­не­ния де­лать про­вер­ку. Также мы объ­яс­ни­ли, по­че­му мы можем по­лу­чить невер­ные (по­сто­рон­ние) корни: из ра­вен­ства квад­ра­тов не сле­ду­ет ра­вен­ство ар­гу­мен­тов, од­на­ко из ра­вен­ства ар­гу­мен­тов сле­ду­ет ра­вен­ство квад­ра­тов.

И самое глав­ное: после ре­ше­ния ир­ра­ци­о­наль­но­го урав­не­ния все­гда необ­хо­ди­ма про­вер­ка кор­ней ме­то­дом их под­ста­нов­ки в ис­ход­ное урав­не­ние.

 Источник конспекта: http://interneturok.ru/ru/school/algebra/8-klass/kvadratnye-uravneniya-prodolzhenie/irratsionalnye-uravneniya?konspekt&chapter_id=16

Источник видео: http://www.youtube.com/watch?v=u0SAYndCm6A

Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень

Примеры решения иррациональных уравнений

Начнем с решения несложного и довольно типичного иррационального уравнения, возведение обеих частей которого в квадрат приводит к квадратному уравнению, не имеющему корней.

Вот пример, в котором все корни уравнения, полученного из исходного иррационального уравнения путем возведения его обеих частей в квадрат, оказываются посторонними для исходного уравнения. Вывод: оно не имеет корней.

Следующий пример чуть сложнее. Его решение, в отличие от двух предыдущих, требует возведения обеих частей уже не в квадрат, а в шестую степень, и это приведет уже не к линейному или квадратному уравнению, а к кубическому уравнению. Здесь проверка нам покажет, что все три его корня будут корнями иррационального уравнения, заданного изначально.

А здесь пойдем еще дальше. Для избавления от корня придется возводить обе части иррационального уравнения в четвертую степень, что в свою очередь приведет к уравнению четвертой степени. Проверка покажет, что лишь один из четырех потенциальных корней будет искомым корнем иррационального уравнения, а остальные будут посторонними.

Три последних примера являются иллюстрацией следующего утверждения: если при возведении обеих частей иррационального уравнения в одну и ту же четную степень получается уравнение, имеющее корни, то последующая их проверка может показать, что

• 
  либо все они являются посторонними корнями для исходного уравнения, и оно не имеет корней,
• 
  либо среди них вообще нет посторонних корней, и все они являются корнями исходного уравнения,
• 
  либо посторонними являются лишь некоторые из них.

Пришло время перейти к решению простейших иррациональных уравнений с нечетным показателем корня, то есть, уравнений . Здесь напомним, что при возведении обеих частей уравнения в одну и ту же нечетную степень не требуется проводить отсеивание посторонних корней.

Знание этого факта позволяет на законных основаниях не проводить отсеивание посторонних корней при решении иррационального уравнения . Тем более в данном случае проверка связана с «неприятными» вычислениями. Посторонних корней и так не будет, так как проводится возведение в нечетную степень, а именно в куб, что является равносильным преобразованием. Понятно, что проверку можно и выполнить, но больше для самоконтроля, чтобы дополнительно убедиться в правильности найденного решения.

Пример

Решить иррациональное уравнение методом возведения обеих частей в одну и ту же степень.

Смотреть решение

Теперь пришло время взглянуть на возведение в одну и ту же степень обеих частей уравнения с общих позиций. По сути, при решении иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень используется уже известный нам общий подход: исходное уравнение путем каких-либо преобразований преобразуется в более простое уравнение, оно преобразуется в еще более простое, и так далее, вплоть до уравнения, которое мы в состоянии решить. Понятно, что если в цепочке таких преобразований мы прибегаем к возведению обеих частей уравнения в одну и ту же степень, то можно сказать, что мы действуем по одноименному методу возведения обеих частей уравнения в одну и ту же степень. Остается лишь разобраться, какие именно преобразования и в какой последовательности нужно проводить для решения иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень.

Вот общий подход к решению иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень:

• 
  Во-первых, нужно перейти от исходного иррационального уравнения к более простому уравнению, чего обычно позволяет добиться циклическое выполнение следующих трех действий:
  • 
    Уединение радикала (или аналогичные приемы, например, уединение произведения радикалов, уединение дроби, числителем и/или знаменателем которой является корень, позволяющие при последующем возведении обеих частей уравнения в степень избавиться от корня).
  • 
    Возведение обеих частей уравнения в одну и ту же степень.
  • 
    Упрощение вида уравнения.

• 
  Во-вторых, нужно решить полученное уравнение.
• 
  Наконец, если в процессе решения были переходы к уравнениям-следствиям (в частности, если проводилось возведение обеих частей уравнения в четную степень), то нужно отсеять посторонние корни.

Решим пример, в котором уединение радикала приводит иррациональное уравнение к простейшему виду, после чего остается выполнить возведение обеих частей в квадрат, решить полученное уравнение и отсеять посторонние корни при помощи проверки.

Пример

Решить иррациональное уравнение , пользуясь возведением обеих частей в одну и ту же степень.

Смотреть решение

Следующее иррациональное уравнение может быть решено путем уединения дроби с радикалом в знаменателе, избавиться от которого позволяет последующее возведение в квадрат обеих частей уравнения. А дальше все просто: решается полученное дробно-рациональное уравнение и делается проверка, исключающая попадание в ответ посторонних корней.

Довольно характерными являются иррациональные уравнения, в записи которых присутствуют два корня. Они обычно с успехом решаются методом возведения обеих частей уравнения в одну и ту же степень. Если корни имеют одинаковую степень, и кроме них нет других слагаемых, то для избавления от радикалов достаточно уединить радикал и выполнить возведение в степень один раз, как в следующем примере.

Пример

Решите уравнение методом возведения обеих частей в одну и ту же степень.

Смотреть решение

А вот пример, в котором также два корня, помимо них также нет никаких слагаемых, но степени корней различны. В этом случае после уединения радикала целесообразно возводить обе части уравнения в степень, освобождающую от обоих радикалов сразу. В качестве такой степени выступает, например, наименьшее общее кратное (НОК) показателей корней. В нашем случае степени корней равны 2 и 3, НОК(2, 3)=6, поэтому, мы будем возводить обе части в шестую степень. Заметим, что можно действовать и по стандартному пути, но в этом случае нам придется дважды прибегать к возведению обеих частей в степень: сначала во вторую, затем в третью. Покажем оба способа решения.

В более сложных случаях, решая иррациональные уравнения методом возведения обеих частей уравнения в одну и ту же степень, к возведению в степень приходится прибегать два раза, реже – три раза, еще реже — большее число раз. Первое иррациональное уравнение, иллюстрирующее сказанное, содержит в записи два радикала и еще одно слагаемое.

Решение следующего иррационального уравнения тоже требует двух последовательных возведений в степень. Если не забывать уединять радикалы, то двух возведений в степень достаточно, чтобы избавиться от трех присутствующих в его записи радикалов.

Метод возведения обеих частей иррационального уравнения в одну и ту же степень позволяет справляться и с иррациональными уравнениями, в которых под корнем, содержится еще один корень. Вот решение характерного примера.

Пример

Решите иррациональное уравнение методом возведения обеих частей в одну и ту же степень

Смотреть решение

Наконец, прежде чем переходить к разбору следующих методов решения иррациональных уравнений, нужно обязательно отметить тот факт, что возведение обеих частей иррационального уравнения в одну и ту же степень может в результате дальнейших преобразований дать уравнение, имеющее бесконечное множество решений. Уравнение, имеющее бесконечно много корней, получается, например, в результате возведения в квадрат обеих частей иррационального уравнения и последующего упрощения вида полученного уравнения. При этом по понятным причинам мы не имеем возможности выполнить проверку подстановкой. В таких случаях приходится либо прибегать к другим способам проверки, либо отказаться от метода возведения обеих частей уравнения в одну и ту же степень в пользу другого метода решения, например, в пользу метода, предполагающего переход от иррационального уравнения к уравнению с модулем.

Мы рассмотрели решения наиболее характерных иррациональных уравнения методом возведения обеих частей уравнения в одну и ту же степень. Изученный общий подход позволяет справиться и с другими уравнениями, если для них вообще подходит этот метод решения.

Создание уравнений и формул — Служба поддержки Office

Для набора новой формулы с нуля нажмите Alt += на клавиатуре.

Или

Выберите Вставка > Формула и выберите Вставить новую формулу в нижней части встроенной коллекции формул. Вставится заполнитель, в котором можно ввести формулу.

Вставка флажка или другого символа

Добавление формулы в коллекцию

1. Выделите формулу, которую нужно добавить.

2. Щелкните стрелку вниз и выберите Сохранить как новую формулу… .

3. В диалоговом окне Создание нового стандартного блока введите имя формулы.

4. В списке коллекции выберите пункт Формулы.

5. Нажмите кнопку ОК.

Для изменения или правки созданных ранее формул:

1. Выберите формулу для открытия вкладки Работа с формулами в ленте.

   
   

2. Выберите Конструктор, чтобы увидеть инструменты для добавления в формулу различных элементов. Можно добавить или изменить следующие элементы формулы.

   • В группе Символы находятся математические символы. Чтобы увидеть все символы, нажмите кнопку Еще.
     
     чтобы увидеть другие наборы символов, щелкните стрелку в правом верхнем углу коллекции.

   • В группе Структуры представлены структуры, которые можно вставить. Просто выберите элемент, а затем замените заполнители в структуре (штрихпунктирные прямоугольники) нужными значениями.

   • Параметр Профессиональный отображает формулу в профессиональном формате, оптимизированном для отображения. Параметр Линейный отображает формулу как исходный текст, который при необходимости можно использовать для внесения изменений в формулу. Параметр «Линейный» отображает формулу в формате UnicodeMath или в формате LaTeX, который можно выбрать в блоке «Преобразования». 

   • Преобразовать в формат «Профессиональный» или «Линейный» можно все формулы в документе или только одну, если выбрать математическую зону или навести курсор на формулу.  

На устройствах с поддержкой сенсорного ввода и пера можно писать формулы пером или пальцем. Для рукописного ввода формулы

1. Выберите Рисование > Преобразовать рукописный фрагмент в математические символы, а затем выберите Рукописное уравнение в нижней части встроенной галереи.

2. С помощью пера или пальца введите математическую формулу от руки. Если у устройства нет сенсорного экрана, напишите уравнение с помощью мыши. Вы можете выделять части формулы и редактировать их по мере ввода, а затем с помощью окна предварительного просмотра проверять, правильно ли Word распознает то, что вы написали.

3. Завершив ввод, щелкните Вставить, чтобы преобразовать текст, который вы только что написали, в формулу.

Методы решения уравнений: замены, подстановки, примеры, тесты

Тестирование онлайн

Потерянные и посторонние корни

К потере корней может привести сокращение обеих частей уравнения на общий множитель.

Посторонние корни могут появится при умножении обеих частей уравнения на множитель, содержащий неизвестное.

При возведении обеих частей уравнения в квадрат (или любую четную степень) могут появляться посторонние корни.

Посторонние корни могут появляться при решении иррационального уравнения, поэтому лучше выполнять проверку.

Метод замены переменной

В ряде случаев решение уравнения можно упростить введением новой переменной (нового неизвестного).

Например, уравнение вида

где a, b, c — числа, называется биквадратным. Решается введением замены x²=t

Метод замены используют не только при решении биквадратных уравнений.

Сложные замены переменной

Основная трудность решения задач методом подстановки заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.

Очень сложные замены переменной

Графический способ решения уравнений

Графический способ решения уравнений f(x)=g(x) заключается в следующем: строят в одной системе координат графики двух функций y=f(x) и y=g(x) и находят абсциссы точек пересечения графиков. Абсциссы точек пересечения графиков и являются корнями уравнения.

Преобразуем выражение a⁴+b⁴=(a+b)⁴:

При решении уравнения f(x)=g(x) можно исследовать функции y=f(x) и y=g(x) на монотонность.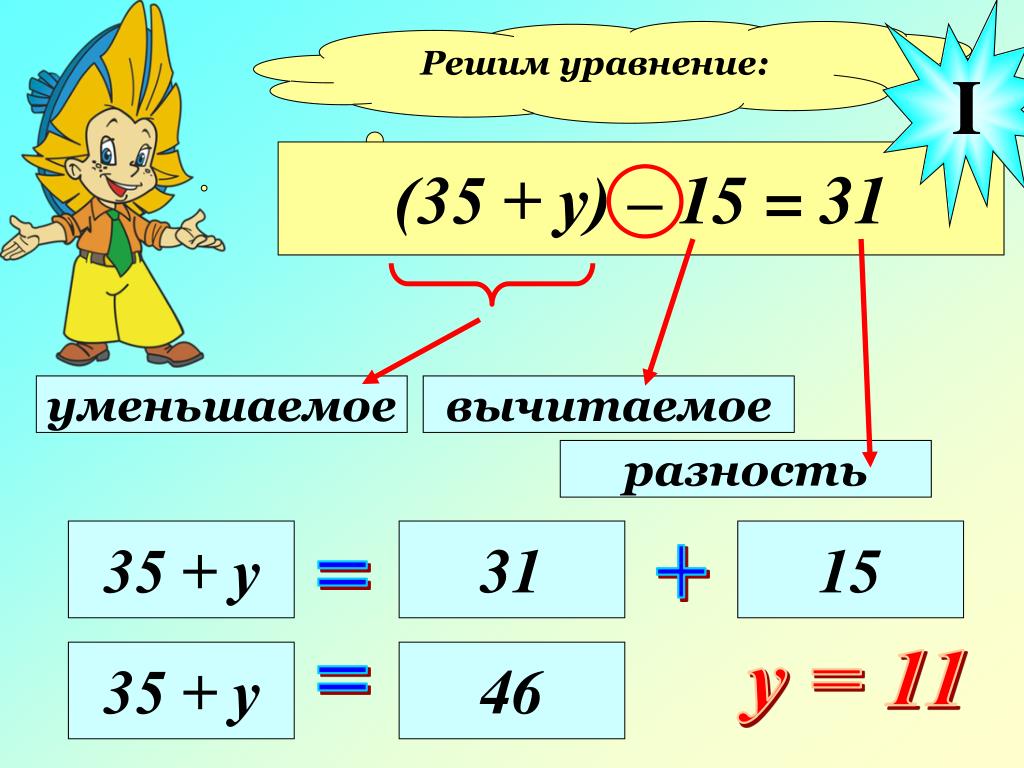 Если одна из этих функций на промежутке монотонно убывает, а другая функция монотонно возрастает, то уравнение или имеет один корень, или вообще не имеет корней. Корень уравнения можно найти методом подбора или графическим методом.

Если функция y=f(x) возрастает, а y=g(x) убывает на промежутке , и при этом f(a)>g(a), то корней нет.

Примеры уравнений вида f(f(x))=x, где f(x) — некоторая функция:

1. Любой корень уравнения f(x)=x является корнем уравнения f(f(x))=x;

2. Если функция f(x) возрастает на некотором множестве и значения x и значения функции f(x) принадлежат этому множеству, то уравнения f(x)=x и f(f(x))=x равносильны на этом множестве.

Для убывающей функции f(x) правило 2 применить нельзя.

Суть метода состоит в замене переменной х тригонометрической функцией, например . Решение исходного уравнения сводится к решению тригонометрического уравнения. Но тригонометрическое уравнение обычно имеет бесконечное множество решений, а исходное — конечное.

Неравенство Коши.

Неравенство Бернулли.

Равенство достигается при x=0 или n=1.

Неравенство Коши-Буняковского.

Равенство достигается в том и только в том случае, когда существует положительная константа a такая, что x₁=ay₁, x₂=ay₂,…,x_n=ay_n.

Решение иррациональных уравнений

Решение  иррациональных уравнений.

В этой статье мы поговорим о способах решения простейших иррациональных уравнений.

Иррациональным  уравнением  называется уравнение, которое содержит неизвестное под знаком корня.

Давайте рассмотрим два вида иррациональных уравнений, которые очень похожи на первый взгляд, но по сути  сильно друг от друга отличаются.

 (1)

и

  (2)

В первом уравнении   мы видим, что  неизвестное стоит под знаком корня третьей степени. Мы можем извлекать корень нечетной степени из отрицательного числа, поэтому в этом уравнении нет никаких ограничений ни на выражение, стоящее под знаком корня, ни на выражение, стоящее в правой части уравнения.  Мы можем возвести обе части уравнения в третью степень, чтобы избавиться от корня. Получим равносильное уравнение:

При возведении правой и левой части уравнения в нечетную степень  мы можем не опасаться  получить посторонние корни.

Пример 1. Решим уравнение 

Возведем обе части уравнения в третью степень. Получим равносильное уравнение:

Перенесем все слагаемые в одну сторону и вынесем за скобки х:

Приравняем каждый множитель к нулю, получим:

,   ,    

Ответ: {0;1;2}

Посмотрим внимательно на второе  уравнение: . В левой части уравнения стоит квадратный корень, который принимает только  неотрицательные значения. Поэтому, чтобы уравнение имело решения, правая часть тоже должна быть неотрицательной. Поэтому на правую часть уравнения накладывается условие:

— это условие существования корней.

Чтобы решить уравнение такого вида, нужно обе части уравнения возвести в квадрат:

 (3)

Возведение в квадрат может привести к появлению посторонних корней, поэтому нам надо учесть ОДЗ уравнения:

 (4)

Однако, неравенство (4) следует из условия (3): если в правой части равенства стоит квадрат какого-то выражения, а квадрат любого выражения может принимать только неотрицательные значения, следовательно левая часть тоже должна быть неотрицательна. Поэтому условие (4) автоматически следует из условия (3) и наше уравнение  равносильно системе:

Пример 2. Решим уравнение:

.

Перейдем к равносильной системе:

Решим первое уравнение системы и проверим, какие корни удовлетворяют неравеству.

,   

Неравеству удовлетворяет только корень 

Ответ: x=1

Внимание! Если мы в процессе решения  возводим обе части уравнения в квадрат, то нужно помнить, что могут появиться посторонние корни. Поэтому либо нужно переходить к равносильной системе, либо в конце решения СДЕЛАТЬ ПРОВЕРКУ: найти корни и подставить их в исходное уравнение.

Пример 3. Решим уравнение:

Чтобы решить это уравнение, нам также нужно возвести обе части в квадрат. Давайте в этом уравнении не будем заморачиваться с ОДЗ и условием существования корней, а просто в конце решения сделаем проверку.

Воозведем обе части уравнения в квадрат:

Перенесем слагаемое, содержащее корень влево, а все остальные слагаемые вправо:

Еще раз возведем обе части уравнения в квадрат:

По тереме Виета:

,   

Сделаем проверку. Для этого подставим найденные  корни в исходное уравнение. Очевидно, что при   правая часть исходного уравнения отрицательна, а левая положительна.

При  получаем верное равенство.

Ответ: 

И.В. Фельдман, репетитор по математике.

Тема урока: «Иррациональные уравнения»

Важным моментом в подготовке к итоговой
аттестации является организация обобщающего
повторения. Умения решать уравнения
отрабатывается в течение всего школьного курса
математики. Иррациональные уравнения, как
правило, вызывают затруднения, поэтому требуют
хорошего знания теоретического материала,
умения проводить исследования различных
ситуаций.

Большинство ошибок связано с формальным и
поверхностным усвоением учащимися основных
понятий и методов решения иррациональных
уравнений. У большинства учащихся единственным
устойчивым знанием является применение метода
возведения обеих частей уравнения в одну и ту же
степень, при этом часто забывают делать проверку
найденных корней. Для многих этот метод является
единственным.

Предлагаемый материал позволяет следующие:

• возместить отсутствие единого обобщения по
  данной теме в курсе алгебры 11-го класса;
• повторить основные теоретические понятия;
• закрепить основные способы решения
  иррациональных уравнений;
• закрепить нестандартные способы решения
  иррациональных уравнений.

Иррациональные уравнения.

Определение. Уравнение с одной переменной f(x)=g(x)
называется иррациональным, если хотя бы одна
функция f(x) или g(x) содержит переменную x
под знаком радикала.

При решении иррациональных уравнений
используют тождественные преобразования,
применяют метод возведения обеих частей
уравнения в одну и ту же степень, а также метод
введения новых переменных.

Теорема. Если возвести обе части уравнения f(x)=g(x)
в натуральную степень n, то полученное
уравнение fⁿ(x)=gⁿ(x) является
следствием данного уравнения.

Основными причинами появления посторонних
корней является возведение обеих частей
уравнения в одну и ту же чётную степень,
расширение области определения и др. По этим
причинам необходимой частью решения
иррационального уравнения является проверка,
либо использование области определения
заданного уравнения.

1. Метод возведения обеих частей уравнения в
одну и ту же степень.

Пример 1. Решить уравнение

Решение. Возведя обе части уравнения в
квадрат, получим

Сделав проверку, убеждаемся, что оба они
являются его корнями. Это уравнение служит
примером того, что возведение в квадрат
исходного уравнения не всегда приводит к
появлению посторонних корней.

Ответ:

Пример 2. Решить уравнение

Решение. Найдём область определения
уравнения: [2; ?). Возведём обе части уравнения в
квадрат, уединим затем полученный радикал и
возведём ещё раз в квадрат. Получим корни
уравнения

После проверки получим корень уравнения

Ответ:

Пример 3. Решить уравнение

Решение. Уравнение перепишем так:
Возведём обе части в квадрат, получим

x=2 проверить нетрудно, а
проверять громоздко. Однако заметим, что при
этом значении отрицательно. Значит, не
является решением уравнения.

Ответ: х=2.

2. Метод введения новых переменных.

Пример 4. Решить уравнение

Решение. Умножив обе части уравнения на 2,
получим:

Обозначив получим:

Далее,

Ответ:

Пример 5. Решить уравнение:

Решение. Обозначим тогда

Составим систему уравнений:

Решением системы является (0; 2) и (2; 0). Таким
образом, решение данного уравнения свелось к
решению следующей совокупности систем
уравнений:

и

Решив эту совокупность, находим

Ответ: -15; 1.

3. Искусственные приёмы решения иррациональных
уравнений.

Пример 6. Решить уравнение

Решение. Умножим обе части уравнения на
выражение

После преобразования уравнение примет вид:

-
корень уравнения. Теперь решим уравнение

Почленно сложив это уравнение с данным, придем
к уравнению:

Решая это уравнение методом возведения в
квадрат, получим Но, х=-4 посторонний корень.

Ответ: 0; 4.

Заменой неизвестной величины решение
иррациональных уравнений можно свести к решению
тригонометрических уравнений.

При этом полезно помнить:

Если в уравнение входит то замена или

Если в уравнение входит то замена

Если в уравнение входит то или

Пример 7. Решить уравнение

Решение. Сделаем замену получим:

Так как то

и

Учитывая, что получим Поэтому,

Ответ:

4. Использование монотонности функции.

Иногда при решении уравнений не видно
преобразований, которые позволяют увидеть
замену или применить один из известных способов,
хотя сразу виден один или более корней.

Пример 8. Решить уравнение

Можно решить это уравнение путем двукратного
возведения в квадрат. Но рассмотрим другой метод:

Подберём один или несколько корней уравнения.

Докажем, что других корней нет или найти
остальные корни.

После проверки — корень уравнения. Так как
функция возрастает в области определения, а
монотонная функция принимает каждое своё
значения один раз, то других корней уравнение не
имеет.

Ответ:1.

Пример 9. Решить уравнение

Решение. При проверке — корень уравнения. Для
того, чтобы использовать свойство монотонности
функции, преобразуем левую часть уравнения.

Так как функция убывает в области определения,
то -
единственный корень.

Ответ: 1.

Устно.

Доказать, что уравнения не имеют корней:

Дополнительные уравнения.

1.
Ответ: 4. Новые переменные.

2.
Ответ: 6. Возведение в квадрат.

3.
Ответ: 0. Возведение в квадрат.

4.
Ответ: -2; 2. Искусственный способ.

5.
Ответ 0; 2. Замена.

6.
Ответ: Замена.

7.
Ответ: К тригонометрическому уравнению.

8. Сколько корней на имеет уравнение

Ответ: 3 корня..

9.
Ответ: 1. Монотонность.

10.
Ответ: 1. Монотонность.

Материалы этой статьи будут полезны при
подготовке к итоговой аттестации и ЕГЭ, а также
при изучении данной темы.

Уравнение и его корни: определения, примеры

После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.

Понятие уравнения

Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:

Определение 1

Уравнением называется равенство с неизвестным числом, которое нужно найти.

Принято обозначать неизвестные маленькими латинскими буквами, например, t, r, m др., но чаще всего используются x, y, z. Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.

Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x=5, y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x+7=38, z−4=2, 8·t=4, 6:x=3.

После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7·(x−1) =19, x+6·(x+6·(x−8))=3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x+2+4·x−2−x=10. Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x·(8+1)−7=8, 3−3=z+3 или 8·x−9=2·(x+17).

Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.

В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:

Определение 2

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

То есть, к примеру, выражение x+3=6·x+7 – это уравнение с переменной x, а 3·y−1+y=0 – уравнение с переменной y.

В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:

Определение 3

Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.

К примеру, равенство вида 3,7·x+0,6=1 является уравнением с одной переменной x, а x−z=5 – уравнением с двумя переменными x и z. Примером уравнения с тремя переменными может быть выражение x2+(y−6)2+(z+0,6)2=26.

Корень уравнения

Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.

Пример 1

Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a+1=5 мы заменим букву числом 2, то равенство станет неверным, а если 4, то получится верное равенство 4+1=5.

Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.

Определение 4

Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.

Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.

Пример 2

Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a+1=5. Согласно определению, корнем в данном случае будет 4, потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2+1=5.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.

Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0·x=5. Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0.

Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.

Пример 3

Так, в уравнении x−2=4 есть только один корень – шесть, в x2=9 два корня ­­– три и минус три, в x·(x−1)·(x−2)=0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.

Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅. Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня -2, 1 и 5, то пишем -2, 1, 5 или {-2, 1, 5}.

Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y, а корнями являются 2 и 7, то мы пишем y=2 и y=7. Иногда к буквам добавляются нижние индексы, например, x1=3, x2=5. Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N, целых ­– Z, действительных – R. Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x∈Z, а если любое действительное от единицы до девяти, то y∈1, 9.

Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.

Определение 5

Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.

Поясним определение на примерах.

Пример 4

Допустим, у нас есть выражение x+y=7, которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4, то равенство станет верным, значит, мы нашли решение.

Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как (3,4).

На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.

Введение в алгебру | SkillsYouNeed

Многие люди думают, что уравнений и алгебра им недоступны — мысль о необходимости работать с уравнениями наполняет их страхом. Однако не стоит бояться уравнений.

Хорошая новость заключается в том, что уравнения на самом деле являются относительно простыми концепциями, и с небольшой практикой и применением некоторых простых правил вы можете научиться управлять ими и решать их.

Эта страница предназначена для ознакомления вас с основами алгебры и, надеюсь, с тем, чтобы вы чувствовали себя более комфортно при решении простых уравнений.

Что такое уравнение?

Уравнение — это два выражения по обе стороны от символа, указывающего на их взаимосвязь.

Это отношение может быть равно (=), меньше (<) или больше (>), или может иметь некоторую комбинацию. Например, меньше или равно (≤) или даже не равно (≠) или приблизительно равно (≈). Это известно как равенства символа.

Таким образом, простые уравнения включают 2 + 2 = 4 и 5 + 3> 3 + 4.

Однако, когда большинство людей говорят об уравнениях, они имеют в виду алгебраические уравнения.

Это уравнения, в которых используются как буквы, так и числа. Буквы используются для замены некоторых чисел, если числовое выражение было бы слишком сложным или если вы хотите обобщить, а не использовать конкретные числа. Их также можно использовать, когда вы знаете значения в части уравнения, но другие значения неизвестны, и вам нужно их вычислить.

Алгебраические уравнения решаются путем определения чисел, которые обозначают буквы.

Мы можем превратить два простых уравнения выше в алгебраические, подставив \ (x \) вместо одного из чисел:

2 + 2 = \ (\ boldsymbol {x} \)

Мы знаем, что 2 + 2 = 4, а это значит, что \ (x \) должно быть равно 4.Таким образом, решение уравнения: \ (\ boldsymbol {x} \) = 4 .

5 + 3> 3 + \ (\ boldsymbol {x} \)

Мы знаем, что 5 + 3 = 8. Уравнение говорит нам, что 8 больше, чем (>) 3 + \ (x \).

Нам нужно переставить уравнение так, чтобы \ (x \) находился с одной стороны, а все числа — с другой, иначе мы не сможем найти значение \ (x \). Правило перестановки уравнений: : что вы делаете с одной стороной, вы также должны делать с другой .Подробнее об этом ниже.

Возьмите по 3 с обеих сторон (8 — 3 = 5), тогда уравнение станет

5> \ (\ boldsymbol {x} \)

Мы видим, что \ (x \) должно быть меньше 5 ( \ (x \) <5 ).

Мы не можем сказать более точно, что такое \ (x \) с информацией, которую нам дают. Однако в исходном уравнении, которое мы использовали в качестве нашего примера, мы заменили 4 на \ (x \), что действительно меньше 5.

Нет никакого волшебства в использовании фигурного символа «x» (\ ({x} \)).Вы можете использовать любую букву, которая вам нравится, хотя \ ({x} \) и \ ({y} \) обычно используются для обозначения неизвестных элементов уравнений.

Переменные и константы

Буква, используемая для замены числа в алгебре, называется переменной , потому что каждый раз, когда вы ее используете, она обозначает разные числа.

Это отличается от конкретной буквы, которая всегда используется для замены одного и того же числа, например \ (\ pi \) (pi), которое всегда равно 3.142. Такая буква называется константой .

В алгебраическом уравнении любые заданные числа также являются константами, потому что они всегда остаются неизменными.

Если вам нужно решить уравнение, содержащее константу, вам всегда сообщат ее значение.

Члены уравнения

Член — это часть уравнения, которая отделена от других частей, обычно символом сложения (+) или вычитания (-).

Группа терминов называется выражением, скорее как математическое предложение или описание.Некоторые математические выражения могут выглядеть довольно устрашающе, наполненные цифрами и буквами, некоторые из которых могут быть даже греческими. Однако главное — рассматривать каждый термин отдельно и разбивать его на вещи, которые вам известны или которые вы можете решить. Если вы сделаете это, вы начнете понимать, что это не всегда так сложно, как вы думали вначале.

Термины могут быть просто числами, или они могут быть просто буквами, или они могут быть комбинацией букв и цифр, например 2 \ (\ boldsymbol {x} \), 3 \ (\ boldsymbol {xy} \) или 4 \ (\ boldsymbol {x} \) ² .

В термине, состоящем из букв и цифр, число известно как коэффициент , а буква — это переменная . Коэффициент — это просто «множитель» — он говорит вам, сколько чего-то (переменной) у вас есть в этом термине.

Термины, которые имеют точно такую ​​же переменную, называются , как и термины , и вы можете складывать, вычитать, умножать или делить их, как если бы они были простыми числами. Например:

Уравнение 2 \ (x \) + 3 \ (x \) равно 5 \ (x \), просто 2 лота \ (x \) плюс 3 лота \ (x \), чтобы получить 5 лотов \ (х \) (5 \ (х \)).2 $$

Вы, , не можете складывать или вычитать «непохожие термины». Однако вы можете умножить их, комбинируя переменные и умножая коэффициенты вместе.

Так, например, 3 \ (y \) × 2 \ (x \) = 6 \ (xy \) (потому что 6 \ (xy \) просто означает 6 раз \ (x \) раз \ (y \)) .

Вы можете разделить непохожие члены, превратив их в дроби и сократив их. Начните с цифр, затем с букв.

Так, например:

\ (\ large {6xy ÷ 3x} \)

Преобразование и решение уравнений

Во многих случаях для решения уравнения вам, вероятно, потребуется переставить его.Это означает, что вам нужно переместить термины так, чтобы в итоге вы получили только термины, содержащие \ (x \) с одной стороны символа равенства (например, =,> или <), и все числа с другой.

Этот процесс иногда называют изолирующим \ (x \) .

Вы можете переставлять уравнения с помощью набора простых правил:

1. Что бы вы ни делали с одной стороной уравнения, вы, , должны, , сделать то же самое с другой. Так вы сохраните отношения между ними.Неважно, что вы делаете, убираете ли вы 2, прибавляете 57, умножаете на 150 или делите на \ (x \). Пока вы делаете это с обеих сторон, уравнение остается правильным. Можно представить себе уравнение как набор весов или качелей, которые всегда должны балансировать.

2. На нашей странице Дополнение объясняется, что не имеет значения, в каком порядке вы добавляете, ответ все тот же. Это означает, что вы можете переставить выражение, чтобы собрать вместе термины , похожие на , и упростить сложение.Это относится и к вычитанию , если вы помните из нашей страницы о положительных и отрицательных числах , что вычитание аналогично добавлению отрицательного числа . Так, например, 10-3 = 10 + (-3).

3. Уравнения также работают в соответствии с BODMAS , поэтому не забывайте выполнять вычисления в правильном порядке.

4. Всегда приводите уравнение к простейшей возможной форме: умножайте скобки, делите вниз, исключайте дроби и складывайте / вычитайте все подобные члены.

Рабочих примеров:

Попытайтесь решить эти уравнения для \ (x \), щелкните поля, чтобы увидеть работу и ответы.

$$ \ large {x + 3 = 5 × 4} $$

• Как и в любом другом вычислении, сначала произведите умножение. 5 × 4 = 20
• Итак, \ (x \) + 3 = 20
• Следующий шаг — убрать по три с обеих сторон
• \ (х \) + 3 — 3 = 20 — 3
• 20 — 3 = 17.

Это оставляет вам ответ: \ (x \) = 17

$$ \ large {5 + x + 21 = 3 + 6 × 5} $$

• Сначала выполните вычисления с правой стороны, потому что в нем нет букв.Скобок нет, поэтому сначала умножение, затем сложение.
• 6 × 5 = 30 и 30 + 3 = 33.
• Вычисление слева является сложением, поэтому вы можете перемещать члены, пока не соберете все числа вместе:
  5 + \ (x \) + 21 = \ (x \) + 5 + 21
  и 5 + 21 = 26.
• Итак, теперь у вас есть 26 + \ (x \) = 33
• Теперь можно убрать 26 с обеих сторон
• 26 + \ (х \) — 26 = \ (х \) = 33 — 26
• А 33 — 26 = 7.2 + 5 = 13 — 4} $$
  • Переставьте так, чтобы все числа были на одной стороне, убрав по пять с каждой стороны.
  • Теперь у вас есть
    \ (x \) ² = 13-4-5, поэтому
  • \ (х \) ² = 4
  • Теперь вам нужно извлечь квадратный корень из обеих частей, потому что вы хотите найти значение \ (x \), а не \ (x \) ² .
  • Вы знаете, что 2 × 2 = 4, что означает, что квадратный корень из 4 = 2

  \ (х \) = 2

  ---

  Уравнения и графики

  Любое уравнение, в котором существует связь только между двумя переменными, \ (x \) и \ (y \), можно нарисовать в виде линейного графика, где \ (x \) идет вдоль горизонтальной оси (иногда называемой x- ось) и \ (y \) по вертикальной оси (иногда называемой осью y).

  Вы можете вычислить точки на графике, решив уравнение для конкретных значений \ (x \).

  Примеры:

  \ (\ large {y = 2x + 3} \)

  \ (х \)	0	1	2	3	4	5	6
  расчет	2 (0) + 3	2 (1) + 3	2 (2) + 3	2 (3) + 3	2 (4) + 3	2 (5) + 3	2 (6) + 3
  \ (у \)	3	5	7	9	11	13	15

  Преимущество построения графика уравнения состоит в том, что затем вы можете использовать его для вычисления значения \ (y \) для любого заданного значения \ (x \) или, действительно, \ (x \) для любого заданного значения. \ (y \), глядя на график.2 + х + 4} \)

  Когда \ (x \) = 0, \ (y \) = 0 + 0 + 4 = 4
  , когда \ (x \) = 1, \ (y \) = 1 + 1 + 4 = 6
  , когда \ ( x \) = 2, \ (y \) = 4 + 2 + 4 = 10
  и так далее …

  \ (х \)	0	1	2	3	4	5	6	7	8	9	10
  \ (у \)	4	6	10	16	24	34	46	60	76	94	114

  Экстраполировать

  ---

  Еще одно преимущество построения вашего уравнения на графике состоит в том, что вы можете экстраполировать свои данные (числовую информацию) для получения больших значений \ (x \) или \ (y \).Экстраполяция означает, что вы расширяете свой график, продолжая линию, которую вы нарисовали из своих данных, чтобы оценить значения \ (x \) и \ (y \) за пределами диапазона данных, которые у вас уже есть.

  В первом примере уравнение дает прямую линию, поэтому экстраполировать этот график несложно. Однако необходимо соблюдать осторожность при экстраполяции графика, который не является прямой линией, как во втором примере.

  ---

  Заключение

  На этой странице объясняется, как решать простые уравнения, а также взаимосвязь между уравнениями и графиками, что дает вам альтернативный способ решения уравнений.

  Теперь вы готовы перейти к более сложным уравнениям, включая одновременные уравнения и квадратные уравнения.

  ---

  Сбалансированное химическое уравнение: определение и примеры — видео и стенограмма урока

  Как сбалансировать уравнение

  Практика всегда добивается совершенства. В общем, чтобы сбалансировать уравнение, нам нужно сделать следующее:

  • Подсчитайте количество атомов каждого элемента в реагентах и ​​продуктах.
  • Использовать коэффициенты; при необходимости разместите их перед составами.

  Шаги просты, но это процесс проб и ошибок. Давайте рассмотрим еще несколько примеров уравнений и методов, которые можно использовать для балансировки каждого из них.

  Пример 1

  Это реакция между метаном (Ch5) и кислородом (O2) с образованием диоксида углерода (CO2) и воды (h3O).

  Показанная реакция представляет собой реакцию горения : соединение реагирует с кислородом и образует диоксид углерода и воду.Метод заключается в том, чтобы сначала уравновесить атомы углерода (C), затем атомы водорода (H), а затем атомы кислорода (O).

  В этом случае атомы углерода (C) уже сбалансированы. Итак, теперь мы посмотрим на атомы водорода (H). Есть 4 атома водорода (H) на стороне реагентов и 2 атома водорода (H) на стороне продуктов. Чтобы уравновесить их, мы ставим коэффициент 2 перед h3O.

  Теперь атомы водорода (H) уравновешены.Из-за коэффициента 2 перед h3O всего на стороне продуктов находится 4 атома кислорода (O). Чтобы уравновесить атомы кислорода с обеих сторон, мы ставим коэффициент 2 перед O2. Теперь химическое уравнение сбалансировано.

  Пример 2

  Это реакция между оксидом железа (Fe2O3) и углеродом (C) с образованием железа (Fe) и диоксида углерода (CO2).

  Эта реакция не сбалансирована.Во-первых, нам нужно сбалансировать атомы кислорода. Мы делаем это так, чтобы с каждой стороны было по 6 атомов кислорода. Для этого нам нужно поставить коэффициент 2 перед Fe2O3 и коэффициент 3 перед CO2.

  Теперь, когда атомы кислорода уравновешены, нам нужно сначала уравновесить атомы железа (Fe). Для этого нам нужно поставить коэффициент 4 перед Fe на стороне продуктов. Теперь, когда атомы Fe уравновешены, мы можем уравновесить атомы углерода.Мы делаем это, устанавливая коэффициент 3 перед C на стороне реагентов. Теперь химическое уравнение сбалансировано.

  Пример 3

  При работе с химическими уравнениями с многоатомными ионами , которые представляют собой ионы, состоящие из более чем одного атома, существует специальный метод для уравновешивания химического уравнения.

  Метод состоит в том, чтобы рассматривать многоатомный ион целиком, как если бы это был только один атом.Давайте посмотрим на это химическое уравнение.

  Многоатомный ион в данном случае — PO4 (зеленый). Мы будем рассматривать весь этот многоатомный ион как один атом. Со стороны реагентов есть один ион PO4, а со стороны продуктов — два иона PO4.

  Первый шаг — сбалансировать многоатомные ионы с обеих сторон. Для этого мы ставим коэффициент 2 перед Na3PO4. Атомы натрия (Na) удваиваются, и PO4 теперь сбалансирован с обеих сторон.

  Следующий шаг — уравновесить атомы магния (Mg), натрия (Na) и хлора (Cl). Сначала мы уравновешиваем атомы магния, задав коэффициент 3 перед MgCl2.

  Затем мы уравновешиваем атомы Na и Cl с обеих сторон, помещая коэффициент 6 перед NaCl. В результате получается сбалансированное уравнение:

  Пример 4

  Давайте рассмотрим реакцию между алюминием (Al) и серной кислотой (h3SO4).В этой реакции наш многоатомный ион, который мы будем считать за один атом, — это SO4. Со стороны реагентов имеется один ион SO4, а со стороны продуктов — три иона SO4.

  Сначала нам нужно сбалансировать ионы SO4, и для этого мы ставим коэффициент 3 перед h3SO4.

  Атомы водорода и алюминия неуравновешены. Следующий шаг — уравновесить атомы водорода (H), поставив коэффициент 3 перед h3.

  Последний шаг — уравновесить атомы алюминия (Al). Мы делаем это, помещая коэффициент 2 перед Al. Теперь химическое уравнение сбалансировано.

  Краткое содержание урока

  Согласно закону сохранения массы , масса реагентов должна быть равна массе продуктов, когда происходит химическая реакция. Это означает, что количество различных атомов, участвующих в реагирующих веществах, должно оставаться неизменным после того, как реакция протекает.Там, где есть химическая реакция, есть химическое уравнение. Химическое уравнение необходимо сбалансировать так, чтобы оно подчинялось закону сохранения массы. Сбалансированное химическое уравнение возникает, когда количество различных атомов элементов на стороне реагентов равно количеству атомов на стороне продуктов.

  Уравновешивание химических уравнений — это процесс проб и ошибок. При балансировании химических уравнений нам сначала нужно подсчитать различные атомы на стороне реагентов и на стороне продуктов.Если уравнение не сбалансировано, нам нужно использовать коэффициенты , которые представляют собой числа, которые мы ставим перед реагирующими веществами, чтобы сбалансировать уравнение. Если перед химической формулой нет коэффициента, это означает, что коэффициент равен единице.

  Для реакций горения метод заключается в уравновешивании атомов углерода (C), за которыми следуют атомы водорода (H) и затем атомы кислорода (O). Для атомов, включающих многоатомные ионы, общий метод состоит в том, чтобы считать весь многоатомный ион за один атом, сначала уравновесить их, а затем уравновесить остальные атомы.

  Результаты обучения

  После того, как вы закончите, вы сможете:

  • Вспомнить, как закон сохранения массы требует сбалансированного химического уравнения
  • Укажите шаги, чтобы сбалансировать химическое уравнение
  • Уравновесить химическое уравнение

  Решение рациональных уравнений

  Решение рациональных уравнений
  Вот шаги, необходимые для решения рациональных уравнений:

  Шаг 1 :	Удалите все дроби.При решении рациональных уравнений у вас есть выбор из двух способов исключить дроби. Опция 1; умножьте всю проблему на наименьший общий знаменатель или ЖКД. Вариант 2; вы можете крестить умножение. Вариант 1 подойдет для любой задачи, но вы можете выполнить перекрестное умножение только в том случае, если у вас есть одна дробь, равная одной дроби, то есть если дроби пропорциональны. Щелкните ссылку, чтобы просмотреть шаги по поиску ЖК-дисплея. Обратите внимание, что при решении рациональных уравнений все дроби должны исчезнуть после первого шага.
  Шаг 2 :	Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 :	Решите упрощенное уравнение. Если упрощенное уравнение имеет более высокие степени, например x 2 или x 3 , вы можете решить уравнение, приравняв его к нулю и разложив на множители. Если упрощенная задача не содержит более высоких степеней, тогда решите для x, получив x с одной стороны и числа с другой.
  Шаг 4 :	Проверьте каждое решение. Подставьте каждое решение в знаменатель исходного вопроса и отклоните любые решения, которые приводят к тому, что знаменатель равен нулю, потому что это делает проблему неопределенной. Этот шаг не гарантирует правильного ответа; это только гарантирует, что ответ приемлем.

  Пример 1 — Решить:

  Шаг 1 : Удалите все фракции.В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби.
  Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне.
  Шаг 4 : Проверьте каждое решение.В этом случае единственное число, которое сделало бы проблему неопределенной, — 0. Поскольку наш ответ не равен 0, ответ принимается.

  Пример 2 — Решить:

  Шаг 1 : Удалите все фракции. В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби.
  Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне.
  Шаг 4 : Проверьте каждое решение. В этом случае единственными числами, которые могут сделать проблему неопределенной, являются 3 или –3. Поскольку наш ответ не равен 3 или –3, ответ принят.

  Щелкните здесь для практических задач

  Пример 3 —

  Шаг 1 : Удалите все фракции.В этом случае мы можем либо умножить на ЖК-дисплей, либо крест-накрест, чтобы исключить дроби.
  Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне, потому что члены x 2 будут сокращаться.
  Шаг 4 : Проверьте каждое решение. В этом случае единственные числа, которые делают проблему неопределенной, — это 2 или 5. Поскольку наш ответ — не 2 или 5, ответ принимается.

  Щелкните здесь для практических задач

  Пример 4 —

  Шаг 1 : Удалите все фракции. В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби.
  Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить x на одной стороне и числа на другой стороне.
  Шаг 4 : Проверьте каждое решение. В этом случае единственные числа, которые делают проблему неопределенной, — это 1 или 4.Поскольку наш ответ равен 4, ответ не принимается, что означает:

  Щелкните здесь для практических задач

  Пример 5 —

  Шаг 1 : Удалите все фракции. В этом случае мы можем либо умножить на ЖК-дисплей, либо крест-накрест, чтобы исключить дроби.
  Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить уравнение, равное нулю, и решить его путем факторизации.
  Шаг 4 : Проверьте каждое решение. В этом случае единственные числа, которые делают проблему неопределенной, — это 0 или –12/5. Поскольку наши ответы не равны 0 или –12/5, ответы принимаются.

  Щелкните здесь для практических задач

  Пример 6 —

  Шаг 1 : Удалите все фракции.В этом случае нам нужно умножить на ЖК-дисплей, чтобы исключить дроби.
  Шаг 2 : Упростите полученное уравнение. Чтобы упростить уравнение, вам может потребоваться распределить и объединить похожие термины.
  Шаг 3 : Решите упрощенное уравнение. В этом случае нам нужно получить уравнение, равное нулю, и решить его путем факторизации.
  Шаг 4 : Проверьте каждое решение.В этом случае единственными числами, которые могут сделать проблему неопределенной, являются 1, –1 или –2. Поскольку наши ответы не равны 1, –1 или –2, ответы принимаются.

  Щелкните здесь для практических задач

  4-х шаговое руководство по решению уравнений (часть 2)

  В последнем эпизоде ​​мы узнали немало важных вещей. Во-первых, мы узнали, что печально известный Knot Dude однажды был вызван на своего рода математическую дуэль группой морских строителей пирамид.2, для переменной b . И мы узнали, что при этом Knot Dude разработал простой 4-шаговый метод — первые два шага, которые мы изучили в прошлый раз — для решения уравнений, которые все еще используются!

  Сегодня мы собираемся изучить два последних шага к методу Knot Dude, собрать все вместе и выяснить, как именно Knot Dude решил свою проблему и отправил этих склонных к морю строителей пирамид, потерпев поражение, уплыл …

  Шаг 1. Упростите каждую сторону уравнения

  Как мы узнали в прошлый раз, первый шаг в решении уравнения — сделать уравнение как можно более простым.Это означает, что вам нужно начать с использования золотого правила решения уравнений и порядка операций, PEMDAS, чтобы выражение каждой стороны знака равенства было как можно более простым. В примере, о котором мы говорили в прошлый раз, мы складывали, вычитали, умножали и делили, пока не повернули уравнение

  2 + x — 2 • 5 = 4/2 — x

  в очень упрощенную версию самого себя

  x — 8 = 2- x

  Эти два уравнения могут выглядеть не одинаково, но, как мы убедились в прошлый раз, на самом деле это просто разные способы написания одного и того же основного уравнения!

  Шаг 2: переместить переменную на одну сторону

  Следующим шагом в решении уравнения для конкретной переменной является использование сложения и / или вычитания, чтобы переместить каждую часть уравнения, содержащую переменную, которую вы решаете, в одну сторону от знака равенства. 2

  И это здорово, потому что сейчас мы очень близки к решению для b .

  Страниц

  Значение химического уравнения

  ChemTeam: значение химического уравнения

  Значение химического уравнения

  Как сбалансировать современное химическое уравнение

  Закон сохранения массы

  Вернуться в меню уравнений

  ---

  Химические уравнения дают информацию в двух основных областях.

  Во-первых, они говорят нам, какие вещества вступают в реакцию (те, которые используются) и какие вещества являются продуктами (производятся).

  Во-вторых, коэффициенты сбалансированного уравнения говорят нам, в каком соотношении вещества вступают в реакцию или производятся.

  Последний пункт имеет практические последствия всякий раз, когда химические вещества вступают в реакцию. Например, в большом среднем баке космического челнока на самом деле есть два бака поменьше: в одном находится жидкий кислород, а в другом — жидкий водород. Резервуар с водородом вмещает вдвое больше, чем резервуар для хранения кислорода. Почему?

  Ответ — водород и кислород реагируют в соотношении 2: 1.Для любого кислорода, используемого шаттлом, требуется вдвое больше водорода. Если бы два баллона были равного размера, водородный баллон работал бы всухую, когда кислородный баллон был бы еще наполовину заполнен.

  ---

  Реагенты находятся в левой части химического уравнения, а продукты — в правой.

  Однако вы можете спросить: «Слева и справа от чего?»

  Ответ — стрелка.

  2H ₂ + O ₂ —> 2H ₂ O

  Слева — реагенты — водород и кислород.Мы на мгновение проигнорируем двоих перед водородом.

  Справа товар — вода. Мы также проигнорируем двоих перед водой, но скоро вернемся к этому.

  Имейте в виду, что по обе стороны от стрелки может быть одно, два, три или более веществ, как в этом более сложном (и несбалансированном) уравнении:

  Ca (H ₂ PO ₄ ) ₂ + CaSO ₄ + HF —> Ca ₁₀ F ₂ (PO ₄ ) ₆ + H ₂ SO ₄

  Обычно стрелка заменяется на «производит» или «дает», когда уравнение произносится вслух.

  ---

  Коэффициенты — это числа перед формулами.

  Вот снова пример уравнения:

  2H ₂ + O ₂ —> 2H ₂ O

  Обратите внимание на наличие двойки перед водородом и водой. Они называются коэффициентами. Эти числа дают две очень важные части информации об уравнении. Вы должны понимать и то, и другое, чтобы успешно читать и использовать химические уравнения.

  Во-первых: коэффициенты дают количество молекул (или атомов), участвующих в реакции. В примере реакции две молекулы водорода реагируют с одной молекулой кислорода и образуют две молекулы воды.

  Секунда: коэффициенты дают количество молей каждого вещества, участвующего в реакции. В примере реакции два моля водорода реагируют с одним моль кислорода и образуют два моля воды.

  Только что затронутая точка — CRITICAL .

  Повторим пункт:

  Коэффициенты уравнения говорят нам, сколько моль каждого реагента задействовано, а также сколько моль каждого продукта получается.

  Между прочим, число Авогадро — это множитель между двумя точками выше.

  А как насчет кислорода? Почему перед ним нет коэффициента? Ответ — если коэффициент отсутствует, считайте, что он присутствует.

  ---

  Быстрый просмотр

  При чтении уравнения следует помнить о трех важных вещах.

  Первый: слева реагенты, справа продукты. Которого? Стрелка.

  Два: Коэффициенты — это числа перед каждой формулой. Если номер не отображается, подразумевается единица.

  Три: Коэффициенты говорят нам, сколько молекул (молей) каждого использованного реагента и сколько молекул (молей) каждого полученного продукта.

  ---

  Практические задачи

  Определите реагенты, продукты и коэффициенты этих уравнений:

  1) Zn + 2HCl —> ZnCl ₂ + H ₂

  2) 2KClO ₃ —> 2KCl + 3O ₂

  3) S ₈ + 24F ₂ —> 8SF ₆

  4) 4Fe + 3O ₂ —> 2Fe ₂ O ₃

  5) 2C ₂ H ₆ + 7O ₂ — -> 4CO ₂ + 6H ₂ O

  Ответы

  ---

  Как сбалансировать современное химическое уравнение

  Закон сохранения массы

  Вернуться в меню уравнений

  Шаг за шагом: как решить уравнение?

  Вы пытались решить уравнение и застряли на шаге на полпути? Возникли проблемы с пониманием уравнений или почему они важны? В каждом выпуске «Шаг за шагом» мы объясним, как можно более эффективно подойти к различным концепциям.Уравнения — полезный способ решения неизвестного количества, когда присутствует другая информация. Как следует из названия, уравнения представляют две суммы, которые должны быть равными друг другу. Это одна из первых концепций, с которыми студенты сталкиваются в алгебре, но ключевые навыки, которые вы здесь изучаете, впоследствии применяются на всех уровнях математики, что делает их одним из наиболее важных навыков, которым нужно овладеть.

  Основы

  Итак, в конечном итоге, какова цель решения уравнения? Всякий раз, когда вас просят решить, это означает, что получит переменную (буква, которая заменяет неизвестное число) сама по себе .Итак, наша цель — переместить любые другие числа (и, возможно, другие переменные) от переменной, которую мы хотим решить. В большинстве уравнений присутствует только одна переменная; в конце концов, вы не можете получить число в качестве ответа, если есть еще одно неизвестное количество… но это обсуждение в другой раз.

  Поскольку уравнения представляют две равные величины, воспринимайте их как балансировочную шкалу. При решении уравнения мы хотим, чтобы обе стороны представляли одну и ту же сумму во всей задаче, поэтому всякий раз, когда вы выполняете действие с одной стороны уравнения, вы должны выполнять то же действие с другой стороны уравнения.Один из способов, который вы можете использовать, чтобы помнить об этом, — это нарисовать линию там, где в уравнении стоит знак равенства. Все, что вы делаете на одной стороне линии, необходимо повторить на другой стороне.

  Решение одношаговых уравнений

  В одношаговых уравнениях вам нужно выполнить только одну операцию для решения проблемы. Возьмем уравнение 3x = 18. В левой части у нас 3x, что означает троекратное неизвестное число x. Другими словами, трехкратное неизвестное число равно числу 18, которое находится в правой части уравнения.

  Поскольку наша цель — получить x отдельно, мы хотим отменить 3 слева. Чтобы сократить число, вы должны выполнить противоположную операцию — в этом случае деление противоположно умножению, поэтому мы делим слева на 3.

  Однако, как мы упоминали выше, мы должны постоянно поддерживать равенство в уравнении, поэтому, если мы разделим на 3 в левой части, мы должны разделить на 3 в правой части. Когда вы делите число на себя, оно отменяется и остается 1, так что остается 1 x слева и 6 справа.

  Решение двухшаговых уравнений

  Двухшаговые уравнения требуют двух шагов для решения проблемы. Обычно они требуют, чтобы вы умножали / делили и складывали / вычитали в уравнении. При решении уравнений, требующих двух или более шагов, имейте в виду, что вы обычно будете выполнять порядок операций в обратном порядке, по крайней мере, для некоторых из них. Помните, что PEMDAS означает скобок, экспонент, умножение, деление, сложение, вычитание .В большинстве числовых задач вы должны начать со скобок и продолжить шаги вправо. В уравнениях все наоборот, особенно с деталью MDAS . Вы все равно должны сначала позаботиться обо всем, что указано в скобках, а затем о показателях, но это больше относится к многоступенчатым уравнениям. Однако после этого вы должны переместить любые числа, добавленные или вычтенные к вашей переменной, а затем избавиться от любого умножения или деления, если это применимо. Возьмем уравнение 4x — 2 = 14. Мы хотим сначала переместить -2, поэтому выполняем операцию сложения противоположную.

  Как только это будет сделано, у нас останется 4x = 16. Чтобы избавиться от 4, которое умножается на x, мы должны разделить. X = 4. Имейте в виду, что любые числа рядом с вашей переменной (4 в этой задаче) должны быть последними , которые вы касаетесь в уравнении. Все остальное нужно сначала переместить.

  Решение многоступенчатых уравнений

  Многоступенчатые уравнения похожи на двухступенчатые уравнения. В уравнениях такого типа часто используются круглые скобки или дроби.Сначала вы захотите распределить и обработать любые числа в круглых скобках; Вы должны позаботиться и об экспонентах в это время. Ключевые моменты, которые следует запомнить:

  1. Выполняйте эти уравнения по одному шагу за раз и записывайте каждый шаг. Чем больше вы попытаетесь сделать сразу, тем больше вероятность, что вы ошибетесь и что-то забудете.
  2. Выполните те же действия, что и для двухэтапных уравнений. После того, как вы разберетесь со скобками и показателями степени, начните с любых чисел, которые нужно добавить или вычесть.

  Итак, давайте поработаем над уравнением 3 (2x + 4) = 36.

  Всякий раз, когда рядом с скобками написано число, это означает умножение. Итак, начнем с распределения числа 3 в скобках.

  Остается 6x + 12 = 36. После того, как мы закончили распределение, мы в основном остаемся с двухэтапным уравнением. Как и выше, мы начинаем с отмены сложения, поэтому мы вычитаем 12 с обеих сторон.

  Теперь у нас 6x = 24.Чтобы исключить 6, мы делим на 6 с обеих сторон. Это оставляет нам ответ x = 4.

  Ищете дополнительную практику решения уравнений? Ознакомьтесь с нашими рабочими листами по алгебре! Есть сотни задач, над которыми нужно практиковаться, и мы постоянно добавляем новые. Если после некоторой практики вам все еще нужна помощь, подумайте о том, чтобы позвонить нам и поработать с одним из наших репетиторов по алгебре.

  Как решить два уравнения с двумя неизвестными — I

  Не могли бы вы напомнить, как решить два уравнения с двумя неизвестными? Если да или если вы никогда не знакомы с этой концепцией, я приглашаю вас посмотреть это видео и следующее видео, которое является второй частью этой серии.

  Два уравнения с двумя переменными. До сих пор при изучении алгебраических уравнений мы рассматривали решение отдельных уравнений только с одной переменной. Например, что-то вроде 2x + 7 = 15.

  Что произойдет, если в уравнении есть более одной переменной? Предположим, у нас есть что-то вроде 2x + 3y = 15.

  Итак, что бы значило для кого-то прийти и сказать нам, решить это уравнение? Как найти значения, которые работают в этом уравнении? Ну, конечно, одно возможное значение, если x = 0, тогда y может быть равно 5, так что это было бы решением.Другими словами, если x = 3 и y = 3, x = 6 и y = 1, это также значения, которые заставляют его работать.

  Конечно, нет ограничений на то, что любая переменная должна быть положительной, поэтому другие решения включают (x = 9, y = -1) или (x = -3 и y = +7). И, как вы понимаете, мы могли бы сделать x все более и более отрицательным, а y — все более и более положительным — или наоборот. Так что мы могли получить довольно много подобных решений. Также нет ограничений, что переменные должны быть целыми числами, поэтому другие решения включают такие вещи, как x = 7 1/2 y = 0 или x = 4 и y = 2 1/3.

  Итак, только на этой странице обратите внимание, что у нас есть одно, два, три, четыре, пять, шесть, семь решений для этого. И, безусловно, ясно, что мы можем получить намного больше. Фактически, одно уравнение с двумя переменными обычно имеет бесконечное количество решений. Обратите внимание, что все эти решения, если их построить на графике x-y, лежали бы на прямой линии.

  Чтение диаграммы

  Итак, семь упомянутых нами решений — это семь точек на этой диаграмме. И все они лежат на прямой.Теперь по причинам, которые мы обсудим позже в модуле координатной геометрии, любое отдельное уравнение только с x и y (ни одна из переменных не возведена в степень или дробь) может быть представлено линией в плоскости x-y. Так что прямо сейчас вам не нужно беспокоиться об их графическом отображении. Вам не нужно беспокоиться о том, как вы найдете наклон линии или что-то в этом роде.

  Все, что вам нужно сделать, это просто иметь эту идею, только эту ассоциацию — что уравнение с x и y представлено линией. Это все, что вам нужно знать для этого обсуждения.

  Большая идея номер один

  Итак, первая большая идея заключается в том, что никто не может попросить вас решить одно уравнение с двумя переменными, потому что у него будет бесконечное количество решений. Линия проходит через бесконечное количество точек, и каждая из этих точек является решением.

  Таким образом, никто не может законно попросить вас решить, потому что они просят вас решить бесконечное количество вещей одновременно.

  Теперь предположим, что у нас есть два уравнения, каждое с двумя переменными.Это называется системой уравнений. Значения x и y должны одновременно удовлетворять обоим уравнениям. Что ж, это интересно.

  Если каждое уравнение представляет собой линию, то имеет смысл, что единственная точка, где эти две линии пересекаются, будет единственной точкой, которая удовлетворяет обоим уравнениям. Итак, вы выбираете одну случайную линию и выбираете другую случайную линию, очень велики шансы, что они собираются где-то пересекаться, и они пересекаются в одной точке, и эта одна точка будет решением.

  Большая идея номер два

  С алгебраической точки зрения, когда мы находим это решение, мы находим геометрическую точку, в которой они пересекаются. Итак, большая идея №2 состоит в том, что если у нас есть система двух уравнений с двумя неизвестными, мы обычно можем решить для уникальных значений x и y. Как решить систему уравнений для этих значений? Есть две стратегии.

  Один — это замена, а другой — либо исключение, некоторые источники также называют это линейной комбинацией.Я назову их заменой и устранением . Цель обоих этих методов — свести ситуацию с двумя уравнениями и двумя неизвестными к ситуации с одним уравнением и одним неизвестным, в которой мы уже знаем, как найти решение.

  Метод подстановки

  Итак, что мы делаем, и это часто верно в отношении математики, мы превращаем проблему, которую не знаем, как решить, в проблему, которую мы действительно знаем, как решить. Это очень типично для математики. Итак, метод подстановки.В этом методе мы сначала решаем одно уравнение, либо одно для одной из переменных.

  _{Изображение предоставлено digitalconsumator}

  В этом уравнении мы получим одну переменную на одной стороне уравнения. Итак, есть два уравнения, которые я привел минуту назад, одно из них было x + 2y = 11. И это уравнение, в котором особенно легко получить x само по себе. Что я собираюсь сделать, так это вычесть 2y с обеих сторон, и я получу x = 11-2y. Так что задержитесь на секунду, x = 11-2y.Теперь давайте посмотрим на другое уравнение.

  Мы можем заменить x в другом уравнении выражением, равным x. Это потому, что x = 11-2y означает, что везде, где есть x, мы можем удалить x и заменить его тем, что он равен. Итак, вот другое уравнение, и мы просто снова напишем то же уравнение, но мы заменим это x на 11 минус 2y. Где теперь у нас есть одно уравнение с y.

  Итак, теперь мы просто используем наше обычное решение, мы распределим, объединим

  _{Image by CLS Digital Art}

  как термины, мы вычтем 22 с обеих сторон, мы получим -y = -7 умножить на — 1 получаем y = 7.Итак, теперь мы решили для одного из двух значений, мы решили для y, нам все еще нужно решить для x. Теперь мы подставляем это значение для возврата y в уравнение, которое было решено для x.

  Итак, у нас было x = 11-2y, теперь мы знаем, что y = 7. Итак, мы просто вставим это, 11-14 равно -3. Таким образом, точка x равна -3, y равна положительному 7, что является решением. Обратите внимание, что метод подстановки наиболее полезен, когда в одном из двух уравнений коэффициенты одной из переменных равны положительной 1 или отрицательной 1.

  Дроби и метод исключения

  Если все коэффициенты при x и y в двух уравнениях не равны положительному или отрицательному, то решение для любой переменной приведет к получению дробей, что сделает решение более громоздким. Так, например, предположим, что это наша система. Предположим, мы пытаемся решить первое уравнение относительно x. Хорошо, если мы можем разложить 5y на обе стороны, то делим на 4.

  Сразу попадаем на дроби. Заменить это было бы неинтересно.Да, математически мы могли бы решить уравнение таким образом — и после дробления, но мы предпочитаем не делать этого. В системах, в которых замена не удобна, мы будем использовать исключение. Мы рассмотрим метод исключения в следующем уроке.

  Таким образом, система уравнений, два уравнения с двумя переменными, обычно имеют одно уникальное решение, и опять же, это место, где две линии пересекаются. Вот что мы находим. Мы можем решить либо заменой, либо устранением.Подстановка работает лучше всего, когда одна из переменных имеет коэффициент плюс или минус 1.

  И снова, в следующем уроке мы поговорим об исключении.

  О Майке МГарри

  Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидных черепных дефектов, он настаивает на том, чтобы болеть за Нью-Йорк Метс.