Математика 4 класс Моро

Страница 4.

Задание 1.

Надо сосчитать большое количество пуговиц. Например: 6 сотен, 5 десятков и 5 отдельных пуговиц. Сколько это всего пуговиц?

Решение:

6 сотен — это 6 х 100 = 600;

5 десятков — это 5 х 10 = 50

и 5 отдельных пуговиц, значит:

600 + 50 + 5 = 655 пуговиц всего.

Задание 2.

Назови и запиши числа, какое число называют при счете перед каждым из этих чисел и после него?

9 дес. 9 ед. − 99 (девяносто девять). Перед числом 99 называют 98, а после 100.

9 дес. 0 ед. − 90 (девяносто). Перед числом 90 называют 89, а после 91.

9 сот. 9 дес. 9 ед. − 999 (девятьсот девяносто девять). Перед числом 999 называют 998, а после 1000.

9 сот. 0 дес. 9 ед. − 909 (девятьсот девять). Перед числом 909 называют 908, а после 910.

9 сот. 0 дес. 0 ед. − 900 (девятьсот). Перед числом 900 называют 899, а после 901.

9 сот. 9 дес. 0 ед − 990 (девятьсот девяносто). Перед числом 990 называют 989, а после 991.

Задание 3.

Прочитайте числа, записанные в таблице.

672 (шестьсот семьдесят два) и 206 (двести шесть).

Вопрос: На каком месте, считая справа налево, пишут единицы? десятки? сотни?

Ответ: Единицы пишут на 1 месте, считая справа налево, десятки − на втором, сотни − на третьем.

2) Сколько единиц каждого разряда в числе 672? 206? 400? 890?

Число 672 содержит 6 единиц III разряда 7 единиц II разряда и 2 единицы I разряда.

Число 206 содержит 2 единиц III разряда 0 единиц II разряда и 6 единиц I разряда.

Число 840 содержит 8 единиц III разряда 4 единиц II разряда и 0 единиц I разряда.

Число 400 содержит 4 единиц III разряда 0 единиц II разряда и 0 единиц I разряда.

Число 590 содержит 5 единиц III разряда 9 единиц II разряда и 0 единиц I разряда.

ГДЗ Математика 4 класс Моро, Бантова часть 1, 2 на Решалка

Родители с педагогами продолжают спорить о необходимом объеме заданий на дом для школьников. Когда норма рабочих часов взрослых людей 40 часов в неделю, учеников нагружают по 50 и более. И цифра растет ежегодно. Эта ситуация волнует не только детей, но и родителей, которым приходится проводить все вечера за занятиями. Ведь вариант с репетиторством далеко не каждому по карману. Часто весь материал, который не успели объяснить на уроке, задают на самостоятельное изучение домой. Математика обязательная дисциплина на многих вступительных экзаменах, по ней сдают ЕГЭ и ЭГЕ, а в младших классах изучаются базовые понятия, без которых потом будет сложнее углубиться предметно. Поэтому так важно не допускать пробелов.

Пособие по математике за 4 класс (часть 1, 2)

Чтобы не просиживать вечера напролет за учебниками, стоит побеспокоиться заранее о вспомогательных материалах. Готовые домашние задания помогут быстрее решить практические упражнения, лучше усвоить материал и закрепить алгоритмы решения однотипных задач. Под авторством Моро, Бантовой вышло отличное пособие по математике для 4 класса и ГДЗ по нему есть на Reshalka.com. Это не просто учебник с ответами, а полностью детализированное описание пошагового решения.

2 части пособия, проверенные квалифицированными педагогами

Для 4 класса решебник станет отличным вспомогательным ресурсом, когда по какой-либо причине ребенок отсутствовал на уроке или плохо усвоил определенную тему. Он поможет качественно подготовиться к контрольной работе или экзамену, разобраться по примерам, как решать подобные упражнения.
Для 4 класса готовые домашние задания по математике содержат проверенные решения с ответами. Помимо умножения, деления, сочетания и вычитания, пособие из двух частей авторов Моро и Бантовой обучит приемам вычисления, измерения длины, массы, определения времени, площади фигур. Четвероклассники научатся использовать обобщенные понятия для арифметических и практических задач. Кроме подготовки к занятиям или контрольным срезам, школьники смогут проработать допущенные ошибки, улучшить свою успеваемость. С онлайн-сервисом ГДЗ «Решалка» Ваш ребенок не будет переутомляться, сможет посещать любимые кружки без ущерба оценкам.

Простые задачи на движение. 4 класс

 {module Адаптивный блок Адсенс в начале статьи}

ПРОСТЫЕ ЗАДАЧИ НА ДВИЖЕНИЕ

4 КЛАСС

  Решение простых задач на движение для 4 класса обычно выполняется в одно действие.

  Основной формулой для решения задач такого типа является формула зависимости расстояния пройденного объектом от скорости движения данного объекта и времени движения:

S = v · t

  где S — расстояние (пройденный путь)

  v — скорость объекта (км/ч; м/с)

  t — время, в течение которого объект был в движении.

  В зависимости от условия задачи, существует несколько способов применения основной формулы для решения задач на движение.

  Рассмотрим несколько примеров решения таких задач.

  В задаче на движение могут быть известны скорость движения и время движения, а расстояние (пройденный путь) необходимо найти. В данном случае основная формула применяется в своем первоначальном виде.

  Пример: Скорость грузового поезда 35 км/час. Поезд был в пути 2 часа. Какое расстояние он прошёл?

  Решение: S = v · t = 35 · 2 = 70 (км) — расстояние пройденное поездом.

  Ответ: 70.

  В задаче на движение могут быть известны расстояние и время, а скорость движения необходимо найти. В данном случае из основной формулы выражается скорость движения.

  Пример: Велосипедист проехал 36 км за 2 часа. С какой скоростью он двигался?

  Решение: v = S / t = 36 ÷ 2 = 18 (км/час) — скорость движения велосипедиста.

  Ответ: 18.

  В задаче на движение могут быть известны расстояние и скорость движения, а время в пути необходимо найти. В данном случае из основной формулы нужно выразить время через расстояние и скорость.

  Пример: Охотник верхом на лошади проехал 28 км со скоростью 14 км/час. Сколько времени он потратил на дорогу?

  Решение: t = S / v = 28 ÷ 14 = 2 (часа) — охотник потратил на дорогу.

  Ответ: 2.

  Примеры простых задач на движение для 4 класса:

  1) Расстояние от города до посёлка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 6 км/час?

  2) Мальчик пробежал 20 м за 10 сек. С какой скоростью бежал мальчик?

  3) Крейсер проплыл 80 км со скоростью 40 км/час. Сколько времени он затратил?

  4) Муха летела со скоростью 5 м/сек 15 секунд. Какое расстояние она пролетела?

  5) Грач пролетел 100 м со скоростью 10 м/сек. Сколько времени он был в пути?

  6) За 3 секунды сокол пролетел 78 м. Какова скорость сокола?

  7) Орёл летел со скоростью 30 м/с 6 секунд. Сколько метров пролетел орёл?

  8) Расстояние в 450 км скорый поезд проехал за 5 часов. С какой скоростью ехал поезд?

  9) Лыжник прошёл с одинаковой скоростью 70 км за 5 часов. Какова скорость лыжника?

  10) Туристы проехали 5 часов на лодке со скоростью 12 км/час. Какое расстояние они проплыли?

  11) Расстояние в 240 км мотоциклист проехал со скоростью 40 км/час. За сколько часов мотоциклист проехал это расстояние?

  12) За 2 часа вертолёт пролетел 600 км. С какой скоростью летел вертолёт?

  13) За 3 дня верблюд прошёл 240 км. С какой скоростью шёл верблюд?

  14) Легковой автомобиль проехал 270 км за 3 часа. С какой скоростью ехал автомобиль?

  15) Мотоциклист ехал 4 часа со скоростью 70 км/час. Какое расстояние проехал мотоциклист?

 {module Адаптивный блок Адсенс в конце статьи}

4 класс. Моро. Учебник №1. Ответы к стр. 37

Числа от 1 до 1000

Величины.

Единицы длины

Ответы к стр. 37

151. 1) Прочитай таблицу единиц длины.
            Запиши и запомни её.

        2) Используя эту таблицу, узнай, сколько миллиметров в 1 дм; сколько сантиметров в 1 м. 

1 дм = 100 мм

       3) Во сколько раз 1 м больше, чем 1 мм?

1 м = 1 000 мм. 1 м больше, чем 1 мм в 1 000 раз.

152. Спиши, заполняя пропуски.

620 = 1 000 м             756 = 75 дес. 6 ед.
620 мм = 62 см           756 мм = 75 см 6 мм
620 дм = 62 м             756 дм = 75 м 6 дм   

1 000 см = 10 м
25 000 м = 25 км
6 000 мм = 6 м

153. От двух остановок, расстояние между которыми 1 км, отошли два пешехода. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?

       1) Дополни условие, чтобы чертёж к задаче был таким:

От двух остановок, расстояние между которыми 1 км, отошли навстречу друг другу два пешехода. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?

1) 160 + 140 = 300 (м) — прошли оба пешехода.
1 км = 1 000 м
2) 1 000 — 300 = 700 (м) — расстояние между пешеходами
О т в е т: расстояние между пешеходами стало 700 м.

2) Измени условие задачи, чтобы чертёж стал таким:

От двух остановок, расстояние между которыми 1 км, отошли два пешехода в противоположных направлениях друг к другу. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?

1) 160 + 140 = 300 (м) — прошли оба пешехода.
1 км = 1 000 м
2) 1 000 + 300 = 1 300 (м) — расстояние между пешеходами
О т в е т: расстояние между пешеходами стало 1 300 м.

154. 

200 — 80 : 2 + 6 = 166               905 — 359 • 2 = 187
(300 — 90) : 3 + 7 = 77              801 — 198 • 4 = 9
600 — 120 : (4 + 2) = 580          703 — 135 • 5 = 28

552 : 8 = 69
836 : 4 = 209
978 : 3 = 326

155. Найди правило, по которому составлен ряд чисел, и запиши ещё 3 числа: 24, 23, 21, 18, 17, 15, 12, 11, 9, 6.

24 — 1 = 23, 23 — 2 = 21, 21 — 3 = 18,
18 — 1 = 17, 17 — 2 = 15, 15 — 3 = 12,
12 — 1 = 11, 11 — 2 = 9, 9 — 3 = 6.

1 560 км = 1 км 560 м 

ЗАДАНИЕ НА ПОЛЯХ:
Ребус

_х 106
      9
   954

ГДЗ по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 4 класс

4 класс. Моро. Учебник №1. Ответы к стр. 37

4.1 (81.71%) от 105 голосующих

4 класс. Моро. Учебник №2. Ответы к стр. 21

Числа от 1 до 1000

Что узнали. Чему научились

Ответы к стр.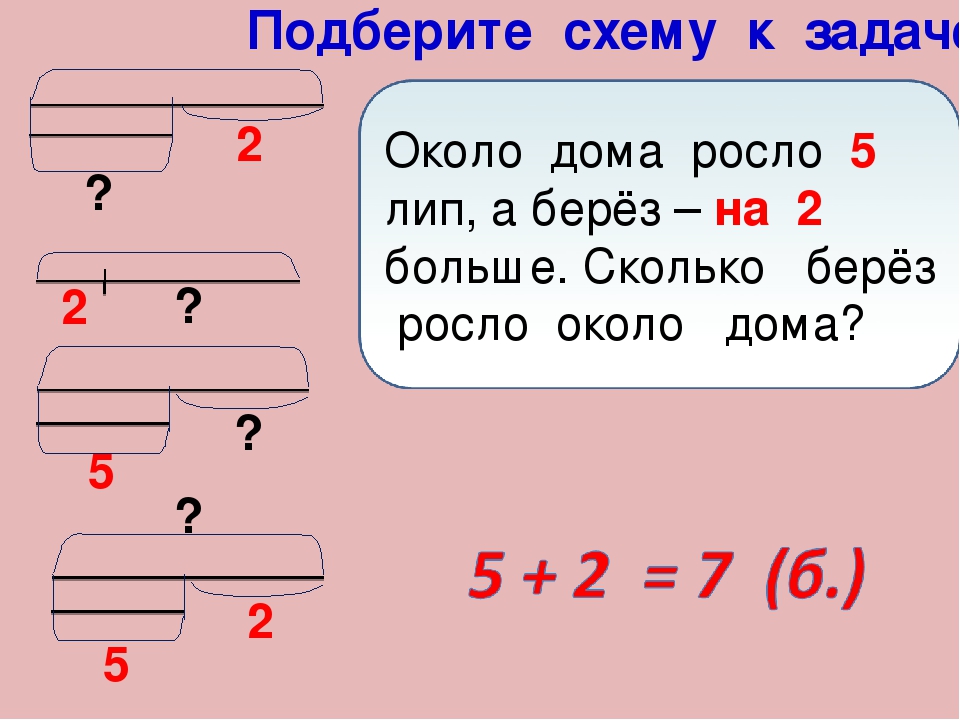 21

10. Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Проверь, какого вида треугольник получился.

Получился прямоугольный треугольник.

11. Вычисли значение выражения α : b, если:
1) α = 7020 и b = 6;     2) α = 17418 и b = 3.

_— 7020|6           
   6      |1170
 _—10                  
     6
   _42
     42
       0       

_— 17418|3           
   15      |5806
    _—24                  
     24
       _18
         18
           0       

12. Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. первый мальчик бежал со скоростью 4 м/с. С какой скоростью бежал второй мальчик?

1) 4 • 10 = 40 (м) − пробежал до встречи первый мальчик
2) 100 − 40 = 60 (м) − пробежал до встречи второй мальчик
3) 60 : 10 = 6 (м/с)
О т в е т: скорость второго мальчика 6 м/с.

13. Товарный поезд прошел 315 км. Он был в пути до остановки 3 ч и после остановки 4 ч. Сколько километров прошел поезд до остановки и сколько после, если он шел с одинаковой скоростью?

1) 3 + 4 = 7 (ч) − общее время в пути
2) 315 : 7 = 45 (км/ч) − скорость поезда
3) 45 • 3 = 135 (км) − прошел поезд до остановки
4) 45 • 4 = 180 (км) − прошел поезд после остановки
О т в е т: поезд прошёл до остановки 135 км, а после остановки 180 км.

14. Отрезок длиной 90 мм разделили сначала на 3 равные части, а затем каждую из них разделили на 2 равные части. На сколько равных частей разделил весь отрезок? Чему равна длина одной шестой части данного отрезка?
Сделай по задаче чертеж и реши ее.

1) 90 : 3 = 30 (мм) – одна часть из трёх
2) 30 : 2 = 15 (мм) – одна часть из двух
3) 90 : 15 = 6 (ч.) – всего
4) 90 : 6 = 15 (мм) – шестая часть
О т в е т: на 6 частей, шестая часть – 15 мм.

15. Молочный завод отправил в магазин 56 ящиков сливочного масла, по 20 кг в каждом. За день продали одну седьмую часть этого масла. Сколько килограммов масла осталось?

1-й способ
1) 56 • 20 = 1120 (кг) − масла отправили всего
2) 1120 : 7 = 160 (кг) − масла продали
3) 1120 − 160 = 960 (кг)
О т в е т: осталось 960 кг масла.

2-й способ
1) 56 : 7 = 8 (ящ.) масла продали
2) 56 – 8 = 48 (ящ.) − масла осталось
3) 48 • 20 = 960 (кг)
О т в е т: осталось 960 кг масла.

16. Расстояние между городом и зимовкой 150 км. Из города к зимовке выехали аэросани и двигались со скоростью 60 км/ч. В это же время навстречу им из зимовки по той же дороге пошел лыжник со скоростью 15 км/ч. На каком расстоянии от зимовки он встретил аэросани?

1) 60 + 15 = 75 (км/ч) − скорость сближения
2) 150 : 75 = 2 (ч) − время до встречи
3) 2 • 15 = 30 (км)
О т в е т: лыжник прошёл 30 км до встречи.

17. Найди ошибки в вычислениях и реши правильно.
1751 : 5 = 35 (ост. 1)     2930 : 7 = 41 (ост. 6)
1983 : 9 = 22 (ост. 3)     40202 : 6 = 670 (ост. 2)

_— 1751|5       
   15    |350
   _—25                
    25
      _1
        0
        1 – ост. 

_— 1983|9       
   18    |220
   _—18                
    18
      _3
        0
        3 – ост. 

_— 2930|7       
   28    |418
    _—13                
       7
      _60
        56
          4 – ост.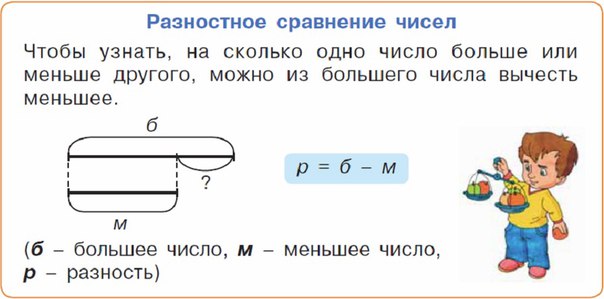  

_— 40202|6         
   36      |6700
    _—42                
     42
         _2
           0
           2 – ост. 

18. 4527 • 50 − 710037 : 9     397 • 600     32340 : 10
      (932 + 17692) : 6 • 80      4030 • 90      56400 : 100

4527 • 50 − 710037 : 9 = 226350 − 78893 = 147457
_— 710037|9               _× 4527
   63       |78893                50
    _—80                        226350
     72
     _80                    _226350
       72                       78893
       _83                   147457
         81
         _27
           27
            0

(932 + 17692) : 6 • 80 = 18624 : 6 • 80 = 3104 • 80 = 248320
_— 18624|6              ₊ 17692
   18      |3104              932
      _—6                       18624
      6
      _24                    _×3104
        24                           80
          0                    248320   

_× 397                _× 4030
      600                   90 
 238200             362700 

32340 : 10 = 3234

56400 : 100 = 564       

19.  Запиши 5 чисел, каждое из которых делится без остатка и на 5, и на 9.

5 • 9 = 45 − значит, на 5 и 9 будут делится все числа которые делятся на 45
1 • 45 = 45
2 • 45 = 90
3 • 45 = 135
4 • 45 = 180
5 • 45 = 225
О т в е т : 45, 90, 135, 180, 225.

ЗАДАНИЕ НА ПОЛЯХ
НАЧЕРТИ УЗОР

Ответы по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 4 класс

4.9
/
5
(
109

голосов
)

учимся работать с таблицей – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)

1. Информационные таблицы

Информационные таблицы содержат данные, которые ученику нужно использовать при выполнении задания. Могут быть указаны площади стран, сведения из биологии, другие показатели. Дети получают задания: «найди информацию», «классифицируй», «расположи по уменьшению» (и возрастанию), «сделай вычисления», «составь вопросы по таблице» и др. Вычисления производятся отдельно.

Примеры заданий

1 класс

(Из проверочных работ. Задание «со звездочкой»)

На даче собрали урожай ягод. Их количество записали в таблицу

Укажите верные утверждения, составленные по таблице.

• Крыжовника больше, чем малины.
• Черники меньше, чем крыжовника.
• Малины столько же, сколько черники.
• Крыжовника больше, чем черники, но меньше, чем клубники.

2 класс

(Из проверочных работ)

В таблице указано расписание движения поездов

Запиши ответ на вопросы.

1. Какой номер поезда Москва — Анапа?
2. В какое время отправляется поезд Москва — Сочи?
3. В какой город поезд отправляется раньше всех?

3 класс

«Моя телефонная книга»

Составь свою телефонную книгу. Расположи абонентов в алфавитном порядке. Какие телефоны экстренных служб обязательно должны быть занесены в книгу?

4 класс

Ответьте на вопросы по таблице, в которой записана длина корней некоторых растений.

1. Какое растение имеет: а) самые длинные корни; б) самые короткие корни?
2. Расставь растения в порядке уменьшения длины корней.
3. На сколько сантиметров корни пшеницы длиннее, чем корни льна?
4. На сколько сантиметров корни гороха короче, чем корни ржи?

Занимательная математика. 1 класс. Рабочая тетрадь

Пособие может быть использовано в начальной школе при проведении занятий математического факультатива, кружка, олимпиады, клуба «Эрудит», интеллектуального марафона и других форм организации внешкольной деятельности учащихся. Задания, включенные в рабочую тетрадь, способствуют формированию у детей самостоятельности, наблюдательности, геометрической зоркости и умения рассуждать, а также создают условия для развития интереса к математике, математического кругозора и эрудиции учащихся.

Купить

2. Справочные таблицы

Справочные таблицы в первом классе показывают числа в пределах 20 с разных точек зрения. И далее, они помогают познакомить учеников с названиями чисел, видами вычислений, разрядами чисел, единицами измерения.

Примеры заданий

1 класс

Назови состав числа 5 по рисунку. Заполни домик.

Найди значение выражений, пользуясь составом числа 5.

2 класс

Рассмотри таблицу чисел от 1 до 100. Назови числа, которые ты знаешь. По какому правилу составлена таблица? Какие числа пропущены?

1. Сколько двузначных чисел начинаются с цифры 7? Назови их.
2. Сколько в таблице круглых чисел? Назови их.
3. Сколько однозначных чисел? Назови их.
4. Сколько двузначных чисел оканчивается цифрой 2? Назови их.

3 класс

Найди значения выражений и запиши их римскими цифрами.

4 класс

Выполни задание по таблице.

Таблица разрядов и классов

1. Сколько классов в таблице? Сколько разрядов?
2. Назови разряды каждого класса.
3. Какие цифры записаны в разряде десятков миллионов?
4. Какие цифры записаны в разряде: единиц, единиц тысяч, единиц миллионов?
5. В каких разрядах записана цифра 3?
6. Назови старший разряд каждого числа.
7. Прочитай второе число. Какой класс не назван?

3. Логические таблицы

Логические таблицы ставят перед учениками логические задачи: проанализировать данные, найти закономерности. Например: «дополни таблицу нужными элементами» (фигурами/числами), «продолжи запись», «сопоставь числа и формулы», «вставь подходящее число из предложенных и сделай вычисление» и т.д.

Примеры заданий

1 класс

Кто быстрее (ты или твой сосед по парте) нарисует фигуру, которую нужно поставить на свободное девятое место?

3 класс

Какие числа пропущены в таблице, если r — радиус окружности, а d — диаметр этой же окружности?

4 класс

Какие высказывания о таблице верные?

1. В первом столбце записаны круглые числа.
2. В первой строке записаны четные двузначные числа.
3. В третьей строке записаны трехзначные числа, которые содержат 9 десятков.
4. В четвертом столбце записаны числа, которые делятся на 3 без остатка.
5. Сумма чисел в первой строке равна 144.

Читайте также:

4. Вычислительные таблицы

Вычислительные таблицы являются формой вычислительного задания, то есть ученики производят вычисления непосредственно в таблице. Так школьники повторяют компоненты действий и составы чисел, работают с множителями, делимыми, разностями, остатками и т.д.

Примеры заданий

1 класс

Какие числа пропущены?

2 класс

Назовите числа, которые пропущены в каждой таблице.

Закончи предложения.

1. Если произведение двух чисел разделить на один из множителей, то получится … .
2. Если делитель умножить на частное, то получится … .
3. Если делимое разделить на частное, то получится … .
4. Если делимое разделить на делитель, то получится … .

3 класс

Какие числа пропущены в таблице?

4 класс

Вычисли устно и расшифруй название науки. Что она изучает?

Математика. 4 класс. Итоговая аттестация. Базовый и повышенный уровни сложности.

Рабочая тетрадь предназначена для оценки результатов деятельности выпускников начальной школы по освоению курса математики. В нее включены 10 вариантов заданий на двух уровнях трудности. В основе многих заданий лежат ситуации из реальной жизни. Пособие окажет учителям начальной школы помощь в организации диагностических процедур.

Купить

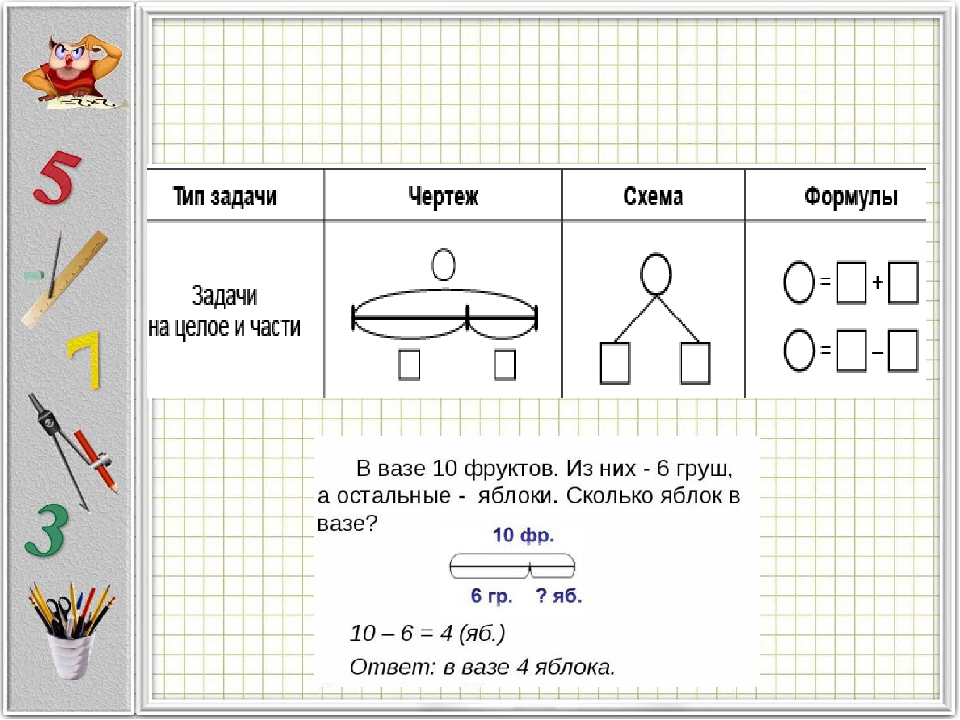
5. Таблицы для решения задач

Таблицы для решения задач подобны вычислительным таблицам, однако используются в заданиях с текстовыми задачами, сопровождаются иллюстрациями, схемами. Такие таблицы часто предусматривают работу с формулами и с пропорциями.

Примеры заданий

1 класс

Составь задачу и реши ее.

2 класс

На пошив спального мешка требуется 4 м ткани. Сколько метров ткани потребуется для 7 спальных мешков? Составь две обратные задачи, используя таблицу.

3 класс

За 5 ластиков Оля заплатила 30 р., а Марина за такие же ластики заплатила 54 р. Сколько ластиков купила Марина?

План решения.

1. Найти цену ластика.
2. Найти количество ластиков, купленных Мариной.

4 класс

Реши задачу, используя таблицу или схему. Машина в первый день за 8 ч проехала 464 км. Во второй день она была в пути 6 часов и двигалась с той же скоростью. Сколько всего километров проехала машина за два дня?

Задание с таблицей из демоверсии ВПР по математике (4 класс)

Проверяемые умения в соответствии с ФГОС:

• Умение работать с таблицами, схемами, графиками диаграммами, анализировать и интерпретировать данные.
• Сравнивать и обобщать информацию, представленную в строках и столбцах несложных таблиц и диаграмм.

Задание:

В спортивных соревнованиях по нескольким видам спорта приняли участие 4 команды. Количество медалей, полученных командами, представлено в таблице. Используя эти данные, ответь на вопросы.

1) Сколько серебряных медалей завоевала команда «Сириус»? 2) Какая команда заняла 3-е место по сумме всех медалей?

Решение: 1) 7 + 8 + 3 = 18 (м.) — «Сириус»; 2) 6 + 4 + 5 = 15 (м.) — «Орион»; 3) 4 + 6 + 7 = 17 (м.) — «Заря»; 4) 3 + 2 + 5 = 10 (м.) — «Весна».

Ответ: 1) 8; 2) Орион.

Вы можете апробировать учебники «Математика» авторства Г. К. Муравина и О. В. Муравиной. Для этого воспользуйтесь акцией «5 учебников бесплатно».

#ADVERTISING_INSERT#

Моро. Решебник 1, 2 часть

ГДЗ по математике для 4 класса Моро – это сборник готовых домашних заданий: решенные задачи, примеры, уравнения, неравенства по учебнику авторитетных российских математиков – М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Его используют в качестве базового пособия для четвероклассников во многих центральных и региональных школах РФ.

Структура ГДЗ по учебнику математики четвертого класса от Моро

В четвертом классе школьная программа изучения предписывает решение задач и примеров с числами от 1 до 1000, умножение и деление столбиком, определение скорости, времени и расстояния.  Именно в 4-м классе закладывается база для изучения углубленных основ арифметики, а после – алгебры, геометрии, химии и физики.

ГДЗ по математике 4 класса Моро, составленные на основе учебника 2015 года в его 4-м издании, включают в себя примеры и задачи на такие темы:

• четыре арифметических действия: сложение, вычитание, умножение, деление;
• диаграммы;
• сложение и вычитание, умножение и деление величин;
• скорость, время, расстояние;
• умножение и деление на числа, оканчивающиеся нулями;
• умножение и деление на двузначное и трёхзначное число;
• числа от 1 до 1000;
• уравнения и неравенства с одной переменной.

В четвертом классе завершается курс средней школы. Ученики переходят на новую степень и должны уметь решать примеры и задачи самостоятельно. Цель решебника по математике к учебнику Моро – представить детальные алгоритмы решений, разъяснить материал, пройденный в классе.

Готовое домашнее задание для 4 класса на сайте ГДЗ Путина поможет не только ученикам, но их родителям, которые часто делают уроки вместе со своими детьми. Это также способ отказаться от услуг репетиторов и платных подготовительных курсов.

Правильные решения от ГДЗ Путина по математике 4 класса к Моро

Чтобы найти решение домашней задачи в интернете, достаточно за пару кликов отыскать нужный решебник. Однако не все сайты предлагают подробные решения и верные ответы. В чем преимущества портала ГДЗ от Путина? Почему именно его часто выбирают ученики младших классов и их родители?

• здесь можно найти несколько вариантов решения одной задачки;
• ответы оформлены по требованиям Минобразования России;
• все примеры с ответами доступны без регистрации и бесплатно;
• информация корректно отображается на телефонах, компьютерах и планшетах.

Перечисленные критерии важны для пользователей ГДЗ по математике 4 класса к учебнику Моро: ученики получают подробные описания решений и могут разобраться со сложными темами, их родители – в любое время проверить домашнюю работу их чад.

Поскольку задачи и примеры приводятся в нескольких вариантах выполнения, то можно выбрать самый понятный и удобный вариант, взять его за основу, разобрать и запомнить.

Решение задач: 4 класс по математике

Приборная панель

4 класс

Решение проблем

Перейти к содержанию

Приборная панель

• Авторизоваться

• Панель приборов

• Календарь

• Входящие

• История

• Помощь

Закрывать

• 
  Мой Dashboard
  
• Оценка 4
• Страницы
• Решение проблем

NE

• Home
• Routines
• Closure
• Resource Bank
• Grade 3 Course
• Grade 4 G / T
• Grade 5 Course
• Grade 4 Curriculum Community
• Grade 4 Family and Community
• Collaborations
• Google Drive

Grade 4 Curriculum

Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут с этим навыком.Мы также поощряем множество упражнений и работу с книгами. Curriculum Home

Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.

Класс 4 | Подсчет

☐ Счетчик пропусков по 1000

4 класс | Сложение

☐ Используйте различные стратегии для сложения чисел до 10 000

4 класс | Вычитание

☐ Используйте различные стратегии для вычитания чисел до 10 000

4 класс | Умножение

☐ Разберитесь в различных значениях умножения

☐ Используйте различные стратегии для умножения двузначных чисел на однозначные числа (с перегруппировкой и без нее)

☐ Используйте различные стратегии для умножения двузначных чисел на двузначные числа (с перегруппировкой и без нее)

☐ Научитесь умножать числа, кратные 10 и 100, на 1000

☐ Понимать, использовать и объяснять ассоциативное свойство умножения

☐ Развивайте свободное владение языком с помощью умножения до 10x

4 класс | Деление

☐ Используйте умножение и деление как обратные операции для решения задач

☐ Используйте различные стратегии для деления двузначных дивидендов на однозначные делители (с остатком и без остатка)

☐ Толковать значение остатков

☐ Понимать различные значения деления

4 класс | Числа

☐ Развить понимание свойств нечетных / четных чисел в результате умножения

☐ Выбрать подходящие вычислительные и операционные методы для решения проблем

☐ Чтение и запись целых чисел в 10,000

☐ Округлить числа от 1000 до ближайшей десятки или до ближайшей сотни

☐ Сравните и закажите номера до 10,000

☐ Поймите структуру разрядных значений десятичной системы счисления:

10 единиц = 1 десятка

10 десятков = 1 сотня

10 сотен = 1 тысяча

10 тысяч = 1 десять тысяч

☐ Распознавать эквивалентные представления чисел до четырех цифр и генерировать их путем разложения и составления чисел

☐ Узнайте, как расширить структуру значений разряда десятичной системы счисления, включив в нее десятичные дроби: десятые, сотые, тысячные…

☐ Округлить десятичные дроби до ближайшего целого числа.

4 класс | Десятичные дроби

☐ Развивайте понимание десятичных дробей как части целого

☐ Сложить и вычесть десятичные дроби до десятых и сотых, используя таблицу сотен

4 класс | Дроби

☐ Сложить и вычесть правильные дроби с общим знаменателем

☐ Выражение десятичных дробей как эквивалент дробей до десятых и сотых

☐ Развивайте понимание дробей как положений на числовых линиях и как делений целых чисел

☐ Распознавать и генерировать эквивалентные дроби (половинки, четверти, трети, пятые, шестые и десятые) с помощью манипуляторов, визуальных моделей и иллюстраций

☐ Используйте конкретные материалы и визуальные модели для сравнения и упорядочивания дробей или дробей единиц с одинаковым знаменателем (с использованием числовой линии и без нее)

☐ Понимать разницу между правильными, неправильными и смешанными дробями

4 класс | Размер

☐ Выберите инструменты и единицы измерения, соответствующие измеренной длине (метрическая)

☐ Используйте линейку для измерения с точностью до метрической единицы (целые сантиметры или целые метры)

☐ Знать и понимать эквивалентные метрические стандартные единицы длины:
10 миллиметров = 1 сантиметр, 100 сантиметров = 1 метр, 1000 метров = 1 километр

☐ Выберите инструменты и единицы измерения, соответствующие массе измеряемого объекта (граммы, килограммы и тонны)

☐ Измерить массу в граммах

☐ Выберите инструменты и единицы измерения, соответствующие измеряемому объему (миллилитры и литры)

☐ Измерьте емкость в миллилитрах и литрах

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой температуре (градусы Цельсия или Фаренгейта)

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой площади (квадратные сантиметры, метры или километры)

☐ Выберите инструменты и единицы измерения, соответствующие измеряемому объему (кубические сантиметры или метры)

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой скорости (скорости) (м / с, км / ч)

☐ Знать и понимать эквивалентные метрические единицы массы: 1000 г = 1 кг, 1000 кг = 1 тонна

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой длине (стандартные единицы США)

☐ Используйте линейку для измерения с точностью до ближайшей стандартной единицы США (целые, 1/2 и 1/4 дюйма, целые футы, целые ярды)

☐ Знать и понимать эквивалентные стандартные единицы длины США:
12 дюймов = 1 фут, 3 фута = 1 ярд, 1760 ярдов = 1 миля

☐ Выберите инструменты и единицы измерения, соответствующие массе измеряемого объекта (унции, фунты и тонны)

☐ Измерить массу в унциях

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой емкости (жидкие унции, чашки и пинты)

☐ Измерьте емкость, используя жидкие унции, чашки и пинты

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой площади (квадратные дюймы, футы или мили)

☐ Выберите инструменты и единицы измерения, соответствующие измеряемому объему (кубические дюймы или футы)

☐ Выберите инструменты и единицы измерения, соответствующие измеряемой скорости (скорости) (кадр / с, миль / ч)

☐ Знать и понимать эквивалентные стандартные единицы массы США: 16 унций = 1 фунт, 2000 фунтов = 1 тонна (короткая)

4 класс | Время

☐ Рассчитайте прошедшее время в днях и неделях, используя календарь

☐ Вычислить прошедшее время в часах и полчаса, не пересекая A.М. / П.М.

4 класс | Геометрия (плоскость)

☐ Определите и назовите многоугольники, учитывая, что их имена связаны с количеством сторон и углов (треугольник, четырехугольник, пятиугольник, шестиугольник и восьмиугольник)

☐ Определение точек и отрезков линий при рисовании плоской фигуры

☐ Определить периметр многоугольника путем сложения сторон

☐ Найдите площадь прямоугольника, посчитав количество квадратов, необходимых для покрытия прямоугольника

☐ Нарисуйте и обозначьте пересекающиеся, перпендикулярные и параллельные линии

☐ Части угла (рука / луч и точка / вершина) и различные способы обозначения угла

☐ Углы классифицируются как острые, прямые, тупые, прямые и отогнутые.

4 класс | Геометрия (твердое тело)

☐ Определение и идентификация вершин, граней и ребер трехмерных фигур

☐ Определить и пронумеровать ребра, вершины и грани трехмерных фигур: куб, цилиндр, сфера, тор, призма, пирамида и конус

4 класс | Pre-Algebra

ate Оценивайте и выражайте отношения, используя открытые предложения за одну операцию

☐ Используйте символы равенства или неравенства (с использованием числовой строки и без нее) для сравнения целых чисел, дробных и десятичных дробей (до сотых)

☐ Найдите значение или значения, которые сделают открытое предложение истинным, если оно содержит символы равенства или неравенства

☐ Описывать, расширять и обобщать числовые (+, -, x, /) и геометрические узоры

☐ Проанализируйте шаблон или целочисленную функцию и сформулируйте правило для данной таблицы или поля ввода / вывода

4 класс | Данные

☐ Разработать исследования для ответа на вопрос из предоставленных данных

☐ Собирать данные с помощью наблюдений, опросов и экспериментов и надлежащим образом записывать

☐ Представляйте данные в виде таблиц, гистограмм и пиктограмм

☐ Чтение и интерпретация линейных графиков

☐ Разрабатывать и делать прогнозы на основе данных

☐ Формулируйте выводы и делайте прогнозы по графикам

☐ Понять точность и прецизионность

4 класс | Оценка

☐ Проверить разумность ответа с помощью оценки

4 класс | Деньги

☐ Внести сдачу, используя комбинированные монеты и суммы в долларах

☐ Чтение и запись десятичных дробей с точностью до сотых, с использованием денег в качестве контекста

☐ Используйте конкретные материалы и визуальные модели, чтобы сравнить и упорядочить десятичные дроби (меньше 1) до сотых в контексте денег

☐ Умножайте десятичные дроби до сотых на целое число, особенно в контексте денег.

☐ Рассчитайте общую стоимость, используя комбинированные суммы в монетах и ​​долларах

Стандарт 4: Математическая модель

Наблюдения в классе

Учителя, развивающие у учащихся способность «моделировать с помощью математики», явно перемещаются между сценариями реального мира и математическими представлениями этих сценариев. Учитель среднего детства может представить сценарий коробок конфет, содержащих несколько вкусов, чтобы помочь ученикам определить пропорции и соотношения вкусов и ингредиентов.Учитель раннего подросткового возраста может представить сравнение различных планов проката DVD с помощью таблицы, спрашивая учащихся, помогает ли таблица напрямую сравнивать планы или элементы сравнения опускаются. Учитель подростков и молодых людей может представить сценарий «фабрики воздушных змеев», в котором продвинутых учеников просят определить условия для создания всегда определенной формы воздушного змея с учетом размеров диагоналей и угла пересечения. Посетите отрывки из видео ниже, чтобы увидеть несколько примеров того, как учителя привлекают студентов к математическому моделированию.

Стандарт

Учащиеся со знанием математики могут применять полученные знания для решения задач, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах учащийся может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.

Связь с практикой в ​​классе

1 класс

Студенты со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации … Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если это не так. выполнила свою задачу.

Лиз О’Нил работает со своими первоклассниками, вовлекая их в составление и разложение чисел в пределах двадцати. Ее ученики играют в игру «Сколько скрываются?» Пары получают пакет с 10 кубиками, бумажную тарелку и лист записи «Сколько человек прячутся». Один из партнеров берет несколько кубиков и «прячет» их под тарелкой. Остальные кладем сверху. Второй партнер использует фреймы предложений, чтобы ответить на вопросы «Какое число вы видите?», «Сколько человек прячется?», «Откуда вы знаете, что __ прячутся»? Кроме того, ответы записываются.Затем роли меняются местами. Партнерская игра дает студентам возможность попрактиковаться в составлении и разложении чисел в пределах десяти. Учащимся, выполнившим исходное задание, предлагается изменить общее количество кубиков на 15 или 20.

Смотрите это видео в контексте всего урока.
(части 2-4)

5 класс

Студенты со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте.В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации … Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл …

Хиллари Льюис-Вольфсен предлагает студентам изучить задачу о пропорциях и соотношениях с помощью стратегии, используемой студентом для организации информации в задаче. В этом ролике она дает студентам «время на личное обдумывание», чтобы снова решить проблему, освежая их воспоминания о проблеме, просит их использовать свои «аналитические листы» для записи своих идей, а затем предлагает им обратиться к партнеру и поделиться им и защитить их мышление.В ходе обсуждения пары делятся мнением, что, по их мнению, стратегия ученика из примера отражает неправильное понимание количественных показателей.

Смотрите это видео в контексте всего урока.

7-8 классы

Студенты со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте. В средних классах учащийся может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе.Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как … таблицы …. Они могут анализировать эти отношения математически, чтобы делать выводы.

Сесилио Димас проводит урок по сравнению трех различных финансовых планов, помогая студентам использовать несколько представлений математических задач: словесное, табличное, графическое и алгебраическое обобщение. В этом ролике Димас соединяется с уроком предыдущего дня, в котором класс «начал разговор об экономическом состоянии нашего мира [и] о принятии ответственных решений, когда мы тратим наши деньги.Его ученики рассказывают, что им предстояло представить различные планы проката DVD в устной и табличной форме.

Смотрите это видео в контексте всего урока.

8 класс

Студенты со знанием математики могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте … Они могут определять важные величины в практической ситуации и отображать свои отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, схемы и формулы.Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл….

Антуанетта Вильярэн начинает свой урок с построения графиков постоянных темпов изменения, анализа целей обучения и математических практик, определения Стандартов для математической практики 1, 3, 6 и 7. Она отмечает, что важно, чтобы ее ученики понимали, как строить математические методы. аргумент, и она делится фреймами предложений и ключевым словарным запасом, которые студенты будут использовать при построении своих аргументов.

Антуанетта представляет модель двух бутылок, прикрепленных друг к другу, чтобы жидкость могла течь между ними, и просит своих учеников разобраться в проблеме, описывая происходящее.

Студенты рассказывают, что по мере уменьшения количества жидкости в верхнем контейнере / призме количество жидкости в нижнем контейнере / призме увеличивается.

Этот клип также относится к стандарту 1 (разбираться в проблемах и настойчиво их решать), стандарту 3 (составлять жизнеспособные аргументы и критиковать рассуждения других), стандарту 6 (уделять внимание точности) и стандарту 7 (искать и делать использование структуры).

Смотрите это видео в контексте всего урока.

Студенты со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте.

Пэтти вводит свой урок, предлагая студентам определить «большие идеи», о которых они должны думать, работая с прямоугольными треугольниками. Студенты делятся своими идеями в паре, и Пэтти отмечает, когда они ссылаются на доступные инструменты и вспомогательные средства, такие как диаграммы привязки, в комнате.В своем комментарии Пэтти отмечает, что этот урок предназначен для развития у студентов способности моделировать математические ситуации. Студенты идентифицируют теорему Пифагора, и Пэтти побуждает их уделять внимание точности и четко общаться. Общаясь в группе, она вовлекает всех учеников, чтобы они дополняли, критиковали, расширяли и разъясняли мысли друг друга. Студенты углубляют свою способность понимать проблему или ситуацию. Пэтти представляет студенческие работы из предыдущей оценки и просит студентов критиковать стратегии и точность этого человека, давая советы каждому образцу ученика о том, как улучшить свой подход.Этот клип также относится к стандарту 1 (разбираться в проблемах и настойчиво их решать), стандарту 3 (составлять жизнеспособные аргументы и критиковать рассуждения других) и стандарту 5 (стратегически использовать соответствующие инструменты).

Смотрите это видео в контексте всего урока.
урок 1 часть

Студенты со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте.

Ученики Пэтти дают советы своим сверстникам о настойчивости и стратегиях, которые они могут использовать, чтобы помочь себе в предстоящем задании по оценке результатов MARS. Она спрашивает: «Что вы делаете, когда застряли? Какие стратегии вам следует попробовать? » Студенты думают, пишут, а затем делятся друг с другом своими стратегиями. Они определяют стратегии, используя якорные диаграммы и калькуляторы, рисуя картинки, консультируясь с коллегами, не торопясь, перепроверив свою работу и убедившись, что она имеет смысл.Этот клип также относится к стандарту 1 (разбираться в проблемах и настойчиво их решать), стандарту 3 (составлять жизнеспособные аргументы и критиковать рассуждения других) и стандарту 5 (стратегически использовать соответствующие инструменты).

Смотрите это видео в контексте всего урока.
урок 2 часть

9–10 классы

Студенты со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте.В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации … Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл …

Кэти Хамфрис ведет расширенное исследование доказательства свойств четырехугольника, помогая студентам научиться исследовать, формулировать, предполагать, обосновывать и в конечном итоге доказывать математические теоремы. В этом ролике Хамфрис представляет задачу, представляя проблему как реальное расследование, в котором производитель воздушных змеев, который «производит только четырехугольные змеи», и должен знать свойства выпуклых четырехугольников, которые всегда будут приводить к заданной форме змея, говоря: «Как делать палки — вот в чем проблема.«Учащиеся работают в группах, чтобы дать рекомендации по созданию прототипов этому производителю, так что каждый раз, когда поступает заказ, производитель всегда будет знать,« какие палочки поставить в комплект и как их собирать ».

Смотрите это видео в контексте всего урока.

Стандартов для математической практики | Инициатива Common Core State Standards

Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учеников.Эти практики опираются на важные «процессы и навыки», имеющие давнюю важность в математическом образовании. Первыми из них являются стандарты процесса NCTM для решения проблем, обоснования и доказательства, коммуникации, представления и связей. Вторые — это направления математической подготовки, указанные в отчете Национального исследовательского совета Сложение : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических концепций, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность).

Стандарты в этой области:

CCSS.Math.Practice.MP1 Разбирайтесь в проблемах и проявляйте настойчивость в их решении.

Учащиеся со знанием математики начинают с объяснения себе значения проблемы и поиска точек входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении.Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.

CCSS.Math.Practice.MP2 Размышляйте абстрактно и количественно.

Учащиеся со знанием математики понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентативными символами, как будто они живут своей собственной жизнью, не обязательно обращая внимание на своих референтов — и возможность контекстуализировать , останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов.

CCSS.Math.Practice.MP3 Создавайте жизнеспособные аргументы и критикуйте рассуждения других.

Студенты со знанием математики понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов.Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.

CCSS.Math.Practice.Модель MP4 с математикой.

Учащиеся со знанием математики могут применять полученные знания для решения задач, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах учащийся может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.

CCSS.Math.Practice.MP5 Стратегически используйте соответствующие инструменты.

Учащиеся со знанием математики рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной мере знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.

CCSS.Math.Practice.MP6 Внимание к точности.

Учащиеся со знанием математики стараются точно общаться с другими. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом. Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме.Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.

CCSS.Math.Practice.MP7 Ищите и используйте структуру.

Студенты, разбирающиеся в математике, внимательно приглядываются, чтобы различить образец или структуру. Например, молодые студенты могут заметить, что три и семь больше равны семи и еще трем, или они могут отсортировать набор фигур в зависимости от того, сколько сторон у них.Позже учащиеся увидят, что 7 × 8 равно хорошо запоминающимся 7 × 5 + 7 × 3, при подготовке к изучению свойства распределения. В выражении x ² + 9 x + 14 старшие ученики могут видеть 14 как 2 × 7 и 9 как 2 + 7. Они осознают значение существующей линии в геометрической фигуре и могут использовать стратегия рисования вспомогательной линии для решения задач. Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или состоящие из нескольких объектов.Например, они могут видеть 5-3 ( x — y ) ² как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y .

CCSS.Math.Practice.MP8 Ищите и выражайте закономерность в повторяющихся рассуждениях.

Студенты, разбирающиеся в математике, замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и придут к выводу, что у них есть повторяющаяся десятичная дробь.Обращая внимание на вычисление наклона, поскольку они неоднократно проверяют, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, ученики средней школы могут абстрагироваться от уравнения ( y — 2) / ( x — 1) = 3. Обратите внимание на регулярность отмены условий при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x ² + x + 1), и ( x — 1) ( x ³ + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.

Соединение стандартов математической практики со стандартами математического содержания

Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты, практикующие математическую дисциплину, должны все активнее заниматься предметом по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы.Разработчики учебных программ, оценок и повышения квалификации должны уделять внимание необходимости увязать математические практики с математическим содержанием в обучении по математике.

Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать практики с содержанием. Студенты, которым не хватает понимания темы, могут слишком сильно полагаться на процедуры.Без гибкой основы для работы они с меньшей вероятностью будут рассматривать аналогичные проблемы, связно представлять проблемы, обосновывать выводы, применять математику к практическим ситуациям, осознанно использовать технологии для работы с математикой, точно объяснять математику другим ученикам, сделайте шаг назад, чтобы получить обзор, или отклонитесь от известной процедуры, чтобы найти ярлык. Короче говоря, непонимание фактически мешает студенту заниматься математической практикой.

В этом отношении те стандарты содержания, которые устанавливают ожидания понимания, являются потенциальными «точками пересечения» между Стандартами математического содержания и Стандартами математической практики.Эти точки пересечения призваны соотносить с центральными и генеративными концепциями школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и концентрации, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и достижений учащихся математика.

Решение проблем: предположение и проверка

Страница 1 из 2

Решение проблем: предположение и проверка

Что это такое?

«Угадай и проверь» — это стратегия решения задач, которую учащиеся могут использовать для решения математических задач, угадывая ответ и затем проверяя, соответствует ли это предположение условиям задачи.Например, следующую задачу лучше всего решить с помощью догадок и проверки:

Из 25 раундов регионального конкурса правописания Mighty Brains сыграли вничью 3 раунда и выиграли на 2 больше, чем проиграли. Сколько раундов выиграли Mighty Brains?

Почему это важно?

Все математики-исследователи используют догадки и проверки, и это один из самых эффективных методов решения дифференциальных уравнений, которые представляют собой уравнения, содержащие неизвестную функцию и ее производные. Предположение математика называется «гипотезой», а оглядываясь назад, чтобы проверить ответ и доказать, что оно верное, называется «доказательством».«Основное различие между решением проблем в классе и математическими исследованиями заключается в том, что в школе обычно существует известное решение проблемы. В исследованиях решение часто неизвестно, поэтому проверка решений является важной частью процесса.

Как Сможете ли вы сделать это?

Предложите учащимся задачу, которую они должны решить, а затем проверить свое предположение, чтобы решить задачу.Например, задача:

Бен знает 100 бейсболистов по имени.Десять — это Ред Сокс. Остальные — Блю Джейс и Даймондбэкс. Он знает имена вдвое больше Даймондбэков, чем Блю Джейс. Сколько Блю Джейс он знает по имени?

Когда учащиеся используют стратегию предположений и проверок, они должны вести записи о том, что они сделали. Было бы полезно попросить их использовать диаграмму или таблицу.

Разберитесь в проблеме

Продемонстрируйте, что первым шагом является понимание проблемы. Это включает в себя поиск ключевой информации, необходимой для поиска ответа.Для этого может потребоваться прочитать задачу несколько раз и / или учащиеся изложат ее своими словами.

Например: «Я знаю, что Diamondbacks вдвое больше, чем Blue Jays. Всего 10 Red Sox. Количество Blue Jays и Diamondbacks должно равняться 90».

Выберите стратегию

Используйте стратегию «Угадай и проверь». Угадай и проверь часто — одна из первых стратегий, которые учащиеся усваивают при решении задач. Это гибкая стратегия, которая часто используется в качестве отправной точки при решении проблемы и может использоваться в качестве подстраховки, когда никакая другая стратегия сразу не очевидна.

Промежуточная алгебра Урок 8: Введение в решение проблем WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения После изучения этого руководства вы сможете: Используйте четырехэтапный процесс Polya для решения словесных задач, связанных с числами, проценты, прямоугольники, дополнительные углы, дополнительные углы, последовательный целые числа и безубыточность. Введение Нравится вам это или нет, собираетесь ли вы мать, отец, учитель, программист, ученый, исследователь, владелец бизнеса, тренер, математик, менеджер, врач, юрист, банкир (список можно продолжать и на), решение проблем везде.Некоторые люди считать что ты либо можешь это сделать, либо нет. Вопреки этому убеждению, это может быть выученная профессия. Даже лучшие спортсмены и музыканты имел немного наставничества и много практики. Вот что это также требует умения решать проблемы. Георгий Поля , г. известен как отец современного решения проблем, провел обширные исследования а также написал множество математических статей и три книги по проблеме решение. Я собираюсь показать вам его метод решения проблем, чтобы помочь вам через эти проблемы. Учебник Как упоминалось выше, я использую четыре шага Полии для решения проблемы решение для показать студентам, как решать задачи со словами. Просто Примечание что ваш учитель математики или учебник по математике могут назвать это немного иначе, но вы увидите, что все это в основном означает одно и то же. Если вы выполните эти шаги, это поможет вам стать более успешный в мир решения проблем. Поля создал свой знаменитый четырехэтапный процесс для решение проблем, , который используется повсюду, чтобы помочь людям в решении проблем: Шаг 1. Разберитесь в проблеме. Иногда проблема заключается в понимании проблема . Если вам неясно, что нужно решить, то, вероятно, вы будет получать неправильные результаты. Чтобы показать понимание проблемы, вы, конечно, должны прочитать проблему осторожно. Звучит достаточно просто, но некоторые люди прыгают с ума и пытаются начать решение проблема до того, как они прочитают всю проблему. Однажды проблема читается, вам нужно перечислить все компоненты и данные, которые вовлеченный. Здесь вы будете назначать свою переменную. Шаг 2: Разработайте план (переведите). Когда вы разрабатываете план (переводите) , вы придумать способ решать проблему. Составление уравнения, построение диаграммы и создание диаграммы — это все способы, которыми вы можете решить свою проблема. В этом уроке мы будем настраивать уравнения для каждого проблема. Вы переведете их так же, как мы это делали в учебнике . 2: Учебник по алгебраическим выражениям и 5: Свойства действительных чисел. Шаг 3: Выполните план (решите). Следующий шаг, выполнить план (решить) , большой.Это где вы решаете уравнение, которое придумали, когда «разрабатываете план» шаг. Все уравнения в этом руководстве будут линейными. Если ты обязательно нужна помощь в их решении, вернитесь к Tutorial 7: Линейные уравнения в одной переменной и просмотрите эту концепцию. Шаг 4. Оглянитесь назад (отметьте и интерпретировать). Возможно, вы знакомы с выражением «не делайте этого». оглядываться’. В решение проблем хорошо, чтобы оглянуться назад (проверить и интерпретировать). . По сути, проверьте, использовали ли вы всю свою информацию и что отвечать имеет смысл. Если ваш ответ подтвердился, убедитесь, что вы написать ваш окончательный ответ с правильной маркировкой. Пример 1 : двойная разница числа, а 1 — это на 4 больше чем этот номер. Найдите номер. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Так как ищем номер, сдадим x = число * Удалить () с помощью dist.опора * Получить все термины x на одной стороне * Инв. суб. 2 прибавить 2 Если вы возьмете двойную разницу 6 и 1, то есть так же, как 4 больше 6, так что это проверка. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Число 6. Пример 2 : Одно число на 3 меньше другого. Если сумма двух чисел равна 177, найдите каждое число. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Ищем два числа, и так как мы можем написать одно число по другому номеру допустим x = другое число ne число на 3 меньше другого числа: x — 3 = одно число * Объединить похожие термины * Инв.суб 3 добавлено 3 * Инв. из мульт. 2 — это div. 2 Если мы сложим 90 и 87 (число 3 меньше 90), мы получим 177. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Одно число — 90. Другое число — 87. Всякий раз, когда вы работаете с проблемой процента, вы нужно убедиться вы пишете свой процент в десятичной форме. Вы делаете это, перемещая десятичный знак процента два слева. Например, 32% в десятичная форма: 0,32 Если вы хотите найти процент некоторых номер, запомнить что «of» представляет собой умножение , поэтому вы должны умножить процентов (в десятичной форме) умноженное на число, от которого вы берете процент. Пример 3 : Найдите 45% от 125. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Мы ищем число, которое составляет 45% от 125, мы позволит x = значение, которое мы есть ищу * Умножить 56.25 — это 45% от 125. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Номер 56,25. Пример 4 : В математическом классе 30 учеников. Примерно 70% сдал последний тест по математике. Сколько студентов сдали последний математика контрольная работа? Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Смотрим, сколько учеников сдали последний тест по математике, сдадим x = количество студенты * Умножить 21 составляет 70% от 30. ИТОГОВЫЙ ОТВЕТ: 21 ученик сдали последний тест по математике. Пример 5 : Я купил новый телевизор в местном магазине электроники для 541,25 доллара США, включая налоги. Если ставка налога составляет 8,25%, найдите цена телевизора до того, как они добавили налог. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Ищем цену на телевизор до того, как добавили налог, сдадим x = цена телевизора до того, как налог был добавлен. * Объединить похожие термины * Инв. В мульт. 1.0825 — это div. от 1.0825 Если добавить 8.25% налога до 500, вы получите 541,25. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Первоначальная цена — 500 долларов США. Следующая формула пригодится для решения пример 6: Периметр прямоугольника = 2 (длина) + 2 (ширина) Пример 6 : На чертеже прямоугольной комнаты длина равна На 1 дюйм больше, чем в 3 раза ширины.Найдите размеры, если периметр должно быть 26 дюймов. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Ищем длину и ширину прямоугольник. С длину можно записать через ширину, допустим w = ширина длина на 1 дюйм больше ширины более чем в 3 раза: 1 + 3 w = длина * Удалить () с помощью dist.опора * Объединить похожие термины * Инв. доп. 2 является суб. 2 * Инв. из мульт. на 8 дел. по 8 Если ширина равна 3, то длина, которая на 1 дюйм больше, чем 3 раз больше ширины должно быть 10.Периметр прямоугольника шириной 3 дюймов, а длина 10 дюймов получается 26. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Ширина 3 дюйма. Длина 10 дюймов. Дополнительные и дополнительные уголки Сумма дополнительных углов составляет 180 градусов. Сумма дополнительных углов составляет 90 градусов. Пример 7: Найдите размер каждого угла на рисунке. ниже. Обратите внимание: поскольку углы составляют прямую линию, они равны дополнительный друг другу. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. На рисунке уже дано, что x = один угол 5 x = другой угол * Объединить похожие термины * Инв.из мульт. на 6 дел. по 6 Если x равно 30, то 5 x = 5 (30) = 150.150 и 30 делают сложить, чтобы быть 180, так что это дополнительные углы. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Два угла: 30 градусов и 150 градусов. Целые числа, идущие подряд — целые числа, следующие за друг друга в заказывать. Например, 5, 6 и 7 — три последовательные целые числа. Если мы позволим x представить первое целое число, как бы мы представили второе подряд целое число в виде x ? Что ж, если мы посмотрим на 5, 6 и 7 — обратите внимание, что 6 — это один больше 5, первое целое число. В общем, мы могли бы представить вторым последовательное целое число на x + 1 . А как насчет третьего целого числа подряд. Ну, обратите внимание, как 7 на 2 больше, чем на 5. В в общем, мы могли бы представить третье последовательное целое число как x + 2. Последовательные ЧЕТНЫЕ целые числа — четные целые числа, следовать друг за другом чтобы. Например, 4, 6 и 8 — три последовательных даже целые числа. Если мы позволим x представить первое ЧЕТНОЕ целое число, как бы мы представили второе подряд четное целое число в виде x ? Обратите внимание, что 6 на два больше, чем 4, первое четное число. В общем, мы могли бы представить вторым последовательное ЧЕТНОЕ целое число на x + 2 . А как же третий подряд четный целое число? Хорошо подмечено как 8 на 4 больше, чем 4. В общем, мы могли бы представить в третьих последовательное ЧЕТНОЕ целое число как x + 4. Последовательные целые нечетные числа — нечетные целые числа, следовать друг за другом чтобы. Например, 5, 7 и 9 — три последовательных нечетные целые числа. Если мы позволим x представить первое целое нечетное число, как бы мы представили второе подряд нечетное целое число в виде x ? Обратите внимание, что 7 на два больше, чем 5, первое нечетное целое число. В общем, мы могли бы представить вторым последовательное нечетное целое число по x + 2. А как насчет третьего подряд нечетного целое число? Ну заметьте как 9 на 4 больше, чем 5. В общем, мы могли бы представить третьим последовательный Целое число ODD как x + 4. Обратите внимание, что распространенное заблуждение состоит в том, что, поскольку мы хотим нечетное число что мы не должны складывать 2, которое является четным числом. Держать в помните, что x представляет ODD число и что следующее нечетное число находится на расстоянии 2, точно так же, как 7 находится на расстоянии 2 от 5, поэтому мы нужно прибавить 2 к первому нечетному числу, чтобы перейти ко второму подряд нечетное число. Пример 8: Сумма трех последовательных целых чисел равна 258. Находить целые числа. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Ищем 3 последовательных целых числа, пускаем x = 1-е целое число подряд x + 1 = 2-е целое число подряд x + 2 = 3-е целое число подряд * Объединить похожие термины * Инв.добавления 3 является подпунктом. 3 * Инв. из мульт. на 3 — div. по 3 Сумма 85, 86 и 87 действительно равна 258. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Три последовательных целых числа: 85, 86 и 87. Пример 9: Возраст трех сестер равен 3 года подряд. целые числа. Если сумма удвоенного 1-го четного целого числа, 3-кратного 2-го четного целого числа, и третье четное целое число 34, найдите каждый возраст. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Ищем 3 ЧЕТЫЕ последовательные целые числа, мы будем пусть x = 1-е последовательное четное целое число x + 2 = 2-е подряд четное целое число x + 4 = 3-е подряд четное целое число * Удалить () с помощью dist.опора * Объединить похожие термины * Инв. доп. 10 является суб. 10 * Инв. из мульт. на 6 дел. по 6 Если мы возьмем сумму, умноженную на два, четыре, три, шесть и 8, мы получаем 34 ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Возраст трех сестер — 4, 6 и 8 лет. Бизнес-проблема: ломка Даже В задаче, связанной с бизнесом, уравнение затрат C — это стоимость производства продукта. В уравнении выручки R — это сумма денег, которые производитель зарабатывает на продукте. Если производитель хочет знать, сколько товаров должно быть проданным, чтобы сломать даже то, что можно найти, установив стоимость равной выручке. Пример 10: Стоимость C to произведем x , количество компакт-дисков будет C = 50 + 5 x . Компакт-диски продаются оптом по 15 долларов за штуку, поэтому выручка в размере рандов равна рандов = 15 x . Узнайте, сколько компакт-дисков нужно изготовить и продать, чтобы их сломать. четный. Убедитесь, что вы внимательно прочитали вопрос несколько раз раз. Мы ищем количество проданных компакт-дисков безубыточность, сдадим x = количество cd’s * Получить все условия x с одной стороны * Инв.из мульт. на 10 — дел. от 10 Когда x равно 5, стоимость и доход как равно 75. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: 5 компакт-дисков. Практические задачи Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшие спортсмены и музыканты получали помощь и много практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики. Чтобы получить от них максимальную отдачу, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ. Практика Задачи 1a — 1g: Решите проблему со словом. 1с. В местном мебельном магазине потрясающий распродажа. Они снижают каждую цену на 45%. Если кушетка у вас есть на глаз стоит 440 долларов после уценки, какой был оригинал цена? Сколько бы вы сэкономили, если бы купили его на этой распродаже? (ответ / обсуждение к 1c) 1г.Прямоугольный сад имеет ширину 8 футов меньше чем вдвое длиннее. Найдите размеры, если периметр 20 ноги. (ответ / обсуждение к 1г) 1д. Сумма дополнительных углов составляет 90 градусов. Находить размер каждого угла на рисунке ниже. Обратите внимание, что поскольку в углы составляют прямой угол, они дополняют друг друга. (ответ / обсуждение к 1e) 1г. Стоимость C to производство x номеров видеомагнитофонов: C = 1000 + 100 x . Видеомагнитофоны продаются оптом по 150 долларов каждый, поэтому выручка определяется по формуле R = 150 x .Узнайте, сколько видеомагнитофонов производитель необходимо производить и продавать, чтобы достичь безубыточности. (ответ / обсуждение до 1 г) Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 1 июля 2011 г. Авторские права на все содержимое (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.

Задачи на умножение слов — урок для 3 класса

Это полноценный урок для третьего класса с обучением и задачами по словам с целью научить детей некоторым основам решения задач умножения слов. Основная идея состоит в том, что у нас есть групп одинакового размера , и детям нужно просто распознавать эти группы, будь то полотенца, кусочки пиццы, шарики или что-то еще.Задачи со словами в уроке также включают сложение и вычитание, поэтому учащимся нужно думать, а не применять данную операцию (умножение), даже не прочитав задачу.

---

Примеры проблем

1. Напишите предложение умножения к каждой задаче и решите.
Вы можете рисовать картинки, чтобы помочь вам.

а) Четверо детей вместе играют в теннис. Всего они принесли по шесть мячей. Сколько всего у них мячей?	б) Семья Смитов состоит из пяти человек.У каждого члена есть небольшое полотенце и банное полотенце. Сколько полотенец вешают в ванной?
в) Семья Джонсов заказывает четыре пиццы. Каждая пицца нарезана на четыре части. Сколько у них кусочков пиццы?	г) В городе три почтовых отделения. В каждом почтовом отделении по пять рабочие. Сколько всего сотрудников в почтовых отделениях?

Проблемы Word с двумя операциями

г.Джонсон обычно ест три раза в день. Как много еды он ест в обычную неделю? Опять же, у нас есть ситуация, когда КАЖДЫЙ ДЕНЬ происходит одно и то же. 7 дней × 3-х разовое питание = _____ нормальное питание неделя.

В эту пятницу он пропустил завтрак. Сколько приемов пищи он ел на этой неделе? Теперь другой день. Это всего лишь ОДИН день, поэтому мы просто вычтите один прием пищи из общего количества. дней раз блюд забрать пропущенный завтрак 7 × 3 – 1 = ______

На следующей неделе он ел три раза в понедельник, Вторник и пятница, а в остальные дни — четыре раза.Сколько раз он ел в течение недели? Теперь мы трижды имеем одну ситуацию, а другую ситуации четыре раза. Мы рассчитываем их отдельно, а затем Добавлять. дней раз блюд и остаток дней раз блюд 3 × 3 + 4 × 4 = ______

Примеры задач

1.Впишите числа к числовым предложениям для каждого
проблема и решаем. Для последних задач напишите числовое предложение
сам. Вы можете написать слова над числами, чтобы описать
числа. Вы также можете рисовать картинки, чтобы помочь вам!

а. Мама купила четыре коробки для яиц, в каждой по шесть яиц. Два яйца были плохими. Сколько хороших яиц получила мамочка? яйцо картонные коробки раз яйца в каждом дубль прочь плохие × – =

б. Johnson’s снова заказал 4 пиццы, разрезанные на четыре части каждая. На этот раз собака съела один кусок. Сколько штук сделал люди едят? номер из пиццы раз штук по штуки по забрать отсюда что съела собака × – =

с. У Джо трое друзей, у всех по пять машинок, и двое друзей, у которых только две машины. Сколько машин у друзей Джо имеют? друзья с 5 легковых автомобилей раз 5 легковых автомобилей и друзей с 2 машины раз 2 легковых автомобиля × + × =

г. На семейном обеденном столе две тарелки на всех и только одна тарелка для маленькой Ханны. На обед пришли 10 человек и Ханна. Сколько тарелок было на столе?

ч. Есть четыре лошади и три человека. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт