Содержание
дискриминант меньше 0
Вы искали дискриминант меньше 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и дискриминант равно 0, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «дискриминант меньше 0».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как дискриминант меньше 0,дискриминант равно 0,если в дискриминанте 0,если дискриминант 0,если дискриминант меньше нуля,если дискриминант равен 0,если дискриминант равен 0 как найти х,если дискриминант равен 0 как решать,если дискриминант равен 0 то,если дискриминант равен 0 то как найти корень формула,если дискриминант равен 0 то формула,если дискриминант равен 0 формула,если дискриминант равен нулю,если дискриминант равен нулю то,если дискриминант равен нулю формула,как решать если дискриминант равен 0,когда дискриминант равен 0,когда дискриминант равен нулю,может ли дискриминант равен 0,формула если дискриминант равен нулю,чему равен х если дискриминант равен 0,что делать если дискриминант меньше 0,что делать если дискриминант равен 0,что делать если дискриминант равен нулю,что делать когда дискриминант равен 0,что если дискриминант равен 0,что если дискриминант равен нулю,что значит если дискриминант равен 0. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и дискриминант меньше 0. Просто введите задачу в окошко и нажмите
«решить» здесь (например, если в дискриминанте 0).
Где можно решить любую задачу по математике, а так же дискриминант меньше 0 Онлайн?
Решить задачу дискриминант меньше 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
DrRacket/Scheme: не порядок — CodeRoad
Я пытаюсь создать программу в схеме (DrRacket) для решения корней квадратного уравнения. У меня также есть функция для решения дискриминанта (функция D). Если дискриминант >0, то корень функции должен иметь на выходе «point pair» (это правильное слово? английский-не мой родной язык) обоих корней. Иначе он должен дать #f на выходе.
У меня также есть функция для решения дискриминанта (функция D). Если дискриминант >0, то корень функции должен иметь на выходе «point pair» (это правильное слово? английский-не мой родной язык) обоих корней. Иначе он должен дать #f на выходе.
(define na2
(lambda (x)
(* x x)))
(define D
(lambda (a b c)
(- (na2 b) (* 4 a c))))
(define roots
(lambda (a b c)
((if (> (D a b c) 0)
(cons (/ (+ (- b) (sqrt (D a b c))) (* 2 a)) (/ (- (- b) (sqrt (D a b c))) (* 2 a)))
#f)))
Это дает мне это:
> (roots 1 3 2)
>: contract violation
expected: real?
given: (-1 . -2)
argument position: 1st
other arguments...:
>
Как видите, правильный вывод есть, но почему ошибка?
Редактировать:
Я исправил опечатку, так как Паракрам Маджумдар помог мне, теперь она дает мне
application: not a procedure;
expected a procedure that can be applied to arguments
given: (-1 . -2)
arguments. ..: [none]
..: [none]
Может кто-нибудь, пожалуйста, сказать, что я делаю не так?
scheme
racket
Поделиться
Источник
SheldonCopper
02 января 2018 в 08:32
1 ответ
- Карта, фильтр, складка в DrRacket / схема
Язык программирования: Scheme / DrRacket В настоящее время мы проходим через map , filter и foldr в моем классе comp sci. Я понимаю, что все три могут быть использованы для создания абстрактных функций, но, честно говоря, я немного смущен разницей между ними и тем, когда я буду использовать каждую…
- Scheme (DrRacket) — оператор cond не работает с рекурсией
Я изучаю схему с использованием DrRacket R5RS. Я думал, что забиваю гвозди в концепции, но я не могу заставить это простое рекурсивное упражнение работать. Я думаю, что это ошибка в DrRacket, но я не уверен. Может ли кто-нибудь увидеть проблему и, надеюсь, объяснить, почему мой код не работает? Я.
 ..
..
2
Как обсуждалось в комментариях, заявление if должно быть написано следующим образом:
(if cond then else)
где будет условие :
(> (D a b c) 0)
Так что в целом это должно быть:
(define roots
(lambda (a b c)
(if (> (D a b c) 0)
(cons (/ (+ (- b) (sqrt (D a b c))) (* 2 a))
(/ (- (- b) (sqrt (D a b c))) (* 2 a)))
#f
)))
Поделиться
Parakram Majumdar
02 января 2018 в 09:10
Похожие вопросы:
DrRacket не запустится
Я пытаюсь начать писать схему в DrRacket. У меня был DrRacket рабочий день в течение короткого периода времени, затем я встал, чтобы пойти за кофе, вернулся, и теперь он не заводится. Вместо того…
Вместо того…
Ошибка в программе Simply Scheme
Я использую программу из книги Simply Scheme: (require (planet dyoo/simply-scheme)) (define (combinations size set) (cond ((= size 0) ‘(())) ((empty? set) ‘()) (else (append (prepend-every (first…
Scheme (Racket) — Библиотеки Циклов
У меня есть DrRacket версия 5.0.2 , я уже потратил около 3 часов на поиски нужных библиотек , чтобы заставить while , dolist и dotimes работать. Я знаю, как их использовать, но просто не могу найти…
Карта, фильтр, складка в DrRacket / схема
Язык программирования: Scheme / DrRacket В настоящее время мы проходим через map , filter и foldr в моем классе comp sci. Я понимаю, что все три могут быть использованы для создания абстрактных…
Scheme (DrRacket) — оператор cond не работает с рекурсией
Я изучаю схему с использованием DrRacket R5RS. Я думал, что забиваю гвозди в концепции, но я не могу заставить это простое рекурсивное упражнение работать. Я думаю, что это ошибка в DrRacket, но я…
Я думаю, что это ошибка в DrRacket, но я…
Добавление языка «Simply Scheme» в DrRacket
Я хочу поработать над этой книгой: http://www.eecs.berkeley.edu/~bh/ss-toc2.html . Но у меня возникли проблемы с тем, чтобы заставить язык Simply Scheme работать. Код не запускается. #lang planet…
Можно ли изменить порядок DrRacket / схема поиска / ссылка на библиотеку?
Я следую инструкциям в 3.3.3 из SICP, чтобы создать таблицу. Вот code_0.scm : ;code_0.scm #lang scheme (require rnrs/base-6) (require rnrs/mutable-pairs-6) (define nil ‘()) (define (make-table)…
В чем разница между foldr и apply in Scheme?
Язык программирования: Scheme/DrRacket Я не вижу никакой разницы в использовании между foldr и apply Может ли кто-нибудь объяснить, чем они отличаются? Насколько я могу судить, Вы можете сделать то…
Схема нарушения контракта в DrRacket
Я следую за лекциями Брайана Харви SICP в archive. org я использую DrRacket v7.4 IDE, чтобы написать свой код схемы. В 06:39 Профессор Брайан Харви показывает, как выбрать первый символ строки. Когда…
org я использую DrRacket v7.4 IDE, чтобы написать свой код схемы. В 06:39 Профессор Брайан Харви показывает, как выбрать первый символ строки. Когда…
Схема / Drracket Число Эйлера
Я пытаюсь реализовать число Эйлера в Drracket aka Scheme. я видел решение с помощью функции поиска, но это путь к сложному. (define (fakultät n) (cond [(= n 0) 0] [(= n 1) 1] [else (* (fakultät (- n…
Решение квадратных неравенств методом интервалов
Универсальным методом решения неравенств по праву считается метод интервалов. Именно его проще всего использовать для решения квадратных неравенств с одной переменной. В этом материале мы рассмотрим все аспекты применения метода интервалов для решения квадратных неравенств. Для облегчения усвоения материала мы рассмотрим большое количество примеров разной степени сложности.
Алгоритм применения метода интервалов
Рассмотрим алгоритм применения метода интервалов в адаптированном варианте, который пригоден для решения квадратных неравенств. Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.
Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.
Перейдем собственно к алгоритму.
У нас есть квадратный трехчлен a·x2+b·x+c из левой части квадратного неравенства. Находим нули из этого трехчлена.
В системе координат изображаем координатную прямую. Отмечаем на ней корни. Для удобства можем ввести разные способы обозначения точек для строгих и нестрогих неравенств. Давайте договоримся, что «пустыми» точками мы будем отмечать координаты при решении строгого неравенства, а обычными точками — нестрогого. Отметив точки, мы получаем на координатной оси несколько промежутков.
Если на первом шаге мы нашли нули, то определяем знаки значений трехчлена для каждого из полученных промежутков. Если нули мы не получили, то производим это действие для всей числовой прямой. Отмечаем промежутки знаками «+» или «-».
Дополнительно мы будем вводить штриховку в тех случаях, когда будем решать неравенства со знаками > или ≥ и < или ≤. В первом случае штриховка будет наноситься над промежутками, отмеченными «+», во втором над участками, отмеченными «-».
В первом случае штриховка будет наноситься над промежутками, отмеченными «+», во втором над участками, отмеченными «-».
Отметив знаки значений трехчлена и нанеся штриховку над отрезками, мы получаем геометрический образ некоторого числового множества, которое фактически является решением неравенства. Нам остается лишь записать ответ.
Остановимся подробнее на третьем шаге алгоритма, который предполагает определение знака промежутка. Существует несколько подходов определения знаков. Рассмотрим их по порядку, начав с наиболее точного, хотя и не самого быстрого. Этот метод предполагает вычисление значений трехчлена в нескольких точках полученных промежутков.
Пример 1
Для примера возьмем трехчлен x2+4·x−5.
Корни этого трехчлена 1 и -5 разбивают координатную ось на три промежутка (−∞, −5), (−5, 1) и (1, +∞).
Начнем с промежутка (1, +∞). Для того, чтобы упростить себе задачу, примем х=2. Получаем 22+4·2−5=7.
7 – положительное число. Это значит, что значения данного квадратного трехчлена на интервале (1, +∞) положительные и его можно обозначить знаком «+».
Для определения знака промежутка (−5, 1) примем x=0. Имеем 02+4·0−5=−5. Ставим над интервалом знак «-».
Для промежутка (−∞, −5) возьмем x=−6, получаем (−6)2+4·(−6)−5=7. Отмечаем этот интервал знаком «+».
Намного быстрее определить знаки можно с учетом следующих фактов.
При положительном дискриминанте квадратный трехчлен с двумя корнями дает чередование знаков его значений на промежутках, на которые разбивается числовая ось корнями этого трехчлена. Это значит, что нам вовсе не обязательно определять знаки для каждого из интервалов. Достаточно провести вычисления для одного и проставить знаки для остальных, учитывая принцип чередования.
При желании, можно и вовсе обойтись без вычислений, сделав выводы о знаках по значению старшего коэффициента. Если a>0, то мы получаем последовательность знаков +, −, +, а если a<0 – то −, +, −.
У квадратных трехчленов с одним корнем, когда дискриминант равен нулю, мы получаем два промежутка на координатной оси с одинаковыми знаками. Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же.
Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же.
Здесь также применим метод определения знака на основе значения коэффициента a: если a>0, то будет +, +, а если a<0, то −, −.
Если квадратный трехчлен не имеет корней, то знаки его значений для всей координатной прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.
Например, если мы возьмем квадратный трехчлен −4·x2−7, он не имеет корней (его дискриминант отрицательный). Коэффициент при x2 есть отрицательное число −4, и свободный член −7 тоже отрицателен. Это значит, что на промежутке (−∞, +∞) его значения отрицательны.
Примеры решения квадратных неравенств
Рассмотрим примеры решения квадратных неравенств с использованием рассмотренного выше алгоритма.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 2
Решите неравенство 8·x2−4·x−1≥0.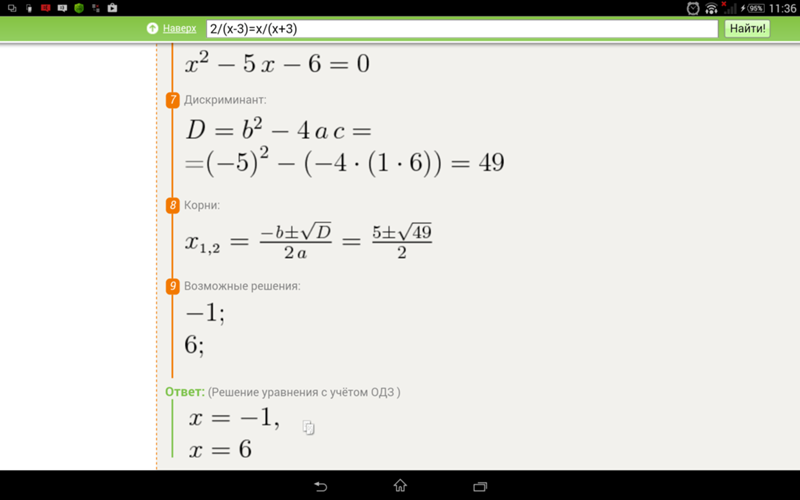
Решение
Используем для решения неравенства метод интервалов. Для этого найдем корни квадратного трехчлена 8·x2−4·x−1. В связи с тем, что коэффициент при х четный, нам будет удобнее вычислить не дискриминант, а четвертую часть дискриминанта: D’=(−2)2−8·(−1)=12.
Дискриминант больше нуля. Это позволяет нам найти два корня квадратного трехчлена: x1=2-129, x1=1-34 и x2=2+128, x2=1+34. Отметим эти значения на числовой прямой. Так как уравнение нестрогое, то на графике мы используем обычные точки.
Теперь по методу интервалов определяем знаки трех полученных интервалов. Коэффициент при x2 равен 8, то есть, положителен, следовательно, последовательность знаков будет +, −, +.
Так как мы решаем неравенство со знаком ≥, то изображаем штриховку над промежутками со знаками плюс:
Запишем аналитически числовое множество по полученному графическому изображению. Мы можем сделать это двумя способами:
(-∞; 1-34]∪[1+34, +∞) или x≤1-34, x≥1+34.
Ответ: (-∞; 1-34]∪[1+34, +∞) или x≤1-34, x≥1+34.
Пример 3
Выполните решение квадратного неравенства -17·x2+2·x-7<0 методом интервалов.
Решение
Для начала найдем корни квадратного трехчлена из левой части неравенства:
D’=12—17·-7=0x0=-1-17×0=7
Это строгое неравенство, поэтому на графике используем «пустую» точку. С координатой 7.
Теперь нам нужно определить знаки на полученных промежутках (−∞, 7) и (7, +∞). Так как дискриминант квадратного трехчлена равен нулю, а старший коэффициент отрицательный, то мы проставляем знаки −, −:
Так как мы решаем неравенство со знаком <, то изображаем штриховку над интервалами со знаками минус:
В данном случае решениями являются оба промежутка (−∞, 7), (7, +∞).
Ответ: (−∞, 7)∪(7, +∞) или в другой записи x≠7.
Пример 4
Имеет ли квадратное неравенство x2+x+7<0 решения?
Решение
Найдем корни квадратного трехчлена из левой части неравенства. Для этого найдем дискриминант: D=12−4·1·7=1−28=−27. Дискриминант меньше нуля, значит, действительных корней нет.
Для этого найдем дискриминант: D=12−4·1·7=1−28=−27. Дискриминант меньше нуля, значит, действительных корней нет.
Графическое изображение будет иметь вид числовой прямой без отмеченных на ней точек.
Определим знак значений квадратного трехчлена. При D<0 он совпадает со знаком коэффициента при x2, то есть, со знаком числа 1, оно положительное, следовательно, имеем знак +:
Штриховку мы могли бы нанести в данном случае над промежутками со знаком «-». Но таких промежутков у нас нет. Следовательно, чертеж сохраняет вот такой вид:
В результате вычислений мы получили пустое множество. Это значит, что данное квадратное неравенство решений не имеет.
Ответ: Нет.
Дискриминант квадратного уравнения
Квадратное уравнение это уравнение которое выглядит как ax2 + dx + c = 0. В нем значение а,в и с любые числа, при этом а не равно нулю.
Все квадратные уравнения разделяются на несколько видов, а именно:
-Уравнения в которых только один корень.
-Уравнения с двумя разными корнями.
-Уравнения в которых корней нет совсем.
Это и различает линейные уравнения в которых корень всегда единый, от квадратных. Для того что бы понять какое количество корней в выражении и нужен Дискриминант квадратного уравнения.
Допустим наше уравнение ax2 + dx + c =0. Значит дискриминант квадратного уравнения —
D = b2 — 4 ac
И это нужно запомнить навсегда. С помощью этого уравнения мы и определяем количество корней в квадратном уравнении. И делаем мы это следующим образом:
— Когда D меньше нуля, в уравнении нет корней.
— Когда D равно нулю, имеется только один корень.
— Когда D больше нуля, соответственно, в уравнении два корня.
Запомните что дискриминант показывает сколько корней в уравнении, не меняя знаков.
Рассмотрим для наглядности:
Нужно выяснить какое количество корней в данном квадратном уравнении.
1) х2 — 8х + 12 = 0
2 )5х2 + 3х + 7 = 0
3) х2-6х + 9 = 0
Вписываем значения в первое уравнение, находим дискриминант.
а = 1, b = -8, c = 12
D = (-8)2 — 4 * 1 * 12 = 64 — 48 = 16
Дискриминант со знаком плюс, значит в данном равенстве два корня.
Делаем тоже самое со вторым уравнением
a = 1, b = 3, c = 7
D = 32 — 4 * 5 * 7 = 9 — 140 = — 131
Значение минусовое, значит корней в данном равенстве нет.
Следующее уравнение разложим по аналогии.
а = 1, b = -6, с = 9
D = (-6)2— 4 * 1 * 9 = 36 — 36 = 0
как следствие имеем один корень в уравнении.
Важно что в каждом уравнении мы выписывали коэффициенты. Конечно это не много длительный процесс, но это помогло нам не запутаться и предотвратило появление ошибок. Если очень часто решать подобные уравнения, то вычисления сможете производить мысленно и заранее знать сколько у уравнения корней.
Рассмотрим еще один пример:
1) х2 — 2х — 3 = 0
2) 15 — 2х — х2 = 0
3) х2 + 12х + 36 = 0
Раскладываем первое
а = 1, b = -2, с = -3
D =(-2) 2 — 4 * 1 * (-3) = 16, что больше нуля, значит два корня, выведем их
х1 = 2+?16/2 * 1 = 3, х2 = 2-?16/2 * 1 = -1.
Раскладываем второе
а = -1, b = -2, с = 15
D = (-2)2 — 4 * 4 * (-1) * 15 = 64, что больше нуля и так же имеет два корня. Выведем их:
х1 = 2+?64/2 * (-1) = -5, х2 = 2-?64/2 *(-1) = 3.
Раскладываем третье
а = 1, b = 12, с = 36
D = 12 2 — 4 * 1 * 36 =0, что равно нулю и имеет один корень
х = -12 + ?0/2 * 1 = -6.
Решать данные уравнения не сложно.
Если нам дано неполное квадратное уравнение. Такое как
1х2 + 9х = 0
2х2 — 16 = 0
Данные уравнения отличаются от тех что были выше, так как оно не полное, в нем нет третьего значения. Но не смотря на это оно проще чем полное квадратное уравнение и в нем дискриминант искать не нужно.
Но не смотря на это оно проще чем полное квадратное уравнение и в нем дискриминант искать не нужно.
Что делать когда срочно нужна дипломная работа или реферат, а времени на его написание нет? Всё это и многое другое можно заказать на сайте Deeplom.by (http://deeplom.by/) и получить высший балл.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
BestMaths
Корни из графиков
Графики трех квадратичных функций показаны ниже.
корней соответствующих квадратных уравнений задаются тем местом, где график пересекает ось x. то есть x- перехватывает.
Корни квадратного уравнения называются действительными корнями , если график пересекает или касается оси x. Эти корни представляют собой реальных чисел.
Если график пересекает ось x НЕ , то уравнение не имеет действительных корней. Уравнение этого типа может быть решено с использованием комплексных или мнимых чисел, которые обычно изучаются в 12-м году обучения (13-й год Новой Зеландии).
Уравнение этого типа может быть решено с использованием комплексных или мнимых чисел, которые обычно изучаются в 12-м году обучения (13-й год Новой Зеландии).
| Графики | |||
| Функция | у = (х + 3) 2 | y = x 2 — 5x + 6 | y = -x 2 + x — 2 |
| Количество и характер корней | Один настоящий корень | Два настоящих корня | Без настоящих корней |
Существует более быстрый способ определения количества корней квадратного уравнения, чем рисование графиков или решение. В этом методе используется дискриминант .
В этом методе используется дискриминант .
Дискриминант
Дискриминант квадратного уравнения ax 2 + bx + c = 0 определяется выражением b 2 — 4ac.
Символ Δ иногда используется в качестве дискриминанта.
Обратите внимание, что дискриминант — это часть квадратной формулы , которая находится под знаком квадратного корня.
Изучая значение дискриминанта, мы можем определить количество и характер корней.
| Если дискриминант равен нулю | b 2 — 4ac = 0 | есть один (повторяющийся) рациональный корень |
| Если дискриминант положительный | b 2 — 4ac> 0 | есть два настоящих корня |
| Если дискриминант отрицательный | b 2 — 4ac <0 | настоящих корней нет |
Если дискриминант представляет собой полный квадрат, например 49 или 100, то корни будут рациональными (дробными) числами.
Примеры:
пример 1 | пример 2 | пример 3 | |
| Уравнение | y = (x + 3) 2 | y = x 2 — 5x + 6 | y = -x 2 + x — 2 |
| a, b и c | а = 1, б = 6, с = 9 | а = 1, б = -5, с = 6 | а = -1, б = 1, с = -2 |
| Дискриминант | b 2 — 4ac = 6 2 — 4x1x9 Дискриминант = 0 | b 2 — 4ac = (-5) 2 — 4x1x6 Дискриминант = 1 | b — 4ac = (1) 2 — 4x-1x-2 Дискриминант = -7 |
| Количество и характер корней | Имеется один повторяющийся настоящий корень | Есть два настоящих корня | Настоящих корней нет |
Дискриминант
Дискриминант
Краткое резюме квадратной формулы
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a, b и c — константы, а a ≠ 0
Для любого такого квадратного уравнения квадратная формула:
| Корни (x 1 , x 2 ) = | -b ± & Sqrt; b2 — 4ac |
| 2a |
Объяснение дискриминанта
В приведенной выше квадратной формуле величина «b 2 — 4ac» , которая находится под знаком квадратного корня, называется дискриминантом квадратного уравнения.
Дискриминант = b 2 — 4ac
Пример вычисления дискриминанта
Для квадратного уравнения x 2 + 4x + 4 = 0 определите определитель
Ответ
x 2 + 5x + 5 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 5, c = 5
Дискриминант = b 2 — 4ac = 5 2 — 4 (1) (5) = 5
Использование дискриминанта
Дискриминант рассказывает о природе корней квадратного уравнения.Корни могут быть реальными, равными или мнимыми.
В зависимости от значения дискриминанта квадратное уравнение может иметь:
◾ два действительных и неравных корня при значении дискриминанта > 0
◾ только один действительный и равный корень при значении дискриминанта = 0
◾ нет настоящих корней т. е. оба корня являются мнимыми, если значение дискриминанта <0
е. оба корня являются мнимыми, если значение дискриминанта <0
Случай I — когда дискриминант> 0
Для квадратного уравнения x 2 — 12x + 32 = 0, определить дискриминант и корни квадратного уравнения
Ответ
Дискриминант = b 2 — 4ac
Здесь a = 1, b = -12, c = 32
Дискриминант = (-12) 2 — 4 (1) (32) = 144 — 128 = 16
Мы знаем, что формула корней квадратного уравнения равна
.
| Корни (x 1 , x 2 ) = | -b ± & Sqrt; b2 — 4ac |
| 2a |
| x 1 = | — (- 12) + & Sqrt; (-12) 2-4 (1) (32) | = 8 |
| 2 (1) |
| x 1 = | — (- 12) — & Sqrt; (-12) 2-4 (1) (32) | = 4 |
| 2 (1) |
Следовательно, для квадратного уравнения x 2 — 12x + 32 = 0, мы получаем два действительных и различных корня — 8 и 4
Следовательно, для Дискриминанта> 0 квадратное уравнение имеет 2 действительных и различных корня
Случай II — Когда Дискриминант = 0
Для квадратного уравнения x 2 — 12x + 36 = 0, определить дискриминант и корни квадратного уравнения
Ответ
Дискриминант = b 2 — 4ac
Здесь a = 1, b = -12, c = 36
Дискриминант = (-12) 2 — 4 (1) (36) = 144 — 144 = 0
Мы знаем, что формула корней квадратного уравнения равна
.
| Корни (x 1 , x 2 ) = | -b ± & Sqrt; b2 — 4ac |
| 2a |
| x 1 = | — (- 12) + & Sqrt; (-12) 2-4 (1) (36) | = 6 |
| 2 (1) |
| x 1 = | — (- 12) — & Sqrt; (-12) 2-4 (1) (36) | = 6 |
| 2 (1) |
Следовательно, для квадратного уравнения x 2 — 12x + 36 = 0, мы получаем только один действительный и равный корень, который равен 6.
Следовательно, для Дискриминанта = 0 квадратное уравнение имеет только один действительный и равный корень
Случай III- Когда Дискриминант <0
Для квадратного уравнения x 2 + 4x + 10 = 0, определить дискриминант и корни квадратного уравнения
Ответ
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 4, c = 10
Дискриминант = (4) 2 — 4 (1) (10) = 16-40 = -24
Мы знаем, что формула корней квадратного уравнения равна
.
| Корни (x 1 , x 2 ) = | -b ± & Sqrt; b2 — 4ac |
| 2a |
| x 1 = | — (4) + & Sqrt; (4) 2-4 (1) (10) | = | — (4) + & Sqrt; -24 |
| 2 (1) | 2 |
| x 1 = | — (4) — & Sqrt; (4) 2-4 (1) (10) | = | — (4) — & Sqrt; -24 |
| 2 (1) | 2 |
Следовательно, для квадратного уравнения x 2 + 4x + 10 = 0, мы не получаем действительных корней
Следовательно, для Дискриминанта <0 квадратное уравнение не имеет действительных корней
Сводка
| Дискриминантное значение Случаи | Корни квадратичной | Факторизация квадратичной |
|---|---|---|
| Дискриминантное значение> 0 | два настоящих отдельных корня | два различных линейных фактора |
| Дискриминантное значение = 0 | два одинаковых настоящих корня | два одинаковых линейных фактора |
| Дискриминантное значение <0 | Настоящих корней нет | Невозможно разложить на множители |
Дискриминант
Дискриминант квадратичной функции — это функция ее коэффициентов, которая раскрывает информацию о ее корнях. 2-4ac $ — это часть формулы квадратного корня.
2-4ac $ — это часть формулы квадратного корня.
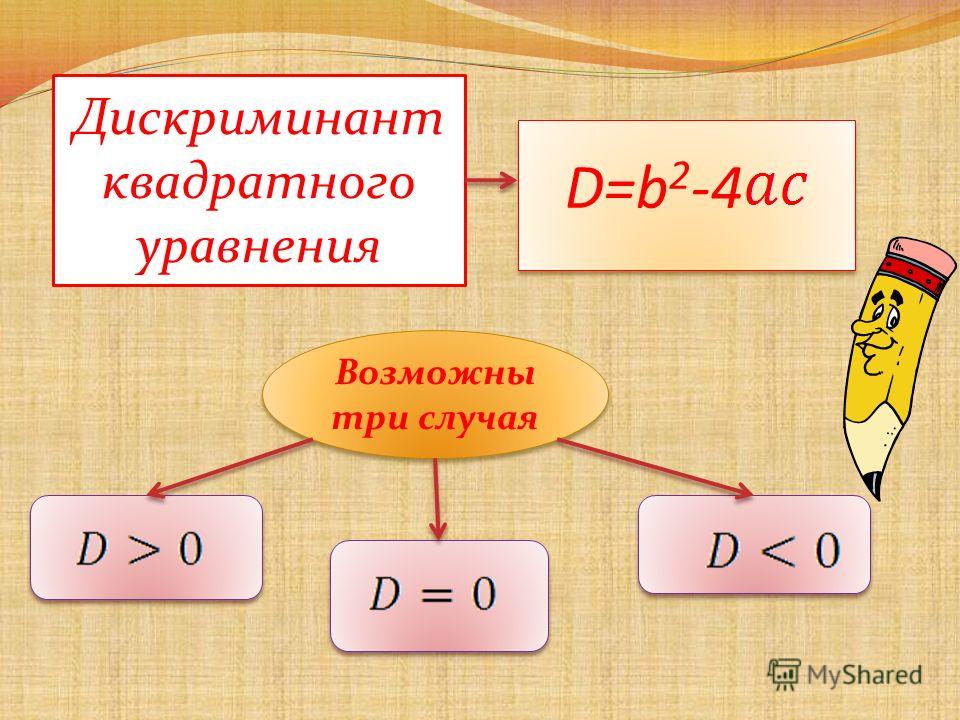
Положительный дискриминант
Если $ {\ Delta} $ положительно, квадратный корень в формуле корней квадратного уравнения положителен, и решения не содержат мнимых чисел.
$ x = {\ dfrac {-b \ pm \ sqrt {\ text {положительное число}}} {2a}} $
Поскольку добавление и вычитание положительного числа приведет к разным значениям, положительный дискриминант дает два различные решения и два различных корня квадратичной функции.
Нулевой дискриминант
Если $ {\ Delta} $ равен нулю, квадратный корень в формуле корней квадратного уравнения равен нулю:
$ x = {\ dfrac {-b \ pm \ sqrt {0}} {2a}}
долларов США
Поскольку добавление нуля и вычитание нуля в квадратном уравнении приводят к одному и тому же результату, существует только один отличный корень квадратичной функции.
Отрицательный дискриминант
Если $ {\ Delta} $ меньше нуля, значение квадратного корня в формуле корней квадратного уравнения отрицательное:
$ x = \ dfrac {-b \ pm \ sqrt {\ text {negative number}}} {2a} $
Это означает, что сам квадратный корень является мнимым числом, поэтому корни квадратичной функции различны и не являются действительными .

 е. положительный)
е. положительный)