В классе 35 учеников из них 20: в классе 35 учеников.Из них :20 школьников занимаются в математическом кружке,11-в — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

в классе 35 учеников.Из них :20 школьников занимаются в математическом кружке,11-в

Берілген сандар қатарының
18;24; 26;28;18
1) арифметикалық ортасын
2)медианасын
3)модасын
4)өзгеріс құлашын табыныз

Вычислите
Помогите очень срочно

розв’яжіть рівняння1)(х)=72)(х)=-4

допоможіть пжжж/жжжж/ж яке з них додатнє а яке зворотнє?????

1. Найдите значение выражения:

mТематичне оцінювання № 11Перпендикулярні і паралельні прямі.Координатна площина. ГрафікиВаріант 11. Перемалюйте в зошит рисунок 27. Про-ведіть через
…

точку С:1) пряму а, паралельну прямій т;2) пряму b, перпендикулярну до прямої т.Рис. 272. Позначте на координатній площині точкиА(-1; 4) і В(-4; — 2). Проведіть відрізок AB. Знайдіть коор-динати точки перетину відрізка AB з віссю абсцис.3. Накресліть тупий кут BDк, позначте на його стороні DKточку М. Проведіть через точку М пряму, перпендикулярнудо прямої DK, і пряму, перпендикулярну до прямої DB.4. Користуючись графіком руху туриста (рис. 28), установіть:SkanВарiант 21. Перемалюйте в зошит рисунок 29. Про-ведіть через точку F:1) пряму а, паралельну прямій с;2) пряму b, перпендикулярну до прямої с.Рис. 292. Позначте на координатній площині точкиС (1; 4) і D(-1; 2). Проведіть відрізок CD. Знайдіть коор-динати точки перетину відрізка CD з віссю ординат.3. Накресліть тупийі кут ОСА, позначте на його стороні САточку Р. Проведіть через точку Р пряму, перпендикулярнудо прямої СА, і пряму, перпендикулярну до прямої Со.4. Користуючись графіком руху вершника (рис. 30),установіть:1) на якій відстані від дому був вершник через 4 год післяпочатку руху;2) скільки часу вершник відпочивав;3) через скільки години після початку руху вершник був за24 км від дому,11816-+12+0-832+1160416S1012120081) на якій відстані від дому був турист через 2 год післяпочатку руху;2) скільки часу турист відпочивав,3) через скільки годин після початку руху турист був за12 км від дому.5. Дано координати трьох вершин прямокутника ABCD:А(-2;-3), B(-2;5) і С(4; 5). 1. Накресліть цей прямокутник.2. Знайдіть координати вершини D.3. Знайдіть координати точки перетину діагоналей прямо-кутника,4. Обчисліть площу і периметр прямокутника, вважаючи,що довжина одиничного відрізка координатних осі дорів-Нюс 1 см.Зобразіть на координатній площині всі точки ( ) такі, що2. — довільне число.0S 10 12Рис. 305.» Дано координати трьох вершин прямокутника ABCD:A(h2 — 3), C(5; 1) і D(5; 3).1. Накресліть це прямокутник.2. Знайдіть координати вершини В.3. Знайдіть координати точки перетину діагоналей прямо-кутника.4. Обчисліть площу і периметр прямокутника, вважаючи,що довжина одиничного відрізка координатних осей порів-Нос 1 см.6.» Зобразіть на координатній площині всі точки) такі по1довільне число

в стаде было 200 животных из них 34% составляли овцы сколько овец было в стаде

Решите уравнение 10+5y=3y -8

катер отплыл от пристани А и проплыл против течения реки. Собственная скорость катера 20 км/ч. 1)какова скорость течения реки? 2) задайте формулой зав
…

исимость росстаяния от времени 3) заполните таблицу СРОЧНО ПОМОГИТЕ!!!!!!!

1)8,*5<8,4* 2)0,**53>0,*5*3* Срочно

Развитие логического мышления среднего звена

Цель: Выявление и развитие математических
способностей у сельских ребят. Развитие
логического мышления.

Работа лагеря — неотъемлемая часть
учебно-воспитательного процесса образования. В
нашем лагере ведется работа по развитию
математических способностей учащихся во
внеурочное время как продолжение учебного
процесса. Работаем над развитием творческого
мышления учащихся, так как умение самостоятельно
мыслить, делать теоретические обобщения,
добывать знания, свободно ориентироваться в
потоке научной информации имеет первостепенное
значение. Теоретическое мышление не является
самостоятельным и изолированным психическим
процессом. Поэтому при планировании занятий в
лагере учителя большое внимание уделяем
развитию логического мышления, смекалки,
воображения, гибкости мышления, развитию
механической и логической памяти с помощью
специальных упражнений и игр.

Формы и методы обучения в летнем
математическом лагере должны соответствовать
возрастным способностям учащихся. Исходя из
этого проводятся математические игры: матбой,
викторины, интеллектуальный марафон, “Что, Где,
Когда?”, математическое лото.

Для формирования устойчивого интереса к
математике необходимы не только математические
игры и занимательные задачи, рассмотрения
собризмов, разгадывания головоломок, но и
проблемность изложения, постановка гипотез,
рассмотрения различных путей решения задач,
доказательство теорем различными методами и
выступления самых учащихся на занятиях.

Для повышения познавательной, творческой
активности учащихся большое значение имеет их
работа и защита рефератов.

Работа над рефератом включает рекомендации по
выбору темы, текущие консультации, проверку и
индивидуальные собеседования.

Темы рефератов учащиеся выбирают сами,
например:

“Дроби на Руси”,

“Из истории нуля”,

“Что такое ломанное число”,

“Как записывали пропорцию

“Геометрические прогрессии в древности”,

“Час веселой математики”,

“Сочинение “Урок Геометрии”,

“Игры со спичками”,

“Исчезновение фигур” и т. д.

Были сделаны наглядные пособия (Настольные
математические игры). В течении семи сезонов было
изготовлено 41 игр. Например: “Волк и овцы”,
“Числовая пирамида”, “Суворовская задача”,
“Мельница”, “Игра 15”, “Игра тактическая
“Фокус”, “Лабиринт”, “Головоломка КИТ”,
“Волшебный круг”, “Маршрут по клеткам” и т. д.
Реферат Семенова Степы написанный во время
летнего математического лагеря под руководством
Унаровой Л. А. Учителя высшей категории,
отличника народного образования на тему “Семь
раз отмерь, один раз отрежь” (Геометрия ножниц). С
этим рефератом выступил на республиканском
семинаре учителей. В городе Якутске 1996 году. За
хороший реферат был приглашен в летний
математический лагерь в г. Якутске.

Тема «Круги Эйлера»

Учебно-воспитательные цели: Тема тесно связана
с алгеброй множеств. Применение кругов Эйлера
придает задачам алгебры множеств наглядность и
простоту. Круги Эйлера с успехом применяются
также в логических задачах для изображения
множеств истинности высказываний и во многих
других случаях. Изображение условий задачи в
виде кругов Эйлера, как правило упрощает и
облегчает путь к решению. Данная тема,
безусловно, расширяет математический кругозор
учащихся обогащает арсенал средств,
используемых в решении разнообразных задач.

Исторические данные:

Леонард Эйлер за свою долгую жизнь (1707-1782 г)
написал более 850 научных работ. В одной из них и
появились эти круги Эйлера. Он написал тогда, что
“они очень подходят для того, чтобы облегчить
наше размышления”.

Задача 1. Пересчитай математиков.

В классе 35 учащихся. Из них 20 занимаются в
математическом кружке, 11 — биологическом кружке,
10 ребят не посещают эти кружки. Сколько биологов
увлекаются математикой?

ОБСУЖДЕНИЕ.

Изобразим эти кружки на большой круг — школьный
двор. В левый круг поместим всех математиков и
обозначим буквой М., а в правой всех биологов и
обозначим буквой Б. В общей части кругов окажутся
те самые биологи -математики, которые нас
интересует. Остальные 10 попросим не входить из
внешнего круга, самого большого. Теперь
подсчитаем всего внутри большого круга 35 ребят,
внутри двух меньших 35 — 10 + 25 внутри
“математического” круга М находится 20 ребят,
значит, в той части “биологического” круга,
которая расположена вне круга М., находится 25-20=5
биологов, непосещающих математический кружок.
Остальные биологи, их 11-5+6 человек, находятся в
общей части кругов МБ. Таким образом, 6 биологов
увлекается математикой.

Вопросы для проверки:

Сколько ребят занимаются только в
математическом кружке и как это показано на
рисунке?

Сколько ребят посещают только один какой-нибудь
кружок?

Задача 2.

В классе 38 человек. Из них 16 в баскетбол, 17 — в
хоккей, 18 — в волейбол. Увлекаются двумя видами
спорта — баскетболом и хоккеем — четверо,
баскетболом и волейболом — трое, волейболом и
хоккеем — пятеро. Трое не увлекаются ни
баскетболом, ни хоккеем, ни волейболом.

А. Сколько ребят не увлекаются одновременно
тремя видами спорта?

Б. Сколько ребят увлекаются лишь одним из этих
видом спорта?

ОБСУЖДЕНИЕ.

Воспользуемся кругами Эйлера. Множество всех
учащихся класса изобразим большим кругом (рис.2)

Внутри которого поместим три меньших круга.
Обозначение: Б -баскетболисты, X — хоккеисты, В -
волейболисты. Число элементов множества БХВ
через у. Из рассмотрения кругов Эйлера видно, что
числа элементов БХВ, БХВ и БХВ равны
соответственно

16-(4+у+3)=9-у, 8-у и 10-у 38= 3+(9-у)+(8-у)+(10-у)-4+3+5+у отсюда У=2

Таким образом двое ребят увлекаются всеми
тремя видами спорта. Складывая количество
элементов непересекающихся множеств, количество
элементов БХВ, БХВ и БХВ т.е. 9-2=7, 8-2=6, 10-2=8, 7+6+8=21 -
увлекаются одним из этих видов спорта.

Тема: Круги Эйлера

В классе 35 учеников. Из них 20 занимается в
математическом кружке, 11 — биологическом, 10 ребят
не посещают эти кружки. Сколько биологов
увлекается математикой ?

В классе 38 человек. Из них 16 играет баскетбол, 17 в
хоккей, 18 в волейбол. Увлекается 2 видами спорта
баскетболом и хоккеем 4, баскетболом и волейболом
3, волейболом и хоккеем 5. Трое не увлекаются ни
баскетболом, ни волейболом, ни хоккеем. Сколько
ребят увлекаются одновременно тремя видами
спорта ?

В классе 40 учеников. Из них 34 подписались на
газету “Кэскил”, 24 — на журнал “Пионер”,
остальные 17 учеников — на газету и на журнал. Есть
ли в классе, те которые не подписались и на
газету, и на журнал ?

В классе мальчики увлекаются собиранием марок.
15 мальчиков собирает марки СНГ, 11 мальчиков -
зарубежные марки, а 6 — и то и другое. Сколько в
классе мальчиков собирают марки ?

Из 32 учеников 12 занимаются в секции волейбола, 15
— в секции баскетбол, а 8 ходят в обеих секциях.
Сколько учеников ходят в секциях ?

В классе 40 учеников. Из них 26 занимаются
баскетболом, 25 плаванием, а 27 — лыжным спортом, 15 -
баскетболом и лыжным спортом, 18 — лыжным спортом и
плаванием. 1 ученик не занимается спортом.
Сколько учеников занимаются в трех видах, а
сколько только одним видом спорта ?

В классе 28 учеников. Из них 4 отличника, 14
спортсменов, 18 певцов. 2 ученика являются
отличником и спортсменом, 10 — певцы и спортсмены,
а один отличник, спортсмен, певец. Сколько
учеников не являются отличником, спортсменом,
певцом.

Решение задач с помощью кругов Эйлера

Давыдова В.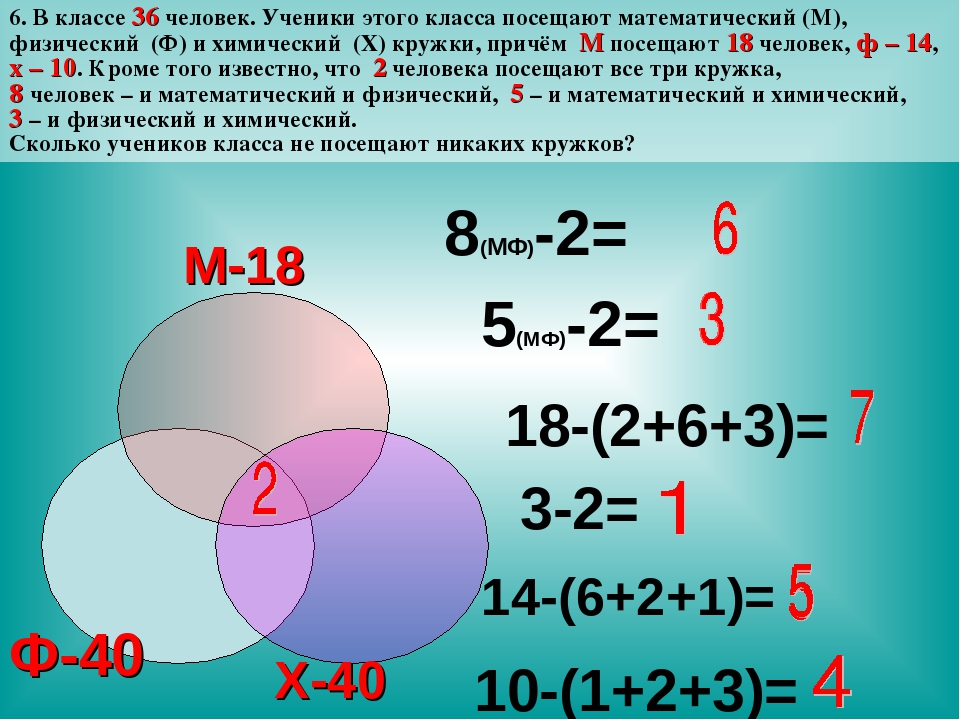 А. 1

1ГБОУ СОШ № 5 «ОЦ «Лидер» г. о. Кинель

Маеренкова В.В. 1

1ГБОУ СОШ № 5 «ОЦ «Лидер» г. о. Кинель

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

1. Введение

Во все времена представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.

Комбинаторика – раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов.

Выбор объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например, конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав [3].

Гипотеза: показать, что решение комбинаторных задач с помощью кругов Эйлера имеет практическое применение.

Проблема: как решение комбинаторных задач с помощью кругов Эйлера помогают в изучении математики и в жизни.

Цель работы: показать широту применения решений комбинаторных задач с помощью кругов Эйлера для привития интереса учащихся к математике.

Задачи:

Познакомиться с историей возникновения науки комбинаторики;

Научиться составлять и решать задачи с помощью кругов Эйлера;

Применять полученные знания в дальнейшем обучении;

Расширить и углубить представление о практическом значении математики в жизни;

Работать с научно-познавательной литературой, анализировать, делать выводы;

Создать собственный банк задач.

Актуальность выбранной темы заключается в необходимости решения комбинаторных задач на уроках математики, применении их в жизни, т.к. они имеют социальную значимость, помогают разобраться в новых веяниях жизни. Основа хорошего понимания комбинаторики – умение считать, думать, рассуждать, находить удачные решения задач.

2. Основная часть

2.1 Решение задач с помощью кругов Эйлера

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью [4].

Круги Эйлера – это тот метод, который наглядно демонстри-рует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Метод Эйлера является незаменимым при решении некоторых задач.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы [3].

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна [2].

Задача №1

В классе учатся 40 человек. Из них по русскому имеют «тройки» 19 человек, по математике – 17 человек и по физике – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека и по физике – 11 человек. Семь человек имеют «тройки» и по математике, и по физике, из них пятеро имеют «тройки и по русскому языку. Сколько людей учатся без «троек»? Сколько людей имеют «тройки» по двум из трёх предметов? [1] Приложение1, Рис. 1

Дальнейшие расчёты не составляют труда.

40-(4+4+11+4+6+2+5)=4 человек учатся без «троек»

6+4+2=12 человек имеют «тройки» по двум предметам

Ответ: 4 человек учатся без «троек», человек имеют «тройки» по двум предметам.

Задача №2

В небольшом городке NN живут 10000 человек. Недавно среди них был проведён опрос «какие машины вам нравятся больше всего?». Результат был таким: 5 000 людям нравятся отечественные машины, 6 000 людям иностранные машины, а 7 тысяч довольны и общественным транспортом. 2000 людям нравятся отечественные машины, но при этом готовы поездить на автобусах. 4000 предпочитаю иностранные машины и автобусы. 2500 людей любят и отечественные и иностранные машины. И только 1000 человек всем довольны. Сколько человек участвовало в опросе? [1]

Решение:

2000 – 1000 = 1000 людей любят только отечественные машины и автобусы

4000 – 1000 = 3000 людей любят только иностранные машины и автобусы

2500 – 1000 = 1500 людей любят и отечественные, и иностранные машины

5 000 людям нравятся отечественные машины, но при этом 1000+1500+1000=3500 людей предпочитают и другие машины, следовательно только отечественные авто любят 500 человек. Также иностранные машины предпочитают 500 людей, а автобусы – 2000 человек. Теперь находим общее количество людей.

3000+1000+500+2000+1000+500+1000=9000 человек

Ответ: 9000 человек участвовали в опросе.

Приложение 1, РИС. 2

Задача №3

На стройке работают 30 рабочих. 17 рабочих строят обувной магазин, 20 рабочих строят парикмахерскую. Сколько рабочих работают на обоих объектах?

Решение:30 – 17= 13 людей строят только обувной магазин. Теперь от 20 отнимем 13 и найдём, что и там, и тут работают только 7 человек. [1] Приложение 1, Рис.3

Задача № 4

Часть туристов разговаривает на английском, а часть на немецком. Английский – 90%, немецкий — 60%. Сколько учеников в классе изучают сразу два языка.

Решение: от всего класса (100%) отнимем английских туристов (90%), получим туристов говорящих только по-английски (10%). А теперь от всех, изучающих немецких (60%), отнимем эти 10%. Получим говорящих на обоих языках (50%).[1] Приложение 2, Рис.4

Задача №5

В классе 30 человек.19-ходят на кружок по математике, 10-на кружок по русскому языку, 1-человек ходит на русский и на математику.

Сколько человек не посещают кружки?

Решение:

19-1=18

10-1=9

30-(18+9+1)=2 человека не посещают ни математику, ни русский.

Приложение 2, Рис.5

Задача № 6

Из 90 детей на футбол ходят 35 детей, на волейбол 28 и на баскетбол 27 детей. На футбол и волейбол ходят одновременно 10 детей, на футбол и баскетбол – 8 детей, на волейбол и баскетбол — 5, на все три – 4. Сколько детей никуда не ходят? [1]

Решение:

10-4=6 ходят на футбол и волейбол

8-4=4 ходят на футбол и баскетбол

5-4=1 ходят на волейбол и баскетбол

На футбол ходят 35 детей, но 4+4+6=14 из них ходят и на другие секции, следовательно, только на футбол ходят 21 ребёнок. Аналогично получаем, что на волейбол ходят 17, а на баскетбол 18. По условию задачи всего 90 детей. 21+17+18+1+4+6+4=71 детей ходят хотя бы на одну секцию, следовательно, 19 детей никуда не ходят.

Приложение 2, Рис. 6

Задача № 7

100 шестиклассников участвовали в опросе, в ходе которого выяснялось, какие пирожки нравятся им нравятся больше: с мясом, с капустой и картошкой. В результате 20 опрошенных выбрали с мясом, 28-с капустой, 12 с картошкой. Выяснилось, что 13 школьников отдают одинаковое предпочтение пирожкам с мясом и капустой, 6-учеников-с мясом и картошкой, 4 ученика с капустой и картошкой, а 9 ребят совершенно равнодушны к пирожкам. Некоторые из школьников ответили, что одинаково любят и мясом, и картошкой, и капустой. Сколько таких ребят? [1]

Решение:

Пусть X – искомое число учеников, любящие все виду пирожков. Тогда: 20+28+12+13+6+4+9+Х=100 Х=6 Приложение 3, Рис. 7

Задача №8

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. [1]

Приложение 3, Рис. 8

Сколько шестиклассников:

1. Являются читателями обеих библиотек;

2. Не являются читателями районной библиотеки;

3. Не являются читателями школьной библиотеки;

4. Являются читателями только районной библиотеки;

5. Являются читателями только школьной библиотеки?

Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.

Решение.

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)

3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)

4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)

5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).

Очевидно, что 2 и 5, а также 3 и 4– равнозначны и ответы на них совпадают.

Задача №9.

Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%? [1]

Решение.

Здесь нет принципиального отличия от решения предыдущей. На готовом рисунке заменим данные: 25 на 85% и 20 на 75%. Учитывая, что все жители дома составляют 100%, заменяем 35 на 100% и получаем готовое решение: 85% + 75% – 100% = 60%.

Ответ: обе газеты выписывают 60% жителей.

Чем более сложная и запутанная логическая задача, связанная с множествами, тем более очевиден эффект от применения кругов Эйлера. Только после составления рисунка их решение становится достаточно очевидным.

Задача №10.

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом? [1] Приложение 3, Рис. 9

Решение.

Д – драмкружок,

Х – хор,

С – спорт.

в круге Д – 27 ребят,

в круге Х – 32 человека,

в круге С – 22 ученика.

Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.

Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,

22 – (5 + 3 + 3) = 11 занимаются только спортом;

70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Ответ: 10 человек и 11 человек.

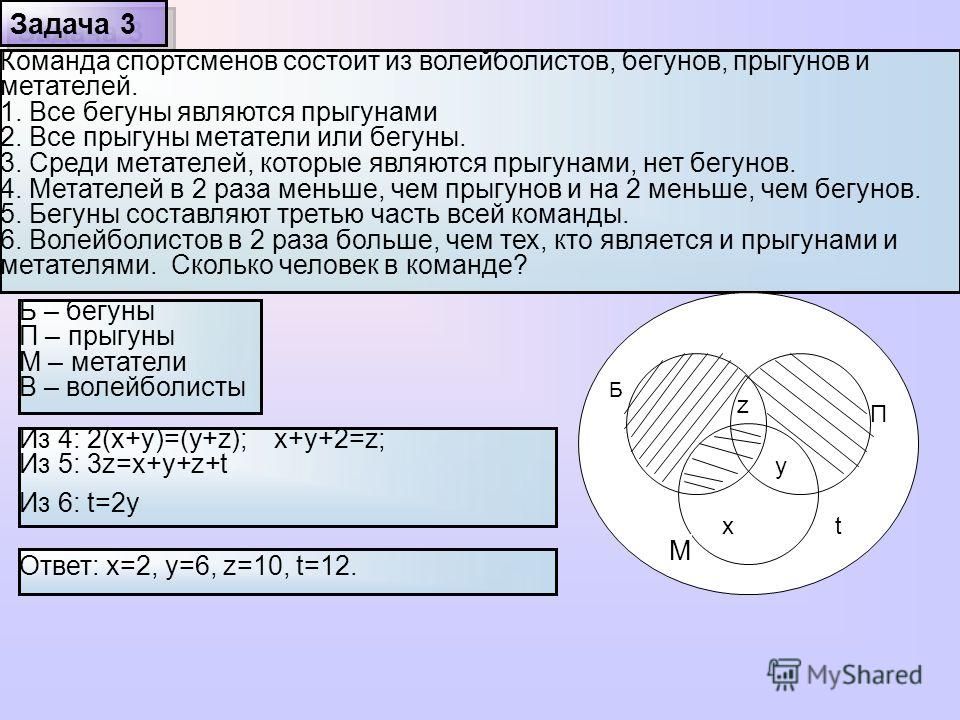
Задача №11.

В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта? [1]

Решение.

1 способ. Для решения опять воспользуемся кругами Эйлера. Приложение 4, Рис. 10

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом – (10 – х) человек, только автобусом и троллейбусом – (9 – х) человек, только метро и автобусом – (12 – х) человек.

Найдем, сколько человек пользуется одним только метро:

20 – (12 – х) – (10 – х) – х = х – 2.

Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:

х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,

отсюда х = 3.

2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.

Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.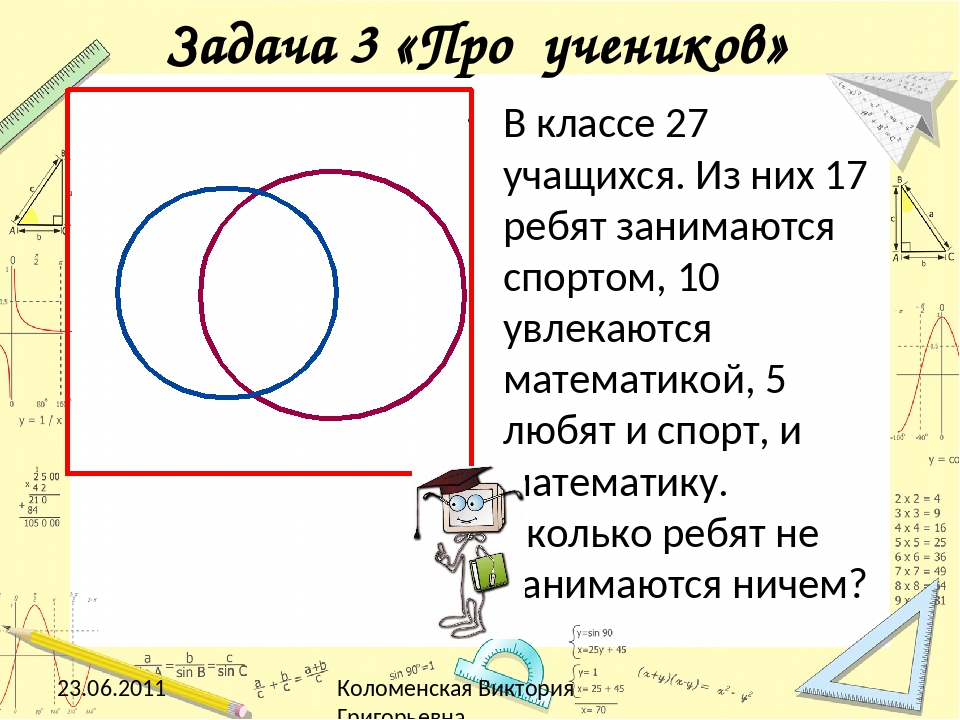

Я проводила опрос среди учащихся 7-х классов. В опросе принимали участие 87 человек.

Результаты социологического опроса представлены на диаграмме. Приложение 5.

Из результатов диаграммы видно, что хотели научиться решать задачи с помощью кругов Эйлера около 80 % учащихся.

2.3 Сборник задач по комбинаторике

Жена попросила своего мужа купить лук, капусту и морковь. Какими различными способами муж мог совершить покупку?

Записанный номер телефона из пяти цифр (5, 3, 4, 7, 2) оказался неверным. Необходимо определить варианты номера телефона.

Сколько трехзначных чисел можно составить из цифр 2,4,6,8 используя в записи числа каждую из них не более одного раза?

Сколько всевозможных вариантов pin-кода надо перебрать, чтобы среди них наверняка был и забытый?

Из группы теннисистов, в которую входят четыре человека – Иванов, Петров, Сидоров и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?

Составьте все возможные трёхзначные числа из указанных цифр,

используя в записи числа каждую из них не более одного раза:

1, 3, 6, 8.

У Арины пять подруг: Катя, Юля, Лиза, Алёна и Таня. Она решила пригласить двух из них в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?

Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

В школьных кружках занимаются 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?

В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?

58 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32 – трамвай, 44 – автобус. 21 человек из них используют метро и трамвай, 31 – метро и автобус, 22 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу?

В 6 А классе 15 человек. В кружок «Эрудит» ходят 5 человек, в кружок «Путь к слову» 13 человек, спортивную секцию посещают 3 человека. Причем 2 человека посещают кружок «Эрудит» и кружок «Путь к слову», «Эрудит» и спортивную секцию, спортивную секцию и «Путь к слову». Сколько человек посещают все три кружка?

В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 — и микроволновку, и телевизор, 15- холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?

В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?

В поход ходили 80 % учеников класса, а на экскурсии было 60 %, причем каждый был в походе или на экскурсии. Сколько процентов класса были и там, и там?

В нашем классе 24 ученика. Все они хорошо провели зимние каникулы.10 человек катались на лыжах, 16 ездили на каток, а 12 — лепили снеговиков. Сколько учеников смогли покататься и на лыжах, и на коньках, и слепить снеговика?

9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 – бананы, апельсины и сливы. Сколько у меня друзей?

В пионерском лагере «Дубки» в смене актива отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. 10 человек были и отличниками и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличники, и спортсмены, и победители олимпиад. Сколько ребят отдыхали в лагере?

У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другте. Угадайте, сколько у меня подруг?

В кондитерском отделе супермаркета посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?

Во дворе стоят машины. Некоторые из них — москвичи, а остальные — жигули. Некоторые из машин красные, а остальные белые. Некоторые из машин новые, а остальные — старые. Известно, что красных москвичей — 3, новых москвичей — 4, а новых красных машин — 5. При этом старых белых москвичей — 2, новых белых жигулей — 1, а старых красных москвичей вообще ни одного. Сколько во дворе новых красных москвичей, если всего машин 21, а старых белых жигулей — 6.

В результате выполнения проектной работы был создан задачник, который состоит из 23 задач и по теории вероятности, и по комбинаторике.

Как видно из моей исследовательской работы, задачи состоят из множества данных. Выстроив данные в единую цепочку, можно увидеть, что решение задач подчиняется одному и тому же способу. Для решения задач, решаемых с помощью кругов Эйлера, был составлен алгоритм, состоящий из следующих этапов:

• Записываем краткое условие задачи.

• Выполняем рисунок.

• Записываем данные в круги (или в диаграмму Эйлера).

• Выбираем условие, которое содержит больше свойств.

• Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).

• Записываем ответ.

Логические задачи заставляют думать, рассуждать, составлять цепочку действий, последовательность, учат алгоритмизации, что немаловажно в современной жизни. А исследовательские работы учат искать информацию из различных источников (включая и интернет) и обрабатывать её, учат находить из большого материала лишь тот, который необходим.

На уроках математики мы решали эти задачи, некоторые из них вызывали у нас затруднение.

3. Заключение

Диаграммы Эйлера — это общее название целого ряда способов графической иллюстрации, широко используемых в различных областях математики: теория множеств, теория вероятностей, логика, статистика, компьютерные науки, и др. Применение кругов Эйлера позволяет даже пятикласснику легко решать задачи, которые обычным путем решаются только в старших классах.

Моя работа заключалась в том, чтобы узнать подробнее об одном из разделов математики — комбинаторике. Я постаралась выяснить, какие комбинаторные методы применяются в наше время. Научилась составлять и решать задачи с помощью кругов Эйлера. В школьных учебниках мало комбинаторных задач. А ведь они включены в олимпиадные задания, ОГЭ и ЕГЭ. Поэтому мне захотелось помочь учителям и ребятам в изучении данной темы. Я надеюсь продолжить работу над этой темой, разработать уже задачи для учащихся старших классов. Самое главное я считаю, что своей работой я заинтересовала и учащихся нашей школы, и учителей. Ведь придумывая самостоятельно задачи, ребята будут развивать в себе еще логическое мышление и творческие способности.

Список использованной литературы

Гусев В. А., Орлов А. И., Розенталь А. Л. Внеклассная работа по математике в 6-8 классах: книга для учителя. М.: Просвещение, 1984– 286с

Савин А. П. Энциклопедический словарь юного математика – М.: Педагогика, 1989. – 352с.

http://ru.wikipedia.org

ПРИЛОЖЕНИЕ 1. Задачи № 1, № 2, № 3

Рис. 1

Рис. 2

Рис. 3

ПРИЛОЖЕНИЕ 2. Задачи № 5, № 6

Рис. 4

Рис. 5

Рис. 6

ПРИЛОЖЕНИЕ 3. Задачи № 7, № 8, № 10

Рис. 7

Рис. 8

Рис. 9

ПРИЛОЖЕНИЕ 4. Задача № 11

Рис. 10

ПРИЛОЖЕНИЕ 5. Результаты социологического опроса

Просмотров работы: 8003

1 использованием формул комбинаторики _Дидактический материал

Приложение 1

Карточки
для активной работы: Деление на пары

Приложение 2

1. Сколько
трехзначных чисел можно составить из цифр 0, 2,4,6,8, используя каждую в записи
числа из них не более одного раза? (Ответ:48)

2.В
классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить
одного дежурного? (Ответ:26)

3.Сколько
существует двузначных чисел, в которых цифра десятков и цифра единиц различные
и нечетные? (Ответ:20)

4.Сколькими
способами читатель может выбрать две книжки из шести имеющихся? (Ответ:15)

5.Сколькими
способами могут сесть в автомобиль 5 человек, каждый из которых может быть
водителем? (Ответ:120)

№	Ответ
1	443=48 трехзначных чисел
2	16+10=26 способами
3
4
5

Приложение 3

Задания
для первой группы

1. Сколькими
способами можно разместить 9 студентов для работы на 9 компьютерах?

2. Сколько
двузначных чисел можно составить из цифр 1,2,3,4 так, чтобы цифры не повторялись?

3.Сколькими
способами можно сшить флаг, состоящий из 3 горизонтальных полос различного цвета, если имеется
материал 10
различных
цветов?

4. На день рождения
приглашено 10 человек. Пришло 6 человек. Сколькими способами можно рассадить
гостей на 10 стульях.

5.Сколькими
способами можно выбрать 2 дежурных из 25 учеников класса? 6.На почтамте имеется
5 видов марок. Сколькими способами можно выбрать из них 3 вида марки?

Задания
для второй группы

1.Сколько
различных пятизначных чисел можно составить из цифр 0,1,2,3,4?

2.На каждой из
десяти карточек записана одна цифра 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Выбирают четыре
карточки и из цифр,
записанных
на них,
составляют
четырёхзначное число.
Сколько
различных четырёхзначных чисел можно составить таким образом?

3.У одного ученика
имеется 7 книг, а у второго – 8 книг. Сколькими способами они могут произвести
обмен книгами два на два?

4.Из 35 учеников
класса 15 – девушки. Сколькими способами из них можно отобрать: 1) девушку и
одного юношу; 2) двух юношей; 3) двух девушек?

5. Сколько среди
четырехзначных чисел, составленных из цифр 3, 5, 7, 9 (без их повторения),
таких, которые начинаются с цифры 3?

Задания
для третьей группы

1.
Сколько
трёхзначных чисел, кратных 5, можно составить из цифр 2, 3, 4, 5, 6, 7 при условии,
что в числе цифры не повторяются?

2.
На книжной полке 8 книг по математике и 5 книг по физике. Сколькими способами
можно взять 3 книги по математике и 2 книги по физике?

3.Сколькими
способами можно переставить буквы в слове логарифм так, чтобы на
втором, четвертом и шестом местах находились гласные буквы?

4.В
комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5
блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга).
Сколькими способами они могут накрыть стол для чаепития (каждый получает чашку,
блюдце и ложку)?

5. Семь мальчиков, в число которых входят Марат и Тимур,
становятся в ряд. Найдите число возможных комбинаций, если:

а)
Марат должен находиться в конце ряда;

б)
Марат должен находиться в начале ряда, а Тимур — в конце ряда;

в)
Марат и Тимур должны стоять рядом.

Презентация — Круги Эйлера

Слайд №2
	№1 Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20-в районной. Сколько шестиклассников: 1. Не являются читателями школьной библиотеки? 2. Не являются читателями районной библиотеки? 3. Являются читателями обеих библиотек? 4. Являются читателями только районной библиотеки? 5. Являются читателями только школьной библиотеки?
Слайд №3
	№2 В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
Слайд №4
	№3 В классе 16 человек любит информатику, а 10 человек любит физкультуру. Учеников, которые любят и физкультуру, и информатику 6. Сколько человек в классе?
Слайд №5
	№4 «Обитаемый остров» и «Стиляги» Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Слайд №6
	№5 «Любимые мультфильмы» Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». 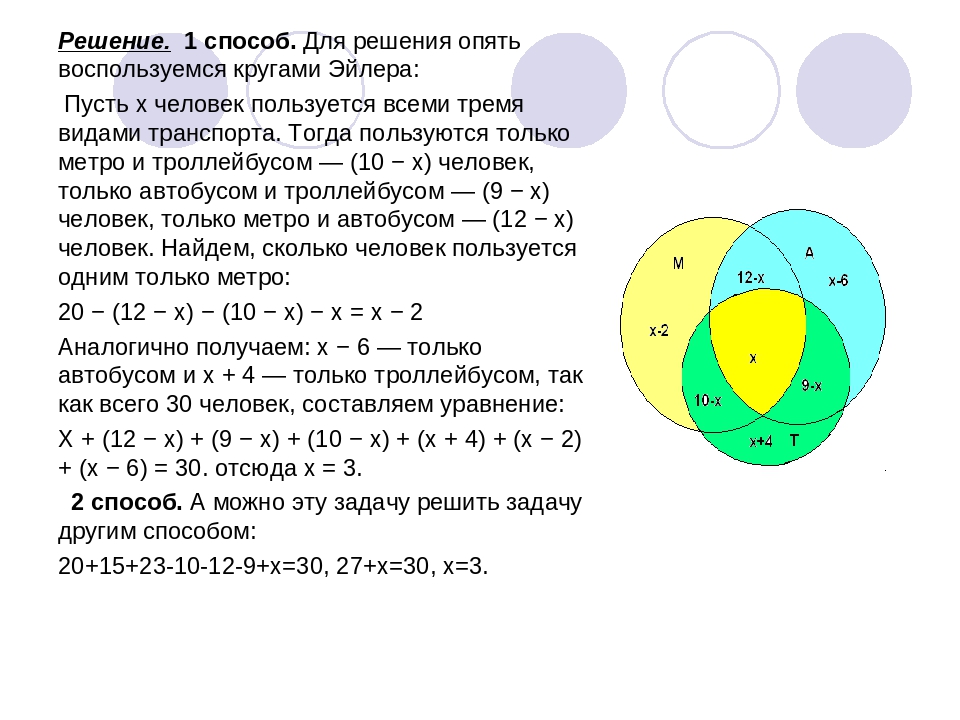Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Слайд №7
	№6 «Мир музыки» В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Слайд №8
	№7 «Гарри Поттер, Рон и Гермиона» На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Слайд №9
	№8 Пионерский лагерь В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
Слайд №10
	№9 Экстрим Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Слайд №11
	№10 На фирме работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
Слайд №12
	№11 Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
Слайд №13
	№12 12 моих одноклассников любят читать детективы, 18 -фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
Слайд №14
	№13 Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
Слайд №15
	№14 Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. 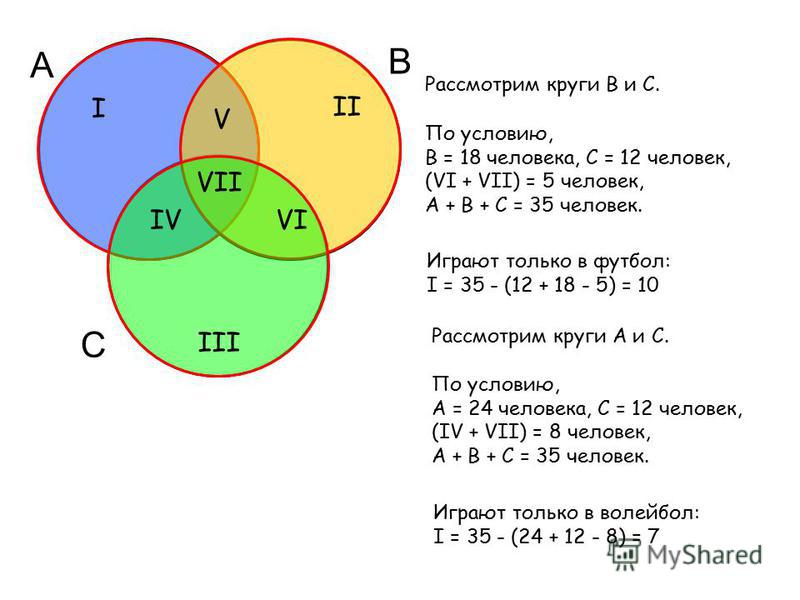Футболом занимается 17 мальчишек, а теннисом – 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
Слайд №16
	№15 65% бабушкиных кроликов любят морковку, 10% любят и морковку, и капусту. Сколько процентов кроликов не прочь полакомиться капустой?
Слайд №17
	№16 В одном классе 25 учеников. Из них 7 любят груши, 11 -черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
Слайд №18
	№17 В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
Слайд №19
	№18 В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
Слайд №20
	№19 Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
Слайд №21
	№20 Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Помощь с практическим заданием по математике и информатике, ЭИОС (edu.pglu.ru)

Задача 1.
9 моих друзей любят хот-дог, 8 – картофель «фри», а 7 – гамбургер, 5 – хот-дог и «фри», 3 – хот-дог и гамбургер, 4 – «фри» и гамбургер, 2 – хот-дог, гамбургер и «фри». Сколько у меня друзей?
Задача 2.
В списке на отдых лагеря «Артек»: 42 отличников, 28 победителей олимпиад и 30 спортсмена. 10 человек были и отличниками и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличники, и спортсмены, и победители олимпиад. Сколько ребят в списке на отдых в лагере?
Задача 3.
В международной компании работают менеджеры, которые знают несколько иностранных языков. 48 менеджеров знают английский, 26 — французский, 28 — немецкий. 8 менеджеров знают английский и немецкий, 8 — английский и французский, 13 — французский и немецкий. 24 менеджера говорят только на русском языке. Сколько менеджеров, знают одновременно три языка: английский, французский и немецкий?
Задача 4.
На олимпиаде по физике школьникам предложили решить три задачи: одну по оптике, одну по механике, одну по молекулярной физике. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по оптике решили 800 участников, по механике — 700, по молекулярной физике — 600. 600 школьников решили задачи по оптики и механики, 500 — по оптики и молекулярной физики, 400 — по механики и молекулярной физики. 300 человек решили задачи по трём темам. Сколько школьников не решило ни одной задачи?
Задача 5.
На олимпиаде по физике школьникам предложили решить три задачи: одну по кинематике, одну по термодинамике, одну по оптике. Результаты олимпиады были следующие: задачу по кинематике решили 400 участников, по термодинамике — 350, по оптике — 300. 300 школьников решили задачи по кинематике и термодинамике, 200 — по кинематике и оптике, 150 — по термодинамике и оптике. 100 человек решили задачи по кинематике, термодинамике и оптике. Сколько школьников решило две задачи?
Задача 6.
Среди студентов-задолжников провели опрос. Был задан вопрос: «Какой предмет у Вас не сдан?». По результатам опроса выяснилось, что у 150 не сдана математика, у 130 – русский язык, у 50 — история. У 60 студентов есть задолженность по математике и русскому языку, у 20 – математика и история, у 30 – русский язык и история. У 70 человек не зачтён иностранный язык. У 10 человек есть нет зачёта по математике, по русскому языку, по истории. Сколько студентов приняли участие в опросе?
Задача 7
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача 8
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников. Сколько учеников пользуются только одним видом транспорта?
Задача 1.
9 моих друзей любят хот-дог, 8- картофель “фри”, а 7- гамбургер., 5- хот-дог и фри, 3- хот-дог и гамбургер, 4- фри и гамбургер, 2- хот-дог, гамбургер и фри. Сколько у меня друзей?
Решение
Введем обозначения
А- друзья которые любят хот- дог , n(A)=9;
B- друзья которые любят картофель фри , n(B)=8;
C- друзья которые любят гамбургер , n(C)=7;
A∩B- друзья которые любят хот- дог и фри , n(A∩B)=5;
A∩С- друзья которые любят хот- дог и гамбургер , n(A∩С)=3;
B∩C- друзья которые любят фри и гамбургер, n(B∩C)=4;
A∩B∩C друзья которые любят хот- дог, гамбургер и фри ,
n(A∩B∩С)=2;
n(A∪B∪C)=n(А)+n(В)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩В∩C)
n(A∪B∪C)=9+8+7-5-3-4+2=14
Ответ: 14 друзей
Задача 2. В списке на отдых лагеря “Артек”:
42 отличников, 28 победителей олимпиад, 30 спортсмена.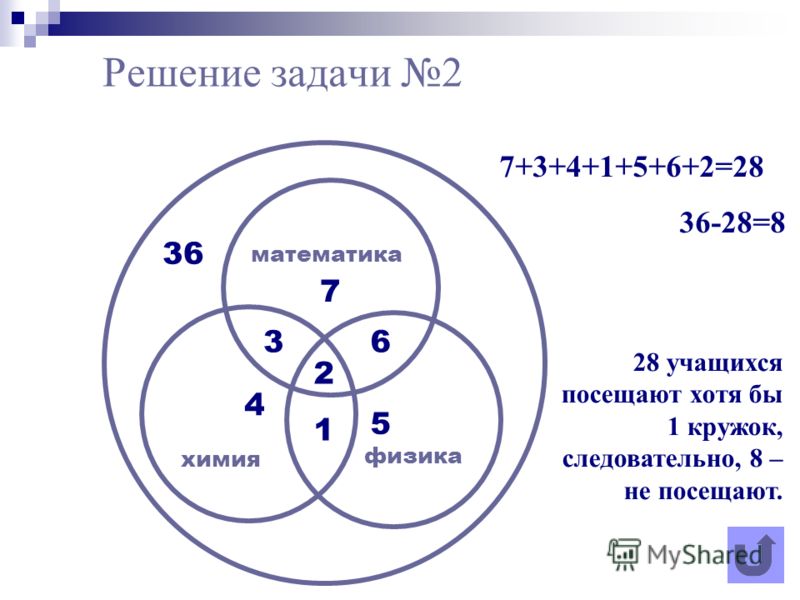 10 человек были и отличниками и победителями олимпиад, 5- отличниками и спортсменами, 8- спортсменами и победителями олимпиад, 3- и отличники, и спортсмены , и победители олимпиад. Сколько ребят в списке на отдых в лагере.
Решение.
Введем обозначения
А- отличники, n(A)=42;
B- победители олимпиад, n(B)=28;
C- спортсмены , n(C)=30;
A∩B-отличники и победители олимпиад, n(A∩B)=10;
A∩С-отличники и спортсмены, n(A∩С)=5;
B∩C-победители олимпиад и спортсмены, n(B∩C)=8;
A∩B∩C-отличники,и спортсмены ,и победители олимпиад ,
n(A∩B∩С)=3;
В списке на отдых в лагере всего найдем по формуле
n(A∪B∪C)=n(a)+n(b)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩b∩C)
n(A∪B∪C)=42+28+30-10-5-8+3=80
Ответ: 80 человек в списке на отдых в лагере.
Задача 4. В олимпиаде по физике школьникам предложили решить три задачи: одну по оптике, одну по механике, одну по молекулярной физике. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по оптике решили 800 участников, по механике -700, по молекулярной физике -600. 600 школьников решили по оптике и механике, 500 – по оптике и молекулярной физике, 400 – по механике и молекулярной физике. 300 человек решили задачи по трем темам. Сколько школьников не решили ни одной задачи?
Решение
Введем обозначения
А- участники, которые решили задачи по оптике, n(A)=800;
B- участники, которые решили задачи по механике, n(B)=700;
C- участники, которые решили задачи по молекулярной физике , n(C)=600;
A∩B- участники, которые решили задачи по оптике и механике, n(A∩B)=600;
A∩С- участники, которые решили задачи по оптике и молекулярной физике n(A∩С)=500;
B∩C-, участники, которые решили задачи по механике и молекулярной физике n(B∩C)=400;
A∩B∩C- по механике, молекулярной физике и оптике
n(A∩B∩С)=300;
Число школьников которые решили хотя бы одну задачу найдем по формуле
n(A∪B∪C)=n(a)+n(b)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩b∩C)
n(A∪B∪C)=800+600+700-600-500-400+300=900
Ни одну задачу не решили 1000-900=100 школьников
Задача 5. На олимпиаде по физике школьникам предложили решить три задачи: одну по кинематике, одну по термодинамике, одну по оптике. Результаты олимпиады следующие: задачу по кинематике решили 400 участников, по термодинамике -350, по оптике -300. 300 школьников решили задачи по кинематике и термодинамике, 200- кинематике и оптике, 150- по термодинамике и оптике. 100 человек решили задачи по кинематике, термодинамике и оптике. Сколько человек решило две задачи
Введем обозначения
А- участники, которые решили задачи по кинематике , n(A)=400;
B- участники, которые решили задачи по термодинамике , n(B)=350;
C- участники, которые решили задачи по оптике , n(C)=300;
A∩B- участники, которые решили задачи по кинематике и термодинамике, n(A∩B)=300;
A∩С- участники, которые решили задачи по кинематике и оптике n(A∩С)=200;
B∩C-, участники, которые решили задачи по термодинамике и оптике n(B∩C)=150;
A∩B∩C- по кинематике, термодинамике и оптике
n(A∩B∩С)=100;
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
Определим количество школьников для всех возможных областей:
0) Область К=0, Т=0, О=0: не определено.
1) Область К=0,Т=0, О=1: 50 школьников.
2) Область К=0, Т=1, О=0: школьников нет.
3) Область К=0, Т=1, О=1: 50 школьников.
4) Область К=1, Т=0, О=0: школьников нет.
5) Область К=1, Т=0, О=1: 100 школьников.
6) Область К=1, Т=1, О=0: 200 школьников.
7) Область К=1, Т=1, О=1: 100 школьников.
Запишем значения областей в таблицу:
К Т О
0 0 0 0 —
1 0 0 1 50
2 0 1 0 0
3 0 1 1 50
4 1 0 0 0
5 1 0 1 100
6 1 1 0 200
7 1 1 1 100

Изобразим значения для всех областей с помощью диаграммы:
Определим х.
х=200+100+50=350.
Получили, 350 школьников решило две задачи.
Задача 6.
Среди студентов-задолжников провели опрос. Был задан вопрос: «Какой предмет у Вас не сдан?». По результатам опроса выяснилось, что у 150 не сдана математика, у 130 – русский язык, у 50 — история. У 60 студентов есть задолженность по математике и русскому языку, у 20 – математика и история, у 30 – русский язык и история. У 70 человек не зачтён иностранный язык. У 10 человек есть нет зачёта по математике, по русскому языку, по истории. Сколько студентов приняли участие в опросе?
Недостаточно данных для решения задачи, потому что 70 студентов у которых не сдан иностранный могли быть и среди тех студентов у которых не сдача по другим предметам.
Введем обозначения
А- студенты, у которых не сдана математика, n(A)=150;
B- студенты, у которых не сдан русский, n(B)=130;
C- студенты, у которых не сдана история , n(C)=50;
A∩B-студенты которые не сдали математику и русский,
n(A∩B)=60;
A∩С- студенты которые не сдали математику и историю,
n(A∩С)=20;
B∩C-студенты которые не сдали русский и историю n(B∩C)=30;
A∩B∩C- студенты которые не сдали русский, математику и историю
n(A∩B∩С)=10;
Число школьников которые решили хотя бы одну задачу найдем по формуле
n(A∪B∪C)=n(a)+n(b)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩b∩C)
n(A∪B∪C)=800+600+700-600-500-400+300=900
Ни одну задачу не решили 1000-900=100 школьников
Задача 7
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Поскольку нам известно, что не менее 20 студентов выполнили двух контрольных работ, сперва находим тех, кто выполнил менее 2 работ.
Для этого поочередно отнимаем от числа выполнивших первую и вторую, вторую и третью, первую и третью работу тех, кто выполнил 2 работы.
Получим:
33 — 20 = 13 студентов.
32 — 20 = 12 студентов.
31 — 20 = 11 студентов.
Находим их общее число.
13 + 12 + 11 = 36 студентов (Выполнили одну из двух работ).
Находим их количество:
36 / 2 = 18 студентов выполнили по 1 контрольной работе.
Задача 8
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников. Сколько учеников пользуются только одним видом транспорта?
Решение
15-6=9 учеников пользуются только метро и автобусом
13-6=7 учеников пользуются только метро и троллейбусом
9-6=3 учеников пользуются только троллейбусом и автобусом
6 учеников пользуются всеми тремя видами транспорта
35-6-9-7-3=10 учеников пользуются одним видом транспорта

«Если бы я мог, но бюджет ограничен». Шерзод Шерматов — об изменениях в системе образования – Газета.uz

Министр народного образования Узбекистана Шерзод Шерматов 22 мая на молодёжном фестивале «Движение пяти инициатив» в Ташкенте заявил о сложности осуществления некоторых изменений в сфере из-за ограничений государственного бюджета.

«Если бы я мог, но бюджет ограничен», — сказал глава МНО, поддержав инициативу дальнейшего проведения неформальных встреч с молодёжью.

«Мне говорят, что в классе должно быть 24 ученика, а не 35. Я бы очень хотел этого. Если подсчитать, то на выполнение одной только этой работы потребуется 9 трлн сумов на один учебный год. На обучение физике и математике выделяется примерно 5−6 трлн сумов. Из-за ограничений бюджета невозможно сделать всё и сразу», — пояснил министр.

Шерзод Шерматов рекомендовал молодым людям, интересующимся предметами STEM (наука, технология, инжиниринг и математика), читать соответствующую литературу на английском языке.

«Те, кто хотят стать хорошими программистами, конечно же, должны выучить английский язык. Например, вы знаете, откуда берутся лучшие IT-новости? Они идут из Кремниевой долины. Затем переводятся на русский язык в течение двух лет, затем — на узбекский язык. Может пройти до четырёх лет, поэтому если мы выпускаем новую книгу по IT, то это будет издание, устаревшее на четыре года», — заявил глава министерства и добавил, что и в других сферах необходимо «поднимать уровень переводчиков».

На встрече с молодёжью выступил также первый заместитель министра туризма и спорта Улугбек Азамов.

Он указал на необходимость увеличения в школах уроков физической культуры, отметив, что «в Узбекистане наименьшее количество часов физкультуры и спорта в средней школе по сравнению с зарубежными странами».

«Молодое поколение необходимо приобщать к спорту с самого детства. Поэтому с 2021—2022 учебного года в школах страны будет увеличено количество уроков физического воспитания до двух часов в неделю», — заявил первый замминистра туризма и спорта.

«Газета.uz» писала, что сегодня в Узбекистане число учеников (6,24 миллиона) значительно превышает проектные мощности школ (5,06 миллиона). Если тенденция продолжится, эта разница может достичь 2 миллионов, отмечал Шерзод Шерматов. Министр объяснял переполненные классы и обучение в две смены ростом населения и переводом школ на 9-летнее образование (в настоящее время в школах вернули 11-летнее образование).

В тесте по математике, сданном 35 учениками, средний балл 9 класс по математике CBSE

Подсказка: Сначала мы запишем уже предоставленные нам данные, а затем оценим все, что можно из них, и посмотрим, какие из вариантов мы могли бы оценить.

Полный пошаговый ответ:
Нам дано, что общее количество учащихся, сдавших тест, составило 35.
Средний балл 15 девочек — 10, а 20 мальчиков — также 10.
Среднее значение — это сумма всех чисел, полученных каждым из студентов, деленная на количество студентов.
Следовательно, средний балл 15 девочек равен 10.
Теперь мы знаем, что сумма всех чисел, полученных каждой из 15 девочек, деленная на 15, равна 10.
Пусть $ {s_g} $ обозначает сумму баллов. получено 15 девушками.
Итак, $ \ dfrac {{{s_g}}} {{15}} = 10 $
Взяв 15 из знаменателя LHS в числитель RHS, мы получим: —
$ \ Rightarrow {s_g} = 10 \ times 15 = 150 $
Это означает, что сумма всех чисел, полученных 15 девушками, равна 150.……. (1)
Эти данные не являются ни одним из вариантов.
Теперь перейдем к следующей предоставленной нам информации о том, что средний балл 20 мальчиков равен 10.
Это означает, что сумма всех чисел, полученных каждым из 20 мальчиков, деленная на 20, равна 10.
Пусть $ {s_b } $ обозначают сумму оценок, полученных 20 мальчиками.
Итак, $ \ dfrac {{{s_b}}} {{20}} = 10 $
Взяв 20 из знаменателя LHS в числитель RHS, мы получим: —
$ \ Rightarrow {s_b} = 10 \ times 20 = 200 $
Это означает, что сумма всех чисел, полученных 20 мальчиками, равна 200.……… .. (2)
Эти данные не являются ни одним из вариантов.
Но если мы закроем (1) и (2), у нас будет сумма оценок мальчиков и девочек.

Итак, правильный ответ — «Вариант В».

Дополнительная информация: Вычисленное «центральное» значение набора чисел в упрощенных терминах называется средним.

Примечание: Учащиеся могут совершить ошибку, не пытаясь объединить две полученные нами информации, и, таким образом, не найти ни одного варианта, если он доступен в вопросе.

В классе из 35 учеников 20 мальчиков и 15 девочек. Студент выбирается случайным образом. Найдите вероятность того, что выбранный ученик (i) мальчик (ii) девочка.

PDF-ФАЙЛ НА ВАШ ЭЛЕКТРОННУЮ ПОЧТУ НЕМЕДЛЕННО ПОКУПКА ЗАМЕТКИ И РЕШЕНИЕ ДЛЯ БУМАГИ. @ Rs. 50 / — каждый (GST extra)

HINDI ENTIRE PAPER SOLUTION

MARATHI PAPER SOLUTION

SSC MATHS I PAPER SOLUTION

SSC MATHS II PAPER SOLUTION

SSCIENCE I PAPER SOLUTION

PSCIENCE

SSCIENCE

БУМАГА НА АНГЛИЙСКОМ ЯЗЫКЕ

SSC & HSC НАВЫК ПИСЬМА НА АНГЛИЙСКОМ ЯЗЫКЕ

УЧЕТНЫЕ ЗАПИСИ HSC

ЗАМЕТКИ HSC OCM

ЗАМЕТКИ ПО ЭКОНОМИКЕ HSC

ЗАМЕТКИ СЕКРЕТАРНОЙ ПРАКТИКИ HSC

НАБОР 2019 Board Paper Solution

A HSCLISH

HSC ENGLISH SET B 2019 21 февраля, 2019

HSC ENGLISH SET C 2019 21 февраля 2019

HSC ENGLISH SET D 2019 21 февраля 2019

СЕКРЕТАРНАЯ ПРАКТИКА (S.P) 2019 25 февраля 2019 г.

HSC XII PHYSICS 2019 25 февраля 2019 г.

ХИМИЯ XII РЕШЕНИЕ HSC 27 февраля 2019 г.

OCM PAPER SOLUTION 2019 27 февраля 2019 г.

HSC MATHS PAPER SOLUTION COMMERCE, 2 марта, 2019

HSC MATHS PAPER SOLUTION SCIENCE 2 марта 2019 г.

SSC ENGLISH STD 10 5 марта 2019 г.

СЧЕТА HSC XII 2019 6 марта 2019 г.

HSC XII BIOLOGY 2019 6 марта 2019 г.

HSC XII ECONOMICS 9th Март 2019 г.

SSC Maths I March 2019 Solution 10th Standard11 марта 2019 г.

SSC MATHS II MARCH 2019 SOLUTION 10TH STD.13 марта 2019 г.

SSC SCIENCE I MARCH 2019 SOLUTION 10TH STD. 15 марта 2019 г.

SSC SCIENCE II МАРТ 2019 РЕШЕНИЕ 10TH STD. 18 марта 2019 г.

РЕШЕНИЕ SSC SOCIENCE I МАРТА 2019 20 марта 2019 г.

РЕШЕНИЕ SSC SOCIENCE II МАРТА 2019 г., 22 марта 2019 г.

XII CBSE — СОВЕТ — МАРТ — 2019 АНГЛИЙСКИЙ — РЕШЕНИЯ QP +, 2 марта 2019 г. 2019

Документы Совета директоров HSC Maharashtra 2020

(стандартный 12-й английский средний)

HSC ECONOMICS МАРТ 2020

HSC OCM МАРТ 2020

СЧЕТА HSC МАРТ 2020

HSC S.П. МАРТ 2020

HSC АНГЛИЙСКИЙ МАРТ 2020

HSC HINDI МАРТ 2020

HSC MARATHI МАРТ 2020

HSC MATHS МАРТ 2020

Документы совета директоров SSC Maharashtra 2020

(стандартная 10-я английская среда)

Английский МАРТ 2020

Хинди МАРТ 2020

Хинди (композитный) МАРТ 2020

Маратхи МАРТ 2020

Математика (Работа 1) МАРТ 2020

Математика (Работа 2) МАРТ 2020

Санскрит МАРТ 2020

Санскрит (композитный) МАРТ 2020

Наука (Документ 1) МАРТ 2020 г.

Наука (Документ 2)

ДОЛЖЕН ПОМНИТЬ Вещи в день экзамена

Готовы ли вы? по грамматике английского языка на школьном экзамене.

Бумажная презентация на экзамене совета директоров

Как получить хорошие оценки на экзаменах совета SSC

Советы, чтобы набрать более 90% оценок на 12-м экзамене

Как писать экзамены по английскому?

Как подготовиться к экзамену совета директоров, когда осталось меньше времени

Как запомнить то, что вы изучаете для экзамена совета директоров

№ 1 Simple Hack, который вы можете попробовать, при подготовке к экзамену совета директоров

Как учиться в классе CBSE 10 мудрых советов по предметам для настольных экзаменов?

Основной процесс регистрации JEE 2020 — Схема экзамена и важные даты

NEET UG 2020 Схема процесса регистрации и важные даты

Как можно подготовиться к двум конкурсным экзаменам одновременно?

8 проверенных советов, как справиться с тревогой перед экзаменом!

КУПИТЬ В PLAY STORE

СКАЧАТЬ НАШЕ ПРИЛОЖЕНИЕ

КАК ПРИОБРЕСТИ НАШИ НОТЫ?

С.P. Важные вопросы для вступительного экзамена 2021

O.C.M. Важные вопросы для вступительного экзамена. 2021

Важные вопросы по экономике для экзамена совета 2021

Банк важных вопросов по химии для экзамена совета 2021

Физика — Раздел I — Банк важных вопросов для экзамена HSC Совета Махараштры

Физика — Раздел II — Наука — Банк важных вопросов для Совета HSC Махараштры Экзамен 2021 г.

Япония сократит количество учеников в начальной школе до 35 к 2025 году

Министр финансов Таро Асо и министр образования Коичи Хагиуда договорились в четверг сократить максимальное количество учеников в классе в государственных начальных школах до 35 к 2025 финансовому году с нынешних 40.

Соглашение было достигнуто в ходе переговоров по соответствующему запросу на финансирование в рамках правительственного проекта бюджета на 2021 финансовый год, который начинается в апреле.

Министерство образования внесет законопроект о необходимом пересмотре закона на очередную сессию Сейма в следующем году, которая состоится в январе.

Правительство будет стремиться обеспечить достаточное количество учителей для работы в меньших классах в течение пяти лет, начиная с апреля 2021 года. Сокращение размеров классов будет осуществляться постепенно, начиная с младших классов.

Максимальное количество учеников начальной школы, которым в настоящее время разрешено учиться в одном классе, составляет 40, за исключением классов первого класса, число которых было сокращено до 35 в 2011 финансовом году.

Запланированный переезд будет включать самый крупный размер класса начальной школы сокращение примерно за 40 лет.

Министерство образования предложило меньшие классы в своем бюджетном запросе на 2021 финансовый год, чтобы снизить риски коронавируса и упростить проведение уроков с использованием компьютеров. Члены Национальной ассоциации губернаторов также стремились к меньшим классам.

Для государственных неполных средних школ министерство также призвало сократить максимальное количество учащихся в классе до 30 с нынешних 40.

Но Министерство финансов неохотно продвигало этот план из-за опасений по поводу расходов на персонал. Меньшие классы «окажут небольшое влияние, если вообще окажут какое-либо влияние на успеваемость детей», заявили в министерстве.

Во времена дезинформации и слишком большого количества информации качественная журналистика как никогда важна.
Подписавшись, вы можете помочь нам понять историю.

ПОДПИШИТЕСЬ СЕЙЧАС

ФОТОГАЛЕРЕЯ (НАЖМИТЕ ДЛЯ УВЕЛИЧЕНИЯ)

процентиль

А

процентиль

представляет собой сравнительный балл между конкретным баллом и баллами остальной группы. Он показывает процент баллов, которые превзошла конкретная оценка. Например, если вы забили

баллов по тесту и ранжируются в

85
^th
процентиль, это означает, что оценка

выше чем

из оценок.

Процентильный ранг рассчитывается по формуле

знак равно

100

(

)

где

желаемый процентиль и

— количество точек данных.

Пример 1:

Если результаты набора учащихся за тест по математике равны

а также

каков процентильный ранг оценки

Расположите числа в порядке возрастания и дайте ранг в диапазоне от

до самого низкого до

к высшему.

Число

Классифицировать

Используйте формулу:

знак равно

100

(

)

знак равно

Таким образом, оценка

имеет

75
^th
процентиль.

Обратите внимание, что если процентильный ранг

целое число,

п
^th
процентилем будет оценка с рангом

когда точки данных расположены в порядке возрастания.

Если

не является целым числом, то

п
^th
процентиль рассчитывается, как показано.

Позволять

быть целой частью и быть десятичной частью

из

.Подсчитайте баллы с рангами

а также

. Умножьте разницу результатов на десятичную часть

. В

п
^th
процентиль — это сумма произведения и оценки с рангом

Пример 2:

Обозначить

35 год
^th
процентиль оценок

а также

Расположите числа в порядке возрастания и дайте ранг в диапазоне от

до самого низкого до

к высшему.

Число

Классифицировать

Используйте формулу:

знак равно

35 год

100

(

)

знак равно

2.45

Целая часть

является

, подсчитайте балл, соответствующий рангам

а также

. Они есть

а также

. Произведение разницы и десятичной части равно

0,45

(

—

)

знак равно

1.35 год

Следовательно

35 год
^th
процентиль

1,35

знак равно

3,35

Что такое ранг в классе? Что такое хороший ранг?

Вы слышали о звании в классе, но не знаете, что это такое? Может быть, вы хотите знать, почему важен классовый ранг или как вы можете определить, что такое хороший классный ранг. И, кстати, что такое хороший классный чин?

У нас есть ответы на все эти вопросы! Читайте дальше, чтобы узнать, что такое звание в классе, как его рассчитывают школы и насколько он важен для вашего будущего.

Что такое ранг в классе?

Классный рейтинг — это способ увидеть, насколько ваши академические достижения соответствуют достижениям ваших одноклассников.

Ваш классный рейтинг определяется путем сравнения вашего среднего балла со средним баллом людей того же класса, что и вы. Итак, если вы младший, и в вашей средней школе 500 учеников, каждый из них получит число от 1 до 500, а человек с наивысшим средним баллом занял первое место. Если в вашем классе 500 человек и ваш классный рейтинг 235, то 234 ваших одноклассника имеют более высокий средний балл, чем вы, 265 одноклассников имеют более низкий средний балл, чем вы, и вы входите в лучшую половину своего класса.

Классный рейтинг пересматривается каждый раз, , будь то семестр или триместр в вашей школе.Таким образом, каждый раз, когда в стенограмму добавляются новые оценки, рейтинг класса обновляется, и ваш рейтинг может повышаться или понижаться.

Как разные школы измеряют рейтинг в классе?

Все методы ранжирования в классе включают присвоение каждому ученику номера в зависимости от того, как его средний балл по успеваемости сравнивается со средним баллом его одноклассников. Однако есть несколько разных способов измерить классовый ранг.

Существует два основных типа классового ранга: взвешенный и невзвешенный. Невзвешенный рейтинг в классе определяет ваш рейтинг на основе вашего невзвешенного среднего балла. Невзвешенный средний балл оценивается по шкале от 0 до 4,0 и не учитывает сложность ваших курсов. Взвешенный рейтинг в классе определяет ваш рейтинг на основе вашего взвешенного среднего балла. Взвешенный средний балл обычно варьируется от 0 до 5,0, и от до учитывается сложность ваших курсов.

Так что это значит для вашего рейтинга? Если вы прошли курсы с отличием или AP, ваш взвешенный классный ранг, вероятно, будет лучше, чем ваш невзвешенный классовый ранг, , даже если вы не получили пятерок на всех этих курсах.Это связано с тем, что более сложные курсы имеют больший вес (обычно 5,0) при расчете среднего балла.

Для невзвешенного ранга в классе человек, который посещает классы обычного уровня и получает в них отличные оценки, будет иметь такой же невзвешенный средний балл и ранг в классе, что и студент, который взял все отличия и классы AP и получил в них пятерки. Для невзвешенного среднего балла каждый A, независимо от сложности курса, засчитывается как 4.0.

Некоторые средние школы предоставляют взвешенный классный ранг, некоторые невзвешенный классовый ранг, а некоторые предоставляют оба рейтинга.Чтобы узнать больше о невзвешенных и взвешенных GPA, прочтите наше руководство по этой теме.

Ваш классовый ранг также определяет ваш классовый процентиль. Если ваша школа не указывает ваш процентиль, это легко вычислить. Разделите свой рейтинг в классе на количество учеников в вашем классе, умножьте на 100, затем вычтите это число из 100. Например, если в вашем классе 600 учеников, и вы занимаетесь 120-м, то вы находитесь в 80-м процентиле потому что (120/600) * 100 = 20, а 100-20 = 80.Вы также входите в лучших 20% своего класса.

Почему важен классный ранг?

Помимо того, что учащиеся узнают, чем они отличаются от своих одноклассников, звание в классе используется по ряду других причин.

# 1: Заявки в колледж

Классный рейтинг позволяет колледжам увидеть, как ваши академические достижения сравниваются с достижениями ваших одноклассников. Например, если вы посещаете среднюю школу, которая дает очень мало оценок, и у вас есть транскрипт, в котором в основном есть оценки B и C, это может сделать ваш средний балл ниже, чем средний балл среднего абитуриента.Однако по вашему высокому классу сотрудники приемной комиссии увидят, что вы были одним из лучших учеников в своем классе, и это укрепит вашу заявку.

И наоборот, если у вас есть отличные оценки, но вы посещали только легкие классы или ходили в среднюю школу, которая дала много пятерок, у вас может быть отличный средний балл, но ваш классный рейтинг не будет особенно высоким, потому что многие ваши одноклассники получили те же оценки, что и вы. сделал.

Звание в классе помогает колледжам анализировать ваш средний балл и дает им больше информации о ваших академических способностях. Некоторые штаты предлагают старшеклассникам гарантированное поступление в государственные университеты, если они имеют определенный классный чин. Например, студентам Флориды гарантируется поступление по крайней мере в один университет штата, если они входят в 20% лучших выпускников своего класса.

# 2: Стипендии

Для получения некоторых стипендий требуется, чтобы кандидаты достигли определенного ранга в классе или процентиля (например, 25% лучших в вашем классе).Как и колледжи, комитеты по стипендиям могут также использовать звание в классе в качестве одного из критериев для оценки академических способностей студента, наряду с GPA и результатами стандартизированных тестов.

# 3: Высшая школа с отличием

Некоторые средние школы присуждают награды выпускникам старших классов, которые достигли определенного звания в классе, например, 10% или 25% лучших в своем классе. Есть также награды для тех, кто занимает верхние строчки в своем классе. Выпускник, занявший первое место в классе, считается прощальным и часто выступает с речью на выпускном.Человек, занявший 2-е место, является салютатором класса.

Почему некоторые школы больше не используют классный рейтинг?

Хотя классный чин уже давно используется колледжами для оценки академических навыков учащихся, в настоящее время только около половины средних школ США предоставляют классный чин.

Есть несколько причин, по которым все больше и больше школ перестают использовать классные чины. Некоторые школы считают, что учащиеся, которые просто пропускают важные процентили, такие как 10% или 25% лучших в своем классе, могут оказаться в несправедливо невыгодном положении с точки зрения стипендий и поступления в колледжи.Например, ученик из лучших 11% своего класса может иметь средний балл, очень похожий на ученика из лучших 9%, но может не получать определенные стипендии или предложения колледжа, потому что он не входит в 10% лучших учеников своего класса. .

Некоторые также считают, что звание в классе не способствует командной работе и сотрудничеству, потому что оно делает учеников слишком конкурентоспособными друг с другом, поскольку они соперничают за повышение своего звания в классе. Некоторые школы также считают, что присвоение ранга в классе побуждает учащихся посещать более легкие классы, чтобы повысить свой рейтинг. вместо того, чтобы бросать вызов самим себе и брать более сложные классы, где они могут не получить пятерку, но могут узнать больше.

Есть также школы, которые больше не присваивают звание каждому ученику, а предоставляют только широкие процентили. Эти процентили могут разделить класс на четверти и показать, входит ли конкретный ученик в 25, 50 или 75% лучших в своем классе. Это позволит вам примерно узнать, насколько хорошо вы успеваете по сравнению с одноклассниками, но вы не будете знать своего точного звания в классе. Некоторые школы также используют процентили, чтобы обозначить, какие учащиеся входят в 10% или 15% лучших учеников своего класса, и не предоставляют процентили для учеников ниже этого порогового значения.

Поскольку меньшее количество средних школ включают это в транскрипты, многие колледжи придают меньшее значение классу при рассмотрении заявлений в колледж. Вместо того, чтобы использовать рейтинг в классе в качестве важного критерия приема, некоторые колледжи вместо этого уделяют больше внимания другим компонентам транскрипта студента, таким как средний балл или строгость пройденных классов.

Вам не нужно будет слишком усердно искать, чтобы найти свой классный ранг.

Как найти свой класс Рейтинг

Чтобы узнать свое звание в классе, сначала проверьте свой последний табель успеваемости или табель средней школы. Ваше звание в классе должно быть указано, обычно внизу страницы. Вы должны увидеть, какой у вас ранг в классе и сколько человек в вашем классе. Ваша школа также может предоставить ваш процентиль, а также указать, является ли ваш рейтинг взвешенным или невзвешенным (или он может предоставлять и то, и другое).

Если вы не можете найти эту информацию или у вас нет доступа к табелям успеваемости или транскриптам, зайдите в офис школы или спросите своего школьного консультанта. Они должны быть в состоянии дать вам ваш классовый чин.Если в вашей школе нет места в классе, они все равно могут дать вам процентильную оценку. Если вам интересно узнать эту информацию, попробуйте спросить что-нибудь вроде: «Я хотел бы узнать свое звание в классе, чтобы иметь лучшее представление о моих шансах на поступление в колледж. Если вы не можете указать мой точный рейтинг, не могли бы вы скажите мне, в какой примерный процентиль я вписываюсь? »

Как определить, в каком процентиле вы находитесь

Многие школы будут указывать ваш процентиль вместе с вашим рангом, но если ваша школа этого не делает, это легко вычислить.Используйте эту формулу:

(1- (ваше звание в классе / количество людей в вашем классе)) * 100 = ваш процентиль

Если ученик занимает 78-е место из 600 учеников своего класса, она подставляет эти числа и получает:

(1- (78/600)) * 100 = 87

Значит, она будет в 87-м процентиле. Помните, процентили показывают, сколько людей вы занимает выше, , поэтому чем выше число, тем лучше. Быть 87-м процентилем означает, что ее классный чин выше 87% классных разрядов ее одноклассников.Вычтя 87 из 100, вы также можете увидеть, что по классному положению этой ученицы она входит в лучших 13% своего класса.

Что делать, если в вашей школе нет ранга в классе?

Только около 60% средних школ по-прежнему используют рейтинг класса, поэтому, если ваша школа не предоставляет рейтинги классов, вы не одиноки.

Некоторые учащиеся опасаются, что, если их школа не предоставит место в классе, это снизит их шансы на поступление в колледж. Однако это неправда. Когда в средней школе не указывается место в классе, колледжи просто изучают другую информацию, такую как средний балл, аттестат зрелости и результаты стандартизированных тестов, чтобы оценить академические способности ученика. Как упоминалось выше, из-за того, что в старших классах меньше школ, они становятся менее важными для приема в колледжи.

Как далеко вы от 4.0? Воспользуйтесь нашим простым инструментом GPA, чтобы определить, насколько хорошо вы должны успевать в будущих классах, чтобы поднять свой средний балл до этого магического числа.

Что такое хороший класс?

Итак, теперь, когда вы знаете, какое у вас звание в классе, какое звание хорошего класса? Этот ответ зависит от множества факторов, в том числе от вашей средней школы и места, где вы собираетесь поступить в колледж, но мы все же можем дать некоторые общие ответы.

Если вы хотите поступить в колледж, ваша минимальная цель должна заключаться в том, чтобы иметь место в классе, которое поместит вас в лучшую половину вашего класса. Итак, если у вас класс 500, вам нужно, чтобы ваш ранг был 249 или выше.Вы, безусловно, можете поступить в колледжи с более низким рейтингом (особенно если вы идете в высококонкурентную среднюю школу и / или магнитную школу), но попадание в лучшую половину вашего класса — хорошая базовая цель, к которой нужно стремиться, поскольку это показывает что вы ученик школы выше среднего.

Если вы хотите поступить в более конкурентоспособный колледж, вам следует стремиться к тому, чтобы в классе вы входили в 25% лучших в своем классе или в 75-й или более высокий процентиль. Для Лиги Плюща и других школ высшего уровня хорошей целью является попадание в класс 10% или 5% лучших.

Помните, однако, что колледжи принимают во внимание множество факторов при подаче заявления в колледж, и ваш классный рейтинг — это лишь часть головоломки. Наличие в целом сильной заявки — с высокими оценками, транскриптом, показывающим, что вы посещали сложные классы, сильные рекомендательные письма и преданность внешкольным занятиям — имеет гораздо большее значение, чем просто ваш классный рейтинг.

Резюме: что нужно знать о ранге в классе

Классный чин — это способ сравнить оценки учащегося с оценками его одноклассников.Студентам дается числовой рейтинг на основе их среднего балла.
Ранг класса может быть взвешенным, невзвешенным или включать только процентили.
Классный чин — это один из критериев, который колледжи используют для определения академических способностей абитуриента.
Некоторые средние школы больше не используют классный рейтинг из-за растущих опасений, что это заставляет учащихся брать менее сложные курсы и ставит учащихся, которые не достигают определенных процентилей, в несправедливое невыгодное положение при поступлении в колледжи.
Звание вашего класса обычно можно найти в школьной справке или табеле успеваемости.
Если ваша средняя школа не включает классный чин, это не повлияет отрицательно на ваши шансы поступить в колледж. В университетах есть много других критериев, таких как ваш средний балл, эссе и результаты стандартизированных тестов, которые помогут принять решение.

Что дальше?

Хотите знать, что еще колледжи ищут в вашей транскрипте? Ознакомьтесь с нашим руководством о том, какая информация содержится в стенограмме средней школы и почему она важна для поступления в колледж.

Хотите повысить свой классный ранг? Прочтите наше руководство по различным стратегиям повышения среднего балла в старшей школе.

Хотите знать, насколько силен ваш средний балл? Узнайте, какой хороший средний балл для колледжа.

Одна из самых важных частей вашего заявления в колледж — это то, какие уроки вы выбираете в старшей школе (в сочетании с тем, насколько хорошо вы успеваете в этих классах). Наша команда экспертов по поступлению в PrepScholar объединила свои знания в это единственное руководство по планированию вашего расписания занятий в средней школе. Мы посоветуем вам, как сбалансировать ваше расписание между обычными курсами и курсами с отличием / AP / IB, как выбрать дополнительные уроки и какие классы вы не можете себе позволить не посещать.

Количество поступающих на бакалавриат Tufts выросло на 35 процентов

Согласно данным, опубликованным Управлением приема на бакалавриат на этой неделе, бакалавриат Tufts привлекает более широкий и разнообразный круг студентов, чем когда-либо прежде.

За место в классе 2025 претендовали более 31 190 претендентов на первый курс, что на 35 процентов больше, чем в прошлом году.Пул кандидатов в этом году также самый разнообразный за всю историю; Впервые цветные студенты составляют большинство абитуриентов в США: 51 процент, сказал JT Duck, декан приемной комиссии и управления зачислением.

На Школу искусств и наук пришлось 24 378 заявок, что на 37 процентов больше, а на Школу инженерии — 5 874 заявок, что на 28 процентов. В Школе изящных искусств в Тафтсе (SMFA) наблюдался рост как по программе бакалавриата изящных искусств, так и по пятилетней комбинированной программе (Arts and Sciences / SMFA), на 31 и 33 процента соответственно.

«Образование Тафтса никогда не было более востребованным, чем сейчас», — говорит Дак, ссылаясь на то, что Тафтс, характеризуемый как совместный и междисциплинарный, объединяет сильные стороны исследовательского университета с гуманитарными науками, инженерией и устоявшейся студией искусств. программа — плюс этика и возможности взаимодействия, которые дает Tisch College of Civic Life.

«Приятно видеть, как студенты сначала с любопытством, а затем с энтузиазмом реагируют, когда мы говорим о Tufts и обо всем, что он может предложить», — говорит Дак.

Duck также объясняет рост числа заявлений частично полностью переосмысленным процессом приема, в том числе политикой факультативного тестирования SAT / ACT (впервые стандартизированные результаты тестов не требовались), а также обязательством университета выполнить 100 процентов продемонстрированных финансовых показателей. необходимость и пристальное внимание к развертыванию цифровых инструментов.

Благодаря протоколам безопасности социального дистанцирования для сдерживания распространения COVID-19 «изменился практически каждый аспект того, как будущие студенты участвуют в процессе поиска вузов, равно как и практически все аспекты того, как приемные комиссии взаимодействуют со студентами», — сказал он.

Среди этих изменений была замена посещения кампуса надежной программой виртуальных туров и информационных сессий. Тафтс, как и большинство университетов, также отменил набор командировок за пределы кампуса, а дни открытых дверей на кампусе превратились в тематическое виртуальное программирование, такое как студенческие панели, виртуальные классы, экскурсии по зданиям и семинары по применению / эссе.

Программа Voices для старшеклассников, заинтересованных в изучении разнообразия и сообщества в Тафтсе, также была преобразована в виртуальное мероприятие на выходных, и все посещения старших классов и ярмарки колледжей также проводились удаленно.

Тем не менее, даже с учетом социального дистанцирования, сотрудники приемной комиссии решили продолжить процесс приема, сказал Дак.

«Мы воспользовались возможностью, чтобы создать веселую и увлекательную переписку по электронной почте и в социальных сетях, и потратили больше времени на общение напрямую с школьными консультантами по электронной почте и вебинарам», — сказал он. «Это позволило нам привлечь больше студентов, чем мы могли бы получить с помощью наших традиционных усилий по набору, почти вдвое увеличив количество потенциальных студентов, с которыми мы общались этой осенью.”

В то время как политика необязательного тестирования и обширное виртуальное программирование способствовали увеличению числа заявлений, тот факт, что студенты были в кампусе в этом осеннем семестре, также произвел положительное впечатление на будущих студентов, сказал Дак.

«Благодаря строгим мерам по охране здоровья и безопасности большинство наших студентов смогли прийти в кампус для виртуальных, гибридных и очных занятий», — сказал он. «То, что семестр прошел так хорошо, является свидетельством силы, устойчивости и гибкости нашего сообщества, упорной работы наших преподавателей и сотрудников, а также приверженности наших студентов благополучию друг друга.”

Вместе с пандемией также было принято решение ввести в конце марта трехлетнюю политику опционального тестирования SAT / ACT. По словам Дака, половина всех претендентов предпочли не выставлять оценки.

«Наша трехлетняя политика дает нам время, чтобы изучить значение экзаменов для нашего процесса принятия решений и их влияние на нашу способность создавать разнообразный пул кандидатов», — сказал он. «Нам не нужно будет сдавать экзамены SAT или ACT еще как минимум два года, и мы продолжим изучать возможность использования стандартизированного тестирования в нашем процессе.”

В результате Приемная комиссия теперь больше полагается на строгость учебной программы, успеваемость в классе и оценки, идеи, почерпнутые из рекомендательных писем, «и то, что мы можем различить из общего академического участия каждого абитуриента с еще большим намерением, чем раньше, для все кандидаты, независимо от того, выставлены ли оценки », — сказал Дак. «Мы делаем это с учетом соответствующего контекста школьного сообщества, в котором учащиеся учатся, а также их уникальных обстоятельств и возможностей.”

Основные приложения класса 2025 включают:

Заявки от чернокожих, коренных и латиноамериканских студентов не отставали от общего пула или превышали его, сказал Дак, отметив, что заявки от чернокожих студентов за последние три года выросли на 89 процентов.

Число заявителей из числа чернокожих увеличилось на 39 процентов в этом году; Latinx на 42 процента; Американские индейцы / коренные жители Аляски — на 35 процентов; и коренной житель Гавайских островов / островов Тихого океана на 35 процентов.

В Tufts наблюдался значительный рост заявок из всех регионов страны, при этом наибольший рост пришелся на Средний Запад (рост на 46 процентов по сравнению с прошлым годом) и Юго-Запад (рост на 43 процента).

Иностранные студенты, определяемые как иностранные граждане без гражданства США, составляют более 6000 заявлений и составляют более 19 процентов от общего числа заявителей, что на 36 процентов больше, чем в прошлом году. В Южной Америке, Африке и Европе наблюдался значительный рост, в то время как Азия оставалась наиболее представленным регионом.

Заявки от студентов первого поколения росли вместе с резервами абитуриентов и составляют 17 процентов от поступающих на первый курс.

Tufts вступает в партнерские отношения с QuestBridge, национальной некоммерческой организацией, деятельность которой направлена на объединение хорошо успевающих студентов с низким доходом с высоко отборными колледжами и университетами. Количество заявок на QuestBridge в Tufts выросло более чем на 35 процентов, а Tufts был сопоставлен с 20 выдающимися учеными QuestBridge в рамках своей программы Early Decision 1.Ожидается, что больше стипендиатов QuestBridge будут поступать в рамках программы Early Decision 2 и регулярных программ принятия решений.

Представлены все 50 штатов, а также округ Колумбия, Пуэрто-Рико, Гуам и Виргинские острова США. Наиболее представленные штаты по порядку — Массачусетс, Нью-Йорк, Калифорния, Нью-Джерси, Коннектикут, Техас, Флорида, Иллинойс, Пенсильвания и Мэриленд.

Наиболее представленные страны по гражданству, каждая из которых направила более 100 заявителей, — это Китай, Индия, Бразилия, Южная Корея, Турция, Канада, Пакистан, Вьетнам, Казахстан, Бангладеш, Гана, Мексика, Кения и Нигерия.

Tufts предлагает два раунда раннего решения. Заявки на раннее решение выросли на 19 процентов.

Забегая вперед, Дак сказал, что кандидаты на раннее решение 2 получат свои решения в начале февраля. Регулярные уведомления о решениях будут выпускаться в конце марта. Вместо ежегодных Jumbo Days на кампусе в апреле, Tufts проведет виртуальный Jumbo Month для зачисленных студентов.

Лауре Фергюсон можно позвонить по телефону [email protected] .

Условия образования — Дошкольное, начальное и среднее образование — Зачисление в начальную и среднюю школу — Учащиеся с ограниченными возможностями

В 2018–19 годах количество учащихся в возрасте от 3 до 21 года, получивших услуги специального образования в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA) было 7,1 миллиона, или 14 процентов всех учащихся государственных школ. Среди студентов, получающих услуги специального образования, 33 процента имели определенные трудности в обучении.

Принятый в 1975 году Закон об образовании лиц с ограниченными возможностями (IDEA), ранее известный как Закон об образовании для всех детей-инвалидов, требует предоставления бесплатного и соответствующего образования в государственных школах для имеющих на это право учащихся в возрасте от 3 до 21 года. Приемлемые студенты — это студенты, определенные группой профессионалов как имеющие инвалидность, которая отрицательно сказывается на успеваемости, и нуждающиеся в специальном образовании и сопутствующих услугах. Сбор данных для мониторинга соблюдения IDEA начался в 1976 году.

С 2000–01 учебного года по 2004–05 годы количество учащихся в возрасте от 3 до 21 года, получивших услуги специального образования в рамках закона IDEA, увеличилось с 6,3 миллиона, или 13 процентов от общего числа учащихся государственных школ, до 6,7 миллиона, или 14 процентов. общее количество учащихся в государственных школах. ¹ Как количество, так и процент студентов, обучающихся в рамках программы IDEA, снизились с 2004–05 по 2011–2012 годы. В период с 2011–2012 по 2018–19 годы количество обслуживаемых учащихся увеличилось с 6,4 миллиона до 7,1 миллиона, а процентная доля учащихся увеличилась с 13 процентов от общего числа учащихся в государственных школах до 14 процентов от общего числа учащихся в государственных школах.

Рисунок 1. Процентное распределение учащихся в возрасте от 3 до 21 года, обучающихся в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA), по типу инвалидности: 2018–19 учебный год

¹ Другие нарушения здоровья включают ограниченную силу, жизнеспособность или бдительность из-за хронических или острых проблем со здоровьем, таких как сердечное заболевание, туберкулез, ревматическая лихорадка, нефрит, астма, серповидно-клеточная анемия, гемофилия, эпилепсия, отравление свинцом, лейкемия или диабет.
ПРИМЕЧАНИЕ. Данные относятся только к 50 штатам и округу Колумбия. Включает данные за 2015–2016 годы для детей в возрасте от 3 до 21 года в Висконсине из-за отсутствия более свежих данных о детях, обслуживаемых в Висконсине. Нарушения зрения, черепно-мозговые травмы и слепоглухота не показаны, поскольку каждое из них составляет менее 0,5% учащихся, обучающихся в рамках программы IDEA. Поскольку категории не показаны, детализация не составляет 100 процентов. Хотя отображаются округленные числа, цифры основаны на неокругленных данных.
ИСТОЧНИК: Министерство образования США, Управление программ специального образования, база данных Закона об образовании лиц с ограниченными возможностями (IDEA), получено 20 февраля 2020 г., из https://www2.ed.gov/programs/osepidea/618-data/state- файлы данных уровня / index.html # bcc; и Национальный центр статистики образования, Национальная модель прогноза охвата начальным и средним образованием, с 1972 по 2029 год. См. сборник статистики образования за 2019 год , таблица 204.30.

В 2018–19 учебном году больший процент учащихся в возрасте от 3 до 21 года получали услуги специального образования в рамках закона IDEA для лечения конкретных нарушений обучаемости, чем для лиц с любым другим типом инвалидности.Конкретная неспособность к обучению — это нарушение одного или нескольких основных психологических процессов, связанных с пониманием или использованием языка, устного или письменного, которое может проявляться в несовершенной способности слушать, думать, говорить, читать, писать, писать по буквам или делать математические расчеты. В 2018–2019 годах около 33 процентов всех учащихся, получивших услуги специального образования, имели определенные трудности в обучении, 19 процентов имели нарушения речи или языка, а 15 процентов имели другие нарушения здоровья (в том числе ограниченные силы, жизнеспособность или бдительность из-за хронических или хронических заболеваний). острые проблемы со здоровьем, такие как сердечная недостаточность, туберкулез, ревматическая лихорадка, нефрит, астма, серповидно-клеточная анемия, гемофилия, эпилепсия, отравление свинцом, лейкемия или диабет).Учащиеся с аутизмом, задержкой в развитии, умственными недостатками и эмоциональными расстройствами составляли от 5 до 11 процентов учащихся, обучающихся в рамках программы IDEA. Учащиеся с множественными нарушениями здоровья, нарушениями слуха, ортопедическими нарушениями, нарушениями зрения, черепно-мозговой травмой и слепоглухотой составляли по 2 или менее процентов от общего числа учащихся в рамках программы IDEA.

Рис. 2. Процент учащихся в возрасте от 3 до 21 года, получивших образование в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA), по расе / этнической принадлежности: 2018–19 учебный год

ПРИМЕЧАНИЕ: На основе общего числа детей, посещающих дошкольные учреждения в государственных школах. до 12 класса по расе / этнической принадлежности.Хотя данные относятся к 50 штатам и округу Колумбия, ограничения данных приводят к включению небольшого (но неизвестного) числа студентов из других юрисдикций. Включает данные за 2015–2016 годы для детей в возрасте от 3 до 21 года в Висконсине из-за отсутствия более свежих данных о детях, обслуживаемых в Висконсине. Категории расы исключают лиц латиноамериканской национальности. Хотя отображаются округленные числа, цифры основаны на неокругленных данных.
ИСТОЧНИК: Министерство образования США, Управление программ специального образования, база данных Закона об образовании лиц с ограниченными возможностями (IDEA), получено 20 февраля 2020 г. с https: // www2.ed.gov/programs/osepidea/618-data/state-level-data-files/index.html#bcc; и Национальный центр статистики образования, Национальная модель прогноза зачисления в начальные и средние школы, с 1972 по 2029 год. См. дайджест по образованию Статистика 2019 , таблица 204.50.

В 2018–19 учебном году процент (от общего числа зачисленных в государственные школы) учащихся в возрасте от 3 до 21 года, получивших услуги специального образования в рамках закона IDEA, различается в зависимости от расы / этнической принадлежности. Процент студентов, обслуживаемых в рамках закона IDEA, был самым высоким среди студентов из числа американских индейцев / коренных жителей Аляски (18 процентов), затем следовали черные студенты (16 процентов), белые студенты и студенты двух или более рас (по 14 процентов каждая), испаноязычные студенты (13 процентов ), Студенты-выходцы с островов Тихого океана (11 процентов) и студенты из Азии (7 процентов).

Среди латиноамериканцев, американских индейцев / коренных жителей Аляски, жителей островов Тихого океана и белых учащихся в возрасте от 3 до 21 года, процент учащихся, получивших услуги специального образования в 2018-19 годах с определенными ограничениями в обучении, в сочетании с процентом, получившим услуги в области речи или языка обесценения составляли 50 и более процентов студентов, обучающихся в рамках закона IDEA. Среди их сверстников, которые были чернокожими, представителями двух или более рас и азиатами, на долю студентов приходилось от 40 до 50 процентов учащихся, обучающихся по программе IDEA.Процентное распределение различных видов услуг специального образования, получаемых учащимися, различается в зависимости от расы / этнической принадлежности. Например, процент учащихся с ограниченными возможностями, получивших услуги в рамках закона IDEA для конкретных нарушений обучаемости, был ниже для азиатских студентов (19 процентов), студентов двух или более рас (29 процентов) и белых студентов (29 процентов), чем для студентов в целом. (33 процента). Однако процент студентов с ограниченными возможностями, получивших услуги в рамках закона IDEA для лечения аутизма, был выше среди азиатских студентов (25 процентов) и студентов двух или более рас (12 процентов), чем среди студентов в целом (11 процентов).² Кроме того, среди студентов, проходящих обучение в рамках закона IDEA, 7 процентов чернокожих студентов и студентов двух или более рас получали услуги по устранению эмоциональных расстройств. Для сравнения, 5 процентов всех студентов, обучающихся в рамках IDEA, получали услуги по устранению эмоциональных расстройств.

Отдельные данные об услугах специального образования для мужчин и женщин доступны только для учащихся в возрасте 6–21 лет, а не в возрасте 3–21 лет. Среди учащихся в возрасте от 6 до 21 года, зачисленных в государственные школы в 2018-19 годах, более высокий процент учащихся мужского пола (18 процентов), чем учащихся девушек (10 процентов), получали услуги специального образования в рамках закона IDEA.Кроме того, процентное распределение учащихся в возрасте от 6 до 21 года, получивших различные виды услуг специального образования в 2018-19 годах, различается по полу. Например, процент студентов, обслуживаемых в рамках IDEA и получивших услуги для лиц с определенными трудностями в обучении, был выше среди учащихся женского пола (44 процента), чем среди студентов мужского пола (34 процента), в то время как процент обучающихся в рамках IDEA, получивших услуги от аутизма, был выше среди мужчин студентов (13 процентов), чем студенток (5 процентов).

Диаграмма 3. Среди учащихся в возрасте 6–21 лет, обучающихся в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA), процентная доля, проводившая разное количество времени в общих классах: осень 2000 г. — осень 2018 г.

ПРИМЕЧАНИЕ. Данные относятся только к 50 штатам и округу Колумбия. Осенью 2016, 2017 и 2018 годов включены данные за осень 2015 года для детей в возрасте от 6 до 21 года в Висконсине из-за недоступности данных за осень 2016, 2017 и 2018 годов для детей, обслуживаемых в Висконсине.Осень 2017 года также включает данные за осень 2016 года для детей в возрасте от 6 до 21 года в Мэне и Вермонте из-за отсутствия данных за осень 2017 года для детей этой возрастной группы, обслуживаемых в этих штатах.
ИСТОЧНИК: Министерство образования США, Управление программ специального образования, база данных Закона об образовании лиц с ограниченными возможностями (IDEA), получено 20 февраля 2020 г., из https://www2.ed.gov/programs/osepidea/618-data/state- level-data-files / index.html # bcc. См. Сборник статистики образования за 2019 год , таблица 204.60.

Данные об образовательной среде также доступны для учащихся в возрасте 6–21 лет, обучающихся в рамках закона IDEA. Около 95 процентов учащихся в возрасте 6–21 лет, прошедших обучение по программе IDEA осенью 2018 года, были зачислены в обычные школы. Три процента учащихся, обучающихся в рамках IDEA, были зачислены в отдельные школы (государственные или частные) для учащихся с ограниченными возможностями; 1 процент был направлен родителями в обычные частные школы; ³ и менее 1 процента каждый находился дома или в больницах, в отдельных жилых помещениях (государственных или частных) или в исправительных учреждениях.Среди всех учащихся в возрасте от 6 до 21 года, обучающихся в рамках закона IDEA, процентная доля, которые проводят большую часть учебного дня (т. Е. 80 или более процентов своего времени) в общеобразовательных классах обычных школ, увеличилась с 47 процентов осенью 2000 года до 64 процентов осенью 2018 года. . Напротив, за тот же период процент учащихся, которые проводят от 40 до 79 процентов учебного дня в общих классах, снизился с 30 до 18 процентов, а процент учащихся, которые проводят менее 40 процентов своего времени в общих классах. снизился с 20 до 13 процентов.Осенью 2018 года процент учащихся, обучающихся в рамках IDEA, которые большую часть учебного дня проводят в общих классах, был самым высоким среди учащихся с речевыми или языковыми нарушениями (88 процентов). Примерно две трети учащихся с особыми нарушениями обучаемости (72 процента), нарушениями зрения (68 процентов), другими нарушениями здоровья (67 процентов), задержками в развитии (66 процентов) и нарушениями слуха (63 процента) проводили большую часть учебного дня. внутри общих классов. Напротив, 17 процентов учащихся с ограниченными интеллектуальными возможностями и 14 процентов учащихся с множественными нарушениями здоровья проводили большую часть учебного дня в общеобразовательных классах.

Данные также доступны для учащихся в возрасте 14–21 лет, обучающихся в рамках закона IDEA, которые бросили школу в 2017–18 учебном году, включая причину выхода. ⁴ Около 414 000 учащихся в возрасте 14–21 лет, обучавшихся в рамках программы IDEA, закончили школу в 2017–2018 годах: более двух третей (73 процента) закончили школу с обычным дипломом средней школы, 16 процентов бросили учебу, 10 процентов получили альтернативный сертификат, ⁵ 1 процент достигли максимального возраста ⁶ для получения услуг специального образования, и менее половины 1 процента умерли.

Диаграмма 4. Среди учащихся в возрасте 14–21 лет, закончивших школу в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA), процент выбывших по определенным причинам в разбивке по расе / этнической принадлежности: 2017–18 учебный год

¹ Получил аттестат об окончании, модифицированный диплом или другой аналогичный документ, но не соответствовал тем же стандартам для окончания учебы, что и для студентов без инвалидности.
ПРИМЕЧАНИЕ: данные на этом рисунке относятся к 50 штатам, округу Колумбия, Бюро образования индейцев, Американскому Самоа, Федеративным Штатам Микронезии, Гуаму, Северным Марианам, Пуэрто-Рико, Республике Палау, Республике Маршалловы острова и США.Южные Виргинские острова. Данные для всех остальных показателей этого показателя относятся только к 50 штатам и округу Колумбия. Включает условные расчеты для отсутствующих или недоступных данных из Вермонта. Категории расы исключают лиц латиноамериканской национальности. Хотя отображаются округленные числа, цифры основаны на неокругленных данных.
ИСТОЧНИК: Департамент образования США, Управление программ специального образования, Закон об образовании для лиц с ограниченными возможностями (IDEA), раздел 618 Продукты данных: файлы данных государственного уровня.Получено 20 февраля 2020 г. с сайта
http://www2.ed.gov/programs/osepidea/618-data/state-level-data-files/index.html. См. Сборник статистики образования за 2019 год , таблица 219.90.

Среди учащихся в возрасте 14–21 лет, проходивших обучение по программе IDEA, которые бросили школу в 2017–18 учебном году, процентное соотношение, окончивших школу с обычным аттестатом средней школы, получивших альтернативный аттестат и выбывших из школы, различается по расе / этнической принадлежности. Процент выбывающих студентов, окончивших школу с обычным дипломом о среднем образовании, был самым высоким среди азиатских студентов (79 процентов) и самым низким среди чернокожих студентов (66 процентов).Процент выбывающих студентов, получивших альтернативный сертификат, был самым высоким среди чернокожих студентов (12 процентов) и самым низким среди студентов из числа американских индейцев / коренных жителей Аляски (4 процента). Процент выбывающих студентов, бросивших учебу в 2017–2018 годах, был самым высоким среди студентов из числа американских индейцев / коренных жителей Аляски (24 процента) и самым низким среди студентов из Азии (7 процентов).

Среди учащихся в возрасте 14–21 лет, проходивших обучение по программе IDEA, которые бросили школу в 2017–18 учебном году, процентное соотношение, окончившее школу с обычным аттестатом средней школы, получившим альтернативный аттестат и выбывшим из школы, также различается по типу инвалидности.Процент выбывающих студентов, окончивших обучение с обычным дипломом о среднем образовании, был самым высоким среди учащихся с речевыми или языковыми нарушениями (86 процентов) и самым низким среди учащихся с множественными ограниченными возможностями (47 процентов). Процент выбывающих студентов, получивших альтернативный сертификат, был самым высоким среди студентов с ограниченными интеллектуальными возможностями (32 процента) и наименьшим среди студентов с нарушениями речи или языка (3 процента). Процент выбывающих студентов, которые бросили учебу в 2017–2018 годах, был самым высоким среди студентов с эмоциональными расстройствами (32 процента) и самым низким среди слепоглухих (5 процентов).

¹ Итоги, представленные в этом индикаторе, включают условные расчеты для состояний, по которым данные были недоступны. См. Справочные таблицы в сборнике статистики образования для получения дополнительной информации. Данные для учащихся в возрасте 3–21 и 6–21 лет, обучающихся в рамках закона IDEA, относятся только к 50 штатам и округу Колумбия. Количество детей, обслуживаемых в процентах от общего числа зачисленных, основано на общем количестве детей, посещающих дошкольные учреждения до 12 класса в государственных школах.
² В 2018–2019 годах необоснованный процент белых учащихся с ограниченными возможностями, получавших услуги по программе IDEA для лечения аутизма, также был выше. чем процент учащихся в целом, но оба округлены до 11 процентов.
³ Учащиеся, зачисленные их родителями или опекунами в обычные частные школы и получающие базовое образование за счет частных ресурсов, но получающие услуги специального образования за счет государства.
⁴ Данные по учащимся в возрасте 14–21 лет, закончившим школу в рамках закона IDEA, относятся к 50 штатам, округу Колумбия, Бюро образования индейцев, Американскому Самоа, Федеративным Штатам Микронезии, Гуаму, Северным Марианам, Пуэрто Рико, Республика Палау, Республика Маршалловы Острова и США.Южные Виргинские острова.
⁵ Получил аттестат об окончании, модифицированный диплом или другой аналогичный документ, но не отвечал тем же стандартам для окончания учебы, что и для студентов без инвалидности.

⁶ Каждый штат определяет максимальный возраст для получения услуг специального образования. На момент сбора этих данных максимальный возраст в штатах обычно составлял от 20 до 22 лет.

Глоссарий

Источник данных

PDF

Загрузите / просмотрите PDF-файл, содержащий этот показатель и соответствующие цифры.(98 КБ)

Справочные таблицы

Таблица 204.30 (сборник за 2019 г.): Дети от 3 до 21 года, обучающиеся в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA), часть B, по типу инвалидности: отдельные годы, 1976-77 гг. до 2018-19 годов
Таблица 204.50 (сборник за 2019 год): Дети от 3 до 21 года, обучающиеся в соответствии с Законом об образовании лиц с ограниченными возможностями (IDEA), Часть B, по возрастным группам и полу, расе / этнической принадлежности и типу инвалидности: 2018- 19
Таблица 204.60 (сборник за 2019 г.): Процентное распределение учащихся в возрасте от 6 до 21 года, получивших образование в соответствии с Законом об образовании для лиц с ограниченными возможностями (IDEA), часть B, по образовательной среде и типу инвалидности: отдельные годы, осень 1989 — осень 2018
Таблица 219.

в классе 35 учеников.Из них :20 школьников занимаются в математическом кружке,11-в

Развитие логического мышления среднего звена

Решение задач с помощью кругов Эйлера

Решение задач с помощью кругов Эйлера

1 использованием формул комбинаторики _Дидактический материал

Презентация — Круги Эйлера

Помощь с практическим заданием по математике и информатике, ЭИОС (edu.pglu.ru)

«Если бы я мог, но бюджет ограничен». Шерзод Шерматов — об изменениях в системе образования – Газета.uz

В тесте по математике, сданном 35 учениками, средний балл 9 класс по математике CBSE

В классе из 35 учеников 20 мальчиков и 15 девочек. Студент выбирается случайным образом. Найдите вероятность того, что выбранный ученик (i) мальчик (ii) девочка.

Япония сократит количество учеников в начальной школе до 35 к 2025 году

ФОТОГАЛЕРЕЯ (НАЖМИТЕ ДЛЯ УВЕЛИЧЕНИЯ)

процентиль

Что такое ранг в классе? Что такое хороший ранг?

Что такое ранг в классе?

Как разные школы измеряют рейтинг в классе?

Почему важен классный ранг?

# 1: Заявки в колледж

# 2: Стипендии

# 3: Высшая школа с отличием

Почему некоторые школы больше не используют классный рейтинг?

Как найти свой класс Рейтинг

Как определить, в каком процентиле вы находитесь

Что делать, если в вашей школе нет ранга в классе?

Что такое хороший класс?

Резюме: что нужно знать о ранге в классе

Что дальше?

Количество поступающих на бакалавриат Tufts выросло на 35 процентов

Условия образования — Дошкольное, начальное и среднее образование — Зачисление в начальную и среднюю школу — Учащиеся с ограниченными возможностями

Глоссарий

Источник данных

PDF

Справочные таблицы

Добавить комментарий Отменить ответ