| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. | |
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа.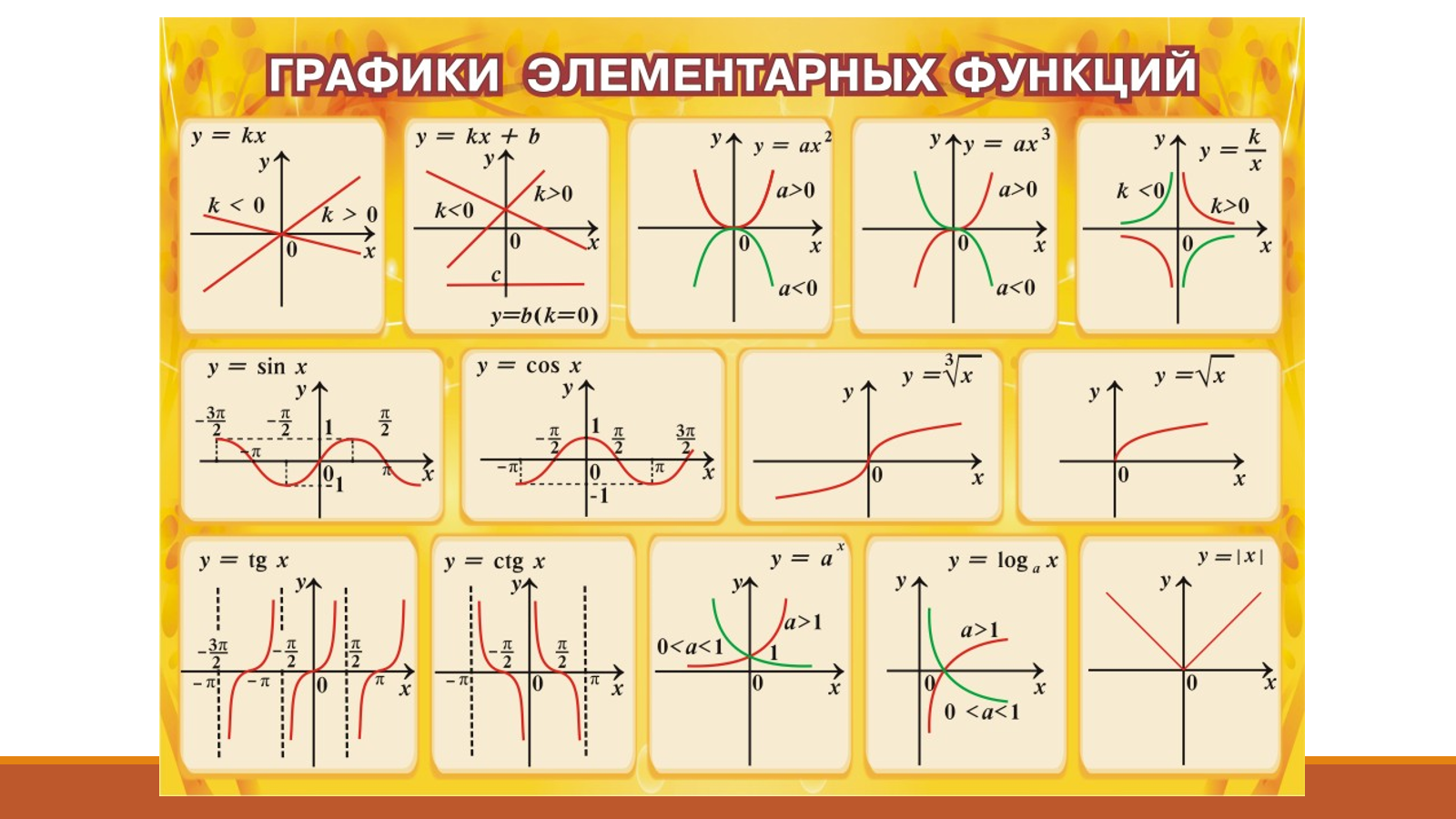 Здесь k = 0.5, b = -1. Здесь k = 0.5, b = -1. | |
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — корень квадратный | y = x1/2 | График функции y = √x | Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590… | |
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). Здесь пример для y = 2x (a = 2 > 1). | |
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. | |
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). | |
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1). | |
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
Функции и графики — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Координаты и базовые понятия о функциях
К оглавлению…
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.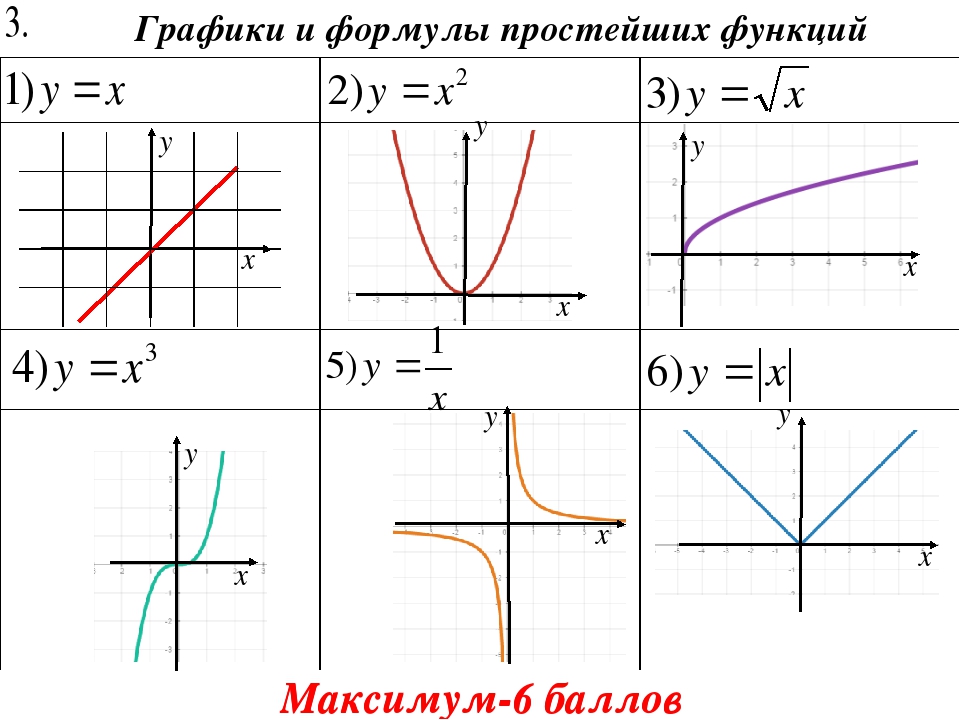
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны.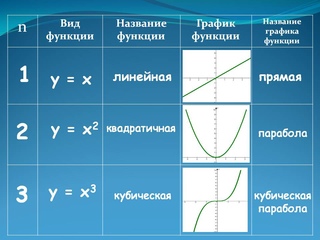 График нечётной функции всегда симметричен относительно начала координат.
График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
К оглавлению…
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):
График квадратичной функции (Парабола)
К оглавлению. ..
..
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x0; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Графики других функций
К оглавлению…
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает.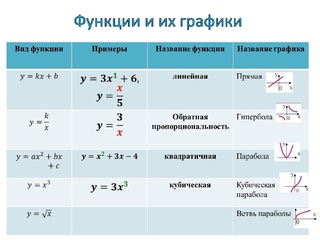 Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x| выглядит следующим образом:
Графики периодических (тригонометрических) функций
К оглавлению…
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:
Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:
График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке.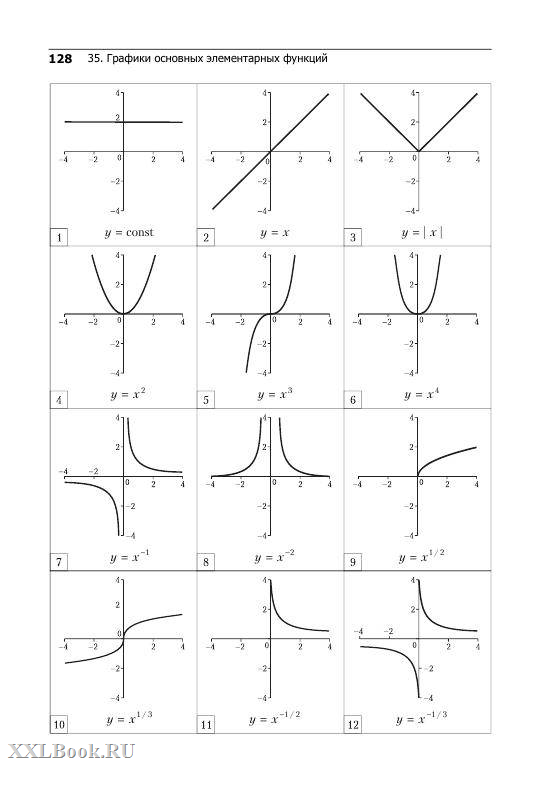 Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. | |
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1. | |
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — корень квадратный | y = x1/2 | График функции y = √x | Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590. .. .. | |
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). | |
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. | |
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). | |
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1). | |
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
Виды графиков | Бета Финанс
Виды графиков
Технический анализ основан на анализе графиков, поэтому наше знакомство с трейдингом и начнем с рассмотрения видов графиков.
Прошло то время, когда котировки записывались вручную в виде цифр на больших досках. Лишь самые «продвинутые» спекулянты чертили по этим котировкам графики и анализировали их. Сейчас все котировки автоматически обрабатываются компьютером и выводятся на монитор в виде готовых графиков цен. Существуют различные виды графиков. Рассмотрим три наиболее популярных вида.
Лишь самые «продвинутые» спекулянты чертили по этим котировкам графики и анализировали их. Сейчас все котировки автоматически обрабатываются компьютером и выводятся на монитор в виде готовых графиков цен. Существуют различные виды графиков. Рассмотрим три наиболее популярных вида.
Первый способ построения графика, наиболее понятный и простой — линейный график. Он строится следующим образом: берутся, например, цены последних сделок каждого часа, наносятся соответствующие ценам и времени точки на график и соединяются линией. В результате получаем линейный график с интервалом в один час.
Можно выбрать любой интервал времени — 1 минута, 10, 15, 30 минут, 1 час, 1 день, месяц, год, а также строить график можно по ценам открытия, наибольших, либо наименьших ценах за интервал.
Рис.1. Линейный график.
Линейный график
Однако, у такого графика, несмотря на его простоту, есть один крупный недостаток: линейный график не раскрывает всю информацию о поведении цены.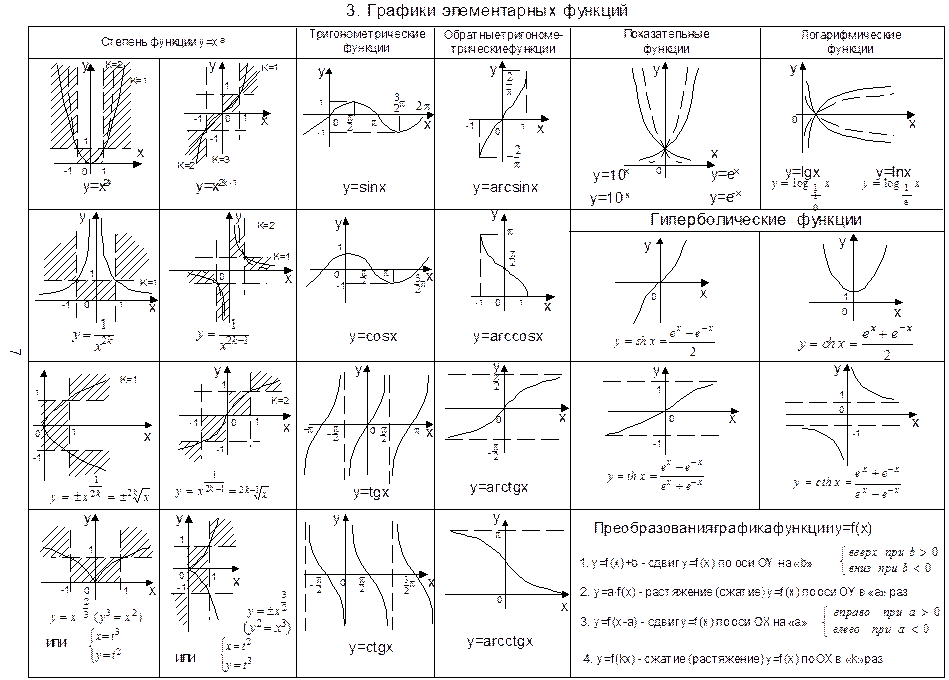 Наибольшая и наименьшая цены периода остаются скрытыми от глаз трейдера.
Наибольшая и наименьшая цены периода остаются скрытыми от глаз трейдера.
Для решения этой проблемы был изобретен другой способ отображения котировок — бары. Бар отражает 4 вида цены — цена открытия (open), наивысшая цена (high), наименьшая цена (low), цена закрытия (close). Иногда цена открытия не отражается на баре, т.к. она часто совпадает с ценой закрытия предыдущего бара.
Рис. 2. Бар.
Бар
Как можно видеть, бары намного информативнее линейного графика. Но визуальное восприятие баров довольно низкое. Обычно вместо баров используют другой вид графиков — японские свечи. Они, также, как и бары показывают 4 вида цены, но отображены они по-другому. Расстояние между открытием и закрытием называется «тело свечи», а хвостики над и под телом свечи — «фитиль». Тело свечи может быть полым (белая (или зеленая) свеча — показывает рост) или заполненным (черная (или красная) свеча — показывает падение). Цена открытия белой свечи ниже цены ее закрытия, у черной свечи, соответственно, наоборот.
Рис.3. Японские свечи.
Японские свечи
Основная масса трейдеров использует приведенные выше 3 вида графиков. Однако, существуют и специфические способы отображения цены, такие как тиковый график, крестики-нолики и пр. Начинать свою карьеру трейдера лучше с японских свечей — они просты для понимания, а также, Вы сможете в дальнейшем строить свою торговлю на сигналах, подаваемых их комбинациями.
Далее: Виды трендов
Виды графиков в техническом анализе с примерами (фото)
Технический анализ в бинарных опционах подразумевает под собой то, что трейдер будет изучать и исследовать ценовые графики. Соответственно, вид графика не один, ведь каждый человек стремится к тому, что ему было комфортно отслеживать изменения котировок нужных активов.
На сегодняшний день есть много видов отображения ценовой линии, но есть три главных вида графиков:
- Линейный;
- Бары;
- Свечи.
Ниже будет разъяснение по каждому из этих графиков, а уже дальше вы сами решите, с каким из них работать. К слову, вы можете протестировать каждый из них здесь же, на странице с живыми графиками.
К слову, вы можете протестировать каждый из них здесь же, на странице с живыми графиками.
Любой график разбит на определенные временные отрезки (таймфреймы), между которыми можно переключаться. Выглядят они следующим образом:
- М1 – 1 минута;
- М5 – 5 минут;
- М15 – 15 минут;
- М30 – 30 минут;
- Н1 – 1 час;
- Н4 – 4 часа;
- D – 1 день;
- W – 1 неделя;
- MN – 1 месяц.
Каждый период означает часть линии графика, например, на свечном графике с таймфреймом М1 — каждая свеча будет равняться одной минуте.
Новейшие платформы могут давать доступ и к другим таймфреймам, к примеру, 2 минуты либо 12 часов. Также там используются следующие виды графиков:
- Каджи;
- Пустые свечи;
- Крестики-нолики;
- Хейкен Аши.
Однако, это довольно частные виды графиков, которые широкого распространения не получили. В целом же любой рынок мира базируется на трех основных графиках, где таймфрейм, например, М5, обозначает, что каждая свеча или бар формируется на экране за 5 минут.
Линейные графики
Линейный график можно назвать самым простым видом, к тому же, он считается основным. Отображается его история посредством линии, которую формирует изменение цены. На графике показывается цена закрытия каждого интервала. Такой вид идеально подходят для краткосрочных сделок на бинарных опционах.
Бары
График с барами уже несколько сложнее линейного, потому как дает больше информации для трейдера. Если в предыдущем отображалась только цена закрытия, то здесь бары показывают также цену открытия. Кроме того, на графике видны точки максимума и минимума, которые еще называют верхними и нижними экстремумами.
- High, H (Хай, точка на самом верху бара) – место, до которого цена может вырасти, называется максимумом.
- Low, L (Лоу, точка внизу бара) – место, до которого цена может опуститься, называется точкой минимума.
- Open, O (штрих слева от бара) – цена, по которой бар открылся.
- Close, C (штрих справа от бара) – цена, на которой бар закрылся.
Японские свечи
График японских свечей по праву считается самым продвинутым и популярным во всем мире. Более того, он наиболее информативен из всех.
Свечи показывают то же самое, что и бары, однако дополняют эту информацию еще и данными о направлении рынка, то есть, о том, какой сейчас тренд. Цвет свечи показывает, какие сейчас на рынке настроения: бычьи или медвежьи. Так, на бычьем рынке свечи либо зеленые, либо белые, а на медвежьем – красные либо черные.
К слову, график с барами тоже может иметь различные цветовые вариации, как и свечной. Однако, в таком случае его уже трудно назвать классическим. Сделано это больше для удобства, потому как в тех же США трейдеры предпочитают пользоваться барами вместо свечей.
Полезные ссылки:
На основе вышеприведенных графиков было придумано огромное количество стратегий, часть из которых желательно применять на каком-либо определенном типе графика. К примеру, стратегия Голова и плечи используется со всеми видами графиков, а стратегия Доджи — только со свечными. Но, как показывает практика, трейдеру стоит испробовать все виды графиков, чтобы подобрать вариант под себя и свою торговую систему.
Но, как показывает практика, трейдеру стоит испробовать все виды графиков, чтобы подобрать вариант под себя и свою торговую систему.
Урок 48. функции. свойства функций и их графики. исследование функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
- функция, аргумент функции, значение функции
- график функции, преобразование графика функции
- свойства функции, исследование свойств функции
Глоссарий по теме урока
Определение
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
у — зависимая переменная, значение функции
Определение
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Определение
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Определение
Функция у = f(х) называется четной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
- для любого х из области определения выполняется равенство f(-х)=f(х).
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=-f(х).
Определение
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Определение
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1<х2, выполняется неравенство у1<у2.
Функция у=f(x) убывает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких что, х1<х2, выполняется неравенство у1>у2.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Дополнительная литература:
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
https://mathb-ege.sdamgia.ru/test?theme=177
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
- Множество значений функции
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
- Четность / нечетность функции
D(y)= — симметрична относительно нуля
,
следовательно, функция четная и ее график симметричен относительно оси ОУ
- Нули функции
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
- Промежутки знакопостоянства
у>0 при
у<0 при
- Монотонность
Найдем производную
Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.
Определим знаки производной в полученных промежутках.
точки -1, 1 – выколоты, 0 — закрашена
Производная положительна, а значит, функция возрастает при .
Производная отрицательна, а значит, функция убывает при
- Экстремум
х=0 – стационарная точка.
В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.
Значение функции в точке максимума
- Дополнительные точки
у(0,5)= у(-0,5)=-5/3; у(2)=у(-2)=5/3; у(3)= у(-3)=5/4
- Отразим найденные свойства графически, построим график функции
2. Решение задачи на оптимизацию
Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.
В решении таких задач выделяют 3 основных этапа:
1 этап. «Перевод» задачи на язык функций:
- вводят независимую переменную х
- выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
- выражают у через х и другие известные величины
- устанавливают по условию задачи границы изменения переменной х
2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.
Рассмотрим план решения на примере задачи.
Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
Решение:
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x2 у. е.
е.
Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x)2 (у.е.)
Всем рабочим нужно заплатить 4x2+(24 — x)2 = 5x2 -48x+576 (у.е.)
Причем 0≤ x ≤ 24, x ϵ N.
2 этап.
Рассмотрим функцию f(x)=5x2-48x+576.
Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x0 = 4,8 .
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
Функции |
у=0 |
у=sin(x+5π/2) |
у=lg(x+10) |
Решение:
- у=0
область определения – множество действительных чисел – симметрична относительно нуля
у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.
Данная функция одновременно четна и нечетна.
- у=sin(x+5π/2)
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
- у=lg(x+10)
логарифмируемое выражение должно быть положительным
x+10>0; x>-10
D(y): x>-10
Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.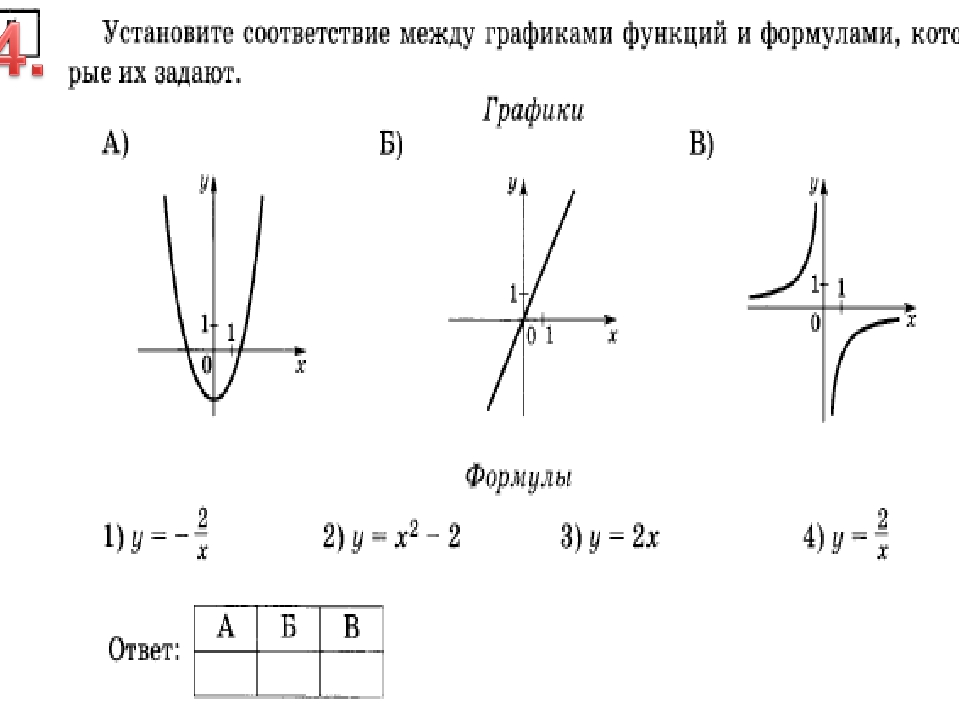
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
Зайдем с другого конца, выразим -f(x):
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
Ответ:
Функции | Четность / нечетность |
у=0 | и четная, и нечетная |
у=sin(x+5π/2) | четная |
у=lg(x+10) | общего вида |
нечетная |
2.
Решение:
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.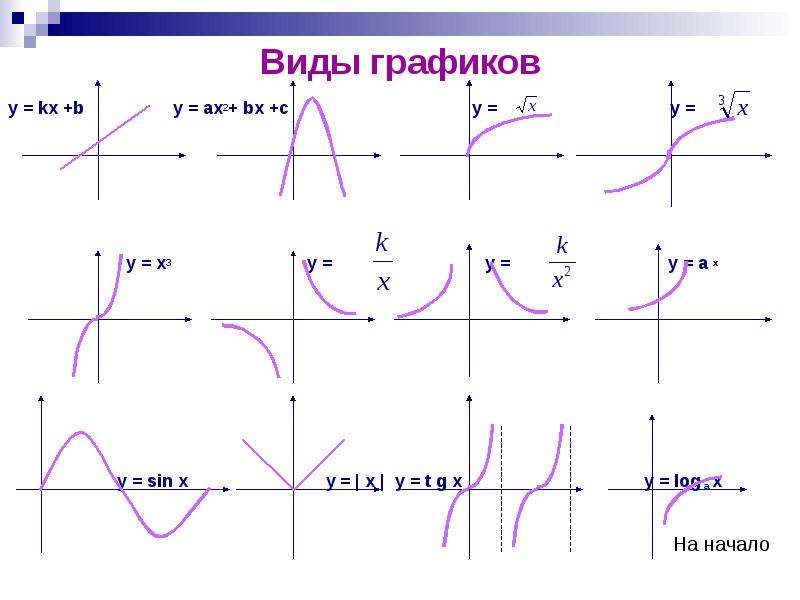
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у<7
Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:
Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.
Выполним построения выделенных функций.
Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.
Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.
Ответ:
Линейная функция. Виды, свойства, графики.
7 класс.
ГЛАВА 2. Функции.
§ 6. Линейная функция.
Линейная функция.
Количество функций неограничено. Однако, существуют функции, которые можно объединить в группы. Они имеют общую формулу, схожие свойства, графиком таких функций является одна и та же кривая. Прежде чем начать рассматривать одну из таких групп функций, введём несколько новых понятий.
Функция называется возрастающей, если большему значению х соответствует большее значение у (т.е. при увеличении х увеличивается у).
Функция называется убывающей, если большему значению х соответствует меньшее значение у (т.е. при увеличении х уменьшается у).
Рассмотрим это на графике.
Фраза «при увеличении х…» означает, что мы рассматриваем график слева направо (также, как пишем и читаем). Если при этом график опускается вниз, то он убывает, если график поднимается вверх, то он возрастает.
На данном рисунке график убывает, если и ; а возрастает, если и .
Это можно записать так:
функция убывает при ;
функция возрастает при .
Теперь введём понятие линейной функции.
Линейной функцией называется функция, вида , где и – некоторые числа.
Например, .
Графиком любой линейной функции является прямая.
В зависимости от значений и , линейная функция разделяется на три вида. Рассмотрим каждый из них.
1. Если , то функция приобретает вид y = b. Такую функцию называют постоянной. Её графиком является прямая, параллельная оси Ox, проходящая через точку (0; b).
Область определения —
Область значений —
Функция является постоянной, поэтому промежутков возрастания и убывания у неё нет
Например, – постоянная функция, графиком является прямая, параллельная оси Ох, проходящая через точку .
Промежутков возрастания и убывания нет.
2. Если , то функция приобретает вид y = kx. Такую функцию называют прямой пропорциональностью. Её графиком является прямая, проходящая через начало координат и точку с произвольно выбранным значением аргумента Если , то прямая составляет с положительным направлением оси Ox острый угол. Если , то прямая составляет с положительным направлением оси Ox тупой угол. Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.
Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.
Область определения —
Область значений —
Если , то функция возрастает при
Если , то функция убывает при .
Например, а) – прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку , и составляющая с положительным направлением оси Ох острый угол, т.к. .
Функция возрастает при .
б) – прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку , и составляющая с положительным направлением оси Ох тупой угол, т.к. .
Функция убывает при .
3. Если , то функция не меняет свой вид . Это линейная функция. Её графиком является прямая, проходящая через точку и точку с произвольно выбранным значением аргумента . Коэффициент играет здесь такую же роль, как и в прямой пропорциональности.
Область определения —
Область значений —
Если , то функция возрастает при
Если , то функция убывает при .
Например, а) – линейная функция, графиком является прямая, проходящая через точки и , и составляющая с положительным направлением оси Ох острый угол, т.к. .
Функция возрастает при .
б) – линейная функция, графиком является прямая, проходящая через точки и , и составляющая с положительным направлением оси Ох тупой угол, т. к. .
к. .
Функция убывает при .
Рассмотрим теперь взаимное расположение графиков линейных функций.
Пусть даны две линейные функции и .
Если , то графики данных функций совпадают.
Если , то графики функций параллельны.
Если , то графики функций пересекаются в точке (или в точке , что то же самое).
Если , то графики пересекаются. Для нахождения координат точки пересечения необходимо решить уравнение: и найденное значение аргумента (х) подставить в любую из двух формул, посчитать полученное числовое выражение. Это и есть ордината точки пересечения графиков.
Например,
и .
 Так как у этих функций коэффициенты равны, то их графики параллельны.
Так как у этих функций коэффициенты равны, то их графики параллельны.
и . Так как у этих функций коэффициенты k разные, а значения одинаковые и равны 1, то графики этих функций пересекаются в точке .
и . У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):
Подставляем найденное значение аргумента в любую из двух функций:
Значит, точка пересечения графиков данных функций .
В завершение конкретизируем значение коэффициента k и числа b в формуле линейной функции:
коэффициент k показывает угол наклона прямой к положительному направлению оси Ох.
 Если , этот угол острый; если , то этот угол тупой;
Если , этот угол острый; если , то этот угол тупой;число b определяет точку пересечения прямой с осью Оу. — точка пересечения.
Из данных функций выбрать линейные:
Назовите коэффициенты k и b линейной функции :
Для функции представлена таблица:
Найдите коэффициент k и заполните таблицу.
Определите вид функции, постройте её график. Найдите область определения и область значений функции, найдите промежутки возрастания и убывания функции.
Не выполняя построения, определить угол наклона прямой к положительному направлению оси Ох и точку пересечения с осью Оу:
Функции заданы формулами . Укажите те из них, графиком которых является прямая, проходящая через начало координат, и постройте эти графики.
Функция задана формулой . Определите:
значение функции, если значение аргумента равно ;
значение аргумента, при котором значение функции равно ;
возрастающей или убывающей является данная функция?
Постройте график функции . Пользуясь графиком, найдите:
значение функции, если значение аргумента равно
значение аргумента, при котором значение функции равно
значения аргумента, при которых функция принимает положительные значения;
промежутки возрастания (или убывания) функции.
Не выполняя построения графика функции , укажите, через какие точки проходит этот график: .
Задайте формулой прямую пропорциональность, если известно, что её график проходит через точку .
Постройте в одной системе координат графики функций и укажите координаты их точки пересечения:
и ;
и .
Не выполняя построения графиков функций ; , определите:
чему равен угловой коэффициент каждой функции;
каково взаимное расположение графиков данных функций;
каковы координаты точек пересечения графиков функций с осями координат.
Не выполняя построения графиков функций , определите:
в какой точке каждый график пересекает ось у; ось х;
чему равен угловой коэффициент каждой функции;
каково взаимное расположение графиков данных функций.
Постройте в одной системе координат графики функций и запишите их область определения и область значений: .
Не выполняя построения, найдите координаты точек пересечения с осями координат графиков функций:
Не выполняя построения графика функции , найдите точку этого графика, у которой:
абсцисса равна ординате;
абсцисса и ордината – противоположные числа.
Найдите , если известно, что график функции проходит через точку .
Найдите , если известно, что график функции проходит через точку .
График функции пересекает оси координат в точках . Найдите значения и .
Все точки графика функции имеют одинаковую ординату, равную . Найдите значения и .
График функции параллелен оси абсцисс и проходит через точку . Найдите значения и .
Постройте графики функций:
Не выполняя построения, найдите точки пересечения графиков функций:
и
и .
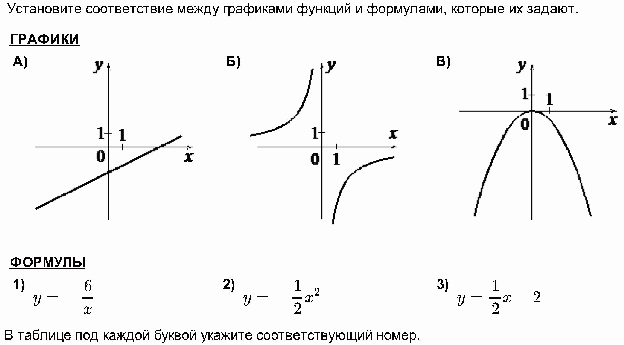
Задайте формулой линейную функцию, график которой изображён на рисунке.
Постройте график функции:
Пересекаются ли графики функций:
и ;
и ?
В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением.
Запишите формулу функции, график которой параллелен графику функции и проходит через точку .
Найдите координаты точки пересечения графиков функций
и
При каком значении параметра а графики функций и
параллельны? Постройте графики этих функций.
При каком значении параметра а графики функций и
параллельны? Постройте графики этих функций.
Постройте прямые, координаты точек которых удовлетворяют уравнению .
Постройте прямые, координаты точек которых удовлетворяют уравнению .
При каком значении k графики линейных функций и имеют более одной общей точки?
Найдите наибольшее и наименьшее значение линейной функции на промежутке .
4
44 типа графиков и диаграмм [и как выбрать лучший]
Популярные типы графиков включают линейные, гистограммы, круговые диаграммы, диаграммы разброса и гистограммы. Графики — отличный способ визуализировать данные и отображать статистику. Например, гистограмма или диаграмма используются для отображения независимых друг от друга числовых данных.
Включение визуализации данных в ваши проекты имеет важное значение при работе со статистикой чисел. Независимо от того, что вы создаете, визуальные эффекты для представления ваших данных могут очень помочь вашей аудитории понять вашу точку зрения.
Но как узнать, какие типы графиков и диаграмм будут лучшими вариантами для вашей отрасли и вашей информации?
Если вы пытаетесь визуализировать рост в отчете о продажах, демонстрировать демографические данные в виде презентации, делиться отраслевой статистикой в инфографике или что-то еще, вам понадобится простой способ продемонстрировать этот контент.
Поскольку мы понимаем, насколько сложно определить, какая именно диаграмма или график лучше всего подходит для визуализации ваших данных, мы составили список из 44 типов графиков, многие из которых могут быть созданы прямо в Visme, чтобы помочь вам. .
Найдите свою отрасль, ознакомьтесь с доступными вам вариантами графиков, затем нажмите кнопку под каждым шаблоном, чтобы начать ввод данных и настройку дизайна для вашего проекта.
44 Типы графиков и диаграмм
Маркетинг
Линейные графики
Линейные диаграммы или линейные графики — это мощные визуальные инструменты, которые иллюстрируют тенденции данных за период времени или конкретную корреляцию. Например, одна ось графика может представлять значение переменной, а другая ось часто отображает временную шкалу.
Каждое значение отображается на диаграмме, затем точки соединяются для отображения тенденции за сравниваемый промежуток времени. Несколько трендов можно сравнить, построив линии разного цвета.
Например, интерес к цифровому маркетингу с течением времени можно легко визуально показать с помощью линейного графика. Просто нанесите каждое количество поисков на временную шкалу, чтобы увидеть тенденцию.
Гистограммы
Самый простой и понятный способ сравнения различных категорий — это классическая гистограмма.Общепризнанный график представляет собой серию полосок разной длины.
На одной оси гистограммы показаны сравниваемые категории, а на другой — значение каждой из них. Длина каждой полосы пропорциональна числовому значению или проценту, которое она представляет.
Например, 4 доллара могут быть представлены прямоугольной полосой длиной четыре единицы, а 5 долларов — полосой длиной пять единиц. Одним беглым взглядом зрители узнают, насколько разные предметы соотносятся друг с другом.
Гистограммы
отлично подходят для визуального представления практически любых типов данных, но они обладают особой силой в маркетинговой индустрии. Графики идеально подходят для сравнения любых числовых значений, включая размеры групп, инвентаризацию, рейтинги и ответы на опросы.
Круговая диаграмма
Круговые диаграммы — это самый простой и эффективный визуальный инструмент для сравнения частей целого. Например, круговая диаграмма позволяет быстро и эффективно сравнивать различные бюджетные ассигнования, сегменты населения или ответы на вопросы маркетинговых исследований.
Разработчики маркетингового контента часто используют круговые диаграммы для сравнения размеров рыночных сегментов. Например, простая круговая диаграмма может четко проиллюстрировать сравнение самых популярных производителей мобильных телефонов по размеру их пользовательской базы.
Аудитория может быстро понять, что стоковая фотография — это наиболее часто используемый визуальный элемент в маркетинге, с оригинальной графикой, такой как та, которую можно создать с помощью Visme, которая занимает второе место.
Мозаика или карты Мекко
Базовые линейные, гистограммы и круговые диаграммы — отличные инструменты для сравнения одной или двух переменных в нескольких категориях, но что происходит, когда вам нужно сравнить несколько переменных или несколько категорий одновременно?
Что, если все эти переменные не являются числовыми? Мозаичный график или график Mekko может быть лучшим выбором.
Возможно, рыночный аналитик, например, хочет сравнить не только размер различных рынков мобильных телефонов. Что, если вместо этого ему или ей нужно сравнить размер пользовательских баз, а также возрастные группы внутри каждой группы?
Мозаичная диаграмма позволит указанному маркетологу четко и прямо проиллюстрировать все переменные.
В приведенном выше примере одна ось диаграммы представляет сравниваемые категории — производителей мобильных телефонов, а другая ось — различные возрастные диапазоны.
Размер и цвет каждого поперечного сечения диаграммы соответствуют сегменту рынка, который он представляет, как показано в легенде диаграммы.
Пирамиды населения
Сегменты рынка часто делятся по возрасту и полу, и пирамида населения является идеальным визуальным представлением этих двух групп.
График обычно принимает форму пирамиды, когда население является здоровым и растет — самые большие группы — самые молодые, и каждый пол уменьшается примерно в равной степени по мере старения населения, оставляя самые маленькие группы в верхней части графика.
Пирамида численности населения, отклоняющаяся от своей классической формы, может указывать на неравномерность численности населения в течение определенного периода, например голод или экономический бум, который привел к увеличению смертности или рождений.
Конечно, пирамиды численности населения не всегда используются для сравнения популяций по возрасту и поэтому не всегда принимают форму тезки на графике.
Маркетолог, например, может использовать этот план для сравнения населения по доходу, весу или IQ, в котором самые маленькие группы часто находятся как наверху, так и внизу.Тем не менее, график четко отображает демографические тенденции и сравнивает размеры двух связанных групп.
Паук-карты
Когда статистику необходимо визуально сравнить три или более количественных переменных, он или она может использовать радарную карту, также известную как паук или звездная карта.
Диаграмма обычно состоит из серии радиусов, каждый из которых представляет отдельную категорию, которые расходятся от центральной точки, как спицы.
Длина каждой «спицы» пропорциональна сравниваемому значению.Для каждой категории спицы затем соединяются линией определенного рисунка или цвета, образуя звездообразную форму с точками, равными количеству категорий.
Результатом является графическое представление, которое позволяет одновременно выявлять тенденции и сравнивать категории.
Бизнес и финансы
графики акций
Источник изображения
Один из самых важных финансовых графиков, графики акций помогают инвесторам отслеживать рынки, определять прибыли и убытки, а также принимать решения о покупке и продаже.
Несмотря на то, что для представления рыночных изменений используются самые разные графики, наиболее распространенной, вероятно, является гистограмма с повернутой основной линейной диаграммой.
Линии просто отслеживают изменения в стоимости конкретной акции или общей рыночной стоимости за определенный период времени. Можно отслеживать и сравнивать несколько акций одновременно, преобразовывая линейный график в диаграмму с накоплением областей или просто используя несколько линий разного цвета.
Блок-схемы
Часто в бизнесе — как и в других отраслях — процесс необходимо представить в виде диаграммы.Блок-схема позволяет упорядочить процесс шаг за шагом, от начала до конца, с целью его анализа, проектирования, документирования или управления.
Эти блок-схемы могут даже иметь несколько начал и концов, с бесчисленными путями и путями между ними.
Хотя простая блок-схема, безусловно, может документировать базовый процесс от A до B и C, диаграммы чаще используются для иллюстрации более сложных последовательностей с множеством решений или условий на этом пути.
Каждый раз, когда выполняется условие, на диаграмме отображаются различные варианты, затем путь продолжается после каждого выбора.
Диаграммы Ганта
Диаграммы Ганта — это особые типы гистограмм, используемые для создания диаграмм проектов и расписаний. Использование цветных полос разной длины отражает не только даты начала и окончания проекта, но также важные события, задачи, вехи и их временные рамки.
Современные диаграммы Ганта также могут иллюстрировать отношения зависимости действий.
Если выполнение командой 3 задачи C, например, зависит от предшествующего завершения задачи B командой 2, диаграмма может отражать не только эту взаимосвязь, но и запланированные даты и крайние сроки для каждой из них.
Контрольные карты
Также широко известная как диаграмма поведения процесса, контрольная диаграмма помогает определить, попадает ли набор данных в средний или заранее определенный диапазон управления.
Часто используется в процессах контроля качества, типичная контрольная диаграмма состоит из точек, нанесенных на две оси, представляющих измерения образцов.
Вычисляется среднее значение каждой точки, а центральная линия на графике соответствует среднему значению. Затем для каждого образца рассчитывается стандартное отклонение от среднего.
Наконец, определены и нанесены на диаграммы верхний и нижний контрольные пределы, чтобы отразить точки, в которых отклонение превышает ожидаемый стандарт.
Карты водопадов
Особенно полезные при бухгалтерском учете и качественном анализе, водопадные диаграммы показывают, как на исходное значение положительно и отрицательно влияют различные факторы.
Например, каскадная диаграмма может четко и эффективно показать, как начальный баланс меняется месяц за месяцем в течение года.
Поскольку они часто выглядят так, как будто столбики плавают по всему графику, водопадные диаграммы иногда называют плавающими кубиками или диаграммами Марио.
Диаграммы иерархии
По внешнему виду похожая на блок-схему, иерархическая диаграмма, также известная как организационная диаграмма или органиграмма, иллюстрирует структуру организации, а также взаимосвязи внутри нее.
Типичная органиграмма компании, например, перечисляет генеральный директор наверху, за которым следуют президенты, вице-президенты, менеджеры и так далее.
Организационная диаграмма может проиллюстрировать цепочку подчинения от любого сотрудника до самого верха. Диаграммы иерархии аналогичным образом используются для представления родословных, научных классификаций, демографии и любых наборов данных с аналогичной разбивкой.
Возьмите приведенную выше диаграмму в качестве примера, где команда проекта организована в виде диаграммы организационной иерархии, чтобы каждый знал, кто их руководитель в проекте.
Техника и технологии
Точечные диаграммы
Диаграмма, также известная как диаграмма рассеяния, состоит из двух осей, каждая из которых представляет набор данных. Например, одна ось может отображать количество миль, пройденных транспортным средством, а вторая ось отображает общее количество использованных галлонов бензина.
Для каждого отобранного транспортного средства его среднее количество миль на галлон представлено точкой, нанесенной на график. После того, как нанесено несколько точек, можно выявить тенденции и сравнить образцы в зависимости от того, сколько цветов представлено на диаграмме.
Участки с решеткой
Иногда статистику необходимо сравнить больше наборов данных, чем может быть представлено одним графиком. Что, если, например, на графике необходимо сравнить не только пройденные мили и использованные галлоны, но также количество шестерен и цилиндров, содержащихся в каждом образце транспортного средства?
Решетчатый график, также называемый решетчатым графиком или графиком, может отображать и сравнивать все эти переменные. В то время как в приведенном выше примере используется серия диаграмм рассеяния, решетчатые диаграммы также обычно содержат серии столбчатых или линейных диаграмм.
Графики функций
Математикам, инженерам и статистикам часто требуется определить значение уравнения, построив график его результата. График функции — это набор всех точек, координаты которых удовлетворяют уравнению.
Следовательно, функция уравнения с переменными x и y будет нарисована на графике с осью x и y . Точно так же уравнение, которое также включает переменную z , необходимо будет нарисовать на трехмерном графике с третьей осью.
Функциональные графы общих форм визуально связаны с соответствующими алгебраическими формулами.
Диаграммы двоичных решений
Бинарное решение — это выбор между двумя альтернативами, поэтому диаграмма бинарных решений иллюстрирует путь от одного решения к другому.
В информатике двоичные решения составляют логический тип данных, в котором два значения связаны с разными действиями в потоке процесса.
За пределами информатики диаграмма бинарных решений все еще может использоваться для иллюстрации любого процесса, в котором действия основаны на выборе между двумя значениями, будь то условия: да или нет, истина или ложь, 1 или 0 или любые другие противоположные значения. выбор.
В конечном итоге выбранный путь будет отображать, как протекал процесс, от начала до конца.
Схема
Схема
Принципиальная схема, как следует из названия, представляет собой визуальное представление электрической цепи. Схема с использованием простых форм и изображений иллюстрирует компоненты и взаимосвязи цепи от начала до конца.
Хотя пути и соединения точны, диаграмма не обязательно отражает пропорциональную пространственную конструкцию цепи.В информатике принципиальные схемы полезны для изображения данных, относящихся как к аппаратному, так и к программному обеспечению.
Графика не только визуализирует пути схемы в буквальном смысле, но они также тесно связаны с вышеупомянутой диаграммой двоичного решения — обе используются для построения схем потоков процессов программирования.
История
Хронология
Возможно, самая понятная из визуализаций данных, временная шкала отслеживает данные за определенный период времени.Важные даты и события выделяются в том месте, где они появляются в хронологической шкале. Временные шкалы можно использовать отдельно или в сочетании с другими визуализациями.
Эта инфографика временной шкалы «История Винсента Ван Гога» — отличный пример того, как вы можете создать временную диаграмму прямо в Visme.
Древовидные диаграммы
Форма иерархической диаграммы, генеалогическое дерево, иллюстрирующее структуру семьи. Он может начинаться с предка, затем изобразить его или ее потомков, их братьев и сестер, браки и детей и так далее.
Родословная, с другой стороны, начинается с человека и показывает его родословную, от родителей до бабушек и дедушек, и продолжается вверх.
Диаграммы солнечных лучей
Тип многоуровневой круговой диаграммы, диаграмма солнечных лучей, используется для иллюстрации иерархических данных с помощью концентрических кругов. Каждое кольцо «солнечных лучей» представляет уровень в иерархии, причем корневой узел представлен центральным кругом, а иерархия движется наружу.
Хотя диаграмму солнечных лучей можно использовать для иллюстрации знакомой иерархии или иерархии компаний, она также может разбивать данные по периодам времени, создавая историческую иерархию.
Различные ветви организации могут быть представлены определенными оттенками, причем разные уровни часто принимают разные оттенки одного и того же цветового семейства. Кольца также могут быть разделены на несколько подразделений на одном организационном уровне.
Фактически, традиционное сложное цветовое колесо, используемое в магазинах красок, является еще одной формой диаграммы солнечных лучей.
Линейные графики
Если временная шкала представляет собой форму графика, то имеет смысл только то, что историки часто используют ее для отображения других данных.Построив уровни иммиграции на временной шкале, полученная гистограмма иллюстрирует демографические тенденции за столетие или дольше с помощью базового линейного графика.
График с накоплением
Диаграммы с областями с накоплением часто используются для отображения изменений нескольких переменных во времени. Например, можно нарисовать несколько линий, чтобы отслеживать изменения населения в различных штатах во времени.
Область под каждой линией может быть окрашена в другой оттенок для обозначения состояния, которое она обозначает, в результате чего получается график, который четко представляет тенденции численности населения, в то же время отображая данные по каждому штату в порядке от наименее к наиболее густонаселенному.
Политология и социология
Гистограммы с накоплением
При изучении групп людей принято сравнивать сразу несколько переменных. В конце концов, гораздо полезнее изучать расовую принадлежность, возраст и пол в дополнение к общей численности населения.
Составная гистограмма сочетает в себе элементы традиционной гистограммы и круговой диаграммы для представления итогов, тенденций и пропорций на одной иллюстрации.
Вместо того, чтобы просто иллюстрировать изменения мирового населения с течением времени с помощью традиционной столбчатой гистограммы, составная гистограмма может также представлять расовый состав населения в течение каждого года и то, как эти пропорции изменились за тот же период.
Решетчатые гистограммы
При представлении данных с тремя переменными дизайнер может попытаться создать трехмерную гистограмму, но добавление дополнительной оси может иногда казаться загроможденным и нечетким, особенно в печатной форме.
Вместо этого дополнительные переменные могут быть представлены в решетчатом или решетчатом формате.
Объединяя серию гистограмм в модульную конструкцию, можно легко сравнивать дополнительные наборы данных. Например, одна столбчатая диаграмма может проиллюстрировать политический распад национальных выборов в Польше за пятилетний период.
Но решетчатая гистограмма может отображать тот же набор данных для 16 европейских стран.
График с накоплением
Диаграммы с областями с накоплением идеально подходят для сравнения значений, для которых обычно требуется несколько линейных графиков. Каждая линия представляет отдельную категорию, а область под каждой линией обычно закрашена определенным цветом, чтобы каждый набор данных можно было легко сравнить.
Например, диаграмма с областями, одна ось которой представляет числовое значение, а другая ось служит временной шкалой, данные для различных категорий с течением времени можно отслеживать и сравнивать с одним графическим изображением.
Многоуровневые круговые диаграммы
Слишком часто дизайнер обнаруживает, что у него больше наборов данных, чем может быть представлено на одном стандартном графике. К счастью, в случае круговой диаграммы несколько слоев данных могут быть представлены без необходимости в нескольких изображениях или решетчатом дизайне.
Например, многоуровневая круговая диаграмма состоит из уровней, каждый из которых представляет отдельный набор данных, и может быть идеальным решением.
Таким образом, хотя для иллюстрации различных источников записанных слов за три разных десятилетия потребуются три традиционных круговых диаграммы, многоуровневая круговая диаграмма может не только заменить все три, но также предлагает более четкое визуальное сравнение каждого года. полученные результаты.
Диаграммы Венна
Классическая диаграмма Венна, также известная как логическая диаграмма, иллюстрирует все возможные логические отношения между заданным набором наборов.
Например, наложение двух или более кругов — в данном случае их три — визуально представляет сходства и различия между социальной, экономической и экологической областями устойчивого развития.
Чем больше кругов используется, тем больше логических выводов можно представить по их перекрытию.Объединенный набор всех данных на диаграмме называется объединением, а области, которые перекрываются, называются пересечениями.
Диаграмма Венна, на которой относительный размер и площадь каждой формы пропорциональны размеру группы, которую она представляет, известна как пропорциональная площади или масштабированная диаграмма Венна.
Наука
Диаграммы рассеяния
Диаграммы рассеяния, также известные как диаграммы рассеяния, представляют собой графики, показывающие взаимосвязь между двумя или более переменными.Графики используют математические координаты для представления двух переменных набора данных.
Данные отображаются на диаграмме рассеивания в виде набора точек, каждая из которых представляет переменные значения, нанесенные на горизонтальную и вертикальную оси. Если точки имеют цветовую кодировку, дополнительная переменная может быть представлена на одной диаграмме.
Построив определенные наборы данных, ученые могут обнаружить тенденции, о которых они иначе могли бы не знать. Например, диаграмма рассеяния может позволить врачу сопоставить частоту сердечных сокращений пациентов в состоянии покоя с показателями их индекса массы тела.
Полученный график показывает, что более высокая частота сердечных сокращений коррелирует с более высоким ИМТ.
Решетчатые линейные графики
Графики
Trellis позволяют ученым изучать сложные наборы данных с множеством переменных, одновременно сравнивая больший объем информации.
В то время как однолинейный график может иллюстрировать ежемесячные наблюдения НЛО в Теннесси за 18-летний период, решетчатый линейный график будет отображать одни и те же данные для всех 50 штатов на одном графике.
Решетчатый линейный график основан на том же принципе, что и его более простой аналог, и отображает тенденции в наборе данных, состоящем из двух переменных — количества наблюдений НЛО и дат — посредством использования точек соединения на двух осях.
Но при объединении нескольких линейных графиков в модульном формате отображается дополнительная переменная — местоположение.
Диаграммы Парето
Иногда простой график не отображает достаточно информации, чтобы сделать необходимый вывод. Диаграмма Парето объединяет гистограмму с линейной диаграммой, чтобы проиллюстрировать не только отдельные значения категорий, но и совокупную сумму всего набора.
Диаграммы
Парето предназначены для выделения наиболее важных факторов.
На диаграмме Парето, которая отслеживает тип и частоту дефектов пищевых продуктов, столбцы показывают общее количество случаев дефектов каждого типа — как указано на одной из осей диаграмм — в то время как линейные диаграммы показывают совокупную частоту всех категорий, от большинства до наименее распространенный.
Результатом является график, который четко отражает наиболее распространенные дефекты пищевых продуктов и какой процент от целого каждый представляет.
Радарные карты
Радиолокационная карта, также обычно называемая паутиной или звездной картой, отображает наборы данных, состоящие из трех или более переменных, на двухмерной графике.Количественное значение каждой переменной отображается на оси, которая обычно начинается в центральной точке диаграммы.
Поскольку переменные каждого элемента нанесены на карту, точки на каждой оси соединяются линией, образуя неправильный многоугольник, который может напоминать или не напоминать звезду или паутину.
Несколько наборов данных можно сравнивать на одном графике радара, каждый из которых имеет свой цвет, обозначенный метками или сопутствующим ключом.
Радиолокационная диаграмма может, например, наглядно сравнить и проиллюстрировать затраты и результаты различных медицинских процедур, поскольку они относятся к нескольким состояниям — и все это на одном графике.
Сферические контурные диаграммы
Источник изображения
Построение планетарных условий на базовом двухосном графике может вызвать проблемы. В конце концов, Земля — это сфера. Вместо этого данные могут быть нанесены на трехосное поле с использованием переменных x, y, и z. Результирующий сюжет, если он будет завершен, примет форму сферы.
Сферический график может, например, выявить тенденции глобальной температуры или количества осадков путем присвоения каждому диапазону значений определенного цвета, а затем нанесения данных на график с точками соответствующего оттенка.
Здоровье и благополучие
Многолинейные графики
Так же, как медицинские симптомы редко бывают изолированными, так же как и анализ биометрических данных. В конце концов, редко одна статистика описывает всю медицинскую картину.
Линейные графики могут отображать несколько наборов данных с линиями разного рисунка или цвета. Например, многолинейный график может проиллюстрировать изменения в ожидаемой продолжительности жизни не только населения в целом, но и для каждого пола и нескольких расовых групп.
Гистограммы с накоплением
Гистограммы с накоплением полезны не только для иллюстрации частей целого. Их также можно использовать для отображения дополнительных переменных.
В то время как базовая гистограмма может отображать, какая часть населения классифицируется как имеющая избыточный вес в течение определенного периода времени, столбчатая диаграмма с накоплением также может отслеживать, какая часть общей численности страдает ожирением.
Блок-схемы
Следование правильному процессу, вероятно, более важно в медицине, чем в любой другой области.В конце концов, если хирург забудет шаг, вы вполне можете истечь кровью, пока спите.
Блок-схемы
часто используются в больницах, клиниках и других медицинских учреждениях для обеспечения единообразного соблюдения надлежащих процедур.
Пиктограммы
В пиктограмме или пиктограмме изображения и символы используются для иллюстрации данных. Например, базовая пиктограмма может использовать изображение солнца для обозначения каждого дня с хорошей погодой в месяце и дождевое облако для обозначения каждого штормового дня.
Поскольку известно, что изображения обладают большей эмоциональной силой, чем необработанные данные, пиктограммы часто используются для представления медицинских данных.
Иллюстрация, которая закрашивает пять из 20 символов человека, чтобы представить 20-процентную смертность, несет более сильное сообщение, например, чем столбик, линия или круговая диаграмма, которые иллюстрируют те же данные.
Анатомические схемы
Медицинские диаграммы часто используются для иллюстрации анатомии, лечения или патологии заболевания, чтобы объяснить лечение пациентов и других лиц, не имеющих обширного биомедицинского опыта.
Хотя медицинские диаграммы считаются сочетанием науки и искусства, они могут быть такими же техническими, как и любой другой количественный график. И независимо от того, насколько подробным является рисунок, анатомические схемы созданы для четкого и эффективного представления данных.
Как и в случае со сложной контурной диаграммой, диаграммы сосредоточены на ключевой информации, даже если она была выбрана из огромного количества медицинских или научных данных.
Многосекторные диаграммы
Так же, как и в случае многоуровневых круговых диаграмм, гистограмм с накоплением и решетчатых диаграмм, многосекционные диаграммы рисуют более подробный портрет набора данных, который они иллюстрируют.
В то время как одна круговая диаграмма может отображать, какая часть общей численности населения имеет определенное состояние, диаграмма с несколькими круговыми диаграммами может разбить эту статистику, чтобы проиллюстрировать не только долю мужчин и долю женщин, но и то, как эти две группы сравниваются. .
Точечные диаграммы
Источник изображения
Может быть сложно графически представить наборы медицинских данных, которые состоят из сотен или более пациентов, как это имеет место в большинстве медицинских исследований.
Но диаграмма рассеяния позволяет представить каждый предмет, нанесенный на график в соответствии с переменными на двух осях диаграммы.
Шаблон, образованный нанесенными точками, может четко определять тенденции в данных. Например, анализируя диаграмму рассеяния, исследователь может легко определить корреляцию между большей продолжительностью жизни и более высоким доходом домохозяйства.
Метеорология и окружающая среда
Контурные графики
Источник изображения
Контурные графики позволяют анализировать три переменных в двухмерном формате. Вместо отображения данных по двум основным осям на графике также отображается третье значение, основанное на затенении или цвете.
Так же, как топографическая карта отображает долготу, широту и высоту в двухмерном дизайне, контурный график показывает значения x , y и z .
С помощью контурного графика, например, климатолог может отобразить не только соленость океана в разные даты, но и его соленость на разных глубинах в эти даты.
Тепловые карты
Источник изображения
Тип контурного графика, тепловая карта, специально предназначенная для отображения различных температур в разных географических точках.Две оси графика — это широта и долгота карты, а третья переменная — температура — представлена спектром цветов.
Хотя чаще всего используются для иллюстрации погоды, тепловые карты также могут отображать веб-трафик, финансовые показатели и почти любые другие трехмерные данные.
Комбинированный модуль с линиями рассеяния
Объединив линейный график с диаграммой рассеяния, метеорологи и другие статистики могут проиллюстрировать взаимосвязь между двумя наборами данных.
Например, высокие и низкие температуры каждого дня в месяце могут отображаться на диаграмме рассеяния, затем может быть добавлен линейный график для построения исторических средних высоких и низких температур за тот же период.
Полученный комбинированный график четко показывает, как диапазон температур каждый день сравнивается со средним историческим значением, и даже показывает тенденции этих измерений за исследуемый период времени.
3D графики
Источник изображения
Технология
теперь позволяет статистикам отображать многомерные наборы данных в истинной форме. Трехмерные графики, созданные с помощью специализированного программного обеспечения, отражают взаимосвязь между тремя переменными, нанесенными на три оси.
Метеоролог может, например, построить график ветрового поля урагана.
Гистограммы
По определению, гистограмма — это особый тип вертикальной гистограммы, на которой представлены числовые данные и их частотное распределение.
Как следует из названия, распределение часто иллюстрируется во времени, но данные также могут быть построены на основе любой хронологической шкалы, такой как температура, высота над уровнем моря или денежное выражение.
Хотя гистограммы обычно представляют собой форму гистограммы, эту концепцию также можно применить к линейным графикам и другим конструкциям, основанным на построении двух осей.
Выберите один из этих типов графиков для создания
Готовы приступить к созданию ваших любимых типов графиков? Создайте бесплатную учетную запись в Visme и начните работу с готовыми шаблонами и простым в использовании графическим движком.
Мы пропустили один из ваших любимых типов графиков? Что вам больше всего нравится создавать с помощью Visme? Дайте нам знать в комментариях ниже!
графиков и диаграмм | SkillsYouNeed
Картинка, как говорят, расскажет тысячу слов.А как насчет графика или диаграммы?
Хороший график или диаграмма может отображать до нескольких абзацев слов. Но как выбрать, какой стиль графика использовать?
На этой странице изложены некоторые основы рисования и создания хороших графиков и диаграмм. Под «хорошими» мы подразумеваем те, которые показывают то, что вы хотите, и не вводят читателя в заблуждение.
Типы графиков
Существует несколько различных типов диаграмм и диаграмм. Четыре наиболее распространенных — это, вероятно, линейные диаграммы, гистограммы и гистограммы, круговые диаграммы и декартовы диаграммы.Обычно они используются и лучше всего подходят для совершенно разных целей.
Вы должны использовать:
Гистограммы для отображения чисел, которые не зависят друг от друга. Примеры данных могут включать такие вещи, как количество людей, которые предпочли китайскую еду на вынос, индийскую еду на вынос и рыбу с жареным картофелем.
Круговая диаграмма , чтобы показать вам, как целое делится на разные части. Например, вы можете захотеть показать, как бюджет был потрачен на разные статьи в конкретном году.
Линейные графики показывают, как числа менялись с течением времени. Они используются, когда у вас есть данные, которые связаны, и для отображения тенденций, например, средней ночной температуры в каждом месяце года.
Декартовы графы имеют числа на обеих осях, что позволяет вам показать, как изменения в одном элементе влияют на другой. Они широко используются в математике, особенно в алгебре и .
Оси
Графики имеют две оси , — линии, проходящие снизу и вверх по бокам.Линия внизу называется горизонтальной или осью x , а линия вверху сбоку называется вертикальной или осью y .
- Ось x может содержать категории или числа. Вы читаете это в нижнем левом углу графика.
- Ось y обычно содержит числа, снова начиная с нижнего левого угла графика.
Числа на оси Y обычно, но не всегда, начинаются с 0 в нижнем левом углу графика и движутся вверх.Обычно оси графика помечены, чтобы указать тип данных, которые они показывают.
Остерегайтесь графиков, на которых ось Y не начинается с 0, поскольку они могут попытаться ввести вас в заблуждение относительно показанных данных (и об этом подробнее на нашей странице, Everyday Mathematics ).
Гистограммы и гистограммы
Гистограммы обычно имеют категории на оси x и числа на оси y (но они взаимозаменяемы). Это означает, что вы можете сравнивать числа в разных категориях.Категории должны быть независимыми, то есть изменения в одной из них не влияют на другие.
Вот сводка «некоторых данных» в таблице данных:
| Некоторые данные | |
| Категория 1 | 4,1 |
| Категория 2 | 2,5 |
| Категория 3 | 3,5 |
| Категория 4 | 4,7 |
И те же данные, отображаемые на гистограмме:
Сразу видно, что этот график дает вам четкое представление о том, какая категория самая большая, а какая самая маленькая.Это дает четкое сравнение между категориями.
Вы также можете использовать график для считывания информации о том, сколько человек входит в каждую категорию, без необходимости возвращаться к таблице данных, которая может или не может быть предоставлена с каждым графиком, который вы видите.
Как правило, вы можете рисовать гистограммы с горизонтальными или вертикальными полосами, потому что это не имеет никакого значения. Стержни не касаются .
Гистограмма — это особый тип гистограммы, где категории — это диапазонов чисел .Таким образом, гистограммы показывают комбинированные непрерывные данные.
Гистограмма — рабочий пример
Вам дан список возрастов в годах, и вам нужно отобразить их на графике.
Возраст:
5, 12, 23, 22, 28, 17, 11, 21, 25, 23, 7, 16, 13, 39, 35, 42, 24, 31, 35, 36, 35, 34, 37, 44, 51, 53, 46, 45 и 57.
Вы можете сгруппировать их по десятилетним возрастным категориям: 0–10, 11–20, 21–30 и так далее:
| Возраст | Количество человек |
| 0-10 | 2 |
| 11-20 | 5 |
| 21-30 | 7 |
| 31-40 | 8 |
| 41-50 | 4 |
| 51-60 | 3 |
Чтобы отобразить эти данные в виде гистограммы, ваша ось x будет пронумерована с точностью до 10 секунд от 0 до вашего наивысшего возраста, ось y от 0 до 8 (наибольшее количество людей в любой группе), и не будет промежутков между полосами , потому что нет промежутков между возрастными диапазонами.
Пиктограммы
Пиктограмма — это особый тип гистограммы. Вместо того, чтобы использовать ось с числами, он использует изображения для представления определенного количества элементов. Например, вы можете использовать пиктограмму для данных о возрасте выше, с изображением человека, чтобы показать количество людей в каждой категории:
Круговая диаграмма
Круговая диаграмма выглядит как круг (или круговая диаграмма), разрезанный на сегменты. Круговые диаграммы используются, чтобы показать, как целое разбивается на части.
Например, эти данные показывают объем продаж за год с разбивкой по кварталам:
| Квартальные показатели продаж | 1 st Qtr | 2 nd Qtr | 3 rd Qtr | 4 th Qtr |
| 8,2 | 3,2 | 1,4 | 1,2 |
Из круговой диаграммы сразу видно, что продажи в первом квартале были намного больше, чем во всех остальных: более 50% от общего годового объема продаж.
За 2-м кварталом было около 25% продаж.
Не зная больше ничего об этом бизнесе, вы можете быть обеспокоены тем, что продажи упали за год.
Круговые диаграммы , в отличие от гистограмм, показывают зависимых данных .
Общие продажи за год должны были произойти в том или ином квартале. Если вы ошиблись в цифрах и первый квартал должен быть меньше, то в одном из других кварталов для компенсации будут добавлены продажи, при условии, что вы не ошиблись с итоговой суммой.
Круговые диаграммы показывают проценты от целого — таким образом, ваша сумма составляет 100%, и сегменты круговой диаграммы имеют пропорциональный размер, чтобы представлять процент от общей суммы. Подробнее о процентах см. На нашей странице: Введение в проценты .
Обычно нецелесообразно использовать круговые диаграммы для более чем 5 или 6 различных категорий. Многие сегменты трудно визуализировать, и такие данные могут быть лучше отображены на диаграмме или графике другого типа.
Линейные графики
Линейные графики обычно используются для отображения зависимых данных и, в частности, тенденций во времени.
Линейные графики отображают количество баллов для каждой категории, которые объединены в линию. Мы также можем использовать данные круговой диаграммы в виде линейного графика.
Еще более очевидно, что продажи резко упали за год, хотя к концу года замедление выровняется. Линейные графики особенно полезны для определения момента времени, в который был достигнут определенный уровень продаж, дохода (или того, что представляет значение y).
В приведенном выше примере предположим, что мы хотим знать, в каком квартале продажи впервые упали ниже 5.Мы можем провести линию напротив точки 5 по оси Y (красная линия в примере) и увидеть, что это было в течение 2 квартала.
Декартовы графы
Декартовы графы — вот что на самом деле имеют в виду математики, когда они говорят о графах. Они сравнивают два набора чисел, один из которых нанесен на ось x, а другой — на ось y. Числа могут быть записаны в виде декартовых координат , которые выглядят как (x, y), где x — это число, считываемое по оси x, а y — число по оси y.
Предупреждение!
Декартовы графы не всегда начинаются с 0; довольно часто (0,0) является средней точкой графика.
Декартов граф — рабочий пример
Джон на два года старше Мэри, и их возраст в сумме равен 12. Какого возраста они оба сейчас?
Мы можем решить эту проблему, проведя две линии: одну из возрастов Джона по сравнению с возрастом Мэри, а другую — из возрастов, которые в сумме дают 12.
Строка 1: (фактический) возраст Джона, когда Мэри разный возраст от 1 до 9
| Возраст Марии | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Возраст Иоанна (= Мария + 2) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Строка 2: Возраст Джона (гипотетический), когда Мэри разный возраст: от 1 до 9 , если их возраст в сумме составляет 12
| Возраст Марии | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Возраст Иоанна (= 12 — Возраст Марии) | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
Изобразив две линии на графике с указанием возраста Марии на оси абсцисс, вы увидите, что есть точка, в которой линии пересекаются.Это единственная точка, в которой а) Джон на два года старше Мэри и б) их возраст в сумме составляет 12. Это должен быть их текущий возраст, который, таким образом, составляет 5 лет для Марии и 7 лет для Иоанна.
Чтобы узнать больше об использовании декартовых графиков для решения математических задач, посетите наши страницы Алгебра и Одновременные и квадратные уравнения .
Рисование графиков с использованием компьютерных пакетов
Для рисования графиков можно использовать различные пакеты компьютерных программ, включая Word и Excel.
Некоторые пакеты чрезвычайно эффективны при эффективном использовании. Однако имейте в виду, что некоторые приложения довольно ограничены в типах диаграмм, которые они могут рисовать, и вы можете не получить полностью те результаты, которые вы ожидали! Вам действительно нужно базовое понимание графиков и диаграмм, чтобы вы могли сравнивать то, что создал компьютер, с тем, что вы хотите показать.
Компьютерные приложения также упрощают создание чрезмерно сложных графиков. Трехмерная круговая диаграмма может выглядеть «круто», но помогает ли она вам или другим людям визуализировать данные? Часто лучше, чтобы графики и диаграммы были простыми, с аккуратным и понятным форматированием.
Дополнительная литература по навыкам, которые вам нужны
Обработка данных и алгебра
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы обработки данных, визуализации данных, базового статистического анализа и алгебры. Книга содержит множество проработанных примеров для улучшения понимания, а также примеры из реальной жизни, чтобы показать вам, насколько полезны эти концепции.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
График стоит…
Независимо от того, как вы решите представить свои данные, как только вы овладеете навыками создания четких графиков и диаграмм, вы почти наверняка обнаружите, что старая поговорка верна: изображение действительно может рассказать тысячу слов.
Независимо от того, стоит ли ваш хорошо нарисованный график тысячу чисел или дюжину, он, безусловно, будет эффективным способом представления ваших данных и демонстрации взаимосвязей или различий между ними.
11 типов графиков и диаграмм + [примеры]
При работе с числами в статистике включение визуализации данных является неотъемлемой частью создания читаемой и понятной сводки набора данных.Неважно, большой это набор данных или маленький, визуализация данных с помощью графиков и диаграмм будет в значительной степени способствовать пониманию вашей аудитории сообщения.
Однако существует множество типов графиков и диаграмм, используемых при визуализации данных, и иногда бывает сложно выбрать, какой тип лучше всего подходит для вашего бизнеса или данных. У каждого из этих графиков есть свои сильные и слабые стороны, которые делают его лучше других в некоторых ситуациях.
Возможно, вам потребуется визуализировать результаты научных исследований, отчет о продажах, отраслевую инфографику или демографическую презентацию.Графики и диаграммы — простые способы демонстрации каждого из этих материалов.
Что такое график?
График — это организованное графическое представление данных. Графики обычно формируются из различных точек данных, которые представляют отношения между двумя или более объектами.
Говорят, картина говорит тысячу слов. С другой стороны, график не только говорит тысячу слов, но и рассказывает миллион историй.
Каждая точка, обводка, цвет или форма на графике имеют разное значение, которое помогает в интерпретации графика.Они бывают разных типов и различаются по структуре: одни имеют только точки, другие — точки, соединенные линиями, и так далее.
Графики и диаграммы — в чем разница?
Хотя иногда используются как взаимозаменяемые, важно отметить разницу между графиками и диаграммами. Вкратце, мы можем сказать, что все графики являются диаграммами, но не все диаграммы являются графиками.
График — это математическая диаграмма, которая изображает взаимосвязь между двумя или более наборами числовых данных за период времени.Основные данные в основном двухмерные с акцентом на необработанные данные, представленные в виде линий, кривых и т. Д.
С другой стороны, диаграммы
— это представление наборов данных с целью помочь пользователю лучше понять информацию. Графики — хороший пример диаграмм, используемых для визуализации данных.
Типы графиков и диаграмм
Для визуализации данных используются различные типы графиков и диаграмм. Однако в этой статье мы рассмотрим 11 основных типов, которые используются для визуализации бизнес-данных.
Гистограмма / график
Гистограмма — это диаграмма, представленная разнесенными прямоугольными полосами, которые описывают точки данных в наборе данных. Обычно он используется для построения дискретных и категориальных данных.
Горизонтальная ось диаграммы представляет категориальные данные, а вертикальная ось диаграммы определяет дискретные данные. Хотя прямоугольные столбцы на гистограмме в основном расположены вертикально, они также могут быть горизонтальными.
Гистограмма
Для горизонтально расположенных прямоугольных полос категориальные данные определяются на вертикальной оси, а горизонтальная ось определяет дискретные данные.
Типы гистограмм
Сгруппированные гистограммы используются, когда в наборах данных есть подгруппы, которые необходимо визуализировать на графике. Каждая подгруппа обычно отличается от другой, закрашивая их разными цветами.
Сложенные гистограммы также используются для отображения подгрупп в наборе данных. Но в этом случае прямоугольные полосы, определяющие каждую группу, накладываются друг на друга.
Это тип столбчатой диаграммы с накоплением, где каждый столбик с накоплением показывает процент своего дискретного значения от общего значения.Общий процент составляет 100%
Преимущества столбчатой диаграммы
- Обобщает большой объем данных в понятной форме.
- Легко доступный для широкой аудитории.
Недостатки гистограммы
- Он не раскрывает ключевые предположения, такие как причины, следствия, закономерности и т. Д.
- Может потребоваться дополнительное объяснение.
Круговая диаграмма
Круговая диаграмма — это круговая диаграмма, используемая для иллюстрации числовых пропорций в наборе данных.Этот график обычно делится на несколько секторов, где каждый сектор представляет долю определенного числового элемента в наборе.
ПИРОГОВАЯ ДИАГРАММА
Так же, как пицца делится на разные части, каждый сектор круговой диаграммы представляет долю элемента в наборе данных. Пропорция определяется степенью сектора и процентной площадью по отношению к площади круга.
Типы круговой диаграммы
Это самый простой тип круговой диаграммы, который также может называться просто круговой диаграммой.
На разнесенной круговой диаграмме один из секторов круга отделен (или разнесен) от диаграммы. Он используется, чтобы сделать акцент на конкретном элементе набора данных.
Как следует из названия, круговая диаграмма — это диаграмма, которая генерирует совершенно новую (обычно небольшую) круговую диаграмму из существующей. Его можно использовать, чтобы уменьшить загроможденность и сделать акцент на определенной группе элементов.
Это похоже на круговую диаграмму с основным отличием в том, что в этом случае создается гистограмма, а не круговая диаграмма.
Это тип круговой диаграммы, представленной в трехмерном пространстве.
Использование круговой диаграммы
- Он суммирует данные в визуально привлекательной форме.
- Это довольно просто по сравнению со многими типами графиков.
Недостатки круговой диаграммы
- Неприменимо для больших наборов данных.
- Невозможно визуализировать группы данных.
Линейный график или диаграмма
Линейные графики представлены группой точек данных, соединенных прямой линией.Каждая из этих точек данных описывает соотношение между горизонтальной и вертикальной осями на графике.
ЛИНИЯ СХЕМА
График может возрастать, опускаться или делать и то, и другое в зависимости от того, какие данные визуализируются. При изучении взаимосвязи между ценой и предложением она снижается, а для мира и спроса — повышается.
При построении линейной диаграммы вы можете решить включать точки данных или нет.
Типы линейного графика
В простом линейном графике на графике отображается только одна линия.Одна из осей определяет независимые переменные, а другая ось содержит зависимые переменные.
Многолинейные графики содержат две или более линий, представляющих более одной переменной в наборе данных. Этот тип графика можно использовать для изучения двух или более переменных за один и тот же период времени.
Составной линейный график — это расширение простого линейного графика, который используется при работе с различными группами данных из более крупного набора данных. Каждая линия в составном линейном графике заштрихована вниз по оси x.
В составном линейном графике каждая группа данных, представленная простым линейным графиком, накладывается одна на другую.
Использование линейного графика
- Это помогает в изучении тенденций данных за определенный период времени.
- Их легко читать и строить.
Недостатки линейного графика
- Его можно использовать только для визуализации данных за короткий период времени.
- Не удобно строить график при работе с дробями и десятичными знаками
Гистограмма Диаграмма
Диаграмма гистограммы
отображает частоту дискретных и непрерывных данных в наборе данных с помощью соединенных прямоугольных полос.Каждая прямоугольная полоса определяет количество элементов, попадающих в заранее определенный интервал классов.
Типы гистограммы
Диаграмма гистограммы подразделяется на разные части в зависимости от их распределения
Гистограмма с нормальным распределением обычно имеет форму колокола. Как следует из названия, это распределение является нормальным и является стандартом для того, как должна выглядеть нормальная гистограмма.
В бимодально распределенной гистограмме у нас есть две группы гистограмм с нормальным распределением.Он формируется в результате объединения двух процессов в наборе данных.
Это асимметричный график со смещением от центра, обычно стремящимся к концу графика. Можно сказать, что гистограмма скошена вправо или влево в зависимости от направления, в котором стремится пик.
Этот тип гистограммы не имеет регулярного паттерна. Он дает множественные пики и также может называться мультимодальным распределением.
Это распределение имеет структуру, аналогичную структуре нормального распределения с большим пиком на одном из его краев, который является отличительным фактором.
Гребневая раздача «гребенчатая» структура , где прямоугольные полосы чередуются между высокими и короткими.
Использование диаграммы гистограммы
- Помогает визуализировать большие объемы данных.
- Он показывает изменение, центрирование и распределение данных.
Минусы
- Он не отображает точные значения в наборе данных.
- Он только визуализирует непрерывные данные.
Диаграмма с областями
Диаграммы с областями используются для коллективного измерения тенденций данных за период времени путем окрашивания области между линейным сегментом и осью x. Проще говоря, диаграмма с областями — это продолжение линейной диаграммы.
Диаграмма с областями
Типы диаграммы с областями
В простой диаграмме с областями цветные сегменты перекрывают друг друга в области диаграммы. Они располагаются друг над другом так, чтобы пересекаться.
На диаграмме с областями с накоплением цветные сегменты накладываются друг на друга так, чтобы они не пересекались.
Это тип диаграммы с областями с накоплением, где площадь, занимаемая каждой группой данных на диаграмме, измеряется в процентах от ее количества от общих данных. Вертикальная ось обычно составляет сто процентов.
Это тип диаграммы с областями, измеряемой в трехмерном пространстве.
Диаграмма использования
- Это визуально привлекательно.
- Дает четкое сравнение различных групп данных.
Минусы
- Может быть трудно читать по сравнению с другими типами данных.
Точечный график или график
Точечный график — это тип графика с точками данных, которые вертикально представлены точечными маркерами. Говорят, что он похож на гистограмму и гистограмму, потому что высота агрегирования каждой группы точечных маркеров равна частоте элементов в определенном интервале классов.
Точечный график
Типы точечных графиков
Этот тип точечной диаграммы использует локальное смещение для предотвращения наложения точек на графике.Этот точечный лот был создан Леландом Уилкинсоном.
Это диаграмма в виде диаграммы рассеяния, на которой данные отображаются вертикально в одном измерении. Его разработал Уильям Кливленд.
Плюсы
- Обычно они очень красочные и визуально привлекательные.
Минусы
- Точки данных загромождаются и становятся нечитаемыми при работе с большими наборами данных.
- Обычно трудно определить частоту по графику
Диаграмма рассеяния
Точечные диаграммы — это диаграммы, используемые для визуализации случайных величин с точечными маркерами, которые представляют каждую точку данных.Эти маркеры обычно разбросаны по области графика графика.
Типы точечной диаграммы
Точечные диаграммы сгруппированы по различным типам в соответствии с корреляцией точек данных. Эти типы корреляции выделены ниже
.
Две группы данных, отображаемые на диаграмме рассеяния, считаются положительно коррелированными, если увеличение одной подразумевает увеличение другой. Можно сказать, что диаграмма рассеяния имеет высокую или низкую положительную корреляцию.
Две группы данных, отображаемые на диаграмме рассеяния, считаются отрицательно коррелированными, если увеличение одной подразумевает уменьшение другой. Можно сказать, что диаграмма рассеяния имеет высокую или низкую отрицательную корреляцию.
Считается, что две группы данных, отображаемых на диаграмме рассеяния, не имеют корреляции, если между ними нет четкой корреляции.
Плюсы
- Он ясно показывает разброс данных
- Ir обычно красочный и визуально привлекательный
Минусы
- Не может дать точной степени корреляции.
- Его можно использовать только для изучения взаимосвязи между двумя переменными.
Пузырьковая диаграмма
Пузырьковая диаграмма — это многомерный график, в котором пузырьки используются для представления точек данных в трех измерениях. Он представляет точки данных с пузырьками, причем первые две переменные определяют положение пузырька по осям x и y, а третья переменная определяет размер пузырька.
Типы пузырьковой диаграммы
Пузырьковые диаграммы
разделены на различные части в зависимости от количества переменных в наборе данных, типа данных, которые он визуализирует, и количества измерений на графике.
Простая пузырьковая диаграмма является самым основным типом пузырьковой диаграммы и эквивалентна обычной пузырьковой диаграмме.
Пузырьки на маркированной пузырьковой диаграмме обычно помечаются для облегчения идентификации, особенно при работе с различными группами данных.
- Пузырьковая диаграмма с несколькими переменными
В пузырьковой диаграмме с несколькими переменными переменные в наборе данных обычно больше 3 (особенно 4). Поэтому четвертую переменную обычно выделяют цветом.
Пузырьковая диаграмма карты обычно используется для иллюстрации данных на карте.
Это пузырьковая диаграмма, созданная в трехмерном пространстве. Пузырьки на трехмерной пузырьковой диаграмме имеют сферическую форму.
Использование пузырьковой диаграммы
- Он может визуализировать до 4-х мерных данных.
- Визуально привлекательный
Минусы
- Не подходит для визуализации больших данных.
- Может быть сложно сразу определить конкретные значения.
Пиктограмма График
Пиктограммный график использует изображения или значки для визуализации небольшого набора дискретных данных. В пиктограмме значок представляет собой заранее заданную единицу и описывает частоту переменных в наборе данных.
Пиктограмма
Плюсы
- Отлично подходит для определения веса.
Минусы
- Невозможно определить данные между точками.
Радарная карта
Радарная диаграмма — это графический метод, используемый для отображения многомерных данных в форме двухмерной диаграммы трех или более количественных переменных, представленных на осях, начиная с одной и той же точки.(Источник: Википедия). Его также называют паутинным графом.
Радарная диаграмма
Типы радиолокационной карты
Это самый простой тип радиолокационной карты, эквивалентный обычной радиолокационной карте. Он состоит из последовательности радиусов, начерченных из центральной точки и соединенных вместе.
Для радиолокационных диаграмм с маркерами каждая точка данных на паутинном графике помечена
На заполненных радарных диаграммах пустое пространство между линиями и центром паутины закрашено.
Использование радарной диаграммы
- Его можно использовать для сравнения нескольких несвязанных переменных в наборе данных.
- Выбросы легко заметить.
Минусы
- Это не подходит для больших наборов данных.
- Он имеет ограниченное применение при анализе данных.
Сплайн-диаграмма
Сплайн-диаграмма — это тип линейной диаграммы, в которой точки данных соединены плавной кривой.
Плюсы
- Их легко нарисовать
- Он может визуализировать квадратичные функции и полиномы
Минусы
- График неудобен при работе с дробями и десятичными знаками.
Как использовать сбор онлайн-данных для графиков и диаграмм с помощью Formplus
Выполните следующие простые шаги, чтобы собрать онлайн-данные для ваших графиков и диаграмм с помощью Formplus.
Создать онлайн-форму n
Чтобы создать новый опрос на Formplus, перейдите к Forms в верхнем меню, затем нажмите кнопку Create Form .
Кроме того, вы можете перейти на панель инструментов , и нажать кнопку Создать новую форму .
Сбор данных для вашего графика
После создания опроса выберите любое из доступных полей формы на левой боковой панели конструктора форм.Выберите поле формы, необходимое для сбора информации для вашего графика, щелкнув или перетащив его в раздел предварительного просмотра в реальном времени.
Настройте свою онлайн-форму
После добавления необходимых полей формы в опрос, нажмите кнопку Сохранить в правом верхнем углу конструктора форм, и вы будете автоматически перенаправлены на страницу Настроить . На этой странице вы можете украсить свой опрос, добавив логотип, цвет, шрифт, фоновое изображение и т. Д.используя встроенные функции Formplus. Кроме того, вы можете добавить свой собственный CSS.
Поделиться и начать сбор данных графика
После настройки опроса по своему вкусу теперь вы можете поделиться с респондентами и собрать необходимые данные для своего графика. С помощью нескольких вариантов совместного использования Formplus вы можете поделиться своим онлайн-опросом по электронной почте, в социальных сетях, с помощью QR-кода и т. Д. Или даже встроить его на свой веб-сайт.
Использование графиков и диаграмм
- В математике и статистике
Графики и диаграммы используются в аналитической геометрии для отображения функций двух или более переменных в декартовых координатах.Они также используются для определения корреляции и регрессии набора статистических данных.
Диаграммы и графики в основном используются при интерпретации данных для понимания набора данных. Диаграммы суммируют информацию в наборе данных, что упрощает процесс интерпретации данных.
Заключение
Существуют разные типы диаграмм, используемых при визуализации данных, каждая из которых используется в разных ситуациях. Ситуация, в которой используются эти графики, в основном зависит от сильных и слабых сторон каждого метода.
Поэтому в одних случаях мы предпочитаем использовать гистограммы, а в других — радарные. Выбор типа диаграммы зависит от усмотрения аналитика данных, но на этот выбор влияют такие факторы, как сильные и слабые стороны, аудитория и т. Д.
Основные типы диаграмм для визуализации данных
Диаграммы являются неотъемлемой частью работы с данными, поскольку они позволяют объединить большие объемы данных в простой для понимания формат.Визуализация данных может помочь в понимании того, кто смотрит на данные впервые, а также передать результаты другим людям, которые не видят необработанные данные. Существует бесчисленное множество типов диаграмм, каждый из которых имеет разные варианты использования. Часто самая сложная часть создания визуализации данных — это выяснить, какой тип диаграммы лучше всего подходит для поставленной задачи.
Ваш выбор типа диаграммы будет зависеть от множества факторов. Какие типы показателей, функций или других переменных вы планируете отображать? Какую аудиторию вы планируете представить — это всего лишь начальное исследование для вас самих или вы представляете более широкую аудиторию? Какой вывод вы хотите, чтобы читатель сделал?
В этой статье мы дадим обзор основных типов диаграмм, которые чаще всего предлагаются инструментами визуализации.С этими диаграммами у вас будет широкий набор инструментов для удовлетворения ваших потребностей в визуализации данных. Рекомендации по выбору каждого из них в зависимости от варианта использования описаны в следующей статье.
Основополагающая четверка
В своей книге «Покажи мне числа» Стивен Фью предлагает четыре основных кодировки для числовых значений, указывая позиционное значение с помощью полос, линий, точек и прямоугольников. Итак, мы начнем с четырех основных типов диаграмм, по одному для каждого из этих способов кодирования значений.
Гистограмма
На гистограмме значения обозначаются длиной столбцов, каждая из которых соответствует измеряемой группе.Гистограммы могут быть ориентированы вертикально или горизонтально; вертикальные гистограммы иногда называют столбчатыми диаграммами. Горизонтальные гистограммы — хороший вариант, когда у вас есть много столбцов для построения или когда метки на них требуют дополнительного места, чтобы их можно было разобрать.
Линейный график
Линейные диаграммы показывают изменения значений при непрерывных измерениях, например, сделанных с течением времени. Движение линии вверх или вниз помогает выявить положительные и отрицательные изменения соответственно. Он также может выявить общие тенденции, чтобы помочь читателю делать прогнозы или прогнозы относительно будущих результатов.Множественные линейные диаграммы также могут привести к появлению других связанных диаграмм, таких как спарклайновый или линейный график.
Диаграмма рассеяния
Диаграмма рассеяния отображает значения двух числовых переменных с использованием точек, расположенных на двух осях: по одной для каждой переменной. Диаграммы разброса — это универсальная демонстрация взаимосвязи между нанесенными на график переменными — независимо от того, является ли эта корреляция сильной или слабой, положительной или отрицательной, линейной или нелинейной. Диаграммы разброса также отлично подходят для определения точек выбросов и возможных пробелов в данных.
Коробчатый участок
Коробчатая диаграмма использует прямоугольники и усы для суммирования распределения значений в измеренных группах. Положение концов прямоугольника и усов показывает области, в которых находится большая часть данных. Чаще всего мы видим коробчатые диаграммы, когда у нас есть несколько групп для сравнения друг с другом; другие диаграммы с более подробной информацией предпочтительнее, когда у нас есть только одна группа для построения.
Таблицы и отдельные значения
Прежде чем переходить к другим типам диаграмм, стоит уделить время тому, чтобы оценить возможность отображения только необработанных чисел.В частности, когда у вас есть только одно число, простое отображение значения является разумным подходом к отображению данных. Когда точные значения представляют интерес для анализа, вы можете включить их в сопроводительную таблицу или с помощью аннотаций в графической визуализации.
Общие вариации
Дополнительные типы диаграмм могут появиться в результате изменения способов использования кодировок или включения дополнительных кодировок. Вторичные кодировки, такие как площадь, форма и цвет, могут быть полезны для добавления дополнительных переменных в более простые типы диаграмм.
Гистограмма
Если группы, изображенные на гистограмме, на самом деле представляют собой непрерывные числовые диапазоны, мы можем сдвинуть столбцы вместе, чтобы создать гистограмму. Длины столбцов на гистограммах обычно соответствуют количеству точек данных, а их шаблоны демонстрируют распределение переменных в ваших данных. Другой тип диаграммы, такой как линейная диаграмма, как правило, используется, когда значение по вертикали не является счетчиком частоты.
Гистограмма с накоплением
Одной из модификаций стандартной столбчатой диаграммы является разделение каждого столбца на несколько столбцов меньшего размера на основе значений второй группирующей переменной, называемой столбчатой диаграммой с накоплением.Это позволяет не только сравнивать значения основных групп, как на обычной гистограмме, но и проиллюстрировать относительную разбивку каждой группы в целом на составные части.
Сгруппированная линейчатая диаграмма
Если, с другой стороны, суббары размещать бок о бок в кластеры, а не хранить их стопками, мы получим сгруппированную гистограмму. Сгруппированная столбчатая диаграмма не позволяет сравнивать итоги основной группы, но гораздо лучше справляется с задачей сравнения подгрупп.
Точечная диаграмма
Точечный график похож на столбчатую диаграмму, поскольку он указывает значения для различных категорийных групп, но кодирует значения на основе положения точки, а не длины столбца. Точечные диаграммы полезны, когда вам нужно сравнить по категориям, но нулевой базовый уровень не является информативным или полезным. Вы также можете думать о точечном графике как о линейном графике с удаленной линией, чтобы его можно было использовать с переменными с неупорядоченными категориями, а не просто с непрерывными или упорядоченными переменными.
Диаграмма с областями
Диаграмма с областями начинается с того же основания, что и линейная диаграмма — точки значений, соединенных линейными сегментами, — но добавляет концепцию гистограммы с затенением между линией и базовой линией. Эту диаграмму чаще всего можно увидеть в сочетании с концепцией стекирования, чтобы показать, как общая сумма менялась с течением времени, а также как менялись вклады ее компонентов.
Диаграмма с двумя осями
Двухосные диаграммы накладываются на две разные диаграммы с общей горизонтальной осью, но могут иметь разные масштабы вертикальной оси (по одной для каждой диаграммы компонентов).Это может быть полезно, чтобы показать прямое сравнение между двумя наборами вертикальных значений, а также включить контекст переменной горизонтальной оси. Обычно используются разные типы базовых диаграмм, такие как комбинация столбцов и линий, чтобы избежать путаницы с разными масштабами осей для каждой диаграммы компонентов.
Пузырьковая диаграмма
Другой способ показать взаимосвязь между тремя переменными — это модификация диаграммы рассеяния. Когда третья переменная является категориальной, точки могут использовать разные формы или цвета для обозначения членства в группе.Если точки данных упорядочены каким-либо образом, точки также можно соединить отрезками линии, чтобы показать последовательность значений. Когда третья переменная имеет числовую природу, именно здесь появляется пузырьковая диаграмма. Пузырьковая диаграмма строится на основе базовой диаграммы рассеяния, поскольку значение третьей переменной определяет размер каждой точки.
Кривая плотности
Кривая плотности или оценка плотности ядра — это альтернативный способ отображения распределения данных вместо гистограммы.Вместо того, чтобы собирать точки данных в интервалы частот, каждая точка данных вносит небольшой объем данных, совокупность которых становится кривой плотности. Хотя кривые плотности могут подразумевать некоторые значения данных, которых не существует, они могут быть хорошим способом сгладить шум в данных, чтобы получить представление о сигнале распределения.
Сюжет для скрипки
Альтернативой подходу коробчатой диаграммы к сравнению распределения ценностей между группами является сценарий скрипки. В сюжете скрипки каждый набор ящиков и усов заменяется кривой плотности, построенной вокруг центральной базовой линии.Это может обеспечить лучшее сравнение форм данных между группами, хотя и проигрывает при сравнении точных статистических значений. Частым вариантом для скрипичных сюжетов является добавление пометок в виде прямоугольников поверх скрипичного сюжета, чтобы получить лучшее из обоих миров.
Тепловая карта
Тепловая карта представляет собой сетку значений на основе двух интересующих переменных. Переменные оси могут быть числовыми или категориальными; сетка создается путем разделения каждой переменной на диапазоны или уровни, такие как гистограмма или гистограмма.Ячейки сетки окрашиваются в зависимости от значения, часто более темными цветами, соответствующими более высоким значениям. Тепловая карта может быть интересной альтернативой диаграмме рассеяния, когда нужно построить много точек данных, но плотность точек не позволяет увидеть истинную взаимосвязь между переменными.
Карты специалиста
Существует множество дополнительных диаграмм, которые кодируют данные другими способами для конкретных случаев использования. Xenographics включает в себя набор некоторых причудливых диаграмм, которые преследовали очень конкретные цели.Тем не менее, некоторые из этих диаграмм имеют достаточно распространенные варианты использования, которые можно считать необходимыми.
Круговая диаграмма
Вы можете быть удивлены, увидев здесь, в разделе «специалистов», круговые диаграммы, учитывая, насколько часто они используются. Однако круговые диаграммы используют необычную кодировку, отображающую значения как области, вырезанные из круглой формы. Поскольку круговая диаграмма обычно не имеет маркировки значений по периметру, обычно трудно получить хорошее представление о точных размерах срезов.Тем не менее, круговая диаграмма и ее родственник — бублик-график — превосходно сообщают читателю, что сравнение частей и целых должно быть основным выводом из визуализации.
Воронкообразная диаграмма
Воронкообразная диаграмма часто встречается в бизнес-контексте, где посетителей или пользователей необходимо отслеживать в конвейерном потоке. Диаграмма показывает, сколько пользователей попадает на каждый этап отслеживаемого процесса, исходя из ширины воронки на каждом этапе деления. Сужение воронки помогает реализовать аналогию, но может сбить с толку истинные коэффициенты конверсии.Гистограмма часто может выполнять те же функции, что и воронкообразная диаграмма, но с более четким представлением данных.
Маркерная диаграмма
Маркированная диаграмма дополняет одну полосу дополнительными отметками, позволяющими контекстуализировать значение этой полосы. Обычно это означает перпендикулярную линию, показывающую целевое значение, но также и затенение фона для дополнительных тестов производительности. Маркированные диаграммы обычно используются для нескольких показателей и более компактны для рендеринга, чем другие типы более причудливых датчиков.
Земельные участки на карте
Существует несколько семейств специализированных графиков, сгруппированных по использованию, но мы закроем эту статью, коснувшись одного из них: картографических или геопространственных графиков. Когда значения в наборе данных соответствуют фактическим географическим местоположениям, может быть полезно нанести их на карту с помощью какой-либо карты. Типичным примером этого типа карты является хороплет, подобный показанной выше. При этом используется подход тепловой карты для изображения значения с помощью цвета, но вместо значений, отображаемых в сетке, они заполняются областями на карте.
Для получения удобного справочного руководства по другим типам диаграмм и о том, когда их следует использовать, ознакомьтесь с нашей бесплатной электронной книгой «Как выбрать правильную визуализацию данных».
16 основных типов диаграмм для визуализации данных, которые вы будете использовать
В эпоху информационного взрыва накапливается все больше и больше данных. Однако эти плотные данные несфокусированы и менее читабельны. Поэтому нам нужна визуализация данных, чтобы облегчить понимание и принятие данных. В отличие от этого, визуализация более интуитивна и значима, и очень важно использовать соответствующие диаграммы для визуализации данных.
В этом посте я расскажу о 16 основных типах диаграмм в визуализации данных и проанализирую их сценарии применения, чтобы помочь вам быстро выбрать тип диаграммы, который отображает характеристики ваших данных. ВНИМАНИЕ !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
ПРИМЕЧАНИЕ: Все графики в статье взяты из средства визуализации данных FineReport.
1. Столбчатая диаграмма
Столбчатая диаграмма использует вертикальные столбцы для отображения числовых сравнений между категориями, при этом количество столбцов не должно быть слишком большим (метки оси могут отображаться неполными, если столбцов слишком много).
Столбчатая диаграмма использует высоту столбца, чтобы отразить разницу в данных, а человеческий глаз чувствителен к разнице в высоте. Ограничение заключается в том, что он подходит только для небольших и средних наборов данных.
Сценарий приложения : сравнение секретных данных
2. Гистограмма
Гистограмма похожа на столбчатую диаграмму, но количество столбцов может быть относительно большим. По сравнению с столбчатой диаграммой положение двух ее осей изменено.
Сценарий приложения : сравнение данных (название категории может быть длиннее, потому что на оси Y больше места)
3. Линейная диаграмма
Линейная диаграмма используется для отображения изменения данных за непрерывное время интервал или временной интервал. Для него характерна тенденция отражать изменения в зависимости от времени или упорядоченных категорий.
Следует отметить, что количество записей данных линейного графика должно быть больше 2, что может использоваться для сравнения тенденций большого объема данных.И лучше не превышать 5 полилиний на одном графике.
Сценарий приложения : тренд объема данных во времени, сравнение трендов ряда
4. Диаграмма с областями
Диаграмма с областями формируется на основе линейной диаграммы. Область между ломаной линией и осью линейной диаграммы заполняется цветом. Цветовая заливка может лучше выделить информацию о тренде.
Цвет заливки диаграммы с областями должен иметь определенную прозрачность.Прозрачность может помочь пользователю увидеть взаимосвязь между разными сериями. Область без прозрачности заставит разные серии перекрывать друг друга.
Сценарий применения : соотношение рядов, соотношение временного тренда
5. Круговая диаграмма
Круговые диаграммы широко используются в различных областях для представления соотношения различных классификаций и сравнения различных классификаций по дуге.
Круговая диаграмма не подходит для нескольких серий данных, потому что по мере увеличения серии каждый срез становится меньше, и, наконец, различие в размерах не очевидно.
Круговая диаграмма также может быть преобразована в многослойную круговую диаграмму, показывающую долю различных категориальных данных, а также отражающую иерархические отношения.
Сценарий применения : соотношение серий, сравнение размеров серии (розовая диаграмма)
6. Точечная диаграмма
На точечной диаграмме показаны две переменные в виде точек в прямоугольной системе координат. Положение точки определяется значением переменной. Наблюдая за распределением точек данных, мы можем сделать вывод о корреляции между переменными.
Для построения точечной диаграммы требуется много данных, иначе корреляция не очевидна.
Сценарий приложения : корреляционный анализ, распределение данных
7. Пузырьковая диаграмма
Пузырьковая диаграмма — это многомерная диаграмма, являющаяся вариантом точечной диаграммы. За исключением значений переменных, представленных осями X и Y, площадь каждого пузырька представляет третье значение.
Следует отметить, что размер пузыря ограничен, и слишком большое количество пузырей затруднит чтение диаграммы.
Сценарий применения : сравнение классифицированных данных, корреляционный анализ
8. Датчик
Датчик в визуализации данных — это своего рода материализованная диаграмма. Масштаб представляет метрику, указатель представляет размер, а угол указателя представляет значение. Он может визуально отображать прогресс или фактическое состояние индикатора.
Датчик подходит для сравнения интервалов.
Он также может быть выполнен в виде кольца или трубки с указанием соотношения.
Сценарий приложения : часы, отображение соотношений
9. Радарная диаграмма
Радарные диаграммы используются для сравнения нескольких квантованных переменных, например для определения того, какие переменные имеют схожие значения или есть экстремальные значения. Они также помогают наблюдать, какие переменные в наборе данных имеют более высокие или более низкие значения. Радарные диаграммы подходят для демонстрации производительности труда.
Радарная диаграмма также имеет стиль столбцов с накоплением, который можно использовать для двустороннего сравнения между классификацией и сериями, а также для представления пропорций.
Сценарий приложения : анализ измерений, сравнение серий, анализ весов серий
10. Рамочная диаграмма
Рамочная диаграмма — это визуальное средство представления иерархии в виде древовидной структуры, которая четко показывает иерархические отношения.
Сценарий приложения : отображение иерархии, отображение процесса
11. Прямоугольная древовидная диаграмма
Прямоугольная древовидная диаграмма подходит для представления данных с иерархическими отношениями, которые могут визуально отражать сравнение между одними и теми же уровнями.По сравнению с традиционной диаграммой древовидной структуры прямоугольная древовидная диаграмма более эффективно использует пространство и имеет функцию отображения пропорций.
Прямоугольные древовидные диаграммы подходят для отображения иерархии с весовыми отношениями. Если нет необходимости отражать пропорции, диаграмма кадра может быть более четкой.
Сценарий приложения : взвешенные данные дерева, доля данных дерева
12. Воронкообразная диаграмма
Воронкообразная диаграмма показывает долю каждого этапа и визуально отражает размер каждого модуля.Подходит для сравнения рейтингов.
В то же время для сравнения можно использовать воронкообразную диаграмму. Мы располагаем несколько воронкообразных диаграмм по горизонтали, и контраст данных также очень четкий.
Сценарий приложения : ранжирование данных, соотношение, сравнение стандартных значений
13. Диаграмма облака слов
Облако слов — это визуальное представление текстовых данных. Это облачная цветная графика, состоящая из словаря. Он используется для отображения большого количества текстовых данных и может быстро помочь пользователям воспринимать наиболее заметный текст.
Для диаграммы облака слов требуется большой объем данных, и степень различения данных относительно велика, иначе эффект не очевиден. И это не подходит для точного анализа.
Сценарий приложения : поиск по ключевым словам
14. Диаграмма Ганта
Диаграмма Ганта визуально показывает время выполнения миссии, фактический прогресс и сравнение с требованиями. Таким образом, менеджеры могут легко понять, как продвигается задача (проект).
Сценарий приложения : ход проекта, изменения состояния с течением времени, процесс проекта
15. Карта
Карта делится на три типа: региональная карта, точечная карта и карта потока.
(1) Региональная карта
Региональная карта — это карта, которая использует цвет для представления распределения определенного диапазона значений на разделе карты.
Сценарий приложения : сравнение и распределение данных
(2) Точечная карта
Точечная карта — это метод представления географического распределения данных путем нанесения точек одинакового размера на географический фон.
Распределение точек позволяет легко понять общее распределение данных, но не подходит, когда вам нужно наблюдать за отдельными конкретными данными.
Сценарий приложения : распределение данных
Но если вы замените точку пузырьком, то карта точек может не только показать распределение, но и приблизительно сравнить размер данных в каждом регионе.
(3) Карта потоков
Карта потоков отображает данные взаимодействия между областью оттока и областью притока.Обычно выражается линией, соединяющей геометрические центры тяжести пространственных элементов. Ширина или цвет линии указывает значение расхода.
Карты потоков помогают проиллюстрировать распределение географической миграции, а использование динамических потоковых линий уменьшает визуальный беспорядок.
Сценарий приложения : поток, распределение и сравнение данных
16. Тепловая карта
Тепловая карта используется для указания веса каждой точки в географической области.Помимо карты в качестве фонового слоя, вы также можете использовать другие изображения. Цвет на тепловой карте обычно относится к плотности.
Сценарий применения : посещение регионов, распределение тепла, распределение различных вещей
Наконец
Все вышеперечисленное — это 16 часто используемых типов диаграмм для визуализации данных. Если вы хотите начать работу с визуализацией данных, я предлагаю вам начать с изучения этих основных диаграмм и практики с помощью простого в использовании инструмента.
Некоторым людям может показаться, что базовые диаграммы слишком просты и примитивны, и они склонны использовать более сложные диаграммы. Однако чем проще диаграмма, тем легче помочь людям быстро понять данные. Разве это не самая важная цель визуализации данных? Поэтому, пожалуйста, не стоит недооценивать эти основные диаграммы. Потому что пользователи с ними больше всего знакомы. Их следует рассматривать как приоритетные, если они применимы.
Раскрытие информации: Автор не имеет личной заинтересованности в упомянутых проектах.
Истории по теме
Теги
Присоединяйтесь к Hacker Noon
Создайте бесплатную учетную запись, чтобы разблокировать свой собственный опыт чтения.
Диаграмма — Типы диаграмм общих данных
Что такое диаграмма данных?
Диаграмма — это визуальное представление данных. Диаграмма может отображать то, что обычно представляет собой таблицу с рядами чисел на картинке. Это позволяет зрителю быстрее улавливать сравнения и тенденции, чем смотреть на необработанные данные.
Типы диаграмм общих данных
Некоторые из наиболее распространенных типов диаграмм данных включают:
Гистограмма
Гистограмма (также известная как гистограмма) показывает различия между категориями или тенденциями во времени, используя длину или высоту столбцов.Они могут быть показаны с помощью вертикальных или горизонтальных полос. Гистограммы имеют две оси. На одной оси показаны категории, а на другой — диапазон значений.
Категории — это качественные группы, такие как типы компаний, месяцы года, продукты и т. Д. Полоса будет представлять каждую категорию, и обычно между каждой полоской есть пробел.
Вот вертикальная гистограмма:
Вот горизонтальная гистограмма:
Существует два более сложных варианта стандартной гистограммы: столбчатая диаграмма с накоплением и столбчатая диаграмма с кластерами или группами.
Гистограмма с накоплением или диаграмма относительных значений
Гистограмма с накоплением позволяет отображать более сложные отношения между наборами данных. Сложенная полоса позволит вам разместить одну или несколько подкатегорий внутри шкалы, при этом все еще показывая общую сумму. Очевидно, что наложение означает, что подкатегории представляют собой часть целого. Например, предположим, что вы хотите сравнить рост набора студентов в конкретный колледж за последнее десятилетие, но хотите провести различие между студентами мужского и женского пола.
Кластерная столбчатая диаграмма
Сгруппированные или сгруппированные гистограммы похожи на гистограммы с накоплением в том, что они позволяют отображать подкатегории в дополнение к обычным категориям на диаграмме. Если столбцы, которые вы хотите сгруппировать, связаны между собой лишь слабо, вам обязательно нужно использовать кластерное представление. Сгруппированные гистограммы также полезны, когда у вас есть более 3 подкатегорий, которые являются частью целого. Если вы попытаетесь сложить 4 или 6 категорий, ваш график будет намного труднее понять из-за всего визуального шума.
Гистограмма
Гистограмма похожа на гистограмму, но вместо сравнения категорий или поиска тенденций с течением времени каждая полоса показывает, как данные распределяются в одной категории. Каждая полоса представляет собой непрерывный диапазон данных или количество частот для определенной точки данных. В приведенном ниже примере гистограммы показано распределение результатов тестов в классе. Мы можем сразу увидеть, что распределение следует традиционной кривой колокола.
Линейный график
Линейная диаграмма (также известная как линейный график) отображает ряд точек данных на графике и соединяет их линиями.Линейная диаграмма особенно полезна при отображении линий тренда с небольшими различиями или с линиями данных, пересекающими друг друга, как показано в примере ниже.
Круговая диаграмма
Круговая диаграмма — это график, который показывает разбивку элементов в наборе в процентах, представляя их как части круговой диаграммы. Ключ к круговой диаграмме в том, что все срезы должны равняться 100%.
Диаграмма с зонами
Диаграмма с областями работает аналогично линейной диаграмме со значениями, отображаемыми с течением времени.Назначение диаграммы с областями — помочь вам сравнить два или более количества, поскольку они составляют часть единого целого. Он хорошо подходит для отображения тенденции, например, если вы хотите сравнить, какой тип продажи автомобилей с течением времени составляет большую часть ваших общих продаж.
Как создать диаграмму
Первый шаг — убедиться, что данные отформатированы правильно.
Если вы собираетесь создать линейный график, диаграмму с областями или гистограмму, отформатируйте данные следующим образом:
Если вы собираетесь создать круговую или кольцевую диаграмму, отформатируйте данные следующим образом:
На вкладке Insert в SmartDraw щелкните Graph и выберите тип графика.
Выберите файл данных для импорта, и SmartDraw автоматически сгенерирует график.
После импорта вы можете легко изменить заголовок, размещение легенды и даже быстро изменить тип графика с помощью опций Edit Graph или просто дважды щелкнув импортированную диаграмму.
Какая диаграмма или график вам подходит? Руководство по визуализации данных
У вас есть данные и вопросы, но как лучше всего визуализировать эти данные, чтобы получить нужные ответы? Преобразование данных в эффективную визуализацию или информационную панель — это первый шаг к тому, чтобы ваши данные оказали влияние.
Как сказал Генри Д. Хаббард, создатель Периодической таблицы элементов: «В графиках есть волшебство. Профиль кривой мгновенно показывает всю ситуацию — историю жизни эпидемии, паники или эпохи процветания. Кривая информирует разум, пробуждает воображение, убеждает ».
Типы диаграмм и графиков
Гистограмма
Гистограммы — одна из наиболее распространенных визуализаций данных. Вы можете использовать их для быстрого сравнения данных по категориям, выделения различий, отображения тенденций и выбросов, а также быстрого выявления исторических максимумов и минимумов.Гистограммы особенно эффективны, когда у вас есть данные, которые можно разделить на несколько категорий.
График
Линейная диаграмма или линейный график соединяет несколько отдельных точек данных, представляя их как одну непрерывную эволюцию. Используйте линейные диаграммы для просмотра тенденций в данных, обычно с течением времени (например, изменения цен на акции за пять лет или просмотров страниц веб-сайта за месяц). В результате получается простой и понятный способ визуализировать изменения одного значения относительно другого.
Круговая диаграмма
Круговые диаграммы удобны для добавления деталей к другим визуализациям.Сама по себе круговая диаграмма не дает зрителю возможности быстро и точно сравнивать информацию. Поскольку зритель должен создавать контекст самостоятельно, ключевые моменты из ваших данных упускаются. Вместо того, чтобы делать круговую диаграмму фокусом вашей информационной панели, попробуйте использовать их для детализации других визуализаций.
Карты
Карты
позволяют легко визуализировать любую информацию о местоположении, будь то почтовые индексы, аббревиатуры штатов, названия стран или ваше собственное геокодирование. Если у вас есть географическая информация, связанная с вашими данными, карты — это простой и убедительный способ показать, как местоположение соотносится с тенденциями в ваших данных.
Карты плотности
Карты плотности
показывают закономерности или относительные концентрации, которые в противном случае могли бы быть скрыты из-за перекрывающейся метки на карте, помогая вам определить местоположения с большим или меньшим количеством точек данных. Карты плотности наиболее эффективны при работе с набором данных, содержащим множество точек данных в небольшой географической области.
Точечная диаграмма
Диаграммы разброса — это эффективный способ исследовать взаимосвязь между различными переменными, показывая, является ли одна переменная хорошим предиктором другой или они имеют тенденцию изменяться независимо.Диаграмма рассеяния представляет множество различных точек данных на одной диаграмме. Затем диаграмму можно улучшить с помощью аналитики, такой как кластерный анализ или линии тренда.
Диаграмма Ганта
Диаграммы
Ганта отображают график проекта или показывают изменения активности во времени. Диаграмма Ганта показывает шаги, которые необходимо выполнить, прежде чем другие смогут начать, а также распределение ресурсов.
Пузырьковая диаграмма
Хотя пузырьки технически не являются отдельным типом визуализации, их использование в качестве метода добавляет детали к диаграммам рассеяния или картам, чтобы показать взаимосвязь между тремя или более показателями.Варьируя размер и цвет кругов, можно создавать визуально привлекательные диаграммы, которые одновременно представляют большие объемы данных.
Древовидная карта
Древовидные карты связывают различные сегменты ваших данных в единое целое. Как следует из названия диаграммы, каждый прямоугольник в древовидной карте подразделяется на меньшие прямоугольники или дочерние ветви в зависимости от его пропорции к целому. Они эффективно используют пространство, чтобы показать общий процент для каждой категории.
Чтобы получить больше типов диаграмм, наглядных примеров, советов и информации, загрузите нашу техническую документацию.В этой статье вы узнаете о различных типах диаграмм (и графиков) — от гистограмм до карт плотности и диаграмм с усами. Вы также узнаете, когда использовать одну диаграмму вместо другой, а также получите советы о том, как использовать эти типы диаграмм для достижения максимального эффекта.
.
