Содержание
Решение
4НСl(г)+О2(г) = 2Н2О(г)+2Cl2(г) при температуре 500 К и постоянном давлении. Изменится ли численное значение теплового эффекта, если реакцию проводить при постоянном объеме ( V =const ) и T =500 K ?
Тепловой эффект реакции при T =500 K рассчитаем по уравнению (1.8), при этом зависимостью теплоемкости от температуры пренебрегаем.
∆H5000 =∆H0298 +∆C0P 298 (500 −298) .
Используя выражение (1.7) и данные из прил., табл. 1, рассчитаем тепловой эффект при 298 К:
∆H0298 = 2∆H0h3O(г) + 2∆H0Cl2 (г) −4∆H0HCl(г) −∆H0O2 =
= 2 (−241,81) +0 −4 (−92,31) −0 = −114,38 кДж.
Изменение теплоемкости ∆C0P 298 рассчитаем по уравнению (1.9) с учетом данных из прил., табл. 1:
∆C0P 298 = 2C0P h3O(г) +2C0P Cl2 (г) −4C0P HCl(г) −C0P O2 =
= 2 33,61+2 33,93 −4 29,14 −29,37 = −10,85 Дж/ К.
Тогда:
∆H5000 = −114380 +(−10,85) (500 −298) = −116,57 кДж.
Если реакцию проводить при постоянном объеме (V =const ), то необходимо рассчитать ∆U5000 . Пользуясь выражением (1.5), запишем
∆U5000 =∆H5000 −∆n RT
Определим изменение числа молей газообразных веществ в реакции:
∆n = 4 −5 = −1. Тогда ∆U5000 = −116,57 −(−1) 8,31 10−3 500 = −112,42 кДж.
Ответ:
∆H5000 = −116,57 кДж. Если реакцию проводить при постоянном объеме, то тепловой эффект станет равным ∆U5000 = −112,42 кДж.
10
Индивидуальные задания
1. Вычислите стандартную энтальпию образования сульфида цинка (ZnS), используя стандартные энтальпии образования веществ, если известно, что тепловой эффект ( ∆H0298 ) реакции
2ZnS(кр)+3О2(г) = 2ZnO(кр)+2SO2(г)
равен минус 855,86 кДж.
2.Рассчитайте тепловой эффект образования AlF3 из простых веществ при температуре 500 К и постоянном давлении. В интервале 298 – 500 К CP ≠ f (T).
3.Вычислите стандартную энтальпию образования газообразного аммиака (Nh4), используя стандартные энтальпии образования веществ, если известно,
что тепловой эффект реакции 4Nh4(г)+3О2(г) = 2N2(г)+6Н2О(г) равен
∆H0х. р. = −1327,04 кДж.
р. = −1327,04 кДж.
4.По стандартным энтальпиям образования веществ вычислите тепловой
эффект реакции СаО(кр)+3С(кр) = СаС2(кр)+СО(г), протекающей при стандартных условиях.
5.Какое соотношение ∆H0 = ∆U0 , ∆H0 < ∆U0 , ∆H0 > ∆U0 справедливо для каждой из приведенных реакций:
4Nh4(г)+3О2(г) = 2N2(г)+6Н2О(г),
С(кр)+2Н2(г) = СН4(г),
2SO2(г)+О2(г) = 2SO3(г).
Ответ необходимо обосновать. Для последней реакции рассчитайте ∆H0298 .
6. Рассчитайте тепловой эффект при Т=1000 К для реакции Н2S(г)+3/2О2(г) = Н2О(г)+SO2(г). В интервале 298 – 1000 К CP ≠ f (T). Можно ли вычислить тепловой эффект данной реакции при T = 2000 K ?
7. Реакция восстановления Fе2О3 алюминием выражается уравнением
Fе2О3(кр)+2Аl(кр) = Аl2О3(кр)+2Fе(кр).
Вычислите тепловой эффект реакции при стандартных условиях, если на восстановление потребовалось 250 г Аl.
8. Вычислите тепловой эффект реакции 4НВr(г)+О2(г) = 2Н2О(г)+2Вr2(г), протекающей при постоянном давлении (Р=const) и Т=600 К. В интервале 298 – 1000 К CP ≠ f (T).
В интервале 298 – 1000 К CP ≠ f (T).
11
9.Рассчитайте тепловой эффект реакции СО(г)+3Н2(г) = СН4(г)+Н2О(г) протекающей при постоянном давлении ( P =101 кПа) и T =800 K (CP ≠ f (T)).
10.Рассчитайте тепловой эффект реакции С(кр)+СО2(г) = 2СО(г), протекающей при постоянном объеме и T =1000 K . В интервале 298 – 1000 К CP ≠ f (T).
11.Реакция восстановления Fе2О3 алюминием выражается уравнением
Fe2О3+2Аl(кр) = Al2О3(кр)+2Fe(кр). При взаимодействии 1 моля атомов Аl с Fe2О3 выделяется 426,74 кДж теплоты. Вычислите стандартную энтальпию образова-
ния Аl2О3.
12.Рассчитайте тепловой эффект реакции 2ZnS(кр)+3О2(г) = 2ZnO(кр)+2SO2(г), протекающей при постоянном давлении ( P =101 кПа) и T =998 K . (CP ≠ f (T)).
13.Рассчитайте количество теплоты, которое выделится при взаимодействии 25 г Na2О с водой при стандартных условиях. Реакция протекает по уравнению
Na2О(кр)+Н2О(ж) = 2NaОН(кр).
14. Рассчитайте количество теплоты, которое будет поглощено при восстановлении 1 кг оксида цинка графитом, происходящем при стандартных условиях по уравнению ZnO(кр)+С(кр) = Zn(кр)+СО(г).
15. Рассчитайте тепловой эффект реакции 4Nh4(Г)+3О2(г) = 2N2(г)+6Н2О(ж), протекающей при стандартном давлении ( P =101 кПа ) и T =323 K . Теплоем-
кость веществ в интервале 298 – 323 К остается постоянной — CP ≠ f (T).
16.Рассчитайте, пользуясь справочными данными (прил., табл. 1), тепловой
эффект реакции 2Сl2(г)+2h3О(г) = 4HCl(г)+О2(г), протекающей при 798 К и стандартном давлении, считая, что теплоёмкости всех веществ в интервале 298 – 798 К не зависят от температуры.
17.При соединении 2,1 г железа с серой выделилось 3,77 кДж теплоты. Рассчитайте стандартную теплоту образования сульфида железа (FeS).
18.При восстановлении 12,7 г CuO углем (с образованием СО) поглощается 8,24 кДж. Рассчитайте ∆H0298 образования CuO.
19.Найдите массу метана, при полном сгорании которого выделяется теплота, достаточная для нагревания 100 г воды от 20 до 30° С. Мольную изобарную теплоемкость воды принять равной 75,3 Дж/моль·К. Реакция протекает по уравнению: СН4(г)+2О2(г) = 2Н2О(ж)+СО2(г).
20.Рассчитайте тепловой эффект реакции ТiО2(кр)+2С(графит) = Тi(кр)+2СО(г), протекающей при стандартном давлении ( P =101 кПа) и T =1000 K . Теплоем-
кость веществ в интервале 298 – 1000 К остается постоянной. Можно ли вычислить тепловой эффект при 2500 К?
12
2. Второй закон термодинамики. Энтропия системы и ее изменение при протекании
физико-химических процессов
Второй закон термодинамики, как и первый, был открыт путем обобщения опытных данных, связанных с тепловыми процессами. Он устанавливает возможность, направление и глубину протекания самопроизвольных процессов. Существует несколько различных, но эквивалентных формулировок второго за-
кона термодинамики:
–быстро или медленно, но всякая система стремится к состоянию равновесия;
–теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому;
–невозможен периодический процесс, единственным результатом которого является превращение теплоты в работу.
Многочисленными наблюдениями над реальными объектами было установлено, что всякая система стремится к переходу в наиболее вероятное состояние, при котором частицы, составляющие систему, расположены в пространстве наиболее беспорядочно. Для описания подобных процессов введена функция состояния — энтропия (S), единицей измерения которой является Дж/моль·К (кДж/моль·К).
Энтропия является количественной мерой степени неупорядоченности (беспорядка) в системе. Все процессы, связанные с плавлением, испарением, диффузией и т.д., ведут к увеличению энтропии. И, наоборот, при конденсации, полимеризации и т.д. энтропия уменьшается. В физико-химических процессах с участием газообразных веществ можно оценить изменение объема. При увеличении объема системы энтропия увеличивается, и наоборот, например, в реакции N2(г)+3Н2(г) = 2NН3(г) объем уменьшается ( ∆V < 0 ), следовательно ∆S < 0 .
Теплота, поглощенная или выделенная системой в обратимом процессе, связана с изменением энтропии и температурой соотношением, которое выражает
математическую запись второго закона термодинамики:
Q = T ∆S или ∆S = Q . | (2.1) |
T |
|
Физический смысл энтропии — количество рассеянной энергии, отне-
сенной к единице температуры (1 К). В отличие от энтальпии и внутренней энергии для большинства веществ определены абсолютные значения энтропии. При этом следует учесть, что энтропия простых веществ не равна нулю. При стандартных условиях энтропия обозначается S0298 .
Изменение энтропии в химических реакциях при стандартных условиях
13
можно рассчитать аналогично изменению энтальпии (1.7):
|
| ∆S0298 =∑n´Sкон0 −∑n′′Sисх0 , | (2.2) |
где n´, n′′ — | коэффициенты, стоящие в уравнении реакции; |
| |
S0 | , S0 | — энтропии продуктов реакции и исходных веществ при стан- | |
кон | исх |
|
|
дартных условиях (прил. , табл. 1).
, табл. 1).
При фазовых превращениях для одного моля вещества изменение энтропии равно:
∆S = | ∆H | превр | , | (2.3) |
| ||||
T |
| |||
| превр |
| ||
где ∆Hпревр — изменение энтальпии превращения, кДж/моль;
Tпревр — температура фазового превращения, К.
Численное значение энтропии зависит от природы веществ, их агрегатного состояния, температуры и числа молей веществ, участвующих в физикохимических процессах.
Зависимость энтропии от температуры в различных процессах выражается приведенными ниже соотношениями:
Изобарные процессы (Р = const): абсолютное значение энтропии для 1 моля вещества:
S0 | =S0 | +C0 |
| ln T2 | , | (2. | |
T | T | P 298 |
| T1 |
| ||
2 | 1 |
|
|
|
|
| |
|
|
|
|
|
| ||
а ее изменение |
|
|
|
|
|
|
|
| ∆S = C0P 298 ln | T2 | , |
| (2.5) | ||
| T1 |
| |||||
|
|
|
|
|
| ||
Изменение энтропии в химических реакциях при любой температуре, отличающейся от стандартной (298 К), в изобарных процессах вычисляется по
уравнению
∆ST0 = ∆S0298 +∆C0P 298 ln | T | . | (2.6) | |
298 | ||||
|
|
|
Изменение теплоемкости в химических реакциях (∆CP) рассчитывается по выражению (1.9).
Изохорные процессы (V = const): абсолютное значение энтропии для 1 моля вещества:
14
а) Ттр.т, Ртр.т б) Тн.т.к, Р = 1 атм; в) Тн.т.к Ртр т. Необходимые для расчета данные возьмите из таблицы… — Контрольная работа #1103438 — Физическая химия
Задание 1 3
Задание 2 3
Задание 3 4
Задание 4 5
Задание 5 6
Список используемой литературы 10
Вариант 7
Задание 1
Вычислите тепловой эффект реакции А при 298 К: а) при Р=const; б) при V=const. Тепловые эффекты образования веществ при стандартных условиях возьмите из справочника [М.]
N2O4=2NO2…
Задание 2
Вычислите тепловой эффект образования вещества А из простых веществ при 298К и стандартном давлении, если известна его теплота сгорания при этой температуре и стандартном давлении. Сгорание происходит до СО2 и Н2О.
Сгорание происходит до СО2 и Н2О.
Пропионитрил C3H5Nж…
Задание 3
Выведите аналитическую зависимость теплового эффекта (Дж) реакции А от температуры, если известен тепловой эффект этой реакции при 298К. Уравнения зависимости Ср = f(T) возьмите из справочника [M]. Вычислите тепловой эффект реакции при температуре Т.
N2O4=2NO2
Т=400…
Задание 4
Рассчитайте изменение энтропии при нагревании (охлаждении) при постоянном давлении в интервале температур от 303К до 473К 80 кг метанола, если известны его температуры плавления и кипения, теплоемкости в твердом, жидком и газообразном состояниях, теплоты плавления и испарения…
Задание 5
По зависимости давления насыщенного пара от температуры и плотности вещества и плотности данного вещества А с молекулярной массой М в твердом и жидком состояниях (dT, и dЖ в кг/м3) в тройной точке (тр.т): 1) постройте график зависимости lg Р от 1/Т; 2) определите по графику координаты тройной точки; 3) рассчитайте среднюю теплоту испарения и возгонки; 4) постройте график зависимости давления насыщенного пара от температуры; 5) определите теплоту плавления вещества при температуре тройной точки; 6) вычислите dT/dP для процесса плавления при температуре тройной точки; 7) вычислите температуру плавления вещества при давлении Р Па; 8) вычислите изменение энтропии, энергий Гиббса и Гельмгольца, энтальпии и внутренней энергии для процесса возгонки 1 моль вещества в тройной точке; 9) определите число термодинамических степеней свободы при следующих значениях температуры и давления: а) Ттр. т, Ртр.т б) Тн.т.к, Р = 1 атм; в) Тн.т.к Ртр т. Необходимые для расчета данные возьмите из таблицы…
т, Ртр.т б) Тн.т.к, Р = 1 атм; в) Тн.т.к Ртр т. Необходимые для расчета данные возьмите из таблицы…
1. Хмельницкий Р.А. Физическая и коллоидная химия. – М.: Высшая школа, 2008.
2. Тиноко И., Зауэр К., Вэнг Дж., Паглиси Дж. Физическая химия. Принципы и применение в биологических науках. – М.: Техносфера, 2005. 744 с.
3. Балезин С.А., Ерофеев Б.В., Подобаев Н.И. Основы физической и коллоидной химии. – М.: Просвещение, 2005.
4. Болдырев А.И. Физическая и коллоидная химия. – М.: Высшая школа, 1983.
5. Кузнецов В.В., Усть-Качинцев В.К. Физическая и коллоидная химия. – М.: Высшая школа, 2006.
6. Кузнецов В.В., Усть-Качинцев В.К. Физическая и коллоидная химия. – М.: Высшая школа, 2006.
7. Балезин С.А. Практикум по физической и коллоидной химии. – М.: Просвещение. 2004.
8. Герасимов Я.И. и др. Курс физической химии: В 2 т. – М.: Химия. ТТ. 1-2, 2009.
9. Киреев В.А. Курс физической химии. – М.: Химия, 2008.
10. Равдель А. А., Пономарева А.М. Краткий справочник физико-химических величин. – Л.: Химия, 2003.
А., Пономарева А.М. Краткий справочник физико-химических величин. – Л.: Химия, 2003.
| Тема: | Вариант 7 Задание 1 Вычислите тепловой эффект реакции А при 298 К: а) при Р=const; б) при V=const. Тепловые эффекты образования веществ при стандартных условиях возьмите из справочника [М.] N2O4=2NO2… Задание 2 Вычислите тепловой эффект образования вещества А из простых веществ при 298К и стандартном давлении, если известна его теплота сгорания при этой температуре и стандартном давлении. Сгорание происходит до СО2 и Н2О. Пропионитрил C3H5Nж… Задание 3 Выведите аналитическую зависимость теплового эффекта (Дж) реакции А от температуры, если известен тепловой эффект этой реакции при 298К. Уравнения зависимости Ср = f(T) возьмите из справочника [M]. Вычислите тепловой эффект реакции при температуре Т. N2O4=2NO2 Т=400… Задание 4 Рассчитайте изменение энтропии при нагревании (охлаждении) при постоянном давлении в интервале температур от 303К до 473К 80 кг метанола, если известны его температуры плавления и кипения, теплоемкости в твердом, жидком и газообразном состояниях, теплоты плавления и испарения.  .. ..Задание 5 По зависимости давления насыщенного пара от температуры и плотности вещества и плотности данного вещества А с молекулярной массой М в твердом и жидком состояниях (dT, и dЖ в кг/м3) в тройной точке (тр.т): 1) постройте график зависимости lg Р от 1/Т; 2) определите по графику координаты тройной точки; 3) рассчитайте среднюю теплоту испарения и возгонки; 4) постройте график зависимости давления насыщенного пара от температуры; 5) определите теплоту плавления вещества при температуре тройной точки; 6) вычислите dT/dP для процесса плавления при температуре тройной точки; 7) вычислите температуру плавления вещества при давлении Р Па; 8) вычислите изменение энтропии, энергий Гиббса и Гельмгольца, энтальпии и внутренней энергии для процесса возгонки 1 моль вещества в тройной точке; 9) определите число термодинамических степеней свободы при следующих значениях температуры и давления: а) Ттр.т, Ртр.т б) Тн.т.к, Р = 1 атм; в) Тн.т.к Ртр т. Необходимые для расчета данные возьмите из таблицы.  .. .. |
| Артикул: | 1103438 |
| Дата написания: | 08.01.2014 |
| Тип работы: | Контрольная работа |
| Предмет: | Физическая химия |
| Оригинальность: | Антиплагиат.ВУЗ — 88% |
| Количество страниц: | 10 |
(PDF) Практические занятие №1
Science: Problems and Innovations”, состоявшейся 30 апреля 2017 г. в г.
Пенза. // МЦНС «Наука и Просвещение», г. Пенза, 2017, Часть 1, № 176. С.
157 – 160.
8. А.А. Yusupkhodjayev, Sh.Т. Khojiev, J.S. Mamirkulov. The analysis of
physic chemical properties of metallurgical molten slags// Сборник статей
Международной научно-практической конференции “Управление социально-
экономическими системами: теория, методология, практика”, состоявшейся
15 июня 2017 г. в г. Пенза. // МЦНС «Наука и Просвещение», г. Пенза, 2017,
в г. Пенза. // МЦНС «Наука и Просвещение», г. Пенза, 2017,
Часть 1, № 190. С. 12 – 15.
9. А.А. Yusupkhodjayev, Sh.Т. Khojiev, G.A. Kimsanboeva. The analysis of
the arch of service of autogenous smelting furnaces during processing of copper
sulfide concentrates// Сборник статей Международной научно-практической
конференции “Управление социально-экономическими системами: теория,
методология, практика”, состоявшейся 15 июня 2017 г. в г. Пенза. // МЦНС
«Наука и Просвещение», г. Пенза, 2017, Часть 1, № 190. С. 16 – 18.
10. А.А. Yusupkhodjayev, Sh.Т. Khojiev, S.B. Mirzajanova. Usage of
reducing-sulfidizing agents in copper-bearing slags depletion// Сборник статей
Международной научно-практической конференции “Управление социально-
экономическими системами: теория, методология, практика”, состоявшейся
15 июня 2017 г. в г. Пенза. // МЦНС «Наука и Просвещение», г. Пенза, 2017,
Часть 1, № 190. С. 19 –21.
С. 19 –21.
11. А.А. Yusupkhodjayev, Sh.Т. Khojiev, J. Usarov. Reasons of copper loss
with slag// Сборник статей Международной научно-практической
конференции “Управление социально-экономическими системами: теория,
методология, практика”, состоявшейся 15 июня 2017 г. в г. Пенза. // МЦНС
«Наука и Просвещение», г. Пенза, 2017, Часть 1, № 190. С.22 –23.
12. А.А. Yusupkhodjayev, Sh.Т. Khojiev, V.K. Nodirov. Modern state of
technology of copper extraction// Сборник статей победителей VIII
Международной научно-практической конференции “Современная
экономика: актуальные вопросы, достижения и инновации”, состоявшейся 20
июня 2017 г. в г. Пенза. // МЦНС «Наука и Просвещение», г. Пенза, 2017,
Часть 2, № 191. С.59 –61.
13. M.M. Yakubov, A.A. Yusupxodjayev, Sh.T. Hojiyev. Eritish jarayonida
misning shlak bilan isrofini kamaytirish yo’llari // Kompozitsion materiallar.
Toshkent, 2017, №1. 18 – 19 b.
14. Yusupkhodjayev A.A., Khojiev Sh.T., Kimsanboeva G.A. Studying of
the clinker coating formed on internal the laying of the oxygen-torch furnace at
fusion of sulphidic copper concentrates // Сборник статей XIII Международной
научно-практической конференции “European research”, состоявшейся 7
декабря 2017 г. в г. Пенза. // МЦНС «Наука и Просвещение», г. Пенза, 2017,
Часть 1, № 248. С. 62 – 65.
15. Samadov A.U., Khojiev Sh.T., Buzurkhanova F.S., Ruziev Z.N.
Perspective method of smelting low-sulfur copper concentrates // Научные
достижения и открития современной молодёжи: сборник статей III
5.3: Энтальпия — Chemistry LibreTexts
Цели обучения
- Знать ключевые особенности функции состояния.
- Использовать закон Гесса и термохимические циклы для расчета изменений энтальпии химических реакций.

И тепло, и работа представляют собой механизмы передачи энергии. Как обсуждалось ранее, термин «тепло» относится к процессу , в котором тело (например, содержимое чайника) приобретает или теряет энергию как прямое следствие того, что его температура отличается от температуры окружающей среды.Точно так же работа относится к передаче энергии без разницы температур. Следовательно, работа, как и энергия, может принимать различные формы, наиболее известные из которых — механическая и электрическая.
- Механическая работа возникает, когда объект перемещается на расстояние \ (Δx \) против противодействующей силы \ (f \): \ [w_ {механика} = f Δx \]
- Электрические работы выполняются, когда тело, имеющее заряд \ (q \), движется через разность потенциалов \ (ΔV \). \ [w_ {электрические} = q \ Delta V \]
Единица измерения — Джоуль.Работа, как и тепло, существует только при передаче энергии. Когда два тела находятся в тепловом контакте и энергия перетекает от более теплого тела к более холодному, этот процесс называется «теплом».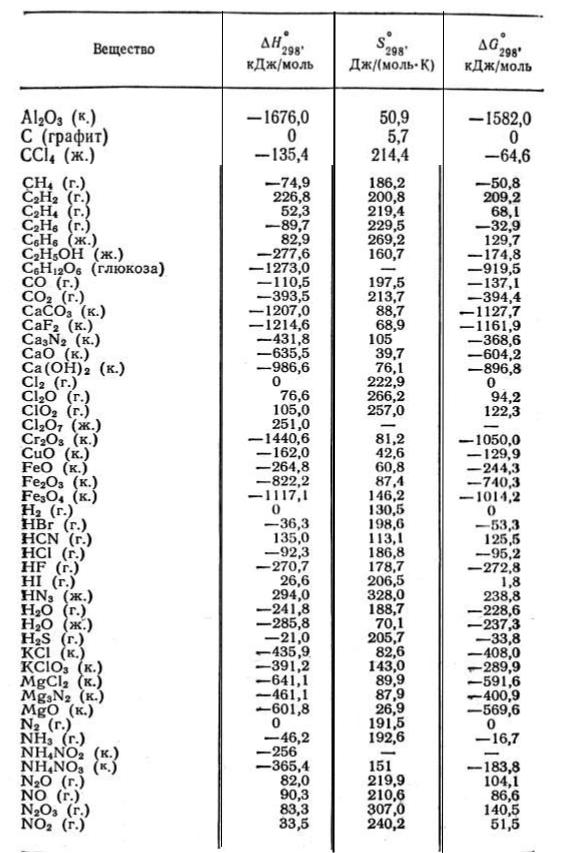 Передача энергии в систему или из системы любым другим способом, кроме тепла, называется «работой».
Передача энергии в систему или из системы любым другим способом, кроме тепла, называется «работой».
Энтальпия как составная функция
Чтобы лучше понять взаимосвязь между тепловым потоком (\ (q \)) и результирующим изменением внутренней энергии (\ (ΔU \)), мы можем рассмотреть два набора ограничивающих условий: реакции, которые происходят при постоянном объеме, и реакции, которые происходят при постоянном давлении.Мы будем предполагать, что работа PV — это единственный вид работы, возможный для системы, поэтому мы можем подставить ее определение (w = -P \ Delta V \) в первый закон термодинамики (\ (\ Delta U = q + w \) )), чтобы получить:
\ [ΔU = q — PΔV \ label {5.2.5} \]
, где убраны индексы.
Если реакция происходит в закрытом сосуде, объем системы фиксирован, а ΔV равно нулю. В этих условиях тепловой поток (часто обозначаемый символом q v для обозначения постоянного объема) должен равняться ΔU:
\ [\ underset {\ textrm {постоянный объем}} {q _ {\ textrm v} = \ Delta U} \ label {5. 3.3} \]
3.3} \]
При постоянном объеме работа в \ (PV \) невозможна, а изменение внутренней энергии системы равно количеству тепла, передаваемому из системы в окружающую среду, или наоборот.
Однако многие химические реакции проводятся не в герметичных контейнерах с постоянным объемом, а в открытых контейнерах при более или менее постоянном давлении около 1 атм. Тепловой поток в этих условиях обозначается символом \ (q_p \) для обозначения постоянного давления.Замена q в уравнении \ (\ ref {5.3.3} \) на \ (q_p \) и преобразование для решения для q p ,
\ [\ underset {\ textrm {постоянное давление}} {q _ {\ textrm p} = \ Delta U + P \ Delta V} \ label {5.3.4} \]
Таким образом, при постоянном давлении тепловой поток для любого процесса равен изменению внутренней энергии системы плюс проделанная работа PV.
Поскольку условия постоянного давления так важны в химии, новая функция состояния, называемая энтальпией (H), определяется как
\ [H = U + PV \]
При постоянном давлении энтальпия системы изменяется следующим образом:
\ [ΔH = ΔU + Δ (PV) = ΔU + PΔV \ label {5. 3.5} \]
3.5} \]
Сравнение двух предыдущих уравнений показывает, что при постоянном давлении изменение энтальпии системы равно тепловому потоку: \ (ΔH = q_p \). Это выражение согласуется с нашим определением энтальпии, где мы заявили, что энтальпия — это тепло, поглощаемое или производимое во время любого процесса, который происходит при постоянном давлении.
При постоянном давлении изменение энтальпии системы равно тепловому потоку: \ (ΔH = q_p \).
Пример \ (\ PageIndex {1} \)
Молярная энтальпия плавления льда при 0.0 ° C и давление 1,00 атм составляет 6,01 кДж, а молярные объемы льда и воды при 0 ° C составляют 0,0197 л и 0,0180 л соответственно. Рассчитайте ΔH и ΔU для таяния льда при 0,0 ° C.
Дано : энтальпия плавления льда, давление и молярные объемы льда и воды
Запрошено : ΔH и ΔU для таяния льда при 0,0 ° C
Стратегия :
- Определите знак q и установите это значение равным ΔH.

- Рассчитайте Δ (PV) на основе предоставленной информации.
- Определите ΔU, подставив вычисленные значения в уравнение \ (\ ref {5.3.5} \).
Решение
A Поскольку при таянии 1 моль льда из окружающей среды поглощается 6,01 кДж тепла, q = +6,01 кДж. Когда процесс осуществляется при постоянном давлении, q = q p = ΔH = 6,01 кДж.
B Чтобы найти ΔU с помощью уравнения \ (\ ref {18.11} \), нам нужно вычислить Δ (PV). Процесс осуществляется при постоянном давлении 1,00 атм, поэтому
\ [\ begin {align} \ Delta (PV) & = P \ Delta V = P (V _ {\ textrm f} -V) = (1.{-3} \; \ mathrm {L \ cdot atm}) (101.3 \; \ mathrm {J / L \ cdot atm}) = — 0,0017 \ textrm {J} \ end {align} \]
C Подставляя вычисленные значения ΔH и PΔV в уравнение 18.11,
ΔU = ΔH — PΔV = 6010 Дж — (−0,0017 Дж) = 6010 Дж = 6,01 кДж
Упражнение \ (\ PageIndex {1} \)
При 298 К и 1 атм преобразование графита в алмаз требует ввода 1,850 кДж тепла на моль углерода. Мольные объемы графита и алмаза составляют 0,00534 л и 0,00342 л соответственно.Рассчитайте ΔH и ΔU для превращения C (графита) в C (алмаз) в этих условиях.
Мольные объемы графита и алмаза составляют 0,00534 л и 0,00342 л соответственно.Рассчитайте ΔH и ΔU для превращения C (графита) в C (алмаз) в этих условиях.
- Ответьте на
ΔH = 1,85 кДж / моль
- Ответ б
ΔU = 1,85 кДж / моль
Связь между ΔH и ΔU
Если ΔH реакции известно, мы можем использовать изменение энтальпии системы (Уравнение \ (\ ref {5.3.5} \)), чтобы вычислить ее изменение внутренней энергии.Когда в реакции участвуют только твердые вещества, жидкости, жидкие растворы или любая их комбинация, объем существенно не изменяется (ΔV = 0). В этих условиях мы можем упростить уравнение \ (\ ref {5.3.5} \) до ΔH = ΔU. Однако, если речь идет о газах, ΔH и ΔU могут значительно отличаться. Мы можем вычислить ΔU из измеренного значения ΔH, используя правую часть уравнения \ (\ ref {5.3.5} \) вместе с законом идеального газа, PV = nRT. Признавая, что Δ (PV) = Δ (nRT), мы можем переписать уравнение \ (\ ref {5.3.5} \) следующим образом:
Признавая, что Δ (PV) = Δ (nRT), мы можем переписать уравнение \ (\ ref {5.3.5} \) следующим образом:
\ [ΔH = ΔU + Δ (PV) = ΔU + Δ (nRT) \ label {5.3.6} \]
При постоянной температуре Δ (nRT) = RTΔn, где Δn — разница между конечным и начальным числом молей газа. Таким образом,
\ [ΔU = ΔH — RTΔn \ label {5.3.7} \]
Для реакций, которые приводят к чистому производству газа, Δn> 0, поэтому ΔU <ΔH. И наоборот, эндотермические реакции (ΔH> 0), которые приводят к чистому потреблению газа, имеют Δn <0 и ΔU> ΔH. Связь между ΔH и ΔU для систем, включающих газы, проиллюстрирована в Примере \ (\ PageIndex {2} \).
Для реакций, приводящих к чистому выделению газа, ΔU <ΔH. Для эндотермических реакций, которые приводят к чистому расходу газа, ΔU> ΔH.
Пример \ (\ PageIndex {2} \): взаимосвязь между ΔH и ΔU в реакциях выделения газа
Сгорание графита с образованием диоксида углерода описывается уравнением
\ [C _ {(графит, s)} + O_ {2 (g)} → CO_ {2 (g)} \]
При 298 К и 1,0 атм ΔH = -393,5 кДж / моль графита для этой реакции, а молярный объем графита равен 0. 0053 L. Что такое ΔU реакции?
0053 L. Что такое ΔU реакции?
Дано : вычисленное химическое уравнение, температура, давление, ΔH и молярный объем реагента
.
Спросил : ΔU
Стратегия :
- Используйте сбалансированное химическое уравнение, чтобы рассчитать изменение количества молей газа во время реакции.
- Подставьте это значение и данные в уравнение \ (\ ref {5.3.7} \), чтобы получить ΔU.
Решение
A В этой реакции образуется 1 моль газа (CO 2 ) и расходуется 1 моль газа (O 2 ).Таким образом, Δn = 1 — 1 = 0.
B Подставляя это вычисленное значение и данные значения в уравнение \ (\ ref {5.3.7} \),
ΔU = ΔH − RTΔn = (- 393,5 кДж / моль) — [8,314 Дж / (моль⋅K)] (298 K) (0)
= (- 393,5 кДж / моль) — (0 Дж / моль) = — 393,5 кДж / моль
Чтобы понять, почему необходимо учитывать только изменение объема газов, обратите внимание, что молярный объем графита составляет всего 0,0053 л. Изменение количества молей газа соответствует изменению объема на 22,4 л / моль газа. газ при стандартной температуре и давлении (STP), поэтому объем потребляемого или производимого газа в этом случае равен (1) (22.4 л) = 22,4 л, что намного, намного больше, чем объем 1 моль твердого вещества, такого как графит.
Изменение количества молей газа соответствует изменению объема на 22,4 л / моль газа. газ при стандартной температуре и давлении (STP), поэтому объем потребляемого или производимого газа в этом случае равен (1) (22.4 л) = 22,4 л, что намного, намного больше, чем объем 1 моль твердого вещества, такого как графит.
Упражнение \ (\ PageIndex {2} \)
Вычислить \ (ΔU \) для преобразования газообразного кислорода в озон при 298 K:
\ [3O_2 (g) \ rightarrow 2O_3 (g). \]
Значение \ (ΔH \) для реакции составляет 285,4 кДж.
- Ответ
288 кДж
Как показано в примере \ (\ PageIndex {2} \), величины ΔH и ΔU для реакций, в которых участвуют газы, обычно довольно схожи, даже если есть чистое производство или потребление газов.
Сводка
Энтальпия — это функция состояния, а изменение энтальпии системы равно сумме изменения внутренней энергии системы и проделанной работы PV. Энтальпия — это функция состояния, изменение которой указывает количество тепла, передаваемого от системы к ее окружению или наоборот, при постоянном давлении. Изменение внутренней энергии системы — это сумма переданного тепла и проделанной работы. При постоянном давлении тепловой поток (q) и внутренняя энергия (U) связаны с энтальпией системы (H).Тепловой поток равен изменению внутренней энергии системы плюс проделанная работа PV. Когда объем системы постоянен, изменения ее внутренней энергии можно рассчитать, подставив закон идеального газа в уравнение для ΔU.
Энтальпия — это функция состояния, изменение которой указывает количество тепла, передаваемого от системы к ее окружению или наоборот, при постоянном давлении. Изменение внутренней энергии системы — это сумма переданного тепла и проделанной работы. При постоянном давлении тепловой поток (q) и внутренняя энергия (U) связаны с энтальпией системы (H).Тепловой поток равен изменению внутренней энергии системы плюс проделанная работа PV. Когда объем системы постоянен, изменения ее внутренней энергии можно рассчитать, подставив закон идеального газа в уравнение для ΔU.
18,6: Изменение энергии Гиббса и равновесие
Δ G имеет значение только для изменений, при которых температура и давление остаются постоянными. Это условия, при которых большинство реакций проводится в лаборатории; система обычно открыта для атмосферы (постоянное давление), и мы начинаем и заканчиваем процесс при комнатной температуре (после того, как все тепло, которое мы добавили или высвободилось в результате реакции, рассеялось. ) Важность функции Гиббса трудно переоценить: она служит единственной главной переменной, которая определяет, возможно ли данное химическое изменение термодинамически. Таким образом, если свободная энергия реагентов больше, чем у продуктов, энтропия мира будет увеличиваться, когда реакция происходит, как написано, и поэтому реакция будет иметь тенденцию происходить спонтанно. И наоборот, если свободная энергия продуктов превышает свободную энергию реагентов, то реакция не будет происходить в указанном направлении, а будет иметь тенденцию протекать в обратном направлении.
) Важность функции Гиббса трудно переоценить: она служит единственной главной переменной, которая определяет, возможно ли данное химическое изменение термодинамически. Таким образом, если свободная энергия реагентов больше, чем у продуктов, энтропия мира будет увеличиваться, когда реакция происходит, как написано, и поэтому реакция будет иметь тенденцию происходить спонтанно. И наоборот, если свободная энергия продуктов превышает свободную энергию реагентов, то реакция не будет происходить в указанном направлении, а будет иметь тенденцию протекать в обратном направлении.
Температурная зависимость от ΔG
При спонтанном изменении энергия Гиббса всегда уменьшается и никогда не увеличивается. Это, конечно, отражает тот факт, что энтропия мира ведет себя прямо противоположным образом (из-за отрицательного знака в члене T Δ S ).
\ [H_2O _ {(l)} \ rightarrow H_2O _ {(s)} \ label {23.5.6} \]
вода ниже точки замерзания испытывает уменьшение своей энтропии, но тепло, выделяемое в окружающую среду, более чем компенсирует это, поэтому энтропия мира увеличивается, свободная энергия H 2 O уменьшается, и процесс продолжается. спонтанно.
спонтанно.
Примечание
При спонтанном изменении энергия Гиббса всегда уменьшается и никогда не увеличивается.
Важным следствием одностороннего нисходящего пути свободной энергии является то, что как только она достигает минимально возможного значения, все чистые изменения прекращаются. Это, конечно, представляет собой состояние химического равновесия. Эти отношения хорошо резюмируются следующим образом:
- ΔG <0: реакция может самопроизвольно идти вправо: \ [A \ rightarrow B \]
- ΔG> 0: реакция может самопроизвольно идти влево: \ [A \ leftarrow B \]
- ΔG = 0: реакция находится в равновесии; количество [A] и [B] не изменится
Напомнить условие самопроизвольного изменения
\ [ΔG = ΔH — TΔS <0 \ label {Master} \]
очевидно, что температурная зависимость Δ G почти полностью зависит от изменения энтропии, связанного с процессом.(Мы говорим «почти», потому что значения Δ H и Δ S сами по себе немного зависят от температуры; оба значения постепенно увеличиваются с температурой). В частности, обратите внимание, что в приведенном выше уравнении знак изменения энтропии определяет, станет ли реакция более или менее спонтанной при повышении температуры. Для любой данной реакции знак Δ H также может быть положительным или отрицательным. Это означает, что существует четыре возможности влияния температуры на спонтанность процесса.
В частности, обратите внимание, что в приведенном выше уравнении знак изменения энтропии определяет, станет ли реакция более или менее спонтанной при повышении температуры. Для любой данной реакции знак Δ H также может быть положительным или отрицательным. Это означает, что существует четыре возможности влияния температуры на спонтанность процесса.
Следующие ниже случаи обобщают эти соотношения для четырех комбинаций знаков Δ H и Δ S . (Обратите внимание, что использование стандартных значений Δ H ° и Δ S ° в примерах реакций здесь не совсем корректно и может привести к ошибочным результатам при общем использовании.)
> 0
В этих условиях члены Δ H и T Δ S будут отрицательными, поэтому Δ G будет отрицательным независимо от температуры.Экзотермическая реакция, энтропия которой возрастает, будет спонтанной при всех температурах.
Пример реакции
\ [C _ {(графит)} + O_ {2 (g)} \ rightleftharpoons CO_ {2 (g)} \]
- Δ H ° = –393 кДж
- Δ S ° = +2.
 9 Дж K –1
9 Дж K –1 - Δ G ° = –394 кДж при 298 К
Положительное изменение энтропии в основном связано с большей массой молекул CO 2 по сравнению с молекулами O 2 .
<0
Если реакция является достаточно экзотермической, она может вызвать отрицательное значение Δ G только при температурах, ниже которых | T Δ S | <| Δ H |. Это означает, что существует температура T = Δ H / Δ S , при которой реакция находится в равновесии; реакция будет протекать только самопроизвольно при ° С при температуре ниже 900 ° С. Замерзание жидкости или конденсация газа — наиболее распространенные примеры этого состояния.
Пример реакции:
\ [3 H_2 + N_2 \ rightleftharpoons 2 NH_ {3 (g)} \]
- ΔH ° = –46,2 кДж
- ΔS ° = –389 Дж · К – 1
- ΔG ° = –16,4 кДж при 298 К
Уменьшение количества молей газа в синтезе аммиака по Хаберу приводит к отрицательному изменению энтропии, делая реакцию самопроизвольной только при низких температурах . Таким образом, более высокое значение T , которое ускоряет реакцию, также снижает ее степень.
Таким образом, более высокое значение T , которое ускоряет реакцию, также снижает ее степень.
> 0
Это обратное предыдущему случаю; увеличение энтропии должно преодолеть недостаток эндотермического процесса, так что TΔS> ΔH. Поскольку влияние температуры должно «усилить» влияние положительного ΔS, процесс будет самопроизвольным при температурах выше T = ΔH / ΔS. (Подумайте о плавлении и кипении.)
Пример реакции:
\ [N_2O_ {4 (g)} \ rightleftharpoons 2 NO_ {2 (g)} \]
- Δ H ° = 55.3 кДж
- Δ S ° = +176 Дж К –1
- Δ G ° = +2,8 кДж при 298 К
Реакции диссоциации обычно являются эндотермическими с положительным изменением энтропии и, следовательно, являются спонтанными при высоких температурах . В конечном итоге все молекулы разлагаются на свои атомы при достаточно высоких температурах.
<0
Поскольку оба Δ H и Δ S работают против него, этот вид процесса не будет происходить самопроизвольно при любой температуре.Вещество А всегда имеет большее количество доступных энергетических состояний и поэтому всегда является предпочтительной формой.
Пример реакции:
\ [½ N_2 + O_2 \ rightleftharpoons NO_ {2 (g)} \]
- Δ H ° = 33,2 кДж
- ΔS ° = –249 Дж К — 1
- Δ G ° = +51,3 кДж при 298 К
Эта реакция не является спонтанной при любой температуре , а это означает, что ее обратная реакция всегда спонтанна .Но поскольку обратная реакция кинетически ингибируется, NO 2 может существовать бесконечно при обычных температурах, даже если он термодинамически нестабилен.
Вышеупомянутые случаи и связанные с ними сюжеты являются важными; не пытайтесь запомнить их, но убедитесь, что вы понимаете и можете объяснить или воспроизвести их для данного набора Δ H и Δ S .
- Их наиболее важными отличительными особенностями являются положение линии Δ H (выше или ниже линии T Δ S ) и наклон последней, который, конечно, зависит от знака Δ S .
- Реакция A → B будет происходить спонтанно только тогда, когда Δ G отрицательное (синие стрелки указывают вниз).
- Из-за небольшой температурной зависимости Δ S , графики T Δ S не совсем прямые, как показано здесь. Точно так же линии, представляющие Δ H , еще более изогнуты.
Два других графика на каждой диаграмме относятся только к химическим соединениям.
- Каждая пара диаграмм уровней энергии отображает относительное расстояние между микроскопическими уровнями энергии в реагентах и продуктах, что отражено величиной Δ S °.(Чем больше энтропия, тем ближе друг к другу квантованные микросостояния.)
- Красная заливка указывает диапазон уровней энергии, доступных для системы при каждой температуре.
 Спонтанное направление реакции всегда будет в том направлении, в котором красная заливка перекрывает большее количество энергетических уровней, что приводит к максимальному распределению тепловой энергии.
Спонтанное направление реакции всегда будет в том направлении, в котором красная заливка перекрывает большее количество энергетических уровней, что приводит к максимальному распределению тепловой энергии. - Обратите внимание, что вертикальные смещения соответствуют Δ H ° для реакции.
- Никогда не забывайте, что именно способность тепловой энергии распространяться в максимально возможное количество этих состояний определяет тенденцию происходящего процесса. Конечно, все это не в масштабе!
Равновесие жидкость-пар
Чтобы лучше понять, как различные компоненты ΔG определяют, происходит ли процесс самопроизвольно, мы теперь рассмотрим простое и знакомое физическое изменение: преобразование жидкой воды в водяной пар. Если этот процесс проводится при 1 атм и нормальной температуре кипения 100.00 ° C (373,15 K), мы можем рассчитать ΔG из экспериментально измеренного значения ΔH vap (40,657 кДж / моль). Для испарения 1 моля воды \ (ΔH = 40,657; Дж \), поэтому процесс сильно эндотермический. \ circ \ textrm C} = \ Delta H-T \ Delta S = \ textrm {40,657 Дж} — [(\ textrm {383.\ circ \ textrm C} = \ Delta HT \ Delta S = \ textrm {40 657 Дж} — [(\ textrm {363,15 K}) (\ textrm {108,96 J / K})] = \ textrm {1088 J} \]
\ circ \ textrm C} = \ Delta H-T \ Delta S = \ textrm {40,657 Дж} — [(\ textrm {383.\ circ \ textrm C} = \ Delta HT \ Delta S = \ textrm {40 657 Дж} — [(\ textrm {363,15 K}) (\ textrm {108,96 J / K})] = \ textrm {1088 J} \]
При 90 ° C ΔG> 0 и вода не превращается самопроизвольно в водяной пар. При использовании всех цифр на дисплее калькулятора при выполнении наших расчетов ΔG 110 ° C = 1090 Дж = −ΔG 90 ° C , как мы и предполагали.
Мы также можем вычислить температуру, при которой жидкая вода находится в равновесии с водяным паром. Вставка значений ΔH и ΔS в определение ΔG (уравнение \ (\ ref {Master} \)), установка ΔG = 0 и решение для T,
0 Дж = 40 657 Дж-Т (108.96 Дж / К)
Т = 373,15 К
Таким образом, ΔG = 0 при T = 373,15 K и 1 атм, что указывает на то, что жидкая вода и водяной пар находятся в равновесии; эта температура называется нормальной температурой кипения воды. При температурах выше 373,15 К ΔG отрицательна, и вода самопроизвольно и необратимо испаряется. Ниже 373,15 К ΔG положительна, и вода самопроизвольно не испаряется. Вместо этого водяной пар при температуре ниже 373,15 К и давлении 1 атм самопроизвольно и необратимо конденсируется в жидкую воду.На рисунке \ (\ PageIndex {1} \) показано, как члены ΔH и TΔS меняются в зависимости от температуры при испарении воды. Когда две линии пересекаются, ΔG = 0 и ΔH = TΔS.
Ниже 373,15 К ΔG положительна, и вода самопроизвольно не испаряется. Вместо этого водяной пар при температуре ниже 373,15 К и давлении 1 атм самопроизвольно и необратимо конденсируется в жидкую воду.На рисунке \ (\ PageIndex {1} \) показано, как члены ΔH и TΔS меняются в зависимости от температуры при испарении воды. Когда две линии пересекаются, ΔG = 0 и ΔH = TΔS.
Рисунок \ (\ PageIndex {1} \): Температурная зависимость ΔH и TΔS для испарения воды. И ΔH, и TΔS зависят от температуры, но линии имеют противоположный наклон и пересекаются при 373,15 K при 1 атм, где ΔH = TΔS. Поскольку ΔG = ΔH — TΔS, при этой температуре ΔG = 0, что указывает на то, что жидкая и паровая фазы находятся в равновесии. Таким образом, нормальная температура кипения воды составляет 373 ° C.15 К. Выше нормальной точки кипения член TΔS больше, чем ΔH, в результате чего ΔG <0; следовательно, жидкая вода самопроизвольно испаряется. Ниже нормальной точки кипения член ΔH больше, чем TΔS, поэтому ΔG> 0. Таким образом, жидкая вода не испаряется самопроизвольно, а водяной пар самопроизвольно конденсируется в жидкость.
Аналогичная ситуация возникает при превращении жидкого яичного белка в твердый при варке яйца. Основным компонентом яичного белка является белок под названием альбумин, который удерживается в компактной упорядоченной структуре большим количеством водородных связей.Их разрушение требует ввода энергии (ΔH> 0), которая превращает альбумин в сильно разупорядоченную структуру, в которой молекулы объединяются в неорганизованное твердое тело (ΔS> 0). При температурах выше 373 K член TΔS преобладает, и ΔG <0, поэтому преобразование сырого яйца в сваренное вкрутую является необратимым и спонтанным процессом при температурах выше 373 K.
Свободная энергия и константа равновесия
Δ G является ключевым для определения того, будет ли реакция иметь место в заданном направлении.Однако оказывается, что в явной оценке Δ G почти никогда не бывает необходимости. Намного удобнее работать с константой равновесия реакции, внутри которой Δ G «спрятано». Это также хорошо, потому что для большинства реакций (тех, которые происходят в растворах или газовых смесях) значение Δ G зависит от пропорций различных компонентов реакции в смеси; это не простая сумма типа «продукты минус реагенты», как в случае с Δ H .
Поскольку ΔH ° и ΔS ° определяют величину ΔG ° и поскольку K является мерой отношения концентраций продуктов к концентрациям реагентов, мы должны иметь возможность выразить K через ΔG ° и наоборот. ΔG равно максимальному количеству работы, которую система может выполнять со своим окружением, претерпевая спонтанное изменение. Для обратимого процесса, который не требует внешней работы, мы можем выразить изменение свободной энергии через объем, давление, энтропию и температуру, тем самым исключив ΔH из уравнения для ΔG.Общая взаимосвязь может быть показана следующим образом (вывод не показан):
\ [\ Delta G = V \ Delta P — S \ Delta T \ label {18.29} \]
Если реакция проводится при постоянной температуре (ΔT = 0), то уравнение \ (\ ref {18.29} \) упрощается до
\ [\ Delta {G} = V \ Delta {P} \ label {18.30} \]
В нормальных условиях зависимость свободной энергии от давления не важна для твердых тел и жидкостей из-за их малых молярных объемов. Однако для реакций с участием газов очень важно влияние давления на свободную энергию.
Предполагая поведение идеального газа, мы можем заменить \ (V \) в уравнении \ (\ ref {18.30} \) на nRT / P (где n — число молей газа, а R — постоянная идеального газа) и выразить \ (\ Delta {G} \) с точки зрения начального и конечного давления (\ (P_i \) и \ (P_f \), соответственно):
\ [\ Delta G = \ left (\ dfrac {nRT} {P} \ right) \ Delta P = nRT \ dfrac {\ Delta P} {P} = nRT \ ln \ left (\ dfrac {P_ \ textrm f } {P_ \ textrm i} \ right) \ label {18.31} \]
Если исходным состоянием является стандартное состояние с P i = 1 атм, то изменение свободной энергии вещества при переходе из стандартного состояния в любое другое состояние с давлением P можно записать следующим образом:
\ [G — G ^ ° = nRT \ ln {P} \]
Это можно изменить следующим образом:
\ [G = G ^ ° + nRT \ ln {P} \ label {18.32} \]
Как вы скоро обнаружите, уравнение \ (\ ref {18.32} \) позволяет связать ΔG ° и K p . Любое соотношение, истинное для \ (K_p \), должно быть истинным и для \ (K \), потому что \ (K_p \) и \ (K \) — это просто разные способы выражения константы равновесия с использованием разных единиц.
Рассмотрим следующую гипотетическую реакцию, в которой все реагенты и продукты являются идеальными газами, а строчные буквы соответствуют стехиометрическим коэффициентам для различных веществ:
\ [aA + bB \ rightleftharpoons cC + dD \ label {18.\ circ + RT \ ln Q \ label {18.35} \]
, где ΔG ° означает, что все реагенты и продукты находятся в своих стандартных состояниях. Для газов в состоянии равновесия (\ (Q = K_p \),), и, как вы узнали в этой главе, ΔG = 0 для системы в состоянии равновесия. Следовательно, мы можем описать взаимосвязь между ΔG ° и K p для газов следующим образом:
\ [0 = ΔG ° + RT \ ln K_p \ label {18.36a} \]
\ [\ color {красный} ΔG ° = −RT \ ln K_p \ label {18.36b} \]
Если продукты и реагенты находятся в своих стандартных состояниях и ΔG ° <0, то K p > 1, и продукты предпочтительнее реагентов.И наоборот, если ΔG °> 0, то K p <1, и реагенты предпочтительнее продуктов. Если ΔG ° = 0, то \ (K_p = 1 \), и ни реагенты, ни продукты не являются предпочтительными: система находится в равновесии.
Примечание
Для самопроизвольного процесса в стандартных условиях \ (K_ {eq} \) и \ (K_p \) больше 1.
Пример \ (\ PageIndex {1} \)
Ранее нами было рассчитано, что ΔG ° = −32,7 кДж / моль N 2 для реакции
\ [N_ {2 (g)} + 3H_ {2 (g)} \ rightleftharpoons 2NH_ {3 (g)} \ nonumber \]
Этот расчет был произведен для реакции в стандартных условиях, то есть со всеми газами, присутствующими при парциальном давлении 1 атм и температуре 25 ° C.Рассчитайте ΔG для той же реакции при следующих нестандартных условиях:
- \ (P _ {\ textrm N_2} \) = 2,00 атм,
- \ (P _ {\ textrm H_2} \) = 7,00 атм,
- \ (P _ {\ textrm {NH} _3} \) = 0,021 атм,
- и T = 100 ° C.
Благоприятствует ли реакция продуктам или реагентам?
Дано : сбалансированное химическое уравнение, парциальное давление каждого вида, температура и ΔG °
Запрошено : предпочтение отдается продуктам или реагентам
Стратегия :
- Используя указанные значения и уравнение \ (\ ref {18.{-7}) \ right] \)
\ (= — 32,7 \ textrm {кДж} + (- 44 \ textrm {кДж}) \)
\ (= — 77 \ textrm {кДж / моль N} _2 \)Поскольку ΔG <0 и Q <1.0, реакция идет спонтанно вправо, как написано, поэтому продукты предпочтительнее, чем реагенты.
Упражнение \ (\ PageIndex {1} \)
Рассчитайте ΔG реакции оксида азота с кислородом с образованием диоксида азота при следующих условиях: T = 50 ° C, P NO = 0,0100 атм, \ (P _ {\ mathrm {O_2}} \) = 0.200 атм и \ (P _ {\ mathrm {NO_2}} \) = 1.00 × 10 −4 атм. Значение ΔG ° для этой реакции составляет -72,5 кДж / моль O 2 . Предпочтительны ли продукты или реагенты?
Ответ : -92,9 кДж / моль O 2 ; реакция происходит спонтанно справа, как написано, поэтому предпочтение отдается продуктам.
Пример \ (\ PageIndex {2} \)
Рассчитайте K p для реакции H 2 с N 2 с образованием NH 3 при 25 ° C. Как вычислено в Примере 10, ΔG ° для этой реакции составляет -32.7 кДж / моль N 2 .
Дано : вычисленное химическое уравнение из примера 10, ΔG ° и температура
.
Спросил : K p
Стратегия:
Подставьте значения ΔG ° и T (в кельвинах) в уравнение \ (\ ref {18.36} \), чтобы вычислить K p , константу равновесия для образования аммиака.
Решение
В примере 10 мы использовали табличные значения ΔG ∘ f для расчета ΔG ° для этой реакции (−32.5 \ nonumber \ end {align} \)
Таким образом, константа равновесия для образования аммиака при комнатной температуре является благоприятной. Однако скорость, с которой реакция протекает при комнатной температуре, слишком мала, чтобы ее можно было использовать.
Упражнение \ (\ PageIndex {2} \)
Рассчитайте K p для реакции NO с O 2 с получением NO 2 при 25 ° C. Как вычислено в упражнении в Примере 10, ΔG ° для этой реакции составляет -70,5 кДж / моль O 2 .
Ответ : 2.{Δn} \ label {18.37} \]
, где Δn — количество молей газообразного продукта за вычетом количества молей газообразного реагента. Для реакций, в которых участвуют только растворы, жидкости и твердые вещества, Δn = 0, поэтому K p = K. Для всех реакций, не связанных с изменением количества молей присутствующего газа, соотношение в уравнении \ (\ ref {18.36b} \) можно записать в более общем виде:
\ [ΔG ° = −RT \ ln K \ label {18.38} \]
Только когда реакция приводит к чистому производству или потреблению газов, необходимо исправлять Уравнение \ (\ ref {18.38} \) для разницы между K p и K. Хотя мы обычно используем концентрации или давления в наших расчетах равновесия, помните, что константы равновесия обычно выражаются безразмерными числами из-за использования активности или летучести в точная термодинамическая работа. Системы, которые содержат газы под высоким давлением или концентрированные растворы, которые существенно отклоняются от идеального поведения, требуют использования летучести или действий, соответственно.о \) .; это довольно мощно. Обратите внимание, что \ (K \) становится больше, когда ΔS ° становится более положительным, что указывает на то, что на величину константы равновесия напрямую влияет тенденция системы двигаться к максимальному беспорядку. Кроме того, K увеличивается с уменьшением ΔH °. Таким образом, на величину константы равновесия также напрямую влияет стремление системы искать состояние с наименьшей возможной энергией.
Примечание
На величину константы равновесия напрямую влияет тенденция системы двигаться к максимальной энтропии и искать состояние с наименьшей возможной энергией.
Чтобы дополнительно проиллюстрировать связь между этими двумя основными термодинамическими концепциями, рассмотрим наблюдение, что реакции спонтанно протекают в направлении, которое в конечном итоге устанавливает равновесие. Как можно показать, построив график изменения свободной энергии в зависимости от степени реакции (например, как отражено в значении Q ), равновесие устанавливается, когда свободная энергия системы минимизирована (Рисунок \ (\ PageIndex {2}) \)). Если присутствует система с реагентами и продуктами, присутствующими в неравновесных количествах ( Q ≠ K ), реакция будет происходить самопроизвольно в направлении, необходимом для установления равновесия.
Рисунок \ (\ PageIndex {2} \): эти графики показывают зависимость свободной энергии от хода реакции для систем, стандартные свободные изменения которых (а) отрицательны, (б) положительны и (в) нулевые. Неравновесные системы будут спонтанно двигаться в любом направлении, необходимом для минимизации свободной энергии и установления равновесия.
ΔG ° и ΔG: прогнозирование направления химических изменений
Мы видели, что нет способа измерить абсолютные энтальпии, хотя мы можем измерить изменения энтальпии (ΔH) во время химической реакции.Поскольку энтальпия является одним из компонентов свободной энергии Гиббса, мы, следовательно, не можем измерить абсолютные свободные энергии; мы можем измерить только изменения в свободной энергии. Стандартное изменение свободной энергии (ΔG °) — это изменение свободной энергии, когда одно вещество или набор веществ в их стандартных состояниях превращается в одно или несколько других веществ, также в их стандартных состояниях. Стандартное изменение свободной энергии можно рассчитать из определения свободной энергии, если известны стандартные изменения энтальпии и энтропии, используя уравнение \ (\ ref {Eq5} \):
\ [ΔG ° = ΔH ° — TΔS ° \ label {Eq5} \]
Если ΔS ° и ΔH ° для реакции имеют один и тот же знак, то знак ΔG ° зависит от относительных величин членов ΔH ° и TΔS °.Важно понимать, что положительное значение ΔG ° для реакции не означает, что никакие продукты не образуются, если реагенты в их стандартных состояниях смешиваются; это означает только то, что при равновесии концентрации продуктов будут меньше концентраций реагентов.
Примечание
Положительное значение ΔG ° означает, что константа равновесия меньше 1.
Пример \ (\ PageIndex {3} \)
Рассчитайте стандартное изменение свободной энергии (ΔG °) при 25 ° C для реакции
\ [H_ {2 (g)} + O_ {2 (g)} \ rightleftharpoons H_2O_ {2 (l)} \ nonumber \]
При 25 ° C стандартное изменение энтальпии (ΔH °) составляет -187.78 кДж / моль, а абсолютные энтропии продуктов и реагентов составляют:
- S ° (H 2 O 2 ) = 109,6 Дж / (моль • К),
- S ° (O 2 ) = 205,2 Дж / (моль • К), а
- S ° (H 2 ) = 130,7 Дж / (моль • К).
Реакция спонтанная, как написано?
Дано : вычисленное химическое уравнение, ΔH ° и S ° для реагентов и продуктов
Запрошено: Спонтанность реакции как написано
Стратегия :
- Рассчитайте ΔS ° по приведенным абсолютным значениям молярной энтропии. \ circ & = — 187.78 \ textrm {кДж / моль} — (\ textrm {298,15 K}) [-226,3 \; \ mathrm {Дж / (моль \ cdot K)} \ times \ textrm {1 кДж / 1000 Дж}] \ nonumber \\ & = — 187,78 \ textrm {кДж / моль} +67,47 \ textrm {кДж / моль} = — 120,31 \ textrm {кДж / моль} \ nonumber \ end {align} \]
Отрицательное значение ΔG ° указывает, что реакция является спонтанной, как написано. Поскольку ΔS ° и ΔH ° для этой реакции имеют один и тот же знак, знак ΔG ° зависит от относительных величин членов ΔH ° и TΔS °. В этом конкретном случае член энтальпии преобладает, указывая на то, что прочность связей, образованных в продукте, более чем компенсирует неблагоприятный член ΔS ° и энергию, необходимую для разрыва связей в реагентах.
Упражнение \ (\ PageIndex {3} \)
Рассчитайте стандартное изменение свободной энергии (ΔG °) при 25 ° C для реакции
\ [2H_2 (g) + N_2 (g) \ rightleftharpoons N_2H_4 (l) \ nonumber \]
. При 25 ° C стандартное изменение энтальпии (ΔH °) составляет 50,6 кДж / моль, а абсолютные энтропии продуктов и реагентов равны S ° (N 2 H 4 ) = 121,2 Дж / (моль • K). , S ° (N 2 ) = 191,6 Дж / (моль • К) и S ° (H 2 ) = 130,7 Дж / (моль • К). Реакция спонтанная, как написано?
Ответ :
Видео решение
149.o_ {f} (реагенты) \ label {Eq7a} \]
где m и n — стехиометрические коэффициенты каждого продукта и реагента в сбалансированном химическом уравнении. Очень большое отрицательное значение ΔG ° указывает на сильную тенденцию к самопроизвольному образованию продуктов из реагентов; однако это не обязательно означает, что реакция будет происходить быстро. Чтобы сделать это определение, нам необходимо оценить кинетику реакции.
Пример \ (\ PageIndex {4} \)
Рассчитайте ΔG ° реакции изооктана с газообразным кислородом с образованием диоксида углерода и воды (описано в примере 7).Используйте следующие данные:
- ΔG ° f (изооктан) = -353,2 кДж / моль,
- ΔG ° f (CO 2 ) = -394,4 кДж / моль, а
- ΔG ° f (H 2 O) = -237,1 кДж / моль. Реакция спонтанная, как написано?
Дано : сбалансированное химическое уравнение и значения ΔG ° f для изооктана, CO 2 и H 2 O
Запрошено : спонтанность реакции, как написано
Стратегия :
Используйте правило «продукты минус реагенты», чтобы получить ΔG ∘ rxn , помня, что ΔG ° f для элемента в его стандартном состоянии равно нулю.По рассчитанному значению определите, является ли реакция спонтанной, как написано.
Решение
Рассчитанное химическое уравнение реакции выглядит следующим образом:
\ [\ mathrm {C_8H_ {18} (l)} + \ frac {25} {2} \ mathrm {O_2 (g)} \ rightarrow \ mathrm {8CO_2 (g)} + \ mathrm {9H_2O (l)} \ nonumber \]
Нам даны значения ΔG ∘ f для всех продуктов и реагентов, кроме O 2 (г). Поскольку газообразный кислород является элементом в своем стандартном состоянии, ΔG ∘ f (O 2 ) равно нулю.\ circ_ \ textrm f (\ mathrm {O_2}) \ right]
\ nonumber \\ & = [(\ textrm {8 mol}) (- 394,4 \ textrm {кДж / моль}) + (\ textrm {9 mol} ) (- 237,1 \ textrm {кДж / моль})]
\ nonumber \\ & — \ left [(\ textrm {1 mol}) (- 353,2 \ textrm {кДж / моль}) + \ left (\ dfrac {25 } {2} \; \ textrm {mol} \ right) (0 \ textrm {кДж / моль}) \ right]
\ nonumber \\ & = — 4935.9 \ textrm {kJ} (\ textrm {на моль} \ mathrm {C_8H_ {18}}) \ nonumber \ end {align} \)Поскольку ΔG ° является большим отрицательным числом, существует сильная тенденция к самопроизвольному образованию продуктов из реагентов (хотя и не обязательно с высокой скоростью).Также обратите внимание, что величина ΔG ° в значительной степени определяется ΔG ∘ f стабильных продуктов: воды и углекислого газа.
Упражнение \ (\ PageIndex {4} \)
Рассчитайте ΔG ° реакции бензола с газообразным водородом с образованием циклогексана, используя следующие данные
- ΔG ∘ f (бензол) = 124,5 кДж / моль
- ΔG ∘ f (циклогексан) = 217,3 кДж / моль.
Реакция спонтанная, как написано?
Ответ :
Видео решение
Расчетные значения ΔG ° чрезвычайно полезны для предсказания, будет ли реакция происходить самопроизвольно, если реагенты и продукты смешиваются в стандартных условиях.Следует отметить, однако, что очень немногие реакции на самом деле проводятся в стандартных условиях, и рассчитанные значения ΔG ° могут не сказать нам, будет ли данная реакция происходить самопроизвольно в нестандартных условиях. То, что определяет, будет ли реакция происходить спонтанно, — это изменение свободной энергии (ΔG) в реальных экспериментальных условиях, которые обычно отличаются от ΔG °. Если члены ΔH и TΔS для реакции имеют одинаковый знак, например, тогда можно изменить знак ΔG, изменив температуру, тем самым преобразовав реакцию, которая не является термодинамически спонтанной, имеющей K экв. <1 , на тот, который имеет K eq > 1, или наоборот.Поскольку ΔH и ΔS обычно не сильно изменяются с температурой в отсутствие фазового перехода, мы можем использовать табличные значения ΔH ° и ΔS ° для расчета ΔG ° при различных температурах, если фазовое изменение не происходит в диапазоне температур считается.
Примечание
В отсутствие фазового перехода ни \ (ΔH \), ни \ (ΔS \) сильно не изменяются с температурой.
Пример \ (\ PageIndex {5} \)
Рассчитайте ΔG ° (а) и ΔG ° (б) 300 ° C для реакции N 2 (г) + 3H 2 (г) ⇌2NH 3 (г), предполагая, что ΔH и ΔS do не изменяется между 25 ° C и 300 ° C.Используйте эти данные:
- S ° (N 2 ) = 191,6 Дж / (моль • К),
- S ° (H 2 ) = 130,7 Дж / (моль • К),
- S ° (NH 3 ) = 192,8 Дж / (моль • К), а
- ΔH ∘ f (NH 3 ) = -45,9 кДж / моль.
Дано : сбалансированное химическое уравнение, температуры, значения S ° и ΔH ∘ f для NH 3
Запрошено для : ΔG ° и ΔG при 300 ° C
Стратегия :
- Перевести каждую температуру в градусы Кельвина.Затем рассчитайте ΔS ° для реакции. Вычислите ΔH ° реакции, вспомнив, что ΔH ∘ f для любого элемента в его стандартном состоянии равно нулю.
- Подставьте соответствующие значения в уравнение \ (\ ref {Eq5} \), чтобы получить ΔG ° для реакции.
- Предполагая, что ΔH и ΔS не зависят от температуры, подставьте значения в уравнение \ (\ ref {Eq2} \), чтобы получить ΔG для реакции при 300 ° C.
Решение
A Чтобы рассчитать ΔG ° для реакции с использованием уравнения \ (\ ref {Eq5} \), мы должны знать температуру, а также значения ΔS ° и ΔH °.\ circ (\ mathrm {H_2})]
\ nonumber \\ & = [\ textrm {2 моль NH} _3 \ times192.8 \; \ mathrm {Дж / (моль \ cdot K)}]
\ nonumber \\ & — \ left \ {[\ textrm {1 моль N} _2 \ times191.6 \; \ mathrm {J / (моль \ cdot K)}] + [\ textrm {3 моль H} _2 \ times130.7 \; \ mathrm {J / (mol \ cdot K)}] \ right \} \ nonumber \\ & = — 198,1 \ textrm {J / K (на моль N} _2) \ end {align} \ nonumber \]Мы также можем рассчитать ΔH ° для реакции, используя правило «продукты минус реагенты». \ circ_ \ textrm f (\ mathrm {H_2})] \ nonumber \\ & = [2 \ times (-45.\ circ \ nonumber \\ & = (- \ textrm {91,8 кДж}) — (\ textrm {573 K}) (- \ textrm {198,1 J / K}) (\ textrm {1 кДж / 1000 Дж}) = 21,7 \ textrm {кДж (на моль N} _2) \ nonumber \ end {align} \ nonumber \]
В этом примере изменение температуры оказывает большое влияние на термодинамическую спонтанность реакции. В стандартных условиях реакция азота и газообразного водорода с образованием аммиака является термодинамически самопроизвольной, но на практике она слишком медленная, чтобы ее можно было использовать в промышленности. Повышение температуры в попытке ускорить эту реакцию также изменяет термодинамику, заставляя член -TΔS ° преобладать, и реакция больше не является спонтанной при высоких температурах; то есть его K eq меньше единицы.Это классический пример конфликта, встречающегося в реальных системах между термодинамикой и кинетикой, который часто неизбежен.
Упражнение \ (\ PageIndex {5} \)
Рассчитать
- \ (ΔG ° \) и
- \ (ΔG_ {750 ° C} \)
для следующей реакции
\ [2НО _ {(г)} + О_ {2 \; (g)} \ rightleftharpoons 2NO_ {2 \; (g)} \ nonumber \]
, который играет важную роль в формировании городского смога. Предположим, что \ (ΔH \) и \ (ΔS \) не меняются между 25.0 ° C и 750 ° C и используйте эти данные:
- S ° (NO) = 210,8 Дж / (моль • К),
- S ° (O 2 ) = 205,2 Дж / (моль • К),
- S ° (NO 2 ) = 240,1 Дж / (моль • К),
- ΔH ∘ f (NO 2 ) = 33,2 кДж / моль, а
- ΔH ∘ f (NO) = 91,3 кДж / моль.
Ответ
- −72,5 кДж / моль \ (O_2 \)
- 33,8 кДж / моль \ (O_2 \)
Видео решение
Влияние температуры на спонтанность реакции, которая является важным фактором при планировании эксперимента или промышленного процесса, зависит от знака и величины как ΔH °, так и ΔS °.Температуру, при которой данная реакция находится в равновесии, можно рассчитать, установив ΔG ° = 0 в уравнении \ (\ ref {Eq5} \), как показано в примере \ (\ PageIndex {4} \).
Пример \ (\ PageIndex {6} \)
При реакции азота и газообразного водорода с образованием аммиака ΔH ° и ΔS ° отрицательны. Предполагается, что такие реакции будут термодинамически спонтанными при низких температурах, но неспонтанными при высоких температурах. Используйте данные в Примере \ (\ PageIndex {3} \), чтобы вычислить температуру, при которой эта реакция изменяется от спонтанной до несамопроизвольной, предполагая, что ΔH ° и ΔS ° не зависят от температуры.
Дано : ΔH ° и ΔS °
Запрошено : температура, при которой реакция меняется с спонтанной на спонтанную
Стратегия :
Установите ΔG ° равным нулю в уравнении \ (\ ref {Eq5} \) и найдите T, температуру, при которой реакция становится несамопроизвольной.
Решение
В примере \ (\ PageIndex {3} \) мы вычислили, что ΔH ° составляет -91,8 кДж / моль для N 2 , а ΔS ° составляет -198.\ circ} & = \ dfrac {(- \ textrm {91,8 кДж}) (\ textrm {1000 Дж / кДж})} {- \ textrm {198,1 Дж / кДж}} = \ textrm {463 K} \ end {align } \]
Это случай, когда инженер-химик сильно ограничен термодинамикой. Любая попытка увеличить скорость реакции азота с водородом путем повышения температуры приведет к тому, что реагенты будут иметь преимущество перед продуктами с температурой выше 463 К.
Упражнение \ (\ PageIndex {6} \)
ΔH ° и ΔS ° отрицательны для реакции оксида азота и кислорода с образованием диоксида азота.Используйте эти данные для расчета температуры, при которой эта реакция меняется от спонтанной к несамопроизвольной.
Ответ : 792,6 K
Термодинамика и метаморфизм
Расчет границ реакции
Еще одно полезное отношение:
G = H — TS
где G — свободная энергия Гиббса, H — энтальпия, T — абсолютная
температура в Кельвинах, а S — энтропия.Для химической реакции мы можем переписать это как:
ΔG = ΔH
— TΔS
(10)где снова:
ΔG = изменение свободной энергии реакции =
ΣG продукты — ΣG реагентыΔH = изменение энтальпии реакции =
ΣH продукты — ΣH реагентыΔS = изменение энтропии реакции =
ΣS продукты — ΣS реагентыВ целом ΔG, ΔH,
ΔS и ΔV являются
зависит от давления и температуры, но при любом заданном T&P:Если ΔG <0 (отрицательное), химическое реакция будет спонтанной и побежит вправо,
Если ΔG = 0, реагенты находятся в равновесии
с продуктами,и если ΔG> 0 (положительный), реакция
будет работать справа налево.Температурная зависимость G, H и S
Как указано выше, G, H и S зависят от температуры и давления.
Но поскольку G зависит от H и S, обычно удобнее
рассмотрим температурную зависимость H и S, так что если мы знаем H и S
при любой заданной температуре мы можем вычислитьг.
где
C p — теплоемкость при постоянном давлении.Жара
мощность — это количество тепла, необходимое для повышения температуры
вещество по 1 o К.Таким образом:
или
Если
C p не зависит от температуры, тогда дальнейшее интегрирование
результатов:(Примечание
что в целом C p является функцией температуры, а известные
функция температуры может быть вставлена перед интеграцией, но это
вводит осложнения, выходящие за рамки этого курса).Таблицы термодинамических данных обычно сводятся к некоторым известным ссылкам.
температура и давление, чаще всего при температуре 298 К, и
Давление 1 бар (= 0,1 МПа ~ 1 атм). Таким образом, мы, если нам нужно
знать H при некоторой температуре T, отличной от 298 K, мы можем использовать приведенное выше
уравнение для определения H при новой температуре:Для
реакции, приведенное выше уравнение можно переписать как:(11)
Температурная зависимость энтропии S определяется по формуле:
или
Опять же,
если Cp не является функцией T, то интегрирование дает:Или,
поскольку данные обычно доступны при 298 K и 0.1 МПа, для реакции это
можно записать как:(12)
Уравнение 10 затем можно объединить с уравнениями 11 и 12.
чтобы дать зависимость ΔG от температуры:ср
это можно упростить еще больше, если предположить, что для реакции ΔC p
= 0:(13)
Таким образом, используя сделанные выше предположения, теперь мы можем вычислить ΔG
при нашем эталонном давлении P 1 при любой температуре, если мы знаем ΔH
и ΔS
при нашей эталонной температуре 298 К.Гиббса Свободная энергия | Безграничная химия
Стандартные изменения свободной энергии
Стандартная свободная энергия Гиббса рассчитывается с использованием свободной энергии образования каждого компонента реакции при стандартном давлении.
Цели обучения
Рассчитайте изменение стандартной свободной энергии для конкретной реакции.
Основные выводы
Ключевые моменты
- Стандартная свободная энергия вещества представляет собой изменение свободной энергии, связанное с образованием вещества из элементов в их наиболее стабильных формах, существующих в стандартных условиях.\ circ (\ text {reactants}) [/ latex] может использоваться для определения стандартного изменения свободной энергии реакции.
Ключевые термины
- энтальпия : В термодинамике, мера теплосодержания химической или физической системы.
- энтропия : термодинамическое свойство, которое является мерой тепловой энергии системы на единицу температуры, которая недоступна для выполнения полезной работы.
- свободная энергия образования : изменение свободной энергии, которое сопровождает образование 1 моля вещества в его стандартном состоянии из составляющих его элементов в их стандартных состояниях.
Обзор стандартных состояний
Концепция стандартных состояний особенно важна в случае свободной энергии, поэтому уделите время ее обзору. Для большинства практических целей приемлемы следующие определения стандартных состояний:
- Газы: парциальное давление 1 атмосфера.
- Чистые жидкости: жидкость под общим давлением 1 атм.
- Растворенные вещества: эффективная концентрация 1 моль.
- Твердые вещества: чистое твердое вещество под давлением 1 атм.
Отметим также, что на самом деле нет «стандартной температуры», но поскольку в большинстве термодинамических таблиц указаны значения для 298,15 K (25 ° C), эта температура обычно подразумевается. Эти же определения применимы к стандартным энтальпиям и внутренней энергии. Не путайте эти термодинамические стандартные состояния со «стандартной температурой и давлением» (STP), широко применяемой в расчетах газового закона.
Расчет свободной энергии Гиббса
Чтобы использовать энергии Гиббса для предсказания химических изменений, необходимо знать свободные энергии отдельных компонентов реакции.\ circ [/ latex]
Напомним, что символ ° относится к стандартному состоянию вещества, измеренному в условиях давления 1 атм или эффективной концентрации 1 моль и температуры 298K. Другой фактор, который следует иметь в виду, это то, что значения энтальпии обычно даются в [latex] \ frac {\ text {kJ}} {\ text {мол}} [/ latex], а значения энтропии даются в [latex] \ frac { \ text {J}} {\ text {K} \ times \ text {мол}} [/ латекс]. Единицы измерения энергии должны быть одинаковыми для правильного решения уравнения.\ circ (\ text {реагенты}) [/ latex]
Как и в случае стандартной теплоты образования, стандартная свободная энергия вещества представляет собой изменение свободной энергии, связанное с образованием вещества из элементов в их наиболее стабильных формах, поскольку они существуют при стандартных условиях давления 1 атм и 298К. Стандартные свободные энергии Гиббса образования обычно находятся непосредственно из таблиц. Как только значения для всех реагентов и продуктов известны, можно найти стандартное изменение свободной энергии Гиббса для реакции.\ circ (\ text {rxn}) = -257,2 \ \ text {кДж} [/ латекс]
Изменения свободной энергии в химических реакциях
ΔG определяет направление и степень химического изменения.
Цели обучения
Вспомните возможные изменения свободной энергии для химических реакций.
Основные выводы
Ключевые моменты
- Если свободная энергия реагентов больше, чем у продуктов, энтропия мира будет увеличиваться, когда реакция происходит, как написано, и поэтому реакция будет иметь тенденцию происходить спонтанно.
- Если свободная энергия продуктов превышает свободную энергию реагентов, то реакция не происходит.
- Важным следствием одностороннего нисходящего пути свободной энергии является то, что как только она достигает минимально возможного значения, чистое изменение прекращается.
- При спонтанном изменении энергия Гиббса всегда уменьшается и никогда не увеличивается.
Ключевые термины
- спонтанное изменение : Спонтанный процесс — это эволюция системы во времени, в которой она высвобождает свободную энергию (обычно в виде тепла) и переходит в более низкое, более термодинамически стабильное энергетическое состояние.
Направление и степень химических изменений
ΔG определяет направление и степень химического изменения. Помните, что ΔG имеет значение только для изменений, при которых температура и давление остаются постоянными. Это условия, при которых большинство реакций проводится в лаборатории. Система обычно открыта для атмосферы (постоянное давление), и процесс начинается и заканчивается при комнатной температуре (после того, как все тепло, которое было добавлено или высвободилось в результате реакции, рассеивается.)
Важность функции Гиббса трудно переоценить: она определяет, возможно ли данное химическое изменение термодинамически. Таким образом, если свободная энергия реагентов больше, чем у продуктов, энтропия мира будет увеличиваться, и реакция протекает самопроизвольно. И наоборот, если свободная энергия продуктов превышает свободную энергию реагентов, реакция не состоится.
При спонтанном изменении энергия Гиббса всегда уменьшается и никогда не увеличивается.Это, конечно, отражает тот факт, что энтропия мира ведет себя прямо противоположным образом (из-за отрицательного знака в члене TΔS). Вот пример:
[латекс] {\ text {H}} _ {2} \ text {O} (\ text {liquid}) \ rightarrow {\ text {H}} _ {2} \ text {O} (\ text {ice }) [/ латекс]
Вода при температуре ниже нуля градусов Цельсия испытывает снижение своей энтропии, но тепло, выделяемое в окружающую среду, более чем компенсирует это, поэтому энтропия мира увеличивается, свободная энергия H 2 O уменьшается, и процесс происходит самопроизвольно. .
Важным следствием одностороннего нисходящего пути свободной энергии является то, что как только она достигает минимально возможного значения, чистое изменение прекращается. Это, конечно, представляет собой состояние химического равновесия. Эти отношения резюмируются следующим образом:
- [латекс] \ Delta \ text {G} <0 [/ latex]: реакция будет происходить спонтанно справа.
- [латекс] \ Delta \ text {G}> 0 [/ latex]: реакция будет происходить спонтанно слева.
- [латекс] \ Delta \ text {G} = 0 [/ latex]: реакция находится в равновесии и не будет идти ни в одном направлении.
Условия спонтанного изменения
Напомним условие самопроизвольного изменения:
ΔG = ΔH — TΔS <0
, где ΔG = изменение свободной энергии Гиббса, ΔH = изменение энтальпии, T = абсолютная температура и ΔS = изменение энтропии
Очевидно, что температурная зависимость ΔG почти полностью зависит от изменения энтропии, связанного с процессом. (уместно сказать «почти», потому что значения ΔH и ΔS сами по себе немного зависят от температуры; оба постепенно увеличиваются с температурой).В частности, обратите внимание, что в приведенном выше уравнении знак изменения энтропии определяет, станет ли реакция более или менее спонтанной при повышении температуры.
Для любой данной реакции знак ΔH также может быть положительным или отрицательным. Это означает, что существует четыре возможности влияния температуры на спонтанность процесса:
Случай 1: ΔH
<0 и ΔS> 0
В этих условиях оба члена ΔH и TΔS будут отрицательными, поэтому ΔG будет отрицательным независимо от температуры.Экзотермическая реакция, энтропия которой возрастает, будет спонтанной при всех температурах.
Случай 2: ΔH
<0 и ΔS <0
Если реакция достаточно экзотермична, она может привести к отрицательному значению ΔG только при температурах, ниже которых | TΔS | <| ΔH |. Это означает, что существует температура, определяемая [латексом] \ text {T} = \ frac {\ Delta \ text {H}} {\ Delta \ text {S}} [/ latex], при которой реакция находится в равновесии; реакция будет происходить самопроизвольно только ниже этой температуры. Замерзание жидкости или конденсация газа - наиболее распространенные примеры этого состояния.
Случай 3: ΔH> 0 и ΔS> 0
Это обратное предыдущему случаю; увеличение энтропии должно преодолеть недостаток эндотермического процесса, так что TΔS> ΔH. Поскольку влияние температуры должно «усилить» влияние положительного ΔS, процесс будет самопроизвольным при температурах выше [латекса] \ text {T} = \ frac {\ Delta \ text {H}} {\ Delta \ текст {S}} [/ latex]. (Подумайте о плавлении и кипении.)
Случай 4: ΔH> 0 и ΔS
<0
Поскольку оба ΔH и ΔS работают против этого, этот вид процесса не будет происходить самопроизвольно при любой температуре.Вещество А всегда имеет большее количество доступных энергетических состояний и поэтому всегда является предпочтительной формой.
Изменения свободной энергии для нестандартных состояний
Одиночная реакция может иметь бесконечное количество значений ΔG, отражающих бесконечное количество возможных составов между реагентами и продуктами.
Цели обучения
Различия между бесплатными изменениями для стандартных и нестандартных состояний.
Основные выводы
Ключевые моменты
- ΔG ° и ΔG f ° относятся к единичным специфическим химическим изменениям, при которых все компоненты (реагенты и продукты) находятся в своих стандартных состояниях.
- Физический смысл ΔG состоит в том, что он говорит нам, насколько изменилась свободная энергия системы от G ° чистых реагентов.
- Когда ΔG достигает своего минимального значения, состав системы находится на своем равновесном значении.
Ключевые термины
- свободная энергия : разница между внутренней энергией системы и произведением ее энтропии и абсолютной температуры.
- равновесие : состояние реакции, в котором скорости прямой и обратной реакций одинаковы.{\ circ} [/ латекс]. На горизонтальной оси схематично показаны относительные концентрации реагентов и продуктов в любой точке процесса. Обратите внимание, что происхождение соответствует составу, при котором половина реагентов была преобразована в продукты.
ΔG по сравнению с G ° : ΔG отложено по вертикальной оси для двух гипотетических реакций, имеющих противоположные знаки ΔG °.
Обратите внимание на следующее:
- Красная линия слева отображает значения [latex] \ Delta \ text {G} [/ latex] для реакции [latex] \ Delta \ text {G} ^ {\ circ} [/ latex]> 0. .{\ circ} [/ latex], соответствующий составу, при котором [latex] \ Delta \ text {G} [/ latex] = 0 (точка 1).
- На данный момент некоторые продукты образовались, но в составе все еще преобладают реагенты.
- Если реакция начинается в композиции слева от точки 1 на диаграмме, [latex] \ Delta \ text {G} [/ latex] будет отрицательным, и композиция переместится вправо. Точно так же, если реакция начинается с композиции справа от точки 1 на диаграмме, [latex] \ Delta \ text {G} [/ latex] будет положительным, и композиция переместится влево.{\ circ} [/ latex] не означает, что никакие продукты не образуются вообще.
Возможные значения
Напротив, состав химической реакционной системы постоянно изменяется, пока не будет достигнуто состояние равновесия. Следовательно, одна реакция может иметь бесконечное количество значений [latex] \ Delta \ text {G} [/ latex], отражающих бесконечное количество возможных составов между крайними значениями чистых реагентов и чистых продуктов.
В примере реакции [латекс] \ text {A} \ rightarrow \ text {B} [/ latex], изображенной на следующей диаграмме, стандартная свободная энергия продуктов (точка 2) меньше, чем у реагенты (точка 1), поэтому реакция будет происходить самопроизвольно.Это не означает, что каждый моль чистого A превратится в один моль чистого B.
Изменение свободной энергии нестандартного состояния : График [латекса] \ text {G} (\ text {T}, \ text {p}) = \ text {f} (\ xi) [/ latex]. Одна реакция может иметь бесконечное количество значений [latex] \ Delta \ text {G} [/ latex].
Физический смысл [латекса] \ Delta \ text {G} [/ latex] заключается в том, что он сообщает нам, насколько сильно изменилась свободная энергия системы от G ° чистых реагентов (точка 1). По мере того, как реакция идет вправо, состав меняется, и [latex] \ Delta \ text {G} [/ latex] начинает падать.Когда композиция достигает точки 3, [латекс] \ Delta \ text {G} [/ latex] достигает минимального значения, и дальнейшая реакция может вызвать его подъем. Но поскольку свободная энергия может только уменьшаться, но никогда не увеличиваться, этого не происходит. Состав системы постоянно остается на своем равновесном значении.
Давление и свободная энергия
Свободная энергия Гиббса зависит от давления.
Цели обучения
Обсудите взаимосвязь между свободной энергией и давлением.
Основные выводы
Ключевые моменты
- Энергия Гиббса (также называемая ∆G) — это также химический потенциал, который сводится к минимуму, когда система достигает равновесия при постоянном давлении и температуре.
- Уравнение свободной энергии Гиббса зависит от давления.
- Это удобный критерий спонтанности для процессов с постоянным давлением и температурой.
Ключевые термины
- химический потенциал : В термодинамике химический потенциал, также известный как частичная молярная свободная энергия, представляет собой форму потенциальной энергии, которая может поглощаться или высвобождаться во время химической реакции.
Свободная энергия Гиббса измеряет полезную работу, получаемую от термодинамической системы при постоянных температуре и давлении. Как и в механике, где потенциальная энергия определяется как способность совершать работу, так и разные потенциалы имеют разное значение. Свободная энергия Гиббса — это максимальное количество работы без расширения, которое может быть извлечено из замкнутой системы.
Уравнение свободной энергии Гиббса : Уравнение свободной энергии Гиббса зависит от давления.
Когда система переходит из начального состояния в конечное, свободная энергия Гиббса (ΔG) равна работе, которой система обменивается с окружающей средой, за вычетом работы силы давления. Энергия Гиббса (также называемая ∆G) — это также химический потенциал, который сводится к минимуму, когда система достигает равновесия при постоянном давлении и температуре. По сути, это удобный критерий спонтанности для процессов с постоянным давлением и температурой. Следовательно, свободная энергия Гиббса наиболее полезна для термохимических процессов при постоянной температуре и давлении.
Свободная энергия и работа
Свободная энергия Гиббса — это максимальное количество работы без расширения, которое может быть извлечено из замкнутой системы.
Цели обучения
Определите взаимосвязь между свободной энергией Гиббса и работой.
Основные выводы
Ключевые моменты
- Когда система переходит из четко определенного начального состояния в четко определенное конечное состояние, свободная энергия Гиббса, ΔG, равна работе, выполненной / обмененной между системой и ее окружением, за вычетом работы сил давления.
- «Полезная» работа — это чаще всего электромонтажные работы (перемещение электрического заряда через разность потенциалов).
Ключевые термины
- работа : В термодинамике работа, выполняемая замкнутой системой, — это энергия, передаваемая другой системе, которая измеряется внешними обобщенными механическими ограничениями на систему.
Свободная энергия Гибба и «полезная» работа
Энергия Гиббса — это максимальная полезная работа, которую система может выполнять со своим окружением, когда процесс, происходящий внутри системы, является обратимым при постоянной температуре и давлении.Как и в механике, где потенциальная энергия определяется как способность выполнять работу, разные потенциалы имеют разное значение. Свободная энергия Гиббса — это максимальное количество работы без расширения, которое может быть извлечено из замкнутой системы. Работа выполняется за счет внутренней энергии системы. Энергия, которая не извлекается в процессе работы, обменивается с окружающей средой в виде тепла.
Схема работы : Обратимое условие подразумевает wmax и qmin. Невозможность извлечения всей внутренней энергии в качестве работы, по сути, является утверждением Второго Закона.
Название «свободная энергия» для G привело к такой путанице, что многие ученые теперь называют его просто «энергией Гиббса». «Свободная» часть старого названия отражает истоки термодинамики, связанные с паровыми двигателями, с ее интересом к преобразованию тепла в работу. ΔG — это максимальное количество энергии, которое может быть «высвобождено» из системы для выполнения полезной работы. «Полезный» в данном случае относится к работе , а не , связанной с расширением системы. Чаще всего это электрическая работа (перемещение электрического заряда через разность потенциалов), но возможны и другие виды работы.Например, примеры полезной работы без расширения у биологических организмов включают сокращение мышц и передачу нервных импульсов.
Константа равновесия — вводная химия — 1-е канадское издание
Цели обучения
- Объясните важность константы равновесия.
- Постройте выражение для константы равновесия химической реакции.
В середине 1860-х годов норвежские ученые К. М. Гульдберг и П.Вааге отметил особую взаимосвязь между количествами реагентов и продуктов в равновесии. Независимо от того, с каким количеством реагентов они начали, определенное соотношение реагентов и продуктов достигалось при равновесии. Сегодня мы называем это наблюдение законом массового действия. Он связывает количества реагентов и продуктов в равновесии для химической реакции. Для общей химической реакции, протекающей в растворе,
aA + bB ⇄ cC + dD
константа равновесия, также известная как K eq , определяется следующим выражением:
, где [A] — молярная концентрация вещества A в состоянии равновесия и т. Д.Коэффициенты a , b , c и d в химическом уравнении становятся показателями степени в выражении для K eq . K eq — это характерное числовое значение для данной реакции при данной температуре; то есть каждая химическая реакция имеет свою характеристику K экв . Концентрация каждого реагента и продукта в химической реакции при равновесии составляет , относящиеся к ; концентрации не могут быть случайными величинами, но они зависят друг от друга.В числителе выражения для K eq указаны концентрации каждого продукта (сколько бы продуктов ни было), а в знаменателе выражения для K eq указаны концентрации каждого реагента, что приводит к общему значению продуктов по сравнению с реагентами определение для K экв .
Рассмотрим простой пример. Предположим, у нас есть это равновесие:
A ⇄ B
Есть один реагент, один продукт, и коэффициенты для каждого из них всего 1 (предполагается, не записано).Выражение для этого равновесия K eq равно
.
(Понятны экспоненты 1 для каждой концентрации.) Предположим, что числовое значение K экв. для этой химической реакции равно 2,0. Если [B] = 4,0 M, то [A] должно быть равно 2,0 M, чтобы значение дроби равнялось 2,0:
.
По соглашению, единицы понимаются как M и опускаются в выражении K eq . Предположим, [B] было 6.0 M. Чтобы значение K eq оставалось постоянным (в конце концов, оно называется константой равновесия ), тогда [A] должно быть 3,0 M в состоянии равновесия:
Если бы [A] было , а не , равным 3,0 M, реакция не была бы равновесной, и результирующая реакция происходила бы до тех пор, пока это соотношение не стало действительно 2,0. В этот момент реакция находится в равновесии, и любые чистые изменения прекратятся. (Напомним, однако, что прямая и обратная реакции не прекращаются, потому что химическое равновесие динамично.)
То же самое и с более сложными выражениями для K eq ; только математика усложняется. Вообще говоря, учитывая значение для K eq и всех концентраций, кроме одной, в состоянии равновесия, недостающую концентрацию можно вычислить.
Пример 2
При следующей реакции:
H 2 + I 2 ⇄ 2 HI
Если равновесие [HI] равно 0,75 M, а равновесие [H 2 ] равно 0.20 M, каково равновесие [I 2 ], если K eq равно 0,40?
Решение
Начнем с написания выражения K eq . Используя подход продуктов по реагентам , выражение K eq выглядит следующим образом:
Обратите внимание, что [HI] возведено в квадрат из-за коэффициента 2 в сбалансированном химическом уравнении. Подставляя для равновесия [H 2 ] и [HI] и для данного значения K экв. :
Чтобы найти [I 2 ], мы должны сделать некоторую алгебраическую перестановку: разделить 0.40 в обе части уравнения и умножьте обе части уравнения на [I 2 ]. Это приводит к [I 2 ] в числителе левой части и 0,40 в знаменателе правой части:
Solving,
[I 2 ] = 7,0 M
Единицей измерения концентрации является молярность. Это значение для [I 2 ] можно легко проверить, подставив 0,75, 0,20 и 7,0 в выражение для K eq и вычислив: вы должны получить 0.40, числовое значение K eq (и вы это делаете).
Проверьте себя
При следующей реакции:
H 2 + I 2 ⇄ 2 HI
Если равновесие [HI] составляет 0,060 M, а равновесие [I 2 ] равно 0,90 M, каково равновесие [H 2 ], если K eq равно 0,40?
Ответ
0,010 млн
В некоторых типах задач равновесия для определения окончательного ответа необходимо проанализировать квадратные корни, кубические корни или даже более высокие корни.Убедитесь, что вы умеете выполнять такие операции на своем калькуляторе; если вы не знаете, обратитесь за помощью к своему инструктору.
Пример 3
Следующая реакция находится в равновесии:
N 2 + 3 H 2 ⇄ 2 NH 3
K eq при определенной температуре 13,7. Если равновесие [N 2 ] составляет 1,88 M, а равновесие [NH 3 ] составляет 6,62 M, что такое равновесие [H 2 ]?
Решение
Начнем с написания выражения K eq из вычисленного химического уравнения:
Подставляя известные равновесные концентрации и K экв , получается
Алгебраически переставляя и затем вычисляя числовое выражение, получаем
Чтобы найти [H 2 ], нам нужно извлечь кубический корень из уравнения.Выполняя эту операцию, получаем
[H 2 ] = 1,15 M
Вы должны убедиться, что это правильно, используя свой собственный калькулятор, чтобы убедиться, что вы знаете, как правильно делать кубический корень.
Проверьте себя
Следующая реакция находится в равновесии:
N 2 + 3 H 2 ⇄ 2 NH 3
K eq при определенной температуре 13,7. Если равновесие [N 2 ] равно 0.055 M и равновесие [H 2 ] составляет 1,62 M, что такое равновесие [NH 3 ]?
Ответ
1.79 M
Модель K eq была определена ранее в терминах концентраций. Для газофазных реакций K eq также можно определить в терминах парциальных давлений реагентов и продуктов: P i . Для газофазной реакции
aA (г) + bB (г) ⇄ cC (г) + dD (г)
константа равновесия, основанная на давлении, K P , определяется следующим образом:
, где P A — парциальное давление вещества A в состоянии равновесия в атмосферах и т. Д.Как и в случае константы равновесия на основе концентрации, единицы измерения опускаются при подстановке в выражение для K P .
Пример 4
Что такое K P для этой реакции, учитывая равновесное парциальное давление 0,664 атм для NO 2 и 1,09 для N 2 O 4 ?
2 NO 2 (г) ⇄ N 2 O 4 (г)
Решение
Запишите выражение K P для этой реакции:
Затем подставьте равновесные парциальные давления в выражение и вычислите:
Проверьте себя
Что такое K P для этой реакции при равновесных парциальных давлениях 0.44 атм для H 2 , 0,22 атм для Cl 2 и 2,98 атм для HCl?
H 2 + Cl 2 ⇄ 2 HCl
Ответ
91,7
Существует простая взаимосвязь между K eq (на основе единиц концентрации) и K P (на основе единиц давления):
, где R — постоянная закона идеального газа (в единицах л · атм / моль · К), T — абсолютная температура, а Δ n — изменение количества молей газа в уравновешенном состоянии. химическое уравнение, определяемое как n газ, prods — n газ, rcts .Обратите внимание, что это уравнение подразумевает, что если количество молей газа одинаково в реагентах и продуктах, K экв. = K P .
Пример 5
Что такое K P при 25 ° C для этой реакции, если K eq составляет 4,2 × 10 −2 ?
N 2 (г) + 3 H 2 (г) ⇄ 2 NH 3 (г)
Решение
Прежде чем использовать соответствующее уравнение, нам нужно сделать две вещи: преобразовать температуру в градусы Кельвина и определить Δ n .Преобразовать температуру очень просто:
Т = 25 + 273 = 298 К
Чтобы определить изменение количества молей газа, возьмите количество молей газообразных продуктов и вычтите количество молей газообразных реагентов. 2 моль газа в качестве продукта и 4 моль газа в качестве реагента:
Δ n = 2 — 4 = −2 моль
Обратите внимание, что Δ n отрицательно. Теперь мы можем подставить в наше уравнение, используя R = 0,08205 л · атм / моль · К.Единицы измерения опущены для ясности:
К P = (4,2 × 10 −2 ) (0,08205) (298) −2
Solving,
К P = 7,0 × 10 −5
Проверьте себя
Что такое K P при 25 ° C для этой реакции, если K eq равно 98,3?
I 2 (г) ⇄ 2 I (г)
Ответ
2.40 × 10 3
Наконец, мы признаем, что во многих химических реакциях участвуют вещества в твердой или жидкой фазах. Например, конкретная химическая реакция представлена следующим образом:
2 NaHCO 3 (т) ⇄ Na 2 CO 3 (с) + CO 2 (г) + H 2 O ()
Это химическое уравнение включает все три фазы вещества. Этот вид равновесия называется гетерогенным равновесием, потому что присутствует более одной фазы.
Правило для гетерогенных равновесий выглядит следующим образом: Не включайте концентрации чистых твердых веществ и чистых жидкостей в выражения K eq . Только парциальные давления для газообразных веществ или концентрации в растворах включаются в выражения констант равновесия. Таким образом, выражение константы равновесия для этой реакции будет просто
.
КП = PCO 2
, потому что два твердых тела и одна жидкость не появятся в выражении.
Основные выводы
- Каждое химическое равновесие может быть охарактеризовано константой равновесия, известной как K eq .
- Выражения K eq и K P сформулированы как количества продуктов, деленные на количества реагентов; каждая величина (концентрация или давление) возводится в степень своего коэффициента в сбалансированном химическом уравнении.
- Твердые тела и жидкости не фигурируют в выражении для константы равновесия.
Упражнения
Определите закон действия масс .
Что такое константа равновесия химической реакции? Как это устроено?
Запишите выражение K eq для каждой реакции.
a) H 2 + Cl 2 ⇄ 2 HCl
б) НЕТ + НЕТ 2 ⇄ N 2 O 3
4.Запишите выражение K eq для каждой реакции.
а) C 2 H 5 OH + NaI ⇄ C 2 H 5 I + NaOH
b) PCl 3 + Cl 2 ⇄ PCl 5
5. Запишите выражение K P для каждой реакции.
а) 2 H 2 (г) + O 2 (г) ⇄ 2 H 2 O (г)
б) 2 H 2 O 2 (г) ⇄ 2 H 2 O (г) + O 2 (г)
6.Запишите выражение K P для каждой реакции.
а) CH 4 (г) + 2 O 2 (г) ⇄ CO 2 (г) + 2 H 2 O (г)
б) CH 4 (г) + 4 Cl 2 (г) ⇄ CCl 4 (г) + 4 HCl (г)
7. Следующая реакция находится в равновесии:
PBr 3 + Br 2 ⇄ PBr 5
Равновесие [Br 2 ] и [PBr 5 ] равно 2.05 М и 0,55 М соответственно. Если K eq равно 1,65, каково равновесие [PBr 3 ]?
8. В равновесии находится следующая реакция:
CO + Cl 2 ⇄ CoCl 2
Равновесие [CO] и [Cl 2 ] составляет 0,088 М и 0,103 М соответственно. Если K eq равно 0,225, каково равновесие [COCl 2 ]?
9. Следующая реакция находится в равновесии:
CH 4 + 2 Cl 2 ⇄ CH 2 Cl 2 + 2 HCl
Если [CH 4 ] равно 0.250 M, [Cl 2 ] составляет 0,150 M, и [CH 2 Cl 2 ] составляет 0,175 M в равновесном состоянии, что такое [HCl] в равновесии, если K eq равно 2,30?
10. Следующая реакция находится в равновесии:
4 HBr + O 2 ⇄ 2 H 2 O + 2 Br 2
Если [HBr] равно 0,100 M, [O 2 ] равно 0,250 M, а [H 2 O] составляет 0,0500 M в равновесном состоянии, что будет [Br 2 ] в равновесном состоянии, если K eq — это 0.770?
11. Напишите выражение K P для следующей газофазной реакции:
4 NO 2 (г) + O 2 (г) ⇄ 2 N 2 O 5 (г)
12. Напишите выражение K P для следующей газофазной реакции:
ClO (г) + O 3 (г) ⇄ ClO 2 (г) + O 2 (г)
13. Каково равновесное парциальное давление COBr 2 , если равновесные парциальные давления CO и Br 2 равны 0.666 атм и 0,235 атм, а K P для этого равновесия составляет 4,08?
CO (г) + Br 2 (г) ⇄ COBr 2 (г)
14. Каково равновесное парциальное давление O 3 , если равновесное парциальное давление O 2 составляет 0,0044 атм, а K P для этого равновесия составляет 0,00755?
3 O 2 (г) ⇄ 2 O 3 (г)
15. Вычислите K P для этой реакции при 298 K, если K eq = 1.76 × 10 −3 .
3 O 2 (г) ⇄ 2 O 3 (г)
16. Вычислите K P для этой реакции при 310 K, если K eq = 6,22 × 10 3 .
4 NO 2 (г) + O 2 (г) ⇄ 2 N 2 O 5 (г)
17. Вычислите K экв. для этой реакции, если K P = 5.205 × 10 −3 при 660 ° C.
CO (г) + F 2 (г) ⇄ COF 2 (г)
18. Вычислите K экв. для этой реакции, если K P = 78,3 при 100 ° C.
4 HCl (г) + O 2 (г) ⇄ 2 H 2 O (г) + 2 Cl 2 (г)
19. Напишите правильное выражение K eq для этой реакции.
NaOH (водн.) + HCl (водн.) ⇄ NaCl (водн.) + H 2 O ()
20.Напишите правильное выражение K eq для этой реакции.
AgNO 3 (водн.) + NaCl (водн.) ⇄ AgCl (т.) + NaNO 3 (водн.)
21. Напишите правильное выражение K P для этой реакции.
CaCO 3 (т) ⇄ CaO (т) + CO 2 (г)
22. Напишите правильное выражение K P для этой реакции.
C 2 H 2 (г) + 2 I 2 (с) ⇄ C 2 H 2 I 4 (г)
ответы
1.
взаимосвязь между концентрациями реагентов и продуктов химической реакции при равновесии
3.
а)
б)
5.
а)
б)
7.
0,163 млн
9.
0,272 млн
11.
13.
0,639 атм
15.
7,20 × 10 −5 17.
K экв = 3,98 × 10 −1 19.
21.
K P = P CO 2
Энтропия
Энтропия
1. имеет то же значение
независимо от пути, если путь обратимый2. — точное
дифференциал некоторой функции, идентичной энтропии3.
4. для реверсивного
только процесс1.
Энтропия — это функция состояния. Изменение энтропии определяется ее
только начальное и конечное состояния2.
При анализе необратимого процесса нет необходимости проводить прямой
анализ реального обратимого процесса.Заменитель фактический
процесс воображаемым обратимым процессом. Изменение энтропии для мнимой
обратимый процесс такой же, как и необратимый процесс между заданными
конечное и начальное состояния.(а) Поглощение
энергия из резервуара постоянной температурыЭнергию можно добавлять обратимо или
безвозвратно в виде тепла или при выполнении работы.Пример : —
Содержимое большого
резервуар с постоянной температурой, поддерживаемый на уровне 500 К, непрерывно перемешивают
лопастное колесо с приводом от электродвигателя. Оцените изменение энтропии
резервуар, если лопастное колесо работает в течение двух часов от двигателя мощностью 250 Вт.Лопастное колесо переделано
во внутреннюю энергию — необратимый процесс.Представьте себе обратимый процесс с
идентичное добавление энергии(б) Отопление или охлаждение
материидля постоянного объема
отоплениедля постоянного давления
отопление, для постоянного
давление, для постоянного
объем процессаПример : —
Вычислить энтропию
измените, если 1 кг воды при 30 0 C нагреется до 80 0 C при 1
бар давление.Удельная теплоемкость воды составляет 4,2 кДж / кг-K.
(c) Фаза
изменение при постоянной температуре и давленииПример: —
Лед тает при 0 0 C
со скрытой теплотой плавления = 339.92 кДж / кг. Вода закипает при атмосферном давлении
при 100 0 C с h fg = 2257 кДж / кг.(г) Адиабатический
смешиваниеПример: —
Кусок стали
массой 30 кг при 427 0 ° C падает в 100 кг масла при 27 0 ° C.
удельная теплоемкость стали и масла 0.5 кДж / кг-К и 3,0 кДж / кг-К соответственно.
Рассчитайте изменение энтропии стали, нефти и вселенной.T = окончательный
равновесная температура.или T = 319K
Tds отношений
Из определения энтропии,
dQ = Tds
dW = PdV
Следовательно,
TdS = dU + PdV
Или, Tds = du + Pdv
Это известно как первое
Tds or, Уравнение Гиббса .h = u + Pv dh = du + vdP
Следовательно, Tds = dh vdP
ds = (du / T) + (Pdv / T)
ds = (dh / T) (vdP / T)
Изменение состояния на идеальный газ
Если идеальный газ подвергается
изменить с P 1 , v 1 , T 1 на P 2 , v 2 ,
T 2 изменение энтропии можно рассчитать, разработав обратимый
путь, соединяющий два заданных состояния.Рассмотрим два пути по
который может быть переведен из начального состояния, 1 в конечное состояние, 2.Газ в состоянии 1 нагрет
при постоянном давлении до достижения температуры T 2 и затем
обратимо и изотермически доводится до конечного давления P 2 .Путь 1-а: реверсивный,
процесс постоянного давления.Путь а-2: реверсивный,
изотермический путьD с 1-a = dq / T = C p dT / T = C p
ln (Т 2 / Т 1 )D с a-2 = dq / T = (du + Pdv) / T = (Pdv) / T = Rln (v 2 / v а )
(Так как du = 0 для
изотермический процесс)Начиная с P 2 v 2
= P a v a = P 1 v aИли, v 2 / v a = P 1 / P 2
Или, D с a-2 = -Rln (P 2 / P 1 )
Следовательно, D s = D s 1-a + D s a-2
= C p ln (T 2 / T 1 )
Рлн (П 2 / П 1 )Путь 1-b-2: Газ
первоначально в состоянии 1 нагревается при постоянном объеме до конечной температуры T 2
а затем обратимо и изотермически изменяется до конечного давления P 2 .1-б: реверсивный, постоянный
объем процессаб-2: реверсивный, изотермический
процессD s 1-b = C v
ln (Т 2 / Т 1 )D с b-2 = Rln (v 2 / v 1 )
или, D s = C v
ln (T 2 / T 1 ) + Rln (v 2 / v 1 )Приведенное выше уравнение для
Ds также можно вывести следующим образом
манера:ds = (dq / T) R = (du + Pdv) / T = (dh vdP) / T
или,
.


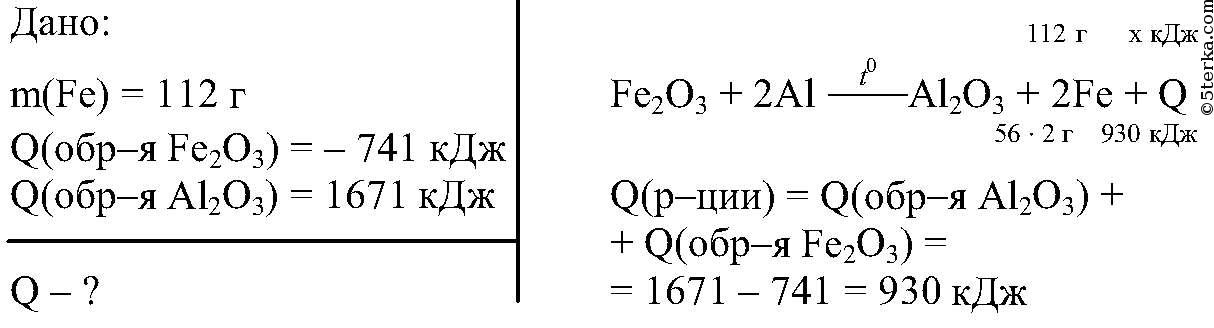 4)
4)