Содержание
По графику функции найти y по x
В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.
Рассмотрим, как по данному графику функции найти y по x.
Рисунок 1
1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.
Решение:
Аргумент — это x, функция — y.
Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.
Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.
От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).
Следовательно, при x=1 y=2.
Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.
Получаем, что при x=3 y=4.
Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.
При x=-3 н=-2.
При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.
Записываем: при x=-1 y=0.
При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.
2) На рисунке 2 изображен график функции y=f(x).
Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.
Рисунок 2
Решение:
Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.
При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.
Пишем: при x=1 y=2.
При x равном -1 и -5 идем сначала вверх, затем — вправо.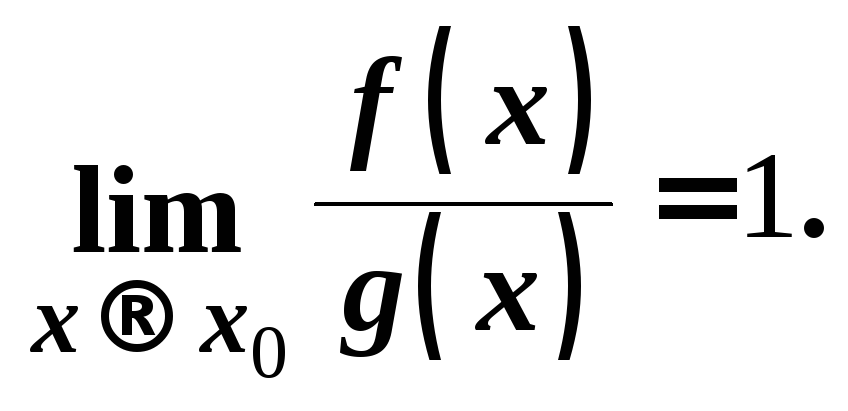
При x= -1 y=4.
При x= -5 y=6.
При иксах равных 3; 5 и 7 идём вниз и влево.
При x=3 y= -3.
При x=5 y= -6.
При x=7 y= -3.
Обратите внимание: различным значениям икса может соответствовать одно значение y:
(при x=3 и x=7 y= -3).
Python/28_func.py at master · Testudinate/Python · GitHub
Python/28_func.py at master · Testudinate/Python · GitHub
Permalink
Cannot retrieve contributors at this time
| Напишите функцию f(x), которая возвращает значение следующей функции, определённой на всей числовой прямой: | |
| f(x)=⎧⎩⎨⎪⎪1−(x+2)2,−x2,(x−2)2+1,при x≤−2при −2<x≤2при 2<x | |
Требуется реализовать только функцию, решение не должно осуществлять операций ввода-вывода. | |
| Sample Input 1: | |
| 4.5 | |
| Sample Output 1: | |
| 7.25 | |
| Sample Input 2: | |
| -4.5 | |
| Sample Output 2: | |
-5. 25 25 | |
| Sample Input 3: | |
| 1 | |
| Sample Output 3: | |
| -0.5 | |
| def f(x): | |
| # put your python code here | |
| if x<=-2: | |
| f=1-(x+2)**2 | |
| elif x>-2 and x<=2: | |
| f=-(x/2) | |
| elif x>2: | |
| f=(x-2)**2+1 | |
| return f |
You can’t perform that action at this time.
You signed in with another tab or window. Reload to refresh your session.
You signed out in another tab or window. Reload to refresh your session.
Бесконечно большие и бесконечно малые функции (Лекция №2)
БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
Функция y=f(x) называется бесконечно
малой при x→a или при x→∞,
если или , т.е. бесконечно малая функция – это функция, предел которой
в данной точке равен нулю.
Примеры.
- Функция f(x)=(x-1)2
является бесконечно малой при x→1, так как (см. рис.). - Функция f(x) = tgx –
бесконечно малая при x→0. - f(x) = ln (1+x)– бесконечно малая при x→0.
- f(x) = 1/x– бесконечно малая при x→∞.
Установим следующее важное соотношение:
Теорема. Если функция y=f(x)
Если функция y=f(x)
представима при x→aв виде суммы постоянного числа b и бесконечно малой величины
α(x): f (x)=b+ α(x)
то .
Обратно, если , то
f (x)=b+α(x),
где a(x) –
бесконечно малая при x→a.
Доказательство.
- Докажем первую часть
утверждения. Из равенства f(x)=b+α(x)
следует |f(x) – b|=| α|.
Но так как a(x) –
бесконечно малая, то при произвольном ε найдется δ – окрестность
точки a,
при всех x из которой, значения a(x)
удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|<
ε. А это и значит, что . - Если , то
при любом ε>0
для всех х
из некоторой δ – окрестность точки a будет |f(x) – b|<
ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.
Рассмотрим
основные свойства бесконечно малых функций.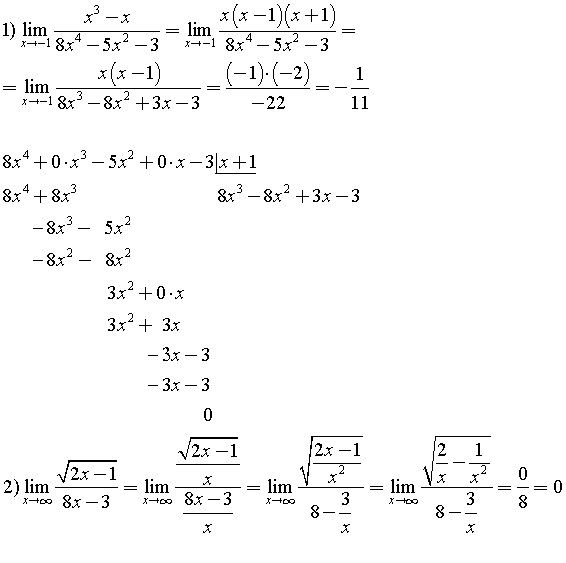
Теорема 1. Алгебраическая сумма двух, трех и вообще любого
конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство. Приведем доказательство для
двух слагаемых. Пусть f(x)=α(x)+β(x),
где и . Нам
нужно доказать, что при произвольном как угодно малом ε>0
найдется δ>0,
такое, что для x, удовлетворяющих
неравенству |x – a|<δ, выполняется |f(x)|<
ε.
Итак, зафиксируем
произвольное число ε>0. Так как по условию теоремы α(x) –
бесконечно малая функция, то найдется такое δ1>0,
что при |x – a|<δ1 имеем |α(x)|<
ε/2. Аналогично, так как β(x) –
бесконечно малая, то найдется такое δ2>0,
что при |x – a|<δ2 имеем | β(x)|<
ε/2.
Возьмем δ=min{ δ1, δ2}.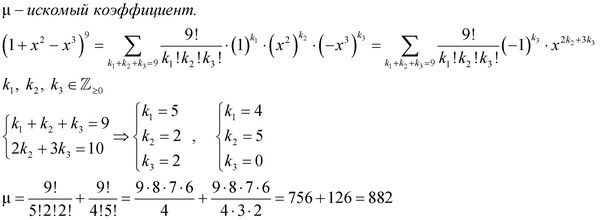 Тогда в окрестности точки a радиуса δбудет выполняться каждое из
Тогда в окрестности точки a радиуса δбудет выполняться каждое из
неравенств |α(x)|<
ε/2 и | β(x)|<
ε/2. Следовательно, в этой окрестности
будет
|f(x)|=| α(x)+β(x)| ≤
|α(x)| + | β(x)| < ε/2
+ ε/2=
ε,
т.е. |f(x)|<ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x)
на ограниченную функцию f(x)
при x→a
(или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x)
ограничена, то существует число М
такое, что при всех значениях x из
некоторой окрестности точки a|f(x)|≤M. Кроме
того, так как a(x) – бесконечно
малая функция при x→a, то для
произвольного ε>0 найдется окрестность точки a, в
которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих
Тогда в меньшей из этих
окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для
случая x→∞ доказательство проводится аналогично.
Из доказанной
теоремы вытекают:
Следствие 1. Если и , то
.
Следствие 2. Если и c=const,
то .
Теорема 3. Отношение бесконечно малой функции α(x)
на функцию f(x),
предел которой отличен от нуля, есть бесконечно малая функция.
Доказательство. Пусть . Тогда 1/f(x)
есть ограниченная функция. Поэтому дробь есть произведение
бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно
малая.
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ
Теорема 1. Если функция f(x)
является бесконечно большой при x→a, то функция 1/f(x)
является бесконечно малой при x→a.
Доказательство. Возьмем произвольное число ε>0 и
Возьмем произвольное число ε>0 и
покажем, что при некотором δ>0 (зависящим от ε) при всех x,
для которых |x – a|<δ, выполняется неравенство , а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно, так как f(x) –
бесконечно большая функция при x→a, то найдется δ>0
такое, что как только |x – a|<δ, так |f(x)|>1/ ε. Но тогда для тех же x.
Примеры.
- Ясно, что при x→+∞ функция y=x2+1 является бесконечно
большой. Но тогда согласно сформулированной выше теореме функция – бесконечно малая при
x→+∞, т.е. . - .
Можно доказать и
обратную теорему.
Теорема 2. Если функция f(x) -
бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x)
является бесконечно большой функцией.
Доказательство
теоремы проведите самостоятельно.
Примеры.
- .
- .
- , так как функции и — бесконечно малые при
x→+∞, то , как сумма бесконечно малых функций есть функция бесконечно
малая. Функция же является суммой
постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для
бесконечно малых функций получаем нужное равенство.
Таким образом,
простейшие свойства бесконечно малых и бесконечно больших функций можно
записать с помощью следующих условных соотношений: A≠ 0
.
ТЕОРЕМЫ О ПРЕДЕЛАХ
Теорема 1. Предел алгебраической суммы двух, трех и вообще
определенного числа функций равен алгебраической сумме пределов этих функций,
т.е.
.
Доказательство. Проведем доказательство для
двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и
g(x)=c+β(x),
где α и β – бесконечно малые функции.
Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) –
функция бесконечно малая, то
.
Пример. .
Теорема 2. Предел произведения двух, трех и вообще конечного
числа функций равен произведению пределов этих функций:
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и
g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть величина постоянная.
Функция bβ + c
α + αβ на основании свойств бесконечно малых функций есть
величина бесконечно малая. Поэтому .
Следствие 1. Постоянный множитель можно выносить за знак предела:
.
Следствие 2. Предел степени равен степени предела:
.
Пример..
Теорема 3. Предел частного двух функций равен частному
пределов этих функций, если предел знаменателя отличен от нуля, т. е.
е.
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно
малые. Рассмотрим частное
.
Дробь является бесконечно
малой функцией, так как числитель есть бесконечно малая функция, а знаменатель
имеет предел c2≠0.
Примеры.
- .
- .
- Рассмотрим . При x→1 числитель дроби стремится к
1, а знаменатель стремится к 0. Но так как , т.е. есть бесконечно малая
функция при x→1, то .
Теорема 4. Пусть даны три функции f(x), u(x) и
v(x),
удовлетворяющие неравенствам u(x)≤f(x)≤ v(x).
Если функции u(x) и
v(x)
имеют один и тот же предел при x→a (или x→∞), то и функция f(x)
стремится к тому же пределу, т.е. если
, то .
Смысл этой
теоремы понятен из рисунка.
Доказательство теоремы 4
можно найти, например, в учебнике: Пискунов Н. С.
Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.
Теорема 5. Если при x→a (или x→∞) функция y=f(x)
принимает неотрицательные значения y≥0 и при этом стремится к
пределу b, то этот предел не может
быть отрицательным: b≥0.
Доказательство. Доказательство проведем
методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль
разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a,
что противоречит условию теоремы.
Теорема 6. Если две функции f(x) и
g(x)
при всех значениях аргумента x
удовлетворяют неравенству f(x)≥ g(x) и
имеют пределы , то имеет место неравенство b≥c.
Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 , или .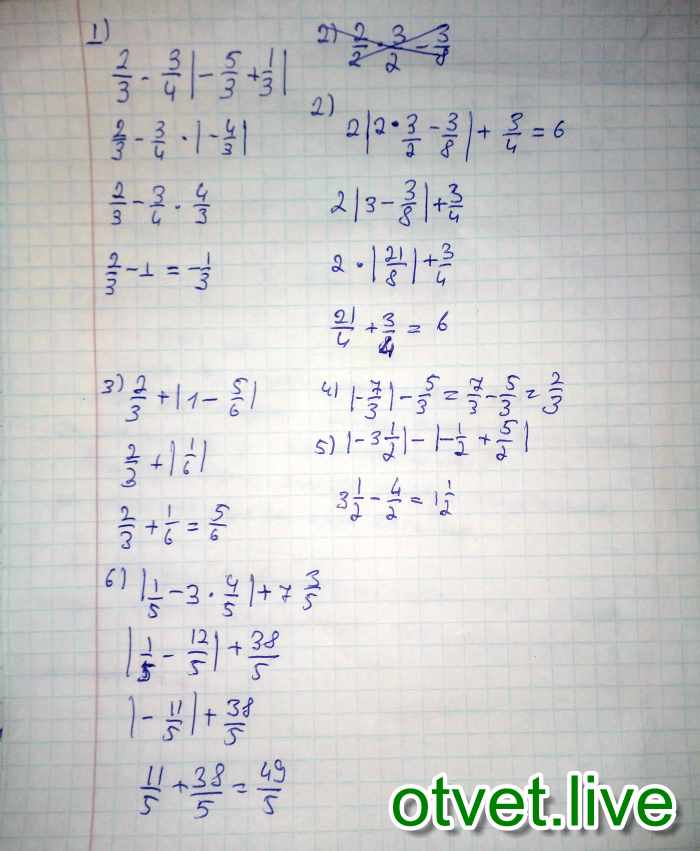
ОДНОСТОРОННИЕ ПРЕДЕЛЫ
До сих пор мы
рассматривали определение предела функции, когда x→a произвольным образом, т.е.
предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако,
довольно часто можно встретить функции, которые не имеют предела при этом
условии, но они имеют предел, если x→a, оставаясь с одной стороны
от а, слева или справа (см. рис.).
Поэтому вводят понятия односторонних пределов.
Если f(x) стремится
к пределу b при x стремящемся
к некоторому числу a
так, что xпринимает только значения, меньшие a, то пишут и называют bпределом функции f(x) в точке a слева.
Таким образом,
число b называется пределом функции
y=f(x)
при x→aслева,
если каково бы ни было положительное число ε,
найдется такое число δ (меньшее a), что для всех выполняется
неравенство .
Аналогично, если x→a и
принимает значения большие a,
то пишут и называют b пределом функции в точке а справа.
Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε,
найдется такое число δ (большее а), что для всех выполняется
неравенство .
Заметим, что
если пределы слева и справа в точке a
для функции f(x)
не совпадают, то функция не имеет предела (двустороннего) в точке а.
Примеры.
- Рассмотрим функцию y=f(x),
определенную на отрезке [0,1] следующим образомНайдем пределы
функции f(x)
при x→3. Очевидно, , а . - .
- .
ТИПЫ НЕОПРЕДЕЛЕННОСТЕЙ И СПОСОБЫ ИХ РАСКРЫТИЯ
Часто при
вычислении пределов какой-либо функции, непосредственное применение теорем о
пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о
Так, например, нельзя применять теорему о
пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем
применять эти теоремы, необходимо тождественно преобразовать функцию, предел
которой мы ищем.
Условные выражения
характеризуют типы
неопределенностей и применяются для обозначения переменных величин, при
вычислении предела которых нельзя сразу применять общие свойства пределов.
Рассмотрим
некоторые приемы раскрытия неопределенностей.
I. Неопределенность
.
- .
- .
При разложении
числителя на множители воспользовались правилом деления многочлена на многочлен
«углом». Так как число x=1
является корнем многочлена x3 – 6x2 + 11x– 6,
то при делении получим - .
II. Неопределенность
.
- .
При вычислении
предела числитель и знаменатель данной дроби разделили на x в старшей степени.
- .
- .
- .
При вычислении
предела воспользовались равенством ,если x<0.
Следующие виды
неопределенностей с помощью алгебраических преобразований функции, стоящей под
знаком предела, сводят к одному из рассмотренных выше случаев или .
III.
Неопределенность 0 ·∞.
.
IV.
Неопределенность ∞ –∞.
- .
Непрерывность функции в точке и на промежутке. С примерами
На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это
с помощью пределов, причем односторонних — правого и левого, которые совсем не страшны, несмотря на
то что записываются как и
.
Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения,
проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия
Если такая линия
начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.
Графически функция непрерывна в точке ,
если её график не «разрывается» в этой точке. График такой непрерывной
функции —
показан на рисунке ниже.
Определение непрерывности функции
через предел. Функция является непрерывной в точке при соблюдении трёх условий:
А могут ли правый и левый пределы хоть когда-нибудь быть не равны, если к значению, к которому
стремится икс, прибавляется или вычитается всего лишь нуль? Могут. Когда и почему — это объяснено на уроке
о точках разрыва функции и их видах.
Если хотя бы одно из перечисленных условий не соблюдено, функция не является
непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на
графике, в которых график прерывается, называются точками разрыва функции. График
График
такой функции , терпящей разрыв в точке x=2 —
на рисунке ниже.
Пример 1. Функция f(x)
определена следующим образом:
Будет ли эта функция непрерывной в каждой из граничных точек её ветвей,
то есть в точках x = 0, x = 1,
x = 3?
Решение. Проверяем все три условия непрерывности функции в каждой
граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из
граничных точек, следует из определения функции. Осталось проверить остальные два условия.
Точка x = 0. Найдём
левосторонний предел в этой точке:
.
Найдём правосторонний предел:
.
Предел функции и значение функции в точке x = 0
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви.
Находим их:
.
Как видим, предел функции и значение функции в точке x = 0
равны. Следовательно, функция является непрерывной в точке x = 0.
Точка x = 1. Найдём
левосторонний предел в этой точке:
.
Найдём правосторонний предел:
Предел функции и значение функции в точке x = 1
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви.
Находим их:
.
Предел функции и значение функции в точке x = 1
равны. Следовательно, функция является непрерывной в точке x = 1.
Точка x = 3. Найдём
левосторонний предел в этой точке:
Найдём правосторонний предел:
Предел функции и значение функции в точке x = 3
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви.
Находим их:
.
Предел функции и значение функции в точке x = 3
равны. Следовательно, функция является непрерывной в точке x = 3.
Основной вывод: данная функция является непрерывной в каждой граничной точке.
Непрерывное изменение функции
можно определить как изменение постепенное, без скачков, при котором малое изменение
аргумента
влечёт малое изменение функции .
Проиллюстрируем это непрерывное изменение функции на примере.
Пусть над столом висит на нитке груз. Под действием этого груза нитка
растягивается, поэтому расстояние l груза от точки
подвеса нити является функцией массы груза m,
то есть l = f(m),
m≥0.
Непрерывность функции на промежутке
Пусть функция y = f(x)
определена в интервале ]a, b[
и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в
интервале ]a, b[. Аналогично
определяется понятие непрерывности функции на промежутках вида
]- ∞, b[,
]a, + ∞[,
]- ∞, + ∞[.
Пусть теперь функция y = f(x)
определена на отрезке [a, b].
Разница между интервалом и отрезком: граничные точки интервала не входят в интервал,
а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой
односторонней непрерывности: в точке a, оставаясь на отрезке [a, b],
мы можем приближаться только справа, а к точке b —
только слева. Функция называется непрерывной на отрезке [a, b],
если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке
a и непрерывна слева в точке b.
Примером непрерывной функции может служить любая из элементарных функций.
Каждая элементарная функция непрерывна на любом отрезке, на котором она определена.
Например, функции и
непрерывны
на любом отрезке [a, b], функция
непрерывна
на отрезке [0, b], функция
непрерывна
на любом отрезке, не содержащем точку a = 2.
Пример 4. Исследовать функцию
на непрерывность.
Решение. Проверяем первое условие. Функция не определена в точках
— 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой
не выполняется. Поэтому данная функция является непрерывной на интервалах
.
Пример 5. Определить, при каком значении
параметра a непрерывна на всей области определения функция
Решение.
Найдём левосторонний предел функции в точке :
.
Найдём правосторонний предел при :
.
Очевидно, что значение
в точке x = 2 должно быть
равно ax:
Ответ: функция непрерывна на всей области определения при
a = 1,5.
К понятию непрерывной функции математика пришла, изучая в первую очередь
различные законы движения. Пространство и время бесконечны, и зависимость, например,
пути s от времени
t, выраженная законом s = f(t),
даёт пример непрерывной функции f(t). Непрерывно
изменяется и температура нагреваемой воды, она также является непрерывной функцией от
времени: T = f(t).
В математическом анализе доказаны некоторые свойства, которыми
обладают непрерывные функции. Приведём важнейшие из этих свойств.
1. Если непрерывная на интервале функция принимает на концах
интервала значения разных знаков, то в некоторой точке этого отрезка она принимает
значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной
как первая теорема Больцано-Коши.
2. Функция f(x),
непрерывная на интервале [a, b],
принимает все промежуточные значения между значениями в концевых точках, то есть,
между f(a) и f(b).
В более формальном изложении это свойство дано в теореме, известной как вторая теорема
Больцано-Коши.
3. Если функция непрерывна на интервале, то на этом интервале она
достигает своего наибольшего и своего наименьшего значения: если m —
наименьшее, а M — наибольшее значение функции
на интервале [a, b], то найдутся
на этом отрезке такие точки и
, что
и
. Теорема,
в которой изложено это свойство, называется второй теоремой Вейерштрасса.
Пример 7. Используя первое из приведённых выше свойств непрерывных
функций, доказать, что уравнение
имеет по меньшей мере один вещественный корень в интервале [1; 2].
Решение.
Пусть .
Вычислим значения функции при x = 1 и x = 2.
.
.
Получили, что функция на концах интервала принимает значения разных знаков:
и , т. е.
Следовательно, в интервале [1; 2]
существует такое число a, при котором
f(a) = 0. То есть, уравнение
имеет по меньшей мере один вещественный корень в данном интервале.
Установление непрерывности функции может быть как самостоятельной задачей,
так и частью Полного исследования функции и построения графика.{-2}$% на множестве $%t\in(-\infty;0)\cup(0;2)$%. При помощи производной можно изучить поведение функции на каждом из двух промежутков, и окажется, что наименьшее значение достигается при $%t=-2$%, и оно равно $%\frac34$%. Поэтому интересующее нас неравенство выполнено при $%a > \frac34$% (можно просто положить $%x=-3$%), и только при таких значениях.
отвечен
21 Июл ’14 0:23
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x).
Основные определения
Начнем, как всегда, с формулировки основных определений.
Определение 1
Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Определение 2
Наименьшее значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Определение 3
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 1
Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] — max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] — max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Пример 2
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Квадратичная функция, как построить Параболу
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x2:
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
x | -2 | -1 | 0 | 1 | 2 |
y | 4 | 1 | 0 | 1 | 4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.
График функции y = –x2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x | -2 | -1 | 0 | 1 | 2 |
y | -4 | -1 | 0 | -1 | -4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax
2 + bx + c.
Разберем общий алгоритм на примере y = 2x2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x2 + 3x — 5.
D = b2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x — 5 = 0
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
Уравнение квадратичной функции имеет вид y = a * (x — x₀)
2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Рассмотрим следующий пример: y = (x — 2) * (x + 1).
Как строим:
- Данный вид уравнения позволяет быстро найти нули функции:
(x — 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.
- Определим координаты вершины параболы:
- Найти точку пересечения с осью OY:
с = ab =(-2) * (1)= -2 и ей симметричная.
- Отметим эти точки на координатной плоскости и соединим плавной прямой.
Чтобы не запутаться во всех графиках, приходите вместе с ребенком на бесплатный урок математики в современную школу Skysmart: порисуем параболы на интерактивной онлайн-доске, разберемся в самых коварных формулах и покажем, что математика может быть увлекательным путешествием.
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найдите число, которое при добавлении к 3 дает 7»
можно записать как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x представляют число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 — это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.
Пример 2 Найдите решение каждого уравнения путем осмотра.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
— эквивалентные уравнения, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.
Если одно и то же количество добавляется или вычитается из обоих элементов
уравнения, полученное уравнение эквивалентно исходному
уравнение.
в символах,
a — b, a + c = b + c и a — c = b — c
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 из каждого члена.
Решение Если вычесть 3 из каждого члена, получится
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 — эквивалентные уравнения, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
, объединив одинаковые термины, а затем добавив по 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим
.
2x + 1-1 = x — 2-1
2x = х — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2х-х = х — 3 — х
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА DIVISION
Рассмотрим уравнение
3x = 12
Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения делятся на одно и то же (ненулевое)
количество, полученное уравнение эквивалентно исходному уравнению.
в символах,
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Разделив оба элемента на -4, получим
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые термины, чтобы получить
5лет = 20
Тогда, разделив каждый член на 5, получим
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
Решение
Сначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединяя одинаковые термины, получаем
3x = -9
Наконец, мы разделим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
в символах,
a = b и a · c = b · c (c ≠ 0)
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
путем умножения каждого члена на 6.
Решение Умножение каждого члена на 6 дает
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.
Пример 2 Решить
Решение Во-первых, умножьте каждый член на 5, чтобы получить
Теперь разделите каждого члена на 3,
Пример 3 Решить.
Решение Во-первых, упростите над дробной чертой, чтобы получить
Затем умножьте каждый член на 3, чтобы получить
Наконец, разделив каждого члена на 5, получим
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.
Шаги по решению уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Во-первых, мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы разделим каждый член на 7, чтобы получить
В следующем примере мы упрощаем над дробной чертой перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы разделим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.
Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть
d = rt
(24) = (3) т
8 = т
Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
из которых по закону симметрии
В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения)
Калькулятор алгебры — это калькулятор, который дает пошаговую помощь по задачам алгебры.
Посмотреть другие примеры »
Заявление об отказе от ответственности:
Этот калькулятор не идеален. Пожалуйста, используйте на свой страх и риск и сообщите нам, если что-то не работает. Спасибо.
Как пользоваться калькулятором
Введите задачу по алгебре в текстовое поле.
(экспонента: «возведена в степень»)
sqrt (квадратный корень) (пример: sqrt (9))
Другие математические символы
Учебное пособие
Прочтите полное руководство, чтобы узнать, как построить графики уравнений и проверить свое домашнее задание по алгебре.Учебное пособие по калькулятору
»
Мобильное приложение
Загрузите мобильное приложение MathPapa! Работает офлайн!
Обратная связь
(Для студентов 13+)
Пожалуйста, используйте эту форму обратной связи, чтобы отправить свой отзыв. Спасибо!
Нужно больше практических задач?
Попробуйте MathPapa
Математическая практика
Решите квадратные уравнения x2-x-1 = 0 Tiger Algebra Solver
Переформатирование ввода:
Изменения, внесенные в ваш ввод, не должны влиять на решение:
(1): «x2» было заменено на «x ^ 2 «.
Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1,1 Факторинг x 2 -x-1
Первый член, x 2 , его коэффициент равен 1.
Средний член, -x, его коэффициент -1.
Последний член, «константа», равен -1
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -1 = -1
Шаг-2: Найдите два множителя -1, сумма которых равен коэффициенту среднего члена, который равен -1.
| -1 | + | 1 | = | 0 |
Наблюдение: Два таких фактора не могут быть найдены !!
Вывод: трехчлен не может быть разложен на множители
Уравнение в конце шага 1:
x 2 - x - 1 = 0
Шаг 2:
Парабола, поиск вершины:
2.1 Найдите вершину y = x 2 -x-1
Параболы имеют высшую или низшую точку, называемую вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 0.5000
Подставляя в формулу параболы 0,5000 для x, мы можем вычислить координату y:
y = 1,0 * 0,50 * 0,50 — 1,0 * 0,50 — 1,0
или y = -1,250
Парабола, графическая вершина и пересечения по оси X:
Корневой график для: y = x 2 -x-1
Ось симметрии (пунктирная линия) {x} = {0,50}
Вершина в точке {x, y} = {0,50, -1,25}
x -Переходы ( Корни):
Корень 1 при {x, y} = {-0,62, 0,00}
Корень 2 при {x, y} = {1,62, 0,00}
Решите квадратное уравнение, заполнив квадрат
2.2 Решение x 2 -x-1 = 0, заполнив квадрат.
Добавьте 1 к обеим сторонам уравнения:
x 2 -x = 1
Теперь умный бит: возьмите коэффициент при x, равный 1, разделите его на два, получив 1/2, и возведите его в квадрат. давая 1/4
Добавьте 1/4 к обеим частям уравнения:
В правой части мы имеем:
1 + 1/4 или, (1/1) + (1/4)
Общий знаменатель две дроби равны 4. Сложение (4/4) + (1/4) дает 5/4
Таким образом, сложив обе стороны, мы, наконец, получаем:
x 2 -x + (1/4) = 5/4
Сложение 1/4 превратила левую часть в полный квадрат:
x 2 -x + (1/4) =
(x- (1/2)) • (x- (1/2)) =
( x- (1/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Так как
x 2 -x + (1/4) = 5/4 и
x 2 -x + (1/4) = (x- (1/2)) 2
то по закону транзитивности,
(x- (1/2)) 2 = 5/4
Мы будем называть это уравнение уравнением. # 2.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x- (1/2)) 2 равен
(x- (1/2)) 2/2 =
(x- (1/2)) 1 =
x- (1/2)
Теперь, применяя принцип квадратного корня к уравнению.# 2.2.1 получаем:
x- (1/2) = √ 5/4
Добавляем 1/2 к обеим сторонам, чтобы получить:
x = 1/2 + √ 5/4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — x — 1 = 0
имеет два решения:
x = 1/2 + √ 5/4
или
x = 1/2 — √ 5/4
Обратите внимание, что √ 5/4 можно записать как
√ 5 / √ 4, что равно √ 5/2
Решите квадратное уравнение с помощью квадратичной формулы
2.3 Решение x 2 -x-1 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = -1
C = -1
Соответственно B 2 — 4AC =
1 — (-4) =
5
Применение квадратичной формулы:
1 ± √ 5
x = ————
2
√ 5, округленное до 4 десятичных цифр, равно 2.2361
Итак, теперь мы смотрим на:
x = (1 ± 2,236) / 2
Два реальных решения:
x = (1 + √5) / 2 = 1,618
или:
x = (1- √5) /2=-0,618
Было найдено два решения:
- x = (1-√5) /2=-0,618
- x = (1 + √5) / 2 = 1,618
Решить квадратично уравнения x2-x + 1 = 0 Tiger Algebra Solver
Переформатирование ввода:
Изменения, внесенные в ваш ввод, не должны влиять на решение:
(1): «x2» было заменено на «x ^ 2».
Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1,1 Факторинг x 2 -x + 1
Первый член равен x 2 , его коэффициент равен 1.
Средний член, -x, его коэффициент -1.
Последний член, «константа», равен +1
Шаг 1: Умножьте коэффициент первого члена на константу 1 • 1 = 1
Шаг 2: Найдите два множителя 1, сумма которых равна коэффициенту среднего члена, который равен -1.
| -1 | + | -1 | = | -2 | ||||||||||||||||||
| 1 | + | 1 | 9049 Наблюдение: Нет двух таких факторов !! Вывод: трехчлен не может быть разложен на множители Уравнение в конце шага 1:x 2 - x + 1 = 0 Шаг 2:Парабола, поиск вершины:2.1 Найдите вершину y = x 2 -x + 1 Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля). Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения. Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины. Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A).В нашем случае координата x равна 0,5000 Подставив в формулу параболы 0,5000 для x, мы можем вычислить координату y: Parabola, Graphing Вершины и пересечения по оси X: Корневой график для: y = x 2 -x + 1 Решите квадратное уравнение, заполнив квадрат2.2 Решение x 2 -x + 1 = 0, заполнив квадрат. Вычтем 1 из обеих частей уравнения: Теперь умный бит: возьмите коэффициент при x, равный 1, разделите его на два, получив 1/2 и, наконец, возведите в квадрат это дает 1/4 Добавьте 1/4 к обеим сторонам уравнения: При сложении 1/4 левая часть завершилась в виде полного квадрата: Мы будем называть это уравнение уравнением. # 2.2.1 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. Обратите внимание, что квадратный корень из Теперь, применяя принцип квадратного корня к уравнению.# 2.2.1 получаем: Добавьте 1/2 к обеим сторонам, чтобы получить: Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное Обратите внимание, что √ 3/4 можно записать как Решить Квадратичное уравнение с использованием квадратичной формулы2.3 Решение x 2 -x + 1 = 0 по квадратичной формуле. Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: В нашем случае A = 1 Соответственно B 2 — 4AC = Применение формулы корней квадратного уравнения: 1 ± √ -3 В наборе действительных чисел отрицательные числа не имеют квадратных корней.Был изобретен новый набор чисел, названный комплексным, чтобы отрицательные числа имели квадратный корень. Эти числа записываются (a + b * i) Оба i и -i являются квадратными корнями из минус 1 Соответственно √ -3 = √ 3, округленное до 4 десятичных цифр, составляет 1,7321 Два мнимых решения: x = ( 1 + √-3) / 2 = (1 + i√ 3) / 2 = 0.5000 + 0,8660i или: Было найдено два решения:
Как найти f (x) — SAT Math Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон Или заполните форму ниже: Уравнение касательной к кривой | Дифференциальное исчисление Нарисуйте график \ (f \) с указанием всех пересечений и точек поворота. {2} — 4x + 3 = 0 \\
Нарисуйте три касательных выше на вашем графике \ (f \). Запишите все наблюдения о трех касательных к \ (f \). Касательная в точке \ (y _ {\ text {int}} \) (синяя линия): градиент положительный, функция увеличивается в этой точке. Касательная в точке поворота (зеленая линия): градиент равен нулю, касательная — горизонтальная линия, параллельная оси \ (x \). Касательная в точке \ (x = \ text {4,25} \) (фиолетовая линия): градиент отрицательный, функция в этой точке убывает. Математическая сцена — Уравнения III — Урок 3Математическая сцена — Уравнения III — Урок 3 — Квадратные уравнения
Урок Как приступить к поиску точек, в которых два графика Мы уже знаем, где найти график Пример 1 Рассчитать точку Рассчитываем точку пересечения по 2х — 1 = х + 1 2х — х = 1 + 1 х = 2 Координата Y теперь может быть найдена f (2) = 2 × 2 — 1 = Точка пересечения — (2, Пример показывает, что мы можем найти точку Решить уравнение графически легко с помощью Пример 2 Решите уравнение x 2 — 2x — 3 = 2x — 3 сначала графически, а затем алгебраически. Рисуем графики f (x) = x 2 — Решает алгебраически: x 2 — 2x — 3 = 2x — 3 x 2 — 4x = 0 х (х — 4) = 0 Получение решений x = 0 и x = 4 . Пример 3 Решите уравнение x 2 — 1 = 2x — 3 Сначала переместите все термины Это дает x 2 — 2x + 2 = 0 Используем формулу корней квадратного уравнения с a = 1, b = Число под знаком квадратного корня: f (x) = x 2 — 1 и правая часть g (x) = 2x — 3. Мы видим, что парабола Пример 4 Решите уравнение x 3 — 3x + 2 = x 2 — Как и в предыдущем примере, мы перемещаем все х 3 — 3x + 2 = x 2 — 2x + 1 x 3 — x 2 — x + 1 = 0 (x 3 — x 2 ) — (x — 1) = 0 x 2 (x — 1) — (x — 1) = 0 (х — 1) (х 2 — (х — 1) (х — 1) (х Расчеты показывают, что их всего два Графики f (x) = Пример 5 Решите уравнение x 2 = x Легко видеть, что x = 0 и x = 1 являются Назовите левую часть f (x) = x 2 и правую часть g (x) = x. На графике видно, что точек всего две
Это дает решение x = 0 и x = 1 . Пример 6 Решите уравнение ln x = x 2 — 1 Это уравнение не так-то просто решить. Если мы График показывает нам, что есть два Обратите внимание, что мы выбираем значения x так, чтобы значения y
Если мы воспользуемся графическим калькулятором, то сможем найти Рисуем графики обеих сторон Еще проще использовать G-Solve (F5) и Теперь выберите Инструменты Пишем D2, Когда Это говорит нам о том, что Попробуйте пройти тест 3 по уравнениям III. Не забудьте использовать контрольный список для . |
