2\) равна \( у=2х.\)
Теперь рассмотрим функцию \(y = 2x \):
Рассмотрим площади треугольников под графиком \(y = 2x.\)
Площадь треугольника равна площади \(\frac{1}{2}\) основания на высоту. Таким образом, ясно, что области под графиком:
\(S_{1} = \frac{1}{2} \times 1 \times 2 = 1\)
\(S_{2} = \frac{1}{2} \times 2 \times 4 = 4\)
\(S_{3} = \frac{1}{2} \times 3 \times 6= 9\)
Итого, можно сказать, что первообразная эквивалентна площади под функцией.
Функция может иметь несколько первообразных.
\(F(x)+C;\)
Докажем что функция может иметь несколько первообразных:
\((F(x)+C) ′ =F ′ (x)+(C) ′ =f(x)+0=f(x).\)
\((F(x)+C) ′ =f(x).\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Содержание
Первообразная и неопределенный интеграл.

Функция $F(x)$ называется первообразной функции $f(x),$ заданной на некотором множестве $X,$ если $F'(x)=f(x)$ для всх $x\in X.$ Если $F(x -)$ первообразная функции $f(x),$ то $\Phi(x)$ является первообразной той же функции в том и только в том случае, когда $\Phi(x)=F(x)+C,$ где $C$ — некоторая постоянная. Совокупность всех первообразных функции $f(x)$ называется неопределенным интегралом от этой функции и обозначается символом $$\int f(x)\,dx.$$ Таким образом, по определению $$\int f(x)\,dx=F(x)+C,$$ где $F(x)$ одна из первообразных функции $f(x)$ а постоянная $C$ принимает действительные значения.
Свойства неопределенного интеграла.
1. $\left(\int f(x)\,dx\right)’=f(x).$
2. $\int f'(x)dx=f(x)+C.$
3. $\int af(x)dx=a\int f(x) dx.\,\,\,\,\,\,a\neq 0.$
4. $\int (f_1(x)+f_2(x))dx=\int f_1(x)\,dx+\int f_2(x)\, dx.$
Таблица основных неопределенных интегралов.
1. $\int dx=x+C$
2. $\int x^{\alpha}dx=\frac{x^{\alpha+1}}{\alpha+1}+C$
3. 2-7}|+c.$
2-7}|+c.$
Понятие и свойства неопределённого интеграла, таблица интегралов
Неопределённый интеграл: 8 фактов, которые надо знать студенту
Факт 1. Интегрирование — действие, обратное дифференцированию, а именно, восстановление
функции по известной производной этой функции.
Восстановленная таким образом функция F(x) называется первообразной для функции f(x).
Определение 1. Функция F(x) называется первообразной для функции f(x)
на некотором промежутке X, если для всех значений x из этого промежутка выполняется
равенство F ‘(x)=f(x), то есть данная функция f(x) является производной
от первообразной функции F(x)..
Например, функция F(x) = sin x
является первообразной для функции f(x) = cos x
на всей числовой прямой, так как при любом значении икса (sin x)’ = (cos x).
Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись
∫
f(x)dx
,
где знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.
Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то
∫
f(x)dx = F(x) +C
, (1)
где C — произвольная постоянная (константа).
Для понимания смысла множества первообразных функции как неопределённого интеграла
уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция — «быть дверью».
Её функция — «быть дверью».
А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции «быть
дверью», то есть её неопределённым интегралом, является функция «быть деревом + С», где С — константа,
которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана
из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции
при помощи формулы, которую мы узнали, изучая производную.
Тогда таблица функций распространённых предметов и соответствующих им первообразных
(«быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и др.) аналогична таблице основных
неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов
перечисляются распространённые функции с указанием первообразных, из которых «сделаны» эти функции. В части
задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых
услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В
В
задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было
использовать табличные интегралы.
Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а
чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно
записывать множество первообразных с произвольной константой C,
например, так: 5x³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку
первообразная может быть функцией, например, 5x³+4 или 5x³+3
и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.
Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x).
Пример 1. Найти множество первообразных функции
Найти множество первообразных функции
Решение. Для данной функции первообразной является функция
так как
Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.
или
(2)
Следовательно, функция — первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции
и вообще
где С – произвольная постоянная. В этом можно убедиться дифференцированием.
Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.
Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.
Теорема (формальное изложение факта 2). Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная.
В следующем примере уже обращаемся к таблице интегралов, которая будет дана
в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы
была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.
Пример 2. Найти множества первообразных функций:
1)
2)
3)
Решение. Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании
Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании
формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу
неопределённых интегралов мы изучим чуть дальше.
1) Применяя формулу (7) из таблицы интегралов при n = 3, получим
2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем
3) Так как
то по формуле (7) при n = -1/4 найдём
Под знаком интеграла пишут не саму функцию f,
а её произведение на дифференциал dx. Это делается прежде всего
для того, чтобы указать, по какой переменной ищется первообразная. Например,
,
;
здесь в обоих случаях подынтегральная функция равна ,
но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта
В первом случае эта
функция рассматривается как функция от переменной x, а во
втором — как функция от z.
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной
в каждой её точке есть заданная функция f(x) абсциссы этой точки.
Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной
точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию
F(x), для которой
F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна
кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена
из неё параллельным переносом вдоль оси Oy.
Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x),
то график функции y=F(x) есть интегральная кривая.
Факт 3. Неопределённый интеграл
геометрически представлен семеством всех интегральных кривых, как на рисунке ниже. Удалённость
каждой кривой от начала координат определяется произвольной постоянной (константой)
интегрирования C.
Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.
(3)
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.
Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
(4)
Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
(5)
Факт 8. Пользусь таблицей неопределённых интегралов,
свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл
любой функции.
Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
Продолжение темы «Интеграл»
Поделиться с друзьями
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2),
Первообразная | ЕГЭ по математике (профильной)
Первообразной для функции $f(x)$ называется такая функция $F(x)$, для которой выполняется равенство: $F'(x)=f(x)$
Таблица первообразных
Первообразная нуля равна $С$
| Функция | Первообразная |
| $f(x)=k$ | $F(x)=kx+C$ |
| $f(x)=x^m, m≠-1$ | $F(x)={x^{m+1}}/{m+1}+C$ |
| $f(x)={1}/{x}$ | $F(x)=ln|x|+C$ |
| $f(x)=e^x$ | $F(x)=e^x+C$ |
| $f(x)=a^x$ | $F(x)={a^x}/{lna}+C$ |
| $f(x)=sinx$ | $F(x)-cosx+C$ |
| $f(x)=cosx$ | $F(x)=sinx+C$ |
| $f(x)={1}/{sin^2x}$ | $F(x)=-ctgx+C$ |
| $f(x)={1}/{cos^2x}$ | $F(x)=tgx+C$ |
| $f(x)=√x$ | $F(x)={2x√x}/{3}+C$ |
| $f(x)={1}/{√x}$ | $F(x)=2√x+C$ |
Если $y=F(x)$ – это первообразная для функции $y=f(x)$ на промежутке $Х$, то $у$ $у=f(x)$ бесконечно много первообразных и все они имеют вид $y=F(x)+C$
Правила вычисления первообразных:
- Первообразная суммы равна сумме первообразных.
 Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$.
Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$. - Постоянный множитель выносится за знак первообразной. Если $F(x)$ — первообразная для $f(x)$, а $k$ – постоянная величина, то $k$ $F(x)$ — первообразная для $k$ $f(x)$.
- Если $F(x)$ — первообразная для $f(x)$, $а, k, b$ — постоянные величины, причем $k≠0$, то ${1}/{k}$ $F(kx+b)$ — это первообразная для $f(kx+b)$.
Пример:
Найти первообразную для функции $f(x)=2sinx+{4}/{x}-{cosx}/{3}$.
Решение:
Чтобы было проще найти первообразную от функции, выделим коэффициенты каждого слагаемого
$f(x)=2sinx+{4}/{x}-{cosx}/{3}=2∙sinx+4∙{1}/{x}-{1/3}∙cosx$
Далее, воспользовавшись таблицей первообразных, найдем первообразную для каждой функции, входящих в состав $f(x)$
$f_1=sinx$
$f_2={1}/{x}$
$f_3=cosx$
Для $f_1=sinx$ первообразная равна $F_1=-cosx$
Для $f_2={1}/{x}$ первообразная равна $F_2=ln|x|$
Для $f_2=cosx$ первообразная равна $F_3=sinx$
По первому правилу вычисления первообразных получаем:
$F(x)=2F_1+4F_2-{1}/{3}F_3=2∙(-cosx)+4∙ln|x|-{1}/{3}∙sinx$
Итак, общий вид первообразной для заданной функции
$F(x)=-2cosx+4ln|x|-{sin x}/{3}+C$
Связь между графиками функции и ее первообразной:
- Если график функции $f (x) > 0$ на промежутке, то график ее первообразной $F(x)$ возрастает на этом промежутке.

- Если график функции $f (x) < 0$ на промежутке, то график ее первообразной $F(x)$ убывает на этом промежутке.
- Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий (или наоборот).
Пример:
На рисунке изображен график функции $y=F(x)$ – одной из первообразных некоторой функции $f(x)$, определенной на интервале $(-3;5)$. Пользуясь рисунком, определите количество решений $f(x)=0$ на отрезке $(-2;2]$
Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий(или наоборот).
Выделим отрезок $(-2;2]$ и отметим на нем экстремумы.
У нас получилось $6$ таких точек.
Ответ: $6$
Неопределенный интеграл
Если функция $у=f(x)$ имеет на промежутке $Х$ первообразную $у=F(x)$, то множество всех первообразных $у=F(x)+С$, называют неопределенным интегралом функции $у=f(x)$ и записывают:
$∫f(x)dx$
Определенный интеграл – это интеграл с пределами интегрирования (на отрезке)
$∫_a^bf(x)dx$, где $a,b$ — пределы интегрирования
Площадь криволинейной трапеции или геометрический смысл первообразной
Площадь $S$ фигуры, ограниченной осью $Oх$, прямыми $х=а$ и $х=b$ и графиком неотрицательной функции $у=f(x)$ на отрезке $[a;b]$, находится по формуле
$S=∫_a^bf(x)dx$
Формула Ньютона — Лейбница
Если функция $у=f(x)$ непрерывна на отрезке $[a;b]$, то справедливо равенство
$∫_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$, где $F(x)$ — первообразная для $f(x)$
Пример:
На рисунке изображен график некоторой функции $у=f(x)$. 2-1={2∙(-8)}/{3}-8-1=-{16}/{3}-9$
2-1={2∙(-8)}/{3}-8-1=-{16}/{3}-9$
$S={2}/{3}-3-(-{16}/{3}-9)={2}/{3}-3+{16}/{3}+9={18}/{3}+6=6+6=12$
Ответ: $12$
Алгебра – 11 класс. Первообразная функция
Дата публикации: .
Первообразная функция. Введение
Ребята, вы умеем находить производные функций, используя различные формулы и правила. Сегодня мы будем изучать операцию, обратную вычислению производной. Понятие производной часто применяется в реальной жизни. Напомню: производная – это скорость изменения функции в конкретной точке. Процессы, связанные с движением и скоростью, хорошо описываются в этих терминах.
Давайте рассмотрим вот такую задачу: «Скорость движения объекта, по прямой, описывается формулой $V=gt$. Требуется восстановить закон движения.
Решение.
Мы хорошо знаем формулу: $S’=v(t)$, где S — закон движения.
Наша задача сводится к поиску функции $S=S(t)$, производная которой равна $gt$. Посмотрев внимательно, можно догадаться, что $S(t)=\frac{g*t^2}{2}$. 2}{2})’+c’=g*t+0=g*t$.
2}{2})’+c’=g*t+0=g*t$.
Ребята, обратите внимание: наша задача имеет бесконечное множество решений!
Если в задаче не задано начальное или какое-то другое условие, не забывайте прибавлять константу к решению. Например, в нашей задаче может быть задано положение нашего тела в самом начале движения. Тогда вычислить константу не трудно, подставив ноль в полученное уравнение, получим значение константы.
Как называется такая операция?
Операция обратная дифференцированию называется – интегрированием.
Нахождение функции по заданной производной – интегрирование.
Сама функция будет называться первообразной, то есть образ, то из чего была получена производная функции.
Первообразную принято записывать большой буквой $y=F'(x)=f(x)$.
Определение. Функцию $y=F(x)$ называется первообразной функции $у=f(x)$ на промежутке Х, если для любого $хϵХ$ выполняется равенство $F’(x)=f(x)$.
Давайте составим таблицу первообразных для различных функции. Ее надо распечатать в качестве памятки и выучить. {\frac{3x+1}{6}}$.
{\frac{3x+1}{6}}$.
3. По заданному закону изменения скорости тела от времени $v=4cos(6t)$ найти закон движения $S=S(t)$, если в начальный момент времени тело имело координату равную 2.
12.1 Антипроизводная
Первообразное — это имя, которое мы иногда (редко) даем операции, идущей в обратном направлении от
производная функции от самой функции. Поскольку производная не определяет функцию полностью
(вы можете добавить любую константу к своей функции, и производная будет такой же), вам нужно добавить дополнительные
информация, чтобы вернуться к явной функции как антипроизводной.
Таким образом, мы иногда говорим, что первообразная функции — это функция плюс произвольная константа.Таким образом
первообразной \ (\ cos x \) является \ ((\ sin x) + c \).
Более распространенное название первообразной — неопределенный интеграл. Это идентичное понятие, просто
другое название для него.
Для этого используется волнистая линия. Таким образом, предложение «первообразная \ (\ cos x \) есть \ ((\ sin x) + c \)»
обычно формулируется так: неопределенный интеграл от \ (\ cos x \) равен \ ((\ sin x) + c \), и это обычно записывается
в виде
\ [\ int \ cos x \; dx = (\ sin x) + c \]
На самом деле это плохая запись.Переменная \ (x \), которая встречается справа, является переменной и представляет
аргумент синусоидальной функции. Символы слева просто говорят, что функция, первообразной которой мы являемся
ищется функция косинуса. Вы избежите путаницы, если выразите это, используя совершенно другой
символ (скажем, \ (y \)) слева, чтобы обозначить это. Правильный способ написать это тогда
\ [\ int \ cos y \; dy = (\ sin x) + c \]
Почему используются эти странные и уродливые обозначения?
Мы делаем это из уважения к традициям. Это обозначение, которое люди использовали на протяжении веков. Мы увидим, почему они
Это обозначение, которое люди использовали на протяжении веков. Мы увидим, почему они
сделал это в следующем разделе.
Первый вопрос, к которому мы обращаемся: если вы дадите мне функцию, скажем \ (g \), и попросите меня найти ее неопределенный
интеграл, как мне это сделать?
Основной ответ на этот вопрос: для этого нет новых уловок. Вы можете работать в обратном направлении от
правила дифференциации и некоторые правила интеграции, и это, по сути, все, что вы можете сделать.Но затем
позволяет интегрировать (находить первообразные) множество полезных функций.
Первообразной суммы нескольких членов является сумма их первообразных. Это следует из того, что
что производная суммы — это сумма производных членов. И аналогично, умножая функцию
на константу умножает свою первообразную на ту же константу.
Используя эти факты, мы можем найти первообразную любого многочлена. {к + 1}} {к + 1} + с \).
{к + 1}} {к + 1} + с \).
Что это за штука \ (+ c \)?
Это напоминание о том, что производная константы равна \ (0 \), поэтому она является антипроизводной как операция, обратная к
производная полностью не определена. Вы можете добавить любую константу к антипроизводной и получить другую.
Некоторые считают, что это было изобретено педантами, чтобы мучить студентов, наказывая их за то, что они иногда игнорируют
этот скучный факт.2} {2} + 7x + c \]
Студенты обычно находят это настолько легким, что, когда они вынуждены находить такое антипроизводное в тесте, часто
их умы уже сосредоточены на следующем вопросе, и они рассеянно забывают и различают вместо этого
анти-дифференциации одного или, возможно, всех терминов. Пожалуйста, избегайте этой ошибки.
Заданий:
Найдите первообразные каждой из следующих функций:
12. {- \ frac {1} {2}} \)
{- \ frac {1} {2}} \)
(проверьте свой ответ, выделив его.)
Знакомство с первообразными | StudyPug
Антипроизводное tanx
Первообразная tanx, возможно, является самым известным тригонометрическим интегралом, с которым у всех возникают проблемы. Это потому, что вам нужно использовать замену u.
Что является первообразной tanx
Давайте посмотрим на функцию, которую мы хотим интегрировать.
Уравнение 1: первообразное tanx pt. 1
Вы можете спросить себя, как я могу использовать замену u? Во-первых, обратите внимание, что tanx может быть изменен на sinx over cosx. Другими словами,
Уравнение 1: первообразное tanx pt. 2
Теперь мы можем использовать замену u.
Пусть u = cosx. Тогда мы можем сказать, что du = -sinx. Обратите внимание, что умножение обеих сторон на отрицательное дает -du = sinx. Таким образом, замена даст нам следующее:
Уравнение 1: первообразное tanx pt. 3
3
Теперь мы можем вынести отрицательный знак из интеграла, что даст нам:
Уравнение 1: первообразное tanx pt. 4
Теперь возникает вопрос, как мне взять первообразную 1 / u? Ну, это то же самое, что брать первообразную 1 / x. Интеграл от 1 / x — это натуральный логарифм от | x |. Другими словами,
Уравнение 1: первообразное tanx pt. 5
Никогда не забывайте добавлять константу c, потому что вы берете первообразную! Наконец, не забывайте, что изначально интеграл выражался через x.Итак, нам нужно изменить нашу первообразную с точки зрения x. Напомним, что u = cosx, поэтому обратная подстановка даст:
Уравнение 1: первообразное tanx pt. 6
, который является неотъемлемой частью tanx.
Поскольку мы обсуждаем триггерные интегралы, почему бы нам не взглянуть на интегралы некоторых триггерных функций? Поскольку tanx представляет собой комбинацию sinx и cosx, почему бы просто не найти их первообразную по отдельности? Давайте продолжим и найдем первообразную sin и первообразную cosx.
Что является первообразной греха
Многие люди просто запоминают, что первообразная sinx — это просто –cosx. Но как именно это получить? Есть несколько способов проиллюстрировать это, но я покажу вам 2 метода.
Метод 1: возврат с использованием производных
Вместо явного нахождения первообразной нашей целью было бы найти функцию, производная которой равна sinx. Если производная функции — это sinx, то должно быть верно, что первообразная функции sinx вернет эту функцию.Хорошо, звучит идеально. Какую функцию мы должны попробовать? Пусть
Уравнение 2: Обратный путь Первообразная sin pt. 1
Обратите внимание, что производная от этого будет:
Уравнение 2: Обратный путь Первообразная sin pt. 2
Видите, мы действительно близки, но вместо sinx у нас –sinx. Как избавиться от негатива? Как насчет того, чтобы взять функцию, которая у нас есть, и добавить лишний отрицательный знак? Это может привести к тому, что у производной будет два отрицательных значения, и она станет положительной. Если мы это сделаем, пусть
Если мы это сделаем, пусть
Уравнение 2: Обратный путь Первообразная sin pt. 3
Теперь производная от этого будет:
Уравнение 2: Обратный путь Первообразная sin pt. 4
Это прекрасно! У нас есть производная sinx, поэтому наша функция является первообразной sinx. Следовательно, антипроизводная sinx равна
Уравнение 2: Обратный путь Первообразная sin pt. 5
Опять же, не забудьте добавить константу c.
Итак, это отличный способ найти первообразные, но некоторые интегралы могут потребовать большого количества предположений.Как лучше найти первообразную греха? Это приводит нас к следующему методу:
Метод 2: используйте теорему Муавра
Этот метод может сбить с толку, если вы не знаете, как использовать комплексные числа. Так что пропустите этот метод, если вы не знаете теорему Муавра. Обратите внимание, что согласно теореме Муавра мы имеем
Уравнение 3: Муавр — первообразная sin pt. 1
Сложение этих двух уравнений дает:
Уравнение 3: Первообразная Муавра sin pt. 2
2
Упрощение правой части приводит к:
Уравнение 3: Муавр — первообразная sin pt.3
Таким образом, разделив обе стороны на 2, получим:
Уравнение 3: Муавр — первообразная sin pt. 4
Мы будем использовать это позже. Теперь вместо того, чтобы складывать оба уравнения, вычтем эти два уравнения.
Вычитание этих двух уравнений даст нам:
Уравнение 3: Муавр — первообразная sin pt. 5
Упрощение правой части даст нам:
Уравнение 3: Муавр — первообразная sin pt. 6
Выделение sinx делением на 2i приведет нас к:
Уравнение 3: Муавр — первообразная sin pt.7
Что мы будем с этим делать? Что ж, вместо того, чтобы брать первообразную греха, мы возьмем первообразную того, что мы видим в правой части уравнения. Это потому, что они абсолютно равны. Следовательно, их первообразные должны давать точно такой же ответ. Следовательно, давайте оценим
Уравнение 3: Муавр — первообразная sin pt. 8
Во-первых, давайте упростим эту задачу, вычленив 1 / 2i из интеграла:
Уравнение 3: Муавр — первообразная sin pt. 9
9
Теперь вычисление интеграла даст нам:
Уравнение 3: Муавр — первообразная sin pt.2 = -1, тогда
Уравнение 3: Муавр — первообразная sin pt. 13
Обратите внимание на то, что из нашего уравнения ранее:
Уравнение 3: Муавр — первообразная sin pt. 14
Следовательно, замена на это приведет нас к окончательному ответу:
Уравнение 3: Муавр — первообразная sin pt. 15
, первородное от греха. Это два метода поиска первородной греха. Теперь перейдем к поиску первообразной cosx.
Какая первообразная у cosx
Опять же, люди запоминают, что первообразная cosx — это sinx.Однако давайте покажем, что это правда, используя два упомянутых ранее метода.
Метод 1: Возврат с использованием производных.
Найдем функцию, производная которой равна cosx. Почему бы нам не сказать это:
Уравнение 4: Обратный поиск Первообразной cos pt. 1
Это отличное предложение, поскольку мы знаем, что производные sin и cos связаны. Теперь, взяв производную от этого, я получу:
Уравнение 4: Обратный ход Первообразной cos pt.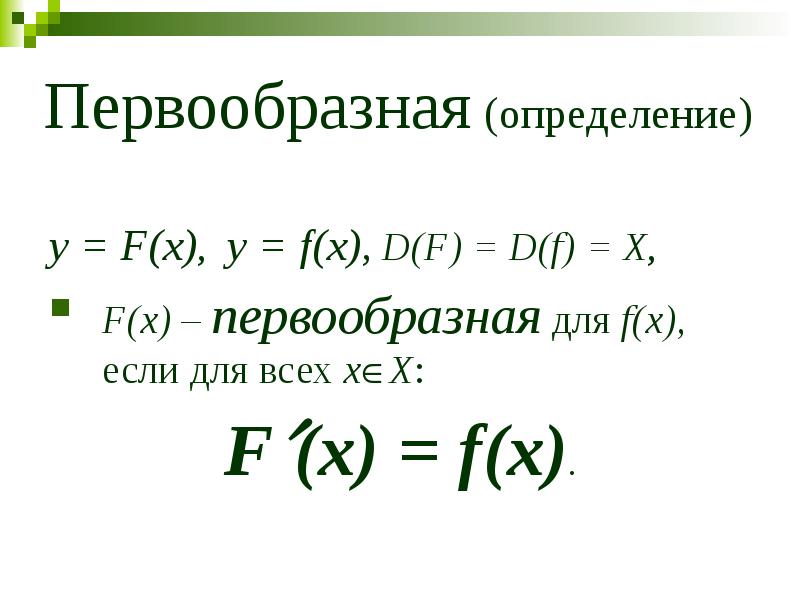 2
2
Обратите внимание, что производная уже дает cosx.Это здорово, потому что нам не нужно вносить какие-либо изменения в функцию. Следовательно, мы знаем, что первообразная cosx равна:
Уравнение 4: Обратный ход Первообразной cos pt. 3
Еще раз не забудьте добавить константу C.
Теперь, если вы не хотите гадать и тестировать, мы можем использовать метод 2.
Метод 2: используйте теорему Муавра
Из ранее мы знаем, что:
Уравнение 5: Первообразная Муавра cosx pt. 1
Опять же, вместо интегрирования cosx, мы вместо этого собираемся найти первообразную правой части уравнения (поскольку они в точности равны).Итак, оценим
Уравнение 5: Первообразная Муавра cosx pt. 2
Вынося за скобки 1/2 интеграла, получаем:
Уравнение 5: Первообразная Муавра cosx pt. 3
Вычисление интеграла приводит к:
Уравнение 5: Первообразная Муавра cosx pt. 4
Распределение 1/2 на каждый член дает:
Уравнение 5: Первообразная Муавра cosx pt. 5
5
Теперь мы можем переписать это уравнение на
.
Уравнение 5: Первообразная Муавра cosx pt. 6
По совпадению, мы знали раньше, что:
Уравнение 5: Первообразная Муавра cosx pt.7
Следовательно, замена этого даст нам
Уравнение 5: Первообразная Муавра cosx pt. 8
, который является первообразной cosx. Если вы хотите узнать больше о первообразных триггерных функций, я предлагаю вам взглянуть на второй раздел этой статьи «Первообразные от триггерных функций»
Теперь, если вам интересно, можно ли взять первообразную обратных тригонометрических функций, тогда ответ — да. Поскольку мы нашли первообразную tanx, sinx и cosx, почему бы нам не найти первообразную их обратных? Давайте посмотрим на arctan.
Что такое первообразная арктана?
Чтобы найти первообразную арктана, мы должны знать, что такое производное арктана. Если вы не знаете, что это такое, рекомендуем вам ознакомиться с этой статьей ниже. Он дает пошаговое решение для поиска производной от arctan. 2), нам нужно использовать замену u.2 ранее, поэтому переключение u обратно на x даст нам:
2), нам нужно использовать замену u.2 ранее, поэтому переключение u обратно на x даст нам:
Уравнение 6: первообразная arctan pt. 9
Отсюда можно сделать вывод, что:
Уравнение 6: первообразная arctan pt. 10
Теперь, если вы заинтересованы в поиске первообразной arcsin и arccosx, взгляните на эти ссылки здесь. Они показывают пошаговое решение для поиска этих первообразных.
http://www.ditutor.com/integration/integral_arccos.html
http://www.ditutor.com/integration/integral_arcsin.html
Обратите внимание, что метод очень прост по отношению к первообразной арктана. Все они требуют использования интеграции по частям.
Первообразная триггерной функции
В этом разделе мы сосредоточимся на поиске первообразной тригонометрических функций, которые являются обратными значениям tanx, sinx и cosx, а также тригонометрическим функциям, для интеграции которых потребуются тождества половинных углов. Обратите внимание, что взаимные триггерные функции и обратные триггерные функции НЕ совпадают. Следовательно, обратные тригонометрические интегралы отличаются от обратных триггерных интегралов. Обратные триггерные интегралы — это те, что мы делали раньше! Следует также отметить, что многие первообразные в этом разделе требуют, чтобы вы также знали производные триггерных функций. Поэтому убедитесь, что вы хорошо их знаете, прежде чем отвечать на эти вопросы. Если вы не очень разбираетесь в них, рекомендуем посмотреть эту ссылку, чтобы попрактиковаться!
Следовательно, обратные тригонометрические интегралы отличаются от обратных триггерных интегралов. Обратные триггерные интегралы — это те, что мы делали раньше! Следует также отметить, что многие первообразные в этом разделе требуют, чтобы вы также знали производные триггерных функций. Поэтому убедитесь, что вы хорошо их знаете, прежде чем отвечать на эти вопросы. Если вы не очень разбираетесь в них, рекомендуем посмотреть эту ссылку, чтобы попрактиковаться!
Что такое первообразная от secx?
Есть несколько способов сделать это, но лучше всего использовать ярлык.Для этого ярлыка нам нужно знать, какова производная от sec. Если вы не знаете, что это такое, вы можете обратиться по этой ссылке.
https://socratic.org/questions/what-is-derivatives-of-y-sec-x
Эта ссылка дает пошаговое решение для производной от sec.
Во-первых, давайте настроим наш интеграл для первообразной secx.
Уравнение 7: первообразная secx pt. 1
Затем мы умножим подынтегральное выражение на secx + tanx / secx + tanx. 2?
2?
Я снова покажу 2 метода.2. Теперь давайте посмотрим на другие взаимные функции.
Что такое первообразная от cscx?
Вы можете попробовать использовать метод, предполагающий возврат с использованием производных, но это может оказаться для вас немного трудным. Вместо этого я собираюсь использовать аналогичный прием, который я использовал ранее для интеграла от secx. Настроив интеграл cscx имеем:
Уравнение 10: первообразная cscx pt. 1
Мы собираемся умножить подынтегральное выражение на cscx + cotx / cscx + cotx.2 пт. 8
, который является интегралом cscx. Теперь давайте посмотрим на нашу последнюю обратную функцию cotx.
Что является первообразной от cotx?
Вы можете подумать, что для получения этого интеграла требуется тот же трюк, что и для получения первообразной от secx и cscx, но на самом деле это другое. Вместо этого при поиске первообразной cotx используется только замена u (очень похожая на первообразную tanx).
Итак, установив наш интеграл, мы имеем:
Уравнение 13: первообразная cotx pt. 1
1
Обратите внимание, что cot x = cos x / sin x, поэтому мы можем изменить наш интеграл на
.
Уравнение 13: первообразная cotx pt. 2
Теперь мы можем использовать замену u. Пусть u = sinx. Тогда du = cosx dx, и подставив их, мы получим
Уравнение 13: первообразная cotx pt. 3
Мы видели это много раз, поэтому оценка дает нам
Уравнение 13: первообразная cotx pt. 4
Напомним, что раньше у нас было u = sinx. Таким образом, преобразование u обратно в x приводит к окончательному ответу:
Уравнение 13: первообразная cotx pt.2x.
Подводя итог, мы нашли интеграл от 6 триггерных функций, а также их интегралы, когда каждая из них возведена в квадрат. Существует бесконечное количество триггерных функций, которые мы можем интегрировать. Так что, если вы ищете интеграл, которого не смогли найти в этой статье, предлагаю вам взглянуть на эту ссылку.
https://en.wikipedia.org/wiki/List_of_integrals_of_trigonometric_functions
К сожалению, он не дает вам пошагового решения, но, по крайней мере, вы найдете решение для своего интеграла. Кроме того, есть предметы, которые мы не рассмотрели, например, гиперболические интегралы. Если вас это интересует, вы можете взглянуть на эту диаграмму первообразных в самом низу.
Кроме того, есть предметы, которые мы не рассмотрели, например, гиперболические интегралы. Если вас это интересует, вы можете взглянуть на эту диаграмму первообразных в самом низу.
http://math3.org/math/integrals/tableof.htm
Интеграл lnx
Теперь, когда мы закончили интегрирование тригонометрических функций, давайте взглянем на натуральный логарифм. Прежде чем перейти к интегралу натурального логарифма, давайте поговорим о том, что такое ln и что интеграция поможет нам найти.x, затем отразите его на линии y = x, чтобы получить график ln. Следовательно, график lnx будет выглядеть так:
График 1: график lnx
Обратите внимание, что единственное, что мы можем вычислить на этом графике без использования калькулятора, это ln, равное 1. Мы видим, что ln1 на графике равно 0. Это потому, что мы знаем, что логарифм 1 с любым основанием равен 0.
Натуральное бревно очень интересно, потому что у него есть особые правила. Эти правила включают в себя правило произведения, правило частного и правило мощности.
Для правила произведения мы можем разделить функцию ln на добавление двух функций ln, если внутренняя часть логарифма является произведением двух или более вещей.у) = yln (x)
Эти свойства будут очень полезны при работе с очень сложными функциями ln. Теперь, когда мы очень хорошо знаем ln, давайте попробуем найти первообразную ln x.
Что такое первообразная lnx?
Сначала мы устанавливаем интеграл lnx:
Уравнение 19: первообразная lnx pt. 1
Как интегрировать lnx? Что действительно трудно заметить, так это то, что вам нужно использовать интеграцию по частям. Напомним, что формула интегрирования по частям:
Уравнение 19: первообразная lnx pt.2
Устанавливаем:
Уравнение 19: первообразная lnx pt. 3
Получение u и интеграция dv даст нам:
Уравнение 19: первообразная lnx pt. 4
Объединение всех четырех из них в формулу интегрирования по частям дает:
Уравнение 19: первообразная lnx pt. 5
Обратите внимание, что вычисление интеграла от ln приводит к окончательному ответу:
Уравнение 19: первообразная lnx pt. 6
6
Обязательно скачайте антидериватную таблицу. Это очень удобно, когда вы учитесь, работаете над заданиями по исчислению или составляете шпаргалку для экзаменов.2 = \ frac {3} {2}, ∫12 xdx = 21 x2∣∣∣∣ 12 = 23,
, поэтому он всегда должен работать со всеми интегралами. Согласно второй фундаментальной теореме исчисления наше утверждение должно быть верным.
Ответ: Интеграция, использованная в опровержении, верна только потому, что f (x) = xf (x) = xf (x) = x непрерывно на интервале (1,2) (1,2) (1,2 ). Вот почему мы можем так интегрироваться. Другими словами, мы только показали, что это верно для конкретного случая. Если функция не является непрерывной на интервале, например f (x) = 1xf (x) = \ frac {1} {x} f (x) = x1 на интервале (−1,1) (- 1,1 ) (- 1,1) (\ big ((обратите внимание, что f (0) f (0) f (0) не определено), \ big),) основная теорема исчисления не может быть применена.+} \ большой (\ ln (x) — \ ln (x) \ big) \\ \\
& = 0.
\ end {align} PV ∫ − 11 x1 dx = ∫ − 10 x1 dx + ∫01 x1 dx = a → 0 − lim ln∣x∣∣∣∣∣ −1a + a → 0 + lim ln∣x∣∣∣∣∣ a1 = (x → 0 + lim ln (x)) — 0 + 0− (x → 0 + lim ln (x)) = x → 0 + lim (ln (x) −ln (x)) = 0,
В этом случае главное значение Коши соответствует тому, что мы ожидали бы, если бы это был правильный интеграл. Тем не менее, это не всегда так. См. Страницу о несобственных интегралах для получения дополнительных примеров главного значения Коши.
Тем не менее, это не всегда так. См. Страницу о несобственных интегралах для получения дополнительных примеров главного значения Коши.
Первообразные в исчислении
Вопросы о понятиях и свойствах первообразных в
исчисления представлены.Эти вопросы были разработаны, чтобы помочь вам лучше понять концепцию и свойства первообразных . Чтобы ответить на приведенные ниже вопросы, вам сначала необходимо просмотреть определения и теоремы, относящиеся к первообразным.
Вопросы с решениямиВопрос 1 Верно или неверно . Вопрос 2 Верно или неверно . Если F (x) является первообразной f (x), то Вопрос 3 Верно или неверно .Первообразное функции f плюс первообразное функции g является первообразным функции f + g. Вопрос 4 Верно или неверно . Первообразная функции f , разделенная на первообразную функции g, является первообразной функции f / g. Дополнительные ссылки по исчислению |
Интегральное и первообразное | математика — это развлечение
У большинства людей неправильное представление о взаимосвязи между «интеграцией» и «принятием первообразных»; они склонны произносить эти слова как синонимы, но есть небольшая разница.
В общем, «Интеграл» — это функция, связанная с исходной функцией, которая определяется ограничивающим процессом. Сузим «интегрирование» более точно до двух частей: 1) неопределенный интеграл и 2) определенный интеграл. Неопределенный интеграл означает интегрирование функции без каких-либо ограничений, но в определенном интеграле есть верхний и нижний пределы, другими словами, мы назвали это интервалом интегрирования.
Пока первообразная как раз означает, что найти функции, производная которых будет нашей исходной функцией.Существует очень небольшая разница между определенным интегралом и первообразной, но явно существует большая разница между неопределенным интегралом и первообразной. Рассмотрим пример:
Рассмотрим пример:
f (x) = x²
Первообразная x² равна F (x) = ⅓ x³.
Неопределенный интеграл равен ∫ x² dx = F (x) = ⅓ x³ + C, что почти является первообразной, за исключением c. (где «C» — постоянное число.)
С другой стороны, пару недель назад мы узнали о фундаментальной теореме исчисления, где нам нужно применить вторую часть этой теоремы к «определенному интегралу».4/4 + 2 также является одним из первообразных. Несмотря на это, когда мы берем неопределенный интеграл, на самом деле мы находим «все» возможные первообразные сразу (поскольку разные значения C дают разные первообразные). Так что между ними есть тонкая разница, но это явно две разные вещи. Вдобавок мы бы сказали, что определенный интеграл — это число, к которому мы можем применить вторую часть фундаментальной теоремы исчисления; но первообразная — это функция, к которой мы могли бы применить первую часть фундаментальной теоремы исчисления.
Математических изображений | Полиномиальные функции и производная (5): Антидифференциация
Есть один важный тип задач, в которых мы знаем производную функции (скорость ее изменения,
наклон его графика), и мы хотим найти функцию. Например, мы знаем скорость и хотим вычислить пространство.
Например, мы знаем скорость и хотим вычислить пространство.
Процесс нахождения функции по ее производной называется антидифференцировкой,
найти примитивную функцию или найти неопределенный интеграл.Как следует из названия, антидифференцировка — это операция, обратная дифференциации.
Использование слова интеграция здесь может показаться странным, потому что проблема интеграции каким-то образом связана с поиском области.
(накопление, суммирование) и дифференциация связаны с мгновенной скоростью изменения или как наклон касательной линии к
график функции. Позже мы увидим, что эти две очень разные проблемы глубоко связаны (Фундаментальная теорема исчисления) и
что в некотором роде интеграция — это процесс, обратный дифференциации.
F (x) называется первообразной (или примитивным, или неопределенным интегралом) функции f (x) на открытом интервале, если производная F равна
f для каждого значения x на интервале.
Обратите внимание, что мы определяем первообразную, а не первообразную. Это потому, что первообразная не уникальна. Тем не менее первообразная
Это потому, что первообразная не уникальна. Тем не менее первообразная
уникальна с точностью до аддитивной константы. Сказано:
Любые две первообразные F и G одной и той же функции f могут отличаться только константой.
Причина в том, что их разность F-G имеет производную 0, а затем F-G является постоянной функцией.
Иногда мы используем особый знак (у Лейбница, знак интегрирования — большая буква s от слова «сумма». Лейбниц использовал следующий знак для обозначения
общий примитив f):
Функция f называется подынтегральной функцией, постоянная C называется постоянной интегрирования.
Символ dx указывает, что мы должны интегрировать по x.
Если мы знаем простые методы дифференцирования, найти какие-то первообразные несложно.Например, легко найти
примитив для постоянной функции:
Мы можем проверить, что в каждой точке производная является исходной постоянной функцией:
Производная полинома степени 1 (линейная функция) является постоянной функцией (степень 0, горизонтальная линия).
Тогда первообразная постоянной функции является линейной функцией.
Первичные производные многочленов-функций тоже просты. Например, базовая линейная функция (функция идентичности):
Проверка результата в одной точке:
Производная многочлена степени 2 (парабола) — это многочлен степени 1 (линейная функция).Тогда примитив линейной функции — это парабола.
Квадратичный многочлен (парабола):
Производная многочлена степени 3 (кубика) — это многочлен степени 2 (парабола).
Тогда первообразная параболы является кубической функцией.
Другой пример, кубический многочлен:
В следующей версии интерактивного приложения вы можете перемещать синюю точку по оси x:
РЕКОМЕНДАЦИИ
Майкл Спивак, Calculus, Third Edition, Publish-or-Perish, Inc.
Том М. Апостол, Calculus, Second Edition, John Willey and Sons, Inc.
БОЛЬШЕ ССЫЛКИ
Производная линейной функции — постоянная функция.
Производная квадратичной функции — это линейная функция, то есть прямая линия.
Производная кубической функции — это квадратичная функция, парабола.
Интегральное понятие ассоциируется с понятием площади. Мы начали рассматривать область, ограниченную графиком функции и осью абсцисс между двумя вертикальными линиями.
Монотонные функции на отрезке интегрируемы. В этих случаях мы можем ограничить ошибку, которую мы допускаем при приближении интеграла с помощью прямоугольников.
Если мы рассматриваем нижний предел интегрирования a как фиксированный и если мы можем вычислить интеграл для различных значений верхнего предела интегрирования b, то мы можем определить новую функцию: неопределенный интеграл от f.
Вычислить площадь по параболе сложнее, чем вычислить площадь по линейной функции.Мы покажем, как аппроксимировать эту область с помощью прямоугольников и что интегральная функция многочлена степени 2 является многочленом степени 3.
Мы можем увидеть некоторые основные понятия об интегрировании, применяемые к общей полиномиальной функции. Интегральные функции от полиномиальных функций — это полиномиальные функции с одной степенью выше, чем исходная функция.
Фундаментальная теорема исчисления говорит нам, что каждая непрерывная функция имеет первообразную, и показывает, как построить ее с помощью интеграла.
Вторая основная теорема исчисления — мощный инструмент для вычисления определенного интеграла (если мы знаем первообразную функции).
В качестве введения в кусочно-линейные функции мы изучаем линейные функции, ограниченные открытым интервалом: их графики подобны отрезкам.
Кусочная функция — это функция, которая определяется несколькими подфункциями. Если каждый кусок является постоянной функцией, то кусочная функция называется кусочно-постоянной функцией или ступенчатой функцией.
Непрерывная кусочно-линейная функция определяется несколькими отрезками или лучами, соединенными без скачков между ними.
Интеграл степенных функций был известен Кавальери от n = 1 до n = 9. Ферма смог решить эту задачу, используя геометрические прогрессии.
Две точки определяют прямую линию. Как функцию мы называем это линейной функцией. Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки. Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.
Степень с натуральными показателями — простые и важные функции. Их обратные функции — это степени с рациональными показателями (радикал или корень n-й степени)
Многочлены степени 2 — это квадратичные функции. Их графики — параболы. Чтобы найти точки пересечения по оси x, мы должны решить квадратное уравнение. Вершина параболы — это максимум минимума функции.
Многочлены степени 3 — это кубические функции. Реальная кубическая функция всегда пересекает ось x хотя бы один раз.
Мы можем рассматривать полиномиальную функцию, проходящую через серию точек плоскости. Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
Увеличивая степень, полином Тейлора все больше и больше приближает экспоненциальную функцию.
Увеличивая степень, полином Тейлора все больше и больше приближает функцию синуса.
Правила интеграции
Интеграция
Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.Его часто используют, чтобы найти область под графиком функции .
Первое правило, которое необходимо знать, — интегралы и производные противоположны!
Иногда мы можем вычислить интеграл
, потому что мы знаем соответствующую производную.
Правила интеграции
Вот наиболее полезные правила с примерами ниже:
| Общие функции | Функция | Интегральный |
|---|---|---|
| Константа | ∫a dx | топор + C |
| переменная | ∫x dx | x 2 /2 + C |
| Квадрат | ∫x 2 dx | x 3 /3 + C |
| Взаимное | ∫ (1 / x) dx | ln | x | + C |
| Экспоненциальная | ∫e x dx | e x + C |
| ∫a x dx | a x / ln (a) + C | |
| ∫ln (x) dx | x ln (x) — x + C | |
| Тригонометрия (x в радианах) | ∫cos (x) dx | грех (х) + С |
| ∫sin (x) dx | -cos (x) + С | |
| мкс 2 (x) dx | загар (x) + C | |
| Правила | Функция | Интегральный |
| Умножение на константу | мкф (х) дх | c∫f (x) dx |
| Правило мощности (n ≠ −1) | ∫x n dx | x n + 1 n + 1 + C |
| Правило о сумме | ∫ (ж + г) dx | ∫f dx + ∫g dx |
| Правило разницы | ∫ (ж — г) dx | ∫f dx — ∫g dx |
| Интеграция по частям | См. Интеграцию по частям Интеграцию по частям | |
| Правило замещения | См. Интеграцию заменой | |
Примеры
Пример: какой интеграл от sin (x)?
Из приведенной выше таблицы он указан как −cos (x) + C
Записывается как:
∫sin (x) dx = −cos (x) + C
Пример: каков интеграл от 1 / x?
Из приведенной выше таблицы это указано как ln | x | + C
Записывается как:
∫ (1 / x) dx = ln | x | + C
Вертикальные стержни || по обе стороны от x означает абсолютное значение, потому что мы не хотим давать отрицательные значения функции натурального логарифма ln .
Правило мощности
Пример: Что такое ∫x
3 dx?
Возникает вопрос: «Какой интеграл x 3 ?»
Мы можем использовать правило мощности, где n = 3:
∫x n dx = x n + 1 n + 1 + C
∫x 3 dx = x 4 4 + C
Пример: Что такое ∫√x dx?
√x — это также x 0. 5
5
Мы можем использовать правило мощности, где n = ½:
∫x n dx = x n + 1 n + 1 + C
∫x 0,5 dx = x 1,5 1,5 + C
Умножение на константу
Пример: Что такое ∫6x
2 dx?
Мы можем вынести 6 за пределы интеграла:
∫6x 2 dx = 6∫x 2 dx
А теперь используйте правило мощности на x 2 :
= 6 x 3 3 + C
Упростить:
= 2x 3 + C
Правило суммы
Пример: Что такое ∫cos x + x dx?
Используйте правило суммы:
∫cos x + x dx = ∫cos x dx + ∫x dx
Найдите интеграл каждого (используя таблицу выше):
= грех х + х 2 /2 + С
Правило разницы
Пример: Что такое ∫e
w — 3 dw?
Используйте правило разницы:
∫e w — 3 dw = ∫e w dw — ∫3 dw
Затем вычислите интеграл каждого (используя таблицу выше):
= e w — 3w + C
Правила суммы, разности, постоянного умножения и мощности
Пример: Что такое ∫8z + 4z
3 — 6z 2 dz?
Используйте правило суммы и разности:
∫8z + 4z 3 — 6z 2 dz = ∫8z dz + ∫4z 3 dz — ∫6z 2 dz
Постоянное умножение:
= 8∫z dz + 4∫z 3 dz — 6∫z 2 dz
Правило мощности:
= 8z 2 /2 + 4z 4 /4 — 6z 3 /3 + C
Упростить:
= 4z 2 + z 4 — 2z 3 + C
Интеграция по частям
См.

 Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$.
Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$.
 Если F (x) — первообразная f (x), а c — любая константа, то F (x) + c также первообразная f (x).
Если F (x) — первообразная f (x), а c — любая константа, то F (x) + c также первообразная f (x).

