Моторизированные позиционеры для выравнивания волокна серии U от Luminos с разрешением по осям XY 10 нм

03.06.2021

В позиционерах сверхвысокого разрешения серии U от компании Luminos используется сверхточный привод с линейным шаговым двигателем, обеспечивающий лучший в отрасли двунаправленный люфт 0,1 мкм с возможностью инкрементного перемещения с разрешением менее 10 нм по осям X и Y. Позиционеры обеспечивают полный диапазон перемещения по осям XYZ 2,5х2,5х12,7 мм и отличаются значительными улучшениями по сравнению с другими позиционерами Luminos.

Позиционеры серии U представляют значительный скачок в возможностях автоматизации, обеспечивая пятикратное увеличение разрешения и увеличение скорости в 12 раз при увеличении диапазона хода двигателя в 25 раз. Производительность намного превосходит требования по выравниванию одномодового волокна SMF-28. При использовании шагового двигателя нет необходимости в компенсации замкнутого контура или в позиционерах с точной регулировкой, а также в дополнительных контроллерах.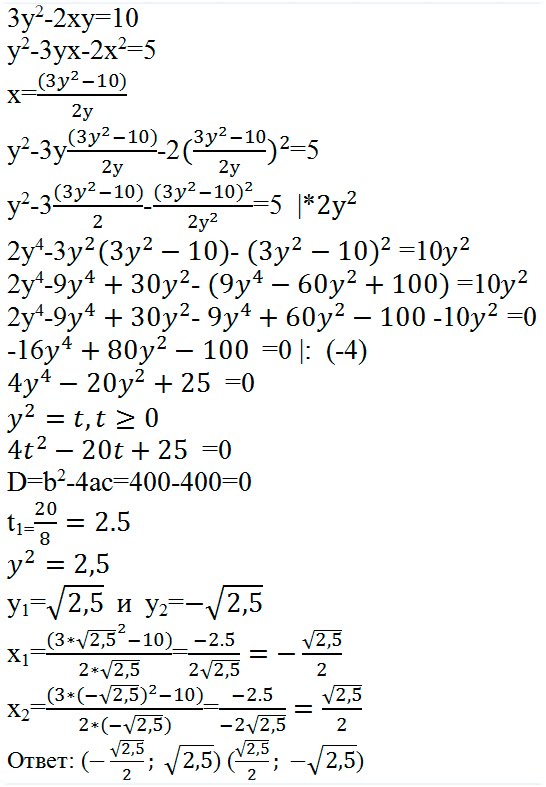 Можно легко настроить SM волноводы с точностью до 0,01 дБ без компенсации люфта.

В серию U входят:

Выравнивание волокна, не требующее пьезодвигателя.

В индустрии фотоники принято считать, что выравнивание должно разрешаться примерно до 1% размера пучка или диаметра модового поля (MFD). Для юстировки SMF-28 с MFD 10 мкм разрешение 100 нм обычно приемлемо. С появлением современных планарных фотонных устройств возрастает потребность в выравнивании все меньших и меньших волноводных структур, иногда даже размером до 2 мкм.

В связи с этим для позиционеров необходим новый стандарт разрешения около 20 нм. Большинство основных производителей столиков для позиционирования предлагают системы автоматического выравнивания, в которых используются позиционеры с грубым и точным перемещением с несколькими уровнями контроллеров, чтобы соответствовать требованиям разрешения. Большинство из них имеют электропривод с люфтом до 5-10 мкм. Поэтому использование пьезопозиционеров приводит к увеличению сложности системы.

Сверхмалый люфт.

Позиционеры Luminos уникальные в отрасли, обеспечивают стабильные характеристики с помощью встроенной платформы позиционирования без трения, что позволяет приводам работать с равномерной нагрузкой. При юстировке волноводов по осям X И Y обычно требуется более чем в 5 раз более высокое разрешение, чем по оси Z. Позиционеры Luminos используют запатентованную технологию Ratio Drive по осям выравнивания X и Y. Все актюаторы XYZ перемещаются на 12,5 мм, однако на автоматических позиционерах Luminos серии U X и Y перемещаются на 2,5 мм под управлением двигателя. Это приводит к 5-кратному увеличению точности по наиболее важным осям X и Y, обеспечивая невероятно низкий двунаправленный люфт 0,1 мкм с разрешением 10 нм без использования пьезодвигателей.

Юстировка фотонного волновода.

Чувствительность бокового выравнивания.

Чтобы понять уровень точности, необходимый для юстировки фотонных волноводов, рассмотрим эталон: одномодовое оптическое волокно SMF-28 с 10-мкм диаметром модового поля (MFD). На рисунке 1 показано, как концы двух волоконно-оптических волноводов будут перемещаться в направлении X для проверки оптических потерь в зависимости от бокового выравнивания. Обычно одно волокно подключается к источнику излучения, а другое — к измерителю мощности. Оптические потери одинаково чувствительны к боковому перемещению в направлениях X и Y для SMF-28. По мере того, как промышленность движется к усовершенствованным устройствам с планарными оптическими волноводами, все чаще встречаются планарные волноводы с MFD 2-3 мкм. Для систем позиционирования становится еще более важным иметь запас.

На рисунке 2 показан график зависимости оптических потерь от бокового выравнивания оптических волокон SMF-28 в диапазоне +/- 1 мкм от идеального выравнивания. Большинство измерителей оптической мощности имеют разрешение 0,01 дБ, что соответствует целевому диапазону смещения по оси X 0,46 мкм.  Если бы система позиционирования имела двунаправленный люфт менее 0,46 мкм, тогда было бы возможно написать программное обеспечение для оптимизации, которое бы не полагалось на компенсацию люфта. Также стала бы возможной разработка системы позиционирования, которая не должна переключаться между грубым и точным управлением перемещением. Большинство двигателей на рынке, которые могут соответствовать требованиям, указанным на рисунке 2, представляют собой сложные устройства с замкнутым контуром с энкодерами или составные приводы с шаговыми двигателями, часто со встроенными дополнительными пьезодвигателями. Позиционеры Luminos предлагают множество преимуществ. Позиционеры Luminos серии U обеспечивают уникальную для рынка архитектуру позиционирования. Компания предлагает единственные позиционеры, которые могут обеспечить двунаправленный люфт 0,1 мкм по осям X и Y с помощью простых элементов управления пошаговым двигателем. Юстировка волновода без использования пьезоэлектрических двигателей или энкодеров. Фактически, рисунок 2 показывает, что есть запас точности для требований юстировки SMF-28. 

Чувствительность осевого совмещения

На рисунке 3 показано, как будут перемещены концы двух оптических волокон для проверки оптических потерь в сравнении с осевым выравниванием. Предполагается, что оптические волокна идеально выровнены по осям X и Y, и изменяется только положение Z. Измерения потерь, показанные на рисунках 2 и 4, были проведены с иммерсионной жидкостью между концами оптических волокон, чтобы устранить эффекты интерференции Френеля.

На рисунке 4 представлены оптические потери в зависимости от размера осевого зазора, оптические потери гораздо менее чувствительны к осевому смещению, чем к поперечному, как показано на рисунке 2.  Разница в значении для смещения 0,01 дБ измеряется как 3,76 мкм против 0,46 мкм. Эта различная чувствительность выравнивания может быть значительной для оптических волокон с малой числовой апертурой. Система Ratio Drive, работает с тщательно спроектированными приводные механизмы изгиба без трения по осям X и Y. Также Ratio Drive от Luminos отличается повышенной стабильностью. Когда двигатели слегка нагреваются, любое результирующее изменение положения, вызванное термическим воздействием, также уменьшается на то же отношение. В результате позиционеры Luminos являются более стабильными по сравнению с другими двигателями, они поддерживают очень стабильную регулировку при простое в течение длительных периодов времени, даже нескольких дней.

Рисунок 3. Перемещение двух концов оптического волокна по оси Z.

Рисунок 4. Зависимость оптических потерь от размера осевого зазора.

Компания «Специальные Системы. Фотоника» является партнером Luminos и оказывает техническую поддержку по всей линейке продукции Luminos на территории России и ЕАЭС.

Вы можете получить любую дополнительную информацию о продукции и технологиях Luminos, обратившись к специалистам нашей компании.

Возврат к списку

S-3-X-Y: как выглядит линейка автомобилей Tesla

15 Марта, 2019,
15:00

7531

15 марта Илон  Маск показал электрический кроссовер Tesla Model Y. Модель уже назвали «самой важной в истории Tesla» и говорят, что она станет настоящей проверкой популярности автопроизводителя. В честь анонса, редакция AIN.UA рассказываем о линейке автомобилей Tesla, которые уже продаются, продавались или появятся в ближайшем будущем. 

Tesla Model S

Первые поставки: 2012 год

Цена: от $79 000

Первый по-настоящему серийный автомобиль компании. Это пятидверный хэтчбек с полным приводом. Машина несколько раз меняла характеристики и конфигурации: поначалу существовали как версии с одним электродвигателем, так и машины с аккумуляторами на 40-60 кВт*ч. Со временем от их использования отказались, а дизайн обновили в соответствии с видом Model 3. Автомобиль разгоняется до 100 км/час за 4,2 секунды и в максимальной конфигурации может проехать 540 км на одном заряде.

Ранее Tesla обещала закрыть продажи автомобилей с емкость менее 100 кВт*ч, однако этого не произошло — на официальном сайте все еще доступна версия на 75 кВт*ч по цене от $79 000. До 2017 года автомобиль также поставлялся с пожизненным безлимитом на зарядку с помощью фирменным станций Supercharger. Все модели, выпущенные после этого срока, получают лишь 400 кВт на год — за остальные придется доплатить по стандартным расценкам.

Tesla Model X

Первые поставки: 2015 год

Цена: от $88 000

Первый электрический кроссовер Tesla, построенный на базе Model S. Полноприводный автомобиль с недавних пор продается только с батареей на 100 кВт и стоит от $88 000. Машина способна проехать на одном заряде до 475 км. Отличительная особенность — автоматические задние двери по конструкции «крыльев сокола», которые поднимаются вверх. Это облегчает посадку и экономит место — в сравнении с дверями традиционной конструкции, для Model X нужно на 30 см меньше свободного пространства.

Компания позиционирует Model X как семейный автомобиль: об этом говорит как третий ряд сидений (до семи мест), так и два просторных багажных отделения и возможность кроссовера тянуть прицеп массой до 2 тонн. Кроме того, Tesla делает большую ставку на безопасность машины: у Model X идеальные результаты в тестах на безопасность и самый высокий в классе коэффициент аэродинамического сопротивления.

Tesla Model 3

Первые поставки: 2018 год

Цена: от $35 000

Самый доступный автомобиль в истории Tesla, с помощью которого она намерена выйти на массовый рынок. После дебюта в 2018 году, машина занимает большую часть в структуре продаж компании. Автопроизводитель не сразу пришел к выпуску самой бюджетной комплектации: сначала в продаже появились модели Long Range с увеличенной батареей и ценой. Стандартная конфигурация, стоимостью от $35 000, обеспечивает запас хода в 350 км и разгон до 100 км/час за 5,6 секунд. 

Производство Model 3 — главный вызов Tesla на 2018-2019 годы. Ранее компания задействовала дополнительную сборочную линию на фабрике во Фримонте, а сам Маск задерживался на производстве до полуночи, мотивируя других сотрудников следовать его расписанию.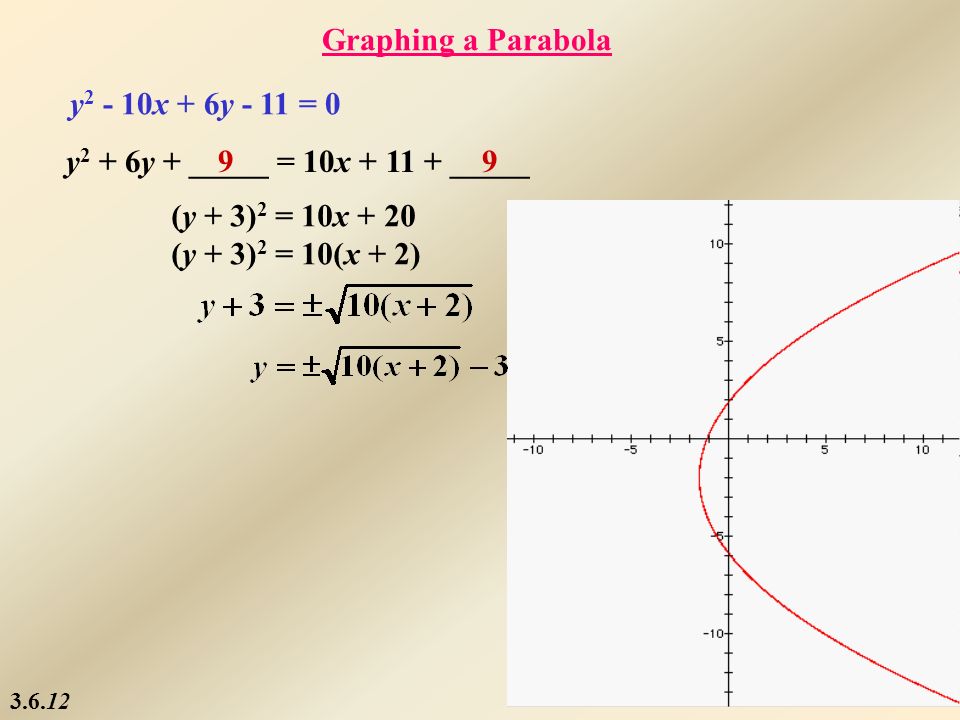 В планах предпринимателя — выйти на темп в 5000 автомобилей/неделю.

Tesla Model Y

Первые поставки: 2020 год (запланировано)

Цена: от $39 000

Второй кроссовер в истории Tesla, построенный на базе Model 3. Как и другие модели, эта получила несколько конфигураций со своими сроками поставками.

Первой, осенью 2020 года, на рынок выйдет версия с максимальным запасом хода — 480 км за $47 000. Затем последует полноприводный вариант за $51 200 и скоростная версия за $60 000. Желающим купить базовую Model Y (370 км хода и $39 000) придется подождать до 2021 года. У машины три ряда сидений и семь посадочных мест, два багажника и 5-звездочные оценки в краш-тестах — все это маркировка для семейного позиционирования. 

Лайнап выпуска Model Y

Model Y будет разгоняться до 100 км/час за 3,5 секунды. По словам Маска, если приобрести версию со всеми дорожными датчиками, «машина будет способна на что угодно после софтверных обновлений» — очевидно, речь идет о полноценном автопилоте.

Tesla Roadster (2008)

Tesla Roadster 2008

Первые поставки: 2008 год

Снят с продажи: 2012 год

Цена на старте продаж: от $109 000

Первый автомобиль Tesla, созданный в партнерстве со спортивным автопроизводителем Lotus на базе шасси Lotus Elise. Машину производили с 2008 по 2012 годы — изначально контракт между Tesla и Lotus был подписан всего на 2500 экземпляров. Позже Tesla выпускала минорные обновления Roadster: версии 2,5 и 3,0. В них улучшали аэродинамику, ставили новые комплектующие и наращивали емкость аккумулятора.

Последняя актуальная на данный момент модель может проехать на одном заряде до 644 км. Автомобиль разгоняется до 201 км/час, дальнейшее ускорение принудительно ограничили. Скорость старта от 0 до 100 км/час — менее 4 секунд, а на полную зарядку батареи уйдет до 4 часов.

Tesla Roadster (2020)

Первые поставки: 2020 год (запланирован)

Цена: от $200 000

Tesla Roadster 2020

В 2020 году в серийное производство должна поступить новая модель Roadster, построенная на платформе седана Tesla Model 3. Это будет четырехместный спорткар с тремя электродвигателями и батареей на 200 кВт*ч.

При таком аккумуляторе, машина должна проезжать до 1000 км на одном заряде и разгоняться от 0 до 100 км/час за 1,9 сек. По словам Илона Маска, Roadster покажет «унизительное поражение бензиновых автомобилей».

Первую 1000 родстеров продают в эксклюзивной версии по цене $250 000 — сумму нужно перечислить в первые 10 дней после оформления заказа. Стандартная конфигурация обойдется в $200 000 и потребует «всего» $50 000 на депозите в пользу Tesla.

Tesla Semi

Начало поставок: 2019 год (запланировано)

Цена на старте продаж: от $150 000 (ориентировочно)

Электрический тягач с четырьмя двигателями  от Model 3, мощность двигателя и подробные спецификации неизвестны. Автомобиль будет поставлять в двух конфигурациях (на 480 км и 800 км хода). Водительское место находится по центру, управление осуществляется с помощью устойчивого к влаге и пыли сенсорного экрана. 2 + 2

Поскольку отношение не равно, это дифференциальное уравнение не является точным.

Следующий шаг — найти функцию u (x, y) u (x, y) u (x, y), которая сделает уравнение u (x, y) (p (x, y) dx + q (x, y) dy ) = 0 u (x, y) (p (x, y) dx + q (x, y) dy) = 0 u (x, y) (p (x, y) dx + q (x, y) dy ) = 0 становится точным дифференциальным уравнением.

u (x, y) u (x, y) u (x, y) называется интегрирующим фактором, и его будет намного легче найти, если это только функция x или только функция y.

u (x, y) u (x, y) u (x, y) является только функцией x, если ∂ p (x, y) ∂ y — ∂ q (x, y) ∂ xq (x, y) ∂ p ( x, y) y — q (x, y) xq (x, y) \ frac {\ frac {\ частичный p (x, y)} {\ частичный y} — \ frac {\ частичный q (x , y)} {\ частичный x}} {q (x, y)} имеют только переменную x, и это только функция y, если ∂ q (x, y) ∂ x — ∂ p (x, y) ∂ yp ( x, y ∂ q (x, y) ∂ x — ∂ p (x, y) ∂ yp (x, y \ frac {\ frac {\ частичный q (x, y)} {\ частичный x} — \ frac { \ частный p (x, y)} {\ частичный y}} {p (x, y} имеет только переменную y. 6 = C, где CCC — постоянная.

(Я впервые провожу более 3 часов, чтобы написать ответ в кворе. Ввод латекса и убедитесь, что никакая ошибка в ответе не занимает много времени, особенно если вы не знакомы с латексом).

XY-L10A: модуль контроля зарядки аккумуляторных батарей | hardware

Модуль зарядки XY-L10A [1] подойдет для зарядки любых аккумуляторных батарей (литиевых, свинцово-кислотных, стартерных) в диапазоне напряжений от 6V до 48V током зарядки до 10A (максимальный ток зарядки ограничен параметрами контактов используемого реле). Основное его достоинство — он очень недорогой (можно купить на AliExpress по цене примерно $6) и обладает достаточным набором функций для создания автоматического зарядного устройства.

Примечание: в продаже есть также модули XY-L30A с более мощным реле, его контакты рассчитаны на ток до 30A.

Модуль может отображать на LCD напряжение, процент заряда батареи, время зарядки батареи. Для работы необходим источник тока с выходным напряжением, достаточным для зарядки батареи. Реализовано автоматическое управление зарядкой по уровню напряжения батареи и времени зарядки. Параметры батареи и процесса заряда можно устанавливать с помощью кнопок и индикатора LCD. Есть возможность ввода и вывода параметров через последовательный порт.

[Описание принципа работы]

Устройство получает питание от источника постоянного тока напряжением 6V .. 60V. Этот же источник тока используется как силовое для заряда аккумуляторной батареи, поэтому начальное напряжение батареи не должно быть меньше 5V, иначе напряжения не хватит для устойчивого работы модуля XY-L10A. Схема подключения источника тока и батареи:

[Настройка параметров батареи]

Перед зарядом батареи нужно установить её минимальное (volt-LI) и максимальное (volt-HI) напряжение. По этим значениям вычисляются и отображаются проценты заряда батареи.

% заряда = 100% * (напряжение_батареи — volt-LI) / (volt-HI — volt-LI)

Максимальное напряжение также используется для определения момента прекращения зарядки.

[Настройка времени зарядки]

Кроме контроля верхнего напряжения заряжаемой аккумуляторной батареи есть еще второй способ прекращения процесса зарядки: истечение заданного времени. По умолчанию эта функция отключена, что определяется параметром времени —:—h, в этом состоянии зарядка продолжается без ограничения по времени, пока напряжение на батарее не достигнет заданного максимального уровня.

Для того, чтобы функция ограничения зарядки по времени начала работать, необходимо установить ненулевое время в диапазоне от минимального 1 минута (00:01h) до максимального 100 часов (99:59h).

Процедура установки параметров:

a) Нажмите и удерживайте кнопку SET несколько секунд для входа в меню установки параметров.
b) Переключайтесь между настраиваемыми параметрами короткими нажатиями на кнопку SET.
с) После того, как параметр выбран, его можно поменять кнопками UP и DOWN. Короткое нажатие изменит параметр на один шаг, долгое нажатие приведет к быстрому изменению параметра. Для изменения всех нужных параметров повторяйте шаги b) и c).
d) После того, как все параметры установлены, нажмите и удерживайте кнопку SET несколько секунд для выхода из меню установки параметров.

Описание работы основного интерфейса:

1. Короткие нажатия кнопки SET позволяют просмотреть текущую установку параметров.
2. Короткое нажатие на кнопку UP переключает дисплей с отображения процентов зарядки на время зарядки.
3. Короткое нажатие на кнопку DOWN включит или выключит реле, которое дает ток заряда на батарею. Если реле может быть замкнуто, то на экране в качестве напоминания будет отображаться OFF.
4. Долгое нажатие на кнопку UP включит режим малого потребления энергии (режим экономии). Когда режим экономии включен, через 10 минут отсутствия активности в интерфейсе подсветка индикатора LCD выключится.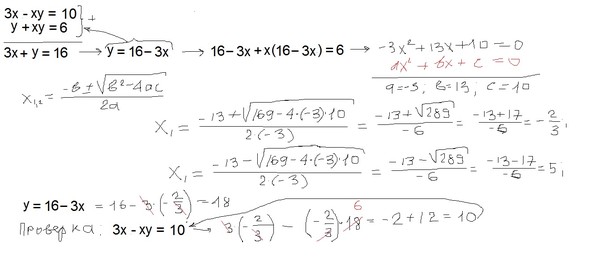 Если режим экономии выключен, то подсветка включена всегда.
5. Длительное нажатие на кнопку SET переключит модуль в режим установки параметров.

[Выгрузка параметров через последовательный порт]

Для подключения последовательного порта необходим преобразователь USB — TTL UART. Его сигналы приема и передачи нужно подключить к контактам RX и TX модуля XY-L10A:

Для порта UART установите параметры 115200, 8, 1 (скорость 115200 бод, 8 бит данных, 1 стоп-бит, без контроля четности).

Команды управления модулем:

Команда	Функция
on	Замкнуть контакты реле (запуск заряда батареи)
off	Разомкнуть контакты реле (прервать заряд батареи)
start	Начать выгрузку данных
stop	Остановить выгрузку данных
read	Прочитать установки параметров
dw10. 0	Установить нижний предел напряжения батареи (volt-LI)
up20.0	Установить верхний предел напряжения батареи (volt-HI)
xx:yy	Установить количество часов (xx) и минут (yy) времени заряда батареи (OP). После истечения этого времени зарядка прекратится.

Формат команды выгрузки данных: напряжение батареи + процент зарядки + время зарядки + состояние зарядки.

12.0V,020%,00:10,OP

[Дополнительные функции]

Запись времени зарядки: при входе в режим отображения времени миганием будет показано время зарядки. Автоматическое определение неправильного ввода параметров: если volt-LI >= volt-HI, то будет отображаться мигающая надпись ERR (ошибка). Определение подключения батареи: если батарея не подключена, то будет отображаться тест NbE (Not Battery Error).

 [Устранение проблем, FAQ]

Q01: Какие параметры должны быть у подключаемого источника питания? На какое напряжение можно заряжать батареи?
A01: Источник питания для зарядки аккумулятора и питания модуля должен быть источником постоянного тока (тока, не напряжения!) с напряжением в диапазоне от 6V до 60V. Источник тока — это означает, что ток на выходе должен автоматически ограничиваться до нужно предела, необходимого для успешного заряда батареи. Идеальный вариант — лабораторный импульсный источник питания с ограничением тока [2, 3], однако это может быть даже простой трансформатор на нужное напряжение с выпрямителем и сглаживающим конденсатором на выходе выпрямителя. Также в качестве источника тока можно использовать простейшие не автоматические зарядные устройства, работающие по принципу ограничения тока.

Напряжение этого источника тока должно быть на несколько вольт выше напряжения заряжаемой батареи. Например, для заряда 12V автомобильного аккумулятора напряжение источника тока должно быть не меньше 15V. Поскольку модуль контроля заряда XY-L10A получает питание от того же самого источника тока, существуют пределы напряжения для него. Минимальный предел 6V и максимальный предел 60V определяются параметрами внутреннего стабилизатора напряжения модуля XY-L10A.

С помощью модуля XY-L10A можно заряжать батареи в диапазоне от напряжений от 6V до 48V.

Q02: Почему заряд быстро прекращается, LCD мигает?
A02: Источник тока выдает слишком большой ток, который не подходит для заряжаемой батареи, либо сама батарея вышла из строя. Для правильной зарядки используйте подключайте заряжаемую батарею короткими и толстыми проводами, чтобы модуль XY-L10A мог правильно контролировать напряжение батареи. Правильно подбирайте ток зарядки — обычно он выбирается в 10 раз меньше емкости батареи. Например для зарядки батареи емкостью 20 А/ч (AH) выбирают ток заряда около 2..3A. Имейте в виду, что слишком большой ток может привести к перегреву батареи и даже к её взрыву (это особенно актуально для Li-Po батарей).

Q03: Можно ли реализовать контроль напряжения батареи с её автоматической подзарядкой?
A03: Модуль XY-L10A работает по принципу контроля напряжения. Если, например, установить нижний предел напряжения 12.0V и верхний предел 14.5V, то когда напряжение 12V-батареи упадет ниже этого предела, то реле замкнется и начнется автоматическая зарядка батареи от внешнего источника тока. Зарядка будет продолжаться, пока напряжение на батарее не достигнет уровня 14.5V, после чего реле разомкнется и заряд автоматически прекратится.

Q04: Можно ли заряжать 24V батарею от 12V источника тока? Или 12V батарею от 48V источника постоянного тока?
A04: 24V батарею от 12V заряжать не получится, потому что напряжение источника тока должно быть гарантированно выше напряжения заряжаемой батареи. От 48V заряжать 12V батарею можно, но только в том случае, если ток на выходе 48V будет ограничиваться до необходимого тока заряда. Помните, что в модуле XY-L10A нет никакого ограничения тока, он реализует только контролирующие функции.

[Ссылки]

1. XY-L10A site:aliexpress.com.
2. Источники питания компании RD.
3. Ремонт блока питания Б5-47.

2 $ — Обмен стека математики

Сеть обмена стеков

Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0

3. +0

6. Авторизоваться
   Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил
5 лет, 3 месяца назад

Просмотрено
92 раза

$ \ begingroup $

Закрыто. 2-2 \ cdot (-10) =… $

Создан 19 марта 2016, 21:41.

Роман83Римский83

17.5k 33 золотых знака2323 серебряных знака6262 бронзовых знака

$ \ endgroup $

Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками арифметика или задайте свой вопрос.

Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie

Настроить параметры

Систем линейных уравнений — Бесплатная математическая справка

Системы линейных уравнений имеют место, когда существует более одного связанного математического выражения.Например, в \ (y = 3x + 7 \) есть только одна линия со всеми точками на этой линии, представляющая набор решений для приведенного выше уравнения.

Когда вам задают 2 уравнения в одном и том же вопросе и просят решить для единственного ответа, вы можете визуализировать проблему как две линии на одной плоскости xy. Следующие два уравнения изображены на одной плоскости xy:

$$ y = 3x + 5 $$
$$ y = — x $$

Решение любого уравнения — это место пересечения ОБЕИХ уравнений на плоскости xy.Это место встречи называется Точкой пересечения. Если у вас есть линейное уравнение и квадратное уравнение в одной плоскости xy, могут быть ДВЕ ТОЧКИ, где график каждого уравнения будет встречаться или пересекаться. Вот геометрический вид:

Вот пример двух уравнений с двумя неизвестными переменными:

Пример

$$ x + y = 10 $$
$$ 3x + 2y = 20 $$

Есть три метода решения нашего пробного вопроса.

• 1) Решаем графически
• 2) Мы можем решить это алгебраически
• 3) Мы также можем решить это с помощью алгебраического исключения

Решу вопрос всеми 3 способами.Метод 1. Решить графически:

Чтобы решить графически, лучше всего записать ОБА уравнения в форме пересечения наклона или в форме: \ (y = mx + b \), где m = наклон, а b = точка пересечения y в качестве первого шага. Таким образом, \ (x + y = 10 \) становится \ (y = — x + 10 \) (форма пересечения наклона). Затем \ (3x + 2y = 20 \) становится \ (y = — \ frac {3x} {2} + 10 \) при записи в форме пересечения наклона.

Затем нарисуйте две линии, ведущие к точке пересечения. Построив эти линии, вы обнаружите, что ОБА уравнения пересекаются в точке (0,10).Точка (0,10) означает, что если вы подставите x = 0 и y = 10 в ОБЕИ исходные уравнения, вы обнаружите, что это решает оба уравнения. Вот как эти два уравнения выглядят на плоскости xy:

Метод 2: Решить алгебраически

Шагов:

1) Решите относительно x или y в первом уравнении (\ (x + y = 10 \)). Решу за у. Итак, \ (x + y = 10 \) становится \ (y = -x + 10 \).

2) Подставьте значение y (то есть -x + 10) во второе уравнение, чтобы найти x. Наше второе уравнение было \ (3x + 2y = 20 \) и после подстановки становится \ (3x + 2 (-x + 10) = 20 \)

Далее: Решите относительно x.

$$ 3x -2x + 20 = 20 $$
$$ x + 20 = 20 $$
$$ x = 0 $$

3) Подставьте x = 0 в ЛЮБОЕ исходное уравнение, чтобы найти значение y. Я буду использовать наше второе уравнение.

$$ 3x + 2y = 20 $$
$$ 3 (0) + 2y = 20 $$
$$ 0 + 2y = 20 $$
$$ y = 10 $$

Итак, наша точка пересечения снова (0,10).

Метод 3: Алгебраическое исключение

Этот метод имеет дело с сопоставлением переменных для ELIMINATE или устранением одной. Имейте в виду, что какую переменную удалить в первую очередь — это ваш выбор.

ЦЕЛЬ: исключить x и решить вместо y или наоборот. Вернемся к нашим исходным уравнениям.

В нашем втором 3x + 2y = 20, вы можете исключить 3x, умножив -3 на КАЖДЫЙ член в нашем первом уравнении (x + y = 10).

x + y = 10
3x + 2y = 20

-3 (x) + -3 (y) = -3 (10)
3x + 2y = 20

-3x + -3y = -30
3x + 2y = 20

ВНИМАНИЕ, что -3x и 3x исключаются. Вижу это? Понять, почему? И вот почему: отрицательный плюс положительный = ноль.

Теперь у нас есть это:

-3y = -30
2y = 20

-3y + 2y = -30 + 20

-y = -10

y = 10.

Далее: чтобы найти x, мы подставляем y = 10 в ЛЮБОЕ из исходных уравнений. К настоящему времени вы должны увидеть, что наш ответ для x будет НУЛЬ.

Вот он:

Я буду использовать x + y = 10

x + 10 = 10

x = 0. {3}

3.8 Неявное дифференцирование — Исчисление Том 1

Задачи обучения

• Найдите производную сложной функции, используя неявное дифференцирование.
• Используйте неявное дифференцирование, чтобы определить уравнение касательной.

Мы уже изучили, как найти уравнения касательных к функциям и скорости изменения функции в определенной точке. Во всех этих случаях мы имели явное уравнение для функции и явно дифференцировали эти функции.Предположим вместо этого, что мы хотим определить уравнение касательной к произвольной кривой или скорость изменения произвольной кривой в точке. В этом разделе мы решаем эти проблемы, находя производные функций, которые неявно определяются в терминах.

В большинстве математических дискуссий, если зависимая переменная является функцией независимой переменной, мы выражаем через. Если это так, мы говорим, что это явная функция из. Например, когда мы пишем уравнение, мы явно определяем в терминах.С другой стороны, если связь между функцией и переменной выражается уравнением, где не выражается полностью через, мы говорим, что уравнение неявно определяет через. Например, уравнение неявно определяет функцию.

Неявное дифференцирование позволяет нам находить наклоны касательных к кривым, которые явно не являются функциями (они не проходят проверку вертикальной линии). Мы используем идею, что части являются функциями, которые удовлетворяют данному уравнению, но на самом деле это не функция.

Как правило, уравнение неявно определяет функцию, если функция удовлетворяет этому уравнению. Уравнение может неявно определять множество различных функций. Например, функции

, и, которые проиллюстрированы на (Рисунок), являются всего лишь тремя из многих функций, неявно определяемых уравнением.

Рисунок 1. Уравнение неявно определяет множество функций.

Если мы хотим найти наклон прямой, касательной к графику в точке, мы можем вычислить производную функции в точке.С другой стороны, если нам нужен наклон касательной в точке, мы можем использовать производную от. Однако не всегда легко найти функцию, неявно определяемую уравнением. К счастью, метод неявного дифференцирования позволяет нам найти производную неявно определенной функции, даже не решая ее явно. Процесс поиска с использованием неявного дифференцирования описан в следующей стратегии решения проблем.

Использование неявной дифференциации

Предполагая, что это неявно определяется уравнением, найти.

Решение

Следуйте шагам стратегии решения проблем.

Использование неявной дифференциации и правила продукта

Предполагая, что это неявно определяется уравнением, найти.

Решение

Использование неявного дифференцирования для нахождения второй производной

Найдите, если.

Найти для, неявно определенного уравнением.

Решение

Ключевые понятия

• Мы используем неявное дифференцирование, чтобы найти производные от неявно определенных функций (функций, определяемых уравнениями).
• Используя неявное дифференцирование, мы можем найти уравнение касательной к графику кривой.

Глоссарий

неявное дифференцирование

— это метод вычисления функции, определяемой уравнением, который достигается путем дифференцирования обеих сторон уравнения (не забывая рассматривать переменную как функцию) и решения для

Полиномиальные тождества

Когда у нас есть сумма (разность) двух или трех чисел в степени 2 или 3 и нам нужно снять скобки, мы используем полиномиальные тождества
(короткие формулы умножения) :

(x + y) ² = x ² + 2xy + y ²
(x — y) ² = x ² — 2xy + y ²

Пример 1. Если x = 10, y = 5a
(10 + 5a) ² = 10 ² + 2 · 10 · 5a + (5a) ² = 100 + 100a + 25a ²

Пример 2: если x = 10 и y равно 4
(10-4) ² = 10 ² -2 · 10 · 4 + 4 ² = 100-80 + 16 = 36

Верно и обратное:
25 + 20a + 4a ² = 5 ² + 2 · 2 · 5 + (2a) ² = (5 + 2a) ²

Последствия вышеуказанных формул:

(-x + y) ² = (y — x) ² = y ² — 2xy + x ²
(-x — y) ² = (- (x + y)) ² = (x + y) ² = x ² + 2xy + y ²

Формулы 3 степени:

(x + y) ³ = x ³ + 3x ² y + 3xy ² + y ³
(x — y) ³ = x ³ — 3x ² y + 3xy ² — y ³

Пример: (1 + ² ) ³ = 1 ³ + 3.1 ² .a ² +
3.1. (A ² ) ² + (a ² ) ³ = 1 + 3a ² + 3a ⁴ + a ⁶

(x + y + z) ² = x ² + y ² + z ² + 2xy + 2xz + 2yz
(x — y — z) ² = x ² + y ² + z ² — 2xy — 2xz + 2yz

Фактор Правила

x ² — y ² = (x — y) (x + y)

x ² + y ² = (x + y) ² — 2xy
или
x ² + y ² = (x — y) ² + 2xy

Пример: 9a ² — 25b ² = (3a) ² — (5b) ² =
(3a — 5b) (3a + 5b)

x ³ — y ³ = (x — y) (x ² + xy + y ² )
x ³ + y ³ = (x + y) (x ² — ху + у ² )

Если n натуральное число

x ⁿ — y ⁿ = (x — y) (x ^n-1 + x ^n-2 y +. 2 + 20 $

3) Решите уравнение: x ² -25 = 0
Решение: x ² -25 = (x — 5) (x + 5)
=> мы должны решить следующие 2 уравнения:
x — 5 = 0 или x + 5 = 0
, поэтому уравнение имеет два решения: x = 5 и x = -5.

Связанные ресурсы:

Викторина о полиномиальных тождествах

Упрощение полиномиальных выражений — проблемы с решениями

Факторинговые полиномы — проблемы с решениями

Полиномиальные тождества на форуме

Рациональные формы Пошаговое решение математических задач

ГЛАВА 4
Рациональные формы

4.1 Введение

Под рациональной формой мы будем понимать алгебраическое выражение вида P / Q, где P и Q — многочлены от одной или нескольких переменных, а Q не равно нулю. Многочлен P назовем числителем рациональной формы, а Q — знаменателем.
В главе 1 мы указали, что если a, b и c — любые три действительных числа с b! = 0 и c! = 0, то, поскольку c / c = 1,

(ac) / (bc) = (a) / (b) (c) / (c) = a / b

Это показывает нам, что любой ненулевой множитель может быть исключен как из числителя, так и из знаменателя дроби.2-ху + х-у)

= ((х-у) (х-у)) / (у (у-х) — (у-х))

= ((х-у) (х-у)) / ((у-х) (у-1))

=

= (х-у) / ((- 1) (у-1))

= (х-у) / (1-у)

4.2 Умножение рациональных форм

Если a, b, c и d — действительные числа с b! = 0 и d! = 0, то

a / b * c / d = (ac) / (bd)

Мы применяем это правило к рациональным формам. Произведение двух рациональных форм — это рациональная форма, числитель которой является произведением числителей, а знаменатель — произведением знаменателей.2-3с + 2)

=

= ((s-2) (s + 1)) / ((s-3) (s-1))

Давайте посмотрим, как наш математический решатель умножает эту и подобные задачи. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.

4.3 Разделение рациональных форм

Если a, b, cand d — действительные числа с b! = 0, c! = 0 и d! = 0, то

(а) / (б) ÷ c / d = a / b * d / c

Мы применяем это правило к рациональным формам и действуем, как в 4.2.

Пример 1.2)

= [((x + 5y) (x + 2y)) / ((x-3y) (x-2y)) * ((x + 3y) (x-2y)) / ((x-5y) (x + 5y)) ((x-5y) (x + 2y)) / ((x + 3y) (x + 2y))

=

= (х + 2у) / (х-3у)

4.4 Сложение и вычитание рациональных форм

Давайте вспомним из главы 1, что для сложения дробей первым делом нужно найти их L.C.D., то есть L.C.M., их знаменателей. Мы рассмотрим метод поиска L.C.M. набора целых чисел.

Пример 1 . Найдите L.2 + с-2 = (с + 2) (с-1)

Поскольку s-1 = (- 1) (1-s), мы используем только один из этих факторов в L.C.M. Следовательно, один L.C.M. это

2 * 3 (1-с) (с + 2)

, а другой L.C.M. это

2 * 3 (с-1) (с + 2)

Всегда есть два L.C.M., один из которых в (-1) раз больше другого.

При сложении рациональных форм мы сначала находим общий знаменатель, а затем выражаем каждую рациональную форму как эквивалентную рациональную форму с этим общим знаменателем. Сумма — это рациональная форма, знаменатель которой является общим знаменателем, а числитель — суммой числителей.2 + 7с + 3) / (2 * 3 (с + 2) (с-1))

= ((2s + 1) (s + 3)) / (6 (s + 2) (s-1))

4,5 Сложные фракции

Под сложной дробью мы подразумеваем любую дробь, числитель или знаменатель (или и то и другое) которой состоит из одной или нескольких рациональных форм. Мы упростим, упростив сначала числитель, затем знаменатель и, наконец, разделив полученные рациональные формы. Это показано на следующих примерах.

Пример 1. Упростить (1 / 3-3 / 2) / (1 / 4-1 / 6).

Упрощая числитель, получаем

1 / 3–3 / 2 = 2 / 6–9 / 6 = — (7/6)

Упрощая знаменатель, получаем

1 / 4–1 / 6 = 3 / 12–2 / 12 = 1/12

Делим, имеем

(1 / 3–3 / 2) / (1 / 4–1 / 6)

= (- (7/6)) / (1/12)

= — (7/6 * 12/1)

= -14

Пример 2.2

Пример 3. Упростить 1 / (1-1 / (1 + 1 / x))

Числитель уже упрощен. Чтобы упростить знаменатель, мы должны сначала упростить 1 / (1 + 1 / x)

1 / (1 + 1 / х)

= 1 / (х / х + 1 / х)

= 1 / ((х + 1) / х)

= 1 * х / (х + 1)

= х / (х + 1)

Таким образом, знаменатель равен

.

1-1 / (1 + 1 / х)

= 1-х / (х + 1)

= (х + 1) / (х + 1) -x / (х + 1)

= (х + 1-х) / (х + 1)

= 1 / (х + 1)

Делим, имеем

1 / (1-1 / (1 + 1 / x))

= 1 / (1 / (х + 1))

= (x + 1) / 1

= х + 1

Пример 4.2

Решение системных уравнений | Уравнения и неравенства

\ (- 10 x = -1 \) и
\ (- 4 х + 10 у = -9 \).

Решить относительно \ (x \):

\ begin {align *}
— 10х = -1 \\
\ поэтому x = \ frac {1} {10}
\ end {выровнять *}

Подставляем значение \ (x \) во второе уравнение и решаем относительно \ (y \):

\ begin {align *}
-4x + 10y & = -9 \\
-4 \ left (\ frac {1} {10} \ right) + 10y & = -9 \\
\ frac {-4} {10} + 10y & = -9 \\
100л & = -90 + 4 \\
y & = \ frac {-86} {100} \\
& = \ frac {-43} {50}
\ end {выровнять *}

Следовательно, \ (x = \ frac {1} {10} \ text {и} y = — \ frac {43} {50} \).

\ (3x — 14y = 0 \) и \ (x — 4y + 1 = 0 \)

Запишите \ (x \) через \ (y \):

\ begin {align *}
3х — 14лет & = 0 \\
3х & = 14л \\
x & = \ frac {14} {3} y
\ end {выровнять *}

Подставьте значение \ (x \) во второе уравнение:

\ begin {align *}
х — 4у + 1 & = 0 \\
\ frac {14} {3} y — 4y + 1 & = 0 \\
14лет — 12лет + 3 & = 0 \\
2у & = -3 \\
y & = — \ frac {3} {2}
\ end {выровнять *}

Подставить значение \ (y \) обратно в первое уравнение:

\ begin {align *}
x & = \ frac {14 \ left (- \ frac {3} {2} \ right)} {3} \\
& = -7
\ end {выровнять *}

Следовательно, \ (x = -7 \ text {и} y = — \ frac {3} {2} \).

\ (x + y = 8 \) и \ (3x + 2y = 21 \)

Запишите \ (x \) через \ (y \):

\ begin {align *}
х + у & = 8 \\
х & = 8 — у
\ end {выровнять *}

Подставьте значение \ (x \) во второе уравнение:

\ begin {align *}
3х + 2у & = 21 \\
3 (8 — у) + 2у & = 21 \\
24 — 3л + 2л & = 21 \\
y & = 3
\ end {выровнять *}

Подставить значение \ (y \) обратно в первое уравнение:

\ [x = 5 \]

Следовательно, \ (x = 5 \ text {и} y = 3 \).

\ (y = 2x + 1 \) и \ (x + 2y + 3 = 0 \)

Запишите \ (y \) через \ (x \):

\ [y = 2x + 1 \]

Подставьте значение \ (y \) во второе уравнение:

\ begin {align *}
х + 2у + 3 & = 0 \\
х + 2 (2х + 1) + 3 & = 0 \\
х + 4х + 2 + 3 & = 0 \\
5x & = -5 \\
х & = -1
\ end {выровнять *}

Подставить значение \ (x \) обратно в первое уравнение:

\ begin {align *}
у & = 2 (-1) + 1 \\
& = -1
\ end {выровнять *}

Следовательно, \ (x = -1 \ text {и} y = -1 \).

\ (5x-4y = 69 \) и \ (2x + 3y = 23 \)

Сделайте \ (x \) предметом первого уравнения:

\ begin {align *}
5х-4л & = 69 \\
5х & = 69 + 4у \\
x & = \ frac {69 + 4y} {5}
\ end {выровнять *}

Подставьте значение \ (x \) во второе уравнение:

\ begin {align *}
2х + 3у & = 23 \\
2 \ left (\ frac {69 + 4y} {5} \ right) + 3y & = 23 \\
2 (69 + 4у) +3 (5) у & = 23 (5) \\
138 + 8л + 15л & = 115 \\
23лет & = -23 \\
\ поэтому y & = -1
\ end {выровнять *}

Подставить значение \ (y \) обратно в первое уравнение:

\ begin {align *}
x & = \ frac {69 + 4y} {5} \\
& = \ frac {69 + 4 (-1)} {5} \\
& = 13
\ end {выровнять *}

Следовательно, \ (x = 13 \ text {и} y = -1 \).

\ (x + 3y = 26 \) и \ (5x + 4y = 75 \)

Сделайте \ (x \) предметом первого уравнения:

\ begin {align *}
х + 3у & = 26 \\
x & = 26 — 3 года
\ end {выровнять *}

Подставьте значение \ (x \) во второе уравнение:

\ begin {align *}
5х + 4у & = 75 \\
5 (26 — 3л) + 4л & = 75 \\
130 — 15л + 4л & = 75 \\
-11л & = -55 \\
\ поэтому y & = 5
\ end {выровнять *}

Подставить значение \ (y \) обратно в первое уравнение:

\ begin {align *}
х & = 26 — 3у \\
& = 26 — 3 (5) \\
& = 11
\ end {выровнять *}

Следовательно, \ (x = 11 \ text {и} y = 5 \).

\ (3x — 4y = 19 \) и \ (2x — 8y = 2 \)

Если мы умножим первое уравнение на 2, то коэффициент при \ (y \) будет одинаковым в обоих уравнениях:

\ begin {align *}
3х — 4л & = 19 \\
3 (2) х — 4 (2) у & = 19 (2) \\
6x — 8 лет & = 38
\ end {выровнять *}

Теперь мы можем вычесть второе уравнение из первого:

\ [\ begin {array} {cccc}
& 6x — 8лет & = & 38 \\
— & (2x — 8y & = & 2) \\ \ hline
& 4x + 0 & = & 36
\ конец {массив} \]

Решить относительно \ (x \):

\ begin {align *}
\ поэтому x & = \ frac {36} {4} \\
& = 9
\ end {выровнять *}

Подставьте значение \ (x \) в первое уравнение и решите относительно \ (y \):

\ begin {align *}
3х-4л & = 19 \\
3 (9) -4y & = 19 \\
\ поэтому y & = \ frac {19-3 (9)} {- 4} \\
& = 2
\ end {выровнять *}

Следовательно, \ (x = 9 \ text {и} y = 2 \).

\ (\ dfrac {a} {2} + b = 4 \) и \ (\ dfrac {a} {4} — \ dfrac {b} {4} = 1 \)

Сделайте \ (a \) предметом первого уравнения:

\ begin {align *}
\ frac {a} {2} + b & = 4 \\
а + 2b & = 8 \\
а & = 8 — 2b
\ end {выровнять *}

Подставьте значение \ (a \) во второе уравнение:

\ begin {align *}
\ frac {a} {4} — \ frac {b} {4} & = 1 \\
а — б & = 4 \\
8 — 2б — б & = 4 \\
3b & = 4 \\
b & = \ frac {4} {3}
\ end {выровнять *}

Подставить значение \ (b \) обратно в первое уравнение:

\ begin {align *}
a & = 8-2 \ left (\ frac {4} {3} \ right) \\
& = \ frac {16} {3}
\ end {выровнять *}

Следовательно, \ (a = \ frac {16} {3} \ text {и} b = \ frac {4} {3} \).

\ (- 10x + y = -1 \) и
\ (- 10x — 2y = 5 \)

Если мы вычтем второе уравнение из первого, то мы сможем решить для \ (y \):

\ [\ begin {array} {cccc}
& -10x + y & = & -1 \\
— & (-10x — 2y & = & 5) \\ \ hline
& 0 + 3г & = & -6
\ конец {массив} \]

Решить относительно \ (y \):

\ begin {align *}
3лет & = -6 \\
\ поэтому y & = -2
\ end {выровнять *}

Подставьте значение \ (y \) в первое уравнение и решите относительно \ (x \):

\ begin {align *}
-10x + y & = -1 \\
-10x — 2 & = -1 \\
-10x & = 1 \\
x & = \ frac {1} {- 10}
\ end {выровнять *}

Следовательно, \ (x = \ frac {-1} {10} \ text {и} y = -2 \).

\ (- 10 x — 10 y = -2 \) и \ (2 x + 3 y = 2 \)

Сделайте \ (x \) предметом первого уравнения:

\ begin {align *}
— 10 х — 10 у = -2 \\
5х + 5у & = 1 \\
5x & = 1 — 5л \\
\ поэтому x = -y + \ frac {1} {5}
\ end {выровнять *}

Подставляем значение \ (x \) во второе уравнение и решаем относительно \ (y \):

\ begin {align *}
2х + 3у & = 2 \\
2 \ left (-y + \ frac {1} {5} \ right) + 3y & = 2 \\
-2y + \ frac {2} {5} + 3y & = 2 \\
y & = \ frac {8} {5}
\ end {выровнять *}

Подставьте значение \ (y \) в первое уравнение:

\ begin {align *}
5х + 5у & = 1 \\
5x + 5 \ влево (\ frac {8} {5} \ right) & = 1 \\
5х + 8 & = 1 \\
5x & = -7 \\
x & = \ frac {-7} {5}
\ end {выровнять *}

Следовательно, \ (x = — \ frac {7} {5} \ text {и} y = \ frac {8} {5} \).

\ (\ dfrac {1} {x} + \ dfrac {1} {y} = 3 \) и \ (\ dfrac {1} {x} — \ dfrac {1} {y} = 11 \)

Переставьте оба уравнения, умножив на \ (xy \):

\ begin {align *}
\ frac {1} {x} + \ frac {1} {y} & = 3 \\
у + х & = 3xy \\\\
\ frac {1} {x} — \ frac {1} {y} & = 11 \\
у — х & = 11xy
\ end {выровнять *}

Сложите два уравнения вместе:

\ [\ begin {array} {cccc}
& y + x & = & 3xy \\
+ & (у — х & = & 11xy) \\ \ hline
& 2y + 0 & = & 14xy
\ конец {массив} \]

Решить относительно \ (x \):

\ begin {align *}
2y & = 14xy \\
у & = 7xy \\
1 & = 7x \\
х & = \ гидроразрыв {1} {7}
\ end {выровнять *}

Подставить значение \ (x \) обратно в первое уравнение:

\ begin {align *}
y + \ frac {1} {7} & = 3 \ left (\ frac {1} {7} \ right) y \\
7у + 1 & = 3у \\
4г & = -1 \\
y & = — \ frac {1} {4}
\ end {выровнять *}

Следовательно, \ (x = \ frac {1} {7} \ text {и} y = — \ frac {1} {4} \).2 + 1 \\
0 & = 0
\ end {выровнять *}

Поскольку это верно для всех \ (x \) в действительных числах, \ (x \) может быть любым действительным числом.

Посмотрите, что происходит с \ (y \), когда \ (x \) очень маленький или очень большой:

Наименьшее значение \ (x \) может быть равно 0. Когда \ (x = 0 \), \ (y = 2- \ frac {3} {2} = \ frac {1} {2} \).2 & = 3 — ab
\ end {выровнять *}

Обратите внимание, что это то же самое, что и второе уравнение

\ (a \) и \ (b \) может быть любым действительным числом, кроме \ (\ text {0} \).

.