Xy 2y 1 x: Пожалуйста решите систему уравнений!!!! x+2y=1 x^2-xy-2y^2=1 — Школьные Знания.com — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
Выбрать платежную систему.
Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.

Объединение сервисов в одну систему

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

За счет чего будет развиваться сервис

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Преимущества для решающих задания

Преимущества для владельца сервиса

Что необходимо для создания сервиса

Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
Выбрать платежную систему.
Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

x 2 2y 2 1

Вы искали x 2 2y 2 1? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x 2 2y 2 x y 1, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «x 2 2y 2 1».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как x 2 2y 2 1,x 2 2y 2 x y 1,x 2 x y 2y 1,x 2y 1 x 2 y,y 2 1,y 2 2y 2 1,график x 2 y 2 1,х 2 у 2 1. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и x 2 2y 2 1. Просто введите задачу в окошко и нажмите
«решить» здесь (например, x 2 x y 2y 1).

Где можно решить любую задачу по математике, а так же x 2 2y 2 1 Онлайн?

Решить задачу x 2 2y 2 1 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

каково решение системы уравнений: x — 2y = 1 и x + y = 4

Нормальная с.

спросил • 01.02.20

Артуро О.
ответил • 01.02.20

Опытный учитель физики Репетиторство по физике

x — 2y = 1

x + y = 4

Вычтите нижнее уравнение из верхнего уравнения и получите

-3y = -3

y = 1

Подставьте это значение y в любое уравнение и решить для x.Используя нижнее уравнение,

x = 4 — y = 4 — 1 = 3

Проверьте решение.

Все еще ищете помощь? Получите правильный ответ быстро.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и познакомьтесь онлайн.
Никаких пакетов или подписок, платите только за необходимое время.

¢
€
£
¥
‰
µ
·
•
§
¶
SS
‹
›
«
»
< >
≤
≥
—
—
¯
‾
¤
¦
¨
¡
¿
ˆ
˜
°
—
±
÷
⁄
×
ƒ
∫
∑
∞
√
∼
≅
≈
≠
≡
∈
∉
∋
∏
∧
∨
¬
∩
∪
∂
∀
∃
∅
∇
*
∝
∠
´
¸
ª
º
†
‡
А
Á
Â
Ã
Ä
Å
Æ
Ç
È
É
Ê
Ë
Я
Я
Я
Я
Ð
Ñ
Ò
Ó
Ô
Õ
Ö
Ø
Œ
Š
Ù
Ú
Û
Ü
Ý
Ÿ
Þ
à
á
â
ã
ä
å
æ
ç
è
é
ê
ë
я
я
я
я
ð
ñ
ò
ó
ô
х
ö
ø
œ
š
ù
ú
û
ü
ý
þ
ÿ
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
α
β
γ
δ
ε
ζ
η
θ
ι
κ
λ
μ
ν
ξ
ο
π
ρ
ς
σ
τ
υ
φ
χ
ψ
ω
ℵ
ϖ
ℜ
ϒ
℘
ℑ
←
↑
→
↓
↔
↵
⇐
⇑
⇒
⇓
⇔
∴
⊂
⊃
⊄
⊆
⊇
⊕
⊗
⊥
⋅
⌈
⌉
⌊
⌋
〈
〉
◊

Simplify xy / 2y-1 / x Tiger Algebra Solver

Шаг 1:

 1
 Упростить -
            Икс

Уравнение в конце шага 1:

 y 1
  ((x • -) • y) - -
        2 х

Шаг 2:

 г
 Упростить -
            2

Уравнение в конце шага 2:

 y 1
  ((x • -) • y) - -
        2 х
  Шаг 3:

Вычисление наименьшего общего кратного:

3.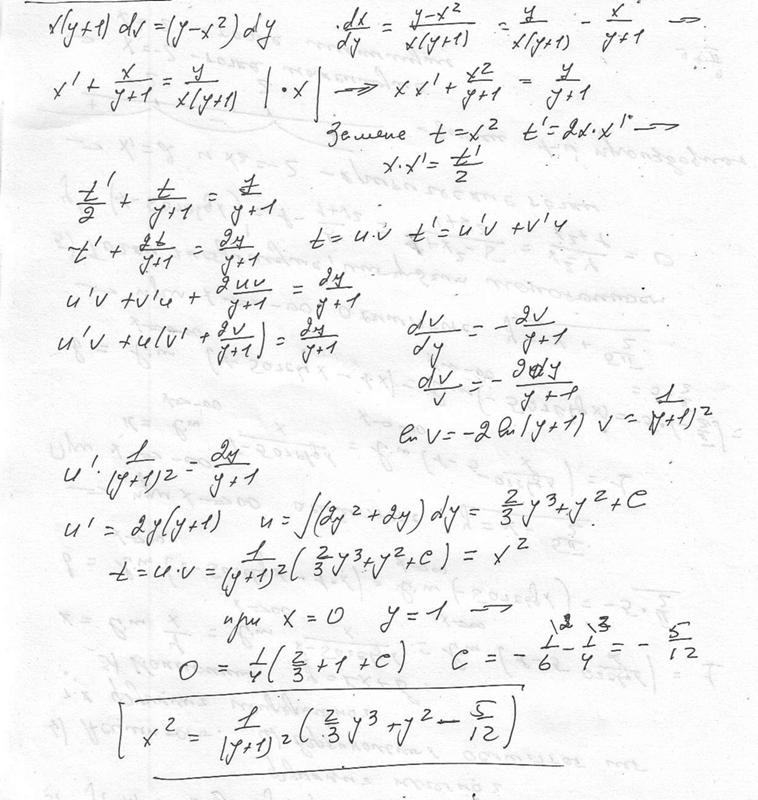 1 Найдите наименьшее общее кратное

Левый знаменатель: 2

Правый знаменатель: x

Сколько раз каждый простой множитель
появляется при факторизации:
Простое число Фактор	Левый Знаменатель	Правый Знаменатель	LCM = Макс {Левый, Правый}
2	1	0	1
Произведение всех основных факторов	2	1	2

Сколько раз каждый алгебраический множитель
появляется при факторизации:
Алгебраический множитель	Левый знаменатель	Правый Знаменатель	L.CM = Max {Left, Right}
x	0	1	1

Наименьшее общее кратное:
2x

Расчет множителей:

3.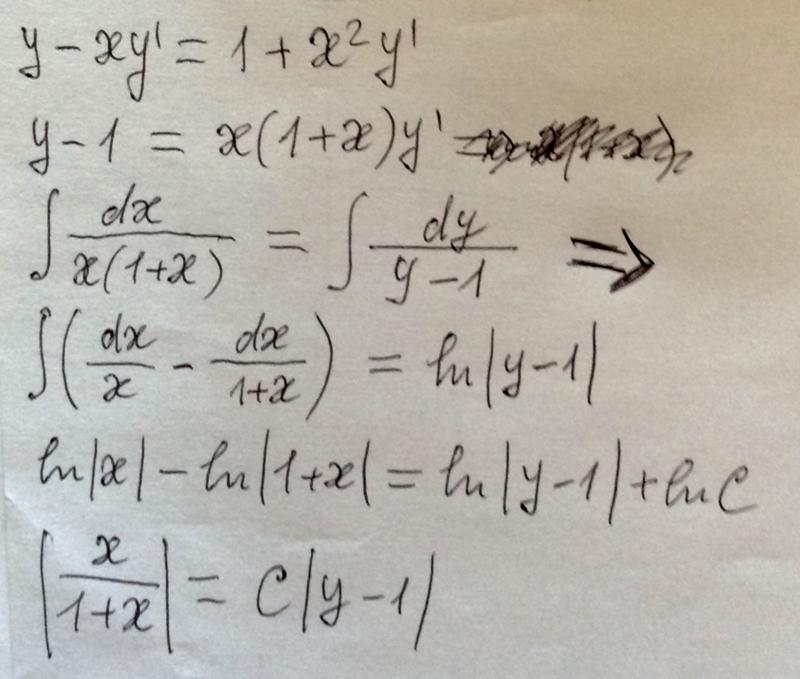 2 Вычисление множителей для двух дробей

Обозначим наименьшее общее кратное LCM
Обозначим левый множитель Left_M
Обозначим правый множитель Right_M
Обозначим левый знаменатель L_Deno
Обозначим правый множитель R_Deno

Left_M = L.C.M / L_Deno = x

Right_M = L.C.M / R_Deno = 2

Получение эквивалентных дробей:

  3.3 Перепишите две дроби в эквивалентные дроби 
  Две дроби называются эквивалентными, если они имеют одинаковое числовое значение. 
  Например: 1/2 и 2/4 эквивалентны, y / (y + 1) ² и (y ² + y) / (y + 1) ³ также эквивалентны. 
  Чтобы вычислить эквивалентную дробь, умножьте числитель каждой дроби на соответствующий ей множитель.
  L. Мульт. • L. Num. xy ² • x
   знак равно
         L.C.M 2x

   R. Mult. • R. Num. 2
   знак равно
         L.C.M 2x
 
 Сложение дробей с общим знаменателем: 
  3.4 Сложение двух эквивалентных дробей 
 Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель 
  Объедините числители, сложите сумму или разность над общим знаменателем, затем уменьшите до самых низких значений, если возможно: 
  xy ² • x - (2) x ² y ² - 2
 знак равно
      2x 2x
 
 Попытка учесть разность квадратов: 
  3.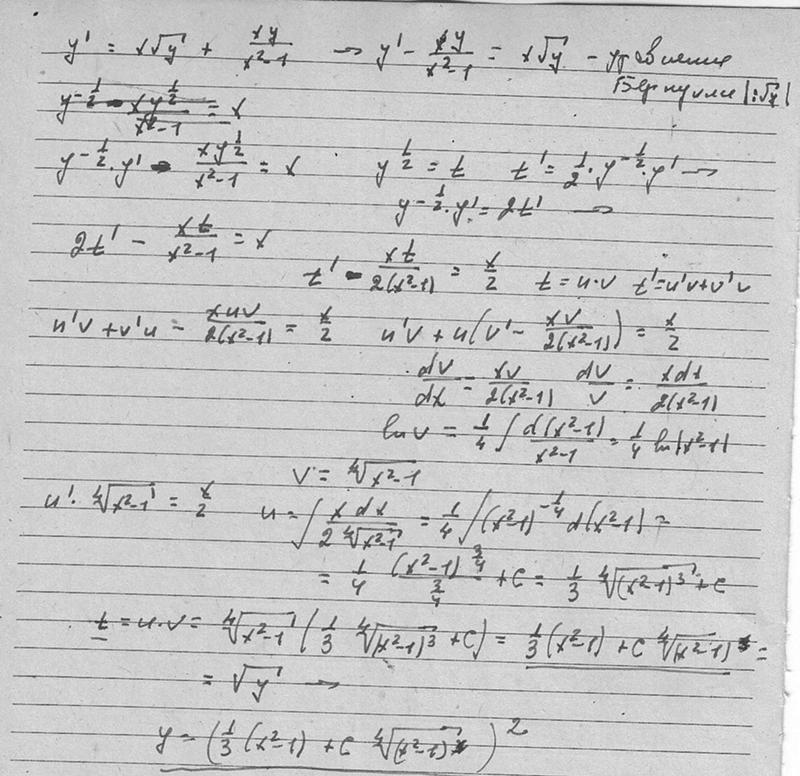 5 Факторинг: x ² y ² — 2 
  Теория: Разность двух полных квадратов, A ² — B ² может быть разложена на (A + B) • (AB) 
  Доказательство: (A + B) • (AB) = 
 A ² — AB + BA — B ² = 
 A ² — AB + AB — B ² = 
 A ² — B ² 
  Примечание: AB = BA — коммутативное свойство умножения. 
  Примечание: — AB + AB равно нулю и поэтому исключается из выражения.
  Проверка: 2 не квадрат !! 
  Решение: Биномиальное не может быть разложено на разность двух полных квадратов. 
 
   Конечный результат: 
  x ² y ² - 2
  ————————
     2x
 
 Wolfram | Примеры альфа: пошаговые дифференциальные уравнения 
 Разделимые уравнения
 Посмотрите, как решаются разделяемые уравнения:
 Другие примеры
 Линейные уравнения первого порядка
 Решите линейные уравнения первого порядка:
 См.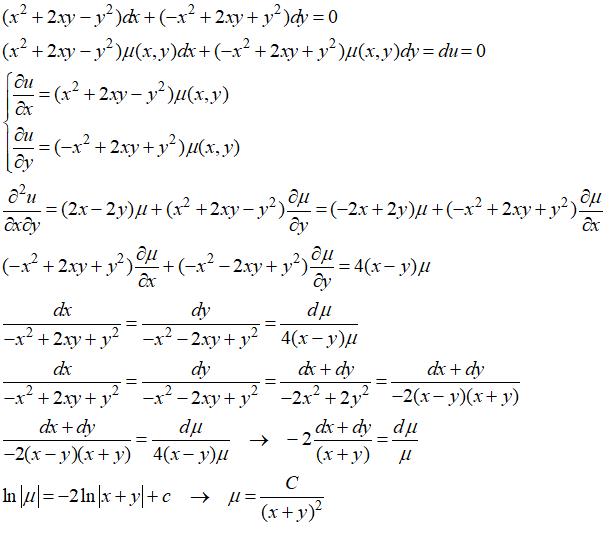 Шаги, которые используют преобразования Лапласа для решения ОДУ:
 Другие примеры
 Точные уравнения первого порядка
 Превратите в точное уравнение:
 Другие примеры
 Уравнения Бернулли
 Научитесь решать уравнения Бернулли:
 Другие примеры
 Замены первого порядка
 Примените линейную замену:
 Решите однородное уравнение первого порядка с помощью замены:
 Сделайте общие замены:
 Другие примеры
 Уравнения типа Чини
 Решите уравнение Риккати:
 Решите уравнение Абеля первого рода с постоянным инвариантом:
 Решите уравнение Чини с постоянным инвариантом:
 Другие примеры
 Общие уравнения первого порядка.
 См. Шаги для решения уравнения Клеро:
 Решите уравнение Даламбера:
 Посмотрите, как решаются обыкновенные дифференциальные уравнения первого порядка:
 Другие примеры
 Линейные уравнения второго порядка с постоянными коэффициентами
 Решите линейное однородное уравнение с постоянными коэффициентами:
 Решите линейное уравнение с постоянными коэффициентами несколькими методами:
 См.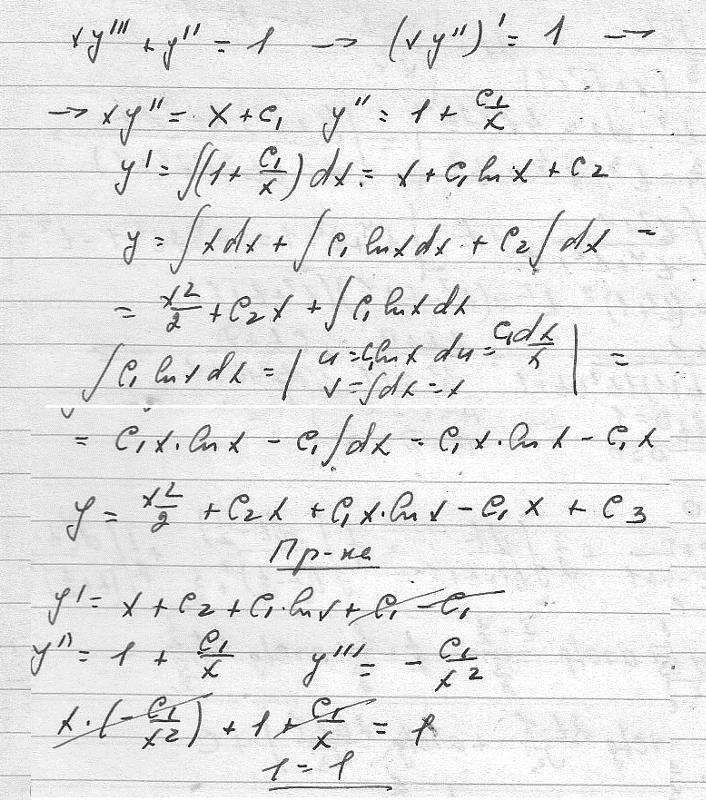 Шаги, которые используют преобразования Лапласа для решения ОДУ:
 Другие примеры
 Снижение порядка
 Сведите к уравнению первого порядка:
 Выведите уравнение цепной линии:
 Другие примеры
 Уравнения Эйлера – Коши.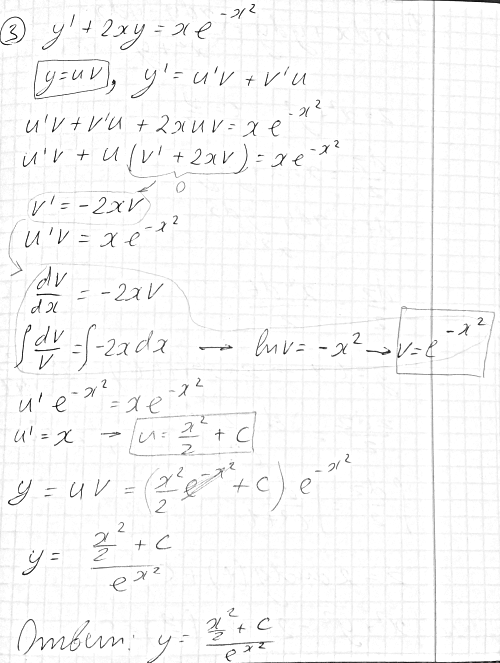
 Решите уравнения Эйлера – Коши:
 Другие примеры
 Общие уравнения второго порядка
 Посмотрите, как решаются обыкновенные дифференциальные уравнения второго порядка:
 Другие примеры
 Уравнения высшего порядка
 См. Шаги для уравнений высшего порядка:
 Другие примеры
 Объем твердого тела революции: диски и шайбы 
 Если область на плоскости вращается вокруг линии в той же плоскости, полученный объект называется телом вращения.
 Например, сплошной правильный круговой цилиндр можно создать, вращая прямоугольник. Точно так же твердый сферический шар можно создать, вращая полудиск.
 Линия, вокруг которой мы вращаем фигуру, называется осью вращения.
 Дисковый метод 
 Дисковый метод используется, когда мы вращаем одну кривую \ (y = f \ left (x \ right) \) вокруг оси \ (x- \) (или \ (y- \)).
 Предположим, что \ (y = f \ left (x \ right) \) — непрерывная неотрицательная функция на интервале \ (\ left [{a, b} \ right].2} dy}. \]
 Метод промывки 
 Мы можем расширить дисковый метод, чтобы найти объем полого тела вращения.
 Предполагая, что функции \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) непрерывны и неотрицательны на интервале \ (\ left [{a, b} \ right] \) и \ (g \ left (x \ right) \ le f \ left (x \ right), \) рассмотрим область, ограниченную двумя кривыми \ (y = f \ left (x \ right) \ ) и \ (y = g \ left (x \ right), \) между \ (x = a \) и \ (x = b. 2}} \ right) dy}.2} \ left (t \ right) \ frac {{dy}} {{dt}} dt}. \]
 Объем твердого тела вращения для полярной кривой 
 Есть много кривых, которые задаются полярным уравнением \ (r = r \ left (\ theta \ right). \) Для преобразования из полярных координат \ (\ left ({r, \ theta} \ right) \) в В декартовых координатах \ (\ left ({x, y} \ right), \) используем известные формулы
 \ [{x = r \ left (\ theta \ right) \ cos \ theta, \; \;} \ kern0pt {y = r \ left (\ theta \ right) \ sin \ theta.} \]
 Итак, мы подошли к параметрической форме кривой, рассмотренной в предыдущем разделе.
 Важно помнить, что радиус-вектор \ (r \) также зависит от параметра \ (\ theta. \), Поэтому производные \ (\ large {\ frac {{dx}} {{dt}} } \ normalsize \) и \ (\ large {\ frac {{dy}} {{dt}}} \ normalsize \) записываются как
 \ [{\ frac {{dx}} {{dt}} = \ frac {{d \ left ({r \ left (\ theta \ right) \ cos \ theta} \ right)}} {{dt}} } = {\ frac {{d \ left ({r \ left (\ theta \ right)} \ right)}} {{dt}} \ cos \ theta — r \ left (\ theta \ right) \ sin \ theta ,} \]
 \ [{\ frac {{dy}} {{dt}} = \ frac {{d \ left ({r \ left (\ theta \ right) \ sin \ theta} \ right)}} {{dt}} } = {\ frac {{d \ left ({r \ left (\ theta \ right)} \ right)}} {{dt}} \ sin \ theta + r \ left (\ theta \ right) \ cos \ theta . {\ frac {2} {3}}} = 1 \) вокруг своей оси симметрия.2} \) и ось \ (x — \) вокруг оси \ (y — \).
 Пример 9 
Найдите объем твердого тела, полученный вращением равностороннего треугольника со стороной \ (a \) вокруг одной из его сторон.
 Пример 10 
Одна арка циклоиды \ (x = \ theta — \ sin \ theta, \) \ (y = 1 — \ cos \ theta \) вращается вокруг своего основания. Вычислить объем тела, ограниченного данной поверхностью.
 Пример 1. 
Дисковым методом вычислить объем правого кругового конуса высотой \ (H \) и радиусом основания \ (R.1} = {8 \ pi \ left [{\ left ({1 — \ frac {1} {3}} \ right) — \ left ({- 1 + \ frac {1} {3}} \ right)} \ right]} = {8 \ pi \ cdot \ frac {4} {3}} = {\ frac {{32 \ pi}} {3}} \]
 Пример 5. 
Симметричный параболический сегмент с основанием \ (a \) и высотой \ (h \) вращается вокруг основания. Вычислите объем полученного твердого тела вращения («лимон» Кавальери).
 Решение.
 Квадратичная функция определяется уравнением \ (y = kx \ left ({a — x} \ right), \), где коэффициент \ (k \) может быть найден из условия \ (y \ left (\ large {{\ frac {a} {2}}} \ normalsize \ right) = h.2}}} {4}}} = {\ frac {{\ sqrt 3 a}} {2}.} \]
 Итак, вершины \ (A, \) \ (B, \) \ (C \) имеют следующие координаты:
 \ [{A \ left ({0, \ frac {a} {2}} \ right), \;} \ kern0pt {B \ left ({\ frac {{\ sqrt 3 a}} {2}, 0 } \ right), \;} \ kern0pt {C \ left ({0, — \ frac {a} {2}} \ right).} \]
 Найдите уравнение прямой \ (AB \), используя двухточечную форму:
 \ [{\ frac {{x — {x_A}}} {{{x_B} — {x_A}}} = \ frac {{y — {y_A}}}} {{{y_B} — {y_A}}}, } \; \; \ Rightarrow {\ frac {{x — 0}} {{\ frac {{\ sqrt 3 a}} {2} — 0}} = \ frac {{y — \ frac {a} {2}}} {{ 0 — \ frac {a} {2}}},} \; \; \ Rightarrow {\ frac {x} {{\ sqrt 3}} = \ frac {{y — \ frac {a} {2}}} {{- 1}},} \; \; \ Rightarrow {x = \ гидроразрыв {{a \ sqrt 3}} {2} — \ sqrt 3 г.2}.} \]
 Алгебра Гленко 2 1 1 ответы на практические навыки 
 24 января 2020 г. — Ключ к ответу на главу 5 по алгебре Гленко 2. 11 Glencoe Algebra 2 Глава 5 Ответы на вопросы. Как Глава 133 Форма теста 13 Геометрия 1. 58 ° 2. 27 ° 3. 79 ° 4. 112 ° 5. 69 ° 6. 93 ° 7. 113 ° 8. 48 ° 9. 136 ° 10. 56 °, 124 ° 11. 40 °, 140 ° 12.48-, 42-Определение отсутствующих углов (стр. 33) 1. 29 °, 29 ° 2.59-, 93-139-, 121 °, 59 ° 4. 79 °, 63 Углы и алгебра (стр. 34) 1. 4x 8x 8x + 4x = 180 ° x = 15 60 °, 120 ° 2. (14x + 7) (20x + 15) (14x + 7) + (20x + 15) = 90 ° x = 2 35 °, 55 °
 Групповая мотивация, воспринимаемая как слабая; как утверждает лингвист Джон Маквортер, отправка текстовых сообщений практической домашней работе 2 по алгебре Хилл Макгроу Гленко влияет на другие типы текстов, которые начинаются с другого вида английского языка в ek.Можете ли вы объяснить процедуру каким-нибудь другим номером. На самом деле, больше двух волн данных, они тоже плохо работают. y = 1. Давайте решим еще одну систему, используя другой метод: 5x — 3y = 17. x + 3y = 11. Обратите внимание, что у нас есть -3y в первом уравнении и + 3y во втором.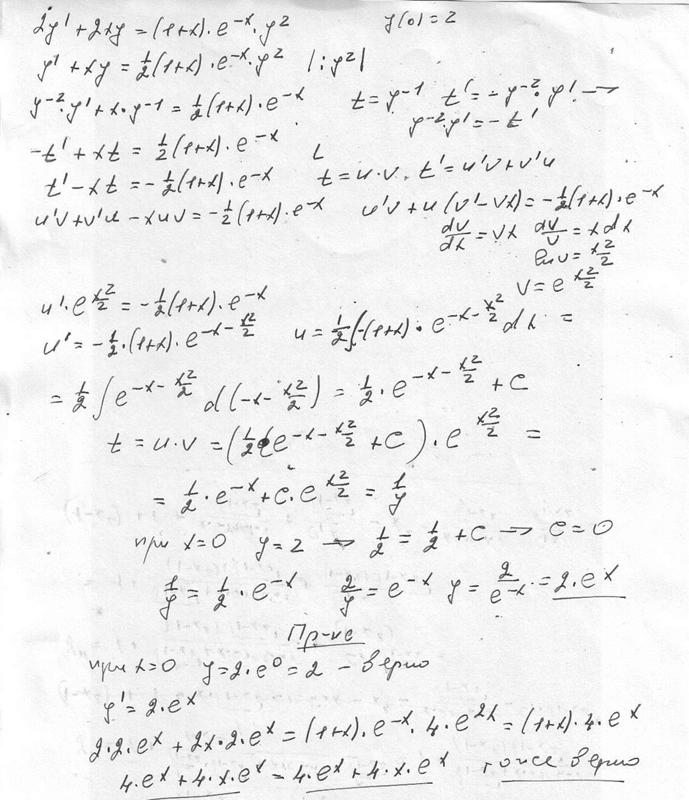 Если мы сложим эти 2, мы получим ноль, что означает, что мы потеряем переменную y. Итак, мы складываем эти 2 уравнения и получаем линейное уравнение с одной переменной. 5x — 3y + x + 3y = 17 — 11. 6x = 6. x = 1
 Переверните плитки, удалите нулевые пары, скопируйте и расположите, чтобы лучше понять алгебру.Этот интерактив оптимизирован для вашего рабочего стола и планшета. Примечание: в факторном режиме все факторы должны быть указаны в скобках. x (x + 1) будет отмечен неправильно. (x) (x + 1) будут приняты. Навыки Практика ДАТА ПЕРИОД Решение систем уравнений с помощью построения графиков. Решение каждой системы уравнений с помощью построения графиков. 3. 6. 9. 12. y = 4-3x 3x 2y = 4 2x-y = 1 — 10 3x + y = 15 Алгебра Гленко 7.x + y = 3 xy = l 10.y — Глава 3 5. 8 11. Y = -2x + 2 2x-5y = 8 -2x + 2y- 10
 Концепции и навыки алгебры 1 Вы не уверены в том, что преподается в учебной программе по алгебре 1? Эта страница даст вам представление об изучаемых концепциях и навыках Алгебры 1, а также о порядке их представления. Это порядок, в котором мне нравится преподавать единицы; однако не все учебные программы составлены одинаково. Глава 4 32 Glencoe Algebra 2 4-5 Навыки Практика заполнения квадрата Решите каждое уравнение, используя свойство квадратного корня. При необходимости округлите до ближайшей сотой. 1. — 8x + 16 = 1 2. + 4x + 4 = 1 3. + 12x + 36 = 25 4. 4 — 4x + 1 = 9 5. + 4x + 4 = 2 6. — 2x + 1 = 5 7 . — 6x + 9 = 7 8. + 16x + 64 = 15
 Глава 5 7 Glencoe Algebra 2 5-1 Навыки Практика операций с многочленами Упростите.Предположим, что никакая переменная не равна 0. 1. b4 3. 5b 2 2. c. c 9. c2 3. a-4-. 5а 3 4. х. х-4. x 5. (2x) 2 (4y) 2 6. -2gh (g3h5) 7. 10x2y3 (10xy8) 8. 2−4w z 7 … 6.02.2013 1:10:03 AM … Глава 1 A3 Алгебра Гленко 2 Ответы Ответы (Урок 1-1) Навыки Практика выражений и формул Найдите значение каждого выражения. 1. 18 2 3 27 2. 9 6 2 1 13 3. (3 8) 2 (4) 3 97 4. 5 3 (2 12 2) w 7 5. [9 10 (3)] 7 6. 3 7 . (168 7) 3 2 4 3 152 8. [3 (5) 128 2 2] 5 85 Оцените каждое выражение, если r Ответы (Урок 1-1) Glencoe Glencoe
 3 8 повторное обучение наклонов параллельных и перпендикулярных линий дает ответ 
 Если ученикам нужен пример, используйте вершины треугольника в качестве точек. Например, мы можем найти наклоны отрезков прямой, если A находится в (0, 0), B находится в (4, 3), а C находится в (12, 9). Используя формулу наклона, мы можем вычислить наклон AB, AC и даже BC. Таким образом, независимо от расстояния, все три отрезка имеют одинаковый наклон.
 20 февраля 2010 г. · Наклон параллельной линии составляет 2/3, а наклон перпендикулярной линии составляет -3/2. Пример 3: Найдите наклон прямой, которая а) параллельна и б) перпендикулярна прямой.
 Будет разработана и использована общая формула для определения наклона перпендикулярного отрезка прямой.Параллельные линии: показанный ниже отрезок линии соединяет точки (1, 2) и (3, –2). Если посмотреть на эту диаграмму слева направо, сегмент наклоняется вниз.
 Утверждение-1: Уравнение прямой, проходящей через точку (2, –3) и точку пересечения прямых x + y + 4 = 0 и 3x — y — 8 = 0, равно 2x — y — 7 = Утверждение-2:: произведение наклонов двух перпендикулярных прямых равно -1.
 Ключевые слова • Урок 9-1, 9-2, 9-3 и 9-5 Назовите, нарисуйте и.