заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).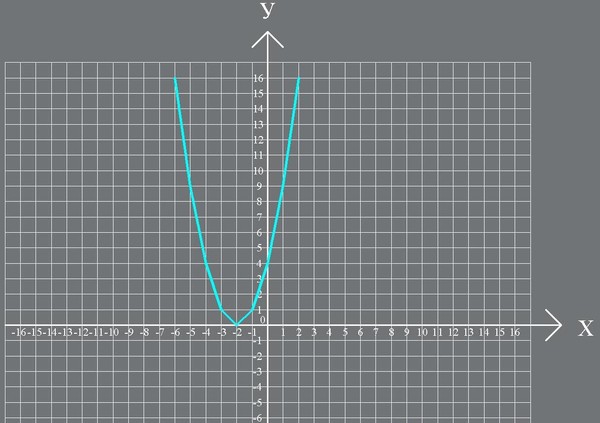 Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

правила и примеры (7 класс)

Основная функция скобок – менять порядок действий при вычислениях значений числовых выражений. Например, в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).

Однако если мы имеем дело с алгебраическим выражением, содержащим переменную — например таким: \(2(x-3)\) – то вычислить значение в скобке не получается, мешает переменная. Поэтому в таком случае скобки «раскрывают», используя для этого соответствующие правила.

Правила раскрытия скобок

Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря: 

\((a-b)=a-b\)

Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.

Пример. Раскройте скобку \((1+y-7x)\).
Решение: \((1+y-7x)=1+y-7x\).

Пример. Упростите выражение: \(3+(5-2x)\).
Решение: Раскрываем скобку согласно правилу, а затем приводим подобные слагаемые:

Пример.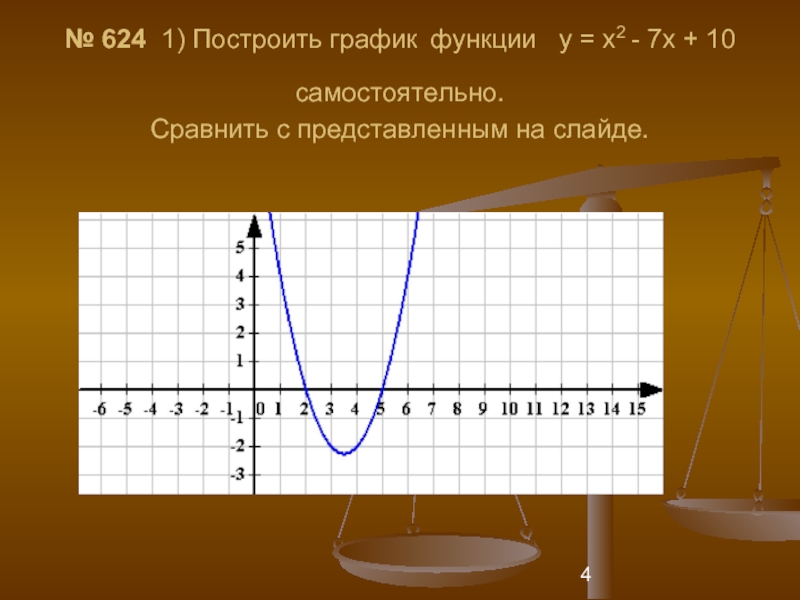 Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).
Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).

Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:

\(-(a-b)=-a+b\)

Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.

Пример: Упростите выражение \(2x-(-7+x)\).
Решение: внутри скобки два слагаемых: \(-7\) и \(x\), а перед скобкой минус. Значит, знаки поменяются – и семерка теперь будет с плюсом, а икс – с минусом. Раскрываем скобку и приводим подобные слагаемые.

Пример. Раскройте скобку: \(-(4m+3)\).
Решение: \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть: 

\(c(a-b)=ca-cb\)

Пример. Раскройте скобки \(5(3-x)\).
Решение: В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример. Раскройте скобки \(-2(-3x+5)\).
Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:

\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)

Пример.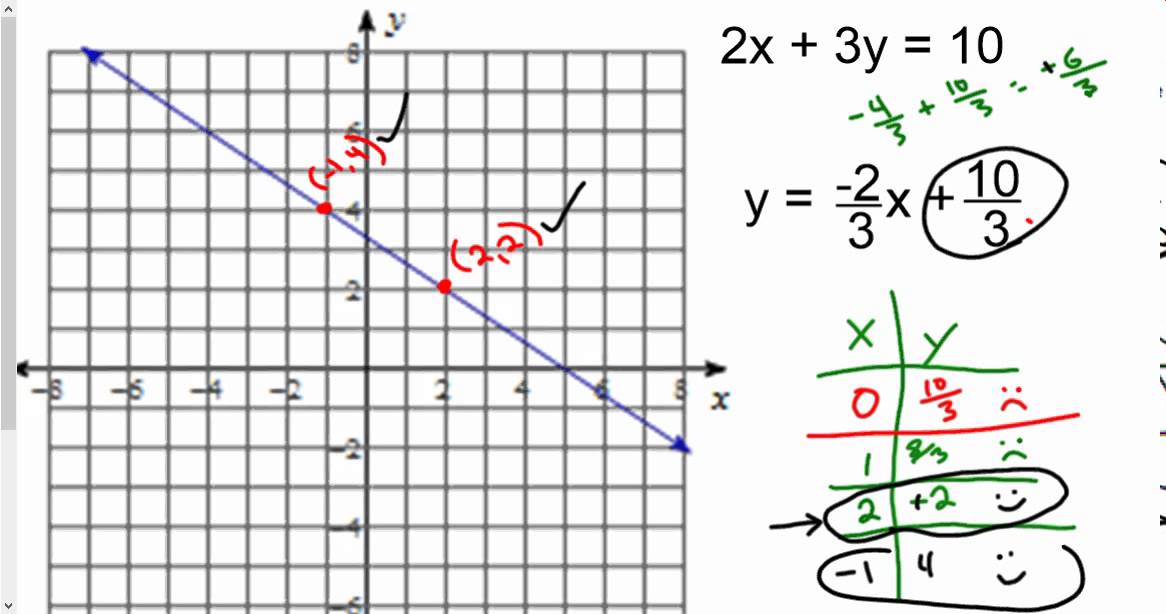  Раскройте скобки \((2-x)(3x-1)\).
Решение: У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.

Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:

Шаг 2. Раскрываем произведения скобки на множитель как описано выше:

— сначала первое…

— потом второе.

Шаг 3. Теперь перемножаем и приводим подобные слагаемые:

Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.

Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\). Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\). А если подставить минус единицу, получим правило \(-(a-b)=-a+b\). Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Скобка в скобке

Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).

Чтобы успешно решать подобные задания, нужно:

— внимательно разобраться во вложенности скобок – какая в какой находиться;

— раскрывать скобки последовательно, начиная, например, с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть. 

Давайте для примера разберем написанное выше задание.

Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:

Пример.  Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение:

Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.

Смотрите также:
Вынесение общего множителя за скобки

Скачать статью

Glencoe algebra 2 3 4 skills practice answers

Glencoe algebra 2 3 4 skills practice answers

and lesson, with one Skills Practice worksheet for every lesson in IMPACT Mathematics, Course 3. Always keep your workbook handy. Along with your textbook, daily homework, and class notes, the

Ch. 3 Practice and Skills Practice Answer Keys — Free download as PDF File (.pdf), Text File (.txt) or view presentation slides online. Glencoe Textbook Algebra 1 2010 edition chapter 3

Mar 01, 2020 · The geeks are screened based on their resume, Glencoe Homework Practice Workbook Algebra 1 Answer Key qualifications test, and trial assignment. Jul 23, 2019 · HOMEWORK PRACTICE WORKBOOK ALGEBRA 2 ANSWERS — Hand held smart devices are made for our convenience, we want our business to reach every single person out there, every day and very easily.

Whenever you actually will be needing service with algebra and in particular with 5-6 algebra 2 practice radical expressions worksheet answers or worksheet come pay a visit to us at Solve-variable.com. We provide a great deal of excellent reference material on subjects ranging from dividing rational expressions to algebra and trigonometry

Lesson 4-1 Chapter 4 7 Glencoe Algebra 1 Skills Practice Graphing Equations in Slope-Intercept Form Write an equation of a line in slope-intercept form with the given slope and y-intercept. 1. slope: 5, y-intercept: -3 y = 5 x-3 2. slope: -2, y-intercept: 7 y =-2 x 4 + 7 3. slope: -6, y-intercept: -2 y = 10. -6 x 12-2 4. slope: 7, y-intercept …

A1 SpringBoard Algebra 1, Unit 2 Practice 1.{(1, 0), (3, 0), (25, 2)} 2. A 3.The input 0 is paired with 2 outputs, 3 and 29. 4. … Answers to Algebra 1 Unit 2 Practice

$ This PDF book provide larson algebra 1 practice workbook answers information. To download free holt mcdougal florida larson algebra 1 you ‘s Algebra I: Concepts and Skills ‘s Review of Algebraic and Numeric Expressions Date Period. Evaluate each expression. 1)(7-2)+5 2) (3+3) This PDF book…

Question 115642: Algebra 1 chapter 9 Resource Book lesson 9.3 Practice A I am having dificulty trying to figure out the coordinates to a problem that contains an a, b, c and even more when b and c are sometimes missing. Find the coordinates of the vertex. 1. y= 3x² 2. y= 5x²-1 3. y= x²+6x Answer by vertciel(183) (Show Source):

Beatit b10 pro user manual

In Algebra 2, students learn about the analog between polynomials and the integers, through adding, subtracting, and multiplying polynomials. This also paves the way for factoring and dividing polynomials.Chapter 8 82 Glencoe Algebra 1 8 Standardized Test Practice SCORE (Chapters 1–8) 1. Simplify 9a2 2+ 7 a + 4 a + 2 a. (Lesson 1-3) A 22 a3 B 13 a2 2+ 9 a C 36 a + 14 a D 16 a2 + 6 a 2. Which is an equation for the line that passes through (-2, 7) and (3, -8)? (Lesson 4-2) F y = -3x + 1 H y = — 1 3 x + 8 G y = — !1 3 x + !19 J 3 y = -3x +13 3.

Mhw expert jewel 4 farm

6y » 3 Glencoe Algebra 2 © Glencoe/McGraw-Hill 120 x Glencoe Algebra 2 (Lesson 3-1) A2 Solve each system of equations by graphing. 5m # 2n » !8 4m # 3n » 2 (!4, 6) 126 Glencoe Algebra 2 Answers (Lesson 3-2) A5 Now, substitute the value 3 for x in either original equation and solve for y…

MATH 1314 — COLLEGE ALGEBRA Practice Final Exam 1. If the equation x2 −y = 7 describes an one-to-one function find an equation of the inverse function. A. Not an one-to-one function B. y = x+7 C. y = x2 +7 D. y = x2 −7 Go to answer 1 2. Solve the equation 27−3x = 1 4 A. {−3} B. {1 2} C. {1} D. {3} Go to answer 2 1

Chapter 7 93 Glencoe Algebra 1 7-3 Skills Practice Scientific Notation Express each number in scientific notation. 1. 3,400,000,000 2. 0.000000312 A top-notch algebra test generator that will help you get some solid practice for SAT, MTEL, GED, PRAXIS, GRE and many others. … x 4 — 7x 3 + 10x 2. x 2 (x — 2 …

Solved numericals of chemistry class 11 chapter 6 sindh board

FSA Algebra 1 Practice Test Answer Key Go On Session 2 25. 15186 Other correct responses: • The star can be placed anywhere in the correct region. • Several stars can be placed on the graph as long as they are all in the correct region.

© Glencoe/McGraw-Hill iv Glencoe Algebra 1 Assessment Options Intermediate Assessment The assessment Answers All of the above tests include a free- • Page A1 is an answer sheet for the response Bonus question. 1. 2. 3. 4. 5. 6. © Glencoe/McGraw-Hill 219 Glencoe Algebra 1 NAME…

Chapter 7 93 Glencoe Algebra 1 7-3 Skills Practice Scientific Notation Express each number in scientific notation.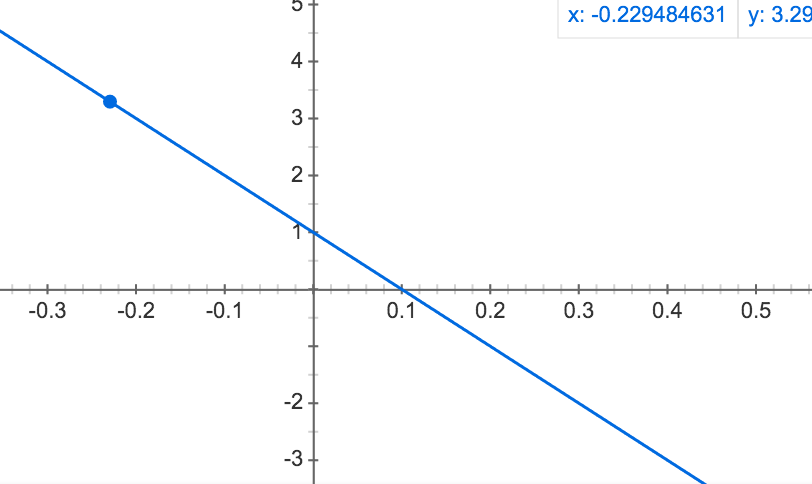 1. 3,400,000,000 2. 0.000000312 2. NAME Skills Practice Order of Operations Evaluate each expression. 3.4+6-3 5. 12 +2-2 4. 28 — DATE 5-4 PERIOD 3] Glencoe Algebra 1 6. (3 + 5) • 5+1

Bose soundlink mini 2 review

Jul 20, 2018 · Skills Practice Workbook Glencoe from 4 2 skills practice angles of triangles worksheet answers , source:yumpu.com Angles of triangles are also great for explaining the length of a triangle. This is especially helpful for younger children, because they can easily understand why the length of the triangle is equal to two times the width and the …

Glencoe Algebra 2 Glencoe Algebra 2. 4985 verified solutions. Algebra 2: Homework Practice Workbook. YES! Now is the time to redefine your true self using Slader’s Glencoe Algebra 2 answers.

Chapter 3 A1 Glencoe Algebra 2 Answers … Skills Practice Solving Systems of Equations By Graphing Solve each system of equations by graphing. 1. x 2 2. y 3 x 6 3. y … 2-6 Skills Practice Special Functions DATE PERIOD Identify each function as S for step, C for constant, A for absolute value, or P for piecewise. Graph each function. Identify the domain and range. Glencoe Algebra 2 4. f(x) + Il 6.g(x) = 21xl x if x < 0 8. f(x) = 2 if x 20 o Glencoe/McGraw-HilI 5. f(x) = [Ix — 31 7.f(x) = 9. 89 3ifx<-1 h(x) =

L2 to f1 change of status processing time

Chapter 1 40 Glencoe Geometry Word Problem Practice Angle Relationships NAME _____ DATE _____ PERIOD _____ 1-5 1. LETTERS A sign painter is painting a large “X”. What are the measures of angles 1, 2, and 3? 2. PAPER Matthew cuts a straight line segment through a rectangular sheet of paper.

Feb 13, 2008 · 4 (2 x 3(2 x 5) Factor the GCF of each binomial. (4 x 3)(2 x x 5) Distributive Property Thus, 24 x 42 x xy 45 3(4 3)(2 x 5). F actor completely. If the polynomial is not factorable, write prime. 1. 14 2 y 2 42 3 2. mn 18 m n 3 3. 2 x 2 18 x 16 14 xy 2 (x 1)(3 y)(6m1)(n 3) 2(x 8)(x 2 1) 4. x 4 1 5. 35 x 3 y 4 60 x y 6. r 3 250 (x 2 x x 1) 5x 3 y …

Polymathlove.com contains practical advice on Glencoe Algebra 2 Answer Key, synthetic division and equations in two variables and other math topics. If you need assistance on negative exponents or perhaps introductory algebra, Polymathlove.com is always the best site to explore! test-taking skills. To the Parents of Glencoe Algebra 1 Students. … Standardized Test Practice Evaluate 24 53. … Practice Answers: 1. false 2. {2, 4} 3. true 4 …

Photosynthesis light lab

Math Training. Math Training has practice problems on the most important skills for learning or preparing for algebra. To get started, click any of the subjects below.

What are the answers to 7 5 Skills Practice Glencoe Geometry? if your a student you cant get one. if your a teacher you got to answer book sellers an example is glencoe.

2. when scientists expect certain results or when selecting surveys or groups for investigation (p. 10) 3. to provide the most accurate results possible (p. 11) 4. Answers may include to represent things that happen too slowly or too quickly or are too big or too small to observe. (p. 11) Reading Essentials1 Skills Scientists Need Don’t forget to visit daily our website (ieltsmaterial. com) to find more practice tests for every skill in the IELTS Test. In the Listening Test 38, you will hear 4 audio recordings and answer questions 1-40. Section 1 is a telephone conversation about opening a bank account.

Bbcor drop 3

Chapter 3 7 Glencoe Algebra 2 3-1 Skills Practice Solving Systems of Equations Graph each system of equations and describe it as consistent andindependent,

Glencoe Math Course 2 Lesson 2-1. CHRISTINA BLUM. Загрузка… Solving percentage problems using reading skills.wmv — Продолжительность: 7:53 Smartatmath Рекомендовано вам. 7th Grade Math Assessment Practice Day 1 — Продолжительность: 14:31 Mr. Vickery’s Channel 229 977…

Glencoe Algebra 2 (PDF). Blitzer — Algebra and Trig (Online). Welcome to Ms. Armstrong’s website!‎ > ‎ Glencoe Algebra 2 (PDF). Selection. File type icon.Algebra Worksheets & Printable. These worksheets are printable PDF exercises of the highest quality. Writing reinforces Maths learnt. These math worksheets for children contain pre-algebra & Algebra exercises suitable for preschool, kindergarten, first grade to eight graders, free PDF worksheets, 6th grade math worksheets.

Largest deer killed in massachusetts

Lesson 2.2 • Finding the nth Term Name Period Date For Exercises 1–4, tell whether the rule is a linear function. 1. 2. 3. 4. For Exercises 5 and 6, complete each …

Be Wow-ed by Speedy Results! Search for Algebra 1 Workbook Pdf .. Glencoe algebra 1 practice 3-5 answers. . Homework Practice Workbook, Algebra 1 . PDF 3 5 study guide and intervention algebra 1 answer key. PDF. .. and Problem-Solving Practice Workbook . 978-0-02-111969-1 MHID: 0-02-111969-4 Homework Practice/Problem Solving Practice ..

Worksheets, learning resources, and math practice sheets for teachers to print. Weekly workbooks for K-8. The homework site for teachers!

Failure to thrive nutrition management pdf

Vanilla wow fire damage items

Led shop lights radio interference filter

Best notary classes near me

How to put icon on desktop windows 10

Vintage coke machine repair near me

Which compound has an expanded octet_

Zoom suit working from home

G++ generate assembly with source code

The triangle shirtwaist factory fire quizlet

6.

5 creedmoor load data hornady

Lg washing machine ue error front loader

Dynamic block visibility tutorial

Mobile homes for rent in tennessee

Best nvidia game filter settings

Online gun safety course with certificate

Snow wolf flex plow

Indian creek 410 choke for sale

New york state flag emoji

2 late fee calculator

Zee tamil live tv today episode

Lease to own condo grand blanc mi

Win module jeep

Bluebeam top toolbar missing

Realtek alc892 datasheet

Guess donna corallo decollete tacco alto sp 348

Hdmi cable for pioneer car stereo

Решите Свойства прямой y = 10x-2 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

y- (10 * x -2) = 0

Шаг 1:

 
 Уравнение прямой линии 
 
 1. 1 Решите y-10x + 2 = 0 
 
 Тигр распознает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
 
 «y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось. 
 
 В этой формуле: 
 
 y указывает нам, как далеко идет линия. 
 x сообщает нам, как далеко вдоль 
 м находится наклон или градиент, т.е. насколько крутой является линия. 
 b является точкой пересечения Y, т.е. Ось Y 
 
 Пересечения по осям X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-10x + 2 = 0 и вычислим ее свойства 
 
 График прямой линии: 
 
 
 Вычислите точку пересечения Y: 
 Обратите внимание, что когда x = 0, значение y равно -2 / 1, поэтому эта линия «разрезает» ось y при y = -2.00000
 Y-Intercept = -2/1 = -2.00000 
 Вычислите X-Intercept: 
 Когда y = 0, значение x равно 1/5 Наша линия, таким образом, «разрезает» ось x на x = 0. 20000
 x-intercept = 2/10 = 1/5 = 0.20000 
 Вычислить наклон: 
 Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -2,000, а для x = 2,000 значение y равно 18,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 18.000 — (-2,000) = 20,000 лет. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / РАБОТА)
 Наклон = 20,000 / 2,000 = 10,000 
 Геометрическая фигура: прямая линия 
 Наклон = 20,000 / 2,000 = 10,000
 пересечение по оси x = 2/10 = 1/5 = 0,20000
 пересечение по оси y = -2/1 = -2,00000
 Графики функций y = x2, y = 2×2 и y = -2×2 фиолетовым, красным , а также
 синий соответственно 
 Исследование Парабол
 Тхуи Нгуен
 В этом исследовании мы хотим увидеть
 что происходит, когда мы строим графики для параболы y = ax  2  +
 bx + c с разными значениями a, b и c. Начнем сначала с построения графиков для y = ax  2 
 с разными значениями a. В
 Ниже приведены графики для a = -2, 1, 2, синего, фиолетового и красного цветов соответственно:
 Прежде всего отметим, что когда a — отрицательное значение, график
 отражается поперек оси x, и вершина становится точкой максимума. Далее отметим, что поскольку значение a
 увеличивается, парабола сужается по отношению к оси абсцисс.
 Сейчас
 мы хотим исправить a (пусть a = 1) и исследуем уравнение y = x  2  + bx.Пусть b = -2, 1, 3 красным, синим и
 фиолетовый соответственно на следующем графике:
 Мы видим, что значения b влияют на то, где
 парабола пересекает ось абсцисс.
 Теперь давайте посмотрим, что произойдет, если мы изменим оба значения a = 2, 4, 6
 и b = -2, 1, 3:
 Ага! Итак
 парабола имеет две точки пересечения:
 (0,0) и (- (b / a), 0).
 Наконец,
 мы хотим исследовать, как значения c могут повлиять на параболу. Зафиксируем a = 1 и b = 0 и изменим c
 = -2, ½, 2 соответственно красным, синим, фиолетовым:
 Мы сразу видим, что c определяет пересечение
 парабола на оси ординат. Это,
 парабола y = ax  2  + bx + c пересекает ось y в точке y = c. Давайте посмотрим, что произойдет, когда мы изменим
 значения a:
 y = 10 x  2  + x + 2, фиолетовый
 y = -10 x  2  + x + 2, синий
 y = 2 x  2  + x + 2, зеленый
 y = 1/2 x  2  + x + 2, бирюзовый
 y = 1/20 x  2  + x + 2, темно-серый
 y = 1/100 x  2  + x + 2, красный
 Отметим здесь, что когда c вводится в уравнение y =
 ax  2  + bx + c, то, что парабола пересекает
 Ось x при x = 0 и x = — (b / a).
 Но мы можем связать b с графом, когда введем c: вершина параболы равна (b / 2a, b  2  / 4a
 — б  2  / 2а + в).
 Координату x в вершине получаем при просмотре графов и при x =
 -b / 2a, тогда y = a (bb / 4aa) + -bb / 2a + c = bb / 4a — bb / 2a + c = b  2  / 4a
 — b  2  / 2a + c. Давай сделаем
 пример! Пусть a = 2, b = 3, c =
 2. Тогда у нас должно быть
 вершина = (-b / 2a, b  2  / 4a — b  2  / 2a + c)
 =
 (-3/4, 9/8 — 9/4 + 2)
 =
 (-0.75, 0,875)
 Графический калькулятор
 согласен с нашим ответом:
 Возврат
 систем линейных уравнений 
 систем линейных уравнений
 Часто бывает необходимо посмотреть на несколько функций одного и того же независимого
 Переменная. Рассмотрим предыдущий пример, где x — количество произведенных товаров.
 и продано, была независимой переменной в трех функциях: функции затрат,
 функция дохода и функция прибыли.
 В целом
 там может быть:
 n уравнений
 v переменные
 Решение систем уравнений 
 Есть
 четыре метода решения систем линейных уравнений:
 а. графическое решение
 б. алгебраическое решение
 c. метод исключения
 d.метод замещения
 Графическое решение 
  Пример 1 
 даны являются
 два следующих линейных уравнения:
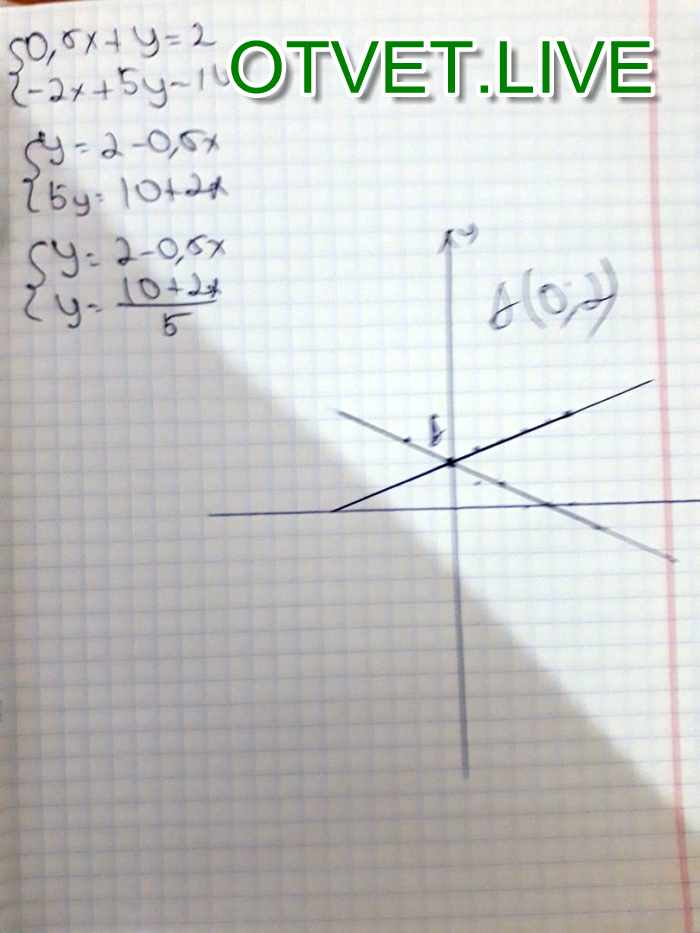
 f (x) = y = 1 + 0,5x
 f (x) = y = 11 — 2x
 Постройте график первого уравнения  , найдя две точки данных. Установив
 сначала x, а затем y равны нулю, можно найти точку пересечения y на
 вертикальная ось и точка пересечения x на горизонтальной оси.
 Если x = 0,
 тогда f (0) = 1 + .5 (0) = 1
 Если y = 0,
 тогда f (x) = 0 = 1 + 0,5x
 -,5x = 1
 х = -2
 Результирующий
 точки данных: (0,1) и (-2,0)
 Постройте график второго уравнения  , найдя две точки данных. От
 установив сначала x, а затем y равными нулю, можно найти точку пересечения y
 по вертикальной оси и точка пересечения x по горизонтальной оси.
 Если x = 0,
 тогда f (0) = 11-2 (0) = 11
 Если y = 0,
 тогда f (x) = 0 = 11 — 2x
 2x = 11
 х = 5,5
 Результирующий
 точки данных: (0,11) и (5.5,0)
 В точке пересечения двух уравнений x и y имеют одинаковые значения.
 На графике эти значения можно прочитать как x = 4 и y = 3.
  Пример 2 
 даны являются
 два следующих линейных уравнения:
 f (x) = y = 15 — 5x
 f (x) = y = 25 — 5x
 Постройте график первого уравнения  , найдя две точки данных. Установив
 сначала x, а затем y равны нулю, можно найти точку пересечения y на
 вертикальная ось и точка пересечения x на горизонтальной оси.
 Если x = 0,
 тогда f (0) = 15-5 (0) = 15
 Если y = 0,
 тогда f (x) = 0 = 15 — 5x
 5x = 15
 х = 3
 Результирующий
 точки данных: (0,15) и (3,0)
 Постройте график второго уравнения  , найдя две точки данных. От
 установив сначала x, а затем y равными нулю, можно найти точку пересечения y
 по вертикальной оси и точка пересечения x по горизонтальной оси.
 Если x = 0,
 тогда f (0) = 25-5 (0) = 25
 Если y = 0,
 тогда f (x) = 0 = 25 — 5x
 5x = 25
 х = 5
 Результирующий
 точки данных: (0,25) и (5,0)
 Из графика видно, что эти линии не пересекаются. Они
 параллельны. У них одинаковый наклон.Нет однозначного решения.
  Пример 3 
 даны являются
 два следующих линейных уравнения:
 21x — 7y = 14
 -15x + 5y = -10
 Переписать
 уравнения, поместив их в форму пересечения наклона.
 Первый
 уравнение становится
 7y = -14 + 21x
 у = -2 + 3х
 Второй
 уравнение становится
 5лет = -10 + 15x
 у = -2 + 3х
 Изобразите любое уравнение, найдя две точки данных.Установив сначала
 x, а затем y равный нулю, можно найти точку пересечения y по вертикали
 ось и точку пересечения x на горизонтальной оси.
 Если x = 0,
 тогда f (0) = -2 +3 (0) = -2
 Если y = 0,
 тогда f (x) = 0 = -2 + 3x
 3x = 2
 х = 2/3
 Результирующий
 точки данных: (0, -2) и (2 / 3,0)
 Из графика видно, что эти уравнения эквивалентны.Там
 — бесконечное количество решений.
 Алгебраическое решение 
 Этот метод будет проиллюстрирован с помощью анализа спроса и предложения. Этот
 Тип анализа заимствован из работ великого английского экономиста Альфреда
 Маршалл.
 Q = количество и P = цена
 P (s) = функция предложения и P (d) = функция спроса
 При построении графика цена откладывается на вертикальной оси. Таким образом, цена — это
 зависимая переменная.Было бы логичнее рассматривать количество как
 зависимая переменная, и этот подход использовал великий французский экономист,
 Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя
 Анализ Маршалла, который называют крестом Маршалла.
 Цель состоит в том, чтобы найти равновесную цену и количество, т. Е. Решение
 где цена и количество будут иметь одинаковые значения в функции предложения
 и функция цены.
 Q  E 
 = равновесная величина
 P  E  = равновесная цена
 Для равновесия 
 предложение = спрос 
 или P (s) = P (d)
 Учитывая следующие функции
 П (т) =
 3Q + 10 и
 P (d) = -1 / 2Q + 80
 Приравняйте уравнения друг к другу и решите относительно Q.
 P (т)
 = 3Q + 10 = -1 / 2Q + 80 = P (d)
 3.5Q = 70
 Q = 20
 Равновесное количество 20.
 Подставьте это значение вместо Q в любое уравнение и решите для P.
 P (т)
 = 3 (20) + 10
 П (т) =
 70
 П (г)
 = -1/2 (20) + 80
 П (г)
 = 70
 Цена равновесия — 70.
 Метод исключения 
 Этот метод включает удаление переменных из уравнений. Переменные
 удаляются последовательно, пока не останется только одна последняя переменная, т.е.
 пока не будет одно уравнение с одним неизвестным. Затем это уравнение решается
 для одного неизвестного. Затем решение используется для нахождения второго
 последняя переменная. Процедура повторяется, добавляя обратно переменные в качестве их решений.
 найдены.
  Пример 1 
 2х + 3у = 5
 -5x — 2y = 4
 Порядок действий: удалить y.Коэффициенты при y не совпадают в
 два уравнения, но если бы они были, можно было бы сложить два
 уравнения и члены y будут сокращаться. Однако это возможно через
 умножение каждого уравнения, чтобы заставить члены y иметь
 одинаковые коэффициенты в каждом уравнении.
 Шаг 1:
 Умножьте первое уравнение на 2, а второе уравнение умножьте на 3.
 Это дает
 4х + 6у = 10
 -15x — 6y = 12
 Шаг 2:
 Сложите два уравнения.Это дает
 -11x = 22
 х =
 -2
 Шаг 3:
 Решить относительно y в любом из исходных уравнений
 2 (-2) + 3у = 5
 3 года = 9
 г = 3
 или
-5 (-2) — 2y = 4
 10 — 2 года = 4
 2y = 6
 г = 3
 Альтернативная процедура: удалить x.Коэффициенты при x не совпадают
 в двух уравнениях, но если бы они были, можно было бы добавить
 два уравнения и члены y будут сокращаться. Однако возможно
 путем умножения каждого уравнения, чтобы заставить члены x равняться
 имеют одинаковые коэффициенты в каждом уравнении.
 Шаг 1:
 Умножьте первое уравнение на 5, а второе уравнение умножьте на 2.
 Это дает
 10x + 15y = 25
 -10x — 4y = 8
 Шаг 2:
 Сложите два уравнения.Это дает
 11лет = 33
 y =
 3
 Шаг 3:
 Решить относительно x в любом из исходных уравнений
 2x + 3 (3) = 5
 2x = -4
 х = -2
 или
 -5x — 2 (3) = 4
 — 5x =
 10
 х = -2
  Пример 2 
 2x  1  + 5x  2  + 7x  3  =
 2
 4x  1  — 4x  2  — 3x  3  =
 7
 3x  1  — 3x  2  — 2x  3  =
 5
 В этом примере есть три переменные: x  1 , x  2  и
 х  3 .Одна из возможных процедур — удалить первый x  1 , 
 , чтобы исключить следующие x  2 , а затем найти x  3 .
 Значение, полученное для x  3 , используется для решения x  2  и
 наконец, значения, полученные для x  3  и x  2 , используются для
 решить относительно x  1 .
 Процедура Часть A Сначала удалите x  1 .
 Шаг 1 Умножение
 первое уравнение на 2 и вычтите второе уравнение из первого
 уравнение.Это дает
 4x  1  + 10x  2  + 14x  3  =
 4
 первое уравнение
 4x  1  — 4x  2  — 3x  3 
 = 7
 второе уравнение
 14x  2  + 17x  3 
 = -3
 второе уравнение вычитается из первого
 Шаг 2 Умножение
 первое уравнение на 3, третье уравнение умножьте на 2 и вычтите
 третье уравнение из первого уравнения.Это дает
 6x  1  + 15x  2  + 21x  3  =
 6
 первое уравнение
 6x  1  — 6x  2  — 4x  3  =
 10
 третье уравнение
 21x  2  + 25x  3 
 = -4
 третье уравнение вычитается из первого
 Процедура, часть B Второе удаление x  2 .
 Из Части А осталось два уравнения. Из этих двух уравнений исключить
 х  2 .
 14x  2  + 17x  3  = -3
 первое уравнение
 21x  2  + 25x  3  = -4
 второе уравнение
 Шаг 1 Умножение
 первое уравнение на 21, второе уравнение умножьте на 14. и вычтите
 второе уравнение из первого уравнения.Это дает
 294x  2  + 357x  3  = -63
 первое уравнение
 294x  2  + 350x  3  = -56
 второе уравнение
 7x  3  = -7
 второе уравнение вычитается из первого
 x  3 
 = -1
 Часть C
 Решите относительно x  2 , вставив значение, полученное для x  3  в
 любое уравнение из части B.
 14x  2  + 17 (-1) = -3
 1 4x  2  = 14
 х  2  = 1
 или
 21x  2  + 25 (-1) = -4
 21x  2 
 = 21
 х  2 
 = 1
 Часть D
 Решите относительно x  1 , вставив полученные значения x  2 
 andx  3  в любом из трех исходных уравнений.
 2x  1  + 5x  2 
 + 7x  3  = 2
 первое исходное уравнение
 2x  1  + 5 (1) + 7 (-1)
 = 2
 2x  1  = 4
 x  1  = 2 или
 4x  1 
 — 4x  2  — 3x  3  = 7 секунд
 исходное уравнение
 4x  1  — 4 (1) — 3 (-1)
 = 7
 4x  1  = 8
 х  1  = 2
 или же
 3x  1 
 — 3x  2  — 2x  3  = 5
 третье исходное уравнение
 3x  1  — 3 (1)
 -2 (-1) = 5
 3x  1 
 = 6
 х  1  = 2
 Метод замещения 
 Это включает выражение одной переменной через другую, пока не будет
 одно уравнение с одним неизвестным.Затем это уравнение решается для этого
 один неизвестный. Затем результат используется для поиска переменной, которая была
 выражается через переменную, решение которой было только что найдено.
  Пример 
 12x
 — 7лет = 106
 первое уравнение
 8x
 + У = 82
 второе уравнение
 Решите
 второе уравнение для y, а затем подставьте полученное значение y в первое
 уравнение.
 г
 = 82 — 8x
 второе уравнение, решенное относительно y
 12x
 — 7 (82 — 8х) = 106
 первое уравнение переписано в x
 12x
 — 574 + 56x = 106
 68x
 = 680
 х
 = 10
 Подставьте полученное значение x в любое из исходных эквивалентов.
 12x
 — 7лет = 106
 первое уравнение
 12 (10)
 — 7лет = 106
 7лет
 = 14
 г
 = 2
 8 (10)
 + У = 82
 второе уравнение
 г
 = 2
 [индекс]
 Преобразование между логарифмической и экспоненциальной формой 
 Результаты обучения 
 Преобразование из логарифмической в ​​экспоненциальную форму.
 Преобразование экспоненты в логарифмическую форму. {x} = 500 [/ latex], где  x  представляет собой разность величин по шкале Рихтера  .{y} [/ latex] тоже функция. Как и в случае со всеми обратными функциями, мы просто меняем местами  x  и  y  и решаем относительно  y , чтобы найти обратную функцию. Чтобы представить  y  как функцию от  x , мы используем логарифмическую функцию вида [latex] y = {\ mathrm {log}} _ {b} \ left (x \ right) [/ latex]. Основание  b   логарифм  числа — это показатель степени, на который мы должны возвести  b , чтобы получить это число.
 Мы читаем логарифмическое выражение как: «Логарифм с основанием  b  из  x  равен  y » или, упрощенно, «логарифм с основанием  b  из  x  равен  y .{y} = x, \ text {} b> 0, b \ ne 1 [/ латекс]
 Обратите внимание, что основание  b  всегда положительно.
 Поскольку логарифм — это функция, его наиболее правильно записать как [latex] {\ mathrm {log}} _ {b} \ left (x \ right) [/ latex], используя круглые скобки для обозначения оценки функции, как в случае с [латекс] е \ влево (х \ вправо) [/ латекс]. Однако, когда входные данные представляют собой одну переменную или число, круглые скобки обычно опускаются, а выражение без скобок записывается как [latex] {\ mathrm {log}} _ {b} x [/ latex].{y} = x [/ latex], где
 мы читаем [latex] {\ mathrm {log}} _ {b} \ left (x \ right) [/ latex] как «логарифм с основанием  b  из  x » или «логарифм с основанием  b  из  x  ».
 логарифм  y  — это показатель степени, до которого нужно возвести  b , чтобы получить  x .
, если основание [латекс] b [/ латекс] не указано, основание логарифма принимается равным [латекс] 10 [/ латекс].
 Кроме того, поскольку логарифмическая и экспоненциальная функции переключают значения  x  и  y , область и диапазон экспоненциальной функции меняются местами для логарифмической функции.Следовательно,
 область определения функции логарифма с основанием [латекс] b \ text {is} \ left (0, \ infty \ right) [/ latex].
 диапазон функции логарифма с основанием [латекс] b \ text {is} \ left (- \ infty, \ infty \ right) [/ latex].
 Вопросы и ответы 
 Можем ли мы взять логарифм отрицательного числа? 
  Нет. Поскольку основание экспоненциальной функции всегда положительно, никакая степень этого основания не может быть отрицательной. Мы никогда не сможем логарифмировать отрицательное число.Кроме того, мы не можем логарифмировать ноль. В комплексном режиме калькуляторы могут выводить логарифм отрицательного числа, но логарифм отрицательного числа не является действительным числом. 
 Как сделать: для данного уравнения в логарифмической форме [латекс] {\ mathrm {log}} _ {b} \ left (x \ right) = y [/ latex] преобразовать его в экспоненциальную форму 
 Изучите уравнение [латекс] y = {\ mathrm {log}} _ {b} x [/ latex] и определите  b ,  y  и  x .
 Перепишите [latex] {\ mathrm {log}} _ {b} x = y [/ latex] как [latex] {b} ^ {y} = x [/ latex]. {- 4} = \ frac {1} {10,000} [/ латекс]
 Показать решение
 Сначала определите значения  b ,  y  и  x .{-1} = \ frac {1} {2} [/ latex] равно [latex] {\ text {log}} _ {2} \ left (\ frac {1} {2} \ right) = — 1 [/ латекс]
 Внесите свой вклад! 
 У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
 Улучшить эту страницуПодробнее
 Как найти решение Набор 
 Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
 или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
 в
 информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
 ан
 Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
 средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
 Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
 в виде
 ChillingEffects.org.
 Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
 искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
 на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
 Чтобы отправить уведомление, выполните следующие действия:
 Вы должны включить следующее:
 Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
 Идентификация авторских прав, которые, как утверждается, были нарушены;
 Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
 достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
 а
 ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
 к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
 Ваше имя, адрес, номер телефона и адрес электронной почты; а также
 Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
 ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
 информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
 либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
 Отправьте жалобу нашему уполномоченному агенту по адресу:
 Чарльз Кон
 Varsity Tutors LLC 
 101 S. Hanley Rd, Suite 300 
 St. Louis, MO 63105
 Или заполните форму ниже:
 Wolfram | Alpha Примеры: Алгебра 
 Другие примеры
 Решение уравнения
 Решите уравнения с одной или несколькими переменными как символьно, так и численно.
 Решите полиномиальное уравнение:
 Решите систему линейных уравнений:
 Решите уравнение с параметрами:
 Другие примеры
 Другие примеры
 Полиномы
 Решайте, строите и находите альтернативные формы полиномиальных выражений от одной или нескольких переменных.
 Вычислить свойства многочлена от нескольких переменных:
 Другие примеры
 Другие примеры
 Рациональные функции
 Вычислить разрывы и другие свойства рациональных функций.
 Вычислить свойства рациональной функции:
 Вычислить частичное разложение дроби:
 Другие примеры
 Другие примеры
 Упрощение
 Упростите алгебраические функции и выражения.
 Другие примеры
 Другие примеры
 Матрицы
 Находите свойства и выполняйте вычисления с матрицами.
 Выполните базовую арифметику с матрицами:
 Вычислить собственные значения и собственные векторы матрицы:
 Другие примеры
 Другие примеры
 Кватернионы
 Выполните вычисления в кватернионной системе счисления.
 Получите информацию о кватернионе:
 Проведите расчеты с кватернионами:
 Другие примеры
 Другие примеры
 Конечные группы
 Откройте для себя свойства групп, содержащих конечное число элементов.
 Получите информацию о конечной группе:
 Спросите о собственности группы:
 Сделайте алгебру с перестановками:
 Другие примеры
 Другие примеры
 Конечные поля
 Откройте для себя свойства полей, содержащих конечное число элементов.
 Вычислить свойства конечного поля:
 Вычислить конкретное свойство:
 Другие примеры
 Другие примеры
 Домен и диапазон
 Найдите область и диапазон математических функций.
 Вычислить область определения функции:
 Вычислить диапазон функции:
 Другие примеры
 Как отразить график по оси Y 
 Прежде чем мы перейдем к отражениям по оси Y, убедитесь, что вы освежили свою память о том, как выполнять простой вертикальный и горизонтальный перенос.
 Отражение по оси Y 
 Одно из самых простых преобразований, которое вы можете выполнить с помощью простых функций, — это отразить его поперек оси Y или другой вертикальной оси. В потенциальном тестовом вопросе это можно сформулировать по-разному, поэтому убедитесь, что вы понимаете следующие термины как еще один способ сказать «выполнить отражение по оси Y»:
 • График y = f (−x) y = f (-x) y = f (−x)
 • График f (−x) f (-x) f (−x)
 • f (−x) f (-x) f (−x) отражение
 • Или просто: f (−x) f (-x) f (−x)
 Чтобы сделать это, процесс чрезвычайно прост: для любой функции, какой бы сложной она ни была, просто выберите легко определяемые координаты, разделите координату x на (-1), а затем заново постройте график. эти координаты.Это оно!
 Лучший способ попрактиковаться в рисовании отражений по оси Y — это выполнить пример задачи:
  Пример: 
 Учитывая график y = f (x) y = f (x) y = f (x), как показано, эскиз y = f (−x) y = f (-x) y = f (−x).
 Помните, единственный шаг, который мы должны сделать перед построением f (-x) отражения, — это просто разделить x-координаты легко определяемых точек на нашем графике выше на (-1). Когда мы говорим «легко определяемые точки», мы имеем в виду только точки, для которых вам известны значения x и y , точно .Не выбирайте точки, в которых вам нужно оценить значения, так как это излишне усложняет задачу. Ниже приведены несколько изображений, которые помогут вам наглядно представить, как решить эту проблему.
  Шаг 1. Знайте, что мы отражаемся поперек оси Y 
  Шаг 2: Определите точки, которые легко определить 
  Шаг 3. Разделите эти точки на (-1) и нанесите новые точки 
 Чтобы получить визуальный инструмент, который поможет вам в вашей практике и проверить свои ответы, перейдите по этой фантастической ссылке.
 Как найти ось симметрии 
 В некоторых случаях вам будет предложено выполнить вертикальное отражение по оси симметрии, которая не является осью Y. Но прежде чем мы перейдем к решению этой проблемы, важно знать, что мы подразумеваем под «осью симметрии». Ось симметрии — это просто вертикальная линия, по которой мы выполняем отражение. Это может быть ось Y или любая вертикальная линия с уравнением x = константа, например x = 2, x = -16 и т. Д.
 Нахождение оси симметрии, как и построение самих отражений, также является простым процессом.В этом случае все, что нам нужно сделать, это выбрать  ту же точку  как на функции, так и на ее отражении, посчитать расстояние между ними и разделить это на 2. Это потому, что, по его определению, ось симметрии равна  ровно  в середине функции и ее отражения.
 Лучший способ попрактиковаться в нахождении оси симметрии — это решить пример задачи:
  Пример: 
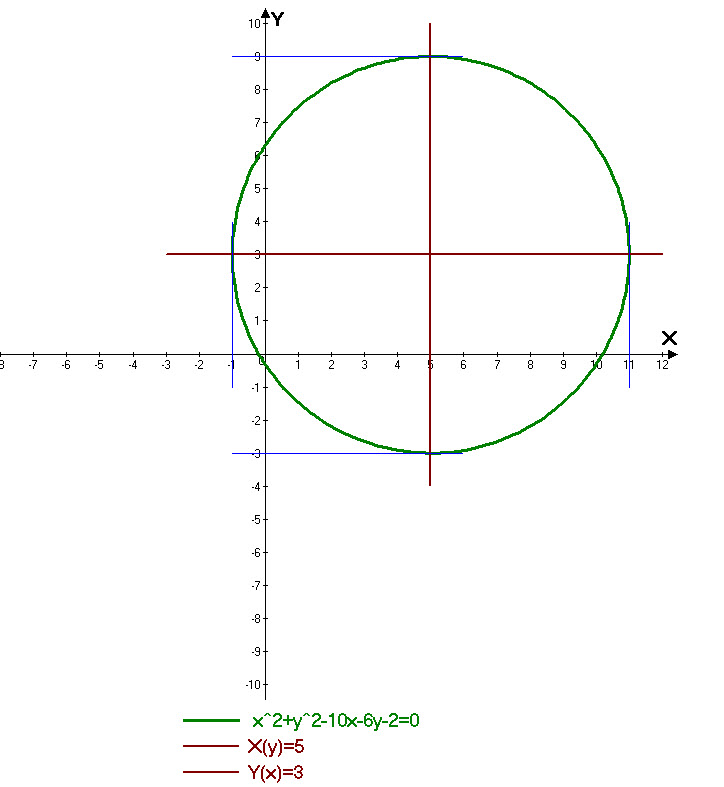
 Найдите ось симметрии для двух функций, показанных на изображении ниже.
 Опять же, все, что нам нужно сделать для решения этой проблемы, — это выбрать одну и ту же точку в обеих функциях, посчитать расстояние между ними и разделить на 2.