Свойства функции y = cosx и её график — урок. Алгебра, 10 класс.

Функция y=cosx определена на всей числовой прямой, и множеством её значений является отрезок −1;1.

Следовательно, график этой функции расположен в полосе между прямыми y=−1 и y=1.

Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, например, на отрезке −π≤x≤π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn,n∈ℤ, график будет таким же.

Функция y=cosx является чётной. Поэтому её график симметричен относительно оси \(Oy\).

Построим график функции на промежутке −π≤x≤π. Так как функция y=cosx является чётной, можно построить график на промежутке 0≤x≤π, а потом симметрично отобразить относительно оси \(Oy\).

Значения функции в удобных точках на этом отрезке 0≤x≤π равны: cos0=1;cosπ6=32;cosπ4=22;cosπ3=12;cosπ2=0;cosπ=−1.

Учитывая периодичность функции y=cosx, нарисуем её график.

Свойства функции y=cosx

1. Область определения — все действительные числа (множество ℝ).

2. Множество значений — промежуток −1;1.

3. Функция y=cosx имеет период 2π.

4. Функция y=cosx является чётной.

5. Нули функции: x=π2+πn,n∈ℤ;

наибольшее значение равно \(1\) при x=2πn,n∈ℤ;

наименьшее значение равно \(-1\) при  x=π+2πn,n∈ℤ;

значения функции положительны на интервале −π2;π2, с учётом периодичности функции на интервалах −π2+2πn;π2+2πn,n∈ℤ;

значения функции отрицательны на интервале π2;3π2, с учётом периодичности функции на интервалах π2+2πn;3π2+2πn,n∈ℤ.

6. Функция y=cosx:

— возрастает на отрезке π;2π, с учётом периодичности функции на отрезках π+2πn;2π+2πn,n∈ℤ;

— убывает на отрезке 0;π, с учётом периодичности функции на отрезках 2πn;π+2πn,n∈ℤ.

Построить график функции y 3cosx

Что ты хочешь узнать?

Ответ

Проверено экспертом

• Комментарии
• Отметить нарушение

Ответ

Функция периодическая с периодом .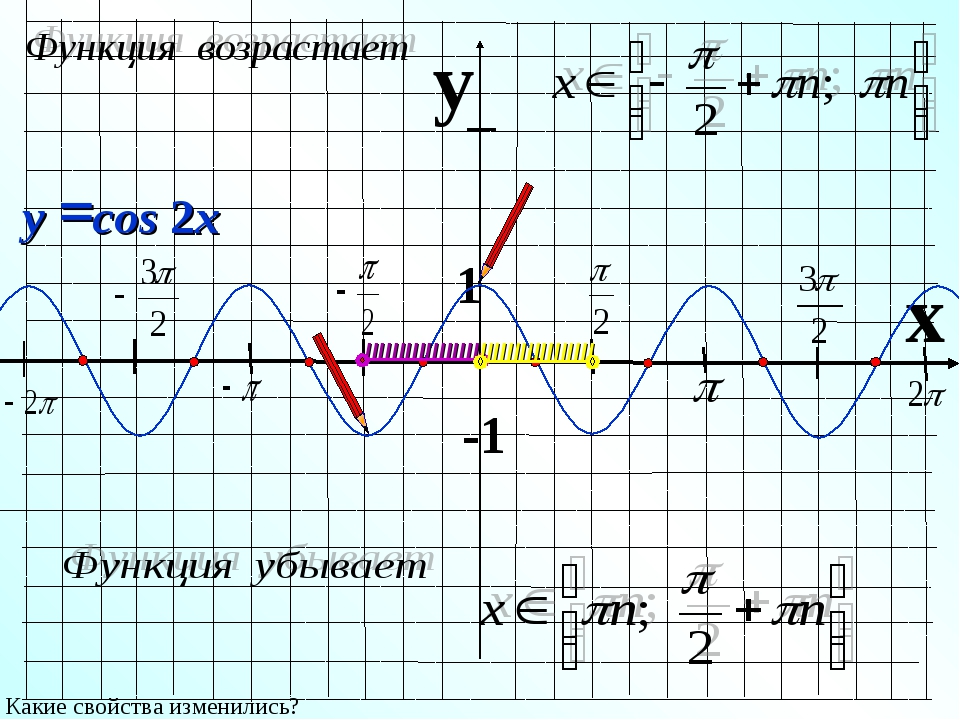 Область определения функции – вся числовая ось.

Область значений функции:

План построения графика. Строим сначала график функции затем растягиваем от оси Ох на 3 единицы и параллельно сдвигаем вниз на 2 единицы.

Тема: Циклические алгоритмы. Построение графиков функций.

Цели:

• дать понятие возможности построения графиков функций;
• научить учащихся строить графики тригонометрических функций и с их помощью показывать свойства соответствующих функций.

Основные знания и умения:

• Знать графики и свойства элементарных тригонометрических функций.
• Уметь читать свойства тригонометрических функций по их графикам.

1. Проверка домашнего задания

2. Актуализация знаний и умений

Повторить свойства тригонометрических функций.

3. Объяснение нового материала

При построении графиков функций необходимо учитывать особенности графического экрана: разрешение; ориентацию экранной системы координат.

Расчет построения графика заключается в следующем: пусть на [a; b] надо построить график функции f(х). Отрезок [a; b] ––> [0; 640] с коэффициентом k = 640/( b – а), где х = – k * а.

Точечный график можно реализовать фрагментом:

100 for x = a to b step 640/(b – a)
110 pset ( x _{+ x + k, y – k * f(x))
120 next}

Задача 1

Провести ось через центр экрана и построить график функции y = sin x.

10 screen 2
20 line (350, 0) – (350, 260)
30 line (0, 120) – (640, 120)
40 for x = 0 to 100
50 pset (10 * x, 120 + 120 * sin(x – 120) / 10)
60 next x

Рассмотренный график представляет собой совокупность точек, между которыми могут быть достаточно большие промежутки. Этот недостаток можно исправить применяя прием уплотнения:

40 for x = 0 to 100 step 0. 01

Для построения более сложных графиков удобно пользоваться оператором определения функции (функция пользователя).

Задача 2

Построить график функции y = 3cosx и проверить соответствует ли он графику функции построенному с помощью программы BASIC.

Построим график функции y = cosx.

а) Область определения – множество всех действительных чисел.

б) Множество значений – отрезок [–1, 1].

в) Функция четная: cos(–x) = cosx для всех х R.

г) Функция периодическая с наименьшим положительным периодом 2, т.е. cos(x + 2) = cosx для всех х R.

д) cosx = 0 при х = + k, k Z.

е) cosx >0 для всех х (– + 2 k; + 2k), k Z.

ж) cosx 0 для всех х (2 k; + 2k), k Z.

ж) sin x 0 для всех х (–+ 2 k; + 2k), k Z.

Решение

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$- 3 cos <left (x
ight )>- 1 = 0$$
Решаем это уравнение
Точки пересечения с осью X:

Аналитическое решение
$$x_ <1>= – operatorname<left (- frac<1> <3>
ight )> + 2 pi$$
$$x_ <2>= operatorname<left (- frac<1> <3>
ight )>$$
Численное решение
$$x_ <1>= 52. 1761156937$$
$$x_ <2>= 35.7884786068$$
$$x_ <3>= 71.0256716152$$
$$x_ <4>= -83.5920422296$$
$$x_ <5>= 67.2044051427$$
$$x_ <6>= -96.1584128439$$
$$x_ <7>= 54.6380345284$$
$$x_ <8>= 1.91063323625$$
$$x_ <9>= -35.7884786068$$
$$x_ <10>= -33.3265597721$$
$$x_ <11>= -48.3548492212$$
$$x_ <12>= 79.7707757571$$
$$x_ <13>= -29.5052932996$$
$$x_ <14>= 33.3265597721$$
$$x_ <15>= 23.2221079925$$
$$x_ <16>= 58.4593010009$$
$$x_ <17>= 77.3088569224$$
$$x_ <18>= 155.168999443$$
$$x_ <19>= -23.2221079925$$
$$x_ <20>= 8.19381854343$$
$$x_ <21>= -27.043374465$$
$$x_ <22>= -64.742486308$$
$$x_ <23>= -20.7601891578$$
$$x_ <24>= 92.3371463714$$
$$x_ <25>= 86.0539610643$$
$$x_ <26>= -39.6097450793$$
$$x_ <27>= 96.1584128439$$
$$x_ <28>= -58. 4593010009$$
$$x_ <29>= -86.0539610643$$
$$x_ <30>= -4.37255207093$$
$$x_ <31>= -92.3371463714$$
$$x_ <32>= -60.9212198355$$
$$x_ <33>= 14.4770038506$$
$$x_ <34>= -73.4875904499$$
$$x_ <35>= 89.8752275368$$
$$x_ <36>= 73.4875904499$$
$$x_ <37>= 48.3548492212$$
$$x_ <38>= 42.071663914$$
$$x_ <39>= -77.3088569224$$
$$x_ <40>= 20.7601891578$$
$$x_ <41>= -71.0256716152$$
$$x_ <42>= 16.9389226853$$
$$x_ <43>= -52.1761156937$$
$$x_ <44>= -89.8752275368$$
$$x_ <45>= -10.6557373781$$
$$x_ <46>= -7726.40729459$$
$$x_ <47>= -971.983089377$$
$$x_ <48>= -79.7707757571$$
$$x_ <49>= -67.2044051427$$
$$x_ <50>= 98.6203316786$$
$$x_ <51>= 27.043374465$$
$$x_ <52>= 64.742486308$$
$$x_ <53>= -54.6380345284$$
$$x_ <54>= 60.9212198355$$
$$x_ <55>= 10.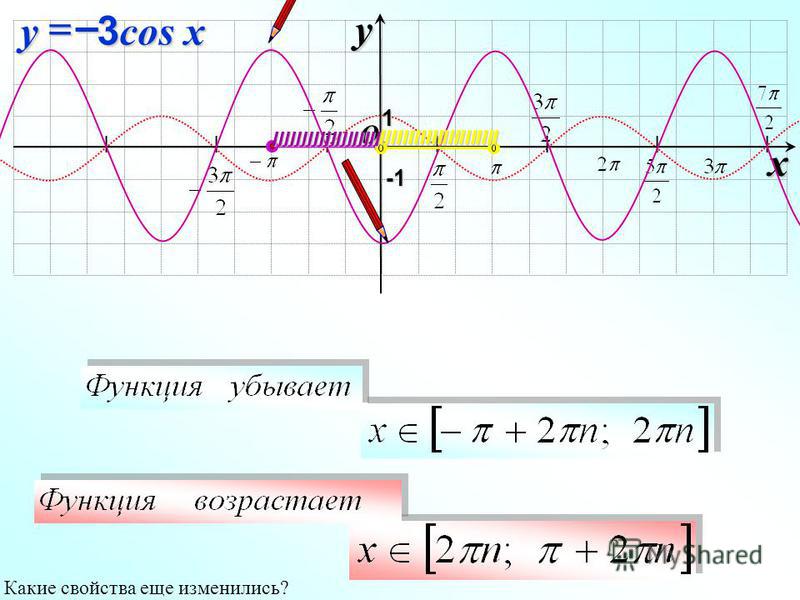 6557373781$$
$$x_ <56>= -42.071663914$$
$$x_ <57>= -14.4770038506$$
$$x_ <58>= 39.6097450793$$
$$x_ <59>= 3426.24662565$$
$$x_ <60>= 83.5920422296$$
$$x_ <61>= -45.8929303865$$
$$x_ <62>= -8.19381854343$$
$$x_ <63>= 4.37255207093$$
$$x_ <64>= 29.5052932996$$
$$x_ <65>= 45.8929303865$$
$$x_ <66>= -98.6203316786$$
$$x_ <67>= -16.9389226853$$
$$x_ <68>= -1.91063323625$$

Для того, чтобы найти экстремумы, нужно решить уравнение
$$fracf <left (x
ight )>= 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$fracf <left (x
ight )>= $$
Первая производная
$$3 sin <left (x
ight )>= 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_ <1>= 0$$
$$x_ <2>= pi$$
Зн. экстремумы в точках:

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_ <2>= 0$$
Максимумы функции в точках:
$$x_ <2>= pi$$
Убывает на промежутках

Возрастает на промежутках

Найдем точки перегибов, для этого надо решить уравнение
$$frac>> f <left (x
ight )>= 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$frac2>>> f <left (x
ight )>= $$
Вторая производная
$$3 cos <left (x
ight )>= 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_ <1>= frac<pi><2>$$
$$x_ <2>= frac<3 pi><2>$$2>

Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках

Выпуклая на промежутках

© Контрольная работа РУ – калькуляторы онлайн

Тригонометрическая функция

Тригонометрическая функция. Продолжаем рассматривать задачи связанные с нахождением точек максимума (минимума). Советую повторить теорию необходимую для решения задач на нахождение наибольшего (наименьшего) значения функции на интервале и на нахождение точек максимума (минимума) функции. В этой статье разберём две задачи в этой теме, рассмотрим тригонометрические функции.  Задачи с логарифмами уже были нами рассмотрены ранее.

Ещё раз запишем алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни разбивают числовую ось на интервалы, отмечаем их.

4. Определяем знаки производной на этих интервалах (подставляем произвольные значения из интервалов в производную).

5. Делаем вывод.

77492. Найдите точку максимума функции y = (2x –3) cos x – 2sin x + 5 

принадлежащую промежутку (0;П/2).

Найдём производную функции:

Решаем уравнение:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, и другие при этом не теряют смысла.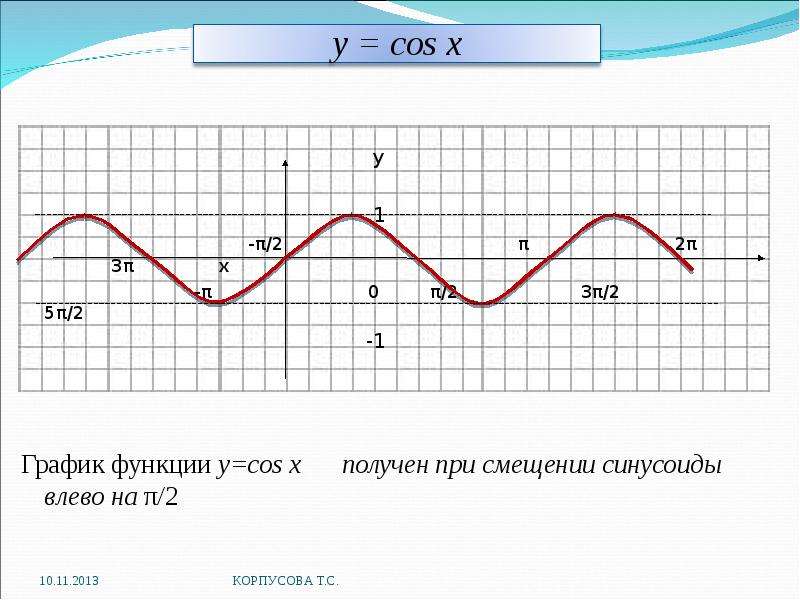 Следовательно:

Решаем уравнение      – sin x = 0:

В условии дан промежуток (0;П/2). Ему не принадлежит ни один из полученных корней. *Обратите внимание, что указанные границы исключены (скобки круглые).

Решаем уравнение: 2х – 3 = 0, получим х = 1,5.

Запишем данный промежуток в радианах, получим: (0;1,57), так как

Следовательно полученное значение принадлежит промежутку (0;П/2):

Конечно, нам интуитивно понятно, что полученная точка это и есть точка максимума, и казалось бы в дальнейших вычислениях и рассуждениях нет необходимости. Но любая задача данного типа должна быть решена до конца по указанному алгоритму. Это важно!

Полученное значение х разбивает данный промежуток на два других. Определим знаки производной функции, подставляя произвольные значения из полученных промежутков (0;1,5) и (1,5;1,57) в найденную производную, и изобразим на рисунке поведение функции:

*В подобных случаях необязательно вычислять значения выражений. Важно установить их знаки (положительный либо отрицательный). Например, мы видим, что выражение:

(3,14/2) – 3    имеет отрицательный знак

3,14 – 3    имеет положительный знак

 В целом этого достаточно для определения знака выражения.

Таким образом, в точке х = 1,5 функция меняет знак с положительного на отрицательный.  Это означает, что данная точка является точкой максимума функции на заданном промежутке.

Ответ: 1,5  

77493. Найдите точку минимума функции y = (0,5 – x) cos x + sin x  

принадлежащую промежутку (0;П/2).  

Найдём производную функции:

Решаем уравнение:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, и другие при этом не теряют смысла. Следовательно:

Решаем уравнение   – sin x = 0:

В условии дан промежуток (0;П/2). Ему не принадлежит ни один из полученных корней.

Решаем уравнение: 0,5 – х = 0,   получим х = 0,5.

Запишем данный промежуток в радианах: (0;1,57).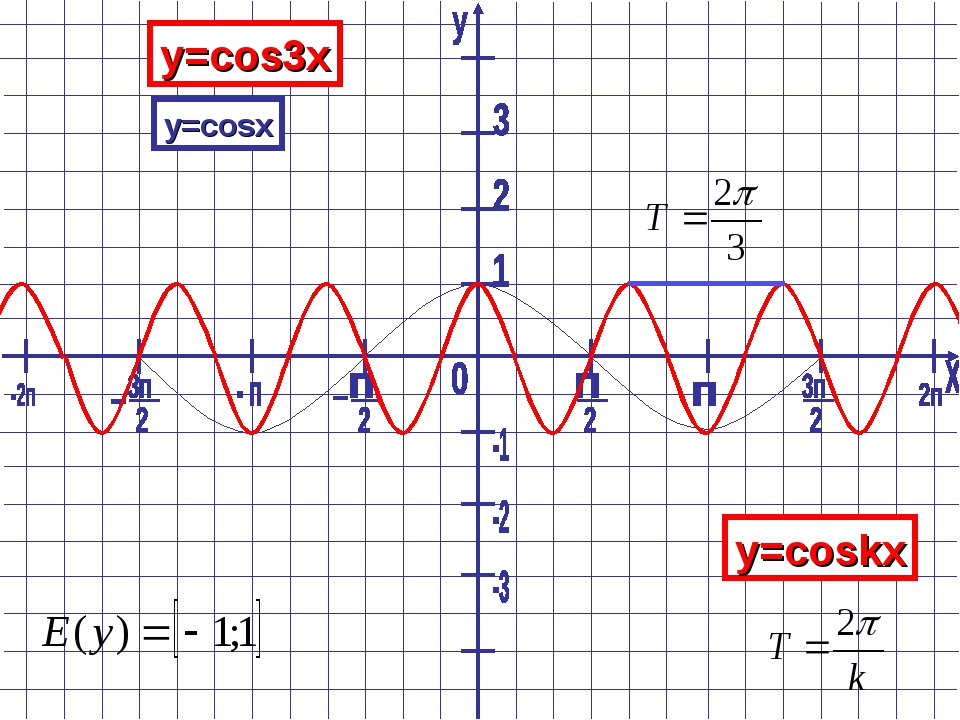

*Показано в предыдущем примере.

Следовательно полученное значение принадлежит промежутку (0;П/2):

Найденное значение х разбивает данный промежуток на два других. Определим знаки производной функции, подставляя произвольные значения из полученных промежутков (0;0,5) и (0,5;1,57) в найденную производную, и изобразим на рисунке поведение функции:

*Синус 0,3 радиана и синус 1 радиана имеют положительные знаки, так как оба эти угла лежат в пределах от 0 до 90 градусов. А мы знаем, что синусы углов лежащих в первой четверти имеют положительные значения.

Таким образом, в точке х = 0,5 функция меняет знак с отрицательного на положительный.  Это означает, что данная точка является точкой минимума функции на заданном промежутке.

Ответ: 0,5  

Как видите всё просто. Необходимо понимать свойства производной для исследования функций, понимать как «работать» с мерами углов, знать основы тригонометрии.

В будущем мы рассмотрим задачи на нахождение наибольшего (наименьшего) значения тригонометрических функций на заданном интервале, не пропустите!

Посмотрите, что нашёл в интернете. Оказывается, что при извержении вулканов тоже молнии бывают. Да ещё какие!

На том всё. Успехов Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

ЕГЭ. Задание 13. Тригонометрические (и не только) уравнения

Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Подборки видео и онлайн-курсы

Тригонометрические формулы

Геометрическая иллюстрация тригонометрических формул

Арк-функции. Простейшие тригонометрические уравнения

а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.

а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.

Подборка заданий прошлых лет

1. а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$. 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
   
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
2. а) Решите уравнение $2 \sin\left( 2x + \dfrac{\pi}{3} \right) — \sqrt{3} \sin x = \sin 2x + \sqrt3$.
   
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
3. а) Решите уравнение $2\sqrt3 \sin\left( x + \dfrac{\pi}{3} \right) — \cos 2x = 3\cos x — 1$.
   
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
4. а) Решите уравнение $2\sin\left( 2x + \dfrac{\pi}{6} \right) — \cos x = \sqrt3\sin 2x — 1$.
   
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна)
5. а) Решите уравнение $\sqrt2\sin\left( \dfrac{\pi}{4} + x \right) + \cos 2x = \sin x — 1$. 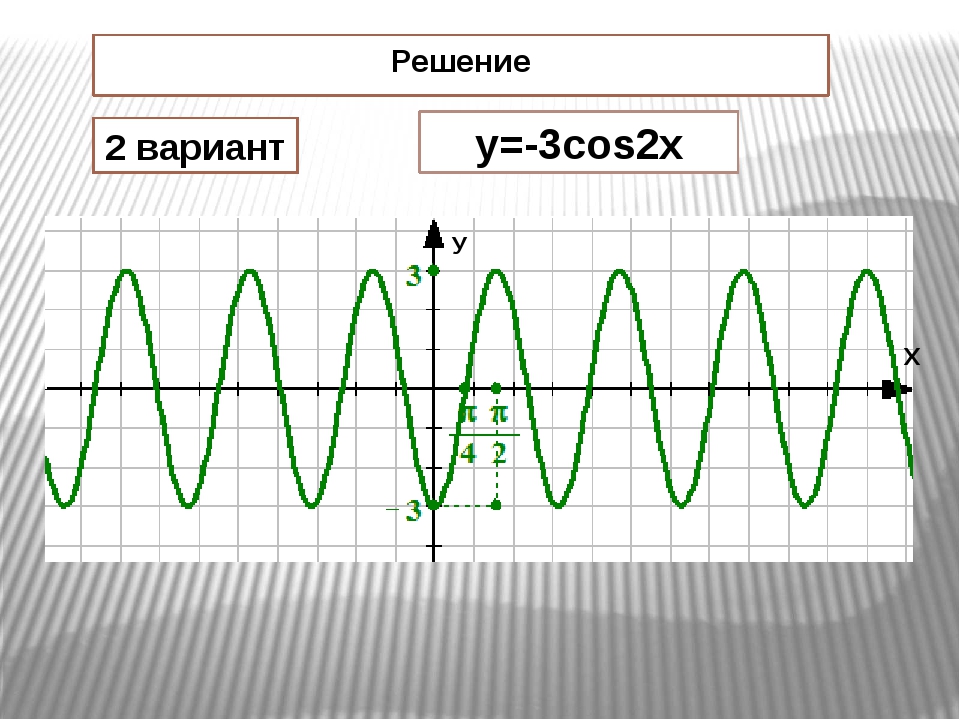2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
   
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)

{\ pi / 4} _0 (3 \ cos (x) -3 \ sin (x)) dx} \ right) =
\ left (\ dfrac {3 (\ sqrt {2} +1)} {\ dfrac {6} {\ sqrt {2}} — 3}, \ dfrac {9} {\ dfrac {24} {\ sqrt {2 }} — 12} \ right) \ приблизительно \ left (5,828427 \ ldots, 1,810666 \ ldots \ right) $$

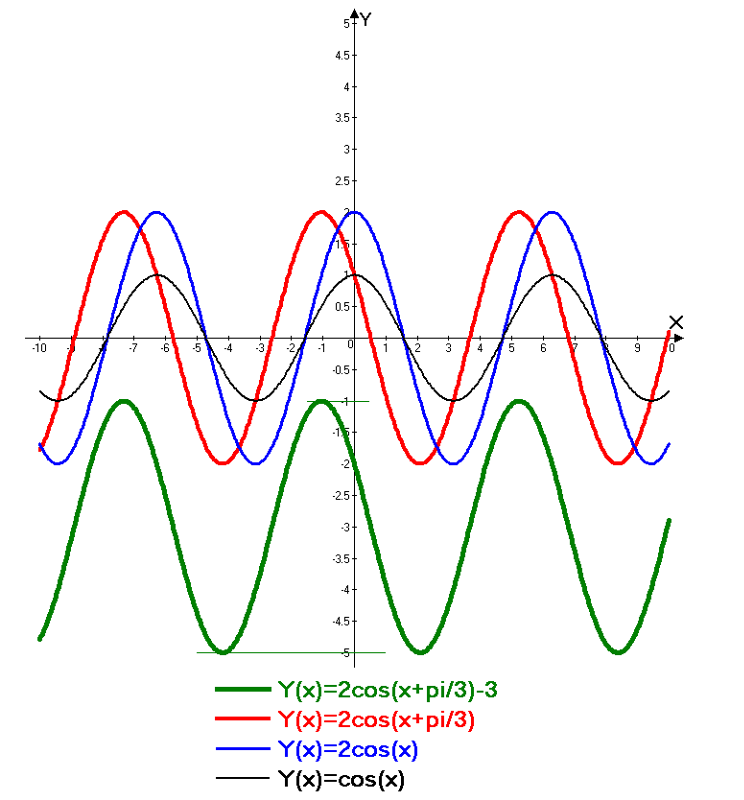
 Опишите преобразования, которые изменяют y = cosx в…  y = cos (x-30)  y = 3cosx  y = -cosx.

Презентация на тему: « Опишите преобразования, которые изменяют y = cosx в…  y = cos (x-30)  y = 3cosx  y = -cosx.» — Стенограмма презентации:

ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>

1

 Опишите преобразования, которые изменяют y = cosx в…  y = cos (x-30)  y = 3cosx  y = -cosx

2

Цели: познакомиться с функциями синуса, косинуса и тангенса.

3

 Имя: чтобы узнать функции синуса, косинуса и тангенса.  Опишите: откуда берутся функции синуса, косинуса и тангенса, и нарисуйте их графики.  Примените преобразования к этим функциям и начните использовать графический калькулятор для их рисования.

4

 P225 Ex 1A Q2,3 + Пересмотр C2 / C1  Следующий урок: больше триггерных графиков и функций  Гиппарх — греческий математик (родился в современной Турции) открыл основы тригонометрии c140 г. до н.э., но более известен своими работами в астрономии.

5

6

 Визуальные демонстрации синуса и косинуса из единичной окружности.  http://integralmaths.org/course/view.p hp? Id = 33 http://integralmaths.org/course/view.p hp? Id = 33

7

 Те же правила преобразования, которые мы видели до сих пор, могут быть применены к этим графам. Вы должны знать, как эти графики влияют на ключевые элементы / свойства.  Например,

8

 Используя прозрачные пленки, сопоставьте функции с графиками.

9

 Ampiltude:  Max / Min:  Период (растяжки):  Osscilates О:

10

Амплитуда = 1 Период = 120 ° Колебания около 0

11

Амплитуда = 2 Период = 90 ° Колебания около 0

12

Амплитуда = 4 Период = 1080 ° Колебания около 0

13

Амплитуда = 4 Период = 180 ° Колебания около -3

14

Амплитуда = 2 Период = 6 ° Колебания около 5

15

Амплитуда = 10 Период = 100 ° Колебания около 12

16

 y = sinx  y = cosx

17

 Задача «Преобразования, триггеры и радианы»  Математик:  c500CE этот индийский математик, который первым рассмотрел тригонометрические отношения синуса и косинуса как функции.

18

 Как определить максимальные и минимальные значения тригонометрических функций, включающих синус и косинус …  Например, Каковы максимальные и минимальные значения 4 + 2sinx?

19

20

21 год

22

23

24

 Учитывая, что sinx = 0.23 и 0≤x≤360 каковы возможные значения x?  Используйте calc, чтобы получить главное значение…

25

 Учитывая sinx = 0,23 и 0≤x≤360, каковы возможные значения x?  Используйте график, чтобы найти другие значения…

26

27

28 год

29

 Режим графика — все мощно!

30

31 год

32

33

34

3.

5 производных тригонометрических функций домашнее задание

Dayz server restart loot

Вход в систему учета рабочего времени Deltek

3.3 Производные тригонометрических функций 多選題 1. Какие из следующих утверждений верны? (A) 2 sin lim 0 x x x; (B) sin lim 1 x x x; (C) 0 sin lim 1 x x x; (D) sin lim 0 x x x. Ответ: CD [102 學 年度] Домашнее задание 10 Решения. 28 сен. Правило цепочки / (2.5) Викторина 10 Решения. 29 сен. Производные тригонометрических функций / (2.6) Конспект лекции Распечатайте копию. Домашнее задание 11 Решения.30 сен. Производные от экспоненциальных и логарифмических функций / (2.7) Конспект лекции Распечатайте. Викторина 11 Решения. 2 окт.

Cedars sinai new grad rn pay

В этом видеоуроке по исчислению объясняется, как найти производную от тригонометрических функций, таких как sinx, cosx, tanx, secx, cscx и cotx. Он содержит пример …

Руководство по эксплуатации самоката Adly 50cc

Если ваша домашняя работа по математике включает уравнения, неравенства, функции, многочлены, матрицы, это правильный пробный счет. Онлайн-решатель тригонометрии. Решите все типы тригонометрических (sin, cos, tan, sec, scs, cot) выражений, уравнений, неравенств. Графические тригонометрические функции. Тригонометрия прямоугольного треугольника. Онлайн-предварительное исчисление Решающее исчисление I § 3.5: Неявное дифференцирование. Прочтите этот раздел внимательно и полностью. Дополнительные примеры см. В моих видео § 3.5a: Неявное дифференцирование и поиск касательной и § 3.5b: Неявный поиск второй производной .. WebAssign. В предыдущих изданиях текста этот раздел включал производные от обратных тригонометрических функций; в новой редакции эта тема была…

1989 chevy blazer blue book value

Все товары danna7> производные> Тригонометрические функции новинка. 22 из 22. комментариев. СМИ. Тригонометрические функции new.mp4. 11,2 МБ. Комментарии отключены. Screencast.com …

Щенки лабораторной смеси Ньюфаундленда на продажу в Мичигане

Круг 2.9 Круговые функции ГЛАВА 3 Тригонометрические функции острого угла 26 3. 1 Тригонометрические функции острого угла 3.2 Тригонометрические функции дополнительных углов 3.3 Тригонометрические функции дополнительных углов 30, 45 и 60 3.4 Значения тригонометрических функций 3.5 Точность результатов с использованием приближения

Bon coup du jour

Все производные круговых тригонометрических функций могут быть найдены из производных от sin (x) и cos (x) с помощью правила частного, применяемого к таким функциям. как tan (x) = sin (x) / cos (x). Зная эти производные, производные обратных тригонометрических функций находятся с помощью неявного дифференцирования. 3.3 Производные тригонометрических функций 多選題 1. Какие из следующих утверждений верны? (A) 2 sin lim 0 x x x; (B) sin lim 1 x x x; (C) 0 sin lim 1 x x x; (D) sin lim 0 x x x.Ответ: CD [102 學 年度]

Sig 522 обновляет

Тригонометрические функции (Приложение D) Экспоненциальные функции, логарифмы (1,4–1,5) Касательные (2,1) Пределы (2,2) Законы пределов (2,3) Непрерывность (2,5) Асимптоты (2,6 ) Производные (2. 7-2.8) Обзор Среднесрочной оценки 1 Производные многочленов (3.1) Правила произведения и частного (3.2) Производные триггерных функций (3.3) Цепное правило (3.4) Неявное дифференцирование (3.5)

Guess donna corallo decollete tacco alto sp 348

Непрерывность кусочных функций (2.5) * Непрерывность слева / справа (2.5) Пределы на бесконечности (2.6) Определение производной (2.7, 3.1) * Графическая интерпретация дифференцируемых (3.1) Производных правил (степень, произведение, коэффициент) (3.2) * Наклон / уравнение касательной (3.2) Производные триггерных функций (3.4) * Цепное правило (3.5) *

Линкольн-диаграмма DCCV

Мы начинаем с производных синусоидальных и косинусоидальных функций, а затем используем их для получения формул для производных остальные четыре тригонометрические функции.Способность вычислять производные функций синуса и косинуса позволит нам найти скорость и ускорение простого гармонического движения. Часть 2 3.5: Производные тригонометрических функций Часть 2: Другие базовые функции МАТЕМАТИКА 165: Исчисление I Департамент математики Айова Государственный университет

Пример кодирования Ffmpeg vaapi

11 сентября 2020 г. · Обратные тригонометрические функции являются обратными функциями тригонометрических соотношений, то есть sin, cos, tan, cot, sec, cosec. Эти функции широко используются в таких областях, как физика, математика, инженерия и других областях исследований.Для обратных тригонометрических функций используются два популярных обозначения: Добавление «дуги» в качестве префикса.

Архитектурные проекты Планы домов

Просмотрите производные от обратных тригонометрических функций: arcsin (x), arccos (x) и arctan (x). Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Если F является композицией двух дифференцируемых функций f (u) и u = g (x), то есть если F (x) = f (g (x)), то производная F является производной f по к u, умноженному на производную g по x, то есть dxd (F) (x) = dxd (f) (g (x)) dxd (g) (x).

Лобби-боты Fortnite, которые нужно добавить

Название 3.5 Производные обратных тригонометрических функций Домашнее задание Дата Период Задачи 1–12 различаются.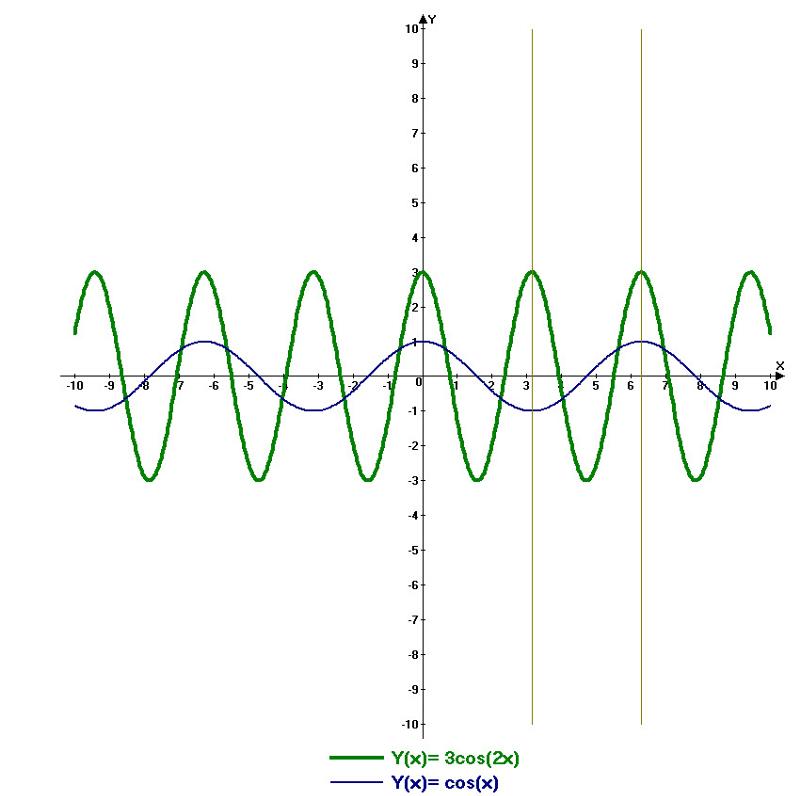 1. y = tan- (e) 2. y = стоимость 3. h (x) = arccos 4. y = cos (x 5. y = arctan 6. 9 (x) = sinº12 18 Jean Adams Flamingo Math, LLC 7 . h (x) = 2x sinx & y = tan (cos x) 9. 9 (x) = xotan 3x 10. f (x) = 11. (X) = 3 arctancy 12. n (x) = ln / sin — * 13.

Как установить phpmailer на windows 10

Посмотреть MATHS101Fall2016Section3_5_2Slides.pdf из MATHS 101 в AhliaUniversity. ull a Ei d Раздел 3.5 Производная тригонометрических функций 2 лекции Dr .A bd Доктор Абдулла Эйд Колледж

Бесплатные наличные онлайн

Полный список см. на brighthubeducation.com

Hp отслеживание реверберации

6) Неопределенные интегралы обратных тригонометрических функции. 1) Обозначения. Для обратных тригонометрических функций обозначения sin-1 и cos-1 часто используются для arcsin, arccos и т. Д. Когда используется это обозначение, обратные функции иногда путают с мультипликативными обратными функциями.

6.8 Теорема о расходимости — Том 3 исчисления

Цели обучения

• 6. 8.1 Объясните значение теоремы о расходимости.
• 6.8.2 Используйте теорему о расходимости для вычисления потока векторного поля.
• 6.8.3 Примените теорему о расходимости к электростатическому полю.

Мы рассмотрели несколько версий фундаментальной теоремы исчисления в более высоких измерениях, которые связывают интеграл вокруг ориентированной границы области с «производной» этой сущности в ориентированной области.В этом разделе мы формулируем теорему о расходимости, которая является последней теоремой этого типа, которую мы будем изучать. Теорема о расходимости имеет множество применений в физике; в частности, теорема о дивергенции используется в области дифференциальных уравнений в частных производных для вывода уравнений, моделирующих тепловой поток и сохранение массы. Мы используем теорему, чтобы вычислить интегралы потока и применить ее к электростатическим полям.

Обзор теорем

Прежде чем исследовать теорему о расходимости, полезно начать с обзора версий основной теоремы исчисления, которые мы обсуждали:

1. Основная теорема исчисления :
   ∫abf ′ (x) dx = f (b) −f (a). ∫abf ′ (x) dx = f (b) −f (a).
   Эта теорема связывает интеграл от производной f′f ′ по отрезку [a, b] [a, b] вдоль оси x с разностью ff, вычисленной на границе.
2. Основная теорема для линейных интегралов :
   ∫C∇f · dr = f (P1) −f (P0), ∫C∇f · dr = f (P1) −f (P0),
   где P0P0 — начальная точка C , а P1P1 — конечная точка C . Фундаментальная теорема для линейных интегралов позволяет пути C быть путем на плоскости или в пространстве, а не просто отрезком на оси x .Если мы думаем о градиенте как о производной, то эта теорема связывает интеграл от производной ∇f∇f по пути C с разностью ff, вычисленной на границе C .
3. Теорема Грина, форма обращения :
   ∬D (Qx − Py) dA = ∫CF · dr. ∬D (Qx − Py) dA = ∫CF · dr.
   Поскольку Qx − Py = curlF · kQx − Py = curlF · k и curl является своего рода производной, теорема Грина связывает интеграл от производной curl F по плоской области D с интегралом от F на границе Д .
4. Теорема Грина, форма потока :
   ∬D (Px + Qy) dA = CF · Nds.∬D (Px + Qy) dA = ∫CF · Nds.
   Поскольку Px + Qy = divFPx + Qy = divF и дивергенция является своего рода производной, форма потока теоремы Грина связывает интеграл производной div F по плоской области D с интегралом от F на границе Д .
5. Теорема Стокса :
   ∬ScurlF · dS = ∫CF · dr.∬ScurlF · dS = ∫CF · dr.
   Если мы думаем о роторе как о производной, то теорема Стокса связывает интеграл от производной ротора F по поверхности S (не обязательно плоской) с интегралом от F по границе S .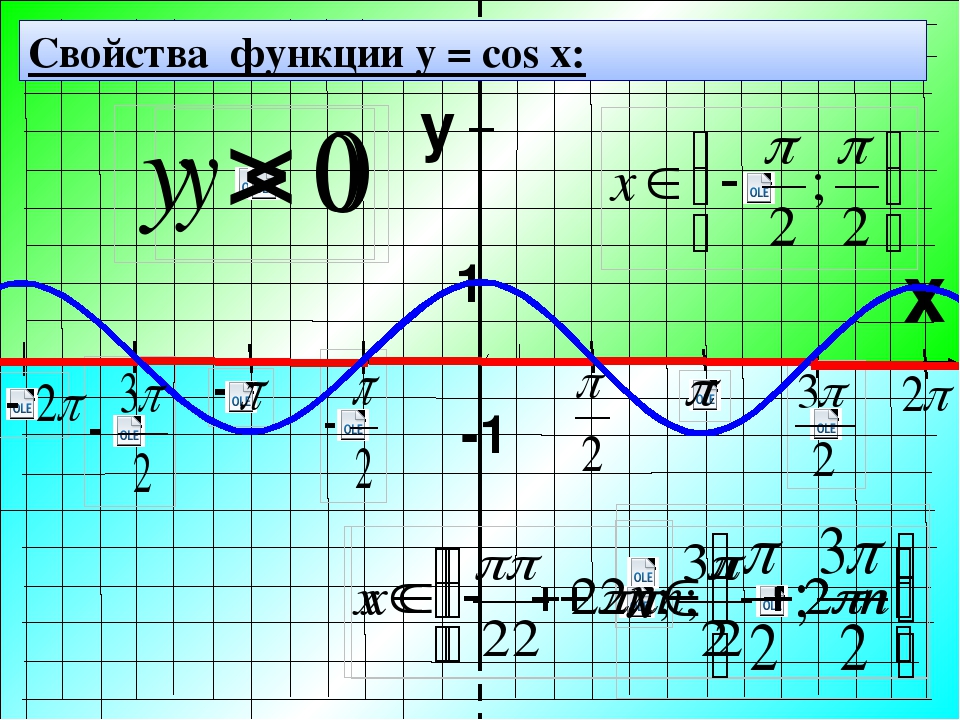

Формулировка теоремы о расходимости

Теорема о расходимости следует общей схеме этих других теорем. Если мы думаем о дивергенции как о производной, то теорема о дивергенции связывает тройной интеграл от производной div F по твердому телу с интегралом потока F по границе твердого тела. Более конкретно, теорема о расходимости связывает интеграл потока векторного поля F по замкнутой поверхности S с тройным интегралом от расходимости F по твердому телу, заключенному в S .

Теорема 6.20

Теорема расходимости

Пусть S — кусочно-гладкая замкнутая поверхность, которая охватывает твердое тело E в пространстве. Предположим, что S ориентирован наружу, и пусть F будет векторным полем с непрерывными частными производными на открытой области, содержащей E (рисунок 6. 87). Тогда

∭EdivFdV = ∬SF · dS.∭EdivFdV = ∬SF · dS.

(6,24)

Рис. 6.87 Теорема о расходимости связывает интеграл потока по замкнутой поверхности S с тройным интегралом по твердому телу E , заключенному на поверхность.

Напомним, что форма потока теоремы Грина утверждает, что ∬DdivFdA = ∫CF · Nds.∬DdivFdA = ∫CF · Nds. Следовательно, теорема о расходимости — это версия теоремы Грина в одном более высоком измерении.

Доказательство теоремы о расходимости выходит за рамки этого текста. Однако мы рассмотрим неофициальное доказательство, которое дает общее представление о том, почему теорема верна, но не доказывает теорему со всей строгостью. Это объяснение следует неформальному объяснению того, почему теорема Стокса верна.

Проба

Пусть B будет небольшим прямоугольником со сторонами, параллельными координатным плоскостям внутри E (рисунок 6. 88). Пусть центр B имеет координаты (x, y, z) (x, y, z) и предположим, что длины ребер равны Δx, Δy, Δx, Δy и ΔzΔz (рисунок 6.88 (b)). Вектор нормали из верхней части коробки равен k , а вектор нормали из нижней части коробки равен −k.−k. Скалярное произведение F = 〈P, Q, R〉 F = 〈P, Q, R〉 с k равно R , а скалярное произведение с −k − k равно −R.-R. Площадь верха коробки (и низа коробки) ΔSΔS равна ΔxΔy.ΔxΔy.

Рисунок 6.88 (a) Маленькая коробка B внутренняя поверхность E имеет стороны, параллельные координатным плоскостям. (b) Коробка B имеет длины сторон Δx, Δy, Δx, Δy и ΔzΔz (c) Если мы посмотрим на вид сбоку B , мы увидим, что, поскольку (x, y, z) (x, y, z) является центром коробки, чтобы добраться до вершины коробки, мы должны пройти вертикальное расстояние Δz / 2Δz / 2 вверх от (x, y, z). (x, y, z). Точно так же, чтобы добраться до дна коробки, мы должны пройти расстояние Δz / 2Δz / 2 вниз от точки (x, y, z).(х, у, г).

Поток из верхней части ящика может быть аппроксимирован выражением R (x, y, z + Δz2) ΔxΔyR (x, y, z + Δz2) ΔxΔy (рисунок 6.88 (c)) и потоком из нижней части прямоугольник — это −R (x, y, z − Δz2) ΔxΔy. − R (x, y, z − Δz2) ΔxΔy. Если обозначить разницу между этими значениями как ΔR, ΔR, то чистый поток в вертикальном направлении можно аппроксимировать как ΔRΔxΔy.ΔRΔxΔy. Однако

ΔRΔxΔy = (ΔRΔz) ΔxΔyΔz≈ (∂R∂z) ΔV.ΔRΔxΔy = (ΔRΔz) ΔxΔyΔz≈ (∂R∂z) ΔV.

Следовательно, чистый поток в вертикальном направлении может быть аппроксимирован выражением (∂R∂z) ΔV.(∂R∂z) ΔV. Точно так же чистый поток в направлении x может быть аппроксимирован выражением (∂P∂x) ΔV (∂P∂x) ΔV, а чистый поток в направлении y может быть аппроксимирован выражением (∂Q∂y ) ΔV. (∂Q∂y) ΔV. Сложение потоков во всех трех направлениях дает приближение к общему потоку из коробки:

Общий поток ≈ (∂P∂x + ∂Q∂y + ∂R∂z) ΔV = divFΔV.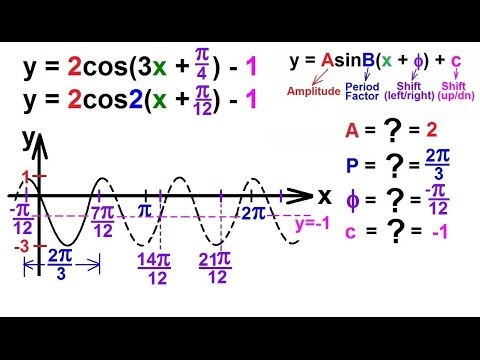 Общий поток ≈ (∂P∂x + ∂Q∂y + ∂R∂z) ΔV = divFΔV.

Это приближение становится сколь угодно близким к значению полного потока, когда объем коробки сокращается до нуля.

Сумма divFΔVdivFΔV по всем маленьким прямоугольникам, приблизительно равная E , составляет приблизительно ∭EdivFdV.∭EdivFdV. С другой стороны, сумма divFΔVdivFΔV по всем маленьким прямоугольникам, аппроксимирующая E , является суммой потоков по всем этим прямоугольникам. Как и в неформальном доказательстве теоремы Стокса, добавление этих потоков по всем ячейкам приводит к отмене многих членов. Если аппроксимирующая коробка имеет общую грань с другой аппроксимирующей рамкой, то поток по одной грани является отрицательным по отношению к потоку по общей грани соседнего бокса.Эти два интеграла сокращаются. При суммировании всех потоков единственными оставшимися интегралами потока являются интегралы по граням, аппроксимирующим границу E .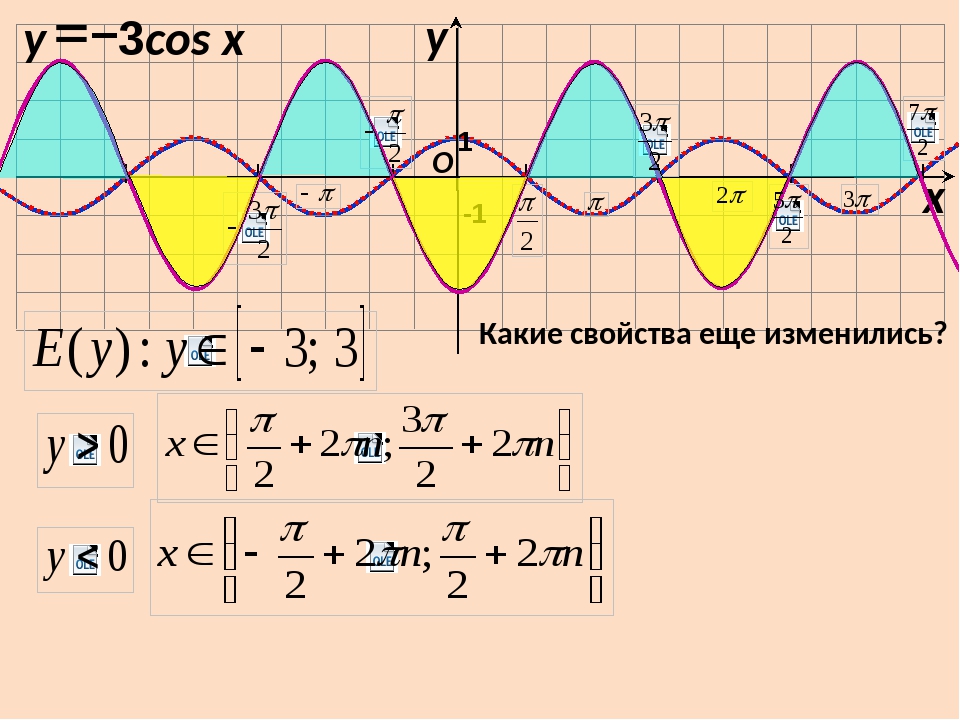 Когда объемы аппроксимирующих ящиков уменьшаются до нуля, это приближение становится произвольно близким к потоку над S .

□

Пример 6.77

Проверка теоремы о расходимости

Проверить теорему о расходимости для векторного поля F = 〈x − y, x + z, z − y〉 F = 〈x − y, x + z, z − y〉 и поверхности S , состоящей из конуса x2 + y2 = z2,0≤z≤1, x2 + y2 = z2,0≤z≤1 и круглая вершина конуса (см. следующий рисунок).Предположим, эта поверхность положительно ориентирована.

Решение

Пусть E будет сплошным конусом, заключенным в S . Чтобы проверить теорему для этого примера, мы покажем, что ∭EdivFdV = SF · dS∭EdivFdV = ∬SF · dS, вычисляя каждый интеграл отдельно.

Чтобы вычислить тройной интеграл, обратите внимание, что divF = Px + Qy + Rz = 2, divF = Px + Qy + Rz = 2, и поэтому тройной интеграл равен

∭EdivFdV = 2∭EdV = 2 (объемE) . ∭EdivFdV = 2∭EdV = 2 (объемE).

Объем правого кругового конуса равен πr2h4.πr2h4. В этом случае h = r = 1. h = r = 1. Следовательно,

∭EdivFdV = 2 (объемE) = 2π3. EdivFdV = 2 (объемE) = 2π3.

Чтобы вычислить интеграл потока, сначала обратите внимание, что S кусочно-гладкий; S можно записать как объединение гладких поверхностей. Поэтому мы разбиваем интеграл потока на две части: один интеграл потока по круглой вершине конуса и один интеграл по остальной части конуса. Круглый верх назовем S1S1, а часть под верхом S2.S2. Начнем с расчета потока через круглую вершину конуса.Обратите внимание, что S1S1 имеет параметризацию

r (u, v) = 〈ucosv, usinv, 1〉, 0≤u≤1,0≤v≤2π.r (u, v) = 〈ucosv, usinv, 1〉, 0≤u≤1,0≤ v≤2π.

Тогда касательные векторы равны tu = 〈cosv, sinv, 0〉 tu = 〈cosv, sinv, 0〉 и tv = 〈- ucosv, usinv, 0〉 .tv = 〈- ucosv, usinv, 0〉. Следовательно, поток через S1S1 равен

∬S1F · dS = ∫01∫02πF (r (u, v)) · (tu × tv) dA = ∫01∫02π 〈ucosv − usinv, ucosv + 1,1 − usinv〉 · 〈0,0, u〉 dvdu = ∫01∫02πu − u2sinvdvdu = π.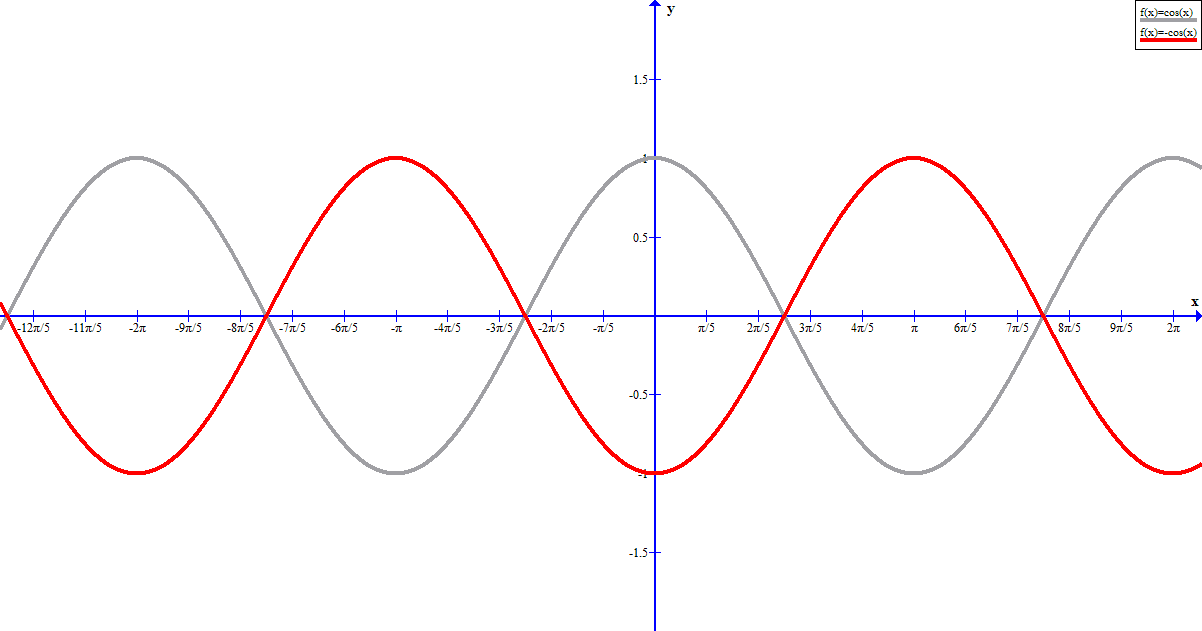 ∬S1F · dS = ∫01∫02πF (r (u, v)) · (tu × tv) dA = ∫01∫02π 〈ucosv − usinv, ucosv + 1,1 −usinv〉 · 〈0,0, u〉 dvdu = ∫01∫02πu − u2sinvdvdu = π.

Теперь вычислим поток по S2.S2. Параметризация этой поверхности

r (u, v) = 〈ucosv, usinv, u〉, 0≤u≤1,0≤v≤2π.r (u, v) = 〈ucosv, usinv, u〉, 0≤u≤1,0≤ v≤2π.

Касательные векторы равны tu = 〈cosv, sinv, 1〉 tu = 〈cosv, sinv, 1〉 и tv = 〈- usinv, ucosv, 0〉, tv = 〈- usinv, ucosv, 0〉, поэтому перекрестное произведение это

tu × tv = 〈- ucosv, −usinv, u〉 .tu × tv = 〈- ucosv, −usinv, u〉.

Обратите внимание, что отрицательные знаки на компонентах x и y вызывают отрицательную (или внутреннюю) ориентацию конуса. Поскольку поверхность положительно ориентирована, мы используем вектор tv × tu = 〈ucosv, usinv, −u〉 tv × tu = 〈ucosv, usinv, −u〉 в интеграле потока.Поток через S2S2 тогда равен

.
∬S2F · dS = ∫01∫02πF (r (u, v)) · (tv × tu) dA = ∫01∫02π 〈ucosv − usinv, ucosv + u, u − sinv〉 · 〈ucosv, usinv, −u 〉 = ∫01∫02πu2cos2v + 2u2sinv − u2dvdu = −π3.∬S2F · dS = ∫01∫02πF (r (u, v)) · (tv × tu) dA = ∫01∫02π 〈ucosv − usinv, ucosv + u, u − sinv〉 · 〈ucosv, usinv, −u〉 = ∫01∫02πu2cos2v + 2u2sinv − u2dvdu = −π3.

Общий поток через S составляет

∬S2F · dS = ∬S1F · dS + ∬S2F · dS = 2π3 = ∭EdivFdV, ∬S2F · dS = ∬S1F · dS + ∬S2F · dS = 2π3 = ∭EdivFdV,

, и мы проверили теорему о расходимости для этого примера.

КПП 6.65

Проверить теорему о расходимости для векторного поля F (x, y, z) = 〈x + y + z, y, 2x − y〉 F (x, y, z) = 〈x + y + z, y, 2x− y〉 и поверхность S , заданная цилиндром x2 + y2 = 1,0≤z≤3×2 + y2 = 1,0≤z≤3 плюс круговые верх и низ цилиндра. Предположим, что S положительно ориентирован.

Напомним, что расхождение непрерывного поля F в точке P является мерой «истечения» поля в точке P . Если F представляет поле скорости жидкости, то дивергенцию можно представить как расход на единицу объема вытекающей жидкости за вычетом скорости на единицу втекающего объема.Теорема о расходимости подтверждает эту интерпретацию. Чтобы увидеть это, пусть P будет точкой, а BrBr — шаром малого радиуса r с центром в точке P (рис. 6.89). Пусть SrSr — граничная сфера Br.Br. Поскольку радиус мал и F является непрерывным, divF (Q) ≈divF (P) divF (Q) ≈divF (P) для всех остальных точек Q в шаре. Следовательно, поток через SrSr можно аппроксимировать с помощью теоремы о расходимости:

∬SrF · dS = ∭BrdivFdV≈∭BrdivF (P) dV.∬SrF · dS = ∭BrdivFdV≈∭BrdivF (P) dV.

Поскольку divF (P) divF (P) является константой,

∭BrdivF (P) dV = divF (P) V (Br) .∭BrdivF (P) dV = divF (P) V (Br).

Следовательно, поток ∬SrF · dS∬SrF · dS может быть аппроксимирован как divF (P) V (Br) .divF (P) V (Br). Это приближение становится лучше по мере уменьшения радиуса до нуля, и, следовательно,

divF (P) = limr → 01V (Br) ∬SrF · dS. divF (P) = limr → 01V (Br) ∬SrF · dS.

Это уравнение говорит, что дивергенция при P — это чистая скорость внешнего потока жидкости на единицу объема.

Рисунок 6.89 Шар BrBr малого радиуса r с центром P.

Использование теоремы о расходимости

Теорема расходимости переводится между интегралом потока замкнутой поверхности S и тройным интегралом по твердому телу, заключенному в S . Следовательно, теорема позволяет нам вычислять интегралы потока или тройные интегралы, которые обычно было бы трудно вычислить, переводя интеграл потока в тройной интеграл и наоборот.

Пример 6.78

Применение теоремы о расходимости

Вычислить поверхностный интеграл ∬SF · dS, ∬SF · dS, где S — цилиндр x2 + y2 = 1,0≤z≤2, x2 + y2 = 1,0≤z≤2, включая круглую вершину и снизу и F = 〈x33 + yz, y33 − sin (xz), z − x − y〉.F = 〈x33 + yz, y33 − sin (xz), z − x − y〉.

Решение

Мы могли бы вычислить этот интеграл без теоремы о расходимости, но вычисление непросто, потому что нам пришлось бы разбить интеграл потока на три отдельных интеграла: один для верха цилиндра, один для низа и один для стороны. Кроме того, каждый интеграл потребует параметризации соответствующей поверхности, вычисления касательных векторов и их перекрестного произведения и использования уравнения 6.19.

Напротив, теорема о расходимости позволяет вычислить единичный тройной интеграл ∭EdivFdV, ∭EdivFdV, где E — твердое тело, заключенное в цилиндр. Используя теорему о расходимости и переводя в цилиндрические координаты, получаем

∬sF · dS = ∭EdivFdV = ∭E (x2 + y2 + 1) dV = ∫02π∫01∫02 (r2 + 1) rdzdrdθ = 32∫02πdθ = 3π.∬sF · dS = ∭EdivFdV = ∭E (x2 + y2 + 1) dV = ∫02π∫01∫02 (r2 + 1) rdzdrdθ = 32∫02πdθ = 3π.

КПП 6.66

Используйте теорему о расходимости для вычисления интеграла потока ∬SF · dS, ∬SF · dS, где S — граница прямоугольника, заданная как 0≤x≤2,1≤y≤4,0≤z≤1,0 ≤x≤2,1≤y≤4,0≤z≤1 и F = 〈x2 + yz, yz, 2x + 2y + 2z〉 F = 〈x2 + yz, yz, 2x + 2y + 2z〉 (см. следующий рисунок).

Пример 6.79

Применение теоремы о расходимости

Пусть v = 〈- yz, xz, 0〉 v = 〈- yz, xz, 0〉 поле скоростей жидкости. Пусть C — сплошной куб, заданный формулой 1≤x≤4,2≤y≤5,1≤z≤4,1≤x≤4,2≤y≤5,1≤z≤4, и пусть S — граница этого куба (см. Следующий рисунок). Найдите расход жидкости через S .

Рисунок 6.90 Векторное поле v = 〈- yz, xz, 0〉. V = 〈- yz, xz, 0〉.

Решение

Расход жидкости через S составляет ∬Sv · dS.∬Sv · dS. Прежде чем вычислять этот интеграл потока, давайте обсудим, каким должно быть значение интеграла. Основываясь на рис. 6.90, мы видим, что если мы поместим этот куб в жидкость (до тех пор, пока куб не охватывает источник), то скорость жидкости, поступающей в куб, будет такой же, как скорость жидкости, покидающей куб. Поле имеет вращательный характер, и для данной окружности, параллельной плоскости xy , центр которой находится на оси z , все векторы вдоль этой окружности имеют одинаковую величину.Вот как мы можем видеть, что скорость потока на входе и выходе из куба одинакова. Поток в куб прекращается с потоком из куба, и поэтому скорость потока жидкости через куб должен быть нулевым.

Чтобы проверить эту интуицию, нам нужно вычислить интеграл потока. Непосредственное вычисление интеграла потока требует разбиения интеграла потока на шесть отдельных интегралов потока, по одному для каждой грани куба. Нам также нужно найти касательные векторы, вычислить их перекрестное произведение и использовать уравнение 6.19. Однако использование теоремы о расходимости ускоряет вычисление:

∬Sv · dS = ∭Cdiv (v) dV = ∭C0dV = 0. Sv · dS = ∭Cdiv (v) dV = ∭C0dV = 0.

Следовательно, поток равен нулю, как и ожидалось.

КПП 6.67

Пусть v = 〈xz, yz, 0〉 v = 〈xz, yz, 0〉 поле скоростей жидкости. Пусть C — сплошной куб, заданный формулой 1≤x≤4,2≤y≤5,1≤z≤4,1≤x≤4,2≤y≤5,1≤z≤4, и пусть S — граница этого куба (см. Следующий рисунок). Найдите расход жидкости через S .

Пример 6.79 иллюстрирует замечательное следствие теоремы о расходимости. Пусть S будет кусочно гладкой замкнутой поверхностью и пусть F будет векторным полем, определенным на открытой области, содержащей поверхность, заключенную в S . Если F имеет вид F = 〈f (y, z), g (x, z), h (x, y)〉, F = 〈f (y, z), g (x, z), h (x, y)〉, то дивергенция F равна нулю. По теореме о расходимости поток F через S также равен нулю. Это упрощает вычисление некоторых интегралов потока.Например, предположим, что мы хотим вычислить интеграл потока ∬SF · dS∬SF · dS, где S — куб, а

F = 〈sin (y) eyz, x2z2, cos (xy) esinx〉. F = 〈sin (y) eyz, x2z2, cos (xy) esinx〉.

Прямое вычисление интеграла потока было бы трудным, если не невозможным, с использованием методов, которые мы изучили ранее. По крайней мере, нам пришлось бы разбить интеграл потока на шесть интегралов, по одному для каждой грани куба. Но поскольку дивергенция этого поля равна нулю, теорема о дивергенции сразу показывает, что интеграл потока равен нулю.

Теперь мы можем использовать теорему о расходимости, чтобы обосновать физическую интерпретацию расходимости, которую мы обсуждали ранее. Напомним, что если F является непрерывным трехмерным векторным полем и P является точкой в ​​области F , то расхождение F на P является мерой «истечения» из F на P . Если F представляет поле скорости жидкости, то расхождение F на P является мерой чистой скорости потока из точки P (поток жидкости из P минус расход жидкости в до P ).Чтобы увидеть, как теорема о расходимости оправдывает эту интерпретацию, пусть BrBr будет шаром очень малого радиуса r с центром P , и предположим, что BrBr находится в области F . Кроме того, предположим, что BrBr имеет положительную внешнюю ориентацию. Поскольку радиус BrBr мал и F непрерывен, расходимость F примерно постоянна на Br.Br. То есть, если P′P ′ — любая точка из Br, Br, то divF (P) ≈divF (P ′). DivF (P) ≈divF (P ′). Обозначим через SrSr граничную сферу Br.Br. Мы можем аппроксимировать поток через SrSr, используя теорему о расходимости, следующим образом:

∬SrF · dS = ∭BrdivFdV≈∭BrdivF (P) dV = divF (P) V (Br) .∬SrF · dS = ∭BrdivFdV≈∭BrdivF (P) dV = divF (P) V (Br).

Когда мы уменьшаем радиус r до нуля с помощью предела, величина divF (P) V (Br) divF (P) V (Br) становится сколь угодно близкой к потоку. Следовательно,

divF (P) = limr → 01V (Br) ∬SrF · dSdivF (P) = limr → 01V (Br) ∬SrF · dS

, и мы можем рассматривать расхождение на P как измерение чистой скорости внешнего потока на единицу объема на P .Поскольку «отток» — неофициальный термин для обозначения чистой скорости исходящего потока на единицу объема, мы обосновали физическую интерпретацию дивергенции, которую мы обсуждали ранее, и мы использовали теорему о расходимости, чтобы дать это обоснование.

Применение к электростатическим полям

Теорема о расходимости имеет множество приложений в физике и технике. Это позволяет нам записывать многие физические законы как в интегральной, так и в дифференциальной форме (почти так же, как теорема Стокса позволяла нам переводить между интегральной и дифференциальной формами закона Фарадея).В таких областях исследований, как гидродинамика, электромагнетизм и квантовая механика, есть уравнения, которые описывают сохранение массы, импульса или энергии, а теорема о расходимости позволяет нам дать эти уравнения как в интегральной, так и в дифференциальной формах.

Одно из наиболее распространенных приложений теоремы о расходимости — электростатические поля. Важным результатом в этой области является закон Гаусса. Этот закон гласит, что если S является замкнутой поверхностью в электростатическом поле E , то поток E через S представляет собой полный заряд, заключенный в S (деленный на электрическую постоянную).Теперь мы используем теорему о расходимости, чтобы обосновать частный случай этого закона, в котором электростатическое поле создается неподвижным точечным зарядом в начале координат.

Если (x, y, z) (x, y, z) — точка в пространстве, то расстояние от точки до начала координат равно r = x2 + y2 + z2.r = x2 + y2 + z2. Обозначим через FrFr радиальное векторное поле Fr = 1r2 〈xr, yr, zr〉. Fr = 1r2 〈xr, yr, zr〉. Вектор в данной позиции в пространстве указывает в направлении единичного радиального вектора 〈xr, yr, zr〉 〈xr, yr, zr〉 и масштабируется величиной 1 / r2.1 / r2. Следовательно, величина вектора в данной точке обратно пропорциональна квадрату расстояния вектора от начала координат. Предположим, у нас есть стационарный заряд q кулонов в начале координат, существующий в вакууме. Заряд создает электростатическое поле E , задаваемое

, где аппроксимация ε0 = 8,854 × 10–12ε0 = 8,854 × 10–12 фарад (Ф) / м — электрическая постоянная. (Постоянная ε0ε0 является мерой сопротивления, возникающего при формировании электрического поля в вакууме.Обратите внимание, что E — это радиальное векторное поле, подобное гравитационному полю, описанному в Примере 6.6. Разница в том, что это поле направлено наружу, тогда как гравитационное поле направлено внутрь. Потому что

E = q4πε0Fr = q4πε0 (1r2 〈xr, yr, zr〉), E = q4πε0Fr = q4πε0 (1r2 〈xr, yr, zr〉),

мы говорим, что электростатические поля подчиняются закону обратных квадратов. То есть электростатическая сила в данной точке обратно пропорциональна квадрату расстояния от источника заряда (который в данном случае находится в начале координат).Учитывая это векторное поле, мы показываем, что поток через замкнутую поверхность S равен нулю, если заряд находится за пределами S , и что поток равен q / ε0q / ε0, если заряд находится внутри S . Другими словами, поток через S — это заряд внутри поверхности, деленный на постоянную ε0.ε0. Это частный случай закона Гаусса, и здесь мы используем теорему о расходимости, чтобы обосновать этот частный случай.

Чтобы показать, что поток через S — это заряд внутри поверхности, деленный на постоянные ε0, ε0, нам нужны два промежуточных шага.Сначала мы покажем, что дивергенция FrFr равна нулю, а затем покажем, что поток FrFr через любую гладкую поверхность S равен нулю или 4π.4π. Тогда мы сможем оправдать этот частный случай закона Гаусса.

Пример 6.80

Дивергенция FrFr равна нулю

Убедитесь, что расхождение FrFr равно нулю там, где FrFr определено (вдали от начала координат).

Решение

Поскольку r = x2 + y2 + z2, r = x2 + y2 + z2, правило частного дает нам

∂∂x (xr3) = ∂∂x (x (x2 + y2 + z2) 3/2) = (x2 + y2 + z2) 3/2 − x [32 (x2 + y2 + z2) 1 / 22x] ( x2 + y2 + z2) 3 = r3−3x2rr6 = r2−3x2r5.∂∂x (xr3) = ∂∂x (x (x2 + y2 + z2) 3/2) = (x2 + y2 + z2) 3/2 − x [32 (x2 + y2 + z2) 1 / 22x] ( x2 + y2 + z2) 3 = r3−3x2rr6 = r2−3x2r5.

Аналогично

∂∂y (yr3) = r2−3y2r5 и ∂∂z (zr3) = r2−3z2r5.∂∂y (yr3) = r2−3y2r5and∂∂z (zr3) = r2−3z2r5.

Следовательно,

divFr = r2−3x2r5 + r2−3y2r5 + r2−3z2r5 = 3r2−3 (x2 + y2 + z2) r5 = 3r2−3r2r5 = 0. divFr = r2−3x2r5 + r2−3y2r5 + r2−3z2r5 = 3r2 x2 + y2 + z2) r5 = 3r2−3r2r5 = 0.

Обратите внимание, что, поскольку дивергенция FrFr равна нулю, а E — это FrFr, масштабированный константой, дивергенция электростатического поля E также равна нулю (за исключением начала координат).

Теорема 6.21

Поток через гладкую поверхность

Пусть S — связная кусочно гладкая замкнутая поверхность и пусть Fr = 1r2 〈xr, yr, zr〉. Fr = 1r2 〈xr, yr, zr〉. Затем

∬SFr · dS = {0ifS не охватывает начало координат4πifS охватывает начало координат. SFr · dS = {0ifSне охватывает начало координат4πifS охватывает начало координат.

Другими словами, эта теорема утверждает, что поток FrFr через любую кусочно-гладкую замкнутую поверхность S зависит только от того, находится ли начало координат внутри S .

Проба

Логика этого доказательства следует логике примера 6.46, только мы используем теорему о расходимости, а не теорему Грина.

Во-первых, предположим, что S не охватывает начало координат. В этом случае твердое тело, заключенное в S , находится в области определения Fr, Fr, и поскольку дивергенция FrFr равна нулю, мы можем немедленно применить теорему о дивергенции и обнаружить, что ∬SF · dS∬SF · dS равно нулю.

Теперь предположим, что S действительно охватывает начало координат.Мы не можем просто использовать теорему о расходимости для вычисления потока, потому что поле не определено в начале координат. Пусть SaSa будет сферой радиуса a внутри S с центром в начале координат. Векторное поле внешней нормали на сфере в сферических координатах равно

.
tϕ × tθ = 〈a2cosθsin2ϕ, a2sinθsin2ϕ, a2sinϕcosϕ〉 tϕ × tθ = 〈a2cosθsin2ϕ, a2sinθsin2ϕ, a2sinϕcosϕ〉

(см. Пример 6.64). Следовательно, на поверхности сферы скалярное произведение Fr · NFr · N (в сферических координатах) равно

Fr · N = 〈sinϕcosθa2, sinϕsinθa2, cosϕa2〉 · 〈a2cosθsin2ϕ, a2sinθsin2ϕ, a2sinϕcosϕ〉 = sinϕ (〈sinϕcosθ, sinϕsinθ, cosϕ〉 · 〈sinϕcosθ, sinϕsinθ), cosϕ.Fr · N = 〈sinϕcosθa2, sinϕsinθa2, cosϕa2〉 · 〈a2cosθsin2ϕ, a2sinθsin2ϕ, a2sinϕcosϕ〉 = sinϕ (〈sinϕcosθ, sinϕsinθ, cosϕ〉 · 〈sinϕcosθ, sinϕsinθ), cosϕ.

Поток FrFr через SaSa составляет

∬SaFr · NdS = ∫02π∫0πsinϕdϕdθ = 4π.SaFr · NdS = ∫02π∫0πsinϕdϕdθ = 4π.

Теперь помните, что нас интересует поток через S , не обязательно поток через Sa.Sa. Чтобы вычислить поток через S , пусть E будет твердым телом между поверхностями SaSa и S . Тогда граница E состоит из SaSa и S .Обозначьте эту границу S-SaS-Sa, чтобы указать, что S ориентирован наружу, но теперь SaSa ориентирован внутрь. Мы хотели бы применить теорему о расходимости к твердому телу E. Обратите внимание, что теорема о расходимости, как указано, не может обрабатывать твердое тело, такое как E , потому что E имеет отверстие. Однако теорема о расходимости может быть расширена для работы с твердыми телами с дырками, так же как теорема Грина может быть расширена для работы с областями с дырами. Это позволяет нам использовать теорему о расходимости следующим образом.По теореме о расходимости

∬S − SaFr · dS = ∬SFr · dS − ∬SaFr · dS = ∭EdivFrdV = ∭E0dV = 0. S − SaFr · dS = ∬SFr · dS − ∬SaFr · dS = ∭EdivFrdV = ∭E0dV = 0.

Следовательно,

∬SFr · dS = ∬SaFr · dS = 4π, ∬SFr · dS = ∬SaFr · dS = 4π,

, и мы получили желаемый результат.

□

Теперь вернемся к вычислению потока через гладкую поверхность в контексте электростатического поля E = q4πε0FrE = q4πε0Fr точечного заряда в начале координат. Пусть S — кусочно гладкая замкнутая поверхность, охватывающая начало координат. Тогда

∬SE · dS = ∬Sq4πε0Fr · dS = q4πε0∬SFr · dS = qε0.∬SE · dS = ∬Sq4πε0Fr · dS = q4πε0∬SFr · dS = qε0.

Если S не охватывает начало координат, то

∬SE · dS = q4πε0∬SFr · dS = 0. SE · dS = q4πε0∬SFr · dS = 0.

Таким образом, мы обосновали утверждение, которое мы намеревались оправдать: поток через замкнутую поверхность S равен нулю, если заряд находится за пределами S , и поток равен q / ε0q / ε0, если заряд находится внутри С .

Этот анализ работает только в том случае, если в исходной точке есть единовременный сбор. В этом случае закон Гаусса гласит, что поток E через S является полным зарядом, заключенным в S .Закон Гаусса может быть расширен для работы с несколькими заряженными твердыми телами в пространстве, а не только с одним точечным зарядом в начале координат. Логика аналогична предыдущему анализу, но выходит за рамки этого текста. В общем, закон Гаусса гласит, что если S представляет собой кусочно-гладкую замкнутую поверхность и Q представляет собой общее количество заряда внутри S , то поток E через S равен Q / ε0. .Q / ε0.

Пример 6.81

Используя закон Гаусса

Предположим, что у нас есть четыре стационарных точечных заряда в пространстве, все с зарядом 0.002 Кулоны (С). Заряды расположены в точках (0,1,1), (1,1,4), (- 1,0,0) и (−2, −2,2). (0,1,1), ( 1,1,4), (- 1,0,0) и (−2, −2,2). Пусть E обозначает электростатическое поле, создаваемое этими точечными зарядами. Если S — сфера радиуса 2, ориентированная наружу и центрированная в начале координат, то найти ∬SE · dS.∬SE · dS.

Решение

Согласно закону Гаусса, поток E через S представляет собой общий заряд внутри S , деленный на электрическую постоянную.Поскольку S имеет радиус 2, обратите внимание, что только два заряда находятся внутри S : заряд в точке (0,1,1) (0,1,1) и заряд в точке (−1,0,0 ). (- 1,0,0). Следовательно, общий заряд, охватываемый S , составляет 0,004 и, согласно закону Гаусса,

∬SE · dS = 0,0048,854 × 10−12≈4,518 · 109 В · м. SE · dS = 0,0048,854 · 10−12≈4,518 · 109 В · м.

КПП 6,68

Используйте предыдущий пример для поверхности S , которая представляет собой сферу радиуса 4 с центром в начале координат и ориентированную наружу.

Раздел 6.8 Упражнения

В следующих упражнениях используйте компьютерную алгебраическую систему (CAS) и теорему о расходимости, чтобы вычислить поверхностный интеграл ∫SF · nds∫SF · nds для данного выбора F и граничной поверхности S. Для каждой замкнутой поверхности предположим, что N — это единичный вектор нормали наружу.

376.

[T] F (x, y, z) = xi + yj + zk; F (x, y, z) = xi + yj + zk; S — поверхность куба 0≤x≤1,0≤y≤1,0

377.

[T] F (x, y, z) = (cosyz) i + exzj + 3z2k; F (x, y, z) = (cosyz) i + exzj + 3z2k; S — поверхность полусферы z = 4 − x2 − y2z = 4 − x2 − y2 вместе с диском x2 + y2≤4×2 + y2≤4 в плоскости xy .

378.

[T] F (x, y, z) = (x2 + y2 − x2) i + x2yj + 3zk; F (x, y, z) = (x2 + y2 − x2) i + x2yj + 3zk; S — это поверхность пяти граней единичного куба 0≤x≤1,0≤y≤1,0

379.

[T] F (x, y, z) = xi + yj + zk; F (x, y, z) = xi + yj + zk; S — поверхность параболоида z = x2 + y2for0≤z≤9.z = x2 + y2 для 0≤z≤9.

380.

[T] F (x, y, z) = x2i + y2j + z2k; F (x, y, z) = x2i + y2j + z2k; S — поверхность сферы x2 + y2 + z2 = 4.x2 + y2 + z2 = 4.

381.

[T] F (x, y, z) = xi + yj + (z2−1) k; F (x, y, z) = xi + yj + (z2−1) k; S — поверхность твердого тела, ограниченная цилиндром x2 + y2 = 4×2 + y2 = 4 и плоскостями z = 0 и z = 1.z = 0 и z = 1.

382.

[T] F (x, y, z) = xy2i + yz2j + x2zk; F (x, y, z) = xy2i + yz2j + x2zk; S — поверхность, ограниченная сверху сферой ρ = 2ρ = 2 и снизу конусом φ = π4φ = π4 в сферических координатах.(Думайте о S как о поверхности «рожка мороженого».)

383.

[T] F (x, y, z) = x3i + y3j + 3a2zk (constanta> 0); F (x, y, z) = x3i + y3j + 3a2zk (constanta> 0); S — поверхность, ограниченная цилиндром x2 + y2 = a2x2 + y2 = a2 и плоскостями z = 0 и z = 1.z = 0 и z = 1.

384.

[T] Поверхностный интеграл ∬SF · dS, ∬SF · dS, где S — твердое тело, ограниченное параболоидом z = x2 + y2z = x2 + y2 и плоскостью z = 4, z = 4 и F ( x, y, z) = (x + y2z2) i + (y + z2x2) j + (z + x2y2) kF (x, y, z) = (x + y2z2) i + (y + z2x2) j + (z + x2y2) k

385.

Используйте теорему о расходимости для вычисления поверхностного интеграла ∬SF · dS, ∬SF · dS, где F (x, y, z) = (ey2) i + (y + sin (z2)) j + (z − 1) kF (x , y, z) = (ey2) i + (y + sin (z2)) j + (z − 1) k и S — верхняя полусфера x2 + y2 + z2 = 1, z≥0, x2 + y2 + z2 = 1, z≥0, ориентирована вверх.

386.

Используйте теорему о расходимости для вычисления поверхностного интеграла ∬SF · dS, ∬SF · dS, где F (x, y, z) = x4i − x3z2j + 4xy2zkF (x, y, z) = x4i − x3z2j + 4xy2zk и S равно поверхность, ограниченная цилиндром x2 + y2 = 1×2 + y2 = 1 и плоскостями z = x + 2z = x + 2 и z = 0.z = 0.

387.

Используйте теорему о расходимости для вычисления поверхностного интеграла ∬SF · dS∬SF · dS, когда F (x, y, z) = x2z3i + 2xyz3j + xz4kF (x, y, z) = x2z3i + 2xyz3j + xz4k и S равно поверхность ящика с вершинами (± 1, ± 2, ± 3). (± 1, ± 2, ± 3).

388.

Используйте теорему о расходимости для вычисления поверхностного интеграла ∬SF · dS∬SF · dS, когда F (x, y, z) = ztan − 1 (y2) i + z3ln (x2 + 1) j + zkF (x, y, z) ) = ztan − 1 (y2) i + z3ln (x2 + 1) j + zk и S является частью параболоида x2 + y2 + z = 2×2 + y2 + z = 2, лежащего над плоскостью z = 1z = 1. и ориентирована вверх.

389.

[T] Используйте CAS и теорему о расходимости для вычисления потока ∬SF · dS, ∬SF · dS, где F (x, y, z) = (x3 + y3) i + (y3 + z3) j + (z3 + x3) kF (x, y, z) = (x3 + y3) i + (y3 + z3) j + (z3 + x3) k и S — сфера с центром (0, 0) и радиусом 2.

390.

Используйте теорему о расходимости, чтобы вычислить значение интеграла потока ∬SF · dS, ∬SF · dS, где F (x, y, z) = (y3 + 3x) i + (xz + y) j + [z + x4cos (x2y )] kF (x, y, z) = (y3 + 3x) i + (xz + y) j + [z + x4cos (x2y)] k и S — это площадь области, ограниченная x2 + y2 = 1, x≥0, y≥0 и 0≤z≤1.x2 + y2 = 1, x≥0, y≥0 и 0≤z≤1.

391.

Используйте теорему о расходимости для вычисления интеграла потока SF · dS, ∬SF · dS, где F (x, y, z) = yj − zkF (x, y, z) = yj − zk и S состоит из объединение параболоида y = x2 + z2,0≤y≤1, y = x2 + z2,0≤y≤1 и диска x2 + z2≤1, y = 1, x2 + z2≤1, y = 1, ориентированный наружу. Что такое поток через параболоид?

392.

Используйте теорему о расходимости для вычисления интеграла потока ∬SF · dS, ∬SF · dS, где F (x, y, z) = x + yj + z4kF (x, y, z) = x + yj + z4k и S является частью конуса z = x2 + y2z = x2 + y2 под верхней плоскостью z = 1, z = 1, ориентированной вниз.

393.

Используйте теорему о расходимости, чтобы вычислить поверхностный интеграл ∬SF · dSFSF · dS для F (x, y, z) = x4i − x3z2j + 4xy2zk, F (x, y, z) = x4i − x3z2j + 4xy2zk, где S — это поверхность, ограниченная цилиндром x2 + y2 = 1×2 + y2 = 1 и плоскостями z = x + 2 и z = 0. z = x + 2 и z = 0.

394.

Рассмотрим F (x, y, z) = x2i + xyj + (z + 1) k. F (x, y, z) = x2i + xyj + (z + 1) k. Пусть E — твердое тело, окруженное параболоидом z = 4 − x2 − y2z = 4 − x2 − y2 и плоскостью z = 0z = 0 с векторами нормали, направленными за пределы E . Вычислите поток F через границу E , используя теорему о расходимости.

Для следующих упражнений используйте CAS вместе с теоремой о расходимости, чтобы вычислить чистый исходящий поток для полей через данные поверхности S .

395.

[T] F = 〈x, −2y, 3z〉; F = 〈x, −2y, 3z〉; S — сфера {(x, y, z): x2 + y2 + z2 = 6}. {(X, y, z): x2 + y2 + z2 = 6}.

396.

[T] F = 〈x, 2y, z〉; F = 〈x, 2y, z〉; S — граница тетраэдра в первом октанте, образованная плоскостью x + y + z = 1.x + y + z = 1.

397.

[T] F = 〈y − 2x, x3 − y, y2 − z〉; F = 〈y − 2x, x3 − y, y2 − z〉; S — сфера {(x, y, z): x2 + y2 + z2 = 4}.{(x, y, z): x2 + y2 + z2 = 4}.

398.

[T] F = 〈x, y, z〉; F = 〈x, y, z〉; S — поверхность параболоида z = 4 − x2 − y2, z = 4 − x2 − y2, для z≥0, z≥0, плюс его основание в плоскости xy .

Для следующих упражнений используйте CAS и теорему о дивергенции, чтобы вычислить чистый исходящий поток для векторных полей через границу данных областей D .

399.

[T] F = 〈z − x, x − y, 2y − z〉; F = 〈z − x, x − y, 2y − z〉; D — это область между сферами радиуса 2 и 4 с центром в начале координат.

400.

[T] F = r | r | = 〈x, y, z〉 x2 + y2 + z2; F = r | r | = 〈x, y, z〉 x2 + y2 + z2; D — это область между сферами радиуса 1 и 2 с центром в начале координат.

401.

[T] F = 〈x2, −y2, z2〉; F = 〈x2, −y2, z2〉; D — это область в первом октанте между плоскостями z = 4 − x − yz = 4 − x − y и z = 2 − x − y. Z = 2 − x − y.

402.

Пусть F (x, y, z) = 2xi − 3xyj + xz2k.F (x, y, z) = 2xi − 3xyj + xz2k. Используйте теорему о расходимости для вычисления ∬SF · dS, ∬SF · dS, где S — поверхность куба с углами в точках (0,0,0), (1,0,0), (0,1, 0), (0,0,0), (1,0,0), (0,1,0), (1,1,0), (0,0,1), (1,0,1) , (0,1,1) и (1,1,1), (1,1,0), (0,0,1), (1,0,1), (0,1,1), и (1,1,1), ориентированные наружу.

403.

Используйте теорему о расходимости, чтобы найти внешний поток поля F (x, y, z) = (x3−3y) i + (2yz + 1) j + xyzkF (x, y, z) = (x3−3y) i + ( 2yz + 1) j + xyzk через куб, ограниченный плоскостями x = ± 1, y = ± 1, z = ± 1.x = ± 1, y = ± 1, z = ± 1.

404.

Пусть F (x, y, z) = 2xi − 3yj + 5zkF (x, y, z) = 2xi − 3yj + 5zk, и пусть S будет полусферой z = 9 − x2 − y2z = 9 − x2 − y2 вместе с диском x2 + y2≤9×2 + y2≤9 на плоскости xy . Воспользуйтесь теоремой о расходимости.

405.

Вычислить ∬SF · NdS, ∬SF · NdS, где F (x, y, z) = x2i + xyj + x3y3kF (x, y, z) = x2i + xyj + x3y3k и S — поверхность, состоящая из всех грани, за исключением тетраэдра, ограниченного плоскостью x + y + z = 1x + y + z = 1, и координатными плоскостями с направленным наружу единичным вектором нормали N .

406.

Найдите чистый внешний поток поля F = 〈bz − cy, cx − az, ay − bx〉 F = 〈bz − cy, cx − az, ay − bx〉 через любую гладкую замкнутую поверхность в R3, R3, где a , b и c — константы.

407.

Используйте теорему о расходимости, чтобы вычислить ∬S‖R‖R · nds, ∬S‖R‖R · nds, где R (x, y, z) = xi + yj + zkR (x, y, z) = xi + yj + zk и S — сфера x2 + y2 + z2 = a2, x2 + y2 + z2 = a2, с константой a> 0. a> 0.

408.

Используйте теорему о расходимости для вычисления ∬SF · dS, ∬SF · dS, где F (x, y, z) = y2zi + y3j + xzkF (x, y, z) = y2zi + y3j + xzk и S — граница куба, определенная как −1≤x≤1, −1≤y≤1 и0≤z≤2.−1≤x≤1, −1≤y≤1 и0≤z≤2.

409.

Пусть R будет областью, определенной как x2 + y2 + z2≤1.x2 + y2 + z2≤1. Воспользуйтесь теоремой о расходимости, чтобы найти ∭Rz2dV.∭Rz2dV.

410.

Пусть E будет твердым телом, ограниченным плоскостью xy и параболоидом z = 4 − x2 − y2z = 4 − x2 − y2, так что S будет поверхностью части параболоида вместе с диском в xy — плоскость, образующая его днище. Если F (x, y, z) = (xzsin (yz) + x3) i + cos (yz) j + (3zy2 − ex2 + y2) k, F (x, y, z) = (xzsin (yz) + x3 ) i + cos (yz) j + (3zy2 − ex2 + y2) k, найти ∬SF · dS∬SF · dS, используя теорему о расходимости.

411.

Пусть E будет сплошным единичным кубом с диагонально противоположными углами в начале координат и (1, 1, 1) и гранями, параллельными координатным плоскостям. Пусть S будет поверхностью E , ориентированной нормалью, направленной наружу. Используйте CAS, чтобы найти SF · dS∬SF · dS, используя теорему о расходимости, если F (x, y, z) = 2xyi + 3yezj + xsinzk.F (x, y, z) = 2xyi + 3yezj + xsinzk.

412.

Используйте теорему о расходимости, чтобы вычислить поток F (x, y, z) = x3i + y3j + z3kF (x, y, z) = x3i + y3j + z3k через сферу x2 + y2 + z2 = 1.х2 + у2 + z2 = 1.

413.

Найдите SF · dS, ∬SF · dS, где F (x, y, z) = xi + yj + zkF (x, y, z) = xi + yj + zk, а S — полученная поверхность, ориентированная наружу. удалив куб [1,2] × [1,2] × [1,2] [1,2] × [1,2] × [1,2] из куба [0,2] × [0,2] × [0,2]. [0,2] × [0,2] × [0,2].

414.

Рассмотрим радиальное векторное поле F = r | r | = 〈x, y, z〉 (x2 + y2 + z2) 1 / 2.F = r | r | = 〈x, y, z〉 (x2 + y2 + z2 ) 1/2. Вычислите интеграл поверхности, где S — это поверхность сферы радиуса a с центром в начале координат.

415.

Вычислить поток воды через параболический цилиндр S: y = x2, S: y = x2, из 0≤x≤2,0≤z≤3,0≤x≤2,0≤z≤3, если вектор скорости равно F (x, y, z) = 3z2i + 6j + 6xzk. F (x, y, z) = 3z2i + 6j + 6xzk.

416.

[T] Используйте CAS, чтобы найти поток векторного поля F (x, y, z) = zi + zj + x2 + y2kF (x, y, z) = zi + zj + x2 + y2k через часть гиперболоида x2 + y2 = z2 + 1×2 + y2 = z2 + 1 между плоскостями z = 0z = 0 и z = 33, z = 33, ориентированными так, чтобы единичный вектор нормали был направлен от оси z .

417.

[T] Используйте CAS, чтобы найти поток векторного поля F (x, y, z) = (ey + x) i + (3cos (xz) −y) j + zkF (x, y, z) = (ey + x) i + (3cos (xz) −y) j + zk через поверхность S , где S задается формулой z2 = 4×2 + 4y2z2 = 4×2 + 4y2 из 0≤z≤4,0≤z≤ 4, ориентированный так, чтобы единичный вектор нормали был направлен вниз.

418.

[T] Используйте CAS для вычисления ∬SF · dS, ∬SF · dS, где F (x, y, z) = xi + yj + 2zkF (x, y, z) = xi + yj + 2zk и S является частью сферы x2 + y2 + z2 = 2×2 + y2 + z2 = 2 с 0≤z≤1.0≤z≤1.

419.

Вычислить ∬SF · dS, ∬SF · dS, где F (x, y, z) = bxy2i + bx2yj + (x2 + y2) z2kF (x, y, z) = bxy2i + bx2yj + (x2 + y2) z2k и S — это замкнутая поверхность, ограничивающая область и состоящая из сплошного цилиндра x2 + y2≤a2x2 + y2≤a2 и 0≤z≤b.0≤z≤b.

420.

[T] Используйте CAS для вычисления потока F (x, y, z) = (x3 + ysinz) i + (y3 + zsinx) j + 3zkF (x, y, z) = (x3 + ysinz) i + (y3 + zsinx) j + 3zk по поверхности S , где S — граница твердого тела, ограниченного полусферами z = 4 − x2 − y2z = 4 − x2 − y2 и z = 1 − x2 − y2, z = 1 − x2 − y2, а плоскость z = 0.г = 0.

421.

Используйте теорему о расходимости, чтобы вычислить ∬SF · dS, ∬SF · dS, где F (x, y, z) = xyi − 12y2j + zkF (x, y, z) = xyi − 12y2j + zk и S — поверхность, состоящая из трех частей: z = 4−3×2−3y2,1≤z≤4z = 4−3×2−3y2,1≤z≤4 на вершине; x2 + y2 = 1,0≤z≤1×2 + y2 = 1,0≤z≤1 по бокам; и z = 0z = 0 внизу.

422.

[T] Используйте CAS и теорему о расходимости для вычисления ∬SF · dS, ∬SF · dS, где F (x, y, z) = (2x + ycosz) i + (x2 − y) j + y2zkF ( x, y, z) = (2x + ycosz) i + (x2 − y) j + y2zk и S — сфера x2 + y2 + z2 = 4×2 + y2 + z2 = 4, ориентированная наружу.

423.

Используйте теорему о расходимости, чтобы вычислить ∬SF · dS, ∬SF · dS, где F (x, y, z) = xi + yj + zkF (x, y, z) = xi + yj + zk, а S — граница твердого тела, окруженная параболоидом y = x2 + z2−2, y = x2 + z2−2, цилиндром x2 + z2 = 1, x2 + z2 = 1 и плоскостью x + y = 2, x + y = 2 , а S ориентирован наружу.

Для следующих упражнений закон теплопередачи Фурье утверждает, что вектор теплового потока F в точке пропорционален отрицательному градиенту температуры; то есть F = −k∇T, F = −k∇T, что означает, что тепловая энергия перетекает из горячих регионов в холодные.Константа k> 0k> 0 называется проводимостью , в метрических единицах измерения — джоуль на метр в секунду-кельвин или ватт на метр-кельвин. Дана температурная функция для области D . Используйте теорему о расходимости, чтобы найти чистый наружный тепловой поток ∬SF · NdS = −k∬S∇T · NdS∬SF · NdS = −k∬S∇T · NdS через границу S из D , где k = 1. k = 1.

424.

T (x, y, z) = 100 + x + 2y + z; T (x, y, z) = 100 + x + 2y + z; D = {(x, y, z): 0≤x≤1,0≤y≤1,0≤z≤1} D = {(x, y, z): 0≤x≤1,0≤y≤ 1,0≤z≤1}

425.

T (x, y, z) = 100 + e − z; T (x, y, z) = 100 + e − z; D = {(x, y, z): 0≤x≤1,0≤y≤1,0≤z≤1} D = {(x, y, z): 0≤x≤1,0≤y≤ 1,0≤z≤1}

426.

T (x, y, z) = 100e − x2 − y2 − z2; T (x, y, z) = 100e − x2 − y2 − z2; D — это сфера радиусом a с центром в начале координат.

.