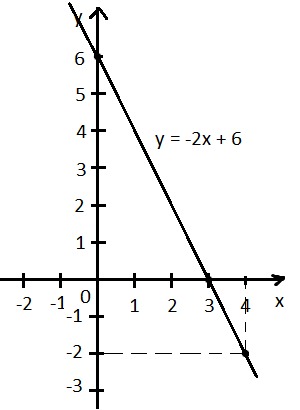Y 3x 6 график: Mathway | Популярные задачи — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Постройте график линейной функции y = 3x — 6 и с его помощью решите неравенство : a) 3x — 6 > 0; б) 3x

Решение смотри в фотографии

1) Нужно обозначить время от А до В: 30/(15+х) — это например, если по течению реки, где х — скорость реки, 30 — расстояние между пунктами, (15+х) — скорость лодки по течению.

2) Время от В до А: 30/(15-х) — это против течения, х — скорость реки. Аналогично.

3) Общее время, затраченное на путь: 4ч40 мин минус 30 мин = 4ч10мин = 25/6 ч.

4) Составим уравнение: Время по течению + время против течения = затраченное время на путь: 30/(15+х) + 30/(15-х) = 25/6.

5) Получившееся уравнение решить как дробное рациональное, домножив на общий знаменатель и получится квадратное уравнение, которое легко решить. Дальше дело техники

4 месяца назад

а) Координаты вершины (3. 2+1)

Значение функции

Begin25. Найти значение функции y = 3x⁶ − 6x² − 7 при данном значении x.

Запишем нашу функцию так:

y = 3(xx²)² — 6x² — 7.

Тогда имеем первый вариант решения:

Код Pascal

var
  x, y: real;

begin
  write('x = ');
  readln(x);
  y := 3 * sqr(x * sqr(x)) - 6 * sqr(x) - 7;
  writeln('y = ', y);
  readln
end.

Далее запишем функцию в виде:

y = 3t(t² — 2) — 7,

где t = x². Имеем второй вариант решения:

Код Pascal

var
  x, y: real;

begin
  write('x = ');
  readln(x);
  x := sqr(x); { <-- Вычисляем квадрат числа }
  y := 3 * x * (sqr(x) - 2) - 7;
  writeln('y = ', y);
  readln
end.

Begin26. Найти значение функции y = 4(x−3)⁶ − 7(x−3)³ + 2 при данном значении x.

Запишем нашу функцию так:

y = 4t² — 7t + 2,

где t = (x-3)³. Тогда имеем код (только вместо t используем x):

Код Pascal

var
  x, y: real;

begin
  write('x = ');
  readln(x);
  x := x - 3; { <-- Уменьшаем x на 3 }
  x := x * sqr(x); { <-- Вычисляем третью степень числа x }
  y := 4 * sqr(x) - 7 * x + 2;
  writeln('y = ', y);
  readln
end.

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий.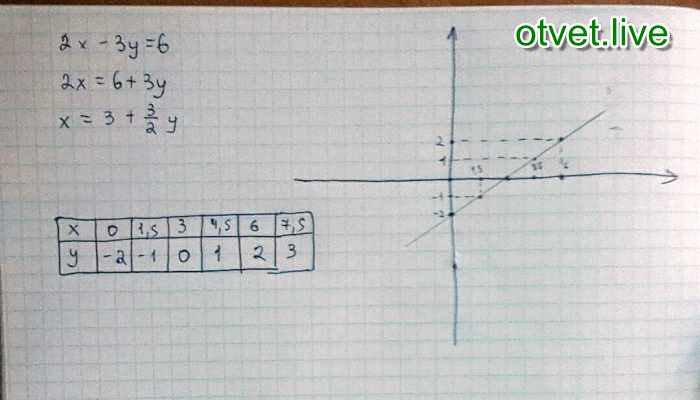 Он будет включать:

решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).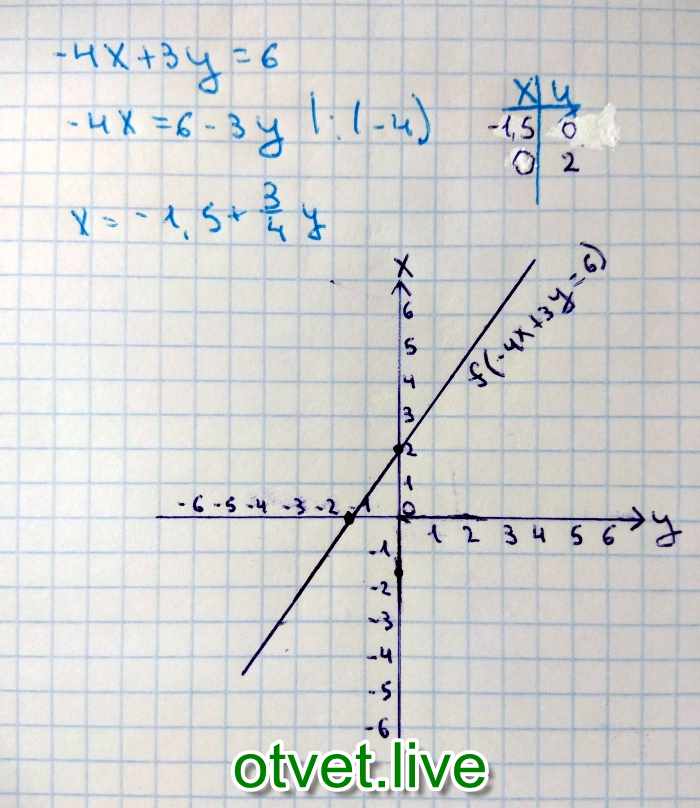 Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.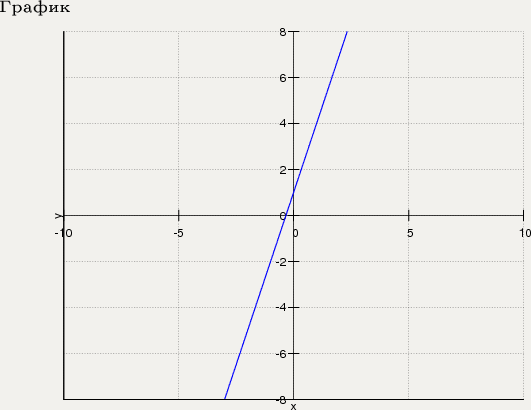

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
Выбрать платежную систему.
Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Что такое угловой коэффициент линейной функции?

☰

Линейная функция y = kx + m, когда m = 0 принимает вид y = kx. В таком случае можно заметить, что:

Если x = 0, то и y = 0. Следовательно, график линейной функции y = kx проходит через начало координат не зависимо от значения k.
Если x = 1, то y = k.

Рассмотрим различные значения k, и как от этого меняется y.

Если k положительно (k > 0), то прямая (график функции), проходя через начало координат, будет лежать в I и III координатных четвертях. Ведь при положительном k, когда x положителен, то y также будет положителен. А когда x отрицателен, y также будет отрицательным. Например, для функции y = 2x, если x = 0.5, то y = 1; если же x = –0.5, то y = –1.

Теперь при условии положительного k рассмотрим три разных линейных уравнения. Пусть это будут: y = 0.5x и y = 2x и y = 3x. Как меняется значение y при одном и том же x? Очевидно оно возрастает вместе с k: чем больше k, тем больше y. А это значит, прямая (график функции) при большем значении k будет иметь больший угол между осью x (осью абсцисс) и графиком функции. Таким образом от k зависит, под каким углом пересекает прямая ось x, и отсюда о k говорят как об угловом коэффициенте линейной функции.

Теперь изучим ситуацию, когда k x положителен, то y будет отрицателен; и наоборот: если x y > 0. Таким образом график функции y = kx при при k

Допустим, имеются линейные уравнения y = –0.5x, y = –2x, y = –3x. При x = 1 получим y = –0.5, y = –2, y = –3. При x = 2 получим y = –1, y = –2, y = –6. Таким образом, чем больше k, тем больше y, если x положительно.

Однако если x = –1, то y = 0.5, y = 2, y = 3. При x = –2 получим y = 1, y = 4, y = 6. Тут с уменьшением значения k возрастает y при x

График функции при k

Графики функций типа y = kx + m отличаются от графиков y = km лишь параллельным смещением.

Взаимное расположение графиков линейных функций

1. Взаимное расположение графиков линейных функций

№
Этап урока
содержание
время
1
Организационны
й момент
Ознакомиться с планом урока
1
2
Проверка знаний
Опрос п.14, п.15, п.16.
5
3
Устная работа
Актуализация знаний
5
4
Изучение нового
материала
Ввести условие пересечения и
параллельности графиков двух
линейных функций
6
5
Тренировочное
упражнение
Формировать умение использовать
условие пересечения и
параллельности графиков двух
линейных функций
18
6
Проверочная
работа
Проверить полученные знания
6
7
Подведение
итогов урока, д. з.
Обобщить теоретические сведения,
полученные на уроке

3. 1. Немного теории

• Что называют функцией?
• Какую функцию называют линейной?
• Что является графиком линейной
функции?
• Что показывает коэффициент К ?
• О чем говорит значение коэффициента
b?

4. Какой из приведенных ниже графиков является графиком функции y=3x-6

y
y
-2
y
2
x
-6
x
6
x
-6
y
3
-6
x

5. 2. Как построить график линейной функции?

Дана функция:
y=3x+5
1. Выберем пару значений для
независимой переменной и найдём
соответствующие значения функции.
Заполним таблицу:
x
0
2
y
5
11
2. Отметим полученные точки на
координатной плоскости.
3. Проведём через отмеченные
точки прямую линию, подпишем
график функции.
11
А
Y=3x+5
7
В
2 3

6. Даны две линейные функции y=0,9x-1 y=0,8x+1.

Выясним будут ли пересекаться графики этих функций, если будут, то каковы

координаты
точки пересечения.
Это можно сделать двумя способами:
1 способ.
• Построить графики
данных функций и найти
их точку пересечения.
• Если необходимо,
продолжить графики до
их пересечения и найти
координаты точки
пересечения.
2 способ
• Составить и решить уравнение,
приравняв правые части
формул:
• 0,9x-1 =0,8x+1
• 0,9х-0,8х=1+1
• 0,1х=2
• Х=2:0,1
• Х=20
• Y=0,9∙20-1=17
• M(20;17) точка пересечения
графиков данных функций.

7. Построим графики данных функций:

Y=0,8x+1
y=0,9x-1
x
0
10
y
-1
8
Y=0,9x-1
y=0,8x+1.
x
0
10
y
1
9

8. ВНИМАНИЕ!

• Откроем учебник на странице 73;
• Рассмотрим рисунки 36 и 38;
• Прочитаем правило выделенное
пунктирной рамкой, запишем его в тетрадь.

9.

Тренировочное задание №1

• y=2,3x-7 , k1=2,3
Выясните
• y=2,3x+3,1, k2=2,3,
взаимное
расположение • К1=к2,
графиков
функций
следовательно
графики
y=2,3x-7
данных
функций
y=2,3x+3,1
параллельны.

10. Тренировочное задание №2

• y=-6x+1 , k1=-6
• y=3x-8, k2=3,
• К1≠к2,
• следовательно графики данных
Выясните
взаимное
расположение
функций пересекаются.
• Составим и решим уравнение:
графиков
-6x+1=3x-8.
функций
Х=1,
y=-5,
y=-6x+1 y=3x-8
• М(1;-5) точка
пересечения графиков
данных функций.

11. 4. Найдите координаты точки пересечения графиков указанных линейных функций, используя 1 способ

1 вариант
2 вариант
• Выясните взаимное
• Выясните взаимное
расположение
расположение
графиков функций
графиков
Y= -2x+5 и y=5x+3,
функцийY=3x-3 и
найдите координаты
y=-4x -10 ,найдите
точки пересечения,
координаты точки
если такая есть.
пересечения если
такая есть.

12. 1 вариант

1. В заданных функциях y=3x-3
(к1=3) и y=-4x-10 (к2=-3,5)
коэффициенты к1 и к2 не равны,
значит графики данных функций
пересекаются.
2. Построим график второй функции
y=3x-3
-2 -1
Y=-4x-10
x
0
2
y
-3
3
3. Построим график второй функции
y=-4x-10
x
0
-2
y
-10
-2
Y=3x-3
y
3
0
1 2
-5
A
-6
9
-10
x

13. 2 вариант

y
2 вариант
1. В заданных функциях y=-2x-5
(к1=-2) и y=5x+3 (к2=5)
коэффициенты к1 и к2 не равны,
значит графики данных функций
пересекаются.
2. Построим график второй
функции y=-2x-5
x
0
-3
y
-5
1
3. Построим график второй
функции y=5x+3
1
-1
-3
-2
0
0
-2
y
3
-7
x
-2,5
R
Y=-2x-5
Y=5x+3
-5
-7
x
3

14.

Графики линейных функций могут располагаться относительно друг друга следующим образом:

Графики линейных функций
могут пересекаться(к1 ≠ к2)
Графики линейных функций могут
быть параллельны друг другу(к1 = к2)
y
10
y
Y=-2x+10
10
6
6
A
2
1
-2
0 1
Y=-2x+10
4,5
Y=-x+6
10
2
1
x
-2
0 1
Y=-2x+6
4
10
x

15. Итог урока

• В каком случае графики линейных функций
пересекаются?
• В каком случае графики линейных функций
параллельны?
• В каком случае угол наклона графика
линейной функции к оси Ох будет острым?
• В каком случае угол наклона графика
линейной функции к оси Ох будет тупым?

Линейная функция y = kx — урок. Алгебра, 7 класс.

Рассматривая линейную функцию вида $y=kx + m$, особо выделяют случай, когда $m=0$.

Тогда линейная функция принимает вид $y=kx$.

Графиком линейной функции $y=kx$ является прямая, проходящая через начало координат.

Важно уметь переходить от аналитической модели $y=kx$ к геометрической и, наоборот, от геометрической к аналитической модели.

Например, рассмотрим прямую, изображённую на рисунке.

Эта прямая является графиком линейной функции $y=kx$, так как проходит через начало координат. Нужно лишь определить значение коэффициента $k$.

Из формулы линейной функции $y=kx$ получим, что k=yx.

Чтобы определить коэффициент $k$, необходимо выбрать некоторую точку на прямой и вычислить частное ординаты и абсциссы заданной точки.

Прямая проходит через точку $M(4; 2)$, следовательно получим 24=0,5. Значит, $k=0,5$, и данная прямая является графиком линейной функции $y=0,5x$.

Если в формуле $y=kx$ вместо $x$ подставим $1$, то получим $y=k$. Это означает, что прямая $y=kx$ проходит через точку $(1; k)$. Поэтому график линейной функции можно строить по двум точкам: $(0;0)$ и $(1; k)$.

Иногда вместо точки $(1; k)$ удобнее взять другую точку.

Коэффициент $k$ определяет угол между прямой и положительным направлением оси $x$.

Если $k>0$, то этот угол острый (как на первом рисунке), а

если $k<0$, то этот угол тупой (как на втором рисунке).

Поэтому коэффициент $k$ в записи $y=kx$ называют угловым коэффициентом.

Обобщая сведения о линейных функциях, можно сделать вывод:

прямая, служащая графиком линейной функции $y=kx + m$, параллельна прямой, служащей графиком линейной функции $y=kx$.

На рисунке показаны параллельные прямые с одним и тем же коэффициентом $k = 4$.

Поэтому коэффициент $k$ в записи $y=kx + m$ также называют угловым коэффициентом, и

если $k>0$, то прямая $y=kx + m$ образует с положительным направлением оси $x$ острый угол;

если $k<0$, то этот угол тупой.

Параграф 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

Работу выполнил: Косярский А. А. студент группы 45.2

Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

1. Понятие числовой функции

Числовой функцией с областью определения D называется зависимость, при которой каждому числу x
из множества D (области определения) ставится в соответствие единственное число y.
Записывается это соотвествие так: y=f(x)
Обозначения и термины
D(f) — область определения
E(f) — область значений
x — аргумент (независимая переменная)
y — функция (зависимая переменная)
f — функция
f(x0) — значение функции f в точке x0

2. График функции

Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x
«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x

3. Возрастающие и убывающие функции

Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2) < f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

4. Чётные и нечётные функции

Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy

Функция f(x) нечётная:
если f(-x) = -f(x)
для любых x из области определения.
График нечётной функции симметричен относительно начала координат

Объяснение и обоснование

1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.

Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.

Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).

Область определения функции f — это множество тех значений, которые
может принимать аргумент x. Она обозначается D(f).

Область значений функции f — это множество, состоящее из всех чисел
f(x), где x принадлежит области определения. её обозначают E(f).

Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.

Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).

Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]

2. График функции. Напомним, что
графиком функции y = f(x) называется множество точек
координатной плоскости с координатами (x;f(x)), где первая координата
x «пробегает» всю область определения функции, а вторая координата —
это соответствующее значение функции f точке x.

На рисунках к пункту 4 табицы 2 приведены графики функций y = x²
и y = 1/x, а на рисунке 11 — график функции y = |x|.

Приведём также график функции y = [x], где [x] — обозначение
целой части числа x, то есть наибольшего целого числа,
не превосходящего x (рис. 12). Область определения этой функции
D(y) = R — множество всех действительных чисел, а область
значений E(y) = Z — множество всех целых чисел.

На рисунке 13 приведён график ещё одной числовой функции y = {x},
где {x} — обозначение дробной части числа x ( по определению
{x} = x — [x]).

3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.

Функция f(x) называется возрастающей на множестве P, если
большему значению аргумента из этого множества соответствует
большее значение функции.

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) > f(x1).
Например, функция f(x) = 2x возрастающая ( на всей области
определения — на множестве R), поскольку при x2 > x1 имеем
2⋅ > 2⋅, то есть f(x2) > f(x1). У возрастающей
функции при увеличении аргумента соотвествующие точки графика
поднимаются (рисунок 14).

На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).

Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) < f(x1).

Например, функция f(x) = -2x убывающая ( на всей области
определения — на множестве R), поскольку при x2 > x1 имеем
-2⋅ < -2⋅, то есть f(x2) < f(x1). У убывающей
функции при увеличении аргумента соотвествующие точки графика
опускаются (рисунок 16).

Рассматривая график функции y = x² (рис. 17), видим, что
на всей области определения эта функция не является ни возрастающей,
ни убывающей. Однако можно выделить промежутки области определения,
где эта функция возрастает и где убывает. Так как на промежутке
(-∞;0] — убывает, а на промежутке [0;+∞) функция
y = x² возрастает.(Докажите самостоятельно).

отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.

Если функция возрастает, то большему значению функции
соответствует большее значение аргумента.
Если функция убывает, то большему значению функции
соответствует меньшее значение аргумента.

Обоснуем первое из этих свойств методом от противного. Пусть
функция f(x)возрастает и f(x2) > f(x1). Допустим, что
аргумент x2 не больше аргумента x1, то есть x2≤x1.
Из этого предположения получаем: если x2≤x1 и f(x)
возрастает, то f(x2)≤f(x1), что противоречит
условию f(x2) > f(x1). Таким образом, наше предположение
неверно, и если f(x2) > f(x1), то x2 > x1, ч.т.д.
Аналогично обосновывается и второе свойство.

Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.

4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).

Например, функция y = x² (то есть функция f(x) = x²) —
чётная, поскольку f(-x) = (-x)² = x² = f(x).

Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.

Например, график четной функции y = x² (рис. 17)
симметричен относительно Oy.
Функция f называется нечётной, если для любого x из её области определения
f(-x) = -f(x).
Например, функция y = 1/x ( то есть функция f(x) = 1/x) — нечётная,
поскольку f(-x) = 1/(-x) = -1/x = -f(x).

Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.

Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ:

1. Что называется числовой функцией? Приведите примеры таких функций.
2. На примерах объясните, что такое область определния функции и область
значений функции. Какие ограничения необходимо учесть при нахождении
области определения функции y = √x/x ? Найдите её область определения.
3. Что называется графиком функции y = f(x)? Приведите примеры.
4. Какая функция называется возрастающей? Приведите примеры.
5. Какая функция называется убывающей? Приведите примеры.
6. Какая функция называется чётной? Приведите примеры. Как расположен
график чётной функции на координатной плоскости? Приведите примеры.
7. Какая функция называется нечётной? Как расположен график нечётной
функции на координатной плоскости? Приведите примеры.

УПРАЖНЕНИЕ 1. Найдите область определения функции: 1.y = x² + x 2.y = x/(x² + x) 3. y= √(x+5)
РЕШЕНИЕ 1) Ограничений для нахождения значений выражения x² + x нет, таким образом D(y) = R. 2) Область определения функции y = x/(x² + x) задаётся ограничением x² + x ≠ 0, поскольку знаменатель не может быть равным нулю. Выясним, когда x² + x = 0. Имеем x(x + 1) = 0, x = 0 или x = -1. Тогда область определения можно задать ограничениями x ≠ 0, x ≠ -1 или записать так: D(y) = (-∞;-1) ∪ (-1;0) ∪ (0;+∞) 3) Область определения функции y= √(x+5) задаётся ограничением x + 5 ≥ 0, то есть x ≥ -5, поскольку под знаком квадратного корня должно стоять неотрицательное выражение. Таким образом, D(y) = [-5;+∞)	КОММЕНТАРИЙ Поскольку все функции заданы формулами, то их области определения — это множество всех значений переменной x, при которых формула имеет смысл, то есть имеет смысл выражение, которое стоит в правой части формулы y = f(x). В курсе алгебры встречались только два ограничения, которые необходимо учитывать при нахождении области определения: 1)если выражение записано в виде дроби A/B, то знаменатель B ≠ 0 2)если запись выражения содержит квадратный корень √ A, то подкоренное выражение A ≥ 0. В других случаях, которые вам приходилось рассматривать, областью определения выражения были все действительные числа.
УПРАЖНЕНИЕ 2. Найдите область определения функции: y = x² — 3
РЕШЕНИЕ Составим уравнение x² — 3 = a. Оно равносильно уравнению x² = a +3, которое имеет решения, если a + 3 ≥ 0, то есть при a ≥-3. Все эти числа и составят область значений функции. Таким образом, область значений заданной функции E(f) = [-3;+∞), то есть y ≥ -3.	КОММЕНТАРИЙ Обозначим значение заданной функции f(x) ( то есть x² — 3) через a и выясним, для каких a можно найти соответствующее значение x ( при этом значении x значение f(x) = a). Тогда все числа a, для которых существует хотя бы один корень уравнения f(x) = a, войдут в область значений функции f(x). Множество всех таких a и составит область значений функции.
УПРАЖНЕНИЕ 3. Докажите, что при k ≠ 0 областью значений линейной функции y = kx + b является множество всех действительных чисел.
ДОКАЗАТЕЛЬСТВО Если kx + b = a (где k ≠ 0), то решение этого уравнения x = (a — b)/k существует для любого a ∈ R (k ≠ 0 по условию). Таким образом, значением заданной функции может быть любое действительное число. Итак, ее область значений E(f) = R.	КОММЕНТАРИЙ Обозначим значение заданной функции f(x), то есть kx + b, через a и выясним, для каких a можно найти соответствующее значение x, такое, что f(x) = a. Множество всех таких значений a и будет составлять область значений функции f(x).
УПРАЖНЕНИЕ 4. Докажите, что линейная функция y = kx + b при k > 0 является возрастающей, а при k < 0 — убывающей.
ДОКАЗАТЕЛЬСТВО Пусть x2 > x1 (тогда x2 — x1 >0). Рассмотрим разность f(x2) — f(x1) = kx2 + b — (kx1 + b) = k(x2 — x1). Поскольку x2 — x1 > 0, то при k > 0 имеем f(x2) — f(x1) > 0, таким образом, f(x2) > f(x1) и, значит, функция возрастает. При k < 0 имеем f(x2) — f(x1) < 0, таким образом, f(x2) < f(x1), значит, функция убывает.	КОММЕНТАРИЙ Для обснования возрастания или убывания функцииполезно помнить, что для доказательства неравенсства f(x2) > f(x1) или f(x2) < f(x1) достаточно найти знак разноссти f(x2) — f(x1). 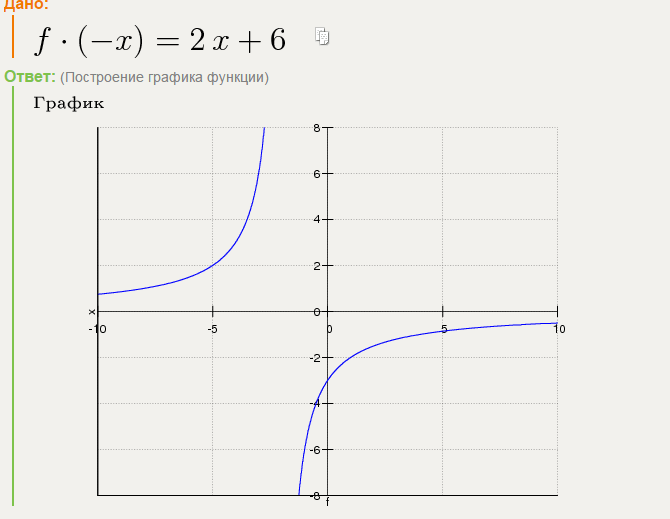Функция f(x) = kx + b будет возрастающей, если из неравенства x2 > x1 будет следовать неравенство f(x2) > f(x1), а для доказательства последнего неравенства достаточно найти знак разности f(x2) — f(x1) (аналогичные рассуждения применимы и для убывания функции)
УПРАЖНЕНИЕ 5. Докажите, что: 1.Сумма двух возрастающих на множестве P функций всегда является возрастающей функцией на этом множестве. 2.Сумма двух убывающих на множестве P функций всегда является убывающей функцией на этом множестве.
ДОКАЗАТЕЛЬСТВО 1) Пусть функции f(x) и g(x) являются возрастающими на одном и том же множестве P. Если x2 > x1, то f(x2) > f(x1) и g(x2) > g(x1). Складывая почленно эти нервенства, получаем: f(x2) + g(x2) > f(x1) + g(x1) Это и означает, что сумма двух возрастающих функций есть функция возрастающая. 2) Пусть функции f(x) и g(x) являются убывающими на одном и том же множестве P. 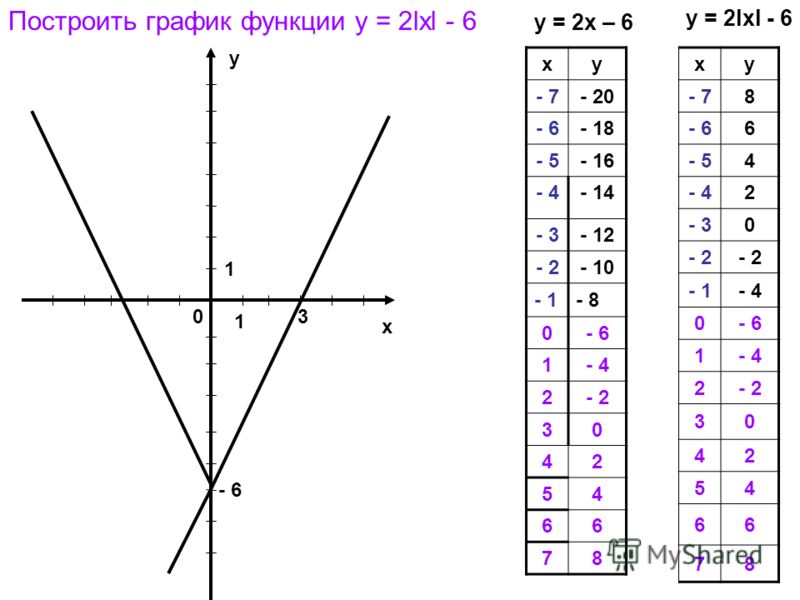Если x2 > x1, то f(x2) < f(x1) и g(x2) < g(x1). Складывая почленно эти нервенства, получаем: f(x2) + g(x2) < f(x1) + g(x1) Это и означает, что сумма двух убывающих функций есть функция убывающая.	КОММЕНТАРИЙ Для доказательства того, что сумма двух возрастающих функций f(x) и g(x) является возрастающей функцией, достаточно доказать, что на множестве P из неравенства x2 >x1 следует неравенство: f(x2) + g(x2) > f(x1) + g(x1) Аналогино, для доказательства того, что сумма двух убывающих функций f(x) и g(x) является убывающей функцией, достаточно доказать, что на множестве P из неравенства x2 > x1 следует неравенство: f(x2) + g(x2) < f(x1) + g(x1)
УПРАЖНЕНИЕ 6. Докажите, что возрастающая или убывающая функция принимает каждое свое значение только в одной точке её области определения.
ДОКАЗАТЕЛЬСТВО Пусть функция f(x) является возрастающей и f(x1) = f(x2) (1) Допустим x1 ≠ x2. Если x1 ≠ x2, то x1 > x2 или x1 x2 имеем f(x1) > f(x2), что противоречит равенству (1). Таким образом, наше предположение неверно, и равенство f(x1) = f(x2) возможно только при x1 = x2. То есть возрастающая функция принимает каждое свое значение только в одной точке её области определения. Аналогично доказывается утверждение и для убывающей функции.	КОММЕНТАРИЙ Докажем это утверждение методом от противного. Для этого достаточно допустить, что выполняется противоположное утверждение (функция может принимать одно и то же значение хотя бы в двух точках), и получить противоречие. Это будет означать, что наше предположение неверно, а верно данное утверждение.
УПРАЖНЕНИЕ 7. Исследуйте, какие из данных функций являются четными, какие нечётными, а какие ни чётными, ни нечётными. 1. y = 1/(x + 1) 2. y = x² 3. y = x³ + x
РЕШЕНИЕ 1) Область определения функции y = 1/(x+1): x ≠ -1, то есть она не симметрична относительно точки O (точка x = 1 принадлежит области определения, а точка x = -1 — нет). Таким образом, заданная функция не является ни чётной, ни нечётной. 2) Область определения функции y = x²: D(y) = R, то есть она симметрична относительно точки O. f(-x)=(-x) ² = x ²$; = f(x), следовательно, функция чётная. 3) Область определения функции y = x³ + x: D(y) = R, то есть она симметричная относительно точки . f(-x)=(-x)² + (-x) = — (x³ + x) = -f(x), значит функция нечётная.	КОММЕНТАРИЙ Для исследования функции y = f(x) на чётность или нечётность достаточно, во-первых, убедиться, что область опредления этой функции симметричная относительно точки O ( вместе с каждой точкой x содержит и точку -x), и, во-вторых, сравнить значения f(-x) и f(x).

5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x⁵ 5) y = √(x)

6. Докажите, что на заданном промежутке функция возрастает:
1) y = -2/x, где x > 0 2) y = 1/x, где x < 0

7. Обоснуйте, что заданная функция является убывающей (на её области определения):
1) y = -3x 2) y = -x -1 3) y = -x³ 4) y = -x⁵

8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x < 0 2) y = 5/x, где x > 0

9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.

10. Используя утверждения, приведённые в примере 5, укажите какие из данных функций являются возрастающими, а какие — убывающими.
1) y = x³ + x 2) y = -x -x⁵ 3) y = x + √ (x) 4) y = -x³-x⁵

11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.

12. Обоснуйте, что заданная функция является чётной:
1) y = x⁶ 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x⁴)

13. Обоснуйте, что заданная функция является нечётной:
1) y = x⁵ 2) y = -1/x³ 3) y = x |x| 4) y = x³ — x

Решите Свойства прямой y = 3x-6 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

y- (3 * x -6) = 0

Шаг 1:

Уравнение прямой линии

1.1 Решите y-3x + 6 = 0

Тигр распознает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).

«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.

В этой формуле:

y указывает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является точкой пересечения Y, т.е. Ось Y

Пересечения по осям X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-3x + 6 = 0 и вычислим ее свойства

График прямой линии:

Вычислите точку пересечения Y:

Обратите внимание, что когда x = 0, значение y равно -6 / 1, поэтому эта линия «разрезает» ось y при y = -6.00000

 Y-Intercept = -6/1 = -6.00000

Вычислите X-Intercept:

Когда y = 0, значение x равно 2/1 Наша линия поэтому «разрезает» ось x в точке x = 2.00000

 x-intercept = 6/3 = 2

Вычислить наклон:

Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -6,000, а для x = 2,000 значение y равно -0,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на -0.000 — (-6,000) = 6.000 в год. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / ПЕРЕДАЧА)

 Наклон = 6.000 / 2.000 = 3.000

Геометрическая фигура: прямая линия

Наклон = 6. 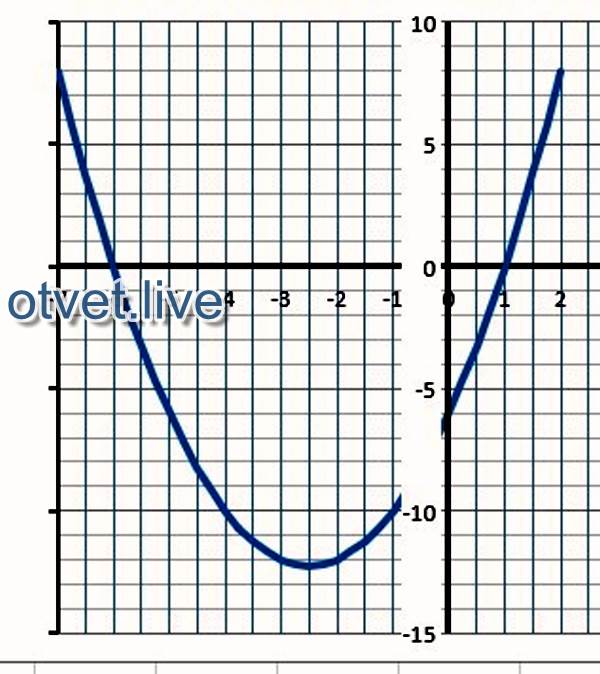000 / 2.000 = 3.000
пересечение по оси x = 6/3 = 2
пересечение по оси y = -6/1 = -6,00000

Уравнение точки и наклона линии

Форма «точка-наклон» уравнения прямой:

Уравнение полезно, когда мы знаем:

одна точка на линии: (x ₁, y ₁)
и уклон линии: м ,

и хотите найти другие точки на линии.

Сначала поиграйте с ним (переместите точку, попробуйте разные уклоны):

Теперь давайте узнаем больше.

Что это означает?

(x ₁, y ₁) — известная точка

м — уклон трассы

(x, y) — любая другая точка на линии

Разобраться в этом

Исходя из уклона:

Уклон м =
изменение в год
изменение в x
знак равно
г — г ₁
х — х ₁

Начиная с уклона:

переставляем так:

чтобы получить это:

Итак, это просто формула наклона по-другому!

Теперь давайте посмотрим, как его использовать.

Пример 1:

уклон «м» = 3 1 = 3

y — y ₁ = m (x — x ₁)

Мы знаем m, а также знаем, что (x ₁, y ₁) = (3,2), поэтому мы имеем:

Это отличный ответ, но мы можем немного его упростить:

г — 2 = 3х — 9

у = 3х — 9 + 2

у = 3х — 7

Пример 2:

м =
−3
1
= −3

y — y ₁ = m (x — x ₁)

Мы можем выбрать любую точку для (x ₁, y ₁), поэтому давайте выберем (0,0), и у нас будет:

у — 0 = −3 (х — 0)

Что можно упростить до:

Пример 3: Вертикальная линия

Какое уравнение представляет собой вертикальная линия?
Наклон не определен!

На самом деле, это особый случай , и мы используем другое уравнение, например:

Каждая точка на линии имеет координату x 1. 5 ,
, поэтому его уравнение: x = 1,5

А как насчет y = mx + b?

Возможно, вы уже знакомы с формой «y = mx + b» (называемой формой уравнения линии с пересечением наклона).

Это то же уравнение, но в другой форме!

Значение «b» (называемое точкой пересечения оси y) — это место, где линия пересекает ось y.

Таким образом, точка (x ₁, y ₁) фактически находится в (0, b)

, и уравнение принимает следующий вид:

Начнем с y — y ₁ = m (x — x ₁)

(x ₁, y ₁) на самом деле (0, b): y — b = m (x — 0)

Это: y — b = mx

Положите b на другую сторону: y = mx + b

Учебное пособие по использованию калькулятора по алгебре

— MathPapa

Это учебное пособие по использованию калькулятора по алгебре , пошагового калькулятора по алгебре.

Решение уравнений

Сначала перейдите на главную страницу калькулятора алгебры. В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить.

Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле.

После того, как вы введете выражение, Калькулятор алгебры распечатает пошаговое объяснение того, как решить 3x + 2 = 14.

Примеры

Чтобы увидеть больше примеров задач, которые понимает калькулятор алгебры, посетите
Страница примеров.2.

Вычисление выражений

Калькулятор алгебры может вычислять выражения, содержащие переменную x.

Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите вставить для x.
Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6.

Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y.Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4).

Проверка ответов для решения уравнений

Так же, как калькулятор алгебры можно использовать для вычисления выражений,
Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x.

В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Поскольку ответ правильный, в калькуляторе алгебры отображается зеленый знак равенства.

Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно».

Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенные точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Пример: x + y = 7; х + 2у = 11 @ (3,4).

Режим планшета

Если вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру.

Статьи по теме

Вернуться к калькулятору алгебры »

Графические уравнения с программой« Пошаговое решение математических задач »

Язык математики особенно эффективен для представления отношений
между двумя или более переменными. В качестве примера рассмотрим пройденное расстояние
через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час.Мы можем представить эту взаимосвязь как

1. Словесное предложение:
Пройденное расстояние в милях равно сороккратному количеству пройденных часов.
2. Уравнение:
d = 40r.
3. Таблица значений.
4. График, показывающий зависимость между временем и расстоянием.

Мы уже использовали словесные предложения и уравнения для описания таких отношений;
В этой главе мы будем иметь дело с табличным и графическим представлениями.

7.1 РЕШЕНИЕ УРАВНЕНИЙ ОТ ДВУХ ПЕРЕМЕННЫХ

ЗАКАЗАННЫЕ ПАРЫ

Уравнение d = 40f объединяет расстояние d для каждого момента времени t. Например,

если t = 1, то d = 40
, если t = 2, то d = 80
, если t = 3, то d = 120

и так далее.

Пара чисел 1 и 40, рассматриваемая вместе, называется решением
уравнение d = 40r, потому что когда мы подставляем 1 вместо t и 40 вместо d в уравнении,
мы получаем верное утверждение. Если мы согласны ссылаться на парные номера в указанном
порядок, в котором первое число относится ко времени, а второе число относится к
расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и
скоро.Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и
вторые числа в парах как компоненты. В соответствии с этим соглашением решения
Уравнение d — 40t — это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению.
Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны

(0,0), (1,40), (2,80), (3,120), (4,160) и (5,200)

Такие пары иногда отображаются в одной из следующих табличных форм.

В любом конкретном уравнении, включающем две переменные, когда мы присваиваем значение одной
переменных определяется значение другой переменной и, следовательно,
зависит от первого.Удобно говорить о переменной, связанной с
первый компонент упорядоченной пары как независимая переменная и переменная
связанный со вторым компонентом упорядоченной пары в качестве зависимой переменной. Если в уравнении используются переменные x и y, подразумевается, что заменить —
элементы для x являются первыми компонентами и, следовательно, x — независимая переменная и
замены y являются вторыми компонентами и, следовательно, y является зависимой переменной.
Например, мы можем получить пары для уравнения

, подставив конкретное значение одной переменной в уравнение (1) и решив для
другая переменная.

Пример 1

Найдите недостающий компонент, чтобы заказанная пара была решением для

2х + у = 4

а. (0 ,?)

г. (1 ,?)

г. (2 ,?)

Решение

, если x = 0, то 2 (0) + y = 4
y = 4

, если x = 1, то 2 (1) + y = 4
y = 2

, если x = 2, то 2 (2) + y = 4
y = 0

Три пары теперь могут отображаться как три упорядоченные пары

(0,4), (1,2) и (2,0)

или в табличной форме

ЯВНО ВЫРАЖАЮЩИЙ ПЕРЕМЕННУЮ

Мы можем добавить -2x к обоим членам 2x + y = 4, чтобы получить

-2x + 2x + y = -2x + 4
y = -2x + 4

В уравнении (2), где y есть само по себе, мы говорим, что y явно выражается через
из х. Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
потому что зависимая переменная явно выражается через независимые
Переменная.

Например, в уравнении (2) выше

, если x = 0, то y = -2 (0) + 4 = 4
, если x = 1, то y = -2 (1) + 4 = 2
, если x = 2, то y = -2 (2) + 4 = 0

Мы получаем те же пары, которые мы получили с помощью уравнения (1)

(0,4), (1,2) и (2,0)

Мы получили уравнение (2) добавлением одинаковой величины -2x к каждому члену
уравнения (1), таким образом получая y само по себе.В общем, мы можем написать эквивалент
уравнения с двумя переменными, используя свойства, которые мы ввели в главе 3,
где мы решали уравнения первой степени с одной переменной.

Уравнения эквивалентны, если:

Одно и то же количество прибавляется к равным количествам или вычитается из них.
Равные количества умножаются или делятся на одинаковое ненулевое количество.

Пример 2

Решите 2y — 3x = 4 явно для y через x и получите решения для x = 0,
х = 1 и х = 2.

Решение
Во-первых, добавляя 3x к каждому члену, получаем

2y — 3x + 3x = 4 + 3x
2y = 4 + 3x (продолжение)

Теперь, разделив каждый член на 2, получим

В этой форме мы получаем значения y для заданных значений x следующим образом:

В этом случае три решения: (0, 2), (1, 7/2) и (2, 5).

ОБОЗНАЧЕНИЕ ФУНКЦИЙ

Иногда мы используем специальные обозначения для наименования второго компонента упорядоченного
пара, которая связана с указанным первым компонентом.Символ f (x), который часто бывает
используется для обозначения алгебраического выражения в переменной x, также может использоваться для обозначения
значение выражения для конкретных значений x. Например, если

f (x) = -2x + 4

, где f (x) играет ту же роль, что и y в уравнении (2) на странице 285, тогда f (1)
представляет значение выражения -2x + 4, когда x заменяется на 1

f (l) = -2 (1) + 4 = 2

Аналогично

f (0) = -2 (0) + 4 = 4

f (2) = -2 (2) + 4 = 0

Символ f (x) обычно называют обозначением функции.

Пример 3

Если f (x) = -3x + 2, найти f (-2) и f (2).

Решение

Замените x на -2, чтобы получить
f (-2) = -3 (-2) + 2 = 8

Замените x на 2, чтобы получить
f (2) = -3 (2) + 2 = -4

7.2 ГРАФИК ЗАКАЗАННЫХ ПАР

В разделе 1.1 мы видели, что каждое число соответствует точке на линии. Simi-
Как правило, каждая упорядоченная пара чисел (x, y) соответствует точке на плоскости. К
граф упорядоченной пары чисел, мы начинаем с построения пары перпендикулярных
числовые линии, называемые осями.Горизонтальная ось называется осью x, вертикальная ось
называется осью Y, а точка их пересечения называется началом координат. Эти топоры
разделите плоскость на четыре квадранта, как показано на рисунке 7.1.

Теперь мы можем присвоить упорядоченную пару чисел точке на плоскости, указав
на перпендикулярное расстояние точки от каждой из осей. Если первый
составляющая положительная, точка лежит правее вертикальной оси; если отрицательный, это
лежит слева.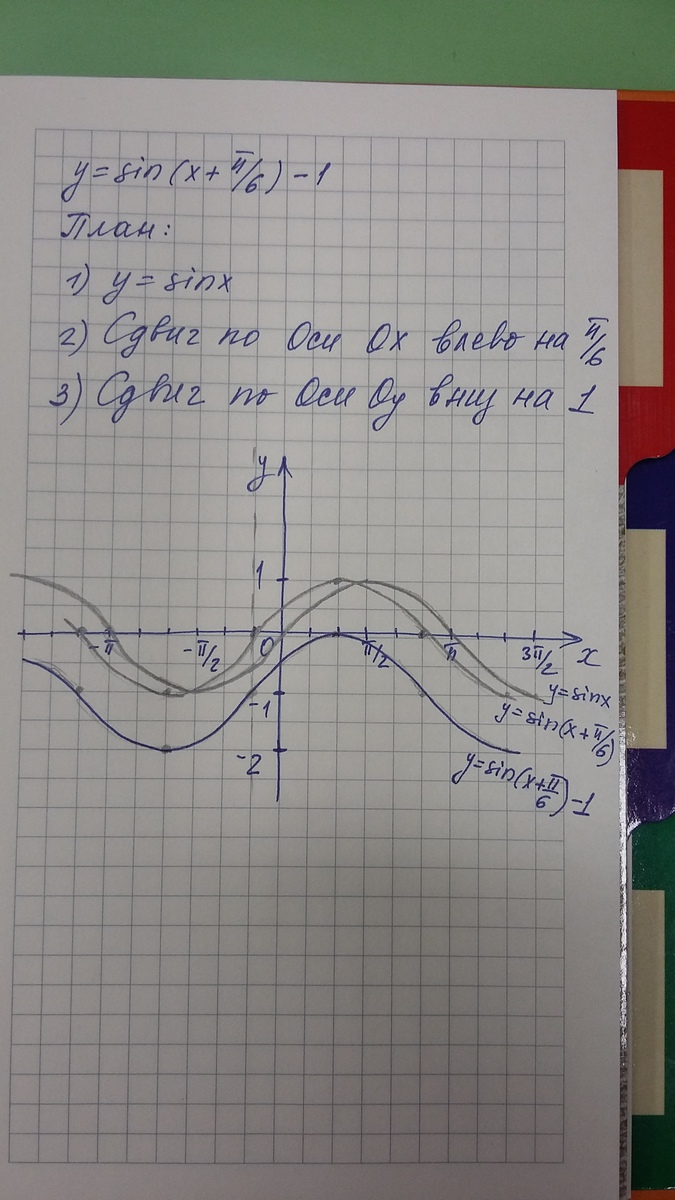 Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу.

Пример 1

График (3, 2), (-3, 2), (-3, -2) и (3, -2) в прямоугольной системе координат.

Решение
График (3, 2) находится на 3 единицы правее
ось y и на 2 единицы выше оси x;
график (-3,2) лежит на 3 единицы слева от
ось y и на 2 единицы выше оси x;
график (-3, -2) лежит на 3 единицы слева от
ось y и на 2 единицы ниже оси x;
график (3, -2) лежит на 3 единицы правее
ось y и на 2 единицы ниже оси x.

Расстояние y, на котором точка расположена от оси x, называется ординатой.
точки, а расстояние x, на котором точка расположена от оси y, называется
абсцисса точки. Абсцисса и ордината вместе называются прямоугольником.
Гулярные или декартовы координаты точки (см. рисунок 7.2).

7.3 ИЗОБРАЖЕНИЕ УРАВНЕНИЙ ПЕРВОГО УРОВНЯ

В разделе 7.1 мы видели, что решение уравнения с двумя переменными является упорядоченным
пара. В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени

у = х + 2

, положив x равным 0, -3, -2 и 3. Затем

для x = 0, y = 0 + 2 = 2
для x = 0, y = -3 + 2 = -1
для x = -2, y = -2 + 2-0
для x = 3, y = 3 + 2 = 5

и получаем решения

(0,2), (-3, -1), (-2,0) и (3,5)

, который может отображаться в табличной форме, как показано ниже.

Если мы изобразим точки, определенные этими
упорядоченные пары и проведите прямую через
их, мы получаем график всех решений
y = x + 2, как показано на рисунке 7.3. Это,
каждое решение y = x + 2 лежит на прямой,
и каждая точка на линии — это решение
у = х + 2.

Графики уравнений первой степени в двух
переменные всегда прямые; следовательно,
такие уравнения также называются линейными
уравнения.

В приведенном выше примере значения, которые мы использовали для
x были выбраны случайным образом; мы могли бы использовать
любые значения x, чтобы найти решения уравнения.Графики любых других упорядоченных пар, которые являются решениями уравнения, также будут
быть на линии, показанной на рисунке 7.3. Фактически, каждое линейное уравнение с двумя переменными
имеет бесконечное количество решений, график которых лежит на прямой. Однако мы только
нужно найти два решения, потому что для определения
прямая линия. Третий балл можно получить как проверку.

Чтобы построить уравнение первой степени:

Постройте набор прямоугольных осей, показывающих масштаб и переменную, представляющую
отправляется каждой осью.
Найдите две упорядоченные пары, которые являются решениями уравнения для построения графика
присвоение любого удобного значения одной переменной и определение соответствующего
значение другой переменной.
Изобразите эти упорядоченные пары.
Проведите прямую линию через точки.
Проверьте, построив график третьей упорядоченной пары, которая является решением уравнения и
убедитесь, что он лежит на линии.

Пример 1

Постройте уравнение y = 2x — 6.

Решение
Сначала мы выбираем любые два значения x, чтобы найти связанные значения y.
Мы будем использовать 1 и 4 для x.
Если x = 1, y = 2 (1) — 6 = -4
, если x = 4, y = 2 (4) — 6 = 2
Таким образом, два решения уравнения:
(1, -4) и (4, 2).
Затем мы строим график этих упорядоченных пар и проводим прямую линию через точки, как показано
на рисунке. Мы используем стрелки, чтобы показать, что
линия тянется бесконечно далеко в обоих направлениях.
Любая третья упорядоченная пара, удовлетворяющая
Уравнение можно использовать в качестве проверки:
, если x = 5, y = 2 (5) -6 = 4
Затем отметим, что график (5, 4) также лежит на линии
. Чтобы найти решения уравнения, как мы уже отмечали, часто проще всего сначала решить
явно для y через x.

Пример 2

График x + 2y = 4.

Решение
Сначала решаем y через x, чтобы получить

Теперь мы выбираем любые два значения x, чтобы найти соответствующие значения y. Мы будем использовать
2 и 0 для x.

Таким образом, двумя решениями уравнения являются (2, 1) и (0, 2).

Затем мы графически отображаем эти упорядоченные пары и
проведите через точки прямую, как
показано на рисунке.

Любая третья упорядоченная пара, удовлетворяющая
уравнение можно использовать как проверку:

Заметим, что график (-2, 3) также
лежит на линии.

ОСОБЫЕ СЛУЧАИ ЛИНЕЙНЫХ УРАВНЕНИЙ

Уравнение y = 2 можно записать как

0x + y = 2

и может рассматриваться как линейное уравнение в двух
переменные, у которых коэффициент при x равен 0. Некоторые
решения 0x + y = 2 равны

(1,2), (-1,2) и (4,2)

Фактически, любая упорядоченная пара вида (x, 2) является
решение (1).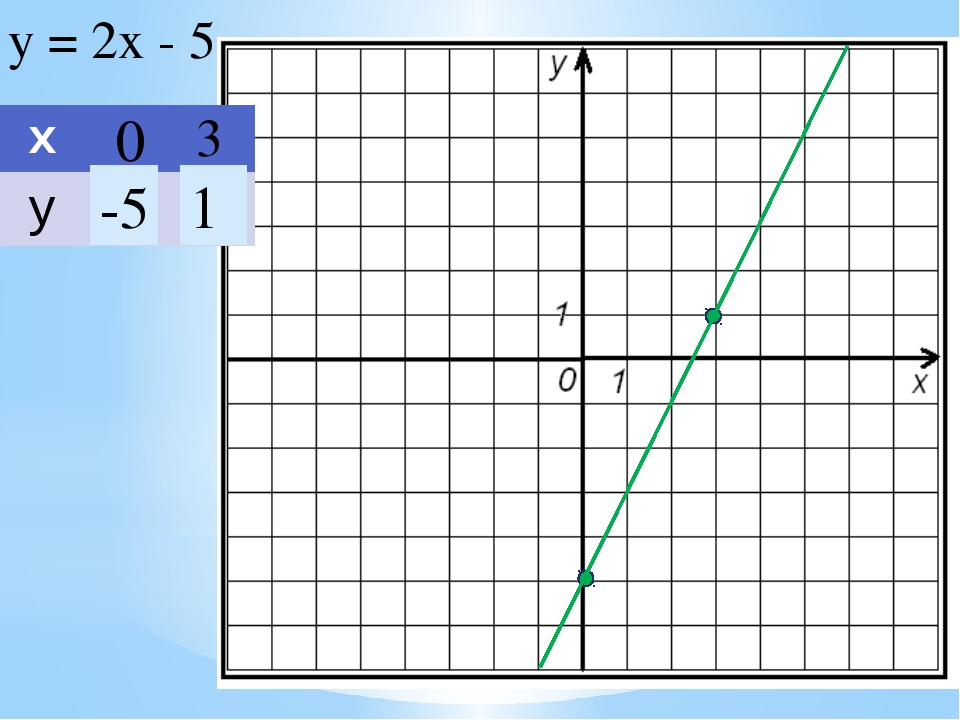 Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4.

Точно так же уравнение, такое как x = -3, может
записывается как

х + 0у = -3

и может рассматриваться как линейное уравнение в двух
переменные, у которых коэффициент при y равен 0.

Некоторые решения x + 0y = -3 являются
(-3, 5), (-3, 1) и (-3, -2). Фактически любой
упорядоченная пара вида (-3, y) является решением
из (2). Построение графика решений дает вертикальную
линия, как показано на рисунке 7.5.

Пример 3

График

а. y = 3
б. х = 2

Решение
а. Мы можем записать y = 3 как Ox + y = 3.
Некоторые решения: (1, 3), (2,3) и (5, 3).

б. Мы можем записать x = 2 как x + Oy = 2.
Некоторые решения: (2, 4), (2, 1) и (2, -2).

7.4 МЕТОД ПЕРЕСЕЧЕНИЯ ГРАФИКА

В Разделе 7.3 мы присвоили значения x в уравнениях с двумя переменными, чтобы найти
соответствующие значения y.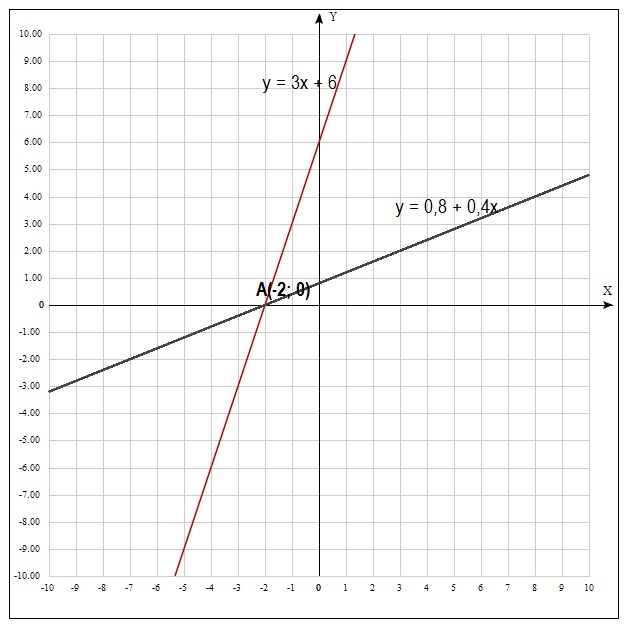 Решения уравнения с двумя переменными, равные
как правило, легче всего найти те, в которых первый или второй компонент
0. Например, если мы заменим 0 на x в уравнении

3x + 4y = 12

у нас

3 (0) + 4y = 12
y = 3

Таким образом, решением уравнения (1) является (0, 3).Мы также можем найти упорядоченные пары, которые
решения уравнений с двумя переменными путем присвоения значений y и определения
соответствующие значения x. В частности, если мы подставим 0 вместо y в уравнение (1), мы
получить

3x + 4 (0) = 12
x = 4

и второе решение уравнения (4, 0). Теперь мы можем использовать упорядоченные пары
(0, 3) и (4, 0) для построения графика уравнения (1). График представлен на рисунке 7.6. Уведомление
что линия пересекает ось x в точке 4 и ось y в точке 3. По этой причине число
4 называется пересечением по оси x графа, а число 3 — точкой пересечения по оси y.

Такой способ построения графика линейного уравнения называется пересечением.
метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.

Пример 1

График 2x — y = 6 методом пересечения.

Решение
Мы находим точку пересечения с x, подставляя 0 вместо y в уравнение, чтобы получить

2x — (0) = 6
2x = 6
x = 3

Теперь мы находим точку пересечения по оси Y, подставляя
для x в уравнении, чтобы получить

2 (0) — y = 6
-y = 6
y = -6

Упорядоченные пары (3, 0) и (0, -6) являются решениями 2x — y = 6.Графическое изображение этих
точки и соединив их прямой линией, получим график 2x — y = 6.
Если график пересекает оси в или около начала координат, метод перехвата не работает.
удовлетворительно. Затем мы должны построить график упорядоченной пары, которая является решением уравнения
и чей график не является началом координат или не слишком близок к началу координат.

Пример 2

График y = 3x.

Решение
Мы можем заменить 0 на x и найти
y = 3 (0) = 0
Аналогичным образом, заменив 0 на y, мы получим
0 = 3.x, x = 0
Таким образом, 0 является пересечением по оси x и точкой пересечения по оси y.

Так как одной точки недостаточно для графического = 3x, мы прибегаем к методам, изложенным в
Раздел 7.3. Выбирая любое другое значение для x, скажем 2, мы получаем

у = 3 (2) = 6

Таким образом, (0, 0) и (2, 6) являются решениями
уравнение. График y = 3x показан на
верно.

7,5 НАКЛОН ЛИНИИ

ФОРМУЛА НАКЛОНА

В этом разделе мы изучим важное свойство линии.Мы назначим
число к линии, которую мы называем уклоном, что даст нам меру «крутизны»
или «направление» линии.

Часто бывает удобно использовать специальные обозначения для различения прямоугольников.
Гулярные координаты двух разных точек. Мы можем обозначить одну пару координат
на (x ₁, y ₁ (читается «x sub one, y sub one»), связанный с точкой P ₁, и второй
пара координат по (x ₂, y ₂), связанная со второй точкой P ₂, как показано на рисунке
7.7. Обратите внимание на рис. 7.7, что при переходе от P ₁ к P ₂ вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y ₂ — y ₁, а изменение по горизонтали (или
расстояние по горизонтали) составляет x ₂ — x ₁.

Отношение вертикального изменения к горизонтальному называется крутизной
линия, содержащая точки P ₁ и P ₂. Это соотношение обычно обозначают m. Таким образом,

Пример 1

Найдите наклон прямой, содержащей два
точки с координатами (-4, 2) и (3, 5) как
показано на рисунке справа.

Решение
Обозначим (3, 5) как (x ₂, y ₂) и (-4, 2)
как (x ₁, y ₁). Подставляя в уравнение (1)
дает

Обратите внимание, что мы получим тот же результат, если подставим -4 и 2 вместо x ₂ и y ₂ и 3 и
5 для x ₁ и y ₁

Линии с различным уклоном показаны на Рисунке 7.8 ниже. Наклоны линий, которые
вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз
справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), что, поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y ₂ — y ₁ равно нулю для любых двух
точек, а наклон линии просто

Также обратите внимание (рисунок 7.8c), что, поскольку все точки на вертикали имеют одинаковое значение x,
x ₂ — x ₁ равняется нулю для любых двух точек. Однако

не определено, поэтому вертикальная линия не имеет наклона.

ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ

Рассмотрим линии, показанные на рисунке 7.9. Линия l ₁ имеет наклон m ₁ = 3, а линия l ₂ имеет наклон
уклон м ₂ = 3. В данном случае

Эти линии никогда не пересекаются и называются параллельными линиями. Теперь рассмотрим строки
показано на рисунке 7.10. Линия l ₁ имеет наклон m ₁ = 1/2, а линия l ₂ имеет наклон m ₂ = -2.
В данном случае

Эти линии пересекаются, образуя прямой угол, и называются перпендикулярными линиями.

В общем, если две линии имеют уклон и м2:

₁

₂

₁

₂

7.6 УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ

ФОРМА POINT-SLOPE

В разделе 7.5 мы нашли наклон прямой по формуле

Допустим, мы знаем, что линия проходит через точку (2, 3) и имеет наклон 2.Если обозначить любую другую точку на прямой как P (x, y) (см. Рис. 7.1а), наклоном
формула

Таким образом, уравнение (1) — это уравнение прямой, проходящей через точку (2, 3), и
имеет уклон 2.

В общем, допустим, мы знаем, что линия проходит через точку P ₁ (x ₁, y ₁ и имеет
уклон м. Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через
формула наклона

Уравнение (2) называется формой точечного уклона для линейного уравнения.В уравнении (2),
m, x ₁ и y ₁ известны, а x и y — переменные, которые представляют координаты
любая точка на линии. Таким образом, всякий раз, когда мы знаем наклон линии и точки на
линии, мы можем найти уравнение линии, используя уравнение (2).

Пример 1

Линия имеет наклон -2 и проходит через точку (2, 4). Найдите уравнение прямой.

Решение
Замените -2 вместо m и (2, 4) вместо (x ₁, y ₁) в уравнении (2)

Таким образом, прямая с наклоном -2, проходящая через точку (2, 4), имеет уравнение
у = -2х + 8.Мы могли бы также записать уравнение в эквивалентной форме y + 2x = 8,
2x + y = 8 или 2x + y — 8 = 0.

ФОРМА НАКЛОНА

Теперь рассмотрим уравнение прямой с наклоном m и точкой пересечения оси y b, как показано на
Рисунок 7.12. Подставив 0 вместо x ₁ и b вместо y ₁ в форме точечного наклона линейного
уравнение, имеем

y — b = m (x — 0)
y — b = mx

или

y = mx + b

Уравнение (3) называется формой пересечения наклона
для линейного уравнения.Наклон и пересечение по оси Y
можно получить непосредственно из уравнения в
эта форма.

Пример 2 Если линия имеет уравнение

, то наклон линии должен быть -2, а точка пересечения оси Y — 8. Аналогично,
график

г = -3x + 4

имеет наклон -3 и точку пересечения по оси Y 4; и график

имеет наклон 1/4 и точку пересечения по оси Y -2.

Если уравнение не записано в форме x = mx + b и мы хотим знать наклон
и / или точку пересечения с y, мы переписываем уравнение, решая относительно y через x.

Пример 3

Найдите наклон и точку пересечения оси Y 2x — 3y = 6.

Решение
Сначала мы решаем y через x, добавляя -2x к каждому члену.

2x — 3y — 2x = 6 — 2x
— 3y = 6 — 2x

Теперь, разделив каждого члена на -3, мы получим

Сравнивая это уравнение с формой y = mx + b, отметим, что наклон m (величина
коэффициент при x) равен 2/3, а точка пересечения оси y равна -2.

7.7 ПРЯМОЕ ИЗМЕНЕНИЕ

Частный случай уравнения первой степени с двумя переменными дается

y = kx (k — постоянная)

Такая связь называется прямой вариацией.Мы говорим, что переменная y изменяется
непосредственно как x.

Пример 1

Мы знаем, что давление P в жидкости изменяется прямо пропорционально глубине d ниже
поверхность жидкости. Мы можем обозначить это соотношение в символах как

P =

кД

В прямом варианте, если мы знаем набор условий для двух переменных, и если
мы также знаем другое значение для одной из переменных, мы можем найти значение
вторая переменная для этого нового набора условий.

В приведенном выше примере мы можем решить для константы k, чтобы получить

Поскольку отношение P / d постоянно для каждого набора условий, мы можем использовать соотношение
для решения задач, связанных с прямым изменением.

Пример 2

Если давление P напрямую зависит от глубины d и P = 40, когда d = 10, найдите P, когда
d = 15.

Решение
Поскольку отношение P / d является постоянным, мы можем подставить значения для P и d и получить
пропорция

Таким образом, P = 60 при d = 15.

7,8 НЕРАВЕНСТВА В ДВУХ ПЕРЕМЕННЫХ

В разделах 7.3 и 7.4 мы построили уравнения с двумя переменными. В этом разделе мы
построит график неравенств по двум переменным. Например, рассмотрим неравенство

у ≤ -x + 6

Решения — это упорядоченные пары чисел, которые «удовлетворяют» неравенству.Это,
(a, b) является решением неравенства, если неравенство является истинным утверждением после того, как мы
заменим a на x и b на y.

Пример 1

Определите, является ли данная упорядоченная пара решением y = -x + 6.

а. (1, 1)
б. (2, 5)

Решение
Упорядоченная пара (1, 1) является решением, потому что, когда 1 заменяется на x, а 1
подставив вместо y, мы получим

(1) = — (1) + 6, или 1 = 5

, что является верным утверждением. С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем

(5) = — (2) + 6, или 5 = 4

, что является ложным заявлением.

Чтобы построить график неравенства y = -x + 6, сначала построим график уравнения y = -x + 6
показано на рисунке 7.13. Обратите внимание, что (3, 3), (3, 2), (3, 1), (3, 0) и т. Д., Связанные
с точками, находящимися на линии или под ней, являются решениями неравенства
y = -x + 6, тогда как (3,4), (3, 5) и (3,6), связанные с точками над
линии не являются решениями неравенства. Фактически, все упорядоченные пары, связанные с
точки на линии или ниже являются решениями y = — x + 6. Таким образом, каждая точка на или
под чертой находится на графике.Мы представляем это, закрашивая область под
линия (см. рисунок 7.14).

В общем, чтобы построить график неравенства первой степени с двумя переменными в виде
Ax + By = C или Ax + By = C, сначала строим график уравнения Ax + By = C и
затем определите, какая полуплоскость (область выше или ниже линии) содержит
решения. Затем закрашиваем эту полуплоскость. Мы всегда можем определить, какая половина
плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C)
и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением
учитывая неравенство.Если да, то закрашиваем полуплоскость, содержащую контрольную точку; иначе,
заштриховываем вторую полуплоскость. Часто (0, 0) — удобная контрольная точка.

Пример 2

График 2x + 3y = 6

Решение
Сначала построим линию 2x + 3y = 6 (см. График a). Используя начало координат как контрольную точку,
мы определяем, является ли (0, 0) решением 2x + 3y ≥ 6. Поскольку утверждение

2 (0) + 3 (0) = 6

ложно, (0, 0) не является решением и мы закрашиваем полуплоскость, не содержащую
начало координат (см. график b).

Когда линия Ax + By = C проходит через начало координат, (0, 0) не является допустимым тестом
точка, так как она находится на линии.

Пример 3

График y = 2x.

Решение
Начнем с построения линии y = 2x (см. График a). Поскольку линия проходит через
начало координат, мы должны выбрать другую точку не на линии в качестве нашей тестовой точки. Мы будем
используйте (0, 1). С выписки

(1) = 2 (0)

верно, (0, 1) — решение, и мы закрашиваем полуплоскость, содержащую (0, 1) (см.
график б).

Если символ неравенства — ‘, точки на графике Ax + By = C
не являются решениями неравенства. Затем мы используем пунктирную линию для графика
Ax + By = C.

РЕЗЮМЕ ГЛАВЫ

Решение уравнения с двумя переменными — это упорядоченная пара чисел. в
упорядоченная пара (x, y), x называется первым компонентом, а y называется вторым
составная часть. Для уравнения с двумя переменными переменная, связанная с первой
компонент решения называется независимой переменной, а переменная
связанный со вторым компонентом, называется зависимой переменной.Обозначение функции f (x) используется для обозначения алгебраического выражения в x. Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x.
Пересечение двух перпендикулярных осей в системе координат называется
происхождение системы, и каждая из четырех областей, на которые делится плоскость
называется квадрантом. Компоненты упорядоченной пары (x, y), связанной с
точки на плоскости называются координатами точки; x называется абсциссой
точки, а y называется ординатой точки.
График уравнения первой степени с двумя переменными представляет собой прямую линию. То есть каждый
упорядоченная пара, которая является решением уравнения, имеет график, лежащий на линии, и
каждая точка в строке связана с упорядоченной парой, которая является решением
уравнение.
Графики любых двух решений уравнения с двумя переменными могут быть использованы для
получить график уравнения. Однако два решения уравнения в двух
переменные, которые обычно легче всего найти, — это те, в которых либо первая, либо
второй компонент равен 0.Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось ординат и называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.
Наклон линии, содержащей точки P ₁ (x ₁, y ₁) и P ₂ (x ₂, y ₂), определяется как
Две прямые параллельны, если они имеют одинаковый наклон (м ₁ = м ₂).
Две прямые перпендикулярны, если произведение их наклонов равно — l (m ₁ * m ₂ = -1).
Форма точки-наклона прямой с наклоном m, проходящей через точку (x ₁, y ₁)
это
г — г ₁ — м (х — х ₁)
Форма точки пересечения с уклоном линии с уклоном m и точкой пересечения по оси y равна
y = mx + b
Взаимосвязь, определяемая уравнением вида
y = kx (k постоянная)
называется прямой вариацией.
Решением неравенства с двумя переменными является упорядоченная пара чисел, которая,
при подстановке в неравенство делает неравенство истинным утверждением. В
График линейного неравенства от двух переменных представляет собой полуплоскость.
Символы, представленные в этой главе, появляются на внутренней стороне передней обложки.

Системы линейных уравнений — Бесплатная математическая справка

Системы линейных уравнений имеют место, когда существует более одного связанного математического выражения.Например, в \ (y = 3x + 7 \) есть только одна линия со всеми точками на этой линии, представляющая набор решений для приведенного выше уравнения.

Когда вам задают 2 уравнения в одном и том же вопросе и просят решить для единственного ответа, вы можете визуализировать проблему как две линии на одной плоскости xy. Следующие два уравнения изображены на одной плоскости xy:

$$ y = 3x + 5 $$
$$ y = — x $$

Решение любого уравнения — это место пересечения ОБЕИХ уравнений на плоскости xy.Это место встречи называется Точкой пересечения. Если у вас есть линейное уравнение и квадратное уравнение в одной плоскости xy, могут быть ДВЕ ТОЧКИ, где график каждого уравнения будет встречаться или пересекаться. Вот геометрический вид:

Вот пример двух уравнений с двумя неизвестными переменными:

Пример

$$ x + y = 10 $$
$$ 3x + 2y = 20 $$

Есть три метода решения нашего пробного вопроса.

1) Решаем графически
2) Мы можем решить это алгебраически
3) Мы также можем решить это с помощью алгебраического исключения

Решу вопрос всеми 3-мя способами.Метод 1. Решить графически:

Чтобы решить графически, лучше всего записать ОБА уравнения в форме пересечения наклона или в форме: \ (y = mx + b \), где m = наклон, а b = точка пересечения y в качестве первого шага. Таким образом, \ (x + y = 10 \) становится \ (y = — x + 10 \) (форма пересечения наклона). Затем \ (3x + 2y = 20 \) становится \ (y = — \ frac {3x} {2} + 10 \) при записи в форме пересечения наклона.

Затем нарисуйте две линии, ведущие к точке пересечения. Построив эти линии, вы обнаружите, что ОБА уравнения пересекаются в точке (0,10).Точка (0,10) означает, что если вы подставите x = 0 и y = 10 в ОБЕИ исходные уравнения, вы обнаружите, что это решает оба уравнения. Вот как эти два уравнения выглядят на плоскости xy:

Метод 2: Решить алгебраически

Шагов:

1) Решите относительно x или y в первом уравнении (\ (x + y = 10 \)). Решу за у. Итак, \ (x + y = 10 \) становится \ (y = -x + 10 \).

2) Подставьте значение y (то есть -x + 10) во второе уравнение, чтобы найти x. Наше второе уравнение было \ (3x + 2y = 20 \) и после подстановки становится \ (3x + 2 (-x + 10) = 20 \)

Далее: Решите относительно x.

$$ 3x -2x + 20 = 20 $$
$$ x + 20 = 20 $$
$$ x = 0 $$

3) Подставьте x = 0 в ЛЮБОЕ исходное уравнение, чтобы найти значение y. Я буду использовать наше второе уравнение.

$$ 3x + 2y = 20 $$
$$ 3 (0) + 2y = 20 $$
$$ 0 + 2y = 20 $$
$$ y = 10 $$

Итак, наша точка пересечения снова (0,10).

Метод 3: Алгебраическое исключение

Этот метод имеет дело с сопоставлением переменных для ELIMINATE или устранением одной. Имейте в виду, что какую переменную удалить в первую очередь — это ваш выбор.

ЦЕЛЬ: исключить x и решить вместо y или наоборот. Вернемся к нашим исходным уравнениям.

В нашем втором 3x + 2y = 20, вы можете исключить 3x, умножив -3 на КАЖДЫЙ член в нашем первом уравнении (x + y = 10).

x + y = 10
3x + 2y = 20

-3 (x) + -3 (y) = -3 (10)
3x + 2y = 20

-3x + -3y = -30
3x + 2y = 20

ВНИМАНИЕ, что -3x и 3x исключаются. Вижу это? Понять, почему? И вот почему: отрицательный плюс положительный = ноль.

Теперь у нас есть это:

-3y = -30
2y = 20

-3y + 2y = -30 + 20

-y = -10

y = 10.

Далее: чтобы найти x, мы подставляем y = 10 в ЛЮБОЕ из исходных уравнений. К настоящему времени вы должны увидеть, что наш ответ для x будет НУЛЬ.

Вот он:

Я буду использовать x + y = 10

x + 10 = 10

x = 0.

Вы видите то, что вижу я? Да, я снова нашел ту же самую точку пересечения, которая составляет (0,10).

Г-н Фелиз
(c) 2005

Напишите уравнение прямой, параллельной или перпендикулярной данной прямой

Если мы знаем уравнение прямой, мы можем использовать то, что мы знаем о наклоне, чтобы написать уравнение прямой, параллельной или перпендикулярной данной прямой.

Написание уравнений параллельных линий

Предположим, например, нам дано следующее уравнение.

[латекс] f \ влево (x \ вправо) = 3x + 1 [/ латекс]

Мы знаем, что наклон линии, образованной функцией, равен 3. Мы также знаем, что точка пересечения y- равна (0, 1). Любая другая линия с наклоном 3 будет параллельна f ( x ). Таким образом, линии, образованные всеми следующими функциями, будут параллельны f ( x ).

[латекс] \ begin {case} g \ left (x \ right) = 3x + 6 \ hfill \\ h \ left (x \ right) = 3x + 1 \ hfill \\ p \ left (x \ right) = 3x + \ frac {2} {3} \ hfill \ end {case} [/ latex]

Предположим, мы хотим написать уравнение прямой, параллельной f и проходящей через точку (1, 7). Мы уже знаем, что наклон равен 3. Нам просто нужно определить, какое значение для b даст правильную линию. Мы можем начать с уравнения для линии в форме точки наклона, а затем переписать его в форме точки пересечения наклона.

[латекс] \ begin {case} y- {y} _ {1} = m \ left (x- {x} _ {1} \ right) \ hfill \\ y — 7 = 3 \ left (x — 1 \ right) \ hfill \\ y — 7 = 3x — 3 \ hfill \\ \ text {} y = 3x + 4 \ hfill \ end {case} [/ latex]

Итак, [латекс] g \ left (x \ right) = 3x + 4 [/ latex] параллелен [latex] f \ left (x \ right) = 3x + 1 [/ latex] и проходит через точку (1 , 7).

Как сделать: учитывая уравнение функции и точку, через которую проходит ее график, напишите уравнение прямой, параллельной данной линии, которая проходит через данную точку.

Найдите наклон функции.
Подставьте указанные значения либо в общее уравнение угла наклона, либо в уравнение пересечения угла наклона для прямой.
Упростить.

Пример 9: Поиск прямой, параллельной заданной

Найдите прямую, параллельную графику [латекса] f \ left (x \ right) = 3x + 6 [/ latex], которая проходит через точку (3, 0).

Решения

Наклон данной прямой равен 3. Если мы выберем форму пересечения уклона, мы можем заменить м = 3, x = 3 и f ( x ) = 0 в точку пересечения наклона. форму, чтобы найти точку пересечения y- .

[латекс] \ begin {case} g \ left (x \ right) = 3x + b \ hfill \\ \ text {} 0 = 3 \ left (3 \ right) + b \ hfill \\ \ text {} b = -9 \ hfill \ end {case} [/ latex]

Линия, параллельная f ( x ), которая проходит через (3, 0), равна [latex] g \ left (x \ right) = 3x — 9 [/ latex].

Написание уравнений перпендикулярных прямых

Мы можем использовать очень похожий процесс, чтобы написать уравнение для линии, перпендикулярной данной линии. Однако вместо того, чтобы использовать один и тот же наклон, мы используем отрицательную величину, обратную данному наклону.Предположим, нам дана следующая функция:

[латекс] f \ влево (x \ вправо) = 2x + 4 [/ латекс]

Наклон линии равен 2, и его отрицательная обратная величина равна [латекс] — \ frac {1} {2} [/ latex]. Любая функция с наклоном [латекс] — \ frac {1} {2} [/ latex] будет перпендикулярна f ( x ). Таким образом, линии, образованные всеми следующими функциями, будут перпендикулярны f ( x ).

[латекс] \ begin {case} g \ left (x \ right) = — \ frac {1} {2} x + 4 \ hfill \\ h \ left (x \ right) = — \ frac {1} { 2} x + 2 \ hfill \\ p \ left (x \ right) = — \ frac {1} {2} x- \ frac {1} {2} \ hfill \ end {case} [/ latex]

Как и раньше, мы можем сузить наш выбор для конкретной перпендикулярной линии, если знаем, что она проходит через данную точку.Предположим, что мы хотим написать уравнение прямой, которая перпендикулярна f ( x ) и проходит через точку (4, 0). Мы уже знаем, что наклон [латекс] — \ frac {1} {2} [/ latex]. Теперь мы можем использовать точку, чтобы найти точку пересечения y , подставляя заданные значения в форму пересечения линии с наклоном и решая для b .

[латекс] \ begin {case} g \ left (x \ right) = mx + b \ hfill \\ 0 = — \ frac {1} {2} \ left (4 \ right) + b \ hfill \\ 0 = -2 + b \ hfill \\ 2 = b \ hfill \\ b = 2 \ hfill \ end {case} [/ latex]

Уравнение для функции с наклоном [латекс] — \ frac {1} {2} [/ latex] и точкой пересечения y- 2 равно

[латекс] g \ left (x \ right) = — \ frac {1} {2} x + 2 [/ latex].

Итак, [латекс] g \ left (x \ right) = — \ frac {1} {2} x + 2 [/ latex] перпендикулярен [латексу] f \ left (x \ right) = 2x + 4 [/ латекс] и проходит через точку (4, 0). Имейте в виду, что перпендикулярные линии могут не выглядеть явно перпендикулярными на графическом калькуляторе, если мы не используем функцию квадратного масштабирования.

Вопросы и ответы

Горизонтальная линия имеет нулевой наклон, а вертикальная линия имеет неопределенный наклон. Эти две линии перпендикулярны, но произведение их наклонов не равно –1. Не противоречит ли этот факт определению перпендикулярных линий?

№Для двух перпендикулярных линейных функций произведение их угловых коэффициентов равно –1. Однако вертикальная линия не является функцией, поэтому определение не противоречит.

Как сделать: учитывая уравнение функции и точку, через которую проходит ее график, напишите уравнение линии, перпендикулярной данной линии.

Найдите наклон функции.
Определите отрицательную обратную величину уклона.
Подставьте новый наклон и значения для x и y из предоставленной пары координат в [latex] g \ left (x \ right) = mx + b [/ latex].
Решите относительно b .
Напишите уравнение линии.

Пример 10: Нахождение уравнения перпендикулярной прямой

Найдите уравнение линии, перпендикулярной [латексу] f \ left (x \ right) = 3x + 3 [/ latex], которая проходит через точку (3, 0).

Решение

Исходная линия имеет наклон м. = 3, поэтому наклон перпендикулярной линии будет обратной обратной величиной [латекс] — \ frac {1} {3} [/ latex]. Используя этот наклон и данную точку, мы можем найти уравнение для прямой.

[латекс] \ begin {case} g \ left (x \ right) = — \ frac {1} {3} x + b \ hfill \\ \ text {} 0 = — \ frac {1} {3} \ left (3 \ right) + b \ hfill \\ \ text {} 1 = b \ hfill \\ \ text {} b = 1 \ hfill \ end {case} [/ latex]

Линия, перпендикулярная к f ( x ), которая проходит через (3, 0), равна [latex] g \ left (x \ right) = — \ frac {1} {3} x + 1 [/ latex] .

Попробуй 5

Учитывая функцию [латекс] h \ left (x \ right) = 2x — 4 [/ latex], напишите уравнение для линии, проходящей через (0, 0), которая равна

а.параллельно h ( x )
b. перпендикулярно к h ( x )

Решение

Как сделать: даны две точки на линии и третья точка, напишите уравнение перпендикулярной линии, проходящей через точку.

Определите наклон линии, проходящей через точки.
Найдите отрицательное значение, обратное наклону.
Используйте форму откоса-пересечения или форму точки-наклона, чтобы написать уравнение, подставляя известные значения.
Упростить.

Пример 11: Нахождение уравнения прямой, перпендикулярной заданной прямой, проходящей через точку

Линия проходит через точки (–2, 6) и (4, 5). Найдите уравнение перпендикулярной прямой, проходящей через точку (4, 5).

Решение

По двум точкам данной линии мы можем вычислить наклон этой линии.

[латекс] \ begin {case} {m} _ {1} = \ frac {5 — 6} {4- \ left (-2 \ right)} \ hfill \\ = \ frac {-1} {6} \ hfill \\ = — \ frac {1} {6} \ hfill \ end {case} [/ latex]

Найдите отрицательное значение, обратное наклону.

[латекс] \ begin {case} {m} _ {2} = \ frac {-1} {- \ frac {1} {6}} \ hfill \\ = -1 \ left (- \ frac {6} {1} \ right) \ hfill \\ = 6 \ hfill \ end {case} [/ latex]

Затем мы можем найти точку пересечения y- прямой, проходящей через точку (4, 5).

[латекс] \ begin {case} g \ left (x \ right) = 6x + b \ hfill \\ 5 = 6 \ left (4 \ right) + b \ hfill \\ 5 = 24 + b \ hfill \\ -19 = b \ hfill \\ b = -19 \ hfill \ end {case} [/ latex]

Уравнение для прямой, которая перпендикулярна прямой, проходящей через две заданные точки, а также проходит через точку (4, 5):

[латекс] y = 6x — 19 [/ латекс]

Попробуй 6

Линия проходит через точки (–2, –15) и (2, –3).Найдите уравнение перпендикулярной прямой, проходящей через точку (6, 4).

Решение

6.3 построение графика с использованием рабочего листа перехватов

Мы можем построить квадратное уравнение, если мы знаем следующее: — положение вершины — расположение оси симметрии (aos) — открывается ли она вверх или вниз — несколько точек (включая y-перехват) На следующих слайдах мы обсудим стратегии для поиска каждого из них и попробуем построить график одной функции.

9.Используйте наклон и точку пересечения по оси Y, чтобы построить график уравнения 3 1 4 — + = x y. 10. Используйте наклон и точку пересечения по оси Y, чтобы построить график уравнения –3x + 2 y = 7. 11. Используйте точку пересечения по оси x и точку пересечения по оси Y, чтобы построить график 3 x — 5 y = 15.

Рабочий лист 6.3, день 2. 1. Жук и муравей идут по прямой линии по столу из положения A в положение B: Жук в момент времени t: A = (–1, 5) и B = (1, –2) Муравей в момент времени t: A = (4, –3) и B = (–3, 1) a. Встречает ли жук (и ест) муравья? Приведенный график может помочь. б.Установите два набора параметрических уравнений для моделирования этой ситуации.

Урок предназначен для обучения студентов через нанесение неравенств на числовую линию и использование пересечений по осям X и Y для построения графиков линейных уравнений на координатной сетке. Затем на уроке учащиеся изобразят линейные неравенства и правильно закрасят область решения на координатной сетке.

А пока используйте информацию выше, чтобы ответить на следующие вопросы. (После того, как вы ответите на все вопросы, вы сможете сделать набросок.) (a) Где график p (t) будет пересекать оси x? Решение: Поскольку p (t) является функцией, она только один раз перехватывает вертикальную ось x при (t, x) = (0, — 0,25).

Форма пересечения линии с наклоном — это один из первых способов решения уравнения линии. И в основном то, что это есть, y = mx + b, m относится к наклону или крутизне графика, а b — это точка пересечения y. Теперь вспомните, как мы находим перехват, если для других вещей мы добавляем 0.

Урок 6-2 Форма пересечения наклона 319 Каждая точка на графике уравнения представляет собой упорядоченную пару, которая делает уравнение истинным.График линейного уравнения — это линия, обозначающая все решения уравнения. Вы можете использовать наклон и точку пересечения по оси Y, чтобы построить линию. Графические уравнения График y = 3x-1. График y = -2. Смотрите слева.