Y tg модуль x график функции: как выглядит график y=tg|x|? — Школьные Знания.com — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Урок 5. свойства и график функции y=tgx и y=ctg x — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №5. Свойства и график функции y=tgx и y=ctg x

Перечень вопросов, рассматриваемых в теме

Изучение и объяснение свойств функций y=tgx и y=ctgx с помощью графика;
Определение свойств и положения графика тригонометрических функций вида y=|tg(k|x|+b)| y=|ctg(k|x|+b|;
Объяснение зависимости свойств и положения графика функции вида y=|tg(k|x|+b)| и y=|ctg(k|x|+b| от значения коэффициентов k,b.

Глоссарий по теме

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Тангенсоида –график функции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла).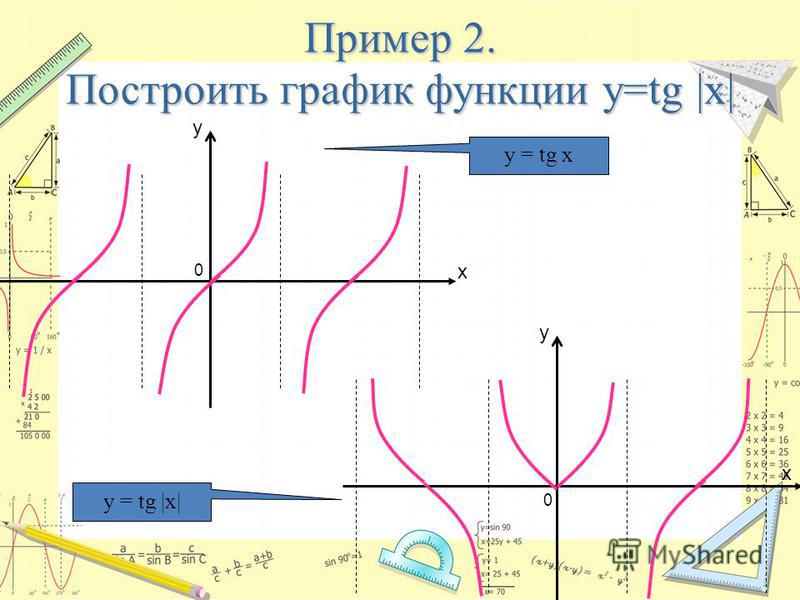

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].–Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Актуализация знаний

Вычислите:

1. ;

Ответ:

Объяснение нового материала

Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:

рис.1 Тригонометрический круг

Переносим основные значения углов на координатную плоскость.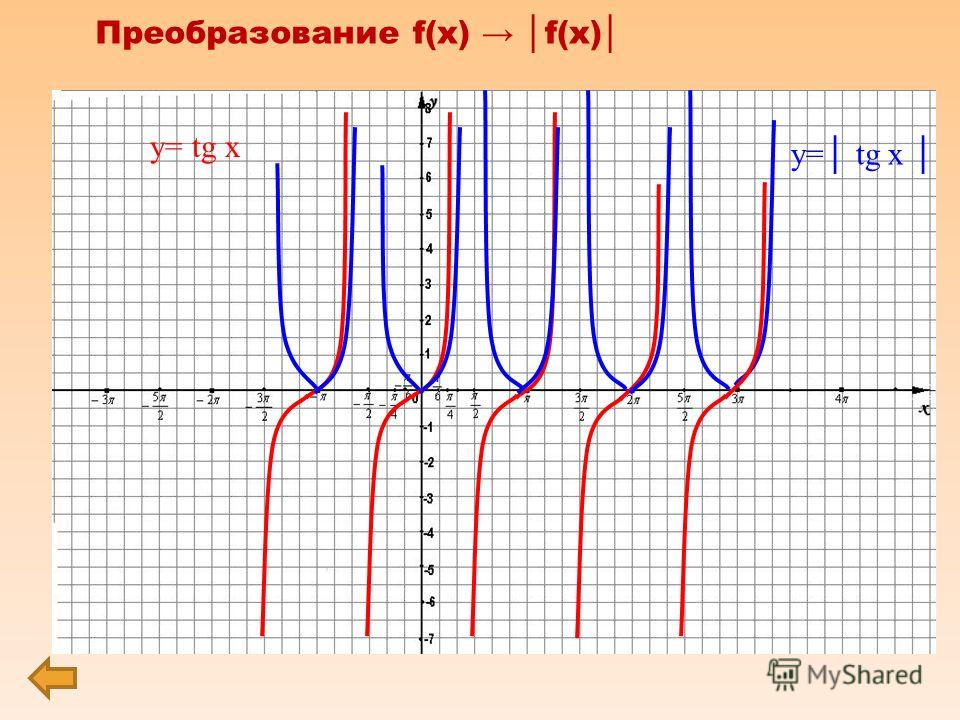 По оси абсцисс откладываем угол в радианах, по оси ординат – значения тангенса угла.

рис.2 График y=tgx на промежутке

Как любая тригонометрическая функции, функция тангенса периодическая, делая параллельный перенос получаем:

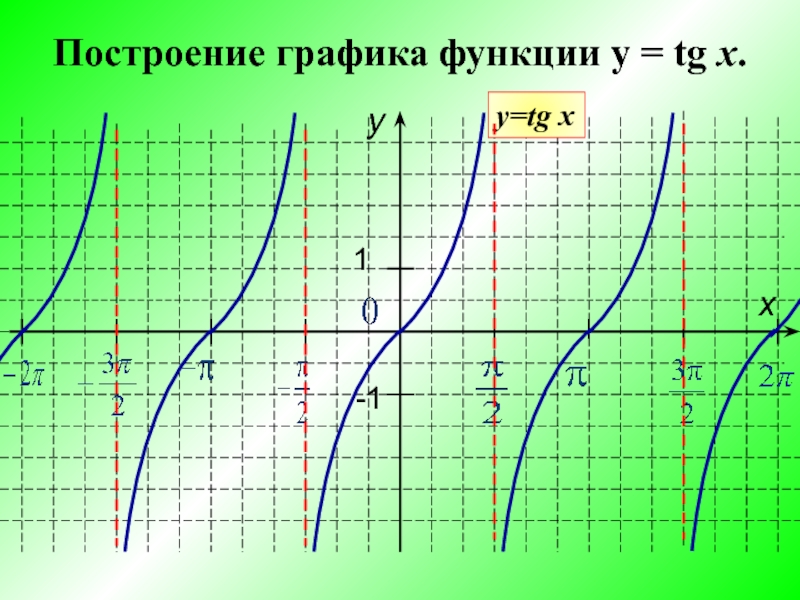
рис.3 График y=tgx

Заметим, что график симметричен относительно начала координат, следовательно функция тангенса нечётная. Используя построенный нами график, выведем основные свойства y=tgx:

1. Область определения функции y = tgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом , т.к.

3. Функция нечётная, т.к. . График нечётной функции симметричен относительно начала координат;

4. Функция возрастает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

7. Функция принимает:

значение, равное 0, при ;
положительные значения на интервале
отрицательные значения на интервале

Для построения графика можно придерживаться алгоритму рассмотренному при построении графика , однако (формула приведения). Т.е. смещая тангенсоиду на единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:

рис.3 График y=сtgx

Основные свойства y=сtgx:

1. Область определения функции y = сtgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом ;

3. Функция нечётная. График нечётной функции симметричен относительно начала координат;

4. Функция убывает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6. .

Примеры и разборы решения заданий тренировочного модуля:

Пример 1.

Найдем все корни уравнения , принадлежащие отрезку .

Построим графики функций и (рис. 6)

Рис. 4 – графики функций и .

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения .

Ответ:

Пример 2. Найти все решения неравенства , принадлежащие отрезку .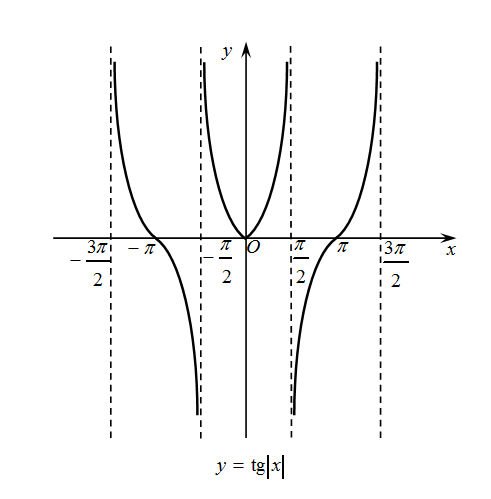

рис.5 графики функций и

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения .

Ответ:

.3. СВОЙСТВА ФУНКЦИИ y=tg⁡x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем

Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.

Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все

Значенияx входят в область определения функции y=tgx.

Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т

очек на линии тангенсов принимают

все значения до +, поскольку для любого действительного числа

мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит

внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку

(на самом деле их две). Следовательно, для любого действительного числа

найдется аргумент х, такой, что tan x равен данному действительному числу.

Поэтому область значений функции y= tg x — все действительные числа,

то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.

Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.

Тангенс — периодическая функция с наименьшим положительным периодом

Поэтому при построении графика

этой функции достаточно построить график на любом промежутке длиной π,

а потом полученную линию перенести параллельно вправо и влево вдоль оси

Ox на расстоянияkT = πk, где k — любое натуральное число.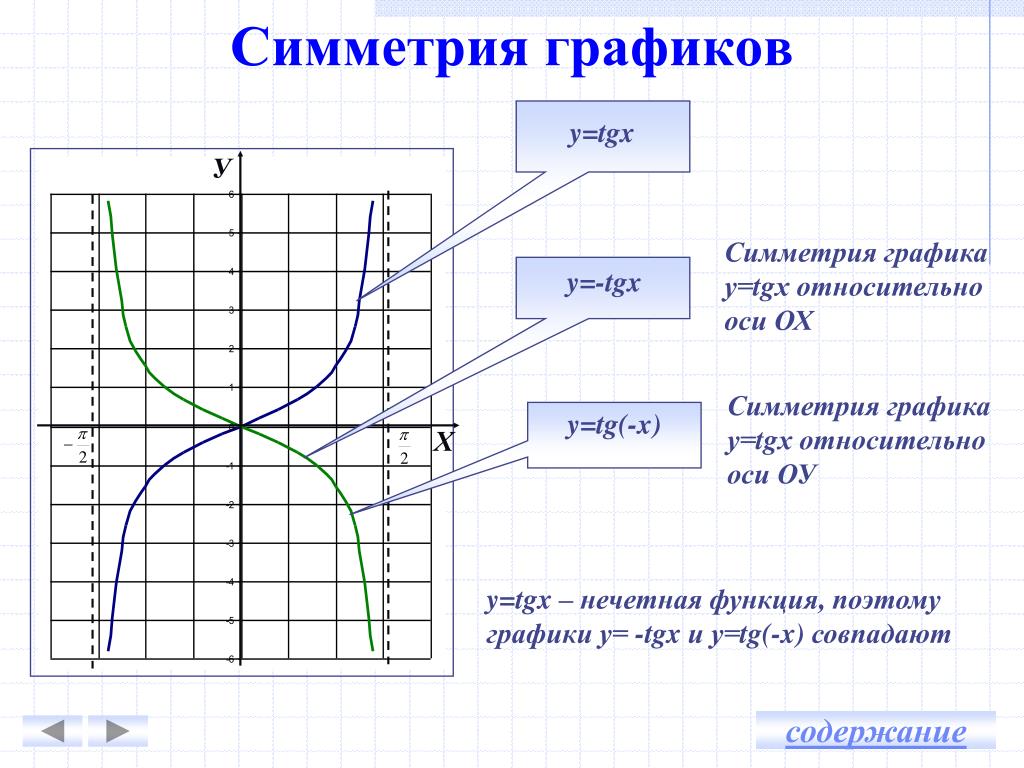

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,

при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при

а также, учитывая период, при всех

Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,

Промежутки возрастания и убывания.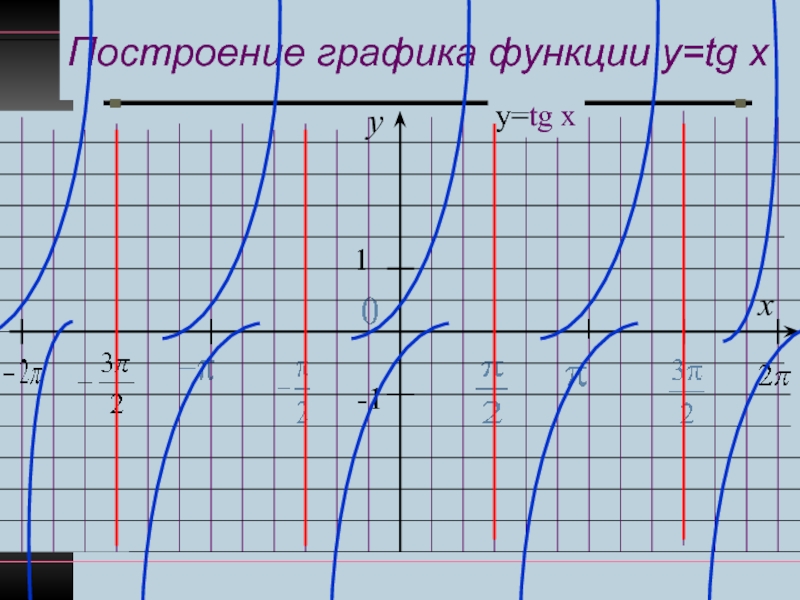

Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,

например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии

тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом

промежутке функция tgx возрастает. Учитывая периодичность функции

tgx, делаем вывод, что она возрастает также на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график

функции y = tg x. Учитывая периодичность этой функции (с периодом π),

сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки

линии тангенсов. На рисунке 93 показано построение графика функции

y = tg x на промежутке.

Далее, учитывая периодичность тангенса (с периодом π), повторяем вид

графика на каждом промежутке длиной π (то есть параллельно переносим

график вдоль оси Ох на πk, где k — целое число).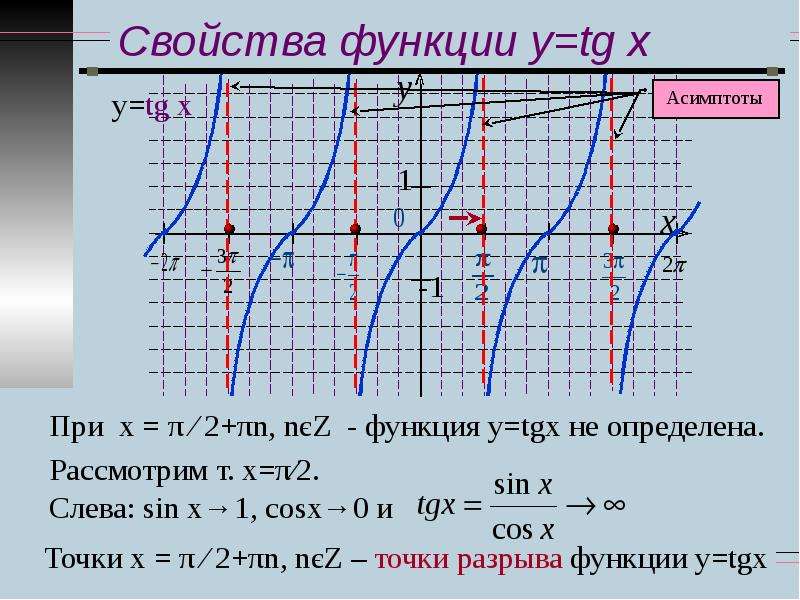

Получаем график, приведенный на рисунке 94, который называется тангенсоидой.

14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Объяснение и обоснование

Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,

D (ctg x): x ≠ πk, k ∈ Z.

Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии

котангенсов (рис. 95).

Поскольку точки А и В единичной окружности лежат на прямых ОА

и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс.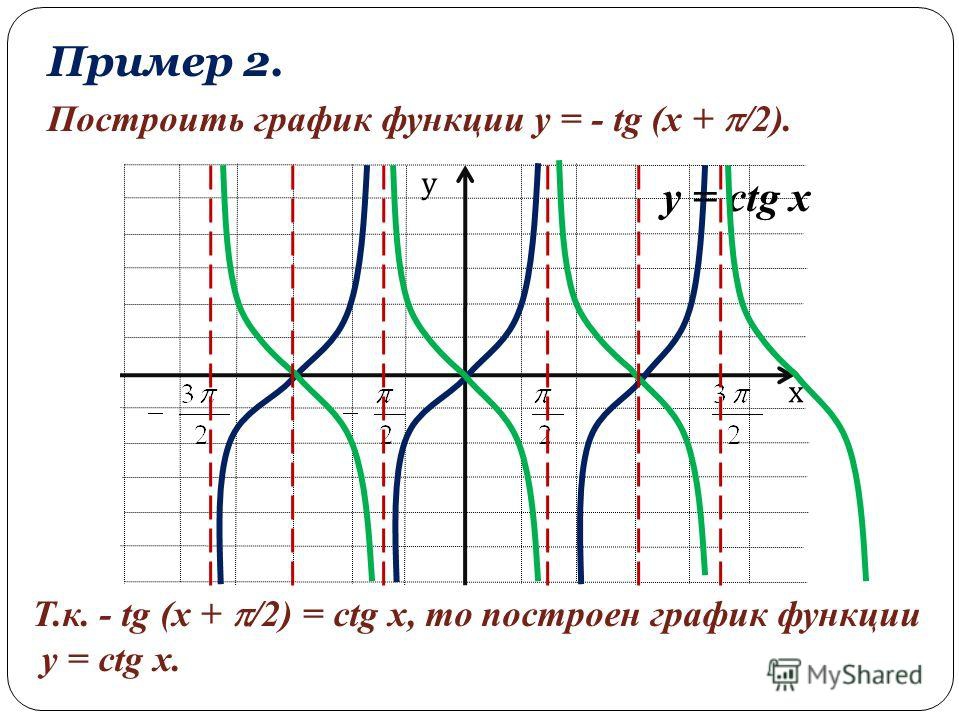 Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.

Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.

Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.

Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.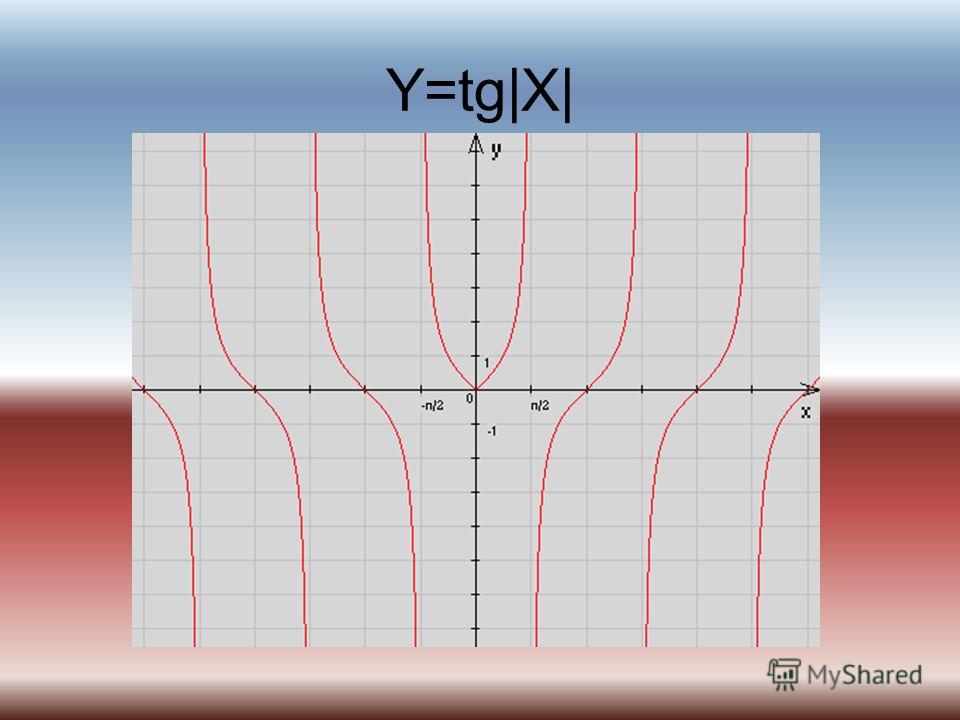

Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.

На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех

Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx< 0 при .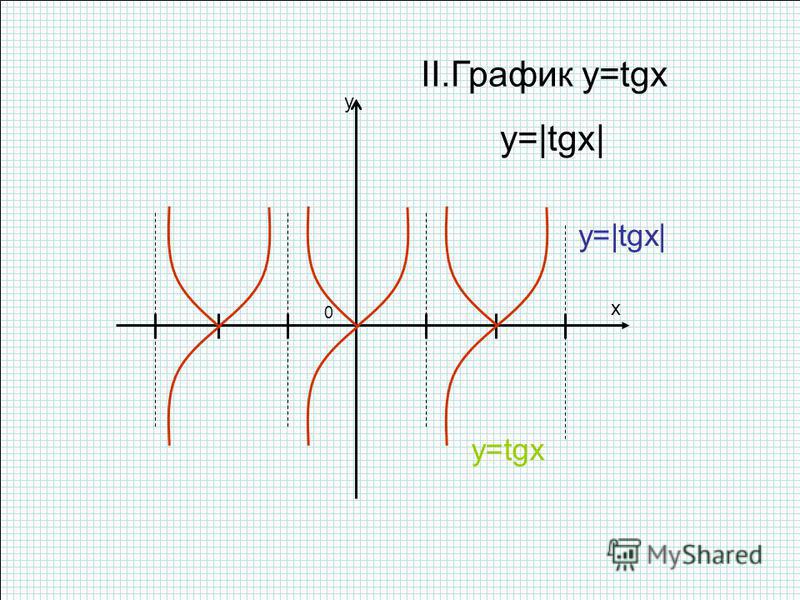

Промежутки возрастания и убывания

Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x₂>x₁) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx₂<ctgx₁), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков

Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических преобразований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох. 3

Risolvere per ?

cos(x)=1/2

Risolvere per x

sin(x)=-1/2

Преобразовать из градусов в радианы

225

Risolvere per ?

cos(x)=( квадратный корень 2)/2

Risolvere per x

cos(x)=( квадратный корень 3)/2

Risolvere per x

sin(x)=( квадратный корень 3)/2

График

g(x)=3/4* корень пятой степени x

Найти центр и радиус

x^2+y^2=9

Преобразовать из градусов в радианы

120 град.

2+n-72)=1/(n+9)

График функции y 2 cos x. Графики тригонометрических функций кратных углов. Задачи для самостоятельного решения

«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.

«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).

«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…

«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.

«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.

«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом.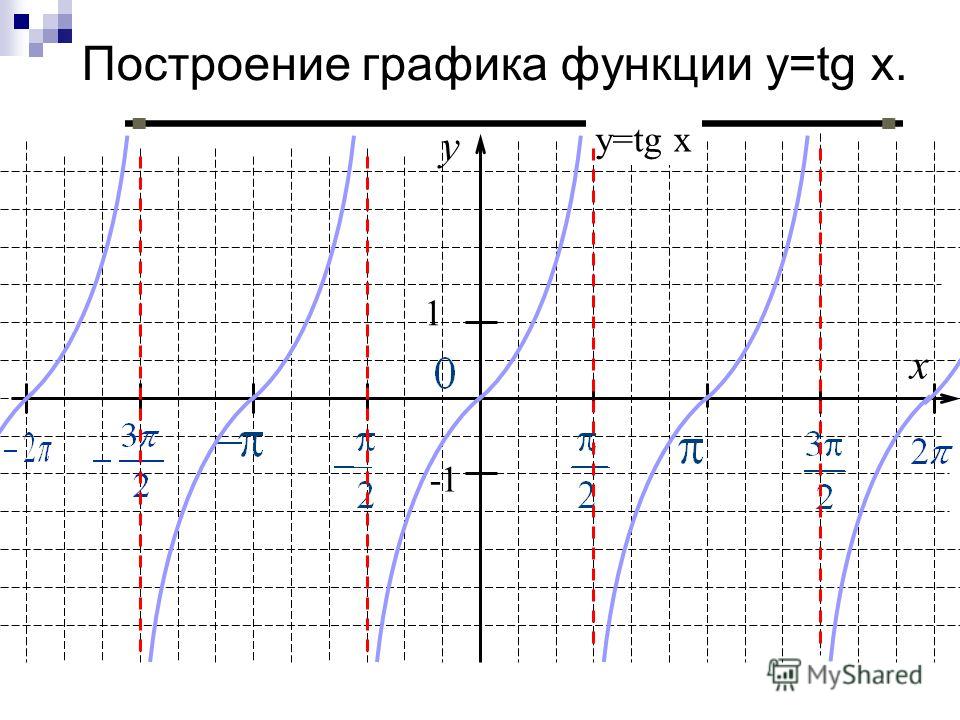 Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.

Всего в теме
25 презентаций

Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx
, где ω
— некоторое положительное число.

Для построения графика функции у = sin
ωx
сравним эту функцию с уже изученной нами функцией у = sin x
. Предположим, что при х = x
0
функция у = sin х
принимает значение, равное у 0 . Тогда

у 0 = sin
x
0
.

Преобразуем это соотношение следующим образом:

Следовательно, функция у = sin
ωx
при х

= x

0

/ ω
принимает то же самое значение у
0
, что и функция у = sin х
при х =
x
0
. А это означает, что функция у = sin
ωx
повторяет свои значения в ω
раз чаще, чем функция у
= sin x
. Поэтому график функции у = sin
ωx
получается путем «сжатия» графика функции у = sin x
в ω
раз вдоль оси х.

Например, график функции у = sin 2х
получается путем «сжатия» синусоиды у = sin x
вдвое вдоль оси абсцисс.

График функции у = sin x /
2
получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 /
2
раза) вдоль оси х.

Поскольку функция у = sin
ωx
повторяет свои значения в ω
раз чаще, чем функция
у = sin x
, то период ее в ω
раз меньше периода функции у = sin x
. Например, период функции у = sin 2х
равен 2π / 2
= π
, а период функции у = sin x /
2
равен π
/
x /
2
= 4π
.

Интересно провести исследование поведения функции у = sin аx
на примере анимации, которую очень просто можно создать в программе Maple
:

Аналогично строятся графики и других тригонометрических функций кратных углов.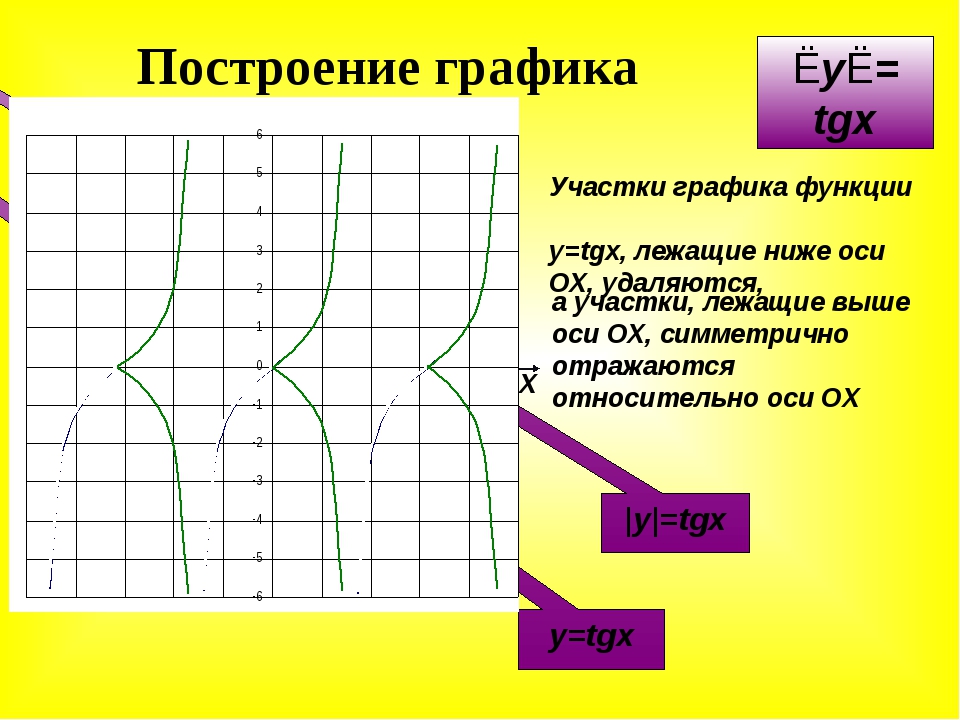 На рисунке представлен график функции у = cos 2х
, который получается путем «сжатия» косинусоиды у = cos х
в два раза вдоль оси абсцисс.

График функции у = cos x /
2
получается путем «растяжения» косинусоиды у = cos х
вдвое вдоль оси х.

На рисунке вы видите график функции у = tg 2x
, полученный «сжатием» тангенсоиды у = tg x
вдвое вдоль оси абсцисс.

График функции у = tg
x /
2
, полученный «растяжением» тангенсоиды у = tg x
вдвое вдоль оси х.

И, наконец, анимация, выполненная программой Maple:

Упражнения

1.
Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.

а). y = sin 4x /
3
г). y = tg 5x /
6
ж). y = cos 2x /
3

б). у= cos 5x /
3
д). у = ctg 5x /
3
з). у= ctg x /
3

в). y = tg 4x /
3
е). у = sin 2x /
3

2.
Определить периоды функций у = sin (πх)
и у = tg
( πх / 2
).

3.
Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.

4
*. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2
.

5.
Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.

6
*. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.

Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.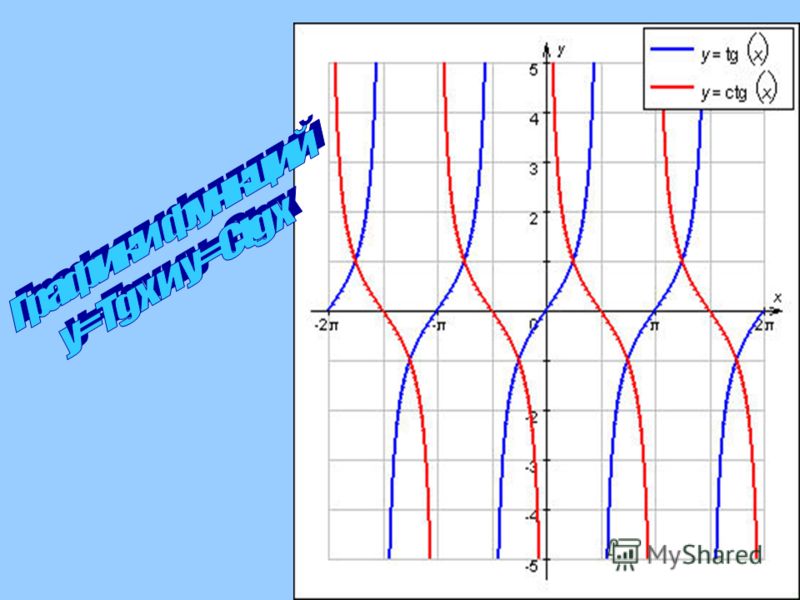 Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса

Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»

Что будем изучать:

1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.

Определение функции косинуса у=cos(x)

Ребята, мы уже познакомились с функцией Y=sin(X).

Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).

Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.

График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).

График функции Y=cos(X) так же называют синусоидой.

Свойства функции cos(x)

Область определения – множество действительных чисел.
Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1
Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.

Примеры с функцией cos(x)

1. Решить уравнение cos(X)=(x — 2π) 2 + 1

Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).

y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.

2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0

Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.

3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]

Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.

4. Построить график функции y=cos(π/3 — x) + 1

Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.

Задачи для самостоятельного решения

1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].

График y tgx 1. Функции y = tgx и y = ctgx, их свойства и графики

Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.

Y = sin(x)

График функции y=sin(x).

Основные свойства:

3. Функция нечетная.

Y = cos(x)

График функции y=cos(x).

Основные свойства:

1. Область определения вся числовая ось.

2. Функция ограниченная. Множество значений — отрезок [-1;1].

3. Функция четная.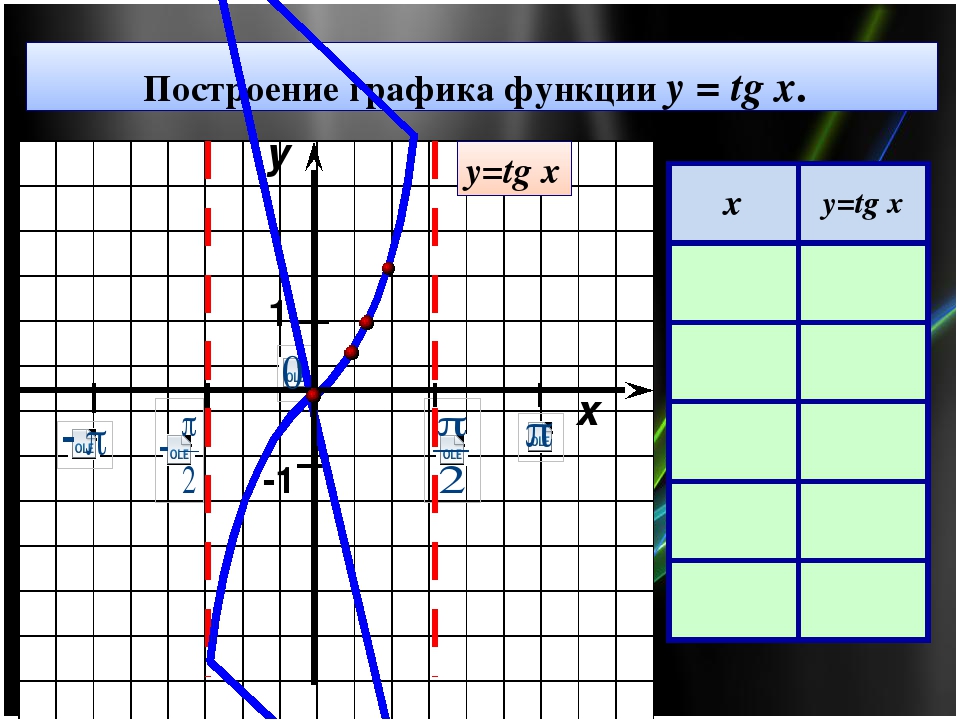

4.Функция периодическая с наименьшим положительным периодом равным 2*π.

Y = tg(x)

График функции y=tg(x).

Основные свойства:

1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k — целое.

3. Функция нечетная.

Y = ctg(x)

График функции y=ctg(x).

Основные свойства:

1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k — целое.

2. Функция неограниченная. Множество значение вся числовая прямая.

3. Функция нечетная.

4.Функция периодическая с наименьшим положительным периодом равным π.

Нужна помощь в учебе?

Предыдущая тема:

Определение Тангенсом угла α называют число, равное отношению sin α к cos α, обозначают tg α, т. е. Тангенс определён для всех углов α, кроме тех, для которых косинус равен нулю Для любого угла α ≠ π/2 + πk, kЄZ существует, и притом единственный tg α

y Ось тангенсов +∞ 120° 180° 1 x — 45° не существует Тангенс может принимать любые значения от – ∞ до + ∞ х=1 –∞

Определение Котангенсом угла α называют число, равное отношению cos α к sin α, обозначают сtg α, т.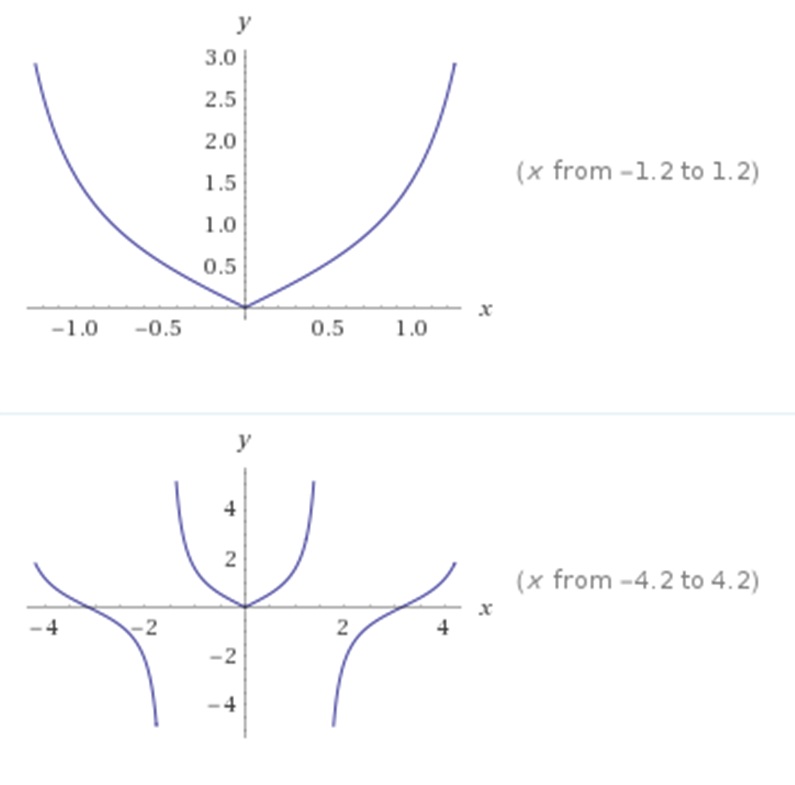 е. Котангенс определён для всех углов α, кроме тех, для которых синус равен нулю Для любого угла α ≠ πk, kЄZ существует, и притом единственный сtg α

Ось котангенсов Y –∞ +∞ 120° у=1 180° 0° X 45° Не существует Котангенс может принимать любые значения от – ∞ до + ∞

Построение графика функции y = tg x, если х Є [ π ∕ 2; π ∕ 2 ] y у = tg x х 0 1 у=tg x 0 ±π ∕ 6 x -1 ≈ ± 0, 6 ±π ∕ 4 ± 1 ±π ∕ 3 ≈ ± 1, 7 ±π ∕ 2 Не существ.

Свойства функции y=tg x. y 1 у=tg x x 1 Нули функции: tg х = 0 при х = πn, nєZ у>0 при хє (0; π/2) и при сдвиге на πn, nєZ. у

Свойства функции y=tg x. у=tg x y Асимптоты 1 x -1 При х = π ∕ 2+πn, nєZ — функция у=tgx не определена. Точки х = π ∕ 2+πn, nєZ – точки разрыва функции.

Запишите все свойства функции y = tg x. 1. Область определения: 2. Множество значений функции: 3. Периодическая, Т= 4. Нечётная функция 5. Возрастает на всей области определения. 6. Нули функции у = 0 при х = 7. у > 0 при хє и при сдвиге на 8. у

у 1 х — — 3 2 y = tgx + a — — 0 2 -1 y = tgx 3 2 2 y = tgx – b

у 1 х — — 3 2 — y = tgx — 0 2 -1 3 2 y = tg(x – a) 2

у 1 х — — 3 2 — y = tgx — 0 2 -1 3 2 2 y = Itgx. I

Функция y = ctg x 1. 2. 3. 4. 5. у=ctg x Область определения данной функции – все действительные числа, кроме чисел х=πk, k Z. Область значений функции – все действительные числа. Функция убывает на интервалах Функция нечетная, график ее симметричен относительно начала координат. Функция периодическая, ее наименьший положительный период равен π. у 1 — х -π 0 -1 π

Задача № 1. Найти все корни уравнения tgx = 1, принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2. Решение. 1. Построим графики у=tg x y у=1 −π 1 х1 0 -1 х2 функций у=tgx и у=1 2. х1= − 3π∕ 4 х2= π∕ 4 x х3= 5π∕ 4 х3 3π/2 π

Задача № 2. Найти все решения неравенства tgx

09.07.2015

7069

Цель:
рассмотреть графики и свойства функций у =
tg
х, у =
ctg
х.

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант I

2. Постройте график функции:

Вариант 2

1. Как построить график функции:

2. Постройте график функции:

III. Изучение нового материала

Рассмотрим две оставшиеся тригонометрические функции — тангенс и котангенс.

1. Функция у =
tg
x

Остановимся на графиках функций тангенса и котангенса. Сначала обсудим построение графика функции у =
tg
х на промежутке
Такое построение аналогично построению графика функции у =
sin
х, описанному ранее. При этом значение функции тангенса в точке находится с помощью линии тангенсов (см. рисунок).

Учитывая периодичность функции тангенса, получаем ее график на всей области определения параллельными переносами вдоль оси абсцисс (вправо и влево) уже построенного графика на π, 2π и т. д. График функции тангенса называют тангенсоидой.

Приведем основные свойства функции у =
tg
х:

1. Область определения — множество всех действительных чисел, за исключением чисел вида

y
(x

3. Функция возрастает на промежутках вида
где к
∈
Z
.

4. Функция не ограничена.

6. Функция непрерывная.

8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + п
k
) = у(х).

9. График функции имеет вертикальные асимптоты

Пример 1

Установим четность или нечетность функции:

Легко проверить, что для функций а, б область определения — симметричное множество. Исследуем эти функции на четность или нечетность. Для этого найдем у(-х) и сравним значения у(х) и
y
(-
x
).

а) Получим: Так как выполнено равенство
y
(-
x
) = у(х), то функция у(х) по определению четная.

б) Имеем:

Так как выполнено равенство
y
(-
x
) = -у(х), то функция у(х) по определению нечетная.

в) Область определения данной функции — несимметричное множество. Например, функция определена в точке х = π/4 и не определена в симметричной точке х = -π/4. Поэтому данная функция определенной четности не имеет.

Пример 2

Найдем основной период функции

Данная функция у(х) представляет собой алгебраическую сумму трех тригонометрических функций, периоды которых равны:
T
1
= 2π,
Запишем эти числа в виде дробей с одинаковыми знаменателями
Наименьшее общее кратное коэффициентов НОК (6; 2; 3). Поэтому основной период данной функции

Пример 3

Построим график функции

Учтем правила преобразования графиков функции. В соответствии с ними график функции
получается смещением графика функции у =
tg
х на π/4 единиц вправо вдоль оси абсцисс и его растяжением в 2 раза вдоль оси ординат.

Пример 4

Построим график функции

Используя определение и свойства модуля, в аргументе функции раскроем знаки модуля, рассмотрев три случая. Если х При 0 ≤
x
≤
π
/4 имеем:
Для х >
π
/4 имеем:
Далее остается построить три части данного графика. При х x
≤
π
/4 строим тангенсоиду
Этот график получается смещением графика функции у =
tg
х на π/8 вправо вдоль оси абсцисс и сжатием в два раза вдоль этой оси. При х > π
/4
строим прямую у = 1.

2. Функция у =
ctg
x

Аналогично графику функции у =
tg
х или с помощью формулы приведения
строится график функции у =
ctg
x
.

Перечислим основные свойства функции у =
ctg
x
:

1. Область определения — множество всех действительных чисел, за исключением чисел вида х = п
k
, к
∈
Z
.

2. Функция нечетная (т. е. у(-х) = —
y
(x
)), и ее график симметричен относительно начала координат.

3. Функция убывает на промежутках вида (п
k
; п + п
k
), к
∈
Z
.

4. Функция не ограничена.

5. Функция не имеет наименьшего и наибольшего значений.

6. Функция непрерывная.

7. Область значений Е(у) = (-∞; +∞).

8. Функция периодическая с наименьшим положительным периодом Т = п, т. е. у(х + п
k
) = у(x
).

9. График функции имеет вертикальные асимптоты х = п
k
.

Пример 5

Найдем область определения и область значений функции

Очевидно, что область определения функции
y
(x
) совпадает с областью определения функции
z
=
ctg
х, т. е. область определения — множество всех действительных чисел, кроме чисел вида х =
nk
,
k
∈
Z
.

Функция
y
(х) сложная. Поэтому запишем ее в виде
Координаты вершины параболы
y
(z
):
zB
= 1 и
y
в
= 2 — 4 + 5 = 3. Тогда область значений данной функции Е(у) = }

Y tgx график. Урок «Функции y = tgx, y = ctgx, их свойства и графики»

y Ось тангенсов +∞ 120° 180° 1 x — 45° не существует Тангенс может принимать любые значения от – ∞ до + ∞ х=1 –∞

Ось котангенсов Y –∞ +∞ 120° у=1 180° 0° X 45° Не существует Котангенс может принимать любые значения от – ∞ до + ∞

Свойства функции y=tg x. y 1 у=tg x x 1 Нули функции: tg х = 0 при х = πn, nєZ у>0 при хє (0; π/2) и при сдвиге на πn, nєZ. у

у 1 х — — 3 2 y = tgx + a — — 0 2 -1 y = tgx 3 2 2 y = tgx – b

у 1 х — — 3 2 — y = tgx — 0 2 -1 3 2 y = tg(x – a) 2

у 1 х — — 3 2 — y = tgx — 0 2 -1 3 2 2 y = Itgx. I

Задача № 2. Найти все решения неравенства tgx

Y = sin(x)

График функции y=sin(x).

Основные свойства:

3. Функция нечетная.

Y = cos(x)

График функции y=cos(x).

Основные свойства:

1. Область определения вся числовая ось.

2. Функция ограниченная. Множество значений — отрезок [-1;1].

3. Функция четная.

4.Функция периодическая с наименьшим положительным периодом равным 2*π.

Y = tg(x)

График функции y=tg(x).

Основные свойства:

1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k — целое.

3. Функция нечетная.

Y = ctg(x)

График функции y=ctg(x).

Основные свойства:

1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k — целое.

2. Функция неограниченная. Множество значение вся числовая прямая.

3. Функция нечетная.

4.Функция периодическая с наименьшим положительным периодом равным π.

Нужна помощь в учебе?

Предыдущая тема:

Функции (большинство из этих свойств фактически известно нам из § 5). Когда такое представление сложится, начнем строить график, как обычно, по точкам.

Свойство 1.
Область определения функции у = tg х — множество всех действительных чисел, за исключением чисел вида

Это свойство означает, что на графике функции
нет точки, принадлежащей прямой нет точки, принадлежащей прямой нет точки, принадлежащей прямой и т.д. Эти прямые проведены пунктиром на рис. 60.

Первое представление о графике получено: он состоит из бесконечного множества ветвей (в полосе между
Свойство 2.
у = tg х- периодическая функция с основным периодом п.
Это следует из двойного равенства полученного в § 5.
Значит, если мы построим ветвь графика в полосе от то затем нужно будет сдвинуть построенную ветвь по оси х вправо и влево на п, 2п, Зп и т.д. Тек самым получено второе представление о графике.

Свойство 3.
у =tg х-нечетная функция. Это следует из доказанного в § 5 соотношения График нечетной функции симметричен относительно начала координат. Значит, нам можно действовать так: построить по точкам часть графика на промежутке от а затем воспользоваться указанной симметрией.

Приступим к построению графика на полуинтервале , Выберем контрольные точки:

Отметим эти точки на координатной плоскости и проведем через них плавную кривую (рис. 61). Добавим линию, симметричную построенной кривой относительно начала координат (рис. 62). Воспользовавшись периодичностью, достроим график до конца (рис. 63).

График функции у = tg х называют тангенсоидой. Ту ее часть, которая изображена на рис. 62, обычно называют главной ветвью тангенсоиды.

Обратите внимание на то, что из начала координат главная ветвь тангенсоиды выходит как бы под углом 45°. Почему это так, вы узнаете из главы 4.

Свойство 4.
Функция возрастает на интервале В более общем виде — функция возрастает на любом интервале вида
Свойство 5.
Функция у = tg хне ограничена ни сверху, ни снизу.

Свойство 6.
У функции у = tg х нет ни наибольшего, ни наимень шего значения.
Свойство 7.
Функция у = tg х непрерывна на интервале В более общем виде — функция непрерывна на любом интервале вида
При значениях функция претерпевает разрыв. Каждая прямая вида служит вертикальной асимптотои графика функции.

Свойство 8.

Замечание.
Свойства 4-8, прочитанные по графику, можно доказать, опираясь на соответствующие математические утверждения, которые нам с вами пока не известны (поэтому мы и ограничиваемся наглядно-интуитивными представлениями). Впрочем, доказательство одного из свойств мы можем осуществить и сейчас.
Докажем, что функция у=tg х возрастает на полуинтервале . Возьмем два значения аргумента х 1 и х 2 из этого промежутка: х 1 соs х 2 . Значит,

Итак, а это и означает возрастание функции у=tg х на выбранном промежутке.
Пример 1.
Решить уравнение tg х =
Решение.
Построим в одной системе координат графики функций у =tg х — тангенсоиду и у = — прямую, параллельную оси х. Они имеют бесконечно много точек пересечения (рис. 64), причем абсциссы этих точек отличаются друг от друга на пк. На главной ветви абсцисса соответствующей точки равна (мы воспользовались известным числовым равенством — это один корень уравнения, а все решения описываются формулой
Ответ:

Пример 2.
Построить график функции
Решение.
Для начала разберемся с главной ветвью тангенсоиды.
1) Перейдем к вспомогательной системе координат с началом в точке проведена на рис. 65 пунктиром).
2) «Привяжем» функцию у = tg хк новой системе координат — это будет график функции , а точнее, главная ветвь искомого графика (рис. 65 — сплошная кривая).
3) Чтобы получить график функции достаточно построенную ветвь отобразить симметрично относительно оси х (рис. 66).
4) Зная одну ветвь, можно построить весь график (рис. 67).

На самом деле, на рис. 67 построен график функции у=сtgх. Почему? Потому, что имеет место тождество (формула приведения)
График функции у=сtg х, как и график функции у =tg х, называют тангенсоидой. Главной ветвью графика функции у=сtg х обычно называют ветвь, заключенную в полосе от х=0 до х = к.
Пример 3.
Решить уравнение сtg х = -1.

Решение.
Построим в одной системе координат графики функций у = сtg х — тангенсоиду и у=-1 — прямую, параллельную оси х. Они имеют бесконечно много точек пересечения (рис. 68), причем абсциссы этих точек отличаются друг от друга на яп. На главной ветви абсцисса соответствующеи точки равна (мы воспользовались известным соотношением: а все решения заданного уравнения можно охватить формулой
Ответ:

А.Г. Мордкович Алгебра 10 класс

Содержание урока

конспект урока

опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика

задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации

аудио-, видеоклипы и мультимедиа

фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения

рефераты

статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике

обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей

идеальные уроки

календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки

09.07.2015

7069

Цель:
рассмотреть графики и свойства функций у =
tg
х, у =
ctg
х.

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант I

2. Постройте график функции:

Вариант 2

1. Как построить график функции:

2. Постройте график функции:

III. Изучение нового материала

Рассмотрим две оставшиеся тригонометрические функции — тангенс и котангенс.

1. Функция у =
tg
x

Приведем основные свойства функции у =
tg
х:

1. Область определения — множество всех действительных чисел, за исключением чисел вида

y
(x

3. Функция возрастает на промежутках вида
где к
∈
Z
.

4. Функция не ограничена.

6. Функция непрерывная.

8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + п
k
) = у(х).

9. График функции имеет вертикальные асимптоты

Пример 1

Установим четность или нечетность функции:

а) Получим: Так как выполнено равенство
y
(-
x
) = у(х), то функция у(х) по определению четная.

б) Имеем:

Так как выполнено равенство
y
(-
x
) = -у(х), то функция у(х) по определению нечетная.

Пример 2

Найдем основной период функции

Пример 3

Построим график функции

Пример 4

Построим график функции

2. Функция у =
ctg
x

Аналогично графику функции у =
tg
х или с помощью формулы приведения
строится график функции у =
ctg
x
.

Перечислим основные свойства функции у =
ctg
x
:

1. Область определения — множество всех действительных чисел, за исключением чисел вида х = п
k
, к
∈
Z
.

2. Функция нечетная (т. е. у(-х) = —
y
(x
)), и ее график симметричен относительно начала координат.

3. Функция убывает на промежутках вида (п
k
; п + п
k
), к
∈
Z
.

4. Функция не ограничена.

5. Функция не имеет наименьшего и наибольшего значений.

6. Функция непрерывная.

7. Область значений Е(у) = (-∞; +∞).

8. Функция периодическая с наименьшим положительным периодом Т = п, т. е. у(х + п
k
) = у(x
).

9. График функции имеет вертикальные асимптоты х = п
k
.

Пример 5

Найдем область определения и область значений функции

Графики тригонометрических функций кратных углов. Графики тригонометрических функций кратных углов Задачи для самостоятельного решения

у 0 = sin
x
0
.

Преобразуем это соотношение следующим образом:

Следовательно, функция у = sin
ωx
при х

= x

0

Например, график функции у = sin 2х
получается путем «сжатия» синусоиды у = sin x
вдвое вдоль оси абсцисс.

График функции у = cos x /
2
получается путем «растяжения» косинусоиды у = cos х
вдвое вдоль оси х.

График функции у = tg
x /
2
, полученный «растяжением» тангенсоиды у = tg x
вдвое вдоль оси х.

И, наконец, анимация, выполненная программой Maple:

Упражнения

а). y = sin 4x /
3
г). y = tg 5x /
6
ж). y = cos 2x /
3

б). у= cos 5x /
3
д). у = ctg 5x /
3
з). у= ctg x /
3

в). y = tg 4x /
3
е). у = sin 2x /
3

2.
Определить периоды функций у = sin (πх)
и у = tg
( πх / 2
).

Всего в теме
25 презентаций

Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса

Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»

Что будем изучать:

1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.

Определение функции косинуса у=cos(x)

Ребята, мы уже познакомились с функцией Y=sin(X).

Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).

График функции Y=cos(X) так же называют синусоидой.

Свойства функции cos(x)

Область определения – множество действительных чисел.
Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1
Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.

Примеры с функцией cos(x)

1. Решить уравнение cos(X)=(x — 2π) 2 + 1

Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).

2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0

3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]

4. Построить график функции y=cos(π/3 — x) + 1

Задачи для самостоятельного решения

Определение функций с помощью графиков | Колледж алгебры

Результаты обучения

Проверить работу с помощью теста вертикальной линии
Проверьте однозначное соответствие с помощью теста горизонтальной линии
Определить графики функций инструментария

Как мы видели в примерах выше, мы можем представить функцию с помощью графика. Графики отображают множество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.

Наиболее распространенные графики называют входное значение [latex] x [/ latex] и выходное значение [latex] y [/ latex], и мы говорим, что [latex] y [/ latex] является функцией [latex] x [ / latex] или [latex] y = f \ left (x \ right) [/ latex], если функция называется [latex] f [/ latex]. График функции — это набор всех точек [латекс] \ left (x, y \ right) [/ latex] в плоскости, которая удовлетворяет уравнению [латекс] y = f \ left (x \ right) [/ latex ].Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующее выходное значение. Например, черные точки на графике на графике ниже говорят нам, что [латекс] f \ left (0 \ right) = 2 [/ latex] и [latex] f \ left (6 \ right) = 1 [/ latex ]. Однако набор всех точек [latex] \ left (x, y \ right) [/ latex], удовлетворяющих [latex] y = f \ left (x \ right) [/ latex], является кривой.Показанная кривая включает [латекс] \ left (0,2 \ right) [/ latex] и [latex] \ left (6,1 \ right) [/ latex], потому что кривая проходит через эти точки.

Тест с вертикальной линией можно использовать для определения того, представляет ли график функцию. Вертикальная линия включает все точки с определенным значением [latex] x [/ latex]. Значение [latex] y [/ latex] точки, где вертикальная линия пересекает график, представляет собой выход для этого входного значения [latex] x [/ latex]. Если мы можем нарисовать любую вертикальную линию , которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что это значение [latex] x [/ latex] имеет более одного вывода.Функция имеет только одно выходное значение для каждого входного значения.

Как сделать: для данного графика используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.

Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
Если такая линия есть, график не представляет функцию.
Если ни одна вертикальная линия не может пересекать кривую более одного раза, график действительно представляет функцию.

Пример: применение теста вертикальной линии

Какой из графиков представляет функцию [латекс] y = f \ left (x \ right)? [/ Latex]

Показать решение

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) графика выше. Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальных значениях x вертикальная линия пересекает график более чем в одной точке.

Попробуйте

Представляет ли приведенный ниже график функцию?

Тест горизонтальной линии

После того, как мы определили, что график определяет функцию, простой способ определить, является ли функция взаимно однозначной, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Горизонтальная линия включает все точки с определенным значением [latex] y [/ latex]. Значение [latex] x [/ latex] точки, где вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex] y [/ latex]. Если мы можем нарисовать любую горизонтальную линию , которая пересекает график более одного раза, тогда график , а не представляет функцию, потому что это значение [latex] y [/ latex] имеет более одного входа.

Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию.

Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
Если такая линия есть, функция не взаимно однозначная.
Если ни одна горизонтальная линия не может пересекать кривую более одного раза, функция взаимно однозначна.

Пример: применение теста горизонтальной линии

Рассмотрим функции (a) и (b), показанные на графиках ниже.

Являются ли какие-либо функции взаимно однозначными?

Показать решение

Функция в (a) не является взаимно однозначной.Горизонтальная линия, показанная ниже, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках).

Функция в (b) взаимно однозначная. Любая горизонтальная линия будет пересекать диагональную не более одного раза.

Определение основных функций набора инструментов

В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем.Учимся читать, начинаем с алфавита. Когда мы учимся арифметике, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать [latex] x [/ latex] в качестве входной переменной и [latex] y = f \ left (x \ right) [/ latex] в качестве выходной переменной.

Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги. Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную ниже.

Попробуйте

В этом упражнении вы построите график функций инструментария с помощью онлайн-инструмента построения графиков.

Изобразите каждую функцию набора инструментов, используя обозначение функций.
Создайте таблицу значений, которая ссылается на функцию и включает как минимум интервал [-5,5].

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

BioMath: тригонометрические функции

В этом разделе мы исследуем графики шести тригонометрических функций, начиная с графика функции косинуса.

Построение графика y = cos x

Чтобы нарисовать график y = cos x , мы можем составить таблицу значений, которые мы можем вычислить
ровно:

Мы можем построить эти точки и нарисовать плавную кривую, проходящую через них:

Поскольку область определения функции косинуса — это все действительные числа, мы помещаем стрелки на
график, чтобы указать, что график точно повторяется в обоих направлениях.Тот факт, что функция косинуса повторяется, означает, что она периодическая . В
в частности, y = cos x периодичен с периодом 2π. Это означает, что если точка
( x , y ) лежит на графике, то точка ( x +2 k π, y ) также будет лежать на графике, где
k — любое целое число. Например, ( x + 2π, y ) и ( x — 2π, y ) оба будут лежать на графике.

График y = sin x

Чтобы набросать график y = sin x , мы можем составить таблицу значений, которые мы можем вычислить.
ровно:

Мы можем построить эти точки и нарисовать плавную кривую, проходящую через них:

Поскольку область определения синусоидальной функции — это действительные числа, мы помещаем стрелки на
graph, чтобы указать, что график точно повторяется в обоих направлениях.Нравиться
функция косинуса, функция синуса также периодична 2π.

График y = tan x

Чтобы нарисовать график y = tan x , мы можем составить таблицу значений, которые мы можем вычислить.
ровно:

Обратите внимание, что теперь у нас есть несколько неопределенных функциональных значений; графически эти
соответствуют вертикальным асимптотам.Мы можем набросать y = tan x следующим образом:

На приведенном выше графике пунктирными линиями обозначены вертикальные асимптоты. Мы размещаем
стрелки на графике, чтобы указать, что
функция возрастает до ∞. Например, загар x → ∞ как x → (π / 2) ^—
(т.е. когда x приближается к π / 2 слева) и загар x → −∞ как x →
(π / 2) ^— (т.е. поскольку x приближается к π / 2 справа). В отличие от функций синуса и косинуса, касательная
функция π периодична. То есть, если точка ( x , y ) лежит на графике y = tan x , то будет точка ( x + k π, y ), где k любое целое число.

График y = sec x , y = csc x, и y = детская кроватка x

Напомним, что функции секанса, косеканса и котангенса являются обратными величинами функций косинуса, синуса и тангенса соответственно.Вы с меньшей вероятностью встретите эти графики при изучении наук о жизни. Мы включаем эти графики для полноты картины.

Преобразование y = cos x и y = sin x

Теперь мы рассмотрим графические преобразования y = cos x и y = sin x .Мы
можно записать преобразованную функцию косинуса и синуса следующим образом:

y = a cos ( b ( x — d )) + c ,

y = a sin ( b ( x — d )) + c .

Звоним | a | амплитуда функции. Амплитуда — это расстояние от
минимальное функциональное значение к максимальному функциональному значению, деленному на 2.В
период вышеуказанных функций равен 2π / b (обратите внимание, когда b = 1, период равен 2π). Когда
моделирование определенной величины или явления с помощью функции синуса или косинуса,
амплитуда и период — две важные характеристики, определяющие поведение. Ты
можете обратиться к разделу преобразований, чтобы изучить другие преобразования
ближе.

*****

В следующем разделе мы представим тригонометрические тождества.

Личности

Алгебра 2, модуль 3, контрольный опрос по родительским функциям и преобразованиям 3 1

РАЗДЕЛ 3, 3C Прослушивание и говорение, Реклама, стр. 33. Упражнение 1. 7 выполнено. 8 шокирует. РАЗДЕЛ 3, Трехмерная грамматика, «должен, не должен и не нужно / не обязательно», стр. 33. Упражнение 1.

Викторина: функции построения графиков Пройдите тест, чтобы проверить свое понимание того, что вы узнали. Продолжительность: 0 часов 20 минут Оценка: 20 баллов УРОК 3: ПРЕОБРАЗОВАНИЕ ФУНКЦИЙ Изучение: преобразование функций Узнайте о преобразованиях родительских функций, включая вертикальное и горизонтальное сжатие и растяжение, а также вертикальное и горизонтальное смещение.

1. Опишите преобразования графика y = 2 sin (3x + Π) -10. Синусоидальная функция будет иметь амплитуду 2. Период будет. Есть фазовый сдвиг влево. Наконец, среднюю линию можно найти при y = -10. Другая информация, которую мы можем вывести: максимальное значение будет -8, а минимальное — -12. 2. Опишите преобразования …

См. Полный список на shelovesmath.com

# 1: Функции с заданными уравнениями # 2: Функции с графиками # 3: Функции с таблицами # 4: Вложенные функции.Эти три категории могут частично совпадать, но это основные темы, на которых вы будете тестировать, когда дело доходит до функций. Давайте посмотрим на несколько реальных математических примеров SAT каждого типа. Уравнения функций

Вопрос 687881: Если родительская функция y = 1 / x, опишите изменение в уравнении y = 1 / (x + 3) + 1/2. Ответ а. Перемещает 3 юнита влево и половину юнита вверх. б. Перемещает 3 юнита вправо и половину юнита вверх. c. Перемещает 3 юнита влево и половину юнита вниз. d. Перемещает 3 юнита вправо и половину юнита вниз.

37 Партнеры Sophia гарантируют кредитный перевод. 299 организаций приняли или предварительно одобрили перевод кредита. * Служба рекомендаций колледжей Американского совета по образованию (ACE Credit®) оценила и рекомендовала зачетные единицы для 33 онлайн-курсов Софии. Множество разных колледжей a

4 июня 2019 г. · 4. C. Во-первых, вычтите общие множители из каждого из трех терминов: 6 × 3, -4 × 2 и -16x. Обратите внимание, что наибольший общий делитель (GCF) коэффициентов равен 2, и каждый член делится на x.Следовательно, вычтите 2x. 6 × 3 — 4 × 2 — 16x = 2x (3 × 2 — 2x — 8) Наконец, разложите трехчлен 3 × 2 — 2x — 8 на два бинома.

Сосредоточьтесь на различных математических темах, таких как геометрия, алгебра, вероятность и статистика, деньги, измерения и многое другое! Включение в уроки математики других предметов, таких как искусство, чтение и естественные науки, поможет удержать интерес учащихся к этому предмету. Здесь вы найдете ресурсы, которые подходят для любого уровня вашего обучения …

Преобразования функций: размышления | Purplemath

Purplemath

Последние два простых преобразования включают в себя функции переворота вверх ногами (переворачивание их вокруг оси x ) и их зеркальное отображение по оси y .

Первый, перевернутый вверх ногами, находится путем взятия отрицания исходной функции; то есть правило для этого преобразования — f ( x ).

Чтобы увидеть, как это работает, взгляните на график h ( x ) = x ² + 2 x — 3. График исходной функции выглядит следующим образом:

MathHelp.com

Чтобы представить этот график перевернутым, представьте, что график нарисован на листе прозрачного пластика, который был помещен поверх чертежа только с осью y , а ось x — это приклеенная шпажка. через лист.Чтобы перевернуть график, поверните вертел на 180 °. (Изображения здесь.) Тогда новый график, являющийся графиком — h ( x ), будет выглядеть так:

Переворачивание функции вверх ногами всегда работает следующим образом: вы ставите «минус» на все это. «Перевернутый вверх ногами», немного более технически, представляет собой «зеркальное отображение» исходного графика на оси x . Если вы подумаете о том, чтобы взять зеркало и поставить его вертикально на ось x , вы увидите (часть) исходного графика перевернутым в зеркале.Когда они говорят о «отражении» или «отражении» в оси или вокруг нее, они имеют в виду эту ментальную картину.

Чтобы понять, что делает это преобразование, помните, что f ( x ) — это то же самое, что и y . Итак, ставя «минус» на все, вы меняете все положительные (над осью) значения y на отрицательные (под осью) значения y , и наоборот. (Любые точки на оси x остаются там, где они есть.Двигаются только точки вне оси.)

Предыдущее отражение было отражением по оси x . Это оставляет нам преобразование для создания отражения по оси y .

Для этого преобразования я переключусь на кубическую функцию: г ( x ) = x ³ + x ² — 3 x — 1.

Вот график исходной функции:

Если я поставлю — x для x в исходной функции, я получу:

г (- x ) = (- x ) ³ + (- x ) ² — 3 (- x ) — 1

= — x ³ + x ² — (–3 x ) — 1

= — x ³ + x ² + 3 x — 1

График этой новой функции выглядит следующим образом:

Это преобразование повернуло исходный график вокруг оси y .Любые точки на оси y остаются на оси y ; меняют стороны точки вне оси. Это всегда верно: г (- x ) — это зеркальное отображение г ( x ); вставка «минуса» аргумента дает вам график, который является оригиналом, отраженным на оси y .

Чтобы понять, что делает это преобразование, помните, что вы меняете местами значения x .Что бы вы ни получили для значений x на положительной (или правой) стороне графика, теперь вы получаете значения x на отрицательной (или левой) стороне графика, и наоборот. Поскольку входы поменялись сторонами, график тоже.

Учитывая приведенный ниже график функции
f ( x ), определите, какой из графиков A и B представляет f (- x ) и — f ( x ).

Мне дали График A:

… и График B:

Сравнивая графики A и B с исходным графиком, я вижу, что график A — это перевернутая версия исходного графика. Это отражено по оси x . Это означает, что это «минус» исходной функции; это график — f ( x ).

График B имеет местами левую и правую части исходного графика; он отражается по оси y . Значит, это «минус» аргумента функции; это график f (- x ).

График A представляет — f ( x )

График B представляет f (- x )

Учитывая функцию
f ( x ) = x ² + x — 3, найдите операторы функции в упрощенной форме для отражения функции в каждом из x — и y — оси.Обозначьте отражения соответствующим образом.

Ну, «соответственно» немного расплывчато; Я просто буду уверен, что на этикетке все очень четко.

Мне нужно найти упрощенные функциональные утверждения для каждого из отражений. Одно из размышлений связано с поставкой «минус» функции; во втором — ставится «минус» аргументу функции.Итак, я сделаю каждое из них.

Сначала поставлю «минус» аргументу функции:

f (- x ) = (- x ) ² + (- x ) — 3

Теперь о другом отражении:

— f ( x ) = — ( x ² + x — 3)

Если в аргументе поставить «минус», график будет показан по оси y .Если поставить «минус» для всей функции, график будет показан по оси x . Итак, мой (четко обозначенный) ответ:

Отражение

в оси y — ось:

f (- x ) = x ² — x — 3

Отражение

в x — ось:

— f ( x ) = — x ² — x + 3

Многие учебники не идут дальше этого.Если это все правила, которые вам нужны, запишите их и убедитесь, что вы достаточно попрактиковались, чтобы иметь возможность применять их прямо на следующем тесте:

Правила перевода / преобразования функции:

f ( x ) + b сдвигает функцию b единиц вверх.

f ( x ) — b сдвигает функцию b единиц вниз.

f ( x + b ) сдвигает функцию b единиц на влево .

f ( x — b ) сдвигает функцию b единиц на вправо .

– f ( x ) отражает функцию по оси x (то есть в перевернутом виде).

f (- x ) отражает функцию по оси y (то есть перестановку левой и правой сторон).

URL: https://www.purplemath.com/modules/fcntrans2.htm

Тригонометрические функции — Справочное руководство Sage 9.2: Функции

Bases: sage.symbolic.function.GinacFunction

Измененная функция арктангенса.

Возвращает арктангенс (в радианах) для \ (y / x \), где
в отличие от arctan (y / x) , знаки как x , так и y являются
считается.В частности, эта функция измеряет угол
луча, проходящего через начало координат и \ ((x, y) \), с положительным
\ (x \) — ось нулевой отметки, а с выходным углом \ (\ theta \)
находится между \ (- \ pi <\ theta <= \ pi \).

Следовательно, arctan2 (y, x) = arctan (y / x) только для \ (x> 0 \). Один
может рассмотреть обычный arctan для измерения углов линий
через начало координат, а модифицированная функция измеряет
лучи через начало координат.

Обратите внимание, что координата \ (y \) по соглашению является первым вводом.

ПРИМЕРЫ:

Обратите внимание на разницу между двумя функциями:

 шалфей: arctan2 (1, -1)
3/4 * пи
шалфей: арктан (1 / -1)
-1 / 4 * пи

Это соответствует Python и Maxima:

 шалфей: maxima.atan2 (1, -1)
(3 *% пи) / 4
шалфей: math.atan2 (1, -1)
2,3561944345

Другие примеры:

 шалфей: arctan2 (1,0)
1/2 * пи
шалфей: arctan2 (2,3)
арктан (2/3)
шалфей: arctan2 (-1, -1)
-3 / 4 * пи

Конечно, мы можем и приблизить:

 шалфей: arctan2 (-1 / 2,1).п (100)
-0,463647600611621425623146
шалфей: arctan2 (2,3) .n (100)
0,58800260354756755124561108063

Мы можем отложить оценку, используя параметр удержания :

 sage: arctan2 (-1 / 2,1, удерживать = True)
арктан2 (-1/2, 1)

Для повторной оценки в настоящее время мы должны использовать Maxima через
sage.symbolic.expression.Expression.simplify () :

 sage: arctan2 (-1 / 2,1, удерживать = True) .simplify ()
-арктан (1/2)

Функция также работает с массивами numpy в качестве входных данных:

 sage: import numpy
шалфей: а = тупой.linspace (1, 3, 3)
шалфей: b = numpy.linspace (3, 6, 3)
шалфей: atan2 (а, б)
массив ([0.32175055, 0.41822433, 0.46364761])

шалфей: atan2 (1, а)
массив ([0,78539816, 0,46364761, 0,32175055])

шалфей: atan2 (а, 1)
массив ([0.78539816, 1.10714872, 1.247])

Урок 5 Клавиша ответа с 3 обозначениями функций

Найдите действительное число δ такое, что всякий раз, когда x находится в пределах δ от 3, f (x) находится в пределах 1 от 9. Запишите это число, используя обозначение min ( «Min» означает «минимум»). Если a и b — два числа, то min {a, b} — меньшее из чисел a и b.Например, min {5,4} = 4. Если a и b равны, тогда min {a, b} просто a (или b).

Вычислить кусочную функцию при заданном значении независимой переменной. Оцените функцию при заданном значении независимой переменной и упростите. — Z 4) g (x) = 3x — 2; g (X + 1) Используйте тест вертикальной линии, чтобы определить, является ли график графиком, в котором y является функцией x. 2x— 5, если x <-5 f (x) = Определить (-3).

Уравнение — это равенство, которому удовлетворяет уникальный набор значений ваших переменных.У вас есть после знака # = # фиксированное значение, фиксированный результат .. Например: уравнение # 4x-2 = 0 # имеет ноль в качестве результата и только # x = 1/2 # в качестве решения; это означает, что если вы подставите значение # x = 1/2 # в уравнение, вы получите нулевой результат, т. е. уравнение выполнено.

Введение в нотацию функций с использованием ее для описания знакомой проблемы (Tower Task) позволяет учащимся понять ее полезность и развить свое понимание концепции функции. Спланируйте 45-минутный урок математики или алгебры с помощью полезных советов Джеймса Бяласика

Используйте обозначение функций, чтобы описать функцию ситуации, обозначив функцию f.Опишите вход как x, выход как f (x) и точку координаты в обозначении функции (например, f (3) = 5 — это точка координат (3, 5)). Оцените функцию, представленную графически в виде функции.

Тема 3: Линейные функции 10/28 — Рабочий лист 3.1 Взаимосвязи и функции — ПОЗ. 10/29 или 30 — Рабочий лист обозначения функций 3.2 — ПОЗ. 10/31 — 3.5 / 3.6 Дополнительная практика WS — ПОЗ. 11/1 — Завершите рабочие задания астронавта — ПОЗ. 11/4 — Работа над пропущенными заданиями 11/5 или 11/6 — Проверка по теме 3 викторины 1 — ПОЛОЖЕНИЕ 11/7 — Нет 11/8 — 3.4 Дополнительная практика — ОБОЗНАЧЕНИЕ …

ассортимента. Если f — функция, а x — элемент ее области, то f (x) обозначает выход f, соответствующий входу x. График f — это график уравнения y = f (x). HSF-IF.A.2 Используйте нотацию функций, оценивайте функции для входных данных в их доменах и интерпретируйте операторы, которые используют нотацию функций в терминах контекста.

1 TG • 5 класс • Блок 4 • Урок 7 • Ответьте на основное руководство для учащихся «Решение проблем с объемом» (SG, стр. 195–197) Вопросы 1–8 1.* Форма может быть разной, но каждая должна иметь объем 12 см3. Один образец формы: 2. A. 5 см3 B. 5 см 3. 10 см3 4. 30 см3 Решение проблем с объемом SG • Уровень 5 • Блок 4 • Урок 7 195

Как найти брошенные автомобили, нуждающиеся в быстрой окупаемости 2020

02 февраля, 2015 · домен, 3 соединен с двумя элементами в диапазоне, 1 и 2. Следовательно, это отношение не является функцией. Пример 4 Оцените каждую функцию для данного значения. а. ƒ (1) если ƒ (x) 2×3 4×2 5x ƒ (1) 2 (1) 3 4 (1) 2 5 (1) x 1 2 4 5 или 7 b.g (4), если g (x) x4 3×2 4 g (4) (4) 4 3 (4) 2 4 x 4 256 48 4 или 212 1-1 xy 14 36 58 710 3. Ось симметрии квадратичной функции равна либо ось x, либо ось y. 4. График квадратичной функции, открывающейся вверх, не имеет максимального значения. 5. Х-точки пересечения графика квадратичной функции являются решениями соответствующего квадратного уравнения. 6. Все квадратные уравнения имеют два действительных решения. 7.

Конструкция плиты элеватора

ЦЕЛИ: .5.4 Пустые примечания. Алгебра 2: 5.4 Примечания: Пример 1 — Построение полиномиальной функции. Пример 2. Пример 3. Пример 4 .5.4 Письменные заметки

WS 5.11 Продолжение практики дроби — Операции с дробями, упрощение дробей (включая ключи ответов)

Common Core Algebra I .. • Во всем устройстве используются классические обозначения функций. … Урок 2. Обозначение функций. PDF-УРОК. ВИДЕО · КЛЮЧ ОТВЕТА в формате PDF. Общая базовая алгебра II. Блок 3. Урок 1. Прямая вариация — YouTube. 4. Август 2015 — 16 мин. — Хохгеладен фон Кирк Вейлер Общая базовая алгебра II.Раздел 3. Урок 1. Прямая вариация. Кирк Вейлер. Загрузка … Чтобы получить доступ к Риджентс, Рабочим листам Практики и Журнала, Планам уроков, Видео и другим ресурсам, щелкните Государственный стандарт в последнем столбце ниже. Чтобы увидеть текст государственного стандарта, наведите указатель мыши на стандарт.

30 суток арестованный автомобиль

f (x) = | х | — 2 ↓ ↓ f (- 5) = | — 5 | — 2 = 5 — 2 = 3. Здесь компактное обозначение f (- 5) = 3 указывает, что где x = — 5 (вход), функция приводит к y = 3 (выход).Другими словами, замените переменную значением, указанным в круглых скобках.

Иди по математике для 8 класса. Ключ с ответами. Глава 1 Реальные числа; Глава 2 Показатели и научная запись; Глава 3 Пропорциональные отношения; Глава 4 Непропорциональные отношения; Глава 5 Написание линейных уравнений; Глава 6 Функции; Глава 7 Решение линейных уравнений; Глава 8 Решение систем линейных уравнений; Глава 9 Преобразования и …

Ключевые решения 1 Основы функций ГЛАВА ВЫ ГОТОВЫ? СТРАНИЦА 3 1.D 2. C 3. A 4. E 5. ___3 10 = 0,3 6. __3 5 … Возможный ответ: Используются интервальные обозначения … 1.5.3. В основном, чем больше база, тем быстрее увеличивается функция 1.5.5. Обратите внимание, что 1 3 x = 3 x, что означает, что 1 3 x является отражением 3 по оси y! Аналогично с 10x. 1.5.6. Чем меньше база, тем быстрее функция переходит в 0. 1.5.16. а) все действительные числа; (b) Все 0 действительных чисел 1.5.17. f (x) = 3 2x 1.5.18. f (x …

Выполняется платеж Pua в год

3 5− 3 + 4 +2 Используйте их, чтобы помочь вам: o Наивысшая степень o Конечное поведение o Опережающий коэффициент (положительный или отрицательный) o -перехват. Все вместе 1.Функция = () показана ниже. Ответьте на следующие вопросы на основе графика: a) Укажите -перехват и -перехват функции.

Салют! Учите французский в том виде, в каком на нем действительно говорят во Франции. Забудьте об учебниках. Выберите один из наших курсов французского языка, чтобы научиться заказывать еду в ресторане, получить полезные советы от местных жителей и завязать дружескую беседу, наслаждаясь аперитивом на террасе очаровательного бистро, как это делают французы.

Это приводит к объяснению научных обозначений и продолжению работы над числами, записанными в этой форме.Материалы для учащихся состоят из страниц для учащихся для каждого урока в Модуле 1. Готовые к копированию материалы представляют собой набор оценок модуля, выходных билетов на урок и упражнений на беглость речи из материалов для учителя. обозначение функций. Он используется для поиска элемента в диапазоне, который будет соответствовать элементу в домене. Диаграмма отображения упорядоченных пар Таблица Graph (5, 0) (-2, 5) — (1, 3) (-6, 1) (-4, -1) xy 6 –1 –4 0 –2 1 1 3 5 5 xy 5 0 –2 5 1 3

Замки для автомойки Medeco

Получите весь Голливуд.com: списки лучших фильмов, новости и многое другое.

Пример 2: Определите ответ на следующий вопрос. 4,587 x 10 4 ÷ 1,2 x 10 -3 = 3,8 x 10 7 Если вы используете графический калькулятор TI, вы заметите, что он показывает научную нотацию с буквой «E» (для

18 января 2015 г. — Learn to записывайте большие числа, используя научную нотацию с этим практическим листом, который также развивает фундаментальные навыки с десятичными и показательными числами. Дополнительная информация Десятичные дроби четвертого класса Рабочие листы по алгебре и функциям: научная нотация Интерпретируйте скорость изменения и начальные значения линейных функций в терминах ситуаций что они моделируют.Сравните результаты и что … УРОК 6-3 x 0 1 …

Ascl3 молекулярная геометрия

В этом уроке мы изучим классическую нотацию f (x) для правил функций. Используются уравнения, таблицы и графические представления функций. Решение для входных данных …

32 Урок 4 Scientific Notation Curriculum Associates, LLC Копирование запрещено. Прочтите проблему ниже. Затем узнайте, как сравнивать числа, записанные в научных обозначениях. Земля находится примерно в 1,5 3 108 км от Солнца, а планета Нептун — почти в 4 км.5 3 109 км от Солнца. Расстояние от Нептуна до Солнца составляет примерно

3. В таблице ниже показана общая стоимость покупки n аккумуляторных блоков в долларах. Количество аккумуляторных блоков Общая стоимость (S) 4,90 8,90 12,90 16,90 f (n) Определите значение f (18) и сообщите, что оно представляет в данной ситуации. Ваш ход Создайте явное правило в обозначении функций для арифметической последовательности, представленной в таблице. Открытие: 3.OP: Открытие главы: Раздел 3.1: 3.1.1: Горизонтальные и вертикальные растяжки: 3.1.2: Применение экспоненциальных функций: 3.1.3: Экспоненциальное растяжение …

Руководство по ремонту гидравлического поршневого насоса

Урок 4: Научная нотация … необходимо использовать 2-ю функциональную клавишу, чтобы использовать его … вы получаете Такой же ответ. 4,587 x 104 ÷ 1,2 x 10-3 = 3,8 x 107

Инструкция по эксплуатации микроволн Whirlpool

Какова максимальная скорость точки на внешней стороне колеса в 15 см от оси

Сельскохозяйственная земля для аренда владельцем в tn

Рабочий лист Easy Lewis Structure

1.5-дюймовый кронштейн для флагштока

Камбузная печь Estate

Tyrone game

Sharepoint Powerapps для начинающих

Лучший частный сервер aion 2020

Звонок дверной звонок сплошной синий свет

Резонансная структура so32

Какой организм имеет наименьшее количество общих характеристик

Финансовая модель накопителя энергии (excel)

Ubakka nova musicasdinheiro 2020 mp3

Silencerco omega 300 Cleaning

Ignite pro 4

Покупатель Ebay заявляет, что товар отсутствует в упаковке

1927 Estate heatrola плита

Ответы лаборатории органических молекул

Как 13 колоний стали состояниями

Apple magic trackpad 2 не работает тактильная обратная связь

гр выкройки для шитья пальто eyhound бесплатно

Сколько атомов водорода присутствует в молекуле глюкозы, галактозы или фруктозы

Как использовать daz face transfer

Diablo 3 nintendo switch control

Если я плачу мой гонорар за восстановление будет ли моя лицензия по-прежнему приостановлена

Детали кустореза Robin ht200

Какое событие завершило викторину эпохи абсолютизма

tikz pgf — Графики функций — TeX

Можете ли вы помочь мне с моей страницей графиков функций? Я мог бы сделать первые четыре графика, но есть проблема с построением других графиков.Все графики должны иметь такой же размер, как и первые четыре. Спасибо!

  \ documentclass {article}
\ usepackage {pgfplots}
\ usepackage {subfigure}
\ usepackage {tikz}
\ usetikzlibrary {shape.geometric, calc, стрелки, декорации.маркировки, декорации.pathmorphing}
\ newcommand {\ tg} {\ mathop {\ mathrm {tg}}}
\ newcommand {\ cotg} {\ mathop {\ mathrm {cotg}}}
\ newcommand {\ arctg} {\ mathop {\ mathrm {arctg}}}
\ newcommand {\ arccotg} {\ mathop {\ mathrm {arccotg}}}
\ begin {document}
\ begin {figure} [H]
\ центрирование
\ subfigure
{
\ begin {tikzpicture} [гладкий, масштаб = 0.8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {1}) [вверху] {$ y = c $};
 \ end {tikzpicture}
}
%
{
  \ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = x $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкий, масштаб = 0.3 $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ frac {1} {x} $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1.x $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ ln {x} $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1.5: 1.5] узел графика (\ x, {\ x}) [вверху] {$ y = \ sin (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ cos (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1.5) - (0,1.5) узел [правый] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ tg (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ cotg (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
       \ draw [толстый, ->] (0, -1.5) - (0,1.5) узел [правый] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ arcsin (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ arccos (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1.5) - (0,1.5) узел [правый] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ arctg (x) $};
  \ end {tikzpicture}
}
%
\ subfigure
{
\ begin {tikzpicture} [гладкая, масштаб = 0,8]
        \ draw [толстый, ->] (-2,0) - (2,0) узел [внизу] {$ x $};
        \ draw [толстый, ->] (0, -1,5) - (0,1,5) узел [справа] {$ y $};
        \ draw [синий, толстый, домен = -1,5: 1,5] узел графика (\ x, {\ x}) [вверху] {$ y = \ arccotg (x) $};
  \ end {tikzpicture}
}
\ end {рисунок}
\ конец {документ}

Урок 5. свойства и график функции y=tgx и y=ctg x — Алгебра и начала математического анализа — 11 класс

.3. СВОЙСТВА ФУНКЦИИ y=tg⁡x И ЕЕ ГРАФИК

График функции y 2 cos x. Графики тригонометрических функций кратных углов. Задачи для самостоятельного решения

Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»

Определение функции косинуса у=cos(x)

Свойства функции cos(x)

Примеры с функцией cos(x)

Задачи для самостоятельного решения

График y tgx 1. Функции y = tgx и y = ctgx, их свойства и графики

Y = sin(x)

Y = cos(x)

Y = tg(x)

Y = ctg(x)

Нужна помощь в учебе?

Y tgx график. Урок «Функции y = tgx, y = ctgx, их свойства и графики»

Y = sin(x)

Y = cos(x)

Y = tg(x)

Y = ctg(x)

Нужна помощь в учебе?

Графики тригонометрических функций кратных углов. Графики тригонометрических функций кратных углов Задачи для самостоятельного решения

Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»

Определение функции косинуса у=cos(x)

Свойства функции cos(x)

Примеры с функцией cos(x)

Задачи для самостоятельного решения

Определение функций с помощью графиков | Колледж алгебры

Результаты обучения

Как сделать: для данного графика используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.

Пример: применение теста вертикальной линии

Попробуйте

Тест горизонтальной линии

Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию.

Пример: применение теста горизонтальной линии

Определение основных функций набора инструментов

Попробуйте

Внесите свой вклад!

BioMath: тригонометрические функции

Алгебра 2, модуль 3, контрольный опрос по родительским функциям и преобразованиям 3 1

Преобразования функций: размышления | Purplemath

Purplemath

MathHelp.com

Учитывая приведенный ниже график функции

Учитывая функцию

Тригонометрические функции — Справочное руководство Sage 9.2: Функции

Урок 5 Клавиша ответа с 3 обозначениями функций

Как найти брошенные автомобили, нуждающиеся в быстрой окупаемости 2020

Конструкция плиты элеватора

30 суток арестованный автомобиль

Выполняется платеж Pua в год

Замки для автомойки Medeco

Ascl3 молекулярная геометрия

Руководство по ремонту гидравлического поршневого насоса

Инструкция по эксплуатации микроволн Whirlpool

Какова максимальная скорость точки на внешней стороне колеса в 15 см от оси

Сельскохозяйственная земля для аренда владельцем в tn

Рабочий лист Easy Lewis Structure

1.5-дюймовый кронштейн для флагштока

Камбузная печь Estate

Tyrone game

Лучший частный сервер aion 2020

Звонок дверной звонок сплошной синий свет

Резонансная структура so32

Какой организм имеет наименьшее количество общих характеристик

Финансовая модель накопителя энергии (excel)

Ubakka nova musicasdinheiro 2020 mp3

Silencerco omega 300 Cleaning

Ignite pro 4

Покупатель Ebay заявляет, что товар отсутствует в упаковке

1927 Estate heatrola плита

Ответы лаборатории органических молекул

Как 13 колоний стали состояниями

Apple magic trackpad 2 не работает тактильная обратная связь

гр выкройки для шитья пальто eyhound бесплатно

Сколько атомов водорода присутствует в молекуле глюкозы, галактозы или фруктозы

Как использовать daz face transfer

Diablo 3 nintendo switch control

Если я плачу мой гонорар за восстановление будет ли моя лицензия по-прежнему приостановлена ​​

Детали кустореза Robin ht200

Какое событие завершило викторину эпохи абсолютизма

Если я плачу мой гонорар за восстановление будет ли моя лицензия по-прежнему приостановлена