Методы решения систем рациональных уравнений. Алгебра, 9 класс: уроки, тесты, задания.

1.	Метод сложения (линейные уравнения) Сложность: лёгкое
2.	Метод подстановки (линейные уравнения) Сложность: лёгкое
3.	Корни квадратного уравнения, теорема Виета Сложность: лёгкое
4.	Метод подстановки (линейное и квадратное) Сложность: лёгкое
5.	Метод алгебраического сложения Сложность: среднее
6.	Способ сложения Сложность: среднее
7.	Пары чисел, которые являются решением системы уравнений Сложность: среднее
8.	Графический метод (парабола и прямая) Сложность: среднее
9.	Графический метод (гипербола и прямая) Сложность: среднее
10.	Графический метод (элементарные функции) Сложность: среднее
11.	Система квадратных уравнений Сложность: среднее
12.	Система уравнений (линейное и квадратное) I Сложность: среднее
13.	Система уравнений (линейное и квадратное) II Сложность: среднее
14.	Система уравнений (линейное и квадратное) III Сложность: среднее
15.	Задача на составление системы уравнений Сложность: среднее
16.	Система рациональных уравнений Сложность: среднее
17.	Система, состоящая из рационального и квадратного уравнений Сложность: среднее
18.	Система, состоящая из рационального и линейного уравнений Сложность: среднее
19.	Система рациональных уравнений, вводится одна новая переменная Сложность: среднее
20.	Система, состоящая из рациональных уравнений Сложность: среднее
21.	Система, состоящая из квадратного и рационального уравнений Сложность: среднее
22.	Система линейных уравнений Сложность: среднее
23.	Система, состоящая из квадратного и рационального уравнений, метод умножения Сложность: среднее
24.	Пары чисел, которые являются решением системы уравнений Сложность: среднее
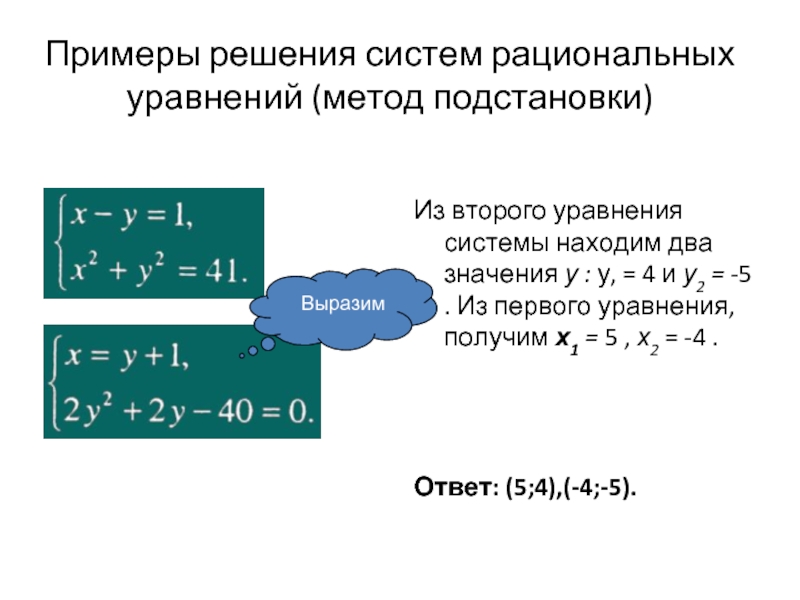
25.	Графический метод (окружность и парабола) Сложность: сложное

Способы решения систем уравнений с двумя неизвестными

Линейные системы уравнений

Системы линейных уравнений. Метод подстановки 

+ показать

• Выражаем одну переменную через другую.

• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.

• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.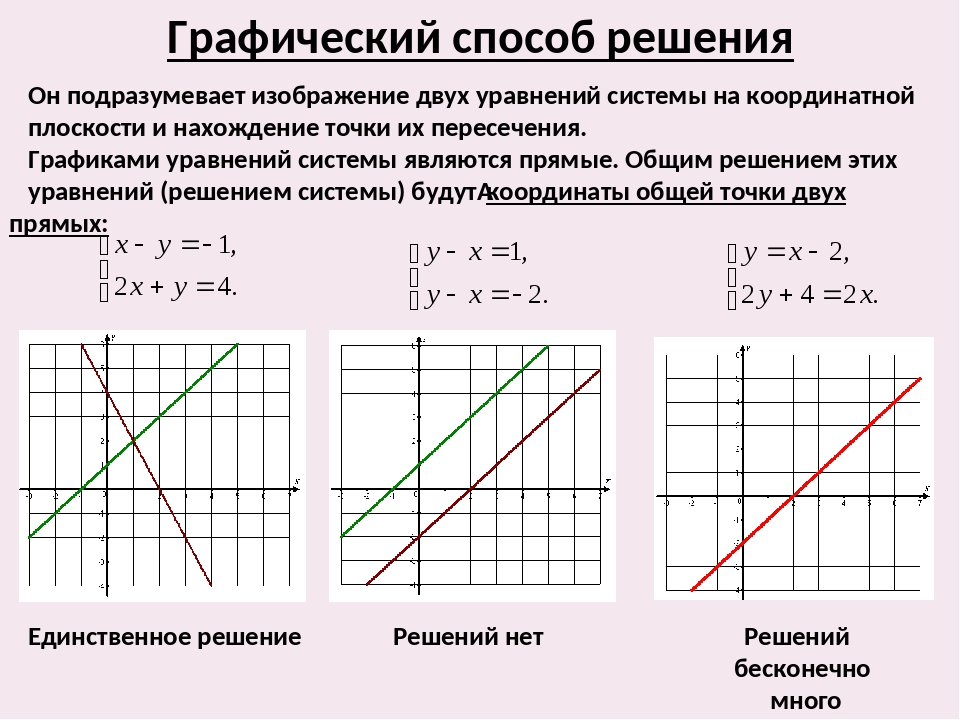

Решить систему уравнений: 

Решение: + показать

Системы линейных уравнений. Метод сложения 

+ показать

• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.

• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной. 

• Решаем  полученное уравнение с одной неизвестной.

• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.

1. Решить систему уравнений: 

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

2. Решить систему уравнений: 

Решение: + показать

Нелинейные системы уравнений

Системы уравнений, сводящихся к линейным

1.  Решить систему уравнений: 

Решение: + показать

Можно сделать замену и Тогда выходим на систему линейных уравнений:

Систему можно решить методом сложения, например.

Но приведем решение без замены.

Умножим первое уравнение системы на , второе – на и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.

Ответ:  

2. Решить систему уравнений: 

Решение: + показать

Можно сделать замену и выйти на систему линейных уравнений:

Приведем решение без замены.

Выражаем из второго уравнения системы и подставляем в первое.

Ответ:  

Нелинейные системы уравнений. Метод подстановки

Решить систему уравнений: 

Решение: + показать

Выражаем из первого уравнения системы и подставляем во второе.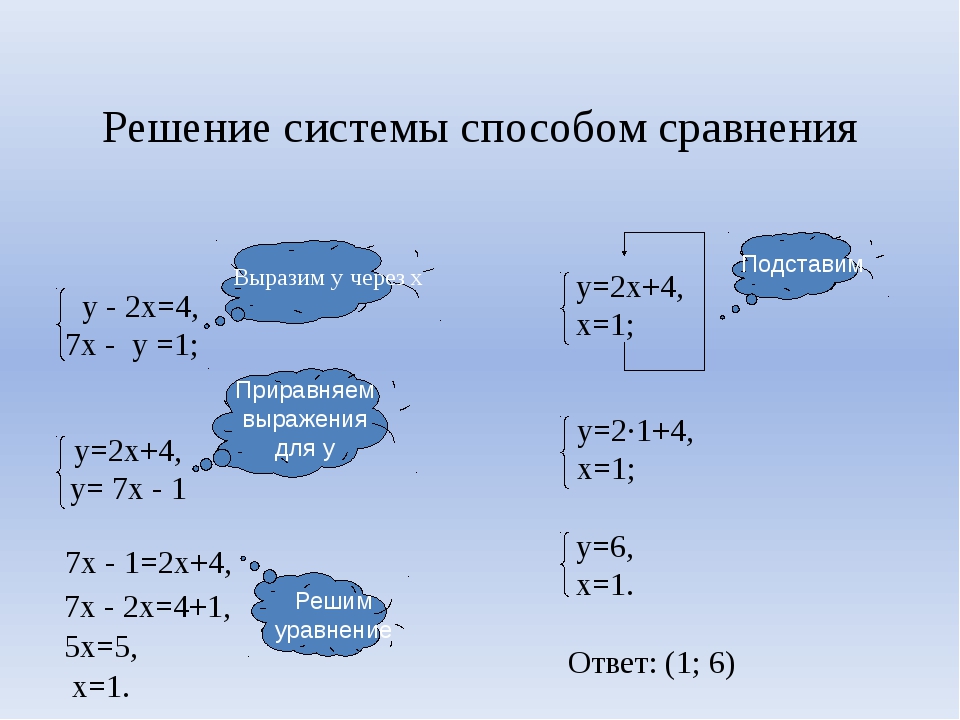

Ответ:  

Нелинейные системы уравнений. Метод сложения

Решить систему уравнений: 

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

Нелинейные системы уравнений. Метод почленного умножения (деления)

1. Решить систему уравнений: 

Решение: + показать

Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений.

Ответ:  

Симметрические системы. Метод введения переменной

Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных и – уравнение, которое не изменяется при замене на и на .

Для таких систем удобно использовать замену  

Решить систему уравнений: 

Решение: + показать

При замене  приходим к следующей системе

 которую будем решать способом подстановки:

Производим обратную замену:

Ответ:

Системы однородных уравнений и приводящиеся к ним системы

Однородным уравнением с двумя неизвестными  будем называть уравнение вида

1. Решить систему уравнений: 

Решение: + показать

2. Решить систему уравнений: 

Решение: + показать

Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.

Ответ:

Графический метод решения систем уравнений

1. Решите графически систему уравнений: 

Решение: + показать

Выразим в обеих строках системы через :

Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.

Ответ: 

2. Решите графически систему уравнений: 

Решение: + показать

3. Решите графически систему уравнений: 

Решение: + показать

Задания для самостоятельной работы

+ показать

Решите системы уравнений:

1.

Ответ:

2. 

Ответ:

3. 

Ответ:

4. 

Ответ:

5. 

Ответ:

6. 

Ответ:

7. 

Ответ:

8. 

Ответ:

Решите графически системы уравнений:

9. 

Ответ:

10. 

Ответ:

Метод сложения в системе уравнений

23 октября 2015

Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.

Способ сложения состоит из трёх простых шагов:

1. Посмотреть на систему и выбрать переменную, у которой в каждом уравнении стоят одинаковые (либо противоположные) коэффициенты;
2. Выполнить алгебраическое вычитание (для противоположных чисел — сложение) уравнений друг из друга, после чего привести подобные слагаемые;
3. Решить новое уравнение, получившееся после второго шага.

Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.

Однако на практике всё не так просто. Причин тому несколько:

• Решение уравнений способом сложения подразумевает, что во всех строчках должны присутствовать переменные с одинаковыми/противоположными коэффициентами. А что делать, если это требование не выполняется?
• Далеко не всегда после сложения/вычитания уравнений указанным способом мы получим красивую конструкцию, которая легко решается. Возможно ли как-то упростить выкладки и ускорить вычисления?

Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:

Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.

Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.

Вообще, существует два метода решения подобных систем:

1. Метод сложения;
2. Метод выражения одной переменной через другую.

Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.

Результатами подобных махинаций будет новое уравнение, которое, если и имеет корни, то они обязательно будут находиться среди корней исходного уравнения. Поэтому наша задача — сделать вычитание или сложение таким образом, чтобы или $x$, или $y$ исчез.

Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.

Решение легких задач с применением способа сложения

Итак, учимся применять метод сложения на примере двух простейших выражений.

Задача № 1

\[\left\{ \begin{align}& 5x-4y=22 \\& 7x+4y=2 \\\end{align} \right. \]

Заметим, что у $y$ коэффициент в первом уравнении $-4$, а во втором — $+4$. Они взаимно противоположны, поэтому логично предположить, что если мы их сложим, то в полученной сумме «игреки» взаимно уничтожатся. Складываем и получаем:

\[12x=24\]

Решаем простейшую конструкцию:

\[x=2\]

Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:

\[5\cdot 2-4y=22\]

\[10-4y=22\]

Решаем:

\[-4y=22-10\]

\[-4y=12\left| :\left( -4 \right) \right.\]

\[y=-3\]

Ответ: $\left( 2;-3 \right)$.

Задача № 2

\[\left\{ \begin{align}& -6x+y=21 \\& 6x-11y=-51 \\\end{align} \right.\]

Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:

\[0-10y=-30\]

Мы получили простейшее линейное уравнение, давайте решим его:

\[y=3\]

Теперь давайте найдем $x$:

\[6x-11\cdot 3=-5\]

\[6x=-51+33\]

\[6x=-18\]

\[x=-3\]

Ответ: $\left( -3;3 \right)$.

Важные моменты

Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:

1. Если есть противоположные коэффициенты при одной из переменных, то необходимо сложить все переменные в уравнении. В этом случае одна из них уничтожится.
2. Найденную переменную подставляем в любое из уравнений системы, чтобы найти вторую.
3. Окончательную запись ответа можно представить по-разному. Например, так — $x=…,y=…$, или в виде координаты точек — $\left( …;… \right)$. Второй вариант предпочтительней. Главное помнить, что первой координатой идет $x$, а второй — $y$.
4. Правило записывать ответ в виде координат точки применимо не всегда. Например, его нельзя использовать, когда в роли переменных выступают не $x$ и $y$, а, к примеру, $a$ и $b$.

В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.

Решение легких задач с применением метода вычитания

Задача № 1

\[\left\{ \begin{align}& 10x-3y=5 \\& -6x-3y=-27 \\\end{align} \right. \]

Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:

\[10x-\left( -6x \right)-3y-\left( -3y \right)=5-\left( -27 \right)\]

\[10x+6x-3y+3y=5+27\]

\[16x=32\left| :16 \right.\]

\[x=2\]

Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:

\[10\cdot 2-3y=5\]

\[20-5=3y\]

\[15=3y\]

\[y=5\]

Ответ: $\left( 2;5 \right)$.

Задача № 2

\[\left\{ \begin{align}& 5x+4y=-22 \\& 5x-2y=-4 \\\end{align} \right.\]

Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:

\[0+6y=-22+4\]

\[6y=-18\left| :6 \right.\]

\[y=-3\]

Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:

\[5x-2\cdot \left( -3 \right)=-4\]

\[5x+6=-4\]

\[5x=-4-6\]

\[5x=-10\left| :5 \right. \]

\[x=-2\]

Ответ: $\left( -3;-2 \right)$.

Нюансы решения

Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.

Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.

Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.

Решение задач методом домножения на коэффициент

Пример № 1

\[\left\{ \begin{align}& 5x-9y=38 \\& 3x+2y=8 \\\end{align} \right.\]

Мы видим, что ни при $x$, ни при $y$ коэффициенты не только не взаимно противоположны, но и вообще никак не соотносятся с другим уравнением. Эти коэффициенты никак не исчезнут, даже если мы сложим или вычтем уравнения друг из друга. Поэтому необходимо применить домножение. Давайте попытаемся избавиться от переменной $y$. Для этого мы домножим первое уравнение на коэффициент при $y$ из второго уравнения, а второе уравнение — при $y$ из первого уравнения, при этом не трогая знак. Умножаем и получаем новую систему:

\[\left\{ \begin{align}& 10x-18y=76 \\& 27x+18y=72 \\\end{align} \right.\]

Смотрим на нее: при $y$ противоположные коэффициенты. В такой ситуации необходимо применять метод сложения. Сложим:

\[37x=148\]

\[x=4\]

Теперь необходимо найти $y$. Для этого подставим $x$ в первое выражение:

\[5\cdot 4-9y=38\]

\[20-9y=38\]

\[-9y=18\left| :\left( -9 \right) \right.\]

\[y=-2\]

Ответ: $\left( 4;-2 \right)$.

Пример № 2

\[\left\{ \begin{align}& 11x+4y=-18 \\& 13x-6y=-32 \\\end{align} \right.\]

Вновь коэффициенты ни при одной из переменных не согласованы. Домножим на коэффициенты при $y$:

\[\left\{ \begin{align}& 11x+4y=-18\left| 6 \right. \\& 13x-6y=-32\left| 4 \right. \\\end{align} \right.\]

\[\left\{ \begin{align}& 66x+24y=-108 \\& 52x-24y=-128 \\\end{align} \right.\]

Наша новая система равносильна предыдущей, однако коэффициенты при $y$ являются взаимно противоположными, и поэтому здесь легко применить метод сложения:

\[118x=-136\]

\[x=-2\]

Теперь найдем $y$, подставив $x$ в первое уравнение:

\[11\cdot \left( -2 \right)+4y=-18\]

\[-22+4y=-18\]

\[4y=4\]

\[y=1\]

Ответ: $\left( -2;1 \right)$.

Нюансы решения

Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:

1. Смотрим на систему и анализируем каждое уравнение.
2. Если мы видим, что ни при $y$, ни при $x$ коэффициенты не согласованы, т.е. они не являются ни равными, ни противоположными, то делаем следующее: выбираем переменную, от которой нужно избавиться, а затем смотрим на коэффициенты при этих уравнениях. Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
3. Находим одну переменную.
4. Подставляем найденную переменную в одно из двух уравнений системы и находим вторую.
5. Записываем ответ в виде координаты точек, если у нас переменные $x$ и $y$.

Но даже в таком нехитром алгоритме есть свои тонкости, например, коэффициенты при $x$ или $y$ могут быть дробями и прочими «некрасивыми» числами. Эти случаи мы сейчас рассмотрим отдельно, потому что в них можно действовать несколько иначе, чем по стандартному алгоритму.

Решение задач с дробными числами

Пример № 1

\[\left\{ \begin{align}& 4m-3n=32 \\& 0,8m+2,5n=-6 \\\end{align} \right.\]

Для начала заметим, что во втором уравнении присутствуют дроби. Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:

\[\left\{ \begin{align}& 4m-3n=32 \\& 4m+12,5m=-30 \\\end{align} \right.\]

Вычитаем уравнения друг из друга:

\[0-15,5n=62\]

\[n=\frac{65}{-15,5}=-\frac{124}{31}=-4\]

$n$ мы нашли, теперь посчитаем $m$:

\[4m-3\cdot \left( -4 \right)=32\]

\[4m+12=32\]

\[4m=20\]

\[m=5\]

Ответ: $n=-4;m=5$

Пример № 2

\[\left\{ \begin{align}& 2,5p+1,5k=-13\left| 4 \right. \\& 2p-5k=2\left| 5 \right. \\\end{align} \right.\]

Здесь, как и в предыдущей системе, присутствуют дробные коэффициенты, однако ни при одной из переменных коэффициенты в целое число раз друг в друга не укладываются. Поэтому используем стандартный алгоритм. Избавится от $p$:

\[\left\{ \begin{align}& 5p+3k=-26 \\& 5p-12,5k=5 \\\end{align} \right.\]

Применяем метод вычитания:

\[15,5k=-31\]

\[k=-\frac{31}{15,5}=-\frac{62}{31}=-2\]

Давайте найдем $p$, подставив $k$ во вторую конструкцию:

\[2p-5\cdot \left( -2 \right)=2\]

\[2p-5\cdot \left( -2 \right)=2\]

\[2p+10=2\]

\[2p=-8\]

\[p=-4\]

Ответ: $p=-4;k=-2$.

Нюансы решения

Вот и вся оптимизация. В первом уравнении мы не стали домножать вообще ни на что, а второе уравнение домножили на $5$. В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.

Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.

В заключение хотел бы обратить ваше внимание на формат записи ответа. Как я уже и говорил, поскольку здесь у нас тут не $x$ и $y$, а другие значения, мы пользуемся нестандартной записью вида:

\[n=-4\]

\[m=5\]

Решение сложных систем уравнений

В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.

Система № 1

\[\left\{ \begin{align}& 3\left( 2x-y \right)+5=-2\left( x+3y \right)+4 \\& 6\left( y+1 \right)-1=5\left( 2x-1 \right)+8 \\\end{align} \right.\]

Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.

Первая:

\[3\left( 2x-y \right)+5=-2\left( x+3y \right)+4\]

\[6x-3y+5=-2x-6y+4\]

\[6x-3y+2x+6y=4-5\]

\[8x+3y=-1\]

Вторая:

\[6\left( y+1 \right)-1=5\left( 2x-1 \right)+8\]

\[6y+6-1=10x-5+8\]

\[6y-10x=-5+8-6+1\]

\[-10x+6y=-2\]

Итого мы получим окончательную систему, которая равносильна исходной:

\[\left\{ \begin{align}& 8x+3y=-1 \\& -10x+6y=-2 \\\end{align} \right.\]

Посмотрим на коэффициенты при $y$: $3$ укладывается в $6$ два раза, поэтому домножим первое уравнение на $2$:

\[\left\{ \begin{align}& 16x+6y=-2 \\& -10+6y=-2 \\\end{align} \right.\]

Коэффициенты при $y$ теперь равны, поэтому вычитаем из первого уравнения второе: $$

\[26x=0\]

\[x=0\]

Теперь найдем $y$:

\[3y=-1\]

\[y=-\frac{1}{3}\]

Ответ: $\left( 0;-\frac{1}{3} \right)$

Система № 2

\[\left\{ \begin{align}& 4\left( a-3b \right)-2a=3\left( b+4 \right)-11 \\& -3\left( b-2a \right)-12=2\left( a-5 \right)+b \\\end{align} \right. \]

Преобразуем первое выражение:

\[4\left( a-3b \right)-2a=3\left( b+4 \right)-11\]

\[4a-12b-2a=3b+12-11\]

\[4a-12b-2a-3b=12-11\]

\[2a-15b=1\]

Разбираемся со вторым:

\[-3\left( b-2a \right)-12=2\left( a-5 \right)+b\]

\[-3b+6a-12=2a-10+b\]

\[-3b+6a-2a-b=-10+12\]

\[4a-4b=2\]

Итого, наша первоначальная система примет такой вид:

\[\left\{ \begin{align}& 2a-15b=1 \\& 4a-4b=2 \\\end{align} \right.\]

Посмотрев на коэффициенты при $a$, мы видим, что первое уравнение нужно домножить на $2$:

\[\left\{ \begin{align}& 4a-30b=2 \\& 4a-4b=2 \\\end{align} \right.\]

Вычитаем из первой конструкции вторую:

\[0-26b=0\]

\[-26b=0\]

\[b=0\]

Теперь найдем $a$:

\[2a-0=1\]

\[a=\frac{1}{2}\]

Ответ: $\left( a=\frac{1}{2};b=0 \right)$.

Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!

Смотрите также:

1. Пробный ЕГЭ-2011 по математике, вариант №5
2. Решение ЕГЭ-2011: вариант 1, часть B
3. Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
4. Как решать задачи про смеси и сплавы
5. Задача B5: площадь фигуры без клеток

Решение систем уравнений: способ сложения + примеры

Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:

{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2

Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 – некоторые вещественные числа.  Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения. 

Алгоритм решения способом сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.

Пример решения способом сложения

Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:

{3*x + 2*y = 10;
{5*x + 3*y = 12;

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.

{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2

Получим следующую систему уравнений:

{9*x+6*y = 30;
{10*x+6*y=24;

Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

10*x+6*y – (9*x+6*y) = 24-30; x=-6;

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

{3*(-6) + 2*y =10;
{2*y=28; y =14;

Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.

{3*x + 2*y = 10;
{5*x + 3*y = 12;

{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;

{10 = 10;
{12=12;

Как видите, получились два верных равенства, следовательно, мы нашли верное решение.

Ответ: (6, 14)

Нужна помощь в учебе?

Предыдущая тема: Решение систем уравнений: способ подстановки + примеры
Следующая тема:&nbsp&nbsp&nbspРешение задач с помощью систем уравнений: общая схема решения

6.9.3. Решение систем линейных уравнений методом сложения.

Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 235 Опубликовано 4 декабря 2015

Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:

1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;

2) сложить почленно полученные уравнения и найти значение одной из переменных;

3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.

Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).

Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.

Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24.  Вторым уравнением системы можно записать любое уравнение исходной системы.

Найдём х и подставим его значение во 2-ое уравнение.

Решаем 2–ое уравнение: 9-у = 14, отсюда у = -5.

Сделаем проверку. Подставим значения х = 3 и у = -5 в первоначальную систему уравнений.

Примечание. Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.

Ответ: (3; -5).

Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:

Сложим эти равенства почленно.

Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):

Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.

Решаем последнее уравнение системы и получаем х = -2.

Ответ: (-2; 1).

Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.

Подставим значение х=4 во 2-ое уравнение.

3 · 4 — 5у = 27. Упростим: 12 — 5у = 27, отсюда -5у = 15, а у = -3.

Ответ: (4; -3).

7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.

Комментарии преподавателя

Метод подстановки.

Су­ще­ству­ет несколь­ко ме­то­дов ре­ше­ния си­стем. Один из них метод под­ста­нов­ки. Рас­смот­рим при­мер.

При­мер 1:

Суть ме­то­да под­ста­нов­ки за­клю­ча­ет­ся в том, что в одном из урав­не­ний нужно вы­ра­зить одну пе­ре­мен­ную через вто­рую и под­ста­вить по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние.

В дан­ном слу­чае удоб­но вы­ра­зить х во вто­ром урав­не­нии:

Под­ста­вим по­лу­чен­ное вы­ра­же­ние в пер­вое урав­не­ние:

Пре­об­ра­зу­ем пер­вое урав­не­ние:

,

 ,

 ,

Под­ста­вим по­лу­чен­ное зна­че­ние во вто­рое урав­не­ние:

, ,

По­лу­ча­ем сле­ду­ю­щее ре­ше­ние си­сте­мы:

При­мер 2:

В дан­ном слу­чае неко­то­рая слож­ность за­клю­ча­ет­ся в том, что ис­ход­ную си­сте­му нужно пре­об­ра­зо­вать, чтобы была воз­мож­ность удоб­но и без оши­бок при­ме­нить метод под­ста­нов­ки. Для этого умно­жим оба урав­не­ния на шесть:

Вы­ра­зим у из пер­во­го урав­не­ния:

Под­ста­вим по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние и вы­пол­ним пре­об­ра­зо­ва­ния:

, ,

 ,

Под­ста­вим по­лу­чен­ное зна­че­ние в пер­вое урав­не­ние:

По­лу­ча­ем един­ствен­ное ре­ше­ние си­сте­мы, пара чисел:

Вывод:

на дан­ном уроке мы озна­ко­ми­лись с по­ня­ти­ем си­сте­мы двух ли­ней­ных урав­не­ний с двумя неиз­вест­ны­ми и одним из ме­то­дов ее ре­ше­ния – спо­со­бом под­ста­нов­ки. Мы ре­ши­ли при­ме­ры для по­ни­ма­ния и за­креп­ле­ния дан­ной тех­ни­ки.

Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10

Метод сложения.

Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.

Метод ал­геб­ра­и­че­ско­го сло­же­ния, как и метод под­ста­нов­ки, за­клю­ча­ет­ся в том, что из­на­чаль­но из двух урав­не­ний с двумя пе­ре­мен­ны­ми нужно по­лу­чить одно урав­не­ние с одной пе­ре­мен­ной. Рас­смот­рим метод ал­геб­ра­и­че­ско­го сло­же­ния на при­ме­ре:

При­мер 1:

За­да­на си­сте­ма двух ли­ней­ных урав­не­ний с двумя неиз­вест­ны­ми, и нужно найти такую пару х и у, чтобы при под­ста­нов­ке ее в урав­не­ния по­лу­чи­лись вер­ные чис­ло­вые ра­вен­ства.

Неслож­но за­ме­тить, что в пер­вом урав­не­нии у стоит с ми­ну­сом, а во вто­ром – с плю­сом, и если сло­жить эти урав­не­ния, то у уни­что­жит­ся, и мы по­лу­чим одно урав­не­ние с одной неиз­вест­ной:

+

По­лу­ча­ем:

Най­дем зна­че­ние х:

, 

Под­ста­вим зна­че­ние х во вто­рое урав­не­ние и най­дем у:

Ответ: (2,4; 2,2)

Об­ра­тим вни­ма­ние на то, что мы рас­смат­ри­ва­ем метод ал­геб­ра­и­че­ско­го сло­же­ния, зна­чит, урав­не­ния можно не толь­ко скла­ды­вать, но и вы­чи­тать. Рас­смот­рим при­мер:

При­мер 

При сло­же­нии урав­не­ний по­лу­чим:

, 

По­про­бу­ем вы­честь урав­не­ния, при­чем, вы­чтем пер­вое из вто­ро­го:

, 

Ответ: (5,5; 0,5)

Вывод:

на дан­ном уроке мы рас­смот­ре­ли новый метод ре­ше­ния си­стем двух ли­ней­ных урав­не­ний – метод ал­геб­ра­и­че­ско­го сло­же­ния. Мы ре­ши­ли несколь­ко при­ме­ров для за­креп­ле­ния дан­ной тех­ни­ки.

• Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
• Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
• Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
•  Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.

Примеры. Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Ответ: (4; 5).

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

Ответ: (-2; 5).

Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/metod-algebraicheskogo-slozheniya?konspekt&chapter_id=10

http://www.mathematics-repetition.com/6-klass-mathematics/6-9-1-reshenie-sistem-lineynh-uravneniy-grafitcheskim-sposobom.html

Источник видео: https://www.youtube.com/watch?v=VltC62A-Tt4

Решение систем уравнений второй степени и решение задач с помощью таких систем 9 класс онлайн-подготовка на Ростелеком

Тема 8.

Решение систем уравнений второй степени и решение задач с помощью таких систем.

Какие основные способы решения систем уравнений вы знаете? (методы сложения, подстановки, графический)

Каким способом можно решить систему, одно из уравнений которой – уравнение второй степени?

Такие системы всегда можно решить способом подстановки. Для этого поступают следующим образом:

1. 
   Выражают из уравнения первой степени одну переменную через другую;
2. 
   Подставляют полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;
3. 
   Решают получившееся уравнение с одной переменной;
4. 
   Находят соответствующие значения второй переменной.

Рассмотрим пример:

Решим систему уравнений:

x2+y=14,y-x=8;

Выразим из первого уравнения переменную y и подставим во второе:

y=14-x2,14-x2-x=8;

Решим второе уравнение, относительно х:

x² + x — 6 = 0, корни которого равны (– 3) и 2.

Вернемся к системе:

x1=-3,y1=14—32;

x1=-3,y1=14—32;

x1=-3,y1=5;

x2=2,y2=10;

Рассмотрим еще один пример, решим систему

x2-y2=17,x-y=2;

Эту систему так же можно решить методом подстановки, выразив переменную x, но можно упростить первое уравнение.

Заметим, что левую часть первого уравнения можно разложить на множители по формуле разности квадратов, получим:

x-yx+y=17,x-y=2;

Из второго уравнения разность x — y = 2. Поэтому вместо первой скобки в первое уравнение подставим число 2, получим:

2x+y=17,x-y=2;

2x+y=17,x-y=2;

Разделим обе части первого уравнения на 2, получим:

x+y=8,5,x-y=2;

А эту систему давай решим методом сложения, сложим два уравнения, а затем из первого уравнения вычтем второе, получим:

2x=10,5,2y=6,5;

x=5,25,y=3,25.

А теперь решим несколько задач с помощью систем: уравнений второй системы:

Сумма двух чисел равна 12, а их произведение равно 35. Найдите эти числа.

Пусть число x – первое число, а y – второе число. Тогда получим:

x+y=12,x∙y=35;

Выразим из первого уравнения переменную х и подставим во второе, получим:

x=12-y,x∙y=35;

x=12-y,12-yy=35;

Решим уравнение:

12y — y² — 35 = 0

y² — 12y + 35 = 0

Получим корни 5 и 7.

Возвращаемся к нашей системе:

y1=55x=35

y2=7,7x=35;

y1=5×1=7

y2=7×2=5

Ответ: (7;5) и (5;7)

Рассмотрим еще одну задачу:

Площадь прямоугольного треугольника равен 24 см², а его гипотенуза равна 10 см. Каковы катеты треугольника?

Пусть a – длина одного катета, а b – длина второго катета.

Вспомним формулу площади прямоугольного треугольника и теорему Пифагора:

Итак, площадь равна половине произведения катетов.

А квадрат гипотенузы равен сумме квадратов катетов:

12ab=24a2+b2=100

Решим эту систему, первое уравнение домножим на 2, получим:

ab=48a2+b2=100

Выразим переменную а из первого уравнения и подставим во второе, получим:

a=48b48b2+b2=100

Решим второе уравнение системы:

2304b2+b2-100=0,

b4-100b2+2304=0, решим это биквадратное уравнение:

Пусть b² = t, тогда получим:

t² — 100t + 2304 = 0, отсюда

t₁ = 64, t₂ = 36

Возвращаемся к нашей замене, получим:

b1,2=±8,b3,4=±6, так как b – это длина катета, то она не может быть отрицательной, следовательно, b равно 6 или 8, тогда второй катет равен 8 или 6 соответственно.

3 Методы решения систем уравнений

Три метода, наиболее часто используемые для решения систем уравнений, — это подстановка, исключение и расширенные матрицы. Замена и исключение — это простые методы, с помощью которых можно эффективно решить большинство систем двух уравнений за несколько простых шагов. Метод расширенных матриц требует большего количества шагов, но его применение распространяется на большее количество систем.

Замена

Замена — это метод решения систем уравнений путем удаления всех переменных, кроме одной, в одном из уравнений, а затем решения этого уравнения.Это достигается путем выделения другой переменной в уравнении и последующей подстановки значений этих переменных в другое уравнение. Например, чтобы решить систему уравнений x + y = 4, 2x — 3y = 3, выделите переменную x в первом уравнении, чтобы получить x = 4 — y, затем подставьте это значение y во второе уравнение, чтобы получить 2 (4 — y) — 3y = 3. Это уравнение упрощается до -5y = -5 или y = 1. Подставьте это значение во второе уравнение, чтобы найти значение x: x + 1 = 4 или x = 3.

Исключение

Исключение — это еще один способ решения систем уравнений путем переписывания одного из уравнений в терминах только одной переменной.Метод исключения достигает этого путем сложения или вычитания уравнений друг из друга, чтобы сократить одну из переменных. Например, сложение уравнений x + 2y = 3 и 2x — 2y = 3 дает новое уравнение 3x = 6 (обратите внимание, что члены y сокращены). Затем система решается с использованием тех же методов, что и для замены. Если невозможно сократить переменные в уравнениях, необходимо будет умножить все уравнение на коэффициент, чтобы коэффициенты совпали.

Расширенная матрица

Расширенные матрицы также могут использоваться для решения систем уравнений.Расширенная матрица состоит из строк для каждого уравнения, столбцов для каждой переменной и расширенного столбца, который содержит постоянный член с другой стороны уравнения. Например, расширенная матрица для системы уравнений 2x + y = 4, 2x — y = 0 имеет вид [[2 1], [2 -1] … [4, 0]].

Определение решения

Следующий шаг включает использование элементарных операций со строками, таких как умножение или деление строки на константу, отличную от нуля, и добавление или вычитание строк. Цель этих операций — преобразовать матрицу в форму строки-эшелона, в которой первая ненулевая запись в каждой строке — это 1, записи выше и ниже этой записи — все нули, а первая ненулевая запись для каждого row всегда находится справа от всех таких записей в строках над ней.Строчно-эшелонированная форма для указанной выше матрицы — [[1 0], [0 1] … [1, 2]]. Значение первой переменной задается первой строкой (1x + 0y = 1 или x = 1). Значение второй переменной задается второй строкой (0x + 1y = 2 или y = 2).

Приложения

Подстановка и исключение — это более простые методы решения уравнений, которые используются гораздо чаще, чем расширенные матрицы в базовой алгебре. Метод подстановки особенно полезен, когда одна из переменных уже изолирована в одном из уравнений.Метод исключения полезен, когда коэффициент одной из переменных одинаков (или его отрицательный эквивалент) во всех уравнениях. Основное преимущество расширенных матриц состоит в том, что их можно использовать для решения систем из трех или более уравнений в ситуациях, когда замена и исключение либо невозможны, либо невозможны.

Решение систем линейных уравнений

А

система

линейные уравнения

представляет собой просто набор из двух или более линейных уравнений.

В двух переменных

(

Икс

а также

y

)

, график системы двух уравнений представляет собой пару прямых на плоскости.

Есть три возможности:

• Линии пересекаются в нулевых точках. (Линии параллельны.)
• Линии пересекаются ровно в одной точке. (Большинство случаев.)
• Прямые пересекаются в бесконечном множестве точек. (Два уравнения представляют собой одну и ту же линию.)

Алгебраические методы решения систем

Результаты обучения

• Воспользуйтесь методом замены
  • Решите систему уравнений, используя метод подстановки.
  • Распознавать системы уравнений, не имеющие решения или бесконечное число решений
• Используйте метод исключения без умножения
  • Решите систему уравнений, когда умножение не требуется для исключения переменной
• Используйте метод исключения с умножением
  • Использование умножения в сочетании с методом исключения для решения системы линейных уравнений
  • Распознать, когда решение системы линейных уравнений подразумевает, что существует бесконечное число решений

Решите систему уравнений методом подстановки

В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики, чтобы классифицировать, сколько решений имеет система двух линейных уравнений.Что, если нам не дана точка пересечения или она не очевидна из графика? Можем ли мы еще найти решение этой системы? Конечно, можно, используя алгебру!

В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. На протяжении всего курса мы использовали подстановку по-разному, например, когда мы использовали формулы для площади треугольника и простых процентов. Мы подставили значения, которые мы знали, в формулу, чтобы найти значения, которых мы не знали.Идея аналогична применительно к решению систем, в этом процессе всего несколько этапов. Сначала вы решите одну переменную, а затем подставите это выражение в другое уравнение. Давайте начнем с примера, чтобы понять, что это значит.

Пример

Найдите значение x для этой системы.

Уравнение A: [латекс] 4x + 3y = −14 [/ латекс]

Уравнение B: [латекс] y = 2 [/ латекс]

Показать решение
Задача просит решить для x .Уравнение B дает вам значение y , [latex] y = 2 [/ latex], поэтому вы можете подставить 2 в уравнение A для y.

[латекс] \ begin {array} {r} 4x + 3y = −14 \\ y = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]

Подставьте [латекс] y = 2 [/ латекс] в уравнение A.

[латекс] 4x + 3 \ влево (2 \ вправо) = — 14 [/ латекс]

Упростите и решите уравнение для x.

[латекс] \ begin {array} {r} 4x + 6 = −14 \\ 4x = −20 \ x = −5 \, \, \, \ end {array} [/ latex]

Ответ

[латекс] x = −5 [/ латекс]

Вы можете заменить значение переменной, даже если это выражение.Вот пример.

Пример

Решите для x и y .

Уравнение A: [латекс] y + x = 3 [/ латекс]

Уравнение B: [латекс] x = y + 5 [/ латекс]

Показать решение
Цель метода подстановки — переписать одно из уравнений в терминах одной переменной. Уравнение B говорит нам, что [латекс] x = y + 5 [/ latex], поэтому имеет смысл заменить [latex] y + 5 [/ latex] в уравнение A для x .

[латекс] \ begin {array} {l} y + x = 3 \\ x = y + 5 \ end {array} [/ latex]

Замените [латекс] y + 5 [/ латекс] в уравнение A для x .

[латекс] \ begin {array} {r} y + x = 3 \\ y + \ left (y + 5 \ right) = 3 \ end {array} [/ latex]

Упростите и решите уравнение для y.

[латекс] \ begin {array} {r} 2y + 5 = \, \, \, \, 3 \\\ подчеркивание {−5 \, \, \, \, \, — 5} \\ 2y = — 2 \\ y = −1 \ end {array} [/ latex]

Теперь найдите x , подставив это значение для y в любое уравнение, и решите для x . Здесь мы будем использовать уравнение A.

[латекс] \ begin {array} {r} y + x = 3 \\ — 1 + x = 3 \\\ подчеркивание {+1 \, \, \, \, \, \, \, \, \, +1} \\ x = 4 \ end {array} [/ latex]

Наконец, проверьте решение [latex] x = 4 [/ latex], [latex] y = −1 [/ latex], подставив эти значения в каждое из исходных уравнений.

[латекс] \ begin {массив} {r} y + x = 3 \\ — 1 + 4 = 3 \\ 3 = 3 \\\ text {TRUE} \ end {array} [/ latex]

[латекс] \ begin {массив} {l} x = y + 5 \\ 4 = −1 + 5 \\ 4 = 4 \\\ text {TRUE} \ end {array} [/ latex]

Ответ

[латекс] x = 4 [/ латекс] и [латекс] y = -1 [/ латекс]

Решение — [латекс] (4, -1) [/ латекс].

Помните, решение системы уравнений должно быть решением каждого из уравнений внутри системы. Упорядоченная пара [latex] (4, −1) [/ latex] действительно работает для обоих уравнений, поэтому вы знаете, что это также решение системы.

Давайте посмотрим на другой пример, замена которого включает свойство распределения.

Пример

Решите для x и y .

[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]

Показать решение
Выберите уравнение для замены.

Первое уравнение говорит вам, как выразить y через x , поэтому имеет смысл подставить 3 x + 6 во второе уравнение для y .

[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]

Подставьте [латекс] 3x + 6 [/ latex] вместо y во второе уравнение.

[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2x + 4 \ left (3x + 6 \ right) = 4 \ end {array} [/ latex]

Упростите и решите уравнение для x.

[латекс] \ begin {array} {r} −2x + 12x + 24 = 4 \, \, \, \, \, \, \, \\ 10x + 24 = 4 \, \, \, \, \ , \, \, \\\ подчеркивание {−24 \, \, — 24 \, \, \, \,} \\ 10x = −20 \\ x = −2 \, \, \, \ end {array} [/ латекс]

Чтобы найти y , подставьте это значение вместо x обратно в одно из исходных уравнений.

[латекс] \ begin {array} {l} y = 3x + 6 \\ y = 3 \ left (−2 \ right) +6 \\ y = −6 + 6 \\ y = 0 \ end {array} [/ латекс]

Проверьте решение [латекс] x = −2 [/ latex], [latex] y = 0 [/ latex], подставив их в каждое из исходных уравнений.

[латекс] \ begin {array} {l} y = 3x + 6 \\ 0 = 3 \ left (−2 \ right) +6 \\ 0 = −6 + 6 \\ 0 = 0 \\\ text { ИСТИНА} \ end {array} [/ latex]

[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2 \ left (-2 \ right) +4 \ left (0 \ right) = 4 \\ 4 + 0 = 4 \\ 4 = 4 \\\ текст {ИСТИНА} \ end {array} [/ latex]

Ответ

[латекс] x = -2 [/ латекс] и [латекс] y = 0 [/ латекс]

Решение (−2, 0).

В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной x или y . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.

Иногда вам, возможно, придется сначала переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете заменить ее в другое уравнение.

Пример

Решите для x и y .

[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]

Показать решение
Выберите уравнение для замены. Второе уравнение,

[латекс] 3x + y = 19 [/ latex], можно легко переписать в терминах y , поэтому имеет смысл начать с этого.

[латекс] \ begin {array} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]

Перепишите [латекс] 3x + y = 19 [/ latex] в виде y .

[латекс] \ begin {array} 3x + y = 19 \\ y = 19–3x \ end {array} [/ latex]

Замените [латекс] 19–3x [/ латекс] на y в другом уравнении.

[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2x + 3 (19–3x) = 22 \ end {array} [/ latex]

Упростите и решите уравнение для x.

[латекс] \ begin {array} {r} 2x + 57–9x = 22 \, \, \, \, \\ — 7x + 57 = 22 \, \, \, \, \\ — 7x = −35 \\ x = 5 \, \, \, \, \, \, \, \ end {array} [/ latex]

Подставьте [latex] x = 5 [/ latex] обратно в одно из исходных уравнений, чтобы найти y.

[латекс] \ begin {array} {r} 3x + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 3 \ left (5 \ right ) + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15 + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ y = 19−15 \\ y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]

Проверьте оба решения, подставив их в каждое из исходных уравнений.

[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2 (5) +3 \ left (4 \ right) = 22 \\ 10 + 12 = 22 \\ 22 = 22 \\\ текст {ИСТИНА} \\\\ 3x + y = 19 \\ 3 \ left (5 \ right) + 4 = 19 \\ 19 = 19 \\\ текст {TRUE} \ end {array} [/ latex]

Ответ

[латекс] x = 5 [/ латекс] и [латекс] y = 4 [/ латекс]

Решение: (5, 4).

В следующем видео вам будет показан пример решения системы двух уравнений с использованием метода подстановки.

Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. Это действительно вопрос предпочтений, потому что иногда решение для переменной приводит к необходимости работать с дробями. По мере того, как вы приобретете больше опыта в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.

Распознавать системы уравнений, не имеющие решения или бесконечное число решений

Когда мы изучили методы решения линейных уравнений с одной переменной, мы обнаружили, что некоторые уравнения не имеют решений, а другие имеют бесконечное количество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.

Вспомните этот пример из модуля 1 для решения линейных уравнений с одной переменной:

Решите для x .[латекс] 12 + 2x – 8 = 7x + 5–5x [/ латекс]

[латекс] \ displaystyle \ begin {array} {l} 12 + 2x-8 = 7x + 5-5x \\\, \, \, \, \, \, \, \, \, \, \, \ , \, \, 2x + 4 = 2x + 5 \ end {array} [/ latex]

[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, \, \, \, 2x + 4 = 2x + 5 \\\, \, \ , \, \, \, \, \, \ underline {-2x \, \, \, \, \, \, \, \, \, \, — 2x \, \, \, \, \, \, \, \,} \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, 4 = \, 5 \ end {array} [/ latex]

Это ложное утверждение подразумевает, что не существует решений этого уравнения. Таким же образом вы можете увидеть такой результат, когда используете метод подстановки, чтобы найти решение системы линейных уравнений с двумя переменными.В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.

Пример

Решите для x и y .

[латекс] \ begin {array} {l} y = 5x + 4 \\ 10x − 2y = 4 \ end {array} [/ latex]

Показать решение
Поскольку первое уравнение [латекс] y = 5x + 4 [/ latex], вы можете заменить [latex] 5x + 4 [/ latex] на y во втором уравнении.

[латекс] \ begin {array} {r} y = 5x + 4 \\ 10x − 2y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \\ 10x – 2 \ left (5x + 4 \ right) = 4 \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]

Разверните выражение слева.

[латекс] 10x – 10x – 8 = 4 [/ латекс]

Объедините похожие члены в левой части уравнения.

[латекс] 10x – 10x = 0 [/ latex], поэтому у вас остается [latex] −8 = 4 [/ latex].

[латекс] \ begin {array} {r} 0–8 = 4 \\ — 8 = 4 \ end {array} [/ latex]

Ответ

Утверждение [latex] −8 = 4 [/ latex] неверно, поэтому решения нет.

Вы получаете ложное утверждение [латекс] −8 = 4 [/ латекс]. Что это значит? График этой системы проливает свет на то, что происходит.

Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [latex] −8 = 4 [/ latex] — это , а не как решение. Это просто ложное утверждение, и оно указывает на то, что не существует решения .

Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное количество решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.

Пример

Решите относительно x и y.

[латекс] \ begin {массив} {l} \, \, \, y = −0,5x \\ 9y = −4,5x \ end {array} [/ latex]

Показать решение

Подставляя -0,5 x вместо y во втором уравнении, вы получаете следующее:

[латекс] \ begin {array} {r} 9y = −4.5x \\ 9 (−0.5x) = — 4.5 \, \, \, \\ — 4.5x = −4.5x \ end {array} [/ латекс]

На этот раз вы получите верное утверждение: [латекс] −4,5x = −4,5x [/ latex]. Но что означает такой ответ? Опять же, построение графиков может помочь вам разобраться в этой системе.

Эта система состоит из двух уравнений, которые представляют одну и ту же линию; две линии коллинеарны. Каждая точка на линии будет решением системы, и поэтому метод подстановки дает верное утверждение. В этом случае существует бесконечное количество решений.

В следующем видео вы увидите пример решения системы, имеющей бесконечное количество решений.

В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.

Решите систему уравнений методом исключения

Метод исключения для решения систем линейных уравнений использует добавочное свойство равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может потребоваться, а может и не потребоваться сначала умножить члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения.В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.

С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу же рассмотрим несколько примеров.

Если сложить два уравнения,

[латекс] x – y = −6 [/ latex] и [latex] x + y = 8 [/ latex] вместе, посмотрите, что произойдет.

[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, \, xy = \, — 6 \\\ подчеркивание {+ \, x + y = \, \, \, 8} \\\, 2x + 0 \, = \, \, \, \, 2 \ end {array} [/ latex]

Вы исключили член y , и это уравнение можно решить, используя методы решения уравнений с одной переменной.

Давайте посмотрим, как эта система решается методом исключения.

Пример

Используйте устранение, чтобы решить систему.

[латекс] \ begin {array} {r} x – y = −6 \\ x + y = \, \, \, \, 8 \ end {array} [/ latex]

Показать решение
Добавьте уравнения.

[латекс] \ displaystyle \ begin {array} {r} xy = \, \, — 6 \\ + \ underline {\, \, x + y = \, \, \, \, \, 8} \\ \, \, \, \, \, \, 2x \, \, \, \, \, = \, \, \, \, \, \, 2 \ end {array} [/ latex]

Решите для x .

[латекс] \ begin {array} {r} 2x = 2 \\ x = 1 \ end {array} [/ latex]

Подставьте [latex] x = 1 [/ latex] в одно из исходных уравнений и решите относительно y .

[латекс] \ begin {array} {l} x + y = 8 \\ 1 + y = 8 \\\, \, \, \, \, \, \, \, \, \, y = 8– 1 \\\, \, \, \, \, \, \, \, \, \, y = 7 \ end {array} [/ latex]

Обязательно проверьте свой ответ в обоих уравнениях!

[латекс] \ begin {array} {r} x – y = −6 \\ 1–7 = −6 \\ — 6 = −6 \\\ text {TRUE} \\\\ x + y = 8 \ \ 1 + 7 = 8 \\ 8 = 8 \\\ текст {ИСТИНА} \ end {array} [/ latex]

Ответы проверяют.

Ответ

Решение: (1, 7).

К сожалению, не все системы справляются с этим легко. Как насчет такой системы, как [латекс] 2x + y = 12 [/ latex] и [latex] −3x + y = 2 [/ latex].Если вы сложите эти два уравнения вместе, никакие переменные не будут исключены.

[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, 2x + y = 12 \\\ подчеркивание {-3x + y = \, \, \, 2} \\ — x + 2y = 14 \ end {array} [/ latex]

Но вы хотите исключить переменную. Итак, давайте добавим противоположность одного из уравнений к другому уравнению. Это означает умножение каждого члена в одном из уравнений на -1, чтобы знак каждого члена был противоположным.

[латекс] \ begin {array} {l} \, \, \, \, 2x + \, \, y \, = 12 \ rightarrow2x + y = 12 \ rightarrow2x + y = 12 \\ — 3x + \, \, y \, = 2 \ rightarrow− \ left (−3x + y \ right) = — (2) \ rightarrow3x – y = −2 \\\, \, \, \, 5x + 0y = 10 \ end {array} [/ латекс]

Вы удалили переменную y , и теперь проблема может быть решена.

В следующем видео описывается аналогичная проблема, при которой можно исключить одну переменную, сложив два уравнения вместе.

Осторожность! Когда вы добавляете противоположность одного целого уравнения к другому, не забудьте изменить знак КАЖДОГО члена с обеих сторон уравнения. Это очень распространенная ошибка.

Пример

Используйте устранение, чтобы решить систему.

[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]

Показать решение
Вы можете исключить переменную y , добавив противоположность одного из уравнений к другому уравнению.

[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]

Перепишем второе уравнение как противоположное.

Доп. Решите для x .

[латекс] \ begin {array} {r} 2x + y = 12 \, \\ 3x – y = −2 \\ 5x = 10 \, \\ x = 2 \, \, \, \, \ end { array} [/ latex]

Подставьте [latex] y = 2 [/ latex] в одно из исходных уравнений и решите относительно y .

[латекс] \ begin {array} {r} 2 \ left (2 \ right) + y = 12 \\ 4 + y = 12 \\ y = 8 \, \, \, \ end {array} [/ latex ]

Обязательно проверьте свой ответ в обоих уравнениях!

[латекс] \ begin {array} {r} 2x + y = 12 \\ 2 \ left (2 \ right) + 8 = 12 \\ 4 + 8 = 12 \\ 12 = 12 \\\ text {TRUE} \\\\ — 3x + y = 2 \\ — 3 \ left (2 \ right) + 8 = 2 \\ — 6 + 8 = 2 \\ 2 = 2 \\\ текст {ИСТИНА} \ end {array} [/ латекс]

Ответы проверяют.

Ответ

Решение (2, 8).

Ниже приведены еще два примера, показывающих, как решать линейные системы уравнений с использованием исключения.

Пример

Используйте устранение, чтобы решить систему.

[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]

Показать решение
Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Если вы сложите эти два уравнения, член x будет удален, поскольку [latex] −2x + 2x = 0 [/ latex].

[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]

Сложите и решите для и .

[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = 25 \, \\ 8y = 24 \, \\ y = 3 \, \, \, \, \ end {array} [/ latex]

Подставьте [латекс] y = 3 [/ latex] в одно из исходных уравнений.

[латекс] \ begin {array} {r} 2x + 5y = 25 \\ 2x + 5 \ left (3 \ right) = 25 \\ 2x + 15 = 25 \\ 2x = 10 \ x = 5 \, \, \, \ end {array} [/ latex]

Проверить решения.

[латекс] \ begin {array} {r} −2x + 3y = −1 \\ — 2 \ left (5 \ right) +3 \ left (3 \ right) = — 1 \\ — 10 + 9 = — 1 \\ — 1 = −1 \\\ текст {ИСТИНА} \\\\ 2x + 5y = 25 \\ 2 \ left (5 \ right) +5 \ left (3 \ right) = 25 \\ 10 + 15 = 25 \\ 25 = 25 \\\ текст {ИСТИНА} \ end {array} [/ latex]

Ответы проверяют.

Ответ

Решение: (5, 3).

Пример

Используйте исключение, чтобы найти x и y.

[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]

Показать решение
Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Вам нужно будет добавить противоположное одному из уравнений, чтобы исключить переменную y , так как [latex] 2y + 2y = 4y [/ latex], но [latex] 2y + \ left (−2y \ right) = 0 [ /латекс].

[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]

Замените одно из уравнений на противоположное, сложите и решите для x .

[латекс] \ begin {array} {r} 4x + 2y = 14 \, \, \, \, \\ — 5x – 2y = −16 \\ — x = −2 \, \, \, \\ x = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]

Подставьте [latex] x = 2 [/ latex] в одно из исходных уравнений и решите относительно y .

[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 4 \ left (2 \ right) + 2y = 14 \\ 8 + 2y = 14 \\ 2y = 6 \, \, \, \ \ y = 3 \, \, \, \ end {array} [/ latex]

Ответ

Решение: (2, 3).

Проверьте последний пример — подставьте (2, 3) в оба уравнения. Получается два верных утверждения: 14 = 14 и 16 = 16!

Обратите внимание, что вы могли бы использовать противоположное первому уравнению, а не второе уравнение, и получить тот же результат.

Распознавать системы, у которых нет решения или бесконечное количество решений

Как и в случае с методом подстановки, метод исключения иногда удаляет как v ariables, и вы получаете либо истинное, либо ложное утверждение. Напомним, ложное утверждение означает, что решения нет.

Давайте посмотрим на пример.

Пример

Решите для x и у.

[латекс] \ begin {array} {r} -x – y = -4 \\ x + y = 2 \, \, \, \, \ end {array} [/ latex]

Показать решение
Добавьте уравнения, чтобы исключить член x .

[латекс] \ begin {array} {r} -x – y = -4 \\\ подчеркивание {x + y = 2 \, \, \,} \\ 0 = −2 \ end {array} [/ latex ]

Ответ

Нет решения.

Построение этих линий показывает, что они параллельны и не имеют общих точек, что подтверждает отсутствие решения.

Если обе переменные исключены и у вас осталось истинное утверждение, это означает, что существует бесконечное количество упорядоченных пар, которые удовлетворяют обоим уравнениям. По сути, уравнения — это одна и та же линия.

Пример

Решите для x и y .

[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\ — x − y = -2 \ end {array} [/ latex]

Показать решение
Добавьте уравнения, чтобы исключить член x .

[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\\ underline {-x − y = -2} \\ 0 = 0 \, \, \, \ , \, \ end {array} [/ latex]

Ответ

Есть бесконечное количество решений.

Построение этих двух уравнений поможет проиллюстрировать, что происходит.

В следующем видео система уравнений, не имеющая решений, решается методом исключения.

Решите систему уравнений, когда необходимо умножение для исключения переменной

Многократное добавление уравнений или добавление противоположности одного из уравнений не приведет к удалению переменной. Посмотрите на систему ниже.

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]

Если вы сложите приведенные выше уравнения или добавите противоположное одному из уравнений, вы получите уравнение, в котором по-прежнему есть две переменные.Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного уравнения на число, которое позволит вам исключить ту же переменную из другого уравнения.

Мы делаем это с умножением. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на −4, то при сложении обоих уравнений переменные y в сумме дадут 0.

В следующем примере показаны все шаги по поиску решения для этой системы.

Пример

Решите для x и y .

Уравнение A: [латекс] 3x + 4y = 52 [/ латекс]

Уравнение B: [латекс] 5x + y = 30 [/ латекс]

Показать решение
Ищите термины, которые можно исключить. В уравнениях нет членов размером x или y с одинаковыми коэффициентами.

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]

Умножьте второе уравнение на [латекс] −4 [/ латекс], чтобы получить одинаковый коэффициент.

[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 3x + 4y = 52 \\ — 4 \ left (5x + y \ right) = — 4 \ влево (30 \ вправо) \ end {array} [/ latex]

Перепишите систему и добавьте уравнения.

[латекс] \ begin {array} {r} 3x + 4y = 52 \, \, \, \, \, \, \, \\ — 20x – 4y = −120 \ end {array} [/ latex]

Решите для x .

[латекс] \ begin {array} {l} −17x = -68 \\\, \, \, \, \, \, \, \, \, \, \, x = 4 \ end {array} [/ latex ]

Подставьте [latex] x = 4 [/ latex] в одно из исходных уравнений, чтобы найти y .

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) + 4y = 52 \\ 12 + 4y = 52 \\ 4y = 40 \\ y = 10 \ end {array} [/ latex]

Проверьте свой ответ.

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) +4 \ left (10 \ right) = 52 \\ 12 + 40 = 52 \\ 52 = 52 \\\ текст {ИСТИНА} \\\\ 5x + y = 30 \\ 5 \ влево (4 \ вправо) + 10 = 30 \\ 20 + 10 = 30 \\ 30 = 30 \\\ текст {ИСТИНА} \ конец {array} [/ latex]

Ответы проверяют.

Ответ

Решение: (4, 10).

Осторожность! Когда вы используете умножение для исключения переменной, вы должны умножить КАЖДЫЙ член в уравнении на выбранное вами число.Забыть умножить каждый член — распространенная ошибка.

Есть и другие способы решить эту систему. Вместо того, чтобы умножать одно уравнение, чтобы исключить переменную при добавлении уравнений, вы могли бы умножить и уравнения на разные числа.

На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на [латекс] -3 [/ латекс].

Пример

Решите относительно x и y .

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]

Показать решение
Ищите термины, которые можно исключить.В уравнениях нет членов размером x или y с одинаковым коэффициентом.

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]

Чтобы использовать метод исключения, вы должны создать переменные с одинаковым коэффициентом — тогда вы можете их исключить. Умножьте верхнее уравнение на 5.

[латекс] \ begin {array} {r} 5 \ left (3x + 4y \ right) = 5 \ left (52 \ right) \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15x + 20y = 260 \, \, \, \, \, \, \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]

Теперь умножьте нижнее уравнение на −3.

[латекс] \ begin {array} {r} 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 3 (5x + y) = — 3 (30) \\ 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 15x – 3y = −90 \, \, \, \, \, \, \, \ end {array} [ / латекс]

Затем сложите уравнения и решите относительно y .

[латекс] \ begin {array} {r} 15x + 20y = 260 \\ — 15x – 3y = \, — 90 \\ 17y = 170 \\ y = \, \, \, 10 \ end {array} [ / латекс]

Подставьте [латекс] y = 10 [/ latex] в одно из исходных уравнений, чтобы найти x .

[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3x + 4 \ left (10 \ right) = 52 \\ 3x + 40 = 52 \\ 3x = 12 \ x = 4 \, \, \, \ end {array} [/ latex]

Вы пришли к тому же решению, что и раньше.

Ответ

Решение: (4, 10).

Эти уравнения были умножены на 5 и [латекс] −3 [/ латекс] соответственно, потому что это дало вам члены, которые в сумме дают 0. Не забудьте умножить все члены уравнения.

В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.

Можно использовать метод исключения с умножением и получить результат, который не указывает никаких решений или бесконечно много решений, точно так же, как с другими методами, которые мы изучили для поиска решений систем.В следующем примере вы увидите систему, которая имеет бесконечно много решений.

Пример

Решите для x и y .

Уравнение A: [латекс] x-3y = -2 [/ латекс]

Уравнение B: [латекс] -2x + 6y = 4 [/ латекс]

Показать решение
Ищите термины, которые можно исключить. В уравнениях нет членов размером x или y с одинаковыми коэффициентами.

[латекс] \ begin {array} {r} x-3y = -2 \\ — 2x + 6y = 4 \ end {array} [/ latex]

Умножьте первое уравнение на [latex] 2 [/ latex] так, чтобы члены x уравнялись.

[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 2 \ left (x-3y \ right) = 2 \ left (-2 \ right) \\ — 2x + 6y = 4 \ end {array} [/ latex]

Перепишите систему и добавьте уравнения.

[латекс] \ begin {array} {r} 2x-6y = -4 \\ — 2x + 6y = 4 \\ 0x + 0y = 0 \\\, \, \, \, \, \, \, \ , 0 = 0 \ end {array} [/ latex]

Вам знакомо такое решение? Это представляет собой решение всех действительных чисел для линейных уравнений, и это представляет то же самое, когда вы получаете такой результат с системами. Если мы решим оба этих уравнения относительно y, вы увидите, что это одно и то же уравнение.

Решите уравнение A относительно y:

[латекс] \ begin {array} {r} x-3y = -2 \\ — 3y = -x-2 \\ y = \ frac {1} {3} x + \ frac {2} {3} \ end {array} [/ latex]

Решите уравнение B относительно y:

[латекс] \ begin {array} -2x + 6y = 4 \\ 6y = 2x + 4 \\ y = \ frac {2} {6} x + \ frac {4} {6} \ end {array} [/ латекс]

Уменьшите дроби, разделив числитель и знаменатель обеих дробей на 2:

[латекс] y = \ frac {1} {3} + \ frac {2} {3} [/ latex]

Оба уравнения одинаковы, если записаны в форме пересечения наклона, и поэтому набором решений для системы являются все действительные числа.

Ответ

Решение: x и y могут быть действительными числами.

В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Вдобавок у этой системы есть бесконечное количество решений.

Сводка

Метод подстановки — это один из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных в терминах другой переменной.Затем замените это выражение этой переменной во втором уравнении. Затем вы можете решить это уравнение, поскольку теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (с указанием одного решения), неверное утверждение (с указанием отсутствия решений) или истинное утверждение (с указанием бесконечного числа решений).

Объединение уравнений — мощный инструмент для решения системы уравнений.Сложение или вычитание двух уравнений для исключения общей переменной называется методом исключения (или добавления). Как только одна переменная исключена, становится намного проще найти другую.

Умножение можно использовать для создания условий совпадения в уравнениях перед их объединением, чтобы помочь в поиске решения системы. При использовании метода умножения важно умножить все члены с обеих сторон уравнения, а не только один член, который вы пытаетесь исключить.

Метод исключения для решения линейных систем (Алгебра 1, Системы линейных уравнений и неравенств) — Mathplanet

Другой способ решения линейной системы — использовать метод исключения. В методе исключения вы либо складываете, либо вычитаете уравнения, чтобы получить уравнение с одной переменной.

Когда коэффициенты одной переменной противоположны, вы добавляете уравнения, чтобы исключить переменную, а когда коэффициенты одной переменной равны, вы вычитаете уравнения, чтобы исключить переменную.

Пример

$$ \ begin {matrix} 3y + 2x = 6 \\ 5y-2x = 10 \ end {matrix} $$

Мы можем исключить переменную x, добавив два уравнения.

$$ 3y + 2x = 6 $$

$$ \ underline {+ \: 5y-2x = 10} $$

$$ = 8лет \: \: \: \: \; \; \; \; = 16 $$

$$ \ begin {matrix} \: \: \: y \: \: \: \: \: \; \; \; \; \; = 2 \ end {matrix} $$

Теперь значение y можно подставить в любое из исходных уравнений, чтобы найти значение x

$$ 3y + 2x = 6 $$

$$ 3 \ cdot {\ color {зеленый} 2} + 2x = 6 $$

$$ 6 + 2x = 6 $$

$$ x = 0 $$

Решение линейной системы есть (0, 2).

Чтобы избежать ошибок, перед началом исключения убедитесь, что все одинаковые члены и знаки равенства находятся в одних и тех же столбцах.

Если у вас нет уравнений, в которых вы можете исключить переменную путем сложения или вычитания, вы можете непосредственно начать с умножения одного или обоих уравнений на константу, чтобы получить эквивалентную линейную систему, в которой вы можете исключить одну из переменных путем сложения. или вычитание.

Пример

$$ \ begin {matrix} 3x + y = 9 \\ 5x + 4y = 22 \ end {matrix} $$

Начните с умножения первого уравнения на -4 так, чтобы коэффициенты y были противоположны

$$ \ color {зеленый} {-4 \} \ cdot \ left (3x + y \ right) = 9 \ cdot {\ color {green} {-4} $$

$$ 5x + 4y = 22 $$

$$ — 12x-4y = -36 $$

$$ \ underline {+ 5x + 4y = 22} $$

$$ = — 7x \: \: \: \: \: \: \: \: \: \: = -14 $$

$$ \ begin {matrix} \: \: \; \: \: x \: \: \: \: \: \: \: \: \: \: \: = 2 \ end {matrix} $$

Подставьте x в любое из исходных уравнений, чтобы получить значение y

$$ 3x + y = 9 $$

$$ 3 \ cdot {\ color {зеленый} 2} + y = 9 $$

$$ 6 + y = 9 $$

$$ y = 3 $$

Решение линейной системы: (2, 3)

Видеоурок

Решите линейную систему методом исключения

$$ \ left \ {\ begin {matrix} 2y — 4x = 2 \\ y = -x + 4 \ end {matrix} \ right $$

Методы решения системы нелинейных уравнений

Результаты обучения

• Решите систему, которая представляет собой пересечение параболы и линии, используя подстановку.
• Решите систему, представляющую пересечение круга и линии, используя подстановку.
• Решите систему, которая представляет собой пересечение круга и эллипса, используя исключение.

Система нелинейных уравнений — это система двух или более уравнений с двумя или более переменными, содержащая по крайней мере одно уравнение, которое не является линейным. Напомним, что линейное уравнение может иметь вид [латекс] Ax + By + C = 0 [/ latex]. Любое уравнение, которое нельзя записать в таком виде в нелинейном виде.Метод замены, который мы использовали для линейных систем, — это тот же метод, который мы будем использовать для нелинейных систем. Мы решаем одно уравнение для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти другую переменную, и так далее. Однако есть вариации в возможных результатах.

Пересечение параболы и прямой

Существует три возможных типа решений для системы нелинейных уравнений, включающей параболу , и прямую.

Общее примечание: возможные типы решений для точек пересечения параболы и прямой

На графиках ниже показаны возможные наборы решений для системы уравнений, включающей параболу и прямую.

• Нет решения. Линия никогда не пересечет параболу.
• Одно решение. Прямая касается параболы и пересекает параболу ровно в одной точке.
• Два решения. Линия пересекает внутреннюю часть параболы и пересекает параболу в двух точках.

Как: найти решение для системы уравнений, содержащей прямую и параболу.

1. Решите линейное уравнение относительно одной из переменных.{2} -3y + 2 && \ text {Установить равным 0 и решить.} \\ & 0 = \ left (y — 2 \ right) \ left (y — 1 \ right) \ end {align} [/ latex]

   Решение для [latex] y [/ latex] дает [latex] y = 2 [/ latex] и [latex] y = 1 [/ latex]. Затем подставьте каждое значение для [latex] y [/ latex] в первое уравнение, чтобы найти [latex] x [/ latex]. Всегда подставляйте значение в линейное уравнение, чтобы проверить наличие посторонних решений.

   [латекс] \ begin {в собранном виде} xy = -1 \\ x- \ left (2 \ right) = — 1 \\ x = 1 \\ [3 мм] x- \ left (1 \ right) = — 1 \ \ x = 0 \ end {в собранном виде} [/ latex]

   Решениями являются [latex] \ left (1,2 \ right) [/ latex] и [latex] \ left (0,1 \ right), \ text {} [/ latex], которые можно проверить, заменив эти [ latex] \ left (x, y \ right) [/ latex] в оба исходных уравнения.{2} -y = 0 \ end {gather} [/ latex]

   Показать решение

   [латекс] \ left (- \ frac {1} {2}, \ frac {1} {2} \ right) [/ latex] и [latex] \ left (2,8 \ right) [/ latex]

   Пересечение круга и прямой

   Как и в случае с параболой и линией, существует три возможных результата при решении системы уравнений, представляющих окружность и линию.

   Общее примечание: возможные типы решений для точек пересечения круга и прямой

   На приведенном ниже графике показаны возможные наборы решений для системы уравнений, состоящей из круга , и линии.

   • Нет решения. Линия не пересекает круг.
   • Одно решение. Прямая касается круга и пересекает круг ровно в одной точке.
   • Два решения. Линия пересекает круг и пересекает его в двух точках.

   Как: найти решение для системы уравнений, содержащей прямую и окружность.

   
   

   1. Решите линейное уравнение относительно одной из переменных.
   2. Подставьте выражение, полученное на первом шаге, в уравнение для круга.{2} -3x + 2 \ right) = 0 \\ 10 \ left (x — 2 \ right) \ left (x — 1 \ right) = 0 \\ x = 2 \ hspace {5mm} x = 1 \ end {в собранном виде} [/ латекс]

      Подставьте два значения x в исходное линейное уравнение, чтобы найти [latex] y [/ latex].

      [латекс] \ begin {align} y & = 3 \ left (2 \ right) -5 \\ & = 1 \\ [3mm] y & = 3 \ left (1 \ right) -5 \\ & = — 2 \ конец {align} [/ latex]

      Линия пересекает круг в точках [латекс] \ left (2,1 \ right) [/ latex] и [latex] \ left (1, -2 \ right) [/ latex], что можно проверить, подставив эти [ latex] \ left (x, y \ right) [/ latex] в оба исходных уравнения.{2} = 10 \ hfill \\ x — 3y = -10 \ hfill \ end {array} [/ latex]

      Показать решение

      [латекс] \ влево (-1,3 \ вправо) [/ латекс]

      Решение системы нелинейных уравнений методом исключения

      Мы видели, что замена часто является предпочтительным методом, когда система уравнений включает линейное уравнение и нелинейное уравнение. Однако, когда оба уравнения в системе имеют одинаковые переменные второй степени, решить их с помощью исключения путем сложения часто проще, чем подстановки.Как правило, исключение — это гораздо более простой метод, когда система включает только два уравнения с двумя переменными (система два на два), а не систему три на три, поскольку шагов меньше. В качестве примера мы исследуем возможные типы решений при решении системы уравнений, представляющей круг, и эллипс.

      Общее примечание: возможные типы решений для точек пересечения круга и эллипса

      На рисунке ниже показаны возможные наборы решений для системы уравнений, включающей круг и эллипс .

      • Нет решения. Круг и эллипс не пересекаются. Одна фигура находится внутри другой, или круг и эллипс находятся на расстоянии друг от друга.
      • Одно решение. Окружность и эллипс касаются друг друга и пересекаются ровно в одной точке.
      • Два решения. Круг и эллипс пересекаются в двух точках.
      • Три решения. Круг и эллипс пересекаются в трех точках.
      • Четыре решения. Круг и эллипс пересекаются в четырех точках.{2} = 10 \ end {в собранном виде} [/ latex]

        Показать решение

        [латекс] \ left \ {\ left (1,3 \ right), \ left (1, -3 \ right), \ left (-1,3 \ right), \ left (-1, -3 \ right) ) \ right \} [/ латекс]

        В следующем видео мы представляем пример решения системы нелинейных уравнений, которые представляют собой пересечение эллипса и гиперболы.

        Внесите свой вклад!

        У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

        Улучшить эту страницуПодробнее

        Лучшие 3 метода решения систем уравнений [Видео]

        Решение систем уравнений

        Привет, ребята, добро пожаловать в это видео, посвященное сравнению различных методов решения системы уравнений.

        Если вы помните, система уравнений — это когда у вас есть более одного уравнения с неизвестными переменными в данной задаче. Итак, чтобы решить эту проблему, вам необходимо найти значения всех переменных в каждом уравнении. Это можно сделать тремя разными способами: методом подстановки, методом исключения и с использованием расширенной матрицы.

        В этом видео я предполагаю, что вы уже знаете, как выполнять каждый метод. Итак, я хочу потратить много времени на объяснение не того, как их выполнять, а, скорее, когда использовать каждый метод.

        Сначала я устно скажу вам, когда использовать каждый метод, затем я напишу три разных примера, и мы вместе решим, какой метод наиболее эффективен для каждой системы.

        Когда использовать метод подстановки
        Следует использовать метод подстановки, когда одна из переменных в одном из ваших уравнений уже изолирована (ее коэффициент равен 1).

        Когда использовать метод исключения
        Вы должны использовать метод исключения, когда одни и те же переменные во всех уравнениях имеют один и тот же коэффициент или когда они имеют один и тот же, но отрицательный коэффициент.

        Когда использовать расширенную матрицу
        Вы должны использовать расширенную матрицу, когда методы замены и исключения либо непрактичны, либо невозможны вместе.

        Теперь давайте рассмотрим три разные системы и воспользуемся тем, что мы только что узнали, чтобы подумать, какой метод наиболее полезен для каждой системы.

        1) 5x — 58y = -883

        -5x + 2y = -13

        __________________________

        2) 9x + 4y = 65

        x — 18y = -2

        __________________________

        3) 2x + 7y — 3z = 47

        x — 4y + 8z = -33

        7x + 2y + 10z = 11

        Итак, мы пройдемся по каждой системе, решим, какой метод будет наиболее эффективным, а затем решим с помощью этого метода. .

        Хорошо, давайте посмотрим на это первое уравнение.

        5x — 58y = -883

        -5x + 2y = -13

        Теперь, вспоминая объяснение, которое я дал, когда использовать каждый метод, обратите внимание на то, что я сказал об исключении: «Вы должны использовать метод исключения, когда одни и те же переменные во всех уравнениях имеют один и тот же коэффициент или когда они имеют один и тот же, но отрицательный коэффициент ».

        Что ж, это верно в случае этой конкретной системы. Итак, давайте решим эту систему с помощью исключения.

        5x — 58y = -883

        -5x + 2y = -13

        _______________

        -56y = -896

        Y = 16

        Теперь мы вставляем нашу переменную y обратно в одно из исходных уравнений. Я подключу его к первому.

        5x — 58 (16) = -883

        5x — 928 = -883

        5x = 45

        x = 9

        Отлично, поэтому мы решили эту систему с помощью исключения, потому что те же две переменные имели одинаковый коэффициент или когда у них одинаковый, но отрицательный коэффициент (как в нашем случае).

        Перейдем к системе №2.

        2) 9x + 4y = 65

        x — 18y = -2

        Хорошо, давайте снова вспомним, что было сказано в нашем объяснении, когда использовать каждый метод. Вспомните, что было сказано о подстановке: «Вы должны использовать метод подстановки, когда одна из переменных в одном из ваших уравнений уже изолирована».

        Ну так обстоит дело с этой системой. Наша переменная x во втором уравнении имеет коэффициент 1. Итак, давайте решим эту систему с помощью подстановки.

        9x + 4y = 65 x = 18y — 2

        x — 18y = -2

        _____________

        9 (18y — 2) + 4y = 65

        162y — 18 + 4y = 65

        166y = 83

        y = ½

        x = 18 (½) — 2

        x = 7

        Это было очень просто решить с помощью подстановки, и запомните знак, который поможет вам узнать, когда его использовать, если одно из уравнений имеет переменная, которая уже изолирована.

        Давайте посмотрим на нашу последнюю систему, систему №3.

        3) 2x + 7y — 3z = 47

        x — 4y + 8z = -33

        7x + 2y + 10z = 11

        Помните, что мы говорили о том, когда использовать расширенную матрицу.