Содержание
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
Определение 1
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
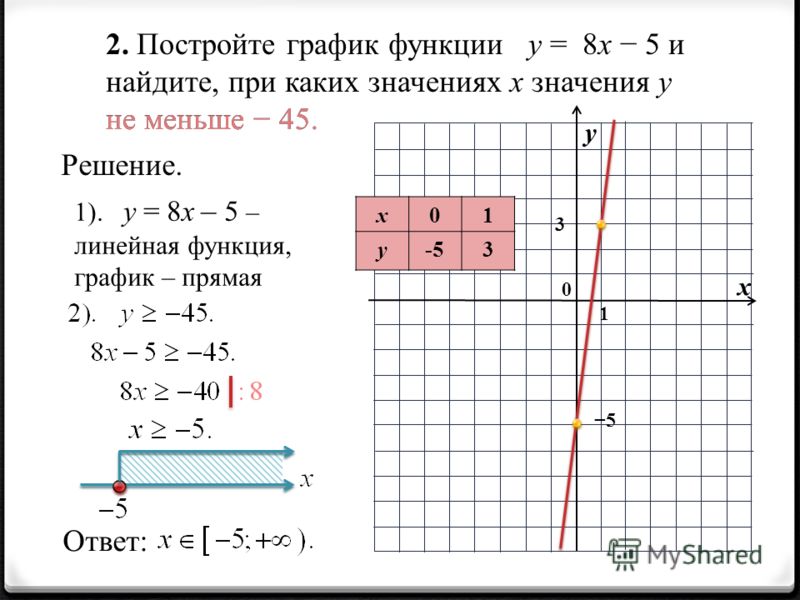
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Пример 1
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Для нахождения области определения произведения функций необходимо применять правило:
Определение 2
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2является арктангенсом, f3– логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x)является -∞, +∞D(f)=D(f).
Получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x — [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Пример 3
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Пример 4
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5
Найти область определения y=ln x2.
Решение
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.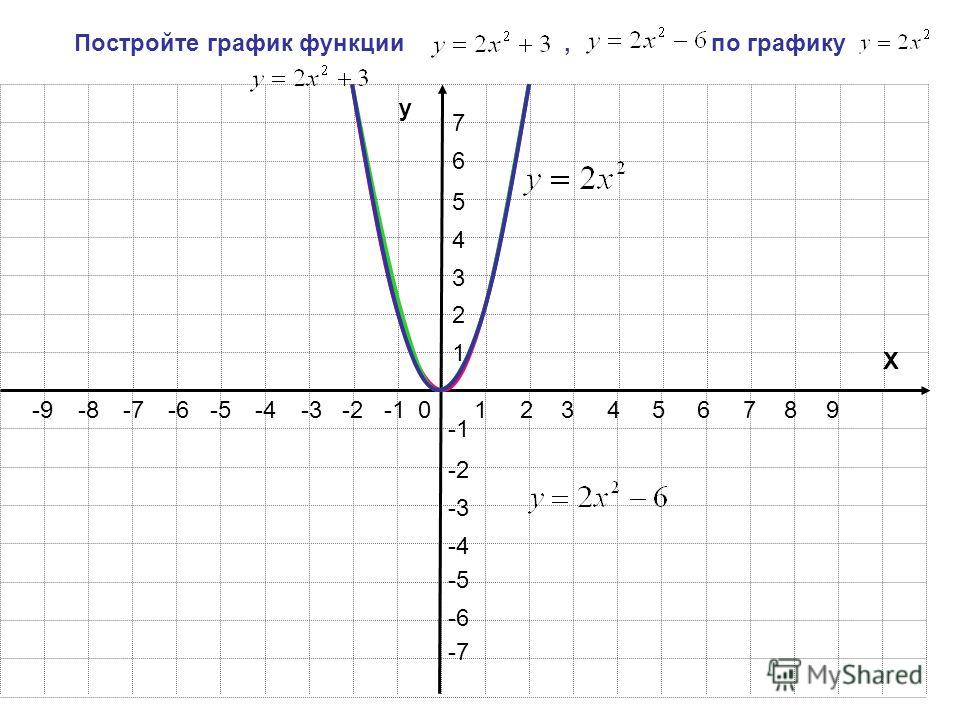
Ответ: (−∞, 0)∪(0, +∞).
Пример 6
Найти область определения функции y=(arcsin x)-12.
Решение
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Пример 7
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 8
Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Область определения логарифма с переменной в основании
Определение 3
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), …, D(fn) |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C — число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) — многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n — четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок: |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Рисунок: |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок: |
Найти точку пересечения графиков линейных функций
☰
Если даны две линейные функции вида y = kx + m, то их графики (прямые) могут вообще не пересекаться, если параллельны друг другу. Во всех остальных случаях они будут пересекаться в одной точке.
Графики двух линейных функций параллельны друг другу, если имеют одинаковый угловой коэффициент (k) и различное значение m (если и m будет одно и то же, то это будет одна и та же функция). Действительно, ведь k определяет угол между осью x и прямой, а значит у графиков линейных функций, отличающихся лишь значением m, угол с осью абсцисс один и тот же, и, следовательно, графики будут параллельны. Пример: графики функций y = 2x – 3 и y = 2x + 1 параллельны и, следовательно, не пересекаются.
Если две линейные функции имеют различные k, но одинаковые m, то они пересекаются в точке (0; m). Действительно, если x = 0, то независимо от того, чему равен k, y становится равен m. Пример: y = –1.3x + 8 и y = 2.1x + 8.
Если две линейные функции имеют различные и k и m, то они пересекаются в какой-то точке, которую можно найти графическим способом. Сначала на координатной плоскости чертится одна прямая, затем вторая, далее находится их точка пересечения. Для того, чтобы начертить прямую линейной функции, надо найти две точки, которые принадлежат прямой. Для этого берут два различных x и вычисляют y. Это нужно сделать для каждой из двух функция. При этом не обязательно брать одинаковые x. Следует брать те, вычислять с которыми удобнее, или их будет проще нанести на координатную плоскость.
Для того, чтобы начертить прямую линейной функции, надо найти две точки, которые принадлежат прямой. Для этого берут два различных x и вычисляют y. Это нужно сделать для каждой из двух функция. При этом не обязательно брать одинаковые x. Следует брать те, вычислять с которыми удобнее, или их будет проще нанести на координатную плоскость.
Также можно решить уравнение. Ведь точка пересечения — это та точка, где у обоих функций одинаковы x и y. Если y одинаковы, то правая часть одного уравнения равна правой части другой. То есть их можно приравнять и найти значение x, при котором это равенство верно. А далее, имея x, можно вычислить y, через любую из функций. Пример:
Даны y = 4x – 5 и y = –2x + 1
4x – 5 = –2x + 1
4x + 2x = 1 + 5
6x = 6
x = 1
y = 4 * 1 – 5 = –1 или y = –2 * 1 + 1 = –1
Таким образом точка пересечения (1; –1).
Экзамен по алгебре в 9-м классе «Функции»
№1.
Найдите все значения k, при которых
прямая y=kx пересекает в трех различных точках
график функции
Решение
Построим график данной функции. Прямые y=2x+1 и
Прямые y=2x+1 и
y=2x-3 параллельны ,т.к. у них одинаковый угловой
коэффициент , равный 2. Прямая y= — 1 параллельна оси
абсцисс.
| y=2x+1, | y=2x — 3. |
| y(0)= 1, y(-1)= -1, | y(0)= — 3, y(1)= — 1. |
Прямая n задана уравнением y=2x. Для
нахождения уравнения прямой l необходимо
подставить координаты точки А(-1; -1) в уравнение
y=kx.
-1=(-1)k. Отсюда k=1. Уравнение прямой l
имеет вид y=kx.
Для того чтобы искомая прямая m
пересекала график данной функции в трех
различных точках (рис.1), она должна располагаться
между прямыми n и l. При этом 1 < k < 2.
Ответ: 1< k < 2.
Рисунок 1
№2
Постройте график функции y = f(x), где
При каких значениях m прямая y = m имеет с
графиком этой функции три общие точки?
Решение.
1. Графиком функции является парабола.
а) Ветви параболы направлены вниз.
б)
(–1;2) – координаты вершины параболы.
в) Ось Оx:
y = 0
D = 4 + 4 = 8
–
координаты точек пересечения параболы и оси Оx
(оси абсцисс).
Ось Оy:
x = 0
y = 1
(0;1) – координаты точки пересечения параболы и
оси Оy(оси ординат).
2. Графиком функции является парабола.
а) Ветви параболы направлены вверх.
б)
– координаты
точки вершины параболы.
в) Ось Оx:
D = 4 + 20 = 24
–
координаты точек пересечения параболы и оси
Оx(оси абсцисс).
Ось Оy:
x = 0
y = – 5
(0; – 5) – координаты точки пересечения параболы
и оси Оy(оси ординат).
Найдём дополнительные точки для точного
построения графика функции :
Найдём дополнительные точки для точного
построения графика функции :
График данной функции (рис. 2) только в трёх
2) только в трёх
точках пересекают прямые
y = m при – 6 < m < – 2.
Ответ: – 6 < m < – 2.
Рисунок 2
№ 3.
Постройте график функции y=¦ (x) , где
При каких значениях m прямая y = m имеет с
графиком этой функции две общие точки?
Решение.
Построим график данной функции. Для
этого проведем исследования.
1. Графиком функции y= — x — 4x – 3 является парабола, ветви которой
направлены вниз. Найдем координаты вершины
параболы:
x= = — 2, y= y( — 2 ) = -4+8-3= 1.
Определим точки пересечения параболы
с осями координат:
x=0, y = -3; y=0, x= -
3, x= — 1. y (-4)= -16+16-3= — 3.
2. Графиком функции y= x + 1 является прямая.
y ( — 1 )= 0 , y (1) = 2.
3. Графиком функции y= является гипербола. В нашем случае
Графиком функции y= является гипербола. В нашем случае
достаточно построить одну ветвь гиперболы , т.к.
нам нужна часть гиперболы при x > 1. y(1) = 2, y(2)= 1,
y(4)=0,5.
График данной функции (рис.3) только в двух
точках пересекает прямая y=0 и прямые y=m при 1<m<2.
Ответ: m=0 и 1<m<2.
Рисунок 3
№ 4.
Постройте график функции y = .
При каких значениях x выполняется
неравенство y ? 3 ?
Решение.
- Найдем область определения функции:
- Преобразуем выражение, задающее функцию:
- Построим прямую y= -(x + 1)= — x – 1 и “ выколем ” на
ней точки, абсциссы которых равны 0 и 2 (рис.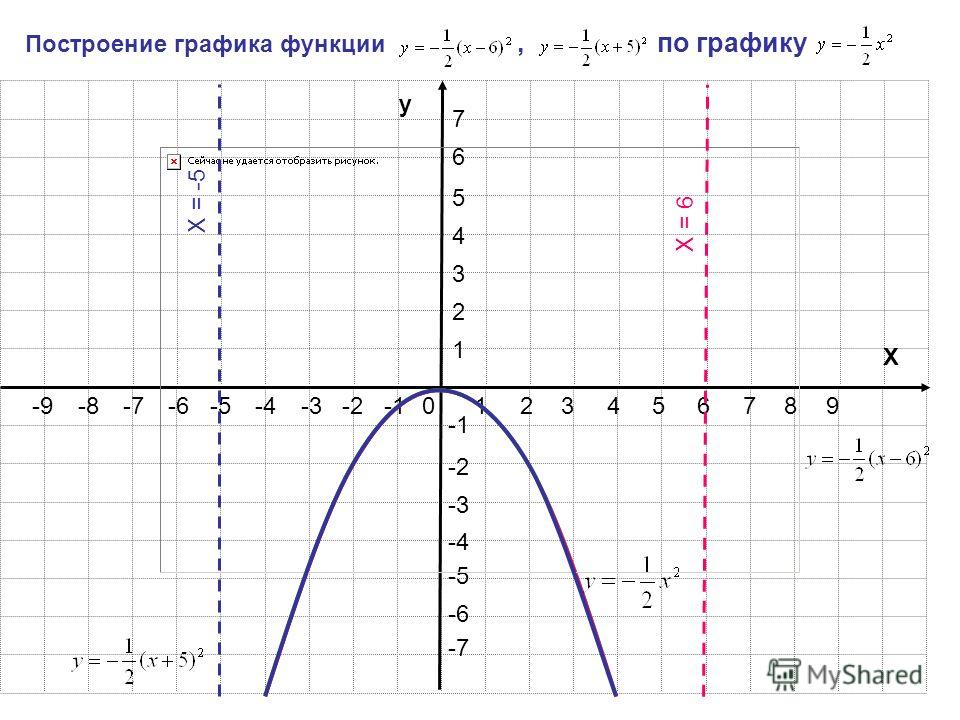 4).
4). - Решим неравенство y? 3 с помощью
графика:
2x — x 0, x (2 – x) 0, x 0, x 2.
y = =
— (x + 1),
x, x=2, x= — 1.
y(- 4) = 3, y(0) = -1, y( 2) = -3.
— 4 x < 0,
0<x<2, x>2.
Рисунок 4
Ответ: [- 4; 0) E (0; 2) E (2; + ? ).
№ 5.
Постройте график функции y= .
Решение.
1. Найдем область определения данной функции:
x+6x+8 0 ,
x+6x+8
=0, x= -4, x= -2.
Значит, областью определения является
множество всех действительных чисел , кроме – 4 и
– 2.
2. Для разложения числителя на множители решим
уравнения :
а) x+7x+12=0,
б) x+3x+2=0,
x= — 3, x= — 4 ; x= — 2, x= -1.
3. Упростим данную функцию:
y= =
(x+3)(x+1)=x+4x+3 .
4.Исследуем полученную квадратичную
функцию: графиком функции y = x+4x+3 является парабола , ветви которой
направлены вверх, вершина её имеет координаты x= — 2, y= -1; точки пересечения с осями координат -
x=0, y=3; y=0 при x=-3 и x=-1.
5. Построим параболу и “выколем” на ней точки,
абсциссы которых равны — 4 и – 2, поскольку при
этих значениях переменной исходная функция не
определена (рис.5).
y(- 4)=16-16+3=3, y(1)= 1+4+3=8.
Рисунок 5
№ 6.
Постройте график функции y= .
Решение.
1. Найдем область определения данной функции:
2. Упростим данную функцию:
y== ==x+1.
3. Построим прямую y=x+1 на промежутках (- 1; — 1) и (1; + ) (рис.6).
y( -1) = 0, y(1) = 2.
Рисунок 6
№ 7.
Задайте аналитически функцию, график
которой изображен на рисунке 7.
Решение.
Ломаная состоит из двух звеньев, одно из них
является графиком линейной функции y=kx+b при x 2, а другое – графиком
линейной функции при x > 2.
В каждом случае необходимо найти k и b.
Для этого необходимо на каждом из звеньев
выбрать по две точки, подставить их координаты в
уравнение линейной функции и решить две
получившиеся системы уравнений относительно k и
b.
1)На левом звене возьмем точки с координатами
(-2;0) и (2; -6).
решая
эту систему получаем b= — 3, k = — 1,5.
Рисунок 7
Получим уравнение прямой y= -1,5 x–3 при x 2.
2) На второй части ломаной возьмем точки с
координатами (2; — 6) и (4;0).
вычитая из
второго уравнения первое, получим k=3, а b= — 12.
Получим уравнение прямой y= 3x – 12 при x > 2.
Зададим теперь заданную графически функцию
аналитически:
Решите Свойства прямой y = 5-2x Tiger Algebra Solver
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:
y- (5-2 * x) = 0
Шаг 1:
Уравнение прямой линии
1. 1 Решите y + 2x-5 = 0
1 Решите y + 2x-5 = 0
Тигр распознает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.
В этой формуле:
y указывает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является точкой пересечения Y, т.е. Ось Y
Пересечения по осям X и Y и наклон называются свойствами линии. Теперь мы построим график линии y + 2x-5 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения Y:
Обратите внимание, что когда x = 0, значение y равно 5 / 1, поэтому эта линия «разрезает» ось y при y = 5.00000
Y-intercept = 5/1 = 5.00000
Вычислить X-Intercept:
Когда y = 0, значение x равно 5/2 Наша линия, таким образом, «срезает» ось x в точке x = 2. 50000
50000
x -intercept = 5/2 = 2.50000
Вычислить наклон:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно 5.000, а для x = 2.000 значение y равно 1.000. Итак, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 1.000 — 5.000 = -4.000 лет. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / РАБОТА)
Наклон = -4,000 / 2,000 = -2,000
Геометрическая фигура: прямая линия
- Наклон = -4,000 / 2,000 = -2,000
- пересечение по оси x = 5/2 = 2,50000
- пересечение по оси y = 5/1 = 5,00000
Поиск линейных уравнений
Для любой точки на линии и ее наклона мы можем найти уравнение этого линия. Начните с применения формулы наклона к заданной точке (x1, y1) и переменной точке (x, y).
Уравнение y − y1 = m (x − x1) называется формой точечного уклона линии Любую невертикальную прямую можно записать в форме y − y1 = m (x − x1), где м — наклон. и (x1, y1) — любая точка на прямой. Любое невертикальное линейное уравнение может быть записано в этой форме. Это полезно для нахождения уравнения прямой с учетом наклона и любого упорядоченного парного решения.
и (x1, y1) — любая точка на прямой. Любое невертикальное линейное уравнение может быть записано в этой форме. Это полезно для нахождения уравнения прямой с учетом наклона и любого упорядоченного парного решения.
Пример 7: Найдите уравнение прямой с наклоном m = 12, проходящей через (4, −1).
Решение: Используйте форму «точка-наклон», где m = 12 и (x1, y1) = (4, −1).
На этом этапе мы должны выбрать представление уравнения нашей линии либо в стандартной форме, либо в форме пересечения наклона.
В этом учебнике мы представим наши линии в форме пересечения уклона. Это облегчает построение графиков в будущем.
Пример 8: Найдите уравнение прямой, проходящей через (−5, 3) с наклоном m = −25.
Решение: Подставьте (−5, 3) и m = −25 в форму точечного наклона.
Всегда важно понимать, что происходит геометрически.Сравните ответ для последнего примера с соответствующим графиком ниже.
Понимание геометрии важно, потому что вам часто будут предлагать графики, по которым вам нужно будет определить точку на линии и наклон.
Решение: Между точками (1, 1) и (3, 0) мы можем видеть, что подъем равен -1 единице, а пробег равен 2 единицам. Наклон линии равен m = riserun = −12 = −12. Используйте это и точку (3, 0), чтобы найти следующее уравнение:
Пример 10: Найдите уравнение прямой, проходящей через (-1, 1) и (7, -1).
Решение: Начните с вычисления наклона по формуле наклона.
Затем подставьте в форму «точка-уклон», используя одну из указанных точек; не имеет значения, какая точка используется. Используйте m = −14 и точку (−1, 1).
Попробуй! Найдите уравнение прямой, проходящей через (4, −5) и (−4, 1).
Тематические упражнения
Часть A: Форма пересечения уклона
Определите наклон и точку пересечения y .
1. 5x − 3y = 18
2. −6x + 2y = 12
3. x − y = 5
4. −x + y = 0
5. 4x − 5y = 15
6. −7x + 2y = 3
7. y = 3
8. y = −34
9. 15x − 13y = −1
10. 516x + 38y = 9
11. −23x + 52y = 54
12. 12x − 34y = −12
Часть B: Поиск уравнений в форме пересечения уклона
Учитывая наклон и точку пересечения y , определите уравнение прямой.
13. м = 1/2; (0, 5)
14. м = 4; (0, -1)
15. м = −2/3; (0, −4)
16. м = −3; (0, 9)
17. м = 0; (0, -1)
18. м = 5; (0, 0)
По графику найдите уравнение в форме углового пересечения.
19.
20.
21.
22.
23.
24.
Найдите уравнение, учитывая наклон и точку.
25. м = 2/3; (−9, 2)
26. м = −1/5; (5, −5)
27. м = 0; (−4, 3)
28. м = 3; (−2, 1)
29. м = −5; (−2, 8)
30. м = −4; (1/2, −3/2)
31. м = −1/2; (3, 2)
32. м = 3/4; (1/3, 5/4)
33. м = 0; (3, 0)
34. м не определено; (3, 0)
Дайте две точки, найдите уравнение прямой.
35. (−6, 6), (2, 2)
(−6, 6), (2, 2)
36. (−10, −3), (5, 0)
37. (0, 1/2), (1/2, -1)
38. (1/3, 1/3), (2/3, 1)
39. (3, −4), (−6, −7)
40. (−5, 2), (3, 2)
41. (−6, 4), (−6, −3)
42. (−4, −4), (−1, −1)
43. (3, −3), (−5, 5)
44. (0, 8), (−4, 0)
Часть C: Уравнения с использованием формы точечного уклона
Найдите уравнение, учитывая наклон и точку.
45. м = 1/2; (4, 3)
46. м = −1/3; (9, −2)
47. м = 6; (1, −5)
48. м = −10; (1, −20)
49. м = −3; (2, 3)
50. м = 2/3; (−3, −5)
51. м = −3/4; (−8, 3)
52. м = 5; (1/5, −3)
53. м = −3; (-1/9, 2)
м = −3; (-1/9, 2)
54. м = 0; (4, −6)
55. м = 0; (−5, 10)
56. м = 5/8; (4, 3)
57. м = −3/5; (−2, −1)
58. м = 1/4; (12, −2)
59. м = 1; (0, 0)
60. м = −3/4; (0, 0)
Учитывая график, используйте формулу угла наклона точки, чтобы найти уравнение.
61.
62.
63.
64.
65.
66.
Используйте формулу угла наклона точки, чтобы найти уравнение прямой, проходящей через две точки.
67. (−4, 0), (0, 5)
68. (-1, 2), (0, 3)
(-1, 2), (0, 3)
69. (−3, −2), (3, 2)
70. (3, −1), (2, −3)
71. (−2, 4), (2, −4)
72. (−5, −2), (5, 2)
73. (−3, −1), (3, 3)
74. (1, 5), (0, 5)
75. (1, 2), (2, 4)
76. (6, 3), (2, −3)
77. (10, −3), (5, −4)
78.(−3, 3), (−1, 12)
79. (4/5, -1/3), (-1/5, 2/3)
80. (5/3, 1/3), (−10/3, −5/3)
81. (3, -1/4), (4, -1/2)
82. (0, 0), (−5, 1)
83. (2, −4), (0, 0)
84. (3, 5), (3, −2)
85. (−4, 7), (−1, 7)
86. (−8, 0), (6, 0)
Часть D: Приложения
87. Джо следил за своими счетами за сотовый телефон в течение последних двух месяцев.Счет за первый месяц составил 38 долларов США за 100 минут использования. Счет за второй месяц составил 45,50 долларов за 150 минут использования. Найдите линейное уравнение, которое дает общий ежемесячный счет, основанный на минутах использования.
Счет за второй месяц составил 45,50 долларов за 150 минут использования. Найдите линейное уравнение, которое дает общий ежемесячный счет, основанный на минутах использования.
88. Компания за первый год своей деятельности выпустила 150 учебных пособий на общую сумму 2 350 долларов США. В следующем году компания выпустила еще 50 руководств по цене 1450 долларов. Используйте эту информацию, чтобы найти линейное уравнение, которое дает общую стоимость производства учебных пособий из количества выпущенных руководств.
89. Фермер, выращивающий кукурузу в Калифорнии, смог произвести 154 бушеля кукурузы с акра через 2 года после начала своей деятельности. В настоящее время после 7 лет работы он увеличил урожайность до 164 бушелей с акра. Используйте эту информацию, чтобы написать линейное уравнение, которое дает общую урожайность с акра на основе количества лет эксплуатации, и используйте его для прогнозирования урожайности на следующий год.
90. Веб-мастер заметил, что количество зарегистрированных пользователей неуклонно растет с начала рекламной кампании.До того, как начать рекламировать, у него было 1200 зарегистрированных пользователей, а после 3 месяцев рекламы у него теперь есть 1590 зарегистрированных пользователей. Используйте эти данные, чтобы написать линейное уравнение, которое дает общее количество зарегистрированных пользователей с учетом количества месяцев после начала рекламы. Используйте уравнение, чтобы спрогнозировать количество пользователей за 7 месяцев рекламной кампании.
Веб-мастер заметил, что количество зарегистрированных пользователей неуклонно растет с начала рекламной кампании.До того, как начать рекламировать, у него было 1200 зарегистрированных пользователей, а после 3 месяцев рекламы у него теперь есть 1590 зарегистрированных пользователей. Используйте эти данные, чтобы написать линейное уравнение, которое дает общее количество зарегистрированных пользователей с учетом количества месяцев после начала рекламы. Используйте уравнение, чтобы спрогнозировать количество пользователей за 7 месяцев рекламной кампании.
91. Автомобиль, купленный новым, стоил 22 000 долларов и был продан 10 лет спустя за 7 000 долларов. Напишите линейное уравнение, определяющее стоимость автомобиля с учетом его возраста в годах.
92. Старинные часы были куплены в 1985 году за 1500 долларов и проданы на аукционе в 1997 году за 5700 долларов. Составьте линейное уравнение, моделирующее значение часов в годах с 1985 года.
Часть E: Темы дискуссионной доски
93. Обсудите достоинства и недостатки формы «точка-наклон» и формы « y «.
Обсудите достоинства и недостатки формы «точка-наклон» и формы « y «.
94. Изучите и обсудите линейную амортизацию. Что представляют собой наклон и пересечение y в линейной модели амортизации?
Линейные отношения и их графическое отображение Пошаговое решение математических задач
ЛИНЕЙНЫЕ ОТНОШЕНИЯ
В этом разделе мы исследуем один из простейших типов отношений — линейное отношение.Каждое линейное отношение имеет график, который представляет собой прямую линию, поэтому нам нужно найти только две точки на графике, чтобы нарисовать его. Примеры линейных отношений: y = 2x + 3, y = x и 3x + 2y = 6
ЛИНЕЙНАЯ СВЯЗЬ Линейная связь двух переменных — это связь, которую можно записать в форме
y = ax + b,
где a и b — действительные числа.
Примечание Линейные отношения часто записываются в форме Ax + By = C, где A, B и C действительны, а A и B одновременно не равны 0. Это называется стандартной формой линейного отношения.
Это называется стандартной формой линейного отношения.
В уравнении Ax + By = C любое число может использоваться для x или y, поэтому как область, так и диапазон линейного отношения, в котором ни один Anor B не равен 0, являются набором действительных чисел (-inf, inf),
ИЗОБРАЖЕНИЕ ЛИНЕЙНЫХ ОТНОШЕНИЙ . График линейной зависимости можно найти, построив не менее двух точек. Две точки, которые особенно полезны для построения графика линии, обнаруживаются с помощью точек пересечения. X-точка пересечения — это значение x, при котором график пересекает ось x.Пересечение оси y — это значение y, при котором график пересекает ось y. Поскольку y = 0 на оси x, пересечение с x можно найти, установив y равным 0 в уравнении и решив относительно x. Точно так же точка пересечения по оси Y находится путем установки x = 0 в уравнении и решения относительно y.
Пример 1 ИЗОБРАЖЕНИЕ ЛИНЕЙНОЙ СВЯЗИ С ПОМОЩЬЮ ПЕРЕСЕЧЕНИЙ
График 3x + 2y = 6.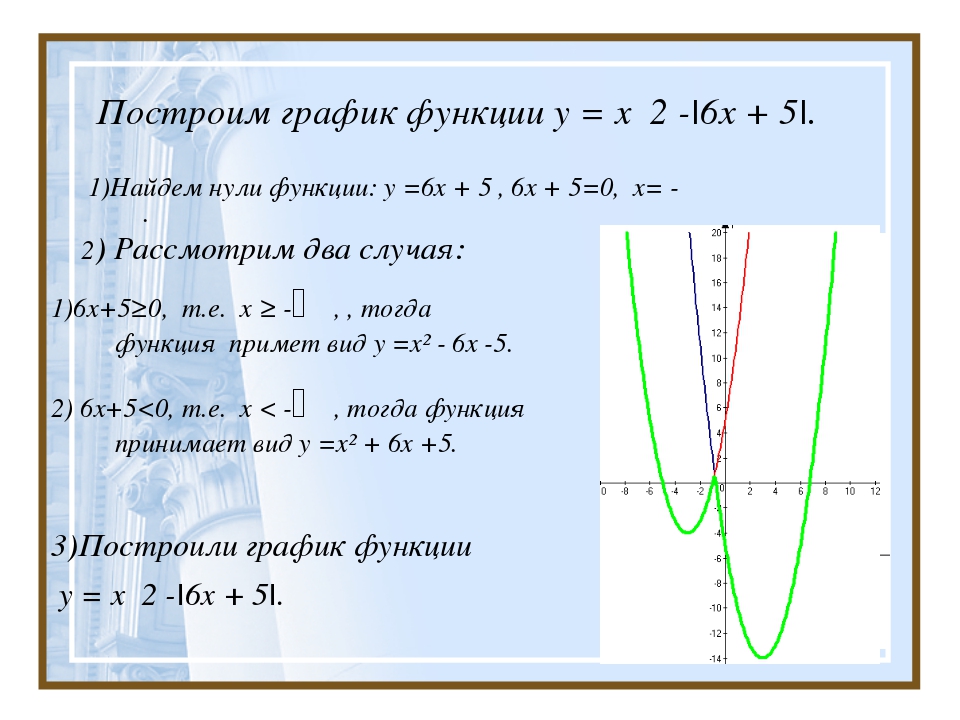
Используйте точки пересечения. Угол пересечения оси y равен
, если положить x = 0.
3,0 + 2у = 6
2y = 6
y = 3
Для точки пересечения по оси x, пусть y = 0, получаем
3x + 2.0 = 6
3x = 6
x = 2.
График (0,3) и (2,0) дает график на рисунке 3.7. Третий пункт при желании можно найти как проверку.
Давайте посмотрим, как наш математический решатель создает графики этой и подобных задач. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
Пример 2 ИЗОБРАЖЕНИЕ ГОРИЗОНТАЛЬНЫХ И ВЕРТИКАЛЬНЫХ ЛИНИЙ
(а) График y = -3.
Поскольку y всегда равно -3, значение y никогда не может быть 0. Это означает, что график не имеет точки пересечения по оси x. Единственный способ, при котором прямая линия не может быть пересечена по оси x, — это быть параллельной оси x, как показано на рисунке 3.8. Обратите внимание, что область определения этого линейного отношения — (-inf, inf), но диапазон — {-3}.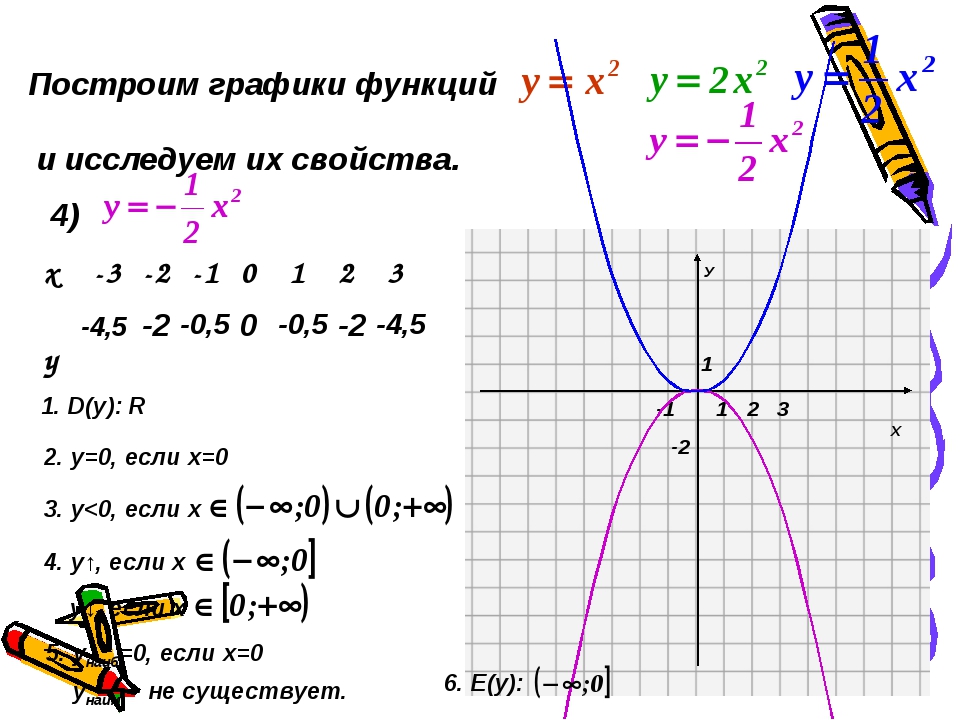
(б) График x = -3.
Здесь, поскольку x всегда равно -3, значение x никогда не может быть 0, и график не имеет точки пересечения по оси y. Используя рассуждения, аналогичные рассуждениям в части (a), мы обнаруживаем, что этот график параллелен оси y, как показано на рисунке 3.9. Область этого отношения — {-3}, а диапазон — (-inf, inf),
.
Из этого примера мы можем заключить, что линейная связь вида y = k имеет в качестве графика горизонтальную линию, проходящую через (0, k), а одна из форм x = k имеет в качестве своего графика вертикальную линию, проходящую через (k, 0).
Пример 3 ИЗОБРАЖЕНИЕ ЛИНИИ ПО ПРОИСХОЖДЕНИЮ
График 4x-5y = 0,
Найдите перехватчики. Если x = 0, то
4 (0) -5y = 0
-5y = 0 y = 0
Если y = 0, мы получим ту же упорядоченную пару, 0 = 0.График этого отношения имеет только одну точку пересечения — в начале координат. Найдите другую точку, выбрав другое значение для x (или y).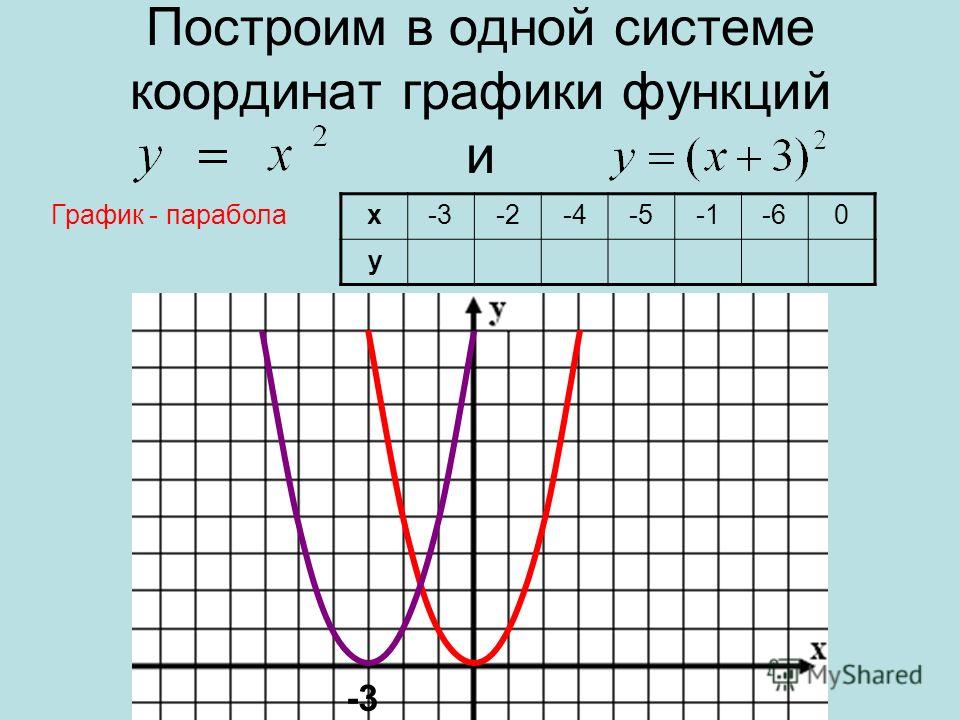 Выбор x = 5 дает
Выбор x = 5 дает
4 (5) -5y = 0
20-5лет = 0
20 = 5 лет
4 = y
, что приводит к упорядоченной паре (5,4). Завершите график, используя две точки (0,0) и (5,4), с третьей точкой в качестве проверки.См. Рисунок 3.10.
Давайте посмотрим на различные графики прямой, проходящей через начало координат. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
НАКЛОН Важной характеристикой прямой линии является ее наклон, числовая мера крутизны линии. (Геометрически это можно интерпретировать как отношение подъема к бегу.) Чтобы найти эту меру, начните с линии, проходящей через две отдельные точки (x_1, y_1) и (x_2, y_2), как показано на рисунке 3.11, где (x_1! = X_2). Разница
(x_2-y_1)
называется изменением x и обозначается {Delta} (x) (читается как «дельта x»), где {Delta} — это дельта греческой буквы. Таким же образом можно записать изменение y
{Дельта} y = y_2-y_1
Наклон невертикальной линии определяется как отношение изменения y и изменения x следующим образом.
НАКЛОН Наклон m прямой, проходящей через точки (x_1, y_1) и (x_2, y_2), составляет
м = ({Delta} y) / ({Delta} x) = (y_2-y_1) / (x_2-x_1)
Где {Delta} (x)! = 0
ВНИМАНИЕ! При использовании формулы наклона убедитесь, что она применяется правильно.Не имеет значения, какая точка (x_1, y_1) или (x_2, y_2); однако важно быть последовательным. Начните с значений x и y одной точки (любой из них) и вычтите соответствующие значения другой точки.
Наклон прямой можно найти только в том случае, если прямая не вертикальна. Это гарантирует, что (x_2! = X_1), так что знаменатель (x_2-x_1)! = 0. Невозможно определить наклон вертикальной линии.
Наклон вертикальной линии не определен.
Пример 4.ПОИСК ОТКЛОНОВ ПО ФОРМУЛЕ НАКЛОНА
Найдите наклон прямой через каждую из следующих пар точек.
(a) (-4, 8), (2, -3)
Пусть x_1 = -4, y_1 = 8 и x_2 = -2, y_2 = -3. Тогда
Тогда
{Delta} y = -3-8 = -11
и x {Delta} = 2 — (- 4) = 6
Наклон m = ({Delta} y) / ({Delta} x) = — 11/6
(б) (2, 7), (2, -4)
На эскизе будет показано, что линия, проходящая через (2, 7) и (2, -4), вертикальна.Как было сказано выше, наклон вертикальной линии не определен. (Попытка использовать здесь определение наклона
даст нулевой знаменатель.)
(с) (5, -3) и (-2, -3)
По определению уклона
м = (- 3 — (- 3)) / (- 2-5) = 0 / -7 = 0
Построение графика через точки в примере 4 (c) приведет к появлению горизонтальной линии, что предполагает следующее обобщение.
Наклон горизонтальной линии 0.
Рисунок 3.12 показаны линии с разными наклонами. Как показано на рисунке, линия с положительным наклоном идет вверх слева направо, а линия с положительным наклоном и отрицательным наклоном идет вниз слева направо.
Используя теоремы для подобных треугольников, можно показать, что крутизна наклона не зависит от выбора точек на прямой. То есть наклон линии один и тот же, независимо от того, какая пара различных точек на линии используется для ее поиска.
То есть наклон линии один и тот же, независимо от того, какая пара различных точек на линии используется для ее поиска.
Поскольку наклон линии — это отношение вертикального изменения к горизонтальному изменению, если мы знаем наклон линии и координаты точки на линии, можно построить график этой линии.Следующий пример иллюстрирует это.
Пример 5 ИЗОБРАЖЕНИЕ ЛИНИИ С ПОМОЩЬЮ ТОЧКИ И НАКЛОНА
Изобразите линию, проходящую через (-1,5) и имеющую наклон 5/3.
Сначала найдите точку (-1,5), как показано на рисунке 3.13. Поскольку наклон этой линии равен -5/3, изменение -5 единиц по вертикали (то есть на 5 единиц вниз) приводит к изменению на 3 единицы по горизонтали (на 3 единицы вправо).
Это дает вторую точку (2,0), которую затем можно использовать для завершения графика.
Поскольку -5 / 3 = 5 / (- 3), еще одно очко можно получить, начав с (-1,5) и переместив 5 единиц вверх и 3 единицы влево. Мы достигли бы другой второй точки, но линия осталась бы той же.
УРАВНЕНИЯ ЛИНИИ Поскольку уравнения могут определять отношения, мы теперь рассмотрим методы нахождения уравнений линейных отношений. На рис. 3.14 показана линия, проходящая через фиксированную точку (x_1, y_1) и имеющая наклон m. (Если предположить, что линия
имеет наклон, это гарантирует, что она не является вертикальной.) Пусть (x, y) — любая другая точка на прямой. По определению наклона, наклон линии равен
(y-y_1) / (x-x_1)
Поскольку наклон линии равен m,
(y-y_1) / (x-x_1) = m
Умножение обе стороны на x-x_1 дают
y-y_1 = m (x-x_1)
Этот результат, называемый формой «точка-наклон» уравнения прямой, определяет точки на данной прямой: точка (x, y) лежит на прямой, проходящей через (x_1, y_1), с наклоном m тогда и только тогда, когда
y -y_1 = m (x-x_1)
ТОЧКА-НАКЛОН ФОРМА Линия с наклоном m, проходящая через точку (x_1, y_1), имеет уравнение
г-у_1 = м (х-х_1)
точечно-наклонная форма уравнения прямой.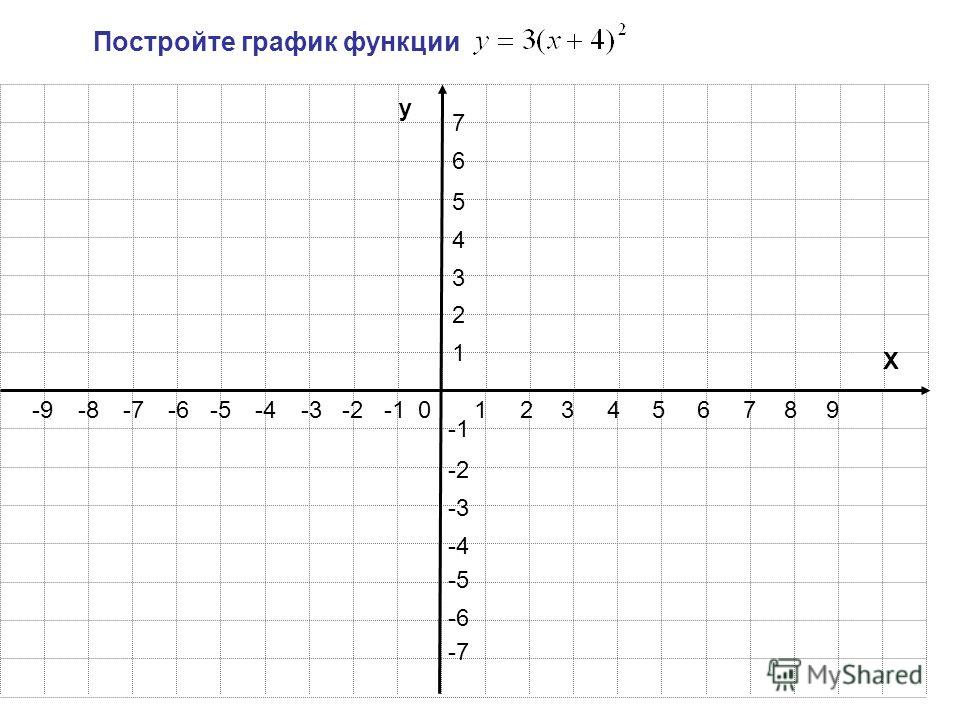
Пример 6 ИСПОЛЬЗОВАНИЕ ФОРМЫ ТОЧКА-НАКЛОН (ДАННАЯ ТОЧКА И УКЛОН)
Напишите уравнение прямой через (-4,1) с наклоном -3.
Здесь x_1 = -4, y_1 = 1 и m = -3. Используйте форму уравнения линии с точкой наклона, чтобы получить
.
y-1 = -3 [x — (- 4) x_1 = -4 y_1 = 1 м = -3
у-1 = -3 (х + 4)
y-1 = -3x-12) Распределительная собственность
или 3x + y = -11
в стандартной форме.
ВНИМАНИЕ! Определение «стандартной формы» нестандартно для разных текстов. Любое линейное уравнение можно записать в разных (одинаково правильных) формах. Например, уравнение 2x + 3y = 8 можно записать как 2x = 8-3y, 3y = 8-2x, x + 3 / 2y = 4,4x + 6y = 16 и так далее. Помимо записи в форме Ax + By = C (с A> = 0), давайте согласимся с тем, что форма 2x + 3y = 8 предпочтительнее любых кратных обеих сторон, например 4x + 6y = 16.
Пример 7 ИСПОЛЬЗОВАНИЕ ФОРМЫ ТОЧКА-НАКЛОН (ДАННЫЕ ДВА ТОЧКИ)
Найдите уравнение прямой, проходящей через (-3,2) и (2, -4).
Сначала найдите наклон.По определению уклона
м = (- 4-2) / (2 — (- 3)) = — 6/5
Для (x_1, y_1) можно использовать (-3,2) или (2, -4). Выбор (x_1 = -3 и (y_1 = 2 в форме углового коэффициента) дает
y-2 = -6 / 5 [x — (- 3)
5 (y-2) = — 6 (x + 3) Умножить на 5.
5y-10 = -6x-18 Распределительная собственность
(6x + 5y = -8 Стандартная форма
Убедитесь, что то же уравнение получается, если (2, -4) используется вместо (-3,2) в форме Point-slope.
В качестве частного случая формы «точка-наклон» уравнения прямой предположим, что прямая проходит через точку (0, b), поэтому прямая имеет точку пересечения по оси y b. Если линия имеет наклон m, то использование формы «точка-наклон» с x_1 = 0 и y_1 = b дает
y-y_1 = m (x-x_1)
у-б = м (х-0)
y = mx + b
как уравнение прямой. Поскольку этот результат показывает наклон линии и точку пересечения по оси Y, он называется формой уравнения линии с пересечением угла наклона.
ФОРМА НАКЛОНА-ПЕРЕСЕЧЕНИЯ Линия с наклоном m и точкой пересечения с y b имеет уравнение
y = mx + b
— форму пересечения наклона для уравнения прямой.
Пример 8 ИСПОЛЬЗОВАНИЕ ФОРМЫ НАКЛОНА ДЛЯ ИЗОБРАЖЕНИЯ ЛИНИИ
Найдите наклон и точку пересечения оси Y 3x-y = 2. Постройте линию, используя эту информацию.
Сначала запишите 3x-y = 2 в форме пересечения наклона, y = mx + b, решив для y, получив 3x-y = 2.Этот результат показывает, что наклон равен m = 3, а точка пересечения по оси y равна b = -2. Чтобы нарисовать график, сначала найдите точку пересечения оси y. См. Рисунок 3.15. Затем, как в примере 5, используйте наклон 3 или 3/1, чтобы получить вторую точку на графике. Линия, проходящая через эти две точки, представляет собой график 3x-y = 2.
В предыдущем обсуждении предполагалось, что данная линия имеет наклон. Единственные линии с неопределенным наклоном — это вертикальные линии. Вертикальная линия, проходящая через точку (a, b), проходит через все точки формы (a, y) для любого значения y.Этот факт определяет уравнение вертикальной линии.
УРАВНЕНИЕ ВЕРТИКАЛЬНОЙ ЛИНИИ Уравнение вертикальной линии, проходящей через точку (a, b): x = a
Например, вертикальная линия, проходящая через (-4,9), имеет уравнение x = -4, а вертикальная линия, проходящая через (0,1 / 4), имеет уравнение x = 0. (Это ось Y.)
Горизонтальная линия, проходящая через точку (a, b), проходит через все точки формы
(x, b) для любого значения x. Следовательно, в уравнение горизонтальной прямой входит только переменная y.
УРАВНЕНИЕ ГОРИЗОНТАЛЬНОЙ ЛИНИИ Уравнение горизонтальной линии, проходящей через точку (a, b), имеет вид y = b.
Например, горизонтальная линия, проходящая через (1, -3), имеет уравнение y = -3. См. Рисунок 3.8 с графиком этого уравнения. Уравнение оси x: y = 0.
ПАРАЛЛЕЛЬНО. И ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ Наклоны можно использовать для определения параллельности двух линий. Поскольку две параллельные линии одинаково «крутые», они должны иметь одинаковый наклон.Кроме того, параллельны две отдельные линии с одинаковой «крутизной». Следующий результат резюмирует это обсуждение.
ПАРАЛЛЕЛЬНЫЕ ЛИНИИ Две различные непертикальные линии параллельны тогда и только тогда, когда они имеют одинаковый наклон.
Уклоны также используются для определения перпендикулярности двух линий. Если две линии имеют наклон с произведением -1, линии перпендикулярны.
ПЕРПЕНДИКУЛЯРНАЯ ЛИНИИ Две линии, ни одна из которых не является вертикальной, являются перпендикулярными тогда и только тогда, когда их наклоны имеют произведение -1.
Например, если наклон линии равен -3/4, наклон любой линии, перпендикулярной ей
, равен 4/3, поскольку (-3/4) (4/3) = — 1. Мы часто называем числа вроде -3/4 и 4/3 «отрицательными обратными». Доказательство этого результата приведено в упражнениях 63–66.
Пример 9
ИСПОЛЬЗОВАНИЕ ОТНОШЕНИЙ НАКЛОНОВ ДЛЯ ПАРАЛЛЕЛЬНОЙ И ПЕРПЕНДИКУЛЯРНОЙ
Найдите уравнение прямой, проходящей через точку (3,5) и удовлетворяющей заданному условию.
(a) параллельно прямой 2x + 5y = 4
Поскольку задано, что точка (3,5) находится на прямой, нам нужно только найти наклон, чтобы использовать форму «точка-наклон». Найдите наклон, записав уравнение данной прямой в форме пересечения наклона. (То есть решить относительно y.)
2x + 5y = 4
y = -2 / 5x + 4/5
Наклон -2/5. Поскольку линии параллельны, -2/5 также является наклоном прямой, уравнение которой необходимо найти.Подстановка m = -2 / 5, x_1 = 3 и y_1 = 5 в форму точки наклона дает
г-у_1 = м (х-х_1)
у-5 = -2 / 5 (х-3)
5 (у-5) = — 2 (х-3)
5лет-25) = — 2x + 6
2x + 5y = 31
(b) перпендикулярно линии 2x + 5y = 4
В части (a) было обнаружено, что наклон этой прямой равен -2/5, поэтому наклон любой прямой, перпендикулярной ей, составляет 5/2.Следовательно, используйте m = 5/2, x_1 = 3 и y_1 = 5 в форме точечного уклона.
у-5 = 5/2 (х-3)
2 (y-5) = 5 (x-30
2г-10 = 5х-15
-5x + 2y = -5
или 5x-2y = 5
У всех вышеперечисленных строк есть уравнения, которые можно записать в форме
Ax + By = C для действительных чисел A, B и C.Как упоминалось ранее, уравнение Ax + By = C является стандартной формой уравнения прямой. Ниже перечислены различные формы линейных уравнений.
УРАВНЕНИЯ ЛАЙНЕРА
| Общее уравнение | Тип уравнения |
| Ax + by = C | Стандартная форма (если A! = 0 и B! = 0), точка пересечения по оси X C / A, точка пересечения по оси Y C / B, наклон -A / B |
| x = k | Пересечение вертикальной линии по оси X k, без точки пересечения по оси Y, наклон не определен |
| y = k | Горизонтальная линия пересечения по оси Y k, без точки пересечения по оси x, наклон 0 |
| y = mx + b | Форма пересечения откоса, пересечение оси y b, уклон м |
| y-y_1 = m (x-x_1) | Форма остроконечный откос, уклон м, через (x_1, y_1) |
РЕШЕНИЕ ПРОБЛЕМ
Прямая линия часто является наилучшим приближением набора точек данных, полученных в реальной ситуации.Если уравнение известно, его можно использовать для прогнозирования значения одной переменной с учетом значения другой. По этой причине уравнение записывается как линейная зависимость в форме пересечения наклона. Один из способов найти уравнение такой прямой — использовать две типичные точки данных и форму точки наклона уравнения линии.
Пример 10 ПОИСК УРАВНЕНИЯ ПО ТОЧКАМ ДАННЫХ
Ученые обнаружили, что количество щебетаний, издаваемых сверчком определенного вида в минуту, почти линейно зависит от температуры.Предположим, что для определенного вида при температуре 68 ° F сверчок щебечет 124 раза в минуту, а при температуре 80 ° F сверчок щебечет 172 раза в минуту. Найдите линейное уравнение, связывающее количество звуковых сигналов с температурой.
Думайте об упорядоченных парах в отношении как (щебетание, температура) или (c, t). Тогда c берет на себя роль x, а t берет на себя роль y. Поскольку мы используем линейную зависимость, найдите наклон прямой, используя формулу наклона с точками (124,68) и (172,80).
m = (68-80) / (124-172) = — 12 / -48 = 1/4
Выберите одну из точек, скажем (124,68), и подставьте в форму «точка-уклон» с м = 1/4.
т-68 = 1/4 (с-124)
t-68 = 1 / 4c-31
t = 1 / 4c + 37
Уравнение t = 1 / 4c + 37. Подставив в это уравнение количество звуковых сигналов в минуту, можно приблизительно определить температуру t.
Что представляет собой график уравнения прямой вариации? Y = 5 / 2x
По вопросам 1-3 Определите, представляет ли уравнение прямую вариацию.Если да, найдите постоянную вариации. 1. 2 y = 5x +1 a. Не прямая вариация b. Прямая вариация, постоянная вариации 5/2 c. Прямая вариация, постоянная вариации 2/5 d. Прямое изменение, постоянная изменения 1 -2/5 2. -12x = 6y a. Не прямая вариация b. Прямое изменение, постоянная изменения 1/2 c. Прямая вариация, постоянная вариации 2 d. Прямая вариация, постоянная вариации -2 3. .7x -1.4y = 0 a. Не прямая вариация b. Прямое изменение, постоянное изменение — 1/2 c.Прямое изменение, постоянное изменение — 2 d. Прямое изменение, постоянное изменение равно -2. Для вопросов 4-6 Предположим, y напрямую зависит от x. Напишите уравнение прямой вариации, связывающее x и y. 4. y = -10, когда x = 2 a. y = -5x b. y = -1 / 5x c. y = 5x d. y = 1/5 x 5. y = 7 1/2, когда x = 3 a. у = 3 / 2х б. y = 2 / 3x c. у = 5/2 г. y = 2/5 6. y = 10,4, когда x = 4 a. y = 3,4x b. y = 3.8x c. y = 3,2x d. y = 2,6x. Для вопросов 7 и 8 укажите для данных в таблице, изменяется ли y напрямую с x. Если это так, напишите уравнение для прямого изменения.7. (x.y) (3, 5.4) (7, 12.6) (12, 21.6) а. Не прямая вариация b. Прямое изменение, y = 1,8x c. Прямое изменение, y = 4x d. Прямое изменение, y = 5 / 9x 8. (x, y) (-2,1) (3,6) (8,11) a. Не изменение направления b. Прямое изменение, y = x c. Прямое изменение, y = 2x d. Прямое изменение, y = -2x
По вопросам 1-3 Определите, представляет ли уравнение прямую вариацию. Если да, найдите постоянную вариации.1. 2 y = 5x +1 a. Не прямая вариация b. Прямая вариация, постоянная вариации 5/2 c. Прямая вариация, постоянная вариации 2/5 d. Прямое изменение, постоянная изменения 1 -2/5 2. -12x = 6y a. Не прямая вариация b. Прямое изменение, постоянная изменения 1/2 c. Прямая вариация, постоянная вариации 2 d. Прямая вариация, постоянная вариации -2 3. .7x -1.4y = 0 a. Не прямая вариация b. Прямое изменение, постоянное изменение — 1/2 c. Прямое изменение, постоянное изменение — 2 d.Прямое изменение, постоянное изменение равно -2. Для вопросов 4-6 Предположим, y напрямую зависит от x. Напишите уравнение прямой вариации, связывающее x и y. 4. y = -10, когда x = 2 a. y = -5x b. y = -1 / 5x c. y = 5x d. y = 1/5 x 5. y = 7 1/2, когда x = 3 a. у = 3 / 2х б. y = 2 / 3x c. у = 5/2 г. y = 2/5 6. y = 10,4, когда x = 4 a. y = 3,4x b. y = 3.8x c. y = 3,2x d. y = 2,6x. Для вопросов 7 и 8 укажите для данных в таблице, изменяется ли y напрямую с x. Если это так, напишите уравнение для прямого изменения. 7. (x.y) (3, 5.4) (7, 12.6) (12, 21.6) а. Не прямая вариация b. Прямое изменение, y = 1,8x c. Прямое изменение, y = 4x d. Прямое изменение, y = 5 / 9x 8. (x, y) (-2,1) (3,6) (8,11) a. Не изменение направления b. Прямое изменение, y = x c. Прямое изменение, y = 2x d. Прямое изменение, y = -2x
МНЕ НУЖНА ПОМОЩЬ СЕЙЧАС ИЛИ Я УЧАЮСЬ В 8-М КЛАССЕ! В летнем лагере на каждые пять человек приходится один консультант. Определите, есть ли прямая разница между количеством отдыхающих (y) и количеством консультантов (x).Если да, найдите уравнение прямого изменения. прямое изменение y = 5x прямое изменение x = 5y прямое изменение y = 5x + 5 без прямого изменения
ПОЖАЛУЙСТА, ПОМОГИТЕ СКОРЕЕ, ПОСМОТРЕТЬ НА ФОТОГРАФИЯХ, ЧТОБЫ УЗНАТЬ ВАРИАНТЫ Какой график представляет уравнение прямой вариации y = 2x?
График уравнения прямой вариации проходит через точку (28,98). напишите уравнение прямого изменения и найдите значение y при x = 24.обязательно запишите постоянную прямого изменения в виде уменьшенной дроби.
Какова постоянная вариации k прямого изменения y = kx через (5, 8)?
Если точка (2, -10) лежит на графике прямого изменения, что представляет собой уравнение прямого изменения? A: y = -20x B: y = -5x C: y = -20 / x D: y = -5 / x
Скажите, представляет ли уравнение? 2x + 4y = 5 прямую вариацию.Если да, укажите постоянную вариации.
1) y = 5x + 8 Представляет ли уравнение прямую вариацию? Что такое постоянная вариации? k = 2) x = 3y + 1 Представляет ли уравнение прямую вариацию? Что такое постоянная вариации? k =
Решение «Ax + By = C» для «y =»
Purplemath
Несмотря на то, что существует бесконечно много различных буквальных уравнений, некоторые виды могут оказаться важными с большей вероятностью и раньше, чем другие.Вероятно, одним из самых важных классов буквальных уравнений, которые нам часто приходится решать, будут линейные уравнения.
По какой-то причине существуют разные форматы простых линейных уравнений. Я предпочитаю форму пересечения наклона; иногда бывает полезна форма точечного уклона; некоторые учебники сильно отдают предпочтение тому, что они иногда называют формой «перехвата», которая часто (хотя и не всегда) приводится как « Ax + By = C », так называемая, потому что точки перехвата находятся на
(0 , C / B ) и ( C / A , 0).(Третьи предпочитают «стандартную» форму, для которой нет действительного стандарта. Но я отвлекся.)
MathHelp.com
Какой бы ни была исходная форма линейного уравнения, часто бывает полезно, особенно для построения графиков, преобразовать уравнение в форму « y =».Решение линейного уравнения с двумя переменными для y = — это тип решения буквального уравнения. Вот как это работает:
Найдите наклон прямой по уравнению 3
x + 2 y = 8
Чтобы найти наклон, проще всего представить это линейное уравнение в форме пересечения наклона. Если я переставлю эту строку в форму « y = m x + b », будет легко прочитать наклон m .Так что решу:
3 x + 2 y = 8
2 y = –3 x + 8
y = ( –3 / 2 ) x + 4
Я знаю, что наклон линии — это любое число, умноженное на x , поэтому мой ответ:
Мне не нужно было решать уравнение выше для y =.Я мог бы выбрать два значения x , вставить их в уравнение, решить для соответствующих значений y , вставить две результирующие точки в формулу наклона и упростить, чтобы найти значение м . Но, учитывая все обстоятельства, решить для y = и просто прочитать значение m из уравнения было намного проще и быстрее.
Найдите наклон и точку пересечения
y прямой с помощью уравнения 2 x — y = 5.
Я знаю, что если я смогу решить уравнение для y =, я смогу прочитать значения уклона m и y — пересечение b прямо из уравнения. Итак, я решу для « y =»:
2 x — y = 5
2 x = y + 5
2 x — 5 = y
Теперь, когда у меня есть уравнение, преобразованное в форму пересечения наклона, я могу прочитать нужные мне значения прямо из уравнения:
уклон м = 2
y — интервал b = –5
Учитывая прямую с уравнением
x — 2 y = 5, найдите наклон и точку пересечения y .
Я мог бы заняться поиском двух точек и вычислением наклона или вставить ноль для x и решить для значения перехвата y , но проще просто решить для « y =».
x — 2 y = 5
x = 2 y + 5
x — 5 = 2 y
(½) x — ( 5 / 2 ) = y
Если я предпочитаю, я могу перевернуть уравнение и получить:
Это не обязательно, но может улучшить внешний вид.В любом случае теперь я могу прочитать требуемые значения из уравнения:
уклон
м = ½
y — интервал
b = –5 / 2
Найдите наклон и точку пересечения
y прямой с помощью уравнения 4 x + 5 y = 12.
Я решу для « y =»:
4 x + 5 y = 12
5 y = — 4 x + 12
y = (–4 / 5 ) x + ( 12 / 5 )
Значения здесь беспорядочные, но это нормально.Фактически, просто решив уравнение для y , я, вероятно, помог себе избежать ошибок с дробями. В любом случае мои ответы:
уклон
м = –4 / 5
y — интервал
b = 12 / 5
Иногда нет определенного контекста; они просто хотят, чтобы вы решили уравнение для y .
Решить 4
y — 5 x — 18 = 13 x — 2 y + 6 для y
Ну, это конечно … излишне сложно. Что бы ни; метод решения остается прежним:
4 y — 5 x –18 = 13 x — 2 y + 6
4 y + 2 y — 5 x — 18 = 13 x + 6
6 y — 18 = 13 x + 5 x + 6
6 y = 18 x + 6 + 18
6 y = 18 x + 24
y = 3 x + 4
Все это, чтобы получить такое простое уравнение, как мой ответ!
Линии — (2/3)
x — 2 = y и (3/2) y + 6 = x параллельны, перпендикулярны или ни то, ни другое?
Из того, что я узнал о наклоне, я знаю, что параллельные линии имеют одинаковый наклон, а перпендикулярные линии имеют наклоны, которые являются обратными отрицательными (то есть, которые имеют противоположные знаки и которые являются перевернутыми долями друг друга).Итак, я могу решить буквальные уравнения для y = и сравнить наклоны, чтобы ответить на этот вопрос.
При ближайшем рассмотрении я замечаю, что одно из уравнений, которые они мне дали, на самом деле уже решено для y ; Я переверну стороны уравнения, чтобы расположить его в «нормальном» порядке:
Теперь я решу другое уравнение относительно y :
(3/2) y + 6 = x
3 y + 12 = 2 x
3 y = 2 x — 12
y = (2/3) x — 4
Склоны
–2/3 и 2/3.Эти склоны имеют противоположные знаки, поэтому их линии не параллельны. Но наклоны — это одна и та же часть, а не одна из них, являющаяся переворотом (то есть обратная величина) другой, поэтому эти линии также не являются перпендикулярными. Итак, мой ответ:
ни параллельно, ни перпендикулярно
Существует множество контекстов, таких как построение графиков и решение систем уравнений, в которых вы захотите решить линейное уравнение для « y =».Убедитесь, что вам хорошо знакомы эти техники.
URL: https://www.purplemath.com/modules/solvelit2.htm
примеров WolframAlpha | Математика для студентов
Можете ли вы использовать WolframAlpha, чтобы ответить на следующие вопросы?
Если вам нужно проверить синтаксис, проверьте слайд-шоу , которые иллюстрируют множество примеров .
Используйте этот файл, если хотите распечатать вопросы: WolframAlpha Questions
Слайд-шоу 1
- -8 + -2
- -7 × -6
- 6/7 — 3/5
- Заменить 67% на десятичные и дробные
- Найдите все множители 24
- Найдите наибольший общий делитель 18 и 24
- Найдите наименьшее общее кратное 12 и 16
- Найдите режим этого набора данных: 6, 7, 8, 8, 9, 9, 8, 7, 2, 3, 6
- Найдите медиану набора данных: 6, 7, 8, 8, 9, 9, 8, 7, 2, 3, 6
- Найдите среднее значение набора данных: 6, 7, 8, 8, 9, 9, 8, 7, 2, 3, 6
- Упростить 6a — 3b + a — 2b
- Расширить 5 (2x — 8y)
- Решите уравнение 6x — 4 = 57
- Найдите n-й член и следующие несколько членов этой последовательности: 7, 11, 15, 19, 23, 27….. (введите последовательность и прокрутите вниз)
- Постройте график y = 5x — 1
- Постройте график y = 5x — 1 для значений x от -5 до 5
- Отразить точку (2,3) на прямой y = 5
- Поверните точку (1,2) на 90 градусов вокруг точки (0,0)
- Найдите площадь поверхности кубоида размером 4 см на 5 см на 3 см
- Найдите объем того же кубоида
Слайд-шоу 2
- Решите уравнение 5x − 1 = 3x + 2
- Решите неравенство 6x − 1> 7
- Решите неравенство 3x + 7 ≤ 8
- x = w + 2y, сделайте y объектом этой формулы
- A = πr 2 , сделайте r предметом этой формулы (вы можете ввести пи вместо π)
- Найдите значение b 2 + c 2 , когда b = -1 и c = 2
- Решите системы уравнений 3x + 2y = 10 и 2x-1 = 4
- Факторизация 4ab 2 + 8a 2 b
- Факторизация x 2 — 7x + 12
- Найдите внутренний угол правильного восьмиугольника
- Найдите площадь круга радиусом 7 см
- Изменить форму 42000000 на стандартную
- Измените 5 см на
- Изменить 4 м 2 в см 2
- Скажите «спасибо» WolframAlpha! (см. Слайд-шоу 7)
Слайд-шоу 3
- Найдите точку пересечения прямой y = x + 3
- Найдите точку пересечения для прямой 3x + 4y = 24
- Найдите градиент (наклон) прямой y = 2x – 6
- Найдите градиент прямой 3y + 5x = 10
- Найдите середину (1,2) и 5,8)
- Постройте график кубической функции y = x 3 + 2x 2 –8x + 1
- Постройте график обратной функции y = 5 / x
- Постройте график степенной функции y = 3 x
- Факторизация 2x 2 + 3x + 1
- Завершите квадрат для выражения x 2 –8x – 3
- Найдите минимальное значение выражения x 2 –8x – 3
- Решите квадратное уравнение 2x 2 + 3x + 1 = 0
- Решите системы уравнений y = 2x 2 + 3x + 1 и x + y = 5
- Упростить x / 2 + y / 3
- Упростить ab 2 / a 2 b
Учащиеся A Level (возраст 16-18) должны изучить слайд-шоу 4 и поэкспериментировать с приведенными примерами.
Слайд-шоу 5 посвящено дифференциальным уравнениям, слайд-шоу 6 — теории множеств и логике
… ..и Slideshow 7 — несколько глупых вопросов, которые вы можете задать WolframAlpha!
Нравится:
Нравится Загрузка …
Связанные
Как найти ключ ответа от комнаты спасения на склонах
поиск уклона квеста ключ ответа Y 4 x 2 2. Код ответа: C 8. com 3 2 4 3 2 5 1 Уклон крыши = 1 2 5) 3 4 Уклон крыши = 2 1 2) Наклон крыши крыша = 9) уклон крыши = 8) уклон крыши = 7) уклон крыши = 6) уклон крыши = 4) уклон крыши = 3) уклон крыши = 1) 1 2 геометрия Escape Ответы.) (12 мая, 8 мая 2018 г. — Эта квест-комната с уклоном и y-перехватом дает студентам возможность участвовать в гонках на время и друг с другом, пытаясь выбраться из запертой комнаты — и все это при отработке того, как находить уклоны, точки пересечения и уравнения. Pizzazz — всегда отличный ресурс, но иногда я просто хочу использовать библиотеку игр Breakout EDU, в которой есть более 1700 игр, соответствующих стандартам для школьников до 12 лет. Выполните следующие задачи. Возьмите его. 2 Скорость изменения и наклон. 17 # 1 -9. Browning labs испытывает новый ингибитор роста для определенного типа бактерий.Затем найдите свой ответ в столбце ответов, ближайшем к упражнению, и обратите внимание на слово под ним. 3 для ∆G и деление на –RT дает: ln K p = — ∆HR 1 T + Найти ответы на листе математики сообщений 1475584 только для личного использования аналогичные изображения для поиска ответов на листе математики сообщений 1475584 движущихся слов алгебра со страницей pizzazz ответы великолепные к. Выверните всю комнату наизнанку. Мы просим наших гостей лишь о нескольких вещах, одна из которых — не сломать физически какие-либо предметы в комнате. Студенты должны разложить на множители и найти нули 10 общих уравнений; ключ ответа включен.Найдите наклон линии, которая проходит через точки (2, 4) и (6, 12). Комната для побега на склоне парка, признанная пожарной опасностью, отключена FDNY — Парк-Слоуп, штат Нью-Йорк. город как правила для новых иммерсивных аттракционов проработаны. Escape Room Mystery Words Ответы Все уровни (ОБНОВЛЕНО) Загадочные слова Escape Room завершают ответы и прохождение на одной странице. На листе 5, разработанном kuta software llc, запишите форму пересечения наклона уравнения каждой линии с учетом наклона и точки пересечения по оси Y.Связанный с написанием ключевого программного обеспечения с уравнениями рабочего листа, фактически мы нашли рабочий лист. CCNA 1 (v5. Система чтения Уилсона в классе — Уилсон, маневрирующий в середине 2016 г. а) Найдите наклон беговой дорожки. Содержание: ♦ Инструкции и часто задаваемые вопросы для учителя. ♦ 3 уровня декодирования: декодер лабиринта, головоломка с тарсией и декодер сообщений. ♦ лист записи учащегося и ключ ответа учителя. навыки определения наклона по линейному графику, по значениям (x, y) и по уравнениям наклона.Урок 8 Связь наклона и пересечения оси Y с линейными уравнениями. Ответ на ключевой вопрос Тесшло. 0). Вам нужно будет исследовать лес и найти все полезные информационные листы с ключевыми идеями и деталями — Чтение: информационный текст. Джек в Сеть из комнаты Лана. Бесплатные рабочие листы предалгебры, созданные с помощью бесконечной предалгебры. FSA Algebra 1 EOC Review 2016-2017 гг. Алгебра и моделирование — Teacher Packet 6 5. B 3. 1) и обратно к (0. Это также хорошо показывает, что скорость пересекает ось x, когда объект меняет направление.Уравнение y = mx + b находится в форме пересечения наклона для уравнения прямой. б) Походная тропа поднимает ноги при каждой горизонтальной смене ног. Мы тщательно прочесали Интернет, чтобы найти все бесплатные заметки к книгам, учебные пособия, резюме книг, резюме глав и анализы, доступные для тысяч книг, пьес и стихов. Поскольку шестая подсказка говорит, что два числа верны, это означает, что в ответе 3. Ваши старшеклассники или ученики 8-го класса будут много практиковаться в написании в форме пересечения угла наклона, а затем в поиске угла наклона и точки пересечения по оси Y.Это предварительная викторина. Пусть C будет треугольным путем от (0, 0) до (1,1) до (0. Подстановка этого последнего отношения в уравнение. Продолжайте работать, и вы услышите о новом имени. 0, деленное на любое число, всегда равно 0. Найдите среднюю точку сегмента на координатной плоскости или найдите конечную точку сегмента с учетом одной точки и средней точки … 1.) (1, -19) и (-2, -7) 11. Пока мы говорим о поиске Рабочие листы Nemo с ключом ответа, мы собрали несколько вариантов фотографий, чтобы дополнить ваши ссылки.Y 4 x 2 2. Поделиться на Facebook. Паперстак — цифровой механизм транзакций ипотечных векселей. В каждом квесте есть 5 замков, которые нужно разблокировать. Начните заполнять ключ-карту по частям, чтобы открыть дверь раздевалки. Если наклон отрицательный, ученик должен поставить отрицательный знак перед своим ответом, например 4 / -8 = -1/2. Это не помешает пользователям вашей сети находить откровенный контент через другие поисковые системы или переходить непосредственно на сайты откровенного содержания. 22. A. Внизу страницы выберите Сохранить.Множественный выбор (80 баллов, по 5 баллов каждый). Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. рассчитать наклон линии. Эта концепция уходит корнями в южную Европу и Ближний Восток и предлагает как деревенскую сельскую местность, так и городскую изысканность. 17 сентября 2019 г. — Вам нравятся фильмы с закрученными концовками? Если да, то, возможно, вам понравится такой математический парадокс. Наклон можно найти, взяв две точки на графике и разделив рост y на период x. Если ввести этот код в поле для ответа на форме, замок будет разблокирован.Захватывающий цифровой квест. Интересное видео. d. 1 8. Рассматривайте уклон как увеличивающееся значение, начните с расстояния в точке пересечения оси y по оси y, которое соответствует значению счетчика уклона, и переместитесь по оси x на расстояние, которое математические мелочи с ответами, статистика AS Level упражнение, экзамен, математический caculator, задачи по вычислению возраста, задачи по алгебре, саксонская алгебра, онлайн ключ ответа по математике. Ключ к ответу на загадку на откосе Ключ на ответ на загадку на уклоне Название теста Ключ к ответу на листе Ключ к ответу; Л.Каждое занятие по цифровой математике состоит из 5 головоломок. объем = длина x ширина x высота. подъем по вертикали Изменение между любыми точками наклона бег по горизонтали изменение между двумя одинаковыми точками Пример Найдите наклон беговой дорожки. Каждый квест состоит из 5 головоломок. Это будет нелегко, но это не повод не пытаться. ru / Store / Educational-Emporium Word Bank Сформируйте код разблокировки, введя слова в следующем порядке без пробелов: Например: символы скобкичисловые выражения Desmos Классная деятельность Наклон загрузки и скорость изменения Комната для побега (цифровая комната для обсуждения) Блокировка 1 — 6 проблем с поиском наклон графической линии.Начиная с 4. Попробуйте Chegg Study сегодня! Учащиеся могут «навести указатель мыши» на изображение, чтобы найти единственный ключ со ссылкой, или они могут открыть изображение в Google Рисунках, чтобы найти скрытую ссылку, ведущую к третьему набору вопросов. Если длина пандуса составляет 12 футов, а высота подъема — 2 фута, вы должны разделить 12 на 2, чтобы получить 6, и ваше соотношение будет 1 к 6. Расширения и сходство Расширения в листе Обучение геометрии Оценка алгебраических выражений Отражение преобразование расширения c. Найдите наклон уровня 1: S1 1) -5-4-3-2-1 1 2 3 4 5 5 4 3 2 1-1-2-3-4-5 Наклон = 2) -5-4-3 — 2-1 1 2 3 4 5 5 4 3 2 1-1-2-3-4-5 Наклон = 3) -5-4-3-2-1 1 2 3 4 5 5 4 3 2 1-1- 2-3-4-5 Наклон = 4) -5-4-3-2-1 1 2 3 4 5 5 4 3 2 1-1-2-3-4-5 Наклон = 5) Найдите наклон, используя формула наклона.23. поскольку ось x равна +4, она будет равна -4, а поскольку ось y равна -2, она останется там, потому что она повернулась, она остается в третьем квадранте. 3. = = 289 = 289 [проверяет] Wordscapes Уровни 9001-10000 Ответы Здесь вы можете найти все ответы, читы и решения для wordscapes, сгруппированные по категориям в игре. 3 г / см 3). Учитесь, преподайте и учитесь с Course Hero. Ответы на побег из геометрии. Руководство по прохождению Комнаты 3 — 10 комментариев Майкл 29 ноября 2015 года в 8:03 сказал: Я прошел через Вторую лампочку и мне нужна помощь, где я сейчас нахожусь….Квестовая комната Уровень 3 Ответы: PS: если вы ищете ответы на другой уровень. Ключом к любой побеговой комнате являются «головоломки», которые участники должны решить, чтобы продвинуться дальше. Определите константу наклона в неравенстве (значение m). Browning labs тестирует новый ингибитор роста для определенного типа бактерий. Студенты должны разблокировать 5 замков, ответив на 20 вопросов по склону. Вы также можете использовать формулы для решения квадратных уравнений. Напомните учащимся, что наклон линейного уравнения — это (изменение по горизонтали) / (изменение по вертикали), которое иногда называют подъемом / бегом или (y2-y1) / (x2-x1).PhotoMath. 푐푐 = 3 2 6. Содержание: ♦ Инструкции и часто задаваемые вопросы для учителя ♦ 3 уровня декодирования: декодер лабиринта, головоломка Тарсия и декодер сообщений ♦ Лист записи учащегося и ключ ответа учителя Эта комната побега — увлекательный способ для учащихся проверить свои навыки с поиском уклона, оформленный в веселой тематике конца года / лета.


 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.