Содержание
Задачи по физике и математике с решениями и ответами
Задача по математике — 4125
Около окружности описана трапеция $ABCD$, боковая сторона $AB$ перпендикулярна основаниям, $M$ — точка пересечения диагоналей трапеции. Площадь треугольника $CMD$ равна $S$. Найдите радиус окружности.
Подробнее
Задача по математике — 4126
Площадь равнобедренной трапеции, описанной около окружности, равна $S$, а высота трапеции в два раза меньше её боковой стороны. Найдите радиус окружности.
Подробнее
Задача по математике — 4127
В равнобедренную трапецию вписана окружность. Докажите, что отношение площади трапеции к площади круга равно отношению периметра трапеции к длине окружности.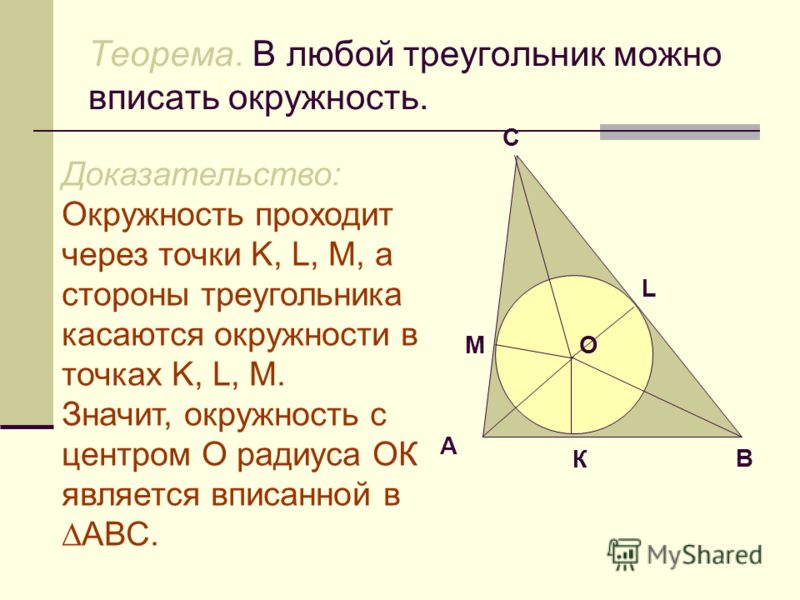
Подробнее
Задача по математике — 4128
Около окружности радиуса 1 описана равнобедренная трапеция, площадь которой равна 5. Найдите площадь четырёхугольника, вершинами которого служат точки касания окружности и трапеции.
Подробнее
Задача по математике — 4129
Около окружности радиуса $R$ описана трапеция. Хорда, соединяющая точки касания окружности с боковыми сторонами трапеции, равна $a$. Хорда параллельна основанию трапеции. Найдите площадь трапеции.
Подробнее
Задача по математике — 4130
Около окружности радиуса $R$ описана равнобедренная трапеция $ABCD$; $E$ и $K$ — точки касания этой окружности с боковыми сторонами $AD$ и $BC$. {\circ}$. Докажите, что $EK$ параллельно $AB$ и найдите площадь трапеции $ABKE$.
{\circ}$. Докажите, что $EK$ параллельно $AB$ и найдите площадь трапеции $ABKE$.
Подробнее
Задача по математике — 4131
В некоторый угол вписана окружность радиуса 5. Хорда, соединяющая точки касания, равна 8. К окружности проведены две касательные, параллельные хорде. Найдите стороны полученной трапеции.
Подробнее
Задача по математике — 4132
Основания трапеции равны 4 и 16. Найдите радиусы окружностей, вписанной в трапецию и описанной около неё, если известно, что эти окружности существуют.
Подробнее
Задача по математике — 4133
В параллелограмме $ABCD$ с углом $A$, равным $60^{\circ}$, проведена биссектриса угла $B$, пересекающая сторону $CD$ в точке $E$.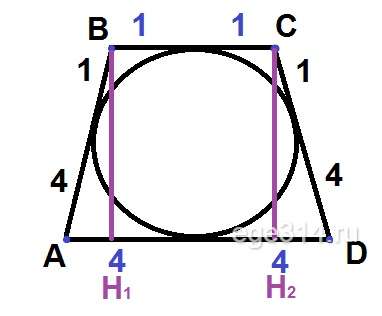 {\circ}$, вписана окружность радиуса $R$. Вторая окружность, лежащая вне треугольника, касается стороны $BC$ и продолжений двух других сторон. Найдите расстояние между центрами этих окружностей.
{\circ}$, вписана окружность радиуса $R$. Вторая окружность, лежащая вне треугольника, касается стороны $BC$ и продолжений двух других сторон. Найдите расстояние между центрами этих окружностей.
Подробнее
Задача по математике — 4135
В параллелограмме лежат две окружности, касающиеся друг друга и трёх сторон параллелограмма каждая. Радиус одной из окружностей равен 1. Известно, что один из отрезков стороны параллелограмма от вершины до точки касания равен $\sqrt{3}$. Найдите площадь параллелограмма.
Подробнее
Задача по математике — 4136
Прямая, перпендикулярная двум сторонам параллелограмма, делит его на две трапеции, в каждую из которых можно вписать окружность. Найдите острый угол параллелограмма, если его стороны равны $a$ и $b$ $(a\lt b)$.
Подробнее
Задача по математике — 4137
Средняя линия равнобедренной трапеции равна 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно $\frac{7}{13}$. Найдите высоту трапеции.
Подробнее
Задача по математике — 4138
Боковые стороны трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно $5:11$. Найдите основания трапеции.
Подробнее
Задача по математике — 4139
Найдите радиус окружности, описанной около прямоугольного треугольника, если радиус окружности, вписанной в него, равен 3, а катет равен 10.
Подробнее
|
Задания для самостоятельной работы
ОГЭ Задание № 17 Вписанные и описанные четырёхугольники
Задания для самостоятельной работы
Читайте также: Рекомендуемые страницы: Вам нужно быстро и легко написать вашу работу? Тогда вам сюда…
Поиск по сайту
| Поиск по сайту:
|
27.
 Окружность. Круг. Вписанные и описанные многоугольники
Окружность. Круг. Вписанные и описанные многоугольники
Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
а, b — касательные,
Решение: 2.
а) R=5 см, AD=8 см, ВС=6 см. б) R=10 см, AD=16 см, ВС=12 см.
Решение:
а) Возможны два случая: хорды лежат по одну сторону от центра окружности и по разные. Рассмотрим оба.
О1О2— расстояние между хордами.
1) Рассмотрим треугольник ВОС — равнобедренный (ОВ=ОС=R), следовательно ОО2 является высотой и медианой и СО2=ВО2=ВС:2=3 см. По теореме Пифагора найдем ОО2: ОО22=ОС2-СО22=25-9=16, ОО2=4 см.
2) Рассмотрим треугольник АОD — равнобедренный (ОD=ОA=R), следовательно ОО1 является высотой и медианой и AО1=DО1=AD:2=4 см. По теореме Пифагора найдем ОО1: ОО12=ОA2-AО12=25-16=9, ОО1=3 см.
По теореме Пифагора найдем ОО1: ОО12=ОA2-AО12=25-16=9, ОО1=3 см.
3) В случае, когда хорды лежат по одну сторону от центра О1О2=4-3=1 см.
В случае, когда хорды лежат по разные стороны от центра, то О1О2=4+3=7 см.
Ответ: 1 см или 7 см.
5. а) В равнобедренном треугольнике угол при вершине равен 120°, боковая сторона равна 6 см. Найдите радиус описанной окружности.
Ответ 12 см.
6. Радиус окружности равен 6 см.
а) Найдите длину дуги, которая содержит 120°.
б) Найдите площадь сектора, если его центральный угол равен 150°.
Решение:
а) l=πR*α : 180=π*6*120 : 180= 4π см.
Ответ: 4π см
7.
 а) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 10 см. Одна из сторон треугольника равна 16 см. Найдите площадь треугольника.
а) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 10 см. Одна из сторон треугольника равна 16 см. Найдите площадь треугольника.б) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 25 см. Одна из сторон треугольника равна 14 см. Найдите площадь треугольника.
Решение:
а) Дано: Δ АВС; w(O,R) — описана около Δ АВС;
R=10 см; ВС=16 см.
Найти S треугольника АВС.
1) Если сторона вписанного треугольника лежит на диаметре, то этот треугольник прямоугольный. АС=2R=20 см.
2) По теореме Пифагора найдем АВ: АВ2=АС2-ВС2=400-256=144, АВ=12 см.
3) Найдем площадь треугольника: S=AB*BC : 2=12*16:2=96 см2.
Ответ: 96 см2.
8.
 Найдите угол х:
Найдите угол х:Решение:
а) 1) Найдем длину дуги АВ:
∠АСВ — вписанный в окружность и он равен половине дуги АВ, следовательно дуга АВ равна 50°*2=100°.
2) Угол между хордой СВ и касательной, проходящей через точку С равен половине дуги, которая находится внутри угла, тогда дуга ВС равна 75°*2=150°.
3) Найдем дугу СА:
дуга СА=360°-дуга АВ — дуга ВС=360°-100°-150°=110°.
4) ∠АВС — вписанный в окружность и равен половине дуги СА, т.е. ∠АВС =110°:2=55°.
Ответ: 55°.
9. а) Радиус описанной около треугольника окружности равен 10 см. Две стороны треугольника равны 12 см и 20 см.
 Найдите площадь треугольника.
Найдите площадь треугольника.б) Радиус описанной около треугольника окружности равен 18,5 см. Две стороны треугольника равны 37 см и 12 см. Найдите площадь треугольника.
Решение:
а)
1) Так как одна из сторон треугольника ( 20 см) в два раза больше радиуса (10 см) описанной окружности, то она лежит на диаметре и треугольник является прямоугольным.
2) АС = 20 см; АВ=12 см. Найдем по теореме Пифагора ВС: ВС2=АС2-АВ2=400-144=256, ВС=16 см.
3) Найдем площадь треугольника: S=AB*BC : 2=12*16:2=96 см2.
Ответ: 96 см2.
10. а) Окружность радиуса 5 см вписана в равнобедренную трапецию с боковой стороной 16 см. Найдите площадь трапеции.
б) Окружность вписана в равнобедренную трапецию с боковой стороной 8 см и площадью 48 см2.
 Найдите радиус окружности.
Найдите радиус окружности.Решение:
а)
Дано: АВСD — равнобедренная трапеция;
АВ=СD=16 см; w(O,R) — описана около трапеции; R=5 см.
Найти S трапеции ABCD.
1) Т.к. в трапецию вписана окружность, то AD+DC=AB+CD=6+6=12 см — сумма оснований трапеции.
2) Высота равна двум радиусам вписанной окружности: КМ=2R=10 см.
3) Найдем площадь трапеции:
S=(AD+DC)*KM:2=12*10:2=60 см2
Ответ: 60 см2
11. а) Найдите площадь прямоугольной трапеции, если точка касания окружности, вписанной в прямоугольную трапецию делит большую боковую сторону на отрезки 4 см и 9 см.
б) Окружность, вписанная в прямоугольную трапецию, точкой касания делит большую боковую сторону на отрезки 4 см и 16 см. Найдите площадь трапеции.
Решение:
а)
Дано: ABCD -прямоугольная трапеция;
CF= 4 см; FD=9 см.
Найти: S трапеции ABCD — ?
1) Рассмотрим треугольники ОКС и OFC, они равны по третьему признаку равенства треугольников:
OK=OF как радиусы;
СF=CK как отрезки касательных, проведенных из одной точки;
ОС — общая сторона.
Тогда ∠КСО=∠FCO и СО — биссектриса ∠KCF.
2) Рассмотрим треугольники ОMD и OFD, они равны по третьему признаку равенства треугольников:
OM=OF как радиусы;
DM=DF как отрезки касательных, проведенных из одной точки;
ОD — общая сторона.
Тогда ∠MDО=∠FDO и DО — биссектриса ∠MDF.
3) Сумма углов трапеции равна 360°, т.к. ∠А=∠В=90°, то ∠С +∠D=360°-180°=180°.
∠OCF + ∠ODF= (∠A + ∠D):2=180°:2=90°. Тогда в треугольнике OCD ∠COD=180°-90°=90°.
4) Треугольник OCD — прямоугольный. OF2=CF*FD=4*9=36. OF=6 см — радиус вписанной окружности.
АВ=2r=12 см.
5) Т.к. трапеция описана около окружности, то AD+DC=AB+CD=12+(4+9)=25 см — сумма оснований трапеции.
6) Найдем площадь трапеции:
S=(AD+DC)*KM:2=25*12:2=150 см2.
Ответ: 150 см2.
12. Найдите угол х:
Решение:
а)
1) Найдем сумму углов А и С:
∠А + ∠С=180° —∠С=180°-70°=110°.
2) Центр вписанной окружности — точка пересечения биссектрис треугольника, тогда ∠ОАС=∠ВАС:2 и ∠ОСА=∠ВСА:2.
Сумма углов ОАС и ОСА равна половине суммы углов А и С и равна 55°.
3) Найдем угол х:
Сумма углов треугольника АОС равна 180°, тогда ∠х=180°-(∠ОАС+∠ОСА)=180°-55°=125°.
Ответ: 125°.
13. а) Доказать, что если в равнобедренную трапецию можно вписать окружность, то квадрат высоты трапеции равен произведению ее оснований.
б) Доказать, что если в прямоугольную трапецию можно вписать окружность, то площадь трапеции равна произведению оснований.
Решение:
а)
Дано: AВCD — равнобедренная трапеция;
окружность вписана в трапецию.
Доказать: ВК2=ВС*АD.
Доказательство:
1) Обозначим основание ВС — а, основание AD — b. ВС=КМ и АК=(AD-DC):2=(b-a):2.
2) Т.к. в трапецию вписана окружность, то АВ+CD=DC+AD=a+b, а т.к. трапеция равнобедренная, то АВ=(a+b):2.
3) Найдем высоту ВК трапеции:
треугольника АВК — прямоугольный и по теореме Пифагора BK2=AB2-AK2
Следовательно, BK2=BC*AD. Что и требовалось доказать.
14. а) Стороны треугольника равны 9 см и 6 см, угол между ними равен 60°. Найдите площадь круга, ограниченного окружностью, описанной около треугольника.
б) Сторона треугольника равна 9 см, угол, прилежащий к ней равен 60°. Площадь круга, ограниченного окружностью, описанной около треугольника равна 39π см2. Найдите вторую сторону, которая прилежит к заданному углу. (№ 5.5.47 [7])
(№ 5.5.47 [7])
Решение:
а)
Дано: АВС — треугольник;
АВ=6 см; АС=9 см; ∠ВАС=60.
Найти: S круга, ограниченного описанной окружностью.
1) Найдем сторону ВС:
по теореме косинусов ВС2=АВ2+АС2+2АВ*АС*cos∠A=36+81-2*6*9*0,5=63.
2) Найдем площадь треугольника АВС:
S=(AB*AC*sin ∠A) :2=(6*9*sin 60) :2,
3) Найдем радиус описанной окружности:
вписанная в многоугольник или угол
Определения
Окружность \(S\) вписана в угол \(\alpha\), если \(S\) касается сторон угла \(\alpha\).
Окружность \(S\) вписана в многоугольник \(P\), если \(S\) касается всех сторон \(P\).
В этом случае многоугольник \(P\) называется описанным около окружности.
Теорема
Центр вписанной в угол окружности лежит на его биссектрисе.
Доказательство
Пусть \(O\) – центр некоторой окружности, вписанной в угол \(BAC\). Пусть \(B’\) – точка касания окружности и \(AB\), а \(C’\) – точка касания окружности и \(AC\), тогда \(OB’\) и \(OC’\) – радиусы, проведённые в точки касания, следовательно, \(OC’\perp AC\), \(OB’\perp
AB\), \(OC’ = OB’\).
Значит, треугольники \(AC’O\) и \(AB’O\) – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда \(\angle CAO = \angle BAO\), что и требовалось доказать.
Теорема
В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.
Доказательство
Проведем биссектрисы углов \(\angle A\) и \(\angle B\). Пусть они пересеклись в точке \(O\).
Т.к. \(O\) лежит на биссектрисе \(\angle A\), то расстояния от точки \(O\) до сторон угла равны: \(ON=OP\).
Т.к. \(O\) также лежит на биссектрисе \(\angle B\), то \(ON=OK\). Таким образом, \(OP=OK\), следовательно, точка \(O\) равноудалена от сторон угла \(\angle C\), следовательно, лежит на его биссектрисе, т.е. \(CO\) – биссектриса \(\angle C\).
Таким образом, точки \(N, K, P\) равноудалены от точки \(O\), то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.
Данная окружность единственна, т.к. если предположить, что существует другая вписанная в \(\triangle ABC\) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.
Таким образом, попутно была доказана следующая теорема:
Следствие
Биссектрисы треугольника пересекаются в одной точке.
Теорема о площади описанного треугольника
Если \(a,b,c\) – стороны треугольника, а \(r\) – радиус вписанной в него окружности, то площадь треугольника \[S_{\triangle}=p\cdot r\] где \(p=\dfrac{a+b+c}2\) – полупериметр треугольника.
Доказательство
\(S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle AOB}+S_{\triangle
BOC}=\frac12OP\cdot AC+\frac12 ON\cdot AB+\frac12 OK\cdot BC\).
Но \(ON=OK=OP=r\) – радиусы вписанной окружности, следовательно,
\[S_{\triangle ABC}=\frac12 r (AC+AB+BC)=p\cdot r\]
Следствие
Если в многоугольник вписана окружность и \(r\) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на \(r\): \[S_{\text{опис.мног-к}}=p\cdot r\]
Теорема
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство
Необходимость. Докажем, что если в \(ABCD\) вписана окружность, то \(AB+CD=BC+AD\).
Пусть \(M,N,K,P\) – точки касания окружности и сторон четырехугольника. Тогда \(AM, AP\) – отрезки касательных к окружности, проведенные из одной точки, следовательно, \(AM=AP=a\). Аналогично, \(BM=BN=b, \ CN=CK=c, \ DK=DP=d\).
Аналогично, \(BM=BN=b, \ CN=CK=c, \ DK=DP=d\).
Тогда: \(AB+CD=a+b+c+d=BC+AD\).
Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Проведем биссектрисы углов \(\angle A\) и \(\angle B\), пусть они пересекутся в точке \(O\). Тогда точка \(O\) равноудалена от сторон этих углов, то есть от \(AB, BC, AD\). Впишем окружность в \(\angle A\) и \(\angle B\) с центром в точке \(O\). Докажем, что эта окружность будет касаться и стороны \(CD\).
Предположим, что это не так. Тогда \(CD\) либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).
Проведем касательную прямую \(C’D’ \parallel CD\) (как показано на рисунке). Тогда \(ABC’D’\) – описанный четырехугольник, следовательно, \(AB+C’D’=BC’+AD’\).
Т.к. \(BC’=BC-CC’, \ AD’=AD-DD’\), то:
\[AB+C’D’=BC-CC’+AD-DD’ \Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD\]
Получили, что в четырехугольнике \(C’CDD’\) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, \(CD\) касается окружности.
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.
Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то \(a+x>d\) и \(b+c>x\). Складывая данные неравенства, получим: \(a+x+b+c>d+x \Rightarrow a+b+c>d\). Следовательно, сумма любых трех сторон всегда больше четвертой стороны.
Теоремы
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.
Доказательство
1) Рассмотрим параллелограмм \(ABCD\), в который вписана окружность. Тогда \(AB+CD=BC+AD\). Но в параллелограмме противоположные стороны равны, т.е. \(AB=CD, \ BC=AD\). Следовательно, \(2AB=2BC\), а значит, \(AB=BC=CD=AD\), т.е. это ромб.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.
2) Рассмотрим прямоугольник \(QWER\). Т.к. прямоугольник является параллелограммом, то согласно первому пункту \(QW=WE=ER=RQ\), т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.
Задание №1207. Тип задания 16. ЕГЭ по математике (профильный уровень)
а) План решения.
1. Сделаем чертёж, считая для определённости, что AD>BC (для пункта а) это не имеет значения).
2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.
3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать по теореме синусов для \triangle ABD.{\circ}, равен половине гипотенузы). Отсюда \frac{O_1N}x=\frac{2O_1N}{O_1N-x} , \frac1x =\frac2{O_1N-x} , O_1N-x=2x, x= \frac13 O_1N= \frac13\cdot \frac12 MN= \frac16\cdot \frac {a\sqrt 3} 2= \frac{a\sqrt 3}{12} , x=\frac{a\sqrt 3}{12} , то есть O_2T=\frac{a\sqrt 3}{12}.
3. \frac{CD}{O_2T} = \frac a{\left( \dfrac{a\sqrt 3}{12} \right)} = 4\sqrt 3.
Радиус вписанного круга Калькулятор | Радиус вписанного круга Расчет
Радиус вписанного круга в равнобедренную трапецию на заданной высоте
Радиус вписанной окружности в равнобедренную трапецию с учетом оснований
Радиус вписанной окружности квадрата с заданной стороной
Радиус вписанной окружности правильного многоугольника с заданной стороной и числом сторон
Радиус вписанной окружности правильного шестиугольника с заданной стороной
Радиус вписанной окружности прямоугольного треугольника с учетом катетов и гипотенузы
Радиус вписанной окружности равностороннего треугольника с заданной стороной
Радиус вписанной окружности ромба заданной высоты
Радиус вписанной окружности ромба по диагоналям
Радиус вписанной окружности ромба по диагоналям и стороне
Радиус вписанной окружности ромба с заданной стороной и углом
Радиус вписанной окружности ромба с учетом большей диагонали и стороны
Радиус вписанной окружности ромба с учетом большей диагонали и угла
Радиус вписанной окружности ромба с учетом меньшей диагонали и стороны
Радиус вписанной окружности ромба с учетом меньшей диагонали и угла
Радиус вписанной окружности треугольника по всем трем сторонам
Радиус круга, вписанного в равнобедренный треугольник с учетом стороны b и высоты.
Радиус круга, вписанного в равнобедренный треугольник, с заданной стороной и углом.
Радиус окружности, вписанной в равнобедренный треугольник с заданной стороной a и высотой.
Радиус окружности, вписанной в равнобедренный треугольник с заданными сторонами
Радиус окружности, вписанной в равнобедренный треугольник со стороной b и углом.
Задача 4 (описанный четырехугольник)
В равнобедренную трапецию АВСD с основаниями AD и ВС вписана окружность, СН – высота трапеции.
а) Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.
б) Найдите диагональ АС, если известно, что средняя линия трапеции равна , а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.
Решение.
а) 1) Пусть точки K и L – точки касания окружности оснований трапеции, тогда
ОК = ОL = rвпис
2) ΔBOK=ΔHOL по катету(см. пункт 1) и острому углу (углы OBK и LHO равны как накрест лежащие при BC II AD и секущей BH. Поэтому ВО = ОН.
3) Центр вписанной в трапецию окружности лежит на пересечении биссектрис внутренних углов трапеции. Данная трапеция ABCD – равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и ΔСОК равны (по катету и острому углу)
4) Из 2) и 3) следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного треугольника ΔВСН. О – центр описанной около треугольника окружности. Следовательно О принадлежит ВН (его середина). Пункт а) доказан.
б) Для доказательства пункта б) сделаем дополнительный чертеж
1) Пусть MN – средняя линия трапеции. Точка О принадлежит MN и О – её середина, поэтому МО =
2) АО – биссектриса, углы МАО и RAO равны, углы RAO и МОА раны как накрест лежащие. ΔАМО – равнобедренный, АМ=МО= . Тогда АВ = 2АМ=
3) ∠AOD=135° (по условию), ∠OAD+∠ODA=45°. Значит, ∠BAD=∠CDA=45°. Пусть BR перпендикулярен AD. BR = AR=
4) Пусть CD1 II BD и точка D1 лежит на прямой AD. Четырехугольник ВСD1D – параллелограмм. CD1=BD (противоположные стороны), BD=AC(диагонали равнобедренной трапеции). Тогда СD1=BD=AC.
5) 1 – равнобедренный, AD1 – основание. АD1=AD+DD1=AD+BC=2MN=2 . CH=BR= . По теореме Пифагора из ΔCHА: AC= = 2= = 3
Ответ: АС = 3.
Задача 5
В треугольнике АВС угол ВАС равен 60°, угол АВС равен 45°. Продолжения высот треугольника АВС пересекают описанную около него окружность в точках M, N, P.
а) Докажите, что треугольник MNP прямоугольный.
б) Найдите площадь треугольника MNP, если ВС=12.
Повторить. Свойство вписанных углов; теорему синусов.
Решение.
а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и P соответственно.
Тогда вписанные углы PNB и PCB опираются на одну и ту же дугу, поэтому
Аналогично,
Значит,
Следовательно, треугольник MNP прямоугольный. Пункт а) доказан.
б) Угол MNA равен углу NBA , угол APM равен углу ACP (вписанные углы, опирающиеся на одну дугу).
Тогда
Следовательно, = 30°.
Пусть R – радиус описанной окружности треугольника АВС. По теореме синусов
Тогда
=
Следовательно,
Ответ:
Geometry Problem Solver — трапеция
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Трасса 1
Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Рассчитайте периметр и площадь трапеции.
Колея 2
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 80 см, имеет меньшее основание 50 см.Рассчитайте периметр.
Трасса 3
Прямоугольная трапеция имеет высоту 40 м, основание большее 80 м, меньшее основание 50 м. Рассчитайте периметр и площадь трапеции.
Трасса 4
Равнобедренная трапеция с основанием больше 80 см, имеет меньшее основание 50 см, имеет площадь 1300 см. Рассчитайте высоту трапеции.
Колея 5
Прямоугольник трапеции имеет площадь 1500 см; имеет высоту 30 см.Вычисляет сумму двух оснований.
Колея 6
Равнобедренная трапеция имеет площадь 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Колея 7
Равнобедренная трапеция имеет периметр 150 см; имеет основание больше 50 см; имеет меньшую базу 30 см. Рассчитайте длину скошенной стороны.
Трасса 8
Равнобедренная трапеция имеет периметр 150 см, меньшее основание 30 см, наклонную сторону 35 см.Рассчитайте длину более длинного основания.
Колея 9
Равнобедренная трапеция имеет периметр 150 см, основание больше 50 см, наклонную сторону 35 см. Рассчитайте длину более короткого основания.
Колея 10
Прямоугольная трапеция имеет основание больше 50 см, имеет меньшее основание 30 см; имеет наклонную сторону 35 см. Рассчитайте периметр и площадь.
Колея 11
Прямоугольник трапеции имеет периметр 180 см; имеет основание больше 60 см, имеет наклонную сторону 50 см; имеет высоту 40 см.Рассчитайте длину более короткого основания.
Колея 12
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет высоту 40 см. Рассчитайте длину более длинного основания.
Колея 13
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет высоту 40 см; имеет базу больше 60 см. Рассчитайте длину скошенной стороны.
Колея 14
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет базу больше 60 см.Рассчитывает длину высоты.
Колея 15
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет высоту 4 см. Рассчитайте меньшую базу.
Колея 16
Равнобедренная трапеция имеет меньшее основание 14 см; имеет скошенную сторону 5 см; имеет высоту 4 см. Вычисляет большую базу.
Колея 17
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет выступ скошенной стороны на большее основание 3 см.Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет меньшее основание 14 см; имеет наклонную сторону 5 см. Имеет экранирование наклонной стороны на большем основании 3 см. Рассчитайте периметр.
Трасса 19
Равнобедренная трапеция имеет площадь 2400 см, высоту 40 см, основы составляют треть от другой. Определите периметр.
Дорожка 20
Трапеция образована квадратом и треугольником.Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, вычислите площадь трапеции.
Колея 21
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание больше 90 см, имеет меньшее основание, равное 2/3 большего основания. Рассчитайте периметр.
Колея 22
Прямоугольная трапеция эквивалентна 1/4 квадрата с периметром 160 см.Учитывая, что высота трапеции составляет 20 см и 6 см, вычислите площадь прямоугольника, размеры которого совпадают с размерами оснований трапеции.
Колея 23
Трапециевидный прямоугольник, описанный по кругу, длина скошенной стороны составляет 40 см, а высота равна 3/5 наклонной стороны. Рассчитайте периметр и площадь трапеции.
Дорожка 24
Площадь трапециевидного прямоугольника составляет 2250 см.Зная, что разница размеров проекции наклонной стороны на большее основание и высоты составляет 15 см, а их соотношение составляет 3/4, рассчитайте периметр трапеции.
Трасса 25
Периметр равнобедренной трапеции 250 см, высота 30 см, меньшее основание на 4/7 больше, чем косая сторона. Вычислите площадь трапеции.
Колея 26
Большая база прямоугольной формы трапеции со скошенной стороной под углом 45; зная, что основания 25 см и 15 см, вычисляет площадь трапеции.
Трасса 27
Равнобедренная трапеция ABCD образована тремя равнобедренными равнобедренными треугольниками, периметр каждого из которых равен 170 см, а наклонная сторона равна 6/5 основания. Рассчитайте периметр трапеции.
Дорожка 28
Равнобедренная трапеция ABCD имеет площадь 900 см. Основание AB является двойным, его высота составляет 20 см. Определите площадь треугольника ACD
Track 29
В равнобедренной трапеции площадь составляет 1032 см, а два основания имеют размер 61 см и 25 см соответственно.Вычислите меру высоты и периметра.
Колея 30
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Две базы размером 50 см и 30 см соответственно определяют периметр и площадь трапеции.
Track 31
В равнобедренной трапеции сумма и разница размеров двух оснований составляет соответственно 74 см и 14 см. Вычисляет площадь и периметр трапеции, зная, что наклонная сторона равна 25 см.
Колея 32
Периметр равнобедренной трапеции 176 см. Зная, что меньшее основание составляет 4/3 наклонной стороны, а большее основание составляет 19/10 меньшего основания, вычисляется площадь трапеции.
Трасса 33
Каждая из наклонных сторон равнобедренной трапеции составляет треть меньшего основания. Зная, что периметр равен 230 см, а наибольшее основание — 105 см, вычисляется размер меньшего основания и площадь трапеции.
Колея 34
В прямоугольной трапеции нижняя диагональ перпендикулярна наклонной стороне. Зная, что эта диагональная линия и наклонная сторона 24 см и 18 см соответственно, найдите периметр и площадь трапеции.
Колея 35
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Рассчитайте периметр трапеции, зная, что высота равна 11,56 см, а площадь равна 462.42 см.
Направляющая 36
В трапеции главное основание и вспомогательное основание имеют длину 55 см и 30 см, а периметр — 140 см. Определяет длину наклонных сторон, зная, что одна составляет 6/5 другой.
Колея 37
Разница между основаниями равнобедренной трапеции составляет 30 см, меньшее основание — 5/8 большего основания, периметр — 180 см. Рассчитывает размер наклонных сторон.
Track 38
Из равнобедренной трапеции вы знаете, что: а) высота составляет 20 см.б) разница между двумя базами 30 см. в) основание больше 80 см. Рассчитайте периметр и площадь трапеции.
Трасса 39
Периметр трапеции, имеющей высоту 34,60 см, составляет 203,49 см. Вычислите площадь трапеции, зная, что наклонные стороны образуют с большим основанием острые углы шириной 45 и 60.
Дорожка 40
Площадь трапециевидного прямоугольника составляет 1080 квадратных сантиметров, а высота — 24 см.Рассчитайте размеры двух оснований, зная, что периметр равен 140 см.
Колея 41
Периметр равнобедренной трапеции составляет 152 см, а длина скошенной стороны — 26 см. Вычислите высоту и площадь трапеции, зная, что меньшее основание имеет длину 40 см.
Направляющая 42
В прямоугольной трапеции основное основание, меньшее основание и высота имеют длину соответственно 60 см, 50 см и 24 см. Вычисляет площадь и периметр трапеции.
Трасса 43
Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, что, в свою очередь, равно высоте, составляющей 50 см.
Трасса 44
Сумма оснований трапеции 80 см, основание 5/3 другого, высота 2/3 вспомогательного основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что одна диагональ равна 25/16 другой.
Трасса 45
Трапеция образована квадратом со стороной 48 см и двумя треугольниками, катет которых совпадает с одной из двух противоположных сторон квадрата.Гипотенуза двух треугольников составляет 60 см и 50 см соответственно. Рассчитайте периметр и площадь трапеции.
Колея 46
Разносторонняя трапеция имеет периметр 180 см; вычисляет все стороны, зная, что AB = 8/5 DC, DC — AB = 30 см, AD = 2/5 DC.
Track 47
У равнобедренной трапеции ABCD основание CD составляет 15/22 большего основания, наклонные стороны превышают 7 см 3/5 меньшего основания, периметр составляет 124 см. Какой район?
Направляющая 48
Большее основание, высота и наклонная сторона прямоугольника до трапеции соответственно размером 80 см, 48 см и 50 см.Рассчитайте периметр и площадь трапеции.
Колея 49
Окружность имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют размер соответственно 96 см и 28 см. Вычисляет площадь и периметр трапеции, в основе которой лежат две хорды.
Трасса 50
Равнобедренная трапеция имеет высоту 20 м, основание больше 80 м, меньшее основание 50 м.Вычислите радиус круга, описанного трапецией.
Трасса 51
Трапеция имеет основания для диаметра окружности длиной 50 см и параллельную ей веревку длиной 30 см. Рассчитайте периметр и площадь трапеции.
Дорожка 52
В круге радиусом 50 см сделайте две параллельные хорды, расположенные на противоположных сторонах относительно центра и на расстоянии 14 см и 48 см от него соответственно. Вычисляет площадь и периметр трапеции, у которой есть основания для двух струн.
Колея 53
Прямоугольник и равнобедренная трапеция равны по высоте, периметр прямоугольника 140 см, разница размеров прямоугольника между ними 30 см, наклонная сторона трапеции 25 см. Вычислить:
размер оснований прямоугольника;
протяженность оснований трапеции;
площадь трапеции и прямоугольника;
периметр трапеции.
Направляющая 54
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует наклонной стороне, зная, что площадь трапеции составляет 1320 см.
Дорожка 55
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 28 и 8 см. Вычислите периметр, площадь и две диагонали.
Направляющая 56
Прямоугольная трапеция имеет высоту 24 см и основания соответственно 18 и 10 см. Вычислите периметр, площадь и две диагонали.
Колея 57
Прямоугольная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Трасса 58
Равнобедренная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Трасса 59
Равнобедренная трапеция имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Дорожка 60
Прямоугольник трапеции имеет площадь 336 см, сумма оснований 28 см.Рассчитайте высоту.
Колея 61
Равнобедренная трапеция имеет большее основание 50 см, меньшее основание 30 см. Рассчитайте высоту, зная, что наклонная сторона равна 26 см.
Колея 62
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Колея 63
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см.Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 64
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Рассчитайте радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Колея 65
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 66
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Рассчитайте диаметр круга на трапеции, зная, что высота составляет 48,75 дюйма.
Колея 67
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите длину круга, окружающего трапецию, зная, что высота составляет 48,75 дюйма.
Колея 68
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см.Вычислите площадь описанной круговой трапеции, зная, что высота составляет 48,75 дюйма.
Колея 69
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите:
площадь круга, описанного трапецией, зная, что высота 48,75 дюйма;
расстояние от центра хорды AB;
расстояние от центра каната CD;
длина дуги АВ;
длина дуги CD;
центральный угол АОБ;
центральный угол ХПК;
площадь кругового сектора AOB; площадь кругового сектора наложенным платежом.
Направляющая 70
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1320 см.
Направляющая 71
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 1320 см.
Направляющая 72
Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Дорожка 73
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Трасса 74
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см.Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 75
Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Дорожка 76
Прямоугольник трапеции имеет большое основание 60 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь круга, имеющего изопериметрическую окружность трапеции.
Направляющая 77
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Колея 78
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Трасса 79
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 80
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует малой диагонали, зная, что площадь трапеции составляет 1320 см.
Трасса 81
Равнобедренная трапеция имеет высоту 10 см и основания, которые являются одним из 7/17 другого. Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 240 см.
Дорожка 82
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Трасса 83
Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 и 50 см.Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Дорожка 84
Прямоугольник в форме трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Трасса 85
Равнобедренная трапеция имеет площадь 240 см и основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 86
Равнобедренная трапеция имеет периметр 186 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Трасса 87
Равнобедренная трапеция имеет большое основание 70 см, малое основание 50 см, высоту 24 см. Вычислите площадь круга, имеющего изопериметрическую окружность трапеции.
Track 88
Рассчитайте площадь и периметр разносторонней трапеции, зная, что большее основание составляет 80 см, а меньшее основание — 50 см, а наклонные стороны имеют длину соответственно 30 см и 20 см.
Колея 89
Равнобедренная трапеция имеет меньшее основание 8,4 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 90
Прямоугольная трапеция имеет меньшее основание 19,2 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 91
Прямоугольник в форме трапеции имеет наклонную сторону 18 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 92
Равнобедренная трапеция имеет наклонную сторону 18 см и выступание наклонной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 93
Равнобедренная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 94
Прямоугольная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 95
Прямоугольная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 96
Равнобедренная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 97
Периметр равнобедренной трапеции составляет 204 см, а каждая наклонная сторона — 30 см.Вычислите площадь и протяженность оснований, зная, что большее — это 5/3 второстепенного.
Колея 98
Более крупное основание равнобедренной формы трапеции со скошенной стороной под углом 45; зная, что основания 35 см и 15 см, вычисляет площадь и периметр трапеции.
***********
Задачи оптимизации в 2D-геометрии
В геометрии существует множество задач, в которых мы хотим найти наибольшее или наименьшее значение функции.В качестве функции мы можем рассматривать периметр или площадь фигуры или, например, объем тела. В качестве независимой переменной функции мы можем взять параметр фигуры или тела, такой как длина стороны, угол между двумя сторонами и т. Д. После того, как функция составлена, необходимо исследовать ее на предмет экстремальных значений, используя производные. Важно помнить, что функции в таких задачах обычно существуют на конечном интервале, который определяется геометрией системы и / или условиями задачи.
В этой теме мы рассматриваем задачи оптимизации, связанные с \ (2D \) геометрией.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Точка \ (A \ left ({a, b} \ right) \) задана в первом квадранте координатной плоскости. Проведите через эту точку прямую линию, которая отсекает от первого квадранта треугольник с наименьшей площадью (рис. \ (1a \)).
Пример 2
Найдите основание \ (a \) равнобедренного треугольника с ногами \ (b \) так, чтобы вписанный круг имел наибольшую возможную площадь (рис. \ (2a \)).
Пример 3
Фермер хочет оградить прямоугольное поле забором и разделить его пополам забором, параллельным одной из сторон (рис. \ (3a \)). Общая длина забора составляет \ (L. \). Какая самая большая площадь поля?
Пример 4
Равнобедренная трапеция описана вокруг окружности радиуса \ (R \) (рисунок \ (4a \)). При каком базовом угле \ (\ alpha \) площадь заштрихованной области наименьшая?
Пример 5
Окна имеют форму прямоугольника и завершаются полукругом (рис. \ (5a \)).2} \) и оси \ (x \) — (рисунок \ (6a \)). Найдите как можно большую площадь прямоугольника.
Пример 7
Найдите максимально возможную площадь прямоугольника, вписанного в полукруг радиуса \ (R \), одна из сторон которого совпадает с диаметром полукруга (рисунок \ (7a \)).
Пример 8
На окружности радиуса \ (R \) задана точка \ (A \) (рисунок \ (8a \)). Хорда \ (BC \) параллельна касательной в точке \ (A. \). Определите расстояние между точкой \ (A \) и хордой \ (BC \), на котором треугольник \ (ABC \) имеет наибольшее расстояние. область.
Пример 9
\ (A \ left ({1,0} \ right) \) и \ (B \ left ({5,0} \ right) \) — точки на оси \ (x — \) (рисунок \ (9a \ )). Найдите координату \ (y — \) точки \ (M \ left ({0, y} \ right) \) на оси \ (y — \) так, чтобы угол \ (\ theta = \ angle AMB \ ) имеет максимально возможное значение.
Пример 10
Два канала шириной \ (a \) и \ (b \) соединены друг с другом под прямым углом (рисунок \ (10a \)). Определите максимальную длину бревен, которые могут перемещаться по этой системе каналов.2}}} = 1. \]
Найдите стороны прямоугольника с наибольшей площадью.
Пример 13
Найдите точку \ (M \ left ({x, y} \ right) \) на графике \ (f \ left (x \ right) = \ sqrt x \), ближайшую к \ (A \ left ({ a, 0} \ right) \), где \ (a \) — положительное вещественное число (рисунок \ (13a \)).
Пример 14
Длина высоты, отсчитываемой от гипотенузы прямоугольного треугольника, равна \ (h \) (рисунок \ (14a \)). Определите самую короткую длину медианы, проведенной к самому длинному отрезку.
Пример 15
Картина высотой \ (a \) вешается на стену таким образом, чтобы ее нижний край был на \ (h \) единиц выше уровня глаз. На каком расстоянии \ (x \) наблюдатель должен стоять от стены, чтобы он был наиболее подходящим для просмотра картины (рисунок \ (15a \))?
Пример 16
Прямоугольник вписан в полукруг радиуса \ (R \), одна из сторон которого совпадает с диаметром полукруга (рис. \ (16a \)). Найдите максимальный периметр прямоугольника.2} \), предполагая, что \ (x \ gt 0 \), ближайший к \ (B \ left ({0, b} \ right) \), где \ (b \) — положительное вещественное число (рисунок \ (17a \ )).
Пример 18
Две стороны параллелограмма лежат на сторонах треугольника, а одна вершина параллелограмма принадлежит третьей стороне треугольника (рис. \ (18a \)). Найдите условия, при которых площадь параллелограмма наибольшая.
Пример 19
Равнобедренная трапеция имеет углы основания 45 градусов и периметр \ (L \) (рисунок \ (19a \)).Какая самая большая площадь трапеции?
Пример 1.
Точка \ (A \ left ({a, b} \ right) \) задана в первом квадранте координатной плоскости. Проведите через эту точку прямую линию, которая отсекает от первого квадранта треугольник с наименьшей площадью (рис. \ (1a \)).
Решение.
Рисунок 1а.
Рассмотрим треугольники \ (OBC \) и \ (MBA. \). Эти треугольники подобны. Следовательно, имеет место соотношение
\ [{\ frac {{OC}} {{MA}} = \ frac {{OB}} {{MB}} \; \;} \ kern0pt {\ text {или} \; \; \ frac {y } {b} = \ frac {x} {{x — a}},} \]
, где координаты \ (x \) и \ (y \) удовлетворяют неравенствам \ (x> a, \) \ (y> b.2}}}.}
\]
Функция \ (S \ left (x \ right) \) имеет критические точки \ (x = 0, \) \ (x = a, \) \ (x = 2a. \) Поскольку \ (x> a, \) решением является точка \ (x = 2a. \) При прохождении через нее производная меняет знак с минуса на плюс, т.е. \ (x = 2a \) является точкой минимума функции \ (S \ left (x \ справа). \)
Найдите другой катет треугольника:
\ [\ require {cancel}
y = \ frac {{bx}} {{x — a}} = \ frac {{b \ cdot 2a}} {{2a — a}} = \ frac {{2 \ cancel {a} b}} {\ cancel {a}} = 2b.
\]
Таким образом, треугольник с наименьшей площадью имеет катеты, равные \ (2a \) и \ (2b. \)
Пример 2.
Найдите основание \ (a \) равнобедренного треугольника с ногами \ (b \) так, чтобы вписанный круг имел наибольшую возможную площадь (рис. \ (2a \)).
Решение.
Пусть площадь \ (A \) треугольника будет максимальной целевой функцией.
Рисунок 2а.
Из аналогичных треугольников \ (\ треугольник OMC \) и \ (\ треугольник CDB \) получаем
\ [{\ frac {{CB}} {{CO}} = \ frac {{DB}} {{OM}}} \]
или
\ [{\ frac {b} {{h — r}} = \ frac {{\ frac {a} {2}}} {r}}, \]
где \ (a \) — основание, \ (h \) — высота, \ (b \) — катет равнобедренного треугольника, \ (r \) — радиус вписанной окружности.2}}}} {2}} = {- b \ pm b \ sqrt 5.} \]
Есть только один нетривиальный положительный корень:
\ [a = b \ sqrt 5 — b = {b \ left ({\ sqrt 5 — 1} \ right)}. \]
Используя тест первой производной, мы находим, что \ (a = b \ left ({\ sqrt 5 — 1} \ right) \) является точкой максимума. Следовательно, равнобедренный треугольник имеет наибольшую площадь, когда \ (a = b \ left ({\ sqrt 5-1} \ right). \)
Рисунок 2b.
Пример 3.
Фермер хочет оградить прямоугольное поле забором и разделить его пополам забором, параллельным одной из сторон (рис. \ (3a \)).Общая длина забора составляет \ (L. \). Какая самая большая площадь поля?
Решение.
Рисунок 3а.
Длина забора определяется по формуле
\ [L = 3y + 2x, \]
где \ (x \) и \ (y \) — стороны прямоугольника.
Отсюда следует, что
\ [y = \ frac {{L — 2x}} {3}. \]
Тогда площадь прямоугольника записывается как функция одной переменной:
\ [{A = xy} = {x \ cdot \ frac {{L — 2x}} {3}} = {\ frac {L} {3} x — \ frac {2} {3} {x ^ 2 }. 2} \ left ({4 — \ pi} \ right).\]
Пример 5.
Окна имеют форму прямоугольника и завершаются полукругом (рис. \ (5a \)). Периметр окна равен \ (P. \). Определите радиус полукруга \ (R \), через который проникает наибольшее количество света.
Решение.
Рисунок 5а.
Очевидно, одна сторона прямоугольника равна \ (2R. \). Обозначим другую сторону как \ (y. \). Периметр окна равен
.
\ [P = \ pi R + 2R + 2y. \]
Отсюда находим \ (y: \)
\ [y = \ frac {1} {2} \ left [{P — \ left ({\ pi + 2} \ right) R} \ right].2}} \ ne 0}
\ end {array}} \ right., \;} \ Rightarrow {\ left \ {{\ begin {array} {* {20} {l}}
{а = \ sqrt 2 R} \\
{a \ ne 2R}
\ end {array}} \ right ..} \]
У нас есть две критические точки \ (a = \ sqrt {2} R \) и \ (a = 2R, \), но, как и во второй точке \ (a = 2R \), площадь прямоугольника равна нулю, далее мы будет рассматривать только первую точку \ (a = \ sqrt {2} R. \)
Производная положительна слева от этой точки и отрицательна справа. 2}.} \]
Гусев-Литивиненко-Мордкович-Решение-Геометрических задач-Мир-1988 — Математика — 12
сторона B C в точке D. Найдите AC, если известно, что C D = 2 см и A B = B C = 6 см. 165. На стороне A B треугольника A B C по диаметру построена окружность, пересекающая AC в точке D и B C в точке E. Найдите AC и B C если известно, что A B = 3 см, A D. D C = 1: 1, а B E. Е С = 7: 2. 166. Отрезок B D - это высота треугольника A B C, а D E - это высота. медиана треугольника B C D.В треугольник B D E вписан круг, касающийся сторона B E в точке K и сторона D E в точке M. Найдите углы треугольник A B C, если A B = B C = 8 см и K M = 2 см. 167. В треугольнике A B C начерчены высота A D и окружность радиуса A D. с центром в точке A. Найдите длину дуги этого круга, лежащего внутри треугольник, если B C = a, Z_5 = P и Z.C = y. 44 гл., 1. П л а н е Геометрия 168. Докажите, что радиус окружности, касающейся гипотенузы и расширение катетов прямоугольного треугольника равно сумме длин гипотенуза и радиус окружности, вписанной в треугольник.169. Биссектрисы A D и C K треугольника A B C пересекаются в точках точка 0, а K D = 1 см. Найдите углы и две другие стороны треугольника. K D O, если известно, что точка B лежит на окружности, описанной треугольник K D O. 170. Окружность касается сторон A C и B C треугольника A B C и имеет центр. tre на A B. Найдите радиус круга, если A C = 48 см, B C = 140 см и A B = 148 см. 171. В треугольнике A B C, D - середина o i A C, E - середина B C.Окружность, описанная вокруг треугольника C D E, проходит через центр тяжести треугольник A B C. Найдите длину медианы C K, если A B = c. 172. Найдите соотношение между сторонами a, b и c треугольника A B C. если известно, что вершина C, центроид M и середины сторон A C и B C лежат в одном круге. 173. Вписан в равнобедренный треугольник A B C с углом B, равным 120 °. представляет собой полукруг радиусом (3 3 + V 21) см с центром на A C. Обращается к Полукруг - это касательная, пересекающая боковые стороны A B и B C в точках D и E соответственно.L A B C = стр. IV. Круг и четырехугольник 176. Докажите, что если есть вписанный и описанный круг для трапеции, то высота трапеции - среднее геометрическое между его базы. 177. Основания равнобедренной трапеции равны 21 см и 9 см, и высота до 8 см. Найдите радиус описанной окружности. 178. Основания равнобедренной трапеции - это a и b, а острый угол это. Найдите радиус описанной окружности. 179. Две вершины квадрата лежат на окружности радиуса R, а две другие - на круге. касательная к этой окружности.Найдите сторону квадрата. 180. Острый угол A ромба A B C D равен a. Найдите соотношение радиуса вписанной окружности в ромб до радиуса вписанной окружности в треугольнике A B C. 181. Вокруг окружности описана равнобедренная трапеция. Найдите его углы если известно, что отношение боковой стороны трапеции к ее меньшей база равна k. 182. Вокруг окружности очерчена трапеция с острыми углами а и р. Найдите отношение периметра трапеции к длине окружности круг.183. (a) Докажите теорему Птолемея: необходимое и достаточное условие того, что выпуклый четырехугольник вписывается в круг в том смысле, что сумма произведений двух пар противоположных сторон равны произведению диагоналей; в другими словами, если противоположные стороны вписанного в круг четырехугольника равны равны a и b, c и m, а диагонали - d x и d 2, тогда ab + c m = d xd 2; (б) используя теорему Птолемея, докажите постановку задачи 146. 184. Докажите, что сумма произведений высот остроугольного треугольника а их отрезки от ортоцентра до вершины равны половине суммы квадратов сторон.П. 3. Круги 45 185. Построен на гипотенузе прямоугольного треугольника, как на стороне квадрата. (вне треугольника). Центр квадрата присоединяется к вершине правой угол треугольника. На какие сегменты делится гипотенуза, если катеты равно 21 см и 28 см? 186. Круг касается двух соседних сторон квадрата и разделяет каждую из две другие его стороны на два сегмента по 2 см и 23 см. Найдите радиус круг. 187. Вписан ромбом A B C D со стороной 4 см и углом B A D равным до 60c - круг.К этой окружности проведена касательная, пересекающая A B в точке M и A D в точке P. Найдите M B и P D, если M P = 2 см. 188. Отношение радиуса окружности, описанной вокруг трапеции, к радиус вписанной окружности равен k. Найдите острый угол трапеция. 189. В круг вписан четырехугольник A B C D, диагонали которого равны взаимно перпендикулярны и пересекаются в точке E. Прямая линия, проходящая через точку E перпендикулярно A B пересекает C D в точке M.Находить E M, если A D = 8 см, A B = 4 см и Z _ C D B = a. 190. В круг вписан четырехугольник A B C D, диагонали которого равны взаимно перпендикулярны и пересекаются в точке E. Прямая линия, проходящая через точку E и середину стороны C D пересекает A B в точке H. Найдите H B, если E D = 6 см, B E = 5 см и / L A D B = a. 25191. В выпуклом четырехугольнике A B C D сторона A B равна -, сторона 25 1 B C на 12 -, сторона C D на 6 -. Известно, что угол D A B острый, 64 4 3 63 угол A D C тупой, sin Z.D A B = - и cos / L A B C = - -. Круг 5 бо с центром в 0 касается сторон B C, C D и A D. Найдите длину линии сегмент OC. V. Разные проблемы 192. От точки C к окружности проведены две касательные C A и C B, образующие угол 60 °. В криволинейный треугольник, образованный этими касательные и малая дуга A B. Докажите, что длина этой дуги равна окружность вписанного круга. 193. Прямоугольник со сторонами 36 см и 48 см разделен на два треугольника. gles по диагонали.В каждый из этих треугольников вписан круг. Найти расстояние между их центрами. 194. Два круга радиусом 16 см и 9 см касаются друг друга снаружи. Com Рассчитайте радиус окружности, вписанной в криволинейный треугольник, заключенный в между окружностями и их общей внешней касательной. 195. Хорда длиной 6 см разделяет круг на два сегмента. Квадрат В меньший сегмент вписано 2 см сбоку. Найдите радиус круга. 196. Две окружности радиуса R расположены так, чтобы расстояние между ними центров равно R.На пересечении кругов вписан квадрат. Находить сторона квадрата. 197. Окружность вписана в сектор окружности, имеющий угол 2а. Находить отношение радиусов вписанной окружности и сектора. 198. Вписанная в сектор A O B окружность радиуса R с центральным углом. a - правильный треугольник, одна из вершин которого лежит в середине дуги A B, а два других по радиусам OA
Площадь трапеции — формула, примеры, решения
Студенты должны выполнять различные домашние задания по геометрии.Однако наибольшие трудности возникают у учеников средней школы, потому что они изучали только математику и алгебру, а также геометрию. Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции. Сегодня мы поговорим конкретно о трапециях, нахождении площади и считая ее одной из важнейших теорем.
Трапеция — что это за фигура?
Трапеция — это четырехугольник, у которого две параллельные стороны и две непараллельные стороны.Параллельные стороны называются основаниями трапеций, а две другие — боковыми сторонами. Высота трапеции — это расстояние между линиями, на которых лежат основания трапеции, любого общего перпендикуляра этих линий. Середина трапеции — это отрезок, соединяющий середины сторон.
Характеристики трапеции
Если в трапецию вписан круг, то сумма основ всегда совпадает с суммой сторон: a + b = c + d, а средняя линия всегда равна полусумме сторон:
Равнобедренная трапеция — это трапеция, стороны которой равны AB = CD.Тогда диагонали AC = BD и углы при основании равны:
Из всех трапеций только равнобедренную трапецию можно описать окружностью, если сумма противоположных прямых углов равна 180 °. В равнобедренной трапеции расстояние от верха одного основания до выступа противоположного верха, который непосредственно связан с основанием, всегда точно соответствует средней линии.
Прямоугольная трапеция — это трапеция, имеющая базовый угол 90 °.
Теорема: площадь трапеции
Чтобы вычислить площадь произвольного многоугольника, мы делаем следующее: делим многоугольник на треугольники и находим площадь треугольника.Сумма площадей этих треугольников равна площади многоугольника. Используя эту технику, мы выводим формулу для расчета площади свободной трапеции. Условимся называть высоту трапеции перпендикуляром, проведенным из любой точки одного из оснований к прямой, содержащей другое основание. На рисунке ниже мы указали, что отрезок линии BH соответствует высоте трапеции ABCD:
На основании этого получаем теорему: «Площадь трапеции равна произведению полусуммы ее оснований на высоту.»Основываясь на формуле площади, мы можем доказать эту теорему.
Дана трапеция: ABCD, AD и BC — длины оснований, BH — высота.
Докажите: площадь этой трапеции ABCD будет равна S = ½ (AD + BC) · BH.
Доказательство: начертите диагональ BD. Он делит трапецию на два треугольника ABD и BCD. Это означает, что периметр трапеции ABCD будет равен сумме площадей этих треугольников.
В треугольнике ABD: AD — основание, а BH — высота.В треугольнике BCD: BC — основание.
Нарисуем высоту ДК. Площадь S треугольника ABD = 1/2 AD · BH; площадь S треугольника BCD = 1/2 BC · DK. Поскольку BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.
Расчет площадей в прошлые времена
Еще 4–5 тысяч лет назад вавилоняне умели определять площадь трапеции в квадратных единицах.Древние египтяне 4000 лет назад использовали почти те же приемы, что и мы: сумму параллельных сторон делили пополам и умножали на высоту.
Определение площадей геометрических фигур — одна из древнейших практических задач. Люди не сразу нашли правильный подход к своему решению. Один из самых простых и доступных способов вычисления площадей открыл Евклид. При расчете площадей он использовал простую технику, называемую методом разбиения.
Расчет площадей в современном мире
Сегодня существует множество формул для расчета длин сторон, вершин, параллельных оснований и трапеции с площадью.Мы рассмотрим самые основные из них. Приведенные ниже формулы просты в использовании, но если вам сложно понять и вам нужна помощь в выполнении домашних заданий, вы всегда можете связаться с нашей службой. Опытные авторы проконсультируют вас по всем задачам, и вы значительно улучшите свою успеваемость.
Формула для вычисления площади трапеции по основанию и высоте
Дана произвольная трапеция. Чтобы найти его площадь, воспользуемся следующей формулой:
В этой формуле:
- а, б — основание трапеции;
- hh — высота трапеции.
Представьте, что нам нужно найти область трапеции с известными основаниями, численно равными 10 см и 8 см. Также всем известная высота, 6 см в длину.
Решение:
Сразу подставляем числа в имеющуюся формулу и вычисляем значение:
Ответ: 54 квадратных сантиметра.
Формула площади трапеции у основания и осевой линии
Следует отметить, что средняя линия трапеции составляет половину суммы ее оснований.Таким образом, нахождение области через осевую линию — не что иное, как метод, аналогичный первому. Постольку:
В этой формуле:
- S = 1 ч;
- l — средняя линия трапеции;
- h — высота.
Предположим, нам нужно найти область трапеции, если известно, что средняя линия равна 5 см, а высота трапеции в два раза больше ее высоты.
Решение:
Найдите высоту трапеции:
h = 2 ⋅ 5 = 10
Площадь:
S = l ⋅ h = 5 ⋅ 10 = 50 см.кв.
Ответ: 50 кв. сантиметров
Формула площади трапеции через радиус вписанной окружности и угол
Этот футляр подходит только для равнобедренной трапеции:
В этой формуле:
- r — радиус вписанной окружности;
- α — угол между основанием и стороной.
Предположим, нам дан радиус вписанной окружности в трапецию, равный 4 см.Угол α равен 90 градусам. Нам нужно найти площадь трапеции.
Решение:
По формуле:
Ответ: 64 квадратных сантиметра.
Формула площади трапеции через диагонали и угла между ними
Существует простая формула для определения площади трапеции по диагоналям и угла между ними:
В этой формуле:
- d1, d2 — диагонали трапеции;
- α — угол между диагоналями.
Пусть две диагонали трапеции равны 20 см и 7 см. Когда они пересекаются, они образуют угол в 30 градусов. Нам нужно найти площадь трапеции.
Решение:
- d1 = 20;
- d2 = 7;
- α = 30 °.
Площадь:
Ответ: 35 квадратных сантиметров.
Трапеции и созвездия
Трапеция встречается не только в домашних заданиях по математике.Этот рисунок можно найти при изучении созвездий. Выдающийся астеризм весеннего неба — трапеция Льва, наблюдаемая по вечерам с февраля по май. Эта фигура находится в зодиакальном созвездии Лев, образуя тело животного, и по форме напоминает трапецию.
Четыре яркие звезды созвездия α, β, γ и δ расположены на вершинах трапеции — тела льва. А голова льва образована звездами, расположенными в форме серпа.Отсюда и название — трапеция Льва.
Трапеции в экспериментальной физике Посмотреть
Союз физики и математики предполагает непрерывное движение науки вперед. В физике ученые проводят эксперименты, суть которых становится полностью ясной только после математического анализа. Многие отрасли математики обязаны своим происхождением и дальнейшим развитием новым физическим экспериментам. В качестве примера рассмотрим школьные лабораторные работы по физике.
Постановка вопроса: Рассмотрим фигуру — произвольную трапецию ABCD.Нарисуйте две ее диагонали AC и BD, которые делят трапецию на четыре треугольника — ABO, BCO, CDO и DAO. Треугольники ABO и CDO равны:
Формулировка цели экспериментальной работы: с помощью взвешивания доказать, что массы треугольников, полученных по диагоналям и сторонам трапеции, равны.
Ход лабораторных работ:
- Учащимся необходимо взять с собой: лист бумаги, линейку, карандаш, ластик, ножницы.
- Учащиеся рисуют параллельные линии с помощью прямоугольных линеек.
- Учащимся нужно построить пять различных трапеций и нарисовать диагональ.
- Учащиеся ножницами вырезают из трапеции треугольники, которые имеют одну сторону трапеции.
- На весах учащиеся взвешивают разрезанные треугольники ABO и CDO.
- Студенты записывают полученные результаты в таблицу и сравнивают.
Как видите, знания о трапеции пригодятся вам в физике и других науках.
В трапецию вписан круг PQRS Если PS QR 25 класс 9 по математике CBSE
Подсказка : Из данных размеров мы видим, что две непараллельные стороны равны, перпендикуляр при падении образует квадрат и два равных прямоугольных треугольника (поскольку углы квадрата равны 90 °), затем с использованием геометрии и Пифагора По теореме мы можем найти длину диаметра.2} $ где,
H = гипотенуза
P = перпендикуляр
B = основание
прямоугольного треугольника.
Полный пошаговый ответ :
Даны длины сторон этой трапеции:
PS = QR = 25 см
PQ = 18 см
SR = 32 см
Пусть AB будет диаметром круг внутри трапеции.
Поскольку две непараллельные стороны этой трапеции (PS и QR) равны, это равнобедренная трапеция. 2}} = \ sqrt {576} $
PX = 24 см
Из (1)
PX = AB
$ \ Rightarrow $ AB = 24, и это диаметр круга.
Следовательно, длина диаметра круга на данном рисунке равна 24 см.
Примечание : Прямой угол представляет собой угол измерения 90 °, и Пифагор может применяться только к прямоугольным треугольникам. Помните:
Трапеция также называется трапецией, и ее разные типы:
Справа: Имеет пару прямых углов
Равнобедренная: Две непараллельные стороны равны по длине
Масштаб: Ни углы, ни стороны не равны.
Ни один многоугольник не имеет такой же площади, как разница между вписанными и описанными окружностями.
Вот доказательство существования контрпримера.
Дан многоугольник, назовите его площадь $ A $. Пусть $ A_R $ — это площадь описанной окружности, $ A_r $ — площадь вписанной окружности, а $ A_ \ Delta $ — разность $ A_R — A_r $. Мы хотим найти такой многоугольник, что $ A = A_ \ Delta $. Я покажу, что есть такой четырехугольник, а именно трапеция.
Сначала рассмотрим единичный квадрат с площадью $ A = 1 $. Его вписанная окружность имеет площадь $ \ pi / 4 $, а его описанная окружность имеет площадь $ \ pi / 2 $, поэтому $ A_ \ Delta = \ pi / 4 <1 = A $. Теперь вытяните одну сторону, чтобы получилась равнобедренная трапеция (см. Рис).2/4} {4a} - \ frac {a} {4} \ right) $$
По общему признанию, это немного беспорядочно, но мы можем использовать теорему о промежуточном значении. Вместо того, чтобы искать $ a $, который удовлетворяет $ A = A_ \ Delta $, нам нужно найти только один с $ A Поскольку равнобедренная трапеция представляет собой непрерывную деформацию квадрата, применима теорема о промежуточном значении, и должно быть некоторое значение $ a $ между $ 1 $ и $ 2 $ с $ A = A_ \ Delta $.2 $$ % PDF-1.4 xref 1114 0 объект
По мере увеличения $ x $ $ r $ уменьшается, увеличивая разность площадей окружностей. Площадь шестиугольника, похоже, тоже уменьшается, так что будет какая-то точка, в которой будет получено равенство.
%
987 0 объект
>
эндобдж
987 128
0000000016 00000 н.
0000003880 00000 н.
0000003965 00000 н.
0000004211 00000 п.
0000005077 00000 н.
0000005132 00000 н.
0000005182 00000 п.
0000005260 00000 н.
0000005336 00000 п.
0000005413 00000 н.
0000005488 00000 н.
0000005566 00000 н.
0000005822 00000 н.
0000009241 00000 н.
0000009615 00000 н.
0000010018 00000 п.
0000010365 00000 п.
0000010635 00000 п.
0000011000 00000 н.
0000011371 00000 п.
0000017973 00000 п.
0000018474 00000 п.
0000018886 00000 п.
0000019119 00000 п.
0000023885 00000 п.
0000024246 00000 п.
0000024648 00000 п.
0000024923 00000 п.
0000025579 00000 п.
0000026016 00000 п.
0000026255 00000 п.
0000026705 00000 п.
0000027451 00000 п.
0000028221 00000 п.
0000028643 00000 п.
0000028694 00000 п.
0000028745 00000 п.
0000028784 00000 п.
0000028835 00000 п.
0000028886 00000 п.
0000030537 00000 п.
0000030827 00000 п.
0000031112 00000 п.
0000031317 00000 п.
0000031697 00000 п.
0000031755 00000 п.
0000032105 00000 п.
0000032412 00000 п.
0000033363 00000 п.
0000033536 00000 п.
0000033907 00000 п.
0000034322 00000 п.
0000034491 00000 п.
0000035370 00000 п.
0000035870 00000 п.
0000037347 00000 п.
0000037493 00000 п.
0000039952 00000 н.
0000040250 00000 п.
0000040598 00000 п.
0000041142 00000 п.
0000041657 00000 п.
0000041718 00000 п.
0000041781 00000 п.
0000043288 00000 п.
0000044499 00000 н.
0000044695 00000 п.
0000045815 00000 п.
0000045869 00000 п.
0000047007 00000 п.
0000047386 00000 п.
0000047650 00000 п.
0000048547 00000 п.
0000049099 00000 н.
0000059599 00000 н.
0000071328 00000 п.
0000074146 00000 п.
0000077438 00000 п.
0000078722 00000 п.
0000084809 00000 п.
0000087502 00000 п.
0000093451 00000 п.
0000099307 00000 п.
0000100263 00000 н.
0000103669 00000 н.
0000104237 00000 п.
0000104820 00000 н.
0000105372 00000 п.
0000105967 00000 н.
0000106547 00000 н.
0000106659 00000 п.
0000108106 00000 п.
0000108348 00000 п.
0000108691 00000 п.
0000108754 00000 н.
0000109651 00000 п.
0000109871 00000 н.
0000110162 00000 п.
0000110393 00000 п.
0000110550 00000 н.
0000114240 00000 н.
0000115835 00000 н.
0000117391 00000 н.
0000117561 00000 н.
0000117707 00000 н.
0000117868 00000 н.
0000118042 00000 н.
0000118215 00000 н.
0000118385 00000 н.
0000118555 00000 н.
0000118701 00000 н.
0000121269 00000 н.
0000121438 00000 н.
0000121584 00000 н.
0000121730 00000 н.
0000121900 00000 н.
0000122046 00000 н.
0000124006 00000 н.
0000124178 00000 н.
0000125255 00000 н.
0000126383 00000 н.
0000143982 00000 н.
0000145717 00000 н.
0000146923 00000 н.
0000164522 00000 н.
0000166287 00000 н.
0000167823 00000 н.
0000002856 00000 н.
трейлер
] / Предыдущее 2012440 >>
startxref
0
%% EOF
> поток
h ެ ole qci = (; BYi) AтYqi-Ņ \ i — nN Չ * F / h% 5 ً؋ X | i.

 Найдите высоту этой трапеции.
Найдите высоту этой трапеции. Найдите высоту этой трапеции.
Найдите высоту этой трапеции.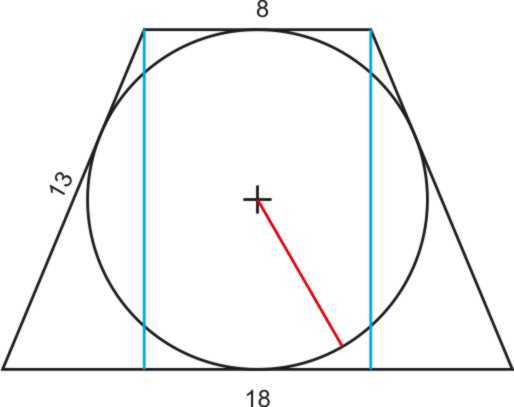 Ответ дайте в градусах.
Ответ дайте в градусах. Найдите радиус окружности, описанной около этого квадрата.
Найдите радиус окружности, описанной около этого квадрата.
 Найдите радиус окружности, описанной около этого квадрата.
Найдите радиус окружности, описанной около этого квадрата.
 Найдите радиус окружности, вписанной в этот квадрат.
Найдите радиус окружности, вписанной в этот квадрат.