Содержание
3.Линейная функция вида y = kx + b
Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).
Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.
Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось.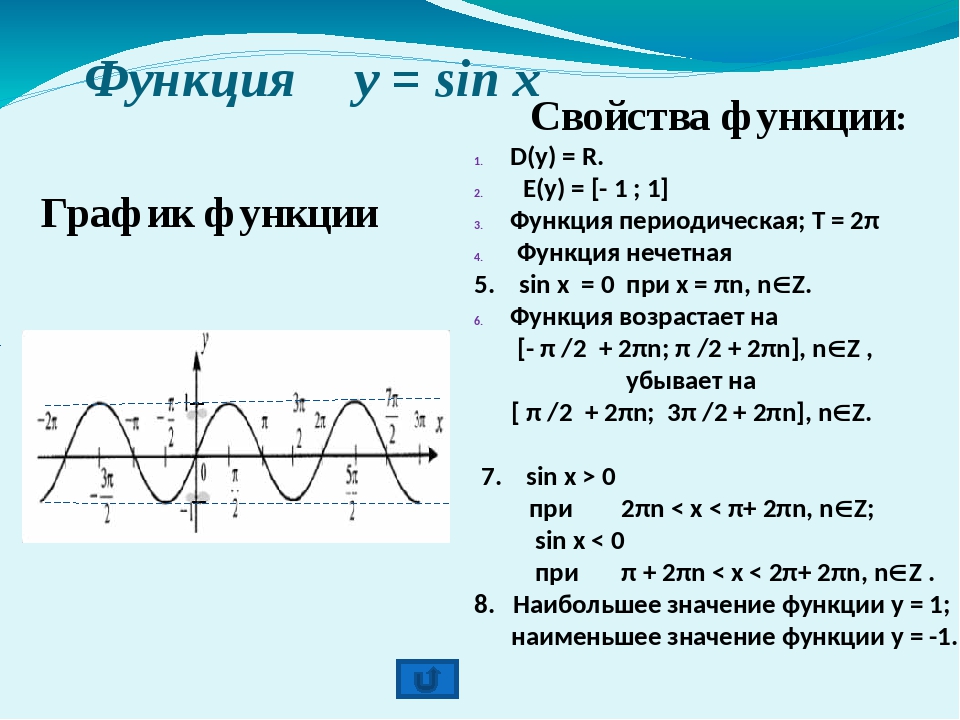 Если k = 0, то область значений линейной функции состоит из числа b;
Если k = 0, то область значений линейной функции состоит из числа b;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.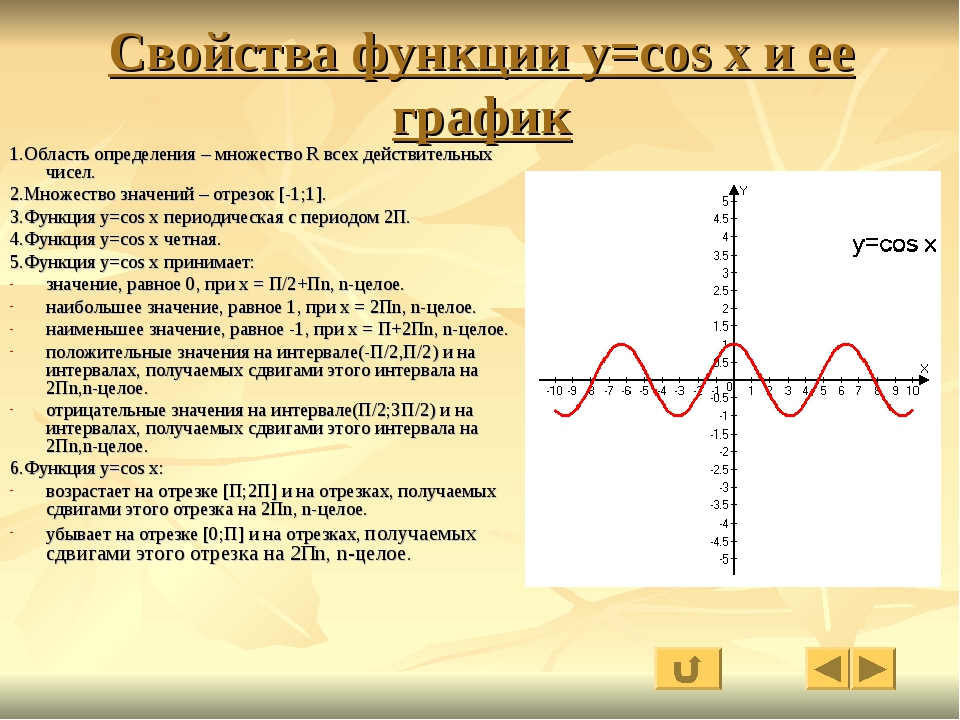
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при x из (-∞; -b/k).
b) k < 0; kx + b < 0, kx < -b, x < -b/k.
y = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b < 0; y = kx + b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k < 0, следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая.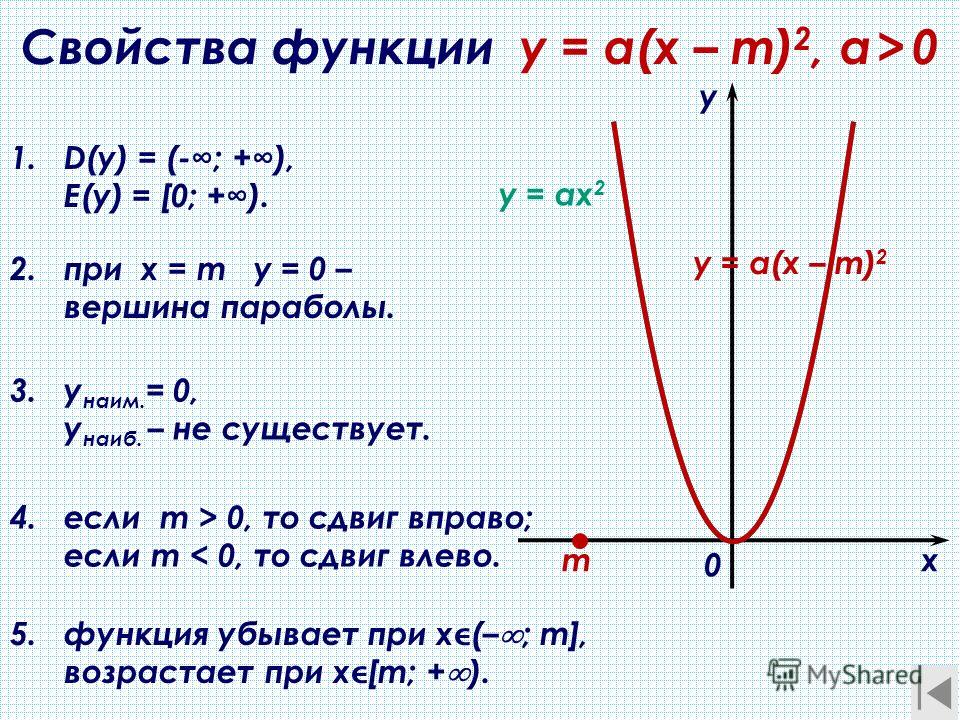 Для построения прямой
Для построения прямой
достаточно знать две точки. Положение прямой на координатной плоскости
зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует.
Что такое функция? Обозначение функций, область функции, диапазон функций
Здесь мы обсудим:
- Что такое функция
- Обозначение функции
- область функции
- диапазон функции
Function
Если значение y зависит от другого значения x таким образом, что каждое значение x определяет только одно значение y, мы говорим, что y есть функцией x
y=4x+1 определяет y как функцию x потому что каждое значение x соответствует только одному значению y.
| x | Value of y = 4x + 1 |
| 2 | 9 |
| 1 | 5 |
| 0 | 1 |
| -1/4 | 0 |
| √3 | 4√3 + 1 |
В следующем примере y не есть функцией x, так как каждому значению x соответствует два значения y.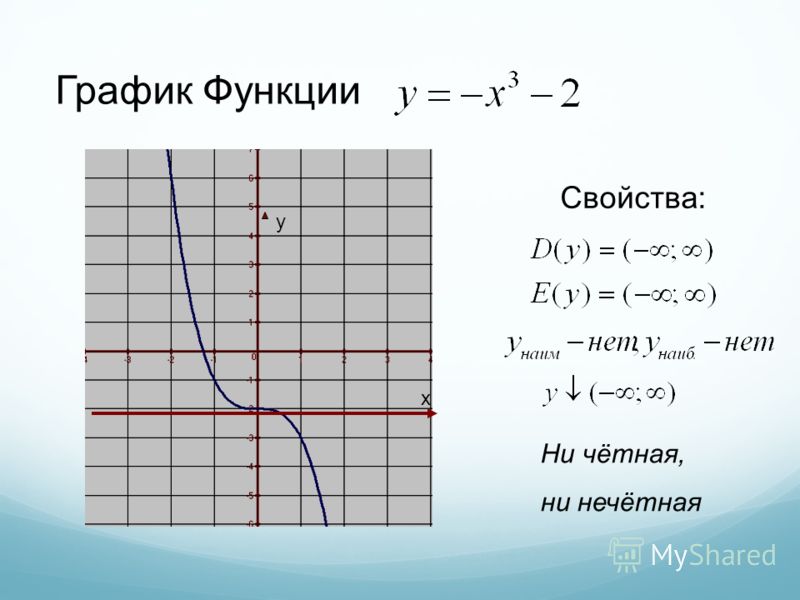
y = ± √x
if x = 4
y = ±√4
y = 2 и y = -2
Если мы используем букву f для обозначения функции, тогда уравнение
y = f(x)
y есть функцией x
Хотя f есть общепринятым символом для обозначения функции, любой символ может быть использован для обозначения функции. Тогда
y = F(x)
y = g(x)
y = h(x)
Пример
φ(x) = 1/(x3 — 1)
Then
φ( 3√7) = 1/(x3 = 1/( 3√7)3 — 1) = 1/(7 — 1) = 1/6
φ(1) = 1/[(1)3 — 1] = 1/0 Undefined
Пример
F(x) = 2x2 — 1
F(d) = 2(d)2 — 1
F(t — 1) = 2(t — 1)2 — 1
= 2(t2 -2t + 1) -1
= 2t2 — 4t + 1
g(c) = c2 — 4c
g(x) = x2 — 4x
Диапазон функции
Для каждого значения, данного независимой переменной из диапазона функции, мы получаем соответствующее значение y.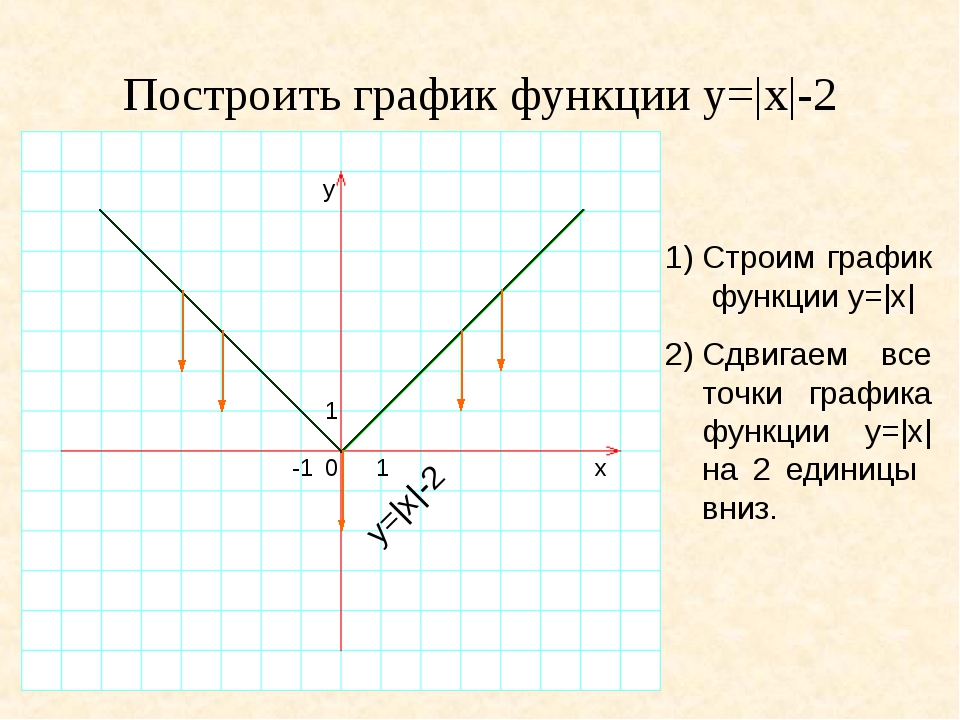
Множество всех таких значений y называется диапазоном функции
Пример
h(x) = 1/[(x — 1)/(x — 3)]
Область есть
(-∞, 1) ∪ (1, 3) ∪ (3, +∞)
Пример
h(x) = (x2 — 4)/(x — 2) = [(x — 2)(x + 2)]/(x — 2) = (x + 2) x ≠ 2
f(x) = x2
Записывается как:
y = x2
Естественная область
Если функция определена формулой, и явной области не определено, то понятно, что область состоит из всех действительных чисел, для которых формула имеет смысл, а функция имеет реальное значение. Такая область называется естественной областью функции.
Пример
y = (x + 1)/(x — 1) — Естественная область функции — все действительные числа кроме 1
Решите для y
x = (y + 1)/(y — 1) — Диапазон функции — все действительные числа кроме 1
Определение функций с разрывом
Область определения функции y(x)
Областью определения называют множество значений аргумента при котором существует значение функции и обозначают или . Областью значений называют множество чисел, которые принимает функция при прохождении аргументом всех значений из области определения.
Областью значений называют множество чисел, которые принимает функция при прохождении аргументом всех значений из области определения.
Ее обозначают или . Графически обе области хорошо иллюстрирует следующий рисунок
Для схематической функции рассматриваемые области принимают значения
Методика нахождения области определения для всех функций одна и та же: нужно выявить точки при которых функция не существует, а затем исключить из множества действительных чисел . В результаты получим набор промежутков или интервалов, точки, которые образуют область определения.
Особенности элементарных функций
1) Если функция имеет вид полинома то ее областью определения будет вся действительная ось или . Такая функция определена повсюду.
2) Дробно рациональная функция , где – полиномы, областью определения имеет значения аргумента при которых знаменатель не превращается в ноль. Сначала находим решения уравнения, если те существуют, вырезаем из множества действительных значений.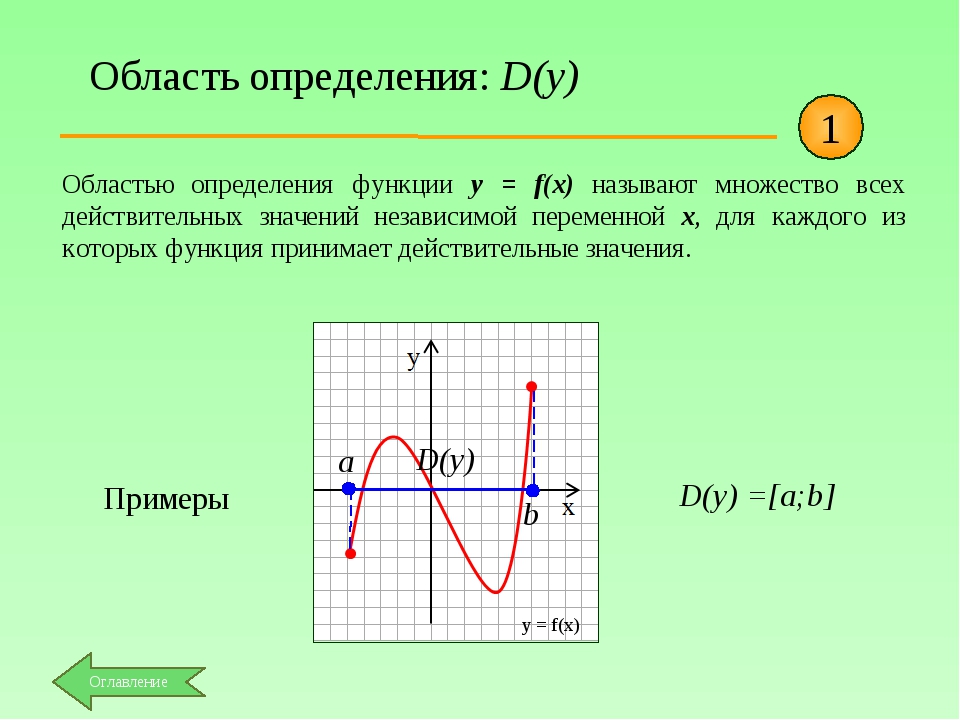 В результате получим набор интервалов
В результате получим набор интервалов
где – корни уравнения .
3) Функция содержит корень парного степени . В таком случае областью определения будут точки , при которых подкоренная функция принимает неотрицательные значения, т.е. решения неравенства .
4) Если корень содержит знаменатель
то область определения определяют из строгого неравенства .
5) Если в знаменателе имеем корень нечетной степени
то область определения находим из условия .
5) Если является логарифмом от другой функции , то по свойству логарифма область определения находим из условия . Как правило, это будет интервал или несколько интервалов.
6) Экспонента областью определения имеет множество аргументов , для которых определена . Например, функция определена на всей действительной оси.
7) Простые тригонометрические функции (косинус и синус) определены на всем множестве действительных чисел .
8) Тангенс и котангенс областями определения имеют интервалы, граничащих между собой точками
для первой функции и
для второй, т.е.
В случаях когда при аргументах есть множители , точки в которых функция не существует следует определять из условия
Подобным образом и для котангенса
9) Следует отметить, что обратные тригонометрические функции — арксинус и арккосинус областями значений имеют отрезок . Для отыскания областей определения необходимо решить двойное неравенство
Например, для функции имеем неравенство с которого получим
При суперпозиции функций, то есть когда задана их комбинацию, нужно находить область определения каждой из функций, после чего — сечение найденных областей.
Пример.
Решение.
Область определения первого слагаемого находим из неравенства
Второй и третий дадут следующий вклад
Сечением найденных областей будет интервал
—————————————
Находите области определения по приведенной выше схеме, выключайте все лишние промежутки и точки и не допускайте ошибок. Помните, что установление областей определения — это одно из самых простых заданий при исследовании функции.
Помните, что установление областей определения — это одно из самых простых заданий при исследовании функции.
Посмотреть материалы:
Исправление ошибки #Н/Д в функции ВПР
В этом разделе описаны наиболее распространенные причины неправильного результата для функции ВЛП и рекомендации по использованию функций ИНДЕКС и ВЫБОРПОЗ.
Совет: Кроме того, обратитесь к краткому справочнику: советы по устранению неполадок с #NA в удобном PDF-файле. Вы можете поделиться PDF-файлом с другими людьми или распечатать его для справки.
Проблема: искомое значение не находится в первом столбце аргумента
таблица
Одно из ограничений функции В. — она может искать значения только в левом большинстве столбцов в массиве таблицы. Если искомого значения нет в первом столбце массива, вы увидите ошибку #N/Д.
— она может искать значения только в левом большинстве столбцов в массиве таблицы. Если искомого значения нет в первом столбце массива, вы увидите ошибку #N/Д.
В следующей таблице нам нужно узнать количество проданной капусты.
Ошибка #N/Д, так как искомого значения «Капуста» отображается во втором столбце («Продукты») аргумента table_array A2:C10. В этом случае Excel ищет его в столбце A, а не в столбце B.
Решение:вы можете попытаться исправить ошибку, настроив в внося изменения в столбец. Если это невозможно, попробуйте передвигать столбцы. Это также может быть нецелесообразным, если в больших или сложных электронных таблицах значения ячеев являются результатом других вычислений или могут быть другие логические причины, по которым вам просто не удается переместить столбцы. Решением является использование сочетания функций ИНДЕКС и ПОИСКПОЧ, которые могут искать значения в столбце независимо от их положения в таблице подытогов. См. следующий раздел.
Если это невозможно, попробуйте передвигать столбцы. Это также может быть нецелесообразным, если в больших или сложных электронных таблицах значения ячеев являются результатом других вычислений или могут быть другие логические причины, по которым вам просто не удается переместить столбцы. Решением является использование сочетания функций ИНДЕКС и ПОИСКПОЧ, которые могут искать значения в столбце независимо от их положения в таблице подытогов. См. следующий раздел.
Вместо них можно использовать индекс и MATCH
Функции
ИНДЕКС и ВЫБОРПОЗ являются хорошими вариантами для многих случаев, когда в функции ВРОТ не соответствует вашим требованиям. Главное преимущество index и MATCH заключается в том, что вы можете искать значения в столбце в любом месте таблицы подытогов. Индекс возвращает значение из указанной таблицы или диапазона в соответствии с его позицией. Возвращает относительную позицию значения в таблице или диапазоне. Используйте функции ИНДЕКС и MATCH вместе в формуле, чтобы найти значение в таблице или массиве, указав относительное положение значения в таблице или массиве.
Возвращает относительную позицию значения в таблице или диапазоне. Используйте функции ИНДЕКС и MATCH вместе в формуле, чтобы найти значение в таблице или массиве, указав относительное положение значения в таблице или массиве.
Существует несколько преимуществ использования индексов и СОВПАДЕНИЙ вместо В ПРОСМОТР:
-
При этом возвращаемая величина не должна быть в том же столбце, что и столбец подытов. Это отличается от внося данной информации в диапазон, в котором возвращаемая величина должна быть в указанном диапазоне. Почему это важно? При использовании функции ВПР вам нужно знать номер столбца, содержащего значение. Хотя это не кажется сложным, это может оказаться утомительным, если у вас большая таблица и вам нужно подсчитать количество столбцов. Кроме того, при добавлении или удаление столбца в таблице необходимо повторно уложиться и обновить col_index_num столбца. При использовании функций ИНДЕКС и ПОИСКПОЗ не нужно подсчитывать столбцы.
Кроме того, при добавлении или удаление столбца в таблице необходимо повторно уложиться и обновить col_index_num столбца. При использовании функций ИНДЕКС и ПОИСКПОЗ не нужно подсчитывать столбцы. -
С помощью функций ИНДЕКС и MATCH можно указать либо строку, либо столбец в массиве, либо оба этих столбца. Это означает, что значения можно искать по вертикали и по горизонтали. -
С помощью функций ИНДЕКС и ПОИСКПОЗ можно находить значения в любом столбце. В отличие от В ПРОСМОТР, где можно искать только значение в первом столбце таблицы, они будут работать, если искомая величина находится в первом столбце, последнем столбце или в любом другом месте между ними. -
Они обеспечивают гибкость создания динамической ссылки на столбец, содержащий возвращаемое значение. Это означает, что вы можете добавлять столбцы в таблицу, не нарушая индекс и MATCH. С другой стороны, при добавлении столбца в таблицу в нее не будет добавлена вся в нее ВРУ, поскольку она создает статическую ссылку на таблицу.
С другой стороны, при добавлении столбца в таблицу в нее не будет добавлена вся в нее ВРУ, поскольку она создает статическую ссылку на таблицу. -
Они предлагают более гибкие возможности. Они могут найти точное совпадение или значение, большее или меньшее искомой величины. ВПР ищет только наиболее близкое (по умолчанию) или точное значение. Кроме того, функция ВПР предполагает, что первый столбец в таблице отсортирован в алфавитном порядке, и возвращает первое наиболее близкое совпадение, поэтому вы можете получить не те данные, которые ожидали.
Синтаксис
Для построения синтаксиса функций ИНДЕКС и MATCH необходимо использовать аргумент массива или ссылки функции ИНДЕКС и вложенный в нее синтаксис ФУНКЦИИ MATCH. В этом случае будет отформатовка:
=ИНДЕКС(массив или ссылка; ПОИСКПОЗ(искомое_значение;массив;[тип_совпадения])
Заменим ВЛОПУ на примере выше с помощью индекса или MATCH. Синтаксис будет выглядеть следующим образом:
Синтаксис будет выглядеть следующим образом:
=ИНДЕКС(C2:C10;ПОИСКПОЗ(B13;B2:B10;0))
Что означает:
=ИНДЕКС(возвращает значение из C2:C10, которое будет СООТВЕТСТВОВАТЬ(Капуста, которая находится в массиве B2:B10, где возвращаемая величина является первым значением, соответствующим «Капуста»).
Формула ищет в C2:C10 первое значение, соответствующее значению Капуста (B7), и возвращает значение в ячейке C7 (100).
Проблема: не найдено точное совпадение
Если аргумент range_lookup ложь ( ложь) и ВЛОП не может найти точное совпадение в данных, возвращается ошибка #N/Д.
Решение:если вы уверены в том, что в вашей книге есть необходимые данные, и вам не нужно их найти, убедитесь, что в ячейках, на которые имеется ссылка, нет скрытых пробелов или непечатаемых символов. Кроме того, убедитесь, что ячейки должны следовать за правильным типом данных. Например, ячейки с числами должны быть отформатированы какчисловые, а не текстовые.
Кроме того, для очистки данных в ячейках можно использовать функцию CLEAN или TRIM.
Проблема: искомое значение меньше, чем наименьшее значение в массиве
Если range_lookup имеет значение ИСТИНА, а искомого значения меньше, чем наименьшее значение в массиве, вы увидите ошибку #N/Д. Функция ищет приблизительное совпадение в массиве и возвращает ближайшее значение, которое меньше искомого.
В приведенном ниже примере искомое значение равно 100, но в диапазоне B2:C10 нет значений меньше 100, поэтому возникает ошибка.
Решение.
-
Исправьте искомое значение.
-
Если вам не удается изменить искомые значения и вам нужна большая гибкость, думайте об использовании индексов и НАЙТИПОЗ вместо ВРОТ. См. раздел выше в этой статье. Они позволяют находить значения больше или меньше искомого, а также равные ему. Дополнительные сведения см. в предыдущем разделе этой статьи.
Проблема: столбец подстановки не отсортирован в порядке возрастания
Если range_lookup имеет вид ИСТИНА и один из столбцов подзагоков не отсортен в порядке возрастания (A–Z), вы увидите ошибку #N/A.
Решение.
-
Измените функцию ВПР так, чтобы искать точное совпадение. Для этого укажите для аргумента диапазон_поиска значение ЛОЖЬ. Для этого не требуется сортировка.
-
Для поиска значения в несортированной таблице можно также использовать функции ИНДЕКС и ПОИСКПОЗ.
Проблема: значение является большим числом с плавающей запятой
При наличии в ячейках значений времени или больших десятичных чисел Excel возвращает ошибку «#Н/Д» из-за точности чисел с плавающей запятой. Числа с плавающей запятой включают цифры после десятичной запятой. (Excel хранит значения времени в качестве чисел с плавающей за точкой. ) В Excel нельзя хранить числа с очень большими плавающей точкой, поэтому для правильной работы функции числа с плавающей за дробной частью необходимо округлять до 5 десятичных дробных.
) В Excel нельзя хранить числа с очень большими плавающей точкой, поэтому для правильной работы функции числа с плавающей за дробной частью необходимо округлять до 5 десятичных дробных.
Решение. Округлите числа до 5 десятичных разрядов с помощью функции ОКРУГЛ.
У вас есть вопрос об определенной функции?
Задать вопрос на форуме сообщества, посвященном Excel
Помогите нам улучшить Excel
У вас есть предложения по улучшению следующей версии Excel? Если да, ознакомьтесь с темами на портале пользовательских предложений для Excel.
См. также
Функции и их аргументы | Python 3 для начинающих и чайников
В этой статье я планирую рассказать о функциях, именных и анонимных, инструкциях def, return и lambda, обязательных и необязательных аргументах функции, функциях с произвольным числом аргументов.
Именные функции, инструкция def
Функция в python — объект, принимающий аргументы и возвращающий значение. Обычно функция определяется с помощью инструкции def.
Определим простейшую функцию:
def add(x, y):
return x + yИнструкция return говорит, что нужно вернуть значение. В нашем случае функция возвращает сумму x и y.
Теперь мы ее можем вызвать:
>>> add(1, 10)
11
>>> add('abc', 'def')
'abcdef'Функция может быть любой сложности и возвращать любые объекты (списки, кортежи, и даже функции!):
>>> def newfunc(n): ... def myfunc(x): ... return x + n ... return myfunc ... >>> new = newfunc(100) # new - это функция >>> new(200) 300
Функция может и не заканчиваться инструкцией return, при этом функция вернет значение None:
>>> def func(): ... pass ... >>> print(func()) None
Аргументы функции
Функция может принимать произвольное количество аргументов или не принимать их вовсе. Также распространены функции с произвольным числом аргументов, функции с позиционными и именованными аргументами, обязательными и необязательными.
>>> def func(a, b, c=2): # c - необязательный аргумент
... return a + b + c
...
>>> func(1, 2) # a = 1, b = 2, c = 2 (по умолчанию)
5
>>> func(1, 2, 3) # a = 1, b = 2, c = 3
6
>>> func(a=1, b=3) # a = 1, b = 3, c = 2
6
>>> func(a=3, c=6) # a = 3, c = 6, b не определен
Traceback (most recent call last):
File "", line 1, in
func(a=3, c=6)
TypeError: func() takes at least 2 arguments (2 given)Функция также может принимать переменное количество позиционных аргументов, тогда перед именем ставится *:
>>> def func(*args): ... return args ... >>> func(1, 2, 3, 'abc') (1, 2, 3, 'abc') >>> func() () >>> func(1) (1,)
Как видно из примера, args — это кортеж из всех переданных аргументов функции, и с переменной можно работать также, как и с кортежем.
Функция может принимать и произвольное число именованных аргументов, тогда перед именем ставится **:
>>> def func(**kwargs):
... return kwargs
...
>>> func(a=1, b=2, c=3)
{'a': 1, 'c': 3, 'b': 2}
>>> func()
{}
>>> func(a='python')
{'a': 'python'}В переменной kwargs у нас хранится словарь, с которым мы, опять-таки, можем делать все, что нам заблагорассудится.
Анонимные функции, инструкция lambda
Анонимные функции могут содержать лишь одно выражение, но и выполняются они быстрее. Анонимные функции создаются с помощью инструкции lambda. Кроме этого, их не обязательно присваивать переменной, как делали мы инструкцией def func():
>>> func = lambda x, y: x + y
>>> func(1, 2)
3
>>> func('a', 'b')
'ab'
>>> (lambda x, y: x + y)(1, 2)
3
>>> (lambda x, y: x + y)('a', 'b')
'ab'lambda функции, в отличие от обычной, не требуется инструкция return, а в остальном, ведет себя точно так же:
>>> func = lambda *args: args >>> func(1, 2, 3, 4) (1, 2, 3, 4)
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
| ||||
Комплект кодирующих адаптеров M22-XC-Y для изменения функции фиксации переключателей
216407 Комплект кодирующих адаптеров M22-XC-Y для изменения функции фиксации переключателей
ПОСТАВЩИК:
ООО «Локальные системы»
Адрес: РБ, 220090, г. Минск, Логойский тракт 22, офис 303а;
Минск, Логойский тракт 22, офис 303а;
Телефон: +375 17 247-19-99
ИНН: 190465237 / КПП: 37597808
Банковские реквизиты:
р/с BY96ALFA30122209810140270000 в ЗАО «Альфа-Банк» г. Минск
БИК ALFABY2X
Комплект кодирующих адаптеров M22-XC-Y для изменения функции фиксации переключателей
Артикул: 216407
На складе 15 шт.
Технические характеристики
Оплата и Доставка
Каталог : Автоматизация, контроль, управление и визуализация
Категория : Светосигнальная арматура
Бренд : Eaton
Линейка продукции : Titan
Тип изделия : адаптер
Срок поставки под заказ : 6-8 недель
ОПЛАТА
Обращаем Ваше внимание на то, что мы работаем только с юридическими лицами и индивидуальными предпринимателями по безналичному расчету. Отгрузка товара происходит после получения предоплаты на расчетный счет ООО «Локальные системы».
Отгрузка товара происходит после получения предоплаты на расчетный счет ООО «Локальные системы».
ДОСТАВКА
Возможные варианты доставки купленного Вами товара:
Способ доставки вы сможете выбрать при оформлении заказа.
Получить товар на условиях самовывоза можно после подтверждения поступления 100% оплаты на расчетный счет продавца. После получения оплаты наши сотрудники в кратчайшие сроки скомплектуют заказ, и по готовности Вы получите SMS-уведомление на мобильный телефон. Вам останется только забрать товар!
Стоимость доставки:
Доставка в пределах территории РБ осуществляется за счет продавца.
Разгрузочные работы осуществляются силами покупателя.
Вопросы по срокам или вариантам доставки, наличию товара, заказам Вы можете уточнить у Вашего менеджера либо по телефону: +375 (17) 247-19-99.
похожие товары
с этим товаром покупают
Коммерческое предложение действительно на 15. 05.2021 г.
05.2021 г.
Товар успешно добавлен в корзину
Ok
| Когда вы пытаетесь построить график такой функции, как 3x + y = 10, будет проще, если функция будет решена для y. В этом уроке мы обсудим, как это сделать. Чтобы решить функцию для y, вы используете те же шаги, что и для обычного уравнения. Единственная разница в том, что у вас есть другая переменная, которую, возможно, нужно переместить. Помните, чтобы переместить что-то добавленное, добавьте противоположное с обеих сторон. Чтобы переместить что-то умноженное или разделенное, сделайте обратное с обеих сторон. Давайте работать с нашим примером: 3x + y = 10. Решение относительно y означает, что мы должны получить y сами по себе. Следовательно, мы должны все остальное перенести на другую сторону. Итак, давайте сначала определим, что нужно переместить. 3x находится на той же стороне, что и y, поэтому его нужно переместить. 3x-3x + y = 10-3x Слева 3x-3x = 0, поэтому они исчезают. Справа 10 и -3x не похожи на термины, поэтому мы не можем их объединить, и мы почти закончили. Нам просто нужно переставить правую часть так, чтобы она имела стандартный вид. (Этот формат известен как форма пересечения наклона.) y = 10-3x y = -3x + 10 Давайте еще пару примеров: 1) 2y = 3x-8 В этом случае 2 умножается на y, поэтому мы переместим его на 2) 5x + 3y = 12 В этой задаче мы должны переместить как 5x, так и 3. Затем мы должны переместить 3, разделив каждый член на 3. (Обратите внимание, что отрицательный результат остался с) Практика: Решите каждую функцию для y. 1) y-4x = 8 2) 3y = 6x-12 3) -2y = 3x-10 4) 3x + 5y = 10 5) -6x-y = 2 Ответы: |
Функции и уравнения: f (x) равно y и более
Я хотел поговорить о функциональной алгебре, которая, естественно, будет включать ссылку на обозначение функций.
Итак, вот что разочаровывает в написании этого блога. Я стараюсь включать ссылки на другие сайты, которые объясняют концепцию, чтобы мне не пришлось изобретать велосипед для моей читающей аудитории.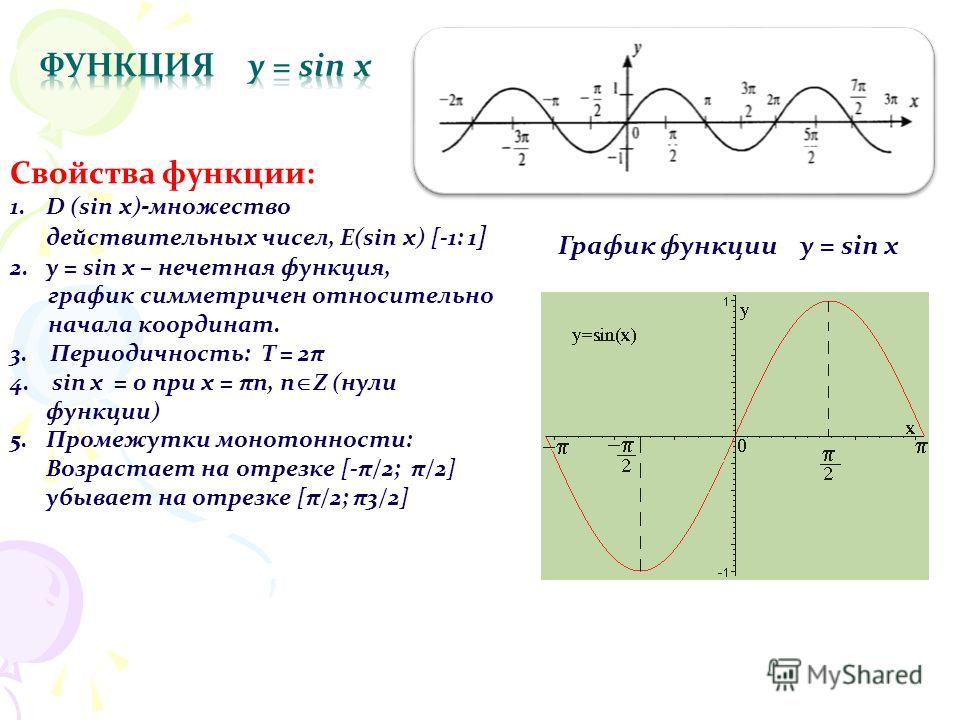 Но гугл дает мне следующие результаты: бесполезные ссылки, которые не более чем говорят: «f (x) то же самое, что и y». Это не математика. Это подготовка к тесту. И нет ничего плохого в подготовке к тестам, но каждый из этих сайтов якобы предназначен для обучения математике, и эй, я не математик, но разве мы не должны объяснять, что f (x) означает ?
Но гугл дает мне следующие результаты: бесполезные ссылки, которые не более чем говорят: «f (x) то же самое, что и y». Это не математика. Это подготовка к тесту. И нет ничего плохого в подготовке к тестам, но каждый из этих сайтов якобы предназначен для обучения математике, и эй, я не математик, но разве мы не должны объяснять, что f (x) означает ?
Кто-то где-то говорит: «Видите, вот почему нам нужны учителя со специальностями по математике, а не по английскому языку, получившие 800 баллов в секции количественного анализа GRE.Вы не можете заменить математику пониманием , которое приходит с изучением этих важных принципов ». Кто-то где-то не прав. Раньше я думал, что в ранние годы, пока у меня не было слишком много разговоров вроде этого:
Я обращаюсь к учителю математического анализа AP, КТО ВЫПУСКАЕТ МАТЕМАТИЮ: Эй, что вы скажете своим детям о нотации функций?
А. П. Учитель математического анализа, ОСОБЕННЫЙ МАТЕМАТИЕЙ: f (x) совпадает с y.
Я, озадаченный: Ну. Ага. Но я имею в виду, почему мы разработали нотацию функций, для чего она служит тому, что не может служить….
А.П. Учитель математики, ОСОБЕННЫЙ МАТЕМАТИЕЙ: Это просто обозначения. Не путайте.
Я: Я не запутался. Но они служат разным целям, и я просто стараюсь точно запечатлеть…
А.П. Учитель математики, ОСОБО ИЗУЧЕННЫЙ МАТЕМАТИЕЙ: Они не служат разным целям. Это просто обозначение f (x) то же самое, что и y.
Я: Хорошо.
По моему опыту, очень немногие учителя математики, ДЕЙСТВИТЕЛЬНО ОСНОВНЫЕ ПО МАТЕМАТИКЕ, тоже заботятся об этих вещах. Мой приятель по пиву — исключение (а теперь он заведующий отделом), и он единственный учитель математики, которого я нашел до сих пор, который интересовался моей работой по этому предмету.
Учебники? Макдугалл Лителл, у CPM есть много таких функциональных машин. Но никаких объяснений. У Холта получается немного лучше, но я не понимал этого, пока не понял, что искал.
Так что трачу больше времени на поиск хорошей ссылки. В противном случае мне придется потратить много времени на то, чтобы выяснить, как правильно или хотя бы безобидно объяснить обозначение функций, чтобы люди, читающие этот блог, не заставляли меня напоминать им, что, черт возьми, я специализируюсь на английском, а не на математик! На это нужно время. Еще не время тратить . Я не хочу рассказывать вам, что такое нотация функций, так, чтобы это прошло проверку экспертов. Я хочу рассказать, как я использую нотацию функций для обучения алгебре функций. Но я не могу обойтись без объяснения обозначений функций, чего я не собирался делать. Это приводит к тому, что многие записи в блогах занимают гораздо больше времени, чем следовало бы. Первоначальная цель моего поста по функциональной алгебре заключалась в том, чтобы сделать небольшой бросок.
Я начал писать этот пост почти месяц назад и зашел в тупик, пытаясь охарактеризовать объяснение.Вам может быть интересно, почему я объясняю то, чего не понимаю, но на самом деле это не так. Я просто не знаю, как это назвать. И это хорошо для преподавания, а не для письма, поэтому я часами пытаюсь найти правильный запрос. Который занимал меня буквально до сегодняшнего дня.
Я просто не знаю, как это назвать. И это хорошо для преподавания, а не для письма, поэтому я часами пытаюсь найти правильный запрос. Который занимал меня буквально до сегодняшнего дня.
Всего пятнадцать минут назад (когда я писал это предложение) я наконец нашел ядро в этом обсуждении нотации функций до Эйлера, в котором кто-то пишет:
но [Ньютон] называет их уравнениями, а не функциями, и по общему признанию (написанные так, как они есть), это именно то, чем они являются.Кажется, все, что мы сегодня написали бы как функцию, Ньютон описал словами, например:
HA. Я узнал кое-что, чего раньше не понимал полностью: функция и уравнение — это не одно и то же. Поиск в Google «в чем разница между уравнением и функцией» привел меня к нужным веб-сайтам. Теперь я понимаю, что искал не просто объяснение обозначений функций, а скорее, почему и когда мы используем функции вместо уравнений.
Вот объяснение того, что я пытался сказать.
Итак, мои исследования окупились. На практике то, что я делал на этом уроке, — это знакомство с операциями функций и нотацией функций как способом преодоления ограничений при использовании уравнений.
На практике то, что я делал на этом уроке, — это знакомство с операциями функций и нотацией функций как способом преодоления ограничений при использовании уравнений.
************************************************ *****************
Сами нужно еще 15 долларов, чтобы купить новую толстовку с капюшоном, которую он хочет. Но если Сами пропускает толстовку, ему нужно всего три доллара, чтобы купить билет в пиццерию в пятницу. Если у Сами есть x долларов, сколько денег в пересчете на x понадобится Сэми, если он хочет и толстовку с капюшоном, и билет на пиццу?
Первое, что думают дети, это то, что Сами нужно на 18 долларов больше.
Хорошо, у Сами есть 20 долларов. Сколько стоит худи? 35 долларов. Сколько стоит корм для пиццы? 23 доллара. Насколько … ох. Ха, говорят дети. Ему нужно намного больше, чем 18 долларов.
В зависимости от того, насколько я себя чувствую, я могу получить фальшивые деньги. Отсчитываю 20 долларов, отдаю тихому ученику. Сколько еще за толстовку? Отсчитайте еще 15 долларов. А теперь как насчет… Примерно тогда студент получает это: вам нужно 20 долларов дважды по .
Сколько еще за толстовку? Отсчитайте еще 15 долларов. А теперь как насчет… Примерно тогда студент получает это: вам нужно 20 долларов дважды по .
Итак, мы переходим к доске и моделируем два разных уравнения для каждой покупки.
у = х + 15
у = х + 3
Итак, если мы получаем и то, и другое, что мы делаем? Добавим, класс припев.
А, вот и новая морщинка. Дети уже некоторое время добавляют уравнения в системах. Итак, я говорю: давайте попробуем сложить эти уравнения.
2у = 2х + 18.
Это правда? Мы тестируем его с 20 долларами, и дети понимают, что правая сторона «работает» (то есть мы получаем 68 долларов), но левая сторона говорит, что нам все еще нужно разделить на 2, что было бы… неправильно.
«Итак, мы находимся в пределах одного уравнения. Уравнение говорит нам, что два выражения занимают одну и ту же точку на числовой прямой — то есть, в конце концов, что означает «равно» ».
«Но когда мы используем несколько переменных в уравнениях, тогда уравнение становится связью между двумя переменными, условием« если-то ». Если y = x + 15, , то точка (3, 18) является решением, потому что установка x = 3 и y = 18 создает уравнение, в котором обе стороны занимают одну и ту же точку на числовой прямой. Если 3x + 2y = 12, , тогда (2,3) является решением, потому что установка x = 2, y = 3 и т. Д. »
Если y = x + 15, , то точка (3, 18) является решением, потому что установка x = 3 и y = 18 создает уравнение, в котором обе стороны занимают одну и ту же точку на числовой прямой. Если 3x + 2y = 12, , тогда (2,3) является решением, потому что установка x = 2, y = 3 и т. Д. »
Но в уравнении переменные — это значения. Таким образом, в случае саамов мы не можем рассматривать y как точку сбора. Мы не можем отслеживать зависимую переменную, потому что она, очевидно, изменяется на . Значение y в первом уравнении отличается от значения y во втором уравнении. Если бы мы хотели разделить их, мы могли бы использовать две разные переменные, например z = x + 15 и y = x + 3.Или мы могли бы пронумеровать ys: y 1 = x + 15, y 2 = x + 3.
«Использование языка функций устраняет многие из этих ограничений».
«Во-первых, по логике. Функции существенно отличаются от уравнений: функция — это выход . Уравнение — это связь между переменными. Да, y = x + 3 и f (x) = x + 3 дают одинаковые результаты, поэтому мы, учителя, всегда говорим вам помнить, что «y и f (x) — одно и то же». Однако f (x) — это не переменная, а выход.Итак, когда мы добавляем две функции, мы добавляем выходы. Помните также, что функция даже не обязательно должна быть уравнением, как в примере кода мобильного телефона.
Да, y = x + 3 и f (x) = x + 3 дают одинаковые результаты, поэтому мы, учителя, всегда говорим вам помнить, что «y и f (x) — одно и то же». Однако f (x) — это не переменная, а выход.Итак, когда мы добавляем две функции, мы добавляем выходы. Помните также, что функция даже не обязательно должна быть уравнением, как в примере кода мобильного телефона.
Тогда есть обозначение функций, изобретенное Эйлером. Обозначение функций позволяет использовать уникальные имена, обычно состоящие из одной буквы. Но этого не должно быть. Вы можете проявить изобретательность с названиями букв и вводимыми значениями ».
«Обозначение функций также стало более элегантным и эффективным. Вместо того, чтобы говорить «если x = 7», вы можете просто сказать f (3).После определения функции с именем «f» можно вводить все, что угодно, даже другое выражение, например f (a + 7). А затем вместо того, чтобы говорить «y =» и решать относительно x, напишите f (x) = 3 ».
«Итак, давайте назовем кассу Сэмми c , а затем создадим функцию h для толстовки и p для корма для пиццы.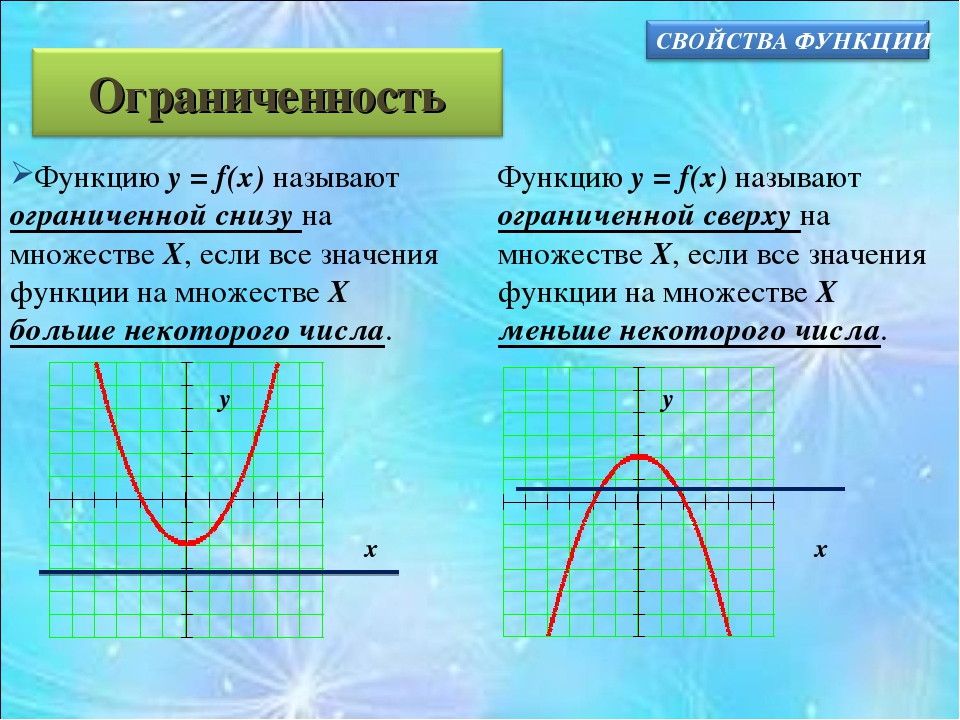
h (c) = c + 15
p (c) = c + 3
В обоих случаях c представляет деньги, которые есть у Сами, поэтому входное значение одинаково. Но выходное значение зависит от используемой функции.”
«Это небольшая разница. Но скольким вам говорили, что f (x) то же самое, что y? » Связка поднятых рук.
«Ага. И во многом это так. Но вам должно быть интересно, почему, если это одно и то же, мы учим вас нотации функций ». Множество кивков.
«Итак, по мере того, как вы перейдете к продвинутой математике, вы начнете узнавать другие причины, по которым мы иногда используем функции, а иногда — уравнения. На данный момент достаточно знать, что обозначение функций позволяет нам отслеживать различные результаты.
«Как только мы сможем это сделать, мы сможем создать целую математику с функциями. Их можно складывать, вычитать, умножать. У них есть обратные операции ».
«Но тогда почему мы используем уравнения?»
«Ну, с одной стороны, функции не работают хорошо с системами . Помните, что когда мы решаем системы, мы — это , ожидая, что и x, и y (и любые другие переменные) будут равны. Функции не справляются с этим. Таким образом, вы увидите, что мы переключаемся между уравнениями и функциями по мере необходимости.”
Когда вам нужно добавить выражения, отлично подойдут функции. Итак, теперь мы можем сложить h (c) и g (c).
h (c) + p (c) = (x + 15) + (x + 3) = 2x + 18
«Поскольку мы добавляем результатов и имеем уникальный способ отслеживания каждого результата, мы можем добавить их должным образом. Помните также, что, поскольку функция не обязательно должна быть уравнением, я могу складывать или вычитать результаты, даже не имея уравнения. Если a (x) = 9 и b (y) = 17, тогда b (y) — a (x) равно 8, и мне не нужно заботиться о том, генерируются ли a (x) и b (y) выражение, или правило, или код, или случайная случайность — конечно, при условии, что эта случайная случайность — только одна для каждого входа.”
************************************************ *****************************
Я знаю. Вам интересно, почему я просто не следую словам учителя математического анализа AP «f (x) то же самое, что и y». Что ж, оказывается, что операции с функциями — большая часть предварительного вычисления, поэтому они будут использовать это позже.
А пока я практикуюсь с обозначением функций (я украл это наугад). Недостаточно. Дети действительно не узнают этого позже. Но, по крайней мере, они этому подвержены.
Затем я перехожу к сложению и вычитанию линейных функций.Обычно я просто кладу проблемы на доску.
Образец теста:
Вот тестовый вопрос:
И отсюда я перехожу к линейному умножению функций (также известному как квадратичность) и, в конечном итоге, к рациональным выражениям (линейное деление функций).
Как и обучение конгруэнтности с изометриями, я не могу утверждать, что лучше использовать функции для дальнейшей работы с линейными и квадратными уравнениями. Мне он кажется более… элегантным, может быть?
Но исполнение еще не совсем так.Это первый год, когда я по-настоящему учил всю эту последовательность: введение функций, сложение / вычитание / запись функций, умножение функций, обратные функции, рациональные выражения. Написание этого показало очевидное улучшение. До сих пор моя функциональная иллюстрация была отдельным уроком. Позже я ввожу понятие сложения функций и при этом обращаюсь к нотации функций.
Это глупо, теперь, когда я смотрю на это. В будущем я представлю функции, а затем перейду к их обозначениям.Я могу потратить на это день или два, так рано пройти викторину. Затем я могу вернуться к линейным уравнениям или неравенствам (размещение гибкое), а затем вызвать сложение и вычитание функций с уже охваченными обозначениями функций.
Знаете, что раздражает? Огромные усилия, описанные в начале этого поста, чтобы выяснить, как описать то, чему я учил, привели меня к этому. Огромные усилия были потрачены исключительно на то, чтобы написать этот пост. О чем я беспокоился. Изучая, как описывать нотацию функций для моих читателей, я узнал, что правильный способ охарактеризовать мою работу — это различие между функциями и уравнениями, и это привело к идее улучшения последовательности.
Это что-то вроде сообщения-заполнителя. Очевидно, я сейчас в курсе. Мой блок линейных уравнений какое-то время находится в хорошей форме. Это дает мне много возможностей, чтобы добавить изюминки, ввести более сложные темы в предмет, который хорошо знают студенты. Между тем, линейное умножение функций оказалось отличным введением в квадратику. Так что теперь я собираю все это воедино.
Далее в этой последовательности: пост, который я действительно хотел написать, о моем введении в квадратику.
Извините за медленное количество сообщений в последнее время. Я сделал пять в апреле, потом поленился.
Нравится:
Нравится Загрузка …
Связанные
Функции Разделы: Функции и отношения, Домен и диапазон Есть «Отношение» Функция Вернемся Отношение
Сейчас «Тест вертикальной линии» Глядя на
Эта характеристика
Сейчас «Есть Думай обо всем С другой То есть да, Вверх | 1 | 2 | Возвращаться
|
Определение функции
Показать общее уведомление
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Пол
6 мая 2021 г.
Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-4: Определение функции
Теперь нам нужно перейти ко второй теме этой главы. Однако, прежде чем мы это сделаем, нам нужно сделать быстрое определение.
Определение отношения
Отношение — это набор упорядоченных пар. 2} — 4 \).Вот упорядоченные пары, которые мы использовали.
\ [\ left ({- 2,5} \ right) \, \, \, \, \ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3 } \ right) \, \, \, \, \ left ({1, — 4} \ right) \, \, \, \, \ left ({2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4,5} \ right) \]
Любые из следующих отношений являются отношениями, потому что они состоят из набора упорядоченных пар.
\ [\ begin {align *} & \ left \ {{\ left ({- 2,5} \ right) \, \, \, \, \ left ({- 1,0} \ right) \, \, \, \, \, \ left ({2, — 3} \ right)} \ right \} \\ & \ left \ {{\ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3} \ right) \, \, \, \, \ left ({2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4,5} \ right)} \ right \} \\ & \ left \ {{\ left ({3,0} \ right) \, \, \, \ , \ left ({4,5} \ right)} \ right \} \\ & \ left \ {{\ left ({- 2,5} \ right) \, \, \, \, \ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3} \ right) \, \, \, \, \ left ({1, — 4} \ right) \, \ , \, \, \ left ({2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4, 5} \ right)} \ right \} \ end {align *} \]
Конечно, есть еще много отношений, которые мы могли бы сформировать из списка упорядоченных пар выше, но мы просто хотели перечислить несколько возможных отношений, чтобы привести некоторые примеры.Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим.
Теперь вы, вероятно, спрашиваете, почему мы заботимся об отношениях, и это хороший вопрос. Некоторые отношения очень специфичны и используются почти на всех уровнях математики. Следующее определение говорит нам, какие отношения являются этими особыми отношениями.
Определение функции
Функция — это отношение, для которого каждое значение из набора первых компонентов упорядоченных пар связано ровно с одним значением из набора вторых компонентов упорядоченной пары.
Ладно, это полный рот. Посмотрим, сможем ли мы понять, что это значит. Давайте посмотрим на следующий пример, который, надеюсь, поможет нам во всем этом разобраться.
Пример 1 Следующее отношение является функцией.
\ [\ left \ {{\ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3} \ right) \, \, \, \, \ left ( {2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4,5} \ right)} \ right \} \]
Показать решение
Из этих упорядоченных пар мы получаем следующие наборы первых компонентов ( i.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{0, — 3,0,5} \ right \} \]
Для набора вторых компонентов обратите внимание, что «-3» встречается в двух упорядоченных парах, но мы указали его только один раз.
Чтобы понять, почему это отношение является функцией, просто выберите любое значение из набора первых компонентов. Теперь вернитесь к отношению и найдите каждую упорядоченную пару, в которой это число является первым компонентом, и перечислите все вторые компоненты из этих упорядоченных пар.Список вторых компонентов будет состоять ровно из одного значения.
Например, давайте выберем 2 из набора первых компонентов. Из отношения мы видим, что существует ровно одна упорядоченная пара с 2 в качестве первого компонента, \ (\ left ({2, — 3} \ right) \). Следовательно, список вторых компонентов (, т.е. список значений из набора вторых компонентов), связанный с 2, представляет собой ровно одно число -3.
Обратите внимание, что нас не волнует, что -3 является вторым компонентом второго упорядоченного номинала в отношении.Это вполне приемлемо. Мы просто не хотим, чтобы было больше одной упорядоченной пары с 2 в качестве первого компонента.
Мы рассмотрели одно значение из набора первых компонентов для нашего быстрого примера, но результат будет таким же для всех остальных вариантов. Независимо от выбора первых компонентов с ним будет связан ровно один второй компонент.
Следовательно, это отношение является функцией.
Чтобы действительно почувствовать, что нам говорит определение функции, мы, вероятно, должны также проверить пример отношения, которое не является функцией.
Пример 2 Следующее отношение не является функцией.
\ [\ left \ {{\ left ({6,10} \ right) \, \, \, \, \ left ({- 7,3} \ right) \, \, \, \, \ left ({ 0,4} \ right) \, \, \, \, \ left ({6, — 4} \ right)} \ right \} \]
Показать решение
Не беспокойтесь о том, откуда взялось это отношение. {{\ mbox {st}}}} {\ mbox {components:}} \ left \ {{6, — 7,0} \ right \} \ hspace {0.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{10,3,4, — 4} \ right \} \]
Из набора первых компонентов выберем 6. Теперь, если мы перейдем к соотношению, мы увидим, что есть две упорядоченные пары с 6 в качестве первого компонента: \ (\ left ({6,10} \ right) \ ) и \ (\ left ({6, — 4} \ right) \). Список вторых компонентов, связанных с 6, будет: 10, -4.
Список вторых компонентов, связанных с 6, имеет два значения, поэтому это отношение не является функцией.
Обратите внимание на тот факт, что если мы выбрали -7 или 0 из набора первых компонентов, то в списке вторых компонентов, связанных с каждым из них, будет только одно число. Это не имеет значения. Тот факт, что мы нашли даже одно значение в наборе первых компонентов с более чем одним вторым компонентом, связанным с ним, достаточно, чтобы сказать, что это отношение не является функцией.
В качестве последнего комментария к этому примеру отметим, что если мы удалим первую и / или четвертую упорядоченную пару из отношения, у нас будет функция!
Итак, надеюсь, у вас есть хоть какое-то представление о том, что нам говорит определение функции.
Теперь, когда мы заставили вас пройти собственно определение функции, давайте дадим еще одно «рабочее» определение функции, которое будет гораздо более полезным для того, что мы здесь делаем.
Фактическое определение работает с отношением. Однако, как мы видели с четырьмя отношениями, которые мы привели до определения функции, и с отношением, которое мы использовали в примере 1, мы часто получаем отношения из какого-либо уравнения.
Важно отметить, что не все отношения основаны на уравнениях! Отношение из второго примера, например, было просто набором упорядоченных пар, которые мы записали для этого примера, и не было получено из какого-либо уравнения.Это также может быть верно для отношений, которые являются функциями. Они не обязательно должны исходить из уравнений.
Однако, как бы то ни было, все функции, которые мы собираемся использовать в этом курсе, основаны на уравнениях. Поэтому давайте напишем определение функции, которая признает этот факт.
Прежде чем мы дадим «рабочее» определение функции, мы должны указать, что это НЕ фактическое определение функции, данное выше. Это просто хорошее «рабочее определение» функции, которое связывает вещи с видами функций, с которыми мы будем работать в этом курсе.
«Рабочее определение» функции
Функция — это уравнение, для которого любой \ (x \), который можно вставить в уравнение, даст ровно один \ (y \) из уравнения.
Вот оно. Это определение функций, которые мы собираемся использовать, и, вероятно, будет легче понять, что оно означает.
Прежде чем мы исследуем это, обратите внимание, что мы использовали фразу «\ (x \), который может быть подключен» в определении.Это имеет тенденцию означать, что не все \ (x \) могут быть включены в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако на этом этапе просто помните, что мы не можем делить на ноль, и если мы хотим, чтобы действительные числа были исключены из уравнения, мы не можем извлечь квадратный корень из отрицательное число. Итак, с этими двумя примерами ясно, что мы не всегда сможем подставить каждое \ (x \) в какое-либо уравнение.
Далее, имея дело с функциями, мы всегда будем предполагать, что и \ (x \), и \ (y \) будут действительными числами.Другими словами, мы на некоторое время забудем о том, что знаем что-либо о комплексных числах, пока будем заниматься этим разделом.
Хорошо, теперь давайте вернемся к определению функции и рассмотрим несколько примеров уравнений, которые являются функциями, и уравнений, которые не являются функциями.
Пример 3 Определите, какие из следующих уравнений являются функциями, а какие нет. 2} = 4 \)
Показать все решения Скрыть все решения
Показать обсуждение
«Рабочее» определение функции гласит, что если мы возьмем все возможные значения \ (x \), подставим их в уравнение и решим для \ (y \), мы получим ровно одно значение для каждого значения \ ( Икс\).На этом этапе игры может быть довольно сложно на самом деле показать, что уравнение является функцией, поэтому в основном мы будем обсуждать его. С другой стороны, часто довольно легко показать, что уравнение не является функцией.
a \ (y = 5x + 1 \) Показать решение
Итак, нам нужно показать, что независимо от того, какое \ (x \) мы подставляем в уравнение и решаем для \ (y \), мы получим только одно значение \ (y \). Также обратите внимание, что значение \ (y \), вероятно, будет различным для каждого значения \ (x \), хотя это не обязательно.
Давайте начнем с того, что подставим некоторые значения \ (x \) и посмотрим, что произойдет.
\ [\ begin {align *} x & = — 4: \ hspace {0,25 дюйма} & y & = 5 \ left ({- 4} \ right) + 1 = — 20 + 1 = — 19 \\ x & = 0: \ hspace {0,25 дюйма} & y & = 5 \ left (0 \ right) + 1 = 0 + 1 = 1 \\ x & = 10: \ hspace {0,25 дюйма} & y & = 5 \ left ({ 10} \ right) + 1 = 50 + 1 = 51 \ end {align *} \]
Итак, для каждого из этих значений \ (x \) мы получили одно значение \ (y \) из уравнения.Но этого недостаточно, чтобы утверждать, что это функция. Чтобы официально доказать, что это функция, нам нужно показать, что она будет работать независимо от того, какое значение \ (x \) мы подставляем в уравнение.
Конечно, мы не можем подставить в уравнение все возможные значения \ (x \). Это просто невозможно физически. Однако давайте вернемся и посмотрим на те, которые мы подключили. Для каждого \ (x \) после подключения мы сначала умножили \ (x \) на 5, а затем прибавили к нему 1.2} + 1 = 9 + 1 = 10 \ end {align *} \]
А теперь давайте немного подумаем о том, что мы делали с оценками. Сначала мы возводили в квадрат значение \ (x \), которое мы подключили. Когда мы возводим в квадрат число, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение.
Итак, похоже, что это уравнение также является функцией.
Обратите внимание, что получить одинаковое значение \ (y \) для разных \ (x \) — это нормально.2} & = 10 + 1 = 11 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \ sqrt {11} \ end {align *} \]
Теперь помните, что мы решаем для \ (y \), и это означает, что в первом и последнем случаях выше мы фактически получим два разных значения \ (y \) из \ (x \), и поэтому это уравнение НЕ является функцией.
Обратите внимание, что у нас могут быть значения \ (x \), которые приведут к единственному \ (y \), как мы видели выше, но это не имеет значения. Если даже одно значение \ (x \) дает более одного значения \ (y \), при решении уравнения не будет функцией. 2} = 4 \ hspace {0.2} = 4 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \, 2 \]
Итак, это уравнение не является функцией. Напомним, что из предыдущего раздела это уравнение круга. Круги никогда не бывают функциями.
Надеюсь, эти примеры позволили вам лучше понять, что такое функция.
Теперь нам нужно перейти к так называемой нотации функции . Обозначения функций будут широко использоваться в большинстве оставшихся глав этого курса, поэтому важно понимать их.2} — 5x + 3 \]
Буква, которую мы используем, не имеет значения. Важна часть «\ (\ left (x \ right) \)». Буква в скобках должна соответствовать переменной, используемой справа от знака равенства.
Очень важно отметить, что \ (f \ left (x \ right) \) на самом деле не более чем действительно причудливый способ записи \ (y \). Если вы запомните это, вы можете обнаружить, что работать с обозначениями функций становится немного проще.
Кроме того, это НЕ умножение \ (f \) на \ (x \)! Это одна из наиболее распространенных ошибок, которые люди допускают, когда впервые сталкиваются с функциями.2} — 5x + 3 \]
и спросите, каково его значение для \ (x = 4 \). В терминах обозначений функций мы будем «спрашивать» об этом, используя обозначение \ (f \ left (4 \ right) \). Итак, когда в скобках есть что-то, кроме переменной, мы действительно спрашиваем, каково значение функции для этой конкретной величины.
Теперь, когда мы говорим значение функции, мы действительно спрашиваем, каково значение уравнения для этого конкретного значения \ (x \). Вот \ (f \ left (4 \ right) \).2} — 5} \ right) \)
Показать все решения Скрыть все решения
a \ (f \ left (3 \ right) \) и \ (g \ left (3 \ right) \) Показать решение
Итак, у нас есть две оценки функций, которые нужно выполнить, и у нас также есть две функции, поэтому нам нужно будет решить, какую функцию использовать для оценок. Главное здесь — обратить внимание на букву перед круглой скобкой. Для \ (f \ left (3 \ right) \) мы будем использовать функцию \ (f \ left (x \ right) \), а для \ (g \ left (3 \ right) \) мы будем использовать \ (g \ влево (х \ вправо) \).2} — 2 \ влево ({- 10} \ вправо) + 8 = 100 + 20 + 8 = 128 \]
Убедитесь, что здесь вы правильно разбираетесь с негативными признаками. Теперь второй.
\ [g \ left ({- 10} \ right) = \ sqrt {- 10 + 6} = \ sqrt {- 4} \]
Мы достигли разницы. Напомним, когда мы впервые начали говорить об определении функций, мы заявили, что будем иметь дело только с действительными числами. Другими словами, мы подставляем только действительные числа и хотим, чтобы в качестве ответов возвращались только действительные числа.2} — 2 \ влево (0 \ вправо) + 8 = 8 \]
Опять же, не забывайте, что это не умножение! По какой-то причине ученикам нравится думать об этом как об умножении и получать нулевой ответ. Будь осторожен.
d \ (f \ left (t \ right) \) Показать решение
Остальные оценки теперь будут немного другими. Как показывает этот, нам не нужно просто указывать числа в скобках. Однако оценка работает точно так же. Мы вставляем символы \ (x \) справа от знака равенства в скобки.2} — 2t + 8 \]
Обратите внимание, что в этом случае это почти то же самое, что и наша исходная функция, за исключением того, что на этот раз мы используем \ (t \) в качестве переменной.
e \ (f \ left ({t + 1} \ right) \) и \ (f \ left ({x + 1} \ right) \) Показать решение
Теперь давайте немного посложнее, или, по крайней мере, они кажутся более сложными. Однако все не так плохо, как может показаться. Сначала мы оценим \ (f \ left ({t + 1} \ right) \). Этот работает точно так же, как и предыдущая часть.2} + 1} \ end {выровнять *} \]
Оценка функций — это то, чем мы будем много заниматься в следующих разделах и главах, поэтому убедитесь, что вы можете это сделать. Вы обнаружите, что несколько последующих разделов будет очень трудным для понимания и / или выполнения работы, если вы не имеете хорошего представления о том, как работает оценка функций.
Пока мы говорим об оценке функций, мы должны теперь поговорить о кусочных функциях . На самом деле мы уже видели пример кусочной функции, даже если в то время мы не называли его функцией (или кусочной функцией).Вспомните математическое определение абсолютной величины.
\ [\ left | х \ право | = \ left \ {{\ begin {array} {* {20} {l}} x & {{\ mbox {if}} x \ ge 0} \\ {- x} & {{\ mbox {if}} x
Это функция, и если мы используем обозначение функции, мы можем записать ее следующим образом:
\ [f \ left (x \ right) = \ left \ {{\ begin {array} {* {20} {l}} x & {{\ mbox {if}} x \ ge 0} \\ {- x} & {{\ mbox {if}} x
Это также пример кусочной функции. Кусочная функция — это не что иное, как функция, которая разбита на части, и какой фрагмент вы используете, зависит от значения \ (x \).2} + 4} & {{\ mbox {if}} t \ le — 4} \\ {10} & {{\ mbox {if}} — 4 15} \ end {array}} \ right. \]
оценивают каждое из следующих действий.
- \ (g \ left ({- 6} \ right) \)
- \ (g \ left ({- 4} \ right) \)
- \ (г \ влево (1 \ вправо) \)
- \ (g \ left ({15} \ right) \)
- \ (g \ left ({21} \ right) \)
Показать все решения Скрыть все решения
Показать обсуждение
Прежде чем приступить к оценкам, обратите внимание, что мы используем разные буквы для функции и переменной, чем те, которые мы использовали до этого момента.Это не повлияет на работу оценки. Не зацикливайтесь на том, чтобы видеть \ (f \) для функции и \ (x \) для переменной, что вы не сможете решить любую проблему, в которой нет этих букв.
Теперь, чтобы выполнить каждую из этих оценок, первое, что нам нужно сделать, это определить, какому неравенству удовлетворяет число, и оно будет удовлетворять только одному неравенству. Когда мы определяем, какому неравенству удовлетворяет число, мы используем уравнение, связанное с этим неравенством.2} + 4 = 52 \]
c \ (g \ left (1 \ right) \) Показать решение
В этом случае число 1 удовлетворяет среднему неравенству, поэтому мы будем использовать среднее уравнение для оценки. Эта оценка часто вызывает проблемы у студентов, несмотря на то, что на самом деле это одна из самых простых оценок, которые мы когда-либо проводим. Мы знаем, что оцениваем функции / уравнения, подставляя номер переменной. В этом случае нет переменных. Это не проблема. Поскольку переменных нет, это просто означает, что мы на самом деле ничего не подключаем, и получаем следующее:
\ [g \ left (1 \ right) = 10 \]
d \ (g \ left ({15} \ right) \) Показать решение
Опять же, как и со второй частью, нам нужно быть немного осторожнее с этой.В этом случае число удовлетворяет среднему неравенству, так как это число со знаком равенства в нем. Затем, как и в предыдущей части, мы получаем
\ [g \ left ({15} \ right) = 10 \]
Не радуйтесь тому факту, что предыдущие две оценки имели одинаковое значение. Иногда это будет происходить.
e \ (g \ left ({21} \ right) \) Показать решение
Для окончательной оценки в этом примере число удовлетворяет нижнему неравенству, поэтому мы будем использовать нижнее уравнение для оценки.
\ [g \ left ({21} \ right) = 1 — 6 \ left ({21} \ right) = — 125 \]
Кусочные функции не так часто возникают в классе алгебры, однако они возникают в нескольких местах в более поздних классах, поэтому вам важно понимать их, если вы собираетесь перейти к большему количеству математических классов.
В качестве последней темы нам нужно вернуться и коснуться того факта, что мы не всегда можем подключить каждый \ (x \) к каждой функции. Мы кратко говорили об этом, когда давали определение функции, и мы видели пример этого, когда оценивали функции.Теперь нам нужно взглянуть на это немного подробнее.
Во-первых, нам нужно избавиться от пары определений.
Домен и диапазон
Область уравнения — это набор всех \ (x \), которые мы можем вставить в уравнение и получить действительное число для \ (y \). Диапазон уравнения — это набор всех \ (y \), которые мы когда-либо можем получить из уравнения.
Обратите внимание, что мы действительно имели в виду использовать уравнение в определениях выше вместо функций.Это действительно определения уравнений. Однако, поскольку функции также являются уравнениями, мы также можем использовать определения функций.
Определение диапазона уравнения / функции для многих функций может быть довольно трудным, поэтому мы не будем вдаваться в подробности. Здесь нас гораздо больше интересует определение областей функций. Согласно определению, домен — это набор всех \ (x \), которые мы можем подключить к функции и получить действительное число. На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \ left ({x + 5} \ right) \ left ({x — 2} \ right) = 0 \ hspace {0,25in} x = — 5, \, \, x = 2 \ ]
Итак, мы получим деление на ноль, если подставим \ (x = — 5 \) или \ (x = 2 \). Это означает, что нам нужно избегать этих двух чисел. Однако все остальные значения \ (x \) будут работать, поскольку они не дают деления на ноль. Тогда домен
\ [{\ mbox {Домен: все действительные числа, кроме}} x = — 5 {\ mbox {и}} x = 2 \]
b \ (f \ left (x \ right) = \ sqrt {5 — 3x} \) Показать решение
В этом случае у нас не будет задач деления на ноль, так как у нас нет дробей.У нас действительно есть квадратный корень в задаче, поэтому нам нужно позаботиться о том, чтобы извлечь квадратный корень из отрицательного числа.
Эта часть будет работать немного иначе, чем предыдущая. В этой части мы определили значение (я) \ (x \), которого следует избегать. В этом случае напрямую получить домен будет так же просто. Чтобы избежать квадратных корней из отрицательных чисел, все, что нам нужно сделать, это потребовать, чтобы
\ [5 — 3x \ ge 0 \]
Это довольно простое линейное неравенство, которое мы должны решить на данный момент.2} + 4}} \) Показать решение
В этом случае у нас есть дробь, но обратите внимание, что знаменатель никогда не будет равен нулю для любого действительного числа, поскольку x 2 гарантированно будет положительным или нулевым, и добавление 4 к этому будет означать, что знаменатель всегда будет минимум 4. Другими словами, знаменатель никогда не будет равен нулю. Итак, все, что нам нужно сделать, это позаботиться о квадратном корне в числителе.
Для этого нам потребуется,
\ [\ begin {align *} 7x + 8 & \ ge 0 \\ 7x & \ ge — 8 \\ x & \ ge — \ frac {8} {7} \ end {align *} \]
Теперь мы можем фактически подставить любое значение \ (x \) в знаменатель, однако, поскольку у нас есть квадратный корень в числителе, мы должны убедиться, что все \ (x \) удовлетворяют неравенство выше, чтобы избежать проблем.2} — 16}} \) Показать решение
В этой заключительной части нам нужно беспокоиться как о квадратном корне, так и о делении на ноль. Давайте сначала позаботимся о квадратном корне, поскольку это, вероятно, наложит наибольшее ограничение на значения \ (x \). Итак, чтобы квадратный корень оставался довольным ( т.е. не было квадратного корня из отрицательных чисел), нам потребуется это,
\ [\ begin {align *} 10x — 5 & \ ge 0 \\ 10x & \ ge 5 \\ x & \ ge \ frac {1} {2} \ end {align *} \]
Итак, по крайней мере, нам нужно потребовать, чтобы \ (x \ ge \ frac {1} {2} \), чтобы избежать проблем с квадратным корнем.2} — 16 = \ left ({x — 4} \ right) \ left ({x + 4} \ right) = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = — 4, \, \, х = 4 \]
Теперь обратите внимание, что \ (x = — 4 \) не удовлетворяет неравенству, которое нам нужно для квадратного корня, и поэтому значение \ (x \) уже исключено квадратным корнем. 3 — 1
являются функциями, потому что каждое значение x дает другое значение y .В графических терминах функция — это отношение, в котором первые числа в упорядоченной паре имеют одно и только одно значение в качестве второго числа, другой части упорядоченной пары.
Проверка упорядоченных пар
Упорядоченная пара — это точка на координатном графике x — y со значениями x и y. Например, (2, −2) — это упорядоченная пара с 2 в качестве значения x и −2 в качестве значения y . При наличии набора упорядоченных пар убедитесь, что ни одно значение x не имеет более одного парного значения y .Когда задан набор упорядоченных пар [(2, −2), (4, −5), (6, −8), (2, 0)], вы знаете, что это не функция, потому что x -Значение — в данном случае — 2, имеет более одного значения y . Однако этот набор упорядоченных пар [(−2, 4), (−1, 1), (0, 0), (1, 1), (2, 4)] является функцией, потому что y -value может иметь более одного соответствующего значения x .
Решение для Y
Относительно легко определить, является ли уравнение функцией, решив для y .2 = 9
имеет два возможных ответа (3 и −3).
Тест вертикальной линии
Определить, является ли отношение функцией на графике, относительно легко с помощью теста вертикальной линии. Если вертикальная линия пересекает отношение на графике только один раз во всех местах, отношение является функцией. Однако, если вертикальная линия пересекает отношение более одного раза, отношение не является функцией. При использовании теста вертикальной линии все линии, кроме вертикальных, являются функциями.Круги, квадраты и другие замкнутые формы не являются функциями, но параболические и экспоненциальные кривые — это функции.
Использование диаграммы ввода-вывода
На диаграмме ввода-вывода отображается вывод или результат для каждого ввода или исходного значения. Любая диаграмма ввода-вывода, где у входа есть два или более разных выхода, не является функцией. Например, если вы видите число 6 в двух разных входных пространствах, а результат — 3 в одном случае и 9 в другом, отношение не является функцией.Однако, если два разных входа имеют одинаковый выход, все еще возможно, что отношение является функцией, особенно если задействованы квадратные числа.
Область и диапазон функции
Определения домена и диапазона
Домен
Домен а
функция — это полный набор возможных значений
независимой переменной.
На простом английском языке это определение означает:
Домен — это совокупность всех возможных
x -значения, которые сделают функцию
«работа» и выдаст действительные значения y .
При нахождении домена запомните:
- Знаменатель (внизу) дроби не может быть
ноль - Число под знаком квадратного корня должно быть
положительный в этом разделе
Пример 1а
Вот график y = sqrt (x + 4):
12345-1-2-3-4123xy
Домен: `x> = — 4`
Область определения этой функции — x ≥ −4, так как x не может быть меньше −4.Чтобы понять, почему, попробуйте в вашем калькуляторе некоторые числа меньше, чем «−4» (например, «−5» или «−10»), и некоторые числа больше, чем «−4» (например, «−2» или «8»). Единственные, которые «работают» и дают нам ответ, — это те, которые больше или равны «−4». Это сделает число под квадратным корнем положительным.
Примечания:
- Закрашенный кружок в точке `(-4, 0)`. Это указывает на то, что домен «запускается» в этот момент.
- Мы видели, как рисовать подобные графики в разделе 4 «График функции».2 = х — 2.
Как найти домен
В общем, мы определяем область каждой функции, ища те значения независимой переменной (обычно x ), которые разрешено использовать для . (Обычно нам нужно избегать 0 в нижней части дроби или отрицательных значений под знаком квадратного корня).
Диапазон
Серия из
функция — это полный набор всех возможных
результирующих значений зависимой переменной ( y, обычно ) после того, как мы подставили домен.
На простом английском языке это определение означает:
Диапазон — это результат
y- значений, которые мы получаем после подстановки всех возможных значений x .
Как найти ассортимент
- Диапазон функции — это разброс возможных значений y (от минимального значения y до максимального y -значения)
- Подставьте различные значения x в выражение для y на
посмотреть, что происходит.(Спросите себя: всегда ли и положительны? Всегда отрицательны? Или, может быть, не равны определенным значениям?) - Убедитесь, что вы ищете минимум и максимум значения y .
- Нарисуйте эскиз ! В математике картина стоит тысячи слов.
Пример 1б
Вернемся к примеру выше, `y = sqrt (x + 4)`.
Мы замечаем, что кривая находится либо на горизонтальной оси, либо над ней.Независимо от того, какое значение x мы попробуем, мы всегда получим нулевое или положительное значение y . Мы говорим, что диапазон в этом случае равен y ≥ 0.
12345-1-2-3-4123xy
Диапазон: `y> = 0`
Кривая продолжается всегда вертикально, за пределы того, что показано на графике, поэтому диапазон — это все неотрицательные значения `y`.
Пример 2
График кривой y = sin x показывает, что диапазон находится между -1 и 1.
12345-1-2-3-4-5-6-71-1xy
Диапазон: `-1
Область y = sin x — это «все значения x », поскольку нет никаких ограничений на значения для x . (Введите любое число в функцию «sin» в вашем калькуляторе. Любое число должно работать и даст вам окончательный ответ от -1 до 1.)
Эксперимент с калькулятором и наблюдение кривой показывают, что диапазон составляет y между -1 и 1.Мы могли бы записать это как −1 ≤ y ≤ 1.
Откуда взялся этот график? Мы узнаем о графиках sin и cos позже в Графах греха x и cos x
Примечание 1: Поскольку мы предполагаем, что для значений x должны использоваться только действительные числа, числа, которые приводят к делению на ноль или к мнимым числам (которые возникают при нахождении квадратного корня из отрицательное число) не включаются.В главе «Комплексные числа» более подробно рассказывается о мнимых числах, но мы не включаем такие числа в эту главу.
Note 2: При выполнении примеров квадратного корня многие люди спрашивают: «Разве мы не получаем 2 ответа, один положительный и один отрицательный, когда мы находим квадратный корень?» Квадратный корень имеет не более одного значения, а не два. См. Это обсуждение: Квадратный корень 16 — сколько ответов?
Примечание 3: Мы говорим о домене и диапазоне функций , которые имеют не более , одно значение y для каждого значения x , а не отношений (которые могут иметь более одного .).
Поиск домена и диапазона без использования графика
Всегда намного легче определить домен и диапазон, считывая его с графика (но мы должны убедиться, что мы увеличиваем и уменьшаем масштаб графика, чтобы убедиться, что мы видим все, что нам нужно увидеть).
Однако у нас не всегда есть доступ к программному обеспечению для построения графиков, и для построения эскиза графика обычно в любом случае сначала требуется знать о разрывах и так далее.
Как упоминалось ранее, ключевые вещи, которые нужно проверить:
- Под знаком квадратного корня нет отрицательных значений
- В знаменателе (внизу) дроби нет нулевых значений
Пример 3
Найдите домен и диапазон функции `f (x) = sqrt (x + 2) / (x ^ 2-9),` без использования графика.2-9`, которое, как мы понимаем, можно записать как `(x + 3) (x-3)`. Таким образом, наши значения для `x` не могут включать` -3` (из первой скобки) или `3` (из второй).
В любом случае нам не нужно беспокоиться о «-3», потому что на первом этапе мы решили, что «x> = -2».
Таким образом, домен для этого случая — `x> = -2, x! = 3`, который мы можем записать как` [-2,3) uu (3, oo) `.
Для определения диапазона мы рассматриваем верхнюю и нижнюю части дроби отдельно.
Числитель: Если `x = -2`, верхняя часть имеет значение` sqrt (2 + 2) = sqrt (0) = 0`.2-9) `приближается к` 0`, поэтому `f (x)` переходит в `-oo`, когда приближается к` x = 3`.
Для `x> 3`, когда` x` просто больше, чем `3`, значение дна чуть больше` 0`, поэтому `f (x)` будет очень большим положительным числом.
Для очень большого `x` верхний край большой, но нижний будет намного больше, поэтому в целом значение функции будет очень маленьким.
Итак, мы можем заключить, что диапазон равен `(-oo, 0] uu (oo, 0)`.
Посмотрите на график (который мы все равно рисуем, чтобы убедиться, что мы на правильном пути):
Показать график
Мы можем видеть на следующем графике, что действительно домен равен «[-2,3) uu (3, oo)» (который включает «-2», но не «3»), а диапазон — «все значения из `f (x)`, кроме `F (x) = 0`.2-9) `.
Сводка
В общем, мы определяем домен по
ищем те значения независимой переменной (обычно x ), которые мы разрешили использовать . (Мы должны избегать 0 в нижней части дроби или отрицательных значений под знаком квадратного корня).
Диапазон находится путем нахождения результирующих значений y после замены возможных значений x .
Упражнение 1
Найдите домен и диапазон для каждого из следующих.2+ 2`.
Ответ
Домен: Функция
f ( x ) = x 2 + 2
определен
для всех реальных значений x (поскольку нет ограничений на значение x ).
Следовательно, область `f (x)` равна
«все действительные значения x «.
Диапазон: Поскольку x 2 никогда не бывает отрицательным,
x 2 + 2 никогда не меньше `2`
Следовательно, диапазон `f (x)` равен
«все действительные числа` f (x) ≥ 2` «.
Мы видим, что x может принимать любое значение на графике, но результирующие значения y = f ( x ) больше или равны 2.
123-1-2-312345678910-1xf (x)
Диапазон: `y> = 2`
Домен: Все `x`
Примечание
- Важно обозначить оси как при рисовании графиков. Это помогает понять, что представляет собой график.
- Мы видели, как рисовать такие графики в Графике функции.
(б) `f (t) = 1 / (t + 2)`
Ответ
Домен: Функция
`f (t) = 1 / (t + 2)`
не определено для т =
-2, так как это значение приведет к делению на ноль. (Внизу дроби будет 0.)
Следовательно, домен из f ( t ) равен
«все
вещественные числа кроме -2 «
Диапазон: Независимо от того, насколько большим или малым становится т ,
f ( t ) никогда не будет равно нулю.
[ Почему? Если мы попытаемся решить уравнение относительно 0, произойдет следующее:
`0 = 1 / (t + 2)`
Умножаем обе стороны на ( t + 2) и получаем
`0 = 1`
Это невозможно.]
Таким образом, диапазон из f ( t ) равен
«все
вещественные числа кроме нуля ».
Мы можем видеть на графике, что функция не определена для «t = -2» и что функция (значения y ) принимает все значения, кроме «0». 2 + 4` для
`x> 2`
Ответ
Функция `f (x)` имеет область из
«все действительные числа,` x> 2` «, как определено в вопросе.(Здесь не используются квадратные корни из отрицательных чисел или деления на ноль.)
Чтобы найти диапазон :
- Когда `x = 2`,` f (2) = 8`
- Когда x увеличивается с `2`,` f (x) `становится
больше, чем `8` (попробуйте подставить некоторые числа, чтобы понять, почему)
Следовательно, диапазон — «все действительные числа,` f (x)> 8` «
Вот график функции с открытым кружком в точке «(2, 8)», указывающим, что домен не включает «x = 2», а диапазон не включает «f (2) = 8».
123456510152025xf (x) (2, 8)
Домен: Все `x> 2`
Диапазон:
Все `f (x)> 8`
Функция является частью параболы. [Подробнее о параболе.]
Упражнение 2
Мы запускаем шар в воздух и находим
высота h , в метрах, как функция времени
т , в секундах, равно
ч = 20 т — 4,9 т 2
Найдите домен и диапазон для функции
ч ( т ).
Ответ
Как правило, отрицательные значения времени не имеют
имея в виду. Кроме того, нам нужно предположить, что снаряд попадает в землю, а затем останавливается — он не уходит под землю.
Итак, нам нужно рассчитать, когда он упадет на землю. Это будет, когда h = 0. Итак, решаем:
20 т — 4,9 т 2 = 0
Факторинг дает:
(20 — 4,9 т ) т = 0
Это верно, когда
`t = 0 \» s «`,
или
`t = 20/4.9 = 4.082 текст (ы) `
Следовательно, домен функции h равен
«все реально
значения t такие, что `0 ≤ t ≤ 4.082`»
Из выражения функции видно, что это парабола с вершиной вверх. (Это имеет смысл, если вы думаете о подбрасывании мяча вверх. Он поднимается на определенную высоту, а затем падает обратно.)
Какое максимальное значение ч ? Воспользуемся формулой максимума (или минимума) квадратичной функции.
Значение т , которое дает максимум
`t = -b / (2a) = -20 / (2 xx (-4.9)) = 2.041 с`
Таким образом, максимальное значение —
.
20 (2,041) — 4,9 (2,041) 2 = 20,408 м
Наблюдая за функцией h , мы видим, что когда t увеличивается, h сначала увеличивается до максимума.
20,408 м, затем ч снова уменьшается до нуля, как и ожидалось.
Следовательно, диапазон h равен
«все реально
числа, `0 ≤ h ≤ 20,408`»
Вот график функции h :
1234565101520-5-й (t)
Домен: `0
Диапазон:
`0
Функции, определяемые координатами
Иногда у нас нет непрерывных функций. Что нам делать в этом случае? Давайте посмотрим на пример.
Упражнение 3
Найдите область и диапазон функции, заданной координатами:
`{(−4, 1), (−2, 2.5), (2, −1), (3, 2)} `
Ответ
Область — это просто следующие значения x : `x = {−4, −2, 2, 3}`
Диапазон состоит из следующих значений `f (x)`: `f (x) = {−1, 1, 2, 2.5}`
Вот график нашей разрывной функции.
1234-1-2-3-41234-1-2-3-е (т) (3, 2) (2, -1) (- 4, 1)
(-2, 2,5)
2 — Типы
Раздел 2
Типы функций
Часто используемые функции в экономике:
Линейная функция: Каждый член содержит не более одной переменной, а показатель степени переменной равен \ (1 \).{n} $$
Здесь \ (a_ {1}, \ cdots, a_ {n} \) — коэффициенты.
(Быстрый вопрос: может ли \ (a_ {n} \) быть равным нулю, если функция является полиномиальной функцией степени n?)
Рациональная функция:
$$ f (x) = \ frac {g (x)} {h (x)} \ qquad \ qquad \ color {red} {(g (x) \ neq 0, \; \; h (x) \ neq 0)} $$
Другими часто используемыми функциями в экономике являются естественные экспоненциальные функции и натуральные логарифмические функции и т. Д. (Пожалуйста, см. Рекомендуемую книгу, чтобы узнать больше об экспоненциальных и логарифмических функциях.{x} \) — экспоненциальная функция.
\ (y = \ ln \; x \) — логарифмическая функция.
Дополнительные примеры см. В рекомендованной книге.
Построение графика функции
Когда мы, , рисуем график функции , мы обычно помещаем независимую переменную на горизонтальную ось, а зависимую переменную — на вертикальную. Если у нас есть две переменные в функции, одна — зависимая переменная, другая — независимая переменная, например, \ (y = f (x) \), мы можем нарисовать график, используя два измерения или ось в декартовой плоскости с помощью координаты \ ((x, y) \).Все точки на графике \ (y = f (x) \) удовлетворяют уравнению \ (y = f (x) \).
Хотя во время экзамена ваше имя и номер ученика важны для вашей идентификации, также важно указать каждую ось, используя соответствующую переменную для определения функции. На рисунке 2 мы представляем графики некоторых часто используемых функций.

 Что такое угловой коэффициент линейной функции? Сбор и использование персональной информации
Что такое угловой коэффициент линейной функции? Сбор и использование персональной информации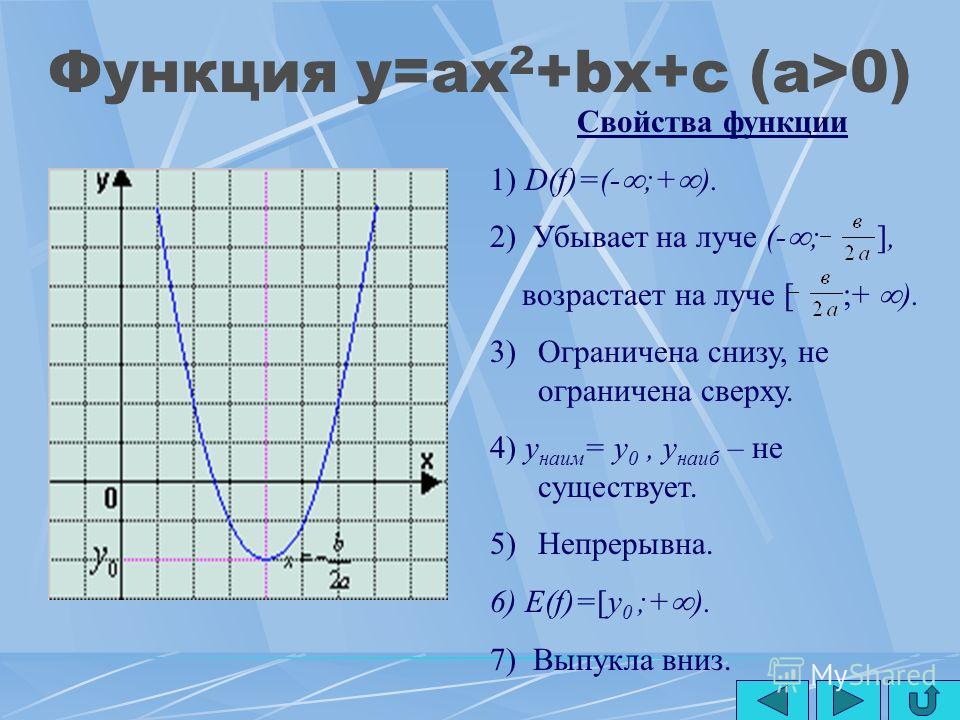
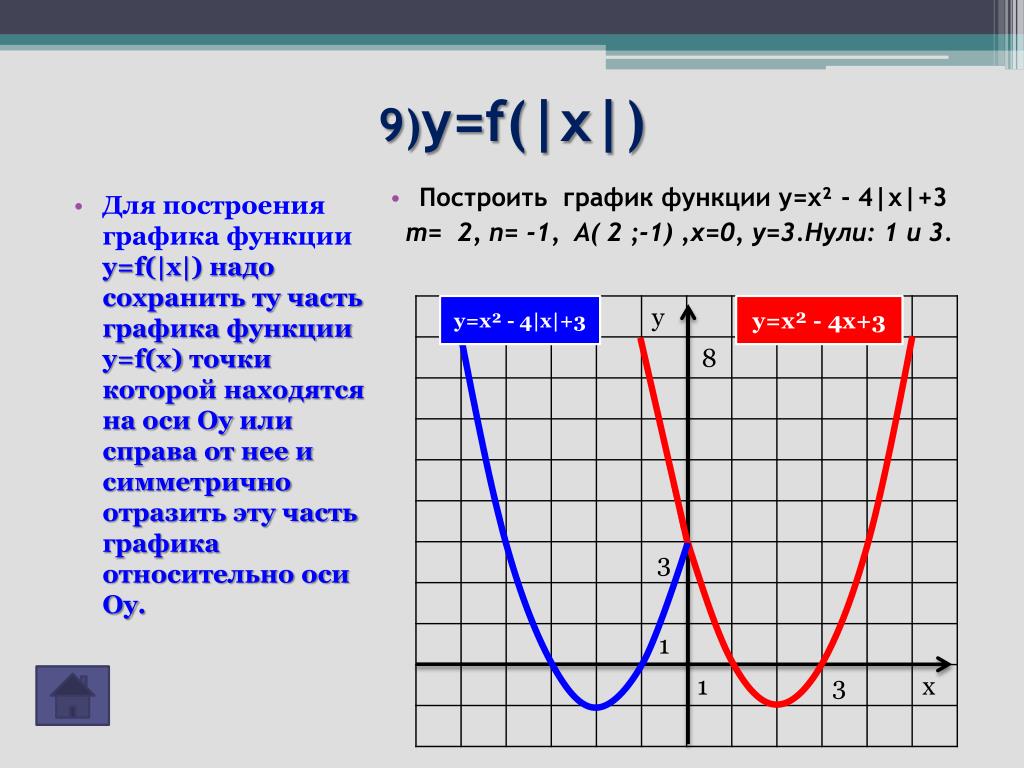

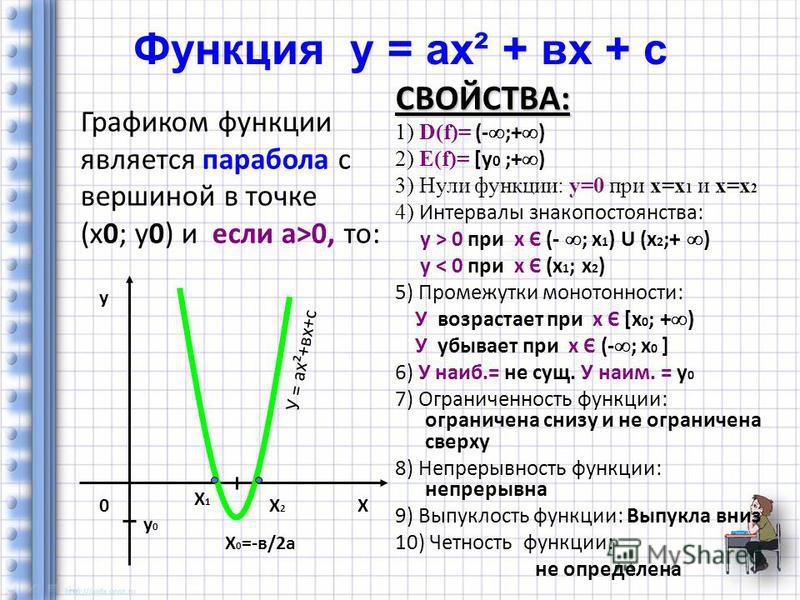 Точки экстремума (повторение). Критические точки функции Точки экстремумов.
Точки экстремума (повторение). Критические точки функции Точки экстремумов. Тема урока: Тест: найти производную функции. Уравнение касательной. Флюксия. 10 класс. Расшифруйте, как исаак ньютон назвал производную функцию.
Тема урока: Тест: найти производную функции. Уравнение касательной. Флюксия. 10 класс. Расшифруйте, как исаак ньютон назвал производную функцию.

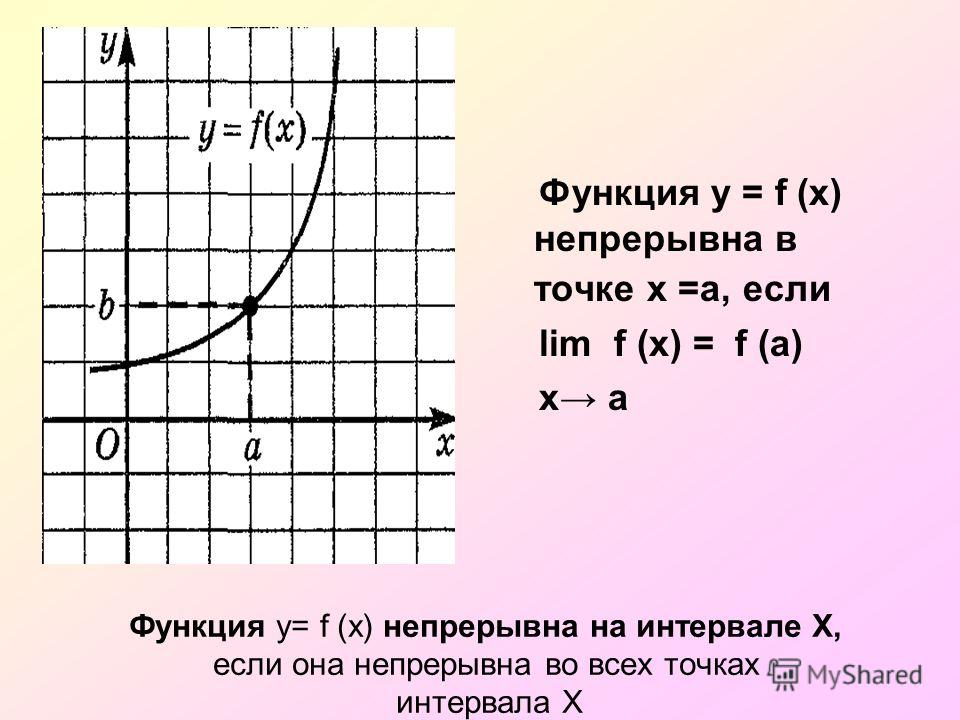

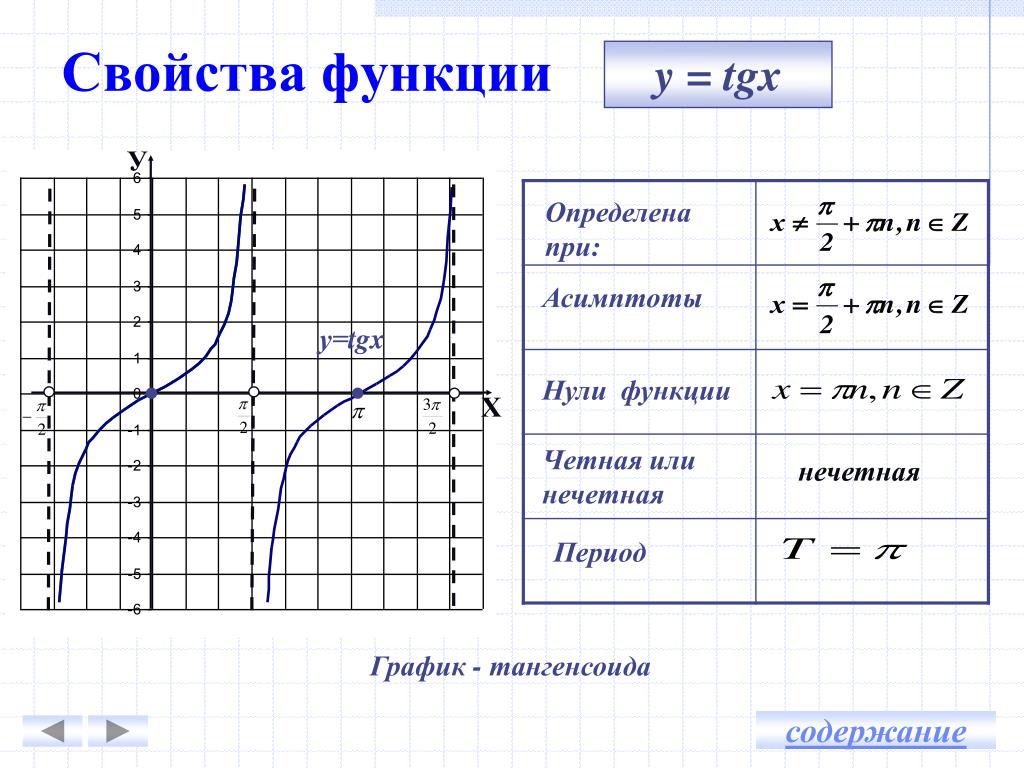

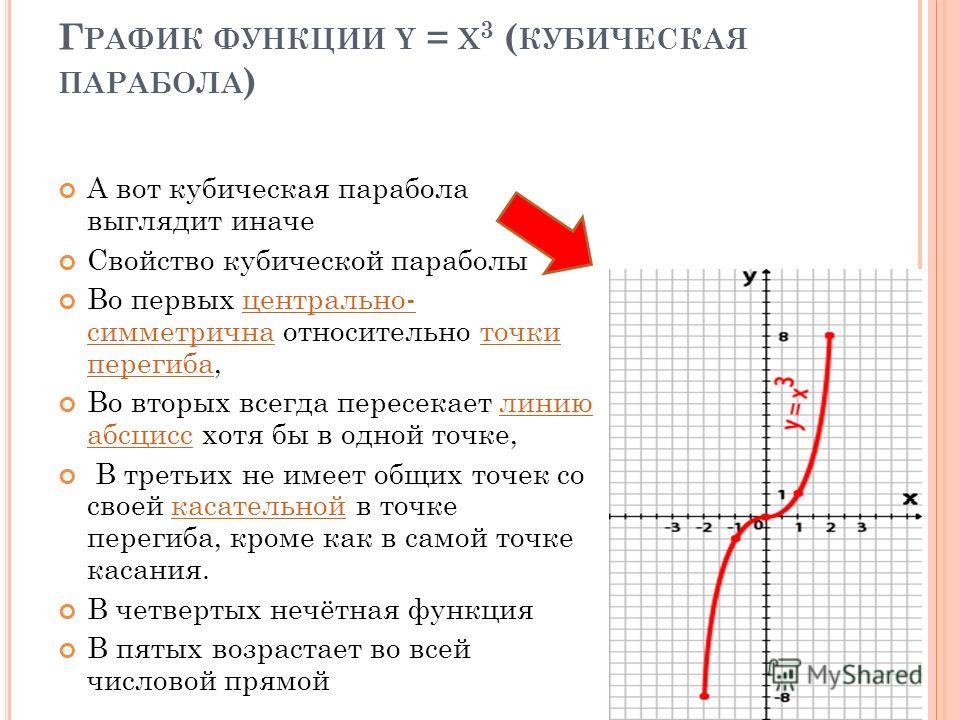
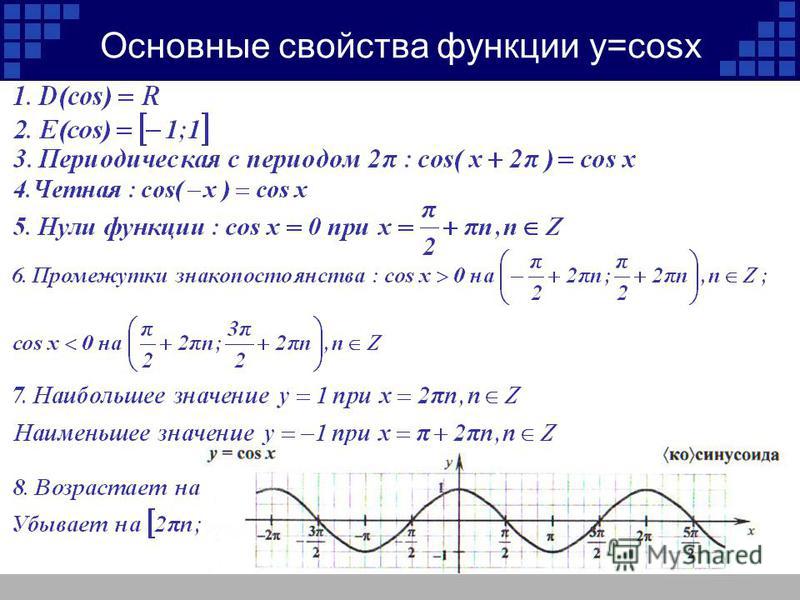 5, b
5, b
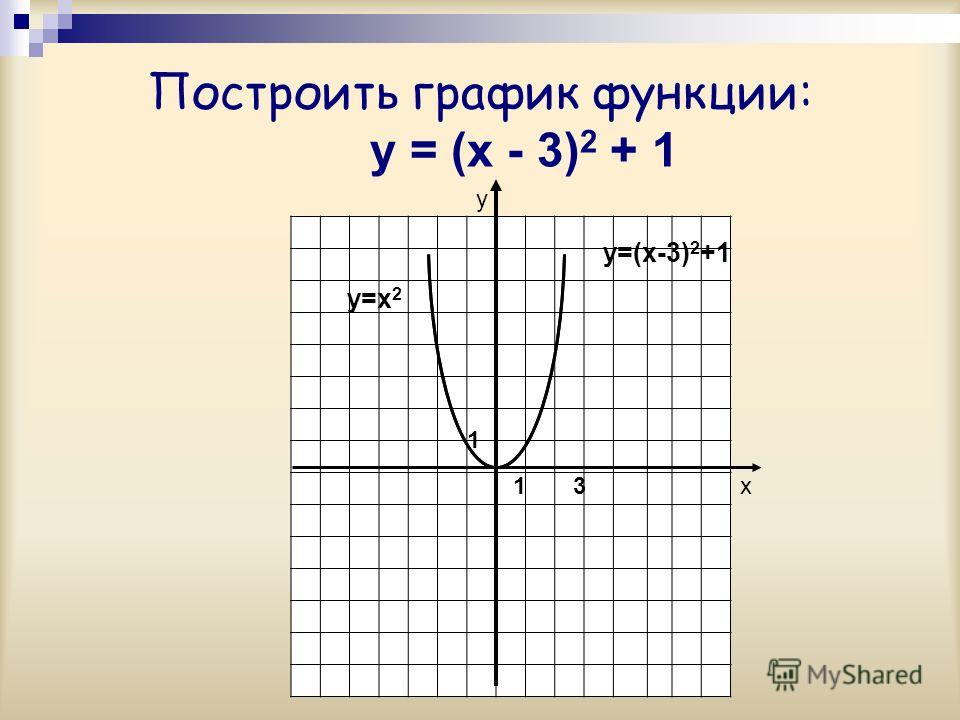 Здесь пример для y = 0,5 x
Здесь пример для y = 0,5 x Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». К y добавляется 3x. (Обратите внимание, что не имеет значения, что 3 и x умножаются. Все, что имеет значение, — это отношение к y, которое является сложением.) Поскольку 3x добавляется, мы добавим противоположное к обеим сторонам: -3x.
К y добавляется 3x. (Обратите внимание, что не имеет значения, что 3 и x умножаются. Все, что имеет значение, — это отношение к y, которое является сложением.) Поскольку 3x добавляется, мы добавим противоположное к обеим сторонам: -3x.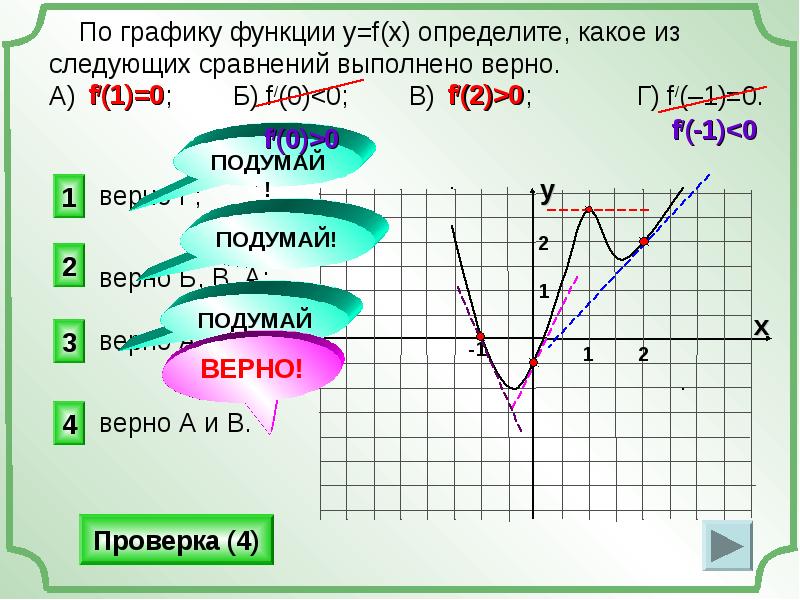 Как и раньше, мы
Как и раньше, мы 