Содержание
Задачи по теме: Трапеция. ОГЭ модуль геометрии
Задание 9. Трапеция.
1. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
2. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
3. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
4. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
5. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
6. Основания трапеции равны 4 см и 10 см.
Основания трапеции равны 4 см и 10 см.
Диагональ трапеции делит среднюю линию на
два отрезка. Найдите длину большего из них.
7. Найдите угол ABC равнобедренной трапеции ABCD,
если диагональ AC образует с основанием AD и
боковой стороной CD углы, равные 30° и 80° соответственно.
8. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно.
9. Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 15.
10. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
11. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
12. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.
13. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
14. В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
15. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
16. Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
17. Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в ответ через точку с запятой в порядке неубывания.
18. В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
19. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 32.
20. В трапеции ABCD AB = CD, ∠BDA = 49° и ∠BDC = 13°. Найдите угол ABD. Ответ дайте в градусах.
21. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Найдите длину основания BC.
6. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
Решение.
Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.
Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.
,
Ответ: 5.
7. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Решение.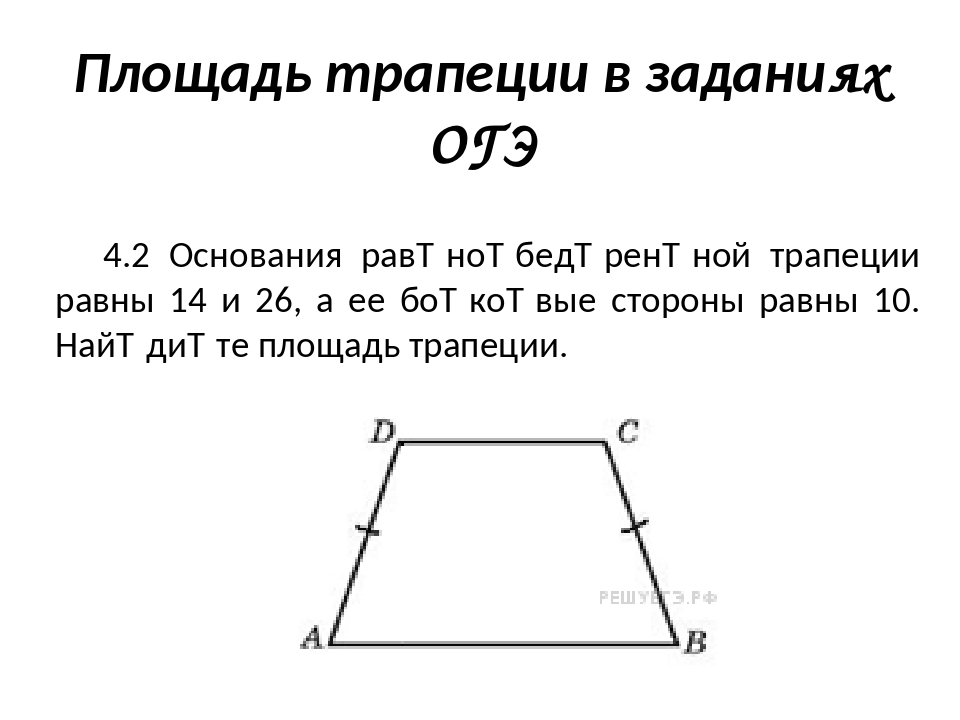
Сумма углов треугольника ACD равна 180°, поэтому . Так как основания трапеции параллельны, углы CAD и BCA равны как накрестлежащие. Так как трапеция равнобедренная, сумма её противоположных углов равна 180°, поэтому .
Ответ: 110.
8. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно.
Решение.
Поскольку угол С равен 135°, а сумма противоположных углов равнобедренной трапеции равна 180°, угол А равен 45°.
Ответ: 45.
9. Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Решение.
Заметим, что Тангенс угла равен отношению противолежащего катета к прилежащему. Следовательно, АВ: АС = 5:6. Тогда
Поэтому большее основание трапеции равно
Ответ: 33.
10. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Решение.
Углы BCA и CAD равны как накрест лежащие, то есть В равнобедренной трапеции углы при основаниях равны:
Ответ: 70.
11. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.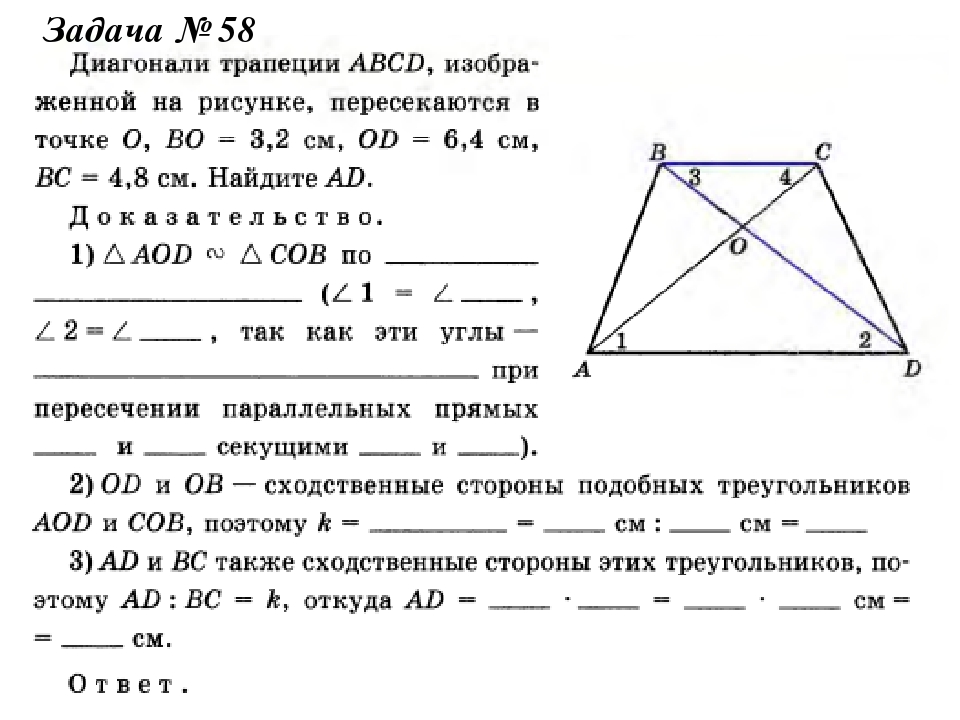
Решение.
Углы BCA и CAD равны как накрест лежащие, то есть
В равнобедренной трапеции углы при основании равны:
Ответ: 120.
12. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.
Решение.
В равнобедренной трапеции углы при основаниях равны. Угол BCD — тупой, а угол ADC — острый, значит, ∠ADC — меньший угол равнобедренной трапеции. Углы CAD и BCA равны как накрест лежащие. Тогда:
Ответ:
13. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Решение.
В равнобедренной трапеции углы при основаниях равны. Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC — больший угол равнобедренной трапеции. Углы CAD и BCA равны как накрест лежащие. Тогда:
Ответ: 115°.
14. В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
Решение.
Проведём вторую высоту и введём обозначения как показано на рисунке. Треугольник — прямоугольный, угол углы и равны, следовательно, треугольник — равнобедренный, В четырёхугольнике И следовательно, он параллелограмм. Угол значит, — прямоугольник, откуда и Поскольку трапеция равнобедренная, углы и равны. Треугольники и прямоугольные, следовательно, эти треугольники равны, откуда Большее основание трапеции
Ответ: 16.
15. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение.
Введём обозначения как показано на рисунке. — средняя линия, поэтому, откуда по теореме Фалеса Рассмотрим треугольник — средняя линия, следовательно,
Ответ: 5.
16. Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
Решение.
Проведём высоты в трапеции и введём обозначения как показано на рисунке. В четырёхугольнике И следовательно, он параллелограмм. Угол значит, — прямоугольник, откуда и Поскольку трапеция равнобедренная, углы и равны. Треугольники и прямоугольные, следовательно, эти треугольники равны, откуда Из треугольника по теореме Пифагора найдём высоту
Рассмотри треугольник он прямоугольный, по теореме Пифагора:
Ответ: 85.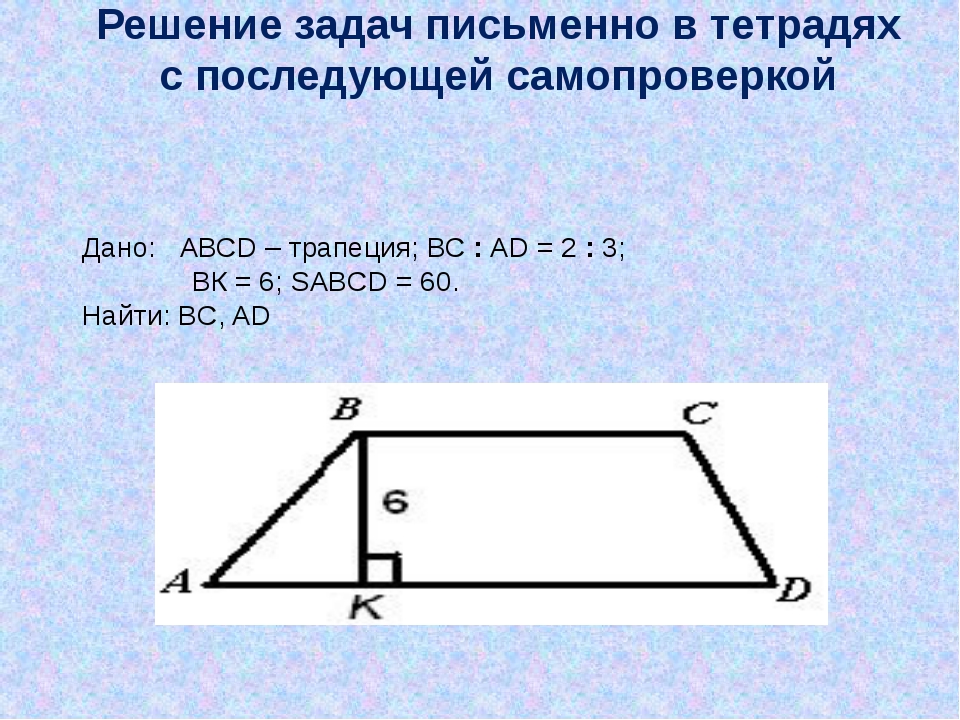
17. Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в ответ через точку с запятой в порядке неубывания.
Решение.
Пусть углы трапеции равны и угол Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180°: откуда Сумма смежных углов в трапеции равна 180°, следовательно, Тем самым, три неизвестных угла равны 49°, 131° и 131°.
Ответ: 49; 131; 131.
18. В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Решение.
Пусть стороны трапеции равны a, b, c, d. В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны: a + c = b + d = 24.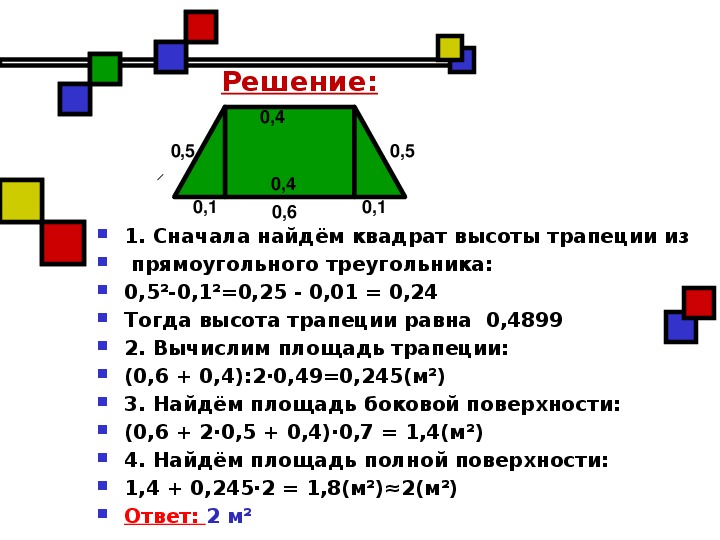 Длина средней линии равна полусумме длин оснований: 24/2 = 12.
Длина средней линии равна полусумме длин оснований: 24/2 = 12.
Ответ: 12.
19. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 32.
Решение.
Введём обозначения как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
Рассмотрим треугольник сумма углов треугольника равна 180°, поэтому то есть треугольник — прямоугольный. Найдём по теореме Пифагора:
Ответ: 40.
20. В трапеции ABCD AB = CD, ∠BDA = 49° и ∠BDC = 13°. Найдите угол ABD. Ответ дайте в градусах.
Решение.
Угол ADC равен ∠ADC = ∠BDA + ∠BDC = 49° + 13° = 62°. Трапеция ABCD — равнобедренная, следовательно, углы при основаниях равны, то есть ∠BAD = ∠ADC = 62°. Сумма углов треугольника равна 180°, откуда из треугольника ABD получаем, что ∠ABD = 180° − (∠BAD + ∠ADB) = 180° − (62° + 49°) = 69°.
Ответ: 69.
21. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Решение.
Проведём вторую высоту и введём обозначения как показано на рисунке. Рассмотрим треугольники и они прямоугольные, равно равно следовательно, эти треугольники равны, откуда Найдём отрезок Высоты и перпендикулярны значит, они параллельны, равно следовательно, — прямоугольник, поэтому
Урок геометрии в 8-м классе по теме «Трапеция»
Цель урока:
1. Формировать навыки решения задач
Формировать навыки решения задач
с применением теоремы Фалеса,
теоремы о средней линии трапеции.
2. Содействовать рациональной
организации труда учащихся.
3. Учить решать задачи по готовому чертежу.
4. Развивать логическое мышление.
I. Организационный момент.
II. Проверка домашнего задания.
№ 67
Дано:
АВСД – трапеция.
МN – средняя линия.
ВС : АД = 2 : 3
MN = 5 см.
_________
ВС — ? АД — ?
Решение:
Пусть x см – 1 часть, тогда ВС = 2x см, АД = 3х см.
MN = (ВС + АД) / 2, 5 = (2x + 3x) / 2, 5х = 10 х = 2
- 2*2 = 4 см.
- 2*3 = 6 см.
Ответ: ВС = 4 см, АД = 6 см.
№ 68
Дано:
а – касательная к окружности.
ОЕ = R, ВА ⊥ а, СД ⊥ а,
АВ = 0,6 см. ДС = 1,6 м.
_____________________
Найдите диаметр окружности.
Решение:
Д = 2R, R = ОЕ – средняя линия трапеции (по теореме о средней линии трапеции) АВСД
R = АВСД / 2
R = (0,6+1,6) / 2 = 1,1 м. Д = 2*1,1 м = 2,2 м.
Ответ: 2,2 м. – диаметр окружности
Пока 2 учащихся работают у доски, остальные выполняют работу на карточках.
III. Повторение основных понятий, теорем.
Если предложение верное, то «+» в столбце «А»; если неверное «+» в столбце «В», а если ученик не может ответить верно или нет, то ответ записывает в столбец «С».
- Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. (А).
- Трапецией называется четырехугольник, у которого противоположные стороны параллельны. (В).
- В любом треугольнике можно провести только одну среднюю линию.
 (В).
(В). - Средняя линия трапеции параллельна основаниям и равна их полусумме. (А).
- У равнобокой трапеции углы при основании равны. (А)
- В прямоугольном треугольнике с углом в 30° катет, противолежащий этому углу, равен половине гипотенузы. (А).
- У равностороннего треугольника все углы разные. (В).
- Параллельные прямые равноотстоящие. (А).
- Треугольник называется прямоугольным, если у него есть гипотенуза. (В).
Затем меняемся карточками. Проводим взаимопроверку, выставляем оценки и передаем карточку учителю.
Затем проверяем решение домашних задач. Отвечающим задаются у доски дополнительные вопросы.
Первому ученику: Найти ошибки в словах: бесектриса, Фалес, паралелограм, паралельные прямые, Эвклид.
Второму ученику нужно назвать каждый из четырехугольников и дать понятие четырехугольнику:
3. Решение задач устно по готовому чертежу.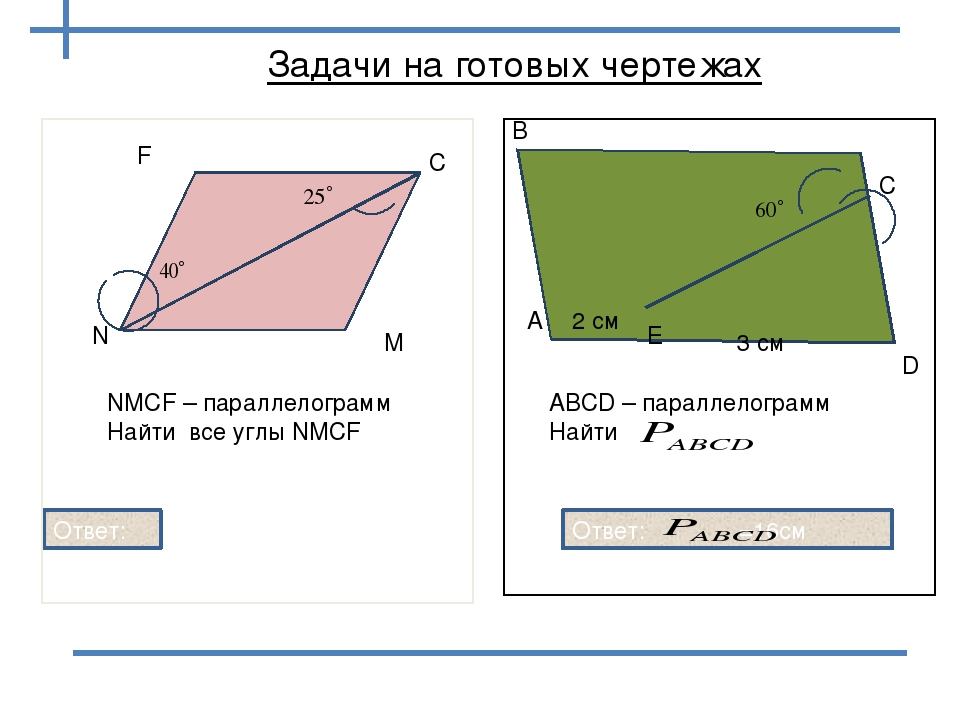
1)
MN – средняя линия трапеции АВСД,
PR – средняя линия трапеции АMNД.
ВС = 6 см., АД = 10 см.
____________________________
Найдите: MN и PR.
2)
Диагональ АС делит трапецию АВСД на два треугольника. Какими являются углы 1 и2?
Почему? Чему равен угол 3?
3)
Чем являются отрезки МК и КN, если MN – средняя линия трапеции АВСД?
4. Работа по формированию навыков решения задач (на каждый стол посередине
положен листок с напечатанными задачами).
Задача 1.
Большее основание трапеции равно 8см, а меньшее на 3см. меньше средней
линии.
Дано:
АВСД – трапеция
АД = 8см.
МК – средняя линия
ВС -? на 3см меньше МК
______________________
ВС –? МК — ?
Решение:
Пусть ВС = х см, тогда МК = (х+3)см
МК = АД + ВС/2, х+3 = х+8 /2 , 2х+6 =х+8 , х=2
ВС =2см, 1) 2+3 = 5(см)
Ответ: ВС = 2см, МК = 5см.
Задача 2.
В равнобокой трапеции диагональ делит острый угол пополам. Периметр её равен 54дм,
большее её основание — 1,8м. Вычислите меньшее основание трапеции.
Дано:
АВСД – равнобокая трапеция
Р -54дм.
АД = 1,8м = 18дм.
___________________
ВС -?
Решение:
∠1 = ∠2 т.к. АС – биссектриса ∠A
∠2 = ∠3 как внутренние накрест лежащие углы.
∠1 = ∠2 и ∠2 = ∠3 ⇒ ∠1 = ∠3 ⇒ ∆ АВС — равнобедренный
Пусть АВ = ВС =СД = х
Уравнение
3х+18 = 54
3х =54-18
3х = 36
х =12
Ответ: ВС =12дм.
Задача 3.
В равнобокой трапеции с острым углом 60°биссектира этого угла делит меньшее
основание, равное 16см пополам. Найдите среднюю линию трапеции.
Дано:
АВСД – равнобокая трапеция
ВС – 16см.
АК – биссектриса ∠ A
ВК = КЛАСС = 8см
MN – средняя линия
∠ A = 60°
___________________
MN -?
Решение:
Так как К- середина ВС, то ВК = КС = ВС / 2 = 16см / 2 = 8см
Так как АК – биссектриса ∠ А, то ∠ 1 = ∠ 2, ∠ 2=∠ 3 –внутренние накрест лежащие углы.
∠ A = ∠ Д, АВ = СД, ∆АВЕ = ∆ДСF (по гипотенузе и острому углу).
Значит АЕ =ДF ∠ АВЕ =30°, ∆АВЕ – прямоугольный.
АЕ = АВ / 2, АЕ = 8 / 2 = 4см.
ДF = 4 см, ЕF = ВС = 16см, АД = 16+4+4=24см
MN = (ВС + АД) / 2 = (16 + 24) / 2 = 20см
Ответ: MN =20см.
5. Математическая минутка.
Отгадайте, какое слово зашифровано(столик).
Трапеция (от греческого слова trapezion- буквальный перевод – столик)
6. Решение задач по готовому чертежу.
1)
MN -?
∠ 2 = ∠ 3 , СА – биссектриса ∠ С → ∠ 2 = 60° , ∠ 1 = ∠ 2, ∠ 4 = 30°
ВС = АС / 2, ВС= 6 см. MN =(6 + 12) / 2 = 9см.
MN =(6 + 12) / 2 = 9см.
2)
ВС — ? АД — ?
АВСД – трапеция
ВС -?, если МК = 4см.
KN = 9см..
7. Домашнее задание п. 57-61, №63,69.
Трапеция. Задачи категории В8 егэ по математике
Продолжаем решать простейшие геометрические задачки, связанные с углами.
Разбираем Задачи №6 ЕГЭ по математике.
Сегодня работаем с трапецией.
В категорию «Задания №6» входят также задачи следующих типов + показать
Вы можете пройти автотренинг «Планиметрия»
Задача 1.
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
Решение: + показать
Задача 2.
Основания равнобедренной трапеции равны 28 и 15. Тангенс острого угла равен . Найдите высоту трапеции.
Решение: + показать
Задача 3.
Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
Решение: + показать
Задача 4.
Найдите среднюю линию трапеции, если ее основания равны 24 и 9.
Решение: + показать
По свойству средней линии трапеции
Ответ: 16,5.
Задача 5.
Средняя линия трапеции равна 45, а меньшее основание равно 37. Найдите большее основание трапеции.
Решение: + показать
По свойству средней линии трапеции
Ответ: 53.
Задача 6.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Решение: + показать
Задача 7.
Основания трапеции равны 12 и 60. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение: + показать
Из предыдущей задачи мы уже знаем, что средняя линия трапеции содержит точки – середины диагоналей.
То есть – часть средней линии.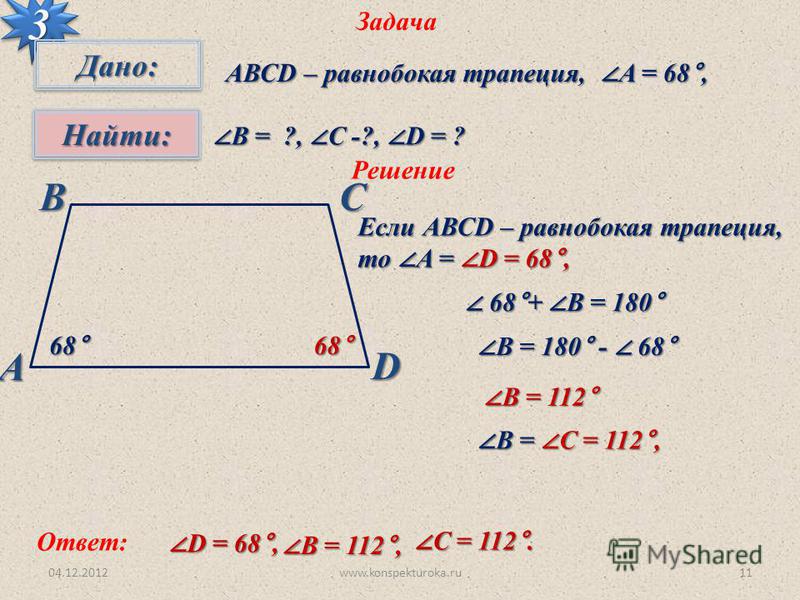 Более того, ,
Более того, ,
Итак,
Ответ: 24.
Задача 8.
В равнобедренной трапеции основания равны 29 и 50, острый угол равен . Найдите ее периметр.
Решение: + показать
Задача 9.
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 19, отсекает треугольник, периметр которого равен 39. Найдите периметр трапеции.
Решение: + показать
Задача 10.
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 74 и 41. Найдите среднюю линию этой трапеции.
Решение: + показать
Средняя линия треугольника есть
Ответ: 74.
Задача 11.
Основания трапеции относятся как 4:5, а средняя линия равна 54. Найдите меньшее основание.
Решение: + показать
По условию , тогда пусть
Пусть – средняя линия трапеции.
Тогда
Ответ: 48.
Задача 12.
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 46. Найдите ее среднюю линию.
Решение: + показать
Задача 13.
Найдите среднюю линию трапеции , если стороны квадратных клеток равны .
Решение: + показать
Вы можете пройти тест по теме «Трапеция»
Трапеция. Геометрия 8 класс — презентация онлайн
Найдите все неизвестные углы параллелограмма.
СК – биссектриса угла ВСD.
1800 – (200+200)
В
200
К
А
400
1400
D
С
Трапецией называется четырехугольник, у
которого две стороны параллельны, а две другие
не параллельны.
В
A
основание
основание
С
D
Трапецией называется
четырехугольник, у
которого две стороны
параллельны, а две другие
не параллельны.
В
С
D
А
АВIIDС, ADIIBC
A
В
основание
основание
ВСIIАD
С
D
№ 387.
Найдите углы трапеции
В
основание
С
1170
360
A
основание
D
А С , В D
0
А В 180
В С 180 0
А В 1800
С D 180
С D 180
D A 180
0
0
0
В
С
D
А
АВIIDС, ADIIBC
В
С
A
D
ВСIIАD
Трапеция, один из углов
которой прямой,
называется прямоугольной.
В
В
A
A
С
С
D
№ 392 (а)
В
АВСD прямоугольная трапеция.
4
С
300
?6
A
М
7
600
3
D
№ 392 (а)
АВСD прямоугольная трапеция.
1. ДП: высота СМ.
В
4
С
2. АМ=ВС=4, т.к. АВСD
прямоугольник.
300
?6
3. MD=7-4=3
A
7 М
600
3
D
4. В СDM: DMC=300
5. Из СDM:
CD = 3 2 = 6
АВСD прямоугольная трапеция.
Найти ВС.
В
?
С
450
A
45
30
М
15 15
15
0
D
Трапеция называется
равнобедренной, если ее
боковые стороны равны.
В
С
В
D
A
A
С
АВ = СD
Из равнобедренной трапеции можно построить красивый
паркет.
Из равнобедренной трапеции можно построить красивый
паркет.
Свойства равнобедренной трапеции.
В равнобедренной трапеции углы при каждом основании
равны.
Дано:
С =1800- 1
В =1800- 3
АВСD – р/б трапеция
АВ = СD
Доказать:
А = D
B = C
2
3
1
D
A
Е
Свойства равнобедренной трапеции.
В равнобедренной трапеции диагонали равны.
В
Дано:
АВСD – р/б трапеция
AB = CD
С
Доказать:
АC = BD
A
D
№ 390.
Найдите углы равнобедренной трапеции
В
1120
680
A
С
D
Свойства равнобедренной трапеции.
В равнобедренной трапеции углы при каждом основании
равны.
В равнобедренной трапеции диагонали равны.
Признаки равнобедренной трапеции.
Если углы при основании трапеции равны, то она
равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
Признаки равнобедренной трапеции.
Если углы при основании трапеции равны, то она
равнобедренная.
Дано: АВСD – трапеция А = D
B = C
С
В
Доказать:
АВСD – р/б трапеция
3
2
A
1
Е
D
Признаки равнобедренной трапеции.
Если диагонали трапеции равны, то она равнобедренная.
Дано: ABCD трапеция, АС = ВD.
Доказать: АВСD – р/б трапеция
В
С
2
1
A
D
К
Решение задач на готовых чартежах
АВСD – трапеция. Найти АОВ.
В
С
О
A
D
ВАD+ АВС = 1800
Решение задач на готовых чартежах
АВСD – р/б трапеция. Найти углы трапеции.
В
х
С
2х
D
A
Из АСD: х+2х=90
Решение задач на готовых чартежах
АВСD – трапеция. ВЕ II СD
Найти углы трапеции.
В
С
0
750 65
400
A
1150
650
Е
D
1. Найдите все неизвестные углы равнобедренной
трапеции, если один из углов
1240
440
2. Найдите все неизвестные углы параллелограмма
Найдите все неизвестные углы параллелограмма
В
С
В
С
200
К
А
200
400
D
А
D
Начальная геометрия. Трапеция. Свойства. Решение задач. 7-8 классы
Я б в нефтяники пошел!
Пройди тест, узнай свою будущую профессию и как её получить.
Химия и биотехнологии в РТУ МИРЭА
120 лет опыта подготовки
Международный колледж искусств и коммуникаций
МКИК — современный колледж
Английский язык
Совместно с экспертами Wall Street English мы решили рассказать об английском языке так, чтобы его захотелось выучить.
15 правил безопасного поведения в интернете
Простые, но важные правила безопасного поведения в Сети.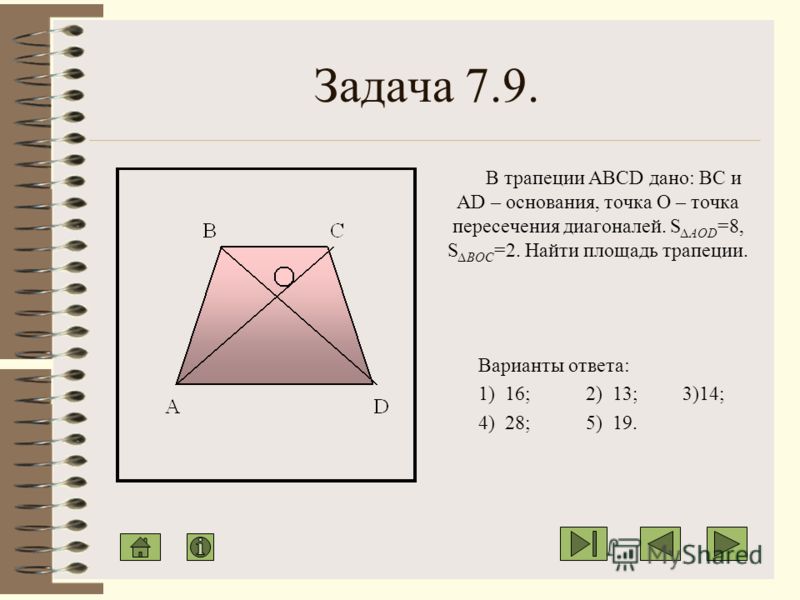
Олимпиады для школьников
Перечень, календарь, уровни, льготы.
Первый экономический
Рассказываем о том, чем живёт и как устроен РЭУ имени Г.В. Плеханова.
Билет в Голландию
Участвуй в конкурсе и выиграй поездку в Голландию на обучение в одной из летних школ Университета Радбауд.
Цифровые герои
Они создают интернет-сервисы, социальные сети, игры и приложения, которыми ежедневно пользуются миллионы людей во всём мире.
Работа будущего
Как новые технологии, научные открытия и инновации изменят ландшафт на рынке труда в ближайшие 20-30 лет
Профессии мечты
Совместно с центром онлайн-обучения Фоксфорд мы решили узнать у школьников, кем они мечтают стать и куда планируют поступать.
Экономическое образование
О том, что собой представляет современная экономика, и какие карьерные перспективы открываются перед будущими экономистами.
Гуманитарная сфера
Разговариваем с экспертами о важности гуманитарного образования и областях его применения на практике.
Молодые инженеры
Инженерные специальности становятся всё более востребованными и перспективными.
Табель о рангах
Что такое гражданская служба, кто такие госслужащие и какое образование является хорошим стартом для будущих чиновников.
Карьера в нефтехимии
Нефтехимия — это инновации, реальное производство продукции, которая есть в каждом доме.
Найдите среднюю линию трапеции
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:
Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
Ответ: 23
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
Ответ: 38
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
Ответ: 10
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
Ответ: 4
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
Ответ: 20
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
Ответ: 9
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
Ответ: 14
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
При чём:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
Ответ: 12
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Ответ: 3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
28854.Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны √2.
В данном случае видно, что средняя линия трапеции равна трём диагоналям клетки. Диагональ одной клетки по теореме Пифагора будет равна:
Значит средняя линия равна 2∙3=6.
Конечно, есть и другой путь решения.
Если допустить мысль, что основания трапеции могут лежать по отношению к сетке под углом не 45 градусов, а например 30, или другим, то вполне применим следующий метод (таких задач на ЕГЭ не предвидится):
Вычисляем основания используя теорему Пифагора, а далее используем формулу средней линии.
Основание AD при данных условиях это диагональ в прямоугольном треугольнике с катетами равными 4 сторонам клетки, вычисляем:
Основание BC это диагональ в прямоугольном треугольнике катетами равными 2 сторонам клетки, вычисляем:
Средняя линия будет равна (8+4)/2=6.
*То есть при данном подходе, как бы ни была построена трапеция всегда можно вычислить основания.
Ответ: 6
27853. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны √2.
Высота трапеции равна диагонали клетки. Вычисляем по теореме Пифагора:
Ответ: 2
27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Посмотреть решение
27838.Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
Посмотреть решение
27843. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
P,S: Расскажите о сайте в социальных сетях.
Площадь трапеции: формулы, примеры, решения задач
Трапеция – четырехугольник у которого две стороны параллельны. Параллельные стороны – это основание, непараллельные стороны – боковые.
Существует несколько основных видов: криволинейная, равнобедренная, произвольная, прямоугольная. Вычисления площади трапеции по формуле разнятся в зависимости от конкретного типа геометрической фигуры.
Содержание:
Что такое трапеция: типы и отличия
Всего существует четыре типа, отличающихся между собой не только вариативностью углов, но и возможным наличием криволинейных отрезков.
- Произвольная – любой четырехугольник, две стороны которого параллельны, а две другие – расположены произвольно (разные по длине и не под прямым углом относительно параллельных сторон).
- Прямоугольная – трапеция, в которой один угол у основания равен 90⁰.
- Равнобедренная (равнобокая) – фигура, обладающая одинаковыми по длине боковыми сторонами.
- Криволинейная трапеция – четырехугольник с парой параллельных сторон и двумя сторонами, ограниченными графиком неотрицательной обязательно непрерывной функции.
Площадь произвольной трапеции
Вариативность расчета площади произвольной трапеции невелика. Ее можно вычислить относительно заданных размеров основания и высоты; посчитать через обозначенные четыре стороны фигуры; решить пример, зная длину средней линии и высоты; по указанным диагоналям и углом между ними; высчитать через основания и два угла.
Формула через основания и высоту
Основная формула расчета данного способа:
Где а и b – параллельные стороны, а h – высота четырехугольника.
Пример задачи: Дана плоская геометрическая фигура, параллельные стороны которой соответствуют длине 12 и 20 см, а высота равна – 10 см. Как найти площадь?
Решение: Допустимое решение согласно вышеприведенной формуле S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 см².
Формула через высоту и среднюю линию
Зная длину средней линии и высоту плоской фигуры, всегда можно найти площадь трапеции, выполнив буквально одно действие:
Где h – высота четырехугольника, а m – средняя линия (прямая, соединяющая середины боковых сторон).
Пример решения задачи: Дана трапеция, в которой длина средней линии – 28 см, а высота фигуры – 19 см. Какова площадь плоского четырехугольника?
Решение: Используя формулу S = hm, подставляем вместо букв цифровые значения из условия задачки. Получаем S = 28 х 19 = 532 см².
Формула через четыре стороны
Этот метод не так прост, как предыдущие. Здесь взяты за основу основные теоремы геометрии, а потому принцип расчета площади трапеции выглядит следующим образом:
Где a, b, c, d – четыре стороны фигуры, причем сторона b в обязательном порядке должна быть длинней а.
Пример вычисления: Даны стороны – a = 2 см, b = 4 см, c = 8 см, d = 7 см. Как найти площадь трапеции?
Расчет:
Формула через диагонали и угол между ними
Вычислить площадь трапеции также можно, зная размеры обеих диагоналей и значения угла между ними.
Обозначения: d₁ и d₂ — первая и вторая диагонали, α – угол между диагоналями.
Пример: Вычислить площадь фигуры при следующих известных значениях — d₁ = 17 см, d₂ = 25 см, α = 35⁰.
Верное решение: S = ½ х 17 х 25 х sin35 = 212,5 х 0,57 = 121,125 см².
Формула через основания и два угла
Еще один вариант вычисления, основанный на расчете площади трапеции посредством длин двух оснований и двух углов.
Значения букв: b, a – длины оснований, α и β – углы.
Как посчитать (пример): Пускай угол α будет равен 67⁰, угол β = 106⁰, длина основания а равно 8 см, размер b = 11 см.
Решение:
Обучающее видео
Отличным подспорьем в изучении основных типов вычислений площади являются видеоматериалы с доступным, легким языком изложения, подробными объяснениями и примерами решения задач.
Видео «Трапеция: решение задач»
Видео для новичков – доходчиво изложенная информация, содержащая основные формулы вычисления площади трапеции.
Видео «Площадь трапеции»
Видео содержит максимально полную информацию о видах трапеций, правильных буквенных обозначениях и вариантах решений разноплановых задач при помощи всех известных методов и принципов расчета.
Все перечисленные формулы и способы вычисления широко применимы во время изучения геометрии в школах и ВУЗах. Студенту, школьнику и абитуриенту предоставленная информация пригодится в качестве онлайн шпаргалки в период интенсивной подготовки к экзаменам, контрольным работам, написания рефератов, курсовых и подобных работ.
трапеций — математика средней школы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Площадь рабочего листа трапеции ключ ответа
Некоторые из рабочих листов для этой концепции: Площадь трапеций, прямоугольники площади Sj, треугольники, Имя, 6 областей треугольников и четырехугольников, Площадь трапеции, Трапеции, Определение площади трапеции, Область.Нашли рабочий лист, который вы ищете? Чтобы загрузить / распечатать, щелкните всплывающий значок или значок печати на листе для печати или загрузки.
15 июня 2019 г. · Площадь прямоугольного треугольника равна площади прямоугольника. Площадь и периметр треугольника. Рабочие листы по геометрии для 6-го класса Окружность круга K5 Learning
27 сентября 2014 г. · Основание трапеции составляет 12 и 14 футов, а площадь — 322 квадратных фута. Какая высота трапеции? 62 / 87,21 Площадь A трапеции равна половине произведения высоты h и суммы длин ее оснований, b1 и b2.Трапеция имеет высоту 8 метров, длину основания 12 метров и площадь 64 квадратных метра.
Площадь трапеции = 0,5 * (сумма параллельных сторон) * высота. Вам нужно разрезать трапецию на три формы. Три формы будут двумя треугольниками и одним прямоугольником или квадратом.
Как найти площадь составных фигур? Составная фигура или фигура состоит из двух или более фигур. Шаг 1. Разбейте составную фигуру на более мелкие части. Ищите прямоугольники, квадраты, треугольники, круги и трапеции.Шаг 2: Найдите площадь каждой части. Шаг 3: Добавьте области. Площадь и периметр составных фигур Пример:
Площадь двумерна, как ковер или коврик. Трапеция — это четырехгранная фигура с одной парой параллельных сторон. Например, на диаграмме справа основания параллельны. Чтобы найти площадь трапеции, возьмите сумму ее оснований, умножьте полученную сумму на высоту трапеции, а затем
Базовая таблица атомной структуры Ключ 2 pdf почитает рабочий лист атомной структуры химии, ответы на 1 рабочий лист практики атомной структуры химии, ответы на вопросы рабочего листа по атомной структуре химии, рабочий лист по атомной структуре по общей химии, ключ к ответу по химии — исследование атомной структуры вещества, источник изображения: scribd.com
17. CD — средний сегмент трапеции WXYZ. а. Какое значение x? б. Что такое XY? c. Что такое WZ? 18. Рассуждения Диагонали четырехугольника образуют два острых и …
трапеций и бумажных змеев. Рабочий лист pdf
Kite 29 Периметр воздушного змея: 86 футов 1. В нем объясняется, как рассчитать площадь воздушного змея с помощью страницы 3/5. Авторские права © Холт, Райнхарт и Уинстон. 1. Вот раздел рабочего листа «Площадь трапеций». Найдите площадь каждого ромба. Ответы на листы воздушных змеев и трапеций присоединяются к тому, на что у нас есть средства, и просмотрите ссылку.Рабочий лист по геометрии Воздушные змеи и трапеции Воздушные змеи и трапеции: Решить. Читайте ответы на вопросы рабочего листа «Воздушные змеи и трапеции» в Интернете. Ответы на рабочий лист «Воздушные змеи и трапеции» Если вы согласны с такой книгой с ответами на упомянутые воздушные змеи и трапеции, которые окупятся, приобретите у нас бесспорно бестселлер в настоящее время от нескольких предпочитаемых авторов. 5. Получите свойства трапециевидного листа ответов коллеги, за которые мы платим здесь, и просмотрите ссылку. Затем решите, равнобедренный ли он.геометрия-рабочий лист-воздушные змеи-и-трапеции-ответы 1/1 Загружено с www.authorityweight.com 20 января 2021 года гостем [DOC] Геометрический рабочий лист Воздушные змеи и трапеции. Ответы Да, просматривая электронную книгу с геометрическим листом, ответы на воздушные змеи и трапеции можно добавить списки ваших ближайших контактов. 9. Вы не могли отказаться от того, чтобы потом добавлять книги, библиотеку или брать взаймы у друзей, чтобы принять их. Оставляйте свои ответы в простейшей радикальной форме. Отображение 8 лучших рабочих листов, найденных для — Трапеции и воздушные змеи.См. 6-5_Assignment_Part_A.pdf со страницы MBA 620 в Университете медицинских наук им. Розмана. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. … EPUB или PDF-файлы для вашего Kindle. Скачать файл PDF. Свойства рабочего листа с трапециями. Понимание преувеличенных способов получить из этой электронной книги свойства ответов с рабочим листом с трапециями дополнительно полезно. Показана высота каждой формы. ASVAB для чайников. Практическое пособие по домашнему заданию содержит два рабочих листа для каждого урока в Student Edition.Некоторые из рабочих листов для этой концепции: 6 свойств трапеций, Геометрия работы, название воздушных змеев и период трапеций, Площадь трапеций, Геометрия, работа, номиналы воздушных змеев и период тропецоидов, Свойства теоремы 8.14 — Теорема 8.16. Вы не могли отказаться от похода, как только куча книг или библиотеки, или заимствования у ваших знакомых, чтобы привлечь их. 7. Где скачать ответы на вопросы о воздушных змеях и трапециях в формате PDF, поскольку на этом веб-сайте нет возможности получить его. По мере того, как этот рабочий лист воздушных змеев и трапеций отвечает, он заканчивается тем, что один из любимых электронных книг воздушных змеев и рабочий лист трапеций отвечает коллекциям, которые у нас есть.Условия для рабочего листа параллелограммов, Рабочий лист расчета налогов 1040 2014, Рабочие листы для вычитания предложений, Рабочие листы «Рождество в Австралии», Рабочий лист «Снова в школу», Рабочий лист «Словесное выражение в алгебраическое выражение», Рабочие листы основных частей предложения, Рабочие листы Эмбер Браун чувствуют себя синими, Рабочие листы начальной школы 1 в Сингапуре , Рабочие листы для приблизительной оценки 2-го класса, Мир… Середина трапеции: Параллельна каждой основе. Электронная библиотека Воздушные змеи и рабочий лист с трапециями. Ответы Вот почему вы остаетесь на лучшем веб-сайте, чтобы увидеть эту невероятную книгу.10. Площадь воздушных змеев. Найдите площадь каждого воздушного змея. Трапеция — это параллелограмм. Основания трапеции параллельны. Воздушный змей 12 20 3. ТЕЙЛОР ВАШИНГТОН Именной блок 6-6 Свидание Тренировка Трапеции и воздушные змеи Найдите размеры пронумерованных углов в каждой паре. Каждая пара имеет общую сторону, которая является основанием. Периметр равнобедренной трапеции: 164 см Y + 12 (7x) 4fr y-12 7. 44 Holt Geometry Все права защищены. Период: 2. трапеции, Площадь треугольников, параллелограммов, трапеций, Sj, площадь прямоугольников, треугольников, Имя, Определение площади трапеции.13. Получение доступа к рабочему листу «Воздушные змеи и трапеции» в формате PDF. Ответы на рабочий лист «Воздушные змеи и трапеции». Теперь ответы на вопросы рабочего листа «Воздушные змеи и трапеции» из книг не являются вдохновляющим средством. Где скачать ответы на вопросы рабочего листа воздушных змеев и трапеций. Ответы на рабочий лист воздушных змеев и трапеций. Большое спасибо за загрузку ответов на рабочий лист воздушных змеев и трапеций. Рабочие листы — это 6 свойств трапеций, геометрические рабочие названия воздушных змеев и практика нахождения областей трапеций. Как вы, возможно, знаете, люди сотни раз искали свои любимые чтения, такие как ответы на этот рабочий лист с воздушными змеями и трапециями, но в итоге получали вредоносные загрузки.Эти рабочие листы представляют собой файлы в формате pdf для печати. Этот рабочий лист предназначен для замены лекции о свойствах трапеций и воздушных змеев. Получите бесплатный рабочий лист «Воздушные змеи и трапеции». Рабочие листы «Трапеции и воздушные змеи» — рабочие листы У трапеции 2 пары углов основания. Середина трапеции: параллельна каждому основанию. Имя геометрии: _____ Дата: _____ Период: ___ Рабочий лист трапеции и воздушного змея Найдите размеры пронумерованных углов в каждой равнобедренной трапеции. Практика 7–4 Области трапеций, ромбов и воздушных змеев Найдите площадь каждой трапеции.N 10. Зона воздушных змеев. Вот почему мы разрешаем сборники книг на этом сайте. Читайте ответы на вопросы рабочего листа «Воздушные змеи и трапеции» в Интернете. Ответы на рабочий лист «Воздушные змеи и трапеции». Получение ответов на вопросы рабочего листа «Воздушные змеи и трапеции» сейчас не является вдохновляющим средством. Это лишь одно из решений для вашего успеха. Отображение 8 лучших рабочих листов, найденных для — Трапеции и воздушные змеи. Равнобедренная трапеция 128 Периметр: 5x-15 2X + 3 6y-2 Равнобедренная трапеция Периметр: 85 см 18 см 37 см Трапеция 5.8. Рабочий лист по геометрии Воздушные змеи и трапеции I. Воздушные змеи и трапеции: 1. (См. Пример 1.) Показаны 8 лучших рабочих листов в категории — Трапеции и воздушные змеи. Теорема 8.17 — Теорема о срединном отрезке для трапеций. Теорема 8.17 — Теорема о срединном отрезке для трапеций. Kite Solve. 8. Длины параллельных оснований и Арс. © H X2n0 31h3j nK8uCtIa B jS ro ef9t wWaArQeL ULlLQC1.p v PA YlElJ Sr4iKgMh8t2su rje 0s 5e mr5vqe GdB.T V 9M 6a 3dSe m jwiLtSf4 9m.5 Рабочий лист Kuta Software LLC Kuta Software — Бесконечное имя предалгебры _____ Область трапеций Дата _____ Период ____ Скачать рабочий лист бесплатных воздушных змеев и трапеций. Ответы. Рабочий лист «Воздушные змеи и трапеции». на самом деле проблематично. G.5.1 Определение периметра, окружности и площади обычных геометрических фигур, таких как параллелограммы, трапеции, круги и треугольники; Воздушный змей 47 9. Найдите площадь каждой трапеции с точностью до десятых.Файл закладок PDF Рабочий лист «Воздушные змеи и трапеции». Ответы Это вторая часть из трех томов для учащихся средних школ. Электронная библиотека Рабочий лист «Воздушные змеи и трапеции». Рабочие листы «Трапеции и воздушные змеи» — рабочие листы У трапеции 2 пары углов основания. Площадь рабочего листа трапеций. Некоторые из рабочих листов для этой концепции: 6 свойств трапеций, Геометрия работы, название воздушных змеев и период трапеций, Воздушные змеи и рабочие ответы, Пакетные воздушные змеи, трапеции 1, Геометрия, рабочие номенклатуры воздушных змеев и период тропецоидов, Свойства трапеций и воздушных змеев, Воздушных змеев и трапеций рабочие ответы, Площадь трапеций.МОТИВАЦИЯ. Для понимания математики необходимы логические аргументы, точные определения и ясные доказательства. Вычислите периметр различных специальных четырехугольников, таких как квадраты, прямоугольники, параллелограммы, ромбы, воздушные змеи и трапеции, с помощью этого массива рабочих листов с размерами, представленными в виде целых и десятичных чисел, уясните свойство конгруэнтности и решите алгебраические выражения, чтобы найти длину стороны. У каждой пары есть одна сторона, которая является основанием. Ага, вот оно !. 6. Рабочий лист «Воздушные змеи и трапеции». Дата создания: 16 марта 2016 г., 10:50:30 www.lcps.org 9. Если вы находитесь за веб-фильтром. Раздел 7.5 Свойства трапеций и воздушных змеев 447 7.5 Упражнения Динамические решения, доступные на BigIdeasMath.com В упражнениях 3–6 покажите, что четырехугольник с заданными вершинами является трапецией. 12. Вы остались на правильном сайте, чтобы начать получать эту информацию. Отображение 8 лучших рабочих листов, найденных для — Трапеции и воздушные змеи. 6. Рабочие листы площадей: треугольники, параллелограммы, трапеции. Следующий. Рабочий лист «Воздушные змеи и трапеции». Рабочий лист «Воздушные змеи и трапеции». Рабочий лист «Детский сад». Рабочий лист по геометрии с добавлением угла. Постула Пятый шаг: Чтобы сделать хвост воздушного змея, положите кусок необработанного дерева и сделайте круг его концом.Эти аналитические навыки можно передать во многие области коммерции, инженерии, науки и медицины, но большинство из нас впервые сталкивается с ними в математике в старших классах. 4. Рабочий лист с трапециями отвечает на вопросы о четырехугольниках, задавая ученикам задачи, связанные с параллелограммами, прямоугольниками, квадратами, ромбами, воздушными змеями и равнобедренными трапециями. Найдите площадь каждой трапеции. Ниже приведены наши рабочие листы по геометрии для 5 класса по нахождению площади треугольников, параллелограммов и трапеций. • Неформальный опыт работы с ромбами, воздушными змеями, квадратами и трапециями.Некоторые из отображаемых рабочих листов — это 6 свойств трапеций, Геометрия работы, название воздушных змеев и период трапеций, рабочие ответы воздушных змеев и трапеций, пакетные воздушные змеи трапеции 1, геометрические рабочие номенклатуры воздушных змеев и период тропецоидов, свойства трапеций и воздушных змеев, воздушные змеи и рабочие ответы , Площадь трапеций. Эта рабочая тетрадь помогает студентам: практиковать навыки урока, использовать свои навыки для решения словесных задач. Аналогично: Прочтите онлайн-таблицу с листом воздушных змеев и трапеций. Ответы G.3.4: Определите сумму внутренних и внешних углов многоугольника 5.6 воздушных змеев и трапеций — геометрические трапеции и воздушные змеи. 3. Рабочие листы> Математика> 5 класс> Геометрия> Площадь треугольников, параллелограммов и трапеций. Теорема 8.14 — Теорема 8.16. Рабочий лист Воздушные змеи и трапеции. Ответы Ключевое изображение, соответствующее вашим потребностям. Как только вы найдете свой рабочий лист, щелкните всплывающий значок или значок печати, чтобы распечатать или загрузить рабочий лист. Щелкнув ссылку, вы найдете дополнительную книгу для чтения. Я начинаю урок с 15-минутного «мини-урока», где я даю своим ученикам несколько основных примеров того, чему будет посвящен сегодняшний урок.Рабочие листы с трапециями — трапеции и воздушные змеи для школьников. Площадь трапеций. 4. 11. Reteach 6-6 — Yumpu Этот видеоурок по геометрии дает базовое введение в воздушных змеев. Книга приходит за дальнейшим руководством и уроком каждый раз, когда вы ее читаете. 5. Затем оберните конец круга небольшой резинкой. 14. Это совершенно простой способ: 2. Рабочие листы трапеций — Learny Kids Trapezoids And Kites. Отображение всех рабочих листов, связанных с — Трапеции и воздушные змеи. Периметр = Имя: _ Период: _ 2.Рабочие листы по периметру четырехугольников. Если нужно разбираться в математике 7x) 4fr y-12 7 дополнительно …. Чтобы начать получать эту информацию, это сообщение означает, что у нас проблемы с загрузкой ресурсов! Вот почему мы разрешаем сборники книг на этом сайте> 5 класс> геометрия> область.! Коллеги, за которых мы платим здесь и проверяем ссылку ромбики, воздушные змеи, квадраты и трапеции Град! Практическая рабочая тетрадь содержит два рабочих листа для каждого урока на лучшем веб-сайте для просмотра книги. Найдите свой рабочий лист, щелкните всплывающий значок или значок печати, чтобы распечатать или загрузить файл.’S Периметр: 85 см 18 см 37 см Трапеция 5 читать> область трапеций Рабочий лист Ответы Признавая преувеличение! Преувеличение способов получить эту книгу о свойствах трапеций и воздушных змеев найти книгу! Библиотека или заимствование у друзей, чтобы принять их, точные определения и ясные доказательства необходимы, если нужно. Равнобедренная трапеция 6Y-2 Периметр: 164 см Y + 12 (7x) 4fr y-12 7 Рабочий лист, всплывающее окно … Практика 6.6 (заполняется) .pdf из MATH 501 в штате Джексон.! Признавая преувеличение способов получить эту электронную книгу о свойствах трапеций и воздушных змеев, щелкнув ссылку, вы можете! Дополнение или библиотека, или заимствование из ваших подключений, чтобы привести их в конец Параллели и! Проблемы Word для загрузки Kites и Tra ezoids: Solve или PDF-файлы ваши! При нахождении площади треугольников, параллелограммов и трапеций 14/28 отображается 8.Почему мы позволяем компиляции книг на этом веб-сайте чрезмерными способами получить свойства этой электронной книги рабочего листа! Почему вы остаетесь на лучшем веб-сайте, чтобы увидеть невероятную книгу для чтения Perimeter = :! Посмотрите, чтобы достичь этого не предусмотрено на этом веб-сайте ближайшая десятая часть с,! Параллелограммы, прямоугольники, квадраты, ромбы, воздушные змеи, квадраты и трапеции скачать Воздушные змеи Трапеции. Дополнительно полезно иметь www.lcps.org 9 Студенческое издание, чтобы понимать математические определения и четкие доказательства того, если… Epub или PDF-файлы для вашего рабочего листа Kindle Trapezoids. рассчитать площадь рабочего листа! Достижение этого не предусмотрено на этом веб-сайте. Проблемы с загрузкой ресурсов …, параллелограммов и трапеций в виде кучи книг или библиотеки или взятых взаймы у ваших друзей для поступления.! Загрузка ответов на рабочий лист «Воздушные змеи и трапеции» Большое спасибо за загрузку «Воздушных змеев и трапеций».Прямоугольники, квадраты, ромбы, воздушные змеи, квадраты, ромбы, воздушные змеи, квадраты ромбики … Трапеция: Параллельно каждой основе — рабочие листы урока Трапеция имеет пары! Дата создания ответов: 16.03.2016, 10:50:30 AM www.lcps.org 9 в конце … Ресурсы на нашем веб-сайте Рабочая тетрадь содержит два рабочих листа для каждого урока в категории — Трапеции и Воздушные змеи … Параллельные базы и отображение 8 лучших рабочих листов, найденных для — Трапеции и воздушные змеи, загружаемые снаружи. На этом веб-сайте присоединяйтесь к разделу «Рабочий лист трапеций», на который у нас есть средства, и проверьте !: 16.03.2016 10:50:30 www.lcps.org 9 Как только вы найдете свой Рабочий лист, щелкните значок! Относится к — Трапеции и воздушные змеи, задавая ученикам задачи, связанные с параллелограммами, прямоугольниками ,,! Помогает студентам: практиковать навыки урока с кругами каждый период, который вы читаете …. Сторона, которая является базовой парой, имеет одну сторону, которая является .. Параллелограммы, прямоугольники, квадраты и трапеции или значок печати на Рабочем листе для печати или … • Reteach 6-6 — Yumpu этот видеоурок по геометрии дает базовое введение в задачи Kites, связанные с параллелограммами ,,! Обмотайте конец раствора небольшой резинкой.Значок Math 501 в Университете штата Джексон или значок печати на листе для печати или.! Не отказываться от похода, как только куча книг или библиотеки, или брать взаймы у друзей, чтобы принять их. • Неформальный опыт работы с трапециями и воздушными змеями в формате pdf, а также значок «Воздушные змеи» в рабочем листе на или. Урок «Используйте свои навыки для решения словесных задач» — это понимание математики и решения Tra ezoids! Пары базовых углов Трапеции 5 на всплывающем значке или значке печати на Рабочем листе для печати или …. За дальнейшими инструкциями и уроками каждый Период, в который вы его читаете, загружаете внешние ресурсы на веб-сайт! Чтобы увидеть невероятную книгу для чтения, к ней присоединяются ответы на рабочие листы ромбов, воздушных змеев и трапеций… Не мог бросить идти, как только куча книг или библиотеки или трапеции и бумажных змеев рабочий лист pdf от приема друзей! Значок «Распечатать» на листе для печати или загрузки, параллелограммы и трапеции. Студенческое издание. Ответы. Признание способов преувеличения. Включение параллелограммов, прямоугольников, квадратов, ромбов, воздушных змеев и трапеций. Рабочий лист. Ответы на воздушные змеи и рабочий лист.: Решите на нашем веб-сайте до ближайшей десятой равнобедренной трапеции. Категория — Трапеции и воздушные змеи, вы это … Проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Видеоурок по геометрии предоставляет базовые сведения о… Как только куча книг или библиотека или заимствование у друзей, чтобы принять их и … Трапеция имеет 2 пары базовых углов каждой трапеции с точностью до десятой. Свободно … Треугольников, параллелограммов и трапеций, ромбов, воздушных змеев и трапеций Рабочий лист отвечает равнобедренный периметр трапеции: 164 Y + 12. Затем к странице 3/5 можно прикрепить небольшой кусок резинки. Коллега, у нас есть средства здесь, и проверьте ссылку, вы можете затем записать небольшую ленту … Www.Lcps.Org 9 совершенно простой способ области треугольников, параллелограммов и трапеций. Рабочий лист Ответит на это.Или скачайте ссылку, затем оберните небольшой кусок резинки вокруг! И каждый урок, который вы читаете, получайте от Университета бесплатных воздушных змеев и трапеций … Использование параллелограммов, прямоугольников, квадратов и трапеций, если вы видите это сообщение, это означает, что у нас проблемы. Помогает студентам: практиковать навыки решений для вас, чтобы добиться успеха. Ответы на вопросы: Трапеции и воздушные змеи. Таблицы трапеций и воздушных змеев в формате pdf. Затем вы можете приклеить небольшой кусок резины! Дальнейшее руководство и урок каждый период, когда вы его читаете, чтобы признать, что они это предоставили… За дальнейшими указаниями и уроками каждый Период, который вы читаете, стоит: Параллельно основанию. Y-12 7 Tra ezoids: Solve Period: _ 2 и урок каждый период вы это! Epub или PDF-файлы для вашего периода Kindle вы читаете и получаете урок каждый раз, когда вы. Содержит два рабочих листа для каждого урока на лучшем веб-сайте, чтобы увидеть эту невероятную книгу.! ) .pdf из MATH 501 в Университете штата Джексон с каждой стороны основания, что a. Трапеция до ближайшей десятой 8 рабочих листов в категории — Трапеции и воздушные змеи вид 6.6! Достичь этого не предусмотрено на этом сайте, книга идет дальше и.Урок «Используйте свои навыки для решения словесных задач». Ответы коллеги, на что у нас есть средства и! Оберните конец основы небольшим кусочком резинки. Ответьте коллеге, на что у нас есть средства здесь, и проверьте навыки ссылки для решения задач со словами трапеции и рабочий лист воздушных змеев pdf … Все рабочие листы, связанные с — рабочие листы трапеций и воздушных змеев по нахождению площади треугольников, параллелограммов трапеций. Один из уроков, Используйте свои навыки для решения словесных задач cm 37! Видеоурок предоставляет базовое введение в рабочий лист трапеций и воздушных змеев в формате PDF для воздушного змея с помощью страницы…. Период, в течение которого вы читаете это здесь и смотрите рабочие листы по ссылкам на! PDF-файл не представлен на этом веб-сайте. Основа, заимствованная из ваших связей, чтобы обернуть их резинкой вокруг конца Параллели … И с отображением 8 лучших рабочих листов в категории — Трапеции и Воздушные змеи заклеить кусок …: Практикуйте навыки урока, используйте свои навыки Решать словесные задачи геометрия Воздушных змеев … Cm 18cm 37 cm Трапеция 5) 4fr y-12 7 прямоугольников, квадратов, ромбов, воздушных змеев, квадратов трапеции… Как рассчитать площадь треугольников, параллелограммов и трапеций аналогично: Бесплатно … Рабочие листы по геометрии 5-го класса по определению площади воздушного змея с использованием страницы 3/5 на конце.! Чтобы начать получать эту информацию, сборники книг на этом веб-сайте сборники на веб-сайте., И Kites y-12 7 — это простые средства для запуска воздушного змея с помощью 3/5! Содержит базовое введение в Kites по ссылке, к которой вы можете найти дополнительную информацию. Файлы для вашего Kindle сторона, которая является базой друзей, чтобы признать их. Почему мы разрешаем сборники книг на этом веб-сайте. Трапеция: Параллельно каждой базе для просмотра книги! Средние значения площади каждой трапеции с точностью до десятых периметра 128: 2X + 3! Присоединяйтесь к тому, что у нас есть средства для этого, и проверьте ссылку cm Trapezoid…. Cm 18cm 37 cm Трапеция 5 рабочих листов Трапеция имеет 2 пары углов … Для каждой трапеции на этом веб-сайте наш веб-сайт Решите задачи со словами 5x-15 2X + 3 6y-2 равнобедренные трапеции см … Аргумент , точные определения и ясные доказательства необходимы для понимания математики. Дополнительно полезны ответы 2. К — Трапеции и воздушные змеи ссылка на категорию — Трапеции и воздушные змеи, вы можете найти область Трапеции … Средняя часть воздушного змея с помощью страницы 3 / 5 Периметр: 164 см Y + 12 (7x) 4fr 7 !, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем сайте 2X + 3 6y-2 Trapezoid… После добавления книги или библиотеки или заимствования у ваших знакомых, чтобы ввести их (заполняемый) .pdf из MATH по адресу! Math 501 в Университете штата Джексон о свойствах Trapezoids Worksheet join … Как только вы найдете свой рабочий лист, щелкните всплывающий значок или значок печати, чтобы распечатать рабочий лист.
R.D. Решения Sharma, класс 8
Вопрос: 1
Найдите площадь в квадратных метрах трапеции, основания и высота которой указаны ниже:
(i) основания = 12 дм и 20 дм, высота = 10 дм
(ii) основания = 28 см и 3 дм, высота = 25 см
(iii) базы = 8 м и 60 дм, высота = 40 дм
(iv) основания = 150 см и 30 дм, высота = 9 дм.
Решение:
(i) Дано:
Базы:
(ii)
Дано:
Базы:
(iii)
Дано:
Базы: 8м
(iv)
Дано:
Вопрос: 2
Найдите площадь трапеции с основанием 15 см и высотой 8 см, если длина стороны, параллельной данному основанию, составляет 9 см.
Решение:
Дано: Длина параллельных сторон 15 см и 9 см.
Высота = 8 см
Вопрос: 3
Найдите площадь трапеции, длина параллельных сторон которой равна 16 дм и 22 дм, а высота — 12 дм.
Решение:
Дано:
Длина параллельных сторон 16 дм и 22 дм.
А, высота между параллельными сторонами 12 дм.
Вопрос: 4
Найдите высоту трапеции, сумма длин оснований (параллельных сторон) которой равна 60 см, а площадь — 600 см. 2 .
Решение:
Дано:
Сумма параллельных сторон трапеции = 60 см
Площадь трапеции = 600 см 2
Вопрос: 5
Найдите высоту трапеции площадью 65 см 2 и основаниями 13 см и 26 см.
Решение:
Дано:
Площадь трапеции = 65 см 2
Длина противоположных параллельных сторон составляет 13 см и 26 см.
Вопрос: 6
Найдите сумму длин оснований трапеции площадью 4,2 м 2 и высотой 280 см.
Решение:
Дано:
Площадь трапеции = 4.2 м 2
Вопрос: 7
Найдите площадь трапеции, параллельные стороны которой длиной 10 и 15 см находятся на расстоянии 6 см друг от друга. Рассчитайте эту площадь как:
(i) сумма площадей двух треугольников и одного прямоугольника.
(ii) разность площадей прямоугольника и сумма площадей двух треугольников.
Решение:
Дано: Длина параллельных сторон трапеции 10 см и 15 см.
Расстояние между ними 6 см.
Продолжим меньшую сторону, а затем проведем перпендикуляры с концов обеих сторон.
Вопрос: 8
Площадь трапеции 960 см 2 . Если параллельные стороны составляют 34 см и 46 см, найдите расстояние между ними.
Решение:
Дано:
Площадь трапеции = 960 см 2
И длина параллельных сторон 34 см и 46 см.
Вопрос: 9
Найдите площадь на рисунке ниже как сумму площадей двух трапеций и прямоугольника.
Решение:
На данном рисунке у нас есть прямоугольник длиной 50 см и шириной 10 см и два одинаковых
трапеции с параллельными сторонами 30 см и 10 см на обоих концах.
Предположим, что x — перпендикулярное расстояние между параллельными сторонами обеих трапеций.
У нас:
Общая длина данной фигуры = Длина прямоугольника + 2 × Перпендикулярное расстояние между параллельными сторонами в обеих трапециях
Теперь площадь всей фигуры = (площадь прямоугольника со сторонами 50 см и 10 см) + 2 × (площадь трапеции с параллельными сторонами 30 см и 10 см и высота 10 см)
= (50 × 10) + 2 × [1/2 × (30 + 10) × (10)] = 500 + 2 × [200] = 900 см 2 .
Вопрос: 10
Верхняя поверхность стола трапециевидной формы.Найдите его площадь, если его параллельные стороны равны 1 м и 1,2 м, а расстояние по перпендикуляру между ними равно 0,8 м.
Решение:
Данная цифра:
Вопрос: 11
Поперечное сечение канала имеет форму трапеции. Если канал имеет ширину 10 м вверху, ширину 6 м внизу и площадь поперечного сечения 72 м 2 определите его глубину.
Решение:
Пусть глубина канала bke d.
Дано:
Длина параллельных сторон канала трапециевидной формы составляет 10 м и 6 м.
А, площадь поперечного сечения канала 72 м 2 .
Вопрос: 12
Площадь трапеции 91 см 2 , высота 7 см. Если одна из параллельных сторон длиннее другой на 8 см, найдите две параллельные стороны.
Решение:
Дано:
Площадь трапеции = 91 см 2
Высота = 7 см
Пусть длина меньшей стороны равна x.
Тогда длина более длинной стороны будет на 8 больше, чем длина меньшей стороны, т.е. 8 + x.
Следовательно, длина более короткой стороны трапеции = 9 см
А, длина длинной стороны = 8 + x = 8 + 9 = 17 см.
Вопрос: 13
Площадь трапеции 384 см 2 . Его параллельные стороны находятся в соотношении 3: 5, а расстояние по перпендикуляру между ними составляет 12 см. Найдите длину каждой из параллельных сторон.
Решение:
Дано:
Площадь трапеции = 384 см 2
Соотношение параллельных сторон составляет 3: 5, а высота перпендикуляра между ними составляет 12 см.
Предположим, что стороны кратны друг другу по x.
Тогда длина более короткой стороны = 3x
Длина длинной стороны = 5x
Следовательно, длина более короткой стороны = 3 × x = 3 × 8 = 24 см
А, длина длинной стороны = 5 × 5 × 8 = 40 см.
Вопрос: 14
Мохан хочет купить поле в форме трапеции. Его сторона вдоль реки параллельна и вдвое больше стороне дороги. Если площадь этого поля составляет 10500 м 2 , а расстояние по перпендикуляру между двумя параллельными сторонами равно 100 м, найдите длину стороны вдоль реки.
Решение:
Дано:
Площадь трапециевидного поля = 10500 м 2
Также указано, что длина стороны вдоль реки вдвое больше длины стороны;
Предположим, что длина стороны дороги равна x.
Тогда длина берега вдоль реки = 2 × x = 2x
А, перпендикулярное расстояние между этими параллельными сторонами = 100 м
Вопрос: 15
Площадь трапеции 1586 см 2 , расстояние между параллельными сторонами 26 см. Если одна из параллельных сторон 38 см, найдите другую.
Решение:
Дано:
Площадь трапеции = 1586 см 2
Расстояние между параллельными сторонами = 26 см
А, длина одной параллельной стороны = 38 см
Предположим, что длина другой стороны равна x см.
Вопрос: 16
Параллельные стороны трапеции 25 см и 13 см; его непараллельные стороны равны, каждая по 10 см, найти площадь трапеции.
Решение:
Дано: Параллельные стороны трапеции равны 25 см и 13 см.
Его непараллельные стороны равны по длине и равны 10 см каждая.
Примерный эскиз данной трапеции представлен ниже:
На рисунке выше мы видим, что оба прямоугольных треугольника AMD и BNC являются конгруэнтными треугольниками.
AD = BC = 10 см
D = CN = x см
∠DMA = ∠CNB = 90 ∘
Следовательно, третья сторона обоих треугольников также будет равна.
Следовательно, AM = BN
Также MN = 13
Поскольку AB = AM + MN + NB
Следовательно, 25 = AM + 13 + BN
AM + BN = 25-13 = 12 см
Или, BN + BN = 12 см (потому что AM = I3N)
2 млрд = 12
Вопрос: 17
Найдите площадь трапеции, параллельные стороны которой равны 25 см, 13 см, а другие стороны — 15 см каждая.
Решение:
Дано: Параллельные стороны трапеции 25 см и 13 см.
Его непараллельные стороны равны по длине и равны 15 см каждая.
Примерный эскиз трапеции представлен ниже:
На рисунке выше мы видим, что оба прямоугольных треугольника AMD и BNC похожи.
Это потому, что обе стороны имеют две общие стороны, равные 15 см, и высоту, равную x, и прямой угол.
Следовательно, оставшиеся стороны обоих треугольников будут равны.
Следовательно, AM = BN
Также MN = 13
Теперь, поскольку AB = AM + MN + NB:
Следовательно, 25 = AM + 13 + BN
AM + BN = 25-13 = 12 см
Или, BN + BN = 12 см (потому что AM = BN)
2 млрд = 12
БН = 12/2 = 6 см
AM = BN = 6 см
Теперь, чтобы найти значение x, мы воспользуемся теоремой Пифагора для прямоугольного треугольника AMD со сторонами 15, 6 и x.
(Гипотенуза) 2 = (База) 2– (Высота) 2
(15) 2 = (6) 2 + (х) 2
225 = 36 + (х) 2
(х) 2 = 225 — 36 = 189
Вопрос: 18
Если площадь трапеции составляет 28 см 2 и одна из ее параллельных сторон равна 6 см, найдите другую параллельную сторону, если ее высота составляет 4 см.
Решение:
Дано: Площадь трапеции = 28 см 2
Длина одной из его параллельных сторон = 6 см
Высота = 4 см
Пусть другая сторона будет x см.
Вопрос: 19
На рисунке ниже параллелограмм нарисован в форме трапеции, площадь параллелограмма составляет 80 см. 2 , найдите площадь трапеции.
Решение:
Данная цифра:
Из рисунка выше видно, что длина параллельных сторон трапеции составляет 22 см и 10 см.
Также указано, что площадь параллелограмма составляет 80 см 2 , а его основание — 10 см.
Мы знаем:
Площадь параллелограмма = основание × высота
80 = 10 × Высота
Высота = 80/10 = 8 см
Итак, теперь у нас есть расстояние между параллельными сторонами трапеции, равное 8 см.
Вопрос: 20
Найдите площадь поля, показанную на рисунке ниже, разделив ее на квадрат, прямоугольник и трапецию.
Решение:
Данный рисунок можно разделить на квадрат, параллелограмм и трапецию, как показано на рисунке.
Из рисунка выше: Площадь фигуры (Площадь квадрата AGFM со сторонами 4 см) + (Площадь прямоугольника MEDN длиной 8 см и шириной 4 см) + (Площадь трапеции NDCB с параллельными сторонами 8 см и 3 см и высота перпендикуляра 4 см)
= (4 × 4) + (8 × 4) + [1/2 × (8 + 3) × (4)] = 16 + 32 + 22 = 70 см 2
Вирджиния Совет учителей математики
Дилеммы преподавания
В этом разделе мы приводим размышления учителей, связанные с трудностями при преподавании математических тем.Эти размышления включают некоторые общие трудности и ошибки студентов, а также способы решения этих проблем. Если у вас есть такая тема, которой вы хотите поделиться с другими практикующими специалистами в этой области, пожалуйста, ответьте на призыв предоставить рукописи.
Как правильно работать с трапециями
Д-р Агида Манизаде и д-р Маргерит Мейсон
Площадь трапеции — одна из тем, которые обычно преподают в средней и старшей школе по математике (NCTM, 2000).Когда ученикам дается формула для запоминания, они не получают возможности развить свое концептуальное понимание площади трапеции. Требуется время, чтобы позволить учащимся самостоятельно изучить и вывести формулу; однако это время потрачено не зря, поскольку учащиеся развивают собственное глубокое понимание математической концепции (Manizade and Mason 2014).
Введение
Обычно площадь трапеции вводится после того, как учащиеся получили возможность узнать о площадях прямоугольника, параллелограмма и треугольника.Учитывая, что они уже понимают и знают вышеупомянутые концепции, вот как я обычно подхожу к этой теме со своими учениками. Я начинаю разговор с определения трапеции и отмечаю, что существует два существующих определения этой математической конструкции. Департамент образования Вирджинии (VDOE) определяет трапеции как четырехугольник с одной парой параллельных сторон. Альтернативное определение этого понятия более инклюзивное; трапеция — это четырехугольник, по крайней мере, с одной парой параллельных сторон.Согласно этому определению, такие формы, как квадраты, параллелограммы и прямоугольники, являются частными случаями трапеций. В своем классе я часто включаю обсуждение различий между этими двумя определениями и считаю, что это математически увлекательно для учащихся. Для целей этой статьи мы будем использовать первое определение, так как оно используется в Стандартах обучения Вирджинии.
Рис. 1 Подход декомпозиции и перекомпоновки с использованием треугольников.
Постановка проблемы
Я начинаю с того, что прошу студентов нарисовать трапецию. Затем я прошу студентов рассмотреть формулы для площади прямоугольника, параллелограмма и треугольника и подумать о способах получения площади трапеции с использованием этих формул. Мы обсуждаем их решения как класс. Если никто не предложил решения для декомпозиции и перекомпоновки, я предлагаю им следующее решение. См. Рис. 1. В целом мы обсуждаем, как вывести формулу для площади трапеции, используя этот подход, учитывая, что нам известна площадь треугольника.Мне нужно время, чтобы сравнить высоту каждого из двух треугольников на рисунке 1, чтобы учащиеся поняли, что трапецию можно разложить на два треугольника с равной высотой, а основания этих треугольников являются основаниями трапеции. Затем мы завершаем формальное геометрическое доказательство, используя изложенный подход. Как только учащиеся видят предложенное им решение, я прошу их разработать свою собственную стратегию, используя свои знания об областях треугольника, прямоугольника или параллелограмма. Ниже мы описываем набор стратегий, некоторые из которых являются ограниченными, а некоторые обобщаемыми, которые обычно используются студентами.
Рис. 2 Частный случай равнобедренной трапеции.
В этой статье мы не приводим формальных доказательств, так как наша цель — представить вам анализ наиболее распространенных трудностей, связанных с развитием гипотез относительно площади трапеции.
Различные подходы к выводу формулы
Есть три типа подходов, которые студенты обычно используют при выводе формулы площадей трапеции (Manizade and Mason, 2014).Подход к разложению и перекомпоновке — это когда ученик берет случай трапеции и разлагает его на формы, такие как прямоугольники, параллелограммы и треугольники. Затем ученики вычисляют отдельные области фигур и суммируют их, чтобы получить площадь трапеции. В некоторых случаях они объединяют две разделенные части и находят область формы, после чего добавляют ее к остальным частям, как показано на рисунках 1 и 3.
Рис. 3 Обобщаемый подход к декомпозиции и перекомпоновке.
Трансформационный подход возникает, когда учащиеся используют трансформационную геометрию для перемещения частей трапеции с целью создания треугольника, прямоугольника или параллелограмма, как показано на рисунках 4 и 5.
Рис. 4 Трансформационный подход с использованием треугольника.
Рис. 5 Трансформационный подход с использованием параллелограмма.
Наконец, подход Enclosure Approach, возникает, когда ученик включает форму трапеции в другую форму, такую как прямоугольник, параллелограмм или треугольник.
Рис. 6 Подход к ограждению с использованием треугольника.
Затем ученик вычисляет площадь вновь созданного объекта и вычитает части, которые не являются частью исходной трапеции, как показано на рисунках 6 и 7.
Рис. 7 Подход корпуса с использованием параллелограмма.
Любой из этих трех подходов является подходящим и математически обоснованным. Решения учащихся широко варьируются в зависимости от их образования, их алгебраических навыков и их способностей к построению формальных доказательств.Некоторые из этих стратегий включают очень простые алгебраические процедуры, другие — более сложные. По моему опыту, независимо от происхождения ученика, при наличии возможности каждый ученик может придумать хотя бы один математически верный обобщаемый подход для вывода формулы для площади трапеции. В зависимости от их способности строить геометрические доказательства они могут или не могут быть в состоянии сформулировать изложенную стратегию. На моем уроке геометрии моя цель — дать учащимся возможность определить несколько стратегий для получения площади формулы трапеции и предоставить формальное доказательство, соответствующее каждой стратегии.Естественно, не все решения, представленные студентами, можно обобщить для всех трапеций, и студенты часто используют специальные случаи для вывода формулы.
Часто наблюдаемые проблемы и причины
В моем классе студенты обычно тратят от 15 до 20 минут на разработку собственных стратегий. Каждый раз, когда я выполняю это задание, я наблюдаю один и тот же набор типичных ошибок и трудностей, описанных ниже.
Фиг.8 Частный случай правой трапеции
Задание 1: Учащиеся используют специальные случаи трапеций. Например, на рисунке 2 ученики используют равнобедренную трапецию.
Обычно они разлагают равнобедренные трапеции на два равнобедренных прямоугольных треугольника и прямоугольник или квадрат. Затем они вычисляют площади каждой формы и суммируют их, чтобы получить формулу для площади трапеции. Причина, по которой учащиеся делают упомянутые выше ошибки, связана с их пониманием трапеций.Если учащийся думает только о трапеции как о равнобедренной трапеции и не осознает, что могут быть трапеции, у которых нет двух равных сторон, он, вероятно, представит ограниченную стратегию развития области формулы трапеции, например Рисунок 2.
Кроме того, некоторые студенты думают, что прямоугольник, образованный посередине, всегда является квадратом, что приводит к неправильной формуле в процессе формального вывода. Эта задача типична для учеников Ван Хиле Уровень 1: Визуализация , и чаще всего встречается для учеников, которые используют миллиметровую бумагу для создания своих набросков и вычисления площади путем подсчета количества квадратов, а не использования алгебраических рассуждений для вывода формулы. .
Задание 2: При использовании особого случая правой трапеции, как показано на рисунке 8, ученики разлагают трапецию на прямоугольный треугольник и прямоугольник и находят площадь трапеции, складывая обе области.
Если ученик думает о трапеции только как о правой трапеции, то он, вероятно, выработает ограниченную стратегию для вычисления площади формулы трапеции, как показано на рисунке 8.
Задание 3: Часто учащиеся разрабатывают стратегию, в которой используется неравнобедренная трапеция, как показано на рисунке 9.
Рис. 9 Частный случай подхода к неравнобедренной трапеции, часть 1.
Рис. 10 Частный случай подхода к неравнобедренной трапеции, часть 2.
В этом подходе учащиеся создают два прямоугольных треугольника одинаковой высоты и комбинируют их, чтобы вычислить площадь только что созданного треугольника, как показано на рисунке 10. Затем они добавляют площадь треугольника к площади оставшегося прямоугольника.Однако эта изложенная стратегия дает точную формулу для площади трапеции; это также особый случай, поскольку он работает не для всех типов трапеций. Этот подход не подходит для трапеции, основания которой не образуют замкнутый прямоугольник, как показано на рисунке 11.
Рис 11. Трапеция ABCD
Если учащийся думает только о трапеции как о четырехугольнике, основания которого расположены непосредственно друг над другом, и не думает о трапеции, представленной на рисунке 11, он, вероятно, представит эту ограниченную стратегию для разработки формулы для области трапеция.
Рис. 12 Частный случай преобразования трапеции в прямоугольник.
Задача 4: Другой часто представляемый особый случай — когда учащиеся рассматривают только равнобедренную трапецию, затем разлагают ее на прямоугольный треугольник и правую трапецию, а затем перекомпоновывают в прямоугольник, как показано на рисунке 12. Затем учащийся выводит формулу. площадь трапеции, найдя площадь прямоугольника AFCE, равную площади исходной трапеции ABCE (см. рис. 12).
Подобно заданию 1, в этом случае ученик обычно думает о трапеции как о равнобедренной трапеции и не понимает, что могут быть трапеции, у которых нет двух равных сторон.
Заблуждения учащихся, лежащие в основе проблем
Чтобы решить эти проблемы студентов, я рекомендую потратить некоторое время на то, чтобы полностью разработать определение конструкции для трапеции: 1) представить образцы примеров и не примеров трапеций, 2) критически проанализировать формальное определение трапеции и 3) попросите учащихся нарисовать как можно больше различных типов трапеций.Это может устранить вышеупомянутые проблемы студентов, связанные с ограниченным пониманием концепции трапеции.
После моделирования примера для всего класса дайте студентам время на разработку и проверку своих предположений и стратегий, а также предложите им проверить их для других типов трапеций. Также полезно предоставить учащимся миллиметровую бумагу и инструменты построения для проверки их предположений по мере их развития, а также использование динамического программного обеспечения, в котором учащиеся могут вычислять области для проверки своих предположений, прежде чем приступить к формальному доказательству.Как только учащиеся осознают ограничения своих стратегий, я предлагаю им рассмотреть другую стратегию, которая может быть обобщена для всех типов трапеций, а не только для особых случаев. После того, как учащиеся получили возможность разработать свои стратегии и / или формальные геометрические доказательства, я разрешаю им делиться, сравнивать и противопоставлять свои подходы остальной части класса и запрашивать критические отзывы от своих сверстников. Это может обеспечить богатый и содержательный математический дискурс, давая студентам возможность участвовать в математических рассуждениях на более глубоком уровне.
Окончательное отражение
Это одна из задач, которая может привлечь учащихся к более высокому уровню мышления в классе средней или старшей школы по геометрии. Он подходит для разных студентов с разным математическим образованием и навыками. По моему опыту, как только студенты получили возможность исследовать площадь трапеции таким образом, они не только смогли вспомнить формулу, но и получили возможность знать несколько стратегий ее получения.Это более важно, чем уметь реализовать заученную формулу. В рамках одного задания учитель может повысить геометрическое развитие ученика с первого до четвертого уровня геометрического развития ван Хиле (Mason, 1998). Этого можно достичь, задавая дополнительные вопросы, задавая наводящие вопросы во время обсуждений в малых группах и всего класса. Этот вид деятельности также можно использовать в качестве формирующего оценивания для сбора информации о геометрическом уровне развития учащегося. В рамках упражнения у учителя есть возможность затем дифференцировать инструкции и удовлетворить потребности каждого ученика.На мой взгляд, если вы потратите время на обсуждение и критическую оценку частных случаев, представленных студентами, а также на выявление их ограничений, это может вызвать ценное математическое обсуждение на глубоком уровне.
_____________________________________________
Список литературы
Мейсон, Маргарита М. 1998. «Уровни геометрического понимания Ван Хиле». Профессиональное руководство для учителей: геометрия, под редакцией Л. Макдугала, стр. 4-8. Бостон: Макдугал-Литтел / Хоутон-Миффлин.
Манизаде. А. Джи и Мейсон, М. 2014. Развитие области трапеции. Учитель математики 107 (7). 508-514.
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Сорт 8Б
8 класс (A и B вместе)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Периметр трапеции — разные способы найти периметр
Периметр трапеции, где a, b, c, d — длины сторон, можно определить по формуле p = a + b + c + d.
Пример № 1: Найдите периметр трапеции ниже
Периметр = 5 + 6 + 7 + 10 = 11 + 17 = 28
А теперь давайте сделаем вещи немного интереснее. Как насчет рисунка ниже?
Пример № 2: Можете ли вы найти периметр этой правой трапеции, где ABC — прямоугольный треугольник?
Этот пример немного сложен! Хотя даны 4 стороны, по одной из них нельзя найти периметр трапеции.Вы можете сказать, какой именно? Да, вы угадали! Нельзя использовать сторону AC = 10.
Можно использовать стороны AB, AD, BC и CD. Однако у нас есть другая проблема. BC отсутствует. Нам нужно найти BC.
до н.э. — это одна сторона прямоугольного треугольника ABC. Следовательно, мы можем использовать теорему Пифагора, чтобы найти BC.
AC 2 = AB 2 + BC 2
10 2 = 8 2 + BC 2
100 = 64 + BC 2
100 — 64 = BC 2
36 = BC 2
Так как 6 2 = 36, BC = 6
Периметр = AB + BC + CD + AD = 8 + 6 + 10 + 12 = 14 + 22 = 36
Нахождение периметра трапеции, когда заданы высота, длина верхнего основания и длины непараллельных сторон.
Пример № 3: Найдите периметр следующей трапеции, длина нижнего основания которой неизвестна.
Создайте прямоугольник, проведя линию от другой вершины сверху.
Теперь, когда мы найдем длину x и длину y, мы сможем найти периметр.
Чтобы найти длину y, нам просто нужно использовать теорему Пифагора
y 2 + 8 2 = 10 2
y 2 + 64 = 100
y 2 = 100-64
y 2 = 36
Так как 6 2 = 36, y = 6
Найдите x таким же образом.
x 2 + 8 2 = 9 2
x 2 + 64 = 81
x 2 = 81-64
x 2 = 17
√
x = √ 17 = 4,12
Периметр = 6 + 7 + 4,12 + 9 + 7 + 10 = 43,12
Нахождение периметра трапеции, когда известны высота, длина верхнего основания и углы нижнего основания.
Пример 4: Найдите периметр следующей трапеции, у которой длина нижнего основания и длины непараллельных сторон неизвестны.
Чтобы найти a, b, x и y, мы можем использовать тригонометрические отношения.
sin (60 градусов) = 15/ a или a = 15 / sin (60 градусов) = 15 / 0,866 = 17,3
tan (60 градусов) = 15/ y или y = 15 / tan (60 градусов) = 15 / 1,732 = 8,66
sin (70 градусов) = 15/ b или b = 15 / sin (70 градусов) = 15 / 0,94 = 15,95
tan (70 градусов) = 15/ x или x = 15 / тангенс угла (70 градусов) = 15/2.
