Содержание
Н и НН в прилагательных
В прилагательных пишется как одна буква -Н-, так и -НН-. Правильный выбор сделаем, определив, от слова какой части речи и с помощью каких суффиксов образуются прилагательные.
Для того чтобы выбрать одну и две буквы -Н- в написании имен прилагательных, определим, с помощью каких суффиксов они образованы от существительных или глаголов несовершенного и совершенного вида.
Написание -Н- и -НН- в прилагательных, образованных от существительных
Если прилагательное образовано от существительного с помощью суффиксов -ан-, -ян-, -ин-, то эти суффиксы пишутся с одной буквой -Н-, например:
- песок — песчаный пляж;
- рожь — ржаной хлеб;
- береста — берестяное лукошко;
- серебро — серебряный крестик;
- осёл — ослиный крик;
- соловей — соловьиное пение.

Обратим внимание, что коренное «н» пишется в прилагательных:
Запомним написание слов-исключений:
- олово — оловянный
- дерево — деревянный
- стекло — стеклянный
Прилагательные образуются от существительных с помощью суффиксов -онн- и -енн-, например:
- лекция — лекционный курс;
- станция — станционное здание;
- клятва — клятвенное обещание;
- бритва — бритвенный прибор.
Качественные прилагательные с суффиксом -енн- могут выражать большую меру признака:
- толстенный фолиант
- тяжеленный мешок
- широченный пояс
- высоченный баскетболист
- здоровенный мужчина.
Исключение составляет слово «ветреный» (день, человек, приятель). Однако приставочные образования этого прилагательного пишутся с -НН-:
- безветренный
- подветренный
- наветренный
- обветренный
- проветренный
- заветренный.
С -НН- пишутся прилагательные, если суффикс -н- присоединяется к основе существительного, заканчивающейся тоже на «н»:
- осень — осенний день;
- длина — длинные тени;
- балкон — балконные перила;
- цена — ценный камень;
- кухня — кухонный комбайн.
В прилагательных, которые образованы от существительных на -мя, напишем -НН-, так как они образованы от основы косвенных падежей этих существительных, оканчивающейся на «н», например:
- время — нет времени — времен-н-ой;
- темя — вид темени — темен-н-ой;
- имя — зову по имени — имен-н-ой;
- семя — много семени — семен-н-ой.
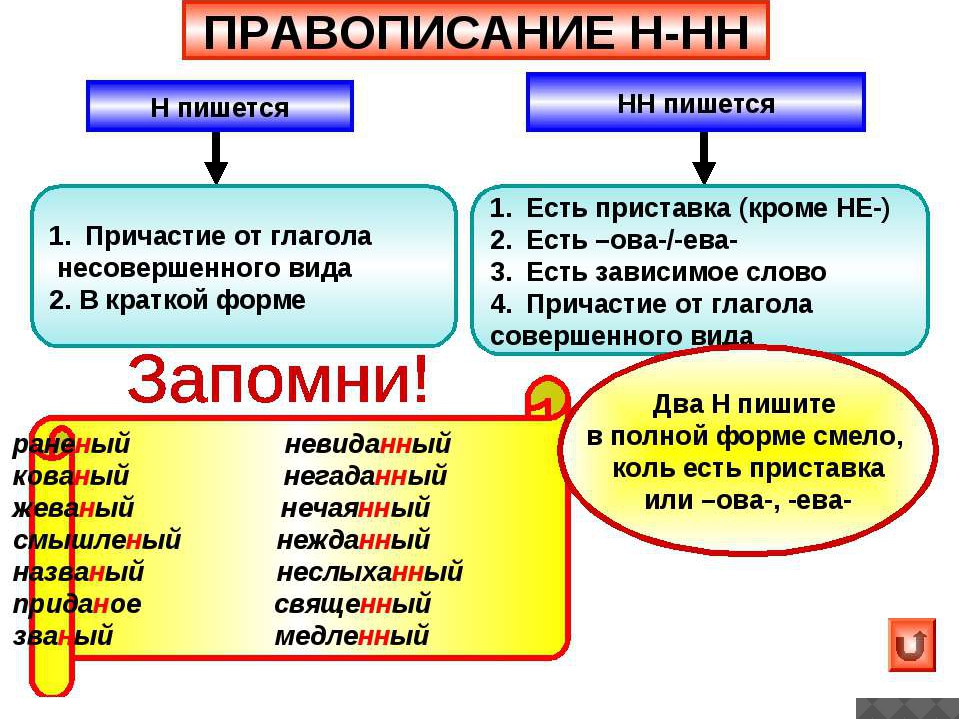
Написание -Н- и -НН- в прилагательных, образованных от глаголов
Чтобы выбрать написание -Н- или -НН- в прилагательных, образованных от глаголов, определяем вид глагола. Если производящим является бесприставочный глагол несовершенного вида (что делать?), то отглагольное прилагательное пишется с -Н-, например:
Если производящим является бесприставочный глагол несовершенного вида (что делать?), то отглагольное прилагательное пишется с -Н-, например:
- грузить — гружёный вагон;
- сеять — сеяная мука;
- плести — плетёная корзина,
- метить — меченый атом;
- точить — точёная ложка.
Наличие приставки не- и полу- не меняет написания прилагательного:
- носить — ношеный — неношеный костюм,
- ранить — раненый — нераненый солдат,
- грузить — гружёный — полугружёный самосвал.
У таких слов в предложении не должно быть зависимых слов.
Дополнительный материал
Поинтересуемся, как отличить отглагольное прилагательное от причастия.
Сравним:
Плетёная корзина полна румяных яблок.
Плетённые дедушкой корзинки были нарасхват на базаре.
Если же производящим является глагол совершенного вида (что сделать?) с приставкой, то прилагательное имеет в написании -НН-, например:
- растерянное лицо
- обиженный вид
- умеренный климат
- усиленное питание
- уверенный тон
- отчаянный крик
- возвышенный стиль.
В прилагательных, имеющих в морфемном составе суффиксы -ова-/ева-, -ирова-, пишется -НН-:
- прессовать — прессованный;
- взволновать — взволнованный;
- рисковать — рискованный;
- очаровать — очарованный;
- никелировать — никелированный;
- натренировать — натренированный;
- иллюстрировать — иллюстрированный.
Обратим внимание на написание бесприставочных глаголов «кованый», «жёваный», «клёваный».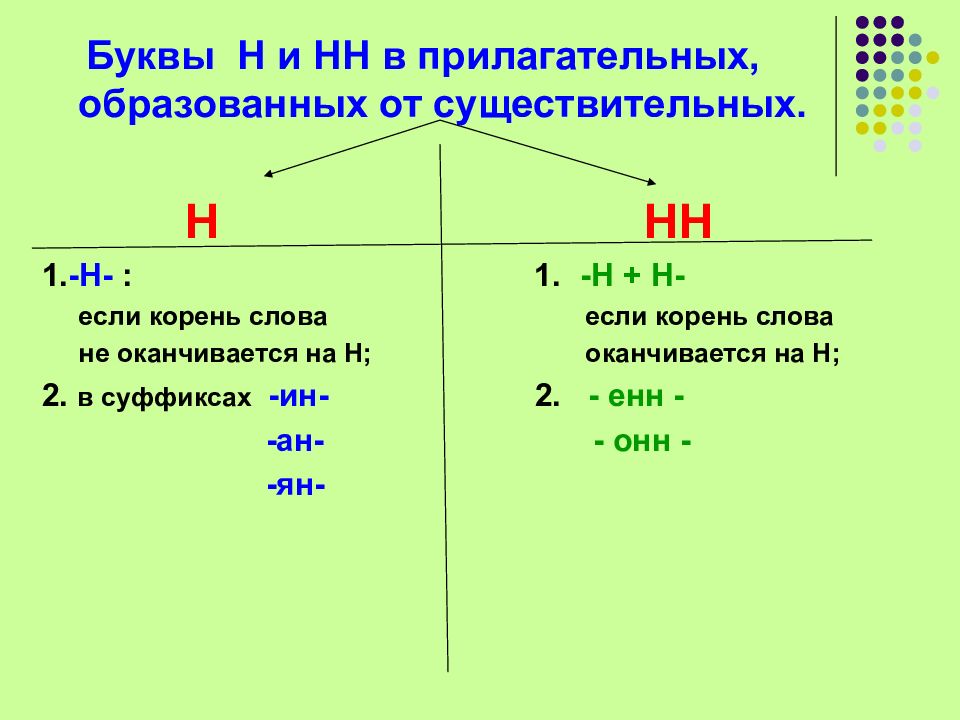
Правописание -Н- и -НН- в кратких формах прилагательных
Краткие формы прилагательных сохраняют написание -Н- или -НН-, которое существует в их полных формах.
Сегодня погода очень ветрена.
Его лицо обиженно и растерянно.
Девушка тактична и воспитанна.
Алгоритм определения написания -Н- или -НН- в прилагательных
Чтобы правильно написать прилагательное с -Н- или -НН-, выясним сначала его форму, полную или краткую. Затем определим, от существительного или глагола образовано рассматриваемое слово. Если производящим является существительное, обращаем внимание на его основу и суффикс, с помощью которого образовано прилагательное.
Если прилагательное является отглагольным, выясняем вид глагола, обратив внимание, есть ли приставка в его морфемном составе, а также учитываем словообразовательные суффиксы.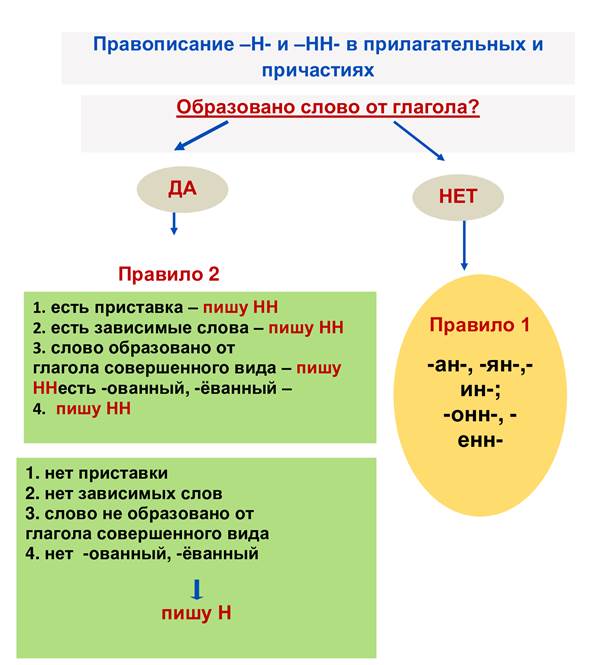
Схематично алгоритм определения написания -Н- или -НН- в именах прилагательных и причастиях выглядит так:
| Определим, в какой форме стоит прилагательное: | |||
| полной | краткой | ||
| Две буквы в окончании (красивая) | Одна буква в окончании (красива, красив) | ||
| Выясним, от какой части речи образовано слово: от существительного или от глагола. | |||
| Полная форма | |||
| Прилагательные от существительных | Прилагательные от глаголов ( причастия) | ||
| -Н- | -НН- | -Н- | -НН- |
| -ан, -ян, -ин лев — львиный ! Стеклянный | -онн, -енн революция — революционный ! Ветреный | без приставки мороженый сом (от морозить) | с приставкой замороженный сом |
| Н+Н = сон+ный НО! К первообразным также относятся слова: | не, полу… не считать! немороженый | зависимое слово мороженный мамой сом | |
| МЯ = енн временный (время) | суф. -ова-, -ева-, -ирова- маринованный ! кованый, жёваный, клёваный ! желанный, нечаянный, нежданный, негаданный | ||
| Краткая форма | |||
| Значение действия (что сделаны?) — «Н» воспитаны отцом, взволнованы бурей | Значение признака (каковы?) — см. на полную форму: сколько «н» в полной, столько и в краткой. Они воспитанны и образованны (воспитанные и образованные).  | ||
Видеоурок
Скачать статью: PDF
Правописание н и нн в глаголах
Пишутся с нн суффиксы полных форм страдательных причастий прошедшего времени: -нн- и -ённ- (-енн-). Соотносительные с ними по форме прилагательные пишутся в одних случаях тоже с нн в суффиксе, в других – с одним н.
1. Пишутся с нн причастия и прилагательные на -ованный, -ёванный, -еванный (образованные от глаголов на -овать, -евать ), например: балованный, корчёванный, линованный, малёванный, организованный; выкорчеванный, избалованный, намалёванный, разлинованный, реорганизованный.
2. Пишутся также с нн причастия не на -ованный (-ёванный, – еванный ) глаголов совершенного вида и соотносительные с ними прилагательные; подавляющее большинство таких глаголов содержит приставку.
- Примеры форм, образованных от приставочных глаголов: выбеленный, выстиранный, довязанный, изжаренный, исписанный, окрашенный, очищенный, обруганный, покрашенный, подсчитанный, распутанный, сделанный.
- Перечень форм исконно бесприставочных глаголов, а также некоторых глаголов, приставка в которых может быть выделена только этимологически: брошенный, данный, конченный, купленный, лишённый, пленённый, прощённый, пущенный, решённый, хваченный, явленный; встреченный, затеянный, обиженный, обретённый, обязанный, посещённый, снабжённый.

По этому правилу пишутся и формы двувидовых (имеющих значение и совершенного, и несовершенного вида) глаголов венчать, завещать, обещать, казнить, родить: венчанный, завещанный, обещанный, казнённый, рождённый.
Исключения. Пишутся с одним н соотносительные с причастными формами прилагательные в составе следующих устойчивых сочетаний: конченый человек, названый брат, названая сестра, посажёный отец, посажёная мать, Прощёное воскресенье .
3. Причастия не на -ованный (-ёванный, -еванный ) глаголов несовершенного вида (они образуются только от бесприставочных глаголов) и соотносительные с ними прилагательные пишутся по-разному: причастия с нн, прилагательные – с одним н, например: гружённые дровами повозки, жаренная на масле рыба, писанная маслом картина, стриженные парикмахером волосы и коротко стриженные волосы, крашенные зелёной краской скамейки, давно не метённый пол, ещё не белённые стены, уже не раз считанные деньги, деланное много раз предложение ; но: гружёная баржа, жареная рыба, писаная красавица, стриженые волосы, крашеные скамейки, метёный пол, белёные стены, считаные минуты, деланое равнодушие ; аналогично вязанный и вязаный, глаженный и глаженый, плетённый и плетёный, чищенный и чищеный ; так же пишутся: жёванный и жёваный, клёванный и клёваный, кованный и кованый.
По этому правилу пишутся формы двувидовых глаголов контузить, крестить и ранить . Ср.: контуженный в голову боец, тяжело раненный солдат, раненный в ногу солдат, только что крещённый младенец , но: контуженый командир, раненый солдат, крещёный ребёнок.
Как раз и навсегда научиться правильно писать н и нн
Эта заметка адресована тем, кто все еще не научился определять, сколько букв н писать в том или ином слове. Или тем, кто на десятый раз перечитывает правила и не может их понять. Заварите себе чай, сделайте бутерброды. Разговор будет серьезным.
Интересные и каверзные задания по русскому языку
Общие советы
Как понизить вероятность правильного написания
Легко. Писать наугад или потому, что так «красиво» выглядит. Или первое и второе одновременно.
Как повысить вероятность правильного написания
Не ленитесь и не пропускайте ни один из пунктов алгоритма. Только тогда вы доведете навык определения количества букв н в слове до автоматизма.
Высший пилотаж — определять количество
н на ходу.
Сможете, но не сразу.
Последовательность действий
Для начала всегда определяем часть речи. Делать это нужно по вопросу, который мы задаем к слову.
- Имя существительное — кто? что?
- Имя прилагательное — какой?
- Краткое прилагательное — каков?
- Наречие — как?
- Причастие — какой?
- Краткое причастие — каков?
- Отглагольное прилагательное — какой?
У вас уже назрел вопрос: как различать те части речи, которые отвечают на один и тот же вопрос?
Имена прилагательные и причастия
Прилагательное образовано от существительного, а причастие образовано от глагола.
Длинный — это прилагательное, потому что отвечает на вопрос какой? и образовано от существительного длина.
Усыпанный — это причастие, потому что отвечает на вопрос какой? и образовано от глагола усыпать.
Кстати, еще у причастий есть характерные суффиксы. В формах настоящего времени: -ущ-, -ющ-, -ащ-, -ящ-, -ем-, -ом-, -им-. В формах прошедшего времени: -вш-, -ш-, -ин-, -т-, -енн-, -ённ-, -нн-. Эти суффиксы используются как дополнительная проверка того, правильно ли вы определили часть речи.
Причастия и отглагольные прилагательные
Теперь у нас еще одна проблема: и причастия, и отглагольные прилагательные образованы от глагола. Оба отвечают на вопрос какой?. Как их различать?
Во-первых, отглагольное прилагательное образовано от глагола несовершенного вида, а причастие образовано от глагола совершенного вида.
Как определить вид глагола? Легко. Если он отвечает на вопрос что делать?, то вид несовершенный (обозначает незавершенное действие). Если он отвечает на вопрос что сделать?, то вид совершенный (обозначает завершенное действие).
Во-вторых, у отглагольных прилагательных отсутствуют зависимые слова.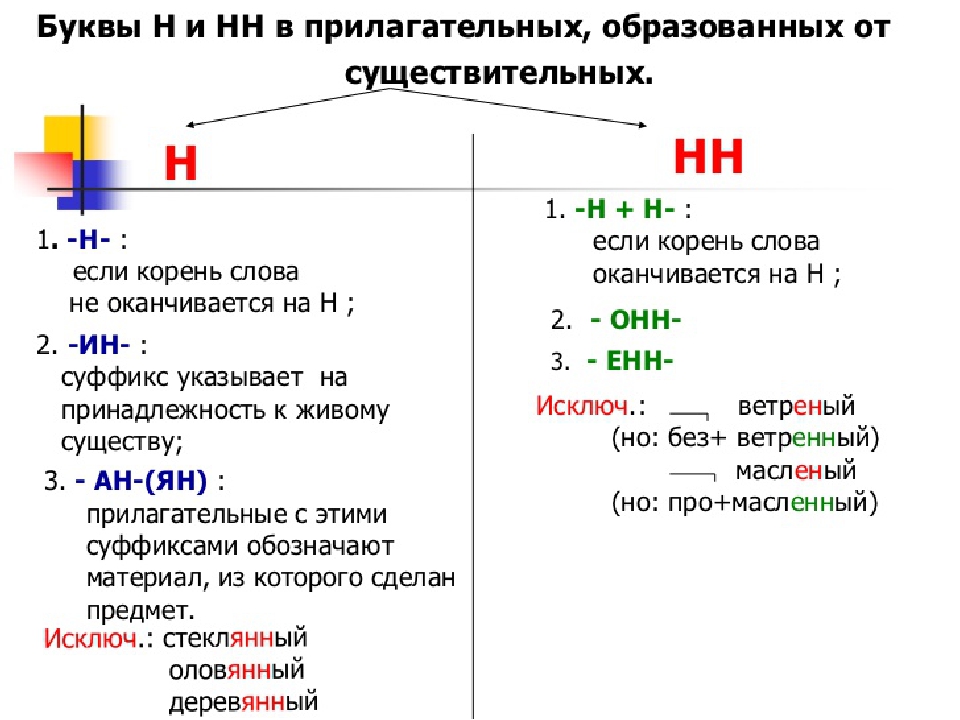
Зависимое слово — это слово, к которому можно задать вопрос от главного слова.
Попробуйте самостоятельно определить, какое из этих слов является причастием, а какое — отглагольным прилагательным: решенная задача, груженая машина.
Ответ. Решенная — причастие. Вот все аргументы: оно отвечает на вопрос какой?; образовано от глагола решить; этот глагол совершенного вида, потому что отвечает на вопрос что сделать?.
Груженая — отглагольное прилагательное. И вот почему: отвечает на вопрос какой?; образовано от глагола грузить; этот глагол несовершенного вида, потому что отвечает на вопрос что делать?; зависимые слова отсутствуют.
Для того, чтобы отглагольное прилагательное стало причастием, достаточно сделать одно из двух:
- Добавить зависимое слово.
Груженная человеком машина. Груженная кем? — человеком. Теперь это причастие.
Теперь это причастие. - Изменить вид глагола.
Загруженная машина. Образовано от глагола загрузить, который отвечает на вопрос что сделать? и потому относится к совершенному виду.
Краткие прилагательные и краткие причастия
Последовательность действий такая:
- Осознали, что слово отвечает на вопрос каков?.
- Думаем, от какой полной формы слово образовано.
- Определяем часть речи у полной формы (отличия имен прилагательных от причастий читаем выше).
Вот таблица для наглядности.
| Прилагательное | Причастие | |
| Полное | Дорога длинная | Усыпанный листьями |
| Краткое | Дорога длинна | Усыпан листьями |
Ура. Теперь мы знаем, к какой части речи относится наше слово.
Применяем правила
Посмотрите, как всё просто, когда мы знаем часть речи:
| Причастие | Краткое причастие | Отглагольное прилагательное |
| нн | н | н |
| Высушенные фрукты | Фрукты высушены | Сушеные фрукты |
| Сваренный картофель | Картофель сварен | Вареный картофель |
Мы также пишем две буквы н в причастиях с суффиксами -ова- и -ева-.
В слове асфальтированный пишем нн, потому что имеется суффикс -ова-.
Следите за тем, чтобы -ова- или -ева- были именно суффиксами. В словах кованый и жеваный таких суффиксов нет. В них есть корни ков- и жев-. В этих словах пишется одна буква н, потому что они относятся к отглагольным прилагательным.
Еще нужно запомнить слова: нежданный, негаданный, виданный, невиданный, виденный, читанный, слыханный, неслыханный, желанный. Просто запомните их.
Осталось разобраться с именами прилагательными, именами существительными и наречиями.
В прилагательных и существительных пишем одну н только в одном случае: если имеется суффикс -ан-, -ян-, -ин-: кожаный, серебряный, куриный, песчаник. Исключения: стеклянный, оловянный, деревянный.
В прилагательных пишем нн в следующих случаях:
- В суффиксах -онн-, -енн-: станционный, временный.

- Если слово образовано от существительного, основа которого заканчивается на -н: туманный.
Обратите на второй пункт особое внимание. Без него вы бы написали в слове туманный одну букву н, поскольку там суффикс -ан-. Но в этом слове нет суффикса -ан-! Почему? Потому что -ан- является частью корня. Слово образовано от существительного туман, основа которого заканчивается на н. По аналогии пишутся прилагательные карманный, длинный, лимонный и многие другие. Не забывайте про это правило.
Слова ветреный, масленый, масляный не являются прилагательными, поскольку образованы от глаголов: ветрить, маслить. Тут всё работает по правилам отглагольных прилагательных и причастий. Или просто запомните, что эти три слова пишутся с одной буквой н. В остальных случаях уже с двумя (ветреный, безветренный).
Окей. Как быть с краткими прилагательными?
Тут всё просто: в них пишется столько же букв н, сколько и в полных.
| Полное прилагательное | Краткое прилагательное |
| Мысли туманные | Мысли туманны |
| Яблоки румяные | Яблоки румяны |
Как быть с наречиями?
Тут та же история. Пишем столько же н, сколько в слове, от которого наречие образовано.
Медленно — наречие, потому что отвечает на вопрос как?. Образовано от прилагательного медленный. В этом прилагательном мы пишем нн в суффиксе -енн-, поэтому и в наречии пишем так же.
Внимание! Наречие может быть образовано не только от прилагательного, но и от других частей речи. Например, путано объяснять. Логика здесь хитрая. Наречие путано образовано от слова путаный, которое является отглагольным прилагательным (отвечает на вопрос какой?; нет зависимых слов; образовано от глагола несовершенного вида путать).
Поскольку путаный — отглагольное прилагательное, то в нем мы пишем одну н. А раз так, то и в наречии, которое от него образовано, пишем столько же.
Небольшое упражнение. Объясните постановку н-нн в предложении.
Маринованные грибы, поджаренная колбаса, масленые ржаные лепешки, сгущенное молоко, говяжья печенка, печеный картофель, немного вывалянный в золе, и глоток напитка, настоянного на каком-то диковинном снадобье, покажутся вкусными на свежем воздухе самому сверхизысканному гурману.
Одна и две буквы Н в суффиксах прилагательных
Урок русского языка.
Тема: Одна и две буквы Н в суффиксах прилагательных.
Задачи урока:
Образовательные: объяснить правописание одной и двух букв Н в прилагательных, образованных от существительных, выработать умение правописания одной и двух букв Н в прилагательных, образованных от существительных.
Развивающие: развивать навыки устной и письменной речи, навыки работы с ИКТ. Продолжить работу над развитием логического мышления; способствовать развитию способностей и умений учащихся самостоятельно добывать знания, систематизировать и применять их на практике.
Продолжить работу над развитием логического мышления; способствовать развитию способностей и умений учащихся самостоятельно добывать знания, систематизировать и применять их на практике.
Воспитательные: воспитание любви к родному языку, воспитание культуры интеллектуального труда, формирование умения чувствовать красоту слова.
Тип урока: усвоение новых знаний.
Оборудование: мультимедийная презентация.
Ход урока.
Организационный момент.
(Слайд № 1)
Слово учителя:
— Здравствуйте, ребята. Начинаем урок русского языка. Откройте тетради, запишите число (сегодня 17 января), классная работа.
Мотивация учебной деятельности.
Слово учителя:
— Прочитаем эпиграф нашего урока.
Ученики читают эпиграф:
«Знания — сила!»
Слово учителя:
— Как вы понимаете это выражение? В чем сила знаний?
Ответы учеников.
Слово учителя:
— Сегодня на уроке вы будете получать новые знания. Как вы думаете, где они вам пригодятся?
Ответы учеников.
Слово учителя:
— Желаю вам удачи.
(Слайд № 2)
Самоопределение к деятельности.
Слово учителя:
— Ребята, отгадайте загадку, текст которой вы видите на ваших карточках и на экране.
Текст загадки:
Он летает серебряной стаей
И сверкает на лету.
Звездочкой стеклянной тает
На ладони и во рту.
Он на солнышке сияет,
В лунном свете – голубой.
Он за ворот и в карманы
Залетает к нам с тобой.
Ответы учеников: снег.
Слово учителя:
— Выпишите из текста имена прилагательные.
Ученики выписывают прилагательные, в суффиксах которых присутствует буква н..
Слово учителя:
— Прочитайте вслух выписанные прилагательные.
Ученики читают: серебряной, стеклянной, лунном.
Слово учителя:
— Выделите в выписанных именах прилагательных суффиксы. Проверим выполненную работу.
Ответы учеников:
Серебряный – суффикс ян, стеклянной – янн, лунном – н.
Слово учителя:
— Сколько букв Н вы записали в выделенных суффиксах?
Ответы учеников:
В суффиксе слова серебряный одна буква н, стеклянный – две, лунном – одна.
Слово учителя:
— Проверим, все ли правильно выделили суффиксы.
Слово учителя:
— Посмотрим на экран.
(Слайд № 3)
Слово учителя:
— Почему так получилось?
Учащиеся затрудняются с ответом.
Слово учителя:
— Подумайте и сформулируйте тему нашего урока.
Предполагаемые ответы учащихся:
Одна и две буквы Н в суффиксах имен прилагательных.
Слово учителя:
— Запишите тему урока в тетрадь. Ее можно списать из учебника со страницы 29.
(Слайд № 4)
Слово учителя:
— Каковы цели нашего урока?
Предполагаемые ответы учащихся:
Познакомиться с правилами написания одной и двух букв Н в суффиксах имен прилагательных, научиться правильно писать прилагательные одной и двумя буквами Н в суффиксах, знать, от чего зависит выбор одной и двух букв Н в суффиксах имен прилагательных.
Изучение нового материала.
Слово учителя:
— Для решения сложившейся проблемы предлагаю объединиться в пары и проанализировать данные прилагательные. Работа с карточками.
(Слайд № 5)
Слово учителя:
— Попробуйте ответить на вопрос: в каких именах прилагательных пишется одна буква Н? В каких две буквы Н?
Для удобства слова объединены в группы, а суффиксы выделены определенным цветом.
Туман – туманный; карман – карманный, сон – сонный, длина – длинный, цена – ценный.
Утро – утренний, экскурсия – экскурсионный, мужество – мужественный, традиция – традиционный, авиация – авиационный.
Орел – орлиный, журавль – журавлиный, шерсть – шерстяной, кожа –кожаный, сова – совиный.
Предполагаемые ответы учащихся:
В первой группе основа слова заканчивается на Н, в суффиксе прилагательных одна буква Н, в имени прилагательном будем писать две буквы Н.
Во второй группе в прилагательных, образованных от имен существительных при помощи суффиксов -ОНН, -ЕНН пишется две буквы Н.
В третьей группе в прилагательных, образованных от имен существительных при помощи суффиксов -ИН, -АН (-ЯН), пишется одна буква Н.
Слово учителя:
— Давайте убедимся, что мы сделали правильный вывод о правописании одной и двух букв Н в суффиксах прилагательных, образованных от существительных.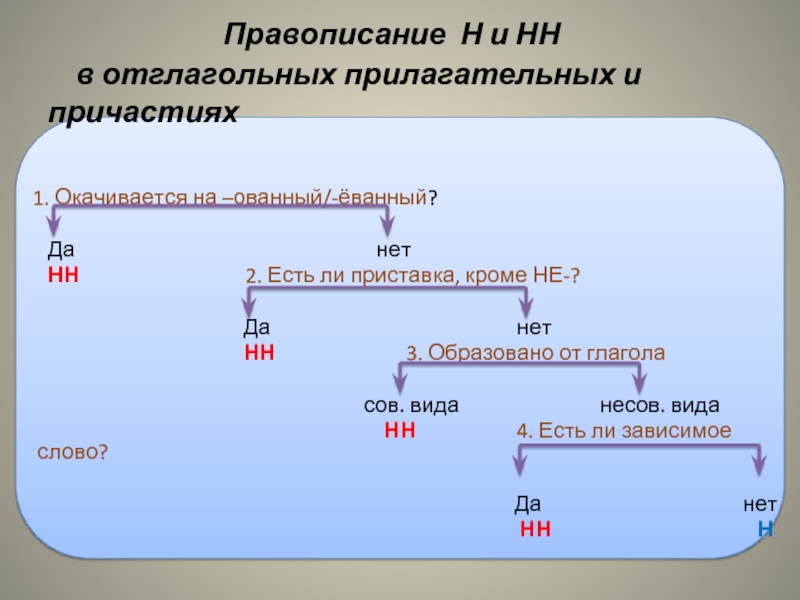
Откройте ваши учебники на странице 29, прочитайте правило №38.
(Слайд № 6)
Учащиеся читают правило про себя, затем вслух.
Слово учителя:
— Подтвердились ли ваши предположения? Что нового вы узнали?
Предполагаемые ответы учащихся:
Существуют слова-исключения: ветреный (день), оловянный, стеклянный, деревянный.
Слово учителя:
— Как графически обозначена орфограмма?
Закрепление изучаемого материала.
(Слайд № 7)
Слово учителя:
— Как мы будем рассуждать при выборе написания одной и двух букв Н в суффиксах прилагательных, образованных от существительных. Давайте составим алгоритм наших действий.
Заполним таблицу. На ваших партах лежат шаблоны. Ваша задача – вписать в таблицу недостающее:
1. Определяю, относится ли слово к исключениям
Да Нет
2. Определяю, от какой части речи образовано прилагательное
3. Определяю, как образовано прилагательное
С помощью суффиксов
–енн-, -онн- С помощью суффиксов
-ин-, -ян-, -ан- От основы на
–н-
Слово учителя:
— Перечитайте правило на странице 29.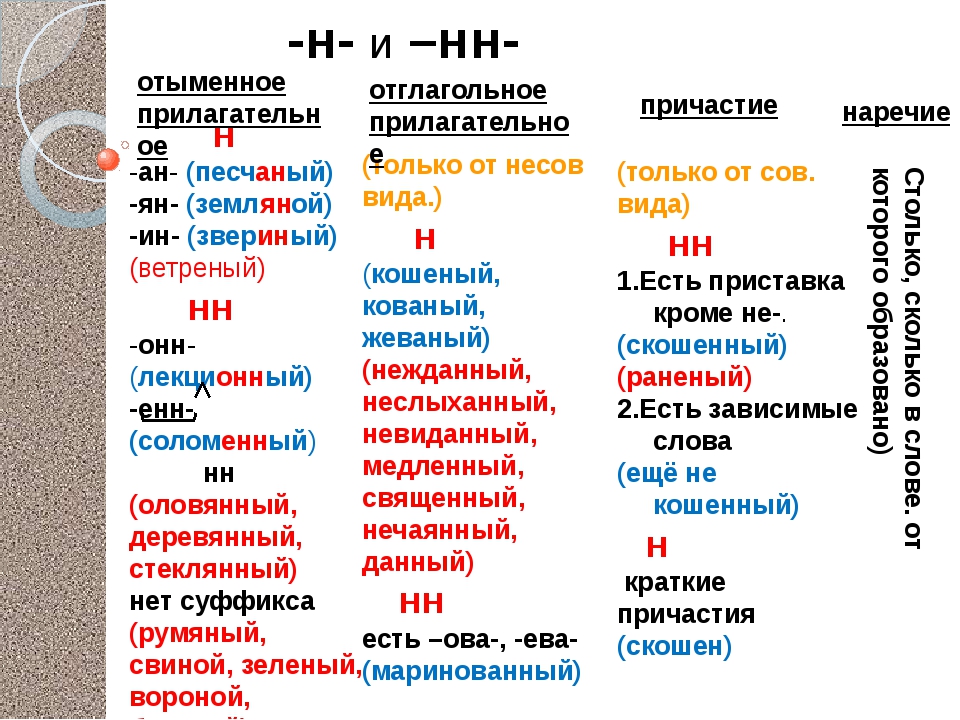
— Что нужно выяснить о прилагательном прежде, чем применять правило?
Предполагаемые ответы учащихся:
Выяснить, не относится ли оно к исключениям?
Слово учителя:
— Назовите все исключения.
Предполагаемые ответы учащихся:
Слова-исключения: ветреный (день), оловянный, стеклянный, деревянный.
Слово учителя:
— Если прилагательное относится к исключениям (да), то его нужно запомнить.
Учащиеся записывают в таблицу под словом «да» «пишу по памяти».
Слово учителя:
— Если прилагательное не относится к исключениям, то нужно определить, от какой части речи оно образовано: от существительного или глагола. Прилагательные, образованные от глаголов, мы будем изучать позже.
Что нужно делать, если прилагательное образовано от существительного?
Предполагаемые ответы учащихся:
Определить, с помощью каких суффиксов образовано прилагательное. Если с помощью суффиксов –енн, -онн, в прилагательном пишем две буквы Н; с помощью –ин, -ан, -ян, пишем одну букву ; от существительного с основой на Н – пишем две буквы Н.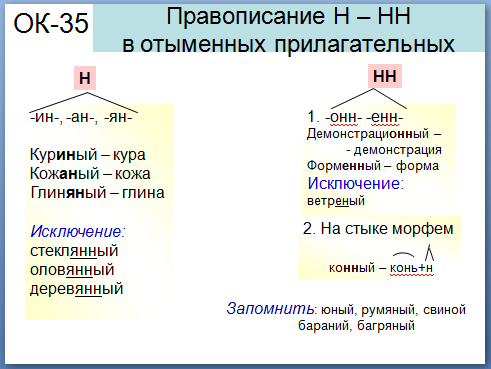
Слово учителя:
— Мы получили таблицу, содержащую алгоритм действий.
(Слайд № 8)
1. Определяю, относится ли слово к исключениям
Да Нет
Пишу по памяти 2. Определяю, от какой части речи образовано прилагательное
От существительного
3. Определяю, как образовано прилагательное
С помощью суффиксов
–енн-, -онн- С помощью суффиксов
-ин-, -ян-, -ан- От основы на
–н-
Пишу –нн- Пишу –н- Пишу –нн-
Слово учителя:
— Давайте потренируемся. На доске вы видите четыре конверта, на каждом из них надпись. Ваша задача – положить карточку с прилагательным в соответствующий конверт, аргументируя свой выбор. Итак: выбираем карточку и комментируем свой выбор.
Слова: стеклянный, оловянный, деревянный, ржаной, муравьиный, сонный, ветреный, длинный, лимонный, телефонный, журавлиный, клюквенный, утренний, тыквенный, станционный.
Слово учителя:
— После проведенной работы расскажите своими словами правило о правописании одной и двух букв Н в прилагательных, образованных от существительных.
Предполагаемые ответы учащихся.
Физкультминутка. (Слайд № 9)
(Слайд № 10)
Слово учителя:
— Предлагаю закрепить полученные знания и заполнить магический квадрат. Подумайте, сколько букв Н следует писать в суффиксах существительных. Впишите одну или две буквы Н в соответствующую клеточку.
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
Слова для работы:
1) кожа…ый
2) багря…ый
3) ястреби…ый
4) глиня…ый
5) песча…ый
6) оловя…ый
7) гуси…ый
8) обществе…ый
9) лошади…ый
10) искусстве…ый
11) тыкве…ый
12) операцио…ый
13) травя…ой
14) обеде…ый
15) письме…ый
16) насте…ый
17) ледя…ой
18) экскурсио…ый
19) овся…ый
20) бесчисле…ый
21) шерстя…ой
22) нефтя…ой
23) петуши…ый
24) пчели…ый
25) ветре…ый
Слово учителя:
— Закрасьте клеточки, в которые вы вписали одну букву Н.
Получившееся изображение должно напоминать прибор, который отсчитывает время.
(Слайд № 11)
1 н 2 н 3 н 4 н 5 н
6 нн 7 н 8 нн 9 н 10 нн
11 нн 12 нн 13 н 14 нн 15 нн
16 нн 17 н 18 нн 19 н 20 нн
21 н 22 н 23 н 24 н 25 н
(Слайд №12)
Слово учителя:
— Как видите, у нас сегодня много творческих заданий. Следующее из них называется творческий диктант.На ваших столах лежат карточки, на которых записаны словосочетания. Образуйте от выделенных существительных прилагательные, объясните графически выбор суффикса.
Учащиеся по очереди работают у доски.
пальто из кожи, кофта из шерсти, островок из песка,
фартук из льна, хлеб из ржи, чашка из глины, кисель из клюквы,
шар из стекла, солдатики из олова, суп из тыквы, яд змеи,
трели соловья, тропа зверя, грива льва, яйцо курицы,
автобус для экскурсий, нож для кухни, дом из камня
(Слайд № 13)
Ответы:
пальто из кожи — кожаное пальто
кофта из шерсти – шерстяная кофта
островок из песка – песчаный островок
фартук из льна – льняной фартук
хлеб из ржи – ржаной хлеб
чашка из глины – глиняная чашка
кисель из клюквы – клюквенный кисель
шар из стекла – стеклянный шар
солдатики из олова – оловянные солдатики
суп из тыквы – тыквенный суп
яд змеи – змеиный яд
трели соловья – соловьиные трели
тропа зверя – звериная тропа
грива льва – львиная грива
яйцо курицы – куриное яйцо
автобус для экскурсий – экскурсионный автобус
нож для кухни – кухонный нож
дом из камня – каменный дом
Рефлексия:
(Слайд № 14)
Слово учителя:
— Ребята, что нового вы сегодня узнали на уроке? С каким новым правилом вы познакомились? Чему вы научились?
Домашнее задание:
(Слайд № 15)
1) Подготовить сообщение о правописании одной и двух букв Н в суффиксах имен прилагательных, образованных от имен существительных.
2) Выполнить задание на карточках.
Слово учителя:
— Ребята, спасибо за работу. Я искренне надеюсь, что наш сегодняшний урок обогатил вас новыми знаниями.
Он летает серебряной стаей
И сверкает на лету.
Звездочкой стеклянной тает
На ладони и во рту.
Он на солнышке сияет,
В лунном свете – голубой.
Он за ворот и в карманы
Залетает к нам с тобой.
————————————————————————————————
Он летает серебряной стаей
И сверкает на лету.
Звездочкой стеклянной тает
На ладони и во рту.
Он на солнышке сияет,
В лунном свете – голубой.
Он за ворот и в карманы
Залетает к нам с тобой.
11 слов с одной и двумя «Н», которые мы не можем запомнить со школы
Помните лингвистическую шутку про жарен (н)ую картошку с грибами? В ней говорится, что количество «Н» в слове здесь зависит от того, в какой момент вы добавили грибы: сразу или сперва жарили картошку и грибы по отдельности, а потом положили в одну тарелку. Так вот, это никакие не шутки, а чистая правда! Ещё больше отглагольных прилагательных, причастий и других частей речи с «Н» и «НН» — в нашем новом выпуске «Грамотности».
Так вот, это никакие не шутки, а чистая правда! Ещё больше отглагольных прилагательных, причастий и других частей речи с «Н» и «НН» — в нашем новом выпуске «Грамотности».
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
Правильно: Печёные яблоки
Правильно: Печённые в микроволновке яблоки
Главная боль всех сомневающихся в количестве «Н» — это причастия и отглагольные прилагательные. Напомним, как отличить одно от другого. Если при слове есть зависимые слова или оно произошло от глагола совершенного вида, если в нём есть суффиксы «-ова-»/«-ева-» или любая приставка, кроме «не-» — перед вами причастие. И писать в нём нужно две «Н». Если ничего из перечисленного к слову не относится, скорее всего, это прилагательное и писать следует одну «Н».
А теперь вернёмся к нашим «печёным яблокам». В первом примере ничего из перечисленного мы не наблюдаем — значит, это прилагательное, пишем одну «Н». Но! Если мы, к примеру, решим запечь яблоки в микроволновке (да, так правда делают!) и захотим подчеркнуть это, у нас будут уже «печённые в микроволновке яблоки», где есть зависимое слово, а значит, и вторая «Н», потому что теперь это причастие.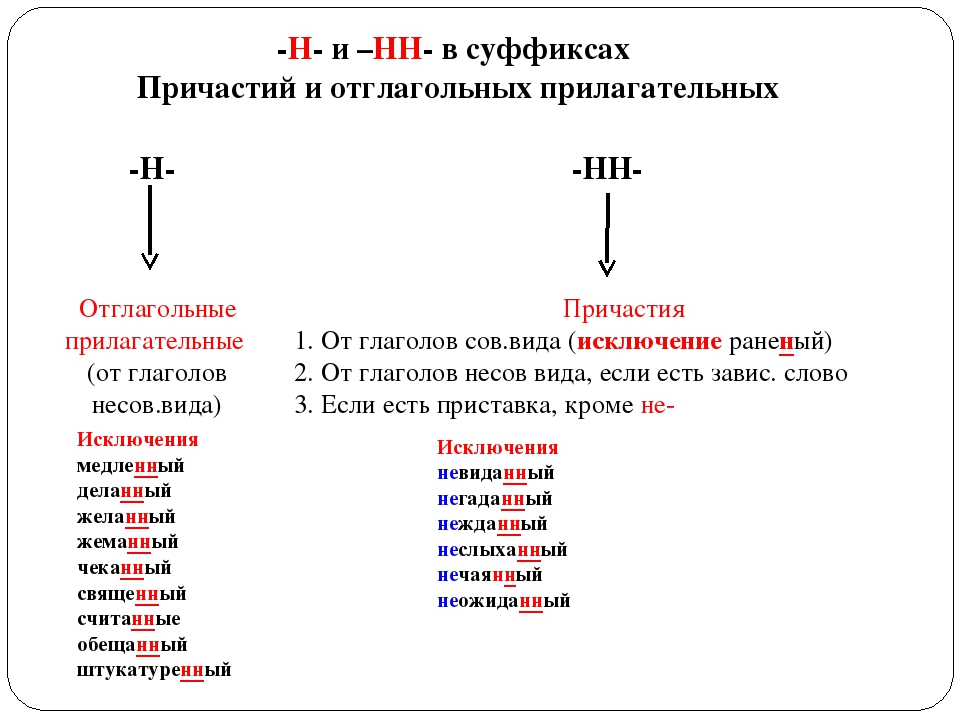
Правильно: Путаница
Надеемся, мы ещё вас не запутали! По запросу «путанница» Google выдаёт больше 60 тысяч результатов. И хоть мы и начали с существительного, тут снова придётся обратиться к причастиям и отглагольным прилагательным. «Путаница» образовано от прилагательного «путаный», а если в прилагательном пишется одна «Н», в существительном тоже сохраняется одна согласная.
Правильно: Спутанные провода
Не самое приятное словосочетание во всех отношениях — но сейчас мы всё распутаем! Мы решили не ходить далеко от прилагательного «путаный» и показать, как на написание слова влияет приставка. Да, так просто: видите приставку — смело пишите две «Н»: «спутанные», «запутанные», «перепутанные» и так далее.
Правильно: А ты смышлёный!
Слышали про смышлёного студента ВШЭ, который придумал название для транспортной карты Перми? Он назвал её «Пермская езда» и набрал больше всего лайков. Но в финал всё равно не прошёл: сокращенное название «П-езда» оказалось неоднозначным.
Про сокращения в русском языке мы расскажем как-нибудь в другой раз, а пока разберёмся с прилагательным. Приставка в слове есть — но это тот случай, когда правилу следовать как раз не нужно, потому что слово считается исключением и пишется с одной «н».
Правильно: До ЕГЭ остались считаные дни
Без паники! Время до ЕГЭ ещё есть, так что «Н» и «НН» вы ещё повторить успеете. Начнём с занимательной статистики: по запросу «считанные дни» в «Яндексе» больше 74 тысяч показов месяц и всего 130 показов (!) по этому же запросу, но с одной «Н». То есть почти ничего! Скорее всего, ошибка в слове возникла из-за того, что раньше слово «считаные» в значении «очень немногие» считалось исключением и действительно писалось с двумя «Н». Но сегодня оно подпадает под общее правило как прилагательное, образованное от глагола несовершенного вида «считать», и пишется с одной «Н».
Это ещё не всё! Вы же не забыли про зависимые слова? Если рядом с нашим словом появляется зависимое, например «считанные кассиром деньги», пишем его уже с двумя «Н» и относим к причастиям.
Правильно: Это подлинник или копия?
«Это неповторимый оригинал или жалкая пародия?» — написали бы любители мемов и не думали бы над количеством «Н». Но вот в приёмной комиссии вузов, куда летом выпускники понесут документы, вряд ли пользуются такими словами! Так что придётся разбираться. Обратимся к этимологии слова.
В интернете и даже некоторых словарях происхождение слова «подлинник» связывают с названием якобы специальных палок на Руси — «подлинников», с помощью которых пытали и добивались истины. Но как говорит лингвист Андрей Зализняк в своей лекции, в таком значении слова «подлинник» нет ни в одном источнике. Он склоняется к другой, более логичной версии с точки зрения языка. Прилагательное «подлинный» произошло от существительного «подлина» с помощью суффикса «н». Так на Руси называли подкладку одежды, нижнюю часть.
Почему же сегодня мы называем «подлинником» оригинальный документ, текст, картину? В древних текстах прилагательное «подлинный» встречается в сочетании с существительным «грамота», а существительное «подлинник» — в словосочетании «по подлинникам и спискам». То есть речь здесь идёт о чём-то исходном и списанном.
То есть речь здесь идёт о чём-то исходном и списанном.
Правильно: Немереное количество ошибок!
Совсем без ошибок, конечно, получается не всегда — но надеемся, сегодня вы разберётесь с причастиями и отглагольными прилагательными раз и навсегда. Прилагательное «немереное» образовано от глагола несовершенного вида «мерить», а приставка «не-», как мы знаем, на написание отглагольных прилагательных не влияет.
Снова помним про зависимые слова: в словосочетании «не меренный никем пиджак» в слове появляется вторая «Н», а после «не» заслуженно занимает своё место пробел.
Правильно: Незваный, неписаный
Ещё два отглагольных прилагательных, в которых легко ошибиться. В «Яндексе», например, число показов в месяц по запросам «неписаный» и «неписанный» примерно одинаково. Но мы с вами уже знаем всё про приставку «не-» и не поддадимся на уловку! Тут тоже работает классическая схема: если появляются зависимые слова, значит, перед вами причастие — и пишется в нём уже две «Н», например: «никем не званный гость», «не писанная мною картина».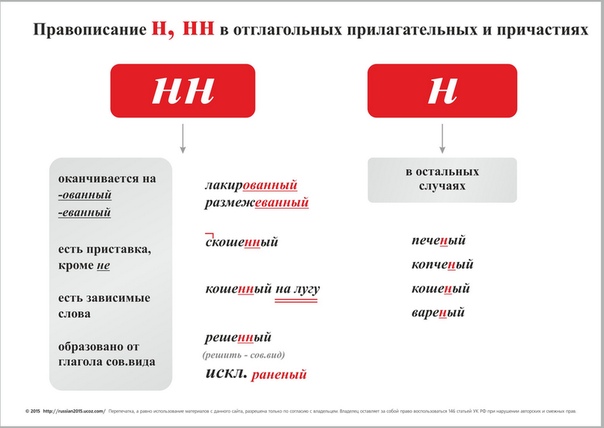 А вот слова «нежданный», «негаданный», «невиданный» и некоторые другие придётся запомнить — это исключения.
А вот слова «нежданный», «негаданный», «невиданный» и некоторые другие придётся запомнить — это исключения.
Правильно: Балованный ребёнок
«Хватит бАловаться!» — говорите вы ребёнку и тут же подаёте плохой пример. Сразу отвечаем на ваш вопрос: да, Карлсон в известном мультфильме тоже не самый грамотный персонаж. Потому что ударение в слове «баловать» падает на последний слог, а в других формах глагол звучит так: «баловАться», «балУю», «баловАл», «балУемся».
Но вернёмся к нашему прилагательному (ударение в нём, кстати, падает на второй слог — балОванный). По правилу двойное «Н» пишется во всех прилагательных глагольного происхождения, оканчивающихся на «-ованный», «ёванный-» — так что здесь без сомнений пишите две «Н». А вот на «кованый» и «жёваный» правило не распространяется: «ов» и «ёв» в этих словах относятся к корню, а не к суффиксу.
Правильно: Казённый язык
Казённый язык плох не только тем, что далёк от живой речи. Часто в нём попросту очень много неграмотных конструкций и форм: «согласно приказа», «договора» вместо «договоры» и вот это «Вы» с большой буквы где вздумается. Надеемся, вы так не пишете! А ещё верим, что вы знаете, почему в прилагательном «казённый» пишется две «Н». Но на всякий случай напомним, что, если прилагательное образовано с помощью суффикса «-н-», а его основа тоже заканчивается на «Н» — удваиваем согласную.
Надеемся, вы так не пишете! А ещё верим, что вы знаете, почему в прилагательном «казённый» пишется две «Н». Но на всякий случай напомним, что, если прилагательное образовано с помощью суффикса «-н-», а его основа тоже заканчивается на «Н» — удваиваем согласную.
Правописание Н и НН в прилагательных, образованных от имени существительного (отыменных)
В русском языке написание H и HH в прилагательных зависит от того, от какой части речи образовано рассматриваемое слово. Чтобы понять, когда пишется одна и две буквы Н в суффиксах прилагательных, определите – перед вами отглагольное прилагательное, причастие или прилагательное, образованное от существительного (отыменное).
Прилагательные, образованные от существительного (отыменные)
Н пишется:
в прилагательных, образованных от существительных с помощью суффиксов -ин-, -ан-,-ян-.
Например: кожаный, земляной, серебряный, львиный
Исключения: стеклянный, оловянный, деревянный
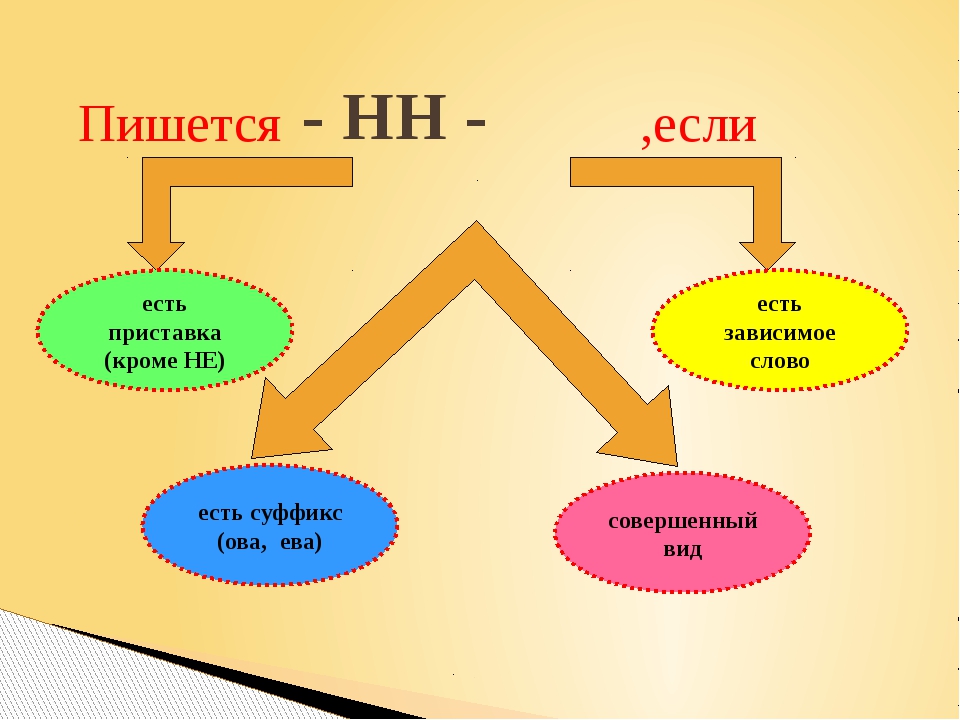
НН пишется:
1) в прилагательных, образованных от имен существительных и прилагательных с помощью суффиксов -енн-, -онн-.
Например: революциОННый, соломЕННый, здоровЕННый
Исключение: ветреный
(но это слово перестаёт быть исключением, когда к нему добавляется приставка: БЕЗветрЕННый, ЗАветрЕННый)
2) в прилагательных, образованных от существительных с основой на -н при помощи суффикса -н-.
Например: длинный, туманный, чугунный
3) Когда суффикс -енн- в прилагательных образует слова от существительных на -мя
имя – имена – именной,
племя – племена – племенной,
время – времена – временный,
пламя – пламени – пламенный
Прилагательные бараний, тюлений, свиной и подобные пишутся с одной н, так как они образованы от существительных с основой на н путем прибавления суффикса -j- (йот).
Прилагательные пряный, румяный, юный пишутся с одной н, так как это непроизводные прилагательные.
Важно! К словам с одной Н, которые стоит запомнить, относятся:
румяный, пряный, пьяный, юный, синий, поганый, зеленый, свиной, вороний, бараний, единый, тюлений, буланый, фазаний, павлиний, сазаний, рьяный, багряный.
таблица с правилами правописания суффиксов отглагольных прилагательных и существительных и задания для этого
В именах прилагательных одна буква Н пишется в суффиксах -ИН-, -АН-, -ЯН-. Например: лебединый (в суффиксе -ИН— пишется одна буква Н), кожаный (в суффиксе -АН- пишется одна буква Н), шерстяной (в суффиксе -ЯН- пишется одна буква Н).
Запомнить три суффикса, в которых пишется одна буква Н, очень легко. Надо знать первую букву алфавита и последнюю – А и Я. Добавляем к ним по одной букве Н и получаем суффиксы – АН, ИН, ЯН.
Н и нн в суффиксах имен прилагательных. видеоурок. русский язык 6 класс
Можно выучить стишок, который поможет запомнить суффиксы имен прилагательных, которые пишутся с одной буквой Н.
- Для прилагательных давно
- Записано в ученых книжках,
- Когда АН, ИН, ЯН, то Н одно
- И больше никаких излишков.
Суффикс —ИН-называют «звериным».При помощи суффикса ИН образуются имена прилагательные от одушевленных существительных, обозначающих животных, насекомых, птиц.
- МЫШИНЫЙ = МЫШЬ + ИН
- КОМАРИНЫЙ = КОМАР + ИН
- СОЛОВЬИНЫЙ = СОЛОВЕЙ + ИН
- В прилагательных МЫШИНЫЙ,КОМАРИНЫЙ, СОЛОВЬИНЫЙ пишется «звериный» суффикс —ИН— с одной буквой Н.
- Суффиксы —АН-, -ЯН— пишутся в именах прилагательных, обозначающих материал, из которого сделан предмет:
- КОЖАНЫЙ= КОЖА + АН
- ПЕСЧАНЫЙ= ПЕСОК + АН
- СЕРЕБРЯНЫЙ= СЕРЕБРО + ЯН
- ШЕРСТЯНОЙ= ШЕРСТЬ + ЯН
- ГЛИНЯНЫЙ = ГЛИНА + ЯН
Имена прилагательные КОЖАНЫЙ, ПЕСЧАНЫЙ, СЕРЕБРЯНЫЙ, ШЕРСТЯНОЙ, ГЛИНЯНЫЙ пишутся с одной буквой Н, так как суффикс в них начинается с букв А, Я.
Следует запомнить три прилагательных, суффикс которых начинается с буквы Я, но букв Н в нем пишется не одна, а две. Это слова-исключения: ДЕРЕВЯННЫЙ, ОЛОВЯННЫЙ, СТЕКЛЯННЫЙ.
Запомнить слова-исключения помогает следующая загадка про ОКНО:
поверхность стеклянная, рама деревянная, ручка оловянная.
2. Две буквы НН в суффиксах прилагательных
Две буквы Н пишутся в именах прилагательных, суффиксы которых начинаются с буквы О или Е. Например, РЕДАКЦИОННЫЙ, ТРАДИЦИОННЫЙ, СОЛОМЕННЫЙ, КЛЮКВЕННЫЙ.
Запомнить суффикс —ОНН- с НН помогает ООН – Организация Объединенных Наций.
Известно, что суффикс -ОНН- – фанат ООН.
Он во всем стремится быть максимально похожим на ООН. Правда, разница между ними заметна сразу: у суффикса —ОНН-две буквы Н, а у его кумира ООН две буквы О.
С помощью суффикса —ОНН-, в котором пишутся две буквы Н, образуются имена прилагательные чаще всего иноязычного происхождения. Например, КОМИССИОННЫЙ, РЕДАКЦИОННЫЙ, ТРАДИЦИОННЫЙ, РЕВОЛЮЦИОННЫЙ
Две буквы Н пишутся в суффиксе -ЕНН-.
Имена прилагательные с суффиксом —ЕНН- чаще всего образуются от существительных, основа которых оканчивается на несколько согласных: ИСКУССТВЕННЫЙ, КЛЮКВЕННЫЙ, ЖИЗНЕННЫЙ, ОГНЕННЫЙ, БОЛЕЗНЕННЫЙ.
В русском языке есть слово-исключение, суффикс которого начинается с буквы Е, однако букв Н в нем пишется не две, а одна. Это слово ВЕТРЕНЫЙ:
- ВЕТРЕНЫЙ ДЕНЬ
- ВЕТРЕНЫЙ ЮНОША
- В слове ВЕТРЕНЫЙ пишется одна буква Н!
- Однако если в слове ВЕТРЕНЫЙ появляется приставка БЕЗ, то букв Н согласно правилу пишется две.

- БЕЗВЕТРЕННАЯ НОЧЬ (в слове есть приставка)
- Запомнить правописание слов ВЕТРЕНЫЙ и БЕЗВЕТРЕННЫЙ помогает следующее стихотворение.
- ВетрЕНый юноша, ветрЕНый день!
- Запомнить можно без труда:
- Одну лишь Н пишу всегда!
- БезветрЕННые утро, день иль ночь!
- Не применяя правил знанья,
- Пиши две Н без колебанья!
3. Две буквы Н на стыке морфем
Две буквы Н пишутся в именах прилагательных, образованных при помощи суффикса Н от существительных с основой на букву Н:
- РАВНИННЫЙ = РАВНИНА+ Н
- ДЛИННЫЙ = ДЛИНА + Н
- ИСТИННЫЙ = ИСТИНА + Н
- ДИКОВИННЫЙ= ДИКОВИНА + Н
- БЛИННЫЙ = БЛИН + Н
- Следующее стихотворное правило помогает написать в имени прилагательном удвоенную букву Н.

- ТумаН одно имеет Н,
- Но если город стал тумаН+Ный,
- В основе Н и суффикс Н,
- И получается НН,
- Запомни этот случай странный.
4. Следует запомнить
В русском языке есть несколько слов, не имеющих суффикса Н и очень от этого страдающих. Эти слова часто путают и ошибочно пишут в них удвоенную НН.
Запомните: в словах ЕДИНЫЙ, ЗЕЛЕНЫЙ, ПРЯНЫЙ, РУМЯНЫЙ, ЮНЫЙ, СВИНОЙ пишется одна буква Н, которая является частью корня.
5. Анализируем примеры
Определим, сколько букв Н пишется в следующих именах прилагательных и почему:
- ГУСИНЫЙ (в этом слове имеется «звериный» суффикс -ИН-, в котором пишется одна буква Н),
- ТЕЛЕФОННЫЙ (это прилагательное образовано от существительного ТЕЛЕФОН, основа которого оканчивается на букву Н. Прибавляется суффикс Н. Поэтому слово ТЕЛЕФОННЫЙ мы пишем с двумя буквами Н),
- СОЛОМЕННЫЙ (суффикс этого прилагательного начинается с буквы Е, поэтому мы пишем НН),
- ЛЬНЯНОЙ (суффикс этого прилагательного начинается с буквы Я и обозначает материал, из которого сделан предмет, поэтому пишем одну букву Н),
- ВЕТРЕНЫЙ (это слово-исключение, в котором пишется одна буква Н),
- ИНФЕКЦИОННЫЙ (суффикс этого прилагательного начинается с буквы О, поэтому мы пишем НН),
- СТЕКЛЯННЫЙ (это слово-исключение, которое входит в загадку про окно; поэтому пишем НН).

6. Алгоритм написания Н, НН в суффиксах прилагательных
Выбирая Н, НН для написания в суффиксе, можете воспользоваться алгоритмом.
Источник: https://interneturok.ru/lesson/russian/6-klass/tema/n-i-nn-v-suffiksah-imen-prilagatelnyh
Правописание Н и НН в прилагательных и причастиях. Н в суффиксах
Правописание Н или НН в прилагательных и причастиях в русском языке зависит от грамматических особенностей слова и от способа его образования.
Различают отыменные прилагательные — образованные от существительных (балкон — балконный, лев — львиный), а также отглагольные прилагательные и причастия (рисованный — рисовать, мороженый — морозить, поношенный — поносить).
Н и нн в прилагательных, образованных от существительных (отыменных прилагательных)
НН пишется в прилагательных, образованных от существительных, если:
- НН пишется, если прилагательное образовано при помощи суффиксов -онн-, -енн-:революционный, лиственный, торжественный, утренний.
 Исключения: с одной Н пишется масляный, ветреный.При добавлении приставки снова пишется НН: безветренный, подветренный.
Исключения: с одной Н пишется масляный, ветреный.При добавлении приставки снова пишется НН: безветренный, подветренный. - НН пишется, если одну букву н дает суффикс, а другую — основа:бетонный, ценный, именной
Исключение. С одной Н пишутся слова: багряный, бараний, буланый, вороний, единый, зеленый, павлиний, поганый, пряный, пьяный, румяный, рьяный, свиной, синий, тюлений, фазаний, юный
Одна Н пишется в прилагательных, образованных от существительных, если:
- Если прилагательное образовано с помощью суффиксов -ин-, -ан-, ян-: лев — львиный, соль — соляной, кожа — кожаный, платина — платиновый, полотно — полотняный
Исключения: с НН пишутся слова оловянный, стеклянный, деревянный
В кратких прилагательных Н и НН пишутся так же, как в полных формах:юный студент — студент юн, зеленые деревья — деревья зелены, длинная дорога — дорога длинна
Написание отглагольных прилагательных не меняется в составе сложных слов:мороженый — свежемороженый, стриженый — гладкостриженый
Н и нн в причастиях и отглагольных прилагательных
Написание Н и НН в суффиксах прилагательных и причастий зависит от наличия приставок, зависимых слов, а также от вида глагола — совершенного или несовершенного:
- НН пишется в страдательных причастиях прошедшего времени, которые образованы от глаголов несовершенного вида, если есть зависимые слова:читанный неоднократно роман, раненный в перестрелке солдат — раненый солдат, крашенная белой краской стена — крашеная стена, груженный углем вагон — груженый вагон
- НН пишется в прилагательных и причастиях, образованных от глаголов с приставками: заброшенный, замороженный, присыпанный
Исключение: одно Н пишется, если это приставки не- и полу-:полумороженный, неубранный, незваный
При этом НН пишется в словах нечаянный, нежданный, негаданный:
- НН пишется в образованных от глаголов совершенного вида, обозначающих завершенное действие:собранный, обрезанный, купленный, решенный
- Исключения: крещеный, раненый, смышленый
- НН пишется в причастиях и прилагательных на -ованный, -еванный:лакированный, рифмованный, образованный, рискованный
- НН пишется в причастиях и прилагательных с суффиксами -ова-, -ева-, -ирова-:асфальтированный, маринованный, пролонгированный
Одна Н пишется:
- Если отглагольное прилагательное образовано от глагола несовершенного вида без приставки при помощи суффиксов -ен-, -н- и не имеет зависимых слов:мороженый, топленый, плетеный
- Исключения — деланный, желанный, действенный и другие.
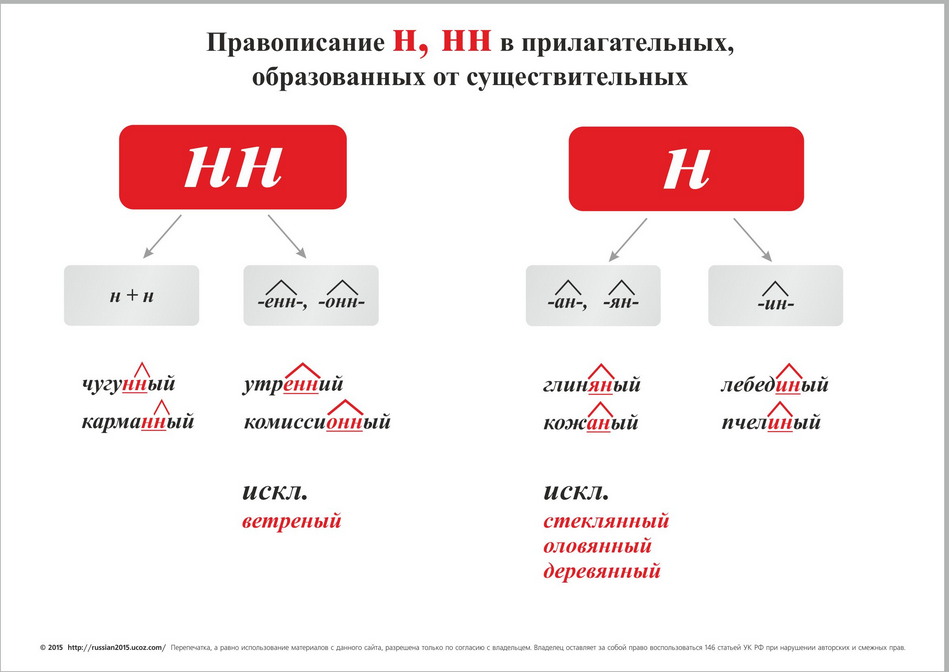
- В кратких причастиях всегда пишется одна Н:убран, достроен, поглажен
Одна Н пишется в прилагательных кованый, жёваный, клёваный. Не путайте их с причастиями, где есть приставки и пишется НН: подкованный, разжёванный, исклёванный.
Н и нн в существительных и наречиях, образованных от причастий и прилагательных:
- В существительных и наречиях, образованных от причастий и отглагольных прилагательных, пишется столько Н, сколько их было в производящей основе:воспитанник — воспитанный, избранник — избранный, священник — священный
- Н и НН в существительных:вареник — вареный, копчености — копченый мороженое — мороженый воспитанность — воспитанный, приданое — это слово-исключение
- Н и НН в наречиях:организованно — организованный путано — путаный удивленно — удивленный
Как это все запомнить?
Пользуйтесь следующим списком действий:
- Определите, от какой части речи образовано слово — от глагола или от существительного?
- Если от существительного: смотрите на суффикс и основу.

- Если от глагола, смотрите на приставку, зависимое слово, суффиксы.
- Смотрите, краткая или полная форма причастия и прилагательного.
Примеры предложений с Н и НН в прилагательных и причастиях
Роняет лес багряный свой убор. (А.С. Пушкин)
Небо все было засеяно звездами. (Н.В. Гоголь)
Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рожденья. (И.С. Тургенев)
Каждый почтенный господин солидной наружности, нанимавший извозчика, на глаза мои тотчас же обращался в почтенного отца семейства. (Ф.М. Достоевский)
Проедешь две-три версты — городок, — кирпичная островерхая кирка, мощеная площадь с каменным колодцем… (А.Н. Толстой)
Дядя Миша мог совершить самый неожиданный, даже необдуманный поступок. (А. Рыбаков)
Был сдержан и официален, разговор был краток. (Д. Гранин)
Широкое звездное небо, посеребренная звездным светом туманная даль лугов прояснились и стали зримыми. (В. Солоухин)
(В. Солоухин)
Источник: https://www.anews.com/p/111864816-pravopisanie-n-i-nn-v-prilagatelnyh-i-prichastiyah-odno-i-dva-n-v-suffiksah/
k \ cdot m $ — Обмен стеками по математике
Сеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
- Авторизоваться
Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.
Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
4к раз
$ \ begingroup $
На этот вопрос уже есть ответы здесь :
Закрыт 4 года назад. k \ cdot m $, где $ m $ — целое нечетное число, а $ k \ geq 0 $.
k \ cdot m $, где $ m $ — целое нечетное число, а $ k \ geq 0 $.
Я знаю, что если $ n $ — целое число, его можно записать в форме $ n = \ frac {a} {b} $ для двух целых чисел $ a $ и $ b $. Кроме того, $ m $ можно записать как $ m = 2c + 1 $ для целого числа c, поскольку оно нечетное. Но я не знаю, как использовать это, чтобы придумать доказательство. Кроме того, я должен показать, что $ n $ — неотрицательное целое число
Создан 21 сен.
SBSSBS
44933 серебряных знака88 бронзовых знаков
$ \ endgroup $
1
$ \ begingroup $
Рассмотрим следующий алгоритм, имеющий на входе $ n \ geq 1 $.к \ cdot м.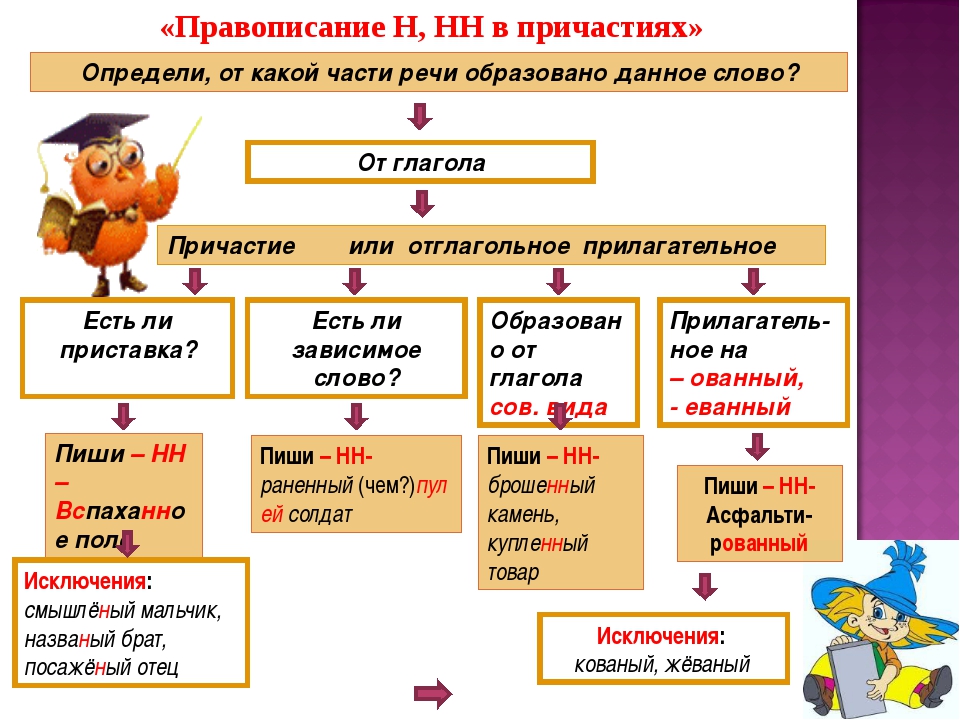 0 = 1 $, если $ 2 $ не является делителем $ n $).
0 = 1 $, если $ 2 $ не является делителем $ n $).
Создан 21 сен.
Эмилио НоватиЭмилио Новати
58.5k44 золотых знака4040 серебряных знаков9999 бронзовых знаков
$ \ endgroup $
5
Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.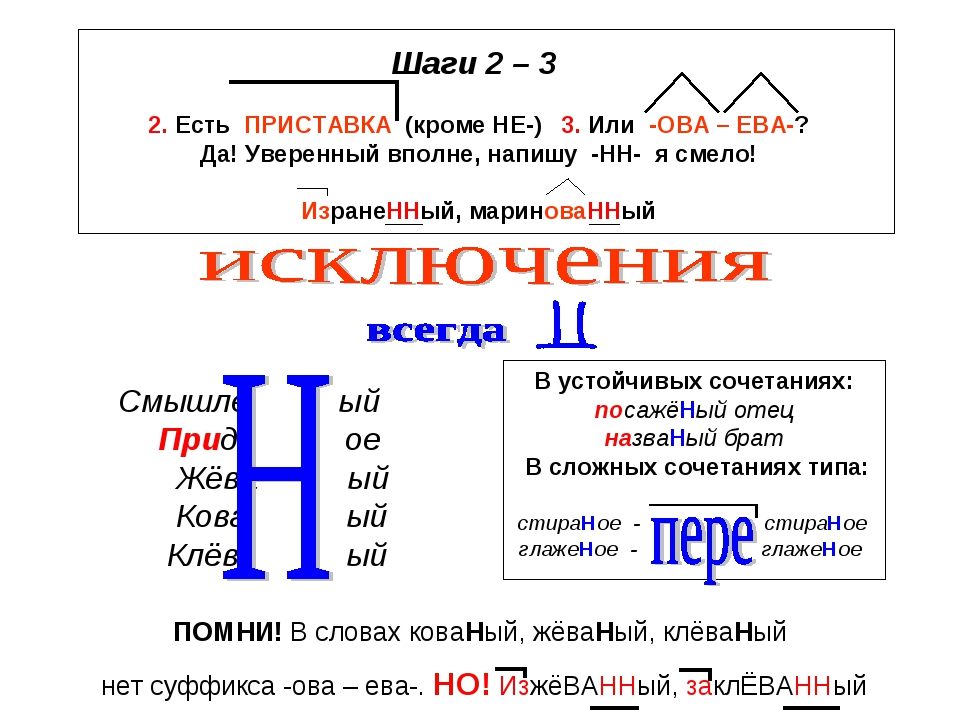
Принимать все файлы cookie
Настроить параметры
последовательностей и серий — Доказательство $ 1 + 2 + 3 + 4 + \ cdots + n = \ frac {n \ times (n + 1)} 2 $
Собираем как можно больше доказательств? Запишите серию рекурсивно:
$$ S (n) = S (n — 1) + n \ tag {1} $$
Заменить $ n \ на n + 1 $:
$$ S (n + 1) = S (n) + n + 1 \ tag {2} $$
Уравнение (2) вычесть Уравнение (1) :
$$ S (n + 1) — S (n) = S (n) + 1 — S (n — 1) \ tag {3} $$
И напишите:
$$ \ begin {case}
S (n + 1) & = 2S (n) -S (n-1) + 1 \\
S (n) & = S (n) \ end {case} \ tag {4} $$
Которая теперь может быть записана в матрице форме:
$
\ begin {bmatrix} S (n + 1) \\ S (n) \ end {bmatrix} =
\ begin {bmatrix} 2 & -1 \\ 1 & 0 \ end {bmatrix}
\ begin {bmatrix} S (n) \\ S (n-1) \ end {bmatrix} +
\ begin {bmatrix} 1 \\ 0 \ end {bmatrix}
\ tag {5} $$
А затем преобразование аффинного уравнения (5) в линейное уравнение (6) :
$
\ begin {bmatrix} S (n + 1) \\ S (n + 0) \\ 1 \ end {bmatrix} =
\ begin {bmatrix} 2 & -1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix}
\ begin {bmatrix} S (n) \\ S (n-1) \\ 1 \ end {bmatrix}
\ tag {6} $$
И закрывая уравнение:
$
\ begin {bmatrix} S (n + 1) \\ S (n) \\ 1 \ end {bmatrix} =
\ begin {bmatrix} 2 & -1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix} ^ n
\ begin {bmatrix} S (1) \\ S (0) \\ 1 \ end {bmatrix}
\ tag {6} $$
Затем находим Jordan из матрицы 3×3:
$$ \ begin {align}
\ begin {bmatrix} S (n + 1) \\ S (n) \\ 1 \ end {bmatrix} & =
\ left (\ begin {bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix}
\ begin {bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \ end {bmatrix}
\ begin {bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix} ^ {- 1} \ right) ^ n
\ begin {bmatrix} S (1) \\ S (0) \\ 1 \ end {bmatrix}
знак равно
\ begin {bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix}
\ begin {bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \ end {bmatrix} ^ n
\ begin {bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix} ^ {- 1}
\ begin {bmatrix} S (1) \\ S (0) \\ 1 \ end {bmatrix}
знак равно
\ begin {bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix}
\ begin {bmatrix} 1 & \ binom {n} {1} & \ binom {n-1} {2} \\ 0 & 1 & \ binom {n} {1} \\ 0 & 0 & 1 \ end { bmatrix}
\ begin {bmatrix} 0 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}
\ begin {bmatrix} S (1) \\ S (0) \\ 1 \ end {bmatrix}
\ end {align}
\ tag {7} $$
И перемножая матрицы:
$$ \ begin {bmatrix} S (n + 1) \\ S (n) \\ 1 \ end {bmatrix} =
\ begin {bmatrix}
\ frac {(2n + 2) S (1) — 2nS (0) + {n} ^ {2} + n} {2} \\
\ frac {2nS (1) + (2–2n) S (0) + {n} ^ {2} -n} {2} \\
1
\ end {bmatrix} \ tag {8} $$
И учитывая, что $ S (0) = 0 $ и $ S (1) = 1 $, мы получаем:
$$ S (n) = \ frac {n ^ 2 + n} {2} \ tag {9} $$
Суммирование
— Доказательство $ \ sum_ {i = 0} ^ n 2 ^ i = 2 ^ {n + 1} -1 $ по индукции.

Начальный комментарий: Во-первых, +1 за усилие. Ваши вопросы почти всегда показывают многое из этого. Кроме того, я вижу, что вы пытаетесь активно улучшить, основываясь на подобных вопросах, где вы явно пытаетесь реализовать советы, данные пользователями здесь. Замечательно. Основываясь на нескольких ваших вопросах, во всяком случае на ваших индукционных, кажется, что одна из главных проблем, с которыми вы сталкиваетесь, заключается в том, чтобы на самом деле хорошо написать доказательство (то есть сделать его ясным, отполированным и т. Д.). Таким образом, в конце этого поста я предоставлю вам шаблон для написания индукционных доказательств, адаптированный из «Справочника по математической индукции » Дэвида Гандерсона (что-то мне подсказывает, кстати, что вам действительно понравится эта книга).{n + 1} -1} {r-1}. \ tag {1}
$$
Ваша конкретная проблема решается установкой $ r = 2 $ в $ (1) $. Я действительно доказал $ (1) $ по индукции некоторое время назад, но я не могу найти этот вопрос (либо он был удален, либо я просто не могу его найти). Тем не менее, вы должны хотя бы знать, что ваша проблема действительно связана с экземпляром более общего сценария.
Тем не менее, вы должны хотя бы знать, что ваша проблема действительно связана с экземпляром более общего сценария.
Ваша конкретная проблема: Я собираюсь предоставить то, что я считаю хорошим описанием вашей конкретной проблемы (примечание: читайте, только если вы хотите полное решение).{k + 2} -1,
\ end {align}
мы видим, что следует правая часть $ S (k + 1) $. На этом индуктивный шаг завершен.
Таким образом, по математической индукции для всех $ n \ geq 0 выполняется S (n) $. $ \ Box $
Шаблон: Как и было обещано, вот шаблон, который вы можете использовать с этого момента, должен очень помочь вам в написании четких индукционных доказательств.
17. Натуральные числа и индукция — логика и доказательство 3.18.4 документация
Эта глава знаменует собой переход от абстрактного к конкретному.Рассмотрение математической вселенной с точки зрения множеств, отношений и функций дает нам полезные способы размышления о математических объектах и структурах и отношениях между ними. Однако в какой-то момент нам нужно начать думать о конкретных математических объектах и структурах, и натуральные числа — хорошее место для начала. Математик девятнадцатого века Леопольд Кронекер однажды провозгласил: «Бог создал целые числа; все остальное — дело рук человека ». Под этим он имел в виду, что натуральные числа (и целые числа, которые мы также обсудим ниже) являются фундаментальным компонентом математической вселенной, и что многие другие объекты и структуры, представляющие интерес, могут быть построены из них.
Однако в какой-то момент нам нужно начать думать о конкретных математических объектах и структурах, и натуральные числа — хорошее место для начала. Математик девятнадцатого века Леопольд Кронекер однажды провозгласил: «Бог создал целые числа; все остальное — дело рук человека ». Под этим он имел в виду, что натуральные числа (и целые числа, которые мы также обсудим ниже) являются фундаментальным компонентом математической вселенной, и что многие другие объекты и структуры, представляющие интерес, могут быть построены из них.
В этой главе мы рассмотрим натуральные числа и основные принципы, которые ими управляют. В главе 18 мы увидим, что даже базовые операции, такие как сложение и умножение, могут быть определены с помощью описанных здесь средств, а их свойства вытекают из этих основных принципов. Однако наша презентация в этой главе останется неформальной. В главе 19 мы увидим, как эти принципы проявляются в теории чисел, одном из старейших и наиболее почтенных разделов математики.
17.1. Принцип индукции
Набор натуральных чисел — это набор
\ [\ mathbb {N} = \ {0, 1, 2, 3, \ ldots \}. \]
В прошлом мнения расходились относительно того, должен ли набор натуральных чисел начинаться с 0 или 1, но в наши дни большинство математиков принимают их за начало с 0. Логики часто называют функцию \ (s (n) = n + 1 \) функция-преемник , поскольку она отображает каждое натуральное число \ (n \) на следующее за ним. Что делает натуральные числа особенными, так это то, что они сгенерированы числом ноль и функцией-преемником, то есть единственный способ построить натуральное число — это начать с \ (0 \) и применить функцию-преемник до конечного много раз.С фундаментальной точки зрения, здесь существует опасность зайти в круг, потому что неясно, как мы можем объяснить, что значит применить функцию «конечное число раз», не говоря о самих натуральных числах. Но следующий принцип, известный как принцип индукции , описывает это существенное свойство натуральных чисел некруглым образом.
Принцип индукции. Пусть \ (P \) — любое свойство натуральных чисел.Предположим, что \ (P \) имеет ноль, и всякий раз, когда \ (P \) имеет натуральное число \ (n \), то оно имеет своего преемника \ (n + 1 \). Тогда \ (P \) выполняется для любого натурального числа.
Это отражает образ натуральных чисел, порождаемых нулем и последующей операцией: покрывая нулевой и последующий случаи, мы заботимся обо всех натуральных числах.
Принцип индукции дает рецепт для доказательства того, что каждое натуральное число обладает определенным свойством: показать, что \ (P \) выполняется для любого натурального числа, показать, что оно верно для \ (0 \), и показать, что всякий раз, когда оно выполняется некоторого числа \ (n \), то имеет место \ (n + 1 \).Эта форма доказательства называется доказательством по индукции . Первая требуемая задача называется базовым случаем , а вторая требуемая задача называется вводным этапом . Шаг индукции требует временной фиксации натурального числа \ (n \), предполагая, что \ (P \) выполняется для \ (n \), а затем показывает, что \ (P \) выполняется для \ (n + 1 \). В этом контексте предположение, что \ (P \) выполняется для \ (n \), называется индуктивной гипотезой .
Шаг индукции требует временной фиксации натурального числа \ (n \), предполагая, что \ (P \) выполняется для \ (n \), а затем показывает, что \ (P \) выполняется для \ (n + 1 \). В этом контексте предположение, что \ (P \) выполняется для \ (n \), называется индуктивной гипотезой .
Вы можете представить доказательство по индукции как метод одновременного сбивания бесконечного потока домино.{n + 2} — 1. \ end {split} \]
В обозначениях логики первого порядка, если мы напишем \ (P (n) \), чтобы обозначить, что \ (P \) выполняется для \ (n \), мы могли бы выразить принцип индукции следующим образом:
\ [P (0) \ клин \ forall n \; (P (n) \ to P (n + 1)) \ to \ forall n \; P (n). \]
Но обратите внимание, что принцип индукции гласит, что аксиома имеет значение для каждого свойства \ (P \), что означает, что мы должны правильно использовать универсальный квантор и для этого:
\ [\ forall P \; (P (0) \ клин \ forall n \; (P (n) \ to P (n + 1)) \ to \ forall n \; P (n)). \]
\]
Количественная оценка свойств выводит нас из области логики первого порядка; поэтому индукция — это принцип второго порядка.
Образец доказательства по индукции еще более естественно выражается следующим естественным правилом дедукции:
Вам следует подумать о том, как некоторые доказательства в этой главе могут быть представлены формально с использованием естественной дедукции.
В качестве другого примера доказательства по индукции выведем формулу, которая для любого конечного множества \ (S \) определяет количество подмножеств \ (S \).n \) подмножества \ (S \).
Доказательство. Воспользуемся индукцией по \ (n \). В базовом случае есть только один набор с элементами \ (0 \), пустой набор, и есть ровно одно подмножество пустого набора, как требуется.
В индуктивном случае предположим, что \ (S \) имеет \ (n + 1 \) элементов. Пусть \ (a \) — любой элемент из \ (S \), и пусть \ (S ‘\) — множество, содержащее оставшиеся \ (n \) элементы. Чтобы подсчитать подмножества \ (S \), мы разделим их на две группы.
Чтобы подсчитать подмножества \ (S \), мы разделим их на две группы.
Сначала рассмотрим подмножества \ (S \), не содержащие \ (a \).{n + 1} \) подмножеств \ (S \), если требуется.
Мы видели, что существует соответствие между свойствами домена и подмножествами домена. Для каждого свойства \ (P \) натуральных чисел мы можем рассмотреть набор \ (S \) натуральных чисел с этим свойством, а для каждого набора натуральных чисел мы можем рассмотреть свойство нахождения в этом наборе. Например, мы можем говорить о свойстве быть четным или говорить о множестве четных чисел. При таком соответствии принцип индукции можно представить следующим образом:
Принцип индукции. Пусть \ (S \) — любой набор натуральных чисел, содержащий \ (0 \) и замкнутый относительно операции преемника. Тогда \ (S = \ mathbb {N} \).
Здесь утверждение, что \ (S \) «закрыто относительно операции-преемника», означает, что всякий раз, когда число \ (n \) находится в \ (S \), то же самое и \ (n + 1 \).
17.2. Варианты индукции
В этом разделе мы рассмотрим варианты принципа индукции, которые часто бывают полезными. Важно понимать, что каждый из них может быть оправдан с использованием принципа индукции, изложенного в последнем разделе, поэтому их не нужно рассматривать как фундаментальные.
Первый — это не очень хорошая встряска: вместо того, чтобы начинать с \ (0 \), мы можем начать с любого натурального числа, \ (m \).
Принцип индукции от начальной точки. Пусть \ (P \) — любое свойство натуральных чисел, и пусть \ (m \) — любое натуральное число. Предположим, что \ (P \) имеет место для \ (m \), и всякий раз, когда \ (P \) имеет натуральное число \ (n \), большее или равное \ (m \), то оно верно для его преемника \ (п + 1 \). Тогда \ (P \) выполняется для любого натурального числа, большего или равного \ (m \).{n + 1}. \ end {split} \]
В качестве другого примера давайте выведем формулу для суммы углов в выпуклом многоугольнике. Многоугольник называется выпуклым , если каждая линия между двумя вершинами остается внутри многоугольника. Мы примем без доказательства визуально очевидный факт, что любой выпуклый многоугольник с более чем тремя сторонами можно подразделить на треугольник и выпуклый многоугольник с одной стороной меньше, а именно, закрывая любые две последовательные стороны, чтобы образовать треугольник. Мы также примем без доказательства основной геометрический факт, что сумма углов любого треугольника равна 180 градусам.
Многоугольник называется выпуклым , если каждая линия между двумя вершинами остается внутри многоугольника. Мы примем без доказательства визуально очевидный факт, что любой выпуклый многоугольник с более чем тремя сторонами можно подразделить на треугольник и выпуклый многоугольник с одной стороной меньше, а именно, закрывая любые две последовательные стороны, чтобы образовать треугольник. Мы также примем без доказательства основной геометрический факт, что сумма углов любого треугольника равна 180 градусам.
Теорема. Для любого \ (n \ geq 3 \) сумма углов любого выпуклого \ (n \) — угольника равна \ (180 (n — 2) \).
Доказательство. В базовом случае, когда \ (n = 3 \), это сводится к утверждению, что сумма углов в любом треугольнике равна 180 градусам.
Для шага индукции предположим, что \ (n \ geq 3 \), и пусть \ (P \) — выпуклый \ ((n + 1) \) — угольник. Разделите \ (P \) на треугольник и \ (n \) — угольник. По индуктивным предположениям сумма углов \ (n \) — угольника равна \ (180 (n-2) \) градусам, а сумма углов треугольника равна \ (180 \) градусам.Меры этих углов вместе составляют сумму углов \ (P \), в сумме \ (180 (n-2) + 180 = 180 (n-1) \) градусов.
По индуктивным предположениям сумма углов \ (n \) — угольника равна \ (180 (n-2) \) градусам, а сумма углов треугольника равна \ (180 \) градусам.Меры этих углов вместе составляют сумму углов \ (P \), в сумме \ (180 (n-2) + 180 = 180 (n-1) \) градусов.
Для нашего второго примера мы рассмотрим принцип полной индукции , также иногда известной как полная индукция .
Принцип полной индукции. Пусть \ (P \) будет любым свойством, которое удовлетворяет следующему: для любого натурального числа \ (n \), всякий раз, когда \ (P \) выполняется для каждого числа, меньшего, чем \ (n \), оно также выполняется для \ (n \).Тогда \ (P \) выполняется для любого натурального числа.
Обратите внимание, что нет необходимости выделять особый случай для нуля: для любого свойства \ (P \), \ (P \) имеет место для всех натуральных чисел, меньших нуля, по той тривиальной причине, что нет любой! Так, в частности, любое такое свойство автоматически имеет нулевое значение.
Заметьте также, что если такое свойство \ (P \) выполняется для каждого числа, меньшего, чем \ (n \), то оно также выполняется для каждого числа, меньшего, чем \ (n + 1 \) (почему?). Итак, для такого \ (P \) из обычного принципа индукции следует, что для любого натурального числа \ (n \), \ (P \) выполняется для любого натурального числа, меньшего, чем \ (n \).Но это всего лишь окольный способ сказать, что \ (P \) выполняется для любого натурального числа. Другими словами, мы обосновали принцип полной индукции с помощью обычной индукции.
Чтобы использовать принцип полной индукции, мы просто должны позволить \ (n \) быть любым натуральным числом и показать, что \ (P \) выполняется для \ (n \), предполагая, что оно выполняется для каждого меньшего числа. Сравните это с обычным принципом индукции, который требует от нас показать \ (P (n + 1) \), предполагая только \ (P (n) \). Следующий пример использования этого принципа дословно взят из введения к этой книге:
Теорема. Каждое натуральное число, большее или равное 2, может быть записано как произведение простых чисел.
Каждое натуральное число, большее или равное 2, может быть записано как произведение простых чисел.
Доказательство. Продолжаем индукцией по \ (n \). Пусть \ (n \) будет любым натуральным числом больше 2. Если \ (n \) простое число, мы закончили; мы можем рассматривать саму \ (n \) как продукт с одним множителем. В противном случае \ (n \) составно, и мы можем написать \ (n = m \ cdot k \), где \ (m \) и \ (k \) меньше, чем \ (n \), но больше 1. По Согласно индуктивной гипотезе каждое из \ (m \) и \ (k \) может быть записано как произведение простых чисел:
\ [\ begin {split} m = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \\
k = q_1 \ cdot q_2 \ cdot \ ldots \ cdot q_v.\ end {split} \]
Но тогда у нас
\ [п = m \ cdot k = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \ cdot q_1 \ cdot
q_2 \ cdot \ ldots \ cdot q_v. \]
Мы видим, что \ (n \) — произведение простых чисел, что и требовалось.
Наконец, мы рассмотрим другую формулировку индукции, известную как принцип наименьшего элемента.
Принцип наименьшего элемента. Предположим, что \ (P \) — некоторое свойство натуральных чисел, и предположим, что \ (P \) имеет место для некоторого \ (n \).Тогда существует наименьшее значение \ (n \), для которого выполняется \ (P \).
Фактически, используя классические рассуждения, это эквивалентно принципу полной индукции. Чтобы убедиться в этом, рассмотрим противоположность приведенного выше утверждения: «если не существует наименьшего значения, для которого выполняется \ (P \), то \ (P \) не имеет никакого натурального числа». Пусть \ (Q (n) \) будет свойством «\ (P \) не соответствует , а не для \ (n \)». Утверждение, что не существует наименьшего значения, для которого выполняется \ (P \), означает, что для каждого \ (n \), если \ (P \) выполняется в \ (n \), то оно имеет некоторое число, меньшее, чем \ ( п \); и это эквивалентно утверждению, что для каждого \ (n \), если \ (Q \) не выполняется в \ (n \), то существует меньшее значение, для которого \ (Q \) не выполняется . И , что эквивалентно утверждению, что если \ (Q \) выполняется для каждого числа, меньшего, чем \ (n \), то это верно и для \ (n \). Точно так же утверждение, что \ (P \) не выполняется ни для какого натурального числа, равносильно утверждению, что \ (Q \) выполняется для любого натурального числа. Другими словами, заменив принцип наименьшего элемента на противоположный и заменив \ (P \) на «not \ (Q \)», мы получим принцип полной индукции. Поскольку каждое утверждение эквивалентно своему противоположному, и каждый предикат имеет свою отрицательную версию, эти два принципа одинаковы.
И , что эквивалентно утверждению, что если \ (Q \) выполняется для каждого числа, меньшего, чем \ (n \), то это верно и для \ (n \). Точно так же утверждение, что \ (P \) не выполняется ни для какого натурального числа, равносильно утверждению, что \ (Q \) выполняется для любого натурального числа. Другими словами, заменив принцип наименьшего элемента на противоположный и заменив \ (P \) на «not \ (Q \)», мы получим принцип полной индукции. Поскольку каждое утверждение эквивалентно своему противоположному, и каждый предикат имеет свою отрицательную версию, эти два принципа одинаковы.
Поэтому неудивительно, что принцип наименьшего элемента можно использовать почти так же, как принцип полной индукции. Вот, например, формулировка предыдущего доказательства в этих терминах. Обратите внимание, что это сформулировано как доказательство от противоречия.
Теорема. Каждое натуральное число, большее 2, может быть записано как произведение простых чисел.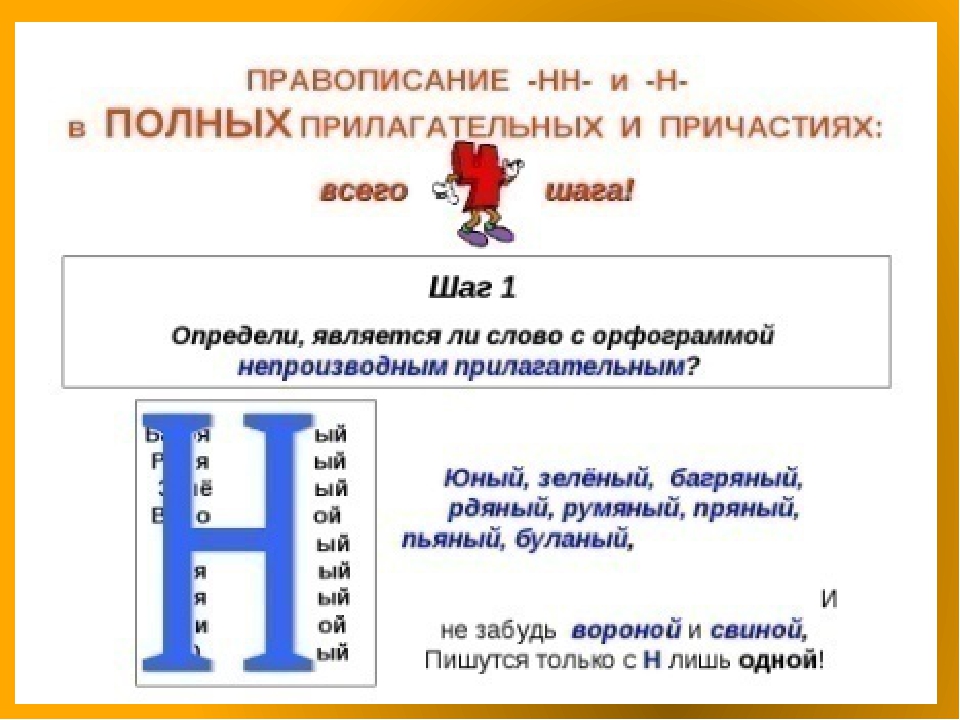
Доказательство. Предположим противное, что некоторое натуральное число, большее или равное 2, не может быть записано как произведение простых чисел.По принципу наименьшего элемента есть наименьший такой элемент; назовите это \ (n \). Тогда \ (n \) не является простым числом, и, поскольку оно больше или равно 2, оно должно быть составным. Следовательно, мы можем написать \ (n = m \ cdot k \), где \ (m \) и \ (k \) меньше, чем \ (n \), но больше 1. По предположению о \ (n \) каждый \ (m \) и \ (k \) можно записать как произведение простых чисел:
\ [\ begin {split} m = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \\
k = q_1 \ cdot q_2 \ cdot \ ldots \ cdot q_v. \ end {split} \]
Но тогда у нас
\ [п = m \ cdot k = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \ cdot q_1 \ cdot
q_2 \ cdot \ ldots \ cdot q_v.\]
Мы видим, что \ (n \) является произведением простых чисел, что противоречит тому факту, что \ (n \) не может быть
написано как произведение простых чисел. n \).
n \).
Что более интересно, так это то, что два вышеуказанных условия определяют все значения \ (f \), то есть есть ровно одна функция, удовлетворяющая приведенной выше спецификации. Фактически, не имеет значения, что \ (f \) принимает значения в натуральных числах; он может принимать значения в любом другом домене. Все, что необходимо, — это значение \ (f (0) \) и способ вычислить значение \ (f (n + 1) \) в терминах \ (n \) и \ (f (n) \ ). Это то, что утверждает принцип определения с помощью рекурсии:
Принцип определения посредством рекурсии .Пусть \ (A \) — любое множество, и предположим, что \ (a \) находится в \ (A \), и \ (g: \ mathbb {N} \ times A \ to A \). Тогда существует единственная функция \ (f \), удовлетворяющая следующим двум пунктам:
\ [\ begin {split} f (0) & = a \\
f (n + 1) & = g (n, f (n)). \ end {split} \]
Принцип рекурсивного определения предъявляет сразу два утверждения: во-первых, что существует функция \ (f \), удовлетворяющая приведенным выше предложениям, и, во-вторых, что любые две функции \ (f_1 \) и \ (f_2 \) удовлетворяют эти предложения равны, то есть они имеют одинаковые значения для всех входных данных. В примере, с которого мы начали этот раздел, \ (A \) — это просто \ (\ mathbb {N} \) и \ (g (n, f (n)) = 2 \ cdot f (n) \).
В примере, с которого мы начали этот раздел, \ (A \) — это просто \ (\ mathbb {N} \) и \ (g (n, f (n)) = 2 \ cdot f (n) \).
В некоторых аксиоматических рамках принцип рекурсивного определения может быть оправдан с помощью принципа индукции. В других случаях принцип индукции можно рассматривать как частный случай принципа рекурсивного определения. На данный момент мы будем просто считать, что оба они являются фундаментальными свойствами натуральных чисел.
В качестве другого примера рекурсивного определения рассмотрим функцию \ (g: \ mathbb {N} \ to \ mathbb {N} \), рекурсивно определяемую следующими предложениями:
\ [\ begin {split} g (0) & = 1 \\
g (n + 1) & = (n + 1) \ cdot g (n) \ end {split} \]
Попробуйте вычислить первые несколько значений.Развернув определение, мы видим, что \ (g (n) = 1 \ cdot 2 \ cdot 3 \ cdot \ ldots \ cdot (n-1) \ cdot n \) для каждого \ (n \); действительно, определение с помощью рекурсии обычно является правильным способом сделать выражения с использованием «…» точными. Значение \ (g (n) \) читается как «\ (n \) факториал» и записывается \ (n! \).
Значение \ (g (n) \) читается как «\ (n \) факториал» и записывается \ (n! \).
Действительно, обозначение суммирования
\ [\ sum_ {i и обозначение продукта \ [\ prod_ {i также можно сделать точным с помощью рекурсивных определений.Например, функция \ (k (n) = \ sum_ {i \ [\ begin {split} k (0) & = 0 \\ Индукция и рекурсия — это взаимодополняющие принципы, и обычно способ доказать что-то о рекурсивно определенной функции — это использовать принцип индукции. Например, следующая теорема дает формулы для суммы \ (1 + 2 + \ ldots + n \) в терминах \ (n \). Теорема.2 + 3n + 2} {2} \\ Существует столько же вариаций принципа рекурсивного определения, сколько и вариаций принципа индукции. \ [\ begin {split} \ mathrm {fib} (0) & = 0 \\ Вычисляя значения \ (\ mathrm {fib} \) на \ (0, 1, 2, \ ldots \), получаем \ [0, 1, 1, 2, 3, 5, 8, 13, 21, \ ldots \] Здесь после второго числа каждое последующее число представляет собой сумму двух предшествующих ему значений.Это известно как последовательность Фибоначчи , а соответствующие числа известны как числа Фибоначчи . Обычное математическое представление будет писать \ (F_n \) вместо \ (\ mathrm {fib} (n) \) и указывать последовательность следующими уравнениями: \ [F_0 = 0, \ quad F_1 = 1, \ quad F_ {n + 2} = F_ {n + 1} + F_n \] Но теперь вы можете распознать такую спецификацию как неявное обращение к принципу определения посредством рекурсии. Мы просим вас доказать некоторые факты о последовательности Фибоначчи в упражнениях ниже. Фактически, мы можем даже использовать принцип рекурсивного определения, чтобы определить самые основные операции с натуральными числами и показать, что они обладают свойствами, которые мы ожидаем от них. С фундаментальной точки зрения мы можем охарактеризовать натуральные числа как набор \ (\ mathbb {N} \) с выделенным элементом \ (0 \) и функцией \ (\ mathrm {succ} (m) \) , который для каждого натурального числа \ (m \) возвращает его преемника . Они удовлетворяют следующему: \ (0 \ neq \ mathrm {succ} (m) \) для любого \ (m \) в \ (\ mathbb {N} \). Для каждого \ (m \) и \ (n \) в \ (\ mathbb {N} \), если \ (m \ neq n \), то \ (\ mathrm {succ} (m) \ neq \ mathrm {succ} (п) \). Другими словами, \ (\ mathrm {succ} \) — это инъективный . Если \ (A \) — любое подмножество \ (\ mathbb {N} \) со свойством, что \ (0 \) находится в \ (A \), и всякий раз, когда \ (n \) находится в \ (A \ ), то \ (\ mathrm {succ} (n) \) находится в \ (A \), тогда \ (A = \ mathbb {N} \). Последний пункт можно переформулировать как принцип индукции: Предположим, что \ (P (n) \) — любое свойство натуральных чисел, такое, что \ (P \) выполняется для \ (0 \), и для любого \ (n \) \ (P (n) \) влечет \ (P (\ mathrm {succ} (п)) \).Тогда каждое \ (P \) выполняется любого натурального числа. Помните, что этот принцип можно использовать для обоснования принципа определения рекурсией: Пусть \ (A \) — любое множество, \ (a \) — любой элемент из \ (A \), и пусть \ (g (n, m) \) — любая функция из \ (\ mathbb {N} \ раз A \) к \ (A \). Тогда существует единственная функция \ (f: \ mathbb {N} \ to A \), удовлетворяющая следующим двум пунктам: Мы можем использовать принцип рекурсивного определения для определения сложения с помощью следующих двух предложений: \ [\ begin {split} m + 0 & = m \\ Обратите внимание, что мы фиксируем \ (m \) и рассматриваем это как функцию от \ (n \).Если мы напишем \ (1 = \ mathrm {succ} (0) \), \ (2 = \ mathrm {succ} (1) \) и т. Д., Легко доказать \ (n + 1 = \ mathrm {succ} (n) \) из определения сложения. Мы можем перейти к определению умножения, используя следующие два предложения: \ [\ begin {split} m \ cdot 0 & = 0 \\ Мы также можем определить функцию-предшественницу с помощью \ [\ begin {split} \ mathrm {pred} (0) & = 0 \\ Мы можем определить усеченное вычитание на \ [\ begin {split} m \ dot — 0 & = m \\ С помощью этих определений и принципа индукции можно доказать все следующие тождества: \ (n \ neq 0 \) подразумевает \ (\ mathrm {succ} (\ mathrm {pred} (n)) = n \) \ (0 + n = n \) \ (\ mathrm {succ} (m) + n = \ mathrm {succ} (m + n) \) \ ((m + n) + k = m + (n + k) \) \ (т + п = п + т \) \ (m (n + k) = mn + mk \) \ (0 \ cdot n = 0 \) \ (1 \ cdot n = n \) \ ((mn) k = m (nk) \) \ (mn = нм \) Здесь мы сделаем первые пять, а оставшиеся оставим в качестве упражнений. Предложение. Для каждого натурального числа \ (n \), если \ (n \ neq 0 \), то \ (\ mathrm {succ} (\ mathrm {pred} (n)) = n \). Доказательство. По индукции по \ (n \). Мы исключили случай, когда \ (n \) равно \ (0 \), поэтому нам нужно только показать, что утверждение верно для \ (\ mathrm {succ} (n) \). Но в этом случае у нас есть \ (\ mathrm {succ} (\ mathrm {pred} (\ mathrm {succ} (n)) = \ mathrm {succ} (n) \) по второму определяющему предложению функции-предшественника Предложение. Для каждого \ (n \), \ (0 + n = n \). Доказательство. По индукции по \ (n \). У нас есть \ (0 + 0 = 0 \) по первому определяющему предложению для сложения. И, предполагая \ (0 + n = n \), мы имеем \ (0 + \ mathrm {succ} (n) = \ mathrm {succ} (0 + n) = n \), используя второе определяющее предложение для сложения. Предложение. Для каждого \ (m \) и \ (n \), \ (\ mathrm {succ} (m) + n = \ mathrm {succ} (m + n) \). Доказательство. Зафиксируйте \ (m \) и используйте индукцию по \ (n \). Тогда \ (n = 0 \), мы имеем \ (\ mathrm {succ} (m) + 0 = \ mathrm {succ} (m) = \ mathrm {succ} (m + 0) \), используя первое определение пункт для дополнения.Предполагая, что утверждение верно для \ (n \), имеем \ [\ begin {split} \ mathrm {succ} (m) + \ mathrm {succ} (n) & = \ mathrm {succ} (\ mathrm {succ} (m) + n) \\ , используя индуктивную гипотезу и второе определяющее предложение для сложения. Предложение. Для любых \ (m \), \ (n \) и \ (k \), \ ((m + n) + k = m + (n + k) \). Доказательство. По индукции по \ (k \).Случай, когда \ (k = 0 \), прост, и на шаге индукции имеем \ [\ begin {split} (m + n) + \ mathrm {succ} (k) & = \ mathrm {succ} ((m + n) + k) \\ , используя индуктивную гипотезу и определение сложения. Предложение. Для каждой пары натуральных чисел \ (m \) и \ (n \), \ (m + n = n + m \). Доказательство. По индукции по \ (n \). Базовый случай легко получить, используя второе предложение выше. На индуктивном шаге имеем \ [\ begin {split} m + \ mathrm {succ} (n) & = \ mathrm {succ} (m + n) \\ , используя третье предложение выше. Продолжая, как в предыдущем разделе, мы можем установить все основные свойства натуральных чисел, которые играют роль в повседневной математике.Суммируем основные из них: \ [\ begin {split} m + n & = n + m \ quad \ text {(коммутативность сложения)} \\ В обычном математическом аргументе или вычислении они могут использоваться без явного обоснования.У нас также есть следующие объекты недвижимости: Мы можем определить \ (m \ le n \), «\ (m \) меньше или равно \ (n \)», чтобы обозначить, что существует \ (k \) такое, что \ (m + k = п \). Если мы это сделаем, нетрудно показать, что отношение «меньше или равно» удовлетворяет всем следующим свойствам для каждого \ (n \), \ (m \) и \ (k \): \ (n \ le n \) ( рефлексивность ) если \ (n \ le m \) и \ (m \ le k \), то \ (n \ le k \) ( транзитивность ) если \ (n \ le m \) и \ (m \ le n \), то \ (n = m \) ( антисимметрия ) для всех \ (n \) и \ (m \), либо \ (n \ le m \), либо \ (m \ le n \) истинно ( совокупность ) если \ (n \ le m \), то \ (n + k \ le m + k \) если \ (n + k \ le m + k \), то \ (n \ le m \) если \ (n \ le m \), то \ (nk \ le mk \) если \ (m \ ge n \), то \ (m = n \) или \ (m \ ge n + 1 \) \ (0 \ ле п \) Помните из главы 13, что первые четыре элемента утверждают, что \ (\ le \) является линейным порядком.Обратите внимание, что когда мы пишем \ (m \ ge n \), мы имеем в виду \ (n \ le m \). Как обычно, мы можем определить \ (m Предложение. Для каждого \ (m \), \ (m + 1 \ not \ le 0 \). Доказательство. В противном случае у нас было бы \ ((m + 1) + k = (m + k) + 1 = 0 \) для некоторого \ (k \). В частности, взяв \ (m = 0 \), мы имеем \ (1 \ not \ le 0 \). Предложение. Мы имеем \ (m Доказательство. Предположим, \ (m В другом направлении предположим \ (m + 1 \ le n \). Тогда \ (m \ le n \). У нас также есть \ (m \ ne n \), так как если бы \ (m = n \), у нас было бы \ (m + 1 \ le m + 0 \) и, следовательно, \ (1 \ le 0 \); противоречие . Аналогичным образом мы можем показать, что \ (m \ (n если \ (n для всех \ (n \) и \ (m \), либо \ (n если \ (n если \ (k> 0 \) и \ (n если \ (m> n \), то \ (m = n + 1 \) или \ (m> n + 1 \) для всех \ (n \), \ (n = 0 \) или \ (n> 0 \) Первые три элемента означают, что \ (<\) является строгим линейным порядком, а указанные выше свойства означают, что \ (\ le \) является связанным линейным порядком в смысле, описанном в разделе 13.1. Доказательство . Мы докажем некоторые из этих свойств, используя предыдущую характеризацию отношения «меньше чем». Первое свойство очевидно: мы знаем \ (n \ le n + 1 \), и если бы у нас было \ (n + 1 \ le n \), мы должны были бы иметь \ (n = n + 1 \), противоречие. . Для второго свойства предположим \ (n Что касается третьего, мы знаем, что либо \ (n \ le m \), либо \ (m \ le n \).Если \ (m = n \), все готово, в противном случае мы имеем либо \ (n Для четвертого, если \ (n + 1 \ le m \), мы имеем \ (n + 1 + k = (n + k) + 1 \ le m + k \), как требуется. Для пятого предположим, что \ (k> 0 \), то есть \ (k \ ge 1 \). Если \ (n Остальные доказательства оставляем читателю в качестве упражнения. Вот некоторые дополнительные свойства \ (<\) и \ (\ le \): \ (n \ (n + 1> n \) если \ (n если \ (n \ le m \) и \ (m если \ (m> n \), то \ (m \ ge n + 1 \) если \ (m \ ge n \), то \ (m + 1> n \) если \ (n + k если \ (nk Это подтверждается приведенным выше.Более того, набор принципов, которые мы только что рассмотрели, можно использовать для обоснования основных фактов о натуральных числах, которые снова обычно принимаются как должное в неформальных математических аргументах. Предложение. Если \ (n \) и \ (m \) — натуральные числа такие, что \ (n + m = 0 \), то \ (n = m = 0 \). Доказательство. Сначала докажем, что \ (m = 0 \). Мы знаем, что \ (m = 0 \) или \ (m> 0 \). Предположим, что \ (m> 0 \). Тогда \ (n + m> n + 0 = n \). Поскольку \ (n \ ge 0 \), заключаем, что \ (n + m> 0 \), что противоречит тому факту, что \ (n + m = 0 \).Поскольку \ (m> 0 \) приводит к противоречию, мы должны иметь \ (m = 0 \). Теперь мы можем легко заключить, что \ (n = 0 \), поскольку \ (n = n + 0 = n + m = 0 \). Следовательно, \ (n = m = 0 \). Предложение. Если \ (n \) — такое натуральное число, что \ (n <3 \), то \ (n = 0 \), \ (n = 1 \) или \ (n = 2 \). Доказательство. В этом доказательстве мы неоднократно используем то свойство, что если \ (m> n \), то \ (m = n + 1 \) или \ (m> n + 1 \). Поскольку \ (2 + 1 = 3> n \), заключаем, что либо \ (2 + 1 = n + 1 \), либо \ (2 + 1> n + 1 \).В первом случае заключаем \ (n = 2 \), и все готово. Во втором случае заключаем \ (2> n \), откуда следует, что либо \ (2 = n + 1 \), либо \ (2> n + 1 \). В первом случае заключаем \ (n = 1 \), и все готово. Во втором случае мы заключаем \ (1> n \) и в последний раз обращаемся к общему принципу, представленному выше, чтобы заключить, что либо \ (1 = n + 1 \), либо \ (1> n + 1 \). В первом случае заключаем \ (n = 0 \), и все снова готово. Во втором случае заключаем, что \ (0> n \).Это приводит к противоречию, поскольку теперь \ (0> n \ ge 0 \), следовательно, \ (0> 0 \), что противоречит иррефлексивности \ (> \). Натуральные числа предназначены для подсчета дискретных величин, но у них есть досадный недостаток: можно вычесть \ (n \) из \ (m \), если \ (n \) меньше или равно \ (m \ ), но не если \ (m \) больше, чем \ (n \). Набор из целых чисел , \ (\ mathbb {Z} \) дополняет натуральные числа отрицательными значениями, чтобы можно было выполнять вычитание полностью: \ [\ mathbb {Z} = \ {\ ldots, -3, -2, -1, 0, 1, 2, 3, \ ldots \}.\] В следующей главе мы увидим, что целые числа могут быть расширены до рациональных чисел , , действительных чисел , и комплексных чисел , , каждое из которых служит полезным целям. Однако при работе с дискретными величинами целые числа уведут нас довольно далеко. Вы можете представить себе целые числа как состоящие из двух копий натуральных чисел, положительной и отрицательной, с общим нулем. И наоборот, когда у нас есть целые числа, вы можете думать о натуральных числах как о состоящих из неотрицательных целых чисел, то есть целых чисел, которые больше или равны \ (0 \).Большинство математиков стирают различие между ними, хотя мы увидим, что в Lean, например, натуральные числа и целые числа представляют два разных типа данных. Большинство свойств натуральных чисел, перечисленных в последнем разделе, также имеют целые числа, но не все. Например, это уже не тот случай, когда \ (n + 1 \ neq 0 \) для каждого \ (n \), поскольку утверждение ложно для \ (n = -1 \). В другом примере это не тот случай, когда каждое целое число либо равно \ (0 \), либо больше, чем \ (0 \), поскольку это не соответствует отрицательным целым числам. Ключевым свойством, которым обладают целые числа, которое отличает их от натуральных чисел, является то, что для каждого целого числа \ (n \) существует значение \ (- n \) со свойством \ (n + (-n) = 0 \). Значение \ (- n \) называется отрицанием \ (n \). Мы определяем вычитание \ (n — m \) как \ (n + (-m) \). Для любого целого числа \ (n \) мы также определяем абсолютное значение из \ (n \), записанное \ (| n | \), как \ (n \), если \ (n \ geq 0 \), и \ (- n \) в противном случае. Мы больше не можем использовать доказательство индукцией по целым числам, потому что индукция не распространяется на отрицательные числа.Но мы можем использовать индукцию, чтобы показать, например, что свойство имеет место для каждого неотрицательного целого числа. Более того, мы знаем, что каждое отрицательное целое число является отрицанием положительного. В результате доказательства, включающие целые числа, часто разбиваются на два случая: один случай охватывает неотрицательные целые числа, а другой случай — отрицательные. Запишите принцип полной индукции, используя обозначения символьной логики. Также напишите таким образом принцип наименьшего количества элементов и используйте логические манипуляции, чтобы показать, что они эквивалентны.2 \) как \ (F_ {n + 2} (F_ {n + 1} + F_n) \). Докажите \ (\ sum_ {i Подтвердите следующие две личности: Совет: используйте индукцию по \ (n \) и докажите оба сразу. На шаге индукции раскройте \ (F_ {2n + 3} = F_ {2n + 2} + F_ {2n + 1} \) и аналогично для \ (F_ {2n + 4} \). Особенно сложно доказать второе уравнение. Используйте индуктивную гипотезу и первое тождество, чтобы упростить левую часть, и многократно разверните число Фибоначчи с наивысшим индексом и упростите уравнение, которое вам нужно доказать.0 \) считается степенью 2. Пусть \ (V \) будет непустым набором целых чисел такой, что выполняются следующие два свойства: Если \ (x, y \ in V \), то \ (x — y \ in V \). Если \ (x \ in V \), то каждое кратное \ (x \) является элементом \ (V \). Докажите, что существует некоторый \ (d \ in V \), такой, что \ (V \) равен множеству кратных \ (d \). Подсказка: используйте принцип наименьшего количества элементов. Дайте неформальное, но подробное доказательство того, что для любого натурального числа \ (n \), \ (1 \ cdot n = n \), используя доказательство по индукции, определение умножения и теоремы, доказанные в разделе 17.4. Покажите, что умножение распределяется по сложению. Другими словами, докажите, что для натуральных чисел \ (m \), \ (n \) и \ (k \), \ (m (n + k) = m n + m k \). Вам следует использовать определения сложения и умножения, а также факты, доказанные в Разделе 17.4 (но не более того). Аналогичным образом докажите, что умножение ассоциативно. Вы можете использовать любой из фактов, доказанных в Разделе 17.4 и предыдущем упражнении. Докажите, что умножение коммутативно.{nk} \). Следуя примеру из Раздела 17.5, докажите, что если \ (n \) — натуральное число и \ (n <5 \), то \ (n \) - одно из значений \ (0, 1, 2, 3 \) или \ (4 \). Докажите, что если \ (n \) и \ (m \) — натуральные числа и \ (n m = 1 \), то \ (n = m = 1 \), используя только свойства, перечисленные в Разделе 17.5. Это сложно. Сначала покажите, что \ (n \) и \ (m \) больше \ (0 \) и, следовательно, больше или равны \ (1 \). Затем покажите, что если один из них больше, чем \ (1 \), то \ (n m> 1 \). Докажите любые другие утверждения в Разделе 17.5, которые были заявлены без доказательств. Докажите следующие свойства отрицания и вычитания для целых чисел, используя только свойства отрицания и вычитания, указанные в Разделе 17.6. Если \ (n + m = 0 \), то \ (m = -n \). \ (- 0 = 0 \). Если \ (- n = -m \), то \ (n = m \). \ (т + (п — т) = п \). \ (- (n + m) = -n — m \). Если \ (m Если \ (m \ (п \ cdot (-m) = -nm \). \ (п (m — k) = нм — nk \). Если \ (n Предположим, у вас есть бесконечная шахматная доска с натуральными числами, написанными в каждой клетке. Значение в каждом квадрате — это среднее значение четырех соседних квадратов.Докажите, что все значения на шахматной доске равны. Докажите, что каждое натуральное число можно записать как сумму различных непоследовательных чисел Фибоначчи. Например, \ (22 = 1 + 3 + 5 + 13 \) не допускается, поскольку 3 и 5 — последовательные числа Фибоначчи, но разрешено \ (22 = 1 + 21 \). Индукция Разделы: Введение, Пуск н … и: Так (*) Предположим, для 2 + 2 2 + 2 3 + 2 4 +… + 2 к Пуск п 2 + 2 2 Затем (*) Обратите внимание на эту распространенную технику: Пуск н Так (*) Пуск п 12 + 23 …которая правая Этот не запускается Пуск н Затем 4 n с 20 Допустим, для n Пуск п Левая сторона [4 k ] + 4 <[2 k ] + 4 Начиная с k 2 к + 4 <2 к + 2 к Тогда 4 ( к +1) Затем Пуск н Тогда выражение Предположим, для n Пуск п Тогда: 8 к +1 = 8 к (8 3) + 3 (8 к 3 к ) Первый член в 8 k (5) Затем (*) << Предыдущая
Вверх | 1 Цитируйте эту статью Стапель, Елизавета. Поделитесь этой страницей! Алгебра — это использование картинок или букв для обозначения чисел. Речь идет об установлении взаимосвязи между разными числами. Например, если N представляет собой число, то N + 9 — это число, которое на 9 больше N. Итак, если N представляет собой число 3, тогда N + 9 — это число 12. Если N представляет собой число 7, то N + 9 — это число 16. Вот 2 важных термина, которые вы должны понять: Алгебраическое выражение и Алгебраическое уравнение. В предыдущем примере N + 9 называется алгебраическим выражением, потому что N может представлять любое число . Если мы запишем это так: N + 9 = 12, мы запишем алгебраическое уравнение. В уравнении N представляет собой конкретное число , а не любое число. N + 9 = 12 означает, что N — число, которое при добавлении к 9 должно дать ответ 12. Таким образом, N может быть только числом 3 , потому что только 3 + 9 равно 12. An алгебраическое выражение говорит нам о взаимосвязи между числами. Алгебраическое уравнение сообщает нам конкретное число, которое дает определенный результат. Перейти к примеру. Поскольку буквы, используемые в алгебре, являются числами, мы можем работать с ними так же, как мы работаем с числами. Пример: M + M = 2M или 1M + 1M = 2M Это означает, что добавленное к самому себе число дает ответ, который вдвое превышает число. Если вы не уверены, просто замените действительные числа как M: 2 + 2 = 4 [M равно 2, а 4 — дважды 2] 3 + 3 = 6 [M равно 3, а 6 равно дважды из 3] Неважно, какое число вы выбрали для M, результат все равно будет вдвое больше этого числа. Таким образом, 2M означает 2 группы M. 2 группы M также могут означать 2 x M.Таким образом, 2 x M = 2M также верно. Аналогично, 5 x H = 5H, и так далее. Просто убедитесь, что в алгебре используется та же буква. Таким образом: R + R + 3R = 5R верно , но R + T = 2RT неверно, потому что R и T представляют два разных числа. Дополнительные примеры: 4S — S = 3S 5 x T = 5T 4N + N — 3N = 2N При работе с алгеброй и числами нам приходится решать их отдельно. Пример 1 2 + N + 2 + 4N = 2 + 2 + N + 4N = 4 + 5N Пример 2 5 — A — 3 + 2A = 5 — 3 + 2A — A = 2 + A Помните, что при работе с алгеброй применяются обычные Правила операций.2 $ — это 225 — 196 = 29 $ Вы можете выразить 22 из 30 чисел как разность двух полных квадратов. В этих решениях наблюдается закономерность: все нечетные числа могут быть представлены разностью двух полных квадратов, а также всех чисел, дающих целое число при делении на четыре. Джошуа из школы Святого Иоанна использовал алгебру, чтобы показать, как могут быть образованы нечетные числа и числа, кратные четырем: Вы можете составить каждое нечетное число, беря последовательные квадраты.2 $. Если $ 2 $ можно записать как разность двух квадратов, то $ (a + b) = 2 $ и $ (a — b) = 1 $, так как $ 2 $ является простым числом, и очевидно, что $ a — b Таким образом, решая одновременные уравнения, $ b = 2 — a $, поэтому $ a — (2 — a) = 1 $, $ 2a = 3 $ и $ a = \ frac {3} {2} $. Таким образом, $ 2 $ нельзя представить как разность двух целых квадратов. Этот метод можно обобщить для любого простого числа $ p $, решив $ (a + b) = p $ и $ (a — b) = 1 $ Любое квадратное число $ n $ можно также записать как разность двух квадратов, взяв $ a = \ sqrt {n} $ и $ b = 0 $. Как правило, число может быть записано как разность двух квадратов, если у него есть два множителя одинаковой четности, поскольку, если $ a + b $ нечетно, а $ a — b $ четно, при сложении двух уравнений мы получит нечетные $ 2a $, поэтому решение не будет целым.2 $ можно переписать в виде $ (a + b) (a-b) $. Это говорит нам о том, что разница между двумя факторами всегда будет, даже если число может быть записано в этой форме. Теперь, чтобы получить четную разницу, нам нужно, чтобы либо $ u $, и $ v $ были нечетными, либо оба были четными. Следовательно, любое число с двумя четными или нечетными множителями может быть записано в этой форме. Это оставляет числа, которые всегда будут иметь один нечетный и один четный множители. Это означает, что $ u $ может быть разделено на два и все равно будет четным, и в то же время $ v $ может быть увеличено вдвое, чтобы оно также стало четным. Это означает, что $ x $ имеет пару факторов, которые оба являются четными, и поэтому могут быть записаны как разность двух квадратов. Если оба множителя нечетные, будет получена и четная разница, поэтому, если при разложении на простые множители $ x $ нет двоек, то x можно записать как разность двух квадратов. Это оставляет случай, когда в факторизации на простые множители приходится ровно одна $ 2 $. Это означает, что один фактор должен содержать $ 2 $, а не другой, и что этими факторами нельзя манипулировать описанным выше способом. Это всегда будет оставлять коэффициенты с нечетной разницей, предполагая, что $ x $ не может быть записано как разность двух квадратов.
k (n + 1) & = k (n) + f (n) \ end {split} \]
& = \ frac {(n + 1) (n + 2)} {2}. \ end {split} \] Например, по аналогии с принципом полной индукции, мы можем указать значение \ (f (n) \) в терминах значений, которые \ (f \) принимает на всех входах, меньших, чем \ (n \). Когда, например, \ (n \ geq 2 \), следующее определение определяет значение функции \ (\ mathrm {fib} (n) \) в терминах двух ее предшественников:
Например, по аналогии с принципом полной индукции, мы можем указать значение \ (f (n) \) в терминах значений, которые \ (f \) принимает на всех входах, меньших, чем \ (n \). Когда, например, \ (n \ geq 2 \), следующее определение определяет значение функции \ (\ mathrm {fib} (n) \) в терминах двух ее предшественников:
\ mathrm {fib} (1) & = 1 \\
\ mathrm {fib} (n + 2) & = \ mathrm {fib} (n + 1) + \ mathrm {fib} (n) \ end {split} \] 17,4. Определение арифметических операций
m + \ mathrm {succ} (n) & = \ mathrm {succ} (m + n) \ end {split} \]
m \ cdot \ mathrm {succ} (n) & = m \ cdot n + m \ end {split} \]
\ mathrm {pred} (\ mathrm {succ} (n)) & = n \ end {split} \]
m \ dot — (\ mathrm {succ} (n)) & = \ mathrm {pred} (m \ dot — n) \ end {split} \]
& = \ mathrm {succ} (\ mathrm {succ} (m + n)) \\
& = \ mathrm {succ} (m + \ mathrm {succ} (n)) \ end {split} \]
& = \ mathrm {succ} (m + (n + k)) \\
& = m + \ mathrm {succ} (n + k) \\
& = m + (n + \ mathrm {succ} (k))) \ end {split} \]
& = \ mathrm {succ} (п + т) \\
& = \ mathrm {succ} (n) + m \ end {split} \] 17,5. Арифметика с натуральными числами
m + (n + k) & = (m + n) + k \ quad \ text {(ассоциативность сложения)} \\
n + 0 & = n \ quad \ text {($ 0 $ — нейтральный элемент для сложения)} \\
n \ cdot m & = m \ cdot n \ quad \ text {(коммутативность умножения)} \\
m \ cdot (n \ cdot k) & = (m \ cdot n) \ cdot k \ quad \ text {(ассоциативность умножения)} \\
n \ cdot 1 & = n \ quad \ text {($ 1 $ — нейтральный элемент для умножения)} \\
n \ cdot (m + k) & = n \ cdot m + n \ cdot k \ quad \ text {(дистрибутивность)} \\
n \ cdot 0 & = 0 \ quad \ text {($ 0 $ — поглощающий элемент для умножения)} \ end {split} \] 17,6. Целые числа
17,7. Упражнения
Индукционные доказательства: рабочие примеры
Доказательства: отработанные примеры (стр.
3 из 3)
Примеры того, где индукция не работает, Примеры работы
Для n
> 1,
2 + 2 2 + 2 3 + 2 4 +… + 2 n
= 2 n +1 2
= 1. Тогда:
работает для n
= 1.
n = k ,
что (*)
держит; то есть
= 2 к +1 2
= к + 1.
+ 2 3 + 2 4 + … + 2 к + 2 к +1
= [2 + 2 2 + 2 3 + 2 4
+ … + 2 к ] + 2 к +1
= [2 k +1 2] + 2 k +1
= 22 к +1 2
= 2 1 2 k +1 2
= 2 к + 1 + 1 2
= 2 ( к +1) +1 2
работает по н
= к + 1.
В « n »
= k + 1 »
шаг, обычно хороший первый шаг — записать всю формулу в
условия к
+1, а затем перерыв
выкл. « н
= k «деталь,
так что вы можете заменить его любым предположением, которое вы сделали о n
= k в предыдущем
шаг.Затем вы манипулируете, упрощаете и пытаетесь переставить вещи, чтобы
получить правую часть формулы через k
+ 1.
Для n
> 1,
12 + 23 + 34 + … + ( n ) ( n +1) = ( n ) ( n +1) ( n +2) / 3
= 1.Авторские права
Элизабет Стапель 2000-2011 Все права защищены
держится для
n = 1. Предположим,
для n
= k , что
(*)
держит; то есть предположим, что
= k + 1.
левая часть (*)
тогда дает нам:
+ 34 +… + ( к ) ( к +1) + ( к +1) (( к +1) +1)
= [12 + 23 + 34 + … + ( k ) ( k +1)] + ( k +1) (( k +1) +1)
= [( k ) ( k +1) ( k +2) / 3] + ( k +1) (( k +1) +1)
= ( k ) ( k +1) ( k +2) / 3 + ( k +1) ( k +2)
= ( к ) ( к +1) ( к +2) / 3 + 3 ( к +1) ( к +2) / 3
= ( к +3) ( к +1) ( к +2) / 3
= ( к +1) ( к +2) ( к +3) / 3
= ( к +1) (( к +1) +1) (( к +1) +2) / 3
сторона (*).
Тогда (*)
работает для всех
п
> 1.
Для n
> 5,
4 n <2 n .
в n
= 1, и включает
неравенство вместо уравнения.(Если вы построите график 4 x
и 2 x
по тем же осям, вы поймете, почему мы должны начинать с n
= 5 вместо
обычный
n = 1.)
= 5.
= 45 = 20 и
2 n
= 2 5 = 32.
<32, тогда (*)
держится на n
= 5.
= k , что
(*)
держит; то есть предположим, что
4 к <2 к
= к + 1.
из (*)
дает нам 4 ( к
+ 1) = 4 к + 4,
и, по предположению,
> 5,
затем 4
<32 <
2 к .Тогда получаем
= 22 к = 2 1 2 к = 2 к +1
<2 к +1 ,
а также (*)
удерживается для n
= к + 1.
(*)
вмещает для всех
п
> 5.
Для всех n
> 1,
8 n
3 n
делится на 5.
= 1.
8 n
3 n
оценивается в 8 1
3 1 = 8 3 = 5,
что явно делится на 5.
= k , что
(*)
держит; то есть 8 k
3 к
делится на 5.
= к + 1.
3 к +1 = 8 к +1 38 к
+ 38 к 3 к +1
= 8 к (5) + 3 (8 к 3 к )
+ 3 (8 k 3 k ) есть
5
как множитель (явно), а второй член делится на 5
(по предположению).Поскольку мы можем разложить на множитель 5
из обоих членов, то все выражение, 8 k (5)
+ 3 (8 к 3 к ) = 8 к +1
3 к +1 ,
должно делиться на 5.
вмещает для n
= k + 1, и
таким образом для всех n
> 1.
| 2 | 3 | Возвращаться
в индекс
как:
«Индукционные доказательства: рабочие примеры». Purplemath .
Доступно по телефону
https://www.purplemath.com/modules/inductn3.htm .
Проверено [Дата] [Месяц] 2016 Алгебра
Работа с алгеброй
30: не работает
Сложение уравнений дает $ 2a = p + 1 $, поэтому $ a = \ frac {p + 1} {2} $.Поскольку $ a — b = 1 $, $ b = a-1 $, поэтому $ b = \ frac {p + 1} {2} — 1 = \ frac {p-1} {2} $. Таким образом, любое нечетное простое число можно записать как разность двух квадратов.
Предположим, что $ u $ и $ v $ — два множителя $ x $ такие, что $ u = a + b $ и $ v = a — b $.
Вычитая два уравнения, получаем $ u — v = 2b $.
Если $ v $ является нечетным множителем $ x $, оно должно иметь разложение на простые множители только нечетных чисел.
Предположим, что $ u $ является четным делителем $ x $ и содержит более одного $ 2 $ в своем разложении на простые множители.