Содержание
Решение задач с процентами
Решение задач на проценты Урок 3 5 класс
Учитель Истомина Т.Г.
Подведем итоги
Все решения задач на проценты делятся на три типа :
- нахождение процента от числа;
- нахождение числа по его проценту;
- сколько процентов одно число составляет от другого.
На следующих слайдах будут приведены примеры решения задач на каждый из типов.
учитель Истомина Т.Г.
Нахождение процента от числа
Чтобы найти процент от числа, надо :
1) выразить проценты обыкновенной или десятичной дробью;
2) умножить данное число на эту дробь.
Пример: найдём 18% от 300 .
I способ. Выполним действия.
Сначала найдём 1% от числа 300: 300:100=3 .
Полученное число умножим на число процентов:
3⋅18=54.
Итак: 18% от 300 равно 54.
II способ. Представим проценты в виде десятичной дроби:
18%=0,18; умножим данную дробь на это число
0,18⋅300=54.
учитель Истомина Т.Г.
Пример оформления задач:
Задача 1
Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие? Решение:
Найдем 60% от 500 (общее количество насосов). 1) 60 % = 0,6 2) 500 · 0,6 = 300 (насосов) высшей категории качества.
Ответ: 300 насосов.
учитель Истомина Т.Г.
Пример оформления задач:
Задача 1
Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие? Решение:
Сколько насосов высшей категории качества изготовило предприятие? Решение:
Найдем 60% от 500 (общее количество насосов). 1) 60 % = 0,6 2) 500 · 0,6 = 300 насосов высшей категории качества.
Ответ: 300 насосов высшей категории качества.
учитель Истомина Т.Г.
Нахождение числа по его проценту
Чтобы найти число по его проценту , надо:
1) выразить проценты обыкновенной или десятичной дробью;
2) разделить данное число на полученную дробь.
Задача . За контрольную по математике в пятом классе отметку «5» получили четверо учеников, что составляет 16% от всех учеников класса. Сколько учеников в классе?
I способ:
Найдём, какая часть всех учащихся класса приходится на 1%:
1) 4 : 16 = 0,25.
Все ученики класса составляют целое: 100%.
Умножим найденное число на 100:
2) 0,25⋅100=25 (уч)
Ответ: в классе 25 учеников.
учитель Истомина Т.Г.
Нахождение числа по его проценту
Задача . За контрольную по математике в пятом классе отметку «5» получили четверо учеников, что составляет 16% от всех учеников класса. Сколько учеников в классе?
II способ .
Выразим проценты обыкновенной или десятичной дробью и
количество учеников, которые получили отметку «5», разделим на эту дробь:
1) 16% = 0,16
2) 4:0,16=25 (уч)
Ответ: в классе 25 учеников.
учитель Истомина Т.Г.
Пример оформления задач:
Задача 1
На олимпиаде школьная команда набрала 72 очка. Сколько очков можно набрать на олимпиаде, если набранные командой очки составляют 80% из всех возможных?
Решение:
1) 72 : 80 = 0,9 (очков) 1% от всех возможных очков;
2) 0,9 * 100 = 90 (очков).
Ответ: на олимпиаде можно набрать 90 очков.
учитель Истомина Т.Г.
Пример оформления задач:
Задача 2
За зиму медведь Вини Пух съел 16 горшочков меда. Сколько горшочков меда заготовил Вини Пух, если у него осталось 20% всех его запасов?
Решение:
- 100 – 20 = 80% — меда съел за зиму Вини Пух;
Так как 16 горшков съел Винни, то найдем 1%
2) 16 : 80 = 0,2 (меда) 1% от всего меда;
3) 0,2 * 100 % = 20 (гор).
Ответ: на зиму Вини Пух заготовил 20 горшочков меда
учитель Истомина Т.Г.
Сколько процентов одно число составляет от другого
Запомните!
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100% .
Задача:
Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?
Решение:
О чем спрашивают? О незрелых арбузах. Значит, 16 делим на общее количество арбузов и умножаем на 100% .
Значит, 16 делим на общее количество арбузов и умножаем на 100% .
1) 16 : 200 * 100 = 0,08 * 100 = 8%
Ответ: 8% — составляют незрелые арбузы
от всех арбузов.
учитель Истомина Т.Г.
Домашнее задание :
Устно: п.40 прочитать. Выучить правила и ответить на вопросы в конце параграфа
Письменно: № 758, №761, №763
учитель Истомина Т.Г.
Решение более сложных задач на проценты. на Сёзнайке.ру
В курсе 7-11 класса практически отсутствуют задачи на проценты. Так как эти задачи можно решать с помощью уравнений и систем уравнений, то их необходимо включать в курс алгебры при изучении данных тем.
Задача 1. (решаемая с помощью уравнения, сводимого к линейному)
В растворе содержится 40% соли. Если добавить 120 г соли, то в растворе будет содержаться 70% соли. Сколько граммов соли было в растворе первоначально?
Сколько граммов соли было в растворе первоначально?
Решение:
Пусть x г весь первоначальный раствор, тогда
0.4x г – соли в первоначальном растворе,
(x + 120) г – стало раствора,
(0,4x + 120) г – стало соли в растворе, которая теперь составляет 70% раствора, т.е. 0,7 от всего раствора, составляем уравнение:
0,4x +120 = 0,7(x + 120), решив которое получим
x = 120
120 · 0,4 = 48 (г)
Ответ: 48 г.
Задача 2. (решаемая с помощью уравнения, сводимого к квадратному)
В сплаве золота с серебром содержится 80 г золота. К сплаву добавили 100 г чистого золота. Содержание золота в сплаве повысилось на 20%. Сколько серебра было в сплаве?
Решение:
|
Было:
|
Стало:
| ||
|
серебро
|
золото
|
серебро
|
золото
|
|
x г
|
80 г
|
x г
|
180 г
|
Пусть x г – серебра в сплаве, тогда
(x + 80) г – масса первоначального сплава,
(x + 180) г – масса нового сплава,
80/(x+80) г – часть золота в первом сплаве,
180/(x+180) г – часть золота во втором сплаве,
Т. к. содержание золота повысилось на 20% (т.е. на 1/5), составляем уравнение:
к. содержание золота повысилось на 20% (т.е. на 1/5), составляем уравнение:
180/(x+180)-80/(x+80)=1/5
решая которое получим
x- 240x + 14400 = 0
(x – 120) = 0
x = 120
Ответ: 120 г.
Задача 3. (решаемая с помощью системы уравнений)
Вычислите массу и пробу сплава серебра с медью, зная, что сплавив его с 3 кг чистого серебра, получим сплав 900-й пробы (т.е. в сплаве 90% серебра), а сплавив с 2 кг сплава 900-й пробы, получим сплав 840-й пробы.
Решение:
Пусть x кг – масса сплава, y% — серебра в сплаве, тогда
(y : 100) · x = 0,01xy (кг) – серебра в сплаве,
(x + 3) кг – нового первого сплава,
(0,01xy + 3) кг – серебра в новом первом сплаве.
Т.к. серебра в новом первом сплаве 90%, составляем уравнение:
0,01xy + 3 = 0,9(x + 3).
(x + 2) кг – масса второго сплава,
2 кг сплава 900-й пробы будут содержать 0,9 · 2 = 1,8 (кг) серебра, тогда
(0,01xy + 1,8) кг – масса серебра во втором сплаве.
Т.к. серебра во втором сплаве 84%, составляем уравнение:
0,01xy + 1,8 = 0,84(x + 2).
Получаем систему уравнений:
0,01xy + 3 = 0,9(x + 3) x = 3
0,01xy + 1,8 = 0,84(x + 2) y = 80
Ответ: 3 кг 800-ой пробы
Задача 4. (решаемая с помощью системы уравнений)
Фабрика должна была сшить 360 костюмов. В первые 8 дней она перевыполняла план на 20%, а в остальные на 25%. Сколько дней работала фабрика, если всего сшито 442 костюма?
Решение:
Пусть x костюмов должна была сшить фабрика за один день,
y дней должна была работать.
Т.к. всего должно было быть сшито 360 костюмов, составляем уравнение:
xy = 360.
1,2x · 8 костюмов сшили за первые 8 дней,
1,25x(y — 8) костюмов сшили за остальные дни.
Т.к. всего сшито 442 костюма, составляем уравнение:
1,2x · 8 + 1,25x(y — 8) = 442.
Получаем систему уравнений:
xy = 360 x = 20
1,2x · 8 + 1,25x(y — 8) = 442 y = 18
Ответ: 18 дней
Задача 5. (решаемая с помощью алгебраических выражений)
(решаемая с помощью алгебраических выражений)
Процесс очищения воды в водохранилище от содержания в ней тяжелых металлов состоит из четырех этапов. На каждом этапе содержание уменьшается на определенное количество процентов к их количеству на предыдущем этапе:
на 1-ом – на 25%
на 2-ом – на 20%
на 3-ем – на 15%
на 4-ом – на 10%
На сколько процентов в результате уменьшается их количество?
Решение:
Пусть x – количество воды, тогда оставшееся количество тяжелых металлов после очистки:
На 1-ом этапе – 0,75x
На 2-ом этапе – 0,8 · (0,75x) = 0,6x
На 3-ем этапе – 0,85 · (0,6x) = 0,51x
На 4-ом этапе – 0,9 · (0,51x) = 0,459x.
Таким образом всего ушло x — 0,459x = 0,541x, т.е. 54,1% тяжелых металлов.
Ответ: 54,1%
Задача 6. (решаемая комбинированным способом)
В январе завод выполнил 105% месячного плана выпуска готовой продукции, а в феврале дал продукции на 4% больше, чем в январе.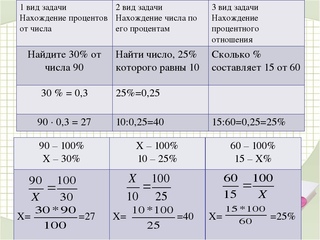 На сколько процентов завод перевыполнил двухмесячный план выпуска продукции?
На сколько процентов завод перевыполнил двухмесячный план выпуска продукции?
Решение:
Пусть x – месячный план, тогда
1,05x – выпущено в январе,
1,04 · (1,05x) = 1,092x – выпущено в феврале, а всего за два месяца выпущено
1,05x + 1,092x = 2,142x.
Таким образом двухмесячный план 2x, а фактически выполнено 2,142x, т.е.
2x – 100%
2,142x – y%
y = (2,142x · 100) : (2x) = 107,1%, т.е. план перевыполнен на 7,1%.
Ответ: 7,1%
Задача 7. (решаемая логическими рассуждениями)
В одном из городов Украины часть жителей говорит только по-русски, часть только по-украински, часть говорит и по-русски и по-украински. Известно, что 90% жителей говорит по-русски, а 80% по-украински. Какой процент жителей этого города говорит на обоих языках?
Решение:
На каждых 100 жителей – 90 говорит по-русски, значит, 10 не говорит по-русски, т.е. 10 говорит только по-украински. Известно, что из каждых 100 жителей говорит по-украински 80 человек, из них, как мы выяснили, 10 человек говорит только по-украински, следовательно из этих 80 знают еще и русский 80 – 10 = 70 человек, т.е. 70%
Известно, что из каждых 100 жителей говорит по-украински 80 человек, из них, как мы выяснили, 10 человек говорит только по-украински, следовательно из этих 80 знают еще и русский 80 – 10 = 70 человек, т.е. 70%
Ответ: 70%
Задачи на проценты. Бесплатная онлайн игра
  Эта математическая онлайн игра-тренажёр поможет научиться считать проценты для чисел от 10 до 1000.
  Отключить звук можно нажав на специальный значок «Динамик» в левом нижнем углы игры.
Процент — это сотая часть числа. Обозначается специальным значком процента — %
Как делать расчёт процентов в уме?
  В общем случае, чтобы найти проценты от какого-либо числа надо это число разделить на 100 и результат деления умножить на количество процентов. Например, чтобы найти 30% от 250, надо 250 поделить на сто (получим 2,5) и потом 2,5 умножить на 30. В результате получится 75. Таким образом, 30% от 250 = 75. Такой способ подходит для расчётов в уме. Но многие проценты можно посчитать проще.
Такой способ подходит для расчётов в уме. Но многие проценты можно посчитать проще.
- 1% — это сотая часть числа. Деля число на 100, мы как раз и получаем один процент.
- 10% — это десятая часть числа. Значит, чтобы найти десять процентов от числа, надо это число разделить на 10.
- 20% — это пятая часть числа. Чтобы вычислить двадцать процентов от числа, его надо разделить на 5.
- 25% — одна четвёртая или четверть числа. Чтобы вычислить двадцать пять процентов от числа, его надо разделить на 4.
- 50% — половина. Если разделить число на 2, то как раз и получим пятьдесят процентов от него.
Как просто искать 75 и 80 процентов предлагаю тебе подумать самому.
Решение процентов на калькуляторе
На калькуляторе проценты можно считать двумя простыми способами.
- С помощью десятичных дробей. Чтобы найти X% от числа A, мы число A умножаем на X делённое на 100. То есть, ища 37% от 98, мы 98 умножаем на 0,37.
 Или ища 128% от 65, мы 65 умножаем на 1,28.
Или ища 128% от 65, мы 65 умножаем на 1,28. - Используя специальную кнопку %. На разных моделях калькуляторов работа этой кнопки немного отличается, поэтому разберись с этим вопросом самостоятельно:-)
Правила игры
В игре представлены задачи на вычисление процентов. Выбери правильный ответ и перетащи его мышкой в мигающую область. Перетаскивать шарик нужно удерживая левую кнопку мышки.
За каждый правильный ответ ты будешь получать один балл. За неправильный — у тебя будет отниматься сразу два балла.
Как быстро научиться считать проценты. Простая методика
Расчётом процентов следует заниматься регулярно. Лучше всего каждый день по несколько минут. С начала попробуй набрать 15-20 баллов. Для первого дня такого результата будет вполне достаточно.
В следующие дни постарайся улучшать свои результаты и набирать на один-два балла больше чем вчера. Если ты хочешь научиться хорошо считать проценты, то занимайся регулярно. Лучше всего — каждый день по несколько минут. Нажми одновременно клавиши «CTRL» и «D» и добавь эту страницу в закладки. И у тебя всегда будет лёгкий доступ к этой онлайн-игре.
Нажми одновременно клавиши «CTRL» и «D» и добавь эту страницу в закладки. И у тебя всегда будет лёгкий доступ к этой онлайн-игре.
Когда ты сможешь быстро и почти без ошибок набирать 25 баллов, твои навыки в изучении процентов уже можно будет оценить как «хорошие». Ну а получение тобою 50 баллов — отличный результат!
Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)
Эта игра предназначена и чрезвычайно полезна для детей от 5 до 15 лет. Но может быть полезной и взрослым:-) Она развивает не только навыки расчёта процентов, как может показаться на первый взгляд. Во время игры также развивается внимание, память. А ещё тренажер «Изучение процентов» развивает мелкую моторику у детей и укрепляет мышцы кисти руки.
Дополнение для любознательных
Кроме одной сотой числа (процента), есть еще и специальное название для одной тысячной числа. Это — промилле. Обозначается похожим на знак процента знаком ‰. Очень часто в промилле измеряют концентрацию растворов и уклоны местности.
Очень часто в промилле измеряют концентрацию растворов и уклоны местности.
Разместить ссылку на игру на сайте, блоге, форуме (HTML код):
Разместить игру на своем сайте:
Создатель сайта будет благодарен Вам, если оцените данную игру. (Это можно сделать вверху страницы.) Ну а Вашим комментариям будет рад вдвойне:-)
p
Простые задачи по интересам с решениями
Задача 1:
Человек кладет 5000 долларов на банковский счет, который платит 6% простых процентов в год. Определите стоимость его депозита через 4 года.
Решение:
Формула для простых процентов:
I = Prt
Здесь P = 5000, t = 4, r = 6%
Подставим эти значения в формулу выше
I = 5000 ⋅ 6/100 ⋅ 4
I = 1200
Формула для определения накопленной стоимости:
= основная сумма + проценты
= 5000 + 1200
= 6200
Следовательно, величина его депозита после 4 лет составляет 6200 долларов.
Задача 2:
Глен получил от банка ссуду на сумму 2250 долларов. Через шесть месяцев он выплатил 2295 долларов и закрыл ссуду. Найдите процентную ставку.
Решение:
Проценты = Сумма — Основная сумма
I = 2295-2250
I = 45
Формула для простых процентов:
I = Prt
Дано: Срок составляет 6 месяцев.
В формуле простых процентов мы используем период времени в годах.Но период времени, указанный в вопросе, исчисляется месяцами.
Итак, изменим данный период времени в годах.
6 месяцев = 6/12 лет
6 месяцев = 1/2 года
Итак, период времени составляет 1/2 года.
Формула для простых процентов:
I = Prt
Здесь I = 45, P = 2250, t = 1/2
Подставим эти значения в формулу выше
45 = 2250 ⋅ r ⋅ 1 / 2
45 = 1125 ⋅ r
Разделите обе части на 1125.
45/1125 = r
0,04 = r
Чтобы преобразовать десятичную дробь 0,04 в процент, умножьте ее на 100.
0,04 ⋅ 100% = r
4% = r
Следовательно, процентная ставка 4%.
Задача 3:
Человек инвестирует 16 500 долларов в казначейские билеты двух видов, которые приносят 7,5% и 6% годовых. Через два года он зарабатывает 2442 доллара на процентах. Сколько он вкладывает по ставке 6%?
Решение:
Пусть «x» будет суммой, инвестируемой по ставке 6%.
Тогда сумма, вложенная в счет 7,5%, составит
= 16500 — x
Дано: Через два года общая сумма процентов, полученных на обоих счетах, составит 2442 доллара.
Итак, имеем
Процентная ставка 6% + Процентная ставка 7,5% = 2442
x ⋅ 6/100 ⋅ 2 + (16500 — x) ⋅ 7,5 / 100 ⋅ 2 = 2442
x ⋅ 0,06 ⋅ 2 + (16500 — x) ⋅ 0,075 ⋅ 2 = 2442
0,12x + (16500 — x) ⋅ 0,15 = 2442
0,12x + 2475 — 0.15x = 2442
2475 — 0,03x = 2442
2475-2442 = 0,03x
33 = 0,03x
Разделить обе стороны на 0,03
33 / 0,03 = x
3300/3 = x
1100 = X
Таким образом, сумма инвестиций по ставке 6% составляет 1100 долларов США.
Задача 4:
Человек вложил 25 200 долларов в два счета, по которым ежегодно выплачиваются 5% и 10% годовых. Сумма инвестирования по ставке 10% составляет 110% от суммы инвестирования по ставке 5%.По прошествии трех лет он зарабатывает 2442 доллара в виде процентов. Сколько он вложил по ставке 5%?
Решение:
Пусть «x» будет суммой, инвестируемой по ставке 5%.
Тогда сумма, вложенная в счет 10%, составляет
= 110% от x
= 1,10 ⋅ x
= 1,1x
Дано: Через три года общая сумма процентов, полученных на обоих счетах, составит 5760 долларов.
Итак, у нас есть
Процентная ставка 5% + Процентная ставка 10% = 5760
x ⋅ 5/100 ⋅ 3 + 1.1x ⋅ 10/100 ⋅ 3 = 5760
x ⋅ 0,05 ⋅ 3 + 1,1x ⋅ 0,1 ⋅ 3 = 5760
0,15x + 0,33x = 5760
0,48x = 5760
Разделите обе стороны на 0,48
x = 5760 / 0,48
x = 576000/48
x = 12000
Следовательно, сумма инвестирования по ставке 5% составляет 12000 долларов США.
Задача 5:
В простых процентах денежная сумма удваивается за 10 лет. Найдите количество лет, которое потребуется, чтобы утроиться.
Решение:
Пусть P — это сумма вложенных денег.
Дано: Сумма денег удваивается через 10 лет
Тогда P станет 2P через 10 лет.
Теперь мы можем рассчитать проценты за десять лет, как показано ниже
Из приведенного выше расчета P — это проценты за первые 10 лет.
В случае простых процентов заработанные проценты будут одинаковыми каждый год.
Таким образом, проценты, полученные в следующие 10 лет, также будут равны P.
Это объясняется ниже.
Следовательно, для того, чтобы принципал стал тройным, потребуется 20 лет.
Задача 6:
В простых процентах денежная сумма составляет 6200 долларов через 2 года и 7400 долларов через 3 года. Найдите директора.
Решение:
Через 2 года мы получаем 6200 долларов
Через 3 года мы получаем 7400 долларов
Из этих двух данных мы можем получить проценты, заработанные в 3-м году, как указано ниже.
В простых процентах проценты будут одинаковыми за каждый год.
Исходя из этого, мы можем рассчитать основную сумму, как указано ниже.
Следовательно, основная сумма составляет 3800 долларов.
Помимо того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Словарные задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейными неравенствами
Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времени
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
с использованием длинного корня видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Сложные проценты | Финансы и рост
9.3 Сложные проценты (EMA6N)
Сложные проценты позволяют получать проценты по процентам. В случае простых процентов проценты приносят только первоначальные инвестиции, а в случае сложных процентов первоначальные инвестиции и проценты, полученные по ним, приносят проценты.
В случае простых процентов проценты приносят только первоначальные инвестиции, а в случае сложных процентов первоначальные инвестиции и проценты, полученные по ним, приносят проценты.
Сложные проценты выгодны для вложения денег, но не для получения кредита.
- Сложные проценты
Сложные проценты — это проценты, полученные на основную сумму и накопленные проценты.
Рассмотрим пример \ (\ text {R} \, \ text {1 000} \), инвестированного на \ (\ text {3} \) лет в банк, который платит \ (\ text {5} \% \) па сложные проценты.
На конец первого года накопленная сумма составляет
\ begin {align *}
{A} _ {1} & = P \ left (1 + i \ right) \\
& = \ text {1 000} \ left (1 + \ text {0,05} \ right) \\
& = \ текст {1 050}
\ end {выровнять *}
Сумма \ ({A} _ {1} \) становится новой основной суммой для расчета накопленной суммы в конце второго года.{3}
\ end {выровнять *}
Вы видите закономерность?
Используя формулу для простых процентов, мы можем разработать аналогичную формулу для сложных процентов.
При начальном сальдо \ (P \) и процентной ставке \ (i \) сальдо на конец первого года составляет:
\ [\ text {Конечный баланс после} 1 \ text {год} = P \ left (1 + i \ right) \]
Это то же самое, что и простой процент, потому что он покрывает только один год. Это конечное сальдо становится начальным сальдо на второй год инвестирования.{п} \\
\ text {Где:} & \\
A & = \ text {накопленная сумма} \\
P & = \ text {основная сумма} \\
i & = \ text {проценты в виде десятичной дроби} \\
n & = \ text {количество лет}
\ end {align *}
Рабочий пример 5: Сложные проценты
Mpho хочет инвестировать \ (\ text {R} \, \ text {30 000} \) в счет, который предлагает сложную процентную ставку \ (\ text {6} \% \) годовых. Сколько денег будет на счету по истечении \ (\ text {4} \) лет?
Запишите известные переменные
\ begin {align *}
P & = \ text {30 000} \\
я & = \ текст {0,06} \\
п & = 4
\ end {align *}
Запишите формулу
\ begin {align *}
A & = P {\ left (1 + i \ right)} ^ {n}
\ end {align *}
Подставьте значения
\ begin {align *}
A & = \ text {30 000} {\ left (1 + \ text {0,06} \ right)} ^ {4} \\
& = \ text {37 874,31}
\ end {align *}
Напишите окончательный ответ
Mpho будет иметь \ (\ text {R} \, \ text {37 874,31} \) на счете в конце \ (\ text {4} \) лет. {2} \\
{2} \\
\ sqrt {\ frac {\ text {10 000}} {\ text {5 000}}} & = 1 + i \\
\ sqrt {\ frac {\ text {10 000}} {\ text {5 000}}} — 1 & = i \\
я & = \ текст {0,4142}
\ end {align *}
Напишите окончательный ответ и комментарий
Чарли нужно найти счет, который предлагает сложную процентную ставку \ (\ text {41,42} \% \) p.а. для достижения желаемого роста. Типичный сберегательный счет дает доход примерно \ (\ text {2} \% \) в год. а агрессивный инвестиционный портфель дает доход примерно \ (\ text {13} \% \) в год. Поэтому кажется маловероятным, что Чарли сможет инвестировать свои деньги под процентную ставку \ (\ text {41,42} \% \) годовых.
Сила сложных процентов (EMA6P)
Чтобы проиллюстрировать, насколько важны «проценты на проценты», мы сравниваем разницу в конечных сальдо для инвестиций, приносящих простые проценты, и инвестиций, приносящих сложные проценты.Рассмотрим сумму в \ (\ text {R} \, \ text {10 000} \), вложенную в течение \ (\ text {10} \) лет, по процентной ставке \ (\ text {9} \% \) па
Конечное сальдо по инвестициям, приносящим простые проценты, составляет
. {10} \\
{10} \\
& = \ text {R} \, \ text {23 673,64}
\ end {выровнять *}
Мы наносим рост двух инвестиций на один и тот же набор осей и отмечаем существенное различие в скорости их изменения: простой процент представляет собой прямолинейный график, а сложный процент — экспоненциальный график.
Легче увидеть огромную разницу в темпах роста, если мы увеличим временной период до \ (\ text {50} \) лет:
Имейте в виду, что это хорошие новости и плохие новости. При получении процентов на вложенные деньги сложные проценты помогают этой сумме расти в геометрической прогрессии. Но если деньги взяты взаймы, накопленная сумма долга также будет расти в геометрической прогрессии.
Это видео объясняет разницу между простыми и сложными процентами. Обратите внимание, что в видео используются доллары, но расчет рандов такой же.
Видео: 2Gh4
Высокие оценки по математике — залог вашего успеха и дальнейших планов. Проверьте себя и узнайте больше о практике Сиявулы. {\ text {3}} \\
{\ text {3}} \\
& = \ text {R} \, \ text {9 327,76}
\ end {align *}
Никола хочет вложить деньги под сложную процентную ставку \ (\ text {11} \% \) p.5} & = P \\
P & = \ text {R} \, \ text {59 345,13}
\ end {выровнять *}
Тобека хочет вложить деньги под сложную процентную ставку \ (\ text {11,8} \% \) годовых.
Сколько денег нужно вложить, если она хочет достичь суммы в \ (\ text {R} \, \ text {30 000} \) за \ (\ text {2} \) лет? Округлите свой ответ до ближайшего ранда.
Внимательно прочтите вопрос и запишите данную информацию:
\ begin {align *}
A & = \ text {R} \, \ text {30 000} \\
P & =? \\
i & = \ frac {\ text {11,8}} {\ text {100}} = \ text {0,118} \\
п & = 2
\ end {выровнять *}
Чтобы определить сумму, которую она должна инвестировать, нам нужно сделать \ (P \) предметом формулы:
\ begin {align *}
А & = Р (1 + я) ^ п \\
\ frac {A} {(1 + i) ^ n} & = P \\
\ frac {\ text {R} \, \ text {30 000}} {(1+ \ text {0,118}) ^ {\ text {2}}} & = P \\
P = & \ text {R} \, \ text {24 001,46}
\ end {выровнять *}
Она должна вложить \ (\ text {R} \, \ text {24 002,00} \). {\ text {7}}} & = P \\
{\ text {7}}} & = P \\
P = & \ text {R} \, \ text {17 941,84} \\
\ text {Следовательно, ответ:} & \ text {R} \, \ text {17 942,00}
\ end {align *}
Морган инвестирует \ (\ text {R} \, \ text {5 000} \) в счет, на котором выплачивается единовременная сумма в конце \ (\ text {5} \) лет.5 \\
\ sqrt [5] {\ frac {\ text {7 500}} {\ text {5 000}}} & = (1 + i) \\
\ sqrt [5] {\ frac {\ text {7 500}} {\ text {5 000}}} — 1 & = i \\
я & = \ текст {0,0844717712}
\ end {выровнять *}
Процентная ставка \ (\ text {8,45} \% \) в год
Кабир инвестирует \ (\ text {R} \, \ text {1 790} \) в счет, на котором выплачивается единовременная сумма в конце \ (\ text {9} \) лет.
Если он получит \ (\ text {R} \, \ text {2 613,40} \) в конце периода, какую сложную процентную ставку банк предложил ему? Дайте правильный ответ с точностью до одного десятичного знака. {\ frac {1} {\ text {7}}} — 1 \\
{\ frac {1} {\ text {7}}} — 1 \\
& = \ текст {0,018} \\
& = \ text {1,8} \% \ text {в год}
\ end {align *}
проблем со словами интереса
проблем со словами интереса
Проблемы со словом «интерес»
Сначала несколько определений:
Основная сумма деньги, вложенные на счет
Проценты деньги, выплачиваемые за инвестирование
главный
Простые проценты проценты, рассчитываемые с использованием
формула Проценты = (Основная сумма) × (Ставка) ×
(Время).Эта формула часто обозначается I = PRT. Если время равно
через год формула становится I = PR.
В наиболее интересных задачах мы постараемся найти
сумма денег (основная сумма), вложенная на каждый из двух банковских счетов. Помогать
найдем эти вещи, нам сообщат общую сумму вложенных денег
и общая сумма процентов, выплаченных по двум счетам.
Давайте посмотрим на пример типичной проблемы со словом интереса.
Сэм вкладывает 6000 долларов в два банковских счета. Один из
Один из
на счетах выплачивается 8% годовых, а на другом счете — 10%.
в год. Если общий процент, полученный от инвестиций, составляет 560 долларов после
в год, сколько денег было вложено в каждый счет?
Что мы должны найти в этой проблеме? Последний
Часть проблемы дает нам ответ на этот вопрос.Мы пытаемся
чтобы узнать, сколько денег было вложено в каждую учетную запись.
Давайте определим переменную. Мы не знаем сколько денег
был вложен в любую учетную запись, поэтому примите решение использовать x, чтобы
представляют собой сумму денег, вложенную в первый счет (тот, который
зарабатывает 8% в год). Как мы называем сумму денег, вложенных в
второй аккаунт? Мы могли бы дать ему другое имя переменной, например y, но
в этой главе мы собирались ограничить наши проблемы одной переменной.
Итак, представьте: Сэм несет стек в 6000 долларов в
первый банк и говорит: «Я хотел бы положить x долларов на счет, который
платит 8% годовых «. Затем кассир снимает x долларов с
Затем кассир снимает x долларов с
свои 6000 долларов, а Сэм кладет оставшиеся деньги в другой банк. Помнить
что для вас значили слова «забрать», когда вы были в начальной школе
студент-математик? Вычесть, верно ?? Так что «забери x долларов из 6000 долларов» можно
можно записать символически как 6,000-x.Вот сколько денег вложено в
второй банк.
При проблемах с процентами часто бывает полезно использовать диаграмму
систематизировать информацию в задаче. Хорошо промаркируйте верхнюю часть
график с двумя объектами, которые искали (деньги, вложенные под 8% и
деньги, вложенные под 10%), и хорошо пометьте сторону графика
две части информации, которую предоставляет проблема (основной
и заработанные проценты). Поскольку проблема дает нам информацию о
общая сумма основного долга и общий процент, а также столбец для итогов.
| деньги под 8% | деньги под 10% | всего | |
| основной | |||
| проценты |
На данный момент нам известно следующее:
х долларов было вложено под 8%
6000 х долларов было вложено под 10%
Общая сумма вложенных средств составила 6000 долларов США.
общая сумма полученных процентов составила 560 долларов США
Давайте поместим эту информацию в нашу диаграмму:
| деньги под 8% | деньги под 10% | всего | |
| основной | Икс | 6000 — х | 6000 |
| проценты | 560 |
Чтобы заполнить поля процентов, помните, что через один год
время I = PR.Итак, в каждом поле процентов мы умножаем сумму основного долга.
вкладывается в этот счет по процентной ставке, полученной на эти деньги. Сейчас
наша диаграмма выглядит так:
| деньги под 8% | деньги под 10% | всего | |
| основной | Икс | 6000 — х | 6000 |
| проценты | . 08x 08x | 0,10 (6000 х) | 560 |
Наше уравнение исходит из последней строки на графике. С
проценты, полученные на первом счете, плюс проценты, заработанные на
второй счет должен равняться общей сумме процентов, мы можем написать:
.08x + .10 (6000 x) = 560
Чтобы решить уравнение, сначала умножьте обе части
уравнения на 100, чтобы убрать десятичные дроби.Помните, умножение
на 100 сдвинет одну десятичную запятую в каждом члене вправо на два разряда.
100 [0,08x + 0,10 (6000 x)] = 100 [560]
8x + 10 (6000 x) = 56000
8x + 60,000 10x = 56,000
-2x + 60 000 = 56 000
-2x = -4,000
х = 2,000
Поскольку x представляет собой сумму денег, вложенных в
По первому счету можно сказать, что 2000 долларов было вложено под 8%.
Нам нужно решить проблему. Нас спросили, сколько
Нас спросили, сколько
деньги были вложены в каждый счет, и, поскольку мы еще не знаем, сколько
деньги были вложены под 10%, у нас есть только половина нашего ответа. В соответствии с
на нашем графике сумма денег, вложенных во второй счет, равна
до 6000- x, поэтому
6000 x = 6000 2000 = 4000
$ 4000 вложено под 10%
Прежде чем мы оставим эту проблему, давайте проверим наш ответ с помощью
слова проблемы:
| слов | чек |
| $ 6000 вложено во все | 2 000 + 4 000 = 6 000 |
| 560 долл. США было получено в виде процентов | Процентный доход 8%: .08 (2,000) = 160 Процентный доход по ставке 10%: 0,10 (4,000) = 400Общий процент заработанных процентов: 160 + 400 = 560 |
Наши ответы проверяют. Были сделаны!
Были сделаны!
Калькулятор сложных процентов — WebMath
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике … Исчисление, Производное вычисление, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование площади, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение , Правые треугольники, Ветер, Рисунок
Формула сложного процента — определение, вывод формулы, приложения и проблемы с решениями
Давайте узнаем, что такое сложные проценты.
 Сложные проценты определяются как проценты, начисленные на основную сумму долга и проценты, накопленные за предыдущий период времени.
Сложные проценты определяются как проценты, начисленные на основную сумму долга и проценты, накопленные за предыдущий период времени.Сложные проценты отличаются от простых процентов.
В простых процентах проценты не добавляются к основной сумме при расчете процентов в течение следующего периода, в то время как в сложных процентах проценты добавляются к основной сумме для расчета процентов.
Сложные проценты (CI) = основная сумма (1 + ставка / 100) n — основная сумма |
где P равно основной сумме, R равно процентной ставке, T равно времени (период)
[Изображение будет загружено в ближайшее время]
Еще немного о сложных процентах
Сначала мы поймем концепцию и то, что такое сложные проценты, а затем перейдем к формуле сложных процентов. Теперь проценты можно определить как сумму, которую мы рассчитываем на предоставленную нам основную сумму. Но в сложных процентах мы рассчитываем проценты на основную сумму и проценты, накопленные за предыдущий период.
Теперь проценты можно определить как сумму, которую мы рассчитываем на предоставленную нам основную сумму. Но в сложных процентах мы рассчитываем проценты на основную сумму и проценты, накопленные за предыдущий период.
По сути, сложные проценты — это проценты на проценты! Таким образом, в этом методе, вместо выплаты процентов, они реинвестируются и становятся частью основной суммы долга.
Как вы могли заметить в простых процентах, сумма процентов остается неизменной для каждого периода.В случае сложных процентов дело обстоит иначе. Поскольку предыдущая сумма процентов реинвестируется, размер процентов каждый год незначительно увеличивается. Вот почему у нас есть целая отдельная формула сложных процентов, чтобы помочь нам рассчитать сложные проценты за любой конкретный год.
Формула сложных процентов в математике:
Сумма = основная сумма (1 + ставка / 100) n |
, где P равно основной сумме, ставка равна ставке Проценты, n равно времени (Период)
Вывод формулы сложного процента
Чтобы лучше понять концепцию, давайте взглянем на вывод формулы сложного процента. Здесь мы возьмем нашу основную сумму, равную 1 рупии, и постепенно будем приближаться к годовой процентной ставке.
Здесь мы возьмем нашу основную сумму, равную 1 рупии, и постепенно будем приближаться к годовой процентной ставке.
Год 1
Процентная ставка по 1 рупии за 1 год равна r / 100 = i (предполагается)
Процентная ставка после года 1 равна Pi
FV (Окончательное значение) после года 1 равно P + Pi = P (1 + i)
год 2
год t
Окончательное значение (сумма) после года «t» равно P (1 + i ) t
Теперь подставляя фактические значения, мы получаем Окончательное значение равно (1 + R / 100) t
CI = FV — P равно P (1 + R / 100) t — P
Это вывод по формуле сложного процента
Заявки на сложный процент
Вот некоторые из приложений, представляющих сложный процент:
Увеличение или уменьшение населения.

Рост бактерий.
Повышение стоимости предмета.
Амортизация стоимости объекта.
Теперь, когда у нас есть некоторая ясность в отношении концепции и значения сложных процентов и формулы сложных процентов в математике, давайте попробуем решить некоторые задачи сложных процентов с решениями, чтобы углубить наше понимание предмета.
Проблемы со сложными процентами с решениями
Вопрос 1) Было обнаружено, что количество бактерий определенного вида увеличивается со скоростью 5% в час.Каков будет рост бактерий через 3 часа, если изначально было 6000?
Решение) Поскольку популяция бактерий увеличивается со скоростью 5% в час,
Мы знаем формулу для расчета суммы, формулу сложных процентов в математике
Сумма = Основная сумма (1 + R / 100) n
Таким образом, население в конце 3 часов = 6000 (1 + 3/100) 3
= 6000 (1 + 0,03) 3 = 6000 (1,03) 3 = 6556,36 рупий
Вопрос 2) Г-н А решил открыть банковский счет и выбрал вариант сложного процента по ставке 10%. Вложил 10 тысяч за 3 года. По истечении трех лет, сколько денег он получит и каковы будут проценты. Проценты начисляются ежегодно.
Вложил 10 тысяч за 3 года. По истечении трех лет, сколько денег он получит и каковы будут проценты. Проценты начисляются ежегодно.
Решение) Поскольку у нас уже есть формула для будущей суммы стоимости, давайте подставим значения в формулу сложных процентов в математике
FV = (1 + R / 100) t
FV = 10000 (1 + 10/100) 5
FV = 10000 (1,1) 5
FV = 16,105
CI = FV — P = 6,105 / —
Вопрос 3) Г-н Б. одолжил деньги своему сыну с 8% CI, рассчитываемым каждые полгода.Если он одолжил 1000 / — на 2 года, сколько он вернет через 2 года?
Решение) Поскольку CI рассчитывается раз в полгода
Окончательное значение = P (1 + R / 100) t
FV = 1000 (1 + 4/100) 4
FV = 1000 (1,17)
FV или сумма = 1170 / —
Простые и сложные процентные задачи | GMAT GRE Maths Tutorial
Щелкните здесь, чтобы посмотреть это содержательное видео.
Лучшие университеты мира
Принцип комплексного роста широко используется в финансовом мире для преобразования небольших сбережений в большую совокупность с течением времени.Это также основная идея, лежащая в основе таких тем MBA, как временная стоимость денег и оценка дисконтированного денежного потока (DCF) .
Узнайте о простых и сложных процентах, поскольку они понадобятся вам не только для вступительных экзаменов, но и в реальном мире, особенно после того, как вы станете богатым и знаменитым.
Простые и сложные процентные задачи и решения
Вот список некоторых основных определений и формул для решения задач по проценту.
Принципал : Это сумма денег, взятых в долг или взятых взаймы.
Проценты : Это дополнительные деньги, уплаченные за взятие денег в качестве ссуды. Часто это выражается в процентах.
Скажем, процент составляет 10% по ссуде в размере рупий. 100. Тогда процент в сумме рупий. 10 и в конце года сумма, подлежащая выплате, составляет рупий. 110.
10 и в конце года сумма, подлежащая выплате, составляет рупий. 110.
Время : Это период времени, на который деньги ссужаются, или период времени, в течение которого деньги должны быть возвращены с процентами.
Простой процент
Как следует из названия, расчет простых процентов довольно прост. Умножьте основную сумму на количество лет и процентную ставку.
Простая формула процента:
Простая процентная ставка = основная сумма * Время * процентная ставка / 100
Сокращенно SI = PTR / 100
Сложные проценты
В сложных процентах основная сумма с процентами после первой единицы времени становится основной суммой для следующей единицы.
Скажем, при ежегодном начислении в течение 2 лет основная сумма долга с начисленными в конце первого года процентами становится основной суммой долга на второй год.
Формула сложных процентов:
Сумма = основная сумма * [1 + процентная ставка / 100] Период времени
Сокращенно: Сумма = P * [1 + R / 100] т , при ежегодном начислении.
Иногда проценты также рассчитываются раз в полгода или квартал.
При начислении раз в полгода или раз в полгода
Сумма = P [1 + (R / 2) / 100] 2т
При начислении ежеквартально
Сумма = P [1 + (R / 4) / 100] 4t
Приведенная стоимость основной суммы долга через t лет определяется по формуле:
P / [1+ R / 100] т
Примеры проблем и решений
Давайте поработаем над некоторыми примерами, чтобы понять концепции и различия.
Задача 1. Сумма рупий. 25000 становится рупий. 27250 в конце 3-х лет при расчете по простым процентам. Найдите процентную ставку.
Решение :
Простой процент = 27250 — 25000 = 2250
Время = 3 года.
SI = PTR / 100 → R = SI * 100 / PT
R = 2250 * 100/25000 * 3 → R = 3%.
Задача 2. Найдите текущую стоимость рупий. 78000 со сроком погашения 4 года под 5% годовых.
Решение :
Сумма с процентами через 4 года = рупий.78000
Следовательно, простой процент = 78000 — основная сумма долга.
Пусть основная сумма будет p.
78000 — p = p * 4 * 5/100 → p = 13000
Основная сумма = 78000 — 13000 = рупий. 65000
Задача 3. Определенная основная сумма рупий. 15000 через 2,5 года и рупий. 16500 через 4 года по той же процентной ставке. Найдите процентную ставку.
Решение :
Сумма станет 15000 через 2,5 года и 16500 через 4 года.
Простой процент за (4-2.5) лет = 16500-15000
Следовательно, СИ за 1,5 года = рупий. 1500.
СИ за 2,5 года = 1500 / 1,5 * 2,5 = 2500
Основная сумма = 15000 — 2500 = Rs. 12500.
Процентная ставка = 2500 * 100/12500 * 2,5 → R = 8%.
Задача 4. Найдите сложные проценты на рупиях. 3000 под 5% на 2 года, начисляются ежегодно.
Решение :
Сумма с CI = 3000 (1+ 5/100) 2 = рупий. 3307,5
3307,5
Следовательно, CI = 3307.5 — 3000 = рупий. 307,5
Задача 5. Найдите сложные проценты на рупиях. 10000 по ставке 12% на 1 год, начисляются каждые полгода.
Решение :
Сумма с CI = 10000 [1+ (12/2 * 100)] 2 = рупий. 11236
Следовательно, CI = 11236 — 10000 = Rs. 1236
Задача 6. Разница между SI и CI, начисляемая ежегодно на определенную денежную сумму в течение 2 лет под 8% годовых, составляет Rs. 12.80. Найдите директора.
Решение :
Пусть основная сумма будет x.
SI = x * 2 * 8/100 = 4x / 25
CI = x [1+ 8/100] 2 — x → 104x / 625
Следовательно, 104x / 625 — 4x / 25 = 12,80
Решение, которое дает x, Principal = Rs. 2000.
Задача 7. Найдите простой процент на рупиях. 5000 по определенной ставке, если сложный процент на ту же сумму за 2 года составляет рупий. 253,125.
Решение :
Пусть процентная ставка будет r.
5000 [1+ r / 100] 2 = 5000 + 253,125
→ [1 + r / 100] 2 = 5253,125 / 5000
Решение, которое дает
[1+ r / 100] 2 = 1681/1600
→ 1 + г / 100 = 41/40
→ г = 2,5
Следовательно, SI = 5000 * 2 * 2,5 / 100 = Rs. 250.
Задача 8. Определенная сумма становится рупий. 5760 через 2 года и рупий. 6912 за 3 года. Какова основная сумма и процентная ставка?
Решение :
Проценты на рупий.5760 на 1 год = 6912 — 5760 = Rs. 1152
Следовательно, процентная ставка на 1 год = 100 * 1152/5760 * 1 = 20%
Пусть главный будет p.
Тогда Принципал = p [1+ 20/100] 2 = 5760
Решение, которое дает Принципал = Rs. 4000
Задача 9. Сколько времени потребуется определенной сумме, чтобы увеличить ее на 30% при ставке 15% простых процентов?
Решение :
Пусть основной будет рупий. х
Простой процент = x * 30/100 = 3x / 10
T = 100 * SI / PR = 100 * 3x / 10 / x * 15 = 2%
В качестве альтернативы, это может быть решено путем рассмотрения основной суммы в рупиях. 100. Тогда простой процент становится рупий. 30.
100. Тогда простой процент становится рупий. 30.
Тогда T = 100 * 30/100 * 15 = 2%
Простая и сложная викторина по интересам: решите эти проблемы
Проблема 1
Кредитор одолжил рупий. 1000 под 3% в год и рупий. 1400 под 5% годовых. Сумма должна быть возвращена ему, когда общая сумма процентов достигнет рупий. 350. Найдите количество лет.
A. 3.5
B. 3.75
C. 4
D. 4.5
Ответ 1
А.
Пояснение
(1000 * t * 3/100) + (1400 * t * 5/100) = 350 → t = 3,5
Задача 2
Найдите настоящую стоимость рупий. 20872,5 со сроком погашения через 2 года по ставке 10%.
A. 17500
B. 17520
C. 17750
D. 17250
Ответ 2
Д.
Пояснение :
Текущая стоимость = 20872,5 / [1+ 10/100] 2
Пройдите эти очень доступные онлайн-курсы по Simple & Compound Interest. Щелкните ниже.
Щелкните ниже.
Простой процент — GeeksforGeeks
- Сумма, которая ссужается / депонируется, называется основной суммой
- Деньги, генерируемые основной суммой, называются процентами. Это деньги, полученные в результате заимствования / кредитования.
- Простые проценты — это проценты, начисляемые на основную сумму, а не на совокупную сумму.
- Простой процент, SI = P x R x T / 100, где P — основная сумма, R — процентная ставка за единицу периода времени, а T — период времени.
- Окончательная сумма = Основная сумма + SI
Примеры задач
Вопрос 1: Каким будет годовой процент, начисленный на депозит в размере рупий. 10 000 в банке, который платит 4% годовых по простым процентам?
Решение: Здесь P = 10000, R = 4, T = 1
=> SI = P x R x T / 100
=> SI = 10000 x 4 x 1/100
=> SI = 400
Таким образом , годовой процент будет рупий. 400
Вопрос 2: Денежная сумма составляет рупий. 28 000 через 2 года под простую процентную ставку 20% годовых. Найдите сумму.
28 000 через 2 года под простую процентную ставку 20% годовых. Найдите сумму.
Решение: Здесь A = 28000, T = 2, R = 20
=> A = P + SI
=> A = P + (P x R x T / 100)
=> A = P [1 + (R x T / 100)]
=> 28000 = P [1 + 0,4]
=> P = 28000 / 1,4
=> P = 20000
Таким образом, требуемая сумма составляет Rs. 20,000
Вопрос 3: Мужчина занял определенную сумму денег из расчета 6% годовых на первые два года, 9% годовых на следующие три года и 14% годовых на период после 5 лет. годы.Если он заплатит общую сумму рупий. 22 800 по истечении 9 лет, найдите сумму, которую он занял.
Решение: Пусть сумма займа будет P.
=> SI на первые 2 года + SI на следующие 3 года + SI на следующие 4 года = 22800
=> (P x 6 x 2/100) + (P x 9 x 3/100) + (P x 14 x 4/100) = 22800
=> 95 P / 100 = 22800
=> P = 24000
Таким образом, сумма займа = рупий. 24,000
Вопрос 4: При какой годовой процентной ставке сумма денег будет трижды за 10 лет?
Решение: Сумма = основная сумма + SI
Если сумма денег будет в три раза больше основной суммы через 10 лет, SI будет в два раза больше основной суммы.
=> SI = 2 x P
=> (P x R x T / 100) = 2 XP
=> R x T / 100 = 2
=> R x T = 200
=> R x 10 = 200
=> R = 20%
Таким образом, требуемая процентная ставка составляет 20%
Вопрос 5: Простой процент на денежную сумму через 5 лет под 12% годовых составляет Rs. На 400 меньше, чем простые проценты, начисленные на ту же сумму через 7 лет под 10% годовых. Найдите сумму.
Решение: Пусть сумма будет P.
=> SI через 5 лет под 12% годовых = P x 12 x 5/100 = 0.6 P
=> SI через 7 лет под 10% годовых = P x 10 x 7/100 = 0,7 P
Теперь по вопросу
0,7 P — 0,6 P = 400
=> 0,1 P = 400
= > P = 4000
Таким образом, необходимая сумма составляет Rs. 4000
Вопрос 6: Сумма рупий. 1000 ссудили двум людям: одному по ставке 5%, другому по ставке 8%. Если простой процент по истечении одного года составляет рупий. 62, найдите сумму, ссужаемую по каждой ставке.
Решение: Пусть сумма ссуды под 5% будет P.
=> Сумма, предоставленная под 8% = 1000 — P
Теперь, согласно вопросу,
SI для 5% + SI для 8% = 62
=> (P x 5 x 1/100) + ((1000 — P ) x 8 x 1/100) = 62
=> 5 P + 8 (1000 — P) = 6200
=> 5 P + 8000 — 8 P = 6200
=> 3 P = 1800
=> P = 600
Таким образом, сумма ссуды под 5% = P = Rs. 600
Сумма взаймы под 8% = 1000 — P = Rs. 400
Задачи по простому интересу | Set-2
Эта статья была предоставлена Nishant Arora
Пожалуйста, напишите комментарии, если у вас есть какие-либо сомнения по теме, обсуждаемой выше, или если вы столкнулись с трудностями в любом вопросе, или если вы хотите обсудить другие вопросы, кроме упомянутых выше.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше
Вниманию читателя! Не прекращайте учиться сейчас. Получите все важные математические концепции для соревновательного программирования с курсом Essential Maths for CP по доступной для студентов цене.
