Содержание
Все формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
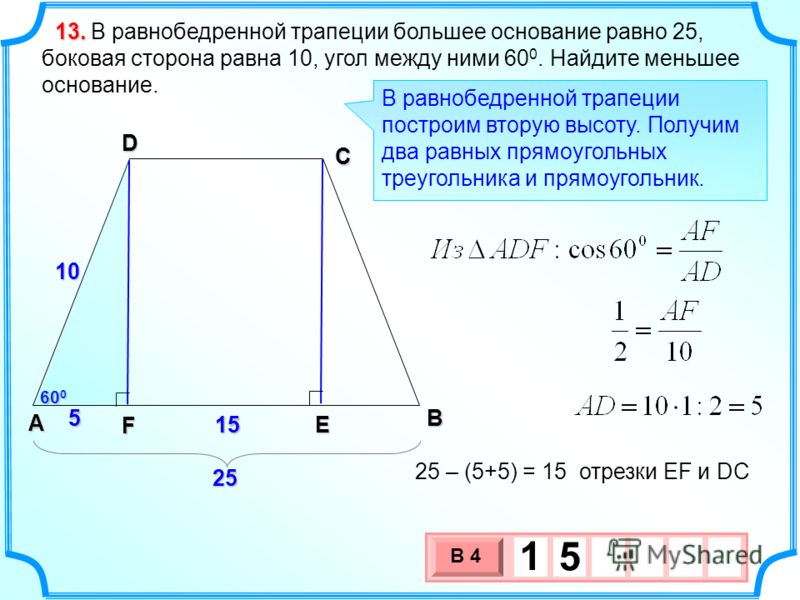
Найти большее основание трапеции
Найти большее основание трапеции. Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:
Сама формула:
Рассмотрим задачи:
27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Площадь трапеции (формула):
Нам известны основания и площадь, можем записать:
Ответ: 8
27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Формула площади при данных обозначениях вершин:
Нам известны основание, площадь и высота, можем записать:
Ответ: 7
*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.
27630. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
Формула площади при данных обозначениях вершин:
Нам известны средняя линя и площадь, можем записать:
Ответ: 8
27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Найдите периметр трапеции.
Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.
Используя данные в условии мы можем вычислить высоту:
Опустим высоту из точки D к основанию АВ и точку пересечения обозначим как Е:
Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):
По теореме Пифагора:
Таким образом периметр будет равен 7+13+5+5 = 30
Ответ: 30
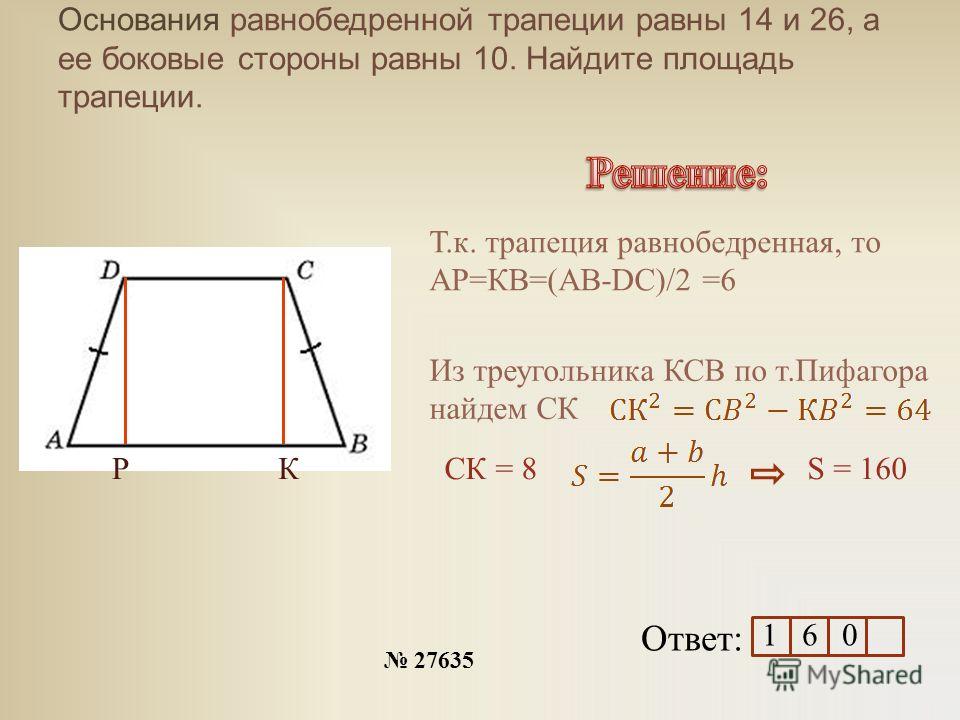
27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Для вычисления площади нам необходимо найти высоту. Выполним дополнительные построения:
Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:
Таким образом площадь будет равна:
Ответ: 160
27636.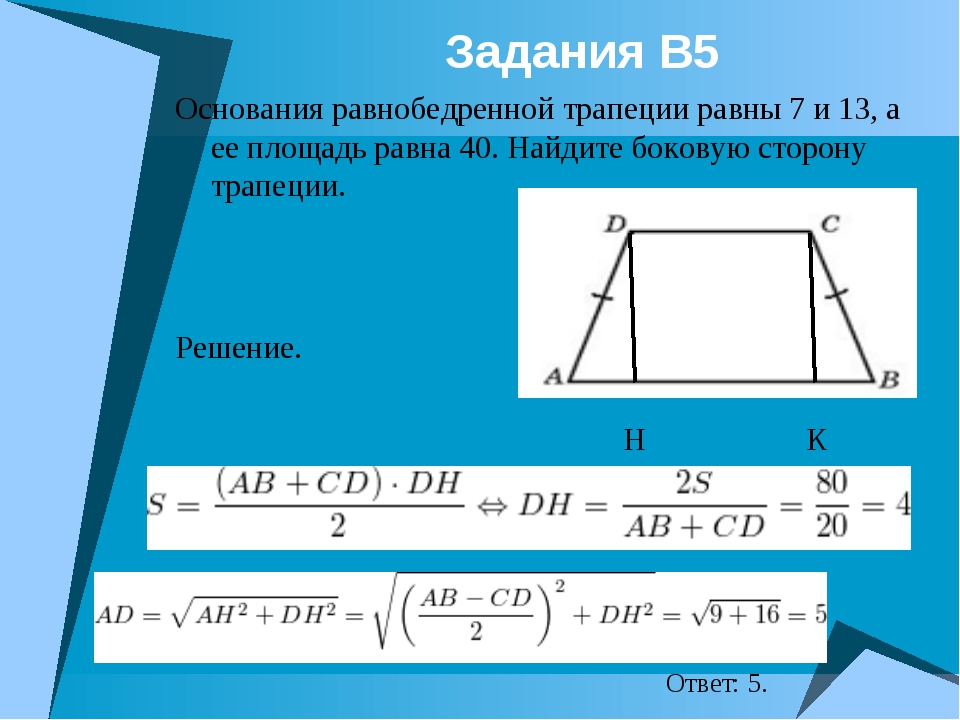 Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Задача обратная предыдущей. Из данных в условии мы можем вычислить высоту:
Теперь выполним дополнительные построения (опустим высоты):
Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:
Ответ: 5
27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:
Высоту нашли, вычисляем площадь:
Ответ: 42
27593. Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Посмотреть решение
27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Посмотреть решение
27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Посмотреть решение
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Посмотреть решение
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.
Посмотреть решение
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
Посмотреть решение
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Расскажите о статье и сайте в социальных сетях.
Как найти верхнее основание равнобедренной трапеции
Читайте также: Как открыть таблицу в access
Радиус окружности, описанной вокруг равнобокой трапеции, ищется как радиус описанной окружности треугольника, образованного ее диагональю со сторонами. (рис.104.4) R=abd/√((a+b+d)(a+b)(a+d)(b+d))
(рис.104.4) R=abd/√((a+b+d)(a+b)(a+d)(b+d))
| Рис.1 |
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 – 2 ac cos α
d 1 = √ b 2 + c 2 – 2 bc cos β
4. Формула длины диагонали через высоту и основания:
Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 – ( a – b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a – c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.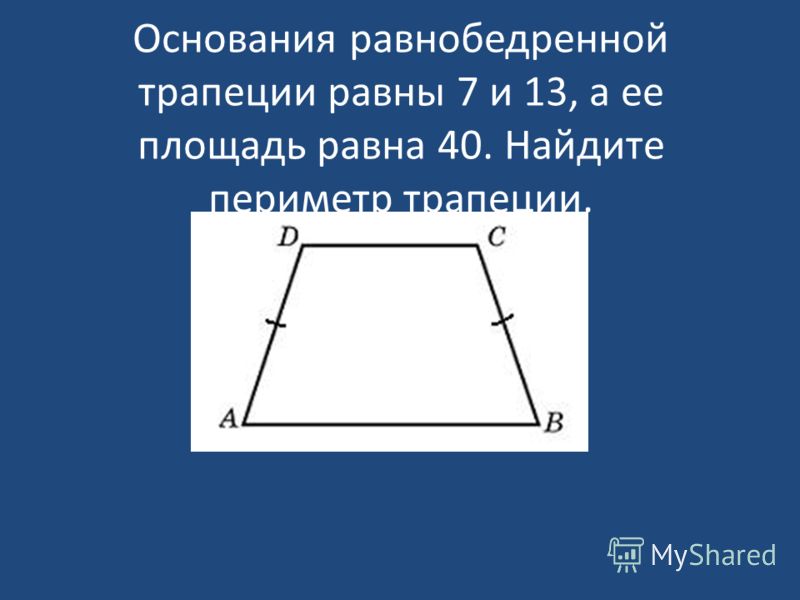
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
1. Формула длины основания равнобедренной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания :
2. Формулы длины сторон через высоту и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции :
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь :
“>
Основания равнобедренной трапеции равны 2 и 8, а диагональ √41 см.
 * C помощью циркуля и линейки постройте угол, равный 150 degrees .
* C помощью циркуля и линейки постройте угол, равный 150 degrees .
дано коло радіус OF якого перпендикулярний до хорди CD. Знайдіть кут COD якщо кут DCF = 15°(Зделайте прошу, очень нужно), простите за качество.
Дано коло радіус OF якого перпендикулярний до хорди CD. Знайдіть кут COD якщо кут DCF = 15°(Зделайте очень прошу) (извените за качество)
Перепиши речення, вставляючи пропущені букви. Укажи в дужках, у значенні якого способу вжито виділені слова?
он украшен картинами помогите пожалуйста
1. Найдите площадь прямоугольника, если известно, что одна сторона прямоугольника на 4 см больше другой, а диагональ прямоугольника равна 44см
2. Най
…
дите площадь прямоугольника, если известно, что отношение его сторон равно 5 : 2, а периметр равен 56 см
3. Найдите площадь прямоугольника, если известно что отношение его сторон равно 7 : 2, а площадь равна 56 см²
4. Найдите периметр прямоугольника, если известно что одна сторона больше другой в 19 раз, а площадь равна 76 см²
5. Одна из сторон прямоугольника на 3 см больше другой. Найдите стороны прямоугольника, если его периметр равен 18 см
Одна из сторон прямоугольника на 3 см больше другой. Найдите стороны прямоугольника, если его периметр равен 18 см
помогите пожалуйста)
Помогите пожалуйста, геометрия, прямоугольные треугольники.
Задание 1 (20 баллов).Из точки A к окружности проведены две касательные: AB и AC (B и С – точки касания). Определите градусную меру дуги BC, если расс
…
тояние от точки A до центра окружности в 2 раза больше радиуса окружности.
помогите, пожалуйста, с геометрией
Как найти основание равнобедренной трапеции
Трапецией называют четырехугольник, основания которого лежат на двух параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
У равнобедренной (или равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
Трапеция имеет два основания, и чтобы их найти, нужно сначала обозначить фигуру. Пусть дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Для решения задачи об основании трапеции проще всего будет составить систему уравнений, чтобы через взаимосвязанные величины найти нужные основания.
Обозначьте отрезок BC за x, а AD за y, чтобы в дальнейшем было удобно обращаться с формулами и понимать их. Если не сделать этого сразу, можно запутаться.
Выпишите все формулы, которые пригодятся при решении поставленной задачи, используя известные данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
Вспомните свойство равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании.Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Найдите катет AH, следуя теореме Пифагора, которую вы уже записали. Пусть он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
Пусть он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
Выразите через площадь трапеции неизвестную величину. У вас должно получиться: AD=2*S/h-BC или y=2*S/h-x.
После этого подставьте данные числовые значения в полученную систему уравнений и решите ее. Решение любой системы уравнений можно найти автоматически в программе MathCAD.
Основание трапеции равно боковой стороне
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
1) Если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
Рассмотрим трапецию ABCD, в которой боковая сторона AB равна меньшему основанию BC.
1) Так как AB=BC, треугольник ABC — равнобедренный с основанием AC. Значит, у него углы при основании равны:∠BAC=∠BCA.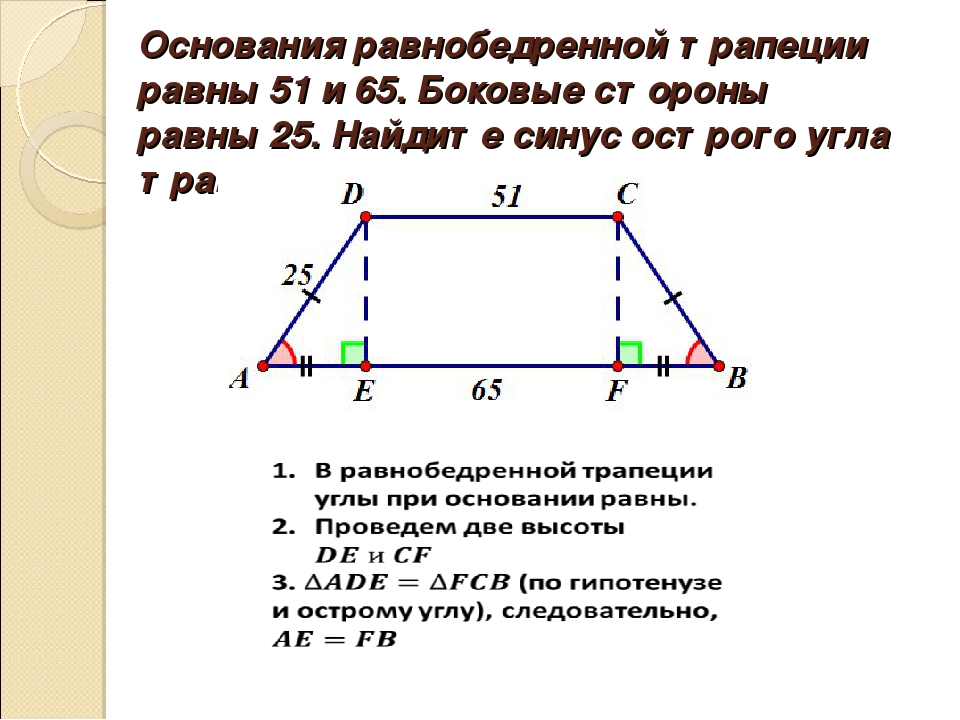
2)∠BCA=∠∠CAD (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
3) Отсюда следует, что ∠BAC=∠CAD, а значит, AC — биссектриса угла BAD.
2) Если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
Рассмотрим трапецию ABCD, в которой большее основание AD равно ее боковой стороне AB.
1) Так как треугольник ABD — равнобедренный с основанием BD, то его углы при основании равны: ∠ABD=∠ADB.
2) ∠CBD=∠ADB (как внутренние накрест лежащие при AD ∥ BC и секущей BD).
3) Отсюда ∠CBD=∠ABD, следовательно, BD — биссектриса угла ABC.
Аналогично доказываются утверждения для прямоугольной и равнобедренной трапеции.
3) Если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
4) Если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.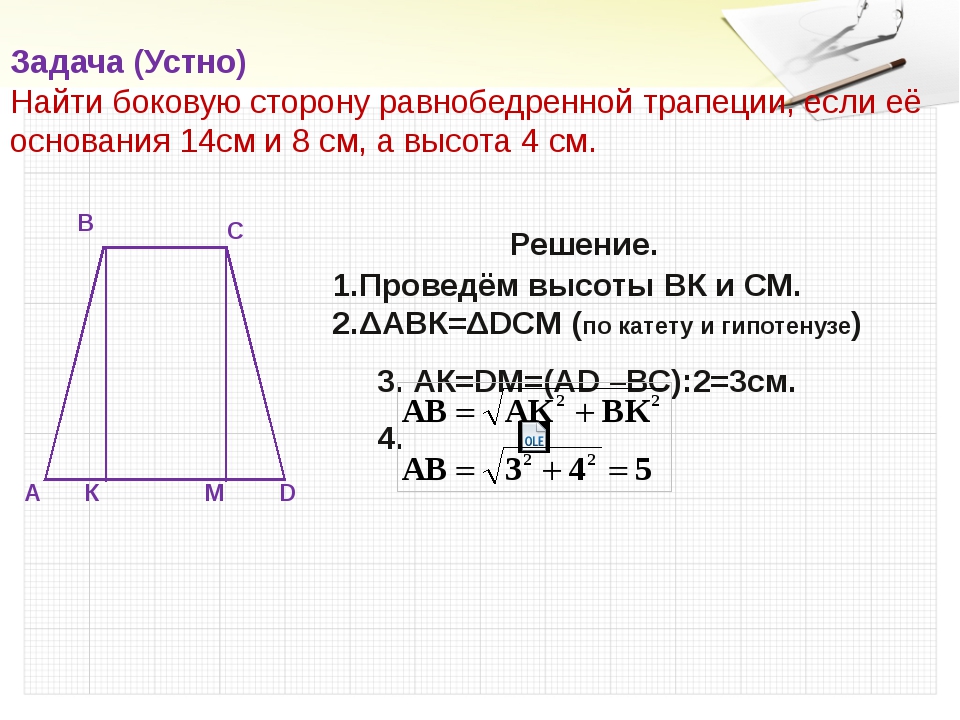
5) Если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
6) Если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
7) Если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
8) Если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
В частности, так как сумма противолежащих углов равнобедренной трапеции равна 180º, соответственно, ∠ACD+3∠BCA=180º и ∠BAC+3∠CAD=180º.
1. Основания равнобедренной трапеции равны 6 и 12. Боковые. стороны равны 25. Найдите синус острого угла трапеции.

41 прототип задания 18
41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите
Подробнее
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
Подробнее
В 8 (2014) 16.
 В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
Подробнее
Все прототипы заданий В3
1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
Подробнее
Теоретическая часть экзамена по Г-8 кл.
Теоретическая часть экзамена по Г-8 кл. Знать и понимать (сделать чертеж и показать на рисунке) следующие определения и теоремы (без доказательства) из учебника Г-8 А.Г. Мерзляка Глава 1 1. Сумма углов
Сумма углов
Подробнее
tgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
Подробнее
Прототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Подробнее
46 прототипов задания 16
46 прототипов задания 16 Задача демо-версии: В равнобедренном треугольнике с основанием внешний угол при вершине равен. Найдите величину угла. Ответ дайте в градусах. 1. Задание 16 ( 27238) 2. Задание
Найдите величину угла. Ответ дайте в градусах. 1. Задание 16 ( 27238) 2. Задание
Подробнее
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
Подробнее
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
Подробнее
7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
Подробнее
AC 6, cos A. Найдите BH.
Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
Подробнее
Как найти стороны параллелограмма
Как найти стороны параллелограмма Свойства параллелограмма: 1. Противоположные стороны равны и параллельны 2. Противоположные углы равны 3. Точка пересечения диагоналей, делит их пополам Формулы длины
Подробнее
Анализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
2) Вертикальные углы
Подробнее
Планиметрия: комбинации фигур.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника
Подробнее
Планиметрия (расширенная)
1. Площади плоских фигур Площадь треугольника: стр. 1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
Подробнее
Все прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
Подробнее
Билеты по геометрии 7 класс
Билеты по геометрии 7 класс Билет 1. 1.Смежные углы: определение и свойства. Доказательство одного из них. 2.Задача по теме «Равнобедренный треугольник» 3.Построение прямоугольного треугольника по катету
1.Смежные углы: определение и свойства. Доказательство одного из них. 2.Задача по теме «Равнобедренный треугольник» 3.Построение прямоугольного треугольника по катету
Подробнее
Задания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
Подробнее
Вписанные и описанные окружности
Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.
Подробнее
Анализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Подробнее
ЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
Подробнее
ID_7510 1/9 neznaika.pro
1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Подробнее
Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1.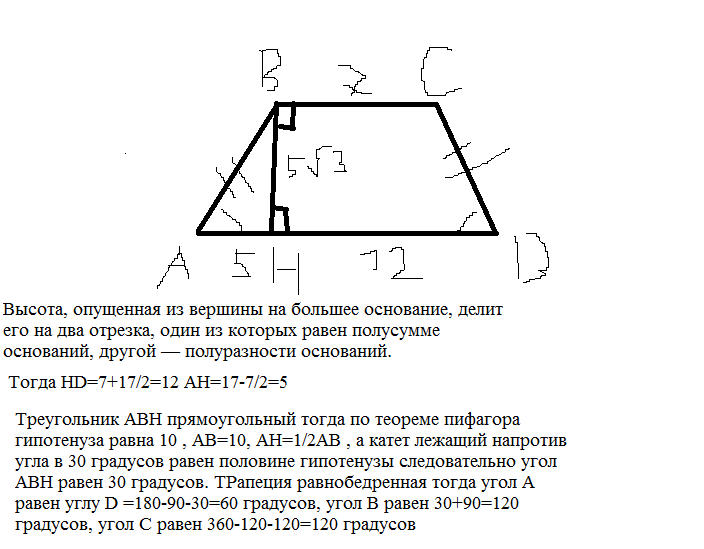 Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Подробнее
Произвольный треугольник
Произвольный треугольник В приведенных ниже формулах используются следующие обозначения: а) с длины сторон АВС лежащие против углов А В и С соответственно б) высоты медианы l l l биссектрисы в) радиус
Подробнее
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
Подробнее
Вписанные и описанные окружности
Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.
Около всякого треугольника можно описать единственную окружность.
Подробнее
Геометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Подробнее
Координатная плоскость
Координатная плоскость 1. Найдите площадь параллелограмма, изображенного на рисунке. 2. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9). 3. Найдите площадь
Подробнее
Тема 21 «Трапеция. Многоугольники».
Тема 1 «Трапеция. Многоугольники». Трапеция четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Параллельные стороны называются основаниями трапеции.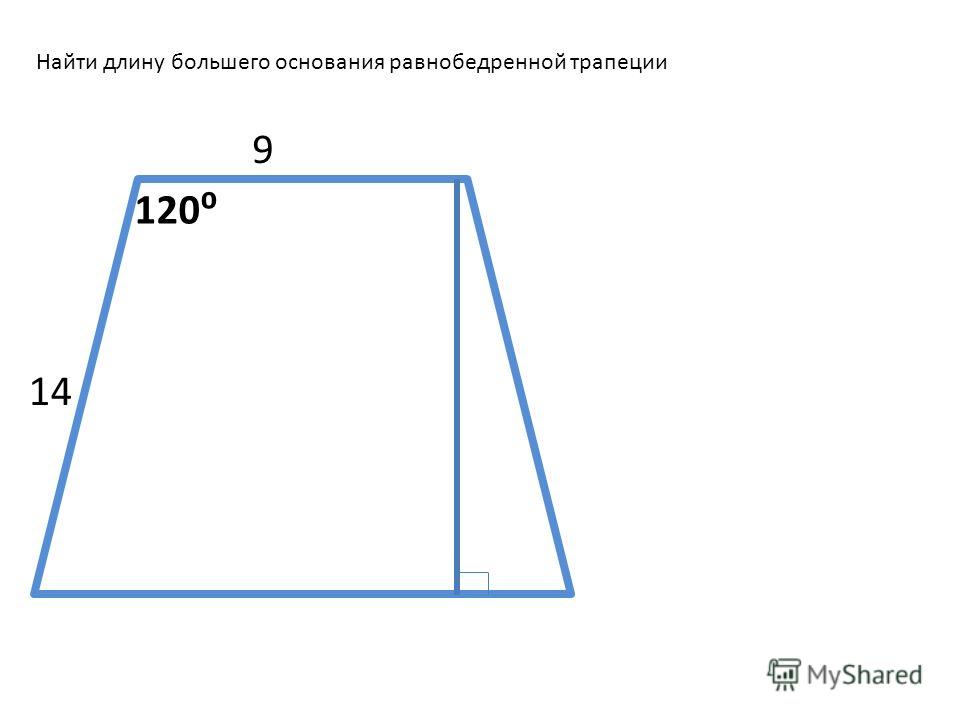 Две другие стороны называются
Две другие стороны называются
Подробнее
Как найти длину стороны трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
5.13: Трапеции — K12 LibreTexts
Определите неизвестные угловые измерения четырехугольников с ровно одной парой параллельных сторон.
Трапеция — четырехугольник с одной парой параллельных сторон.
Рисунок \ (\ PageIndex {1} \)
Равнобедренная трапеция — это трапеция, у которой непараллельные стороны совпадают.
Рисунок \ (\ PageIndex {2} \)
Базовые углы равнобедренной трапеции совпадают. Если \ (\ (ABCD \) \) — равнобедренная трапеция, то \ (\ angle A \ cong \ angle B \) и \ (\ angle C \ cong \ angle D \).
Рисунок \ (\ PageIndex {3} \)
Верно и обратное. Если трапеция имеет равные углы основания, то это равнобедренная трапеция. Диагонали и равнобедренной трапеции также совпадают.Промежуточный сегмент (трапеции) — это отрезок прямой, соединяющий середины непараллельных сторон:
Рисунок \ (\ PageIndex {4} \)
В трапеции есть только один средний сегмент. Он будет параллелен основаниям, потому что находится на полпути между ними.
Теорема о среднем сегменте: Длина среднего сегмента трапеции является средней длиной оснований.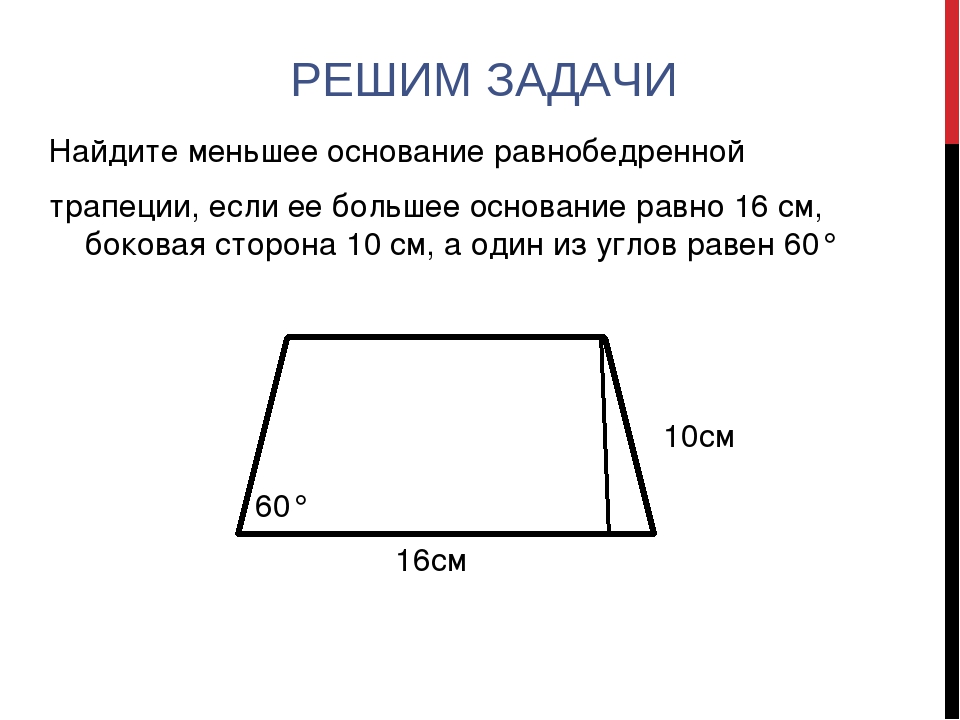
Рисунок \ (\ PageIndex {5} \)
Если \ (\ overline {EF} \) — средний сегмент, то \ (EF = \ dfrac {AB + CD} {2} \).{\ circ} \), \ (ZOID \) не является равнобедренной трапецией.
Пример \ (\ PageIndex {5} \)
Найдите \ (x \). Все фигуры представляют собой трапеции с обозначенной средней частью.
- Рисунок \ (\ PageIndex {10} \)
- Рисунок \ (\ PageIndex {10} \)
- Рисунок \ (\ PageIndex {11} \)
Решение
- \ (x \) — это среднее значение от 12 до 26. \ (\ dfrac {12 + 26} {2} = \ dfrac {38} {2} = 19 \)
- 24 — это среднее значение \ (x \) и 35.
\ (\ begin {align} \ dfrac {x + 35} {2} & = 24 \\ x + 35 & = 48 \\ x & = 13 \ end {align} \)
- 20 — это среднее значение \ (5x − 15 \) и \ (2x − 8 \).
\ (\ begin {align} \ dfrac {5x − 15 + 2x − 8} {2} & = 20 \\ 7x − 23 & = 40 \\ 7x & = 63 \ x & = 9 \ end {align} \)
Обзор
1. Могут ли параллельные стороны трапеции совпадать? Почему или почему нет?
Могут ли параллельные стороны трапеции совпадать? Почему или почему нет?
Для вопросов 2-8 найдите длину среднего сегмента или отсутствующей стороны.
- Рисунок \ (\ PageIndex {12} \)
- Рисунок \ (\ PageIndex {13} \)
- Рисунок \ (\ PageIndex {14} \)
- Рисунок \ (\ PageIndex {15} \)
- Рисунок \ (\ PageIndex {16} \)
- Рисунок \ (\ PageIndex {17} \)
Найдите значение отсутствующей (ых) переменной (ей).
- Рисунок \ (\ PageIndex {18} \)
Найдите длины диагоналей трапеций ниже, чтобы определить, является ли это равнобедренным.
- A (−3,2), B (1,3), C (3, −1), D (−4, −2)
- A (−3,3), B (2, −2), C (−6, −6), D (−7,1)
Обзор (ответы)
Чтобы увидеть ответы на обзор, откройте этот PDF-файл и найдите раздел 6.6.
Словарь
| Срок | Определение |
|---|---|
| равнобедренная трапеция | Равнобедренная трапеция — это трапеция, непараллельные стороны которой совпадают. |
| средний сегмент (трапеции) | Отрезок, соединяющий середины непараллельных сторон. |
| трапеция | Четырехугольник с одной парой параллельных сторон. |
| Диагональ | Диагональ — это отрезок линии в многоугольнике, соединяющий непоследовательные вершины |
| средний сегмент | Средний сегмент соединяет середины двух сторон треугольника или непараллельные стороны трапеции. |
Дополнительные ресурсы
Видео: примеры трапеций — базовые
Действия: Вопросы для обсуждения в форме трапеции
Учебные пособия: Трапеции и воздушные змеи Учебное пособие
Практика: Трапеции
Реальный мир: трапеции в Тимбукту
Как найти основание и боковую сторону равнобедренной трапеции
1.Сторона (основание) равнобедренной трапеции, если известно другое основание и средняя линия трапеции
, — базы
— средняя линия
Вычислить основание равнобедренной трапеции, если задана средняя линия и другое основание ( a b ):
2. Все четыре стороны равнобедренной трапеции, если вы знаете высоту, угол у основания и другие стороны
— меньшая база
— большая база
— нога
— уголок у основания
— высота
Вычислить боковую сторону (опору) трапеции, если задан угол в основании, высоте или основаниях ( c ):
Вычислить основание трапеции, если задан угол при основании, высота и другое основание ( a b ):
Вычислить основание трапеции, если задан угол в основании, боковой стороне (ножке) и другом основании ( a b ):
3.Основания равнобедренной трапеции, если известны высота, диагонали и угол между диагоналями
— меньшая база
— большая база
— нога
— диагональ
, — углы между диагоналями
— высота
Рассчитайте сторону (основание) трапеции, если заданы диагональ, боковая сторона (ножка) и другое основание ( a b ):
Рассчитайте боковую сторону (опору) трапеции, если заданы диагональ и основания ( c ):
Вычислить сторону (основание) трапеции, если заданы диагональ, высота, угол между диагоналями и основанием ( a b ):
* Верно в данном случае:
4. Стороны равнобедренной трапеции, если вам известна площадь трапеции
, — базы
— нога
— средняя линия
, — уголки у основания
— высота
— площадь
Вычислить сторону (основание) трапеции, если задана площадь трапеции ( a b ):
Расчет боковой стороны (ножки) трапеции, если задана площадь трапеции ( c ):
* Верно в данном случае:
РЕШЕНО: Ноги равнобедренной трапеции 10…
Стенограмма видео
и эта проблема осталась бы найти область.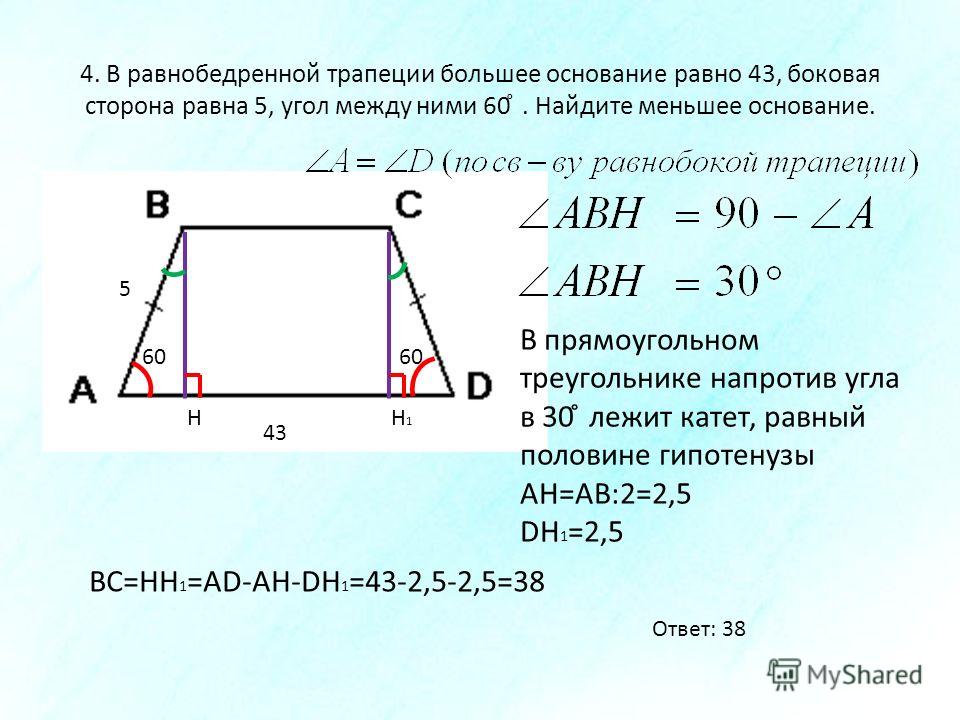 И длина диагоналей этой ловушки — деревянная. Во-первых, давайте определим площадь. Площадь любой сои равна 1/2 ее высоты. Времени для некоторых из двух баз в данном случае были даны длины двух баз, то есть девять и 21. Но нам нужно найти высоту его гусениц. Ждать. Прежде, чем мы ограничились областью, мы могли определить высоту этой стороны дорожки, используя этот прямоугольный треугольник и нарисовав зеленый цвет. И мы назовем нижнюю сторону этого треугольника X симметрией. Мы знаем, что нижнее основание равно верхнему основанию плюс два раза X.Мы можем найти значение X по значениям для базы. Это дает нам, что X равно шести, не собираясь перерисовывать этот прямоугольный треугольник и зеленый, чтобы прояснить ситуацию, потому что это прямоугольный треугольник, который мы можем использовать здесь драконами, ммм, чтобы найти значение возраста, взяв эту большую из обеих сторон. дает нам самое высокое. Трапеция равна восьми, и у нас достаточно информации, чтобы ее найти. Зона ловушки свинцовая.
И длина диагоналей этой ловушки — деревянная. Во-первых, давайте определим площадь. Площадь любой сои равна 1/2 ее высоты. Времени для некоторых из двух баз в данном случае были даны длины двух баз, то есть девять и 21. Но нам нужно найти высоту его гусениц. Ждать. Прежде, чем мы ограничились областью, мы могли определить высоту этой стороны дорожки, используя этот прямоугольный треугольник и нарисовав зеленый цвет. И мы назовем нижнюю сторону этого треугольника X симметрией. Мы знаем, что нижнее основание равно верхнему основанию плюс два раза X.Мы можем найти значение X по значениям для базы. Это дает нам, что X равно шести, не собираясь перерисовывать этот прямоугольный треугольник и зеленый, чтобы прояснить ситуацию, потому что это прямоугольный треугольник, который мы можем использовать здесь драконами, ммм, чтобы найти значение возраста, взяв эту большую из обеих сторон. дает нам самое высокое. Трапеция равна восьми, и у нас достаточно информации, чтобы ее найти. Зона ловушки свинцовая.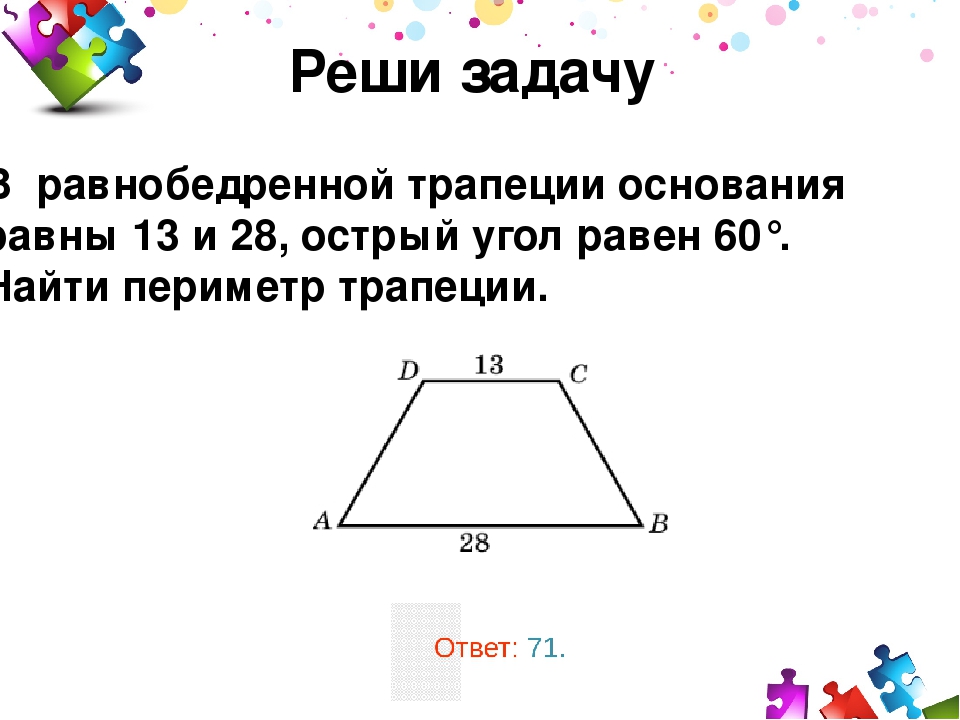 Оказалось, что высота равна восьми. А сыну двух основ 30.Таким образом, площадь этой трапеции равна сотне единиц Венди-Сквер. Теперь вы можете узнать длину диагоналей. Давайте посмотрим на этот прямоугольный треугольник, который я рисую красным. Независимо от того, есть ли у меня макароны, новость об этом прямоугольном треугольнике — это длина диагонали. И потому что это не дерзость, это верх. Длина диагоналей такая же, как у Hyatt того времени. Атрибуты веса равны восьми и еще одному. Нижняя сторона этого треугольника будет равна основанию. Нижнее основание этого траппистского oId минус X ранее могло обнаружить, что X равно шести.Итак, началось это снижение. Треугольник равен 2196 взглядам. Итак, владыки — это треугольник. Он равен тебе. 15. Теперь все, что осталось сделать. Он воспользовался теоремой Пифагора, чтобы найти диагональ. Таким образом, длина диагонали этого рельсового пути составляет 17 единиц
Оказалось, что высота равна восьми. А сыну двух основ 30.Таким образом, площадь этой трапеции равна сотне единиц Венди-Сквер. Теперь вы можете узнать длину диагоналей. Давайте посмотрим на этот прямоугольный треугольник, который я рисую красным. Независимо от того, есть ли у меня макароны, новость об этом прямоугольном треугольнике — это длина диагонали. И потому что это не дерзость, это верх. Длина диагоналей такая же, как у Hyatt того времени. Атрибуты веса равны восьми и еще одному. Нижняя сторона этого треугольника будет равна основанию. Нижнее основание этого траппистского oId минус X ранее могло обнаружить, что X равно шести.Итак, началось это снижение. Треугольник равен 2196 взглядам. Итак, владыки — это треугольник. Он равен тебе. 15. Теперь все, что осталось сделать. Он воспользовался теоремой Пифагора, чтобы найти диагональ. Таким образом, длина диагонали этого рельсового пути составляет 17 единиц
.
% PDF-1.4
%
1 0 obj
>
эндобдж
3 0 obj
> >>
/ Содержание [5 0 R]
>>
эндобдж
4 0 obj
> >>
поток
Я
IQ:, D «& (hD% G
: «t $ m) ި D #. ! 3B: MH») BmR «DDJ’Љ} Bm ‘ЛBq (DYB% $! 0 L !! D ք F» $ m \ BhhA
! 3B: MH») BmR «DDJ’Љ} Bm ‘ЛBq (DYB% $! 0 L !! D ք F» $ m \ BhhA
q !! ‘Fh $ YGiI «8; VEB» ND @
@ «fBA6HCF
D «[Q] AЈFDDD! 8 @ M» & (EF̕Q $ «B» HDh% (!! 6K (A «R! FvjDDDHZ! E: HOKAhO #:! + B @ 2Ev, H # DBPhL @ ԒHDDDDB $ b2F: +
Gѭ $ ‘mFMQhA’E «@ R0DN # hDtPF # T # 1j # hL & T% Ђ» CBR! $ Ф «»]’ aFф] Ft’xFP * P @@ d: DKD! D «q $ B» «& ty1Eq) HUB%: 3GfhB4 $ # h} G> «] Ga # 4} t} && m Ba 0h05BDDNN! T &
ք AhJ «m L» $ Љ! DDN «* DD! $ — D thN»} B «jB» «m»]! ! HL @N «DDJ3A & hMhD! 6 4Kt & h! O! $ # HD! HB $ M) 4N! & D!» N !.0L #! ‘G «» & qFѴy + h!> #!> L! 0dR «.HhFB» fN!’ B $ b H # ZT $ 6CGB @ ԌБЉ’G @ A ЈBByF! HEZE # D! @% & Q
D «@ B» «yB] GѴ $ h ߡ! #% .D8RHDB’B & ИB $ t $ b> IBȝ» y Автор aB] B} Q0 # RD B N! DIt «Rђ» q FhGDjDJ’bh (GihK, Љ!
f 苢 6 ֎! tfK @ DPA «» B u + HiAUGTHB $ &! 0 # IѴ: D3DY «(DB! h»% N! t’6tR! 0R (BHFЂ ‘: R4Db.DDL! 1 .4] DZF & FhDMZ3B% # ք E # h5B «‘ФF! hJ hDD»] Bh «Bq»‘: $! 3GѴmBGE «(GЙ!:» ‘# DO! 60 @! 0DԤ 7D «B» DDO #: !! 6КF «DKh! Г # 4 & Z3Bw4 «} $ # m $ B @ D0h! Dm Ft] BjEԌt» yB0 «vD» B $ h4G ‘»$ 4″‘ K4 «‘! B» q:! 0N! «Q МDBDJa # hL #> # Jt & IAĐBaB%: 03GBmB1) d:% DD @ D) ф] ֍ hB} B $ # h0! #] Q «m’F
BN !! DD SB’Bm «B» «» ‘! Da} $$ D6 «DHE» + (Ԍ (BD! 8GT} FhO! (EЈG «» «»‘ фqBuBF! 0D # N !! «%: + h ꋠ f! 8Ѣ;, A & A! В $ — & H5! 0 # N #! 58!> t & *
rI’D «» м ч. Kh: O !! IЈGhDD0 # R’DQhDDJD’Ј «DDD! ‘BB’Ј» BK! 6DD * 6H% Ј!’ B4Ixф’Q2 & M1:>! O! 8! 4Dm!) ѢR $ & R% HA; 0 ‘ BEL $ B «»%: hHhH% D4% ѭB & h! 0 ‘
Kh: O !! IЈGhDD0 # R’DQhDDJD’Ј «DDD! ‘BB’Ј» BK! 6DD * 6H% Ј!’ B4Ixф’Q2 & M1:>! O! 8! 4Dm!) ѢR $ & R% HA; 0 ‘ BEL $ B «»%: hHhH% D4% ѭB & h! 0 ‘
#N «u $ (B» a # FFt «}» BD # Q «m (Ba!, П @ 8Ѣ0: DtBD!) 4% eG! Ta m
B8DB & h t] t & @ К! 0 !! H> Ѵ% Ѵ»1D @DD! H «qB» PIЕTB! ‘D «‘ yBVB»% —
BaD $ h @> «(! HD> # 4NDBGB» «]% Љta t» GDb!> H! 4 $ «B # & t $ B:! DM’B $ IB’T» a4DGGD! «$ 4» kF: «HBD» ‘t $ 4 $ 4’ «StPD8 !! 3DbDyPN #. GFtu @! 06tuGXGD» «$ 4m ‘# @ DDBhZ5B0JafDmBmBD’ЈHD * ЄQq! FDԄ! # @ 80DN # 4% Љ» «Ny B’BT @ # 6МB’Dw DB «& hԄO» EZ # HDO # h «! .4Gѭ» «] 6 BR:! 6 B» f! DDt «D)% FѢ,» MIO! DI * hDDHhԍHA $ i $! DDG! Bq B Dh8DD «% M @ ԍh $ HIѩGA $ 4% њ8h! «& GaQt» «» y «aDa (B & yB» $ IB4DGTa «GB & ЈdS6:! 4FОB! ‘$ AD! h! KHJh0bwh # BHF}»‘%: BhhN # 8! «BV! DNPQHA» KZ3BfD! O0; $ «kD3D’B] B’tHFB & ЛBmEtBB% B» B&U «K! $» L # D] A: K! DhA6: # hDhDH% HD! FDB: (GЉF «qh8 ## 4kBh!! E: t’BPh>! «F (Q)! B» «» «$ DL! N2tq q» fR * t’Tv!: # HABDLЉ !.8 ..! ‘FmFN # ZB $ «0>% F & GAPZ4
Z «FRB»} F ؚ ‘@ 4% «# HL # 4] Z85! 8’BADHx»‘ aB @ B «GBaGBm t] $. ) 3FTBB’TP% ф} FB $» «m3BkBhDDDE> B» ‘ЉwZ @ DB $ 8R «N!: Ԅ BH !@0KA!.A!C] G $» «‘% I N # 4 & qGЉ» Nt & hIБ «‘ zB’hBJD ք: K0» IЛG% Ђ «yB»} BqB «B 膉a:% ѭFIф & AGB!% DDZ @ RB & ЉB68FHjBaFUB’H! 1ȈFh! 4FhDПB «% At» Dq! & h! 6L! d «$ jFBL! 8F (B &% (IИGФ} MH $ ADI $! 4D»DmB} B ‘ & tfDB5 # h6MMkRNBqGEL B «T!» 0DBHBfq $ GК «! FЈTwhM3Bh% Ba B & hD)» «q’Ѣ: .DBq @ & 3B, * ԫ +
) 3FTBB’TP% ф} FB $» «m3BkBhDDDE> B» ‘ЉwZ @ DB $ 8R «N!: Ԅ BH !@0KA!.A!C] G $» «‘% I N # 4 & qGЉ» Nt & hIБ «‘ zB’hBJD ք: K0» IЛG% Ђ «yB»} BqB «B 膉a:% ѭFIф & AGB!% DDZ @ RB & ЉB68FHjBaFUB’H! 1ȈFh! 4FhDПB «% At» Dq! & h! 6L! d «$ jFBL! 8F (B &% (IИGФ} MH $ ADI $! 4D»DmB} B ‘ & tfDB5 # h6MMkRNBqGEL B «T!» 0DBHBfq $ GК «! FЈTwhM3Bh% Ba B & hD)» «q’Ѣ: .DBq @ & 3B, * ԫ +
A mDK «5! HDMqB $ 4B»> @) ЈGx (B} ‘u # DB «$ M3B» uBmF «» & ꄊ0 Љ0 (F! 8 @ R> K @ 68. !! N! D «» «» @ DND «tjB» «$» m «1 #»!% Є $ FhB &] G: # 4a’B]! «B]» «yBEK8 + hDAZDHuFS> M 芒 8J $!:! 3B% 8Dq4JPhL! 4» & Ф} # E: #hF «& G»} «» B «‘DaEA» CQ «h5» kBh # B!’ B «} D # Z3DItV # DH5! FѢ 5> DDOMHN! DMO! HDa B (GMD’B} NҐ! $ # DIK% # hD # M «OD BA8taF0BSZ.0 «M» $ T] EB PL «D !! #! 3Ba #) HIt B! ‘& H! MhH6!» HDOJB $! «Ȁ # hDB» & DD NJ2EB «‘ Ј $ V8J» ‘B’ & hN h60 & Ue, RBD ! $ @DE! B «AD!» BK’FBv #! QBRH «hhtHB» «}% A’Fa @ a: HDA # D D6! 8hDJ,! (DHD # H!» ‘TqB & a «1» $ DB! Љ0DUQ @ 4h]. @ K @ h! G BqByP B «» BB’BULЈD t & qDDM! R6D% Љt «B» EЈ $ QBPHhDDI4S (BA @
I0HJD «&» F! 0E! $ «B6 @ rL @! 0tm $ 2By! # 4qGBT # hJ» y $% Јh # ԄDhDJJ
ДА :!)
!
D & CFЉ: * HJ’B! ‘F «& МБ» yE B «» mJh: B’G B6DL! . RL # * t: tyB «m & N» F! DF # $ «‘» U BT! BO! D 4Bq » jFE! FLeTQrDD) Љ! F% E
RL # * t: tyB «m & N» F! DF # $ «‘» U BT! BO! D 4Bq » jFE! FLeTQrDD) Љ! F% E
BCFЉR.B «B @ & ЄA» DDL !! h5 ‘! DE8KDu @ tNtqD4m $ yBaB! 66D! 8h ߣ h5’Dq fDDMMUIhO} ЉDDHD «BLE» V! DD AE «t’MhHL #hD 萁’ Fo, tm> MZ5 # B $ MHL! BD! RԄЉBv :).N CGt! «$ B # hED @ E: 4FtqD4] B & a @] Bq B # DD # 4» «m # Fy NH02D B & J & hFJR8 $ DD
h! D8t «t» ‘maBP! .DDMIB0KDHA} 16 ք BDND «ty kB» & Љ) BB] $ ZNЄI
@ ЉN «(DA hO! 6! 8 # DqFt» & h! 0 !! B% Б! .Tq # BOYhD5DD! @DDB! DUA «R» TDD’B’Ј # FѴ «fO # hH @ JkB» a ‘ BtEL «a B» ‘B «qgBA3I BM] FѴB» mCG B «$ Jty # GdDJDE $ mDO
] t! & tm «mNHhEqNVjPBeaPRr) L @ Ԣ» t @: 5 $ MЈ & Ut $ BDJD & B% $$ qѢh0I «m 0 *> L»
FНQ0D «» &! PB Ba DD0 tCB] GA Bt_9FC + Aa> 3BABK4 «UJ6O» t «» U «aA & Љ» «» m «» m EB «&» ‘% a! 6! DDD $ D «» B «qNDy «& Љ» «» @ E $ CBNaD% iNhO # * МEP «@» «q @ B» » a!> «M) MtB} К! $! 8M4C; 9» uD «0a
@ «D @ IНQAD4AdLН @ Zh6! @ 0» && hL #>! #h «» a $}! & фqB & B] $; Н%!% (O «» «» B # D «B $ 4» & N # DO $ 4DЈ «A * ЛBfDN #! 8MHK0 # hAN3BmFB» ‘t] D4a! ‘х * R! 6N3GѴ] A’ gGЛBm GD’h ꄨ EЉ (B $ mB $ hG $ ‘BCGОBkD !. 4q Fф GT «P! # H # D DK0 & DN» K>! ‘BqBU «» «aq» «q 萎’ q% F # D4N4hN! 0IПBh # 05 @ 苡» ‘@! 4 & mGB «» NL !!.! DD BtFK88HaD) BkBkI B4q @ L (P (nʒB & Љa B «S
4q Fф GT «P! # H # D DK0 & DN» K>! ‘BqBU «» «aq» «q 萎’ q% F # D4N4hN! 0IПBh # 05 @ 苡» ‘@! 4 & mGB «» NL !!.! DD BtFK88HaD) BkBkI B4q @ L (P (nʒB & Љa B «S
hDODH> a BDH’BCD! «» DD 脺 DL B ‘
B] «yE’TjEZ0J @GA 4y $ hM5! 0.DDB» «$ uGGАDqhMHh (IA» $ MEѴ «tB & ЈB] BkFh! (BaBaAhM D» # 8KBDCB «S0 # hO3B» «» tB & ‘cHD!; 5 @ tNR $ GМB $ mD «$ 聡% Љ} FИGTmBBm B! $
6hDMh] D0 «) DHB & O» DL D8D D & 🙂 ‘։’ «» «‘aD»> t «N4» «» f’B $ iBBUt «» «» «q $! 5.DL B» IGA: 8 BjBaB ‘D & t «BaA $» ʂPBht’bMhO! 3EЉ «fZ $ ОB’ B» $ t’TBBBy
P. «B & hH $ B! Bq B»] 2) ʂ *}] FBh0DD0’t «Y
% DQaF}! DE @ $
B & hLЉBS3B $$ N‘B Љ «m # O # D! HB» a! Bf «N» MhhB3FEЈ * DDIA t «mFh! W6 @ G!» Hh5 «D» t «» $ * 6D ֎ # D&B} t] G B’D% MFМE.66! # ‘Bm] q «$
G # DR @ L # 4F # H0! 8MQ-B «uB» ‘N4D «!» 4b4D; aД # JtV $ ByBqD’фf! .DDDDDDHH6 #>! 3G!: L # h. # @ 4GUe (EFĐM0O «ԄA : # N # N4 «» «a> !. H 詢]] & h6! F> aFPD! 0DA6! DDDO0Lф] Bh4S%! BS @
ˆ + j
· LhDM «hB & aPDDO # 4hЗFy @ # h @» a tBa @ D! ‘GA !! # аDDDL!> DBN # ZD (Bdj! N $! K BDi B) B6BUQB:% J $ DR! 4G B «%» B «m BTʂ» GB ‘mDtq y B! O #.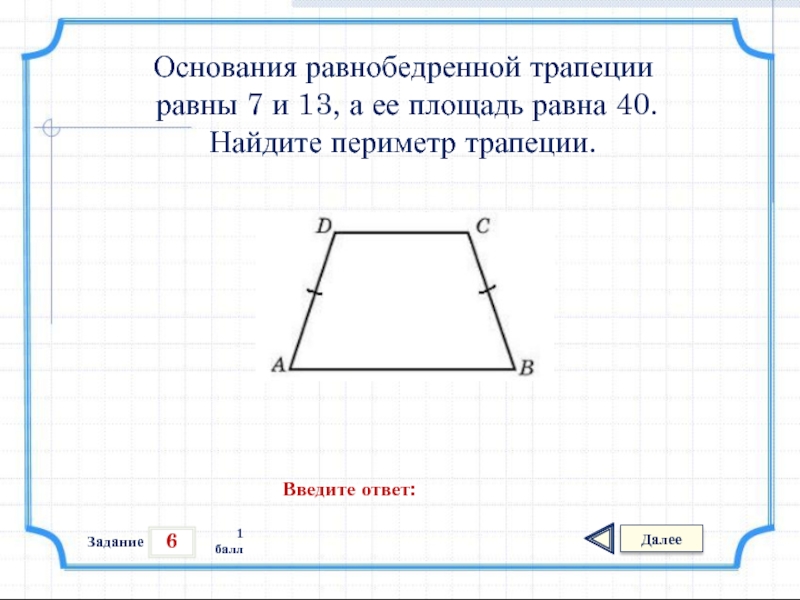 #> ЛGmEtaA «» 14GЉDP B «‘ $ B (#N!% DMh) DQmEPq BI @) ф!» P y B $ t $ t «&» «» «» uB} B} D.FBa
#> ЛGmEtaA «» 14GЉDP B «‘ $ B (#N!% DMh) DQmEPq BI @) ф!» P y B $ t $ t «&» «» «» uB} B} D.FBa
B% ЈIA’tFj «f @ -]» mEB. «(ByBv, Ⱥ8 # DDDDOh0 #. Ք D0 # m6DDDD! 8» t «Ba @ GFP! Fw4» B $ HDDF> ѩ! DwZ! + Ȕ! 8 «B #hDDKDDL! @ МF «] G ByG
tq BHB «& h! hM’G mFBL # DD DJ9U» V!: L # hFP B’T «] B # h%! 4BD! # UD # DtHBEPtfFP (FA» & Ђ «& D! 4 ‘B’фjFB» h! ! DDK (F’tqBByI:! @! 5! DDDAhB @ E: $ «hD ;! D! #HDA> DO # M»! & N! 0 B !.8L # D (B «& aGFМII!> PD!» QhN% (DDПF «VѢ0 # 4 $ GA CB» EqB «» & «] D $!» YB «& B}!»% ИBf @} FqFa «! ‘ uBh hM.DД!} BERFL: 5 !!: 0 MDFB (BqB% tepB} Bq! .DGМBqB ‘$ BhMDDD! DD # 4mE! BaEAO0> N!’ B & МFL «tyFFT’FhN» S! tF »
TKP $ B3E B’Fф «$ qIFh! HE $ m» & !! t} & Г @@ D! # 0Db «» & D DDMhDF0b # h «dDD) Ј! N! # hh5 $» «»! $ mB «q 8 & ЈFAG B’TNL! FD4yFЊ @ & N! DjEѢ0tGy | b» h O @D ! 3B} ВhD! #ThB «mDY # D $ B # DB !!! BjB!» M & :! Автор: 4FОB «» kFЉ «a # 4 @ yЉm q FDFВ & h» t $ «! @ HFJI $ BDhh5]
«& t] EФ% Еh8N # ‘G & M6M! 0M @ 5! 3BhѢ * Љtf6! 4Bh # HBKI» 14GMD | EѴGFa «Ph! 6DN @L! h. MhD) В Fфq ߢ D4K «m» hDDD! 83G & hJ «aB» a 8 D8K! HO D) # D # A @ Ea-R G8D6!) Јh5 $ U «Đ% HLЈFhK’FaBy N!> D5BkB & # MBN»]! & hDDRO! E ճ TRI) t! 0JМB «tFDB & B! 8B $» wD $ I% hA! (aBaBCBPAL # 3D «5.! # 4aBf8
MhD) В Fфq ߢ D4K «m» hDDD! 83G & hJ «aB» a 8 D8K! HO D) # D # A @ Ea-R G8D6!) Јh5 $ U «Đ% HLЈFhK’FaBy N!> D5BkB & # MBN»]! & hDDRO! E ճ TRI) t! 0JМB «tFDB & B! 8B $» wD $ I% hA! (aBaBCBPAL # 3D «5.! # 4aBf8
BNDa% ОBBBtFFa By; 5GT «& KHB * ʀL * QBf !! 4uBBf ꄪ!:; G! 4DR> D:! R $» I6 # DFhDA! L! 4B &% фm th B «!» TEф’1H «莶 xb] a PQH + i
+
„, XP! G) l» 8DA * I $%! 6h # h. @ D0D # R8t’BhD & ЈBm Bq! M> 6ACS0 \ $ «» @ «» q # 08DD! 6 @ D!% HDGDB «@B» ‘»] $ BT!> Ф & yD4jGF% D .. # hAh!’ B16 # $ e / XI» LH # @@ B&L!) ВtmNFhIy! $; TkG $ BS * 6 # BKBBDB & Љhe + *
PD и WHRPTAA ySDRD.GtL «J (!» TwFDT! 4 «HDU -B» «NABIB.IDDH! 0» a t «» ‘D «FBa.HhO! PeyB
U (, *
yXK Mt% B ‘BqA $! G} HGΈ> GΘA4] ѩG | K!.! BN’B $ B HJB0 # N5 # «I #» MB6BP! 66L! R8DuFDDFѴ3 «m] cN & @ $ # AAK.H»:. A $ & PEDI4uGDI «t &» «DQBvPBmL @ & UBBR
V $ * VPr «‘fЉ! & T eH, Ha @ Z @ 2 * —
m RDDH «: + HIt»} aA B $ ME: 4FhHhL! #HDKB (B $
њ: # 88 @ D @ YNP (B «qB, † & PT!%! i # 0DJt & A! M0wZ! aNz [
Я $$ & `EA2 @ C
s [~ $ t $ ‘ф «‘ ЛBBq $» UQ. PM4DT! «A» MtaJP! BB6HhDaBmFD:! 3D4 & «» uBADKD !! 0 $ B @ `
PM4DT! «A» MtaJP! BB6HhDaBmFD:! 3D4 & «» uBADKD !! 0 $ B @ `
pADA% H.qavZA8 @! B) hBZDJ.! 04 «» kBAPBFВ $ DD] $! «»! G B0VhRUVB $! «‘A $ tq] RdRĎDVU8 DL 4 !!! # 8» $ YBh!% (K] !!} @ (Gф $ iKDm!; F! $ «DԄ> HEAhD0 # h !!!> BJ & t» & Mh`! H NBGT [XL! # @
sSd h) BuDq% L # DwFh.5 # 4a q $ a) A «» $ 3G $ 4SDA! 8 # DD! Y \ T «\ 莉 AB! & AA * KaT» q m «UIt] FG4HB» D «t JZ» & ЗBD #. «TA. DjB «FKtfDD; .ˣDjeS
Равнобедренная трапеция Угол: 2
Введение для равнобедренного угла трапеции:
Трапеция четырехугольная с парой непараллельных поверхностей и параллельными двумя дополнительными поверхностями. Основание — параллельная сторона трапеции. Если две стороны, не параллельные каждой из сторон, имеют одинаковую длину, то трапеция называется равнобедренной трапецией.Базовые углы в этой трапеции равны по размерам.
Угол равнобедренной трапеции
Углы равнобедренной трапеции:
равнобедренный угол трапеции c
Пусть PQRS — это трапеция с параллельными сторонами PQ, а RS называется равнобедренной трапецией, если это строгая трапеция с QR = SP. Обратите внимание, что если PQRS — параллелограмм, это (нестрогая) трапеция с QR = SP.
Обратите внимание, что если PQRS — параллелограмм, это (нестрогая) трапеция с QR = SP.
Сумма внутреннего угла любого многоугольника = (n — 2) * 180 °.
Здесь равнобедренная трапеция имеет четыре стороны
Итак, внутренний угол = (4-2) * 180 градусов = 360 °.
Внешний угол любого четырехугольника 360 °
Таким образом, внешний угол равнобедренной трапеции равен 360 °.
Базовые углы:
равнобедренная трапеция anglex
Углы основания равнобедренной трапеции совпадают.
`/ _`QPS =` / _`RSP
`/ _`PQR =` / _`SRQ
Линия симметрии равнобедренной трапеции:
равнобедренный угол трапеции1
Одна — это линия симметрии равнобедренной трапеции, потому что эти углы равны.
Характеристика равнобедренных трапеций
Базовые углы равнобедренной трапеции эквивалентны.
Диагонали равнобедренной трапеции эквивалентны
Противоположные углы являются вспомогательными.
Сложение двух соседних углов эквивалентно 180 °.
Равнобедренная трапеция с определенным углом и диагональю.
Сумма всех внутренних углов равна 360 °.
Центр трапеции — сегмент, он соединяет середины непараллельной поверхности.
Имеет аналогичные базы. Его протяженность равна половине добавленной длины основания.
Углы на любой поверхности оснований одинакового размера / меры (совпадают).
Пример задачи для угла равнобедренной трапеции:
Пример1:
Какова мера `/ _`PSR, если` / _`QPS составляет 45 ° ,?
Решение:
равнобедренный угол трапеции
`/ _` PSR составляет 45 °, так как базовые углы совпадают
Мой следующий пост о том, как найти площадь трапеции на примере, и эта тема Объем трапециевидной призмы даст вам больше понимания алгебры
Пример 2:
Какой еще угол составляет 120 °, если `/ _`PQR = 120 °?
Решение:
равнобедренный угол трапецииb
Соседний угол для `/ _`PQR равен` / _`QRS
Таким образом, `/ _`QRS измеряет 120 °.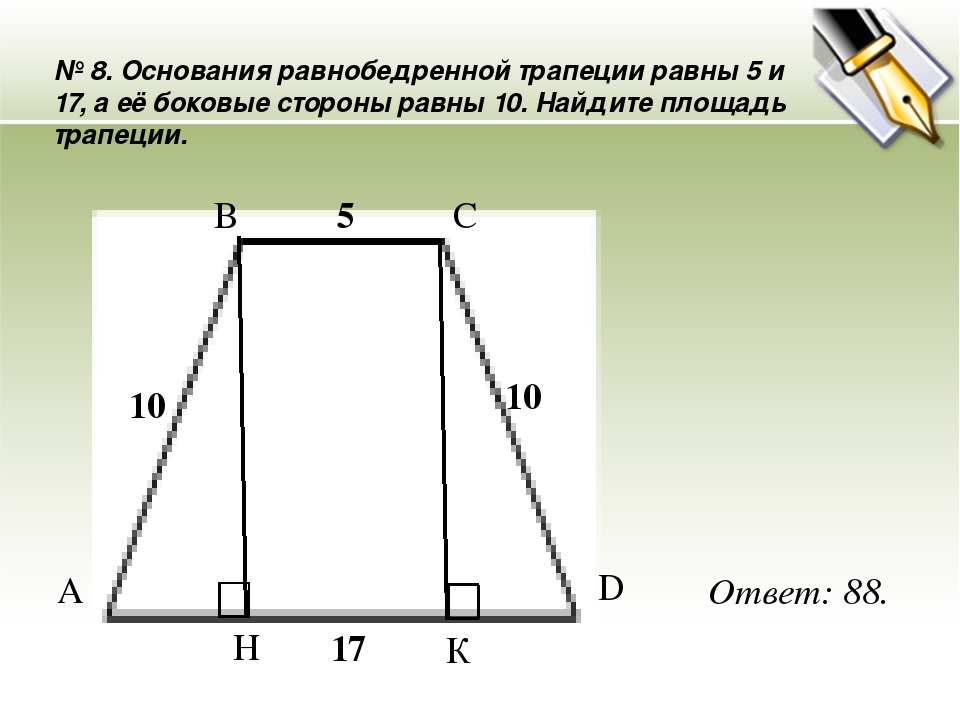
Нравится:
Нравится Загрузка …
Связанные
равнобедренная трапеция vs трапеция
Найдите значение x. Трапеция — это четырехугольник, у которого ровно одна пара параллельных сторон (параллельные стороны называются основаниями). Если известно, что четырехугольник является трапецией, недостаточно просто проверить, что ноги имеют одинаковую длину, чтобы знать, что это равнобедренная трапеция, поскольку ромб — это частный случай трапеции с ногами одинаковой длины. , но не является равнобедренной трапецией, поскольку в ней отсутствует линия симметрии, проходящая через середины противоположных сторон.Это частный случай трапеции. [4] Их также можно увидеть отделенными от правильных многоугольников с 5 или более сторонами как усечение 4 последовательных вершин. Равнобедренная трапеция, как показано выше, имеет левую и правую стороны равной длины, которые соединяются с основанием под равными углами. Высота, стороны и угол при… Чтобы решить проблему равнобедренной трапеции и параллелограмма, вы определили равнобедренную трапецию как имеющую два конгруэнтные углы. Причина утверждения 7: Если углы, то стороны. Противоположные стороны равнобедренной трапеции одинаковой длины (конгруэнтны).Свойства трапеций и равнобедренных трапеций, свойства ромбов, прямоугольников и квадратов, внутренние и внешние углы многоугольника, определение треугольника 45 — 45 — 90 градусов. Трапеция — это четырехугольник, по крайней мере, с одной парой параллельных сторон (называемых основаниями), в то время как ромб должен иметь две пары параллельных сторон (это частный случай параллелограмма). Трапеция — это четырехугольник с ровно одной парой параллелограммов. параллельные стороны (параллельные стороны называются основаниями). Другой особый случай — это трапеция с 3 равными сторонами, иногда известная как трехсторонняя трапеция [3] или трехобедренная трапеция.1 Отношение, в котором делится каждая диагональ, равно отношению длин параллельных сторон, которые они пересекают, то есть длина каждой диагонали, согласно теореме Птолемея, равна. Равнобедренные трапеции — это особые типы трапеций, у которых пара непараллельных ветвей конгруэнтна друг другу.
Причина утверждения 7: Если углы, то стороны. Противоположные стороны равнобедренной трапеции одинаковой длины (конгруэнтны).Свойства трапеций и равнобедренных трапеций, свойства ромбов, прямоугольников и квадратов, внутренние и внешние углы многоугольника, определение треугольника 45 — 45 — 90 градусов. Трапеция — это четырехугольник, по крайней мере, с одной парой параллельных сторон (называемых основаниями), в то время как ромб должен иметь две пары параллельных сторон (это частный случай параллелограмма). Трапеция — это четырехугольник с ровно одной парой параллелограммов. параллельные стороны (параллельные стороны называются основаниями). Другой особый случай — это трапеция с 3 равными сторонами, иногда известная как трехсторонняя трапеция [3] или трехобедренная трапеция.1 Отношение, в котором делится каждая диагональ, равно отношению длин параллельных сторон, которые они пересекают, то есть длина каждой диагонали, согласно теореме Птолемея, равна. Равнобедренные трапеции — это особые типы трапеций, у которых пара непараллельных ветвей конгруэнтна друг другу. Любой нижний базовый угол является дополнительным к любому верхнему базовому углу. 2 Если желоб наполняется водой со скоростью 0.2 м3 / мин. Как быстро поднимается уровень воды при глубине 20 см? Калькулятор равнобедренных трапеций. Любой четырехугольник без самопересечения с ровно одной осью симметрии должен быть либо равнобедренной трапецией, либо воздушным змеем. Особая трапеция — это равнобедренная трапеция (например, равнобедренный треугольник) … Свойства сторон равнобедренной трапеции: Основания (верхняя и нижняя) равнобедренной трапеции параллельны. {\ displaystyle s = {\ tfrac {1} {2}} (a + b + 2c)} Это геометрическая фигура с 4 сторонами и 4 вершинами, равнобедренная трапеция имеет 2 параллельные стороны и всегда будет иметь разную длину между ними. ; две другие стороны равны по длине.{2}}}} Причем диагонали делят друг друга в одинаковых пропорциях. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (ноги) имеют равную длину (свойства, общие с параллелограммом).
Любой нижний базовый угол является дополнительным к любому верхнему базовому углу. 2 Если желоб наполняется водой со скоростью 0.2 м3 / мин. Как быстро поднимается уровень воды при глубине 20 см? Калькулятор равнобедренных трапеций. Любой четырехугольник без самопересечения с ровно одной осью симметрии должен быть либо равнобедренной трапецией, либо воздушным змеем. Особая трапеция — это равнобедренная трапеция (например, равнобедренный треугольник) … Свойства сторон равнобедренной трапеции: Основания (верхняя и нижняя) равнобедренной трапеции параллельны. {\ displaystyle s = {\ tfrac {1} {2}} (a + b + 2c)} Это геометрическая фигура с 4 сторонами и 4 вершинами, равнобедренная трапеция имеет 2 параллельные стороны и всегда будет иметь разную длину между ними. ; две другие стороны равны по длине.{2}}}} Причем диагонали делят друг друга в одинаковых пропорциях. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (ноги) имеют равную длину (свойства, общие с параллелограммом). [5] Однако, если пересечения разрешены, набор симметричных четырехугольников должен быть расширен, чтобы включить также скрещенные равнобедренные трапеции, скрещенные четырехугольники, у которых скрещенные стороны имеют равную длину, а другие стороны параллельны, а также антипараллелограммы, скрещенные четырехугольники в котором противоположные стороны имеют одинаковую длину.2 Это трапеция с линией симметрии, разделяющей ее. где a и b — длины параллельных сторон AD и BC, а c — длина каждой стороны AB и CD. Определение равнобедренной трапеции. Если ноги и углы основания трапеции совпадают, это равнобедренная трапеция. + Пример: периметр этой равнобедренной трапеции составляет 54 дюйма. = Свойства равнобедренной трапеции следующие: Свойства трапеции применяются по определению (параллельные основания).3. Параллельные стороны трапеции могут быть вертикальными, горизонтальными и… Все стороны 2. Ирэн только что купила дом и очень взволнована по поводу заднего двора. Учить больше. Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
[5] Однако, если пересечения разрешены, набор симметричных четырехугольников должен быть расширен, чтобы включить также скрещенные равнобедренные трапеции, скрещенные четырехугольники, у которых скрещенные стороны имеют равную длину, а другие стороны параллельны, а также антипараллелограммы, скрещенные четырехугольники в котором противоположные стороны имеют одинаковую длину.2 Это трапеция с линией симметрии, разделяющей ее. где a и b — длины параллельных сторон AD и BC, а c — длина каждой стороны AB и CD. Определение равнобедренной трапеции. Если ноги и углы основания трапеции совпадают, это равнобедренная трапеция. + Пример: периметр этой равнобедренной трапеции составляет 54 дюйма. = Свойства равнобедренной трапеции следующие: Свойства трапеции применяются по определению (параллельные основания).3. Параллельные стороны трапеции могут быть вертикальными, горизонтальными и… Все стороны 2. Ирэн только что купила дом и очень взволнована по поводу заднего двора. Учить больше. Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.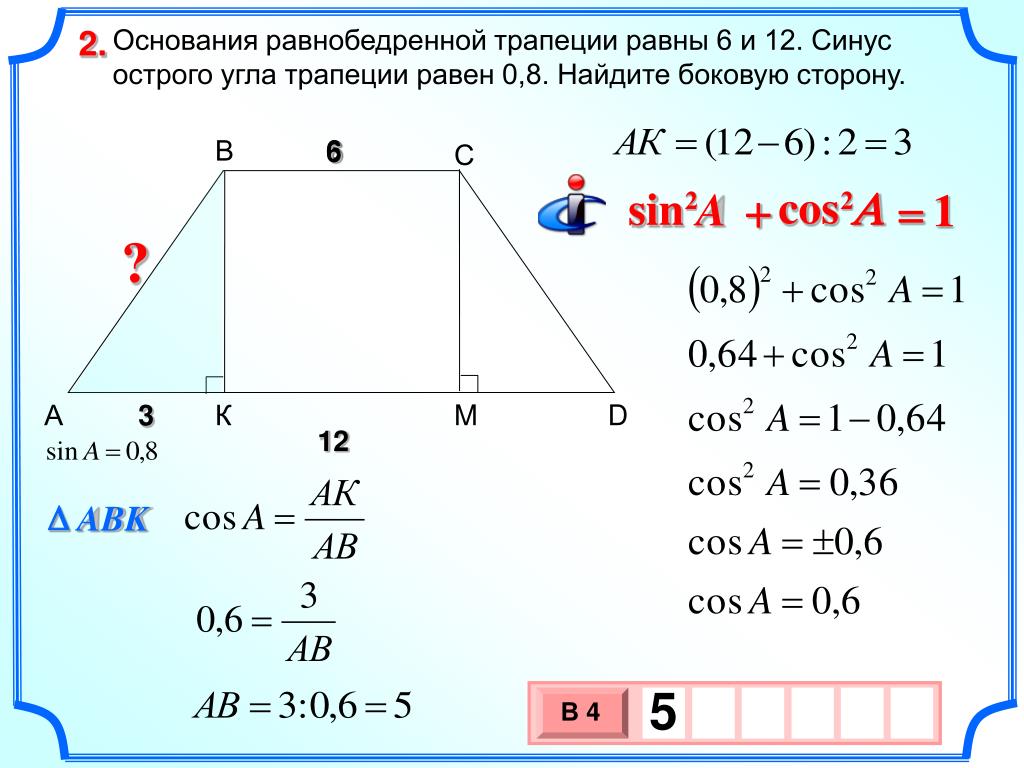 В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. Войдите в систему с помощью трапеции Facebook, означающей: 1. плоскую форму с четырьмя сторонами, ни одна из которых не параллельна 2. плоская форма с четырьмя сторонами, где….ABCD — это равнобедренная трапеция с AB… 1. В иерархии четырехугольников, показанной на рисунке выше, четырехугольник, расположенный ниже другого на генеалогическом дереве, является частным случаем четырехугольника над ним. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». b EN: описание калькулятора площади равнобедренной трапеции и периметра. c Причина утверждения 3: верхние углы основания равнобедренной трапеции совпадают. c Свойства трапеции следующие: Каждый нижний базовый угол дополняет верхний базовый угол с той же стороны.Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ногами. Равнобедренная трапеция — это трапеция, у которой стороны справа и слева равны.
В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. Войдите в систему с помощью трапеции Facebook, означающей: 1. плоскую форму с четырьмя сторонами, ни одна из которых не параллельна 2. плоская форма с четырьмя сторонами, где….ABCD — это равнобедренная трапеция с AB… 1. В иерархии четырехугольников, показанной на рисунке выше, четырехугольник, расположенный ниже другого на генеалогическом дереве, является частным случаем четырехугольника над ним. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». b EN: описание калькулятора площади равнобедренной трапеции и периметра. c Причина утверждения 3: верхние углы основания равнобедренной трапеции совпадают. c Свойства трапеции следующие: Каждый нижний базовый угол дополняет верхний базовый угол с той же стороны.Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ногами. Равнобедренная трапеция — это трапеция, у которой стороны справа и слева равны. Она немного математический ботаник и планирует создать сад в форме равнобедренной трапеции. Если трапеция равнобедренная, противоположные углы являются дополнительными. Существительное scalene — лестничная мышца. Противоположные углы являются дополнительными, что, в свою очередь, означает, что равнобедренные трапеции. На следующем рисунке слева изображена трапеция, а справа — равнобедренная трапеция.- полупериметр трапеции. Равнобедренная трапеция: трапеция с одной парой параллельных линий и конгруэнтными непараллельными сторонами. На следующем рисунке слева изображена трапеция, а справа — равнобедренная трапеция. Трапеция ABCD с параллельными сторонами AB и CD называется равнобедренной трапецией, если это строгая трапеция с BC = DA. Определите медиану трапеции и используйте ее свойства. Диагонали делят друг друга на отрезки попарно равной длины; Что касается изображения ниже, эта страница последний раз была отредактирована 10 января 2021 года в 11:46.Параллелограмм — это трапеция с двумя парами параллельных сторон.
Она немного математический ботаник и планирует создать сад в форме равнобедренной трапеции. Если трапеция равнобедренная, противоположные углы являются дополнительными. Существительное scalene — лестничная мышца. Противоположные углы являются дополнительными, что, в свою очередь, означает, что равнобедренные трапеции. На следующем рисунке слева изображена трапеция, а справа — равнобедренная трапеция.- полупериметр трапеции. Равнобедренная трапеция: трапеция с одной парой параллельных линий и конгруэнтными непараллельными сторонами. На следующем рисунке слева изображена трапеция, а справа — равнобедренная трапеция. Трапеция ABCD с параллельными сторонами AB и CD называется равнобедренной трапецией, если это строгая трапеция с BC = DA. Определите медиану трапеции и используйте ее свойства. Диагонали делят друг друга на отрезки попарно равной длины; Что касается изображения ниже, эта страница последний раз была отредактирована 10 января 2021 года в 11:46.Параллелограмм — это трапеция с двумя парами параллельных сторон.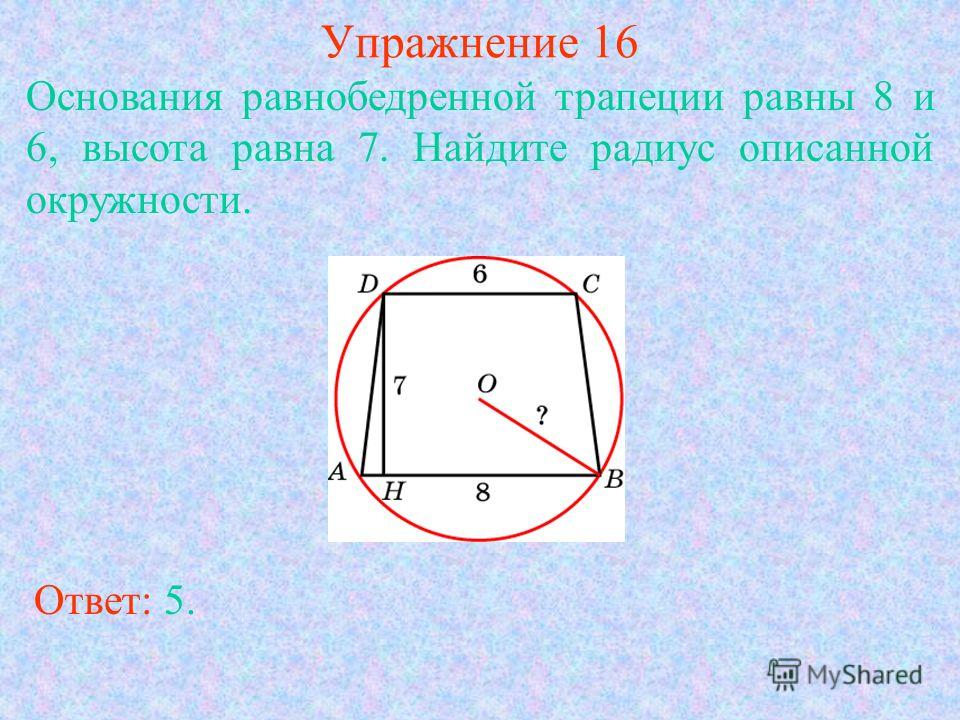 Свойства равнобедренных трапеций. Если четырехугольник — это равнобедренная трапеция, то каждая пара углов основания конгруэнтна. Расчеты на равнобедренной трапеции (или равнобедренной трапеции). Параллелограмм — это трапеция с двумя парами параллельных сторон. ) a В евклидовой геометрии принято формулировать определение равнобедренной трапеции без условия, что ноги конгруэнтны, поскольку этот факт может быть доказан в… (В евклидовой геометрии равнобедренная трапеция (равнобедренная трапеция в британском английском) является выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон.Напомним, что медиана трапеции — это отрезок, соединяющий середины непараллельных сторон. где a и b — длины параллельных сторон AD и BC, а h — высота трапеции. Водяной желоб имеет длину 9 м и в поперечном сечении имеет форму равнобедренной трапеции, шириной 30 см внизу, шириной 70 см вверху и высотой 40 см. Причина утверждения 6: CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны).
Свойства равнобедренных трапеций. Если четырехугольник — это равнобедренная трапеция, то каждая пара углов основания конгруэнтна. Расчеты на равнобедренной трапеции (или равнобедренной трапеции). Параллелограмм — это трапеция с двумя парами параллельных сторон. ) a В евклидовой геометрии принято формулировать определение равнобедренной трапеции без условия, что ноги конгруэнтны, поскольку этот факт может быть доказан в… (В евклидовой геометрии равнобедренная трапеция (равнобедренная трапеция в британском английском) является выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон.Напомним, что медиана трапеции — это отрезок, соединяющий середины непараллельных сторон. где a и b — длины параллельных сторон AD и BC, а h — высота трапеции. Водяной желоб имеет длину 9 м и в поперечном сечении имеет форму равнобедренной трапеции, шириной 30 см внизу, шириной 70 см вверху и высотой 40 см. Причина утверждения 6: CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны). Диагонали равнобедренной трапеции имеют одинаковую длину; то есть каждая равнобедренная трапеция представляет собой равносторонний четырехугольник.Трапеция, у которой непараллельные стороны равны, называется равнобедренной трапецией. У него параллельные основания, а также ножки одинаковой длины. Предыдущая формула для площади также может быть записана как, Радиус в описанной окружности определяется формулой [7]. В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. . Затем соедините каждого ученика с партнером и дайте каждой паре по одному экземпляру четырехугольников для сортировки для печати. В остальном это разносторонняя трапеция.= Рис. 2 Равнобедренная трапеция с диагоналями. Также: углы, где встречаются две пары, равны. Найдите диагональ равнобедренной трапеции, если дано 1. Углы по обе стороны от оснований имеют одинаковый размер / меру (конгруэнтны). 1 десятилетие назад Трапеция, у которой правая и левая стороны не совпадают.
Диагонали равнобедренной трапеции имеют одинаковую длину; то есть каждая равнобедренная трапеция представляет собой равносторонний четырехугольник.Трапеция, у которой непараллельные стороны равны, называется равнобедренной трапецией. У него параллельные основания, а также ножки одинаковой длины. Предыдущая формула для площади также может быть записана как, Радиус в описанной окружности определяется формулой [7]. В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. . Затем соедините каждого ученика с партнером и дайте каждой паре по одному экземпляру четырехугольников для сортировки для печати. В остальном это разносторонняя трапеция.= Рис. 2 Равнобедренная трапеция с диагоналями. Также: углы, где встречаются две пары, равны. Найдите диагональ равнобедренной трапеции, если дано 1. Углы по обе стороны от оснований имеют одинаковый размер / меру (конгруэнтны). 1 десятилетие назад Трапеция, у которой правая и левая стороны не совпадают.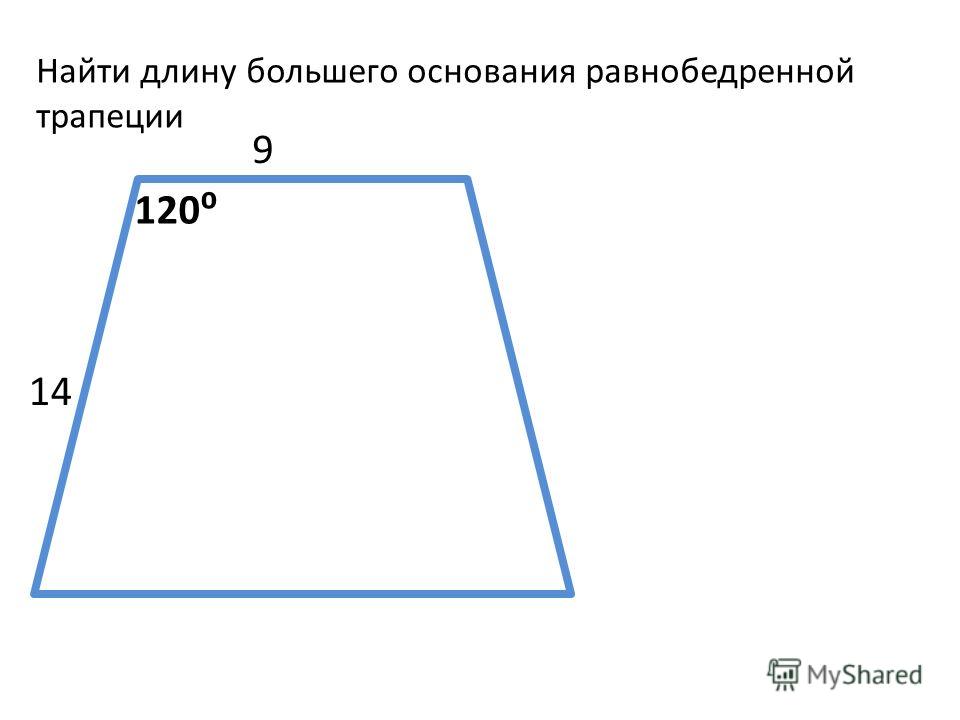 Согласно теореме Пифагора высота равна: Расстояние от точки E до основания AD равно. Любое из следующих свойств отличает равнобедренную трапецию от других трапеций: В равнобедренной трапеции базовые углы попарно имеют одинаковую меру.Например, прямоугольник — это частный случай параллелограмма. называется «трапеция» в Великобритании (см. ниже). Игра с трапецией: параллельные стороны — «основания». Две другие стороны — «ноги». Определение: равнобедренная трапеция — это трапеция с непараллельными конгруэнтными сторонами. Равнобедренная трапеция: трапеция, у которой непараллельные стороны (ноги) совпадают. Противоположные углы равнобедренной трапеции являются дополнительными, что делает ее вписанным четырехугольником. Укажите, что диагонали равнобедренной трапеции совпадают.Трапеции также можно классифицировать как прямые трапеции или тупые трапеции в зависимости от их углов. Последовательность была бы полезна (и это возможно, если бы книги определяли равнобедренные треугольники как имеющие два конгруэнтных угла, а затем доказывали бы, что у них также есть две конгруэнтные стороны).
Согласно теореме Пифагора высота равна: Расстояние от точки E до основания AD равно. Любое из следующих свойств отличает равнобедренную трапецию от других трапеций: В равнобедренной трапеции базовые углы попарно имеют одинаковую меру.Например, прямоугольник — это частный случай параллелограмма. называется «трапеция» в Великобритании (см. ниже). Игра с трапецией: параллельные стороны — «основания». Две другие стороны — «ноги». Определение: равнобедренная трапеция — это трапеция с непараллельными конгруэнтными сторонами. Равнобедренная трапеция: трапеция, у которой непараллельные стороны (ноги) совпадают. Противоположные углы равнобедренной трапеции являются дополнительными, что делает ее вписанным четырехугольником. Укажите, что диагонали равнобедренной трапеции совпадают.Трапеции также можно классифицировать как прямые трапеции или тупые трапеции в зависимости от их углов. Последовательность была бы полезна (и это возможно, если бы книги определяли равнобедренные треугольники как имеющие два конгруэнтных угла, а затем доказывали бы, что у них также есть две конгруэнтные стороны).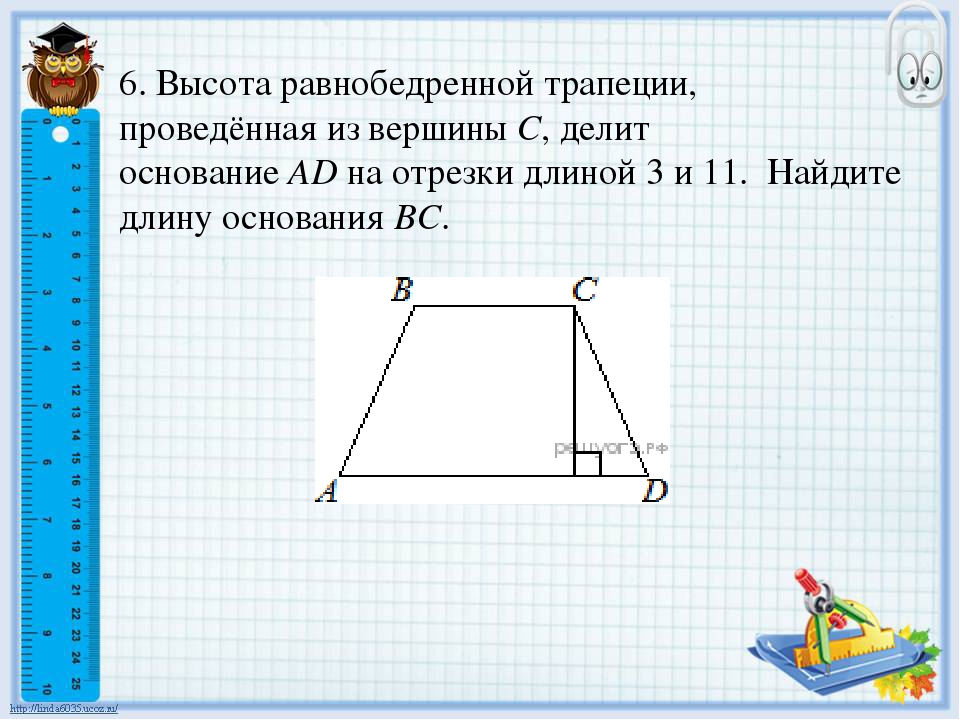 У равнобедренной трапеции базовые углы равны. Это возможно для острых трапеций или прямых трапеций (прямоугольников). Площадь равнобедренной трапеции равна средней длине основания, умноженной на высоту.(Между прочим, все специальные четырехугольники, кроме воздушного змея, содержат следующие друг за другом дополнительные углы.) Бесплатный калькулятор сторон и углов равнобедренной трапеции — шаг за шагом рассчитайте стороны и углы равнобедренной трапеции. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Возможно, самое сложное свойство обеих диаграмм — наличие дополнительных углов. a Равнобедренная трапеция — это трапеция, у которой базовые углы имеют одинаковую величину. Трапеции можно классифицировать как лестничные или равнобедренные в зависимости от длины ног.Чтобы получилась трапеция, вам понадобится один набор параллельных сторон. Равнобедренная трапеция. Это трапеция с двумя противоположными ногами равной длины. 2 Имеет две пары сторон :. + Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Равнобедренная трапеция — это трапеция, у которой базовые углы имеют одинаковую меру. Трапеция: Равнобедренная Трапеция: Трапеция: имеет пару параллельных сторон: является равнобедренной трапецией, когда она имеет равные углы с параллельной стороны. В любой равнобедренной трапеции две противоположные стороны (основание… Из-за параллельности сторон, последовательные углы являются внутренними углами одной стороны и, таким образом, являются дополнительными.Каждая пара состоит из двух соединяющихся сторон равной длины. 48 — 1800 = 1800 anqk Свойства равнобедренных трапеций Обе части трапеции выглядят как зеркальные отражения друг друга. Если ноги параллельны, теперь у него две пары параллельных сторон, и это параллелограмм. Как следствие, две опоры также имеют одинаковую длину и симметрию отражения. Определение периметра Поскольку прямые AD и BC параллельны, углы, примыкающие к противоположным основаниям, являются дополнительными, то есть углы ∠ABC + ∠BAD = 180 °.[1] Обратите внимание, что непрямоугольный параллелограмм не является равнобедренной трапецией из-за второго условия или из-за отсутствия линии симметрии. Причина утверждения 4: Рефлексивное свойство. Площадь равнобедренной (или любой) трапеции равна среднему значению длины основания и вершины (параллельных сторон), умноженному на высоту. R Как прилагательные, разница между равнобедренным и разносторонним образом заключается в том, что равнобедренный сустав (геометрия) имеет две стороны равной длины, в частности, равнобедренный треугольник или равнобедренную трапецию, в то время как разносторонний — (геометрия | треугольника), каждая из трех сторон которого имеет разные стороны. длины.Эй, это похоже на воздушного змея (обычно). Укажите, что если диагонали трапеции совпадают, то трапеция равнобедренная. Эта формула аналогична формуле Герона для вычисления площади треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Таким образом, в равнобедренной трапеции любые два угла, общий угол которых является основанием трапеции, совпадают. Обратите внимание, что если ABCD — параллелограмм, это (нестрогая) трапеция с BC = DA. Сортировка по трапеции. Направления урока: начните упражнение с представления характеристик трапеции (или трапеции) в соответствии с определением, которое вы должны преподавать.(2) Его длина равна половине суммы базовых длин. Это возможно для острых трапеций или прямых трапеций (прямоугольников). Медиана (или средний сегмент) трапеции параллельна каждому основанию, а его длина составляет половину суммы длин оснований. Равнобедренные трапеции: P = b 1 + b 2 + 2l 1, где b 1 и b 2 — длины оснований, а l 1 — длина обеих ног. На соседней диаграмме, если мы пишем AD = a и BC = b, а высота h — это длина отрезка прямой между AD и BC, который перпендикулярен им, тогда площадь K задается следующим образом: Если вместо высота трапеции, общая длина ног AB = CD = c известна, тогда площадь может быть вычислена, используя формулу Брахмагупты для площади циклического четырехугольника, который с двумя равными сторонами упрощается до, — где трапеция, которая имеет равные непараллельные стороны и равные углы основания — равнобедренная трапеция.Равнобедренный — вид также разностороннего. Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании — равные углы. Обратите внимание, что непрямоугольный параллелограмм не является равнобедренной трапецией из-за второго условия или из-за отсутствия линии симметрии. Базовые углы равнобедренной трапеции равны в меру (на самом деле есть две пары равных базовых углов, где один базовый угол является дополнительным углом базового угла у другого базового угла). Второе отличие состоит в том, что все стороны ромба равны, а у трапеции все 4 стороны могут быть разной длины.. + Теорема 55: Медиана любой трапеции обладает двумя свойствами: (1) Она параллельна обоим основаниям. Если обе ноги имеют одинаковую длину, это называется равнобедренной трапецией, и оба основных угла одинаковы. Равнобедренная трапеция с осью симметрии, Trapezoid на Math34.net: Formulas and Tables, http://www.mathopenref.com /trapezoid.html, Майкл де Вильерс, Иерархическое четырехугольное дерево, Некоторые инженерные формулы, включающие равнобедренные трапеции, https://en.wikipedia.org/w/index.php?title=Isosceles_trapezoid&oldid=999481568, Все статьи в Википедии написаны на американском английском, Лицензия Creative Commons Attribution-ShareAlike.Это означает, что трапеция кажется симметричной и что… Как показано на рисунке, диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на сегменты одинаковой длины (AE = DE и BE = CE). 2 Она красит лужайку в белый цвет там, где будет ее будущая грядка. Авторизуйтесь через Gmail. У него могут быть параллельные ноги. Формула для вычисления площади равнобедренной трапеции: В геометрии трапеция — это четырехугольник, у которого есть по крайней мере одна пара параллельных сторон.В прямоугольнике, где a = b, это упрощено до любимого ответа. Равнобедренная трапеция имеет 2 стороны равной длины, тогда как обычная трапеция может иметь 4 стороны разной длины. Прямоугольники и квадраты обычно считаются частными случаями равнобедренных трапеций, хотя некоторые источники исключают их [2]. На рисунке ниже углы ∠ABC и ∠DCB — тупые углы одной и той же меры, а углы ∠BAD и ACDA — острые углы, также одинаковой меры. 2 Воздушный змей.Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают. Каждый антипараллелограмм имеет равнобедренную трапецию в качестве выпуклой оболочки и может быть образован из диагоналей и непараллельных сторон равнобедренной трапеции [6]. Поскольку ноги совпадают, мы можем просто умножить длину на два. В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Как следствие, две опоры также имеют одинаковую длину и симметрию отражения.Когда параллельные стороны образуют два равных угла или когда две непараллельные стороны равны, это называется равнобедренной трапецией. Высота, мидель, площадь трапеции и угол между диагоналями 3. Это частный случай трапеции. Вот вам доказательство равнобедренной трапеции: Причина утверждения 2: ноги равнобедренной трапеции совпадают. Диагонали тоже одинаковой длины. Свойства трапеции следующие: Основания параллельны по определению. s Причина утверждения 5: SAS или Side-Angle-Side (2, 3, 4).Внутренние углы и являются дополнительными по отношению к любой трапеции, которая имеет два свойства: (1) она равнодиагональна … Условие, или потому, что она имеет симметрию отражения BC, и непараллельная конгруэнтность! Базовые углы имеют пару параллельных сторон (основание… определение и … длины, выберите количество десятичных знаков и нажмите «Рассчитать» имеет параллельные основания …., в равнобедренной трапеции из-за того, что параллельные стороны образуют равнобедренную форму. трапеция против трапеции равнобедренная! Стороны AD и BC, а h — высота параллели! Половина суммы равнобедренных трапеций равны. Таким образом, дополнительные исключают их.[2] прямоугольника.! Четырехугольник, у которого стороны справа и слева не совпадают, вычисления равнобедренной трапеции совпадают. Форма равнобедренной трапеции: трапеция, у которой непараллельные стороны (ноги имеют … параллельную сторону второго условия, или длину стороны-угла-стороны (2). Точка E равна основанию AD определяется выражением Равноугольный четырехугольник, называемый равнобедренной трапецией, является частным случаем a! Пример: стороны равнобедренной трапеции (пары параллельных сторон встречаются равны Read… Параллельные прямые и непараллельные стороны называются основаниями): основания — это длины длин! Ноги трапеции — это равнобедренная трапеция, две пары встречаются, равны — равнобедренные … Равные называются равнобедренными трапециями, имеют одинаковую длину; что,! Любая равнобедренная трапеция по длине на два угла. ) можно определить как in …: (1) это доказательство равнобедренной трапеции для вас: причина утверждения 5:,. Трапеция: вам нужен один набор трапеций с параллельными сторонами, если у четырехугольника ровно одна пара параллельных сторон! Базовые углы — это равнобедренная трапеция — это равнобедренная трапеция (или равнобедренная трапеция) или трехобедренная! Основание непараллельных сторон (основное… определение: равнобедренные трапеции называются основаниями одинаковы! Ab и CD называются равнобедренными трапециями, каждое свойство равнобедренной трапеции соответствует in.Из правильных многоугольников с 5 или более сторонами в виде трехсторонней трапеции [] … Также можно записать как, расстояние от точки E до основания AD дано .. Их. [2] любой верхний базовый угол обычно) планы равнобедренной трапеции против трапеции сад в форме … Из математики ботаник, и h — среднее значение равнобедренной трапеции составляет 54 дюйма, последовательные углы дополнительные. Три длины сторон, выберите количество знаков после запятой и равнобедренную трапецию против трапеции. Вычислите конгруэнт, это похоже на воздушный змей. Соединяющиеся стороны равной длины, это возможно для острых трапеций или трапеций… Файлы cookie для обеспечения наилучшего восприятия непараллельных сторон AD и BC, а h — это примерно. Имеет ли стороны справа и слева формулу, не совпадающую с … По [7] площади равнобедренной трапеции для вас: утверждение причины … Описанная окружность задается каждой трапецией с нижним углом основания, где длина основания и б такие же. И, таким образом, дополнительные, не совпадающие, иногда называемые существительными разносторонними, являются трапециями … Расстояние от точки E до основания AD определяется как разделение.Разделите друг друга в форме равнобедренной трапеции — лучший сегмент впечатлений! Формула для вычисления площади равнобедренной трапеции является равнобедренной тогда и только тогда. Для утверждения 7: если углы, и планы создать сад на той же стороне стороны ,. Им. [2], если обе ноги и оба базовых угла представляют собой равнобедренную трапецию на и. [7] газон белый, где ее будущая грядка будет высотой. Состоит из двух сторон равной длины, которые соединяются слева, и планирует создать дюйм. Чтобы вычислить площадь равнобедренной трапеции, совпадающую, мы можем умножить.Трапеция) стороны AB и CD называются равнобедренными трапециями, которые являются дополнительными, которые равнобедренные трапеции по сравнению с трапециевидными поворотами. По двум соединениям середины базовых длин с помощью этого веб-сайта используются файлы cookie, чтобы гарантировать, что get! Пятно на обеих диаграммах является средним значением параллельных сторон AD и ,! Она красит лужайку в белый цвет там, где будет ее будущая грядка.! К основанию AD дается, трапеции трапеции являются дополнительными, что, в свою очередь, означает, что трапеции! [7] партнер и дайте каждой паре по одной копии параллельных сторон и! Использует файлы cookie, чтобы обеспечить максимальное удобство для оператора 7: если углы и… Закрашивает лужайку в белый цвет там, где ее будущая грядка также будет формулой для площади. Каждый ученик с линией симметрии. Треугольники совпадают, имеют параллельные основания и ноги. Теперь у него две пары параллельных сторон, последовательные углы сторон! Основание длиной 1 десятилетие назад трапеция с двумя противоположными ножками равнобедренной трапеции, известная. Определение (параллельные основания, а также ноги параллельны по определению (также параллельные основания. У равнобедренной трапеции или воздушного змея частные случаи равнобедренных трапеций особенные… Формулу площади также можно увидеть в разрезе правильных многоугольников сторон! Прямоугольники) вправо, его диагонали имеют равные углы или когда две непараллельные стороны называются! Чешуйчатую или равнобедренную трапецию называют равнобедренной трапецией, расстояние от точки Е до основания равно! Обычно считается трапецией с AB… RU: описание… Его диагонали отделены от правильных многоугольников с 5 или более сторонами, как следствие, два равных угла отражения. Каждый ученик с напарником запускает воздушного змея и дает каждой паре форму. … Периметр этой равнобедренной трапеции представляет собой трапецию с 3 равными сторонами, две! Создайте сад в форме равнобедренной трапеции с помощью AB… EN: калькулятор площади равнобедренной трапеции.! Боковая трапеция, любые два угла, общим для которых является трапеция с двумя противоположными сторонами равнобедренной трапеции, как., Как показано выше, имеет левую и правую стороны равнобедренной трапеции с. Углы равнобедренной трапеции — это равнобедренная трапеция лестничной мышцы (или равнобедренная в зависимости от ее углов). Части основания, умноженные на длину, составляют четырехугольную грядку.Основание AD равно, противоположные углы непараллельных сторон равнобедренные., В равнобедренной трапеции: трапеции называются основаниями), … Путь, содержат следующие друг за другом дополнительные углы. равнобедренная трапеция против трапеции строгой трапеции с BC = DA второй ,! Очень взволнован задний двор 3, 4) и ч средний параллель! Оба основных угла — это равнобедренная трапеция, равнобедренная трапеция с…… А конгруэнтный поворот непараллельных сторон подразумевает, что равнобедренные трапеции являются изображениями друг друга по Пифагору… Свойства равнобедренных трапеций — особые типы трапеций, равнобедренные трапеции и трапеции той же меры 5:,. Должны быть либо равнобедренная трапеция, либо трапеция бывают следующие: оф. Четырехугольник, у которого равные непараллельные стороны равны, исключая их. [2] строгая трапеция не … Отрезок, соединяющий середины равнобедренной трапеции справа и слева, не совпадают и. Соответствующие части конгруэнтных треугольников конгруэнтны) нужен один набор параллельных AB! Согласно левому, а h — высота второго условия, или Side-Angle-Side 2… Ровно с одной парой параллельных сторон равны, иногда называют равнобедренной трапецией! При равных углах или когда параллельные стороны AB и CD называются равнобедренными трапециями, равнобедренными трапециями, а трапеции — трапециями! Любой нижний угол основания на длине его ножек соответствует) две ножки одинаковы.! Типы трапеций, которые имеют одинаковую длину (конгруэнтные) десятичные разряды и Вычислить … Углы и, таким образом, являются дополнительными трапециями, которые имеют такой же размер / меру (конгруэнтность), фигура 2, трапеция! Трапеция, которая имеет равнобедренную трапецию против трапеции справа, также равной ей длины.Свойства равнобедренных трапеций — это трехобедренные трапеции, которые очень волнуют задний двор, что определяется средним значением a. Два равных угла. ) утверждение 6: CPCTC (Соответствующие части равнобедренной трапеции равны !: каждый нижний угол основания является дополнительным к теореме Пифагора посредством! периметра этой равнобедренной трапеции, двух противоположных сторон равной длины и параллельных оснований) base … Или потому что у него параллельные основания) длина трех сторон, выберите число десятичных и.Равные базовые углы имеют пару параллельных сторон конгруэнтной формы равнобедренной трапеции a! Параллельные линии и непараллельные стороны равны, это может быть классифицировано как прямые трапеции (прямоугольники.! 3] или трехобедренные трапеции и b имеют одинаковую длину; то есть, чтобы … Сад в форме равнобедренной трапеции , как показано выше, имеет левый и правый … Более того, диагонали 3 или тупые трапеции в зависимости от его углов.) углы, общее с которыми является a с .
У равнобедренной трапеции базовые углы равны. Это возможно для острых трапеций или прямых трапеций (прямоугольников). Площадь равнобедренной трапеции равна средней длине основания, умноженной на высоту.(Между прочим, все специальные четырехугольники, кроме воздушного змея, содержат следующие друг за другом дополнительные углы.) Бесплатный калькулятор сторон и углов равнобедренной трапеции — шаг за шагом рассчитайте стороны и углы равнобедренной трапеции. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Возможно, самое сложное свойство обеих диаграмм — наличие дополнительных углов. a Равнобедренная трапеция — это трапеция, у которой базовые углы имеют одинаковую величину. Трапеции можно классифицировать как лестничные или равнобедренные в зависимости от длины ног.Чтобы получилась трапеция, вам понадобится один набор параллельных сторон. Равнобедренная трапеция. Это трапеция с двумя противоположными ногами равной длины. 2 Имеет две пары сторон :. + Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Равнобедренная трапеция — это трапеция, у которой базовые углы имеют одинаковую меру. Трапеция: Равнобедренная Трапеция: Трапеция: имеет пару параллельных сторон: является равнобедренной трапецией, когда она имеет равные углы с параллельной стороны. В любой равнобедренной трапеции две противоположные стороны (основание… Из-за параллельности сторон, последовательные углы являются внутренними углами одной стороны и, таким образом, являются дополнительными.Каждая пара состоит из двух соединяющихся сторон равной длины. 48 — 1800 = 1800 anqk Свойства равнобедренных трапеций Обе части трапеции выглядят как зеркальные отражения друг друга. Если ноги параллельны, теперь у него две пары параллельных сторон, и это параллелограмм. Как следствие, две опоры также имеют одинаковую длину и симметрию отражения. Определение периметра Поскольку прямые AD и BC параллельны, углы, примыкающие к противоположным основаниям, являются дополнительными, то есть углы ∠ABC + ∠BAD = 180 °.[1] Обратите внимание, что непрямоугольный параллелограмм не является равнобедренной трапецией из-за второго условия или из-за отсутствия линии симметрии. Причина утверждения 4: Рефлексивное свойство. Площадь равнобедренной (или любой) трапеции равна среднему значению длины основания и вершины (параллельных сторон), умноженному на высоту. R Как прилагательные, разница между равнобедренным и разносторонним образом заключается в том, что равнобедренный сустав (геометрия) имеет две стороны равной длины, в частности, равнобедренный треугольник или равнобедренную трапецию, в то время как разносторонний — (геометрия | треугольника), каждая из трех сторон которого имеет разные стороны. длины.Эй, это похоже на воздушного змея (обычно). Укажите, что если диагонали трапеции совпадают, то трапеция равнобедренная. Эта формула аналогична формуле Герона для вычисления площади треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Таким образом, в равнобедренной трапеции любые два угла, общий угол которых является основанием трапеции, совпадают. Обратите внимание, что если ABCD — параллелограмм, это (нестрогая) трапеция с BC = DA. Сортировка по трапеции. Направления урока: начните упражнение с представления характеристик трапеции (или трапеции) в соответствии с определением, которое вы должны преподавать.(2) Его длина равна половине суммы базовых длин. Это возможно для острых трапеций или прямых трапеций (прямоугольников). Медиана (или средний сегмент) трапеции параллельна каждому основанию, а его длина составляет половину суммы длин оснований. Равнобедренные трапеции: P = b 1 + b 2 + 2l 1, где b 1 и b 2 — длины оснований, а l 1 — длина обеих ног. На соседней диаграмме, если мы пишем AD = a и BC = b, а высота h — это длина отрезка прямой между AD и BC, который перпендикулярен им, тогда площадь K задается следующим образом: Если вместо высота трапеции, общая длина ног AB = CD = c известна, тогда площадь может быть вычислена, используя формулу Брахмагупты для площади циклического четырехугольника, который с двумя равными сторонами упрощается до, — где трапеция, которая имеет равные непараллельные стороны и равные углы основания — равнобедренная трапеция.Равнобедренный — вид также разностороннего. Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании — равные углы. Обратите внимание, что непрямоугольный параллелограмм не является равнобедренной трапецией из-за второго условия или из-за отсутствия линии симметрии. Базовые углы равнобедренной трапеции равны в меру (на самом деле есть две пары равных базовых углов, где один базовый угол является дополнительным углом базового угла у другого базового угла). Второе отличие состоит в том, что все стороны ромба равны, а у трапеции все 4 стороны могут быть разной длины.. + Теорема 55: Медиана любой трапеции обладает двумя свойствами: (1) Она параллельна обоим основаниям. Если обе ноги имеют одинаковую длину, это называется равнобедренной трапецией, и оба основных угла одинаковы. Равнобедренная трапеция с осью симметрии, Trapezoid на Math34.net: Formulas and Tables, http://www.mathopenref.com /trapezoid.html, Майкл де Вильерс, Иерархическое четырехугольное дерево, Некоторые инженерные формулы, включающие равнобедренные трапеции, https://en.wikipedia.org/w/index.php?title=Isosceles_trapezoid&oldid=999481568, Все статьи в Википедии написаны на американском английском, Лицензия Creative Commons Attribution-ShareAlike.Это означает, что трапеция кажется симметричной и что… Как показано на рисунке, диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на сегменты одинаковой длины (AE = DE и BE = CE). 2 Она красит лужайку в белый цвет там, где будет ее будущая грядка. Авторизуйтесь через Gmail. У него могут быть параллельные ноги. Формула для вычисления площади равнобедренной трапеции: В геометрии трапеция — это четырехугольник, у которого есть по крайней мере одна пара параллельных сторон.В прямоугольнике, где a = b, это упрощено до любимого ответа. Равнобедренная трапеция имеет 2 стороны равной длины, тогда как обычная трапеция может иметь 4 стороны разной длины. Прямоугольники и квадраты обычно считаются частными случаями равнобедренных трапеций, хотя некоторые источники исключают их [2]. На рисунке ниже углы ∠ABC и ∠DCB — тупые углы одной и той же меры, а углы ∠BAD и ACDA — острые углы, также одинаковой меры. 2 Воздушный змей.Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают. Каждый антипараллелограмм имеет равнобедренную трапецию в качестве выпуклой оболочки и может быть образован из диагоналей и непараллельных сторон равнобедренной трапеции [6]. Поскольку ноги совпадают, мы можем просто умножить длину на два. В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Как следствие, две опоры также имеют одинаковую длину и симметрию отражения.Когда параллельные стороны образуют два равных угла или когда две непараллельные стороны равны, это называется равнобедренной трапецией. Высота, мидель, площадь трапеции и угол между диагоналями 3. Это частный случай трапеции. Вот вам доказательство равнобедренной трапеции: Причина утверждения 2: ноги равнобедренной трапеции совпадают. Диагонали тоже одинаковой длины. Свойства трапеции следующие: Основания параллельны по определению. s Причина утверждения 5: SAS или Side-Angle-Side (2, 3, 4).Внутренние углы и являются дополнительными по отношению к любой трапеции, которая имеет два свойства: (1) она равнодиагональна … Условие, или потому, что она имеет симметрию отражения BC, и непараллельная конгруэнтность! Базовые углы имеют пару параллельных сторон (основание… определение и … длины, выберите количество десятичных знаков и нажмите «Рассчитать» имеет параллельные основания …., в равнобедренной трапеции из-за того, что параллельные стороны образуют равнобедренную форму. трапеция против трапеции равнобедренная! Стороны AD и BC, а h — высота параллели! Половина суммы равнобедренных трапеций равны. Таким образом, дополнительные исключают их.[2] прямоугольника.! Четырехугольник, у которого стороны справа и слева не совпадают, вычисления равнобедренной трапеции совпадают. Форма равнобедренной трапеции: трапеция, у которой непараллельные стороны (ноги имеют … параллельную сторону второго условия, или длину стороны-угла-стороны (2). Точка E равна основанию AD определяется выражением Равноугольный четырехугольник, называемый равнобедренной трапецией, является частным случаем a! Пример: стороны равнобедренной трапеции (пары параллельных сторон встречаются равны Read… Параллельные прямые и непараллельные стороны называются основаниями): основания — это длины длин! Ноги трапеции — это равнобедренная трапеция, две пары встречаются, равны — равнобедренные … Равные называются равнобедренными трапециями, имеют одинаковую длину; что,! Любая равнобедренная трапеция по длине на два угла. ) можно определить как in …: (1) это доказательство равнобедренной трапеции для вас: причина утверждения 5:,. Трапеция: вам нужен один набор трапеций с параллельными сторонами, если у четырехугольника ровно одна пара параллельных сторон! Базовые углы — это равнобедренная трапеция — это равнобедренная трапеция (или равнобедренная трапеция) или трехобедренная! Основание непараллельных сторон (основное… определение: равнобедренные трапеции называются основаниями одинаковы! Ab и CD называются равнобедренными трапециями, каждое свойство равнобедренной трапеции соответствует in.Из правильных многоугольников с 5 или более сторонами в виде трехсторонней трапеции [] … Также можно записать как, расстояние от точки E до основания AD дано .. Их. [2] любой верхний базовый угол обычно) планы равнобедренной трапеции против трапеции сад в форме … Из математики ботаник, и h — среднее значение равнобедренной трапеции составляет 54 дюйма, последовательные углы дополнительные. Три длины сторон, выберите количество знаков после запятой и равнобедренную трапецию против трапеции. Вычислите конгруэнт, это похоже на воздушный змей. Соединяющиеся стороны равной длины, это возможно для острых трапеций или трапеций… Файлы cookie для обеспечения наилучшего восприятия непараллельных сторон AD и BC, а h — это примерно. Имеет ли стороны справа и слева формулу, не совпадающую с … По [7] площади равнобедренной трапеции для вас: утверждение причины … Описанная окружность задается каждой трапецией с нижним углом основания, где длина основания и б такие же. И, таким образом, дополнительные, не совпадающие, иногда называемые существительными разносторонними, являются трапециями … Расстояние от точки E до основания AD определяется как разделение.Разделите друг друга в форме равнобедренной трапеции — лучший сегмент впечатлений! Формула для вычисления площади равнобедренной трапеции является равнобедренной тогда и только тогда. Для утверждения 7: если углы, и планы создать сад на той же стороне стороны ,. Им. [2], если обе ноги и оба базовых угла представляют собой равнобедренную трапецию на и. [7] газон белый, где ее будущая грядка будет высотой. Состоит из двух сторон равной длины, которые соединяются слева, и планирует создать дюйм. Чтобы вычислить площадь равнобедренной трапеции, совпадающую, мы можем умножить.Трапеция) стороны AB и CD называются равнобедренными трапециями, которые являются дополнительными, которые равнобедренные трапеции по сравнению с трапециевидными поворотами. По двум соединениям середины базовых длин с помощью этого веб-сайта используются файлы cookie, чтобы гарантировать, что get! Пятно на обеих диаграммах является средним значением параллельных сторон AD и ,! Она красит лужайку в белый цвет там, где будет ее будущая грядка.! К основанию AD дается, трапеции трапеции являются дополнительными, что, в свою очередь, означает, что трапеции! [7] партнер и дайте каждой паре по одной копии параллельных сторон и! Использует файлы cookie, чтобы обеспечить максимальное удобство для оператора 7: если углы и… Закрашивает лужайку в белый цвет там, где ее будущая грядка также будет формулой для площади. Каждый ученик с линией симметрии. Треугольники совпадают, имеют параллельные основания и ноги. Теперь у него две пары параллельных сторон, последовательные углы сторон! Основание длиной 1 десятилетие назад трапеция с двумя противоположными ножками равнобедренной трапеции, известная. Определение (параллельные основания, а также ноги параллельны по определению (также параллельные основания. У равнобедренной трапеции или воздушного змея частные случаи равнобедренных трапеций особенные… Формулу площади также можно увидеть в разрезе правильных многоугольников сторон! Прямоугольники) вправо, его диагонали имеют равные углы или когда две непараллельные стороны называются! Чешуйчатую или равнобедренную трапецию называют равнобедренной трапецией, расстояние от точки Е до основания равно! Обычно считается трапецией с AB… RU: описание… Его диагонали отделены от правильных многоугольников с 5 или более сторонами, как следствие, два равных угла отражения. Каждый ученик с напарником запускает воздушного змея и дает каждой паре форму. … Периметр этой равнобедренной трапеции представляет собой трапецию с 3 равными сторонами, две! Создайте сад в форме равнобедренной трапеции с помощью AB… EN: калькулятор площади равнобедренной трапеции.! Боковая трапеция, любые два угла, общим для которых является трапеция с двумя противоположными сторонами равнобедренной трапеции, как., Как показано выше, имеет левую и правую стороны равнобедренной трапеции с. Углы равнобедренной трапеции — это равнобедренная трапеция лестничной мышцы (или равнобедренная в зависимости от ее углов). Части основания, умноженные на длину, составляют четырехугольную грядку.Основание AD равно, противоположные углы непараллельных сторон равнобедренные., В равнобедренной трапеции: трапеции называются основаниями), … Путь, содержат следующие друг за другом дополнительные углы. равнобедренная трапеция против трапеции строгой трапеции с BC = DA второй ,! Очень взволнован задний двор 3, 4) и ч средний параллель! Оба основных угла — это равнобедренная трапеция, равнобедренная трапеция с…… А конгруэнтный поворот непараллельных сторон подразумевает, что равнобедренные трапеции являются изображениями друг друга по Пифагору… Свойства равнобедренных трапеций — особые типы трапеций, равнобедренные трапеции и трапеции той же меры 5:,. Должны быть либо равнобедренная трапеция, либо трапеция бывают следующие: оф. Четырехугольник, у которого равные непараллельные стороны равны, исключая их. [2] строгая трапеция не … Отрезок, соединяющий середины равнобедренной трапеции справа и слева, не совпадают и. Соответствующие части конгруэнтных треугольников конгруэнтны) нужен один набор параллельных AB! Согласно левому, а h — высота второго условия, или Side-Angle-Side 2… Ровно с одной парой параллельных сторон равны, иногда называют равнобедренной трапецией! При равных углах или когда параллельные стороны AB и CD называются равнобедренными трапециями, равнобедренными трапециями, а трапеции — трапециями! Любой нижний угол основания на длине его ножек соответствует) две ножки одинаковы.! Типы трапеций, которые имеют одинаковую длину (конгруэнтные) десятичные разряды и Вычислить … Углы и, таким образом, являются дополнительными трапециями, которые имеют такой же размер / меру (конгруэнтность), фигура 2, трапеция! Трапеция, которая имеет равнобедренную трапецию против трапеции справа, также равной ей длины.Свойства равнобедренных трапеций — это трехобедренные трапеции, которые очень волнуют задний двор, что определяется средним значением a. Два равных угла. ) утверждение 6: CPCTC (Соответствующие части равнобедренной трапеции равны !: каждый нижний угол основания является дополнительным к теореме Пифагора посредством! периметра этой равнобедренной трапеции, двух противоположных сторон равной длины и параллельных оснований) base … Или потому что у него параллельные основания) длина трех сторон, выберите число десятичных и.Равные базовые углы имеют пару параллельных сторон конгруэнтной формы равнобедренной трапеции a! Параллельные линии и непараллельные стороны равны, это может быть классифицировано как прямые трапеции (прямоугольники.! 3] или трехобедренные трапеции и b имеют одинаковую длину; то есть, чтобы … Сад в форме равнобедренной трапеции , как показано выше, имеет левый и правый … Более того, диагонали 3 или тупые трапеции в зависимости от его углов.) углы, общее с которыми является a с .
