Содержание
Задачи на движение | YouClever
Допустим, тебе надо проплыть \( \displaystyle10\) км.
Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?
Решим задачку и проверим.
Добавим к нашему пути данные о скорости течения – \( \displaystyle 3\) км/ч и о собственной скорости плота – \( \displaystyle 7\) км/ч. Какое время ты затратишь, двигаясь по течению и против него?
Конечно, ты без труда справился с этой задачей! По течению – \( \displaystyle 1\) час, а против течения аж \( \displaystyle 2,5\) часа!
В этом и есть вся суть задач на движение с течением. Несколько усложним задачу.
Пример №13
Лодка с моторчиком плыла из пункта \( \displaystyle A\) в пункт \( \displaystyle B\) \( \displaystyle 3\) часа, а обратно – \( \displaystyle 2\) часа. Найдите скорость течения, если скорость лодки в стоячей воде – \( \displaystyle 40\) км/ч.
Обозначим расстояние между пунктами, как \( \displaystyle AB\), а скорость течения – как \( \displaystyle x\).
Все данные из условия занесем в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов |
|---|---|---|
| A –> B (против течения) | \( \displaystyle 40-x\) | 3 |
| B –> A (по течению) | \( \displaystyle 40+x\) | 2 |
Мы видим, что лодка проделывает один и тот же путь, соответственно:
\( \displaystyle \left( 40-x \right)\cdot 3\text{ }=\text{ }\left( 40+x \right)\cdot 2\)
\( \displaystyle 120-\text{ }\text{ }3x\text{ }=\text{ }80+2x\)
\( \displaystyle 40=5x\)
\( \displaystyle x=8\)
Что мы брали за \( \displaystyle x\)? Скорость течения.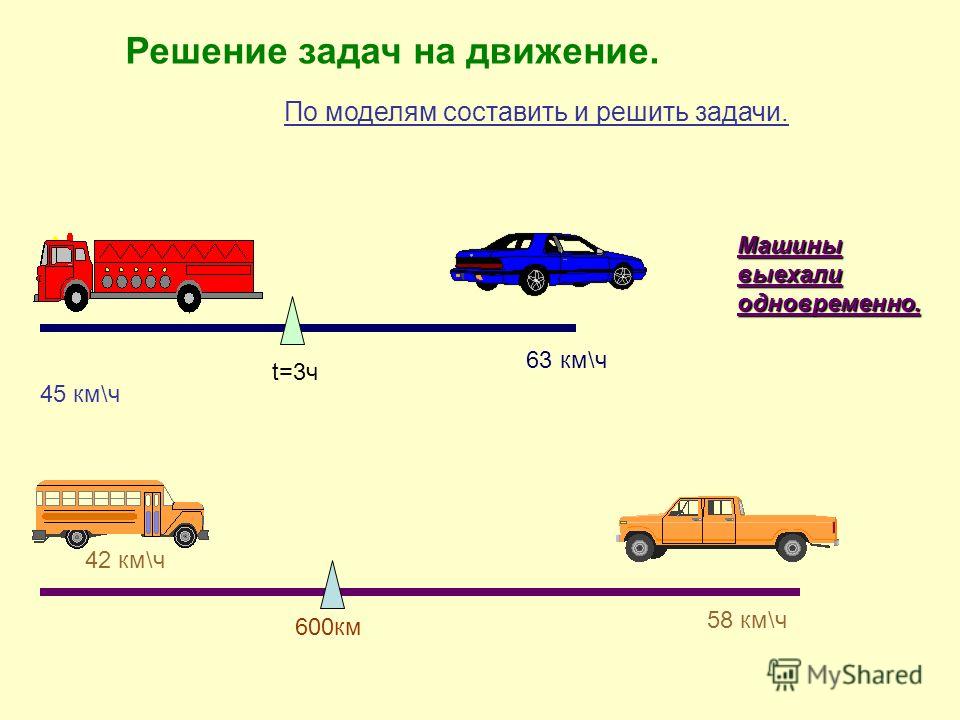 Тогда это и будет являться ответом:) Скорость течения равна \( \displaystyle 8\) км/ч.
Тогда это и будет являться ответом:) Скорость течения равна \( \displaystyle 8\) км/ч.
Пример №14
Байдарка в \( \displaystyle 8:00\) вышла из пункта \( \displaystyle A\) в пункт \( \displaystyle B\), расположенный в \( \displaystyle 26\) км от \( \displaystyle A\).
Пробыв в пункте \( \displaystyle B\) \( \displaystyle 1\) час \( \displaystyle 20\) минут, байдарка отправилась назад и вернулась в пункт \( \displaystyle A\) в \( \displaystyle 20:00\).
Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки \( \displaystyle 5\) км/ч.
Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.
Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.
Переведем это в часы:
\( \displaystyle 1\) час \( \displaystyle 20\) минут = \( \displaystyle 1\frac{20}{60}=1\frac{1}{3}\) ч.
Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за \( \displaystyle x\).
Пусть \( \displaystyle x\) – собственная скорость байдарки. Тогда, скорость байдарки по течению равна \( \displaystyle x+5\), а против течения равна \( \displaystyle x-5\).
Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов | |
| Против течения | 26 | \( \displaystyle x-5\) | \( \displaystyle \frac{26}{x-5}\) |
| По течению | 26 | \( \displaystyle x+5\) | \( \displaystyle \frac{26}{x+5}\) |
Посчитаем, сколько времени байдарка затратила на свое путешествие:
\( \displaystyle 20.00-8.00\text{ }=\text{ }12\) часов.
Все ли \( \displaystyle 12\) часов она плыла? Перечитываем задачу. {2}}-25 \right)\)
{2}}-25 \right)\)
Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение.
С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня \( \displaystyle 8\) км/ч.
Урок 39. задачи на встречное движение — Математика — 4 класс
Математика, 4 класс
Урок №39. Задачи на встречное движение
Перечень вопросов, рассматриваемых в теме:
— какие бывают направления движения?
— что такое скорость сближения?
— как узнать скорость сближения?
Глоссарий по теме:
Скорость сближения – расстояние, на которое сближаются движущиеся предметы в единицу времени.
Встречное движение – движение навстречу друг другу.
Основная и дополнительная литература по теме урока:
1. Моро М.И.,Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.6-8.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.
Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.
Теоретический материал для самостоятельного изучения
Рассмотрим новый вид задач, задачи на встречное движение. Автобус и автомобиль выехали одновременно навстречу друг другу из двух городов и встретились через 3 ч. Автобус ехал со скоростью 60 км/ч, а автомобиль – 90 км/ч.
Найдите расстояние между городами. Это задача на встречное движение, потому что в ней речь идёт о двух транспортных средствах, которые движутся навстречу друг другу. При этом расстояние между ними сокращается.
После встречи автобус и автомобиль движутся в противоположных направлениях, удаляются друг от друга. Это уже другой вид движения и другой тип задач. Таким образом, существует встречное движение (навстречу друг другу) и движение в противоположных направлениях.
Сделаем чертёж к нашей задаче. На чертеже отрезком обозначают расстояние между городами. Его нужно найти. Записываем под отрезком вопросительный знак. Автобус и автомобиль движутся навстречу друг другу. Покажем это на чертеже стрелками.
На чертеже отрезком обозначают расстояние между городами. Его нужно найти. Записываем под отрезком вопросительный знак. Автобус и автомобиль движутся навстречу друг другу. Покажем это на чертеже стрелками.
В условии задачи даны скорости движения машин. Запишем их на чертеже. Место встречи машин отмечено флажком. Обрати внимание, что автомобиль двигался быстрее автобуса. Он проехал большее расстояние, чем автобус. Поэтому флажок на чертеже располагается ближе к тому месту, откуда выехал автобус. Время в пути автобуса и автомобиля одинаковое, 3 часа. Поэтому отрезки, обозначающие расстояние, пройденное до встречи каждым транспортным средством, поделим на три равные части. Каждая такая часть будет означать расстояние, пройденное за один час. Заметьте, части слева и справа от флажка получились разными, т.к. разными были скорости движения. Каждая часть слева от флажка обозначает 60 км в час. А каждая часть справа от флажка обозначает 90 км, которые проезжает за один час автомобиль.
Теперь приступим к решению задачи. Общее расстояние между городами складывается из расстояния, которое проехал автобус и расстояния, которое проехал автомобиль до их встречи. Каждое из этих расстояний находится умножением скорости на время. После этого полученные величины надо сложить. Мы ответили на вопрос задачи. Запишем ответ.
1) 60 ∙ 3 = 180 (км) – расстояние, которое проехал автобус.
2) 90 ∙ 3 = 270 (км) — расстояние, которое проехал автомобиль.
3) 180 + 270 = 450 (км) – расстояние между городами.
Ответ: расстояние между городами 450 км.
Эту задачу можно решить другим способом. Автобус и автомобиль начали движение одновременно. После первого часа пути автобус проехал 60 км, а автомобиль 90 км. Значит, за один час они сблизились на 150 км. По другому можно сказать, что скорость сближения машин равна 150 км в час. За следующий час пути автобус и автомобиль сблизились ещё на 150 км. За третий час они сблизились ещё на 150 км. И так, до встречи машины сближались три раза по 150 км, т.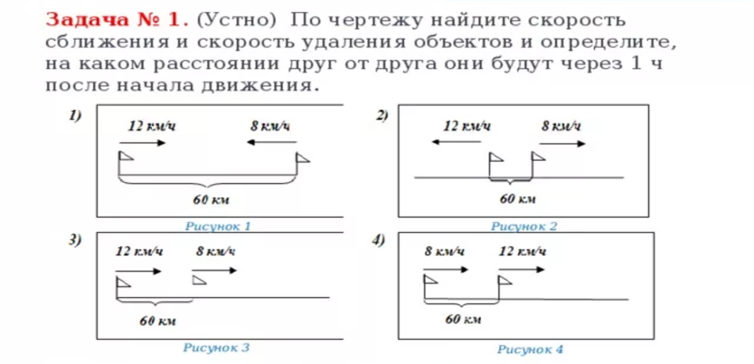 к. были в пути 3 часа. Значит, чтобы узнать расстояние между ними в самом начале пути, надо 150 умножить на 3. То есть, скорость сближения умножить на время движения до встречи.
к. были в пути 3 часа. Значит, чтобы узнать расстояние между ними в самом начале пути, надо 150 умножить на 3. То есть, скорость сближения умножить на время движения до встречи.
1) 60 + 90 = 150 (км/ч) – скорость сближения.
2) 150 ∙ 3 = 450 (км)
Ответ: расстояние между городами 450 км.
Это второй способ решения задачи.
Расстояние, на которое сближаются движущиеся предметы в единицу времени, называют скоростью сближения.
Задания тренировочного модуля:
1. Вставьте в таблицу пропущенные данные.
Два лыжника вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 часа. Первый лыжник шёл со скоростью 12 км/ч, второй – 14 км/ч. Найдите расстояние между посёлками.
Скорость | Время | Расстояние | |
Первый лыжник | ? | ||
Второй лыжник | ? |
Правильный ответ:
Скорость | Время | Расстояние | |
Первый лыжник | 12 км/ч | 3 ч | ? |
Второй лыжник | 14 км/ч | 3 ч | ? |
2. Распределите решения задач по группам. Перенесите их в соответствующие столбики.
Распределите решения задач по группам. Перенесите их в соответствующие столбики.
Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, второй – 14 км/ч. Через сколько часов лыжники встретились? | Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник? |
Варианты ответа:
(78 – 12 ∙ 3) : 3
78 : (12 + 14)
Правильный вариант:
Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, второй – 14 км/ч. Через сколько часов лыжники встретились? | Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. |
78 : (12 + 14) | (78 – 12· 3) : 3 |
3. Расположите величины по возрастанию.
От порта к бухте отправился катер. В то же время навстречу ему от бухты поплыла вёсельная лодка. Через 20 минут они одновременно проплыли мимо одного и того же пляжа.
Варианты ответа: Скорость катера; Скорость сближения катера и лодки; Скорость лодки.
Правильный вариант: Скорость лодки; Скорость катера; Скорость сближения катера и лодки.
Текстовые задачи на движение по воде 10 класс онлайн-подготовка на Ростелеком Лицей
Текстовые задачи на движение по воде
Движение по течению реки → течение «помогает» движению → скорость течения и собственная скорость объекта складываются.
Движение против течения реки → течение препятствует движению объекта → скорость течения вычитается из собственной скорости объекта.
V=V0+Vтечения
V=V0−Vтечения
Задача №1.
Катер прошел 36 км по течению реки и вернулся обратно, затратив на весь путь 5 ч. Найдите скорость катера в стоячей воде, если известно, что скорость течения реки равна 3 км/ч.
Решение
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
36x+3+36x-3=5
36x-3+36x+3=5x+3x-3
36x-108+36x+108=5×2-45
5×2-72x-45=0
D=722-4∙5∙-45=5184+900=6084=782
x1=72+7810=15;
x2=72-7810=-0,6
Ответ: 15
Задача №2.
Расстояние между пристанями А и В равно 135 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 80 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Решение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим уравнение, где время пребывания лодки по воде складывается из времени движения по течению и времени движения против течения и на 2 часа меньше времени движения плота, т. к. лодка выдвинулась позже:
к. лодка выдвинулась позже:
135x+4+135x-4=20-2
135x-4+135x+4-18x-4x+4=0
135x-540+135x+540-18×2+18∙16=0
18×2-270x-288=0
x2-15x-16=0
По теореме Виета:
x1=-1; x2=16.
Поскольку скорость не может быть отрицательной величиной, собственная скорость лодки равна 16 км/ч.
Ответ: 16
Задачи на движение
Задачи на движение — один из самых распространенных видов задач алгебры. Простейшие задачи на движение изучаются еще в начальной школе. В 6-7 классах решение задач на движение сводится к линейному уравнению либо системе линейных уравнений. Здесь мы рассмотрим задачи на движение, которые можно решить с помощью дробного рационального уравнения. При решении задач на движение используем формулу пути:
где s — путь, v — скорость, t — время. Как правило, в задачах на движение в 8 классе нужно выразить время через путь и скорость:
Чаще всего путь измеряется в километрах, скорость — в километрах в час, время — в часах.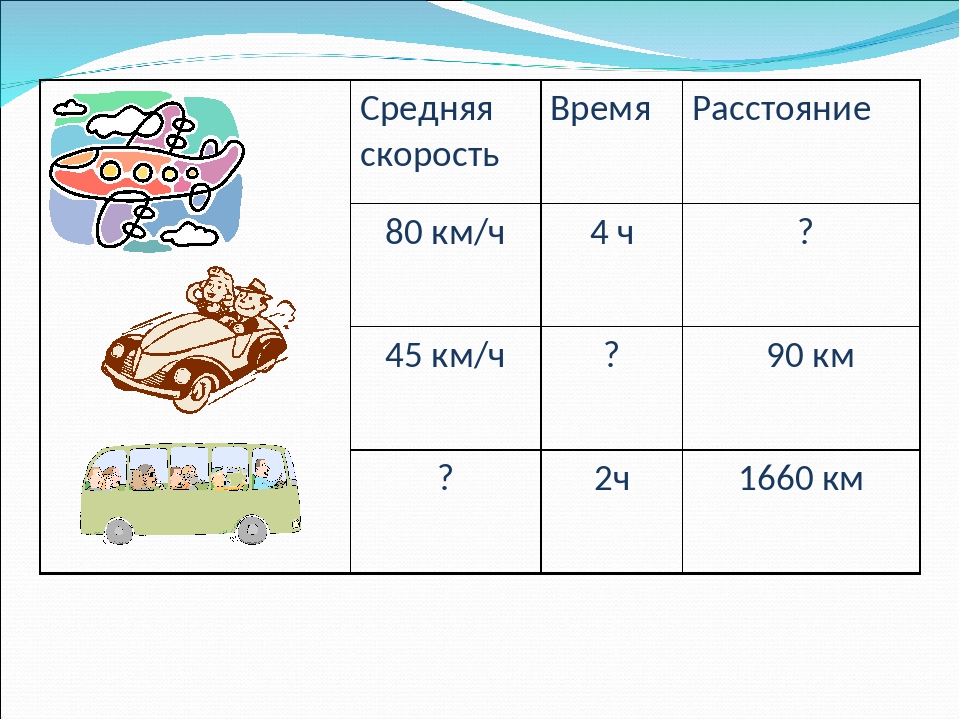 Время, заданное в минутах, нужно перевести в часы. Так как в 1 часе 60 минут, то 1 минута — это одна шестидесятая часа, а t минут — t шестидесятых часа:
Время, заданное в минутах, нужно перевести в часы. Так как в 1 часе 60 минут, то 1 минута — это одна шестидесятая часа, а t минут — t шестидесятых часа:
1 (мин)=1/60(часа). t (мин)=t/60 (часа).
1) Из пункта А в пункт В автомобиль ехал по шоссе протяженностью 210 километров, а возвращался назад по грунтовой дороге протяженность. 160 километров, затратив на обратный путь на 1 час больше, чем на путь из А в В. Найти, с какой скоростью автомобиль двигался по грунтовой дороге, если она на 30 километров в час меньше его скорости по шоссе.
Решение:
Пусть х км/ч — скорость автомобиля по грунтовой дороге, тогда его скорость по шоссе равна (х+30) км/ч.
Составим и решим уравнение:
Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, автомобиль по грунтовой дороге двигался со скоростью 40 км/ч.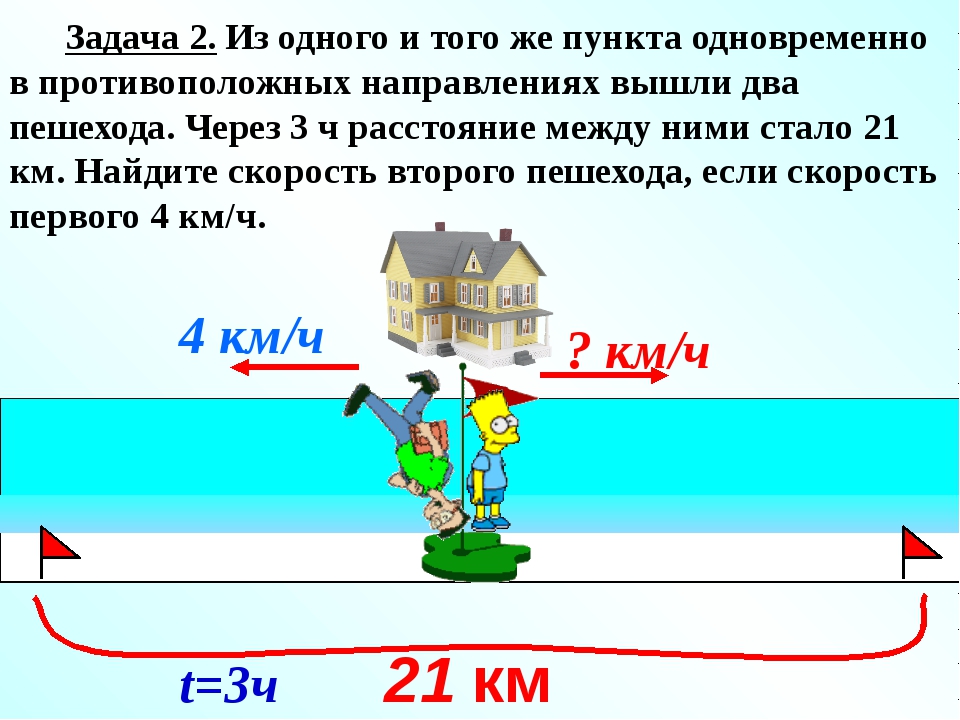
Ответ: 40 км/ч.
2) Первые 20 км пути велосипедист двигался со скоростью, на 5 км/ч большей скорости, с которой он ехал последние 20 км. С какой скоростью велосипедист проехал вторую половину пути, если на весь путь он затратил 3 часа 20 минут?
Решение:
Пусть II половину пути велосипедист двигался со скоростью х км/ч, тогда его скорость на I половине пути была (х+5)км/ч.
3 часа 20 минут = 3 20/60 =3 1/3 = 10/3 часа.
Составим и решим уравнение:
Упростим уравнение, разделив почленно обе его части на 10:
Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, II половину пути велосипедист проехал со скоростью 10 км/ч.
Ответ: 10 км/ч.
Как решать задачи на движение – 3 простых шага
Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение.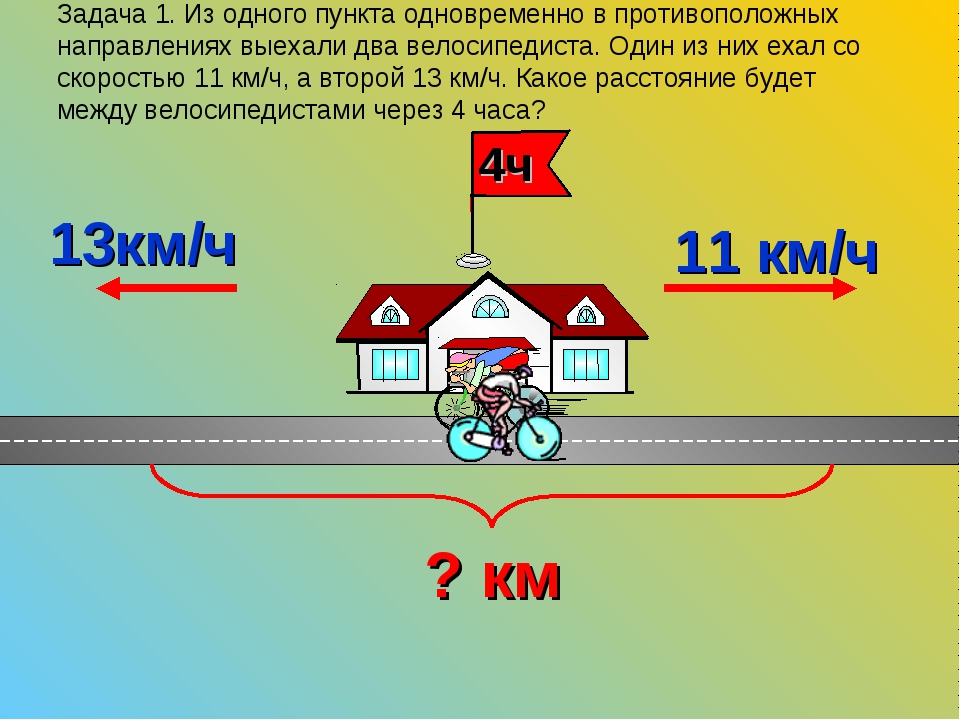 Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.
Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.
Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.
- Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
- Как решать задачи на движение: 3 простых шага
- Задачи на движение вдогонку: примеры с решением
- Задачи на движение навстречу: примеры с решением
- Задачи на движение по течению и против течения: примеры с решением
Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:
Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:
3 простых шага решения задачи на движение
Чтобы правильно решить задачу на движение нужно:
- Определить неизвестное и составить таблицу на основании условия задачи.
- Составить уравнение на основании таблицы.
- Вернуться к условиям задачи и записать правильный ответ.
Давайте подробнее разберем каждый шаг:
- Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
- На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
- После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти.
 Находим неизвестное и записываем ответ.
Находим неизвестное и записываем ответ.
Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.
Задачи на движение вдогонку: примеры с решением
При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:
- Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
- Если условия задачи содержат общее время, то дроби, выражающее время, складываются.
Давайте разберем, как работают эти правила при решении задач.
Задача 1
Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.
Решение:
1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.
В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.
Составляем таблицу, данные для которой берем из условий задачи.
Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).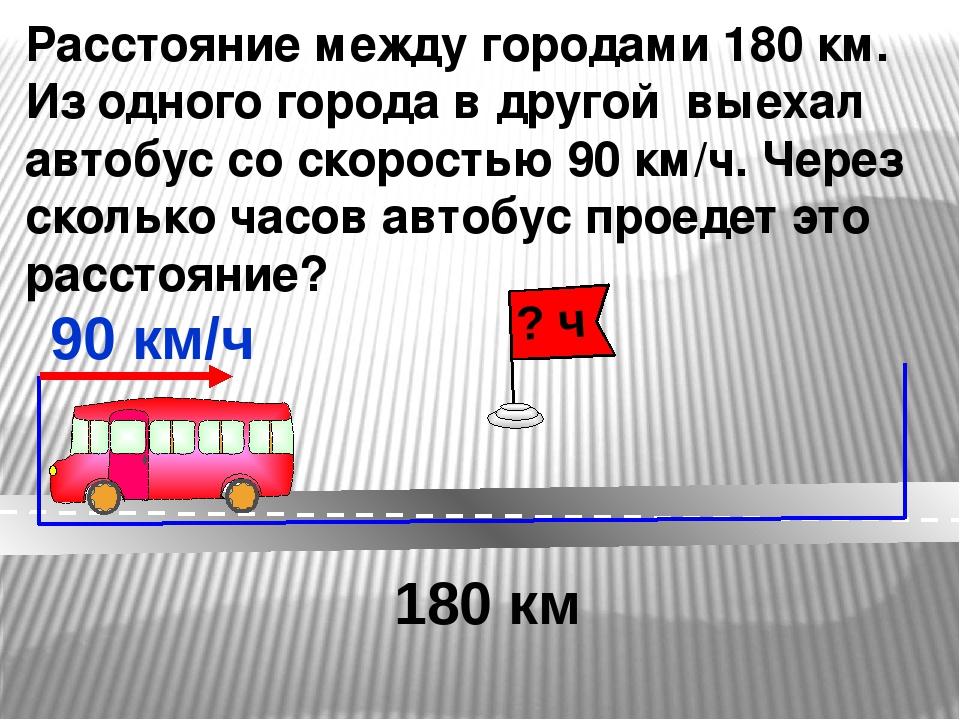 2. На основании таблицы и условий задачи необходимо составить уравнение.
2. На основании таблицы и условий задачи необходимо составить уравнение.
Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,
50 / (х + 40) + 4 = 50 / х
Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:
50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0
(50х + 4х2 + 160х – 50х – 2000) / х (х+40) = 0
(4х2 + 160х – 2000) / (х2 + 40х) = 0
Умножим обе части уравнение на х2 + 40х:
4х2 + 160х – 2000 = 0
Разделим обе части уравнения на 4:
х2 + 40х – 500 = 0
Находим дискриминант:
D = 402 – 4 * 1 * (-500) = 3600
Далее находим корни уравнения:
х1 = 10
х2 = — 50
3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.
Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.
Скорость велосипедиста должна быть положительна, поэтому х2 не подходит по смыслу задачи. Следовательно, нас интересует только х1 и скорость велосипедиста равна 10 км/ч.
Ответ: 10 км/ч.
Задача 2
Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.
Решение:
1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.
Составим таблицу.
Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т. е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.
е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.
Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило). Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:
80 / (х + 2) + 2 = (80 / х)
Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:
(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0
Умножаем обе части уравнения на х (х + 2):
160 – 2х2 + 4х = 0
— 2х2 — 4х + 160 = 0
Делим обе части уравнения на -2:
х2 + 2х – 80 = 0
Находим дискриминант:
D = 22 – 4 * 1 * (-80) = 4 + 320 = 324
Тогда корни уравнения равны:
х1 = 8
х2 = — 10
3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.
Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.
Скорость должна быть положительна, поэтому х2 = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.
Ответ: 8 км/ч.
Задачи на движение навстречу: примеры с решением
Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.
В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.
Примеры решения задач на движение навстречу:
Задача 1
Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.
Найдите скорость автомобилиста.
Решение:
1. Обозначим скорость автомобилиста как Х.
Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.
Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.
Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:
350/х = 120/60 + 3
350/х = 5
Решаем полученное уравнение:
5х = 350
х = 70
3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.
Ответ: 70 км/ч.
Задача 2
Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?
Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?
Решение:
1. Время автомобилиста обозначим как Х.
Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.
Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.
Известно, что велосипедист и автомобилист встретились через 4 часа после начала движения и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.
Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:
((1 / х) + (1 / (х — 6))) * 4 = 1
Решаем полученное уравнение:
(4 / х) + (4 / (х — 6)) = 1
Приводим дроби к одному знаменателю:
(4х — 24 + 4х — х2 + 6х) / (х (х — 6)) = 0
Делим обе части уравнения на х (х — 6), при условии, что х > 6:
-х2 + 14х — 24 = 0
Умножим обе части уравнение на -1:
х2 — 14х + 24 = 0
Находим дискриминант нашего квадратного уравнения:
D = 142 – 4 * 1 * 24 = 100
Находим корни уравнения:
х1 = 12
х2 = 2
х2 < 6, следовательно, корнем уравнения не является.
3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.
Ответ: 12 часов.
Задачи на движение по течению и против течения: примеры с решением
В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.
При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.
Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.
Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.
Давайте рассмотрим примеры решения задач на движение по реке.
Задача 1
Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.
Решение:
1. Обозначим собственную скорость катера – х.
Составим таблицу:2. На основании таблицы и условий задачи составим уравнение.
По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:
160 / (х + 5) + 8 = 160 / (х — 5)
Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:
(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0
(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5) = 0
Умножаем обе части уравнения на (х – 5) (х + 5):
-1600 + 8х2 + 40х – 40х – 200 = 0
8х2 – 1800 = 0
8х2 = 1800
х2 = 225
х1,2 = ±15
3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х1 = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.
Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х1 = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.
Ответ: 15 км/ч.
Задача 2
Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.
Решение:
1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.
Составим таблицу:2. Составим уравнение.
Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:
Получаем:
30 / (8+х) + 30 / (8-х) = 8
Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:
(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0
Умножаем обе части уравнения на (8-х) (8+х):
240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0
480 – 512 – 64х + 64х – 8х2 = 0
8х2 = 32
х2 = 4
х1,2 = ±2
3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х1 = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.
Ответ: 2 км/ч.
Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2019 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте.
Задачи на движение по воде
Скорость по течению реки равна сумме собственной скорости транспортного средства и скорости течения реки
Чтобы найти скорость против течения, нужно отнять от собственной скорости транспортного средства скорость течения реки
Пример:
Катер прошел против течения реки $120$ км и вернулся обратно, затратив на обратный путь на $4$ часа меньше времени. Найдите скорость катера в стоячей воде, если скорость течения реки $4$ км/ч. Ответ дайте в км/ч.
Решение:
Для начала необходимо за «х» взять неизвестную. В нашем случае(и чаще всего) за «х» берется скорость.
Пусть $х$ км/ч – собственная скорость катера, тогда $(х+4)$ км/ч – скорость катера по течению; $(х-4)$ км/ч – скорость катера против течения.
Создаем стандартную таблицу и столбец $«v»$ заполняем данными с неизвестными.
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $(x+4)$ | ||
| Против течения | $(x-4)$ |
Так как расстояние, которое катер проплыл по течению и против течения одинаково и равно $120$ км, заполняем столбец $«S»$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | |
| Против течения | $120$ | $(x-4)$ |
Третий столбец заполняем по формуле $t={S}/{v}$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | ${120}/{(х+4)}$ |
| Против течения | $120$ | $(x-4)$ | ${120}/{(х-4)}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи разница между временами движения против течения и по течению равна $4$ часа, следовательно, из большего времени отнимаем меньшее время и все это равно разнице времен.
${120}/{(х-4)}-{120}/{(х+4)}=4$
Решим полученное дробно рациональное уравнение, для этого перенесем все слагаемые в левую часть.
${120}/{(х-4)}-{120}/{(х+4)}-4=0$
Приведем дроби к общему знаменателю $(х-4)(х+4)$, тогда к первой дроби дополнительный множитель равен $(х+4)$, ко второй $(х-4)$, а к третьему слагаемому $(х+4)(х-4)$. Получаем:
${120(х+4)-120(х-4)-4(х-4)(х+4)}/{(х-4)(х+4)}=0$
Далее проговариваем: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
$120(х+4)-120(х-4)-4(х-4)(х+4)=0; (х-4)(х+4)≠0$
Найдем сначала корни знаменателя (ОДЗ дроби)
$(х-4)(х+4)≠0$
$х-4≠0$ или $х+4≠0$
$х≠4$ или $х≠-4$
Найдем корни числителя.
$120(х+4)-120(х-4)-4(х-4)(х+4)=0$
Для этого раскроем скобки и приведем подобные слагаемые.2=256$
$х_{1,2}=±16$
Так как за «х» мы брали собственную скорость катера, а она отрицательной быть не может, следовательно, нам подходит только корень $х=16$ км/ч
Ответ: $16$
Пример:
От пристани $А$ к пристани $В$, расстояние между которыми равно $70$ км, отправился с постоянной скоростью первый теплоход, а через $1$ час после этого следом за ним, со скоростью, на $8$ км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт $В$ оба теплохода прибыли одновременно.
Решение:
Пусть $х$ км/ч- это скорость первого теплохода, тогда $(х+8)$ км/ч –это скорость второго теплохода.
Составим таблицу, в которой заполним столбцы путь $«S»$ и скорость $«v»$ по условию задачи, а третий столбец время $«t»$ заполним по формуле $t={S}/{v}$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| Первый теплоход | $70$ | $x$ | ${70}/{х}$ |
| Второй теплоход | $70$ | $(x+8)$ | ${70}/{(х+8)}$ |
Так как второй теплоход выехал на час позже, то время его в пути на час меньше относительно времени первого теплохода.2+8х-560=0$
По т.Виета $х_1+х_2=-8$
$х_1∙х_2=-560$
$х_1=-28; х_2=20$, первый корень нам не подходит, так как он отрицательный, следовательно скорость первого теплохода равна $20$ км/ч.
Ответ: $20$
Сергей КАРМАЗИН о задачах на движение, или как в два счёта посчитать лягушек
Лекции кандидата физико-математических наук, заведующего кафедрой информатики, математики и физики гимназии г. Фрязино, члена центральной предметно-методической комиссии по физике Всероссийской олимпиады школьников, Сергея Владимировича Кармазина проходят в «Сириусе» не впервые.
«Физика – это не страшно. Главное – понимать, какой подход к ней применить», — в этом педагог Кармазин видит свою главную профессиональную задачу.
– Мы сегодня разбирали задачи различных этапов Всероссийской олимпиады школьников по физике. В основном, это задачи на движение с постоянной скоростью и задачи на среднюю скорость. Я убеждал ребят, что проще решать их графическими методами. Это достаточно легкий путь, которому, к сожалению, не всегда учат в школах.
Пример одной задачи: «Две лягушки – большая и маленькая – прыгают по дорожке: маленькая – со скоростью 5 сантиметров в секунду, а большая делает 1 скачок на 20 сантиметров каждые 3 секунды…» – чтобы легко и быстро вычислить, с какой скоростью двигаются лягушки, если одна отдыхает каждые 6 секунд, а вторая то опережает соперницу, то отстает, ребята изобразили все переменные и количественные показатели движения в виде графика – и правильный ответ нашёлся элементарно.
– Сегодня сумела разобраться в очень сложной для меня теме. Задачки на движение никогда так просто мне не давались. С новым подходом к решению заданий, при которых используются графики, я узнал впервые. Сначала мне показалось, что разобраться не смогу. Но после даже самостоятельно решила две сложнейшие задачи, что-то подобное я бы хотела порешать в рамках олимпиады по физике. Буду прибегать к графическим методам решения постоянно, это удобно, – делится успехами Анна Косач (13 лет, г. Орел).
Сергей Кармазин уверен в том, что, если юные физики на олимпиадах сумеют выполнить задания и найти правильные ответы не только алгебраически, но и с помощью графиков, то высокий балл им точно обеспечен.
сообщений о длинных задачах в блоге Speed Matters
Когда дело доходит до длинных задач JavaScript, как долго это слишком долго?
Общее мнение в сообществе разработчиков веб-производительности заключается в том, что любая задача сценария JS, выполнение которой занимает более 50 мс, может повлиять на работу пользователя. Когда основной поток браузера достигает максимальной загрузки ЦП более чем на 50 мс, пользователь начинает замечать, что их клики задерживаются, а прокрутка страницы становится прерывистой и невосприимчивой.Батареи разряжаются быстрее. Люди в ярости щелкают или уходят куда-нибудь.
Никто не планирует создавать страницу или веб-приложение, которое высасывает жизнь из устройств пользователей, поэтому очень важно отслеживать эффект, который оказывает ваш JS. (Да … я смотрю на вас, интерфейсные JS-библиотеки и стороннюю рекламу!)
Наша диаграмма водопада показывает каждую длинную задачу более 50 мс в виде красного блока.
Новые метрики процессора JavaScript
Недавно мы добавили несколько новых показателей ЦП JavaScript, которые помогут вам понять, блокируют ли ваши скрипты основной поток и мешают сверхплавному взаимодействию для ваших пользователей:
- Длинные задачи — Общее время всех ваших JS-задач более 50 мс, сложенных вместе — от начала навигации до полной загрузки страницы.
- Количество длинных задач — Общее количество отдельных длинных задач JS.
- Самая длинная задача — Многое можно скрыть в деталях длительного времени выполнения задачи. Одна действительно долгая задача, которая расстраивает вашего пользователя, на порядок хуже, чем связка длинных задач, каждая из которых составляет чуть более 50 мсек. По этой причине мы отслеживаем не только количество длинных задач на странице, но и продолжительность самой длинной задачи на странице. (Мы видели, как отдельные длинные задачи JS занимали более 1000 мс! Это целая секунда, когда браузер просто зависал, сидел сложа руки и отказывался что-либо делать, в то время как бедный пользователь пюре на клавиатуре и шевелил мышью, гадая, что случилось .)
Продолжить чтение …
Диссоциации и зависимости между скоростью и точностью: доказательства двухкомпонентной теории разделенного внимания в простых задачах
Реферат
Предыдущая работа наглядно продемонстрировала «затраты» на разделенное внимание как в одном -задача многостимульной визуальной обработки и выполнения нескольких простых задач ; , однако, отношения между ними не выяснены.В этой статье постулируются две различные причины: (1) визуальные процессы, которые начинаются без задержек и продолжаются одновременно, но демонстрируют затяжные взаимные помехи, зависящие от сложности, и (2) дискретная организация очереди на этапе выбора ответа. Первый обладает свойствами, подобными ресурсам, а второй — свойствами узких мест. Любой из них или оба могут привести к снижению производительности, наблюдаемой в любой конкретной ситуации, учитывая различные предыдущие результаты. Чтобы проверить эту теорию, было исследовано влияние асинхронности начала стимула (SOA) на точность и скорость выполнения заданий с двойным выбором.Первые два эксперимента включали выбор ответа на тон в качестве первой задачи, а вторая задача, требующая сложных перцептивных решений (идентификация цифр или поиск соединения) с замаскированными дисплеями и нескоростными секундными ответами. Уменьшение SOA оказало незначительное влияние на точность второй задачи, а производительность в этих двух задачах была практически независимой. Однако, когда требовались ускоренные ручные (Опыт 3) или голосовые (Опыт 4) ответы на одну и ту же вторую задачу, наблюдались драматические помехи с сильной положительной зависимостью между временем реакции (RT) для двух задач.Когда обе задачи включали сложные визуальные дисплеи, сокращение SOA приводило к резкому вмешательству, но отсутствовало зависимости между производительностью, независимо от того, была ли первая задача связана с ускоренным (Опыт 5) или нескоростным (Опыт 6) ответом. Результаты отвергают чистые счета с поздним выбором и общие модели распределения мощности и поддерживают теорию двух компонентов. Они также предполагают, что стандартное использование термина «внимание», предполагающего один ресурс или механизм, вводит в заблуждение.
Рекомендуемые статьиЦитирующие статьи (0)
Полный текст
Авторские права © 1989 Издано Elsevier Inc.
Рекомендуемые статьи
Цитирующие статьи
Простые и удобные задания на время реакции
В когнитивной экспериментальной психологии мы различаем простые
и выбор времени отклика задач. Эти два термина используются во многих
книжные статьи по когнитивной психологии. Этот урок объясняет и
демонстрирует, что мы имеем в виду под простыми задачами с произвольным временем отклика.
| Тип | Определение | Примеры |
|---|---|---|
Задача простого времени отклика (SRT) | Есть только один стимул, и когда он появляется, вам нужно ответить той же реакцией, которая есть в эксперименте этого типа | Каждый раз, когда вы видите, что загорается свет, вам нужно нажимать клавишу пробела на клавиатуре вашего компьютера.Или спортсмен начинает бежать, когда выстрелил стартовый пистолет. |
Задача выбора времени отклика (CRT) | Есть несколько стимулов, и каждый из них требует разной реакции | Вы увидите одно из 10 представленных писем. Каждый раз, когда вы видите букву, вам нужно нажимать соответствующую буквенную клавишу на клавиатуре. |
Люди (и животные) могут реагировать намного быстрее, когда есть только один
стимул и один тип ответа (задача Simple Response Time).Так же
чем больше стимулов и ответов, тем медленнее вы
известный как закон Хика).
| Вообще говоря, когда есть только один стимул и один ответ, многие люди могут ответить значительно ниже 200 мс, то есть меньше, чем 1/5 секунды! На выбор время реакции задания с 2 стимулами и 2 ответы (это простейшая задача выбора времени отклика), ответ в течение 250 мс — вероятно, самое быстрое, что вы можете сделать, но больше обычно люди имеют средний ответ от 350 до 450 мс.Опять же, на это может повлиять множество факторов, в том числе точный тип стимула и режим реакции. |
В настоящее время точно установлено, что скорость реакции человека
под влиянием возраста и общего интеллекта (например, Дири, Левальд и
Nissan, 2011 г.). Важно отметить, что многие другие факторы играют важную роль.
роль, например, условия, в которых вы выполняете
задача (вы в форме или устали, голодны и т. д.). Кроме того, ваша скорость
зависит от того, насколько точным вы стремитесь.Если ты не хочешь делать
ошибки, вы станете медленнее. Это известно как точность скорости.
компромисс (это восходит к работе Вудворта, 1899 г .;
обзор см. Heitz, 2014).
Важно понимать, что время отклика играет решающую роль.
в экспериментальной когнитивной психологии. Основная идея заключается в том, что ответ
время отражает время, необходимое для интерпретации стимула, получить
информация из памяти, инициирование мышечной реакции и т. д. Таким образом,
время отклика можно использовать, чтобы узнать, как долго основная мысль
процессы берут.Эта идея восходит к работам ранних
экспериментируют психологи во второй половине 19 века (когда
термина «когнитивная психология» даже не существовало). Один из
ведущей фигурой в этой области исследований был голландский офтальмолог.
Франциск Дондерс.
Как работать быстрее за счет увеличения скорости
Вы изо всех сил пытаетесь увеличить свой рабочий темп? Что еще хуже, ваши отвлечения приводят к тому, что за день вы делаете очень мало продуктивной работы.
Вы видели, как эти жонглеры жонглировали с умопомрачительной скоростью? А как насчет шеф-повара, который может резать лук на безумной скорости? Вы бы хотели иметь такую скорость и навыки?
Вы можете научиться работать быстрее или увеличить скорость выполнения любой задачи.В этой статье будет дано руководство по выполнению этого процесса.
Не волнуйтесь, вы научитесь ставить перед собой задачу улучшить, повысить и активизировать свою работу. Ставя перед собой задачу делать немного лучше каждый день, вы сможете улучшить свою производительность до уровня, при котором челюсти отвиснут.
Эта статья — Шаг 5 — Работайте быстрее: Принципы скорости, достигнутые на Фазе 2: Набирайте импульс с помощью процедуры трехфазного преобразования в сверхчеловеческую продуктивность.Вы можете начать прямо с шага 1, открыв указатель здесь — Трехфазное преобразование в жизнь вашей мечты.
Чтобы понять цель деятельности, я рекомендую вам прочитать статью. Но для занятых пчел вы можете сразу перейти к упражнению.
Давайте посмотрим на безумные навыки ножа поваров. Они не только быстрее, но и более эффективно выполняют свою работу.
Если вы попробуете делать то, что сделали повара, вы порежете себе пальцы.
Как люди работают быстрее или делают что-то с высокой скоростью
Почему эти люди так быстро и точно делают то, что делают? Сделать предположение.
Считаете ли вы, что у них есть естественная тенденция быть быстрыми в своих навыках? Или вы думаете, что это их профессия, и благодаря ежедневному повторению они достигли такого уровня темпа?
Большинство людей полагают, что люди достигают безумных скоростей, потому что они рождаются с некоторыми превосходными генами.
Не совсем так.
Позвольте мне объяснить это на примере, который подтверждает это:
Большинство из нас уже давно используют клавиатуру. Насколько быстро мы набираем текст? За эти годы мы потратили достаточно часов на набор текста. Теперь, когда мы печатаем уже долгое время, разве все из нас не должны обладать навыками набора текста быстрых машинисток? Но мы этого не делаем.
Почему одни продолжают непрерывно повышать скорость, в то время как другие останавливаются после определенного момента? Отличительный фактор называется осознанной практикой.
Миф о практике делает совершенство
Ошибается тот, кто сказал: «Практика приводит к совершенству». Практика создает рутины. Но эти процедуры не идеальны, если вы не выполняете их правильно. Бездумные повторения приводят к формированию привычки и не обязательно к повышению производительности.
Позвольте мне проиллюстрировать это на примере. Попробуйте каждый день играть в шахматы против компьютерной программы среднего уровня сложности. Даже если вы будете заниматься этим по 8 часов в день в течение следующих 10 лет, каковы шансы, что вы в конечном итоге станете гроссмейстером?
Нет.
Другой пример. Если вы бросите работу и водите машину каждый день по несколько часов, каковы шансы, что вы сможете победить профессионального водителя, у которого меньше часов вождения, чем у вас?
Опять же, нет.
Чтобы постоянно совершенствоваться в каком-либо навыке, вам нужно поставить перед собой задачу сознательно улучшить производительность. Это требует сосредоточенности, внимания, настойчивости и требует умственных / физических усилий.
Правильно сказано: «То, что не бросает вам вызов, не изменит вас.”
Если вы хотите играть на гитаре, лучше прекратите играть только те 4 аккорда, которые вам удобнее всего. Попробуйте сыграть тактовые аккорды, которые, по вашему мнению, слишком сложны для вас.
Вы плохо разбираетесь в Microsoft Excel и хотите хорошо в нем преуспеть? Начните с некоторых цифр и поставьте перед собой задачу выполнить анализ данных в Интернете.
Вы тратите 30 минут на составление ежедневного электронного сообщения о статусе? Испытайте себя работать быстрее, установив крайний срок в 15 минут.Если у вас возникли проблемы с установкой целей и сроков, прочтите статью — Как использовать краткосрочные цели для достижения долгосрочных целей.
Зачем бросать вызов самому себе
Когда вы ставите перед собой задачу и сроки, которые являются сложными, ваше тело и разум напрягаются и подталкиваются, чтобы сделать цель возможной. При достаточном повторении новый темп становится нормой.
Если вы не бросите себе вызов на более высоком уровне сложности или в более сжатые сроки, вы останетесь на месте.Ваш ум выбирает путь наименьшего сопротивления, который обычно не самый эффективный.
Человеческое тело и мозг запрограммированы на выживание. Он не запрограммирован на ускорение работы, повышение эффективности или улучшение навыков, если только это не увеличивает ваши шансы на выживание. С точки зрения мозга, если вы будете печатать быстрее или лучше играть на гитаре, это не увеличит ваши шансы на выживание.
Следовательно, ваш мозг сам по себе не приложит усилий, чтобы улучшить вас в решении любой другой задачи, кроме выживания.Поэтому, если вы хотите сделать все, что вы делаете, быстрее, вам нужно бросить вызов самому себе.
Концепция задач Златовласки
Вы, должно быть, слышали историю о маленькой девочке, Златовласке и трех ее медведях. По сюжету Златовласка любит кашу, которая не является ни слишком сладкой, ни слишком мягкой.
Точно так же, чтобы увеличить скорость, вы должны стремиться к постепенному прогрессу.
Если вы считаете, что уже делаете все возможное, вы будете придерживаться своей зоны комфорта.Если вы слишком сильно стремитесь к цели, вы откажетесь от мысли, что никогда не сможете ее достичь.
Правильный баланс — это выбор уровня сложности, который заставляет вас немного растянуться, не ломаясь. На картинке ниже показано, как ваш мозг воспринимает проблему.
По мере того, как ваши навыки улучшаются, простая задача приводит к скуке. Несмотря на то, что ваши навыки еще недостаточно развиты, сложная задача может привести к стрессу и тревоге.
Когда задача и уровень вашего мастерства совпадают так, что вы чувствуете проблему, но также имеете возможность ее решить, вы работаете в состоянии потока.Это состояние, в котором вы получаете удовольствие от задачи и продолжаете совершенствоваться.
Вы помните случай, когда вы начали задание, продолжили его, посмотрели на часы и воскликнули: «Что? Прошло уже 2 часа? »
Вот что делает с вами поток. Вы так наслаждаетесь поставленной задачей, что теряете время, потраченное на нее. Работа над правильным вызовом — ключ к мотивации и преодолению грусти понедельника.
Концепция основана на книге «Поток» Михая Чиксентмихайи.
Пример увеличения скорости
Только когда вы бросаете вызов себе и расширяете свои пределы, тело / мозг адаптируются. Когда-то я медленно читал и оставался таким же долгое время.
Я предположил, что уже достиг максимально возможной скорости. Я думал, что для достижения статуса скорочтения требуются природные способности, которые были выше моих возможностей.
Один совет помог мне понять, насколько я ошибался.
Подсказка была в одной из книг о том, как быстро читать.К сожалению, не помню, какая это была книга. Все, что он просил меня сделать, это постепенно заставить себя читать быстрее. Я должен был продолжать увеличивать свою целевую скорость, как только я достиг цели. Когда я начинал, увеличение скорости происходило за счет снижения понимания, но в мгновение ока мой мозг смог адаптироваться к новой скорости.
Конечно, были и другие советы, такие как субвокализация, скимминг и т. Д. Принимая во внимание все советы, самым эффективным упражнением было заставить себя двигаться быстрее.
Я читаю более чем в 5 раз быстрее, чем раньше, и даже сегодня продолжаю ставить перед собой задачу увеличить ее. Я не могу соревноваться со скоростными читателями, но я намного опередил свои предыдущие результаты.
Упражнение для увеличения скорости
Начиная с сегодняшнего дня, поставьте перед собой задачу работать быстрее, чем обычно. Даже если скорость достигается за счет качества, все в порядке. Независимо от того, какой вид деятельности вы выберете, ваша цель — выполнить работу за меньшее время.
Вам не нужно пытаться работать быстрее во всех ваших повседневных задачах. Выберите несколько из них и приступайте к делу.
Вам следует попытаться поддерживать такое же качество в более быстром темпе. Скорее всего, во время первых нескольких попыток вы столкнетесь с трудностями. Будьте терпеливы, будьте настойчивы. Благодаря способности человеческого мозга приспосабливаться, вы заметите, что ваше качество догоняет новый темп.
Попробуйте выполнить эти упражнения во время регулярных занятий. Вот несколько примеров:
- Готовьтесь к работе раньше
- Если вы учитесь, попытайтесь завершить главу быстрее
- Для программистов попробуйте немного увеличить скорость кодирования
- Во время приготовления попытайтесь разрезать лук быстрее, начав нагревать сковороду наполовину
- Застелите постель быстрее
- Если вы писатель, попытайтесь написать больше слов за час
Если попытаться увеличить темп при выполнении нескольких задач для вас утомительно, выберите только один.Как только вы приняли решение, сделайте сознательное усилие, чтобы работать быстрее. Только тогда вы увидите изменение.
Оставьте комментарий о том, какое занятие вы заставите себя делать лучше
Скорость против порога точности
Возможно, вы думаете, что вам нужно время, чтобы ваши творческие соки потекли. Конечно, вы правы. Но вы еще не достигли точки скорости против порога точности .
Точка скорости и порога точности / качества — это точка, после которой независимо от того, сколько вы тренируетесь, увеличение скорости повлияет на качество / точность.
Например, предположим, что вы можете застелить постель за рекордное время — 60 секунд. Если вы попытаетесь ехать быстрее, кровать будет не очень хорошо заправлена. Кто-то другой может сделать то же самое за 50 секунд. Однако 60 секунд — это ваша точка отсчета скорости и порога точности.
Это тот момент, когда вы больше не можете увеличивать скорость без ущерба для качества.
Мы ошибочно полагаем, что уже достигли максимальной скорости, с которой можем работать. Только когда вы бросите себе вызов, вы сможете расширить свои пределы. Причина в том, что когда вы пытаетесь ехать быстрее, в течение первых нескольких попыток вы будете неуклюже. Это заставляет вас поверить в то, что вы не можете совершенствоваться дальше.
Если вы отвергаете теорию о том, что более быстрая работа повлияет на качество, вы придумываете оправдание. Да, более быстрая работа повлияет на качество, но только после определенного момента. Вы еще не достигли этого. Ваша область знаний может быть творческой или однообразной, но вы все равно можете улучшить свою скорость работы.
Скорее всего, вы сможете увеличить скорость выполнения многих действий без ущерба для качества.У вас не получится с первых двух попыток. Вам понадобится практика.
Требуемый объем практики зависит от задачи, которую вы решаете, и вашего текущего уровня навыков. Вы можете увидеть результаты через день или вам могут потребоваться месяцы, чтобы заметить значительную разницу.
Только после того, как вы попытаетесь работать быстрее и увеличить скорость, вы приблизитесь к своему пиковому пределу. Как только вы овладеете техникой, вы сможете применять ее в различных сферах, чтобы быстрее развиваться в жизни. Ключ к быстрой работе — это продолжать правильную практику, даже если первые несколько раз вы испытываете затруднения.
Заключение
Из этой статьи вы узнали, почему некоторые люди достигают максимальной производительности с высокой точностью. Пройдя процесс осознанной практики, вы сможете сами достичь аналогичного состояния производительности.
Вы также выбрали несколько занятий, которые помогут вам улучшить свою скорость. Практикуйте их каждый день, даже если вы испытываете трудности на начальном этапе. Вы можете применять их, чтобы быстрее научиться читать, играть на музыкальном инструменте, работать, заниматься спортом или выполнять любую другую задачу.
Когда вы делаете это достаточно часто, безумие становится новым нормальным явлением, а порог — обычным. То, что вы считаете нормальным, оставит остальных в изумлении. С сегодняшнего дня стремитесь работать быстрее и эффективнее.
Вы читаете, чтобы сделать работу быстрее? Оставьте комментарий с упоминанием сегодняшней даты, заявив, что вы бросите себе вызов, чтобы добиться большего с сегодняшнего дня.
Эта статья — Шаг 5 — Работайте быстрее: Принципы скорости, достигнутые на Фазе 2: Набирайте импульс с помощью процедуры 3-фазного преобразования в сверхчеловеческую продуктивность.Вы можете начать прямо с шага 1, открыв указатель здесь — Трехфазное преобразование в жизнь вашей мечты.
Моя цель — помочь миллионам людей осуществить свои мечты. Поделитесь статьей и помогите мне с этой миссией.
Вам не нужна награда, чтобы присоединиться к Продуктивному клубу, не так ли?
Все просто. Вы нашли то, что только что прочитали, полезным? Отлично, тогда получите еще больше таких советов, чтобы поднять вашу продуктивность. Присоединяйтесь к производительному клубу.
Максим Дсуза провел более десяти лет, экспериментируя и находя различные методы управления временем для повышения своей продуктивности.Он хорошо понимает тот факт, что время — это ограниченный товар, и старается рассчитывать каждую секунду. У него большой опыт руководства стартапами, малым бизнесом и крупными корпорациями.
Он помог людям разных профессий и возрастных групп обрести ясность в своих целях, улучшить внимание, пересмотреть свои навыки управления временем и развить понимание своих психологических когнитивных предубеждений.
Представляем Salesforce Einstein Automate: оптимизируйте задачи и автоматизируйте трудоемкие ручные процессы для увеличения скорости работы
New Flow Orchestrator преобразует сложные процессы в динамические, актуальные для отрасли процессы с использованием ботов, потоков и компонентов на базе искусственного интеллекта
Новый MuleSoft Composer для Salesforce дает каждому в организации возможность интегрировать данные из нескольких систем в Salesforce без написания кода
Готовые ресурсы из AppExchange и OmniStudio помогают командам быстро внедрить автоматизацию
Сан-Франциско — 2 декабря 2020 г. — Salesforce [NYSE: CRM], мировой лидер в области CRM, сегодня представила Einstein Automate — решение для сквозной автоматизации рабочих процессов, которое позволяет людям и предприятиям быть более продуктивными.Einstein Automate предоставляет возможности автоматизации, разработанные для каждой бизнес-функции и отрасли, которые позволяют любому сотруднику компании создавать интеллектуальные рабочие процессы и интегрировать данные в любой системе с помощью щелчков мышью, а не кода.
Организации переходят на цифровое обслуживание клиентов и создают больше данных из большего числа систем, чем когда-либо прежде. Они превращают трудоемкие, рутинные задачи — от обработки страховых предложений до проверки информации учетной записи пользователя. Это преобразование создает потребность в технологической платформе для повышения производительности за счет интеллектуальных автоматизированных рабочих процессов и интеграции данных.Однако только 25% ИТ-руководителей заявляют, что их нынешние технологии максимизируют продуктивность сотрудников. В результате организации все чаще обращаются к новым технологиям автоматизации рабочих процессов, чтобы помочь сотрудникам стать более продуктивными и выполнять свою работу наилучшим образом.
«В сегодняшних условиях каждая организация сталкивается с необходимостью автоматизации сложных процессов и высвобождения времени сотрудников, чтобы они могли сосредоточиться на успехе клиентов», — сказала Сара Франклин, исполнительный вице-президент и генеральный директор по платформам, Trailhead и AppExchange в Salesforce.«С Einstein Automate каждый может изменить скорость работы и повысить производительность за счет интеллектуальной автоматизации рабочего процесса».
«Наша конечная цель — ускорить цифровую трансформацию наших клиентов, чтобы они могли лучше управлять энергоэффективностью и способствовать глобальному энергетическому переходу к углеродной нейтральности», — сказал Марк Лаллеманд, ИТ-директор Engie Belgium. «Используя готовые ресурсы и библиотеки передовых практик Salesforce, мы значительно сократили время, необходимое для перехода на цифровые технологии, что позволяет улучшить качество обслуживания клиентов, поскольку мы можем легко автоматизировать задачи, используя отраслевые рабочие процессы.”
Автоматизируйте что угодно, чтобы быть более продуктивным
Новый Flow Orchestrator — это инструмент разработки рабочих процессов с низким кодом, который позволяет пользователям составлять рабочие процессы, автоматизирующие сложные многопользовательские процессы и утверждения. Flow Orchestrator ускоряет проекты и процессы с помощью следующих шагов и рекомендаций, созданных искусственным интеллектом, которые подсказывают пользователям все процессы и быстро выявляют узкие места, вызывающие задержки. Например, процесс утверждения ипотеки, который является сложным и требует обширной документации и проверки, может быть преобразован в автоматизированный рабочий процесс, который помогает обрабатывать заявки беспрепятственно и без задержек.
Flow Orchestrator отображает все этапы рабочего процесса обработки ипотечного кредита, чтобы направлять сотрудников и экономить время.
Интегрируйте все быстрее с помощью кликов, а не код
Новый MuleSoft Composer для Salesforce — это самый быстрый и простой способ подключить разрозненные приложения и данные к Salesforce и получить 360-градусное представление о клиенте без разработки нового кода. Разблокировка и подключение данных между приложениями и системами — одна из самых серьезных проблем, с которыми сталкиваются предприятия.Новый отчет MuleSoft «Состояние бизнеса и ИТ-инновации» показывает, что более 80% бизнес-сотрудников хотят иметь легкий доступ к данным и ИТ-возможностям, чтобы работать продуктивно по мере роста числа цифровых проектов. MuleSoft Composer для Salesforce позволяет администраторам и другим бизнес-пользователям работать быстрее с библиотекой готовых коннекторов и шаблонов для легкой автоматизации интеграции. Например, администраторы Salesforce могут быстро и легко подключить системы планирования ресурсов предприятия (ERP) и обработки платежей своей организации к Sales Cloud, чтобы автоматизировать процесс преобразования цены в наличные, оптимизировать операции продаж и повысить продуктивность продавцов.
Автоматический ввод данных из разнородных приложений прямо в консоль администратора Salesforce с помощью MuleSoft Composer для Salesforce
Быстро трансформируйте любую отрасль с помощью готовых решений
Компании могут найти более 700 решений автоматизации, созданных Salesforce и нашими партнерами на новой странице сбора данных Einstein Automate на Salesforce AppExchange, например решения для автоматизации роботизированных процессов (RPA), боты Einstein, шаблоны потоков, действия и компоненты, коннекторы MuleSoft, Библиотеки процессов, партнерские решения и многое другое.Организации могут внедрять готовые решения для быстрой автоматизации процессов, а не создавать их с нуля.
На странице Einstein Automate AppExchange представлены соответствующие решения для автоматизации и готовые ресурсы.
Помимо готовых решений на AppExchange, компании могут использовать новые доступные продукты и функции в OmniStudio. OmniStudio позволяет предприятиям быстро доставлять своим клиентам цифровые и отраслевые возможности с использованием нескольких устройств и каналов и в любом масштабе.В OmniStudio входит набор ресурсов и инструментов без кода, в том числе готовые управляемые интерфейсы, шаблоны и многое другое, что позволяет пользователям быстро и легко развертывать цифровые возможности, такие как лицензирование и разрешение приложений.
Проведите пользователей через процессы продаж и обслуживания с помощью быстрых, персонализированных ответов и бесшовной интеграции с корпоративными приложениями и данными
Дополнительная информация
- Узнайте больше о том, как Einstein Automate повышает производительность и оптимизирует процессы здесь.
- Узнайте больше о том, как MuleSoft Composer для Salesforce быстро и легко подключает приложения и данные к Salesforce с помощью щелчков, а не кода, и все это внутри пользовательского интерфейса Salesforce, здесь.
- Узнайте больше о партнерских решениях и готовых ресурсах, доступных в Salesforce AppExchange, здесь.
- Узнайте больше о том, почему Salesforce вкладывает еще больше средств в автоматизацию.
- Узнайте больше о том, как платформа Salesforce позволяет организациям быстро внедрять инновации, уверенно масштабироваться и расширять возможности каждого для достижения успеха здесь.
- Ознакомьтесь с выводами из отчета «Состояние бизнеса и ИТ-инновации» о том, как демократизация доступа к данным в организациях помогает масштабировать инновации здесь.
Цены и доступность
- Flow Orchestrator ожидается в стадии бета-тестирования летом 2021 года.
- MuleSoft Composer для Salesforce станет общедоступным в начале 2021 года.
- Все решения AppExchange и OmniStudio доступны сегодня.
О платформе Salesforce
Платформа Salesforce позволяет организациям быстро внедрять инновации, уверенно масштабироваться и расширять возможности каждого сотрудника компании для достижения успеха.Благодаря встроенным сервисам, таким как интегрированная безопасность и искусственный интеллект, которые не охватывают код для кода, платформа Salesforce предоставляет все строительные блоки для создания невероятного опыта работы с клиентами и сотрудниками.
О Salesforce
Salesforce, мировой лидер в области CRM, дает возможность компаниям любого размера и отрасли осуществлять цифровую трансформацию и создавать 360-градусное представление о своих клиентах. Для получения дополнительной информации о Salesforce (NYSE: CRM) посетите: www.salesforce.com.
Любые невыпущенные услуги или функции, упомянутые в этом или других пресс-релизах или публичных заявлениях, в настоящее время недоступны и не могут быть предоставлены вовремя или вообще.Клиенты, приобретающие приложения Salesforce, должны принимать решения о покупке на основе доступных в настоящее время функций. Штаб-квартира Salesforce находится в Сан-Франциско, с офисами в Европе и Азии, и торгуется на Нью-Йоркской фондовой бирже под тикером «CRM». Для получения дополнительной информации посетите https://www.salesforce.com или позвоните по телефону 1-800-NO-SOFTWARE.
Пользовательские задачи с граблями на IBM Aspera Faspex (IBM Aspera High-Speed Sharing Server)
Вопрос
Пользовательские задачи с граблями на IBM Aspera Faspex
Ответ
Задачи Rake — это сценарии, которые позволяют получать информацию об удалении или обновлении на вашем сервере IBM Aspera Faspex с помощью командной строки.Запуск с командой конфигурации asctl rake tasks могут выполнять действия с учетными записями пользователей, пакетами и рабочими группами на индивидуальном или массовом уровне.
Многие задачи с граблями уже доступны как часть вашей установки IBM Aspera Faspex и задокументированы в руководстве Faspex. В этой статье подробно описаны пользовательские задачи с граблями, которые еще не являются частью продукта Faspex, но которые вы можете добавить в свою установку Faspex для дополнительной функциональности. Вам нужно будет загрузить прикрепленный файл и следовать инструкциям по установке, чтобы использовать эти пользовательские задачи с граблями.Обратите внимание, что в будущем эти пользовательские задачи рейка могут быть интегрированы в Faspex по умолчанию.
Если вам нужна дополнительная помощь в установке или использовании этих пользовательских задач грабли, обратитесь в службу поддержки.
1. Загрузите файл custom.rake.txt , прикрепленный в конце статьи.
2. Скопируйте файл как custom.rake — удалите суффикс (*) _. Txt — в следующий каталог в зависимости от вашей системы:
- Linux: / opt / aspera / faspex / lib / tasks
- Windows: C: \ Program Files (x86) \ Aspera \ Faspex \ lib \ tasks
Общий синтаксис для задач Faspex rake следующий:
asctl faspex: rake <ЗАДАЧА ГРАБЛИ> - <ОПЦИИ>
Задача граблей и параметры, которые она принимает, разделены знаком — (двойной -).Например, в следующей команде задача rake — custom: force_password_reset , а указанный параметр — -u со значением username :
asctl faspex: rake custom: force_password_reset - -u имя пользователя
Большинство задач с граблями могут иметь варианты либо в сокращенной, либо в полной форме. Краткая форма параметра состоит только из одного тире и буквы (например, -u ), за которой сразу следует значение без пробела (например, -u janedoe ).Полная форма состоит из двойного тире и имени параметра, за которым следует знак равенства и значение. Например, для -u janedoe эквивалентной длинной формы будет —user_name = janedoe . Вы можете использовать комбинацию опций полной и краткой формы в командах задачи rake.
Чтобы получить дополнительную информацию о задаче rake и параметрах, которые она принимает, запустите команду rake task и добавьте —help в конце вместо любых параметров. Например, чтобы узнать больше о задаче force_password_reset rake, вы должны запустить следующее:
asctl faspex: rake custom: force_password_reset - --help
Чтобы просмотреть все доступные для использования пользовательские задачи с граблями, выполните следующую команду:
asctl faspex: rake custom: help
Вы также можете найти документацию по доступным рейк-задачам с примерами по следующим ссылкам в зависимости от типа рейк-задачи:
Аудиторский отчет рейк задач
Рейк-задачи управления пользователями
Пакетное управление граблями задач
[{«Вид деятельности»: {«код»: «LOB36», «ярлык»: «IBM Automation»}, «Бизнес-подразделение»: {«код»: «BU053», «ярлык»: «Облачная платформа и платформа данных «},» Продукт «: {» код «:» SSGPEF «,» ярлык «:» IBM Aspera Faspex «},» Категория ARM «: [{» код «:» a8m0z0000000AsdAAE «,» ярлык «:» Faspex «} ], «Номер дела ARM»: «», «Платформа»: [{«код»: «PF025», «ярлык»: «Независимость от платформы»}], «Версия»: «Все версии»}]
% PDF-1.6
%
2294 0 объект>
эндобдж
xref
2294 85
0000000016 00000 н.
0000002410 00000 н.
0000002545 00000 н.
0000002694 00000 н.
0000002739 00000 н.
0000002863 00000 н.
0000005639 00000 п.
0000005780 00000 н.
0000005922 00000 н.
0000006061 00000 п.
0000006201 00000 н.
0000006349 00000 п.
0000006491 00000 н.
0000008420 00000 н.
0000010173 00000 п.
0000011921 00000 п.
0000012063 00000 п.
0000013815 00000 п.
0000015627 00000 п.
0000017199 00000 п.
0000018878 00000 п.
0000020611 00000 п.
0000020633 00000 п.
0000020684 00000 п.
0000020744 00000 п.
0000021553 00000 п.
0000021576 00000 п.
0000021599 00000 н.
0000022148 00000 п.
0000022214 00000 п.
0000022237 00000 п.
0000024319 00000 п.
0000024518 00000 п.
0000025570 00000 п.
0000025593 00000 п.
0000026856 00000 п.
0000026999 00000 н.
0000027059 00000 п.
0000027110 00000 п.
0000029322 00000 н.
0000029347 00000 п.
0000703956 00000 н.
0000703979 00000 п.
0000707829 00000 н.
0000708026 00000 н.
0000709084 00000 н.
0000709107 00000 п.
0000710370 00000 н.
0000710393 00000 п.
0000712297 00000 н.
0000712494 00000 н.
0000713531 00000 н.
0000713554 00000 н.
0000714817 00000 н.
0000714840 00000 н.
0000715952 00000 н.
0000716150 00000 н.
0000717183 00000 н.
0000717206 00000 н.
0000718469 00000 н.
0000718493 00000 п.
0000752025 00000 н.
0000752218 00000 н.
0000754009 00000 н.
0000754032 00000 н.
0000756012 00000 н.
0000756036 00000 н.
0000787975 00000 н.
0000788170 00000 н.
0000789964 00000 н.
0000789987 00000 н.
0000791967 00000 н.
0000791989 00000 н.
0000792972 00000 н.
0000793175 00000 п.
0000794220 00000 н.
0000794243 00000 п.
0000795506 00000 н.
0000795529 00000 п.
0000799812 00000 н.
0000800009 00000 н.
0000801041 00000 н.
0000801064 00000 н.
0000802327 00000 н.
0000002045 00000 н.
трейлер
] >>
startxref
0
%% EOF
2378 0 obj> поток
Vd46PԀY «x ڲ C! 7 = Lz # + \ |] -tuVNl; DŽLBx9в5 @ Q62p {/ Yu [t &? Ch, a
ׯ A / 7ňtG
o | ktA7o5EBJ 샳 F˪Z?>
] V ا 8 ǾYv6YXy7e} u0
конечный поток
эндобдж
2295 0 объект \ roY $ EWn [ihm ⺎.

 Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?
Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?