Содержание
Ошибка 404. Страница не найдена!
Уважаемые родители будущих первоклассников!
График приема родителей c 01.04.2021г:
понедельник 14.00-17.00
среда 14.00-17.00
пятница 14.00-17.00
С 01.09.2021 года в гимназии будут открыты 4 первых класса.
Количество мест в первых классах — 112.
Прием документов начинается с 01.04.2021 г.
ИЗМЕНЕНИЯ ПОДАЧИ ЗАЯВЛЕНИЙ НА СДАЧУ ОГЭ В 2021
Дубненские выпускники 9-х классов смогут подать заявление на сдачу основного государственного экзамена (далее-ОГЭ) дистанционно. Подробнее>>
Уважаемые учащиеся и родители!
Уважаемые родители!
В соответствии с Приказом Министерства просвещения Российской Федерации от 02.09.2020 № 458 «Об утверждении Порядка приема на обучение по образовательным программам начального общего, основного общего и среднего общего образования» информируем Вас об изменении сроков приема заявлений в первый класс на 2021-2022 учебный год.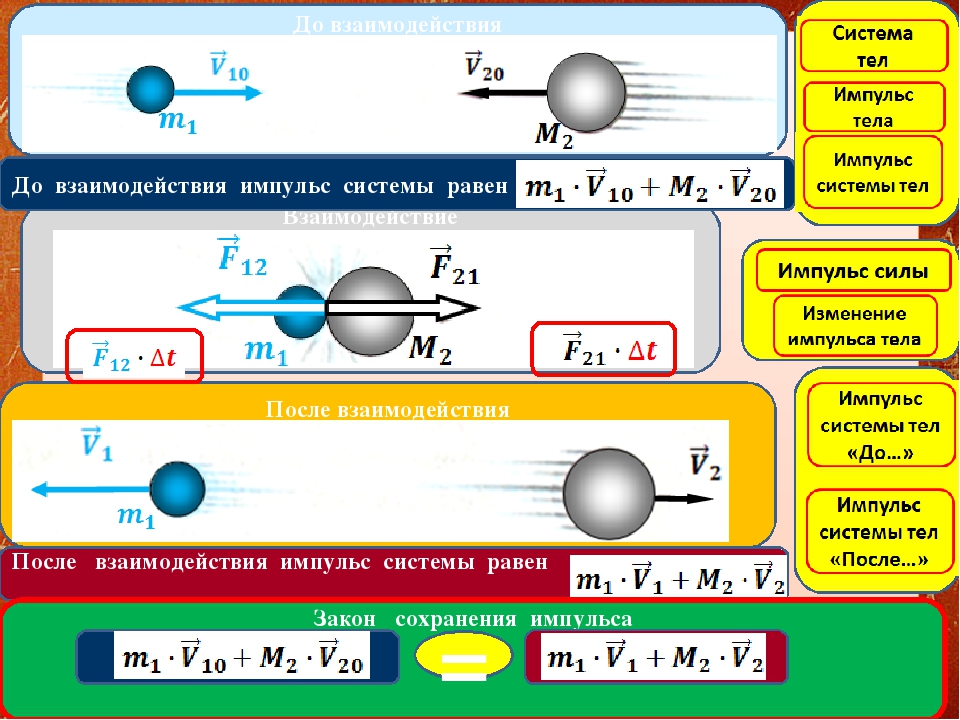
Уважаемые родители!
Информируем вас о том, что записаться на «Родительский контроль» — проект по оценке качества питания в школах — в Подмосковье теперь можно в режиме онлайн. Сделать это можно на Школьном портале региона. Регистрация проходит быстро — вся процедура займет не более трех минут.
— Нужно перейти во вкладку «Родительская»;
— Перейти в раздел «Школьное питание»;
— Выбрать желаемую дату и время;
— Нажать кнопку «Записаться».
Школа автоматически получит заявку и в назначенное время родителя будет ожидать классный руководитель или ответственный за питание.
Проект «Билет в будущее»
Билет в будущее» — это проект ранней профессиональной ориентации школьников 6−11 классов.
Кампания проекта проходит с июля по ноябрь 2020 года. Родителю и ребенку нужно пройти регистрацию на Платформе проекта по адресу https://bilet.worldskills.ru/, у каждого будет свой личный кабинет, в котором будут отражаться результаты участия.
Инструкция для регистрации .pdf
Подготовка к егэ
Приказ №164 от 29.05.2020г. «Об организации подготовки к ЕГЭ в режиме онлайн в 2020г».pdf
График консультаций ЕГЭ в режиме онлайн. pdf
Приказ №166 от 29.05.2020 «О внесении изменений в приказ №142 от 29.04.2020 «Об организации сотрудников гимназии №11 с 01.06.2020 по 14.06.2020г.» .pdf
внимание
Приказ №151а от 12.05.2020 «О внесении изменений в приказ №142 от 29.04.2020 «Об организации сотрудников гимназии №11 с 06.04.2020 по 31.05.2020» .pdf
Приказ №142 от 29.04.2020 «О внесении изменений в приказ №136 от 06.04.2020 «Об организации сотрудников гимназии №11 с 06. 04.2020 по 30.04.2020» .pdf
04.2020 по 30.04.2020» .pdf
Северное инспекторское отделение Центра ГИМС ГУ МЧС России по Московской области информирует
Сейчас на территории Подмосковья действует режим самоизоляции и покидать дома без острой необходимости запрещается, а прогулки у воды без присмотра взрослых могут стоить жизни. К сожалению, не все родители объясняют своим детям, что же означает этот режим, и к каким последствиям могут привести прогулки.
Самоизоляция – это комплекс ограничительных мер для населения, которые вводит правительство на определенный срок для борьбы с распространением опасного заболевания.
Граждан просят соблюдать режим: не выходить на улицу без острой необходимости, ограничить контакты с другими людьми и соблюдать все рекомендации по профилактике вирусных заболеваний, предложенные медицинским сообществом.
Уважаемые родители и дети просим Вас не пользоваться береговой зоной водоемов и не нарушать режим самоизоляции.
Берегите себя и своих близких!!!
Приказ №136 от 06. 04.2020 «Об организации работы сотрудников гимназии №11 с 06.04.2020г. по 30.04.2020г » .pdf
04.2020 «Об организации работы сотрудников гимназии №11 с 06.04.2020г. по 30.04.2020г » .pdf
Приказ №134 от 03.04.2020 «О переходе на обучение с использованием электронного обучения и дистанционных образовательных программ» .pdf
Регламент организации дистанционного обучения в Гимназии №11
Дорогие участники образовательного процесса, учащиеся, учителя, родители! Познакомьтесь с регламентом организации дистанционного обучения .pdf
Изменения в Постановлении Губернатора Московской области
Уважаемые родители и ученики! Согласно постановлению Губернатора Московской области №171-ПГ от 02.04.2020 образовательный процесс в Гимназии №11 с 06.04.2020 по 30.04.2020 будет осуществляться с использованием электронного обучения и дистанционных образовательных технологий .pdf
О режиме повышенной готовности в гимназии №11
20 марта на сайте гимназии опубликован приказ №122 » О введении режима повышенной готовности в гимназии №11″ . pdf
pdf
меры профилактики гриппа и ОРВИ
Уважаемые родители!
Ежегодно в конце зимы и начале весны увеличивается число заболевших гриппом и ОРВИ. Давайте отнесемся к здоровью наших детей в этот период с особым вниманием. Узнать более подробно о мерах профилактики данных заболеваний:
https://www.rospotrebnadzor.ru/about/info/news_time/news_details.php?ELEMENT_ID=13566
УВАЖАЕМЫЕ РОДИТЕЛИ! ПРИМИТЕ УЧАСТИЕ В ОПРОСЕ
Родителям будущих первоклассников!
График приема родителей: (приказ.pdf)
1 февраля 2020г. — с 09.00 до 17.00 (обед 13.00-14.00)
2 февраля 2020г. — с 09.00 до 17.00 (обед 13.00-14.00)
с 03.02.2020 — 30.06.2020г. с с 09.00 до 18.00 (обед 13.00-14.00) с понедельника по пятницу
С 1 февраля 2020 года начинается прием заявлений от родителей (законных представителей) на зачисление детей в 1 класс 2020 – 2021 учебного года в электронном виде для граждан, проживающих на закрепленной территории, посредством Портала государственных и муниципальных услуг Московской области https://uslugi. mosreg.ru/.
mosreg.ru/.
Подробнее по ссылке>>
Учитель шахмат
Департамент государственной политики в сфере общего образования Министерства Просвещения РФ информирует о проведении конкурса «Учитель шахмат», организатором которого является Общероссийская общественная организация «Федерация шахмат России». Заявки на участие в конкурсе принимаются до 15 апреля 2019 года.
Показать/скрыть
Форму заявки можно скачать по ссылке. Конкурсные материалы принимаются с 16 апреля до 30 июня 2019 года. Форму для прикрепления конкурсных материалов можно скачать здесь. Контактное лицо: руководитель проекта «Шахматный всеобуч России» Костьев Александр Николаевич, тел. 8(968)732-00-74, адрес электронной почты: [email protected].
Урок мужества
1 марта 2019 г. во всех классах школы пройдет Урок мужества. В этот день будет проходить торжественная церемония награждения детей-лауреатов Всероссийской общественной инициативы «Горячее сердце».
Показать/скрыть
Целью такого урока является формирование у школьников готовности к общественной полезной деятельности, преодолению сложных ситуаций в семье или ограничений здоровья.
Лауреатами «Горячего сердца» являются дети, которые спасли людей при пожарах, помогли оказавшимся в беде или в сложной ситуации, участвовали в борьбе с распространением наркотиков, а также добились успеха в различных видах деятельности, несмотря на ограничения здоровья.
Методические рекомендации
Ребята и их родители!
Приглашаем вас принять участие в увлекательных конкурсах! Зарегистрируйтесь на сайте https://www.prav-pit.ru/, если есть вопросы, обращайтесь за помощью к координатору конкурса в гимназии №11социальному педагогу Волковой Елене Ивановне.
01.11.2018 – 15.06.2019
Конкурс семейной фотографии. Участники конкурса должны подготовить семейный фотоплакат, демонстрирующий важность здорового образа жизни.
15.10.2018 – 30.08.2019
Фотоконкурс “Воспитываем здоровых и счастливых”. Участвуйте конкурсе и размещайте свои фотографии, рассказывающие о том, как в вашей семье воспитывают здоровых и счастливых!
Авторы фотографий, за которых проголосует больше всего посетителей сайта, получат главный приз — 3 дневную экскурсионную поездку в Москву.
ЕСИА Условия успешной авторизации на Школьном портале через ЕСИА (только для пользователей старше 14 лет)
1.Наличие Подтверждённой учётной записиЕСИА (подробно о том, как и где подтвердить учётную запись ЕСИА, рассказано здесь)
2.Наличие учётной записи в системе «Школьный портал»
3.Совпадение ФИО и СНИЛС в учётных записях ЕСИА и системы «Школьный портал»
ВНИМАНИЕ! В случае отсутствия СНИЛС в учетной записи необходимо выполнить связывание своих учетных записей вручную. Как это сделать: https://helpschool.mosreg.ru/hc/ru/articles/360001467547
Уважаемые родители!
Информацию о приеме в кружки и секции дополнительного образования на 2018/2019 уч.г. можно посмотреть в разделе Родителям
Уважаемые учащиеся!
Предлагаем вам ознакомиться с материалами и принять участие в VIII Всероссийском конкурсе социальной рекламы «Новый взгляд». Подробнее…
Уважаемые учащиеся и родители!
Министерство здравоохранения Московской области в рамках подготовки к Всемирному Дню сердца предлагает ознакомиться с видео-роликом о первых признаках инсульта «УДАР», а также на сайте службы медицинской профилактики Московской области пройти анкетирование и ознакомиться с полезной информацией о факторах риска развития инсульта.
Решение задач по физике на законы сохранения им пульса и энергии
Автор: Горбушин Николай Николаевич
Решение задач на законы сохранения импульса и механической энергии (10 класс).
Выполнил
Горбушин Николай Николаевич
Идентификатор:300 339 209
Разминка
. Два тела движутся по взаимно перпендикулярным пересекающимся прямым, как показано на рисунке.
Модуль импульса первого тела равен , а второго тела равен . Чему равен модуль импульса системы этих тел после их абсолютно неупругого удара?
1) 2) 3) 4)
Если при увеличении модуля скорости материальной точки величина ее импульса увеличилась в 4 раза, то при этом кинетическая энергия
1) увеличилась в 2 раза
2) увеличилась в 4 раза
3) увеличилась в 16 раз
4) уменьшилась в 4 раза
Танк движется со скоростью , а грузовик со скоростью .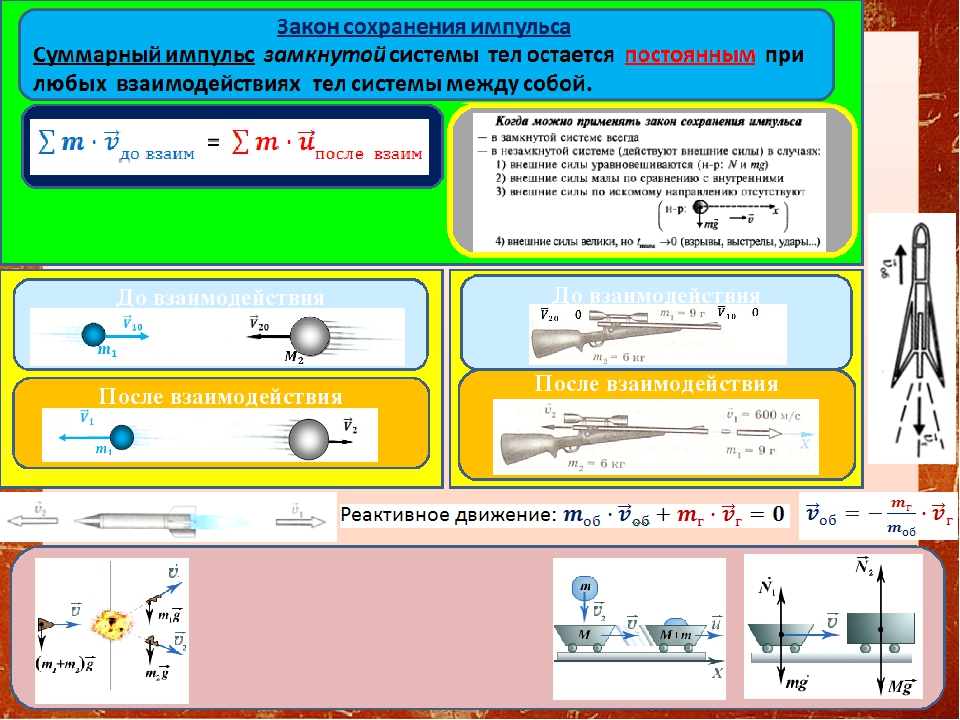 Масса танка . Отношение величины импульса танка к величине импульса грузовика равно 2,25. Масса грузовика равна
Масса танка . Отношение величины импульса танка к величине импульса грузовика равно 2,25. Масса грузовика равна
1) 1 500 кг
2) 3 000 кг
3) 4 000 кг
4) 8 000 кг
Гладкая лёгкая горка массой M с двумя вершинами высотой h и 4h, покоится на гладкой горизонтальной поверхности стола (см. рис.). На правой вершине горки лежит массивная шайба массой m. От незначительного толчка шайба начинает соскальзывать с горки в лево. Чему будет равна скорость шайбы, когда она окажется на левой вершине горки? При движении тел шайба не отрывается от горки, а горка — от стола.
Используя какие законы физики эту задачу можно решить?
В этой задаче рассматривается неравномерное криволинейное движение тела, причём равнодействующая приложенных к телу сил изменяется со временем: действующая, например, на монету сила тяжести остаётся постоянной, а вот сила нормальной реакции со стороны горки изменяется и по модулю, и по направлению. Исследовать такие сложные движения с помощью законов Ньюто на в рамках школьного курса физики не удаётся. Поэтому единственный способ решать такие задачи – это использовать законы сохранения механической энергии и импульса.
Исследовать такие сложные движения с помощью законов Ньюто на в рамках школьного курса физики не удаётся. Поэтому единственный способ решать такие задачи – это использовать законы сохранения механической энергии и импульса.
Но их можно использовать только в замкнутой системе. Система тел горка–шайба НЕ ЗАМКНУТА: шайба взаимодействует с Землёй, а горка – не только с Землёй, но и со столом.
Как быть?
Абсолютно замкнутых систем тел в природе вообще не существует. Закон сохранения механической энергии можно применять, во-первых, тогда, когда внешними силами, то есть силами взаимодействия тел данной системы с другими телами, можно пренебречь по сравнению с внутренними силами, то есть силами, действующими между телами самой системы. А в нашем случае тел на самом деле не два, а три, потому что в систему взаимодействующих тел входит ещё и Земля. В нашей задаче главными «действующими лицами» являются горка, шайба и Земля. Действия других, «внешних», тел мы считаем пренебрежимо малыми. Во вторых важно, чтобы среди внутренних сил системы не было силы трения. Вследствие трения механическая энергия уменьшается, превращаясь во внутреннюю энергию: тела нагреваются. Слова гладкая горка и гладкий стол подразумевают, что трением можно пренебречь.
Во вторых важно, чтобы среди внутренних сил системы не было силы трения. Вследствие трения механическая энергия уменьшается, превращаясь во внутреннюю энергию: тела нагреваются. Слова гладкая горка и гладкий стол подразумевают, что трением можно пренебречь.
Внешние силы, действующие на горку и шайбу, – это сила тяжести и сила нормальной реакции со стороны стола. Но обе эти силы направлены вертикально. По этому горизонтальная проекция каждой из них равна нулю. А это означает, что они не могут изменить горизонтальную проекцию суммарного импульса нашей системы горка–шайба.
Следовательно при решении этой задачи мы можем использовать эти законы.
Идея решения
В начальном состоянии шайба и горка покоятся: их скорости, v и V соответственно, равны нулю. Поэтому равен нулю и импульс каждого из этих тел. Следовательно, равна нулю и проекция p1x их суммарного импульса на ось x.
Когда шайба находится на левой вершине, её скорость направлена влево, поэтому проекция её импульса на ось x отрицательна. Но проекция суммарного импульса системы горка-шайба на ось x по-прежнему остаётся равной нулю. Это означает, что проекция импульса горки на ось x положительна, то есть горка движется, причём вправо.
Но проекция суммарного импульса системы горка-шайба на ось x по-прежнему остаётся равной нулю. Это означает, что проекция импульса горки на ось x положительна, то есть горка движется, причём вправо.
Используя законы сохранения энергии и импульса, получим систему двух уравнений с двумя неизвестными — это скорость горки и скорость шайбы в конечном состоянии (когда шайба находится на левой вершине). Из этой системы уравнений найдём конечную скорость шайбы.
План решения
1. Запишем закон сохранения импульса для системы горка–шайба.
2. Запишем закон сохранения механической энергии для данной системы.
3. Из полученной системы уравнений найдём скорость шайбы.
Подробное решение
1. Как использовать закон сохранения импульса?
Проекция суммарного импульса системы горка–шайба на ось x сохраняется, то есть остаётся равной нулю. mvx + MVx=0
Выведем соотношение для модулей скорости шайбы и горки с учётом выбранного направления оси x.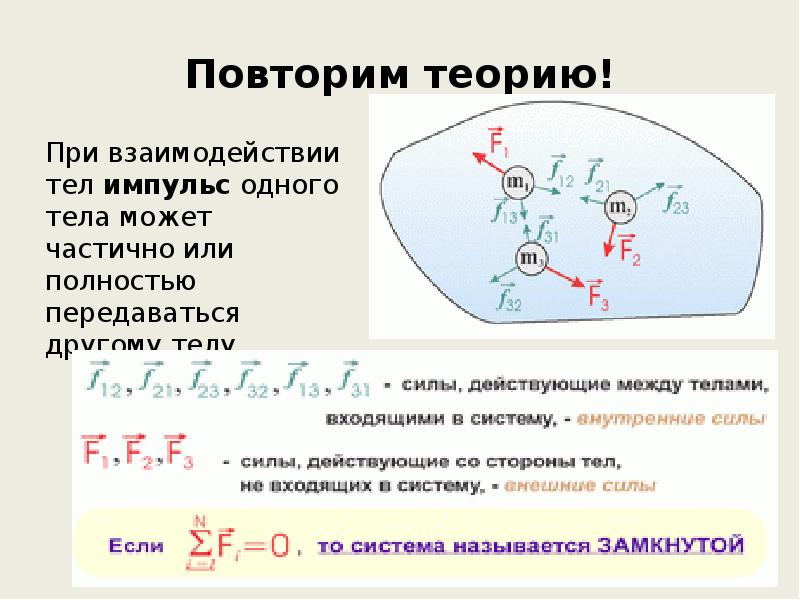
2. Как использовать закон сохранения энергии?
В начальном состоянии суммарная кинетическая энергия Ek1 системы равна нулю: горка и шайба покоятся. Потенциальная энергия системы Ep1 в начальном состоянии определяется массой шайбы и высотой, на которой находится шайба. Полная механическая энергии системы равна сумме кинетической и потенциальной энергии.
Запишем выражение для суммарной кинетической энергии Ek2 системы в конечном состоянии: оба тела — горка и шайба — движутся (в противоположные стороны) , поэтому каждое из них обладает кинетической энергией.
Запишем выражение для потенциальной энергии Ep2 системы. Запишем выражение для полной механической энергии E2 системы в конечном состоянии.
Согласно закону сохранения энергии
:
3. Как составить и решить систему уравнений?
Из второго уравнения:
Подставим в первое уравнение и получим:
Ответ
Задачи для самостоятельного решения
1. В системе, изображенной на рисунке, масса левого груза, лежащего на гладкой горизонтальной плоскости, равна m = 3 кг. Масса правого груза, скользящего по плоскости с некоторой скоростью V, равна M = 6 кг. Грузы соединены неупругим невесомым ненатянутым вначале шнуром, таким, что после его натяжения скорости грузов выравниваются. Сколько процентов начальной кинетической энергии системы будет потеряно во время выравнивания скоростей тел?
В системе, изображенной на рисунке, масса левого груза, лежащего на гладкой горизонтальной плоскости, равна m = 3 кг. Масса правого груза, скользящего по плоскости с некоторой скоростью V, равна M = 6 кг. Грузы соединены неупругим невесомым ненатянутым вначале шнуром, таким, что после его натяжения скорости грузов выравниваются. Сколько процентов начальной кинетической энергии системы будет потеряно во время выравнивания скоростей тел?
Решение.
В горизонтальном направлении система тел не подвергается действию внешних сил, и по закону сохранения импульса суммарная горизонтальная проекция импульса тел системы сохраняется: MV = (m+M)v, где v – скорость системы после выравнивания скоростей тел в результате их неупругого взаимодействия через шнур.
Начальная кинетическая энергия системы равна
Потери ΔEк кинетической энергии системы в процессе выравнивания скоростей тел равны разности кинетических энергий тел системы до и после их взаимодействия:
Таким образом, во время выравнивания скоростей тел будет потеряно
начальной кинетической энергии системы.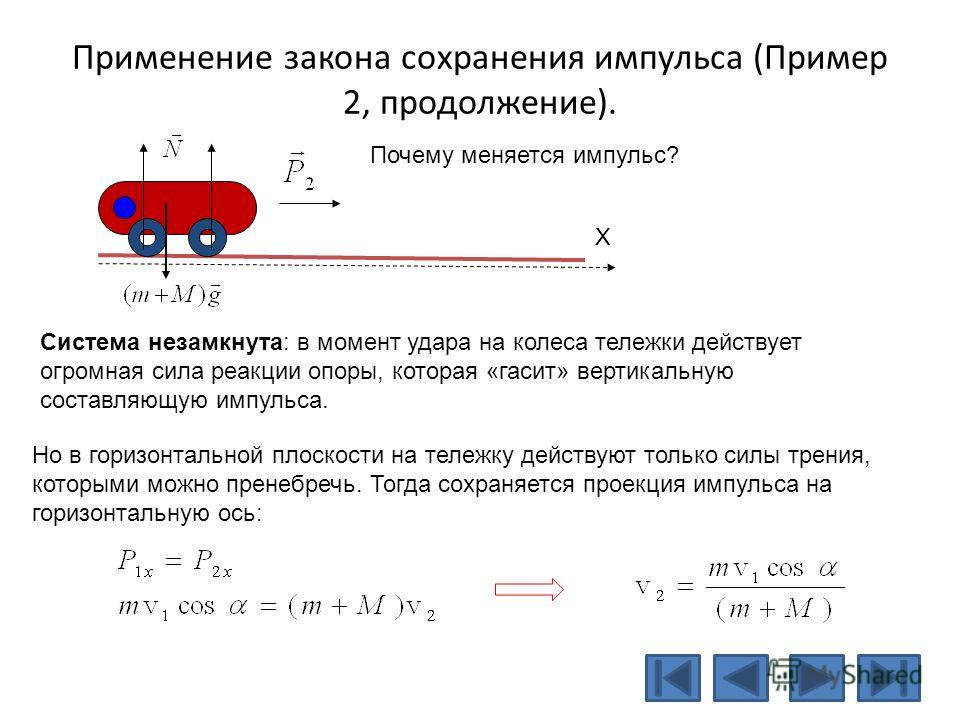
Ответ:
2. Снаряд массой 4 кг, летящий со скоростью 400 м/с, разрывается на две равные части, одна из которых летит в направлении движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличилась на величину . Скорость осколка, летящего по направлению движения снаряда, равна 900 м/с. Найдите .
Решение.
Введем обозначения: — масса снаряда до взрыва; — модуль скорости снаряда до взрыва; — модуль скорости осколка, летящего вперед; — модуль скорости осколка, летящего назад.
Система уравнений для решения задачи:
Выразим из первого уравнения: и подставим во второе уравнение. Получим:
.
Отсюда следует:
Ответ:
3.Снаряд, движущийся со скоростью , разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна . Найдите массу m осколка.
В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна . Найдите массу m осколка.
Решение.
Для системы выполняются законы сохранения импульса и энергии (не механической энергии, а просто энергии, так как в данном случае внутренняя энергия взрывчатого вещества переходит в кинетическую энергию осколков):
Здесь — скорость второго осколка после взрыва. Решая систему из двух уравнений, для массы осколка получаем
Ответ:
comments powered by HyperComments
Импульс. Закон сохранения импульса — Электронный учебник по законам сохранения
Задача 1
Вдоль оси Ох движется тело массой m=1 кг со скоростью V0= 2 м/с. Вдоль направления движения действует сила F = 4 Н в течение некоторого времени t = 2 с. Определите скорость тела после окончания действия этой силы.
Вдоль направления движения действует сила F = 4 Н в течение некоторого времени t = 2 с. Определите скорость тела после окончания действия этой силы.
Для решения этой задачи в первую очередь важно вспомнить о том, что такое импульс, импульс тела .
Рис. 1. Выбор системы отсчета
Вспоминая, что импульс силы – это изменение импульса тела, запишем следующее выражение: .
Теперь уравнение согласуем с выбранной системой отсчета. Сила F при проекции на ось Х будет с положительным знаком, а значит: .
Затем, преобразовав это уравнение, выделив из него ту скорость, которую нужно определить, запишем следующее выражение: .
Ответ: 10 м/с.
Задача 2
Тележка с человеком на ней движется вдоль прямой со скоростью 2 м/с. Человек спрыгивает с тележки в горизонтальном направлении, противоположном направлению движения тележки, со скоростью 1 м/с. Определите скорость тележки после того, как с нее спрыгнул человек. Масса человека в 1,5 раза больше, чем масса тележки.
Рис. 2. Проекции импульса тел на ось Х
В первом случае, обратите внимание, и тележка, и человек едут вместе, значит, скорость у них одинакова, мы можем записать для данной системы отсчета, связанной с осью Ох, следующее выражение: .
Затем, когда человек спрыгивает с тележки, импульс этих двух тел можно записать следующим образом: .
Знак минус показывает, что скорость человека направлена в противоположную сторону, а скорость тележки со знаком плюс будет направлена в ту же сторону, что и первоначальная скорость, т.е. вдоль оси Ох.
Записав эти выражения для начального состояния и состояния после взаимодействия, воспользуемся законом сохранения импульса.
По закону сохранения импульса импульс в первом случае будет равен импульсу во втором случае: Р0х = Рх..
Записав это соотношение, переписываем, раскрываем скобки выражений: (m1+m2).V1=-m2.V2+m1.V¢1.
Скорость V¢1 и нужно определить. Выразим массу человека через массу тележки, но так, чтобы масса была выражена в одних единицах: (m1+1,5 m1). V1=-1,5m1.V2+m1.V¢1.
V1=-1,5m1.V2+m1.V¢1.
Массу m1 мы можем вынести за скобку и сократить: 2,5 m1.V1=-1,5 m1.V2+m1.V¢1. Когда подставляем значения для скоростей, получаем ответ: .
м
Эта задача хорошо иллюстрирует реактивное движение. Человек, который спрыгнул с тележки в противоположную сторону, увеличил скорость самой тележки. Не правда ли, это хорошо сочетается с тем, как из ракеты вырываются с некоторой скоростью газы и придают дополнительную скорость оболочке, т.е. самой ракете.
Задача 3
Шарик массой m1=1 кг. скользит по идеально гладкой поверхности со скоростью v1=4 м/с и абсолютно упруго сталкивается с таким же по размеру шариком массой m2=3 кг. Определите скорость шариков после удара?
Определите скорость шариков после удара?
Решение:
По закону сохранения импульса при абсолютно неупругом ударе .
ОХ:
Ответ: 1 м/с
Задача 4
Мячик массой 70 г. падает на пол под углом 600 к нормали и под таким же углом отскакивает без потери скорости. Определите импульс суммарной силы, действовавшей на мячик во время удара, если его скорость равна 30 м/с.
Решение:
Покажем на рисунке изменения скорости мячика в процессе удара:
Запишем 2-й закон Ньютона
По построению определяем, что . Величина импульса суммарной силы, действовавшей на мячик во время удара, равна
Ответ:
Задача 5
Мальчик массой 40 кг, стоя на коньках кидает камень массой 1 кг со скоростью 8 м/с. под углом 600 к горизонту. Определите скорость, с которой мальчик начнет двигаться по льду в результате броска?
Решение:
На систему мальчик — камень не действуют ни какие горизонтальный силы. В инерциальной системе отчета, связанной с землей, проекция суммарного импульса системы на горизонтальную ось должны оставаться неизменной:
В инерциальной системе отчета, связанной с землей, проекция суммарного импульса системы на горизонтальную ось должны оставаться неизменной:
Скорость мальчика после броска
Ответ: 0.1 м/с
Задача 6
Два мальчика массами 40 кг. и 50 кг. неподвижно стоят на горизонтальной поверхности на роликовых коньках и держатся за концы невесомой веревки. Затем первый из них начинает тянуть веревку со скоростью 0.09 м/с. С какой скоростью относительно земли будет двигаться второй мальчик?
Решение:
Обозначим скорости, с которыми мальчики будут относительно земли, через и , тогда их в проекции на ось ОХ:
Внешние силы, действующие в системе мальчик — веревка, уравновешивают друг друга, поэтому выполняется закон сохранения импульса:
В проекции на ось ОХ:
Скорость второго мальчика относительно земли
Ответ: 0.04 м/с
Задача 7
Снаряд в верхней точке своей траектории разорвался на два осколка с массами m1=3 кг и m2=5 кг.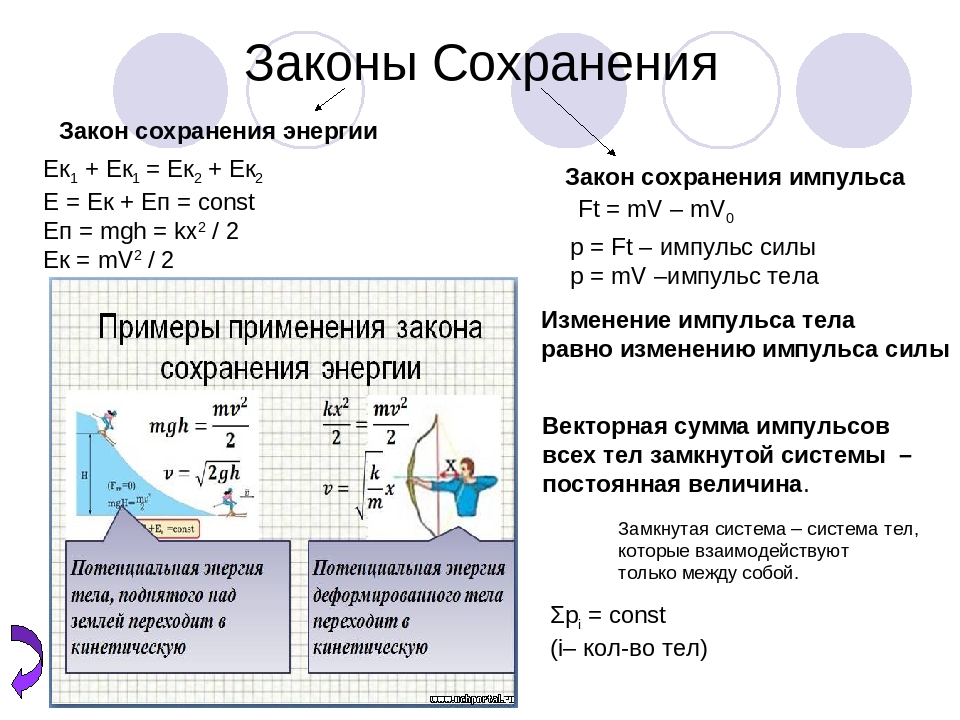 Скорость снаряда непосредственно перед разрывом равнялась v0=600 м/с, скорость большего осколка сразу после разрыва равнялась v2=800 м/с, а направление ее совпало с направлением движения снаряда перед разрывом. Определите скорость малого осколка сразу после разрыва.
Скорость снаряда непосредственно перед разрывом равнялась v0=600 м/с, скорость большего осколка сразу после разрыва равнялась v2=800 м/с, а направление ее совпало с направлением движения снаряда перед разрывом. Определите скорость малого осколка сразу после разрыва.
Решение:
Выберем за положительное направление скорости снаряда v0и запишем закон сохранения импульса.
Значит, и меньший осколок летел в том же направлении.
Ответ:
Задачи Закон сохранения энергии и импульса
Карточка «Законы сохранения энергии. Импульс тела»
1 уровень
1. Что означает буква m и v в формуле p=mv ? Запишите ответ в тетрадь
2. Найдите и выпишите формулы кинетической и потенциальной энергии. Выясните, что означает каждая буква в формуле. Запишите формулу полной механической энергии
3. Вспомните перевод единиц 1 т= 1000 кг, 1 ч=3600с , км/ч: 3,6= м/с,
2 уровень.
1. Используя правило выражения, выразите из формулы E=mgh высоту.
(пример, 10=2*5 => 5=10/2)
2. Используя формулу для нахождения импульса , решите задачу:
Найти импульс шара массой 2кг, если он движется со скоростью 5 м/с
3. Используя формулу потенциальной энергии, решите задачу:
Тело массой 50 кг подняли на высоту 0,5м . Чему равна его потенциальная энергия?
3 уровень.
1. Грузовик массой 5т может развивать скорость 90 км/ч. К грузовику цепляют тележку массой 3т. Чему равна максимальная скорость грузовика в этом случае?
2. Найти начальную скорость мяча , если после удара теннисиста он взлетел на 25м
4 уровень.
1. Вагон, массой 10т , въезжает на сортировочную горку высотой 0,5 м. При этом скорость вагона уменьшается с 14,4 км/ч до 9км/ч. Рассчитайте полную механическую энергию вагона на горке, его изменение импульса. Какое количество энергии пошло на совершение работы?
5 уровень.
1. Истребитель Су-35 массой 19т , движется со скоростью 1260 км/ч и выстреливает ракетой массой 100кг , скорость которой относительно самолета 720км/ч. Ракета покидает самолет в течении 0,2с Найти: силу отдачи ракеты, на сколько уменьшилась скорость самолета при выстреле, импульс ракеты относительно земли, ее полную энергию, если высота самолета над землей 8000м.
Карточка «Законы сохранения энергии. Импульс тела»
1 уровень
1. Что означает буква m и v в формуле p=mv ? Запишите ответ в тетрадь
2. Найдите и выпишите формулы кинетической и потенциальной энергии. Выясните, что означает каждая буква в формуле. Запишите формулу полной механической энергии
3. Вспомните перевод единиц 1 т= 1000 кг, 1 ч=3600с , км/ч: 3,6= м/с,
2 уровень.
1. Используя правило выражения, выразите из формулы E=mgh высоту.
(пример, 10=2*5 => 5=10/2)
2. Используя формулу для нахождения импульса , решите задачу:
Найти импульс шара массой 2кг, если он движется со скоростью 5 м/с
3. Используя формулу потенциальной энергии, решите задачу:
Тело массой 50 кг подняли на высоту 0,5м . Чему равна его потенциальная энергия?
3 уровень.
1. Грузовик массой 5т может развивать скорость 90 км/ч. К грузовику цепляют тележку массой 3т. Чему равна максимальная скорость грузовика в этом случае?
2. Найти начальную скорость мяча , если после удара теннисиста он взлетел на 25м
4 уровень.
1. Вагон, массой 10т , въезжает на сортировочную горку высотой 0,5 м. При этом скорость вагона уменьшается с 14,4 км/ч до 9км/ч. Рассчитайте полную механическую энергию вагона на горке, его изменение импульса. Какое количество энергии пошло на совершение работы?
5 уровень.
1. Истребитель Су-35 массой 19т , движется со скоростью 1260 км/ч и выстреливает ракетой массой 100кг , скорость которой относительно самолета 720км/ч. Ракета покидает самолет в течении 0,2с Найти: силу отдачи ракеты, на сколько уменьшилась скорость самолета при выстреле, импульс ракеты относительно земли, ее полную энергию, если высота самолета над землей 8000м.
Сохранение энергии: задачи заочной школы МФТИ
Сложные, интересные задачи, после решения которых вы будете чувствовать себя гуру закона сохранения энергии)))
Задача 1. Космический корабль (КК) движется по околоземной орбите. Чему равна работа силы земного тяготения за время половины одного оборота КК вокруг Земли?
Так как энергия корабля осталась неизменной, то и работа, равная ее изменению, равна нулю.
Задача 2. Какую работу – положительную или отрицательную – мы совершаем: 1) растягивая пружину? 2) сжимая её?
И растягивая пружину, и сжимая ее, мы сообщаем ей потенциальную энергию. Иными словами, совершаем работу. Работа в обоих случаях ненулевая, положительная. Не путайте эту работу с работой силы упругости!
Задача 3. Недеформированную пружину сжали на 1 см, совершив при этом работу 10 Дж. Какую минимальную работу нужно совершить дополнительно, чтобы сжать её ещё на 1 см?
Определим работу как изменение потенциальной энергии пружины. Тогда
Нужно определить жесткость пружины. Сделаем это, использовав первую формулу.
Тогда:
Ответ: 30 Дж.
Задача 4. В каком случае двигатель автомобиля должен совершить большую полезную работу – при разгоне автомобиля с места до скорости 10 км/ч или далее при увеличении скорости от 10 км/ч до 20 км/ч?
Аналогично решению предыдущей задачи определим работу как изменение энергии. Тогда разность меньше, чем разность :
Задача 5. У какого из грузовиков, гружёного или порожнего, больше тормозной путь при одинаковой скорости в начале торможения? Торможение производится только задними колёсами. Нагрузка равномерно распределена по всем четырём колёсам. Коэффициент трения между покрышками и дорогой одинаков для обоих грузовиков. Сопротивление воздуха не учитывать.
Так как масса груженого автомобиля больше, чем пустого, энергия такого автомобиля больше. Чтобы снизить скорость до нуля, придется произвести большее изменение энергии для груженого автомобиля, поэтому и совершенная работа будет больше. Но и “пятно контакта” у груженой машины больше. Подкрепим это формулами:
То есть ускорение не зависит от массы, следовательно, тормозной путь при одинаковой начальной скорости тоже одинаков.
Ответ: тормозные пути равны.
Задача 6. Какую полезную работу совершает двигатель автомобиля «Жигули» массой т во время разгона на первых м пути, если это расстояние автомобиль проходит, двигаясь равноускоренно, за время с? Коэффициент сопротивления движению .
Коэффициент сопротивления – такой коэффициент, который учитывает как силу трения об асфальт, так и сопротивление воздуха. Поскольку мы знаем, как работать с силой трения, то будем считать этот коэффициент коэффициентом трения (сведем все сопротивление к силе трения).
Тогда можно записать по второму закону:
Здесь – сила тяги автомобиля, она же – «полезная часть» силы трения, – сила сопротивления.
Ускорение автомобиля найдем как
Можно было и так:
Конечная скорость равна
Работа, совершенная двигателем, равна кинетической энергии автомобиля плюс работа против силы сопротивления:
Результат будет тот же.
Ответ: 195 кДж.
Задача 7. Какую полезную мощность развивает автомобиль из предыдущей задачи в конце 10-й секунды своего движения?
Мгновенную мощность в конце 10-ой секунды вычислим по формуле
Здесь – скорость в конце 10 секунды.
Ответ: 39 кВт.
Задача 8. Шарик для игры в настольный теннис радиусом мм и массой г погружён в воду на глубину см. Когда шарик отпустили, он выпрыгнул из воды на высоту см. Сколько энергии перешло в теплоту вследствие трения шарика о воду? Сопротивлением воздуха пренебречь. Считать, что количество энергии, перешедшей в теплоту, равно работе силы сопротивления воды, взятой с противоположным знаком: .
Сначала шарик находился в покое. В момент достижения им максимальной высоты подъема он снова неподвижен, но уже на другой высоте относительно первоначальной точки. То есть потенциальная энергия шарика изменилась, а кинетическая – нет. Изменение кинетической энергии – сумма работ, совершенных всеми силами. В воде на шарик действует сила Архимеда, сила тяжести и сила сопротивления воды. В воздухе – только сила тяжести. Работа силы тяжести отрицательна и равна
Работа силы сопротивления воды также отрицательна:
Работа силы Архимеда равна
Тогда:
По условию,
Ответ: мДж.
Задача 9. На какую высоту выпрыгнул бы из воды шарик для игры в пинг-понг из задачи 8, если бы вода не оказывала сопротивление движению шарика? Сопротивлением воздуха пренебречь.
Исключим из уравнений работу силы сопротивления. В этом случае
Работа силы тяжести отрицательна и равна
Работа силы Архимеда равна
Изменение кинетической энергии – сумма работ, совершенных всеми силами:
Ответ: 55 см.
Задача 10. Льдина площадью м и толщиной м плавает в воде. Какую минимальную работу надо совершить, чтобы полностью погрузить льдину в воду?
Так как , то
Где = объем льдины, – объем погруженной части.
Тогда
Глубина погружения льдины
«Недогруженными» остались см.
При погружении льдины будет меняться сила Архимеда. Именно против нее мы будем совершать работу. Поэтому для вычислений нужно взять среднюю силу. Кроме того, в расчет возьмем не полную силу, а только тот «излишек», который возникнет в результате полного погружения льдины в воду, и, чтобы усреднить, поделим его пополам (на самом деле нужно считать интеграл с соответствующими пределами, но мы же с вами в школе):
Ответ: 8 Дж.
Задача 11. Поперёк шоссе лежит бревно массой и длиной . Чтобы освободить дорогу, бревно пытаются перетащить на траву, прикладывая силу вдоль бревна. Бревно перетащили лишь наполовину длины. Какую минимальную работу при этом совершили? Коэффициенты трения бревна об асфальт и о траву равны и соответственно.
Эту задачу я решала «по отдельности». Предположим, что ширина шоссе , и бревно занимает его от края до края. Первая половина бревна, потихоньку съезжая с асфальта, въезжала на траву. Коэффициент трения плавно менялся с до , тогда средний равен . Масса половины бревна , перетащили на , тогда работа по перетаскиванию равна
Теперь вторая половина. Она ехала только по асфальту, коэффициент трения не менялся, масса , перетащили на , тогда работа по перетаскиванию равна
Полная работа по перетаскиванию бревна равна
Ответ: .
Задача 12. Брусок массой 0,5 кг лежит на наклонной плоскости, образующей с горизонтом угол (). Брусок соединен с вершиной наклонной плоскости недеформированной пружиной жёсткостью 64 Н/м. Какую скорость надо сообщить бруску вверх вдоль наклонной плоскости, чтобы он вернулся и остановился в начальной точке? Коэффициент трения между бруском и плоскостью 0,8.
Когда бруску сообщили скорость, то ему сообщили кинетическую энергию. Брусок стал двигаться вверх. При этом он терся о поверхность: тратил энергию на преодоление силы трения. Кинетическая энергия постепенно переходила в потенциальную энергию бруска (он поднимался выше по плоскости) и пружины (она сжималась). Теперь можно записать это уравнением:
Или, выражая высоту подъема через длину пройденного бруском расстояния,
Для силы реакции опоры плоскости можно записать, что , а для силы трения тогда
Теперь брусок станет двигаться вниз. Его потенциальная энергия и потенциальная энергия сжатой пружины будут переходить в работу силы трения. То есть
Сократим на :
Отсюда определим :
Подставим в уравнение (1):
Подставим числа:
Ответ: м/с.
Задача 13. (МФТИ, 2008) На гладкой горизонтальной поверхности стола покоятся незакреплённые горки массами и . На вершине горки массой на высоте лежит монета массой (рис.). От незначительного толчка монета съезжает с горки в направлении другой горки. На какую максимальную высоту сможет подняться монета на горке массой ? Поверхности горок гладкие. Горки имеют плавный переход к поверхности стола. Шайба не отрывается от поверхностей горок, а поступательно движущиеся горки – от стола. Направления всех движений находятся в одной вертикальной плоскости.
Запишем закон сохранения импульса. Сначала общая масса монетки и горки покоилась, а затем монетка съехала вперед, а горка – назад:
Откуда получим, что
Теперь запишем закон сохранения энергии. Потенциальная энергия монетки перешла в кинетическую энергию монетки и горки (монетка полностью съехала вниз):
Подставляя ранее полученное отношение скоростей монетки и горки, имеем:
Найдем теперь скорость монетки на столе перед заездом на вторую горку:
Снова обращаемся за помощью к закону сохранения импульса:
Откуда
И снова составим закон сохранения энергии. Кинетическая энергия монетки переходит в ее потенциальную энергию, а также в кинетическую энергию горки:
Откуда
Подставим скорость второй горки из закона сохранения импульса:
Ответ: .
Задача 14. На пути тележки массой , скользящей по гладкому горизонтальному столу со скоростью , находится незакреплённая горка высотой и массой . Тележка по горке, а также горка по столу скользят без трения. Скорость тележки недостаточна, чтобы преодолеть горку. На какую максимальную высоту поднимется тележка? Какие скорость и приобретут тележка и горка, когда тележка съедет с горки, не добравшись до вершины?
Запишем закон сохранения импульса:
Теперь запишем закон сохранения энергии. Кинетическая энергия тележки перейдет в ее потенциальную, а также в кинетическую энергию системы горка – тележка:
Откуда
Теперь тележка съезжает с горки. По закону сохранения импульса
По закону сохранения энергии
После преобразований данного выражения, которые я не хочу приводить, получим скорость горки:
Вообще, получается два корня, один из которых . Этот корень подразумевает, что , то есть тележка преодолела всю горку: при въезде толкнула горку вперед, при скатывании – назад, и горка осталась неподвижной. Этот корень по условию не подойдет нам.
Из закона сохранения импульса найдем скорость тележки:
Ответ: , скорость горки , скорость тележки .
Задача 15. При движении автомобиля на подъёме с углом наклона поверхности дороги к горизонту () у него устанавливается скорость при полезной мощности автомобиля кВт. При движении автомобиля по горизонтальному участку дороги при той же полезной мощности у него устанавливается скорость . Какую полезную мощность должен развивать автомобиль при спуске с углом наклона поверхности дороги () со скоростью ? Сила сопротивления движению автомобиля пропорциональна квадрату его скорости.
Так как сила сопротивления движению пропорциональна квадрату скорости, то можно записать
Работа по преодолению этой силы будет равна
А мощность
– коэффициент.
Кроме того, работа совершается и против силы тяжести (в первом случае), а в третьем, наоборот, сила тяжести нам будет помогать.
Работа против силы тяжести (при подъеме) будет равна:
Требуемая в этом случае дополнительная мощность
– коэффициент.
Общая мощность в первом случае равна
Теперь рассмотрим второй случай.
Так как по условию , то
Откуда
Теперь, наконец, случай движения вниз по склону. Работа по преодолению силы сопротивления
Работа силы тяжести (при спуске) будет равна:
Требуемая в этом случае дополнительная мощность
– все тот же коэффициент.
Общая мощность в третьем случае равна
Подставим , определив эту величину:
Подставим , имеем:
Ответ: .
Задача 16. Ракета массой с работающим двигателем неподвижно «зависла» над землей. Скорость вырывающихся из ракеты газов равна . Какова мощность двигателя ракеты?
Ракета «зависла», следовательно,
Здесь – сила давления газов на ракету. Тогда импульс, сообщаемый газу (ведь ракета действует на газы с такой же точно силой) равен
Но с другой стороны этот импульс равен :
Кроме того, работа двигателя равна кинетической энергии вылетевших газов:
Мощность двигателя – скорость совершения работы – равна
Подставим ранее найденный импульс:
Ответ:
Задачи на законы сохранения в механике
Законы сохранения – фундаментальные физические законы. Учитесь решать задачи на эту тему? Отлично! В этой статье мы разберем несколько примеров решений таких задач.
Наш телеграм – это полезная и интересная информация для студентов всех специальностей. Присоединяйтесь!
Задачи на тему «Законы сохранения в механике»
Задача №1. Закон сохранения энергии
Условие
На какую высоту поднимется тело, подброшенное вертикально вверх, с начальной скоростью 10 м/с? При решении задачи не учитывается сопротивление воздуха.
Решение
По закону сохранения энергии, начальная кинетическая энергия брошенного тела будет равна его потенциальной энергии в наивысшей точке подъема.
Ответ: 5,1м
Задача №2. Закон сохранения импульса
Условие
Определите скорости двух шаров массами m1 и m2 после центрального абсолютно упругого удара. Скорости шаров до удара v1 и v2 соответственно
Решение
В задаче применяется закон сохранения импульса. Запишем его в векторном виде и в проекции на горизонтальную ось в соответствии с рисунком:
Теперь запишем закон сохранения энергии:
Преобразуем полученные выражения:
Воспользуемся формулами сокращенного умножения, разделим правые и левые части системы друг на друга и получим:
Подставим выраженное значение u2 в первое уравнение для закона сохранения импульса и получим:
Ответ: см. решение
Задача №3. Закон сохранения энергии
Условие
Спусковую пружину игрушечного пистолета сжали на 5 см, при вылете шарик массой 20 г приобрел скорость 2 м/с. Необходимо рассчитать, какова жесткость пружины
Решение
Потенциальная энергия деформированной пружины переходит в кинетическую энергию шарика
Ответ: 32 Н/м
Задача №4. Закон сохранения момента импульса
Условие
Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определите, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдёт ближе к центру на расстояние, равное половине радиуса платформы.
Решение
Так как в системе человек–платформа сумма моментов сил тяжести и реакции опоры равна нулю, для решения задачи можно применить закон сохранения момента импульса
Запишем моменты инерции системы в начальном и конечном состояниях, затем подставим результат во второе выражение:
Ответ: угловая скорость увеличится в 1,43 раза.
Задача №5. Закон сохранения энергии
Условие
При растяжении пружины на 20 см она приобрела потенциальную энергию упругодеформированного тела 20 Дж. Какова жесткость пружины?
Решение
Потенциальная энергия пружины вычисляется по формуле
Ответ: 1000 Н/м
Кстати! Для наших читателей действует скидка 10% на любой вид работы
Вопросы на законы сохранения
Вопрос 1. Что такое механическая система тел?
Ответ. Механическая система – это совокупность материальных точек (тел), движения которых взаимосвязаны.
Вопрос 2. Какая механическая система называется замкнутой?
Ответ. Замкнутой называется механическая система, на которую не действуют внешние силы. Такая система не взаимодействует с внешними телами, не входящими в нее.
Вопрос 3. В каких механических системах выполняются законы сохранения импульса, энергии и момента импульса?
Ответ. Законы сохранения импульса, энергии и момента импульса выполняются в замкнутых механических системах.
Вопрос 4. Сформулируйте закон сохранения момента импульса
Ответ. Момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Вопрос 5. Каково философское значение законов сохранения?
Ответ. Законы сохранения показывают неуничтожимость и несотворимость движущейся материи со всеми её свойствами в процессах её перехода из одной формы в другую. Другими словами, движение материи вечно и лишь переходит из одной формы в другую.
Такая точка зрения характерна для диалектического материализма.
Законы сохранения в механике
В физике, точнее в механике, можно выделить три фундаментальных закона сохранения:
- Закон сохранения импульса.
- Закон сохранения энергии.
- Закон сохранения момента импульса.
Формулировка закона момента импульса дана выше, в разделе «Вопросы». Кстати, для понимания физической сути момента импульса рекомендуем сначала почитать о том, что такое момент инерции.
Нужна помощь в решении задач и выполнении любых других заданий? Обращайтесь в профессиональный студенческий сервис.
Презентация к уроку 10 класса «Решение задач на законы сохранения импульса и энергии» | Презентация урока для интерактивной доски по физике (10 класс) на тему:
Слайд 1
Обобщение темы «Законы сохранения в механике». Автор: Маху О.С., учитель физики
Слайд 2
Цели и задачи урока: создание условий для глубокого усвоения системы знаний по законам сохранения в механике; повторить основные теоретические положения по теме “Законы сохранения в механике”; закрепить навыки решения задач .
Слайд 3
Импульс тела Модуль p=mv Направление p v Единица измерения кг •м /с Закон сохранения импульса m 1 v 1 +m 2 v 2 =m 1 v 1 `+m 2 v 2 `
Слайд 4
Механическая работа Условия совершения F ≠0,s≠0, α ≠ 9 0 0 Формула A=F ·s·cos α Единица измерения Дж Графическая интерпретация Мощность Теорема о кинети- ческой энергии A= Δ E k Теорема о потен- циальной энергии A=- Δ E p Формула N=A/t Единица измерения Вт Формула при v=const N=F ·v·cos α F x x А
Слайд 5
Общий закон сохранения и превращения энергии Энергия Внутренняя Единицы Дж Механическая Потенциальная Кинетическая Поднятого тела Деформированного тела Формула E p =mgh Формула E p =kx 2 /2 Формула E k =mv 2 /2 Закон сохранения энергии E k1 +E p1 =E k2 +E p2
Слайд 6
Решение задач. Задача 1 1. Арт. установка на горизонтальной поверхности выстреливает под углом 60 0 к горизонту. Масса снаряда 100кг, его скорость при вылете из дула 300м/с. С какой скоростью начнет откатываться установка, если она не закреплена, а ее масса 10 4 кг?
Слайд 8
Дано: Угол а= 6 0 градусов m₁ = 10 4 кг V ₂ = 3 00м/c m₂ = 1 00кг Найти V ₁ =?
Слайд 9
Р ешение Импульс снаряда равен P = m₂ V ₂ = 100*300 = 30000 кг*м/с . Горизонтальная составляющая равна Рг = Р* cos α = 30000* cos 60 = 30000*0.5 = 15000 кг*м/с — она действует на пушку. Тогда скорость откатывания пушки равна V ₁ = Pг / m ₁ = 15000 / 10000 = 1.5 м/с..
Слайд 10
Задача 2 Движение материальной точки описывается уравнением х = 5 — 8t + 4t2. Приняв ее массу равной 2 кг, найти импульс через 2 с и через 4 с после начала отсчета времени, а также силу, вызвавшую это изменение импульса.
Слайд 11
Дано Найти:
Слайд 12
Р ешение х = 5 — 8t + 4t²
Слайд 13
Задача 3 Тело свободно падает с высоты Н. Определите, на какой высоте кинетическая энергия равна трети потенциальной .
Слайд 14
Р ешение Е П = m . g . H m . g . H = m . g . h + m . g . h h = H h= 0,75H
Слайд 15
Задача 3 С лодки массой 200 кг, движущейся со скоростью 1 м/с, ныряет мальчик массой 50 кг, двигаясь в горизонтальном направлении. Какой станет скорость лодки после прыжка мальчика, если он прыгает: а) с кормы со скоростью 4 м/с; б) с носа со скоростью 2 м/с; в) с носа со скоростью 6 м/с?
Слайд 16
Дано Найти V’
Слайд 17
Решение При v=—4 м/с, При v = 2 м/с, При v = 6 м/с ,
Слайд 18
Задача 4 В воде с глубины 5 м поднимают до поверхности камень объемом 0,6 м3. Плотность камня 2500 кг/м3. Найти работу по подъему камня.
Слайд 19
Дано Найти А
Слайд 20
Решение m= ϸ *v
Слайд 21
Найти КПД наклонной плоскости длиной 1 м и высотой 0,6 м, если коэффициент трения при движении по ней тела равен 0,1.
Слайд 22
Дано Найти: η
Слайд 23
Решение
Слайд 24
Задание на дом: Итоги 5, 6 глав учебника Г.Я. Мякишева «Физика 10».
Сохранение импульса и энергии
Сохранение импульса и энергии
ПРИМЕЧАНИЕ
В этом руководстве описывается лаборатория
эксперимент проводился в течение 1996–1997 учебного года. Значительный
с тех пор были внесены изменения, и руководство использовалось во время
текущий учебный год еще НЕ доступен в Интернете.
Печатные копии можно приобрести в книжном магазине.
Назначение
Для экспериментальной проверки законов сохранения количества движения.
и энергия.В частности вам подойдет:
- Часть А. Линейный путь (установка в помещении 266)
- Первый закон Ньютона
- Упругие столкновения
- Неупругие столкновения
- (по желанию). Проверка Первого закона Ньютона с помощью кинестетика
Корзина.
- Часть Б. Баллистический маятник (установка в помещении 267)
Введение
Законы сохранения энергии и импульса относятся к числу
самые фундаментальные и полезные законы физики.Они помогают в решении
многих проблем механики и часто возникают во многих областях
науки. Эти законы говорят, что если нет чистых сил
на системе, то эта система будет иметь тот же импульс, p =
mv, всегда. Кроме того, если нет внешних или внутренних
силы, действующие в системе или на нее, то энергия этой системы
останется постоянным. В этих законах сохранения скрыт Первый закон Ньютона.
законы. Первый закон Ньютона гласит, что покоящиеся тела останутся
в состоянии покоя, пока на них не действуют никакие силы, а движущиеся тела
будут оставаться в движении до тех пор, пока на них не действуют никакие силы.Как один
Как видите, Первый закон Ньютона — это утверждение о сохранении
импульса и энергии. Вещи остаются прежними, пока они
остались одни.
Несмотря на свою фундаментальность, законы сохранения
часто трудно наблюдать в обычном опыте, в первую очередь
из-за наличия трения. Трение между движущимися телами
и их окружение означает, что есть внешние силы, действующие
на систему, следовательно, законы сохранения не действуют.
Итак, для соблюдения законов сохранения необходимо исключить трение.
как можно больше.
Эта лаборатория будет заниматься в первую очередь законами сохранения как
они применяются к столкновениям между материальными объектами. Эти столкновения
можно разделить на два разных класса; упругих столкновений
и неупругих столкновений . Если кинетическая энергия частицы
то же самое до и после столкновения, то столкновение
считается эластичным. Обратите внимание на ссылку на частицы. Твердый
тела не частицы, но имеют структуру. Если столкновение,
однако оставляет там структуру без изменений, их можно лечить
как частицы.Для другого типа столкновения энергия будет течь
между двумя объектами, и кинетическая энергия не будет сохранена.
В этом случае говорят, что столкновение неупругое. Обратите внимание, что
при отсутствии трения импульс будет сохраняться в
оба типа столкновений.
В одном измерении условия до и после эластичного
столкновение двух тел массой м 1 и
м 2 , начальные скорости v 1i и
v 2i , и конечные скорости v 1f
и v 2f , задаются
(кинетическая энергия)
(Импульс)
Для неупругого столкновения справедливо только уравнение импульса.
Prelab Домашнее задание
Предварительная домашняя работа должна выполняться дома и передаваться
lab TA, прежде чем вы начнете лабораторию.
1) Маленький шар массой м 1 и скоростью v 1i имеет упругий столкновение с большим неподвижным объектом.
массой м 2 . Покажите, что скорость v 1f
шара и v 2f большого объекта
после столкновения в пересчете на две массы v 1i
2) Для предыдущей задачи покажите, что скорость
мяч переворачивается после столкновения, если неподвижный объект
чрезвычайно большой, m 2 уходящий в бесконечность.Указывать
пределы скоростей.
Часть A: Трек:
Фиг.1
Для этих экспериментов вы будете использовать гусеницу с тележками.
которые имеют колеса с очень низким коэффициентом трения. Расстановка пути с тележкой
использованный в экспериментах показан на рисунке 1. Вы сможете
для измерения временных интервалов движения тележки с помощью таймеров Photo Gate
(см. раздаточный материал по таймерам фотоэлементов), из которого вы можете рассчитать
скорость тележки.Это электронный таймер с управлением
прерыванием невидимого инфракрасного светового луча, когда
телега проезжает ворота. Если объект длиной L прерывает
луч за промежуток времени t при прохождении через ворота,
тогда дается средняя скорость объекта за это время
по
(3,1)
Это основное измерение, которое вы сделаете в этом эксперименте.
Измеряя скорость тележек до и после различных
столкновений, а также взвешивания тележек вы сможете
вычислить энергию и импульс и проверить законы сохранения.
Работа таймеров:
Полное описание таймеров см. В раздаточном материале.
Работа и настройка трека:
Есть несколько вещей, которые необходимо сделать для подготовки к
эксперименты. Самое главное — проверить, исправна ли дорожка.
уровень. Для этого предусмотрены уровни. Возьмите один и поместите
это над ногами следа на одном конце следа. Первое место
по всей длине трассы и наблюдаем за «пузырем» уровня.Вы хотите, чтобы этот пузырек был точно посередине. Если это не так,
отрегулируйте ножки гусеницы, поворачивая винты в основании
ног. Когда пузырек окажется в середине уровня, повторите
эта процедура на противоположном конце дорожки с уровнем
снова по длине. После того, как оба конца были отрегулированы, повторите это
снова на обоих концах с уровнем по ширине дорожки.
Убедитесь, что один из конечных упоров находится на правом конце
гусеница, а пусковая установка находится слева от гусеницы (см. рис.2). Описание пусковых установок см. В раздаточном материале. Двигаться
концевой упор и пусковую установку, ослабьте винты сбоку и
задвиньте их на место. Наконец, выровняйте два фотоэлемента на одинаковом расстоянии.
друг от друга, убедившись, что дисплей обращен к вам. В
трасса оснащена рулеткой, чтобы расстояния могли
быть измеренным. Поместите первые фото-ворота на расстоянии 50 см от пусковой установки.
Поместите вторую фотокамеру на расстоянии примерно 100 см от пусковой установки, чтобы
что два фото-воротника находятся на расстоянии около 50 см друг от друга.
Фиг.2
Обратимся к тележкам. Один конец тележки
имеет магнит внутри, а другой конец имеет поршень и липучку
полоски, обозначенные на рисунке как «накладки на крючок и ворс» (см. рис. 3). Ты
будет использовать поршень для упругих столкновений и липучку для
неупругие столкновения. Может случиться так, что липучка будет
не слипаются хорошо. Чтобы проверить это, вдавите поршень во все
путь на обеих тележках.Соедините две тележки на липучках.
заканчивается. Если они плохо держатся, можно придать липучке шероховатость.
многократно складывая тележки вместе и разводя их.
Убедитесь, что тележки не имеют дефектов, проверив их на
трек. Поместите каждую тележку на рельсы, убедившись, что
колеса находятся в пазах. Дайте каждой тележке небольшой толчок и посмотрите
насколько хорошо он движется по трассе. Должны быть минимальные потери в
скорость по трассе. Если есть заметная потеря скорости,
еще раз проверьте уровень дорожки.Если это нормально, проверьте
колеса тележки и обратитесь за помощью к ТА.
Фиг.3
Обзор
Дорожка будет использоваться для создания различных коллизий между
тележки. Столкновения будут организованы так, чтобы изначально
движущаяся тележка пройдет через ворота для фотографий, прежде чем столкнется с другой.
объект, чтобы измерить начальную скорость. После столкновения
тележка снова пройдет через фото-ворота, чтобы измерить
конечная скорость.С этими измеренными скоростями, а также
измеренные массы, импульс и кинетическая энергия тележек
до и после столкновения можно рассчитать и сравнить.
Будут предприняты шаги для устранения систематических ошибок в этом
эксперимент. Будут измерены приблизительные эффекты трения.
Пусковые установки используются таким образом, чтобы начальные условия последовательных испытаний
можно воспроизвести.
Процедура эксперимента A.1: Ньютоны
Первый закон
Цель этого эксперимента — проверить Первый закон Ньютона,
в котором говорится, что объект останется в своем состоянии движения
до тех пор, пока на объект не действуют никакие силы.В этом случае тележка
движение без трения не изменит его скорость при движении
по трассе.
1) Поместите две прямоугольные гири на одну из
тележки. Поместите картонную полоску между двумя массами по длине.
чтобы он плотно прилегал.
2) Вы должны измерить длину картона и взвесить
тележка с массой и картоном. Запишите эти измерения.
3) Зафиксируйте высоту фото ворот так, чтобы луч прервался
по картону.Для этого поднесите тележку к каждому из
фото ворот и отрегулируйте высоту кронштейна так, чтобы он
картон, который устанавливает таймер. Вы можете регулировать высоту
фотозатвора, повернув винт на стойке и сдвинув
кронштейн вверх или вниз. Убедитесь, что вы настроили оба фото
ворота.
4) Отрегулируйте пусковое устройство тележки так, чтобы на шкале было 3,2 см.
взведен. Вы можете отрегулировать компрессию, ослабив винт
на фиксирующем зажиме и сдвинув его в нужное положение.Возьмите один из
тележки и поднесите к пусковой установке. Убедитесь, что пусковая установка
направлен в центр тележки. Убедитесь, что тележка
колеса находятся в пазах гусеницы. Запустите тележку, потянув
шнурок на пусковой установке. После того, как он прошел через оба
фото ворота, остановите тележку и запишите отображаемое время
на фото ворота.
5) Повторите шаг 4 еще два раза, всего три попытки.
6) Повторите шаги 4 и 5, на этот раз с фрикционным блоком.
масс.Поместите кусок картона в паз на
фрикционный блок (вам может понадобиться два, чтобы плотно прилегать). Убеждаться
вы записываете новую массу тележки.
Процедура эксперимента A.2: эластичный
Столкновения
Для этого эксперимента вы создадите упругие столкновения с
две тележки. Вы изучите все возможные сценарии; два
Тележки одинаковой массы сталкиваются, тележки меньшей массы сталкиваются
с тележкой большей массы сталкивается тележка большей массы
с одной меньшей массой и тележкой, сталкивающейся с бесконечным
масса (концевые упоры).Важно, чтобы вы установили пусковые установки
к описанным настройкам. Эти настройки демонстрируют каждый сценарий
Лучший.
1) Поместите одну из тележек с двумя прямоугольными гирями.
на нем и картон, помещенный, как и прежде, между двумя фотографиями
ворот, примерно в трех четвертях пути до вторых ворот с фотографиями.
Установите пусковую установку на 3,5 см. Поместите другую тележку с трением
блок и картон в позиции для запуска. Убеждаться
что поршни тележек обращены друг к другу и что поршни
все выходят.
2) Запустите тележку к неподвижной тележке, которая находится в
середина. Тележка пройдет через ворота для фотографий и оттолкнется
стационарной тележки. Затем две тележки пройдут через свои
соответствующие фото ворота. Запишите начальное время, когда тележка
потребовалось пройти фото ворот и времени телеги
потребовалось пройти через ворота после столкновения. Помни это
время, отображаемое в памяти, — это общее время. Вы должны вычесть
чтобы получить актуальный второй раз.
3) Повторите эту процедуру еще два раза.
4) Повторите шаги 1-3, но на этот раз обе тележки должны иметь
на них блокируется трение, поэтому их массы равны. Установите пусковую установку
до 2см.
5) Повторите шаги 1-3, но на этот раз запускаемую вами тележку
должна иметь две массы, а тележка посередине должна иметь
блок трения. Отрегулируйте пусковую установку на 3 см.
6) Повторите шаги 1-3 еще раз, но на этот раз используйте только один
тележка сталкивается с упором.Переместите фото-ворота на противоположный
конец дорожки разнесен таким же образом. Сдвиньте пусковую установку примерно
100 см от текущего положения. Установите пусковую установку на 3,5 см. Двигаться
тележку на место и запустите ее. Запишите отображаемое время
на обоих фото воротах до и после столкновения.
Процедура эксперимента A.3: Неупругие
Столкновения
Этот последний эксперимент со столкновениями будет иметь дело с неупругими столкновениями.
Повторите процедуру для части B, но на этот раз конец липучки
тележки должны быть обращены вперед.При каждом столкновении тележки
должны сталкиваться и слипаться. Когда тележки проезжают
фото ворот вместе, луч сломается только тогда, когда
картон проходит насквозь. Это означает, что будет место, где
балка не разорвана, поэтому убедитесь, что вы измерили длину
две картонные части и не длина двух
тележки.
Процедура эксперимента A.4: необязательно
Вы и ваш партнер с третьим лицом повторите эксперимент.
продемонстрированный вами ТА.Инструкции по проведению этого эксперимента
находится в раздаточном материале, который вам даст ваш ТА.
Анализ данных для части A.1
Цель всех испытаний — сравнить начальный импульс
тележек с конечным импульсом, а также начальный
кинетическая энергия до финала. Это будет сделано путем разделения
конечное значение импульса по начальному, давая дробь
сохраняющегося импульса. Если выполняются законы сохранения,
это должно быть равно единице.Результаты меньше единицы указывают на то, что
импульс был потерян. Таким же образом доля кинетической энергии
то, что сохраняется, будет найдено.
Первый закон Ньютона гласит, что если нет действующей силы
на объекте его импульс не изменится. Используйте данные, которые у вас есть
записаны, чтобы проверить это путем вычисления доли импульса
сохраняется в каждом испытании. Поскольку тележка одна, ее масса
и коэффициент длины вне этого отношения, который тогда будет
(3.2)
, где t i и t f — более ранние и более поздние
временные интервалы соответственно. Кинетическая энергия также должна быть сохранена.
рассчитать сохраняемую дробь,
(3,3)
Наличие любых внешних сил, таких как трение или сила тяжести,
создаст систематическую ошибку во всех дальнейших измерениях. К
получить приблизительную оценку эффекта, рассчитать
средняя доля начальной энергии и импульса, потерянных для вашего
данные.Для этого сначала усредните все коэффициенты импульса и все
отношения кинетической энергии, рассчитанные выше, (чтобы получить среднее
дроби сохранены), затем вычтите эти результаты из единицы (чтобы
получить среднюю потерянную дробь),
(3,4)
(3,5)
Эти результаты будут использованы при анализе ошибок.
Анализ данных для части A.2
Рассчитайте доли импульса и кинетической энергии, которые
сохранялась во всех столкновениях; то есть вычислить
(3.5)
(3,6)
Скорость и импульс имеют направление, поэтому подайте им знаки
ваш расчет (т.е. право положительно). Вы сделали три попытки
каждый, усредните эти результаты.
Анализ данных для части A.3
Снова найдите среднюю долю сохраняемых импульса и энергии.
В этом случае v 1f и v 2f одинаковы (поскольку
тележки соединены вместе).
Анализ ошибок для детали A
Если законы сохранения верны, это все равно неразумно
ожидать, что вычисленные дроби будут иметь значение ровно один,
из-за экспериментальных ошибок.Ошибки в измерениях длины и времени
окажет лишь небольшое влияние на результаты. Систематическая ошибка
вызвано трением Более важно. Как только убытки обнаружены,
нам нужно будет знать, сколько можно отнести к трению, прежде чем
вывод законов сохранения не соблюдались. Потери
из-за трения были рассчитаны для испытаний в части A (с
уравнение 3.4 и 3.5). Хотя это не даст точной ошибки
из-за трения он не должен быть больше, чем в несколько раз.
Итак, если результаты отличаются от единицы не более чем на три или
в четыре раза превышающие потери, обнаруженные для части A, мы можем предположить, что эти различия
скорее всего из-за трения.Решите, какие законы сохранения были
проверено в каждой части.
Часть B: Скорость снаряда
В этом эксперименте скорость снаряда при выходе из него
пружинный пистолет будет измеряться двумя способами. Во-первых, сохранение
законы будут использоваться несколько тонким способом для определения скорости.
Для сравнения он также будет измерен с использованием движения снаряда.
Деталь B1 Измерение скорости с помощью
Баллистический маятник
Рисунок 3.3
Пружинным пистолетом мяч попадает в ловушку, предназначенную для качания.
как маятник (рисунок 3.3). Когда мяч пойман, комбинация
мяча и ловца становятся качелями маятника. Хотя
столкновение между мячом и ловушкой неупругое и
энергия не сохраняется , импульс есть. С ловцом
в состоянии покоя начальный импульс системы обеспечивается
мяч, выстрелил со скоростью v b . Сразу после
мяч пойман, импульс, который возникает из-за движения центра
массы маятника, собранного из ловителя и шара, имеющего
скорость v p .Сохранение импульса требует
это то же самое,
(3,7)
, где m и M — массы мяча и
маятник соответственно.
После того, как мяч пойман, энергия объединенного мяча и
система улавливания сохранена. Первоначально центр масс находится в
высота h 1 , скорость v p . Как он движется
вверх против силы тяжести, кинетическая энергия преобразуется
в потенциальную энергию.Механизм защелки фиксирует его в самом верху
точка, h 2 , где вся начальная кинетическая энергия
маятник был использован для изменения потенциала
энергия,
(3,8)
, который можно определить, измерив увеличение высоты
ч = ч 1 — ч 2 ч.
центр масс сборки. Значение начальной скорости
мяча,
(3.9)
Процедура для Части B1
Убедитесь, что ваше устройство надежно закреплено и не
двигаться во время эксперимента. Убедитесь, что основание выровнено
и при необходимости отрегулируйте. Шаровая опора на штанге пистолета
через отверстие через его диаметр. Убедитесь, что это подходит гладко
на вашем аппарате. Убедитесь, что уловитель шариков выровнен
с пружинным пистолетом.
Рисунок 3.4
1) Измерьте и запишите вес вашего мяча. Чтобы удалить
шарик из ловителя, пальцем поднимите пружину защелки
при выталкивании сзади. Мяч должен выходить легко.
Не сгибайте пружину назад, иначе она может сломаться.
2) Взвесьте маятник. Для этого аккуратно откручиваем конус.
несущий винт до тех пор, пока маятник не освободится. Заменить маятник
и аккуратно, но надежно затяните конический подшипник на место.
3) Чтобы взвести пистолет, сначала поместите маятник на стойку, чтобы
убери это с дороги. Затем, установив мяч на стержень,
надавите на шар, пока спусковой крючок не защелкнется.
4) При свободном подвешивании маятника измерьте высоту
Индикатор центра масс (ЦМ) от основания.
5) Начиная с неподвижного маятника, выстрелите мячом в
ловушка девять раз ( будьте осторожны , чтобы не получить руку
попал в ружье, когда вы стреляете из него) и измерьте высоту
C.М. Индикатор от базы каждый раз. Это не всегда будет
быть таким же.
Часть B2: Измерение скорости снарядом
движение
Рисунок 3.5
Если ловитель убран с его пути, мяч упадет.
свободно после того, как он покидает пистолет. Он будет следовать по параболической дуге
пока он не ударится о столешницу, пройдя горизонтальное расстояние L
при падении на вертикальное расстояние h.Уравнения снаряда
движение можно использовать для анализа движения в этих направлениях,
как показано на рисунке 3.5. Комбинируя два уравнения, чтобы исключить
времени, тогда начальная скорость мяча будет
(3,10)
Процедура для Части B2
Убедитесь, что аппарат надежно закреплен и выровнен по уровню.
блок на столе. Уберите маятник с пути и
потренируйтесь стрелять мячом из пистолета над столом.Примечание
где мяч приземляется. Остерегайтесь диких выстрелов.
1) Наклейте кусок белой бумаги на поверхность стола.
где мяч приземляется. Накройте его копировальной бумагой, карбоновой стороной
вниз, чтобы точка удара мяча оставила след.
2) Установив шар и отпустив пистолет, найдите положение.
на столешнице прямо под центром мяча и отметьте
это с куском ленты.
3) Измерьте высоту от дна мяча до
столешница.
4) Огонь пять выстрела, маркировка и нумерация каждого
ударов.
5) Измерьте дальность L каждого из этих снимков со своей ленты.
отметка.
Анализ данных для Части B1
Рассчитать среднее увеличение высоты центра масс.
маятника и его стандартная ошибка (от стандартного отклонения
измерений). Используйте эти данные для расчета начальной скорости
шара и его погрешность (см. Приложение по анализу ошибок).Ты
Можно предположить, что в массах нет ошибки.
Анализ данных для части B2
Рассчитайте средний диапазон L и его ошибку [Delta] L из
стандартное отклонение. Сделайте разумную оценку [Delta] h,
возможная ошибка в измерении вашего роста. Рассчитать начальную
скорость мяча по измерениям h и L. Вычислить
ошибка начальной скорости [Дельта] v b
полученный этим методом. Результат распространения ошибок
(см. Приложение по анализу ошибок) —
(3.11)
Сравните полученные вами результаты для начальной скорости
мяч двумя разными способами . Последовательны ли они
в пределах ваших ошибок? Можете ли вы учесть расхождения?
9.3 Сохранение линейного импульса — University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Объясните значение выражения «сохранение импульса»
- Правильно определить, закрыта ли система
- Определите систему, импульс которой сохраняется
- Математически выразить сохранение импульса для данной системы
- Вычислить неизвестную величину, используя закон сохранения количества движения
Вспомните третий закон Ньютона: когда два объекта масс m1m1 и m2m2 взаимодействуют (что означает, что они прикладывают силы друг к другу), сила, которую объект 2 применяет к объекту 1, равна по величине и противоположна по направлению силе, которую прикладывает объект 1. на объекте 2.Пусть:
- F → 21 = F → 21 = сила на m1m1 от m2m2
- F → 12 = F → 12 = сила на м2 м2 от m1m1
Тогда в символах третий закон Ньютона говорит:
F → 21 = −F → 12m1a → 1 = −m2a → 2.F → 21 = −F → 12m1a → 1 = −m2a → 2.
9,10
(Напомним, что эти две силы не отменяются, потому что они применяются к разным объектам. F21F21 заставляет m1m1 ускоряться, а F12F12 заставляет m2m2 ускоряться.)
Хотя величины сил, действующих на объекты, одинаковы, ускорения нет, просто потому, что массы (в общем) разные.Следовательно, изменения скорости каждого объекта различны:
Дв → 1дт ≠ дв → 2дт. dv → 1дт ≠ дв → 2дт.
Однако произведения массы и изменения скорости равны (по величине):
m1dv → 1dt = −m2dv → 2dt.m1dv → 1dt = −m2dv → 2dt.
9,11
На этом этапе неплохо было бы убедиться, что вы ясно понимаете физический смысл производных в уравнении 9.3. Из-за взаимодействия скорость каждого объекта изменяется на величину dv .Кроме того, взаимодействие происходит в интервале времени dt , что означает, что изменение скоростей также происходит в течение dt . Этот временной интервал одинаков для каждого объекта.
Предположим на время, что массы объектов не меняются во время взаимодействия. (Мы ослабим это ограничение позже.) В этом случае мы можем перетянуть массы внутрь производных:
ddt (m1v → 1) = — ddt (m2v → 2) ddt (m1v → 1) = — ddt (m2v → 2)
9,12
и, следовательно,
dp → 1dt = −dp → 2dt.dp → 1dt = −dp → 2dt.
9,13
Это говорит о том, что скорость изменения импульса одинакова для обоих объектов. Массы разные, и изменения скорости разные, но скорость изменения произведения м и v → v → одинаковы.
Физически это означает, что во время взаимодействия двух объектов (m1andm2m1andm2) у обоих объектов изменился импульс; но эти изменения идентичны по величине, хотя и противоположны по знаку.Например, импульс объекта 1 может увеличиться, что означает, что импульс объекта 2 уменьшается точно на такую же величину.
В свете этого давайте переписываем уравнение 9.12 в более понятной форме:
dp → 1dt + dp → 2dt = 0. dp → 1dt + dp → 2dt = 0.
9,14
Это говорит о том, что во время взаимодействия, хотя импульс объекта 1 изменяется, и импульс объекта 2 также изменяется, эти два изменения компенсируют друг друга, так что общее изменение количества движения двух объектов вместе равно нулю.
Поскольку общий суммарный импульс двух объектов вместе никогда не меняется, мы могли бы записать
ddt (p → 1 + p → 2) = 0 ddt (p → 1 + p → 2) = 0
9,15
, откуда следует, что
p → 1 + p → 2 = константа. p → 1 + p → 2 = константа.
9,16
Как показано на рисунке 9.14, общий импульс системы до и после столкновения остается неизменным.
Рис. 9.14. Перед столкновением два бильярдных шара движутся с импульсами p → 1p → 1 и p → 2p → 2. Полный импульс системы — это их сумма, как показано красным вектором, помеченным слева p → totalp → total.После столкновения два биллиардных шара движутся с разными импульсами p → ′ 1p → ′ 1 и p → ′ 2p → ′ 2. Однако общий импульс не изменился, как показано красной векторной стрелкой p → ‘totalp →’ total справа.
Обобщая этот результат на N объектов, получаем
p → 1 + p → 2 + p → 3 + ⋯ + p → N = constant j = 1Np → j = constant. p → 1 + p → 2 + p → 3 + ⋯ + p → N = постоянный j = 1Np → j = постоянная.
9,17
Уравнение 9.17 — это определение полного (или чистого) импульса системы из N взаимодействующих объектов, а также утверждение, что полный импульс системы объектов постоянен во времени или, лучше сказать, сохраняется.
Законы о сохранении
Если значение физической величины постоянно во времени, мы говорим, что величина сохраняется.
Требования к сохранению импульса
Однако есть одна сложность. Для сохранения импульса система должна соответствовать двум требованиям:
- Масса системы должна оставаться постоянной во время взаимодействия.
Когда объекты взаимодействуют (прикладывают силы друг к другу), они могут передавать массы друг другу; но любая масса, которую приобретает один объект, уравновешивается потерей этой массы другим.Таким образом, общая масса системы объектов остается неизменной с течением времени:
[dmdt] system = 0. [dmdt] system = 0. - Чистая внешняя сила, действующая на систему, должна быть равна нулю.
Когда объекты сталкиваются, взрываются и перемещаются, они оказывают друг на друга силу. Однако все эти силы являются внутренними по отношению к системе, и, таким образом, каждая из этих внутренних сил уравновешивается другой внутренней силой, равной по величине и противоположной по знаку. В результате изменение количества движения, вызванное каждой внутренней силой, компенсируется другим изменением количества движения, равным по величине и противоположным по направлению.Следовательно, внутренние силы не могут изменить общий импульс системы, потому что сумма изменений равна нулю. Однако, если есть некоторая внешняя сила, которая действует на все объекты (гравитация, например, или трение), то эта сила изменяет импульс системы в целом; другими словами, импульс системы изменяется под действием внешней силы. Таким образом, для сохранения импульса системы мы должны иметь
F → ext = 0 → .F → ext = 0 →.
Система объектов, отвечающая этим двум требованиям, называется закрытой системой (также называемой изолированной системой).Таким образом, ниже показан более компактный способ выразить это.
Закон сохранения импульса
Общий импульс закрытой системы сохраняется:
∑j = 1Np → j = константа. J = 1Np → j = постоянная.
Это утверждение называется Законом сохранения количества движения. Наряду с сохранением энергии это одна из основ, на которой стоит вся физика. Все наши экспериментальные данные подтверждают это утверждение: от движения скоплений галактик до кварков, составляющих протон и нейтрон, и во всех промежуточных масштабах. В закрытой системе общий импульс никогда не меняется.
Обратите внимание, что абсолютно могут быть внешними силами, действующими на систему; но для того, чтобы импульс системы оставался постоянным, эти внешние силы должны уравновешиваться, так что чистая внешняя сила равна нулю. Все бильярдные шары на столе имеют весовую силу, действующую на них, но веса уравновешиваются (компенсируются) нормальными силами, поэтому нет чистой силы .
Значение «системы»
Система (механическая) — это совокупность объектов, движение которых (кинематика и динамика) вас интересует.Если вы анализируете отскок мяча от земли, вас, вероятно, интересует только движение мяча, а не Земли; Таким образом, мяч — это ваша система. Если вы анализируете автокатастрофу, две машины вместе составляют вашу систему (рис. 9.15).
Рис. 9.15 Две машины вместе образуют систему, которая должна быть проанализирована. Важно помнить, что содержимое (масса) системы не изменяется до, во время или после взаимодействия объектов в системе.
Стратегия решения проблем
Сохранение импульса
Использование сохранения импульса требует четырех основных шагов.Первый шаг имеет решающее значение:
- Обозначьте замкнутую систему (общая масса постоянна, чистая внешняя сила не действует на систему).
- Запишите выражение, представляющее полный импульс системы до «события» (взрыва или столкновения).
- Запишите выражение, представляющее общий импульс системы после «события».
- Установите эти два выражения равными друг другу и решите это уравнение для получения желаемой величины.
Пример 9.6
Встречающиеся тележки
Две тележки в лаборатории физики катятся по ровной дороге с незначительным трением. На концах этих тележек есть небольшие магниты, поэтому при столкновении они слипаются (рис. 9.16). Первая тележка имеет массу 675 граммов и катится вправо со скоростью 0,75 м / с; второй имеет массу 500 грамм и катится со скоростью 1,33 м / с, также вправо. Какова скорость двух соединенных тележек после столкновения?
Рис. 9.16 Две лабораторные тележки сталкиваются и слипаются после столкновения.
Стратегия
У нас столкновение. Нам даны массы и начальные скорости; нас спрашивают окончательную скорость. Все это предполагает использование сохранения импульса в качестве метода решения. Однако мы можем использовать его только в том случае, если у нас есть закрытая система. Таким образом, мы должны быть уверены, что выбранная нами система не подвергается действию чистой внешней силы и что ее масса не изменяется в результате столкновения.
Определение системы как две тележки соответствует требованиям для закрытой системы: общая масса двух тележек определенно не меняется, и хотя тележки определенно действуют друг на друга, эти силы являются внутренними по отношению к системе, поэтому они не меняют импульс системы в целом..
Значение
Принципы, применимые к двум лабораторным тележкам, одинаково применимы ко всем объектам любого типа и размера. Даже для фотонов концепции импульса и сохранения импульса по-прежнему имеют решающее значение даже в этом масштабе. (Поскольку они безмассовые, импульс фотона определяется совсем иначе, чем импульс обычных объектов. Вы узнаете об этом, когда изучите квантовую физику.)
Проверьте свое понимание 9.3
Предположим, что вторая тележка поменьше изначально двигалась влево.Каким был бы знак конечной скорости в этом случае?
Пример 9.7
Прыгающий супербол
Супербол массой 0,25 кг падает с высоты h = 1,50 мh = 1,50 м над полом. Он подпрыгивает без потери энергии и возвращается на исходную высоту (рис. 9.17).
- Каково изменение импульса супербара при отскоке от пола?
- Каким было изменение импульса Земли из-за столкновения шара с полом?
- Как изменилась скорость Земли в результате этого столкновения?
(Этот пример показывает, что вы должны быть осторожны при определении вашей системы.)
Рис. 9.17 Супербар падает на пол (t0t0), ударяется об пол (t1t1), отскакивает (t2t2) и возвращается на исходную высоту (t3t3).
Стратегия
Поскольку нас спрашивают только об изменении количества движения мяча, мы определяем нашу систему как мяч. Но это явно не закрытая система; гравитация применяет к мячу направленную вниз силу во время его падения, а нормальная сила, исходящая от пола, создает силу во время отскока. Таким образом, мы не можем использовать сохранение импульса в качестве стратегии.Вместо этого мы просто определяем импульс мяча непосредственно перед его столкновением с полом и сразу после него и вычисляем разницу. У нас есть масса шара, поэтому нам нужны его скорости.
Решение
- Поскольку это одномерная задача, мы используем скалярную форму уравнений. Пусть:
- p0 = p0 = величина импульса мяча в момент времени t0t0, момент, когда он был выпущен; так как он был сброшен из состояния покоя, это ноль.
- p1 = p1 = величина импульса мяча в момент времени t1t1, момент непосредственно перед тем, как он упадет на пол..
У нас нет простого способа рассчитать импульс после отскока. Вместо этого мы рассуждаем, исходя из симметрии ситуации.
Перед отскоком мяч начинает с нулевой скорости и падает на 1,50 м под действием силы тяжести, достигая некоторого количества движения непосредственно перед тем, как упасть на землю. На обратном пути (после отскока) он начинается с некоторой инерцией, поднимается на те же 1,50 м, что и упал, и заканчивается с нулевой скоростью. Таким образом, движение после отскока было зеркальным отображением движения до отскока.. - Каким было изменение импульса Земли из-за столкновения шара с полом?
Ваш инстинктивный ответ вполне мог быть либо «нулевым; Земля слишком массивна, чтобы этот крошечный шарик мог повлиять на нее »или, возможно,« больше нуля, но совершенно незначительно ». Но нет — если мы переопределим нашу систему как Супербол + Земля, тогда эта система будет замкнута (без учета гравитационного притяжения Солнца, Луны и других планет в солнечной системе), и, следовательно, полное изменение импульс этой новой системы должен быть нулевым..
Это изменение скорости Земли на равно совершенно незначительно.
Значение
Важно понимать, что ответ на часть (c) — это не скорость; это изменение скорости, а это совсем другое дело. Тем не менее, чтобы вы почувствовали, насколько мало это изменение скорости, предположим, что вы двигались со скоростью 4,7 × 10–25 м / с4,7 × 10–25 м / с. С такой скоростью вам потребуется около 7 миллионов лет, чтобы преодолеть расстояние, равное диаметру атома водорода.
Проверьте свое понимание 9,4
Было бы изменение импульса мяча большим, меньшим или таким же, если бы он столкнулся с полом и остановился (без отскока)?
Было бы изменение импульса мяча большим, меньшим или таким же, если бы он столкнулся с полом и остановился (без отскока)?
Пример 9,8
Хоккей 1
Две хоккейные шайбы одинаковой массы находятся на плоской горизонтальной хоккейной площадке. Красная шайба неподвижна; синяя шайба перемещается на 2.На 5 м / с влево (рисунок 9.18). Он сталкивается с неподвижной красной шайбой. Масса шайб 15 г. После столкновения красная шайба движется влево со скоростью 2,5 м / с. Какова конечная скорость синей шайбы?
Рисунок 9.18 Столкновение двух одинаковых хоккейных шайб. Верхняя диаграмма показывает шайбы за момент до столкновения, а нижняя диаграмма показывает шайбы в момент после столкновения. Чистая внешняя сила равна нулю.
Стратегия
Нам говорят, что у нас есть два сталкивающихся объекта, нам сообщают массы и начальные скорости, а также одну конечную скорость; нас просят указать обе конечные скорости.Сохранение импульса кажется хорошей стратегией. Определите систему как две шайбы; нет трения, поэтому у нас замкнутая система.
Прежде чем вы посмотрите на решение, как вы думаете, какой будет ответ?
Конечная скорость синей шайбы будет:
- ноль
- 2,5 м / с влево
- 2,5 м / с вправо
- 1,25 м / с влево
- 1,25 м / с вправо
- что-то другое
Решение
Определите направление + x , чтобы оно указывало вправо.v → bf = 0.
Значение
Очевидно, две шайбы просто обменялись моментом. Синяя шайба передала весь свой импульс красной шайбе. Фактически, это то, что происходит при аналогичном столкновении, когда m1 = m2.m1 = m2.
Проверьте свое понимание 9,5
Даже если бы было какое-то трение о лед, все равно можно было бы использовать сохранение импульса для решения этой проблемы, но вам нужно будет наложить дополнительное условие на задачу. Что это за дополнительное условие?
Пример 9.9
Посадка
Philae
12 ноября 2014 г. Европейское космическое агентство успешно посадило зонд под названием Philae на комету 67P / Чурюмова / Герасименко (рис. 9.19). Однако во время приземления зонд на самом деле приземлился три раза, потому что он дважды отскочил. Давайте посчитаем, насколько изменилась скорость кометы в результате первого отскока.
Рис. 9.19 Художественная визуализация Philae , приземляющейся на комету. (кредит: модификация работы Немецкого аэрокосмического центра DLR / Flickr)
Определим вверх как направление + y , перпендикулярное поверхности кометы, и y = 0y = 0, чтобы быть на поверхности кометы.
Стратегия
Нас спрашивают, насколько изменилась скорость кометы, но мы мало что знаем о комете, кроме ее массы и ускорения, которое вызывает ее сила тяжести. Однако нам, , говорят, что посадочный модуль Philae сталкивается (приземляется) с кометой и отскакивает от нее. Столкновение предлагает импульс как стратегию решения этой проблемы.
Если мы определим систему, которая состоит как из Philae , так и из кометы 67 / P, то на эту систему не действует чистая внешняя сила, и, таким образом, импульс этой системы сохраняется.(Мы пренебрегаем гравитационной силой Солнца.) Таким образом, если мы вычислим изменение количества движения посадочного модуля, мы автоматически получим изменение количества движения кометы. Кроме того, изменение скорости кометы напрямую связано с изменением ее импульса в результате «столкновения» с ней посадочного модуля.
Решение
Пусть p → 1p → 1 — это импульс Philae в момент непосредственно перед приземлением, а p → 2p → 2 — его импульс сразу после первого отскока. Тогда его импульс перед приземлением был
p → 1 = Mpv → 1 = (96 кг) (- 1..
Значение
Это очень небольшое изменение скорости, примерно одна тысячная миллиардной доли метра в секунду. Однако важно то, что это , а не ноль.
Проверьте свое понимание 9.6
Изменения количества движения для Philae и кометы 67 / P были равны (по величине). Были ли импульсы, испытанные Philae и кометой, равны? А как насчет сил? А как насчет изменений кинетической энергии?
Сохранение импульса
Сохранение импульса — фундаментальная концепция физики.
вместе с
сохранение энергии
и
сохранение массы.Импульс определяется как масса объекта, умноженная на скорость
объекта.
Сохранение импульса утверждает, что,
внутри некоторой проблемной области количество импульса остается постоянным;
импульс не создается и не уничтожается, а только изменяется
за счет действия сил , как описано у Ньютона.
законы движения.
Работать с импульсом труднее, чем с массой и энергией, потому что
импульс — это
векторная величина
имеющий как величину, так и направление. Импульс сохраняется во всех трех
физические направления одновременно.Еще сложнее иметь дело с
газ
потому что силы в одном направлении могут влиять на импульс в другом направлении
из-за столкновений многих молекул.
На этом слайде мы представим очень и очень упрощенную задачу потока.
где свойства меняются только в одном направлении.
Проблема дополнительно упрощается, если рассмотреть установившийся поток, который
не меняться со временем и ограничивая силы только теми
связанный с
давление.
Имейте в виду, что реальных проблем с потоком очень много.
более сложный
чем этот простой
пример.
Рассмотрим течение газа через область, в которой свойства течения
только изменение в одном направлении, которое мы назовем «х». Газ попадает в домен
на станции 1 с некоторой скоростью u и некоторым давлением p
и выходит на станции 2 с другим значением
скорости и давления. Для простоты будем считать, что
плотность r остается постоянной в пределах области
и что область A , через которую
расход газа также остается постоянным.Расположение станций 1 и 2 разделено.
на расстоянии del x . (Дельта — маленький треугольник на слайде
и это греческая буква «д». Математики часто используют этот символ для обозначения
изменение или изменение количества. Шрифт веб-печати не поддерживает
греческие буквы, поэтому мы будем называть его просто «дель».)
Изменение с расстоянием обозначается как градиент
чтобы избежать путаницы с изменением во времени, которое называется ставкой .
Градиент скорости обозначен как del u / del x ;
изменение скорости на
изменение расстояния.Итак, на станции 2 скорость определяется скоростью
на 1 плюс градиент, умноженный на расстояние.
u2 = u1 + (del u / del x) * del x
Аналогичное выражение дает давление
на выходе:
p2 = p1 + (del p / del x) * del x
Ньютона
второй закон движения состояний
что сила F равна изменению количества движения с
уважение ко времени. Для объекта постоянной массы
м это сводится к массе, умноженной на ускорение a .Ускорение — это изменение скорости с изменением времени.
(дель у / дель т) . Потом:
F = m * a = m * (del u / del t)
Сила в этой проблеме
происходит из-за градиента давления. Поскольку давление — это сила на единицу площади,
чистая сила, действующая на нашу область жидкости, равна давлению, умноженному на площадь
выход минус давление, умноженное на площадь у входа.
F = — [(p * A) 2 — (p * A) 1] = m * [(u2 — u1) / del t]
Знак минус у
начало этого выражения используется потому, что газы движутся из области
от высокого давления до области низкого давления; если давление увеличивается с
x скорость уменьшится.Подставляя наши выражения для скорости
и давление:
— [{(p + (del p / del x) * del x} * A) — (p * A)] = m * [(u + (del u / del x) * del x — u) /
дель т]
Упрощать:
— (del p / del x) * del x * A = m * (del u / del x) * del x / del t
Отметив, что (del x / del t) — это
скорость и масса равна плотности r, умноженной на объема (площадь, умноженная на del x):
— (del p / del x) * del x * A = r * del x * A * (del u / del x) * u
Упрощать:
— (del p / del x) = r * u * (del u / del x)
дель п / дел х и дел у / дел х
представляют градиенты давления и скорости.Если мы уменьшим нашу область до различных размеров, эти градиенты станут дифференцированными:
— dp / dx = r * u * du / dx
Это одномерная устойчивая форма
Уравнение Эйлера.
Интересно отметить, что падение давления
жидкости (член слева) пропорционален как значению
скорость и градиент скорости.
Решение этого уравнения импульса дает нам вид
динамическое давление
что появляется в
Уравнение Бернулли.
Действия:
Экскурсии с гидом
Основные уравнения динамики жидкости:
Навигация..
- Руководство для начинающих Домашняя страница
Импульс и энергия — Практика — Физический гипертекст
Здесь мы приводим начальные условия для двух сталкивающихся объектов.
| ∑ p = | м 1 в 1 | + | м 2 в 2 |
| ∑ p = | (8 кг) (+ 6 м / с) | + | (4 кг) (- 9 м / с) |
| ∑ p = | +12 кг м / с | ||
| ∑ К = | ½ м 1 v 1 2 | + | ½ м 2 v 2 2 |
| ∑ К = | ½ (8 кг) (6 м / с) 2 | + | ½ (4 кг) (9 м / с) 2 |
| ∑ К = | 306 Дж | ||
Импульс — это векторная величина, поэтому полный импульс определяется векторной суммой.Поскольку импульсы двух объектов противоположны, один из них будет отрицательным. Поскольку положительные ответы предпочтительнее отрицательных, давайте выберем правильное направление в качестве положительного. Это дает нам общий импульс +12 кг · м / с. С энергией, являющейся скаляром, гораздо легче обращаться, особенно здесь, поскольку единственная энергия, которая имеет значение, — кинетическая (которая всегда положительна). Полная механическая энергия этой системы в 306 Дж.
Первый результат, который мы рассмотрим, состоит в том, что два объекта слипаются и движутся вправо.
| ∑ p ′ = | ( м 1 + м 2 ) в ′ |
| ∑ p ′ = | (8 + 4 кг) (+ 1 м / с) |
| ∑ p ′ = | +12 кг м / с |
| ∑ K ′ = | ½ ( м 1 + м 2 ) v ′ 2 |
| ∑ K ′ = | ½ (8 + 4 кг) (1 м / с) 2 |
| ∑ K ′ = | 6 Дж |
Это разумный результат, поскольку начальный общий импульс положительный (справа).Расчеты показывают, что конечный общий импульс все еще составляет +12 кг м / с, но конечная полная энергия значительно упала до относительно низкого значения 6 Дж. Импульс был сохранен, но механическая энергия была потеряна. Это классический пример неупругого столкновения . (Некоторые даже назвали бы это полностью неупругим столкновением ). Потерянная энергия, вероятно, пошла на пластическую деформацию двух объектов (учитывая искаженные края, показанные на диаграмме).
Здесь два объекта разделились после столкновения и движутся в противоположных направлениях.Каждый движется медленнее, чем до столкновения. Это намекает на потерю механической энергии.
| ∑ p ′ = | м 1 в 1 ′ | + | м 2 в 2 ′ |
| ∑ p ′ = | (8 кг) (- 1 м / с) | + | (4 кг) (+ 5 м / с) |
| ∑ p ′ = | +12 кг м / с | ||
| ∑ K ′ = | ½ м 1 v 1 2 | + | ½ м 2 v 2 2 |
| ∑ K ′ = | ½ (8 кг) (1 м / с) 2 | + | ½ (4 кг) (5 м / с) 2 |
| ∑ K ′ = | 54 Дж | ||
Импульс был сохранен, как и должно быть, но механическая энергия была потеряна, что привело к неупругому столкновению .Поскольку было сохранено больше энергии, чем в предыдущем исходе, некоторые назвали бы это частично неупругим столкновением . Потерянная энергия не имеет большого значения и не нарушает закон сохранения энергии. При таком исходе энергия не была уничтожена. Он просто превратился в форму, которую нелегко увидеть нашими глазами — внутреннюю энергию. Когда кинетическая энергия преобразуется во внутреннюю энергию, либо температура системы увеличивается, либо в ней происходит фазовый переход (например, плавление). Подробнее о внутренней энергии мы поговорим позже в этой книге.
Этот результат аналогичен предыдущему, только теперь объекты перемещаются немного быстрее. Тем не менее, их скорость после столкновения ниже, чем раньше.
| ∑ p ′ = | м 1 в 1 ′ | + | м 2 в 2 ′ |
| ∑ p ′ = | (8 кг) (- 3 м / с) | + | (4 кг) (+ 9 м / с) |
| ∑ p ′ = | +12 кг м / с | ||
| ∑ K ′ = | ½ м 1 v 1 2 | + | ½ м 2 v 2 2 |
| ∑ K ′ = | ½ (8 кг) (3 м / с) 2 | + | ½ (4 кг) (9 м / с) 2 |
| ∑ K ′ = | 198 Дж | ||
Импульс был сохранен, а энергия потеряна, но в меньшей степени, чем в предыдущем исходе.Из всех исходов до сих пор это неупругое столкновение является наименее неупругим. Назвать его частично неупругим или частично упругим на самом деле не имеет значения.
Здесь мы видим упругое столкновение . (Некоторые даже назвали бы это совершенно упругим столкновением .)
| ∑ p ′ = | м 1 в 1 ′ | + | м 2 в 2 ′ |
| ∑ p ′ = | (8 кг) (- 4 м / с) | + | (4 кг) (+ 11 м / с) |
| ∑ p ′ = | +12 кг м / с | ||
| ∑ K ′ = | ½ м 1 v 1 2 | + | ½ м 2 v 2 2 |
| ∑ K ′ = | ½ (8 кг) (4 м / с) 2 | + | ½ (4 кг) (11 м / с) 2 |
| ∑ K ′ = | 306 Дж | ||
И импульс, и полная механическая энергия системы были сохранены.Полная кинетическая энергия двух объектов после столкновения такая же, как и раньше. В макроскопическом мире такого исхода никогда бы не было. Результаты выше показывают предел того, что может случиться. То есть макроскопические объекты всегда будут иметь меньше общей механической энергии после столкновения, чем прежде. Никогда не больше или равно.
Такой исход трудно объяснить.
| ∑ p ′ = | м 1 в 1 ′ | + | м 2 в 2 ′ |
| ∑ p ′ = | (8 кг) (- 6 м / с) | + | (4 кг) (+ 15 м / с) |
| ∑ p ′ = | +12 кг м / с | ||
| ∑ K ′ = | ½ м 1 v 1 2 | + | ½ м 2 v 2 2 |
| ∑ K ′ = | ½ (8 кг) (- 6 м / с) 2 | + | ½ (4 кг) (15 м / с) 2 |
| ∑ K ′ = | 594 Дж | ||
Импульс был сохранен, но механическая энергия увеличилась.Как это могло случиться? Откуда взялась дополнительная энергия? Поскольку это проблема общих объектов, мы можем придумывать всевозможные объяснения. Возможно, на одном из объектов была сжатая пружина, или химическая взрывчатка, или два объекта были небольшими млекопитающими, которые оттолкнулись друг от друга после столкновения. Я думаю, что «изобретать» было подходящим выбором с моей стороны, чтобы описать то, что мы здесь делаем. Этот результат кажется невероятным , поскольку он нарушает закон сохранения механической энергии способом, отличным от предыдущих результатов.
Этот результат тоже вызывает недоумение.
| ∑ p ′ = | м 1 в 1 ′ | + | м 2 в 2 ′ |
| ∑ p ′ = | (8 кг) (- 8 м / с) | + | (4 кг) (+ 5 м / с) |
| ∑ p ′ = | −44 кг м / с | ||
| ∑ K ′ = | ½ м 1 v 1 2 | + | ½ м 2 v 2 2 |
| ∑ K ′ = | ½ (8 кг) (8 м / с) 2 | + | ½ (4 кг) (5 м / с) 2 |
| ∑ K ′ = | 306 Дж | ||
В этом исходе была сохранена механическая энергия (что бывает редко, но возможно), но импульс — нет.Для этого потребуется импульс извне системы. Поскольку описание этой проблемы не упоминает о существовании или даже возможности третьего объекта, мы должны были бы сделать вывод, что этот результат невозможен , поскольку он нарушает сохранение линейного количества движения.
Сохранение импульса: определение, уравнение и примеры
Любой, кто когда-либо играл в пул, знаком с законом сохранения импульса, осознают он это или нет.
Закон сохранения количества движения является фундаментальным для понимания и предсказания того, что происходит, когда объекты взаимодействуют или сталкиваются. Этот закон предсказывает движение бильярдных шаров и определяет, попадет ли этот восьмой шар в угловую лузу или нет.
Что такое моментум?
Импульс определяется как произведение массы и скорости объекта. В форме уравнения это часто записывается как p = mv .
Это векторная величина, что означает, что с ней связано направление.Направление вектора импульса объекта совпадает с направлением его вектора скорости.
Импульс изолированной системы — это сумма импульсов каждого отдельного объекта в этой системе. Изолированная система — это система взаимодействующих объектов, которые никаким образом не взаимодействуют ни с чем другим. Другими словами, на систему не действует чистая внешняя сила.
Изучение общего количества движения в изолированной системе важно, потому что оно позволяет вам делать прогнозы того, что произойдет с объектами в системе во время столкновений и взаимодействий.
Что такое законы сохранения?
Прежде чем приступить к пониманию закона сохранения количества движения, важно понять, что подразумевается под «сохраняющейся величиной».
Сохранить что-либо — значит каким-то образом предотвратить отходы или потерю. В физике говорят, что величина сохраняется, если она остается постоянной. Возможно, вы слышали это выражение, относящееся к сохранению энергии, то есть к понятию, что энергия не может быть ни создана, ни уничтожена, а только изменяет форму.Следовательно, его общее количество остается постоянным.
Когда мы говорим о сохранении количества движения, мы говорим о том, что общее количество количества движения остается постоянным. Этот импульс может передаваться от одного объекта к другому в изолированной системе и по-прежнему считаться сохраняющимся, если общий импульс в этой системе не изменяется.
Второй закон движения Ньютона и закон сохранения количества движения
Закон сохранения количества движения может быть выведен из второго закона движения Ньютона.Напомним, что этот закон связывает чистую силу, массу и ускорение объекта следующим образом: F net = ma .
Уловка здесь состоит в том, чтобы представить эту чистую силу как действующую на систему в целом. Закон сохранения количества движения применяется, когда результирующая сила, действующая на систему, равна 0. Это означает, что для каждого объекта в системе единственные силы, которые могут быть приложены к нему, должны исходить от других объектов внутри системы или же отменяться. как-нибудь.
Внешними силами могут быть трение, сила тяжести или сопротивление воздуха.Они должны либо не действовать, либо им необходимо противодействовать, чтобы создать силу нетто в системе 0.
Вы можете начать деривацию с оператора F net = ma = 0 .
м в данном случае — это масса всей системы. Рассматриваемое ускорение — это чистое ускорение системы, которое относится к ускорению центра масс системы (центр масс — это среднее местоположение всей массы системы.)
Чтобы чистая сила была равна 0, тогда и ускорение должно быть 0. Поскольку ускорение — это изменение скорости во времени, это означает, что скорость не должна изменяться. Другими словами, скорость постоянна. Отсюда получаем утверждение, что мв см = константа.
Где v см — скорость центра масс, определяемая по формуле:
v_ {cm} = \ frac {m_1v_1 + m_2v_2 + …} {m_1 + m_2 + .. .}
Итак, теперь оператор сокращается до:
m_1v_1 + m_2v_2 +… = \ text {constant}
Это уравнение, описывающее сохранение количества движения. Каждый член — это импульс одного из объектов в системе, и сумма всех импульсов должна быть постоянной. Другой способ выразить это:
m_1v_ {1i} + m_2v_ {2i} + … = m_1v_ {1f} + m_2v_ {2f} + …
Где нижний индекс i относится к начальному values и f до конечных значений, обычно происходящих до, а затем после какого-либо взаимодействия, такого как столкновение между объектами в системе.
Упругие и неупругие столкновения
Причина, по которой закон сохранения импульса важен, заключается в том, что он может позволить вам найти неизвестную конечную скорость или что-то подобное для объектов в изолированной системе, которые могут столкнуться друг с другом.
Существует два основных способа возникновения такого столкновения: упругий или неупругий.
Совершенно упругое столкновение — это столкновение, при котором сталкивающиеся объекты отскакивают друг от друга. Этот тип столкновения характеризуется сохранением кинетической энергии.2
Если кинетическая энергия сохраняется, то сумма кинетических энергий всех объектов в системе должна оставаться постоянной как до, так и после любых столкновений. Использование сохранения кинетической энергии вместе с сохранением количества движения может позволить вам решить более одной конечной или начальной скорости в сталкивающейся системе.
Совершенно неупругое столкновение — это столкновение, при котором два объекта сталкиваются, прилипают друг к другу и затем перемещаются как единая масса. Это также может упростить задачу, потому что вам нужно определить только одну конечную скорость вместо двух.
В то время как импульс сохраняется при обоих типах столкновений, кинетическая энергия сохраняется только при упругом столкновении. Большинство реальных столкновений не являются ни идеально эластичными, ни совершенно неупругими, но находятся где-то посередине.
Сохранение углового момента
В предыдущем разделе было описано сохранение количества движения. Есть еще один тип импульса, применимый к вращательному движению, который называется угловым моментом.
Так же, как и в случае количества движения, сохраняется и угловой момент.Угловой момент зависит от массы объекта, а также от того, насколько далеко эта масса от оси вращения.
Когда фигурист вращается, вы увидите, как он вращается быстрее по мере приближения рук к телу. Это потому, что их угловой момент сохраняется только в том случае, если их скорость вращения увеличивается пропорционально тому, насколько близко они подносят руки к центру.
Примеры задач сохранения импульса
Пример 1: Два бильярдных шара одинаковой массы катятся навстречу друг другу.Один движется с начальной скоростью 2 м / с, а другой — со скоростью 4 м / с. Если их столкновение совершенно упругое, какова конечная скорость каждого шара?
Решение 1: При решении этой задачи важно выбрать систему координат. Поскольку все происходит по прямой, вы можете решить, что движение вправо является положительным, а движение влево — отрицательным. Предположим, что первый мяч движется вправо со скоростью 2 м / с. Тогда скорость второго мяча составляет -4 м / с.2 = 20
Алгебраическое решение системы дает следующие решения:
v_ {if} = -4 \ text {m / s} v_ {2f} = 2 \ text {m / s}
Вы заметите, что поскольку два шара имели одинаковую массу, они, по сути, обменивались скоростями.
Пример 2: Автомобиль весом 1200 кг, движущийся на восток со скоростью 20 миль в час, врезается головой в грузовик весом 3000 кг, движущийся на запад со скоростью 15 миль в час. Два автомобиля слипаются при столкновении. С какой конечной скоростью они движутся?
Решение 2: Одна вещь, на которую следует обратить внимание в отношении этой конкретной проблемы, — это блоки.В системе СИ для количества движения используются кг · м / с. Однако вам дана масса в кг и скорость в милях в час. Обратите внимание, что пока все скорости указаны в согласованных единицах, преобразование не требуется. Когда вы решите окончательную скорость, ваш ответ будет в милях в час.
Начальный импульс системы можно выразить как:
m_cv_ {ci} + m_tv_ {ti} = 1200 \ times 20 — 3000 \ times 15 = -21 000 \ text {kg} \ times \ text {mph}
Конечный импульс системы может быть выражен как:
(m_c + m_t) v_f = 4200v_f
Закон сохранения количества движения говорит вам, что эти начальные и конечные значения должны быть равны.Вы можете вычислить конечную скорость, установив начальный импульс равным конечному импульсу, решив конечную скорость следующим образом:
4200v_f = -21000 \ implies v_f = \ frac {-21000} {4200} = -5 \ text { mph}
Пример 3: Покажите, что кинетическая энергия не была сохранена в предыдущем вопросе, связанном с неупругим столкновением между автомобилем и грузовиком.
Решение 3: Начальная кинетическая энергия этой системы была:
\ frac {1} {2} m_cv_ {ci} ^ 2 + \ frac {1} {2} m_tv_ {ti} ^ 2 = \ frac {1} {2} (1200) (20) ^ 2 + \ frac {1} {2} (3000) (15) ^ 2 = 557 500 \ text {кг (миль / ч)} ^ 2
Окончательная кинетическая энергия системы была:
\ frac {1} {2} (m_c + m_t) v_f ^ 2 = \ frac {1} {2} (1200 + 3000) 5 ^ 2 = 52,500 \ text {кг (миль / ч) } ^ 2
Поскольку начальная полная кинетическая энергия и полная конечная кинетическая энергия не равны, можно сделать вывод, что кинетическая энергия не сохранялась.
Сохранение импульса | физика
Сохранение количества движения , общий закон физики, согласно которому величина, называемая импульсом, которая характеризует движение, никогда не изменяется в изолированном наборе объектов; то есть полный импульс системы остается постоянным. Импульс равен массе объекта, умноженной на его скорость, и эквивалентен силе, необходимой для остановки объекта за единицу времени. Для любого массива из нескольких объектов полный импульс — это сумма отдельных импульсов.Однако есть особенность в том, что импульс является вектором, включающим как направление, так и величину движения, так что импульсы объектов, движущихся в противоположных направлениях, могут сокращаться, давая общую сумму, равную нулю.
Британская викторина
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Перед запуском полный импульс ракеты и ее топлива равны нулю. Во время запуска нисходящий импульс расширяющихся выхлопных газов по величине равен восходящему импульсу восходящей ракеты, так что общий импульс системы остается постоянным — в данном случае нулевым значением. При столкновении двух частиц сумма двух импульсов до столкновения равна их сумме после столкновения. Какой импульс одна частица теряет, другая получает.
Закон сохранения количества движения в изобилии подтвержден экспериментом и может быть даже математически выведен на основе разумного предположения, что пространство однородно, то есть что в законах природы нет ничего, что выделяло бы одно положение в пространстве как особенное по сравнению с с любым другим.
Существует аналогичный закон сохранения для углового момента, который описывает вращательное движение практически так же, как обычный импульс описывает линейное движение. Хотя точное математическое выражение этого закона несколько сложнее, примеры его многочисленны. Например, всем вертолетам для стабилизации требуется как минимум два гребных винта (ротора). Корпус вертолета вращался бы в противоположном направлении, чтобы сохранить угловой момент, если бы наверху был только один горизонтальный пропеллер.В соответствии с принципом сохранения углового момента фигуристы вращаются быстрее, когда они тянут руки к своему телу, и медленнее, когда они их вытягивают.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Сохранение углового момента также было тщательно установлено экспериментально, и можно показать математически, что оно следует из разумного предположения, что пространство однородно относительно ориентации, то есть что в законах природы нет ничего, что выделяло бы одно направление в пространстве. пространство как особенное по сравнению с любым другим.
Понимание сохранения импульса — Физика средней школы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.
