Содержание
Урок по алгебре 8 класс по теме «Решение задач на движение по реке»
Урок алгебры, 8 класс.
Тема:
«Решение задач, на движение по реке, составлением дробных рациональных уравнений».
Учитель Иванова Л. А.
МБОУ «СОШ № 14» г. Выборг
Тема урока: «Решение задач на движение по реке».
Цель: формирование программных знаний с учётом дифференцируемого подхода;
Задачи:
1. Образовательные:
2. Развивающие:
развитие памяти и речи на языке предмета;
развитие умения преодолевать трудности при решении рациональных уравнений и заданий, связанных с использованием дробно-рациональных уравнений;
развитие познавательного интереса, умения переносить знания в новые условия.
3. Воспитательные:
воспитание внимания, аккуратности, чёткости записи;
умения работать в паре и самостоятельно, оказывать помощь товарищу, умение провести самооценку и оценить деятельность товарищей.
Оборудование: компьютер, презентация, раздаточный материал: тест, карточка-помощник по решению дробных рациональных уравнений, карточка-помощник по составлению уравнения по условию задачи.
Ход урока.
1 этап. Проверка домашней задачи из учебника Магницкого (слайд №2).
2 этап. Повторение темы «Квадратные корни». Тест из шести заданий, повышающегося уровня сложности, таким образом, каждый может проявить себя. Самопроверка (слайд №4-5).
3 этап.
1) Подготовка к изучению нового материала. Устная фронтальная работа (слайд № 7, 8).
2) Изучение нового материала. Решение задач на движение по реке.
Задача № 1(слайд №9).
Турист проехал на моторной лодке вверх по реке 25 км, а обратно спустился на плоту. В лодке он плыл на 10 ч меньше, чем на плоту. Найдите скорость течения, если скорость лодки в стоячей воде 12 км/ч.
Учитель: Что нужно, чтобы решить задачу?
Ученик: Составить математическую модель задачи, используя таблицу.
Учитель: Какие величины должны быть в нашей таблице?
Заполнение таблицы на доске и в тетради. Выявление логических связей. Составление уравнения. Решение уравнения. Отбор корней на предмет условия задачи.
s
v
t
По течению реки (плот)
25 км
х
Против течения реки (лодка)
25 км
12-х
Скорость теч. реки
Х км/ч
Собственная скорость лодки
12 км/ч
Ответ: скорость течения реки 2 км/ч.
3) Физкультминутка.
4) Учитель: А теперь поговорим о задачах древнего Китая (слайды № 10,11).
5) Составить уравнение по условию задачи № 629 (работа в парах, карточка-помощник). Самопроверка (слайд № 9). Дорешать задачу дома.
6) Самостоятельное решение задач по уровням. 1 уровень №628, 2 уровень № 627 (дополнительно № 703). Проверка учителем.
5 этап. Домашнее задание № 629, 636(а), Китайская задача.
Итог урока.
Задача №703
Моторная лодка прошла 35 км вверх по реке и на 18 км поднялась по ее притоку, затратив на весь путь 8ч. Скорость течения в реке на 1 км/ч меньше скорости течения в ее притоке. Найдите скорость течения в реке, если скорость лодки в стоячей воде 10 км/ч?
s
v
t
Против течения реки
35
(10-х)
8 ч
Против течения притока
18
(10-х-1)
Скорость теч. реки
x
Скорость теч.в притоке
X+1
Собственная скорость лодки
10 км/ч
Составим уравнение, решим его.
Ответ: скорость течения реки 3 км/ч.
Карточка-помощник по составлению уравнения.
s
v
t
По течению реки
Против течения
Собственная скорость лодки (скорость лодки в стоячей воде)
Скорость течения реки
Заполните таблицу.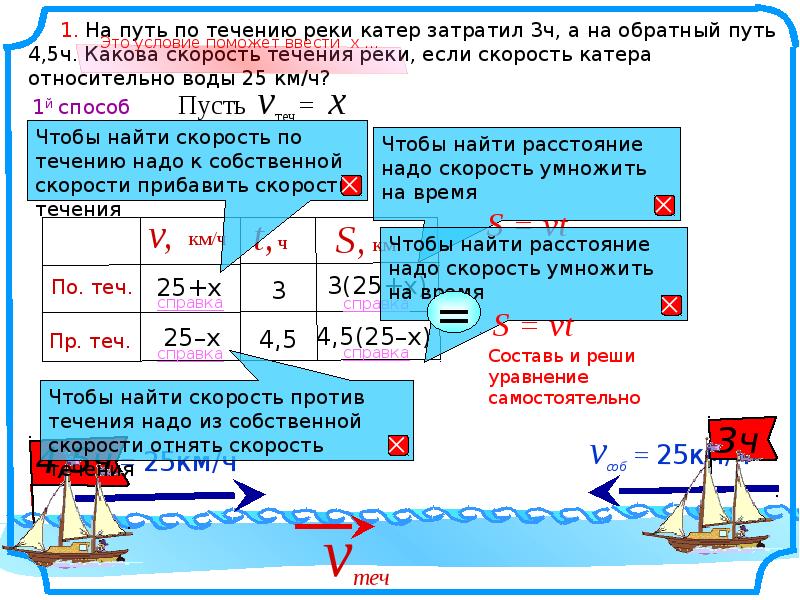 Для этого внимательно читая текст задачи, постепенно заполните столбец s.
Для этого внимательно читая текст задачи, постепенно заполните столбец s.
В столбце v введите переменную х (для этого посмотрите на вопрос задачи, что необходимо найти), заполните остальные строчки, используя правило нахождения скорости лодки по течению реки и против течения. Заполните последний столбец, используя правило нахождения времени через расстояние и скорость. Что еще известно по условию задачи? Как это использовать, чтобы составить уравнение? Составьте уравнение.
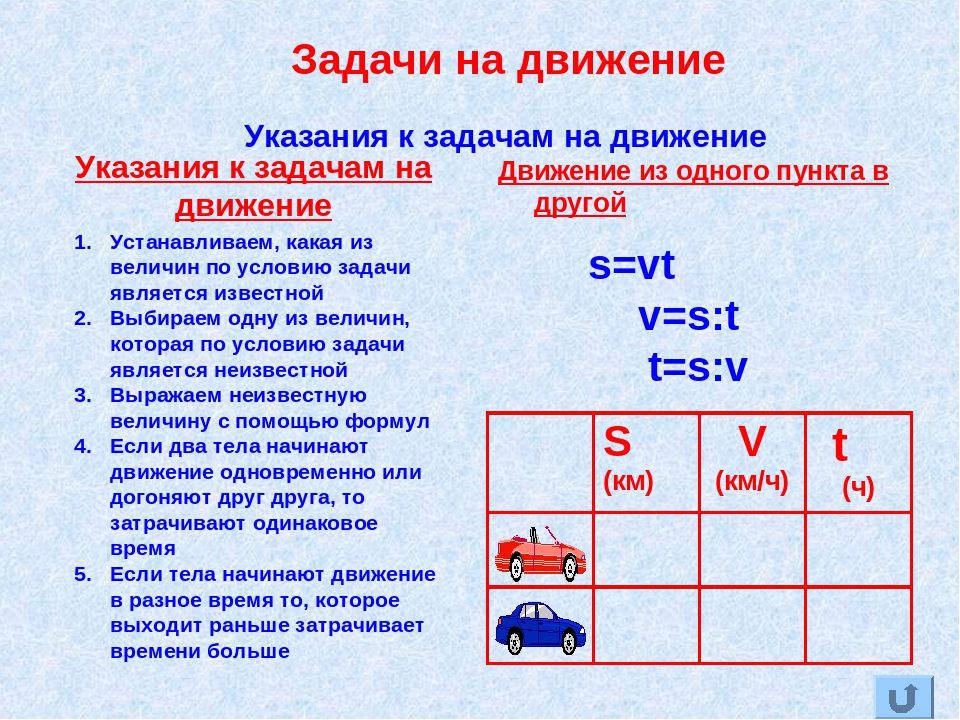
Задачи на движение
Задачи на движение — один из самых распространенных видов задач алгебры. Простейшие задачи на движение изучаются еще в начальной школе. В 6-7 классах решение задач на движение сводится к линейному уравнению либо системе линейных уравнений. Здесь мы рассмотрим задачи на движение, которые можно решить с помощью дробного рационального уравнения. При решении задач на движение используем формулу пути:
где s — путь, v — скорость, t — время. Как правило, в задачах на движение в 8 классе нужно выразить время через путь и скорость:
Как правило, в задачах на движение в 8 классе нужно выразить время через путь и скорость:
Чаще всего путь измеряется в километрах, скорость — в километрах в час, время — в часах. Время, заданное в минутах, нужно перевести в часы. Так как в 1 часе 60 минут, то 1 минута — это одна шестидесятая часа, а t минут — t шестидесятых часа:
1 (мин)=1/60(часа). t (мин)=t/60 (часа).
1) Из пункта А в пункт В автомобиль ехал по шоссе протяженностью 210 километров, а возвращался назад по грунтовой дороге протяженность. 160 километров, затратив на обратный путь на 1 час больше, чем на путь из А в В. Найти, с какой скоростью автомобиль двигался по грунтовой дороге, если она на 30 километров в час меньше его скорости по шоссе.
Решение:
Пусть х км/ч — скорость автомобиля по грунтовой дороге, тогда его скорость по шоссе равна (х+30) км/ч.
Составим и решим уравнение:
Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, автомобиль по грунтовой дороге двигался со скоростью 40 км/ч.
Значит, автомобиль по грунтовой дороге двигался со скоростью 40 км/ч.
Ответ: 40 км/ч.
2) Первые 20 км пути велосипедист двигался со скоростью, на 5 км/ч большей скорости, с которой он ехал последние 20 км. С какой скоростью велосипедист проехал вторую половину пути, если на весь путь он затратил 3 часа 20 минут?
Решение:
Пусть II половину пути велосипедист двигался со скоростью х км/ч, тогда его скорость на I половине пути была (х+5)км/ч.
3 часа 20 минут = 3 20/60 =3 1/3 = 10/3 часа.
Составим и решим уравнение:
Упростим уравнение, разделив почленно обе его части на 10:
Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, II половину пути велосипедист проехал со скоростью 10 км/ч.
Ответ: 10 км/ч.
Решение задач с помощью квадратных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей
Решение задач с помощью квадратных уравнений.
При решении любой задачи необходимо сначала перевести её условие на математический язык, составить нужное уравнение (или не одно, а несколько уравнений – систему уравнений), а затем решить его. Поговорим о таких задачах, в которых уравнения будут получаться не линейные, как это было раньше, а квадратные. Или сводящиеся к квадратным.
Три основных типа текстовых задач в математике – на движение, на работу и на смеси. На смеси очень редко бывают задачи, сводящиеся к квадратным уравнениям, так что о них сейчас говорить не будем. Рассмотрим задачу на движение.
Задача 1. Катер прошел 5 км по течению реки и 8 км по озеру, затратив на весь путь 1 час. Скорость течения равна 3 км/ч. Найти скорость катера по течению.
В подобных задачах лучше всего за х брать то, что спрашивают. Тогда мы не ошибемся, если, найдя х, сразу запишем его в ответ.
Итак, пусть х км/ч – скорость катера по течению. Тогда скорость катера по озеру меньше ровно на скорость течения – ведь в озере течения нет. Значит, по озеру катер двигался со скоростью (х-3) км/ч. При этом мы также знаем пути, которые катер прошёл по реке и по озеру. Вспомним уравнение движения: S = vt. Найдем время по формуле t = s:v. Время движения по озеру 8:(x-3), а по реке 5:x.
Значит, по озеру катер двигался со скоростью (х-3) км/ч. При этом мы также знаем пути, которые катер прошёл по реке и по озеру. Вспомним уравнение движения: S = vt. Найдем время по формуле t = s:v. Время движения по озеру 8:(x-3), а по реке 5:x.
Чтобы было удобнее, запишем все данные в следующую таблицу.
|
|
S, км
|
v, км/ч
|
t, ч
|
|
По течению
|
5
|
x
|
5x
|
|
По озеру
|
8
|
x-3
|
8x-3
|
Теперь вспомним, что в общей сложности катер плыл 1 час, получаем уравнение:
8x-3+5x=1 .
Умножим обе части уравнения на x(x-3) и приравняем числители при условии x(x-3)≠0.
8x+5x-3=x(x-3)
8x+5x-15=x2-3x
x2-16x+15=0
D=(-16)2-4∙1∙15=256-60=196
D=14
x1=—16-142=1
x2=—16+142=15
Первый ответ не подходит, так как скорость катера по течению не может быть меньше скорости течения. Значит, ответ: 15 км/ч.
Универсальный алгоритм для решения текстовых задач:
- Переписать условие на математический язык.
- Составить уравнение или систему уравнений.
- Решить полученное уравнение или систему.
- Проанализировать полученное решение и записать ответ.
Так, в рассмотренной задаче про катер получилось два значения неизвестной, и чисто алгебраически оба они являются решениями уравнения (системы). Однако для одного из значений скорость катера против течения реки получается отрицательной – это и есть анализ: в ответ записываем только второе значение.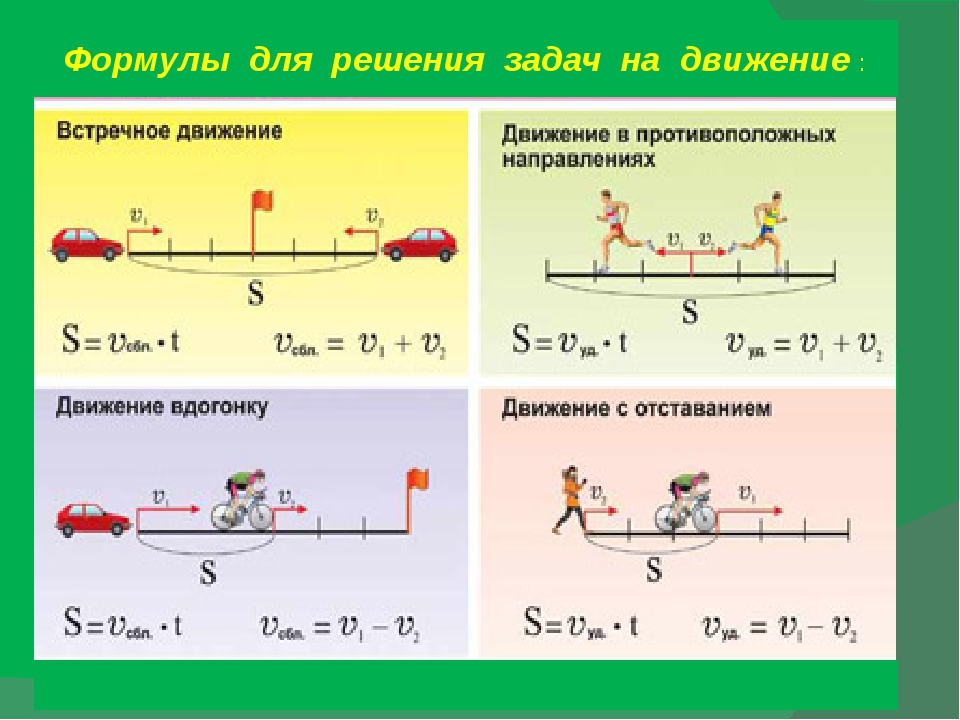
Задача 2. Бассейн наполняется двумя трубами за 10 часов. За сколько часов наполнит бассейн первая труба, если она это делает на 15 ч быстрее, чем вторая?
Для начала вспомним формулу для вычисления объёма проделанной работы: А = vt. Обрати внимание на то, что здесь есть полное соответствие задачам на движение: путь – объём работы, скорость – производительность, время – время.
Эту задачу можно решить по алгоритму. Сначала перепишем условие на математическом языке.
Работа по наполнению бассейна объёмом A выполнена двумя трубами одновременно с общей скоростью v1+v2 за время t = 10 ч.
Первая труба наполняет бассейн (объём работы A) со скоростью v1 за время t1.
Вторая труба наполняет бассейн (объём работы A) со скоростью v2 за время t2.
Разница между временем t2 и временем t1 равна 15 (t2>t1 на 15 ч).
Обрати внимание на то, что в подобных задачах на совместную работу производительности складывать можно, а времена – нет.
Второй шаг – составляем систему:
A=10v1+v2A=v1t1A=v2t2t2-t1=15
Так как трубы заполняют один и тот же бассейн, то есть выполняют одинаковую работу, то можно принять работу за 1. Обрати внимание, речь не идет об 1 литре или кубометре, 1 в данном случае – это 1 бассейн. Так что и производительность в этом случае будет измеряться не в литрах в час, а в бассейнах в час, то есть какую часть бассейна заполнит труба за час.
Третий шаг – решаем систему:
110=v1+v2A1t1=v1A1t2=v2At2=15+t1
Получаем:
1t1+1t1+15=110
Умножим обе части на 10t1(t1+15)
10t1+15+10t1=t1(t1+15)
10t1+150+10t1=t12+15t1
t12-5t1-150=0
Решая уравнение, получим два корня: 15 и -10.
И теперь анализ: время не может быть отрицательным, так что ответ – 15 часов.
Урок 29. решение задач с помощью квадратных уравнений — Алгебра — 8 класс
Тема: Решение задач с помощью квадратных уравнений.
Содержание модуля (краткое изложение модуля):
Задача №1.
Иван Иванович приехал в магазин покупать изгородь для своего дачного участка, имеющего прямоугольную форму, но забыл его размеры. Какой длины изгородь надо купить Ивану Ивановичу, если единственное, что он помнит, это площадь участка – 750 м2, и то, что длина участка на 5 метров больше ширины?
Пусть ширина участка будет х. Чаще всего удобнее брать за х меньшую из неизвестных величин. Тогда длина участка составит х + 5.
Площадь прямоугольника S = х • (x + 5)
x • (x + 5) = 750,
x2 + 5x — 750 = 0.
Найдем дискриминант этого уравнения и его корни.
a = 1, b = 5, c = -750
D = b2 — 4ac
D = 52 — 4 • 1 • (-750) = 25 + 3000 = 3025 = 552
x1,2 = (-5 ± √3025)/(2 • 1), x1 = (-5 — 55)/2 или x2 = (-5 + 55)/2.
x1 = -30 или x2 = 25
Первый из найденных корней является посторонним по смыслу задачи, значит, ширина участка будет равна 25 м. Следовательно, длина окажется равной 25 + 5 = 30 м.
Следовательно, длина окажется равной 25 + 5 = 30 м.
Теперь Иван Иванович может рассчитать периметр своего участка.
P = 2 • (25 + 30) = 110 м
Необходимо купить 110 м изгороди.
Задача №2.
Известно, что в прямоугольном треугольнике один из катетов на 4 сантиметра меньше гипотенузы, а другой – на 2 сантиметра меньше гипотенузы. Найдем длину гипотенузы.
Пусть гипотенуза треугольника будет равна х см. Тогда бОльший катет будет равен х – 2 см, а меньший х – 4 см.
По теореме Пифагора
x2 = (x — 2)2 + (x — 4)2
Упростим полученное уравнение, используя формулу квадрат разности.
x2 = x2 — 4x + 4 + x2 — 8x + 16
x2 = 2x2 — 12x + 20
x2 — 12x + 20 = 0
Решив полученное квадратное уравнение, найдем два корня.
x1 = 2, x2 = 10
2 является посторонним корнем по смыслу задачи, т. к. в этом случае один из катетов получится равным 0, а второй будет отрицательным. Значит, гипотенуза треугольника равна 10 см, а его катеты 8 см и 6 см.
к. в этом случае один из катетов получится равным 0, а второй будет отрицательным. Значит, гипотенуза треугольника равна 10 см, а его катеты 8 см и 6 см.
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Предварительные навыки
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.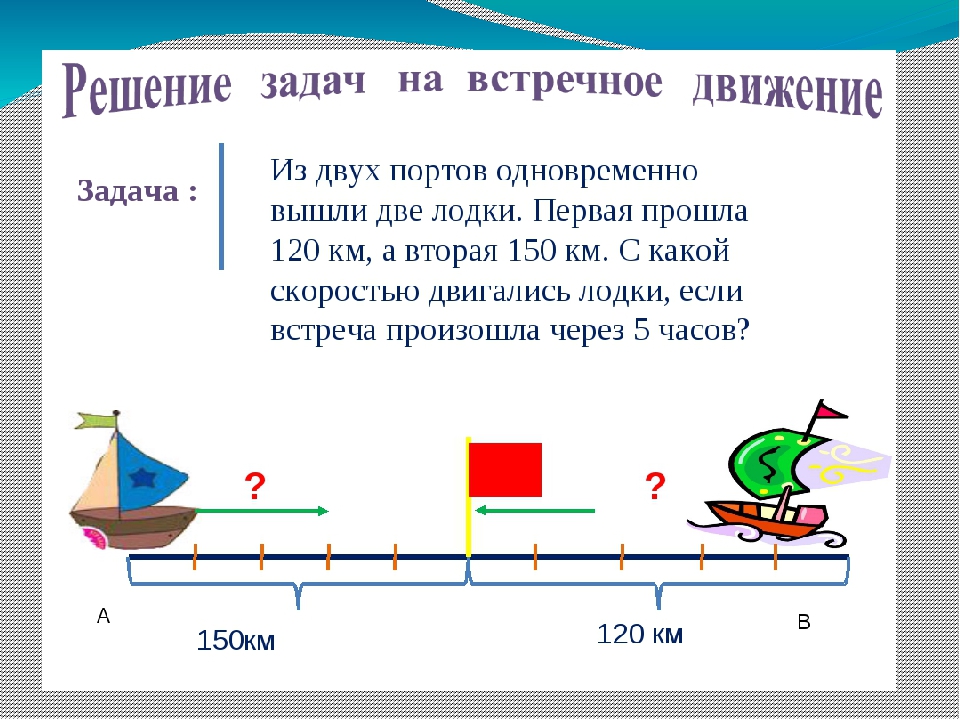
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.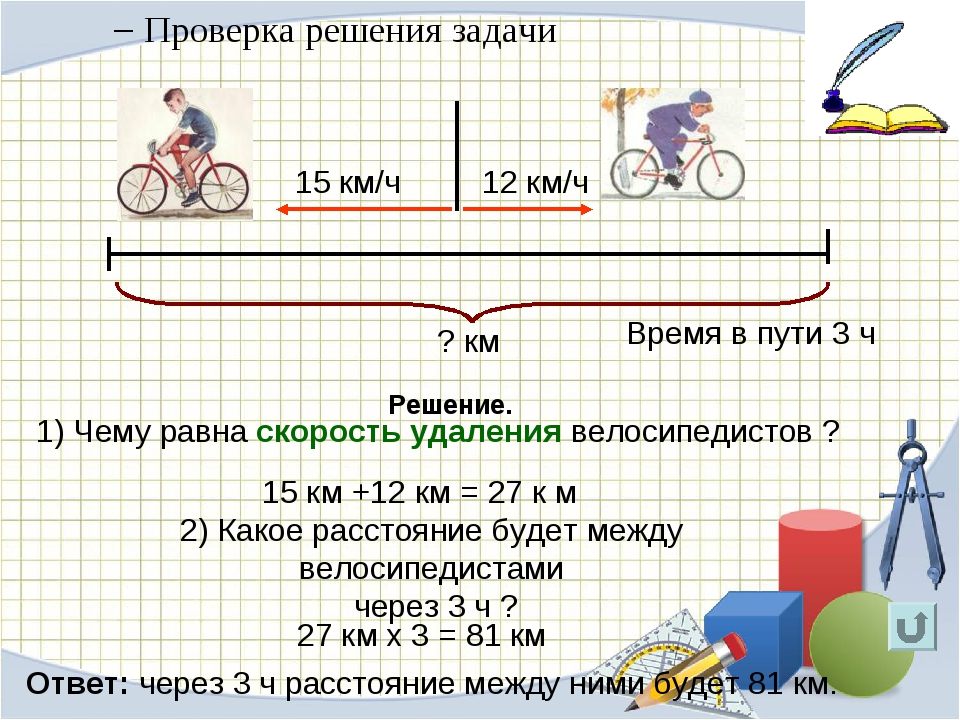
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту.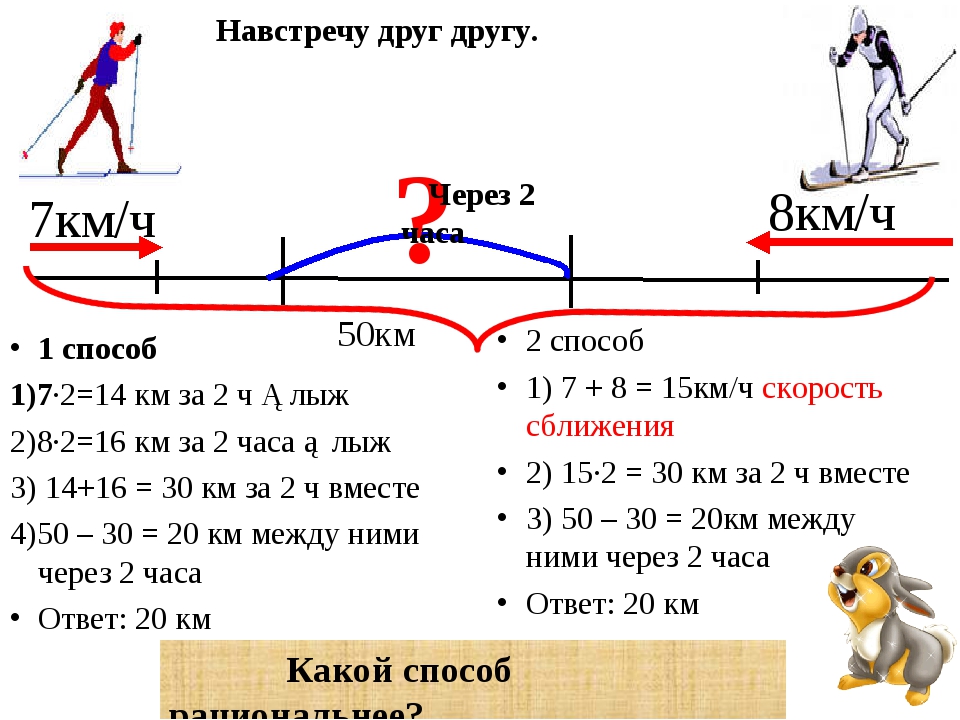 За две минуты он пройдет в два раза больше, то есть 160 метров
За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5.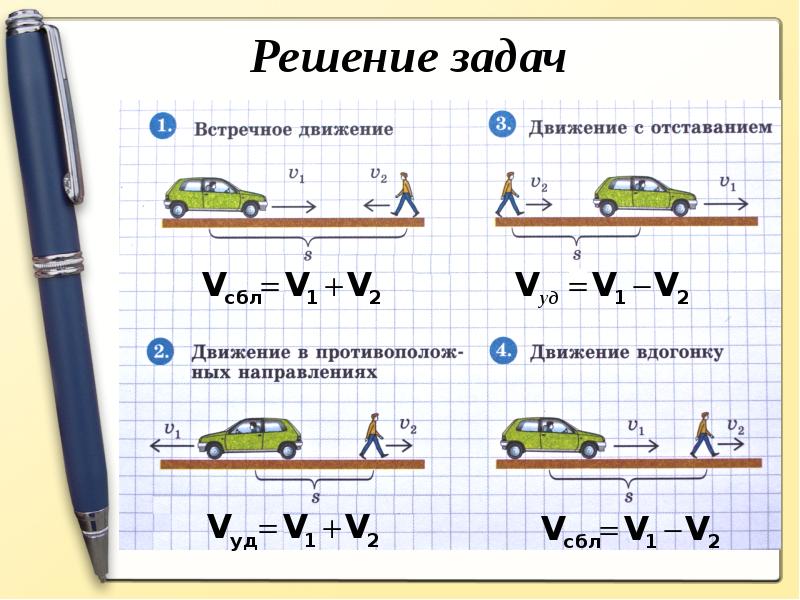 Двигаясь по течению реки, за 6 часов лодка
Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч.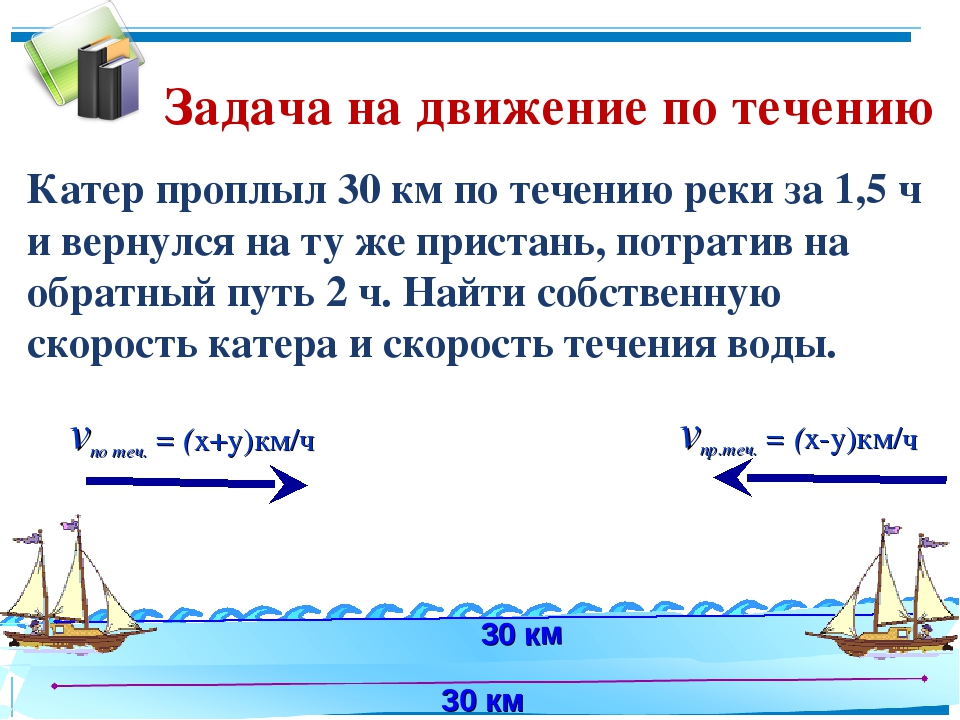 Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста.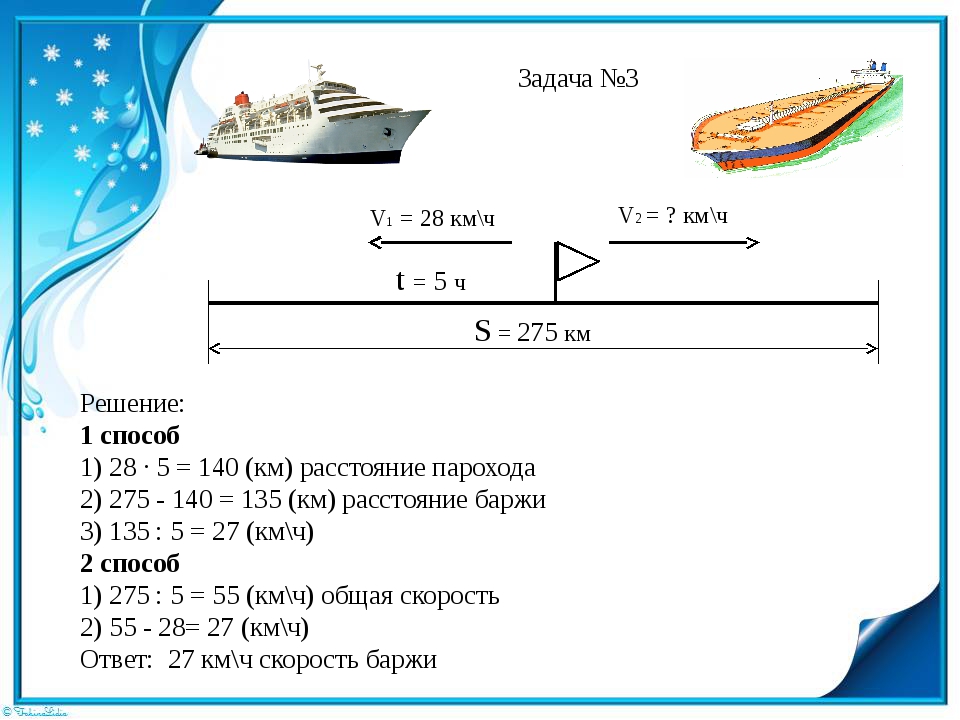 Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы.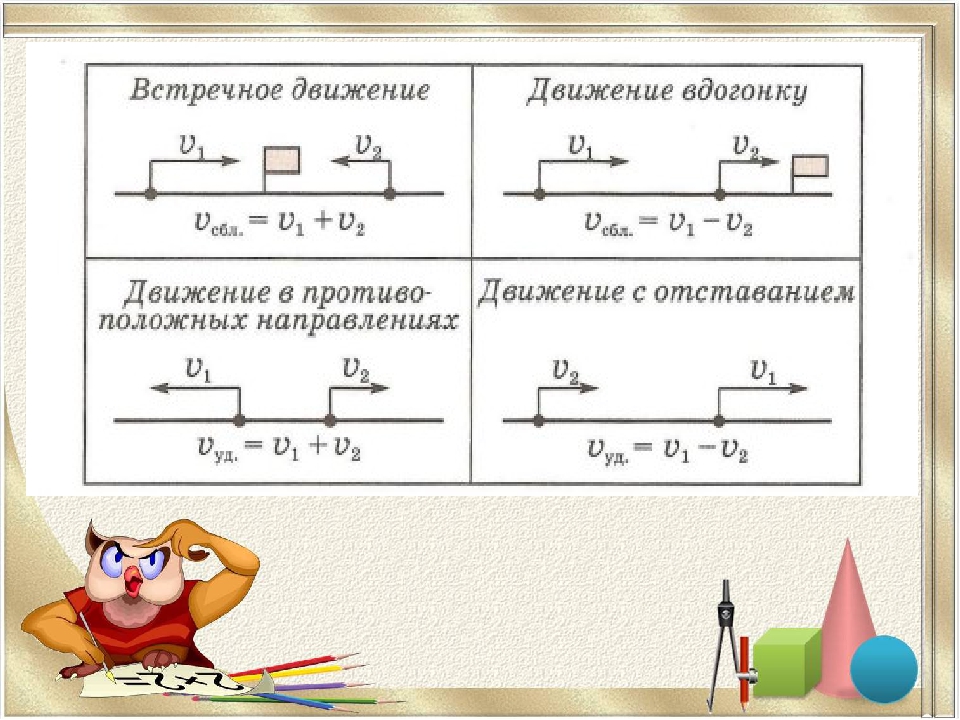 Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
ПЛАН КОНСПЕКТ ОТКРЫТОГО УРОКА ПО МАТЕМАТИКЕ 8 КЛ Тема «Решение задач с помощью рациональных уравнений»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ ДАГЕСТАН
МКОУ «ТЕМИРАУЛЬСКАЯ СОШ»
ПЛАН КОНСПЕКТ ОТКРЫТОГО УРОКА
ПО МАТЕМАТИКЕ 8 КЛ
УРОК ПОДГОТОВИЛА
УЧИТЕЛЬ МАТЕМАТИКИ
МКОУ «ТЕМИРАУЛЬСКАЯ СОШ»
ИСМАИЛОВА А.А.
ДАТА ПРОВЕДЕНИЯ:
Цели урока:
1) обобщить и систематизировать материал по теме: «Рациональные уравнения»;
2) научить составлять дробно – рациональные уравнения по условию задачи;
3) умение определять соответствуют ли найденные корни уравнения условию задачи;
4) закрепить умение решать задачи с помощью дробно – рациональных уравнений;
5) умение выбора способа решения текстовой задачи.
6) познакомить учащихся с методом подобия при решении текстовых задач, который так же приводит к составлению дробного рационального уравнения.
Тип урока: урок ознакомления и первичного закрепления нового материала.
Формы обучения: индивидуальная, коллективная.
Средства обучения: раздаточный материал к уроку, учебник, доска, методическое пособие.
Структура урока:
-
Организационный момент. -
Актуализация ранее полученных знаний: фронтальная беседа + самостоятельная работа + устная работа. -
Ознакомление с новым материалом и его первичное закрепление. -
Итоги урока.
Ход урока:
-
Организационный момент. -
А) Фронтальная работа. Ответить на вопросы:-
Какие уравнения называют рациональными уравнениями? -
Что называют корнем уравнения с неизвестным х? -
Что значит решить уравнение? -
Какие уравнения называют равносильными? -
По какому правилу решают рациональные уравнения? Что может произойти при отклонении от этого правила?
-
Б) Самостоятельная работа по теме: «Решение дробно-рациональных уравнений». Взаимопроверка – 4 варианта. Работа выполняется на листочках. Ответы записаны на обратной стороне доски. В ходе выполнения работы учащиеся определяют для себя алгоритм решения дробных рациональных уравнений. На каждой парте – таблица – напоминание «Алгоритм решения дробных рациональных уравнений». (Приложение ).
|
|
|
|
|
|
О т в е т ы:
I вариант: , (; ).
II вариант: (; )
III вариант: ( )
IV вариант: , (; ).
В) Устная работа. Составить уравнение для решения задачи:
-
Расстояние между городами скорый поезд, идущий со скоростью 90 км/ч, проходит на 1,5 ч быстрее товарного, который идет со скоростью 60 км/ч. Каково расстояние между городами?
Ответ:
-
Ученику и мастеру дано задание изготовить одинаковое количество деталей. Мастер, изготовляя 18 деталей в час, затратил на выполнение задания на 3 ч меньше, чем ученик, который изготавливал лишь 12 деталей в час. Сколько деталей было заказано?
Ответ:
-
Знаменатель дроби на 2 больше числителя. Если числитель увеличить на 15, а знаменатель – на 3, то получится число . Найдите дробь.
Ответ: .
-
Ознакомление с новым материалом
Схема решения задачи с помощью уравнения. (Приложение ).
-
Анализ условия; -
Выделения двух ситуации;
-
Введение неизвестной величины; -
Установление зависимости между данными задачи и неизвестной величиной; -
Составление уравнения; -
Решение уравнения; -
Запись ответа.
При решении задач составлением уравнения за х можно принять любое
неизвестное.
Решаем задачу № 387 из учебника. (Алгебра – 8 класс/ С.М.Никольский)
К доске вызываются четыре ученика, чтобы записать условие задачи и составить уравнение четырьмя способами:
I – ученик за х принимает скорость 1-го автомобиля;
II – ученик принимает за х скорость 2-го автомобиля;
III – ученик за х принимает время 1-го автомобиля;
IV – ученик принимает за х время 2-го автомобиля.
Учащиеся записывают в тетрадь условия четырьмя способами, а решают одним, в соответствии со своим вариантом.
I с п о с о б.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение:
II с п о с о б.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение:
III c п о с о б.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение:
Задача № 29 из методического пособия по математике А.В. Шевкина «Текстовые задачи. 7 – 9 классы, часть2».
Две старушки вышли одновременно навстречу друг другу из двух городов. Они встретились в полдень и достигли чужого города: первая в 4 ч по полудни, а вторая – в 9 ч. Нужно узнать, когда они вышли из своих городов.
1) Данную задачу заранее предлагаю учащимся решить в парах. Заслушиваем комментарии по решению задачи учащимся. Задача решена составлением дробного рационального уравнения.
Уравнение: , где х – время старушек до встречи, а весь путь пройден за 1. (Ответ: в 6 часов).
-
Объясняю решение данной задачи методом подобия, построив графики движения старушек.
Р е ш е н и е: Изобразим график движения старушек и применим метод подобия.
Пусть старушки до встречи шли х ч.
АD – промежуток времени движения первой старушки. СВ – промежуток времени движения второй старушки. КL – отсекает промежутки времени движения старушек до встречи. На рисунке АL – промежуток времени движения до встречи.
Расстояние
С К 4 D
I
N
II
А х L 9 В Время движения
-
Рассмотрим и : подобен по двум углам. -
Рассмотрим и , они подобны по двум углам. -
Из подобия двух пар треугольников следует, что и , т.е. -
Составим и решим уравнение: ()
Это уравнение имеет единственный положительный корень, удовлетворяющий условию задачи. — это время движения старушек до встречи.
-
Выясним, в какое время старушки вышли из своих городов:
.
Ответ: старушки из своих городов вышли в 6 ч утра.
Как мы видим, метод подобия приводит к более простому решению.
-
Итоги урока.
Домашнее задание: № 388 (а), № 390, № 392 — решить задачу двумя способами: 1) стандартным способом и 2) методом подобия.
| Класс | Название урока | Ссылка на учебные материалы | |
| 7 | Числовые выражения | https://resh.edu.ru/subject/lesson/7261/main/248922/ | |
| 7 | Буквенные выражения | https://resh.edu.ru/subject/lesson/7258/main/248957/ | |
| 7 | Сравнение значений выражений | https://onliskill.ru/video/1844-algebra-7-klass-sravnenie-znachenii-vyrazhenii.html | |
| 7 | Основные свойства действительных чисел | https://resh.edu.ru/subject/lesson/7230/main/248010/ | |
| 7 | Тождество. Тождественные преобразования выражений | https://resh.edu.ru/subject/lesson/1166/ | |
| 7 | Уравнения первой степени с одним неизвестным. Линейные уравнения с одним неизвестным | https://resh.edu.ru/subject/lesson/7277/main/248200/ | |
| 7 | Решение линейных уравнений с одним неизвестным | https://resh.edu.ru/subject/lesson/7278/main/248165/ | |
| 7 | Решение задач с помощью линейных уравнений | https://resh.edu.ru/subject/lesson/7274/main/248060/ | |
| 7 | Обобщение и систематизация знаний по теме «Линейные уравнения» | https://resh.edu.ru/subject/lesson/7280/main/247870/ | |
| 7 | Понятие функции и графика функции | https://resh.edu.ru/subject/lesson/3139/main/ | |
| 7 | Функция y = x и её график | https://resh.2 и её график | https://resh.edu.ru/subject/lesson/2908/main/ |
| 7 | Понятие многочлена. Свойства многочленов | https://resh.edu.ru/subject/lesson/7256/main/247975/ | |
| 7 | Сумма и разность многочленов | https://resh.edu.ru/subject/lesson/7254/main/247920/ | |
| 7 | Произведение одночлена и многочлена | https://resh.edu.ru/subject/lesson/7253/main/248795/ | |
| 7 | Произведение многочленов | https://resh.edu.ru/subject/lesson/7262/main/248762/ | |
| 7 | Способ группировки | https://resh.edu.ru/subject/lesson/1069/ | |
| 7 | Обобщение и систематизация знаний по теме «Одночлены, многочлены» | https://resh.edu.ru/subject/lesson/7251/main/248430/ | |
| 7 | Квадрат суммы | https://resh.edu.ru/subject/lesson/7250/main/269675/ | |
| 7 | Квадрат разности | https://resh.edu.ru/subject/lesson/7264/main/269690/ | |
| 7 | Выделение полного квадрата | https://resh.edu.ru/subject/lesson/7249/main/248585/ | |
| 7 | Разность квадратов | https://resh.edu.ru/subject/lesson/7265/main/248445/ | |
| 7 | Сумма кубов. Разность кубов | https://resh.edu.ru/subject/lesson/7248/main/269620/ | |
| 7 | Куб суммы. Куб разности | https://resh.edu.ru/subject/lesson/7247/main/247675/ | |
| 7 | Целое выражение | https://resh.edu.ru/subject/lesson/7263/main/248688/ | |
| 7 | Числовое значение целого выражения. Тождественное равенство целых выражений | https://resh.edu.ru/subject/lesson/7252/main/248725/ | |
| 7 | Применение формул сокращённого умножения. Разложение многочленов на множители | https://resh.edu.ru/subject/lesson/7266/main/247640/ | |
| 7 | Обобщение и систематизация знаний по теме «Формулы сокращённого умножения» | https://resh.edu.ru/subject/lesson/7246/main/248360/ | |
| 7 | Уравнения первой степени с двумя неизвестными | https://resh.edu.ru/subject/lesson/7273/main/248025/ | |
| 7 | Линейная функция и её график | https://resh.edu.ru/subject/lesson/1340/ | |
| 7 | Графический способ решения линейных уравнений | https://resh.edu.ru/subject/lesson/1212/ | |
| 7 | Система уравнений первой степени с двумя неизвестными | https://resh.edu.ru/subject/lesson/7279/main/247780/ | |
| 7 | Решение задач при помощи уравнений первой степени | https://resh.edu.ru/subject/lesson/7271/main/249248/ | |
| 7 | Обобщение и систематизация знаний по теме «Линейные уравнения» | https://resh.edu.ru/subject/lesson/7280/main/247870/ | |
| 7 | Сбор и группировка статистических данных | https://resh.edu.ru/subject/lesson/1556/main/ | |
| 7 | Наглядное представление статистической информации | https://resh.edu.ru/subject/lesson/1988/main/ | |
| 7 | Случайная изменчивость. Примеры случайной изменчивости | https://resh.edu.ru/subject/lesson/1556/main/ | |
| 7 | Дисперсия и среднее квадратичное отклонение | https://resh.edu.ru/subject/lesson/3409/main/ | |
| 8 | Рациональные выражения | https://resh.edu.ru/subject/lesson/2907/main/ | |
| 8 | Преобразование рациональных выражений. Построение графика функции y = k/x | https://infourok.ru/videouroki/3050 | |
| 8 | Основное свойство дроби. Сокращение дробей | https://resh.edu.ru/subject/lesson/1549/main/ | |
| 8 | Сложение и вычитание дробей с одинаковыми знаменателями | https://resh.edu.ru/subject/lesson/1550/main/ | |
| 8 | Сложение и вычитание дробей с разными знаменателями | https://resh.edu.ru/subject/lesson/1967/main/ | |
| 8 | Умножение дробей. Возведение в степень | https://resh.edu.ru/subject/lesson/1968/main/ | |
| 8 | Деление дробей | https://resh.edu.ru/subject/lesson/1969/main/ | |
| 8 | Преобразование рациональных выражений | https://resh.edu.ru/subject/lesson/1970/main/ | |
| 8 | Функция y = 1/x и её график | https://resh.edu.ru/subject/lesson/2909/main/ | |
| 8 | Функция y = k/x и её график | https://resh.edu.ru/subject/lesson/2501/main/ | |
| 8 | Решение уравнений графическим способом | https://resh.2 = а | https://resh.edu.ru/subject/lesson/1973/main/ |
| 8 | Нахождение приближенных значений квадратного корня | https://resh.edu.ru/subject/lesson/2916/main/ | |
| 8 | Функция у = √х и её график | https://resh.edu.ru/subject/lesson/2917/main/ | |
| 8 | Квадратный корень из произведения и дроби | https://resh.edu.ru/subject/lesson/2915/main/ | |
| 8 | Квадратный корень из степени | https://resh.edu.ru/subject/lesson/1974/main/ | |
| 8 | Вынесение множителя за знак корня. Внесение множителя под знак корня | https://resh.edu.ru/subject/lesson/2913/main/ | |
| 8 | Преобразование выражений, содержащих квадратные корни | https://resh.edu.ru/subject/lesson/1975/main/ | |
| 8 | Квадратные уравнения. Неполные квадратные уравнения | https://resh.edu.ru/subject/lesson/1976/main/ | |
| 8 | Решение квадратных уравнений вида ax2+bx+c = 0. Формула корней квадратного уравнения | https://resh.edu.ru/subject/lesson/3137/main/ | |
| 8 | Решение приведённых квадратных уравнений. Теорема Виета | https://resh.edu.ru/subject/lesson/1552/main/ | |
| 8 | Решение задач с помощью квадратных уравнений | https://resh.edu.ru/subject/lesson/1977/main/ | |
| 8 | Решение дробных рациональных уравнений | https://resh.edu.ru/subject/lesson/1978/main/ | |
| 8 | Решение задач с помощью рациональных уравнений | https://resh.edu.ru/subject/lesson/1979/main/ | |
| 8 | Уравнения с параметром. Контрольный урок | https://resh.edu.ru/subject/lesson/1980/main/ | |
| 8 | Числовые неравенства. Свойства числовых неравенств | https://resh.edu.ru/subject/lesson/1983/main/ | |
| 8 | Сложение и умножение числовых неравенств | https://resh.edu.ru/subject/lesson/1984/main/ | |
| 8 | Погрешность и точность приближения | https://resh.edu.ru/subject/lesson/1985/main/ | |
| 8 | Множества чисел | https://resh.edu.ru/subject/lesson/1553/main/ | |
| 8 | Пересечение и объединение множеств | https://resh.edu.ru/subject/lesson/1986/main/ | |
| 8 | Числовые промежутки | https://resh.edu.ru/subject/lesson/3407/main/ | |
| 8 | Решение неравенств с одной переменной | https://resh.edu.ru/subject/lesson/2578/main/ | |
| 8 | Решение систем неравенств с одной переменной | https://resh.edu.ru/subject/lesson/1987/main/ | |
| 8 | Доказательство неравенств | https://resh.edu.ru/subject/lesson/3408/main/ | |
| 8 | Определение степени с целым показателем. Свойства степени с целым показателем | https://resh.edu.ru/subject/lesson/7242/main/248570/ | |
| 8 | Стандартный вид числа | https://resh.edu.ru/subject/lesson/7269/main/248095/ | |
| 8 | Сбор и группировка статистических данных | https://resh.edu.ru/subject/lesson/1556/main/ | |
| 8 | Наглядное представление статистической информации | https://resh.edu.ru/subject/lesson/1988/main/ | |
| 8 | Дисперсия и среднее квадратичное отклонение | https://resh.edu.ru/subject/lesson/3409/main/ | |
| 8 | Вероятности событий | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3883737 | |
| 8 | Случайные опыты и случайные события | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795185 | |
| 8 | Элементарные события. Равновозможные элементарные события | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795141 | |
| 8 | Благоприятствующие элементарные события | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795141 | |
| 8 | Опыты с равновозможными элементарными событиями | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795141 | |
| 8 | Противоположное событие. Диаграммы Эйлера | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/1238874 | |
| 8 | Объединение и пересечение событий | https://uchebnik.mos.ru/my_materials/material_view/atomic_objects/5795009 | |
| 8 | Несовместные события. Правило сложения вероятностей | https://uchebnik.n | https://resh.edu.ru/subject/lesson/3182/main/ |
| 9 | Корень n-ой степени | https://resh.edu.ru/subject/lesson/1558/main/ | |
| 9 | Повторительно-обобщающий урок «Функции и их свойства, квадратный трехчлен» | https://resh.edu.ru/subject/lesson/1992/main/ | |
| 9 | Дробно-линейная функция и её график | https://resh.edu.ru/subject/lesson/2912/main/ | |
| 9 | Степень с рациональным показателем | https://resh.edu.ru/subject/lesson/2911/main/ | |
| 9 | Квадратный трёхчлен и его корни | https://resh.edu.ru/subject/lesson/1557/main/ | |
| 9 | Разложение квадратного трёхчлена на множители | https://resh.edu.ru/subject/lesson/1991/main/ | |
| 9 | Повторительно-обобщающий урок «Функции и их свойства, квадратный трёхчлен» | https://resh.edu.ru/subject/lesson/1992/main/ | |
| 9 | Некоторые приёмы решения целых уравнений | https://resh.edu.ru/subject/lesson/1997/main/ | |
| 9 | Дробные рациональные уравнения | https://resh.edu.ru/subject/lesson/2741/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Уравнения с одной переменной» | https://resh.edu.ru/subject/lesson/2575/main/ | |
| 9 | Решение уравнений графическим способом (8 класс) | https://resh.edu.ru/subject/lesson/1548/main/ | |
| 9 | Решение задач с помощью рациональных уравнений (8 класс) | https://resh.edu.ru/subject/lesson/1979/main/ | |
| 9 | Решение неравенств второй степени с одной переменной | https://resh.edu.ru/subject/lesson/3118/main/ | |
| 9 | Решение неравенств методом интервалов | https://resh.edu.ru/subject/lesson/1996/main/ | |
| 9 | Некоторые приёмы решения целых уравнений | https://resh.edu.ru/subject/lesson/1997/main/ | |
| 9 | Неравенства с двумя переменными | https://resh.edu.ru/subject/lesson/2574/main/ | |
| 9 | Системы неравенств с двумя переменными | https://resh.edu.ru/subject/lesson/2001/main/ | |
| 9 | Уравнение с двумя переменными и его график | https://resh.edu.ru/subject/lesson/2740/main/ | |
| 9 | Решение систем уравнений второй степени | https://resh.edu.ru/subject/lesson/1999/main/ | |
| 9 | Решение задач с помощью систем уравнений второй степени | https://resh.edu.ru/subject/lesson/2000/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Уравнения и неравенства с двумя переменными» | https://resh.edu.ru/subject/lesson/2739/main/ | |
| 9 | Последовательности | https://resh.edu.ru/subject/lesson/2003/main/ | |
| 9 | Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии | https://resh.edu.ru/subject/lesson/2004/main/ | |
| 9 | Характеристическое свойство арифметической прогрессии | https://resh.edu.ru/subject/lesson/1561/main/ | |
| 9 | Формула суммы первых n членов арифметической прогрессии | https://resh.edu.ru/subject/lesson/2005/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Арифметическая прогрессия» | https://resh.edu.ru/subject/lesson/2006/main/ | |
| 9 | Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии | https://resh.edu.ru/subject/lesson/2007/main/ | |
| 9 | Свойство геометрической прогрессии | https://resh.edu.ru/subject/lesson/2008/main/ | |
| 9 | Формула суммы n первых членов геометрической прогрессии | https://resh.edu.ru/subject/lesson/1562/main/ | |
| 9 | Метод математической индукции | https://resh.edu.ru/subject/lesson/2122/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Геометрическая прогрессия» | https://resh.edu.ru/subject/lesson/2121/main/ | |
| 9 | Целое уравнение и его корни | https://resh.edu.ru/subject/lesson/2573/main/ | |
| 9 | Некоторые приёмы решения систем уравнений второй степени с двумя переменными | https://resh.edu.ru/subject/lesson/2002/main/ | |
| 9 | Повторительно-обобщающий урок по теме «Неравенства с одной переменной» | https://resh.edu.ru/subject/lesson/1998/start/ | |
| 9 | Решение сложных задач на движение | https://resh.edu.ru/subject/lesson/1377/ | |
| 9 | Решение сложных текстовых задач на работу | https://resh.edu.ru/subject/lesson/1376/ | |
| 9 | Решение сложных текстовых задач на проценты | https://resh.edu.ru/subject/lesson/1344/ | |
| 9 | Графический способ решения систем уравнений | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3976540 | |
| 9 | Правило умножения. Примеры комбинаторных задач | https://infourok.ru/videouroki/1400 | |
| 9 | Перестановки. Факториал числа | https://infourok.ru/videouroki/1401 | |
| 9 | Правило умножения и перестановки в задачах на вычисление вероятностей | https://infourok.ru/videouroki/1406 | |
| 9 | Сочетания | https://infourok.ru/videouroki/1403 | |
| 9 | Испытания Бернулли. Вероятность событий в испытаниях Бернулли | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/2091951 | |
| 9 | Треугольник Паскаля | https://oblako-media.ru/behold/0bhpfZgZIAk/treugolynik-paskalya-1-postroenie-sverhu-vniz/ | |
| 9 | Примеры случайных величин. Распределение вероятностей случайной величины | http://specclass.ru/v0179_tv05_sluchaynaya_velichina_zakon_raspredeleniya/#comments | |
| 9 | Математическое ожидание случайной величины | http://specclass.ru/v0065_teorver_task_mat_ojidanie_dispersiya/ | |
| 9 | Понятие о законе больших чисел | https://clck.ru/MWUec |
Заданий по математике для 8-х классов
Какие математические навыки должны быть у ученика, поступающего в среднюю школу?
Вы поступаете в среднюю школу и беспокоитесь о том, какими математическими навыками вам следует обладать? Ты в 8 классе и скоро собираешься пойти в Большой Дом? Несомненно, поступление в среднюю школу требует сильных математических и аналитических навыков. Они имеют жизненно важное значение при работе со сложными статистическими и математическими концепциями. Помимо академических кругов, математические знания повышают способность к суждениям и логике в повседневной жизни.Независимо от того, насколько хорошо вы успели учиться в предыдущих классах, в старшей школе вам необходимо улучшить и улучшить свои математические навыки.
Ниже приведены математические навыки, которые вам необходимо получить до поступления в среднюю школу.
Значение и операции с числами: Чтобы иметь дело со всеми арифметическими аспектами, вам необходимо хорошо разбираться в концепции абсолютных чисел, порядке операций, соотношении и пропорциях, а также в концепции действительных, рациональных и комплексных чисел.
Алгебра, функции и моделирование: Использование алгебраических моделей очень распространено в инженерной и технологической областях при разработке бюджетов и исследовании неизвестных величин.Этот навык также требует умения переводить слова в числа.
Геометрия: Этот навык требует интерпретации основных геометрических понятий, понимания соответствующих или совпадающих ангелов. Определение длины дуги, объема и площади всех двумерных форм.
Вероятность и статистика: при интерпретации и систематизации данных для вывода количественных данных наличие вероятности и статистические навыки необходимы для старшей школы.
По мере того, как учащиеся переходят из 8-го класса в среднюю школу, мы наблюдаем повышенный уровень математической тревожности среди учащихся в целом.Это может быть связано с усиленным тестированием и обобщенными оценками. Социальное давление также побуждает студентов подчиняться общему утверждению о том, что им не нравится математика или что это слишком сложно. Легче сказать, что тогда нужно протолкнуться и приложить максимум усилий. Вы увидите, что ученики склонны избегать вещей, которых они боятся или имеют негативный опыт. Как и у людей всех возрастов. Вы можете помочь преодолеть это как учитель или родитель, создав позитивную среду, в которой математика будет рассматриваться как увлекательная задача.Это также помогает студентам, которые борются в небольших группах или один на один. Самая важная вещь, о которой нужно помнить, — это всегда быть рядом с учениками, отвечать на вопросы и моделировать позитивную математическую среду. Когда что-то не считается невозможным, у студентов будет лучший образ мышления, с которым можно будет работать.
Задачи и решения по математическим словам
Проблема 1
Днем продавец продал в два раза больше груш, чем утром.
Если он продал в тот день 360 килограммов груш, сколько?
килограммов он продал утром, а сколько днем?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет килограммами, которые он
продал утром.Затем днем он продал по 2 доллара за килограммы. Итак
итого $ x + 2x = 3x $. Это должно быть равно 360.
$ 3x = 360 $
$ x = \ frac {360} {3}
$ x = 120 $
Следовательно, продавец продал утром 120 кг и 2 \ cdot 120 = 240 $ кг днем.
Задача 2 Мэри, Питер и Люси собирали каштаны. Мэри собрала в два раза больше каштанов, чем Питер. Люси выбрала
На 2 кг больше Питера. Вместе они собрали 26 кг каштанов. Сколько килограммов набрал каждый из них?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранной Питером суммой.Затем Мэри и Люси выбрали $ 2x $ и $ x + 2 $ соответственно.
Итак,
$ x + 2x + x + 2 = 26
$ 4x = 24
$ x = 6 900 $ 21 Таким образом, Питер, Мэри и Люси выбрали 6, 12 и 8 кг соответственно.
Задача 3
София закончила $ \ frac {2} {3} $ книги. Она подсчитала, что закончила на 90 страниц больше, чем еще не прочитала. Как долго ее книга?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет общим количеством страниц в книге, тогда она закончила $ \ frac {2} {3} \ cdot x $ страниц.
Тогда у нее осталось $ x- \ frac {2} {3} \ cdot x = \ frac {1} {3} \ cdot x $ страниц.
$ \ frac {2} {3} \ cdot x- \ frac {1} {3} \ cdot x = 90 $
$ \ frac {1} {3} \ cdot x = 90 $
$ x = 270 $
Итак, в книге 270 страниц.
Задача 4
Поле можно обработать 6 тракторами за 4 дня. Когда 6 тракторов работают вместе, каждый из них пашет.
120 га в сутки. Если два трактора были перенесены на другое поле,
тогда оставшиеся 4 трактора могут вспахать то же поле за 5 дней.Сколько гектаров в день будет обрабатывать один трактор?
Нажмите, чтобы увидеть решение
Решение:
Если каждый из тракторов за 6 долларов пашет 120 долларов гектаров в день, и они завершат работу за 4 доллара.
дней, то все поле будет: 120 $ \ cdot 6 \ cdot 4 = 720 \ cdot 4 = 2880 $ га. Давайте
предположим, что каждый из четырех тракторов обрабатывал $ x $ гектаров в день. Таким образом, за 5 дней вспахано
$ 5 \ cdot 4 \ cdot x = 20 \ cdot x $ га, что равняется площади всего поля, 2880 га.
Итак, получаем $ 20x = 2880 $
$ x = \ frac {2880} {20} = 144 $. Таким образом, каждый из четырех тракторов будет обрабатывать 144 гектара в день.
Задача 5
Студент выбрал число, умножил его на 2, затем вычел 138 из результата и получил 102. Какое число он выбрал?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранным им числом, тогда
$ 2 \ cdot x — 138 = 102 $
$ 2x = 240 $
$ x = 120 $
Задача 6
Я выбрал число и разделил его на 5.Затем я вычел из результата 154 и получил 6. Какое число я выбрал?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранным мной числом, тогда
$ \ frac {x} {5} -154 = 6 $
$ \ frac {x} {5} = 160 $
$ x = 800 $
Задача 7
Расстояние между двумя городами 380 км. В этот же момент легковой автомобиль и грузовик начинают движение навстречу друг другу из
разные города. Они встречаются через 4 часа. Если автомобиль движется на 5 км / ч быстрее грузовика, какова их скорость?
Нажмите, чтобы увидеть решение
Решение:
Основная идея, используемая в задачах такого типа, заключается в том, что расстояние равно скорости, умноженной на время $ S = V \ cdot t $.
| В (км / ч) | т (час) | S (км) | |
| Автомобиль | х + 5 | 4 | 4 (х +5) |
| Грузовик | Х | 4 | 4x |
4 $ (x + 5) + 4x = 380
$ 4x + 4x = 380-20 $
$ 8x = 360 $
$ x = \ frac {360} {8}
$ x = 45
$
Следовательно, скорость грузовика составляет 45 долларов за км / час, а скорость автомобиля — 50 долларов за км / час.
Задача 8
Одна сторона прямоугольника на 3 см короче другой стороны. Если увеличить длину каждой стороны на 1 см, то площадь прямоугольника
увеличится на 18 см 2 . Найдите длины всех сторон.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет длиной большей стороны $ x \ gt 3 $, тогда длина другой стороны будет $ x-3 $ см. Тогда площадь S 1 = x (x — 3) см 2 .
После увеличения длины сторон они станут $ (x +1) $ и $ (x — 3 + 1) = (x — 2) $ см в длину.2 + x — 2x — 2
$ 2x = 20
$ x = 10 $.
Итак, стороны прямоугольника равны $ 10 $ см и $ (10 — 3) = 7 $ см в длину.
Задача 9
В первый год две коровы дали 8100 литров молока. Второй год их производство увеличилось.
на 15% и 10% соответственно, а общее количество молока увеличилось до
9100 литров в год. Сколько литров молока давалось от каждой коровы за год?
Нажмите, чтобы увидеть решение
Решение:
Пусть x будет количеством молока первой коровы.
произведен в течение первого года.Затем вторая корова в тот год произвела (8100 — x) литров молока. На второй год каждая корова произвела
столько же молока, сколько в первый год плюс прибавка на 15 \% $ или 10 \% $.
Итак, 8100 $ + \ frac {15} {100} \ cdot x + \ frac {10} {100} \ cdot (8100 — x) = 9100 $
Следовательно, 8100 $ + \ frac {3} {20} x + \ frac {1} {10} (8100 — x) = 9100 $
$ \ frac {1} {20} x = 190 $
$ x = 3800 $
Следовательно,
коровы дали 3800 и 4300 литров молока в первый год и 4370 долларов и 4730 долларов за литр молока во второй год, соответственно.
Проблема 10
расстояние между станциями A и B — 148 км. Экспресс отправился со станции A в сторону станции B со скоростью 80 км / ч. В то же
В это время товарный поезд покинул станцию B в сторону станции A со скоростью 36 км / час. Они встретились на станции C в 12 часов, и к тому времени
экспресс остановился на промежуточной станции на 10 мин, а грузовой поезд остановился на 5 мин. Найдите:
а) Расстояние между станциями C и B.
б) Время, когда грузовой поезд покинул станцию B.
Нажмите, чтобы увидеть решение
Решение
a) Пусть x будет расстоянием между
станции B и C. Тогда расстояние от станции C до станции A составляет $ (148 — x) $ км. К моменту встречи на станции C экспресс
ехал $ \ frac {148-x} {80} + \ frac {10} {60} $ часов, а грузовой поезд ехал $ \ frac {x} {36} + \ frac {5} {60} $ часов . Поезда ушли одновременно, так что:
$ \ frac {148 — x} {80} + \ frac {1} {6} = \ frac {x} {36} + \ frac {1} {12} $. Общий знаменатель чисел 6, 12, 36, 80 равен 720.Тогда
$ 9 (148 — x) +120 = 20x + 60 $
$ 1332 — 9x + 120 = 20x + 60 $
$ 29x = 1392 $
$ x = 48 $.
Следовательно, расстояние между станциями B и C составляет 48 км.
б) К моменту встречи на станции С фрахт
поезд ехал $ \ frac {48} {36} + \ frac {5} {60} $ часов, то есть 1 доллар в час и 25 долларов в минуту.
Следовательно, он покинул станцию B на отметке $ 12 — (1 + \ frac {25} {60}) = 10 + \ frac {35} {60} $ часов, то есть в 10:35.
Задача 11
Сьюзен едет из города А в город Б.После двух часов езды она
заметила, что она преодолела 80 км и подсчитала, что если она
двигаясь с той же скоростью, она опаздывала на 15 минут. Так
она увеличила скорость на 10 км / ч и прибыла в город B на 36 минут раньше
чем она планировала.
Найдите расстояние между городами A и B.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет расстоянием между A и B. Поскольку Сьюзен преодолела 80 км за 2 часа, ее скорость составила $ V = \ frac {80} {2} = 40 $ км / час.
Если бы она продолжила движение с той же скоростью, то опоздала бы на 15 $ минут, т.е. запланированное время в пути составляет $ \ frac {x} {40} — \ frac {15} {60} $ hr.
Остальное расстояние $ (x — 80) $ км. $ V = 40 + 10 = 50 $ км / час.
Итак, она преодолела расстояние между A и B за $ 2 + \ frac {x — 80} {50} $ ч, и это оказалось на 36 минут меньше, чем планировалось.
Таким образом, запланированное время было $ 2 + \ frac {x -80} {50} + \ frac {36} {60} $.
Когда мы выравниваем выражения для запланированного времени, мы получаем уравнение:
$ \ frac {x} {40} — \ frac {15} {60} = 2 + \ frac {x -80} {50} + \ frac {36} {60} $
$ \ frac {x — 10} {40} = \ frac {100 + x — 80 + 30} {50} $
$ \ frac {x — 10} {4} = \ frac {x +50} {5} $
$ 5x — 50 = 4x + 200 $
$ x = 250 $
Итак, расстояние между городами A и B составляет 250 км.
Задача 12
Чтобы доставить заказ вовремя, предприятие должно производить 25 деталей в день. После изготовления 25 частей в день по 3
дней компания начала производить на 5 деталей больше в день, а к последнему дню работы было произведено на 100 деталей больше, чем планировалось.
Узнайте, сколько деталей изготовила компания и сколько дней это заняло.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством дней, в течение которых компания проработала. Тогда 25x — это
количество деталей, которые они планировали сделать.При новом уровне добычи они
сделано:
$ 3 \ cdot 25 + (x — 3) \ cdot 30 = 75 + 30 (x — 3) $
Следовательно: 25 $ x = 75 + 30 (x -3) — 100 $
$ 25x = 75 + 30x -90 — 100 $
$ 190 -75 = 30x -25 $
$ 115 = 5x $
$ x = 23 $
Итак, компания проработала 23 дня, и они заработали 23 $ \ cdot 25 + 100 = 675 $ штук.
Задача 13
В седьмом классе 24 ученика. Решили посадить на заднем дворе школы березы и розы. Пока каждая девочка посадила по 3
роз, каждые три мальчика посадили по 1 берёзе.К концу дня они посадили растения за 24 доллара. Сколько берез и роз было посажено?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством роз. Тогда количество берез составляет 24 $ — x $, а количество мальчиков — $ 3 \ times (24-x) $. Если каждая девочка посадила 3
роз, в классе $ \ frac {x} {3} $ девочек.
Мы знаем, что в классе 24 ученика. Следовательно, $ \ frac {x} {3} + 3 (24 — x) = 24 $
$ x + 9 (24 — x) = 3 \ cdot 24 $
$ x +216 — 9x = 72 $
$ 216 — 72 = 8x $
$ \ frac {144} {8} = x $
$ x = 18 $
Итак, ученики посадили 18 роз и 24 — x = 24 — 18 = 6 берез.
Задача 14
Автомобиль выехал из города A в сторону города B, двигаясь со скоростью V = 32 км / час. После 3 часов в пути водитель остановился на 15 минут в городе C.
на закрытой дороге ему пришлось изменить маршрут, увеличив поездку на 28 км. Он увеличил скорость до V = 40 км / час, но все равно опоздал на 30 минут. Находим:
а) Расстояние, которое преодолела машина.
b) Время, которое потребовалось, чтобы добраться от C до B.
Щелкните, чтобы увидеть решение
Решение:
Из постановки задачи мы не знаем, была ли 15-минутная остановка в городе C запланирована или она была запланирована.
непредвиденный.Итак, мы должны рассмотреть оба случая.
1 корпус . Остановка была запланирована. Рассмотрим только поездку из C в B, и пусть $ x $ будет количеством часов, в течение которых водитель
потратил на эту поездку.
Тогда расстояние от C до B равно $ S = 40 \ cdot x $
км. Если бы водитель мог использовать первоначальный маршрут, ему потребовалось бы $ x — \ frac {30} {60} = x — \ frac {1} {2} $ часов, чтобы проехать от C до B. Расстояние от C до B.
согласно первоначальному маршруту $ (x — \ frac {1} {2}) \ cdot 32 $ км, и это
расстояние на $ 28 $ км короче, чем $ 40 \ cdot x $ км.Тогда у нас есть уравнение
$ (x — 1/2) \ cdot 32 + 28 = 40x $
$ 32x -16 +28 = 40x $
$ -8x = -12 $
$ 8x = 12 $.
$ x = \ frac {12} {8} $
$ x = 1 \ frac {4} {8} = 1 \ frac {1} {2} = 1 \ frac {30} {60} = 1 час. 30 минут.
Итак, автомобиль преодолел расстояние от C до B за 1 час 30 минут.
Расстояние от A до B составляет $ 3 \ cdot 32 + \ frac {12} {8} \ cdot 40 = 96 + 60 = 156 $ км.
2-й корпус. Водитель не планировал остановку в C. Предположим, ему потребовалось $ x $ часов.
добраться из Ц в Б.Тогда расстояние $ S = 40 \ cdot x $ км. Потребовалось $ x — \ frac {30} {60} — \ frac {15} {60} = x — \ frac {45} {60} = x — \ frac {3} {4} $ h, чтобы проехать от C к Б.
расстояние от C до B составляет $ 32 (x — \ frac {3} {4}) $ км, что на $ 28 $ км короче, чем $ 40 \ cdot x $, т.е.
$ 32 (x — \ frac {3} {4}) + 28 = 40x $
$ 32x — 24 +28 = 40x $
$ 4 = 8x $
$ x = \ frac {1} {2} \ text {hr} \ cdot x = 30 \ text {min}. $ Тогда Время в пути из С в Б — 30 мин.
Пройденное расстояние равно $ 3 \ cdot32 + \ frac {1} {2} \ cdot 40 = 96 + 20 = 116 км $.
Задача 15
Если фермер хочет вовремя вспахивать сельскохозяйственное поле, он должен вспахивать 120 гектаров в день. По техническим причинам он пахал всего 85 гектаров в день, следовательно, ему пришлось пахать на 2 дня больше, чем планировалось, и он
осталось еще 40 га. Какова площадь фермерского поля и сколько дней фермер изначально планировал работать?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством дней в первоначальном плане. Таким образом, все поле составляет 120 $ \ cdot x $ га.Фермеру приходилось работать x + 2 доллара в день, и он
вспахали 85 долларов (x + 2) гектаров, оставив 40 гектаров невыпаханными. Тогда у нас есть уравнение:
$ 120x = 85 (x + 2) + 40 $
$ 35x = 210 $
$ x = 6 $.
Итак, фермер планировал завершить работу за 6 дней, а площадь фермерского поля составляет 120 $ \ cdot 6 = 720 $ гектаров.
Задача 16
Столяр обычно делает определенное количество
запчасти за 24 дня. Но он смог увеличить свою производительность на 5 деталей в день, и поэтому он
не только закончил работу всего за 22 дня, но и сделал 80 дополнительных деталей.Сколько частей
плотник обычно делает в день, а сколько штук он делает за 24 дня?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством деталей, которые плотник обычно изготавливает ежедневно. За 24 дня он заработал $ 24 \ cdot x $ штук. Его новая дневная норма производства составляет x + 5 долларов за штуку и в
$ 22 $ дней он сделал $ 22 \ cdot (x + 5) $ деталей. Это на 80 больше, чем $ 24 \ cdot x $. Следовательно
уравнение:
$ 24 \ cdot x + 80 = 22 (x +5) $
$ 30 = 2x $
$ x = 15 $
Обычно он делает 15 деталей в день, а за 24 дня он зарабатывает 15 $ \ cdot 24 = 360 $ частей.
Задача 17
Байкер преодолел половину расстояния между двумя городами за 2 часа 30 минут.
После этого он увеличил скорость на 2 км / час. Вторую половину дистанции он преодолел за 2 часа 20 минут. Найдите расстояние между двумя городами
и начальная скорость байкера.
Нажмите, чтобы увидеть решение
Решение:
Пусть x км / час будет начальной скоростью
байкером, то его скорость во второй части поездки составляет x + 2 км / час.
Половина расстояния между двумя городами равна $ 2 \ frac {30} {60} \ cdot x $ км и $ 2 \ frac {20} {60} \ cdot (x + 2) $ км.Из уравнения: $ 2 \ frac {30} {60} \ cdot x = 2 \ frac {20} {60} \ cdot (x + 2) $
получаем $ x = 28 $ км / час.
Начальная скорость байкера — 28 км / ч.
Половина расстояния между двумя городами составляет
$ 2 ч 30 мин \ раз 28 = 2,5 \ раз 28 = 70 $.
Итак, расстояние 2 $ \ умноженное на 70 = 140 $ км.
Задача 18
Поезд преодолел половину расстояния между станциями A и B со скоростью 48 км / час, но затем ему пришлось остановиться на 15 мин. Составить
из-за задержки он увеличил свою скорость на $ \ frac {5} {3} $ м / сек и прибыл на станцию B вовремя.Найдите расстояние между двумя станциями и скорость поезда после остановки.
Нажмите, чтобы увидеть решение
Решение:
Сначала определим скорость поезда после остановки. Скорость
было увеличено на $ \ frac {5} {3} $ м / сек $ = \ frac {5 \ cdot 60 \ cdot 60} {\ frac {3} {1000}} $ км / час = $ 6 $ км / час. Следовательно
новая скорость 48 $ + 6 = 54 $ км / час. Если на покрытие первого
половины расстояния, то на преодоление расстояния требуется $ x — \ frac {15} {60} = x — 0,25 $ ч.
вторая часть.
Итак, уравнение: $ 48 \ cdot x = 54 \ cdot (x — 0,25) $
$ 48 \ cdot x = 54 \ cdot x — 54 \ cdot 0,25 $
$ 48 \ cdot x — 54 \ cdot x = — 13,5 $
$ -6x = — 13,5 $
$ x = 2,25 $ ч.
Все расстояние составляет
$ 2 \ умножить на 48 \ умножить на 2,25 = 216 $ км.
Задача 19
Элизабет может выполнить определенную работу за 15 дней, а Тони — только 75%.
эта работа в одно и то же время. Тони работал один в течение нескольких дней, а затем к нему присоединилась Элизабет, так что они закончили остаток работы.
работа за 6 дней, работаем вместе.
Сколько дней проработал каждый из них и какой процент работы каждый из них выполнил?
Нажмите, чтобы увидеть решение
Решение:
Сначала мы найдем дневную производительность каждого рабочего. Если мы рассмотрим
всю работу как единицу (1), Элизабет выполняет $ \ frac {1} {15} $ работы в день, а Тони выполняет 75 \% $ из $ \ frac {1} {15} $, т.е.
$ \ frac { 75} {100} \ cdot \ frac {1} {15} = \ frac {1} {20} $. Предположим, что Тони работал один
за $ x $ дней. Затем он в одиночку выполнил $ \ frac {x} {20} $ всей работы.За работой
вместе в течение 6 дней двое рабочих закончили $ 6 \ cdot (\ frac {1} {15} + \ frac {1} {20}) = 6 \ cdot \ frac {7} {60} = \ frac {7} { 10} $ работы.
Сумма $ \ frac {x} {20} $ и $ \ frac {7} {10} $ дает нам всю работу, то есть $ 1 $. Получаем уравнение:
$ \ frac {x} {20} + \ frac {7} {10} = 1 $
$ \ frac {x} {20} = \ frac {3} {10} $
$ х = 6 $. Тони проработал 6 + 6 = 12 дней
и Элизабет работала за 6 долларов в день. Часть работы сделана
это $ 12 \ cdot \ frac {1} {20} = \ frac {60} {100} = 60 \% $ для Тони и $ 6 \ cdot \ frac {1} {15} = \ frac {40} {100} = 40 \% $ для Элизабет.
Задача 20
Фермер планировал вспахать поле, выполнив 120
га в сутки. После двух дней работы он увеличил свою дневную производительность на 25% и закончил работу на два дня раньше срока.
а) Какова площадь поля?
б) За сколько дней фермер выполнил свою работу?
c) Через сколько дней фермер планировал завершить работу?
Нажмите, чтобы увидеть решение
Решение:
Прежде всего мы найдем новую суточную производительность
фермер в гектарах в сутки: 25% от 120 гектаров
$ \ frac {25} {100} \ cdot 120 = 30 $ га, поэтому 120 $ + 30 = 150 $ га
новая ежедневная продуктивность.Пусть x будет запланированным количеством
дней, отведенных на работу. Тогда хозяйство будет 120 \ cdot x $ га. На
с другой стороны, мы получим ту же площадь, если добавим 120 $ \ cdot 2 $ гектаров к
150 $ (х -4) $ га. Тогда мы получаем уравнение:
$ 120x = 120 \ cdot 2 + 150 (x -4) $
$ x = 12 $
Итак, изначально предполагалось, что работа займет 12 дней, но на самом деле поле было вспахано за 12-2 дней. = 10 дней.
Площадь поля 120 $ \ cdot 12 = 1440 $ га.
Задача 21
Чтобы покосить травяное поле, бригада косилок планировала обрабатывать 15 гектаров в день.Через 4 рабочих дня они увеличили дневную производительность на
$ 33 \ times \ frac {1} {3} \% $ и закончил работу на 1 день раньше запланированного срока.
A) Какова площадь травяного поля?
Б) Сколько дней понадобилось, чтобы косить все поле?
C) Сколько дней изначально было запланировано для этой работы?
Подсказка : Смотрите задачу 20 и решайте сами.
Ответ: А) 120 га; Б) 7 дней; В) 8 дней.
Задача 22
Поезд идет от станции A до станции B.Если поезд отправляется со станции А
со скоростью 75 км / час, прибывает на станцию B на 48 минут раньше запланированного. Если бы он двигался со скоростью 50 км / час, то к запланированному времени прибытия бы
осталось еще 40 км до станции B. Найти:
A) Расстояние между двумя станциями;
B) Время, необходимое поезду, чтобы добраться из пункта A в пункт B по расписанию;
C) Скорость поезда по расписанию.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет запланированным временем поездки из пункта А в пункт Б.Тогда расстояние
между A и B можно найти двумя способами. С одной стороны, это расстояние составляет $ 75 (x — \ frac {48} {60}) $ км. С другой стороны, это 50 $ + 40 $ км. Таким образом, мы получаем уравнение:
$ 75 (x — \ frac {48} {60}) = 50x + 40 $
$ x = 4 $ час — это запланированное время в пути. В
расстояние между двумя станциями 50 $ \ cdot 4 + 40 = 240 $ км. Тогда скорость, которую поезд должен поддерживать, чтобы идти по расписанию, составляет $ \ frac {240} {4} = 60 $ км / час.
Задача 23
Расстояние между городами A и B составляет 300 км.Один поезд отправляется из города А, а другой — из города.
город B, оба уезжают в один и тот же момент времени и направляются друг к другу. Мы знаем, что один из них на 10 км / час быстрее другого. Находить
скорости обоих поездов, если через 2 часа после отправления расстояние между ними составляет 40 км.
Нажмите, чтобы увидеть решение
Решение:
Пусть скорость более медленного поезда будет $ x $ км / час. Тогда скорость
более быстрый поезд стоит (x + 10) $ км / час. За 2 часа они преодолевают 2x $ км и 2 (x +10) $ км соответственно.Поэтому, если они еще не встретились, весь
расстояние от A до B составляет $ 2x + 2 (x +10) +40 = 4x + 60 $ км. Однако если
они уже встретились и продолжили движение, расстояние будет $ 2x + 2 (x + 10) — 40 = 4x — 20 $ км.
Таким образом, мы получаем следующие уравнения:
$ 4x + 60 = 300 $
$ 4x = 240 $
$ x = 60 $ или
$ 4x — 20 = 300 $
$ 4x = 320 $
$ x = 80 $
Отсюда скорость более медленного поезда составляет 60 долларов США км / час или 80 долларов США км / час, а скорость
более быстрый поезд стоит 70 долларов за км / час или 90 долларов за км / час.
Задача 24
Автобус едет из города А в город Б.Если скорость автобуса составляет 50 км / час, он прибудет в город B на 42 минуты позже запланированного срока. Если автобус увеличивается
его скорость составляет $ \ frac {50} {9} $ м / сек, он прибудет в город B на 30 минут раньше запланированного срока. Находим:
A) Расстояние между двумя городами;
B) Планируемое время прибытия автобуса в B;
C) Скорость автобуса по расписанию.
Нажмите, чтобы увидеть решение
Решение:
Сначала определим скорость автобуса после ее увеличения. Скорость
увеличено на $ \ frac {50} {9} $ м / сек $ = \ frac {50 \ cdot60 \ cdot60} {\ frac {9} {1000}} $ км / час $ = 20 $ км / час.Следовательно, новая скорость составляет $ V = 50 + 20 = 70 $ км / час. Если $ x $ — количество часов по расписанию, то со скоростью 50
км / ч автобус едет из пункта A в пункт B за $ (x + \ frac {42} {60}) $ час. Когда скорость автобуса составляет $ V = 70 $ км / час, время в пути составляет $ x — \ frac {30} {60} $ час. потом
$ 50 (x + \ frac {42} {60}) = 70 (x- \ frac {30} {60}) $
$ 5 (x + \ frac {7} {10}) = 7 (x- \ frac { 1} {2}) $
$ \ frac {7} {2} + \ frac {7} {2} = 7x -5x $
$ 2x = 7 $
$ x = \ frac {7} {2} $ час.
Итак, автобус должен проехать 3 доллара за час 30 долларов за минуту.
Расстояние между двумя городами составляет $ 70 (\ frac {7} {2} — \ frac {1} {2}) = 70 \ cdot 3 = 210 $ км, а запланированная скорость составляет $ \ frac {210} {\ гидроразрыв {7} {2}} = 60 $ км / час.
Онлайн-курс алгебры для средней школы | Математика в 8 классе
Этот список является репрезентативным для материалов, предоставленных или используемых в этом курсе. Имейте в виду, что фактически используемые материалы могут отличаться в зависимости от школы, в которую вы записаны, и от того, проходите ли вы курс как независимое обучение.
Чтобы получить полный список материалов, которые будут использоваться в этом курсе вашим зачисленным студентом, посетите MyInfo . Все списки могут быть изменены в любое время.
Объем и последовательность: Документы «Объем и последовательность» описывают , что охватывает курс (объем), а также порядок , в котором рассматриваются темы (последовательность). В этих документах перечислены учебные цели и навыки, которые необходимо освоить.K12 Объем и последовательность документов для каждого курса включают:
Обзор курса
Студенты развивают беглость алгебры, приобретая навыки, необходимые для решения уравнений и выполнения операций с числами, переменными, уравнениями и неравенствами. Они также изучают основные понятия абстракции и обобщения, которые делает возможной алгебра. Студенты учатся использовать числовые свойства для упрощения выражений или обоснования утверждений; описывать множества с обозначением множеств и находить объединение и пересечение множеств; упрощать и оценивать выражения, включающие переменные, дроби, показатели степени и радикалы; работать с целыми числами, рациональными числами и иррациональными числами; создавать графики и решать уравнения, неравенства и системы уравнений.Они учатся определять, является ли отношение функцией, и как описывать его область и диапазон; использовать факторинг, формулы и другие методы для решения квадратных и других полиномиальных уравнений; формулировать и оценивать достоверные математические аргументы, используя различные типы рассуждений; и преобразовать текстовые задачи в математические уравнения, а затем использовать уравнения для решения исходных задач. Ожидается, что студенты, изучающие алгебру, овладеют навыками и концепциями, представленными в курсе предварительной алгебры K12 (или его эквиваленте).
вернуться наверх
Краткое содержание курса
СЕМЕСТР ОДИН
Раздел 1: Основы алгебры
Английское слово algebra и испанское слово algebrista происходят от арабского слова al-jabr , что означает «восстановление». В средневековье цирюльник часто называл себя альгебристом. Альгебрист также был костоправом, который восстанавливал или фиксировал кости. Сегодня математики используют алгебру для решения задач.Алгебра может находить решения и «исправлять» определенные проблемы, с которыми вы сталкиваетесь.
- Введение в семестр
- Выражений
- Переменные
- Перевод слов в переменные выражения
- Уравнения
- Перевод слов в уравнения
- Запасные наборы
- Решение проблем
Раздел 2: Свойства действительных чисел
Есть много разных типов чисел. Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел.Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
- Номер строки
- Наборы
- Сравнение выражений
- Количество объектов недвижимости
- Измерение, точность и оценка
- Распределительная собственность
- Алгебраическое доказательство
- Противоположности и абсолютное значение
Раздел 3: Операции с действительными числами
Есть много разных типов чисел.Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел. Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
- Дополнение
- Вычитание
- Умножение
- Взаимные и деление
- : проблемы с числами
Приложения
Раздел 4: Решение уравнений
Греческого математика Диофанта часто называют «отцом алгебры».В его книге «Арифметика » описаны решения 130 проблем. Он не открыл все эти решения сам, но он собрал множество решений, которые были найдены греками, египтянами и вавилонянами до него. Некоторым людям давным-давно явно нравилось заниматься алгеброй. Это также помогло им — и может помочь вам — решить множество реальных проблем.
- Уравнения сложения и вычитания
- Уравнения умножения и деления
- Узоры
- Множественные преобразования
- Переменные с обеих сторон уравнения
- Формулы преобразования
- Оценка решений
- Стоимость проблем
Раздел 5: Устранение неравенств
Каждый математик знает, что 5 меньше 7, но когда y Что общего между чертежом в масштабе, шестерней велосипеда и распродажей в местном магазине? Все они представляют проблемы, которые можно решить с помощью уравнений с дробями. Приложения Вы, наверное, слышали фразу: «Вот где я провожу черту!» В алгебре это выражение можно понимать буквально.Линейные функции и их графики играют важную роль в нескончаемом стремлении к моделированию реального мира. При встрече два человека часто обмениваются рукопожатием или здороваются.Как только они начнут разговаривать друг с другом, они смогут узнать, что у них общего. Что происходит, когда встречаются две линии? Они что-нибудь говорят? Наверное, нет, но всякий раз, когда встречаются две линии, вы знаете, что у них есть по крайней мере одна общая точка. Определение точки, в которой они встречаются, может помочь вам решить проблемы в реальном мире. Солнечная батарея — это небольшая машина, которая поглощает солнечную энергию и вырабатывает электричество.Математическая функция — это машина, которая принимает число на входе и производит другое число на выходе. Есть много видов функций. У некоторых есть графики, которые выглядят как линии, в то время как у других есть графики, которые изгибаются как парабола. Функции также могут принимать другие формы. Не у каждой функции есть график, похожий на линию или параболу. Не у каждой функции есть уравнение. Важно помнить, что если вы поместите какой-либо действительный ввод в функцию, вы получите единственный результат. Рациональные числа очень уравновешенные? Сложно ли рассуждать с иррациональными числами? Не совсем, но у рациональных и иррациональных чисел есть что-то общее и то, что их отличает. Подобно тому, как поезд строится из соединения вагонов, полином строится путем объединения терминов и их связывания знаками плюс или минус.Вы можете выполнять основные операции с многочленами так же, как вы складываете, вычитаете, умножаете и делите числа. Многочлен — это выражение, в котором есть переменные, представляющие числа. Число может быть разложено на множители, так что вы должны иметь возможность разложить на множители многочлен, верно? Иногда можно, а иногда нет.Поиск способов записать многочлен как произведение множителей может быть весьма полезным. Решение уравнений может помочь вам найти ответы на многие проблемы повседневной жизни.Линейные уравнения обычно имеют одно решение, но как насчет квадратных? Как их решить и как выглядят решения? Приложения Приложения У дроби всегда есть число в числителе и знаменателе.Однако на самом деле эти числа могут быть выражениями, представляющими числа, а это значит, что вы можете делать с дробями всевозможные интересные вещи. Дроби с переменными выражениями в числителе и знаменателе могут помочь вам решить многие проблемы. Профессионалы используют логические рассуждения по-разному.Подобно тому, как юристы используют логические рассуждения для формулирования убедительных аргументов, математики используют логические рассуждения для формулирования и доказательства теорем. Освоив использование индуктивного и дедуктивного рассуждений, вы сможете приводить и понимать аргументы во многих областях. Пример счетчика Два дополнительных раздела обеспечивают дополнительную курсовую работу.«Измерение и геометрия» предоставляет некоторые из основных предметов для начинающих студентов-геометров, а «Счет, вероятность и статистика» обеспечивает прочную основу для дальнейших исследований в области статистики и вероятности. Тесселяция — это способ повторения формы снова и снова, чтобы покрыть плоскую поверхность. Художник Мауриц Корнелис (М.К.) Эшер был очарован мозаикой. Он использовал мозаику и геометрические идеи, такие как точки, сегменты, углы и конгруэнтность, чтобы создать множество красивых и интересных произведений искусства. Сколько кукурузы может получить фермер с акра земли? Какие страны экспортируют больше всего кукурузы? Как цена на кукурузу изменилась с течением времени и как она изменится в будущем? Данные повсюду вокруг нас.Хорошо понимая вероятность и статистику, люди могут принимать более обоснованные решения. наверх Всего уроков: вернуться наверх Вы здесь: На главную → Рабочие листы → Линейные уравнения Здесь вы найдете неограниченное количество распечатываемых рабочих листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html.Вы можете настроить рабочие листы, включив в них одношаговые, двухэтапные или многоступенчатые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Рабочие листы подходят для курсов предварительной алгебры и алгебры 1 (6-9 классы). Вы можете выбрать из СЕМЬ основных типов уравнений, от простых до сложных, описанных ниже (например, одношаговые уравнения, переменные с обеих сторон или необходимость использования свойства распределения). Настройте рабочие листы, используя генератор ниже. Каждый рабочий лист генерируется случайным образом и поэтому уникален.Ключ ответа генерируется автоматически и помещается на вторую страницу файла. Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — и то, и другое легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Сделать рабочий лист html ». Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе. Иногда созданный рабочий лист не совсем то, что вам нужно. Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами: Формат Рабочие листы для упрощения выражений Рабочие листы для вычисления выражений с переменными Рабочие листы для написания выражений с переменными из словесных выражений Рабочие листы по линейным неравенствам Ключ к учебным пособиям по алгебре Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй.Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 расширяют охват действительной системы счисления. => Узнать больше Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон Или заполните форму ниже: Раздел 6: Применение дробей
Раздел 7: Линейные уравнения и неравенства
Раздел 8: Системы уравнений
Раздел 9: Обзор семестра и тест
СЕМЕСТР ВТОРОЙ
Раздел 1: Взаимосвязи и функции
Раздел 2: Рационалы, иррациональные элементы и радикалы
Раздел 3: Работа с многочленами
Раздел 4: Факторинговые многочлены
Раздел 5: Квадратичные уравнения
Раздел 6: Рациональные выражения
Раздел 7: Логика и рассуждение
Раздел 8: Обзор семестра и тест
ДОПОЛНИТЕЛЬНЫЕ УСТАНОВКИ
A – 1: Измерение и геометрия
A – 2: Подсчет, вероятность и статистика
Количество уроков и расписание
Бесплатные рабочие листы по линейным уравнениям (6-9 классы, предалгебра, алгебра 1)
Основные инструкции к рабочим листам
Рабочие листы готовые
См. Также
Операции и алгебраическое мышление — MAP 8th Grade Math
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
в виде
ChillingEffects.org.
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Решение многоступенчатых линейных уравнений | Purplemath
Purplemath
На предыдущих двух страницах мы рассмотрели решение одношаговых линейных уравнений; то есть уравнения, которые требуют одного сложения или вычитания или требуют одного умножения или деления.Однако для решения большинства линейных уравнений требуется более одного шага. Какие шаги следует предпринять и в каком порядке?
Для многоступенчатых линейных уравнений мы будем использовать те же шаги, что и ранее; единственная разница в том, что мы не закончим после одного шага. Нам все равно придется сделать еще хотя бы один шаг. В каком порядке нужно делать эти шаги? Что ж, это будет меняться в зависимости от уравнения, но есть несколько общих рекомендаций, которые могут оказаться полезными.
MathHelp.com
Переменная находится в левой части (LHS) уравнения.Сейчас он умножается на семь, а затем к нему прибавляется два. Мне нужно отменить «семь раз» и «плюс два».
Нет правила о том, какую операцию «отменить» я должен выполнить в первую очередь. Однако, если я сначала разделю на 7, я определенно сделаю дроби. Лично я предпочитаю избегать дробей, если это возможно, поэтому я почти всегда делаю любой плюс / минус перед любым умножением / делением. В любом случае мне, возможно, придется иметь дело с дробями, но, по крайней мере, я могу отложить их до конца своей работы.
Начиная с «плюс два», я вычту два из каждой части уравнения. Только тогда я разделю на семь. Моя работа выглядит так:
7x + 2 = -54
-2 -2
————
7x = -56
— —
7 7
х = -8
Делая сначала плюс / минус, я избегал дробей.Как видите, в ответе не используются дроби, поэтому я сделал себе одолжение, сделав деление последним. Мое решение:
Форматирование вашего домашнего задания и демонстрация вашей работы способом, который я сделал выше, по моему опыту, достаточно универсально приемлемы. Однако (предупреждение!) Также неплохо переписать окончательный ответ в конце каждого упражнения, как показано (фиолетовым цветом) выше. Не ждите, что ваш оценщик потратит время на то, чтобы покопаться в вашей работе и попытаться понять, какой вы, вероятно, хотели ответить.Отформатируйте свою работу так, чтобы ее смысл был ясен.
В этом уравнении переменная (в левой части) умножается на минус пять, а затем из нее вычитается семерка. В надежде (как всегда!) Избежать дробей, я сначала добавлю семь к каждой стороне уравнения. Только тогда я разделю на минус пять. Моя работа выглядит так:
-5x — 7 = 108
+7 +7
————-
-5x = 115
— —
-5-5
х = -23
Я аккуратно показал свои работы.Сейчас однозначно перепишу свое решение по окончании работы:
Переменная (в левой части уравнения) умножается на тройку, а затем из нее вычитается девятка. Сначала я позабочусь о девяти, а затем о трех:
3x — 9 = 33
+9 +9
————
3x = 42
— —
3 3
х = 14
В этом случае, опять же, в моем решении нет дробей:
В этом уравнении у меня есть два члена в левой части, которые содержат переменные.Итак, мой первый шаг — объединить эти «похожие термины» слева. Тогда я могу решить:
Итак, теперь мое уравнение:
Даже если поначалу это могло показаться более сложным, на самом деле это одношаговое уравнение. Я решу, разделив на двенадцать:
12x = 72
— —
12 12
х = 6
Мой ответ:
В этом уравнении у меня есть члены с переменными по обе стороны от уравнения.Чтобы решить, мне нужно получить все эти переменные члены на одной стороне уравнения.
Нет правила, определяющего, какой из двух элементов мне следует переместить: 4 x или 6 x . Однако из опыта я узнал, что, чтобы избежать отрицательных коэффициентов для моих переменных, я должен переместить член x с меньшим коэффициентом. Это означает, что в данном случае я вычту 4 x из левой части в правую:
4x — 6 = 6x
-4x -4x
————-
-6 = 2x
И теперь у меня есть одношаговое уравнение, которое я решу, разделив его на два:
Мое решение:
В приведенном выше упражнении переменная (в моей работе) оказалась в правой части уравнения.Это нормально. Переменная не «обязательна», чтобы оказаться в левой части уравнения; мы просто привыкли видеть это там. Таким образом, результат «–3 = x » совершенно нормален и означает то же самое, что и « x = –3».
Однако (предупреждение!) Я слышал, что некоторые инструкторы настаивают на том, чтобы переменная помещалась в левую часть уравнения в окончательном ответе . (Нет, я не выдумываю.) Таким образом, даже если «–3 = x » совершенно верно в работе, эти инструкторы сочтут это «неправильным», если вы оставите ответ таким образом.Если у вас есть какие-либо сомнения относительно предпочтений вашего инструктора по форматированию, спросите сейчас.
Решить 8
x — 1 = 23-4 x
В этом уравнении у меня есть переменные по обе стороны от уравнения, а также свободные числа по обе стороны. Мне нужно получить переменные термины с одной стороны, а свободные числа — с другой.Поскольку я хотел бы избежать отрицательных коэффициентов для моих переменных, я перемещу меньшее из двух членов; а именно –4 x , который сейчас находится справа. Чтобы получить нечеткие числа на стороне, противоположной переменным членам, я перемещу –1, который в настоящее время находится в левой части. Не существует определенного «правильного» порядка выполнения этих шагов; поскольку они оба являются предметом сложения, люди обычно делают их вместе за один шаг. Сначала я сделаю переменные, а затем свободные числа:
8x — 1 = 23 — 4x
+ 4x + 4x
——————
12x — 1 = 23
+1 +1
————
12x = 24
На данный момент у меня есть одношаговое уравнение, для решения которого требуется одно деление:
12x = 24
— —
12 12
х = 2
Тогда мой ответ:
Если бы в приведенном выше описании я сделал первые два шага за один раз, это выглядело бы так:
8x — 1 = 23 — 4x
+ 4x +1 +1 + 4x
——————
12x = 24
— —
12 12
х = 2
Вероятно, когда вы только начинаете, делать каждый шаг отдельно.Но как только вы освоитесь с процессом (и надежно придете к правильным значениям), не стесняйтесь начинать комбинировать некоторые шаги.
Решить 5 + 4
x — 7 = 4 x -2 — x
Это уравнение очень запутанное! Прежде чем я смогу решить, мне нужно объединить одинаковые члены с обеих сторон уравнения:
5 + 4 x — 7 = 4 x -2 — x
(5-7) + 4 x = (4 x -1 x ) — 2
–2 + 4 x = 3 x — 2
Теперь, когда я упростил каждую часть уравнения, я могу решить.
-2 + 4x = 3x — 2
-3x -3x
——————
-2 + 1x = -2
+2 +2
——————
1x = 0
Я добавил (обычно неустановленный) 1 к члену переменной в правой части исходного уравнения, чтобы помочь мне отслеживать то, что я делал; это не «необходимо». И этого не ожидается в окончательном ответе, который правильно сформулирован как:
Для x вполне нормально иметь нулевое значение.Ноль — допустимое решение. Не говорите, что это уравнение «не имеет решения»; у него действительно есть решение, которое составляет x = 0.
Решить 0,2
x + 0,9 = 0,3 — 0,1 x
Это уравнение решает так же, как и все другие линейные уравнения, которые я сделал. Просто выглядит на хуже из-за десятичных знаков.Но это легко исправить!
Какое бы ни было наибольшее количество десятичных знаков в любом из коэффициентов, я могу умножить с обеих сторон на «1» с последующим этим количеством нулей. В этом случае у всех десятичных знаков есть один десятичный разряд, поэтому я умножу его на 10:
.
10 (0,2 x + 0,9) = 10 (0,3 — 0,1 x )
10 (0,2 x ) + 10 (0,9) = 10 (0,3) — 10 (0,1 x )
2 x + 9 = 3 — 1 x
Теперь я могу решить как обычно:
2x + 9 = 3 — 1x
+ 1x + 1x
——————
3х + 9 = 3
-9-9
————
3x = -6
— —
3 3
х = -2
Тот факт, что в исходном уравнении были десятичные знаки, не означает, что я застрял с ними.Сохраните этот трюк на потом; это пригодится.
Между прочим, если бы коэффициент с наибольшим количеством десятичных разрядов имел два десятичных знаков, то я бы умножил обе части уравнения на 100; для трех десятичных знаков я бы умножил на 1000; и так далее.
Решить
Крик! Дроби! Но, как и с десятичными знаками в предыдущем упражнении, мне не нужно зацикливаться на дробях.В этом случае я буду производить умножение, чтобы «очистить» знаменатели, что даст мне более удобное уравнение для решения.
Чтобы упростить вычисления для уравнений с дробями, я сначала умножу обе части на общий знаменатель различных дробей. Для этого уравнения общий знаменатель равен 12, поэтому я умножу все на 12 (или, при умножении на дробь, я умножу на
12/1):
Теперь работать с этим уравнением гораздо удобнее.Я продолжу свое решение, вычтя меньшие 2 x с любой стороны:
3x + 12 = 2x + 6
-2x -2x
——————
1x + 12 = 6
-12-12
——————
1x = -6
Я удалю 1 из переменной, когда напишу свой окончательный ответ:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении многоступенчатого линейного уравнения.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)
URL: https: //www.purplemath.com / modules / solvelin3.htm
Двухэтапная викторина по уравнениям
Решение и графическое отображение двухэтапных неравенств Стандарты CC 7.EE.4b Использование переменных для представления величин в реальных или математических задачах и построение простых уравнений и неравенств для решения реальных или математических задач. и построить простые уравнения и неравенства для решения проблем, рассуждая о величинах.
Решение уравнений 8 Решение многоступенчатых уравнений Так же, как автомобилю для движения требуется бензин, давайте потренируемся в некоторых необходимых навыках, прежде чем переходить к решению многоступенчатых уравнений.Упростите каждое выражение, используя свойство распределения и / или комбинируя похожие термины.
09 июля 2014 · Linear Equations — [6:05] видео объяснение уравнений в форме AX + B = C; Линейные уравнения в одной переменной — игровая викторина Quia, в которой учащимся предлагается решить одно- и двухэтапные линейные уравнения и простые алгебраические пропорции, чтобы выиграть 1 000 000 долларов. Модель
Двухэтапные уравнения Использование с Уроком 11-1 11-1 КЛЮЧЕВЫЕ ПОМНИТЕ • 0 • + 0 • В уравнении выражения с обеих сторон от знака равенства эквивалентны.В лабораторной работе 2–5 вы узнали, как решать одношаговые уравнения с использованием плиток алгебры. Вы также можете использовать плитки алгебры для решения двухэтапных уравнений. При решении двухэтапного уравнения проще всего выполнить
Двухэтапные уравнения Практические задачи с ответами — ChiliMath Рабочие листы с двухэтапными уравнениями содержат огромную коллекцию печатных страниц с практическими занятиями для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби.
