Содержание
Задачи по термодинамике с подробными решениями
Задачи по термодинамике с решениями
Изменение внутренней энергии при теплообмене. Теплота сгорания топлива.
5.1.1 Тело нагрелось на 5 К, поглотив 10 кДж теплоты. Чему равна его теплоемкость?
5.1.2 На сколько градусов нагреется вода массой 0,5 кг, если ей сообщить 16,8 кДж тепла?
5.1.3 Сколько тепла выделится при сгорании 2 кг бензина?
5.1.4 На сколько увеличилась внутренняя энергия 1 кг воды при нагревании её на 2 К?
5.1.5 Сколько тепла было передано льдинке массой 50 г, если она нагрелась на 3 К?
5.1.6 Какая установится температура воды после смешивания 39 л воды при 20 C и 21 л при 60 C?
5.1.7 Железный стержень массой 5 кг, нагретый до 550 C, опускается в воду. Сколько теплоты
5.1.8 Сколько литров воды при 100 C нужно добавить к воде при 20 C, чтобы получить
5.1.9 В стакане было 50 г воды при температуре 20 C. В него долили 100 г воды при температуре
5.1.10 Реактивный самолет пролетает с постоянной скоростью 250 м/с путь 1800 км, затрачивая
5. 1.11 Гусеничный трактор развивает номинальную мощность 60 кВт и при этой мощности
1.11 Гусеничный трактор развивает номинальную мощность 60 кВт и при этой мощности
5.1.12 В стакане имеется 250 г воды при температуре 80 C. На сколько понизится температура
5.1.13 Воду массой 4,65 кг, взятую при температуре 286 К, нагревают до 308 К погружением куска
5.1.14 Определить удельную теплоемкость трансформаторного масла, если для нагревания 5 т
5.1.15 Тепловая нагрузка горелки водонагревателя равна 25 МДж/ч, вместимость бака 80 л
5.1.16 В электрическом чайнике мощностью 800 Вт можно вскипятить 1,6 л воды, имеющей
5.1.17 Для закалки стальную деталь, нагретую до 1073 К, массой 0,5 кг опустили в воду массой 10 кг
5.1.18 Мощность, развиваемая двигателем самолета на скорости 900 км/ч, равна 3 МВт. При этом
5.1.19 Определите расход бензина автомобилем на 1 км пути при скорости 72 км/ч. Мощность
5.1.20 Горячее тело, температура которого 70 C, приведено в соприкосновение с холодным телом
5.1.21 Для экономии энергии стальной бак массой 4 кг заменили стальной сеткой массой 1,5 кг
5. 1.22 Смешали 24 кг цемента при температуре 5 C с 30 л воды при температуре 35 C. Определить
1.22 Смешали 24 кг цемента при температуре 5 C с 30 л воды при температуре 35 C. Определить
5.1.23 Для приготовления ванны необходимо смешать холодную воду при 11 C и горячую
5.1.24 Автомобиль расходует 5,67 кг бензина на 50 км пути. Определить мощность, развиваемую
5.1.25 Алюминиевый сосуд содержит 118 г воды при температуре 20 C. Кусок железа массой
5.1.26 Автомобиль, движущийся со средней скоростью 72 км/ч, развивает силу тяги 2500 Н
5.1.27 Определить КПД нагревателя, расходующего 80 г керосина на нагревание 3 л воды
5.1.28 На спиртовке нагревали воду массой 100 г от 16 до 71 C. При этом был сожжен спирт массой
5.1.29 Медное тело, нагретое до 100 C, опущено в воду, масса которой равна массе тела
5.1.30 На сколько километров пути хватит 40 л бензина автомобилю, движущемуся со скоростью
5.1.31 В ванне находится 400 л воды при температуре 30 C. Из крана вытекает горячая вода
5.1.32 Чтобы нагреть 1,8 кг воды от 18 C до кипения на горелке с КПД 25%, потребовалось
5. 1.33 У какого из тел теплоемкость больше и во сколько раз: у куска свинца массой 1 кг или
1.33 У какого из тел теплоемкость больше и во сколько раз: у куска свинца массой 1 кг или
5.1.34 Для определения удельной теплоёмкости 0,15 кг вещества, взятого при температуре 100 C
5.1.35 Сколько керосина необходимо сжечь, чтобы 50 л воды нагреть от 20 C до кипения? КПД
5.1.36 На зажженную спиртовку с КПД 60% поставили сосуд с 500 г воды при 20 C. Через какое
5.1.37 Какое количество керосина потребовалось бы сжечь, чтобы вывести спутник массой
5.1.38 Какую массу керосина потребовалось бы сжечь, чтобы вывести спутник массой 1000 кг
5.1.39 В стеклянный сосуд массой 120 г, имеющий температуру 20 C, налили горячую воду
5.1.40 В батарею водяного отопления вода поступает при 80 C по трубе площадью поперечного
5.1.41 Газовая нагревательная колонка потребляет 1,8 м3 метана (Ch5) в час. Найти температуру
5.1.42 Какую массу керосина нужно сжечь, чтобы вывести спутник массой 1000 кг на круговую
5.1.43 Некоторая установка, выделяющая мощность 30 кВт, охлаждается проточной водой
5. 1.44 Теплоизолированный сосуд разделен на две части перегородкой, не проводящей тепла
1.44 Теплоизолированный сосуд разделен на две части перегородкой, не проводящей тепла
5.1.45 Ванну емкостью 100 литров необходимо заполнить водой, имеющей температуру 30 C
5.1.46 В калориметр налили 500 г воды, имеющей температуру 40 C, и положили кусок льда
5.1.47 В сосуд, содержащий 1 кг льда при температуре 0 C, влили 330 г воды при температуре 50 C
5.1.48 Слой льда толщиной 4,2 см имеет температуру 0 C. Какова минимальная толщина слоя воды
5.1.49 В калориметр, содержащий 100 г льда при температуре 0 C, налили 150 г воды, имеющей
Фазовые переходы
5.2.1 Сколько требуется энергии для испарения 4 кг воды, взятой при температуре кипения?
5.2.2 Из 450 г водяного пара с температурой 373 К образовалась вода. Сколько теплоты
5.2.3 Сколько тепла выделится при конденсации 10 г пара и охлаждении получившейся воды
5.2.4 Монету из вещества с плотностью 9000 кг/м3 и удельной теплоёмкостью 0,22 кДж/(кг*К)
5.2.5 На сколько возрастёт потенциальная энергия взаимодействия между молекулами
5. 2.6 Кусок свинца массой 1,6 кг расплавился наполовину при сообщении ему количества
2.6 Кусок свинца массой 1,6 кг расплавился наполовину при сообщении ему количества
5.2.7 В теплоизолированном сосуде находится вода при 273 К. Выкачивая из сосуда воздух
5.2.8 На нагревание 5 кг воды от 303 К до кипения и на обращение в пар при температуре
5.2.9 Сколько было затрачено бензина в нагревателе с КПД 32%, если с его помощью 4 кг воды
5.2.10 При охлаждении 40 кг жидкого олова, взятого при температуре плавления 505 К
5.2.11 Нагретый алюминиевый куб положили на лёд, и он полностью погрузился в лёд. До какой
5.2.12 Водяной пар массой 200 кг при температуре 100 C пропустили через воду при температуре
5.2.13 Комок мокрого снега массой 0,3 кг поместили в 1,2 л воды при температуре 21 C. После того
5.2.14 В калориметре находится 1 кг льда при -40 C. В него впускают 1 кг пара при 120 C
5.2.15 Под невесомым поршнем в цилиндре находится 1 кг воды при температуре 0 C. В воду
5.2.16 Сколько энергии нужно затратить, чтобы 6 кг льда при -20 C обратить в пар
5. 2.17 В сосуд, содержащий 10 кг льда при 0 C, влили 3 кг воды при 90 C. Какая установится
2.17 В сосуд, содержащий 10 кг льда при 0 C, влили 3 кг воды при 90 C. Какая установится
5.2.18 В теплоизолированный сосуд малой теплоёмкости налили 0,4 кг воды при 293 К и положили
5.2.19 В холодильник, потребляющий мощность 200 Вт, поместили воду массой 2 кг
5.2.20 Через воду, имеющую температуру 10 C, пропускают водяной пар при 100 C. Сколько
5.2.21 Струя стоградусного водяного пара направляется на кусок льда массой 10 кг
5.2.22 В 5 кг воды, температура которой 288 К, опущен 1 кг льда с температурой 270 К. Какая
5.2.23 В литр воды при 20 C бросили комок мокрого снега массой 250 г. Когда весь снег растаял
5.2.24 Колба, теплоемкостью которой можно пренебречь, содержит 600 г воды при 80 C
5.2.25 На электрической плитке мощностью 600 Вт находится чайник с двумя литрами воды
5.2.26 В условиях Севера пресную воду получают из снега. Сколько дров нужно израсходовать
5.2.27 Тающий лёд массой 0,5 кг погрузили в калориметр с 0,3 кг воды при температуре 80 C
5. 2.28 При замораживании некоторого вещества в холодильнике потребовалось 4 мин для того
2.28 При замораживании некоторого вещества в холодильнике потребовалось 4 мин для того
5.2.29 В ведре находится смесь воды со льдом массой m=10 кг. Ведро внесли в комнату
5.2.30 В сосуд с водой объемом 0,25 л при 20 C поместили 50 г расплавленного свинца
5.2.31 В сосуд, содержащий 2,3 кг воды при 20 C, бросают кусок стали, который передаёт воде
5.2.32 Калориметр содержит 250 г воды при температуре 15 C. В воду бросили 20 г мокрого
5.2.33 В калориметр теплоёмкостью 1254 Дж/К бросили 30 г мокрого снега
5.2.34 Сосуд, содержащий воду, внесли в теплую комнату, причем за 15 мин температура
5.2.35 Алюминиевый чайник массой 0,4 кг, в котором находится 2 кг воды при 10 C
5.2.36 В латунный калориметр массы 0,3 кг , содержащий 1 кг воды при 18 C, опускается
5.2.37 В калориметр, содержащий 1,5 кг воды при 20 C, положили 1 кг льда, имеющего
5.2.38 В сосуд с водой объемом 0,25 л при 20 C поместили 50 г расплавленного свинца
Изменение внутренней энергии тела при совершении работы
5. 3.1 Стальной шар падает с высоты 15 м. При ударе о землю вся накопленная им энергия
3.1 Стальной шар падает с высоты 15 м. При ударе о землю вся накопленная им энергия
5.3.2 Многократное перегибание алюминиевой проволоки массой 2 г нагревает её на 40 C
5.3.3 На сколько температура воды у основания водопада с высотой 20 м больше
5.3.4 С какой скоростью должна лететь свинцовая пуля, чтобы при ударе о препятствие
5.3.5 При трении двух тел, теплоёмкости которых по 800 Дж/К, температура через 1 мин
5.3.6 Найти высоту, на которой потенциальная энергия груза массой 1000 кг равна количеству
5.3.7 Чему равна высота водопада, если температура воды у его основания на 0,05 C больше
5.3.8 С какой высоты упал свинцовый шар, если при падении изменение его температуры
5.3.9 Две одинаковых льдинки летят навстречу друг другу с одинаковыми скоростями
5.3.10 Вода падает с высоты 60 м. На сколько температура воды внизу водопада выше
5.3.11 С какой скоростью должна лететь льдинка при 0 C, чтобы при резком торможении
5.3.12 Снежок, летящий со скоростью 20 м/с, ударяется в стену. Какая часть его расплавится
Какая часть его расплавится
5.3.13 Стальной шар, падая свободно, достиг скорости 41 м/с и, ударившись о землю
5.3.14 Свинцовая пуля массой 10 г, летящая горизонтально со скоростью 100 м/с, попадает
5.3.15 Свинцовая пуля, летящая со скоростью 430 м/с, пробивает стену, причем скорость
5.3.16 При выстреле вертикально вверх свинцовая пуля ударилась о неупругое тело
5.3.17 Свинцовая пуля пробивает доску, при этом её скорость падает с 400 до 200 м/с
5.3.18 Свинцовая пуля, летящая горизонтально со скоростью 500 м/с, пробивает
5.3.19 С какой скоростью должна лететь свинцовая пуля, чтобы расплавиться при ударе
5.3.20 Железный метеорит влетает в атмосферу Земли со скоростью 1,5·103 м/с
5.3.21 Сани массы 300 кг равномерно движутся по горизонтальной снежной поверхности
5.3.22 Найти работу газа, совершенную в процессе 1-2-3
5.3.23 Найти работу газа в процессе 1-2-3
5.3.24 Найти работу газа в процессе 1-2
5.3.25 Укажите, в каком из случаев работу внешних сил по изменению состояния идеального газа
Внутренняя энергия идеального газа.
 Работа газа при изменении объема.
Работа газа при изменении объема.
5.4.1 Какова температура одноатомного идеального газа, если известно, что внутренняя энергия
5.4.2 На сколько увеличится внутренняя энергия 1,5 моль гелия при нагревании на 40 К?
5.4.3 Газ, занимающий объем 6,6 л, расширяется при постоянном давлении 515 кПа
5.4.4 При сжатии газа внешними силами была совершена работа 12 кДж. Какую работу
5.4.5 Газ, занимающий объем 460 л при температуре 280 К, нагрели до 295 К. Найти работу
5.4.6 Углекислый газ массой 220 г имеет температуру 290 К. Определить работу газа
5.4.7 Определить работу, которую совершает газ при изобарном нагревании на 50 C, если он
5.4.8 Газ был нагрет изобарно от 285 до 360 К. Какую работу совершил при этом газ
5.4.9 160 г гелия нагревают от 50 до 60 C. Найти работу газа при постоянном давлении
5.4.10 Рассчитайте внутреннюю энергию одноатомного идеального газа в количестве 3 моль
5.4.11 Какую работу совершил гелий массой 40 г при его изобарном нагревании на 20 К?
5. 4.12 На сколько изменится внутренняя энергия восьми молей идеального одноатомного газа
4.12 На сколько изменится внутренняя энергия восьми молей идеального одноатомного газа
5.4.13 Вычислить работу, которую совершают 2 моля идеального газа при изобарном
5.4.14 Каково давление одноатомного газа, занимающего объем 2 л, если его внутренняя
5.4.15 На сколько изменится давление идеального одноатомного газа, если его внутреннюю
5.4.16 Во сколько раз изменится внутренняя энергия идеального газа, если его давление
5.4.17 Внутренняя энергия одноатомного газа массой m при температуре T равна U
5.4.18 На сколько градусов надо нагреть газ, чтобы его объем увеличился вдвое по сравнению
5.4.19 Какая масса водорода находится в цилиндре под поршнем, если при изобарном
5.4.20 Один моль газа, имевший начальную температуру 300 К, изобарно расширился
5.4.21 Какую работу совершил водород массой 3 г при изобарном нагревании на 100 К?
5.4.22 19 м3 воздуха имеют температуру 50 C. Какую работу совершит воздух, расширяясь
5.4.23 В координатах давление-объем график процесса в идеальном одноатомном газе имеет
5. 4.24 Объем 120 г кислорода при изобарном нагревании увеличился в два раза. Определите
4.24 Объем 120 г кислорода при изобарном нагревании увеличился в два раза. Определите
5.4.25 В цилиндре под тяжелым поршнем находится 20 г углекислого газа. Газ нагревается
5.4.26 На диаграмме T (температура) – V (объем) график процесса представляет собой прямую
5.4.27 Над идеальным газом проводят два замкнутых процесса. Какое соотношение
5.4.28 Некоторая масса газа, занимающего объем 0,01 м3, находится при давлении 0,1 МПа
5.4.29 Кислород массой 0,3 кг при температуре 320 К охладили изохорно так, что его давление
5.4.30 Некоторое количество газа нагревается от температуры 300 до 400 К. При этом объем газа
5.4.31 Газ изобарно увеличился в объеме в три раза при давлении 3000 кПа. Определить
5.4.32 В цилиндре находится газ, удерживаемый в объеме 1 м3 силой тяжести поршня и силой
5.4.33 Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают
5.4.34 Определите работу, совершаемую одним молем газа за цикл, если
5.4.35 В сосуде объемом 2 л находится гелий при давлении 100 кПа и температуре 200 К
5. 4.36 Два одинаковых сосуда, содержащих одинаковое число молекул азота, соединены
4.36 Два одинаковых сосуда, содержащих одинаковое число молекул азота, соединены
5.4.37 Два сосуда, содержащие одинаковое количество атомов гелия, соединены краном
5.4.38 Два одинаковых сосуда, содержащие одинаковое число молекул азота, соединены
5.4.39 Два теплоизолированных сосуда соединены трубкой с закрытым краном. В первом
Первый закон термодинамики. Тепловой двигатель
5.5.1 Газ при изотермическом расширении получил 10 кДж теплоты. Чему равна
5.5.2 Какое количество теплоты получил гелий массой 1,6 г при изохорном нагревании
5.5.3 В адиабатическом процессе газ совершил работу 50 кДж. Чему равно приращение
5.5.4 Сколько тепла получил газ, если известно, что для его сжатия была совершена работа
5.5.5 При адиабатном расширении внутренняя энергия газа уменьшилась на 120 Дж. Какую
5.5.6 При изохорном нагревании 10 г неона его температура увеличилась на 205 К
5.5.7 Какое количество теплоты сообщили гелию массой 640 г при изобарном нагревании
5. 5.8 Определить, какое количество теплоты надо сообщить неону массой 400 г, чтобы
5.8 Определить, какое количество теплоты надо сообщить неону массой 400 г, чтобы
5.5.9 Какой процесс произошёл при сжатии идеального газа, если работа, совершаемая
5.5.10 При постоянном давлении 5 молям одноатомного газа сообщили теплоту 10 кДж
5.5.11 В закрытом сосуде объемом 2,5 л находится гелий при температуре 17 C и давлении
5.5.12 Один моль идеального газа, находящегося при температуре T0, нагревают. Какое
5.5.13 Закрытый баллон емкостью 50 л содержит аргон под давлением 200 кПа. Каким
5.5.14 Криптон массой 1 г был нагрет на 100 К при постоянном давлении. Какое количество
5.5.15 При изобарном расширении газа на 0,5 м3 ему было передано 0,26 МДж теплоты
5.5.16 В изотермическом процессе газ совершил работу 2 кДж. На сколько увеличится
5.5.17 Какой график соответствует процессу, в котором температура газа изменяется только
5.5.18 Количество теплоты, передаваемое газу, одинаково. В каком газовом процессе нагрев
5.5.19 Сколько молей одноатомного газа нагрели на 10 К, если количество подведенной
5. 5.20 Один моль одноатомного идеального газа нагревается при постоянном объеме
5.20 Один моль одноатомного идеального газа нагревается при постоянном объеме
5.5.21 При нагревании 1 кг неизвестного газа на 1 К при постоянном давлении требуется
5.5.22 При изобарном расширении 40 г гелия его объем увеличили в два раза. Начальная
5.5.23 Идеальный одноатомный газ в количестве 5 моль сначала охлаждают
5.5.24 Один моль идеального одноатомного газа находится при нормальных условиях. Какое
5.5.25 При расширении одноатомного газа от 0,2 до 0,5 м3 его давление росло линейно
5.5.26 Двигатель Дизеля, КПД которого равен 35%, за некоторое время выбросил в атмосферу
5.5.27 Коэффициент полезного действия тепловой машины 20%. Какую работу совершает
5.5.28 Определить коэффициент полезного действия теплового двигателя, если температура
5.5.29 Идеальная тепловая машина совершает за цикл работу 1 кДж и отдаёт холодильнику
5.5.30 В идеальной тепловой машине температура нагревателя в три раза выше температуры
5.5.31 Во сколько раз максимально возможный КПД газовой турбины больше максимально
5. 5.32 Идеальная тепловая машина совершает работу 200 Дж, при этом холодильнику
5.32 Идеальная тепловая машина совершает работу 200 Дж, при этом холодильнику
5.5.33 Каков КПД идеальной паровой турбины, если пар поступает в турбину при температуре
5.5.34 КПД тепловой машины равен 15%. Какое количество теплоты передано от нагревателя
5.5.35 В результате циклического процесса газ совершил работу 100 Дж и передал
5.5.36 Тепловая машина работает по циклу Карно. Температура нагревателя 400 C
5.5.37 Газ в идеальной тепловой машине 70% теплоты, полученной от нагревателя
5.5.38 Идеальная тепловая машина, работающая по циклу Карно, получает от нагревателя
5.5.39 В идеальной тепловой машине за счёт каждого килоджоуля теплоты, получаемой
5.5.40 Двигатель работает по циклу Карно. Во сколько раз изменится его КПД, если при
5.5.41 Тепловой двигатель работает по циклу Карно. Количество теплоты, отдаваемое
5.5.42 Тепловая машина имеет максимальный КПД 35%. Определить температуру нагревателя
5.5.43 Коэффициент полезного действия тепловой машины равен 25%.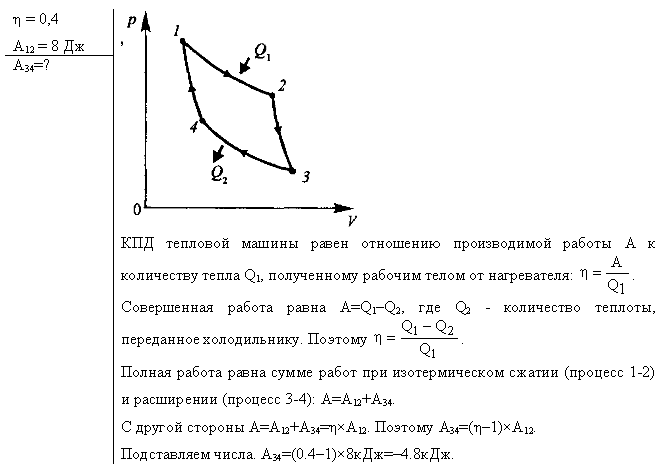 В результате её
В результате её
5.5.44 Тепловая машина с максимально возможным КПД имеет в качестве нагревателя
5.5.45 Один моль одноатомного газа совершает цикл, состоящий из двух изохор и двух изобар
5.5.46 Над одним молем идеального газа совершают цикл, показанный на рисунке
5.5.47 В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ
5.5.48 При изобарном расширении гелия совершена работа, равная 500 Дж. Какое
5.5.49 Если в некотором процессе газу сообщено 900 Дж теплоты, а газ при этом совершил
5.5.50 В каком из представленных на рисунке процессов AB, протекающих в данной массе газа
5.5.51 Два моля идеального газа совершают замкнутый цикл, изображенный на рисунке
5.5.52 В некотором процессе газу сообщено 800 Дж теплоты, а его внутренняя энергия
5.5.53 В некотором процессе газу сообщено 900 Дж теплоты, а его внутренняя энергия
5.5.54 На p-V диаграмме изображен цикл, проводимый с одноатомным идеальным газом
5.5.55 В идеальном тепловом двигателе за счёт каждого килоджоуля энергии, полученной
5. 5.56 Холодильник идеального теплового двигателя имеет температуру 27 C. Как изменится
5.56 Холодильник идеального теплового двигателя имеет температуру 27 C. Как изменится
5.5.57 Холодильник идеального теплового двигателя имеет температуру 27 C. Как изменится
5.5.58 Идеальный тепловой двигатель совершает за один цикл работу 30 кДж
5.5.59 Температура нагревателя идеального теплового двигателя равна 327 C, а температура
( 35 оценок, среднее 4.54 из 5 )
Вы можете поделиться с помощью этих кнопок:
Задачи по термодинамике с решением для вузов
В этой статье подробно разберем решение нескольких задач из разных разделов термодинамики.
Наш телеграм – это полезная информация для всех студентов каждый день, присоединяйтесь.
Задачи по термодинамике с решениями
Прежде чем начать, вспомним, какие задачи мы уже решали раньше:
Также напомним, что прежде чем начинать решать задачи, полезно ознакомиться с общей памяткой, а при решении держать под рукой полезные формулы.
Задача №1 на уравнение состояния газа
Условие
Кислород массой m=0.032кг находится в закрытом сосуде под давлением p=0,1МПа при температуре T=290К. После нагревания давление в сосуде повысилось в 4 раза. Определите: 1) объем сосуда; 2) температуру, до которой газ нагрели; 3) количество теплоты, сообщенное газу.
Решение
Запишем уравнение состояния газа и найдем объем:
При изохорном процессе:
Сообщенное газу количество теплоты:
Зная, что для двухатомного кислорода число степеней свободы молекулы i=5, вычислим:
Ответ: 1) 24 л, 2) 1160 К, 3) 578.4 Дж.
Задача №2 на цикл Карно
Условие
Идеальный газ совершает цикл Карно при температурах нагревателя 400 К и холодильника 290 К. Во сколько раз увеличится коэффициент полезного действия цикла, если температура нагревателя возрастёт до 600 К?
Решение
Коэффициент полезного действия цикла Карно:
Коэффициенты полезного действия цикла Карно при разных температурах нагревателя соответственно:
Найдём отношение коэффициентов:
Следовательно, коэффициент полезного действия цикла Карно увеличится в 1,88 раза. -21 Дж.
-21 Дж.
Задача №4 на внутреннюю энергию газа
Условие
Один моль одноатомного идеального газа изобарно расширяется от объема 5 литров до 10 литров при давлении в 202 кПа. Как изменилась внутренняя энергия газа в этом процессе?
Решение
Для одноатомного газа i=3. Для внутренней энергии идеального газа запишем, выражая температуру через уравнение Клапейрона-Менделеева:
Ответ: 1515 Дж
Задача №5 на изопроцессы
Условие
Кислород, занимающий при давлении р1 объем V1, расширяется в n раз. Определите конечное давление и работу, совершаемую газом. Рассмотрите следующие процессы:
- Изобарный.
- Изотермический.
- Адиабатный.
Решение
1) При изобарном процессе давление не меняется, работа газа:
2) при изотермическом процессе:
Работа газа:
3) уравнение адиабаты:
Ответ: см.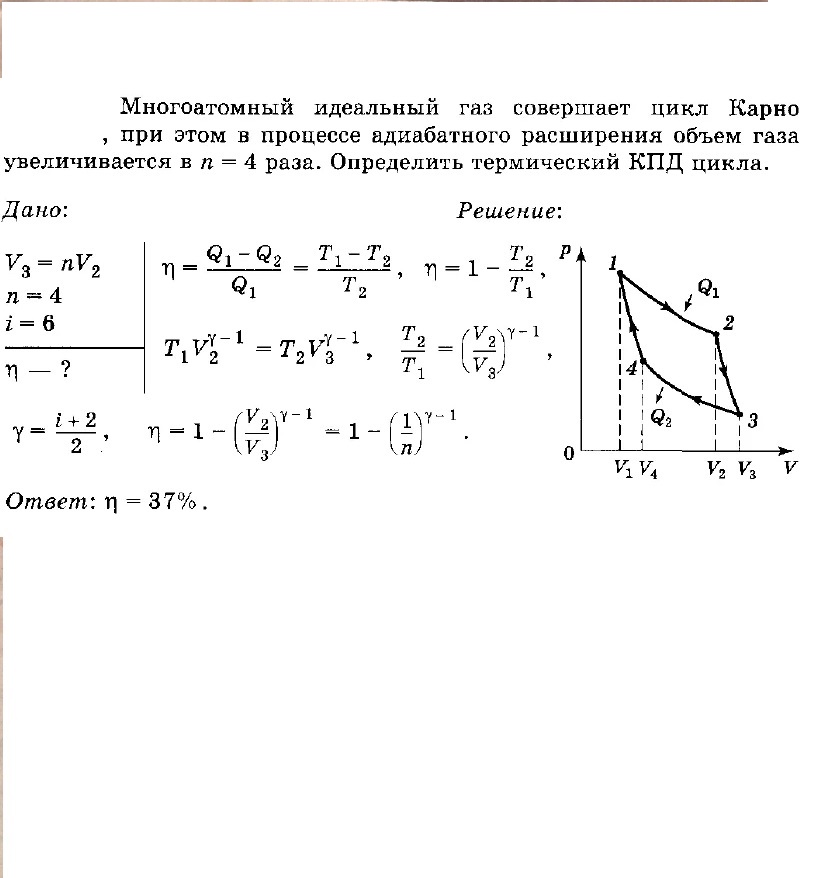 выше
выше
Вопросы по термодинамике
Вопрос 1. Сформулируйте первое начало термодинамики.
Ответ. Первое начало термодинамики гласит:
Теплота, полученная системой, идет на изменение ее внутренней энергии и на совершение системой работы против внешних сил.
В другой формулировке первое начало утверждает невозможность построения вечного двигателя первого рода.
Вопрос 2. Что такое идеальный газ?
Ответ. Идеальный газ – это математическая модель газа, в которой соударения между молекулами газа абсолютно упруги, между молекулами не действуют силы притяжения или отталкивания, потенциальной энергией взаимодействия молекул можно пренебречь.
В расширенной модели идеального газа его молекулы имеют сферическую форму
Вопрос 3. Что такое термодинамическая система?
Ответ. Термодинамическая система – это физическая система, состоящая из из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Такую систему можно описать статистическими законами.
Такую систему можно описать статистическими законами.
Вопрос 4. Сформулируйте второе начало термодинамики.
Ответ. У второго начало терможинами есть несколько формулировок. Вот одна из них:
Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому.
Вопрос 5. Что такое теплоемкость?
Ответ. Теплоемкость – физическая величина, численно равная количеству теплоты, которое необходимо передать телу, чтобы увеличить его температуру на 1 градус.
Если у вас есть вопросы по термодинамике, на которые вы ищете ответы, оставляйте их в комментариях. А если не получается решить какую-то задачу, спросите у экспертов профессионального студенческого сервиса, они обязательно помогут.
|
Конспект урока по теме «Решение задач по термодинамики»
Конспект на тему «Решение задач по теме «Основы термодинамики»
Тема занятия. Решение задач по теме «Основы термодинамики».
Решение задач по теме «Основы термодинамики».
Цель учебного занятия. Выработать алгоритм решения задач по теме «Основы термодинамики» через активное включение учеников в самостоятельную работу.
Задачи.
Образовательные:
1. Работая с упражнениями определить алгоритм решения задач по теме «Основы термодинамики».
2. В ходе решения задач закрепить полученные теоретические знания о расчете количества теплоты различных тепловых процессов.
Воспитания:
1. Продолжить привитие навыков коллективной работы, товарищеской взаимопомощи;
2. В ходе решения задач воспитывать самостоятельность, настойчивость и терпение.
Развития:
1. продолжить развитие интереса к предмету;
2. развивать вычислительные навыки при решении задач;
3. развивать самостоятельность школьников при объяснении решения примеров.
Форма учебного занятия: практическое занятие.
Фома организации работы: индивидуальная, групповая, индивидуально-групповая.
Образовательные технологии: проблемное обучение.
Ход урока.
Для успешного решения задач по данной теме необходимо знать закон сохранения энергии для термодинамики. Его же называют первым началом. Суть его состоит в том, что, когда термодинамическая система получает извне какое-то количество теплоты, то часть энергии добавляется к внутренней энергии системы, а другая возвращается в процессе совершения системой работы наружу, то есть:
,
где все величины алгебраические.
Для идеального газа изменение внутренней энергии , где i = 3 – степень свободы молекул, для реального газа i зависит от строения молекулы. Так для двухатомной молекулы i = 5, для трехатомной – i = 6 и т.д.
Работу A газ совершает только при изменении объема, т.е. . Надо сказать, что мы получаем три случая, когда один из членов первого начала термодинамики равен 0.
Q = 0 – это адиабатический процесс, изменение состояния происходит без обмена энергией с внешней средой. A = -ΔU.
ΔU = 0 – это изотермический процесс, так как внутренняя энергия не изменяется, а, значит не изменяется и температура. Q = A = pΔV, T = const.
A = 0 – это изохорический процесс, так как газ не совершает работу, а значит и не меняет объема. , V = const.
Наконец, изобарический процесс, в котором энергия расходуется на изменение внутренней энергии и на работу. , p = const.
Также необходимо знать еще 4 формулы, которые помогут нам в решении задач:
Количество теплоты, которое поглощается при нагревании или выделяется при охлаждении , где с – удельная теплоемкость, т.е. сколько теплоты понадобится передать или отнять у единицы массы вещества для изменения его температуры на 1o.

Также различают Cv – теплоемкость при постоянном объеме и Cp — теплоемкость при постоянном давлении. Причем и . Соответственно, удельные теплоемкости будут и , где μ – количество вещества в молях.Количество теплоты, которое поглощается при плавление или выделяется при кристаллизации Q = λm, где λ – удельная теплота плавления.
Количество теплоты, которое поглощается при парообразовании или выделяется при конденсации Q = rm, где r — удельная теплота парообразования.
Количество теплоты, которое выделяется при сгорании вещества Q = qm, где q — удельная теплота сгорания.
Все эти удельные величины берутся из справочных таблиц.
В системе, которая не взаимодействует с внешней средой, т.е. в замкнутой, между элементами системы происходит исключительно теплообмен:
где — вся полученная тепловая энергия, — вся отданная тепловая энергия – это закон теплового равновесия.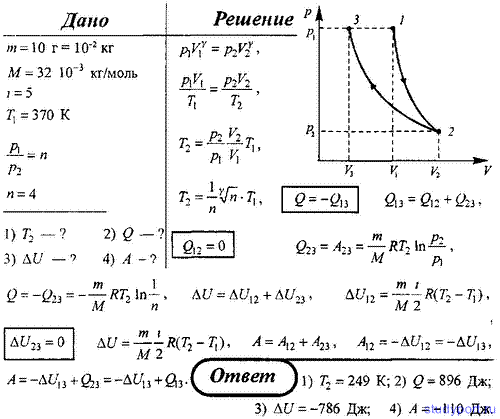
В итоге все задачи по термодинамике решаются следующим образом:
Перевести все заданные величины в единицы СИ.
Определить вид происходящего процесса, т.е., какие параметры остаются неизменными – T, V или P, определить, какие тела входят в замкнутую систему в теплообменных процессах и что с ними происходит.
Выбрать из справочника необходимые табличные удельные величины или рассчитать, зная степени свободы молекул и молярные массы веществ.
Применяя формулы, описанные выше, а так же формулы из других разделов физики, решить задачу.
Ниже рассмотрим пару примеров решения задач.
Задача 1. Закрытый сосуд содержит 14 г азота, давление p1 = 0.1 МПа, а температура t = 27oC.
Когда сосуд нагрели, давление увеличилось впятеро. Какая была конечная температура азота? Найти емкость сосуда V и количество теплоты Q, затраченное на нагревание.
Какая была конечная температура азота? Найти емкость сосуда V и количество теплоты Q, затраченное на нагревание.
Решение.
Состояние азота до нагревания (1), после нагревания (2).
Так как сосуд закрыт, процесс изохорический, т.е. V = const и все тепло уходит на изменение внутренней энергии азота.
Найдем конечную температуру азота:
Решая совместно (1) и (2), получаем:
л.
Количество теплоты, полученное азотом:
Дж,
где Дж/(моль · K). i = 5, т.к. молекула азота состоит из 2 атомов.
Задача 2. Сколько нужно сжечь керосина, чтобы полностью испарить 100 г воды, температура которой 20oC? К.П.Д. керосинового нагревателя η = 0,2.
Решение.
Тепловая энергия сгорания керосина Qк = qmк, с учетрм К.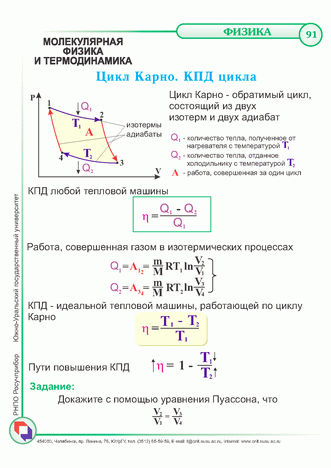 П.Д. Qк = ηqmк, q = 40.8 · 106Дж/кг – для керосина. Керосин горит и отдает энергию. Вода поглощает энергию, нагреваясь от 20 до 100oС. Qн = cm(T2 — T1), с = 4.187 · 103 Дж/(кг · К) – удельная теплоемкость воды. Далее энергия расходуется на парообразование. Qп = rm, r = 2256 · 103 Дж/кг – удельная теплота парообразования воды.
П.Д. Qк = ηqmк, q = 40.8 · 106Дж/кг – для керосина. Керосин горит и отдает энергию. Вода поглощает энергию, нагреваясь от 20 до 100oС. Qн = cm(T2 — T1), с = 4.187 · 103 Дж/(кг · К) – удельная теплоемкость воды. Далее энергия расходуется на парообразование. Qп = rm, r = 2256 · 103 Дж/кг – удельная теплота парообразования воды.
Составляем уравнение теплового баланса Qк — Qн — Qп = 0:
Откуда кг.
Задача№1
Тело нагрелось на 5 К, поглотив 10 кДж теплоты. Чему равна его теплоемкость?
Дано:
ΔT=5 К, Q=10 кДж, C−?
Решение задачи:
Теплоемкость C — это физическая величина, показывающая какое количество теплоты нужно затратить, чтобы изменить температуру тела на 1 К (или 1° C).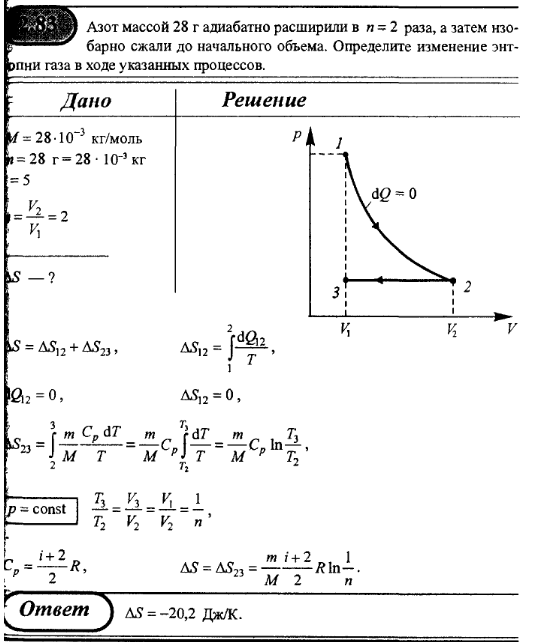 Не путайте теплоемкость C с удельной теплоемкостью c — первая относится ко всему телу, а вторая — к единице массы.
Не путайте теплоемкость C с удельной теплоемкостью c — первая относится ко всему телу, а вторая — к единице массы.
Значит её можно определить по формуле:
C=QΔT
Посчитаем ответ:
C=10⋅1035=2000Дж/К=2кДж/К
Ответ: 2 кДж/К.
Задача2
Какая установится температура воды после смешивания 39 л воды при 20° C и 21 л при 60° C?
Дано:
V1=39 л, t1=20∘ C, V2=21 л, t2=60∘ C, t−?
Решение задачи:
Понятно, что объем воды V2, имеющий более высокую температуру t2, после смешения передаст часть теплоты объему воды V1 c более низкой температурой t1, которая за счёт этой теплоты нагреется. В конце вся вода будет иметь некоторую температуру t.
Запишем уравнение теплового баланса:
Q1=Q2
Здесь Q1 — количество теплоты, полученное водой объемом V1 при нагревании до температуры t, а Q2 — количество теплоты, отданное водой объемом V2 при охлаждении до температуры t.
cm1(t—t1)=cm2(t2—t)
Выразим массы как произведение плотности воды на объем:
cρV1(t—t1)=cρV2(t2—t)
V1(t—t1)=V2(t2—t)
Теперь раскроем скобки, в одной части равенства соберем все члены с множителем t, вынесем его за скобки и выразим его.
V1t—V1t1=V2t2—V2t
V1t+V2t=V2t2+V1t1
t(V1+V2)=V2t2+V1t1
t=V1t1+V2t2V1+V2
Переводить объемы и температуры в систему СИ нет смысла — ответ мы получим в градусах Цельсия.
t=39⋅20+21⋅6039+21=34∘C=307К
Ответ: 307 К.
Задача№3
Чтобы нагреть 1,8 кг воды от 18° C до кипения на горелке с КПД 25%, потребовалось 92 г горючего. Найти удельную теплоту сгорания горючего.
Дано:
m1=1,8 кг, t1=18∘ C, η=25%, m2=92 г, q−?
Решение задачи:
Запишем формулу определения КПД (коэффициента полезного действия), он равен отношению полезной работы к затраченной работе.
η=AпAз(1)
Полезная работа горелки Aп равна количеству теплоты, которое требуется для нагревания воды от температуры t1до температуры кипения tк (при нормальном атмосферном давлении tк=100∘ C).
Aп=cm1(tк—t1)(2)
Удельная теплоёмкость воды c равна 4200 Дж/(кг·°C).
Затраченная работы Aз равна количеству теплоты, которое выделяется при сгорании горючего массой m2, поэтому:
Aз=qm2(3)
Подставим выражения (2) и (3) в формулу (1), тогда имеем:
η=cm1(tк—t1)qm2
Выразим искомую удельную теплоту сгорания q:
q=cm1(tк—t1)ηm2
Переведём КПД η в доли единиц, а массу горючего m2 в килограммы, далее произведем расчет численного ответа.
25%=0,25
92г=0,092кг
q=4200⋅1,8⋅(100—18)0,25⋅0,092=26953043,5Дж/кг≈27МДж/кг
Вероятнее всего, что горючим в горелке является спирт.
Ответ: 27 МДж/кг.
Задача4
Автомобиль, движущийся со средней скоростью 72 км/ч, развивает силу тяги 2500 Н. Коэффициент полезного действия двигателя автомобиля равен 25%. Сколько он тратит бензина в час?
Дано:
υ=72 км/ч, F=2500 Н, η=25%, t=1 ч, m−?
Решение задачи:
Если в задаче говорится о коэффициенте полезного действия (КПД), то при решении задачи первым делом записывают формулу определения КПД. КПД двигателя η — это отношение полезной работы Aп к затраченной работе Aз, то есть:
η=AпAз(1)
Так как каждый малый промежуток времени вектор силы тяги сонаправлен с вектором перемещения, то полезную работу Aп можно найти по формуле:
Aп=FS
В этой формуле S — пройденный путь, который легко найти из выражения:
S=υt
Aп=Fυt(2)
Затраченная работа Aз равна количеству теплоты, которое выделяется при сгорании бензина, поэтому верна формула:
Aз=qm(3)
Подставим выражения (2) и (3) в формулу (1), тогда мы получим:
η=Fυtqm
Выразим искомую массу бензина m:
m=Fυtηq
Удельная теплота сгорания бензина q равна 46 МДж/кг. Переведём скорость автомобиля в м/с, КПД — в доли единицы, а время работы — в секунды:
Переведём скорость автомобиля в м/с, КПД — в доли единицы, а время работы — в секунды:
72км/ч=72⋅10001⋅3600м/с=20м/с
25%=0,25
1ч=3600с
Численный ответ к задаче равен:
m=2500⋅20⋅36000,25⋅46⋅106=15,65кг
Ответ: 15,65 кг.
Домашнее задание.
1.Определить удельную теплоемкость трансформаторного масла, если для нагревания 5 т масла от 70° до 75° C требуется 50,6 МДж количества теплоты.
Решение задач по Термодинамике. Заказать решение задач по теме термодинамика
Спасибо за скорость и качество!
Понравилось обслуживание в личном кабинете на сайте. Все очень быстро, чётко. Отвечали оперативно на все мои вопросы и быстро подготовили решение. Мне нужно было не срочно получить задачки, до конца сессии просто сдать. Но получилось так, что я принесла все листики уже через пару дней!)
5,0 rating based on 521 ratings
Спасибо большое!
В работу вносятся правки, и это отлично! Мое счастье, что вовремя сообразила. В первый раз сдавала, препод не принял ответы без проставленных методов решения. Типа, надо объяснять, как я пришла к такому выводу. Написала менеджеру на сайте, вопрос был решен через день, добавили развернутые ответы.
В первый раз сдавала, препод не принял ответы без проставленных методов решения. Типа, надо объяснять, как я пришла к такому выводу. Написала менеджеру на сайте, вопрос был решен через день, добавили развернутые ответы.
5,0 rating based on 521 ratings
Ооочень благодарна Вам!
Уважаемые сотрудника сайта. Я ооочень рада что Вы мне помогаете с учёбой. Постоянно у Вас заказываю решение по сопромату, термодинамике, матанализу и другим непонятным предметам))). Вообщем спасибо огромное, вы мне помогаете получить высшее образование. Еще хотелось бы Вас попросить о скидках ))
5,0 rating based on 521 ratings
Заочникам тоже помогут! Спасибо
Пришлось сдать вступительные и начать учиться на заочке. Честно – я уже в возрасте и уделять время на учебу нет желания. Решил воспользоваться — написал на решаем онлайн, сотрудники быстро ответили, проконсультировали. Теперь заказываю решение задач только у них
5,0 rating based on 521 ratings
На удивление недорого и качественно!
Только поступил на 1-ый курс. Наткнулся на проблему – никто не хотел мне помогать с учёбой и домашнем заданием. Решил обратиться к интернету. Очень долго искал подходящий сайт по решение домашних задач. Но везде очень много берут денег и не понятно за что. Самый недорогой сервис – решаем онлайн.
5,0 rating based on 521 ratings
Заказываю все решения по эконом теории только в решаем онлайн
Что в школе, что в университете училась на пять. Но тут наткнулась на предмет, с который у меня ну ни как не выходит разобраться, а тем более понять. Тут у наших ребят подслушала, что решения по различным предметам заказывают, где то в сети. Обратилась и заказываю все решения по эконом теории у вас!
5,0 rating based on 521 ratings
Убедился в качественном сервисе 5+
Заказывал решение задач на разных сайтах. Постоянно были проблемы с выполнением. То преподаватели были не довольны, при этом мне не переделывали решение. То не вовремя скинут задачу и опять же не были довольны мной преподы. Наткнулся на сайт решаемонлайн – стал систематично заказывать только тут.
5,0 rating based on 521 ratings
Скорость и удобство порадовали
Меня смутило, что некуда приложить условия, на сайте только email и имя. Однако после открылся личный кабинет, где я нашла все нужые вкладки. Отправила фотографию с заданием и села ждать. Ответили моментально, прислали цену и сказали, что нашли автора. Я в восторге от скорости.
5,0 rating based on 521 ratings
Морока с Гражданским правом решена на отлично!
Работаю, воспитываю двоих детей одна. Параллельно учусь на заочке. Времени катастрофически не хватает ни на что. На учебе была на гране вылета из-за предмета гражданское право, накопилось много хвостов. Подружка посоветовала обратиться к ребятам из решаемонлайн. В общем они еще и диплом написали!
5,0 rating based on 521 ratings
Сессия для Бухгалтера теперь без проблем ребята!)
Катастрофически не хватает времени! Учусь на бухгалтера и каждую сессию получаю эти пресловутые задачки. Спасибо вам за помощь с работами! Я всегда оформлялась за несколько дней до сдачи, чтобы успеть получить, проверить, распечатать и сдать. Радуют цены, т.к. за учебу итак плачу денежку немалую.
5,0 rating based on 521 ratings
Кто не любит писать сочинения тогда вам сюда!
Очень люблю точные науки. С цифрами мне проще работать. Поэтому я поступил на физмат. Но оказывается весь первый курс у нас продолжают преподавать школьную программу по русскому языку и литературе. Ненавижу писать сочинения. Спасибо однокурснику – показал сайт на котором быстро, качественно!
5,0 rating based on 521 ratings
Незаменимые помощники!
После 9 класса поступил в колледж. Случайно узнал о сайте решаемонлайн – делают за тебя всю домашнюю работу быстро и не дорого. Одногруппники о таком сайте не знают. Стал всем ребятам предлагать помощь в домашнем задании, при этом перенаправляю на работников сайта!
5,0 rating based on 521 ratings
Закрыл сессию на отлично благодаря Вам!
Спасибо вам, дорогие друзья, за помощь! Для меня было жизненно важно закрыть сессию и сдать все экзамены, чтобы получить стипендию. Но я вообще, ну никак не успевала сдать парочку задач по макроэкономике, списывать было не вариант. Мне решили все за один день, по демократичной цене!
5,0 rating based on 521 ratings
Мастера на все руки!
Всю свою сознательную жизнь программировал на С++, а тут преподаватель задал задачку на языке Phynton. Не стал долго заморачиваться и написал ребятам из решаемонлайн – был очень удивлен когда они взялись за работу и через день прислали решение задачи. При этом денег практически не взяли!
5,0 rating based on 521 ratings
Оперативный сервис!
На последних курсах просто некогда заниматься заданиями, которые выдаются на дом. Итак куча дел, а я должен видеть ночами и помимо основной работы и диплома писать задачки. Нашел сайт, где буду заказывать ответы для галочки, а получил настоящих друзей со скидками и супербыстрой реакцией! Спасибо!
5,0 rating based on 521 ratings
Спасибо! Очень выручили
Компьютер для меня — это настоящая черная дыра, умею только то, что делает среднестатистический пользователь. Задали сделать видео с музыкой из своих фоток, а я только накачала вирусов, пока искала программку. Посоветовали обратиться к специалистам, нашла ваш сайт. Спасибо за готовое задание!
5,0 rating based on 521 ratings
Ваш выпускник!)
На втором курсе учиться очень сложно. Я не успевал ничего из-за новых предметов и жуткого расписания занятий. Именно тогда с вами познакомился и стал заказывать мелкие задачки, которые делать не хотелось (или попросту не хватало часов в сутках). Сейчас выпускаюсь и хочу сказать спасибо за поддержку
5,0 rating based on 521 ratings
Обратился впервые – компания не подвела!
На потоке знакомый подкинул идею – что бы самому не заморачиваться с выполнением задач по термодинамики, можно заказать где-то в интернете. Наткнулся на reshaemonline. Предоставил всю методичку, решения скидывают по мере необходимости, еще ни разу не подводили.
5,0 rating based on 521 ratings
Теперь матанализ не зло!
Мне нужно было срочно решить несколько задач по матанализу, иначе ждало отчисление. От безысходности полез в интернет и начал оставлять заявки везде, где предлагаются услуги помощи студентам. Тут мне ответили быстрее всех, я оформил заказ и получил файлик с готовым решением в этот же день. Спасибо!
5,0 rating based on 521 ratings
Большое спасибо!
Медикам особенно тяжело учиться… я частенько обращаюсь за помощью, чтобы закрыть неважные предметы и уделить время учебе по специальности. Задачи по генетике — это зло, но мне не пришлось ими заниматься. 🙂 Я просто передал специалистам нежелаемые дела и получил море свободного времени для написания
5,0 rating based on 521 ratings
Благодарю за помощь!
Медикам особенно тяжело учиться… я частенько обращаюсь за помощью, чтобы закрыть неважные предметы и уделить время учебе по специальности. Задачи по генетике — это зло, но мне не пришлось ими заниматься. 🙂 Я просто передал специалистам нежелаемые дела и получил море свободного времени для написания
5,0 rating based on 521 ratings
Электронный архив РГППУ: 100 задач по физике. Методика решения задач : учебное пособие для поступающих в вузы и втузы. Ч. 1. Механика. Молекулярная физика и термодинамика : учебное пособие
Please use this identifier to cite or link to this item:
https://elar.rsvpu.ru/handle/123456789/2095
| Title: | 100 задач по физике. Методика решения задач : учебное пособие для поступающих в вузы и втузы. Ч. 1. Механика. Молекулярная физика и термодинамика : учебное пособие |
| Other Titles: | 100 задач по физике. Методика решения задач : учебное пособие для поступающих в вузы и втузы. Ч. 1. Механика. Молекулярная физика и термодинамика |
| Authors: | Бухарова, Г. Д. |
| Issue Date: | 1995 |
| Publisher: | Уральский государственный профессионально-педагогический университет |
| Citation: | Бухарова, Г. Д. 100 задач по физике. Методика решения задач : учебное пособие для поступающих в вузы и втузы. Ч. 1. Механика. Молекулярная физика и термодинамика / Г. Д. Бухарова ; Урал. гос. проф.-пед. ун-т. — Екатеринбург : Издательство УГППУ, 1995. — 171 с. |
| Abstract: | В пособии рассмотрены вопроси методики решения физических задач. Приведены краткий теоретический материал по механике, молекулярной физике и термодинамике и подробное решение 100 задач этих разделов курса физики средней школы. Пособие окажет помощь учащимся при подготовке к вступительному экзамену по физике в вузы и втузы. |
| Keywords: | ЗАДАЧИ ПО ФИЗИКЕ РЕШЕНИЕ ЗАДАЧ ПО ФИЗИКЕ МОЛЕКУЛЯРНАЯ ФИЗИКА ЗАДАЧИ ПО ТЕРМОДИНАМИКЕ МЕТОДИКА РЕШЕНИЯ ЗАДАЧ |
| Appears in Collections: | Образовательные ресурсы РГППУ |
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
| Submit Date | Title | Author(s) |
|---|---|---|
| 8-Jun-2021 | Образовательное право : учебное пособие | Ожиганова, М. В. |
| 8-Jun-2021 | Внедрение в современный учебный процесс инновационных технологий обучения : монография | Фоминых, М. В.; Ускова, Б. А.; Ветлугина, Н. О.; Лузянина, Т. В. |
| 8-Jun-2021 | Проектирование основных и дополнительных образовательных программ в сфере физической культуры и спорта : учебное пособие | Кетриш, Е. В. |
| 8-Jun-2021 | Профилактика и преодоление профессиональных деформаций специалистов по социальной работе : учебное пособие | Заглодина, Т. А. |
| 8-Jun-2021 | Социально-психологические аспекты жизненного самоопределения человека : монография | Бастракова, Н. С. |
| 8-Jun-2021 | Стратегическое целеполагание как фактор конкурентоспособности предпринимательских структур : монография | Мокроносов, А. Г.; Журавлев В. С. |
| 8-Jun-2021 | Обеспечение качества машиностроительной продукции : учебное пособие | Гузанов, Б. Н.; Большакова, М. Ю.; Соколова, Т. Б.; Мигачева, Г. Н. |
| 8-Jun-2021 | Развитие ремесленной деятельности как социально-экономического явления: монография | Гаврилов, Д. Е.; Мокроносов, А. Г. |
| 8-Jun-2021 | Введение в курс «Философия и история образования» : учебное пособие для вузов | Чапаев, Н. К. |
| 5-Mar-2021 | Диалектика педагогики: настоящее в прошлом, прошлое в настоящем: монография | Чапаев, Н. К. |
| 5-Mar-2021 | Профессиональное самоопределение личности как построение смыслов будущего: монография | Щипанова, Д. Е. |
| 5-Mar-2021 | Коммуникативная компетенция и ее развитие у студентов вуза в условиях преемственности образования: монография | Стурикова, М. В. |
| 5-Mar-2021 | Психолого-педагогический практикум: учебное пособие | Курочкина, И. А.; Шахматова, О. Н. |
| 5-Mar-2021 | Профессионально-педагогическое и профессионально-техническое образование в России : К столетию становления и развития. 1920–2020 гг.: сборник документов: в 3 томах. Т. 3: Профессионально-техническое и профессионально-педагогическое образование в региональном разрезе: Свердловская область : учебное пособие | — |
| 5-Mar-2021 | Высшая школа в процессах общественного воспроизводства: социально-философский анализ: монография | Шмурыгина, О. В. |
| 7-Dec-2020 | Социально-экономическая статистика : учебное пособие | Логинова, С. Л. |
| 7-Dec-2020 | Проектирование и расчет ленточного конвейера : учебно-методическое пособие | Каменских, С. Ф.; Осьмушкин, С. С.; Каржавин, В. В. |
| 7-Dec-2020 | Дипломное проектирование в профессионально-педагогическом вузе : учебно-методическое пособие | Осипова, И. В.; Ларионова, М. Б.; Новоселова, А. Е. |
| 7-Dec-2020 | Колористика : учебное пособие | Анисимова, Е. В.; Фирсанова, О. В. |
| 7-Dec-2020 | Педагогические технологии в музыкально-компьютерной деятельности студентов : монография | Коновалов, А. А.; Буторина, Н. И. |
CHM 112 Практические задачи по термодинамике Ответы
CHM 112 Практические задачи по термодинамике Ответы
1. Почему изменение энтропии в системе не всегда является надежным предиктором того,
процесс, вызывающий изменение, является спонтанным?
Ответ
Второй закон гласит, что процесс является спонтанным, если система и окружение имеют
увеличение энтропии. Таким образом, даже если данная система имеет уменьшение энтропии (что свидетельствует о несистематичности),
если имеется достаточное увеличение энтропии окружающей среды, тогда процесс может быть спонтанным.
2. Чем похожа константа равновесия K eq и чем она отличается от K c и K p ?
Ответ
Константа термодинамического равновесия K eq формально записывается в терминах активности,
безразмерное количество. Активность приблизительно выражена с использованием концентраций раствора в молярных единицах.
(деленное на 1 M для удаления единиц) и парциальное давление газа в единицах атм (деленное на 1 атм
удалить блоки).K c записывается исключительно с точки зрения молярности, а K p записывается
исключительно с точки зрения парциальных давлений. K eq может смешивать «единицы».
3. Для каждой из следующих реакций укажите, ожидаете ли вы, что энтропия системы
увеличивать или уменьшать. Если вы не можете сказать, проверив уравнение, объясните почему.
( a ) CH 3 OH ( л ) → CH 3 OH ( г )
( b ) N 2 O 4 ( г ) → 2 NO 2 ( г )
( c ) CO ( г ) + H 2 O ( г ) → CO 2 ( г )
+ H 2 ( г )( d ) 2 KClO 3 ( с ) → 2 KCl ( с ) + 3 O 2 ( г )
( e ) CH 3 COOH ( л ) → CH 3 COOH ( с )
( f ) N 2 ( г ) + O 2 ( г ) → 2 NO ( г )
( г ) N 2 H 4 ( л ) → N 2 ( г )
+ 2 ч 2 ( г )( ч ) 2 NH 3 ( г ) + H 2 SO 4 ( водн. )
→ (NH 4 ) 2 SO 4 ( водн. )
Ответ
( a ) CH 3 OH ( л ) → CH 3 OH ( г )
Энтропия S увеличивается из-за большего количества молей газообразных продуктов.
( b ) N 2 O 4 ( г ) → 2 NO 2 ( г )
Энтропия S увеличивается из-за большего количества молей газообразных продуктов.
( c ) CO ( г ) + H 2 O ( г ) → CO 2 ( г )
+ H 2 ( г )
Невозможно предсказать изменение энтропии, потому что количество молей газообразных продуктов и реагентов одинаково.
( d ) 2 KClO 3 ( с ) → 2 KCl ( с ) + 3 O 2 ( г )
Энтропия S увеличивается из-за большего количества молей газообразных продуктов.
( e ) CH 3 COOH ( л ) → CH 3 COOH ( с )
ΔS ° <0 (уменьшение энтропии), поскольку реакция идет от жидкости к твердому.
( f ) N 2 ( г ) + O 2 ( г ) → 2 NO ( г )
ΔS ° ~ 0 (небольшое изменение энтропии), поскольку реакция идет от 2 молей газов до 2 молей газов.
( г ) N 2 H 4 ( л ) → N 2 ( г ) + 2 H 2 ( г )
ΔS °> 0 (увеличение энтропии), поскольку реакция идет от жидкости к 3 молям газов.
( ч ) 2 NH 3 ( г ) + H 2 SO 4 ( водн. )
→ (NH 4 ) 2 SO 4 ( водн. )
ΔS ° <0 (уменьшение энтропии), так как реакция идет из жидкости + 2 моля газы до полностью жидкого состояния.
4. На основании рассмотрения изменений энтропии, почему так трудно исключить
загрязнение окружающей среды, такое как загрязнение подземных вод водорастворимым метил трет -бутиловым эфиром?
Ответ
Загрязнение вызвано случайным и массовым удалением предметов, ситуацией с высокой энтропией.
Чтобы устранить загрязнение, необходимо вызвать обратный процесс, чтобы энтропия системы
теперь становится отрицательным, что требует большого положительного изменения энтропии для окружающей среды и большого расхода энергии.
5. Ожидаете ли вы, что каждая из следующих реакций будет спонтанной при
низкие температуры, высокие температуры, все температуры или совсем не? Объяснять.
( a ) PCl 3 ( г ) + Cl 2 ( г ) →
PCl 5 ( г ) ΔH ° = –87,9 кДж( b ) 2 NH 3 ( г ) →
N 2 ( г ) + 3 H 2 ( г ) ΔH °
= +92,2 кДж( c ) 2 N 2 O ( г ) →
2 N 2 ( г ) + O 2 ( г )
ΔH ° = –164.1 кДж( d ) H 2 O ( г ) + ½O 2 ( г ) →
H 2 O 2 ( г ) ΔH ° = +105,5 кДж( e ) CH 4 ( г ) + O 2 ( г ) → CO 2 ( г )
+ 2 H 2 O ( г ) ΔH ° = –802,3 кДж( f ) 2 CO ( г ) + O 2 ( г ) →
2 CO 2 ( г ) ΔH ° = –566.0 кДж
Ответ
( a ) PCl 3 ( г ) + Cl 2 ( г ) →
PCl 5 ( г ) ΔH ° = –87,9 кДж
ΔS °, по прогнозам, будет отрицательным, поскольку имеется меньше молей газообразных продуктов.
чем реактивы. Таким образом, при низких температурах будет преобладать энтальпия (TΔS ° мала) и
реакция будет спонтанной (ΔH ° <0), а при высокой температуре энтропия
преобладает, и реакция становится неспонтанной (TΔS ° становится большой и отрицательной).
( b ) 2 NH 3 ( г ) →
N 2 ( г ) + 3 H 2 ( г ) ΔH ° = +92,2 кДж
ΔS °, по прогнозам, будет положительным, поскольку имеется больше молей газообразных продуктов.
чем реактивы. Таким образом, при низких температурах будет преобладать энтальпия (TΔS ° мала) и
реакция будет несамопроизвольной (ΔH °> 0), а при высокой температуре энтропия
преобладает, и реакция становится спонтанной (TΔS ° становится большим и положительным).
( c ) 2 N 2 O ( г ) →
2 N 2 ( г ) + O 2 ( г ) ΔH ° = –164,1 кДж
ΔS °, по прогнозам, будет положительным, поскольку имеется больше молей газообразных продуктов.
чем реактивы. Таким образом, при низких температурах будет преобладать энтальпия (TΔS ° мала)
и реакция будет спонтанной (ΔH ° <0), в то время как при высокой температуре
энтропия доминирует, и реакция также является спонтанной (TΔS ° становится большим и положительным).Следовательно, ожидается, что реакция будет спонтанной при всех температурах.
( d ) H 2 O ( г ) + ½O 2 ( г ) →
H 2 O 2 ( г ) ΔH ° = +105,5 кДж
ΔS ° будет отрицательным (1,5 моль газов в реагентах, но только 1 моль газов в
продукта) и ΔH ° положительно, поэтому ΔG ° будет положительным при всех температурах.
Таким образом, реакция никогда не бывает спонтанной.
( e ) CH 4 ( г ) + O 2 ( г ) →
CO 2 ( г ) + 2 H 2 O ( г ) ΔH ° = –802.3 кДж
ΔS ° будет положительным (2 моля газов в реагентах, но 3 моля газов в продукте)
и ΔH ° отрицательно, поэтому ΔG ° будет отрицательным при всех температурах.
Таким образом, реакция протекает самопроизвольно при всех температурах.
( f ) 2 CO ( г ) + O 2 ( г ) →
2 CO 2 ( г ) ΔH ° = –566,0 кДж
ΔS ° будет отрицательным (3 моля газов в реагентах, но только 2 моля
газов в продукте) и ΔH ° отрицательно, поэтому ΔG ° будет отрицательным при
низкие температуры и положительные при высоких температурах.Таким образом, реакция протекает самопроизвольно только при низкой температуре.
6. Используйте данные из Таблицы термодинамических величин.
для определения значений ΔG ° для следующих реакций при 25 ° C.
( a ) C 2 H 4 ( г ) + H 2 ( г )
→ С 2 H 6 ( г )( b ) SO 3 ( г ) + CaO ( с ) → CaSO 4 ( с )
Ответ
( a ) C 2 H 4 ( г ) + H 2 ( г )
→ С 2 H 6 ( г )
ΔG f ° (C 2 H 6 ( g )) = –32.89 кДж / моль
ΔG f ° (H 2 ( г )) = 0,00 кДж / моль
ΔG f ° (C 2 H 4 ( г )) = 68,12 кДж / моль
, поэтому ΔG ° = [–32,89] — [68,12 + 0,00] = –101,01 кДж
( b ) SO 3 ( г ) + CaO ( с ) → CaSO 4 ( с )
ΔG f ° (CaSO 4 ( с )) = –1322 кДж / моль
ΔG f ° (CaO ( с )) = –604.0 кДж / моль
ΔG f ° (SO 3 ( г )) = –371,1 кДж / моль
, поэтому ΔG ° = [–1322] — [–604,0 + –371,1] = –347 кДж
7. Используйте данные из Таблицы термодинамических величин.
для определения ΔH ° и ΔS ° при 298 K для следующей реакции. потом
определить ΔG ° двумя способами и сравнить результаты.
CS 2 ( л ) + 3 O 2 ( г ) → CO 2 ( г )
+ 2 СО 2 ( г )
Ответ
Энтальпия реакции находится из энтальпий образования:
ΔH f ° (CS 2 ( l )) = 89.70 кДж / моль
ΔH f ° (O 2 ( г )) = 0 кДж / моль
ΔH f ° (CO 2 ( г )) = –393,5 кДж / моль
ΔH f ° (SO 2 ( г )) = –296,8 кДж / моль
ΔH ° = [(–393,5) + 2 (–296,8)] — [(89,70) + 3 (0)] = –1076,8 кДж
Энтропия реакции находится из стандартных энтропий:
S ° (CS 2 ( л )) = 151,3 Дж / моль · K
S ° (O 2 ( г )) = 205.0 Дж / моль · K
S ° (CO 2 ( г )) = 213,6 Дж / моль · K
S ° (SO 2 ( г )) = 248,1 Дж / моль · K
ΔS ° = [(213,6) + 2 (248,1)] — [(151,3) + 3 (205,0)] = –56,5 Дж / К
Один из способов найти ΔG ° — использовать свободную энергию образования:
ΔG f ° (CS 2 ( l )) = 65,27 кДж / моль
ΔG f ° (O 2 ( г )) = 0 кДж / моль
ΔG f ° (CO 2 ( г )) = –394.4 кДж / моль
ΔG f ° (SO 2 ( г )) = –300,2 кДж / моль
ΔG ° = [(–394,4) + 2 (–300,2)] — [(65,27) + 3 (0)] = –1060,1 кДж
Другой способ найти свободную энергию реакции — использовать энтальпию и изменения энтропии:
ΔG ° = ΔH ° — TΔS ° = –1076,8 — (298) (–0,0565) = –1060,0 кДж
Как и требовалось, свободные энергии Гибба в пределах экспериментальной ошибки одинаковы.
8. Используйте данные из Таблицы термодинамических величин.
для определения ΔH ° и ΔS ° при 298 K для следующей реакции.Затем определите
ΔG ° двумя способами и сравните результаты.
C ( графит ) + H 2 O ( г ) → CO ( г ) + H 2 ( г )
Ответ
C ( графит )
ΔH f ° = 0,00 кДж / моль
S ° = 5,74 Дж / моль · K
ΔG f ° = 0,00 кДж / моль
H 2 O ( г )
ΔH f ° = –241.8 кДж / моль
S ° = 188,7 Дж / моль · K
ΔG f ° = –228,6 кДж / моль
CO ( г )
ΔH f ° = –110,5 кДж / моль
S ° = 197,6 Дж / моль · K
ΔG f ° = –137,2 кДж / моль
H 2 ( г )
ΔH f ° = 0,00 кДж / моль
S ° = 130,6 Дж / моль · K
ΔG f ° = 0,00 кДж / моль
ΔH ° = [–110,5 + 0.0] — [0,0 + –241,8] = 131,3 кДж
ΔS ° = [197,6 + 130,6] — [5,74 + 188,7] = 133,8 Дж / К = 0,1338 кДж / К
ΔG ° = [–137,2 + 0,0] — [0,0 + –228,6] = 91,4 кДж
ΔG ° = 131,3 — (298) (0,1338) = 91,4 кДж
Оба метода дают одинаковую ΔG °, как и должно быть.
9. Оценить нормальное кипение гептана, C 7 H 16 , учитывая, что при этом
температура ΔH ° vapn = 31,69 кДж / моль.
Ответ
Используйте правило Траутона: ΔS ° vpn = ΔH ° vpn / T bp ≈ 87 Дж / моль · K
так T т.н. = ΔH ° vapn / (87 Дж / моль · K) =
(31690 Дж / моль) / (87 Дж / моль · K) = 364 K = 91 ° C.
10. Нормальная температура кипения Br 2 ( л ) составляет 59,47 ° C. Оценивать
ΔH ° vapn брома. Сравните свой результат со значением на основе
по данным Таблицы термодинамических величин.
Ответ
Правило Траутона предполагает, что ΔH ° vapn =
87 Дж / моль · K × T т.н. = (87) (273,15 + 59,47) = 29000 Дж / моль = 29 кДж / моль.
Для использования данных из Таблицы термодинамики
Кол-во, используйте реакцию:
Br 2 ( л ) → Br 2 ( г )
с ΔH f ° (Br 2 ( l )) = 0 кДж / моль и ΔH f °
(Br 2 ( л )) = 30.91 кДж / моль, поэтому ΔH ° =
ΔH ° vapn = [30,91] — [0] = 30,91 кДж / моль.
Учитывая приблизительный характер правила Траутона, оценка и экспериментальное значение очень похожи.
11. Напишите выражения K eq для следующих реакций. Какие из них, если таковые имеются
выражения соответствуют константам равновесия, которые мы ранее обозначили как
K c , K p , K a и так далее?
( a ) 2 NO ( г ) + O 2 ( г )
→
←
2 НО 2 ( г )( b ) MgSO 3 ( с )
→
←
MgO ( с )
+ СО 2 ( г )( c ) HCN ( водн. ) + H 2 O ( л )
→
←H 3 O + ( водн. ) + CN — ( водн. )
Ответ
( a ) 2 NO ( г ) + O 2 ( г )
→
←
2 НО 2 ( г )
( b ) MgSO 3 ( с )
→
←
MgO ( с ) + SO 2 ( г )
( c ) HCN ( водн. ) + H 2 O ( л )
→
←
H 3 O + ( водн. )
+ CN — ( водн. )
12.Используйте данные из Таблицы термодинамических величин, чтобы
определить K p при 298 K для этих реакций.
( a ) 2 SO 2 ( г ) + O 2 ( г )
→
←
2 SO 3 ( г )( b ) CH 4 ( g ) + 2 H 2 O ( g )
→
←
CO 2 ( г ) + 4 H 2 ( г )
Ответ
( a ) 2 SO 2 ( г ) + O 2 ( г )
→
←
2 SO 3 ( г )
ΔG f ° (SO 3 ( г )) = –371.1 кДж / моль
ΔG f ° (SO 2 ( г )) = –300,2 кДж / моль
ΔG f ° (O 2 ( г )) = 0 кДж / моль
ΔG ° = [2 (–371,1)] — [2 (–300,2) + (0)] = –141,8 кДж
ΔG ° = –RTlnK p
–141800 = — (8,314) (298) lnK p
K p = e 57,23 = 7,2 × 10 24
( b ) CH 4 ( g ) + 2 H 2 O ( g )
→
←
CO 2 ( г ) + 4 H 2 ( г )
ΔG f ° (CO 2 ( г )) = –394.4 кДж / моль
ΔG f ° (H 2 ( г )) = 0 кДж / моль
ΔG f ° (CH 4 ( г )) = –50,75 кДж / моль
ΔG f ° (H 2 O ( г )) = –228,6 кДж / моль
ΔG ° = [(–394,4) + 4 (0)] — [(–50,75) + 2 (–228,6)] = 113,6 кДж
ΔG ° = –RTlnK p
113600 = — (8,314) (298) lnK p
K p = e –45,85 = 1,2 × 10 –20
13.Используйте данные из Таблицы термодинамических величин.
определить K p при 298 K для этих реакций.
( a ) 2 N 2 O ( г ) + O 2 ( г )
→
←
4 НЕТ ( г )( b ) 2 NH 3 ( г ) + 2 O 2 ( г )
→
←
N 2 O ( г ) + 3 H 2 O ( г )
Ответ
( a ) 2 N 2 O ( г ) + O 2 ( г )
→
←
4 НЕТ ( г )
ΔG ° f (NO ( г )) = 86.57 кДж / моль
ΔG ° f (O 2 ( г )) = 0,00 кДж / моль
ΔG ° f (N 2 O ( г )) = 104,2 кДж / моль
ΔG ° = [4 (86,57)] — [2 (104,2) + 0,0] = 137,9 кДж
137900 = — (8,314) (298) lnK p
lnK p = –55,7
K p = e –55. 7 = 6 × 10 –25
( b ) 2 NH 3 ( г ) + 2 O 2 ( г )
→
←
N 2 O ( г ) + 3 H 2 O ( г )
ΔG ° f (N 2 O ( g )) = 104.2 кДж / моль
ΔG ° f (H 2 O ( г )) = –228,6 кДж / моль
ΔG ° f (NH 3 ( г )) = –16,48 кДж / моль
ΔG ° f (O 2 ( г )) = 0,00 кДж / моль
ΔG ° = [104,2 + 3 (–228,6)] — [2 (–16,48)
+ 2 (0,00)] = –548,6 кДж
–548600 = — (8,314) (298) lnK p
lnK p = 221,4
K p = e 221. 4 = 1 × 10 96
14.Перечисленные ниже термодинамические данные относятся к 298 К. Используйте эти данные и данные.
из Таблицы термодинамических величин
для определения K экв при 45 ° C для реакции
CO 2 ( г ) + SF 4 ( г )
→
←
CF 4 ( г ) + SO 2 ( г )
ΔH f °, кДж / моль
S °, Дж моль –1 K –1
SF 4 ( г )
–763
299,6
CF 4 ( г )
–925
261.6
Ответ
Найдите энтальпию реакции при 298 K:
ΔH f ° (CF 4 ( г )) = –925 кДж / моль
ΔH f ° (SO 2 ( г )) = –296,8 кДж / моль
ΔH f ° (SF 4 ( г )) = –763 кДж / моль
ΔH f ° (CO 2 ( г )) = –393,5 кДж / моль
ΔH ° = [(–925) + (–296,8)] — [(–393,5) + (–763)] = –65 кДж
Найдите энтропию реакции при 298 K:
S ° (CF 4 ( г )) = 261.6 Дж / моль · K
S ° (SO 2 ( г )) = 248,1 Дж / моль · K
S ° (SF 4 ( г )) = 299,6 Дж / моль · K
S ° (CO 2 ( г )) = 213,6 Дж / моль · K
ΔS ° = [(261,6) + (248,1)] — [(213,6) + (299,6)] = –3,5 Дж / К
Предполагая, что ΔH ° и ΔS ° не изменяются значительно между 298 K и 318 K (45 ° C):
ΔG ° = ΔH ° — TΔS ° = –65 — (318) (- 0,0035)
= –64 кДж = –64000 Дж
ΔG ° = –RTlnK экв
–64000 = — (8.314) (318) lnK экв
К экв = e 24,2 = 3 × 10 10
15. Следующую реакцию проводят в промышленном масштабе для получения тионилхлорида,
химическое вещество, используемое при производстве пестицидов.
SO 3 ( г ) + SCl 2 ( л )
→
←
OSCl 2 ( л ) + SO 2 ( г )
Термодинамические данные, перечисленные ниже, относятся к 298 К.Используйте эти данные и данные из
Таблица термодинамических величин к
определить температуру, при которой K экв = 1,0 × 10 15 для реакции.
ΔH f °, кДж / моль
S °, Дж моль –1 K –1
SCl 2 ( л )
–5,0
184
OSCl 2 ( л )
–245,6
121
Ответ
ΔH ° f (SO 2 ( г )) = –296,8 кДж / моль
ΔH ° f (SO 3 ( г )) = –395.7 кДж / моль
ΔH ° f (SCl 2 ( г )) = –50,0 кДж / моль
ΔH ° f (OSCl 2 ( г )) = –245,6 кДж / моль
ΔH ° = [–245,6 + –296,8] — [–395,7 + –50,0] = –96,7 кДж
S ° (SO 2 ( г )) = 248,1 Дж / моль · K
S ° f (SO 3 ( г )) = 256,6 Дж / моль · K
S ° f (SCl 2 ( г )) = 184 Дж / моль · K
S ° f (OSCl 2 ( г )) = 121 Дж / моль · K
ΔS ° = [121 + 248.1] — [256,6 + 184] = –72 Дж / К
— (8,314) Tln (1,0 × 10 15 ) = –96700 — T (–72)
–287T = –96700 + 72T
–359T = –96700
T = 269 K (= –4 ° C)
16. Несколько раз мы делали предположение, что ΔH °
и ΔS ° мало изменяются с температурой. Почему мы не можем сделать
такое же предположение о ΔG °? Если принять, что ΔH ° 298
и ΔS ° 298 не изменяются с температурой, возможно ли
чтобы реакция, которая не является спонтанной в стандартных условиях, стала
самопроизвольно как при более высокой, так и при более низкой температуре? Объяснять.
Ответ
Поскольку ΔG ° = ΔH ° — TΔS °, энергия Гиббса изменяется
линейно с температурой. Если ΔS ° большое значение, то ΔG ° может измениться
значительно с температурой.
Если изменение энтальпии и изменение энтропии постоянны по отношению к
температура и реакция не является спонтанной в стандартных условиях, реакция может
не становятся самопроизвольными и при более высокой и более низкой температуре. Например, если оба
изменение энтальпии и изменение энтропии отрицательны, реакция может быть несамопроизвольной
в стандартных условиях и может стать самопроизвольным при более низкой температуре; однако это
сценарий не допускает спонтанности при более высоких температурах (изменение энергии Гибба всегда
положительный после достижения определенной температуры).
17. Ниже приведены значения K p при различных температурах реакции,
2 SO 2 ( г ) + O 2 ( г )
→
←
2 SO 3 ( г ).
При 800 К, К p = 9,1 × 10 2 ; при 900 К, К p =
4,2 × 10 1 ; при 1000 К, К p = 3,2; при 1100 К, К p
= 0,39; а при 1170 К K p = 0,12. Постройте сюжет, чтобы определить
ΔH ° для этой реакции.
Ответ
Уравнение Вант-Гоффа таково, что наклон ln K eq по сравнению с 1 / T
график равен –ΔH ° / R.
Наклон графика = 22700, поэтому ΔH ° = –R × наклон = — (8,314) × (22700)
= –189000 Дж / моль = –189 кДж / моль
18. Используйте термодинамические данные, чтобы определить K экв. для следующей реакции
Mg (OH) 2 ( с ) + 2 NH 4 + ( водн. )
→
←
Mg 2+ ( водн. ) + 2 NH 3 ( водн. )
+ 2 H 2 O ( л )
Затем получите K eq из других табличных констант равновесия и сравните результаты.
Ответ
ΔG f ° (Mg 2+ ( водн. )) = –454,8 кДж / моль
ΔG f ° (NH 3 ( водн. )) = –26,57 кДж / моль
ΔG f ° (H 2 O ( l )) = –237,2 кДж / моль
ΔG f ° (NH 4 + ( водн. )) = –79,31 кДж / моль
ΔG f ° (Mg (OH) 2 ( s )) = –833,9 кДж / моль
ΔG ° = [(–454.8) + 2 (–26,57) +2 (–237,2)] — [(–833,9) + 2 (–79,31)] = 10,2 кДж
ΔG ° = –RTlnK экв
10200 = — (8,314) (298) lnK экв
K экв = e –4,12 = 1,6 × 10 –2
Чтобы использовать опубликованные константы равновесия, необходимо использовать серию реакций:
Mg (OH) 2 ( с )
→
←
Mg 2+ ( водн. )
+ 2 OH — ( водн. ) K sp
= 1,8 × 10 –11
NH 4 + ( водн. ) + H 2 O ( л )
→
←
H 3 O + ( водн. ) + NH 3 ( водн. )
К а = 5.6 × 10 –10
NH 4 + ( водн. ) + H 2 O ( л )
→
←
H 3 O + ( водн. ) + NH 3 ( водн. )
K a = 5,6 × 10 –10
H 3 O + ( водн. ) + OH — ( водн. )
→
←
2 H 2 O ( л )
K c = 1 / K w
= 1 / 1,0 × 10 –14 = 1,0 × 10 14
H 3 O + ( водн. ) + OH — ( водн. )
→
←
2 H 2 O ( л ) K c
= 1 / K w = 1/1.0 × 10 –14 = 1,0 × 10 14
Суммирование реакций дает желаемую реакцию с
K c = K sp × K a × K a × 1 / K w × 1 / K w =
(1,8 × 10 –11 ) (5,6 × 10 –10 ) (5,6 × 10 –10 )
(1,0 × 10 14 ) (1,0 × 10 14 ) = 5,6 × 10 –2
Две константы равновесия имеют одинаковый порядок величины, но различаются примерно в 3 раза.5.
Это не так уж и плохо.
19. Используйте термодинамические данные, чтобы получить значение K sp для Ag 2 SO 4 ,
и сравните свой результат с результатом, найденным в таблице констант произведения растворимости.
Ответ
Реакция:
Ag 2 SO 4 ( с )
→
←
2 Ag + ( водн. ) +
СО 4 2– ( водн. )
ΔG ° f (SO 4 2–) = –744.5 кДж / моль
ΔG ° f (Ag + ) = 77,11 кДж / моль
ΔG ° f (Ag 2 SO 4 ) = –618,5 кДж / моль
ΔG ° = [2 (77,11) + –744,5] — [–618,5] = 28,2 кДж
ΔG ° = –RTln K экв = –RTlnK sp
28200 = — (8,314) (298) ln K sp
ln K sp = –11,4
K sp = e –11. 4 = 1 × 10 –5
Из таблицы K sp = 1.4 × 10 –5 ; два значения одинаковы, в пределах погрешности.
Термодинамика — проблемы и решения
Первый закон термодинамики
1. На основании графика P-V ниже, каково отношение работы, выполняемой газом в процессе I, к работе, выполняемой газом в процессе II?
Известный:
Процесс 1:
Давление (P) = 20 Н / м 2
Начальный объем (V 1 ) = 10 литров = 10 дм 3 = 10 x 10 -3 м 3
Конечный объем (V 2 ) = 40 литров = 40 дм 3 = 40 x 10 -3 м 3
Процесс 2:
Процесс (P) = 15 Н / м 2
Начальный объем (V 1 ) = 20 литров = 20 дм 3 = 20 x 10 -3 м 3
Конечный объем (V 2 ) = 60 литров = 60 дм 3 = 60 x 10 -3 м 3
Разыскивается: Соотношение выполненных работ по газу
Решение:
Работа, выполняемая газом в процессе I:
W = P ΔV = P (V 2 –V 1 ) = (20) (40-10) (10 -3 м 3 ) = (20) (30) (10 -3 м 3 ) = (600) (10 -3 м 3 ) = 0.6 м 3
Работа, выполняемая газом в процессе II:
W = P ΔV = P (V 2 –V 1 ) = (15) (60-20) (10 -3 м 3 ) = (15) (40) (10 -3 м 3 ) = (600) (10 -3 м 3 ) = 0,6 м 3
Соотношение работы, совершаемой газом в процессе I и процессе II:
0,6 м 3 : 0,6 м 3
1: 1
2.
На основании приведенного ниже графика, какую работу выполняет газообразный гелий в процессе AB?
Известный:
Давление (P) = 2 x 10 5 Н / м 2 = 2 x 10 5 Паскаль
Начальный объем (V 1 ) = 5 см 3 = 5 x 10 -6 м 3
Конечный объем (V 2 ) = 15 см 3 = 15 x 10 -6 м 3
Разыскивается: Работы по газу в процессе AB
Решение:
Вт = ∆P ∆V
W = P (V 2 — V 1 )
W = (2 x 10 5 ) (15 x 10 -6 -5 x 10 -6 )
W = (2 x 10 5 ) (10 x 10 -6 ) = (2 x 10 5 ) (1 x 10 -5 )
Вт = 2 Джоуля
3.
На основании приведенного ниже графика, какая работа выполняется в процессе a-b?
Известный:
Начальное давление (P 1 ) = 4 Па = 4 Н / м 2
Конечное давление (P 2 ) = 6 Па = 6 Н / м 2
Начальный объем (V 1 ) = 2 м 3
Конечный объем (V 2 ) = 4 м 3
Требуются: работы выполнены Я обрабатываю а-б
Решение:
Работа, выполненная газом = площадь под кривой a-b
W = площадь треугольника + площадь прямоугольника
Вт = ½ (6-4) (4-2) + 4 (4-2)
Вт = ½ (2) (2) + 4 (2)
Вт = 2 + 8
Вт = 10 Дж
4.На основании приведенного ниже графика показано, какие работы выполняются в процессе A-B-C-A.
Решение:
Работа (Вт) = Площадь треугольника A-B-C
W = ½ (20-10) (6 x 10 5 — 2 x 10 5 )
W = ½ (10) (4 x 10 5 )
Вт = (5) (4 x 10 5 )
W = 20 x 10 5
Вт = 2 x 10 6 Джоуль
Тепловой двигатель
5. Двигатель поглощает 2000 джоулей тепла при высокой температуре и выделяет 1200 джоулей тепла при низкой температуре.Каков КПД двигателя?
Известный:
Подвод тепла (Q H ) = 2000 Дж
Тепловая мощность (Q L ) = 1200 Дж
Работа, выполненная двигателем (Вт) = 2000 — 1200 = 800 Дж
Требуется: КПД (д)
Решение:
e = W / Q H
е = 800/2000
e = 0,4 x 100%
e = 40%
Двигатель Карно
6.Двигатель поглощает тепло при 960 Кельвинах, а двигатель отводит тепло при 576 Кельвинах. Какой КПД у двигателя.
Известный:
Высокая температура (T H ) = 960 K
Низкая температура (T L ) = 576 K
Требуется: КПД (д)
Решение:
КПД двигателя Карно = 0,4 x 100% = 40%
7. Согласно приведенному ниже графику, работа двигателя составляет 6000 Джоулей.Какое тепло выделяется двигателем за каждый круг?
Известный:
Работа (Вт) = 6000 Дж
Высокая температура (T H ) = 800 Кельвин
Низкая температура (T L ) = 300 Кельвинов
Разыскивается: тепла, отводимого двигателем
Решение :
КПД Карно (идеальный):
Тепло, поглощаемое двигателем Карно:
W = e Q 1
6000 = (0.625) Q 1
Q 1 = 6000 / 0,625
Q 1 = 9600
Тепло, выделяемое двигателем Карно:
Q 2 = Q 1 — W
Q 2 = 9600 — 6000
Q 2 = 3600 Дж
8. КПД двигателя Карно составляет 40%. Если тепло поглощается при 727 ° C, то какова низкая температура.
Известный:
КПД (е) = 40% = 40/100 = 0.4
Высокая температура (T H ) = 727 o C + 273 = 1000 K
Требуется: Низкотемпературный
Решение:
T L = 600 Кельвин — 273 = 327 o C
9. На основании приведенного ниже графика, если двигатель поглощает 800 Дж тепла, какую работу выполняет двигатель.
Известный:
Высокая температура (T H ) = 600 Кельвинов
Низкая температура (T L ) = 250 Кельвинов
Подвод тепла (Q 1 ) = 800 Дж
Требуются: Работа (Вт)
Решение:
КПД двигателя Карно:
Выполнено работ по двигателю:
W = e Q 1
Вт = (7/12) (800 Дж)
Вт = 466.7 Джоуль
10. Высокая температура двигателя Карно составляет 600 К. Если двигатель поглощает 600 Дж тепла, а низкая температура составляет 400 К, то какую работу выполняет двигатель.
Известный:
Низкотемпературный (T L ) = 400 K
Высокая температура (T H ) = 600 K
Подвод тепла (Q 1 ) = 600 Дж
Требуется: Работа выполнена двигателем Карно (W)
Решение:
КПД двигателя Карно:
Выполнена работа двигателя Карно:
W = e Q 1
Вт = (1/3) (600) = 200 Дж
Первый закон термодинамики — проблемы и решения
1.В систему добавляется 3000 Дж тепла, и система выполняет 2500 Дж работы. Как меняется внутренняя энергия системы?
Известный:
Тепло (Q) = +3000 Джоуля
Работа (Вт) = +2500 Дж
Разыскивается: изменение внутренней энергии системы
Решение:
Уравнение первого начала термодинамики
ΔU = Q-W
Условные обозначения:
Q положительный, если в систему добавлено тепло
Вт положительно, если работа выполняется системой
Q отрицательный, если тепло покидает систему
Вт отрицательно, если в системе ведутся работы
Изменение внутренней энергии системы:
ΔU = 3000-2500
ΔU = 500 Дж
Внутренняя энергия увеличивается на 500 Дж.
2. 2000 Дж добавляется к системе и 2500 Дж работы выполняется в системе. Как меняется внутренняя энергия системы?
Известный:
Тепло (Q) = +2000 Джоуль
Работа (Вт) = -2500 Дж
Разыскивается: изменение внутренней энергии системы
Решение:
ΔU = Q-W
ΔU = 2000 — (- 2500)
ΔU = 2000 + 2500
ΔU = 4500 Дж
Внутренняя энергия увеличивается на 4500 Дж.
3. 2000 Дж тепла уходит из системы и 2500 Дж работы выполняется в системе. Как меняется внутренняя энергия системы?
Известный:
Тепло (Q) = -2000 Джоуль
Работа (Вт) = -3000 Джоуль
Разыскивается: изменение внутренней энергии системы
Решение:
ΔU = Q-W
ΔU = -2000 — (- 3000)
ΔU = -2000 + 3000
ΔU = 1000 Дж
Внутренняя энергия увеличивается на 4500 Дж.
Вывод:
— Если в систему добавлено тепло, внутренняя энергия системы увеличивается
— Если тепло покидает систему, внутренняя энергия системы уменьшается
— Если работа выполняется системой, то внутренняя энергия системы уменьшается
— Если работа ведется в системе, то внутренняя энергия системы увеличивается
Задачи термодинамики
На этой странице я собрал сборник задач термодинамики, чтобы помочь вам лучше понять термодинамику.Эти задачи призваны помочь вам понять некоторые основы, не вдаваясь в подробности. Термодинамика — довольно странный предмет, который не всегда легко связать с реальным миром, как, скажем, теорию динамики. Вот почему я выбрал задачи, которые имеют хоть какое-то практическое значение.
Проблема № 1
Изначально газ содержится внутри изолированного контейнера A, при начальных условиях P 1 , V 1 , m и T 1 .Эти величины представляют собой давление, объем, массу и температуру соответственно. Затем открывается клапан, который позволяет газу свободно расширяться в изолированный контейнер B, который изначально пустой. После того, как газ осядет, конечные условия газа следующие: P 2 , V 2 , m и T 2 . В термодинамике процесс называется обратимым, если он не производит энтропии. Это означает, что процесс может происходить в обратном направлении.Объясните, почему описанный процесс необратим.
См. Ответ
Проблема № 2
В емкость закачивают воздух с относительной влажностью 30% при 20 ° C. Какое максимальное давление внутри емкости, чтобы вода не конденсировалась внутри емкости? Предположим, что температура воздуха внутри контейнера составляет 20 ° C.
См. Ответ
Проблема № 3
Для всех тепловых двигателей максимальная мощность работы ( Вт, ) связана с максимальной подводимой тепловой энергией ( Q ) следующим уравнением:
, где T H — температура источника тепла, а T L — температура радиатора, которая представляет собой температуру «оставшейся» тепловой энергии после работы, извлеченной из процесса. .Обе температуры указаны в единицах Кельвина.
Термин в скобках обозначает термический КПД процесса, широко известный как КПД Карно.
В приложении, включающем двигатель Стирлинга (тип теплового двигателя, показанный ниже), параболическая тарелка используется для концентрации солнечной энергии на приемнике двигателя. Используя приведенное выше уравнение, почему это может производить больше выходной мощности, чем использование неконцентрированной солнечной энергии в качестве источника тепла, собираемой на той же площади, что и тарелка.
См. Ответ
Источник: http://www.stirlingenergy.com
Проблема № 4
Пар с температурой 350 ° C и давлением 1 МПа течет по трубе. Какая энтальпия пара?
См. Ответ
Проблема № 5
Вихревая трубка, также известная как вихревая трубка Ранка-Хилша, представляет собой механическое устройство без движущихся частей, которое разделяет сжатый газ на горячий и холодный потоки.Согласно данным производителя, сжатый воздух поступает в вихревую трубку с температурой 20 ° C и манометрическим давлением 700 кПа. Из левой части трубки выходит холодный воздух при температуре -18 ° C и атмосферном давлении. Горячий воздух выходит из правой стороны трубки при температуре 105 ° C и атмосферном давлении. Отношение массового расхода между холодным потоком и входящим потоком составляет 0,70. Возможны ли эти спецификации?
См. Ответ
Проблема № 6
Пневматический автомобиль приводится в движение сжатым воздухом под высоким давлением, хранящимся в резервуаре.Бак под давлением соединен с пневматическим двигателем. Объем резервуара составляет 0,3 м 3 , а начальная температура и давление воздуха внутри резервуара 20 ° С и 30 МПа соответственно. Используя онлайн-ресурсы, проанализируйте эффективность Air Car.
См. Ответ
Проблема № 7
Башня падения — популярный аттракцион в парках развлечений. Чтобы сделать поездку максимально энергоэффективной, можно настроить электродвигатель и систему рекуперативных аккумуляторов, в которой энергия аккумулятора используется для приведения в действие электродвигателя, чтобы поднять гонщиков на вершину поездки.Когда гонщики спускаются по трассе, «падающая» энергия используется для подзарядки аккумулятора. Учитывая, что трение неизбежно, объясните, почему эта поездка является примером необратимого процесса.
См. Ответ
Источник: https://commons.wikimedia.org/wiki/File:Freefall_moviepark.png
Проблема № 8
Ученые предполагают, что развитые инопланетные цивилизации будут использовать большой процент энергии своей родительской звезды.Это приведет к образованию большого количества отработанного тепла в огромных масштабах, которое может быть обнаружено с помощью телескопов здесь, на Земле. Объясните, почему эта теория имеет смысл с точки зрения термодинамики, на примере нашей цивилизации.
См. Ответ
Ответы на проблемы термодинамики
Ответ на проблему №1
Поскольку контейнеры изолированы, теплопередача между газом и внешней средой не происходит, а поскольку газ свободно расширяется в контейнер B, нет сопротивления, «толкающего» его, что означает, что с газом не происходит никакой работы. расширяется.В результате внутренняя энергия газа остается неизменной до и после расширения. Чтобы вернуть газ в исходное состояние, его нужно сжать обратно в контейнер A. Это неизбежно происходит против силы сопротивления (создаваемого газом), а это означает, что для этого требуется работа. Это добавило бы энергии газу, тем самым увеличив его внутреннюю энергию, в результате чего температура и давление газа были бы выше, чем его начальная температура и давление (внутри контейнера A).Затем его необходимо охладить, чтобы вернуть его к условиям P 1 и T 1 . Это добавит тепла в окружающую среду, что увеличит энтропию. Следовательно, газ не может быть возвращен в исходное состояние в обратных условиях, и поэтому процесс, описанный в задаче, не является обратимым.
Ответ на проблему №2
Для воздуха при атмосферном давлении и температуре 20 ° C, содержащего водяной пар с относительной влажностью 30%, парциальное давление водяного пара составляет P w = 0.30 × P г (согласно определению относительной влажности), где P г — давление насыщенного водяного пара. Ссылаясь на таблицу термодинамики, содержащую свойства насыщенной воды (H 2 O), P g = 0,002338 МПа. Итак, P w = 0,30 × 0,002338 = 0,0007 МПа. Мы хотим рассчитать давление воздуха внутри контейнера так, чтобы P w = P g .Это означает, что парциальное давление водяного пара внутри контейнера равно давлению насыщенного водяного пара (при 20 ° C). Если мы увеличим давление воздуха на некоторое количество M , то парциальное давление водяного пара, присутствующего в воздухе, увеличится на такое же кратное M (на основе закона парциальных давлений Дальтона). Следовательно, M = 0,002338 / 0,0007 = 3,34. Максимальное давление внутри контейнера тогда составляет 3,34 × (атмосферное давление) = 340 кПа, приблизительно, для атмосферного давления = 101.3 кПа. При таком давлении водяной пар начнет конденсироваться внутри емкости (при температуре точки росы 20 ° C). Обратите внимание, что наличие конденсата внутри контейнера может быть нежелательным, так как это может вызвать коррозию или рост плесени. Этого можно избежать, поддерживая давление внутри контейнера ниже 340 кПа, чтобы не происходила конденсация воды.
Ответ на проблему № 3
Согласно уравнению для КПД Карно, большая разница температур между источником тепла и радиатором приводит к большей выходной мощности (более высокой тепловой эффективности).А меньшая разница температур приводит к более низкой выходной мощности (более низкому тепловому КПД). Вот почему для выработки солнечной тепловой энергии желательно фокусировать солнечный свет с большой площади на небольшой площади. Результатом является намного более высокая температура источника тепла и, как следствие, гораздо более высокий тепловой КПД, что означает гораздо более высокую выходную мощность для двигателя. Например, коллектор с площадью поверхности A, который собирает тепловую энергию от солнца для запуска теплового двигателя, намного менее эффективен (и производит гораздо меньше энергии), чем тепловой двигатель, который использует ту же энергию, но в концентрированной форме.Другими словами, фокусирование солнечного света, падающего на точку A, на маленькую точку и использование этой энергии для запуска теплового двигателя намного эффективнее и производит больше энергии, чем использование несфокусированного солнечного света, падающего на коллектор. Чем больше вы сможете сфокусировать тепловую энергию, тем больше энергии вы получите. Вот почему тарелки Стирлинга, которые фокусируют солнечный свет в определенную точку, производят больше энергии, чем параболические желоба, которые фокусируют солнечный свет вдоль линии (при условии, что оба используют одну и ту же область воздействия солнца). В чашках Стирлинга фокусная температура выше, чем в параболических желобах, поэтому они более эффективны.
Ответ на проблему №4
Это можно определить, посмотрев непосредственно на таблицы перегретого пара. Для данных температуры и давления энтальфия составляет 3157,7 кДж / кг.
Ответ на проблему № 5
Пусть m i будет массовым расходом воздуха на входе, m c будет массовым расходом воздуха на холодном выходе и m h будет массовым расход воздуха на горячем выходе.
Во-первых, проверьте Первый закон термодинамики (который представляет собой уравнение баланса энергии), предполагая установившийся режим и адиабатический процесс, в котором имеется незначительная передача тепла к или от воздуха, когда он течет через вихревую трубку, поэтому мы не делаем этого. t необходимо учитывать вклад энергии за счет теплопередачи.Это разумное предположение, поскольку воздух быстро проходит через вихревую трубку. Кроме того, в вихревую трубку не добавляется и не отводится рабочая энергия. У нас есть
м i h i — ( м c h c + m h h h ) = 0
Где:
h i — энтальпия воздуха на входе
h c — энтальпия воздуха на холодном выходе
ч ч — энтальпия воздуха на горячем выходе
Разделите полученное выше уравнение на м i .Мы получили
h i — ( m c / m i ) h c — ( m h / m i ) h h = 0
Сейчас, м c / м i = 0,70 и м h / м i = 0,30.
Ссылаясь на термодинамическую таблицу, содержащую энтальпию воздуха,
При 20 ° C и 801.3 кПа (рабочее давление 700 кПа), ч i = 293 кДж / кг
При -18 ° C и 101,3 кПа, ч c = 255 кДж / кг
При 105 ° C и 101,3 кПа, ч ч = 379 кДж / кг
Подставьте значения в левую часть приведенного выше уравнения и посмотрите, равно ли оно 0. Получаем
293 — (0,70) (255) — (0,30) (379) = 0,8
Это не совсем равно 0, но находится в пределах диапазона ошибки округления.
Следующим шагом является проверка второго закона термодинамики (который представляет собой уравнение производства энтропии), снова предполагая установившееся состояние и адиабатический процесс, в котором нет передачи тепла к воздуху или от воздуха, когда он течет через вихревую трубу. , поэтому нам не нужно учитывать производство энтропии за счет теплопередачи.У нас есть
S = ( m c s c + m h s h ) — m i s i
Где:
S i — полное производство энтропии
с i — энтропия воздуха на входе
s c — энтропия воздуха на холодном выходе
с ч — энтропия воздуха на горячем выходе
Разделите полученное выше уравнение на м i .Мы получили
S / м i = ( м c / м i ) s c + ( m h / m i ) с ч — с i
Ссылаясь на термодинамическую таблицу, содержащую энтропию воздуха,
При 20 ° C и 801,3 кПа (рабочее давление 700 кПа), с i = 6,3 кДж / (кг · K)
При -18 ° C и 101.3 кПа, с c = 6,7 кДж / (кг · К)
При 105 ° C и 101,3 кПа, с ч = 7,1 кДж / (кг · К)
Подставьте значения в правую часть приведенного выше уравнения и посмотрите, больше ли оно 0. Это будет означать, что процесс производит энтропию и физически возможен с точки зрения термодинамики. Мы получили
(0,70) (6,7) + (0,30) (7,1) — 6,3 = 0,52
Это больше 0. Итак, исходя из первого и второго законов термодинамики, процесс физически осуществим.Но это, однако, не говорит вам о том, что это возможно с технологической точки зрения, точно так же, как эффективность Карно для теплового двигателя только говорит вам о том, что теоретически возможно с учетом ограничений термодинамики. Он не сообщает вам, что возможно, исходя из других ограничений, например, из-за технологических ограничений. Кроме того, этот анализ не говорит вам, как работает вихревая трубка, что является совершенно другим обсуждением, на самом деле довольно сложным.
Ответ на проблему №6
Используя термодинамику, мы можем оценить эффективность воздушной машины следующим образом:
КПД воздушной машины равен 100 × (выходная энергия) / (входная энергия).Подводимая энергия равна количеству энергии, необходимой для заполнения резервуара сжатым воздухом. Давайте предположим идеальный изотермический (постоянная температура) процесс, при котором сжатый воздух, закачиваемый в резервуар, поддерживается как можно ближе к температуре окружающего воздуха. Это сводит к минимуму энергию откачки, необходимую для нагнетания воздуха в резервуар. Это достигается за счет охлаждения сжатого воздуха перед его поступлением в резервуар. Если воздух не охлаждается одновременно с закачкой в резервуар, он достигнет очень высокой температуры, что потребует большей энергии откачки, чем более холодный воздух.Нагрев воздуха за счет сжатия является фундаментальным свойством газов (который здесь можно смоделировать как идеальный газ, где PV = mRT). Если сжать воздух в меньший объем, он будет нагреваться.
Важно отметить, однако, что (при отсутствии воздушного охлаждения) дополнительная входная (накачивающая) энергия приведет к дополнительной выходной энергии при вождении автомобиля, но только в том случае, если нагретый воздух в баке может поддерживать его температуру. Но на самом деле нагретый воздух остывал бы до температуры окружающей среды.И эта дополнительная энергия накачки будет напрасной (то есть она не будет восстановлена в фазе движения). Это одна из причин, по которой мы должны охлаждать воздух как можно ближе (в практических пределах) к температуре окружающей среды, когда он входит в резервуар. Это достигается за счет многоступенчатого охлаждения.
При изотермической перекачке воздуха в резервуар (идеальная) подводимая энергия составляет E в = P 1 В 1 лн (P 2 / P 1 ), где P 1 и V 1 — начальное (атмосферное) давление и начальный объем воздуха соответственно, а P 2 — давление воздуха после его закачки в резервуар.Из приведенного выше уравнения идеального газа и учитывая изотермический процесс, P 1 V 1 = P 2 V 2 , где V 2 — объем резервуара. Затем мы можем вычислить V 1 = 90 м 3 .
Подставляя P 1 = 0,1 МПа (атмосферное давление), P 2 = 30 МПа и V 1 = 90 м 3 в приведенное выше уравнение, мы вычисляем E в = 51,3 МДж (мегаджоули) .
Теперь, на самом деле воздух несколько нагревается между ступенями охлаждения, так что это «вынуждает» компрессор использовать больше 51.3 МДж для закачки воздуха в бак. По данным Европейского форума топливных элементов, реальный коэффициент полезного действия для многоступенчатого охлаждения составляет 48% (ссылка: http://www.efcf.com/reports/E14.pdf). Таким образом, фактическая входная энергия составляет евро в = 51,3 / 0,48 = 107 МДж .
Попав в резервуар, воздух охладится до тех пор, пока его температура не достигнет температуры окружающей среды. Энергия воздуха в этой точке составит 51,3 МДж.
Обратите внимание, что 51,3 МДж на больше, чем на фактическая энергия, которая будет извлечена из резервуара для питания автомобиля.Это связано с термодинамическими (физическими) потерями (форма термодинамической необратимости). Чтобы сохранить эти потери на минимальном уровне, необходимо, чтобы воздух нагревался при расширении внутри двигателя после выхода из резервуара. Поскольку воздух имеет тенденцию остывать при расширении, лучше поддерживать его температуру как можно более высокой, используя окружающий воздух в качестве источника тепла. Другими словами, мы хотим поддерживать температуру (расширяющегося) воздуха как можно ближе к его температуре внутри резервуара.Если это можно сделать идеально, то извлеченная энергия будет точно равна 51,3 МДж. Но на самом деле это не так. Воздух неизбежно остывает, поэтому, чтобы противодействовать этому, используется многоступенчатый нагрев для нагрева расширяющегося воздуха, когда он выходит из бака и попадает в двигатель.
По данным Европейского форума топливных элементов, реальный коэффициент полезного действия для многоступенчатого нагрева составляет 84% (ссылка: http://www.efcf.com/reports/E14.pdf). Таким образом, фактическая выходная энергия E out = 51.3 × 0,84 = 43 МДж .
Следовательно, термодинамический КПД Air Car составляет 100 × (E из / E в ) = 40%.
Ответ на проблему № 7
Процесс, не производящий энтропии, является обратимым процессом, потому что его также можно заставить происходить в обратном направлении. В этом случае прямое направление процесса — это движение, которое поднимается (что снижает заряд батареи), а обратное направление — это движение, возвращающееся вниз (что увеличивает заряд в аккумуляторе).Заряд не может быть полностью возвращен в аккумулятор после завершения поездки, потому что трение, присутствующее в поездке, преобразует часть энергии аккумулятора в тепловую энергию, которая теряется в окружающей среде (которая производит энтропию), и ее нельзя восстановить. Следовательно, поездка (по пути вверх или вниз) не является обратимым процессом.
Ответ на проблему № 8
Если инопланетяне где-то во Вселенной используют значительную часть звездной энергии для питания своей цивилизации, в результате будет образовываться очень большое количество отработанного тепла, которое будет находиться в средней инфракрасной части электромагнитного спектра.Это неизбежное следствие законов термодинамики. Энергия не может быть уничтожена, она может только изменять форму, и обычно после использования энергия превращается в отходящее тепло. Возьмем, к примеру, машину; большая часть энергии топлива теряется в виде тепла, а оставшаяся энергия используется для движения автомобиля (т. е. выполнения полезной работы). Однако для движения автомобиля необходимо преодолеть трение с дорогой и воздухом, а также внутреннее трение двигателя и других движущихся частей автомобиля. В конце концов, это тоже приводит к потере тепла.Таким образом, практически вся энергия автомобильного топлива превращается в отработанное тепло. Вы можете утверждать, что тот же принцип применим к инопланетянам, использующим значительную долю звездной энергии. Эта энергия используется, чтобы «что-то сделать», и после того, как эта задача или задачи будут выполнены, и если предположить, что энергия нигде не накапливается, эта энергия в конечном итоге превратится в отработанное тепло в средней инфракрасной области. Вы можете пойти гораздо глубже, чтобы объяснить точные причины, но это основное следствие законов термодинамики.
Вернуться на страницу Вопросы по физике
Вернуться на Реальные проблемы физики домашняя страница
пожаловаться на это объявление
Практические проблемы и решения термодинамики — Видео и стенограмма урока
Автомобильные двигатели
Автомобили — почти неотъемлемая часть нашей повседневной жизни.Люди, которым приходится много водить, могут принять решение о том, на каком автомобиле ехать, исходя из того, насколько хорошо двигатель автомобиля может экономить бензин. К сожалению, большая часть бензина, которую мы покупаем для питания двигателя нашей машины, только нагревает двигатель. Давайте посмотрим, как автомобильный двигатель превращает бензин в движение.
Внутри двигателя автомобиля находятся цилиндры и поршни. Поршни представляют собой металлические части цилиндрической формы, которые перемещаются вверх и вниз внутри цилиндра. К нижней части поршня прикреплен шатун, который прикреплен к коленчатому валу.Коленчатый вал соединен с маховиком, который вращает шестерни трансмиссии при включении. Трансмиссия по сути поворачивает колеса, и ваша машина едет по дороге. Нам нужно сосредоточить внимание на том, что происходит внутри цилиндра.
Бензин и воздух воспламеняются внутри цилиндра, когда поршень находится в верхней части цилиндра. При повышении температуры увеличивается беспорядок в системе, что выражается в увеличении энтропии. Взрывающийся газ хочет расширяться во всех направлениях, но толстый металл стенки цилиндра не позволяет этого.Только молекулы, направленные на поршень, толкают его вниз, в конечном итоге заставляя колеса автомобиля двигаться.
Энергия молекул, которые не заставляют поршень двигаться, идет на нагревание цилиндра. Часть энергии молекул, которые ударяются о поршень, также теряется на тепло. Это приводит нас непосредственно к обсуждению эффективности двигателя.
КПД двигателя
Рассматриваемый нами тепловой двигатель работает на потоке тепловой энергии. Температурный градиент — это разница температур между двумя отдельными местами.Представьте разницу между температурой внутри цилиндра при работающем двигателе и температурой выхлопных газов. Выхлоп теплый, но температура внутри цилиндра очень высокая. Тепло, выходящее из выхлопных газов, теряет энергию Давайте посмотрим на эту диаграмму на вашем экране, которая показывает концептуальный поток тепла в тепловом двигателе.
Мы можем рассчитать эффективность теплового двигателя, используя тепло, выделяемое горящим топливом, и тепло, выходящее через выхлоп.Уравнение:
В этом уравнении:
- QH — тепло в системе
- QC — тепло, покидающее систему
Обе температуры должны быть в градусах Кельвина. Определим КПД некоторых тепловых двигателей.
Давайте сначала рассмотрим пример бензинового двигателя. Вот наша подсказка: температура воспламененного бензина внутри цилиндра автомобильного двигателя составляет около 503 К.Температура выхлопных газов двигателя составляет 298 К. Каков КПД двигателя?
Вот наше решение: QH = 503 K , QC = 298 K
Таким образом, используя наше уравнение эффективности, мы только что узнали:
Важно отметить, что это теоретический КПД бензинового двигателя. Мы проигнорировали другие недостатки, которые значительно снижают общую эффективность.
Давайте теперь рассмотрим пример с паровой машиной. Паровые двигатели работают за счет сжигания топлива до кипения воды. Затем пар используется для перемещения поршней. Вот наша подсказка: у парового двигателя внутренняя температура 373 К. Температура выхлопных газов составляет 298 К. Каков КПД двигателя?
Вот наше решение: QH = 373 K , QC = 298 K
Как и раньше, давайте воспользуемся формулой эффективности. В данном случае:
Опять же, это теоретическое значение.Фактическая эффективность намного меньше.
Итоги урока
Давайте рассмотрим, что мы узнали. Энтропия — часть второго закона термодинамики. Это определяется как тенденция системы становиться более неупорядоченной и случайной. Тепловые двигатели работают по концепции температурного градиента , который представляет собой разницу температур между двумя отдельными местами. Топливо сгорает, выделяя тепло. Тепло заставляет газ расширяться и используется для выполнения работы, перемещая поршень.Выхлоп содержит тепло, которое не использовалось для работы. Когда частицы газа нагреваются, они хотят расширяться. Не все частицы газа ударяются о поршень. Некоторые ударяются о стенки цилиндра, что только увеличивает температуру цилиндра.
Теоретический КПД теплового двигателя можно рассчитать на основе его внутренней температуры в зависимости от температуры выхлопных газов.
Проблемы и решения по термодинамике
1 11 — Термодинамика Тепло и теплоемкость 1) 2) TA> TB TA TB Q TA = TB = T Исторически считалось, что тепло является своего рода жидкостью (калорийностью), но на самом деле это форма энергии Одна калория (1 кал) определяется как количество тепла, необходимое для повышения температуры 1 г воды на 1 ° C (или 1 ° K).Для небольших изменений температуры ∆T существует линейная зависимость TmcTCQ ∆ = ∆ = C — теплоемкость в кал / ° C c — удельная теплоемкость в кал / (г ° C) По определению c = 1 кал / (г ° C) для воды. Вводя воду в тепловой контакт с другими материалами и, таким образом, позволяя теплу течь от одного к другому, и измеряя изменения температуры обоих материалов, можно определить теплоемкость других веществ. У большинства из них c меньше, чем у воды. BA A B PHY166 Осень 2005 г. Тепло Q передается от более горячего тела к более холодному, пока температура не уравновесится 2 Задача: В одном эксперименте студент бросает 100 г свинца [cL = 0.0305 кал / (г ° C)] при 0 ° C в 1 литр воды при 100 ° C. В другом эксперименте она добавляет 100 г воды при 0 ° C в 1 л воды при 100 ° C. Сравните полученные значения температуры в обоих случаях. Решение: рассмотрим общий случай добавления веществ с теплоемкостью cA и cB, массами mA и mB и температурами TA и TB. Полученная температура равна T. Тепло течет от A к B, таким образом, сумма тепла, полученного A и на B равно нулю: () () BBBAAABBBAAABA TTcmTTcmTcmTcmQQ — + — = ∆ + ∆ = + = 0 Решая это уравнение для T, получаем BBAA BBBAAA cmcm TcmTcm T + + = Теперь для первого эксперимента CT ° = −≅ + = × + = × + × × × + × × = 695.99) 00305.01 (100 00305.01 1100 1000 / 0305.01001 1100 0305.010011000 00305.010010011000 1 Для второго эксперимента CT ° = + = × + = × + × × × + ×× = 91.90 1.01 1100 1000/11001 1100 110011000 0110010011000 2 ( Охлаждение примерно на 9 ° C) (очень небольшой охлаждающий эффект) 5 Первый закон термодинамики VPWQWQU ∆ — + = + = ∆ dis Здесь ∆U — изменение внутренней энергии системы (потенциальная энергия за счет взаимодействия молекул плюс их кинетическая энергия) Q — тепло, получаемое системой Wdiss — это так называемая диссипативная работа (например, работа трения и перемешивания), которая эквивалентна теплу −P∆V — это так называемая конфигурационная работа над телом, полученная ниже Вывод конфигурационной работы (если тело расширяется, ∆l> 0, работа над телом отрицательная): l∆ F SVPlPSlFW ∆− = ∆− = ∆− =, поскольку PSF = и VlS ∆ = ∆ (Обобщенный закон сохранения энергии ) S — площадь поперечного сечения 6 Теперь рассмотрим процессы с постоянным объемом, ∆V = 0 и Wdiss = 0.В этом случае первый закон термодинамики имеет вид QU = ∆. Для идеальных газов (разреженных газов) потенциальная энергия пренебрежимо мала, и, таким образом, U — кинетическая энергия, пропорциональная температуре. Из кинетической теории одноатомных газов (предыдущая лекция) следует TkNNU B2 3 == ε Используя определение теплоемкости и формулу для U, получаем TCTkN B ∆ = ∆2 3 или теплоемкость при постоянном объеме BkNC 2 3 = Двухатомные газы (молекулы, состоящие из двух атомов) и многоатомные газы дополнительно обладают кинетической энергией вращения, поэтому их внутренняя энергия и теплоемкость выше.Это кинетическая энергия, соответствующая линейному движению в трех разных направлениях в пространстве. 7 Если газ термически изолирован так, что Q = 0 (адиабатический процесс) и с газом совершается отрицательная работа W <0 (газ расширяется), его внутренняя энергия U уменьшается, а температура T также уменьшается. Напротив, адиабатическое сжатие газа приводит к повышению его температуры. По этой причине адиабатический процесс описывается более крутой кривой на диаграмме P-V, чем изотермический процесс.Изотермический процесс в идеальном газе сохраняет его внутреннюю энергию, таким образом, Q + W = 0, и вся положительная работа, выполняемая при сжатии газа, отдается в виде тепла, Q <0. PV Адиабатический процесс, Q = 0 Изотермический процесс, T = const
Задача термодинамики — обзор
2.3 Уравнение состояния
В целом термодинамика касается веществ во всех трех фазах: твердой, жидкой и газовой. Большинство термодинамических проблем обычно связаны с газами или парами, например, при горящих пожарах, хотя некоторые из возникающих термодинамических проблем могут в некоторых случаях касаться жидкостей и твердых тел.Такие проблемы обычно связаны с интенсивными и экстенсивными свойствами систем. При определении взаимосвязи между различными свойствами вещества в дальнейшем следует исходить из того, что интенсивные свойства одинаковы во всей рассматриваемой системе, что означает, что система находится в термическом и механическом равновесии. Когда система находится в тепловом, механическом и химическом равновесии, говорят, что система находится в состоянии термодинамического равновесия.Другими словами, можно сказать, что, хотя интенсивные свойства могут быстро меняться от места к месту, система может термодинамически адаптироваться к новым условиям так быстро, что изменения фактически мгновенны. Следовательно, система всегда остается в термодинамическом равновесии.
Согласно Куо (1986), интенсивное свойство может быть определено как свойство, которое не изменяется при увеличении размера системы путем добавления к нему любого количества систем, идентичных исходной системе, в то время как расширенное свойство свойство , наоборот, можно определить как свойство, которое увеличивается пропорционально размеру системы в таком процессе.
Интенсивными свойствами, обычно обнаруживаемыми в движущейся жидкости, являются плотность (ρ), давление ( p ), удельная внутренняя энергия ( e ) и температура ( T ), в то время как другие переменные, такие как объем ( V ), масса ( м ), полная энтальпия ( ч ) и другие, как правило, рассматриваются как экстенсивные свойства. Использование термодинамического равновесия обеспечивает средства, с помощью которых состояние вещества обычно может быть описано в терминах только двух термодинамических переменных или интенсивных свойств.Для идеального газа или следующее широко используемое уравнение состояния, подчиняющееся законам двух известных исследователей, Бойля и Чарльза, равно
(2.3.1) pV = nRuT
, где R u — универсальная газовая постоянная (8,31431 кДж кмоль −1 K −1 ). Установка давления p = 101325 Па, T = 273,15 K (0 o C) и n = 1 моль, В = 0,022414 м 3 .Для идеальных газов этот объем представляет собой общий объем, который будет занят 28 г N 2 (азот), 32 г O 2 (кислород), 44 г CO 2 (диоксид углерода), 18 г H 2 O (водяной пар) или 16 г CH 4 (метан).
Плотность или концентрацию газа можно определить согласно
(2.3.2) ρ = нМВ = pMRuT
, где M — молекулярная масса газовой смеси. Для воздуха можно показать, что один моль соответствует молекулярной массе 0.02895 кг. Для давления p = 101325 Па и температуры T = 0 o C (273,15 K) плотность будет 1,292 кг м -3 .
Процесс горения при пожаре обычно вызывает значительные изменения температуры окружающей среды в результате образования многих продуктов горения при высоких температурах. Для потока реагирующей жидкости в химическом равновесии количество молей для каждого химического вещества обычно может быть выражено известным материалом с объемом V и температурой T :
(2.3.3) ni * = f (V, T)
, где верхний индекс * обозначает равновесные значения. Уравнение состояния системы в равновесии принимает вид
(2.3.4) p = f (V, T, n1 *, n2 *,…, nN *)
Из закона парциальных давлений Дальтона p i , выражение для смеси термически совершенных газов в термодинамическом равновесии, таким образом, может быть альтернативно дано аналогично уравнению (2.3.1) как:
(2.3.5) p = ∑ipi = 1V∑i = 1Nni * RuT
давление смеси для системы, находящейся в химическом неравновесном состоянии, можно просто представить, удалив верхний индекс * в уравнении (2.3.5).
Газы, текущие с высокой скоростью, обычно относятся к сжимаемым потокам . Здесь плотность резко меняется в широком диапазоне давлений, а также температур в поле течения. В таких потоках уравнение состояния обеспечивает необходимую связь между уравнением сохранения энергии и уравнениями сохранения массы и количества движения. Также существует ряд ситуаций, когда газы, текущие с низкой скоростью, ведут себя как несжимаемые жидкости .Плотность остается неизменной, и поток жидкости, таким образом, можно решить, только рассматривая уравнения, относящиеся к сохранению массы и количества движения. Для других низкоскоростных потоков, типичных для горящих пожаров, они, тем не менее, считаются слабосжимаемыми . Термин слабо относится к последствиям изменения плотности, на которое в основном влияют существенные колебания температуры из-за химических реакций в поле потока, но не из-за изменений давления, поскольку давление остается относительно неизменным в окружающей среде.

 На сколько изменилась внутренняя энергия газа и какая работа была совершена им?
На сколько изменилась внутренняя энергия газа и какая работа была совершена им?





 Эта энергия весьма велика. Но изменения средней температуры земной атмосферы, самой Земли практически не происходит. Это объясняется тем, что Земля выбрасывает в космос в среднем такое же количество тепла, какое получает извне.
Эта энергия весьма велика. Но изменения средней температуры земной атмосферы, самой Земли практически не происходит. Это объясняется тем, что Земля выбрасывает в космос в среднем такое же количество тепла, какое получает извне. На сколько градусов повысится температура большой капли по сравнению с температурой маленьких капель? Радиус каждой маленькой капельки – 1 мм.
На сколько градусов повысится температура большой капли по сравнению с температурой маленьких капель? Радиус каждой маленькой капельки – 1 мм.
 Следовательно, мы можем массу выразить либо через объем маленькой капельки v и количество капелек, либо через объем большой капли V. m = ρV = ρNv.
Следовательно, мы можем массу выразить либо через объем маленькой капельки v и количество капелек, либо через объем большой капли V. m = ρV = ρNv.