3

6

Risolvere per ?

cos(x)=1/2

7

Risolvere per x

sin(x)=-1/2

8

Преобразовать из градусов в радианы

225

9

Risolvere per ?

cos(x)=( квадратный корень 2)/2

10

Risolvere per x

cos(x)=( квадратный корень 3)/2

11

Risolvere per x

sin(x)=( квадратный корень 3)/2

12

График

g(x)=3/4* корень пятой степени x

13

Найти центр и радиус

x^2+y^2=9

14

Преобразовать из градусов в радианы

120 град. 2+n-72)=1/(n+9)

Таблица степеней 🆕

Основные понятия

Степень числа — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.

Показатель степени всегда натуральное число — это значит, что его можно использовать при счете или перечислении предметов:

• aⁿ = a * a *…* a, где a — основание степени,
• n — натуральный показатель степени.

Запись читается, как «a» в степени «n».

Вот пример для наглядности:

• 3⁵ = 3 * 3 * 3 * 3 * 3 = 243

Эту запись можно прочитать тремя способами:

• 3 в 5 степени;
• пятая степень числа три;
• возвести число три в пятую степень.

Свойства степеней

Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры.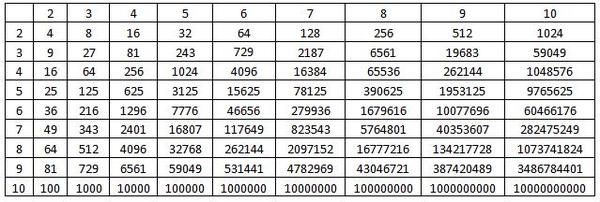 Удобно использовать вместе с таблицей степеней и таблицей умножения.

a1 = а a0 = 1 (a ≠ 0) a-n = 1 : an am * an = am+n am : an = am-n (a * b)n = an * bn (am)n = am*n (a : b)n = an : bn

Таблица степеней от 1 до 10

Таблица степеней — это перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Ниже приведены два вида таблиц, выберите ту, которая удобнее для вас — скачайте на телефон или распечатайте и положите в учебник.

Как найти необходимые значения в этой таблице:

• В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
• В первой строке находим показатель степени. Запомним найденный столбец.
• На пересечении строки и столбца находится ответ.

В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.

А если ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Вот несколько подходящих:

Алгебра — предмет серьезный: при переходе в новый класс багаж формул и правил будет только увеличиваться. Поэтому важно запоминать все последовательно и практиковаться на примерах.

Решение задач

Задание 1. Упростить и решить выражение 5²* 5³.

Как решаем:

5² * 5³ = 5²⁺³ = 5⁵ = 3125

Задание 2. Упростить и решить выражение 2⁴* 3³* 2⁵.

Как решаем:

2⁴ * 3³ * 2⁵ = 2⁴⁺⁵ * 3³ = 2⁹ * 3³ = 512 * 27 = 13824

Задание 3. Найти 36⁴.

Как решаем:

При условии, что у нас есть только таблица до 10, разложим основание степени на множители:

36⁴ = 6⁴ * 6⁴ = 1296 * 1296 = 1679616

36⁴ = 6⁴ * 6⁴ = 6⁸ = 1679616

Запомнить все и сразу бывает сложно, но чем больше задачек решит ваш ребенок, тем меньше придется заглядывать в шпаргалки. Запишитесь на бесплатный вводный урок в детскую онлайн-школу Skysmart. Мы подобрали тысячи увлекательных заданий: от простых логических загадок до хитрых головоломок, над которыми интересно подумать. 

Сумма пятой степени | Формулы с примерами

1. 2⁵ + 3⁵ = (2 + 3) • (2³ • 3 + 2² • 3² — 2 • 3³ + 3⁴) =


5 • (16 — 8 • 3 + 4 • 9 — 2 • 27 + 81) =


5 • (16 — 24 + 36 — 54 + 81) =


5 • 55 = 275 ;


a = 2⁵ ;


b = 3⁵ ;

2. 7⁵ + 5⁵ = (7 + 5) • (7⁴ — 7³ • 5 + 7² • 5² — 7 • 5³ + 5⁴) =


12 • (2 401 — 343 • 5 + 49 • 25 — 7 • 125 + 625) =


12 • (2 401 — 1 715 + 1 225 — 875 + 625) =


12 • 1 661 = 19 932 ;


a = 7⁵ ;


b = 5⁵ ;

3. 3⁵ + 3⁵ = (3 + 5) • (3⁴ — 3³ • 5 + 3² • 5² — 3 • 5³ + 5⁴) =


8 • (81 — 27 • 5 + 9 • 25 — 3 • 125 + 625) =


8 • (81 — 135 + 225 — 375 + 625) =


8 • 421 = 3 368 ;


a = 3⁵ ;


b = 5⁵ ;

Решите уравнение (x+2)^5=32 ((х плюс 2) в степени 5 равно 32)

Дано уравнение
$$\left(x + 2\right)^{5} = 32$$
Т. {5 i p} = 1$$
Используя формулу Эйлера, найдём корни для p
$$i \sin{\left (5 p \right )} + \cos{\left (5 p \right )} = 1$$
значит
$$\cos{\left (5 p \right )} = 1$$
и
$$\sin{\left (5 p \right )} = 0$$
тогда
$$p = \frac{2 \pi}{5} N$$
где N=0,1,2,3,…
Перебирая значения N и подставив p в формулу для z
Значит, решением будет для z:
$$z_{1} = 2$$
$$z_{2} = — \frac{1}{2} + \frac{\sqrt{5}}{2} — 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$z_{3} = — \frac{1}{2} + \frac{\sqrt{5}}{2} + 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$z_{4} = — \frac{\sqrt{5}}{2} — \frac{1}{2} — 2 i \sqrt{- \frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$z_{5} = — \frac{\sqrt{5}}{2} — \frac{1}{2} + 2 i \sqrt{- \frac{\sqrt{5}}{8} + \frac{5}{8}}$$
делаем обратную замену
$$z = x + 2$$
$$x = z — 2$$

Тогда, окончательный ответ:
$$x_{1} = 0$$
$$x_{2} = — \frac{5}{2} + \frac{\sqrt{5}}{2} — 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$x_{3} = — \frac{5}{2} + \frac{\sqrt{5}}{2} + 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$x_{4} = — \frac{5}{2} — \frac{\sqrt{5}}{2} — 2 i \sqrt{- \frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$x_{5} = — \frac{5}{2} — \frac{\sqrt{5}}{2} + 2 i \sqrt{- \frac{\sqrt{5}}{8} + \frac{5}{8}}$$

Степень числа.

Квадрат и куб числа 5 класс онлайн-подготовка на Ростелеком Лицей

Степень числа. Квадрат и куб числа.

Мы знаем, что сумму 2 + 2 + 2 + 2 + 2 можно записать короче с помощью умножения, получится 2*5, где 2 – слагаемое, 5 – количество одинаковых слагаемых.

Аналогично произведение 2 * 2 * 2 * 2 * 2 можно записать короче. Для этого используется степень:

2 * 2 * 2 * 2 * 2 =2⁵

Запись 2⁵ читают “два в пятой степени”. Здесь 2 – основание степени; 5 – показатель степени; 2⁵ – степень.

Запишем произведения в виде степени:

4 * 4 * 4 = 4³

3 * 3 * 3 = 3³

2 * 2 * 2 * 2 * 2 * 2 = 2⁶

Вторую степень числа принято называть иначе. Произведение 5 * 5 называют квадратом числа 5 и обозначают 5².

n² = n * n – квадрат числа.

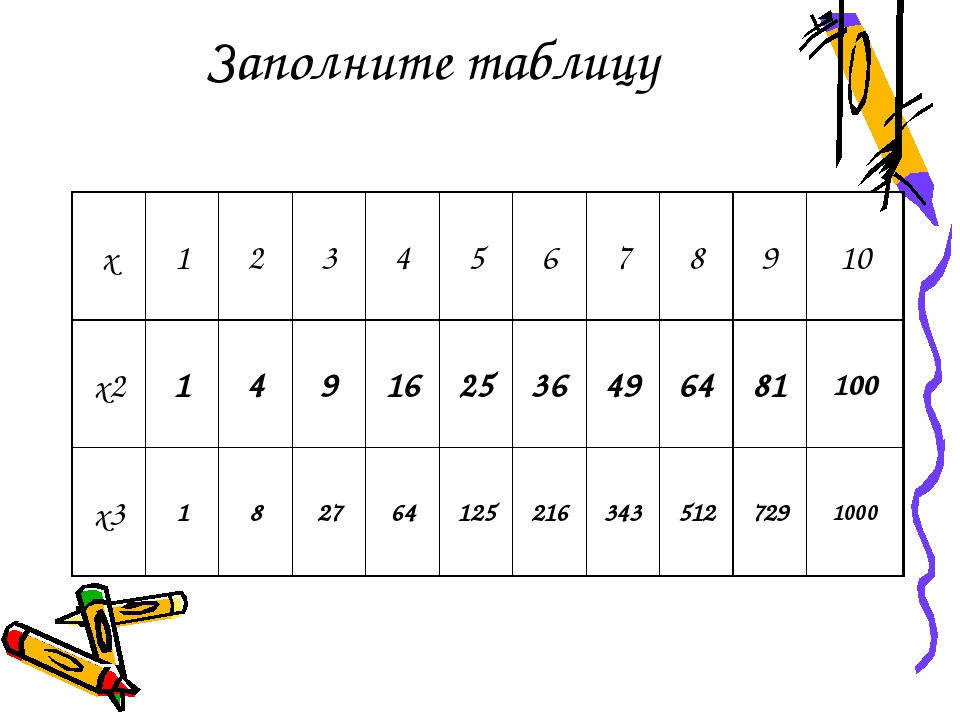
Рассмотрим таблицу квадратов первых десяти натуральных чисел.

2² = 4, 3² = 9 и т. д.

n	1	2	3	4	5	6	7	8	9	10
n2	1	4	9	16	25	36	49	64	81	100

Третья степень числа также имеет свое особое название. Произведение 7 * 7 * 7 называют кубом числа 7 и обозначают 7³.

n³ = n * n * n – куб числа.

Рассмотрим таблицу кубов первых десяти натуральных чисел.

2³=8, 3³=27, 4³=216 и т.д.

n	1	2	3	4	5	6	7	8	9	10
n 3	1	8	27	64	125	216	343	512	729	1000

Первую степень числа обычно не пишут: 3¹=3; 5¹=5 и т. д.

Таблица степеней

Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.

Калькулятор степеней

Вычислить
Очистить

\begin{align}
\end{align}

С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».

---

Таблица степеней от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
1n	1	1	1	1	1	1	1	1	1	1
2n	2	4	8	16	32	64	128	256	512	1024
3n	3	9	27	81	243	729	2187	6561	19683	59049
4n	4	16	64	256	1024	4096	16384	65536	262144	1048576
5n	5	25	125	625	3125	15625	78125	390625	1953125	9765625
6n	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7n	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8n	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9n	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10n	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

---

Таблица степеней от 1 до 10

11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1	21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024	31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049	41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576	51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176	71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249	81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824	91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401	101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000

Теория

Степень числа – это сокращенная запись операции многократного умножения числа самого на себя. Само число в данном случае называется — основанием степени, а количество операций умножения — показателем степени.

aⁿ = a×a … ×a

запись читается: «a» в степени «n».

«a» — основание степени

«n» — показатель степени

Пример:

46 = 4 × 4 × 4 × 4 × 4 × 4 = 4096

Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.

Скачать таблицу степеней

• Нажмите на картинку чтобы посмотреть в увеличенном виде.
• Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.

Возведение в степень | Кодкамп

Квадратный корень: math.

sqrt () и cmath.sqrt

math модуль содержит math.sqrt() -функции , который может вычислить квадратный корень из любого числа (которые могут быть преобразованы в float ) , и результат всегда будет float :

import math

math.sqrt(9)                # 3.0
math.sqrt(11.11)            # 3.3331666624997918
math.sqrt(Decimal('6.25'))  # 2.5

 

math.sqrt() функция вызывает ValueError , если результат будет complex :

math.sqrt(-10)              
 

ValueError: ошибка математического домена

math.sqrt(x) быстрее , чем math.pow(x, 0.5) или x ** 0.5 , но точность результатов является то же самое. cmath модуль очень похож на math модуля, за исключением того , что можно вычислить комплексные числа , и все его результаты в виде + би исключением. Он может также использовать . sqrt() :

import cmath

cmath.sqrt(4)  # 2+0j
cmath.sqrt(-4) # 2j

 

Что с j ? j является эквивалентом квадратного корня из -1. Все числа можно записать в виде a + bi или в этом случае a + bj. реальная часть числа , как 2 в 2+0j . Так как она не имеет мнимую часть, b равно 0. b представляет собой часть мнимой части числа , как 2 — в 2j . Поскольку нет никакой реальной части в этом, 2j также можно записать в виде 0 + 2j .

Экспонирование с использованием встроенных функций: ** и pow ()

Возведение может быть использован с помощью встроенного pow -функции или ** оператора:

2 ** 3    # 8
pow(2, 3) # 8

Для большинства (все в Python 2.x) арифметических операций тип результата будет типом более широкого операнда. Это не верно для ** ; следующие случаи являются исключениями из этого правила:

Основание: int , показатель: int < 0 :

2 ** -3
# Out: 0. 125 (result is a float) 

Это также верно для Python 3.x.

Перед Python 2.2.0, это поднял ValueError .

Основание: int < 0 или float < 0 , показатель: float != int

(-2) ** (0.5)  # also (-2.) ** (0.5)# Out: 0.125 (result is a float) 
Out: (8.659560562354934e-17+1.4142135623730951j) (result is complex)

operator модуль содержит две функции, которые эквивалентны ** -оператора:

import operator
operator.pow(4, 2)      # 16
operator.__pow__(4, 3)  # 64

 

или можно напрямую вызвать __pow__ метод:

val1, val2 = 4, 2
val1.__pow__(val2)      # 16
val2.__rpow__(val1)     # 16
# in-place power operation isn't supported by immutable classes like int, float, complex:
# val1.__ipow__(val2)    

Экспонирование с использованием математического модуля: math.pow()

math модуль содержит другой math.pow() функцию. Разница в встроено pow() -функции или ** оператора является то , что результат всегда float :

import math
math.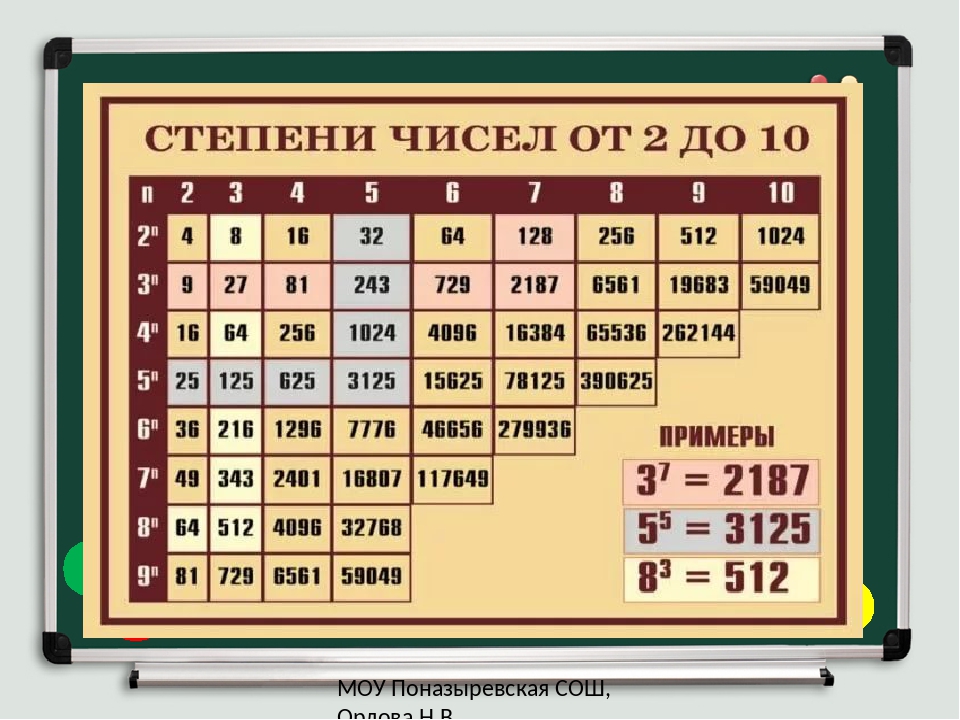 pow(2, 2)    # 4.0
math.pow(-2., 2)  # 4.0

 

Что исключает вычисления со сложными входами:

math.pow(2, 2+0j) 
 

Ошибка типа: невозможно преобразовать сложное в плавающее

и вычисления, которые привели бы к сложным результатам:

math.pow(-2, 0.5)
 

ValueError: ошибка математического домена

Экспоненциальная функция: math.exp () и cmath.exp ()

Как math и cmath модуль содержит число Эйлера: е и использовать его с встроено pow() -функции или ** -оператором работает в основном как math.exp() :

import math

math.e ** 2  # 7.3890560989306495
math.exp(2)  # 7.38905609893065

import cmath
cmath.e ** 2 # 7.3890560989306495
cmath.exp(2) # (7.38905609893065+0j)

Однако результат отличается и использованием экспоненциальной функция непосредственно является более надежной , чем с встроенным базовым возведением в степень math. ------------

Магические методы и возведение в степень: построение, математика и математика

Предположим, у вас есть класс, который хранит чисто целочисленные значения:

class Integer(object):
    def __init__(self, value):
        self.value = int(value) # Cast to an integer

    def __repr__(self):
        return '{cls}({val})'.format(cls=self.__class__.__name__,
                                     val=self.value)

    def __pow__(self, other, modulo=None):
        if modulo is None:
            print('Using __pow__')
            return self.__class__(self.value ** other)
        else:
            print('Using __pow__ with modulo')
            return self.__class__(pow(self.value, other, modulo))

    def __float__(self):
        print('Using __float__')
        return float(self.value)

    def __complex__(self):
        print('Using __complex__')
        return complex(self.value, 0)

 

Использование встроенной pow функции или ** оператор всегда вызывает __pow__ :

Integer(2) ** 2                 # Integer(4)
# Prints: Using __pow__
Integer(2) ** 2. 5               # Integer(5)
# Prints: Using __pow__
pow(Integer(2), 0.5)            # Integer(1)
# Prints: Using __pow__  
operator.pow(Integer(2), 3)     # Integer(8)
# Prints: Using __pow__
operator.__pow__(Integer(3), 3) # Integer(27)
# Prints: Using __pow__

 

Второй аргумент __pow__() метод может подаваться только с помощью builtin- pow() или путем непосредственного вызова метода:

pow(Integer(2), 3, 4)           # Integer(0)
# Prints: Using __pow__ with modulo
Integer(2).__pow__(3, 4)        # Integer(0) 
# Prints: Using __pow__ with modulo  

 

В то время как math -функции всегда преобразовать его в float и использовать флоат-вычисления:

import math

math.pow(Integer(2), 0.5) # 1.4142135623730951
# Prints: Using __float__

 

cmath -функции попытаться преобразовать его в complex , но может также Откат к float , если нет явного преобразования в complex :

import cmath

cmath. exp(Integer(2))     # (7.38905609893065+0j)
# Prints: Using __complex__

del Integer.__complex__   # Deleting __complex__ method - instances cannot be cast to complex

cmath.exp(Integer(2))     # (7.38905609893065+0j)
# Prints: Using __float__ 

Ни math , ни cmath будет работать , если также __float__() -метод отсутствует:

del Integer.__float__  # Deleting __complex__ method

math.sqrt(Integer(2))  # also cmath.exp(Integer(2))
 

Ошибка типа: требуется плавающее число

Модульное возведение в степень: pow() с 3 аргументами

Обеспечение pow() с аргументами 3 pow(a, b, c) оценивает модульного возведения в степень а б мод C:

pow(3, 4, 17)   # 13

# equivalent unoptimized expression:
3 ** 4 % 17     # 13

# steps:
3 ** 4          # 81
81 % 17         # 13

 

Для встроенных типов использование модульного возведения в степень возможно только в том случае, если:

• Первый аргумент является int
• Второй аргумент является int >= 0
• Третий аргумент является int != 0

Эти ограничения также присутствуют в Python 3. x

Например, можно использовать 3-аргумент форму pow определить модульную обратную функцию:

def modular_inverse(x, p):
    """Find a such as  a·x ≡ 1 (mod p), assuming p is prime."""
    return pow(x, p-2, p)

[modular_inverse(x, 13) for x in range(1,13)]
# Out: [1, 7, 9, 10, 8, 11, 2, 5, 3, 4, 6, 12]

 

Корни: n-корень с дробными показателями

В то время как math.sqrt функция предусмотрена для конкретного случая квадратных корней, это часто бывает удобно использовать оператор возведения в степень ( ** ) с дробными показателями для выполнения п-корневые операции, как кубические корни.

Обратное возведение в степень является возведением в степень по взаимности экспоненты. Таким образом, если вы можете кубизировать число, указав его в показателе степени 3, вы можете найти корень куба в числе, указав его в показателе 1/3.

>>> x = 3
>>> y = x ** 3
>>> y
27
>>> z = y ** (1. 0 / 3)
>>> z
3.0
>>> z == x
True 

Вычисление больших целочисленных корней

Несмотря на то, что Python изначально поддерживает большие целые числа, получение n-го корня очень больших чисел может привести к сбою в Python.

 x = 2 ** 100
cube = x ** 3
root = cube ** (1.0 / 3)

 

OverflowError: long int слишком велико для преобразования в float

При работе с такими большими целыми числами вам нужно будет использовать пользовательскую функцию для вычисления n-го корня числа.

def nth_root(x, n):
    # Start with some reasonable bounds around the nth root.
    upper_bound = 1
    while upper_bound ** n <= x:
        upper_bound *= 2
    lower_bound = upper_bound // 2
    # Keep searching for a better result as long as the bounds make sense.
    while lower_bound < upper_bound:
        mid = (lower_bound + upper_bound) // 2
        mid_nth = mid ** n
        if lower_bound < mid and mid_nth < x:
            lower_bound = mid
        elif upper_bound > mid and mid_nth > x:
            upper_bound = mid
        else:
            # Found perfect nth root. 
            return mid
    return mid + 1

x = 2 ** 100
cube = x ** 3
root = nth_root(cube, 3)
x == root
# True

образуют полиномиальную функцию пятой степени с действительными коэффициентами, так что 5i, 1-3i и -3 являются нулями, а f (0) = 1500

Привет, Джессика.

Чтобы получить искомый многочлен, нам нужно добавить несколько фрагментов информации.

ВСЕ КОМПЛЕКСНЫЕ КОРНИ ПАРЫ. Таким образом, они намеренно опустили два корня, чтобы проверить, знаете ли вы, что вам нужно найти «другой» корень для каждого комплексного числа.

Два корня являются комплексно сопряженными.Это означает, что если один — «5i», другой — «-5i». Если у вас «1-3i», другой — «1 + 3i»

Теперь у вас есть 5 корней, и вы можете составить полином пятой степени.

Корни:

x = 5i, x = -5i, x = 1-3i, x = 1 + 3i, x = -3

Для каждого «x =» переместите все в левую сторону, чтобы они стали множителями, а не нулями.

х-5i = 0, х + 5i = 0, х-1 + 3i = 0, х-1-3i = 0, х + 3 = 0

Теперь ваши факторы:

(x-5i) (x + 5i) (x-1-3i) (x-1 + 3i) (x + 3)

Умножьте первые два и получите

(x-5i) (x + 5i) = x ² + (5x) i — (5x) i — 25i ²

Средние члены взаимно отменяют друг друга

25i ² = (25) (- 1) = -25

Таким образом, получается (x ² — (-25)) = x ² +25

3-й и 4-й члены, умноженные вместе, дают:

(x-1 + 3i) (x-1-3i) =

x ² — x — (3x) i — x + 1 + 3i + (3x) i — 3i — 9i ²

Обратите внимание, что все термины «i» исчезли.

9i ² = (9) (- 1) = -9

— (3x) i отменяется с (3x) i

-3i отменяется с 3i

Все, что осталось, — настоящие.

x ² — 2x — (- 9)

х ² — 2х + 9

Теперь у вас есть все реальные коэффициенты для работы:

Ваш оригинал: (x-5i) (x + 5i) (x-1-3i) (x-1 + 3i) (x + 3)

Стало: (x ² + 25) (x ² -2x + 9) (x + 3)

Умножьте первые два.Затем умножьте этот результат на оставшийся множитель (x + 3)

(x ² +25) (x ² — 2x + 9) =

x ⁴ — 2x ³ + 9x ² + 25x ² — 50x + 225

Это упрощается до:

x ⁴ — 2x ³ + 34x ² — 50x + 225

Последний шаг — умножить это на (x + 3), и вы получите многочлен 5-й степени

.

(x + 3) (x ⁴ — 2x ³ + 34x ² — 50x + 225) =

x ⁵ -2x ⁴ + 34x ³ -50x ² + 225x + 3x ⁴ -6x ³ + 102x ² — 150x +675

Комбинируйте одинаковые термины, чтобы получить окончательный ответ, полином 5-й степени со всеми действительными коэффициентами:

x ⁵ + x ⁴ + 28x ³ + 52x ² + 75x +675

теория Галуа — Решение уравнений 5-й степени или выше

Для общих уравнений deg $ k> 4 $ можно использовать,

1. Функции Фукса
2. Тета-функции
3. Интегралы Меллина

Для заданных натуральных чисел $ m, n $ и $ m + n = k $, если общее уравнение deg $ k $ может быть решено определенным методом, из этого следует, что общие уравнения deg $ m, n $ тоже может быть.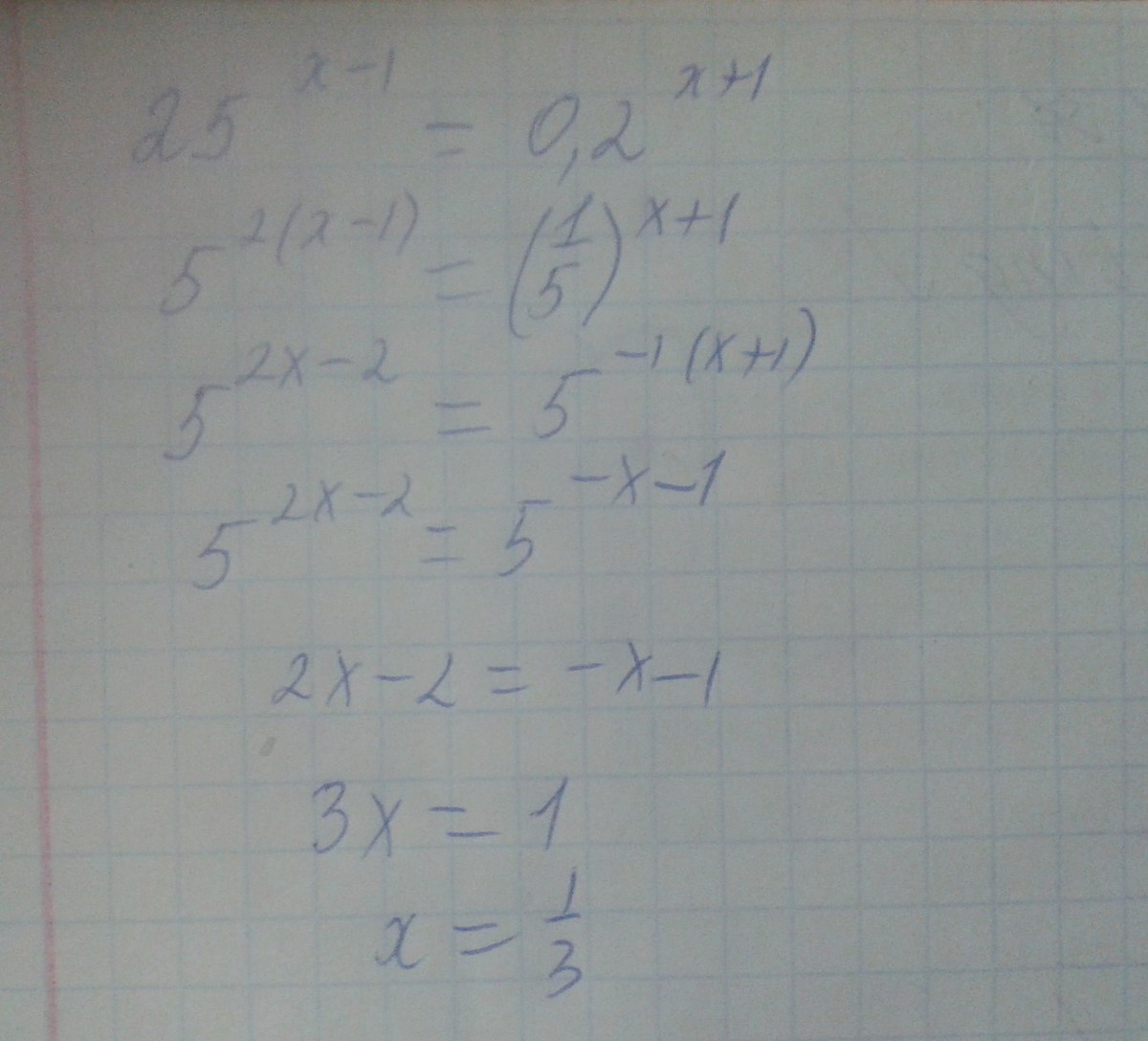 2} \ big)} \ tag {4} $$

, где $ \ lambda (\ tau) $ — эллиптическая лямбда-функция , $ \ eta (\ tau) $ — эта функция Дедекинда , $ K (k) $ — полный эллиптический интеграл первого рода , а $ \, _ 2F_1 $ — гипергеометрическая функция .

(Примечание: при извлечении корня 4-й степени из $ x_i $ следует быть осторожным, чтобы добавить правильную степень корня 4-й степени из единицы $ \ zeta_4 = \ exp (2 \ pi i / 4) $, особенно когда коэффициенты квадратичных сложны.3 $$

тогда,

$$ x = \ pm \ sqrt {\ frac {4u-1} {3u-3}} $$

, где выбран соответствующий знак квадратного корня. (Это более простая формула, чем предыдущая редакция.)

Обратите внимание на разницу между (4) и (5), поскольку последнее — это Теория эллиптических функций Рамануджана с сигнатурой 3 . Это дает один корень кубики, и некоторые модификации $ \ tau $, вероятно, могут дать два других корня.

полиномов — Как решить уравнения пятой степени эллиптическими функциями?

Чтобы решить общую квинтику с использованием эллиптических функций, можно сократить ее до Форма Бринга-Джеррарда ,

$$ x ^ 5-x + d = 0 \ tag {1} $$

преобразование, которое может быть выполнено в радикалах. 3 + \ ddots}}}} $$

изучал Рамануджан (у которого также был свой метод решения решаемых квинтик).

Введение и терминология — Подготовка к оценке TSI

Полиномы — это алгебраические выражения, которые включают действительные числа и переменные. В переменных нельзя использовать деление и квадратные корни. Переменные могут включать только сложение, вычитание и умножение.

Многочлены содержат более одного члена. Многочлены — это суммы одночленов.

Одночлен имеет один член: 5 y или –8 x ² или 3.
Двучлен имеет два члена: –3 x ² + 2 или 9 y — 2 y ²
Трехчлен имеет 3 члена: –3 x ² + 2 +3 x , или 9 y -2 y ² + y

Степень члена — это показатель степени переменной: 3 x ² имеет степень 2.
Если у переменной нет показателя степени — всегда имейте в виду, что есть «1» e.г., x = x ¹

Полиномы обычно записываются в порядке убывания членов. Обычно первым пишется самый большой член или член с наивысшим показателем в полиноме. Первый член полинома называется главным членом. Когда термин содержит показатель степени, он сообщает вам степень этого члена.

Вот пример трехчленного многочлена:

6 x ² — 4 xy + 2 xy ² — Этот трехчленный многочлен имеет ведущий член второй степени.Он называется многочленом второй степени и часто называется трехчленом.

9 x ⁵ — 2 x + 3 x ⁴ — 2 — Этот четырехчленный полином имеет главный член пятой степени и член четвертой степени. Он называется полиномом пятой степени.

3 x ³ — это алгебраическое выражение с одним термином, которое на самом деле называется одночленом .

Пример 1. Определите, является ли каждое выражение полиномом. Если это так, классифицируйте каждый многочлен по соответствующему типу (одночлен, двучлен или трехчлен) и укажите степень.

а) 3 x –2 — 5x + 2

б) x ² — 5

в) 8 x ⁵ — 3 x ³ -2 x ² + 6

г) а ⁴ -16 б ⁴

Решение.

a) 3 x –2 — 5x + 2 не представляет собой многочлен, поскольку первый показатель степени –1 не является целым числом. б)

x ² -5 — бином второй степени.

в)

8 x ⁵ -3 x ³ -2 x ² + 6 представляет полином пятой степени.

d) a ⁴ -16 b ⁴ — бином четвертой степени.

Обвинения в отношении наркотиков пятой степени. Серьезное преступление.

Хотя обвинения в преступлениях, связанных с наркотиками пятой степени, являются наименее серьезными, они по-прежнему являются обвинениями в совершении тяжких преступлений. Вы можете столкнуться с суровыми последствиями, включая серьезные штрафы и тюремное заключение, если вас обвинят в преступлении, связанном с наркотиками пятой степени. Ниже приводится подробный отчет о незаконном поведении и связанных с ним наказаниях.

Обвиняется в преступлении, связанном с наркотиками? Свяжитесь с Olson Defense сегодня, чтобы получить бесплатную консультацию по телефону 952.835.1088.

Торговля преступлениями.

Лицо виновно в преступлении, связанном с наркотиками, в пятой степени и в случае признания виновным может быть приговорено к лишению свободы на срок не более пяти лет или к выплате штрафа в размере не более 10 000 долларов США, или и того, и другого, если:

1. лицо незаконно продает одну или несколько смесей, содержащих марихуану или тетрагидроканнабинолы (ТГК), за исключением небольшого количества марихуаны, без вознаграждения; или
2. лицо незаконно продает одну или несколько смесей, содержащих контролируемое вещество, включенное в Список IV.

За исключением случаев, предусмотренных в пункте (c), если лицо виновно в преступлении, связанном с наркотиками, пятой степени, и осуждение является последующим осуждением за употребление наркотиков, осужденное лицо должно быть передано в распоряжение комиссара исправительных учреждений или местного исправительное учреждение на срок от шести месяцев до десяти лет и, кроме того, может быть приговорено к уплате штрафа в размере не более 20 000 долларов, если:

1. лицо незаконно продает одну или несколько смесей, содержащих марихуану или тетрагидроканнабинолы (ТГК), за исключением небольшого количества марихуаны, без вознаграждения; или
2. лицо незаконно продает одну или несколько смесей, содержащих контролируемое вещество, включенное в Список IV.

До вынесения приговора прокурор может подать ходатайство о вынесении приговора без учета минимального обязательного наказания, установленного пунктом (b). Ходатайство должно сопровождаться заявлением о его причинах. При представлении ходатайства или по собственной инициативе суд может приговорить лицо без учета обязательного минимального наказания, если суд обнаружит в протоколе существенные и веские причины для этого.

Хранение и другие преступления.

• (a) Лицо виновно в преступлении, связанном с наркотиками, пятой степени, и в случае признания его виновным может быть приговорено к лишению свободы на срок не более пяти лет или к выплате штрафа в размере не более 10 000 долларов США, либо к тому и другому, если:

1. лицо незаконно владеет одной или несколькими смесями, содержащими контролируемое вещество, включенное в Список I, II, III или IV, за исключением небольшого количества марихуаны; или
2. лицо приобретает, пытается достать, обладает или контролирует контролируемое вещество любым из следующих способов:

• (i) мошенничество, обман, введение в заблуждение или уловки;
• (ii) использование вымышленного имени или предоставление ложной информации; или
• (iii) ложное присвоение титула или ложное представление любого лица, которое должно быть производителем, оптовиком, фармацевтом, врачом, доктором остеопатии, имеющим лицензию на медицинскую практику, дантистом, ортопедом, ветеринаром или другим уполномоченным лицом с целью получения контролируемое вещество.

• (b) За исключением случаев, предусмотренных в параграфе (c), если лицо виновно в преступлении, связанном с употреблением запрещенных веществ, пятой степени и осуждение является последующим осуждением за употребление запрещенных веществ, осужденное лицо должно быть передано уполномоченному по исправительным учреждениям. или местному исправительному учреждению на срок от шести месяцев до десяти лет и, кроме того, может быть приговорен к уплате штрафа в размере не более 20 000 долларов, если:

1. лицо незаконно владеет одной или несколькими смесями, содержащими контролируемое вещество, включенное в Список I, II, III или IV, за исключением небольшого количества марихуаны; или
2. лицо приобретает, пытается достать, обладает или контролирует контролируемое вещество любым из следующих способов:

• (i) мошенничество, обман, введение в заблуждение или уловки;
• (ii) использование вымышленного имени или предоставление ложной информации; или
• (iii) ложное присвоение титула или ложное представление любого лица, которое должно быть производителем, оптовиком, фармацевтом, врачом, доктором остеопатии, имеющим лицензию на медицинскую практику, дантистом, ортопедом, ветеринаром или другим уполномоченным лицом с целью получения контролируемое вещество.

• (c) До вынесения приговора прокурор может подать ходатайство о вынесении приговора без учета минимального обязательного наказания, установленного в параграфе (b). Ходатайство должно сопровождаться заявлением о его причинах. При представлении ходатайства или по собственной инициативе суд может приговорить лицо без учета обязательного минимального наказания, если суд обнаружит в протоколе существенные и веские причины для этого.

Свяжитесь с Olson Defense и узнайте о своих правах, связанных с обвинениями в совершении преступлений, связанных с наркотиками 5 ^{-й степени} .

Миннеаполис Юрист пятой степени по делам о нападениях | Адвокат защиты от нападения Сент-Пол, Миннесота | Адвокаты пятой степени защиты от нападения Стиллуотер | McKee & Associates — Присяжные поверенные

Миннеаполис, адвокат пятой степени по делам о нападениях

Нападение пятой степени является серьезным преступлением в штате Миннесота.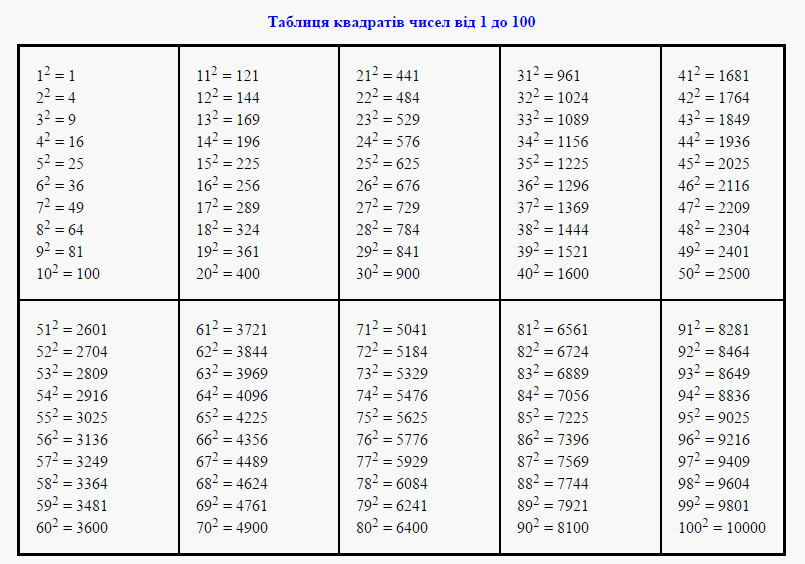 Если вам или вашему знакомому предъявлено обвинение в совершении преступления, немедленно позвоните адвокату по уголовным делам Барри Макки. В этих вопросах время часто играет решающую роль! Барри Макки — юрист с большим опытом защиты дел о нападениях в Миннесоте, который может помочь вам (или вашему близкому) прийти к наилучшему исходу дела.

Что такое нападение пятой степени?

Закон 609.224 Миннесоты определяет нападение пятой степени в Миннесоте.Нападение пятой степени — бесспорно, наиболее распространенное нападение. Это может быть обвинено в проступке, тяжком проступке или уголовном преступлении.

Статут Миннесоты 609.224, подраздел 1 объясняет Нападение пятой степени за проступок :

«Кто бы ни совершил одно из следующих действий, совершает нападение и виновен в проступке:

(1) совершает действие с намерением вызвать у другого человека страх немедленных телесных повреждений или смерти; или

(2) умышленно причиняет или пытается причинить телесные повреждения другому лицу. ”

Статут Миннесоты 609.224, подраздел 2 определяет Пятую степень Нападение за грубое правонарушение следующим образом:

Лицо, совершившее одно из следующих действий, совершает нападение и виновно в тяжком проступке, если оно совершено против той же жертвы в течение десяти лет с момента предыдущего квалифицированного обвинения в правонарушении, связанного с домашним насилием, или судебного решения о правонарушении лицо:

(1) совершает действие с намерением вызвать у другого человека страх немедленных телесных повреждений или смерти; или

(2) умышленно причиняет или пытается причинить телесные повреждения другому лицу.”

Статут Миннесоты 609.224, подраздел 4 определяет Пятую степень Нападение на преступление :

(a) Лицо, нарушающее положения раздела 1 в отношении одной и той же жертвы в течение десяти лет с момента первого из двух или более предыдущих обвинений в совершении преступления, связанного с домашним насилием, или судебных решений о правонарушении, виновно в совершении уголовного преступления.

(b) Тот, кто нарушает положения раздела 1 в течение трех лет с момента первого из двух или более предыдущих обвинительных приговоров за преступление, связанное с домашним насилием, или судебных решений о правонарушении, виновен в совершении уголовного преступления.

Каковы уголовные наказания за нападение пятой степени?

Штрафы за Нападение пятой степени зависят от того, на кого напали, от типа совершенного нападения и количества предыдущих квалифицированных нападений. Осуждение за нападение за мисдиминор пятой степени наказывается максимальным наказанием в виде тюремного заключения на срок до 90 дней и штрафом в размере 1000 долларов США или и тем, и другим. Осуждение за тяжкий проступок за нападение пятой степени наказывается тюремным заключением на срок до 356 дней и штрафом в размере 3000 долларов или и тем, и другим.Наконец, лицо, признанное виновным в нападении пятой степени тяжкого преступления, может быть приговорено к тюремному заключению на срок до 5 лет или выплате штрафа в размере 10 000 долларов, либо к тому и другому одновременно.

Важно отметить, что лица, осужденные за нападение пятой степени, не всегда отбывают максимально возможное тюремное заключение или платят максимально возможный штраф; однако некоторое время в тюрьме обычно бывает после осуждения за нападение пятой степени. Более того, лица, осужденные за нападение пятой степени, скорее всего, будут подвергнуты испытательному сроку на длительный период и будут обязаны соблюдать все правила и положения об испытательном сроке.Если имеет место нарушение условного осуждения, то человеку, возможно, придется заплатить больше штрафов или отбыть больше времени в тюрьме или тюрьме.

Каковы неуголовные последствия осуждения за нападение пятой степени?

Напряжение. Для большинства людей одним из неприятных последствий любого уголовного обвинения является стресс. Уголовное обвинение является стрессом для обвиняемого, его или ее семьи и друзей. Стресс возникает из-за незнания юридического процесса и правил; смущение от обвинения в преступлении и необходимости обращаться в суд; расходы, связанные с рассмотрением уголовных обвинений, неудобства DANCO или других приказов о запрете контактов, а также опасения, что исход дела находится вне контроля ответчика.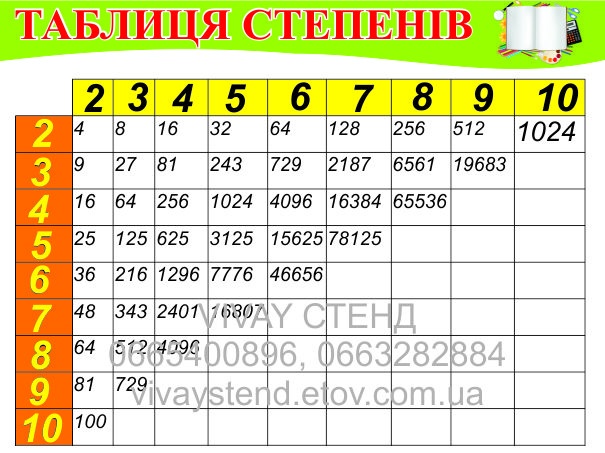 Будет ли вынесен тюремный срок? Если так, то как долго? Будут ли штрафы, если да, то сколько? Нужно ли будет дело до суда? Сколько все это будет стоить? Я потеряю работу?

Вред занятости / перспективам занятости. Согласно закону Миннесоты, некоторые работодатели могут уволить сотрудника из-за судимости. Кроме того, в заявлении о приеме на работу соискателя часто спрашивают, был ли он осужден за преступление. К сожалению, нападение пятой степени является преступлением и должно быть раскрыто в заявлении о приеме на работу.Более того, обвинительный приговор за нападение пятой степени наверняка обнаружится при проверке криминального прошлого.

Пробационный / пробационные нарушения. Суд вынесет постановление об условном осуждении за нападение пятой степени. Испытательный срок может быть интенсивным или неинтенсивным и приводить к ограничениям на поездки и другим ограничениям. Если обвиняемый в нападении уже находится на испытательном сроке по другому делу, то обвинительный приговор может повлечь за собой нарушение условного срока по любым другим делам, по которым обвиняемый в настоящее время находится на испытательном сроке.

Оценка гнева и использования химических веществ. Большинство судей приказывают человеку, осужденному за нападение пятой степени, пройти оценку по управлению гневом. Кроме того, если обвиняемый употреблял алкоголь или наркотики в связи с инцидентом, судья, скорее всего, также прикажет ответчику пройти оценку использования химических веществ.

После завершения процесса оценки судья (или сотрудник службы пробации) рассмотрит оценку и связанные с ней рекомендации.Затем судья, как часть постановления о вынесении приговора, приказывает обвиняемому выполнить все рекомендации оценки. Например, если оценка управления гневом рекомендует, чтобы обвиняемый посещал определенный класс управления гневом, то ответчик должен посещать этот конкретный урок (и платить за него). Более того, если обвиняемый не выполняет рекомендации оценки, то судья может установить, что обвиняемый нарушил испытательный срок и должен отбыть срок в тюрьме.

Какая защита от нападения пятой степени?

Как и во всех уголовных делах, в зависимости от обстоятельств дела обвиняемому могут быть доступны средства защиты. Общий список защит включает: самозащиту, защиту других, интоксикацию, непроизвольное опьянение, безумие, необходимость, жестокое обращение и некоторые другие. Свяжитесь с адвокатом Миннесоты по уголовным делам Барри Макки, чтобы узнать, какие меры защиты могут применяться в вашем случае.

Почему вам следует связаться с адвокатом штата Миннесота по нападениям пятой степени Барри Макки?

Барри Макки — адвокат по уголовным делам с более чем 40-летним опытом ведения дел о нападениях. Он знает склонности прокуроров и судей, закон, защиту и знает, как добиться наилучшего результата в вашем деле.Если с Барри Макки свяжутся на достаточно раннем этапе процесса, ему часто удастся снять или смягчить уголовные обвинения.

Раздел 609.3451 — УГОЛОВНОЕ СЕКСУАЛЬНОЕ ПОВЕДЕНИЕ ПЯТОЙ СТЕПЕНИ, Минн. Стат. § 609.3451

Ток до 2021 года, c. 12

Раздел 609.3451 — ПРЕСТУПНОЕ СЕКСУАЛЬНОЕ ПОВЕДЕНИЕ ПЯТОЙ СТЕПЕНИ Подраздел 1. Определение преступления.

Лицо виновно в преступном сексуальном поведении пятой степени:

(1) , если это лицо вступает в половую связь без согласия; или (2) лицо занимается мастурбацией или непристойным показом гениталий в присутствии несовершеннолетнего в возрасте до 16 лет, зная или имея основания знать, что несовершеннолетний присутствует.

Для целей этого раздела «сексуальный контакт» имеет значение, указанное в разделе 609.341, подраздел 11, параграф (а), пункты (i), (iv) и (v). Сексуальный контакт также включает умышленное снятие или попытку снятия одежды, закрывающей интимные части или нижнее белье заявителя, и прикосновение заявителя к интимным частям актера без согласия актера, если действие совершается с сексуальным или агрессивным намерением.

Суб. 2. Грубый проступок.

Лицо, осужденное по подразделу 1, может быть приговорено к лишению свободы на срок не более одного года или к выплате штрафа в размере не более 3000 долларов, либо к тому и другому.

Суб. 3. Уголовное преступление. (a) Лицо виновно в совершении тяжкого преступления и может быть приговорено к тюремному заключению на срок не более семи лет или к выплате штрафа в размере не более 14 000 долларов США или того и другого, если лицо нарушит этот раздел в течение семи лет после : (1) судимость за нарушение подпункта 1, пункта (2), преступления, описанного в пункте (b), или закона другого штата в соответствии с любым из этих правонарушений; или (2) первая из двух или более судимостей за нарушение подпункта 1, пункта (1) или закона другого штата в соответствии с этим правонарушением. (b) Ранее судимость за нарушение статьи 609.342; 609,343; 609.344; 609,345; 609.3453; 617.23, подраздел 2, пункт (2) или подраздел 3; или 617.247 может использоваться для усиления уголовного наказания, как предусмотрено в параграфе (а).

Minn. Stat. § 609.3451

1988 c 529 s 2; 1990 c 492 с 1; 1995 c 226 ст. 2 с 19; 1996 c 408 ст.