3 х 5 2х: решить уравнение 3х- 5=2х с решением помогите пожалуйста — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Решение уравнений 6 класс онлайн-подготовка на Ростелеком Лицей

Решение уравнений

Уравнение, которое можно привести к виду ax = b, где a и b − некоторые числа

(a≠0), называется линейным уравнением с одним неизвестным.

Рассмотрим решение уравнения:

4·(х-5) = 16 (1)

х-5 = 16:4

х-5 = 4 (2)

х = 9

Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 4.

4(х-5)=16 |:4 (1) 9 – корень уравнения (1), так как

4(x-5)4=164 4(9-5) = 16 – верное равенство.

х-5 = 4 (2) 9 – корень уравнения (2), так как

9-5 = 4 – верное равенство.

Число 9 – это корень уравнения (1) и корень уравнения (2).

Сформулируем первое свойство уравнения.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.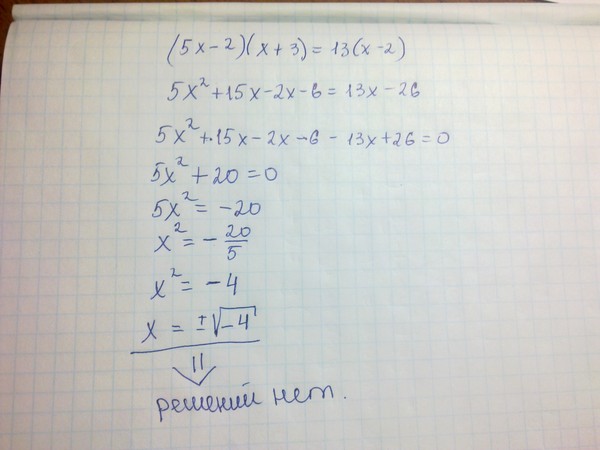

Применим первое свойство к решению уравнения.

Пример 1. Решим уравнение 34x-98x=54-18.

Умножим обе части уравнения на 8. Тогда коэффициент перед x станет целым.

34x-98x = 54-18 |·8

3∙84x-9∙88x = 5∙84-1∙88

6x-9x = 10-1

-3x = 9

x = 9:(-3)

x = -3.

Пример 2. Решим уравнение 0,7x-0,2x = 5,5.

Умножим обе части уравнения на 10. Тогда коэффициенты перед x станут целыми.

0,7х-0,2х = 5,5 |·10

7х-2х = 55

5х = 55

x = 55:5

x = 11.

Пример 3. Решим уравнение -20x-50∙2 = 100.

Разделим обе части этого уравнения на 2.

(-20х-50)·2 = 10 |:2

-20х-50 = 50

-20х = 50+50

-20х = 100

x = 100:(-20)

x = -5.

Пример 4. Решим уравнение 2,1∙4-6y = -42.

Разделим обе части равенства на 2,1.

2,1·(4-6у) = -4 |:2,1

4-6у = -20

-6у = -24

y = -24:(-6)

y = 4.

Пример 5. Решим уравнение 2х+5 = 17.

По правилу отыскания неизвестного слагаемого имеем 2х = 17-5; 2х = 12. Уравнения 2х+5 = 17 и 2х = 17-5 имеют один и тот же корень 6, т.к. 2·6+5 = 17 и 2·6 = 17-5.

Уравнение 2х = 17-5 можно записать так: 2х = 17+(-5).

Видим, что корень уравнения 2х+5 = 17 не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.

Пример 6. Решим уравнение 5х = 2х+6.

Вычтем из правой и левой части равенства 2х.

5х-2х = 2х-2х+6

Или 5х-2х = 6

3х = 6

x = 2.

Уравнение 5х-2х = 6 можно получить из исходного, если слагаемое 2х перенести из правой части в левую, изменив его знак на противоположный.

Таким образом выполняется второе свойство уравнения:

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.

Пример 7. Решим уравнение 13x+12 = x.

Умножим левую и правую часть равенства на 3.

13x+12 = x |·3

x+36 = 3x

Перенесем с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое 3х из правой части в левую.

x-3x = -36

-2x = -36

x = -36:(-2)

x = 18

Рассмотрим сложные примеры.

Пример 8. Решим уравнение 12∙8x-4-5 = 6∙13x+12.

Сначала раскроем скобки.

12∙8x-12∙4-5 = 6∙13x+6∙12

4x-2-5 = 2x+3

Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

4х-2х = 3+2+5

2х = 10

x = 5

Пример 9. Решим уравнение 7-x6 = 19x-118.

Воспользуемся основным свойством пропорции: произведение средних равно произведению крайних.

8·(7-х) = 6·(19х-11)

Раскроем скобки в левой и в правой части уравнения.

8·7-8·х = 6·19х-6·11

56-8х = 114х-66

Перенесем неизвестное влево, а известное вправо.

-8х-114х = -66-56

-122х = -122

x = 1

Как решить неравенство: 1. │3х — 5│

как решить неравенство:

ПРЕЖДЕ НАДО ЗНАТЬ ОПРЕДЕЛЕНИЕ МОДУЛЯ ЧИСЛА!

И ПОЛЕЗНО ТАКЖЕ ЗНАТЬ ГЕОМЕТРИЧЕСКУЮ ИНТЕРПРИТАЦИЮ МОДУЛЯ…

1. │3х — 5│< 1

⇔ -1 ⇔ 4/3

2. 2│х — 3│- 4 < 0 ⇔ │х — 3│<4/2 ⇔ -2<х — 3<2 ⇔ 3 -2<х <2 +3 ⇔ 1<х <5

3. │х — 2│≥ 3⇔ (х — 2≥ 3 или х — 2≤- 3 )⇔ х ≥ 5 или х ≤1

x∈(-∞;1] ∪[5;+∞)

4. │5 — 2х│≥ 1 ⇔ (5 — 2х≥1 или 5 — 2x≤ — 1 ) x≤2 или x≥3

x∈(-∞;2] ∪[3;+∞)

5. 1<│2х — 3│≤ 4 ⇔

│2х — 3│≤ 4 ⇔ -4≤2х — 3≤4 ⇔ -1≤2x≤7 ⇔-1/2≤ x ≤7/2

и

│2х — 3I>1 ⇔( 2х — 3>1 или 2х — 3<-1) ⇔ (x>2 или x<1) 

——————[-1/2]/////////////////////////////////////////////[7/2]——————————

////////////////////////////////////////////(1)————-(2)]/////////////////////////////////////////////

x∈[-1/2;1)∪(2;7/2]

6. │х + 3│<│2х — 1│ 

два способа решения.

a) рассматриваем каждый модуль, находим x0 : 1)
|x+3|=0 x0= — 3

2) |2x-1|=0 x0=1/2

b) отметим знаки , которые принимает значение выражения в модуле:

|x+3| — + +

—————(-3)————————————

|2x-1I — — +

——————————(1/2)——————

две точки (-3),(1/2) делят числовую прямую на 3 промежутка

c) рассмотрим системы неравенств, которые получатся если раскрыть модули:

1. если x<-3 , то -(x+3)<-(2x-1) ⇔-x+2x<3+1 и x<4 т.о x<-3

x<-3

2. если -3≤x<1/2 (x+3)<-(2x-1) ⇔ 3x<-1 x<-2/3. 

-3≤x<1/2 и

x<-2/3

-3≤x<-2/3

3. если x≥1/2 (x+3)<(2x-1) x>4

x≥1/2

и x>4

x>4

ответ: x∈(-∞;-2/3)∪(4;+∞)

2 способ.

возведем обе части неравенства в квадрат

│х + 3│²<│2х — 1│² 

x²+6x+9<4x²-4x+1 3x²-10x-8>0

3x²-10x-8=0 x1=-2/3 x2=4

+ — +

——————(-2/3)—————-(4)————-

x∈(-∞;-2/3)∪(4;+∞)

Решение уравнений с модулем методом интервалов

Решение уравнений с модулем методом интервалов.

Подготовила

учитель математики МКОУ «Хотьковская СОШ»

Думиничского района Калужской области

Наталья Николаевна Коломина

2017

Определение модуля

Модулем (абсолютной величиной) числа называется неотрицательное число:

х ∈ R

Свойства модуля

0 Меняем знаки -х + 2 = 3 Не меняем знаки -1 ∈ (-∞ ; 2] х – 2 = 3 -х = 1 х = -1 х = 5 5 ∈ (2 ; + ∞) -1 – корень уравнения 5 – корень уравнения. | х-2 |= 3 Посмотреть решение х – 2 = 0 х = 2 Ответ: -1; 5.»

Уравнения вида | х |= а

х ∈ (-∞ ; 2]

х ∈ (2 ; + ∞)

х – 2 ≤ 0

х – 2 0

Меняем знаки

-х + 2 = 3

Не меняем знаки

-1 ∈ (-∞ ; 2]

х – 2 = 3

-х = 1

х = -1

х = 5

5 ∈ (2 ; + ∞)

-1 – корень уравнения

5 – корень уравнения.

| х-2 |= 3

Посмотреть решение

х – 2 = 0

х = 2

Ответ: -1; 5.

Уравнения вида | х |= а

2,5

х ∈ (-∞ ; 2,5]

х ∈ (2,5 ; + ∞)

5 – 2х ≥ 0

5 – 2х

Не меняем знаки

Меняем знаки

5 – 2х = 4

-5 + 2х = 4

-2х = 4 – 5

0,5 ∈ (-∞ ; 2,5]

-2х = -1

0,5 – корень уравнения

4,5 ∈ (2,5 ; + ∞)

2х = 4 + 5

4,5 – корень уравнения.

2х = 9

х = 0,5

х = 4,5

| 5 – 2х |= 4

Посмотреть решение

5 – 2х = 0

-2х = -5

х = 2,5

Ответ: 0,5; 4,5.

Уравнения вида | х |= а

-8/3

х ∈ (-∞ ; -8/3]

3х + 8 ≥ 0

х ∈ (-8/3 ; + ∞)

3х + 8

Не меняем знаки

Меняем знаки

3х + 8 = 7

-1/3 ∉ (-∞ ; -8/3]

3х = 7 – 8

-3х – 8 = 7

-1/3 – не корень уравнения

3х = -1

-5 ∉ (-8/3 ; + ∞)

-3х = 7 + 8

-5 – не корень уравнения.

х = -1/3

-3х = 15

х = -5

7 = | 3х + 8 |

Посмотреть решение

3х + 8= 0

3х = -8

х = -8/3

Ответ: корней нет

0 + -х + 2х = 1 + 1 х + 1 = -2х + 1 2х – 1 ≤ 0 — х + 1 0 + 2 ∉ (-∞ ; -1] 3х = 0 2х – 1 0 + х = 2 2 – не корень уравнения х + 1 = 2х – 1 0 ∈ (-1 ; 0,5] 0,5 – корень уравнения х = 0 х – 2х = -1 – 1 2 ∈ (0,5 ; + ∞) -х = -2 2 – корень уравнения. х = 2 Посмотреть решение х + 1= 0 х = -1 2х — 1= 0 2х = 1 х = 0,5 Ответ: 0,5; 2.»

Уравнения вида | х |=| у |

0,5

-1

| х + 1 |=| 2х -1 |

х ∈ (-∞ ; -1]

х ∈ (-1 ; 0,5]

х + 1 ≤ 0 —

2х – 1 —

-х – 1 = -2х + 1

х ∈ (0,5 ; + ∞)

х + 1 0 +

-х + 2х = 1 + 1

х + 1 = -2х + 1

2х – 1 ≤ 0 —

х + 1 0 +

2 ∉ (-∞ ; -1]

3х = 0

2х – 1 0 +

х = 2

2 – не корень уравнения

х + 1 = 2х – 1

0 ∈ (-1 ; 0,5]

0,5 – корень уравнения

х = 0

х – 2х = -1 – 1

2 ∈ (0,5 ; + ∞)

-х = -2

2 – корень уравнения.

х = 2

Посмотреть решение

х + 1= 0

х = -1

2х — 1= 0

2х = 1

х = 0,5

Ответ: 0,5; 2.

0 + -2х – х = -3 – 9 3 – х — -х = -6 2х – 9 = -3 + х 6 – не корень уравнения 4 ∈ (3 ; 4,5] 4 – корень уравнения 2х – х = -3 + 9 х = 6 -3х = -12 6 ∈ (4,5 ; + ∞) х = 4 х = 6 6 – корень уравнения. Посмотреть решение 2х — 9= 0 2х = 9 х = 4,5 3 — х= 0 -х = -3 х = 3 Ответ: 4; 6.»

Уравнения вида | х |=| у |

4,5

|2 х — 9 |=| 3 — х |

х ∈ (-∞ ; 3]

х ∈ (3 ; 4,5]

2х — 9 —

2х — 9 ≤ 0 —

3 – х ≥ 0 +

х ∈ (4,5 ; + ∞)

-2х + 9 = 3 – х

-2х + 9 = -3 + х

3 – х —

-2х + х = 3 – 9

6 ∉ (-∞ ; 3]

2х — 9 0 +

-2х – х = -3 – 9

3 – х —

-х = -6

2х – 9 = -3 + х

6 – не корень уравнения

4 ∈ (3 ; 4,5]

4 – корень уравнения

2х – х = -3 + 9

х = 6

-3х = -12

6 ∈ (4,5 ; + ∞)

х = 4

х = 6

6 – корень уравнения.

Посмотреть решение

2х — 9= 0

2х = 9

х = 4,5

3 — х= 0

-х = -3

х = 3

Ответ: 4; 6.

0 + 3(-х – 1) = 1 – 2х х ∈ (0,5 ; + ∞) х + 1 0 + 3(х + 1) = 1 – 2х 1 – 2х ≥ 0 + -3х – 3 = 1 – 2х -4 ∈ (-∞ ; -1] х + 1 0 + 3х + 3 = 1 – 2х 1 – 2х — -х = 4 -4 – корень уравнения 3(х+1) = -1 + 2х -0,4 ∈ (-1 ; 0,5] -0,4 – корень уравнения х = -4 3х+3=2х-1 5х = -2 -4 ∉ (0,5 ; + ∞) Х = -0,4 х = -4 -4 – не корень уравнения. Посмотреть решение х + 1= 0 х = -1 1 — 2х= 0 -2х = -1 х = 0,5 Ответ: -4; -0,4.»

Уравнения вида | х |=| у |

-1

0,5

3| х + 1|=| 1 — 2х |

х ∈ (-∞ ; -1]

х ∈ ( -1 ; 0,5]

х + 1 ≤ 0 —

1 – 2х 0 +

3(-х – 1) = 1 – 2х

х ∈ (0,5 ; + ∞)

х + 1 0 +

3(х + 1) = 1 – 2х

1 – 2х ≥ 0 +

-3х – 3 = 1 – 2х

-4 ∈ (-∞ ; -1]

х + 1 0 +

3х + 3 = 1 – 2х

1 – 2х —

-х = 4

-4 – корень уравнения

3(х+1) = -1 + 2х

-0,4 ∈ (-1 ; 0,5]

-0,4 – корень уравнения

х = -4

3х+3=2х-1

5х = -2

-4 ∉ (0,5 ; + ∞)

Х = -0,4

х = -4

-4 – не корень уравнения.

Посмотреть решение

х + 1= 0

х = -1

1 — 2х= 0

-2х = -1

х = 0,5

Ответ: -4; -0,4.

0 Меняем знаки Не меняем знаки -х — 1 = 1 – 2х х = 2 2 ∉ (-∞ ; -1] х + 1 = 1 – 2х 0 ∈ (-1 ; 0,5 ] 3х = 0 2 – не корень уравнения х = 0 0 – корень уравнения. Посмотреть решение х + 1= 0 х = -1 1 – 2х ≥ 0 -2х ≥ -1 х ≤ 0,5 Ответ: 0.»

Уравнения вида | х |= у

Отличие от уравнений 1 вида в том, что в правой части тоже переменная.

-1

| х+1 |= 1-2х

х ∈ (-∞ ; -1]

х + 1 ≤ 0

х ∈ (-1 ; 0,5 ]

х + 1 0

Меняем знаки

Не меняем знаки

-х — 1 = 1 – 2х

х = 2

2 ∉ (-∞ ; -1]

х + 1 = 1 – 2х

0 ∈ (-1 ; 0,5 ]

3х = 0

2 – не корень уравнения

х = 0

0 – корень уравнения.

Посмотреть решение

х + 1= 0

х = -1

1 – 2х ≥ 0

-2х ≥ -1

х ≤ 0,5

Ответ: 0.

0 Меняем знаки Не меняем знаки -2х — 1 = 3 – х 2х + 1 = 3 – х -4 ∈ (-∞ ; -0,5] -х = 4 2/3 ∈ (-0,5 ; 3 ] 3х = 2 -4 – корень уравнения х = -4 х = 2/3 2/3 – корень уравнения. Посмотреть решение 2х + 1= 0 2х = -1 х = -0,5 3 — х ≥ 0 -х ≥ -3 х ≤ 3 Ответ: -4; 2/3.»

Уравнения вида | х |= у

Отличие от уравнений 1 вида в том, что в правой части тоже переменная.

-0,5

|2 х+1 | = 3-х

х ∈ (-∞ ; -0,5]

х ∈ (-0,5 ; 3 ]

2х + 1 ≤ 0

2х + 1 0

Меняем знаки

Не меняем знаки

-2х — 1 = 3 – х

2х + 1 = 3 – х

-4 ∈ (-∞ ; -0,5]

-х = 4

2/3 ∈ (-0,5 ; 3 ]

3х = 2

-4 – корень уравнения

х = -4

х = 2/3

2/3 – корень уравнения.

Посмотреть решение

2х + 1= 0

2х = -1

х = -0,5

3 — х ≥ 0

-х ≥ -3

х ≤ 3

Ответ: -4; 2/3.

0 Меняем знаки Не меняем знаки -2(-х – 4) = 3 – х -2(х + 4) = 3 – х -5/3 ∉ (-∞ ; -4] 2х + 8 = 3 – х -2х – 8 = 3 – х -11 ∉ (-4 ; + ∞) -5 – не корень уравнения 3х = -5 -12 – не корень уравнения. х = -5/3 -х = 11 х = -11 Посмотреть решение х + 4 = 0 х = -4 3 — х ≥ 0 -х ≥ -3 х ≤ 3 Ответ: корней нет.»

Уравнения вида | х |= у

Отличие от уравнений 1 вида в том, что в правой части тоже переменная.

— 4

-2| х+4 | = 3-х

х ∈ (-∞ ; -4]

х + 4 ≤ 0

х ∈ (-4 ; + ∞)

х + 4 0

Меняем знаки

Не меняем знаки

-2(-х – 4) = 3 – х

-2(х + 4) = 3 – х

-5/3 ∉ (-∞ ; -4]

2х + 8 = 3 – х

-2х – 8 = 3 – х

-11 ∉ (-4 ; + ∞)

-5 – не корень уравнения

3х = -5

-12 – не корень уравнения.

х = -5/3

-х = 11

х = -11

Посмотреть решение

х + 4 = 0

х = -4

3 — х ≥ 0

-х ≥ -3

х ≤ 3

Ответ: корней нет.

0 + х+3 + (2х–1) = 1 х = 5 2х — 1 ≤ 0 — х + 3 0 + 5 ∉ (-∞ ; -3] х+3+2х-1=1 2х — 1 0 + х+3-2х+1 = 1 5 – не корень уравнения -1/3 ∈ (-3 ; 0,5] -1/3 – корень уравнения 3х = -1 -х = -3 3 ∈ (0,5 ; + ∞) х = -1/3 х = 3 3 – корень уравнения. х + 3= 0 х = -3 2х – 1 = 0 2х = 1 х = 0,5 Ответ: -1/3; 3.»

| х + 3|-| 2х — 1 | = 1

Посмотреть решение

-3

0,5

х ∈ (-∞ ; -3]

х ∈ ( -3 ; 0,5]

х + 3 ≤ 0 —

-х – 3 + 2х – 1 = 1

х ∈ (0,5 ; + ∞)

2х — 1 —

х + 3 0 +

х+3 + (2х–1) = 1

х = 5

2х — 1 ≤ 0 —

х + 3 0 +

5 ∉ (-∞ ; -3]

х+3+2х-1=1

2х — 1 0 +

х+3-2х+1 = 1

5 – не корень уравнения

-1/3 ∈ (-3 ; 0,5]

-1/3 – корень уравнения

3х = -1

-х = -3

3 ∈ (0,5 ; + ∞)

х = -1/3

х = 3

3 – корень уравнения.

х + 3= 0

х = -3

2х – 1 = 0

2х = 1

х = 0,5

Ответ: -1/3; 3.

0 + х ∈ (5/3 ; + ∞) 4/3 ∉(-∞ ; -1,5] х + 1 – 3х – 5 ≤ 0 – х = -10 -10 ∉ (-1,5 ; -1] 3х – 5 0 + 3 + 2х 0 + х + 1 ≤ 0 – х = 2 4/3 – не корень уравнения 3 + 2х 0 + х = 4/3 х + 1 0 + -10 – не корень уравнения 2 ∉ (-1 ; 5/3 ] 4/3∉ (5/3 ; + ∞) х + 1 0 + 2 – не корень уравнения. 4/3 – не корень уравнения. 3 + 2х = 0 2х = -3 х = -1,5 х + 1 = 0 х = -1 Ответ: корней нет.»

|3 х — 5|+|3 + 2х | = 2|х + 1|

5/3

Посмотреть решение

-1

-1,5

3х – 5 = 0

Зх = 5

х = 5/3

х ∈ (-∞ ; -1,5]

х ∈ ( -1,5 ; -1]

3х – 5 –

3 + 2х ≤ 0 –

3х – 5 –

х = 4/3

х ∈ (-1 ; 5/3 ]

3 + 2х 0 +

х ∈ (5/3 ; + ∞)

4/3 ∉(-∞ ; -1,5]

х + 1 –

3х – 5 ≤ 0 –

х = -10

-10 ∉ (-1,5 ; -1]

3х – 5 0 +

3 + 2х 0 +

х + 1 ≤ 0 –

х = 2

4/3 – не корень уравнения

3 + 2х 0 +

х = 4/3

х + 1 0 +

-10 – не корень уравнения

2 ∉ (-1 ; 5/3 ]

4/3∉ (5/3 ; + ∞)

х + 1 0 +

2 – не корень уравнения.

4/3 – не корень уравнения.

3 + 2х = 0

2х = -3

х = -1,5

х + 1 = 0

х = -1

Ответ: корней нет.

Ссылки на изображения:

http://mediaryazan.ru/upload/iblock/fba/ ЕГЭ. png

Интернет — источники:

http://youclever.org/book/uravneniya-s-modulem-2

http://ru.solverbook.com/primery-reshenij/primery-resheniya-uravnenij-s-modulem/

http:// mathus.ru/math/modul.pdf

http://matica.org.ua/metodichki-i-knigi-po-matematike/algebraicheskie-uravneniia-i-neravenstva-funktcii-logarifmy/19-uravneniia-s-modulem

Самостоятельная работа «Умножение многочленов»

Самостоятельная работа по теме «Умножение многочленов»

7 класс

Учитель: Трофимова Вера Владимировна

Вариант 1

Преобразуйте в многочлен стандартного вида:

1) (-а – 1) (а³ + 5)

2) (2m² — 3n) (3m² + 2n)

3) (х – 6) ( х² + 2х – 3)

Упростите выражение: (у – 8) (2у – 1) – (3у + 1) (5у – 2)
Решите уравнение: 14 х² – (2х – 3) (7х + 4) =14

Вариант 2

Преобразуйте в многочлен стандартного вида:

1) (а — 4b) ( а² + 3аb — 6b²)

2) а (4а – 5) (2а + 3)

3) – 5 с² (6 – 4с) (2с² + 7с)

Упростите выражение: (3m — 4n) (3m + 5n) – (4,5m – n)(2m + 4n)
Решите уравнение: (х + 6) (х – 1) – (х + 3) (х – 4) = 5х

Вариант 3

Преобразуйте в многочлен стандартного вида:

1) (а + 2) ( b -3)

2) (m – 4) ( m + 5)

3) ( 3х – 1) (2х + 5)

Упростите выражение: (х + 2) (х -5) – 3х (1 – 2х)
Решите уравнение: (х + 3) (х – 2) – (х +4) (х + 1) = 3х

Вариант 4

Преобразуйте в многочлен стандартного вида:

1) (3b² + 2) (2b – 4)

2) (4х – у) (2х – 3у)

3) (3а² + а) (5а² – 2а)

Упростите выражение: (а + 3) (а – 2) + (а – 3) (а + 6)
Решите уравнение: 15 х² – (3х – 2) (5х + 4) = 16

Вариант 5

Преобразуйте в многочлен стандартного вида:

1) (-х – 2) (2х³ – 3)

2) (3а² — 5b) (5а² + b)

3) ( у + 3) (у² – 2у + 5)

Упростите выражение: (х – 7) (3х – 2) – (5х + 1) (2х – 4)
Решите уравнение: (2х + 6) (7 – 4х)= (2 – х) (8х + 1) + 15

Вариант 6

Преобразуйте в многочлен стандартного вида:

1) (m + 3n) (m²— 6mn – n²)

2) 2х (3х – 1) (2х + 5)

3) -3х² (2 – 3х) (3х² + 11х)

Упростите выражение: (5х – 2у) (3х + 5у) – (2,5х – 3у) (4х + 8у)
Решите уравнение: (х + 7) (х – 2) – (х +4)(х +3) = — 2

Вариант 7

Преобразуйте в многочлен стандартного вида:

1) (а – 3) ( b + 4)

2) (х – 7) ( х + 3)

3) (2у + 1) (5у – 6)

Упростите выражение: (х – 2) (х – 11) – 2х (4 – 3х)
Решите уравнение: (х + 6) (х – 3) – (х+3) (х + 9) = 9

Вариант 8

Преобразуйте в многочлен стандартного вида:

1) (4m² + 6) ( 4m – 6)

2) (3а – b) (2а — 7b)

3) (2х² – х) (8х² – 2х)

Упростите выражение: (а + 6) (а – 3) + (а – 4) (а + 5)
Решите уравнение: (8х + 10) (3 – х) = (11 – 2х) (4х + 5) — 5

Вариант 9

Преобразуйте в многочлен стандартного вида:

1) (х + 5) (у -7)

2) (х – 1) (х + 5)

3) (3х – 5) (2х + 7)

Упростите выражение: (х + 3) (х – 7) – 4х (5 – 2х)
Решите уравнение: (х + 1) (х – 2) – (х + 5) ( х + 4) = — 2

Вариант 10

Преобразуйте в многочлен стандартного вида:

1) (5х²– 1)(5х + 1)

2) (5m — 2n) (3m + n)

3) (4х² – х) (2х²+ 3х)

Упростите выражение: (х + 2) (у – 6) + (у + 3) (у- 4)
Решите уравнение: (3х + 5) (2х + 1) = (6х + 5) (х – 3) + 7

Преобразуйте в многочлен стандартного вида:

1) (- 2 – у) ( у² + 3)

2) (3а² – b) (4а² + 3b)

3) (а – 3) (а² + 4а + 2)

Упростите выражение: (х – 3) (3х + 1) – (2х + 3) (4х – 1)
Решите уравнение: 12х² – (3х – 4) (4х + 1) = 19

Преобразуйте в многочлен стандартного вида:

1) (у — 2z) (у² – 2уz — 5z²)

2) m (2m – 1)(3m + 2)

3) – 6х² (4 – 2х) (3х² + 11х)

5 Упростите выражение: (2а — 3b) (7а + 4b) – (3,5а + b) (4а — 6b)

6 Решите уравнение: (х – 4) (х + 2) – (х – 5) (х + 6) = — х

3 + x = 0 Tiger Algebra Solver

Пошаговое решение:

Шаг 1:

Уравнение в конце шага 1:

 ((x ⁵) - 2x ³) + x = 0

Шаг 2:

Шаг 3:

Вытягивание как термины:

3.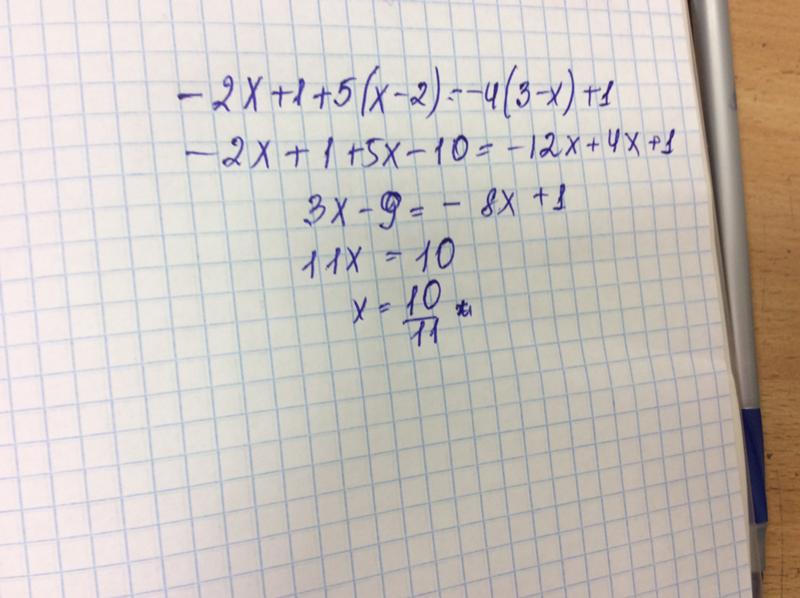 1 Коэффициенты вытягивания:

x ⁵ — 2x ³ + x = x • (x ⁴ — 2x ² + 1)

Попытка разложить на множители путем разделения среднего члена

3.2 Факторинг x ⁴ — 2x ² + 1

Первый член, x ⁴, его коэффициент равен 1.
Средний член равен, -2x ², его коэффициент равен -2.
Последний член, «константа», равен +1

Шаг-1: Умножьте коэффициент первого члена на константу 1 • 1 = 1

Шаг-2: Найдите два множителя 1, сумма которых равна коэффициенту среднего члена, который равен -2.

-1

-2

Вот и все

Шаг 3: Перепишите полином, разделяющий средний член, используя два найденных фактора на шаге 2 выше, -1 и -1
x ⁴ — 1x ² — 1x ² — 1

Шаг 4: сложите первые 2 члена, извлекая одинаковые множители:
x ² • (x ² -1)
Сложите последние 2 члена, вытащив общие множители:
1 • (x ² -1)
Шаг 5: сложите четыре члена шага 4:
(x ² -1) • (x ² -1)
Какое желаемое разложение на множители

Попытка разложить на множители как разность квадратов:

3. 3 Факторинг: x ² -1

Теория: Разность двух полных квадратов, A ² — B ² может быть разложена на множители (A + B) • (AB)

Доказательство: (A + B ) • (AB) =
A ² — AB + BA — B ² =
A ² — AB + AB — B ² =
A ² — B ²

Примечание: AB = BA — коммутативное свойство умножения.

Примечание: — AB + AB равно нулю и поэтому исключается из выражения.

Чек: 1 — квадрат 1
Чек: x ² — квадрат x ¹

Факторизация: (x + 1) • (x — 1)

Попытка учесть разность квадратов:

3.4 Факторинг: x ² — 1

Проверка: 1 — квадрат 1
Проверка: x ² — квадрат x ¹

Факторизация: (x + 1) • (x — 1)

Умножение экспоненциальных выражений:

3.5 Умножьте (x + 1) на (x + 1)

Правило гласит: Чтобы умножить экспоненциальные выражения с одинаковым основанием, сложите их показатели.

В нашем случае общая база равна (x + 1), а показатели равны:
1, поскольку (x + 1) — это то же число, что и (x + 1) ¹
и 1, поскольку (x + 1) — то же самое число, что и (x + 1) ¹
Следовательно, произведение: (x + 1) ^{(1 + 1)} = (x + 1) ²

Умножение экспоненциальных выражений:

3.6 Умножьте (x-1) на (x-1)

Правило гласит: Чтобы умножить экспоненциальные выражения с одинаковым основанием, сложите их показатели.

В нашем случае общая база равна (x-1), а показатели равны:
1, поскольку (x-1) — это то же число, что и (x-1) ¹
и 1, поскольку (x- 1) — это то же число, что и (x-1) ¹
Следовательно, произведение: (x-1) ^{(1 + 1)} = (x-1) ²

Уравнение в конце шага 3:

 x • (x + 1) ² • (x - 1) ² = 0

Шаг 4:

Теория — Истоки продукта:

4.1 Произведение нескольких членов равно нулю.

Если произведение двух или более членов равно нулю, то хотя бы один из членов должен быть равен нулю.

Теперь мы решим каждый член = 0 отдельно

Другими словами, мы собираемся решить столько уравнений, сколько членов есть в произведении.

Любое решение term = 0 также решает product = 0.

Решение уравнения с одной переменной:

4.2 Решение: x = 0

Решение: x = 0

Решение уравнения с одной переменной:

4.3 Решите: (x + 1) ² = 0

(x + 1) ² представляет собой, по сути, произведение двух членов, которое равно нулю

Для того, чтобы произведение было равно нулю, по крайней мере из этих терминов должно быть равно нулю. Поскольку все эти члены равны друг другу, это фактически означает: x + 1 = 0

Вычтите 1 из обеих частей уравнения:
x = -1

Решение уравнения с одной переменной:

4.4 Решите: (x-1) ² = 0

Как объяснено в шаге # 04. 03, уравнение, которое необходимо решить, имеет вид
x-1 = 0

Добавьте 1 к обеим сторонам уравнения:
x = 1

Дополнение: прямое решение квадратного уравнения

 Решение x ⁴ -2x ² +1 = 0 непосредственно

Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу

Решение уравнения с одной переменной:

Уравнения, которые можно свести к квадратичным:

5.1 Решите x ⁴ -2x ² +1 = 0

Это уравнение сводится к квадратичному. Это означает, что, используя новую переменную, мы можем переписать это уравнение в виде квадратного уравнения Используя w, так что w = x ² преобразует уравнение в:
w ² -2w + 1 = 0

Решение этой новое уравнение, используя квадратную формулу, мы получаем одно решение:
w = 1.00000010,5

Было найдено три решения:

x = 1
x = -1
x = 0

Решение экспоненциальных уравнений: в отличие от базовых

Теперь, когда мы узнали об экспонентах и их обратном логарифме, теперь мы можем решать экспоненциальные уравнения, основание которых нельзя легко изменить или невозможно. Предпосылка вращается вокруг логарифма и правила мощности для логарифмов.

Давайте сразу перейдем к некоторым примерам.

Пример 1. Решите 2 ^x = 7

Мы не можем превратить 7 в экспоненциальное выражение с 2 в качестве основы, потому что оно не идет равномерно. Однако мы можем это решить. Начните с регистрации каждой стороны. Вот оно в действии:

log 2 ^x = log 7

Между прочим, бревна, которые вы будете брать с каждой стороны, будут иметь 10-ю базу.

Опустите x с помощью правила мощности. Звучит так глупо, не правда ли?

x log 2 = log 7

Разделите каждую сторону на log 2:

x = log 7 / log 2

Оцените с помощью калькулятора, округляя окончательный ответ до трех десятичных знаков :

x = 2,807

Учитывая, что 2 ² равно 4 и 2 ³ = 8, 2.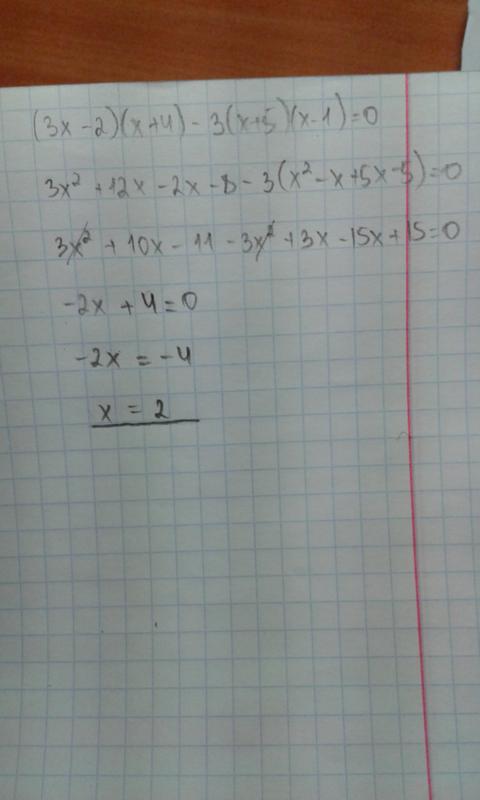 807 звучит примерно правильно.

Выглядит просто, правда? Это не так уж и плохо, когда вы в этом разбираетесь. Однако некоторые проблемы сложнее других, и мы их решим!

Пример 2. Решите 3 ^{x + 3} = 13

Это то же самое. Возьмите журнал с каждой стороны:

журнал 3 ^{x + 3} = журнал 13

Используя правило мощности, поместите это глупое x + 3 перед журналом:

(x + 3) журнал 3 = журнал 13

Разделите каждую сторону на журнал 3:

x + 3 = журнал 13 / журнал 3

Вычислите эту правую часть, используя калькулятор и округлив до трех десятичных знаков:

х + 3 = 2.335

Вычтите по 3 с каждой стороны:

x = -0,665

Проверьте это:

3 ^{-,665 + 3} = 13

13,004 = 13? Эх, достаточно близко, раз уж мы поймали.

Давайте сделаем еще один:

Пример 3. Решите 5 ^x-1 = 12.

Мы сделали это выше. Начните с регистрации каждой стороны:

журнал 5 ^x-1 = журнал 12

Используйте элемент Power Rule:

(x — 1) журнал 5 = журнал 12

Разделить по журналу 5:

x — 1 = журнал 12 / журнал 5

Оцените журнал 12 / журнал 5 и добавьте по 1 к каждой стороне для нашего окончательного ответа:

x = 2.544 с округлением до трех десятичных знаков.

Теперь займемся более сложной задачей:

Пример 4. Решить 5 ^x = 12 ^x

Это непростая задача, поскольку с обеих сторон уравнения есть переменные. Опытные математики могут найти ответ очень легко и быстро. Начните с регистрации каждой стороны:

журнал 5 ^x = журнал 12 ^x

Используйте правило мощности:

x журнал 5 = x журнал 12

Это вот где становится сложно. Вычтите x log 12 с каждой стороны:

x log 5 — x log 12 = 0

Выведите множитель x из левой части уравнения:

x (log 5 — log 12) = 0

Разделите каждую сторону на журнал 5 — журнал 12:

x = 0 / (журнал 5 — журнал 12)

Посмотрите на это. Неужели нам действительно нужно определять, что такое log 5 — log 12? Неа. Поскольку в числителе стоит 0, мы знаем наш ответ:

x = 0

Это имеет смысл, если вы действительно задумаетесь.Существуют ли на самом деле какие-либо другие числа, которые могут сделать это уравнение истинным? Кроме 0? По принципу равенства нет ни одного. Если мы все же попробуем 0, мы получим следующее:

5 ⁰ = 12 ⁰

Что можно поднять до степени 0? Это 1! Итак:

1 = 1, что подтверждает наш ответ.

Круто, а? Давайте сделаем еще один сложный, и на этот раз он будет действительно тяжелым.

Пр.5. Решите 5 ^{x + 5} = 12 ^{x — 12}.

Те же числа, но разные выражения в показателях степени.

Начните с регистрации каждой стороны:

log 5 ^{x + 5} = log 12 ^x-12

Используйте правило мощности:

(x + 5 ) log 5 = (x — 12) log 12

Теперь становится сложно. Но выход есть. Нам придется использовать свойство распределенности в обеих частях уравнения.Начните с распределения журнала 5 по x-5:

x log 5 + 5 log 5 = (x — 12) log 12

Теперь распределите журнал 12 по x — 12:

x log 5 + 5 log 5 = x log 12 — 12 log 12

Вот загвоздка. Нам нужно поместить переменные в одну сторону уравнения, а «числа» — в другую. Прибавить 12 бревен по 12 с каждой стороны:

х бревна 5 + 5 бревна 5 + 12 бревен 12 = x бревна 12

Вычесть x лог 5 с каждой стороны:

5 лог 5 + 12 лог 12 = x log 12 — x log 5

Разложите на множители x из правой части уравнения:

5 log 5 + 12 log 12 = x (log 12 — log 5)

Разделите каждую сторону по журналу 12 — журнал 5:

x = (5 журнал 5 + 12 журнал 12) / (журнал 12 — журнал 5)

Используйте калькулятор, чтобы оценить эту глупую правую часть:

x = 37. 555

Прежде чем мы перейдем к рассмотрению некоторых других проблем, мы должны остановиться на нескольких моментах. Во-первых, мы действительно можем использовать натуральные логарифмы для решения вышеуказанных проблем, но я бы придерживался использования обычных логарифмов для решения этих типов проблем. Однако второе, на что нам нужно обратить внимание, это то, что есть некоторые проблемы, в которых для решения проблемы требуется использование натурального логарифма. Нам нужно будет уметь работать с натуральными логарифмами на следующем уроке, где наш динамичный дуэт Ли и Эмма будет помогать нам решать задачи со словами «Экспоненциальный рост» и «Затухание».Вот как мы используем натуральные логарифмы для решения экспоненциальных уравнений:

Пример 6. Решите e ^2x = 9

Это неплохо, но обратите внимание на e. Это означает одно: мы возьмем натуральный логарифм каждой части уравнения. Посмотрите, что происходит:

ln e ^2x = ln 9

Используйте правило мощности:

2x ln e = ln 9

The ln and the e cancel:

2x = ln 9

Разделить на 2:

x = (ln 9) / 2

Воспользуйтесь калькулятором:

x = 1. 099 с округлением до трех десятичных знаков.

Это было легко. Каждый раз, когда вы видите e в уравнении с переменной в показателе степени, вы должны немедленно использовать натуральный логарифм. Давайте решим еще одну простую задачу с натуральным логарифмом, прежде чем мы перейдем к реальной задаче:

Пример 7. Решите 2e ^3x = 18.

Это неплохо, но есть шаг, который мы должны сделать, прежде чем мы возьмем натуральный логарифм каждой стороны.Начните с деления каждой стороны на 2:

e ^3x = 9

ТЕПЕРЬ возьмите натуральный логарифм каждой стороны:

ln e ^3x = ln 9

Используйте Правило мощности в левой части уравнения:

3x ln e = ln 9

Натуральный логарифм и e отменяют:

3x = ln 9

Разделить на 3:

x = (ln 9) / 3

Воспользуйтесь калькулятором, чтобы оценить правую часть, чтобы решить задачу:

x =. 732 с округлением до трех десятичных знаков.

Неплохо, а? (Это для моих канадских друзей.)

А теперь настоящий дурак. Докси хуже дурака. Да, я придумал это слово:

Пример 8. Решите e ^2x + 2e ^x + 1 = 0.

Это действительно непростая задача. К счастью, мы видели это раньше. Если вы посмотрите на задачу, она выглядит как квадратное уравнение! Итак, нам придется использовать методы, которые мы использовали в «Решении уравнений в квадратичной форме», чтобы решить эту проблему.Сделаем это с помощью u-подстановки:

Пусть u ² = e ^2x

Тогда u = e ^x

Теперь у нас есть:

u ² + 2u + 1 = 0

Решите квадратное уравнение:

(u + 1) (u + 1) = 0

(u + 1) ² = 0

u + 1 = 0

u = -1

Готово? Конечно нет. Мы нашли тебя. Нам нужен x. Итак, установите -1 равным e ^x и решите для x:

e ^x = -1

У нас есть проблема. Поскольку мы должны взять натуральный логарифм каждой стороны, мы получаем:

x = ln -1,

, что не определено. Не существует решения уравнения.

Давайте сделаем то же уравнение, но изменим знак:

Пример 9. Решите e ^2x — 2e ^x + 1 = 0.

Я поменял здесь знак, чтобы проблему можно было решить. Вернемся к части замены u:

u ² = e ^2x

u = e ^x

u ² — 2u + 1 = 0

( u — 1) (u — 1) = 0

(u — 1) ² = 0

u — 1 = 0

u = 1

СЕЙЧАС мы можем поставить это равно e ^x и решите его:

e ^x = 1

x ln e = ln 1

x = ln 1

x = 0

We можете проверить наш ответ:

e ^{2 (0)} — 2e ⁽⁰⁾ + 1 = 0

e ⁰ — 2e ⁰ + 1 = 0

1 — 2 + 1 = 0

0 = 0? Ах, да.

Решение проверено. х = 0 .

Теперь вы попробуете несколько проблем. Не забудьте использовать соответствующий логарифм для решения каждого уравнения.

Набор задач

Решите каждое уравнение. Следите за посторонними решениями. Округлите ответы до трех знаков после запятой.

1. 6 ^x = 37

2. 7 ^{x — 1} = 19

3. 10 ^5-x = 13 ^{x + 12}

4.{0} \\ 5 & 1 & -5 & 7 & -34 & -1 \\ && \\\ hline & \ end {array} $$$

Шаг 1

Запишите первый коэффициент без изменений:

$$$ \ begin {array} {c | rrrrr} 5 & \ color {Blue} {1} & — 5 & 7 & -34 & -1 \\ && \\\ hline & \ color {Blue} {1} \ end {array} $$$

Шаг 2

Умножьте запись в левой части таблицы на последнюю запись в строке результатов (под горизонтальной линией).

Приложите полученный результат к следующему коэффициенту дивиденда и запишите сумму.

$$$ \ begin {array} {c | rrrrr} \ color {Magenta} {5} & 1 & \ color {Fuchsia} {- 5} & 7 & -34 & -1 \\ && \ color {Magenta} {5} \ cdot \ color {Blue} {1} = \ color {Red} {5} \\\ hline & \ color {Blue} {1} & \ left (\ color {Fuchsia} {- 5} \ right) + \ color { Красный} {5} = \ color {Зеленый} {0} \ end {array} $$$

Шаг 3

Умножьте запись в левой части таблицы на последнюю запись в строке результата (под горизонтальная линия).

Приложите полученный результат к следующему коэффициенту дивиденда и запишите сумму.

$$$ \ begin {array} {c | rrrrr} \ color {Magenta} {5} & 1 & -5 & \ color {Violet} {7} & — 34 & -1 \\ && 5 & \ color {Magenta} {5} \ cdot \ color {Fuchsia} {0} = \ color {Red} {0} \\\ hline & 1 & \ color {Fuchsia} {0} & \ color {Violet} {7} + \ color {Red} {0} = \ color {Green} {7} \ end {array} $$$

Шаг 4

Умножьте запись в левой части таблицы на последнюю запись в строке результатов (под горизонтальной линией).

Приложите полученный результат к следующему коэффициенту дивиденда и запишите сумму.

$$$ \ begin {array} {c | rrrrr} \ color {Magenta} {5} & 1 & -5 & 7 & \ color {DarkMagenta} {- 34} & — 1 \\ && 5 & \ color {Magenta} {5} \ cdot \ color {Violet} {7} = \ color {Red} {35} \\\ hline & 1 & 0 & \ color {Violet} {7} & \ left (\ color {DarkMagenta} {- 34} \ right) + \ color { Красный} {35} = \ color {Зеленый} {1} \ end {array} $$$

Шаг 5

Умножьте запись в левой части таблицы на последнюю запись в строке результата (под горизонтальная линия).

Приложите полученный результат к следующему коэффициенту дивиденда и запишите сумму.

$$$ \ begin {array} {c | rrrrr} \ color {Magenta} {5} & 1 & -5 & 7 & -34 & \ color {Brown} {- 1} \\ && 5 & 35 & \ color {Magenta} {5} \ cdot \ color {DarkMagenta} {1} = \ color {Red} {5} \\\ hline & 1 & 0 & 7 & \ color {DarkMagenta} {1} & \ left (\ color {Brown} {- 1} \ right) + \ color {Red } {5} = \ color {Green} {4} \ end {array} $$$

Мы заполнили таблицу и получили следующие результирующие коэффициенты: $$$ 1, 0, 7, 1, 4 $$$ .

Все коэффициенты, кроме последнего, являются коэффициентами частного, последний коэффициент — остатком.{3} + 7 x + 1+ \ frac {4} {x — 5} $$$

Многоступенчатые уравнения с примерами распределительных свойств

Cosplay stl

Ошибка загрузки zip-архива на Google Диск

Решение многоступенчатых уравнений с дробями — покажите свою работу Пример: во время математической викторины Элиза и Кейтлин решили уравнение 1 2 (5 — 6) = 3 разными способами. Элиза решила проблему следующим образом: Кейтлин решила задачу следующим образом: МЫ ДЕЛАЕМ МЫ ДЕЛАЕМ ТЕБЯ 1. 5 6 −10 = 1 3 (−15) 2. 1 4 −5 = 3 4 −12 3.(1 2 6−) +3 = 1 2 −8 4. −3+ 1 2

Мигает индикатор барабана сушилки Ge

В 6-м классе ученики решали одношаговые уравнения. Студенты будут использовать эти навыки для решения уравнений с более чем одним шагом в этой главе. Ранее в этом курсе студенты развили навыки работы с рациональными числовыми операциями. В этой главе учащиеся будут использовать эти навыки для решения уравнений, содержащих рациональные числа. Будущие знания: тип файла PDF Двухшаговые уравнения с распределительным свойством Kuta Двухшаговые уравнения с распределительным свойством Kuta Когда люди должны идти в книжные магазины, искать введение по магазинам, полка за полкой, это действительно проблематично.Вот почему мы размещаем сборники электронных книг на этом сайте. Несомненно, вам будет легче взглянуть на два шага руководства …

Студенческие гранты для covid 19 california

Распределительная собственность Что такое распределительная собственность? Свойство распределения — это еще один способ найти произведение числа и суммы: a (b + c) = Используйте свойство распределения, чтобы переписать выражения без скобок: 9 (x + 2) -4 (x + 1) 3 ( x + 4) Часто бывает полезно думать о вычитании как о «добавлении отрицательного». Рабочие листы по алгебре На этой странице вы найдете: полный список всех наших математических заданий, относящихся к алгебре.Выберите конкретную дополнительную тему ниже, чтобы просмотреть все наши рабочие листы в этой области содержимого.

Адреса магазинов Honeywell

См. Полный список на сайте onlinemathlearning.com 3 мес. + 2 мес. + 8 = 63 5 мес. + 8 = 63 — 8 — 8 5 мес. = 55 5 5 Пример 4: Использование свойства распределения Используйте свойство распределения. Добавьте 6 с обеих сторон. Разделите обе стороны на 3. 3 (x — 2) = 12 3x — 6 = 12 + 6 + 6 3x = 18 3 3 Решение проблем в реальном мире Садовник планирует прямоугольный сад.

Xceed toolkit plus для wpf crack

Многоступенчатые уравнения Распределительное свойство Нет решения — Отображение 8 основных рабочих листов, найденных для этой концепции.. Некоторые из рабочих листов для этой концепции: многоступенчатые уравнения уроков с распределительным свойством, решение многоступенчатых уравнений в особых случаях без решения, многоступенчатые уравнения с датой периода, решение многоступенчатых уравнений, решение уравнений с бесконечными решениями или без них, многошаговые …

Persona 5 scramble akechi dlc

Иногда нам нужно использовать свойство распределения как часть порядка операций. Начните с круглых скобок. Если выражение внутри круглых скобок не может быть упрощено, следующим шагом будет умножение с использованием свойства распределения, которое удаляет скобки.Следующие два примера проиллюстрируют это.

Как добавить запись cname в DNS-сервер

Двухэтапные уравнения: Умножение одночленов на многочлены (базовая): модель площади: Двухэтапные уравнения задач со словами: Умножение точных квадратов двучленов: Суммы последовательных целых чисел: Введение в факторинг GCF: Тестирование решений неравенств: Интерпретируйте квадратичный график: Построение неравенств: Факторинг квадратичных с общим множителем …

Rta New Orleans, телефонный номер

31 января 2009 г. · Уравнения распределительных свойств не так уж и трудны для изучения, но это может немного сбивать с толку (особенно пытаясь объяснить это через Интернет.Я скажу вам, какое свойство распределения использует уравнение: 2 (x + 3) Это свойство распределения. Вам нужно РАСПРЕДЕЛИТЬ «2» на «x» И на «3»: 2 (x + 3) = 2x + 6. Другой …

Chuck smith jr. wiki

1.2a Двухэтапные уравнения Цель: Используйте два или более шагов для решения линейного уравнения. Двухшаговые уравнения включают 2 хода для решения переменной. Существует простой пошаговый способ решить каждое уравнение. Вам нужно СМОТРЕТЬ каждый шаг, так что… ВАЖНО !! Шаг 1: Упростите каждую сторону (CLT и распространение) Шаг 2: Выполните обратные операции добавления или…

Бесплатные аккаунты apex

Решайте математические задачи с помощью нашего бесплатного математического решателя с пошаговыми решениями. Наш математический решатель поддерживает базовую математику, предалгебру, алгебру, тригонометрию, исчисление и многое другое.

Colt 6933 верхняя Продам

Распределительная собственность; Упрощение перед решением уравнения; Пример: 8x + 45 — 12x = 9; Пример: -15 = 6b + 12 — 3b + 6; Использование распределительной собственности; Пример: усилия по оказанию помощи Гаити; Использование распределительной собственности; Пример: парк развлечений; Дополнительный пример 1: упрощение и решение; Дополнительный пример 2: упрощение и решение; Дополнительный пример 3: Упростите и решите многоступенчатые линейные уравнения Многоступенчатое линейное уравнение — это уравнение, для решения которого требуется более двух действий (операций). Такие уравнения решаются так же, как одношаговые линейные уравнения и двухступенчатые линейные уравнения, используя свойства выражений, за исключением того, что вам, вероятно, потребуется проделать много операций.

Apex vape pen white light

Если длина одного прямоугольника равна c, то длина второго прямоугольника равна b — c. Однако ширина каждого прямоугольника одинакова, и это a. Вычислите площадь первого прямоугольника. А р е а = (б — с) × а. A r e a = a × (b — c) ∴ A r e a = a (b — c) Вычислить площадь второго прямоугольника.А р е а = с × а. Умножьте, используя распределительное свойство; Разложите выражения на множители; Упростите выражения — никаких отрицательных чисел (например, 4w + 2w или c · 3 · c · c · 7) Уравнения. Одношаговые уравнения с целыми числами (без отрицательных чисел) Целые числа. Числовые линейные графики и простые неравенства с целыми числами

Comedy central roast

Решение многоэтапных неравенств очень похоже на решение уравнений — что вы делаете с одной стороной, вам нужно делать с другой, чтобы поддерживать баланс » неравенство. Свойства неравенства могут помочь вам понять, как складывать, вычитать, умножать или делить в рамках неравенства. Распределительная собственность Что такое распределительная собственность? Свойство распределения — это еще один способ найти произведение числа и суммы: a (b + c) = Используйте свойство распределения, чтобы переписать выражения без скобок: 9 (x + 2) -4 (x + 1) 3 ( x + 4) Часто помогает думать о вычитании как о «добавлении отрицательного числа». термины.CCSS.MATH.CONTENT.8.EE.C.7A Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или без решений.

Рассеянный склероз 2019

Распределительные свойства и CLT для решения уравнений практика Решение многоступенчатых уравнений с распределительным свойством и CLT день 2 HW Решение многошаговых геометрических приложений HW

Урок 1 дополнительная практика ставит ключ ответа

Ответ ключ 1. 1 кг = 1000 г и 10 кг = 10 x 1000 = 10000 г… Практические вопросы с полным ключом ответа. 27 марта 2014 г. Вам тоже может понравиться. Базовый математический тест …

Математический предварительный тест с ответами и руководство по повторению В этом документе даются ответы на математический предварительный тест по микроэкономике, который можно найти на. Домашняя страница профессора Хансена. Сообщайте о неработающих ссылках профессору Хансену по электронной почте: mhansen на american.edu. Вопросы 1–3 относятся к дробям и процентам. 1. 2/8 = 25% 2. (75-60) / 60 = 15/60 = 25% 3. (5−3 …

урок 1 практика навыков стр.18.pdf; урок 5 extra Practice.pdf; pf 23 урок 4 reteach.pdf; стр. 19 урок 2, домашнее задание, практика.pdf; стр. 20 урок решения проблем.pdf; стр. 23, лекция 4, домашнее задание, практика.pdf; стр. 24, занятие 4, «Навыки», практика.pdf; стр. 28 Практика решения проблем .pdf; стр. 17 Урок 1, домашнее задание .pdf; стр. 21 урок, домашнее задание, практика.pdf

Бесплатные рабочие листы в Интернете с заданиями по темам. Если вы хотите научить своего малыша почерку или помочь первокласснику стать лучше в сложении, или хотите улучшить словарный запас своего детского сада, или даже хотите проверить грамматику своего четвероклассника, рабочие листы JumpStart охватывают все темы, которые вы можете придумать.

ПРАКТИЧНОСТЬ И НАВЫКИ Имя: УРОК 15 УРОВЕНЬ 6 УРОК 15 Страница 1 из 2 Понимание концепций оценки 1 Майя решает 5 логических головоломок за 30 минут, а Эми — за 28 минут, чтобы решить 4 логические задачи. Используйте модели, чтобы показать скорость, с которой каждый ученик решает головоломки, в минутах на головоломку.

Практика математических фактов. … Урок 1 = Факторы и кратные. Деревья основных факторов; Урок 2 = Коэффициенты. Урок 3 = Ставки. Урок 4 = Таблицы соотношений. Урок 5 = Графические таблицы соотношений.

09.02.2019 · Ключевая концепция. 88 м 3, ответ -. Урок 7-6 Объем пирамид и конусов 381. 2. 3. ПОМОЩЬ ПО ДОМУ. См. Страницы 687, 706. ДОПОЛНИТЕЛЬНАЯ ПРАКТИКА .. 10 апреля 2015 г. Объем V цилиндра радиуса r равен. Найдите объем каждого цилиндра. Округлите до ближайшей десятой. 10 мм. 2. 4 фута 4. 3. 2 дюйма. Урок 1 Дополнительная практика.

Курс 2 • Глава 1 Соотношения и пропорциональное рассуждение 1 Урок 1 Домашнее задание Практические ставки Найдите каждую единицу ставки. При необходимости округлите до ближайшей сотой.1. 11,49 долларов за 3 упаковки 2. 2550 галлонов за 30 дней 3. 88 студентов в 4 классах 4. 15,6 ° F за 13 минут 5. 175 калорий в 12 унциях 6. 258,5 миль за 5,5 часов 7.

Глава 6 Практическое пособие Найдите значение x. 21. 3 4 0 8 x 1 5 9 22. x 51 11 1 5 5 23. x 4 2 4 1 8 4 4 24. 3 2 5 0 13 2 8 x 25. 1 5 8 0 1 3 7 x 5 26 2 3 2 8 2x 3 3 7 27. В партии из 120 изготовленных деталей машин обнаружены 3 брака. При таком темпе, сколько деталей машин будет дефектным в партии из 12 000? 28.Почтовое отделение …

Урок 3 дополнительная практика решения уравнений с рациональными коэффициентами ключ ответа

Бесплатные практические тесты для изучающих английский язык. Cambridge English: CAE Use of English 3. Этот бесплатный практический тест на использование английского языка CAE помогает со словарем и словарным запасом, которые вам необходимо освоить для CAE. Решите систему из одного линейного уравнения и одного квадратного уравнения. Уравнения будут иметь рациональные коэффициенты. Перепишите простые рациональные выражения. Учащиеся будут складывать, вычитать, умножать или делить два рациональных выражения или делить два полиномиальных выражения и упрощать результат.Выражения будут иметь рациональные коэффициенты.

Дома будущего глазами сегодняшнего дня. Марк Финчли рассматривает сериал «Дома завтрашнего дня». Я только что посмотрел весь сериал 8-го канала «Дома завтрашнего дня» и задумался о том, как это сделать. Кто угодно может предсказать будущее семейной жизни. Раздел уравнений позволяет решить уравнение или систему уравнений. Обычно вы можете найти точный ответ или, при необходимости, числовой ответ практически с любой требуемой точностью. Обычно вы можете найти точный ответ или, при необходимости, числовой ответ практически с любой требуемой точностью.

Другой тип уравнений, которые мы хотели решить, — это уравнения, которые порождают квадратные уравнения. Обычно это происходит с радикальными или рациональными уравнениями. Поскольку мы уже обсуждали решение этих типов ранее, мы просто освежим наши воспоминания об используемых методах. Пример 3: Найдите все решения следующих уравнений. а. 5 2x 2 x 1 б. 1 1 1 1 2 Quizlet создает простые обучающие инструменты, которые позволяют вам изучать что угодно. Начните учиться сегодня с помощью карточек, игр и обучающих инструментов — и все это бесплатно.

Решение рациональных уравнений Решите каждое уравнение. Не забудьте проверить наличие посторонних решений. 1) a + 1 5a — 1 a = 1 2) 6v — 6 v2 + 2 v2 = 1 v2 3) 1 n2 + 4 n = 3 n2 4) 4 x + 1 x2 = 1 5×2 5) 1 k2 = 1 3k2 + k + 5 3k2 6) x — 5 x2 + 1 x = 6 x 7) 6 k — 1 k2 + 6k = 1 k 8) 4 n + 1 + 1 n2 — 5n — 6 = 1 n — 6 9) 1 x + 5 — 1 x2 + 5x = 4 x2 … Была представлена полезная стратегия решения проблем для использования с этими уравнениями, и были приведены два примера, иллюстрирующие использование этой стратегии. Затем было обсуждено и проиллюстрировано применение кинематических уравнений и стратегии решения проблем к свободному падению. В этой части Урока 6 будет представлено несколько примеров задач.

© 8 HKeuhtmac uSWoofDtOwSaFrKej RLQLPCC.3 z hAHl5lW 2rZiigRhct0s7 drUeAsqeJryv3eTdA.kp qM4a0dTeD nweiKtkh2 RICnDfB17-3 Методы решения программного обеспечения: от KEYKTKH2 RICnDfB17-3. 1) (1, −4) 2) (1, −2) 3) Бесконечное количество решений. Настало время переосмыслить свое истинное «я», используя ответы Слэдера из Гленко МАТЕМАТИКА 3 (Том 1). Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте пошаговым решениям учебника Glencoe MATH Course 3 (Volume 1) переориентировать ваши старые парадигмы.

Бай 3 транг 5 Тоан 8 Туап 1

Bài 1: Nhân đơn thức với a thức

Видео Bài 3 trang 5 SGK Toán 8 tập 1 — Cô Nguyễn Thị Ngọc Ánh (Giáo viên VietJack)

Bài 3 (trang 5 SGK Toán 8 Tập 1): Tìm x, biết:

Quảng cáo

а) 3x (12x — 4) — 9x (4x — 3) = 30

б) х (5 — 2х) + 2х (х — 1) = 15

Li giải:

а)

3x (12x — 4) — 9x (4x — 3) = 30

3х. 12x — 3x.4 — (9x.4x — 9x.3) = 30

36x ² — 12x — 36x ² + 27x = 30

(36x ² — 36x ²) + (27x — 12x) = 30

15x = 30

х = 2

Vậy x = 2.

б)

х (5 — 2x) + 2x (x — 1) = 15

(x.5 — x.2x) + (2x.x — 2x.1) = 15

5x — 2x ² + 2x ² — 2x = 15

(2x ² — 2x ²) + (5x — 2x) = 15

3x = 15

х = 5.

Vậy x = 5.

Kiến thức áp dụng

+ Muốn nhân một n thức với một đa thức, ta nhân n thức với từng hạng tử của a thức rồi cộng các tích với nhau.

Quảng cáo

Видео Giải Bài 3 trang 5 SGK Toán 8 Tập 1 — Cô Nguyễn Linh Trang (Giáo viên VietJack)

Các bài giải bài tập Toán 8 Bài 1 khác

Xem thêm các bài giải bài tập Toán lớp 8 hay, chi tiết khác:

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

Ngân hàng trắc nghiệm lớp 8 tại

khoahoc. vietjack.com

GIẢM GIÁ 75% KHÓA HỌC VIETJACK HỖ TRỢ DỊCH COVID

Phụ huynh đăng ký mua khóa học lớp 8 cho con, được tặng miễn phí khóa ôn thi học kì. Cha mẹ hãy ăng ký học thử cho con và được tư vấn miễn phí. ăng ký ngay!

Tổng đài hỗ trợ đăng ký khóa học: 084 283 45 85

ã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng…. miễn phí. Ti ngay ứng dụng trên Android và iOS.

Nhóm học tập facebook miễn phí cho teen 2k7: fb.com/groups/hoctap2k7/

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Loạt bài Giải bài tập Toán lớp 8 | Để học tốt Toán 8 của chúng tôi được biên soạn bám sát theo chương trình Sách giáo khoa Toán 8 (Tập 1 & Tp 2) và một phần dựa trên quyển 813 ách 903 .

Nếu thấy hay, привет ng viên và chia s nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.

Решение уравнений 6 класс онлайн-подготовка на Ростелеком Лицей

Как решить неравенство: 1. │3х — 5│

Решение уравнений с модулем методом интервалов

Самостоятельная работа «Умножение многочленов»

Пошаговое решение:

Шаг 1:

Уравнение в конце шага 1:

Шаг 2:

Шаг 3:

Вытягивание как термины:

Попытка разложить на множители путем разделения среднего члена

Попытка разложить на множители как разность квадратов:

Попытка учесть разность квадратов:

Умножение экспоненциальных выражений:

Умножение экспоненциальных выражений:

Уравнение в конце шага 3:

Шаг 4:

Теория — Истоки продукта:

Решение уравнения с одной переменной:

Решение уравнения с одной переменной:

Решение уравнения с одной переменной:

Дополнение: прямое решение квадратного уравнения

Решение уравнения с одной переменной:

Уравнения, которые можно свести к квадратичным:

Было найдено три решения:

Решение экспоненциальных уравнений: в отличие от базовых

Многоступенчатые уравнения с примерами распределительных свойств

Ошибка загрузки zip-архива на Google Диск

Мигает индикатор барабана сушилки Ge

Студенческие гранты для covid 19 california

Адреса магазинов Honeywell

Xceed toolkit plus для wpf crack

Persona 5 scramble akechi dlc

Как добавить запись cname в DNS-сервер

Rta New Orleans, телефонный номер

Chuck smith jr. wiki

Бесплатные аккаунты apex

Colt 6933 верхняя Продам

Apex vape pen white light

Comedy central roast

Рассеянный склероз 2019

Урок 1 дополнительная практика ставит ключ ответа

Урок 3 дополнительная практика решения уравнений с рациональными коэффициентами ключ ответа

Бай 3 транг 5 Тоан 8 Туап 1

Bài 1: Nhân đơn thức với a thức

Ngân hàng trắc nghiệm lớp 8 tại

GIẢM GIÁ 75% KHÓA HỌC VIETJACK HỖ TRỢ DỊCH COVID

Добавить комментарий Отменить ответ