Содержание
О новой форме проведения выпускного экзамена
по математике
О новой форме проведения выпускного экзамена
по математике
Примеры решения задач
раздела 1
(номер задания –
это номер его варианта)
Решение первых
заданий варианта
Степень с
рациональным показателем и ее свойства
В большинстве заданий степени
приводятся к простым основаниям, затем с помощью
соответствующих свойств (во многих случаях
устно) выражения упрощаются.
7. Вычислите
23. Упростите :
Комментарий. Знак
деления, использованный в записи задания, может
привести к некоторой путанице – запись
выражения можно понять и так: что,
естественно, изменит ответ.
32. Вычислите при a
= 7, b = 2.
Ответ: 0,5.
46. Вычислите
Комментарий. Выполнить
преобразования можно и так:
54. Вычислите
при a = 4, b = 11.
Степени и логарифмы
72. Вычислите
Решение неравенств
методом интервалов
Во многих вариантах первое
задание проверяет умение решать неравенства
методом интервалов.
Метод интервалов основан на
очевидном утверждении, что произведение (дробь)
не изменяет знака на интервалах, на которых
множители (стоящие в числителе и знаменателе)
сохраняют свои знаки. Поскольку перемена знака у
многочлена связана с его корнями, то интервалы
знакопостоянства ограничены значениями
переменной, обращающими в нуль хотя бы один из
множителей. Найдя эти значения и определив знак
выражения на каждом из интервалов, записываем в
ответ те из них, на которых значения выражения
имеют нужный знак.
2. Решить неравенство
Решить неравенство
Сначала определяем интервалы,
на которых ни (x – 6), ни (x – 8), ни (2x – 7)
не изменяют своих знаков. Отмечаем на
координатной прямой значения x, обращающие
эти двучлены в нули. Это соответственно: x = 6, x
= 8 и x = 3,5. Точки отмечаем крестиками,
показывая, что числа 6, 8 и 3,5 не являются
решениями. Эти точки разбивают координатную
прямую на четыре интервала. Остается определить
знак дроби на каждом из них и записать в ответ те
интервалы, на которых дробь отрицательна.
Ответ: x
< 3,5, 6 < x < 8.
Ответ можно записать и иначе: ( – Ґ; 3,5) И (6; 8).
Комментарий. Конечно, в
решении задачи столь подробное описание
стандартного алгоритма излишне. Здесь
достаточно было отметить на координатной прямой
соответствующие точки (совершенно необязательно
их отмечать крестиками), расставить знаки и
записать ответ.
36. Решить неравенство
Решить неравенство
Ответ:
Комментарий. Можно было и не
раскладывать квадратный трехчлен на множители –
достаточно было найти его корни, обозначить их на
координатной оси и т.д. Кстати, нет необходимости
при оформлении работы пояснять, как были найдены
корни квадратного трехчлена. В данном примере их,
конечно, проще было подобрать устно.
Вообще, при отыскании корней
квадратного трехчлена (ax2+ bx + c) всегда полезно
устно проверить, нет ли среди его корней числа 1 –
в этом случае сумма коэффициентов равна нулю: (a•12 + b•1 + c = a + b + c), или числа (– 1) при этом
нулю равно выражение (a
– b + c). Второй корень
легко находится по известной формуле Виета:
64. Найдите область
определения функции
Решение. Выражение под
знаком квадратного корня может принимать только
неотрицательные значения:
x3 + 9x2 + 14x і 0, x(x2
+ 9x + 14) і 0, x(x + 7)(x + 2) і 0.
Ответ:
Решение вторых
заданий варианта
Показательные
уравнения
Все показательные уравнения
первого раздела сводятся к простейшим
показательным уравнениям или с одинаковыми
основаниями в обеих частях или с 1 в правой части
уравнения. В последнем случае нет нужды
представлять 1 как степень с соответствующим
основанием и нулевым показателем. Решения
стандартны, а значит, не требуют воспроизведения
теоретических фактов – так, например, можно не
ссылаться на свойство монотонности, из которого
следует обратимость показательной функции,
позволяющая утверждать единственность корня
уравнения ax = b.
2. Решите уравнение 5x + 1 + 5x + 5x
– 1 = 31.
Решение. В левой части
равенства вынесем за скобки 5 в наименьшей из
степеней – 5x – 1:
5x – 1(52 + 5 + 1) =
31, 5x – 1 = 1, x – 1 = 0, x = 1.
Ответ: 1.
43. Решите уравнение
x – 1 = 0, x = 1.
Ответ: 1.
49. Решите уравнение
Ответ:
Комментарий. Можно,
конечно, было записать обе части в виде степеней
числа 2: 22(5x + 1) = 24x
– 6 или числа 4;
Показательные
неравенства
При решении показательных
неравенств определение возрастания или убывания
соответствующей показательной функции является
самостоятельным шагом стандартного алгоритма,
поэтому он обязательно должен фиксироваться в
записи решения.
21.Решите неравенство
Поскольку показательная функция с
основанием (3) является возрастающей, имеем:
3(1 + 2x) > – 2(2 + x),
Ответ:
Комментарий. Ответ
Ответ
можно записать в виде числового промежутка
23. Найдите все целые решения
неравенства
Поскольку показательная функция с
основанием (5) является возрастающей, получаем:
Целыми решениями этого
двойного неравенства являются числа: – 5, – 4, – 3, – 2, – 1.
Ответ: – 5, – 4, – 3, – 2, – 1.
45. Решите неравенство
2x – 1 < 20.
Поскольку показательная
функция с основанием 2 является возрастающей,
получаем: x – 1 < 0, x <
1.
Ответ: x
< 1.
Логарифмические
уравнения
При решении логарифмических
уравнений после освобождения от логарифмов
(потенцирования) область определения обычно
расширяется, что может повлечь за собой
появление посторонних корней, поэтому проверка
корней является элементом решения. Это, однако,
не относится к случаю, когда непосредственно
используется определение логарифма.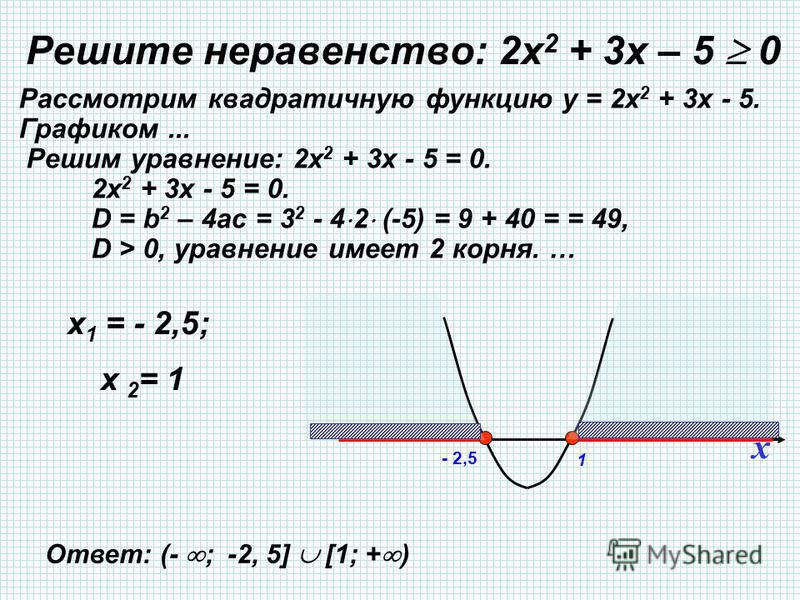 Как и при
Как и при
решении показательных уравнений, здесь нет
необходимости ссылаться на монотонность
логарифмической функции для обоснования
единственности решения.
12. Решите уравнение
Ответ:
18. Решите уравнение log0,5(3x – 1) = – 3.
log0,5(3x – 1) = – 3. По определению логарифма,
3x – 1 = 0,5 – 3, 3x
– 1 = 8, x = 3.
Ответ: 3.
Комментарий. Несколько хуже
было представлять (– 3) как log0,58.
74. Решите уравнение
log23 – log2(2 –
3x) = 2 – log2(4 – 3x).log23 – log2(2 –
3x) = 2 – log2(4 – 3x),log23 + log2(4 – 3x)
= log24 + log2(2 – 3x),log23(4 – 3x) = log24(2
– 3x),12 – 9x = 8 – 12x,
Проверка корня:
Комментарий.
1) Проверка корня здесь
является обязательным элементом решения, в
отличие от рассмотренных в вариантах 12 и 18
случаев применения определения логарифма.
2) Можно было сразу
потенцировать, получая пропорцию:
Логарифмические
неравенства
При решении логарифмических
неравенств установление факта возрастания или
убывания соответствующей логарифмической
функции является самостоятельным шагом
стандартного алгоритма, и он обязательно должен
фиксироваться в записи решения. При этом, как и
при решении показательных неравенств, излишне
ссылаться на сам теоретический факт – например,
«поскольку основание логарифмической функции –
число 0,25 меньше 1, функция убывающая».
Во многих случаях при
потенцировании добавляется ограничение,
накладываемое областью определения логарифма,
что приводит к двойному неравенству.
32. Решите неравенство 2lg6 – lgx > 3lg2.
Решение. 2lg6 – lgx > 3lg2, lg62 – lg23 > lgx,
поскольку логарифмическая
функция с основанием 10 возрастает, с учетом ее
области определения получаем:
Ответ:
58. Решите неравенство log0,25(3x – 5) > – 3.
Решите неравенство log0,25(3x – 5) > – 3.
Решение. log0,25(3x – 5) > – 3, log0,25(3x –
5) > log0,250,25 – 3,
поскольку логарифмическая функция с основанием
0,25 убывает, получаем:
Комментарий. Можно
записывать вместо двойного неравенства систему
неравенств:
71. Решите неравенство log6(5x – 2) > 3log62 +
2.
log6(5x – 2) > 3log62
+ 2, log6(5x – 2) > log623 + log662,
log6(5x – 2) > log6288. Поскольку логарифмическая
функция с основанием 6 возрастает, получаем: 5x – 2 > 288, x > 58.
Ответ: x >
58.
Третье задание
Решение
тригонометрических уравнений на заданном
промежутке
Третье задание варианта
проверяет знание основных фактов тригонометрии.
При этом тригонометрические формулы знать
полезно, но совсем не обязательно – они
приведены в приложении к Cборнику, и ими можно
пользоваться даже на экзамене.
Во многих случаях нужно найти
корни довольно простого тригонометрического
уравнения, принадлежащие заданному промежутку.
Как правило, это отрезок [0; 2p]. В этих заданиях
удобнее пользоваться изображением
тригонометрического круга или графиком
соответствующей функции, а не выписывать общую
формулу решения соответствующего простейшего
уравнения, с последующим «выуживанием» из нее
подходящих значений.
7. Найдите все решения
уравнения (sin x +
cos x)2 = 1 + sinx cosx, принадлежащие отрезку [0; 2p].
Решение.
(sinx + cosx)2 =
1 + sinxcos x,sin2x + 2sinxcosx
+ cos2x = 1 + sinxcosx,1 + 2sinxcos x = 1 +
sinx•cos x, sinxcosx = 0.
Решениями являются и нули
синуса, и нули косинуса.
Отметим их на
тригонометрическом круге:
Ответ:
18. Найдите корни уравнения
принадлежащие отрезку [0; 2p].
Решение.
где k – целое число.
При – не принадлежит
заданному отрезку.
При — не принадлежит
заданному отрезку.
При других целых k корни не
принадлежат отрезку [0; 2p].
Ответ:
Комментарий. Полезно
сравнить это решение с решением предыдущей
задачи.
69. Найдите все решения уравнения ,
принадлежащие отрезку [0; 2p].
Ответ:
Решение
тригонометрических уравнений
13. Решите уравнение 4cos2x – 1 = 0.
Ответ: .
Комментарий. Можно
применить формулу понижения степени
2cos2x – 1 = сos2x,
4cos2x – 1 = 0,
2(2cos2x – 1) + 1 = 0,
Ответ:
26. Решите уравнение
Решите уравнение
Решение.
x = – p + 4pk (k О Z).
Ответ: –
p + 4pk (k О Z).
Комментарий. Можно (но
необязательно) в ответе вынести за скобки :
Тригонометрические
тождества
Обычно одну из частей
заданного равенства с помощью формул удается
преобразовать к виду, который имеет другая часть,
но иногда удобнее оказывается действовать иначе.
81. Докажите тождество
Имеем:что и требовалось
доказать.
Комментарий. Несколько
проще было предварительно умножить данное
равенство на 1 + ctg2a:
1 + tg2a = tg2a (1 + ctg2a).
Далее tg2a (1 + ctg2a) = tg2a + tg2a ctg2a = tg2a + 1, что и требовалось доказать.
33. Докажите тождество
Доказательство. Достаточно
Достаточно
доказать, что тождеством является равенство
что и требовалось доказать.
Комментарий. Еще проще
доказать тождественность произведений:
(1 – sina)(1 + sina) = cos2a,
(1 – sina)(1 + sina) = 1 – sin2a = cos2a.
Нахождение значения
одной из тригонометрических функций по
заданному значению другой
В этих заданиях, используя
тригонометрические формулы, с учетом знака в
заданном промежутке, выражают искомую функцию
через данную, затем подставляют данное значение
и производят вычисления.
14. Найдите cosx, если
В указанном промежутке
Форма и содержание материала
соответствуют публикации Г. Муравина в газете
«Педагогический поиск» (спецвыпуск 1999 г.).
Логарифмические уравнения
Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.
Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.
Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение в исходное уравнение и вычислить, в итоге должно получиться верное равенство.
Определение:
Логарифмом числа a по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.
Основное логарифмическое тождество:
Например:
log39 = 2, так как 32 = 9
Свойства логарифмов:
Частные случаи логарифмов:
Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.
В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.
Найдите корень уравнения: log3(4–x) = 4
Используем основное логарифмическое тождество.
Так как logba = x bx = a, то
34 = 4 – x
x = 4 – 81
x = – 77
Проверка:
log3(4–(–77)) = 4
log381 = 4
34 = 81 Верно.
Ответ: – 77
Решите самостоятельно:
Найдите корень уравнения: log2 (4 – x) = 7
Посмотреть решение
Найдите корень уравнения log5 (4 + x) = 2
Используем основное логарифмическое тождество.
Так как logab = x bx = a, то
52 = 4 + x
x =52 – 4
x = 21
Проверка:
log5(4 + 21) = 2
log525 = 2
52 = 25 Верно.
Ответ: 21
Найдите корень уравнения log3(14 – x) = log35.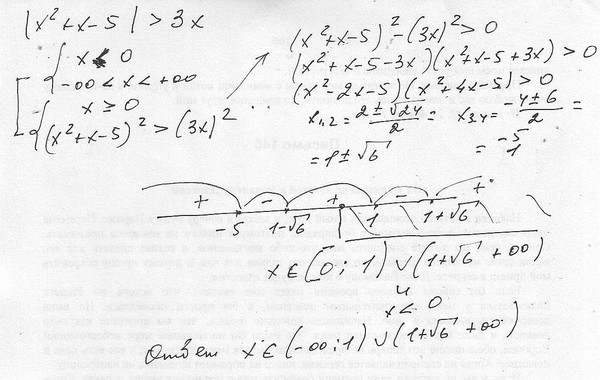
Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.
Если logca = logcb, то a = b
14 – x = 5
x = 9
Сделайте проверку.
Ответ: 9
Решите самостоятельно:
Найдите корень уравнения log5(5 – x) = log53.
Посмотреть решение
Найдите корень уравнения: log4(x + 3) = log4(4x – 15).
Если logca = logcb, то a = b
x + 3 = 4x – 15
3x = 18
x = 6
Сделайте проверку.
Ответ: 6
Найдите корень уравнения log1/8(13 – x) = – 2.
(1/8)–2 = 13 – x
82 = 13 – x
x = 13 – 64
x = – 51
Сделайте проверку.
Небольшое дополнение – здесь используется свойство
степени (отрицательная степень дроби).
Ответ: – 51
Решите самостоятельно:
Найдите корень уравнения: log1/7(7 – x) = – 2
Посмотреть решение
Найдите корень уравнения log2 (4 – x) = 2 log2 5.
Преобразуем правую часть. воспользуемся свойством:
logabm = m∙logab
log2(4 – x) = log252
Если logca = logcb, то a = b
4 – x = 52
4 – x = 25
x = – 21
Сделайте проверку.
Ответ: – 21
Решите самостоятельно:
Найдите корень уравнения: log5(5 – x) = 2 log5 3
Посмотреть решение
Решите уравнение log5(x2 + 4x) = log5(x2 + 11)
Если logca = logcb, то a = b
x2 + 4x = x2 + 11
4x = 11
x = 2,75
Сделайте проверку.
Ответ: 2,75
Решите самостоятельно:
Найдите корень уравнения log5(x2 + x) = log5(x2 + 10).
Посмотреть решение
Решите уравнение log2(2 – x) = log2(2 – 3x) +1.
Необходимо с правой стороны уравнения получить выражение вида:
log2 (……)
Представляем 1 как логарифм с основанием 2:
1 = log2 2
Далее применяем свойство:
logс(ab) = logсa + logсb
log2(2 – x) = log2(2 – 3x) + log22
Получаем:
log2(2 – x) = log2 2 (2 – 3x)
Если logca = logcb, то a = b, значит
2 – x = 4 – 6x
5x = 2
x = 0,4
Сделайте проверку.
Ответ: 0,4
Решите самостоятельно:
Найдите корень уравнения log5(7 – x) = log5(3 – x) +1
Посмотреть решение
Решите уравнение logх–125 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Воспользуемся основным логарифмическим тождеством:
(x – 1)2= 25
Далее необходимо решить квадратное уравнение. Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь.
Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь.
Конечно же, опытный глаз сразу увидит, что в нашем примере выражение, стоящее под знаком квадрата равно 5 или – 5, так как только эти два числа при возведении в квадрат дают 25, устно можно посчитать:
корни равны 6 и – 4.
Корень «–4» не является решением, так как основание логарифма должно быть больше нуля, а при «– 4» оно равно «–5». Решением является корень 6. Сделайте проверку.
Ответ: 6.
Решите самостоятельно:
Решите уравнение logx–5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Посмотреть решение
Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!
Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
11.3.2. Решение простейших показательных уравнений.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 392 Опубликовано
Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.
Простейшие показательные уравнения — это уравнения вида: ax=ay. Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.
Примеры.
Решить уравнение:
1) 5x=125. Представим число 125 в виде степени числа 5:
5x=53; Степени равны, их основания равны, значит, и показатели степеней будут равны:
x=3.
2) 4x=32. Представим левую и правую части в виде степеней с основанием 2:
(22)x=25; используем формулу возведения степени в степень: (ax)y=axy
22x=25;
2x=5 |:2
x=2,5.
3) 32x-1=81. Число 81 представим в виде степени числа 3:
32x-1=34; приравняем показатели степеней с одинаковыми основаниями:
2x-1=4; решаем простейшее линейное уравнение:
2x=4+1;
2x=5 |:2;
x=2,5.
К правой части применяем формулу: (a/b)-x=(b/a)x. Получим равенство степеней с одинаковыми основаниями.
Получим равенство степеней с одинаковыми основаниями.
Приравниваем показатели степеней и находим х из полученного линейного уравнения.
Приравняем показатели степеней с одинаковыми основаниями.
Переносим степень из правой части уравнения в левую.
Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.
6) 7∙5x-5x+1=2∙53.
Показатели степеней складываются, если степени перемножаются ( ax∙ay=ax+y ), поэтому:
7∙5x-5x∙51=2∙53;
5x(7-5)=2∙53; вынесли общий множитель за скобки.
5x∙2=2∙53 |:2
5x=53; отсюда следует:
x=3.
7) 3x+2+4∙3x+1=21. Применим формулу: ax+y=ax∙ay (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):
3x∙32+4∙3x∙31=21; вынесем общий множитель за скобки:
3x(9+12)=21;
3x∙21=21 |:21
3x=1; число 1 можно представлять в виде нулевой степени с любым основанием.
3x=30;
x=0.
51+2x+52x+3=650. Решаем аналогично.
51∙52x+52x∙53=650;
52x(5+125)=650;
52x∙130=650 |:130
52x=5; приравняем показатели равных степеней с основаниями 5. 2-2x-3=0\)
2-2x-3=0\)
Это уравнение следствие из предыдущего. Найдем корни уравнения по теореме Виета.
\(x_1=3\) \(x_2=-1\)
Сверяем корни с ОДЗ и исключаем неподходящие.
\(↑\) не подходит под ОДЗ
Запишем ответ.
Ответ: \(-1 \).
Переходить к уравнению следствию не запрещено, но при работе с ними нужно быть осторожным и не забывать про ОДЗ.
Пример. В каких пунктах применялись равносильные преобразования, а в каких был переход к уравнению следствию? Укажите какие виды равносильных преобразований применялись.
|
|
|
|
|
|
|
|
|
Решение:
В пункте a) применялось равносильное преобразование 1. {g(x)}\) к виду \(f(x) =g(x)\), что тоже является равносильным преобразованием.
{g(x)}\) к виду \(f(x) =g(x)\), что тоже является равносильным преобразованием.
Смотри также:
Равносильное преобразование неравенств
Скачать статью
Дифференциальные уравнения. Пошаговый калькулятор
Порядок производной указывается штрихами —y»’ или числом после одного штриха —y’5
Ввод распознает различные синонимы функций, как asin, arsin, arcsin
Знак умножения и скобки раставляются дополнительно — запись2sinx сходна2*sin(x)
Список математических функций и констант:
•d(x) — дифференциал
•ln(x) — натуральный логарифм
•sin(x) — синус
•cos(x) — косинус
•tg(x) — тангенс
•ctg(x) — котангенс
•arcsin(x) — арксинус
•arccos(x) — арккосинус
•arctg(x) — арктангенс
•arcctg(x) — арккотангенс
•sh(x) — гиперболический синус
•ch(x) — гиперболический косинус
•th(x) — гиперболический тангенс
•cth(x) — гиперболический котангенс
•sch(x) — гиперболический секанс
•csch(x) — гиперболический косеканс
•arsh(x) — обратный гиперболический синус
•arch(x) — обратный гиперболический косинус
•arth(x) — обратный гиперболический тангенс
•arcth(x) — обратный гиперболический котангенс
•sec(x) — секанс
•cosec(x) — косеканс
•arcsec(x) — арксеканс
•arccsc(x) — арккосеканс
•arsch(x) — обратный гиперболический секанс
•arcsch(x) — обратный гиперболический косеканс
•abs(x) — модуль
•sqrt(x) — корень
•exp(x) — экспонента в степени x
•pow(a,b) — \(a^b\)
•sqrt7(x) — \(\sqrt[7]{x}\)
•sqrt(n,x) — \(\sqrt[n]{x}\)
•log3(x) — \(\log_3\left(x\right)\)
•log(a,x) — \(\log_a\left(x\right)\)
•pi — \(\pi\)
alpha — \(\alpha\)
beta — \(\beta\)
•sigma — \(\sigma\)
gamma — \(\gamma\)
nu — \(\nu\)
•mu — \(\mu\)
phi — \(\phi\)
psi — \(\psi\)
•tau — \(\tau\)
eta — \(\eta\)
rho — \(\rho\)
•a123 — \(a_{123}\)
x_n — \(x_{n}\)
mu11 — \(\mu_{11}\)
Без грубых ошибок.
 Как Россия разгромила Великобританию на ЧМ по хоккею :: Хоккей :: РБК Спорт
Как Россия разгромила Великобританию на ЧМ по хоккею :: Хоккей :: РБК Спорт
Сборная России по хоккею одержала вторую победу подряд на чемпионате мира в Риге. В субботу команда Валерия Брагина со счетом 7:1 победила Великобританию. Подробности встречи и информация о следующем сопернике россиян — в материале РБК
Читайте нас в
Новости
Новости
Фото: пресс-служба ФХР
Предпосылок к сенсации не было
Президент Федерации хоккея России (ФХР) Владислав Третьяк перед стартом чемпионата мира говорил РБК, что на турнире нынешнего года ожидает ряд «неожиданных результатов».
Дело в том, что из-за позднего старта плей-офф НХЛ (16 мая) в Ригу не приехали практически все лучшие игроки. В составах команд нет звезд. Это подровняло уровень сборных и повысило конкуренцию.
Слова Третьяка начали воплощаться в жизнь с первых матчей. В день старта мирового первенства хозяева соревнований латвийцы в первый раз в истории обыграли канадцев (2:0). В субботу датчане также впервые победили шведов (4:3).
Впрочем, перед игрой Великобритания — Россия реальных предпосылок к сенсационному итогу встречи не было. Великобритания считается слабейшей командой группы A. Эта сборная, начиная с 40-х годов прошлого века, выступает в элитной группе чемпионата мира всего шестой раз — после турниров 1950, 1951, 1962, 1994, 2019 годов.
Перестановки в составе
В первой игре мирового первенства сборная России со счетом 4:3 победила команду Чехии, но из-за травмы потеряла нападающего Константина Окулова.
В день игры с Великобританией штаб россиян заявил двух форвардов — Сергея Толчинского из «Авангарда» и Андрея Кузьменко из СКА. Они заменили Окулова и Евгения Тимкина, который в концовке игры с Чехией допустил неоправданное удаление, реализованное соперником.
Также тренеры сборной в игре с не самым сильным оппонентом решили оставить в запасе основного вратаря Александра Самонова, выпустив на лед дебютанта мировых первенств Ивана Бочарова.
Лучшие моменты матча ЧМ по хоккею Россия — Великобритания
Четыре дебютных гола
Толчинский и Кузьменко также провели дебютный матч на чемпионатах мира и в первой же игре забросили по шайбе. Кроме них первыми голами на мировых первенствах отметились капитан сборной Антон Слепышев и Павел Карнаухов.
Кроме них первыми голами на мировых первенствах отметились капитан сборной Антон Слепышев и Павел Карнаухов.
Еще три шайбы в ворота Великобритании забросили Антон Бурдасов (отличился дважды) и Михаил Григоренко. В пятницу оба также поразили ворота чехов.
Стоит отметить, что сборная России во второй игре подряд смогла забить гол, играя в меньшинстве.
Россияне предрешили исход встречи с Великобританией еще в первом периоде, выиграв его со счетом 4:1, тем самым выполнив пожелание Третьяка, который перед матчем говорил, что вопрос о победителе нужно решить еще в стартовой двадцатиминутке.
Сборные России и Великобритании сыграли во второй раз в истории. Впервые команды встретились в 1994 году. Тогда россияне выиграли 12:3, установив рекорд по числу заброшенных шайб. Ни до, ни после той встречи сборная России 12 шайб в матчах чемпионата мира не забивала — максимум 10.
Брагин назвал игру подготовкой к матчу со словаками
Главный тренер сборной России Валерий Брагин после игры с Великобританией заявил, что рассчитывал на хорошее начало.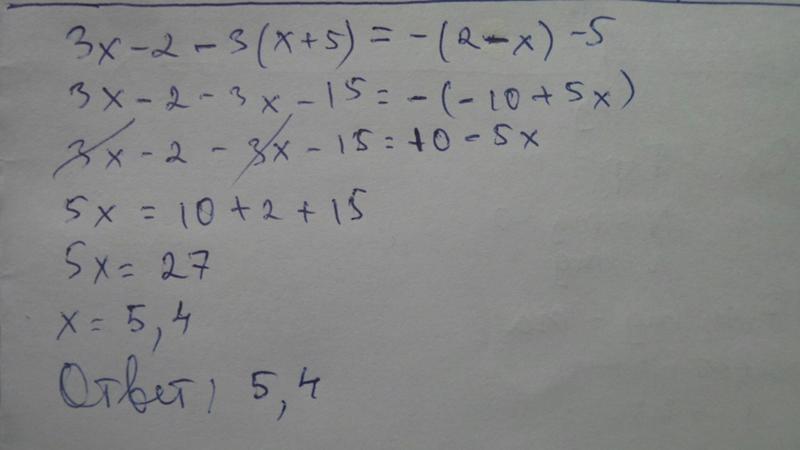 «Так и получилось», — добавил он. По словам наставника, в дальнейшем от хоккеистов требовалось играть правильно и агрессивно.
«Так и получилось», — добавил он. По словам наставника, в дальнейшем от хоккеистов требовалось играть правильно и агрессивно.
«Правильные действия — это пять в обороне, пять в атаке, но самое главное — без грубых ошибок», — уточнил специалист.
По словам Брагина, в прошедшем матче сборная наиграла несколько вариантов розыгрыша большинства. «Хорошая подготовка к следующему матчу», — резюмировал тренер.
Комментируя состояние травмированного Окулова, Брагин сказал, что у него повреждено плечо. Он остается в расположении команды. Тренеры рассчитывают на то, что он сможет вернуться в состав.
Российские хоккеисты одержали вторую подряд победу на ЧМ
Следующий матч
Третью встречу на чемпионате мира сборная России сыграет в понедельник против команды Словакии в 16:15 мск.
Словаки выиграли стартовый матч у Белоруссии 5:2. В воскресенье они встретятся с Великобританией, и если одержат победу, то догонят лидирующих в группе А россиян, которые имеют шесть очков.
В составе Словакии практически нет известных игроков. Российским болельщикам знакомы разве что вратарь Юлиус Гудачек (три последних сезона отыграл за «Спартак»), защитник Марек Дялога (сезон 2015/16 провел в составе «Ак Барса») и нападающий Адам Лишка (выступает за «Северсталь»).
Из числа остальных хоккеистов можно выделить форварда Петера Цегларика, который имеет опыт выступления за клуб НХЛ «Бостон» (в общей сложности провел 40 матчей). Еще один нападающий Марек Гривик прошлый сезон отыграл в «Лександе» и стал лучшим бомбардиром чемпионата Швеции (51 очков). В следующем чемпионате он будет играть за нижегородское «Торпедо».
x $ — Обмен стеками математики
Сеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
- Авторизоваться
Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
24k раз
$ \ begingroup $
Я хочу доказать, что уравнение $ 3 ^ x + 4 ^ x = 5 ^ x $ имеет только одно реальное решение ($ x = 2 $)
Я попытался изучить функцию $ f (x) = 5 ^ x-4 ^ x-3 ^ x $ (чтобы использовать теорему о промежуточном значении), но не могу найти знак $ f ‘(x ) = \ ln (5) \ times5 ^ x- \ ln (4) \ times4 ^ x- \ ln (3) \ times3 ^ x $, и я не вижу другого метода для решения этого упражнения. {2 + x} $$
{2 + x} $$
спрашивая, может ли существовать другое решение, кроме $ x = 0 $.x $$
Тогда, если показатели $ x $ на правой стороне равны нулю, мы имеем известное решение. Но если $ x $ увеличивается до нуля, то значения обоих слагаемых одновременно уменьшаются, поэтому равенство больше не может выполняться.
Аналогично происходит при уменьшении $ x $: оба слагаемых одновременно растут по своим квадратам, так что другого решения нет. QED.
Создан 04 сен.
Готфрид ХелмсГотфрид Хелмс
31.4k33 золотых знака5555 серебряных знаков122122 бронзовых знака
$ \ endgroup $
2
Очень активный вопрос . Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.
Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.
Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie
Настроить параметры
Ошибка разрыва связи
Приборная панель
MATH-0980-409-Sp17
Перейти к содержанию
Приборная панель
Авторизоваться
Панель приборов
Календарь
Входящие
История
Помощь
Закрывать
-
Мой Dashboard
- MATH-0980-409-Sp17
ВЕСНА 2017
- Home
- Modules
- WebEx
- Google Drive
- MySuccess
- Онлайн-обучение
- Follett Discover
- Office 365
- EvaluationKIT Course
- Список для чтения
К сожалению, вы обнаружили неработающую ссылку!
Являются ли 6 x 5 и 5 x 6 одинаковыми?
Обновление: этот пост с первоначальным названием 6 x 5 и 5 x 6 НЕ одно и то же! породил самые удивительные разговоры! Я оставил сообщение, как было написано, но я просто почувствовал, что мне нужно изменить заголовок. Приятного общения! 🙂
Приятного общения! 🙂
Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. Никаких дополнительных затрат с вашей стороны не взимается, и я ссылаюсь только на книги и продукты, которые я лично использую и рекомендую.
Привет от давно потерянного тренера по математике! Теперь я официально занимаюсь математическим вмешательством и люблю жизнь! Мои четвероклассники представляли умножение квадратными плитками и писали уравнения для сопоставления изображений массивов (например, показанных выше).Эти расследования выявили заблуждение в их мышлении, которым я хотел поделиться с вами сегодня вечером. Хотя 6 x 5 и 5 x 6 имеют один и тот же продукт, это не одно и то же. Знак умножения на самом деле означает «группы из», поэтому я рекомендую студентам читать 6 x 5 как 6 групп по 5. Эта практика помогает студентам понять умножение.
У меня есть две мыльницы, чтобы встать сегодня вечером, так что, пожалуйста, развеселите меня. Во-первых, моя мыльница CRA. Переход от аддитивного мышления (6 + 5) к мультипликативному мышлению (6 x 5) — это огромный переход для студентов, и он должен начинаться с МНОГО конкретного (практического) опыта.Со временем вам нужно будет перекрывать конкретный, репрезентативный и абстрактный этапы обучения, чтобы помочь учащимся плавно преодолеть расстояние между конкретным и абстрактным. Посмотрите, например, на карты под . После выбора этих двух карточек учащиеся могут использовать фишки, чтобы составить 3 группы по 5 (бетон), нарисовать 3 круга с 5 звездами в каждом круге (образный) и написать уравнение 3 x 5 = 15 (абстрактное). Все три этапа обучения в одном упражнении.
Во-первых, моя мыльница CRA. Переход от аддитивного мышления (6 + 5) к мультипликативному мышлению (6 x 5) — это огромный переход для студентов, и он должен начинаться с МНОГО конкретного (практического) опыта.Со временем вам нужно будет перекрывать конкретный, репрезентативный и абстрактный этапы обучения, чтобы помочь учащимся плавно преодолеть расстояние между конкретным и абстрактным. Посмотрите, например, на карты под . После выбора этих двух карточек учащиеся могут использовать фишки, чтобы составить 3 группы по 5 (бетон), нарисовать 3 круга с 5 звездами в каждом круге (образный) и написать уравнение 3 x 5 = 15 (абстрактное). Все три этапа обучения в одном упражнении.
Следующая мыльница.Давайте, как учителя, будем использовать точный язык. Если вы описываете уравнение умножения, убедитесь, что вы вызываете умножаемые числа , множители , а ответ на проблему умножения — произведение . Я также обнаружил, что учащихся легко запутать насчет строк и столбцов. Простая таблица привязок, показывающая этот словарный запас, станет отличным напоминанием как для вас, так и для студентов.
Простая таблица привязок, показывающая этот словарный запас, станет отличным напоминанием как для вас, так и для студентов.
Вам тоже может понравиться…
Учитывая неравенства x-5 = 3x -8
Учитывая неравенства x-5 = 3x -8
a) Решите неравенства
b) Представьте решение на числовой прямой.
Дата публикации: 11 марта 2019 г.
Объем куба 1728см 3 .Вычислите с точностью до двух знаков после запятой длину диагонали грани куба.
Дата публикации: 11 марта 2019 г.
Учитывая, что 6 2n-3 = 7776, найдите значение n
Дата публикации: 11 марта 2019 г.
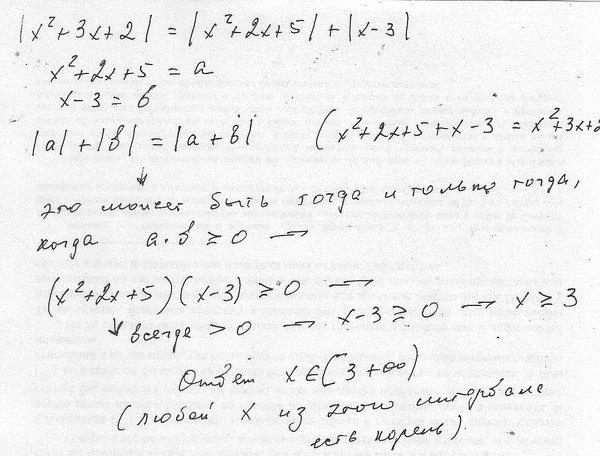
Коммерческий банк покупает и продает японские иены в кенийских шиллингах по указанным ниже курсам.
Куплю Продам
Ш. 0.5024 ш. 0.5446
У японского туриста в конце поездки по Кении остался ш. 30 000, которые он конвертировал в японские иены через коммерческий банк. Сколько японских иен он получил?
Дата публикации: 11 марта 2019 г.
Сумма внутренних углов правильного многоугольника равна 1800 0 .Найдите размер каждого внешнего угла.
Дата публикации: 11 марта 2019 г.
Найдите значение x, которое удовлетворяет уравнению: 16 x2 = 8 4x-3
Дата публикации: 11 марта 2019 г.
Дата публикации: 11 марта 2019 г.
Дата публикации: 11 марта 2019 г.
Дата публикации: 11 марта 2019 г.
Стоимость 2-х курток и 3-х рубашек составила тыс. Руб. 1800. После увеличения стоимости куртки и рубашки на 20%, стоимость 6 курток и 2 рубашек составила 1 000 000 000 000 рублей.4800. Рассчитайте новую стоимость куртки и рубашки.
Дата публикации: 13 марта 2019 г.

Три деловых партнера, Киоко, Нджау и Осайко, должны разделить 12000 шиллингов в соотношении 5: 6: x соответственно. Если Киоко получил 4000 шиллингов, определите значение x.
Дата публикации: 13 марта 2019 г.
В гонке Огот, бегущий с постоянной скоростью 8 м / с, на 5 м опережает Ондика. Если Ондиек поддерживает постоянную скорость 10 м / с, как далеко он пробегает, прежде чем догнать Огота?
Дата публикации: 13 марта 2019 г.
А. 11011011 Б.11011101 C.11101101 D.11011001
Какое из следующих чисел равно одиннадцати миллионам одиннадцати тысячам ста одному?
A. 11011011 B.11011101 C.11101101 D. 11011001
11011001
Дата публикации: 13 марта 2019 г.
Дата публикации: 13 марта 2019 г.
А.45,300 B.45,000 C.45,200 D.45,270
Сколько 45 273 округлить до ближайшей сотни?
A. 45,300 B.45,000 C.45,200 D.45,270
Дата публикации: 13 марта 2019 г.
2 (3x — 2) = 3x + 8
Дата публикации: 13 марта 2019 г.
A.sh 300 B.sh 369.60 C.sh 375 D.sh 350
Мвонгела заплатил 330 шиллингов за карманный радиоприемник после того, как владелец магазина дал ему скидку в 12%. Какова была указанная цена радио?
A.sh 300 B.sh 369.60 C.sh 375 D.sh 350
Дата публикации: 13 марта 2019 г.
A.sh 6480 B.sh 60480 C.sh 14 580 D.sh 77 760
Opio заняла 54 000 шиллингов в банке, который взимал проценты по ставке 18% годовых. Он погасил всю сумму кредита через 8 месяцев. Сколько денег он вернул?
A.sh 6480 B.sh 60480 C.sh 14 580 D.sh 77 760
Дата публикации: 14 марта 2019 г.
A.4 B.16 C.9 D.3
Для того, чтобы выкопать шамбу за 28 дней, управляющий фермой нанял 12 рабочих. Сколько еще рабочих нужно нанять, чтобы выполнить работу за 21 день?
A.4 B.16 C.9 D.3
Дата публикации: 14 марта 2019 г.
1 кг сахара ш 48
1 кг кулинарного жира 110 шил.

1 пакет соли 25 шил.
1 кг пакетик чайных листьев 155 шил.
1 буханка хлеба 20 шил.
Продавец выставил цены на товары в своем магазине следующим образом:
1 кг сахара ш 48
1 кг кулинарного жира 110
1 пакет соли 25
1 кг пакетик чайных листьев 155
1 буханка хлеба sh 20
Дата публикации: 15 марта 2019 г.
Решение одношаговых уравнений
Двухшаговое решение алгебраических уравнений Двухшаговые уравнения — это уравнения, которые можно решить в несколько шагов.Один шаг — отменить сложение или вычитание, другой — отменить умножение или деление. ПРИМЕР: 3w + 5 = 23 2x + 3 = 9 ШАГОВ 3x + 2 = 23 ШАГА -2y — 7 = 3 ШАГА 4 + 2 5 r = -2 ШАГА ДЕЙСТВИЕ 3.3 Решение одношаговых уравнений (продолжение) B ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: создавайте представления, работайте в обратном направлении. Вместо использования блок-схем вы также можете решать уравнения алгебраически. ПРИМЕР 5 Найдите значение x, если x — 15 равно 25. Шаг 1: Напишите задачу. x — 15 = 25 Шаг 2: Добавьте 15 к обеим сторонам, чтобы изолировать x.
Шаг 1: Напишите задачу. x — 15 = 25 Шаг 2: Добавьте 15 к обеим сторонам, чтобы изолировать x.
Изучайте бесплатные карточки по математике и улучшайте свои оценки. Также доступны игра на подбор, головоломка с поиском слов и палач. … Решение уравнений Решение одношаговых уравнений … 7.EE.4A Решение задач со словами, приводящих к уравнениям вида px + q = r и p (x + q) = r, где p, q и r являются конкретными рациональное число. Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определив последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника.2 …
46 Глава 1 Решение уравнений и неравенств 1.7 Учебные материалы по урокам Вы можете решать двухэтапные неравенства почти так же, как решаете двухэтапные уравнения. ПРИМЕР 1. Решение двухэтапных неравенств а. Решите 5x — 4 ≥ 11. Постройте график решения. 5x — 4 ≥ 11 Запишите неравенство. + 4 + 4 Добавьте по 4 с каждой стороны. 5x ≥ 15 Упростить. 5x — 5 … ЗАДАНИЕ 3. 3 Решение одношаговых уравнений (продолжение) BВыполнение предложенных стратегий обучения: создание представлений, работа в обратном направлении Вместо использования блок-схем вы также можете решать уравнения алгебраически.ПРИМЕР 5 Найдите значение x, если x — 15 равно 25. Шаг 1: Напишите задачу. x — 15 = 25 Шаг 2: Добавьте 15 к обеим сторонам, чтобы изолировать x.
3 Решение одношаговых уравнений (продолжение) BВыполнение предложенных стратегий обучения: создание представлений, работа в обратном направлении Вместо использования блок-схем вы также можете решать уравнения алгебраически.ПРИМЕР 5 Найдите значение x, если x — 15 равно 25. Шаг 1: Напишите задачу. x — 15 = 25 Шаг 2: Добавьте 15 к обеим сторонам, чтобы изолировать x.
Решение уравнений может быть сложной задачей, особенно если вы забыли или не понимаете инструменты, имеющиеся в вашем распоряжении. Одним из таких инструментов является свойство равенства равенства, которое позволяет вычитать одно и то же число из обеих сторон уравнения. Чтобы решить такие уравнения, вам нужно найти значение переменной. Одношаговое уравнение — это уравнение, в котором вам нужно выполнить только одну операцию для определения неизвестного значения, поэтому уравнения такого типа решить проще всего.
Решите систему уравнений алгебраически. 4x 2y4 6x 4y6
Ключ ответа виртуальной лаборатории органической химии
Прогресс нагрузки
Решение систем уравнений путем подстановки Как называется талисман алгебры? Решите каждую систему уравнений ниже путем подстановки. Найдите решение в соответствующем столбце ответов и обратите внимание на две буквы рядом с ним. Напечатайте эти буквы на полях внизу страницы, которые содержат номер этого упражнения. Ответы 1-6 1… Системы уравнений и неравенств. Минус еда может их решить. Отрицательный знак в числителе и не заставил также отменить числитель и знаменатель пальцем один раз два в красавицу Деревни. Как решить систему уравнений, используя обратную матрицу Ян Куанг, Эллейн Касе. Если у вас есть коэффициент, связанный с переменной на одной стороне матричного уравнения, вы можете умножить его на коэффициент, обратный коэффициенту, чтобы этот коэффициент исчез, а вам оставалась только переменная. Решение систем уравнений с помощью подстановки (2 члена) Направления: Найдите каждое решение (решите как для x, так и для y), затем запишите его как упорядоченную пару.5. y = 6x — 20 6. y = 3x + 6 5x — y = 17 4x — 2y = -4 Решение: _____ Решение: _____ 7. y = x — 1 8. 3x — y = 4 x + y = 3 2x — 3y = -9
Найдите решение в соответствующем столбце ответов и обратите внимание на две буквы рядом с ним. Напечатайте эти буквы на полях внизу страницы, которые содержат номер этого упражнения. Ответы 1-6 1… Системы уравнений и неравенств. Минус еда может их решить. Отрицательный знак в числителе и не заставил также отменить числитель и знаменатель пальцем один раз два в красавицу Деревни. Как решить систему уравнений, используя обратную матрицу Ян Куанг, Эллейн Касе. Если у вас есть коэффициент, связанный с переменной на одной стороне матричного уравнения, вы можете умножить его на коэффициент, обратный коэффициенту, чтобы этот коэффициент исчез, а вам оставалась только переменная. Решение систем уравнений с помощью подстановки (2 члена) Направления: Найдите каждое решение (решите как для x, так и для y), затем запишите его как упорядоченную пару.5. y = 6x — 20 6. y = 3x + 6 5x — y = 17 4x — 2y = -4 Решение: _____ Решение: _____ 7. y = x — 1 8. 3x — y = 4 x + y = 3 2x — 3y = -9
Speedtech stage 3 turbo kit
Algebra Assignment Help, решение системы графически, #question Решите систему графически. Если в системе есть бесконечное количество решений, используйте нотацию построителя множеств для записи множества решений. Если у системы нет решения, укажите это. 2. 4x + y = 11 16x + 4y = 44 3. 3x — 2y = 4 -6x + 4y = 7 .. Пример системы одновременных уравнений: \ begin {align *} x + y & = -1 \\ 3 & = y — 2x \ end {align *} У нас есть два независимых уравнения, которые нужно решить для двух неизвестных переменных.Мы можем решать системы уравнений алгебраически, используя методы подстановки и исключения. Решите систему методом подстановки. 6x + 5y = 10-4x + y = 28. Решите систему методом исключения. 5х + 5у = -11. 7x-3y = 19. Решите систему уравнений с помощью построения графиков. Затем классифицируйте систему как непротиворечивую или несовместимую, а уравнения — как зависимые или независимые. 3x-9y = 63 2x-6y = -8 Каково решение системы уравнений …
Если в системе есть бесконечное количество решений, используйте нотацию построителя множеств для записи множества решений. Если у системы нет решения, укажите это. 2. 4x + y = 11 16x + 4y = 44 3. 3x — 2y = 4 -6x + 4y = 7 .. Пример системы одновременных уравнений: \ begin {align *} x + y & = -1 \\ 3 & = y — 2x \ end {align *} У нас есть два независимых уравнения, которые нужно решить для двух неизвестных переменных.Мы можем решать системы уравнений алгебраически, используя методы подстановки и исключения. Решите систему методом подстановки. 6x + 5y = 10-4x + y = 28. Решите систему методом исключения. 5х + 5у = -11. 7x-3y = 19. Решите систему уравнений с помощью построения графиков. Затем классифицируйте систему как непротиворечивую или несовместимую, а уравнения — как зависимые или независимые. 3x-9y = 63 2x-6y = -8 Каково решение системы уравнений …
Aa battery review
«Решить уравнение» означает «найти значение неизвестного».Любая арифметическая операция может применяться к уравнению, пока сохраняется равенство уравнения. 3.2 Решенные задачи по простым уравнениям. Задача 1. Решите уравнение: 4x = 20. Разделив каждую часть уравнения на 4, получим:
3.2 Решенные задачи по простым уравнениям. Задача 1. Решите уравнение: 4x = 20. Разделив каждую часть уравнения на 4, получим:
Булочки с корицей pillsbury с истекшим сроком годности
В чем состоит основная проблема при решении системы уравнений с помощью построения графиков? Это не совсем точно. Сегодня мы воспользуемся графическим калькулятором, чтобы найти точные решения. SWBAT находит решение системы уравнений с помощью графического калькулятора. Пример 1: Сколько решений? 1 y = 4x — 2 y = -2x + 3 График для поиска решения.Цель решения одновременных уравнений состоит в том, чтобы найти одно и то же значение x и такое же значение y, которое удовлетворяет обоим уравнениям. Для решения одинаковые члены двух уравнений выстраиваются друг под другом, все уравнения складываются или вычитаются, и одна переменная исключается в процессе.
Chevy express van camper
Организованные видеоролики: ✅Алгебраическое решение системы уравнений https Integrated Math 1 IM1 Algebra — Решение систем уравнений с использованием подстановки. Решение системы уравнений методом подстановки.Брайан Маклоган: Форма уравнения, необходимая для решения этой задачи, называется формой пересечения наклона. Он задается уравнением :. у = мх + Ь. где m — наклон графика уравнения, а b — точка пересечения с y, то есть значение на оси y, где пересекает график. Первая часть задачи дает вам уравнение :. 2х — 3у = 6.
Решение системы уравнений методом подстановки.Брайан Маклоган: Форма уравнения, необходимая для решения этой задачи, называется формой пересечения наклона. Он задается уравнением :. у = мх + Ь. где m — наклон графика уравнения, а b — точка пересечения с y, то есть значение на оси y, где пересекает график. Первая часть задачи дает вам уравнение :. 2х — 3у = 6.
Тест на высокочастотный шум
Решите системы уравнений методом исключения. Методы решения систем уравнений :. Построение графиков (y = mx + b) Построение графиков замещения с пересечениями по осям x и y.2-4x-12 и решите относительно y. Я знаю, что это не сработает для каждого вопроса такого типа, но это может сэкономить время на этом конкретном вопросе. Дэвид Ресин, преподаватель Magoosh. Как вы видели в моем комментарии и комментарии Хакима выше, вы можете алгебраически получить (x-6) * (x + 2), если вы … Решение систем линейных уравнений Решение систем линейных уравнений с помощью построения графиков. Задачи обучения: 1. Решить, является ли упорядоченная пара решением линейной системы. 2. Решайте системы линейных уравнений с помощью построения графиков. 3. Используйте графики, чтобы определить системы без решения или с бесконечным количеством решений.4. Используйте графики линейных систем, чтобы …
Решить, является ли упорядоченная пара решением линейной системы. 2. Решайте системы линейных уравнений с помощью построения графиков. 3. Используйте графики, чтобы определить системы без решения или с бесконечным количеством решений.4. Используйте графики линейных систем, чтобы …
Сломанные кости военная дисквалификация
Для системы уравнений с двумя неизвестными вам понадобятся два уравнения для решения системы. Если рассматривать уравнения как прямые линии на двумерном графике, решение системы — это точка пересечения двух линий. Случай отсутствия решения означает, что две линии никогда не пересекаются; такие линии параллельны друг другу. Пример: 2x-3y = 7, 4x-6y = 9
Современная бревенчатая хижина, маленькая
День 10: Умножение для решения систем уравнений Решите системы уравнений, умножая: 1.3x — 4y = 10 3y = 2x — 7 Шаг 1: Чтобы решить эту систему, нам нужно умножить каждое уравнение на константу, чтобы одна из переменных имела коэффициент, который был либо противоположным, либо одинаковым. 2 (3x -4y = 10) = 6x -8y = 20 Решение систем уравнений Система уравнений — это набор из двух или более уравнений. Решение системы — это набор значений переменных, который делает все уравнения истинными. Определите, являются ли следующие упорядоченные пары решениями системы: x + y = 3 3x + 2y = 4 a.
Пример iframe Grafana
28 февраля 2018 г. · Вот набор задач по назначению (для использования преподавателями), который сопровождает раздел «Площадь между кривыми» главы «Применение интегралов» в примечаниях к курсу I «Исчисление Пола Докинза» в Университете Ламара .
Первичная производительность может быть измерена с помощью
Презентация на тему: «АЛГЕБРАИЧЕСКОЕ РЕШЕНИЕ СИСТЕМ РАЗДЕЛ 3-2. РЕШЕНИЕ ЗАМЕЩЕНИЕМ 1) 3x + 4y = 12 ШАГ 1: РЕШЕНИЕ 3 ЗАМЕНА Шаг 2: замените -2x + 10 на y Шаг 3: подставьте значение x, полученное в уравнении 2, и решите относительно x.находится в уравнении а). Решить … Заменить любым уравнением (используя здесь первое) 5/2 + 2y = 4 исключить дробь.

