Содержание
Корень квадратный из числа
Мы с вами уже уяснили себе, что каждому математическому действию соответствует аналогичное, но обратное по направлению действие.
Для сложения таким обратным действием является вычитание, для умножения — деление. Теперь попробуем выяснить, какое действие является обратным для возведения в степень. Поскольку возведение в степень — это многократное умножение, то, очевидно, обратным действием будет многократное деление.
Например, 32 можно разделить на 2 и получить 16, затем 16 разделить на 2 и получить 8; затем 8 разделить на 2 и получить 4; затем 4 разделить на 2 и получить 2; наконец, затем 2 разделить на 2 и получить 1. В краткой форме эти действия можно записать как 32:2:2:2:2:2=1. (Наша задача заключалась в том, чтобы добраться до 1.) Поскольку мы произвели деление 5 раз и добрались до 1, то можно сказать, что 2 — это корень пятой степени из 32.
Если мы рассмотрим число 81, то увидим, что 81:3:3:3:3=1, таким образом, 3 является корнем четвертой степени из 81. (Почему, собственно, корнем? Откуда взялось это слово? Это можно объяснить таким образом: число 32 растет из основания 2, а 81 — из основания 3 так же, как растение произрастает из корней.)
(Почему, собственно, корнем? Откуда взялось это слово? Это можно объяснить таким образом: число 32 растет из основания 2, а 81 — из основания 3 так же, как растение произрастает из корней.)
Такая математическая операция обозначается как $\sqrt{}$. На разнообразие корней указывает число в верхней левой части корня. Так, корень пятой степени из 32 можно записать как $\sqrt[5]{32}$, корень четвертой степени из 81 можно записать как $\sqrt[4]{81}$. Значок $\sqrt{ }$ называется знаком радикала, а числа, содержащие корни, называются радикалами. Слово «радикал» пришло к нам из латыни, где оно означает просто «корень».
Мы редко встречаемся с корнями высоких степеней, чаще всего приходится иметь дело с операциями, обратными возведению во вторую степень, то есть в квадрат. Извлечение корня второй степени называется извлечением квадратного корня, а $\sqrt[2]{}$ называется квадратным корнем, причем двойка слева часто опускается. В дальнейшем под значком $\sqrt{}$ без цифры в верхнем левом углу мы всегда будем иметь в виду квадратный корень. 5=32$, это означает, что если 32 пять раз разделить на 2, то результатом будет 1. (Если мы возвели число в какую-то степень, нетрудно пойти в обратном порядке.)
5=32$, это означает, что если 32 пять раз разделить на 2, то результатом будет 1. (Если мы возвели число в какую-то степень, нетрудно пойти в обратном порядке.)
На практике арифметический метод определения корней заключается в серии обратных действий. Попробуем извлечь квадратный корень из 625. Схема вычислений будет следующей:
Первую цифру ответа, 2, мы получаем подбором. Мы знаем, что 2×2=4, это ближайшее возможное число, меньшее 6, поскольку 3×3=9, что больше 6. Затем проводим вычитание и выносим две цифры вместо одной, как это принято при обычном делении в столбик. (Если бы мы извлекали кубический корень, мы выносили бы три цифры, в случае корня четвертой степени — четыре цифры и так далее.) Чтобы получить следующую цифру, надо разделить 225 на 45. Цифру 45 вы получаете, удваивая первую цифру ответа, что дает вам 4. Вторая цифра должна быть равна второй цифре вашего ответа, таким образом, ее тоже можно найти подбором, так, чтобы получить число, ближайшее к 225. 2$ — это $1\frac{24}{25}$, а нам нужно получить число $1\frac{25}{25}$, то есть 2.
2$ — это $1\frac{24}{25}$, а нам нужно получить число $1\frac{25}{25}$, то есть 2.
Но можно получить и более точный ответ. Если помножить дробное число $1\frac{41}{100}$ на себя самое, мы получим $1\frac{9881}{10000}$, что гораздо ближе к 2. Может показаться, что, если делать более точные вычисления, мы рано или поздно найдем точное значение дробного числа, которое является корнем квадратным из 2, хотя, возможно, это будет очень сложное число.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
методы умножения, примеры с объяснением
Известно, что знак корня является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
Пример
Пример 1: 18×2=?
Пример 2: 10×5=?
Пример 3: 33×93=?
Далее необходимо перемножить числа под корнем.
Пример
Пример 1: 18×2=36
Пример 2: 10×5=50
Пример 3: 33×93=273
Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Пример
Пример 1: 36=6. 36 — квадратный корень из шести (6×6=36).
Пример 2: 50=(25×2)=(5×5)×2=52.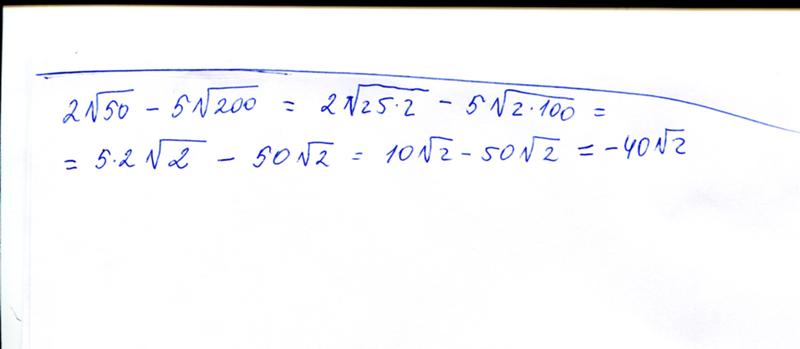 Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.
Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 273=3. Кубический корень из 27 равен 3: 3×3×3=27.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Метод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
Пример
Пример 1: 32×10=3?3×1=3
Пример 2: 43×36=12?4×3=12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример
Пример 1: 32×10=3(2×10)=320
Пример 2: 43×36=12(3×6)=1218
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример
Пример 1: 320=3(4×5)=3(2×2)×5=(3×2)5=65
Пример 2: 1218=12(9×2)=12(3×3)×2=(12×3)2=362
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
Пример
Необходимо найти НОК показателей для следующего выражения:
53×22
Показатели равны 3 и 2. Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3, и на 2). Для умножения корней необходим показатель 6.
Записать каждое выражение с новым показателем:
56×26
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 53 необходимо умножить 3 на 2, чтобы получить 6. А в выражении 22 — наоборот, необходимо умножить на 3, чтобы получить 6.
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2, а втором — 2 в степень 3:
2→56=5263→26=236
Возвести в степень выражения и записать результат под знаком корня:
526=(5×5)6=256236=(2×2×2)6=86
Перемножить числа под корнем:
(8×25)6
Записать результат:
(8×25)6=2006
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Определение корня n-ой степени. Свойства арифметического корня n-ой степени 9 класс онлайн-подготовка на Ростелеком
Тема 15.
Определение корня n-ой степени. Свойства арифметического корня n-ой степени.
Давай вспомним, что квадратным корнем из числа а называется такое число, квадрат которого равен а. Аналогично определяется корень любой натуральной степени n.
Аналогично определяется корень любой натуральной степени n.
Итак, корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.
Например, корнем пятой степени из 32 является число 2, так как 25=32, корнем четвертой степени из 81 является каждое из чисел 3 и -3, так и 34=81 и (-3)4=81. Корень второй степени принято называть квадратным корнем, а корень третьей степени – кубическим корнем.
Если n — нечетное число, то выражение an имеет смысл при любом a; если n — четное число, то выражение an имеет смысл при a≥0.
Из определения корня n-ой степени следует, что при всех значениях а, при которых выражение anимеет смысл, верно равенствоann=a.
Определение: Арифметическим корнем n-ой степени из неотрицательного числа а называется неотрицательное число, n-ая степень которого равна а.
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень. Например,
-83=-83=-2
Значит, при любом положительном a и нечетном n верно равенство:
-an=-an
Решим уравнение: x6 = 7. Корнями уравнения служат числа, шестая степень которых равна 7. И таких чисел два: 76 и -76.
Решим уравнение x3 = 27. Уравнение имеет единственный корень, это число, третья степень которого равна 27, то есть 273=3.
Рассмотрим свойства арифметического корня n-ой степени.
-
Если a≥0 и b≥0, то abn=anbn
Корень из неотрицательных множителей равен произведению корней из этих множителей.
Например, найдем значение выражения 16∙814=164∙814=2∙3=6
-
Если a≥0 и b>0, то abn=anbn
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Например, найдем значение выражения 210273=64273=643273=43=113.
-
Если n и k – натуральные числа и a≥0, то akn=ank -
Если n,k и m – натуральные числа и a≥0, то amknk=amn
Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
Рассмотрим некоторые примеры.
Вычислим значение выражения:
1353∙253=135∙253=27∙5∙253=27∙1253=3∙5=15
5106212∙526=510∙212∙526=512∙2126=10126=102=100
8-373∙8+373=8-378+373=64-373=273=3
Арифметический корень / math5school.ru
Арифметический корень
Свойства корней
Значения некоторых корней n-й степени
Таблица квадратных корней натуральных чисел от 1 до 99
Таблица кубических корней натуральных чисел от 1 до 99
Арифметический корень
Арифметическим корнем n-й степени из неотрицательного числа a называется неотрицательное число b, n-я степень которого равна a.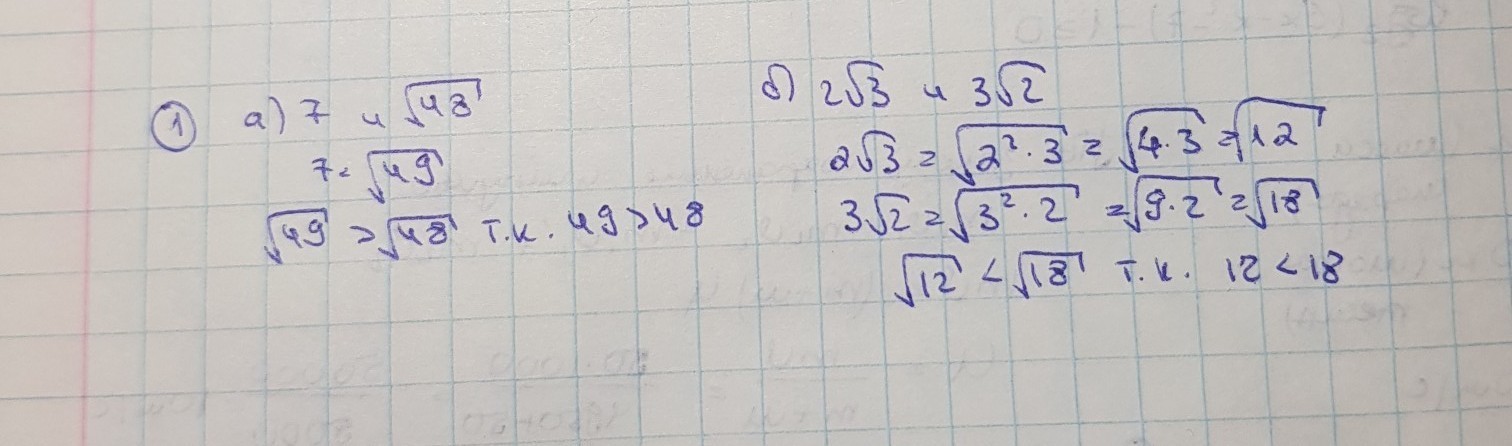
Записывается так:
Эта запись означает, что bn = a, где b и a – неотрицательные числа.
Число n называется показателем степени корня, число а – подкоренным выражением, b – значением арифметического корня n-й степени. Операция нахождения значения корня называется извлечением корня.
Корней чётной степени из отрицательных чисел не существует.
Корнем нечётной степени из отрицательного числа а называется такое отрицательное число b, которое при его возведении в эту нечётную степень равно числу а.
Для корней нечётной степени справедливо равенство:
Свойства корней
Для положительных а и b, натуральных n и k (n ≥ 2, k ≥ 2), целого m выполняются следующие соотношения.
Кроме того, для любого числа а верно:
Значения некоторых корней
n-й степени
| 3√8 = 2 | 4√16 = 2 | 5√32 = 2 | 6√64 = 2 | 7√128 = 2 | 8√256 = 2 | 9√512 = 2 | 10√1024 = 2 |
| 3√27 = 3 | 4√81 = 3 | 5√243 = 3 | 6√729 = 3 | 7√2187 = 3 | 8√6561 = 3 | 9√19683 = 3 | 10√59049 = 3 |
| 3√64 = 4 | 4√256 = 4 | 5√1024 = 4 | 6√4096 = 4 | 7√16384 = 4 | 8√65536 = 4 | 9√262144 = 4 | 10√1048576 = 4 |
| 3√125 = 5 | 4√625 = 5 | 5√3125 = 5 | 6√15625 = 5 | 7√78125 = 5 | 8√390625 = 5 | 9√1953125 = 5 | 10√9765625 = 5 |
| 3√216 = 6 | 4√1296 = 6 | 5√7776 = 6 | 6√46656 = 6 | 7√279936 = 6 | 8√1679616 = 6 | 9√10077696 = 6 | 10√60466176 = 6 |
| 3√343 = 7 | 4√2401 = 7 | 5√16807 = 7 | 6√117649 = 7 | 7√823543 = 7 | 8√5764801 = 7 | 9√40353607 = 7 | 10√282475249 = 7 |
Смотрите также:
Таблицы чисел
Алгебраические тождества
Степени
Логарифмы
Графики элементарных функций
Построение графиков функций геометрическими методами
Тригонометрия
Таблицы значений тригонометрических функций
Треугольники
Четырёхугольники
Многоугольники
Окружность
Площади геометрических фигур
Прямые и плоскости
Многогранники
Тела вращения
от арифметики до высшей математики
Спускаемся от высоких степеней к низким
Мы с вами уже уяснили себе, что каждому математическому действию соответствует аналогичное, но обратное по направлению действие.
Для сложения таким обратным действием является вычитание, для умножения — деление. Теперь попробуем выяснить, какое действие является обратным для возведения в степень. Поскольку возведение в степень — это многократное умножение, то, очевидно, обратным действием будет многократное деление.
Например, 32 можно разделить на 2 и получить 16, затем 16 разделить на 2 и получить 8; затем 8 разделить на 2 и получить 4; затем 4 разделить на 2 и получить 2; наконец, затем 2 разделить на 2 и получить 1. В краткой форме эти действия можно записать как 32 : 2 : 2 : 2 : 2 : 2 = 1. (Как и в случае деления, которое мы изучали в третьей главе, наша задача заключалась в том, чтобы добраться до 1.) Поскольку мы произвели деление 5 раз и добрались до 1, то можно сказать, что 2 — это корень пятой степени из 32.
Если мы рассмотрим число 81, то увидим, что 81 : 3 : 3 : 3 : 3 = 1, таким образом, 3 является корнем четвертой степени из 81. (Почему, собственно, корнем? Откуда взялось это слово? Это можно объяснить таким образом: число 32 растет из основания 2, а 81 — из основания 3 так же, как растение произрастает из корней. )
)
Такая математическая операция обозначается как ?. На разнообразие корней указывает число в верхней левой части корня. Так, корень пятой степени из 32 можно записать как 5?32 . корень четвертой степени из 81 можно записать как 4?81. Значок ? называется знаком радикала, а числа, содержащие корни, называются радикалами. Слово «радикал» пришло к нам из латыни, где оно означает просто «корень».
Мы редко встречаемся с корнями высоких степеней, чаще всего приходится иметь дело с операциями, обратными возведению во вторую степень, то есть в квадрат. Извлечение корня второй степени называется извлечением квадратного корня, а 2? называется квадратным корнем, причем двойка слева часто опускается. В дальнейшем под значком ? без цифры в верхнем левом углу мы всегда будем иметь в виду квадратный корень.
Что же такое квадратный корень из числа? 25 — это квадрат 5, таким образом, можно сказать, что 5 — это квадратный корень из 25, или ?25 = 5. Поэтому следует говорить «пять — это корень второй степени из 25», но обычно употребляют формулировку «квадратный корень». (Точно так же корень третьей степени называют кубическим корнем.)
Поэтому следует говорить «пять — это корень второй степени из 25», но обычно употребляют формулировку «квадратный корень». (Точно так же корень третьей степени называют кубическим корнем.)
Следующая проблема заключается в том, чтобы выяснить, как найти корень такой- то из некоего числа. Здесь можно идти путем от противоположного. Предположим, мы знаем, что 25 = 32, это означает, что если 32 пять раз разделить на 2, то результатом будет 1. (Если мы возвели число в какую-то степень, нетрудно пойти в обратном порядке.)
На практике арифметический метод определения корней заключается в серии обратных действий. Попробуем извлечь квадратный корень из 625. Схема вычислений будет следующей:
Первую цифру ответа, 2, мы получаем подбором. Мы знаем, что 2 ? 2 = 4, это ближайшее возможное число, меньшее 6, поскольку 3 ? 3 = 9, что больше 6. Затем проводим вычитание и выносим две цифры вместо одной, как это принято при обычном делении в столбик. (Если бы мы извлекали кубический корень, мы выносили бы три цифры, в случае корня четвертой степени — четыре цифры и так далее.) Чтобы получить следующую цифру, надо разделить 225 на 45. Цифру 45 вы получаете, удваивая первую цифру ответа, что дает вам 4. Вторая цифра должна быть равна второй цифре вашего ответа, таким образом, ее тоже можно найти подбором, так, чтобы получить число, ближайшее к 225. Цифра 5 подходит наиболее точно, так как 5 ? 45 = 225.
(Если бы мы извлекали кубический корень, мы выносили бы три цифры, в случае корня четвертой степени — четыре цифры и так далее.) Чтобы получить следующую цифру, надо разделить 225 на 45. Цифру 45 вы получаете, удваивая первую цифру ответа, что дает вам 4. Вторая цифра должна быть равна второй цифре вашего ответа, таким образом, ее тоже можно найти подбором, так, чтобы получить число, ближайшее к 225. Цифра 5 подходит наиболее точно, так как 5 ? 45 = 225.
Этот процесс может показаться вам очень трудным, и вы будете совершенно правы. Вычислять корни чисел арифметическим способом очень трудно, но результаты оказываются полезными при различных расчетах.
Рассмотрим следующий пример. Чему равен ?2 ? Какое число надо возвести в квадрат, чтобы получить 2?
Мы можем сразу определить, что среди целых чисел такого числа нет, ведь 1 ? 1 = 1, а 2 ? 2 = 4. Первое число слишком мало, а второе слишком велико. Следовательно, ответ будет дробным числом.
А может ли вообще существовать квадратный корень в виде дробного числа? Почему же нет? Согласно нашему определению экспоненциальных выражений (12/5)2 — это 12/5 ? 12/5, и ответом является число 124/25. А это, в свою очередь, означает, что ?124/25 равен 12/5. Теперь мы убедились, что не только квадратный корень может быть дробным числом, но и квадрат числа также может быть дробным числом. И в обоих случаях справедливы те же правила, что и в случае целых чисел.
А это, в свою очередь, означает, что ?124/25 равен 12/5. Теперь мы убедились, что не только квадратный корень может быть дробным числом, но и квадрат числа также может быть дробным числом. И в обоих случаях справедливы те же правила, что и в случае целых чисел.
Кроме того, случайно оказалось, что число 124/25, будучи умноженным на себя самое, дает результат, близкий к 2. Отсюда следует, что 12/5 близко к ?2. Только 1/25 отделяет нас от искомого ответа, так как (12/5)2 — это 124/25, а нам нужно получить число 125/25, то есть 2.
Но можно получить и более точный ответ. Если помножить дробное число 141/100 на себя самое, мы получим 19881/10000, что гораздо ближе к 2. Может показаться, что, если делать более точные вычисления, мы рано или поздно найдем точное значение дробного числа, которое является корнем квадратным из 2, хотя, возможно, это будет очень сложное число.
Но так ли это, вот в чем вопрос.
Сравниваем линии
Впервые поиском корня квадратного из 2 занялись еще математики Древней Греции. Как я вам уже говорил, они в первую очередь были геометрами, их интересовали соотношения длин отрезков геометрических фигур. Например, если провести диагональ в прямоугольнике, как показано на рисунке, то в каком соотношении будут находиться длина диагонали и длины сторон прямоугольника? Очевидно, что диагональ длиннее, но насколько? Древние греки хотели найти ответ на этот вопрос.
Предположим, мы сравниваем два отрезка. Длина одного из них 2 см, а длина другого — 1 см. Следовательно, мы можем сказать, что длины отрезков соотносятся как 2 к 1, или один отрезок в два раза длиннее другого. Длина одного из отрезков 4 см, а длина другого — 2 см, то можно сказать, что длины отрезков соотносятся как 4 к 2.
В обоих случаях длина одного из отрезков вдвое больше длины другого отрезка. С точки зрения математика, соотношение величин представляет гораздо больший интерес, чем их абсолютные значения. Не так важно, что в одном случае длины равны 4 и 2 см, а в другом 48 и 24 см. Математик в обоих случаях обратит внимание на то, что длина одного отрезка вдвое больше длины другого, то есть соотносятся как 2 к 1.
Не так важно, что в одном случае длины равны 4 и 2 см, а в другом 48 и 24 см. Математик в обоих случаях обратит внимание на то, что длина одного отрезка вдвое больше длины другого, то есть соотносятся как 2 к 1.
Прямоугольник с диагональю
Самое удобное — представить соотношение величин в виде дроби. Если длина одного отрезка равна 2 см, а длина другого — 1 см, значит, их соотношение равно 2/1. Если длина одного отрезка равна 48 см, а длина другого 24 см, значит, их соотношение равно 48/24 или 2/1, если мы разделим обе части на 24.
Дробь, представляющая собой отношение двух однотипных величин, называется соотношением. (Этими величинами могут быть и длины отрезков, и объемы сосудов, и веса двух человек и так далее.)
Разумеется, соотношение может не быть таким простым, как 2 : 1. Предположим, длина одного отрезка равна одному сантиметру, а длина другого — 19/10 сантиметра.
Тогда соотношение равно 19/10/1. Это выражение можно упростить, умножив верхнюю и нижнюю части на 10. Тогда получим, что соотношение равно 19/10.
Это выражение можно упростить, умножив верхнюю и нижнюю части на 10. Тогда получим, что соотношение равно 19/10.
Соотношение любых двух чисел, выраженных дробными числами, может быть представлено как отношение двух целых чисел. Например, у нас есть два отрезка, длина одного из них — 24/17 сантиметра, а длина другого — 113/15 сантиметра. Соотношение этих двух отрезков можно представить в виде дроби — 24/17/113/15. Если мы умножим числитель и знаменатель этой пугающе сложной дроби на 127?, то получим то же соотношение в виде целых чисел, то есть 285/238.
(Гораздо проще было бы воспользоваться десятичными дробями, но в Древней Греции они не были известны. А если мы последуем по тому же пути, по которому древние математики познавали мир, наше путешествие будет значительно интереснее.)
Теперь можно вернуться к нашему прямоугольнику. Нас интересует соотношение длин сторон прямоугольника и длин диагонали, то есть мы решаем ту же задачу, что и греческие математики в древности. Поскольку прямоугольник разделяется диагональю на две абсолютно симметричные части, мы можем упростить задачу и отбросить одну половину фигуры, предположим, левую. У нас остался так называемый прямоугольный треугольник.
Поскольку прямоугольник разделяется диагональю на две абсолютно симметричные части, мы можем упростить задачу и отбросить одну половину фигуры, предположим, левую. У нас остался так называемый прямоугольный треугольник.
Прямоугольный треугольник с гипотенузой
Еще за много столетий до наших дней египтяне на основе практического опыта установили, что если одна сторона прямоугольного треугольника равна 3 единицам, а другая — 4 единицам, то длина гипотенузы составит 5 единиц. В этом случае соотношение гипотенузы и одной из сторон равно 5/4 для более длинной стороны и 5/3 для более короткой.
Греки подошли к задаче с более общих позиций. Им важно было найти закономерность, то есть соотношение длин сторон прямоугольника и длин диагонали для любого прямоугольного треугольника.
Как гласит история, великий греческий математик Пифагор такую закономерность открыл. Он установил, что для любого прямоугольного треугольника верно следующее утверждение: сумма квадратов сторон равна квадрату гипотенузы. Это утверждение получило название теоремы Пифагора. Теорема до сих пор носит имя великого грека, хотя теперь мы знаем, что еще за 600 лет до Пифагора древним китайцам уже было известно это соотношение.
Это утверждение получило название теоремы Пифагора. Теорема до сих пор носит имя великого грека, хотя теперь мы знаем, что еще за 600 лет до Пифагора древним китайцам уже было известно это соотношение.
Проверим теорему для треугольника со сторонами 3 и 4. Квадрат одной из сторон равен 3 ? 3 = 9, квадрат другой стороны равен 4 ? 4 = 16. Сумма квадратов равна: 9 + 16 = 25, то есть квадрат гипотенузы равен 25, следовательно, гипотенуза равна 5.
Рассмотрим другой треугольник со сторонами 5 и 12.
Сумма квадратов сторон этого треугольника равна 5 ? 5 + 12 ? 12 = 25 + 144 = 169. Следовательно, 169 — это квадрат гипотенузы. Тогда гипотенуза равна ?169, или 13, поскольку 13 ? 13 = 169.
Для этого треугольника соотношение гипотенузы к стороне равно 13/5 для короткой стороны и 13/12 для длинной стороны.
Теорема Пифагора
Используя теорему Пифагора, можно найти соотношение гипотенузы и любой из сторон любого прямоугольного треугольника.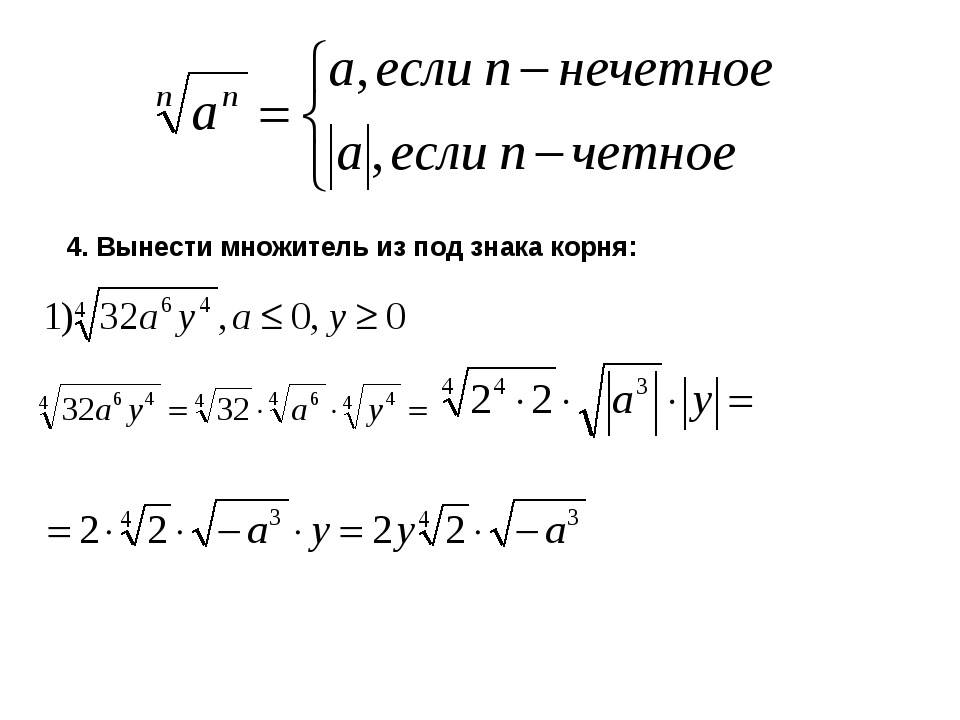 Математики Древней Греции могли вздохнуть спокойно, задача была решена. Самое главное заключалось в том, что теорема распространялась на все прямоугольные треугольники, в том числе, разумеется, и на равносторонние, то есть на прямоугольные треугольники, у которых обе стороны равны. А нас сейчас интересуют именно такие треугольники.
Математики Древней Греции могли вздохнуть спокойно, задача была решена. Самое главное заключалось в том, что теорема распространялась на все прямоугольные треугольники, в том числе, разумеется, и на равносторонние, то есть на прямоугольные треугольники, у которых обе стороны равны. А нас сейчас интересуют именно такие треугольники.
Один из них представлен на рисунке.
Равносторонний прямоугольный треугольник
Максимально упростим задачу и предположим, что стороны треугольника равны 1. Тогда квадрат стороны равен 1 ? 1, а сумма квадратов сторон равна 1 ? 1 + 1 ? 1 = 2. Согласно теореме Пифагора квадрат гипотенузы равен 2, а гипотенуза равна соответственно ?2.
Казалось бы, теперь грекам осталось сделать совсем немного. Надо было только найти такую дробь, которая являлась бы ?2, а потом представить ее в виде соотношения целых чисел, и можно праздновать победу. Но все оказалось гораздо сложнее.
Дроби, которых не существует
Ранее в этой главе мы с вами показали, что 12/5 близко к ?2. Если бы оно точно равнялось ?2, задача была бы решена. Тогда соотношение 12/5/1, которое можно превратить в соотношение целых чисел 7/5, умножив верхнюю и нижнюю части дроби на 5, и было бы искомой величиной.
Если бы оно точно равнялось ?2, задача была бы решена. Тогда соотношение 12/5/1, которое можно превратить в соотношение целых чисел 7/5, умножив верхнюю и нижнюю части дроби на 5, и было бы искомой величиной.
Но, к сожалению, 12/5| не является точной величиной ?2. Более точный ответ, 141/100, дает нам соотношение 141/100. Еще большей точности мы достигаем, когда приравниваем ?2 к 1207/500. В этом случае соотношение в целых числах будет равно 707/500. Но и 1207/500 не является точным значением корня квадратного из 2. Греческие математики потратили массу времени и сил, чтобы вычислить точное значение ?2, но это им так и не удалось. Они не смогли представить соотношение ?2/1 в виде соотношения целых чисел.
Наконец, великий греческий математик Евклид доказал, что, как бы ни увеличивалась точность подсчетов, получить точное значение ?2 невозможно. Не существует такой дроби, которая, будучи возведена в квадрат, даст в результате 2. Говорят, что первым к этому заключению пришел Пифагор, но этот необъяснимый факт настолько поразил ученого, что он поклялся сам и взял со своих учеников клятву хранить это открытие в тайне. Однако, возможно, эти сведения не соответствуют действительности.
Говорят, что первым к этому заключению пришел Пифагор, но этот необъяснимый факт настолько поразил ученого, что он поклялся сам и взял со своих учеников клятву хранить это открытие в тайне. Однако, возможно, эти сведения не соответствуют действительности.
Но если число ?2/1 не может быть представлено в виде соотношения целых чисел, то и никакая дробь, содержащая ?2, например ?2/2 или 4/?2, также не может быть представлена в виде соотношения целых чисел, поскольку все такие дроби могут быть преобразованы в ?2/1, умноженное на какое нибудь число. Так, ?2/2 = ?2/1 ? 1/2. Или ?2/1 ? 2 = 2?2/1, что можно преобразовать, умножив верхнюю и нижнюю части на ?2, и получить 4/?2. (Не следует забывать, что независимо от того, что представляет собой число ?2 , если мы умножим его на ?2, то получим 2.)
Поскольку число ?2 нельзя представить в виде соотношения целых чисел, оно получило название иррационального числа. С другой стороны, все числа, которые можно представить в виде соотношения целых чисел, называются рациональными. Рациональными являются все целые и дробные числа, как положительные, так и отрицательные.
Как оказалось, большинство квадратных корней являются иррациональными числами. Рациональные квадратные корни есть только у тех чисел, входящих в ряд квадратных чисел, о которых мы говорили в шестой главе. Эти числа называются также идеальными квадратами. Рациональными числами являются также дроби, составленные из этих идеальных квадратов. Например, ?(17/9) является рациональным числом, так как ?(17/9) = ?16/?9 = 4/3 или 11/3 (4 — это корень квадратный из 16, а 3 — корень квадратный из 9).
Тот факт, что многие квадратные корни являются иррациональными числами, нисколько не умаляет их значения, в частности, число ?2 очень часто используется в различных инженерных и научных расчетах. Это число можно вычислить с той точностью, которая необходима в каждом конкретном случае. Способ вычисления был описан ранее в этой главе, и вы можете получить это число с таким количеством знаков после запятой, на которое у вас хватит терпения.
Например, число ?2 можно определить с точностью до шести десятичных знаков: ?2 = 1,414214. Эта величина не очень сильно отличается от истинного значения, поскольку 1,414214 ? 1,414214 = 2,000001237796. Этот ответ отличается от 2 на величину, едва превышающую одну миллионную. Поэтому значение ?2, равное 1,414214, считается вполне приемлемым для решения большинства практических задач. В том случае, когда требуется большая точность, нетрудно получить столько значащих цифр после запятой, сколько необходимо в данном случае.
Однако если вы проявите редкостное упрямство и попробуете извлекать квадратный корень из числа 2 до тех пор, пока не добьетесь точного результата, вы никогда не закончите своей работы. Это бесконечный процесс. Сколько бы десятичных знаков после запятой вы ни получили, всегда останется еще несколько.
Этот факт может поразить вас так же сильно, как и превращение 1/3 в бесконечную десятичную дробь 0,333333333… и так бесконечно или превращение 1/7 в 0,142857142857142857… и так далее бесконечно. На первый взгляд может показаться, что эти бесконечные десятичные дроби и иррациональные квадратные корни — это явления одного порядка, но это совсем не так. Ведь у этих бесконечных дробей есть дробный эквивалент, в то время как у ?2 такого эквивалента нет. А почему, собственно? Дело в том, что десятичным эквивалентом 1/3 и 1/7, а также бесконечного числа других дробей являются периодические бесконечные дроби.
В то же время десятичный эквивалент ?2 является непериодической дробью. Это утверждение справедливо также для любого иррационального числа.
Проблема заключается в том, что любая десятичная дробь, которая является приближенным значением корня квадратного из 2, представляет собой непериодическую дробь. Как далеко мы ни продвинемся в расчетах, любая дробь, которую мы получим, будет непериодической.
Представьте себе дробь с огромным количеством непериодических цифр после запятой. Если вдруг после миллионной цифры вся последовательность десятичных знаков повторится, значит, десятичная дробь — периодическая и для нее существует эквивалент в виде отношения целых чисел. Если у дроби с огромным количеством (миллиарды или миллионы) непериодических десятичных знаков в какой-то момент появляется бесконечная серия повторяющихся цифр, например …55555555555…, это также означает, что данная дробь — периодическая и для нее существует эквивалент в виде отношения целых чисел.
Однако в случае иррациональных чисел их десятичные эквиваленты полностью непериодические и не могут превратиться в периодические.
(Разумеется, вы можете задать мне следующий вопрос: «А кто может знать и сказать наверняка, что происходит с дробью, скажем, после триллионного знака? Кто может гарантировать, что дробь не станет периодической?» Существуют способы неопровержимо доказать, что иррациональные числа являются непериодическими, но такие доказательства требуют сложного математического аппарата, поэтому мы не сможем разобрать их в нашей книжке. Но если бы вдруг оказалось, что иррациональное число становится периодической дробью, это означало бы полный крах основ математических наук. И на самом деле это вряд ли возможно.)
Существование дробей
Теперь рассмотрим следующее выражение: (24)2. Такая запись означает, что 24 следует возвести в квадрат. Число 24 — это 2 ? 2 ? 2 ? 2, или 16. Далее, 16 в квадрате — это 16 ? 16, или 256. Таким образом, (24)2 = 256. Но 256 — это также 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2, или 28. Следовательно, (24)2 = 28.
Если вы произведете подобные действия с различными экспоненциальными выражениями, различающимися как основанием, так и показателем степени, вы сможете убедиться, что существует правило, общее для всех экспоненциальных выражений: при возведении экспоненциального числа в степень показатели степени перемножаются. Это означает, что, не производя расчетов, мы всегда можем сказать следующее: (35)2 = 310, а (78)7 = 756 и так далее.
Если это утверждение верно, то, очевидно, оно будет верно и для дробного показателя степени. Рассмотрим число (24)?.
Следуя правилу перемножения экспонент, получим (24)? = 22. Далее, поскольку 24 = 16, а 22 = 4, то мы можем утверждать, что 161/2 = 4.
Но мы также знаем, что 4 — это квадратный корень из 16, значит, возведение числа в степень ? равносильно извлечению из этого числа квадратного корня. Другими словами, 161/2 = ?16.
Далее, следуя этому правилу, можно утверждать, что 161/3= 3?16, 161/4 = 4?16 и так далее. Теперь мы ввели в обиход дробные экспоненты, о которых я обещал вам рассказать еще в шестой главе. Обратите внимание, ?2 невозможно представить в виде конечной дроби, но можно — в виде экспоненциального выражения с дробной экспонентой.
Что же означает дробная экспонента? Например, выражение 163/2 — это то же самое, что (163)1/2, поскольку 3 ? 1/2 = 3/2. Следовательно, 163/2 = ?163.
Или, обобщая, можно сказать, что в случае дробной экспоненты основание возводится в степень, равную числителю экспоненты, и из него извлекается корень, равный знаменателю экспоненты.
Следовательно, 2567/235 — это корень 235-й степени из 2, возведенных в 567-ю степень.
Очевидно, такие дробные экспоненты очень громоздки. А нельзя ли перейти на десятичные дроби? Ведь мы помним, что 1/2 — это 0,5, так что вместо 41/2 можно написать 40,5. Любая десятичная экспонента имеет свое значение. Например, 25,175—это 2207/40, поскольку 5,175 = 207/40. В свою очередь, число 2207/40 получается при возведении 2 в степень 207 и извлечении из полученного результата корня 40-й степени. (Можно поменять местами операции. Если мы сначала извлечем из 2 корень 40-й степени, а затем возведем этот промежуточный результат в 207-ю степень, мы получим тот же окончательный результат. Это утверждение вы легко можете проверить на более простом примере, например на выражении 43/2. Квадратный корень из 43— это ?64, что равно 8. В то же время куб ?4 равен 23, что также равно 8.)
Значение выражения 2207/40 (или любого другого выражения, где экспонента является целым, дробным, десятичным, положительным или отрицательным числом) может быть вычислено при помощи соответствующих математических методов. При этом вам не пришлось бы двести семь раз перемножать 2 или искать путем последовательных приближений корень сороковой степени. 2207/40 = 36,126.
Эта величина приблизительная, поскольку 2207/40 является иррациональным числом, как и большинство выражений с дробными или десятичными экспонентами. Десятичный эквивалент 2207/40 — это бесконечная непериодическая дробь, но мы всегда можем получить столько десятичных знаков после запятой, сколько требуется в соответствии с требованиями по точности конкретных вычислений.
Используя любое число в виде основания экспоненциального выражения, мы можем составить соответствующее экспоненциальное выражение для любого другого числа. Теперь мы можем вернуться к моей задаче об умножении 7 ? 17, которая возникла у нас еще в шестой главе. Число 7 можно представить как 22,81, как 31,77 или как 51,21 (существуют специальные методы для вычисления экспоненциальных эквивалентов), в то же время 17 равно 24,08, 32,58 или 51,76. Теперь задачу умножения можно свести к сложению: 7 ? 17 = 22,81 ? 24,08 = 22,81+4,08 = 26,89, или 31,77 ? 32,58 = 34,35, или 51,21 ? 51,76= 52,97. Все эти числа, 26,89, 34,35, 52,97, приблизительно равны между собой и приблизительно равны 119, это и есть ответ.
Конечно, было бы гораздо проще просто перемножить 7 ? 17 вместо того, чтобы находить значения экспоненциальных выражений. Кроме того, вместо точного ответа мы получим приближенный. Однако посмотрим, что будет дальше. Возможно, этот метод окажется незаменимым. Обратим внимание на основания экспоненциальных выражений. Мы выбрали 2, 3 или 5. А почему не выбрать число 10, ведь 10 — это основа нашей системы счета.
Урок 32. буквы а и о в корне -кас- – -кос — — Русский язык — 6 класс
Русский язык
6 класс
Урок № 32
Буквы а – о в корне -кас- – -кос-
Перечень вопросов, рассматриваемых по теме:
1. Понятие «чередующаяся гласная в корне».
2. Понятие «чередование гласных в корне».
3. Суффикс после корня.
4. Значение слова.
5. Алгоритм работы с чередующимися гласными в корне.
Тезаурус
Чередование гласных в корне – такое явление, при котором в корнях с одним и тем же лексическим значением пишутся разные гласные.
Чередующиеся гласные – безударные гласные внутри корней, которые невозможно проверить ударением, так как зависят они от значения, положения в слове или соседствующих морфем.
Список литературы
Обязательная литература:
1. Ладыженская Т. А., Русский язык. 6 класс. В 2-х частях. Ч. 1. // Ладыженская Т. А., Баранов М. Т., Тростенцова Л. А. и др. – М.: Просвещение, 2016. – с. 104-105.
Дополнительная литература:
1. Розенталь Д. Э. Справочник по русскому языку. Орфография и пунктуация. – М.: Оникс 21 век, Мир и Образование, 2016. – с. 7.
Теоретический материал для самостоятельного изучения
Давайте рассмотрим несколько слов: прикасаться, коснулся, косить (траву), косой (заяц), прикосновение, касался. Какие из них объединены значением и каким? Конечно, это слова прикасаться, коснулся, прикосновение, касался, так как у них общее значение «дотрагиваться до кого-либо или чего-либо».
Давайте разберём их по составу. Как можно разбить эти 4 слова на 2 группы по 2 слова? На основе какого признака? Если за корнем с чередующейся есть суффикс -а-, то писать следует -кас-, при отсутствии – -кос-.
Давайте вместе разберём несколько примеров. Слово прикасаясь имеет значение «дотрагиваясь» и после корня имеет суффикс -а-, поэтому в корне пишем букву а.
Обратимся к другому примеру.
Косой прыгал среди невысоких кустов.
В предложении есть слово косой. Оно не имеет значения дотрагиваться, обозначая косость, то есть это не корень с чередованием, а проверяемая гласная в корне.
Давайте проверим себя. Какие буквы вы бы вставили в слова: к_саться, прик_снуться, к_сой, прик_сание, к_снуться, к_солапый, прик_сновение, прик_саться, сенок_силка, к_сательная, песчаная к_са, неприк_сновенный.
Какие из этих слов не относятся к правилу? Конечно, слова косой, косолапый, сенокосилка и песчаная коса не относятся к нашему правилу, потому что имеют иное лексическое значение. Косой и косолапый проверяются словом косо; сенокосилка – косит, а песчаная коса – косами.
Всё же остальные слова имеют значение «дотрагиваться». Применим к ним правило.
Касаться: вставляем А, так как есть суффикс -а- за корнем.
Прикоснуться: вставляем О, так как нет суффикса -а- за корнем.
Прикасание: вставляем А, так как есть суффикс -а- за корнем.
Коснуться: вставляем О, так как нет суффикса -а- за корнем.
Прикосновение: вставляем О, так как нет суффикса -а- за корнем.
Прикасаться: вставляем А, так как есть суффикс -а- за корнем.
Касательная: вставляем А, так как есть суффикс -а- за корнем.
Неприкосновенный: вставляем О, так как нет суффикса -а- за корнем.
Какие ещё чередующиеся корни вы знаете? В 5 классе вы изучили корни -лаг-/-лож- и -рос-/-раст-/-ращ-. Какие из них похожи на изучаемый? Конечно, -лаг-/-лож-, так как тоже зависит от наличия или отсутствия последующего суффикса -а-. А от чего зависят -рос-/-раст-/-ращ-? От последующей согласной буквы после чередующейся гласной.
Когда мы работаем с чередующимися гласными в корне, очень важно помнить все особенности этих корней: у одних правописание зависит от ударения, у других – от наличия или отсутствия суффикса, у третьих – от значения корня, а у четвёртых – от буквы в корне.
Примеры заданий из Тренировочного модуля
1. Единичный выбор
Подберите правильное лексическое значение слову.
Точка касания:
Прямая, имеющая общую точку с кривой
Так говорят о запасе, который нельзя расходовать
Дотрагиваться
Общее место стыковки
Разбор задания: надо вчитаться в значения слов, обратить внимание на слово точка.
Правильный ответ: точка касания – общее место стыковки.
2. Выбор элемента из выпадающего списка.
Выберите правильное утверждение.
Слова касаться, коснулся, неприкосновенный в корне имеют:
а) проверяемую безударную гласную;
б) непроверяемую безударную гласную;
в) чередующуюся безударную гласную.
Разбор задания: корни -кас- и -кос- зависят от последующей гласной. Правильный ответ: в
Гемисекция корня зуба
Пораженный инфекцией корень является существенной угрозой для костной ткани челюсти и здоровья ротовой полости. Удаление зуба – не единственная процедура, позволяющая избавится от проблемы.
Специалисты во многих случаях, чтобы сохранить зуб, используют гемисекцию – ампутацию корня зуба.
Показания
Перечень показаний к гемисекции не так широк. Процедуру проводят, если:
- невозможна терапия из-за отсутствия доступа к очагу по тем или иным причинам;
- зубной канал непроходим из-за гранулемы;
- в полости дна или корне наблюдается перфорация.
Процедура относится к направлению хирургическая стоматология и проводится в случаях, когда консервативная терапия не приводит к положительной динамике, а также при наличии инфекционных очагов, чрезмерного поражения зуба кариозным процессом, фрактуры корня.
Тут форма голубая
Противопоказания
Гемисекцию корня зуба не проводят в случае наличия только одного корня и при поражении всех корней. Также, процедура не проводится, если корни зуба срослись, потому что нет возможности отделить здоровую ткань от пораженной. Оперативное вмешательство противопоказано пожилым людям, и пациентам, которые имеют такие заболевания, как сахарный диабет, злокачественные новообразования, нарушение работы почек, а также болезни, поражающие сердечно-сосудистую систему.
Преимущества и недостатки
Если у пациента есть показания к ампутации корня, то специалист имеет возможность спасти зуб с помощью процедуры, которая характеризуется следующими достоинствами:
- позволяет избежать удаления зуба;
- практически не вызывает осложнений;
- сохраняется костная ткань, позволяющая проводить имплантацию.
Операция имеет и ряд недостатков. Показание к операции ампутация корня и собственно последующая процедура ведут к тому, что зуб остается без одного из корней, а значит, не может служить опорой для протезов. После процедуры срок службы зуба ограничен и, чтобы его продлить – нельзя чрезмерно нагружать место гемисекции, а это не всегда удобно.
Этапы
Гемисекция – достаточно объемное по времени хирургическое вмешательство, которое длится около 2-х часов. В процессе операции используется местная или общая анестезия. При выборе методики удаления корня учитываются индивидуальные особенности здоровья пациента и результаты обследования.
Удаление корня зуба на нижней челюсти
Сам процесс делится на несколько основных фаз:
Распиливание коронки зуба до уровня бифуркация
Такой подход позволяет отделить здоровые ткани от части коронки и пораженного корня.
Удаление части зуба с одним из корней
Часть поврежденного зуба и корень удаляются после проведения сепарации.
Выскабливание патологически измененных тканей
Образовавшуюся после удаления корня полость выскабливают, чтобы очистить лунку от омертвевших и пораженных тканей.
Заполнение лунки Коллапаном
Очищенная полость наполняется Коллапаном для предупреждения образования грануляционной ткани. Материал биосовместим и практически никогда не отторгается.
Стоит отметить, что цена гемисекции зуба достаточно доступна, поэтому, если специалист рекомендует процедуру, то стоит попытаться сохранить зуб.
Послеоперационный период
Естественно, после всех этапов гемисекции возможно появление болевых ощущений, которые снимаются с помощью обезболивающих препаратов. Перед приемом лекарств следует в обязательном порядке проконсультироваться со своим стоматологом.
Спустя неделю после оперативного вмешательства большинство пациентов чувствуют себя значительно лучше. После процедуры нет нужды в стационарном лечении, но использование общего наркоза вынуждает пациента оставаться в клинике некоторое время. Терапия, включающая курс антибиотиков, назначается при риске возникновения воспалительного процесса. Стоматолог лично назначает курс приема препаратов, время их приема следует строго соблюдать даже в случае хорошего самочувствия.
Рана должна быть в покое определенное время, поэтому необходимо питаться только мягкой пищей, не стоит жевать прооперированной стороной и не следует физически перегружаться. В обязательном порядке нужно посещать стоматологическую клинику для проведения профилактических осмотров. При появлении тревожной симптоматики и болей следует незамедлительно обратиться к специалистам.
Стоимость гемисекции корня зуба в Profident Junior
☑️ Гемисекция | 2000 грн |
квадратный корень из 32 — Как найти квадратный корень из 32?
Прежде чем мы начнем, давайте разберемся в значении квадратного корня. Символ квадратного корня записывается как √ и является неотъемлемой частью математики. Как только вы поймете основы нахождения квадратного корня из числа, вы сможете решить любую задачу, связанную с квадратным корнем. В этом коротком уроке мы узнаем о квадратном корне из 32. 32 не является точным квадратным числом. Следовательно, квадратный корень из 32 является иррациональным числом. Мы будем использовать такие методы, как разложение на простые множители и деление, и узнаем, как найти квадратный корень из 32.Мы также сосредоточимся на некоторых решенных примерах, основанных на квадратном корне из 32
.
Давайте посмотрим, что такое квадратный корень из 32:
- Квадратный корень из 32: √32 = 5,65685424 …
- Квадрат 32: 32² = 1024
Что такое квадратный корень из 32?
Квадратный корень любого числа x можно записать как √x. Пусть существует такое число a, что x = a × a. Теперь это можно также записать как: a² = x или a = √x.Следовательно, a называется вторым корнем x.
- Теперь, если x = 32, то a = √32 является квадратным корнем из 32. В простейшей радикальной форме √32 = √ (16 × 2) = 4√2
- В десятичной форме √32 = 5,657
Является ли квадратный корень из 32 рациональным или иррациональным?
Квадратный корень из 32 — это иррациональное число с бесконечными цифрами.
√32 = 5,65685424…
Квадратный корень из 60 нельзя записать в виде p / q, следовательно, это иррациональное число.
Как найти квадратный корень из 32?
Есть два основных метода, которые мы используем, чтобы найти квадратный корень от 32 до
.
- Прайм-факторизация
- Длинное деление
Есть и другие методы, о которых можно узнать больше, нажав здесь
Основная факторизация
- Чтобы найти квадратный корень из 32, мы сначала выразим его через простые множители.
32 = 2 × 2 × 2 × 2 × 2. - Далее, это может быть уменьшено до
32 = 16 × 2 - Наконец, отсюда очень легко найти корень этого,
√32 = √ (16 × 2)
√32 = 4√2
= 4 × 1,414
= 5,656
Следовательно, квадратный корень из 3 равен 5,656
Длинный дивизион
- Шаг 1: Поместите черту над 32. Мы также соединяем нули в десятичных дробях парами по 2 слева направо.
- Шаг 2: Найдите такое число, что при умножении его на само полученное произведение будет меньше или равно 32.
Мы знаем, что 5 × 5 равно 25 и меньше 32. Теперь давайте разделим 32 на 5 - Шаг 3: Давайте поставим десятичную точку и пары нулей и продолжим наше деление.
Теперь сложите делитель 5 с самим собой, и сумма станет начальной цифрой нашего следующего делителя. - Шаг 4: Выберите число на месте единицы для нового делителя так, чтобы его произведение с тем же числом было меньше или равно 700.
Если поставить 6 вместо единицы, то получится меньше 700.Получаем 106 × 6 = 636. - Продолжаем делать те же шаги, пока не получим требуемое количество десятичных знаков.
.
Итак, наше длинное деление теперь выглядит так:
Изучите квадратные корни с помощью иллюстраций и интерактивных примеров
- Корень квадратный из 32 ≈ 5,656
- Квадратный корень из 32 в простейшей радикальной форме равен 4√2
- √32 иррационально. Его настоящие корни +5,656 и -5.656
Часто задаваемые вопросы о квадратном корне из 32
Что такое квадратный корень из 32?
Квадратный корень из 32 равен √32 = 5,656
Что такое квадрат 32?
Квадрат 32 равен 32² = 1024
Что такое упрощенный квадратный корень из 32?
Квадратный корень из 32 в упрощенном виде равен 4√2.
Является ли квадратный корень из 32 рациональным числом?
Квадратный корень из 32 — это иррациональное число, так как оно не заканчивается.Его нельзя выразить в форме p / q, что и составляет рациональное число.
Какова степень корня 32?
Показатель степени, если корень 32 равен 32 1/2 .
Квадратный корень из 32 (√32)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 32. Начнем с определения, а затем ответим на некоторые общие
вопросы о квадратном корне из 32. Затем мы покажем вам различные способы вычисления квадратного корня из 32 с учетом и без
компьютер или калькулятор.У нас есть чем поделиться, так что приступим!
Корень квадратный из 32 определения
Квадратный корень из 32 в математической форме записывается со знаком корня, например, √32. Мы называем это квадратным корнем из 32 в радикальной форме.
Квадратный корень из 32 — это величина (q), которая при умножении сама на себя будет равна 32.
√32 = q × q = q 2
Является ли 32 идеальным квадратом?
32 — это полный квадрат, если квадратный корень из 32 равен целому числу.Как мы подсчитали дальше
На этой странице квадратный корень 32 не является целым числом.
32 — не идеальный квадрат.
Квадратный корень из 32 является рациональным или иррациональным?
Квадратный корень из 32 является рациональным числом, если 32 — это полный квадрат. Это иррациональное число, если оно не является полным квадратом.
Поскольку 32 не является полным квадратом, это иррациональное число. Это означает, что ответ на «квадратный корень из 32?» будет бесконечное число
десятичных знаков.Десятичные дроби не прерываются, и вы не можете преобразовать их в точную дробь.
√32 — иррациональное число
Можно ли упростить квадратный корень из 32?
Вы можете упростить 32, если можете сделать 32 внутри корня меньше. Мы называем этот процесс «упрощением сурда».
Квадратный корень из 32 можно упростить.
√32 = 4√2
Как вычислить квадратный корень из 32 с помощью калькулятора
Самый простой и утомительный способ вычислить квадратный корень из 32 — это использовать калькулятор!
Просто введите 32, а затем √x, чтобы получить ответ.Мы сделали это с помощью нашего калькулятора и получили следующий ответ
с 9 десятичными числами:
√32 ≈ 5,656854249
Как вычислить квадратный корень из 32 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT (32) в ячейку, чтобы получить квадратный корень из 32.
Ниже приведен результат с 13 знаками после запятой. Мы называем это квадратным корнем из 32 в десятичной форме.
КОРЕНЬ (32) ≈ 5,6568542494924
Каков квадратный корень из 32 с округлением?
Квадратный корень из 32, округленный до ближайшей десятой, означает, что вам нужна одна цифра после десятичной точки.Квадратный корень из 32, округленный до сотых, означает, что вы
хотите две цифры после десятичной точки. Квадратный корень из 32, округленный до ближайшей тысячной, означает, что вам нужны три цифры после десятичной точки.
10-я: √32 ≈ 5,7
100-я: √32 ≈ 5,66
1000-я: √32 ≈ 5,657
Что такое квадратный корень из 32 в виде дроби?
Как мы уже говорили выше, поскольку квадратный корень из 32 является иррациональным числом, мы не можем преобразовать его в точную дробь.Однако мы можем преобразовать его в приблизительную дробь, используя квадратный корень из 32, округленный до ближайшей сотой.
√32
≈ 5,66 / 1
≈ 566/100
≈ 5 33/50
Что такое квадратный корень из 32, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробной степенью. Квадратный корень из 32 — не исключение. Вот правило и ответ
в «квадратный корень из 32, преобразованный в основание с показателем степени?»:
√b = b ½
√32 = 32 ½
Как найти квадратный корень из 32 методом деления в длину
Здесь мы покажем вам, как вычислить квадратный корень из 32, используя метод длинного деления с точностью до одного десятичного знака.Это потерянный
искусство того, как они вычисляли квадратный корень из 32 вручную до того, как были изобретены современные технологии.
Шаг 1)
Установите 32 пары из двух цифр справа налево и присоедините один набор 00, потому что нам нужен один десятичный разделитель:
Шаг 2)
Начиная с первого набора: наибольший полный квадрат, меньший или равный 32, равен 25, а квадратный корень из 25 равен 5. Таким образом, поместите 5 вверху и 25 внизу следующим образом:
Шаг 3)
Вычислите 32 минус 25 и запишите разницу ниже.Затем перейдите к следующему набору чисел.
Шаг 4)
Удвойте число, выделенное зеленым сверху: 5 × 2 = 10. Затем используйте 10 и нижнее число, чтобы решить эту задачу:
10? ×? ≤ 700
Знаки вопроса «пустые» и такие же «пустые». Методом проб и ошибок мы обнаружили, что наибольшее число «пробел» может быть 6.
Теперь введите 6 сверху:
Это оно! Ответ сверху. Квадратный корень из 32 с точностью до одной десятичной дроби равен 5,6.
Квадратный корень числа
Введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 32 на этой странице.
Банкноты
Помните, что отрицательное умножение на отрицательное равняется положительному. Таким образом, квадратный корень из 32 не дает только положительного ответа.
то, что мы объяснили выше, но также и отрицательный аналог.
На этой странице мы часто упоминаем точные квадратные корни. Вы можете использовать список идеальных квадратов
для справки.
Квадратный корень из 33
Вот следующее число в нашем списке, о котором у нас есть столь же подробная информация о квадратном корне.
Авторские права |
Политика конфиденциальности |
Заявление об ограничении ответственности |
Контакт
Таблица квадратов и квадратных корней
Что такое квадратный корень и почему нам это нужно?
Квадратный корень из числа — это число, которое при умножении само на себя дает желаемое значение.Так, например, квадратный корень из 49 равен 7 (7×7 = 49). Сам процесс умножения числа раз называется возведением в квадрат .
Числа, квадратные корни которых являются целыми числами (или, точнее, положительными целыми числами), называются точными квадратными числами. Числа с десятичными знаками не являются точными квадратными корнями.
Все положительные числа будут иметь положительное число в качестве квадратного корня, называемого главным, и отрицательное число. Все эти числа известны как действительные числа.
Все отрицательные числа будут иметь комплексное число в качестве квадратного корня.Комплексное число — это число, умноженное на i. i — это «мнимый» квадратный корень из -1. Это называется мнимым, но для математиков оно существует.
Как нам выписать квадратные корни?
Уравнение квадратного корня записывается с использованием знака корня или символа корня (?). Число, из которого мы хотим получить корень, идет после или под хвостом радикала (например,? 3, если мы хотим найти квадратный корень из 3). Число после корня называется подкоренным.На калькуляторе вместо радикала вы можете увидеть «sqrt».
Для чего мы используем квадратные корни?
Это может быть немного сложно представить, но квадратные корни — одни из самых полезных чисел. Функции квадратного корня очень важны для уравнений физики всех видов. Они также полезны для статистики; статистики всегда используют квадратные корни при анализе корреляции между разными точками данных.
Список идеальных квадратов
Используйте эту таблицу, чтобы найти квадраты и квадратные корни чисел от 1 до 100 .
Эту таблицу также можно использовать для вычисления квадратных корней из больших чисел.
- Например, если вы хотите найти квадратный корень из 2000 , ищите в среднем столбце , пока не найдете число, наиболее близкое к 2000. Число в среднем столбце, которое ближе всего к 2000, равно 2,025 .
- Теперь посмотрите на число слева от от 2,025 , чтобы найти его квадратный корень. Квадратный корень из 2025 равен 45 .
- Следовательно, приблизительный квадратный корень из 2000 составляет 45 .
Чтобы получить более точное число, вам понадобится калькулятор (44,721 — это более точный квадратный корень из 2000).
Готовитесь к длительной учебной сессии? Возможно, вас заинтересует наш список лучших настольных стульев 2020 года.
| НОМЕР | КВАДРАТ | КВАДРАТНЫЙ КОРЕНЬ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 4 | 1.414 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 9 | 1,732 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 16 | 2,000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 25 | 2,236 | 0 6329 | 49 | 2.646 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 64 | 2,828 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 81 | 3.000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 100 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 121 | 3,317 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 144 | 3,464 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 169 | 3,606 |
|
