Содержание
Геометрическая прогрессия на примерах
Геометрическая прогрессия не менее важная в математике по сравнению с арифметической. Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают
Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя прогрессия является монотонной последовательностью, причем если это последовательность чисел является монотонно убывающей и при монотонно возрастающей. Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
Общий член геометрической прогрессии вычисляют по формуле
Сумма n первых членов геометрической прогрессии определяют по формуле
Рассмотрим решения классических задач на геометрическую прогрессию. Начнем для понимания с простейших.
Начнем для понимания с простейших.
Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.
Решение: Запишем условие задачи в виде
Для вычислений используем формулу n-го члена геометрической прогрессии
На ее основе находим неизвестные члены прогрессии
Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом
Пример 2. Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.
Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения
Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле
На этом задача решена.
Пример 3. Геометрическая прогрессия задана двумя ее членами . Найти десятый член прогрессии.
Найти десятый член прогрессии.
Решение:
Запишем заданные значения через формулы
По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем
Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим
Если полученное значение умножить на шестой член, получим десятый
Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
Пример 4. Геометрическая прогрессия задано рекуррентными формулами
Найти знаменатель геометрической прогрессии и сумму первых шести членов.
Решение:
Запишем заданные данные в виде системы уравнений
Выразим знаменатель разделив второе уравнение на первое
Найдем первый член прогрессии из первого уравнения
Вычислим следующие пять членов для нахождения суммы геометрической прогрессии
Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель
В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам. Наконец найденные значения добавить.
Наконец найденные значения добавить.
Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Похожие материалы:
формула n-го члена прогрессии 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 12.
Геометрическая прогрессия.
Давай рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:
2; 22; 23; 24; 25; …
Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической последовательности.
Давай дадим определение: Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Другими словами, последовательность (bn)– геометрическая прогрессия, если для любого натурального n выполняются условия:
bn ≠ 0 и bn+1 = bn⋅ q,где q – некоторое число. Значит, в последовательности натуральных степеней числа 2, для любого натурального n верно равенство bn+1 = bn⋅ 2, то есть q=2.
Из определения геометрической прогрессии следует, что отношение ее любого члена, начиная со второго, к предыдущему равно q, то есть bn+1bn=q
Это равенство верно при любом натуральном n.
Число q – называют знаменателем геометрической прогрессии, который всегда отличен от 0.
Чтобы задать геометрическую прогрессию достаточно указать ее первый член и знаменатель.
Например:
Если b1 = 2 и q = 3, то мы получим геометрическую прогрессию:
2, 6, 18, 54, …
Если и b1 = 3 и q = -2, то мы получим геометрическую прогрессию:
3, -6, 12, -24,…
Если b1 = 5 и q = 1, то получим геометрическую прогрессию:
5, 5, 5,…
Зная первый член и знаменатель геометрической прогрессии, можно последовательно найти второй, третий и вообще любой член прогрессии:
b2=b1∙q
b3=b2∙q=b1∙q∙q=b1q2
b4=b3∙q=b1∙q2∙q=b1q3
Значит, чтобы найти n-ый член надо первый член умножить на знаменатель в степени на единицу меньше, то есть
bn=b1qn-1
Это и есть формула n-го члена геометрической прогрессии.
Рассмотрим пару примеров:
Найти девятый член геометрической прогрессии:
-2; 4; -8;…
В данном случае: b1=-2,q=4-2=-2
b9=b1q8=-2∙-28=-2∙256=-512
Ответ: -512
Найдите первый член геометрической прогрессии, если шестой член равен 9, а знаменатель равен 3.
b6=b1∙q5
9=b1∙35
b1=935=127
Ответ: 127
Геометрическая прогрессия обладает следующим свойством:
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению последующего и предыдущего ее членов (произведению своих соседей)
То есть bn2=bn+1∙bn-1
Например, надо найти третий член геометрической прогрессии, если известно, что ее второй член равен 6, а четвертый – равен 24.
Давай воспользуемся этим свойством геометрической прогрессии, тогда
b32=b2∙b4
b32=6∙24=144
b3=±12
Ответ: 12 или –12.
Урок 38. формула суммы первых n членов геометрической прогрессии — Алгебра — 9 класс
Напомним, что геометрической прогрессией называется последовательность ненулевых чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. Это число называют знаменателем геометрической прогрессии. Из определения следует, что знаменатель геометрической прогрессии отличен от нуля.
Зная первый член и знаменатель, можно найти любой член геометрической прогрессии по его номеру. Это позволяет сделать формула n-го члена.
Мы выяснили, что последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого её члена, начиная со второго, равен произведению предыдущего и последующего членов. Это свойство геометрической прогрессии называется её характеристическим свойством.
Более того, квадрат любого члена геометрической прогрессии, начиная с некоторого, равен не только произведению своих непосредственных соседей, но и произведению членов прогрессии, находящихся от него на одинаковом расстоянии.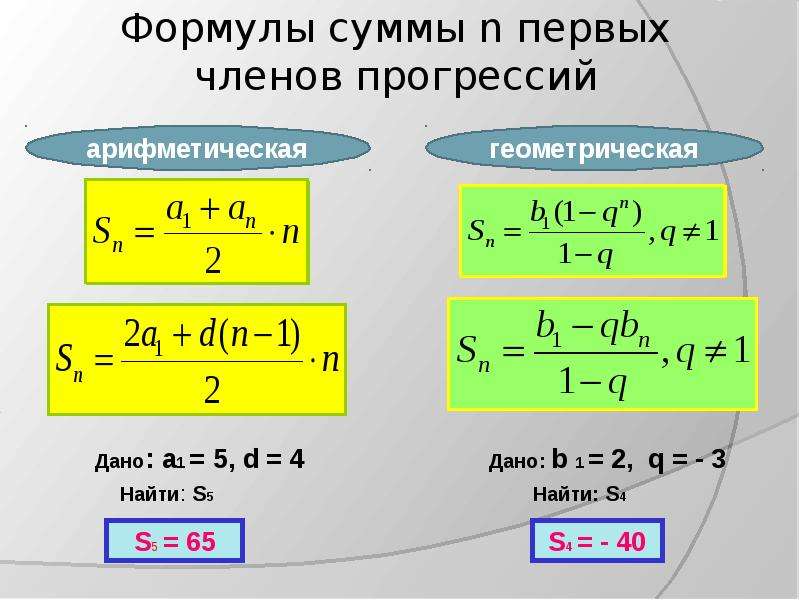
Например, квадрат 10-го члена геометрической прогрессии равен произведению 9-го и 11-го членов, а также 8-го и 12-го, 7-го и 13-го, … 1-го и 19-го.
Обозначим сумму первых n членов геометрической прогрессии как эс энное и запишем эту сумму.
Умножим полученное равенство на знаменатель прогрессии q.
Учитывая, что a1q = a2, a2q = a3, a3q = a4 … an-1q = an, получаем равенство 2.
Вычитаем из равенства 2 равенство 1.
При q, не равном единице, делим обе части равенства на q минус 1 и получаем формулу суммы n первых членов геометрической прогрессии.
Вернёмся к задаче, которую мы решали в начале урока. Найдём количество зёрен, которые попросил в награду у принца создатель шахмат: на первую клетку шахматной доски он просил положить одно зерно, на каждую следующую в два раза больше зёрен, чем на предыдущую.
Заметим, что эти числа образуют геометрическую прогрессию с первым членом 1 и знаменателем 2. В этой прогрессии 64 члена – по количеству клеток на шахматной доске. На последнюю клетку нужно было положить 2 в 63-й степени зёрен.
А общее количество зёрен равно сумме первых 64-х членов данной геометрической прогрессии.
Вычислим приближённо массу всего зерна. Заметим, что 2 в десятой степени равно 1024, округлим до 1000. Тогда в награду изобретателю нужно дать 16, умноженное на 10 в 18-й степени зёрен.
Масса одного пшеничного зерна составляет примерно 0,06 грамма.
Масса всех зёрен должна составить примерно 10 в 12-й степени тонн, то есть триллион тонн. Однако, такого количества пшеницы не собрало человечество за все годы своего существования.
По полученной формуле можно находить сумму n первых членов геометрической прогрессии, если известны её первый и n-й члены, знаменатель и количество членов. Но далеко не всегда нам известен n-й член. И не обязательно его находить.
Воспользуемся формулой n – го члена геометрической прогрессии и выведем ещё одну формулу суммы первых n членов – через первый член и знаменатель геометрической прогрессии.
Найдём сумму первых семи членов геометрической прогрессии с первым членом 4400 и знаменателем –0,1.
Сумма первых шести членов геометрической прогрессии равна 364, её знаменатель равен 3. Найдём первый член.
Запишем формулу суммы n первых членов геометрической прогрессии, подставим в неё известные величины, решим полученное уравнение.
Первый член геометрической прогрессии равен 1.
Конспект урока по геометрии «Геометрическая прогрессия. Формула n-го члена геометрической прогрессии» 9 класс
Цели урока:
Образовательная: формирование понятия геометрической прогрессии, умений работать с формулой nго члена геометрической прогрессии, сформировать навыки применения формулы при выполнении упражнений;
Развивающая: продолжить развитие математического мышления, умений применять ранее изученный материал о последовательностях, развивать интеллектуальные умения: сравнивать, делать выводы, выявлять закономерности, анализировать;
Воспитательная: воспитание правильного отношения к своему здоровью, внимания, чувства ответственности и общематематической культуры.
Тип урока: объяснение нового материала.
Формы работы: фронтальная, индивидуальная, самостоятельная
Методы контроля: устный
План урока
I Организационный момент
II Повторение пройденного материала. Подготовка к изучению нового материала
III Изучение нового материала
IV Физ.минутка
V Закрепление учебного материала
VI Задание на дом
VII Рефлексия. Подведение итогов урока
Оборудование: компьютер, интерактивная доска, презентация «Геометрическая прогрессия», учебник «Алгебра 9» , Мордкович А.Г.
I Организационный момент.(2 мин)
Цель: проверить готовность учащихся и кабинета к работе, выявить отсутствующих; создать положительный настрой учащихся к работе.
Метод : беседа
Здравствуйте, ребята! Садитесь. Проверьте, пожалуйста, наличие у вас учебника, тетради, ручки, дневника. Дежурный , сообщите об отсутствующих.
Дежурный , сообщите об отсутствующих.
Ребята! Французский писатель Анатоль Франс однажды заметил «Учиться можно только весело…чтобы переваривать знания, надо поглощать их с аппетитом» Так давайте, сегодня, на уроке будем следовать совету писателя. Будем внимательны, активны , будем поглощать знания с желанием, ведь они пригодятся вам в дальнейшей жизни.
— Какую тему мы изучали с вами на прошлых уроках? ( арифметическая прогрессия)
-Повторим определение (называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом , которое называется разностью d).
— Что ещё знаем и умеем находить для арифметической прогрессии? (d, n-й член, сумму n-первых членов)
Из сказанного сформулируем девиз сегодняшнего урока
« Прогрессио – движение вперёд!»
Ход урока
II.Повторение пройденного материала. Подготовка к изучению нового материала.
Цель: актуализировать знания учащихся, которые необходимы для сознательного восприятия нового материала; организовать фронтальную деятельность класса; развивать быстроту реакций, математическое мышление, умение правильно понимать вопрос.
Задачи учителя: предложить и решить примеры, с помощью которых учащимся будет легче воспринимать новый материал.
Форма работы: устная, фронтальная, индивидуальная.
Найдите значение выражения: 2n , при n= 1, 2, 3, 4,…, составьте последовательность
Ответы : 2,4,8, 16 ….
а) Найдите три первых члена последовательности, заданной условиями:
с1 = 10, сn+1 = 5 сn.
б) Чему равно значение выражения: ;
в) Назовите член последовательности, который следует за C5 ; Сn ; Сn+1?
г) Назовите член последовательности, который предшествует С5 ;Сn+1;Сn-2 ?
3. а) Вставьте в числовую последовательность число вместо вопросительного знака: 1. 7;?; 13; 16;
а) Вставьте в числовую последовательность число вместо вопросительного знака: 1. 7;?; 13; 16;
2. 5; 15; 25;?;
3. 4; 8;?; 32;
б) Выявите закономерность, которой подчиняются числа в каждой последовательности?
III Изучение нового материала.
Цель: познакомить учащихся с определением геометрической прогрессии и формулой n–го члена геометрической прогрессии; формировать умения и навыки распознавать геометрическую прогрессию и применять формулу n – го члена при выполнении упражнений.
Задачи учителя: создать условия для восприятия учащимися новых понятий изучаемого материала; добиваться усвоения методов воспроизведения изучаемого материала; отрабатывать умения; делать выводы.
Метод: проблемно-исследовательский.
Форма работы: письменная, устная работа, работа с учебником.
На доске записана последовательность 4; 8; 16; 32;
— Посмотрите, ребята, на данную последовательность, что вы про неё можете сказать?
— В дальнейшем все последовательности чисел, для которых, устанавливается нами открытая закономерность, будем называть геометрической прогрессией.
Итак, тема сегодняшнего урока «Геометрическая прогрессия. Формула n-го члена геометрической прогрессии».
Давайте вместе аналогично определению арифметической прогрессии попробуем дать определение геометрической прогрессии :
называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго равен предыдущему члену, умноженному на одно и то же число.
bn+1 = bnq
где bn ≠ 0, q – некоторое число.
— Ребята, запишите данную формулу в тетрадь и выразите q из формулы. q – будем называть знаменателем геометрической прогрессии.
Запомните! q0.
Вывод формулы n-го члена геометрической прогрессии.
(у доски будет работать ученик)
Цель: показать непосредственное следствие формулы n- го члена геометрической прогрессии из её определения.
bn= b1qn-1
Пример 2.
а) В геометрической прогрессии b1 = 12, q = . Найти b4.
б) В геометрической прогрессии b1 = -2, q=3. Найти b5.
— Что нам известно?
— Что надо найти?
— Какую формулу будем использовать?
Решение:
а) b4 = b1q3 = 12 )3 =)3 = =
б) b5 = b1q4 = -2 34 = -2 81= — 162(самостоятельно)
3. Сообщение о показательной функции.
Если bn= b1qn-1 = b1qn : q; bn = qn при m = , получим ; bn = m qn
Т. к. n – находится в показателе , то функцию вида ; у = m qх называют показательной, т.е. геометрическую прогрессию можно рассматривать как показательную на множестве N.
к. n – находится в показателе , то функцию вида ; у = m qх называют показательной, т.е. геометрическую прогрессию можно рассматривать как показательную на множестве N.
Применение показательной функции в природе.
В жизни нередко приходится встречаться с такими фактами, когда скорость
изменения какой-либо величины пропорциональна самой величине (размножение
бактерий, ход химической реакции и т. д.). В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид: y= у0ах
По закону показательной функции размножалось бы все живое на Земле, если
бы для этого имелись благоприятные условия, то есть не было естественных врагов
и было вдоволь пищи.
В природе, технике и экономике встречаются многочисленные процессы, в
ходе которых значение величины меняется в одно и то же число раз, то есть по
закону показательной функции. Эти процессы называются процессами
органического роста или органического затухания. Например, рост бактерий в
идеальных условиях соответствует процессу органического роста; радиоактивный
распад вещества – процессу органического затухания. Законам органического роста подчиняется рост вклада в Сберегательном банке, восстановление гемоглобина в крови, донора или раненого, потерявшего много крови, рост дрожжей, ферментов, микроорганизмов.
В природе и технике часто можно наблюдать процессы, которые подчиняются
законам выравнивания, описываемым показательной функцией. Например,
температура чайника изменяется со временем .Процессы выравнивания также можно наблюдать при включении и выключении электрического тока в цепи при падении тел в воздухе с парашютом. В биологии процесс выравнивания встречается при разрушении адреналина в крови; о работе
почек судят по их способности выводить радиоактивные вещества, количество
которых уменьшается по показательному закону.
Вы все слышали о цепных реакциях, теорию которых в 20-ых годах описал
молодой химик Н.Н.Семенов, а потом развили ученые-атомщики. Как управлять
этим процессом в мирных целях? На этот вопрос можно ответить только при
помощи знаний о показательной функции.
При прохождении света через мутную среду каждый слой этой среды
поглощает строго определенную часть падающего на него света.
Подобный же закон будет характеризовать процесс поглощения газа соответствующей средой, изменение скорости ветра и т.п.
Как видите во всех приведенных выше исследованиях использовалась
показательная функция.
IV. Физ.минутка
Цель: восстановление работоспособности учащихся, воспитание правильного отношения к своему здоровью.
— А сейчас немного отдохнём.
В весенний период идёт распространение вируса ГРИППА, ОРВИ . Недаром в народе говорят, что инфекция распространяется с геометрической прогрессией. Есть много различных способов профилактики и лечения ОРЗ.
Есть много различных способов профилактики и лечения ОРЗ.
— Какие профилактические мероприятия вы проводите?
Раз — подняться, подтянуться
Два — согнуться, разогнуться
Три — в ладоши три хлопка, головою три кивка.
На четыре — ноги шире.
Пять — руками помахать
Шесть — за стол тихонько сесть.
V. Закрепление учебного материала
Цель: закрепить и проверить практическое применение геометрической прогрессии при решении примеров и теста.
Задачи учителя: выработать умения применять новые знания, создать условия для понимания нового материала и правильного воспроизведения.
Метод: комбинированный.
Форма работы: письменная, практическая.
1.Повторение курса 9 класса.
Методы решения систем № 514 ( стр 107) Ответ:0,5 и 72
Решение упражнений из открытого банка ФИПИ.
В этом году вам предстоит пройти ГИА . Предлагаю выполнить несколько упражнений, которые позволят подготовиться к экзамену.
Взаимопроверка. Критерии оценивания:
3упр. – оценка «5»
2упр.– оценка «4»
1 упр. – оценка «3»
0 упр. – оценка «2».
Ф.И._________________________
I вариант
№ 1.Из последовательностей выбрать геометрическую прогрессию:
1. 3;6;9;…
2. 3; 9; 27;
3. 7; 12; 33;…
4. -8; -11; -34;…
№ 2. Найти b4 геометрической прогрессии bn=
Ответ:
№ 3. Сколько отрицательных членов данной последовательности
сn= n2 – 16 ?
Ответ:
Ф.И.____________________
II вариант
№ 1.Из последовательностей выбрать геометрическую прогрессию:
1. 10; 14; 18;…
2. 4; 13; 24;…
4; 13; 24;…
3. —3; -6; -9; …
4. 4; 16;64;…
№ 2. Найти b3 геометрической прогрессии bn=
Ответ:
№ 3. Сколько положительных членов данной последовательности
сn= 25 — n2 ?
Ответ:
Существует древняя история, а вместе с ней и задача, про шахматную доску. Однажды создатель шахмат показал правителю страны свое изобретение. А правителю настолько понравилось, что он разрешил мудрецу попросить для себя любую награду. Тот попросил заплатить за первую клетку доски 1 зерно пшеницы (или риса), за вторую — 2, и так далее: за каждую клетку вдвое больше предыдущей. Правитель быстро согласился, но через некоторое время узнал, что не может расплатиться с изобретателем…
И не удивительно, ведь уже подсчитано, что сумма данной геометрической прогрессии составляет 18 446 744 073 709 551 615 зерен.( 20-значное число). Это примерно в 1800 раз больше, чем в мире собирают за год, это даже больше, чем весь урожай, собранный за всю историю человечества!
Что нужно знать для определения количества зёрен? Сумма n-первых членов геометрической прогрессии.
Изучим её на следующем уроке.
VI Задание на дом
Цель: проверить усвоение материала урока.
Задачи учителя: сообщить домашнее задание, разъяснить методику его выполнения.
Форма работы: индивидуальная, дифференцированная.
Задание на дом. П. 16, п.5-повторение
«3» №476 (б), 484(б)
«4» №495(б)
«5» №512
VII Рефлексия. Подведение итогов урока
Цель: подведение итогов урока, развитие у учащихся навыков самоконтроля.
Задача учителя: дать оценку успешности достижения цели и наметить перспективу на будущее.
— Что нового мы узнали на уроке?
Мне хочется вернуться к нашему девизу «Прогрессио – движение вперёд!
Учащимся предлагается поставить на значок + на линии в том месте, которое отражает их отношение к занятию и степень участия в уроке:
1. Я считаю, что занятие было интересным___________________скучным.
2.Я научился многому ______________________малому.
3. Я думаю, что слушал других внимательно__________________невнимательно.
4. Я принимал участие в дискуссии часто________________________редко.
5. Результатами своей работы на уроке я доволен_________________не доволен.
Как вы думаете, а мы сегодня добились прогресса?
В чём заключается наш прогресс?
(Оценки за урок)
Всего вам хорошего! Спасибо за урок!
Геометрическая прогрессия
Вопросы
занятия:
· повторить основные понятия, связанные с
геометрической прогрессии;
· повторить формулу для нахождения суммы первых n
членов геометрической прогрессии;
· повторить понятие бесконечно убывающей
геометрической прогрессии.
Материал
урока
Определение.
Геометрической прогрессией
называется последовательность отличных от нуля чисел, каждый член которой, начиная
со второго, равен предыдущему члену, умноженному на одно и то же число.
Для задания геометрической прогрессии достаточно
задать её первый член и значение знаменателя q.
Рассмотрим пример.
Пример.
Получим формулу n—ого
члена геометрической прогрессии.
Она позволит найти любой член геометрической
прогрессии, зная её первый член и номер искомого члена.
Пример.
Пример.
Пример.
Пример.
Как и в случае просто последовательностей,
геометрическая прогрессия бывает возрастающей и убывающей.
Рассмотрим геометрическую прогрессию, состоящую из
степеней числа три.
Таким свойством обладает любая геометрическая
прогрессия.
Квадрат любого члена геометрической прогрессии,
начиная со второго, равен произведению предыдущего и последующего членов.
Другими словами, любой член геометрической
прогрессии равен среднему геометрическому предыдущего и последующего членов.
Справедливо и обратное утверждение.
Если в последовательности чисел, отличных от нуля,
квадрат каждого члена, начиная со второго, равен произведению предыдущего и
последующего членов, то эта последовательность является геометрической
прогрессией.
Рассмотрим пример.
Пример.
Рассмотрим пример.
Пример.
Можно сказать, что данная последовательность является
геометрической прогрессией.
Рассмотрим геометрическую прогрессию:
Запишем сумму эн первых членов геометрической
прогрессии.
Формулу, записанную в таком виде, на практике
использовать удобнее.
Решим несколько примеров.
Пример.
Рассмотрим ещё один пример.
Пример.
Для бесконечно убывающей последовательности сумма
первых n членов равна:
Рассмотрим пример.
Пример.
Итоги урока
Сегодня на уроке, мы повторили основные понятия,
связанные с геометрической прогрессией, повторили формулу для нахождения суммы
первых эн членов геометрической прогрессии, рассмотрели несколько задач.
Формула суммы n первых членов геометрической прогрессии + примеры
Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число.
Геометрическая прогрессия обозначается b1,b2,b3, …, bn, … .
Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.
Монотонная и постоянная последовательность
Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … . 8 -1))/(3-1) = 19 680.
8 -1))/(3-1) = 19 680.
Нужна помощь в учебе?
Предыдущая тема: Определение геометрической прогрессии: формула n-го члена прогрессии
Следующая тема:   Сумма бесконечной геометрической прогрессии при |q|
Геометрическая прогрессия | umath.ru
Определение геометрической прогрессии
Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.
То есть геометрическая прогрессия определяется рекуррентным соотношением
Итак, для n-го члена геометрической прогрессии справедлива формула
Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Доказательство. Из определения геометрической прогрессии
Следовательно,
откуда
Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.
Сумма первых n членов геометрической прогрессии
Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :
(1)
Умножим это равенство на :
или
(2)
Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как имеем
или
(3)
Так как то формулу (3) можно переписать в виде
(4)
Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.
Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии
По формуле (3) получаем
Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.
Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогресcии выражается формулой
(5)
Геометрическая серия
А
геометрическая серия
это
ряд
чьи родственные
последовательность
геометрический. Это результат добавления
термины
из
геометрическая последовательность
.
Пример 1:
Конечная геометрическая последовательность:
1
2
,
1
4
,
1
8
,
1
16
,
…
,
1
32768
Связанные конечные геометрические ряды:
1
2
+
1
4
+
1
8
+
1
16
+
…
+
1
32768
Написано в сигма-нотации:
∑
k
знак равно
1
15
1
2
k
Пример 2:
Бесконечная геометрическая последовательность:
2
,
6
,
18
,
54
,
…
Связанные бесконечные геометрические серии:
2
+
6
+
18
+
54
+
…
Написано в сигма-нотации:
∑
п
знак равно
1
∞
(
2
⋅
3
п
—
1
)
Конечный геометрический ряд
Чтобы найти сумму конечного геометрического ряда, используйте формулу
S
п
знак равно
а
1
(
1
—
р
п
)
1
—
р
,
р
≠
1
,
где
п
это количество терминов,
а
1
это первый член и
р
это
обычное отношение
.
Пример 3:
Найдите сумму первых
8
члены геометрического ряда, если
а
1
знак равно
1
а также
р
знак равно
2
.
S
8
знак равно
1
(
1
—
2
8
)
1
—
2
знак равно
255
Пример 4:
Находить
S
10
, десятая частичная сумма бесконечного геометрического ряда
24
+
12
+
6
+
…
.
Сначала найдите
р
.
р
знак равно
а
2
а
1
знак равно
12
24
знак равно
1
2
Теперь найдите сумму:
S
10
знак равно
24
(
1
—
(
1
2
)
10
)
1
—
1
2
знак равно
3069
64
Пример 5:
Оценивать.
∑
п
знак равно
1
10
3
⋅
(
—
2
)
п
—
1
(Вы находите
S
10
для сериала
3
—
6
+
12
—
24
+
…
, обыкновенное отношение которого
—
2
.)
S
п
знак равно
а
1
(
1
—
р
п
)
1
—
р
S
10
знак равно
3
[
1
—
(
—
2
)
10
]
1
—
(
—
2
)
знак равно
3
(
1
—
1024
)
3
знак равно
—
1023
Бесконечная геометрическая серия
Чтобы найти сумму бесконечного геометрического ряда, имеющего отношения с
абсолютная величина
меньше единицы, используйте формулу,
S
знак равно
а
1
1
—
р
,
где
а
1
это первый член и
р
это обычное отношение.
Пример 6:
Найдите сумму бесконечного геометрического ряда
27
+
18
+
12
+
8
+
…
.
Первая находка
р
:
р
знак равно
а
2
а
1
знак равно
18
27
знак равно
2
3
Затем найдите сумму:
S
знак равно
а
1
1
—
р
S
знак равно
27
1
—
2
3
знак равно
81 год
Пример 7:
Найдите сумму бесконечного геометрического ряда
8
+
12
+
18
+
27
+
…
если он существует.
Первая находка
р
:
р
знак равно
а
2
а
1
знак равно
12
8
знак равно
3
2
С
р
знак равно
3
2
не меньше единицы, ряды не сходятся.То есть в нем нет суммы.
Явные формулы для геометрических последовательностей
Результаты обучения
- Напишите рекурсивную формулу для последовательности чисел.
- Дайте два члена геометрической последовательности, найдите третий.
- Решите прикладную задачу, используя геометрическую последовательность.
Использование рекурсивных формул для геометрических последовательностей
Рекурсивная формула позволяет нам найти любой член геометрической последовательности, используя предыдущий член.Каждый член является продуктом обычного отношения и предыдущего члена. Например, предположим, что обычное отношение равно 9. Тогда каждый член в девять раз больше предыдущего. Как и в любой рекурсивной формуле, необходимо указать начальный член.
Общее примечание: рекурсивная формула для геометрической последовательности
Рекурсивная формула для геометрической последовательности с общим соотношением [латекс] r [/ латекс] и первым членом [латекс] {a} _ {1} [/ latex]:
[латекс] {a} _ {n} = r \ cdot {a} _ {n — 1}, n \ ge 2 [/ латекс]
Как сделать: учитывая первые несколько членов геометрической последовательности, напишите ее рекурсивную формулу.
- Укажите первоначальный срок.
- Найдите обычное отношение, разделив любой термин на предыдущий.
- Подставляет обычное отношение в рекурсивную формулу геометрической последовательности.
Пример: использование рекурсивных формул для геометрических последовательностей
Напишите рекурсивную формулу для следующей геометрической последовательности.
[латекс] \ влево \ {6,9,13.5,20,25, \ точки \ вправо \} [/ латекс]
Показать решение
Первый член равен 6.Обычное отношение можно найти, разделив второй член на первый член.
[латекс] r = \ dfrac {9} {6} = 1,5 [/ латекс]
Подставьте обычное соотношение в рекурсивную формулу для геометрических последовательностей и определите [латекс] {a} _ {1} [/ latex].
[латекс] \ begin {align} & {a} _ {n} = r \ cdot {a} _ {n — 1} \\ & {a} _ {n} = 1.5 \ cdot {a} _ {n — 1} \ text {for} n \ ge 2 \\ & {a} _ {1} = 6 \ end {align} [/ latex]
Анализ решения
Последовательность точек данных следует экспоненциальному шаблону.Обычное отношение также является основой экспоненциальной функции.
Вопросы и ответы
Должны ли мы разделить второй член на первый член, чтобы найти обычное отношение?
Нет. Мы можем разделить любой член в последовательности на предыдущий. Однако чаще всего делят второй член на первый член, потому что это часто самый простой метод определения общего отношения.
Попробуй
Напишите рекурсивную формулу для следующей геометрической последовательности.
[латекс] \ left \ {2, \ dfrac {4} {3}, \ dfrac {8} {9}, \ dfrac {16} {27}, \ dots \ right \} [/ latex]
Показать решение
[латекс] \ begin {align} & {a} _ {1} = 2 \\ & {a} _ {n} = \ frac {2} {3} \ cdot {a} _ {n — 1} \ текст {for} n \ ge 2 \ end {align} [/ latex]
Использование явных формул для геометрических последовательностей
Поскольку геометрическая последовательность является экспоненциальной функцией, область определения которой является набором положительных целых чисел, а обычное отношение является основой функции, мы можем написать явные формулы, которые позволят нам находить определенные термины.{3} && \ text {Divide} \\ & r = 2 && \ text {Решите для общего отношения} \ end {align} [/ latex]
Найдите второй член, умножив первый член на обыкновенное отношение.
[латекс] \ begin {align} {a} _ {2} & = 2 {a} _ {1} \\ & = 2 \ left (3 \ right) \\ & = 6 \ end {align} [/ латекс]
Анализ решения
Обычное отношение умножается на первый член один раз, чтобы найти второй член, дважды, чтобы найти третий член, трижды, чтобы найти четвертый член, и так далее.Десятый член можно найти, умножив первый член на обыкновенное отношение девять раз или умножив на обыкновенное отношение в девятой степени.
Попробуй
Учитывая геометрическую последовательность с [латексом] {a} _ {2} = 4 [/ latex] и [latex] {a} _ {3} = 32 [/ latex], найдите [latex] {a} _ {6 }[/латекс].
Показать решение
[латекс] {a} _ {6} = 16 \ text {,} 384 [/ латекс]
Пример: написание явной формулы для
n -го члена геометрической последовательности
Напишите явную формулу для члена [latex] n \ text {th} [/ latex] следующей геометрической последовательности.{n} [/ латекс]
Пример: решение прикладных задач с помощью геометрических последовательностей
В 2013 году количество учеников в малой школе составляет 284 человека. По оценкам, количество учеников будет увеличиваться на 4% каждый год.
- Напишите формулу для численности учащихся.
- Оцените численность студентов в 2020 г.
Показать решение
- Ситуацию можно смоделировать геометрической последовательностью с начальным семестром 284. Контингент студентов составит 104% по сравнению с предыдущим годом, поэтому обычное отношение равно 1.{n} [/ латекс]
- Количество просмотров будет около 333.
Следующее видео представляет собой короткий урок по некоторым темам, затронутым в этом уроке.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
геометрических последовательностей и серии
Геометрические последовательности
Геометрическая последовательность — последовательность чисел, в которой каждое последующее число является произведением предыдущего числа и некоторой константы r ., или геометрическая прогрессия. Используется при обращении к геометрической последовательности., представляет собой последовательность чисел, в которой каждое последующее число является произведением предыдущего числа и некоторой константы r .
an = ran − 1 Геометрическая последовательность
И поскольку anan − 1 = r, постоянный множитель r называется общим отношением Константа r , которая получается делением любых двух последовательных членов геометрической последовательности; anan − 1 = r .. Например, следующая геометрическая последовательность,
9,27,81,243,729…
Здесь a1 = 9, а соотношение между любыми двумя последовательными членами равно 3.Можно построить общий член an = 3an − 1, где,
a1 = 9a2 = 3a1 = 3 (9) = 27a3 = 3a2 = 3 (27) = 81a4 = 3a3 = 3 (81) = 243a5 = 3a4 = 3 (243) = 729 ⋮
В общем, с учетом первого члена a1 и общего отношения r геометрической последовательности мы можем записать следующее:
a2 = ra1a3 = ra2 = r (a1r) = a1r2a4 = ra3 = r (a1r2) = a1r3a5 = ra3 = r (a1r3) = a1r4 ⋮
Отсюда мы видим, что любую геометрическую последовательность можно записать в терминах ее первого элемента, ее общего отношения и индекса следующим образом:
an = a1rn − 1 Геометрическая последовательность
Фактически, любой общий член, являющийся экспонентой в числах n , является геометрической последовательностью.
Пример 1
Найдите уравнение для общего члена данной геометрической последовательности и используйте его для вычисления 10 th члена: 3,6,12,24,48…
Решение:
Начнем с нахождения общего отношения,
г = 63 = 2
Обратите внимание, что соотношение между любыми двумя последовательными членами равно 2. Последовательность действительно представляет собой геометрическую прогрессию, где a1 = 3 и r = 2.
an = a1rn − 1 = 3 (2) n − 1
Следовательно, мы можем записать общий член an = 3 (2) n − 1, а член 10 th можно вычислить следующим образом:
a10 = 3 (2) 10−1 = 3 (2) 9 = 1,536
Ответ: an = 3 (2) n − 1; а10 = 1,536
Термины между данными элементами геометрической последовательности называются средними геометрическими. Термины между данными элементами геометрической последовательности..
Пример 2
Найдите все члены геометрической последовательности между a1 = −5 и a4 = −135. Другими словами, найдите все геометрические средние между 1 -м и 4 -м членами.
Решение:
Начнем с нахождения общего отношения r . В данном случае нам даны первый и четвертый слагаемые:
an = a1rn − 1 Используйте n = 4.a4 = a1r4−1a4 = a1r3
Подставляем a1 = −5 и a4 = −135 в приведенное выше уравнение, а затем решаем относительно r .
−135 = −5r327 = r33 = r
Затем используйте первый член a1 = −5 и общее отношение r = 3, чтобы найти уравнение для n -го члена последовательности.
an = a1rn − 1an = −5 (3) n − 1
Теперь мы можем использовать an = −5 (3) n − 1, где n — положительное целое число, чтобы определить пропущенные члены.
a1 = −5 (3) 1−1 = −5⋅30 = −5a2 = −5 (3) 2−1 = −5⋅31 = −15a3 = −5 (3) 3−1 = −5⋅32 = −45} средние геометрические a4 = −5 (3) 4−1 = −5⋅33 = −135
Ответ: −15, −45,
Первый член геометрической последовательности не может быть указан.
Пример 3
Найдите общий член геометрической последовательности, где a2 = −2 и a5 = 2125.
Решение:
Чтобы определить формулу для общего члена, нам нужны a1 и r. Нелинейная система с этими переменными может быть сформирована с использованием данной информации и an = a1rn − 1:
{a2 = a1r2−1a5 = a1r5−1 ⇒ {−2 = a1r2125 = a1r4 Используйте a2 = −2. Используйте a5 = 2125.
Решите относительно a1 в первом уравнении,
{−2 = a1r ⇒ −2r = a12125 = a1r4
Подставляем a1 = −2r во второе уравнение и решаем: r .
2125 = a1r42125 = (- 2r) r42125 = −2r3−1125 = r3−15 = r
Обратный заменитель, чтобы найти a1:
a1 = −2r = −2 (−15) = 10
Следовательно, a1 = 10 и r = −15.
Ответ: an = 10 (−15) n − 1
Попробуй! Найдите уравнение для общего члена данной геометрической последовательности и используйте его для вычисления 6 -го члена : 2,43,89,…
Ответ: an = 2 (23) n − 1; а6 = 64243
Геометрическая серия
Геометрический ряд Сумма членов геометрической последовательности.представляет собой сумму членов геометрической последовательности. Например, сумма первых 5 членов геометрической последовательности, определенной как an = 3n + 1, выглядит следующим образом:
S5 = Σn = 153n + 1 = 31 + 1 + 32 + 1 + 33 + 1 + 34 + 1 + 35 + 1 = 32 + 33 + 34 + 35 + 36 = 9 + 27 + 81 + 243 + 729 = 1089
Можно добавить 5 натуральных чисел. Однако задача добавления большого количества терминов не стоит. Поэтому далее мы разработаем формулу, которую можно использовать для вычисления суммы первых n членов любой геометрической последовательности.В целом
Sn = a1 + a1r + a1r2 +… + a1rn − 1
Умножая обе стороны на r , мы можем написать,
rSn = a1r + a1r2 + a1r3 +… + a1rn
Вычитая эти два уравнения, получаем
Sn-rSn = a1-a1rnSn (1-r) = a1 (1-rn)
Если предположить, что r ≠ 1, деление обеих сторон на (1 − r), приводит нас к формуле для n -й частичной суммы геометрической последовательности Сумма первых n членов геометрической последовательности, заданной формулой: Sn = a1 (1 − rn) 1 − r, r ≠ 1.:
Sn = a1 (1 − rn) 1 − r (r ≠ 1)
Другими словами, n -я частичная сумма любой геометрической последовательности может быть вычислена с использованием первого члена и общего отношения. Например, чтобы вычислить сумму первых 15 членов геометрической последовательности, определенной как an = 3n + 1, используйте формулу с a1 = 9 и r = 3.
S15 = a1 (1 − r15) 1 − r = 9⋅ (1−315) 1−3 = 9 (−14,348,906) −2 = 64,570,077
Пример 4
Найдите сумму первых 10 членов заданной последовательности: 4, −8, 16, −32, 64,…
Решение:
Определите, существует ли общее соотношение между данными терминами.
г = −84 = −2
Обратите внимание, что отношение между любыми двумя последовательными членами равно -2; следовательно, данная последовательность является геометрической последовательностью. Используйте r = −2 и тот факт, что a1 = 4, чтобы вычислить сумму первых 10 членов,
Sn = a1 (1 − rn) 1 − rS10 = 4 [1 — (- 2) 10] 1 — (- 2) = 4 (1−1,024) 1 + 2 = 4 (−1,023) 3 = −1,364
Ответ: S10 = −1,364
Пример 5
Вычислить: Σn = 162 (−5) n.
Решение:
В этом случае нас просят найти сумму первых 6 членов геометрической последовательности с общим членом an = 2 (−5) n.Используйте это, чтобы определить член 1 st и обыкновенное отношение r :
а1 = 2 (−5) 1 = −10
Чтобы показать, что существует общее отношение, мы можем использовать следующие друг за другом следующие термины:
r = anan − 1 = 2 (−5) n2 (−5) n − 1 = (- 5) n− (n − 1) = (- 5) 1 = −5
Используйте a1 = −10 и r = −5, чтобы вычислить частичную сумму 6 th .
Sn = a1 (1 − rn) 1 − rS6 = −10 [1 — (- 5) 6] 1 — (- 5) = — 10 (1−15,625) 1 + 5 = −10 (−15,624) 6 = 26 040
Ответ: 26 040
Попробуй! Найдите сумму первых 9 членов заданной последовательности: −2, 1, −1 / 2,…
Ответ: S9 = −171128
Если общее отношение r бесконечной геометрической последовательности является дробью, где | r | <1 (то есть -1
1− (110) 2 = 1−0,01 = 0,991− (110) 4 = 1−0,0001 = 0,99991− (110) 6 = 1−0,000001 = 0,999999
Здесь мы видим, что этот коэффициент становится все ближе и ближе к 1 для все больших значений n . Это иллюстрирует идею предела, важную концепцию, широко используемую в математике более высокого уровня, которая выражается с помощью следующих обозначений:
limn → ∞ (1 − rn) = 1, где | r | <1
Читается, что «предел (1-rn), поскольку n приближается к бесконечности, равен 1.«Хотя это дает предварительный обзор того, что должно произойти в вашем продолжающемся изучении математики, на данный момент мы заинтересованы в разработке формулы для специальных бесконечных геометрических рядов. Рассмотрим n -ю частичную сумму любой геометрической последовательности,
Sn = a1 (1 − rn) 1 − r = a11 − r (1 − rn)
Если | r | <1, то существует предел частичных сумм, когда n приближается к бесконечности, и мы можем написать
Sn = a11 − r (1 − rn) ⇒n → ∞ S∞ = a11 − r⋅1
Следовательно, сходящийся геометрический ряд — это бесконечный геометрический ряд, где | r | <1, сумма которого определяется формулой: S∞ = a11 − r.бесконечный геометрический ряд, где | r | <1; его сумму можно рассчитать по формуле:
S∞ = a11 − r
Пример 6
Найдите сумму бесконечного геометрического ряда: 32 + 12 + 16 + 118 + 154 + ⋯
Решение:
Определить обычное отношение,
г = 1232 = 12⋅23 = 13
Поскольку знаменатель r = 13 является дробью от -1 до 1, это сходящийся геометрический ряд.Используйте первый член a1 = 32 и обыкновенное отношение, чтобы вычислить его сумму.
S∞ = a11 − r = 321− (13) = 32 23 = 32⋅32 = 94
Ответ: S∞ = 94
Примечание : В случае бесконечного геометрического ряда, где | r | ≥1, ряд расходится, и мы говорим, что нет суммы. Например, если an = (5) n − 1, то r = 5, и мы имеем
S∞ = Σn = 1∞ (5) n − 1 = 1 + 5 + 25 +
Мы видим, что эта сумма неограниченно растет и не имеет суммы.
Попробуй! Найдите сумму бесконечного геометрического ряда: Σn = 1∞ − 2 (59) n − 1.
Ответ: −9/2
Повторяющаяся десятичная дробь может быть записана как бесконечный геометрический ряд, значащий коэффициент которого равен степени 1/10. Таким образом, формулу сходящегося геометрического ряда можно использовать для преобразования повторяющегося десятичного числа в дробь.
Пример 7
Запишите в виде дроби: 1.181818…
Решение:
Начните с определения повторяющихся цифр справа от десятичной дроби и перепишите их в геометрической прогрессии.
0,181818… = 0,18 + 0,0018 + 0,000018 +… = 18100 + 1810 000 + 181 000 000 +…
В этой форме мы можем определить общее отношение,
г = 1810,000 18100 = 1810,000 × 10018 = 1100
Обратите внимание, что соотношение между любыми двумя последовательными членами равно 1100. Используйте это, а также тот факт, что a1 = 18100, чтобы вычислить бесконечную сумму:
S∞ = a11 − r = 181001− (1100) = 1810099100 = 18100⋅10099 = 211
Следовательно, 0.181818… = 211 и имеем
1,181818… = 1 + 211 = 1211
Ответ: 1211
Пример 8
Определенный мяч отскакивает назад на две трети высоты, с которой он упал. Если этот мяч изначально падает с высоты 27 футов, приблизьте общее расстояние, которое он пролетит.
Решение:
Мы можем вычислить высоту каждого последующего отскока:
27⋅23 = 18 футов Высота первого отскока 18⋅23 = 12 футов Высота второго отскока 12⋅23 = 8 футов Высота третьего отскока
Общее расстояние, которое проходит мяч, складывается из расстояний, на которые мяч падает, и расстояний, на которые мяч поднимается.Расстояния, на которые падает мяч, образуют геометрическую серию
.
27 + 18 + 12 + ⋯ Дистанция падения мяча
, где a1 = 27 и r = 23. Поскольку r представляет собой дробную часть от -1 до 1, эту сумму можно рассчитать следующим образом:
S∞ = a11 − r = 271−23 = 2713 = 81
Следовательно, мяч падает на общую дистанцию 81 фут. Расстояния, на которые мяч поднимается, образуют геометрическую серию
.
18 + 12 + 8 + ⋯ Расстояние подъема мяча
, где a1 = 18 и r = 23.Вычислите эту сумму аналогично:
S∞ = a11 − r = 181−23 = 1813 = 54
Следовательно, мяч поднимается на общую дистанцию 54 фута. Приблизительно общее пройденное расстояние, сложив общее расстояние подъема и падения:
81 + 54 = 135 футов
Ответ: 135 футов
Основные выводы
- Геометрическая последовательность — это последовательность, в которой отношение r между последовательными членами является постоянным.
- Общий член геометрической последовательности может быть записан в терминах его первого члена a1, общего отношения r и индекса n следующим образом: an = a1rn − 1.
- Геометрический ряд — это сумма членов геометрической последовательности.
- Частичная сумма n геометрической последовательности может быть вычислена с использованием первого члена a1 и общего отношения r следующим образом: Sn = a1 (1-rn) 1-r.
- Бесконечная сумма геометрической последовательности может быть вычислена, если общее отношение представляет собой дробь от -1 до 1 (то есть | r | <1) следующим образом: S∞ = a11-r.Если | r | ≥1, то суммы не существует.
Тематические упражнения
−3.6, −4,32, −5,184,…
Найдите общий член и используйте его для определения 20-го члена в последовательности: 1, x2, x24,…
Найдите общий член и используйте его для определения 20-го члена в последовательности: 2, −6x, 18×2,…
Количество клеток в культуре определенных бактерий удваивается каждые 4 часа.Если изначально присутствует 200 ячеек, напишите последовательность, которая показывает популяцию ячеек после каждых n -го 4-часового периода в течение одного дня. Напишите формулу, которая дает количество ячеек после любого 4-часового периода.
Определенный мяч отскакивает назад на половине высоты, с которой он упал. Если этот мяч изначально падает с 12 футов, найдите формулу, которая дает высоту мяча при отскоке n и используйте ее, чтобы найти высоту мяча при отскоке 6 th .
Для геометрической последовательности, определяемой рекуррентным соотношением an = 4an − 1, где a1 = 2 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общего отношения r .
Учитывая геометрическую последовательность, определяемую рекуррентным соотношением an = 6an − 1, где a1 = 12 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общего отношения r .
a4 = −2.4 × 10−3 и a9 = −7,68 × 10−7
a2 = −20 и a5 = −20 000
Часть A: Геометрические последовательности
Запишите первые 5 членов геометрической последовательности с учетом ее первого члена и общего отношения. Найдите формулу для его общего члена.
Учитывая геометрическую последовательность, найдите формулу для общего члена и используйте ее, чтобы определить 5 -й член в последовательности.
Учитывая члены геометрической последовательности, найдите формулу для общего члена.
Найдите все геометрические средние между заданными членами.
∑n = 155n
∑n = 16 (−4) п
∑k = 1102k + 1
∑k = 1142k − 1
∑k = 110−2 (3) к
∑k = 185 (−2) к
∑n = 152 (12) n + 2
∑n = 14−3 (23) п
∑n = 1∞2 (13) n − 1
∑n = 1∞ (15) п
∑n = 1∞3 (2) n − 2
∑n = 1∞ − 14 (3) n − 2
∑n = 1∞12 (−16) п
∑n = 1∞13 (−25) п
Предположим, вы согласились работать за гроши в день в течение 30 дней.Вы заработаете 1 пенни в первый день, 2 пенни во второй день, 4 пенни в третий день и так далее. Сколько всего пенни вы заработаете в конце 30-дневного периода? Какая сумма в долларах?
Первоначальная ставка в рулетке 100 долларов делается (красное поле) и проигрывает. Чтобы компенсировать разницу, игрок удваивает ставку, делает ставку 200 долларов и проигрывает.Опять же, чтобы компенсировать разницу, игрок удваивает ставку до 400 долларов и проигрывает. Если игрок продолжает удваивать свою ставку таким образом и проигрывает 7 раз подряд, сколько всего он проиграет?
Определенный мяч отскакивает назад на половину высоты, с которой он упал. Если этот мяч изначально падает с 12 футов, приблизьте общее расстояние, которое он пролетит.
Мяч для гольфа отскакивает от цементного тротуара на три четверти высоты, с которой он упал. Если мяч изначально падает с 8 метров, приблизьте общее расстояние, которое он пролетит.
Структурированное поселение ежегодно приносит сумму в долларах, представленную как n , в соответствии с формулой pn = 6000 (0.80) п — 1. Какова общая сумма дохода от урегулирования через 10 лет?
Начните с квадрата, каждая сторона которого составляет 1 единицу, начертите еще один квадрат, соединив середины каждой стороны. Продолжайте писать квадраты таким образом до бесконечности, как показано на рисунке:
Найдите сумму площадей всех квадратов на рисунке.(Подсказка: начните с поиска последовательности, сформированной с использованием площадей каждого квадрата.)
Часть B: геометрическая серия
Рассчитайте указанную сумму.
Запишите как смешанное число.
∑n = 150 (3n − 5)
∑n = 125 (4−8n)
∑n = 112 (−2) n − 1
∑n = 1∞5 (−12) n − 1
∑n = 1405
∑n = 1∞0.6n
Часть C: Последовательности и серии
Определите последовательность как арифметическую, геометрическую или ни то ни другое. Укажите общее различие или соотношение, если оно существует.
Определите последовательность как арифметическую или геометрическую, а затем вычислите указанную сумму.
Рассчитайте указанную сумму.
Используйте методы, описанные в этом разделе, чтобы объяснить, почему 0,999… = 1.
Постройте геометрическую последовательность, где r = 1. Исследуйте n -ю частичную сумму такой последовательности.Какие выводы мы можем сделать?
Часть D: Обсуждение
ответы
1, 5, 25, 125, 625; ан = 5n − 1
2, 6, 18, 54, 162; ан = 2 (3) п − 1
2, -6, 18, -54, 162; ан = 2 (−3) п − 1
3, 2, 43, 89, 1627; ан = 3 (23) п − 1
1.2, 0,72, 0,432, 0,2592, 0,15552; ан = 1,2 (0,6) п − 1
an = — (- 23) n − 1, a5 = −1681
ан = −3.6 (1,2) n − 1, a5 = −7,46496
400 ячеек; 800 ячеек; 1600 ячеек; 3200 ячеек; 6400 ячеек; 12800 ячеек; pn = 400 (2) n − 1 ячеек
1,073,741,823 пенни; 10 737 418 долларов.23
Арифметическая геометрическая последовательность
Последовательность означает приказ.Теперь дело в том, что такое последовательность и как она связана с предметом математики. Арифметическая последовательность — это числа, которые складываются или вычитаются. Геометрическая прогрессия переходит от одного члена к другому и умножается или делится. Результат — общая ценность. Как показано на рисунке ниже, в арифметической последовательности разница (d) всегда является стандартным значением 7. В геометрических рядах общее значение всегда равно 2. Арифметическая последовательность представляет собой сложение (или вычитание) в заданном порядке. Геометрическая последовательность — это умножение (или деление) в заданном порядке.
Изображение будет загружено в ближайшее время
Формула арифметической последовательности
Давайте разберемся с формулой арифметической последовательности. В арифметической последовательности один член переходит к следующему, всегда добавляя — например, 1, 2, 3, 4, 5… .10 и так далее. Здесь, в этой последовательности, каждое число переходит ко второму числу путем добавления (или вычитания 1). Давайте рассмотрим несколько примеров, чтобы лучше понять. 2, 5, 8, 11, 14… .это арифметическая последовательность, когда каждый шаг добавляет 3. То же самое верно и для обратного порядка (при вычитании).Например. 7, 3, -1, -5… представляет собой арифметическую последовательность, поскольку каждый шаг вычитает 4.
Важно отметить, что число, которое добавляется или вычитается на каждом уровне арифметической последовательности, называется разностью (d) . Причина в том, что если вы сложите или вычтете (также известное как поиск разницы), вы всегда получите одно и то же общее значение. См. Рис. 2 ниже
Изображение будет загружено в ближайшее время
Формула геометрической последовательности
Геометрическая последовательность или геометрическая последовательность — это геометрический порядок.Мы получаем результаты, умножая члены геометрической последовательности. Проще говоря, геометрическая последовательность перемещается от одного члена к другому путем умножения (или деления) на одно и то же общее значение или число. Например, 2, 4, 8, 16, 32… — геометрический ряд. Причина в том, что каждый шаг умножается на два. Давайте возьмем другой пример, 81, 27, 9, 3, 1… это геометрическая последовательность, поскольку каждый шаг делится (или умножается) на число 3.
Важно отметить, что общее число, которое умножается или делится на каждый шаг геометрической последовательности называется отношением r.Это связано с тем, что если вы разделите или найдете отношение следующих друг за другом членов, вы получите обычное или стандартное соотношение. См. Рис. 3 ниже.
Изображение будет добавлено в ближайшее время
Арифметическая геометрическая прогрессия
Арифметическая прогрессия — это серия или последовательность чисел, в которой каждый член выводится из следующего члена путем добавления или вычитания фиксированного или общего числа, называемого общей разностью d. Например, ряд 9, 6, 3, 0, -3 и т. Д. Представляет собой арифметическую прогрессию с -3 в качестве стандартной разности.Прогрессия -3, 0, 3, 6, 9 — это пример арифметической прогрессии (AP), в которой общее различие равно трем d.
Установленная форма AP — a, a + d, a + 2d, a + 3d и… .so on. N-й член будет
an = a + (n -1) d
Геометрическая прогрессия — это ряд, в котором каждый член получается умножением или делением следующего члена на фиксированное или общее число. Например, ряды 8, 4, -2, 1, -1/2… — это геометрическая прогрессия (GP), для которой -1/2 — обычное отношение.
Установленная форма GP: a, ar, ar2, ar3, ar4… и так далее. N-й член будет an = ar (n-1)
Пример -1
Вычислите общую разность и следующий член следующего ряда:
3, 11, 19, 27, 35…
. найти общую разницу d. можно подобрать любую пару. Начнем с вычитаний.
11-3 = 8
19-11 = 8
27-19 = 8
35-27 = 8
На всем протяжении разница составляет 8, поэтому общая разница равна 8.
У нас 5 терминов. Нам нужно найти следующий или шестой член. Мы можем узнать, добавив общую разницу к пятому члену, 35 + 8 = 43.
шестой член = 43 и общая разница = 8
Пример -2
Найдите общее отношение и 7-й член следующей последовательности
2/9, 2/3, 2, 6, 18.
Мы возьмем 6/2 = 3 и 18/6 = 3, общее отношение равно 3, поэтому r = 3
У нас 5 членов, мы должны найти 6-й, а затем 7-й член.
Итак, a6 = 18 x 3 = 54
a7 = 54 x 3 = 162, ответ — обычное отношение r = 3 и седьмой член = 162.
12.3 Геометрические последовательности и ряды — промежуточная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли последовательность геометрической
- Найдите общий член (n-й член) геометрической последовательности
- Найдите сумму первых nn членов геометрической последовательности
- Найдите сумму бесконечного геометрического ряда
- Применение геометрических последовательностей и рядов в реальном мире
Будьте готовы 12.7
Прежде чем начать, пройдите тест на готовность.
Упростить: 2432.2432.
Если вы пропустили эту проблему, просмотрите Пример 1.24.
Будьте готовы 12,8
Оцените: ⓐ 3434 ⓑ (12) 4. (12) 4.
Если вы пропустили эту проблему, просмотрите Пример 1.19.
Будьте готовы 12.9
Если f (x) = 4 · 3x, f (x) = 4 · 3x, найти ⓐ f (1) f (1) ⓑ f (2) f (2) ⓒ f (3) .f (3).
Если вы пропустили эту проблему, просмотрите Пример 3.49.
Определить, является ли последовательность геометрической
Теперь мы готовы рассмотреть второй особый тип последовательности, геометрическую последовательность.
Последовательность называется геометрической последовательностью, если соотношение между последовательными членами всегда одинаково. Отношение между последовательными членами в геометрической последовательности составляет r , обычное отношение, где n больше или равно двум.
Геометрическая последовательность
Геометрическая последовательность — это последовательность, в которой соотношение между последовательными членами всегда одинаково.
Отношение между последовательными членами, anan-1, anan-1, составляет r , общее отношение . n больше или равно двум.
Рассмотрим эти последовательности.
Пример 12.21
Определите, является ли каждая последовательность геометрической. Если да, укажите обычное отношение.
ⓐ 4,8,16,32,64,128,… 4,8,16,32,64,128,…
ⓑ −2,6, −12,36, −72,216,… −2,6, −12,36, −72,216,…
ⓒ 27,9,3,1,13,19,… 27,9,3,1,13,19,…
Чтобы определить, является ли последовательность геометрической, мы находим соотношение показанных последовательных членов.
ⓐ
| Найдите соотношение следующих друг за другом членов. | 4,8,16,32,64,128,… 841683216643212864222224,8,16,32,64,128,… 84168321664321286422222 |
| Последовательность геометрическая. Обычное отношение r = 2.r = 2. |
ⓑ
| Найдите соотношение следующих друг за другом членов. | −2,6, −12,36, −72,216,… 6−2−12636−12−7236216−72−3−2−3−2−3−2,6, −12,36, −72,216,… 6−2−12636−12−7236216−72−3−2−3−2−3 |
| Последовательность не геометрическая.Нет общего соотношения. |
ⓒ
| 27,9,3,1,13,19,… 27,9,3,1,13,19,… | |
| Найдите соотношение следующих друг за другом членов. | 9273 11 1313139273 11 13131313 |
| Последовательность геометрическая. Обычное отношение r = 13. r = 13. |
Попробовать 12,41
Определите, является ли каждая последовательность геометрической. Если да, укажите общее соотношение.
ⓐ 7,21,63,189,567,1,701,… 7,21,63,189,567,1,701,…
ⓑ 64,16,4,1,14,116,… 64,16,4,1,14,116,…
ⓒ 2,4,12,48,240,1,440,… 2,4,12,48,240,1,440,…
Попробовать 12,42
Определите, является ли каждая последовательность геометрической. Если да, укажите общее соотношение.
ⓐ −150, −30, −15, −5, −52,0,… −150, −30, −15, −5, −52,0,…
ⓑ 5,10,20,40,80,160,… 5,10,20,40,80,160,…
ⓒ 8,4,2,1,12,14,… 8,4,2,1,12,14,…
Если мы знаем первый член, a1, a1, и общее отношение, r , мы можем перечислить конечное число членов последовательности.
Пример 12.22
Запишите первые пять членов последовательности, где первый член равен 3, а общее отношение r = −2.r = −2.
Мы начинаем с первого члена и умножаем его на обыкновенный коэффициент. Затем мы умножаем этот результат на обычное отношение, чтобы получить следующий член, и так далее.
a1a2a3a4a533 · (−2) −6 · (−2) 12 · (−2) −24 · (−2) −612−2448a1a2a3a4a533 · (−2) −6 · (−2) 12 · (−2) −24 · (−2) −612−2448
Последовательность: 3, −6,12, −24,48,… 3, −6,12, −24,48,…
Попробуй 12.43
Запишите первые пять членов последовательности, где первый член равен 7, а общее отношение r = −3.r = −3.
Попробовать 12,44
Запишите первые пять членов последовательности, где первый член равен 6, а общее отношение r = −4.r = −4.
Найдите общий член (
n -й член) геометрической последовательности
Подобно тому, как мы нашли формулу для общего члена последовательности и арифметической последовательности, мы можем также найти формулу для общего члена геометрической последовательности.
Давайте запишем несколько первых членов последовательности, где первый член равен a1a1, а общее отношение равно r . Затем мы будем искать образец.
Когда мы ищем шаблон в пяти приведенных выше членах, мы видим, что каждый из терминов начинается с a1.a1.
Первый член a1, a1 не умножается на r . Во втором члене a1a1 умножается на r . В третьем члене a1a1 умножается на r два раза (r · rr · r или r2r2).В четвертом члене a1a1 умножается на r три раза (r · r · rr · r · r или r3r3), а в пятом члене a1a1 умножается на r четыре раза. В каждом члене количество раз, которое a1a1 умножается на , r на единицу меньше количества члена. Это приводит нас к следующим
Общий термин (
n -й член) геометрической последовательности
Общий член геометрической последовательности с первым членом a1a1 и знаменателем r равен
Мы будем использовать эту формулу в следующем примере, чтобы найти четырнадцатый член последовательности.
Пример 12.23
Найдите четырнадцатый член последовательности, в котором первый член равен 64, а общее отношение r = 12.r = 12.
| Чтобы найти четырнадцатый член, a14, a14, , используйте формулу с a1 = 64a1 = 64 и r = 12.r = 12. | an = a1rn − 1an = a1rn − 1 |
| Подставить значения. | a14 = 64 (12) 14−1a14 = 64 (12) 14−1 |
| Упростить. | a14 = 64 (12) 13a14 = 64 (12) 13 |
| a14 = 1128a14 = 1128 |
Попробуй 12.45
Найдите тринадцатый член последовательности, в которой первый член равен 81, а общее отношение r = 13.r = 13.
Попробовать 12,46
Найдите двенадцатый член последовательности, в котором первый член равен 256, а общее отношение r = 14.r = 14.
Иногда мы не знаем общего отношения, и мы должны использовать данную информацию, чтобы найти его, прежде чем мы найдем запрошенный термин.
Пример 12.24
Найдите двенадцатый член последовательности 3, 6, 12, 24, 48, 96,… Найдите общий член последовательности.
Чтобы найти двенадцатый член, мы используем формулу an = a1rn − 1, an = a1rn − 1, и поэтому нам нужно сначала определить a1a1 и общее отношение r .
| 3,6,12,24,48,96,… 3,6,12,24,48,96,… | |
| Первый член — три. | а1 = 3а1 = 3 |
| Найдите общее отношение. | 63126241248249648222226312624124824964822222 |
| Обычное отношение r = 2.г = 2. | |
| Чтобы найти двенадцатый член, a12, a12, используйте формулу с a1 = 3andr = 2.a1 = 3andr = 2. | an = a1rn − 1an = a1rn − 1 |
| Подставить значения. | a12 = 3 · 212−1a12 = 3 · 212−1 |
| Упростить. | a12 = 3 · 211a12 = 3 · 211 |
| a12 = 6,144a12 = 6,144 | |
| Найдите общий термин. | an = a1rn − 1an = a1rn − 1 |
| Мы используем формулу с a1 = 3andr = 2.а1 = 3 и г = 2. | an = 3 (2) n − 1an = 3 (2) n − 1 |
Попробовать 12,47
Найдите девятый член последовательности 6, 18, 54, 162, 486, 1,458,… Затем найдите общий член последовательности.
Попробовать 12,48
Найдите одиннадцатый член последовательности 7, 14, 28, 56, 112, 224,… Затем найдите общий член последовательности.
Найдите сумму первых
n членов геометрической последовательности
Мы нашли сумму как общих последовательностей, так и арифметических последовательностей.Теперь сделаем то же самое для геометрических последовательностей. Сумма Sn, Sn первых n членов геометрической последовательности записывается как Sn = a1 + a2 + a3 + … + an.Sn = a1 + a2 + a3 + … + an. Мы можем записать эту сумму, начав с первого члена, a1, a1, и продолжив умножение на r , чтобы получить следующий член как:
Sn = a1 + a1r + a1r2 + … + a1rn − 1 Sn = a1 + a1r + a1r2 + … + a1rn − 1
Давайте также умножим обе части уравнения на r .
rSn = a1r + a1r2 + a1r3 + … + a1rnrSn = a1r + a1r2 + a1r3 + … + a1rn
Затем мы вычитаем эти уравнения.Мы увидим, что при вычитании все, кроме первого члена верхнего уравнения и последнего члена нижнего уравнения, вычитаются до нуля.
| Sn = a1 + a1r + a1r2 + a1r3 +… + a1rn − 1rSn = a1r + a1r2 + a1r3 +… + a1rn − 1 + a1rn ____________________________________________________ Sn − rSn = a1 − a1rnSn = a1 + a1r-1r + ar1 + arn + arn + a1 + a1r + ar1 + arn + + a1r2 + a1r3 +… + a1rn − 1 + a1rn ____________________________________________________ Sn − rSn = a1 − a1rn | |
| Мы учитываем обе стороны. | Sn (1-r) = a1 (1-rn) Sn (1-r) = a1 (1-rn) |
| Чтобы получить формулу для Sn, Sn, разделите обе части на (1 — r).(1-г). | Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − r |
Сумма первых
n членов геометрического ряда
Сумма Sn, Sn первых n членов геометрической последовательности равна
Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − r
, где a1a1 — первое слагаемое, r — обычное отношение, а r не равно единице.
Мы применяем эту формулу в следующем примере, где даны первые несколько членов последовательности.Обратите внимание, что сумма геометрической последовательности обычно становится очень большой, когда общее отношение больше единицы.
Пример 12.25
Найдите сумму первых 20 членов геометрической последовательности 7, 14, 28, 56, 112, 224,…
Для нахождения суммы воспользуемся формулой Sn = a1 (1 − rn) 1−r.Sn = a1 (1 − rn) 1 − r. Мы знаем, что a1 = 7, a1 = 7, r = 2, r = 2 и n = 20. n = 20.
| Зная a1 = 7, r = 2, a1 = 7, r = 2 и n = 20, n = 20, используйте формулу суммы. | Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − r |
| Подставить значения. | S20 = 7 (1-220) 1-2S20 = 7 (1-220) 1-2 |
| Упростить. | S20 = 7,340,025S20 = 7,340,025 |
Попробовать 12,49
Найдите сумму первых 20 членов геометрической последовательности 3, 6, 12, 24, 48, 96,…
Попробуйте 12,50
Найдите сумму первых 20 членов геометрической последовательности 6, 18, 54, 162, 486, 1,458,…
В следующем примере нам дана сумма в виде суммирования. Хотя сложение всех членов возможно, чаще всего проще всего использовать формулу, чтобы найти сумму первых n членов.
Для использования формулы нам нужно r . Мы можем найти его, выписав несколько первых членов последовательности и найдя их соотношение. Другой вариант — понять, что в обозначении суммирования последовательность записывается в виде ∑i = 1ka (r) i, ∑i = 1ka (r) i, где r — это обычное отношение.
Пример 12.26
Найдите сумму: ∑i = 1152 (3) i.i = 1152 (3) i.
Чтобы найти сумму, мы будем использовать формулу Sn = a1 (1 − rn) 1 − r, Sn = a1 (1 − rn) 1 − r, что требует a1a1 и r .Мы выпишем несколько терминов, чтобы получить необходимую информацию.
Попробуйте 12,51
Найдите сумму: ∑i = 1156 (2) i.i = 1156 (2) i.
Попробуйте 12,52
Найдите сумму: ∑i = 1105 (2) i.i = 1105 (2) i.
Найдите сумму бесконечного геометрического ряда
Если мы возьмем геометрическую последовательность и сложим члены, мы получим сумму, которая называется геометрическим рядом. Бесконечный геометрический ряд — это бесконечная сумма, первый член которой равен a1a1, а обычное отношение равно r и записывается как
.
a1 + a1r + a1r2 +… + a1rn − 1 +… a1 + a1r + a1r2 +… + a1rn − 1 +…
Серия Infinite Geometric
Бесконечный геометрический ряд представляет собой бесконечную сумму, первый член которой равен a1a1, а обычное отношение равно r и записывается как
a1 + a1r + a1r2 +… + a1rn − 1 +… a1 + a1r + a1r2 +… + a1rn − 1 +…
Мы знаем, как найти сумму первых n членов геометрического ряда, используя формулу Sn = a1 (1 − rn) 1 − r.Sn = a1 (1 − rn) 1 − r. Но как найти сумму бесконечной суммы?
Давайте посмотрим на бесконечный геометрический ряд 3 + 6 + 12 + 24 + 48 + 96 +… .3 + 6 + 12 + 24 + 48 + 96 +…. Каждый член становится все больше и больше, поэтому имеет смысл, что сумма бесконечного числа членов становится больше. Давайте посмотрим на несколько неполных сумм по этой серии. Мы видим a1 = 3a1 = 3 и r = 2r = 2
Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rS10 = 3 (1−210) 1−2S30 = 3 (1−230) 1− 2S50 = 3 (1−250) 1−2S10 = 3,069S30 = 3,221,225,469S50≈3,38 × 1015Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1− rS10 = 3 (1-210) 1-2S30 = 3 (1-230) 1-2S50 = 3 (1-250) 1-2S10 = 3,069S30 = 3,221,225,469S50≈3.38 × 1015
По мере того, как n становится все больше и больше, сумма становится все больше и больше. Это верно, когда | r | ≥1 | r | ≥1 и мы называем этот ряд расходящимся. Мы не можем найти сумму бесконечного геометрического ряда, когда | r | ≥1. | R | ≥1.
Давайте посмотрим на бесконечный геометрический ряд, общее отношение которого меньше единицы,
12 + 14 + 18 + 116 + 132 + 164 +… 12 + 14 + 18 + 116 + 132 + 164 +…. Здесь члены становятся все меньше и меньше по мере увеличения n . Давайте посмотрим на несколько конечных сумм для этой серии. Мы видим a1 = 12a1 = 12 и r = 12.г = 12.
Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rS10 = 12 (1− (12) 10) 1−12S20 = 12 (1− ( 12) 20) 1−12S30 = 12 (1− (12) 30) 1−12S10≈.99
375S20≈0,99999
S30≈0,9999999991Sn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rSn = a1 (1 − rn) 1 − rS10 = 12 (1− (12) 10) 1−12S20 = 12 (1− (12) 20) 1−12S30 = 12 (1− (12) 30) 1−12S10≈. 99
375S20≈0,99999
S30≈0,9999999991
Обратите внимание, что сумма становится все больше и больше, но также становится все ближе и ближе к единице. Когда | r | <1, | r | <1, выражение rnrn становится все меньше и меньше. В этом случае мы называем этот ряд сходящимся.Когда n приближается к бесконечности (становится бесконечно большим), rnrn становится все ближе и ближе к нулю. В нашей формуле суммы мы можем заменить rnrn на ноль, и тогда мы получим формулу суммы S для бесконечного геометрического ряда, когда | r | <1. | r | <1.
Sn = a1 (1 − rn) 1 − rS = a1 (1−0) 1 − rS = a11 − rSn = a1 (1 − rn) 1 − rS = a1 (1−0) 1 − rS = a11 − r
Эта формула дает нам сумму бесконечной геометрической последовательности. Обратите внимание, что S не имеет нижнего индекса n , как в SnSn, поскольку мы не добавляем конечное количество членов.
Сумма бесконечного геометрического ряда
Для бесконечного геометрического ряда с первым членом a1a1 и знаменателем r ,
Если | r | <1, сумма равна Если | r | <1, сумма равна
Если | r | ≥1, бесконечный геометрический ряд не имеет суммы. Мы говорим, что ряд расходится. Если | r | ≥1, бесконечный геометрический ряд не имеет суммы. Мы говорим, что серии расходятся.
Пример 12.27
Найдите сумму бесконечного геометрического ряда 54 + 18 + 6 + 2 + 23 + 29 +… 54 + 18 + 6 + 2 + 23 + 29 +…
Чтобы найти сумму, мы сначала должны убедиться, что общее отношение | r | <1 | r | <1, а затем мы можем использовать формулу суммы S = a11 − r.S = a11 − r.
| Найдите общее отношение. | г = 1854 г = 618… г = 1854 г = 618… |
| r = 13r = 13 | r | <1r = 13r = 13 | r | <1 | |
| Определите a1.a1. | а1 = 54а1 = 54 |
| Зная a1 = 54, r = 13, a1 = 54, r = 13, используйте формулу суммы. | S = a11-rS = a11-r |
| Подставить значения. | S = 541-13S = 541-13 |
| Упростить. | S = 81 S = 81 |
Попробуй 12.53
Найдите сумму бесконечного геометрического ряда 48 + 24 + 12 + 6 + 3 + 32 +… 48 + 24 + 12 + 6 + 3 + 32 +…
Попробуйте 12,54
Найдите сумму бесконечного геометрического ряда 64 + 16 + 4 + 1 + 14 + 116 +… 64 + 16 + 4 + 1 + 14 + 116 +…
Интересным вариантом использования бесконечных геометрических рядов является запись повторяющейся десятичной дроби в виде дроби.
Пример 12.28
Запишите повторяющуюся десятичную дробь 0,5–0,5– в виде дроби.
| Записываем 0.5–0,5– показывая повторяющуюся пятерку. | 0,5555555555555… 0,5555555555555… |
| Используйте разряд, чтобы записать это как сумму. | 0,5 + 0,05 + 0,005 + 0,0005 + … 0,5 + 0,05 + 0,005 + 0,0005 + … |
| Это бесконечный геометрический ряд. | |
| Найдите общее отношение. | r = 0,050,5r = 0,0050,05… r = 0,050,5r = 0,0050,05… |
| r = 0,1r = 0,1 | r | <1r = 0,1r = 0,1 | r | <1 | |
| Определить a1.а1. | а1 = 0,5а1 = 0,5 |
| Зная a1 = 0,5, r = 0,1, a1 = 0,5, r = 0,1, используйте формулу суммы. | S = a11-rS = a11-r |
| Подставить значения. | S = 0,51-0,1S = 0,51-0,1 |
| Упростить. | S = 0,50,9S = 0,50,9 |
| Умножьте числитель и знаменатель на 10. | S = 59S = 59 |
| Нас просят найти форму дроби. | 0,5– = 590,5– = 59 |
Попробуй 12.55
Запишите повторяющуюся десятичную дробь 0,4–0,4– в виде дроби.
Попробуйте 12,56
Запишите повторяющуюся десятичную дробь 0,8–0,8– в виде дроби.
Применение геометрических последовательностей и рядов в реальном мире
Одно из применений геометрических последовательностей связано с потребительскими расходами. Если налоговая скидка предоставляется каждому домохозяйству, ее влияние на экономику во много раз превышает сумму индивидуальной скидки.
Пример 12.29
Правительство решило предоставить налоговую скидку в размере 1000 долларов каждому домохозяйству, чтобы стимулировать экономику.Согласно государственной статистике, каждая семья потратит 80% скидки на товары и услуги. Компании и частные лица, получившие выгоду от этих 80%, затем потратят 80% от того, что они получили, и так далее. Результат называется эффектом умножения. Каков общий эффект скидки на экономику?
Каждый раз, когда деньги идут в экономику, 80% их тратится и затем направляется в экономику, чтобы быть потраченным. Опять же, 80% этих денег снова тратится в экономике. Эта ситуация продолжается и приводит нас к бесконечному геометрическому ряду.
1000 + 1000 (0,8) +1000 (0,8) 2 +… 1000 + 1000 (0,8) +1000 (0,8) 2 +…
Здесь первый член равен 1000, a1 = 1000.a1 = 1000. Обычное отношение составляет 0,8,0,8, r = 0,8.r = 0,8. Мы можем оценить эту сумму, поскольку 0,8 <1,0,8 <1. Воспользуемся формулой суммы бесконечного геометрического ряда.
| S = a11-rS = a11-r | |
| Подставьте значения, a1 = 1,000, a1 = 1,000 и r = 0,8.r = 0,8. | S = 1,0001-0,8S = 1,0001-0,8 |
| Оценить. | S = 5,000 S = 5,000 |
Общий эффект от 1000 долларов, полученных каждым домохозяйством, приведет к росту экономики на 5000 долларов.
Попробуйте 12,57
Каков общий эффект на экономику государственной налоговой скидки в размере 1000 долларов США для каждого домохозяйства с целью стимулирования экономики, если каждое домохозяйство потратит 90% скидки на товары и услуги?
Попробуйте 12,58
Каков общий эффект на экономику государственной налоговой скидки в размере 500 долларов для каждого домохозяйства с целью стимулирования экономики, если каждое домохозяйство потратит 85% скидки на товары и услуги?
Мы рассмотрели формулу сложных процентов, в которой основная сумма P инвестируется под процентную ставку r на t лет.Новый баланс, A , равен A = P (1 + rn) ntA = P (1 + rn) nt, когда проценты начисляются n раз в год. Эта формула применяется, когда единовременная сумма была инвестирована авансом, и сообщает нам ее стоимость по истечении определенного периода времени.
Аннуитет — это инвестиция, которая представляет собой последовательность равных периодических вкладов. Мы будем рассматривать аннуитеты, которые выплачивают проценты во время депозита. По мере того, как мы разрабатываем формулу для величины аннуитета, мы собираемся положить n = 1.n = 1. Это означает, что есть один депозит в год.
| А = P (1 + rn) ntA = P (1 + rn) nt | |
| Пусть n = 1.n = 1. | А = P (1 + r1) 1tA = P (1 + r1) 1t |
| Упростить. | А = P (1 + r) tA = P (1 + r) t |
Предположим, что в конце каждого года инвестируется P долларов. Через год этот депозит будет стоить P (1 + r) 1P (1 + r) 1 доллар, а еще через год он будет стоить P (1 + r) 2P (1 + r) 2 доллара. Через t лет он будет стоить A = P (1 + r) tA = P (1 + r) t долларов.
| Конец 1 года | Конец года 2 | Конец года 3 | |
|---|---|---|---|
| Первый депозит P на конец года 1 | п | Сумма через год P (1 + r) 1P (1 + r) 1 | Сумма 2 года спустя П (1 + г) 2П (1 + г) 2 |
| 2-й депозит P на конец года 2 | п | Сумма через год P (1 + r) 1P (1 + r) 1 | |
| 3 рд Депозит P на конец 3 года | п |
Через три года размер аннуитета составляет
Это сумма членов геометрической последовательности, в которой первый член равен P , а общее отношение равно 1 + r.1 + р. Подставляем эти значения в формулу суммы. Будьте осторожны, у нас есть два разных использования r . r в формуле суммы — это обычное отношение последовательности. В данном случае это 1 + r1 + r, где r — процентная ставка.
| St = a1 (1-rt) 1-rSt = a1 (1-rt) 1-r | |
| Подставить значения. | St = P (1− (1 + r) t) 1− (1 + r) St = P (1− (1 + r) t) 1− (1 + r) |
| Упростить. | St = P (1− (1 + r) t) −rSt = P (1− (1 + r) t) −r |
| St = P ((1 + r) t − 1) rSt = P ((1 + r) t − 1) r |
Помните, что наша предпосылка заключалась в том, что один депозит вносился в конце каждого года.
Мы можем адаптировать эту формулу для n депозитов в год, а проценты начисляются n раз в год.
Размер ренты с начислением процентов nn раз в год
Для основной суммы, P , инвестировано в конце периода начисления сложных процентов, с процентной ставкой, r , которая начисляется n раз в год, новый баланс, A, через t лет , это
При = P ((1 + rn) nt − 1) rnAt = P ((1 + rn) nt − 1) rn
Пример 12.30
Новые родители решают вкладывать 100 долларов в месяц в аннуитет для своей маленькой дочери. По счету будет выплачиваться 5% годовых, которые начисляются ежемесячно. Сколько будет на счету ребенка к восемнадцатилетию?
Чтобы найти формулу ренты, At = P ((1 + rn) nt − 1) rn, At = P ((1 + rn) nt − 1) rn, нам нужно идентифицировать P , r , n и t .
| Укажите P , сумму, инвестируемую каждый месяц. | P = 100P = 100 |
| Укажите r , годовую процентную ставку в десятичной форме. | r = 0,05r = 0,05 |
| Укажите n , , сколько раз будет сделан депозит и начисляются проценты каждый год. | п = 12 п = 12 |
| Обозначим т , количество лет. | т = 18 т = 18 |
| Зная P = 100, r = 0,05, n = 12 и P = 100, r = 0,05, n = 12 и t = 18, t = 18, используйте формулу суммы. | At = P ((1 + rn) nt − 1) rnAt = P ((1 + rn) nt − 1) rn |
| Подставить значения. | At = 100 ((1 + 0,0512) 12 · 18−1) 0,0512At = 100 ((1 + 0,0512) 12 · 18−1) 0,0512 |
| Используйте калькулятор для оценки. Обязательно используйте скобки по мере необходимости. | Ат = 34 920,20 Ат = 34 920,20 |
| У ребенка будет 34 920,20 доллара, когда ей исполнится 18 лет. |
Попробуйте 12,59
Новые бабушка и дедушка решают вкладывать 200 долларов в месяц в качестве ренты для своего внука.По счету будет выплачиваться 5% годовых, которые начисляются ежемесячно. Сколько будет на счету ребенка к его двадцать первому дню рождения?
Попробуйте 12.60
Артуро только что получил свою первую постоянную работу после окончания колледжа в возрасте 27 лет. Он решил инвестировать 200 долларов в месяц в IRA (аннуитет). Процентная ставка по аннуитету составляет 8%, которая начисляется ежемесячно. Сколько будет на счету Артуро, когда он выйдет на пенсию в свой шестьдесят седьмой день рождения?
Раздел 12.3 упражнения
Практика ведет к совершенству
Определить, является ли последовательность геометрической
В следующих упражнениях определите, является ли последовательность геометрической, и если да, укажите общее отношение.
127.
3,12,48,192,768,3072,… 3,12,48,192,768,3072,…
128.
2,10,50,250,1250,6250,… 2,10,50,250,1250,6250,…
129.
72,36,18,9,92,94,… 72,36,18,9,92,94,…
130.
54,18,6,2,23,29,… 54,18,6,2,23,29,…
131.
−3,6, −12,24, −48,96,… −3,6, −12,24, −48,96,…
132.
2, −6,18, −54,162, −486,… 2, −6,18, −54,162, −486,…
В следующих упражнениях определите, является ли каждая последовательность арифметической, геометрической или ни одной из них. Если арифметический, укажите общую разницу. Если геометрический, укажите общее отношение.
133.
48,24,12,6,3,32,… 48,24,12,6,3,32,…
134.
12,6,0, −6, −12, −18,… 12,6,0, −6, −12, −18,…
135.
−7, −2,3,8,13,18,… −7, −2,3,8,13,18,…
136.
5,9,13,17,21,25,… 5,9,13,17,21,25,…
137.
12,14,18,116,132,164,… 12,14,18,116,132,164,…
138.
4,8,12,24,48,96,… 4,8,12,24,48,96,…
В следующих упражнениях запишите первые пять членов каждой геометрической последовательности с заданным первым членом и знаменателем.
141.
a1 = −4a1 = −4 и r = −2r = −2
142.
a1 = −5a1 = −5 и r = −3r = −3
Найдите общий член ( n -й член) геометрической последовательности
В следующих упражнениях найдите указанный член последовательности, в которой дан первый член и общее отношение.
145.
Найдите a11a11 при a1 = 8a1 = 8 и r = 3.r = 3.
146.
Найдите a13a13 при a1 = 7a1 = 7 и r = 2.r = 2.
147.
Найдите a10a10 при a1 = −6a1 = −6 и r = −2.r = −2.
148.
Найдите a15a15 при a1 = −4a1 = −4 и r = −3.r = −3.
149.
Найдите a10a10 при a1 = 100000a1 = 100000 и r = 0,1.r = 0,1.
150.
Найдите a8a8 при a1 = 1 000 000 a1 = 1 000 000 и r = 0,01. R = 0,01.
В следующих упражнениях найдите указанный член данной последовательности.Найдите общий термин для последовательности.
151.
Найдите a9a9 последовательности, 9,18,36,72,144,288,… 9,18,36,72,144,288,…
152.
Найдите a12a12 последовательности, 5,15,45,135,405,1215,… 5,15,45,135,405,1215,…
153.
Найдите a15a15 последовательности, −486,162, −54,18, −6,2,… −486,162, −54,18, −6,2,…
154.
Найдите a16a16 последовательности, 224, −112,56, −28,14, −7,… 224, −112,56, −28,14, −7,…
155.
Найдите a10a10 последовательности, 1,0.1,0.01,0.001,0.0001,0.00001,… 1,0.1,0.01,0.001,0.0001,0.00001,…
156.
Найдите a9a9 последовательности, 1000,100,10,1,0.1,0.01,… 1000,100,10,1,0.1,0.01,…
Найдите сумму первых n членов геометрической последовательности
В следующих упражнениях найдите сумму первых пятнадцати членов каждой геометрической последовательности.
157.
8,24,72,216,648,1944,… 8,24,72,216,648,1944,…
158.
7,14,28,56,112,224,… 7,14,28,56,112,224,…
159.
−6,12, −24,48, −96,192,… −6,12, −24,48, −96,192,…
160.
-4,12, -36,108, -324,972,… -4,12, -36,108, -324,972,…
161.
81,27,9,3,1,13,… 81,27,9,3,1,13,…
162.
256,64,16,4,1,14,116,… 256,64,16,4,1,14,116,…
В следующих упражнениях найдите сумму геометрической последовательности.
167.
∑i = 1109 (13) i∑i = 1109 (13) i
168.
∑i = 1154 (12) i∑i = 1154 (12) i
Найдите сумму бесконечного геометрического ряда
В следующих упражнениях найдите сумму каждого бесконечного геометрического ряда.
169.
1 + 13 + 19 + 127 + 181 + 1243 + 1729 +… 1 + 13 + 19 + 127 + 181 + 1243 + 1729 +…
170.
1 + 12 + 14 + 18 + 116 + 132 + 164 +… 1 + 12 + 14 + 18 + 116 + 132 + 164 +…
171.
6−2 + 23−29 + 227−281 +… 6−2 + 23−29 + 227−281 +…
172.
−4 + 2−1 + 12−14 + 18−… −4 + 2−1 + 12−14 + 18−…
173.
6 + 12 + 24 + 48 + 96 + 192 +… 6 + 12 + 24 + 48 + 96 + 192 +…
174.
5 + 15 + 45 + 135 + 405 + 1215 +… 5 + 15 + 45 + 135 + 405 + 1215 +…
175.
1024 + 512 + 256 + 128 + 64 + 32 +… 1024 + 512 + 256 + 128 + 64 + 32 +…
176.
6,561 + 2187 + 729 + 243 + 81 + 27 +… 6,561 + 2187 + 729 + 243 + 81 + 27 +…
В следующих упражнениях запишите каждую повторяющуюся десятичную дробь в виде дроби.
Применение геометрических последовательностей и рядов в реальном мире
Решите проблему с помощью следующих упражнений.
183.
Найдите общий эффект на экономику каждой государственной налоговой скидки для каждого домохозяйства с целью стимулирования экономики, если каждое домохозяйство потратит указанный процент скидки на товары и услуги.
| Налоговая скидка каждому домохозяйству | Процент, потраченный на товары и услуги | Общий эффект на экономику | |
|---|---|---|---|
| ⓐ | 1000 долларов США 1000 долларов США | 85% 85% | |
| ⓑ | 1000 долларов США 1000 долларов США | 75% 75% | |
| ⓒ | $ 1,500 $ 1,500 | 90% 90% | |
| ⓓ | $ 1,500 $ 1,500 | 80% 80% |
184.
Новые бабушка и дедушка решают вкладывать 100 долларов в месяц в качестве ренты для своего внука. По счету будет выплачиваться 6% 6% годовых, которые начисляются ежемесячно (12 раз в год). Сколько будет на счету ребенка к двадцать первому дню рождения?
185.
Беренис только что получила свою первую постоянную работу после окончания колледжа в возрасте 30 лет. Она решила инвестировать 500 долларов в квартал в IRA (аннуитет). Процентная ставка по аннуитету составляет 7% 7%, которая начисляется ежеквартально (4 раза в год).Сколько будет на счету Беренис, когда она выйдет на пенсию в возрасте 65 лет?
186.
Алиса хочет купить дом примерно через пять лет. Она вносит 500 долларов 500 долларов в месяц в аннуитет, который приносит 5% 5% годовых, которые начисляются ежемесячно (12 раз в год). Сколько у Алисы будет первоначальный взнос через пять лет?
187.
Майра только что получила свою первую постоянную работу после окончания колледжа. Она планирует получить степень магистра и поэтому вкладывает 2500 долларов в год из своего годового бонуса в аннуитет.Аннуитет выплачивается 6.5% 6.5% в год и начисляется ежегодно. Сколько она накопит за пять лет, чтобы получить степень магистра?
Письменные упражнения
188.
Объясните своими словами, как определить, является ли последовательность геометрической.
189.
Объясните своими словами, как найти общий член геометрической последовательности.
190.
Объясните своими словами разницу между геометрической последовательностью и геометрической последовательностью.
191.
Объясните своими словами, как определить, есть ли сумма в бесконечном геометрическом ряду и как ее найти.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Последовательности и серии вопросов для девятого класса (9 класс) для тестов и рабочих листов
Вы можете создавать печатные тесты и рабочие листы из этих
Последовательности и серии 9 класса вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.Затем нажмите кнопку «Добавить выбранные вопросы к тесту » перед переходом на другую страницу.
Предыдущая
Страница 1 из 3
След.
Выбрать все вопросы
Найдите следующие три члена последовательности.[математика] 14,34,54,74,94, … [/ математика]
- 114, 134, 154
- 188, 208, 228
- 104, 124, 144
- 84, 104, 124
Предыдущая
Страница 1 из 3
След.
Часть 6: Ряды и последовательности
В этой статье мы рассмотрим ряды и последовательности, которые являются важным навыком в математике в средней школе.
Умение успешно решать простые серии и навыки последовательностей позволяют учащимся заложить прочный фундамент и позволяют им решать более сложные проблемы, с которыми они столкнутся позже.
Сюда входит умение умело решать вопросы, связанные с экспоненциальным ростом / спадом, финансовой математикой и т. Д.
В этой статье мы обсуждаем:
Результаты программы NESA
NESA требует, чтобы студенты владели следующей программой исходы:
- Знайте разницу между последовательностью и серией
- Распознавайте и используйте рекурсивное определение арифметической последовательности: \ (T_ {n} = T_ {n — 1} + d, \ T_ {1} = a \)
- Установите и используйте формулу для члена \ (n ^ {th} \) (где \ (𝑛 \) — положительное целое число) арифметической последовательности: \ (𝑇 = 𝑎 + (𝑛 — 1) 𝑑 \), где \ (𝑎 \) — первый член, а \ (𝑑 \) — общее различие, и признать его линейный характер
- Установите и используйте формулы для суммы первых \ (𝑛 \) членов арифметическая последовательность: \ (S_ {n} = \ frac {n} {2} (a + l) \), где \ (𝑙 \) — последний член в последовательности, а \ (S_ {n} = \ fra c {n} {2} (2a + (n-1) d) \)
- Выявление и использование арифметических последовательностей и арифметических рядов в контекстах, включающих дискретный линейный рост или убывание, например простой процент (ACMMM070)
- Распознавать и использовать рекурсивное определение геометрической последовательности: \ (T_ {n} = rT_ {n-1}, \ T_ {1} = a \) (ACMMM072)
- Установите и используйте формулу для \ (𝑛 ^ {th} \ ) член геометрической последовательности: \ (T_ {n} = ar ^ {n-1} \), где \ (𝑎 \) — первый член, \ (𝑟 \) — общее отношение и \ (𝑛 \) является положительным целым числом и распознает его экспоненциальный характер (ACMMM073)
- Установите и используйте формулу для суммы первых \ (𝑛 \) членов геометрической последовательности: \ (S_ {n} = \ frac {a (r ^ {n})} {1-r} = \ frac {a (r ^ {n} — 1)} {r-1} \) (ACMMM075)
- Выведите и используйте формулу для предельной суммы геометрической серия с \ (| 𝑟 | <1: S = \ frac {a} {1-r} \)
Предполагаемые знания
Учащиеся уже должны быть знакомы с основами арифметики операции и индексы.Это включает в себя возможность распознавать обозначение суммы и использовать основные законы индекса для определения переменных.
Введение в серии и последовательности
Последовательность
Последовательность — это набор чисел, который подчиняется определенному правилу. По сути, последовательность — это упорядоченный список, разделенный запятыми.
Каждое число в последовательности называется термином \ (T_ {n} \), где \ (n \) является числовой позицией числа. Например. \ (3, 6, 9, 12, 15… \)
Последовательность может быть конечной (т. Е.е. количество членов фиксировано) или бесконечно (т. е. когда количество членов в последовательности бесконечно). Бесконечная последовательность заканчивается на «…».
Серия
И наоборот, серия — это сумма членов последовательности.
Т.е. \ (1 + 2 + 3 + 4… \) — это серия, а \ (1, 2, 3, 4… \) — последовательность.
Каждый член в серии отделяется знаком плюса. Следующие обозначения сигма / суммы также могут использоваться для определения ряда:
\ begin {align}
\ sum_ {k = 1} ^ {n} T_ {k}
\ end {align}
Где \ (n \) относится к количеству терминов, а \ (T_ {k} \) относится к правилу / шаблону, за которым следует серия.{2} + 5k — 6 & = 0 \\
(k-1) (k + 6) & = 0 \\
k = 1 \ или \ k = -6
\ end {align}
Однако \ (к> 0 \). Следовательно, 1-й член \ ((T_ {1}) \) равен 0.
Арифметическая прогрессия (AP)
Арифметическая прогрессия — это последовательность или последовательность, в которой каждый член определяется добавлением константы к предыдущему члену:
Арифметическая последовательность : \ (3, 5, 7, 9… \)
Арифметическая последовательность : \ (3 + 5 + 7 + 9… \)
Общая разность
Константа, добавленная к Предыдущий член известен как общая разница, \ (d \)
Общая разница может быть положительной или отрицательной.
Чтобы найти общую разницу в арифметической прогрессии, два последовательных члена вычитаются друг из друга:
\ begin {align}
d = T_ {n} — T_ {n-1}
\ end {align}
Доказательство арифметического ряда
Чтобы доказать арифметический ряд, мы должны доказать, что разница между двумя наборами последовательных членов одинакова. То есть:
\ begin {align}
T_ {2} — T_ {1} = T_ {3} — T_ {2}
\ end {align}
Условия арифметической прогрессии
Ниже приведена формула связаны с членами в арифметической прогрессии:
\ begin {align}
T_ {n} = a + (n-1) d
\ end {align}
Где \ (a \) = первый член, \ ( d \) = общая разница и \ (n \) = количество терминов в AP.
Сумма арифметической прогрессии
Есть две формулы, которые можно использовать для нахождения суммы арифметической прогрессии:
\ begin {align}
S_ {n} = \ frac {n} {2} \ big {(} 2a + (n-1) d \ big {)}
\ end {align}
Где \ (a \) = первый член, \ (d \) = общая разница и \ (n \ ) = количество терминов в AP.
\ begin {align}
S_ {n} = \ frac {n} {2} (a + l)
\ end {align}
Где \ (a \) = первый член, \ (l \) = последний член и \ (n \) = количество терминов в AP.
Задачи, связанные с арифметическими последовательностями
Существуют различные типы задач, связанных с арифметическими последовательностями.
К ним относятся:
- Нахождение суммы
- Нахождение конкретного члена
- Определение общей разности
Пример 2
Первый член арифметического ряда равен 4, а пятый член четырехкратного третьего срок. Найдите общее различие.
Решение 2
Мы знаем, что \ (a = 4 \) и \ (T_ {5} = 4T_ {3} \).Использование формулы для члена в арифметической прогрессии \ (\ big {(} T_ {n} = a + (n-1) d \ big {)} \):
\ begin {align}
T_ {5} & = 4T_ {3} \\
4 + (5-1) d & = 4 \ big {(} 4 + (3-1) d \ big {)} \\
4 + 4d & = 16 + 8d \ \
∴ d & = 3
\ end {align}
Хотите убедиться, что следующей маркой в вашей серии будет Band 6?
Проверьте свои навыки серий и последовательностей с помощью нашего бесплатного рабочего листа!
Геометрическая прогрессия (GP)
Геометрическая прогрессия — это последовательность или последовательность, в которой каждый член находится путем умножения предыдущего члена на константу:
Геометрическая последовательность : \ (5, 25, 125, 625… \ )
Геометрическая серия : \ (5 + 25 + 125 + 625… \)
Общее отношение
Константа, которая умножается на предыдущий член, называется общим отношением \ (r \).{n} — 1)} {r-1}
\ end {align}
Где \ (a \) = первый член, \ (r \) = обычное отношение и \ (n \) = количество термины в ГП.
Предельная сумма
Если \ (- 1 Эта фиксированная константа также известна как предельная сумма / сумма до бесконечности \ ((S _ {\ infty}) \) и является общей суммой этого бесконечного геометрического ряда. Чтобы найти его, мы используем следующую формулу: \ begin {align} Где \ (a \) = первый член, \ (r \) = обычное отношение и \ (-1 Существуют различные типы задач, связанных с геометрическими прогрессиями. К ним относятся: Некоторые вопросы могут даже включать сочетание арифметических и геометрических прогрессий. В этих случаях мы хотим решить две прогрессии отдельно. Пример 3 Популяция цикад в тропических лесах Какаду ежегодно уменьшается на 15%. Однако благодаря реабилитационным программам в начале каждого года вводится 70 дополнительных цикад. В начале 2010 года насчитывалось 1800 насекомых. Сколько насекомых будет в начале 2020 года, если эта закономерность сохранится? Решение 3 4. Рассмотрим серию \ (\ frac {1} {5} + \ frac {1} {25} + \ frac {1} {125} + \ frac {1} {625} +… \) . Найдите предельную сумму. 5. Выразите \ (0. \ dot {2} \) как простейшее рациональное число. 1. \ (360 \) 2. \ (4 \) 3. \ (120 \) 4.
S _ {\ infty} = \ frac {a} {1-r}
\ end {align} Задачи, связанные с геометрическими прогрессиями
\ begin {align}
A_ {2010} & = 1800 \\
A_ {2011} & = 1800 (0.{n} \). Определите \ (S_ {4} \). Решения для проверки концепции
