Содержание
Решение задач с помощью кругов Эйлера | План-конспект урока (алгебра, 5 класс) по теме:
Урок математики в 5 «Б» классе. Провела: учитель I категории Астапова Н.Г
Тема: Решение задач с помощью кругов Эйлера.
Цели:
- Обучающая – познакомить учащихся со способом решения логических задач с помощью кругов Эйлера — Венна
- Развивающая – способствовать развитию логического мышления, памяти, самостоятельности и инициативы при выполнении групповых и индивидуальных заданий.
- Воспитывающая – способствовать формированию информационной культуры учащихся, ответственности в групповой и индивидуальной работе.
Ход урока:
1) Орг. момент.
— Какие геометрические фигуры вы знаете?
— Как вы думаете, как мы их будем сегодня использовать при решении задач?
— Такое применение геометрических фигур, в основном кругов, при решении логических задач ввел Леонардо Эйлер. Тема нашего сегодняшнего урока «Решение задач с помощью кругов Эйлера»
2) Сообщение исторического материала: сообщение делает учащийся из 6 класса.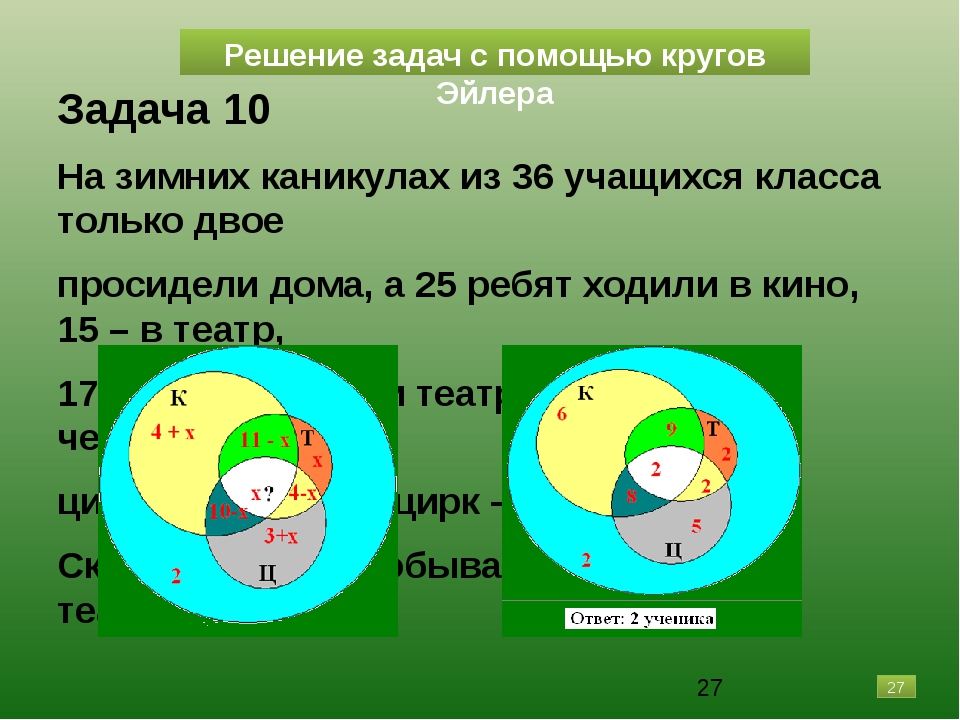
Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).
Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.
Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома.
Леонард Эйлер
(1707 – 1783)
Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы.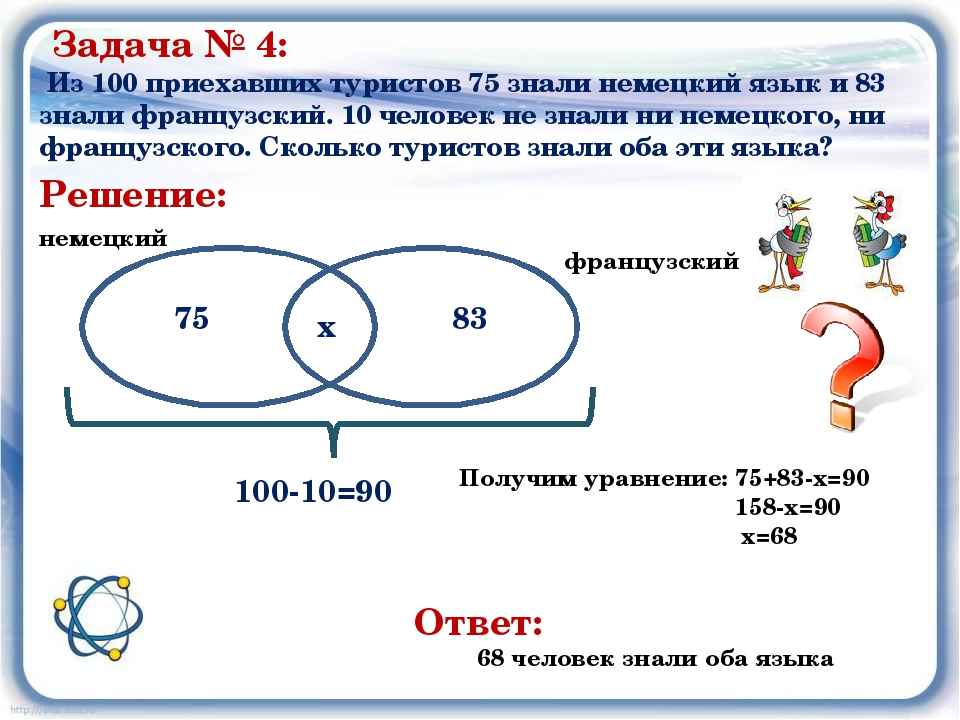 Только теперь он уже диктовал ученикам, которые проводили за него громоздкие вычисления.
Только теперь он уже диктовал ученикам, которые проводили за него громоздкие вычисления.
С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения». Понятно, что слово «круг» здесь весьма условно, множества могут изображаться на плоскости в виде произвольных фигур.
После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году.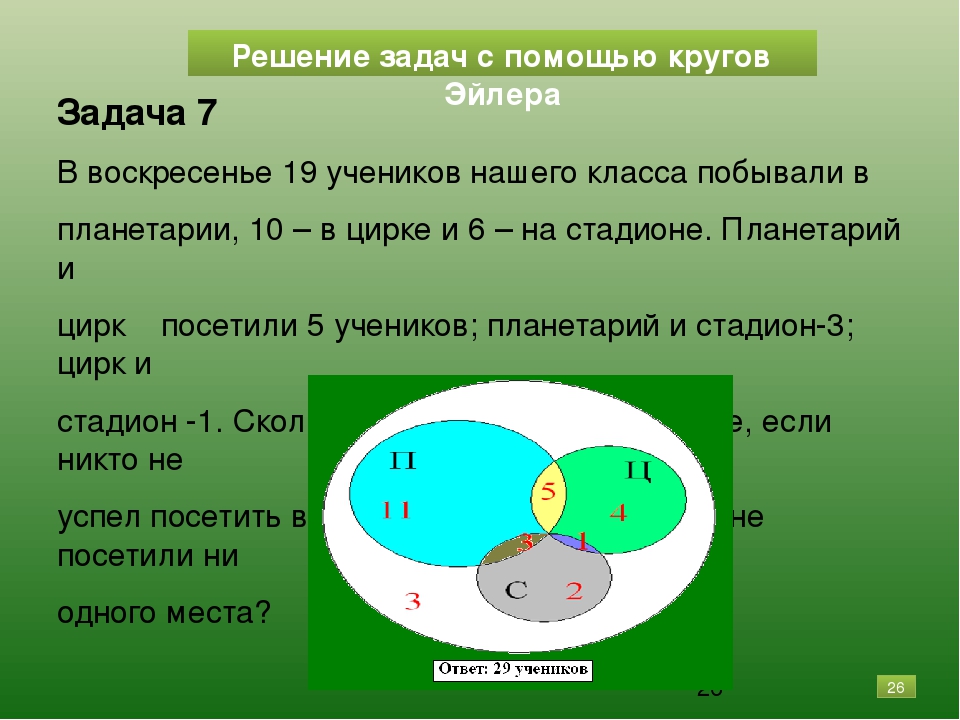 В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.
В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.
3) Пример решения задач:
Задача 1. Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?
Решение: Обратимся к кругам Эйлера:
Изобразим два множества (можно вводить обозначения их не только кругами), так как два вида спорта. В одном я буду фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом. Поскольку некоторые из моих друзей увлекаются и тем и другим видом спорта, то квадраты нарисую так, чтобы у них была общая часть (пересечение). В этой общей части ставим цифру 2. В оставшейся части «футболистов» круга ставим цифру 14 (16 − 2= 14). В свободной части «баскетболистов» круга ставим цифру10 (12 − 2 = 10). А теперь рисунок сам подсказывает, что всего у меня 14 + 2 + 10 = 26 друзей.
Ответ: 26 друзей.
Задача 2. Любимые мультфильмы
Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Решение
В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:
Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».
Задача 3. Гарри Поттер, Рон и Гермиона
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение
Учитывая условия задачи, чертеж будет таков:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ. 8 книг прочитал только Рон.
4) Работа в группах. Самостоятельное решение задач, с последующей проверкой.
1 группа: Пионерский лагерь
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение
Изобразим множества следующим образом:
70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.
Ответ. 5 человек заняты только спортом.
2 группа: Экстрим
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение
Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде.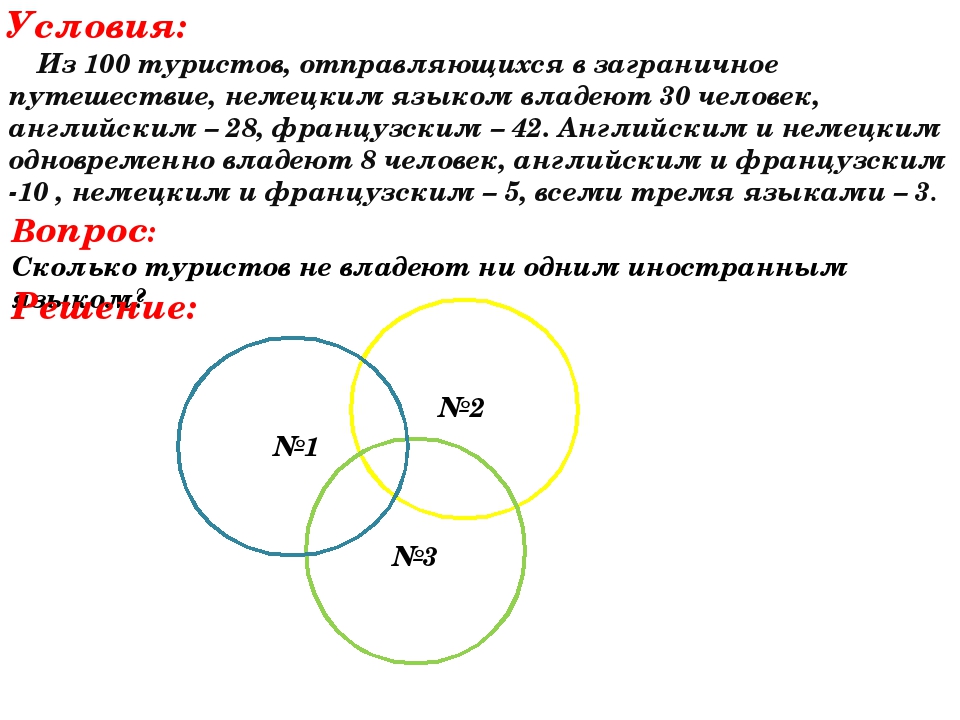 Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
3 группа: «троечники»
В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?
Решение. Нарисуем круги Эйлера. Внутри большего круга, изображающего всех учеников класса, поместим три меньших круга М, Р, И, означающих соответственно математика, русский язык и история.
Дальнейшие расчеты не представляют большого труда. Так как число ребят, имеющих «тройки» по математике и истории, равно 7, то число учеников, имеющих только две «тройки» — по математике и по истории, равно 7-5=2.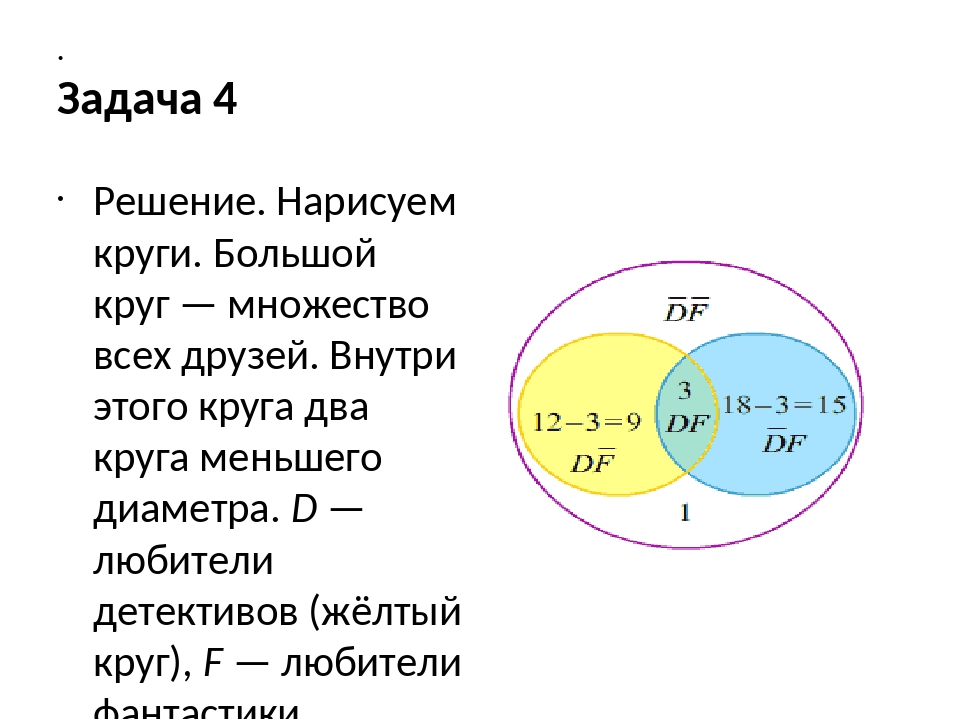 Тогда 17-4-5-2=6 учеников имеют две «тройки» — по математике и по русскому языку, а 22-5-2-11=4 ученика только две «тройки» — по истории и по русскому языку. В этом случае без «тройки» учится 40-22-4-6-4=4 ученика. А имеют «тройки» по двум предметам из трех 6+2+4=12 человек.
Тогда 17-4-5-2=6 учеников имеют две «тройки» — по математике и по русскому языку, а 22-5-2-11=4 ученика только две «тройки» — по истории и по русскому языку. В этом случае без «тройки» учится 40-22-4-6-4=4 ученика. А имеют «тройки» по двум предметам из трех 6+2+4=12 человек.
4 группа: Любители физики
Из 100 семиклассников, выполнивших практическое задание по физике, 75 сделали модели, а 65 эскиз фонтана, а 10 человек ни чего не сделали. Сколько учеников сделали модель и эскиз?
Решение: В большом круге, изображающем 100 семиклассников, поместим 2 меньших круга, изображающих учеников, выполнивших модель и эскиз фонтана. Мы видим, что 90 учеников (100-10)выполнили хотя бы одну часть задания; 15 учеников (90-75) сделали только эскиз фонтана, 75-15=50 – учеников сделали эскиз и фонтан.
Ответ: 50 учеников.
4) Итог урока.
— Чем был для вас полезен сегодняшний урок?
5) Домашнее задание: В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров.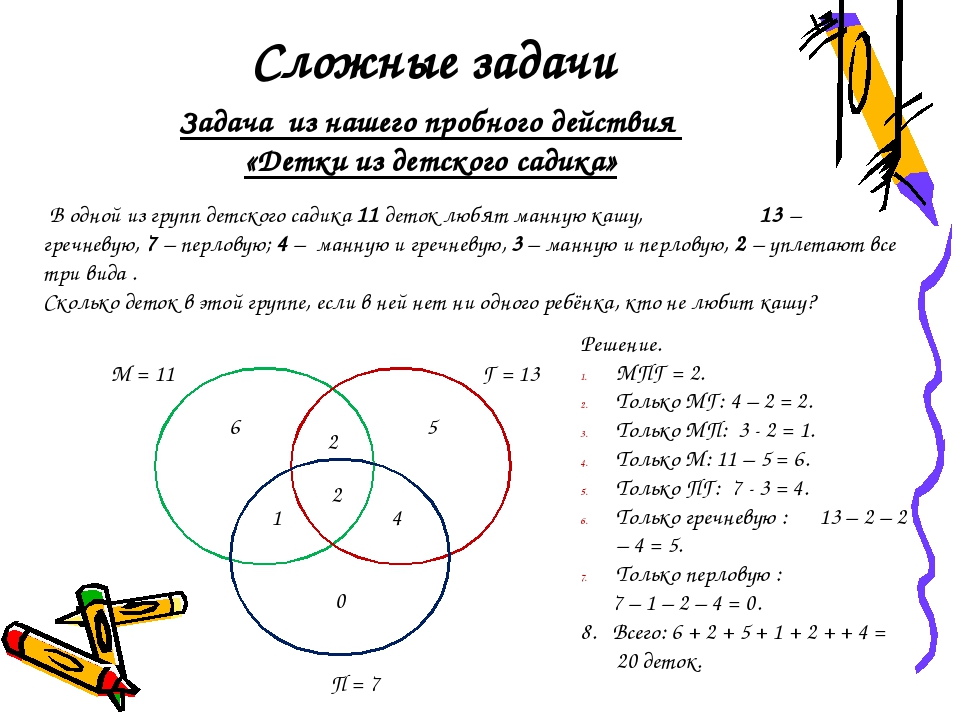 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, ителевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
20 из них купили и холодильник и микроволновку, 19 -и микроволновку, ителевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. |
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? | В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. |
1 группа: Пионерский лагерь
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
2 группа: Экстрим
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
3 группа: «троечники»
В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?
Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?
4 группа: Любители физики
Из 100 семиклассников, выполнивших практическое задание по физике, 75 сделали модели, а 65 эскиз фонтана, а 10 человек ни чего не сделали. Сколько учеников сделали модель и эскиз?
Множества и операции над ними. Решение задач с помощью кругов Эйлера
1. Презентация «Множества и операции над ними. Решение задач с помощью кругов Эйлера»
Автор: учитель математики
МОУ ООШ с. Цепочкино
Саламатова А. Г.
Множества
Множество – совокупность объектов,
объединенных по какому – нибудь признаку.
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
д.
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I — множество иррациональных чисел;
R – множество действительных чисел.
4. Виды множеств
• Равные множества
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}
• Конечные множества
А = {2; 3; 5; 7; 11; 13};
{х | 5
• Бесконечные множества
{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …};
• Пустое множество обозначается символом Ø
4
5. Множества
Задание 1
1) Задайте множество цифр, с помощью которых
записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {- 2, — 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
г) А = {0,1; 0,01; 0,001; 0,0001; …};
д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества: М = {5,4,6},
Р = {4,5,6}, Т = {5,6,7}, S = {4, 6}.
Какое из утверждений неверно?
а) М = Р. б) Р ≠ S. в) М ≠ Т. г) Р = Т.
5
6. Стандартные обозначения
х
А
— знак принадлежности.
«элемент х принадлежит множеству А»;
«х – элемент множества А».
5 N
«5 – число натуральное».
Наряду со знаком принадлежит используют и его
«отрицание» — знак
.
х
А
«элемент х не принадлежит множеству А».
0 N
«нуль не натуральное число»
6
7. Стандартные обозначения
Задание 2
1. Запишите на символическом языке следующее
утверждение:
а) число 10 – натуральное;
б) число – 7 не является натуральным;
в) число – 100 является целым;
г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N; б) -5 Z; в) 2,(45) Q?
3. Верно ли, что:
а) 0,7 {х | х2 – 1
7
8. Стандартные обозначения
А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}.
А
В
«множество А является подмножеством множества В».
Знак « » называют знаком включения.
Пустое множество считают подмножеством любого
множества.
8
9. Стандартные обозначения
Задание 3
1. Даны множества:
А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( или ) так,
чтобы получилось верное утверждение:
а) А … D; б) А … В; в) С … А; г) С … В.
2. Даны три множества А = {1, 2, 3, …, 37}, В = {2, 4, 6, 8, …},
С = {4, 8, 12, 16, …, 36}.
Верно ли, что:
а) А В; б) В С; в) С
А; г) С В?
9
10. Операции над множествами
1) Пересечением множества А и В называют множество,
состоящие из всех общих элементов множеств А и В.
Пересечение множеств А и В обозначают так: А∩В.
Можно записать и так: А∩В = {х | х А и х В}.
Например,
если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то А∩В = {3; 9};
если А = {10; 20; …; 100} и В = {6; 12; 18;…}, то А∩В = {30; 60; 90}.
10
11. Операции над множествами
Задание 4
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11},
Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) А∩В; 2) А∩С; 3) С∩В.
2. Даны множества: А – множества всех натуральных
чисел, кратных 10, В = {1; 2; 3;…, 41}.
Найдите А∩В.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}. Найдите (А∩В)∩С.
11
12. Операции над множествами
2) Объединением множеств А и В называют множество,
состоящее из всех элементов, которые принадлежат хотя
бы одному из этих множеств.
Объединение множеств А и В обозначают так: АUВ.
Можно записать и так: АUВ = {х | х А или х В}.
Например,
если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11},
то АUВ = {1; 3; 5; 7; 9; 11; 12}.
12
13. Операции над множествами
Задание 5
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}.
Найдите (АUВ)UС.
13
14.
 Операции над множествами
Операции над множествами
3) Разность А и В это множество элементов А, не
принадлежащих В.
Разность А и В обозначают так: А\ В.
Например, если А = {2; 4; 6; 8; 10} и В = {5; 10; 15; 20},
то А\ В={2; 4; 6; 8}.
14
15. Операции над множествами
4) Дополнение множества А обозначают так: Ā.
Дополнение множества до множества К: Ā = К\А.
Например, если А = {3; 6; 9; 12} и К = {1; 2; 3; 4; 5; 6; …},
то Ā = {1; 2; 4; 5; 7; 8; 10; 11; 13; …}.
15
16. Решение задач с помощью кругов Эйлера
ЭЙЛЕР Леонард (1707-1783),
российский ученый — математик,
механик, физик и астроном.
16
17. Решение задач с помощью кругов Эйлера
Задача 1
Расположите 4 элемента в двух множествах так, чтобы в
каждом из них было по 3 элемента.
17
18. Решение задач с помощью кругов Эйлера
Задача 2
Множества А и В содержат соответственно 5 и 6 элементов,
а множество А ∩ В – 2 элемента. Сколько элементов в
множестве А U В?
18
19.
 Решение задач с помощью кругов Эйлера
Решение задач с помощью кругов Эйлера
Задача 3
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь
13 семей выписывают и журнал, и газету. Сколько
семей живет в нашем доме?
19
20. Решение задач с помощью кругов Эйлера
Задача 4
На школьной спартакиаде каждый из 25 учеников 9 –го
класса выполнил норматив или по бегу, или по прыжкам в
высоту. Оба норматива выполнили 7 человек, а 11 учеников
выполнили норматив по бегу, но не выполнили норматив
по прыжкам в высоту. Сколько учеников выполнили
норматив: а) по бегу; б) по прыжкам в высоту; в) по
прыжкам при условии, что не выполнен норматив по бегу?
20
21. Решение задач с помощью кругов Эйлера
Задача 5
Из 52 школьников 23 собирают значки, 35 собирают марки,
а 16 – и значки, и марки. Остальные не увлекаются
коллекционированием.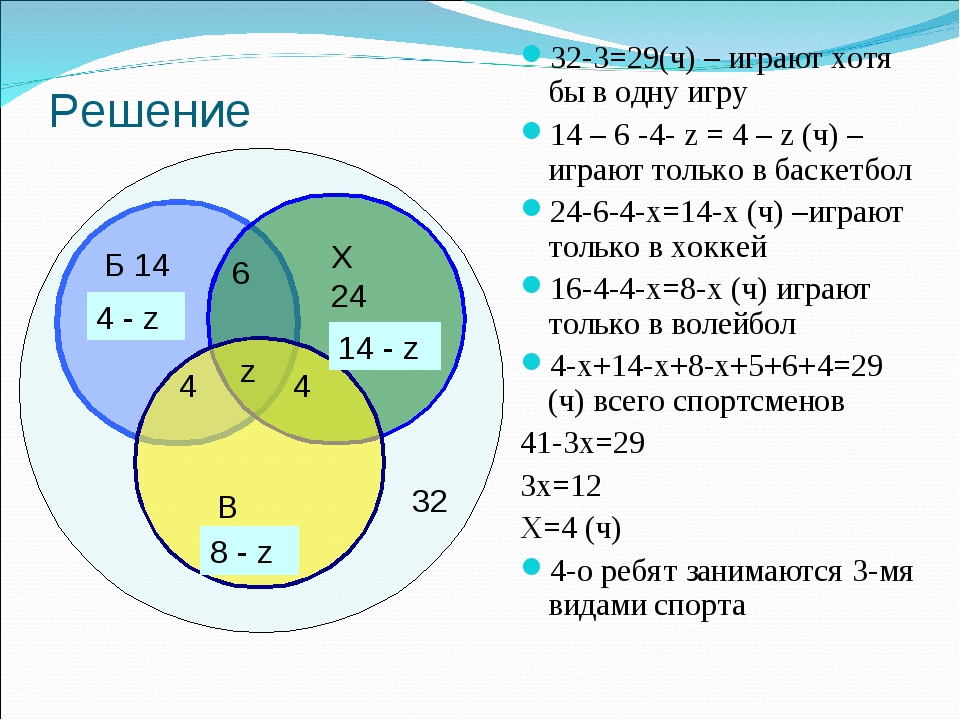 Сколько школьников не
Сколько школьников не
увлекаются коллекционированием?
21
22. Решение задач с помощью кругов Эйлера
Задача 6
Каждый из учеников 9-го класса в зимние каникулы ровно
два раза был в театре, посмотрев спектакли А, В или С. При
этом спектакли А, В, С видели соответственно 25, 12 и 23
ученика. Сколько учеников в классе?
22
23. Решение задач с помощью кругов Эйлера
Задача 7
В воскресенье 19 учеников нашего класса побывали в
планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и
цирк посетили 5 учеников; планетарий и стадион-3; цирк и
стадион -1. Сколько учеников в нашем классе, если никто не
успел посетить все три места, а три ученика не посетили ни
одного места?
23
24. Решение задач с помощью кругов Эйлера
Задача 8
В одном классе 25 учеников. Из них 7 любят груши,
11 – черешню. Двое любят груши и черешню; 6 – груши и
яблоки; 5 – яблоки и черешню. Но есть в классе два ученика,
которые любят всё и четверо таких, что не любят фруктов
вообще. Сколько учеников этого класса любят яблоки?
Сколько учеников этого класса любят яблоки?
24
25. Решение задач с помощью кругов Эйлера
Задача 9
На уроке литературы учитель решил узнать, кто из 40
учеников 9 –го класса читал книги А, В, С. Результаты
опроса выглядели так: книгу А прочитали 25 учеников,
книгу В – 22 ученика, книгу С – 22 ученика; одну из книг А
или В прочитали 33 ученика, одну из книг А или С
прочитали 32 ученика, одну из книг В или С – 31 ученик.
Все три книги прочитали 10 учеников.
Сколько учеников:
а) прочитали только по одной книге;
б) прочитали ровно две книги;
в) не прочили ни одной из указанных книг?
25
26. Решение задач с помощью кругов Эйлера
Задача 9. Решение:
а)
Ответ: 15 учеников
б)
в)
Ответ: 12 учеников
Ответ: 3 ученика
26
27. Решение задач с помощью кругов Эйлера
Задача 10
На зимних каникулах из 36 учащихся класса только двое
просидели дома, а 25 ребят ходили в кино, 15 – в театр,
17 – в цирк.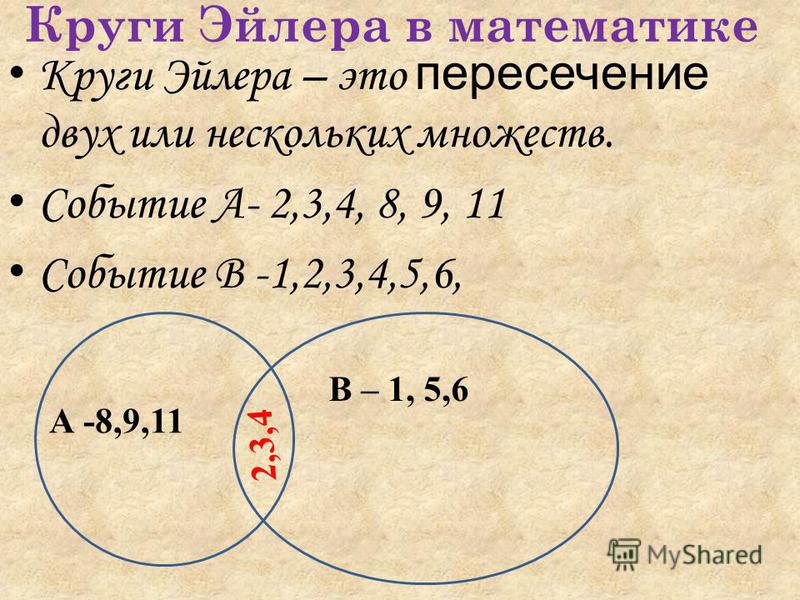 Кино и театр посетили 11 человек, кино и
Кино и театр посетили 11 человек, кино и
цирк – 10, театр и цирк – 4.
Сколько ребят побывало и в кино, и в театре, и в цирке?
27
Литература
[1] Алгебра, 9 класс. В 2 ч. Ч. 2. Задачник для учащихся
общеобразовательных учреждений
/ [А. Г. Мордкович, Л.А. Александрова и др.] -12-е изд.,
испр. — М.: Мнемозина, 2010.
[2] Занимательная математика. 5 – 11 классы. Авт.- сост.
Т.Д. Гаврилова. – Волгоград: Учитель, 2005. – 96 с.
[3] Математика 6 класс: учеб. для общеобразоват.
учреждений / Г.В. Дорофеев, И.Ф.
Шарыгин, С.Б. Суворова и др./; под ред. Г.В. Дорофеева,
И.Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования,
изд-во «Просвещение». – 11 –е изд. — М.: Просвещение,
2010. – 303 с.: ил.
28
Решение задач с помощью кругов Эйлера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение задачи №1
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов. Решение задачи №2
Решение задачи №2
Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множествоПироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500
Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).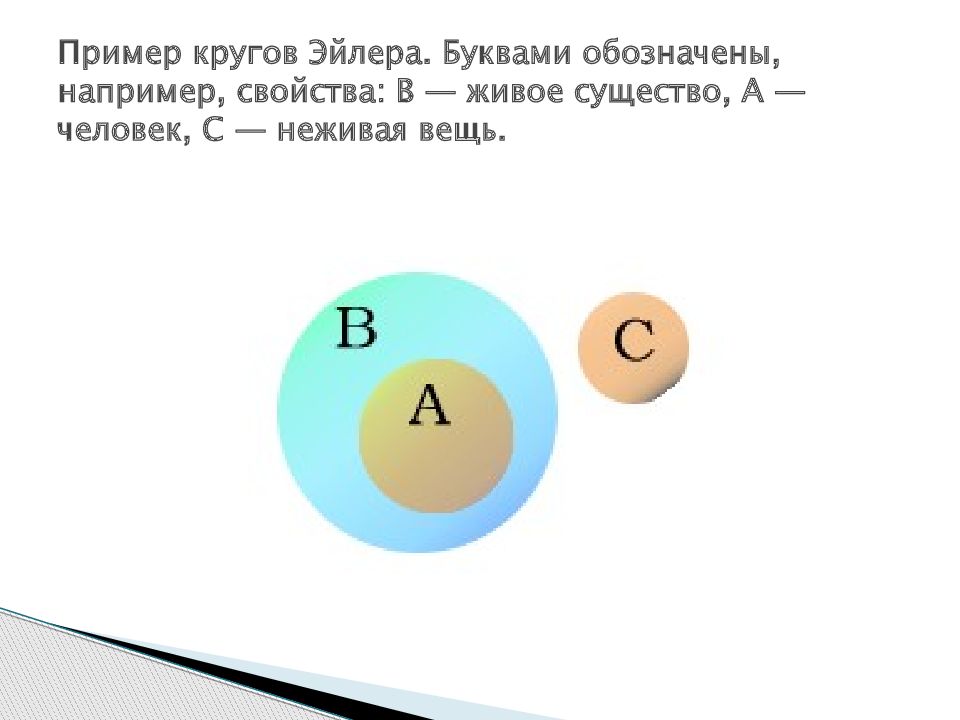
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).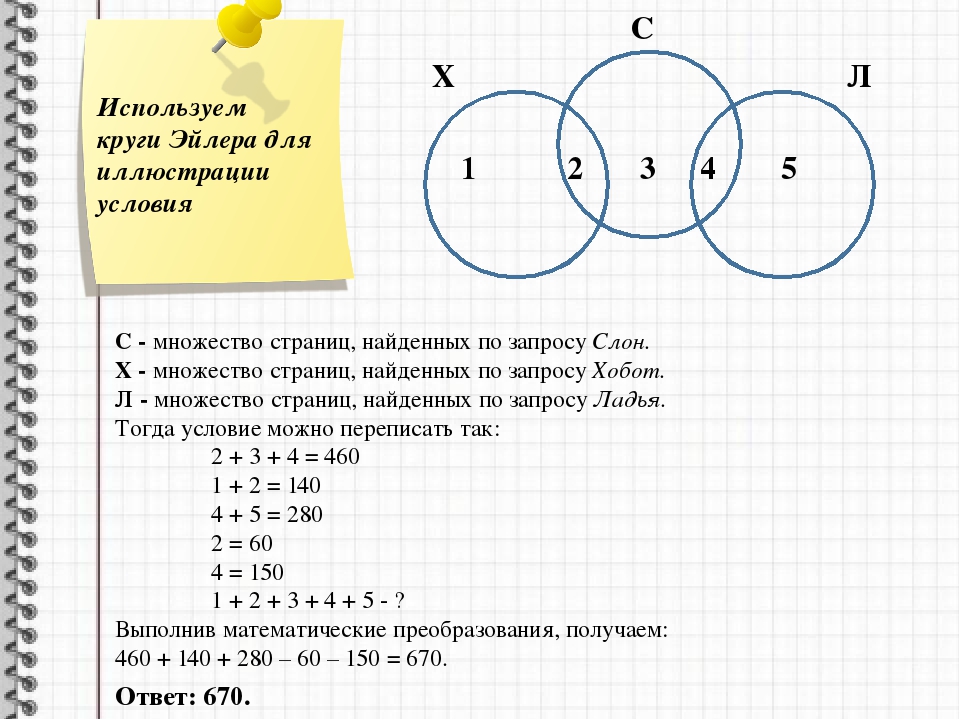
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5
Для решения задачи представим запросы в виде кругов Эйлера.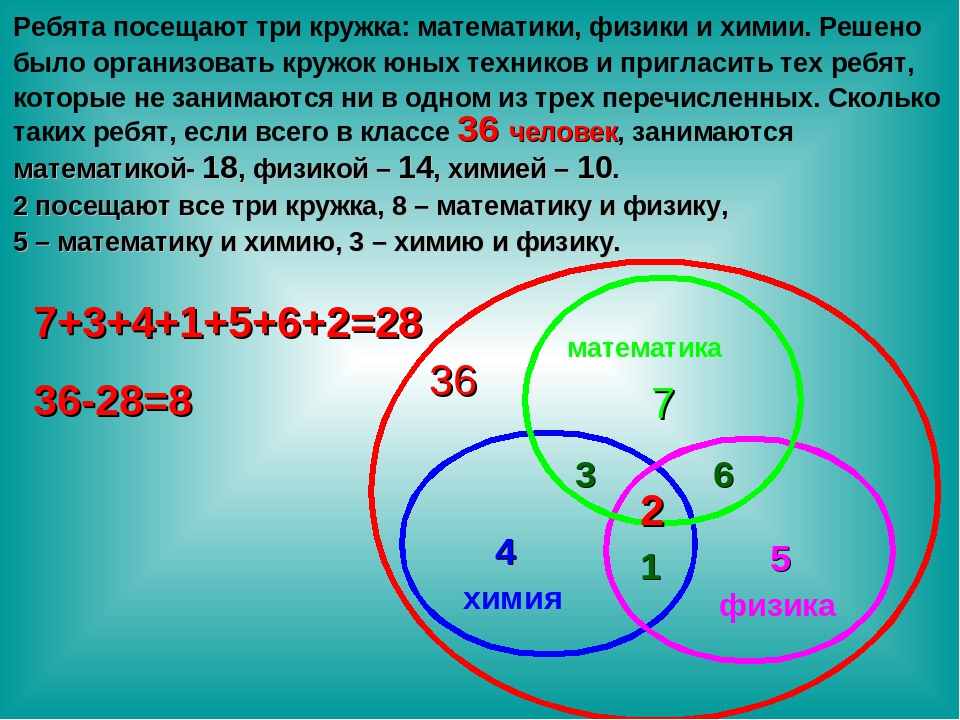
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
Круги эйлера примеры решения.
 Отношения между понятиями. круги эйлера. Изучение нового материала
Отношения между понятиями. круги эйлера. Изучение нового материала
Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).
Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.
Происхождение термина
– это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Пока не очень понятно, верно? Посмотрите на этот рисунок:
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Автор метода — ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.
До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.
Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).
Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.
Зачем нужны круги Эйлера?
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.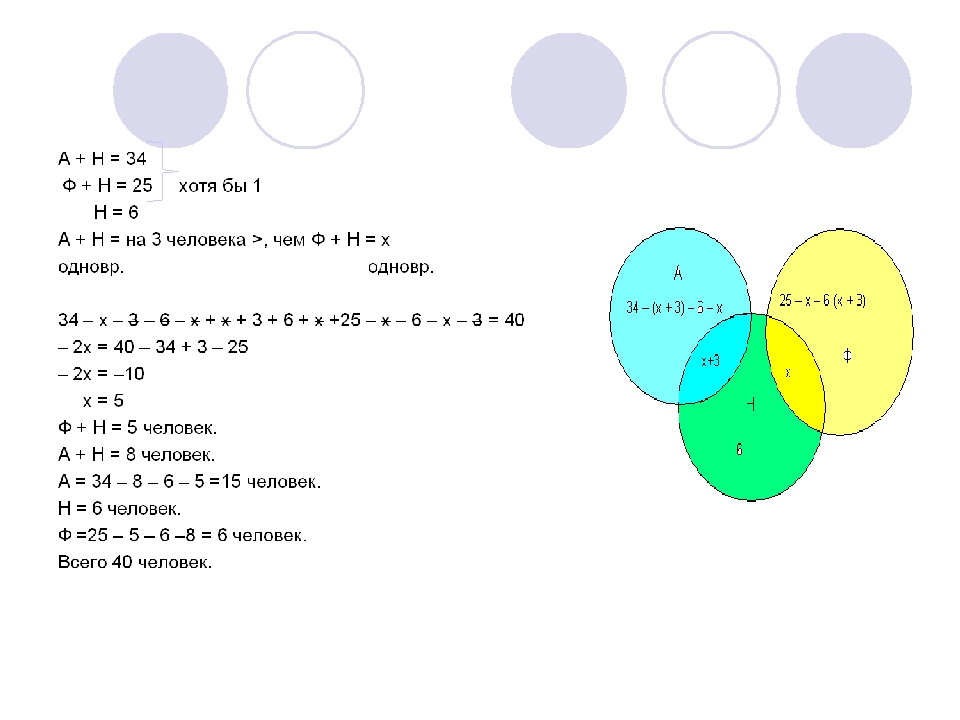
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:
Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Решение задач с помощью кругов Эйлера
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.
Вот на этом сайте — http://logika.vobrazovanie. ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.
ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
Выходит, что:
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».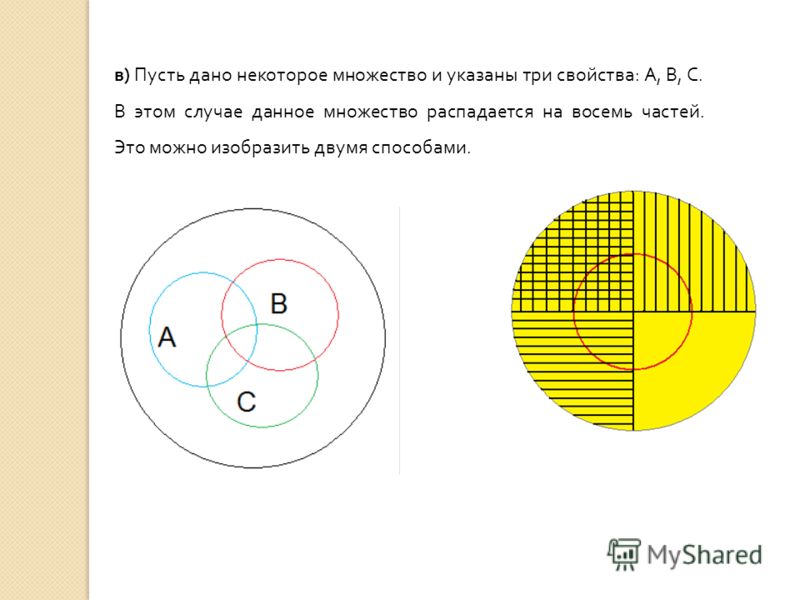
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
А еще давайте рассмотрим задачу
, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.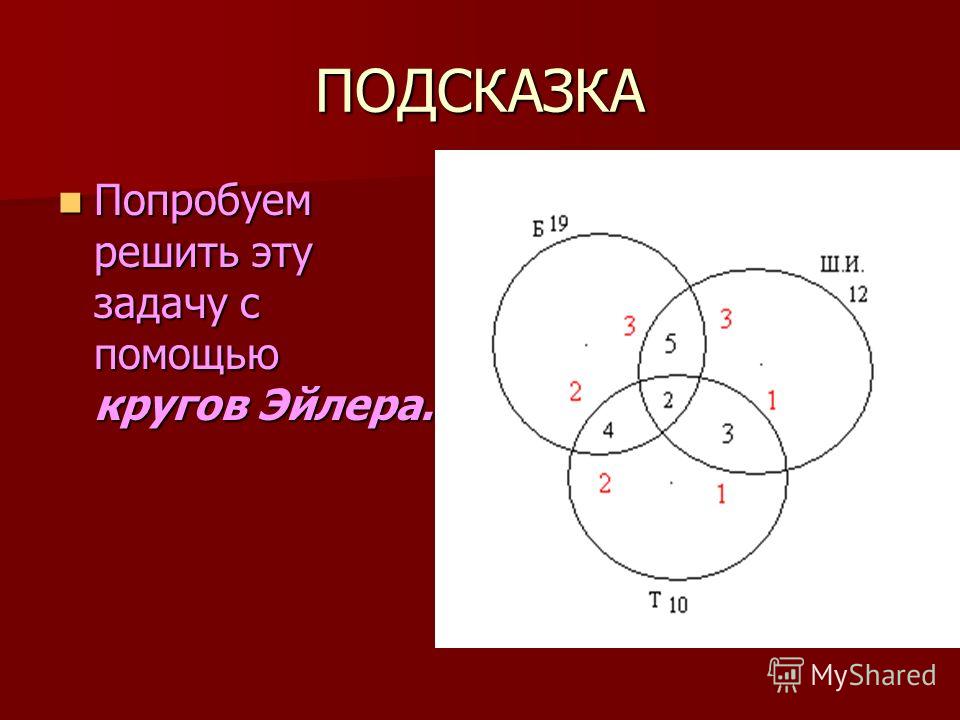
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор
?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор
(обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.
Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Заключение
Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.
Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».
Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Каждый предмет или явление обладает некими свойствами (признаками).
Получается, что составить понятие об объекте означает, прежде всего, умение отличить его от других сходных с ним объектов.
Можно сказать, что понятие — это мысленное содержание слова.
Понятие —
это форма мысли, отображающая предметы в их наиболее общих и существенных признаках.
Понятие — это форма мысли, а не форма слова, так как слово лишь метка, которой мы помечаем ту или иную мысль.
Слова могут быть различны, но при этом обозначать одно и то же понятие. По-русски — «карандаш», по-английски — «pencil», по-немецки — bleistift. Одна и та же мысль в разных языках имеет разное словесное выражение.
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА.
Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ
(«адвокат» и «депутат»; «студент» и «спортсмен»).
В противном случае, понятия считаются НЕСРАВНИМЫМИ
(«крокодил» и «блокнот»; «человек» и «пароход»).
Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ
.
Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).
| ВИД ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ | ИЗОБРАЖЕНИЕ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА |
| РАВНОЗНАЧНОСТЬ (ТОЖДЕСТВЕННОСТЬ) Объёмы понятий полностью совпадают. Т.е. это понятия, которые различаются по содержанию, но в них мыслятся одни и те же элементы объёма. | 1) А — Аристотель В — основатель логики 2) А — квадрат В — равносторонний прямоугольник |
| ПОДЧИНЕНИЕ (СУБОРДИНАЦИЯ) Объём одного понятия полностью входит в объём другого, но не исчерпывает его. | 1) А — человек В — студент 2) А — животное В — слон |
ПЕРЕСЕЧЕНИЕ (ПЕРЕКРЕЩИВАНИЕ) Объёмы двух понятий частично совпадают.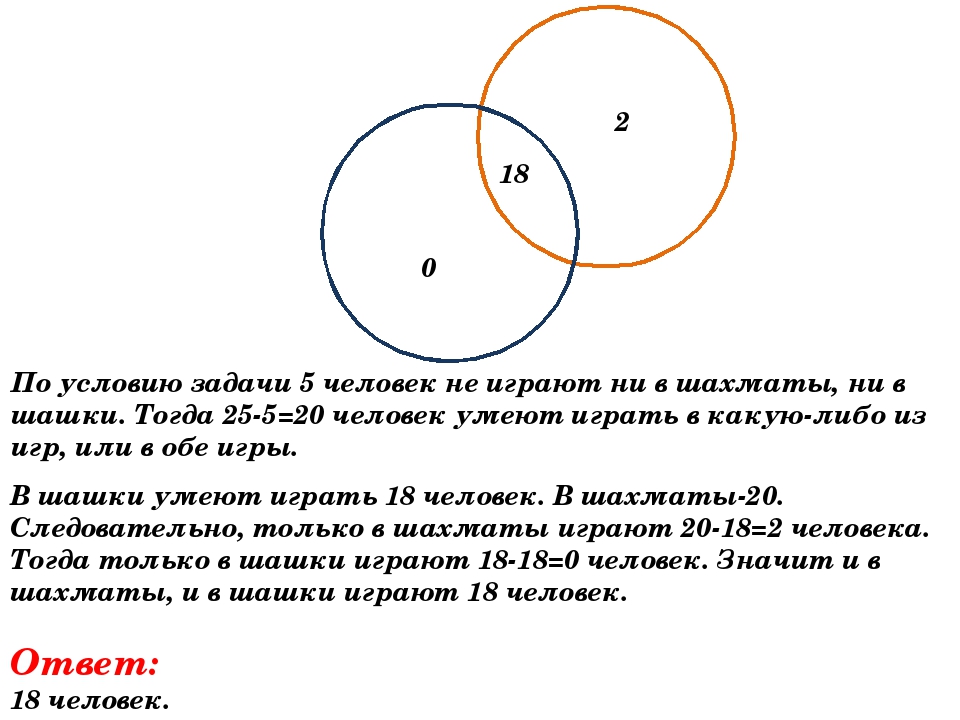 То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них. То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них. | 1) А — юрист В — депутат 2) А — студент В — спортсмен |
| СОПОДЧИНЕНИЕ (КООРДИНАЦИЯ) Понятия, не имеющие общих элементов, полностью входят в объём третьего, более широкого понятия. | 1) А — животное В — кот; С — собака; D — мышь 2) А — драгоценный металл В — золото; С — серебро; D — платина |
| ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ) Понятия А и В не просто включены в объём третьего понятия, а как бы находятся на его противоположных полюсах. То есть, понятие А имеет в своём содержании такой признак, которых в понятии В заменён на противополжный. | 1) А — белый кот; В — рыжий кот (коты бывают и чёрными и серыми) 2) А — горячий чай; холодный чай (чай может быть и тёплым) Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят. |
ПРОТИВОРЕЧИЕ (КОНТРАДИКТОРНОСТЬ) Отношение между понятиями, одно из которых выражает наличие каких-либо признаков, а другое — их отсутствие, то есть просто отрицает эти признаки, не заменяя их никакими другими. | 1) А — высокий дом В — невысокий дом 2) А — выигрышный билет В — невыигрышный билет Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие. |
Упражнение
:
Определите вид отношений по объёму приведённых ниже понятий. Изобразите их с помощью кругов Эйлера .
1) А — горячий чай; В — холодный чай; С — чай с лимоном
Горячий чай (В) и холодный чай (С) — находятся в отношении противоположности.
Чай с лимоном (С) может быть как горячим,
так и холодным, но может быть и, например, тёплым.
2) А
— деревянный; В
— каменный; С
— строение; D
— дом.
Всякое ли строение (С) — дом (D)? — Нет.
Всякий ли дом (D) — строение (С)? — Да.
Что-то деревянное (А) обязательно ли дом (D) или строение (С) — Нет.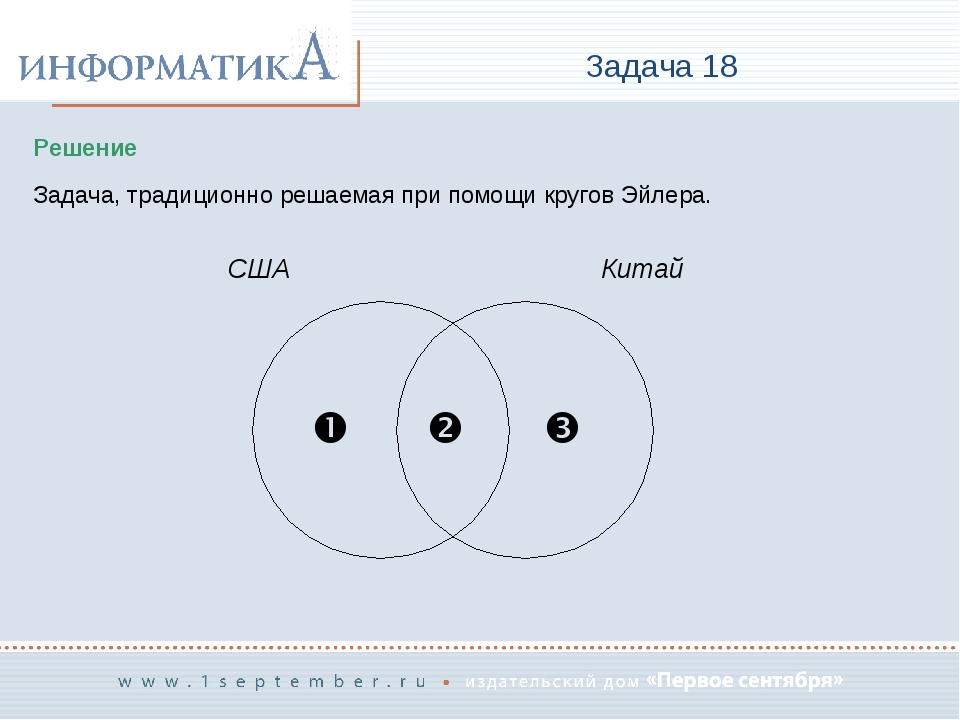
Но можно найти деревянное строение (например, будка),
также можно найти деревянный дом.
Что-то каменное (В) не обязательно дом (D) или строение (С).
Но может быть и каменное строение, и каменный дом.
3) А
— российский город; В
— столица России;
С
— Москва; D
— город на Волге; Е
— Углич.
Столица России (В) и Москва (С) — один и тот же город.
Углич (Е) является городом на Волге (D).
При этом, Москва, Углич, как и любой город на Волге,
являются российскими городами (А)
Задача 1
.
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.
Сколько шестиклассников:
1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?
Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
Решение.
1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)
3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)
4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)
(На схеме правая часть правого круга)
5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).
Очевидно, что 2 и 5
, а также 3 и 4
– равнозначны и ответы на них совпадают
.
При решении данной задачи мы использовали способ ее графического представления при помощи так называемых кругов Эйлера.
Этот способ был предложен Леонардом Эйлером и широко используется при решении логических задач.
Леона́рд Э́йлер
(4(15) апреля 1707, Базель, Швейцария – 7(18) сентября 1783, Санкт-Петербург, Российская империя) – швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Некоторые из его потомков до сих пор живут в России.
Рассмотрим еще один пример.
Задача 2.
Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету.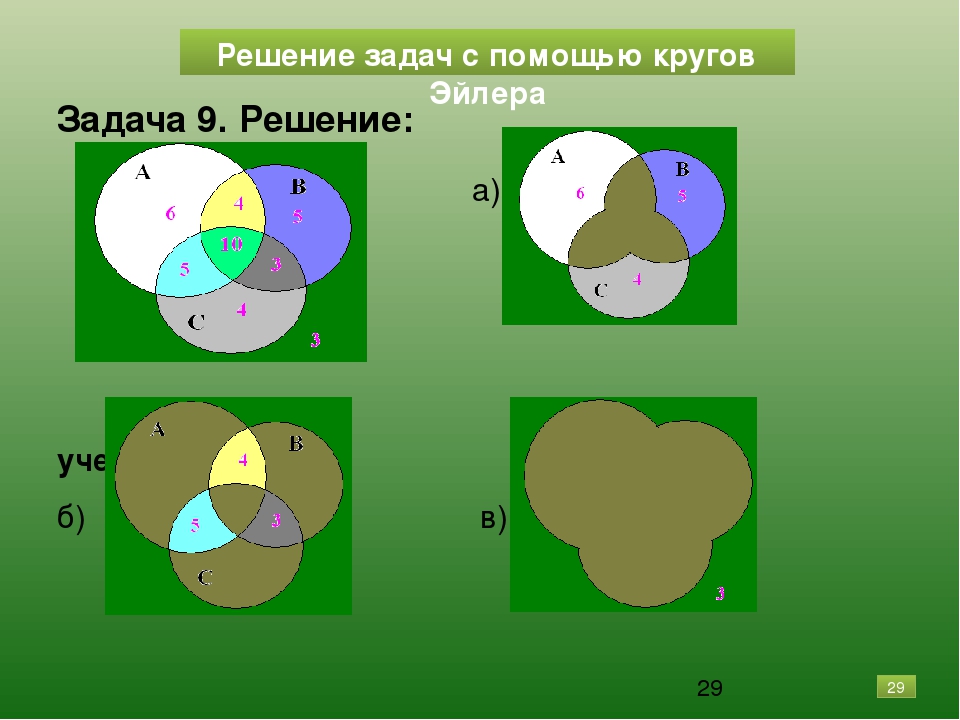 Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?
Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?
Решение.
Здесь нет принципиального отличия от решения предыдущей. На готовом рисунке заменим данные: 25 на 85% и 20 на 75%. Учитывая, что все жители дома составляют 100%, заменяем 35 на 100% и получаем готовое решение: 85% + 75% – 100% = 60%.
Ответ: обе газеты выписывают 60% жителей.
Чем более сложная и запутанная логическая задача, связанная с множествами, тем более очевиден эффект от применения кругов Эйлера. Только после составления рисунка их решение становится достаточно очевидным.
Задача 3.
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение.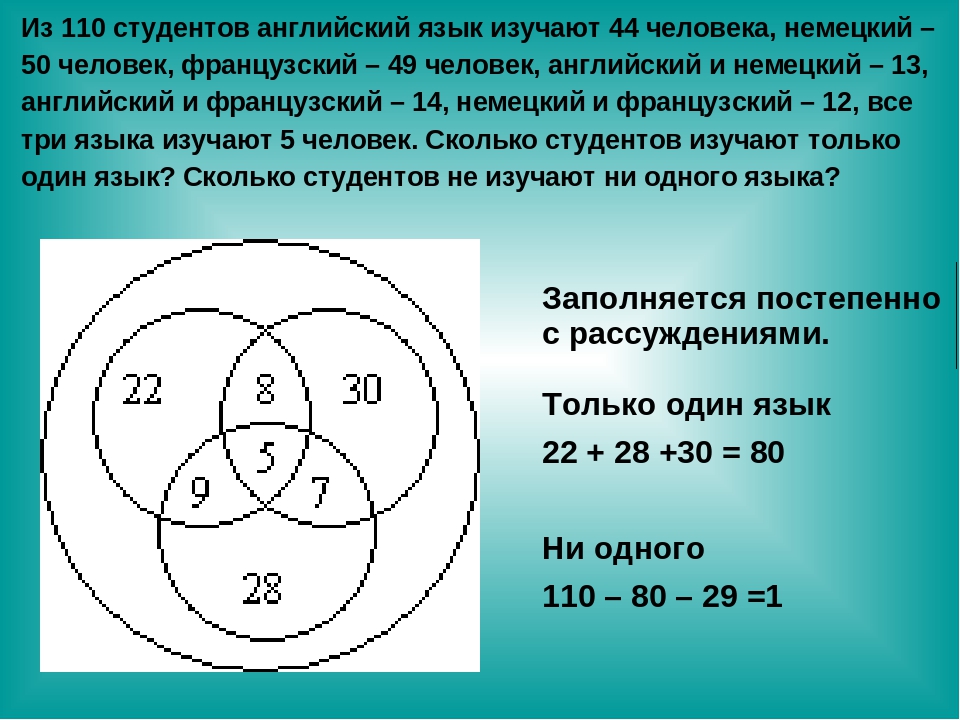
Пусть
Д – драмкружок,
Х – хор,
С – спорт.
Тогда
в круге Д – 27 ребят,
в круге Х – 32 человека,
в круге С – 22 ученика.
Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.
Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,
22 – (5 + 3 + 3) = 11 занимаются только спортом;
70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.
Ответ: 10 человек и 11 человек.
Задача 4.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение.
1 способ.
Для решения опять воспользуемся кругами Эйлера. Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются
только метро и троллейбусом – (10 – х) человек,
только автобусом и троллейбусом – (9 – х) человек,
только метро и автобусом – (12 – х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.
Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
2 способ.
А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3
. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.
Таким образом, получили количество всех учеников в классе.
Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.
Остались вопросы? Не знаете, как решить задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
кругами Эйлера называют фигуры, условно изображающие множества и наглядно иллюстрирующие некоторые свойства операций над множествами. В литературе круги Эйлера иногда называют диаграммами Вен на (или диаграммами Эйлера — Венна). Круги Эйлера, иллюстрирующие основные операции над множествами, представлены на рис. 1.2 (множества, полученные в результате этих операций, отмечены штриховкой).
АПВ
00 АЬВ
Рис. 1.2
Пример 1.8. При помощи кругов Эйлера установим сначаг ла справедливость первого соотношения, выражающего свойство дистрибутивности операций объединения и пересечения множеств,
На рис.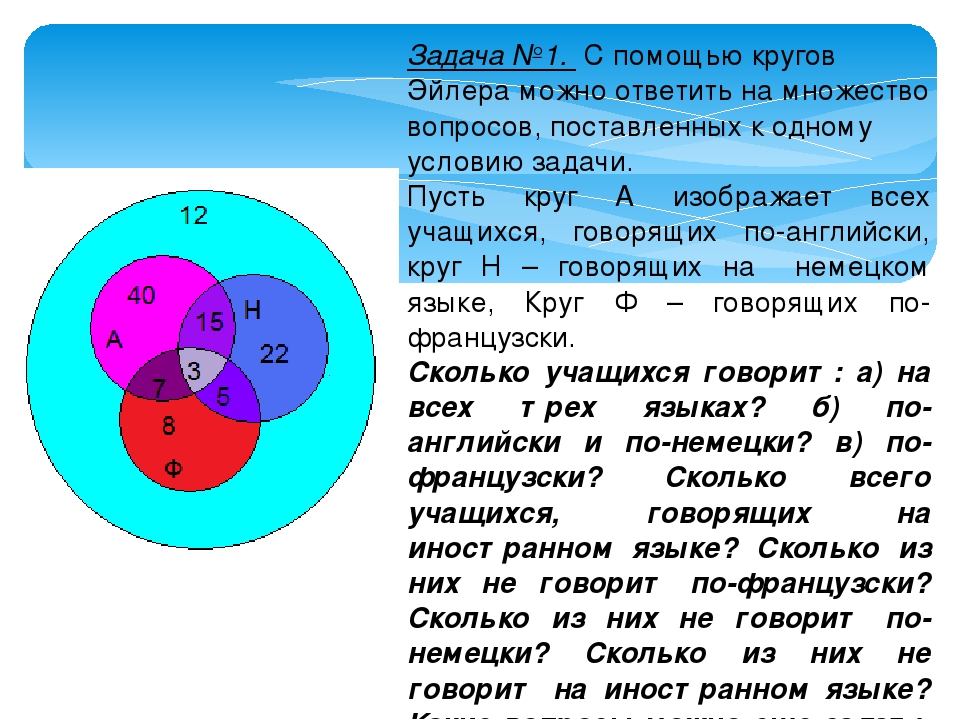 1.3,а вертикально заштрихован круг, изображающий множество А) а горизонтально — область, отвечающая пересечению множеств В и С. В итоге тем или иным способом заштрихована область, изображающая множество A U (БПС). На рис. 1.3,5 вертикально заштрихована область, соответствующая объединению множеств Л и Б, а горизонтально — объединению множеств Л и С, так что обоими способами заштрихована область, изображающая множество (A U В) П (A U С) и совпадающая с областью, заштрихованной каким-либо способом на рис. 1.3,а. Таким образом, круги Эйлера позволяют установить справедливость (1.10).
1.3,а вертикально заштрихован круг, изображающий множество А) а горизонтально — область, отвечающая пересечению множеств В и С. В итоге тем или иным способом заштрихована область, изображающая множество A U (БПС). На рис. 1.3,5 вертикально заштрихована область, соответствующая объединению множеств Л и Б, а горизонтально — объединению множеств Л и С, так что обоими способами заштрихована область, изображающая множество (A U В) П (A U С) и совпадающая с областью, заштрихованной каким-либо способом на рис. 1.3,а. Таким образом, круги Эйлера позволяют установить справедливость (1.10).
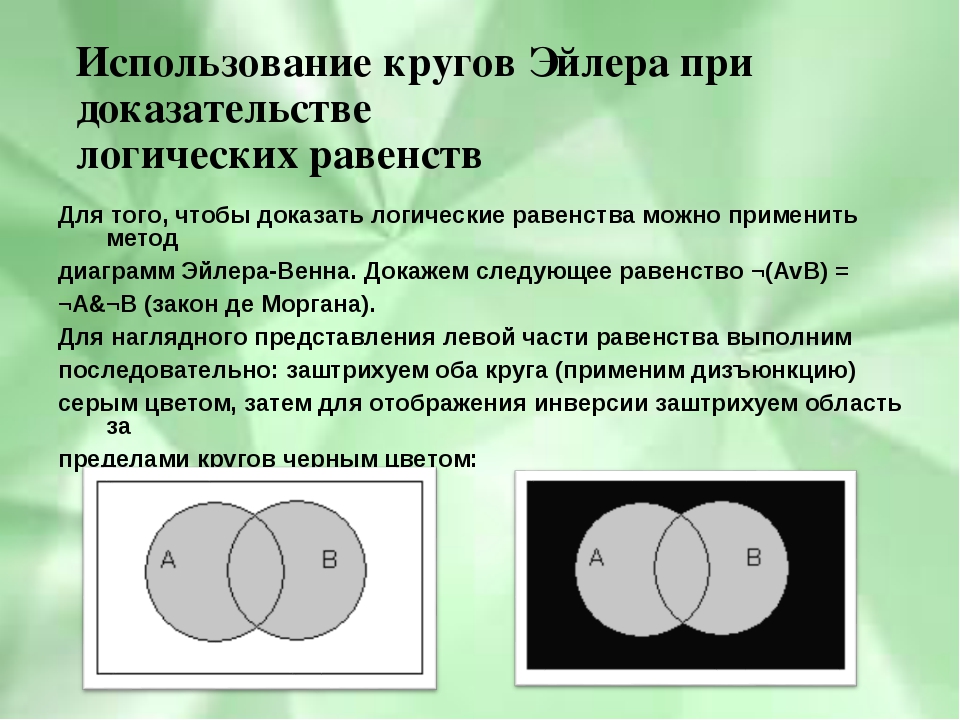
Теперь рассмотрим второй закон де Моргана (1.7)
Заштрихованная на рис. 1.4,а область изображает множество ЛИВ, а незаштрихованная часть прямоугольника Q (внешняя по отношению к заштрихованной) соответствует множеству ЛПВ. На рис. 1.4,5 части прямоугольника 12, заштрихованные вертикально и горизонтально, отвечают соответственно А и В. Тогда множеству Ли В отвечает область, заштрихованная хотя бы одним из указанных способов. Она совпадает с областью, не заштрихованной на рис. 1.4,а и отвечающей множеству ЛПБ, что устанавливает справедливость (1.11).
Она совпадает с областью, не заштрихованной на рис. 1.4,а и отвечающей множеству ЛПБ, что устанавливает справедливость (1.11).
Вопросы и задачи
1.1. Запись m|n, где m,n € Z, означает, что число m нацело делит число п (то — делитель п). Описать заданные множества при условии, что х € N:
1.2. Доказать следующие соотношения и проиллюстрировать их кругами Эйлера:
.
1.3. Установить, в каком отношении (X С Y, X Э У или X = Y) находятся множества X и У, если:
а
Использовать для иллюстрации круги Эйлера.
1.4. Пусть Aj — множество точек, образующих стороны некоторого треугольника, вписанного в заданную окружность. Описать объединение и пересечение всех таких множеств, если треугольники: а) произвольные; б) правильные; в) прямоугольные. Найти
IK и flAi
ieN i en
для заданных семейств множеств:
1.6. Указать, какие из представленных ниже соотношений неверны, и объяснить, почему:
1.7. Указать, какие из множеств равны между собой: .
1.8. Найти множества Ли В, АГ\В, А\В, В\А и изобразить их на числовой прямой, если А = (1.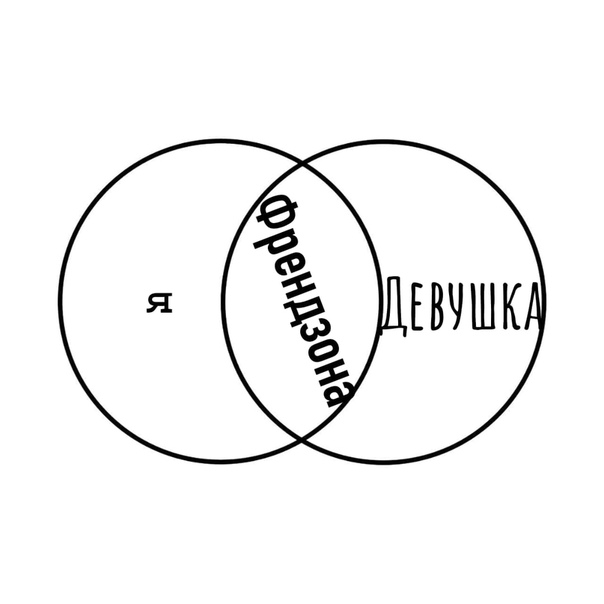 0. Считая отрезок универсальным множеством, найти и изобразить на числовой прямой дополнения множеств: .
0. Считая отрезок универсальным множеством, найти и изобразить на числовой прямой дополнения множеств: .
1.10. По приведенным ниже описаниям множеств людей подберите для каждой записи высказывания на языке множеств подходящую пословицу или поговорку. Надеемся, что это позволит лишний раз проанализировать смысл народных изречений. Например, если Z -множество людей, которые сами как следует не знают того, о чем говорят, то запись х £ Z можно отнести к пословице „Слышал звон, да не знает, где он, поскольку именно так говорят о человеке, наделенном указанным свойством (в данном случае — характеристическим свойством множества Z, см. 1.1).
Множества людей ft — универсальное множество всех людей, Л — добрые, 5е
В — незаурядные, с большими способностями, С — глупые, D — умные,
Е — поступающие по своему, не слушающие советов,
F — связанные корыстными отношениями,
G — много обещающие,
Я — не выполняющие своих обещаний,
J — злоупотребляющие своим служебным положением,
К — слишком важничающие, задающиеся,
L — вмешивающиеся не в свое дело,
М — предприимчивые, ловкие, умеющие устраиваться,
Р — берущиеся за несколько дел сразу,
Q — плодотворно работающие,
S — ошибающиеся,
Т — чувствующие вину и возможность расплаты, U — не добивающиеся результатов, V — выдающие себя своим поведением, W- недальновидные,
X — действующие заодно, не предающие друг друга, У — бывалые, опытные люди.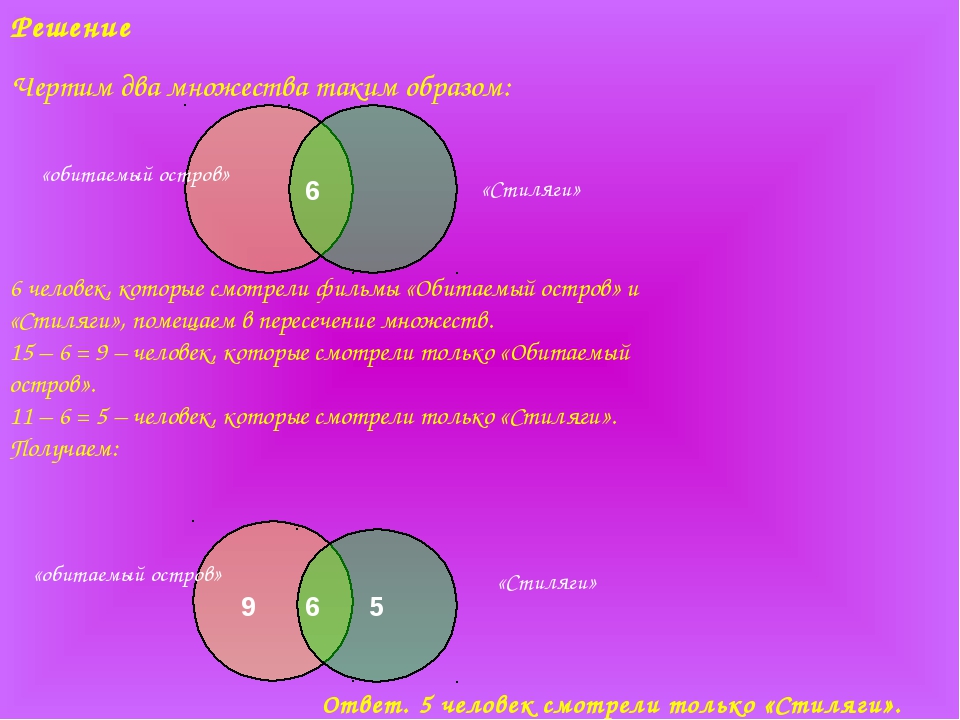 1 + ns, Vs>-1 (неравенство Бернулли).
1 + ns, Vs>-1 (неравенство Бернулли).
1.14. Доказать, что среднее арифметическое п положительных действительных чисел не меньше их среднего геометрического, т.е.
п
1.15. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что это был синий „Бьюик», Джонс — голубой „Крайслер», а Смит — „Форд Мустанг», но не синий. Какого цвета был автомобиль и какой марки, если известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет?
1.1в. Для полярной экспедиции из восьми претендентов А, В, С, Д J5, F, G и Я надо отобрать шесть специалистов: биолога, гидролога, синоптика, радиста, механика и врача. Обязанности биолога могут выполнять Е и G, гидролога — В и F, синоптика — F и G, радиста — С и Д механика — С и Я, врача — А и Д но каждый из них, если будет в экспедиции, сможет выполнять лишь одну обязанность. Кого и кем следует взять в экспедицию, если F не может ехать без
D — без Я и без С, С не может ехать с G, а Д — с В?
Леонард Эйлер –
величайший из математиков,написал более 850 научных работ.
В одной из них и появились эти круги.
Учёный писал, что
«они очень подходят для того, чтобы облегчить наши размышления».
Круги Эйлера
– это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Задача 1
Из 90 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским – 28 чел, французским – 42 чел.
Английским и немецким одновременно владеют 8 человек, английским и французским -10 чел, немецким и французским – 5 чел, всеми тремя языками – 3 чел. Сколько туристов не владеют ни одним языком?
Решение:
Покажем условие задачи графически – с помощью трёх кругов
Ответ:
10 человек.
Задача 2
Многие ребята нашего класса любят футбол, баскетбол и волейбол. А некоторые — даже два или три из этих видов спорта. Известно, что 6 человек из класса играют только в волейбол, 2 – только в футбол, 5 – только в баскетбол. Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти:
Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти:
Сколько всего человек в классе?
Сколько человек умеют играть в футбол?
Сколько человек умеют играть в волейбол?
Задача 3
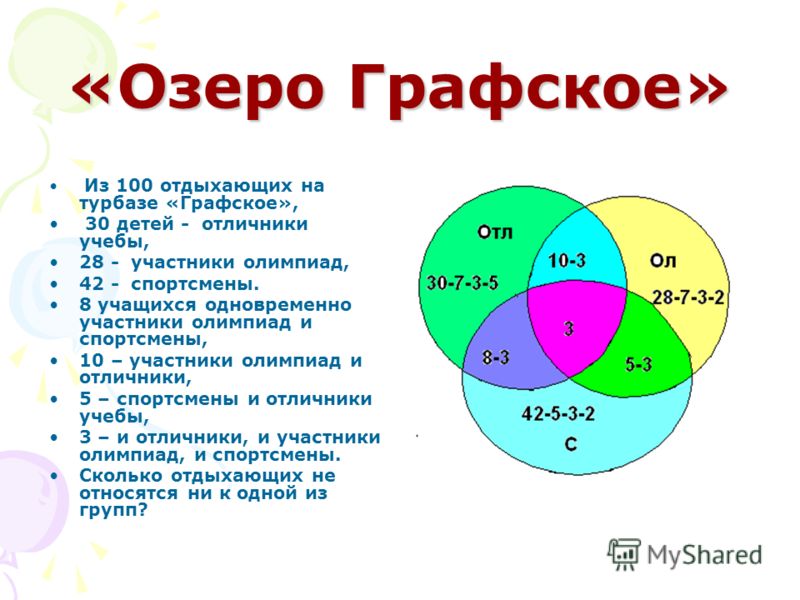
В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, а 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Задача 4
Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – пятеро, в Англии и Франции – 6, во всех трёх странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работает 19 человек, и каждый их них побывал хотя бы в одной из названных стран?
Задача 5
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Задачи для решения учащимися
1.
В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной.
Сколько из них:
а) не являются читателями школьной библиотеки;
б) не являются читателями районной библиотеки;
в) являются читателями только школьной библиотеки;
г) являются читателями только районной библиотеки;
д) являются читателями обеих библиотек?
2. Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?
Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?
3.На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа.
4. В группе туристов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? Если может, то в каком случае?
5. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое, или то и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
6. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек -.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?
Кроме того, известно, что 2 человека посещают все три кружка, 8 человек -.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?
7. После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Решение задач ЕГЭ с помощью кругов Эйлера
Задача 1
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Крейсер & Линкор
?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.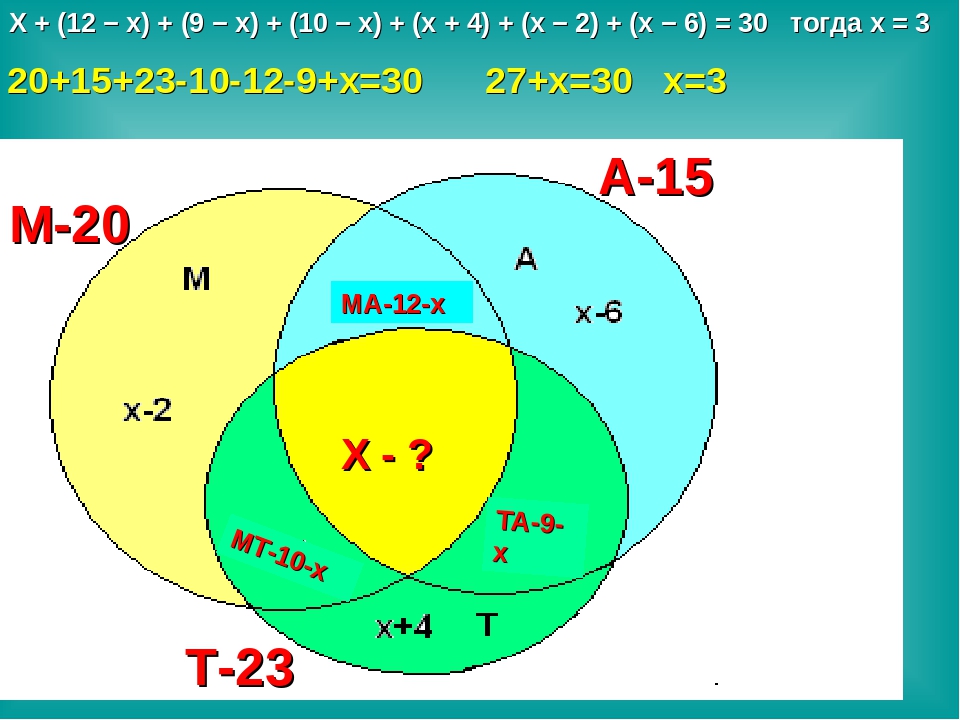
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор
(обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ:
2300 — количество страниц, найденных по запросу
Крейсер & Линкор.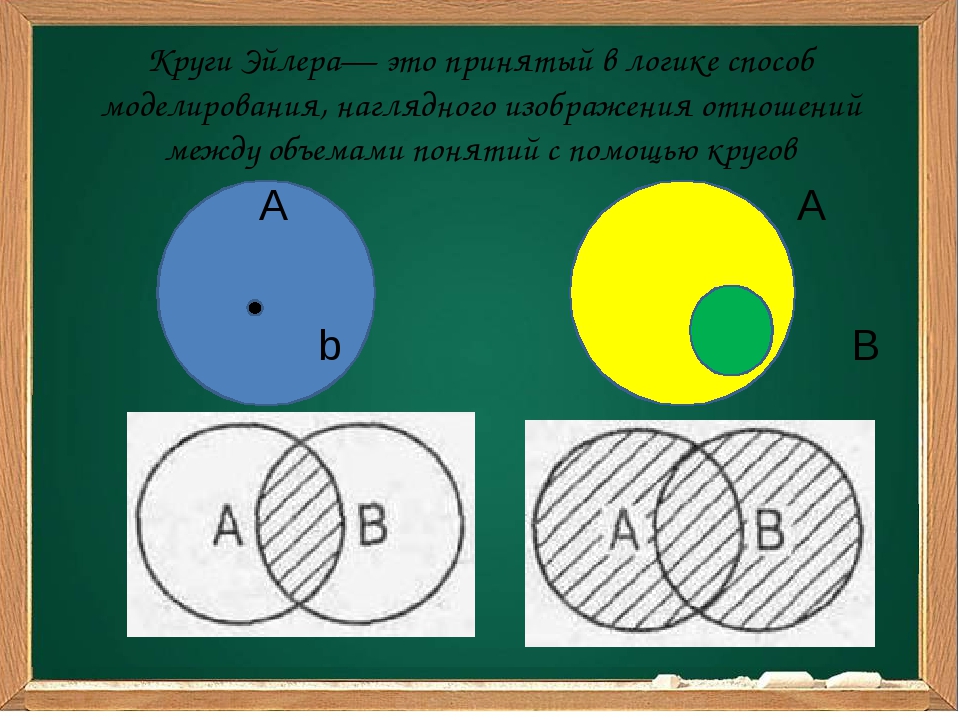
Задача 2
В языке запросов поискового сервера для обозначения
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Торты | Пироги | 12000 |
| Торты & Пироги | 6500 |
| Пироги | 7700 |
Какое количество страниц (в тысячах) будет найдено по запросу Торты
?
Решение
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
А
,
Б
,
В
).
Из условия задачи следует:
Торты
│Пироги
=
А
+
Б
+
В
= 12000
Торты & Пироги =
Б
= 6500
Пироги =
Б
+
В
= 7700
Чтобы найти количество Тортов (Торты =
А
+
Б
), надо найти сектор
А
Торты│Пироги
) отнимем множество Пироги.
Торты│Пироги
– Пироги =
А
+
Б
+
В
-(Б
+
В
) =
А
= 1200 – 7700 = 4300
Сектор
А
равен 4300, следовательно
Торты =
А
+
Б
= 4300+6500 =
10800
Задача 3
|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросуВыпечка
?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение
Для решения задачи отобразим множества
Пироженых
и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А
,
Б
,
В
).
Из условия задачи следует:
Пироженое
& Выпечка =
Б
= 5100
Пироженое
=
А
+
Б
= 9700
Пироженое
│ Выпечка =
А
+
Б
+
В
= 14200
Чтобы найти количество Выпечки (Выпечка =
Б
+
В
), надо найти сектор
В
, для этого из общего множества (Пироженое
│ Выпечка) отнимем множество
Пироженое
.
Пироженое
│ Выпечка –
Пироженное
=
А
+
Б
+
В
-(А
+
Б
) =
В
= 14200–9700 = 4500
Сектор
В
равен 4500, следовательноВыпечка =
Б
+
В
= 4500+5100 =
9600
Задача 4
убывания
Для обозначения
логической операции «ИЛИ» используется символ »
|», а для логической операции «И» — символ «&».
Решение
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (
А
,
Б
,
В
,
Г
).
с
паниели │(терьеры & овчарки) =
Г
+
Б
с
паниели│овчарки
=
Г
+
Б
+
В
спаниели│терьеры│овчарки
=
А
+
Б
+
В
+
Г
терьеры & овчарки =
Б
Расположим номера запросов в порядке убывания количества страниц:
3 2 1 4
Задача 5
В таблице приведены запросы к поисковому серверу.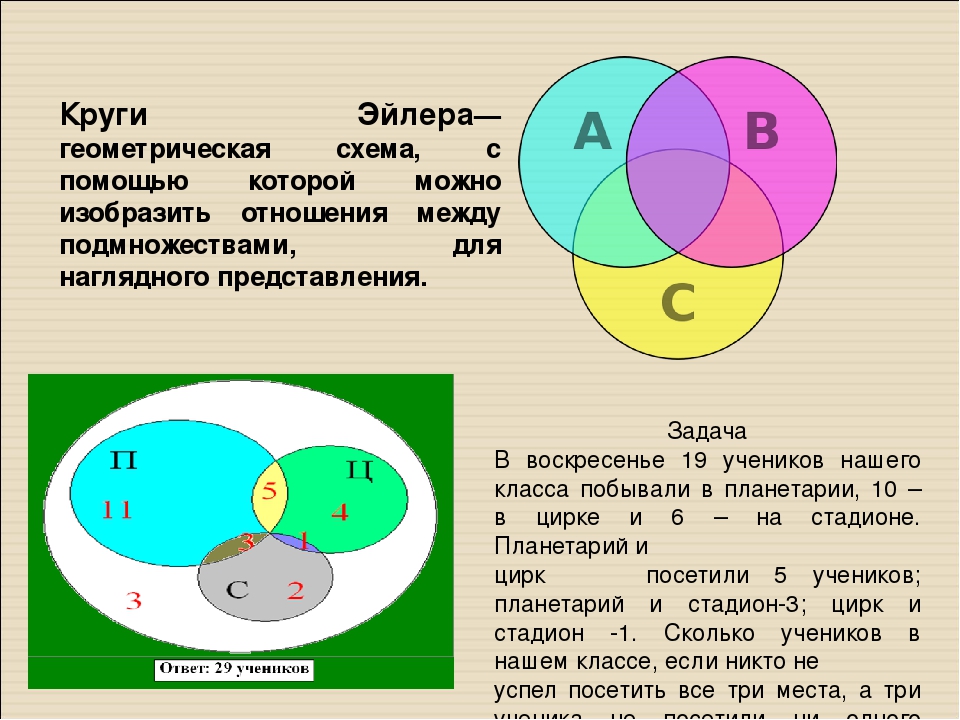 Расположите номера запросов в порядке возрастания
Расположите номера запросов в порядке возрастания
количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения
логической операции «ИЛИ» используется символ »
|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | (классицизм & ампир) |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А
,
Б
,
В
,
Г
).
Преобразим условие задачи в виде суммы секторов:
барокко│
классицизм
│ампир
=
А
+
Б
+
В
+
Г
барокко │(классицизм & ампир) =
Г
+
Б
классицизм
&
ампир =
Б
барокко│
классицизм =
Г
+
Б
+
А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.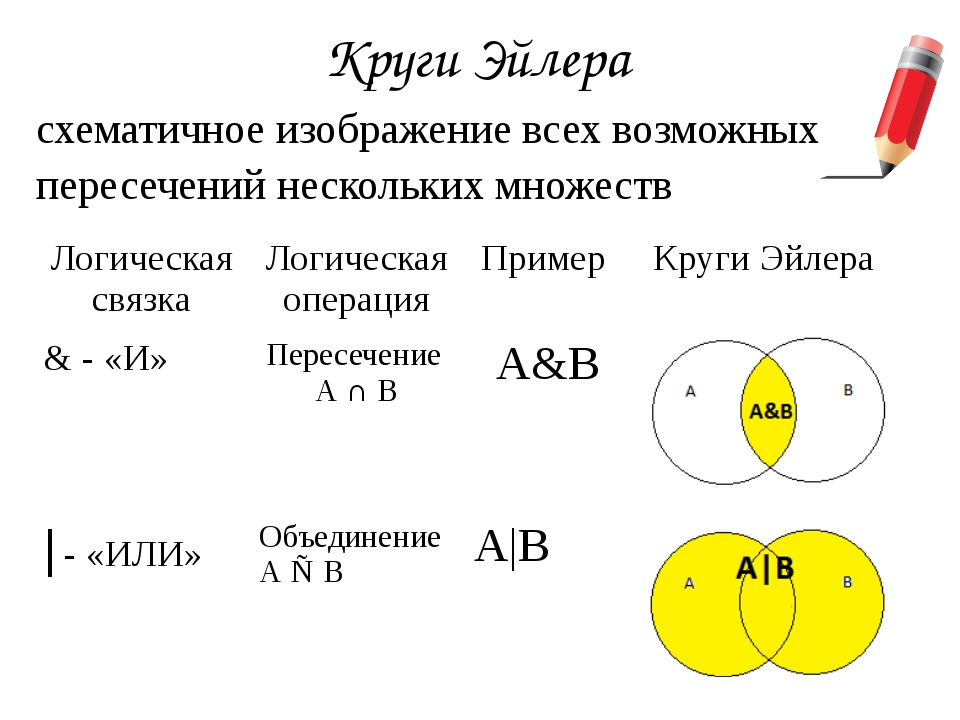
Расположим номера запросов в порядке возрастания количества страниц:
3 2 4 1
Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания
количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения
логической операции «ИЛИ» используется символ »
|», а для логической операции «И» — символ «&».
| 1 | канарейки | щеглы | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение
Для решения задачи представим запросы в виде кругов Эйлера.
K —
канарейки,
Щ – щеглы,
Р – разведение.
| канарейки | терьеры | содержание | канарейки & содержание | канарейки & щеглы & содержание | разведение & содержание & канарейки & щеглы |
Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.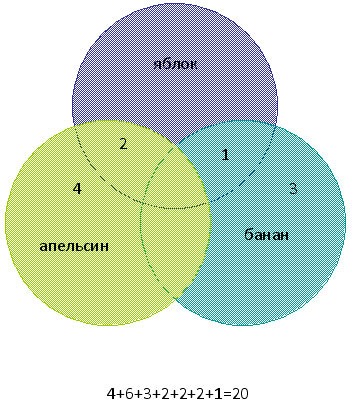
Задача 7 (ЕГЭ 2013)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец
?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Презентация к уроку «Решение задач ЕГЭ с помощью кругов Эйлера-Венна»
библиотека
материалов
Содержание слайдов
Номер слайда 1
http://anisimovaiv.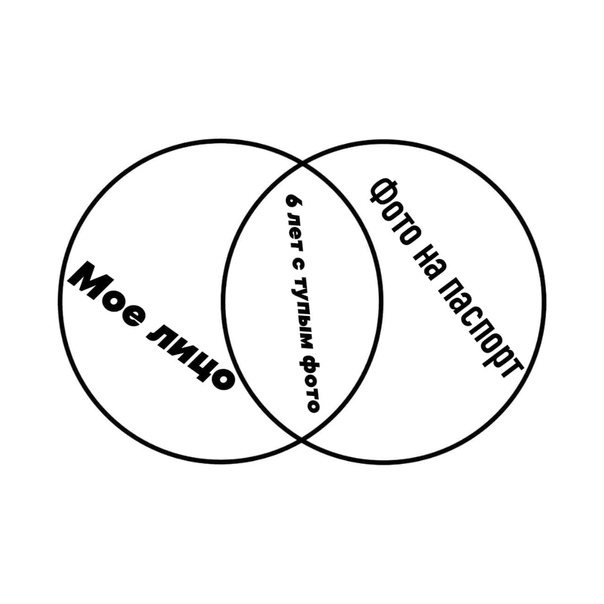 edusite.ru/p32aa1.html
edusite.ru/p32aa1.html
Номер слайда 2
Номер слайда 3
Тема: Решение задач с помощью кругов Эйлера-Венна Цель: Научиться использовать круги Эйлера-Венна при решении задач
Номер слайда 4
Учить всему надо легко, доступно и наглядно.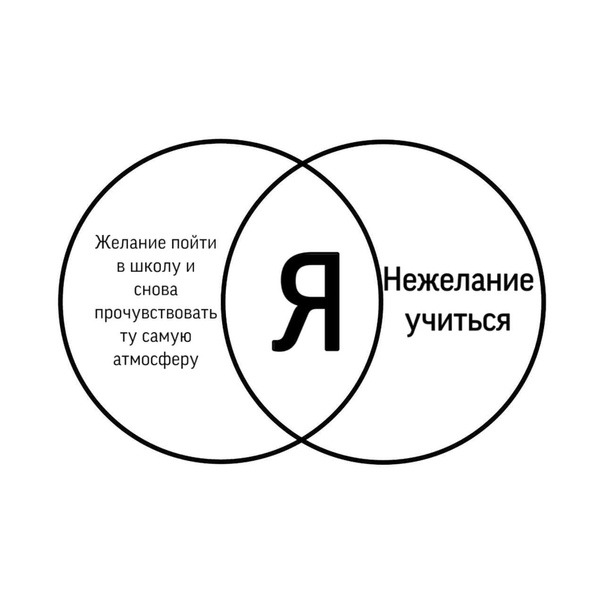 Леонард Эйлер
Леонард Эйлер
Номер слайда 5
Задача №17(ЕГЭ). Запросы для поисковых систем с использованием логических выражений Два поля Три поля с пустым пересечением Три поля Более трёх полей
Номер слайда 6
Экзамен Репетитор 1 2 3 формула включений и исключений NA & B = NA + NB – NA | B Решение: 2=500+370-750=120 Два поля
Номер слайда 7
формула включений и исключений NA & B = NA + NB – NA | B NA = NA & B + NA | B – NB Торты=6500+12000-7700=10800
Номер слайда 8
Вопрос: Как понять пересекаются поля или нет? Три поля с пустым пересечением
Номер слайда 9
Три поля с пустым пересечением Демоверсия ЕГЭ-2020
Номер слайда 10
ПШЕНИЦА ПОЛЕ НАПРЯЖЕННОСТЬ Дано: N1+N2=40 (1) N2+N3+N4=54 (2) N4+N5=44 (3) N2=30 N4=14 N1+N2+N3+N4+N5=? Решение: из (2) N3=54-30-14=10 Напряженность | Поле | Пшеница = N1+N2+N3+N4+N5=40+10+44=94 1 2 3 4 5
Номер слайда 11
Вопрос: Как понять что поля не пересекаются? Ответ: Если в результате конъюнкции двух полей получается 0, эти поля не пересекаются Три поля с пустым пересечением
Номер слайда 12
Три поля с пустым пересечением Открытый банк заданий ЕГЭ-2019 (fipi.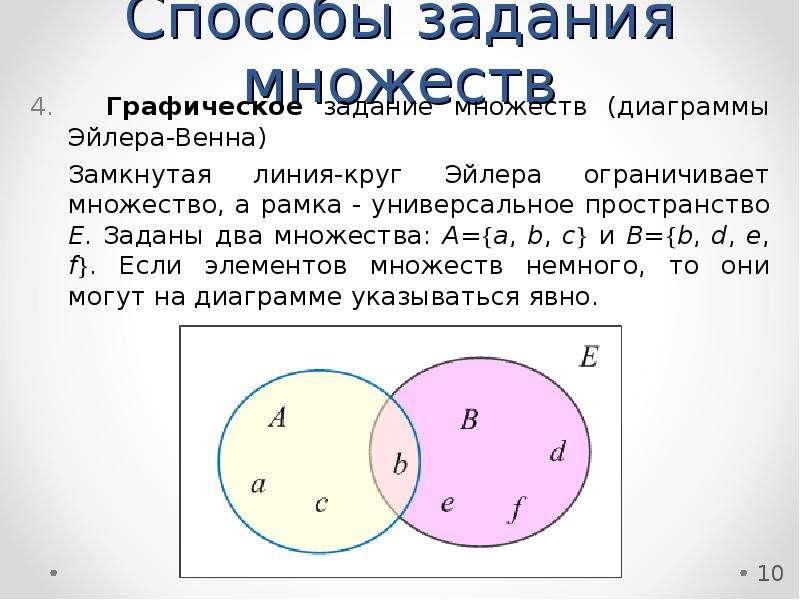 ru)
ru)
Номер слайда 13
ГОРЛО НОС КОРАБЛЬ Дано: N1+N2=35 (1) N4+N5=30 (2) N2+N3+N4=40 (3) N1+N2+N3+N4+N5=70 (4) N2=10 (5) N4=? Решение: N1+N2+N3+N4+N5=70 N3=70-35-30=5 Из (3) находим N4=40-10-5=25 n 4 2 1 3 5
Номер слайда 14
Номер слайда 15
Варианты логических выражений (три поля с пересечением)
Номер слайда 16
Три поля с пересечением Дано: N5=50 (1) N2+N5=150 (2) N4+N5=130 (3) N2+N3+N4+N5+N6+N7=660 (4) N1+N2+N3+N4+N5+N6+N7=900 (5) N1+N2+N4+N5=? Решение: N1=900-660=240 N2=150-50=100 N4=130-50=80 Ночь=N1+N2+N4+N5=240+100+80+50=470
Номер слайда 17
1 1 1 2 3 4 5 6 7 Дано: N5+N6=165 N4+N5=125 N5=80 N4+N5+N6=? Решение: N4=125-80=45 N6=165-80=85 N4+N5+N6=45+80+85=210 Фотон Протон Бозон
Номер слайда 18
Стр. 184 № 5, 6, 7
184 № 5, 6, 7
Решение задач с помощью кругов Эйлера
Текст этой презентации
Слайд 1
Для тех , кому интересно
«Решение задач с помощью кругов Эйлера»
5-6 класс
Слайд 2
Изображение множеств в виде кругов подходит для того, чтобы облегчить рассуждения при решении задач
Слайд 3
Задача:
Все мои друзья занимаются каким-нибудь видом спорта. 17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?
Слайд 4
1.Изобразим два множества , так как два вида спорта. В одном будем фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом
2.Поскольку некоторые из друзей увлекаются и тем и другим видом спорта, то круги нарисуем так, чтобы у них была общая часть (пересечение)
Слайд 5
2
15
12
17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта.
И только двое увлекаются и тем и другим видом спорта.
Расставить числа , согласно условию задачи: 1)В общей части ставим цифру 2(двое увлекаются и тем и другим видом спорта)
2)В оставшейся части «футболистов» круга ставим цифру 15 (17 − 2 = 15). В свободной части «баскетболистов» круга ставим цифру12 (14 − 2 = 12).
футболом
баскетболом
3)Всего друзей 15+2+12=29 Ответ:29 друзей
Слайд 6
Задача: В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
Слайд 7
1.Изобразим три множества , так как три увлечения. В одном будем фиксировать ребят из драмкружка, во втором ребят , которые поют. В третьем будем фиксировать ребят, которые увлекаются спортом.
2.Поскольку некоторые из ребят увлекаются всем , то круги нарисуем так, чтобы у них было пересечение.
Слайд 8
драмкружок
хор
спорт
Слайд 9
драмкружок
хор
спорт
3 спортсмена посещают и драмкружок и хор , поэтому заполняем эту общую часть.
3
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
Слайд 10
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает занятие ребят в драмкружке и хоре.
Слайд 11
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом.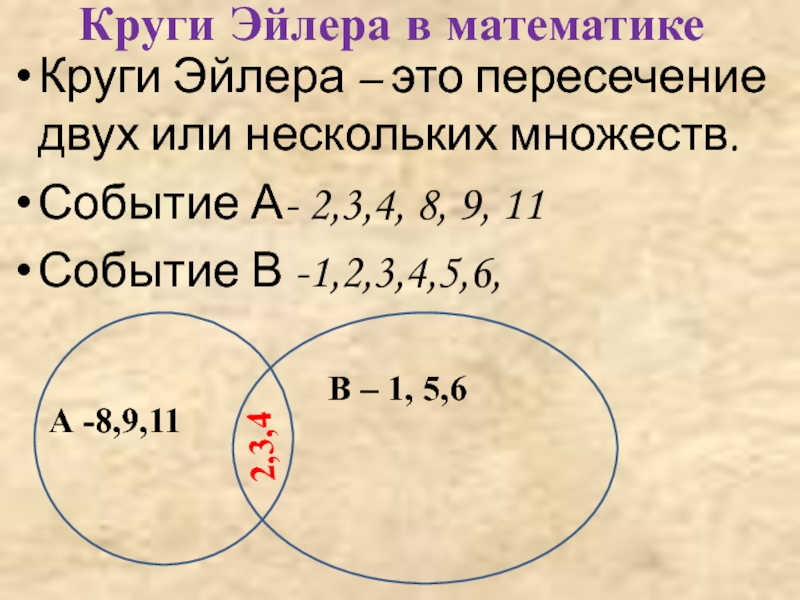 В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 10 ребят из хора . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 7 (10-3=7)
Слайд 12
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
3
7
Слайд 13
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает занятие спортсменов в драмкружке
Слайд 14
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 8 спортсменов . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 5 (8-3=5)
Слайд 15
3
5
драмкружок
хор
спорт
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
Слайд 16
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько спортсменов поют в хоре .
Слайд 17
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в хоре 6 спортсменов . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 3 (6-3=3)
Слайд 18
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
3
3
Слайд 19
драмкружок
хор
спорт
3
7
5
3
Слайд 20
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят в драмкружке
Слайд 21
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 27 занимаются в драмкружке . А так как в предыдущих рассуждениях поставлены числа 3,5,7 ,то в оставшейся части ставим число 12 (27-(3+5+7)=12)
Слайд 22
драмкружок
хор
спорт
3
7
5
12
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
Слайд 23
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят поют в хоре
Слайд 24
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 32 поют в хоре . А так как в предыдущих рассуждениях поставлены числа 3,3,7 ,то в оставшейся части ставим число
19 (32-(3+3+7)=19)
3
7
3
19
Слайд 25
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят занимаются спортом.
Слайд 26
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
По условию 22 человека увлекаются спортом. А так как в предыдущих рассуждениях поставлены числа 3,5,3 ,то в оставшейся части ставим число 11 (22-(3+5+3)=11)
драмкружок
хор
спорт
Слайд 27
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
11
3
5
3
Слайд 28
драмкружок
хор
спорт
3
7
5
3
19
11
12
Слайд 29
Всего занимаются 12+19+11+7+3+3+5=60 человек. Не поют, не увлекаются спортом, не занимаются в драмкружке 70-60=10 человек
Ответ: 10 человек
Слайд 30
Задача:
Из 220 студентов 163 играют в шахматы,175-в футбол,22 человека не играют в эти игры . Сколько студентов одновременно играют в шахматы и в футбол?
шахматы
футбол
х
163-х
175-х
220-22=198(чел)-играют в игры
163-х+х+175-х=198
338-х=198
х=140
140 студентов одновременно играют в шахматы и в футбол
Слайд 31
Реши :
9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы,
2 бананы, апельсины и сливы. Сколько у меня друзей?
Слайд 32
Проверь решение:
бананы
апельсины
сливы
3
2
3
1
2
1
2
3+3+2+1+2+2+1=14 друзей
Ответ:14 друзей
Слайд 33
Домашнее задание:
1.Каждый из членов команды играет либо в футбол , либо в хоккей , либо в футбол и в хоккей . Сколько человек в команде ,если известно , что 18 человек играют в обе игры,22 человека играют в футбол,21 в хоккей?
2.В некоторой школе есть класс увлеченных ребят.Семь учеников из этого класса увлекаются математикой,шесть-физикой,пять-астрономией.Четверо из учеников увлекаются математикой и физикой,трое-математикой и астрономией,двое-физикой и астрономией,а один –и математикой,и физикой,и астрономией.Сколько учеников в классе?
Слайд 34
Проверь:
футбол
хоккей
1)
18
22-18=4
21-18=3
4+18+3=25(чел.)
Ответ:25 человек
Слайд 35
2)
математика
физика
астрономия
1
2
1
1
1
1
3
Ответ:10 человек
1+1+1+1+1+2+3=10(чел)
Слайд 36
Спасибо за внимание
почему один раз увидеть лучше, чем сто раз услышать
Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).
Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.
Происхождение термина
Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Пока не очень понятно, верно? Посмотрите на этот рисунок:
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Автор метода — ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.
До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.
Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).
Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.
Зачем нужны круги Эйлера?
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:
Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Решение задач с помощью кругов Эйлера
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.
Вот на этом сайте — http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
Выходит, что:
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.
Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Заключение
Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.
Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».
Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Искусство решения проблем
Треугольник ABC со светло-оранжевым кружком из девяти точек
девятиконечная окружность (также известная как круг Эйлера или круг Фейербаха ) данного треугольника — это круг, который проходит через 9 «значащих» точек:
«Окружность из девяти точек касается вписанной окружности, имеет радиус, равный половине радиуса описанной окружности, а ее центр — это середина сегмента, соединяющего ортоцентр и центр описанной окружности.»
-hankinjg
То, что такой круг существует — нетривиальная теорема евклидовой геометрии.
Центр девятиконечной окружности — это девятиконечный центр и обычно обозначается.
Окружность из девяти точек касается вписанной окружности, имеет радиус, равный половине радиуса описанной окружности, а ее центр — это середина сегмента, соединяющего ортоцентр и центр описанной окружности, на который также падает центроид.
Его также называют центром Кимберлинга.
Первое доказательство существования
Так как это середина и середина, параллельно.Используя аналогичную логику, мы видим, что это тоже параллельно. Поскольку это середина и середина, параллельна, которая перпендикулярна. Подобная логика дает нам то, что тоже перпендикулярно. Следовательно, это прямоугольник, который представляет собой циклическую фигуру. Диагонали и являются диагоналями описанной окружности. Логика, аналогичная приведенной выше, дает нам прямоугольник с общей диагональю к. Следовательно, описанные окружности двух прямоугольников идентичны. Мы также можем получить, что прямоугольник также находится на круге.
Теперь у нас есть круг с точками,,,, и на нем, с диаметрами, и. Теперь отметим это. Следовательно, и тоже находятся на круге. Теперь у нас есть круг с серединами сторон на нем, три середины отрезков, соединяющих вершины треугольника с его ортоцентром на нем, и три фута высот треугольника на нем. Следовательно, девять точек находятся на окружности, а окружность из девяти точек существует.
Второе доказательство существования
Мы знаем, что отражение ортоцентра относительно сторон и около середин сторон треугольника лежит на описанной окружности.Таким образом, рассмотрим гомотетию с центром с ratio. Он отображает описанную окружность в девятиточную окружность, а вершины треугольника — в его точки Эйлера.
Значит доказано.
См. Также
Эта статья является незавершенной. Помогите нам, расширив его.
Два занятия в классе Эти занятия в классе предназначены для того, чтобы позволить ученикам использовать математические рассуждения для решения задачи и в то же время дать учителю возможность поделиться с классом некоторой историей математики.Эти задания разработаны с учетом потребностей учителя, у которого может не хватать времени на выполнение манипулятивных действий в классе. Как учитель, я считаю, что эти задания хорошо работают в качестве задания «Задача дня», которое можно использовать как «трамплин» для «быстрого старта» дневного урока. Первое упражнение вращается вокруг «кругов Эйлера», а второе сосредоточено на идее принятия мер, очень похожих на те, что задумал Джордж Пойя для решения словесной проблемы. Это попытка улучшить навыки критического мышления учащихся путем изучения проблемы и реализации стратегии поиска решения.Это также способ привнести логику в класс. ЗАДАНИЕ 1: Поездка в кондитерскую Дженнифер любит перекусить. Во время недавнего похода в кондитерскую она купила несколько конфет типа «смешай и сочетай». Всего у нее 16 конфет. Девять содержат карамель; 10 содержат кокосовый орех; и 6 содержат как карамель, так и кокос. Сколько конфет не содержат ни карамели, ни кокоса. Один из подходов к этой проблеме — использовать то, что сейчас называется «диаграммой Венна».«Однако идея использования кругов для иллюстрации проблемы была впервые предложена математиком швейцарского происхождения Леонардом Эйлером (1707–1783). Ему приписывают множество достижений, особенно в области исчисления и теории чисел, но он также известен многими другими достижениями, одно из которых он оставил другому математику, чтобы получить признание. Вместо того, чтобы отдавать должное использованию кругов для иллюстрации утверждений и описания отношений между множествами и называть их «кругами Эйлера», Леонард Эйлер оставил это Джону Венну. чтобы расширить его идеи, и по сей день они называются «диаграммами Венна».» А теперь вернемся к нашей проблеме. Первый шаг для определения решения любой проблемы — убедиться, что оно понятно. Один из способов помочь понять проблему — использовать иллюстрации. Диаграммы Венна — хороший способ проиллюстрировать проблемы. Хорошо, пусть C представляет количество карамельных конфет, тогда n (C) = 9. Пусть Co представляет количество кокосовых конфет, тогда n (Co) = 10. Наконец, пусть (CCo) = 6 (где карамель и кокос конфеты внахлест). Очевидно, что если бы все конфеты были карамельными или кокосовыми, всего было бы 19 конфет.Однако от задачи у Дженнифер осталось всего 16 штук. Из данной информации мы можем построить «круг Эйлера», фактически диаграмму Венна. Очевидно, из диаграммы Венна ясно, что n (CCo) = Общее количество карамели, кокоса ИЛИ обоих равно 13. Поскольку всего 16 конфет, может быть только 3 штуки, которые не содержат ни карамели, ни кокоса. . С использованием настоящих конфет это занятие может стать любимым занятием в классе. Конечно, поскольку кокосовый орех не является любимой конфетой многих студентов, можно заменить его другим вкусом.Также может быть полезно убедиться, что учащиеся понимают основные обозначения при работе с диаграммами Венна и наборами. ЗАДАНИЕ 2: Колени и плавки Во время недавнего сафари в самые глубокие и темные джунгли Африки группа туристов или «исследователей джунглей» и слонов собрала 100 колен и 100 хоботов. Если у каждого туриста было по три чемодана, сколько исследователей джунглей и слонов отправились на сафари? Это задание предназначено для того, чтобы учащийся критически осмыслил процесс математики и подошел к словесной задаче, шаг за шагом.Это также возможность вставить историческую заметку об одном из ведущих мыслителей в области решения проблем, Джордже Поля (1887–1985). Поля, который вырос в Венгрии и из-за прихода к власти Гитлера, приехал в США, где большая часть его работы была сделана в области математических исследований. В 1950-х он начал писать серию книг и проницательных статей о решении проблем. Из его четырех шагов развились многие стратегии решения проблем. Одна из используемых стратегий решения проблем — это стратегия, которую альтернативная средняя школа Хейсвилла применяет в учебной программе и включает в себя следующее:
Один из способов решения этой проблемы или действия — использовать метод «угадать и проверить».Чтобы сделать хорошее предположение, необходимо сделать несколько основных предположений. Во-первых, у слонов четыре (4) колена и один (1) хобот. Во-вторых, у наших «исследователей джунглей» или туристов есть два (2) колена и три (3) туловища, как указано в проблеме. Теперь мы делаем обоснованное предположение.
Этот метод требует много времени, потому что, если вы сделаете неверное предположение, вы можете некоторое время гадать.Возможно, это не самый эффективный способ решения проблемы, но, тем не менее, это метод решения проблемы. Сделав предположение, можно подсчитать общее количество колен и туловищ, чтобы увидеть, были ли выполнены требования для сафари. Если требования соблюдены — хорошее предположение. Если требования не выполняются, продолжайте гадать. Второй подход к этой проблеме — использовать уравнение. Попробуйте следующее, где E представляет слонов, а H представляет людей, K представляет колени, а T представляет хоботы.Еще раз сделаем несколько предположений:
Следовательно, 4E + 2H = 100 (колени) и 1E + 3H = 100 (туловища). Это означает, что E = 100 — 3H (алгебраическая манипуляция) Теперь мы просто составляем уравнение и решаем для одной из переменных, а затем, когда у нас есть одна из переменных, мы подставляем в одно из уравнений и решаем для другой переменной.Начнем с уравнения: 4E + 2H = 100.
и H = 30
Теперь мы знаем, что на сафари участвуют 10 слонов и 30 человек. Уделяя время критическому обдумыванию проблемы, учащийся может найти решение и, таким образом, «решить проблему рассказа» и реализовать базовую структуру решения проблем, представленную Джорджем Поля. Хотя эти упражнения больше похожи на проблемы, они все же дают учителю возможность работать с учениками в области решения основных проблем, используя как минимум два разных метода. Хотя кажется, что им не хватает творчества, эти задачи работают как вопросы типа «Проблема дня», потому что я их использовал и знаю, что они работают. Если вы можете найти место для их использования в своем классе, не стесняйтесь! | Это задание разработано, чтобы помочь студентам всех уровней изучить математические концепции и терминологию на экзаменах.Темы для включения варьируются от сложения и вычитания до расчетов и исторических цифр и определений. Процедура: Разделите класс на две группы. Группы не обязательно Материалы:
Действия: Сложите наборы флешек в той же последовательности на столе вдоль Пусть по два студента из каждой группы выйдут впереди Дайте учащимся временные рамки, соответствующие задаче, По истечении времени студенты должны представить свои работы. Вся группа должна активно участвовать в решениях, если Модификаций: Вы можете попросить студентов ответить на вопросы индивидуально и | Ancient History: Летом середины 1950-х годов матери заставляли нас вздремнуть, потому что отдохнувшие, здоровые дети якобы были менее восприимчивы к полиомиелиту, который в те дни процветал. В семь или восемь лет у нас была настоящая битва за то, чтобы днем отдохнуть перед купанием. Однажды днем, вместо того, чтобы вздремнуть, нам дали возможность спокойно отдохнуть и записать свои числа от одного до тысячи.(Это был замечательный обмен, но вскоре я обнаружил, что аккуратный написание чисел требует больше времени, чем сон.) Когда задача была закончена, мы представили наши списки нашей матери. Она внимательно их изучила, а затем сказала, что дала нам задание показать нам, насколько велик миллион. Она напомнила нам, как трудно было написать от одного до тысячи, а затем объяснила, что нам придется написать тысячу списков, каждый с тысячей чисел, чтобы достичь миллиона. Математическая сила 1 000 x 1 000 = 1 000 000 стала реальной. Следующие упражнения призваны помочь учителям математики и естествознания познакомить учащихся с такими понятиями, как степени, последовательность, счет целых чисел и пропорции. Цель: Выучить квадраты чисел, счет путем сложения степеней двойки и изменения степени при изменении размеров. Цель: Разобраться в том, как числа растут экспоненциально, и получить материальные доказательства, демонстрирующие влияние изменений в измерениях; получать удовольствие от математики. Степень двойки для подсчета целых чисел.
График мощности.
Ханойская башня . На плате есть три колышка и стопка дисков разного размера, обычно от пяти до семи в порядке возрастания. Цель игры — переместить весь стек дисков на другой стержень, также в порядке возрастания. Одновременно можно перемещать только один диск, а больший диск нельзя ставить на меньший. Эдуард Лукас утверждал, что в настоящей Ханойской башне присутствуют
| ||
Проблемы со словами на диаграмме Венна | Мир математики Пасси
Источник изображения: http://img.izismile.com
Слово на диаграмме Венна. Если вы новичок, то в нем очень легко сделать ошибку.
Чрезвычайно важно:
Внимательно прочтите вопрос и запишите всю ключевую информацию.
Знать стандартные части диаграммы Венна
Пошаговая работа
В конце проверьте, правильно ли складываются все числа.
Давайте начнем с простого примера задачи с двумя круговыми диаграммами.
Диаграммы Венна — Word Problem One
«Был опрошен класс из 28 учеников, и их спросили, были ли у них дома когда-нибудь собаки или кошки в качестве домашних животных.
8 студентов сказали, что у них когда-либо была только собака.
6 студентов сказали, что у них когда-либо была только кошка.
10 студентов сказали, что у них есть собака и кошка.
4 студента сказали, что у них никогда не было собаки или кошки.”
Обратите внимание, что слово «только» чрезвычайно важно в задачах со словами на диаграмме Венна.
Поскольку слово «только» есть в тексте нашей задачи, это упрощает задачу.
Поскольку этот вопрос касается собак и кошек, потребуется диаграмма Венна с двумя кругами.
Вот тип диаграммы, который нам понадобится.
Источник изображения: Мир математики Пасси — Copyright 2012
Наша задача очень проста: нам даны все номера элементов, указанных на диаграмме.
Нам не нужно вычислять пропущенные значения.
Все, что нам нужно сделать, это поместить числа из задачи со словами на стандартную диаграмму Венна, и все готово.
Источник изображения: Мир математики Пасси — Copyright 2012
Диаграммы Венна — вторая задача слов
Ответ на этот вопрос будет фактически таким же, как и на вопрос о кошках и собаках в примере 1.
Однако на этот раз нам дают меньше информации, и поэтому мы будем работать над недостающей информацией.
Вот задача 2:
«Был опрошен класс из 28 учеников и их спросили, были ли у них дома когда-нибудь собаки или кошки в качестве домашних животных.
18 студентов сказали, что у них есть собака.
16 студентов сказали, что у них есть кошка.
4 студента сказали, что у них никогда не было собаки или кошки ».
Обратите внимание, что слово «только» чрезвычайно важно в задачах со словами на диаграмме Венна.
В приведенном выше вопросе нигде нет слова «только», и это указывает на то, что нам придется немного поработать.
Вопрос гласит: «18 студентов сказали, что у них есть собака» без слова «только».
Это означает, что сумма круга Собаки равна 18.
Всего 18 студентов по направлению «Собаки» включают людей, у которых есть и кошка, и собака, а также люди, у которых есть только собака.
Некоторые люди, которые не читают этот вопрос внимательно, просто возьмут приведенные выше цифры и поместят их прямо в диаграмму Венна, подобную этой.
Источник изображения: Мир математики Пасси — Copyright 2012
Всегда проверяйте в конце, чтобы сумма чисел равнялась общей сумме «Е».
16 + 18 + 4 = 38, что намного больше, чем сумма «E», равная 28.
Это потому, что у некоторых студентов есть и кошка, и собака. Мы вообще этого не учли.
Другие люди могут подумать, что у нас недостаточно информации, и поэтому решить эту проблему невозможно. Это просто неправда.
Давайте запишем на нашу диаграмму всю полученную информацию.
Источник изображения: Мир математики Пасси — Copyright 2012
Из предоставленной информации мы смогли выяснить, что всего кругов 24.(Например. Все в целом — без кошек и без собак = 28 — 4 = 24.
Это жизненно важная информация, которую мы сейчас используем для работы над остальной частью проблемы.
Давайте сначала определим значение «Только кошки».
Источник изображения: Мир математики Пасси — Copyright 2012
Далее мы рассчитываем количество человек «Только собаки».
Источник изображения: Мир математики Пасси — Copyright 2012
Давайте заполним всю информацию, которую мы уже разработали.
Источник изображения: Мир математики Пасси — Copyright 2012
Все, что нам осталось вычислить, — это количество кошек и собак в центре диаграммы.
Мы можем сделать это любым из трех возможных способов:
Кошки и собаки = Всего кошек — только кошек
или
Кошки и собаки = Всего собак — Только собаки
или
Кошки и собаки = Итого E — Только кошки — Только собаки — (Без кошек и без собак)
Как бы то ни было, ответ — 10.
Итак, вот окончательный ответ на диаграмму Венна.
Источник изображения: Мир математики Пасси — Copyright 2012
При вводе ответов в нашу рабочую тетрадь по математике нам не нужно раскрашивать диаграмму.
Окончательный ответ, подобный следующему, вполне приемлем.
Источник изображения: Мир математики Пасси — Copyright 2012
Мы можем резюмировать шаги, которые мы использовали для решения этой проблемы, следующим образом.
Word, задача два — краткое описание шагов
— Определите, какая информация предоставляется и что необходимо вычислить.
— Всего кругов = E все — (Без кошек и без собак)
— Только кошки = Всего кругов — Всего собак
— Только собаки = Всего кругов — Всего кошек
— Кошки и собаки = Всего кошек — Только кошки
— Наконец, убедитесь, что все числа на диаграмме в сумме равны букве «Е» всего в сумме.
Задача третьего слова — подмножества
«Было опрошено 50 человек, и только 20 человек сказали, что они регулярно едят здоровую пищу, такую как фрукты и овощи.
Из этих 20 здоровых едоков 12 сказали, что они ели овощи каждый день.
Нарисуйте диаграмму Венна, чтобы представить эти результаты ».
Эта задача сильно отличается от двух наших других круговых диаграмм.
Кошки и Собаки сильно отличаются друг от друга, поэтому нам понадобились два отдельных круга.
Однако здоровая пища и овощи не отличаются друг от друга, потому что овощи являются одним из видов здоровой пищи.
Мы говорим, что овощи — это «подмножество» здоровой пищи.
Это означает, что мы не разделяем круги. На самом деле нам нужно нарисовать круги друг в друге вот так.
Источник изображения: Мир математики Пасси — Copyright 2012
В сумме получается 50, и 12 человек, которые включают овощи в свою здоровую пищу, показаны как полностью входящие в круг «Здоровое питание».
Задача четвертого слова — Непересекающиеся наборы
«Нарисуйте диаграмму Венна, которая делит двенадцать месяцев в году на следующие две группы:
Месяцы, название которых начинается с буквы« J », и Месяцы, название которых заканчивается на« бер ».Для ответа вам понадобится диаграмма Венна с двумя кругами «.
Первый шаг — перечислить двенадцать месяцев в году:
Январь — назван в честь Януса, бога дверей и ворот.
Февраль — назван в честь февраля, когда приносились жертвы за грехи.
Март — назван в честь Марса, бога войны.
Апрель — от аперире, латинского «открывать» ( бутоны)
Май — назван в честь Майи, богини роста растений
Июнь — назван в честь Юния, на латыни означает богиня Юнона
Июль — назван в честь Юлия Цезаря в 44 г. до н.э.Ок.
г. Август — назван в честь Августа Цезаря в 8 г. до н. Э.
сентябрь — от septem, латиница для «семь»
октябрь — от octo, латиница для «восьмерки»
ноябрь — от novem, латиница для «девять»
декабрь — от decem, латиница для «десять»
Месяцев, начиная с J = {январь, июнь, июль}
Месяцы, заканчивающиеся на «ber» = {сентябрь, октябрь, ноябрь, декабрь}
У этих двух наборов нет общих элементов, поэтому мы не будем их перекрывать.
Остальные месяцы должны будут выйти за рамки наших двух кругов.
Когда мы закончим, на диаграмме должны быть все двенадцать месяцев.
Заполненная диаграмма Венна показана ниже:
Источник изображения: Мир математики Пасси — Copyright 2012
Задачи Venn Word — Резюме
Мы не включили три круговые диаграммы, так как они будут рассмотрены в отдельном уроке.
Помните, что схема Венна с двумя кругами обычно выглядит следующим образом:
Источник изображения: Мир математики Пасси — Copyright 2012
Помните, что шаги для решения более сложных задач:
Определите, какая информация предоставляется и что необходимо вычислить.
Проверьте, являются ли эти два набора «Подмножествами» или «Непересекающимися» наборами.
Если это «пересекающиеся множества», то могут потребоваться некоторые из следующих формул.
Всего кругов = все E — (не в A и не в B)
Только в A = Итого в обоих кругах — Итого в B
Только в А = Итого по кругу А — Итого на перекрестке (A и B)
Только в B = Итого по обоим кругам — Итого по А
Только в B = Итого по кругу B — Всего на перекрестке (A и B)
на перекрестке (A и B) = всего на B — только на B
на пересечении (A и B) = всего в A — только в A
Наконец, проверьте, что все числа на диаграмме в сумме равны букве «Е» всего в сумме.
Видео о задачах Venn Word
На следующем видео показана типичная задача с двумя кружками.
Вот видео, которое охватывает проблему двух кругов, где нам нужно найти количество элементов, которые находятся (не в «A» и не в «B»).
Вот видео, в котором показано, как решать задачи опроса по диаграмме Венна.
Следующее видео — еще одно очень хорошее видео от YourMathGal о том, как рисовать диаграммы Венна для текстовых задач.
Сопутствующие товары
Введение в диаграммы Венна
Трехкружные диаграммы Венна
Реальные диаграммы Венна
Если вам понравился этот пост, почему бы не получить бесплатную подписку на наш сайт.
Затем вы можете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы узнать, как именно работает бесплатная подписка, щелкните следующую ссылку:
Как работает бесплатная подписка
Если вы хотите представить идею для статьи или стать приглашенным автором в нашем блоге, напишите нам по адресу hotmail, указанному в правой боковой панели этой страницы.
Если вы подписались на «Мир математики Пасси» и хотели бы получить бесплатную версию этого урока в формате PowerPoint, которая на 100% бесплатна для вас как подписчика, напишите нам по следующему адресу:
Пожалуйста, укажите в своем электронном письме, что вы хотите получить бесплатную подписную копию Powerpoint «Проблемы с диаграммами Венна».
Поставьте нам лайк на Facebook
На нашей странице в Facebook есть много дополнительных элементов, которые не публикуются на этом сайте.
Сюда входят предметы, представляющие математический интерес, забавные математические картинки и мультфильмы, а также случайные взгляды на личную жизнь «Пасси».
Проверьте это по следующей ссылке:
https://www.facebook.com/PassysWorldOfMat Mathematics
Пока вы там, ПОНРАВИТЕСЬ на странице, чтобы вы могли получать наши обновления FB в своей ленте новостей Facebook.
Помогите миру расти Пасси
Ежедневно в Passy’s World сотни людей проходят бесплатные уроки математики.
Помогите нам поддерживать эту бесплатную услугу и поддерживать ее рост.
Пожертвуйте любую сумму от 2 долларов и выше через PayPal, щелкнув изображение PayPal ниже. Спасибо!
PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать учетную запись PayPal для обработки транзакции. Это действие не взимает с вас комиссию за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно достигнет Passy’s World.
Наслаждайтесь,
Пасси
Трехкружная диаграмма Венна | Мир математики Пасси
Источник изображения: istockphoto Приобретено Passy’s World
Трехкруговые диаграммы Венна — это шаг вперед по сложности по сравнению с двухкруглыми диаграммами.
В этом уроке мы сначала узнаем, как читать три круговые диаграммы. Затем мы рассмотрим некоторые проблемы со словами.
Чтение трех круговых диаграмм
Музыкальное исследование было проведено с целью выяснить, какие музыкальные жанры нравятся группе людей.
Результаты были помещены на следующую трехкружную диаграмму Венна.
Источник изображения: Мир математики Пасси
Чтобы узнать общее количество опрошенных людей (или значение E = Everything), мы складываем все числа на диаграмме.
Когда мы это сделаем, ответ будет 70.
Это «значение E = Все» также называется «Универсальным набором» всего во вселенной нашей диаграммы.
Если мы хотим найти общее количество людей, которым нравится «рок», мы складываем все числа в круге «рок», включая области, где «рок» перекрывается с другими кругами.
Общее количество рок-людей: 16 + 2 + 8 + 5 = 31 человек.
Мы также можем вычислить вероятность или шансы по нашей диаграмме Венна.
Например, мы обнаружили, что 31 человек из 70 любит рок-музыку.
Итак, если мы выберем любого человека из нашей группы наугад, шансы, или шансы, или вероятность того, что им понравится рок-музыка, будут 31 из 70, или 31/70, или 31/70 x100 = 44%.
Мы можем найти количество людей, которым нравятся все три типа музыки, перейдя в центр нашей диаграммы, где все три круга пересекаются.
Есть 8 человек, которым нравятся все три типа музыки.
Диаграмма Венна Word Problem One
Эта первая проблема довольно проста, поскольку вся необходимая нам информация была предоставлена нам в вопросе.
«Класс из 40 учеников заполнил опрос о том, какие домашние животные им нравятся. Выбор был: кошки, собаки и птицы. Всем понравился хотя бы один питомец.
10 студентам понравились кошки и птицы, но не собаки
6 студентам понравились кошки и собаки, но не птицы
2 студентам понравились собаки и птицы, но не кошки
2 студентам понравились все три питомца
10 студентам понравились только кошки
9 студентам понравились только собаки
1 ученику понравились только птицы
Изобразите эти результаты, используя трехкружную диаграмму Венна.”
Тип трехкружной диаграммы Венна, которая нам понадобится, выглядит следующим образом:
Источник изображения: Мир математики Пасси
Эта задача из трех круговых слов проста.
Все числовые значения для каждого раздела диаграммы были даны нам в вопросе.
Все, что нам нужно сделать, это аккуратно нанести числовые значения на диаграмму.
Нам также нужно проверить, что все числа в сумме дают 40 учеников, когда мы закончим.
Заполненная диаграмма Венна показана ниже.
Источник изображения: Мир математики Пасси
Обратите внимание, что нам не нужно закрашивать и закрашивать круги на диаграммах Венна.
Следующая диаграмма также является правильным и вполне приемлемым ответом.
Источник изображения: Мир математики Пасси
Слово на диаграмме Венна Задача 2
Это более сложная версия Задачи 1, где в тексте вопроса дается меньше
информации.Это означает, что нам нужно будет выполнить
несколько шагов по разработке, чтобы добраться до окончательной завершенной диаграммы.
Источник изображения: Мир математики Пасси
Нам нужна диаграмма Венна того же типа, что и для вопроса 1.
Источник изображения: Мир математики Пасси
Теперь нам нужно внимательно рассмотреть проблему со словом и сразу решить, какую информацию мы можем использовать.
Всегда должны быть какие-то данные, которые мы можем разместить на диаграмме, чтобы начать работу, даже если это может показаться не так уж и много.
Источник изображения: Мир математики Пасси
Когда мы помещаем то, что знаем до сих пор, на диаграмму, мы получаем следующее:
Источник изображения: Мир математики Пасси
Теперь нам нужно проработать другую информацию в словесной задаче, по частям.
Обычно в этих задачах нам нужно работать над перекрывающимися частями в центре диаграммы, а затем продвигаться к внешним частям диаграммы «Только кошки», «Только собаки» и «Только птицы».
Помните: работайте наизнанку.
Вот что мы будем делать дальше.
Источник изображения: Мир математики Пасси
Эта информация относится к следующему разделу диаграммы Венна.
Источник изображения: Мир математики Пасси
Теперь мы можем заполнить ответ «2» в центре нашей диаграммы.
Источник изображения: Мир математики Пасси
Итак, круг птиц почти завершен.
Осталось только проработать раздел «Только птицы», чем мы сейчас и займемся.
Источник изображения: Мир математики Пасси
Теперь мы можем заполнить ответ «1» на нашей диаграмме.
Источник изображения: Мир математики Пасси
Теперь мы закончили круг с птицами.
Затем мы работаем над кругом кошек, следуя точно таким же шагам, как и над кругом с птицами.
Сначала нам нужно поработать с перекрытиями, которые касаются кошек и других животных в центре диаграммы.
Источник изображения: Мир математики Пасси
Эта информация относится к следующему разделу диаграммы Венна.
Источник изображения: Мир математики Пасси
Теперь мы можем заполнить ответ «6» на нашей диаграмме.
Источник изображения: Мир математики Пасси
Мы почти у цели!
Теперь у нас есть только «Только кошки» и «Только собаки», и у нас есть вся необходимая информация для этого.
Источник изображения: Мир математики Пасси
Теперь мы можем поместить ответ «Только кошки» на нашу диаграмму.
Источник изображения: Мир математики Пасси
Нам осталось только разработать «Только собаки».
Источник изображения: Мир математики Пасси
Наша диаграмма для задачи два наконец-то завершена.
Источник изображения: Мир математики Пасси
Обратите внимание, что нам не нужно закрашивать и закрашивать круги на диаграммах Венна.
Следующая диаграмма также является правильным и вполне приемлемым ответом.
Источник изображения: Мир математики Пасси
Сводка проблем со словом в диаграмме Венна
Источник изображения: Мир математики Пасси
Видео с тремя кругами
Вот отличное видео с диаграммами Венна, в котором также объясняется метод «включения / исключения».
Это интересная задача с тремя кругами, в которой они используют таблицу значений, чтобы помочь с разработкой.
Вот видео, в котором показано, как выполнять «Дополнительные наборы» для трех круговых диаграмм.
Сопутствующие товары
Введение в диаграммы Венна
Проблемы со словами на диаграмме Венна
Диаграммы Венна в реальном мире
Если вам понравился этот пост, почему бы не получить бесплатную подписку на наш сайт.
Затем вы можете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы узнать, как именно работает бесплатная подписка, щелкните следующую ссылку:
Как работает бесплатная подписка
Если вы хотите представить идею для статьи или стать приглашенным автором в нашем блоге, напишите нам по адресу hotmail, указанному в правой боковой панели этой страницы.
Если вы подписались на «Мир математики Пасси» и хотели бы получить бесплатную версию этого урока в формате PowerPoint, которая на 100% бесплатна для вас как подписчика, напишите нам по следующему адресу:
Пожалуйста, укажите в своем электронном письме, что вы хотите получить бесплатную подписную копию Powerpoint «Три круга Венна».
Поставьте нам лайк на Facebook
На нашей странице в Facebook есть много дополнительных элементов, которые не публикуются на этом сайте.
Сюда входят предметы, представляющие математический интерес, забавные математические картинки и мультфильмы, а также случайные взгляды на личную жизнь «Пасси».
Проверьте это по следующей ссылке:
https://www.facebook.com/PassysWorldOfMat Mathematics
Пока вы там, ПОНРАВИТЕСЬ на странице, чтобы вы могли получать наши обновления FB в своей ленте новостей Facebook.
Помогите миру расти Пасси
Ежедневно в Passy’s World сотни людей проходят бесплатные уроки математики.
Помогите нам поддерживать эту бесплатную услугу и поддерживать ее рост.
Пожертвуйте любую сумму от 2 долларов и выше через PayPal, щелкнув изображение PayPal ниже. Спасибо!
PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать учетную запись PayPal для обработки транзакции.Это действие не взимает с вас комиссию за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно достигнет Passy’s World.
Наслаждайтесь,
Пасси
Примеры диаграмм Венна для решения проблем
Что такое диаграмма Венна?
Диаграммы
Венна определяют все возможные отношения между наборами множеств. Самые простые диаграммы Венна просто состоят из множества круговых границ, описывающих диапазон множеств.
Пример простой диаграммы Венна
Перекрывающиеся области между двумя границами описывают общие для них элементы, а области, которые не перекрывают друг друга, содержат разные элементы. Диаграммы Венна часто используются в математике, поскольку люди склонны полагать, что они используются только для решения математических задач. Но, как показывает трехкружная диаграмма Венна ниже, ее можно использовать для решения многих других проблем.
Пример диаграммы Венна с 3 кругами
Хотя приведенная выше диаграмма может показаться сложной, на самом деле ее очень легко понять.Хотя диаграммы Венна могут выглядеть сложными при решении бизнес-процессов, понимание значения границ и их обозначения может в значительной степени упростить процесс. Давайте посмотрим на несколько примеров, которые демонстрируют, как диаграммы Венна могут значительно облегчить решение проблем.
Пример 1. Процесс найма в компании
Первый пример диаграммы Венна демонстрирует процесс составления короткого списка сотрудников компании. При составлении короткого списка кандидатов на должность отдел кадров учитывает несколько факторов, таких как опыт, профессиональные навыки и лидерские качества.Все эти качества отличаются друг от друга и могут присутствовать или отсутствовать у некоторых кандидатов. Однако лучшими кандидатами будут те, кто сочетал бы все эти качества.
Как использовать диаграммы Венна для найма людей
Кандидат, обладающий всеми тремя качествами, идеально подходит для вашей организации. Таким образом, используя простые диаграммы Венна, подобные приведенной выше, компания может легко продемонстрировать свои процессы найма и значительно упростить процесс отбора.
Красочную и точную диаграмму Венна, подобную приведенной выше, можно легко создать с помощью нашего программного обеспечения диаграмм Венна, и мы профессионально разработали шаблоны диаграмм Венна, чтобы вы тоже могли быстро приступить к работе.
Пример 2: Инвестиции в местоположение
Второй пример диаграммы Венна идет дальше и рассматривает, как компания может использовать диаграмму Венна для выбора подходящего местоположения офиса. Решение будет основано на экономических, социальных и экологических факторах.
Выбор местоположения офиса с помощью диаграммы Венна
В идеальном сценарии вы найдете место, в котором в равной мере учитываются все вышеперечисленные факторы. Но если вам не удастся найти такое место, вы можете решить, какой фактор для вас наиболее важен. Независимо от приоритета, потому что вы уже перечислили места, принятие решения становится проще.
Пример 3: Выбор работы мечты
Последний пример отражает то, как можно легко ответить на один из самых сложных вопросов жизни с помощью диаграммы Венна.Выбор работы мечты — это то, что ставит в тупик большинство выпускников колледжей, но с помощью единственной диаграммы Венна этот мыслительный процесс можно в значительной степени упростить.
Во-первых, выделите факторы, которые имеют значение при выборе работы мечты, например, то, что вы любите делать, что у вас хорошо получается, и, наконец, потенциал заработка. Хотя большинство из нас мечтают стать знаменитостями и появиться на телевидении, не все одарены актерскими способностями, и этот карьерный путь может быть не самым жизнеспособным. Вместо этого выбор того, что у вас хорошо получается, чем вы любите заниматься, и того, что имеет хороший потенциал заработка, будет наиболее практичным выбором.
Работа мечты Диаграмма Венна
Таким образом, работа, отвечающая всем этим трем критериям, была бы для кого-то работой мечты. Эти три критерия не обязательно должны быть одинаковыми и могут быть изменены в соответствии с индивидуальными требованиями.
Итак, вы видите, что даже самые сложные процессы можно упростить, используя эти простые диаграммы Венна.
Что такое диаграмма Венна с примерами
Что такое
Диаграмма Венна ?
Термин Диаграмма Венна не является чуждым, поскольку у всех нас была математика, особенно теория вероятностей и алгебра.Теперь, для непрофессионала, диаграмма Венна представляет собой наглядную демонстрацию всех возможных реальных отношений между коллекцией различных наборов предметов. Он состоит из нескольких перекрывающихся кругов или овальных форм, каждая из которых представляет собой отдельный набор или предмет.
Диаграммы Венна изображают сложные теоретические отношения и идеи для лучшего и легкого понимания. Эти диаграммы также профессионально используются профессорами для отображения сложных математических концепций, классификации в науке и разработки стратегий продаж в бизнес-индустрии.
Источник изображения : pinterest.com
Эволюция диаграммы Венна
Развитие диаграммы Венна восходит к 1880 году, когда Джон Венн воплотил их в жизнь в статье под названием «О схематическом и механическом представлении суждений и рассуждений». Она была опубликована в Philosophical Magazine и Journal of Science. Джон Венн провел тщательное исследование этих диаграмм и предвидел их формализацию.Он — тот, кто первоначально их обобщил, неудивительно, как они были названы, то есть Диаграммы Венна в 1918 году.
Существует небольшой разрыв между диаграммами Венна и диаграммами Эйлера, изобретенными в 18 веке Леонардом Эйлером, который также приложил руку к ее развитию в 1700-х годах. Джон называл диаграммы кругами Эйлера.
Разработка диаграмм Венна продолжалась и в 20 веке. Например, примерно в 1963 году Д. В. Хендерсон обнаружил существование n-графа Венна, состоящего из n-кратной рациональной симметрии, что указывало на то, что n было простым числом.В последующие годы в эту концепцию углубились еще четыре интеллекта, которые пришли к выводу, что вращательно-симметричные диаграммы Венна существуют только в том случае, если n — простое число.
С тех пор эти диаграммы стали частью сегодняшней учебной программы и иллюстрируют бизнес-информацию. Диаграммы Венна и Эйлера были включены в качестве компонента обучения теории множеств нового математического движения в 1960 году.
Почему диаграммы Венна важны?
Диаграммы Венна полезны в качестве обучающих и учебных пособий для ученых, учителей и профессоров.Они помогают представлять простые математические концепции в начальной школе, а также теории и задачи теоретического характера среди логиков и математиков.
Кроме того, вместе с теорией множеств, диаграммы Венна способствовали более четкому и современному пониманию бесконечных чисел и действительных чисел в математике. Они также способствовали созданию общего языка и системы символов, касающихся теории множеств, среди исследователей и математиков.
Они идеально подходят для иллюстрации сходства и различий между предметами или идеями, когда круги перекрываются или иначе.Эта функция обычно используется в деловой индустрии для поиска и создания ниши на рынке товаров и услуг. Благодаря им предприниматели получают невероятные отчеты о продажах и получают огромную реализованную прибыль.
Вы также можете использовать диаграммы Венна , чтобы принимать важные жизненные решения, например, в какой колледж поступить, в какую школу взять вашего ребенка, какие материалы лучше использовать для конструирования или изготовления одежды, в каком ресторане пообедать и т. Д.
Когда использовать диаграммы Венна?
Вы можете использовать диаграммы Венна , чтобы продемонстрировать взаимосвязи в статистике, логике, вероятности, лингвистике, информатике, организации бизнеса и многих других областях.
В математике Диаграммы Венна — это обучающий инструмент, который объясняет такие математические концепции, как множества, объединения и пересечения. Они также решают серьезные задачи по высшей математике. Вы можете подробно прочитать о них в академических журналах в своей библиотеке и поразиться тому, насколько теория множеств является законченным разделом математики.
Статистики используют идею диаграмм Венна , чтобы предсказать вероятность конкретных событий.То же самое и в области прогнозной аналитики. Наборы выборочных данных сравниваются и исследуются, чтобы выявить их сходства и различия.
Источник изображения : pinterest.com
Они также эффективны при определении логических оснований в аргументах и выводах. Как и в дедуктивном рассуждении, если посылки реальны, а форма аргумента верна, результат должен быть правильным.Диаграмма, аналогичная диаграмме Венна по логике, — это таблица истинности. Он помещает переменные в столбцы, чтобы расшифровать то, что логически возможно. Еще одна диаграмма Рэндольфа, также известная как R-диаграмма, использует линии для объяснения множеств.
Источник изображения : youtube.com
В лингвистике Диаграммы Венна помогают узнать, как языки различаются или соотносятся друг с другом с точки зрения алфавита, гласных, произношения и т. Д.
Источник изображения : slideshare.net
Источник изображения : kdnuggets.com
Диаграммы также полезны в сфере продаж и маркетинга для сравнения и сопоставления продуктов, услуг, процессов и всего, что происходит при организации бизнеса. Они практичны и эффективны в увеличении продаж и прибылей, а также в расширении деятельности предприятий.
Источник изображения : businessbullet.co.uk
Символы на диаграмме Венна
Когда дело доходит до диаграммы Венна, существует множество символов, но мы рассмотрим три.
ꓵ — пересечение двух наборов: показывает элементы, общие для обоих наборов.
Источник изображения : youtube.com
∪ — это представляет собой полная диаграмма Венна.
Источник изображения : math-only-math.com
A ’- обозначает завершение набора A. Он состоит из всего, что не входит в коллекцию.
Источник изображения : mathonline.wikidot.com
Примеры диаграмм Венна
Математика
Первый пример диаграммы Венна относится к математике.Они доступны при освещении тем, посвященных теории множеств и теории вероятностей.
На схеме ниже представлены два набора: A = {1, 5, 6, 7, 8, 9, 10, 12} и B = {2, 3, 4, 6, 7, 9, 11, 12, 13}. Секция, в которой два набора перекрываются, имеет числа, содержащиеся как в наборе A, так и в B, называемом пересечением A и B. Два набора, вместе взятые, дают их объединение, которое включает все объекты в A, B, которые являются { 1 2 3 4 5 6 7 8 9 10 11 12 13}.
Источник изображения : bbc.co.uk
Бизнес
В приведенном ниже примере диаграммы Венна анализируются общие черты и различия в различных областях работы. Менеджеры по персоналу и специалисты по карьерной лестнице используют его, чтобы консультировать людей по вопросам их карьеры.
Источник изображения : pinterest.com
Наука
Ученый использует диаграммы Венна для изучения здоровья человека и лекарств. На иллюстрации ниже вы можете увидеть аминокислоты, жизненно важные для человека.
Источник изображения : researchgate.com
Как создать простую диаграмму Венна за считанные минуты?
Теперь мы будем использовать онлайн-программное обеспечение Edraw Max.В нем есть все основные символы и формы, которые вам нужны, а также множество бесплатных шаблонов Диаграмма Венна, и модный и продвинутый интерфейс, понятный для новичков.
Перед тем, как начать онлайн-диаграмму Венна , вы должны убедиться, что вы:
- Определите цель, которую вы хотите достичь. Имейте четкое представление о том, что вы хотели бы сравнить и для какой цели это сравнение необходимо. Это облегчает определение множеств.
- Просмотрите и найдите список предметов, содержащихся в наборах.
- Просмотрите доступные шаблоны, чтобы получить представление о том, что вы собираетесь рисовать, а затем создайте свою собственную диаграмму Венна , выполнив следующие действия.
Шаг 1: Войдите на веб-сайт программного обеспечения с https://www.edrawmax.com/online/ . Если вы не создавали учетную запись ранее, войдите в систему, используя действительные учетные данные, подтвердите свою учетную запись, а затем войдите в систему.
Шаг 2: Выберите параметры бизнес-диаграммы на вкладке «Доступные шаблоны» и дважды щелкните значок диаграммы Венна, чтобы отобразить пустую страницу, на которой вы будете рисовать.
Шаг 3: На левой панели экрана вы найдете все необходимые символы и формы диаграммы Венна. Перетащите подходящие и поместите их на холст для рисования, чтобы создать диаграмму Венна.
Шаг 4: Сохраните готовую диаграмму Венна в доступных форматах или экспортируйте или поделитесь ею на других платформах прямо с веб-страницы Edraw.
Шаг 5: Настройка. Большинство встроенных фигур предназначены для изменения размера, редактирования и изменения цвета.
Чтобы изменить цвет, коснитесь целевого круга несколько раз и выберите цвет на вкладке быстрого выбора цвета внизу.
Чтобы добавить личную тему и стиль, выберите один из доступных шрифтов, эффектов и цветовых схем. Сделайте уникальную и профессиональную диаграмму Венна, щелкнув то, что вам больше нравится.
Статьи по теме
теория графов | Проблемы и приложения
Теория графов , раздел математики, связанный с сетями точек, соединенных линиями.Теория графов зародилась в развлекательных математических задачах ( см. числовая игра), но превратилась в значительную область математических исследований с приложениями в химии, исследовании операций, социальных науках и информатике.
Подробнее по этой теме
комбинаторика: теория графов
Граф G состоит из непустого набора элементов V (G) и подмножества E (G)…
История теории графов восходит к 1735 году, когда швейцарский математик Леонард Эйлер решил проблему Кенигсбергского моста. Проблема Кенигсбергского моста была старой загадкой, касающейся возможности найти путь через каждый из семи мостов, пересекающих разветвленную реку, протекающую мимо острова, — но без необходимости пересекать мост дважды. Эйлер утверждал, что такого пути не существует. Его доказательство включало только ссылки на физическое устройство мостов, но по существу он доказал первую теорему теории графов.
мосты Кенигсберга
В XVIII веке швейцарского математика Леонарда Эйлера заинтриговал вопрос, существует ли маршрут, который пересекает каждый из семи мостов ровно один раз. Доказав, что ответ отрицательный, он заложил основы теории графов.
Encyclopædia Britannica, Inc.
В теории графов термин график не относится к диаграммам данных, таким как линейные или гистограммы. Вместо этого он относится к набору вершин (то есть точек или узлов) и ребер (или линий), соединяющих вершины.Когда любые две вершины соединяются более чем одним ребром, граф называется мультиграфом. Граф без петель и не более чем с одним ребром между любыми двумя вершинами называется простым графом. Если не указано иное, предполагается, что граф относится к простому графу. Когда каждая вершина соединяется ребром с каждой другой вершиной, граф называется полным графом. При необходимости каждому ребру может быть присвоено направление для создания так называемого ориентированного графа или орграфа.
Важным числом, связанным с каждой вершиной, является ее степень, которая определяется как количество ребер, которые входят в нее или выходят из нее.Таким образом, петля дает 2 степени своей вершины. Например, все вершины простого графа, показанного на диаграмме, имеют степень 2, тогда как все вершины показанного полного графа имеют степень 3. Знание числа вершин в полном графе характеризует его сущность. По этой причине полные графы обычно обозначаются K n , где n обозначает количество вершин, а все вершины K n имеют степень n — 1.(В переводе на терминологию современной теории графов теорему Эйлера о проблеме Кенигсбергского моста можно переформулировать следующим образом: если существует путь вдоль ребер мультиграфа, который пересекает каждое ребро один и только один раз, то существует не более двух вершин нечетная степень; кроме того, если путь начинается и заканчивается в одной и той же вершине, то никакие вершины не будут иметь нечетную степень.)
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Еще одно важное понятие в теории графов — это путь, который представляет собой любой маршрут по краям графа.Путь может следовать за одним ребром непосредственно между двумя вершинами, или он может следовать за несколькими ребрами через несколько вершин. Если есть путь, соединяющий любые две вершины в графе, этот граф называется связным. Путь, который начинается и заканчивается в одной и той же вершине, не пересекая какое-либо ребро более одного раза, называется схемой или замкнутым путем. Схема, которая следует за каждым ребром ровно один раз при посещении каждой вершины, называется схемой Эйлера, а граф называется графом Эйлера. Эйлеров граф связен и, кроме того, все его вершины имеют четную степень.
Схема Эйлера
Граф — это совокупность вершин или узлов и ребер между некоторыми или всеми вершинами. Если существует путь, который пересекает каждое ребро ровно один раз, так что путь начинается и заканчивается в одной и той же вершине, путь известен как эйлеров контур, а граф — как эйлеров граф. Эйлериан относится к швейцарскому математику Леонарду Эйлеру, который изобрел теорию графов в 18 веке.
Encyclopædia Britannica, Inc.
В 1857 году ирландский математик Уильям Роуэн Гамильтон изобрел головоломку (Икосианскую игру), которую позже продал производителю игр за 25 фунтов стерлингов.Головоломка заключалась в том, чтобы найти особый тип пути, позже известный как гамильтонова цепь, вдоль краев додекаэдра (платоново твердое тело, состоящее из 12 пятиугольных граней), который начинается и заканчивается в одном и том же углу, проходя через каждый угол ровно один раз. Маршрут коня ( см. числовая игра: задачи на шахматной доске) — еще один пример развлекательной задачи, включающей гамильтонову схему. Гамильтоновы графы было сложнее охарактеризовать, чем эйлеровы графы, поскольку необходимые и достаточные условия существования гамильтоновой схемы в связном графе до сих пор неизвестны.
Гамильтонова схема
Ориентированный граф, в котором путь начинается и заканчивается в одной и той же вершине (замкнутый цикл), так что каждая вершина посещается ровно один раз, называется гамильтоновой схемой. Ирландский математик XIX века Уильям Роуэн Гамильтон начал систематическое математическое изучение таких графов.
Encyclopædia Britannica, Inc.
Истории теории графов и топологии тесно связаны, и эти две области имеют много общих проблем и методов.Эйлер сослался на свою работу по проблеме Кенигсбергского моста как на пример geometria situs — «геометрии положения», тогда как развитие топологических идей во второй половине XIX века стало известно как analysis situs — « анализ позиции ». В 1750 году Эйлер открыл полиэдральную формулу V — E + F = 2, связывающую количество вершин ( V ), ребер ( E ) и граней ( F ) многогранника (a твердое тело, как упомянутый выше додекаэдр, грани которого являются многоугольниками).Вершины и ребра многогранника образуют граф на его поверхности, и это понятие привело к рассмотрению графов на других поверхностях, таких как тор (поверхность твердого бублика), и к тому, как они делят поверхность на дискообразные грани. Формула Эйлера вскоре была обобщена на поверхности как V — E + F = 2 — 2 г , где г обозначает род или количество «бубликовых отверстий» на поверхности ( см. Эйлерова характеристика). Рассмотрев поверхность, разделенную на многоугольники встроенным графом, математики начали изучать способы построения поверхностей, а позже и более общих пространств, склеивая многоугольники вместе.Это было началом области комбинаторной топологии, которая позже, благодаря работам французского математика Анри Пуанкаре и других, превратилась в так называемую алгебраическую топологию.
Связь между теорией графов и топологией привела к подполе, называемому топологической теорией графов. Важная проблема в этой области касается плоских графов. Это графы, которые можно нарисовать в виде точечных диаграмм на плоскости (или, что то же самое, на сфере) без пересечения ребер, за исключением тех вершин, где они встречаются.Полные графы с четырьмя или менее вершинами являются планарными, а полные графы с пятью вершинами ( K 5 ) или более — нет. Непланарные графы нельзя рисовать на плоскости или на поверхности сферы без пересечения ребер между вершинами. Использование диаграмм из точек и линий для представления графиков фактически выросло из химии 19-го века, где буквенные вершины обозначали отдельные атомы, а соединительные линии обозначали химические связи (со степенью, соответствующей валентности), в которой планарность имела важные химические последствия.Первое использование в этом контексте слова граф приписывается англичанину 19-го века Джеймсу Сильвестру, одному из нескольких математиков, заинтересованных в подсчете специальных типов диаграмм, представляющих молекулы.
Другой класс графов — это совокупность полных двудольных графов K m , n , которые состоят из простых графов, которые можно разбить на два независимых набора по m и n вершин такое, что между вершинами в каждом наборе нет ребер, и каждая вершина в одном наборе соединяется ребром с каждой вершиной в другом наборе.Как и K 5 , двудольный граф K 3,3 не является плоским, опровергая заявление, сделанное в 1913 году английским специалистом по рекреационным проблемам Генри Дудени о решении проблемы «газ-вода-электричество». В 1930 году польский математик Казимеж Куратовский доказал, что любой неплоский граф должен содержать копию определенного типа K 5 или K 3,3 . Хотя K 5 и K 3,3 не могут быть вложены в сферу, они могут быть вложены в тор.Проблема вложения графа касается определения поверхностей, в которые может быть вложен граф, и тем самым обобщает проблему планарности. Только в конце 1960-х годов проблема вложения для полных графов K n была решена для всех n .
Другая проблема топологической теории графов — это проблема раскраски карты. Эта проблема является результатом хорошо известной проблемы четырехцветной карты, которая спрашивает, можно ли раскрасить страны на каждой карте, используя всего четыре цвета таким образом, чтобы страны, разделяющие границу, имели разные цвета.Первоначально заданная в 1850-х годах Фрэнсисом Гатри, тогда студентом Лондонского университетского колледжа, эта проблема имеет богатую историю, наполненную ошибочными попытками ее решения. В эквивалентной теоретико-графовой форме эту проблему можно перевести, чтобы спросить, всегда ли вершины плоского графа можно раскрасить, используя всего четыре цвета, таким образом, чтобы вершины, соединенные ребром, имели разные цвета. Результат был окончательно подтвержден в 1976 году с помощью компьютеризированной проверки почти 2000 специальных конфигураций.Интересно, что соответствующая проблема раскраски, касающаяся количества цветов, необходимых для раскрашивания карт на поверхностях более высокого рода, была полностью решена несколькими годами ранее; например, карты на торе могут потребовать до семи цветов. Эта работа подтвердила, что формула английского математика Перси Хивуда из 1890 года правильно дает эти числа окраски для всех поверхностей, кроме односторонней поверхности, известной как бутылка Клейна, для которой правильное число окраски было определено в 1934 году.

 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? Был ли среди них посетитель, не купивший ничего?
Был ли среди них посетитель, не купивший ничего?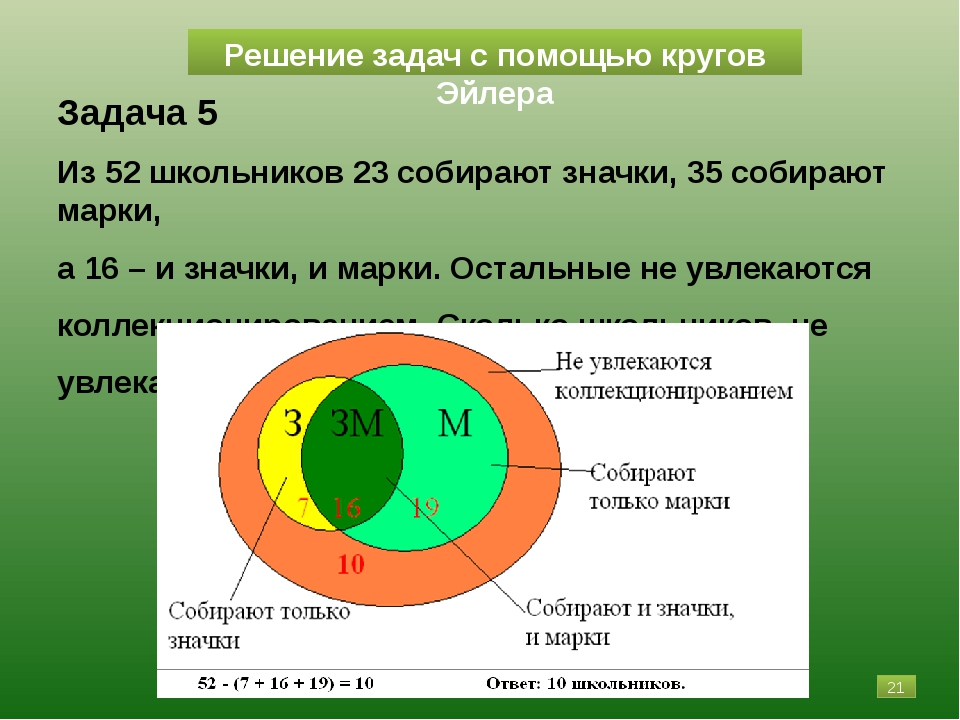 Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? Был ли среди них посетитель, не купивший ничего?
Был ли среди них посетитель, не купивший ничего? Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? Был ли среди них посетитель, не купивший ничего?
Был ли среди них посетитель, не купивший ничего?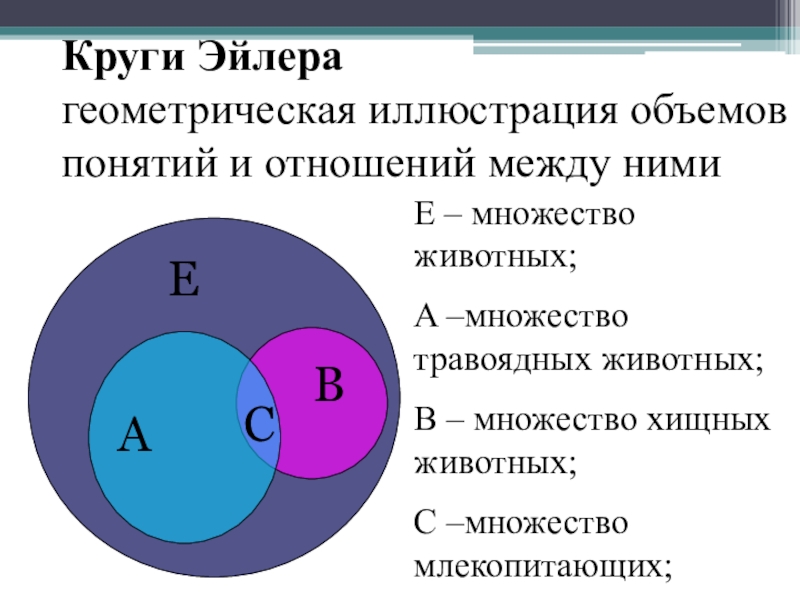 Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?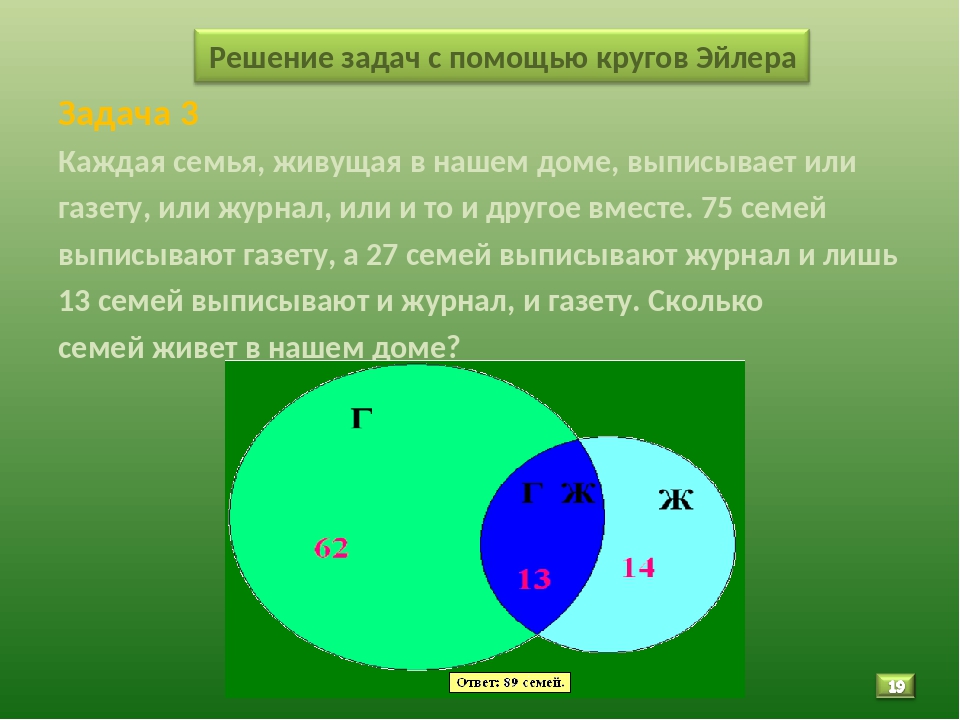 20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
20 из них купили и холодильник и микроволновку, 19 -и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?