Содержание
Урок алгебры в 8-м классе. Тема «Неравенства, содержащие модуль». Повторение
Цель урока: повторить различные
способы решения неравенств с одной переменной и
рассмотреть применение неравенств к решению
задач и упражнений.
Ход урока
- Организационный момент. Постановка цели.
- Индивидуальная работа по карточкам (во время
фронтального опроса).
1 карточка.
Решить неравенства:
1. 6x+2>9-x;
2. 2(x+3)-(x-8)<4.
2 карточка.
Решить неравенства:
1. ;
2. 5x+4>12-(x-3).
3 карточка.
Решить неравенства:
- ;
4 карточка.
Решить неравенства:
1. x-4>12
2.
- Фронтальный опрос
(используются слайды
презентации учителя).
1.Что называется модулем числа а?
2.Решить неравенства
а)
б)
в)
г)
д)
3. на координатной плоскости
изображены графики двух линейных функций. При
каких x значения обеих функций одновременно
положительны? Отрицательны?
Cм. Презентацию, слайды 3–5.
4.Самостоятельная работа (по
вариантам)
Cм. Презентацию, слайд 6.
5. Актуализация опорных знаний.
Учитель. Очень часто при решении
неравенств со знаком модуля возникает
необходимость перейти либо к системе неравенств,
либо к совокупности.
Вопросы?
- Когда неравенство равносильно системе
неравенств? - Когда число а является решением совокупности
неравенств?
Экспресс-опрос (шесть человек
работают у доски по карточкам, а в то же время
остальные учащиеся работают со слайдом, на
котором видно задание каждого ребенка, который
стоит у доски).
Задание представлено в виде теста. По
окончании решения необходимо выбрать правильный
ответ, а букву, соответствующую этому варианту
ответа, занести в соответствующую клетку
кроссворда.
1 вариант.
2 вариант.
3 вариант.
4 вариант.
5 вариант.
6 вариант.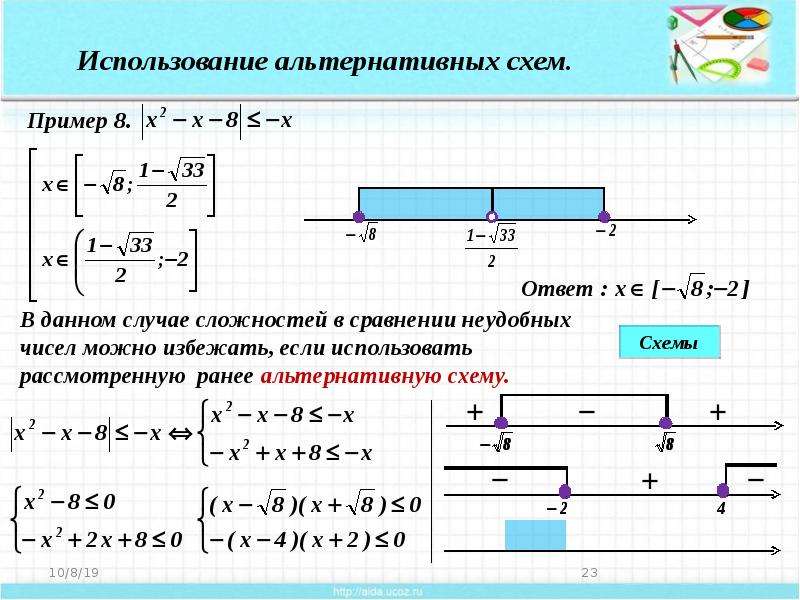
Итак, мы прочли Гарриот, это имя.
Историческую справку о Гарриоте подготовил
ученик.
Томас Гарриот (1560-1621)- английский
математик. Родился в Оксфорде. Образование
получил в Оксфордском университете.
Переписывался с Галиллеем и Кеплером. Развивал
алгебраическую символику, в частности, ввел
знаки > и < , которые сразу были приняты.
Гарриот пользовался для обозначений чисел
строчными буквами алфавита, записывал уравнения
в форме, близкой к современной. В этом отношении
он шел дальше своего друга Франсуа Виета. Гарриот
первый заметил, что число корней уравнения
определяется его степенью и что левая часть
уравнения должна разлагаться на такое же число
линейных множителей. Гарриот строил уравнения по
их корням.
Вопрос: какие существуют способы
решения неравенств с одной переменной?
6. Решение задач и упражнений.
Решение задач и упражнений.
1.Задача. При каких значениях х точки
графика функции лежат выше точек графика функции ?
Задача решается графическим способом.
2.Решить неравенство
Используется аналитический способ
решения.
3.Найти допустимые значения переменной
7. Домашнее задание. Его необходимо
выполнить в виде творческой работы:
- Составить и решить по 2 неравенства со знаком
модуля, решениями которых будут в одном случае
система, а в другом- совокупность неравенств; - Придумать задачу, где применяется неравенство,
а затем рассмотреть графический и аналитический
способы решения этой задачи.
8. Сообщение учащегося из
дополнительной литературы.
Учитель: Неравенства занимают
важное место в курсе алгебры не только 8 класса,
они встретятся нам и в 9 классе, и далее. Но уже
сегодня, используя свойства известных нам
неравенств, можно решать и более сложные задачи.
Ученик: напомним, что для любых двух
действительных чисел а и b справедливо
неравенство
(*)
Причем знак равенства достигается в
том и только случае, когда
Решим задачу. Найти наименьшее
значение функции
В силу неравенства (*)
Таким образом , причем знак равенства
достигается только в том случае, когда х=0. Отсюда
наименьшее значение функции равно 1 при х=0.
9. Итог урока. Оценки.
Учитель. Наш великий соотечественник
Давидов Август Юльевич сказал: “Алгебра учит
рассуждать о величинах. При этом она изображает
При этом она изображает
их буквами и означает особыми знаками
зависимость между ними”.
Вот этим сегодня мы и занимались на
уроке.
Неравенства с модулем. Способы решения неравенств с модулями
Неравенства с модулем
2. Способы решения неравенств с модулями:
2
1. По определению модуля
2. Возведение обоих частей неравенства
в квадрат
3. Замена переменной
4. Раскрытие модуля на промежутке
знакопостоянства
5. Равносильность неравенств системам
6. Важный частный случай
3. 1.По определению модуля
3
| f (x) |
-a
|3x-1|
-7
-6
8
-2
3
8
Ответ: 2;
3
| f (x) |> а
a
5x 2 4
-a
a
5 x 2 4
5 x 2 4
5 x 6
5 x 2
2 6
Ответ : ; ;
5 5
4. 2.Возведение обеих частей в квадрат
4
|x2-1| > |x2-x|
(x2-1)2 > (x2-x)2 — равносильность не нарушена
(x2-1+ x2-x)(x2-1-x2+x) > 0 – разность квадратов
(2×2-x-1)(x-1) > 0
—
+
1
2
+
1
5.
 3.Замена переменной
3.Замена переменной
5
+
-2
0
—
+
3
t
6. 4. Раскрытие модуля на промежутках знакопостоянства
6
|x-1| + |2-x| > 3
x-1
—
2-x
+
1
+
Нули подмодульных выражений: x =1 и x =2
2
+
+
—
а)
б)
в)
x 1
( x 1) 2 x 3
x 1
x 0
1 x 2
x 1 x 3
x 2
x 3 x 3
x 2
x 3
0
1
х ;0
1 x 2
1 3 неверное
Ответ : ;0 3;
2
3
х 3;
7. 5. Равносильность неравенств системам или их совокупности
7
См. решение по определению
Равносильно неравенству:
Можно записать в виде
системы
Неравенство равносильно двум
неравенствам:
Можно записать в виде совокупности
8. 5. Равносильность неравенств системам (примеры)
8
№1
3x | 2 x | 5
№2
5 x 7 | x 2 |
| 2 x | 5 3x
| x 2 | 5 x 7
2 x 5 3 x
2 x 3 x 5
1
x 1 2
x 1 3
4
x 2 5x 7
x 2 7 5x
1
x 2 4
x 5
6
1
Ответ : ( ;1 ]
2
1
Ответ : ( ;2 )
4
9.
 6. Один частный случай
6. Один частный случай
9
x 1
1
x 2
x 1
x 2
ОДЗ : x 2
1
умножим на |x+2|>0 в ОДЗ
| x 1 | | x 2 |
возведем в квадрат, обе части
( x 1 x 2)( x 1 x 2) 0
(2 x 1)( 3) 0
2x 1 0
x 12
для преобразования используем
разность квадратов
Учитывая ОДЗ, получим:
1
Ответ : ( ; 2) ( 2; )
2
Обучающая самостоятельная работа
10
Метод решения
1. По определению модуля
условие
ответы
(-5; 1)
По определению модуля
По определению модуля
По определению модуля
(-∞; −2) ∪ (−2; −0,5)
2. Возведение обеих частей в
квадрат
3. Раскрытие модуля на
промежутках
знакопостоянства
4. Замена переменной
Замена переменной
5. Замена совокупностью
систем
0; 2
11
Алгебра 8: С-46 Уравнения и неравенства
Алгебра 8: С-46 Уравнения и неравенства
РЕШЕНИЯ и ОТВЕТЫ на самостоятельную работу «С-46 Уравнения и неравенства, содержащие переменную под знаком модуля» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже образец варианта № 1 самостоятельной работы по алгебре 8 класса и ответы на оба варианта этой работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы на самостоятельную работу по алгебре адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания.
Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже образец варианта № 1 самостоятельной работы по алгебре 8 класса и ответы на оба варианта этой работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы на самостоятельную работу по алгебре адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания.
Самостоятельная работа Уравнения и неравенства (С-46 В-1).
Нажмите на картинку для увеличения !
Ключевые слова самостоятельной работы:
1. Имеет ли уравнение корни и сколько.
2. Решите уравнение.
3. Решите неравенство и изобразите множество его решений на координатной прямой.
4. Решите неравенство.
5. Сравните с нулем число а, если известно, что…
6. При каких значениях b верно равенство?
7. Решите уравнение.
8. Найдите координаты точек пересечения графиков функций.
9. Решите уравнение.
10. Решите неравенство:
11. Найдите множество решений двойного неравенства.
Ответы на самостоятельную работу «Уравнения и неравенства»
Вариант 1.
Вариант 2
Вы смотрели «Самостоятельная работа Уравнения и неравенства (С-46)» — ГДЗ на контрольную работу по алгебре 8 класс «Уравнения и неравенства, содержащие переменную под знаком модуля» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.: Просвещение» (учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского).
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Макарычев и др.)
№ | Этап занятия | Деятельность преподавателя | Деятельность студентов | ||||||
1 | Орг. | Приветствие учеников. Отмечает присутствующих и отсутствующих. Проверяет подготовку учеников к занятию | Приветствие учителя. Подготовка к занятию | ||||||
2 | Актуализация знаний | Предлагает ученикам ответит на ряд вопросов (проводит фронтальный опрос): 1.Что называют модулем числа? 2.Как с помощью системы записать определение модуля? 3.Перечислить все свойства модуля Предлагает учащимся устно ответить на следующие вопросы: 1) Найдите модуль каждого из чисел: 81; 1,2; -3,6; -74; 0. 2) Найдите значение выражения: а) — б) + в) : г) * 3) Известно, что =7. Чему равен ? 4) Из двух чисел выберите то, у которого модуль больше? а) -700,1 и 0,24 б) -2 и 3 | Отвечают на вопросы преподавателя, тем самым вспоминают тот материал, что изучали в ШКМ в 9-11 классах 1. 2. = 3.Свойства модуля: 1) модуль есть число неотрицательное; 2) модули противоположных чисел равны; 3) модуль разности двух чисел равен расстоянию между точками числовой прямой, соответствующим этим точкам По ходу выполнения устных упражнений студенты, с помощью преподавателя, вспоминают или изучают понятие и определение «модуля» и его основные свойства; В случае затруднения при выполнении заданий, пример разбирается у доски с комментированием более подготовленных студентов или преподавателя | ||||||
3 | Постановка цели и задач занятия | Используя определение модуля и его свойства, можно решить простейшие уравнения и неравенства с модулем Сможете ли вы самостоятельно сформулировать цель нашего занятия, опираясь на то, что мы выполняли ранее? | Ученики формулируют цели и задачи занятия Цель: научиться (овладеть методами) решения уравнений и неравенств, содержащих модуль, | ||||||
4 | Изучение нового материала | Учитель раздает учащимся раздаточный материал, на котором представлена систематизация материала, классификация уравнений и неравенств с модулем в виде таблицы См. | Изучают и анализируют все методы решения уравнений и неравенств с модулем. Обсуждают в парах, с преподавателем моменты, в которых возникают вопросы | ||||||
5. | Первичное закрепление материала | Учитель представляет учащимся задания на слайде См. Приложение 2 Примеры №1 из каждого раздела студенты прорешивают у доски с подробным комментированием и объяснением менее подготовленным студентам; примеры №2 все учащиеся решают самостоятельно, преподаватели и более подготовленные студенты могут оказывать консультации; примеры №3 – домашнее задание Ученик 1: │x2 — 5x│ = 6 Используя правило: , a , Ученик 2: │x2 — 5x│ ≤ 6 Ученик 3: │x2 — 5│ ≥ 4 Используя правило: , a , Ученик 4: │x2 + x – 1│= 2x – 1, x0,5 Используя правило: , g(x) = Ученик 5: 1 Ученик 6: │—x2 + x – 1│= │-x2 + 2x + 3│ Используя правило: , Ученик 7: │x + x2 – 3│≤ │x – 2 + 2x2│ Используя правило: , (f – g)(f + g) 0 Для учеников, которые усвоили алгоритмы и приемы решения уравнений и неравенств, предусмотрены дополнительные задания См. | Используя таблицу с классификацией уравнений и неравенств с модулей, работают над решением заданий, предложенных учителем Внимательно выслушивают комментарии преподавателя, при этом проводят анализ и соответствие тех заданий, что представлены в таблице №2 Планируют свою деятельность на уроке Решение: │x2 — 5x│ = 6 Ответ: Решение: -6 6 Ответ: Решение: Ответ: (- [-1;1] Решение: Ответ: Решение: Ответ: (- Решение: Ответ: Решение: (x + x 2 – 3 + x – 2 + 2 x 2)( x + x 2 – 3 – x + 2 – 2 x 2) ≤ 0 (2 x + 3 x 2 – 5)( – x 2 – 1) ≤ 0 (2 x + 3 x – 5)( x 2 + 1) ≥ 0 (2 x + 3 x 2 – 5) ≥ 0 Ответ: (- | ||||||
6 | Проблемное задание | Преподаватель ставит перед учащимися проблемное задание: решить не по заданной схеме в предложенной таблице, а самостоятельно вывести алгоритм решения уравнений и неравенств, объединив некоторые приемы (примеры 8-9) или выработать «свой» метод – метод замены переменной (пример 10) Пример 8: 2│x – 1│– 3│x + 4│= 1 Пример 9: │x2 – 2x│+ │x – 1│ ≤ x2 Пример 10: (x – 2)2 – 8│x –2│+ 15 = 0 Используя правило: | Студенты объединяются по группам для того, чтобы найти способ решения уравнений и неравенства с модулем методом замены переменной Решение: = 1, = –4
Ответ: Решение: │( x – 2) x │+ │ x – 1│≤ x 2 = 0, = 2, = 1 Ответ: Решение: │x – 2│= t, t 0 и Ответ: | ||||||
7 | Самостоятельная работа | Учитель предлагает ученикам работу по вариантам (примеры №2) См. Приложение 2 (таблица №2) | Самостоятельно выполняют задания, осознают уровень владения навыками решения уравнений и неравенств с модулем | ||||||
8 | Подведение итогов. Рефлексия. Домашнее задание | Подводит итоги занятия.
Предоставляет студентам инструкцию по выполнению домашнего задания (см. Приложение 1 и 2, примеры №3) | Подводят итоги занятия Отвечают осознанно и осмысленно на вопросы учителя, корректируя в дальнейшем свою деятельность на уроке, анализируя свои ошибки и недочеты, свои достижения и успехи Внимательно выслушивают инструкцию к выполнению домашнего задания |
Алгебра 8: С-46 Уравнения и неравенства
Алгебра 8: С-46 Уравнения и неравенства
РЕШЕНИЯ и ОТВЕТЫ на самостоятельную работу «С-46 Уравнения и неравенства, содержащие переменную под знаком модуля» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже образец варианта № 1 самостоятельной работы по алгебре 8 класса и ответы на оба варианта этой работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы на самостоятельную работу по алгебре адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания.
Самостоятельная работа Уравнения и неравенства (С-46 В-1).

Нажмите на картинку для увеличения !
Ключевые слова самостоятельной работы:
1. Имеет ли уравнение корни и сколько.
2. Решите уравнение.
3. Решите неравенство и изобразите множество его решений на координатной прямой.
4. Решите неравенство.
5. Сравните с нулем число а, если известно, что…
6. При каких значениях b верно равенство?
7. Решите уравнение.
8. Найдите координаты точек пересечения графиков функций.
9. Решите уравнение.
10. Решите неравенство:
11. Найдите множество решений двойного неравенства.
Ответы на самостоятельную «Уравнения и неравенства»
Смотреть РЕШЕНИЯ и ОТВЕТЫ на Вариант № 1
Смотреть РЕШЕНИЯ и ОТВЕТЫ на Вариант № 2
Вы смотрели «Самостоятельная работа Уравнения и неравенства (С-46)» — ГДЗ на контрольную работу по алгебре 8 класс «Уравнения и неравенства, содержащие переменную под знаком модуля» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В. И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.: Просвещение» (учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского).
И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.: Просвещение» (учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского).
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Макарычев и др.)
|
1. |
Уравнение с модулем вида |x|=a
|
1 |
|
2. 
|
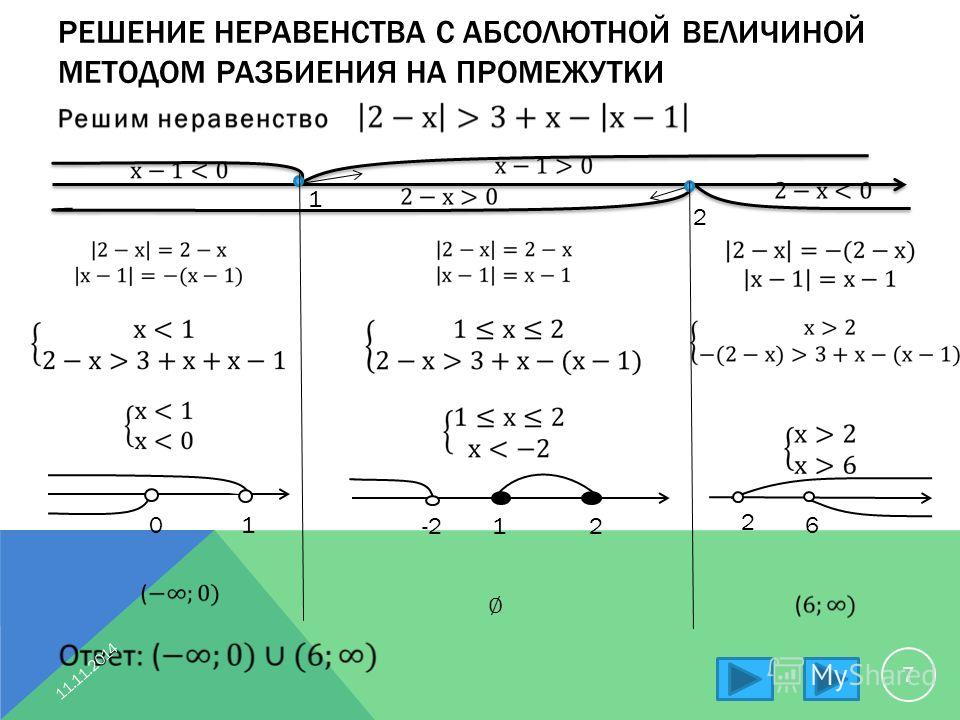
Неравенство с модулем вида |f(x)|< a
|
1 |
|
3. |
Неравенство с модулем вида |f(x)|<0
|
1 |
|
4. 
|
Неравенство с модулем вида |f(x)|≤0
|
1 |
|
5. |
Уравнение с модулем, подобные модули
|
3 |
|
6. 
|
Неравенство с модулем (квадратное неравенство)
|
3 |
|
7. |
Вопросы по равенству с модулем
|
1 |
|
8. 
|
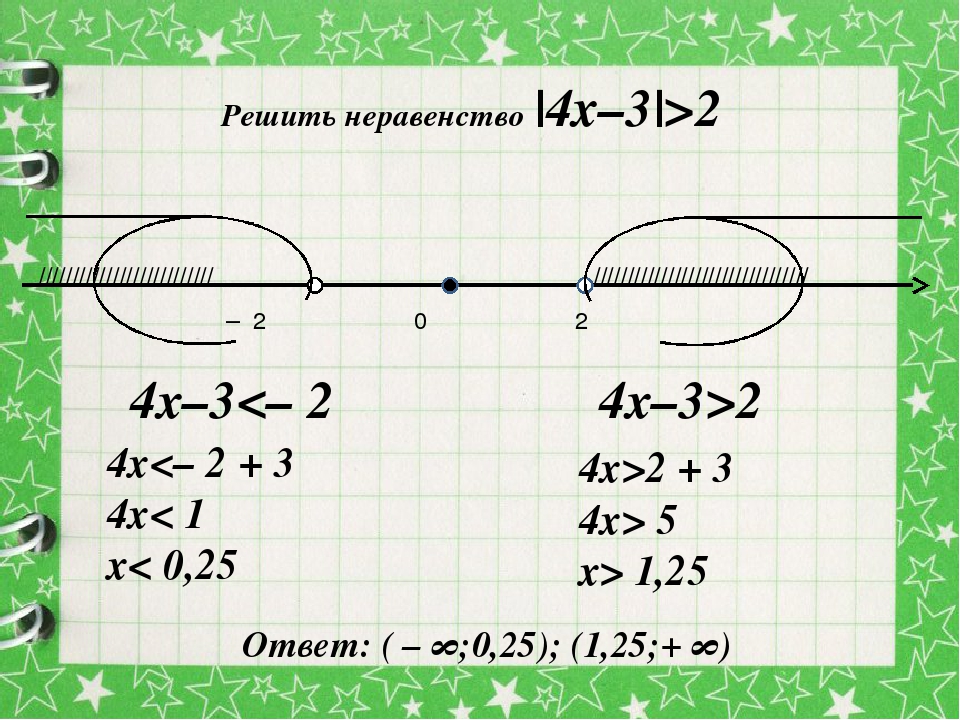
Уравнение с модулем вида |f(x)|=a
|
2 |
|
9. |
Уравнение с модулем вида |f(x)|=|g(x)|
|
3 |
|
10. 
|
Уравнение с двумя модулями
|
3 |
|
11. |
Неравенство с модулем вида |f(x)|≥g(x)
|
5 |
|
12. 
|
Неравенство с модулем вида |f(x)|>a (дробное)
|
6 |
|
13. |
Квадратное уравнение с модулем
|
3 |
Информация
Пробные варианты и вопросы к собеседованию для поступления в лицейские классы.
8 класс
Собеседование по математике в 9 класс (2019 г.)
Учащиеся должны уметь (алгебра):
1.Выполнять действия с действительными числами;
2.Решать уравнения: квадратные, сводящиеся к квадратным, биквадратные, дробно-рациональные, иррациональные;
3.Решать неравенства: системы линейных неравенств, квадратные неравенства (переходом к системе линейных неравенств и графическим способом), решать неравенства методом интервалов, решать неравенства с модулем;
4.Строить графики функций (линейной, квадратичной, обратной пропорциональной зависимости), с заданием по частям;
5.Описывать свойства функций.
Учащиеся должны знать (геометрия):
1.Треугольник, элементы треугольника. Неравенство треугольника. Равенство треугольников, признаки равенства. Подобие треугольников, признаки подобия. Теорема Пифагора и обратная к ней.Свойства и признаки равнобедренного треугольника.Теорема о пропорциональных отрезках. Соотношения между сторонами и углами прямоугольного треугольника.
Теорема Пифагора и обратная к ней.Свойства и признаки равнобедренного треугольника.Теорема о пропорциональных отрезках. Соотношения между сторонами и углами прямоугольного треугольника.
2.Параллельные прямые: определение, свойства, признаки. Теорема Фалеса.
3. Понятие многоугольника, периметра многоугольника, какой многоугольник называется выпуклым; формулы суммы углов выпуклого многоугольника.
4. Четырёхугольники. Параллелограмм, его свойства и признаки. Прямоугольник, ромб, квадрат, их свойства и признаки. Трапеция, средняя линия трапеции. Свойства произвольной и равнобедренной трапеции.
5. Площади многоугольников: площадь треугольника, площадь параллелограмма, площадь ромба, площадь трапеции. Свойства площадей треугольников.
Вопросы для собеседования по физике 9 класс (2019 г.)
Тепловые явления.
1. Тепловое движение, внутренняя энергия, способы её изменения, виды теплопередачи.
2. Расчёт количества теплоты, необходимого для нагревания тела, выделяемого при сгорании топлива.
3. Плавление и отвердевания кристаллических тел. Расчёт количества теплоты.
4. Испарение и конденсация. Насыщенный и ненасыщенный пар. Влажность воздуха.
5. Кипение. Расчёт количества теплоты.
6. Уравнение теплового равновесия.
7. Тепловые двигатели. ДВС. КПД теплового двигателя.
Электрические явления.
1. Электризация, два рода зарядов их взаимодействие, проводники и непроводники электричества, электрическое поле.
2. Делимость электрического заряда. Электрон. Строение атома. Объяснение электрических явлений.
3. Электрический ток, направление тока. Электрическая цепь и её составные части. Роль источника тока. Действия электрического тока.
4. Сила тока. Амперметр, его подключение в цепь.
5. Вольтметр, его подключение в цепь.
6. Сопротивление проводника. Реостаты.
7. Закон Ома для участка цепи.
8. Последовательное и параллельное соединение проводников.
9. Работа и мощность электрического тока. Закон Джоуля-Ленца.
10. Магнитное поле, магнитные линии прямого и кругового тока, электромагниты и их применение.
11. Постоянные магниты. Магнитное поле Земли.
Световые явления.
1. Законы геометрической оптики: прямолинейного распространения, отражения, преломления света.
2. Построение изображений в плоском зеркале.
3. Линзы. Оптическая сила линзы. Формула тонкой линзы. Изображения, даваемое линзой.
4. Глаз как оптическая система. Дефекты глаза и их исправление.
Вопросы для собеседования по информатике 9 класс (2019 г.)
Определение объемов информации. Кодирование информации. Алфавитный подход к определению объемов информации. Передача информации. (учебник Босова 7 — 8 класс)
Системы счисления. (Перевод чисел «2» — «10» с/с)
Алгебра логики: решение неравенств, запросы к поисковому серверу.
Задачи на файловую систему компьютера.
Исполнители «Чертежник, Черепашка, Умножитель и т.п.
Программирование: операторы паскаля для работы с линейными алгоритмами, алгоритмами ветвления, циклическими, результат работы программы (фрагмента программы).
10 класс
Собеседование по математике в 10 класс (2019 г.)
Учащиеся должны уметь(алгебра):
1. Выполнять действия с действительными числами;
2. Решать уравнения: квадратные, сводящиеся к квадратным, биквадратные, дробно-рациональные, иррациональные, степенные, уравнения с модулем, с параметром;
3. Решать неравенства: системы линейных неравенств, квадратные неравенства (переходом к системе линейных неравенств и графическим способом), решать неравенства методом интервалов, решать неравенства с модулем;
4. Строить графики и описывать свойства функций (линейной, квадратичной, обратной пропорциональной зависимости, степенной), с модулем, комбинированных;
5.Решать уравнения графическим способом, в том числе и с параметром.
Учащиеся должны знать (геометрия):
1. Треугольник, элементы треугольника. Неравенство треугольника. Равенство треугольников, признаки равенства. Теорема синусов. Теорема косинусов. Решение треугольников.
2. Параллельные прямые: определение, свойства, признаки. Теорема Фалеса.
3. Четырёхугольники. Параллелограмм, его свойства и признаки. Прямоугольник, ромб, квадрат, их свойства и признаки. Трапеция, средняя линия трапеции. Свойства произвольной и равнобедренной трапеции.
4. Площади многоугольников: площадь треугольника, площадь параллелограмма, площадь ромба, площадь трапеции. Свойства площадей треугольников.
5. Подобие треугольников, признаки подобия.
6. Окружность и её элементы. Центральный и вписанный угол. Касательная и секущая к окружности, их свойства. Длина окружности и площадь круга, площадь кругового сектора.
7. Вписанные и описанные многоугольники: свойства, признаки.
8. Правильные многоугольники: определение, свойства, площадь.
Вопросы для собеседования по информатике 10 класс (2019 г.)
- Определение объемов информации. Кодирование информации. Алфавитный подход к определению объемов информации. Передача информации. (учебник Босова 8 — 9 класс, ОГЭ — Демо)
- Системы счисления. (Перевод чисел «2» — «10» с/с)
- Алгебра логики: решение неравенств, запросы к поисковому серверу.
- Моделирование: графы (напр. схема дорог), таблицы (длина кратчайшего пути), базы данных (работа с фрагментом)
- Файловая система компьютера.
- Работа с электронными таблицами (решение задач).
- Исполнители «Чертежник, Черепашка, Умножитель, Авитоматы и т.п.
- Программирование: операторы паскаля для работы с линейными алгоритмами, алгоритмами ветвления, циклическими, результат работы программы (фрагмента программы). Массивы (обработка массива).
- Организация глобальных сетей. Доступ к файлу.
Вопросы собеседования по физике 10 класс (2019 г.)
Основные понятия кинематики.
- Механическое движение. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Прямолинейное равномерное движение.
- График зависимости координаты точки от времени, график скорости. Относительность механического движения. Сложение скоростей.
- Прямолинейное неравномерное движение. Средняя скорость. Мгновенная скорость. Ускорение. Равноускоренное движение Перемещение при равноускоренном движении. Уравнения движений.
- Свободное падение тел. Движение тела брошенного вертикально.
- Криволинейное движение. Перемещение, скорость и ускорение при криволинейном движении. Движение по окружности. Угол поворота. Радиан. Период. Частота. Угловая и линейная скорости при равномерном движении по окружности. Ускорение при равномерном движении тела по окружности.
- Закон движения тела, брошенного под углом к горизонту, траектория. Дальность полёта и высота подъема.
- Период и частота при движении тела по окружности. Линейная скорость при движении тела по окружности. Угловая скорость при движении тела по окружности. Центростремительное ускорение.
Силы в природе.
- Сила всемирного тяготения. Сила тяжести. Сила упругости. Вес тела. Сила трения.
- Законы сохранения. Статика
- Импульс тела. Импульс силы. Закон сохранения импульса. Реактивное движение.
- Механическая работа Мощность. КПД машин и механизмов.
- Кинетическая энергия. Потенциальная энергия тела поднятого над землей. Потенциальная энергия упруго деформированного тела. Закон сохранения энергии.
- Условие равновесия тел. Центр масс. Центр тяжести.
4. Электромагнитное поле.
Правило буравчика, правило правой руки. Направление силы Ампера и силы Лоренца.
Электромагнитные колебания и волны.
5. Элементы атомной, ядерной физики.
Явление радиоактивности, радиоактивные превращения.
Опыты Резерфорда, строение атома.
Строение ядра, ядерные силы.
Энергия связи, дефект масс.
Ядерные реакции. Деление ядер урана, цепная реакция деления и ее применение.
Термоядерная энергия.
11 класс
Вопросы для собеседования в 11 класс (2019 г.)
Геометрия
- Аксиомы стереометрии, следствия из аксиом стереометрии.
- Параллельные прямые в пространстве: определение и признаки.
- Скрещивающиеся прямые: определение, признаки.
- Свойство скрещивающихся прямых (теорема о существовании плоскости, проходящей через одну из скрещивающихся прямых параллельно другой прямой).
- Параллельность прямой и плоскости: определение, признаки и свойства.
- Параллельность плоскостей: определение, признаки, свойства.
- Перпендикулярность плоскостей: определение, признаки, свойства.
- Перпендикулярность прямой и плоскости: определение и признак.
- Построение сечений многогранников. Метод следа.
- Угол между прямыми (включая скрещивающиеся прямые). Угол между прямой и плоскостью.
- Двугранный угол (определение). Величина двугранного угла. Понятие угламежду пересекающимися плоскостями.
- Трехгранный угол.
- Теорема о трех перпендикулярах и теорема, обратная ей.
- Прямоугольный параллелепипед. Теорема о квадрате диагонали прямоугольного параллелепипеда Теорема о точке пересечения диагоналей параллелепипеда.
- Определение вектора в пространстве. Классификация векторов. Действия над векторами.
Алгебра
- Рациональные уравнения и неравенства. Методы решения.
- Уравнения и неравенства с модулем.Методы решения.
- Иррациональные уравнения и неравенства.Методы решения.
- Построение графиков кусочно-заданных функций, функций, содержащих модуль.
- Многочлены. Теорема Безу, схема Горнера. Уравнения высших степеней.
- Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных.
- Свойства и графики показательной функции.
- Свойства и графики логарифмической функции.
- Свойства и графики степенной функции.
- Основные методы решения показательных уравнений и неравенств.
- Основные методы решения логарифмических уравнений и неравенств.
- Преобразование иррациональных, показательных и логарифмических выражений.
- Использование свойств и графиков функций при решении уравнений и неравенств.
- Применение метода интервалов для решения иррациональных, показательных и логарифмических неравенств.
- Использование функционально-графических представлений для решения и исследования иррациональных уравнений, неравенств, систем уравнений и неравенств.
- Понятия тригонометрических функций.Основные тригонометрические тождества.
- Формулы приведения.
- Синус, косинус и тангенс суммы и разности двух углов.
- Синус и косинус двойного угла. Формулы половинного угла.
- Преобразования суммы тригонометрических функций в произведение и произведения в сумму.
- Выражение тригонометрических функций через тангенс половинного аргумента.
- Преобразования тригонометрических выражений.
- Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Отбор корней тригонометрических уравнений.
- Примеры решения простейших тригонометрических неравенств.
- Решение задач с параметром.
- Область определения и множество значений тригонометрических функций.
- Чётность, нечётность, периодичность тригонометрических функций. Их свойства и графики.
- Обратные тригонометрические функции.
Вопросы для собеседования по физике 11 класс (2019 г.)
Механика
1. Основные понятия кинематики.
2. Уравнения и графики равномерного прямолинейного движения.
3. Уравнения и графики равноускоренного прямолинейного движения.
4. Вращательное движение твёрдого тела.
5. Законы механики Ньютона.
6. Закон всемирного тяготения.
7. Движение тела под действием силы тяжести. Первая космическая скорость.
8. Закон Гука. Сила упругости. Движение тела под действием силы упругости.
9. Силы трения (сопротивления). Движение тела под действием силы трения.
10. Движение тела под действием нескольких сил.
11. Импульс тела. Второй закон Ньютона в импульсной форме. Закон сохранения импульса.
12 Работа силы, мощность, энергия. Работа силы тяжести, силы упругости, силы трения.
13. Условия равновесия тел.
МКТ, термодинамика.
- Основные положения МКТ и их опытные обоснования.
- Основное уравнение МКТ.
- Температура. Энергия теплового движения молекул.
- Уравнение состояния идеального газа. Газовые законы.
- Взаимные превращения жидкостей и газов.
- Кристаллические и аморфные тела
- Основы термодинамики: внутренняя энергия, работа, количество теплоты.
- Первый закон термодинамики и его применение в различных изопроцессах.
- Тепловые двигатели, принцип действия, КПД.
Электродинамика.
1. Электрический ток. Закон Ома для участка цепи.
2. Электрические цепи. Последовательное и параллельное соединение проводников.
3. Работа и мощность тока.
4. Понятие ЭДС . Закон Ома для полной цепи.
5. Электрический ток в металлах. Зависимость сопротивления проводника от температуры. Сверхпроводимость.
6. Электрический ток в жидкостях.
7. Электрический ток в полупроводниках.
8. Электрический ток в вакууме.
9. Электрический ток в газах.
Вопросы для собеседования по информатике 11 класс (2019 г.)
Алгебра логики – таблицы истинности.
Системы счисления (с основаниями 2, 10, 8, 16 и др.).
Использование информационных моделей (таблицы, диаграммы, графики).
Кодирование и декодирование информации (с использованием условий Фано).
Выполнение и анализ простых алгоритмов (автоматы).
Поиск алгоритма минимальной длины для исполнителя.
Анализ программы (с циклами и ветвлениями).
Кодирование текстовой, графической информации, звука, передача информации, пропускная способность канала связи.
Вычисление информационного объема сообщения.
Выполнение алгоритмов для исполнителя (цепочки символов).
Графы. Поиск количества путей.
Составление запросов для поисковых систем с использованием логических выражений.
Линейные неравенства и абсолютные неравенства
Результаты обучения
- Используйте интервальную нотацию для выражения неравенства.
- Используйте свойства неравенств.
- Решите сложные неравенства.
- Решите неравенства абсолютных значений.
Попасть в список почета в большинстве ведущих университетов непросто. Предположим, студенты должны были пройти курс не менее 12 кредитных часов и поддерживать средний балл 3.5 или выше. Как можно математически выразить эти требования к списку почета? В этом разделе мы рассмотрим различные способы выражения различных наборов чисел, неравенств и неравенств по абсолютным значениям.
Как писать о неравенствах и манипулировать ими
Указание решения такого неравенства, как [латекс] x \ ge 4 [/ латекс], может быть достигнуто несколькими способами.
Мы можем использовать числовую линию, как показано ниже. Синий луч начинается с [latex] x = 4 [/ latex] и, как указано стрелкой, продолжается до бесконечности, что показывает, что набор решений включает все действительные числа, большие или равные 4.
Мы можем использовать нотацию конструктора наборов : [latex] \ {x | x \ ge 4 \} [/ latex], что переводится как «все действительные числа x , такие, что x больше или равно 4. ” Обратите внимание, что фигурные скобки используются для обозначения набора.
Третий метод — это обозначение интервала , где наборы решений указываются круглыми или квадратными скобками. Решения для [latex] x \ ge 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex]. Это, пожалуй, самый полезный метод, поскольку он применим к концепциям, изучаемым позже в этом курсе, и к другим курсам математики более высокого уровня.
Основная концепция, которую следует запомнить, заключается в том, что круглые скобки представляют решения больше или меньше числа, а квадратные скобки представляют решения, которые больше или равны или меньше или равны числу. Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле слова и, следовательно, не могут быть «равны». Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [/ латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше чем [latex] 1 [/ latex] включительно.В таблице ниже представлены возможности.
| Указанный набор | Обозначение конструктора множеств | Интервальное обозначение |
|---|---|---|
| Все действительные числа от a до b , за исключением a или b | [латекс] \ {x | a | [латекс] \ левый (а, б \ правый) [/ латекс] | |
| Все действительные числа больше a , но не включая a | [латекс] \ {x | x> a \} [/ латекс] | [латекс] \ left (a, \ infty \ right) [/ latex] |
| Все действительные числа меньше b , но не включая b | [латекс] \ {x | x | [латекс] \ влево (- \ infty, b \ right) [/ латекс] |
| Все действительные числа больше a , включая a | [латекс] \ {x | x \ ge a \} [/ латекс] | [латекс] \ left [a, \ infty \ right) [/ latex] |
| Все действительные числа меньше b , в том числе b | [латекс] \ {x | x \ le b \} [/ латекс] | [латекс] \ влево (- \ infty, b \ right] [/ латекс] |
| Все вещественные числа от a до b , включая a | [латекс] \ {x | a \ le x | [латекс] \ слева [a, b \ справа) [/ латекс] |
| Все вещественные числа от a до b , включая b | [латекс] \ {x | a | [латекс] \ слева (a, b \ справа] [/ латекс] | |
| Все вещественные числа от a до b , включая a и b | [латекс] \ {x | a \ le x \ le b \} [/ латекс] | [латекс] \ слева [a, b \ справа] [/ латекс] |
| Все действительные числа меньше a или больше b | [латекс] \ {x | x b \} [/ латекс] | [латекс] \ left (- \ infty, a \ right) \ чашка \ left (b, \ infty \ right) [/ latex] |
| Все вещественные числа | [латекс] \ {x | x \ text {все вещественные числа} \} [/ latex] | [латекс] \ влево (- \ infty, \ infty \ right) [/ латекс] |
Пример: использование интервальной записи для выражения всех действительных чисел, больше или равных числу
Используйте обозначение интервала, чтобы указать все действительные числа, большие или равные [latex] -2 [/ latex].
Показать решение
Используйте скобку слева от [latex] -2 [/ latex] и скобки после бесконечности: [latex] \ left [-2, \ infty \ right) [/ latex]. Скобка указывает, что [latex] -2 [/ latex] включен в набор со всеми действительными числами от [latex] -2 [/ latex] до бесконечности.
Попробуйте
Используйте обозначение интервала для обозначения всех действительных чисел между [latex] -3 [/ latex] и [latex] 5 [/ latex] включительно.
Показать решение
[латекс] \ влево [-3,5 \ вправо] [/ латекс]
Пример: использование интервальной записи для выражения всех действительных чисел, меньших или равных
a или больше или равных b
Запишите интервал, выражающий все действительные числа, меньшие или равные [latex] -1 [/ latex] или больше или равные [latex] 1 [/ latex].
Показать решение
Для этого примера нам нужно написать два интервала. Первый интервал должен указывать все действительные числа, меньшие или равные 1. Итак, этот интервал начинается с [latex] — \ infty [/ latex] и заканчивается на [latex] -1 [/ latex], что записывается как [latex ] \ left (- \ infty, -1 \ right] [/ latex].
Во втором интервале должны отображаться все действительные числа, большие или равные [латекс] 1 [/ латекс], который записывается как [латекс] \ left [1, \ infty \ right) [/ latex]. Однако мы хотим объединить эти два набора.Мы достигаем этого, вставляя символ объединения, [latex] \ cup [/ latex], между двумя интервалами.
[латекс] \ left (- \ infty, -1 \ right] \ чашка \ left [1, \ infty \ right) [/ latex]
Попробуйте
Выразите все действительные числа меньше [латекс] -2 [/ latex] или больше или равные 3 в интервальной нотации.
Показать решение
[латекс] \ left (- \ infty, -2 \ right) \ чашка \ left [3, \ infty \ right) [/ latex]
Использование свойств неравенств
Когда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как с уравнениями, но не в точности.Мы можем использовать свойство сложения и свойство умножения , чтобы помочь нам решить их. Единственное исключение — когда мы умножаем или делим на отрицательное число, мы должны перевернуть символ неравенства.
Общее примечание: свойства неравенств
[латекс] \ begin {array} {ll} \ text {Свойство добавления} \ hfill & \ text {If} a
Эти свойства также применимы к [латексу] a \ le b [/ latex], [латексу] a> b [/ latex] и [латексу] a \ ge b [/ latex].
Пример: демонстрация свойства сложения
Проиллюстрируйте свойство сложения для неравенств, решив каждое из следующих решений:
- [латекс] x — 15 <4 [/ латекс]
- [латекс] 6 \ ge x — 1 [/ латекс]
- [латекс] x + 7> 9 [/ латекс]
Показать решение
Свойство сложения для неравенств гласит, что если неравенство существует, добавление или вычитание одного и того же числа с обеих сторон не меняет неравенства.
1.
[латекс] \ begin {array} {ll} x — 15 <4 \ hfill & \ hfill \\ x - 15 + 15 <4 + 15 \ hfill & \ text {Добавьте 15 с обеих сторон.} \ Hfill \\ x <19 \ hfill & \ hfill \ end {array} [/ latex]
2.
[латекс] \ begin {array} {ll} 6 \ ge x — 1 \ hfill & \ hfill \\ 6 + 1 \ ge x — 1 + 1 \ hfill & \ text {Добавить 1 с обеих сторон}. \ Hfill \\ 7 \ ge x \ hfill & \ hfill \ end {array} [/ latex]
3.
[латекс] \ begin {array} {ll} x + 7> 9 \ hfill & \ hfill \\ x + 7-7> 9-7 \ hfill & \ text {Вычтите 7 с обеих сторон}.\ hfill \\ x> 2 \ hfill & \ hfill \ end {array} [/ latex]
Попробуйте
Решить [латекс] 3x — 2 <1 [/ латекс].
Пример: демонстрация свойства умножения
Проиллюстрируйте свойство умножения неравенств, решив каждое из следующих решений:
- [латекс] 3x <6 [/ латекс]
- [латекс] -2x — 1 \ ge 5 [/ латекс]
- [латекс] 5-x> 10 [/ латекс]
Показать решение
1.
[латекс] \ begin {array} {l} 3x <6 \ hfill \\ \ frac {1} {3} \ left (3x \ right) <\ left (6 \ right) \ frac {1} {3} \ hfill \\ x <2 \ hfill \ end {array} [/ latex]
2.
[латекс] \ begin {array} {ll} -2x — 1 \ ge 5 \ hfill & \ hfill \\ -2x \ ge 6 \ hfill & \ hfill \\ \ left (- \ frac {1} {2} \ right) \ left (-2x \ right) \ ge \ left (6 \ right) \ left (- \ frac {1} {2} \ right) \ hfill & \ text {Умножить на} — \ frac {1} {2}. \ Hfill \\ x \ le -3 \ hfill & \ text {Обратное неравенство}. \ Hfill \ end {array} [/ latex]
3.
[латекс] \ begin {array} {ll} 5-x> 10 \ hfill & \ hfill \\ -x> 5 \ hfill & \ hfill \\ \ left (-1 \ right) \ left (-x \ right )> \ left (5 \ right) \ left (-1 \ right) \ hfill & \ text {Умножить на} -1.\ hfill \\ x <-5 \ hfill & \ text {Обратное неравенство}. \ hfill \ end {array} [/ latex]
Попробуйте
Решить [латекс] 4x + 7 \ ge 2x — 3 [/ латекс].
Алгебраическое решение неравенств с одной переменной
Как показали примеры, мы можем выполнять те же операции с обеими сторонами неравенства, как и с уравнениями; совмещаем похожие сроки и выполняем операции. Чтобы решить, мы изолируем переменную.
Пример: алгебраическое решение неравенства
Решите неравенство: [латекс] 13 — 7x \ ge 10x — 4 [/ латекс].
Показать решение
Решение этого неравенства аналогично решению уравнения до последнего шага.
[латекс] \ begin {array} {ll} 13 — 7x \ ge 10x — 4 \ hfill & \ hfill \\ 13 — 17x \ ge -4 \ hfill & \ text {Переместите переменные члены в одну сторону неравенства} . \ hfill \\ -17x \ ge -17 \ hfill & \ text {Изолировать термин переменной}. \ hfill \\ x \ le 1 \ hfill & \ text {Разделение обеих сторон на} -17 \ text {отменяет неравенство }. \ hfill \ end {array} [/ latex]
Множество решений задается интервалом [latex] \ left (- \ infty, 1 \ right] [/ latex] или всеми действительными числами, меньшими включительно 1.
Попробуйте
Решите неравенство и запишите ответ, используя интервальную запись: [latex] -x + 4 <\ frac {1} {2} x + 1 [/ latex].
Показать решение
[латекс] \ влево (2, \ infty \ right) [/ латекс]
Пример: решение неравенства с дробями
Решите следующее неравенство и запишите ответ в интервальной записи: [latex] — \ frac {3} {4} x \ ge — \ frac {5} {8} + \ frac {2} {3} x [/ latex ].
Показать решение
Мы начинаем решать так же, как и при решении уравнения.
[латекс] \ begin {array} {ll} — \ frac {3} {4} x \ ge — \ frac {5} {8} + \ frac {2} {3} x \ hfill & \ hfill \\ — \ frac {3} {4} x- \ frac {2} {3} x \ ge — \ frac {5} {8} \ hfill & \ text {Поместите переменные члены на одну сторону}. \ hfill \\ — \ frac {9} {12} x- \ frac {8} {12} x \ ge — \ frac {5} {8} \ hfill & \ text {Запишите дроби с общим знаменателем}. \ hfill \\ — \ frac {17} {12} x \ ge — \ frac {5} {8} \ hfill & \ hfill \\ x \ le — \ frac {5} {8} \ left (- \ frac {12} {17} \ right) \ hfill & \ text {Умножение на отрицательное число отменяет неравенство}. \ hfill \\ x \ le \ frac {15} {34} \ hfill & \ hfill \ end {array} [/ latex]
Множество решений — это интервал [latex] \ left (- \ infty, \ frac {15} {34} \ right] [/ latex].
Попробуйте
Решите неравенство и запишите ответ в интервальной записи: [latex] — \ frac {5} {6} x \ le \ frac {3} {4} + \ frac {8} {3} x [/ latex].
Показать решение
[латекс] \ left [- \ frac {3} {14}, \ infty \ right) [/ latex]
Неравенства составных и абсолютных значений
Сложное неравенство включает два неравенства в одном утверждении. Такое выражение, как [латекс] 4 Решите составное неравенство: [латекс] 3 \ le 2x + 2 <6 [/ латекс]. Показать решение Первый метод — написать два отдельных неравенства: [латекс] 3 \ le 2x + 2 [/ latex] и [latex] 2x + 2 <6 [/ latex]. Решаем их самостоятельно. [латекс] \ begin {array} {lll} 3 \ le 2x + 2 \ hfill & \ text {and} \ hfill & 2x + 2 <6 \ hfill \\ 1 \ le 2x \ hfill & \ hfill & 2x < 4 \ hfill \\ \ frac {1} {2} \ le x \ hfill & \ hfill & x <2 \ hfill \ end {array} [/ latex] Затем мы можем переписать решение в виде составного неравенства, точно так же, как возникла проблема. [латекс] \ frac {1} {2} \ le x <2 [/ латекс] В интервальной записи решение записывается как [latex] \ left [\ frac {1} {2}, 2 \ right) [/ latex]. Второй метод — оставить составное неравенство неповрежденным и выполнить процедуры решения для трех частей одновременно. [латекс] \ begin {array} {ll} 3 \ le 2x + 2 <6 \ hfill & \ hfill \\ 1 \ le 2x <4 \ hfill & \ text {Выделите член переменной и вычтите 2 из всех трех частей }. \ hfill \\ \ frac {1} {2} \ le x <2 \ hfill & \ text {Разделите все три части на 2}.\ hfill \ end {array} [/ latex] Получаем такое же решение: [латекс] \ left [\ frac {1} {2}, 2 \ right) [/ latex]. Решите составное неравенство [латекс] 4 <2x - 8 \ le 10 [/ латекс]. Показать решение [латекс] 6 Решите сложное неравенство с переменными во всех трех частях: [латекс] 3 + x> 7x — 2> 5x — 10 [/ latex]. Показать решение Попробуем первый способ. Запишите два неравенства : [латекс] \ begin {array} {lll} 3 + x> 7x — 2 \ hfill & \ text {and} \ hfill & 7x — 2> 5x — 10 \ hfill \\ 3> 6x — 2 \ hfill & \ hfill & 2x — 2> -10 \ hfill \\ 5> 6x \ hfill & \ hfill & 2x> -8 \ hfill \\ \ frac {5} {6}> x \ hfill & \ hfill & x> -4 \ hfill \\ x <\ frac {5} {6} \ hfill & \ hfill & -4 Набор решений: [latex] -4 Решите составное неравенство: [латекс] 3y <4 - 5y <5 + 3y [/ latex]. Показать решение [латекс] \ left (- \ frac {1} {8}, \ frac {1} {2} \ right) [/ latex] Как мы знаем, абсолютное значение величины — это положительное число или ноль. От исходной точки точка, расположенная в [latex] \ left (-x, 0 \ right) [/ latex], имеет абсолютное значение [latex] x [/ latex], так как находится на расстоянии x единиц.Считайте абсолютное значение расстоянием от одной точки до другой точки. Независимо от направления, положительного или отрицательного, расстояние между двумя точками представляется как положительное число или ноль. Неравенство абсолютного значения — это уравнение вида [латекс] | A | , где A , а иногда B , представляет алгебраическое выражение, зависящее от переменной x. Решение неравенства означает нахождение набора всех значений [latex] x [/ latex] –, которые удовлетворяют задаче.Обычно этот набор представляет собой интервал или объединение двух интервалов и включает диапазон значений. Существует два основных подхода к решению абсолютных неравенств: графический и алгебраический. Преимущество графического подхода в том, что мы можем прочитать решение, интерпретируя графики двух уравнений. Преимущество алгебраического подхода состоит в том, что решения являются точными, поскольку точные решения иногда трудно прочитать с графа. Предположим, мы хотим знать все возможные доходы от инвестиций, если бы мы могли заработать некоторую сумму денег в пределах от 200 до 600 долларов.Мы можем решить алгебраически для набора значений x — , так что расстояние между [latex] x [/ latex] и 600 меньше 200. Мы представляем расстояние между [latex] x [/ latex] и 600 как [ latex] | x — 600 | [/ latex], следовательно, [latex] | x — 600 | \ le 200 [/ latex] или [латекс] \ begin {array} {c} -200 \ le x — 600 \ le 200 \\ -200 + 600 \ le x — 600 + 600 \ le 200 + 600 \ 400 \ le x \ le 800 \ конец {array} [/ latex] Это означает, что наша прибыль составит от 400 до 800 долларов. Для решения неравенств по абсолютным значениям, как и для уравнений с абсолютными значениями, мы записываем два неравенства и затем решаем их независимо. Для алгебраического выражения X и [латекс] k> 0 [/ latex], неравенство по модулю является неравенством вида: [латекс] \ begin {array} {l} | X | Эти утверждения также применимы к [latex] | X | \ le k [/ latex] и [latex] | X | \ ge k [/ latex]. Опишите все значения [latex] x [/ latex] на расстоянии 4 от числа 5. Показать решение Мы хотим, чтобы расстояние между [latex] x [/ latex] и 5 было меньше или равно 4. Мы можем нарисовать числовую линию, чтобы обозначить условие, которое должно быть выполнено. Расстояние от [latex] x [/ latex] до 5 может быть представлено с помощью символа абсолютного значения, [latex] | x — 5 | [/ latex]. Запишите значения [latex] x [/ latex], которые удовлетворяют условию, как неравенство абсолютных значений. [латекс] | x — 5 | \ le 4 [/ латекс] Нам нужно написать два неравенства, так как всегда есть два решения уравнения абсолютного значения. [латекс] \ begin {array} {lll} x — 5 \ le 4 \ hfill & \ text {and} \ hfill & x — 5 \ ge -4 \ hfill \\ x \ le 9 \ hfill & \ hfill & x \ ge 1 \ hfill \ end {array} [/ latex] Если набор решений — [latex] x \ le 9 [/ latex] и [latex] x \ ge 1 [/ latex], то набор решений представляет собой интервал, включающий все действительные числа от 1 до 9 включительно. Итак, [latex] | x — 5 | \ le 4 [/ latex] эквивалентно [latex] \ left [1,9 \ right] [/ latex] в интервальной нотации. Опишите все значения x- на расстоянии 3 от числа 2. Показать решение [латекс] | x — 2 | \ le 3 [/ латекс] Решить [латекс] | x — 1 | \ le 3 [/ latex]. Показать решение [латекс] \ begin {array} {c} | x — 1 | \ le 3 \ hfill \\ \ hfill \\ -3 \ le x — 1 \ le 3 \ hfill \\ \ hfill \\ -2 \ le x \ le 4 \ hfill \\ \ hfill \\ \ left [-2,4 \ right] \ hfill \ end {array} [/ latex] Учитывая уравнение [latex] y = — \ frac {1} {2} | 4x — 5 | +3 [/ latex], определите значения x , для которых значения y отрицательны. Показать решение Мы пытаемся определить, где [latex] y <0 [/ latex], а где [latex] - \ frac {1} {2} | 4x - 5 | +3 <0 [/ latex]. Начнем с выделения абсолютного значения. [latex] \ begin {array} {ll} — \ frac {1} {2} | 4x — 5 | <-3 \ hfill & \ text {Умножьте обе стороны на -2 и отмените неравенство}. \ Hfill \\ | 4x - 5 |> 6 \ hfill & \ hfill \ end {array} [/ latex] Далее решаем [latex] | 4x — 5 | = 6 [/ latex]. [латекс] \ begin {array} {lll} 4x — 5 = 6 \ hfill & \ hfill & 4x — 5 = -6 \ hfill \\ 4x = 11 \ hfill & \ text {или} \ hfill & 4x = — 1 \ hfill \\ x = \ frac {11} {4} \ hfill & \ hfill & x = — \ frac {1} {4} \ hfill \ end {array} [/ latex] Теперь мы можем изучить график, чтобы увидеть, где значения y- отрицательны.Мы наблюдаем, где ветви находятся ниже оси x-. Обратите внимание, что не важно, как именно выглядит график, если мы знаем, что он пересекает горизонтальную ось в точках [latex] x = — \ frac {1} {4} [/ latex] и [latex] x = \ frac {11} {4} [/ latex], и график открывается вниз. Решите [латекс] -2 | k — 4 | \ le -6 [/ latex]. Показать решение [латекс] к \ ле 1 [/ латекс] или [латекс] к \ л 7 [/ латекс]; в обозначении интервала это будет [латекс] \ left (- \ infty, 1 \ right] \ cup \ left [7, \ infty \ right) [/ latex]. Подсказка: Чтобы решить неравенство, данное в приведенной выше задаче, выполните следующие действия: $ \ left | 2х + 4 \ вправо |> 8 $.Мы знаем, что если нам нужно решить модульное неравенство этой формы, $ \ left | x + a \ right |> b $, то мы преобразуем эту модульную форму следующим образом: $ \ left (x + a \ right) b $. Этот результат объединения дает нам решение указанного выше неравенства. Используя это решение, мы также можем нарисовать график. Полное пошаговое решение: Теперь в приведенной выше задаче нам нужны значения, когда y принимает значение больше 8, поэтому мы удалим область на графике выше, где значение y равно меньше или равно 8. На приведенном выше графике, как вы можете видеть, когда значение функции равно 8, появляются два значения x i.е. (2 и -6), поэтому мы удаляем часть BFA из приведенного выше графика, чтобы получить требуемый график. Открытые отверстия в точках A и B предполагают, что при x, равном -6 и 2, y не принимает значения. Итак, мы построили график $ \ left | 2х + 4 \ вправо |> 8 $. Примечание: Как вы можете видеть, график, который мы нарисовали выше, находится в том же интервале, в котором мы вычислили решение неравенства. Решение неравенства $ \ left | 2x + 4 \ right |> 8 $ выглядит следующим образом: Теперь вы можете видеть, что на приведенном выше графике значение x лежит от отрицательной бесконечности до -6 (в которое не входит -6) и от 2 до бесконечности (в котором 2 не входит ). Для $ | x | \ le v $ решить неравенства $ -v \ le x $, а также $ x \ le v $. Вы также можете решить такое уравнение, используя числовую прямую. Итак, вы можете увидеть, нужно ли вам использовать и , или . Для $ | x |> v $ решите неравенства $ x <-v $ или $ x> v $. Эта числовая строка представляет $ | x-95 | \ le 4 $. Имейте в виду следующее: Поскольку неравенства немного сложнее, мы должны каждый раз решать неравенства: $ ~ $ $ | x-23 | \ le 12 $ $ \ begin {array} {rcr} $ \ begin {array} {rcr} Вместе мы имеем $ 11 \ le x $ и $ x \ le 35 $. $ ~ $ \ left | \ frac12x + 5 \ right | \ le 7 $ $ \ begin {array} {rcr} $ \ begin {array} {rcr} Вместе мы имеем $ -24 \ le x $ и $ x \ le 4 $. $ ~ $ $ | x + 6 |> 5 $ $ \ begin {array} {rcr} $ \ begin {array} {rcr} Вместе мы имеем $ x <-11 $ или $ -1 $ ~ $ | 3x-12 | \ ge 9 $ $ \ begin {array} {rcr} $ \ begin {array} {rcr} Вместе мы имеем $ x \ le 1 $ или $ 7 \ le x $. 12 Алгеграфическое определение Геометрический смысл Уравнения абсолютных значений Абсолютное неравенство Геометрический смысл | x — и | ЭТОТ СИМВОЛ | x | обозначает абсолютное значение x , то есть число без знака.| +3 | = 3. | −3 | = 3. Можно сказать, что абсолютное значение числа — это чисто арифметическое значение. Вот алгебраическое определение | x |: Если x ≥ 0, то | x | = х ; if x x | = — х . То есть, если x неотрицательно: | 3 |, то абсолютное значение — это само число. Если x отрицательно: | −3 |, то абсолютное значение будет отрицательным; что делает абсолютное значение положительным. Геометрически, | x | расстояние x от 0. И 3, и −3 — это расстояние из 3 единиц от 0. | 3 | знак равно Проблема 1. Оцените следующее. Чтобы увидеть ответ, наведите указатель мыши на цветную область. Проблема 2.Объясните следующие правила. a) | — x | = | x |. Оба — x и x находятся на одинаковом расстоянии от 0. б) | b — a | = | a — b | b — a — отрицательное значение a — b . (Урок 7). Следовательно, согласно части а) они равны. c) | x | ² = x ² Мы можем удалить столбцы абсолютных значений, потому что левая часть никогда не бывает отрицательной, как и правая часть. Уравнения абсолютных значений | a | = 5. Какие значения могут иметь и ? может быть 5 или -5. Ведь если мы заменим на любым из них, утверждение — уравнение — будет истинным. Итак, любое уравнение выглядит как — | a | = б — имеет два решения a = b или a = — b . Все, что отображается внутри вертикальных полос — a в этом примере — мы называем аргументом абсолютного значения. Либо аргумент будет равен b , либо он будет равен — b . Пример 1. Решите относительно x : | x — 2 | = 8. Решение . x — 2 аргумента. Либо этот аргумент будет равен 8, либо он будет равен -8. x — 2 = 8 или x — 2 = −8. Мы должны решить эти два уравнения. Первый подразумевает х = 8 + 2 = 10. Второй подразумевает х = −8 + 2 = −6. Это два решения: x = 10 или −6. Задача 3. a) Сколько решений имеет уравнение абсолютных значений? б) Запишите их для этого уравнения: | x | = 4. Задача 4. Решите для x . | x + 5 | = 4. Решите эти два уравнения: Проблема 5.Решите относительно x . | 1 — x | = 7. Задача 6. Решите для x . | 2 x + 5 | = 9. Абсолютные неравенства Существует две формы неравенства по абсолютной стоимости. Один с меньше , | a | b, а другой больше , | a |> b . Решаются они по-разному. Вот первый случай. Пример 2. Абсолютное значение меньше . | a | Чтобы это неравенство было истинным, какие значения может иметь a ? Геометрически a меньше 3 единиц от 0. Следовательно, −3 а Это решение. Неравенство будет истинным, если a имеет любое значение от −3 до 3. В общем, если неравенство выглядит так — | a | б. — тогда решение будет выглядеть так: — б а б для любого аргумента a . Пример 3. Для каких значений x будет справедливо это неравенство? | 2 x — 1 | Решение . Аргумент 2 x -1 будет находиться в диапазоне от −5 до 5: −5 х — 1 Надо выделить х . Сначала прибавьте 1 к каждому члену неравенства: −5 + 1 х −4 х Теперь разделите каждый член на 2: -2 х Неравенство будет истинным для любого значения x в этом интервале. Задача 7. Решите это неравенство для x : | x + 2 | −7 х + 2 Вычтите 2 из каждого члена: −7 — 2 х −9 х Задача 8. Решите это неравенство для x : | 3 x — 5 | −10 х — 5 Добавьте 5 к каждому члену: −5 х Разделите каждый член на 3: Проблема 9.Решите это неравенство для x : | 1-2 x | −9 х Вычтите 1 из каждого члена: −10 х Разделите каждый член на −2. Смысл изменится. 5> х > −4. То есть −4 х Пример 4.Абсолютное значение больше . | a | > 3. Для каких значений a это будет верно? Геометрически, a > 3 или a Это форма решения для любого аргумента a : Если | a | > b (и b > 0), , затем a > b или a b. Задача 10. Решите для x : | x | > 5. Проблема 11. Для каких значений x это будет верно? | x + 2 | > 7. Первое уравнение подразумевает x > 5. Второе, x . Задача 12. Решите для x : | 2 x + 5 | > 9. 2 x + 5> 9 или 2 x + 5 Решите эти два уравнения: Проблема 13.Решить относительно x : | 1-2 x | > 9. 1-2 x > 9 или 1-2 x Решите эти два уравнения. При окончательном делении на −2, Геометрический смысл | x — и | Геометрически, | x — и | — это расстояние x от до . | x — 2 | означает расстояние x от 2. Итак, если мы напишем | x — 2 | = 4 мы имеем в виду, что x на 4 единицы больше, чем 2. Пример: решение сложного неравенства
Попробуйте
Пример: решение сложного неравенства с переменной во всех трех частях
Попробуйте
Решение абсолютных неравенств
Общее примечание: Неравенства абсолютных значений
Пример: определение числа в пределах заданного расстояния
Попробуйте
Пример: решение неравенства абсолютного значения
Пример: использование графического подхода для решения неравенств абсолютных значений
Попробуйте
Ключевые понятия
Глоссарий
Как решить и построить график математической формулы класса неравенства 11 по абсолютному значению CBSE
Неравенство формы модуля, заданное в приведенной выше задаче, выглядит следующим образом:
$ \ left | 2x + 4 \ right |> 8 $
Теперь мы собираемся решить указанное выше неравенство, открыв эту модульную форму, и мы получим
$ \ begin {align}
& \ Rightarrow \ left (2x + 4 \ right) & \ Rightarrow \ left (2x + 4 \ right)> 8 \\
\ end {align} $
Решение двух вышеперечисленных неравенств одно за другим, а затем объединение этих двух решений неравенств.
Решая первое неравенство из приведенного выше, мы получаем
$ \ Rightarrow 2x + 4 Вычитая 4 с обеих сторон в приведенном выше выражении, мы получаем
$ \ begin {align}
& \ Rightarrow 2x + 4-4 & \ Rightarrow 2x \ end {align} $
Разделив 2 с обеих сторон, мы получим
$ \ begin {align}
& \ Rightarrow \ dfrac {2x} {2} & \ Rightarrow x \ end {align} $
Решение второго неравенства мы получаем
$ \ Rightarrow 2x + 4> 8 $
Вычитая 4 с обеих сторон, получаем
$ \ begin {align}
& \ Rightarrow 2x + 4-4> 8-4 \\
& \ Rightarrow 2x > 4 \\
\ end {align} $
Разделив 2 с обеих сторон, мы получим
$ \ begin {align}
& \ Rightarrow \ dfrac {2x} {2}> \ dfrac {4} {2} \ \
& \ Rightarrow x> 2 \\
\ end {align} $
Теперь, объединив решение двух вышеупомянутых неравенств, мы получим
$ \ left (x2 \ right) $
Теперь, преобразовав указанные выше неравенства в интервальную нотацию получаем,
Преобразование $ \ left (x $ \ Rightarrow x \ in \ left (- \ infty, -6 \ right) $ 90 475 Преобразуя $ \ left (x> 2 \ right) $ в обозначение интервалов, мы получаем
$ \ Rightarrow x \ in \ left (2, \ infty \ right) $
Теперь объединение двух вышеуказанных интервалов выглядит следующим образом:
$ x \ in \ left (- \ infty, -6 \ right) \ bigcup \ left (2, \ infty \ right) $
Следовательно, решение приведенного выше неравенства выглядит следующим образом:
$ x \ in \ left (- \ infty, -6 \ right) \ bigcup \ left (2, \ infty \ right) $
Теперь мы собираемся нарисовать график приведенного выше неравенства.Для этого в первую очередь построим график функции модуля.
Функция, записанная в модуле, имеет следующий вид:
$ \ left | 2x + 4 \ right | $
График этой функции выглядит следующим образом:
$ x \ in \ left (- \ infty, -6 \ right) \ bigcup \ left (2, \ infty \ right) $
И график, который мы имеем нарисованный выше выглядит следующим образом:
Итак, по сути, графическое представление является доказательством того, что найденное нами решение является правильным. Абсолютные неравенства — проще простого
-12 & \ le & x-23 \\
\ color {# 669900} {+ 23} && \ color {# 669900} {+ 23} \\
11 & \ le & x
\ end {array} $
х-23 & \ le & 12 \\
\ color {# 669900} {+ 23} && \ color {# 669900} {+ 23} \\
х & \ ле & 35
\ end {array} $
-7 & \ le & \ frac12x + 5 \\
\ color {# 669900} {- 5} && \ color {# 669900} {- 5} \\
-12 & \ le & \ frac12x \\
\ color {# 669900} {\ cdot 2} && \ color {# 669900} {\ cdot 2} \\
-24 & \ le & x
\ end {array} $
\ frac12x + 5 & \ le & 7 \\
\ color {# 669900} {- 5} && \ color {# 669900} {- 5} \\
\ frac12x & \ le & 2 \\
\ color {# 669900} {\ cdot 2} && \ color {# 669900} {\ cdot 2} \\
х & \ le & 4
\ end {array} $
х + 6 & <& - 5 \\
\ color {# 669900} {- 6} && \ color {# 669900} {- 6} \\
х & <& - 11
\ end {array} $
х + 6 &> & 5 \\
\ color {# 669900} {- 6} && \ color {# 669900} {- 6} \\
х &> & — 1
\ end {array} $
3x-12 & \ le & -9 \\
\ color {# 669900} {+ 12} && \ color {# 669900} {+ 12} \\
3x & \ le & 3 \\
\ color {# 669900} {\ overline {\ div 3}} && \ color {# 669900} {\ overline {\ div 3}} \\
х & \ le & 1
\ end {array} $
3x-12 & \ ge & 9 \\
\ color {# 669900} {+ 12} && \ color {# 669900} {+ 12} \\
3x & \ ge & 21 \\
\ color {# 669900} {\ overline {\ div 3}} && \ color {# 669900} {\ overline {\ div 3}} \\
х & \ ge & 7
\ end {array} $ Абсолютное значение. Уравнения абсолютных значений
| −3 | = 3. Расстояние в математике никогда не бывает отрицательным.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами! а) | 6 | = 6 б) | −6 | = 6 в) | 0 | = 0 г) | 2-7 | = 5 e) | 8 | + | −4 | = 8 + 4 = 12 е) | −3 | — | −2 | = 3 — 2 = 1 г) 1 — | −1 | = 1 — 1 = 0 ч) −8 + | −7 | = −8 + 7 = −1 i) −4
| −4 | = −4
4 = -1 Дж) (−4) | −4 | =
(−4) · 4 = −16
Два. x + 5 = 4 x + 5 = −4 x = 4–5 х = −4 — 5 x = -1 или х = −9 1- x = 7 1- x = −7 — x = 7–1 — х = −7 — 1 — x = 6 — х = −8 x = −6 или х = 8. 2 x + 5 = 9 2 x + 5 = −9 2 x = 9–5 2 x = −9 — 5 2 x = 4 2 x = −14 x = 2 или х = −7. 2 x > 4 2 x −14 x > 2 или х −7
чувства изменятся. −2 x > 8 −2 х −10 x −4 или х > 5.
x , следовательно, равно −2 или 6.
С другой стороны, если мы напишем
| x — 2 |
мы имеем в виду, что x на меньше , чем на 4 единицы от 2.
Это означает, что x может иметь любое значение в открытом интервале от -2 до 6.
Задача 14. Каков геометрический смысл | x + a |?
Расстояние x от — до .Для, | x + a | = | x — (- a ) |.
| x + 1 |, значит, расстояние x от −1. Например, если
| x + 1 | = 2,
, то x на 2 единицы от -1.
x = −3 или x = 1.
Задача 15. Каково геометрическое значение каждого из следующих утверждений? И поэтому какие значения имеет x ?
а) | x | = 2
x находится на расстоянии 2 единиц от 0.Для, | x | = | x — 0 |. x , следовательно, равно 2 или −2.
б) | x — 3 | = 1
x находится на расстоянии 1 единицы от 3. x , следовательно, равно 2 или 4.
c) | x + 3 | = 1
x — это 1 единица от −3. x , следовательно, равно −4 или −2.
d) | x — 5 | ≤ 2
x меньше или равно 2 единицам от 5. x , следовательно, может принимать любое значение в закрытом интервале от 3 до 7.
Закрытый интервал.
e) | x + 5 | ≤ 2
x меньше или равно 2 единицам от −5. Следовательно, x может принимать любое значение в закрытом интервале от -7 до -3.
Проблема 16. | x — 5 | d. Укажите геометрическое значение этого слова и проиллюстрируйте его числовой прямой.
x попадает в d единиц из 5.
x , следовательно, попадает в интервал между 5 — d и 5 + d .
5- d x
Следующий урок: Экспоненты
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.2 $ = 0 ⇒ a = 0 и b = 0
, т.е. z = 0 + i0 = 0
Итак, | z | = 0, если, z = 0
(III) Абсолют произведения двух комплексных чисел z1 и z2 равен произведению абсолютных значений чисел. т.е.
$ \ left | z1.z2 \ right | $ = $ \ left | z1 \ право. | $ $ \ left | z2 \ right | $
(IV) Абсолют частного двух комплексных чисел z1 и z2 (0) равен частному абсолютных значений делимого и делителя.
$ \ осталось | \ frac {z1} {z2} \ right | $ = $ \ frac {\ left | z1 \ right |} {\ left | z2 \ right |} $
(V) Абсолют суммы двух сопряженных комплексные числа z1 и z2 никогда не могут превышать сумму своих абсолютных значений, т.е. $ \ left | z1 + z2 \ right | $ $ \ leq $ $ \ left | z1 \ right | $ + $ \ left | z2 \ right | $
Это неравенство называется неравенством треугольника .
Математика в 11 классе
От модуля комплексного числа к дому
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Что такое условное и абсолютное неравенство? [Видео]
Условные и абсолютные неравенства
Привет, и добро пожаловать в это видео об условных и абсолютных неравенствах .
До сих пор большая часть изученной вами алгебры включала уравнений , то есть утверждений, показывающих два равных друг другу математических выражения. Например, если посмотреть на 3x + 5 = 17, то, что находится в левой части уравнения, 3x + 5, равно тому, что находится в правой части уравнения, 17.
Иногда, однако, вместо того, чтобы показать, что выражения равны, мы хотим сравнить два выражения, чтобы показать, что одно больше или меньше другого. Эти типы утверждений называются неравенствами, потому что мы не стремимся генерировать два выражения, которые равны друг другу, как мы это делаем с уравнениями. Неравенства изображают выражения, которые обычно не равны .
Есть четыре символа, которые позволяют нам указать, что выражения больше или меньше друг друга.
Этот символ: меньше ». Например, это означает, что три меньше семи. Уловка, позволяющая запомнить, какая сторона больше или меньше, заключается в том, что сторона символа с точкой «меньше», чем открытая сторона, которая кажется «больше».
Следующий символ ->, что означает « больше ». Пример: «8> 2».
Последние два символа очень похожи на первые два:
Этот символ ≤ означает « меньше или равно ».Это почти то же самое, что больше или равно ». Итак, если мы сказали y6, тогда y может включать такие значения, как 7, 10 или 22, но также может включать 6, поскольку y может быть равно шести.
Иногда можно встретить неравенства, содержащие более одного из этих символов. Они называются двойными неравенствами .
Примером может быть 7> x> 2. Это предполагает, что x меньше 7, но больше 2. Это означает, что 3, 4, 5 и 6 будут приемлемыми значениями x.
Как видите, неравенства могут содержать переменные, как и уравнения. И точно так же, как определенные значения переменной делают уравнение правильным, точно так же определенные значения переменных делают неравенства истинными.
Часто только определенные значения переменной удовлетворяют неравенству, в то время как другие значения делают его ложным. Эти типы неравенств называются условными неравенствами , потому что они верны только при определенных условиях.
Чтобы решить условное неравенство, относитесь к нему, как к стандартному уравнению, и решайте для переменной.
Давайте посмотрим на простой пример:
Допустим, вам дали это:
X + 2> 9
Чтобы вычислить значение X, нужно решить это неравенство так же, как и любое другое уравнение. Как вы помните, чтобы определить значение переменной, вы изолируете переменную на одной стороне уравнения, и мы делаем то же самое для неравенства.
Итак, вы вычтете 2 с обеих сторон, и у вас останется:
X> 7
Это означает, что любое значение X выше 7, не включая 7, сделает это неравенство истинным.
Чтобы быстро проверить свой ответ, давайте используем значение 4 для x. Подключите 4 плюс 2 больше девяти, вы получите 6> 9, что неверно. Однако, используя значение 8 для X, вы можете подключить 8 плюс 2, больше 9, что дает 10> 9, что верно. Он больше 7, значит, правильный.
Давайте попробуем более сложный пример.
3x — 7 8 + 2x
Первый шаг — решить относительно X, как и с любым другим уравнением.
Итак, мы начнем с добавления 7 к обеим сторонам, что даст нам: 3x 15 + 2x.Теперь мы собираемся вычесть 2x с обеих сторон, это оставляет нам X 15. Это означает, что любые значения X, равные 15 или ниже, будут работать для этого неравенства.
Есть одно дополнительное правило, которое вы должны помнить при решении неравенств: всякий раз, когда неравенство умножается или делится на отрицательное число, знак неравенства должен быть перевернутым .
Вот быстрый пример, чтобы увидеть это правило в действии:
Давайте решим это неравенство:
-2x + 10> 8
Итак, мы начнем с вычитания 10 с обеих сторон, что даст вам:
-2x> -2
Чтобы изолировать X, мы делим обе стороны на -2.Вот тут-то и вступает в игру наше правило. После деления на два отрицательных мы обычно останемся с X> 1, но мы меняем знак неравенства, давая нам X абсолютные значения , неравенства также могут включать их. Если вам нужно напомнить, абсолютное значение выражает, насколько далеко число от нуля. Неважно, положительное или отрицательное число.
Скажем, у вас было:
| x | — 5
College Algebra WTAMU > Виртуальная математическая лаборатория> Алгебра колледжа Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? Видео на этом сайте были созданы и продюсированы Ким Сьюард и Вирджиния Уильямс Трайс. |

 момент
момент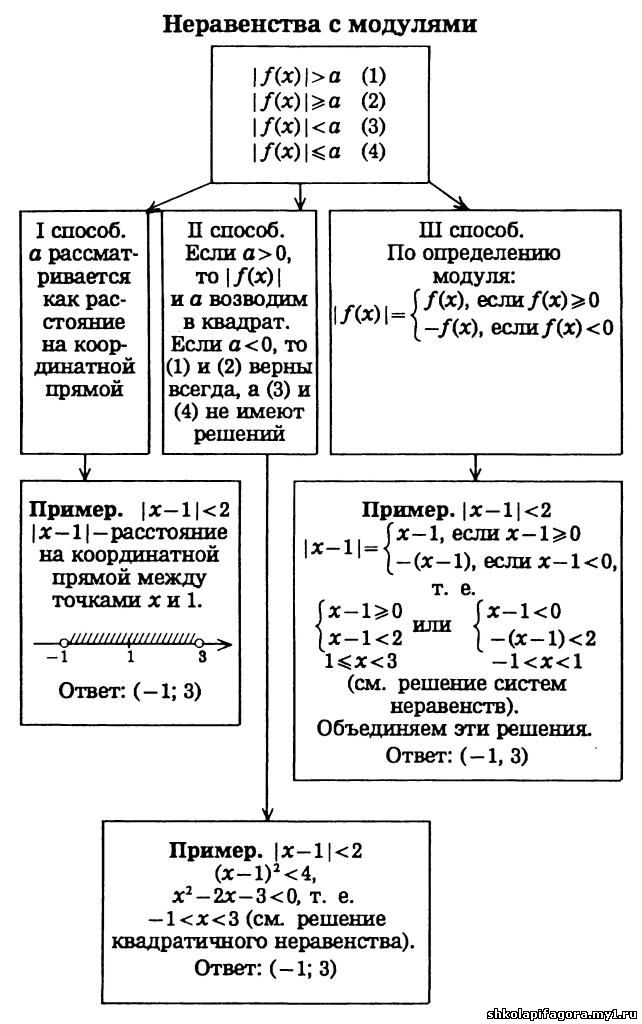 Модуль числа – само это число, если оно не отрицательное, и противоположное ему число, если данное число отрицательное
Модуль числа – само это число, если оно не отрицательное, и противоположное ему число, если данное число отрицательное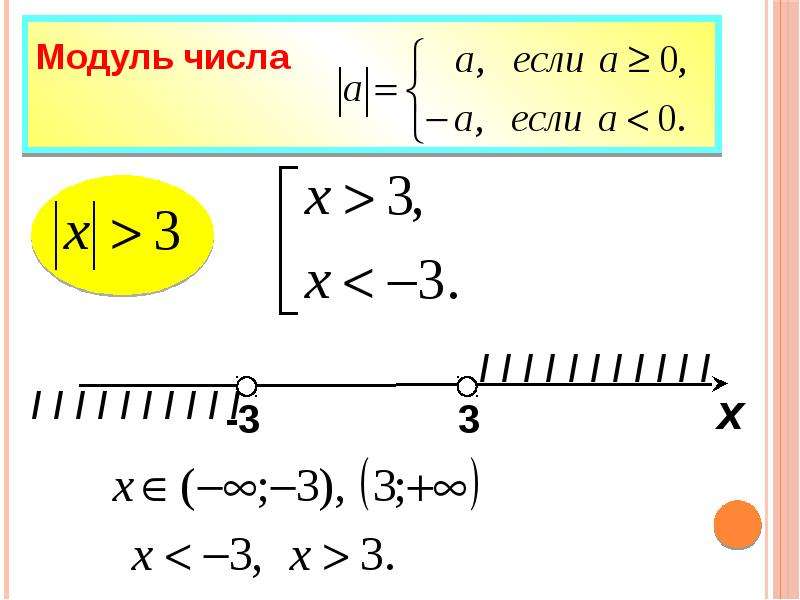 Приложение 1
Приложение 1 Приложение 3
Приложение 3
 Предлагает ученикам ответить на вопросы:
Предлагает ученикам ответить на вопросы: