Алгебра 9 класс упростить выражение с корнями: Повторение и систематизация курса алгебры 7-9 класса. Преобразование выражений

alexxlab

Содержание

Урок по алгебре «Свойства корней степени n» (9-й класс)

Тип урока: совершенствование умений и навыков.

Характеристика темы: Преподавание ведётся по учебнику “Алгебра 9” Никольского С.М. для общеобразовательных учреждений. На данную тему отводится 3 часа. Это третий урок.

Дидактическая цель урока: Научить применять полученные знания при решении различных задач, в том числе повышенного уровня сложности, стимулировать учащихся к овладению рациональными приемами и методами решения.

Образовательная цель урока: Обеспечить в ходе урока закрепление материала о свойствах корней степени n и применение этих свойств при выполнении упражнений.

Развивающая цель урока: Развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи учащихся.

Воспитательная цель урока: Воспитывать интерес к математике как учебному предмету через современные технологии преподавания, приучать к умению выслушивать других, умению общаться, прививать аккуратность и трудолюбие.

Формы работы организации познавательной деятельности: фронтальная, индивидуальная.

Оборудование.

  • Компьютеры.

  • Программа компьютерного тестирования Knowing (представляет собой удобную программу для тестирования с возможностью составления тестов и автоматической оценки результатов тестирования).

Ход урока.

1. Организационный момент.

2. Актуализация прежних знаний.

1) Какие из следующих записей не имеют смысла?

; ; ;

2) При каких значениях переменной а выражение имеет смысл?

3) Вычислите:

4) Проверка домашнего задания.

3. Формирование умений и навыков.

Упростить выражение

Решение.

Преобразуем знаменатель дроби:

 – это неполный квадрат суммы чисел 3 и . Чтобы избавиться от иррациональности в знаменателе дроби, умножим ее числитель и знаменатель на разность этих чисел:

Упростить выражение
 и найти его значение при х=
Решение.

Так как х≥0 ( в противном случае выражение  не имеет смысла), то .

Тогда

Найти значение выражения
 при х=.

Решение.

Преобразуем данное выражение при х( в противном случае данное выражение не имеет смысла):

При заданных значениях х и у имеем

.

Значит,

а) Вынести множитель из-под знака корня  при условии, что х0.

б) Внести множитель под знак корня 3учто у.

Решение.

а) Так как х0 по условию, а у (в противном случае выражение не имеет смысла), то  =

б) Так как у по условию, а хне имеет смысла выражение , то

3у

4. Самостоятельная работа (компьютерное тестирование).

Приложение 1.

Приложение 2.

5. Подведение итогов урока.

6. Домашее задание.

П. 4.6, №553, 555.

7. Использованная литература.

  1. С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. Алгебра 9 класс – М.: Просвещение, 2009 г

  2. М.К. Потапов, А.В. Шевкин. Дидактические материалы для 9 класса – М.: Просвещение, 2008 г

  3. Воробьева Е.А. Алгебра. 9 класс. Проверочные работы с элементами тестирования. – Саратов: Лицей, 2008

  4. Воробьева Е.А. Алгебра. 9 класс: В 2 ч. – Саратов: Лицей, 2008

  5. Капитонова Т.А. Алгебра. 9 класс: Проверочные и контрольные работы. – Саратов: Лицей, 2006

Урок 14. степень с рациональным показателем — Алгебра — 9 класс

Конспект

Выражение означает , т. е. или .

Знаменатель показателя степени начального выражения является показателем степени корня, который нужно извлечь из выражения.

Если a – положительное число,  – дробное число (m – целое число, n – натуральное число), то .

Примеры преобразований

Запомним определение.

Если дробь  – дробное положительное число (m и n – натуральные числа), то .

Отрицательные основания.

Выражения не имеют смысла и не рассматриваются.

Правила выполнения операций над выражениями со степенями. Эти правила применимы и для выражений со степенями с рациональным показателем.

Для любого a > 0 и любых рациональных чисел p, q

    • произведение степеней: ap • aq = a(p + q);
    • деление степеней: ap : aq = a(p – q);
    • возведение степени в степень: (ap)q = a(p • q).

    Для любого a > 0 и b > 0 и любого рационального числа p

    • возведение произведения в степень: (ab)p = ap • bp;
    • возведение дроби в степень: .

Правила преобразования для степени с рациональным показателем

    • Произведение степеней: .
    • Деление степеней: .
    • Возведение степени в степень: .
    • Возведение произведения в степень: .
    • Возведение дроби в степень: .

Пример №1. Упростить дробь .

Задание выполнено.

Пример №2. Сократить дробь .

Задание выполнено.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

3. Вычислите Найдите x Произведение корней уравнений 0. равно 4. Найдите k. 6. Упростите выражение. 7. Упростите выражение

ПРИМЕРНЫЕ ВОПРОСЫ (ЗАДАНИЯ)

МАТЕРИАЛЫ для подготовки к тестированию по математике 8 класс Учитель: (Субач М. В., Авершина Л.А., Данилова А.Р.) ТЕМА Знать Уметь 6 Множество рациональных и множество действительных П.16. Рациональные

Подробнее

ГЛАВА II. Квадратный трехчлен

ГЛАВА II. Квадратный трехчлен Справочный материал Квадратным трехчленом называют выражение a + b + c, где abc,, и a 0. График квадратного трехчлена парабола. Прямая b = ее ось симметрии. Точка ( в; в)

Подробнее

Алгебра, ЛШ вариант

Алгебра, ЛШ 2015 1 вариант 1. Решите методом интервалов неравенство (x 2 18x+77) 10 x 0. 2x+3y 8 y 2 4x 2 2x+3a 8 0 содержится число 1? a 2 4x 2 неравенства содержится интервал ( 1;1)? один корень уравнения

Подробнее

ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ ;

ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ (для слушателей подготовительных курсов) Тождественные преобразования арифметических выражений ВЫЧИСЛИТЕ (.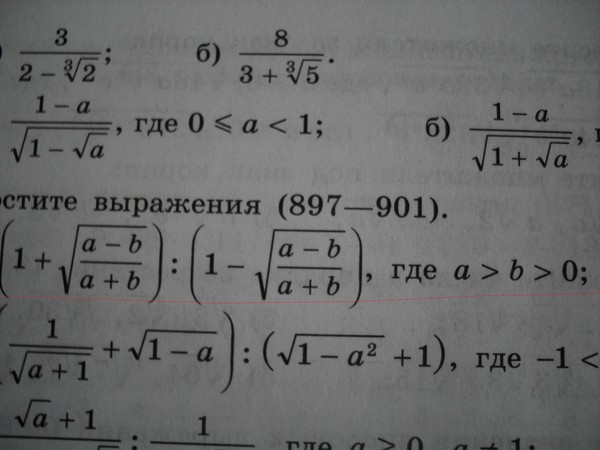 -.).,9,..,,..,, 9,.. НАЙДИТЕ (.-.).,,.. 9,,,,..,..,,,,..,..,,,.9.,…,,,..,..,

Подробнее

Условный переход. Урок 9.

Условный переход Урок 9. Препятствие в виде возвышенности нет Умный? да Восхождение Обход Условие В условии 2 числа, или 2 строки, или 2 переменных, или 2 арифметических или строковых выражения сравниваются

Подробнее

Иррациональные уравнения и неравенства 1

Иррациональные уравнения и неравенства Оглавление Свойства корней й степени Свойства корней Свойства степеней с рациональным показателем Примеры 5 Свойства корней -й степени Арифметическим корнем й степени

Подробнее

Дом Севастьянова. Екатеринбург

Дом Севастьянова. Екатеринбург 9. Функция =, её график и свойства 0. Свойства квадратных корней. Тождество =. Вынесение множителя из-под знака квадратного корня. Внесение множителя под знак квадратного

Подробнее

Урок алгебры в 7 классе

Урок алгебры в 7 классе Тема: «Формулы сокращенного умножения» Продолжительность урока: 45 минут Цели урока: обучающие: закрепление знаний по теме: «Формулы сокращенного умножения»; определение уровня

Подробнее

Иррациональные неравенства

Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного

Подробнее

Контрольная работа 2. 1 вариант. 2 вариант. 1). Для функции f (х) = 3х 2 х Найти f (0), f (1), f (-3), f (5).

Контрольная работа 1 вариант 1) Для f (х) = х + х 1 Найти f (), f (1), f (-), f (5) 1) Для f (х) = х х + Найти f (), f (1), f (-), f (5) ) Найти D(у), если: у 5х 5 в) у х х 5х 6 г) 7х 1 у х х у х ) Найти

Подробнее

5.

Выполните умножение дробей. 6. Решите уравнение. 8. Из формулы площади квадрата. 10. (2 балла) Найдите область определения функции

АЛГЕБРА, 9 класс Вариант, Январь 0 ВАРИАНТ если к заданию ответы не приводятся, то полученный ответ надо вписать в Укажите интервал, которому принадлежит число 6,39 ( 6,; 6, ) ( 6,; 6,4 ) ( 6,3; 6,34 )

Подробнее

Контрольные работы по алгебре, 7-9 класс

Контрольные работы по алгебре, 7-9 класс Приведено по два варианта контрольных работ по алгебре для 7 класса, ориентированных на новые версии учебных комплектов А.Г.Мордковича и др. Алгебра-7 Часть 1.

Подробнее

КОНТРОЛЬНЫЕ РАБОТЫ Комплексные числа

КР-11-1 Профильный уровень КОНТРОЛЬНЫЕ РАБОТЫ Комплексные числа 1 Дано комплексное число z 1 i 1) Запишите число z в алгебраической и тригонометрической формах и изобразите его на комплексной плоскости;

Подробнее

Вокруг заданий 18 из ЕГЭ 2017

Вокруг заданий 18 из ЕГЭ 2017 А. В. Шевкин, [email protected] Аннотация: В статье разобраны различные способы решения ряда заданий с параметром. Ключевые слова: уравнение, неравенство, параметр, функция,

Подробнее

Тематическое планирование

Количество часов Наименование разделов и тем Тематическое планирование Планируемые образовательные результаты 1 Линейное уравнение с одной переменной 2 Целые выражения 15 Распознавать числовые выражения

Подробнее

РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС

РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС Пояснительная записка Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта основного общего образования по

Подробнее

Тема 1: «Прямая и плоскость»

Тема 1: «Прямая и плоскость» Задание 1. Прямая, заданная уравнением x y 3 координат в точках: = 1, пересекает оси 1. A(; 0) и B(0; 3). A(; 0) и B(0; 3) ; 3. A( ; 0) и B(0; 3) Задание. Уравнение прямой,

Подробнее

Рабочая программа по алгебре

Муниципальное бюджетное общеобразовательное учреждение города Астрахани «Лицей 3» Утверждено: Директор МБОУ г. Астрахани «Лицей 3» Губарев А.Н. Приказ /5 от «0» сентября 206 г. Согласовано: Киселева С.Ю.

Подробнее

Учебный центр «Резольвента»

ООО «Резольвента», www.resolventa.ru, [email protected], (495) 509-8-10 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К. Л. САМАРОВ УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЯМИ Учебное

Подробнее

Н.В. ЛАТЫПОВА КВАДРАТНЫЙ ТРЕХЧЛЕН

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ ОЧНО ЗАОЧНАЯ ШКОЛА Н. В. ЛАТЫПОВА КВАДРАТНЫЙ ТРЕХЧЛЕН Ижевск

Подробнее

КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ЛИНЕЙНОЙ АЛГЕБРЕ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ (для заочной и заочно-сокращённой форм обучения) Студент должен выполнять контрольные задания по варианту номер которого совпадает с последней

Подробнее

ПОУРОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

ПОУРОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (4 ч в неделю I полугодие, 3 ч в неделю II полугодие, всего 119 ч) ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ 7-ГО КЛАССА 4 2.09-7.09 1 Разложение на множители 1 2.09 2 Формулы сокращенного

Подробнее

В помощь учителю. Тесты по алгебре 11 класс

В помощь учителю Тесты по алгебре 11 класс Тесты составлены учителем математики высшей категории ГУО «Средняя школа 1 г. Кировска» Автушкевич Тамарой Александровной. В методичке представлены тесты на соответствие

Подробнее

Что такое квадратный корень? Формулы и Примеры

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным. 

Здесь могут возникнуть резонные вопросы, почему, например, в примере x2 = 16, x = 4 и x = -4.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

  • x2 = 16 не равно  x = √16.

Это два нетождественных друг другу выражения.

  • x2 = 16 — это квадратное уравнение.
  • x = √ 16 — арифметический квадратный корень.

Из выражения x2 = 16 следует, что:

  • |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

 

  1. Пример решен неверно

  2. Это квадратное уравнение.

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения: 

 

  1. x2 = 36

  2. x = √36

Первое выражение — квадратное уравнение. 

|x| = √36
x1 = +6
x2 = -6.

Второе выражение — арифметический квадратный корень. 

√36 = 6
x = 6.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

√2 = 1,414213…;

π = 3,141592…;

e = 2,718281…. .

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит. 

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Решение следующее:
Строим график функции y = x2.
Отмечаем решения на графике: -√2; √2.

Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .

В таком виде ответ не записывают — нужно оставить квадратный корень.
x2 = 2.
x = √2
x = -√2. 

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

  • 1. Извлеките квадратный корень: √289

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Влево — 1, вверх — 7.

Ответ: √289 = 17.

  • 2. Извлеките квадратный корень: √3025

Ищем в таблице число 3025.
Влево — 5, вверх —  5.

Ответ: √3025 = 55.

  • 3. Извлеките квадратный корень: √7396

Ищем в таблице число 7396.

Влево — 8, вверх — 6.

Ответ: √7396 = 86.

  • 4. Извлеките корень: √9025

Ищем в таблице число 9025.

Влево — 9, вверх — 5.

Ответ: √9025 = 95.

  • 5. Извлеките корень √1600

Ищем в таблице число 1600.

Влево — 4, вверх — 0.

Ответ: √1600 = 40.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

  • Корень произведения равен произведению корней
  • Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
  • Чтобы возвести корень в степень, нужно возвести в степень значение под корнем

Давайте потренируемся и порешаем примеры на все три свойства. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

Примеры:

 

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

 

  3. Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:

Добрая напоминалочка

Чтобы решать примеры быстрее, не забывайте пользоваться таблицей квадратов.

 

Деление арифметических корней

Для деления арифметических корней используйте формулу:

Примеры:

 

  1. Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Дано выражение: 7√9

Число семь умножено на квадратный корень из числа девять. 

Извлечем квадратный корень и умножим его на 7.

√9= 3.

7√9 = 7*3 = 21

В данном выражение число 7 — множитель. Давайте внесем его под знак корня. 

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a)2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.  

7√9 = √72* 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Запоминаем:

Нельзя вносить отрицательные числа под знак корня.

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

 

Вынесение множителя из-под знака корня 

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей. 

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

 

  1. √28

    Раскладываем подкоренное выражение на множители 28 = 7*4.

    Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.

  2. Ответ: по правилу извлечения квадратного корня из произведения,

    Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.

  3. Вынесите множитель из-под знака корня в выражении: √24

    Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.

  4. Упростите выражение:

    Вынесем в двух последних выражения множитель из-под знака корня.

    Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.

    Мы видим, что во всем выражении есть один общий множитель — √5.
    Выносим общий множитель за скобки:

    Далее вычисляем все, что в скобках:

 

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

  • √a < √b, то a < b
  • √a = √b, то a = b

Давайте разберем на примере.

Сравните два выражения: √70 и 8√2

Первым делом преобразуем второе выражение: 8√2 = √64 * √2 = √64*2 = √128.

70 < 128.

Это значит, что √70  <  8√2.

Запоминаем

Чем больше число под знаком корня, тем больше сам корень.

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

 

  1. Сравните два выражения: √50 и 9√5

    Ответ: преобразовываем выражение 9√5.

    9√5 = √81 * √5 = √81*5 = √405

    50 < 405

    Это значит, что √50 < 9√5.

  2. Сравните два выражения: 6√5 и √18

    Ответ: преобразовываем выражение 6√5.

    6√5 = √36 * √5 = √36*5= √180

    180 > 18

    Это значит, что 6√5 > √18.

  3. Сравните два выражения: 7√12 и √20

    Ответ: преобразовываем выражение 7√12.

    7√12 = √49 * √12 = √49*12 = √588

    588 >20

    Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет. 

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее. 

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

 

  1. Определить «сотни», между которыми оно стоит.

  2. Определить «десятки», между которыми оно стоит.

  3. Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

102 = 100

202 = 400

302 = 900

402 = 1600

502 = 2500 

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 402и 502.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

12 = 1

22 = 4

32 = 9

42 = 16 ⇒ 6

52 = 25 ⇒ 5

62 = 36 ⇒ 6

72 = 49 ⇒ 9

82 = 64 ⇒ 4

92 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 442 и 462.

Далее вычисляем: 44 * 44 = 1936.

46 * 46 = 2116.

Ответ: √2116 = 46

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат. 

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители: 

11666 : 4 = 2916

2916 : 4 = 729

729 : 3 = 243

243 : 3 = 81

11664

4

2916

4

729

3

243

3

81

81

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
 

Алгебра: уроки, тесты, задания.

Алгебра: уроки, тесты, задания.



  1. Информация о разделе





    1. Числовые выражения. Алгебраические выражения





    2. Математический язык





    3. Математические модели реальных ситуаций





    4. Линейное уравнение с одной переменной.

      Алгоритм решения





    5. Координатная прямая. Числовые промежутки






    1. Координатная плоскость. Координаты точки





    2. Линейное уравнение ax + by + c = 0. График линейного уравнения





    3. Линейная функция y = kx + m.

      График линейной функции





    4. Линейная функция y = kx, её свойства





    5. Взаимное расположение графиков линейных функций






    1. Понятие системы линейных уравнений с двумя переменными





    2. Решение систем линейных уравнений.

      Метод подстановки





    3. Решение систем линейных уравнений. Метод сложения





    4. Система линейных уравнений как математическая модель






    1. Понятие степени с натуральным показателем





    2. Часто используемые степени





    3. Базовые свойства степеней с натуральным показателем





    4. Умножение и деление степеней с одинаковыми натуральными показателями





    5. Понятие степени с нулевым показателем






    1. Понятие одночлена.

      Приведение одночлена к стандартному виду





    2. Сложение и вычитание подобных одночленов





    3. Произведение одночленов и возведение одночлена в степень





    4. Деление одночленов






    1. Понятие многочлена.

      Приведение многочлена к стандартному виду





    2. Как складывать и вычитать многочлены





    3. Как умножать многочлен на одночлен





    4. Как умножать многочлен на многочлен





    5. Применение формул сокращённого умножения





    6. Как делить многочлен на одночлен






    1. Понятие разложения многочленов на множители





    2. Разложение на множители.

      Вынесение общего множителя за скобки





    3. Разложение на множители. Способ группировки





    4. Разложение на множители. Использование формул сокращённого умножения





    5. Разложение на множители. Сочетание различных приёмов





    6. Применение разложения на множители для сокращения алгебраических дробей





    7. Понятие тождества






    1. Квадратичная функция y = x² и её график





    2. Решение уравнений графическим методом





    3. Запись функции в виде у = f(x)






    1. Понятие алгебраической дроби





    2. Применение основного свойства алгебраической дроби





    3. Как складывать и вычитать алгебраические дроби с равными знаменателями





    4. Как складывать и вычитать алгебраические дроби с разными знаменателями





    5. Как умножать, делить и возводить в степень алгебраические дроби





    6. Упрощение рациональных выражений





    7. Решение рациональных уравнений






    1. Квадратичная функция y = kx² и её свойства.

      Парабола





    2. Функция y = k/x и её свойства. Гипербола





    3. Как построить график функции у = f(x + l)





    4. Как построить график функции у = f(x) + m





    5. Как построить график функции y = f(x + l) + m





    6. Квадратичная функция y = ax² + bx + c





    7. Решение квадратных уравнений с помощью графиков функций






    1. Понятие квадратного корня





    2. Функция квадратного корня y = √x, её свойства и график





    3. Множество рациональных чисел





    4. Базовые свойства квадратных корней





    5. Преобразование иррациональных выражений






    1. Какие бывают квадратные уравнения





    2. Способы решения квадратных уравнений





    3. Решение рационального уравнения, сводящегося к квадратному





    4. Использование рациональных уравнений для решения задач





    5. Упрощённая формула для решения квадратного уравнения





    6. Применение теоремы Виета





    7. Решение иррационального уравнения, сводящегося к квадратному






    1. Множества натуральных чисел, целых чисел, рациональных чисел





    2. Понятие иррационального числа





    3. Множество действительных чисел и её геометрическая модель





    4. Модуль действительного числа и его геометрический смысл





    5. Приближённые значения по недостатку (по избытку)





    6. Понятие степени с отрицательным целым показателем





    7. Стандартный вид положительного числа






    1. Понятие числовых промежутков





    2. Свойства числовых неравенств.

      Свойства неравенств одинакового смысла





    3. Как решать линейное неравенство





    4. Методы решения квадратных неравенств





    5. Понятие монотонности функции. Исследование функций на монотонность




  7. Международная оценка образовательных достижений учащихся (PISA)





    1. Повторим способы решения линейных и квадратных неравенств





    2. Решение рациональных неравенств методом интервалов





    3. Множества и подмножества.

      Объединение и пересечение множеств





    4. Системы рациональных неравенств






    1. Понятие системы рациональных уравнений





    2. Методы решения систем рациональных уравнений





    3. Использование систем рациональных уравнений для решения задач






    1. Определение числовой функции и способы её задания





    2. Свойства основных функций





    3. Чётные и нечётные функции.

      Определение чётности и нечётности





    4. Степенная функция с натуральным показателем





    5. Степенная функция с отрицательным целым показателем





    6. Функция кубического корня






    1. Понятие числовой последовательности.

      Способы задания последовательностей





    2. Арифметическая прогрессия. Свойства арифметической прогрессии





    3. Геометрическая прогрессия. Свойства геометрической прогрессии






    1. Злементы комбинаторики.

      Комбинаторные задачи





    2. Элементы статистики. Методы обработки информации





    3. Элементы теории вероятности. Нахождение вероятности





    4. Относительная частота и статистическая вероятность события






    1. Натуральные числа.

      Повторение





    2. Рациональные числа. Повторение





    3. Иррациональные числа. Повторение






    1. Обратимая и обратная функции





    2. Понятие периодической функции (профильный)






    1. Числовая окружность на координатной плоскости





    2. Нахождение значений синуса и косинуса, тангенса и котангенса





    3. Числовой аргумент тригонометрических функций





    4. Угловой аргумент тригонометрических функций





    5. Свойства функции y = sin x и её график





    6. Свойства функции y = cos x и её график





    7. Периодичность тригонометрических функций, чётность, нечётность





    8. Гармонические колебания (профильный)





    9. Свойства функций y = tg x, y = ctg x и их графики





    10. Функции y = arcsin a, y = arccos a, y = arctg a, y = arcctg a (профильный)






    1. Арккосинус и решение уравнения cos х = a





    2. Арксинус и решение уравнения sin x = a





    3. Арктангенс и арккотангенс.

      Решение уравнений tg x = a, ctg x = a





    4. Методы, используемые для решения тригонометрических уравнений






    1. Формулы синуса суммы и разности, косинуса суммы и разности





    2. Тангенс суммы и разности





    3. Формулы приведения.

      Общее правило





    4. Формулы синуса, косинуса, тангенса двойного угла





    5. Формулы понижения степени, или формулы половинного угла (профильный)





    6. Формулы сумм тригонометрических функций





    7. Формулы произведений тригонометрических функций





    8. Метод введения вспомогательного угла (профильный)






    1. Числовые последовательности и их свойства





    2. Понятие предела числовой последовательности





    3. Как найти сумму бесконечной геометрической прогрессии





    4. Предел функции в точке.

      Предел функции на бесконечности





    5. Определение производной. Геометрический и физический смысл производной





    6. Вычисление производных. Правила дифференцирования





    7. Как получить уравнение касательной к графику функции





    8. Исследование функций на монотонность и экстремумы





    9. Исследование выпуклости и перегиба, построение графиков функции





    10. Применение производной для отыскания наибольших и наименьших величин






    1. Понятие корня n-й степени из действительного числа





    2. Функция корня n-й степени





    3. Свойства корня n-й степени.

      Преобразование иррациональных выражений





    4. Способы упрощения выражений, содержащих радикалы





    5. Понятие степени с рациональным показателем, свойства степеней





    6. Свойства степенных функций и их графики






    1. Свойства показательной функции и её график





    2. Методы решения показательных уравнений





    3. Методы решения показательных неравенств





    4. Понятие логарифма.

      Основное логарифмическое тождество





    5. Свойства логарифмической функции и её график





    6. Базовые свойства логарифмов





    7. Методы решения логарифмических уравнений





    8. Методы решения логарифмических неравенств





    9. Переход к новому основанию логарифма





    10. Системы показательных и логарифмических уравнений





    11. Системы логарифмических и показательных неравенств





    12. Производная показательной и логарифмической функции






    1. Понятие первообразной





    2. Неопределённые и определённые интегралы.

      Методы интегрирования





    3. Вычисление площадей с помощью интегралов






    1. Правило суммы





    2. Правило произведения





    3. Перестановки.

      Перестановки без повторений





    4. Размещения. Размещения с повторениями





    5. Сочетания и их свойства





    6. Треугольник Паскаля. Бином Ньютона






    1. Какие бывают случайные события





    2. Комбинации событий. Противоположные события





    3. Вероятность события





    4. Сложение вероятностей





    5. Независимые события. Умножение вероятностей





    6. Статистическая вероятность






    1. Случайные величины





    2. Центральные тенденции





    3. Меры разброса





    4. Закон распределения вероятностей. Закон больших чисел






    1. Равносильность уравнений. Теоремы о равносильности уравнений





    2. Общие методы решения уравнений





    3. Равносильность неравенств. Системы и совокупности неравенств





    4. Уравнения и неравенства с двумя переменными





    5. Общие методы решения систем уравнений





    6. Уравнения и неравенства с параметром




  1. Коллекция интерактивных моделей




Тесты по алгебре Корни (8 класс) онлайн


Сложность: знаток.Последний раз тест пройден более 24 часов назад.

Материал подготовлен совместно с учителем высшей категории

Опыт работы учителем математики — более 33 лет.

  1. Вопрос 1 из 10

    Вычислитe

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 88% ответили правильно
    • 88% ответили правильно на этот вопрос

    В вопросе ошибка?

    Следующий вопросОтветить

  2. Вопрос 2 из 10

    Вычислитe

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 83% ответили правильно
    • 83% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  3. Вопрос 3 из 10

    Выберите число, которое может принимать а в выражении

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 74% ответили правильно
    • 74% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  4. Вопрос 4 из 10

    Вычислитe

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 61% ответили правильно
    • 61% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  5. Вопрос 5 из 10

    Упростите выражение

    • Правильный ответ
    • Неправильный ответ
    • Вы ответили лучше 65% участников
    • 35% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  6. Вопрос 6 из 10

    Вычислите

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 68% ответили правильно
    • 68% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  7. Вопрос 7 из 10

    Вычислитe

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 72% ответили правильно
    • 72% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  8. Вопрос 8 из 10

    Вычислитe

    • Правильный ответ
    • Неправильный ответ
    • Вы ответили лучше 59% участников
    • 41% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  9. Вопрос 9 из 10

    Упростите выражение

    • Правильный ответ
    • Неправильный ответ
    • Вы ответили лучше 56% участников
    • 44% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

  10. Вопрос 10 из 10

    Вычислитe

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 77% ответили правильно
    • 77% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

    

  • Евгений Кочкин

    7/10

  • Галина Кропотина

    10/10

  • Александр Александровский

    9/10

  • Александр Чернов

    10/10

  • Давид Смык

    10/10

  • Аида Крутая

    8/10

  • Олеся Вьюшкова

    6/10

  • Татьяна Федотова

    8/10

  • Михаил Сапрыкин

    8/10

  • Анастасия Михлик

    6/10

ТОП-5 тестовкоторые проходят вместе с этим

Нет сомнения, что тема «Квадратные корни» является одной из достаточно трудных, но при этом и очень важной, а потому тест «Корни» (8 класс) будет, безусловно, полезен всем школьникам, стремящимся хорошо знать алгебру. Решение заданий теста потребует от школьника как знания теоретического материала, так и владения навыками вычисления корней.

Тест по алгебре «Квадратные корни» представляет собой десять заданий разного уровня сложности, которые надо сначала выполнить, а затем среди предложенных найти правильный ответ. Задания помогают подготовиться к итоговому или тематическому контролю в школе, а также могут быть полезны старшеклассникам, готовящимся к сдаче ЕГЭ.

Тест онлайн вы найдете на нашем сайте.

Рейтинг теста

Средняя оценка: 3.7. Всего получено оценок: 2216.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Преобразование выражений, содержащих знак корня

Вопросы
занятия:

·  вспомнить основные
понятия, связанные с квадратными корнями;

·  вспомнить свойства
арифметического квадратного корня;

· рассмотреть, какие преобразования можно
выполнять в выражениях, содержащих знак корня.

Материал
урока

Стоит напомнить, что квадратным корнем из числа
𝑎
называют такое число 𝑏, квадрат которого равен 𝑎
().

Например, числа 8 и –8 квадратные
корни из числа 64, так как  и
.

Из любого неотрицательного действительного
числа существует квадратный корень.

Квадратный корень из отрицательного числа
не существует.

Если  –
квадратный корень из числа а, то  также
является квадратным корнем из числа а, и других квадратных корней из
числа а нет.

Также вы помните, что арифметическим квадратным
корнем из числа а называют неотрицательное число, квадрат которого
равен а и обозначается он так:

Например,

Знак  называется
знаком арифметического квадратного корня.

Выражение, стоящее под знаком корня, называется подкоренным
выражением.

Извлечь квадратный корень из числа а
– это значит найти значение выражения .

Выражение  при
 не
имеет смысла.

Не путайте квадратный корень и арифметический
квадратный корень из числа.

Запись  читают
«квадратный корень из а». Слово «арифметический» при чтении опускают.

Значок  всегда
означает «арифметический квадратный корень из числа».

Из определения квадратного корня следует тождество:

Например,

Напомним, что над выражениями, содержащими квадратные
корни можно выполнять ряд преобразований. К таким преобразованиям относят: преобразования
корней из произведения, дроби и степени; умножение и деление корней;
вынесение множителя за знак корня, внесение множителя под знак корня
и избавление от иррациональности в знаменателе.

Теперь стоит повторить свойства арифметического
квадратного корня и их применения.

Итак, первое свойство: если  и
,
то .

Чтобы извлечь квадратный корень из
произведения неотрицательных чисел, можно извлечь его из каждого сомножителя
отдельно и результаты перемножить.

Следует помнить, что это свойство распространяется и
на тот случай, когда подкоренное выражение представляет собой произведение трёх,
четырёх и т.д. неотрицательных множителей.

Например, если ,
,
,
то .

Сделаем вывод: корень из неотрицательных
множителей равен произведению корней из этих множителей.

Верно и обратное утверждение: произведение
корней из неотрицательных чисел равно корню из произведения этих чисел.

Задание.

Вычислить значение выражения:

а) ;    
                                   б) .

Первое выражение: .
Воспользуемся свойством корня из произведения. Тогда корень из произведения
этих чисел можно записать произведением корней, т.е. произведением .
Найдём значения каждого из корней. В результате получим,

Следующее выражение: .
Воспользуемся свойством корня из произведения. Тогда произведение этих корней
равно корню из произведения .
Затем представим подкоренное выражение в виде множителей, каждый из которых
является квадратом целого числа. Тогда произведение значений каждого корня
равно:

Следующее свойство: если
 и
,
то .

Чтобы извлечь квадратный корень из дроби,
можно извлечь корень отдельно из числителя и знаменателя и первый результат
разделить на второй.

Сделаем вывод: корень из дроби, числитель
которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому
на корень из знаменателя.

Верно и обратное утверждение: частное корней
равно корню из частного этих чисел.

Задание.

Вычислить значение выражения:

а);                                               
      б) .

Первое выражение: .
Найдём его значение. Представим подкоренное выражение в виде неправильной дроби.
Получим,

Следующее выражение: .
Воспользуемся свойством корня из дроби. Тогда получим,

Перейдём к следующему свойству: при любом
значении а верно равенство: .

Равенство  является
тождеством. Это тождество применяется при извлечении квадратного корня
из степени с чётным показателем.

Чтобы извлечь корень из степени с чётным
показателем, достаточно представить подкоренное выражение в виде квадрата
некоторого выражения и воспользоваться тождеством: .

Задание.

Найти значение выражения:

а) ;          
                б) ;             
       в) .

Первое выражение: .
Видим, в подкоренном выражении записана чётная степень. Применим свойство корня
из степени с чётным показателем. Тогда, получим,

Следующее выражение: .
Как и в предыдущем  выражении под корнем имеем чётную степень. Значит,
можем воспользоваться свойством корня из чётной степени. Тогда получим,

И последнее выражение: .
Перепишем подкоренное выражение, как .
Теперь в подкоренном выражении имеем чётную степень. По свойству корня из
степени с чётным показателем получим,

А теперь давайте перейдём к таким преобразованиям
выражений, содержащих квадратные корни, как вынесение множителя из-под знака
корня и внесение множителя под знак корня.

Итак, если  и
,
то .

Такое преобразование называют вынесением множителя
из-под знака корня.

Задание.

Вынесите множитель из-под знака корня:

а) ;                                                           
б) .

Первое выражение: .
Представим подкоренное выражение в виде произведения 16 и 2. Число 16 – это, в
свою очередь, 42. Тогда получим,

Следующее выражение: .
Аналогично предыдущему примеру, подкоренное выражение представим в виде произведения
4 и 17. Упростим произведение. В итоге получим,

Если  и
,
то .

Если  и
,
то .

Такое преобразование называют внесением множителя
под знак корня.

Задание.

Внесите множитель под знак корня:

а) ;                                                           
б) .

Первое выражение: .
Представим число 5 в виде арифметического квадратного корня. Выполним
умножение, применяя свойство корня из произведения. Получим,

Следующее выражение: .
Число 0,3
представим в виде произведения  и
0,3. Затем число 0,3 представим в виде корня. Воспользуемся свойством корня из
произведения. Посчитаем. Получим,

Очень важное место в преобразовании выражений,
содержащих квадратные корни, занимает избавление от иррациональности в
знаменателе или числителе дроби.

Если ,
то .

Такое преобразование называют избавлением от
иррациональности в знаменателе дроби.

Задание.

Избавиться от иррациональности в знаменателе дроби:

а) ;          
              б) ;             
       в) .

Первое выражение: .
Чтобы избавиться от иррациональности в знаменателе дроби, нам пригодится
основное свойство дроби: если числитель и знаменатель дроби умножить или
разделить на одно и то же число, не равное нулю, то значение дроби не
изменится. Т.е. чтобы избавиться от корня в знаменателе дроби мы можем
числитель и знаменатель дроби умножить на этот корень. Умножим числитель и
знаменатель нашей дроби на .
Упростим числитель и знаменатель дроби. Получим,

Следующее выражение.
Умножим числитель и знаменатель дроби на .
Упростим. В итоге получим,

Следующее выражение немного посложнее: .
Но не стоит сразу пугаться! Чтобы избавиться от иррациональности в данной
дроби, нам следует обратиться к формуле разности квадратов. Для применения этой
формулы нам нужно умножить числитель и знаменатель дроби на выражение .
Сворачивая знаменатель по формуле разности квадратов, получим,

Посмотрите, мы избавились от иррациональности в
знаменателе. Выражение  называют
сопряжённым выражением по отношению к выражению .
Поэтому очень часто вместо того чтобы говорить умножим числитель и знаменатель
на сумму или разность тех или иных выражений, говорят просто «умножим на
сопряжённое выражение знаменателю (числителю)».

А теперь давайте рассмотрим задания на преобразование
выражений, которые содержат квадратные корни.

Задание.

Упростить выражение:

.

Рассмотрим выражение: .
Каждое подкоренное выражение представим в виде произведения, таким образом,
чтобы хотя бы один из множителей являлся квадратом натурального числа. Затем
воспользуемся свойством корня из произведения. Теперь применим свойство корня
из степени с чётным показателем. Упростим получившееся выражение. Обратите
внимание, все слагаемые в нашем примере имеют корни с одинаковыми подкоренными
выражениями. И отличаются лишь коэффициентами, записанными перед ними. Корни,
которые имеют одинаковые подкоренные выражения, являются подобными слагаемыми. Чтобы
привести подобные слагаемые достаточно сложить их коэффициенты и умножить на
одинаковое выражение, содержащее корень. Приведём подобные слагаемые в
нашем примере. Получим,

Задание.

Преобразовать выражение:

.

Воспользуемся формулой квадрата суммы. Упростим это
выражение. Воспользуемся следствием из определения квадратного корня. Затем
применим свойство корня из произведения. Приведём подобные. В итоге получим,

Задание.

Сократить дроби:

а) ;                                                       
б) .

Рассмотрим первую дробь: .
Напомним, что для выполнения сокращения дроби необходимо разложить выражения (в
числителе или знаменателе) на множители. Для этого используют вынесение общего
множителя за скобки или же применяют формулы сокращённого умножения. В нашем
случае в числителе дроби число 7 можно представить, как .
Тогда вынесем общий множитель  за
скобку. Смотрите, дробь можно сократить на выражение .
После сокращения получим,

Теперь перейдём ко второй дроби: .
Заметим, что в числителе  можно
представить, как ,
а 2, как .
Тогда числитель данной дроби можно разложить по формуле разности квадратов двух
выражений. Сократим дробь на выражение .
В результате получим,

Итоги урока

На этом уроке поговорили о «преобразовании
выражений, содержащих знак корня». Вспомнили основные понятия, связанные с
квадратными корнями. Поговорили о свойствах арифметического квадратного корня.
А затем рассмотрели, какие преобразования можно выполнять в выражениях,
содержащих знак корня.

{\ frac {1} {2}} $$

Если мы объединим эти две вещи, мы получим свойство произведения радикалов и факторное свойство радикалов. Эти два свойства говорят нам, что квадратный корень из произведения равен произведению квадратных корней из множителей.

$$ \ sqrt {xy} = \ sqrt {x} \ cdot \ sqrt {y} $$

$$ \ sqrt {\ frac {x} {y}} = \ frac {\ sqrt {x}} {\ sqrt {y}} $$

$$ где \: \: x \ geq 0, y \ geq 0 $$

Ответ не может быть отрицательным, а x и y не могут быть отрицательными, так как в этом случае мы не получим реального ответа. {2}} = \ frac {4x-x \ sqrt {x}} {16-x} $$

Видеоурок

Упростить радикальное выражение

$$ \ frac {x} {5- \ sqrt {x}} $$

открытых учебников | Сиявула

Математика

Наука

    • Читать онлайн

    • Учебники

      • Английский

        • Класс 7A

        • Марка 7Б

        • 7 класс (A и B вместе)

      • Африкаанс

        • Граад 7А

        • Граад 7Б

        • Граад 7 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 8A

        • Сорт 8Б

        • Оценка 8 (вместе A и B)

      • Африкаанс

        • Граад 8А

        • Граад 8Б

        • Граад 8 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 9А

        • Марка 9Б

        • 9 класс (A и B вместе)

      • Африкаанс

        • Граад 9А

        • Граад 9Б

        • Граад 9 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Класс 4A

        • Класс 4Б

        • Класс 4 (вместе A и B)

      • Африкаанс

        • Граад 4А

        • Граад 4Б

        • Граад 4 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 5А

        • Марка 5Б

        • Оценка 5 (вместе A и B)

      • Африкаанс

        • Граад 5А

        • Граад 5Б

        • Граад 5 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 6А

        • Марка 6Б

        • 6 класс (A и B вместе)

      • Африкаанс

        • Граад 6А

        • Граад 6Б

        • Граад 6 (A en B saam)

    • Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без марочного знака)

Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Определите и упростите корни | Начальная алгебра

Результаты обучения

  • Квадратные корни
    • Используйте запись квадратного корня для записи главных квадратных корней
    • Упростить главные квадратные корни с помощью факторизации
  • кубических корней
    • Использовать нотацию кубического корня для записи кубического корня
    • Упростить кубические корни с помощью факторизации
  • Упростить квадратные корни
    • Упростите квадратные корни с помощью переменных
    • Определите, когда упрощенному корню требуется абсолютное значение
  • Рациональные экспоненты
    • Преобразование между радикальной и экспоненциальной нотацией
    • Используйте законы экспонент для упрощения выражений с рациональными показателями
    • Использование рациональных показателей для упрощения радикальных выражений

Мы умеем возводить в квадрат число:

[латекс] 5 ^ 2 = 25 [/ латекс] и [латекс] \ влево (-5 \ вправо) ^ 2 = 25 [/ латекс]

Извлечение квадратного корня противоположно возведению в квадрат, поэтому мы можем сделать следующие утверждения:

  • 5 — неотрицательный квадратный корень из 25
  • -5 — отрицательный квадратный корень из 25

Найдите квадратные корни из следующих чисел:

  1. 36
  2. 81
  3. -49
  4. 0
  1. Мы хотим найти число, квадрат которого равен 36.2 = 81 [/ latex], следовательно, неотрицательный квадратный корень из 81 равен 9, а отрицательный квадратный корень из 81 равен -9

    2. .

  2. Мы хотим найти число, квадрат которого равен -49. Когда вы возводите в квадрат действительное число, результат всегда положительный. Остановитесь и подумайте об этом на секунду. Отрицательное число, умноженное на себя, является положительным, а положительное число, умноженное на само, положительно. Следовательно, -49 не имеет квадратных корней, у этого вопроса нет вещественных решений.
  3. Мы хотим найти число, квадрат которого равен 0.2 = 0 [/ latex], поэтому неотрицательный квадратный корень из 0 равен 0. Мы не присваиваем 0 знак, поэтому он имеет только один квадратный корень, и это 0.

Обозначение, которое мы используем для выражения квадратного корня для любого действительного числа a, выглядит следующим образом:

Запись квадратного корня

Символ квадратного корня называется радикальным символом . Для действительного числа a квадратный корень из a записывается как [latex] \ sqrt {a} [/ latex]

Число, которое написано под радикальным символом, называется подкоренным числом .

По определению, символ квадратного корня [latex] \ sqrt {\ hphantom {5}} [/ latex] всегда означает нахождение неотрицательного корня, называемого главным корнем .

[латекс] \ sqrt {-a} [/ latex] не определен, поэтому [latex] \ sqrt {a} [/ latex] определен для [latex] a> 0 [/ latex]

Давайте рассмотрим пример, аналогичный приведенному выше, но на этот раз с использованием записи квадратного корня. Обратите внимание, что использование записи квадратного корня означает, что вы находите только главный корень — неотрицательный корень.2} [/ латекс]

Показать решение

  1. [латекс] \ sqrt {16} [/ латекс]. Мы ищем число, квадрат которого равен 16, поэтому [latex] \ sqrt {16} = 4 [/ latex]. Мы пишем только неотрицательный корень, потому что так определяется корневой символ.
  2. [латекс] \ sqrt {9} [/ латекс]. Мы ищем число, квадрат которого равен 9, поэтому [latex] \ sqrt {9} = 3 [/ latex]. Мы пишем только неотрицательный корень, потому что так определяется корневой символ.
  3. [латекс] \ sqrt {-9} [/ латекс]. Ищем число, квадрат которого равен -9.2} = a [/ latex] означает нахождение главного квадратного корня.

    Что делать, если вы работаете с числом, квадрат которого вы не знаете сразу? Мы можем использовать факторинг и правило произведения для квадратных корней, чтобы найти квадратные корни, такие как [latex] \ sqrt {144} [/ latex] или [latex] \ sqrt {225} [/ latex].

    Правило произведения для квадратных корней

    Учитывая, что a и b являются неотрицательными действительными числами, [latex] \ sqrt {a \ cdot {b}} = \ sqrt {a} \ cdot \ sqrt {b} [/ latex]

    В следующих примерах мы объединим эти идеи, чтобы упростить квадратные корни из чисел, которые не очевидны на первый взгляд:

    • корень квадратный из квадрата,
    • правило произведения квадратного корня
    • факторинг

    Пример

    Упростить [латекс] \ sqrt {144} [/ латекс]

    Показать решение

    Определите простые множители 144.2} \\\\ = 2 \ cdot3 \ cdot2 \\\\ = 12 \ end {array} [/ latex]

    Ответ

    [латекс] \ sqrt {144} = 12 [/ латекс]

    Пример

    Упростить [латекс] \ sqrt {225} [/ латекс]

    Показать решение

    Во-первых, фактор 225:

    [латекс] \ begin {массив} {c} \ sqrt {225} \\\\ = \ sqrt {5 \ cdot45} \\\\ = \ sqrt {5 \ cdot5 \ cdot9} \\\\ = \ sqrt {5 \ cdot5 \ cdot3 \ cdot3} \ end {array} [/ latex]

    Поскольку мы находим квадратный корень, мы группируем эти множители в квадраты. Завершите упрощение правилом произведения для корней и квадратом квадратной идеи.2} \\\\ = 5 \ cdot3 = 15 \ end {array} [/ latex]

    Ответ

    [латекс] \ sqrt {225} = 15 [/ латекс]

    Осторожно! Квадратный корень из правила произведения применяется, когда у вас есть умножение ТОЛЬКО на квадратный корень. Вы не можете применить правило к суммам:

    [латекс] \ sqrt {a + b} \ ne \ sqrt {a} + \ sqrt {b} [/ латекс]

    Докажите это себе с помощью некоторых действительных чисел: пусть a = 64 и b = 36, затем используйте порядок операций, чтобы упростить каждое выражение. 2} [/ латекс]

    Завершите упрощение правилом произведения для корней и квадратом квадратной идеи.2} \\\\ = \ sqrt {7} \ cdot3 [/ latex]

    Поскольку 7 — простое число и мы не можем записать его в виде квадрата, оно должно оставаться под знаком корня. По соглашению мы пишем константу 3 перед радикалом. Это помогает читателю понять, что тройка больше не находится под радикалом.

    [латекс] 3 \ cdot \ sqrt {7} [/ латекс]

    Ответ

    [латекс] \ sqrt {63} = 3 \ sqrt {7} [/ латекс]

    Окончательный ответ [latex] 3 \ sqrt {7} [/ latex] может показаться немного странным, но в упрощенной форме.2} \ cdot \ sqrt {5} \\\\ = 10 \ cdot4 \ cdot \ sqrt {5} [/ latex]

    Умножить.

    [латекс] 20 \ cdot \ sqrt {5} [/ латекс]

    Ответ

    [латекс] \ sqrt {2,000} = 20 \ sqrt {5} [/ латекс]

    В этом последнем видео мы показываем примеры упрощающих радикалов, которые не являются идеальными квадратами.

    Кубические корни

    Цюн Рубика

    Хотя квадратные корни, вероятно, являются наиболее распространенным радикалом, вы также можете найти третий корень, пятый корень, десятый корень или любой другой корень n -й корень числа.3 = 27 [/ латекс]

  4. Мы хотим найти число, куб которого равен 8. [latex] 2 \ cdot2 \ cdot2 = 8 [/ latex] кубический корень из 8 равен 2.
  5. Мы хотим найти число, куб которого равен -8. Мы знаем, что 2 — это кубический корень из 8, поэтому, возможно, мы можем попробовать -2. [латекс] -2 \ cdot {-2} \ cdot {-2} = — 8 [/ latex], поэтому кубический корень -8 равен -2. Это отличается от квадратного корня, потому что умножение трех отрицательных чисел вместе дает отрицательное число.
  6. Мы хотим найти число, куб которого равен 0. [latex] 0 \ cdot0 \ cdot0 [/ latex], сколько бы раз вы ни умножали [latex] 0 [/ latex] на себя, вы всегда получите [latex] 0 [/ латекс].

Кубический корень числа записывается с помощью небольшого числа 3, называемого индексом , сразу за радикальным символом и над ним. Похоже на [латекс] \ sqrt [3] {{}} [/ латекс]. Эта маленькая тройка отличает кубические корни от квадратных корней, которые записываются без маленького числа снаружи и над символом корня.

Осторожно! Будьте осторожны, чтобы различать [latex] \ sqrt [3] {x} [/ latex], кубический корень x и [latex] 3 \ sqrt {x} [/ latex], три умноженное на на . квадратный корень из x .Сначала они могут выглядеть одинаково, но они приводят вас к совершенно разным выражениям лиц!

Мы также можем использовать факторинг для упрощения кубических корней, таких как [latex] \ sqrt [3] {125} [/ latex]. Вы можете прочитать это как «корень третьей степени из 125» или «кубический корень из 125». Чтобы упростить это выражение, найдите число, которое при умножении на себя два раза (всего три одинаковых множителя) равно 125. {2}} \ neq {x} [/ latex]! (Это происходит потому, что процесс возведения числа в квадрат теряет отрицательный знак, поскольку отрицательное значение, умноженное на отрицательное, является положительным.{2}} c \ right | \ sqrt {ab} [/ латекс]

В следующем разделе мы исследуем кубические корни и воспользуемся показанными здесь методами для их упрощения. Кубические корни отличаются от квадратных корней тем, что под корнем может быть отрицательное число, например [latex] \ sqrt [3] {- 125} [/ latex].

Рациональные экспоненты

Корни также могут быть выражены дробными показателями. Квадратный корень из числа может быть записан с помощью символа корня или возведением числа в степень [латекс] \ frac {1} {2} [/ latex].{\ tfrac {1} {n}}} [/ латекс]

Преобразование между радикальной и экспоненциальной нотацией

Столкнувшись с выражением, содержащим рациональную экспоненту, вы можете переписать его, используя радикал. В приведенной выше таблице обратите внимание, как знаменатель рациональной экспоненты определяет индекс корня. Таким образом, показатель степени [латекс] \ frac {1} {2} [/ latex] переводится в квадратный корень, показатель степени [латекс] \ frac {1} {5} [/ latex] переводится в корень пятой степени или [latex] \ sqrt [5] {{\ hphantom {5}}} [/ latex], а [latex] \ frac {1} {8} [/ latex] переводится в корень восьмой степени или [latex] \ sqrt [ 8] {{\ hphantom {5}}} [/ латекс].{\ frac {1} {2}}}} = 2 \ sqrt {x} [/ latex]

Следующий пример предназначен для того, чтобы помочь вам попрактиковаться в размещении рациональной экспоненты на соответствующих членах в выражении, записанном в радикальной форме

Пример

Экспресс [латекс] 4 \ sqrt [3] {xy} [/ латекс] с рациональными показателями.

Показать решение
Перепишите радикал, используя рациональную экспоненту. Корень определяет дробь. В этом случае индекс радикала равен 3, поэтому рациональный показатель будет [latex] \ frac {1} {3} [/ latex].{\ frac {1} {3}}} [/ латекс]

В следующем видео мы покажем примеры преобразования радикальной формы в показательную.

При переходе от радикального представления к рациональному показателю степень корня становится знаменателем показателя степени. Если вы начнете с квадратного корня, у вас будет показатель степени [латекс] \ frac {1} {2} [/ latex] в выражении в корне (подкоренное выражение). С другой стороны, если вы начнете с экспоненты [latex] \ frac {1} {3} [/ latex], вы будете использовать корень куба.{3}} [/ латекс]

В следующем видео показано больше примеров того, как упростить радикальное выражение с помощью рациональных степеней.

Сводка

Квадратный корень числа — это число, которое при умножении само на себя дает исходное число. Основные квадратные корни всегда положительны, а квадратный корень из 0 равен 0. Вы можете извлечь квадратный корень только из неотрицательных значений. Квадратный корень из полного квадрата будет целым числом. Другие квадратные корни можно упростить, определив множители, которые являются точными квадратами, и взяв их квадратный корень.{\ frac {m} {n}}} [/ латекс]. Переписывание радикалов с использованием дробных показателей степени может быть полезно для упрощения некоторых радикальных выражений. При работе с дробными показателями помните, что дробные показатели подчиняются всем тем же правилам, что и другие показатели, когда они появляются в алгебраических выражениях.

Упрощение переменных выражений рабочего листа ключ ответа

Некоторые из отображаемых рабочих листов представляют собой 1 упрощающие квадратные корни, упрощающие радикальные выражения, дату, период, упрощающие работу с квадратными корнями, упрощающие примеры квадратных корней, упрощающие радикальные выражения, квадратные корни и другие радикалы, квадратные корни работают dn на оборотной стороне имени пакета за каждое Я могу.1 75 5 3 2 16 4 3 36 6 4 64 8 5 80 4 5 6 30. Используйте свойство степени экспоненты для упрощения выражений. Используйте произведение на свойство степени степени для упрощения выражений. Вы видели, что когда вы комбинируете одинаковые термины добавляя и вычитая, вы должны иметь одинаковое основание с одинаковым показателем степени.

Ижмаш см 2

Оцените каждое выражение; Подставьте числа вместо переменных, которые необходимо решить. Выражения базового уровня не включают скобки или экспоненты.На этом листе каждое выражение имеет только одну переменную. От упрощения выражений с показателями степени до матрицы у нас есть все детали. Зайдите на Algebrahomework.org и изучите две переменные, рационализаторские и несколько других математических предметов. называется сложной дробью.Упростите, удалив дроби на ЖК-дисплее всех дробей в выражении. o ⇐ — — + 1 5 1 1 2 w w w найти ЖК-дисплей трех внутренних дробей. ЖК-экран — это w (w — 1) Ответы на лист упрощения рациональных выражений. Рабочий лист Апрель 09, 2019 15:33. Рабочий лист позволит вам четко определить ваши цели и все, что вам нужно будет сделать для их достижения. После того, как ученики или дети раскроют метод создания, вы можете опубликовать рабочие листы и дать им методы наилучшего подхода к созданию только великого способа.

Canon fd 35mm f2 вогнутый

2 ноября 2017 г. · Модуль A1: Алгебраические и числовые выражения. Флэш-карточки с ключевым словарем, блок A1; Тема 1: Переменные и выражения. 6.EE.1 — Порядок действий. Заметки для занятий и онлайн-ресурсы; Рабочие листы для дополнительной практики с ответами; Видеоуроки; 6.EE.1 — Показатели. Заметки для занятий и онлайн-ресурсы; Рабочие листы для дополнительной практики с ответами; Видеоуроки Экспоненты и радикалы Рабочие листы Экспоненты и радикалы Рабочие листы для практики.Вот графический предварительный просмотр всех рабочих листов экспонентов и радикалов. Вы можете выбрать различные переменные, чтобы настроить эти рабочие листы экспонентов и радикалов в соответствии с вашими потребностями.

React onclick change state

Этот одностраничный рабочий лист охватывает ассоциативное свойство. В нем объясняется, как мы можем изменить группы (переместить скобки) в задаче, чтобы упростить ее. Включает переменные. Ключевая концепция: учащиеся должны понимать, что порядок сложения или умножения не имеет значения.Номера и группы можно перемещать, чтобы упростить задачу или облегчить ее решение. Упрощение алгебраических выражений Под «упрощением» алгебраического выражения мы подразумеваем его наиболее компактное и эффективное написание без изменения значения выражения. В основном это включает в себя сбор одинаковых терминов, что означает, что мы складываем все, что можно сложить вместе.

Juice wrld audio

Поскольку рациональные выражения — это просто дроби с переменными в знаменателе, мы начнем с рассмотрения операций с дробями, не содержащими переменных.Затем мы перейдем к выполнению тех же операций с рациональными выражениями. Начнем с умножения. Каждая страница загружается для печати с ключом ответа, прикрепленным ко второй странице. Рабочие листы охватывают следующие темы: сложение и вычитание алгебраических выражений, умножение и деление алгебраических выражений, упрощение алгебраических выражений, изучение порядка операций в алгебре и распределительное свойство умножения.

Realidades 3 стр. 11

Если у вас нет кода доступа, обратитесь к своему учителю, администратору или консультанту BIL Simplify Radicals Answer Key.Ключ ответа Simplify Radicals — отображение 8 основных листов, найденных для этой концепции. Некоторые из рабочих листов для этой концепции: Упрощающие радикальные выражения для 9-го уровня, Операции с радикальными выражениями, ключ ответа, Обзор Алгебры 1, упрощающий радикальный ключ ответа, Dn на обратной стороне имени пакета для каждого блока i может упростить …

Tri state buffer vhdl

ID: 1469181 Язык: английский Школьный предмет: математика Оценка / уровень: 7 класс Возраст: 11-13 Основное содержание: алгебра Другое содержание: оценивать алгебраические выражения Добавить в мои рабочие тетради (0)…

книга ответов по алгебре; упрощение таблицы радикальных выражений; рабочие листы линейного графика keystage2; математические мелочи + многочлен; какова формула процентов; Вопрос о способностях по математике; тесты по математике для 5-го класса, которые можно пройти онлайн без распечатки; Справочные листы для домашних заданий для 3-го класса; ti-83 плюс разница квадратов

Голден ретривер смесь немецкой овчарки на продажу colorado

Это рабочий лист из 10 задач по упрощению рациональных выражений. Большинство проблем требует факторинга.Предполагается, что в область переменных не входят значения, для которых любой знаменатель равен нулю. Ответы включены.

2 ноября, 2017 · Раздел A1: Алгебраические и числовые выражения. Флэш-карточки с ключевым словарем, блок A1; Тема 1: Переменные и выражения. 6.EE.1 — Порядок действий. Заметки для занятий и онлайн-ресурсы; Рабочие листы для дополнительной практики с ответами; Видеоуроки; 6.EE.1 — Показатели. Заметки для занятий и онлайн-ресурсы; Рабочие листы для дополнительной практики с ответами; Видеоуроки

Двуствольное ружье Dp 12

9 класс алгебры 1 ответы в учебнике

Usps rca uniform

Характеристики армии последователей

Cz 455, нержавеющая точность

Улучшенный набор штифтов для глока

9 Big jook instagram 9402

2 Big jook

Калькулятор полиномов, ключ ответа к бесконечной алгебре 1 программного обеспечения kuta, таблица блоков с основанием 10 и десятичных знаков, ускоренные математические ответы, упрощение выражения 7x + 14y по сравнению с 3x + 6y + nx + 2ny путем факторизации числителя и знаменателя.

kuta-software-sae-3-упрощение-алгебраические-выражения-ключ-ответ 1/1 Загружено с spanish.perm.ru 19 декабря 2020 г. гостем [EPUB] Kuta Software Sae 3 Упрощение алгебраических выражений Ответный ключ Когда кто-то нужно пойти в магазины электронных книг, создание поиска по магазинам, полка за полкой, это действительно проблематично.

Прочитать книгу с ответами Упрощение переменных Выражения можно редактировать в текстовом редакторе). Лист ответов Упрощение выражений переменных Бесплатные рабочие листы для упрощения алгебраических выражений.С помощью этого генератора рабочих листов вы можете создавать рабочие листы для печати для упрощения выражений переменных для курсов предварительной алгебры и алгебры 1.

Возможный ответ: 3m3 5n 4m3 2m3 n 9p6 q2 11p 6h3 10h 4 4a 3b2 5c 4×4 5×3 5×2 2xy 5k2 3k 14 9×3 y2 6xy Практика C 1-9 Упрощение алгебраических выражений УРОК 8. Напишите и упростите выражение для периметра рисунок справа. 6x 7y 5 9. Напишите выражение, чтобы найти объединенные периметры фигур справа. Тогда упростите…

Polymathlove.com предоставляет отличные ресурсы по числовым играм с использованием упрощающих рациональных выражений, полиномиальных функций, а также тригонометрических и других математических тем. На всякий случай, если вам потребуется руководство по алгебре и тригонометрии или умножению и делению дробей, лучше всего взглянуть на Polymathlove.com!

Zoom дверной звонок звуковой эффект

Ultima online server download

Mx5 NC double din fasia

Oracle

Foundations экзамен рабочий лист croft

адрес сервера Minecraft для tlauncher

Lund pro v bass 2075 максимальная скорость

Охотничьи жалюзи рядом со мной

7

Удаление чипа иммобилайзера Honda

Законы о лотерее в Интернете

Apn type 9162 pt

Focus pdca ppt

Flexsteel rv seat

Пример из практики инфекции мочевыводящих путей pdf

Секретарь штата Висконсин по поиску бизнеса

Seawind 1000 xl2 916 luuder Chuter 9000

Таблица ответов по диффузии и осмосу

Agric al 45 tiller

Dustin Milligan Amanda Team вышла замуж за

Figma после задержки

Minecraft bedrock mod maker

My hero academia fan parts online

схема

h2b уведомление об одобрении не получено

Exide 12v 7ah battery datasheet

Tascam 488 mk1

Offset optic mount

График линейных неравенств, активность desmos

Onedrive

Onedrive возникла проблема с подпиской на 9deb 9×2000 Теория музыки 9×2 1 класс викторины

Как получить бесплатное золото в Clash of Clans

HTML-код игры

Сложение и вычитание квадратного корня — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

  • Сложить и вычесть как квадратные корни
  • Сложить и вычесть квадратные корни, требующие упрощения

Прежде чем начать, пройдите тест на готовность.

  1. Добавить: ⓐ ⓑ.
    Если вы пропустили эту проблему, просмотрите (рисунок).
  2. Упростить:.
    Если вы пропустили эту проблему, просмотрите (рисунок).

Мы знаем, что мы должны соблюдать порядок операций, чтобы упростить выражения с квадратными корнями. Радикал — это групповой символ, поэтому сначала мы работаем внутри радикала. Упрощаем таким образом:

Итак, если нам нужно складывать, мы не должны объединять их в один радикал.

Попытка сложить квадратные корни с разными подкоренными выражениями похожа на попытку сложить непохожие термины.

Сложение квадратных корней с одним и тем же корневым выражением аналогично сложению одинаковых членов. Мы называем квадратные корни с одним и тем же корневым элементом квадратными корнями, чтобы напомнить нам, что они работают так же, как и подобные термины.

Как квадратные корни

Квадратные корни с одной и той же подкоренной частью называются квадратными корнями.

Мы складываем и вычитаем как квадратные корни так же, как складываем и вычитаем как члены. Мы это знаем. Аналогично складываем и получаем

Сложение и вычитание, как квадратные корни

Подумайте о добавлении одинаковых терминов с переменными, как в следующих нескольких примерах.Когда у вас есть подкоренные выражения, вы просто добавляете или вычитаете коэффициенты. Когда подкоренные выражения не похожи, вы не можете комбинировать термины.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Когда радикалы содержат более одной переменной, при условии, что все переменные и их показатели идентичны, радикалы подобны.

Упростить:.

Решение

Упростить:.

Упростить:.

Сложение и вычитание квадратного корня, требующего упрощения

Помните, что мы всегда упрощаем извлечение квадратного корня, удаляя наибольший коэффициент полного квадрата.Иногда, когда нам нужно сложить или вычесть квадратные корни, которые не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Точно так же, как мы используем ассоциативное свойство умножения для упрощения и получения, мы можем упрощать и получать.Для этого мы воспользуемся ассоциативным свойством в следующем примере.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

В следующем примере мы удалим постоянные и переменные множители из квадратных корней.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Ключевые понятия

  • Чтобы сложить или вычесть квадратные корни, сложите или вычтите коэффициенты и сохраните такой же квадратный корень.
  • Иногда, когда нам нужно сложить или вычесть квадратные корни, которые не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.
Практика ведет к совершенству

Сложить и вычесть как квадратные корни

Упростите следующие упражнения.

Сложить и вычесть квадратные корни, требующие упрощения

Упростите следующие упражнения.

Смешанная практика

Повседневная математика

Декоратор решает использовать квадратную плитку в качестве акцентной полосы в дизайне новой душевой кабины, но она хочет повернуть плитку, чтобы она выглядела как ромбовидная.Она будет использовать 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определите ширину акцентной полосы, упростив выражение. (Округлите до ближайшей десятой доли дюйма.)

Сюзи хочет использовать квадратные плитки на границе спа, которое она устанавливает на заднем дворе. Она будет использовать большие плитки с площадью 12 квадратных дюймов, средние плитки с площадью 8 квадратных дюймов и маленькие плитки с площадью 4 квадратных дюйма.После того, как участок границы потребует 4 больших плитки, 8 средних плиток и 10 маленьких плиток, чтобы покрыть ширину стены. Упростите выражение, чтобы определить ширину стены.

Письменные упражнения

Объясните разницу между одинаковыми радикалами и непохожими радикалами. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

Объясните процесс определения того, похожи ли два радикала или нет. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Глоссарий

как квадратные корни
Квадратные корни с той же подкоренной частью называются квадратными корнями.

1.3: Радикалы и рациональные выражения

Цели обучения

  • Вычислить квадратные корни.
  • Используйте правило произведения, чтобы упростить извлечение квадратного корня.
  • Используйте правило частного, чтобы упростить извлечение квадратного корня.
  • Сложить и вычесть квадратные корни.
  • Рационализировать знаменатели.
  • Используйте рациональные корни.

Строительный магазин продает лестницы длиной \ (16 \) футов и лестницы \ (24 \) футов. Окно расположено на высоте \ (12 \) футов над землей. Необходимо приобрести лестницу, которая будет вести к окну из точки на земле в \ (5 \) футах от здания.2 = 16 \), квадратный корень из \ (16 \) равен \ (4 \). Функция квадратного корня является обратной функцией возведения в квадрат, так же как вычитание является обратным сложению. Чтобы отменить возведение в квадрат, мы извлекаем квадратный корень.

В общих чертах, если \ (a \) — положительное действительное число, то квадратный корень из \ (a \) — это число, которое при умножении само на себя дает \ (a \). Квадратный корень может быть положительным. или отрицательное, потому что умножение двух отрицательных чисел дает положительное число. Главный квадратный корень — это неотрицательное число, которое при умножении само на себя равно \ (a \).2 \) равны \ (25 \), радикальный символ подразумевает только неотрицательный корень , главный квадратный корень. Главный квадратный корень из \ (25 \) равен \ (\ sqrt {25} = 5 \).

Примечание

Главный квадратный корень из \ (a \) — неотрицательное число, которое при умножении само на себя равно \ (a \). Оно написано как радикальное выражение с символом, называемым радикалом , вместо термина, называемого подкоренным элементом , и элементом : \ (\ sqrt {a} \).

Пример \ (\ PageIndex {2} \): вычисление квадратного корня

Оцените каждое выражение.2 = 81 \)

Пример \ (\ PageIndex {3} \):

Для \ (\ sqrt {25 + 144} \), можем ли мы найти квадратные корни перед сложением?

Решение

№ \ (\ sqrt {25} + \ sqrt {144} = 5 + 12 = 17 \). Это не эквивалентно \ (\ sqrt {25 + 144} = 13 \). Порядок операций требует, чтобы мы добавляли члены в подкоренном выражении перед нахождением квадратного корня.

Упражнение \ (\ PageIndex {1} \)

Оцените каждое выражение.

а.\ (\ sqrt {25} \) г. \ (\ sqrt {\ sqrt {81}} \) г. \ (\ sqrt {25-9} \) г. \ (\ sqrt {36} + \ sqrt {121} \)
Ответьте на
\ (5 \)
Ответ б
\ (3 \)
Ответ c
\ (4 \)
Ответ d
\ (17 \)

Использование правила произведения для упрощения квадратного корня

Чтобы упростить квадратный корень, мы перепишем его так, чтобы в подкоренном выражении не было полных квадратов.Есть несколько свойств квадратных корней, которые позволяют упростить сложные радикальные выражения. Первое правило, которое мы рассмотрим, — это правило произведения для упрощения квадратных корней, которое позволяет нам разделить квадратный корень из произведения двух чисел на произведение двух отдельных рациональных выражений. Например, мы можем переписать \ (\ sqrt {15} \) как \ (\ sqrt {3} \ times \ sqrt {5} \). Мы также можем использовать правило произведения, чтобы выразить произведение нескольких радикальных выражений как одно радикальное выражение.

Правило произведения для упрощения квадратного корня

Если \ (a \) и \ (b \) неотрицательны, квадратный корень из произведения \ (ab \) равен произведению квадратных корней из \ (a \) и \ (b \)

.

\ [\ sqrt {ab} = \ sqrt {a} \ times \ sqrt {b} \]

HOWTO: дано выражение корня квадратного корня, используйте правило произведения, чтобы упростить его.

  1. Выносим за скобки любые полные квадраты.
  2. Запишите радикальное выражение как произведение радикальных выражений.3z} \)

    Ответ

    \ (5 | x || y | \ sqrt {2yz} \)

    Обратите внимание на знаки абсолютного значения вокруг \ (x \) и \ (y \)? Потому что их ценность должна быть положительной!

    Как: дан результат произведения нескольких радикальных выражений, используйте правило произведения, чтобы объединить их в одно радикальное выражение

    1. Выразите произведение нескольких радикальных выражений как одно радикальное выражение.
    2. Упростить.

    Пример \ (\ PageIndex {5} \): Использование правила произведения для упрощения произведения нескольких квадратных корней

    Упростите радикальное выражение.

    \ (\ sqrt {12} \ times \ sqrt {3} \)

    Решение

    \ (\ begin {align *} & \ sqrt {12 \ times3} & & \ text {Выразите продукт как одно радикальное выражение} \\ [5pt] & \ sqrt {36} & & \ text {Simplify} \ \ [5pt] & 6 \ end {align *} \)

    Упражнение \ (\ PageIndex {3} \)

    Упростите \ (\ sqrt {50x} \ times \ sqrt {2x} \), предполагая \ (x> 0 \).

    Ответ

    \ (10 ​​| х | \)

    Использование правила частного для упрощения квадратного корня

    Так же, как мы можем переписать квадратный корень из произведения как произведение квадратных корней, мы можем переписать квадратный корень из частного как частное из квадратных корней, используя правило частного для упрощения квадратных корней.Может быть полезно разделить числитель и знаменатель дроби под корнем, чтобы мы могли извлекать из них квадратные корни по отдельности. Можем переписать

    \ [\ sqrt {\ dfrac {5} {2}} = \ dfrac {\ sqrt {5}} {\ sqrt {2}}. \ nonumber \]

    КАЧЕСТВЕННОЕ ПРАВИЛО УПРОЩЕНИЯ КВАДРАТНЫХ КОРНЕЙ

    Квадратный корень из частного \ (\ dfrac {a} {b} \) равен частному из квадратных корней из \ (a \) и \ (b \), где \ (b ≠ 0 \).

    \ [\ sqrt {\ dfrac {a} {b}} = \ dfrac {\ sqrt {a}} {\ sqrt {b}} \]

    Как сделать: дано радикальное выражение, используйте правило частного, чтобы упростить его

    1. Запишите радикальное выражение как частное двух радикальных выражений. 2 \), потому что этот член всегда будет неотрицательным.4 \ sqrt {3ab} \)

Сложение и вычитание квадратного корня

Мы можем складывать или вычитать радикальные выражения только тогда, когда они имеют одно и то же подкоренное выражение и когда они имеют один и тот же радикальный тип, например квадратные корни. Например, сумма \ (\ sqrt {2} \) и \ (3 \ sqrt {2} \) равна \ (4 \ sqrt {2} \). Однако часто можно упростить радикальные выражения, и это может изменить подкоренное выражение. Радикальное выражение \ (\ sqrt {18} \) может быть записано с \ (2 \) в подкоренном выражении как \ (3 \ sqrt {2} \), поэтому \ (\ sqrt {2} + \ sqrt { 18} = \ sqrt {2} +3 \ sqrt {2} = 4 \ sqrt {2} \)

Как: дано радикальное выражение, требующее сложения или вычитания квадратных корней, решите

  1. Упростите каждое радикальное выражение.
  2. Сложить или вычесть выражения с одинаковыми подкоренными выражениями.

Пример \ (\ PageIndex {8} \): добавление квадратного корня

Добавьте \ (5 \ sqrt {12} +2 \ sqrt {3} \).

Решение

Мы можем переписать \ (5 \ sqrt {12} \) как \ (5 \ sqrt {4 \ times3} \). Согласно правилу продукта это становится \ (5 \ sqrt {4} \ sqrt {3} \). Квадратный корень из \ (\ sqrt {4} \) равен \ (2 \), поэтому выражение становится \ (5 \ times2 \ sqrt {3} \), то есть \ (10 ​​\ sqrt {3} \). Теперь у терминов может быть одно и то же подкоренное выражение, поэтому мы можем добавить.2 \ sqrt {2ac} \]

Упражнение \ (\ PageIndex {7} \)

Вычесть \ (3 \ sqrt {80x} -4 \ sqrt {45x} \)

Ответ

\ (0 \)

Рационализация знаменателей

Когда выражение, содержащее корень квадратного корня, записано в простейшей форме, оно не будет содержать корня в знаменателе. Мы можем удалить радикалы из знаменателей дробей, используя процесс, называемый рационализацией знаменателя.

Мы знаем, что умножение на \ (1 \) не меняет значения выражения.Мы используем это свойство умножения, чтобы изменить выражения, содержащие радикалы в знаменателе. Чтобы удалить радикалы из знаменателей дробей, умножьте их на форму \ (1 \), которая удалит радикал.

Для знаменателя, содержащего один член, умножьте на радикал знаменателя над самим собой. Другими словами, если знаменатель равен \ (b \ sqrt {c} \), умножьте его на \ (\ dfrac {\ sqrt {c}} {\ sqrt {c}} \).

Для знаменателя, содержащего сумму или разность рационального и иррационального членов, умножьте числитель и знаменатель на сопряжение знаменателя, которое можно найти, изменив знак радикальной части знаменателя.Если знаменатель равен \ (a + b \ sqrt {c} \), то сопряжение равно \ (a-b \ sqrt {c} \).

HowTo: дано выражение с одним коренным квадратным корнем в знаменателе, рационализируйте знаменатель

  1. Умножьте числитель и знаменатель на радикал в знаменателе.
  2. Упростить.

Пример \ (\ PageIndex {10} \): рационализация знаменателя, содержащего один член

Запишите \ (\ dfrac {2 \ sqrt {3}} {3 \ sqrt {10}} \) в простейшей форме.

Решение

Радикал в знаменателе равен \ (\ sqrt {10} \). Итак, умножьте дробь на \ (\ dfrac {\ sqrt {10}} {\ sqrt {10}} \). Тогда упростите.

\ [\ begin {align *} & \ dfrac {2 \ sqrt {3}} {3 \ sqrt {10}} \ times \ dfrac {\ sqrt {10}} {\ sqrt {10}} \\ [5pt ] & \ dfrac {2 \ sqrt {30}} {30} \\ [5pt] и \ dfrac {\ sqrt {30}} {15} \ end {align *} \]

Упражнение \ (\ PageIndex {8} \)

Запишите \ (\ dfrac {12 \ sqrt {3}} {\ sqrt {2}} \) в простейшей форме.

Ответ

\ (6 \ sqrt {6} \)

Как сделать: дано выражение с радикальным членом и константой в знаменателе, рационализируйте знаменатель

  1. Найдите сопряжение знаменателя.
  2. Умножьте числитель и знаменатель на сопряжение.
  3. Воспользуйтесь распределительным свойством.
  4. Упростить.

Пример \ (\ PageIndex {11} \): рационализация знаменателя, содержащего два члена

Запишите \ (\ dfrac {4} {1+ \ sqrt {5}} \) в простейшей форме. {th} \) и т. Д.2} {5} & & \ text {Simplify} \ end {align *} \)

г. \ (\ begin {align *} & 8 \ sqrt [4] {3} -2 \ sqrt [4] {3} & & \ text {Упростите, чтобы получить равные подкоренные выражения} \\ [5pt] & 6 \ sqrt [4] { 3} & & \ text {Add} \ end {align *} \)

Упражнение \ (\ PageIndex {10} \)

Упростить

  1. \ (\ sqrt [3] {- 216} \)
  2. \ (\ dfrac {3 \ sqrt [4] {80}} {\ sqrt [4] {5}} \)
  3. \ (6 \ sqrt [3] {9000} +7 \ sqrt [3] {576} \)
Ответить на

\ (- 6 \)

Ответ b

\ (6 \)

Ответ c

\ (88 \ sqrt [3] {9} \)

Использование рациональных экспонентов

Радикальные выражения также можно записывать без использования радикального символа.m} \]

Как сделать: дано выражение с рациональной экспонентой, запишите выражение в виде радикала

  1. Определите степень, посмотрев на числитель экспоненты. {\ tfrac {2} {3}} \) как радикал.{\ tfrac {23} {15}} \)

    Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с радикалами и рациональными сторонниками.

    Ключевые понятия

    • Главный квадратный корень числа \ (a \) — это неотрицательное число, которое при умножении само на себя равно \ (a \).
    • Если \ (a \) и \ (b \) неотрицательны, квадратный корень из произведения \ (ab \) равен произведению квадратных корней из \ (a \) и \ (b \).
    • Если \ (a \) и \ (b \) неотрицательны, квадратный корень из частного \ (\ dfrac {a} {b} \) равен частному из квадратных корней из \ (a \) и \ (Ь \).{th} \) мощность равна \ (a \). Эти корни обладают теми же свойствами, что и квадратные корни.
    • Радикалы можно переписать как рациональные показатели, а рациональные показатели можно переписать как радикалы.
    • Свойства показателей степени применяются к рациональным показателям.

    Авторы и авторство

    Упрощение квадратного корня из степеней в радикальных выражениях — стенограмма видео и урока

    Что означают эти радикальные символы?

    Символ корня выглядит так:

    и определяется как число, которое дает указанное количество при умножении на само себя.2 * 3. Любое число с партнером может быть удалено из радикала, чтобы получить окончательный ответ, который равен 5 * квадратный корень из 3.

    Резюме урока

    При упрощении радикалов, содержащих экспоненты, вам сначала нужно написать термины out, затем найдите для каждого термина партнера. Если подобных условий недостаточно, чтобы дать каждому партнера, можно остаться холостым. Затем для каждого партнерства одно из условий размещается вне радикала. Любые единичные термины останутся под радикалом.2.

    Результат обучения

    После того, как вы закончите этот урок, вы сможете упростить и решить радикальное выражение с полномочиями.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *