2
Содержание
определение, формула, таблица, график, свойства
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
Свойства арккосинуса
Ниже в табличном виде представлены основные свойства арккосинуса с формулами.
Таблица арккосинусов
| x | arccos x (рад) | arccos x (°) |
| -1 | π | 180° |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| 0 | π/2 | 90° |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 1 | 0 | 0° |
microexcel. ru
ru
Arccos 1 корень из 10. Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Что такое арккосинус
Плоскость пересекает
сферу всегда по окружности, которая
может проецироваться на плоскость в
виде эллипса
,окружности
илиотрезка
прямой линии (рис. 70).
Сечение сферы
проецирующей плоскостью
Ω
П
2
Окружность сечения
проецируется на фронтальную плоскость
в отрезок прямой линии С
2 D
2 ,
а на горизонтальную плоскость проекций
в эллипс, большая ось которого равна
диаметру окружности сечения.
Для построения
большой оси А
1 В
1
(горизонтальной проекции, определяем
середину отрезкаС
2 D
2 ,
через точку (А
2 В
2) проводится параллель,
находят горизонтальную проекцию этой
параллели и по линиям связи определяют
на ней точки осиА
1 иВ
1.
Точки 1 и 1,
расположенные на экваторе, являются
границей видимости на П 1 . Точки 2
Точки 2
и 2, расположенные
на главном меридиане, являются границей
видимости на П 3 .
Лекция № 6 аксонометрические проекции
1. Общие сведения.
2. Показатели искажения. 3. Виды
аксонометрических проекций. 4. Построение
окружности в аксонометрии.
1 Общие сведения
При выполнении
технических чертежей часто бывает
необходимым иметь более наглядные
изображения предметов. Для построения
таких изображений применяют
аксонометрические проекции (аксонометрию).
Аксонометрия
–
греческое
слово, состоящее
из двух слов ахсо
n
–
ось
и metreo
– измеряю
.
Способ
аксонометрического проецирования
состоит в том, что предмет вместе с осями
координат, к которым он отнесен в
пространстве, проецируется на какую-либо
плоскость параллельными лучами. Эта
плоскость называется плоскостью
аксонометрических проекций или картинной
плоскостью (рис. 71).
Направление
проецирования не должно совпадать ни
с одной из осей координат, тогда и
изображение получается наглядным.
Кроме наглядности
аксонометрические проекции допускают
и измерение предмета по трем координатным
направлениям.
Построение
изображения предмета выполняется по
каркасу характерных для предмета точек
с учетом свойств параллельного
проецирования: параллельные прямые
остаются на аксонометрических проекциях
параллельными, точки, принадлежащие
линиям, на проекциях принадлежат
аксонометрическим проекциям этих линий.
Все измерения делаются только по осям
или параллельно осям.Характерные
точки строятся по координатам.
К – аксонометрическая
(картинная) плоскость;
S
– направление проецирования.
2 Показатели искажения
Для возможности
использования метода координат в
аксонометрии вводятся показатели
искажения по осям.
На
рис. 72 изображена пространственная
система координат,
единичные
отрезки е
на осях
координат и их проекция в направлении
S
на
некоторую
плоскость К
,
являющуюся
аксонометрической плоскостью
проекций.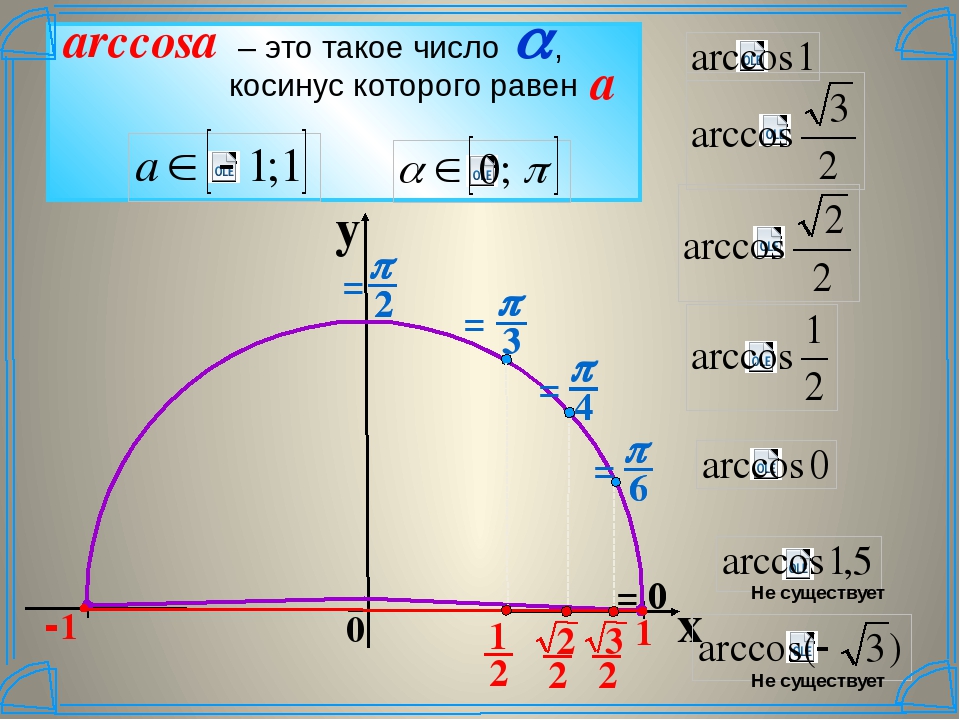 Проекции е
Проекции е
х
,
е
у
,
e
z
отрезка е
на соответствующих
аксонометрических
осях
в
общем случае не равны отрезкуе
и не равны между собой. Отрезкие
х
,
е
у
,
e
z
являютсяединицами
измерения по аксонометрическим осям —
аксонометрическими
единицами (аксонометрическими масштабами).
Отношение
длинны отреза в аксонометрических
проекциях к истинной длине отрезка
называют показателем искажения
(коэффициентом искажения):
.
Зная величину
коэффициента искажения можно построить
аксонометрическое изображение точки
по ее натуральным координатам, пользуясь
следующими формулами:
Х
1 = К
х
Х; У
1 =
К
у
У;
Z
1 =
К
z
Z
.
Показатели искажения
связаны между собой соотношениями:
в прямоугольной
аксонометрии:
К
х
2
К
у
2
К
z
2
=
2,
в косоугольной
аксонометрии:
К
х
2
К
у
2
К
z
2
=
2
с
tg
2 .
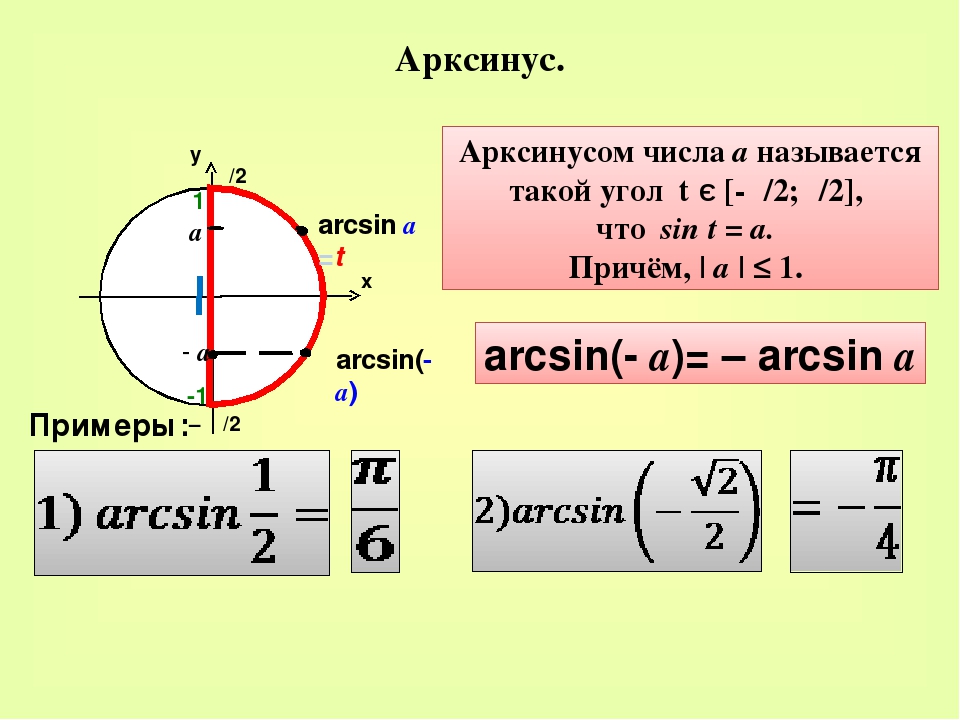
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс
учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно. ) Прямо здесь и сейчас вы в этом убедитесь.
) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы.
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4.
Или arctg(-1,3).
Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4
! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc
sin
0,4
угол,
синус которого
равен 0,4
Как пишется, так и слышится. ) Почти. Приставка arc
) Почти. Приставка arc
означает дуга
(слово арка
знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите. ) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки.
) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки.
Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная
расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных
заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам?
— слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку:
arcsin 0,5 — это угол, синус которого равен 0,5.
Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов
. Вот и все дела: arcsin 0,5 — это угол 30°.
Вот и все дела: arcsin 0,5 — это угол 30°.
Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс…
То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку:
арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1)
— это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные
значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного
значения внутри арккосинуса к положительному
по второй формуле:
Внутри арккосинуса справа уже положительное
значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Урок и презентация на темы: «Арккосинус. Таблица арккосинусов. arccos(0), arccos(1), arccos(2)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Что такое арккосинус?
2. Обозначение арккосинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арккосинуса.
6. Примеры.
Что такое арккосинус?
Ребята, мы с вами уже изучили функцию Y=cos(X), построили ее график и решали некоторые уравнения, например cos(x)= 1/2. Для решения этого уравнения требовалось провести прямую x= 1/2 и
посмотреть, в каких точках она пересекает числовую окружность.
Видно что прямая пересекает окружность в двух точках F и G. Эти точки и являются решением уравнения. Переобозначим F как x1, а G — как x2. Решение уравнения мы нашли довольно легко и определили, что x1 = π/3 + 2πk, а x2 = -π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение cos(x)=4/7.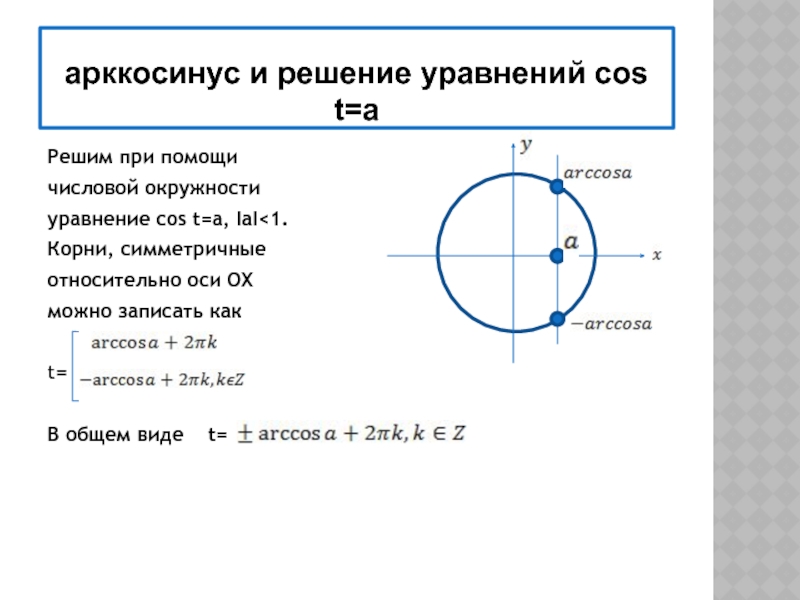 Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности?
Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности?
Обозначение арккосинуса
Давайте внимательно посмотрим на уравнение cos(x)=4/7.
Как мы и говорили, решениями нашего уравнения будут две точки: F=x1+2πk и G=x2+2πk, но, что это за точки? Много лет назад столкнувшись с этой проблемой математики решили, что надо придумать некоторый способ описания решения на математическом языке. И был придуман новый символ – arccos(x). Будем читать как арккосинус.
Тогда решения нашего уравнения запишутся как: x1=arccos(4/7) и x2=-arccos(4/7). И решение в общем виде: x=arccos(4/7) + 2πk и x=-arccos(4/7) + 2πk. Арккосинус — это угол (длина дуги AF, AG), косинус которого равен 4/7.
Немного истории
Символ arccos появляется впервые в 18 веке в работах математика Шерфера и известного французского ученого Жозефа Луи Лагранжа, портрет которого вы видите на этой странице. Несколько ранее понятие арккосинус уже рассматривал Д. Бернули, но записывал его совсем другими символами.
Бернули, но записывал его совсем другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия:
arccos x — это угол (можно сказать и дуга), косинус которого равен x.
Определение арккосинуса.
Если |а|≤ 1, то arccos(a) – это такое число из отрезка , косинус которого равен а.
Если |а|≤ 1, то уравнение cos(x)=a имеет решение: x=±arccos(a) + 2πk
Есть три случая, в которых предпочитают записывать решения более простым способом:
cos(x)=0, то x= π/2 + πk
cos(x)=1, то x= 2πk
cos(x)=-1, то x= π + 2πk
Также стоит записать важное равенство:
Для любого -1 ≤ а ≤ 1 выполняется равенство: arccos(a) + arccos(-a) = π
; при решение заданий удобнее использовать: arccos(-a) = π — arccos(a), где -1 ≤ а ≤ 1
Таблица значений арккосинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арккосинуса
Примеры
1.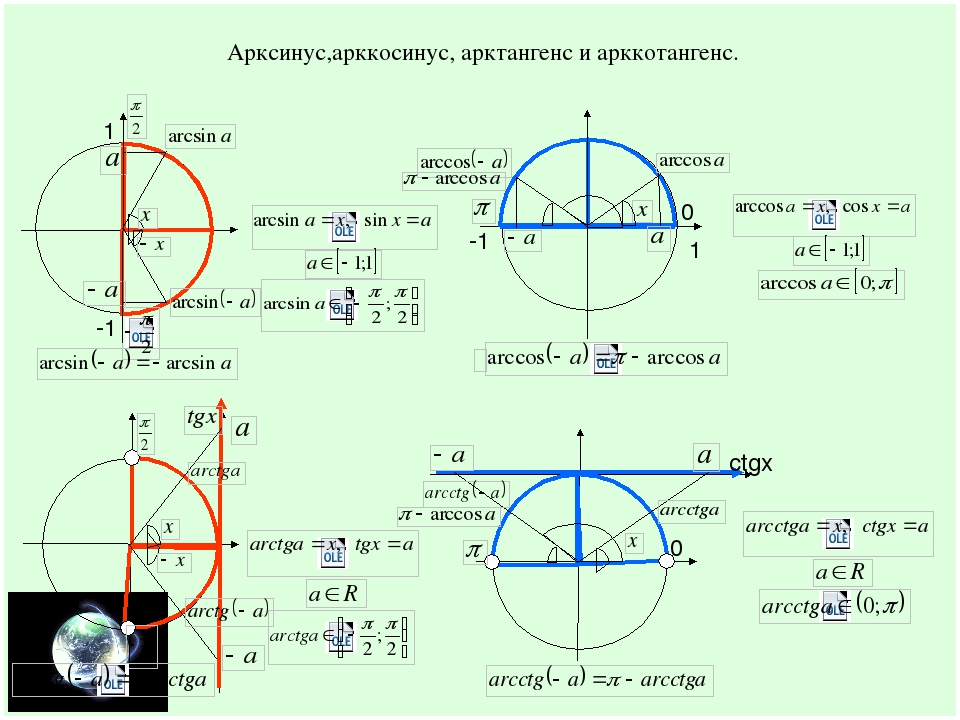 Найти значение функции arccos(-√3/2).
Найти значение функции arccos(-√3/2).
Решение: Пусть arccos(-√3/2)=x, тогда cos(x)=-√3/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=5π/6, т.к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
Ответ: arccos(-√3/2)=5π/6
2. Найти значение функции arccos(√2/2).
Решение: Пусть arccos(√2/2) = x, тогда cos(x)= √2/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=π/4, т.к. cos(π/4)= √2/2 и 0 ≤ π/4 ≤ π.
Ответ: arccos(√2/2)=π/4
3. Найти значение функции arccos(1).
Решение: Пусть arccos(1) = x, тогда cos(x)= 1 и по определению 0≤ x ≤ π. Посмотрим значения косинуса в таблице: значит x=0, т.к. cos(0)= 1 и 0 ≤ 0 ≤ π.
Ответ: arccos(1)=0
4. Решить неравенство cos(x)> -0.3.
Решение: Косинус — это абсцисса точки числовой окружности. Значит необходимо найти такие точки, абсциссы которых больше -0.3. Нарисуем прямую x=-0.3. Она пересекает числовую окружность в двух точках: F и G. Неравенству x>-0.3 соответствуют точки дуги GF.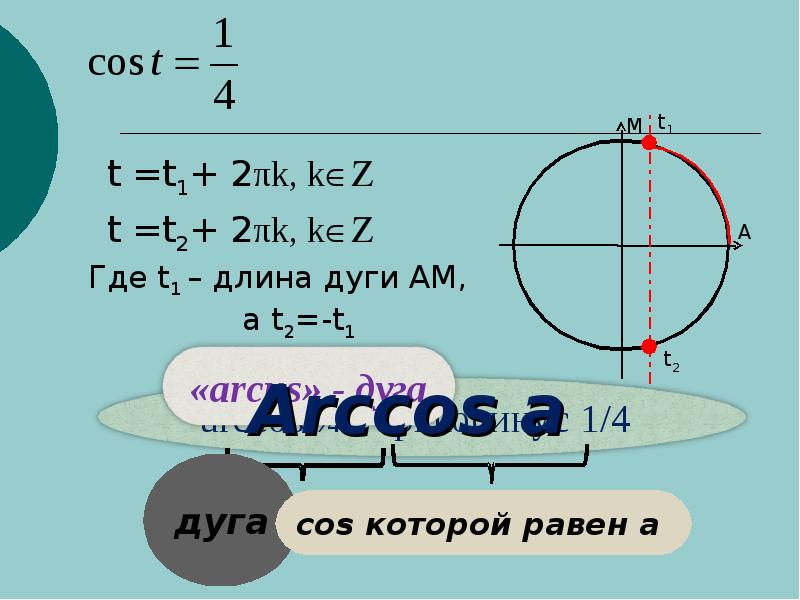 Точкам F и G соответствуют абсциссы:
Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3)
Задачи для самостоятельного решения
1)Вычислить:
а) $arccos(\frac{\sqrt{3}}{2})$,
б) $arccos(-\frac{1}{2})$,
в) $arccos(0)$,
г) $arccos(-0,5)$.
2) Решить уравнения:
а) $cos(x)=-\frac{1}{2}$,
б) $cos(x)=1$,
в) $cos(x)=\frac{\sqrt{3}}{2}$,
г) $cos(x)=0,25$,
д) $cos(x)=-1,2$.
3) Решить неравенства:
а) $cos(x)>0,6$,
б) $cos(x)≤0,2$.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т. п.
п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса
».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a
, arccos(−a)=π−arccos a
, arctg(−a)=−arctg a
и arcctg(−a)=π−arcctg a
.
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12
, а нужно найти значение arccos a
. Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12
.
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a
требуется найти значение арктангенса или арккотангенса этого числа a
или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a
равен π/10
, и нужно вычислить значение арктангенса этого числа a
. Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg
.
Список литературы.
- Алгебра:
Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 - Башмаков М. И.
Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра
и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. - И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М.
Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Чему равен arccos -1/корень 2???
1)80*32=2560 кв м площадь участка
2)2560:8*3=960 кв м площадь сада
3)2560-960=1600 кв м площадь огорода
===================================
36:9*1+56=60 ;)))))))))))))))))
15,67-1,89
Надо решить столбиком если ты не можешь в уме.
ВАЖНО: ставить числа по своим местам.
Что значит по своим местам?
По своим местам значит надо поставить: целые под целые; десятые под десятыми и т.д.
15,67
— 1,89
Схема 1.Дальше мы отнимаем сотые 7 с сотыми 9.
Но 7 меньше чем 9. Значит нужно занять одно число у шести. Если число ноль надо занять у того числа у которого нету нуля. Когда мы занимаем к 7 или другим числам прибавляется ещё 10.
Значит у нас уже не 7 а 17.
Так как 17 больше 9 мы можем отнять.
17-9=8
Дальше мы отнимаем 5 и 8.
Почему 5, потому что мы заняли 1 число. Значит когда мы будем занимать у нас всегда будет отниматься 1.
5 меньше числа 8. Значит делаем по 1 схеме. Только на этот раз числа другие.
У нас теперь получилось 7.
Двигаемся дальше.
5 уже больше чем 1. Значит у нас получится 4: 5-1=4.
А под числом 1 уже ничего нету, значит мы просто переписываем это число.
15,67
— 1,89
______
4,78
Вот так у нас получился правильный ответ.
22лр вот такой будет ответ
192*2=384 г редис
384:3=128 г репа
192+384+128=704 г всех семян
Алгебра – 10 класс.
 Арккосинус, arccos (x)
Арккосинус, arccos (x)
Дата публикации: .
Что будем изучать:
1. Что такое арккосинус?
2. Обозначение арккосинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арккосинуса.
6. Примеры.
Что такое арккосинус?
Ребята, мы с вами уже изучили функцию Y=cos(X), построили ее график и решали некоторые уравнения, например cos(x)= 1/2. Для решения этого уравнения требовалось провести прямую x= 1/2 и
посмотреть, в каких точках она пересекает числовую окружность.
Видно что прямая пересекает окружность в двух точках F и G. Эти точки и являются решением уравнения. Переобозначим F как x1, а G — как x2. Решение уравнения мы нашли довольно легко и определили, что x1 = π/3 + 2πk, а x2 = -π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение cos(x)=4/7. Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности?
Обозначение арккосинуса
Давайте внимательно посмотрим на уравнение cos(x)=4/7.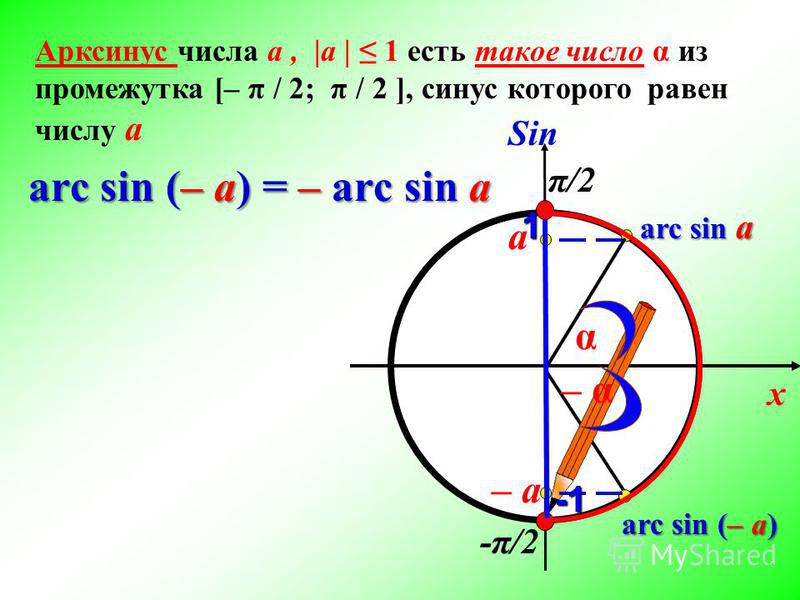
Как мы и говорили, решениями нашего уравнения будут две точки: F=x1+2πk и G=x2+2πk, но, что это за точки? Много лет назад столкнувшись с этой проблемой математики решили, что надо придумать некоторый способ описания решения на математическом языке. И был придуман новый символ – arccos(x). Будем читать как арккосинус.
Тогда решения нашего уравнения запишутся как: x1=arccos(4/7) и x2=-arccos(4/7). И решение в общем виде: x=arccos(4/7) + 2πk и x=-arccos(4/7) + 2πk. Арккосинус — это угол (длина дуги AF, AG), косинус которого равен 4/7.
Немного истории
Символ arccos появляется впервые в 18 веке в работах математика Шерфера и известного французского ученого Жозефа Луи Лагранжа, портрет которого вы видите на этой странице. Несколько ранее понятие арккосинус уже рассматривал Д. Бернули, но записывал его совсем другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия:
arccos x — это угол (можно сказать и дуга), косинус которого равен x.
Определение арккосинуса.
Если |а|≤ 1, то arccos(a) – это такое число из отрезка [0; π], косинус которого равен а.
Если |а|≤ 1, то уравнение cos(x)=a имеет решение: x=±arccos(a) + 2πk
Есть три случая, в которых предпочитают записывать решения более простым способом:
cos(x)=0, то x= π/2 + πk
cos(x)=1, то x= 2πk
cos(x)=-1, то x= π + 2πk
Также стоит записать важное равенство:
Для любого -1 ≤ а ≤ 1 выполняется равенство: arccos(a) + arccos(-a) = π; при решение заданий удобнее использовать: arccos(-a) = π — arccos(a), где -1 ≤ а ≤ 1
Таблица значений косинуса
Таблица значений арккосинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арккосинуса
Примеры
1. Найти значение функции arccos(-√3/2).
Решение: Пусть arccos(-√3/2)=x, тогда cos(x)=-√3/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=5π/6, т. к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
Ответ: arccos(-√3/2)=5π/6
2. Найти значение функции arccos(√2/2).
Решение: Пусть arccos(√2/2) = x, тогда cos(x)= √2/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=π/4, т.к. cos(π/4)= √2/2 и 0 ≤ π/4 ≤ π.
Ответ: arccos(√2/2)=π/4
3. Найти значение функции arccos(1).
Решение: Пусть arccos(1) = x, тогда cos(x)= 1 и по определению 0≤ x ≤ π. Посмотрим значения косинуса в таблице: значит x=0, т.к. cos(0)= 1 и 0 ≤ 0 ≤ π.
Ответ: arccos(1)=0
4. Решить неравенство cos(x)> -0.3.
Решение: Косинус — это абсцисса точки числовой окружности. Значит необходимо найти такие точки, абсциссы которых больше -0.3. Нарисуем прямую x=-0.3. Она пересекает числовую окружность в двух точках: F и G. Неравенству x>-0.3 соответствуют точки дуги GF. Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3)
Задачи для самостоятельного решения
1)Вычислить:
а) $arccos(\frac{\sqrt{3}}{2})$,
б) $arccos(-\frac{1}{2})$,
в) $arccos(0)$,
г) $arccos(-0,5)$.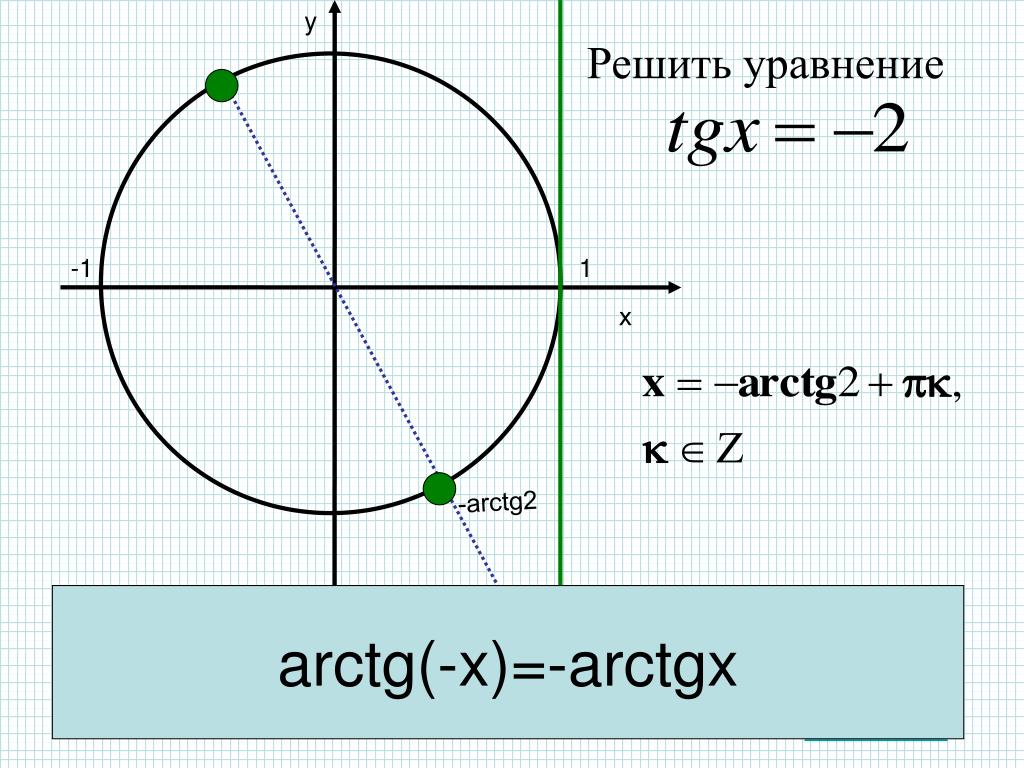
2) Решить уравнения:
а) $cos(x)=-\frac{1}{2}$,
б) $cos(x)=1$,
в) $cos(x)=\frac{\sqrt{3}}{2}$,
г) $cos(x)=0,25$,
д) $cos(x)=-1,2$.
3) Решить неравенства:
а) $cos(x)>0,6$,
б) $cos(x)≤0,2$.
Арксинус, арккосинус и арктангенс угла
К понятиям арксинус, арккосинус, арктангенс, арккотангенс
учащийся народ относится с опаской. Не понимает он эти термины и, стало
быть, не доверяет этой славной семейке.) А зря. Это очень простые
понятия. Которые, между прочим, колоссально облегчают жизнь знающему
человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3).
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3).
Всякие углы бывают.) Просто записать углы можно разными способами.
Можно записать угол через градусы или радианы. А можно — через его
синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка
знаете?), т.к. древние люди вместо углов использовали дуги, но это сути
дела не меняет. Запомните эту элементарную расшифровку математического
термина! Тем более, для арккосинуса, арктангенса и арккотангенса
расшифровка отличается только названием функции.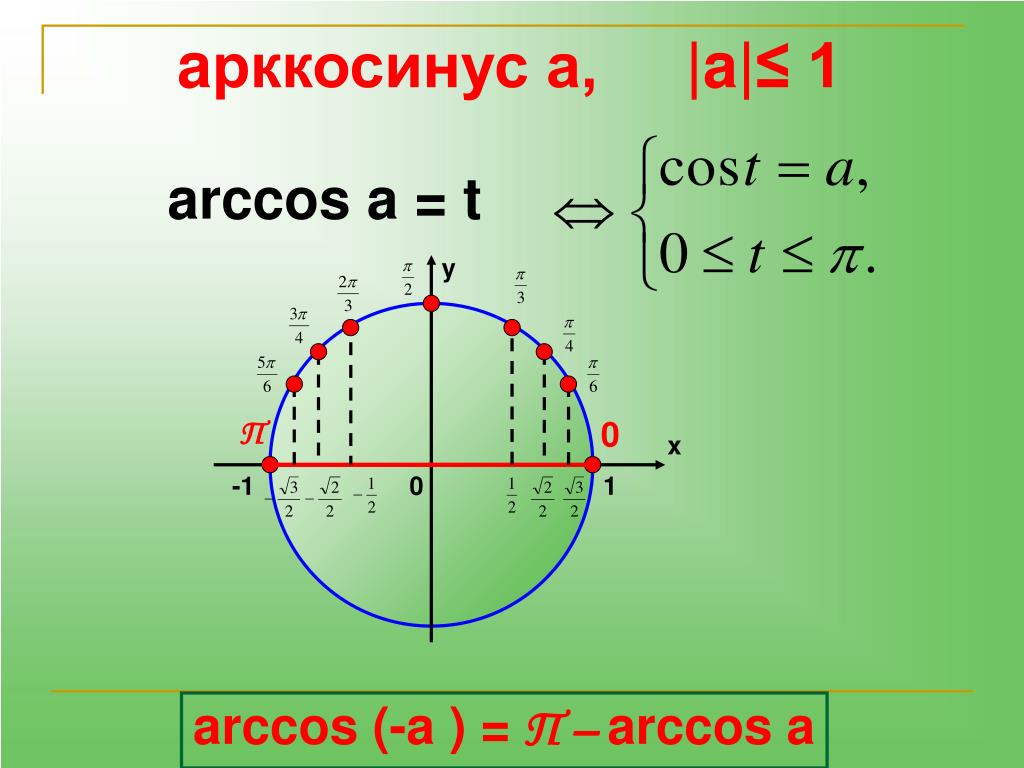
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать
эпических ляпов.) Например, выражение arccos1,8 выглядит вполне
солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой
персональный синус и косинус. И почти у каждого — свой тангенс и
котангенс. Стало быть, зная тригонометрическую функцию, можно записать и
сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы
и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Чтобы печатать меньше.)
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того,
это иногда нужно обязательно делать. Арки — штука простая, но без них
как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да. ..) А сведущий
..) А сведущий
вспомнит заклинание: арксинус — это угол, синус которого… Ну и так
далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё
посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что
и является правильным ответом.
Вот таким образом можно (и нужно) переходить от
арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным
градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные
значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не
проблема. Вот вам простые формулы перехода от отрицательных значений к
положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать.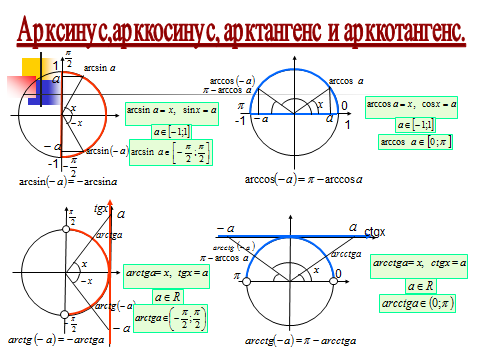 Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Те, кто освоил темы «Тригонометрический круг», и «Отсчёт углов на тригонометрическом круге»
— люди грамотные. И, возможно, уже приготовили мне убойный вопрос.) По
определению, скажем, arcsin 0,5 — это угол, синус которого равен 0,5.
Т.е 30°. Но…
Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:
sin30° = 0,5
sin150° = 0,5
sin390° = 0,5
sin510° = 0,5
И так до бесконечности… Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и ….
Да. Именно так. Арксинус 0,5 — это действительно
Именно так. Арксинус 0,5 — это действительно
бесконечный набор углов. Но обозначается такой арксинус вот как:
Arcsin0,5. С заглавной буквы. В школе такие арксинусы не изучают. В
школе изучают арки с маленькой буквы: arcsin, arccos, arctg, arcctg.
Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и
имеют жёсткие ограничения по величине. Для однозначности.
С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:
arсsin (любой) — это угол, который располагается в интервале:
arсcos (любой) — это угол, который располагается в интервале:
arсtg (любой) — это угол, который располагается в интервале:
arсctg (любой) — это угол, который располагается в интервале:
Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:
Зелёным нарисованы углы, которые пробегают значения от
— Пи/2 до + Пи/2.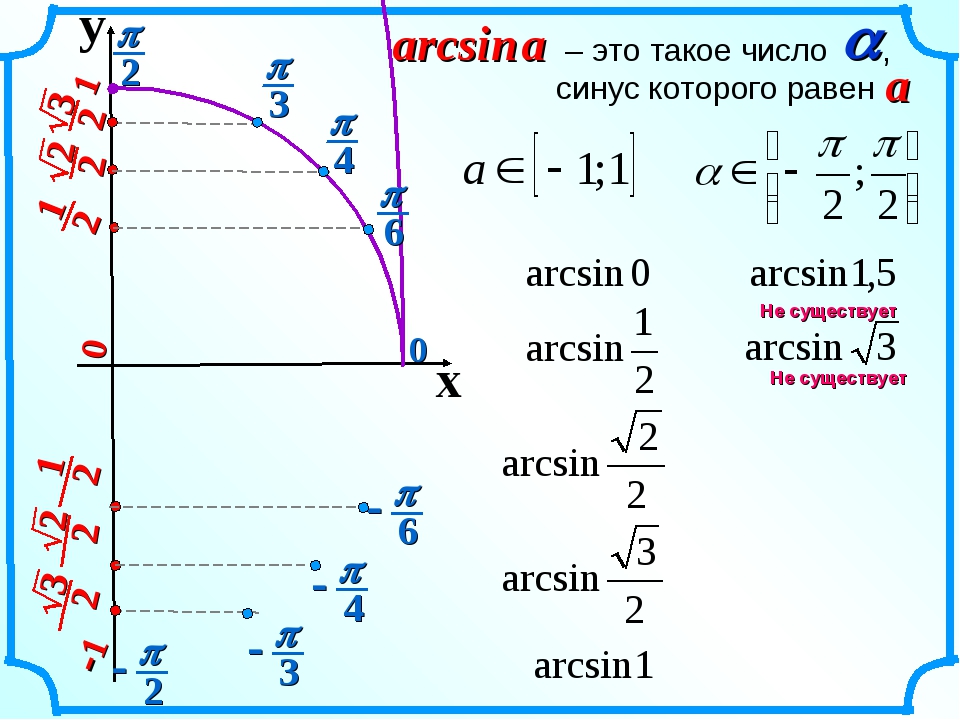 Это и есть разрешённая зона для арксинусов. И никаких
Это и есть разрешённая зона для арксинусов. И никаких
дополнительных оборотов! Строго от -90° до +90°! Никакой arcsin не может
быть равным, например 120°, 180° или 330°. А вот 50°, -65°, 90° или
25° — пожалуйста!
Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только
30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус,
равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого
диапазона.
А теперь наведите курсор мышки на рисунок. Вы увидите
диапазон арктангенсов. Найдите 2 отличия.) Да! Конечные точки на оси ОУ
стали белыми! Это означает, что они не включаются в диапазон
арктангенсов. Арктангенс не может быть равным ±90°. По той простой
причине, что тангенс 90° (и -90°) не существует.
Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):
Надеюсь, зрительная память вас спасёт, если что…)
А зачем все эти арки? — слышу ещё один осторожный вопрос. )
)
Вопрос резонный. В математике просто так, чисто для
красоты, ничего не бывает. Только по острой необходимости!) А вы
попробуйте ответить на такой вопрос:
У какого угла синус равен 0,4?
Для ответа в градусах или радианах вам придётся открывать
таблицы Брадиса, или включать солидный калькулятор. Искать там значение
синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот
синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу…)
А через арксинус мгновенно даётся абсолютно точный ответ: угол, у которого синус равен 0,4 — это arcsin 0,4
! Просто по смыслу арксинуса: arcsin 0,4 — это и есть угол, синус
которого равен 0,4. Разумеется, это не единственный угол, синус которого
равен 0,4, но через арки и все остальные записываются в три секунды.
Этим мы в тригонометрических уравнениях займёмся.
Арксинус, арккосинус — свойства, графики, формулы
Арксинус, arcsin
Определение и обозначения
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ).
 Он имеет область определения –1 ≤ x ≤ 1 и множество значений –π/2 ≤ y ≤ π/2.
Он имеет область определения –1 ≤ x ≤ 1 и множество значений –π/2 ≤ y ≤ π/2.
sin(arcsin x) = x ;
arcsin(sin x) = x .
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат.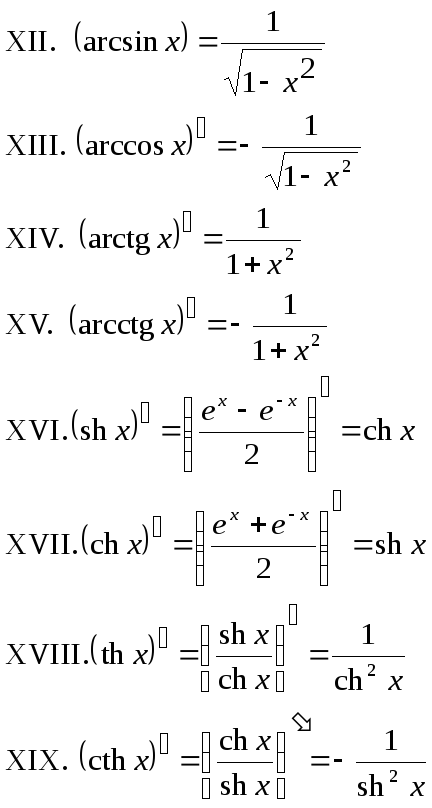 Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.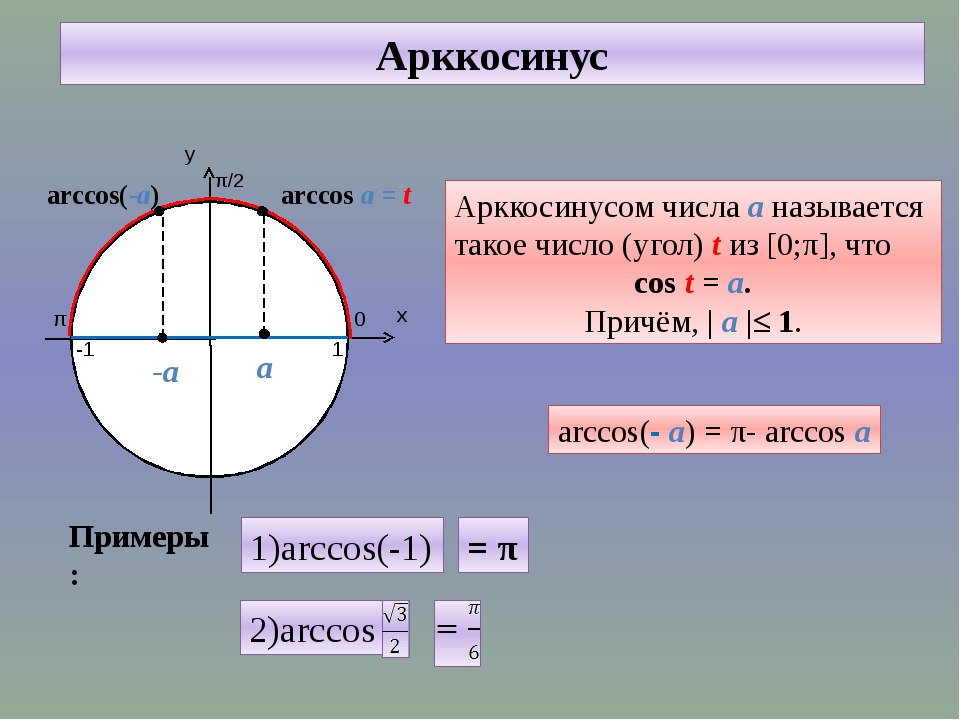
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См.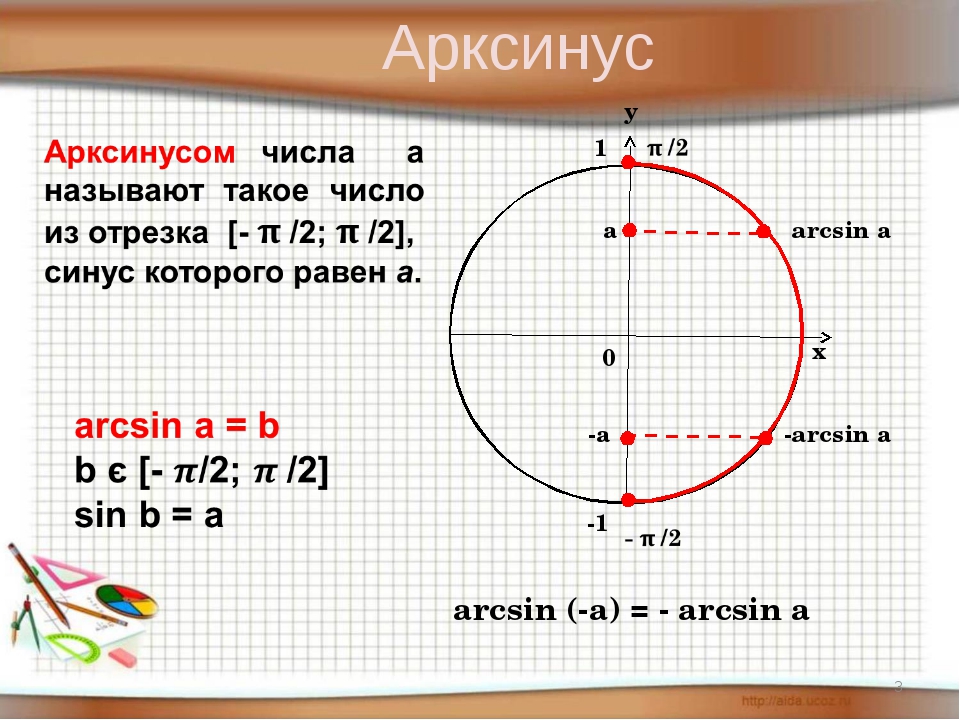 Вывод формул
Вывод формул
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков:
,
где – многочлен степени . Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin t. Интегрируем по частям, учитывая что –π/2 ≤ t ≤ π/2, cos t ≥ 0:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| < 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
Обратный синус, косинус, тангенс
Быстрый ответ:
Для прямоугольного треугольника:
Синус функция sin принимает угол θ и дает отношение против гипотенузы
Функция обратного синуса sin -1 принимает отношение против гипотенузы и дает угол θ
Косинус и тангенс следуют аналогичной идее.
Пример (длина до одного десятичного знака):
sin (35 °) = Противоположно / Гипотенуза
= 2,8 / 4,9
= 0,57 …
sin -1 (противоположно / гипотенуза) = sin -1 (0,57 . ..)
..)
= 35 °
А теперь подробнее:
Синус, косинус и тангенс — все основаны на прямоугольном треугольнике
Это очень похожие функции…
поэтому мы посмотрим на синусоидальную функцию , а затем на обратный синус , чтобы понять, что это такое.
Синусоидальная функция
Синус угла θ равен:
- длина стороны Противоположный угол θ
- делится на длину гипотенузы
Или проще:
sin ( θ ) = Противоположно / Гипотенуза
Пример: Что такое синус 35 °?
Используя этот треугольник (длины до одного десятичного знака): sin (35 °) = Противоположно / Гипотенуза |
Функция синуса может помочь нам решить такие задачи:
Пример: используйте синусоидальную функцию
, чтобы найти «d»
Мы знаем
- Угол наклона кабеля к морскому дну составляет 39 °.

- Длина кабеля 30 м.
И мы хотим знать «d» (расстояние вниз).
Начать с: sin 39 ° = противоположно / гипотенуза
sin 39 ° = d / 30
Поменять местами стороны: d / 30 = sin 39 °
С помощью калькулятора найдите sin 39 °: d / 30 = 0.6293…
Умножить обе стороны на 30: d = 0,6293… x 30
d = 18,88 с точностью до 2 знаков после запятой
Глубина «d» составляет 18,88 м
Функция обратной синусоиды
Но иногда нам нужно найти угол .
Вот где появляется «обратный синус».
Он отвечает на вопрос «какой угол имеет синус, равный противоположному / гипотенузе?»
Символ для обратного синуса — sin -1 , или иногда arcsin .
Пример: найти угол
«a»
Мы знаем
- Расстояние вниз 18,88 м.
- Длина кабеля 30 м.
И мы хотим знать угол «а»
Начать с: sin a ° = противоположно / гипотенуза
sin a ° = 18,88 / 30
Вычислить 18,88 / 30: sin a ° = 0,6293 . ..
..
Какой угол имеет синус, равный 0.6293 …?
Обратный синус нам расскажет.
Обратный синус: a ° = sin −1 (0,6293 …)
С помощью калькулятора найдите sin −1 (0,6293 …): a ° = 39,0 ° (с точностью до 1 знака после запятой)
Угол «а» составляет 39,0 °
Они как вперед, так и назад!
- sin берет угол и дает нам соотношение «противоположное / гипотенуза»
- sin -1 берет отношение «противоположность / гипотенуза» и дает нам угол .
Пример:
Функция синуса: sin ( 30 ° ) = 0,5
Обратный синус: sin −1 ( 0,5 ) = 30 °
Калькулятор
| На калькуляторе вы нажимаете одну из следующих кнопок (в зависимости от марки вашего калькулятора): либо «2ndF sin», либо «shift sin».  |
На вашем калькуляторе попробуйте использовать sin, а затем sin -1 , чтобы увидеть, что произойдет
Больше чем один угол!
Обратный синус показывает только один угол … но есть и другие ракурсы, которые могут сработать.
Пример: два угла, где противоположность / гипотенуза = 0,5
На самом деле существует бесконечно много углов , потому что вы можете продолжать складывать (или вычитать) 360 °:
Помните об этом, потому что бывают случаи, когда вам действительно нужен один из других углов!
Сводка
Синус угла θ равен:
sin ( θ ) = Противоположно / Гипотенуза
и обратный синус:
sin -1 (противоположно / гипотенуза) = θ
А как насчет «кос» и «загар».
 ..?
..?
Идея точно такая же, но с другим соотношением сторон.
Косинус
Косинус угла θ равен:
cos ( θ ) = Соседний / Гипотенуза
И обратный косинус равен:
cos -1 (смежный / гипотенуза) = θ
Пример: найти величину угла a °
cos a ° = Соседний / Гипотенуза
cos a ° = 6,750 / 8,100 = 0.8333 …
a ° = cos -1 (0,8333 …) = 33,6 ° (с точностью до 1 знака после запятой)
Касательная
Тангенс угла θ составляет:
загар ( θ ) = напротив / рядом
Таким образом, обратный тангенс равен:
tan -1 (напротив / рядом) = θ
Пример: Найдите размер угла x °
tan x ° = напротив / рядом
tan x ° = 300/400 = 0.75
x ° = tan -1 (0,75) = 36,9 ° (с точностью до 1 десятичного знака)
Другие названия
Иногда sin -1 называется asin или arcsin
Аналогично cos -1 называется acos или arccos
, а tan -1 называется atan или arctan
Примеры:
- arcsin (y) совпадает с sin -1 (y)
- атан (θ) совпадает с tan -1 (θ)
- и др.
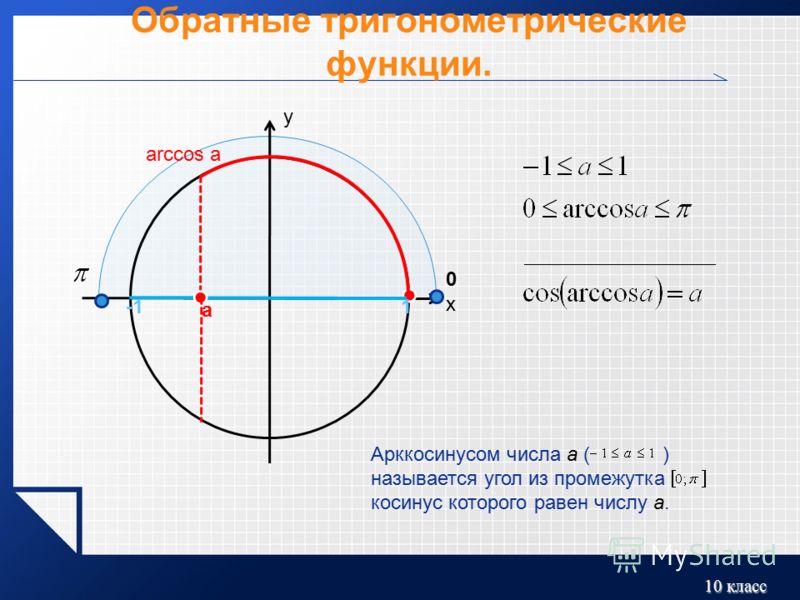
Графики
И, наконец, вот графики синуса, обратного синуса, косинуса и обратного косинуса:
Синус
Обратный синус
Косинус
Обратный косинус
Вы что-нибудь заметили в графиках?
- Они как-то похожи, правда?
- Но обратный синус и обратный косинус не «продолжаются вечно», как синус и косинус …
Давайте посмотрим на примере косинуса.
Вот Косинус и Обратный косинус , нанесенные на тот же график:
Косинус и обратный косинус
Они зеркальные (примерно по диагонали)
Но почему обратный косинус обрезается сверху и снизу (точки на самом деле не являются частью функции) …?
Потому что, чтобы быть функцией, она может дать только один ответ
, когда мы спрашиваем «что такое cos -1 (x)?»
Один ответ или бесконечно много ответов
Но мы видели ранее, что существует бесконечно много ответов , и пунктирная линия на графике показывает это.
Так что да, — это бесконечно много ответов …
… но представьте, что вы вводите 0,5 в свой калькулятор, нажимаете cos -1 , и это дает вам бесконечный список возможных ответов …
Итак, у нас есть правило, что функция может дать только один ответ .
Итак, отсекая это таким образом, мы получаем только один ответ, но мы должны помнить, что могут быть другие ответы .
Касательная и обратная касательная
А вот и функция касательной и арктангенс.Вы видите, как они зеркальные (примерно по диагонали) …?
Касательная
Обратный тангенс
математических слов: обратный косинус
Обратный
Косинус
cos -1
Cos -1
arccos
Arccos
функция, обратная косинусу.
Основная идея : Найти cos -1 (½),
мы спрашиваем «что
угол имеет косинус, равный ½? »
ответ 60 °.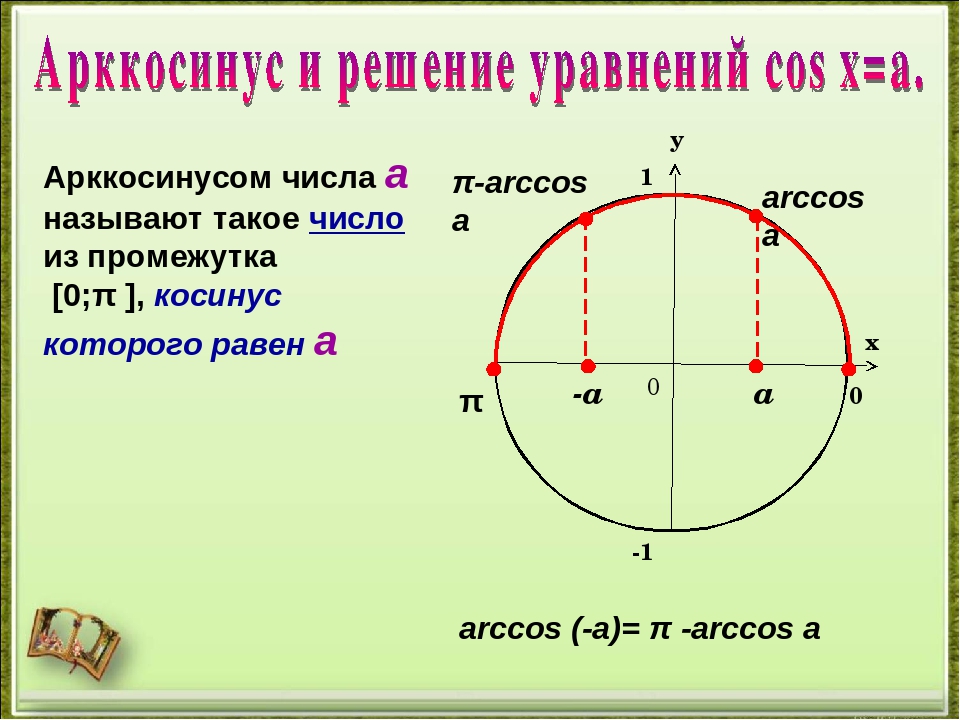 В результате мы говорим cos -1 (½)
В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3.
Подробнее : На самом деле существует много углов, у которых косинус равен ½.
Мы действительно спрашиваем, «какой самый простой, самый основной угол, который
косинус равен ½? »Как и прежде,
ответ 60 °. Таким образом, cos -1 (½)
= 60 ° или cos -1 (½) = π / 3.
Подробности : Что такое cos -1 (–½)?
Мы выбираем 120 °, –120 °, 240 °,
или под другим углом?
Ответ — 120 °.Обратным косинусом выбираем угол в верхней половине блока.
круг. Таким образом, cos -1 (–½)
= 120 ° или
cos -1 (–½) = 2π / 3.
В
другими словами, диапазон cos -1 равен
ограничивается [0, 180 °] или [0, π].
Примечание: arccos означает «арккосинус»,
или радианная мера дуги на окружности, соответствующая
заданное значение косинуса.
Техническое примечание : Поскольку ни одна из шести триггерных функций не синусоида,
косинус, тангенс, косеканс, секанс и котангенс взаимно однозначны,
их инверсии не являются функциями.Каждая триггерная функция может иметь свой
домен ограничен, однако, чтобы сделать его инверсию функцией.
Некоторые математики пишут эти ограниченные триггерные функции и их
переворачивается с заглавной буквы (например, Cos или Cos -1 ).
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не делает различий между заглавными и не заглавными буквами
триггерные функции.
См.
также
обратный
тригонометрия, обратная
триггерные функции, интервальное обозначение
Обратные тригонометрические функции
Вы изучили, как
тригонометрические функции
грех
(
Икс
)
,
потому что
(
Икс
)
, а также
загар
(
Икс
)
может использоваться, чтобы найти неизвестную длину стороны прямоугольного треугольника, если известны длина одной стороны и величина угла.
В
обратные тригонометрические функции
грех
—
1
(
Икс
)
,
потому что
—
1
(
Икс
)
, а также
загар
—
1
(
Икс
)
, используются для нахождения неизвестной меры угла прямоугольного треугольника, когда известны две длины сторон.
Пример 1:
Основание лестницы размещено
3
в футах от
10
— стена высотой до стопы, так чтобы верх лестницы совпадал с верхом стены.Каков угол между лестницей и землей?
Здесь у нас есть прямоугольный треугольник, для которого нам известны длины двух катетов, то есть сторон, противоположных и прилегающих к углу. Итак, мы используем функцию обратной касательной. Если вы введете это значение в калькулятор, установленный в режим «градус», вы получите
загар
—
1
(
10
3
)
≈
73.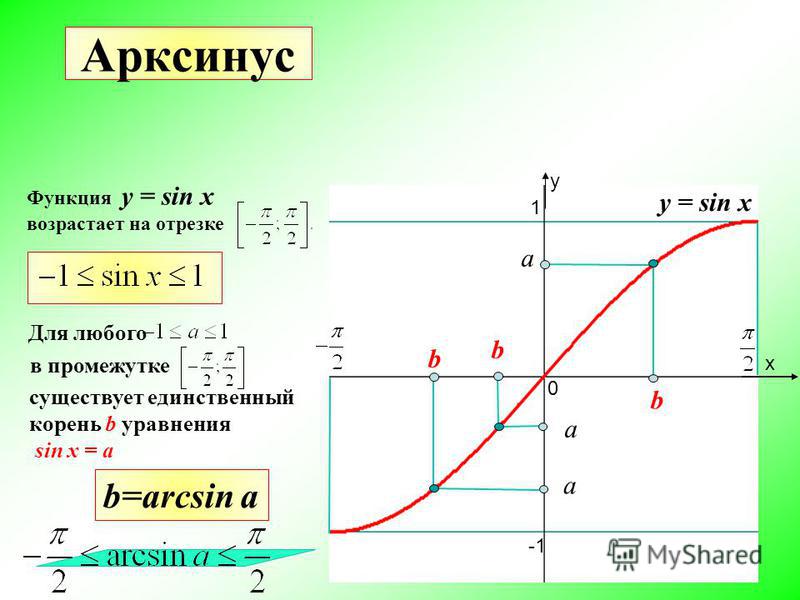 3
3
°
Если у вас установлен калькулятор в радианах, вы получите
загар
—
1
(
10
3
)
≈
1,28
Если вы запомнили отношения длин сторон, которые встречаются в
45
—
45
—
90
а также
30
—
60
—
90
треугольников, вы, вероятно, сможете найти некоторые значения обратных тригонометрических функций без использования калькулятора.
Пример 2:
Находить
потому что
—
1
(
3
2
)
.
Вы можете вспомнить, что в
30
—
60
—
90
треугольник, если гипотенуза имеет длину
1
, то длинная нога имеет длину
3
2
. Поскольку косинус — это отношение смежной стороны к гипотенузе, значение обратного косинуса равно
Поскольку косинус — это отношение смежной стороны к гипотенузе, значение обратного косинуса равно
30
°
, или около
0.52
радианы.
потому что
—
1
(
3
2
)
знак равно
30
°
Графики обратных тригонометрических функций
Все тригонометрические функции
периодические функции
. Таким образом, графики ни у одного из них не проходят
Горизонтальная линия
Тест и так нет
1
—
к
—
1
.Это означает, что ни у одного из них нет обратного, если только
домен
каждого ограничено, чтобы сделать каждый из них
1
—
к
—
1
.
Поскольку графики периодические, если мы выберем подходящую область, мы сможем использовать все значения
диапазон
.
Если мы ограничим область
ж
(
Икс
)
знак равно
грех
(
Икс
)
к
[
—
π
2
,
π
2
]
мы сделали функцию
1
—
к
—
1
.Диапазон
[
—
1
,
1
]
.
(Хотя есть много способов ограничить домен для получения
1
—
к
—
1
функция это согласованный используемый интервал.)
Обозначим
обратная функция
в виде
y
знак равно
грех
—
1
(
Икс
)
. Читается
y
инверсия синуса
Икс
и означает
y
— угол действительного числа, значение синуса которого равно
Икс
.Будьте осторожны с используемыми обозначениями. Надстрочный индекс «
Надстрочный индекс «
—
1
”НЕ является показателем. Чтобы избежать этого обозначения, в некоторых книгах используется обозначение
y
знак равно
Arcsin
(
Икс
)
вместо.
Чтобы построить график, обратный синусоидальной функции, помните, что график — это отражение над линией.
y
знак равно
Икс
функции синуса.
Обратите внимание, что домен теперь является диапазоном, а диапазон теперь является доменом.Поскольку домен ограничен, все положительные значения будут давать
1
ул
угол квадранта и все отрицательные значения дадут
4
th
угол квадранта.
Точно так же мы можем ограничить области определения функций косинуса и касательной, чтобы сделать их
1
—
к
—
1
.
Область определения функции обратного косинуса:
[
—
1
,
1
]
и диапазон
[
0
,
π
]
. Это означает, что положительное значение даст
Это означает, что положительное значение даст
1
ул
угол квадранта и отрицательное значение даст
2
nd
угол квадранта.
Область определения функции обратной касательной:
(
—
∞
,
∞
)
и диапазон
(
—
π
2
,
π
2
)
.Функция, обратная касательной, даст значения в
1
ул
а также
4
th
квадранты.
Тот же процесс используется для нахождения обратных функций для остальных тригонометрических функций — котангенса, секанса и косеканса.
Функция | Домен | Диапазон |
|---|---|---|
грех — 1 ( Икс ) | [ — 1 , 1 ] | [ — π 2 , π 2 ] |
потому что — 1 ( Икс ) | [ — 1 , 1 ] | [ 0 , π ] |
загар — 1 ( Икс ) | ( — ∞ , ∞ ) | ( — π 2 , π 2 ) |
детская кроватка — 1 ( Икс ) | ( — ∞ , ∞ ) | ( 0 , π ) |
сек — 1 ( Икс ) | ( — ∞ , — 1 ] ∪ [ 1 , ∞ ) | [ 0 , π 2 ) ∪ ( π 2 , π ] |
csc — 1 ( Икс ) | ( — ∞ , — 1 ] ∪ [ 1 , ∞ ) | [ — π 2 , 0 ) ∪ ( 0 , π 2 ] |
Обратный косинус и обратный синус
Обратный косинус и обратный синус
Стандартные триггерные функции являются периодическими, то есть они повторяются. Таким образом, одно и то же выходное значение появляется для нескольких входных значений функции. Это делает невозможным построение обратных функций. Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии.
Таким образом, одно и то же выходное значение появляется для нескольких входных значений функции. Это делает невозможным построение обратных функций. Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии.
Чтобы определить обратную функцию, исходная функция должна быть взаимно однозначно . Для существования взаимно однозначного соответствия (1) каждое значение в домене должно соответствовать ровно одному значению в диапазоне, и (2) каждое значение в диапазоне должно соответствовать ровно одному значению в домене.Первое ограничение распространяется на все функции; второй нет. Например, синусоидальная функция не удовлетворяет второму ограничению, поскольку одно и то же значение в диапазоне соответствует многим значениям в домене (см. Рисунок 1).
Рисунок 1
Функция синуса не является взаимно однозначной.
Чтобы определить обратные функции для синуса и косинуса, области этих функций ограничены. Ограничение, которое накладывается на значения домена функции косинуса, составляет 0 ≤ x ≤ π (см. Рисунок 2).Эта ограниченная функция называется косинусом. Обратите внимание на заглавную букву «C» в косинусе.
Рисунок 2
График функции ограниченного косинуса.
Функция обратного косинуса определяется как функция, обратная ограниченной функции косинуса Cos −1 (cos x ) = x ≤ x ≤ π. Следовательно,
Рисунок 3
График функции обратного косинуса.
Тождества для косинуса и обратного косинуса:
Развитие функции обратного синуса аналогично развитию функции косинуса. Ограничение, которое накладывается на значения домена синусоидальной функции, составляет
.
Эта ограниченная функция называется синусом (см. Рисунок 4). Обратите внимание на заглавную букву «S» в синусе.
Рисунок 4). Обратите внимание на заглавную букву «S» в синусе.
Рисунок 4
График ограниченной синусоидальной функции.
Обратная функция синуса (см. Рисунок 5) определяется как функция, обратная ограниченной функции синуса y = Sin x ,
Рисунок 5
График функции обратной синусоиды.
Следовательно,
Идентичности для синуса и обратного синуса:
Графики функций y = Cos x и y = Cos −1 x являются отражениями друг друга относительно линии y = x . Графики функций y = Sin x и y = Sin −1 x также являются отражениями друг друга относительно линии y = x (см. Рисунок 6).
Рисунок 6
Симметрия обратных синуса и косинуса.
Пример 1: Используя рисунок 7, найдите точное значение Cos −1 .
Рисунок 7
Чертеж для примера 1.
Таким образом, y = 5π / 6 или y = 150 °.
Пример 2: Используя рисунок 8, найдите точное значение Sin −1 .
Рисунок 8
Рисунок для примера 2.
Таким образом, y = π / 4 или y = 45 °.
Пример 3: Найдите точное значение cos (Cos −1 0,62).
Используйте тождество косинус-обратный косинус:
Функция обратного косинуса
Функция обратного косинуса
Функция y = cos
-1 x = arccos x и ее график:
Поскольку y = cos -1 x является обратной функцией y = cos x, функция y = cos -1 x тогда и только тогда, когда cos y = x .Но поскольку y = cos x не является взаимно однозначным, его область определения должна быть ограничена, чтобы y = cos -1 x был функцией. Чтобы получить график y = cos -1 x, начните с графика y = cos x. | |
Ограничить область действия функции однозначной областью — обычно используется (выделено красным справа) для cos -1 x. Это оставляет диапазон ограниченной функции неизменным как [-1, 1]. | |
Отразите график поперек линии y = x, чтобы получить график. Обратите внимание, что y = cos -1 x имеет домен [-1, 1] и диапазон. Он строго убывает на всей своей территории. . | |
| Итак, когда вы попросите калькулятор построить график y = cos -1 x, вы получите график, показанный справа.(Окно просмотра составляет [-2, 2] x [-0,5, 3,5].) |
Вычисление y = cos
-1 x:
Вычисление cos -1 x выражений следует той же процедуре, что и вычисление sin -1 x выражений — вы должны знать домен и диапазон функции! Вот пример:
Пример 1: Оценить cos
-1 (-1/2)
Если y = cos -1 (-1/2), то cos y = -1/2.Это уравнение имеет бесконечное количество решений, но только одно из них () находится в диапазоне cos -1 x. Таким образом:
.
Это показано на рисунке справа. Вертикальные красные линии указывают некоторые места, где y = -1/2, но только одно (сплошная красная линия) находится в пределах области y = cos -1 x (что есть).
Производная y = cos
-1 x:
Производная cos -1 x: (Производная по существу такая же, как и для sin -1 x.)
График y = cos -1 x и его производной показан справа. Обратите внимание, что, поскольку cos -1 x является строго убывающей функцией, ее производная всегда отрицательна.
Интегралы, включающие функцию обратного косинуса:
Ну нет! Поскольку производные sin-1x и cos-1x очень похожи (а производная sin-1x проще), стандартной практикой является утверждение:
последнее обновление 6 февраля 2009 г., автор: JL Stanbrough
Функция обратного косинуса — концепция
Поскольку косинус не является взаимно однозначной функцией, диапазон должен быть ограничен значением от 0 до пи, что называется ограниченной косинусной функцией.-1 (x) или arccos (x). Обратные функции меняют местами значения x и y, поэтому диапазон обратного косинуса составляет от 0 до пи, а область — от -1 до 1. При оценке проблем используйте тождества или начинайте с внутренней функции.
Я хочу поговорить об обратной косинусной функции. Начнем с функции y, равной косинусу x. У меня есть график, и вы можете видеть, что y равно косинусу. X — это не функция 1 к 1, и мы можем найти только функции, обратные 1 к 1.Таким образом, мы должны ограничить область определения функции косинуса, и соглашение заключается в том, чтобы ограничить ее этим интервалом от 0 до пи, поэтому позвольте мне нарисовать ограниченную функцию косинуса. Просто эта часть косинусного графика до числа пи и до нуля включительно. Итак, y равен косинусу x для x между 0 и пи, это ограниченная функция косинуса, от 1 до 1, и поэтому мы можем инвертировать его.
И мы называем это обратным y, равным обратному косинусу x, как это читается, этот верхний индекс отрицательный 1 не является показателем, это означает обратный косинус, и эта функция также называется y, равным арккосинусу x.Теперь я хочу изобразить наш косинус или обратный косинус, поэтому я начну с ключевых точек кривой косинуса. У меня 0, 1 пи больше 2, 0 и пи отрицательное 1, это эти 3 ключевые точки, и помните, когда вы строите график обратной функции, вы просто меняете координаты x и y, так что точка 0, 1 становится 1, 0 точка пи больше 2, 0 становится 0 пи больше 2, а точка пи, отрицательная 1, становится отрицательной 1 пи, и это будет где-то здесь. Позвольте мне соединить их, сохранив при этом, что график функции и обратная ей функция должны быть симметричными относительно линии y = x, так что это довольно хороший график.
Теперь очень важна область значений, я отмечу здесь отрицательную единицу, область значений функции обратного косинуса находится между отрицательными 1 и 1, очень важна. И подумайте о том, что функция косинуса может выводить числа только между отрицательными 1 и 1, поэтому имеет смысл, что область определения функции обратного косинуса — это этот интервал, а диапазон будет между 0 и пи, потому что это была область ограниченного функция косинуса и все. Это график области обратного косинуса между отрицательными 1 и 1, диапазон от 0 до пи, и он имеет эти 3 ключевые точки.
Тригонометрическая функция arccos () — обратный косинус — определение математического слова
Тригонометрическая функция arccos () — обратный косинус — определение математического слова — Math Open Reference
Функция arccos является обратной функцией косинуса.
Возвращает угол, косинус которого является заданным числом.
Попробуй это
Перетащите любой
вершине треугольника и посмотрите, как вычисляется угол C с помощью функции arccos ().
Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.Эти обратные функции имеют то же имя, но с дугой впереди.
(На некоторых калькуляторах кнопка arccos может быть обозначена как acos, а иногда и
cos -1 .)
Итак, косинус, обратный cos, равен arccos и т. Д. Когда мы видим «arccos x», мы понимаем его как «угол, косинус которого равен x».
| cos30 = 0,866 | Означает: косинус 30 градусов равен 0,866 |
| arccos 0,866 = 30 | Означает: угол, косинус которого равен 0,866, равен 30 градусам. |
Используйте arccos, если вы знаете косинус угла и хотите узнать фактический угол.
См. Также Обратные функции — тригонометрия
Пример — поиск угла с помощью arccos
На рисунке выше нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что
поэтому нам нужно знать угол, косинус которого равен 0,866, или формально:
С помощью калькулятора находим arccos 0.866 равным 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить
триггерные функции на любой угол, включая большие и отрицательные углы.Но когда мы
Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же косинус.
Например, 45 ° и 360 + 45 ° будут иметь одинаковый косинус. Подробнее об этом см.
Обратные тригонометрические функции.
Чтобы решить эту проблему,
диапазон
обратных триггерных функций ограничены
таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и домен arccos
Напомним, что область определения функции — это набор допустимых входных данных для нее.Диапазон — это набор возможных выходов.
Для y = arccos x:
По соглашению диапазон arccos ограничен от 0 до + 180 °.
Итак, если вы используете калькулятор для решения, скажем, arccos 0,55, из бесконечного числа возможностей он вернет 56,63 °,
тот, который находится в диапазоне функции.
Что попробовать
- На рисунке выше нажмите «сбросить» и «скрыть детали».
- Отрегулируйте треугольник до нового размера
- Используя функцию arccos, вычислите значение угла C из длин сторон
- Нажмите «показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
.
