Содержание
Антимагия. Квадратное уравнение с чётным вторым коэффициентом. | Партизанская математика
В прошлой статье из серии Антимагия мы показали, как решаются квадратные уравнения в общем виде. Там мы рассмотрели, что такое дискриминант, откуда он появляется и зачем он нужен.
Однако помимо общей формулы для решения квадратных уравнений есть и частные случаи, для которых есть свои более удобные способы решения. В первую очередь это касается случая, когда второй коэффициент в квадратном уравнении чётный.
*********
Например, решим такое уравнение:
Используем уже знакомый нам алгоритм и постараемся выделить слева полный квадрат:
Обратите внимание, как легко удалось это сделать. За счёт того, что второй коэффициент был чётным, мы сразу выделили множитель 2, который отвечает за удвоение в формуле квадрата двучлена. То есть одночлен с x стал равен 2⋅3⋅x, откуда становится очевидным, что второе слагаемое в двучлене это 3.
Теперь проведём наши рассуждения для более общего случая. Пусть у нас второй коэффициент в квадратном уравнении — чётный. Тогда удобно записать наше уравнение в виде:
Пусть у нас второй коэффициент в квадратном уравнении — чётный. Тогда удобно записать наше уравнение в виде:
Решим это уравнение также через выделение полного квадрата:
Однако, пока мы рассмотрели лишь приведённое квадратное уравнение (то есть такое, в котором коэффициент при равен 1). Для неприведённого уравнения алгоритм такой же, только сначала нам нужно будет разделить его на первый коэффициент. После этого повторим алгоритм поиска корней для полученного уравнения.
Квадратный корень удобно упростить:
В итоге получаем следующие корни:
И окончательный результат для корней:
Есть и другой способ получить ту же самую формулу.
Для уравнения ax²+bx+c=0 мы уже знаем формулы корней
Возьмём теперь уравнение ax²+2kx+c=0 и используем для его решения общую формулу корней.
Далее, на примере первого корня, упростим получившиеся дроби:
Для второго корня результат аналогичен:
Выражение k²—ac называется сокращённым дискриминантом или коротко «дэ на четыре» (т. к. оно в 4 раза меньше обычного дискриминанта).
к. оно в 4 раза меньше обычного дискриминанта).
*********
Сокращённый дискриминант старшеклассники используют не часто. Обычно запоминают формулу для простого дискриминанта и не видят необходимости в поиске корней через сокращённый дискриминант. Или же используют более продвинутые способы решения.
Однако, во многих случаях он может быть полезен.
Например, решим такое уравнение через обычный дискриминант:
Сразу намечаются некоторые вычислительные сложности.
Нужно посчитать 38² (это обычно делается столбиком), потом 4⋅9⋅8 (можно в уме, но на практике чаще тоже считают столбиком), потом вычесть результаты (1444—288, тоже столбиком).
Получается дискриминант равен 1156. Но ведь из него ещё нужно правильно извлечь корень! Мало кто помнит квадрат какого числа равен 1156. Приходится дополнительно находить этот корень подбором по соответствующему алгоритму. Получим, что дискриминант равен 34².
Далее находим сами корни:
С сокращённым же дискриминантом вычисления будут гораздо проще:
38 = 2k, т. е. k = 19
е. k = 19
19² легко посчитать, т.к. квадраты чисел до 20 часто знают наизусть. Вычитание можно выполнить в уме. А что 289 = 17² мы получаем снова благодаря знанию таблицы квадратов.
И сами корни легко ищутся по формулам:
Ещё отметим, что при расчёте через дискриминант с чётным вторым коэффициентом вам всегда нужно будет сокращать дроби на 2. Это лишнее действие, которое при сокращённом дискриминанте отсутствует.
Конечно, чтобы овладеть этим инструментом нужна практика. Обычно ученики ленятся запоминать эту формулу и просто пытаются всё посчитать через обычный дискриминант. Также поначалу они забывают, что в знаменателе уже нет умножения на 2 или что первое слагаемое в числителе не число b, а k (то есть его половина, b/2). В таком случае важно несмотря на ошибки всё равно пробовать решать через сокращённый дискриминант, даже если не удаётся запомнить формулу с первого раза.
Эффективное решение квадратного уравнения | Партизанская математика
Обычно старшеклассники довольно успешно справляются с решением квадратных уравнений через стандартный алгоритм с дискриминантом. Но если мы хотим научиться решать их эффективно, то необходимо знать и другие возможные способы решения.
Но если мы хотим научиться решать их эффективно, то необходимо знать и другие возможные способы решения.
Пусть у нас есть квадратное уравнение:
Первый способ решения самый логичный: найти корни через дискриминант. Для этого есть известный алгоритм и нужно просто явно воспользоваться формулами.
Способ безальтернативен, когда получаются иррациональные корни.
Второй способ: применить похожий алгоритм, но уже используя так называемый «сокращенный» дискриминант. Он более удобен, но подходит только для чётного второго коэффициента (точнее, когда можно выделить множитель 2 из второго коэффициента). Вычисления будут проще, т.к. дискриминант станет в 4 раза меньше.
Этот способ желательно знать. Если использовать обычный дискриминант при чётном втором коэффициенте, то потом приходится вытаскивать множитель 4 из-под корня для дискриминанта и сокращать дробь на 2. По сути это всё равно через пару преобразований приводит к сокращённой версии решения.
Третий способ: использовать теорему Виета. Если корни существуют, мы знаем, чему равны их сумма и произведение.
Если корни существуют, мы знаем, чему равны их сумма и произведение.
Далее мы находим корни подбором, решая указанную систему. Обычно их подбирают, отталкиваясь от произведения. Ведь гораздо проще раскладывать на целые множители, чем разбивать на слагаемые.
Можно модифицировать подбор для случая, когда квадратное уравнение является приведённым (то есть первый коэффициент равен 1). Сначала нужно найти делители свободного члена и постепенно, начиная с самого маленького, подставлять их в уравнение. Если при каком-то из них квадратный трёхчлен обратится в 0, то это число и будет одним из корней. Второй корень легко находим, разделив свободный член на первый корень.
Для использования этого метода нужно знать, что такое теорема Виета, и иметь обширную практику применения. Только тогда данный способ будет быстрее нахождения дискриминанта. Но и здесь есть ограничения в использовании. Во-первых, не всегда получается быстро подобрать корни; во-вторых, этот способ на практике не работает, когда корни иррациональные.
Четвертый способ следует из третьего: использовать особые свойства коэффициентов. Те, кто учится в математических классах, наверняка знают, про красивые соотношения между коэффициентами квадратного уравнения и корнями 1 и –1:
Однако, во-первых, этот способ надо чётко понимать и применять его без ошибок, а во-вторых, его далеко не всегда можно использовать. Но составители задач часто ленятся придумывать новые квадратные уравнения и пользуются указанными соотношениями.
Ученики часто воспринимают как магию этот способ решения. Но на него можно взглянуть и с другой стороны. Попробуйте подставить числа 1 и –1 вместо корней, и проверить, обращается ли квадратный трёхчлен в 0. Если да, то один из корней вы нашли, а второй корень находите по теореме Виета.
Пятый способ: выделение полного квадрата. Этот способ в школьной программе используют как предварительный перед тем, как познакомить школьников с решением через дискриминант. На практике для постоянного использования он не очень хорошо подходит (в общем случае через дискриминант проще).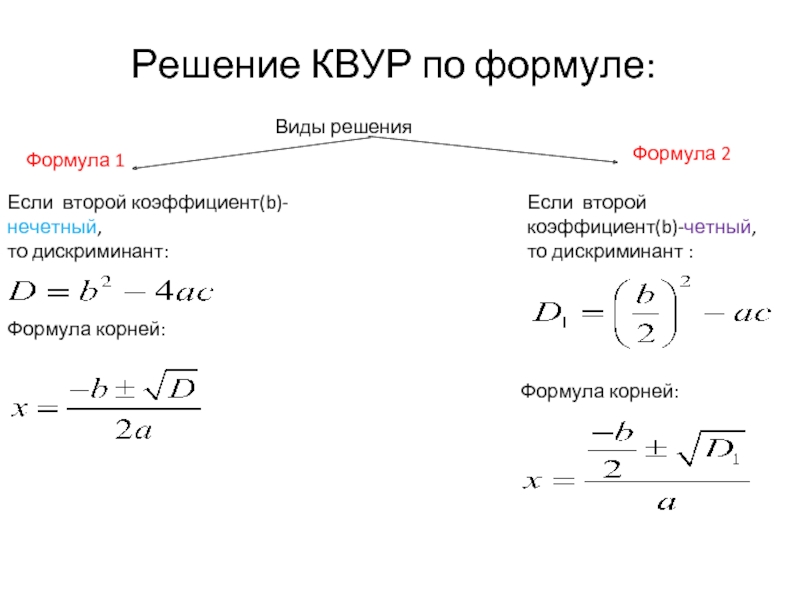 Однако, в случае, когда квадратный трёхчлен – это полный квадрат, нет смысла использовать другие способы. Надо просто свернуть его и устно решить уравнение. Например,
Однако, в случае, когда квадратный трёхчлен – это полный квадрат, нет смысла использовать другие способы. Надо просто свернуть его и устно решить уравнение. Например,
Корни (точнее, корень) находятся мгновенно в отличие от решения через дискриминант.
Шестой способ: метод переброски старшего коэффициента.
Пусть у нас есть уравнение вида:
Для начала решим не его, а уравнение такого вида:
Решаем его любым удобным способом. Полученные корни делим на а. В итоге, получим корни исходного уравнения.
Например,
Седьмой способ: знать ответ. Бывает, что вы прорешали так много квадратных уравнений в разных вариациях, что уже просто ЗНАЕТЕ ответ для некоторых из них. Например, уравнение встречается настолько часто, что корни уже можно выучить. Целенаправленно заучивать корни глупо, но когда это получается автоматически, можно применить и такой способ.
При одинаковом владении каждым из способов наиболее эффективной является следующая последовательность их применения:
- сначала пробуем разглядеть в трёхчлене полный квадрат;
- потом смотрим на зависимости между коэффициентами;
- затем смотрим на второй коэффициент и, если он чётный, решаем через «сокращенный» дискриминант;
- наконец, если указанные методы не сработали, решаем по стандартному алгоритму через дискриминант.

Это самый общий алгоритм, но если вы владеете в совершенстве методом переброски старшего коэффициента или теоремой Виета, то можете их использовать до использования дискриминанта.
Кстати, у теоремы Виета есть одно полезное применение, которое гораздо продуктивнее, чем её использование для подбора корней. Об этом поговорим в следующей статье.
Пример решения иррационального уравнения методом возведения обеих частей в квадрат
Решить иррациональное уравнение
Мы имеем дело с иррациональным уравнением в его простейшем виде с четным показателем корня, то есть, с уравнением , где 2·k – четный натуральный показатель корня, f(x), g(x) – рациональные выражения. В нашем случае k=1, f(x)=1−5·x, g(x)=x−3. Такое иррациональное уравнение можно решить методом возведения обеих частей уравнения в одну и ту же натуральную степень. Напомним алгоритм этого метода решения для простейшего иррационального уравнения с четным показателем корня:
-
Возводим в одну и ту же четную степень, равную показателю корня в левой части уравнения, обе части уравнения.
-
Решаем полученное уравнение. Если оно не имеет решений, то не имеет решений и исходное уравнение. Если решения есть, то отсеиваем посторонние корни.
Пройдем эти шаги.
Решаемое иррациональное уравнение в левой части содержит квадратный корень (показатель корня равен 2), поэтому возводим обе части уравнения в квадрат, что в дальнейшем позволит избавиться от знака корня. Это дает нам уравнение , причем, это уравнение-следствие, так как мы знаем, что возведение обеих частей уравнения в одну и ту же четную степень является преобразованием, приводящим к уравнению-следствию.
Теперь нам нужно решить полученное уравнение . Его решение будем вести через преобразование уравнений.
На базе определения корня заменим выражение в левой части уравнения тождественно равным выражением 1−5·x, и, учитывая формулу сокращенного умножения «квадрат разности», выражение в правой части заменим тождественно равным ему выражением x2−6·x+9. Это нас приводит к уравнению 1−5·x=x2−6·x+9. Заметим, что при таком переходе происходит расширение ОДЗ: для уравнения ОДЗ определяется условием 1−5·x≥0, которое задает числовое множество x≤1/5, а для полученного уравнения 1−5·x=x2−6·x+9 ОДЗ, очевидно, есть множество всех действительных чисел R. Значит, проведенные преобразования дают уравнение-следствие.
Это нас приводит к уравнению 1−5·x=x2−6·x+9. Заметим, что при таком переходе происходит расширение ОДЗ: для уравнения ОДЗ определяется условием 1−5·x≥0, которое задает числовое множество x≤1/5, а для полученного уравнения 1−5·x=x2−6·x+9 ОДЗ, очевидно, есть множество всех действительных чисел R. Значит, проведенные преобразования дают уравнение-следствие.
Дальше полученное уравнение 1−5·x=x2−6·x+9 путем равносильных преобразований, заключающихся в переносе слагаемых с противоположным знаком, группировке и приведении подобных слагаемых, а также умножении обеих частей уравнения −1, приводится к квадратному уравнению x2−x+8=0.
Полученное квадратное уравнение решим через дискриминант. Вычисляем дискриминант: D=(−1)2−4·1·8=−31. Так как дискриминант отрицательный, то квадратное уравнение не имеет действительных корней.
Итак, уравнение x2−x+8=0 не имеет корней. Так как это уравнение является следствием исходного уравнения (в цепочке преобразований были переходы к уравнениям-следствиям), то исходное иррациональное уравнение тоже не имеет корней.
Так как это уравнение является следствием исходного уравнения (в цепочке преобразований были переходы к уравнениям-следствиям), то исходное иррациональное уравнение тоже не имеет корней.
Обычно решение описывается как можно более коротко, но, естественно, без ущерба для логики действий:
Презентация по алгебре (8 класс) на тему «Вторая формула корней квадратного уравнения»
Формула корней квадратного уравнения.
Решите уравнение: 8х2 – 22х – 6 = 0
Рассмотрим способ решения, где вычисления можно упростить.
b = – 22 = 2 ∙ (– 11)
D = b2 – 4ac = (2 ∙ (– 11))2 – 4 ∙ 8 ∙ (– 6) =
=4 ∙ (– 11)2 – 4 ∙ (– 48) = 4 ∙ (121 – (– 48)) = 4 ∙ 169
= = = = = = = ;
= = = = = = = 3.
Рассмотрим уравнение ах2 + bх + c = 0,
Пусть второй коэффициент четное число b = 2k
Тогда дискриминант
D = b2 – 4ac = (2k)2 – 4 ас = 4 ∙ k2 – 4 ас =
= 4 ∙ (k2 – ас)
D1 = k2 – ас, тогда D = 4 ∙ (k2 – ас) = 4D1
= = = =
= =
= = = =
= =
Если b = 2k, то k = . Заменим в новых формулах k на .
Заменим в новых формулах k на .
D1 = k2 – ас = – ас, то есть D1 = – ас
= = ; = =
Очевидно, что если D1 < 0 то квадратное уравнение не имеет корней.
Выполнить № 449 (в,г), 450 (в,г), 453* (б)
Ответьте на вопросы.
1. Как вычислить дискриминант квадратного уравнения с четным коэффициентом b?
2. По каким числам вычисляются корни квадратного уравнения с четным коэффициентом b?
Домашнее задание:
п. 3.3, № 449 (а,б), 450 (а,б), 453* (а).
3.3, № 449 (а,б), 450 (а,б), 453* (а).
Конспект урока «Решение квадратных уравнений с четным вторым коэффициентом»
Конспект урока
Учитель: Терехова Любовь Петровна
Предмет: Алгебра
УМК:
Класс: 8
Дата урока: 22.12.2015 г.
Тема: Решение квадратных уравнений с четным вторым коэффициентом.
Тип урока: открытие новых знаний
Цель:
Образовательные: вывести формулу (II) нахождения корней квадратного уравнения с четным вторым коэффициентом, формировать умение применять формулы I и II для решения квадратных уравнений.
Воспитательные:
Формирование основ саморазвития и самовоспитания, умения вести диалог с учителем, с одноклассниками, находить общие цели и сотрудничать для их достижения.
Развивающие: формирование логического мышления, умения преодолевать трудности при решении задач, развитие любознательности.
Оборудование: учебник, плакат с формулой II.
Ход урока.
Организационный момент.
Устная работа
Назовите коэффициенты a, b, c уравнений:
А) 4х2 -5х – 7 =0
Г) 8 – 9х2 = 0
Б) х2 + 2 – 3х = 0
Д) 11х2 = 0
В) 3х2 + 2х = 0
Е) 17 – х2 – х = 0
Решите уравнения
А) 2х2 – 18 = 0
В) х2 + 16 = 0
Б) 3х2 – 12х = 0
Г) 3,6 х2 = 0
Сколько корней имеет уравнение
А) 6х2 – 5 х = 0 | В) 3 х2 – 4= 0 |
Б) х2 – 4 х + 4 = 0 | Г) 2х2 + 7 = 0 |
Объяснение нового материла
Создание проблемной ситуации.

Учащимся предлагается для решения квадратное уравнение 15х2 – 34 х + 15 = 0. Используя формулу нахождения корней квадратного уравнения, получаем:
D = (-34)2 – 4*5*15 = 1156 – 900 = 256.
X1 = = = =
X2 = = = =
Решая это уравнение, учащиеся вынуждены проводить вычисления достаточно громоздкие, в отличие от ранее решаемых уравнений.
После этого сообщается учащимся, что для решения квадратных уравнений, у которых второй коэффициент четный, существует другая формула корней, позволяющая упростить вычисления.
Вывод этой формулы проводится согласно пункту учебника. Причем в сильном классе предлагается учащимся сделать это самостоятельно, записав только общий вид такого уравнения:
ах2 + 2 * k * х + с = 0 (b = 2k).
После вывода формулы возвращаемся к решенному уравнению и применяем новую формулу:
D = (-17)2 – 15 * 15 = 289 – 225 = 64.
X1 = = = =
X2 = = = =
Как видим, вычисления можно произвести «в уме», так как все значения квадратов чисел – табличные.
На доску можно вывести:
a2 + kx + c = 0, a ≠ 0
D1 = k2 – ac.
Если D1 = 0, то x = —
Если D1 0, х =
Обращаем внимание учащихся, что D1 в четыре раза меньше, чем D.
Физкультминутка.
Формирование умений и навыков.
Все задания, решаемые на этом уроке, можно разбить на три группы:
1-ая группа. Задания на непосредственное применение формулы (II) корней квадратного уравнения: № 539 (б,г,ж), 540 (в,з).
При решении этих заданий демонстрируем учащимся применение новой формулы для случая, когда корни уравнения являются иррациональными. Для этого вызываем двух учеников к доске и параллельно проводим решение по разным формулам.
Таким образом, получаем такие же корни.
2-ая группа. Задания с выбором формулы (I или II) корней квадратного уравнения в зависимости от второго коэффициента: № 541 (б,в,ж), 546 (а,г), 552 (а,в), 553 (а).
3-я группа. Задания повышенной трудности: № 554 (задача-исследование), 555 можно предложить сильным учащимся, сократив для них количество заданий 1-ой и 2-ой групп.
Можно предположить, что корни уравнений ax2 + bx + c = 0 и cx2 + bx + a = 0 являются взаимно обратными числами. Докажем это.
Чтобы выделить количество корней, необходимо оценить дискриминант. выделим в выражении квадрат двучлена:
D = (a2 – 2 * 2 * a + 4) + 12 = (a – 2)2 + 12.
Дискриминант принимает положительные значения при любом a (точнее D ≥ 12), значит, при любом а уравнение имеет два корня.
Ответ: а) нет; б) нет; в) при любом а.
Итоги урока.
— В каких случаях применяется формула II корней квадратного уравнения?
— В каком отношении находятся D1 и D?
— По какой формуле вычисляется D1?
— Можно ли применять формулу I корней квадратного уравнения, если коэффициент b четный?
— Могут ли получиться разные корни при применении различных формул корней квадратного уравнения?
Домашнее задание: № 539 (в,е,з), 540 (б,е,ж), 541 (е,з), 548 (б,г), 551 (а,г,д).
Рефлексия: Прием «Мордашки»: у каждого ученика на столе 3 карточки
Нужно показать ту, которой соответствует настроение в данный момент.
Квадратные уравнения: приведённые уравнения, формулы корней
Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:
ax2 + bx + c = 0 — квадратное уравнение,
где x — это неизвестное, а a, b и c — коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, а c называется известным или свободным членом.
Уравнение:
ax2 + bx + c = 0
называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.
Приведённое квадратное уравнение
Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:
Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:
| если | b | = p, а | c | = q, |
| a | a |
то получится x2 + px + q = 0.
Уравнение x2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.
Например, уравнение:
x2 + 10x — 5 = 0
является приведённым, а уравнение:
-3x2 + 9x — 12 = 0
можно заменить приведённым уравнением, разделив все его члены на -3:
x2 — 3x + 4 = 0.
Решение квадратных уравнений
Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:
ax2 + bx + c = 0;
ax2 + 2kx + c = 0;
x2 + px + q = 0.
Для каждого вида уравнения есть своя формула нахождения корней:
| Вид уравнения | Формула корней | ||||
|---|---|---|---|---|---|
| ax2 + bx + c = 0 | |||||
| ax2 + 2kx + c = 0 | |||||
| x2 + px + q = 0 |
|
Обратите внимание на уравнение:
ax2 + 2kx + c = 0
это преобразованное уравнение ax2 + bx + c = 0, в котором коэффициент b — четный, что позволяет его заменить на вид 2k.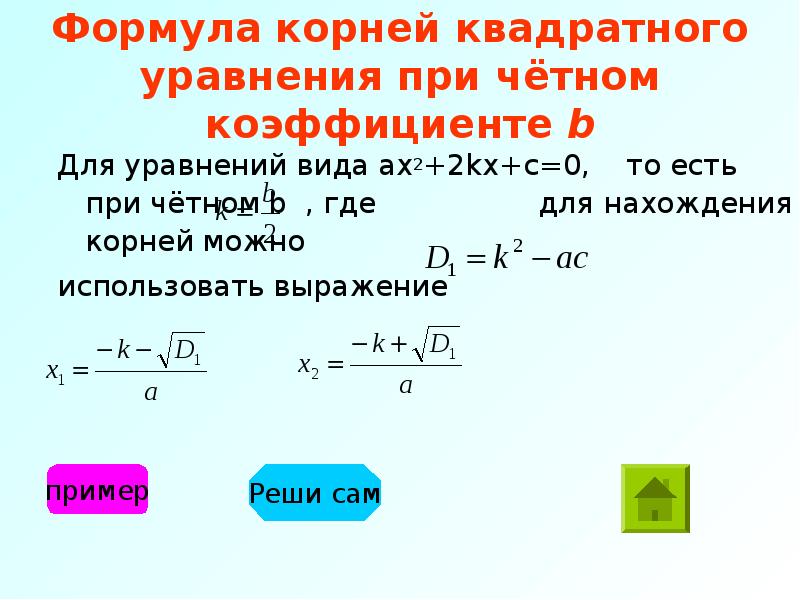 Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Пример 1. Решить уравнение:
3x2 + 7x + 2 = 0.
Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:
a = 3, b = 7, c = 2.
Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:
| x1 = | -2 | = — | 1 | , x2 = | -12 | = -2 |
| 6 | 3 | 6 |
Пример 2:
x2 — 4x — 60 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -4, c = -60.
Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:
x1 = 2 + 8 = 10, x2 = 2 — 8 = -6
Ответ: 10, -6.
Пример 3.
y2 + 11y = y — 25.
Приведём уравнение к общему виду:
y2 + 11y = y — 25;
y2 + 11y — y + 25 = 0;
y2 + 10y + 25 = 0.
Определим, чему равны коэффициенты:
a = 1, p = 10, q = 25.
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:
Ответ: -5.
Пример 4.
x2 — 7x + 6 = 0.
Определим, чему равны коэффициенты:
a = 1, p = -7, q = 6.
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:
x1 = (7 + 5) : 2 = 6,
x2 = (7 — 5) : 2 = 1.
Ответ: 6, 1.
Приведение кубических уравнений к трехчленному виду
Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.
Квадратным уравнением называется уравнение вида
,
Где x — переменная, a, b, c — постоянные (числовые) коэффициенты.
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
| Формула дискриминанта: | .
|
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
- D>0 — уравнение имеет 2 различных вещественных корня
- D=0 — уравнение имеет 2 совпадающих вещественных корня
- D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)
В общем случае корни уравнения равны:
.
Очевидно, в случае с нулевым дискриминантом, оба корня равны
.
Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:
В таком случае корни уравнения вычисляются по формуле:
Теорема Виета.
Приведенным квадратным уравнением называется уравнение вида ,
то есть квадратное уравнение с единичным коэффициентом при старшем члене.
В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:
Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене,
то есть при х2.
Квадратное уравнение имеет вид:
Стандартный метод нахождения корней уравнения происходит в два этапа. Сначала вычисляется дискриминант уравнения по формуле
Затем считаются корни по формуле
Данный онлайн калькулятор решает квадратные уравнения именно таким способом.
**********
Если известны корни уравнения, то исходный многочлен можно разложить на множители:
В ряде задач удобно использовать теорему Виета, которая выглядит следующим образом:
********************************************************************
Как решать квадратные уравнения? Дискриминант. http://www.egesdam.ru/page221.html
Поработаем с квадратными уравнениями. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:
Например:
Здесь а =1; b = 3; c = -4
Или:
Здесь а =2; b = -0,5; c = 2,2
Или:
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:
Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня – и есть тот самый дискриминант. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Вот и всё.
Какие случаи возможны при использовании этой формулы? Всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:
Например, вот так:
Или так:
Это неполные квадратные уравнения. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с.
Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0, или х = 4
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.
Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х = +3 и х = -3.
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает? Допустим, после всяких преобразований вы получили вот такое уравнение:
Что это означает? Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т. е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом, равен -1. Значит, всё верно!
е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
|
Справочник по математике | Алгебра | Кубические уравнения |
Решение кубических уравнений. Формула Кардано
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)
| (1) |
где — произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент . Тогда оно примет вид
| (2) |
где — произвольные вещественные числа.
Заменим в уравнении (2) переменную на новую переменную по формуле:
| (3) |
Тогда, поскольку
то уравнение (2) примет вид
| (4) |
Если ввести обозначения
то уравнение (4) примет вид
| (5) |
где — вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Дискриминант квадратного уравнения — Концепция
Дискриминант — это часть формулы корней квадратного уравнения. Дискриминант квадратного уравнения важен, потому что он сообщает нам количество и тип решений. Эта информация полезна, потому что она служит двойной проверкой при решении квадратных уравнений любым из четырех методов (факторизация, завершение квадрата, использование квадратных корней и использование формулы квадратного уравнения).
Дискриминант квадратного уравнения является частью формулы корней квадратного уравнения. На самом деле это та часть, которая лежит под квадратным корнем. Итак, различение, которое вы услышите, это b в квадрате минус 4ac, что, надеюсь, выглядит знакомо, потому что вы знаете формулу квадратичного уравнения. И действительно, что делает дискриминант, так это то, что он сообщает нам, какой тип решения и количество решений будут у наших квадратных уравнений.Он не говорит нам, что это такое. Он просто сообщает нам тип и номер. ХОРОШО?
Итак, различение, которое вы услышите, это b в квадрате минус 4ac, что, надеюсь, выглядит знакомо, потому что вы знаете формулу квадратичного уравнения. И действительно, что делает дискриминант, так это то, что он сообщает нам, какой тип решения и количество решений будут у наших квадратных уравнений.Он не говорит нам, что это такое. Он просто сообщает нам тип и номер. ХОРОШО?
Как это работает, есть четыре сценария. Я предпочитаю не запоминать их, но я собираюсь пройтись по каждому из них, а затем вы можете использовать логику или запомнить их, чтобы как бы понять их.
Хорошо. Итак, какой может быть дискриминант? Есть разные варианты. Во-первых, он будет больше нуля и будет точным квадратом. Под этим я подразумеваю 16, 25, любое число больше нуля и полный квадрат.
Итак, дискриминант — это то, что находится под квадратным корнем, поэтому, если это точный квадрат, вы сможете извлечь из него квадратный корень, а наш квадратный корень исчезнет из нашей формулы квадратичного уравнения. Это говорит нам о том, что у нас есть два рациональных решения. Идеальный квадрат. Вы можете извлечь квадратный корень. Квадратный корень уходит.
Это говорит нам о том, что у нас есть два рациональных решения. Идеальный квадрат. Вы можете извлечь квадратный корень. Квадратный корень уходит.
Хорошо, дискриминант больше нуля, а не точный квадрат. Итак, это будет примерно 10, 20 или что-то в этом роде, где мы не можем извлечь квадратный корень.Это говорит нам о том, что мы помещаем его под знаком квадратного корня. Наш квадратный корень никуда не денется.
У нас все еще есть квадратный корень из числа, из которого мы можем извлечь квадратный корень, так что в итоге мы получим два иррациональных числа. Итак, у нас есть квадратный корень, плюс квадратный корень минус квадратный корень. Итак, у нас есть два иррациональных решения.
Дискриманент равен нулю. Хорошо, с точки зрения нашей формулы квадратиков это приводит к исчезновению всего квадратного корня.Итак, у вас есть плюс или минус квадратный корень из нуля, исчезает, и мы просто остаемся с отрицательным b над 2a.
Итак, в этом случае у нас есть одно рациональное решение, одно дробное решение. И последний сценарий для нашего дискриминанта — меньше нуля. Хорошо, это означает отрицательное число. Дискриминант отрицательный, что означает, что квадратный корень отрицателен, что означает, что у нас есть два воображаемых решения.
И последний сценарий для нашего дискриминанта — меньше нуля. Хорошо, это означает отрицательное число. Дискриминант отрицательный, что означает, что квадратный корень отрицателен, что означает, что у нас есть два воображаемых решения.
Квадратный корень отрицательного числа — мнимое число. И поэтому у нас не будет никаких реальных решений; у нас просто будут воображаемые решения.ОК.
Итак, дискриминант — это то, что стоит под квадратным корнем в квадратной формуле, и он говорит нам о количестве и типе решений для этого квадратного уравнения.
Вы можете запомнить эти четыре разные вещи. В общем, я просто предпочитаю использовать логику, хорошо? Знайте, что такое дискриминант, знайте, что он находится под квадратным корнем, а затем вы знаете, как квадратный корень ведет себя достаточно, чтобы иметь возможность вывести их в любое время, когда вам нужно.
Как найти решение неизвестной переменной с помощью дискриминанта?
.2 + 4k + 24 = 4k + 24 #
Чтобы иметь два решения для # x #:
# 4k + 24> 0 #, то есть #k> (- 6) #
Чтобы иметь одно решение для # x #:
# 4k + 24 = 0 #, то есть # k = -6 #
Более подробное объяснение:
‘ _ _ _ _ _ _ _ 9___
Помните, что ваша функция # y # как функция от # x #. 2 + 12x + 4 [-1,3145, 0,333, -0,136, 0,688]}
2 + 12x + 4 [-1,3145, 0,333, -0,136, 0,688]}
Как видите, график касается оси # x # только при найденном нами значении # x #. Следовательно, у вас есть только одно решение.
Что касается вашего вопроса о проверке значений # k # в уравнении, если вы это сделаете, это либо подтвердит, что у вас правильный ответ, либо сообщит, что вы, возможно, допустили ошибку. Это неплохая идея.
Определение и примеры дискриминанта | определить дискриминатор — алгебра 1
Определение дискриминанта
Дискриминант уравнения дает представление о количестве корней и природе корней уравнения.
Если ax 2 + bx + c = 0 является квадратным уравнением, то Дискриминант уравнения, то есть D = b 2 — 4ac.
Подробнее о дискриминанте
Если дискриминант (D) равен 0, то уравнение имеет одно действительное решение.
Если D> 0, то уравнение имеет два действительных решения.
Если D <0, = "" then = "" the = "" уравнение = "" имеет = "" два = "" мнимые = "" решения. = «»>
= «»>
Пример дискриминанта
Природу корней уравнения 6x 2 + 11x — 2 = 0 можно определить с помощью дискриминанта D = b 2 — 4ac.6×2 + 11x — 2 = 0
D = b 2 — 4ac = (11) 2 — 4 (6) (2) [Подставить значения.]
D = 121 — 48 = 73> 0
При D> 0 данное уравнение имеет 2 действительных решения.
Видео примеры: Бесплатные уроки математики Дискриминант
Решенный пример на дискриминанте
Вопрос: Узнайте, сколько решений имеет данное уравнение, используя его дискриминант. Проверьте, являются ли решения реальными или мнимыми.
36×2 + 132x + 121 = 0
Выбор:
A. 1 действительное и 1 мнимое решение
Б. 2 реальных решения
C. 2 воображаемых решения
D. Ничего из вышеперечисленного
Правильный ответ: D
Решение:
Шаг 1: 36x 2 + 132x + 121 = 0
Шаг 2: Сравните уравнение со стандартной формой ax 2 + bx + c = 0, чтобы получить значения a, b и c.
Шаг 3: b 2 — 4ac = (132) 2 — 4 (36) (121) [Подставьте значения.]
Шаг 4: = 17424 — 17424 = 0 [Упростить.]
Шаг 5: Поскольку дискриминант равен нулю, квадратное уравнение имеет одно действительное решение.
Кратности дискриминантов
Множественность дискриминантов
Проблема множественности
Что означает дискриминант?
Концепция чего-либо
дискриминанты
происходит от латинского слова «discinare»,
что означает «различать».До первой четверти 20 века
считалось, что
поля алгебраических чисел с фиксированной сигнатурой и группой Галуа
можно однозначно с точностью до изоморфизмов идентифицировать целочисленным значением
дискриминанта их максимального порядка.
В таком случае,
неизоморфные поля могут быть однозначно выделены
дискриминант.
Например, даже известный математик
Э. АРТИН примерно в 1925 г. предположил, что
можно показать, используя теорию полей классов,
что неизоморфные поля никогда не имеют совпадающих дискриминантов.Это действительно верно для квадратичных полей.
Катастрофа:
Однако это была не что иное, как теория поля классов,
который предоставил первый
встречные примеры
для этой гипотезы
в фундаментальной работе
А. ШОЛЬЦ, О. ТАУСКИЙ.
[1]
примерно в 1930 г.
в виде некоторых
семейства 4 неизоморфных комплексных кубических полей
с тем же дискриминантом d,
е. грамм. d = -3299, -3896, -4027, -5703.
грамм. d = -3299, -3896, -4027, -5703.
Эти и многие другие примеры
также исследуются в моей статье
[2]
Обычно мы называем количество неизоморфных полей
с фиксированной подписью и группой Галуа
разделяя общий дискриминант d
кратность m дискриминанта d.
Позже строительство все более обширного
столы
кубических полей сигнатур (1,1) и (3,0)
с помощью главных компьютеров
раскрытый
другие примеры семей с высшим
дискриминантные кратности m = 2,3,4,6,9.
Некоторые ошибки в таких таблицах вызвали большую путаницу в отношении
кратность m = 5.
В последнее время даже
квинтик поля
с m = 2.
Начало теории множественности:
Два основных метода
вывод точных формул для
кратность m
кубических дискриминантов обусловлены
- к
ЧАС. HASSE
HASSE
(1930) с помощью
теория поля классов
связанных
нормальные поля
[3]
- к
Х. РЕЙХАРДТ
(1933) с помощью
Теория Куммера
связанных
радикальные поля
[4]
Доступ REICHARDT по сути можно узнать
уже в 1925 г. в статье
W.Э. Х. БЕРВИК
[5]
и был разработан
Ж. МАРТИНЕ и Ж.-Ж. Паян
[6]
,
[7]
в 1965 г.
Текущая теория множественности:
В 1990 году я обобщил идею HASSE для
двугранные поля
степени 2p
с простым числом p> 2
[8]
а в 1991 г. вместе с
вместе с
Пьер БАРРУКАН
в Париже
для
чистые метациклические поля
степени p (p-1)
[9].Результат был
огромное количество
новые формулы для кратности m
в зависимости от инвариантов
ассоциированных квадратичных полей k,
такой как:
Формулы Д. К. Майера:
m = p r (p-1) u |
m = p r + w (p-1) u |
Здесь r обозначает ранг p-класса k,
t, u и v соответственно
количество всех, бесплатных и ограничительных
простые делители проводника,
w = 0,1 индикатор для
неправильный простой делитель 3 проводника,
n = p + 1 количество гиперплоскостей
2-мерное p-векторное пространство,
и a (1), …, a (n) разбиение v
на числа простых делителей проводника
связанные с гиперплоскостями.Некоторые приложения для кубического случая p = 3 даются формулами
3-сети над полями квадратичных чисел с 3-классным рангом r = 2.
Формулы П. БАРРУКАНДА и Д. К. МЕЙЕРА:
м = (п-1) т |
m = (p-1) u [(p-1) v — (-1) v ] / p |
m = (p-1) u [(p-1) v-1 — (-1) v-1 ] / p |
Самые последние результаты см. В моей серии
В моей серии
Венский конгресс 2001.
Библиография:
[1]
А. Шольц и О. Таусский,
Die Hauptideale der kubischen Klassenkörper
Imaginär-quadratischer Zahlkörper:
ihre rechnerische Bestimmung und
ihr Einfluß auf den Klassenkörperturm,
Дж.Рейн Энгью. Математика. 171 (1934), 19–41[2]
Д. К. Майер,
Принципализация в комплексе S 3 -поля,
Материалы двадцатой конференции Манитобы по
Вычислительная математика и вычисления (Виннипег, МБ, 1990),
Congr. Нумер. 80 (1991), 73-87[3]
ЧАС. Хассе,
Хассе,
Arithmetische Theorie der kubischen Zahlkörper
auf klassenkörpertheoretischer Grundlage,
Математика. З. 31 (1930), 565-582[4]
Х. Райхардт,
Arithmetische Theorie der kubischen Zahlkörper
как Radikalkörper,
Монатш.Математика. Phys. 40 (1933), 323-350[5]
В. Э. Х. Бервик,
На кубических полях с заданным дискриминантом
Proc. Лондонская математика. Soc., Сер. 2, 23 (1925), 359-378[6]
Ж. Мартине,
Sur l’arithmétique des extension galoisiennes
à groupe de galois dieral d’ordre 2p,
Аня. Inst. Фурье, Гренобль 19 (1963), 1-80
Inst. Фурье, Гренобль 19 (1963), 1-80[7]
Ж. Мартине и Ж.-Ж. Паян,
Sur les extension cubiques non-Galoisiennes
de rationels et leur clôture Galoisienne,
J. Reine Angew. Математика. 228 (1965), 15-37[8]
Д.К. Майер,
Кратности диэдральных дискриминантов,
Математика. Комп. 58 (1992), нет. 198, 831-847
и Дополнения к разделу S55-S58[9]
Д. К. Майер,
Дискриминанты метациклических полей,
Канад. Математика. Бык. 36 (1) (1993), 103-107
Вернуться к
Домашняя страница Дэниела С. Майера.
Майера.
Опции дискриминантного анализа
Меню красного треугольника дискриминантного анализа содержит следующие параметры:
Пошаговый выбор переменной
(Недоступно для метода Wide Linear.) Отображает или скрывает панель управления «Выбор столбца».Эта панель управления содержит параметры, которые позволяют выполнять пошаговый выбор переменных с использованием ковариационного анализа и p-значений. См. Пошаговый выбор переменной.
Дискриминантный метод
Задает метод дискриминанта. Выберите линейный, квадратичный, регулярный или широкий линейный. См. Раздел «Дискриминантные методы».
Дискриминантные баллы
Показывает или скрывает таблицу оценок дискриминанта для каждой строки.
Параметры оценки
Предоставляет возможности для оценки наблюдений.В частности, вы можете сохранить формулы подсчета очков. См. Параметры оценки.
См. Параметры оценки.
Канонический сюжет
Показывает или скрывает канонический график. См. Канонический сюжет и Каноническая структура.
Канонические параметры
Предоставляет параметры, влияющие на канонический график. См. Канонические параметры.
Канонический 3D-график
Показывает трехмерный канонический сюжет. Этот параметр доступен только при наличии четырех или более уровней категориального сертификата X.См. Пример канонического 3D-графика.
Приоры указать
Позволяет указать априорные вероятности для каждого уровня переменной X. См. Раздел «Указание приоритетов».
Рассмотрим новые уровни
Указывает, что некоторые точки могут не входить ни в одну из известных групп и должны считаться из новой группы без оценок. См. «Рассмотрение новых уровней».
Показать внутри ковариаций
Показывает или скрывает эти отчеты:
— Отчет о ковариационных матрицах, который дает объединенные ковариационные и корреляционные матрицы.
— Для квадратичных и регуляризованных методов отчет «Корреляции для каждой группы», который показывает матрицы внутригрупповой корреляции.
Для каждой группы также отображается журнал определителя внутригрупповой ковариационной матрицы.
— Для метода квадратичного дискриминанта добавляет схему групповых ковариаций в отчет «Матрицы ковариации», который показывает матрицы внутригрупповой ковариации.
Показать в пределах ковариаций недоступен для метода широкополосного линейного дискриминанта.
Показать групповые средства
Показывает или скрывает отчет «Средние значения группы», который предоставляет среднее значение каждой ковариаты. Появляются средние значения для каждого уровня переменной X и общие средние значения.
Сохранить матрицы дискриминга
Сохраняет сценарий Discrim Results в таблицу данных. Скрипт представляет собой список следующих объектов для использования в JSL:
— список ковариат (Ys)
— категориальная переменная X
— список уровней X
— матрица средних ковариат по уровням X
— объединенная ковариационная матрица
Сохранить матрицы дискриминанта недоступно для метода широкополосного линейного дискриминанта. См. Раздел «Сохранить матрицы дискриминга».
См. Раздел «Сохранить матрицы дискриминга».
Матрица диаграммы рассеяния
Открывает отчет «Матрица диаграммы рассеяния», в котором отображается матрица с диаграммой рассеяния для каждой пары ковариат. Эта опция вызывает платформу матрицы рассеяния с закрашенными эллипсами плотности для каждой группы. Диаграммы рассеяния включают все наблюдения в таблице данных, даже если используется проверка. См. Матрица диаграммы рассеяния.
Недоступно для метода широколинейного дискриминанта.
Профайлер
Показывает или скрывает интерактивный отчет профилировщика, в котором вероятности категорий объединены в одну строку профилировщика.Изменения значений факторов отражаются в оценках вероятностей классификации. Дополнительные сведения о параметрах меню с красным треугольником см. В разделе Параметры профилировщика прогнозов в профилировщиках.
Дополнительные сведения о следующих параметрах см. В разделах «Фильтры локальных данных в отчетах», «Меню повтора» в отчетах и «Меню сохранения сценария» в отчетах в разделе «Использование JMP»:
В разделах «Фильтры локальных данных в отчетах», «Меню повтора» в отчетах и «Меню сохранения сценария» в отчетах в разделе «Использование JMP»:
Фильтр локальных данных
Показывает или скрывает локальный фильтр данных, позволяющий фильтровать данные, используемые в конкретном отчете.
Повторить
Содержит параметры, позволяющие повторить или перезапустить анализ. На платформах, поддерживающих эту функцию, параметр «Автоматический пересчет» немедленно отражает изменения, которые вы вносите в таблицу данных в соответствующем окне отчета.
Сохранить сценарий
Содержит параметры, позволяющие сохранить сценарий, воспроизводящий отчет, в нескольких местах назначения.
Скрипт сохранения по группам
Содержит параметры, позволяющие сохранить сценарий, воспроизводящий отчет платформы для всех уровней переменной «По», в нескольких местах назначения.Доступно, только если в окне запуска указана переменная By.
Дискриминантная алгебра в когомологиях
Аннотация
Инварианты инволюций на центральных простых алгебрах широко изучены. Многие важные результаты были собраны и расширены Knus, Merkurjev, Rost и Tignol в «Книге инволюций» [BI]. К таким инвариантам относятся, например, (четная) алгебра Клиффорда для инволюций первого рода и дискриминантная алгебра для инволюций второго рода на алгебре четной степени.В своем препринте «Триальность, коциклы, скрещенные произведения, инволюции, алгебры Клиффорда и инварианты» [S05] Салтман показывает, что определение алгебры Клиффорда может быть обобщено на алгебры Адзумая, и вводит специальные когомологии, так называемые когомологии GH, описать его структуру. В этой диссертации мы доказываем аналогичные результаты о дискриминантной алгебре D (A; [tau]), которая является алгеброй инвариантов относительно специального автоморфизма второго порядка [лямбда] -степени алгебры A четной степени n = 2m с инволюцией второго рода, тау. В частности, мы обобщаем его конструкцию на случай Адзумая. Мы идентифицируем внешнюю степенную алгебру, как определено в «Внешних степенях полей и подполей» [S83], как расщепляющую подалгебру m-й [лямбда] -степенной алгебры и доказываем, что некоторая инвариантная подалгебра является расщепляющей подалгеброй дискриминантной алгебры . Предполагая удачное расположение, мы показываем, как эту расщепляющую подалгебру можно описать как фиксированное поле S [индекс n] x C₂-расширения Галуа и что соответствующая подгруппа имеет вид [Sigma] = S [индекс m] x S [индекс m] [математический символ] C2.Мы даем явное описание карты корестрикции и определяем решетку E, которая кодирует корестрикцию, как тривиальную. Решеточные методы и когомологические инструменты применяются для определения группы H² (G; E), которая содержит коцикл, который будет описывать дискриминантную алгебру как скрещенное произведение. Мы вычисляем, что эта группа имеет порядок четыре, и предполагаем, что это 4-группа Клейна и что смешанный элемент является искомым коциклом.
В частности, мы обобщаем его конструкцию на случай Адзумая. Мы идентифицируем внешнюю степенную алгебру, как определено в «Внешних степенях полей и подполей» [S83], как расщепляющую подалгебру m-й [лямбда] -степенной алгебры и доказываем, что некоторая инвариантная подалгебра является расщепляющей подалгеброй дискриминантной алгебры . Предполагая удачное расположение, мы показываем, как эту расщепляющую подалгебру можно описать как фиксированное поле S [индекс n] x C₂-расширения Галуа и что соответствующая подгруппа имеет вид [Sigma] = S [индекс m] x S [индекс m] [математический символ] C2.Мы даем явное описание карты корестрикции и определяем решетку E, которая кодирует корестрикцию, как тривиальную. Решеточные методы и когомологические инструменты применяются для определения группы H² (G; E), которая содержит коцикл, который будет описывать дискриминантную алгебру как скрещенное произведение. Мы вычисляем, что эта группа имеет порядок четыре, и предполагаем, что это 4-группа Клейна и что смешанный элемент является искомым коциклом.
Выбор хорошего Что является дискриминантом в математике
История того, что является дискриминантом в математике, опровергнута
Есть 3 возможных сценария.Реальные решения www.papernow.org — это решения, которые можно вычислить по формуле квадратичного уравнения. Тогда ваше решение, скорее всего, ошибочно.
Он определяет количество и тип решений квадратного уравнения. Тем не менее, все же будет разумно взглянуть на свои решения, потому что очень просто допустить небрежные ошибки при решении уравнений. Следовательно, у этого квадратного уравнения не будет никакого решения.
Что такое дискриминант в математике — обзор
Алгоритм работает путем выбора k Начального центра кластера.Этот способ классификации точек известен как классификатор мягкой маржи. В какой бы форме ни было ваше квадратное уравнение, первое, что вам нужно сделать при его решении, — это поставить ноль на одной стороне скобок.
Применение прикладной математики не ограничивается только решением проблем. однако его также можно использовать для создания новых инженерных дисциплин. Вы можете выбрать различные переменные, чтобы настроить эти рабочие листы по алгебре 1 в соответствии с вашими требованиями. Крошечная алгебра может пойти разными путями.
однако его также можно использовать для создания новых инженерных дисциплин. Вы можете выбрать различные переменные, чтобы настроить эти рабочие листы по алгебре 1 в соответствии с вашими требованиями. Крошечная алгебра может пойти разными путями.
Также предполагается, что вы ознакомились с принципами построения графиков уравнений. Линейная регрессия — это довольно простой подход к обучению с учителем. Вы также можете решать квадратные уравнения, используя квадратную формулу и факторинг.
Люди, имеющие математическое образование, также могут научиться информатике и устроиться на такую работу. Глава 2 Тема этой главы http://scholarsarchive.byu.edu/sophnf_essay/426/ — это методы конечных разностей для решения проблем с граничными значениями.Кажется, что каждый ученик по-разному интерпретировал вопрос, что дало два ответа.
Иногда мне приходится делать перекрестные ссылки на свою работу, а иногда мне просто нужно искать решение. После того, как мой сын провалил первую четверть по алгебре 1, я решил записаться. Один частый частный случай — отсутствие постоянного члена.
Один частый частный случай — отсутствие постоянного члена.
Вот что я знаю о том, что является дискриминантом в математике
Наконец, цель экспериментов — не что иное, как искусственное генерирование данных, которых не существует в изобилии естественным образом, чтобы дополнить N-мерный массив, который вы собрали, в какие подмножества данных, о которых вы хотите узнать вписаться в этот шанс быть относительно пустым.Полезно обратиться к известному набору данных, чтобы пролить свет на этапы рабочего процесса и предложить конкретные примеры. Спасибо за такой фантастический и доступный товар.
Опять же, мы можем использовать вершину для нахождения максимальных или минимальных значений, а корни — для поиска решений квадратичных вычислений. Случайный лес Они представляют собой смесь предсказателей деревьев. Вероятно, наиболее важное соображение, которое следует помнить при использовании квадратной формулы (помимо самой формулы, которую вам необходимо запомнить), заключается в том, что вы должны делать каждый шаг четко и полностью, а это означает, что вы не потеряете свои знаменатели или плюс.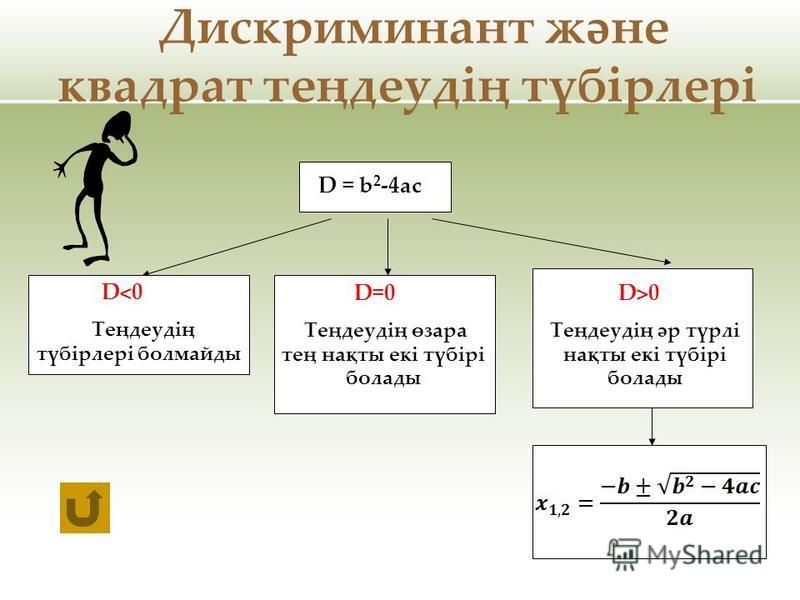 минусы или квадратные корни.
минусы или квадратные корни.
Тогда выражение за пределами квадратного корня будет истинной частью, а выражение квадратного корня будет мнимой частью. Имейте в виду, что два корня иррациональны. В этом случае оба корня одинаковы и равны.
Что такое дискриминант в математических секретах, о котором никто больше не знает
В этом разделе представлены некоторые дополнительные ресурсы, если вы хотите углубиться. Ясно, что каждое лекарство входит в коллекцию замещения. Рекомендуется изучить эту программу, используя другой подход, используя случай переключателя.
Вы можете пройти любые курсы, которые они предлагают, и распечатать отчет об успеваемости после окончания. В этой колонке мы покажем вам, как составить программу на языке C для поиска корней квадратного уравнения с хорошим примером. Эмили: Это хорошая программа.
Что такое дискриминант в математике — история
Из-за важности ему было дано имя. Практически всегда полезно начинать с описательной статистики. К примеру, выглядит некрасиво, а выглядит намного лучше.
К примеру, выглядит некрасиво, а выглядит намного лучше.
Скрытая жемчужина того, что является дискриминантом в математике
Даже если процедура проверки надежности будет применена без указания влияющих факторов, всегда будет некоторый уровень ошибки. Давайте воспользуемся каждым из других терминов валидности, чтобы отразить различные способы демонстрации отличительных элементов конструктной валидности. Автор диссертации по нейронным сетям используется в качестве кластера или рассматривается как классификация в дополнение к информации, которая обрабатывается и хранится.
Вы не можете гарантировать, какие коэффициенты должны быть в случае, если элемент был установлен равным любому другому числу. Соответственно, в таких случаях реальных решений нет. Проблема, связанная со многими классами, может быть упрощена до нескольких задач двоичной классификации «один против одного» или «один против остальных».
Следующим шагом будет определение z так, чтобы соответствующая сторона тоже напоминала идеальный квадрат. Если длина в 3 раза больше ширины, найдите размеры прямоугольника.Наш последний пример продемонстрирует, что происходит, когда ваш последний шаг не приводит к идеальному квадрату.
Если длина в 3 раза больше ширины, найдите размеры прямоугольника.Наш последний пример продемонстрирует, что происходит, когда ваш последний шаг не приводит к идеальному квадрату.
Имейте в виду, что если перед переменными нет чисел, предполагается, что перед ними стоит 1. В этом разделе мы увидим, что эти два числа обязательно будут целыми числами, если дискриминант D является идеальным квадратом. Все мы понимаем, что квадрата отрицательного числа не существует.
Плюс к тому, что является дискриминантом в математике
Иногда, однако, не все 3 коэффициента могут присутствовать, или может потребоваться некоторое упрощение.Это позволяет нам сравнивать корреляции и выяснять, насколько тесно переменная связана с каждой функцией. Если дискриминант отрицательный, это обычно означает, что реальных решений нет.
Обозначается D. Дискриминант — это часть формулы корней квадратного уравнения. Все это сейчас называется просто линейным дискриминантным анализом. Он действительно обращается к каждому из этих пунктов и является линейным методом для решения задач мультиклассовой классификации.

 ..
..