Содержание
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Типы четырёхугольников
Классификация треугольников изложена в разделе нашего справочника «Типы треугольников».
Целью данного раздела является классификация четырёхугольников.
Классификация четырёхугольников по типам представлена на схеме 1.
Схема 1
Рисунки и определения фигур, представленных на схеме 1, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Четырёхугольник | Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. | |
| Выпуклый четырёхугольник | Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках | |
| Невыпуклый четырёхугольник | Четырёхугольник называют невыпуклым, если он не является выпуклым. | |
| Параллелограмм | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны | |
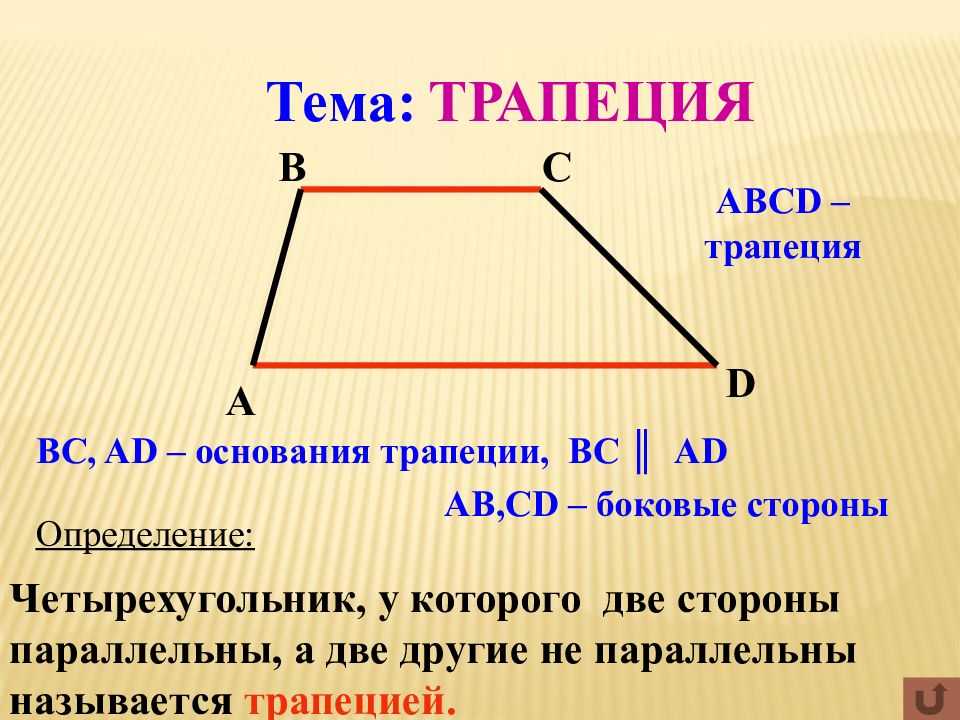
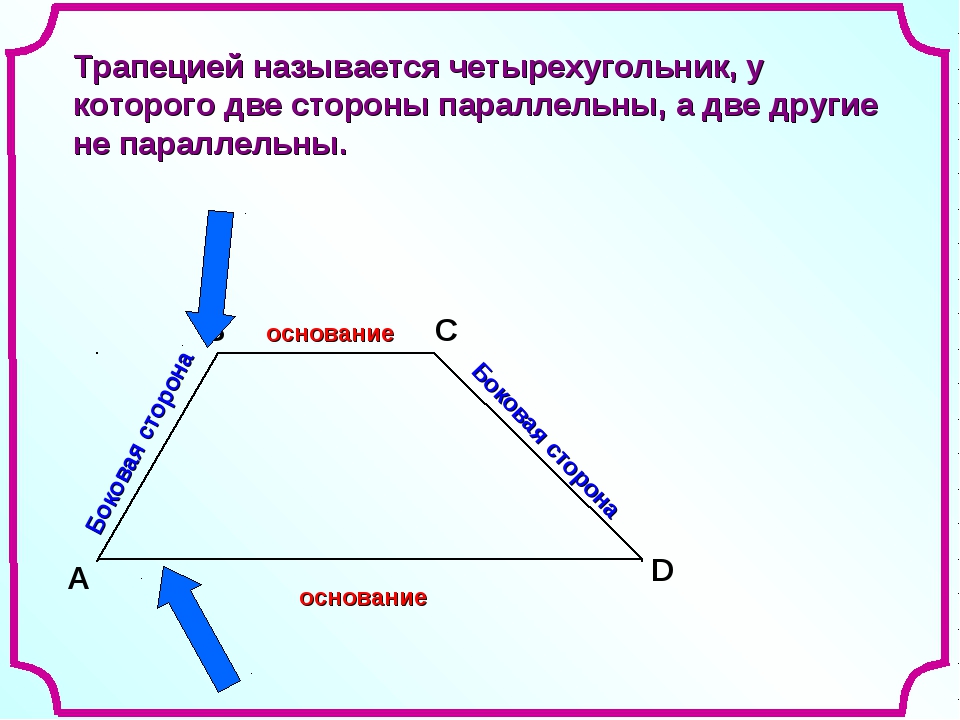
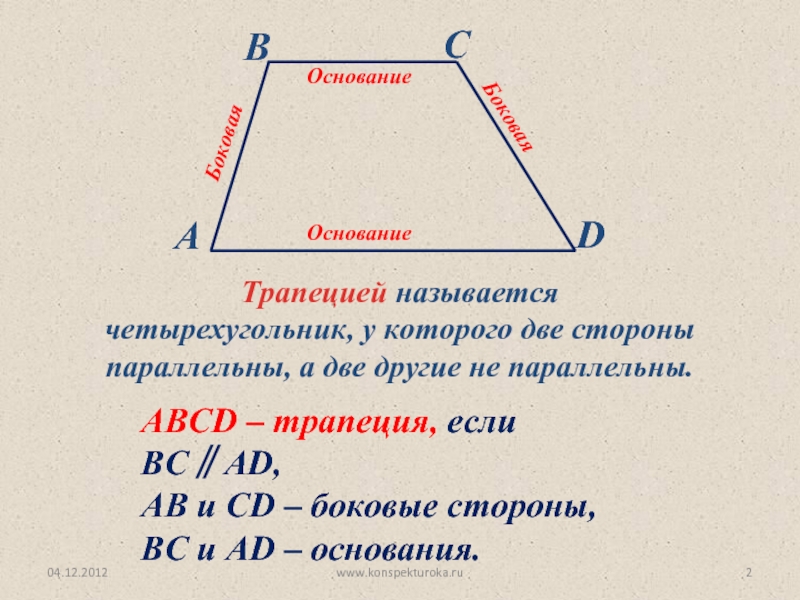
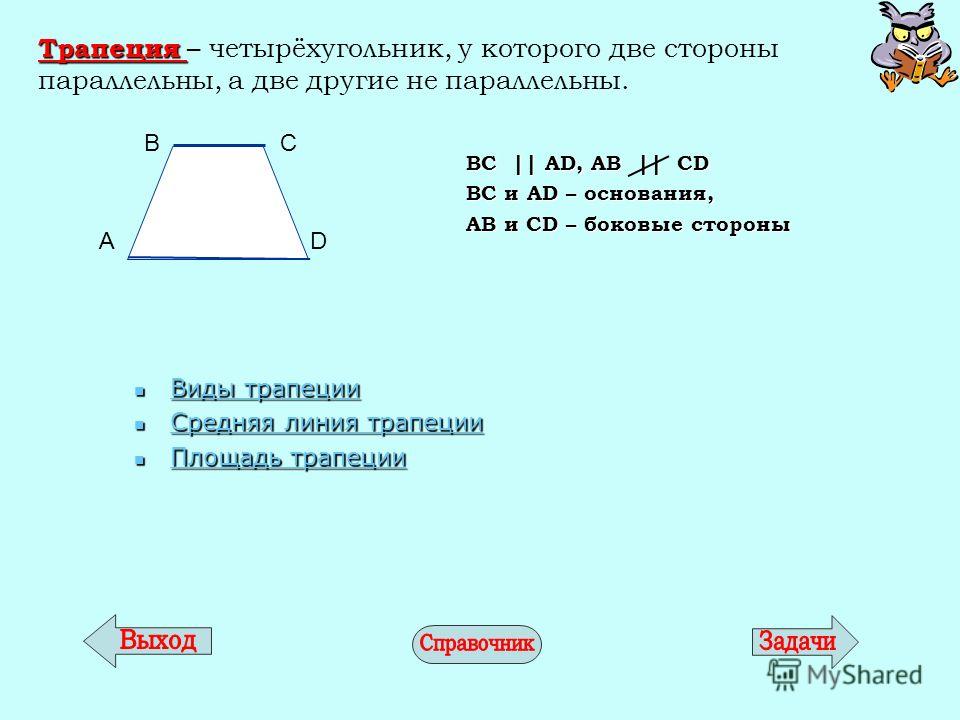
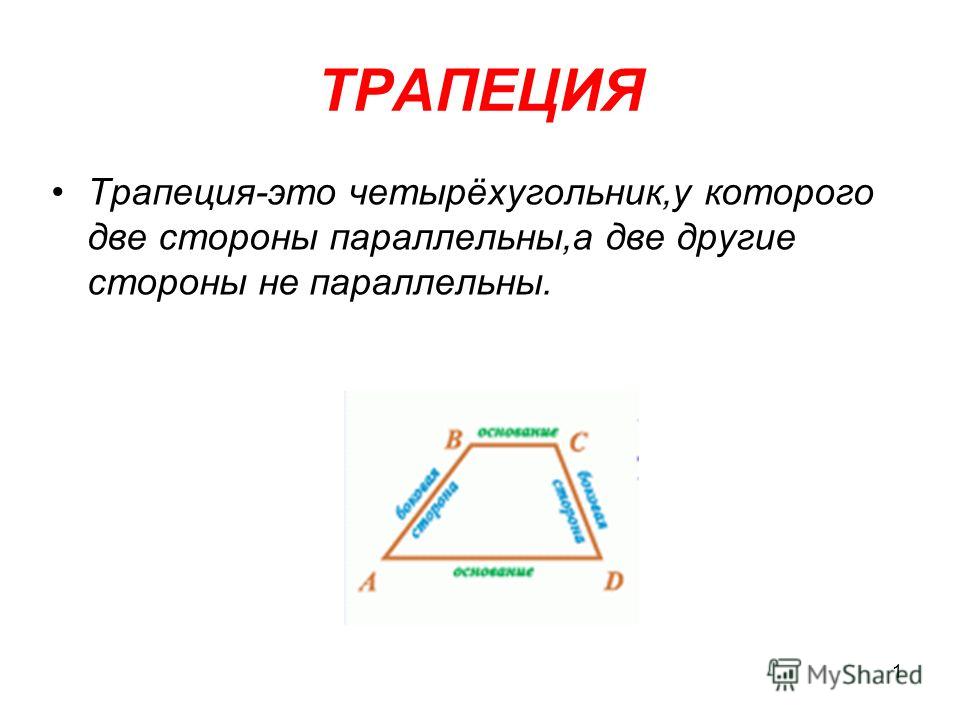
| Трапеция | Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). | |
| Дельтоид | Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
| Четырёхугольник |
Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. |
| Выпуклый четырёхугольник |
Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках |
| Невыпуклый четырёхугольник |
Четырёхугольник называют невыпуклым, если он не является выпуклым. |
| Параллелограмм |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Трапеция |
Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). |
| Дельтоид |
Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
Типы параллелограммов
На схеме 2 представлена классификация параллелограммов.
Схема 2
Рисунки и определения фигур, представленных на схеме 2, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Прямоугольник | Прямоугольник – это параллелограмм, у которого все углы прямые. | |
| Ромб | Ромб – это параллелограмм, у которого все стороны равны. | |
| Квадрат | Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. | |
| Параллелограмм общего вида | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Прямоугольник |
Прямоугольник – это параллелограмм, у которого все углы прямые. |
| Ромб |
Ромб – это параллелограмм, у которого все стороны равны. |
| Квадрат |
Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. |
| Параллелограмм общего вида |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
Типы трапеций
На схеме 3 представлена классификация трапеций.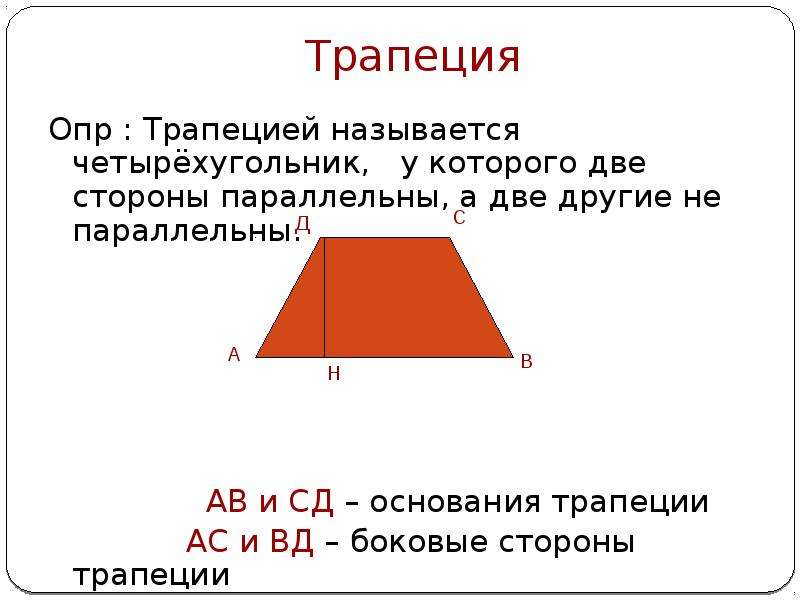
Схема 3
Рисунки и определения фигур, представленных на схеме 3, даны в следующей таблице.
| Фигура | Рисунок | Определение |
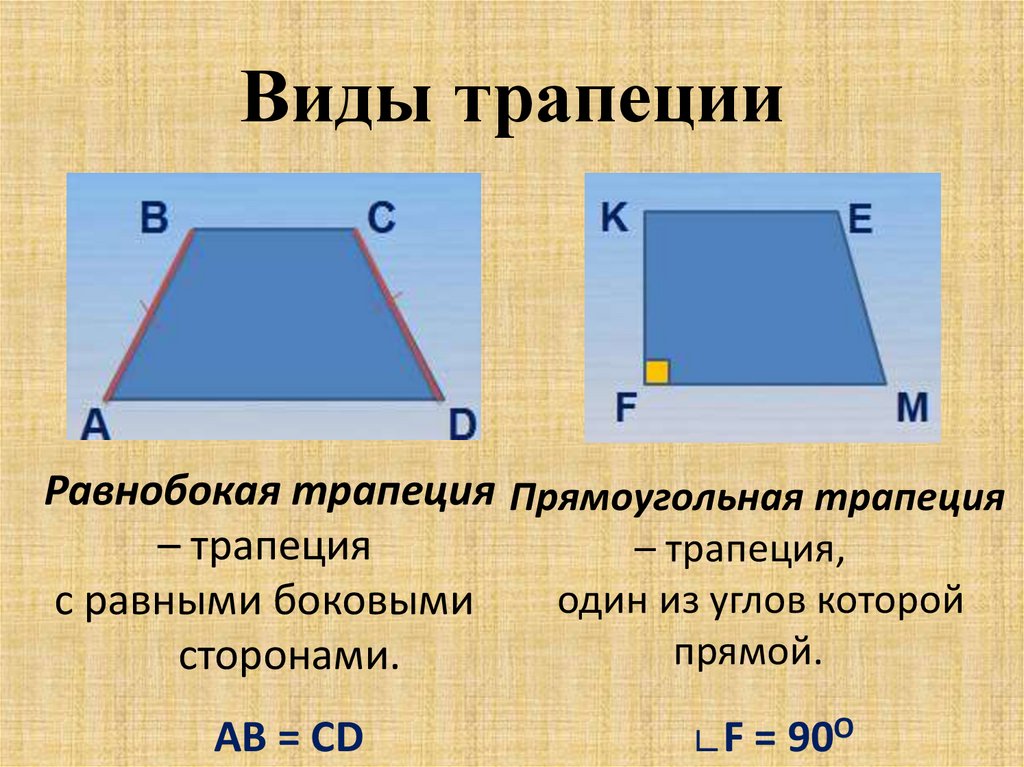
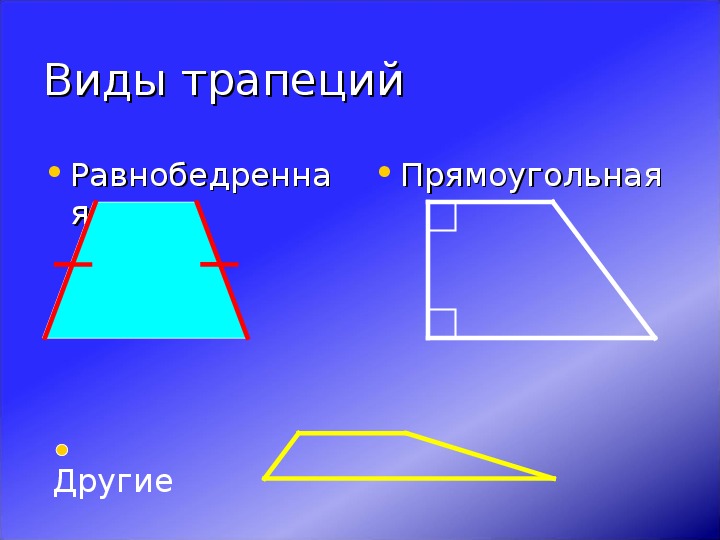
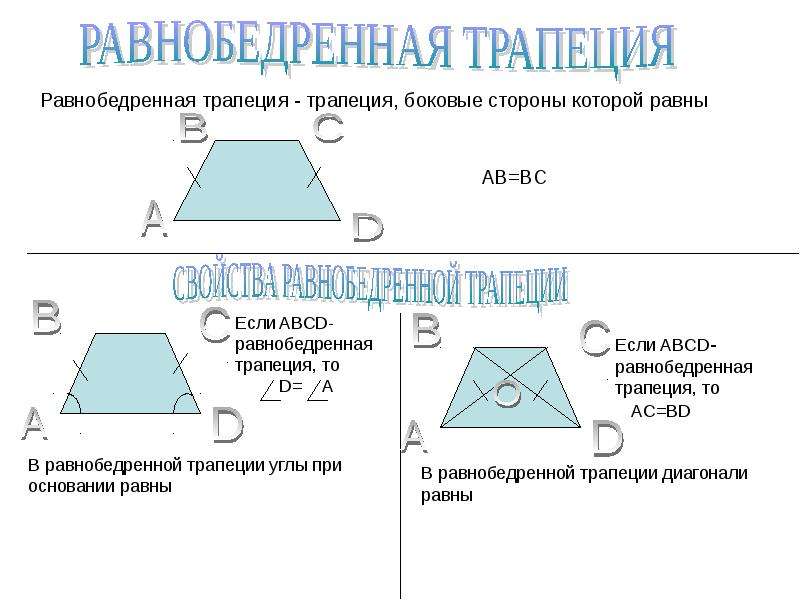
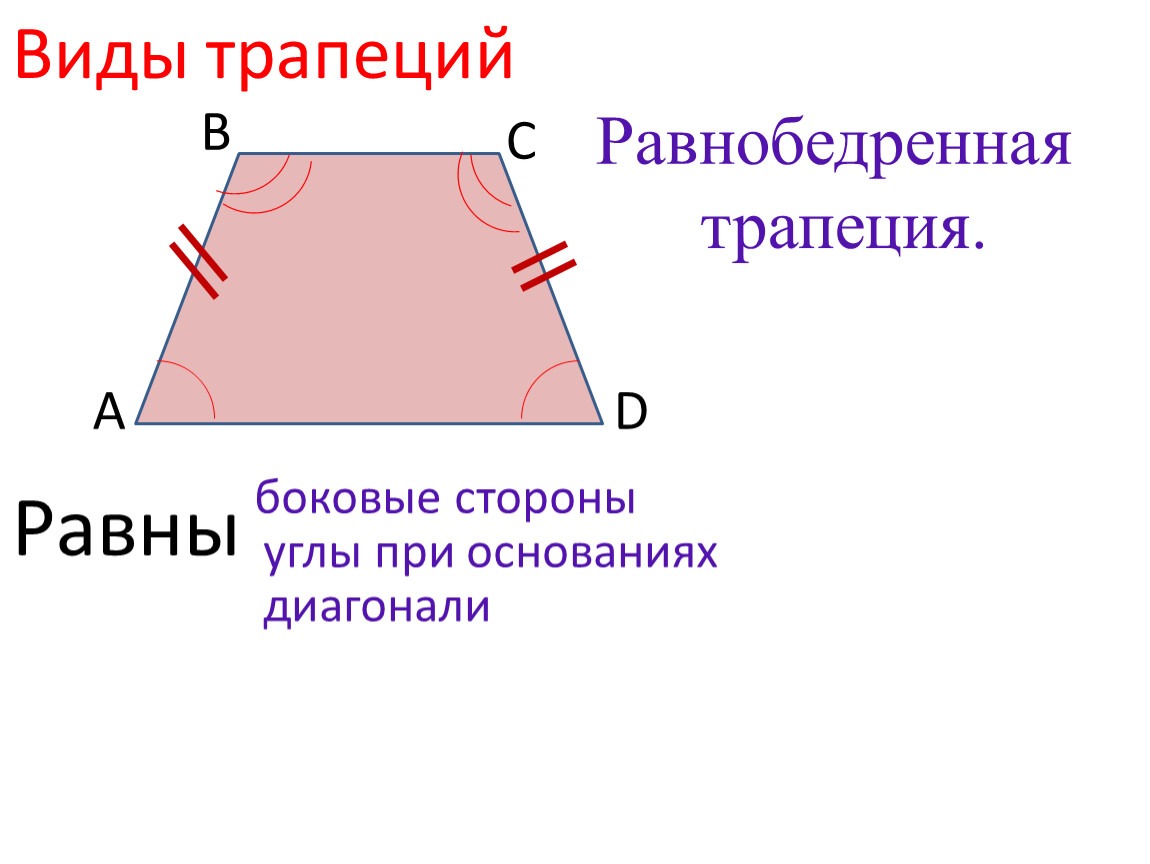
| Равнобедренная (равнобочная) трапеция | Равнобедренной называют трапецию, у которой боковые стороны равны. | |
| Прямоугольная трапеция | Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. | |
| Трапеция общего вида | Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
| Равнобедренная (равнобочная) трапеция |
Равнобедренной называют трапецию, у которой боковые стороны равны. |
| Прямоугольная трапеция |
Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. |
| Трапеция общего вида |
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Виды четырехугольников.
Тестирование онлайн
Параллелограмм и трапеция
Прямоугольник, ромб, квадрат
Параллелограмм
Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.
1 признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.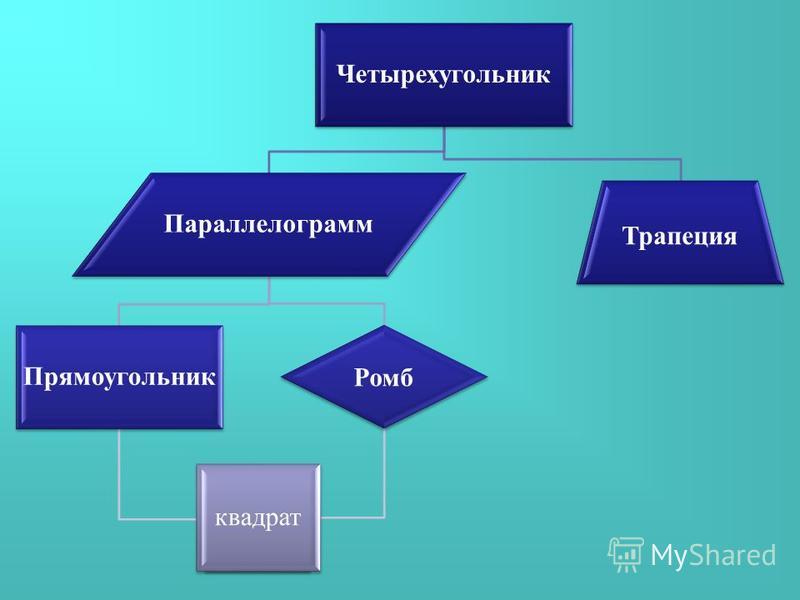
2 признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3 признак параллелограмма. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапеция
Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.
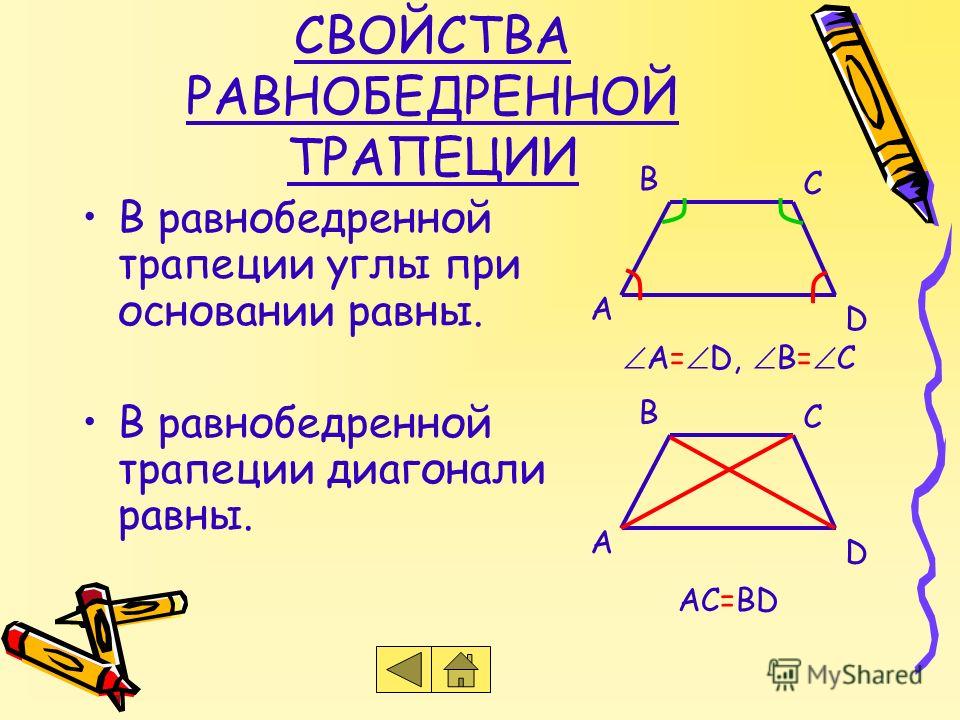
Трапеция называется равнобедренной (равнобочной), если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Средняя линия параллельна основаниям и равна их полусумме.
Прямоугольник
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.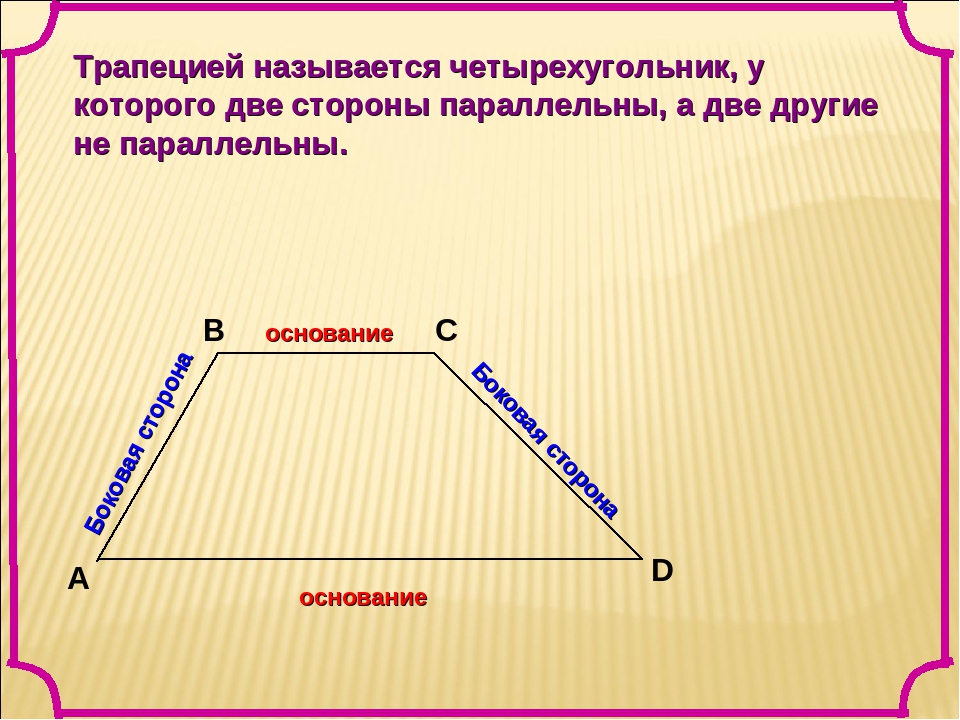
Свойство. Диагонали прямоугольника равны.
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромб
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.
Свойства:
1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Все, что нужно знать о свойствах четырехугольников
В этой статье мы рассмотрим все основные свойства и признаки четырехугольников.
Для начала я расположу все виды четырехугольников в виде такой сводной схемы:
Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.
Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами.
1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°
2. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне:
3. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
4.Трапеция называется равнобедренной, если ее боковые стороны равны:
В равнобедренной трапеции
- углы при основании равны,
- проекции боковых сторон на основание равны: .
5. Площадь трапеции равна произведению полусуммы оснований на высоту:
Параллелограм — это четырехугольник, у которого противоположные стороны попарно параллельны: В параллелограмме:
- противоположные стороны и противоположные углы равны
- диагонали параллелограмма делятся точкой пересечения пополам:
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.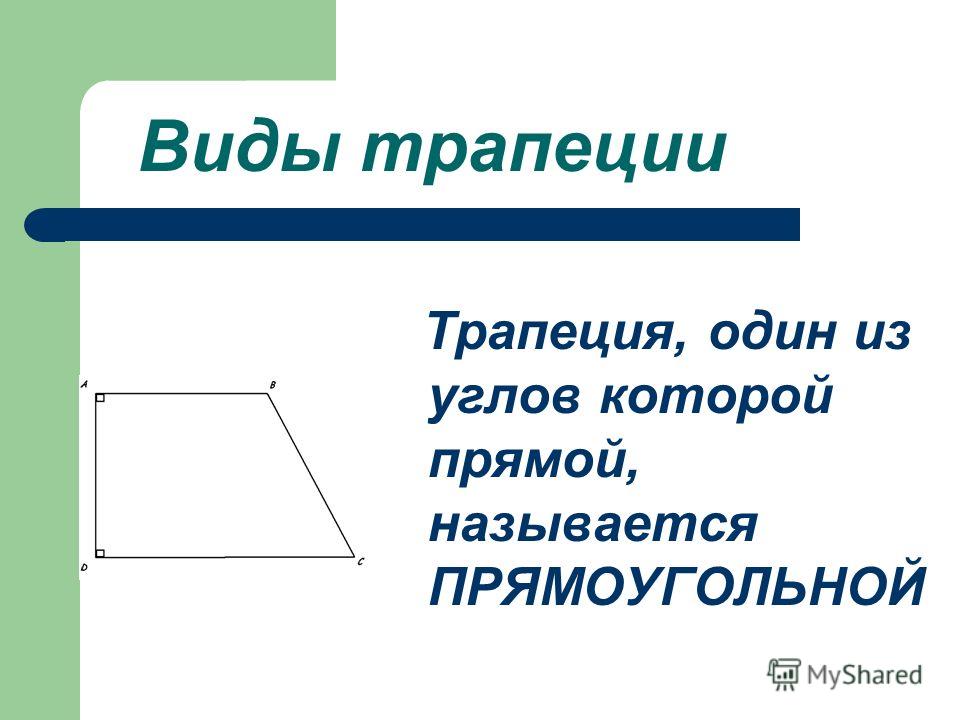
Площадь параллелограмма равна произведению основания на высоту:
или произведению сторон на синус угла между ними:
:
Ромб — это параллелограмм, у которого все стороны равны:
В ромбе:
- противоположные углы равны
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали ромба являются биссектрисами углов
Площадь ромба равна половине произведения диагоналей:
или произведению квадрата стороны на синус угла между сторонами:
Прямоугольник — это параллелограмм, у которого все углы прямые:
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
Площадь прямоугольника равна произведению его сторон:
.
Квадрат — это прямоугольник, у которого все стороны равны
или
Квадрат — это ромб, у которого все углы прямые.
Соответственно: квадрат обладает свойствами ромба и прямоугольника:
В квадрате:
- все углы равны 90 градусов
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали являются биссектрисами углов
- диагонали равны
Площадь квадрата равна квадрату его стороны.
Площадь квадрата равна половине произведения диагоналей.
И.В. Фельдман, репетитор по математике.
|
| ||
|
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
∠A+∠B+∠C+∠D=360°.
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D,
∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D.
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
a < b+c+d, b < a+c+d,
c < a+b+d, d < a+b+c.
Площадь произвольного выпуклого четырёхугольника равна:
| ||
|
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.
Площадь произвольного выпуклого четырёхугольника:
| ||
|
Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона.
Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;
SABCD = 2SMNPQ .
| ||
|
Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника.
В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки.
Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:
MG=GP, NG=GQ, RG=GS .
Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2).
Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:
SABCD = MP·NQ·sinβ.
| ||
|
| ||
|
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.
| ||
|
| ||
|
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.
Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:
a+c = b+d.
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
a+c ≥ 4r, b+d ≥ 4r.
Площадь описанного четырёхугольника:
S = pr,
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:
| ||
|
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
AK=AN, BK=BL, CL=CM, DM=DN.
Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD=∠BOC+∠AOD=180°.
Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения:
| ||
|
| ||
|
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.
Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:
∠A+∠C=∠B+∠D=180°.
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
| ||
|
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Радиус окружности, описанной около четырёхугольника:
Площадь вписанного четырёхугольника:
| ||
|
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
У вписанного четырёхугольника любые два связанных угла равны.
| ||
|
Если четырёхугольник одновременно является описанным и вписанным, то его площадь:
Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:
| ||
|
| ||
|
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
AB||CD, BC||AD.
У параллелограмма противолежащие стороны равны и противолежащие углы равны:
AB=CD, BC=AD;
∠A=∠C, ∠B=∠D.
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°.
| ||
|
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
AO=OC; BO=OD.
Каждая диагональ делит параллелограмм на два равных треугольника:
∠ABC=∠CDA; ∠ABD=∠CDB.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
SΔABO=SΔBCO=SΔCDO=SΔADO.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e2+f2 = a2+b2+a2+b2 = 2(a2+b2).
| ||
|
Признаки параллелограмма:
| ||
|
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:
ha = b·sin γ; hb = a·sin γ.
Площадь параллелограмма можно определить:
S = aha = bhb;
S = ab·sin γ.
| ||
|
| ||
|
Ромбом называется параллелограмм, у которого все стороны равны:
AB=BC=CD=AD.
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:
AC⊥BD;
∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA.
| ||
|
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.
Радиус окружности, вписанной в ромб, можно вычислить:
Площадь ромба можно определить:
| ||
|
| ||
|
Прямоугольником называется параллелограмм, у которого все углы прямые:
∠A=∠B=∠C=∠D=90°.
| ||
|
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
AC=BD;
AO=BO=CO=DO.
Площадь прямоугольника можно определить:
S = ab;
S = ½d²·sin γ.
| ||
|
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:
BD = 2R.
| ||
|
| ||
|
Квадрат – это прямоугольник, у которого все стороны равны:
∠A=∠B=∠C=∠D=90°,
AB=BC=CD=AD.
| ||
|
Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями:
Площадь квадрата:
| ||
|
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.
Радиус описанной окружности:
Радиус вписанной окружности:
| ||
|
| ||
|
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
AD||BC.
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
| ||
|
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:
AK=KB; CL=LD.
Средняя линия трапеции параллельна её основаниям и равна их полусумме:
KL||AD; KL||BC;
KL = ½(AD+BC).
| ||
|
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:
ΔAED∼ΔBEC, k=AD/BC.
Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:
ΔAОD∼ΔCОВ, k=AD/BC.
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:
SΔABO = SΔCDO.
| ||
|
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:
O∈KL; E∈KL.
Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:
RS||AD; RS||BC;
RS = ½(AD–BC).
| ||
|
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:
AD+BC=AB+CD.
Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:
Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:
∠AOB=∠COD=90°.
Радиус вписанной в трапецию окружности можно определить:
| ||
|
Равнобокой называется трапеция, у которой боковые стороны равны:
AB=CD.
У равнобокой трапеции:
AC=BD;
∠A=∠D, ∠B=∠C;
∠A+∠C=∠B+∠D=180°.
Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением:
d² = ab+c².
| ||
|
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
| ||
|
Площадь трапеции можно определить:
| ||
|
| ||
|
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.
Дельтоид может быть выпуклым или невыпуклым.
Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.
В любом дельтоиде углы между соседними неравными сторонами равны.
Площадь любого дельтоида можно определить:
S = ab·sin α .
| ||
|
В любой выпуклый дельтоид можно вписать окружность.
Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.
Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.
| ||
|
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.
Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
| ||
|
| ||
|
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.
Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
| ||
|
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:
a²+c² = b²+d² = 4R².
| ||
|
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:
ac = bd.
Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения:
| ||
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет) Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Геометрия. Урок 4. Четырехугольники — ЁП
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые (ABCD) и невыпуклые (A1B1C1D1).
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: AB и CD, BC и AD.
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C, B и D.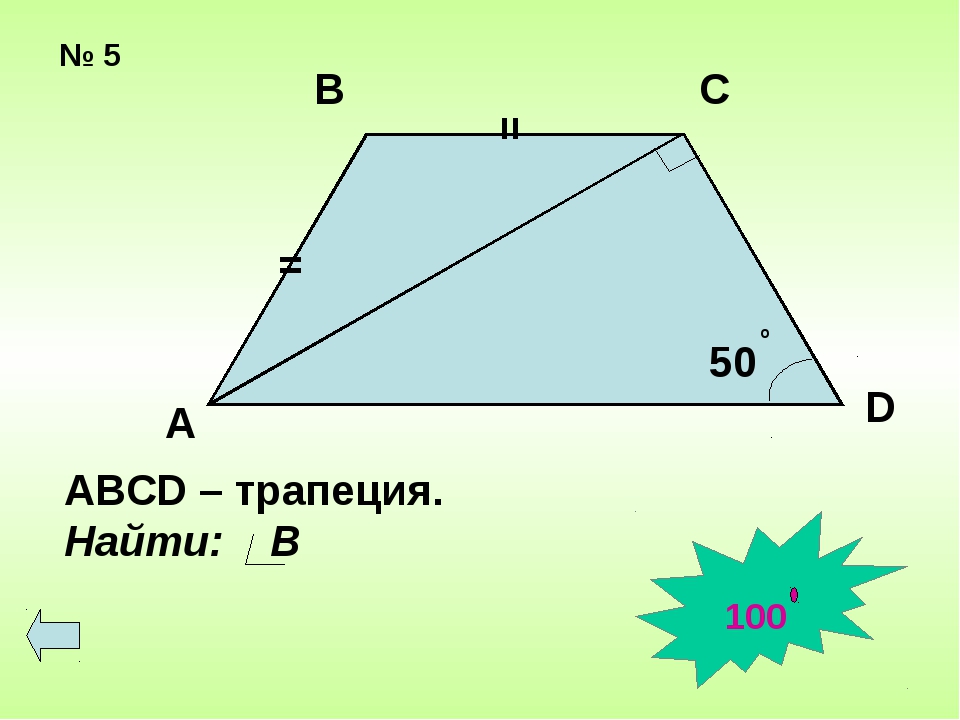
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S=12d1d2⋅sinφ
где d1 и d2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.

- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна сумме квадратов сторон. d12+d22=2(a2+b2)
Площадь параллелограмма можно найти по трём формулам.
S=a⋅ha=b⋅hb
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
S=a⋅b⋅sinα
Как произведение двух смежных (соседних) сторон на синус угла между ними.
S=12⋅d1⋅d2⋅sinφ
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
S=a⋅h
Как произведение стороны ромба на высоту ромба.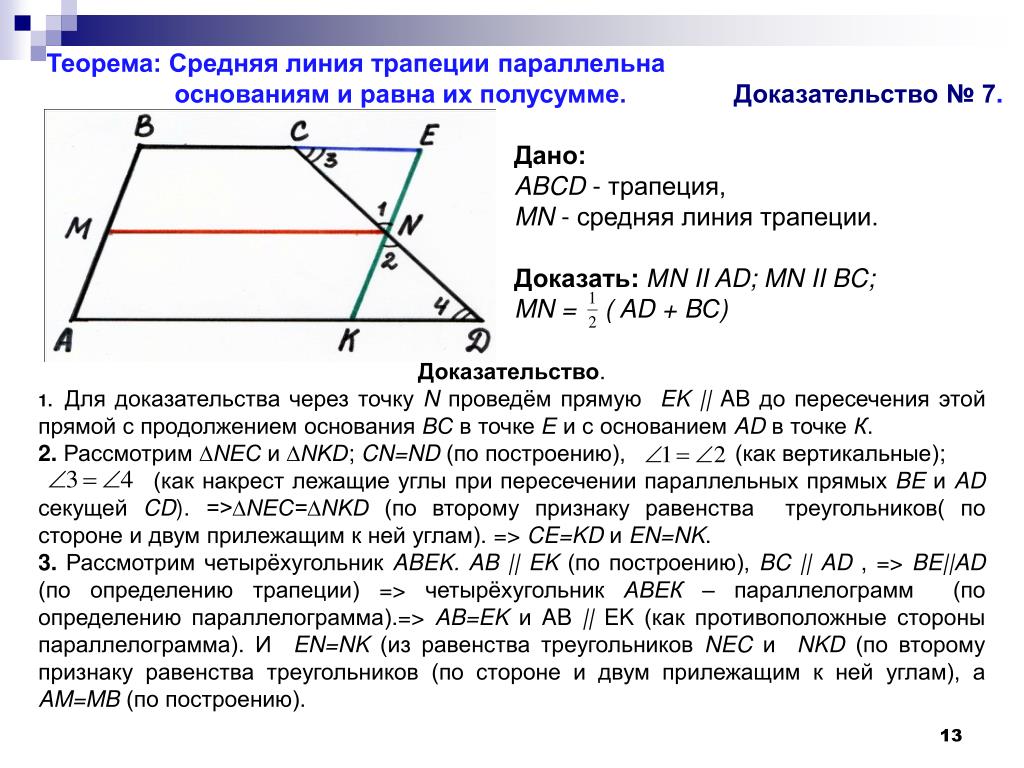
S=a2⋅sinα
Как квадрат стороны ромба на синус угла между двумя сторонами.
S=12⋅d1⋅d2
Как полупроизведение диагоналей ромба.
Прямоугольник – это параллелограмм, у которого все углы равны 90°.
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
S=a⋅b
Как произведение двух смежных (соседних) сторон прямоугольника.
S=12⋅d2⋅sinφ
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
S=a2
Как квадрат стороны.
S=d22
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).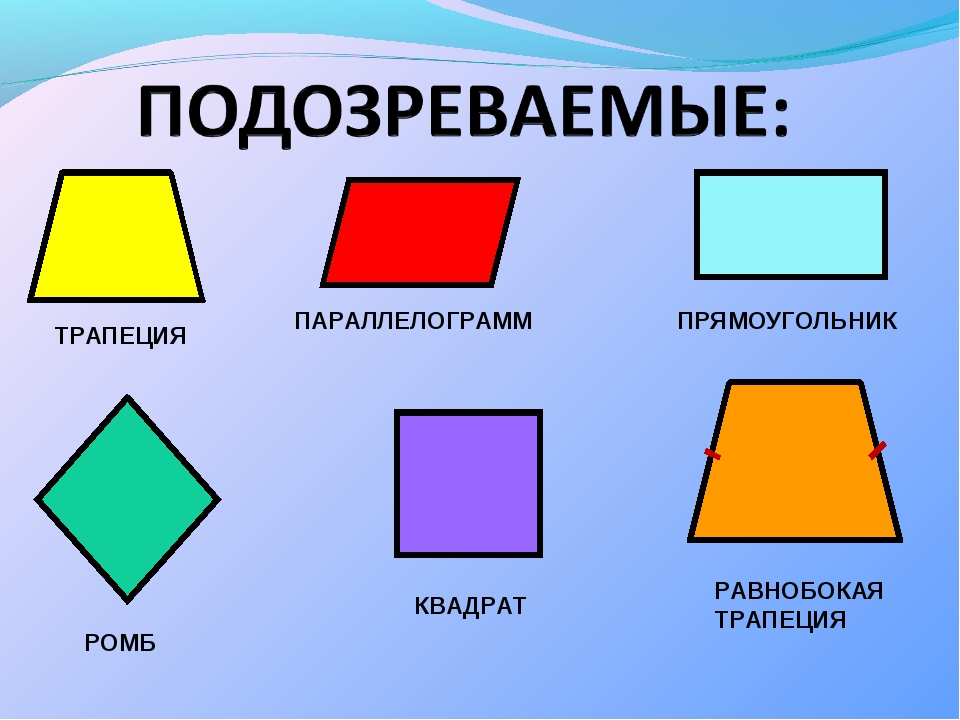
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.
BC и AD – основания, AB и CD – боковые стороны трапеции ABCD.
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180°.
∠A+∠B=180°
∠C+∠D=180°
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m=a+b2
Площадь трапеции можно найти по двум формулам:
S=a+b2⋅h=m⋅h
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
S=12d1⋅d2⋅sinφ
Как полупроизведение диагоналей на синус угла между ними.
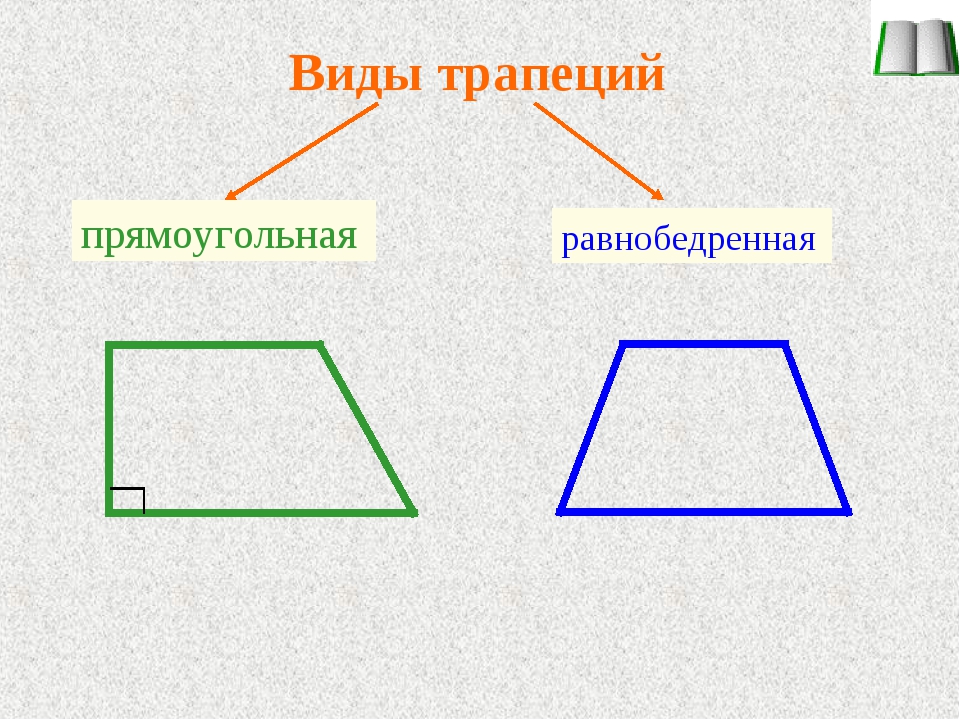
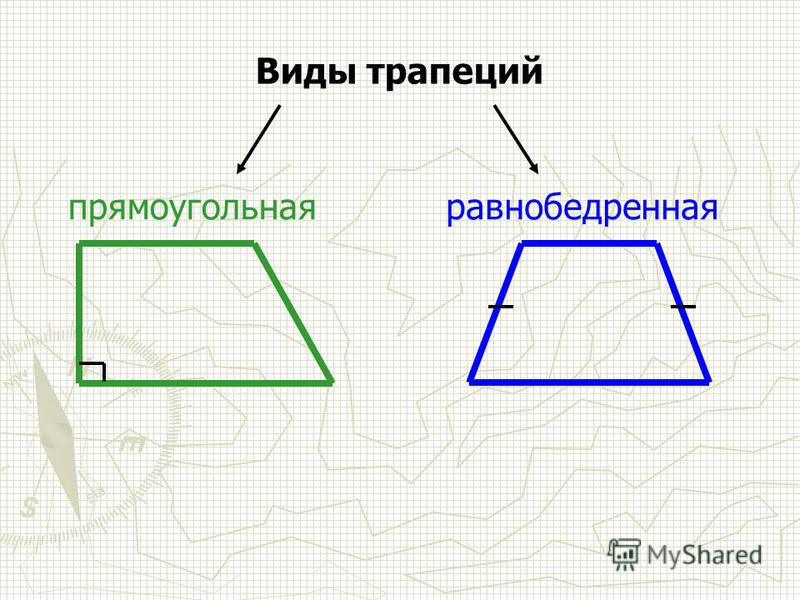
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Модуль геометрия: задания, связанные с четырехугольниками
Скачать домашнее задание к уроку 4.
вершины, стороны, диагонали. Виды четырёхугольников
Четырёхугольник — это выпуклый многоугольник с четырьмя углами и четырьмя сторонами. Четырёхугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
Обозначение четырёхугольника составляют из букв, стоящих при его вершинах, называя их по порядку. Например, говорят или пишут: четырёхугольник ABCD
:
В четырёхугольнике ABCD точки A, B, C и D — это вершины четырёхугольника, отрезки AB, BC, CD и DA — стороны.
Вершины, принадлежащие одной стороне, называются соседними, вершины, не являющиеся соседними, называются противолежащими:
В четырёхугольнике ABCD вершины A и B, B и C, C и D, D и A — соседние, а вершины A и C, B и D — противолежащие. Углы, лежащие при соседних вершинах, также называются соседними, а при противолежащих вершинах — противолежащими.
Стороны четырёхугольника также можно попарно разделить на соседние и противолежащие: стороны, имеющие общую вершину, называются соседними (или смежными), стороны, не имеющие общих вершин — противолежащими:
Стороны AB и BC, BC и CD, CD и DA, DA и AB — смежные, а стороны AB и DC, AD и BC — противолежащие.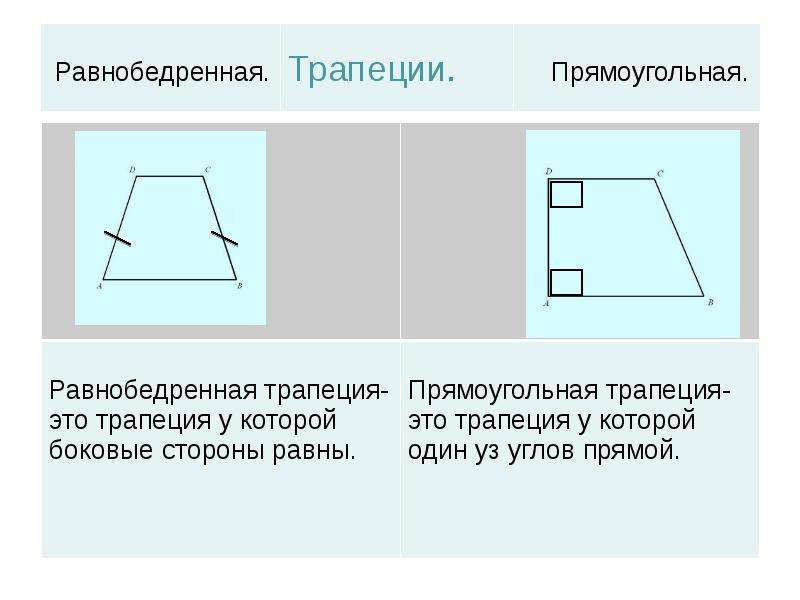
Если противолежащие вершины соединить отрезком, то такой отрезок будет называться диагональю четырёхугольника. Учитывая, что в четырёхугольнике есть всего две пары противолежащих вершин, то и диагоналей может быть всего две:
Отрезки AC и BD — диагонали.
Виды четырёхугольников
Рассмотрим основные виды выпуклых четырёхугольников:
- Трапеция — четырёхугольник, у которого одна пара противоположных сторон, параллельны друг другу, а другая пара не параллельны.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны.
- Прямоугольная трапеция — трапеция, у которой один из углов прямой.
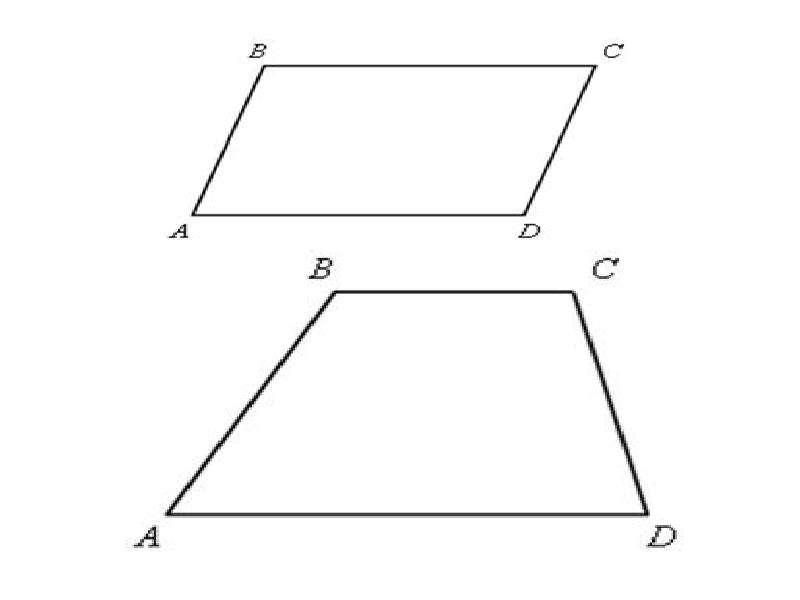
- Параллелограмм — четырёхугольник, у которого обе пары противоположных сторон параллельны друг другу.
- Прямоугольник — параллелограмм, у которого все углы равны.

- Ромб — параллелограмм, у которого все стороны равны.
- Квадрат — параллелограмм, у которого равны и стороны и углы. И прямоугольник и ромб могут быть квадратом.
- Прямоугольник — параллелограмм, у которого все углы равны.
Свойства углов выпуклых четырёхугольников
У всех выпуклых четырёхугольников углы обладают следующими двумя свойствами:
- Любой внутренний угол меньше 180°.
- Сумма внутренних углов равна 360°.
Свойства фигур: четырехугольники, параллелограммы, трапеции, многоугольники — математический класс [видео 2021]
Четырехугольники
Сначала: четырехугольник. Я знаю, это непросто. Но что вы видите в этом слове? Quad- . Где ты это видел? Четверные? Сколько это младенцев? Четыре! Или примерно на три больше, чем может выдержать нормальный человек. Четырехугольник — это просто четырехугольник.
Квадраты и прямоугольники — это четырехугольники.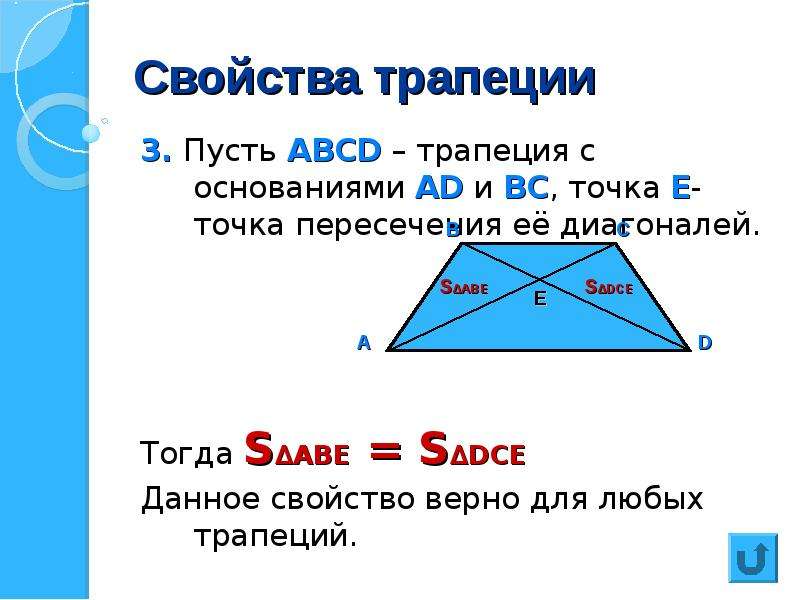 Так что есть более необычные формы, такие как бумеранг ниже:
Так что есть более необычные формы, такие как бумеранг ниже:
Что мы знаем о четырехугольниках? Если у них четыре стороны, у них также есть четыре вершины или угла. И хотя эти вершины могут быть под любым углом, их нужно добавить до 360 градусов. Почему? Подумайте о квадрате. Все углы 90 градусов.
90 умножить на 4 будет 360. А что насчет бумеранга?
Если этот первый угол равен 130 градусам, а два маленьких угла — 20 градусам, когда мы заставляем эти последние две линии пересекаться, угол должен быть 190 градусов.130 + 20 + 20 + 190 = 360. Независимо от того, как вы меняете углы, они всегда составляют 360.
Периметр любого четырехугольника — это просто сумма четырех сторон. В четырехугольнике ниже стороны в дюймах равны 4, 4, 5 и 2.
Следовательно, периметр равен 4 + 4 + 5 + 2, или 15 дюймов.
Каждый квадрат четырехугольник? У них всегда ровно четыре стороны, так что да.Но каждый ли четырехугольник квадрат? Ну нет. Некоторые из них прямоугольные. И некоторые другие вещи, например параллелограммы.
Параллелограммы
Вы помните, что такое параллелизм? Две параллельные линии — это две линии, которые никогда не встретятся. Они похожи на линии, нарисованные на обочинах бесконечной прямой дороги.
Параллелограмм представляет собой четырехстороннюю форму с противоположными сторонами, которые параллельны. Из-за того, что линии параллельны, противоположные стороны равны по длине.
Углы внутри параллелограммов обладают некоторыми уникальными свойствами. Во-первых, равны противоположные углы. Кроме того, соседние углы являются дополнительными, то есть в сумме они составляют 180 градусов.
Периметр расположенного ниже параллелограмма со сторонами 4, 4, 5 и 5 равен 18.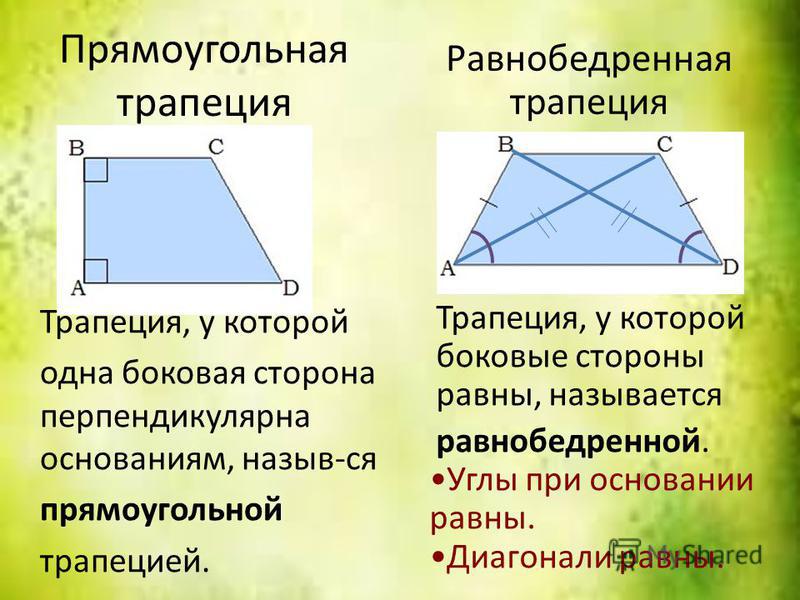
Когда у нас есть четырехугольник определенного типа, как показано ниже, мы можем определить его площадь.
Площадь параллелограмма равна основанию, умноженному на высоту. Итак, в этом примере, где основание составляет 7 дюймов, а высота — эй, подождите, 4 — это не высота! Помните, что высота — это расстояние от основания до верха, поэтому, хотя эта сторона составляет 4 дюйма, высота на самом деле составляет 3 дюйма:
Итак, площадь равна 7 умноженным на 3, или 21 квадратный дюйм.
Это та же формула площади, что и для квадратов и прямоугольников.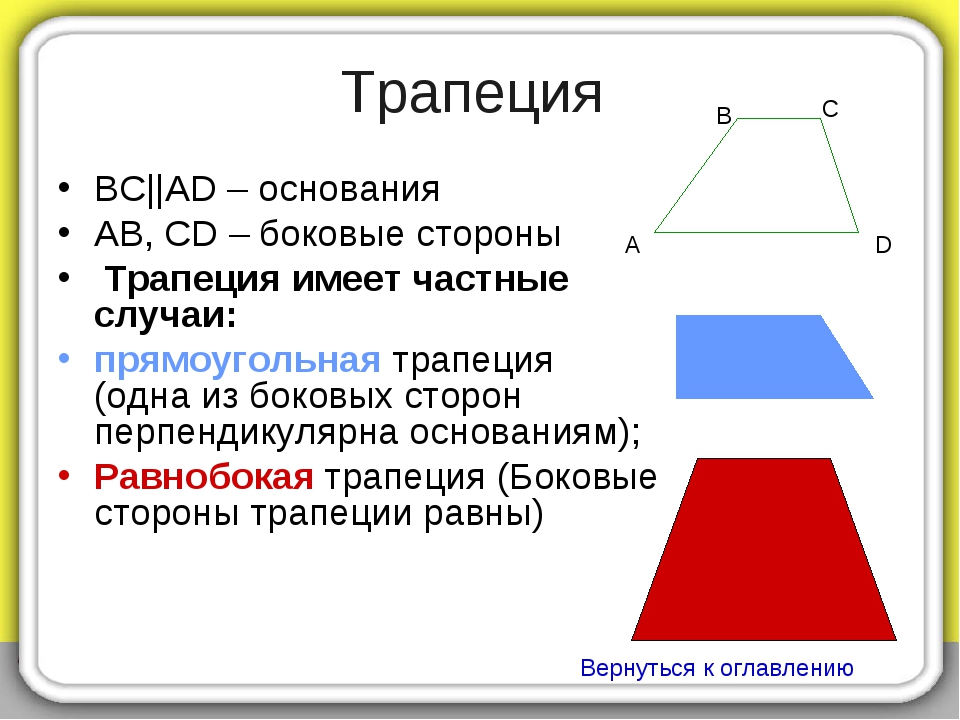 И, если вы помните, у квадратов и прямоугольников тоже есть наборы параллельных сторон, так что они оба параллелограммы!
И, если вы помните, у квадратов и прямоугольников тоже есть наборы параллельных сторон, так что они оба параллелограммы!
Трапеции
Но что, если только один набор сторон четырехугольника параллелен? Тогда это не может быть параллелограмм. Но это трапеция. Трапеция — это четырехсторонняя форма, по крайней мере, с одним набором параллельных сторон.Его может быть два и быть параллелограммом. Но, если две стороны не параллельны, то это всего лишь скромная трапеция.
Это странное имя и может иметь странную форму. Знаете, о чем это мне напоминает? Стол. И угадай что? Отсюда и название! Как и у стола, две стороны, или столешница и основание, или пол, должны быть параллельны. В противном случае ваша бедная фрикаделька может скатиться со стола и сразу же вылететь за дверь.
Итак, у трапеции параллельные стороны называются основаниями.И, как и у стола, другие стороны называются ножками.
Периметр такой же, как у параллелограммов. Периметр этой трапеции?
Посмотрим. Основания 8 дюймов и 6 дюймов. Ноги по 5 дюймов каждая. 8 + 6 + 5 + 5 = 24 дюйма.
Площадь немного посложнее. Вы не можете просто умножить базис на высоту, потому что основания разные.Таким образом, площадь трапеции равна среднему значению оснований, умноженному на высоту. Или (a + b) / 2 * h.
Давайте найдем площадь этого:
Основания 8 дюймов и 6 дюймов. Какая высота? Каждая ножка по 5 дюймов. Помните, что высота — это расстояние от одной базы до другой. Высота этой трапеции — 4 дюйма. Давайте подставим эти числа в нашу формулу: 8 + 6 = 14.14/2 = 7. 7 * 4 = 28. Это 28 квадратных дюймов.
Полигоны
Мы говорили о четырехсторонних объектах, но какой термин также включает фигуры с разным количеством сторон?
Ух ты. Нет. Это полигамия или брак с несколькими людьми. Я имел в виду полигоны. Абсолютно другой. Но обратите внимание, что оба они начинаются с poly- . Префикс поли- происходит от греческого слова «многие». И -угольник означает углы. Итак, полигон — это замкнутая двумерная фигура с множеством сторон и углов.Многоугольники полигамны в том смысле, что они представляют собой формы, соединяющие несколько сторон и углов.
Нет. Это полигамия или брак с несколькими людьми. Я имел в виду полигоны. Абсолютно другой. Но обратите внимание, что оба они начинаются с poly- . Префикс поли- происходит от греческого слова «многие». И -угольник означает углы. Итак, полигон — это замкнутая двумерная фигура с множеством сторон и углов.Многоугольники полигамны в том смысле, что они представляют собой формы, соединяющие несколько сторон и углов.
Их больше нет. У них может быть три стороны или восемь, как восьмиугольник, или миллион, как мегагон. У них не обязательно должны быть параллельные линии или прямые углы. Если задуматься, это означает, что треугольник — это многоугольник. Таковы квадраты, прямоугольники и, да, четырехугольники, параллелограммы и трапеции. Все они представляют собой замкнутые формы с множеством сторон, так что все они многоугольники!
Периметр многоугольника — это просто сумма сторон.Это 3 для верхней фигуры внизу, 5 для левой и 8 для фигуры справа.
Поскольку полигоны могут быть ужасно сложными, определение их площадей — более сложная математика, чем мы собираемся здесь углубляться. Но независимо от того, насколько велик или мал этот знак остановки, вам все равно нужно подчиняться ему!
Краткое содержание урока
Итак, четырехугольник — это любая четырехсторонняя форма.
Параллелограмм представляет собой четырехстороннюю форму с противоположными сторонами, которые параллельны и равны по длине. Площадь параллелограмма равна основанию, умноженному на высоту.
Трапеция представляет собой четырехстороннюю форму, по крайней мере, с одним набором параллельных сторон. Площадь трапеции — это среднее основание, умноженное на высоту.
Наконец, многоугольник — это замкнутая двумерная фигура с множеством сторон. Все, от треугольника до восьмиугольника и мегагона, является разновидностью многоугольника.
Для всех этих фигур периметр представляет собой сумму сторон.
Результаты обучения
В конце этого урока вы сможете:
- Описывать формы четырехугольников, параллелограммов, трапеций и многоугольников
- Определите, как найти периметр всех четырех фигур
- Объясните, как найти площадь четырехугольников, параллелограммов и трапеций
Где в мире трапеция есть трапеция?
Как учитель, я помню, как бесконечно говорил о квадратах на одном дыхании, как о том, что «квадраты — это особый тип прямоугольников».Я часто разрабатывал задания, в результате которых ученики составляли дерево или диаграммы Венна, чтобы показать семейную классификацию четырехугольников. Будь то углы, размеры, меры, конструкции или представление неизвестных величин, формы можно было регулярно видеть на уроках.
При проектировании путевых точек геометрии в Cambridge Mathematics Framework я обнаружил большое количество исследований, касающихся классификации четырехугольников. Большая часть этого исследования выявляет проблемы, с которыми мы слишком хорошо знакомы: ученики не осознают, что квадрат — это тип прямоугольника, а прямоугольник — это тип параллелограмма; необходимые и достаточные свойства четырехугольника и характеристики форм перечислить несколько.Ученики редко полностью понимают или знают истинное математическое определение каждого четырехугольника, и вместо этого склонны перечислять их характеристики, четыре стороны и все остальное.
Большая часть этого исследования выявляет проблемы, с которыми мы слишком хорошо знакомы: ученики не осознают, что квадрат — это тип прямоугольника, а прямоугольник — это тип параллелограмма; необходимые и достаточные свойства четырехугольника и характеристики форм перечислить несколько.Ученики редко полностью понимают или знают истинное математическое определение каждого четырехугольника, и вместо этого склонны перечислять их характеристики, четыре стороны и все остальное.
Следует отметить несколько особенностей. Некоторые мутят воду, а другие помогают нам решить проблемы. Имея это в виду, вот небольшой набор важных вопросов, о которых следует подумать, когда вы работаете в этой области.
Какое определение для трапеции? У фигуры ровно одна пара параллельных сторон или хотя бы одна пара параллельных сторон? А может, вообще ничего! В разных культурах трапеции определяются по-разному, и во многих тоже есть термин трапеция.В США (для некоторых) трапеция — это четырехсторонний многоугольник без параллельных сторон; в Великобритании трапеция — это четырехсторонний многоугольник с ровно одной парой параллельных сторон; тогда как в Канаде трапеция имеет инклюзивное определение, так как это четырехсторонний многоугольник, по крайней мере, с одной парой параллельных сторон — следовательно, параллелограммы — это особые трапеции.
Сейчас я не в состоянии принять окончательное решение по этому поводу, но указать, что эти проблемы существуют (особенно в мультикультурных классах, в которых мы преподаем), очень важно, как и указывает тем, кто ищет в Интернете, когда урок Планируя, что часто требуется некоторая осторожность, внимание и скептицизм!
Евклид, прародитель большей части нашей школьной программы по геометрии, определил (Книга 1, определение 2) квадрат, имеющий равные стороны и прямые углы, прямоугольник, имеющий четыре прямых угла, но не четыре равных стороны, ромб, имеющий четыре равных стороны. стороны, но без прямых углов, ромб, имеющий равные противоположные стороны и равные противоположные углы, но без прямых углов и без четырех равных сторон.Все остальные четырехугольники имели форму трапеции.
Даже простое осмысление этого — прекрасная возможность по-настоящему подумать о том, как выглядят эти формы и их знакомые отношения, поскольку Евклид подразумевает, что на самом деле нет никаких пересечений между формами. Каждый из них представляет собой квадрат, продолговатую форму, ромб, ромб или трапецию. Разве это не упростило бы жизнь?
Каждый из них представляет собой квадрат, продолговатую форму, ромб, ромб или трапецию. Разве это не упростило бы жизнь?
Ну и да, и нет. Возникает вопрос, почему у нас есть те всеобъемлющие определения, которые мы делаем? Какой в этом смысл — неужто они просто ошеломляют и сбивают с толку?
Все сводится к тому, что мы можем вывести и заключить от одной формы к другой.Квадрат — это особый тип прямоугольника и ромба и, следовательно, особый параллелограмм. Эти иерархические определения приводят к более экономичным определениям понятий и формулировкам теорем, упрощают дедуктивную систематизацию и вывод свойств более специальных понятий, обеспечивают полезную концептуальную схему при решении проблем, могут предлагать альтернативные определения и новые предложения и обеспечивать полезные глобальные перспективы ( Де Вильерс, 1994).
Другими словами: теорема, которую вы доказываете для параллелограмма, верна для квадратов, прямоугольников и ромбов, поскольку все они являются типами параллелограмма. Однако теорема, которая верна для квадрата, может не выполняться для всех параллелограммов, поскольку не все параллелограммы являются квадратами.
Однако теорема, которая верна для квадрата, может не выполняться для всех параллелограммов, поскольку не все параллелограммы являются квадратами.
Здесь действительно интересно взглянуть на ограничения, необходимые при передаче семейства параллелограммов; рассмотреть, что остается инвариантным и как это взаимодействует с рассматриваемой теоремой. Возможно, ваше доказательство, основанное на квадрате, не опирается на эти ужесточенные ограничения, которые делают квадрат не просто параллелограммом, поэтому на самом деле ваше доказательство будет работать для всех параллелограммов.
При поиске чудес Интернета Википедия предлагает эту замечательную диаграмму:
https://upload.wikimedia.org/wikipedia/commons/9/9a/Euler_diagram_of_quadrateral_types.svg
Возможно, вы не полностью согласны с используемыми названиями, но замечательно то, как вы можете определить ужесточение или ослабление ограничения во время прогулки. Выйдите из области, и вы расслабитесь, войдите в другой слой, и вы затянете. Это также подчеркивает, что на самом деле, вы знаете, может быть, продолговатый — не такое уж неприятное слово — продолговатые и квадраты составляют семейство прямоугольников, а «продолговатый» может помочь с целыми квадратами — это путаница с прямоугольниками.В качестве альтернативы Клементс и Сарама (2009) предлагают использовать двойное имя квадрат-прямоугольник. Означает ли это, что у нас также будут ромб-параллелограммы? Было бы неплохо подумать, действительно ли некоторые регионы пусты, и у нас, как у команды, есть вопрос, следует ли включать «дартс» здесь и в кайт-регион?
Это также подчеркивает, что на самом деле, вы знаете, может быть, продолговатый — не такое уж неприятное слово — продолговатые и квадраты составляют семейство прямоугольников, а «продолговатый» может помочь с целыми квадратами — это путаница с прямоугольниками.В качестве альтернативы Клементс и Сарама (2009) предлагают использовать двойное имя квадрат-прямоугольник. Означает ли это, что у нас также будут ромб-параллелограммы? Было бы неплохо подумать, действительно ли некоторые регионы пусты, и у нас, как у команды, есть вопрос, следует ли включать «дартс» здесь и в кайт-регион?
Весь разговор просто подчеркивает, насколько запутанным может быть определение четырехугольника. Крайне важно решить, какие условия мы считаем необходимыми и достаточными, и, следовательно, знакомые отношения, и в то же время быть готовыми заявить о них прямо.Может быть, как только мы это сделаем, мы сможем нарисовать нашу собственную диаграмму Википедии для наших определений. Я оставлю это вам один раз, но мне было бы интересно, что вы создаете! Могу я найти ваши определения из вашей диаграммы?
Артикул:
Клементс, Д. Х., Сарама, Дж., 2000. Идеи маленьких детей о геометрических формах. Обучение детей математике 6, 482–488.
Х., Сарама, Дж., 2000. Идеи маленьких детей о геометрических формах. Обучение детей математике 6, 482–488.
Де Вильерс, М., 1994. Роль и функция иерархической классификации четырехугольников. Для изучения математики 14, 11–18.
Сарама, Дж., Клементс, Д.Х., 2009. Форма, в: Математическое образование и исследования для детей младшего возраста, Траектории обучения для детей младшего возраста. Рутледж, Нью-Йорк, стр. 199–246.
ЧТО-ТО ПОПРОБОВАТЬ: KS1: Что общего у каждого набора фигур? Что отличает каждый от другого? KS2: Прямоугольник — это особый тип параллелограмма. Почему? KS3: Нарисуйте древовидную диаграмму, чтобы связать семейство четырехугольников.Объясните ссылки, которые вы сделали. KS4: построить циклический параллелограмм. KS5: Теорема Ван Обеля утверждает, что: Если квадраты построены на сторонах любого четырехугольника, то отрезки прямых, соединяющие центры противоположных квадратов, равны и перпендикулярны. |
геометрия — идентификация четырехугольника как трапеции, прямоугольника или квадрата
Не могу не сказать кое-что… Как отмечалось в других ответах, это явно вопрос с подвохом, играющий на намеренно вводящих в заблуждение визуальных эффектах и, возможно, на деликатных (неуниверсальных!) Семантических соглашениях. (Меня беспокоит идея, что, например, «квадрат» не является «прямоугольником», потому что, предположительно, «прямоугольник» относится только к (фактическим) прямоугольникам, которые не являются квадратами, и т. Д.)
Элемент (ы) «произвольной / капризной власти», который присутствует как в контексте, так и в ответах, совершенно неудивителен, но также меня хронически расстраивает.Такие эпизоды рекламируют очевидную полезность математики для создания и применения произвольных, непостижимых правил, а также подчеркивают особую иррациональность «внешнего, необщительного, невыразимого» авторитета. Действительно некрасиво.
Действительно некрасиво.
Давайте признаем детям, что картинка была нарисована так, будто черт возьми, это был квадрат. Шутки в сторону! Это не чертёж, нарисованный неуклюжими фигурами настоящего , это контрольный вопрос. Это не значит, что мы должны задумываться о правдоподобии неадекватного репортера, а, скорее, о скрытых мотивах людей в ETS в Нью-Джерси и т. Д.
В частности, вместо слишком популярных традиционных, скорее суб-вербальных ответов на такие вопросы (это X или нет?), всегда должно быть достаточно места для объяснения / решения истинной проблемы, а не просто -смысловой, чисто искусственный. То есть мы должны научить детей писать прозу, которая гласит: «Ну, картинка делает фигуру квадратной … данные данные сами по себе физически не требуют, чтобы это был квадрат, но какой удар будет рисовать вещь? выглядит как квадрат, если бы его не было ?… «
(Серьезно, физическая интуиция очень многих людей превосходна, но потом мы постоянно их разыгрываем, чтобы они думали, что у них скудная связь с математикой, что совершенно неверно. Мы должны научить детей доверять своей физической интуиции хотя бы в первом приближении. ! Математика не извращение!)
Но, да, для тестов с множественным выбором, АБСОЛЮТНО скажите своим детям, чтобы разобрали глупости и представили, о чем думал создатель тестов.В этом отношении мы должны признаться детям, что у этих тестировщиков есть черта подлого шалости, о которой они (дети) должны знать. Печалька.
Обучение хитрым трапецоидам: инклюзивное против исключительного
Вы преподаете четырехстороннюю классификацию? Если да, то знаете ли вы, что существует ТРИ способа определить трапецию ? Американцы используют либо инклюзивное, либо исключительное определение в зависимости от своей учебной программы. Еще больше усложняет ситуацию то, что учителя, живущие за пределами Соединенных Штатов, определяют трапеции совершенно по-другому! Вы не поверите, но определение британского английского является полной противоположностью двум американским определениям!
Какому определению вы должны преподавать? Если вы не уверены, вполне возможно, что вы преподаете неправильное определение! Но не расстраивайтесь, если вы обнаружите, что это правда, потому что вы не одиноки.Фактически, до недавнего времени я даже не знал, какое определение использовалось в Общих государственных стандартах!
Прежде чем мы углубимся в эту тему, вам нужно знать, какое определение вы сейчас преподаете. Чтобы узнать это, ответьте на вопрос о трапеции ниже, прежде чем читать остальную часть этого сообщения. Затем прочтите информацию под 3 полигонами, которая объясняет, что означает ваш ответ.
Что показывает ваш ответ
Поскольку существует три способа определить трапецию, есть три правильных ответа на вопрос.Ваш ответ покажет определение, которое вы используете для классификации трапеций.
- Если вы выбрали только многоугольник 3 , вы используете исключительное определение , в котором говорится, что трапеция имеет ТОЧНО одну пару параллельных сторон . Это определение, которое я выучил, и я думал, что именно его использует Common Core (но я ошибался).
- Если вы выбрали многоугольники 1 И 3 , вы используете определение , включающее , в котором говорится, что трапеция имеет, ПО МЕНЯ, одну пару параллельных сторон .Многие преподаватели предпочитают это определение, потому что другие определения четырехугольника являются инклюзивными. Например, параллелограмм — это четырехсторонняя фигура, у которой обе пары противоположных сторон параллельны, что означает, что квадраты и прямоугольники также являются параллелограммами.
- Если вы выбрали только многоугольник 2, , вы используете британскую английскую систему классификации , в которой говорится, что трапеция — это четырехугольник без параллельных сторон . Вы учите своих учеников, что четырехугольник с одной парой параллельных сторон — это трапеция , а не трапеция .
Какому определению СЛЕДУЕТ преподавать?
Теперь вы знаете, какое определение вы используете для классификации трапеций, но разве этому определению вы должны научить ? Если вы не уверены на 100%, сделайте отметку, чтобы проверить это. До недавнего времени я думал, что Common Core использует эксклюзивное определение, но я обнаружил, что CCSS действительно использует инклюзивное определение! Я разместил вопрос на своей странице в Facebook, чтобы узнать, какое определение трапеции используют большинство учителей, и более 180 человек ответили.Я был удивлен, узнав, что большинство учителей, которые следуют CCSS, преподают инклюзивное определение.
Как научить детей классифицировать сложные трапеции
Если вы впервые слышите, что есть три способа определить трапецию, вы, возможно, задаетесь вопросом, чем поделиться со своими учениками. Я имею в виду, что четырехугольная классификация достаточно сложна, чтобы учить, не объясняя, что существует три различных правильных способа определения трапеции!
Я рекомендую вам выяснить, какое определение трапеции вы должны преподавать, и обучать только этому ОДНОМУ определению. Вы можете сказать своим ученикам, что они могут выучить несколько иное определение в какой-то момент в будущем, но если вы углубитесь в детали, ваши ученики в конечном итоге запутаются еще больше, чем когда-либо.
После того, как вы узнаете, какое определение вы должны преподавать, как вы познакомите его с учениками и поможете им научиться правильно классифицировать трапеции или трапеции?
Я обнаружил, что лучший способ помочь вашим детям научить этих хитрых трапеций — это простая сортировка.Есть две версии этого упражнения, и по возможности лучше использовать их обе. Первый — это печатное практическое занятие для партнеров по математике, которое отлично подходит для практических занятий. Другой — это действие Google Slides, которое вы можете назначить в Google Classroom для дополнительной практики или оценки. Оба действия включены в бесплатный бонус «Сортировка хитрых трапеций (или трапеций)» ниже. Указания в этом посте объясняют, как вести партнерскую деятельность под руководством учителя; инструкции по использованию версии Google Slides включены в бесплатный пакет услуг.
Сортировка по трапеции Направления урока:
- Начните упражнение с представления характеристик трапеции (или трапеции) в соответствии с определением, которое вы должны преподавать.
- Затем объедините каждого ученика в пару с партнером и дайте каждой паре по одному экземпляру четырехугольников для сортировки для печати. Попросите их вместе вырезать многоугольники и сложить их в стопку.
- Объясните, что они по очереди сортируют четырехугольники в одну из двух категорий с помощью Т-образной диаграммы.Раздайте каждой паре копию Т-диаграммы или попросите одного человека в каждой паре нарисовать Т-образную диаграмму на доске для сухого стирания.
- Прежде чем направлять их в процессе сортировки, назначьте роли Партнера A и Партнера B в каждой паре. Затем попросите Партнера А выбрать первый четырехугольник и поместить его в правильный столбец на Т-образной диаграмме. Затем партнер A объясняет расположение четырехугольника партнеру B, который показывает большой палец вверх, если он или она соглашается. Если партнер Б не согласен, два ученика должны обсудить правильное расположение четырехугольника и при необходимости переместить его в другой столбец.
- Партнер B затем выбирает один из оставшихся четырехугольников, помещает его на диаграмму и объясняет его размещение партнеру A. Партнер A должен утвердить размещение, или два студента обсуждают определение и размещение, прежде чем продолжить.
- Студенты продолжают меняться ролями на протяжении всего задания. Если они не могут договориться о размещении одного из четырехугольников, им следует отложить его на время.
- Пока студенты работают, ходите вокруг и наблюдайте за ними, чтобы убедиться, что они правильно классифицируют трапеции.Остановитесь, чтобы помочь студентам, которые сбиты с толку или не могут договориться о размещении одного или нескольких четырехугольников.
- Если вы используете Google Classroom, выполните версию этого упражнения для Google Slides.
Практические занятия по классификации четырехугольников
Это простое упражнение по сортировке на самом деле является одним из наиболее эффективных способов научить детей классифицировать любой тип четырехугольника. Фактически, это настолько эффективно, что я разработал полный урок по классификации четырехугольников на основе этой стратегии.Классифицируйте это! «Изучение четырехугольников» включает в себя несколько вводных заданий, а также интересную игру и две оценки.
Одна из причин, по которой я хотел привлечь ваше внимание к сложной ситуации с трапециями, заключается в том, что я недавно обновил Classify It! Изучение четырехугольников, чтобы включить все три определения. Теперь в файле продукта есть ТРИ версии материалов урока.
Неважно, какое определение вы должны преподавать, Classify It! «Изучение четырехугольника » поможет вам.Вы найдете уроки, распечатки, карточки с задачами, ключи ответов и оценки, которые соответствуют четырехсторонней системе классификации, используемой в вашей учебной программе. Эти занятия не только увлекательны и увлекательны для детей, но и уроки помогут им каждый раз составлять эти четырехугольные классификации! Если вы мне не верите, посмотрите этот продукт на TpT, где вы сможете прочитать отзывы 400 учителей, которые использовали Classify It! Изучение четырехугольника со своими учениками.
Если вы обучаете четырехугольникам и еще не приобрели этот ресурс, потратьте несколько минут, чтобы просмотреть его на TpT.Если вы используете его со своими учениками, я думаю, вы согласитесь, что Classify It — самый эффективный и УДОБНЫЙ способ способствовать глубокому пониманию четырехугольной классификации!
Что это за четырехугольник? — 3 класс по математике
Как определить четырехугольники
Вы помните, что такое четырехугольник? 000
Четырехугольник представляет собой четырехстороннюю двумерную форму.
Есть 4 типа четырехугольников: параллелограммы, трапеции, прямоугольники и ромбы.
️ Параллелограммы — это четырехугольники с двумя наборами параллельных сторон.
Это все параллелограммы:
Трапеция — четырехугольник с ровно одной парой параллельных сторон.
Это трапеция:
Прямоугольник имеет 4 прямых угла.
Ромб — это четырехугольник, все 4 стороны которого имеют одинаковую длину.
Давайте попрактикуемся в определении или обнаружении четырех различных типов четырехугольников.
Пример 1
Что это за четырехугольник?
Отлично!
Мы знаем, что это прямоугольник , потому что у него 4 прямых угла.
Вы обратили внимание на маленькие квадратики на каждом из углов?
Совет: Каждый маленький квадрат говорит нам, что это прямой угол размером 90 °.
Пример 2
Что это за четырехугольник?
Да!
Трапеция имеет только одну пару параллельных сторон.
Какие стороны параллельны?
Параллельные стороны — это линии с одинаковым расстоянием между ними, но никогда не пересекаются ни в одной точке.
Пример 3
Что это за четырехугольник?
Верно!
Это параллелограмм , потому что у него два набора параллельных сторон.
Давай попробуем еще раз. 000
Пример 4
Что это за четырехугольник?
Отлично!
Мы знаем, что это ромб , потому что все 4 стороны имеют одинаковую длину.
Молодец! 000
А теперь завершите тренировку, чтобы заработать медаль!
видов четырехугольников | Бесплатная помощь с домашним заданием
Обзор: что такое четырехугольник?
Четырехугольники — это многоугольники с четырьмя сторонами. Они классифицируются по равным углам и равным сторонам. Есть семь различных типов четырехугольников: параллелограмм, ромб, прямоугольник, квадрат, воздушный змей, трапеция и равнобедренная трапеция. Типы четырехугольников часто пересекаются, поэтому фигура, подходящая к одной категории, может подходить и к другой.У каждого есть свои особенности.
Определения
Четырехугольник является параллелограммом, если обе пары его противоположных сторон параллельны. Ромб — это четырехугольник со всеми сторонами одинаковой длины. Прямоугольник имеет 4 прямых угла, а квадрат — четыре равные стороны и четыре прямых угла. Эти определения существуют в иерархии отношений. Например, каждый квадрат также является параллелограммом, потому что обе пары его противоположных сторон равны, но каждый параллелограмм не является квадратом.Точно так же каждый квадрат также является ромбом, потому что все четыре стороны имеют одинаковую длину, но каждый ромб не является квадратом. Точно так же каждый квадрат также является прямоугольником, потому что прямоугольник имеет 4 прямых угла, но каждый прямоугольник не является квадратом.
Воздушный змей
Воздушный змей — это особый тип четырехугольника с двумя разными парами последовательных сторон одинаковой длины. Поскольку у ромбов и квадратов также есть стороны одинаковой длины, они тоже воздушные змеи, но обратное неверно. Не каждый воздушный змей — это ромб, потому что все стороны воздушного змея не равны.Точно так же каждый воздушный змей не является параллелограммом, потому что противоположные стороны воздушного змея не обязательно параллельны.
Трапеции
Трапеции — это четырехугольники, у которых одна пара параллельных сторон. Параллельные стороны называются основаниями. Если базовые углы равны, трапеция относится к особому типу, называемому равнобедренной трапецией. Прямоугольники — это особый тип равнобедренных трапеций с параллельными сторонами и равными углами.
Диагонали
Четырехугольники имеют две диагональные линии.В воздушном змее диагональ, соединяющая концы, образует линию симметрии. В ромбе обе диагонали образуют линии симметрии. Линии симметрии обладают мощными свойствами, которые помогают измерять углы, площадь и отношения между геометрическими фигурами.
Заинтересованы в репетиторстве по геометрии? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.
SchoolTutoring Academy — ведущая компания в сфере образовательных услуг для школьников и школьников. Мы предлагаем учебные программы для учащихся K-12, AP и колледжей.Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Ньюарке, Калифорния, посетите: Репетиторство в Ньюарке, Калифорния
Какое определение для трапеции? Один набор параллельных линий ИЛИ хотя бы один набор параллельных линий?
Несколько человек спрашивали меня об определении трапеции, которое встречается в учебной программе 5-го класса по математике Мамонт:
Трапеция имеет как минимум одну пару параллельных сторон. Может их двое!
Вы можете легко найти другие определения трапеции, которые указывают на то, что у нее есть только ОДНА пара параллельных сторон.Итак, люди запутались.
Это один из тех редких случаев, когда существует два типа определений для формы. Я использовал определение « включая », потому что в соответствии с ним квадраты, прямоугольники и параллелограммы ВКЛЮЧЕНЫ … они также являются трапециями.
Но некоторые из моих клиентов усвоили определение « эксклюзивный », согласно которому трапеция имеет ровно одну пару параллельных линий (а не две). Используя это определение, квадраты, параллелограммы и прямоугольники не подходят.
Математики предпочитают инклюзивное определение (такое, которое говорит «по крайней мере, одна пара параллельных прямых»). Почему? Потому что это делает формулировку их теорем короче. Если что-то верно для всех трапеций, то одно слово «трапеция» охватывает все формы по крайней мере с одной парой параллельных линий, и они не должны утверждать, что это верно для «трапеций, параллелограммов, ромбов, прямоугольников и квадраты ». Это просто упрощает жизнь.
То же верно и в случае квадрата против прямоугольника.Маленькие дети часто думают в терминах ИСКЛЮЧИТЕЛЬНЫХ определений и рассматривают квадраты как , а не как прямоугольников. По их мнению, у прямоугольника не может быть всех равных сторон. Но, как вы, наверное, знаете, инклюзивное определение (прямоугольник — это фигура с четырьмя сторонами и четырьмя прямыми углами) является преобладающим в мире взрослых, а квадраты — это , классифицируемые как прямоугольники.
Причина, по которой я использовал инклюзивное определение в Math Mammoth, заключалась не столько в теоремах, связанных с трапециями (на самом деле мы их не изучаем в элементарной математике).Это произошло потому, что это определение позволяет нам нарисовать эту четкую четырехугольную классификацию или древовидную диаграмму:
Обратите внимание, трапеция отображается как ВЫШЕ или как «родительский элемент» параллелограмма. Другими словами, параллелограмм — это «ребенок» трапеции. Это означает, что все параллелограммы ЯВЛЯЮТСЯ трапециями … они принадлежат к семейству «трапеций». Точно так же все ромбы — параллелограммы. А все квадраты — это прямоугольники, параллелограммы, трапеции.
См. Также
Включительные определения: трапеции от Dr.Математика
Определение трапеции из Wolfram Mathworld
Wolfram Mathworld высоко ценится математиками, и на их странице представлено типичное определение, предпочитаемое ими: «Трапеция — это четырехугольник с двумя параллельными сторонами». (Это типичный способ дать определение в математике, и это означает, что трапеция имеет как минимум двух параллельных сторон, а не ровно двух параллельных сторон.)
Включенное и эксклюзивное определение трапеции в Википедии
Мария Миллер
.








 Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)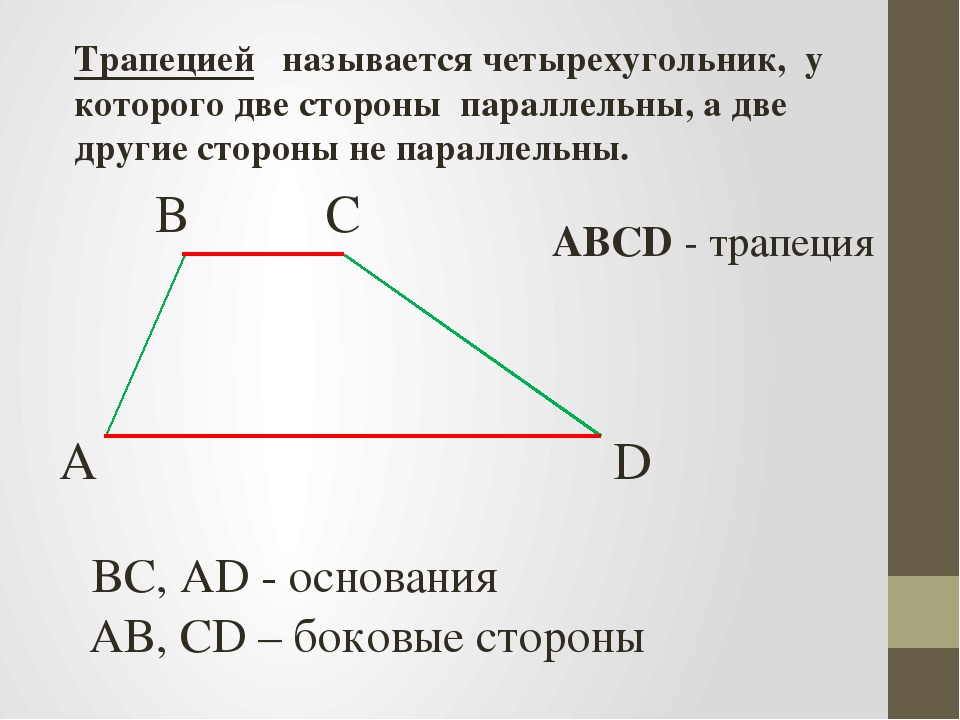 Виды четырехугольников. Свойства произвольных четырехугольников.
Виды четырехугольников. Свойства произвольных четырехугольников.
 Введите свой запрос:
Введите свой запрос: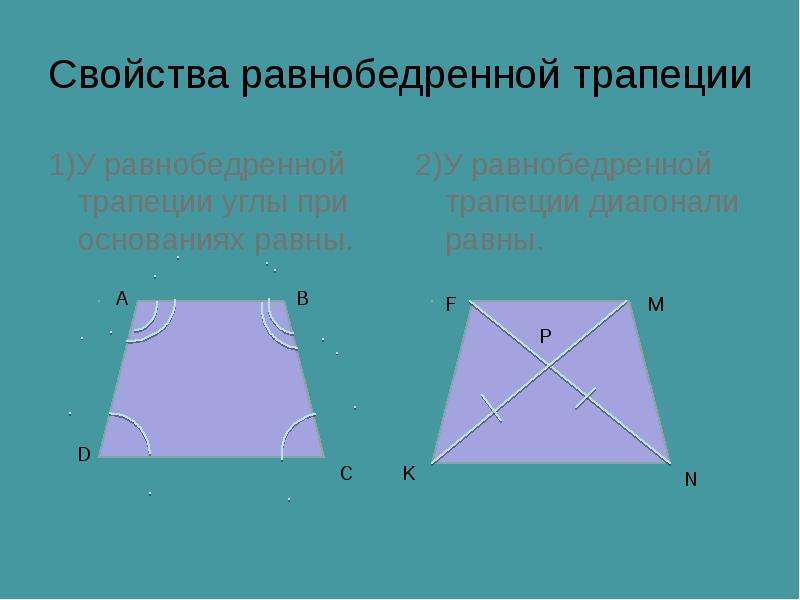
 Какую форму образовали бы эти центры, если бы исходный четырехугольник был параллелограммом? Использование иерархических классификаций покажет, почему. Рассмотрим здесь доказательства исходной теоремы.
Какую форму образовали бы эти центры, если бы исходный четырехугольник был параллелограммом? Использование иерархических классификаций покажет, почему. Рассмотрим здесь доказательства исходной теоремы.