Число Фибоначчи. Почему оно так популярно в природе?

Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.

«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи

Кто такой Фибоначчи?

Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.

В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.

Последовательность Фибоначчи

Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.

Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.

Леонардо Пизанский — тот самый создатель числа Фибоначчи

Читайте также: Найдено самое длинное простое число Мерсенна, состоящее из 22 миллионов цифр

Где используется число Фибоначчи

Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

Что такое золотое сечение

С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.

Так выглядит «золотое сечение»

Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.

Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.

ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!

ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!

Круглов  Н. П. 1

1Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»

Холинова  О.А. 1

1Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Математику называют «царицей всех наук». Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку. Иначе обстоит дело с математикой средневековья. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет для нас сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы (ок. 1170-после 1228), более известный под прозвищем Фибоначчи, который был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

В исследовательской работе рассматриваются числа последовательности Фибоначчи, их свойства, а также, тесно связанный с этой темой, феномен золотого сечения, в котором большинство ученых видят одно из наиболее ярких, давно уже замеченных человеком проявлений гармонии природы. Феномен золотого сечения рассмотрен в работе в общей картине исторического становления архитектуры, на формах живой природы и за пределами предметного мира, в области гармонии и математических абстракций. Он рассмотрен и как объективная характеристика объектов искусства, экономики и т. д.

Общеизвестно, что золотое сечение – это закон пропорциональной связи целого и составляющих это целое частей. Классический пример золотого сечения – деление отрезка в среднепропорциональном отношении, когда целое так относится к большей своей части, как большая часть – к меньшей: (a+b)/b = b/a.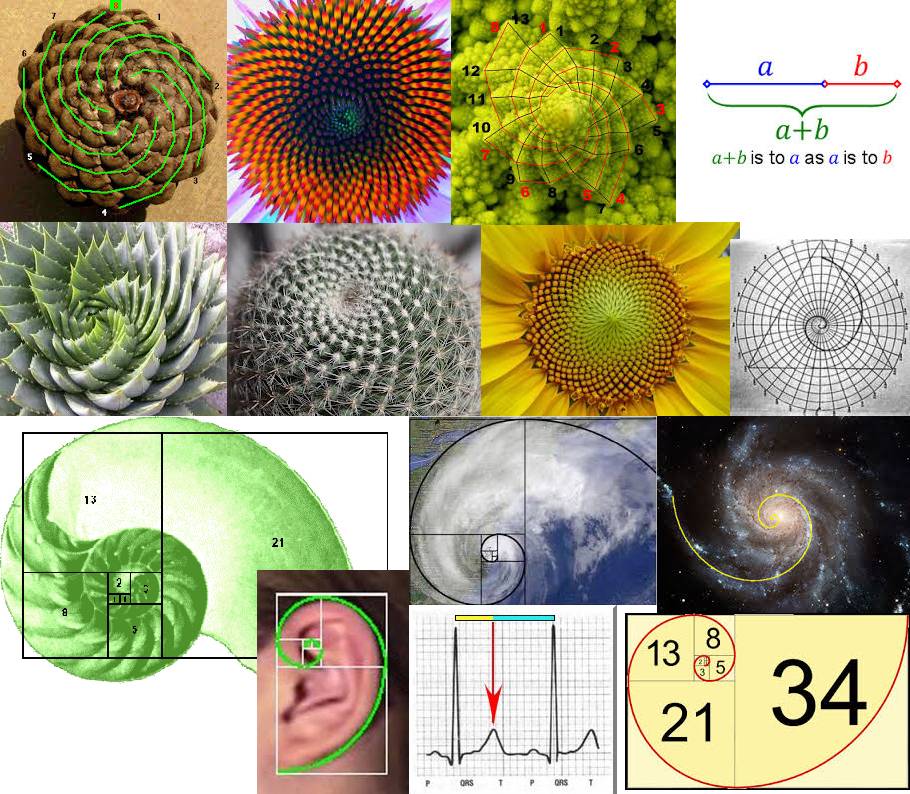 Такая задача имеет решение в виде корней уравнения x² – x – 1 = 0.За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных математических свойств и множество форм выражения пропорции золотого сечения.

Золотое сечение, как и загадочные свойства чисел Фибоначчи, владели мыслью и чувствами многих выдающихся мыслителей прошлого и продолжает волновать умы современников наших не ради самих математических свойств, а потому, что неотделимо от ценности объектов искусства и в то же время обнаруживает себя как признак структурного единства объектов природы. Скульптура, архитектура, музыка, астрономия, биология, психология, техника – вот те сферы, где так или иначе обнаруживает свою жизнь золотое сечение. Современные исследователи находят его при описании строения растений, пропорций тел животных, птиц, человека, в статистике популяций, в строении глаза и строении космоса и т. д.

Сегодня невозможно с абсолютной достоверностью определить, когда и как понятие золотого сечения было выделено в человеческом знании из интуитивной и опытной категорий. Но судить обоснованно, кто прав: те ли, кто относит открытие золотого сечения к цивилизациям древнего Востока (Египет. Индия), или те, кто, подобно Кеплеру, связывает открытие золотого сечения с именем Пифагора, можно, но для этого необходимо владеть базовыми историческими и математическими познаниями.

В эпоху Ренессанса среднепропорциональное отношение именовали Sectio divina – божественной пропорцией. Леонардо да Винчи дает ему имя Sectio aurea (золотое сечение), живое поныне, а много раньше, в 1202 г., открытием ряда Фибоначчи было обнажено фундаментальное свойство золотого сечения – единство аддитивности и мультипликативности.

Сегодня сущность гармонии невозможно выявить ни в биологии, ни в искусстве, ни в абстрактно-математических построениях, если рассматривать их раздельно, – здесь можно лишь наблюдать и осмысливать ее проявления. «Философия, – говорил Галилео Галилей, – написана в той величественной книге, которая постоянно открыта у нас перед глазами (я имею в виду Вселенную), но которую невозможно понять, если не научиться предварительно ее языку и не узнать те письмена, которыми она начертана». «Божественная пропорция – бесценное сокровище, одно из двух сокровищ геометрии», – развивает эту же мысль Кеплер. Действительно, гармония может быть расшифрована лишь на ее собственном языке, отображенном фундаментальными принципами естествознания.

Существуют любопытные закономерности, которые могут быть описаны с помощью математики. Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.

Актуальность данной работы заключается в необходимости исследования чисел Фибоначчи, так как они встречаются нам в различных творениях природы. Знания о них будут полезны во многих науках.

Цель: изучить практическую значимость чисел Фибоначчи

Задачи:

1. Познакомиться с числами Фибоначчи и историей их создания.

2. Рассмотреть рекурентную формулу ряда Фибоначчи.

3. Познакомиться с биографией итальянского математика Леонардо Пизанского (Фибоначчи).  

4. Изучить свойства числового ряда Фибоначчи

5. Проверить на практике  проявление чисел Фибоначчи  в неживой природе, в строении человека и растений.

Предмет исследования — числа Фибоначчи.

Объект исследования — область применения чисел Фибоначчи; свойства чисел Фибоначчи.

Проблема, которую призвано разрешить наше исследование, заключается в том, что мы не знаем и не видим в окружающей нас жизни числовые закономерности, которые укладываются в ряд Фибоначчи.

Изучение этих чисел не предусмотрено уроками математики, поэтому чтобы познакомится с ними подробнее, необходимо  использовать разнообразные источники информации: дополнительную литературу по предмету и интернет ресурсы.

Методы исследования в работе:

теоретический (логическая ступень познания).

эмпирический (наблюдение, эксперимент, измерение).

сравнение.

классификация.

математическое моделирование

практический (расчеты числа фи)

Структура работы: исследовательская работа состоит из введения, двух глав, заключения, списка используемой литературы. Во введении определена актуальность темы, связанная с понятием последовательности ряда Фибоначчи и проявление чисел Фибоначчи  в неживой природе, в строении человека и растений, цели, задачи, объекты и методы исследования. В первой главе описана историческая справка о Леонарде Пизанском, итальянском математике средневековья; последовательность ряда Фибоначчи и его свойства. Во второй главе рассмотрены проявления последовательности Фибоначчи в окружающем мире. Далее следует заключение. В нем определены выводы по проделанной работе. В списке используемых источников перечислена основная литература, которая использовалась в процессе работы.

В теоретической части исследования была изучена литература по данной теме, узнали, как образуется этот ряд, историю его возникновения, какими свойствами он обладает. Рассмотрели разные объекты природы где, обнаруживает себя ряд Фибоначчи. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах, в строении человеческого тела и в строении раковин моллюсков, в океане, в космосе и т.д. В проверке этих фактов заключается практическая часть нашего исследования.

1 Числа Фибоначчи.

1.1.Биография Леонардо Пизанского

Удивительные числа были открыты итальянским математиком средневековья Леонардо Пизанским, более известным под именем Фибоначчи.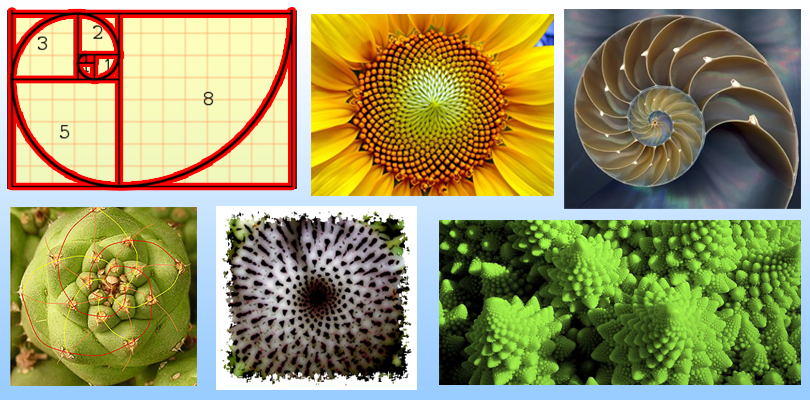    Леонардо Пизанский (Фибоначчи)– это первый крупный математик средневековой Европы. Более известен под прозвищем Фибоначчи, что в переводе с итальянского означает «хороший сын родился».

Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170г. в городе Пиза, в Италии. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты.

Его отец был купцом и государственным вельможей, представителем нового класса бизнесменов. Тогда Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи энергично торговал на северном побережье Африки, по торговым делам часто бывал в Алжире. Благодаря этому ему удалось «устроить» своего сына в одну из арабских школ, где он смог получить превосходное для того времени математическое образование.

Леонардо изучал труды математиков востока, по арабским переводам он ознакомился также с достижениями античных и индийских математиков.

Все эти знания он впитывал в себя как губка. А потом принес их в Европу, он «открыл» арабские цифры вместо римских и десятичную систему счисления для европейцев. Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Libег аЬасi, 1202; до наших дней сохранилась только дополненная рукопись 1228 г.).  Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной и одно из величайших открытий всех времён и народов – десятичную систему счисления.

На протяжении нескольких столетий по труду Фибоначчи ученые знакомились с двумя важнейшими разделами математики – арифметикой и алгеброй и черпали из него задачи и оригинальные методы решения, благодаря чему уже в XV – XVI в. в. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам.

Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи.

Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II.

1.2. Числа Фибоначчи и их свойства.

Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку.

Иначе обстоит дело с математикой средневековья. Кроме Виета, жившего в шестнадцатом столетии, и математиков более близких нам времен школьный курс математики не называет ни одного имени, относящегося к средним векам. Это, конечно, не случайно. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci – сокращенное filius Bonacci, т. е. сын Боиаччи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г.

«Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами. Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, составляющих значительную часть этого трактата. Рассмотрим одну такую задачу, помещенную на стр. 123-124 рукописи 1228 г.

«Сколько пар кроликов в один год от одной пары рождается?»

«Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; из них в этом же месяце будут давать потомство 3 пары, и число пар кроликов в четвертом месяце достигнет 8; из них 5 пар произведут другие 5 пар, которые, сложенные с 8 парами, дадут в пятом месяце 13 пар; из них 5 пар, рожденных в этом месяце, не дают в том же месяце потомства, а остальные 8 пар рождают, так что в шестом месяце оказывается 21 пара; сложенные с 13 парами, которые родятся в седьмом месяце, они дают 34 пары; сложенные с 21 парой, рожденной в восьмом месяце, они дают в этом месяце 55 пар; сложенные с 34 парами, рожденными в девятом месяце, они дают 89 пар; сложенные вновь с 55 парами, которые рождаются в десятом месяце, они дают в этом месяце 144 пары; снова сложенные с 89 парами, которые рождаются в одиннадцатом месяце, они дают в этом месяце 233 пары; сложенные вновь с 144 парами, рожденными в последнем месяце, они дают 377 пар; столько пар произвела первая пара в данном месте к концу одного года.

Действительно, на этих полях ты можешь увидеть, как мы это делаем; именно, мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с. четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев».

Построим алгебраическую модель задачи о кроликах и рассмотрим следующую числовую последовательность: , в которой u₁ = u₂ = 1, а каждый член последовательности, начиная с третьего, равен сумме двух предыдущих членов, то есть при всяком n > 2 выполняется равенство: .

Такие последовательности, в которых каждый член определяется как некоторая функция предыдущих, часто встречаются в математике и называются рекуррентными или, по-русски, возвратными последовательностями. Сам процесс последовательного определения элементов таких последовательностей называется рекуррентным процессом, а равенство (2) – возвратным (рекуррентным) уравнением [2].

Возвратная последовательность, задаваемая условием u₁ = u₂ = 1 и формулой (2) называется последовательностью Фибоначчи, а её члены –

числами Фибоначчи.

Перечислим основные свойства последовательности Фибоначчи.

1) Каждое следующее число, начиная с третьего равно сумме двух предыдущих.

2) Отношение каждого числа к последующему  при увеличении порядкого номера все более и более стремится к 0,618.

3) Отношение каждого числа ряда к предыдущему стремится к 1,618.

Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стремится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду, как арифметическому выражению закона золотого деления.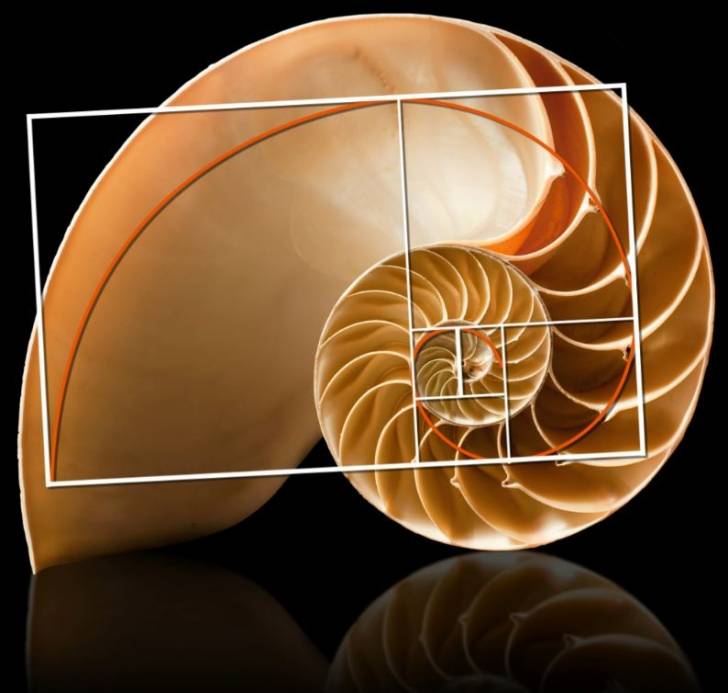

Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.

1.3 Спираль Фибоначчи

Спираль Фибоначчи – это некоторая кривая, которая огибает точку своего центра, приближаясь или удаляясь от неё, все зависит от направления, избранного вами. Эти фигуры могут быть как двухмерными, так и трехмерными, однако, если мы говорим о Фибоначчи, как о рыночной модели, то рассматривать можно только один вариант – двухмерный.

Когда строятся такие фигуры, то используется стартовая точка, построенная на плоскости, радиус выступает в роли непрерывной монотонной функции от угла.

Спираль Фибоначчи, отличается от Золотой пропорции и имеет точку начала. Беря начало в некоторой точке, такая фигура обычно разворачивается бесконечно долго.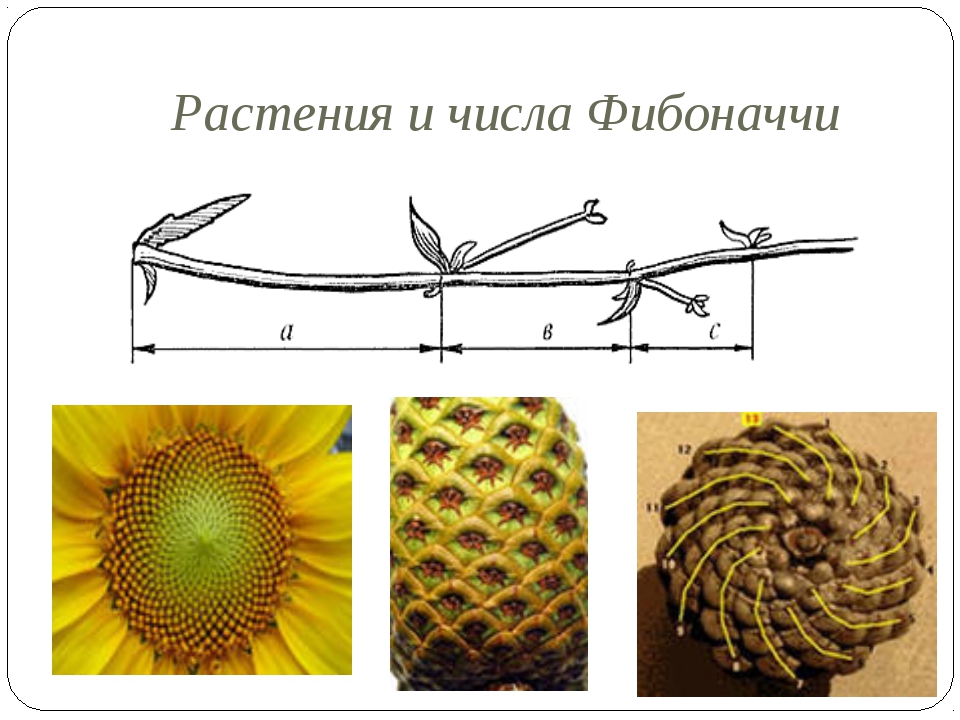

У последовательности Леонардо есть интересные свойства. Ряд Фибоначчи отличается от Золотого Сечения, так как начинается с единицы или нуля и при этом стремится к Золотой пропорции.

Также он постоянно увеличивает точность. В некоторой точке (когда почти достигнута фи =1,618) уже невозможно найти разницу, которая прослеживалась между двумя спиралями. Понимание этого свойства Спирали Фибоначчи и определяет её удивительность.

Это поразительно, однако, строение спирали Фибоначчи можно наблюдать в большом количестве предметов и явлений.

2 Числа Фибоначчи в нашей жизни

2.1 Числа Фибоначчи в природе

С тех пор, как Фибоначчи открыл свою последовательность, были найдены много явлений природы, в которых его последовательность чисел прослеживается очень четко. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи.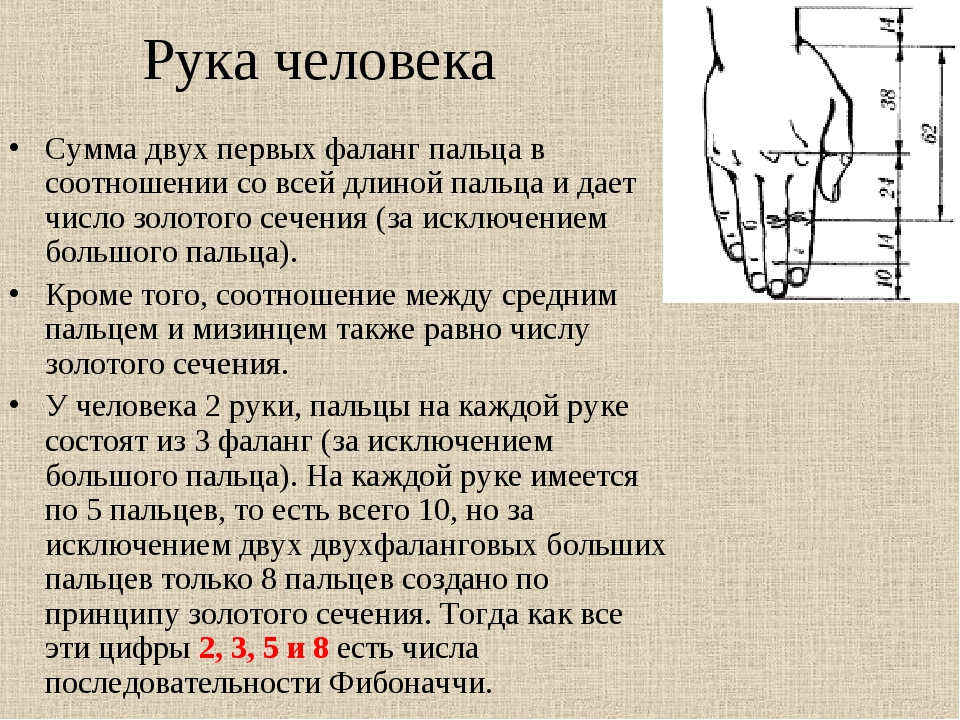 Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис — листорасположение), в числе оборотов на стебле, в числе листьев в цикле  проявляет себя ряд чисел Фибоначчи.

Чёткая, симметричная форма цветов  также   подчинена строгому закону.

У многих цветов количество лепесточков является числами из ряда Фибоначчи.

Встретить числовые закономерности в живой природе  можно в различных спиральных формах, которыми так богат мир растений.  Обычно можно усмотреть два вида спиралей. В одном спирали завиваются по часовой стрелке, а в другом против. Число «правых «и «левых» спиралей часто оказываются соседними числами Фибоначчи

Можно привести множество примеров.

Первый и очень яркий пример – это подсолнухи. Их семена расположены так, чтобы максимально использовать всю площадь соцветия, не теряя ни миллиметра. А расположены они в виде двух пересекающихся спиралей справа налево и наоборот. Пары этих спиралей встречаются разные, у меньших соцветий 13 и 21, 21 и 34, у больших 34 и 55, 55 и 89. И отклонений от этих пар быть не может.

Нечто подобное происходит и с ячейками ананаса: у него 8 правосторонних спиралей, 13 левосторонних и 21 вертикальная. И снова последовательность Фибоначчи.

В сосновой шишке, если хорошо присмотреться, можно увидеть две спирали, закручены одна по часовой стрелкой, а другая против. Число этих спиралей 8 и 13.

Количество лепестков во многих соцветиях совпадает с числами из этой последовательности, например, ирис имеет 3 лепестка, у примулы их 5, у амброзии полыннолистной — 13, у астр бывает 55 или 89 лепестков.

Листья на деревьях и других растениях распределены в последовательности, основанной на золотом числе, таким способом, чтобы получать максимум света и не мешать друг другу.

У многих бабочек отношения размеров грудной и брюшной части тела очень близки к золотому числу.

Раковины моллюсков закручены по спирали, и если измерить ее завитки, то их отношение постоянно и равно 1.618.

Спиралеобразно паук плетет паутину. По спирали закручивается ураган. Стадо северных оленей по тревоге разбегается по спирали. По спирали закручиваются волны, которые разбиваются об берега океана. Молекулы ДНK живых организмов закручены двойной спиралью. Гете называл эту спираль «кривой жизни».

2.2. Числа Фибоначчи в строении животных

Кроме растений, числа Фибоначчи проявляются в строении различных живых организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13.

У хорошо знакомого комара – три пары ног, брюшко делится на 8 сегментов на голове 5 усиков – антенн. И опять мы видим числа 3,5,8, числа последовательности Фибоначчи.

2.3. Числа Фибоначчи в строении человека

Числа Фибоначчи отражают основную закономерность роста организмов, следовательно проявляются и в строении человеческого тела.  Рассмотрим это поподробнее.

У человека одно туловище, одна голова, одно сердце и т. д.  Многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги,  руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. Можно рассмотреть части тела и с другой стороны. У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, только 8 пальцев трехфаланговые. Все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи. (Приложение 1, 2).

Позвоночник человека состоит из 34 позвонков.   Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34. Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.

Числа Фибоначчи можно обнаружить и в «крови» у человека. Так распределение людей по трём  группам крови отвечает отношениям чисел 8/ 21 /3.

Сердечная мышца сокращается до 0,618 от своей изначальной длины и нарушение этого числа при сокращении ведет к болезням сердца.  А это число отражает одно из свойств чисел Фибоначчи. В результате математической обработки экспериментальных медицинских данных, появились отношения чисел, характеризующих сердечный цикл: 0,050; 0,081; 0,131; 0,210; 0,340. Мы видим, что они отражают последовательность ряда чисел Фибоначчи 5, 8, 13, 21, 34. В строении человеческого лица и кисти существуют и иные воплощения ряда Фибоначчи. (Приложение 1, 2).

Этот ряд получается, если провести измерения длин фаланг пальцев  и расстояний между различными частями лица.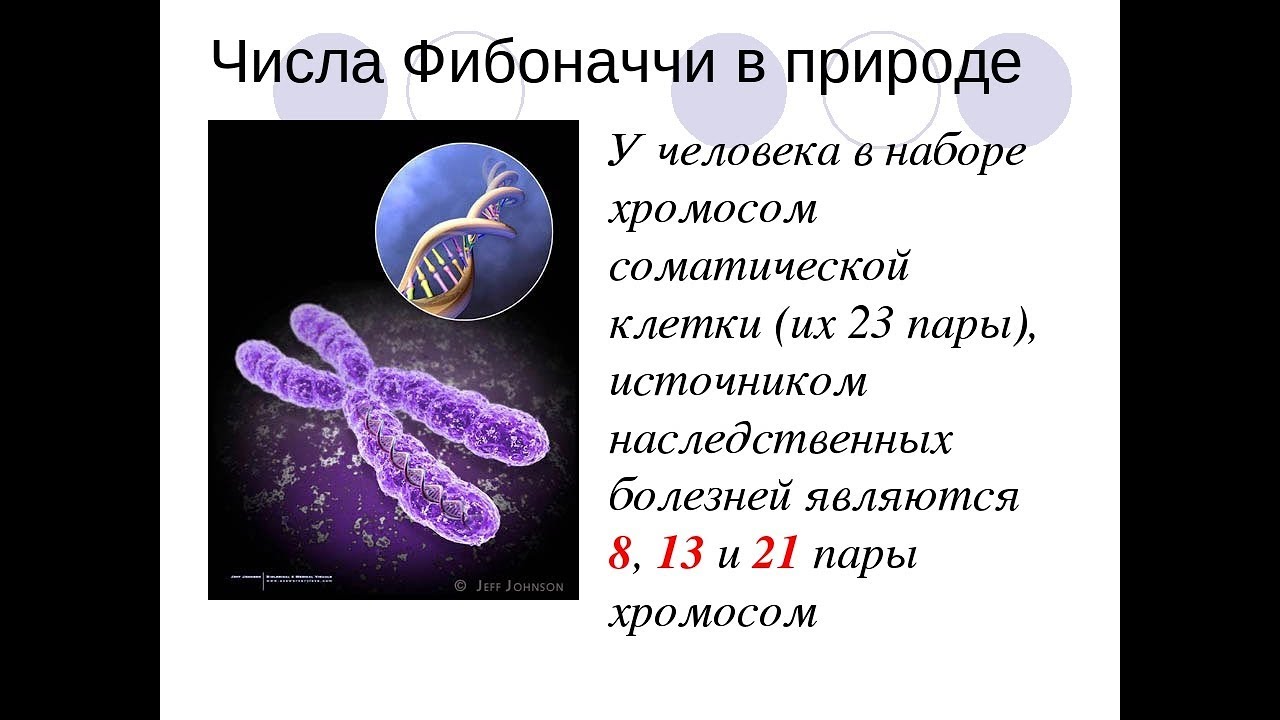

2.4. Числа Фибоначчи и золотой прямоугольник

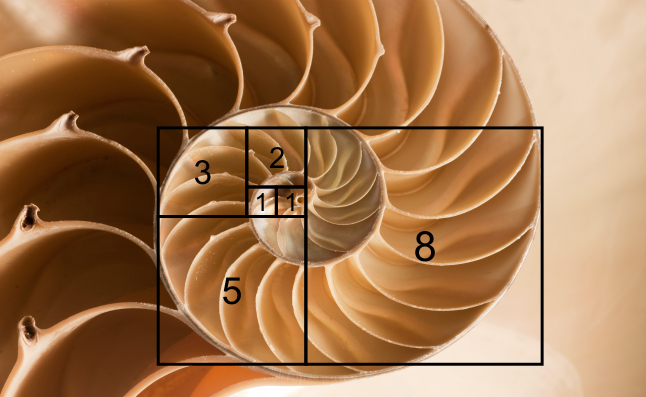
Было отмечено, что числа Фибоначчи тесно связаны со спиралевидным строением многих представителей живой и неживой природы. Чтобы рассмотреть еще несколько таких примеров, необходимо познакомиться с так называемым «золотым прямоугольником». Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров.

Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по спирали, которая называется спираль Фибоначчи.

Эту спираль можно обнаружить  в самых различных и неожиданных предметах и явлениях.

У большинства улиток, которые обладают раковинами, раковина растет в форме  спирали. Раковины улиток подчиняются последовательности  и спирали Фибоначчи.       

Паук плетет паутину спиралеобразно. Интересно, что спиралью  закручиваются ураган, облака циклона и это хорошо видно из космоса.

Числа Фибоначчи оказались и в спирали, описывающей изгиб гребня набегающей волны в океане, и в спирали, убегающей воды в раковине умывальника. Да и живём мы тоже  в спирали, ведь галактика – это спираль, соответствующая спирали Фибоначчи.

На рисунке показаны относительные размеры Земли и Луны в масштабе.

Нарисуем радиус Земли. Проведем отрезок от центральной точки Земли до центральной точки Луны. Нарисуем отрезок для соединения двух данных отрезков, чтобы сформировать треугольник. Получаем золотой треугольник.

Сатурн показывает золотую пропорцию в нескольких ее измерениях

Диаметр Сатурна очень близко находится в отношении золотой пропорции с диаметром колец, как показано зелеными линиями.  Радиус внутренней части колец находится в отношении, очень близком к с внешним диаметром колец, как показано синей линией.

Расстояние планет от Солнца также подчиняется золотой пропорции.

2.5 Числа Фибоначчи в архитектуре

В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.

Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).

Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.

Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.

2.6.Числа Фибоначчи в искусстве

В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики применение закона золотого сечения распространилось на конструирование машин, мебели и пр.

Пропорция, выражаемая числом Ф, по мнению многих исследований, является наиболее приятной для человеческого глаза.

Леонардо де Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с числом Ф. Деление отрезка в отношении Ф он назвал «золотым сечением». В эпоху возрождения «золотое сечение» было очень популярно среди художников, скульпторов и архитекторов. Размеры картины было принято брать такими, чтобы отношение ширины к высоте равнялось Ф. Этот термин сохранился до наших дней, и само «золотое сечение» по прежнему играет важную роль в искусстве. Им руководствовался, например, великий архитектор Ле Корбюзье.

Прямоугольник с таким отношением сторон стали называть «золотым прямоугольником».

Форму «золотого сечения» придавали книгам, столам почтовым открыткам. В дальнейшем книгам и другим бумажным изделиям стали чаще придавать форму прямоугольника с отношением сторон корень из двух. Это связано с тем, что при перегибании такого прямоугольника по средней линии образуются два прямоугольника с тем же соотношением сторон.

Число золотого сечения Ф обладает какой-то странной неуловимостью. Оно появляется в различных проекциях, так и не давая ответа на вопрос, как это число связано с тем или иным явлением. Интерес к мистическому числу Ф достаточно периодичен. Он возникает с обнаружением нового проявления этого числа в каком-либо явлении природы.

Проходит время, и интерес к нему спадает. Но ненадолго. Числу Ф находят всё новое и новое применение, но оно так и остается недоступным для ясного и полного понимания его свойств и степени его влияния на окружающий мир.

2.7. Числа Фибоначчи и фотография

Применительно к фотографическому искусству правило золотого сечения делит кадр двумя горизонтальными и двумя вертикальными линиями на 9 неравных прямоугольников. Чтобы облегчить себе задачу съемки сбалансированных изображений, фотографы немного упростили задачу и стали делить кадр на 9 равных прямоугольников в соответствии с числами Фибоначчи. Так правило золотого сечения трансформировалось в правило третей, которое относится к одному из принципов построения композиции.

В видоискателях современных цифровых камер точки фокусировки расположены на позициях 2/8 или на воображаемых линиях, делящих кадр по правилу золотого сечения.

Наиболее удачным примером для демонстрации является пейзаж. Принцип композиции заключается в том, что небо и суша (либо водная гладь) должны иметь соотношение 1:2. Одну треть кадра следует отвести под небо, а две трети под сушу или наоборот.

Практическое исследование

Вторая часть нашего практического исследования заключается в конкретных подсчетах и измерениях.

Числа Фибоначчи в строении подсолнуха

Первым для изучения мы взяли подсолнух и сосчитали количество спиралей, идущих в одну сторону и количество спиралей в другую сторону. Правых спиралей, они закрашены красным, получилось 34, левых, они закрашены синим – 55. Эти числа 34 и 55 являются соседними в последовательности Фибоначчи.

          Числа Фибоначчи в строении еловой и сосновой шишек

Продолжая исследование, числа, входящие в ряд Фибоначчи мы увидели в сосновых и еловых шишках. Подсчет спиралей выявил следующие результаты. Замечаем две серии   спиралей  Фибоначчи: одна —  по часовой стрелки, другая —  против, их число 8 и 13.

Числа Фибоначчи в строении ананаса

На фотографиях показано как мы  проводили подсчеты чешуек на кожуре ананаса. Нами получены числа: 8 и 13. Как мы снова можем убедиться, эти числа являются членами последовательности Фибоначчи.

Числа Фибоначчи в ветке дерева

Последовательность ответвлений, идущих по стволу растений, мы подсчитывали, рассматривая ветку дерева. Положив её на ватман, мы провели горизонтальные линии, соответствующие пазам выхода веток,  и посчитали их количество. Получили следующие данные: 1,2,3,5,8… Полученный ряд является частью ряда Фибоначчи.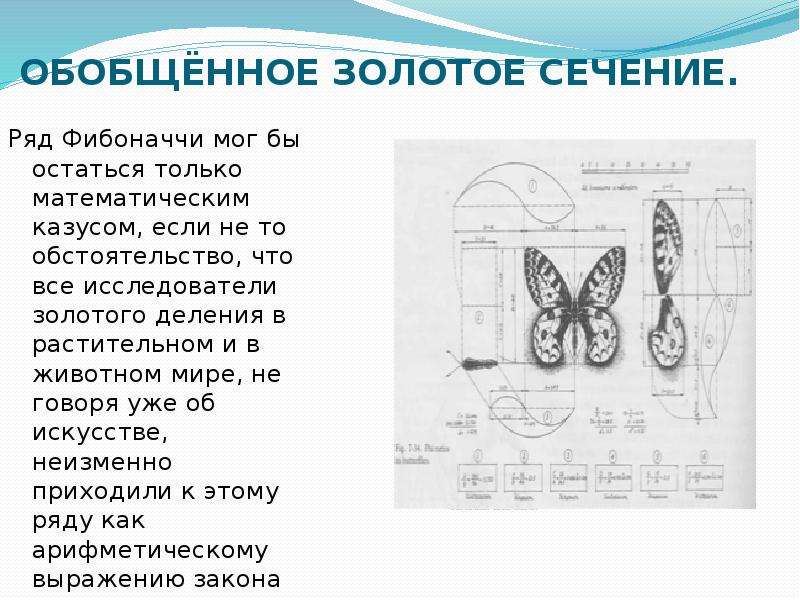

ЗАКЛЮЧЕНИЕ

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве и архитектуре, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их. 

В своей работе, мы, конечно же, не можем до мельчайших подробностей изложить суть этого вопроса, но мы постарались отразить наиболее интересные и весомые аспекты. Мы рассказали о Леонардо Пизанском и дали понятное определение последовательности Фибоначчи; затем, на ярких примерах показали присутствие чисел Фибоначчи и Золотого сечения в разных сферах нашей жизни; выяснили что такое «Закон сохранения света», «Платоновы тела» и как они связаны с последовательностью.

 Золотое сечение и последовательность чисел Фибоначчи помогают учёным описывать строение галактик и планетарных систем, а некоторые социологи начинают их использовать для прогнозирования различных катаклизмов, обусловленных массовой истерией (войн, беспорядков, революций и т.д).

Одна и та же закономерность используется в совершенно разных областях, практически не связанных между собой, а это значит, что она является универсальной.

Экономика, как и другие общественные сферы жизни человека поддаются определенным законам, несмотря на свою определенную непредсказуемость и зависимость от многих факторов современные экономические системы (в теории волнового анализа) поддаются законам «уровней Фибоначчи» построенных на основе одноименной последовательности.

С появлением финансовых рынков математики и статисты попробовали при помощи золотых чисел Фибоначчи строить уровни поддержки и сопротивления.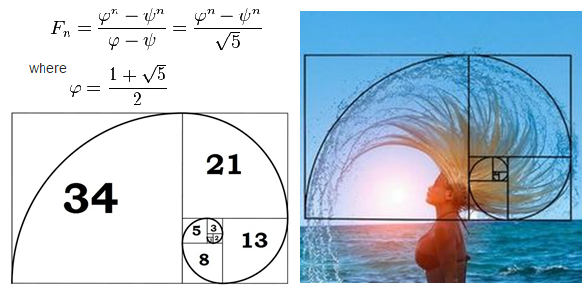 Логично, ведь если поведение социума подчиняется божественной пропорции, разумно предположить, что и в действиях участников рынка также будет прослеживаться данная закономерность.

Как известно, эксперимент оказался удачным, и сегодня золотые числа Фибоначчи на Форекс используются для построения сеток, расширений, вееров, каналов и временных зон. В частности, при помощи первого инструмента можно найти сильные уровни, на которых следует ждать завершения коррекции, сформированной по отношению к последнему импульсу.

Мы убеждены, что данная тема будет актуальна еще долгое время, и будут открываться все новые и новые факты, подтверждающие присутствие и влияние суммационной последовательности Фибоначчи на нашу жизнь.

Список литературы

1. Маркушевич, А. И. Возвратные последовательности. / А. И. Маркушевич.М.: Наука, 1975.

2. Воробьёв, Н. Н. Числа Фибоначчи. / Н. Н. Воробьёв. М.: Наука, 1978.

3. Савин, А. П. Энциклопедический словарь юного математика. / А. П. Савин. М.: Педагогика, 1989.

4. Мохнаткина, К. В. Последовательности в школьном курсе. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 3. Саратов: Научная книга, 2005. С. 63-67.

5. Мохнаткина, К. В. Изучение последовательностей в старших классах. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 4. Саратов: Научная книга, 2005. С. 59-63.

1.http://fb.ru/article/323642/chisla-fibonachchi-i-zolotoe-sechenie-vzaimosvyaz

2.https://studwood.ru/1851811/matematika_himiya_fizika/biografiya_fibonachchi

3.https://multiurok.ru/files/issliedovatiel-skaia-rabota-po-matiematikie-chisla-fibonachchi.html

4.http://fibonachi. gimnaziayanaul.edusite.ru/p11aa1.html

Приложение 1.

Золотые пропорции в частях тела человека.

Приложение 2

Просмотров работы: 1372

Числа Фибоначчи. История. Интересные факты. Использование в повседневной жизни

Числа Фибоначчи и золотое сечение

МОУ «Малыгинская средняя общеобразовательная школа» Числа Фибоначчи и золотое сечение Выполнила ученица 9 «а» класса Кузнецова Юлия под руководством учителя математики Большаковой О.К. «Числа не управляют

Подробнее

Золотое сечение в теле человека

Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение

Подробнее

Рис.

1.Золотой квадрат.

УДК 517.8 ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ А.А. Куликов, студент группы ЭЭб-152, I курс Научный руководитель: А.В. Чередниченко, ассистент Кузбасский государственный технический университет г. Кемерово Что общего

Подробнее

Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21,

Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Такая зависимость получилась в результате

Подробнее

ЧИСЛА ФИБОНАЧЧИ КУРСОВАЯ РАБОТА

Министерство образования и науки Российской федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ

Подробнее

Темы проектов по математике для 5 класса

Темы проектов по математике для 5 класса Алгебраические дроби. В мире процентов. В стране рыцарей и лжецов. Виды уравнений, решаемые в 5-м классе. Возникновение чисел. Вокруг обыкновенных дробей. Графический

Подробнее

Золотое сечение и строение человека

1 Городское соревнование юных исследователей «Шаг в будущее Юниор» Золотое сечение и строение человека Россия, г.сургут, Ульянова Виктория Александровна Муниципальное бюджетное общеобразовательное учреждение

Подробнее

ЗОЛОТОЕ СЕЧЕНИЕ ВОКРУГ НАС

Капустина М.Д., Жапова С.Д. Золотое сечение вокруг нас // Материалы по итогам Всероссийской научно-практической конференции «Молодежь XXI века: образование, наука, инновации», 01-10 марта 2016 г. 0,3 п.

Подробнее

Глава 4.2. Технический анализ: Фибоначчи

Глава 4.2 Технический анализ: Фибоначчи ТЕХНИЧЕСКИЙ АНАЛИЗ: ФИБОНАЧЧИ Анализ Фибоначчи — это инструмент, позволяющий выявить потенциальные уровни поддержки и сопротивления, основываясь на прошлых ценовых

Подробнее

Математическая гармония человеческого тела

Краевая научно-практическая конференция учебно-исследовательских работ учащихся 9-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Математическая гармония человеческого

Подробнее

Система счисления.

Тренер: Аюпов Р.Х.

Система счисления Тренер: Аюпов Р.Х. — Говорили древнегреческие философы, ученики Пифагора, подчеркивая важную роль чисел в практической деятельности. — Это знаковая система, в которой числа записываются

Подробнее

Страничка для влюбленных в математику

Страничка для влюбленных в математику Страницу подготовила учитель математики, директор школы Шмелькова Наталья Александровна Если учитель имеет только любовь к делу, он будет хороший учитель. Если учитель

Подробнее

Древнекитайский символ

Древнекитайский символ Сравните Некоторые современные здания Золотое сечение «Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник

Подробнее

Числа Фибоначчи.

Формула красоты.

Научно исследовательская работа Числа Фибоначчи. Формула красоты. Автор: ученик10 класс Шроо Артур Муниципального бюджетного образовательного учреждения Катановской средней общеобразовательной школы Руководитель:

Подробнее

ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ

ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ ЭТАПЫ РЕШЕНИЯ ЗАДАЧ НА ЭВМ : постановка задачи; математическое описание задачи; выбор и обоснование метода решения; алгоритмизация вычислительного процесса; составление

Подробнее

АСТРОНОМИЯ А С Т Р О Н О М И Я. Кеплер

А С Т Р О Н О М И Я Кеплер 243 Золотое сечение в строении Солнечной системы и Вселенной У каждой планеты имеется минимальный радиус орбиты, но есть и максимальный как у всякого эллипса. Если рассмотреть

Подробнее

Учебный проект «Золотое сечение» Часть I

Муниципальное бюджетное общеобразовательное учреждение Лицей 7 г. Химки Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования: Мизеровская Анна ученица 10 «А» класса

Подробнее

Проект для учеников 8 классов

Проект для учеников 8 классов «Геометрия владеет двумя сокровищами — теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.

Подробнее

МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ

ВГУЗУ «Украинская медицинская стоматологическая академия» Кафедра социальной медицины, организации и экономики здравоохранения с биостатистикой и медицинским правоведением МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ Лектор:

Подробнее

Что такое числа Фибоначчи?

Что такое числа Фибоначчи? Определение. Числа Фибоначчи или Последовательность Фибоначчи числовая последовательность, обладающая рядом свойств. Например, сумма двух соседних чисел последовательности дает

Подробнее

Содержание курса математики в 5 6 классах

Содержание курса математики в 5 6 классах Натуральные числа и нуль Натуральный ряд чисел и его свойства Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками

Подробнее

Анкета для индивидуального пошива

01 РОСТ Измеряется в сантиметрах от пола до макушки. 02 ОБХВАТ ГОЛОВЫ Измеряется в самом широком месте головы: Горизонтально, по кругу, над ушами и бровями 02-А ДЛИНА ГОЛОВЫ ОТ 7 ШЕЙНОГО ПОЗВОНКА ДО НАДБРОВНЫХ

Подробнее

«Подсолнух с целой галактикой» 1

А.Н. Ковалев «Подсолнух с целой галактикой» 1 Аннотация. Рассмотрено уточнение и обобщение модели Фогеля для подсолнуха. Предложена аналогичная формула для одуванчика. Определена формула для разворачивающихся

Подробнее

Урок-игра по теме «Системы счисления»

Урок-игра по теме «Системы счисления» Предмет: информатика и ИКТ Класс: 9 класс Тема учебного занятия: Урок-игра «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции

Подробнее

Природная мера знания

Павел Саввин Природная мера знания Содержание Предисловие…1 1.Божественная пропорция в числовой последовательности Фибоначчи…2 2. Способ исчисления количества знания…3 Приложение Achillea (Золототысячник)…7

Подробнее

Буква слово, цифра число?

1 Буква слово, цифра число? Нина Коптюг, кандидат филологических наук, лауреат 1 Всероссийского конкурса «Дистанционный учитель года РФ», победитель конкурса ПНПО «Лучший учитель РФ», представитель РФ

Подробнее

«Золотое сечение» Часть I

Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования Мизеровская Анна, ученица 10 «А» класса МБОУ Лицей 7 г. Химки Провести исследования по теме «Золотое сечение

Подробнее

Проценты в нашей жизни

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ «ШКОЛА 2048» Проценты в нашей жизни Даниэль Айратович Мустафин, ученик 6 «е» класса Научный

Подробнее

Пояснительная записка

Пояснительная записка Программа по математике разработана, в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра

Подробнее

S = {1, 1, 1, } (1) N = (N раз). (2)

7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у

Подробнее

Высшая математика жизни: где в природе встречаются числа Фибоначчи? | Наука | Общество

Каждый год 23 ноября в мире вспоминают первого крупного математика средневековой Европы Леонардо Пизанского, известного под прозвищем Фибоначчи. Он открыл для современников десятичную арабскую систему счисления и в целом обогатил их знания в точных науках. Но главным его открытием стала последовательность, названная числами Фибоначчи. Её называют удивительной за свойство неожиданно проявляться в самых разных сферах жизни — от биологии до живописи.

Кролики Леонардо Пизанского

Леонардо Пизанский, наиболее известный под прозвищем Фибоначчи (чаще всего имя трактуют как «счастливчик»), родился около 1170 года в итальянском городе Пиза. Его отец был купцом и посещал по торговым делам Алжир, куда привёз сына для изучения математики у арабских учителей. Позднее Фибоначчи сам ездил в Египет, Сирию, Византию и Сицилию, где ещё ближе познакомился с достижениями античных и индийских математиков. На основе полученных там знаний Леонардо написал ряд математических трактатов, ставших революционными для средневековой западноевропейской науки. Самым известным его трудом стала «Книга абака» (абак — это древнеримские счёты).

«Фактически это была энциклопедия математики того времени, — рассказывает кандидат физико-математических наук, доцент Кубанского госуниверситета Эдуард Сергеев. — В ней впервые в Европе была изложена десятичная позиционная система счисления арабов. Там впервые использовались отрицательные числа как долг. Завершалась эта большая книга изложением алгебры и примерами решения практических задач, связанных с торговым делом. В её 12-й главе содержалась знаменитая задача о кроликах. Именно благодаря ей мир узнал о числах Фибоначчи».

Золотое сечение в пятиконечной звезде. Фото: YouTube/ Скриншот

Придуманная средневековым математиком задача предназначалась для расчёта потомства кроликов. По её условию в огороженный со всех сторон загон поместили двух животных для размножения. Вопрос: сколько они могут произвести на свет пар кроликов за год, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару? Ответ — 233 пары. Для поиска решения автор задачи вывел числовой ряд, в котором каждый последующий член равен сумме двух предыдущих. Он выглядит так: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее до бесконечности. Намного позже, уже в XIX веке эту последовательность назвали «числами Фибоначчи».

Дату 23 ноября для неофициального праздника Дня Фибоначчи тоже выбрали исходя из его последовательности. Для этого использовали принятый на Западе календарный формат, при котором цифрами сначала пишут месяц, а потом день. Получается 11/23, что повторяет первые четыре числа из ряда математика: 1, 1, 2, 3.

Но ещё интереснее то, что числовой ряд Фибоначчи нашёл применение во многих областях математики и по сей день удивляет учёных своей универсальностью. Кроме того, с ним также оказались связаны многие явления окружающего мира.

Проявления золотого сечения в природе. Фото: YouTube/ Кадр из видео

Удивительные числа

«В Италии выпускается периодический журнал, который называется „Числа Фибоначчи“, — продолжает Эдуард Сергеев. — Авторы со всего мира пишут для него статьи, связанные с последовательностью Леонардо Пизанского и другими свойствами чисел. И практически каждый год открывают что-то новое. В мои студенческие годы были известны одни свойства чисел Фибоначчи, а сегодня уже появились другие, в том числе совершенно неожиданные. Одно из открытых недавно удивительных свойств чисел Фибоначчи в том, что с определённой периодичностью в них повторяются одни и те же последовательности последних цифр. То есть рост этого ряда не случаен и подчиняется некоему закону, который, видимо, пока недоступен нашему пониманию. Это действительно загадочная вещь».

Поразительные свойства последовательности Фибоначчи в математике сложно объяснить человеку без специальных знаний, но многое можно понять и без формул. Одна из главных особенностей этого «золотого ряда» в том, что отношение каждого последующего его члена к предыдущему неуклонно приближается к показателю 1,618. Математикам он известен как число Фи, но у него есть и много других имён: число Бога, божественная гармония, асимметричная симметрия, золотое сечение (последнее понятие придумал Пифагор). Константу Фи назвали так в честь древнегреческого скульптора Фидия. Еще древние строители знали, что при использовании определённых пропорций здание выглядит максимально красиво и к тому же получается наиболее устойчивым. Коротко золотое сечение определяется так: меньшая часть относится к большей, как большая ко всему целому. В процентном выражении это соответствует показателям 62 и 38.

Спираль Фибоначчи и «золотые» прямоугольники. Фото: Википедия/ Джахобр, CC0, via Wikimedia Commons

«Леонардо Да Винчи тоже был виртуозом золотого сечения, — говорит Эдуард Сергеев. — Эту пропорцию можно найти в его знаменитой „Джоконде“ и других картинах. По тому же принципу я как-то давал своим студентам задачу нарисовать самый красивый эллипс, который только возможен. Для этого нужно рассчитать отношение большого диаметра к меньшему по числу Фи. Это такая константа, к которой удивительным образом сходятся все рекуррентные последовательности».

Отражение «числа Бога» можно найти даже в пропорциях человеческого тела. Расстояние от ног до пупа (центра тела) и от пупа до головы находятся между собой в золотой пропорции. То же самое касается отношения расстояния от пупка до коленей и от коленей до ступней. Число Фи или близкое к нему получится, если вычислить отношение расстояния от плеч до макушки к размеру головы. И лицо кажется тем красивее, чем ближе его пропорции к числу Фи. Именно по этим принципам было создано известное изображение Леонардо да Винчи «Витрувианский человек». Согласно сопроводительным записям самого мастера, он сделал этот рисунок для определения пропорций мужского тела, как это описано в трактате античного архитектора Витрувия «Об архитектуре».

Кстати, учёные также находят математическую взаимосвязь между величиной Фи и числом Пи, которое тоже часто называют загадочным.

«Витрувианский человек» Леонардо да Винчи. Источник: Public Domain

В подсолнухе и в ухе

С рядом Фибоначчи и числом Фи в геометрии связана логарифмическая спираль, которая разворачивается по принципу золотого сечения. Её можно вписать в систему вложенных друг в друга «золотых» прямоугольников с отношением сторон, равным Фи, или описать вокруг неё. А удивляет то, что такие модели часто встречаются в природе. По образу спирали Фибоначчи построены раковины моллюсков Nautilus pompilius и окаменелых аммонитов. Их рост хорошо описывается на основе числа Фи с коэффициентом 2.

Отношение длин трёх витков спирали уха человека точно соответствует Фи и такие же параметры — у раковин некоторых улиток. Недавно узнали, что золотая и другие логарифмические спирали встречаются в роговичном эпителии мышей.

Ещё Леонардо да Винчи и знаменитый немецкий учёный Кеплер обращали внимание на винтовое расположение листьев у растений, напоминающее спираль. Так же растут лепестки у цветов, семечки в подсолнечнике, шишки у хвои, чешуйки на плодах ананаса. Эту закономерность в ботанике называют филлотаксисом, и в формулах листорасположения тоже встречаются числа Фибоначчи, расположенные через одно. Такие свойства определяет генетика, уходящая корнями на клеточный и молекулярный уровни. А полипептидные цепи в молекуле ДНК тоже имеют винтовое расположение. Есть данные, что соотношение длины и ширины у них несёт в себе формулу золотого сечения.

Тот же принцип виден и в строении галактик. Например, наш Млечный Путь имеет несколько рукавов, растущих по принципу логарифмической спирали с шагом примерно 12 градусов. Великий поэт Гёте, который также был естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. И, может быть, не случайно символ спирали присутствовал в культуре многих коренных народов Земли.

«Кеплер говорил, что Бог является хорошим геометром и строит Вселенную по математическим законам, — продолжает Эдуард Сергеев. — И я на сто процентов с этим согласен. Узнавая окружающий мир, всё больше изумляешься и удивляешься. На эти темы очень замечательно пишет астрофизик Марио Ливио. Я читал его книгу „Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса“. Он там рассказывает и о спирали жизни, и о строении ДНК, и о многих других явлениях. Конечно, всё это математика — и ещё какая математика».

Фибоначчи повсюду!. Числа Фибоначчи названы в честь… | by Сергей Базанов | Paradox Review

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.

Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

Числа Фибоначчи: практическое применение — HintFox

Числа Фибоначчи — элементы числовой последовательности.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи), который жил и работал торговцем и математиком в итальянском городе Пизе. Он один из самых прославленных европейских ученых своего времени. Среди его величайших достижений — введение арабских цифр, заменивших римские. Fn =Fn-1 +Fn-2

Математический ряд асимптотически (то есть приближаясь все медленнее и медленнее) стремится к постоянному отношению. Однако это отношение иррационально; оно имеет бесконечную, непредсказуемую последовательность десятичных значений, выстраивающихся после него. Оно никогда не может быть выражено точно.8 или 21 -ИЗ), результат действия выразится в отношении, которое колеблется вокруг иррационального числа 1,61803398875, чуть больше или чуть меньше соседних отношений ряда. Отношение никогда, до бесконечности, не будет точным до последней цифры (даже при использовании самых мощных компьютеров, созданных в наше время). Ради краткости, будем использовать в качестве отношения Фибоначчи число 1,618 и просим читателей не забывать об этой погрешности.

Числа Фибоначчи имеют важное значение и во время выполнения анализа Алгоритм Евклида для определения наибольшего общего делителя двух чисел. Числа Фибоначчи происходят в формулу о диагонали треугольником Паскаля (биномиальных коэффициентов).

Числа Фибоначчи оказались связанными с « золотым сечением».

О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Что же такое « золотое сечение»? Ответ неизвестен до сих пор. Числа Фибоначчи действительно актуальны для теории практики в наше время. Подъем значимости произошел в 20 веке и продолжается до сих пор. Использование чисел Фибоначчи в экономике и информатике и привлекло массы людей к их изучению.

Методика моего исследования заключалась в изучении специализированной литературы и обобщении полученной информации, а так же проведении собственных исследований и выявлений свойств чисел и сферы их использования.

В ходе научных исследования определила само понятия чисел Фибоначчи, их свойства. Так же я выяснила интересные закономерности в живой природе, непосредственно в строении семян подсолнуха.

На подсолнухе семечки выстраиваются в спирали, причем количества спиралей, идущих в другую сторону, различны — они являются последовательными числами Фибоначчи.

На этом подсолнухе 34 и 55.

То же наблюдается и на плодах ананаса, где спиралей бывает 8 и 14. С уникальным свойством чисел Фибоначчи связаны листьев кукурузы.

Дроби вида a/b, соответствующие винтообразному расположению листьев ног стебелька растения, часто являются отношениями последовательных чисел Фибоначчи. Для орешника это отношение равно 2/3, для дуба-3/5, для тополя 5/8, для ивы 8/13 и т. д.

Рассматривая расположения листьев на стебле растений можно заметить, что между каждыми парами листьев (А и С) третья расположено в месте золотого сечения(В)

Ещё интересное свойство числа Фибоначчи является, что произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

В результате исследования я пришла к следующим выводам: числа Фибоначчи — уникальная арифметическая прогрессия, появившаяся в 13 веке нашей эры. Данное прогрессия не теряет своей актуальности, что и подтвердилось в ходе моих исследований. Число Фибоначчи встречаются не то и в программировании и экономических прогнозах, в живописи, архитектуре и музыке. Картины таких известных художников, как Леонардо да Винчи, Микеланджело, Рафаэля и Боттичелли скрывают в себе магию золотого сечения. Даже И. И. Шишкин использовал золотое сечение в своей картине «Сосновая роща».

В это сложно поверить, но золотое сечение встречается и в музыкальных произведениях таких великих композиторов, как Моцарт, Бетховен, Шопен и т. д.

Числа Фибоначчи встречается и в архитектуре. Например, золотое сечение использовалось при строительстве Парфенона и собора Парижской Богоматери

Я обнаружила, что Числа Фибоначчи используются и в наших краях. Например, наличники домов, фронтоны.

Числа Фибоначчи

Звезда. Орбиты планет. Сосновая шишка. Все эти природные формы не случайны. Они связаны с такими понятиями, как золотое сечение и числа Фибоначчи, за которыми стоит некое идеальное математическое соотношение. Когда мы видим что-то красивое, гармоничное, симметричное в природе или искусстве, то, скорее всего, оно имеет «золотое» соотношение частей и целого, близкое к 1,6 — его еще называют «числом бога».

Кто открыл числа Фибоначчи?

Последовательность Фибоначчи выглядит так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711…

Если вы заметили, каждое последующее число равно сумме двух предыдущих. Эту последовательность первым открыл европейцам математик и путешественник Леонардо Пизанский, Фибоначчи было его прозвищем (считается, что оно образовано от слов «сын Боначчи»). В 1202 году он опубликовал монументальный 460-страничный сборник по алгебре и арифметике под названием «Книга абака», основанный на математических знаниях индусов и арабов. Этот труд настолько опережал свое время, что просвещенному человечеству потребовалось еще несколько веков, чтобы осилить и осмыслить эти сведения. Числа Фибоначчи стали применяться в математике в эпоху Возрождения и в Новое время.

Согласно легенде, на бесконечную последовательность чисел, каждое из которых является суммой двух предыдущих, Леонардо натолкнула нехитрая задачка о кроликах. Можете попробовать ее решить и проверить, получится ли у вас нужная последовательность.

Задача о кроликах

1 января у вас в закрытом загоне скрестилась пара кроликов: самка и самец. 1 февраля они произвели на свет детей — самку и самца. Новорожденные кролики становятся зрелой парой через месяц и затем еще через месяц дают жизнь новой разнополой паре животных. Вопрос: сколько пар кроликов у вас будет через год? Учтите, что каждая половозрелая пара дает жизнь только одной паре и в ней всегда один самец и одна самка, все кролики из задачи бессмертны и точно доживут до 1 января следующего года. Посчитали?

Теперь проверьте себя:

1 + 1 = 2

2 + 1 = 3

3 + 2 = 5

5 + 3 = 8

8 + 5 = 13

13 + 8 = 21

21 + 13 = 34

34 + 21 = 55

55 + 34 = 89

89 + 55 = 144

144 + 89 = 233

233+ 144 = 377

Правильный ответ: через год будет 377 пар кроликов.

С точки зрения математики у последовательности Фибоначчи имеется много интересных свойств. Если взять пару соседних чисел из этого ряда и разделить большее число на меньшее, результат будет постепенно приближаться к числу золотого сечения (~1,6).

А что такое золотое сечение?

И тут настало время поговорить о принципе золотого сечения. Так называют идеальное соотношение частей и целого, которое лежит в основе таких понятий, как гармония, красота, идеал. Этим принципом руководствовался Леонардо да Винчи, когда рисовал своего «Витрувианского человека», ему же пытаются соответствовать современные дизайнеры, архитекторы, ювелиры, художники. Золотое сечение встречается и в природе, и в науке, и в технике. И это тот редкий пример, когда математическая формула передает такое сложное понятие, как красота.

Представьте отрезок. Разделите его на два меньших отрезка — a и b, при этом a должно быть равно отношению a:b. Это и будет «золотой» пропорцией. Иными словами, золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок относится к большей части так, как сама большая часть относится к меньшей. В виде формулы вышесказанное можно записать так: (a + b):a=a:b. Золотое сечение выражается числом Ф (фи), оно равно 1,6180339887, но обычно округляется до 1,618 или 1,62. Если выразить золотое сечение в процентном соотношении, то оно составит 62% к 38%.

Где искать золотое сечение?

Математики утверждают, что правило золотого сечения действует и в природе, и в космосе. Наглядный пример красоты и совершенства в природе — это растения и цветы. Внимательные ботаники давно разглядели в многообразии форм растительной жизни четкие математические закономерности: многие природные узоры, орнаменты, формы подчиняются правилу золотого сечения, вернее, одному из его частных случаев — последовательности Фибоначчи.

Многолетние наблюдения ботаников показали, что растения, чья структура или плоды подчиняются правилам золотого сечения, гораздо более выносливы, а не просто красивы. В одном из исследований по шишкам сибирской сосны или кедра было установлено, что если шишки сильно уклоняются от правильного расположения чешуек, то их семена очень слабо жизнеспособны. Иными словами, только у гармоничной красивой шишки будут жизнеспособные семена.

Числа Фибоначчи можно найти даже у себя. Посмотрите на свои руки: на обеих по пять пальцев. Два из них (большие) состоят из двух фаланг, а у остальных восьми — по три фаланги. 2, 3, 5, 8 — это как раз одни из первых чисел последовательности Фибоначчи. Совпадение? Математики считают, что это закономерно — правило золотого сечения действует повсюду.

Даже в космосе можно найти число идеальной пропорции. Возьмем Солнечную систему. Планеты вращаются по траектории эллипса, а значит, у их траекторий есть минимальный и максимальный радиус. Удивительно, но соотношение этих радиусов у всех планет Солнечной системы совпадает с числом золотого сечения, погрешность составляет доли процента. В то же время соотношение орбит планет нашей Солнечной системы очень близко к коэффициенту золотого сечения. Этот факт был известен еще Кеплеру, и, опираясь на него, он пытался построить некую универсальную систему мироздания.

«Золотая пропорция — это не только критерий красоты, — говорит профессор физического факультета МГУ, доктор физико-математических наук Павел Короленко. — Не только явление, которое позволяет проникнуть в суть понятия красивого. Но это и явление, которое несет в себе некую эвристическую ценность. Задает некое направление в исследованиях, проводимых в математике, физике, биологии. Я считаю, что это очень важное достоинство этого феномена».

Подробнее о золотом сечении и числах Фибоначчи рассказывается в фильме канала «Наука» — «В поисках абсолютной гармонии».

Зачем нужна математика?

Единственное существо, которое научилось жить вечно

В поисках эликсира молодости

φ Фибоначчи в людях ★ Фибоначчи

Это отрывок из книги «Мастер Фибоначчи: человек, изменивший математику». Все цитаты занесены в каталог на странице «Цитаты».

Человеческое тело

(Предыдущий раздел: Фибоначчи в космосе и географии )

Купить сейчас на Amazon

Обнаружены те же явления Фи, которые встречаются в объектах природы от раковин улиток до спиралей галактик. в дизайне и строении человеческого тела.Например, улитка уха представляет собой спираль Фибоначчи, как и спираль пуповины. Прогрессия чисел и соотношения Фибоначчи хорошо подходит для описания органического роста в человеческом теле, потому что они обладают свойствами самоподобия и «гномонического роста»; то есть изменяется только размер, а форма остается неизменной. Большинство органов человеческого тела по мере роста сохраняют свою общую форму и пропорции (Sacco).

Простое наблюдение подтверждает, что числа Фибоначчи представлены множеством человеческих частей: одним хоботом, одной головой, одним сердцем и т. Д.Затем идут пары: руки, ноги, глаза, уши. Три представлены количеством костей в каждой ноге и руке и тремя основными частями кисти: запястьем, пястью и набором пальцев, состоящим из трех фаланг, основной, средней и ногтевой. Рассматривая каждый палец в отдельности, длины фаланговых костей соотносятся друг с другом согласно правилу золотой пропорции (Ахтаруззаман и Шафи). Эти размеры позволяют безупречно выполнять и адаптировать «кратковременные движения пальцев» при захвате.В частности, рентгенологические и анатомические исследования показывают, что «длина указательного, длинного и безымянного пальцев соответствует недавно выявленному определенному математическому шаблону, ряду Литтлера, который тесно связан с рядом Фибоначчи» (Йеткин и др.; Хатчисон) и Хатчисон).

К туловищу примыкают пять придатков: руки, ноги и голова; На каждом из них по пять придатков: по пять пальцев рук и стопы; и на лице пять отверстий. Благодаря им пять органов чувств позволяют телу взаимодействовать с окружающим миром: зрение, звук, осязание, вкус и запах.Обратно к руке пять пальцев соединены с пятью пястными костями, составляющими основу ладони, которая связана со структурой запястья. Продолжая считать, человеческая рука вместе с пальцами состоит из восьми частей. Существует 12 пар ребер, но некоторые утверждают (без научных доказательств), что в прошлом у человека было 13 пар ребер. Четырнадцать лицевых костей, шесть костей среднего уха и горло всего 21 кость. Человеческий позвоночник с черепом состоит из 34 костей: восьми костей черепа (Crania), 24 позвонков, одного крестца и одного копчика.Таким образом, основная колонна человеческого тела насчитывает 55 (21 + 34 = 55) костей (Ахтаруззаман и Шафи). Все эти числа — 1, 2, 3, 5, 8, 13, 21, 34 и 55 — являются числами ряда Фибоначчи.

Купить сейчас на Amazon

Человеческое лицо

Говорят, что многие черты «идеального» человеческого лица имеют отношения, равные φ; размерные отношения между глазами, ушами, ртом и носом, например. Отношение высоты всей головы к высоте головы над носом также называется Фи (Ахтаруззаман и Шафи).Другие примеры якобы включают соотношение между общей высотой тела и расстоянием от головы до кончиков пальцев, а также «расстояния от головы до моря и от моря до холма». Затем есть пропорция между предплечьем и плечом и пропорция между кистью и предплечьем; все они, как говорят, следуют правилу золотого сечения (Ахтаруззаман и Шафи).

Стоматологи, заинтересованные в здоровье своих пациентов, изучают взаимосвязь между эстетикой зубов и золотой пропорцией.По словам доктора Стивена Марквардта, выдающегося хирурга-стоматолога из Калифорнии, «высота центрального резца в золотой пропорции равна ширине двух центральных резцов». Стоматологи использовали эту информацию при решении «множества стоматологических эстетических проблем». Были разработаны сетки золотой пропорции, которые показывают соотношение золотого прямоугольника между шириной и высотой восьми зубов переднего эстетического сегмента, резцов. Кроме того, четыре передних зуба, от центрального резца до премоляра, находятся в золотой пропорции друг к другу.В статье «Ширина зубов верхней и нижней челюсти» (1985) доктор МакАртур объяснил, что «среднее отношение верхнего центрального резца к нижнему центральному резцу составляет 1,62». Вскоре после этого, в 1987 году, Шумейкер «написал серию статей, пропагандирующих использование золотой пропорции в качестве дополнения к косметической стоматологии». В статье Аморика «Le nombre d’or» (1989) показано «множество золотых пропорций в цефалометрических записях на различных стадиях роста лица, а также включены геометрические утверждения».

В том же году в журнале «Анналы пластической хирургии » (1989) были представлены исследования Kawakami et al.кто измерил золотую пропорцию баланса между глазами, носом и ртом во внешности типичных японцев и сравнил эти отношения с измерениями у кавказцев. «Каждое соотношение затем использовалось для до- и послеоперационного эстетического анализа» (Каваками).

Подобная цель побудила дантиста Йоша Джефферсона в 1996 году предоставить диаграммы золотой пропорции, цефалометрические записи и компьютерные фотографии в «Красоте лица — установление универсального стандарта», чтобы изобразить идеальную структуру человеческой головы.Он считал, что «возможно, существуют миллиарды примеров божественной пропорции в человеческом теле» и «все живые организмы, включая людей, генетически закодированы, чтобы развиваться и соответствовать божественной пропорции». Целью исследования доктора Джефферсона было установить универсальный стандарт красоты лица независимо от расы, возраста или пола; но его заявленное намерение не состояло в том, чтобы расширять возможности или поддерживать дискриминацию. Он надеялся, что его работа упростит диагностику и лечение несоответствий структуры лица и скелета у пациентов, тем самым улучшив не только их стоматологическое и физическое здоровье, но (как следствие) также их эмоциональное и психологическое здоровье (Джефферсон).

Использование последовательности Фибоначчи для изучения эволюции!

Изучение рук приматов и неприматов может помочь вам понять последовательность Фибоначчи. Кредит: Джефф Грант

Что такое последовательность Фибоначчи?

Узоры можно найти по всему миру. От цепких усиков растения до заросшей росой паутины паука мы можем рассматривать повторяющиеся последовательности как продукт живых систем. Один из паттернов, на котором мы сосредоточимся в этом ресурсе, — это последовательность Фибоначчи.Результатом этой последовательности являются потрясающие завитки и цепкие руки. Просматривая следующее видео, чтобы увидеть его красоту и математическую важность, подумайте над этими двумя вопросами:

1. Можете описать закономерность, о которой шла речь в видео?
2. Доктор Джон Эдмарк рассказал о золотом сечении в природе. Где он сказал, что это появляется? Вы можете придумать другие места, где он мог бы появиться?

Алоэ полифилла. Предоставлено: Shutterstock

Паттерн, описанный в видео, называется последовательностью Фибоначчи.Последовательность Фибоначчи названа в честь Леонардо Фибоначчи, итальянского математика, который писал об этой закономерности в своих журналах, когда наблюдал за размножением кроликов.

Последовательность Фибоначчи работает следующим образом.

Допустим, у вас есть два сегмента определенной длины, A и B, где A больше B.

Если эти два сегмента находятся в последовательности Фибоначчи, большая часть, разделенная на меньшую, будет приблизительно равна 1,618.

Кроме того, если вы возьмете длину A и прибавите ее к длине B, а затем разделите на длину A, вы получите такое же число: 1.618. Это соотношение называется золотым сечением.

Например, следующие числа представляют собой последовательность Фибоначчи: 3, 5, 8,13, 21, 34, 55 и т. Д. Когда мы разделим 5 на 3, мы получим примерно 1,6. Разделите 8 на 5, и вы получите около 1,6. 13 разделить на 8? Опять про 1.6!

Чтобы определить следующее число в последовательности, вы просто суммируете два предыдущих числа. Вы можете повторить этот процесс, чтобы сгенерировать бесконечно длинную последовательность Фибоначчи. Например:

Если вы выберете любые три числа подряд из последовательности Фибоначчи, вы найдете тот же образец.Давайте определим Fn как , любое число в последовательности, а затем определим (n-1) как число, расположенное непосредственно перед Fn, и (n-2) как число, занимающее две позиции перед Fn в последовательности. Для любой последовательности Фибоначчи Fn будет , всегда будет равно (n-1) + (n-2).

Например, давайте посмотрим на последовательность Фибоначчи, начинающуюся с 75, 120, 195. Чтобы найти следующее число в этой последовательности (Fn), вы можете добавить 120 (это n-2) к 195 (n-1) чтобы получить 315 (Fn). Итак, последовательность теперь 75, 120, 195, 315.Теперь у вас есть последовательность Фибоначчи!

Отношение большего числа к меньшему, которое всегда равно 1,6, обозначается греческой буквой Фи (Φ) и называется золотым сечением. Вы можете найти Фи в приведенном выше примере Фибоначчи: 315/195 = 1,615.

Если вы сложите твердые куски дерева, измеренные длиной нескольких последовательных порядковых номеров Фибоначчи, вместе по этой схеме, вы увидите аддитивный эффект, наблюдаемый в видео, где структуры доктора Эдмарка красиво скручиваются друг с другом.

Мы набираем сотрудников для участия в программе SciFri Educator Collaborative 2019! Создавайте потрясающие научные мероприятия, подобные этой, работайте с сотрудниками SciFri и получайте наставничество от коллег-преподавателей. Мы будем принимать заявки до пятницы, 4 января 2019 года, до 17:00 по восточному стандартному времени.

ПРИМЕНИТЬ

15 необычных примеров золотого сечения в природе

Знаменитая последовательность Фибоначчи веками очаровывала математиков, художников, дизайнеров и ученых. Также известное как золотое сечение, его повсеместность и поразительная функциональность в природе говорят о его важности как фундаментальной характеристики Вселенной.

Мы уже говорили о рядах Фибоначчи и золотом сечении, но стоит сделать небольшой обзор. Последовательность Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее до бесконечности. Каждое число представляет собой сумму двух предшествующих ему чисел. Это простой образец, но он кажется своего рода встроенной системой нумерации космоса. Вот 15 поразительных примеров фи в природе.

Леонардо Фибоначчи придумал последовательность при вычислении идеальных пар разложения кроликов в течение одного года.Сегодня его возникающие закономерности и соотношения (phi = 1,61803 …) можно увидеть от микромасштаба до макромасштаба и вплоть до биологических систем и неодушевленных объектов. Хотя золотое сечение не учитывает на каждую структуру или узор из во вселенной, оно, безусловно, играет важную роль. Вот несколько примеров.

1. Лепестки цветов

G / O Media может получать комиссию

Количество лепестков в цветке постоянно соответствует последовательности Фибоначчи. Известные примеры включают лилию, у которой три лепестка, лютики, у которых пять (на фото слева), у цикория 21, у ромашек 34 и так далее.Phi появляется в лепестках из-за идеальной упаковки, выбранной с помощью дарвиновских процессов; каждый лепесток размещается на 0,618034 за оборот (из круга на 360 °), что обеспечивает наилучшее воздействие солнечного света и других факторов.

2. Семенные головки

Головка цветка также подвержена процессам Фибоначчи. Обычно семена производятся в центре, а затем перемещаются наружу, заполняя все пространство. Подсолнухи — отличный пример спиралевидного узора.

В некоторых случаях высевные головки настолько плотно набиты, что их общее количество может достигать 144 и более. И при подсчете этих спиралей общая сумма стремится соответствовать числу Фибоначчи. Интересно, что для оптимизации заполнения требуется крайне иррациональное число (а именно такое, которое не будет хорошо представлено дробью). Фи вполне отвечает всем требованиям.

3. Сосновые шишки

Точно так же семенные коробочки на шишке расположены по спирали. Каждый конус состоит из пары спиралей, каждая из которых поднимается вверх в противоположных направлениях.Количество шагов почти всегда будет соответствовать паре последовательных чисел Фибоначчи. Например, конус 3-5 — это конус, который встречается сзади после трех шагов по левой спирали и пяти шагов по правой.

4. Фрукты и овощи

Аналогичным образом спиралевидные узоры можно найти на ананасах и цветной капусте.

5. Ветви дерева

Последовательность Фибоначчи также можно увидеть в том, как ветви дерева образуются или разделяются. Главный ствол будет расти до тех пор, пока не создаст ветку, которая создаст две точки роста.Затем один из новых стеблей разветвляется на два, а другой находится в состоянии покоя. Этот образец ветвления повторяется для каждого нового стебля. Хороший пример — чиханье. Корневые системы и даже водоросли демонстрируют эту закономерность.

6. Оболочки

Еще один пример — уникальные свойства золотого прямоугольника. Эта форма, прямоугольник, в котором отношение сторон a / b равно золотой середине (фи), может привести к процессу вложенности, который может повторяться до бесконечности и который принимает форму спирали.Это называется логарифмической спиралью, и она изобилует природой.

Раковины улиток и наутилусов следуют по логарифмической спирали, как и улитка внутреннего уха. Его также можно увидеть в рогах некоторых коз и форме паутины некоторых пауков.

7. Спиральные галактики

Неудивительно, что спиральные галактики также следуют знакомому паттерну Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждое из которых представляет собой логарифмическую спираль около 12 градусов. Интересно отметить, что спиральные галактики бросают вызов ньютоновской физике.Еще в 1925 году астрономы поняли, что, поскольку угловая скорость вращения галактического диска меняется с расстоянием от центра, радиальные рукава должны становиться искривленными по мере вращения галактик. Впоследствии, после нескольких оборотов, спиральные рукава должны начать закручиваться вокруг галактики. Но они этого не делают — отсюда так называемая проблема намотки. Казалось бы, звезды снаружи движутся со скоростью выше ожидаемой — уникальная особенность космоса, которая помогает сохранять его форму.

8. Ураганы

9.Лица

Лица, как человеческие, так и нечеловеческие, изобилуют примерами золотого сечения. Рот и нос расположены на золотых сечениях расстояния между глазами и нижней частью подбородка. Подобные пропорции видны сбоку, и даже глаз и ухо (которое следует по спирали).

Стоит отметить, что тело каждого человека индивидуально, но средние значения по популяциям имеют тенденцию к фи. Также было сказано, что чем точнее наши пропорции соответствуют фи, тем более привлекательными воспринимаются эти черты.Например, самые «красивые» улыбки — это те, у которых центральные резцы на 1,618 шире боковых резцов, которые на 1,618 шире клыков и т. Д. Вполне возможно, что с точки зрения эволюции и психологии мы привыкли любить физические формы, соответствующие золотому сечению — потенциальному индикатору репродуктивной пригодности и здоровья.

10. Пальцы

Глядя на длину наших пальцев, можно заметить, что каждая часть — от кончика основания до запястья — больше предыдущей примерно на соотношение фи.

11. Тела животных

Даже наши тела имеют пропорции, соответствующие числам Фибоначчи. Например, расстояние от пупка до пола и от макушки до пупка является золотым сечением. Тела животных демонстрируют аналогичные тенденции, включая дельфинов (глаза, плавники и хвост падают на Золотые сечения), морских звезд, морских ежей, муравьев и медоносных пчел.

12. Репродуктивная динамика

Говоря о медоносных пчелах, они следуют Фибоначчи в других интересных направлениях.Самый яркий пример — это деление количества самок в колонии на количество самцов (самок всегда больше, чем самцов). Обычно ответ очень близок к 1,618. Кроме того, генеалогическое древо медоносных пчел также следует знакомому образцу. У самцов один родитель (самка), а у самок — два (самка и самец). Таким образом, когда дело доходит до генеалогического древа, у мужчин есть 2, 3, 5 и 8 бабушек и дедушек, прабабушек и дедушек, gr-gr-grandparents и gr-gr-grandparents соответственно.По той же схеме у женщин 2, 3, 5, 8, 13 и так далее. И, как уже отмечалось, физиология пчел также довольно хорошо следует по Золотой кривой.

13. Схемы схватки животных

Когда ястреб приближается к своей жертве, его самый резкий вид находится под углом к ​​направлению полета — углом, который совпадает с шагом спирали.

14. Матка

По словам Джаспера Вегутса, гинеколога из университетской больницы Лёвена в Бельгии, врачи могут определить, выглядит ли матка нормальной и здоровой, основываясь на ее относительных размерах — размерах, которые приблизительно соответствуют золотому сечению.Из Guardian :

За последние несколько месяцев он измерил матки 5000 женщин с помощью ультразвука и составил таблицу среднего отношения длины матки к ее ширине для разных возрастных групп.

Данные показывают, что это соотношение составляет около 2 при рождении, а затем оно неуклонно снижается в течение жизни женщины до 1,46, когда она находится в пожилом возрасте.

Доктор Вергутс был взволнован, обнаружив, что, когда женщины наиболее плодовиты, в возрасте от 16 до 20 лет, отношение длины матки к ширине равно 1.6 — очень хорошее приближение к золотому сечению.

«Это первый раз, когда на это смотрят, поэтому я рад, что все получилось так красиво», — сказал он.

15. Молекулы ДНК

Даже микроскопический мир не застрахован от Фибоначчи. Молекула ДНК имеет длину 34 ангстрем и ширину 21 ангстрем для каждого полного цикла двойной спирали. Эти числа, 34 и 21, являются числами в ряду Фибоначчи, и их отношение 1,6190476 близко приближается к Phi, 1.6180339.

Спасибо Calvin Dvorsky за помощь в написании статьи!

Источники и изображения: Вверху: Лоскутников / Shutterstock; Лютик: motorolka / shutterstock, ThinkQuest , Shell , Galaxy: FabulousFibonacci , Американский музей естественной истории и ric : MNN , Faces: Goldennumber и здесь , DNA .

Все в нашей жизни имеет только математические закономерности. | Али | Однако математика

Как может быть, что математика, будучи, в конце концов, продуктом человеческой мысли, независимой от опыта, настолько превосходно соответствует объектам реальности?

Альберт Эйнштейн…

Однажды вечером несколько лет назад я был с друзьями из колледжа на заднем дворе колледжа и говорил о взаимосвязи между наукой и математикой.Один из друзей моих друзей прокомментировал: «Наука не объясняет объекты, она просто описывает их». Это меня крайне удивило, потому что я был почти уверен, что математика и естественные науки — лучшие языки для объяснения того, что происходит во Вселенной.

В ту ночь я увидел, что большинство людей не верят, что «Математика — прекрасный язык Вселенной». Другими словами, для них математика — это не объяснение Вселенной и природы.Я думаю, что такой подход для них нормален, потому что настоящая математика — абстрактное понятие, а не осязаемая вещь , которую можно понюхать, потрогать или съесть. А абстрактность делает математику глубокой и загадочной. Однако все согласны с тем, что человек может развиваться в любое время. И нет верхнего предела числовым способностям человека. Сначала они обнаружили огонь, чтобы согреться. Затем в их доме понадобился свет, и они изобрели электричество и лампочку.Когда им нужно поговорить с кем-то, кто находится за 10000 миль, они просто изобрели Интернет. За всеми этими изобретениями стояла математика.

Конечно, Вселенная не может ни говорить, ни думать. Однако мы, люди, можем читать вселенную. Поскольку существует так много людей, склонных к науке и математике, они могут читать вселенную и находить ответы, а затем описывать вселенную и природу. Мы, нормальные люди, можем также использовать наше воображение как аппарат, чтобы читать вселенную, а также природу.Если мы умеем читать, значит, что-то написано. Чтобы писать, всегда нужен язык. Итак, у вселенной должен быть язык. Буквы — это круги, треугольники, шестиугольники и т. Д. Или этот язык просто содержит шаблоны.

Все в нашей жизни имеет только математические аспекты. Например, я люблю смотреть документальные фильмы о дикой природе. Рассказчики всегда говорят нам, что у многих животных есть полосы или узоры для маскировки. Но почему у леопарда, гепарда или тигра особые рисунки? Взломщик кода Enigma Алан Тьюринг — вы можете посмотреть хороший фильм «Игра в имитацию», чтобы увидеть его жизнь — имел математическую теорию о пятнах леопарда.60 лет назад ему пришла в голову идея, что узоры на животных можно объяснить математикой. * 1

Звезды имеют узоры. И большинство астрологов считают, что наша судьба зависит от узоров звезд. Некоторые астрологи думают, что звезды действительно определяют, кто мы, а другие думают, что звезды влияют на нашу судьбу. Да, такой человек, как я, или ты не можешь контролировать его жизнь. По этой причине люди искали во Вселенной и искали закономерности, раскрывающие их настоящие характеры и судьбу.И когда они что-то находят, это всегда связано с математикой.

Времена года имеют закономерности. Они приходят и уходят. И каждый раз оказывают влияние на природу; меняется климат, животные мигрируют на север или юг, идет дождь, тает снег, земля меняет цвет и т. д. Конечно, времена года не могут творить эти чудеса. У них могут быть только математические закономерности.

Все эти модели показывают нам, что существует разрыв между человеком и вселенной. Эйнштейн много лет размышлял о том, как математика идеально работает в науке.Он все время ломал голову над этим вопросом. Он знал, что математика — это связь, мост или язык для этого разрыва. И на данный момент связь между нами и вселенной делает математику величайшим достижением для людей.

Если вы также присмотритесь к закономерностям нашего мира, вы всегда откроете для себя прекрасную математику. Это на 100% верно, потому что математика находится в наших руках. Приведу несколько конкретных примеров.

Фибоначчи, золотое сечение, спираль, капуста…

Числа природы: последовательность Фибоначчи

Числа природы: последовательность Фибоначчи

Последовательность Фибоначчи всегда привлекала внимание людей, поскольку, помимо особых математических свойств, другие числа, столь широко распространенные, как числа Фибоначчи, не существуют больше нигде в математике: они появляются в геометрии, алгебре, теории чисел и во многих других областях. области математики и даже в природе! Давайте вместе узнаем, что это такое…

Жизнь Фибоначчи
Леонардо Пизано по имени Фибоначчи (Фибоначчи означает filius Bonacii ) родился в Пизе около 1170 года.Его отец, Гульельмо деи Боначчи, богатый пизанский купец и представитель купцов Пизанской республики в районе Буджи в Кабилии (на территории современного северо-восточного Алжира), после 1192 года забрал с собой сына, потому что хотел, чтобы Леонардо был стать купцом.

Источник: Википедия

Таким образом, он заставил Леонардо учиться под руководством мусульманского учителя, который руководил им в изучении методов вычисления, особенно тех, которые касались индо-арабских чисел, которые еще не были введены в Европе.Обучение Фибоначчи началось в Беджая и продолжилось также в Египте, Сирии и Греции, местах, которые он посетил со своим отцом на торговых путях, прежде чем окончательно вернуться в Пизу примерно с 1200 года. В течение следующих 25 лет Фибоначчи посвятил себя написанию математических рукописей: из них Liber Abaci (1202), благодаря которым Европа узнала индо-арабские числа, сегодня нам известны Practica Geometriae (1220), Flos (1225) и Liber Quadratorum (1225). .
Репутация Леонардо как математика стала настолько велика, что император Федерико II попросил аудиенции в Пизе в 1225 году. После 1228 года о жизни Леонардо мало что известно, за исключением того, что он был удостоен звания « Discretus et sapiens magister» Леонардо Биголло »В знак признания большого прогресса, которого он добился в математике. Фибоначчи умер где-то после 1240 года, предположительно в Пизе.

Кролики Фибоначчи и знаменитая последовательность
Liber Abaci , помимо ссылки на индо-арабские числа, которые впоследствии заменили римские цифры, также включали большой набор задач, адресованных торговцам, относительно цен на продукты, расчет прибыли от бизнеса, конвертация валюты в различные монеты, используемые в странах Средиземноморья, а также другие проблемы китайского происхождения.Наряду с этими коммерческими проблемами были и другие, гораздо более известные, которые также оказали большое влияние на более поздних авторов. Среди них наиболее известным, источником вдохновения для многих математиков более поздних веков является следующее: «Сколько пар кроликов родится за год, начиная с одной пары, если каждый месяц каждая пара рождает нового? пара, которая становится репродуктивной со второго месяца? ». Решением этой проблемы является знаменитая «последовательность Фибоначчи»: 0, 1, 1, 2, 3, 5, 8, 13, 21,34,55,89… последовательность чисел, в которой каждый член является суммой предыдущие два.

Источник: Oilproject

Важной характеристикой последовательности является тот факт, что отношение между любым числом и предыдущим в серии стремится к четко определенному значению: 1,618… Это золотое сечение или золотое сечение φ (Phi), которое часто встречается. в природе (чтобы узнать больше: Совершенство улитки).
Когда Фибоначчи проиллюстрировал эту последовательность как решение проблемы «развлекательной математики», он не придал ей особого значения.Только в 1877 году математик Эдуард Лукас опубликовал ряд важных исследований этой последовательности, которые, как он утверждал, обнаружил в Liber Abaci и которые в честь автора он назвал «последовательностью Фибоначчи». Впоследствии количество исследований увеличилось, и были обнаружены многочисленные и неожиданные свойства этой последовательности, настолько, что с 1963 года издается журнал, посвященный исключительно ей, «Ежеквартальный отчет Фибоначчи».

Последовательность Фибоначчи в природе
Наблюдая за геометрией растений, цветов или фруктов, легко распознать наличие повторяющихся структур и форм.Последовательность Фибоначчи, например, играет жизненно важную роль в филлотаксисе, который изучает расположение листьев, ветвей, цветов или семян у растений с основной целью выявить существование регулярных паттернов. Различное расположение природных элементов следует удивительным математическим закономерностям: Д’арси Томпсон заметил, что царство растений имеет любопытное предпочтение определенным числам и определенной спиральной геометрии, и что эти числа и геометрии тесно связаны.
Мы можем легко найти номера последовательности Фибоначчи в спиралях, образованных отдельными цветками в составных соцветиях маргариток, подсолнечника, цветной капусты и брокколи.

У подсолнечника отдельные цветки расположены по изогнутым линиям, которые вращаются по и против часовой стрелки. Источники: Последовательность Фибоначчи в филлотаксисе — Лаура Реста (диссертация по биоматематике)

Кеплер заметил, что на многих типах деревьев листья выровнены по образцу, который включает два числа Фибоначчи. Начиная с любого листа, после одного, двух, трех или пяти витков спирали всегда есть лист, выровненный с первым, и, в зависимости от вида, это будет второй, третий, пятый, восьмой или тринадцатый. лист.

Расположение листьев на стебле. Источники: Последовательность Фибоначчи в филлотаксисе — Лаура Реста (диссертация по биоматематике)

Другой простой пример, в котором можно найти последовательность Фибоначчи в природе, — это количество лепестков цветов. У большинства их три (например, лилии и ирисы), пять (парнасия, плоды шиповника) или восемь (космея), 13 (некоторые маргаритки), 21 (цикорий), 34, 55 или 89 (сложноцветные). Эти числа являются частью известной последовательности Фибоначчи, описанной в предыдущем абзаце.

Ирис, 3 лепестка; парнасия, 5 лепестков; cosmea, 8 лепестков

Бенедетта Палаццо

Источники:
Tesi di Laurea in biomatematica: La successione di Fibonacci nella fillotassi — Laura Resta
Le geometrie delle piante e la successione di Fibonacci — Scientificast

Золотое сечение и числа Фибоначчи не доказывают красоту

Цветки кочана подсолнечника Helianthus расположены по спирали из 34 и 55.Л. Шьямал / Wikimedia Commons

Еще в 1855 году немецкий психолог Адольф Цайзинг опубликовал книгу со смехотворно длинным названием:

Новая теория пропорций человеческого тела, разработанная на основе основного морфологического закона, который оставался до сих пор неизвестным и который пронизывает всю природу и искусство. сопровождается полным обзором преобладающих систем.

Название многословное и излишнее — достаточно, чтобы вызвать смешок — но глупо или нет, книга фактически породила увлечение математиками, философами, художниками, кинематографистами и широкую публику на протяжении почти двух столетий.

Но есть одна проблема: «Он был просто чудаком», — сказал Tech Insider Кейт Девлин, математик и исполнительный директор Стэнфордского института перспективных исследований в области гуманитарных наук и технологий.«Люди зарабатывают деньги, написав эти вещи, а он заработал деньги, и они взлетели».

Цейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении, также называемом последовательностью Фибоначчи, которое, по словам Цейзинга, кажется наиболее «приятным» с научной точки зрения.

Цейзинг далее сказал, что золотое сечение лежит в основе древнегреческой архитектуры и архитектуры эпохи Возрождения, заявив, что эти точные пропорции делают такие конструкции наиболее сбалансированными и приятными для глаз.

Но Девлин говорит, что вера в то, что Золотое сечение существует вне сада, — это просто вера. «Это похоже на креационизм. Вы можете в это поверить, если хотите, но нет никаких доказательств», — говорит Девлин. «Если вы в это верите, значит, вы не занимаетесь наукой».

Сторонники с тех пор пытались доказать, что золотое сечение является фундаментальной характеристикой Вселенной. И хотя математически доказано, что золотое сечение существует в природе, утверждение, что оно существует в человеческом теле, практически не имеет научного подтверждения.

«Многие из тех, кто заявляет об этом, на самом деле имеют бизнес», — говорит Девлин.«Вы можете спуститься в Беверли-Хиллз, и вы найдете людей, которые будут продавать вам стоматологию, основываясь на людях, которые сделают ваши зубы золотым сечением».

LinkedIn

Так что же такое последовательность Фибоначчи и золотое сечение? Последовательность Фибоначчи — это последовательность чисел, каждое из которых представляет собой сумму двух чисел перед ним.

Например, со строкой «0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55», если вы добавите 0 + 1, вы получите 1. Если вы добавите 1 + 1, вы Получите 2. Если вы сложите 1 +2, вы получите 3, и так далее до конца последовательности.

Другой способ описать это — посмотреть на соотношение между двумя числами. Допустим, у вас есть линия, которая разделена на две части, где «a» представляет длину более длинной части линии, а «b» представляет длину более короткой части.

Wikimedia Commons

Считается, что данный набор чисел находится в золотом сечении, если происходит следующее: Если оба отношения a / b и (a + b) / a равны 1.618.

Например, Цейзинг утверждал, что если вы вычислите расстояние между пупком и пальцами ног, а затем разделите его на свой общий рост, вы получите золотое сечение, или 1,6. Цейзинг также утверждал, что вы можете получить такое же соотношение, разделив высоту вашего лица на его ширину. Утверждают, что чем ближе эти измерения к золотому сечению, тем кто-то красивее.

Но, как говорит Девлин, математики не нашли доказательств того, что золотое сечение что-либо доказывает, не говоря уже о красоте, в человеческом теле.

«Скажем так, если завтра кто-нибудь придет с научным объяснением того, почему золотое сечение играет роль в эстетике и во всем остальном, тогда мы все пересмотрим свое мнение», — сказал Девлин. «Но с научной точки зрения нет никаких доказательств». По словам Девлина, нет доказательств того, что вещи, соответствующие этому соотношению, красивее или что это соотношение вообще существует в человеческом теле.

Джон Лемье / Flickr

Однако это не означает, что золотого сечения не существует в природе.

Мы знаем около 25 лет, говорит Девлин, что золотое сечение существует повсюду в мире природы — в таких вещах, как рост растений (например, спиральный узор в подсолнухах), семенные головки и сосновые шишки. Это показали годы чрезвычайно сложных математических расчетов.

Причина его существования сводится к полезности. Поскольку растения выживают за счет оптимизации количества получаемого солнечного света и питательных веществ, многие из них растут по этой идеальной схеме. Например, лепестки некоторых цветов расходятся веером в последовательности Фибоначчи, чтобы получить как можно больше солнечного света.Семена на цветочных головках закручиваются по спирали от центра кнаружи, чтобы заполнить все возможные пространства пропорционально золотому сечению. Наборы спиралей сосновой шишки соответствуют числам Фибоначчи. Примеров в природе предостаточно.

Если вы посмотрите, что нужно для того, чтобы формы этих вещей были оптимальными с точки зрения выживания и естественного отбора, — говорит Девлин, — вы обнаружите, что золотое сечение играет огромную роль, и это также означает, что числа Фибоначчи сыграйте роль ».

Математически доказано, что спирали на сосновой шишке находятся в золотом сечении.Долгота, широта / Flickr

Колючки кактуса с золотой бочкой растут по спирали в соответствии с золотым сечением.Лафлин Элкинд / Wikimedia Commons

Но когда вы пытаетесь применить это к людям, говорит Девлин, теория терпит неудачу, потому что просто нет доказательств того, что мы оптимизированы так же, как растения. В конце концов, люди бывают самых разных форм и размеров.

Не только это, но и соотношение появляется практически во всем, на что вы смотрите.

«Золотое сечение — 1,6. Это настолько распространенное соотношение, что вы можете найти его повсюду», — говорит Девлин. «Обнаружение золотого сечения [в человеческом теле] ничего вам не говорит. Чтобы иметь что-то значимое, вам нужно научное объяснение» того, почему оно существует.

В дополнение к использованию этого соотношения, чтобы «доказать красоту», музыканты пытались заявить о значении Золотого сечения в масштабах фортепианной клавиатуры, художники утверждали, что это соотношение лежит в основе композиции и дизайна, а аналитики рекламировали его значение для игры на пианино. фондовый рынок.

Quora

«К сожалению, вся эта забавная история про художественную галерею, музыку и прочее — просто фальшивка, это сказка», — сказал Девлин.«Вы можете верить в фей, вы можете верить в Санта-Клауса, и миллионы людей верят, но это не делает их правдой».

Хотя мы можем найти золотое сечение в множестве мест в природе, математическое доказательство того, что оно существует где-нибудь во Вселенной, чрезвычайно сложно и требует множества сложных вычислений. Девлин говорит, что он все время получает сообщения от людей, в которых говорится, что они нашли золотое сечение в человеческом теле, но за 25 лет изучения золотого сечения и чисел Фибоначчи он еще не получил ни одного научного доказательства. или математический расчет, подтверждающий любое из этих утверждений.

«Дело не в том, что мы не доказали, что золотое сечение объясняет человеческое тело, дело в том, что мы не доказали это», — говорит Девлин. «Я не говорю, что все это ложно, я говорю, что как ученый, , как они это утверждают, — чушь собачья. Этому просто нет никаких оснований».

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — одна из самых известных формул в математике.

Каждое число в последовательности представляет собой сумму двух предшествующих ему чисел.Итак, последовательность такова: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Математическое уравнение, описывающее его: Xn + 2 = Xn + 1 + Xn

Опора средней школы и студентов, его называют «секретным кодом природы» и «универсальным правилом природы». Говорят, что он определяет размеры всего, от Великой пирамиды в Гизе до культовой морской ракушки, которая, вероятно, украшала обложку вашего школьного учебника математики.

И, скорее всего, почти все, что вы знаете об этом, неверно.

Разрозненная история

Итак, что же на самом деле стоит за этой знаменитой сценой?

Многие источники утверждают, что он был впервые обнаружен или «изобретен» Леонардо Фибоначчи. Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский, сказал Кейт Девлин, математик из Стэнфордского университета. Только в 19 веке историки придумали прозвище Фибоначчи (что примерно означает «сын клана Боначчи»), чтобы отличить математика от другого известного Леонардо Пизанского, сказал Девлин.[Большие числа, определяющие Вселенную]

Но Леонардо Пизанский на самом деле не обнаружил последовательность, — сказал Девлин, который также является автором книги «В поисках Фибоначчи: поиски заново забытого математического гения, изменившего мир» (Принстон University Press, 2017). Древние санскритские тексты, в которых использовалась индуистско-арабская система счисления, впервые упоминают об этом, и те, что предшествуют Леонардо Пизанскому на столетия.

«Это было всегда», — сказал Девлин Live Science.

Однако в 1202 году Леонардо Пизанский опубликовал огромный фолиант «Liber Abaci», математическую «поваренную книгу» о том, как проводить вычисления », — сказал Девлин.«Liber Abaci», написанная для торговцев, излагает индуистско-арабскую арифметику, полезную для отслеживания прибылей, убытков, остатков ссуд и т. Д., Сказал Девлин.

В одном месте книги Леонардо Пизанский вводит последовательность с задачей с участием кроликов. Задача состоит в следующем: начните с кролика-самца и кролика-самки. Через месяц они созревают и производят помет с еще одним кроликом и самкой. Через месяц эти кролики размножаются и выходят, как вы уже догадались, еще один самец и самка, которые также могут спариваться через месяц.(Игнорируйте здесь невероятно невероятную биологию.) Сколько кроликов у вас будет через год? Оказывается, ответ — 144, и формула, использованная для получения этого ответа, теперь известна как последовательность Фибоначчи. [11 самых красивых математических уравнений]

«Liber Abaci» впервые представила последовательность в западном мире. Но после нескольких скудных абзацев о разведении кроликов Леонардо Пизанский никогда больше не упоминал последовательность. Фактически, об этом почти забыли до 19 века, когда математики больше узнали о математических свойствах последовательности.В 1877 году французский математик Эдуард Лукас официально назвал задачу о кролике «последовательностью Фибоначчи», — сказал Девлин.

Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но не такие волшебные, как могут показаться. (Изображение предоставлено Shutterstock)

Воображаемое значение

Но каково именно значение последовательности Фибоначчи? Помимо того, что это изящный инструмент обучения, он обнаруживается в нескольких местах на природе. Однако, по словам Девлина, архитектурой вселенной управляет не какой-то секретный код.

Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение (которое даже не является истинным соотношением, потому что это иррациональное число). Проще говоря, соотношение чисел в последовательности, когда последовательность стремится к бесконечности, приближается к золотому сечению, которое составляет 1,6180339887498948482 … Отсюда математики могут вычислить так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотое сечение. [9 самых значительных чисел в мире]

«Золотое сечение», кажется, действительно отражает некоторые типы роста растений, — сказал Девлин.Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Сосновые шишки имеют золотую спираль, как и семена подсолнечника, согласно «Филлотаксису: системное исследование морфогенеза растений» (Cambridge University Press, 1994). Но столько же растений не соблюдают это правило.

«Это не« единственное Божье правило »для выращивания растений, скажем так, — сказал Девлин.

И, возможно, самый известный пример из всех, морская раковина, известная как наутилус, на самом деле не выращивает новые клетки в соответствии с последовательностью Фибоначчи, сказал он.

Когда люди начинают рисовать связи с человеческим телом, искусством и архитектурой, связи с последовательностью Фибоначчи переходят от призрачных к совершенно вымышленным.

«Требуется большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, большая часть которой является просто повторением одних и тех же ошибок разными авторами», — писал Джордж Марковски, математик, работавший в то время в Университете штата Мэн. в статье 1992 года в College Mathematics Journal.

Большая часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Цайзинга.Цейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. Золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения. С тех пор люди говорят, что золотое сечение можно найти в размерах пирамиды в Гизе, Парфенона, «Витрувианского человека» Леонардо да Винчи и ряда зданий эпохи Возрождения. По словам Девлина, общие утверждения о том, что это соотношение «исключительно приятно» для человеческого глаза, были сформулированы некритически.

Все эти утверждения, когда они проверяются, оказываются в значительной степени ложными, сказал Девлин.

«Мы хорошие распознаватели образов. Мы можем видеть закономерности независимо от того, есть они или нет», — сказал Девлин. «Это все просто принятие желаемого за действительное».

.