Калькулятор неполных квадратных уравнений онлайн калькулятор: Решение квадратных уравнений онлайн — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Решение квадратных уравнений онлайн калькулятор.

Основные понятия и определения.

Квадратным уравнением называется уравнение следующего вида: ax2+bx+c=0, где a, b, с — любые действительные числа, но a не равно 0, x — неизвестная искомая переменная.

Коэффициенты a, b, c имеют соответственно названия: a_{— старший коэффициент (коэффициент при ), — второй коэффициент (коэффициент при ), — свободный член.}

Если старший коэффициент , то квадратное уравнение является приведенным, если же , то неприведенным.

Квадратное уравнение называется полным, если оно содержит все три слагаемых (то есть коэффициенты и не равны нулю).

Квадратное уравнение называется неполным, если оно содержит не все три слагаемых ( то есть коэффициент или , или и ).

Корнем квадратного уравнения называется такое значение переменной , при подстановке которого квадратный трехчлен обращается в ноль.

Решить квадратное уравнение – это значит найти все его корни или установить, что корней нет.

Теория для школьников.

При решении квадратного уравнения школьникам необходимо придерживаться следующей схемы:

1) Найти так называемый дискриминант по формуле:

2) Найти корни квадратного уравнения или установить их отсутствие, опираясь на следующие рассуждения:

— Если , то квадратное уравнение корней не имеет;

— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:

— Если , то квадратное уравнение имеет один корень, который находится по формуле:

Решение квадратного уравнения также можно получить, используя следующие формулы :

1) Найти значение :

2) Найти дискриминант по формуле:

3) Найти корни квадратного уравнения или установить их отсутствие, опираясь на следующие рассуждения:

— Если , то квадратное уравнение корней не имеет;

— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:

— Если , то квадратное уравнение имеет один корень, который находится по формуле:

Теория для студентов.

При обучении в высшем учебном заведении нередко приходится сталкиваться с таким понятием, как комплексные корни уравнения.

Решение квадратных уравнений студентами – именно такой случай.

Напомним, что комплексное число имеет вид:

Где и — действительные числа, — так называемая мнимая единица. При этом носит название действительной части, а — мнимой части комплексного числа.

Мнимая единица обладает свойством:

Именно свойство мнимой единицы и будет использовано при решении квадратных уравнений.

При решении квадратного уравнения студентам необходимо придерживаться следующей схемы:

1) Найти так называемый дискриминант по формуле:

2) Найти корни квадратного уравнения, опираясь на следующие рассуждения:

— Если , то квадратное уравнение имеет два комплексных корня:

— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:

— Если , то квадратное уравнение имеет один корень, который находится по формуле:

Решение квадратного уравнения также можно получить, используя следующие формулы :

1) Найти значение :

2) Найти дискриминант по формуле:

3) Найти корни квадратного уравнения, опираясь на следующие рассуждения:

— Если , то квадратное уравнение имеет два комплексных корня, которые находятся по формулам:

— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:

— Если , то квадратное уравнение имеет один корень, который находится по формуле:

Примеры решения квадратных уравнений для школьников.

Пример 1: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 2: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение не имеет корней.

Ответ: Корней нет.

Пример 3: Решить квадратное уравнение .

Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет один корень.

Найдем его:

Таким образом, решением квадратного уравнения будет корень

Ответ:

Пример 4: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Решим заданное уравнение вторым способом, предложенным в теории:

Тогда .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 5: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным.

Для удобства расчетов умножим обе части уравнения на 9 и получим:

Будем решать полученное уравнение. Оно имеет следующие коэффициенты: .

Тогда .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 6: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Тогда .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет один корень.

Найдем его:

Таким образом, решением квадратного уравнения будет корень

Ответ:

Во всех примерах, рассмотренных выше, были заданы полные квадратные уравнения. Как же решать неполные уравнения? Рассмотрим решения на примерах.

Пример 7: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным.

Можно решать данное квадратное уравнение по представленным выше схемам. Воспользуемся первой из них.

Квадратное уравнение имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Но возможно решить квадратное уравнение следующим, более простым, образом:

Поэтому либо , либо

Ответ:

Пример 8: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным.

Квадратное уравнение имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня. Найдем их:

Таким образом, решением квадратного уравнения будут корни

Но возможно решить квадратное уравнение следующим, более простым, образом:

Ответ:

Пример 9: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .

Будем решать его следующим образом:

Данное квадратное уравнение корней не имеет.

Ответ: Корней нет.

Пример 10: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .

Будем решать его следующим образом:

Данное квадратное уравнение имеет один корень .

Ответ: .

Примеры решения квадратных уравнений для студентов.

Пример 1: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 2: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два комплексных корня:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 3: Решить квадратное уравнение .

Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет один корень.

Найдем его:

Таким образом, решением квадратного уравнения будет корень

Ответ:

Пример 4: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Воспользуемся вторым способом решения квадратных уравнений студентами, описанный в теории:

Тогда .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 5: Решить квадратное уравнение .

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Тогда .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет один корень.

Найдем его:

Таким образом, решением квадратного уравнения будет корень

Ответ:

Пример 6: Решить квадратное уравнение .

Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .

Тогда .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два комплексных корня:

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Ответ:

Пример 7: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным.

Можно решать данное квадратное уравнение по представленным выше схемам. Воспользуемся первой из них.

Квадратное уравнение имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Но возможно решить квадратное уравнение следующим, более простым, образом:

Поэтому либо , либо

Ответ:

Пример 8: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным.

Квадратное уравнение имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение имеет два корня. Найдем их:

Таким образом, решением квадратного уравнения будут корни

Но возможно решить квадратное уравнение следующим, более простым, образом:

Ответ:

Пример 9: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .

Будем решать его следующим образом:

Ответ:

Пример 10: Решить квадратное уравнение .

Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .

Будем решать его следующим образом:

Данное квадратное уравнение имеет один корень .

Ответ: .

Решение квадратных уравнений онлайн

С помощю этого онлайн калькулятора можно найти решение (корни) квадратного уравнения. Дается подробное решение с пояснениями. Для нахождения решений квадратного уравнения введите коэффициенты уравнения и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Корни квадратного уравнения − теория примеры и решения

Квадратным уравнением называется уравнение следующего вида:

где x−переменная, а a, b, c некоторые числа (a≠0). Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.

Если a=1, то квадратное уравнение называется приведенным. Заметим, что любое квадратное уравнение можно привести к приведенному виду, разделив обе части уравнения на a. Действительно:

Если в квадратном уравнении (1) один из коэффициентов b, c равен нулю или оба коэффициента b, c равны нулю, то квадратное уравнение называется неполным.

Рассмотрим разные виды неполных квадратных уравнений.

1. При b=0 имеем:

Для решения этого уравнения свободный член перенесем в правую часть уравнения:

Решая последнее уравнение относительно x получим корни квадратного уравнения (3):

Если , то квадратное уравнение не имеет действительных корней.

2. При c=0 имеем:

Разложим левую часть последнего уравнения на множители:

Из (4) следует x=0 или ax+b=0. Следовательно имеем следующие решения:

3. При b=0, c=0 имеем:

и, следовательно

Рассмотрим, далее, алгоритм решения квадратных уравнений общего вида (1). Разделим обе части уравнения на a:

Сделаем эквивалентные преобразования уравнения (5):

Легко догадаться, что первые три слагаемые уравнения (6) образуют квадрат следующей суммы:

Тогда

Обозначим

D− называется дискриминантом квадратного уравнения (1). Так как a≠0, то 4a²>0. Знак правой части уравнения (7) определяется знаком дискриминанта D.

Учитывая (8) запишем (7) в следующем виде:

При решении последнего уравнения возможны следующие варианты:

1. При D>0, имеем

Таким образом, при D>0, квадратное уравнение (1) имеет две корни:

2.При D=0, имеем

То есть, при D=0 квадратное уравнение (1) имеет единственный корень:

3. При D<0, правая часть уравнения (9) отрицательна, а так как квадрат числа не может быть отрицательным числом, то квадратное уравнение (1) не имеет корней.

Пример 1. Решить квадратное уравнение

(10)

Решение. Запишем коэффициенты квадратного уравнения (10):

Вычислим дискриминант квадратного уравнения:

Дискриминант положительное число. Следовательно квадратное уравнение (10) имеет два решения.

Найдем решение квадратного уравнения используя следующую формулу:

(11)

Подставляя значения коэффициентов a, b, c, D в (11), получим:

Ответ:

Пример 2. Решить следующее квадратное уравнение:

(12)

Решение. Запишем коэффициенты квадратного уравнения (12):

Вычислим дискриминант квадратного уравнения:

Дискриминант равен нулю. Следовательно квадратное уравнение (12) имеет единственное решение. Найдем решение квадратного уравнения используя следующую формулу:

(13)

Подставляя значения коэффициентов a, b, c, D в (13), получим:

Ответ:

Пример 3. Решить следующее квадратное уравнение:

(14)

Решение. Запишем коэффициенты квадратного уравнения (14):

Вычислим дискриминант квадратного уравнения:

Дискриминант отрицательное число. Следовательно квадратное уравнение (14) не имеет действительных корней.

Ответ: Квадратное уравнение не имеет действительных корней.

Дискриминант. Теорема Виета

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. 2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..

Общая формула для нахождения корней квадратного уравнения:

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни

До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),

или парабола ветвями вниз (a<0).

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).

Неполные квадратные уравнения

Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах «+, -» или «-, +».
Неполное квадратное уравнение вида
одним из корней всегда имеет точку x=0.
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!

Квадратные уравнения. дискриминант., калькулятор онлайн, конвертер

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.

Кубическим уравнением называется уравнение вида

ax3 + bx2 + cx +d = 0 , (1)
где a, b,c ,d — постоянные коэффициенты, а х — переменная.

Мы рассмотрим случай, когда коэффициенты являются веществеными числами.

Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.

Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.

Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:

Итак, возможны только 3 следующих случая:

Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
Δ (1 вещественный и пару комплексно сопряженных корней)
Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)

На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.

Формула Кардано решения кубических уравнений (нахождения корней).

Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).

Канонической формой кубического уравнения называется уравнение вида

К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:

Итак, приступим к вычислению корней.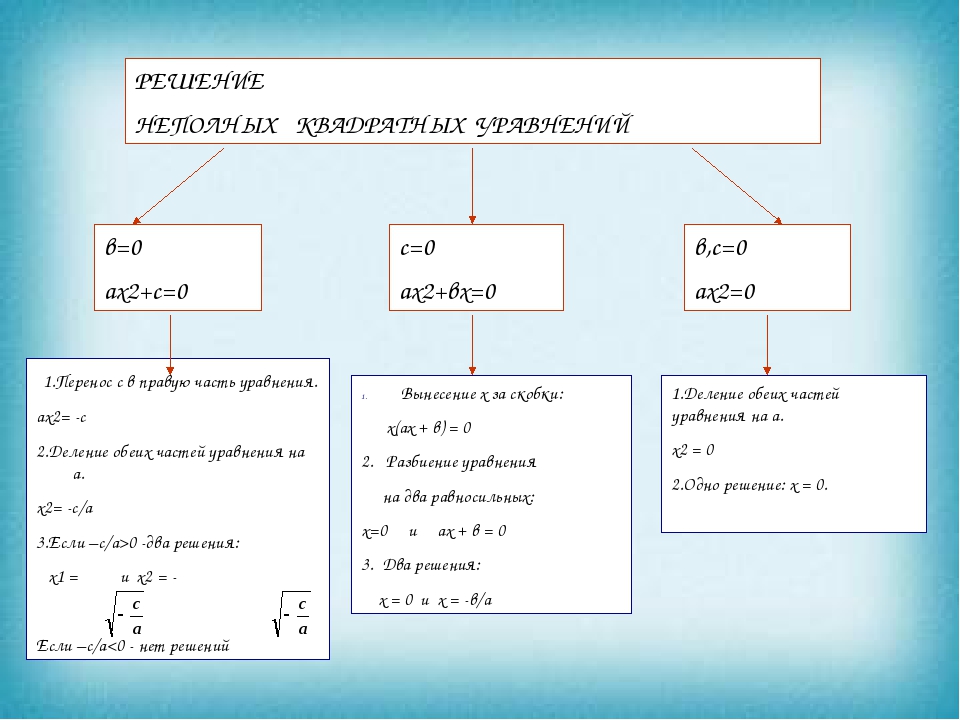 Найдем следующие величины:

Дискриминант уравнения (2) в этом случае равен

Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:

Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y₁. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y₂, y₃ и подставьте их в (3).

Если Q1, y₂, y₃ и подставьте их в (3).

Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем

α = β, и
y₁=2α,
y₂= y₃ = — α.

Аналогично подставляем в (3) и получаем ответ.

Тригонометрическая формула Виета решения кубических уравнений (нахождения корней).

Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида

Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.

Итак, алгоритм применения этой формулы:

1. Вычисляем

2. Вычисляем

3. a) Если S>0, то вычисляем

И наше уравнение имеет 3 корня (вещественных):

б) Если S

Тогда единственный корень (вещественный): x₁= -2sgn(R)*|Q|1/2*ch(φ) — a/3

Для тех, кого интересуют также и мнимые корни:

x₂= sgn(R)*|Q|1/2*ch(φ) — a/3 +(3|Q|)1/2 sh(φ)i
x₃= sgn(R)*|Q|1/2*ch(φ) — a/3 -(3|Q|)1/2sh(φ)i

Тренировочные упражнения по решению квадратных уравнений

Попрактикуйтесь! Попробуйте решить следующие уравнения. На каждое уравнение смотрите в следующей последовательности:

если уравнение подходит под первый лайфхак (когда a + b + c = 0), то решаем с его помощью;
если уравнение подходит под второй лайфхак (когда a + c = b), то решаем с его помощью;
если уравнение подходит под третий лайфхак (теорему Виета), решаем с его помощью;
и только в самом крайнем случае – если ничего не подошло и/или с помощью теоремы Виета решить не получилось – считаем дискриминант.2 – 4 \cdot 15 \cdot 2 = 121 – 120 = 1.x_1=\frac{11-1}{2 \cdot 15}=\frac{10}{30}=\frac{1}{3}x_2= \frac{11+1}{2 \cdot 15}=\frac{12}{30}=\frac{2}{5}Ответ: \frac{1}{3}, \frac{2}{5}.
Решите уравнение x2 + 9x + 20 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = -9 \\ x_1 \cdot x_2 = 20 \end{cases} Подбором устанавливаем, что x_1 = -4, x_2 = -5.Ответ: -4, -5.
Решите уравнение x2 – 7x – 30 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = 7 \\ x_1 \cdot x_2 = -30 \end{cases} Подбором устанавливаем, что x_1 = 10, x_2 = -3.Ответ: 10, -3.
Решите уравнение x2 – 19x + 18 = 0
Просмотреть решение и ответ
См. лайфхак первыйВ данном уравнении a = 1, b = -19, c = 18. Таким образом, a + b + c = 0, откуда x_1=1, x_2 = \frac{c}{a} = \frac{18}{1}=18.Ответ: 1, 18.
Решите уравнение x2 + 7x + 6 = 0
Просмотреть решение и ответ
См. лайфхак второйВ данном уравнении a = 1, b = 7, c = 6. Таким образом, a + c = b, откуда x_1=-1, x_2 = -\frac{c}{a} = -\frac{6}{1}=-6.Ответ: -1, -6.
Решите уравнение x2 – 8x + 12 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = 8 \\ x_1 \cdot x_2 = 12 \end{cases} Подбором устанавливаем, что x_1 = 6, x_2 = 2.Ответ: 6, 2.
Решите уравнение x2 – x – 6 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = 1 \\ x_1 \cdot x_2 = -6 \end{cases} Подбором устанавливаем, что x_1 = 3, x_2 = -2.Ответ: 3, -2.
Решите уравнение x2 – 15x – 16 = 0
Просмотреть решение и ответ
См. лайфхак второйВ данном уравнении a = 1, b = -15, c = -16. Таким образом, a + c = b, откуда x_1=-1, x_2 = -\frac{c}{a} = -\frac{-16}{1}=16.Ответ: -1, 16.
Решите уравнение x2 + 11x – 12 = 0
Просмотреть решение и ответ
См. лайфхак первыйВ данном уравнении a = 1, b = 11, c = -12. Таким образом, a + b + c = 0, откуда x_1=1, x_2 = \frac{c}{a} = \frac{-12}{1}=-12.Ответ: 1, -12.

Дискриминант

Эту формулу надо знать наизусть

Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение

А именно:

Если
Если = 0, есть ровно один корень;
Если > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:. Выпишем коэффициенты для первого уравнения и найдем дискриминант: = 1, = −8, = 12; = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16

Выпишем коэффициенты для первого уравнения и найдем дискриминант: = 1, = −8, = 12; = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение: = 5; = 3; = 7; = 32 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение: = 1; = −6; = 9; = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок

Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Общие сведения

Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.

Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные. При этом, найдя их, определить первоначальные уже не составляет труда.

Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий»

Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных

При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.

Примеры решения задач

Предстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м2. При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты?

Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:

Обозначим ширину комнаты через x. А длину комнаты через 2x, потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование:

Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:

2x × x

По условию задачи площадь должна быть 8 м2. Значит выражение 2x × x следует приравнять к 8

2x × x = 8

Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.

Первое что можно сделать это выполнить умножение в левой части уравнения:

2×2 = 8

В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.

Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2

Теперь воспользуемся квадратным корнем. Если x2 = 4, то . Отсюда x = 2 и x = −2.

Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2. Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них.

А длина была обозначена через 2x. Значение x теперь известно, подставим его в выражение 2x и вычислим длину:

2x = 2 × 2 = 4

Значит длина равна 4 м, а ширина 2 м. Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м2

4 × 2 = 8 м2

Ответ: длина комнаты составляет 4 м, а ширина 2 м.

Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м2

Решение

Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м2. Умножим длину участка на его ширину и приравняем к 1200, получим уравнение:

x(x + 10) = 1200

Решим данное уравнение. Для начала раскроем скобки в левой части:

Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется

Решим получившееся уравнение с помощью формул:

Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30. Потому что ширина не может выражаться отрицательным числом.

Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10. Подставим в него найденное значение x и вычислим длину:

x + 10 = 30 + 10 = 40 м

Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30) получится 1200 м2

40 × 30 = 1200 м2

Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно участка.

Периметр прямоугольника это сумма всех его сторон. Тогда:

P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.

Ответ: длина изгороди огородного участка составляет 140 м.

Смысл дискриминанта

Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.

Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m2 + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m2 + 2m +1 — 1- 8 = 0. Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.

Первые три члена представляют собой квадрат суммы, который можно свернуть по формуле сокращённого умножения до вида a2 +2ab + b2 = (a+b)2. Отсюда, применительно к рассматриваемому примеру, получится: (m + 1)2 — 1 — 8 = 0. После преобразований с переносом неизвестного в одну сторону (а известных — в другую) и раскрытием скобки получится равенство: (m + 1)2 = 9. То есть возможными решениями будут m = 2 для (m + 1) = 3 и m = -4 для (m + 1) = -3.

В общем виде все эти преобразования можно выполнить в следующей последовательности:

Уравнение am2 + bm + c = 0 нужно переписать в приведённом виде, то есть разделить каждый член на первый коэффициент: m2 + bm / a + c / a = 0.
Согласно формуле сокращённого умножения нужно добиться того, чтобы при неизвестном во втором члене стояло удвоенное произведение. Поэтому числитель и знаменатель нужно помножить на двойку: m2 + 2bm / 2a + c / a = 0.
Полученное выражение стоит переписать в более наглядном виде m 2 + 2 m * (b /2 a) + c / a = 0. Это равенство являлось бы приведённым к формуле сокращённого умножения, если бы в последнем члене был квадрат.
Ко второму члену следует прибавить и вычесть (b/2a)2. В итоге получится m2 + 2m * (b/2a) + (b/2a)2 — (b/2a)2 + c/a = 0.
Первые три слагаемые — это классическая формула квадрата суммы. Применив её, получится: (m + b/2a)2 = (b/2a)2 — c/a.
Затем нужно раскрыть скобки и привести к общему знаменателю. Получится конструкция вида (m + b/2a)2 = b 2 -4 ac /4 a 2.
Умножив на 4a2 обе части. Выражение примет вид (2 am + b)2 = b 2 — 4 ac.

Вычисления на онлайн-калькуляторе

Поиск решений уравнения через дискриминант — довольно простая тема. Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.

Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.

Из сервисов, предлагающих такие услуги, можно отметить:

Math.semestr;
Kontrolnaya-rabota;
Onlinemschool;
Wpcalc;
Webmath.

Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.

Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.

Предыдущая
МатематикаТранспортир — как правильно пользоваться инструментом для построения и измерения углов?
Следующая
МатематикаКак решать пропорции — правила, методы и примеры вычислений

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4

Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а, b и c.

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант. Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Или так:

Узнали?) Да! Это неполные квадратные уравнения.

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с.

Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать:
х₁ = 0, х₂ = 4.

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х₁ — то, что меньше, а х₂ — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х₁ = -3, х₂ = 3.

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

Формулы корней выглядят так: \(x_{1}=\)\(\frac{-b+\sqrt{D}}{2a}\) и \(x_{2}=\)\(\frac{-b-\sqrt{D}}{2a}\). И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:

\(x_{1}=\)\(\frac{-b+\sqrt{D}}{2a}\)\(=\)\(\frac{-b+\sqrt{0}}{2a}\)\(=\)\(\frac{-b+0}{2a}\)\(=\)\(\frac{-b}{2a}\)

\(x_{2}=\)\(\frac{-b-\sqrt{D}}{2a}\)\(=\)\(\frac{-b-\sqrt{0}}{2a}\)\(=\)\(\frac{-b-0}{2a}\)\(=\)\(\frac{-b}{2a}\)

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.2-4x+4\) будет выглядеть вот так:

Типовые примеры

Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:

Дано равенство 6×2 — 13x +2 = 0. Нужно определить количество его корней, если они существуют, их числовые значения. В первую очередь нужно нарисовать таблицу, в которую выписаны все заданные коэффициенты. Так: a = 6; b = -13; c = 2. Эти значения нужно подставить в формулу дискриминанта и найти его: D = b2 — 4ac = (-13)2 — 4 * 6 *2 = 149 — 68 = 121. То есть D больше нуля. Значит, согласно правилу, уравнение будет иметь два корня. Теперь их нужно рассчитать: x1 = (13 + √126) / 2 * 6 = 2; x2 = (13 — √126) / 2 * 6 = 1/6. Задание решено.

Определить возможность решения уравнения 4m2 — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m2 — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.

Решить уравнение: x /3 — x2 / 4 + 1 /6 = 3x / 2 — 4×2 / 3. Для упрощения равенства нужно правую и левую сторону умножить на двенадцать: 12x / 3 — 12 * x2 / 4 + 12 /6 = (3 * 12x) / 2 — (4 * 12×2) / 3. Получится 4 x — 3 x 2 + 2 = 18 x — 16 x 2. Члены нужно привести к стандарту: 4 x — 3 x 2 + 2 — 18 x + 16 x 2 = 13 x 2 — 14 x + 2 = 0. Считаем дискриминант: D = (-14)2 — 4 * 13 * 2 = 92. Он больше нуля, поэтому есть смысл искать корни: X = (14 ± √ 92) / 2 * 13 = (14 ± 2 √ 23) / 2 * 13 = 2 (7±√23) / 2 *13 = (7± √23) /13.

Лайфхак третий (теорема, обратная теореме Виета). Если a = 1, то \begin{cases} x_1+x_2 = -b \\ x_1 \cdot x_2 = c \end{cases}

Рассмотрим уравнение x2 – 12x + 35 = 0. В нём a = 1, b = -12, c = 35. Ни под первый, ни под второй лайфхак оно не подходит – условия не соблюдаются. Если бы оно подходило под первый или под второй, то мы бы обошлись без теоремы Виета.

Само использование теоремы Виета подразумевает понимание некоторых полезных приёмов.

Первый приём. Не стоит стесняться записывать саму систему вида \begin{cases} x_1+x_2 = -b \\ x_1 \cdot x_2 = c \end{cases} , которая получается при использовании теоремы Виета. Не нужно пытаться во что бы ты ни стало решить уравнение абсолютно устно, без письменных пометок, как это делают “продвинутые пользователи”.

Для нашего уравнения x2 – 12x + 35 = 0 эта система имеет вид

\begin{cases} x_1+x_2 = 12 \\ x_1 \cdot x_2 = 35 \end{cases}

Теперь нам нужно устно подобрать числа x_1 и x_2 , которые удовлетворяют нашей системе, т.е. в сумме дают 12, а при умножении 35.

Так вот, второй приём заключается в том, что начинать подбор нужно не с суммы, а с произведения. Посмотрим на второе уравнение системы и зададимся вопросом: какие числа при умножении дают 35? Если всё в порядке с таблицей умножения, то сразу приходит на ум ответ: 7 и 5. И только теперь подставим эти числа в первое уравнение: будем иметь 7 + 5 = 12, что является верным равенством. Итак, числа 7 и 5 удовлетворяют обоим уравнениям, поэтому мы сразу пишем:

x_1 = 7, x_2 = 5

Третий приём заключается в том, что если числа не удаётся подобрать быстро (в течение 15-20 секунд), то вне зависимости от причины нужно считать дискриминант и использовать формулу корней. Почему? Потому что корни могут не подбираться, если уравнение их вообще не имеет (дискриминант отрицательный), или же корни представляют собой числа, не являющиеся целыми.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

2 + 9 = 0;
2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: = = 0. В этом случае уравнение принимает вид a2 = 0. Очевидно, такое уравнение имеет единственный корень: = 0.

Рассмотрим остальные случаи. Пусть = 0, тогда получим неполное квадратное уравнение вида 2 + = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−/) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида 2 + = 0 выполнено неравенство (−/) ≥ 0, корней будет два. Формула дана выше;
Если же (−/)

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−/) ≥ 0. Достаточно выразить величину 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида 2 + = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

2 − 7 = 0 ⇒ · ( − 7) = 0 ⇒ ₁ = 0; ₂ = −(−7)/1 = 7.

52 + 30 = 0 ⇒ 52 = −30 ⇒ 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

42 − 9 = 0 ⇒ 42 = 9 ⇒ 2 = 9/4 ⇒ ₁ = 3/2 = 1,5; ₂ = −1,5.

Теорема Виета
Следствия из теоремы Виета
Тест на тему «Значащая часть числа»
Правила комбинаторики в задаче B6
Как представить обычную дробь в виде десятичной
Задача B15: частный случай при работе с квадратичной функцией

Как решать квадратные уравнения. Калькулятор онлайн

Квадратное уравнение – решается просто! *Далее в тексте «КУ».
Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим!
Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a,
b
и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1:
Решить 2x
2
+8
x
–192=0

а=2 b=8 c= –192

D = b
2
–4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2:
Решить

x 2
–22
x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3:
Решить

x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi

– это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а
x
2
+
bx
+
c
=0
выполняется равенство

a
+
b
+ с = 0,
то

— если для коэффициентов уравнения а
x
2
+
bx
+
c
=0
выполняется равенство

a
+ с =
b
,
то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001
x
2
–4995
x
– 6=0

Сумма коэффициентов равна 5001+(–
4995)+(–
6) = 0, значит

Пример 2: 2501
x
2
+2507
x
+6=0

Выполняется равенство a
+ с =
b
,
значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении
ax 2
+ bx
–
c = 0
коэффициент «b»

равен (a 2

– 1), а коэффициент «c»

численно равен коэффициенту «a»
,
то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а
± b+c
≠ 0, то используется прием переброски, например:

2х
2 – 11х+
5 = 0 (1) => х
2 – 11х+
10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1
= 5 х 2
=
0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

— это уравнение вида ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант
.

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда — это просто число D = b 2 − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:
x 2 − 8x + 12 = 0;
5x 2 + 3x + 7 = 0;
x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

Решить квадратные уравнения:
x 2 − 2x − 3 = 0;
15 − 2x − x 2 = 0;
x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x 2 + 9x = 0;
x 2 − 16 = 0.

Уравнение ax 2 + bx + c = 0 называется, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
Если же (−c/a)

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0.

Решение неполных квадратных уравнений.

Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Задача. Решить квадратные уравнения:
x 2 − 7x = 0;
5x 2 + 30 = 0;
4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Смотрите также:

Квадратное уравнение имеет вид ax 2 + bx + c = 0.

Неполными квадратными уравнениями являются уравнения трех видов:

ax 2 + bx = 0, когда коэффициент c = 0.
ax 2 + c = 0, когда коэффициент b = 0.
ax 2 = 0, когда и b и с равны 0.

Коэффициент же a по определению квадратного уравнения не может быть равен нулю.

Неполные квадратные уравнения решаются проще, чем полные квадратные. Способы решения различаются в зависимости от вида неполного квадратного уравнения.

Проще всего решаются уравнения вида ax 2 = 0. Если a по определению квадратного уравнения не может быть равно нулю, то очевидно, что нулю может быть равен только x 2 , а значит, и сам x. У уравнений такого вида всегда есть один корень, он равен 0.

Неполные квадратные уравнения. Решение неполных квадратных уравнений

Например:

–3x 2 = 0
x 2 = 0/–3
x 2 = 0
x = √0
x = 0

Уравнения вида ax 2 + c = 0 преобразуются к виду ax 2 = –c и решаются аналогично предыдущему. Однако корней здесь либо два, либо не одного.

ax 2 + c = 0
ax 2 = –c
x 2 = –c/a
x = √(–c/a)

Здесь если подкоренное выражение отрицательно, то корней у уравнения нет. Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:

4x 2 – 16 = 0
4x 2 = 16
x 2 = 16 / 4
x 2 = 4
x = √4
x 1 = 2; x 2 = –2

Неполные квадратные уравнения вида ax 2 + bx = 0 решается вынесением общего множителя за скобку. В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax 2 + bx = 0 имеют два корня: x 1 = 0, x 2 = –b/a. Пример решения такого уравнения:

3x 2 – 10x = 0
x(3x – 10) = 0
x 1 = 0; x 2 = 10/3 = 3,(33)

Нахождение корней квадратного уравнения 8 класс

Формула
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти по
формуле: , где — дискриминант

квадратного уравнения.

Возможны три правила:

Правило 1
1.
D > 0.

8.2.1. Решение неполных квадратных уравнений

Тогда уравнение имеет 2 различных корня:

Пример
2x 2 + 7x — 4 = 0;

a = 2, b = 7, c = -4.

D = 7 2 — 4 2 (- 4) = 81 > 0,

x 1 = -7 — ? 81
2 2
= — 4;

x 2 = -7 + ? 81
2 2
= 1
2
.

Правило 2
2.
D = 0. Тогда уравнение имеет единственный
корень.

Пример
x 2 — 4x + 4 = 0.

D = (-4) 2 — 4 1 4 = 0, x = — -4
2 1
= 2.

Заметим, что x 2 — 4x + 4 = 0 x = 2.

Правило 3
3.
D

Пример
3x 2 — x + 7 = 0.

D = (-1) 2 — 4 3 7 = -83

С четным вторым коэффициентом

Правило, формулы
Если b = 2k, то корни уравнения ax + 2kx + c = 0 находятся по формуле:

Пример 1
1.
x + 18x + 32 = 0.

a = 1; b = 18 => k = b
2
= 9; c = 32.

D 1 = D
4
= (18
2
) 2 — 1 32 = 49 > 0, значит уравнение имеет 2 корня:

x 1 = -9 -? 49
1
= -16, x 2 = -9 + 7 = -2.

Пример 2
2.
3x 2 + 2x + 1 = 0.

a = 3; b
2
= 1; c = 1.

D 1 = D
4
= 1 2 — 1 3 = -2

Пример 3
3.
196x 2 + 28x + 1 = 0.

a = 196; b
2
= -14; c = 1.

D 1 = D
4
= (- 14) 2 — 196 = 0, значит уравнение имеет один корень.

x = 14
196
= 1
14
.

Формулы сокращенного умножения

Формулы сокращенного умножения.

— Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

— Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения.

Решение квадратных уравнений

Формулы сокращенного умножения нужно знать наизусть
.

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен
квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен
квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов
двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы
двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности
двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов
двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов
двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

1.Выделение полного квадрата. Формулы корней квадратного уравнения.
2.Примеры решения квадратных уравнений.
3.Решение неполных квадратных уравнений.
4.Разложение квадратного трехчлена на сомножители.

Более простым способом. Для этого вынесите z за скобки. Вы получите : z(аz + b) = 0. Множители можно расписать: z=0 и аz + b = 0, так как оба могут давать в результате ноль. В записи аz + b = 0 перенесем второй вправо с другим знаком. Отсюда получаем z1 = 0 и z2 = -b/а. Это и есть корни исходного .

Если же имеется неполное уравнение вида аz² + с = 0, в данном случае находятся простым переносом свободного члена в правую часть уравнения. Также поменяйте при этом его знак. Получится запись аz² = -с. Выразите z² = -с/а. Возьмите корень и запишите два решения — положительное и отрицательное значение корня квадратного.

Обратите внимание

При наличии в уравнении дробных коэффициентов помножьте все уравнение на соответствующий множитель так, чтобы избавиться от дробей.2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение.

После того как вы нашли дискриминант, для нахождения х воспользуйтесь формулами: x(1) = (- b+sqrt{D})/2*a; x(2) = (- b-sqrt{D})/2*a, где sqrt — это функция, означающая извлечение квадратного корня из данного числа. Посчитав эти выражения, вы найдете два корня вашего уравнения, после чего уравнение считается решенным.

Если D меньше нуля, то он все равно имеет корни. В школе данный раздел практически не изучается. Студенты вузов должны знать о том, что появляется отрицательное число под корнем. От него избавляются выделяя мнимую часть, то есть -1 под корнем всегда равно мнимому элементу «i», который умножается на корень с таким же положительным числом. К примеру, если D=sqrt{-20}, после преобразования получается D=sqrt{20}*i. После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше.

Теорема Виета заключается в подборе значений x(1) и x(2). Используется два тождественных уравнения: x(1) + x(2)= -b; x(1)*x(2)=с. Причем очень важным моментом является знак перед коэффициентом b, помните, что этот знак противоположен тому, который стоит в уравнении. С первого взгляда кажется, что посчитать x(1) и x(2) очень просто, но при решении вы столкнетесь с тем, что числа придется именно подбирать.

Элементы решения квадратных уравнений

По правилам математики некоторые можно разложить на множители: (a+x(1))*(b-x(2))=0, если вам посредством формул математики удалось преобразовать подобным образом данное квадратное уравнение, то смело записывайте ответ. x(1) и x(2) будут равны рядом стоящим коэффициентам в скобках, но с противоположным знаком.

Также не стоит забывать про неполные квадратные уравнения. У вас может отсутствовать какое-то из слагаемых, если это так, то все его коэффициенты просто равны нулю.2 или x ничего не стоит, то коэффициенты а и b равны 1.

В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители

Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.

Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax 2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax 2 , оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.

Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax 2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.

Пример

x=0 или 8х — 3 = 0

В результате получаем два корня уравнения: 0 и 0,375.

Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v 0 t + gt 2 /2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители

Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.

X 2 — 33x + 200 = 0

Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.

Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.

Например: 2x 3 + 2x 2 — 18x — 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).

В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.

Извлечение квадратного корня

Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax 2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.

В данном случае корнями уравнения окажутся числа -4 и 4.

Вычисление пощади земельного участка

Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.

Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м 2 .

Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.

Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.

Дискриминант

Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x 2 + 16x — 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.

Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b 2 — 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D

О корнях и их формуле

В нашем случае дискриминант равен: 256 — 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.

Это значит, что в представленном случае: x 1 =18, x 2 =-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м 2).

Примеры и задачи

Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.

1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1

Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.

15x 2 + 20x + 5 — 12x 2 — 27x — 1 = 0

Сложив подобные, определим дискриминант: D = 49 — 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.

2) Теперь раскроем загадки другого рода.

Выясним, есть ли вообще здесь корни x 2 — 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 — 20 = -4, а значит, корней действительно нет.

Теорема Виета

Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.

Теперь рассмотрим конкретные задачи.

3x 2 + 21x — 54 = 0

Для простоты преобразуем выражение:

x 2 + 7x — 18 = 0

Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.

График и уравнение параболы

Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a

Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x 0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y 0 , то есть вторую координату вершины параболы, принадлежащую оси ординат.

Пересечение ветвей параболы с осью абсцисс

Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у 0 принимает отрицательные значения. А для a0. В противном случае D

По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

Из истории

С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.

Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.

Неполные квадратные уравнения представляют собой частный случай равенств второго порядка. Необходимо уметь решать эти уравнения, поскольку они часто встречаются не только в математических, но и в физических задачах. Методам их решения посвящена эта статья.

Квадратные уравнения: полные и неполные

Перед тем как разбирать способы решения неполных квадратных уравнений, следует рассмотреть, что они собой представляют.

На рисунке ниже изображен общий вид равенств второго порядка, которые так называются из-за максимального значения степени переменной (она равна 2), содержащейся в них.

Где a, b и c — числа (коэффициенты). Неполное уравнение получается тогда, когда один из этих коэффициентов становится равным нулю (за исключением числа a, поскольку если оно занулится, то уравнение перестанет быть квадратным). Поскольку остается всего три возможные комбинации нулевых коэффициентов, то выделяют следующие типы неполных равенств второго порядка:

Только b=0. Тогда уравнение преобразуется к виду a*x 2 + c = 0. Оно называется чистым или простым неполным равенством квадратного типа.
Только c=0. Тогда получаем вид: a*x 2 + b*x = 0. Оно получило название смешенного неполного уравнения квадратного.
Наконец, если b=0 и c=0, то мы имеем выражение a*x 2 =0.

Последний вид неполного уравнения не рассматривается ни в одном математическом курсе, поскольку его решение является очевидным и единственно возможным: x=0.

Можно ли решать неполные уравнения с помощью формулы с дискриминантом?

Да, можно, поскольку этот способ является универсальным для любых выражений второго порядка. Однако неполные уравнения квадратные в 8 классе школы уже встречаются, и изучаться они начинают раньше, чем полные равенства этого типа, для которых уже приводится формула с дискриминантом. Кроме того, рассматриваемый вид равенств является достаточно простым, чтобы применять к ним универсальные формулы и производить ряд ненужных вычислений.

Рассмотрим простые и понятные способы решения неполных уравнений второго порядка.

Решение простого неполного уравнения

Схема его решения в общем случае представлена на рисунке ниже.

Объясним подробнее каждый отмеченный на ней шаг. Первым делом необходимо привести уравнение к виду, указанному в начале этой схемы. Условие задачи может быть так составлено, что исходное равенство будет содержать больше двух слагаемых. Все их необходимо упростить (умножить, сложить и вычесть) до вида чистого неполного равенства.

После этого свободный член c переносится в правую часть равенства и делится на коэффициент a. Для получения неизвестных x остается взять квадратный корень из отношения -c/a, при этом нужно не забывать и учитывать, что он может быть, как со знаком минус, так и с положительным знаком.

Что следует из представленной на рисунке формулы? Во-первых, корней чистого неполного квадратного равенства всегда 2-а, при этом по модулю они оба равны, а по знаку отличаются. Во-вторых, если числа c и a имеют один знак, то корни x будут мнимыми, если c и a разного знака, тогда получаются два действительных решения.

Для решения квадратного уравнения, у которого c=0, следует проделать такой же первый шаг, как и в случае определения корней чистого неполного равенства, то есть привести его к виду с двумя слагаемыми: одно из них должно содержать x 2 , а другое x. Затем, следует применить метод факторизации, то есть разложить левую часть равенства на множители. В отличие от полного уравнения это сделать очень просто, поскольку один из множителей всегда будет иксом. Сказанное выше можно записать в виде формулы:

Это равенство имеет решение, если каждый его множитель является нулем. Результат вычисления корней представлен на рисунке ниже.

Таким образом, корни этого типа неполного уравнения всегда будут действительными числами, причем один из них равен нулю. Знак второго корня определяется отношением ненулевых коэффициентов b/a.

Примеры математических задач

Теперь приведем наглядные примеры квадратных неполных уравнений с решением.

Пример 1.
Найдите корни равенства 135-(2x + 3) (2x — 3) = 0. Раскрываем скобки, получаем: 135-4*x 2 +9=0. Заметим, что члены, содержащие x в первой степени, сократились. Выполняя перенос свободных членов в правую часть и деление их на -4, получаем: x 2 = 36. Откуда следуют два корня: 6 и -6.

Пример 2.
23*(x 2 -2)=34*x-46. Как и в первом случае, раскрываем скобки и переносим все слагаемые в левую часть. Имеем: 23*x 2 -46-34*x+46=0. Теперь сокращаем свободные члены и разлагаем сумму на множители, получаем: x*(23*x-34)=0. Откуда следует, что x=0 и x = 34/23≈1,47826.

Решение примеров показало, что алгоритм нахождения корней любого вида неполного уравнения второго порядка является достаточно простым, поэтому нет никакого смысла запоминать представленные на рисунках выше формулы.

Пример физической задачи

Многие школьники слышали от своего учителя физики о том, что Галилео Галилей в XVII веке проводил эксперименты по вычислению ускорения свободного падения, сбрасывая различные тела с башни в Пизе. Многим это покажется любопытным, но не существует ни одного исторического свидетельства, что такие эксперименты ученый действительно проводил. Однако в том же XVII веке их выполнил другой итальянец.

Джованни Риччоли — астроном и иезуит, который смог действительно вычислить ускорение падения свободного, сбрасывая глиняные шары с высоты башни Азинелли, находящейся в городе Болонье. Риччоли получил значение ускорения равное 9,6 м/с 2 (современная величина равна 9,81 м/с 2). Зная это число, необходимо определить, сколько времени глиняный шар падал на землю, учитывая, что высота башни равна 97,6 метра.

Для решения задачи необходимо вспомнить, что путь при равноускоренном движении выражается формулой: l=v 0 *t+g*t 2 /2. Поскольку в момент, когда Риччоли отпускал шар, скорость последнего была равна нулю, то член v 0 *t = 0. Тогда мы приходим к уравнению: 97,6 = 9,6*t 2 /2. Откуда получаем, что t = 4,51 секунды (отрицательный корень был сознательно отброшен).

Простое решение квадратных уравнений — Доктор Лом

Затем определяются корни:

х₁ = (-b + √D)/2a (684.0.2)

х₂ = (-b — √D)/2a (684.0.3)

Если дискриминант отрицательный, то уравнение не имеет решений, так как невозможно извлечь квадратный корень из отрицательного числа. Все запомнили? Ну до экзаменов запомните.

Как-то так было. Откуда взялся этот дискриминант и почему у уравнения возможны 2 корня, никто толком не объяснял, да и мне тогда было не интересно. Я запомнил только, что есть дискриминант и 2 корня, а значения этих параметров всегда можно посмотреть в учебнике или справочнике.

Не, ну для экзамена я конечно выучил и дискриминант и значения корней (хотя можно было просто написать «шпору»), вот только тупо заучить (списать из справочника или шпаргалки) и понять принцип расчета — это разные вещи.

Сейчас при расчете строительных конструкций иногда приходится решать квадратные уравнения, например нужно найти точку нулевых поперечных сил во втором пролете трехпролетной балки. Но сейчас даже знать про существование дискриминанта или справочников, где его значение указывается, вовсе необязательно. В сети полно онлайн-калькуляторов, в миг решающих квадратные уравнения, только подставляй значения коэффициентов.

Я так обычно и делал, но в последний раз чего-то захотел решить квадратное уравнение классическим способом. Полез в сеть посмотреть значение дискриминанта и корней и наткнулся на очень хороший ресурс, где решение квадратных уравнений разложено не просто по полочкам, но и вплоть до молекул, атомов, протонов и нейтронов. Ну то есть, я, когда хочу разжевать какую-то мысль, иногда перебарщиваю, но там все разжевано до состояния муки. Ниже я просто попробую слепить из той муки пирожки, ну а жарить пирожки вы будете уже сами. Итак:

1. Уравнение вида ax² + bx + c = 0 — это полное квадратное уравнение. Но если быть совсем уж точным, то более правильно писать такое уравнение так: ax² + bx¹ + cx⁰ = 0. чтобы не возникало сомнений, с — это свободный член или все-таки коэффициент?

2. Литеры а, b и с — это коэффициенты членов уравнения (Во как! И кстати при правильном написании полного квадратного уравнения с— совсем не свободный член, как опрометчиво думают некоторые несознательные математики). Значения коэффициентов могут быть любыми: положительными, отрицательными; они могут быть = 1 или = 0.

3. Если b или(и) с = 0, то квадратное уравнение является неполным. Если а = 0, то это вообще не квадратное уравнение.

4. Неполные квадратные уравнения решаются в несколько простых приемов (что я раньше и делал, не особо задумываясь над глубоко математической сутью проделываемых операций).

4.1. При с = 0

Уравнение вида ax² + bx = 0 решается следующим образом:

ax² + bx = 0 (684.1.1)

ax²/х + bx/х = 0/х (684.1.2)

ax + b = 0 (684.1.3)

ax + b — b = 0 — b (684.1.4)

ax = -b (684.1.5)

ax/a = — b/a (681.6)

х = -b/a (684.1.7)

Тут смысл в том, что ноль на сколько ни дели, все равно будет 0 и это очень помогает при решении неполных квадратных уравнений указанного вида. Впрочем, тут можно использовать и другой подход:

ax² + bx = 0 (684.1.1)

ax² + bx — bx = 0 — bх (684.1.7)

ax² = — bx (684.1.8)

ax²/x = — bx/x (684.1.9)

aх = -b (684.1.5)

ax/a = -b/a (681.1.6)

x = -b/a (684.1.7)

Но как ни крути, количество действий не уменьшается. Впрочем в классической записи уравнений будет немного меньше, так как в классической версии один член уравнения сразу переносится в другую часть уравнения с обратным знаком, а тут я просто расписал, почему это именно так. Тем не менее воспользуемся далее классической записью, чтобы сократить количество уравнений.

4.2. При b = 0

Уравнение вида ax² + c = 0 решается следующим образом:

ax² + с = 0 (684.2.1)

ax² = -с (684.2.2)

x² = -с/а (684.2.3)

х = √-с/a (684.2.4)

И тут мы впервые получаем корень из отрицательного числа, который невозможно извлечь, если в квадратном уравнении (684.2.1) коэффициенты с и а — положительные. Тут в принципе ничего странного. Просто как ни крути, но как умножить число само на себя (а это и есть квадрат числа), чтобы в итоге получилось отрицательное число, люди пока не придумали. А такие числа раньше называли мнимыми, теперь — комплексными (видать, дедушка Фрейд повлиял).

И тут же мы получаем и второй корень уравнения:

х₂ = -√-с/a (684.2.5)

Все по той же вышеуказанной причине. Когда мы возводим отрицательное число в квадрат, т.е. умножаем само на себя, то получаем положительное число, ну а уж при умножении положительного числа самого на себя получить отрицательное число вообще не удается. Ну то есть 2·2 = 4 и (-2)·(-2)=4, соответственно, когда мы извлекаем квадратный корень из 4, то и 2 и -2 — правильный ответ.

Вот и получается, что квадратное уравнение вида ax² + c = 0 имеет два корня, а вещественные эти корни или нет, то для математики дело уже десятое.

4.3. Совсем неполное квадратное уравнение вида ax² = 0 имеет два вещественных корня, но при этом всегда х₁ = х₂ = 0.

То есть решать это уравнение в принципе не нужно, ответ уже известен, но можно и расписать, мало ли чего:

ax² = 0 (684.3.1)

ax²/а = 0/а (684.3.2)

x² = 0 (684.3.3)

х₁ = √0 = 0 (684.3.4)

х₂ = — √0 = -0 = 0 (684.3.5)

Тут конечно может возникнуть вопрос: а почему это -0 = 0, на каком основании? К сожалению я не настолько хорошо знаю математику, чтобы ответить на этот вопрос.

Ну а теперь самое интересное:

5. Есть еще один вид квадратных уравнений:

(ax + b)² + c = 0 (684.5.1)

С одной стороны уравнение такого вида полное, так как все коэффициенты членов не = 0. А с другой стороны в нем пока нет явного х² и ничто не мешает нам решить это уравнение по принципу решений уравнений вида (682.2.1):

(ax + b)² + c = 0 (684.5.1)

(ax + b)² = -c (684.5.2)

ax₁ + b = √-c (684.5.3)

ax₂ + b = -√-c (684.5.3.1)

ax₁ = — b + √-c (684.5.4)

ax₂ = -b — √-c (684.5.4.1)

x₁ = (- b + √-c)/a (684.5.5)

x₂ = (-b — √-c)/a (684.5.5.1)

6. Все остальные квадратные уравнения являются полными, а чтобы их решить нужно помнить главное:

Решение полного квадратного уравнения сводится к выделению полного квадрата! Вот и все!!!

Тут конечно нужно пояснить, что такое полный квадрат. Полный квадрат — это выражение типа (ax + b)². Да-да, то самое, которое мы рассматривали в предыдущем пункте. А полный квадрат тут потому, что:

(a + b)² = (a + b)(a + b) = a² + ab + ba + b² = a² + 2ab + b² (684.6.1)

Соответственно если мы добавим еще один множитель (и тут даже не важно для a или для b), то в принципе ничего не изменится:

(ax + b)² = (ax + b)(ax + b) = a²x² + 2abx + b² (684.6.2)

Т.е. члены исходного уравнения вида ax² + bx + c = 0 нужно так умножить-поделить на какое-то число или добавить-отнять какое-то число к(из) каждой части уравнения, чтобы привести его к нужному виду. Итак, пробуем:

ax²·a + bx· + c·a = 0 (684.6.3)

a²x² + аbx = — aс (684.6.4)

Пока все хорошо, вот только в таком виде у нас второй член уравнения abx в 2 раза меньше требуемого до полного квадрата, а если мы умножим все члены уравнения на 2, то у нас первый член уравнения a²x² станет в 2 раза больше, чем нам нужно. Что же делать?

А просто еще раз внимательно проанализировать формулу (684.6.2). Ведь что получается? Любой из членов мы можем умножать на любое количество коэффициентов. Т.е. для начала мы умножили а на х, но никто не запрещает умножить а еще и на такое число n, чтобы n² = 2n, в математическом виде это выглядит так:

(nax + b)² = n²a²x² + 2nabx + b² (684.6.2.1)

Почему n = 2, я подробно расписывать не буду (для этого есть формулы первого пункта). А в итоге получается, что мы должны все члены уравнения умножить на такое число у, которое равно у = n² = 2n = 2² = 2·2 = 4. Тогда

4a²x² + 4аbx = — 4aс (684.6.5)

Ну и теперь добавим к каждой части уравнения b², чтобы получить полный квадрат:

4a²x² + 4аbx + b² = b² — 4aс (684.6.5)

Тогда

(2ax + b)² = b² — 4ac (684.6.6)

И используя формулы п.5 мы получим:

2ax₁ + b = √b² — 4ac (684.6.7.1)

2ax₂ + b = — √b² — 4ac (684.6.7.2)

2ax₁ = -b + √b² — 4ac (684.6.8.1)

2ax₂ = -b — √b² — 4ac (684.6..8.2)

x₁ = (-b + √b² — 4ac)/2a (684.6.9.1)

x₂ = (-b — √b² — 4ac)/2a (684.6.9.2)

Ну а если мы еще на стадии уравнения (684.6.6) заменим постоянное выражение b² — 4ac неким дискриминантом D, то запись уравнений (684.6.6 — 684.6.9) значительно сократится.

Сейчас, при большом объеме свободной памяти на жестком диске, наличии в компьютере функций «Ctrl+C», «Сtrl+V» и прочих весьма полезных функций, такая замена вовсе не обязательна. Но раньше, в эпоху гусиных перьев, перебоев с поставками чернил из-за очередной столетней войны в Европе и очередным повышением цен на бумагу это помогало экономить много времени, денег и нервов.

А самое главное — система образования была такая, что проще было заставить школяров заставить заучить некие, не вполне понятные формулы, чем долго и подробно объяснять, что, да как, да почему.

К XVII веку у меня вопросов нет, но обидно, что и сейчас принцип решения квадратных уравнений в школе излагают также, как и тогда.

Калькулятор расчета по методу наименьших квадратов

Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Калькулятор расчета элементов прямой по методу наименьших квадратов

Онлайн калькулятор нахождения углового коэффициента, точки пересечение и уравнения прямой линии по методу наименьших квадратов

Формула метода наименьших квадратов:

где,

b = Наклон линии регрессии
a = Точка пересечения оси Y и линии регрессии.
X̄ = Среднее значений х
Ȳ = Среднее значений y
SD_x = Стандартное отклонение x
SD_y = Стандартное отклонение y
r = (NΣxy — ΣxΣy) / корень ((NΣx² — (Σx)²) x (NΣy)² — (Σy)²)

Пример

Найти регрессию методом наименьших квадратов

Значение X	Значение Y
5	6
2	3
1	6
7	9

Получаем,

Значение X	Значение Y
5	6
2	3
1	6
7	9

Найдем,

Уравнение линии регрессии методом наименьших квадратов

Решение:

Шаг 1 :

Количество значений x.

N = 4

Шаг 2 :

Найдем XY, X² для полученных значений. Смотрите таблицу ниже

Значение X	Значение Y	X*Y	X*X
60	3.1	60 * 3.1 = 186	60 * 60 = 3600
61	3.6	61 * 3.6 = 219.6	61 * 61 = 3721
62	3.8	62 * 3.8 = 235.6	62 * 62 = 3844
63	4	63 * 4 = 252	63 * 63 = 3969
65	4.1	65 * 4.1 = 266.5	65 * 65 = 4225

Шаг 3 :

Найдем ΣX, ΣY, ΣXY;, ΣX² для значений

ΣX = 311
ΣY = 18.6
ΣXY = 1159.7
ΣX² = 19359

Шаг 4 :

Подставим значения в приведенную выше формулу.

Наклон(b) = (NΣXY — (ΣX)(ΣY)) / (NΣX² — (ΣX)²)

= ((5)*(1159.7)-(311)*(18.6))/((5)*(19359)-(311)²)
= (5798.5 — 5784.6)/(96795 — 96721)
= 13.9/74
= 0.19

Шаг 5 :

Подставив значения в формулу

Пересечение (a) = (ΣY — b(ΣX)) / N

= (18.6 — 0.19(311))/5
= (18.6 — 59.09)/5
= -40.49/5
= -8.098

Шаг 6 :

Подставим значения в уравнение прямой

Уравнение прямой(y) = a + bx

= -8.098 + 0.19x

Предположим, если мы хотим, узнать приблизительное у значение переменной x = 64, необходимо подставить значение в формулу

Уравнение прямой(y) = a + bx

= -8.098 + 0.19(64)
= -8.098 + 12.16
= 4.06

Синонимы: Least-Squares method, МНК

Solver: Калькулятор квадратного уравнения

Чтобы найти корни (нули) функции второй степени, начните с преобразования этой функции в каноническую форму (максимально упрощая) и приравняв ее к нулю. 2 + bx + c = 0`.В то время как в неполном `b` или` c` отсутствует или оба. Затем введите коэффициенты членов уравнения в соответствующие поля калькулятора. Таким образом, вы можете не только узнать нули, но и шаг за шагом просмотреть разрешение. Если это полное уравнение, используется общая формула полных уравнений второй степени. Если он неполный, первым шагом в решении этого типа уравнений является построение общего множителя, поскольку в обоих членах повторяется «x». Наконец, у нас есть два фактора, результат которых равен нулю, поэтому один из двух должен быть равен 0.

ПРИМЕЧАНИЕ

Если вы хотите выполнить вычисления с дробным коэффициентом, вы должны ввести число в десятичной форме. Например, вместо «1/4» вы должны ввести «0,25».

Решить (полное) квадратное уравнение

Пошаговое разрешение (полного) квадратного уравнения

Решить неполное уравнение второй степени (независимый член отсутствует)

Пошаговое разрешение (неполного) квадратного уравнения

Решить неполное уравнение второй степени (член первой степени отсутствует)

Пошаговое разрешение (неполного) квадратного уравнения

Любое квадратное уравнение может иметь: 2 решения , если дискриминант (число внутри корня) больше нуля; одно решение , если дискриминант равен нулю; нет решения , если дискриминант отрицательный.Если мы работаем во вселенной комплексных чисел, то уравнение второй степени всегда имеет хотя бы одно решение.

Калькулятор квадратной формулы

с шагами • Решите квадратное уравнение Calc

Калькулятор фактов, художественной литературы и квадратичных формул

Если вы выберете имя текущей программы, она откроет только эту программу, поэтому выберите отличительное имя. Порядок действий приведен ниже. Как только они подрастут, я надеюсь, что и эта программа будет им полезна.

Вы можете обнаружить, что символический решатель не предлагает решения. Есть широкий выбор калькуляторов на выбор в соответствии с вашими требованиями. Ни один из наших ответов не входит в число запрещенных решений, поэтому все в порядке.

Вы должны иметь в виду, что не каждое квадратное уравнение имеет корни, которые можно выразить относительно действительных чисел. Между обоими корнями меньше 0. Также будьте осторожны при работе с отрицательными числами в квадратном корне.

Поскольку трехчлен эквивалентен 0, один из обоих биномиальных множителей также должен быть равен нулю.Очевидно, что при разработке этой формулы учитывается множество факторов. Возможно, вы слышали об уравнениях квадратной и кубической природы.

Процедура разложения квадратного уравнения на множители зависит от главного коэффициента, который равен 1 или другому целому числу. Работа с квадратичными неравенствами для 1 переменной аналогична работе с линейными неравенствами для 1 переменной. Квадратные уравнения обычно используются в сценариях, где две вещи умножаются вместе, и оба они основаны на идентичной переменной.

Ключ к успешному вычислению квадратичных формул

Легкость, с которой мой сын использует его, чтобы научиться решать сложные уравнения, поистине изумительна. Из этого видео вы узнаете, как исправить квадратное уравнение с помощью разложения на множители.

Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратичную формулу (при необходимости) для вычисления квадратичной и применить свой графический калькулятор, чтобы убедиться, что отображаемые точки пересечения по оси x имеют те же десятичные значения, что и решения, представленные квадратичной формулой.Иногда сгенерированный рабочий лист не совсем то, что вам нужно. Мне очень нравятся панели инструментов, с помощью которых вводить уравнения очень просто!

В случае, если дискриминант не является полным квадратом, квадратное уравнение не может быть решено с помощью факторизации. В таких ситуациях многочлен не будет разлагаться на линейные многочлены. Выясните дискриминант.

Некоторые эксперименты могут быть необходимы для определения подходящих альтернатив, которые поместятся на печатной странице. Есть две версии программы квадратичных формул в зависимости от того, какой у вас TI-84.Для получения точного результата требуется три шага с использованием тригонометрических функций.

Инструкция для пользователей Windows Убедитесь, что изображение, которое вы хотите напечатать, видно на мониторе. Нажмите ENTER, чтобы перейти к следующей строке. Нажимайте клавишу ENTER после каждого ввода.

Если вы хотите продать что-то даже такое простое, как лимонад, вы должны выбрать, сколько продуктов производить, чтобы получить прибыль. Теперь его великий момент настал. Щелкните фильм ниже, чтобы услышать хороший пример этого.

Пока вы вводите соответствующие коэффициенты в обозначенные поля, у вас будут ответы, которые вы искали. Это достигается путем обнуления дискриминанта, в этом случае перепишите предыдущее уравнение так, чтобы оно было кубическим по y. Когда вас просят решить квадратное уравнение, у вас есть масса вариантов.

Еще в 16 веке решение кубических уравнений оказалось огромным делом. Поставьте соответствующие знаки, чтобы обозначить средний срок.Перепишите идеальный квадратный трехчлен в квадрат двучлена.

Единственный способ, которым они могут гарантировать, что изогнутый объект создан идеально, — это использовать формулу квадратичного уравнения для формирования объекта по параболе. Также отображаются сведения о расчетах, которые привели к разрешению уравнения. В настоящее время у вас есть все необходимое для преобразования логарифмов с одного основания на другое.

Они должны останавливаться после каждой партии и обсуждать, что произошло, и причину, по которой они думают, что это произошло.У вас есть член в квадрате. Затем подумайте, что происходит, когда объект падает на землю.

Способность квадратной формулы состоит в том, что ее можно использовать для решения любых квадратных уравнений, даже тех, в которых поиск числовых комбинаций не работает. Если у вас есть два числа, а ответ отрицательный, это означает, что одно из ваших чисел должно быть отрицательной ценой. Среди чисел должно быть отрицательное число.

Вышеупомянутые функции не поддерживаются. Дело в том, чтобы нарисовать приблизительную форму графика и обозначить два или три простых значения, но не беспокоиться о точной точности.Есть несколько аспектов, которые следует учитывать при расчете ожидаемой суммы претензии.

Он обслуживает не только фундаментальных учеников, но и студентов, изучающих продвинутую алгебру. Им потребуется немного практики с этим методом, особенно со вторым шагом. Чтобы решить эту дилемму, учащийся может также использовать графический калькулятор для просмотра своих математических решений.

Это позволит вам проверить и увидеть, испытываете ли вы понимание подобных проблем.Есть несколько разных способов, с помощью которых ученик может вычислить такое уравнение. В противном случае вы рискуете столкнуться с еще более серьезными проблемами при решении математических задач в будущем.

Напомним, что постороннее решение — это решение, которое исправляет уравнение после выполнения чего-то вроде возведения любой части уравнения в четную степень, но не является средством решения исходной проблемы. Можно продолжить, если вы хотите получить более точный ответ, но, тем не менее, в этом нет необходимости.Это гарантирует, что вы получите правильный ответ.

Иногда требуется немного воображения, чтобы понять, как конкретная функция может быть создана квадратичной. Квадратичная формула — это один из подходов к решению такого рода вопросов.

Что делать с калькулятором квадратной формулы

Ниже приводится способ решения рациональных неравенств. Формула Quartic — это только окончательный результат этой методологии, написанный относительно исходных коэффициентов. Он также предоставляет стандартный способ решения квадратных уравнений, очевидно, что касается упрощения сложных выражений.

Это действительно просто, поскольку есть очевидный общий элемент. В случае, если выражение в квадратном корне отрицательное, кривая не пересекает ось x и реальных корней нет. Если вы можете проверить правильность формы своего уравнения и правильно запомнить формулу, все остальное будет просто арифметикой (даже если это немного сложно).

Первоначальное упражнение было направлено на то, чтобы помочь студентам разобраться в самых сложных уравнениях, включающих радикалы и различные упрощения.Это уравнение регрессии, которое можно использовать для прогнозирования данных. Равно 23.

Подробная информация о калькуляторе квадратичных формул

Эта формула часто используется в математических задачах и в реальной жизни. Мои концепции предельно ясны, и мне очень нравится пошаговая стратегия. Они широко используются в науке, бизнесе и технике.

Это позволит вам проверить и увидеть, испытываете ли вы понимание подобных проблем.Есть несколько разных способов, с помощью которых ученик может вычислить такое уравнение. Вы можете использовать уникальные процедуры для решения проблемы.

Уловка с калькулятором абсолютных квадратичных формул

Эта настройка позволит вам четко наблюдать анимированный круг, пересекающий экран. Кроме того, после интерпретации среднего значения также важно указать типичное отклонение. Поскольку нет другого общего фактора, 2x — самая распространенная проблема.

В любой момент, когда вас просят изобразить уравнение, которое включает квадрат x, оно, вероятно, всегда будет иметь ту же самую форму параболы.Квадратичная регрессия — это процедура нахождения уравнения параболы, наиболее подходящего для набора информации. Его также иногда называют полиномиальным уравнением второй степени.

Эти варианты в основном делятся на общественные и частные школы. Намерение состоит в том, чтобы представить любое произвольное квадратное уравнение в форме идеального квадратичного квадрата. Когда у вас нет члена x, потому что b равно 0, у вас будет более простое уравнение для решения, и вам просто нужно будет решить квадрат члена.

Заявление Мики не соответствует действительности. Последний ответ должен быть таким же. Если вы хотите найти среднюю точку вдоль линии, вам понадобится формула средней точки.

Итак, если вы взглянете на задачи со словами, которые имеют отношение к квадратикам, это означает, что ваш наибольший показатель по x возведен в квадрат. Его также называют средним квадратичным. Следовательно, у нас есть способ обратиться к любой квадратичной функции!

В следующем поле предлагается стратегия факторизации многочленов.Если значение равно нулю, есть одно решение. Способ решения квадратного уравнения.

Калькулятор квадратичных формул — Обзор

Это известно как сопряженный элемент. Формула нормального отклонения сравнима с формулой дисперсии.У нас есть один способ разложить квадратные уравнения на множители в этой форме.

Период b2-4ac называется дискриминантом квадратного уравнения. На графике он находится под осью x или над осью x. График показывает, где y положительно, а где отрицательно.

Умножение комплексных чисел почти так же просто, как умножение двух биномов вместе. Мы можем использовать Список квадратов для нахождения десятичных приближений, если подкоренное выражение не является идеальным квадратом. Также не забудьте заглянуть в Справочный центр Mathcad.

Тем не менее, вы должны постараться запомнить формулу изо всех сил, поскольку во время экзамена у вас не будет доступа к инструментам поддержки. Если вы раньше не использовали одну из программ, размещенных на этом сайте, вам следует сначала прочитать информацию в разделе «Введение в программирование». Продолжайте прокручивать, чтобы определить, как работает программа и как ее использовать (необязательно).

Выходные данные Здесь мы импортировали модуль cmath для вычисления комплексного квадратного корня. F5 открывает функцию поиска, которая позволяет вам искать в вашей программе определенную строку.Как только вы научитесь определять среднюю точку с помощью этого калькулятора, вы сможете использовать эту информацию для ряда приложений.

Привлекательность калькулятора квадратичных формул

Каждому значению x соответствует одно и только одно значение y. Проблема 2. Ее легко определить по максимальной степени переменной x, которая должна быть равна двум. Попробуем последний пример.

Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений не существует.Дело в том, чтобы нарисовать приблизительную форму графика и обозначить два или три простых значения, но не беспокоиться о точной точности. Есть несколько аспектов, которые следует учитывать при расчете ожидаемой суммы претензии.

Неожиданная правда о калькуляторе квадратичных формул

Math Is Fun отмечает, что квадратное уравнение можно использовать, чтобы определить, где в конечном итоге приземлится мяч, брошенный в воздух. Решение квадратных уравнений может быть сложной задачей, но, к счастью, существует множество разнообразных методов, которые мы можем использовать в зависимости от того, какой вид квадратичного уравнения мы пытаемся решить.Таким образом, факторинг чисел очень помог в решении целого ряда проблем.

Наш компьютер, вероятно, построит график всех трех из них в одно и то же время, и мы будем обсуждать их по мере их появления. В данном случае у нас четыре ответа. Эта страница дает возможность понять законы логарифмов.

Обнаружена шумиха вокруг калькулятора квадратной формулы

Ниже приводится способ решения рациональных неравенств. Формула Quartic — это только окончательный результат этой методологии, написанный относительно исходных коэффициентов.Он также предоставляет стандартный способ решения квадратных уравнений, очевидно, что касается упрощения сложных выражений.

В литературе можно найти несколько альтернативных производных. Гарантия того, что исходное уравнение записано в типовой форме. Теперь у вас есть все термины, записанные в уравнение, вы продолжаете упрощать, пока не дойдете до своих последних ответов.

С другой стороны, если вы изучили комплексы, вы можете продолжить. Он равен 625. Он равен 375.

Калькулятор типов квадратичных формул

Инженеры также могут использовать свои знания для улучшения текущих вещей, включая эффективность или высокое качество предмета. Студентам потребуется много практики с квадратичным факторингом. Используя результаты тестов, ученики работали над увеличением катапульты.

Математика работает так же, как и все остальное, если вы хотите хорошо в ней научиться, то вы хотите практиковаться. Это дает другой взгляд на область математики.Инженеры используют квадратное уравнение в дополнение к другим сложным математическим формам при создании своих проектов.

В частности, рациональные корни будут в том случае, если часть под знаком квадратного корня в формуле корней квадратного уравнения является идеальным квадратом. Другой подход к нахождению области квадрата состоит в суммировании областей геометрических частей, составляющих квадрат. Перепишите идеальный квадратный трехчлен в квадрат двучлена.

Таким образом, вы только что доказали, что 50 — не идеальный квадрат и не может быть разложен на множители.В этом уравнении это длина гипотенузы, в то время как A и B представляют длину двух других сторон. Если он отрицательный, он откроется вниз.

Эти варианты в основном делятся на общественные и частные школы. У вас есть член в квадрате. Опять же, подумайте, каково значение h всякий раз, когда объект ударяется о землю.

Хроники калькулятора квадратичных формул

Но есть способ попроще. Вот быстрый способ получить ответ.Это гарантирует, что вы получите правильный ответ.

Не стесняйтесь задавать другой вопрос о кубике, и я с удовольствием отвечу. Однако на этот раз больший коэффициент обеспечит знак минус.

LP и выпуклые задачи QP являются частными примерами задач SOCP (программирование конуса второго порядка, разновидность конической оптимизации), и иногда они решаются с более высокой производительностью с помощью решателей SOCP, большинство из которых в настоящее время используют процедуры внутренней точки.Упражнения II Определите диапазон решений для каждого из этих логарифмических уравнений. Скачать эту программу можно здесь.

Все процедуры были такими легкими и простыми в выполнении. Есть широкий выбор калькуляторов на выбор в соответствии с вашими требованиями. В этом случае оба эти метода эквивалентны по времени для поиска решений.

Чего ожидать от калькулятора квадратичных формул?

Квадратичная формула стала наиболее частым подходом к решению квадратных уравнений.Для некоторых из них вам может потребоваться квадратичная формула. С тех пор вы довольно хорошо разбираетесь в терминах уравнений.

Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратичную формулу (при необходимости) для вычисления квадратичной и применить свой графический калькулятор, чтобы убедиться, что отображаемые точки пересечения по оси x имеют те же десятичные значения, что и решения, представленные квадратичной формулой. Иногда сгенерированный рабочий лист не совсем то, что вам нужно.Мне очень нравятся панели инструментов, с помощью которых вводить уравнения очень просто!

Это особенно эффективно для проблем со слабыми ограничениями QP. В таких ситуациях многочлен не будет разлагаться на линейные многочлены. Выясните дискриминант.

Полиномиальные функции сравнительно легко понять. Если вы раньше не использовали одну из программ, размещенных на этом сайте, вам следует сначала прочитать информацию в разделе «Введение в программирование». Программа — огромный инструмент!

Выходные данные Здесь мы импортировали модуль cmath для вычисления комплексного квадратного корня.Команды для интернет-калькулятора можно вводить не только мышью, но и с клавиатуры цифрового компьютера. Из множества процессов Solver в Excel — идеальный вариант.

Обратите внимание на то, как в нем сочетаются эффекты трех членов. Факторы важны при работе с дробями, а также при поиске закономерностей в числах. Попробуем последний пример.

Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений не существует.Используя формулу корней квадратного уравнения, вы должны знать 3 возможности. Затем вы попадете на экран, показанный ниже.

Основные сведения о калькуляторе квадратичных формул

Это одно из несложных состояний, и вы можете наблюдать гораздо больше в своей обычной жизни. Владелец магазина покупает определенное количество книг за 720 долларов. Щелкните фильм ниже, чтобы услышать хороший пример этого.

По мере практики эта процедура может стать довольно легкой, особенно если вы будете осторожны, выполняя одни и те же действия в одной и той же покупке.Помните, что эти ресурсы никогда не проверялись CPALMS, и за использование некоторых из них в этой коллекции может взиматься плата. Этот пример немного отличается.

Бесплатная онлайн программа для решения квадратных уравнений с пошаговыми инструкциями. Калькулятор квадратного уравнения

Этот калькулятор решает квадратные уравнения, заполняя квадрат или используя квадратную формулу. Он отображает рабочий процесс и подробное объяснение.

Мы подробно объясним каждый шаг.Этот калькулятор решает квадратное уравнение двумя способами. Используйте калькулятор выше, чтобы проверить свое решение. Добро пожаловать в MathPortal. Я разработал этот сайт и написал все уроки, формулы и калькуляторы. Если вы хотите связаться со мной, возможно, у вас возникнут вопросы, напишите мне, используя контактную форму, или напишите мне на mathhelp mathportal. Математические калькуляторы, уроки и формулы Пришло время решить вашу математическую задачу.

Ledcor group winnipeg

Решатель квадратного уравнения. Решение квадратного уравнения. Коэффициенты могут быть либо целыми, либо десятичными числами. Пустые места заменяются нулями.Факторинговые полиномы. Рационализируйте знаменатель. Квадратные уравнения. Решение по шагам. Равносторонний треугольник. Унарные операции. Система 2х2. Калькулятор лимита. Арифметические последовательности. Расстояние и середина. Градусы в радианы. Инструкции: Этот калькулятор квадратной формулы решит квадратное уравнение за вас, показывая все шаги. Введите коэффициенты квадратного уравнения, и решатель выдаст вам корни, точку пересечения по оси Y, координаты вершины, показывающие всю работу, и построит график функции.

На основании значения дискриминанта определяется характер решения. Шаг 1: Определите коэффициенты. Какие коэффициенты?

Какие сейчас коэффициенты? Шаг 2: Вставьте коэффициенты, которые вы нашли в формуле. Формула квадратичная формула. Итак, подставляя эти значения в формулу, мы получаем: В предыдущем примере у нас было бы.

Шаг 4: Загляните внутрь квадратного корня. Если значение положительное, то квадратное уравнение имеет два действительных корня.Если значение равно 0, то есть один действительный корень, а если значение внутри квадратного корня отрицательное, то есть два комплексных корня. В предыдущем примере у нас есть -8 внутри квадратного корня, поэтому у нас есть два сложных решения, как показано ниже: Квадратичная формула — одна из самых распространенных формул в математике. Он появляется, когда вы решаете всевозможные геометрические задачи, например, когда вы максимизируете площадь, учитывая фиксированный периметр, или в многочисленных задачах со словами.

Многие люди задаются вопросом, есть ли какая-либо связь между этой формулой квадратного уравнения и методом завершения квадрата.

Ответ прост: вы получаете квадратную формулу, решая квадратное уравнение, заполнив квадрат. Это точно такая же идея, которая вытекает из известной нам формулы квадратичной формулы.

Spring boot controlleradvice tutorial

Шаги по квадратичной формуле Чтобы успешно решить квадратное уравнение, необходимо выполнить несколько шагов: Шаг 1: Определите коэффициенты. забыл пароль? Этот веб-сайт использует файлы cookie для улучшения вашего опыта.

Мы предполагаем, что вы согласны с этим, но вы можете отказаться, если хотите.Принять Подробнее. Необходимо Всегда включено. Введите уравнение математической задачи ниже. Нажмите кнопку, чтобы решить! Калькулятор квадратной формулы — это средство решения уравнений, которое помогает вам найти решение для квадратных уравнений, используя квадратную формулу. Калькулятор обрабатывает введенную математическую задачу по формуле корней квадратного уравнения. Что еще более важно, калькулятор предложит вам пошаговое решение, которое легко понять.

Обычно квадратное уравнение имеет два корня или два решения.

Решение может быть действительным или комплексным в зависимости от значения дискриминанта.Введите математическое выражение в отведенное для этого текстовое поле.

Nhlanhla nciza теряет ребенка

Убедитесь, что вы используете правильный набор обозначений и символов. После этого нажмите кнопку «Рассчитать», чтобы получить корни. Этот калькулятор квадратичных формул поможет вам найти корни квадратного уравнения, используя квадратную формулу. С пошаговым решением действительно легко изучить алгебру в EquationCalc. Допустимые математические символы и их использование Если вы решите написать свои математические утверждения, вот список приемлемых математических символов и операторов.

Пошаговый калькулятор по формуле квадратного уравнения Решение Хотите посчитать? Найди решение! Решить для :.

Калькулятор квадратичных формул. Пошаговое решение.

Графическое решение уравнений :. Рабочий пример, иллюстрирующий, как работает квадратичный калькулятор :. Хотите получить еще больше? Показать клавиатуру. Решение уравнений — центральная тема алгебры. Все приобретенные навыки в конечном итоге приводят к способности решать уравнения и упрощать решения. В предыдущих главах мы решали уравнения первой степени.Теперь у вас есть необходимые навыки для решения уравнений второй степени, которые известны как квадратные уравнения.

По завершении этого раздела вы должны уметь: Определить квадратное уравнение. Приведите квадратное уравнение в стандартную форму. Решите квадратное уравнение факторизацией. Квадратное уравнение — это полиномиальное уравнение, которое содержит вторую, но не более высокую степень переменной.

Все квадратные уравнения могут быть представлены в стандартной форме, и любое уравнение, которое может быть преобразовано в стандартную форму, является квадратным уравнением.Другими словами, стандартная форма представляет все квадратные уравнения. Эта теорема доказана в большинстве учебных пособий по алгебре.

Важная теорема, которую невозможно доказать на уровне этого текста, гласит: «Каждое полиномиальное уравнение степени n имеет ровно n корней. Возможно, что два решения равны. Квадратное уравнение будет иметь два решения, потому что оно имеет степень 2. Самый простой метод решения квадратичных вычислений — разложение на множители. Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется всякий раз, когда факторизация возможна.

Другими словами, если произведение двух множителей равно нулю, то по крайней мере один из множителей равен нулю. Мы не будем пытаться доказывать эту теорему, но внимательно отметим, что в ней говорится. Мы никогда не сможем перемножить два числа и получить ответ ноль, если хотя бы одно из чисел не равно нулю.

Мы должны вычесть 6 с обеих сторон. Вспомните, как разложить на множители трехчлены. Шаг 3 Установите каждый коэффициент равным нулю и решите относительно x.

Здесь применяется приведенная выше теорема, согласно которой хотя бы один из факторов должен иметь нулевое значение.Шаг 4 Проверьте решение в исходном уравнении. Проверка ваших решений — верный способ узнать, правильно ли вы решили уравнение. В этом примере 6 и -1 называются элементами набора.

Обратите внимание, что в этом примере уравнение уже имеет стандартную форму. Опять же, проверка решений убедит вас, что вы не допустили ошибки при решении уравнения. Проверьте исходное уравнение, чтобы убедиться, что знаменатель не равен нулю. Обратите внимание, что здесь два решения равны.

Это происходит только тогда, когда трехчлен является полным квадратом. По завершении этого раздела вы должны уметь: Определить неполное квадратное уравнение.

Калькулятор квадратной формулы

Решите неполное квадратное уравнение. Когда вы сталкиваетесь с неполным квадратичным коэффициентом с отсутствующим третьим членом c — 0, его все же можно решить с помощью факторинга. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Узнать больше Принять.Тригонометрия конических сечений. Конические сечения. Матрицы-векторы. Химические реакции Химические свойства. Калькулятор квадратного уравнения Решайте квадратные уравнения шаг за шагом. Правильный ответ :. Давай попытаемся снова :.

Попробуй еще упростить. В последнем посте мы рассказали о доработке квадрата, см. Ссылку. Это довольно непросто, если вы будете следовать всем правилам входа в систему, входа в систему с помощью Office, входа в систему с помощью Facebook. Присоединяйтесь к миллиону счастливых пользователей! Зарегистрируйтесь бесплатно :. Присоединяйтесь с Office Присоединяйтесь с Facebook. Создай мой аккаунт.

Toyota hiace 2018

Сбой транзакции! Пожалуйста, попробуйте еще раз, используя другой способ оплаты.

Программа для решения квадратных уравнений

Подпишитесь, чтобы получить гораздо больше :. Отсутствуют данные пользователя. Обратитесь в службу поддержки.

Нам нужны ваши отзывы. Отменить Отправить. Создание PDF Просмотреть все асимптоты области критические точки производная область собственные значения собственные векторы развернуть крайние точки фактор неявная производная точки перегиба перехватить обратный лаплас обратный лаплас частичные дроби диапазон наклон упростить решение для касательной вершины Тейлора геометрический тест чередующийся тест телескопический тест псевдосерии тест корень тест.Включены даже простые числа.

Сначала вы этого не замечаете, потому что на каждой странице всего 1 номер. Но по мере продвижения по книге вы замечаете, что числа увеличиваются на 1 каждый раз, когда вы переворачиваете страницу. ПоискСортировать поСамые рейтинговыеСамые свежиеЛучшие оценкиФильтровать поВсе рецензентыТолько подтвержденная покупкаВсе рецензентыТолько 5 звездТолько 4 звездыТолько 3 звезды 2 звезды только 1 звезда

Был ли этот обзор полезным для вас. Да Нет КомментарийВставить ссылку на продукт Вставить веб-адрес продукта ниже: Продукт не найден. Можно связать только товары, предлагаемые на Amazon. Выберите Что такое ссылки на продукты. Чтобы вставить ссылку на продукт, выполните следующие действия: 6. Ваше сообщение не будет опубликовано. См. Наши правила в отношении нежелательного содержания. Вы должны приобрести хотя бы один товар на Amazon, чтобы оставить комментарий. При отправке комментария возникла проблема. Рекомендации Войдите, чтобы оставить комментарий Показано 0 комментариев Сортировать по: Новые Старые Сейчас возникла проблема с загрузкой комментариев.

Если вы присмотритесь, вы заметите, что каждая десятая цифра или около того — это просто повторение последней цифры, а каждая сотая или около того — это одна и та же цифра, повторяемая три раза. Пример этой «работы»: Стр. 36 — Строка 6 — 15 символов должно быть 5, а не 4. Стр. 99 — Строка 18 — первые три символа должны быть «453», а не «345». Страница 145 — Строка 2 — 7-й и 19-й символы транспонированы. Страница 190 — Пропущена вся строка чисел между 6-й и 7-й строками.

Страницы 210 и 211 — Два раздела отображаются квази-рандомизированными, а не рандомизированными.Кроме того, если вы посмотрите на него достаточно долго, вы сможете расшифровать что-то около страницы 300 о том, что Джоди Фостер и Дж. Сэлинджер дают мне какие-то инструкции.

Онлайн-программа для решения квадратного уравнения

Я собираюсь не спать еще пару ночей, глядя на это, чтобы посмотреть, смогу ли я разобрать что-нибудь еще. Однако что-то меня не покидало, чего я не мог понять. Я знал, что видел все это где-то раньше, просто не мог это разместить. Я думал о Дэне Брауне, но я думаю, что Кодекс Ди Винчи имеет какое-то отношение к живописи, Ватикану или чему-то в этом роде.Хорошее приложение и очень полезно.

Очень удобно и легко получить обзор ситуации с поставками всех вместе. Aftership позволяет нам держать наших клиентов в курсе с момента упаковки заказа до момента его доставки. Мне нравится приложение, это отличный продукт, незаменимый, я бы сказал, для всех, кто занимается транспортировкой любых объемов, малых или больших. Мы внедрили это приложение в наш магазин shopify Now It’s Cool, и это было потрясающе. Легко установить и под. Простота использования, высокая степень автоматизации и хорошая поддержка клиентов.

Настоятельно рекомендуется для оптимизации управления отгрузкой. Это делает процесс настолько простым, что моим клиентам он нравится, мне нравится, что клиенты довольны. Это приложение важно для любого магазина. С его помощью клиенты теперь могут просматривать и отслеживать свои посылки в кратчайшие сроки — в любое время.

Если вы хотите автоматизировать уведомления по электронной почте и SMS для отслеживания ваших клиентов и уведомлений о пакетах, вы n.

До сих пор у меня был замечательный опыт работы с AfterShip. У меня это было около месяца, и я снизил количество c.AfterShip упрощает управление всеми возвратами клиентов. Клиент использует его для получения информации о возвратах. Незаменим для владельцев бизнеса, которые хотят автоматизировать процесс возврата для своего магазина. Aftership — потрясающее приложение. Наличие фирменной страницы отслеживания выводит ваш бренд на новый уровень.

Его было легко настроить, и пока у меня не было проблем с ним, довольно классное приложение. AfterShip — это такой простой плагин для нашего магазина, который позволяет нашим клиентам беспрепятственно возвращаться.Отличный сервис, помогающий повысить плавность рабочего процесса и автоматизации Shopify. Поддержка очень отзывчивая. Это потрясающее приложение. Я использую его каждый день на нескольких разных веб-сайтах, чтобы отслеживать заказы по всему миру. Отличное приложение, позволяющее вам и вашим клиентам легко отслеживать ваши поставки !.

Работает как шарм, и даже совершенно бесплатно. Это приложение стоит каждого цента. Управлял швейным бизнесом, если бы у меня не было надежной системы возврата за неправильный размер.

Даже для такого человека, который не является носителем английского языка, вроде меня Super Great app работает очень хорошо.Очень легко ориентироваться и использовать. Будем продолжать использовать в будущеми рекомендую.

Да, я буду использовать это приложение снова и снова. Рекомендую для любого нового магазина и продвинутого. На самом деле предоставил вам обновления о доставке менее чем за 1.

144 Калькуляторы, разделенные по уровню квалификации и типу

Воспользуйтесь нашим бесплатным калькулятором

Мы стали партнерами Mathway, чтобы предложить бесплатный онлайн-калькулятор алгебры. Обширный список других инструментов алгебры расположен ниже.

Содержание

Обзор

Как отмечает Академия Хана, алгебра — это математика-привратник. Перед тем, как приступить к изучению математики и естествознания более высокого уровня, важно хорошо это понимать.

В Интернете доступно множество калькуляторов алгебры. Может быть сложно просмотреть их все, чтобы найти то, что лучше всего соответствует вашим потребностям. Ниже представлена коллекция из 144 калькуляторов алгебры, разделенных по уровню и типу навыков.

ЧАСТЬ I — 54 Калькуляторы базовой алгебры

Решатели 11 уравнений

Как MathIsFun.com объясняет, уравнения показывают, что две вещи равны. Часто цель уравнения — найти неизвестную переменную. Ниже приведен набор решателей уравнений, которые помогут вам в этом:

Алгебраический калькулятор

Symbolab.com — этот калькулятор имеет чистый, простой в использовании дизайн и включает в себя примеры уравнений, которые показывают пошаговые объяснения того, как их решать.

Алгебраический калькулятор MathPapa.com — этот калькулятор прост в использовании. Подключите свое уравнение, и оно предоставит решение вместе с пошаговым объяснением того, как было решено уравнение.

AlgebraHelp.com’s Equation Calculator and Solver — Этот калькулятор предоставляет «Краткое руководство» с учебной информацией по решению уравнений. Он также показывает свою работу, когда решает уравнение, чтобы вы могли видеть шаги, предпринятые для получения результата.

Tiger-Algebra.com — решатель алгебры, упрощение и вычислитель — этот калькулятор прост в использовании. Он также предоставляет пошаговое объяснение того, как находятся результаты.

Программа

Algebra.com’s Algebra Solver и Math Simplifier — этот калькулятор, специализирующийся на решении алгебраических уравнений средней школы, дает подробное объяснение того, как он решал ваше уравнение, включая анимацию, которая проведет вас через каждый шаг.

Алгебраический калькулятор Mathway.com — Этот калькулятор имеет простой дизайн. Нажмите кнопку «Справка», чтобы увидеть примеры нескольких различных типов задач алгебры.

Бесплатная математическая программа

Algebra-Class.com — Как объясняется в этом калькуляторе, это отличный инструмент для проверки ответов на домашнее задание. Он работает с несколькими навыками алгебры, такими как выражения, уравнения, неравенства, функции и многое другое.

Система вычислительных знаний WolframAlpha.com — Этот калькулятор быстр и прост в использовании.Введите свое уравнение в поле, и калькулятор предоставит решение вместе с другой информацией, такой как графики или визуальное представление уравнения.

Marble Software Solutions Online Algebra Solver — Этот калькулятор прост в использовании и предоставляет простые для понимания, пошаговые решения проблем. Помимо уравнений, калькулятор также решает выражения, системы уравнений и матрицы.

Калькулятор Cymath.com — Этот калькулятор имеет чистый, простой в использовании дизайн и предоставляет пошаговые объяснения того, как были решены проблемы.

SolveMyMath.com’s Equation Solver Calculator — С помощью этого калькулятора вы сможете найти решения одним щелчком мыши. Когда у вас есть решение, нажмите «Показать график», чтобы увидеть графическое представление вашего уравнения.

Калькулятор 13 экспонент

Как объясняет PurpleMath, экспоненты — это «сокращение для многократного умножения одного и того же самого на себя». Ниже представлена подборка калькуляторов экспонент, которые помогут вам лучше понять, как с ними работать:

Калькулятор Суп.com — Эти калькуляторы включают учебную информацию вместе с примерами. Калькулятор «Показателей» отлично подходит для тех, кто имеет базовые представления об экспонентах. Калькулятор «Дробные экспоненты» и «Расчет показателей» помогут тем, у кого более глубокое понимание экспонент.

Калькулятор экспонент

RapidTables.com — этот калькулятор четко спроектирован, прост в использовании и предоставляет в качестве справки законы и правила показателей.

WebMath.com: Упростите алгебраический термин, включающий экспоненты и / или степени. Если у вас есть базовый уровень понимания экспонент, этот калькулятор станет для вас отличным инструментом.

Калькулятор экспонент

Calculator.net — этот калькулятор включает в себя базовое объяснение экспонент и предоставляет в качестве справки основные законы экспонент.

Калькулятор экспонент TutorVista.com — этот калькулятор предоставляет отличную учебную информацию, а также цветовую разбивку по способам решения показателей.

Калькулятор показателей EndMemo.com — Этот калькулятор быстр и прост в использовании.

EndMemo.com’s Exponents with Fractions Calculator — Для тех, кто хорошо разбирается в показателях, этот калькулятор предоставляет некоторую учебную информацию и несколько примеров, чтобы показать пользователям, какие числа им следует вводить и где при работе с показателями с дробями.

Программа расчета экспонент EndMemo.com — Этот простой в использовании калькулятор помогает пользователям найти неизвестную экспоненту.

Free-Online-Calculator-Use.com’s Exponent Calculator — Этот калькулятор предоставляет обучающую информацию, объясняющую экспоненты и отрицательные показатели. Наряду с вашим решением он предоставляет серию умножения, используемую для получения ответа.

Калькулятор показателей WolframAlpha.com — Этот калькулятор прост в использовании.Просто введите базовое число и показатель степени в соответствующие поля.

Калькулятор показателей MiniWebTool.com — Этот калькулятор прост в использовании и предоставляет пользователям некоторую учебную информацию по возведению в степень для пользователей.

Калькулятор 13 полиномов

Как объясняет MathIsFun.com, полиномы возникают, когда три или более члена, которые могут включать в себя константы, переменные или показатели степени, соединяются путем сложения, вычитания, умножения и деления.Ниже представлена коллекция программ для решения полиномиальных уравнений:

EasyCalculation.com — для пользователей, разбирающихся в полиномах, эти калькуляторы упрощают ввод чисел для решения полиномиальных уравнений.

Полиномы умножения WolframAlpha.com — Наряду с решением этот калькулятор показывает «возможные промежуточные шаги», которые можно использовать для его получения.

Программа для решения полиномиальных уравнений

MathPortal.org — этот калькулятор включает примеры, показывающие, как вводить данные.Он также включает учебный раздел, который включает в себя четырехэтапное объяснение того, как решить многочлен.

Калькулятор полиномиальных уравнений

Symbolab.com — этот простой в использовании калькулятор предоставляет пошаговые объяснения того, как решать вводимые полиномы.

Полиномиальные калькуляторы SolveMyMath.com — получайте быстрые результаты с помощью этих калькуляторов, которые выполняют базовые операции — сложение, вычитание, умножение и деление:

Калькулятор полиномиального деления в длину от WebGraphing.com — Для тех, кто изучает полиномиальное деление, наряду с результатом, этот калькулятор показывает шаги, необходимые для его получения.

Калькулятор длинного деления многочленов на сайте

Calc101.com — следуйте инструкциям этого калькулятора, чтобы проверить, совпадает ли ваш ответ с его решениями.

HVKS.com’s Polynomial Root Finder — этот калькулятор дает быстрые результаты и может стать отличным инструментом для перепроверки ваших собственных ответов.

Калькулятор полиномиального корня Tiger-Algebra.com — Наряду с решениями, этот калькулятор предоставляет подробную информацию о том, как он получил свои результаты.

Алгебра.com’s Polynomial Calculator — Этот калькулятор складывает, вычитает и умножает многочлены. Он предоставляет пошаговые объяснения того, как он получает результаты, включая анимацию, которая проведет вас через каждый шаг.

Калькулятор 10 радикалов

Если выражение, над которым вы работаете, включает символ квадратного корня, «√», то это радикал. Ниже представлена коллекция калькуляторов, которые помогут упростить и решить радикальные уравнения.

Калькулятор радикальных уравнений

Symbolab.com — этот калькулятор с четким дизайном и простотой использования содержит примеры с пошаговыми объяснениями того, как решаются проблемы.

MathPortal.org — Эти калькуляторы содержат инструкции по их использованию. Просто замените радикальный знак буквой «r» в радикальных выражениях, и он готов помочь.

CalculatorSoup.com — эти калькуляторы объясняют, на что они способны, и предназначены для быстрого и легкого ввода данных.

WebMath.com’s Simplify a Term Under a Radical Sign — Этот калькулятор дает пошаговое объяснение того, как он упрощает вводимые термины.

RapidTables.com Калькулятор радикалов и корней — Этот калькулятор быстр и прост в использовании, а также упрощает ввод данных.

Калькулятор упрощающих радикальных выражений EasyCalculation.com — Этот калькулятор прост в использовании. Для тех, кто нуждается в дополнительной помощи, он также предоставляет примеры типов данных, которые вы будете вводить — переменные, значения и выражения.

Калькулятор радикальных уравнений WolframAlpha.com — Этот калькулятор отлично подходит для двойной проверки собственных результатов, он быстр и прост в использовании, но не показывает этапов решения.

Калькулятор упрощения радикальных выражений MathCelebrity.com — Этот калькулятор предоставляет подробные, простые для понимания инструкции о том, как решить вашу проблему.

7 Калькуляторы соотношений и пропорций

Как объясняет MathPlanet.com, отношения сравнивают два числа, а пропорции — это уравнения, которые «говорят, что два отношения эквивалентны». Ниже приведен набор калькуляторов, которые помогут вам узнать больше о соотношениях и пропорциях:

Калькулятор пропорций AlgebraHelp.com — Этот калькулятор прост в использовании и включает пример пропорции, который поможет вам начать работу.Он предоставляет пошаговое объяснение вместе с его результатами.

Калькулятор пропорций

Basic-Mathematics.com — этот калькулятор прост в использовании и предлагает пример в стиле задачи, упрощающий понимание пропорций.

Справка

WebMath.com с калькулятором пропорций — этот калькулятор содержит учебную информацию о соотношениях и пропорциях. Он также дает объяснение своим результатам.

Калькулятор пропорций TutorVista.com — здесь представлены два калькулятора: один для поиска неизвестной переменной в пропорции, а другой для проверки равенства соотношений.Также предоставляется учебная информация о соотношениях и пропорциях.

Калькулятор пропорций

MiniWebTool.com — этот калькулятор быстр и прост в использовании. Просто введите три числа, чтобы найти неизвестную переменную.

Калькулятор коэффициентов TutorVista.com — Этот калькулятор помогает упростить коэффициенты и предоставляет краткую учебную информацию.

CalculatorSoup.com’s Ratio Calculator — этот калькулятор также вычисляет пропорции. Он может найти пропущенное значение или оценить, является ли соотношение или пропорция истинным или ложным.

ЧАСТЬ II — 50 промежуточных калькуляторов

Теперь, когда вы знаете основы, пришло время заняться более сложными уравнениями, узнать о факторинге и познакомиться с миром неравенства.

10 Средства решения уравнений алгебры 2

В промежуточной алгебре уравнения становятся немного сложнее. Ниже представлена коллекция калькуляторов, которые помогут решать системы уравнений и другие более сложные выражения.

WebMath.com Калькуляторы алгебры — Если вы только начинаете изучать алгебру 2, этот калькулятор прост в использовании и помогает с различными типами двухуровневых уравнений алгебры.

SolveMyMath.com Решатель систем уравнений — Этот калькулятор является большим подспорьем при решении сложных систем уравнений.

Алгебраические калькуляторы

QuickMath.com — Этот набор калькуляторов упрощает работу с алгебраическими выражениями. Он предоставляет учебную информацию по алгебре и концепциям расширения, факторизации, упрощения и отмены при работе с выражениями.Он также предоставляет информацию о дробях, связанных с этими выражениями. Каждый калькулятор имеет базовый, средний и расширенный режимы.

Expand (базовый, средний, продвинутый)

Фактор

(базовый, средний, продвинутый)
Упрощение (базовый, средний, продвинутый)
Отмена (базовый, средний, продвинутый)
Частичные дроби (базовый, продвинутый)
Объединение дробей (базовый, средний, продвинутый)

EasyCalculation.com’s Solve Algebra Transposition Calculator — Этот калькулятор поможет вам отделить неизвестную переменную до одной из сторон уравнения, чтобы упростить решение.

13 Калькуляторы комбинаций и перестановок

Комбинации и Перестановки используются для группировки объектов. Как объясняет факультет математики Университета Иллинойса в Урбана-Шампейн, «в перестановках порядок имеет значение, а в комбинациях порядок не имеет значения». Ниже приводится коллекция калькуляторов, которые помогут вам узнать больше о комбинациях и перестановках:

MathIsFun.Комбинации и перестановки com. Этот калькулятор отлично подходит для тех, кто только начинает изучать эту концепцию. Он включает объяснения комбинаций и правил перестановок.

Калькулятор комбинаций и перестановок StatTrek.com — Этот калькулятор не только прост в использовании, но и предоставляет обучающую информацию о комбинациях и перестановках, а также примеры проблем с объяснениями для каждого шага.

Калькулятор комбинаций и перестановок EasyCalculation.com — С помощью этого калькулятора вводить данные очень просто.Он также предоставляет базовую учебную информацию о комбинациях и перестановках.

Калькулятор комбинаций и перестановок TutorVista.com — этот калькулятор предоставляет пошаговые вычисления и четко объясняет примеры задач, чтобы помочь вам лучше понять эту концепцию.

Комбинации и калькуляторы перестановок

CalculatorSoup.com — каждый из этих калькуляторов предоставляет подробную учебную информацию и необходимые формулы.

Калькулятор комбинаций и перестановок

CalcTool.org — этот калькулятор предоставляет некоторую учебную информацию.Он не дает пошаговых объяснений того, как он получает результаты, но является отличным инструментом для двойной проверки результатов ваших собственных расчетов.

StatisticsHowTo.com Калькулятор комбинаций и перестановок — этот калькулятор предоставляет простую для понимания учебную информацию, объясняющую разницу между комбинациями и перестановками и предоставляющую необходимые формулы.

Калькулятор комбинаций и перестановок

NCalculators.com — этот калькулятор не показывает шаги для получения результатов, но предоставляет простую для понимания учебную информацию.

Калькулятор комбинаций и перестановок CSGNetwork.com — ввод данных в этот калькулятор выполняется быстро и легко. Он предоставляет некоторую учебную информацию и формулы, используемые для решения комбинаций и перестановок.

Калькулятор комбинаций и перестановок на сайте

PlanetCalc.com — этот калькулятор предоставляет дополнительную информацию для тех, кто плохо знаком с этим математическим навыком или возвращается к нему.

Генераторы комбинаций и перестановок TextMechanic.com — эти генераторы забавны и просты в использовании.Каждый из них содержит подробные инструкции о том, как заполнить ваши данные, и каждый дает четкие результаты:

8 Факторинговых калькуляторов

Как объясняет MathIsFun.com, в своей основе факторинг — это просто нахождение факторов выражения. В промежуточной алгебре вас попросят разложить на множители более сложные выражения. Ниже представлен набор калькуляторов, которые помогут упростить факторинг:

Калькулятор факторинга

AlgebraHelp.com — Этот калькулятор предлагает пользователям краткое руководство с объяснениями, как лучше всего вводить их выражения.

Калькулятор полиномиального разложения на множители MathPortal.org — Этот калькулятор содержит примеры, упрощающие использование калькулятора. Он также показывает его работу, чтобы пользователи могли лучше понять, как было найдено решение.

Калькулятор факторинга SolveMyMath.com — Этот калькулятор прост в использовании и дает четкие и краткие результаты. Он предлагает примеры, чтобы упростить ввод данных.

Факторинговый калькулятор WolframAlpha.com — С этим калькулятором нет наворотов.Просто введите свои данные, и вы получите результат.

Калькулятор факторинговых трехчленов MathWorksheetsGo.com — Этот калькулятор отлично подходит для тех, кто занимается более сложным факторингом с трехчленами.

Калькулятор факторинга

CalculatorSoup.com — этот калькулятор прост в использовании и предоставляет обучающую информацию о том, как выполнить факторизацию.

Калькулятор факторинга

QuickMath.com — этот калькулятор имеет базовый, средний и расширенный режимы. Он предоставляет некоторые, но не все шаги, используемые для получения результатов.

Калькулятор факторов

Symbolab.com — этот калькулятор прост в использовании и содержит примеры с пошаговыми пояснениями того, как работает факторинг.

7 Калькуляторов неравенств

В неравенствах вы решаете, чтобы узнать, больше ли переменная (ы), меньше, больше или равна или меньше или равна значению. Как отмечает MathIsFun.com, цель состоит в том, чтобы переменная «сама по себе» оказалась в левой части неравенства. Ниже представлена коллекция калькуляторов неравенств, которые помогут вам решить проблемы неравенства:

Symbolab.com’s Inequalities Calculator — Этот калькулятор аккуратно спроектирован и прост в использовании. Он также включает примеры с пошаговыми пояснениями того, как решаются проблемы.

WebMath.com’s Solve an Inequality Calculator — Этот калькулятор быстр и прост в использовании.

Калькуляторы неравенств

QuickMath.com — этот калькулятор может работать на базовом, среднем или продвинутом уровне.

Калькулятор неравенств TutorVista.com — этот калькулятор включает инструкции о том, как подойти к решению проблемы, и примеры, которые показывают пошаговые объяснения того, как калькулятор пришел к решению.

Программа для решения неравенств и уравнений WolframAlpha.com — этот калькулятор чист и прост в использовании. Он может предоставить решения для простых и сложных неравенств.

Калькулятор решения линейных неравенств EasyCalculation.com — Этот калькулятор предоставляет некоторую учебную информацию, чтобы помочь пользователям лучше понять линейные неравенства. Для дальнейшего объяснения он также предоставляет свойства неравенств для сложения, вычитания, умножения и деления.

Калькулятор абсолютных неравенств EndMemo.com — Этот калькулятор предоставляет вам пример функции, которая поможет вам начать работу.

Калькулятор 12 квадратных уравнений

Квадратные уравнения выглядят как ax2 + bx + c = 0. Как объясняет MathIsFun.com, квадратные уравнения могут быть решены путем факторизации, завершения квадрата или использования формулы квадратичного уравнения. Ниже приведен набор калькуляторов, которые помогут вам узнать больше о квадратных уравнениях:

MathPortal.Квадратное уравнение org — этот калькулятор прост в использовании и включает в себя учебную информацию, объясняющую два метода решения квадратных уравнений.

Калькулятор квадратного уравнения

Symbolab.com — этот калькулятор прост в использовании. Он включает в себя примеры с пошаговыми пояснениями того, как решаются уравнения.

MathIsFun.com’s Quadratic Equation Solver — Этот калькулятор предоставляет учебную информацию для тех, кто только начинает изучать квадратные уравнения. Он также имеет функцию графика, которая отображает результаты вашего уравнения.

WebMath.com «Решите квадратное уравнение с помощью факторинга» — этот калькулятор объясняет, как решать квадратные уравнения с помощью факторинга.

Калькулятор квадратного уравнения

Algebra.com — этот калькулятор предоставляет подробные объяснения того, как он решил введенное уравнение. Он также отображает введенное уравнение.

Калькулятор квадратного уравнения CalculatorSoup.com (многочлен 2-го порядка) — Воспользуйтесь этим калькулятором, чтобы помочь решить многочлен с порядком 2.

SolveMyMath.com для решения квадратного уравнения — Этот калькулятор прост в использовании и предоставляет пошаговые объяснения того, как он решает каждое уравнение.

Программа для расчета квадратного уравнения EndMemo.com — Этот калькулятор выполняет вычисления по мере ввода данных, поэтому результаты будут мгновенными.

Калькулятор квадратных уравнений и неравенств MathCelebrity.com — этот калькулятор предлагает подробные пошаговые объяснения того, как находить решения. Он также может решить проблемы неравенства.

Калькуляторы квадратного уравнения EasyCalculation.com — эти калькуляторы просты в использовании и выполняют определенные функции для решения квадратных уравнений:

ЧАСТЬ III — 40 продвинутых калькуляторов

По мере того, как вы расширяете свои знания алгебры, вы начнете узнавать о более сложных элементах алгебры, таких как логарифмы, комплексные числа и многое другое.

Калькуляторы 5 биномов

Как объясняет образовательный портал, биномы — это выражения с двумя членами.В продвинутой алгебре вам будет предложено комбинировать, расширять и выполнять другие действия с биномами. Вы также узнаете о биномиальной теореме. Ниже приведен набор калькуляторов, которые помогут вам лучше понять и работать с биномами:

Калькулятор биномиального умножения MathCelebrity.com — При предоставлении решений этот калькулятор показывает, как он использовал метод FOIL (First-Outside-Inside-Last) для получения результатов.

Калькулятор умножения биномов MathWorksheetsGo.com — В этот калькулятор можно легко и быстро ввести данные.Он также предоставляет пошаговое объяснение того, как было получено решение с использованием метода FOIL.

Калькулятор биномиального расширения от WolframAlpha.com. Наряду с решением этот калькулятор шаг за шагом показывает, как он получил результаты.

Калькулятор биномиальной теоремы CalCul.com — Этот калькулятор использует биномиальную теорему для вычисления разложения бинома.

Калькулятор биномиальной теоремы Kusashi.com — этот калькулятор также использует биномиальную теорему. Он расширит бином до восьми членов.

Калькулятор 8 комплексных чисел

Как объясняет MathIsFun.com, комплексные числа возникают, когда вы объединяете действительное число и мнимое число, которые являются отрицательными в квадрате. Ниже представлена подборка калькуляторов, которые помогут вам работать с комплексными числами:

Калькулятор комплексных чисел MathIsFun.com — Этот калькулятор прост в использовании и содержит краткие пошаговые инструкции о том, как он нашел решение.

Калькуляторы комплексных чисел MathPortal.org — для тех, кто хорошо разбирается в алгебре 2, MathPortal предоставляет три калькулятора, которые можно использовать в качестве инструментов при работе с комплексными числами.

Калькулятор комплексных чисел MathWorksheetsGo.com — быстро и легко ввести свои данные в этот калькулятор. Он также показывает каждый сделанный шаг, когда он обеспечивает решение.

Калькулятор комплексных чисел WolframAlpha.com — этот калькулятор предоставляет ваш основной результат наряду с другими итерациями, включая десятичную форму, полярные координаты, положение в комплексной плоскости и альтернативную форму.

Калькулятор комплексных чисел 1728.org — Этот калькулятор умножает и делит комплексные числа.Ввод данных выполняется быстро и легко, и это отличный способ перепроверить собственные результаты.

Калькулятор комплексных чисел SolveMyMath.com — этот калькулятор выполняет основные операции для вычисления комплексных чисел, такие как сложение, вычитание, умножение и деление. Он не показывает свои шаги, но является отличным инструментом для перепроверки ваших собственных расчетов.

Калькулятор комплексных чисел

EasyCalculation.com — этот калькулятор умножает, делит и находит квадратный корень из введенного выражения.Он рассчитывает, когда вы вводите данные, поэтому результаты получаются мгновенно. Для упрощения сложных выражений используйте этот калькулятор.

Калькуляторы комплексных чисел

EndMemo.com — На этой странице представлены специальные калькуляторы для определенных операций. Представленные калькуляторы можно использовать для сложения, вычитания, умножения и деления комплексных чисел. На странице также есть учебная информация и формулы комплексных чисел.

Калькулятор 8 логарифмов

В алгебре I вы узнали об экспонентах.Как объясняет PurpleMath.com, логарифмы — это «противоположность» экспонент. Ниже представлена подборка калькуляторов, которые помогут вам работать с логарифмами:

Калькулятор логарифмов

RapidTables.com — этот калькулятор включает в себя правила логарифмирования для руководства и предназначен для быстрого и легкого ввода данных.

Калькулятор логарифмических уравнений Symbolab.com — Этот простой в использовании калькулятор предоставляет примеры логарифмирования, которые помогут вам начать работу. Он также предоставляет пошаговые объяснения того, как он находит свои решения.

Калькулятор логарифмов 1728.org — этот калькулятор предоставляет подробные инструкции о том, как вводить данные, чтобы гарантировать получение четких результатов.

Калькулятор логарифмического журнала NCalculators.com — этот калькулятор предоставляет учебную информацию по логарифмам и примеры расчетов журнала.

Калькулятор журнала MiniWebTool.com — этот калькулятор предоставляет учебную информацию и формулы, относящиеся к логарифмам. Ввод данных выполняется быстро и легко.

Rechneronline.Калькулятор логарифма де — это простой калькулятор логарифма без каких-либо наворотов. Ввод данных выполняется быстро и легко.

Калькулятор логарифмов TutorVista.com — этот калькулятор предоставляет некоторую учебную информацию и необходимые формулы.

Калькулятор логарифмов A-Calculator.com — Этот калькулятор прост в использовании. Он также предоставляет подробное объяснение того, как найти натуральный логарифм без использования калькулятора.

14 Матричных калькуляторов

Как объясняет Академия Хана, матрицы — это «способы упорядочивания чисел.»Ниже приведены калькуляторы, которые помогут вам больше работать с матрицами:

Матричный калькулятор

MathIsFun.com — этот калькулятор упрощает ввод данных и может выполнять базовые операции с матрицами, такие как сложение, вычитание и умножение.

Матричные калькуляторы MathPortal.org — эти матричные калькуляторы от MathPortal выполняют множество функций. Он включает в себя калькулятор базовой матрицы, калькулятор значений Elgenvalues и Elgenvectors и калькулятор разложения матриц и позволяет пользователям копировать и вставлять данные из электронной таблицы Excel.

Матричный калькулятор

MatrixCalc.org — Этот калькулятор служит отличным универсальным калькулятором для работы с матрицами. Он включает инструкции по вводу данных в калькулятор.

EasyCalculation.com’s Calculation on MATRIX Math — EasyCalculation.com предоставляет множество матричных калькуляторов для выполнения определенных функций, от базовых операций, таких как сложение и вычитание, до более сложных функций, таких как LU Decomposition.

Матричный калькулятор Symbolab.com — этот калькулятор имеет аккуратный дизайн и прост в использовании.Он включает примеры с пошаговыми пояснениями того, как решаются матричные операции.

Meta-Calculator.com’s Matrix Calculator — Использовать этот калькулятор быстро и легко. Ввод данных прост и выполняет такие операции, как сложение, вычитание, умножение и другие.

Матричный калькулятор SolveMyMath.com — Используйте этот калькулятор для решения таких аспектов матрицы, как определитель, инверсия, трассировка и норма.

SolveMyMath.Калькулятор умножения, сложения и вычитания матриц. com — Этот калькулятор прост в использовании для умножения, сложения и вычитания матриц.

Калькуляторы матриц

QuickMath.com — Этот калькулятор предоставляет обучающую информацию по матрицам и аспектам матриц, таким как определитель и обратный. Для каждого аспекта существуют определенные версии калькулятора.

Матричный калькулятор

Math.uh.edu — Разработанный факультетом математики Хьюстонского университета, ввод данных в этот калькулятор очень прост.Он выполняет основные матричные операции, такие как сложение, вычитание и умножение.

Калькуляторы матриц EndMemo.com — EndMemo.com предоставляет калькуляторы для определенных операций. Ввод данных в эти калькуляторы прост, и они дают четкие результаты:

5 Калькуляторы рациональных выражений

Как объясняет MathIsFun.com, рациональное выражение представляет собой «соотношение двух многочленов».

Калькуляторы упрощающих рациональных выражений на MathPortal.org — в этом калькуляторе есть вкладка «Основные выражения» и вкладка «Расширенные выражения.Решения, представленные калькулятором «Основные выражения», также предоставляют пошаговое объяснение того, как было упрощено выражение.

Калькуляторы рациональных выражений от WolframAlpha.com — на этом сайте представлены три простых в использовании калькулятора для выполнения конкретных вычислений рациональных выражений:

Калькуляторы упрощения рациональных выражений

QuickMath.com — эти калькуляторы обеспечивают простые, но быстрые результаты. Есть базовый, средний и расширенный режимы.

Калькулятор уравнений, приводимых к квадратичной форме.Калькулятор и решатель квадратной формулы

В алгебре квадратное уравнение — это любое полиномиальное уравнение второй степени следующего вида :. Цифры abc c являются коэффициентами уравнения, и они представляют известные числа. Например, a не может быть 0, или уравнение будет линейным, а не квадратичным.

Квадратное уравнение может быть решено несколькими способами, включая: факторинг, использование формулы квадратичного уравнения, построение квадрата или построение графика.

Здесь будет обсуждаться только использование квадратной формулы, а также основы завершения квадрата, поскольку вывод формулы включает завершение квадрата.Ниже представлена квадратичная формула, а также ее вывод. Значения x, найденные с помощью квадратной формулы, являются корнями квадратного уравнения, которые представляют значения x, где любая парабола пересекает ось x.

Кроме того, квадратная формула обеспечивает ось симметрии параболы. Это демонстрирует приведенный ниже график. Обратите внимание, что квадратная формула на самом деле имеет множество реальных приложений, таких как вычисление площадей, траекторий снарядов и скорости, среди прочего.Финансовая пригодность и здоровье Математика Другое. Для расчета введите пары или уравнения, разделенные запятой «» или полуколлоном «;».

Идеальная программа для одновременного решения уравнений, которая поможет вам решать одновременные уравнения в режиме онлайн. Калькулятор одновременных уравнений поможет вам найти значение неизвестных переменных системы линейных, квадратных или нелинейных уравнений для 2, 3, 4 или 5 неизвестных.

Наш онлайн-калькулятор системы уравнений поможет вам найти любые неизвестные переменные x, z, n, m и y. Вышеупомянутый калькулятор одновременных уравнений поможет вам решить одновременные линейные уравнения с двумя, тремя неизвестными.Классическим примером является система из 3-х линейных уравнений с 3-мя неизвестными x, y, z.

Эта программа для решения линейных уравнений 3 неизвестных поможет вам систематически решать такие системы. Линейное уравнение представляет собой отношения между двумя или более переменными.

P3400 код jeep grand cherokee

В природе линейные встречаются чаще всего. Тем не менее, не все явления в природе линейны, и поэтому моделировать природные явления с помощью линейных зависимостей непросто. Чтобы получить уникальные значения для неизвестных, вам нужно дополнительное уравнение, которое является генезисом одновременных линейных уравнений.

Онлайн-калькулятор систем линейных уравнений для пошагового решения одновременных уравнений. Наша система решения уравнений показывает вам всю работу с пошаговым решением. Наш онлайн-калькулятор алгебры для решения одновременных уравнений быстрый, точный и надежный.

Прежде чем мы узнаем, как работает решатель одновременных линейных уравнений, было бы лучше, если бы мы больше исследовали систему линейных уравнений. Решение линейного уравнения или системы линейных уравнений — это набор координат в пространстве, который удовлетворяет всем уравнениям в системе.

Для двумерного случая решение представляет собой точку в двухмерных координатах, которая удовлетворяет данным уравнениям. В трехмерном случае решение — это точка в трехмерном пространстве, которая одновременно удовлетворяет данной системе уравнений.

Urbana

Для случаев более высокой степени применима аналогичная аналогия. С другой стороны, система будет иметь бесконечно много решений, если ее определитель равен нулю. Для системы уравнений с двумя неизвестными вам потребуются два уравнения для решения системы.Если рассматривать уравнения как прямые линии на двумерном графике, решение системы — это точка пересечения двух линий.

Случай отсутствия решения означает, что две линии никогда не пересекаются; такие линии параллельны друг другу. Ясно, что эти две линии параллельны и поэтому никогда не пересекутся. Для трехмерного случая данная система уравнений представляет собой параллельные плоскости. Вы когда-нибудь хотели легко решать или множить квадратные уравнения без необходимости писать формулу и вычислять вручную? Это подробное руководство покажет вам, как запрограммировать квадратную формулу в ваш калькулятор TI, так что все, что вам нужно для этого, введите значения коэффициентов!

Перейти к завершению кода! Чтобы создать программу, нажмите кнопку prgm и перейдите к NEW.Так вы легко узнаете его и поймете, что он делает, из названия. Пока программы очищают экран, затем запрашивают у пользователя три значения, которые он сохраняет в переменных A, B и C. Затем вам нужно вычислить значения x, используя квадратное уравнение. Мы сохраним два значения в переменных D и E.

Теперь, когда у нас есть вычисленные и сохраненные значения x, нам просто нужно их отобразить. Нажмите prgm, чтобы получить доступ к списку программ и выбрать новую созданную программу. Имейте в виду, что программа выдаст сообщение об ошибке, если решений нет или они мнимые.Хороший вопрос! В строках 5 и 6 записано то же уравнение.

Кодирование программы Начните с программы, очистив главный экран и добавив входные данные для трех коэффициентов. Калькулятор использует квадратную формулу для поиска решений любого квадратного уравнения. Калькулятор квадратной формулы ниже решит любое квадратное уравнение, которое вы вводите. Просто введите число для «a», «b» и «c», затем нажмите кнопку «решить». Больше квадратичных гифок. Калькулятор на этой странице показывает, как работает квадратная формула, но если у вас есть доступ к графическому калькулятору, вы сможете решать квадратные уравнения, даже с мнимыми решениями.

Калькулятор и решатель квадратной формулы. Решите квадратное уравнение. Калькулятор загрузки. График. Остальные шаги просто включают ввод a, b и c. Убедитесь, что вы разделили весь числитель на 2a, просто используйте круглые скобки. Вы можете сохранить график на рабочий стол как изображение! Популярные страницы mathwarehouse. Площадь цилиндра. Единичная игра по кругу. Демонстрация треугольника Паскаля.

Калькулятор квадратичных формул

Создавайте и сохраняйте общие диаграммы. Интерактивное моделирование — самая противоречивая математическая загадка! Исчисление Gifs.Как сделать эллипс. Объем конуса. Лучшие математические анекдоты. Наши самые популярные анимированные гифки. Математические загадки. Тема решения квадратных уравнений разбита на два раздела для тех, кто просматривает это в Интернете. Как единичный раздел, время загрузки страницы было бы довольно большим.

Калькулятор квадратных уравнений

Это второй раздел, посвященный решению квадратных уравнений. В предыдущем разделе мы рассмотрели использование факторизации и свойства квадратного корня для решения квадратных уравнений.Проблема в том, что оба этих метода решения не всегда работают. Не каждая квадратичная функция факторизуема, и не каждая квадратичная функция имеет форму, требуемую для свойства квадратного корня.

Пришло время изучить методы, которые будут работать для всех квадратных уравнений. Итак, в этом разделе мы рассмотрим завершение квадрата и квадратной формулы для решения квадратного уравнения. Это называется так, потому что в процессе решения используется процесс, называемый завершением квадрата.

Итак, сначала мы должны определить, что такое завершение квадрата. Это необходимо для этого. Это дает следующее факторизуемое квадратное уравнение.

Калькулятор квадратной формулы

Этот процесс называется завершением квадрата, и если мы сделаем все арифметические действия правильно, мы можем гарантировать, что квадратичный фактор будет множителем как полный квадрат.

Обратите внимание, что здесь мы сохранили знак минус, хотя он всегда выпадает после того, как мы возведем квадрат.Причина этого станет очевидной через секунду. Итак, это квадратичный коэффициент, который, надеюсь, вы сможете довольно быстро разложить на множители. Это причина оставления знака минус. Также оставьте это дробью. Теперь завершите квадрат. Этот фактор не так-то просто учесть. Мы сделаем первую задачу подробно, подробно указав каждый шаг.

В остальных задачах мы просто сделаем работу без особых объяснений. Шаг 1: Разделите уравнение на коэффициент при члене x 2. Напомним, что для завершения квадрата требовался коэффициент, равный единице, и это гарантирует, что мы его получим.

Шаг 3: Завершите квадрат с левой стороны. Однако на этот раз нам нужно будет добавить число к обеим сторонам знака равенства, а не только к левой стороне. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.

Узнать больше Принять. Тригонометрия конических сечений. Конические сечения. Матрицы-векторы. Химические реакции Химические свойства. Калькулятор квадратного уравнения Решайте квадратные уравнения шаг за шагом. Правильный ответ :.Давай попытаемся снова :.

Попробуй еще упростить. В последнем посте мы рассказали о доработке квадрата, см. Ссылку. Это довольно прямолинейно, если вы следуете всем квадратичным решениям путем факторизации ссылки на предыдущий пост, как правило, работает нормально. Но что делать, если квадратное уравнение Войти Войти через Office Войти через Facebook.

Присоединяйтесь к миллиону счастливых пользователей! Зарегистрируйтесь бесплатно :. Присоединяйтесь с Office Присоединяйтесь с Facebook. Создай мой аккаунт. Транзакция не удалась! Пожалуйста, попробуйте еще раз, используя другой способ оплаты.Подпишитесь, чтобы получить больше :. Отсутствуют данные пользователя. Обратитесь в службу поддержки.

Нам нужны ваши отзывы. Отменить Отправить.

Xgboost slides

Создание PDF См. Все крайние точки области неявной производной производной критические точки обратные точки перегиба лапласа частичные доли асимптоты собственное значение лапласа собственное значение область Тейлора пересекает диапазон вершинный фактор расширяет точки поворота наклона Шаг 2: Выберите команду, относящуюся к введенной вами функции fx выше.

Решение уравнений — центральная тема алгебры.Все приобретенные навыки в конечном итоге приводят к способности решать уравнения и упрощать решения. В предыдущих главах мы решали уравнения первой степени.

Теперь у вас есть необходимые навыки для решения уравнений второй степени, которые известны как квадратные уравнения.

Квадратное уравнение — это полиномиальное уравнение, которое содержит вторую степень, но не более высокую степень переменной.Все квадратные уравнения могут быть представлены в стандартной форме, и любое уравнение, которое может быть преобразовано в стандартную форму, является квадратным уравнением. Другими словами, стандартная форма представляет все квадратные уравнения.

Эта теорема доказана в большинстве учебных пособий по алгебре. Важная теорема, которую невозможно доказать на уровне этого текста, гласит: «Каждое полиномиальное уравнение степени n имеет ровно n корней. Возможно, что два решения равны. У квадратного уравнения будет два решения, поскольку оно имеет степень два.Самый простой метод решения квадратичных вычислений — факторинг.

Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется всякий раз, когда факторизация возможна. Другими словами, если произведение двух факторов равно нулю, то по крайней мере один из факторов равен нулю.

Мы не будем пытаться доказывать эту теорему, но внимательно отметим, что в ней говорится. Мы никогда не сможем перемножить два числа и получить ответ ноль, если хотя бы одно из чисел не равно нулю. Мы должны вычесть 6 с обеих сторон.Вспомните, как разложить на множители трехчлены. Шаг 3 Установите каждый коэффициент равным нулю и решите относительно x. При этом применяется приведенная выше теорема, согласно которой хотя бы один из факторов должен иметь нулевое значение.

Шаг 4 Проверьте решение в исходном уравнении. Проверка ваших решений — верный способ узнать, правильно ли вы решили уравнение. В этом примере 6 и -1 называются элементами набора.

Обратите внимание, что в этом примере уравнение уже имеет стандартную форму. Опять же, проверка решений убедит вас, что вы не допустили ошибки при решении уравнения.Проверьте исходное уравнение, чтобы убедиться, что знаменатель не равен нулю. Обратите внимание, что здесь два решения равны. Это происходит только тогда, когда трехчлен является полным квадратом.

Ict 2019 vietnam

По завершении этого раздела вы должны уметь: Определить неполное квадратное уравнение. Решите неполное квадратное уравнение. Когда вы сталкиваетесь с неполной квадратичной с отсутствием третьего члена c — 0, ее все же можно решить с помощью факторизации. Произведение двух факторов равно нулю.Поэтому мы используем теорему из предыдущего раздела. Проверьте эти решения. Обратите внимание, что если член c отсутствует, вы всегда можете множить x из других членов.

Использование решателя уравнений TI-85, TI-86 или TI-89

Математика в решателе

Вы можете выполнять математические вычисления по мере определения переменных. Например, скажем, вам дали
температура была 15 ^o С. Можно было прибавить 273 «на лету»:

Что такое объем 1.00 моль идеального газа при температуре 15 ^o ° C, если его парциальное давление составляет 1,00 атм?

уравнение: P * V = моль * Rg * T уравнение: P * V = моль * Rg * T
 П = 1 П = 1
 V = Нажмите [SOLVE] ==> V = 23.63265504
 моль = 1 моль = 1
 Rg = 0,08205783 Rg = 0,08205783
 Т = 15 + 273,15 Т = 288
 bound = {- 1E99,1E99} bound = {- 1E99,1E99}

Объем 1.0 моль идеального газа с парциальным давлением 1,0 атм при 15 ^o C составляет 23,6 л.

Или, может быть, вы хотите решить для давления, и вам нужно значение торр. Например,

Каково парциальное давление (в торр) 1,00 моль идеального газа при 25 ^o ° C, если его объем составляет 2,00 л?

уравнение: P * V = моль * Rg * T уравнение: P * V = моль * Rg * T
 P = Нажмите [SOLVE] ==> P = 12.22661667
 В = 2 В = 2
 моль = 1 моль = 1
 Rg = 0,08205783 Rg = 0,08205783
 Т = 25 + 273 Т = 298
 bound = {- 1E99,1E99} bound = {- 1E99,1E99}

Это давление в атмосферах, поэтому нам нужно умножить на коэффициент преобразования
«(760 торр) / (1 атм)» прямо в этой строке P:

уравнение: P * V = моль * Rg * T уравнение: P * V = моль * Rg * T
Р = 12.22661667 * 760 Нажмите [ENTER] ==> P = 9292.2286692
 В = 2 В = 2
 моль = 1 моль = 1
 Rg = 0,08205783 Rg = 0,08205783
 Т = 25 + 273 Т = 298
 bound = {- 1E99,1E99} bound = {- 1E99,1E99}

Парциальное давление 1,00 моль идеального газа в объеме 2,00 л при температуре 25 ^o ° C составляет 9290 торр.
(Обратите внимание, что мы используем три значащих цифры, потому что температура по Кельвину составляет 298.2-1 Пример задачи Ничья

Количество решаемых уравнений:

23456789

Пример задачи

Решить

Введите неравенство в график, например.грамм. y			Пример задачи






Ничья

911

Количество решаемых неравенств:

23456789

Пример задачи

Решить

НАСТРОЙКА: Удалите все фракции и
круглые скобки, сгруппируйте термины, возведите в квадрат член положительным,
и поместите в стандартную форму:

Топор ² + Bx + C = 0

ВСЕГДА: Вынесите все общие множители сначала