Содержание
Внеклассный урок — Числовая окружность
Числовая окружность
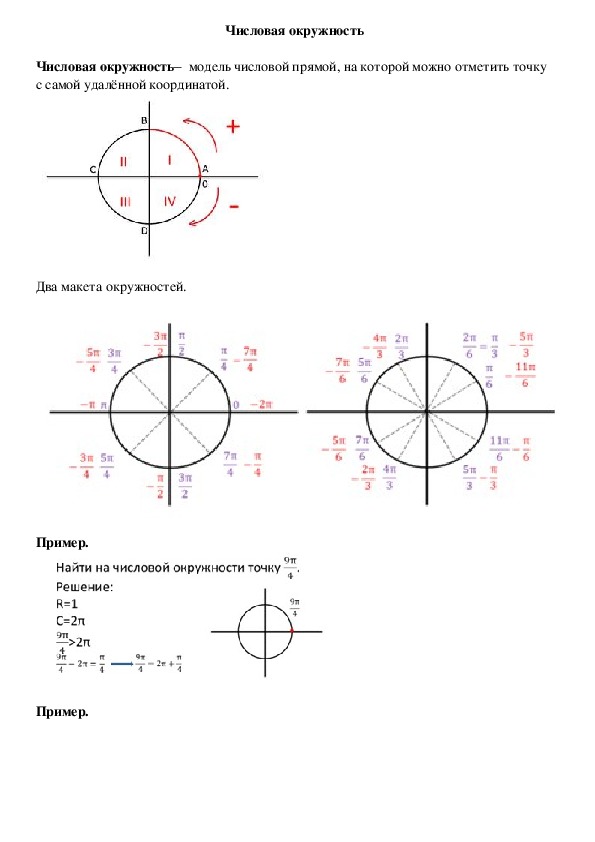
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
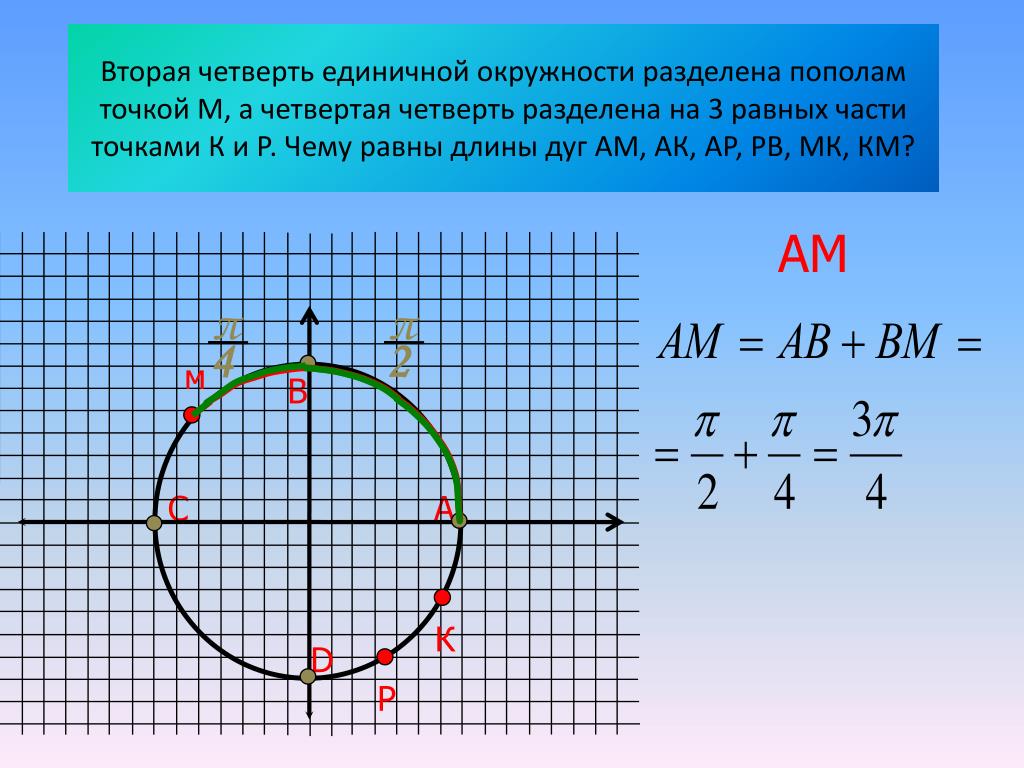
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
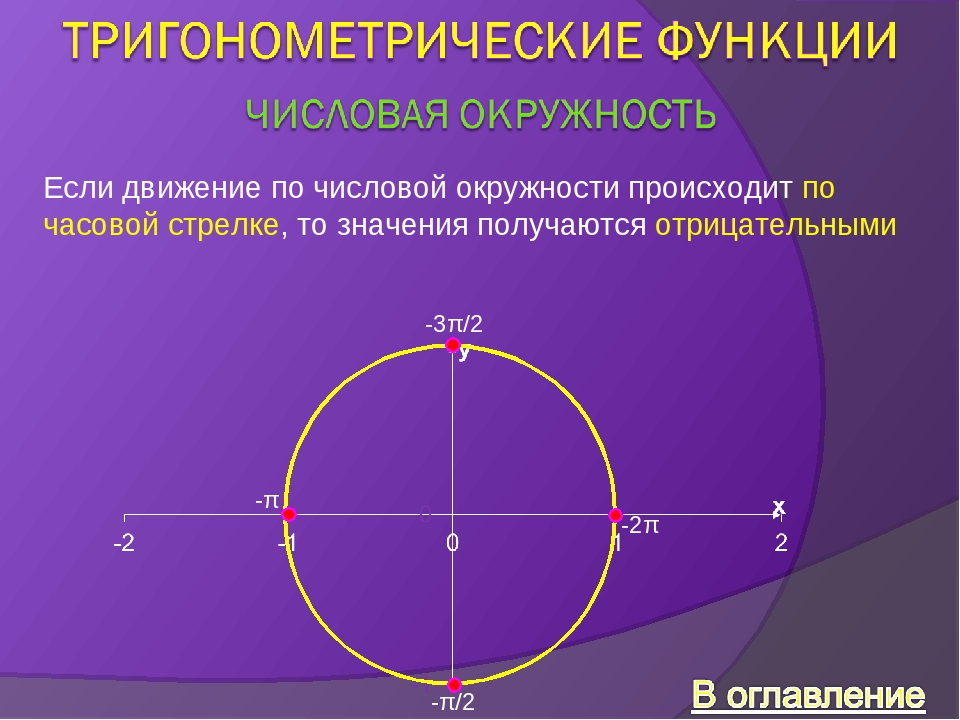
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
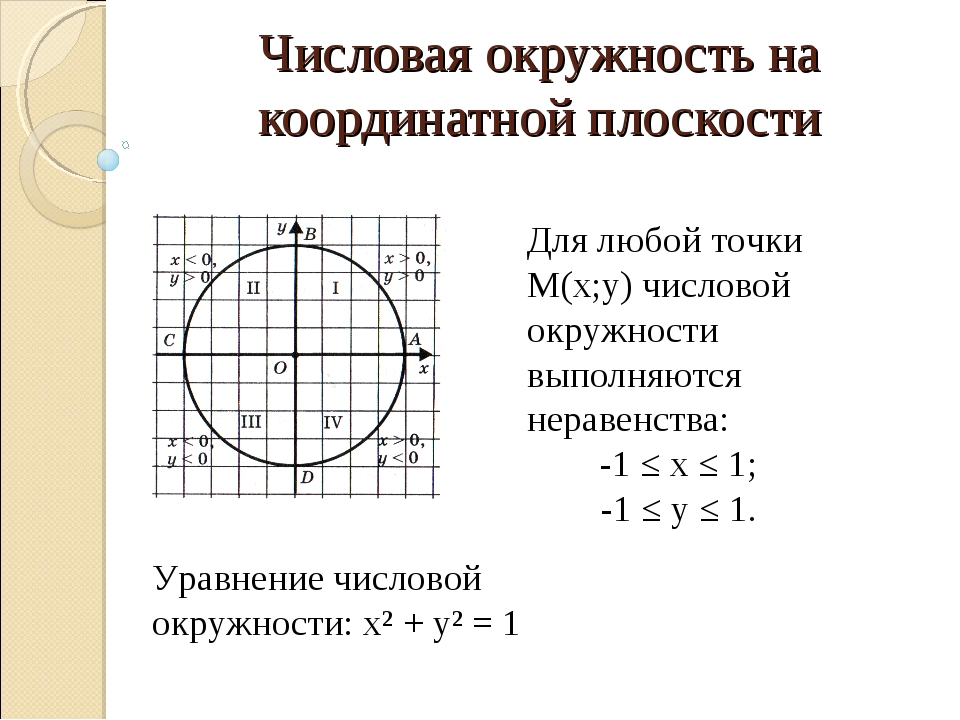
Числовая окружность на координатной плоскости.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
x > 0, y > 0 | x < 0, y > 0 | x < 0, y < 0 | x > 0, y < 0 |
Значение любой точки числовой окружности:
Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: –1 ≤ x ≤ 1; –1 ≤ y ≤ 1 |
Основные величины числовой окружности:
| | |
Окружность | 2π | 360º |
Полуокружность | π | 180º |
Четверть окружности | π | 90º |
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.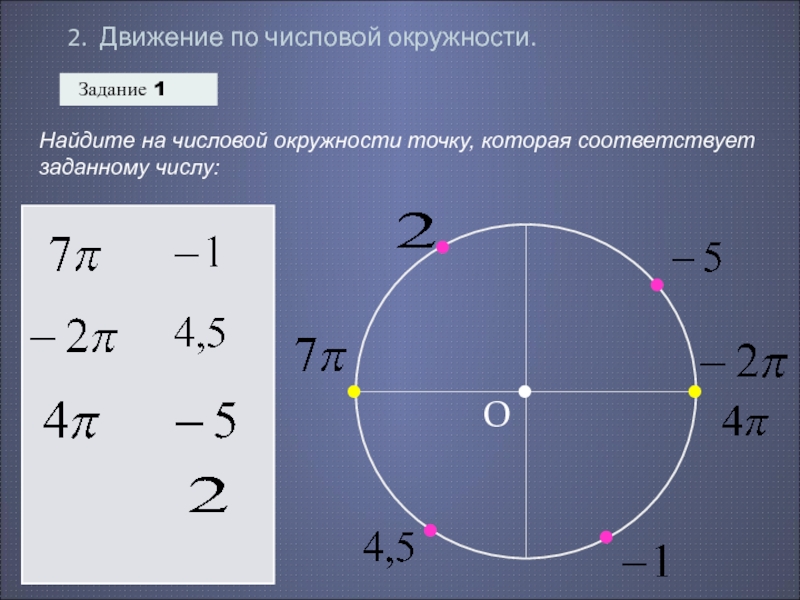
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
— Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей.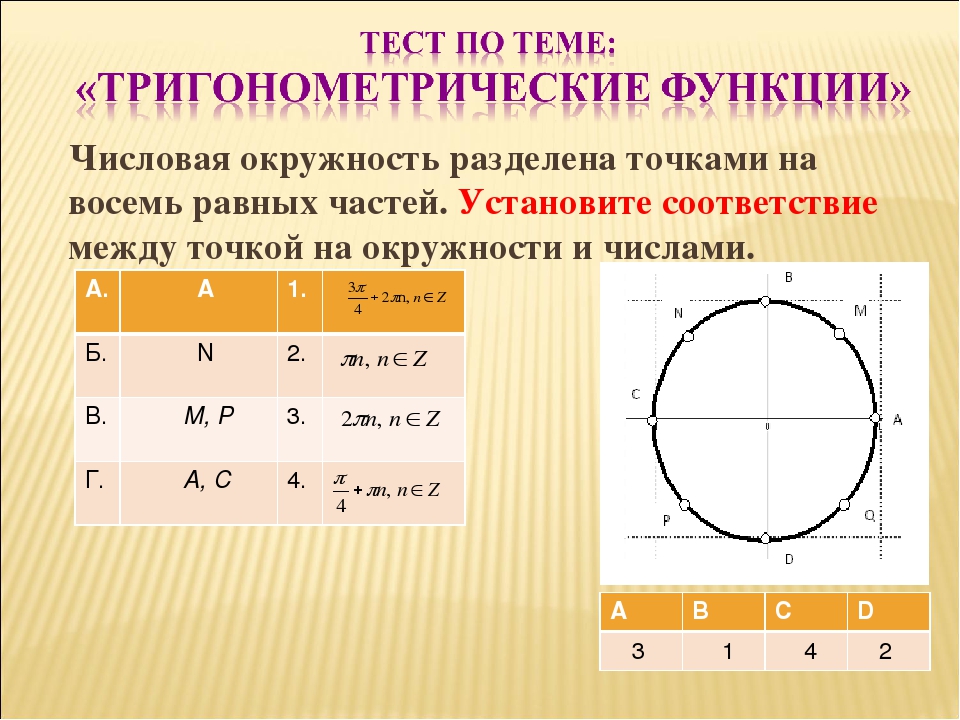
Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.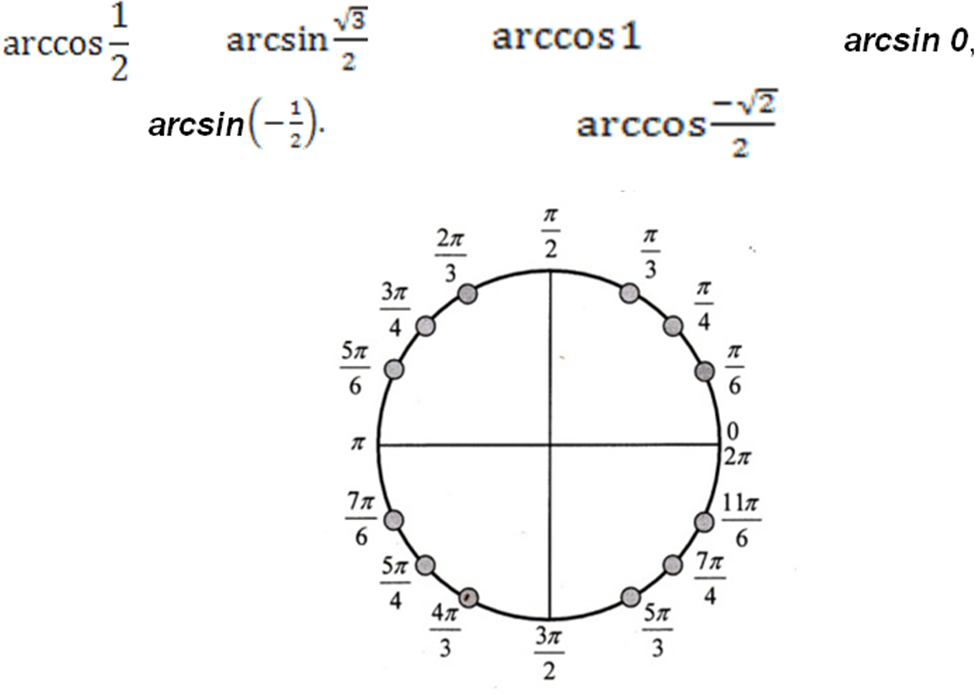
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число: M(t) = M(t + 2πk), где k ∈ Z. Число k называется параметром. |
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
Числовая окружность на координатной плоскости. 10 класс, алгебра
Дата публикации: .
Что будем изучать:
1. Определение.
2. Важные координаты числовой окружности.
3. Как искать координату числовой окружности?
4. Таблица основных координат числовой окружности.
5. Примеры решения задач.
Определение числовой окружности на координатной плоскости
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при $x > 0$, $у > 0$ – в первой четверти;
2) при $х 0$ – во второй четверти;
3) при $х
4) при $х > 0$, $у
Для любой точки $М(х; у)$ числовой окружности выполняются неравенства: $-1
Запомните уравнение числовой окружности: $x^2 + y^2 = 1$.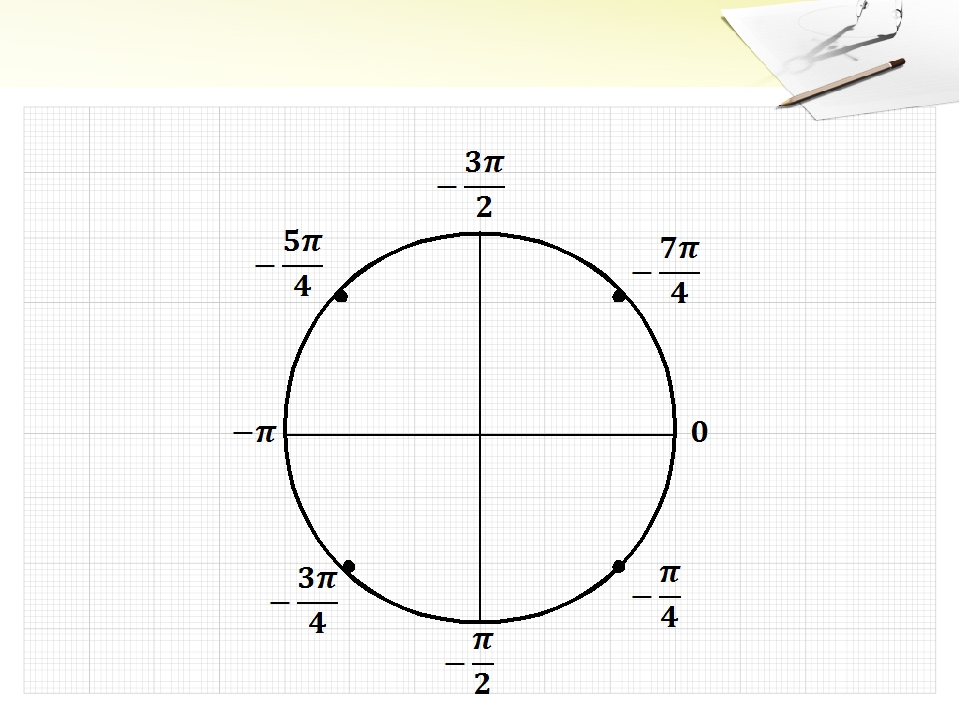
2 = 1, \\ x = y. \end {cases}$
Решив данную систему, получаем: $y = x =\frac{\sqrt{2}}{2}$.
Значит, координаты точки M, соответствующей числу $\frac{π}{4}$, будут $M(\frac{π}{4})=M(\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2})$.
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности
Рассмотрим примеры
Пример 1.
Найти координату точки числовой окружности: $Р(45\frac{π}{4})$.
Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$45\frac{π}{4} = (10 + \frac{5}{4}) * π = 10π +5\frac{π}{4} = 5\frac{π}{4} + 2π*5$.
Значит, числу $45\frac{π}{4}$ соответствует та же точка числовой окружности, что и числу $\frac{5π}{4}$. Посмотрев значение точки $\frac{5π}{4}$ в таблице, получаем:
$P(\frac{45π}{4})=P(-\frac{\sqrt{2}}{2};-\frac{\sqrt{2}}{2})$.
Пример 2.
Найти координату точки числовой окружности: $Р(-\frac{37π}{3})$.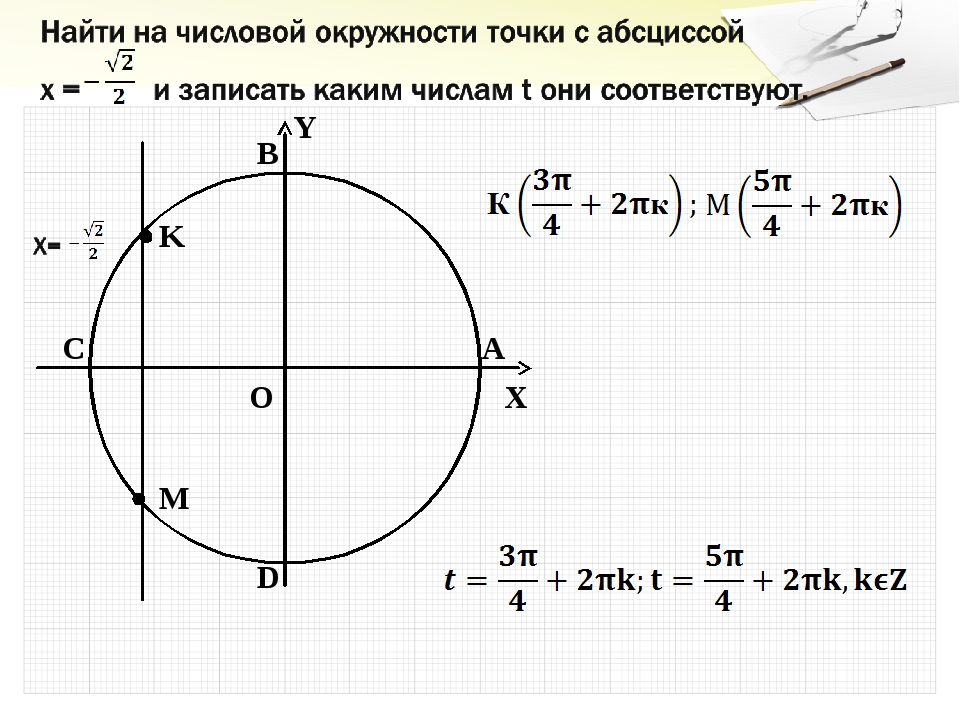
Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$-\frac{37π}{3} = -(12 + \frac{1}{3})*π = -12π –\frac{π}{3} = -\frac{π}{3} + 2π*(-6)$.
Значит, числу $-\frac{37π}{3}$ соответствует та же точка числовой окружности, что и числу $–\frac{π}{3}$, а числу –$\frac{π}{3}$ соответствует та же точка, что и $\frac{5π}{3}$. Посмотрев значение точки $\frac{5π}{3}$ в таблице, получаем:
$P(-\frac{37π}{3})=P(\frac{{1}}{2};-\frac{\sqrt{3}}{2})$.
Пример 3.
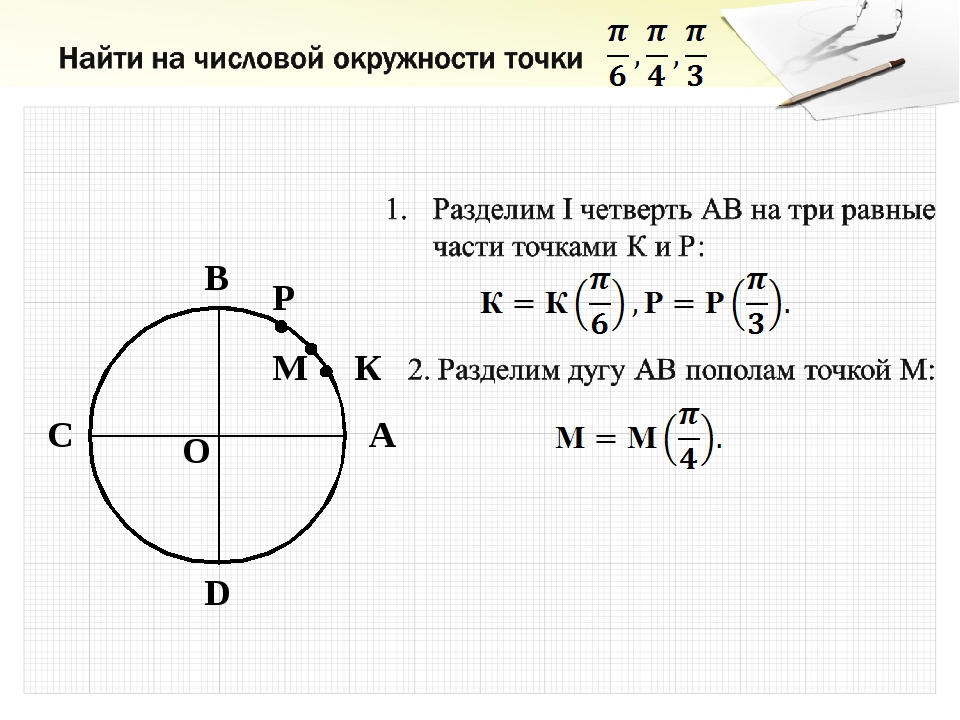
Найти на числовой окружности точки с ординатой $у =\frac{1}{2}$ и записать, каким числам $t$ они соответствуют?
Решение:
Прямая $у =\frac{1}{2}$ пересекает числовую окружность в точках М и Р. Точка М соответствует числу $\frac{π}{6}$ (из данных таблицы). Значит, и любому числу вида: $\frac{π}{6}+2π*k$. Точка Р соответствует числу $\frac{5π}{6}$, а значит, и любому числу вида $\frac{5π}{6} +2 π*k$.
Получили, как часто говорят в таких случаях, две серии значений:
$\frac{π}{6} +2 π*k$ и $\frac{5π}{6} +2π*k$.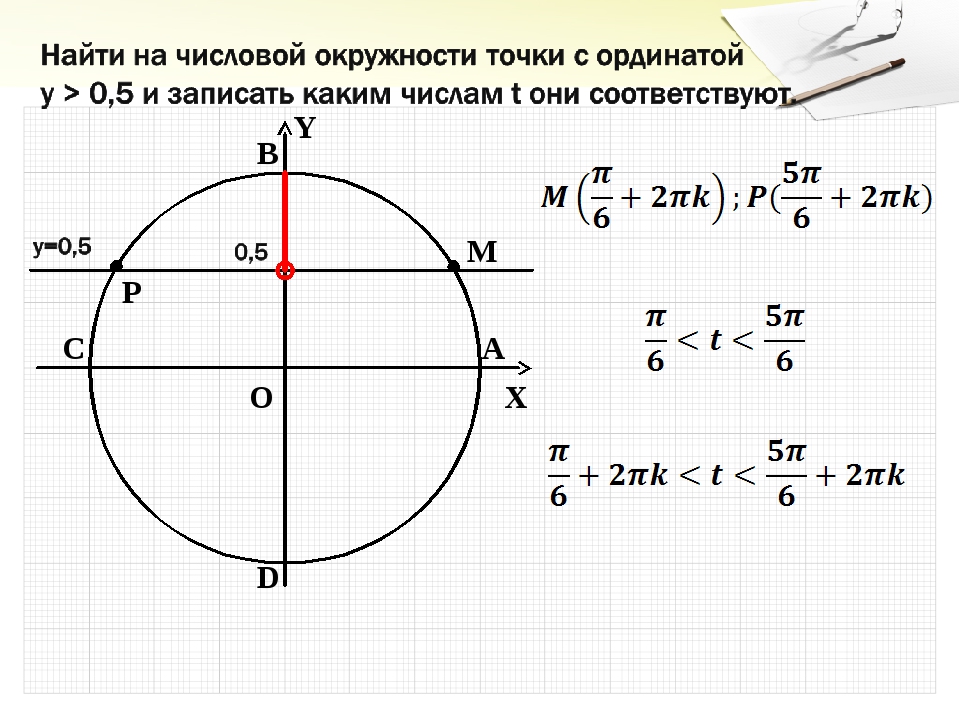
Ответ : $t=\frac{π}{6} +2 π*k$ и $t=\frac{5π}{6} +2π*k$.
Пример 4.
Найти на числовой окружности точки с абсциссой $x≥-\frac{\sqrt{2}}{2}$ и записать, каким числам $t$ они соответствуют.
Решение:
Прямая $x =-\frac{\sqrt{2}}{2}$ пересекает числовую окружность в точках М и Р. Неравенству $x≥-\frac{\sqrt{2}}{2}$ соответствуют точки дуги РМ. Точка М соответствует числу $3\frac{π}{4}$ (из данных таблицы). Значит, и любому числу вида $-\frac{3π}{4} +2π*k$. Точка Р соответствует числу $-\frac{3π}{4}$, а значит, и любому числу вида $-\frac{3π}{4} +2π*k$.
Тогда получим $-\frac{3π}{4} +2 π*k ≤t≤\frac{3π}{4} +2πk$.
Ответ : $-\frac{3π}{4} +2 π*k ≤t≤\frac{3π}{4} +2πk$.
Задачи для самостоятельного решения
1) Найти координату точки числовой окружности: $Р(\frac{61π}{6})$.
2) Найти координату точки числовой окружности: $Р(-\frac{52π}{3})$.
3) Найти на числовой окружности точки с ординатой $у = -\frac{1}{2}$ и записать, каким числам $t$ они соответствуют.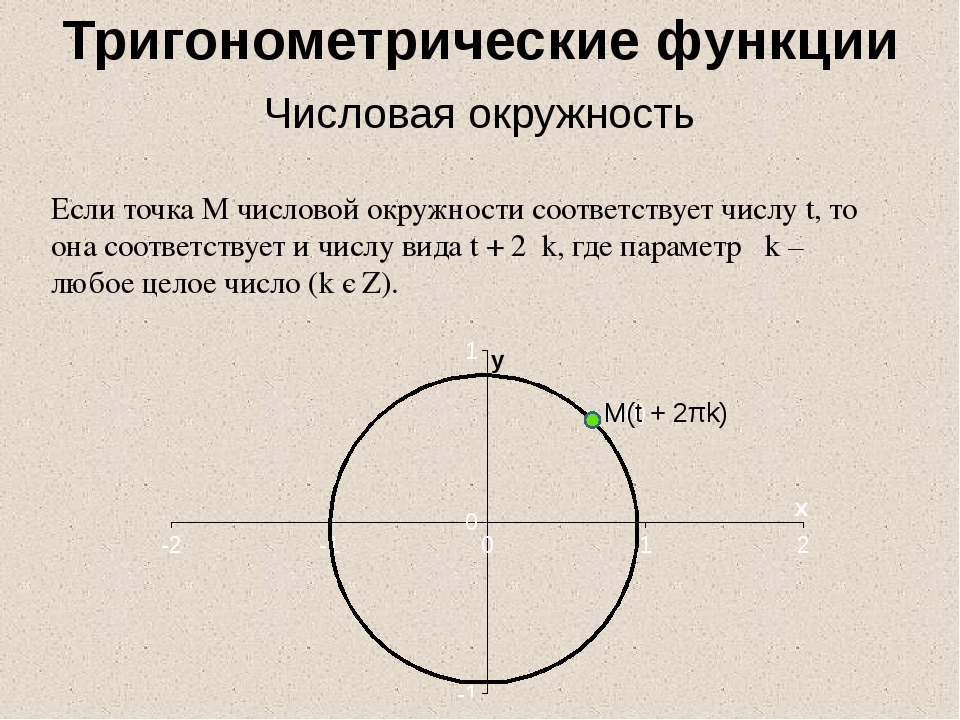
4) Найти на числовой окружности точки с ординатой $у ≥ -\frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
5) Найти на числовой окружности точки с абсциссой $x≥-\frac{\sqrt{3}}{2}$ и записать, каким числам $t$ они соответствуют.
2. Числовая окружность
Единичная
окружность
— это окружность, радиус которой принят
за единицу измерения.
Числовая
окружность
— это единичная окружность с установленным
соответствием между действительными
числами и точками окружности:
Указанное
соответствие можно определить следующим
образом: каждому числу
соответствует такая точка Р
числовой окружности, чтобы дуга ОР
имела длину ||
и была отложена в положительном
направлении если
> 0 и в отрицательном, если
< 0:
Признаки
числовой окружности:
1) начало отсчета
– правый конец горизонтального диаметра;
2) единичный отрезок
– длина радиуса окружности;
3) положительное
направление – против часовой стрелки.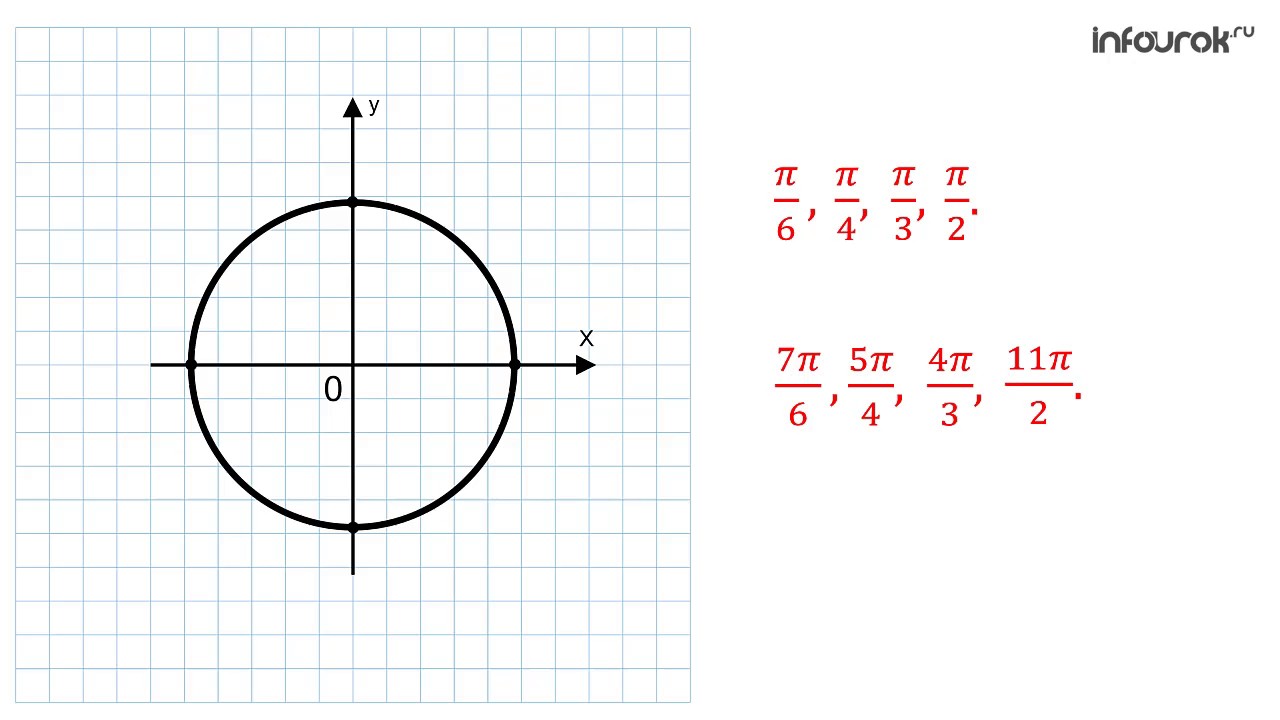
Откладывать
можно дуги какой угодно длины. То есть
числовую окружность можно рассматривать
как окружность радиуса 1, на которую
«намотана» числовая прямая:
3. Радианная мера углов и дуг
Угол
в 1
— это центральный угол, опирающийся на
дугу, длина которой равна части
окружности.
Угол
поворота
— это угол, полученный вращением луча
около его начала О
от начального положения ОА
до конечного положения ОВ.
Угол
в 1 радиан
— это центральный угол, опирающийся на
дугу, длина которой равна радиусу
окружности.
Радианная мера
угла численно равна пути, который
проходит точка по дуге единичной
окружности, на которую опирается этот
угол:
Для связи радианов
и градусов используют развернутый угол:
1. Говорят:
«угол радиан»
или чаще «угол
». Обозначение
«радиан» или «рад», как правило, опускают.
2. Термин
«радианное измерение углов» равносилен
термину «числовое измерение углов»,
т.е. фраза «угол
равен двум радианам» равносильна фразе
«угол
равен числу
2» и даже «угол
равен двум». Поэтому вопрос типа «Чему
равно ?»
некорректен. Нужно спрашивать: «Чему
равен угол
?» (60)
или «Чему равно число ?» (
1,05).
9. Обратные тригонометрические функции
Арксинусом числа
а
называется такое число х
из интервала
,
синус которого равен а.
Арккосинусом
числа а
называется такое число х
из интервала [0; ],
косинус которого равен а.
Арктангенсом
числа а
называется такое число х
из интервала
,
тангенс которого равен а.
Арккотангенсом
числа а
называется такое число х
из интервала (0; ),
котангенс которого равен а.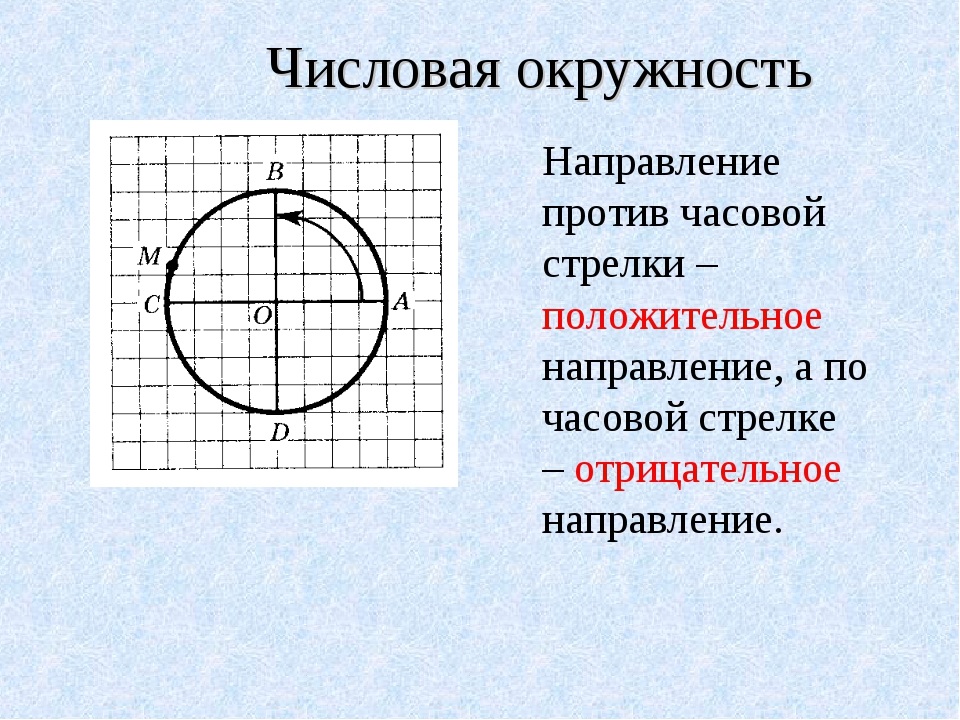
1. Для отрицательных
значений аргумента:
2. Из определения
аркфункции сразу следует, что:
VI. Формулы
половинного аргумента
(знак – по
функции в левой части):
VII. Формулы
сумм:
VIII. Формулы
произведений:
IX. Универсальная
тригонометрическая подстановка:
X. Некоторые
дополнительные формулы:
4. Угол поворота
Полный
оборот
— это угол поворота, равный 2
рад (или 360).
Некоторые
положения конечной точки угла поворота:
Тригонометрические функции. Числовая окружность. Синус и косинус
Определение. Числовой окружностью называется окружность на координатной плоскости с центром в начале координат и единичным радиусом.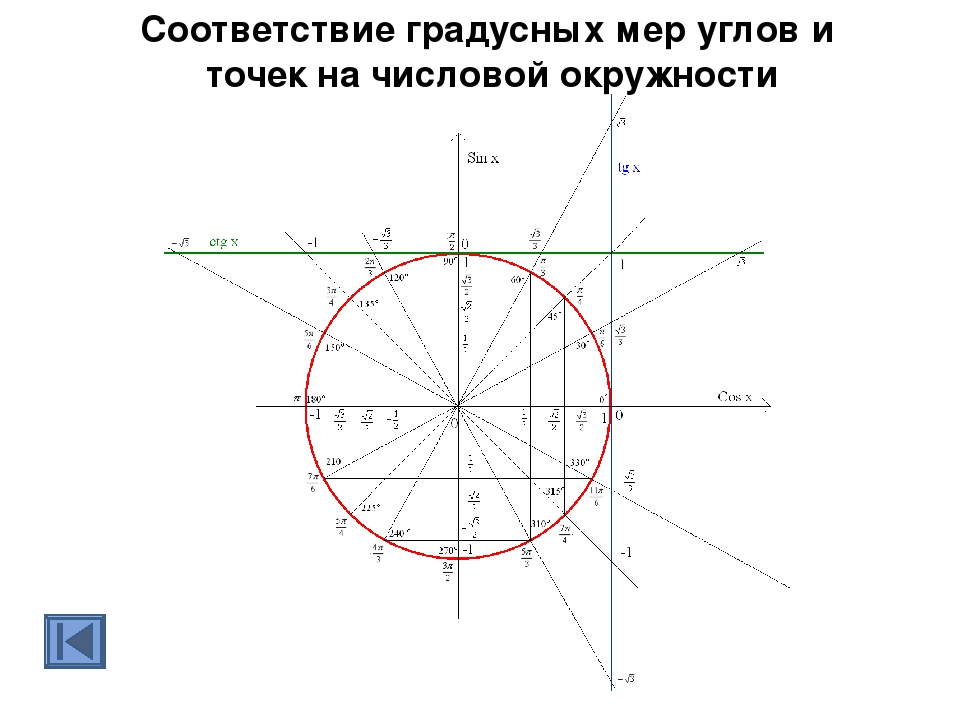
Числовая окружность изображена на рис. 37:
Рис. 37
Иначе говоря, это множество точек координатной плоскости, координаты которых удовлетворяют уравнению .
Представим себе, что точка равномерно движется по числовой окружности против часовой стрелки со скоростью 1.
Будем предполагать, что это движение обладает следующими свойствами ( — положение точки в момент времени ):
1. — точка числовой окружности.
2. .
3. .
4. имеет положительные координаты.
5. , где .
6. расстояние между точками и равно расстоянию между точками и .
Примечание. Расстояние между точками и вычисляется по формуле
Определение синуса и косинуса
Определение. Предположим, что точка равномерно движется по числовой окружности так, что выполняются свойства 1–6. Абсцисса точки называется косинусом числа , ордината — синусом числа .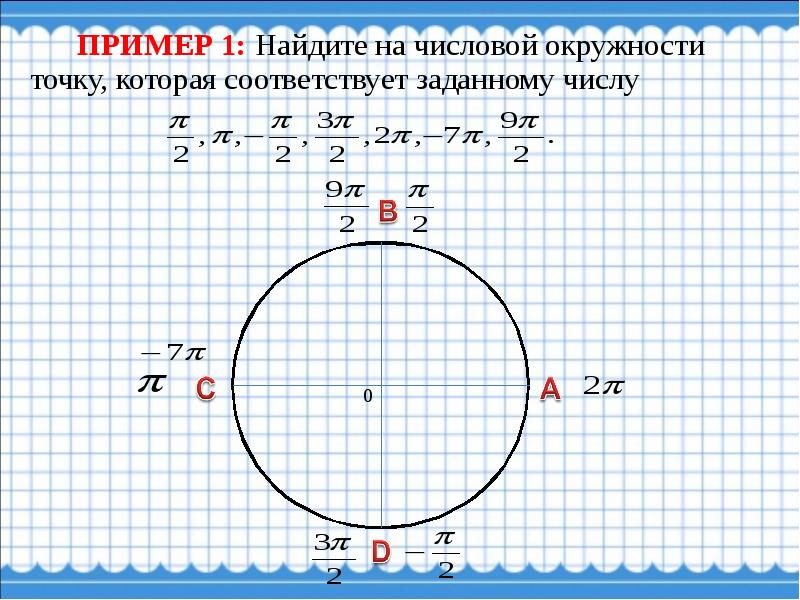
Задачи.
1) Найдите координаты точек .
2) Изобразите на числовой окружности дугу, описываемую движущейся точкой в течение промежутков времени
1. .
2. .
3) Отметьте на числовой окружности положения, которые занимает движущаяся точка в моменты времени
1. , где — целое число.
2. , где — целое число.
4) Расположите в порядке возрастания числа
5) Решите уравнения и неравенства (для этого не нужно знать тригонометрические формулы):
1. .
2. .
3. .
4. .
5. .
Тест. Числовая окружность
Будьте внимательны! У Вас есть 10 минут на прохождение теста.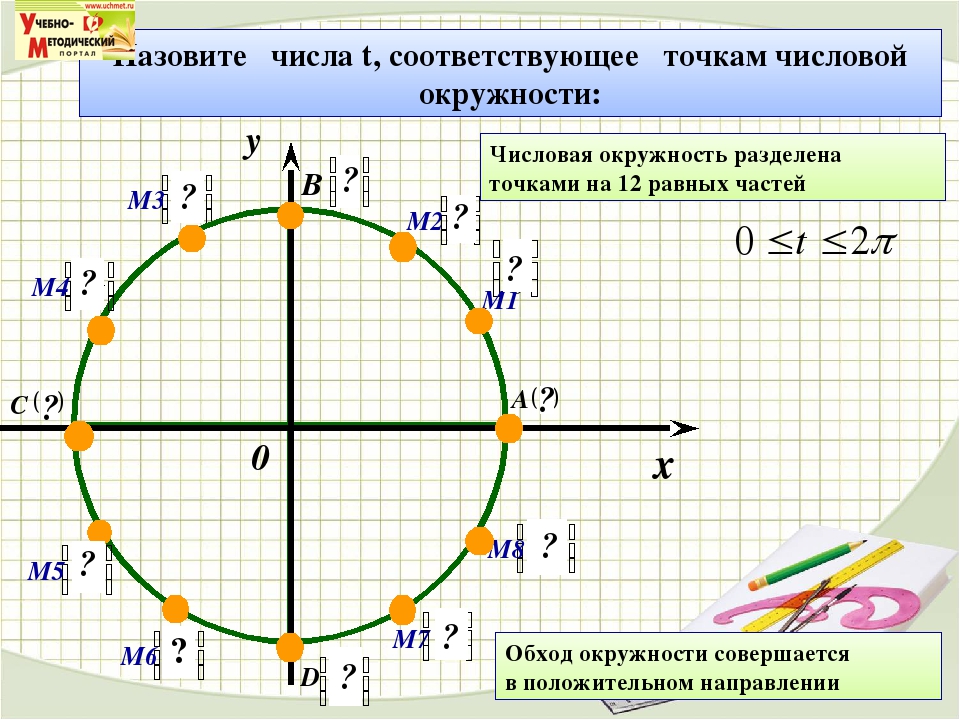
Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
Список вопросов теста
Вопрос 1
Определите, где на числовой окружности находятся точки, соответствующие числам:
Варианты ответов
Вопрос 2
Определите, где на числовой окружности находятся точки, соответствующие числам
Варианты ответов
Вопрос 3
Укажите семейство точек, которому на числовой окружности соответствует точка
Варианты ответов
Вопрос 4
Определите числа, которым соответствует на числовой окружности точка А:
Варианты ответов
Вопрос 5
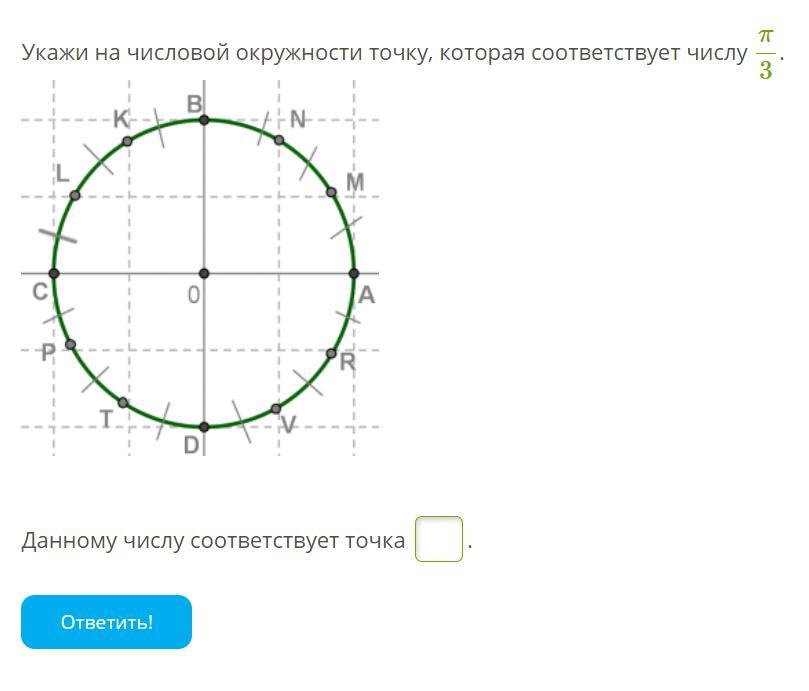
Найдите на числовой окружности точку, которая соответствует числу
.
Ответ запишите заглавной буквой латинского алфавита.
Вопрос 6
Найдите координаты точки числовой окружности
Варианты ответов
Вопрос 7
Существует ли на числовой окружности точка, ордината которой равна 1,2
Варианты ответов
Вопрос 8
Существует ли на числовой окружности точка, ордината которой равна 0,9
Варианты ответов
Вопрос 9
Определите знаки абсциссы и ординаты заданной точки
Варианты ответов
- абсцисса
- ордината
Вопрос 10
Найдите на числовой окружности точку, которая соответствует числу
.
Ответ запишите заглавной буквой латинского алфавита.
Окружность на координатной плоскости
☰
Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).
Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности
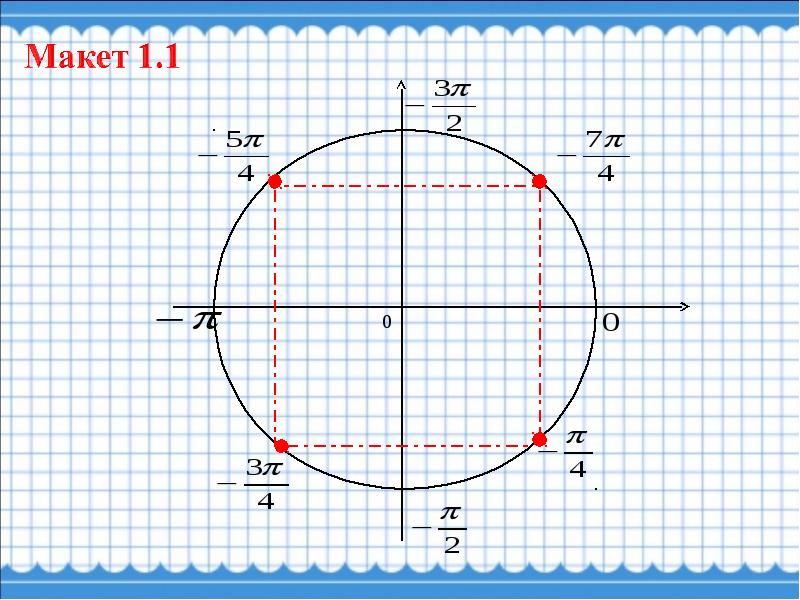
- четвертям — 0 или 2π, π/2, π, (2π)/3,
- серединам четвертей — π/4, (3π)/4, (5π)/4, (7π)/4,
- третям четвертей — π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.
На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности.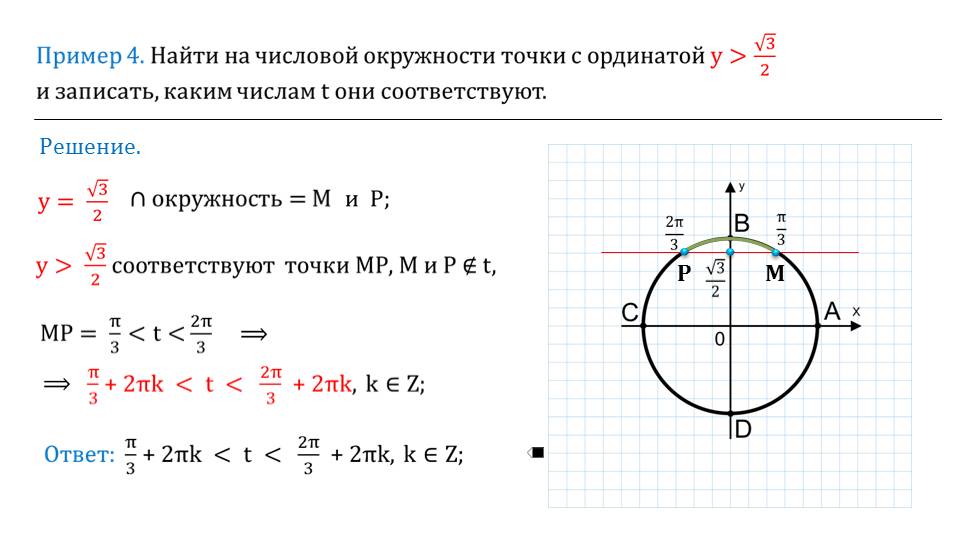
Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0).
Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1).
Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0).
Конец третьей четверти: D ((2π)/3) = D (0; -1).
Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого — это и есть координаты x и y точки окружности.
Четверть окружности составляет 90º. А половина четверти составляет 45º.
Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник.
Из теоремы Пифагора получаем уравнение x2 + y2 = 12. Поскольку x = y, а 12 = 1, то уравнение упрощается до x2 + x2 = 1. Решив его, получаем x = √½ = 1/√2 = √2/2.
Таким образом, координаты точки M1 (π/4) = M1 (√2/2; √2/2).
В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим:
M2 ((3π)/4) = M2 (-√2/2; √2/2)
M3 ((5π)/4) = M3 (-√2/2; -√2/2)
M4 ((7π)/4) = M4 (√2/2; -√2/2)
При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник.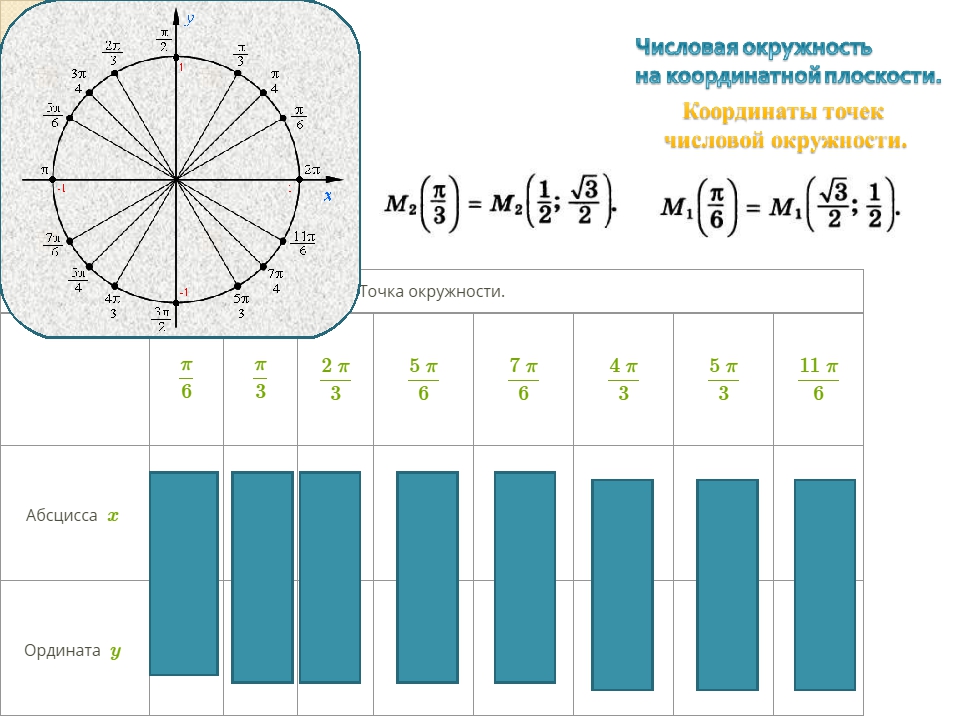
Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½.
Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет:
x2 + (½)2 = 12
x2 = 1 — ¼ = ¾
x = √3/2
Таким образом T1 (π/6) = T1 (√3/2; ½).
Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y. Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T2 (π/3) = T2 (½; √3/2).
Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2.
T3 ((2π)/3) = T3 (-½; √3/2)
T4 ((5π)/6) = T4 (-√3/2; ½)
T5 ((7π)/6) = T5 (-√3/2; -½)
T6 ((4π)/3) = T6 (-½; -√3/2)
T7 ((5π)/3) = T7 (½; -√3/2)
T8 ((11π)/6) = T8 (√3/2; -½)
Единичная окружность в тригонометрии
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка.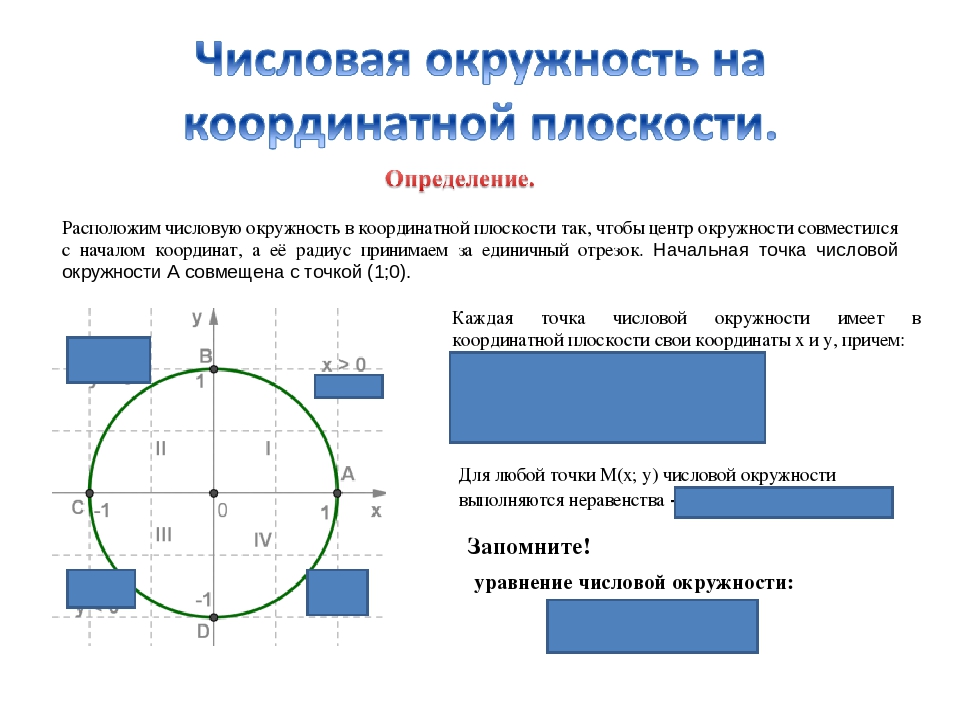
Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы.
2 = 1
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Для чего использовать единичную окружность
- определить синус, косинус, тангенс и котангенс угла
- найти значения тригонометрических функций для некоторых значений числового и углового аргумента
- вывести основные формулы тригонометрии
- вывести формулы приведения
- найти области определения и области значений тригонометрических функций
- определить периодичность тригонометрических функций
- определить четность и нечетность тригонометрических функций
- определить промежутки возрастания и убывания тригонометрических функций
- определить промежутки знакопостоянства тригонометрических функций
- применить радианное измерение углов
- найти значения обратных тригонометрических функций
- решить простейшие тригонометрические уравнения
- решить простейшие неравенства.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!
Цифры в кружке | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2460 | ① | Первая цифра в кружке | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ≈ |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
14159265 … число, известное как Pi 
Вы ходите по кругу диаметром 100 м. Как далеко вы прошли?
.. 
1415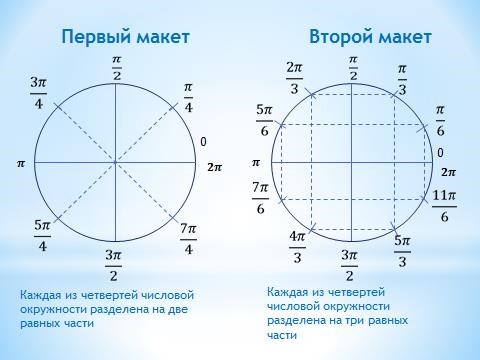
..
Выберите одного ребенка, который войдет в середину круга и пойдет первым.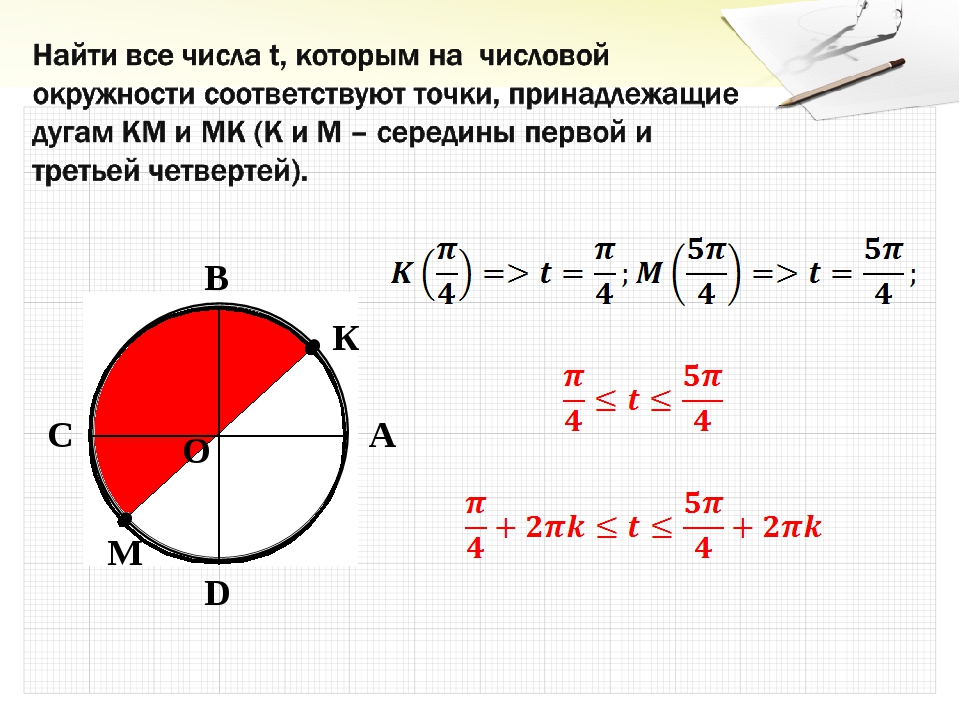
Отличный способ ввести счет для определенной цели, на один меньше, а также делает числа очень наглядными.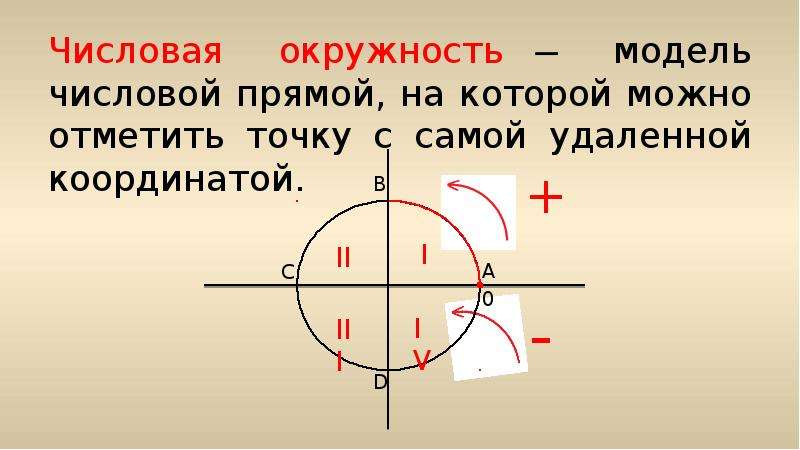
Вы можете заставить их держать растяжки или факелы, чтобы сделать его еще более захватывающим.
Когда дети научатся этому, можно переходить к нечетным числам. С нечетными числами дело в том, что вы получите «остаток» — нечетный.
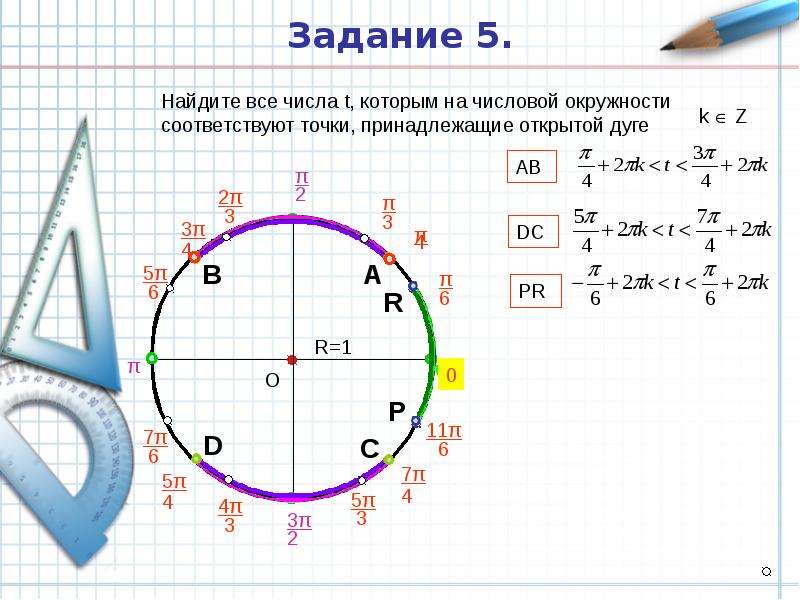
Вы можете узнать о его улучшениях в нашем продукте первого поколения в этой статье. 
