Содержание
Явление самоиндукции — урок. Физика, 9 класс.
Согласно правилу Ленца индукционный ток в замкнутом контуре всегда противодействует своим магнитным полем изменению внешнего магнитного потока, которое вызвало его появление.
Рассмотрим случай, когда явление электромагнитной индукции наблюдается при изменении силы тока, проходящего через катушку с большим количеством витков. Если причина возникновения индукционного тока состоит в возрастании тока, то индукционный ток своим магнитным полем будет противодействовать этому возрастанию.
Убедиться в этом можно на следующем опыте. Соберём цепь из источника тока и двух параллельных ветвей.
Одна из ветвей состоит из последовательно соединённых лампы \(1\) и катушки со стальным сердечником, а другая — из такой же лампы \(2\) и последовательно соединённого с ней резистора. Резистор имеет такое же сопротивление, как и провод катушки. При замыкании ключа лампа \(1\), включённая последовательно с катушкой, загорится позднее, чем лампа \(2\), соединённая с резистором.
При замыкании цепи сила тока нарастает от нуля до некоторого значения. Одновременно растёт и магнитный поток. При этом в катушке создаётся индукционный ток, направленный в соответствии с правилом Ленца противоположно основному току, то есть препятствующий его нарастанию.
В данном случае индукционный ток возник в цепи, которая содержит источник тока, и оказал воздействие на силу тока в этой цепи. Это явление называют явлением самоиндукции.
Самоиндукция — это явление возникновения индукционного тока в цепи при изменении протекающего по цепи тока.
Возникающий индукционный ток называют током самоиндукции.
На участке цепи, содержащий катушку, возник индукционный ток, который препятствовал нарастанию основного тока, создаваемого источником, поэтому лампа загорелась позже, чем лампа соединенная с резистором. Из этого следует, что индуктивность катушки превышает индуктивность резистора.
Индуктивность — это физическая величина, которую обозначают буквой L.
Индуктивность характеризует способность катушки препятствовать нарастанию силы тока.
Обрати внимание!
За единицу измерения индуктивности принят генри (Гн).
L=1 Гн
Различные катушки могут иметь разную индуктивность. Она зависит от:
- размеров и формы катушки;
- числа витков;
- наличия сердечника;
- материала, из которого изготовлен сердечник.
Чем большей индуктивностью обладает катушка, тем с большим запозданием будет загораться лампа.
Явление самоиндукции можно наблюдать и при размыкании цепи. Изменим цепь.
Параллельно источнику тока включены катушка и лампа. При размыкании цепи лампа, перед тем как погаснуть, ярко вспыхивает.
При отключении источника сила тока в цепи уменьшается от некоторого значения до нуля. Одновременно уменьшается и магнитный поток сквозь катушку. При этом в катушке появляется индукционный ток, который должен своим магнитным полем препятствовать уменьшению магнитного потока, то есть индукционный ток должен быть направлен так же, как и первоначальный ток. Поэтому лампа ярко вспыхивает.
Поэтому лампа ярко вспыхивает.
Явление самоиндукции учитывается во многих технических устройствах.
Пример:
если в электрическую цепь в качестве потребителя включены катушки с большой индуктивностью (например обмотки электродвигателя), то при размыкании цепи ток самоиндукции может достигать огромных значений, что в некоторых случаях приводит к возникновению искрового или дугового разряда в воздухе вблизи цепи.
Явление самоиндукции.Индуктивность. Энергия магнитного поля тока. Работа поля. Тесты, курсы по физике
Тестирование онлайн
Явление самоиндукции. Индуктивность. Основные понятия
Явление самоиндукции. Энергия магнитного поля
Явление самоиндукции
Мы уже изучили, что около проводника с током возникает магнитное поле. А также изучили, что переменное магнитное поле порождает ток (явление электромагнитной индукции). Рассмотрим электрическую цепь. При изменении силы тока в этой цепи произойдет изменение магнитного поля, в результате чего в этой же цепи возникнет дополнительный индукционный ток. Такое явление называется самоиндукцией, а ток, возникающий при этом, называется током самоиндукции.
Такое явление называется самоиндукцией, а ток, возникающий при этом, называется током самоиндукции.
Явление самоиндукции — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.
Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.
ЭДС самоиндукции определяется по формуле:
Явление самоиндукции подобно явлению инерции. Так же, как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет явления самоиндукции. Если в цепь, состоящую из двух параллельно подключенных к источнику тока одинаковых ламп, последовательно со второй лампой включить катушку, то при замыкании цепи первая лампа загорается практически сразу, а вторая с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока.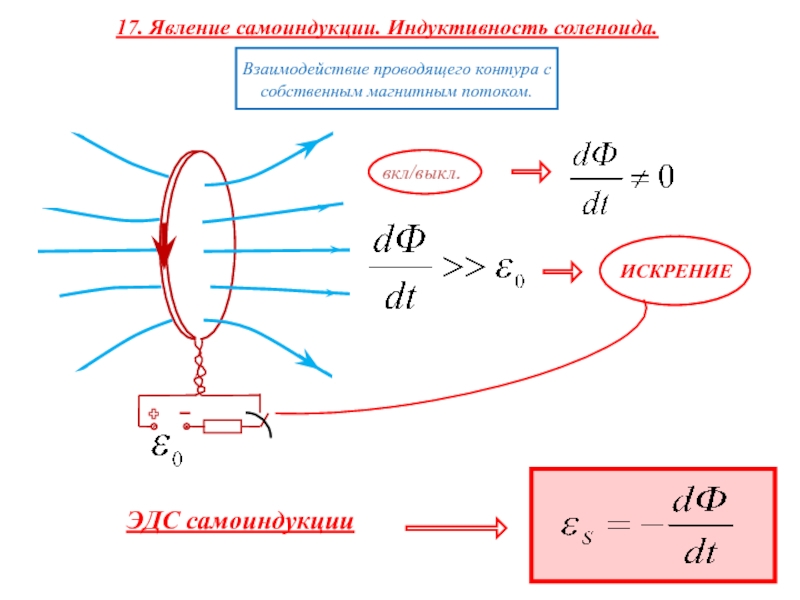 При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки очень часто перегорают при выключении света.
При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки очень часто перегорают при выключении света.
Энергия магнитного поля
Энергия магнитного поля контура с током:
Самоиндукция простыми словами: определение, формулы, примеры
Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.
Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.
Определение
Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.
В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.
Рис. 1. Магнитное поле катушки
Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.
Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.
Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.
Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.
Рис. 2. Явление самоиндукции
Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.
Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).
Рис. 3. Схема опыта с лампочками
Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.
На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.
График на рисунке 4 красноречиво объясняет эффект задержки.
Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности
Обратите внимание на нелинейность изменения силы тока по времени.
Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.
Рис. 5. Возникновение самоиндукции
Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.
В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.
Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.
Формулы
Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:
где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.
Индуктивность
Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.
Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.
Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.
Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.
Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.
Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.
Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.
Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.
Примеры использования на практике
Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.
Работает этот важный узел следующим образом:
- На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.

- Электрическая цепь резко обрывается специальным прерывателем.
- Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
- Искровой разряд зажигает топливную смесь, приводя в движение поршень.
В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.
Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.
В блоках питания электронной аппаратуры таким же способом убирают:
- шумы:
- пульсации;
- нежелательные частоты.
Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.
В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.
В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
Видео в помощь
Самоиндукция
Физика > Самоиндукция
Изучите явление самоиндукции – сила тока, значение, как возникает. Читайте о связи самоиндукции и закона Фарадея, взаимная индуктивность, схема катушки.
Индукцией именуют процесс, где электродвижущая сила индуцируется из-за перемен в магнитном потоке.
Задача обучения
- Охарактеризовать свойства индуктора.
Основные пункты
- В электронике индуктивность выступает характеристикой проводника, где перемены тока вызывают напряжение в самом проводнике и соседних – взаимная индуктивность.
- В законе Ленца написано, что меняющийся электрический ток сквозь цепь с индуктивностью индуцируется пропорционально напряжению, вступающим в сопротивление к изменению тока.
- Взаимная индуктивность – воздействие двух устройств на индицирование ЭДС. Перемена тока в одном индуцирует ЭДС во втором: ЭДС2 = -M ΔI1/Δt (M – взаимная индуктивность между двумя устройствами).
- Самоиндукция – эффект закона Фарадея индукции на себя. Наведенная ЭДС = — L ΔI/Δt.
- Прибор со значительной самоиндукцией – индуктор.
Термины
- Индуктор – пассивный прибор, вводящий индуктивность в электрическую цепь.

- Самоиндукция – соотношение напряжения и перемены тока.
- Взаимная индуктивность – соотношение напряжения в цепи и перемены тока в соседней.
Обзор
Индукцией именуют процесс, где электродвижущая сила индуцируется из-за перемены магнитного потока. В электронике это характеристика проводника, где изменение тока формирует напряжение, как в самом проводнике, так и в соседних. Этот эффект выплывает из двух фундаментальных наблюдений в физике: постоянный ток формирует стабильное магнитное поле и перемены в магнитном поле индуцируют напряжение в соседнем проводнике.
Взаимная индуктивность
Взаимная индуктивность возникает из-за закона индукции Фарадея от одного прибора к другому, вроде передачи энергии от первичной катушки к трансформатору. Ниже представлена схема взаимной индуктивности для катушек тока.
Катушки способны индуцировать ЭДС между собой в качестве неэффективного трансформатора. Взаимная индуктивность (М) указывает на эффективную связь. Перемены тока в первой катушке индуцируют ЭДС во второй
Когда геометрия приборов зафиксирована, то поток меняется переменным током. Поэтому следует заострить внимание на скорости перемены тока как главную причину индукции. В виде формулы:
(M – взаимная индуктивность между двумя устройствами). Минусовый знак выражает закона Ленца. Чем больше взаимная индуктивность M, тем эффективнее сцепление.
Мы наблюдаем здесь симметричность. Если изменить ток I2 во второй катушке, то индуцируем ЭДС1 в первой:
(М – то же самое, что и для обратного процесса). Трансформаторы перемещаются назад с той же эффективностью или взаимной индуктивностью М.
Возможно, что большая взаимная индуктивность не была желательным явлением. Нам хочется, чтобы у трансформатора наблюдалась подобная взаимная индуктивность. Однако, прибор вроде электрической сушилки способен создать опасную ЭДС на корпусе, если взаимная индуктивность между ним и катушками превышает норму. Чтобы уменьшить ее, нужно использовать противодействие катушкам.
Нагревательные катушки электрической сушилки можно проколоть так, чтобы их магнитные поля отменяли друг друга, что снизит уровень взаимной индуктивности
Самоиндукция
Существует и явление самоиндукции, когда индукция влияет на само устройство. К примеру, если ток в катушке увеличивается, то это повторяют поток и магнитное поле, создавая встречную ЭДС, которая сопротивляется уменьшению. Во многих устройствах наблюдается фиксированная геометрия, поэтому перемена потока полностью основывается на изменении тока. Электродвижущая сила в самоиндукции задается по формуле:
(L – самоиндукция устройства). Если мы замечаем значительную самоиндукцию, то сталкиваемся с индуктором.
Символ индуктора
Минусовый знак указывает на закон Ленца, то есть, ЭДС сопротивляется перемене тока. Чем больше самоиндукция, тем сильнее устройство сопротивляется любой перемене тока. К примеру крупная катушка с витками и железным сердечником обладает большой L и не позволит быстро изменить ток.
Соленоиды
Благодаря геометрии можно определить L соленоида и созданное магнитное поле. Однако поле часто формируется сложным, что создает дополнительные проблемы для вычисления. Обычно индуктивность – заданная величина, но в соленоиде все не так, потому что внутри него находится однородное поле. Формула:
Самоиндукция — это… Что такое Самоиндукция?
частный случай явления индукции токов (см. Индукция), а именно индукция тока в проводнике, вызываемая изменением силы тока, протекающего по этому проводнику. Это явление было замечено Фарадеем в 1834 г., три года спустя после его знаменитого открытия индукции токов. Фарадей нашел, что всякое изменение силы тока в проводнике сопровождается возникновением особой электродвижущий силы, которая стремится возбудить в этом проводнике ток, противодействующий происходящему изменению главного тока. Так, при увеличении силы тока в проводнике появляется в нем электродвижущая сила, вследствие которой происходит замедление в возрастании силы тока; при уменьшении силы тока появляется электродвижущая сила, от которой ослабление тока становится также медленнее. Такая электродвижущая сила, возникающая в проводнике при изменении силы тока в нем, называется электродвижущей силой С., а ток, возбуждаемый ею, носит название экстратока. — С. наблюдается особенно хорошо, когда в цепи тока находится катушка, и еще лучше, когда внутри этой катушки помещен железный сердечник. В последнем случае при замыкании цепи ток появляется сначала слабый, а затем только в течение некоторого промежутка времени он, непрерывно возрастая, достигает своей наибольшей силы. При размыкании цепи С. усиливает искру, являющуюся в месте разрыва цепи, и может вызвать весьма сильное физиологическое действие на организм человека или животного, когда тело человека или животного введено в цепь тока. Закон, которому подчинено явление С., тот же, какой управляет вообще явлениями индукции токов. Самоиндукция происходит вследствие того, что при изменении силы тока изменяется магнитный поток, пронизывающий контур этого тока и возбуждающийся самим этим током. Электродвижущая сила С., являющаяся в какой-либо момент времени, равна скорости изменения силы этого магнитного потока, взятой с обратным знаком и соответствующей рассматриваемому моменту времени, или иначе — она равна взятому с обратным знаком и рассчитанному на единицу времени изменению числа линий магнитной индукции, пронизывающих контур данного тока и возбуждающихся этим же током (см. Магнитизм). Обозначая чрез i силу тока, мы можем силу магнитного потока, пронизывающего контур этого тока и возбуждаемого последним, выразить чрез Li. Величина L, зависящая от формы и размеров контура тока, от свойства окружающей среды и в некоторых случаях (когда проводник приготовлен из сильно магнитного металла) от магнитных свойств проводника, носит название коэффициента С. цепи. Согласно вышеприведенному закону, электродвижущая сила С. ε выражается через
ε = d(Li)/dt. . . (1)
и в случае, когда находящиеся в цепи проводники неизменны, т. е. сохраняют свои размеры и форму, а также магнитные свойства этих проводников остаются одинаковыми при различных силах тока и окружающая среда не подвергается никакому изменению, электродвижущая сила С. вычисляется по формуле
ε = —L(di/dt). . . (2)
т. е. при данных условиях коэффициент С. имеет постоянную величину. Принимая во внимание закон Ома и формулу (2), мы получаем для силы тока i, являющегося в какой-либо цепи, которой сопротивление R и коэффициент С. L, от электродвижущей силы Е, выражение
i = [(Е — L)(di/dt)]/R. . . (3)
Отсюда при условии, что Е постоянна, т. е. что ток получается от источника, обладающего постоянной электродвижущей силой (элемент, гальваническая батарея или аккумуляторы), при помощи интегрального исчисления находим
i = (Е/R)[1 — e-(R/L)t].. . (4).
Здесь е обозначает основание Неперовых логарифмов, a t — время, протекшее от момента замыкания цепи до момента, для которого мы определяем силу i. Из формулы (4) видно, что ток достигает своей наибольшей силы Е/R только через бесконечно большое время, но на самом деле величина e—(R/L)t очень быстро становится ничтожно малой и притом тем быстрее, чем больше R и меньше L. Однако для большой величины L, как это будет в том случае, когда в цепи находится электромагнит, продолжительность установления тока может быть немалая. Она может измеряться даже минутами. Когда в цепи находится источник тока, которого электродвижущая сила изменяется гармонически n раз в единицу времени (в секунду), т. е. выражается через Е = Е0Sin2πnt, то для получающегося при этом переменного тока теория дает (см. Переменный ток) формулу
i = Е0(Sin2πnt — θ)/(√[R2 +4π2n2L2]).. . (5)
в которой tgθ = 2πnL/R. Из формулы (5) видно, что в данном случае для опроделения силы тока необходимо знать, кроме величины электродвижущей силы и сопротивления цепи, еще и коэффициент С. цепи. При таком переменном токе кажущееся сопротивление, т. е. величина √(R2 +4π2n2L2) при большой величине L может быть значительно больше R, т. е. того сопротивления, какое оказывает цепь току постоянному. Определение величины L производится в большей части случаев непосредственно путем опыта, так как теория дает возможность только для немногих проводников найти формулу для L. Так, напр., для очень длинной прямой катушки, состоящей из n оборотов, расположенных в одном слое, теоретически выводится формула
L = 4π2(n2/l)S.
В этой формуле S обозначает поперечное сечение катушки. Для длинной прямой катушки, состоящей из n оборотов, расположенных в нескольких слоях, может быть применена формула
L =n2r2/(0,01844r + 0,035l + 0,031d)
в которой r обозначает средний радиус оборотов, l — длину катушки, d — толщину обмотки ее. Для цилиндрического проводника, приготовленного из немагнитного металла и имеющего длину l, а диаметр d, коэффициент С. вычисляется по формуле
L = 2l[log(4l/d) — 0,75]
когда ток распространяется равномерно по всей массе проводника, и по формуле
L = 2l[log(4l/d) — 1]
— когда ток ограничивается только поверхностным слоем проводника. Последняя формула особенно важна в теории вибратора Гертца (см. Гертца явления). Соответственно абсолютной электромагнитной (С. G. S.) системе единиц величина L выражается в сантиметрах. Практическая единица для коэффициентов С., называемая генри или также квадрантом, равняется 109 см.
Опытное сравнение коэффициентов С. двух проводников может быть произведено по способу, аналогичному способу сравнения сопротивлений проводников при помощи мостика Витстона. Составляется цепь по схеме мостика Витстона, при чем в две соседние ветви четырехугольника этой схемы помещаются сравниваемые проводники, в две другие ветви ящики сопротивлений [Образцы сопротивлений обыкновенно принимаются неиндуктивными, т. е полагают, что коэффициенты самоиндукции их равны 0. Вообще у проволоки, сложенной вдвое, можно считать коэффициент С. равным нулю, хотя это не вполне строго.], в диагональную ветвь помещается вторичная обмотка катушки Румкорфа, а в другую диагональную ветвь, т. е. в самый мостик, вводится телефон. Изменением сопротивлений в двух ветвях четырехугольника достигают наконец того, что телефон перестает издавать звуки. В этом случае должно быть L1:L2 = R3:R4. Здесь L1 и L2 обозначают коэффициенты С. проводников, находящихся в ветвях 1 и 2, R3 и R4 — сопротивления ветвей 3 и 4. Об опытном определении абсолютной величины коэффициента С. см. в подробных курсах физики, напр. в соч. И. Боргмана «Основания учения об электрических и магнитных явлениях» (т. II).
И. Боргман.
Что такое самоиндукция простыми словами | Энергофиксик
Здравствуйте уважаемые посетители и гости моего канала! Мы продолжаем с вами говорить просто о сложных вещах, и сегодня пойдет речь о таком любопытном физическом явлении как самоиндукция.
Явление самоиндукции
Явление самоиндукции
Определение
Итак, давайте для начала вспомним (узнаем) определение самоиндукции:
Индукция – это явление возникновения ЭДС индукции в токопроводящем контуре при изменении проходящего по контуру тока. Понятно? Если честно, то не очень. Давайте разбираться что такое самоиндукция по-простому.
Разбираемся по-простому
Итак, давайте начнем с поиска аналогии в окружающем мире: Представьте товарный состав, составленный из бочек наполненных, например, нашим черным золотом (нефтью). Вы прекрасно знаете, что товарный состав не может сразу набрать максимальную скорость и в первое время большая часть энергии локомотива тратится на преодоление инерции состава (набор кинетической энергии) и незначительная часть на преодоление трения.
Точно так же и при торможении, состав не может остановиться мгновенно, ему требуется время для того, чтобы израсходовать запасенную кинетическую энергию.
Товарный состав
Товарный состав
Теперь давайте от железной дороги перейдем к рассмотрению электрической цепи.
Аналогичные процессы протекают в замкнутой цепи при подаче и отключении тока.
Для лучшего понимания давайте рассмотрим вот такую схему экспериментальной установки Джозефа Генри, где катушка и есть «товарный состав».
Схема экспериментальной установки Джозефа Генри
Схема экспериментальной установки Джозефа Генри
Если собрать такую установку и поэкспериментировать, то можно заметить, что одна из лампочек (та, перед которой в цепи расположена катушка) загорается медленнее, чем другая.
Экспериментальная установка в действии
Экспериментальная установка в действии
И все вот почему:
Итак, ключ замкнулся.
По цепи начинает протекать ток.В этот момент в катушке начинает формироваться электромагнитное поле и чем больший ток протекает, тем большее поле формируется.
Получается, что катушка находится в изменяющемся магнитном поле, а это значит, что пронизывающий изменяющий магнитный поток формирует ЭДС индукции и соответственно индукционный ток. А, согласно правилу Ленца, этот сформированный ток будет направлен так, чтобы своим собственным магнитным полем воспрепятствовать изменению магнитного потока, который пронизывает катушку.
То есть проще говоря сформированный ток будет направлен против тока от источника питания, тем самым оказывая ему сопротивление (также как инерция вагонов оказывает сопротивление локомотиву).
При подключении источника тока, ток в цепи устанавливается не мгновенно
При подключении источника тока, ток в цепи устанавливается не мгновенно
А это означает, что сила тока достигнет своего максимального значения не сразу.
Теперь давайте рассмотрим ситуацию, когда ключ размыкается.
В этой ситуации ток в цепи начинает уменьшаться, что приводит к уменьшению магнитного потока через катушку. Это также порождает ЭДС самоиндукции и индукционный ток, только в этом случае индукционный ток направлен в ту же сторону что и ток в цепи, что приводит к замедлению убывания тока в цепи.
То есть ток в цепи не может пропасть мгновенно (состав не остановится сразу), так как есть запасенная энергия в магнитном поле, которую нужно израсходовать (погасить кинетическую энергию состава торможением).
При выключении источника тока, то в цепи пропадает не мгновенно
При выключении источника тока, то в цепи пропадает не мгновенно
Таким образом при любом изменении тока в проводнике формируется электромагнитная индукция, которая формирует индукционный ток текущий таким образом, чтобы воспрепятствовать любому изменению собственного тока в проводнике. Это и есть самоиндукция – частный случай электромагнитной индукции.
Понравилась статья, тогда палец вверх, репост и лайк! Спасибо, что дочитали до конца!
Кто впервые наблюдал явление самоиндукции. Самоиндукция. Энергия самоиндукции, индуктивность
«Физика — 11 класс»
Самоиндукция.
Если по катушке идет переменный ток, то:
магнитный поток, пронизывающий катушку, меняется во времени,
а в катушке возникает ЭДС индукции .
Это явление называют самоиндукцией
.
По правилу Ленца при увеличении тока напряженность вихревого электрического поля направлена против тока, т.е. вихревое поле препятствует нарастанию тока.
При уменьшения тока напряженность вихревого электрического поля и ток направлены одинаково, т.е.вихревое поле поддерживает ток.
Явление самоиндукции подобно явлению инерции в механике.
В механике:
Инерция приводит к тому, что под действием силы тело приобретает определенную скорость постепенно.
Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила.
В электродинамике:
При замыкании цепи за счет самоиндукции сила тока нарастает постепенно.
При размыкании цепи самоиндукция поддерживает ток некоторое время, несмотря на сопротивление цепи.
Явление самоиндукции выполняет очень важную роль в электротехнике и радиотехнике.
Энергия магнитного поля тока
По закону сохранения энергии энергия магнитного поля
, созданного током, равна той энергии, которую должен затратить источник тока (например, гальванический элемент) на создание тока.
При размыкании цепи эта энергия переходит в другие виды энергии.
При замыкании
цепи ток нарастает.
В проводнике появляется вихревое электрическое поле, действующее против электрического поля, созданного источником тока.
Чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля.
Эта работа идет на увеличение энергии магнитного поля тока.
При размыкании
цепи ток исчезает.
Вихревое поле совершает положительную работу.
Запасенная током энергия выделяется.
Это обнаруживается, например, по мощной искре, возникающей при размыкании цепи с большой индуктивностью.
Энергия магнитного поля, созданного током, проходящим по участку цепи с индуктивностью L, определяется по формуле
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Плотность энергии магнитного поля (т. е. энергия единицы объема) пропорциональна квадрату магнитной индукции: w м ~ В 2 ,
аналогично тому как плотность энергии электрического поля пропорциональна квадрату напряженности электрического поля w э ~ Е 2 .
При всяком изменении тока в катушке (или вообще в проводнике) в ней самой индуктируется
ЭДС самоиндукции.
Когда ЭДС в катушке индуктируется за счет изменения собственного магнитного потока, величина этой ЭДС зависит от скорости изменения тока. Чем больше скорость изменения тока, тем больше ЭДС самоиндукции.
Величина ЭДС самоиндукции зависит также от числа витков катушки, густоты их намотки и размеров катушки. Чем больше диаметр катушки, число ее витков и густота намотки, тем больше ЭДС самоиндукции.
Эта зависимость ЭДС самоиндукции от скорости изменения тока в катушке, числа ее витков и размеров имеет большое значение в
электротехнике.
Направление ЭДС самоиндукции определяется по закону Ленца. ЭДС самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока.
Иначе говоря, убывание тока в катушке влечет за собой появление ЭДС самоиндукции, направленной по направлению тока, т. е. препятствующей его убыванию. И, наоборот, при возрастании тока в катушке возникает ЭДС самоиндукции, направленная против тока, т. е. препятствующая его возрастанию.
Не следует забывать, что если ток в катушке не изменяется, то никакой ЭДС самоиндукции
не возникает.
Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку с железным сердечником, так как
железо значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции при его изменении.
Индуктивность
Итак, нам известно, что величина ЭДС самоиндукции в катушке, кроме скорости изменения тока в ней, зависит
также
от размеров катушки и числа ее витков.
Следовательно, различные по своей конструкции катушки при одной и той же скорости изменения тока способны индуктировать в себе различные по величине ЭДС самоиндукции.
Чтобы различать катушки между собой по их способности индуктировать в себе ЭДС самоиндукции, введено понятие
индуктивности катушек
, или коэфициента самоиндукции.
Индуктивность катушки есть величина, характеризующая свойство катушки индуктировать в себе ЭДС самоиндукции.
Индуктивность данной катушки есть величина постоянная, не зависящая как от силы проходящего по ней тока, так и от скорости его изменения.
Генри
— это индуктивность такой катушки (или проводника), в которой при изменении силы тока на 1 ампер в 1 секунду возникает ЭДС самоиндукции в 1 вольт.
На практике иногда нужна катушка (или обмотка), не обладающая индуктивностью. В этом случае провод наматывают на катушку, предварительно сложив его вдвойне. Такой способ намотки называется
бифилярным.
ЭДС взаимоиндукции
Итак, мы знаем, что ЭДС индукции в катушке можно вызвать и не перемещая в ней электромагнит, а изменяя лишь ток в его обмотке.
Но что чтобы вызвать ЭДС индукции в одной катушке за счет изменения тока в другой,
совершенно не обязательно вставлять одну из них внутрь другой, а можно расположить их рядом
И в этом случае при изменении тока в одной катушке возникающий переменный магнитный поток будет пронизывать (пересекать) витки другой катушки и вызовет в ней ЭДС.
Взаимоиндукция дает возможность связывать между собой посредством магнитного поля различные электрические цепи. Такую связь принято называть
индуктивной связью.
Величина ЭДС взаимоиндукции зависит прежде всего от того, с какой скоростью изменяется ток в первой катушке
. Чем быстрее изменяется в ней ток, тем создается большая ЭДС взаимоиндукции.
Кроме того, величина ЭДС взаимоиндукции зависит от величины индуктивности обеих катушек и от их взаимного расположения, а также от
магнитной проницаемости окружающей среды.
Следовательно, различные по своей индуктивности и взаимному расположению катушки и в различной среде способны вызывать одна в другой различные по величине ЭДС взаимоиндукции.
Чтобы иметь возможность различать между собой различные пары катушек по их способности взаимно индуктировать ЭДС, введено понятие о
взаимоиндуктивности
или коэффициенте взаимоиндукции.
Обозначается ся взаимоиндуктивность буквой М. Единицей ее измерения, так же как и индуктивности, служит генри.
Генри — это такая взаимоиндуктивность двух катушек, при которой изменение тока в одной катушке на 1 ампер в 1 секунду вызывает в другой катушке ЭДС взаимоиндукции, равную 1 вольту.
На величину ЭДС взаимоиндукции влияет магнитная проницаемость окружающей среды.
Чем больше магнитная проницаемость среды, по которой замыкается переменный магнитный поток, связывающий катушки, тем сильнее индуктивная связь катушек и больше величина ЭДС взаимоиндукции.
На явлении взаимоиндукции основана работа
такого важного электротехнического устройства, как трансформатор.
Принцип действия трансформатора
Принцип действия трансформатора основан на и заключается в следующем.
На железный сердечник наматывают две обмотки, одну из них соединяют с источником переменного тока, а другую — с потребителем тока (сопротивлением).
Обмотка, соединенная с источником переменного тока, создает в сердечнике переменный магнитный поток, который в другой обмотке индуктирует ЭДС.
Обмотку, соединенную с источником переменного тока, называют первичной, а обмотку, к которой присоединяется потребитель, — вторичной.
Но так как переменный магнитный поток пронизывает одновременно обе обмотки, то в каждой из них индуктируются переменные ЭДС.
Величина ЭДС каждого витка, как и ЭДС всей обмотки, зависит от величины магнитного потока, пронизывающего виток, и скорости его изменения.
Скорость изменения магнитного потока зависит исключительно от частоты
переменного тока, постоянной для данного тока. Постоянна для данного трансформатора также и величина магнитного потока. Поэтому в рассматриваемом трансформаторе ЭДС в каждой обмотке зависит только от количества витков в ней.
Отношение первичного напряжения ко вторичному равно отношению чисел витков первичной и вторичной обмоток. Это отношение называется .
Если к одной из обмоток трансформатора подано напряжение сети, то с другой обмотки будет снято напряжение, большее или меньшее напряжения сети во столько раз, во сколько раз больше или меньше количество витков вторичной обмотки.
Если со вторичной обмотки снимается напряжение, большее, чем поданное к первичной обмотке, то такой трансформатор называется
повышающим.
Наоборот, если со вторичной обмотки снимается напряжение, меньше первичного, то такой трансформатор называется
понижающим.
Каждый трансформатор может быть использован как повышающий и как понижающий.
Коэффициент трансформации обычно указывается в паспорте трансформатора как отношение высшего напряжения к низшему, т. е. он всегда больше единицы.
Явление самоиндукции
Если по катушке идет переменный ток, то магнитный поток, пронизы-вающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет переменный ток. Это явление называют самоиндукцией
.
При самоиндукции проводящий контур играет двоякую роль: по нему протекает ток, вызывающий индукцию, и в нем же появляется ЭДС индукции. Изменяющееся магнитное поле индуцирует ЭДС в том самом проводнике, по которому течет ток, создающий это поле.
В момент нарастания тока напряженность вихревого электрического поля в соответствии с правилом Ленца направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
Это приводит к тому, что при замыкании цепи, содержащей источник постоянной ЭДС, определенное значение силы тока устанавливается не сразу, а постепенно с течением времени (рис. 9). С другой стороны, при отключении источника ток в замкнутых контурах прекращается не мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника, так как изменение тока и его магнитного поля при отключении источника происходит очень быстро.
Явление самоиндукции можно наблюдать на простых опытах. На рисунке 10 показана схема параллельного включения двух одинаковых ламп. Одну из них подключают к источнику через резистор R
, а другую — последовательно с катушкой L
с железным сердечником. При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения.
Появление ЭДС самоиндукции при размыкании можно наблюдать на опыте с цепью, схематически показанной на рисунке 11. При размыкании ключа в катушке L
возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальванометр течет ток (штриховая стрелка), направленный против начального тока до размыкания (сплошная стрелка). Причем сила тока при размыкании цепи превосходит силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции E
is больше ЭДС E
батареи элементов.
Индуктивность
Величина магнитной индукции B
, создаваемой током в любом замкнутом контуре, пропорциональна силе тока. Так как магнитный поток Ф
пропорционален В
, то можно утверждать, что
\(~\Phi = L \cdot I\) ,
где L
– коэффициент пропорциональности между током в проводящем контуре и созданным им магнитным потоком, пронизывающим этот контур. Величину L называют индуктивностью контура или его коэффициентом самоиндукции.
Используя закон электромагнитной индукции, получим равенство:
\(~E_{is} = — \frac{\Delta \Phi}{\Delta t} = — L \cdot \frac{\Delta I}{\Delta t}\) ,
Из полученной формулы следует, что
индуктивность
– это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Индуктивность подобно электроемкости, зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Единицу индуктивности в СИ называют генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В:
1 Гн = 1 В / (1 А/с) = 1 В·с/А = 1 Ом·с
Энергия магнитного поля
Найдем энергию, которой обладает электрический ток в проводнике. Согласно закону сохранения энергии энергия тока равна той энергии, которую должен затратить источник тока (гальванический элемент, генератор на электростанции и др.) на создание тока. При прекращении тока эта энергия выделяется в той или иной форме.
Энергия тока, о которой сейчас пойдет речь, совсем иной природы, чем энергия, выделяемая постоянным током в цепи в виде теплоты, количество которой определяется законом Джоуля-Ленца.
При замыкании цепи, содержащей источник постоянной ЭДС, энергия источника тока первоначально расходуется на создание тока, т. е. на приведение в движение электронов проводника и образование связанного с током магнитного поля, а также отчасти на увеличение внутренней энергии проводника, т.е. на его нагревание. После того как установится постоянное значение силы тока, энергия источника расходуется исключительно на выделение теплоты. Энергия тока при этом уже не изменяется.
Выясним теперь, почему же для создания тока необходимо затратить энергию, т.е. необходимо совершить работу. Объясняется это тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля, которое создается в проводнике благодаря источнику тока. Для того чтобы сила тока стала равной I
, источник тока должен совершить работу против сил вихревого поля. Эта работа и идет на увеличение энергии тока. Вихревое поле совершает отрицательную работу.
При размыкании цепи ток исчезает и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обнаруживается по мощной искре, возникающей при размыкании цепи с большой индуктивностью.
Найдем выражение для энергии тока I
L
.
Работа А
, совершаемая источником с ЭДС E
за малое время Δt
, равна:
\(~A = E \cdot I \cdot \Delta t\) . (1)
Согласно закону сохранения энергии эта работа равна сумме приращения энергии тока ΔW
m и количества выделяемой теплоты \(~Q = I^2 \cdot R \cdot \Delta t\):
\(~A = \Delta W_m + Q\) .2}{2 \cdot \mu_0}\) .
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока. Плотность энергии магнитного поля пропорциональна квадрату магнитной индукции.
Литература
- Жилко В.В. Физика: Учеб. пособие для 10-го кл. общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, А.В. Лавриненко, Л.Г. Маркович. – Мн.: Нар. асвета, 2001. – 319 с.
- Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. – М.: Дрофа, 2005. – 476 с.
Магнитное поле
контура, в котором сила тока изменяется,
индуцирует ток не только в других
контурах, но и в себе самом. Это
явление получило название самоиндукции.
Опытным путём
установлено, что магнитный поток вектора
магнитной индукции поля, создаваемого
текущим в контуре током, пропорционален
силе этого тока:
где L– индуктивность
контура. Постоянная характеристика
контура, которая зависит от его формы
и размеров, а так же от магнитной
проницаемости среды, в которой находится
контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время
dtток в контуре изменится
наdI, то магнитный поток,
связанный с этим током, изменится наdФ
=LdIв результате чего в
этом контуре появится ЭДС самоиндукции:
Знак минус показывает, что ЭДС
самоиндукции (а, следовательно, и ток
самоиндукции) всегда препятствует
изменению силы тока, который вызвал
самоиндукцию.
Наглядным
примером явления самоиндукции служат
экстратоки замыкания и размыкания,
возникающие при включении и выключении
электрических цепей, обладающей
значительной индуктивностью.
Энергия магнитного поля
Магнитное поле
обладает потенциальной энергией, которая
в момент его образования (или изменения)
пополняется за счёт энергии тока в цепи,
совершающего при этом работу против
ЭДС самоиндукции, возникающей вследствие
изменения поля.
Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС
самоиндукциии токIможно считать
постоянными, равняется:
.
(5)
Знак минус указывает, что
элементарная работа совершается током
против ЭДС самоиндукции. Чтобы определить
работу при изменении тока от 0 до I,
проинтегрируем правую часть, получим:
.
(6)
Эта работа численно равна
приросту потенциальной энергии ΔW п магнитного поля, связанного с этой
цепью, т.е.A= -ΔW п.
Выразим энергию магнитного
поля через его характеристики на примере
соленоида. Будем считать, что магнитное
поле соленоида однородно и в основном
расположено внутри его. Подставим в (5)
значение индуктивности соленоида,
выраженное через его параметры и значение
силы тока I, выраженное
из формулы индукции магнитного поля
соленоида:
, (7)
где N – общее число витков
соленоида; ℓ – его длина; S – площадь
сечения внутреннего канала соленоида.
, (8)
После подстановки имеем:
Разделив обе части на V,
получим объёмную плотность энергии
поля:
(10)
или, с учётом, что
получим,
.
(11)
Переменный ток
2.1 Переменный ток и его основные характеристики
Переменным
называется ток, изменяющийся с течением
времени и по величине и по направлению.
Примером переменного тока может служить
потребляемый промышленный ток. Этот
ток является синусоидальным, т.е.
мгновенное значение его параметров
меняются со временем по закону синуса
(или косинуса):
i
= I 0 sinωt,
u =
U 0 sin(ωt
+ φ 0). (12)
Переменный
синусоидальный ток можно получить, если
вращать рамку (контур) с постоянной
скоростью
в однородном
магнитном поле с индукцией B
(рис.5). При этом магнитный поток,
пронизывающий контур, изменяется по
закону
где S– площадь
контура, α = ωt– угол
поворота рамки за время t. Изменение
потока приводит к возникновению ЭДС
индукции
, (17)
направление которой определяется
по правилу Ленца.
Если
контур замкнут (рис.5), то по нему идёт
ток:
.
(18)
График изменения электродвижущей
силыи индукционного токаi
представлен на рис.6.
Переменный
ток характеризуется периодом Т, частотой
ν = 1/Т, циклической частотой
и фазой φ = (ωt
+ φ 0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
Для
характеристики переменного тока вводятся
понятия действующего (эффективного)
значения тока и напряжения. Эффективным
значением силы переменного тока
называется сила такого постоянного
тока, который выделяет в данном проводнике
столько же тепла за время одного периода,
сколько выделяет тепла и данный переменный
ток.
,
. (13)
Приборы, включенные в цепь
переменного тока (амперметр, вольтметр),
показывают эффективные значения тока
и напряжения.
Мы уже изучили, что около проводника с током возникает магнитное поле. А
также изучили, что переменное магнитное поле порождает ток (явление
электромагнитной индукции). Рассмотрим электрическую цепь. При изменении силы
тока в этой цепи произойдет изменение магнитного поля, в результате чего в этой
же цепи возникнет дополнительный индукционный ток
. Такое явление
называется самоиндукцией
, а ток, возникающий при этом, называется
током самоиндукции
.
Явление самоиндукции
— это возникновение в проводящем контуре ЭДС,
создаваемой вследствие изменения силы тока в самом контуре.
Индуктивность контура
зависит от его формы и размеров, от магнитных
свойств окружающей среды и не зависит от силы тока в контуре.
ЭДС самоиндукции определяется по формуле:
Явление самоиндукции подобно явлению
инерции . Так же, как в механике нельзя мгновенно остановить движущееся тело,
так и ток не может мгновенно приобрести определенное значение за счет явления
самоиндукции. Если в цепь, состоящую из двух параллельно подключенных к
источнику тока одинаковых ламп, последовательно со второй лампой включить
катушку, то при замыкании цепи первая лампа загорается практически сразу, а
вторая с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС
самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный
ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз
превысить внешнюю ЭДС. Поэтому электрические лампочки очень часто перегорают при
выключении света.
САМОСТОЯТЕЛЬНАЯ | |||
| Собственная индукция — это явление, при котором изменение электрического тока в Катушка создает наведенную ЭДС в самой катушке. | |||
| МАТЕМАТИЧЕСКАЯ ПРЕДСТАВИТЕЛЬСТВО: | |||
| Собственная наведенная ЭДС в катушке прямо пропорциональна скорости изменения электрический ток в катушке.т.е. | |||
Emf a Или ЭДС Где, | |||
| САМ ИНДУКТИВНОСТЬ | |||
| Собственная индуктивность катушки определяется как отношение самоиндуцированной ЭДС к скорость изменения тока в катушке. | |||
Самостоятельная | |||
Обозначается Единица себя | |||
| ГЕНРИ | |||
| Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com | |||
Я 1 генри = | |||
ПОЯСНЕНИЕ | |||
Рассмотреть | |||
| Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com | |||
Персонализированная обучающая платформа для учащихся K6-K12
Бесплатная Персонализированная обучающая платформа для студентов
Simply Science — это бесплатная персонализированная платформа для обучения детей в возрасте от 6 до 12 классов на основе STEM.Мы — веб-сайт открытого обучения, который побуждает детей понимать концепции и логику в удобном для них темпе, предлагая помощь с помощью интерактивной навигации. Развивайте способности решения проблем, творческий подход к дизайну, логику и наблюдательность, не выходя из дома, бесплатно!
Обучение на основе тем
Наш контент создан специально для привлечения маленьких умов и их любопытства. Разделенные на темы, вы можете выбрать интересующую вас тему и просто узнать все, что вы хотели знать о ней.Упорядоченный, умный и интерактивный с помощью примеров, аналогий и моделирования, Simply Science гарантирует, что вы приложите максимум усилий для мышления!
Знайте свой IQ и SQ
Оцените свою способность обрабатывать информацию. Применяйте рассуждения и науку с помощью быстрого бесплатного теста IQ и SQ. Определите свои сильные и слабые стороны и сосредоточьтесь на своих интересах, чтобы построить свой научный коэффициент, который пробуждает ваше любопытство и облегчает изучение STEM. Наши IQ и SQ указывают на формирующую оценку по естествознанию и математике, которая может продвинуть вас вперед и раскрыть новый потенциал.
Обучение с помощью технологий
Раскройте науку, математику и их загадки с помощью наших уникальных технологий, основанных на исследованиях на основе тем. Отправляйтесь в новый мир с нашими темами полного погружения, наполненными забавными, увлекательными видео, викторинами и персонализированной лентой контента.
Лучшая платформа для внеклассных занятий STEM для учащихся
В то время как формальное школьное и институциональное обучение фокусируется на языках, когнитивном развитии и многих других вещах, Simply Science является вспомогательной идеей учебной программы, обучая учащихся в 6 и 12 классах наукам, технологиям, инженерным наукам и математика.Благодаря междисциплинарному подходу, мероприятиям и ресурсам, ориентированным на воздействие, это идеальное занятие для молодых умов после школы.
Комплексные темы обучения для детей от 9 до 18 лет
Узнавайте что-то новое каждый день, занимайтесь интересами и отвечайте на вопросы, которые всегда заставляли вас задуматься! Педагогика Simply Science поощряет вас исследовать, вводить новшества и применять полученные концепции в повседневной жизни, от базовых концепций до подробных бесед. Наша модель на основе темы гарантирует, что тема охватывает все темы в дисциплинах, которые она затрагивает — математику, науку и технологии, биологию и химию и все, что между ними.
Интерактивный и увлекательный контент и виртуальная помощь
Межотраслевое обучение с сокровищницей ресурсов — мы считаем, что каждый молодой ум должен иметь доступ к связанным и равным возможностям обучения. Наука формирует мир, она всепроникающая и преобразующая. Наши материалы мирового уровня, методология и ресурсы идут рука об руку с учебной программой учебного заведения. Наши виртуальные помощники направляют студентов к ключевым навыкам в темах, чтобы развивать критическое мышление, рассуждение и дизайн.
Объясните феномен самоиндукции ЭДС. и взаимно индуцированная ЭДС.
Самоиндуцированная э.д.с.
Фиг.1
Рассмотрим катушку, имеющую «N» витков и проводящую ток «I», когда переключатель «S» находится в замкнутом положении. Величину тока можно изменять с помощью переменного сопротивления, подключенного последовательно к батарее, катушке и переключателю, как показано на рисунке.
Поток, создаваемый катушкой, соединяется с самой катушкой. Суммарные потокосцепления катушки будут N Φ
Вт-виток.Теперь, если ток «I» изменяется с помощью переменного сопротивления, то создаваемый поток также изменится, из-за чего изменятся и потокосцепления.
Следовательно, согласно закону Фарадея, из-за скорости изменения потоковых связей будет индуцированная ЭДС. в катушке. Таким образом, без физически движущейся катушки или магнитного потока возникает наведенная ЭДС. в катушке. Это явление называется самоиндукцией.
Э.д.с. индуцированная в катушке из-за изменения ее собственного потока, связанного с ней, называется самоиндуцированным e.м.ф.
Динамически индуцированная э.д.с.
Если поток, создаваемый одной катушкой, соединяется с другой катушкой, и из-за изменения этого потока, создаваемого первой катушкой, возникает наведенная ЭДС. во второй катушке, то такая э.д.с. называется взаимно индуцированной ЭДС.
Фиг.2
Рассмотрим две катушки, которые расположены рядом друг с другом, как показано на рисунке. Катушка A имеет N1 витков, а катушка B — N2 витков.Катушка A имеет последовательно включенный переключатель S, переменное сопротивление R и батарею на «E» вольт. К перекрестной катушке B подключен гальванометр для измерения наведенной ЭДС. и ток из-за этого.
Ток через катушку A равен I1, создающему магнитный поток Φ1. Часть этого потока будет связана с катушкой B, т.е. завершит свой путь через катушку B, как показано на рис. 2. Это взаимный поток Φ2.
. Теперь, если ток через катушку A изменить с помощью переменного сопротивления R, то изменится поток Φ1. Из-за этого также изменяется магнитный поток, связанный с катушкой B, который является взаимным потоком Φ2.
По закону Фарадея будет индуцированная ЭДС. в катушке B, которая установит ток через катушку B, который будет обнаружен гальванометром G.
Любое изменение тока через катушку A вызывает ЭДС. в катушке B это явление называется взаимной индукцией и э.д.с. называется взаимно индуцированной ЭДС.
Катушки индуктивности ― Часть 2 Основы индукторов ② | Электроника ABC | TDK Techno Magazine
Поведение индуктора на постоянном токе
Переходная характеристика катушки
Из-за эффекта самоиндукции катушки (индукторы) создают электродвижущую силу (индуктивную электродвижущую силу), которая ориентирована таким образом, чтобы противодействовать изменению тока.Следовательно, когда на катушку подается напряжение, ток не начинает течь сразу, а когда напряжение снимается, ток не прекращается сразу. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения переключателя, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) подключены параллельно, простое замыкание переключателя батареи (напряжение всего несколько вольт) не приведет к включите неоновую лампу.Но если выключатель разомкнут, когда через катушку протекает ток, загорится неоновая лампа. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI / Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, и поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока большой, вызывая создание большой электродвижущей силы, достаточной для зажигания неоновой лампы.
Энергия, запасаемая катушкой
В приведенной выше схеме неоновая лампа может быть зажжена, потому что катушка накапливает энергию. Эта энергия пропорциональна индуктивности катушки и квадрату тока. Когда переключатель установлен в положение OFF, накопленная энергия мгновенно высвобождается, создавая высокую электродвижущую силу.
Поведение катушки переменного тока
Индуктивное реактивное сопротивление (XL)
Катушка (индуктор) плавно пропускает постоянный ток, но имеет сопротивление переменному току.Сопротивление увеличивается по направлению к более высоким частотам. Этот эффект называется индуктивным реактивным сопротивлением (XL) катушки. Следующее соотношение существует между частотой переменного тока (f) и индуктивностью (L).
Форма волны напряжения и тока в цепи переменного тока с катушкой
Переменный ток от коммерческой розетки переменного тока имеет синусоидальную форму.Когда катушка подключена к источнику переменного тока, эффект самоиндукции создает электродвижущую силу, ориентированную таким образом, чтобы противодействовать изменению тока. Таким образом, изменение тока задерживается на 90 градусов (1/4 цикла) по отношению к изменению напряжения.
Намагничивание сердечника и магнитная проницаемость
Кривая намагничивания и магнитное насыщение
Магнитный поток (Φ), создаваемый в катушке, пропорционален индуктивности (L) и протекающему току (I).Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и приложение большого тока приведет к созданию более сильного магнитного потока. Однако есть пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm).
Процесс намагничивания сердечника и изменение магнитной проницаемости
Когда сердечник намагничивается, магнитная проницаемость сердечника изменяется.Как показано на графике ниже, магнитная проницаемость (μ) выражается градиентом кривой намагничивания сердечника (θ). Начальный градиент около начала кривой — это начальная магнитная проницаемость (μ0). Эта начальная магнитная проницаемость — это то, что обычно называют магнитной проницаемостью, и это также значение, которое указано в каталогах для ферритовых материалов. Увеличение тока в катушке и, таким образом, увеличение намагниченности в конечном итоге приведет к тому, что магнитная проницаемость достигнет максимально возможного значения.Это называется максимальной магнитной проницаемостью (мкм), после которой значение снова падает.
Потери на вихревые токи в сердечнике
Когда в катушку подается переменный ток, создается электродвижущая сила, которая противодействует изменению магнитного потока, и в сердечнике течет концентрический ток. Это называется вихревым током, и он лишает систему мощности RI2 (R: сопротивление, I: ток), которая уходит в виде джоулева тепла.Это называется потерей на вихревые токи. У металлических сердечников с низким электрическим сопротивлением потери на вихревые токи более выражены. Ламинированные сердечники, используемые для силовых трансформаторов, представляют собой попытку уменьшить потери на вихревые токи. Однако потери будут увеличиваться по направлению к более высоким частотам, что приведет к выделению большего количества тепла. Поскольку феррит имеет высокое удельное сопротивление, потери на вихревые токи низкие, что делает этот материал пригодным для многих применений, таких как высокочастотные катушки и высокочастотные трансформаторы.
11.2 Самоиндуктивность и индукторы — Введение в электричество, магнетизм и схемы
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Сопоставьте скорость изменения тока с наведенной ЭДС, создаваемой этим током в той же цепи
- Вывести самоиндукцию цилиндрического соленоида
- Вывести самоиндукцию прямоугольного тороида
Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ — да, и это явление называется самоиндуктивностью .
Катушки индуктивности
На рис. 11.2.1 показаны некоторые силовые линии магнитного поля, возникающие из-за тока в кольцевой проволочной петле. Если ток постоянный, магнитный поток через контур также постоянен. Однако, если бы ток изменялся со временем — скажем, сразу после замыкания переключателя — тогда соответственно изменился бы магнитный поток.Тогда закон Фарадея говорит нам, что в цепи будет индуцирована ЭДС, где
(11.2.1)
Поскольку магнитное поле, создаваемое токоведущим проводом, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть
(11.2.2)
(рисунок 11.2.1)
Рисунок 11.2.1 Магнитное поле создается током I в контуре. Если бы он изменялся со временем, магнитный поток, проходящий через петлю, также изменился бы, и в петле была бы индуцирована ЭДС.
Это также можно записать как
(11.2.3)
, где постоянная пропорциональности известна как самоиндуктивности проволочного контура. Если петля имеет витки, это уравнение принимает вид
(11.2.4)
По соглашению, положительное значение нормали к петле связано с током по правилу правой руки, поэтому на рисунке 11.2.1 нормаль направлена вниз. Согласно этому соглашению, в уравнении 11.2.4 положительно, поэтому L всегда имеет положительное значение .
Для петли с витками, поэтому наведенная ЭДС может быть записана в терминах самоиндукции как
(11.2.5)
При использовании этого уравнения для определения проще всего игнорировать знаки и и вычислить как
Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией. Например, помимо проволочной петли, длинный прямой провод имеет самоиндукцию, как и коаксиальный кабель.Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно найти для подключения к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и самоиндукцией, что может иметь нежелательные эффекты.
Элемент схемы, используемый для обеспечения самоиндукции, известен как индуктор. Он представлен символом, показанным на рисунке 11.2.2, который напоминает катушку с проводом, основную форму индуктора.На рисунке 11.2.3 показано несколько типов индукторов, обычно используемых в схемах.
(рисунок 11.2.2)
Рисунок 11.2.2 Символ, используемый для обозначения катушки индуктивности в цепи.
(рисунок 11.2.3)
Рисунок 11.2.3 Различные индукторы. Независимо от того, заключены ли они в капсулу, как показанные три верхних, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой. (кредит: Windell Oskay) Разнообразные индукторы. Независимо от того, заключены ли они в капсулу, как показанные три верхних, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой.(Источник: Windell Oskay)
В соответствии с законом Ленца отрицательный знак в уравнении 11.2.5 указывает, что наведенная ЭДС на катушке индуктивности всегда имеет полярность, которая противодействует изменению тока. Например, если бы ток, протекающий от до на рис. 11.2.4 (а), увеличивался, наведенная ЭДС (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от до уменьшался, то наведенная ЭДС имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (Рисунок 11.2.4 (б)). Наконец, если бы ток через катушку индуктивности был постоянным, в катушке не было бы индуцированной ЭДС.
(рисунок 11.2.4)
Рисунок 11.2.4 Индуцированная ЭДС на катушке индуктивности всегда противодействует изменению тока. Это можно представить себе как воображаемую батарею, заставляющую течь ток, чтобы противодействовать изменению в (а) и усиливать изменение в (б).
Одно из распространенных применений индуктивности состоит в том, чтобы разрешить светофорам определять, когда автомобили ждут на перекрестке.Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет. Аналогичным образом, металлоискатели , используемые для безопасности аэропортов, используют ту же технологию. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал от катушки передатчика вызывает сигнал в приемнике.На самоиндукцию цепи влияет любой металлический предмет на пути (рисунок 11.2.5). Металлоискатели можно настроить на чувствительность, а также они могут определять присутствие металла на человеке.
(рисунок 11.2.5)
Рис. 11.2.5 Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но также могут указывать их приблизительную высоту над полом. (Источник: «Alexbuirds» / Wikimedia Commons)
Большие наведенные напряжения обнаружены в вспышках фотокамер .Во вспышках камеры используются аккумулятор, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. Обратите внимание, что термин «колебание» в физике определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Теперь вспомните (из «Электромагнитная индукция об электромагнитной индукции»), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.Система генератора делает это много раз, когда напряжение батареи повышается до более высокого. (Вы можете услышать пронзительный свист трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки.
ПРОВЕРЬТЕ ПОНИМАНИЕ 11.2
Ток протекает через катушку индуктивности на рисунке 11.2.4 от до, а не от до, как показано. Увеличивается или уменьшается ток, чтобы создать ЭДС, показанную на диаграмме (а)? На диаграмме (б)?
ПРОВЕРЬТЕ ПОНИМАНИЕ 11.3
Изменяющийся ток индуцирует ЭДС в катушке индуктивности. С какой скоростью меняется ток?
Хороший подход к расчету самоиндукции катушки индуктивности состоит из следующих шагов:
Стратегия решения проблем: самоиндуктивность
- Предположим, через катушку индуктивности течет ток.
- Определите магнитное поле, создаваемое током. Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
- Получить магнитный поток,.
- При известном магнитном потоке самоиндукция может быть найдена из уравнения 11.2.4,.
Чтобы продемонстрировать эту процедуру, мы теперь вычисляем самоиндуктивность двух катушек индуктивности.
Цилиндрический соленоид
Рассмотрим длинный цилиндрический соленоид с длиной, площадью поперечного сечения и витками провода. Мы предполагаем, что длина соленоида настолько больше, чем его диаметр, что мы можем считать, что магнитное поле распространяется по всей внутренней части соленоида, то есть мы игнорируем концевые эффекты в соленоиде.При токе, протекающем через катушки, магнитное поле, создаваемое внутри соленоида, составляет
(11.2.6)
, поэтому магнитный поток на один виток равен
(11.2.7)
Используя ??, находим для самоиндукции соленоида
(11.2.8)
Если — количество витков на единицу длины соленоида, мы можем записать уравнение 11.2.8 как
(11.2.9)
где — объем соленоида.Обратите внимание, что самоиндукция длинного соленоида зависит только от его физических свойств (таких как количество витков провода на единицу длины и объема), а не от магнитного поля или тока. Это верно для индукторов в целом.
Прямоугольный тороид
Тороид прямоугольного сечения показан на рисунке 11.2.6. Внутренний и внешний радиусы тороида равны и, а — высота тороида. Применяя закон Ампера так же, как мы это делали в примере 10.4.2 для тороида с круглым поперечным сечением мы находим, что магнитное поле внутри прямоугольного тороида также равно
(11.2.10)
где — расстояние от центральной оси тороида. Поскольку поле внутри тороида изменяется, мы должны вычислить поток путем интегрирования по поперечному сечению тороида. Используя бесконечно малый элемент площади поперечного сечения, показанный на рисунке 11.2.6, получаем
(11.2.11)
(рисунок 11.2.6)
Рисунок 11.2.6 Расчет самоиндукции прямоугольного тороида.
Теперь из уравнения 11.2.11 для самоиндукции прямоугольного тороида получаем
(11.2.12)
Как и ожидалось, самоиндукция — постоянная величина, определяемая только физическими свойствами тороида.
ПРОВЕРЬТЕ ПОНИМАНИЕ 11,4
ПРОВЕРЬТЕ ПОНИМАНИЕ 11,5
(а) Каков магнитный поток через один виток соленоида самоиндукции, когда через него протекает ток? Предположим, что соленоид намотан из проволоки диаметром.(б) Какова площадь поперечного сечения соленоида?
Кандела Цитаты
Лицензионный контент
CC, конкретная атрибуция
- Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Самоиндукция — определение, коэффициент самоиндукции
Что такое самоиндукция?
Явление генерации наведенной ЭДС в катушке всякий раз, когда в той же катушке происходит изменение тока.
Если понимать самоиндукцию практически так:
Рассмотрим катушку L, намотанную на полый деревянный цилиндр. Шофт-железо упаковано в полую область для увеличения магнитного потока, связанного с L.
Две торцевые клеммы подключаются к источнику ЭДС через ключ-ответвитель K.
При нажатии клавиши K ток, протекающий по цепи, увеличивается. По мере его увеличения от нуля до максимума в нем создается наведенная ЭДС из-за явления электромагнитной индукции.Согласно закону Ленца, создаваемая ЭДС противодействует изменению, которое ее вызывает. Следовательно, его направление противоположно направлению тока. Когда ток достигает максимального значения, связь магнитного потока с катушкой становится максимальной. На данном этапе в катушке нет наведенной ЭДС.
При отпускании ключа ток уменьшится с максимального до нуля. Это приводит к уменьшению магнитного потока, связанного с катушкой. Снова настраивается ЭДС. Направление ЭДС, согласно закону Ленца, должно быть таким же, как у тока.
Таким образом, ясно, что индуцированная ЭДС, когда бы она ни появлялась в цепи, противодействует изменению силы тока, протекающего по цепи. Это свойство катушки называется самоиндукцией.
Теперь мы можем определить самоиндукцию как
Самоиндукция цепи определяется как свойство цепи, благодаря которому она имеет тенденцию противодействовать изменению силы тока через нее, индуцируя в себе ЭДС.
Экспериментальная демонстрация самоиндукции
Свойство самоиндукции можно продемонстрировать, подключив лампочку B к двум выводам катушки.ЭДС, индуцированная в катушке, проходит прямо через лампочку и вызывает сильный ток, протекающий по ней.
Следовательно, лампочка дает вспышку света всякий раз, когда присутствует наведенная ЭДС. Яркая вспышка в лампочке при включении и при разрыве цепи свидетельствовала о самоиндукции.
Коэффициент самоиндукции
Пусть магнитный поток связан с цепью благодаря току I.
Где L называется коэффициентом самоиндукции цепи.
Это зависит от
1. Площадь поперечного сечения
2. Количество витков катушки
3. Тип материала, упакованного в рулон
Если I = 1, магнитный поток = L
Коэффициент самоиндукции цепи определяется как магнитный поток, связанный с цепью, когда через цепь протекает единичный ток.
SI Единица коэффициента самоиндукции — Генри
CGS unit коэффициент самоиндукции — abhenry
Важные примечания по самоиндукции
1.Сопротивление R — это мера противодействия электрического тока, в то время как собственная индуктивность L — это мера противодействия изменению тока в цепи.
2. Самоиндукцию часто называют электрической инерцией, поскольку она аналогична механической инерции. В механике инерция противодействует изменению скорости, в то время как самоиндукция противодействует изменению тока в цепи.
3. Идеальной катушкой индуктивности считается катушка с нулевым сопротивлением, в то время как идеальный резистор считается обладающей нулевой самоиндукцией.И идеальный индуктор, и идеальный резистор получить практически невозможно.
4. Идеальный индуктор эквивалентен замкнутому ключу в электрической цепи.
5. Проволока, используемая в ящиках сопротивления, имеет пространственный тип обмотки, называемый неиндуктивной обмоткой. Проволока сначала складывается вдвое, а затем наматывается на лист слюды.
Когда через него протекает ток, направление тока в двух обмотках, расположенных близко друг к другу, будет противоположно друг другу. Таким образом, создаваемое ими магнитное поле будет нейтрализовано.Поскольку в этой области нет результирующего магнитного поля, в проводе не будет наведенной ЭДС при изменении тока в проводе. Таким образом, единственная оппозиция будет носить резистивный характер.
Лактура на самоиндукции
Если у вас есть какие-либо вопросы, вы можете задать их в поле для комментариев.
электромагнетизм — Когда между двумя катушками возникает взаимная индуктивность, всегда ли собственная индуктивность возникает в каждой отдельной катушке?
Когда ток проходит через замкнутый контур, магнитный поток через
площадь поперечного сечения этой петли возникает из-за этого тока.Этот
магнитный поток связан с током соотношением:
$$ \ phi = Li $$
$ L $ называется самоиндукцией контура и зависит от
конфигурация этого цикла. $ L $ остается постоянным, пока конфигурация
петли не изменено.
Если ток в контуре изменяется со временем, магнитный поток через
петля изменяется пропорционально току. Это изменение магнитного потока вызывает
электродвижущая сила (ЭДС), индуцируемая на выводах контура.Это явление называется самоиндукцией . Генерируемая ЭДС определяется выражением
Закон Фарадея как:
$$ e = — \ dfrac {d \ phi} {dt} = — L \ dfrac {di} {dt} $$
Распространенное недоразумение у новичков:
Пусть источник переменного напряжения подключен к круговой петле. Поскольку нынешний
через изменения цепи это вызывает изменение магнитного потока. Этот
изменение магнитного потока действует, чтобы изменить ток в цепи, который затем
изменяет магнитный поток и т. д. i.е. мы вращаемся по кругу.Другими словами, изменение тока $ \ rightarrow $ Изменение магнитного потока
$ \ rightarrow $ снова меняет ток … круг никогда не заканчивается.
Это заблуждение .
Чтобы прояснить, как достигается баланс, рассмотрим напряжение переменного тока, приложенное к
идеальная (нулевое сопротивление) петля. Решим схему, применив КВЛ . В
приложенное напряжение:
$$ V (t) = V_0 \ sin (\ omega t) $$
В этом контуре устанавливается ток $ I (t) $.Заблуждение состоит в том, что
изменение $ V $ вызывает изменение $ I $. Поскольку $ I $ изменяется, магнитный поток
также изменяется, что может вызвать самоиндукцию, изменяя сетевое напряжение на
петля. Следовательно, существующее электрическое поле изменяется, поэтому ток снова будет
поменять и так далее. Но у этого заблуждения есть изъян. По КВЛ сумма
напряжение вокруг контура должно быть нулевым, т.е .:
$$ V (t) + \ text {индуцированная ЭДС} = 0 $$
Удивительный факт заключается в том, что электрическое поле $ 0 $ внутри провода
петля, потому что сопротивление петли составляет $ 0 $.Чтобы ток протекал в
идеальный индуктор не нужен $ E $. Переменный ток существует только для
противодействовать приложенному напряжению.
Мы знаем, что наведенная ЭДС связана с током в контуре следующим образом:
$$ e = — \ dfrac {d \ phi} {dt} = — L \ dfrac {di} {dt} $$
Это соотношение говорит нам, что ток является функцией наведенной ЭДС. С
наведенная ЭДС также является функцией приложенного напряжения, ток является функцией
приложенного напряжения и может быть рассчитано. Это также выражение для
идеальный индуктор и решение, как мы знаем:
$$ I (t) = \ dfrac {V_0} {\ omega L} \ cos (\ omega t) $$
Это объясняет, почему, несмотря на круг рассуждений, ток можно найти
как функция приложенного напряжения.Это потому, что наведенная ЭДС должна быть
равным приложенному напряжению. Фактически, изменения в количествах связаны соотношением
дифференциальное уравнение, решение которого даст нам значение неизвестной
Текущий.
Рассмотрим две петли, как показано:
(источник: Talkingelectronics.com)
Есть две петли, синяя и черная. Когда черная петля отсутствует,
ток в синей петле равен $ i_1 $. Этот ток постоянный и нет
самоиндукция; батарея имеет нулевое напряжение, так как контур идеально
проведение.Пока считайте эту батарею коротким замыканием.
Что происходит, если черная петля размещается рядом с синей петлей? В виде
синяя петля перемещается, чтобы приблизиться к черной петле, магнитный поток через
и синяя, и черная петли меняются со временем. Это приводит к тому, что наведенная ЭДС
появляются в обеих петлях. Обе петли являются идеальными проводниками, поэтому нам не нужны никакие
$ E $ внутри их проводов, чтобы вызвать ток.
Предположим, что начальный ток, протекающий через черный контур, был $ i_2 $.Оба
$ i_1 $ и $ i_2 $ изменятся, когда петли приблизятся друг к другу, но как?
Пусть синяя петля будет петлей $ 1 $, а черная петля будет петлей $ 2 $. Магнитный поток
пересечение черной петли из-за тока в синей петле
$ \ phi_ {12} (x, t) $. Этот поток связан с $ i_1 (t) $ уравнением:
$$ \ phi_ {12} (x, t) = M_ {12} (x) i_1 (t) $$
$ M_ {12} (x) $ — это функция расстояния $ x $ между двумя контурами и их
конфигурация. Этот параметр $ M (x) $ называется взаимной индуктивностью .Если $ x $ равно
не изменится, взаимная индуктивность останется постоянной.
Точно так же контур пересечения магнитного потока $ 1 $ из-за тока в контуре $ 2 $ равен:
$$ \ phi_ {21} (x, t) = M_ {21} (x) i_2 (t) $$
Если обе петли имеют одинаковую конфигурацию, они создают одинаковый узор из
магнитное поле вокруг них при прохождении того же тока. Так
$ M_ {12} (x) = M_ {21} (x) $ для аналогичных циклов и может быть обозначено просто как $ M (x) $ в
тот случай.
Магнитный поток, существующий в контуре $ 1 $ из-за собственного тока $ i_1 $, равен:
$$ \ phi_ {11} (t) = L_1i_i (t) $$
Магнитный поток в контуре $ 2 $ из-за $ i_2 $ равен:
$$ \ phi_ {22} (t) = L_2i_ {2} (t) $$
ЭДС, сгенерированная в цикле $ 1 $ и цикле $ 2 $:
$$ e_ {11} = — \ dfrac {d \ phi_ {11}} {dt} $$
$$ e_ {22} = — \ dfrac {d \ phi_ {22}} {dt} $$
$$ e_ {12} = — \ dfrac {d \ phi_ {12}} {dt} $$
$$ e_ {21} = — \ dfrac {d \ phi_ {21}} {dt} $$
Для удержания KVL условие:
$$ e_ {11} + e_ {21} = 0 = e_ {22} + e_ {12} $$
Но $ e_ {11} $ и $ e_ {22} $ представляют собой самоиндукцию в цикле $ 1 $ и цикле $ 2 $.
соответственно.Итак, $ i_1 $ и $ i_2 $ меняются со временем. И $ \ phi_ {12} $, и
$ \ phi_ {21} $ также изменится из-за изменений в $ i_1 $ и $ i_2 $ и любых изменений
в $ x $. Таким образом, мы можем упростить $ e_ {12} $ как:
$$ e_ {12} = — \ dfrac {d \ phi_ {12}} {dt}
= \ dfrac {d (M (x) i_1 (t))} {dt}
= \ dfrac {dM_ {12}} {dt} i_1 + \ dfrac {di_1} {dt} M_ {12} $$
$ e_ {12} $, индуцированная ЭДС в контуре $ 2 $, создается изменением x и / или
изменение в цикле $ 1 $ current, $ i_1 $. Явления наведения ЭДС в петле
за счет изменения тока в каком-то другом контуре называется взаимоиндукцией .Если
$ L_1 $ маленький, мы можем представить петлю $ 1 $ как стержневой магнит и самоиндукцию.
будет наблюдаться только в цикле $ 2 $. Далее, если мы предположим, что цикл $ 2 $ имеет сопротивление
$ R_2 $ очень большой по сравнению с $ L_2 $, мы не увидим самоиндукции, а просто
Закон Фарадея, т.е. $ e_ {12} = i_2R_2 $.
Теперь давайте рассмотрим ваш конкретный вопрос:
«Когда катушка, подключенная к генератору переменного тока, создает ЭДС в другой поблизости
катушка (взаимная индуктивность), это самоиндукция, одновременно возникающая в обоих
катушки? «
Чтобы проанализировать это, снова рассмотрим предыдущий цикл $ 1 $ и цикл $ 2 $, заменив
Аккумулятор постоянного тока с источником переменного напряжения.
