Содержание
Русский язык 4 класс Канакина и Горецкий
ЧАСТЬ 1
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
101 102 103 104 105 106 107 108 109 110
111 112 113 114 115 116 117 118 119 120
121 122 123 124 125 126 127 128 129 130
131 132 133 134 135 136 137 138 139 140
141 142 143 144 145 146 147 148 149 150
151 152 153 154 155 156 157 158 159 160
161 162 163 164 165 166 167 168 169 170
171 172 173 174 175 176 177 178 179 180
181 182 183 184 185 186 187 188 189 190
191 192 193 194 195 196 197 198 199 200
201 202 203 204 205 206 207 208 209 210
211 212 213 214 215 216 217 218 219 220
221 222 223 224 225 226 227 228 229 230
231 232 233 234 235 236 237 238 239 240
241 242 243 244 245 246 247 248 249 250
251 252 253 254 255 256 257 258 259 260
261 262 263 264 265 266 267 268 269 270
271 272 273 274 275
Задания проверь себя для главы Повторение
1 2
Задания проверь себя для главы Предложение
1 2 3 4
Задания проверь себя для главы Слово в языке
1 2 3 4 5
Задания проверь себя для главы 4
1 2 3 4
Задания наши проекты для главы 4
1 2 3 4
ЧАСТЬ 2
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
101 102 103 104 105 106 107 108 109 110
111 112 113 114 115 116 117 118 119 120
121 122 123 124 125 126 127 128 129 130
131 132 133 134 135 136 137 138 139 140
141 142 143 144 145 146 147 148 149 150
151 152 153 154 155 156 157 158 159 160
161 162 163 164 165 166 167 168 169 170
171 172 173 174 175 176 177 178 179 180
181 182 183 184 185 186 187 188 189 190
191 192 193 194 195 196 197 198 199 200
201 202 203 204 205 206 207 208 209 210
211 212 213 214 215 216 217 218 219 220
221 222 223 224 225 226 227 228 229 230
231 232 233 234 235 236 237 238 239 240
241 242 243 244 245 246 247 248 249 250
251 252 253 254 255 256 257 258 259 260
261 262 263 264 265 266 267 268 269 270
271 272 273 274 275 276 277 278 279 280
281 282 283 284 285 286 287 288 289 290
291 292 293 294 295 296 297 298 299 300
301 302 303 304 305 306 307 308 309 310
311 312 313 314 315 316 317 318 319 320
321 322 323 324 325 326
Задания наши проекты для главы 1
1 2
Задания проверь себя для главы 2
1 2 3
Задания проверь себя для главы: Местоимение
1 2 3
Упражнение наши проекты
1 2 3
Задания проверь себя для главы: Глагол
1 2 3 4 5 6 7
Математика 4 класс Моро
Страница 4.
Задание 1.
Надо сосчитать большое количество пуговиц. Например: 6 сотен, 5 десятков и 5 отдельных пуговиц. Сколько это всего пуговиц?
Решение:
6 сотен — это 6 х 100 = 600;
5 десятков — это 5 х 10 = 50
и 5 отдельных пуговиц, значит:
600 + 50 + 5 = 655 пуговиц всего.
Задание 2.
Назови и запиши числа, какое число называют при счете перед каждым из этих чисел и после него?
9 дес. 9 ед. − 99 (девяносто девять). Перед числом 99 называют 98, а после 100.
9 дес. 0 ед. − 90 (девяносто). Перед числом 90 называют 89, а после 91.
9 сот. 9 дес. 9 ед. − 999 (девятьсот девяносто девять). Перед числом 999 называют 998, а после 1000.
9 сот. 0 дес. 9 ед. − 909 (девятьсот девять). Перед числом 909 называют 908, а после 910.
9 сот. 0 дес. 0 ед. − 900 (девятьсот). Перед числом 900 называют 899, а после 901.
− 900 (девятьсот). Перед числом 900 называют 899, а после 901.
9 сот. 9 дес. 0 ед − 990 (девятьсот девяносто). Перед числом 990 называют 989, а после 991.
Задание 3.
Прочитайте числа, записанные в таблице.
672 (шестьсот семьдесят два) и 206 (двести шесть).
Вопрос: На каком месте, считая справа налево, пишут единицы? десятки? сотни?
Ответ: Единицы пишут на 1 месте, считая справа налево, десятки − на втором, сотни − на третьем.
2) Сколько единиц каждого разряда в числе 672? 206? 400? 890?
Число 672 содержит 6 единиц III разряда 7 единиц II разряда и 2 единицы I разряда.
Число 206 содержит 2 единиц III разряда 0 единиц II разряда и 6 единиц I разряда.
Число 840 содержит 8 единиц III разряда 4 единиц II разряда и 0 единиц I разряда.
Число 400 содержит 4 единиц III разряда 0 единиц II разряда и 0 единиц I разряда.
Число 590 содержит 5 единиц III разряда 9 единиц II разряда и 0 единиц I разряда.
Моро. Решебник 1, 2 часть
ГДЗ по математике для 4 класса Моро – это сборник готовых домашних заданий: решенные задачи, примеры, уравнения, неравенства по учебнику авторитетных российских математиков – М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Его используют в качестве базового пособия для четвероклассников во многих центральных и региональных школах РФ.
Структура ГДЗ по учебнику математики четвертого класса от Моро
В четвертом классе школьная программа изучения предписывает решение задач и примеров с числами от 1 до 1000, умножение и деление столбиком, определение скорости, времени и расстояния. Именно в 4-м классе закладывается база для изучения углубленных основ арифметики, а после – алгебры, геометрии, химии и физики.
ГДЗ по математике 4 класса Моро, составленные на основе учебника 2015 года в его 4-м издании, включают в себя примеры и задачи на такие темы:
- четыре арифметических действия: сложение, вычитание, умножение, деление;
- диаграммы;
- сложение и вычитание, умножение и деление величин;
- скорость, время, расстояние;
- умножение и деление на числа, оканчивающиеся нулями;
- умножение и деление на двузначное и трёхзначное число;
- числа от 1 до 1000;
- уравнения и неравенства с одной переменной.

В четвертом классе завершается курс средней школы. Ученики переходят на новую степень и должны уметь решать примеры и задачи самостоятельно. Цель решебника по математике к учебнику Моро – представить детальные алгоритмы решений, разъяснить материал, пройденный в классе.
Готовое домашнее задание для 4 класса на сайте ГДЗ Путина поможет не только ученикам, но их родителям, которые часто делают уроки вместе со своими детьми. Это также способ отказаться от услуг репетиторов и платных подготовительных курсов.
Правильные решения от ГДЗ Путина по математике 4 класса к Моро
Чтобы найти решение домашней задачи в интернете, достаточно за пару кликов отыскать нужный решебник. Однако не все сайты предлагают подробные решения и верные ответы. В чем преимущества портала ГДЗ от Путина? Почему именно его часто выбирают ученики младших классов и их родители?
- здесь можно найти несколько вариантов решения одной задачки;
- ответы оформлены по требованиям Минобразования России;
- все примеры с ответами доступны без регистрации и бесплатно;
- информация корректно отображается на телефонах, компьютерах и планшетах.

Перечисленные критерии важны для пользователей ГДЗ по математике 4 класса к учебнику Моро: ученики получают подробные описания решений и могут разобраться со сложными темами, их родители – в любое время проверить домашнюю работу их чад.
Поскольку задачи и примеры приводятся в нескольких вариантах выполнения, то можно выбрать самый понятный и удобный вариант, взять его за основу, разобрать и запомнить.
Страница 87 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 1
Вернуться к содержанию учебника
Числа, которые больше 1000. Умножение и деление
Вопрос
Объясни решение примера и сравни подробную и более краткую записи.
Подсказка
Повтори алгоритм письменного деления многозначного числа на однозначное.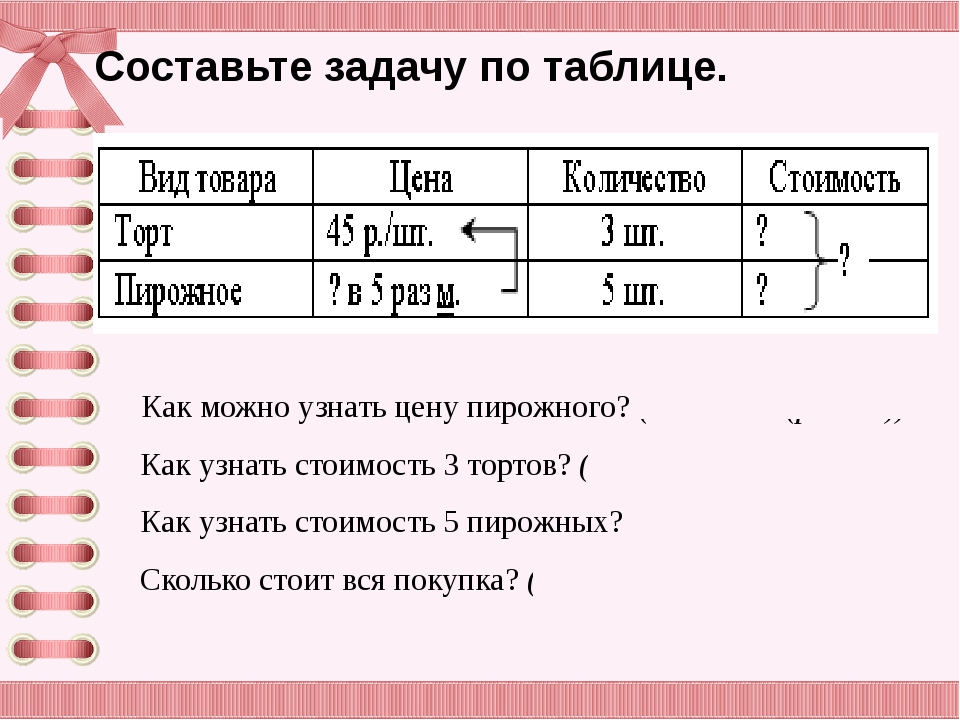
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
404. Вычисли, выполняя подробную или краткую запись.
| 4581 : 9 | 1824 : 3 | 29650 : 5 | 36800 : 8 |
Подсказка
Повтори алгоритм письменного деления многозначного числа на однозначное.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
405. Не вычисляя, назови неверные решения.
Не вычисляя, назови неверные решения.
| 7380 : 9 = 82 | 3010 : 5 = 62 | 56014 : 7 = 8002 |
Реши правильно и выполни проверку умножением.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
406. Реши задачи и сравни их решения.
1) На оклейку двух комнат пошло 108 м обоев. На одну комнату пошло 4 рулона обоев одинаковой длины, на другую — 5 таких же рулонов. Сколько метров обоев пошло на каждую комнату?
2) На оклейку двух комнат пошло 9 рулонов обоев одинаковой длины. На одну комнату пошло 48 м обоев, на другую — 60 м. Сколько рулонов обоев пошло на каждую комнату?
Сколько рулонов обоев пошло на каждую комнату?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
407. Из куска ситца можно сшить 32 детских платья или 16 платьев для взрослых. На каждое детское платье идёт 2 м ситца. Сколько метров ситца идёт на каждое платье для взрослых?
Подсказка
Повтори единицу длины — метр.
Если есть схематический рисунок, таблица или чертёж, краткую запись задачи составлять не нужно.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
408.
| 56182 : 7 | 46800 : 3 • 2 | (17437 — 10297) : 7 |
| 38412 : 6 | 13500 : 5 • 4 | 17437 — 10297 : 7 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
409. Найди периметр квадрата со стороной 3 см 2 мм.
Найди периметр квадрата со стороной 3 см 2 мм.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
410. Петров на 8 лет младше, чем Светлов, но на 3 года старше, чем Денисов. Кто моложе всех? На сколько лет Светлов старше Денисова?
Подсказка
Повтори единицу времени — год.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Найди длину стороны квадрата, периметр которого равен 432 мм.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ребус
Подсказка
Повтори алгоритм письменного деления многозначного числа на однозначное.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
4 класс. Моро. Учебник №1. Ответы к стр. 37
Числа от 1 до 1000
Величины.
Единицы длины
Ответы к стр. 37
151. 1) Прочитай таблицу единиц длины.
Запиши и запомни её.
| 1 км = 1 000 м 1 дм = 10 см 1 м = 10 дм 1 см = 10 мм |
2) Используя эту таблицу, узнай, сколько миллиметров в 1 дм; сколько сантиметров в 1 м.
1 дм = 100 мм
3) Во сколько раз 1 м больше, чем 1 мм?
1 м = 1 000 мм. 1 м больше, чем 1 мм в 1 000 раз.
152. Спиши, заполняя пропуски.
620 = 1 000 м 756 = 75 дес. 6 ед.
6 ед.
620 мм = 62 см 756 мм = 75 см 6 мм
620 дм = 62 м 756 дм = 75 м 6 дм
1 000 см = 10 м
25 000 м = 25 км
6 000 мм = 6 м
153. От двух остановок, расстояние между которыми 1 км, отошли два пешехода. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
1) Дополни условие, чтобы чертёж к задаче был таким:
От двух остановок, расстояние между которыми 1 км, отошли навстречу друг другу два пешехода. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
1) 160 + 140 = 300 (м) — прошли оба пешехода.
1 км = 1 000 м
2) 1 000 — 300 = 700 (м) — расстояние между пешеходами
О т в е т: расстояние между пешеходами стало 700 м.
2) Измени условие задачи, чтобы чертёж стал таким:
От двух остановок, расстояние между которыми 1 км, отошли два пешехода в противоположных направлениях друг к другу.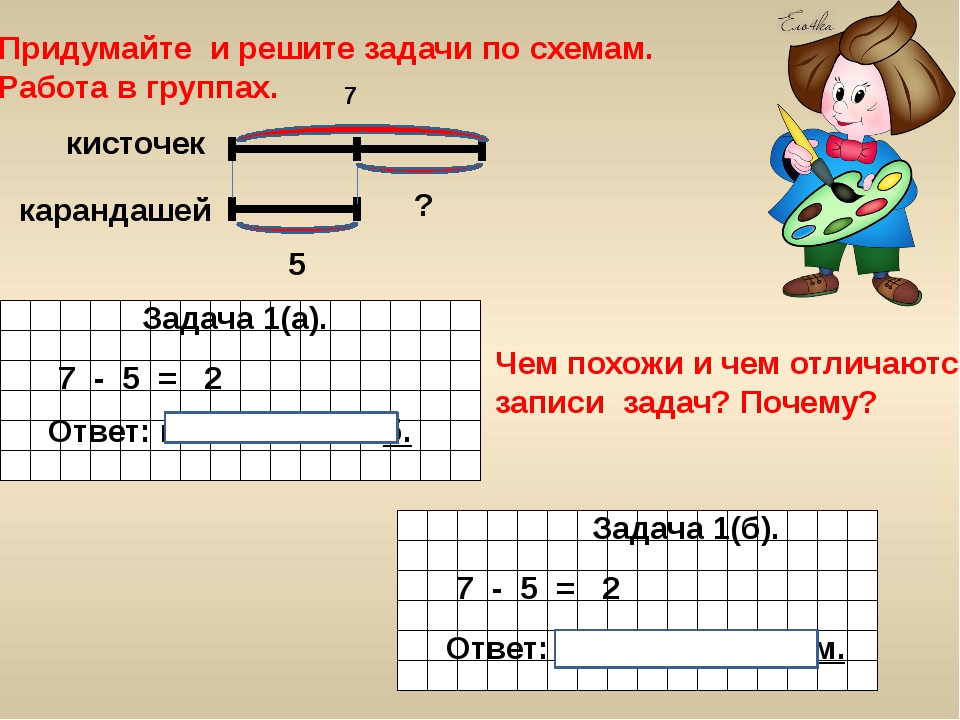 Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
1) 160 + 140 = 300 (м) — прошли оба пешехода.
1 км = 1 000 м
2) 1 000 + 300 = 1 300 (м) — расстояние между пешеходами
О т в е т: расстояние между пешеходами стало 1 300 м.
154.
200 — 80 : 2 + 6 = 166 905 — 359 • 2 = 187
(300 — 90) : 3 + 7 = 77 801 — 198 • 4 = 9
600 — 120 : (4 + 2) = 580 703 — 135 • 5 = 28
552 : 8 = 69
836 : 4 = 209
978 : 3 = 326
155. Найди правило, по которому составлен ряд чисел, и запиши ещё 3 числа: 24, 23, 21, 18, 17, 15, 12, 11, 9, 6.
24 — 1 = 23, 23 — 2 = 21, 21 — 3 = 18,
18 — 1 = 17, 17 — 2 = 15, 15 — 3 = 12,
12 — 1 = 11, 11 — 2 = 9, 9 — 3 = 6.
1 560 км = 1 км 560 м
ЗАДАНИЕ НА ПОЛЯХ:
Ребус
х 106
9
954
ГДЗ по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №1. Ответы к стр. 37
4.1 (81.71%) от 105 голосующих
Открытый урок по математике 4 классе
Тип урока: урок закрепления новых знаний.
Цель: учить учащихся решать задачи на движение.
Задачи:
Образовательная:
-
закреплять навык решения простых задач на движение, -
вырабатывать и совершенствовать прочные вычислительные навыки; -
учить применять на практике ЗУН, полученные в ходе изучения данной темы.
Развивающая:
-
развивать логическое мышление при решении составных задач, -
развивать логическое мышление; -
развивать математическую речь учащихся.
Воспитательная:
-
воспитывать трудолюбие и взаимовыручку.
Регулятивные УУД.
-
Организовывать рабочее место, свою деятельность. -
Принимать и ставить учебно-познавательную задачу. -
Строить логические рассуждения. -
Планировать свои действия.
Познавательные УУД.
-
Использование схем при решении задач.
Коммуникативные УУД.
-
Уметь использовать математическую речь при объяснении своих действий. -
Осуществлять взаимный контроль и оказывать необходимую помощь товарищам.
Оборудование: карточки-маршруты, карточки для работы в парах и для индивидуальной работы; таблицы формул о взаимосвязи скорости, времени и расстояния; пословицы «Тише едешь – дальше будешь», «Делу время – потехе час».
Ход урока
I Организационный момент
Прозвенел опять звонок,
Новый начался урок.
Сели тихо на места-
Вот какая красота!
II. Актуализация знаний
— Обратите внимание на доску. Что написано?
— «Тише едешь – дальше будешь»
_ как эта пословица связана с темой, которую мы изучаем на уроках математики?
— В этой пословице говорится о скорости движения, а мы сейчас как-раз изучаем взаимосвязь между скоростью, временем и расстоянием.
_ Правильно, а поможет нам установить эту взаимосвязь уже известный нам математический язык – формулы.
— Что обозначает формула – v=S:t ? (S=v*t t=S :v)
— Зачем нам нужно знать об этой взаимосвязи? (Чтобы уметь решать задачи на движение)
_ Перед нами стоит задача проплыть по океану задач на движение со скоростью знаний и умений и нигде не сесть на мель.
III. Отработка вычислительных навыков
— Для того, чтобы быстро решать задачи на движение, надо отработать вычислительные навыки. Посмотрите в листы маршрута, которые лежат у вас на партах. Как называется первая гавань?
Как называется первая гавань?
-Устный счёт.
— Начнём его с игры «Молчанка» (заполняют таблицу):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
— Как находили неизвестный множитель?
— Какова связь между нахождением множителя и скорости движения?
-Чтобы найти множитель, надо произведение разделить на известный множитель, а чтобы найти скорость- надо расстояние разделить на время.
-Пронаблюдаем это, решая задачу №27. Составьте условие задачи по первой строке.
— Решите её.
— Составьте условие задачи ко второй строке.
— Решите её.
— Составьте условие задачи к третьей строке.
— А кто сможет ответить на вопрос задачи № 28(1) ? №28(2)?
-Молодцы. Как называется вторая гавань?
— Письменные вычисления.
— Что требуется от нас, чтобы мы не застряли в этой гавани?
— Решим примеры №32(1) по вариантам.
— Какое свойство сложения надо применить, чтобы быстрее и точнее посчитать результат?
— Переместительное.
— Какое число надо написать первым в первом варианте, …..а во втором?
(2 ученика у доски)
278546 354120 14003 72006
+32027 +43264 -3765 +3875
8957 823 10238 75881
319530 398207
— Как связано сложение нескольких слагаемых со средней скоростью?
— Давайте придумаем условие задачи с числами из первого примера. Какие тела могут двигаться с такой скоростью, если эти числа будут выражены в метрах?
Какие тела могут двигаться с такой скоростью, если эти числа будут выражены в метрах?
— Вертолёт, лошадь и человек.
— Человек пролетел первый час на вертолёте со скоростью 278546м, второй час проскакал на лошади со скоростью 32027м, а потом прошёл пешком ещё час со скоростью 8957м. Какова средняя скорость его движения?
— Как решим задачу?
— Теперь наш путь лежит в третью гавань. Как она называется?
— Решение составных задач
— Чем составная задача отличается от простой?
(Она решается в несколько действий)
— Решить какую задачу нам предлагается?
— №28(3)
— Что необычного в этой задаче?
— Составьте условие задачи и поставьте вопрос, если к данному чертежу я добавлю вот это (Показываю новый чертёж) и задам несколько вопросов.
3км/ч 15км/ч
________________________________________________
?
__________________________________________________
— Кто может двигаться с такой скоростью?
— Как двигались лыжники?
— Сколько времени они двигались?
— Теперь слушаю условие задачи.
— Можем ли сразу ответить на вопрос задачи?
— Почему?
— Можно ли найти расстояние первого лыжника?
— Как?
— Можно ли найти расстояние второго лыжника? Как?
— Теперь можно найти ответ на вопрос задачи? Как?
— Запишите решение задачи с пояснениями. (У доски 1 ученик)
— Можно ли решить задачу другим способом? Как?
Физминутка
— Теперь пора и отдохнуть. Я называю величину скоростей, а вы показываете, что можно делать с такой скоростью.
5км/ч – идти, 12км/ч – бежать, 60км/ч – ехать, 280км/ч – лететь, 0км/ч – стоять или сидеть.
— Следующая остановка в гавани Самостоятельности.
— Сможете ли вы самостоятельно решить задачу №30? Прочитайте её и скажите, как с ней связана пословица – «Делу время, потехе час»?
— Правильно, в ней в первую очередь надо найти время движения машины. Как его найти? Запишите решение задачи самостоятельно?
1)13-7=6(ч)-время
2)240:6=40(км/ч)
Ответ:40км/ч- средняя скорость машины.
(Несколько пар получают дополнительную задачу):
«Велосипед проехал за 4 часа расстояние в 64км.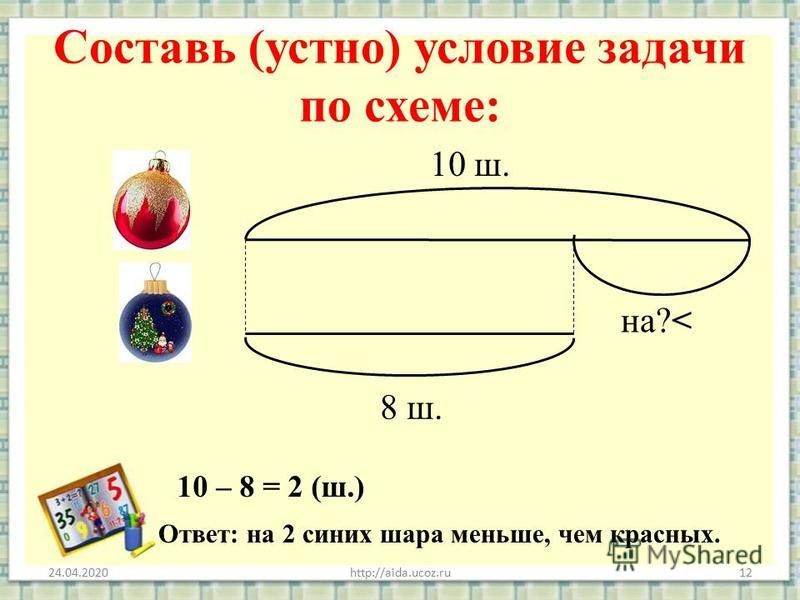 С какой скоростью двигался велосипедист и во сколько времени он выехал из дома, если в пункт назначения он приехал в 11 часов?»
С какой скоростью двигался велосипедист и во сколько времени он выехал из дома, если в пункт назначения он приехал в 11 часов?»
— Проверка. Сколько времени двигалась машина? С какой скоростью?
— Кто справился с дополнительной задачей?
— С какой скоростью ехал велосипедист? (16км/ч) Как найти скорость?
— В какое время он выехал из дома? (7ч)
— Вот мы и попали в гавань Вычислительных надежд. Какое задание в этой гавани? (порядок действий)
— Найдите номер с таким заданием на с.8
-Это №33.
— Решать будем второй столбик по вариантам.
(У доски 2 ученика)
82000-4730*8=44150 93000-8691*7=32163
1)4730 2)82000 1)8691 2)93000
* 8 -37840 * 7 -60837
— Кто успел решить другие примеры?
IV. Домашнее задание
— Потрудились мы на славу. Осталась последняя гавань – Объяснительная.
Осталась последняя гавань – Объяснительная.
Прочитайте задачу №31.
— Можете сразу ответить на вопрос задачи?
— Как нужно рассуждать?
-Решение запишите дома. С.8№31 или №37(на выбор)
V. Рефлексия
— Чему учились?
-Как найти скорость, время, расстояние?
— Кому ещё сложно решать задачи на движение?
-Эту работу мы продолжим на следующих уроках.
Вы заслужили отдых. Урок окончен.
4 класс. Моро. Учебник №2. Ответы к стр. 28
Числа от 1 до 1000
Деление на числа, оканчивающиеся нулями
Деление c остатком на 10, 100, 1000
Ответы к стр. 28
Продолжаем учиться решать задачи, составлять задачи, обратные данной.
95. Из 2 м полотна получается 3 наволочки. Сколько таких наволочек получится из 42 м полотна?
1) 42 : 2 = 21 (раз) − взяли больше полотна
2) 21 • 3 = 63 (н. )
)
О т в е т: 63 наволочки получится из 42 м полотна.
96. В 10 одинаковых банках 16 кг меда. Сколько килограммов меда в 20 таких банках?
1) 20 : 10 = 2 (раза) − взяли больше банок
2) 16 • 2 = 32 (кг)
О т в е т: 32 кг меда в 20 таких банках.
97. Из двух городов выехали одновременно навстречу друг другу два мотоциклиста. Один из них двигался со скоростью 70 км/ч и проехал до встречи 140 км, а другой двигался со скоростью 65 км/ч. Найди расстояние между городами.
Составь и реши задачи, обратные данной.
1) 140 : 70 = 2 (ч) − ехал до встречи первого мотоциклист
2) 65 • 2 = 130 (км) − проехал до встречи второй мотоциклист
3) 140 + 130 = 270 (км)
О т в е т: расстояние между городами 270 км.
1-я обратная задача
Расстояние между городами равно 270 км. Из них выехали одновременно навстречу друг другу два мотоциклиста и встретились через 2 ч. Один из них двигался со скоростью 70 км/ч. Найди скорость второго мотоциклиста?
1) 70 • 2 = 140 (км) − проехал первый мотоциклист
2) 270 − 140 = 130 (км) − проехал второй мотоциклист
3) 130 : 2 = 65 (км/ч)
О т в е т: скорость второго мотоциклиста 65 км/ч.
2-я обратная задача
Из двух городов выехали одновременно навстречу друг другу два мотоциклиста. Один из них двигался со скоростью 70 км/ч и проехал до встречи 140 км, а другой двигался со скоростью 65 км/ч. Сколько км до встречи проехал второй мотоциклист?
1) 140 : 70 = 2 (ч) − ехал до встречи первый мотоциклист
2) 65 • 2 = 130 (км)
О т в е т: 130 км проехал до встречи второй мотоциклист.
98. Запиши равенства и неравенства, проверь, верны ли они.
1) Произведение чисел 293 и 70 равно разности чисел 2900 и 849.
2) Сумма чисел 9391 и 7028 равна частному чисел 82095 и 5.
3) Частное чисел 70236 и 9 меньше их разности.
4) Произведение чисел 8019 и 7 больше их суммы.
1) 293 • 70 = 2900 – 849 – неверно (20510 > 2051)
× 293 _2900
70 849
20510 2051
2) 9391 + 7028 = 82095 : 5 – верно (16419 = 16419)
+9391 — 82095|5
7028 5 |16419
16419 —32
30
_20
20
_9
5
_45
45
0
3) 70236 : 9 < 70236 – 9 – верно (7804 < 70227)
— 70236|9 _ 70236
63 |7804 9
—72 70227
72
_36
36
0
4) 8019 • 7 > 8019 + 7 – верно (56133 > 8026)
× 8019 _8019
7 7
56133 8026
99. Выполни деление с остатком и проверь решение.
Выполни деление с остатком и проверь решение.
1724 : 10 2540 : 100 65032 : 1000
1724 : 10 = 172 (ост. 4)
172 • 10 + 4 = 1724
2540 : 100 = 25 (ост. 40)
25 • 100 + 40 = 2540
65032 : 1000 = 65 (ост. 32)
65 • 1000 + 32 = 65032
100. 140 : 20 8100 : 900 500 + (600 − 3 • 100) : 10
560 : 7 3200 : 800 9000 : (100 − 90) : 9 • 2
140 : 20 = 7 560 : 7 = 80
8100 : 900 = 9 3200 : 800 = 4
500 + (600 − 3 • 100) : 10 = 500 + (600 – 300) : 10 = 500 + 300 : 10 = 500 + 30 = 530
9000 : (100 – 90) : 9 • 2 = 9000 : 10 : 9 • 2 = 900 : 9 • 2 = 100 • 2 = 200
101. У моей мамы рост 164 см. Мой брат на 16 см выше мамы, а я пока на 8 см ниже мамы. Какой у меня рост? Сделай схематический чертеж к задаче и определи, на сколько сантиметров брат выше меня.
Мой брат на 16 см выше мамы, а я пока на 8 см ниже мамы. Какой у меня рост? Сделай схематический чертеж к задаче и определи, на сколько сантиметров брат выше меня.
1) 164 + 16 = 180 (см) – брат
2) 164 – 8 = 156 (см) – я
3) 180 – 156 = 24 (см) – выше брат
Сумма трех чисел 2010. Первое слагаемое 980, оно в 2 раза больше второго. Найди третье слагаемое.
980 : 2 = 490 − второе слагаемое
2010 − (980 + 490) = 2010 − 1470 = 540 − третье слагаемое
ЗАДАНИЕ НА ПОЛЯХ
Ответы по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4.8
/
5
(
303
голоса
)
математических приложений для 4-го класса для iPad, iPhone, Android, Windows 8
iTooch для четвертого класса MathApp Store4. 2
2
Откройте для себя наше математическое приложение для четвероклассников
Четвертый класс — критический год для математиков. Стандарты Common Core State Standard демонстрируют высокий уровень строгости. Ключевые концепции, которые обеспечивают основу для будущего успеха в математике, преподаются в четвертом классе математики. Например, учеников четвертого класса просят формализовать понимание концепций умножения и получить понимание деления и применять эти знания в ситуациях решения проблем.Дроби также являются важной составляющей 4-го класса.
Студенты опираются на предварительные знания о дробных единицах, чтобы понять концепции эквивалентности и выполнять операции с дробями. Студенты впервые сталкиваются с десятичными знаками и должны изучить их отношение к дробям. Четвероклассники также активно работают с двумерными формами для решения задач по геометрии, а также для преобразования измерений в реальных ситуациях. Математика в 4-м классе — это ключевой момент для ознакомления и развития многих навыков, которые потребуются учащимся для достижения успеха на курсах высшей математики, таких как алгебра и геометрия.
Номера и операции
- Значение места
- Заявления о расстановке ценностей
- Номера для заказа
- Округление чисел
- Сложение, многозначное число до 1000
- Вычитание, многозначное от 1000
- Умножение целых чисел
- Стратегии умножения
- Свойства умножения
- Умножение нескольких цифр
- Разделение целых чисел
- Многозначное деление
- Задачи в словах с целыми числами
- Решение проблем 1: Массивы
- Множители и кратные
- Уравнения
- Решение проблемы 2: Использование переменной
- Определение арифметических шаблонов
- Анализ паттернов
- Факты Семьи
- Решение проблем 3: многоэтапные проблемы
- Оценка — Разумность
Дроби и десятичные знаки
- Введение в дроби
- Порядок и сравнение дробей
- Сравнение дробей
- Эквивалентные дроби
- Эквивалентные дроби и сложение
- Решение проблем
- Неправильные дроби и смешанные числа
- Дроби и десятичные знаки
- Дроби и десятичные знаки 2
- Умножение дробей
Измерения и данные
- Истекшее время
- Решение проблем 1
- Использование правильных единиц для оценки
- Объем жидкости
- Метрическая система мер
- Измерение длины и расстояния
- Решение проблем 2
- Линейные участки
- Области и периметр
- Взаимосвязи между измерениями
Графики и статистика
- Линейные графики
- Круговые диаграммы
- Гистограммы
- Таблицы и диаграммы для чтения
- Пиктограммы
Геометрия
- Полигоны
- Симметрия
- Четырехугольники
- Периметр
- Решение проблем 1
- Решение проблем 2
- Линии: перпендикулярные и параллельные
- Уголки
- Треугольники
- Цельные фигуры
- Измерительные углы
Характеристики
Загруженные тысячами вопросов, приложения охватывают официальные образовательные программы и соответствуют Общим основным государственным стандартам.
Это приложение создает отличную динамику игры и стимулы, так что пользователь всегда хочет развиваться дальше в приложении.
Приложения включают в себя доску и калькулятор, чтобы студенты могли писать и вычислять прямо на экране, не выходя из приложения.
К каждой главе прилагается краткое содержание урока, чтобы подчеркнуть основные концепции, которые студенты должны знать, чтобы отвечать на вопросы.
Мгновенно переходите от одного экрана к другому. Перестаньте ждать загрузки информации с сервера: пропускная способность больше не является проблемой.
Приложения автоматически синхронизируются в фоновом режиме, чтобы загружать новые действия при наличии подключения к Интернету.
Право на участие в программе оптовых закупок Apple
(только для iOS)
Вы представитель школы и хотите купить iTooch по программе 4-го класса по математике для всей организации? Хорошие новости! iTooch 4th Grade Math имеет право на участие в программе Apple Volume Purchase Program (VPP) для образовательных учреждений. Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch для 4-го класса вместо того, чтобы покупать контент в нашем приложении для начальной школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами.
Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch для 4-го класса вместо того, чтобы покупать контент в нашем приложении для начальной школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами.
Познакомьтесь с учителями математики 4 класса:
Кортни Локридж
Кортни Локридж, автор 4-го класса по математике iTooch, является директором отдела математического образования в штате Оклахома.Она координирует государственные инициативы в области математики и отвечает за профессиональное развитие и техническую помощь школам и округам Оклахомы во всех областях, связанных с учебной программой и преподаванием математики. Ранее она работала поставщиком технической помощи в Среднем континентальном комплексном центре, финансируемом из федерального бюджета центре технической помощи при Университете Оклахомы. В этой роли она оказывала поддержку агентствам образования штатов в Арканзасе, Канзасе, Миссури и Оклахоме в реализации федеральных инициатив.
В этой роли она оказывала поддержку агентствам образования штатов в Арканзасе, Канзасе, Миссури и Оклахоме в реализации федеральных инициатив.
До переезда в Оклахому она работала педагогом по математике и естественным наукам в двух региональных сервисных центрах в Техасе. В течение этого времени г-жа Локридж обеспечивала постоянное профессиональное развитие и техническую помощь сотням школьных округов, а также работала над разработкой и распространением учебных материалов по математике на территории штата. Прежде чем работать в этой должности, она работала в Техасе классным руководителем в начальных и средних классах и работала специалистом по математике в пятом классе, обеспечивая возможности обучения как для студентов, так и для сотрудников.Кроме того, она провела обучение и подготовку по различным предметам для учителей, прошедших альтернативную сертификацию в региональном сервисном центре в Сан-Антонио, штат Техас.
Кортни также работала в отделе кадров до начала своей карьеры в сфере образования. В настоящее время Кортни завершает диссертацию, чтобы получить степень доктора философии. в области управления образованием, учебной программы и надзора в Университете Оклахомы. Г-жа Локридж получила степень MBA в Техасском университете в Сан-Антонио и получила степень бакалавра в Техасском университете в Остине.Кроме того, г-жа Локридж имеет сертификаты учителя и администратора в Оклахоме и Техасе. Она выступала в качестве рецензента для многочисленных групп по грантам на национальном и государственном уровнях и участвует в национальных и государственных организациях, включая Национальный совет учителей математики, Ассоциацию государственных наблюдателей математики и Совет учителей математики Оклахомы. .
В настоящее время Кортни завершает диссертацию, чтобы получить степень доктора философии. в области управления образованием, учебной программы и надзора в Университете Оклахомы. Г-жа Локридж получила степень MBA в Техасском университете в Сан-Антонио и получила степень бакалавра в Техасском университете в Остине.Кроме того, г-жа Локридж имеет сертификаты учителя и администратора в Оклахоме и Техасе. Она выступала в качестве рецензента для многочисленных групп по грантам на национальном и государственном уровнях и участвует в национальных и государственных организациях, включая Национальный совет учителей математики, Ассоциацию государственных наблюдателей математики и Совет учителей математики Оклахомы. .
Кортни выступала на национальных, региональных, региональных и местных конференциях и писала статьи в профессиональные журналы.В свободное время она любит путешествовать с семьей и играть со своими четырьмя мальчиками в возрасте от 6 месяцев до 12 лет.
Наоми Холл
Наоми Холл, редактор 4-го класса по математике iTooch, имеет степень бакалавра наук. в комплексном естественнонаучном образовании и степень доктора медицины в математике и технологическом образовании. За последние девять лет она преподавала различные курсы естествознания, математики и технологий. Наоми увлечена образованием и любит видеть, как ученики преуспевают и преуспевают в ее классах.
в комплексном естественнонаучном образовании и степень доктора медицины в математике и технологическом образовании. За последние девять лет она преподавала различные курсы естествознания, математики и технологий. Наоми увлечена образованием и любит видеть, как ученики преуспевают и преуспевают в ее классах.
Наоми выросла в Нью-Гэмпшире и прожила там всю свою жизнь.Она любит все времена года, но осень — ее любимое время. Ей нравится проводить время со своей семьей и играть со своими племянницами и племянниками. В свободное время Наоми любит бегать, рисовать, шить и играть на пианино и кларнете.
Вам также могут понравиться эти другие приложения 4-го класса:
4-й класс / начальная школа / английский язык
4-й класс / Начальная школа / Естественные науки
Math
Исследования показывают, что в сфере образования качество преподавания и руководство школой являются двумя наиболее важными факторами в повышении успеваемости учащихся. Чтобы учителя и руководители школьных округов были максимально эффективными, непрерывное профессиональное обучение, направленное на повышение и расширение знаний по содержанию и совершенствование учебных навыков, является обязательным условием внедрения передовых образовательных практик. Приверженность педагогов непрерывному профессиональному обучению огромна, когда речь идет об успеваемости учащихся. Суперинтенданты, школьные администраторы, директора, руководители учителей и учителя разделяют ответственность за стратегии профессионального развития и достижения, которые, как доказано, повышают уровень успеваемости педагогов.LearningForward.org — это международная ассоциация лидеров образования, приверженных школьному образованию.
Чтобы учителя и руководители школьных округов были максимально эффективными, непрерывное профессиональное обучение, направленное на повышение и расширение знаний по содержанию и совершенствование учебных навыков, является обязательным условием внедрения передовых образовательных практик. Приверженность педагогов непрерывному профессиональному обучению огромна, когда речь идет об успеваемости учащихся. Суперинтенданты, школьные администраторы, директора, руководители учителей и учителя разделяют ответственность за стратегии профессионального развития и достижения, которые, как доказано, повышают уровень успеваемости педагогов.LearningForward.org — это международная ассоциация лидеров образования, приверженных школьному образованию.
стандарты профессионального обучения для педагогов и автора
Почему важно профессиональное развитие.
Возможности профессионального обучения переходной математике
Чтобы помочь во внедрении переходной математики, Совет по образованию штата Иллинойс (ISBE) создает следующие возможности для профессионального обучения.
Обновленная библиотека информационных вебинаров будет доступна в январе 2020 года.Вебинары будут длиться примерно 10-20 минут и будут посвящены конкретным темам переходной математики, таким как обзор, пути, советы, ресурсы и переносимость. Вебинары будут доступны на веб-сайте штата по переходной математике, расположенном по адресу
http://www.iltransitionalmath.org/.
В дополнение к серии вебинаров, ISBE предложит серию переходных модулей профессионального обучения математике в режиме онлайн для инструкторов, администраторов и консультантов. Часы профессионального развития доступны по запросу после завершения.
ISBE также доступен для предоставления личного профессионального обучения по запросу с округами, учителями и руководителями учебных программ, партнерами по общественным колледжам, региональными управлениями образования и другими группами, такими как системы образования для трудоустройства (EFE), заинтересованных в изучении переходного обучения математике. и реализация.
и реализация.
Все возможности профессионального обучения и ресурсы, предлагаемые ISBE, являются
бесплатно бесплатно. Для получения дополнительной информации или запроса профессионального опыта обучения в ISBE, пожалуйста, напишите по электронной почте
TrMathSupport @ isbe.сеть.
VDOE :: Математика
Ваш браузер не поддерживает джаваскрипт! Этот сайт использует JavaScript, но полностью работает без него.
Инструкция
Новости и объявления
НОВИНКА! Стандартные документы по математике
Стандартные документы по математике (K-8) были созданы как часть ресурсов Вирджинии LEARNS, чтобы помочь в выявлении контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися.Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.
Теперь доступны
журналов отслеживания учебных стандартов по математике (с 2020-2021 учебного года по 2021-2022 учебный год)!
Журналы отслеживания для оценок от детского сада до алгебры II были разработаны, чтобы помочь учителям определить, какие стандарты учащиеся имели достаточный уровень знаний и опыта в течение 2020-2021 учебного года.Эти журналы могут помочь в принятии решений относительно того, когда и как можно будет познакомиться с новыми стандартами в 2021-2022 учебном году.
Информационные сессии сообщества Инициативы по математике в Вирджинии
В течение следующих нескольких месяцев будет проведена серия одночасовых информационных сессий сообщества VMPI, чтобы дать родителям и членам сообщества возможность узнать больше об Инициативе Вирджиния по математическим путям. Заседания пройдут в следующие даты:
.
- Вторник, 23 марта 2021 г. — Зачем менять инструкции по математике?
- Вторник, 13 апреля 2021 г.
 — Как VMPI влияет на будущее детей Вирджинии?
— Как VMPI влияет на будущее детей Вирджинии? - Вторник, 27 апреля 2021 г. — Основные понятия для 8-10 классов
- Вторник, 25 мая 2021 г. — Программа повышения квалификации в 11–12 классах
Все занятия будут транслироваться в прямом эфире на канале VDOE на YouTube, начало в 18:30 с 20-минутной презентацией членов комитетов по планированию VMPI, а затем координаторы смогут ответить на вопросы сообщества.Вопросы, которые участники хотели бы задать во время занятий, можно задать через форму «Инициатива по математике в Вирджинии». Посетите Инициативу подготовки к математике в Вирджинии (VMPI): отзывы о записях каждого занятия.
Инициатива по программам подготовки к математике в Вирджинии
Инициатива подготовки к математике в Вирджинии (VMPI) — это совместная инициатива Департамента образования Вирджинии (VDOE), Государственного совета высшего образования Вирджинии (SCHEV) и системы общественных колледжей Вирджинии (VCCS). Инициатива поддерживает Профиль выпускника Вирджинии, переопределяя математические пути для студентов в Содружестве, чтобы обратиться к знаниям, навыкам, опыту и характеристикам, которые студенты должны достичь, чтобы добиться успеха в колледже и / или на работе и быть «готовыми к жизни». ”
Инициатива поддерживает Профиль выпускника Вирджинии, переопределяя математические пути для студентов в Содружестве, чтобы обратиться к знаниям, навыкам, опыту и характеристикам, которые студенты должны достичь, чтобы добиться успеха в колледже и / или на работе и быть «готовыми к жизни». ”
Содержание страницы
Стандарты обучения
Математика K-12
Включает:
- Стандарты обучения и рамки учебных программ
- Планы обучения математике (MIP)
- Тестовые чертежи
- Практические задания
Обзор
Стандарты обучения по математике определяют основной академический контент на каждом уровне обучения для последовательного обучения.Содержание стандартов по математике поддерживает следующие пять целей для студентов: научиться решать математические задачи, общаться математически, рассуждать математически, устанавливать математические связи и использовать математические представления для моделирования и интерпретации практических ситуаций.
Коронавирус (COVID-19) —
Учебные ресурсы по математике
Команда математики Министерства образования Вирджинии собрала несколько материалов по математике Learning in Place, , чтобы помочь учителям, родителям и ученикам в это беспрецедентное время.
Стандарты обучения Вирджинии — журналы отслеживания математики (с 2020-2021 учебного года по 2021-2022 учебный год)
Журналы отслеживания учебных стандартов по математике для классов от детского сада до алгебры II были разработаны, чтобы помочь учителям определить, с какими стандартами учащиеся знакомы и имеют достаточный опыт в течение 2020-2021 учебного года.Они могут поддержать решения относительно того, когда и как можно будет познакомиться с новыми стандартами в 2021-2022 учебном году. Документы по математическим стандартам — это документ в формате PDF. (PDF) можно использовать вместе с журналами отслеживания в качестве поддержки при идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися.
Документы по математическим стандартам — это документ в формате PDF. (PDF) можно использовать вместе с журналами отслеживания в качестве поддержки при идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися.
Переходная математика
Стандартные документы по математике — это документ в формате PDF.(PDF) можно использовать вместе с журналами отслеживания в качестве поддержки при идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися. Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.
Обучение на месте — Интернет-ресурсы
В следующем списке приведены некоторые из множества общих онлайн-ресурсов, которые всегда бесплатны для учителей, родителей и учащихся.
| PBS для родителей — включает занятия и игры, которые можно искать по возрасту и теме. | Y | № | № | № |
| Математика перед сном — предлагает родителям онлайн-математические задачи, которые они могут делать каждый день со своими детьми, а также веселые практические игры. | Y | Y | № | № |
GregTangMath — предоставляет игры, головоломки и другие ресурсы для решения задач и математических центров. | Y | Y | № | № |
| Summer Math Challenge – бесплатная программа, которая обеспечивает доступ к ежедневным увлекательным занятиям и ресурсам, разработанным для вашего класса и уровня способностей вашего ученика.Летние математические соревнования 2020 года открылись раньше, чтобы поддержать студентов, которые учатся дома. | Y | Y | Y | № |
| CK-12 — Интернет-учебник, адаптивная практика и видео примеры | Y | Y | Y | Y |
NCTM Illuminations — включает в себя множество интерактивных материалов, которые побуждают учащихся K-12 изучать, изучать и применять математику. Для доступа к ним можно использовать браузеры с поддержкой Java (например, Internet Explorer, Firefox, Chrome или Safari). Для доступа к ним можно использовать браузеры с поддержкой Java (например, Internet Explorer, Firefox, Chrome или Safari). | Y | Y | Y | Y |
| Open Middle — представляет математические задачи, которые заканчиваются одним и тем же ответом, но имеют несколько способов подхода и решения проблемы. | Y | Y | Y | Y |
| Национальная библиотека виртуальных манипуляторов — включает интерактивные манипуляторы и упражнения для студентов по изучению математики. | Y | Y | Y | Y |
PBS Learning Media — включает бесплатные интерактивные материалы, видео и планы уроков. Также включает ресурсы PreK-12 для аварийного закрытия. Также включает ресурсы PreK-12 для аварийного закрытия. | Y | Y | Y | Y |
| Khan Academy Math — предоставляет бесплатные онлайн-уроки.Студентам необходимо создать учетную запись только в том случае, если необходимо сохранить их работу. | Y | Y | Y | Y |
| Вы бы предпочли математику — предлагает студентам построить математический аргумент для выбора между двумя или более вариантами. | Y | Y | Y | Y |
VDOE Desmos Activity Log — включает электронную таблицу для каждого уровня обучения, в которой перечислены действия Desmos, согласованные с SOL, с кратким описанием и прямой ссылкой на действие на веб-странице Desmos Classroom Activity. | № | Y | Y | Y |
| FigureThis! NCTM — предлагает задания и задания по математике для студентов и семей. Некоторые задачи также доступны на испанском языке. Советы для родителей можно найти в Семейном уголке. | № | Y | Y | Y |
Обучение на месте — Интернет-плейлисты eMediaVA
В следующей таблице содержатся ссылки на плейлисты избранных ресурсов eMediaVA, согласованных с классами K-8 2016 Стандарты обучения по математике .Расширенные списки коллекций ресурсов eMediaVA по математике доступны ниже.
Обучение на месте — Дополнительные подборки материалов по математике eMediaVA по классам
Марки К — 2
3-5 классы
6–8 классы
Обучение на месте — VA TV Classroom On-Demand
Blue Ridge PBS, VPM, WETA и WHRO Public Media работали с VDOE над созданием VA TV Classroom для обучения учащихся классов K-10, которые не могут получить доступ к другим возможностям дистанционного обучения из-за отсутствия высокоскоростного Интернета. Эти образовательные программы также доступны по запросу. Сегменты из «Учись и развивайся с WHRO » (классы K-3) и «Продолжай узнавать с WHRO » (классы 4–7) теперь доступны в eMediaVA.
Эти образовательные программы также доступны по запросу. Сегменты из «Учись и развивайся с WHRO » (классы K-3) и «Продолжай узнавать с WHRO » (классы 4–7) теперь доступны в eMediaVA.
Обучение на месте — Предлагаемые автономные мероприятия для вовлечения студентов
Следующий список содержит лишь некоторые из множества ресурсов, которые бесплатно доступны учителям, родителям и учащимся.
Детский сад — 2 класс
- Изобразите виды птиц, которых вы видите у себя во дворе или из окна.(Используйте метки для сбора данных и систематизируйте данные в виде графической или гистограммы.)
- Играйте в математические карточные игры. Например, Go Fish (попробуйте составить пары, которые складываются с 10).
- Измерьте длину своей кровати, используя пять различных нестандартных единиц. Например, в моей кровати 14 туфель, какова длина вашей кровати?
3–5 классы
- Измерьте площадь и периметр каждой комнаты в вашем доме.
 Какие комнаты самые большие, самые маленькие? Составьте список, когда вам нужно знать площадь комнаты? Периметр комнаты?
Какие комнаты самые большие, самые маленькие? Составьте список, когда вам нужно знать площадь комнаты? Периметр комнаты? - Постройте 3 разных бумажных самолетика. Проверьте каждый, чтобы определить, какой из них пролетает наибольшее расстояние. Измерьте расстояние, которое пролетает каждый самолет.
- Играйте в математические карточные игры. Например, Fraction War (каждый человек получает 2 карты и формирует дробь с намерением попытаться сформировать наибольшую дробь).
6-8 классы
- Выберите свой любимый рецепт и пополам. Решите, сколько каждого ингредиента вам понадобится, чтобы приготовить угощение для своей семьи.
- Определите объем и площадь различных предметов в ваших шкафах, например коробок для хлопьев и консервов.
- Используйте магазинную бумагу для продажи, чтобы создать список покупок. Затем найдите общую стоимость ваших товаров с учетом скидок и налога с продаж.
- Играть в математические карточные игры. Например, Порядок операций , каждый человек выбирает четыре карты и использует правила порядка операций, чтобы сделать число как можно ближе к определенному числу.
9–12 классы
- Рассчитайте уклон лестницы (подъем / спуск) и сравните, что произойдет, если высота каждой ступеньки будет увеличиваться или уменьшаться. По каким лестницам легче всего подниматься?
- Оцените объем нескольких предметов неправильной формы в вашем доме, используя то, что вы знаете об объеме и площади поверхности.Что бы произошло с поверхностью, если бы предмет разрезать вертикально пополам?
Ресурсы для профессионального развития
VDOE продолжает обеспечивать профессиональное развитие школьных подразделений и учителей, чтобы поддержать внедрение стандартов обучения математике. Школьным подразделениям и учителям рекомендуется использовать ресурсы профессионального развития для повышения успеваемости учащихся за счет качественного обучения.
Школьным подразделениям и учителям рекомендуется использовать ресурсы профессионального развития для повышения успеваемости учащихся за счет качественного обучения.
- 2019 Развитие более глубокого обучения с помощью разнообразных математических задач — Институт математики
— Институты 2019 года предоставили учителям и руководителям математики возможность повышения квалификации, направленную на выполнение разнообразных математических задач, чтобы поддержать более глубокие возможности обучения для студентов и улучшить учебные программы, разработанные на местном уровне. Материалы институтов были включены для использования учителями и педагогическими коллективами. - Математические стандарты обучения (SOL) 2018 институты — Математические стандарты обучения 2018 институты обеспечивали обучение, ориентированное на внедрение математических стандартов обучения 2016 года; усиление преподавания и изучения математики посредством содействия содержательному математическому дискурсу; и поддержка равных возможностей обучения математике для всех учащихся.
 Продукт Математических институтов 2018 года представляет собой набор онлайн-модулей профессионального развития, предназначенных для использования группой учителей определенного уровня или курса при содействии одного из членов команды.
Продукт Математических институтов 2018 года представляет собой набор онлайн-модулей профессионального развития, предназначенных для использования группой учителей определенного уровня или курса при содействии одного из членов команды. - Институты по стандартизации обучения математике (SOL) 2017 г. — VDOE обеспечил повышение квалификации школьных подразделений и их учителей в поддержку внедрения Стандартов обучения по математике и структуры учебной программы 2016 года. Ресурсы профессионального развития VDOE поддерживают использование эффективных методов преподавания математики.
- Институты стандартов обучения математике (SOL) на 2009-2014 гг. — VDOE обеспечивает целевое профессиональное развитие через институты математики с 2009 года. Эти институты сосредоточились на стандартах обучения по математике 2009 года и были сформулированы пятью целями процесса, чтобы студенты стали математиками. решатели проблем, математически общаются, рассуждают математически, устанавливают математические связи и используют математические представления для моделирования и интерпретации практических ситуаций.

Учебные ресурсы по математике
В дополнение к стандартам, рамкам учебных программ, планам тестов и выпущенным тестам, другие учебные ресурсы включают:
- Algeblocks Training — онлайн-тренинг для учителей, которым либо нужно введение в использование алгебр, либо необходимо заново познакомиться с манипулятивным
- Инициатива готовности к алгебре — информация для подготовки студентов к успеху в алгебре
- Корреляция между VASOL и CCSS. Это таблица в формате Excel.(XLS) — Эта таблица содержит черновик взаимосвязей между детским садом и алгеброй II — 2016 Стандарты обучения Вирджинии (VASOL) для математики с Общими государственными стандартами (CCSS) для математики. Эта корреляция была создана для поддержки преподавателей по всему Содружеству, поскольку они пытаются использовать материалы, которые могут указывать только на соответствие CCSS. Все VASOL и CCSS, а также цели процесса Вирджинии и математические практики CCSS связаны по всей таблице, чтобы упростить перекрестные ссылки.

- Учебные планы по математике с совместным преподаванием — в этих планах используются шесть общих подходов к совместному обучению и содержатся предложения о том, как со-преподаватели могут эффективно использовать опыт каждого учителя для улучшения уроков и занятий в классе с совместным преподаванием. Эти планы совместного обучения были созданы и изменены избранной группой учителей Вирджинии, участвующих в Инициативе «Совершенство для совместного обучения». Эти планы согласовывают обучение с требованиями стандартов обучения по математике 2016 г. и были проверены специалистами VDOE и специалистами по специальному образованию.
- Нарушения обучаемости по математике — Эта страница содержит информацию и ресурсы, а также два новых сопутствующих руководства VDOE:
- Учебные видеоролики для учителей — видеоролики, предоставленные в качестве поддержки для внедрения Стандартов обучения математике штата Вирджиния
- Just in Time Mathematics Quick Checks — Эти формирующие экзамены соответствуют Стандартам обучения математике 2016 года (SOL).
 Эти ресурсы, разработанные учителями и руководителями математики Вирджинии, предназначены для того, чтобы помочь учителям выявлять учащихся с незаконченным обучением и помогать в планировании обучения, чтобы «вовремя» заполнить потенциальные пробелы.По мере того, как в течение учебного года вводится новый контент, учителя могут использовать эти быстрые проверки для выявления и диагностики незавершенного обучения на уровне класса и / или для оценки понимания необходимых знаний, которые могут потребоваться для доступа к контенту на уровне класса. Пробелы в понимании математики учащимися существуют по разным причинам, и эти ресурсы можно использовать, чтобы помочь вернуть учащимся математическое обучение в нужное русло.
Эти ресурсы, разработанные учителями и руководителями математики Вирджинии, предназначены для того, чтобы помочь учителям выявлять учащихся с незаконченным обучением и помогать в планировании обучения, чтобы «вовремя» заполнить потенциальные пробелы.По мере того, как в течение учебного года вводится новый контент, учителя могут использовать эти быстрые проверки для выявления и диагностики незавершенного обучения на уровне класса и / или для оценки понимания необходимых знаний, которые могут потребоваться для доступа к контенту на уровне класса. Пробелы в понимании математики учащимися существуют по разным причинам, и эти ресурсы можно использовать, чтобы помочь вернуть учащимся математическое обучение в нужное русло. - Образцы результатов успеваемости по математике K-3 — Школы ведут учет достижений по математике для каждого ученика K-3, чтобы отслеживать его успеваемость и способствовать успеваемости на экзаменах SOL в третьем классе.Эта запись сопровождает ученика, который переходит в новую школу
- Математика Capstone Информация о курсе — Руководящие документы и ссылки на учебные ресурсы
- по математике — ранее известные как Уроки с расширенным объемом и последовательностью , теперь доступны для классов K-8, алгебры I, геометрии, алгебры II и алгебры, функций и анализа данных.
 Эти учебные планы включают обновленные документы 2009 года, а также недавно разработанные учебные планы, соответствующие Стандартам обучения по математике 2016 года .Учебные планы по математике помогают учителям привести обучение в соответствие со Стандартами обучения по математике 2016 , предоставляя примеры того, как знания, навыки и процессы, содержащиеся в SOL и Curriculum Framework, могут быть представлены учащимся в классе.
Эти учебные планы включают обновленные документы 2009 года, а также недавно разработанные учебные планы, соответствующие Стандартам обучения по математике 2016 года .Учебные планы по математике помогают учителям привести обучение в соответствие со Стандартами обучения по математике 2016 , предоставляя примеры того, как знания, навыки и процессы, содержащиеся в SOL и Curriculum Framework, могут быть представлены учащимся в классе. - Инструмент вертикального сочленения по математике (MVAT) — этот инструмент обеспечивает поддержку в определении концепций, соответствующих Стандартам обучения по математике 2016 (SOL), которые формулируются на разных уровнях обучения математике или на разных курсах.
- Математические настенные карточки со словарным запасом (K-8, Алгебра I, Геометрия, AFDA и Алгебра II) — обеспечивают отображение слов математического содержания и связанных визуальных подсказок для помощи в развитии словарного запаса.
- Rich Mathematical Tasks — (K-8, Algebra I, Geometry, Algebra II) Эти ресурсы предназначены для поддержки учителей во внедрении в их классах «Стандартов обучения по математике 2016» .
 Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.
Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.
Учебные планы
- Программа подготовки к детскому саду штата Вирджиния — многомерная оценка готовности к детскому саду, которая дополняет существующую оценку навыков грамотности учащихся с использованием скрининга фонологической осведомленности на грамотность (PALS) с оценками начальных математических знаний учащихся, саморегуляции и навыки общения.
- Цель ВКРП состоит в том, чтобы школьные подразделения и Содружество имели более полное представление о критических навыках готовности учащихся к школе при поступлении в детский сад.Школы, подразделения и руководители штатов могут использовать данные о готовности для определения приоритетов индивидуальных потребностей учащихся и целевых программ, ресурсов и возможностей профессионального развития учителей.
- В 2018 году Генеральная ассамблея Вирджинии приняла закон, который требует, чтобы все учащиеся детских садов проходили аттестацию с использованием VKRP до конца 2019-2020 учебного года, а затем ежегодно (HB5002, пункт 128, H.
 ).
).
Ресурсы по технологиям и математике
Профессиональные организации
Премиальные программы
- Президентские награды за выдающиеся достижения в преподавании математики и естествознания — Президентская награда за выдающиеся достижения в преподавании математики и естественных наук (PAEMST) — это высшее признание, которое учитель математики или естествознания в детском саду может получить от детского сада до 12-го класса за выдающееся преподавание в Соединенных Штатах.
- Учитель года по математике Уильяма К. Лоури — каждый год Совет учителей математики Вирджинии признает классного учителя начального, среднего, среднего, университетского уровня, а также специалиста / тренера по математике за его или ее выдающуюся работу и достижения в обучение математике.
Начало страницы
Математика | Агентство образования
В 2010 году Вермонт принял Стандартные стандарты штата по математике. CCSS по математике дает студентам четкие и последовательные ожидания, которые определяют, что студенты должны понимать и уметь делать. AOE разработало типовые требования к выпускным экзаменам (PBGR) по математике на основе CCSS. Эти PBGR являются примерами строгих рамок выпуска, основанных на профессиональных знаниях, которым студенты должны соответствовать для выпуска в соответствии с содержанием математики в соответствии с требованиями EQS. Эти стандарты не определяют учебный план или методы обучения. Они также не предназначены для того, чтобы дать новое название старым способам ведения бизнеса, а скорее как основу для поддержки школ, поскольку они обеспечивают эффективное обучение и учебную программу по математике для K-12.
CCSS по математике дает студентам четкие и последовательные ожидания, которые определяют, что студенты должны понимать и уметь делать. AOE разработало типовые требования к выпускным экзаменам (PBGR) по математике на основе CCSS. Эти PBGR являются примерами строгих рамок выпуска, основанных на профессиональных знаниях, которым студенты должны соответствовать для выпуска в соответствии с содержанием математики в соответствии с требованиями EQS. Эти стандарты не определяют учебный план или методы обучения. Они также не предназначены для того, чтобы дать новое название старым способам ведения бизнеса, а скорее как основу для поддержки школ, поскольку они обеспечивают эффективное обучение и учебную программу по математике для K-12.
«Вермонтский портрет выпускника» (PoG) был разработан совместно с преподавателями и студентами для использования в качестве инструмента для анализа и уточнения местных PBGR, включая PBGR по конкретному содержанию, а также в качестве руководства для принятия учебных решений. PoG определяет когнитивные, личные и межличностные навыки и способности, которые студенты должны быть в состоянии продемонстрировать после окончания учебы, с учетом шести атрибутов: учащегося, глобального гражданства, академического мастерства, общения, критического мышления и благополучия.
PoG определяет когнитивные, личные и межличностные навыки и способности, которые студенты должны быть в состоянии продемонстрировать после окончания учебы, с учетом шести атрибутов: учащегося, глобального гражданства, академического мастерства, общения, критического мышления и благополучия.
Портрет выпускника как функция математики
В дополнение к изучению концепций математики, учащийся может также обратиться к характеристикам PoG штата Вермонт посредством изучения математики. Ниже представлена версия PoG, которая показывает, как студент, изучающий математику, будет соответствовать шести атрибутам, описанным в PoG штата Вермонт. Содержащаяся информация в значительной степени основана на показателях эффективности атрибутов PoG штата Вермонт, а также на Практике справедливого преподавания математики, найденной в книге «Катализатор изменений», опубликованной Национальным советом учителей математики.
Ученическое агентство = Собственность + Завидные ожидания + Аутентичный опыт
Учащиеся становятся учениками на всю жизнь, когда они развивают чувство собственности своего обучения. Практикуя навыки моделирования, рассуждения и решения проблем во время аутентичных опытов , учащиеся формируют свою собственную математическую идентичность и начинают соответствовать завышенным ожиданиям . Создание уникальных математических представлений и решений позволяет учащимся стать компетентными в использовании и применении математики в реальных сценариях и отстаивать свои собственные решения с помощью использования данных.
Практикуя навыки моделирования, рассуждения и решения проблем во время аутентичных опытов , учащиеся формируют свою собственную математическую идентичность и начинают соответствовать завышенным ожиданиям . Создание уникальных математических представлений и решений позволяет учащимся стать компетентными в использовании и применении математики в реальных сценариях и отстаивать свои собственные решения с помощью использования данных.
Глобальное гражданство = универсальный язык + сложность + разные культуры
Чтобы стать гражданами мира, учащиеся должны уметь использовать математику для общения и моделирования природных явлений на местном и глобальном уровнях. Математика считается универсальным языком , поскольку структура математического языка одинакова во всем мире. Однако понимание сложностей того, как другие изучают математику, имеет решающее значение для преодоления культурных разрывов, поскольку способ представления математических идей в других странах отличается. Учащиеся, выполняющие соответствующие задачи из различных культур, взаимодействуют с различными идеями и концепциями, которые устраняют предубеждения, неправильные представления и иерархический статус при изучении математических практик и концепций.
Учащиеся, выполняющие соответствующие задачи из различных культур, взаимодействуют с различными идеями и концепциями, которые устраняют предубеждения, неправильные представления и иерархический статус при изучении математических практик и концепций.
Академический уровень = Основные понятия + Применение + Вопросы
Учащиеся, которые понимают основных концепций математики , могут свободно объединять знания и навыки для решения реальных задач. Применение этих концепций к новым и уникальным ситуациям развивает способность учащегося эффективно задавать вопросов и участвовать в математических дискуссиях и решении проблем в жизни после окончания учебы.
Коммуникация = Дискурс + Мультимодальность + Контекст
Чтобы получить более глубокое понимание математики и использовать математические навыки для осмысления своего мира, учащиеся должны общаться посредством дискурса среди сверстников, используя мультимодальные формы средств массовой информации при моделировании математики, одновременно понимая точки зрения других, анализируя их аргументы и подходы к решению проблемы. Учащимся необходимо целенаправленно задавать вопросы, чтобы передать свои знания, пересмотреть собственное мышление и развить позитивную математическую идентичность, позволяющую им представлять свои решения в контексте и в уважительной манере.
Учащимся необходимо целенаправленно задавать вопросы, чтобы передать свои знания, пересмотреть собственное мышление и развить позитивную математическую идентичность, позволяющую им представлять свои решения в контексте и в уважительной манере.
Критическое мышление = решение проблем + оценка + сотрудничество
По мере того, как учащиеся анализируют математическую информацию и предпринимают новаторские решения реальных задач , они развивают необходимые навыки рассуждения, чтобы участвовать в более сложных и требовательных ситуациях. Обнародование мышления учащихся посредством презентации, как независимо, так и в сотрудничестве со своими сверстниками, подтверждает их идеи как достойные оценки и исследования, а также формирует положительную математическую идентичность.Это стимулирует анализ неизвестных ситуаций, чтобы понять, как компоненты работают независимо и вместе, позволяя неизвестному стать известным.
Благополучие = уверенность + компетентность + финансовая независимость
Соединение концептуального понимания с процедурной беглостью позволяет учащемуся укрепить уверенность в своих способностях знать и выполнять математику. Студенты, которые могут ориентироваться в экономических ситуациях — личных, местных и глобальных — и участвовать в ответственном принятии математических решений, демонстрируют свою компетенцию с математикой и финансовой грамотностью, что, в свою очередь, может привести к улучшенным результатам, таким как финансовая независимость .
Стандарты
ресурсов
Информационные бюллетени
Профессиональные организации
- NCSM: Национальный совет наблюдателей за математикой
- NCTM: Национальный совет учителей математики
- VCTM: Совет учителей математики штата Вермонт
Вопросы?
Напишите письмо Райану Паркману или позвоните по телефону (802) 828-6468.
Что заставляет учащихся испытывать трудности с математикой?
Многие дети плохо разбираются в математике, но некоторым ученикам это труднее, чем другим.Это могут быть в остальном умные дети, у которых есть острое чувство логики и рассуждений, но которые все равно плохо справляются с домашними заданиями, тестами и викторинами.
Со временем повторяющаяся неуспеваемость по математике может привести к тому, что ученик потеряет мотивацию и поверит, что он или она «глуп» или плохо разбирается в предмете.
Более того, поскольку математика накапливается, отставание может означать, что учащийся пропускает большую часть того, чему его учат, до конца учебного семестра. Базовые математические навыки важны независимо от того, какую карьеру выбирает человек.
Вот почему так важно выявлять проблемы на ранней стадии. При правильном сочетании условий в классе и стратегий обучения каждый ученик может полностью раскрыть свой потенциал в математике.
Есть ряд причин, по которым у ребенка могут быть проблемы с математикой в школе, от низкой мотивации, вызванной математической тревогой, до плохого понимания того, как применять и выполнять математические операции.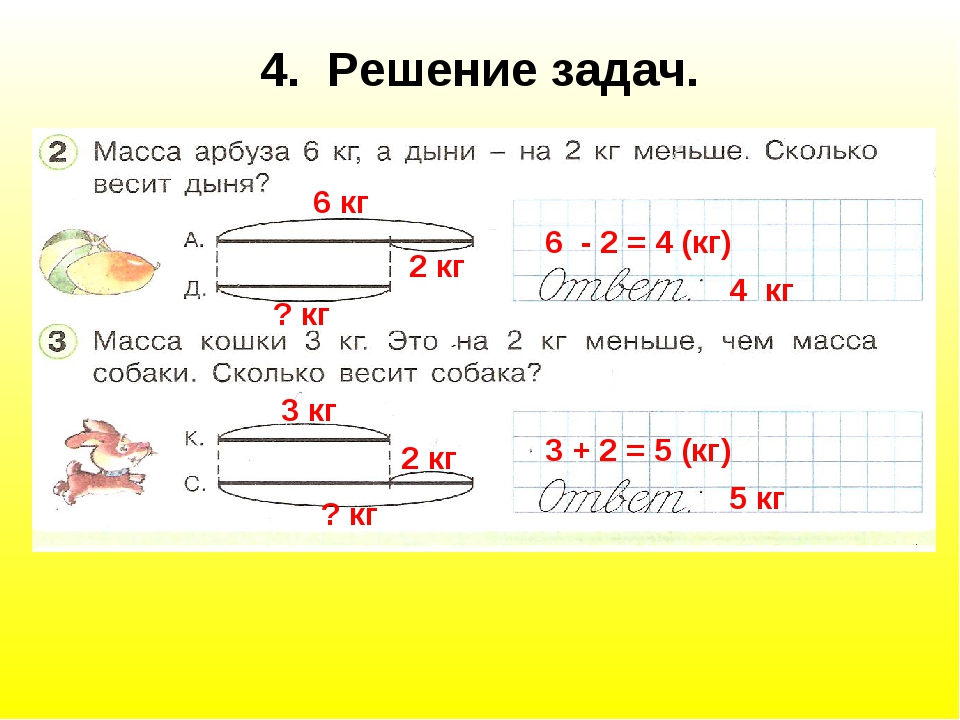 Но иногда первопричина недостаточной успеваемости кроется в чем-то другом, например, в различиях в обучении или проблемах с моторикой.
Но иногда первопричина недостаточной успеваемости кроется в чем-то другом, например, в различиях в обучении или проблемах с моторикой.
Наиболее часто ассоциированным заболеванием является дискалькулия , при котором люди испытывают трудности с выполнением основных вычислений и не могут манипулировать числами так же, как их сверстники.
Однако ученики с дислексией также могут испытывать трудности с математикой в школе из-за трудностей при чтении чисел и проблем с пониманием слов. Они могут менять порядок цифр при выполнении работы на бумаге или правильно решать задачи, но записывать свои ответы неправильным образом.
Дети с СДВ / СДВГ могут выскочить вперед и пропустить шаг или с трудом сосредоточиться и быть не в состоянии проверить свою работу после того, как решат задачу.
Учащиеся с дисграфией и диспраксией , которым трудно писать от руки, могут настолько отвлечься на формирование чисел, что они сделают неосторожные ошибки или выполнят шаги в уравнении в неправильном порядке.
Наконец, дети с расстройствами зрительной обработки могут не обладать навыками визуально-пространственной обработки, которые им необходимы для выравнивания чисел, чтения графиков и выполнения основных геометрических операций.
Как мы относимся к математике
Математика — один из тех предметов, которые плохо понимают как дети, так и взрослые. Это связано с тем, что в то время как дошкольная математика заключается в решении практических задач, обнаружении закономерностей, распознавании форм в вашей среде и обучении счету, обучение математике в средней и старшей школе становится более абстрактным. Он часто фокусируется на заучивании наизусть и решении уравнений из книг — подумайте об арифметике и таблицах умножения — что может оттолкнуть учащихся и заставить их поверить в то, что математические навыки не имеют отношения к их повседневной жизни.
На самом деле, многие студенты жалуются, что математика скучна. Они могут не видеть смысла в изучении алгебры, геометрии или математического анализа в школе. Или они могут спросить, почему им нужно уметь выполнять основные арифметические операции, такие как сложение, вычитание, умножение и деление, вручную, когда ответы можно легко найти с помощью калькулятора или компьютера.
Или они могут спросить, почему им нужно уметь выполнять основные арифметические операции, такие как сложение, вычитание, умножение и деление, вручную, когда ответы можно легко найти с помощью калькулятора или компьютера.
Ответ на этот последний вопрос тройной. Во-первых, у вас не всегда может быть калькулятор; во-вторых, даже если вы это сделаете, понимание того, как и почему нужно делать это для себя, дает более прочную основу для будущего обучения, и в-третьих, выполнение арифметики — это умственная тренировка, которая укрепляет вашу рабочую память.
Числа окружают нас повсюду, и возможность работать с ними быстро и эффективно — это важный жизненный навык. Учтите, что быстрота в арифметике также весьма практична во многих профессиях, от плотника до розничной торговли, ракетостроения и обеспечения своевременного движения поездов!
Однако математика — это гораздо больше, чем арифметика. Многое из того, что входит в решение многоступенчатых задач со словами, — это определение проблемы, выбор подходящего подхода к ее решению (их может быть несколько) и соблюдение правильного порядка действий.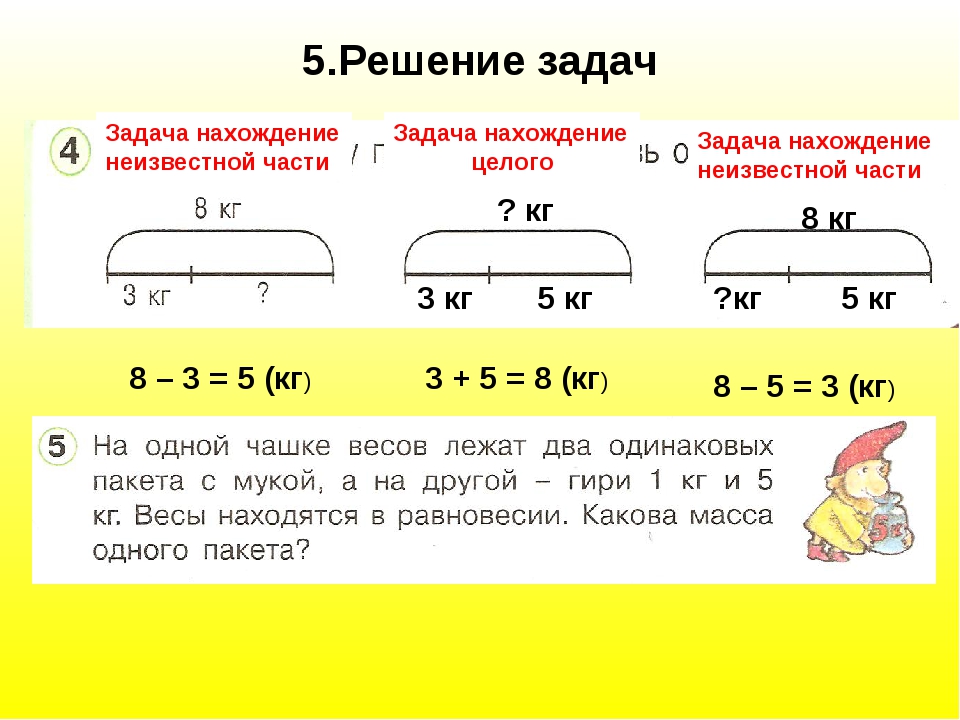
Уяснить фактическую арифметику — ту часть, на которую способен калькулятор — гораздо проще. Это одна из причин, по которой детей просят показывать свою работу, когда они делают домашнее задание или дают ответы на тесте по математике.
В некоторых случаях учителя могут поставить за хорошую работу больше, чем за правильный ответ. Это потому, что именно в развернутой рукописной работе педагоги могут увидеть, как происходит «математическое мышление».
Однако такой подход может оскорбить очень способного ребенка, который интуитивно подскакивает к правильному решению, но не анализирует, как он к нему пришел, или ребенка, которому трудно писать от руки.Признание индивидуальных потребностей и сильных сторон учащихся лежит в основе передового опыта в обучении.
Кто борется с математикой?
- Учащиеся с математической тревогой
Исследования показали, что математика — это предмет, в котором на успех в значительной степени влияют психологические факторы, включая тревогу.
 Беспокойство — это больше, чем просто чувство беспокойства — это химическая реакция в мозге, которая может подавлять когнитивные процессы и вызывать физические симптомы, включая учащенное дыхание, учащенное сердцебиение и потоотделение.
Беспокойство — это больше, чем просто чувство беспокойства — это химическая реакция в мозге, которая может подавлять когнитивные процессы и вызывать физические симптомы, включая учащенное дыхание, учащенное сердцебиение и потоотделение.Беспокойство по математике может привести к тому, что люди, которые в остальном являются сильными учениками, замирают на школьной викторине или экзамене.
У них могут быть трудности с поиском решения проблемы, неправильное понимание вопросов или выполнение гораздо меньшего количества задач, чем они способны. Многие учащиеся, испытывающие тревогу, совершают небрежные ошибки из-за стресса, который они испытывают в данный момент, и, как правило, их оценочная работа по расписанию хуже по качеству, чем классные занятия или задания, выполняемые дома.
Тревога по поводу математики не обязательно связана с плохими математическими способностями, она может влиять на учащихся с любым уровнем способностей — даже на одаренных детей.Тем не менее, это обычно приводит к снижению оценок, что подрывает уверенность учащегося.
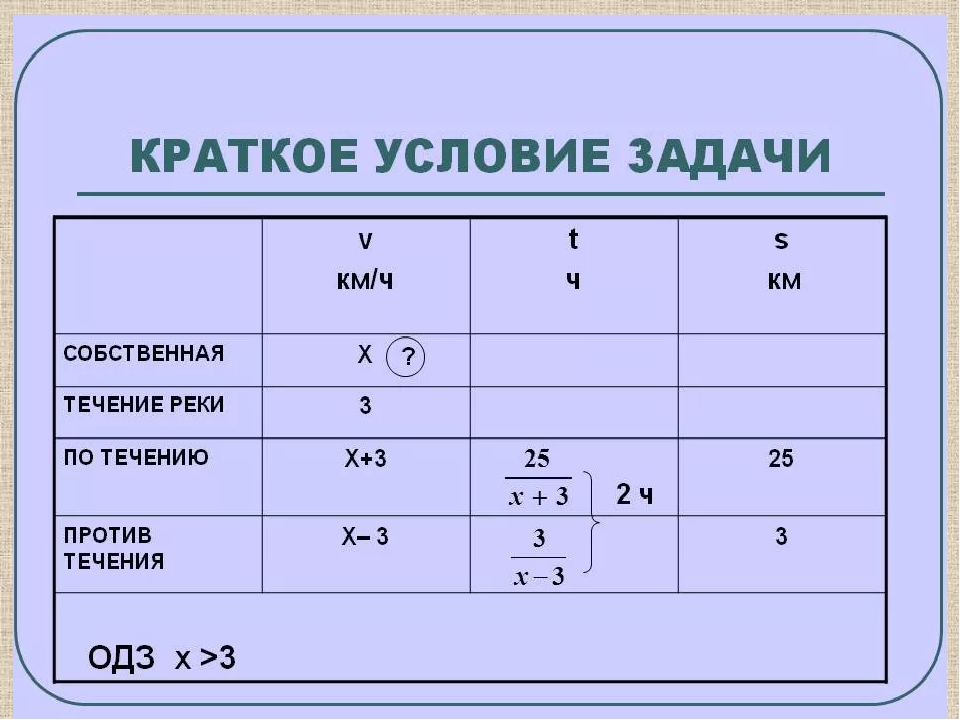
Это несоответствие между оценками и знаниями / навыками может как обескураживать, так и демотивировать учащихся. В худшем случае ребенок может начать проявлять признаки избегания математики и отрицательного отношения к школе и обучению в результате беспокойства.
Стоит отметить, что некоторые учащиеся унаследовали от родителей тревогу и / или избегание математики. В западных обществах нередко можно услышать, как люди выражают неприязнь к математике.Фактически, это стало общепринятым способом обсуждения предмета в США и Великобритании. Это может повлиять на учащихся, которые начинают обесценивать его как предмет или считают приемлемым заниженные ожидания от себя, когда дело касается математики в школе.
Также имейте в виду, что для некоторых учащихся беспокойство по поводу математики является результатом плохой успеваемости из-за неучтенных проблем с обучением или моторикой либо пробелов в их истории обучения.
- Дети с дискалькулией
Учащиеся с дискалькулией плохо справляются с основами арифметики и могут с трудом усваивать математические факты.
 Как и в возрасте до 5 лет, им, возможно, потребовалось больше времени, чем их сверстникам, чтобы овладеть счетом.
Как и в возрасте до 5 лет, им, возможно, потребовалось больше времени, чем их сверстникам, чтобы овладеть счетом.Дискалькулия также может влиять на оценочные способности и пространственное мышление; эти учащиеся могут быть не в состоянии определять время на часах, делать сравнительные суждения о размерах или определять математические символы. Дискалькулия часто сочетается с другими специфическими различиями в обучении, такими как дислексия, а также с проблемами внимания.
ГЛАВНЫЙ СОВЕТ: Калькуляторы — разумная настройка. Поскольку учащиеся с дискалькулией могут быть не в состоянии надежно выполнять вычисления сложения, вычитания, умножения и pision, им может потребоваться использовать калькулятор для решения сложных математических задач.
- Студенты с дислексией
Дислексия — это другой способ обработки в мозгу, который может повысить вероятность того, что ученики переворачивают числа и буквы, меняют числа или меняют их порядок. Например, копирование многозначного числа из одной строки в другую может привести к тому, что учащийся уронит цифру или добавит цифру, которой там не было.
Проблемы могут возникать и при обработке письменной речи, поскольку дислексия влияет на способность ребенка слышать звуки, из которых состоят слова.Это затрудняет чтение и может повлиять на понимание текстовых задач.
Учащимся с дислексией, возможно, придется перечитать абзац несколько раз, чтобы понять его, они могут легко потерять свое место, выполняя упражнения вручную, и им может потребоваться гораздо больше времени, чем их сверстникам, чтобы пройти начальные этапы понимания подсказки. Следовательно, у них останется меньше времени на выполнение фактических вычислений, необходимых для поиска решения.
- Лица с диспраксией
Диспраксия может повлиять на мелкую моторику, необходимую для того, чтобы держать ручку или карандаш.Поскольку большая часть длинных математических формул выполняется вручную, учащиеся с диспраксией могут с трудом показать шаги, которые они использовали, чтобы прийти к ответу.
Человек может легко отвлечься или расстроиться из-за боли при письме и с большей вероятностью бросит или оставит вопрос, прежде чем решить его. Диспраксия также может влиять на планирование и организационные навыки. Поскольку решение более сложных проблем требует определенного планирования того, как вы придете к ответу, учащимся с диспраксией может быть трудно начать.
Они также могут бороться с последовательностью шагов и правильным порядком операций в математике.
- Дети с СДВ / СДВГ
Проблемы с вниманием могут повлиять на математические навыки по-разному. Во-первых, им труднее уделять внимание в классе. Решение математической задачи требует от вас выполнения нескольких шагов; ответ на одну строку сообщает следующую.
Если ученик отвлекается и отвлекается, ему может быть очень сложно проследить за демонстрацией учителя и понять, как было получено определенное число.Сохранение концентрации также является проблемой при выполнении работы вручную и проверке работы после того, как проблема решена .
ПОЛЕЗНЫЙ СОВЕТ: Учащиеся с проблемами внимания могут быть более восприимчивыми к эффектам привязки. Когда вы впервые сталкиваетесь с математической задачей, вам нужно сначала сосредоточиться на понимании того, что от вас просят. Частью сбора важных битов является блокирование любых эффектов привязки от чисел, которые появляются постоянно и пытаются привлечь ваше внимание. Эти числа обычно указываются намеренно, чтобы отвлечь внимание, но они могут быть проблематичными для некоторых учащихся.Вы можете научить детей следить за этими числами, чтобы они могли активно подавлять свои инстинкты и использовать их в качестве ответа.
Дети с СДВГ и гиперактивностью могут спешить с математическими задачами и в результате пропускать шаги или ошибаться с арифметикой. Они могут импульсивно записывать ответы, или их рукописные работы могут быть запутанными и трудными для чтения.
Сложные для расшифровки числа могут сбить с толку как ученика, так и учителя — узнайте больше о том, как трудности с письмом влияют на учеников с СДВ / СДВГ.
- Учащиеся с дисграфией
Одна из самых важных частей решения математической задачи — это способность изложить свои мысли на бумаге. Это сделано для того, чтобы вы могли работать поэтапно, потому что одновременное удержание в голове нескольких вычислений создает нагрузку на когнитивные ресурсы и увеличивает вероятность ошибки.
Однако для учащихся с дисграфией записать «математическое мышление» может быть непросто. Студенты-дисографы могут испытывать трудности с формированием чисел и символов, их пространственной организацией и копированием текста с доски при ведении заметок.
У них может быть беспорядочная и неорганизованная письменная работа, которую им может быть трудно читать и из-за которой они получат неправильный ответ, даже если выбранный ими подход был правильным. Узнайте больше о дисграфии.
- Лица с нарушениями обработки зрения
Учащиеся с нарушениями визуальной обработки могут иметь трудности с математическими задачами, которые включают пространственное мышление, включая геометрию, чтение таблиц, чтение карт, а также различение и идентификацию различных чисел.Узнайте больше о нарушениях обработки зрения.
Как учителя могут сделать занятия по математике более инклюзивными
Сделайте математику актуальной.
Мотивируйте учащихся, показывая им реальные ситуации, связанные с использованием математики вне школьных классов. Объясните, как работает математика, убедите учащихся, что дело не только в арифметике, и побудите их попробовать и почувствовать себя комфортно, пробуя различные подходы к решению проблем, даже если это означает, что они не всегда получают правильный ответ.
Обучайте мультисенсорным способом.
Учитель дает устные объяснения, показывает работу на доске и, если возможно, использует тактильные приспособления, которые ученики могут коснуться и передвигать. Мультисенсорный ввод может помочь в обучении, облегчая учащимся участие в уроке, а также может закрепить материал в памяти. Это особенно важно для облегчения понимания предмета, который может быть довольно абстрактным.
Упражняйте словарный запас заранее.
Некоторым учащимся, особенно тем, кто борется с грамотностью, возможность попрактиковаться в чтении, правописании и наборе математической лексики и определений может облегчить и ускорить выполнение урока, чтение учебника или понимание проблемы в домашнем задании. или в викторинах.
ПОЛЕЗНЫЙ СОВЕТ: Вы когда-нибудь задумывались, как слепой набор может помочь учащимся с математикой? Попробуйте читать и писать по буквам с помощью сенсорного ввода.
Узнать больше
Назначьте друзей для ведения заметок.
Иногда записывать информацию и одновременно обрабатывать ее может утомительно. Также может случиться так, что копирование с доски может привести к тому, что числа будут перенесены или записаны таким образом, что работа больше не имеет смысла. Может быть полезно разрешить ребенку делать заметки с помощью компьютера или объединить их с другом, который ведет заметки.
Разрешить доступ к жилым помещениям.
Если учащемуся диагностировали трудности в обучении, такие как дискалькулия, дислексия или дисграфия, вы можете разрешить им использовать калькулятор для выполнения основных арифметических операций или компьютер, чтобы печатать и отправлять работы.Слепой набор на компьютере часто бывает проще для детей, которым сложно научиться писать от руки.
Дайте учащимся больше времени.
Потребность во времени на обработку в математике может варьироваться между учениками, но детям с трудностями в обучении часто полезно иметь больше времени, чтобы понять концепцию и посмотреть, как она работает. Это также помогает разбить работу на небольшие этапы и дать каждому учащемуся время, необходимое для осмысления линии, на которой он находится, прежде чем перейти к следующей.Увеличение ограничения по времени также может помочь уменьшить беспокойство по поводу математики.
Быстрый повторный колпачок:
Учащиеся с дискалькулией, дислексией, диспраксией, проблемами внимания, дисграфией, проблемами обработки изображений и тревогой могут бороться с математикой.
- Дети с дискалькулией могут затруднить основы арифметики и счета
- Учащиеся с трудностями обработки данных и ADD / ADHD могут иметь проблемы после объяснений учителя в классе
- Учащимся с диспраксией может быть сложно выбрать лучший подход к решению проблемы диспраксия
- Запись, интерпретация и преобразование решения могут быть сложными для учащихся с дислексией и дисграфией
- Учащиеся с математикой тревожно могут испытывать трудности с выполнением заданий по оценке по времени или испытывать недостаток мотивации из-за низкой самооценки или неуверенности.
Сенсорное чтение и написание
Touch-type Read and Spell — это мультисенсорная программа набора текста, которая учит печатать с использованием всего слова и подхода, основанного на звуке.Учащиеся могут использовать модули набора текста по математике, созданные учителями для соответствия учебной программе на разных уровнях обучения. Математические модули TTRS обучают основным определениям и помогают укрепить навыки чтения с листа для ключевых слов. Подход работает как для детей, так и для взрослых, которые испытывают трудности с математикой.
Используйте наши предметы по математике, чтобы подготовиться к предстоящему году, поддержать обучение в классе или просмотреть ранее изученный материал. Печатание может дать учащимся с трудностями в обучении уверенность и навыки, необходимые для достижения успеха!
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 1 июля 2011 г.{-1} $} \). Время определяется путем деления расстояния на скорость. \ [\ text {time} (t) = \ frac {\ text {distance}} {\ text {speed}} \] Когда струи пересекают друг друга: \ begin {align *} Теперь мы знаем расстояние, которое проходит вторая струя, когда она проходит первую струю, мы можем найти время: \ begin {align *} Самолеты преодолеют друг друга за 2 часа.{-1} $} \). Если обе лодки отправятся в путь одновременно, сколько времени им понадобится, чтобы обогнать друг друга? Обратите внимание, что сумма расстояний для двух лодок должна быть равна общему расстоянию, когда лодки встречаются: \ (d_ {1} + d_ {2} = d _ {\ text {total}} \ longrightarrow d_ {1} + d_ {2} = \ text {144} \ text {km} \). Этот вопрос касается расстояний, скорости и времени.Уравнение, связывающее эти значения: Вы хотите знать количество времени, необходимое лодкам, чтобы встретиться — пусть это время будет \ (t \). Затем вы можете написать выражение для расстояния, которое проходит каждая из лодок: Теперь мы можем подставить два выражения для расстояний в выражение для общего расстояния: \ begin {align *} Лодки встретятся через \ (\ text {1} \) час. Звелибанци и Джессика — друзья. Zwelibanzi берет тестовую работу Джессики по гражданским технологиям и не говорит ей, какова ее оценка. Он знает, что Джессика не любит проблемы со словами, поэтому он решает подразнить ее. Звелибанци говорит: «У меня \ (\ text {12} \) оценок больше, чем у вас, и сумма обеих наших оценок равна \ (\ text {148} \». Какие у нас отметки? » Пусть отметкой Звелибанци будет \ (z \), а отметкой Джессики будет \ (j \).потом Подставляем первое уравнение во второе уравнение и решаем: Подстановка этого значения обратно в первое уравнение дает: Кадеш купил \ (\ text {20} \) рубашки на общую сумму \ (\ text {R} \, \ text {980} \). Если большие рубашки стоили \ (\ text {R} \, \ text {50} \), а маленькие — \ (\ text {R} \, \ text {40} \), сколько каждого размера он купить? Пусть \ (x \) будет количеством больших рубашек и \ (20 — x \) количеством маленьких рубашек. Далее отметим следующее:
Мы можем представить стоимость как: \ begin {align *} Поэтому Кадеш покупает \ (\ text {18} \) большие рубашки и \ (\ text {2} \) маленькие рубашки. Диагональ прямоугольника на \ (\ text {25} \) \ (\ text {cm} \) больше его ширины. Длина прямоугольника на \ (\ text {17} \) \ (\ text {cm} \) больше его ширины. Какие размеры у прямоугольника? Пусть длина \ (= l \), ширина \ (= w \) и диагональ \ (= d \). \ (\, следовательно, d = w + 25 \) и \ (l = w + 17 \).{2} — 16w — 336 & = 0 \\ Ширина должна быть положительной, поэтому: width \ (w = \ text {28} \ text {cm} \) length \ (l = (w + 17) = \ text {45} \ text {cm} \) и диагональ \ (d = (w + 25) = \ text {53} \ text {cm} \). Сумма \ (\ text {27} \) и \ (\ text {12} \) равна \ (\ text {73} \) больше, чем неизвестное число.Найдите неизвестный номер. Пусть неизвестное число \ (= x \). \ begin {align *} Неизвестный номер: \ (- \ text {34} \). Группа друзей покупает обед. Вот несколько фактов об их обеде:
Определите индивидуальные цены на обед. Пусть молочный коктейль будет \ (m \), а обертка будет \ (w \). Из предоставленной информации получаем следующие уравнения: \ begin {align *} Подставляем первое уравнение во второе уравнение и решаем относительно \ (w \): \ begin {align *} Подставьте значение \ (w \) в первое уравнение и решите относительно \ (m \): \ begin {align *} Следовательно, молочный коктейль стоит \ (\ text {R} \, \ text {34} \), а упаковка — \ (\ text {R} \, \ text {27} \). Два меньших угла в прямоугольном треугольнике находятся в соотношении \ (1: 2 \). Каковы размеры двух углов? Пусть \ (x = \) наименьший угол. Следовательно, другой угол \ (= 2x \). Нам дан третий угол \ (= 90 ° \). \ begin {align *} Размеры углов: \ (30 ° \) и \ (60 ° \). Длина прямоугольника в два раза больше ширины. {2} & = 64 \\ Но ширина должна быть положительной, поэтому \ (b = 8 \). Подставьте это значение в первое уравнение, чтобы найти \ (l \): \ begin {align *} Следовательно, \ (b = \ text {8} \ text {cm} \) и \ (l = 2b = \ text {16} \ text {cm} \). Если \ (\ text {4} \) раз число увеличивается на \ (\ text {6} \), результат будет на \ (\ text {15} \) меньше квадрата числа. {2} — 4x — 21 & = 0 \\ Нам не сообщают, положительное или отрицательное число.Следовательно, это номер \ (\ text {7} \) или \ (- \ text {3} \). Длина прямоугольника на \ (\ text {2} \) \ (\ text {cm} \) больше, чем ширина прямоугольника. Периметр прямоугольника равен \ (\ text {20} \) \ (\ text {cm} \). Найдите длину и ширину прямоугольника. Пусть длина \ (l = x \), ширина \ (w = x — 2 \) и периметр \ (= p \). \ begin {align *} \ (l = \ text {6} \ text {cm} \) и \ (w = l — 2 = \ text {4} \ text {cm} \). длина: \ (\ text {6} \) \ (\ text {cm} \), ширина: \ (\ text {4} \) \ (\ text {cm} \) У Стивена есть 1 литр смеси, содержащей \ (\ text {69} \% \) соль. Сколько воды нужно добавить Стивену, чтобы получилась \ (\ text {50} \% \) соль? Запишите свой ответ в долях литра. Новый объем (\ (x \)) смеси должен содержать \ (\ text {50} \% \) соль, следовательно: \ begin {align *} Объем новой смеси составляет \ (\ text {1,38} \) литр. Количество воды (\ (y \)), которое нужно добавить: \ begin {align *} Следовательно, необходимо добавить \ (\ text {0,38} \) литров воды.Чтобы записать это как долю литра: \ (\ text {0,38} = \ frac {38} {100} = \ frac {19} {50} \ text {литры} \) Следовательно, необходимо добавить \ (\ frac {19} {50} \ text {литры} \). Сумма двух подряд идущих нечетных чисел равна \ (\ text {20} \), а их разница равна \ (\ text {2} \). Найдите два числа. Пусть числа будут \ (x \) и \ (y \). Тогда два уравнения, описывающие ограничения: \ begin {align *} Добавьте первое уравнение ко второму: \ begin {align *} Подставить в первое уравнение: \ begin {align *} Следовательно, два числа — 9 и 11. Знаменатель дроби на \ (\ text {1} \) больше, чем числитель.Сумма дроби и обратной величины равна \ (\ frac {5} {2} \). Найдите дробь. Пусть числитель будет \ (x \). Значит, знаменатель равен \ (x + 1 \). \ begin {align *} Решить относительно \ (x \): \ begin {align *} Отсюда дробь может быть \ (\ frac {1} {2} \) или \ (\ frac {-2} {- 1} \).Для второго решения мы можем упростить дробь до \ (\ text {2} \), и в этом случае знаменатель не на 1 меньше, чем числитель. Итак, дробь равна \ (\ frac {1} {2} \). Масинди на \ (\ text {21} \) лет старше своей дочери Муливху. Сумма их возрастов равна \ (\ text {37} \). Сколько лет Муливху? Пусть Муливху будет \ (x \) лет.Итак, Масинди \ (x + 21 \) год. \ begin {align *} Муливху \ (\ text {8} \) лет. Цамано сейчас в пять раз старше его сына Мурунвы.Через семь лет Тшамано будет в три раза старше своего сына. Найдите их возраст сейчас. Пусть Мурунве будет \ (x \) лет. Итак, Тшамано \ (5x \) лет. Через \ (\ text {7} \) лет возраст Мурунвы будет \ (x + 7 \). Возраст Тшамано будет \ (5x + 7 \). \ begin {align *} Со Мурунве 7 лет, а Тшамано 35 лет. \ (\ text {7} \) и \ (\ text {35} \) лет. Если сложение числа от одного до трех совпадает с числом, чему будет это число? Пусть число будет \ (x \). Тогда: \ begin {align *} Если треть суммы числа и единицы эквивалентна дроби, знаменателем которой является число, а в числителе два, то какое число? Пусть число будет \ (x \). 2 + х — 6 & = 0 \\ Владелец магазина покупает 40 мешков риса и муки на сумму \ (\ text {R} \, \ text {5 250} \).Если рис стоит \ (\ text {R} \, \ text {150} \) за мешок, а мука стоит \ (\ text {R} \, \ text {100} \) за мешок, сколько мешков муки еду он купил? \ begin {align *} В коробке по 100 кусков синих и зеленых мылов.Синие полосы весят \ (\ text {50} \) \ (\ text {g} \) на полосу, а зеленые полосы \ (\ text {40} \) \ (\ text {g} \) на полосу. Общая масса мыла в ящике составляет \ (\ text {4,66} \) \ (\ text {кг} \). Сколько кусков зеленого мыла в коробке? \ begin {align *} У Лизы 170 бусинок.У нее есть синие, красные и фиолетовые бусины весом \ (\ text {13} \) \ (\ text {g} \), \ (\ text {4} \) \ (\ text {g} \) и \ ( \ text {8} \) \ (\ text {g} \) соответственно. Если красных бусинок вдвое больше, чем синих, и все бусинки весят \ (\ text {1,216} \) \ (\ text {kg} \), сколько бусинок каждого типа есть у Лизы? \ begin {align *} . |
