Вычисление площадей плоских фигур с помощью интеграла

На этом уроке будем учиться вычислять площади плоских фигур, которые
называются криволинейными трапециями.

Примеры таких фигур — на рисунке ниже.

С одной стороны, найти площадь плоской фигуры с помощью определённого интеграла
предельно просто. Речь идёт о площади фигуры, которую сверху ограничивает некоторая кривая, снизу — ось
абсцисс (Ox), а слева и справа — некоторые прямые. Простота в том,
что определённый интеграл функции, которой задана кривая, и есть площадь такой фигуры (криволинейной трапеции).

Но здесь нас подстерегают некоторые важные нюансы, без понимания которых не решить
большинство задач на это практическое приложение определённого интеграла. Учтём эти нюансы и будем во
всеоружии.

Для вычисления площади фигуры нам понадобятся:

1. Определённый интеграл от функции,
   задающей кривую, которая ограничивает криволинейную трапецию сверху. И здесь возникает
   первый существенный нюанс: криволинейная трапеция может быть ограничена кривой не только сверху, но и снизу.
   Как действовать в этом случае? Просто, но это важно запомнить: интеграл в этом случае берётся со знаком
   минус.
2. Пределы интегрирования a и b, которые находим из уравнений прямых, ограничивающих
   фигуру слева и справа: x = a, x = b, где
   a и b — числа.

Отдельно ещё о некоторых нюансах.

Кривая, которая ограничивает криволинейную трапецию сверху (или снизу)
должна быть графиком непрерывной и неотрицательной функции y = f(x).

Значения «икса» должны принадлежать отрезку [a, b]. То есть
не учитываются такие, например, линии, как разрез гриба, у которого ножка вполне вписывается в этот отрезок,
а шляпка намного шире.

Боковые отрезки могут вырождаться в точки. Если вы увидели такую фигуру на чертеже,
это не должно вас смущать, так как эта точка всегда имеет своё значение на оси «иксов». А значит с пределами
интегрирования всё в порядке.

Теперь можно переходить к формулам и вычислениям. Итак, площадь s
криволинейной трапеции может быть вычислена по формуле

 (1).

Если же f(x) ≤ 0 (график функции расположен ниже оси Ox),
то площадь криволинейной трапеции может быть вычислена по формуле

. (2)

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры — функции, соответственно
y = f(x) и y = φ(x), то площадь такой фигуры
вычисляется по формуле

. (3)

Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).

Пример 1. Найти площадь фигуры, ограниченной графиком функции
, осью абсцисс (Ox)
и прямыми x = 1, x = 3.

Решение. Так как y = 1/x > 0
на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):

.

Пример 3. Найти площадь фигуры, ограниченной графиком функции
, осью абсцисс (Ox)
и прямой x = 4.

Решение. Фигура, соответствующая условию задачи — криволинейная трапеция, у которой левый отрезок выродился в
точку. Пределами интегрирования служат 0 и 4. Поскольку ,
по формуле (1) находим площадь криволинейной трапеции:

.

Пример 4. Найти площадь фигуры, ограниченной линиями
,
,
и
находящейся в 1-й четверти.

Решение.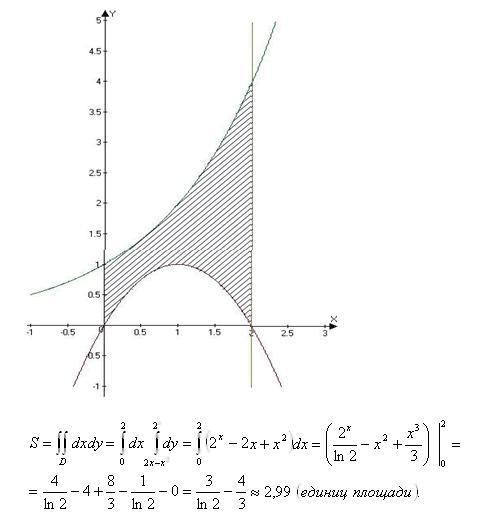 Чтобы воспользоваться формулой (1), представим площадь фигуры,
заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной
трапеции ABC. При вычислении площади треугольника OAB
пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC —
абсциссы точек A и C (A является точкой пересечения прямой OA и
параболы, а C — точкой пересечения параболы с осью Ox).
Решая совместно (как систему) уравнения прямой и параболы, получим

(абсциссу точки A) и
(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично
получим ,
(абсциссы точек
C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:

Пример 5. Найти площадь криволинейной трапеции ACDB,
если уравнение кривой CD
и абсциссы A и B соответственно 1 и 2.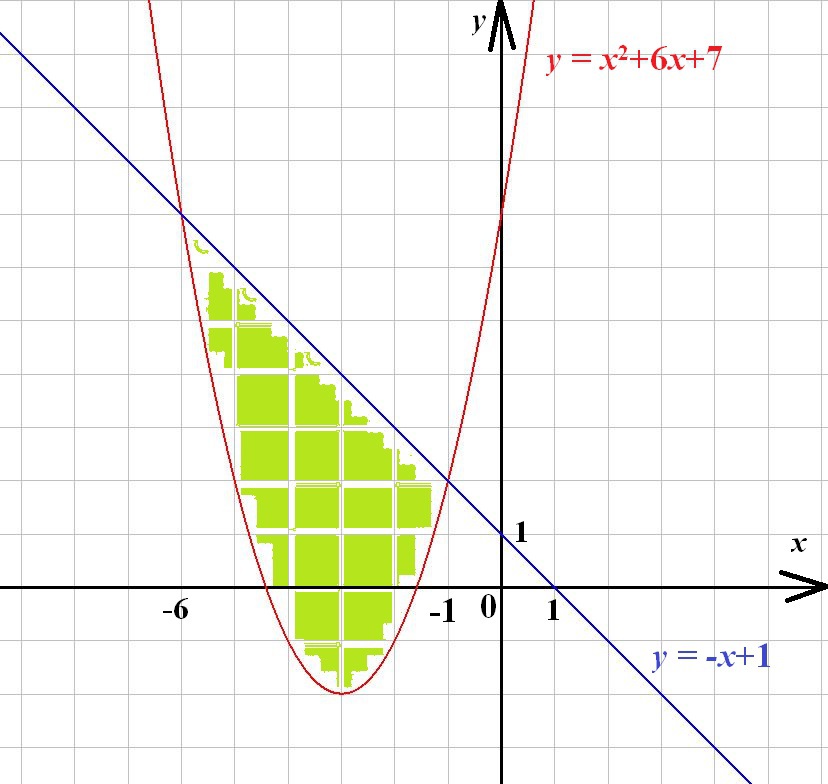

Решение. Выразим данное уравнение кривой через игрек:
Площадь криволинейной
трапеции находим по формуле (1):

.

Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).

Пример 7. Найти площадь, заключённую между осью абсцисс (Ox)
и двумя соседними волнами синусоиды.

Решение. Площадь данной фигуры можем найти по формуле (2):

.

Найдём отдельно каждое слагаемое:

.

.

Окончательно находим площадь:

.

Пример 8. Найти площадь фигуры, заключённой между параболой
и кривой
.

Решение. Выразим уравнения линий через игрек:

Площадь по формуле (2) получим как

,

где a и b — абсциссы точек A и B.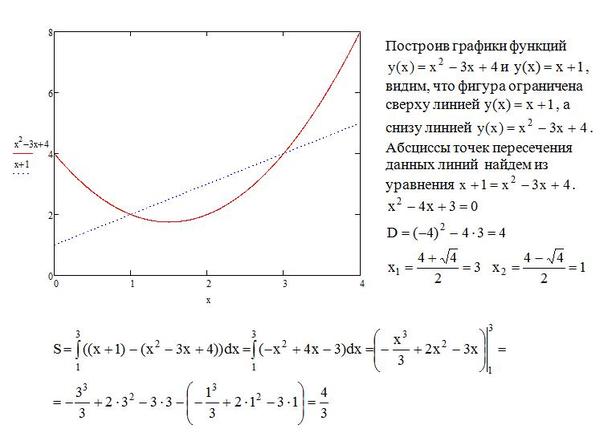 Найдём их,
решая совместно уравнения:

Отсюда

Окончательно находим площадь:

И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3).

Начало темы «Интеграл»

Урок 24. вычисление площадей с помощью интегралов — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №24. Вычисление площадей с помощью интегралов.

Перечень вопросов, рассматриваемых в теме

1) Нахождение площади фигуры, ограниченной графиками функций с помощью определенного интеграла.

2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница

3) Решение задач, с помощью формулы Ньютона – Лейбница

Формула Ньютона – Лейбница

Основная литература:

Колягин Ю.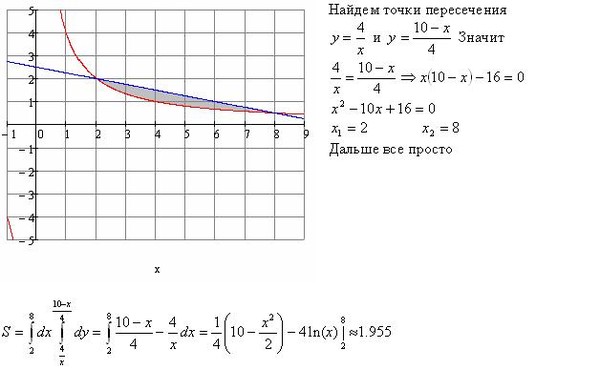 М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым. ( зависит от расположения криволинейной трапеции)

Примеры и разбор решения заданий тренировочного модуля

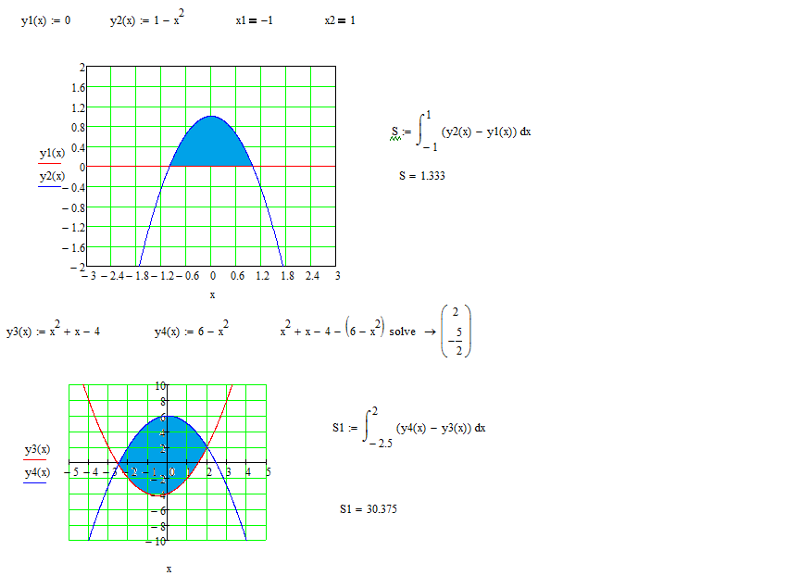
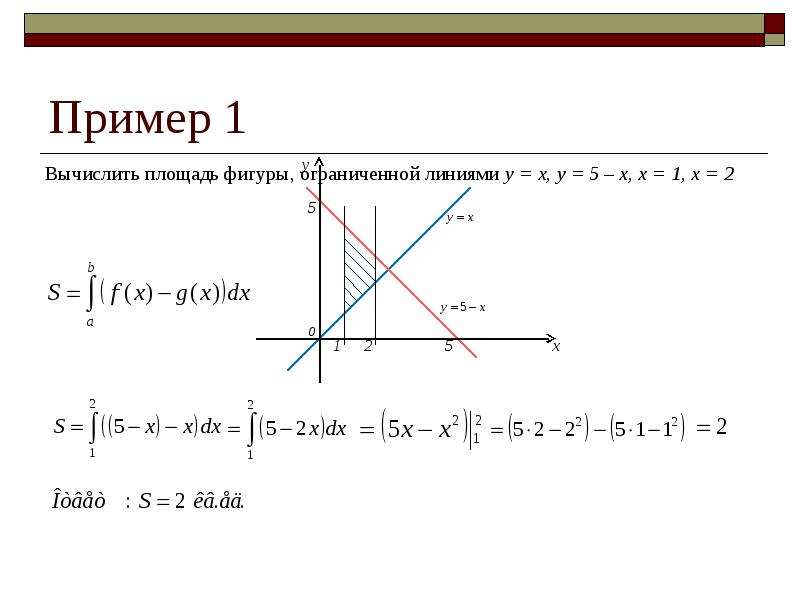
№1 Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2, используя определенный интеграл.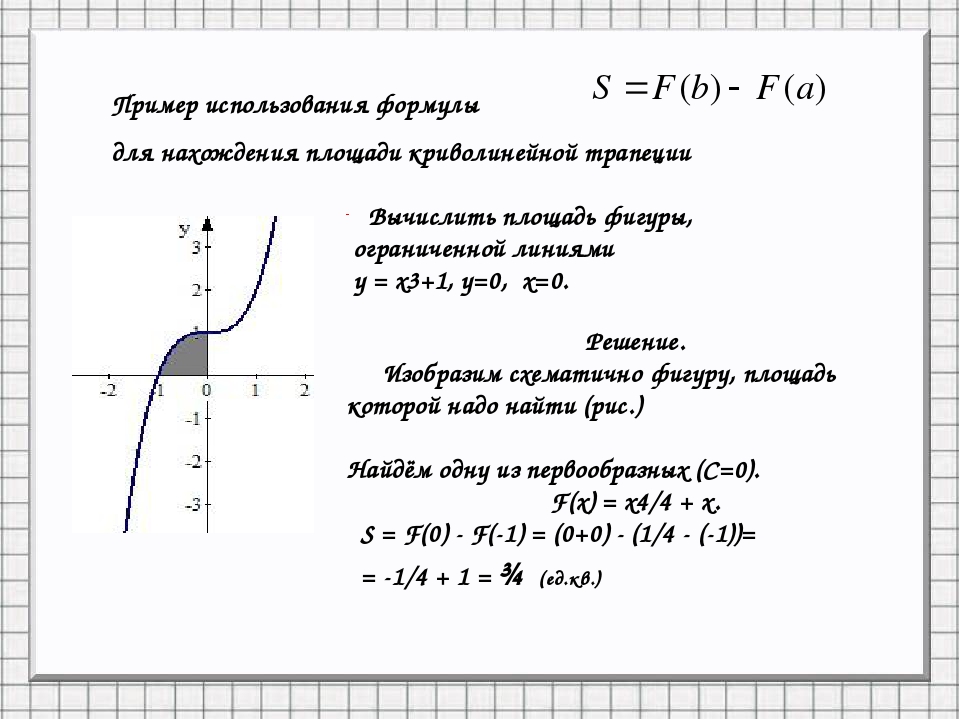

Решение. Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию  F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b).

Затем подставляем значение нижнего предела в первообразную функцию: F(а) .

Рассчитываем разность F(b)  — F(а)    , это и будет ответ

№2. Найти площадь фигуры, ограниченной линиями у=4-х²,у=3х, у=0 и находящейся в 1-й четверти.

Решение: Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию  F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b)  .

Затем подставляем значение нижнего предела в первообразную функцию: F(а) .

Рассчитываем разность F(b)  — F(а)    , это и будет ответ.

Решение. S=S_OAB +S_ABC

№3. Найти площадь криволинейной трапеции (х-1)², ограниченной линиями х=2 и х=1, осью 0х

Решение:

Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию  F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b)  .

Затем подставляем значение нижнего предела в первообразную функцию: F(а) .

Рассчитываем разность F(b)  — F(а), это и будет ответ.

Задание 3. Вычислить площадь фигуры, ограниченной линиями.

0. y
=
x²
– 2x
+ 2,
y
=
x
+ 2.

Решение варианта
0.

Данная
фигура сверху ограничена прямойy
= x
+ 2, снизу параболой y
=
x²
– 2x
+ 2.
Искомую
площадь вычислим по формуле S = 
Пределами
интегрирования будут абсциссы точек
пересечения параболы и прямой. Решая
систему уравнений y
=
x²
– 2x
+ 2,
y
=
x
+ 2 находим:

,

,
т.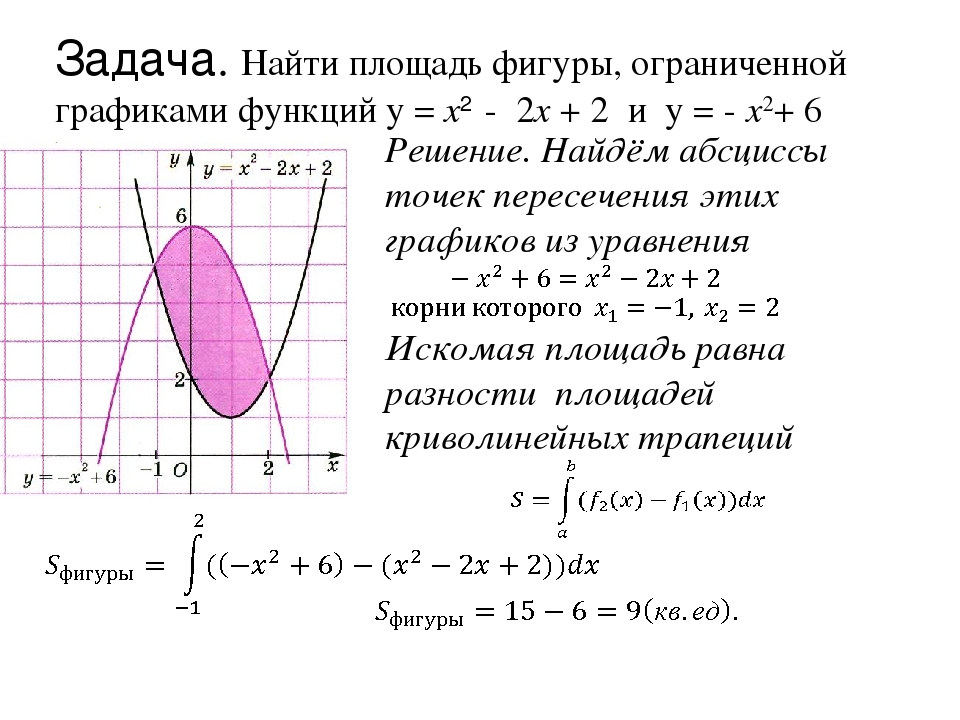 е. a
= 0, b
= 3. Таким
образом получаем:

S
=

=

=

=
=–9 +

Задание 4. Вычислить объем тела, образованного вращением вокруг указанной оси фигуры, ограниченной линиями:

0. y
= sinx,
(0≤x≤),
y =
0, Ox.

Решение варианта
0.

Изобразим указанное
тело на чертеже.

Искомый объем
вычислим по формуле V
=
.
Имеем:

V
=
==
=
.

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.

— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?

— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень.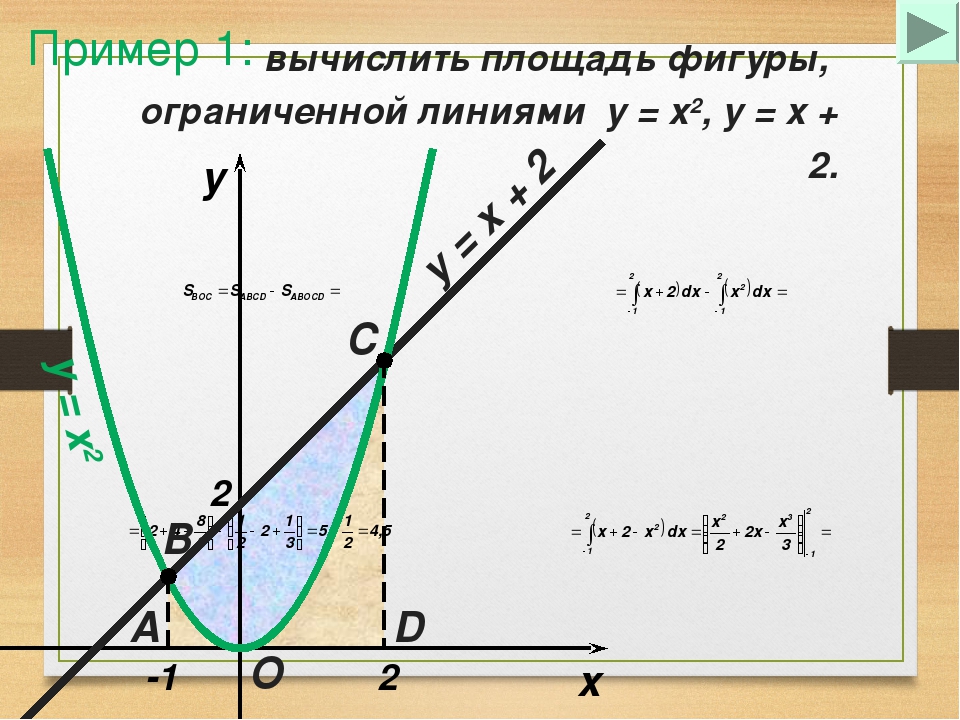 Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.

Как найти площадь фигуры ограниченной линиями

Геометрический смысл определенного интеграла – площадь криволинейной трапеции. Чтобы найти площадь фигуры, ограниченной линиями, применяется одно из свойств интеграла, которое заключается в аддитивности площадей, интегрируемых на одном и том же отрезке функций.

По определению интеграла, он равен площади криволинейной трапеции, ограниченной графиком заданной функции. Когда требуется найти площадь фигуры, ограниченной линиями, речь идет о кривых, заданных на графике двумя функциями f1(x) и f2(x).

Пусть на некотором интервале [a, b] заданы две функции, которые определены и непрерывны. Причем одна из функций графике расположена выше другой. Таким образом, образуется визуальная фигура, ограниченная линиями функций и прямыми x = a, x = b.

Тогда площадь фигуры можно выразить формулой, интегрирующей разность функций на интервале [a, b]. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.

Пример1.
Найти площадь фигуры, ограниченной прямыми линиями y = -1/3·x – ½, x = 1, x = 4 и параболой y = -x² + 6·x – 5.

Решение.
Постройте графики всех линий. Вы можете увидеть, что линия параболы находится выше прямой y = -1/3·x – ½. Следовательно, под знаком интеграла в данном случае должна стоять разность между уравнением параболы и заданной прямой. Интервал интегрирования, соответственно, находится между точками x = 1 и x = 4:
S = ∫(-x² + 6·x – 5 – (-1/3·x – 1/2))dx = (-x² +19/3·x – 9/2)dx на отрезке [1, 4].

Найдите первообразную для полученного подынтегрального выражения:
F(-x² + 19/3x – 9/2) = -1/3x³ + 19/6x² – 9/2x.

Подставьте значения концов отрезка:
S = (-1/3·4³ + 19/6·4² – 9/2·4) – (-1/3·1³ + 19/6·1² – 9/2·1) = 13.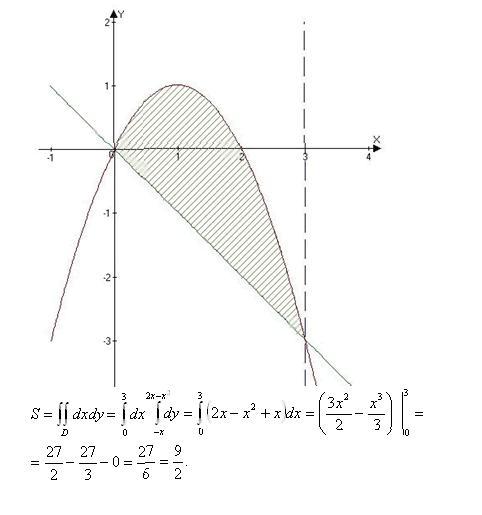

Пример2.
Вычислите площадь фигуры, ограниченной линиями y = √(x + 2), y = x и прямой x = 7.

Решение.
Эта задача является более сложной по сравнению с предыдущей, поскольку в ней нет второй прямой, параллельной оси абсцисс. Это значит, что второе граничное значение интеграла неопределенно. Следовательно, его нужно найти из графика. Постройте заданные линии.

Вы увидите, то прямая линия y = x проходит диагонально относительно координатных осей. А график функции корня – это положительная половина параболы. Очевидно, что линии на графике пересекаются, поэтому точка пересечения и будет нижним пределом интегрирования.

Найдите точку пересечения, решив уравнение:
x = √(x + 2) → x² = x + 2 [x ≥ -2] → x² – x – 2 = 0.

Определите корни квадратного уравнения с помощью дискриминанта:
D = 9 → x1 = 2; x2 = -1.

Очевидно, что значение -1 не подходит, поскольку абсцисса токи пересечения – положительная величина. Следовательно, второй предел интегрирования x = 2.(3/2)) = 59/6.

Методы вычисления площади фигуры, ограниченной линиями

Существует тип задач из области высшей математики, в которых нужно вычислить площадь фигуры, ограниченной линиями. В этом случае необходимо использовать интегралы. Однако в интернете слишком много неправильных методов решения. Это может существенно замедлить обучение, поэтому следует запомнить алгоритм нахождения площади.

Общие сведения

Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.

Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.

Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.

Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.

Информация об интегралах

С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.

Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:

Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.

Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.

Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.

Для нахождения первообразной используется специальная таблица интегралов:

Рисунок 1. Таблица интегралов и их первообразные.

В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).

Криволинейные фигуры

Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.

Рисунок 2. Фигуры с криволинейными сторонами.

Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.

Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.

Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).

Способы вычисления и рекомендации

Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.

Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.

Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.

Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.

Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:

Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.

Основной алгоритм

При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:

Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.

Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.

Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.

Следующим шагом является правильное изображение прямых. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой.

После всех операций образуется фигура, которая ограничена линиями. Ее необходимо заштриховать. После этого вычисляется неопределенный интеграл заданной функции. Необходимо воспользоваться табличными значениями первообразных на рисунке 2. Однако здесь есть небольшой нюанс: константу записывать нет необходимости.2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).

Для определения значения площади криволинейной фигуры (трапеции) необходимо использовать определенные интегралы. При решении нужно внимательно следить за знаками и первообразными из таблицы на рисунке 1.

Предыдущая

МатематикаФормулы площадей всех фигур

Следующая

МатематикаКорень уравнения — определение в математике, формулы нахождения

1.1: Площадь между двумя кривыми

1. Последнее обновление

2. Сохранить как PDF

1. Площадь, ограниченная двумя функциями от \ (y \)
2. Приложение
3. Авторы и авторства

Напомним, что площадь под кривой и над осью x может быть вычислена с помощью определенного интеграла.1 \\ & = \ big (- \ dfrac {3} {4} + \ dfrac {3} {2} \ big) — \ big (\ dfrac {3} {4} — \ dfrac {3} {2} \ big) \\ & = \ dfrac {3} {2} \ end {align *}. \]

Приложение

Пусть \ (y = f (x) \) будет функцией спроса на продукт, а \ (y = g (x) \) будет функцией предложения. Затем мы определяем точку равновесия как пересечение двух кривых. Излишек потребителя определяется площадью выше равновесного значения и ниже кривой спроса, в то время как излишек производителя определяется площадью ниже равновесного значения и выше кривой предложения.х \) и \ (у = 2х +1 \).

Авторы и авторство

Область между двумя функциями | Суперпроф

В этой статье мы обсудим, как вычислить площадь между двумя функциями. Мы специально сконцентрируемся на том, как вычислить площадь между кривой и прямой линией и площадь между двумя кривыми.

Область между двумя функциями

Область между двумя функциями равна площади функции, расположенной выше, за вычетом области функции, расположенной ниже.Математически мы можем обозначить эту область следующим образом:

Лучшие преподаватели математики, доступные

Первый урок бесплатно

Область между кривой и прямой

Теперь давайте разберемся, как вычислить площадь между кривой и прямой линией. прямая линия через следующие примеры

Пример 1

Найдите площадь пространства, ограниченного параболой

и прямой линией, проходящей через точки A (-1, 0) и B (1, 4).

Решение

Шаг 1. Найдите уравнение прямой линии

На этом этапе мы вычислим уравнение прямой, проходящей через две точки A и B. Для этого сначала мы должны вычислить наклон прямой, проходящей через точки A (-1, 0) и B (1, 4). Для вычисления наклона мы будем использовать следующую формулу:

Подставьте значения точек A и B в приведенную выше формулу:

Теперь подставьте этот наклон в уравнение точки пересечения ниже:

Следовательно, уравнение прямой y = 2x + 2.

Шаг 2 — Нарисуйте график

На этом шаге мы нарисуем график функции

и линию следующим образом:

Шаг 3 — Вычислите границы

Точки пересечения линии параболы будут границами или пределами функции. Как видно из приведенного выше графика, линия пересекает параболу в точках

и. Следовательно, это пределы функции.

Шаг 4 — Вычисление определенного интеграла

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующей форме:

Перепишите функцию

, используя правило суммы / разности определенных интегралов, например:

Чтобы вычислить определенный интеграл, мы сначала найдем первообразную функции.Первообразная функции — это

Теперь используйте основную теорему исчисления:

Замените 2 и 0 в первообразной функции следующим образом:

Пример 2

Вычислите площадь фигуры ограниченный функцией

и линиями y = x, при x = 0 и x = 2.

Решение

Шаг 1 — Нарисуйте график

В этом примере нам уже дано уравнение линии y = Икс.Следовательно, нам не нужно его рассчитывать. Мы просто начнем с наброска графика функций

и.

На приведенном выше графике вы можете видеть, что от x = 0 до x = 1 прямая линия проходит над параболой, а от x = 1 до x = 2 прямая линия проходит под параболой. Следовательно, мы будем вычислять площади, используя эти пределы выше и ниже параболы отдельно.

Шаг 2 — Вычислите границы

Границы или пределы графика уже указаны в этом примере, они равны 0 и 1.

Шаг 3 — Вычислить определенный интеграл

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующей форме:

Область, где прямая линия находится над параболой:

Найдите первообразную функции. Первообразная функции —

Используйте основную теорему исчисления:

Замените 1 и 0 в первообразной функции следующим образом:

Область, где прямая линия находится ниже параболы:

Найдите первообразную функции.3} {3} —

В следующем разделе мы увидим, как вычислить площадь между двумя кривыми по их уравнениям.

Площадь между двумя кривыми

Следующие примеры позволят вам понять, как рассчитать площадь между двумя кривыми.

Пример 1

Найдите область, ограниченную графиками функций

и

Решение

Шаг 1 — Нарисуйте график

Шаг 2 — Найдите границы

Чтобы определить, где расположены графики двух кривых пересекаются друг с другом, приравняем уравнения двух кривых:

или

Отсюда границы

и 0.

Шаг 3 — Вычислить определенный интеграл

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующей форме:

Найдите первообразную функции . Первообразная функции —

Используйте основную теорему исчисления:

Подставив

и 0 в первообразную функции, мы получим следующее значение площади:

Пример 2

Найдите площадь между двумя кривые

и.

Решение

Выполните следующие действия, чтобы рассчитать площадь.

Шаг 1 — Нарисуйте график

График двух кривых приведен ниже:

Шаг 2 — Найдите границы

Вычислите границы функции по уравнению, как следующие уравнения:

или

Следовательно, границы функции равны 0 и 2.

Шаг 3 — Вычислить определенный интеграл

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов для записи функции в следующем виде:

Найдите первообразную функции.Первообразная функции —

Используйте основную теорему исчисления:

Замените 2 и 0 в первообразной функции:

4a. Объем Solid of Revolution путем интеграции (дисковый метод)

М. Борна

Токарный станок

Многие твердые объекты, особенно сделанные на токарном станке , имеют круглое поперечное сечение и изогнутые стороны.
На этой странице мы видим, как найти тома таких объектов с помощью интеграции.

Предметы, изготовленные на токарном станке …

Пример 1

Рассмотрим область, ограниченную прямой y = 3x, осью x и x = 1:

График y = 3x с заштрихованной областью под «кривой» между «x = 0» и «x = 1».

Когда заштрихованная область поворачивается на 360 ° вокруг оси «x», создается объем.

Полученное твердое тело представляет собой конус:

Область под кривой «y = 3x» от «x = 0» до «x = 1», повернутой вокруг оси «x», показывая типичный диск.2dx`

где:

`y = f (x)` — уравнение кривой, площадь которой вращается

`a` и` b` — границы вращаемой области

`dx` показывает, что область вращается вокруг оси` x`

ПРИМЕЧАНИЕ: На этой странице мы используем только дисковый метод и метод шайбы (где мы разрезаем форму на круглые срезы),
а затем познакомьтесь с методом Shell). 3` (Проверяет ОК.2] dx`

На следующем общем графике y_2 выше y_1. Нижний и верхний пределы для области, которая должна быть повернута, обозначены вертикальными линиями в точках «x = a» и «x = b».

Площадь, ограниченная кривыми y_1 и y_2 и линиями x = a и x = b, включая типичный прямоугольник .xyab

`y_2`

`y_1`

Площадь, ограниченная кривыми `y_1` и` y_2` и линиями `x = a` и` x = b`.

Когда мы вращаем такую ​​фигуру вокруг оси и делаем срезы, в результате получается шайба формы (с круглым отверстием посередине).2` (нижняя кривая), `y = x + 1` (линия вверху) и` x = 0`, показывая типичный прямоугольник.

Нижний предел интегрирования равен «x = 0» (поскольку в вопросе указано «x ≥ 0»).

Затем нам нужно найти место пересечения кривых, чтобы мы знали верхний предел интегрирования.

Приравнивая 2 выражения и решая:

2 x ² = x + 1

2 x ² — x — 1 = 0

(2 x + 1) ( x — 1) = 0

x = 1 (поскольку нам нужно учитывать только x ≥ 0. 3`

`~~ 8.2 = 4` в квадранте I, повернутом вокруг оси `y`.

Ответ

Мы понимаем, что это эллипс. Вопрос говорит нам, что интересующая нас область находится только в первом квадранте.

Эллипс x ² + 4 y ² = 4, показывающий часть, ограниченную кривой, x = 0, x = 2 и ось x .

Из диаграммы мы видим, что пределы ограниченной области составляют y = 0 и y = 1.3`

Приложения

1. Объем винной бочки

Винная бочка имеет радиус в верхней части 30 см и радиус в середине 40 см. Высота бочки 1 м. Каков объем бочки (в л), если предположить, что форма сторон параболическая?

Ответ

Положим бочку набок, чтобы облегчить алгебру:

Парабола с вершиной в точке `(0, 40)` и проходящая через `(50, 30)`.

Нам нужно найти уравнение параболы с вершиной в точке `(0, 40)` и проходящей через `(50, 30)`. 2) / (250) + 40`

Нам нужно найти объем бочки, который образуется, когда мы вращаем эту параболу между x = -50 и x = 50 вокруг оси x .2ч.

Интересно, что Архимед (тот, кто, как известно, выпрыгнул из ванны и побежал по улице с криком «Эврика! Я понял») использовал этот подход, чтобы найти объемы сфер около 200 г. до н. Э. Этот метод был почти забыт до начала 1700-х годов, когда исчисление было разработано Ньютоном и Лейбницем.

Мы видим, как решить проблему, используя оба подхода.

Объем историческим методом:

Ответ

Поскольку дыня симметрична, мы можем вычислить объем одной половины дыни, а затем удвоить наш ответ.3` или `9.161 \» L «`. Это примерно то же самое, что мы получили, нарезав арбуз и увеличив объем ломтиков.

[См. Также Архимед и площадь параболического сегмента.]

Решенных проблем | PDF | Совместно непрерывные случайные переменные

5.2.5 Решенные проблемы

Проблема
Пусть $ X $ и $ Y $ — совместно непрерывные случайные величины с совместной PDF
\ begin {уравнение}
\ nonumber f_ {X, Y} (x, y) = \ left \ {
\ begin {array} {l l}
cx + 1 & \ quad x, y \ geq 0, x + y

1. Показать диапазон $ (X, Y) $, $ R_ {XY} $ в плоскости $ x-y $.{1-y} 3x + 1 \ hspace {5pt} dx \\
   \ nonumber & = \ frac {1} {2} (1-y) (5–3y), \ hspace {10pt} \ textrm {for} y \ in [0,1].
   \ end {align}
   Таким образом, мы имеем
   \ begin {уравнение}
   \ nonumber f_Y (y) = \ left \ {
   \ begin {array} {l l}
   \ frac {1} {2} (1-год) (5–3 года) & \ quad 0 \ leq y \ leq 1 \\
   & \ quad \\
   0 & \ quad \ text {в противном случае}
   \ end {array} \ right.
   \ end {уравнение}
2. Чтобы найти $ P (Y

Проблема
Пусть $ X $ и $ Y $ — совместно непрерывные случайные величины с совместной PDF
\ begin {уравнение}
\ nonumber f_ {X, Y} (x, y) = \ left \ {
\ begin {array} {l l}
6e ^ {- (2x + 3y)} & \ quad x, y \ geq 0 \\
& \ quad \\
0 & \ quad \ text {в противном случае}
\ end {array} \ right.{-5y} dy \\
\ nonumber & = \ frac {3} {5}.
\ end {align}

Проблема
Пусть $ X $ — непрерывная случайная величина с PDF
\ begin {уравнение}
\ nonumber f_X (x) = \ left \ {
\ begin {array} {l l}
2x & \ quad 0 \ leq x \ leq 1 \\
& \ quad \\
0 & \ quad \ text {в противном случае}
\ end {array} \ right.
\ end {уравнение}
Мы знаем, что при $ X = x $ случайная величина $ Y $ равномерно распределена на $ [- x, ​​x] $.

1. Найдите совместный PDF-файл $ f_ {XY} (x, y) $.3) $.

• Решение
  • 1. Сначала отметим, что по предположению
       \ begin {уравнение}
       \ nonumber f_ {Y | X} (y | x) = \ left \ {
       \ begin {array} {l l}
       \ frac {1} {2x} & \ quad -x \ leq y \ leq x \\
       & \ quad \\
       0 & \ quad \ text {в противном случае}
       \ end {array} \ right.
       \ end {уравнение}
       Таким образом, мы имеем
       \ begin {уравнение}
       \ nonumber f_ {XY} (x, y) = f_ {Y | X} (y | x) f_X (x) = \ left \ {
       \ begin {array} {l l}
       1 & \ quad 0 \ leq x \ leq 1, -x \ leq y \ leq x \\
       & \ quad \\
       0 & \ quad \ text {в противном случае}
       \ end {array} \ right.3} {2x} \ right) 2x dx \ hspace {20pt} \ textrm {поскольку} Y | X = x \ hspace {5pt} \ sim \ hspace {5pt} Uniform (-x, x) \\
       \ nonumber & = \ frac {1} {2}.
       \ end {align}

Проблема
Пусть $ X $ и $ Y $ — две совместно непрерывные случайные величины с совместной PDF
\ begin {уравнение}
\ nonumber f_ {X, Y} (x, y) = \ left \ {
\ begin {array} {l l}
6xy & \ quad 0 \ leq x \ leq 1, 0 \ leq y \ leq \ sqrt {x} \\
& \ quad \\
0 & \ quad \ text {в противном случае}
\ end {array} \ right.\ end {уравнение}

1. Показать $ R_ {XY} $ в плоскости $ x-y $.
2. Найдите $ f_X (x) $ и $ f_Y (y) $.
3. Независимы ли $ X $ и $ Y $?
4. Найдите условную PDF $ X $ при $ Y = y $, $ f_ {X | Y} (x | y) $.
5. Найдите $ E [X | Y = y] $ для $ 0 \ leq y \ leq 1 $.
6. Найдите $ \ textrm {Var} (X | Y = y) $ для $ 0 \ leq y \ leq 1 $.

• Решение
  • 1. Рисунок 5.9 показывает $ R_ {XY} $ в плоскости $ x-y $.

       Рисунок 5.2 \ leq 1 \}.
       \ end {align}
       Предположим, что мы выбираем точку $ (X, Y) $ равномерно случайным образом в $ D $. То есть совместная PDF $ X $ и $ Y $ определяется выражением
       \ begin {уравнение}
       \ nonumber f_ {XY} (x, y) = \ left \ {
       \ begin {array} {l l}
       \ frac {1} {\ pi} & \ quad (x, y) \ in D \\
       & \ quad \\
       0 & \ quad \ text {в противном случае}
       \ end {array} \ right.
       \ end {уравнение}
       Пусть $ (R, \ Theta) $ — соответствующие полярные координаты, как показано на рисунке 5.10. Обратное преобразование дается формулой
       \ begin {уравнение}
       \ nonumber \ left \ {
       \ begin {array} {l}
       X = R \ cos \ Theta \\
       Y = R \ sin \ Theta
       \ end {array} \ right.\ end {уравнение}
       где $ R \ geq 0 $ и $ — \ pi

       Рисунок 5.10: Полярные координаты

       • Решение
         • Здесь $ (X, Y) $ совместно непрерывны и связаны с $ (R, \ Theta) $ взаимно однозначным соотношением. Воспользуемся методом преобразований (теорема 5.1). Функция $ h (r, \ theta) $ задается формулой
           \ begin {уравнение}
           \ nonumber \ left \ {
           \ begin {array} {l}
           х = h_1 (г, \ тета) = г \ соз \ тета \\
           у = ч_2 (г, \ тета) = г \ грех \ тета
           \ end {array} \ right.
           \ end {уравнение}
           Таким образом, мы имеем
           \ begin {align}
           \ nonumber f_ {R \ Theta} (r, \ theta) & = f_ {XY} (h_1 (r, \ theta), h_2 (r, \ theta)) | J | \\
           \ nonumber & = f_ {XY} (r \ cos \ theta, r \ sin \ theta) | J |.\ end {align}
           где
           \ begin {align}
           \ nonumber J = \ det \ begin {bmatrix}
           \ frac {\ partial h_1} {\ partial r} & \ frac {\ partial h_1} {\ partial \ theta} \\
           & \\
           \ frac {\ partial h_2} {\ partial r} & \ frac {\ partial h_2} {\ partial \ theta} \\
           \ end {bmatrix}
           = \ det \ begin {bmatrix}
           \ cos \ theta & -r \ sin \ theta \\
           & \\
           \ sin \ theta & r \ cos \ theta \\
           \ end {bmatrix}
           = г \ соз ^ 2 \ тета + г \ грех ^ 2 \ тета = г.\ end {align}
           Мы делаем вывод, что
           \ begin {align}
           \ nonumber f_ {R \ Theta} (r, \ theta) & = f_ {XY} (r \ cos \ theta, r \ sin \ theta) | J | \\
           \ nonumber & = \ left \ {
           \ begin {array} {l l}
           \ frac {r} {\ pi} & \ quad r \ in [0,1], \ theta \ in (- \ pi, \ pi] \\
           & \ quad \\
           0 & \ quad \ text {в противном случае}
           \ end {array} \ right.
           \ end {align}
           Обратите внимание, что сверху мы можем написать
           \ begin {align}
           \ nonumber f_ {R \ Theta} (r, \ theta) = f_R (r) f _ {\ Theta} (\ theta),
           \ end {align}
           где
           \ begin {уравнение}
           \ nonumber f_R (r) = \ left \ {
           \ begin {array} {l l}
           2r & \ quad r \ in [0,1] \\
           & \ quad \\
           0 & \ quad \ text {в противном случае}
           \ end {array} \ right.\ end {уравнение}
           \ begin {уравнение}
           \ nonumber f_ \ Theta (\ theta) = \ left \ {
           \ begin {array} {l l}
           \ frac {1} {2 \ pi} & \ quad \ theta \ in (- \ pi, \ pi] \\
           & \ quad \\
           0 & \ quad \ text {в противном случае}
           \ end {array} \ right. 2 $.{1}

           $

           При установке лимитов получаем,

           $ = (1 + 1) — \ left (\ dfrac {1} {3} + \ dfrac {1} {3} \ right) $

           $ = 2- \ dfrac {2} {3}

           $

           $ A = \ dfrac {4} {3}

           $

           Томов Революции

           Объемы тел вращения

           Вы также можете использовать определенный интеграл, чтобы найти объем твердого тела, который получается вращением плоской области вокруг горизонтальной или вертикальной линии, которая не проходит через плоскость.Этот тип твердого тела будет состоять из одного из трех типов элементов — дисков, шайб или цилиндрических оболочек, каждый из которых требует разного подхода к установке определенного интеграла для определения его объема.

           Дисковый метод

           Если ось вращения является границей плоской области, а поперечные сечения взяты перпендикулярно оси вращения, то вы используете дисковый метод , чтобы найти объем твердого тела. Поскольку поперечное сечение диска представляет собой круг с площадью π r ² , объем каждого диска равен его площади, умноженной на его толщину.Если диск перпендикулярен оси x , то его радиус должен быть выражен как функция от x . Если диск перпендикулярен оси y , то его радиус должен быть выражен как функция от y .

           Объем ( V ) твердого тела, созданный путем вращения области, ограниченной y = f (x ) и осью x на интервале [ a, b ] относительно x Ось

           Если область, ограниченная x = f (y ) и осью y на [ a, b ], вращается вокруг оси y , то ее объем ( V ) равен

           Обратите внимание, что f (x ) и f (y ) представляют собой радиусы дисков или расстояние между точкой на кривой и осью вращения.

           Пример 1: Найдите объем твердого тела, образованный путем вращения области, ограниченной y = x ² и осью x на [−2,3] относительно оси x . .

           Поскольку ось x является границей области, вы можете использовать дисковый метод (см. Рисунок 1).

           Рисунок 1 Диаграмма для примера 1.

           Объем ( V ) твердого тела

           Метод мойки

           Если ось вращения не является границей плоской области, а поперечные сечения взяты перпендикулярно оси вращения, вы используете метод с шайбой , чтобы найти объем твердого тела.Думайте о шайбе как о «диске с отверстием» или как о «диске с диском, удаленным из его центра». Если R — радиус внешнего диска, а r — радиус внутреннего диска, тогда площадь шайбы будет π R ² — π r ² , и ее объем будет быть его площадью, умноженной на толщину. Как отмечалось при обсуждении дискового метода, если шайба перпендикулярна оси x , то внутренний и внешний радиусы должны быть выражены как функции от x .Если шайба перпендикулярна оси y , тогда радиусы должны быть выражены как функции от y .

           Объем ( V ) твердого тела, созданный путем вращения области, ограниченной y = f (x ) и y = г (x ) на интервале [ a, b ], где f (x ) ≥ г (x ), примерно ось x составляет

           Если область, ограниченная x = f (y ) и x = g (y ) на [ a, b ], где f (y ) ≥ g (y ) вращается вокруг оси y , тогда его объем ( V ) равен

           Еще раз обратите внимание, что f (x ) и g (x ) и f (y ) и g (y ) представляют собой внешний и внутренний радиусы шайб или расстояние между точкой на каждой кривой до ось вращения.

           Пример 2: Найдите объем твердого тела, полученный путем вращения области, ограниченной y = x ² + 2 и y = x + 4 относительно оси x .

           Поскольку y = x ² + 2 и y = x + 4, получается, что

           Графики будут пересекаться в точках (–1,3) и (2,6) с x + 4 ≥ x ² + 2 на [–1,2] (Рисунок 2).

           Рисунок 2 Диаграмма для примера 2.

           Поскольку ось x не является границей области, вы можете использовать метод шайбы, а объем ( V ) твердого тела равен

           Метод цилиндрической оболочки

           Если поперечные сечения твердого тела взяты параллельно оси вращения, то для определения объема твердого тела будет использован метод с цилиндрической оболочкой .Если цилиндрическая оболочка имеет радиус r и высоту h, , то ее объем будет в 2π rh раз больше ее толщины. Подумайте о первой части этого продукта (2π rh ) как о площади прямоугольника, образованного путем разрезания оболочки перпендикулярно ее радиусу и плоского расположения. Если ось вращения вертикальна, то радиус и высота должны быть выражены в формате x . Если же ось вращения горизонтальна, то радиус и высота должны быть выражены в единицах y .

           Объем ( V ) твердого тела, образованный вращением области, ограниченной y = f (x ) и осью x на интервале [ a, b ], где f ( x ) ≥ 0, примерно по оси y —

           Если область, ограниченная x = f (y ) и осью y на интервале [ a, b ], где f (y ) ≥ 0, вращается вокруг x ‐ ось, то его объем ( V ) равен

           Обратите внимание, что x и y в подынтегральных выражениях представляют радиусы цилиндрических оболочек или расстояние между цилиндрическими оболочками и осью вращения.Коэффициенты f (x ) и f (y ) представляют высоту цилиндрических оболочек.

           Пример 3: Найдите объем твердого тела, полученный путем вращения области, ограниченной y = x ² и осью x [1,3] относительно оси y .