Содержание
Трапеция
Сегодня на уроке мы познакомимся с геометрической
фигурой, которую называют трапецией.
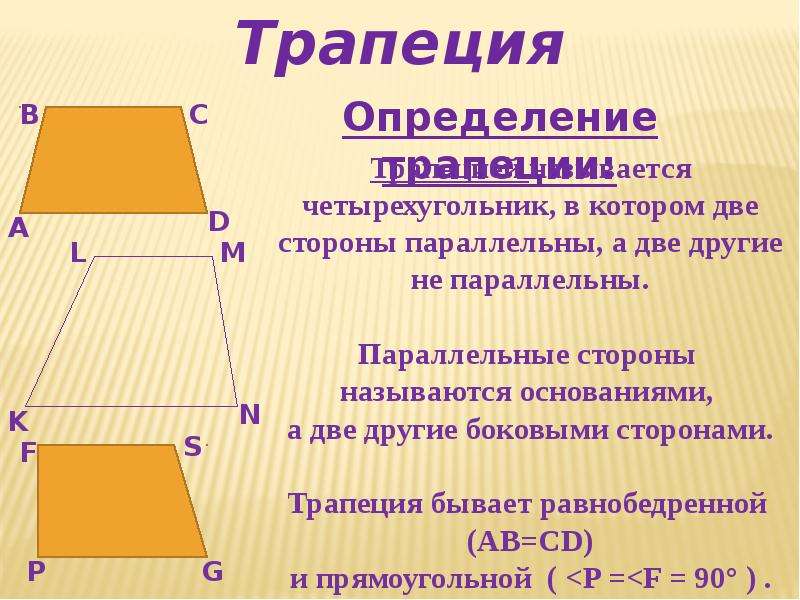
Итак, трапецией называется четырёхугольник, у
которого две стороны параллельны, а две другие – нет.
Параллельные стороны трапеции называются основаниями.
А не параллельные – боковыми сторонами.
Перпендикуляр, проведённый из любой точки одного из
оснований на другое основание или его продолжение, называется высотой
трапеции.
Трапеция, у которой есть прямой угол, называется прямоугольной.
Следует отметить, что, так как основания AB
и CD параллельны, прямая BC
–
секущая, а сумма односторонних углов равна 180º, то и угол BCD
также равен 90º.
Трапеция, у которой боковые стороны равны,
называется равнобедренной.
Далее мы рассмотрим некоторые свойства и признаки равнобедренной
трапеции.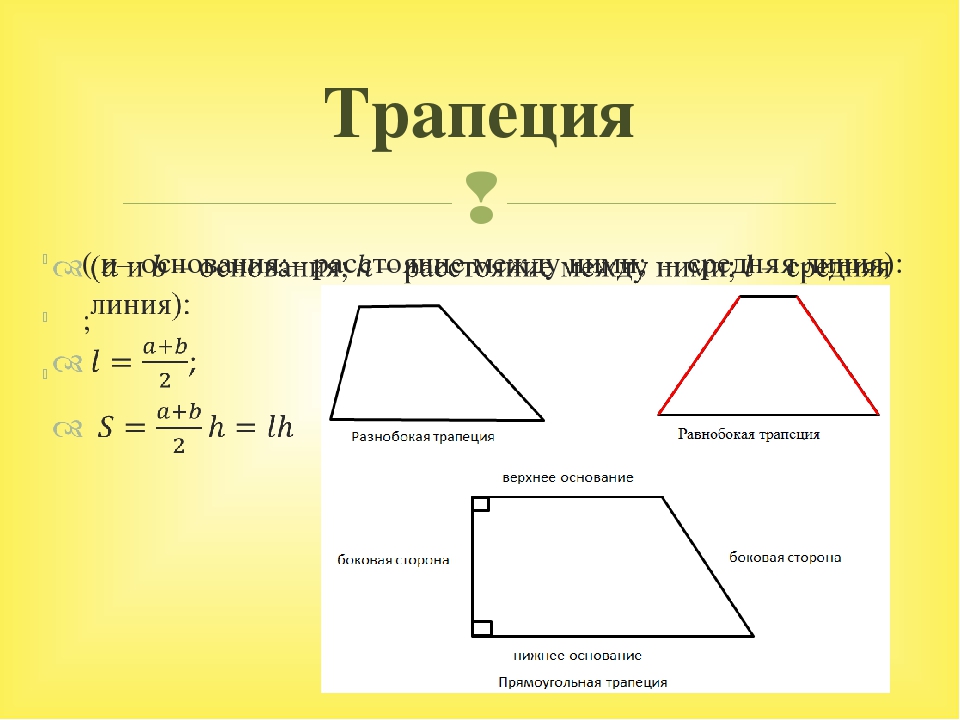
Теорема. Свойство углов равнобедренной трапеции. Углы
при основании равнобедренной трапеции равны.
Доказательство.
Рассмотрим прямоугольные и .
, так как – равнобедр.
трапеция,
.
по катету и
гипотенузе.
Следовательно, .
Теорема доказана.
Теорема. Свойство диагоналей равнобедренной
трапеции. Диагонали равнобедренной трапеции равны.
Доказательство.
Рассмотрим и .
, так как – равнобедр.
трапеция,сторона – общая,
как углы при
основании равнобедр. трапеции.
по первому
признаку.
Следовательно, .
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если
у трапеции углы при основании равны, то она равнобедренная.
Доказательство.
Рассмотрим прямоугольные и .
по условию.
.
по катету и
противолежащемуострому углу.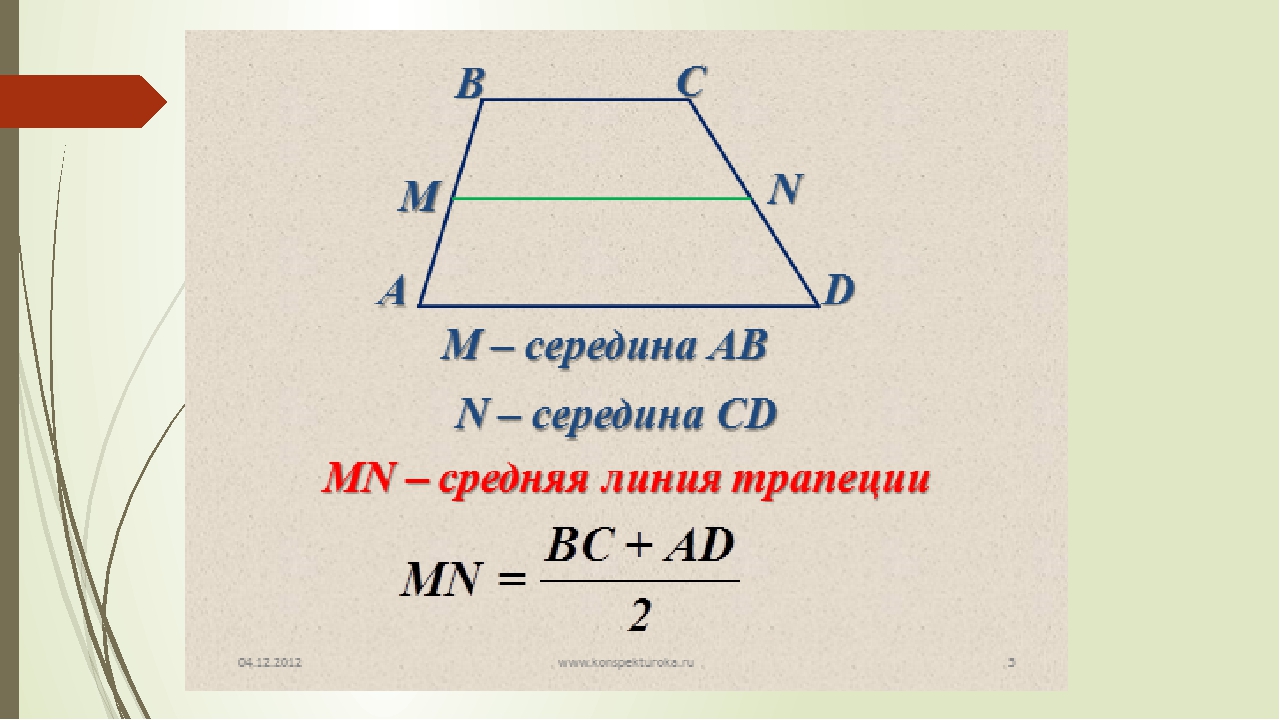
Следовательно, .
Тогда трапеция –
равнобедренная.
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если
у трапеции диагонали равны, то она равнобедренная.
Доказательство.
Рассмотрим прямоугольные и .
по условию,.
по катету и гипотенузе.
Следовательно, .
Рассмотрим и .
по
условию,сторона – общая,.
по первому
признаку.
Следовательно, .
Тогда трапеция –
равнобедренная.
Теорема доказана.
А теперь решим несколько задач.
Задача. – трапеция, у
которой . . Найдите
градусную меру .
Решение.
Так как , то трапеция –
равнобедренная.
как углы при
основании равнобедр. трапеции.
, –
внутр. односторонние при и секущей , то есть
,
,
,
.
Ответ: .
Задача.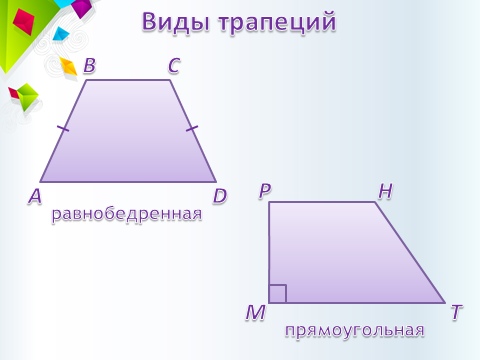 В прямоугольной
В прямоугольной
трапеции проведена
диагональ . , . Найдите
градусную меру .
Решение.
как накр.
лежащие при и секущей ,то есть .
,следовательно, –
равнобедренный, тогда .
Для : ,
,
,
.
Ответ: .
Урок по геометрии «Трапеция»(8 класс)
Дата:
Тема урока: Трапеция.
Цели урока:
Образовательная:
Ввести понятие трапеции и ее элементов, познакомить учащихся видами трапеций;
Рассмотреть некоторые свойства и признаки равнобедренной трапеции;
Научить учащихся применять полученные знания в процессе решения задач.
Развивающая:
Развитие у детей умения обобщать, логически мыслить, применять в своих рассуждениях аналогию, наблюдение, рационально применять свои знания;
Воспитательная:
Воспитание интереса к математике с помощью элементов занимательности, знакомства с историей возникновения понятия «трапеция»
Тип урока: урок изучения нового материала и первичное закрепление знаний.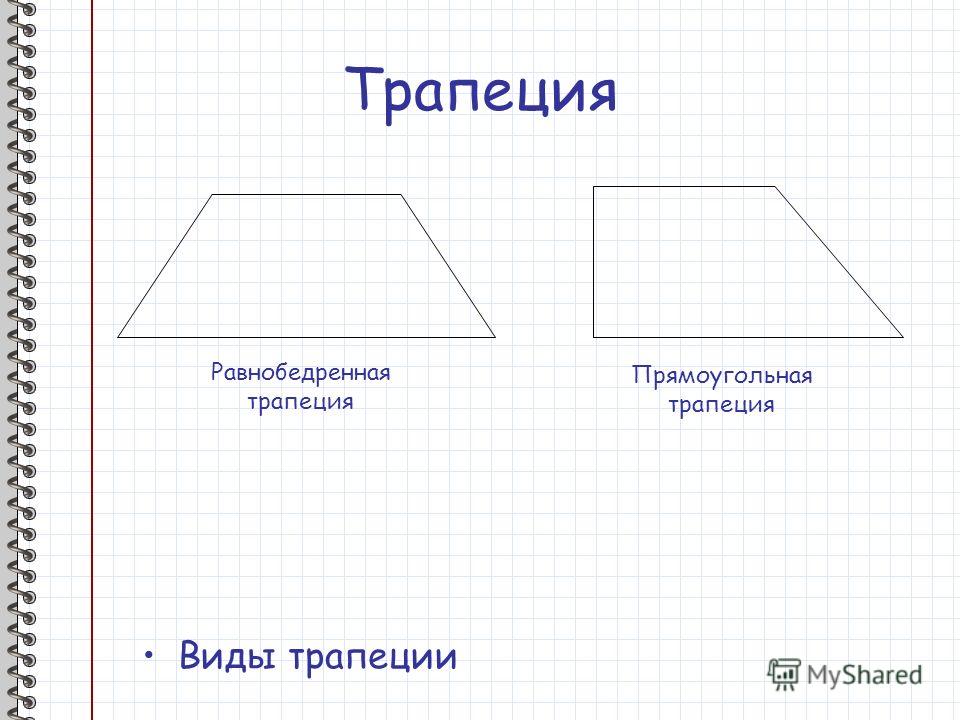
Оборудование: слайды из презентации к уроку, проектор, карточка-тест.
Содержание урока:
Организационный момент (1 мин)
Актуализация опорных знаний (5-7 минут)
Сообщение цели и темы урока. (2-3 минуты)
Изучение нового материала (15 – 20 минут)
Ввести понятие трапеции, ее оснований и боковых сторон.
Ввести понятия равнобедренной трапеции, прямоугольной трапеции.
Изучение свойств равнобедренной трапеции.
Закрепление изученного материала (решение задач на готовых чертежах)
(10-12 минут)Самостоятельная работа в виде теста (3- 4 минуты)
Подведение итогов урока. Рефлексия (2 – 3 минуты)
Домашнее задание (1 минута)
Ход урока:
Организационный момент
Учитель: Здравствуйте, ребята. Сегодня на уроке мы продолжаем изучение одного из важнейших разделов геометрии – изучение четырехугольников.
Сегодня на уроке мы продолжаем изучение одного из важнейших разделов геометрии – изучение четырехугольников.
Эта тема является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем.
Актуализация опорных знаний
Попробуем систематизировать все, что мы знаем о четырехугольниках.
Слайд 1
Ребята, посмотрите, пожалуйста, на слайд.
На доске представлена схема изучения геометрии 8 класса, но все понятия потеряли свои места. Ваша задача – восстановить порядок изучения материала.
Вспомогательные вопросы:
— Какие бывают четырехугольники? [Выпуклые и невыпуклые]
— Какой четырехугольник называется выпуклым? [четырехугольник – называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины]
— Что вы можете сказать о сумме углов четырехугольника? [Сумма всех углов равна 360°]
— С каким четырехугольником мы уже познакомились?[Параллелограммом]
— Дайте определение параллелограмма? [Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны]
— Какие свойства параллелограмма мы изучили? [В параллелограмме противоположные стороны и углы равны ]; [Диагонали параллелограмма точкой пересечения делятся пополам]
— Какие признаки мы изучили?
[Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм]
[Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм]
[Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм]
— Для чего необходимо использовать признаки, а для чего применять свойства?
[Свойство — это характерная особенность, присущая только этой геометрической фигуре. Признак — это характерная особенность, по которой ищут в многообразии других фигур именно эту].
Признак — это характерная особенность, по которой ищут в многообразии других фигур именно эту].
Молодцы! Вы хорошо справились с заданием!
Сообщение цели и темы урока.
Слайд 2
На доске вы видите разные виды четырехугольников.
— Как вы думаете, у всех ли четырехугольников противоположные стороны параллельны? (Выслушиваются ответы учеников).
-А может ли существовать четырехугольник, у которого только одна пара сторон параллельна?
— А как такие четырехугольники называются?
Итак, какова тема нашего урока? [Трапеция]
— Запишем тему урока: Трапеция.
Мы уже изучили параллелограмм, вспомнили с вами структуру изучения темы? По аналогии с параллелограммом, скажите, что мы узнаем о трапеции?
[Сегодня на уроке мы познакомиться с еще одним видом четырехугольников – трапецией, узнаем о её видах, свойствах и признаках; научимся применять эти свойства и признаки при решении задач.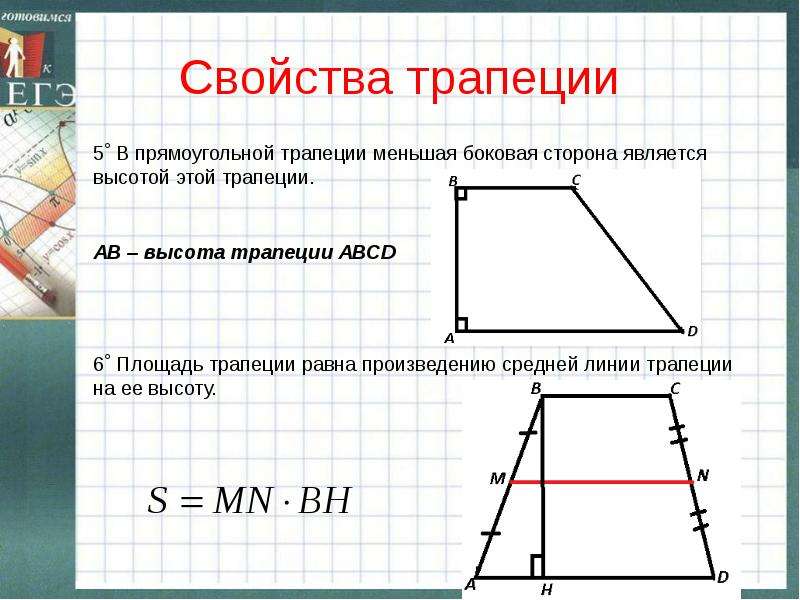 ]
]
Изучение нового материала
— Правильно, а сейчас послушаем рассказ подготовленный Самуйленковым Степаном и узнаем, почему этот четырехугольник — носит такое название?
Понятие трапеции формировалось в течение длительного периода времени. «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посейдона. Сначала трапецией называли любой четырехугольник, не являющийся параллелограммом . Именно в таком смысле термин «трапеция» использовал Евклид в своих «Началах». Лишь в XVIII в. это слово приобретает современный смысл.
«Трапеция» — слово греческого происхождения, означавшее в древности «столик» (по гречески «трапедзион» означает столик, обеденный стол).
— Спасибо, Степа! [Сообщение оценки]
Ввести понятие трапеции, ее оснований и боковых сторон.
В тетрадях и на доске рисунок и записи
Слайд 3
— Ребята, посмотрите на трапецию и дайте определение трапеции самостоятельно.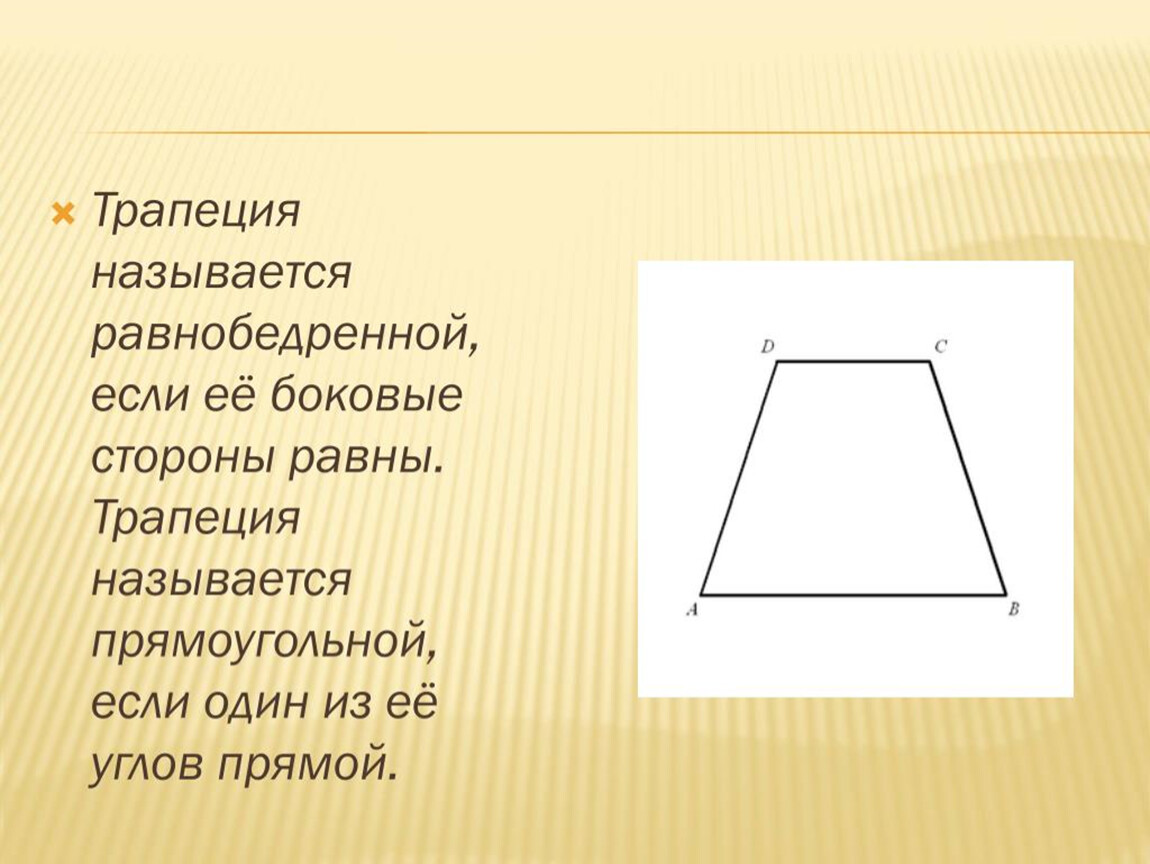 [Выслушиваются ответы учеников].
[Выслушиваются ответы учеников].
— Проверьте себя, прочитайте определение в учебнике. ( страница 103)
— Как называются параллельные стороны? [Основания]
Как называются две другие стороны? [боковые стороны]
— Параллельные стороны не могут быть равными? [ Нет, так как в противном случае мы имели бы параллелограмм]
— Правильно, поэтому одну из них мы назовем большим, вторую – малым основаниями трапеции.
2. Ввести понятия равнобедренной трапеции, прямоугольной трапеции. В тетрадях и на доске рисунки и записи. Слайд 4.
— Какие стороны у трапеции могут быть равными? [Боковые]
В зависимости от длин боковых сторон и их расположения трапеции могут быть различных видов. Рассмотрим виды трапеции.
В 7 классе мы изучали треугольник, у которого две равные стороны. Как он называется? [равнобедренный]
Как называется трапеция, которой боковые стороны равны? [равнобедренная]
Слайд 5.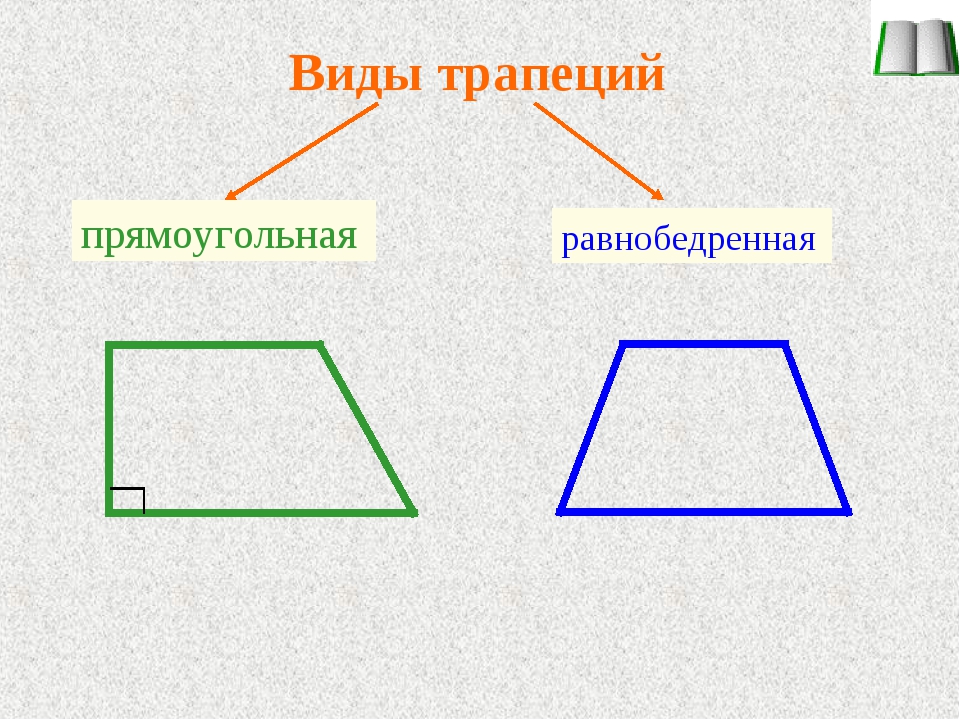
— Следующий вид трапеции — прямоугольная трапеция.
Дайте определение прямоугольной трапеции самостоятельно.
Подведем итог: Трапеция – это …[ответ учащихся]
Трапеции бывают …[ответ учащихся]
Какая трапеция называется равнобедренной? прямоугольной …[ответ учащихся]
Изучение свойств равнобедренной трапеции.
— Равнобедренная трапеция обладает основными свойствами. Эти свойства мы выведем, решая задачу.
Рассмотрим задачу с учебника №388(а)
№ 388 (а).
В равнобедренной трапеции углы при основании равны.
1. Дополнительные построения: СЕ||АВ.
2. ABСЕ – параллелограмм (СЕ||АВ, АЕ||ВС) => АВ=СЕ.
3. АВ=СЕ=СD=> СЕD равнобедренный => 1=2.
4. Так как АВ||СЕ, то 3=2 – как соответственные => 3=1.
5. В=180º-3=180º-1=С.
Ч.т.д.
В ходе решения задачи, учитель задает наводящие вопросы:
При решении задач, мы используем свойства и признаки уже изученных фигур.
 Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.]
Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.]Что вы можете сказать о четырехугольнике ABСЕ? [ABСЕ – параллелограмм (СЕ||АВ, АЕ||ВС) => АВ=СЕ.]
Рассмотрим другую фигуру – треугольник СЕD. Какой это треугольник? [Равнобедренный, т.к. АВ=СЕ=СD].
Какими свойствами обладает равнобедренный треугольник? [В равнобедренном треугольнике углы при основании равны, значит 1=2.]Скажите, можно ли утверждать что 3 = 2? Как называются эти углы?
Итак, если 1=2 , а 2=3 значит 3=1Мы доказали равенство углов при большем основании. Как доказать, что В=С?
Что вы можете сказать о А и В? [односторонние]. Что мы знаем про односторонние углы? [сумма односторонних углов равна 180]
Слайд 6. № 388 (б) прочитать задачу.
— Доказательство этого свойства, вы проведете дома самостоятельно.
В тетрадях и на доске рисунок и записи:
Слайд 7.
— Сформулируйте утверждения, обратные свойствам равнобедренной трапеции. Как называются эти обратные свойства? [признаки равнобедренной трапеции]
Закрепление изученного материала (решение задач на готовых чертежах)
Сейчас я предлагаю вам узнать имя ученого, спрятанного за сеткой задач. При правильном ответе сектор открывается и появляется часть изображения.
Много интересного рассказывают про этого учёного. Вот, например, один случай. Учёный, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит»
Этот учёный сформулировал следующие теоремы: а) Вертикальные углы равны; б) В равнобедренном треугольнике углы при основании равны; в)Если на одной стороне угла отложить равные отрезки, и провести через них параллельные прямые, то и на другой стороне угла отложатся равные отрезки.
Слайд 8
Ответы:
( слева – направо, 1 ряд – 2 ряд )
1) Е = N = 80;M = 100.
2) F = 90;M=115
3) К =F = 55;M=R= 125;
4) B = 110;M=130
5) D = 55;C=125;F = 105
6) C = 120;A=60;B = 120
При отсутствии времени количество задач сократить, решив их на следущем уроке.
Самостоятельная работа в виде теста
Слайд 9.
ТЕСТ
Определить вид четырехугольника если он имеет:
Трапеция
Паралле-лограмм
Равнобед-ренная
Прямо-угольная
Разносто-ронняя
два прямых угла и все стороны разные
+
два разных острых угла и все разные стороны
+
два одинаковых тупых угла и две одинаковые боковые стороны
+
противоположные стороны равны и углы равны
+
Подведение итогов урока.
 Рефлексия.
Рефлексия.
Ребята, что нового вы узнали на уроке?
Что было особенно интересно?
На что еще необходимо обратить внимание?Домашнее задание
П. 44, записи в тетрадях, № 388(б), № 390.
Придумать и решить задачу на использование свойства или признака трапеции.
Трапеция
Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара противолежащих сторон параллельна.
Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон трапеции.
Элементы трапеции
- Параллельные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
- Трапеция, у которой боковые стороны равны, называется равнобедренной.
- Трапеция, у которой один из углов «прямой», называется прямоугольной.
Основные свойства трапеции
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
\[ AB + CD = BC + AD \]
Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
\[ AK = KB, AM = MC, BN = ND, CL = LD \]
Средняя линия трапеции параллельна основаниям и равна их полусумме:
\[ m = \dfrac{a + b}{2} \]
Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой. 2 \]
2 \]
Формулы длин сторон трапеции
Формула длины оснований трапеции через среднюю линию и другую основу:
\[ a = 2m — b , b = 2m — a \]
Формулы длины основ трапеции через высоту и углы при нижнем основании:
\[ a = b + h · (ctg \alpha + ctg \beta) , b = a — h · (ctg \alpha + ctg \beta)\]
Формулы длины основ трапеции через боковые стороны и углы при нижнем основании:
\[ a = b + c·cos \alpha + d·cos \beta, b = a — c·cos \alpha — d·cos \beta \]
Формулы боковых сторон трапеции через высоту и углы при нижнем основании:
\[ с = \dfrac{h}{sin \alpha } , d = \dfrac{h}{sin \beta } \]
Формулы длины средних линий трапеции
Формула определения длины средней линии через длины оснований:
\[ m = \dfrac{a + b}{2} \]
Формула определения длины средней линии через площадь и высоту:
\[ m = \dfrac{S}{h} \]
Формулы длины высоты трапеции
Формула высоты трапеции через сторону и прилегающий угол при основании:
\[ h = c·sin α = d·sin β \]
Формула высоты трапеции через диагонали и углы между ними:
\[ h = sin γ \cdot \dfrac{d_1\cdot d_2}{a + b} = sin δ \cdot \dfrac{d_1\cdot d_2}{a + b} \]
Формула высоты трапеции через диагонали, углы между ними и среднюю линию:
\[ h = sin γ \cdot \dfrac{d_1 \cdot d_2}{2m 2m} = sin δ · \dfrac{d_1}{d_2} \]
Формула высоты трапеции через площадь и длины оснований:
\[ h = \dfrac{2S}{a + b} \]
Формула высоты трапеции через площадь и длину средней линии:
\[ h = \dfrac{2S}{m} \]
Формулы длин диагоналей трапеции
Формулы длин диагоналей трапеции по теореме косинусов:
\[ d_1 = \sqrt{a^2 + d^2 — 2ad·cos β} \]
\[ d_2 = \sqrt{a^2 + c^2 — 2ac·cos β} \]
Формулы длин диагоналей трапеции через четыре стороны:
\[ d_1 = \sqrt{d^2 + ab — \dfrac{a(d^2 — c^2)}{a — b} } \]
\[ d_2 = \sqrt{c^2 + ab — \dfrac{ a(c^2 — d^2) }{a — b} } \]
Формулы длин диагоналей трапеции через высоту:
\[ d_1 = \sqrt{h^2 + (a — h · ctg β)^2} = \sqrt { h^2 + (b + h · ctg α)^2} \]
\[ d_2 = \sqrt{h^2 + (a — h · ctg α)^2} = \sqrt{h^2 + (b + h · ctg β)^2} \]
Формулы длин диагоналей трапеции через сумму квадратов диагоналей:
\[ d_1 = \sqrt{c^2 + d^2 + 2ab — d_2^2} \]
\[ d_2 = \sqrt{c^2 + d^2 + 2ab — d_1^2} \]
Формулы площади трапеции
Формула площади трапеции через основания и высоту:
\[ S = \dfrac{ (a + b) · h }{2} \]
Формула площади трапеции через среднюю линию и высоту:
\[ S = m · h \]
Формула площади трапеции через диагонали и угол между ними:
\[ S = \dfrac{d_1d_2}{2} · sin γ = \dfrac{d_1d_2}{2} · sin δ \]
Формула площади трапеции через четыре стороны:
\[ S = \dfrac{a + b}{2}\sqrt{c^2 — \left\lgroup\dfrac{(a — b)^2 + c^2 — d^2)}{2\cdot (a — b)} \right\rgroup ^2 } \]
Формула Герона для площади трапеции
\[ S = \frac{a + b}{\left|a-b\right| } \sqrt{(p — a)(p — b)(p — a — c)(p — a — d)} \]
где \( p = \dfrac{a + b + c + d}{2} \) — полупериметр трапеции.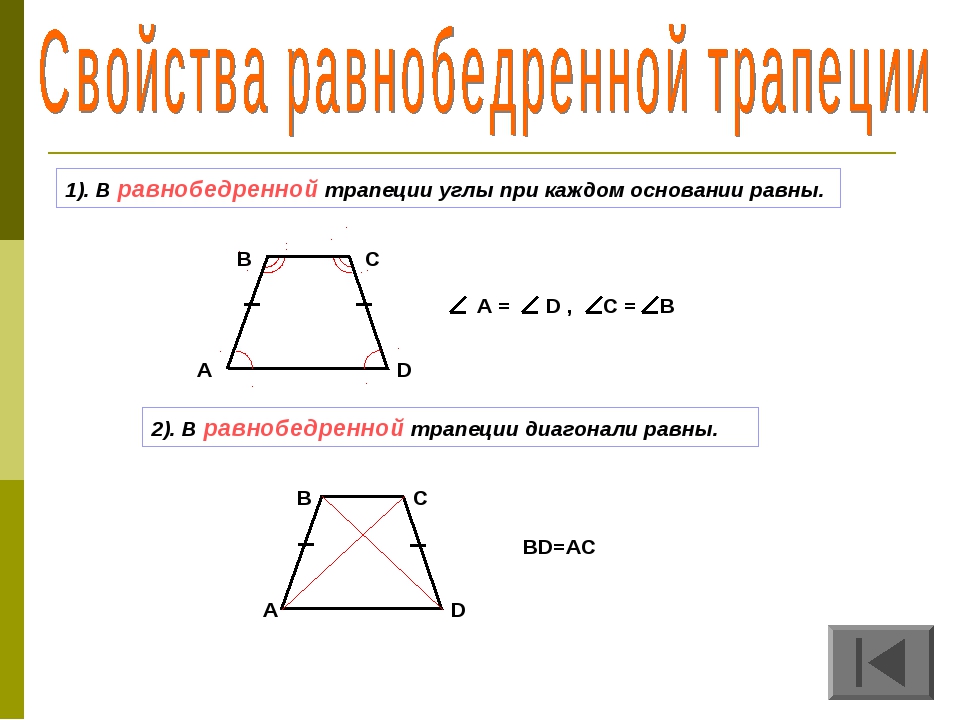
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsbox
Урок геометрии в 8 классе по теме «Трапеция»
ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ
ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»
Учитель Математики Высшей категории
ТРАПЕЦИЯ
Цель:
- Ввести понятие трапеции, её элементов, виды трапеций.
- Рассмотреть некоторые свойства трапеции.
- Применение знаний при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Кроссворд.
Ключевое слово кроссворда – является темой нашего урока.
Любой многоугольник разделяет плоскость на две части, одна из которых называется …
Четырехугольник, у которого противоположные стороны попарно параллельны.
Отрезок, соединяющий любые две не соседние вершины многоугольника.
Сумма длин всех сторон многоугольника.
Две вершины многоугольника, принадлежащие одной стороне, называются…
В конце урока каждый ученик ждет хорошую …
Две несмежные стороны четырехугольника называются …
Любой многоугольник разделяет плоскость на две части, одна из которых внутренняя, а другая
Ответы:
III. Новый материал.
Трапеция – (от греч. trapezion, букв. – столик).
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Виды трапеции.
Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная – трапеция, один из углов которой прямой.
Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Работа в группах.
Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
Свойства равнобедренной трапеции.
Теорема. В равнобедренной трапеции углы при каждом основании равны.
Доказательство.
Проведем СЕ АВ.
ABCD – параллелограмм (АВ СЕ, ВС AD).
CD = AB = CE, СDE – равнобедренный, СDЕ = СЕD.
АВ СЕ, тогда СЕD = ВАЕ, СDЕ = СЕD = ВАЕ.
ABC = 180° – СDЕ = 180° – ВАЕ = BCD.
Теорема. В равнобедренной трапеции диагонали равны.
Доказательство.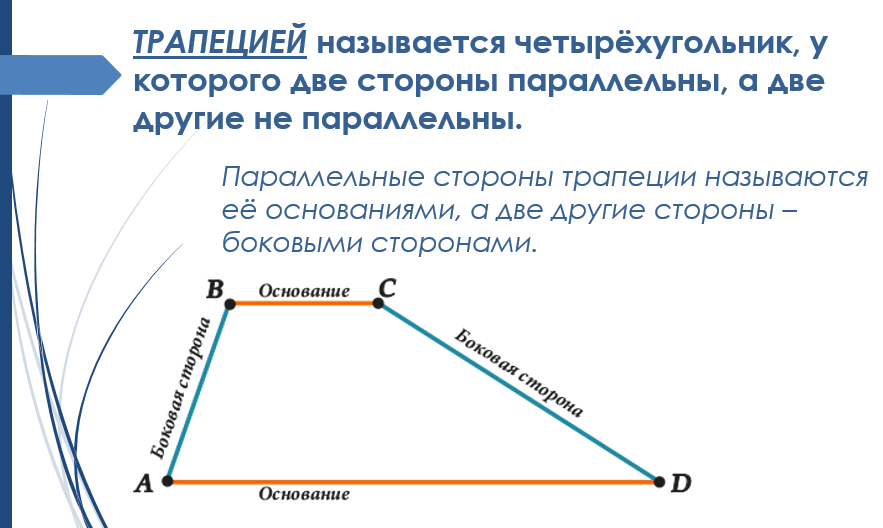
ABC = DСВ (АВ = С, ВС – общая сторона, АВС = ВСD) тогда АС = ВD.
Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.
Признаки равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
1. Если углы при основании трапеции равны, то она равнобедренная.
Доказательство.
Проведем ЕС АВ.
ABCЕ – параллелограмм, тогда АВ СЕ, А = СЕD, СЕD – равнобедренный (D = СЕD), тогда СЕ = СD.
АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.
2. Если диагонали трапеции равны, то она равнобедренная.
Доказательство.
Проведем СК ВD.
ВСКD – параллелограмм (т.к. СК ВD, ВС АК).
АСК – равнобедренный, т.к. АС = ВD = СК, САD = СDА.
СК ВD, ВDА = СКD, тогда САD = СКD.
АВD = DСА, т.к. АС=ВD, АD – общая сторона, САD = СКD, тогда АВ = СD, т. е. АВСD – равнобедренная трапеция.
е. АВСD – равнобедренная трапеция.
IV. Закрепление.
Решение задач по готовым чертежам.
F = 65° Найти: В, С, D. | |
ВС = 10, СD = 15, А = 60° Найти: АD. |
V. Итог урока:
VI. Домашнее задание.
Параграф 44, вопросы: 10-11, №386, №388.
Урок геометрии в 8 классе на тему «Трапеция» – УчМет
Приложение № 1
На какие группы
можно разделить данные четырехугольники?
Ответ:
Первая группа – 1, 3, 5, 7; вторая – 2, 4 и
6.
Почему
объединили в одну группу фигуры 1, 3, 5 и
7? [Ответ: четырехугольники имеют две
пары параллельных сторон].
Почему
объединили 2, 4 и 6? [Ответ: у четырехугольников
две стороны параллельны, а две другие
не параллельны].
Приложение № 2
Разгадайте
кроссворд. Определите ключевое слово
нашего урока.
Сумма длин всех
сторон четырехугольника.
Единица
измерения сторон четырехугольника.
Ответ:
Приложение
3
1)
Ознакомиться с материалом по теме
«Трапеция» (с. 43 – 44, до определения
средней линии трапеции).
2)
Сделать рисунки и соответствующие
записи в тетрадях.
2)
Работа со словарем: Что такое трапеция?
(толковый словарь С.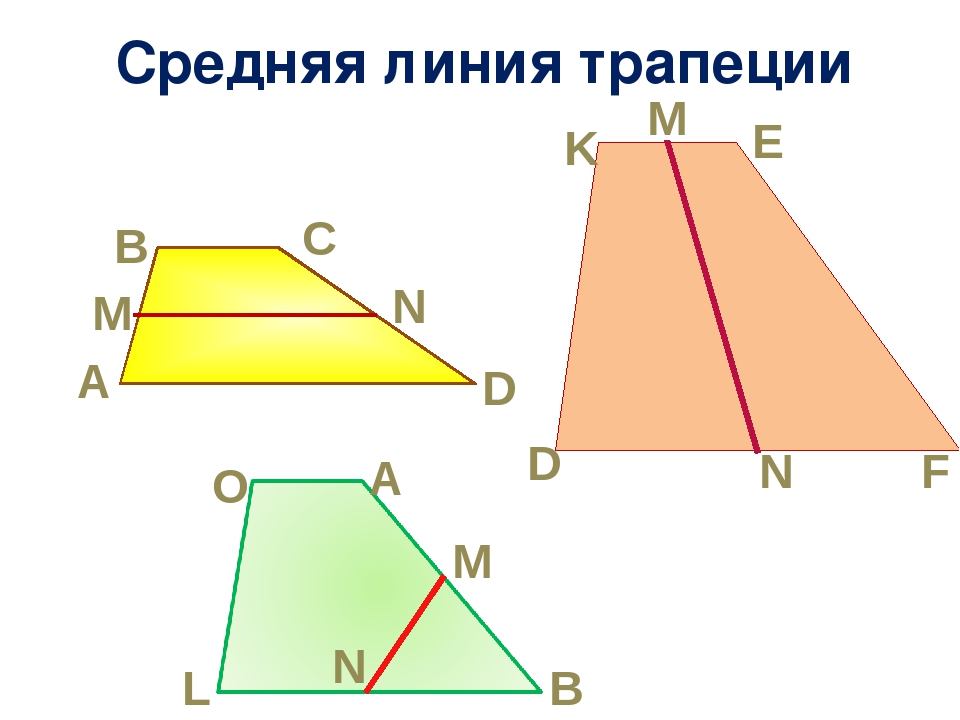 И. Ожегова, словарь
И. Ожегова, словарь
иностранных слов русского языка А.Н.
Чудинова, словарь синонимов, современная
энциклопедия).
3)
Ответить соседу по парте на вопросы (В:
1 – 6, с. 46):
—
Какой четырехугольник называется
трапецией?
—
Какие стороны трапеции называют
основаниями? Боковыми сторонами?
—
Что называют высотой трапеции?
—
Какие существуют виды трапеций?
—
Какую трапецию называют равнобокой?
—
Какую трапецию называют прямоугольной?
4)
Что вы можете сказать об углах, прилежащих
к боковой стороне трапеции?
Приложение
4
Ответ:
Задача
1:
Задача
2:
Приложение
№ 5
№ 216
Начертите
по клеткам тетради трапецию: 1) равнобокую;
2) прямоугольную; 3) не являющуюся ни
прямоугольной, ни равнобокой; 4) у которой
один из углов при основании острый, а
другой тупой.
№ 218 (Устно)
Найдите
на рисунке трапеции, укажите их основания
и боковые стороны.
[Ответ: а)
АВСК, АК и ВС – основания, АВ и КС –
боковые стороны; AМСD,
МС и AD – основания, АМ и
CD – боковые стороны; б) АВDE, ВD и АЕ –
основания, АВ и DE – боковые стороны; в)
АВСК, ВС и АК – основания, АВ и СК –
боковые стороны, АМСD, МС и АD – основания,
АМ и СD – боковые стороны]
№ 220 (Устно)
Периметр
равнобоковой трапеции равен 52 см,
основания – 13 см и 21 см. Найдите боковую
сторону трапеции. [9 см; 9 см]
№ 222
Найдите углы
А и С трапеции ABCD с основаниями AD и ВС,
если В
= 1320,
D
= 240.
[Ответ:480;
1560]
№ 223
Найдите углы
трапеции АВСD, прилежащие к боковой
стороне АВ, если угол А меньше угла В на
380 [Ответ: 710; 1090]
Приложение
№ 6
§
8, В: 1 – 6. Практические задания: № 217,
Практические задания: № 217,
219. Задачи: № 221, 224, 227.
По желанию:
Из плотной бумаги вырежьте квадрат и
разделите его так, как показано на
рисунке. Из трех получившихся треугольников
сложите трапецию.
Трапеция / Четырехугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Трапеция
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Многоугольник
Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Прямоугольник
Ромб и квадрат
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 391,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 392,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 518,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 522,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 723,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 725,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 861,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1007,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1073,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2021
Пользовательское соглашение
Copyright
О площади трапеции в сферической геометрии Текст научной статьи по специальности «Математика»
УДК 514.132
О ПЛОЩАДИ ТРАПЕЦИИ В СФЕРИЧЕСКОЙ ГЕОМЕТРИИ
Г. А. Байгонакова, Д. Ю. Соколова
ON THE AREA OF A TRAPEZOID IN SPHERICAL GEOMETRY
G. A. Baigonakova, D. Yu. Sokolova
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты 12-01-90701-моб_ст и 12-01-00210-а) и Совета по грантам при президенте Российской Федерации (гранты МК-4447.2012.1 и НШ-921.2012.1). d — длины сторон четырёхугольника, a р =——————————— его полупериметр. Формулу Брах-
магупты и её доказательство можно найти в книге [7, с. 90]. Во втором случае площадь трапеции находится через длины её сторон элементарными вычислениями по формуле, приведённой ниже.
Отметим, что для сферического четырёхугольника формула площади через длины его сторон и диагонали была получена в монографии [4, с. 165]. Она имеет следующий вид.
Теорема 1. Площадь S сферического четырёхугольника ABCD со сторонами a,b,c,d и диагоналями e, f находится из соотношения:
e f a c b d e f a c b d
o (sin — sin — + cos—cos — cos — cos —)(sin — sin — — cos — cos — + cos — cos —) /14
sin2 ± _ 24 22 2 2 2 4 22 2 2. (1)
7 7
4 a b c d
4cos — cos — cos—cos —
2 2 2 2
Напомним [3], что выпуклый четырехугольник вписан в окружность тогда и только тогда, когда выполнено равенство
. e . f . a . c . b . d
sin—sin — _ sin—sin— + sin—sin—
2 4 2 2 2 2
Подставляя это соотношение в формулу (1) получим следующий сферический аналог формулы Брахмагупты [4, с. 46].
Следствие. Площадь S вписанного в окружность сферического четырёхугольника ABCD со сторонами
a, b, c, d находится по формуле:
. =—-2——2_———-2 d 2 .
4 a b c d
cos — cos — cos — cos —
2 2 2 2
В гиперболическом случае варианты формул Брахмагупты для вписанного четырехугольника представлены в работе [2]. Формула площади трапеции на гиперболической плоскости через длины её сторон получена в работе одного из авторов [8].
Цель настоящей статьи — перенести результаты работы [8] на сферический случай. Все приведённые ниже результаты будут сформулированы для сферической плоскости с гауссовой кривизной к = 1. Необходимые сведения по сферической геометрии приведены в книге [5].
2. Основной результат
Определение. Выпуклый четырехугольник ABCD называется трапецией, если для его внутренних углов справедливо соотношение
ZA + ZB = ZC + ZD. d. При b = d, как и в евклидовой геометрии (случай параллелограмма), площадь трапеции не определяется по длинам её сторон.
Для вычисления площади трапеции нам потребуется следующая теорема. В гиперболическом случае она доказана в работе Ф. В. Петрова [6].
Теорема 2. Пусть ABCD — выпуклый четырёхугольник в сферической геометрии. Тогда следующие два свойства эквивалентны:
(г) ZBAD + ZABC = ZADC + ZDCB.
(гг) Z CAD + Z CBD = ZBCA + ZBDA.
Доказательство. Выведем (ii), предполагая (i). Пусть точка E симметрична точке D относительно середины AB , и точка F симметрична точке A относительно середины CD , тогда равны пары треугольников: AABE = ABAD и ACDA = ABDA (рис. 2.)
По двум сторонам и углу между ними равны DEBC и DFCB
( ZEBC = 2р — (ZCBA + ZABE) = = 2р — (ZCBA + ZDAB) =
= 2р — (ZBCD + ZCDA) =
= 2р — (ZBCD + ZDCF) = ZFCB).
Значит, EC = FB, и по трем сторонам равны треугольники DFBD = DACE, так что ZFDB = ZCAE. Откуда из равенств ZFDC = ZDCA и ZBAE = ZDBA следует, что ZDBA + ZCAB = ZBDC + ZDCA. Вычитая последнее равенство из (i), получаем (ii).
Для вывода (i) из (ii) надо рассмотреть точку, симметричнуюD относительно середины AC , и точку, симметричную A относительно BD середины, и провести аналогичные рассуждения.
Заметим, что каждое из свойств (i) и (ii) равносильно тому, что четырехугольник ABCD является трапецией с основаниями BCи AD. Вычитая из первого равенства второе, получим, что справедлива следующая лемма.
Лемма. Для трапеции ABCD справедливо соотношение
ZDBA + ZCAB = ZBDC + ZDCA
В силу формулы Гаусса-Бонне площади треугольников AOB и COD находятся по формулам:
SAOB = ZCAB + ZABD + ZAOB — p, SGOD = ZACD + ZCDB + ZCOD — p.
Учитывая утверждение леммы и равенство вертикальных углов ZAOB = ZCOD, получим, что
AOB °COD-
Отсюда непосредственно заключаем, что имеют место равенства площадей SaDB = SaDC и
Sabc = SBCD . Обозначим через S(a,b, с) площадь сферического треугольника с длинами сторон a, b, с.
Переписывая полученные два равенства в терминах длин сторон, установим, что справедливо следующее следствие.
Следствие. Для площадей треугольников с соответствующими сторонами выполнены равенства
\S (a, d, f) = S (с, d, e),
[S (b, a, e) = S (b, c, f). (3)
Из работы [5] известна следующая формула для площади S сферического треугольника со сторонами
Ja + b + c b + c — a
tan———tan——-tan
4 4 , (4)
a—b+c a+b—c
tan———tan——-,
4 4
которая элементарными преобразованиями приводиться к следующему сферическому аналогу формулы Билински [1]
S(a,b, c) cos(a) + cos(b) + cos(c) + 1
2 a b c
4 cos — cos — cos — 2 2 2
(5)
Положим с(а) = соя (2) и я (а) = вт(2). Подставляя равенство ео8(а) = 2с2(а) — 1 в уравнение (5), получим, что система уравнений (3) эквивалентна следующей:
с2(а) + с?(б) + с2(/) — 1 с2(с) + с?(б) + с2(е) — 1
с(а)с(/) с(с)с(е)
c2(а) + c2(b) + c2(e) — 1 _ c2(c) + c2(b) + c2(/) — 1 (6)
с(а)с(е) с(с)с(/)
Решая эту систему на компьютере относительно с(е)с(/) и , получим следующее предложение.
с(/)
Предложение. Длины сторон и диагоналей трапеции связаны соотношениями
с(е)с(/) = с(а)с(с) — з(Ь)з(с1),
с(е) с(с)з(Ь) — с(а)з(С) (7)
с(/) с(а)з(Ь) — с(с)з(сС)
Из данной системы уравнений находятся выражения для длин диагоналей трапеции ЛВОБ :
^) = fwM ~ ^) «“)c(c) — »(%№)• (8)
c(a )s(b) — c(c)s(d)
c2(f) = c(a)s(b) — C(C)a(d) (c(a)c(c) — s(b)s(d)). (9)
c(c)s(b) — c(a)s(d)
Сформулированное предложение потребуется для доказательства теоремы о площади трапеции. Теорема 3. Площадь S сферической трапеции ABCD со сторонами a, b, c, d находится из соотношения:
. 2 b + d . a + b — c — d . a + b + c — d . —a + b + c — d . a — b + c + d „ sin ———-sin—————-sin——————sin——————sin——————
tan’2 — =———2—————4——————-4——————-4——————-4——-.
4 ,2 b — d a — b — c — d a — b + c — d a + b — c + d a + b + c + d
2
sin———-cos———————-cos———————cos———————cos —
4
Замечание. Евклидов вариант формулы, выражающий квадрат площади трапеции через её стороны, находится элементарными вычислениями из геометрических соображений и имеет вид:
(b + d )2(a + b — c — d )(a + b + c — d)(—a + b + c — d )(a — b + c + d)
E 16(b — d)2
Отметим также, что tan2 S » (-E-)2 при достаточно малых величинах a, b, c, d.
4 4
Доказательство. Рассмотрим трапецию ABCD, изображенную на рисунке 1. Для вычисления её площади воспользуемся формулой (1) и представим ее в следующем виде:
sin2 — = (s 0)(f))2 — (c(a )c(c) — c (b )c (d ))2 (10)
4 4c (a )c (b )c (c )c (d)
Вычисляя выражение (s(e)s(f))2 = (1 — c2(e))(1 — c2(f)) по формулам (8), (9) и подставляя полученное значение в (10), после упрощения на компьютере получим:
. 2 b + d . a + b — c + d . a + b + c — d . a — b — c + d . a — b + c + d „ sin ————sin————-sin——————sin—————-sin——————
sin2 — =—————————————————————————————————————2-4-4-4-4-. (11)
4 c(b)c(d )(c(c)s(b) — c(a)s(d ))(c(c)s(d) — c(a)s(b))
Далее,
. 2 b — d a — b — c — d a — b + c — d a + b — c + d a + b + c + d
„ sin ——————————cos—————————————cos—————————————-cos——————————————-cos—————————————-
■ S
cos2 — =————————————————————————————————2-4-4-4-4-. (12)
4 c(b)c(d)(c(c)s(b) — c(a)s(d))(c(a)s(b) — c(c)s(d))
Поделив (11) на (12), имеем утверждение теоремы
. 2 b + d . a + b — c — d . a + b + c — d . —a + b + c — d . a — b + c + d „ sin ———sin—————sin—————sin——————sin—————
tan2S =———2—————4——————4——————4——————4——.
4 . 2 b — d a — b — c — d a — b + c — d a + b — c + d a + b + c + d
sin——-cos—————cos—————cos—————cos—————
2 4 4 4 4
Что и требовалось доказать.
Литература
1. Bilinski, S. Zur Begründung der elementaren Inhaltslehre in der hyperbolischen Ebene / S. Bilinski // Math. Ann. — 1969.
2. Mednykh, A. D. Brahmahupta formula for cyclic quadrilaterals in the hyperbolic plane / A. D. Mednykh // Sib. Electron. Math. Reports. — 2012 to appear.
3. Valentine, J. E. An Analogue of Ptolemy’s Theorem in Spherical Geometry / J. E. Valentine // Amer. Math. Monthly. — 1970. — Vol. 77.
4. M’Clelland, W. J. A Treatise on Spherical Trigonometry with application to Spherical Geometry and Numerous Examples. Part II / W. J. M’Clelland, T. Preston. — London: Macmillian and Co,1886.
5. Алексеевский, Д. В. Геометрия пространств постоянной кривизны / Д. В. Алексеевский, Э. Б. Винберг, А. С. Солодовников // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. — М.: ВИНИТИ. — 1988. — Т. 29.
6. Петров, Ф. В. Вписанные четырехугольники и трапеции в абсолютной геометрии / В. Ф. Петров // Математическое просвещение. — Сер. 3. — 2009. — Вып. 13.
7. Понарин, Я. П. Элементарная геометрия. Планиметрия / Я. П. Понарин. — М.: МЦНМО, 2004. — Т. 1.
8. Соколова, Д. Ю. О площади трапеции на плоскости Лобачевского / Д. Ю. Соколова // Сиб. электрон. мат. изв. — 2012.
Информация об авторах:
Байгонакова Галия Аманболдыновна — аспирант кафедры математического анализа ГАГУ, т. 8(913) 691-8816, e-mail: [email protected].
Bajgonakova Galiya Amanboldynovna — post-graduate student at the Department of Mathematical Analysis of Gorno-Altaysk State University.
Соколова Дарья Юрьевна — аспирант лаборатории теории функции Института математики им. С. Л. Соболева СО РАН, т. 8(913) 460-2823, e-mail: from [email protected].
Sokolovа Daria Yurievna — post-graduate student at the Laboratory of Function theory of S. L. Sobolev Institute of Mathematics of the Siberian Branch of the RAS.
трапеций — расширенная геометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Трапеция | Блог по математике ∞
Трапеция — это плоская форма с четырьмя прямыми сторонами. Две стороны параллельны друг другу и противоположны друг другу. Трапеция не должна быть маленькой фигурой, поскольку длина сторон и углы могут сильно различаться.В то время как некоторые люди думают, что трапеция — это термин, зарезервированный исключительно для учебников по математике, реальные примеры трапециевидных форм можно найти в сумках, опорах мостовых ферм, банках для попкорна и некоторых музыкальных инструментах, таких как гитарные цимбалы. .
Студенты иногда путаются, когда дело доходит до определения площади трапеции, просто потому, что они не знают, как правильно обозначить форму, чтобы они могли вставить правильные числа в формулу. Эти ключевые факты помогут определить правильные числа для использования в формуле для определения площади трапеции:
Две стороны, идущие параллельно друг другу, называются основаниями.
Две другие стороны называются ножками.
Расстояние между двумя базами называется высотой или высотой.
При нахождении площади трапеции необходимо следовать простой формуле. Если вы укажете правильные числа в формуле и не сделаете простых ошибок при сложении, делении и умножении, вы легко сможете прийти к окончательному ответу. Формула выглядит следующим образом:
Площадь = a + b x h
2
Верхняя базовая линия обозначается как «a.”
Нижняя базовая линия обозначается буквой «b».
Высота обозначается как «h».
Пример. Предположим, у нашей трапеции есть основания длиной 6 метров и 8 метров и высотой 4 метра, поэтому наша формула будет выглядеть следующим образом.
6 м + 8 м x 4 м
2
Шаг 1: Сначала необходимо сложить две базы. Итак, мы говорим 5м + 8м = 14м.
Шаг 2: Разделите число, полученное при сложении оснований, на 2.Итак, вы скажете 14, разделенное на 2, что равно 7.
Шаг 3: возьмите 7 и умножьте на «h», что равно 4.
Ответ: Ответ на эту проблему — 28 м2
При поиске площади трапеции важно не перепутать числа и поставить их на их законное место в формуле, чтобы можно было найти нужную область. Если вы перепутаете одно число, вы получите совершенно неправильный ответ, даже если вы знаете правильную формулу.
Трапеции обычно встречаются в дизайне мебели, такой как столы, и в других объектах, таких как знаки.Есть много причин, по которым человеку может потребоваться найти область объекта, например, планирование строительного проекта, покраска и изготовление покрытия для стола.
Интересный факт:
Часто возникает путаница, когда дело доходит до значения трапеции и того, что этот термин означает в США и Великобритании. В США этот термин означает четырехугольник с одной парой параллельных сторон, в то время как в Великобритании трапеция не имеет параллельных сторон.
трапеций — математика для 3-го класса
Научитесь определять трапеции
Вы помните, что такое параллелограмм? 🤔
👉 Это квадрилатера л с двумя парами противоположных сторон, которые параллельны .
Есть еще один тип четырехугольника с одним набором параллельных сторон. Это называется трапеция !
Трапеция — четырехугольник с одной парой параллельных сторон.
Как мы можем определить, является ли изображение трапецией? 🤔
Мы можем проследить противоположные стороны и посмотреть, пересекаются ли они в какой-либо точке!
Давайте попробуем проверить эту цифру:
Сначала обведем верхнюю и нижнюю стороны. Эти линии противоположны.
Мы видим, что они никогда не коснутся !
У нас есть одна пара параллельных сторон.
Теперь обведем левую и правую стороны.
Вы видите, как они пересекаются в определенной точке?
Эта форма имеет только одну пару параллельных линий.
Это трапеция! ✅
Давайте посмотрим на другую фигуру:
Верхняя и нижняя линии параллельны.
Левая и правая линии параллельны.
Имеется более чем одной пары параллельных линий этой формы.
Это форма , а не трапеция. ❎
Попробуем еще одну фигуру.
Это форма трапеции?
Да! Только верх и низ параллельны. Левая и правая не параллельны друг другу!
Это форма трапеции. ✅
Что насчет этого?
Верхняя и нижняя линии параллельны. Левая и правая стороны также параллельны.
Это , а не трапеция. ❎
Отличная работа! Теперь вы знаете, как определить трапецию.
Смотри и учись
💪 Теперь можно переходить к практике!
Трапеция | Encyclopedia.com
Трапеция в плоской геометрии представляет собой четырехсторонний двумерный многоугольник с двумя параллельными сторонами (основаниями) неравной длины. Многоугольник — это любая двухмерная геометрическая фигура, образованная тремя или более прямыми сторонами. Перпендикулярное расстояние между основаниями называется его высотой (или высотой).Непараллельные стороны называются ножками. Среда — это линия от середины одной ноги до середины другой ноги. Площадь трапеции вычисляется путем умножения высоты на среднюю.
С четырьмя сторонами трапеция представляет собой четырехугольник, как квадрат, прямоугольник или параллелограмм. Однако, в отличие от этих форм, трапеция не обязательно имеет параллельные стороны. Другими словами, все прямоугольники являются трапециями, но не все трапеции являются прямоугольниками.
Трапеция — это подмножество трапеций, у которых по крайней мере две стороны параллельны; параллелограмм — один из примеров трапеции.Наиболее распространенное изображение трапеции, которую часто путают с трапецией, — это фигура с двумя параллельными гранями, одна длиннее другой. Две параллельные стороны трапеции называются базовыми линиями, а более длинная из двух называется основанием. Если две непараллельные стороны имеют одинаковую длину, трапеция называется равнобедренной трапецией (рис. 1).
Одно из важных математических применений трапеции — это математика. По сути, исчисление можно использовать для определения площади под кривой.Математики могут аппроксимировать эту область серией трапеций — одна сторона вдоль оси x, две стороны поднимаются параллельно оси y, а последняя сторона наклонена для аппроксимации наклона кривой. По мере того, как трапеция становится все более и более узкой, приближение увеличивается.
КЛЮЧЕВЫЕ ТЕРМИНЫ
Параллелограмм — четырехугольник, противоположные стороны которого параллельны.
Трапеция —Трапеция, две противоположные стороны которой параллельны.
точнее.Расчетный интеграл предполагает, что трапеция становится все более узкой, чтобы получить точную площадь под кривой.
Кристин Левотски
Q&A: Определение трапеции
Вопрос: Почему вы решили использовать эксклюзивное определение трапеции?
Ответ: Как следует из вопроса, существует более одного определения трапеции. Математики определяют трапеции одним из двух способов:
Согласно включительному определению, все параллелограммы (включая прямоугольники, квадраты и ромбы) являются трапециями.Используя исключительное определение, это не так.
При определении того, какое определение использовать, мы подумали о нескольких вещах:
- В большинстве учебников начальной школы используется исключительное определение, а в Общих основных государственных стандартах не указывается, какое определение следует использовать. На боковой панели прогрессий по геометрии указано, что большинство колледжей / университетов используют инклюзивное определение, но математические цели на этом уровне разные.
- Использование исключительного определения имеет математический смысл в начальных классах.Он поддерживает одну из основных математических целей работы с двумерной геометрией в Investigations 3 — заставить учащихся глубже задуматься о классификации двумерных фигур и о том, как изменение атрибута или свойства может изменить способ классификации формы. . Поскольку это определение определяет трапеции как отличные от параллелограммов, оно интересным образом усложняет иерархию 4-сторонних двумерных фигур — учащимся необходимо определять не только параллельные стороны, но и количество параллельных сторон.
Людей часто удивляет наличие двух конкурирующих определений. Разве математика не должна быть точной и иметь «один правильный ответ»? Это может быть интересное расследование для учеников четвертого или пятого класса, которым часто интересно узнавать о таких математических разногласиях. «Что произойдет, если мы изменим правила и воспользуемся определением трапеции, которое говорит:« , по крайней мере, одна пара параллельных сторон »? Как это изменит ваши категории и какие формы в них содержатся?
Мы рады, что у нас есть место, которое дает нам возможность отвечать на общие вопросы с мест.Есть вопросы, на которые вы хотите получить ответы? Свяжитесь с нами по электронной почте.
Главная | | Геометрия Четырехугольник | Электронная почта | Добавить комментарий |
Формула трапеции — Изучите формулу для расчета различных параметров с помощью формулы трапеции
Трапеция, также известная как трапеция, представляет собой четырехсторонний многоугольник или четырехугольник.У него есть один набор противоположных сторон, которые параллельны, и набор непараллельных сторон. Параллельные стороны известны как основания, а непараллельные стороны известны как ноги трапеции.
Существуют разные типы трапеций: равнобедренная трапеция, правая трапеция и разносторонняя трапеция.
- Трапеция с двумя непараллельными сторонами одинаковой длины называется равнобедренной трапецией.
- Правая трапеция — это трапеция, имеющая как минимум два прямых угла.
- Правая равнобедренная трапеция — это трапеция, которая одновременно является правой и равнобедренной трапециями. В евклидовой геометрии такие трапеции автоматически являются прямоугольниками.
Давайте подробнее рассмотрим формулы трапеции.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом в решении проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Забронируйте бесплатный пробный курс
Что такое формула трапеции?
Мы будем изучать следующую формулу трапеции
Формула для вычисления периметра трапеции
Периметр трапеции определяется как сумма всех ее сторон или полная граница трапеции.Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте посмотрим на формулу Трапеции
.
Периметр трапеции рассчитывается путем нахождения суммы всех сторон, то есть AB + BC + CD + DA
Периметр трапеции = Сумма всех сторон = a + b + c + d
Формула для расчета площади трапеции
Площадь определяется как площадь или область, занятая трапецией.Рассмотрим трапецию ABCD, как показано ниже.
Площадь трапеции определяется по формуле:
Площадь трапеции = (1/2) × h × (a + b)
где,
- a = более короткое основание
- b = более длинное основание
- h = Расстояние или высота между двумя основаниями
Давайте посмотрим на применение формулы трапеции в следующих решенных примерах.
Пример 1: Если периметр трапеции составляет 60 см, а три ее стороны составляют 15 см, 20 см и 16 см соответственно, найдите размер четвертой стороны с помощью формулы трапеции.
