2
Содержание
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
 Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Алгебра и начала анализа в 10-м классе «Решение тригонометрических уравнений»
Цель: закрепить навык решения
тригонометрических уравнений.
Работа учащихся состоит из нескольких этапов.
Чтобы получить оценку “3”, необходимо пройти 4
этапа, чтобы получить оценку “4” — 5 этапов, чтобы
получить оценку “5” — 6 этапов. На каждом этапе
ученик встретится с указаниями учителя о том, что
нужно знать и уметь, или краткими пояснениями к
выполнению заданий.
Прочитав указания учителя, ученик выполняет
самостоятельные работы данного этапа, проверяет
ответы, сверяя с ответами, которые предоставляет
учитель. Если допущены ошибки, то ученик их
Если допущены ошибки, то ученик их
исправляет и решает задания другого варианта,
аналогичные тем, где он допустил ошибки. После
этого можно переходить к следующему этапу.
1 этап.
Цель: закрепить решение простейших
тригонометрических уравнений.
Указания учителя.
Вспомните основные правила решения
тригонометрических уравнений.
(учебник А.Н.Колмогорова и др. с. 69 – 73)
Выполните письменно самостоятельную
работу (10 минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) cos x = 1/2 | 1) sin x = -1/2 |
| 2) sin x = -/2 | 2) cos x = /2 |
| 3) tg x = 1 | 3) ctg x = -1 |
| 4) cos (x+)
= 0 | 4) sin (x – /3) = 0 |
| 5) 2 cos x = 1 | 5) 4 sin x = 2 |
| 6) 3 tg x = 0 | 6) 5 tg x = 0 |
| 7) sin 4x = 1 | 7) cos 4x = 0 |
2 этап.

Цель: закрепить умения решать
тригонометрические уравнения методом сведения к
квадратному.
Указания учителя.
Метод сведения к квадратному состоит в том, что,
пользуясь изученными формулами, надо
преобразовать уравнение к такому виду, чтобы
какую-то функцию (например, sin x или cos x) или
комбинацию функций обозначить через y, получив
при этом квадратное уравнение относительно y.
Пример. 4 – cos2 x = 4 sin x
Так как cos2 x = 1 – sin2 x, то
4 – (1 – sin2 x) = 4 sin x,
3 + sin2 x = 4 sin x,
sin2 x — 4 sin x + 3 = 0,
Пусть y = sin x, получим уравнение
y 2 — 4 y +3 = 0
у1=1; у2=3.
sin x =1 или sin x = 3,
x = /2 + 2 n, n= Z, решений нет.
Ответ: x = /2 + 2 n, n= Z.
Выполните письменно самостоятельную работу (10
минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) tg2 x — 3 tg x + 2 = 0; | 1) 2 + cos2 x — 3 cos x = 0; |
| 2) 2 cos2 x + 5 sin x – 4 = 0; | 2) 4 — 5 cos x — 2 sin2 x =0; |
| 3) (1 — cos 2x)/2 + 2 sin x = 3; | 3) (1 — cos 2x)/2 + 2 sin x = 3. |
3 этап.
Цель: закрепить навык решения
тригонометрических уравнений методом
разложения на множители.
Указания учителя.
Под разложением на множители понимается
представление данного выражения в виде
произведения нескольких множителей. Если в одной
части уравнения стоит несколько множителей, а в
другой – 0, то каждый множитель приравнивается к
нулю. Таким образом, данный множитель можно
представить в виде совокупности более простых
уравнений.
Пример. 2 sin3 x — cos 2x — sin x = 0
Сгруппируем первый член с третьим, а cos 2x = cos2
x — sin2 x.
(2sin3 x — sin x) – (cos2 x — sin x) = 0,
Вынесем из выражения, стоящего в первой скобке
sin x, а cos2 x = 1 — sin x.
sin x (2sin2 x – 1) – (1 — 2 sin2 x) = 0,
sin x (2sin2 x – 1) + (2 sin2 x — 1) = 0,
(2 sin2 x — 1) • ( sin x + 1) = 0.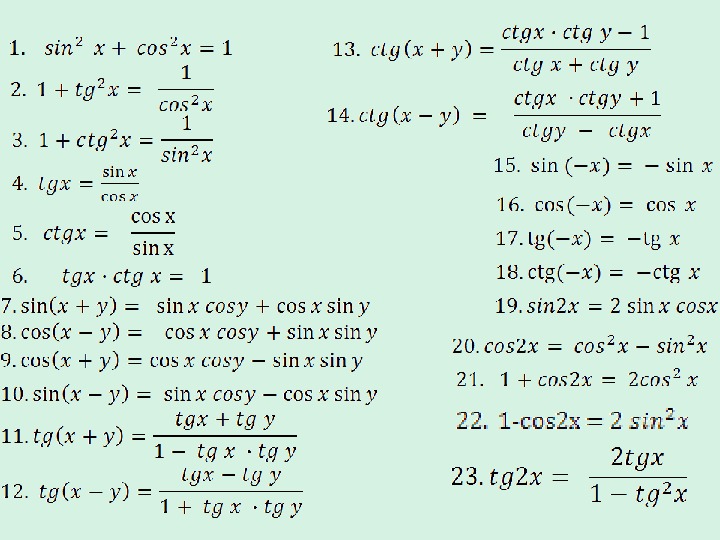
| 2 sin2 x – 1 = 0 | или | sin x + 1 = 0 |
| sin2 x = 1/2, | sin x = — 1 | |
| sin x = ±1/v2 |
Ответ: x1 = ± /4 + n, n = Z, x2 = — /2 +2k, k = Z.
Выполните письменно самостоятельную работу (10
минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) sin2 x — sin x = 0, | 1) ctg2 x — 4 ctg x = 0, |
| 2) 3 cos x + 2 sin 2x = 0, | 2) 5 sin 2x — 2 sin x = 0.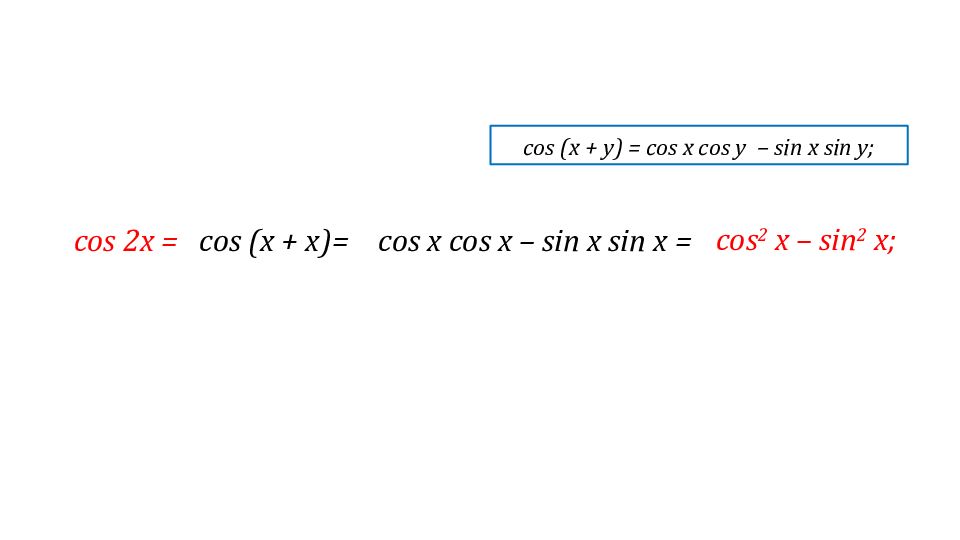 |
4 этап.
Цель: закрепить навык решения однородных
уравнений
Указания учителя.
Однородными называются уравнения вида a sin x + b cos
x = 0,
a sin2 x + b sin x cos x + c cos2 x = 0, и т.д., где a, b,
c – числа.
Пример 1. 5 sin x — 2 cos x = 0
Поделим обе части уравнения cos x (или на sin x).
Предварительно докажем,
что cos x 0 (или
sin x 0). (Пусть cos
x = 0, тогда 5 sin x — 2 • 0 = 0, т.е. sin x = 0; но этого не может
быть, так как sin2 x + cos2 x = 1).
Значит, можно делить на cos x:
5 sin x /cos x — 2 cos x / cos x = 0 / cos x. Получим уравнение
5 tg x – 2 = 0
tg x = 2/5,
x = arctg 2/5 + n, n =
Z.
Ответ: x = arctg 2/5 + n, n = Z.
Аналогично решаются однородные уравнения вида
a sin2 x + b sin x cos x + c cos2 x = 0, их решение
начинается с того, что обе части уравнения
делятся на cos2 x (или на sin2 x).
Пример 2. 12 sin2 x + 3 sin 2x — 2 cos2 x = 2.
Данное уравнение не является однородным, но его
можно преобразовать в однородное, заменив 3 sin 2x
на 6 sin x cos x и число 2 на 2sin2 x + 2cos2 x.
Приведя подобные члены, получим уравнение
10sin2 x + 6sin x cos x — 4 cos2 x = 0.
(Пусть cos x = 0, тогда 10sin2 x = 0, чего не может
быть, т.к. sin2 x + cos2 x = 1, значит, cos x 0).
Разделим обе части уравнения на cos2 x.
10 tg2 x +6 tg x — 4 = 0,
tg x = -1 или tg x = 2/5,
x = — /4 + n, n = Z, x = arctg 2/5 + k, k = Z.
Ответ: x1 = — /4 + n, n =
Z, x2 = arctg 2/5 + k, k = Z.
Выполните письменно самостоятельную работу (10
минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) sin x — cos x = 0, | 1) 5sin x +6cos x = 0, |
| 2) sin2 x — sin 2x = 3 cos2 x, | 2) 3sin2 x — 2sin 2x +5cos2 x = 2. |
5 этап.
Указания учителя.
Вы прошли 4 этапа, теперь вам самостоятельно
придется выбрать метод решения уравнений.
Вспомните основные тригонометрические формулы.
(Учебник А.Н.Колмогорова и др. с. 7 — 9)
Выполните письменно самостоятельную работу (20
минут)
Решите уравнения:
6 этап.
Указания учителя.
Молодцы! Вы прошли 5 этапов. Целью вашей
дальнейшей работы является применение своих
знаний и умений в более сложных ситуациях.
Выполните письменно самостоятельную работу
(Задания даются в одном варианте, т.к. их решают
не все учащиеся. Время, отводимое на эту работу,
определяется учителем (ситуацией на уроке)).
Решите уравнения:
- sin 6x + cos 6x = 1 — sin 3x,
- 29 — 36 sin2 (x – 2) — 36 cos (x – 2) = 0,
- 2sin x cos x + – 2 cos
x — v3 sin x = 0, - sin 4x = 2 cos2 x – 1,
- sin x (sin x + cos x ) = 1,
- 1/(1 + cos2 x) + 1/(1 + sin2 x) =16/11.

Подсказки:
- Воспользуйтесь формулой двойного угла для sin 6x,
cos 6x. - Обозначьте x – 2 = y, решите уравнение, сведя его к
квадратному с помощью формулы sin2 y = 1 — cos2
y. - Сгруппируйте первое и третье слагаемое,
примените разложение на множители. - Воспользуйтесь формулой двойного угла для sin 4x,
cos 4x, формулой понижения степени 2cos2 x – 1 = cos
2x. - Раскройте скобки, примените основное
тригонометрическое тождество. - Приведите дроби к общему знаменателю, затем
используйте основное тригонометрическое
тождество sin2 x + cos2 x = 1, сведите
уравнение к квадратному.
Оцените свои работы самостоятельно.
Домашнее задание:
Если вы выполнили задания всех этапов, то дома
№ 163-165 – любое уравнение (учебник А.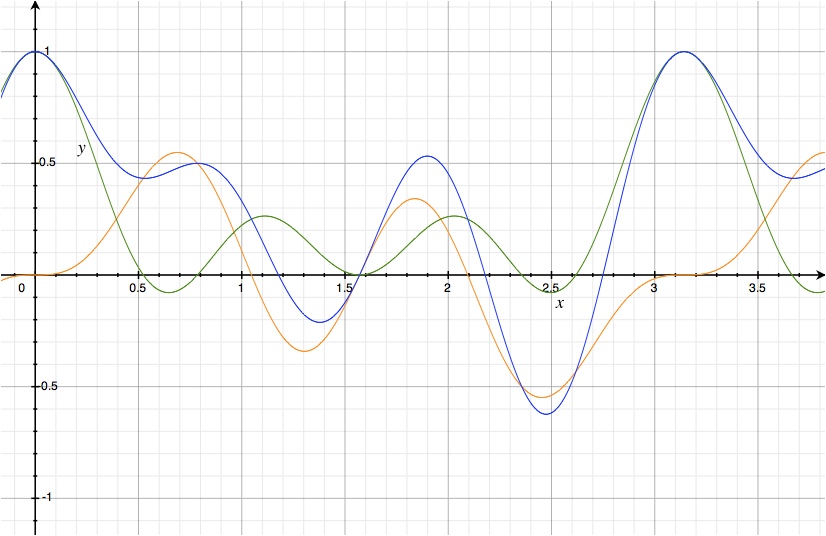 Н.Колмогорова
Н.Колмогорова
и др. с. 333)
Если вы выполнили задания 5 этапов, то дома
задания 6 этапа.
Если вы выполнили задания 4 этапов, то дома
задания 5 этапа, и т.д.
Все формулы по тригонометрии
Все
формулы по тригонометрии
Основные
тригонометрические тождества
sin2x +
cos2x =
1
tgx ctgx =
1
tg2x + | = | 1 |
cos2x |
ctg2x + | = | 1 |
sin2x |
Формулы
двойного аргумента
sin2x =
2sinx cosx
sin2x | = | 2tgx | = | 2ctgx | = | 2 |
1 | 1 | tgx + |
cos2x =
cos2 —
sin2x =
2cos2x —
1 = 1 — 2sin2x
cos2x | = | 1 | = | ctg2x — | = | ctgx — |
1 | ctg2x + | ctgx + |
tg2x | = | 2tgx | = | 2ctgx | = | 2 |
1 | ctg2x — | ctgx — |
ctg2x | = | ctg2x — | = | ctgx — |
2ctgx | 2 |
Формулы
тройного аргумента
sin3x =
3sinx —
4sin3x
cos3x =
4cos3x —
3cosx
tg3x | = | 3tgx — |
1 |
ctg3x | = | ctg3x — |
3ctg2x — |
Формулы
половинного аргумента
sin2 | x | = | 1 |
2 | 2 |
cos2 | x | = | 1 |
2 | 2 |
tg2 | x | = | 1 |
2 | 1 |
ctg2 | x | = | 1 |
2 | 1 |
tg | x | = | 1 | = | sinx |
2 | sinx | 1 |
ctg | x | = | 1 | = | sinx |
2 | sinx | 1 |
Формулы
квадратов тригонометрических функций
sin2x | = | 1 |
2 |
cos2x | = | 1 |
2 |
tg2x | = | 1 |
1 |
ctg2x | = | 1 |
1 |
sin2 | x | = | 1 |
2 | 2 |
cos2 | x | = | 1 |
2 | 2 |
tg2 | x | = | 1 |
2 | 1 |
ctg2 | x | = | 1 |
2 | 1 |
Формулы
кубов тригонометрических функций
sin3x | = | 3sinx — |
4 |
cos3x | = | 3cosx + |
4 |
tg3x | = | 3sinx — |
3cosx + |
ctg3x | = | 3cosx + |
3sinx — |
Формулы
тригонометрических функций в четвертой
степени
sin4x | = | 3 |
8 |
cos4x | = | 3 |
8 |
Формулы
сложения аргументов
sin(α
+ β) = sinα cosβ + cosα sinβ
cos(α
+ β) = cosα cosβ — sinα sinβ
tg(α | = | tgα |
1 |
ctg(α | = | ctgα |
ctgα |
sin(α
— β) = sinα cosβ — cosα sinβ
cos(α
— β) = cosα cosβ + sinα sinβ
tg(α | = | tgα |
1 |
ctg(α | = | ctgα |
ctgα |
Формулы
суммы тригонометрических функций
sinα | = 2sin | α | ∙ cos | α |
2 | 2 |
cosα | = 2cos | α | ∙ cos | α |
2 | 2 |
(sinα
+ cosα)2 =
1 + sin2α
tgα | = | sin(α |
cosα |
ctgα | = | sin(α |
sinα |
Формулы
разности тригонометрических функций
sinα | = 2sin | α | ∙ cos | α |
2 | 2 |
cosα | = -2sin | α | ∙ sin | α |
2 | 2 |
(sinα
— cosα)2 =
1 — sin2α
tgα | = | sin(α |
cosα |
ctgα | = – | sin(α |
sinα |
Формулы
произведения тригонометрических функций
sinα | = | cos(α |
2 |
sinα | = | sin(α |
2 |
cosα | = | cos(α |
2 |
tgα | = | cos(α | = | tgα |
cos(α | ctgα |
ctgα | = | cos(α | = | ctgα |
cos(α | tgα |
tgα | = | sin(α |
sin(α |
тригонометрических идентичностей | Purplemath
Purplemath
В математике «тождество» — это всегда истинное уравнение. Они могут быть «тривиально» истинными, например « x = x », или практически истинными, например, « a 2 + b 2 = c 2 » теоремы Пифагора прямоугольные треугольники.Существует множество тригонометрических отождествлений, но следующие из них вы, скорее всего, увидите и будете использовать.
Они могут быть «тривиально» истинными, например « x = x », или практически истинными, например, « a 2 + b 2 = c 2 » теоремы Пифагора прямоугольные треугольники.Существует множество тригонометрических отождествлений, но следующие из них вы, скорее всего, увидите и будете использовать.
Базовый и пифагорейский, сумма углов и разность, двойной угол, полуугол, сумма, произведение
MathHelp.com
Нужен индивидуальный курс математики?
K12 | Колледж | Подготовка к тесту
Основные и пифагорейские тождества
Обратите внимание на то, что триггерный коэффициент «со- (чего-то)» всегда является обратной величиной некоторого «несовместимого» отношения.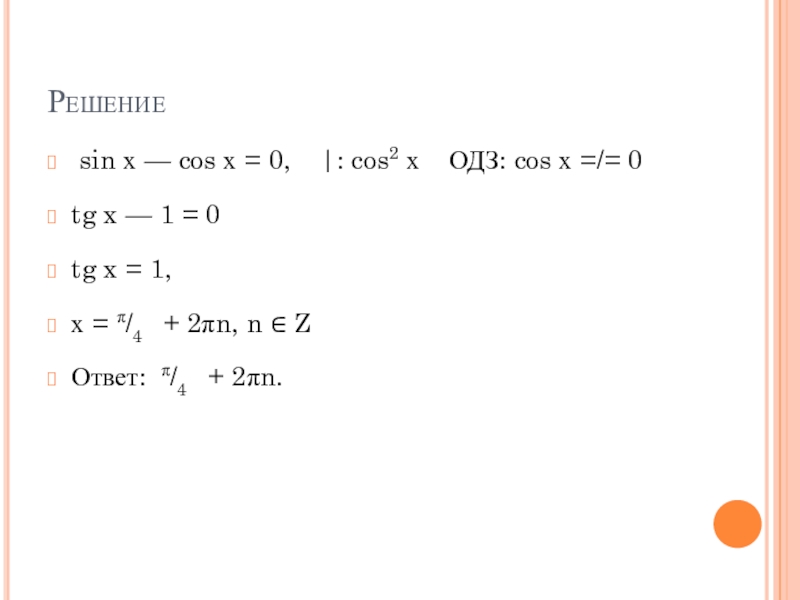 Вы можете использовать этот факт, чтобы понять, что косеканс идет с синусом, а секанс — с косинусом.
Вы можете использовать этот факт, чтобы понять, что косеканс идет с синусом, а секанс — с косинусом.
Следующие (в частности, первая из трех ниже) называются «пифагорейскими» идентичностями.
sin 2 ( т ) + cos 2 ( т ) = 1
загар 2 ( т ) + 1 = сек 2 ( т )
1 + детская кроватка 2 ( т ) = csc 2 ( т )
Обратите внимание, что все три тождества включают в себя возведение в квадрат и число 1.Вы можете ясно увидеть взаимосвязь Пифагора и Терема, если вы рассмотрите единичную окружность, где угол составляет t , «противоположная» сторона — sin ( t ) = y , «смежная» сторона — cos ( t ) = x , а гипотенуза равна 1.
У нас есть дополнительные идентификаторы, связанные с функциональным статусом триггерных соотношений:
sin ( –t ) = — sin ( t )
cos ( –t ) = cos ( t )
тангенса ( –t ) = — тангенса ( т )
Обратите внимание, в частности, что синус и тангенс являются нечетными функциями, симметричными относительно начала координат, а косинус — четной функцией, симметричной относительно оси y .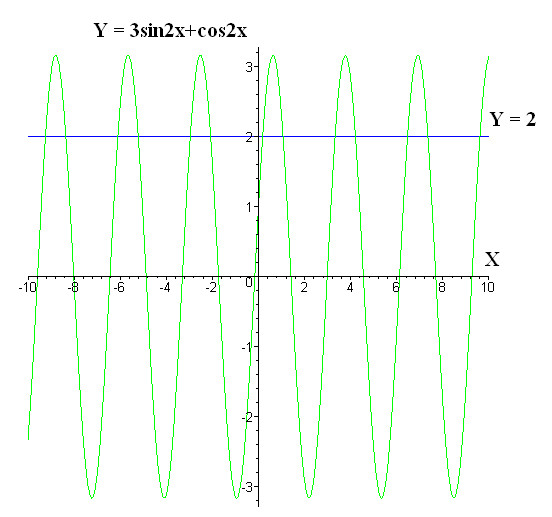 Тот факт, что вы можете вынести знак «минус» аргумента за пределы (для синуса и тангенса) или полностью исключить его (для косинуса), может быть полезным при работе со сложными выражениями.
Тот факт, что вы можете вынести знак «минус» аргумента за пределы (для синуса и тангенса) или полностью исключить его (для косинуса), может быть полезным при работе со сложными выражениями.
Тождества суммы углов и разности
sin (α + β) = sin (α) cos (β) + cos (α) sin (β)
sin (α — β) = sin (α) cos (β) — cos (α) sin (β)
cos (α + β) = cos (α) cos (β) — sin (α) sin (β)
cos (α — β) = cos (α) cos (β) + sin (α) sin (β)
Кстати, в указанных выше тождествах углы обозначаются греческими буквами.Буква типа «а», «а», называется «альфа», что произносится как «аль-фу». Буква b-типа, «β», называется «бета», что произносится как «BAY-tuh».
Двойные углы идентификации
sin (2 x ) = 2 sin ( x ) cos ( x )
cos (2 x ) = cos 2 ( x ) — sin 2 ( x ) = 1-2 sin 2 ( x ) = 2 cos 2 ( x ) — 1
Полуугловые идентичности
Вышеупомянутые идентичности могут быть переформулированы путем возведения квадратов каждой стороны и удвоения всех угловых мер.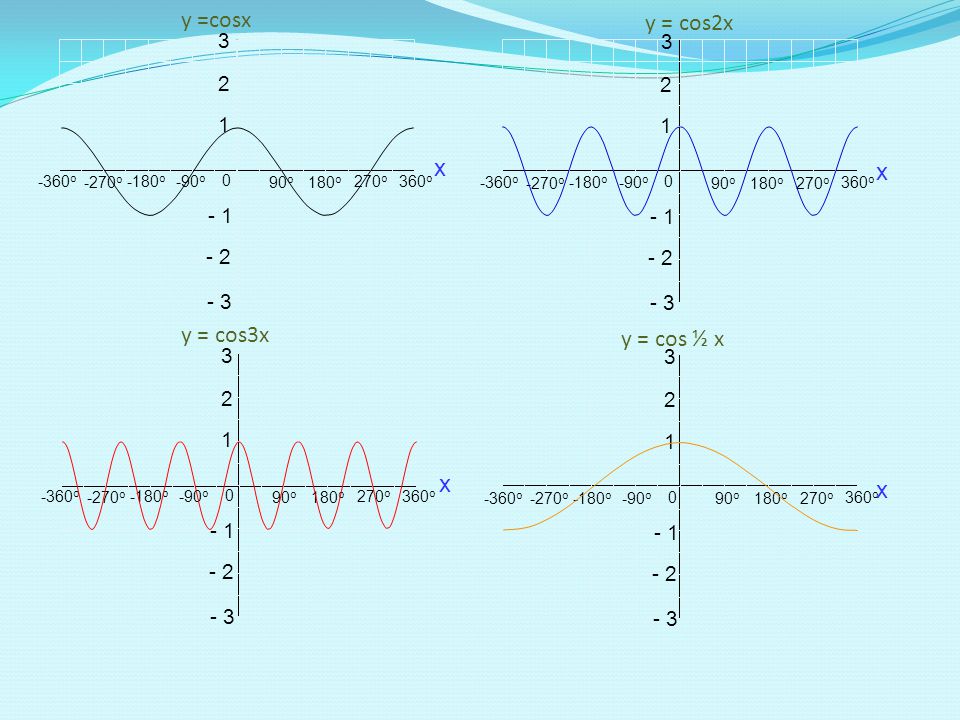 Результаты следующие:
Результаты следующие:
sin 2 ( x ) = ½ [1 — cos (2 x )]
cos 2 ( x ) = ½ [1 + cos (2 x )]
Партнер
Сумма идентификаторов
Обозначения продукта
Вы будете использовать все эти тождества или почти все эти тождества для доказательства других триггерных тождеств и для решения тригонометрических уравнений.2 (y) $? — Обмен стеками математики
Сеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
- Авторизоваться
Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
4к раз
$ \ begingroup $
Для 4. 2 (x)) = \? $
2 (x)) = \? $
Создан 20 дек.
ронноронно
6,1122020 серебряных знаков4848 бронзовых знаков
$ \ endgroup $
3
$ \ begingroup $
На первый вопрос отвечает ronno.Что касается вашего второго вопроса, вы можете увидеть, что это правда, просто упростив правую часть каждого уравнения.
Создан 20 дек.
математика
1,955 11 золотой знак 9999 серебряных знаков254254 бронзовых знака
$ \ endgroup $
$ \ begingroup $
Если кто-то принимает эти три личности:
$$
\ грех ^ 2 \ тета + \ соз ^ 2 \ тета = 1
$$
$$
\ грех (х + у) = \ грех х \ соз у + \ соз х \ грех у
$$
$$
\ соз (х + у) = \ соз х \ соз у — \ грех х \ грех у
$$
Затем следует большой класс других личностей, включая те, что указаны в вашем вопросе.
Теперь, почему человек должен принять три вышеупомянутых личности? Я не знаю их исторических доказательств, хотя первое обычно приписывают пифагору. Способ доказательства этих тождеств зависит от того, как $ \ textbf {определяет} $ концепции $ \ sin $ и $ \ cos $.
Я предпочитаю определение бесконечных рядов, а методы, которые я бы использовал для доказательства этих тождеств, основаны на идеях анализа (включая исчисление) и использовании комплексных чисел.Это определенно не тот способ, которым эти идентичности были исторически доказаны, но я считаю, что это более фундаментальный способ их понимания.
Создан 20 дек.
R RR R
1,9449 серебряных знаков1515 бронзовых знаков
$ \ endgroup $
1
Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками тригонометрия или задайте свой вопрос.
 2x) dy = 0 $
2x) dy = 0 $
Я помогал кому-то над некоторыми математическими задачами, когда возник дикий вопрос.2x) dy = 0 $$
Моя работа
Мне удалось поискать в Интернете, как найти решение дифференциального уравнения, показанного выше, но я не понимаю, как это сделать.
Возможно, мы могли бы переписать приведенное выше дифференциальное уравнение в форму
$$ M (x, y) dx + N (x, y) dy = 0 $$
С помощью приведенной выше формы мы могли бы увидеть, является ли данное дифференциальное уравнение разделяемым по переменным, однородным или точным типом.
Проверка данного дифференциального уравнения как разделимого на переменную:
№нФ (х, у) $$
Сами члены должны быть однородными, если дифференциальные уравнения однородны.
Нет. Мы не можем. Приведенное выше дифференциальное уравнение неоднородно.
Проверка данного дифференциального уравнения, если оно точного типа:
Необходимым условием точности дифференциального уравнения является
$$ \ frac {\ partial M} {\ partial y} = \ frac {\ partial N} {\ partial x} $$
Итак, получаем выражение для $ \ frac {\ partial M} {\ partial y} $:
$$ \ frac {\ partial M} {\ partial y} = \ frac {\ partial} {\ partial y} (\ cos y \ sin2x) $$
$$ \ frac {\ partial M} {\ partial y} = \ sin 2x \ frac {\ partial} {\ partial y} (\ cos y) $$
$$ \ frac {\ partial M} {\ partial y} = \ sin 2x (- \ sin y) $$
$$ \ frac {\ partial M} {\ partial y} = — \ sin y \ sin 2x $$
Итак, получаем выражение для $ \ frac {\ partial N} {\ partial x} $:
$$ \ frac {\ partial N} {\ partial x} = \ frac {\ partial} {\ partial x} (\ cos ^ 2y — \ cos ^ 2x) $$
$$ \ frac {\ partial N} {\ partial x} = 0 — \ frac {\ partial} {\ partial x} (\ cos ^ 2x) $$
$$ \ frac {\ partial N} {\ partial x} = 0 — \ frac {\ partial} {\ partial x} \ left (\ frac {1} {2} + \ frac {1} {2} \ cos 2x \ вправо) $$
$$ \ frac {\ partial N} {\ partial x} = \ sin 2x $$
Мы видим, что $ \ frac {\ partial M} {\ partial y} \ neq \ frac {\ partial N} {\ partial x} $, поэтому данное дифференциальное уравнение также не является точным . 2
2
Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке.
Помните, что значение производной в данной точке равно наклону касательной в этой точке. Помните также, что неявное дифференцирование означает, что вы берете производную всего этого, помните, что y является функцией x, поэтому вы должны использовать правило цепочки всякий раз, когда вы дифференцируете y. Итак, поехали.
d / dx [ysin (2x)] = d / dx [xcos (2y)] Нам понадобится Правило произведения с обеих сторон.
y · cos (2x) · 2 + y ‘· sin (2x) = x (-sin (2y) · 2y’) + 1 · cos (2y)
Небольшая очистка дает нам 2y · cos (2x) + y ‘· sin (2x) = -2xy’ · sin (2y) + cos (2y) Теперь мы необходимо, чтобы члены y ‘находились на одной стороне, а другие члены — на другой стороне: y’ · sin (2x) + 2xy ‘· sin (2y) = cos (2y) — 2y · cos (2x) Выносим за множитель y ‘: y’ [sin (2x) + 2xsin (2y)] = cos (2y) — 2ycos (2x) y ‘= [cos (2y) — 2ycos (2x)] / [sin (2x) + 2xsin (2y)] Оцените это на (π / 2, π / 4) (cos (π / 2) — (π / 2) cos (π)) / (sinπ + πsin (π / 2)) = (0 — (π / 2) (- 1)) / (0 + π (1)) = (π / 2) / π = 1/2 Таким образом, наклон касательной линии равен 1/2 Используйте точечный наклон форма уравнения прямой: yy 1 = m (xx 1 ) y — π / 4 = 1/2 (x — π / 2) y = 1 / 2x — π / 4 + π / 4 Итак, y = 1/2 x — уравнение касательной в точке (π / 2, π / 4)График квадрата синуса (x)
График квадрата синуса (x) | математикатестподготовка. ком
ком
назад к вопрос и ответ по математике
- Шаг 1. Найдите выражение sin 2 x
- Использование формул двойного угла: cos 2x = cos 2 x — sin 2 x, обозначьте его как уравнение (1)
- Использование тождеств Пифагора: sin 2 x + cos 2 x = 1
- Подставляем cos 2 x = 1 — sin 2 x в уравнение (1), затем
- cos 2x = 1 — sin 2 x — sin 2 x
- cos 2x = 1-2sin 2 x.
- Выразите sin 2 x в левой части уравнения, тогда
- 2sin 2 x = 1 — cos 2x, разделите коэффициент 2 в каждом пункте уравнения
- sin 2 x = 1/2 — (1/2) cos 2x
- , таким образом, получаем выражение sin 2 x
- Шаг 2: Постройте график y = (1/2) cos 2x
- Примечание: для функции периода y = A cos (Bx + C) ее амплитуда равна A.
 период T = 2 pi / B и фазовый сдвиг C.
период T = 2 pi / B и фазовый сдвиг C. - В данном случае его амплитуда A = 1/2, период T = 2 pi / 2 = pi и фазовый сдвиг C = 0
- Шаг 3. Постройте график y = — (1/2) cos 2x
- Отразите график y = (1/2) cos2x по оси x, чтобы получить график y = — (1/2) cos2x
- Шаг 4: Нарисуйте два графика, например y 1 = 1/2 и y 2 = — (1/2) cos2x, чтобы сложить их.
- Когда x = 0, y = 1/2 + (-1/2) cos2x = 1/2 + (- 1/2) = 0
- Когда x = pi / 4, y = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = pi / 2, y = 1/2 + (-1/2) cos2x = 1/2 + 1/2 = 1
- Когда x = 3pi / 4, y = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = pi, y = 1/2 + (-1/2) cos2x = 1/2 + (- 1/2) = 0
- Когда x = 5pi / 4, y = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = 3pi / 2, y = 1/2 + (-1/2) cos2x = 1/2 + 1/2 = 1
- Когда x = 7pi / 4.
 у = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
у = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2 - Когда x = 2pi, y = 1/2 + (-1/2) cos2x = 1/2 + (- 1/2) = 0
- Следовательно, график y = 1/2 + [- (1/2) cos 2x] выглядит следующим образом:
- Сводка:
- График y = sin 2 x является суммой графика y = 1/2 и графика y = (-1/2) cos2x
- Сумма графика y = 1/2 и графика y = (-1/2) cos2x является графиком y = (-1/2) cos2x, перемещающимся на 1/2 единицы.
.
