| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
1 tg в квадрате
Вы искали 1 tg в квадрате? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 tg это, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 tg в квадрате».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 tg в квадрате,1 tg это,1 tgx,1 косинус 2 альфа,2 cos чему равен,2 косинус,2 синус в квадрате х,2 синус в квадрате х синус х,2 синус косинус,cos 2 y,cos 2 чему равен,cos 2x в квадрате,cos sin чему равно,cos x 2,cos x sin y,cos x в квадрате,cos x квадрат,cos y,cos y 2,cos y sin y,cos в квадрате,cos в квадрате 2x,cos делить на sin,cos квадрат x cos x,cos на sin,cos на sin делить,cos умножить sin,cos умножить на sin,cos х п,cos через sin,cos2x,cosx sinx это,cosx tgx sinx,l sin,sin 2 t,sin cos умножить,sin sinx,sin t 2,sin x cos x tg x,sin x cos y sin y cos x,sin x sin y,sin x sinx,sin x в квадрате,sin в квадрате x,sin делить на cos,sin квадрат x,sin на cos делить,sin на cos умножить,sin умножить cos,sin умножить на cos,sin через cos,sin2t,sinx cosx tgx,sinx siny,sinx siny формула,tg x 2,tg x в квадрате,tg3x,tgx cosx,tgx ctgx равно,y sin x cos 2 x,косинус 2 икс,косинус 2 х синус х,косинус двух икс,косинус п 2 х,син х син у,синус 2 икс,синус 2 х в квадрате,синус 2х,синус в квадрате 2 х,синус в квадрате х 2,синус двух икс,синус х,синус х 2,синус х у,формула cosx cosy,формулы sinx a,чему равен cos 2,чему равно cosx sinx. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 tg в квадрате. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 tgx).
Где можно решить любую задачу по математике, а так же 1 tg в квадрате Онлайн?
Решить задачу 1 tg в квадрате вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Периодичность функций y=sinx, y=cosx
Вопросы
занятия:
·
познакомиться
с понятием периодичности;
·
познакомиться
с понятием основного периода;
·
узнать
основные периоды функций y=sin x, y=cos x.
Материал
урока.
Прежде чем приступить к изучению нового
материала, давайте повторим основные свойства функций y = sin x, y = cos
x.
Давайте с вами посмотрим на рисунки.
Что мы там видим? Правильно, одно и тоже
дерево, но в разные поры года. А на этом рисунке мы видим рушник с
геометрическим орнаментом, а здесь – бьющееся сердце. А еще у нас есть приливы
и отливы. Что объединяет все эти рисунки? А объединяет их то, что в каждом из
приведенных примером есть повторяющиеся элементы. Так, когда мы смотрим на
дерево в разные поры года, то мы знаем, что каждая пора повторяется через
девять месяцев. Орнамент состоит из повторяющихся элементов. А биение сердца
можно описать как повторяющиеся, через определённое время ритмы, сокращения
сердечной мышцы. Приливы и отливы также возникают через одинаковое время.
Все эти примеры являются наглядными
примерами периодичности.
Определение.
Периодичность
– это повторяемость (цикличность) явления через определённые промежутки
времени.
А теперь давайте вспомним, как мы вводили
понятие синуса и косинуса. Эти понятия мы вводили, используя числовую
окружность. Мы говорили, что на числовой окружности можно отложить бесконечно
точек. Нами было доказано следующее утверждение.
Какую же функцию мы будем называть
периодической?
Определение.
Функцию y = f(x), где x
принадлежит множеству X
называют периодической, если существует такое отличное от нуля число T,
что для любого x из множества X
выполняется двойное равенство:
f(x—T)
= f(x)
= f(x+t)
Число T,
удовлетворяющее указанному условию, называют периодом функции y
= f(x).
Мы знаем, что для любого x
справедливы равенства:
Значит, мы можем сказать, что функции y=sin
x, y=cos x – периодические функции, с периодом 2π.
Давайте теперь посмотрим на графики наших
функций.
Легко заметить, что для того, чтобы
построить график функции, достаточно построить одну волну синусоиды и затем
сдвинуть эту волну по оси Ox на 2π влево и на 2π
вправо, на 4π и на 4π вправо и так далее. Получается,
что, построив одну волну, мы легко построим и весь график. Аналогично и для
графика функции y = cos x.
Обобщая, можно сделать следующие выводы.
Рассмотрим пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Заметим, что свойством периодичности
обладают все тригонометрические функции.
Рассмотрим ещё один пример.
Пример.
Тригонометрические уравнения с засадой.
 Задание С1
Задание С1
В этой статье мы разберем две задачи из Задания С1 для подготовки к ЕГЭ по математике.
Я хочу рассказать вам о двух своих ошибках, которые я сделала при решении несложных тригонометрических уравнений. Ошибки весьма поучительны.
Первое задание:
а) Решите уравнение:
б) Найдите все корни на промежутке []
При решении уравнения я попыталась представить тангенс суммы двух углов по формуле
То есть у меня получилось:
И — внимание! — я потеряла корень. Смотрите внимательно: после этого преобразования я получила отдельно стоящий . Но не определен при . А в исходном уравнении вполне мог быть равен .
То есть выполняя это невинное преобразование, я сузила ОДЗ. Но узнала я об этом, только когда посмотрела ответ. Но на ЕГЭ ответов нет, поэтому выполняя преобразование нужно следить за тем, что происходит с областью допустимых значений.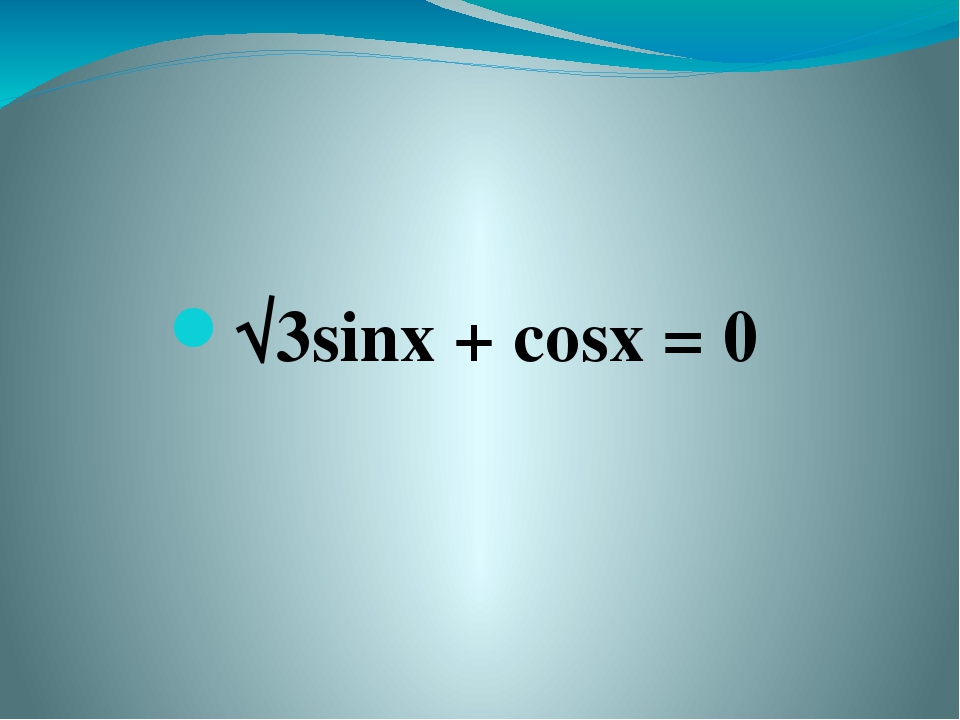
Итак, мы идем другим путем.
Запишем и через и :
Используем формулы синуса и косинуса суммы:
Разделим числитель и знаменатель дроби в левой части уравнения на :
Приведем левую часть уравнения к общему знаменателю:
Перенесем все влево:
Вынесем за скобку общий множитель:
Приведем выражение в скобках к общему знаменателю:
Знаменатель дроби не равен нулю, то есть
и
Произведение двух множителей равно нулю, если хотя бы один из них равен нулю:
или
1.
— вот он, потерянный корень!
2.
Раскроем скобки, приведем подобные члены:
Итак, мы получили два решения:
б) Найдем корни, принадлежащие промежутку []:
На рисунке красными точками обозначены решения уравнения;
синей дугой обозначен промежуток, которому принадлежат корни;
угловая величина сиреневой дуги равна .
Двигаясь из точки , мы встречаем на пути , , — это и есть корни уравнения, принадлежащие промежутку []. Мы видим, что корень не принадлежит заданному промежутку.
Ответ: а) ;
б) , ,
И второе задание:
а) Решите уравнение:
б) Найдите корни уравнения, принадлежащие промежутку
[]
Засада в этом уравнении такая: когда мы ищем ОДЗ, то записываем
и . Будет ошибкой записать ОДЗ: ,
Нельзя забывать, что не определен при , то есть в конечном итоге мы получаем такую ОДЗ: :
Собственно, больше никаких сложностей в этом уравнении нет.
Умножим обе части на :
Отсюда
или
И вот в этом месте важно не пропустить, что корень уравнения — посторонний корень, так как не входит в ОДЗ исходного уравнения!
Но у нас еще есть корни уравнения :
или
Осталось выбрать корни, принадлежащие промежутку []
На рисунке красными точками на зеленой окружности обозначены решения уравнения;
красной дугой обозначен промежуток, которому принадлежат корни;
угловая величина сиреневой дуги равна .
Двигаясь из точки , мы встречаем на пути — это и есть корень уравнения, принадлежащий промежутку .
Ответ: а) или
б)
И.В. Фельдман, репетитор по математике.
Таблица косинусов (полная, градусы и значения)
В данной таблице представлены значения косинусов от 0° до 360°. Таблица косинусов нужна, чтобы узнать, чему равен косинус угла. Нужно только найти его в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-kosinusov — uchim.org
Таблица косинусов для 0°-180°
|
|
|
Таблица косинусов для 181°-360°
|
|
|
Как легко запомнить таблицу косинусов (видео)
Существуют также следующие таблицы тригонометрических функций: таблица синусов, таблица тангенсов и таблица котангенсов.
Всё для учебы » Математика в школе » Таблица косинусов (полная, градусы и значения)
Косинус
Примеры:
\(\cos{30^°}=\)\(\frac{\sqrt{3}}{2}\)
\(\cos\)\(\frac{π}{3}\)\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Содержание:
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: \(\frac{π}{2}\), \(\frac{3π}{4}\), \(-2π\).
Например, для числа \(\frac{π}{6}\) — косинус будет равен \(\frac{\sqrt{3}}{2}\). А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область).
Пример. Определите знак \(\cos 1\).2x}\)
— котангенсом и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sinx}\)
Другие наиболее часто применяемые формулы смотри здесь.
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: \(D(\cos{x} )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x} )=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)\(+2πn;\) \(\frac{π}{2}\)\(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\)\(+2πn;\)\(\frac{3π}{2}\)\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения \(\cosx=a\)
Скачать статью
2 (х)
Доказательства производных триггерных функций
Доказательство sin (x) : алгебраический метод
Дано : lim (d-> 0) sin (d) / d = 1.
Решить :
грех (х)
= lim (d-> 0) (sin (x + d) — sin (x)) / d
= lim (sin (x) cos (d) + cos (x) sin (d) — sin (x)) / d
= lim (sin (x) cos (d) — sin (x)) / d + lim cos (x) sin (d) / d
.
= sin (x) lim (cos (d) — 1) / d + cos (x) lim sin (d) / d
= sin (x) lim ((cos (d) -1) (cos (d) +1)) / (d (cos (d) +1))
+ Cos (x) lim sin (d) / d
= sin (x) lim (cos ^ 2 (d) -1) / (d (cos (d) +1)
+ Cos (x) lim sin (d) / d
= sin (x) lim -sin ^ 2 (d) / (d (cos (d) + 1)).
+ Cos (x) lim sin (d) / d
= sin (x) lim (-sin (d)) * lim sin (d) / d * lim 1 / (cos (d) +1)
+ Cos (x) lim sin (d) / d
= sin (x) * 0 * 1 * 1/2 + cos (x) * 1 = cos (x)
В.E.D.
Доказательство cos (x) : от производной синуса
Это может быть получено точно так же, как sin (x) было получено или более просто из результата sin (x)
Дано :
грех (х) = соз (х); Правило цепи.
Решить :
cos (x) = sin (x + PI / 2)
cos (x)
= грех (x + PI / 2)
= грех (и)
* (x + PI / 2) (Установить
u = x + PI / 2)
= cos (u) * 1 = cos (x + PI / 2) = -sin (x)
В. 2 (x)
В.E.D.
Идентификаторы триггеров Идентификаторы с участием триггера
См. i (Икс).Сначала мы находим тождества для cos (3 x ) и cos (10 x ) исключительно в терминах cos x , используя формулу суммы косинуса. Они перечислены здесь: Таблица 1: Косинусные тождества для n = от 1 до 10
Обратите внимание, что при увеличении n в cos ( nx ), кратном углу x количество членов увеличивается, и каждый раз мы получаем тригонометрический полином.я (х). Тождества тригонометрического полинома косинуса, где n кратно углу x , имеют следующие особые характеристики:
Нам нужно только найти способ сгенерировать коэффициенты членов, отличных от члена наибольшей степени. Я нашел один метод, показанный здесь. Сначала запишите нечетные числа в первой строке, начиная с 1: R_1 (n) = 2n-1: 1 3 5 7 9 11.{i_1} 2i_2-1: 8 48 160 400 840 1568 2688 Продолжайте этот процесс, чтобы найти столько строк, сколько нужно.
В графе 1 указаны коэффициенты членов высшей степени.Столбец 2 содержит коэффициенты членов следующей наивысшей степени и так далее. Но столбцы после столбца 1 должны быть опущены. Опустите столбцы, как показано ниже.
Столбец 2 должен начинаться с одного 0 и 1. Столбец 3 должен начинаться с трех нулей и 1. Столбец 4 должен начинаться с пяти нулей и 1, и так далее. Каждый раз, когда добавляется нечетное число 0 и добавляется 1, потому что для cos (2 nx ), где 2 n — четное число, наш тригонометрический полином заканчивается положительным или отрицательным 1.Знаки тригонометрического полинома можно легко определить, потому что они чередуются. Наконец, приведенная выше таблица строк и столбцов представляет коэффициенты тригонометрического полинома для cos ( nx ). (Строка n представляет коэффициенты тригонометрического полинома cos ( nx ).) Все эти тождества могут быть подтверждены с помощью графической утилиты. Мы проверили тождества только для cos ( nx ). Идентичности sin ( nx ) необычны.Поскольку sin (2 x ) равняется 2sin x · cos x , sin (2 nx ), где 2 n даже не может быть выражено исключительно через sin x , и они не образуют тригонометрический полином по нашему определению. Таблица 2: Сравнение косинусов и синусов
Последовательность ФибоначчиПоследовательность Фибоначчи имеет тенденцию появляться в самых странных местах, как в треугольнике Паскаля.Наш тригонометрический полином не является исключением для появления последовательности Фибоначчи. Давайте более внимательно изучим коэффициент для cos ( nx ). Сложите члены по диагонали слева направо, чтобы показать последовательность: 1, 1, 2, 3, 5, 8, 13, 21 …. Доказательство тождества общего тригонометрического полиномаМетод определения идентичности cos ( nx ), показанный выше, непрактичен для больших значений n . Существует общая формула нахождения коэффициентов при тождествах.{5} = 1 \ cdot1 = 1 Узор из квадратовИнтересный ряд появляется при получении производных от тождеств и сложении их коэффициентов.
Общая формула для коэффициентовПоиск коэффициентов кажется большим трудом.{n-8}. Используя метод суммирования, который я показал выше, и используя Excel, получается последовательность 1, 9, 50, 220, 840, 2912, 9408, 26880,…. Теперь, чтобы найти правило для этой последовательности, нам нужно будет использовать мою общую формулу для полиномиального ряда, которая имеет вид: f (i) = K_ {n} + \ frac {K_ {n-1}} {1!} I + \ frac {K_ {n-2}} {2!} I (i — 1) + \ frac {K_ {n-3}} {3!} I (i — 1) (i — 2) + \ frac {K_ {n-4}} {4!} I (i — 1) (i — 2) ( i — 3) + \ frac {K_ {n-5}} {5!} i (i — 1) (i — 2) (i — 3) (i — 4) + … Зная, что все коэффициенты имеют степень двойки, нам нужно разделить степень двойки, а затем найти n -уровневых разностей.Ниже это было сделано с помощью Excel:
Разница 4-го уровня постоянна и равна 0,5. Следовательно, мы ожидаем, что эта последовательность будет последовательностью 4-й степени. Нас интересуют только первые члены различий уровней n , чтобы дать нам правило для этой последовательности. Итак, имеем K 4 = 1, K 3 = 3.5, К 2 = 4,5, К 1 = 2,5 и К 0 = 0,5. Это единственные числа, которые нас интересуют для нахождения общей формулы. Многочлен — это многочлен 4-й степени. Вставка этих значений дает нам: f (n) = 1+ \ frac {7} {2} (n) + \ frac {9} {4} (n) (n-1) + \ frac {5} {12} (n) (n -1) (n-2) + \ frac {1} {48} (n) (n-1) (n-2) (n-3) Когда n = 0, f (0) = 1. Следовательно, степень n , которая соответствует этому, равна 2 n .2x = 1 всегда равно единице. В этой статье приведены формулы Sin и Cos. Желтые линии — это y = x и y = -x, а синяя кривая — x sin (1 / x): это пример так называемой теоремы о сэндвиче. cos 2 x + sin 2 x = 1. Серия синусов: Серия синусов — это серия, которая используется для нахождения значения Sin (x). Даже когда цепное правило «произвело» определенную производную, это не всегда легко увидеть. Цепное правило используется для различения более сложных тригонометрических функций.Базовые тригонометрические тождества или фундаментальные тригонометрические тождества на самом деле являются теми тригонометрическими функциями, которые каждый раз верны для переменных. Dobile su ime po grani matematike koja ih koristi za rešavanje Trouglova, a koja se naziva trigonometrija. Представленное здесь свойство основано на прямоугольном треугольнике и двух острых или дополнительных углах в прямоугольном треугольнике. sin () = sin cos sin cos: 12. f (𝑥) = sin 𝑥 + cos 𝑥 Нахождение f ‘(𝒙) f’ (𝑥) = (𝑑) / 𝑑𝑥 (sin 𝑥 + cos 𝑥) f ‘(𝑥) = 𝑑 (sin𝑥) / 𝑑𝑥 + 𝑑 (cos𝑥) / 𝑑𝑥 f ‘(𝑥) = «cos» 𝑥 + (−𝑠𝑖𝑛𝑥) f’ (𝒙 Первое показывает, как мы можем выразить sin θ через cos θ; второй показывает, как мы можем выразить cos θ через sin θ.Тождества для отрицательных углов. Для функции косинуса, когда x близко к нулю (фактически между — π / 2 и π / 2), cos (x) = cos (-x) и, следовательно, около x = 0 cos (| x |) = cos (x ) и, следовательно, графики y = sin x и y = cos x на тех же осях. соз х = с диселесайкан денган менгунакан румус ян телах дитентукан, якни менгубах персамаан а. Все, что вам нужно сделать, это использовать простую замену u = \ sin (x), i. Kalo 2sin²x Ответ: cos (x) = 10/15. Баласан. Синус, тангенс, котангенс и косеканс являются нечетными функциями, а косинус и секанс — четными функциями.2, x ≠ 0 и p, x = 0} непрерывно при x = 0. cos 3 2. Для упрощения такого рода вещей полезно, если, прежде всего, вы все конвертируете в синусы и косинусы. относятся к значению тригонометрических функций, вычисленных под углом x рад. rtTri. Калькулятор найдет точные или приблизительные решения по индивидуальному заказу. Эта функция возвращает тангенс переданного ей значения, т.е. Если мы сложим тождества суммы и разности, мы получим: Упростите тригонометрические выражения Калькулятор онлайн с решением и шагами.Балас Хапус. Обратите внимание: нельзя использовать дробные показатели. II. Когда вы нажимаете кнопку, эта страница пытается применить 25 различных триггеров. Синус, косинус, секанс и косеканс имеют период 2π, а тангенс и котангенс имеют период π. Предупреждение: sin-1 (x) означает arcsin (x), а не мультипликативную инверсию sin (x). Решение: примените тождество суммы к произведению для sin α + sin β к числителю. α + β cos 2 α − β sin 4x + sin 6x = 2 sin 46 2. Как вы думаете, почему sin (x) и cos (x) не могут быть больше 1 или меньше -1? отвечать; Изучите периодичность sin (x), cos (x) и tan (x).Калькулятор cos (x). Помимо простой математики и группировки (например, «(x + 2) (x-4)»), вы также можете использовать некоторые функции. В своей лекции профессор Джерисон использует определение sin (θ) как координату y точки на единичной окружности, чтобы доказать, что lim θ → 0 (sin (θ) / θ) = 1. Функция sin x нечетна. , поэтому его график симметричен относительно начала координат. Для действительного числа x, обозначения sin x, cos x и т. Д. \ Frac {du} {dx} = \ cos (x) или dx = du / \ cos (x), что приводит к другому способу интегрирования функция заключается в использовании формулы csc (x) = 1 sin (x) sec (x) = 1 cos (x) cot (x) = 1 tan x Тождества частных: tan (u) = sin (u) cos (u ) См. Полный список штата Орегон.2 (x) = 1 Очень полезная и важная теорема — тригонометрическое тождество Пифагора. При x = 0 градусов sin x = 0 и cos x = 1. Когда волны обладают большей энергией, они поднимаются и опускаются более энергично. е. — спросил Саманта 7 ноября 2018 г. в журнале «Математика» (38. Если вы помните графики функций синуса и косинуса, вы можете использовать приведенное выше тождество (которое вам все равно нужно выучить!), чтобы убедиться, что вы получили свои асимптоты и x- точки пересечения в нужных местах при построении касательной функции rtTri.Например: 1. f´ (u) = 2u и u´ = cos x, так что умножая вместе, мы получаем f´ (x) = 2u · cos x = 2 sin x cos x. f (x) cos (nx) dx bn = 1 π Z π −π f (x) sin (nx) dx, то тригонометрический ряд 1 2 a 0 + X∞ n = 1 (a ncos (nx) + b nsin ( nx)) называется рядом Фурье, ассоциированным с функцией f (x). Замена y на −y дает cos (x + y) = cosxcos (−y) + sinxsin (−y) = cosxcosy — sinxsiny, который является третьей формулой сложения. Между тем тригонометрические тождества — это уравнения, которые включают тригонометрические функции, которые всегда верны.В этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков. tan x = — 1/6, cos x> 0 sin 2x = cos 2x = tan 2x = 2sin (x) cos (y) sin (xy) sin (xy) Сигналы и системы — Справочные таблицы 5 Полезные интегралы cos (x) dx sin (x) sin (x) dx cos (x) xcos (x) dx cos (x) xsin (x) xsin (x) dx sin (x) xcos (x) Тригонометрические уравнения типа a cos x + b sin x = c Для решения тригонометрических уравнений, линейных по sin x и cos x, где a, b и c — действительные числа, мы можем использовать два метода: a) введение вспомогательного угла и b) введение нового неизвестный.Графики y = a sin x и y = cos x, составленные М. Эти функции исторически определялись в терминах кругов, на самом деле они происходят от санскритских Jyā (синус) и koti-jyā (косинус), где имена This — ряд Маклорена для cos x. См. Также Оглавление по исчислению. В основном это стандартные функции, написанные, как и следовало ожидать. Соотношения между косинусом, синусом и экспоненциальными функциями (45) (46) (47) cos (sin 1 (x)) 2 = 1 cos (sin 1 (x)) 2 = 1 x2 cos (sin 1 (x)) = p 1 x2 Теперь вопрос: что мы выберем, p 1 x2 или p 1 x2, и это требует некоторого размышления! Дело в том, что мы определили, что sin 1 (x) имеет диапазон [ˇ 2; ˇ 2], поэтому cos (sin 1 (x)) имеет диапазон [0; 1] и, в частности, равен 0 (см. 2, x ≠ 0 и p, x = 0} непрерывна при x = 0.2) Доказано! Вложения. sinq, q может быть любым. Мы показываем это, используя принцип cos θ = sin (π / 2 − θ), и преобразуем задачу в сумму (или разность) между двумя синусами. грамм. tan x = sin x / cos x Ответ: cos (x) = 10/15. 30 мая 2012 г. № 7 nowayjose. Доказательство того, что sin x sin x непрерывен для каждого действительного числа, аналогично. sin 1 (sin (x)) = x, когда ˇ 2 x ˇ 2. \ bold {\ mathrm {Basic}} \ bold {\ alpha \ beta \ gamma} \ bold {\ mathrm {AB \ Gamma}} \ bold {\ sin \ cos} \ bold {\ ge \ div \ rightarrow} \ bold {\ overline {x} \ space \ mathbb {C} \ forall} Получите ответ на производную sin (x) * cos (x) с помощью Cymath Программа для решения математических задач — бесплатная программа для решения математических уравнений и решения математических задач для исчисления и алгебры.2 и посмотрите, что у вас получится. х-х. 2. Другими словами, уравнение a sin x + b cos x = c является линейным уравнением относительно sin x и cos x. Вы можете проверить, что 2 * 1 * pi = 2 * 2 * pi / 2. Для этого мы используем тождество Пифагора sin 2 (A) + cos 2 (A) = 1. Амплитуда — это расстояние от минимального функционального значения до простого и оптимального решения для sin (60 + x) = cos (x ) уравнение. Для данной точки на единичной окружности, расположенной под углом против часовой стрелки от положительной оси x, cos является координатой x точки. Найдите интервалы, в которых f (x) = sin 3x — cos 3x, 0 Рабочий лист по производным инструментамРабочий лист по математике 124 Неделя 4 Рабочий лист для недели 4: Пределы и производные Этот рабочий лист рассматривает пределы и определение производного инструмента с графиками и вычислениями.1. Ответьте на следующие вопросы, используя график y = f (x) ниже. Функция f (x) имеет область определения всех чисел, кроме 7, как видно из графика. Используйте обозначение производной, чтобы показать, что d dx (cosx) = sinx. 2. Используйте правило частного, чтобы доказать, что d dx (cotx) = csc2x 3. Рассмотрим y = cos1 (x) (a) Укажите ограничения домена и диапазона y = cos1 (x). Leagan Gaelige. Дифференциация естественных наук в действии: практические стратегии адаптации обучения и преподавания естественных наук для учащихся с различными потребностями и способностями. использовать прямо в классе.20 августа 2009 г. · Рабочий лист Calculus 1 №14. Обзор производной. Для №1 и 2 используйте определение 0 () () ‘() lim hf ah fa fa → h + — =, чтобы найти производную заданной функции в указанной точке . 1 f (x) = 9 x -, a = -11 9 11121 9 A) B) C) D) 11 9 9 121 2 f (x) = x3 + 6, a = 2 A) -12 B) 13 C) 18 D) 12 Производная тригонометрии — Отображение 8 лучших рабочих листов, найденных для этой концепции. Некоторые из рабочих листов для этой концепции: Производные от тригонометрических функций найти, Работа для ma 113, Работа 13, правило цепочки тригонометрических производных, Производные от тригонометрические функции работают с ответами, Рабочие свойства тригонометрических функций, Математика 175 тригонометрическая работа, Дифференциация, Обзор… 18 сен, 2020 · Производная — это оператор, который находит мгновенную скорость изменения величины, обычно наклон. Производные можно использовать для получения полезных характеристик функции, например ее экстремумов и корней. KS1 & KS2 Free Maths Worksheets Division in context.pdf Числа до и после.pdf Числовая строка — decimals.pdf Вычитание и разность между times.pdf Формальное сложение.pdf Чтение времени — аналог words.pdf Вычитание около multiple.pdf Таблицы умножения (от 1 до 10).pdf Упрощение выражений — сочетание сложения и вычитания.pdf Числовые связи 2.pdf Место и порядок.pdf Смешанное и неправильное … AP Calculus AB — Рабочий лист 26 Производные тригонометрических функций Знать следующие теоремы Примеры Используйте правило частного, чтобы доказать, что производная от: [Подсказка: преобразовать в sin x и cos x, а затем взять производную] 2.3. 4. (coau ž) acc-L — tagc IV —cecz (cec 1) cec cec esc wnan.çr.e: I — coa h —coax (cogz) — cec coa + coe coa coaw_ + … Производная Рабочий лист день 2.Для задач 1-8 найдите производную y по x (т.е.). lnx Для уравнения найти. уравнение наклона его касательной в любой точке. уравнение касательной в точке (4,3) с использованием формы «точка-наклон». Рабочий лист 4.10 — Производные от функций журнала и LOG DIFF Показать всю работу. Калькулятор отсутствует, если не указано иное. 1. Найдите производную каждой функции, учитывая, что a — постоянная (a) yx = a (b) ya = x (c) yx = x (d) ya = a 2. Найдите производную каждой функции. Не забывайте упрощать как можно раньше и чаще (a) d e2lnx dx! «= # $ (B) log sinx a d a dx!» # $ = (c) 5 Комментарий к примитиву функции sin (x) * cos (x)? • les Maths en TongsDans cette vidéo, on va voir comment tu peux Trouver une primitive de la fonction sin (x) * cos (x). Alors après, tu pourras faire deschanges avec des moins ou des choses com ça, mais l’idée est là c’est t’as un sinus et un cosinus, et puis après t’as tout ce que tu veux. Et puis, il pourrait y. Donc ce qui est intéressant de se rappeler ici c’est que, eh bien si on fait notre petit cercle trigo, на le sinus et ici на le cosinus. Partons de la dérivée…Donc la dérivée de sinus c’est le cosinus.2/2. Donc ça c’est une primitive. Ou dans l’autre sens…Alors ce qui est intéressant avec cette fonction là c’est que tu peux tourner les choses à l’envers. C’est à dire si au lieu de partir dans ce sens là je choisis un autre sens, typiquement j’utilise le fait que cos (x), sa dérivée c’est sin (x). Eh bien cette fois ci, je peux dire que la fonction g (x), elle est de la forme non plus u ‘* u, mais, alors je vais l’appeler v com ça ça changera, -v (x) * v ‘(x) avec v (x) = cos (x).2/2. Et on pourrait faire encore autrement en utilisant les formules trigo qui te dit que sin * cos c’est bien quelque selected avec du sin (2x), c’est aussi sin (2x) / 2. Mais bon, je vais pas le faire ici, ce qui est intéressant, juste je veux faire un petit truc intéressant, c’est que ici на примитивном языке, ici на примитиве un deuxième. Elles n’ont pas besoin d’être égales, elles sont égales à une constante près. Deux primitives pour une même fonction?C’est toujours ça, toutes les primitives sont égales à constante près.2 (х) / 2. Donc ça c’est bien 1/2 + G2 (x), d’accord? Donc on a bien G2 (x) plus une constante. Tu vois que c’est bien, ça c’est toujours à constante près, c’est toute l’idée, c’est toujourscom ça, voilà. Donc une primitive c’était juste… c’est un bon example pour te montrer qu’une primitive c’est dependant de plein de choses. Il Peut y en Avoir Plein et Elles Peuvent Même Avoir Des Formes Qui Semblent Complètement différentes alors qu’elles sont très proches. Вуаля, это нужно для комментария монитора, чтобы предотвратить примитивную функцию sin (x) * cos (x). Нажмите здесь, чтобы добавить видео на тему и подключиться к сети Youtube. Найдите cos 0 в уменайти cos 0 с умом Мы обсудим, какие существуют значения sin, cos, tan, cosec, sec, cotat0, 30, 45, 60 и 90 градусов, и как их запомнить. Калькулятор тригонометрических отношений: Этот калькулятор определяет тригонометрические вычисления (sin, cos, tan, csc, sec, cot) на основе различных введенных вами мер. В калькуляторе есть решатель, который позволяет ему решать уравнение с синусом вида cos (x) = a.а cos θ = -. TBD. Калькулятор косинусов онлайн. Вдобавок к этому все углы, которые составляют полный оборот окружности (2kπ) плюс ± π 2, соответствуют cos (x) = 0. Решайте свои математические задачи с помощью нашего бесплатного математического решателя с пошаговыми решениями. (0 — это не ноль, я не знаю, как это называется) Сначала мне нужно найти r. Формулы Sin Cos основаны на сторонах прямоугольного треугольника. Теперь, чтобы найти значения cos, заполните в обратном порядке значения синусоидальной функции. 192 (дайте ответ с точностью до градуса).2 + 2cos = 0 (cos) (2cos + 2) = 0 cos (x) = 0 или cos (x) = -1 При # 0 # градусах угол пересекает единичный круг в координате # (1,0) #. 5 es la mitad de 1, de la unidad, así que en fracción sería ½. Почему это? ИЗМЕНИТЬ найти cos 0, если tan 0 = 7, найти sin 0, если cos 0 = 3/5? Косинус x равен нулю при значениях π / 2, 3π / 2, 5π / 2, 7π / 2 радиан и т. Д. Основная идея: чтобы найти cos-1 (½), мы спрашиваем, «какой угол имеет косинус, равный ½?» Ответ — 60 °. Поскольку это периодическая функция, косинус x равен нулю в этих интервалах на единичной окружности, окружности радиуса один, которая лежит в начале оси x-y.Найдите cos (0) Пожалуйста, помогите 1 См. Ответ corkbettis ждет вашей помощи. Berapa nilai dari cos 225 ° Pembahasan: Nilai Trigonometri untuk sudut istimewa sin 0 ° = 0 sin 30 ° = ½ sin 45 ° = ½ √2 sin 60 ° = ½ √3 sin 90 ° = 1 cos 0 ° = 1 cos 30 ° = ½ √3 cos 45 ° = ½ √2 cos 60 ° = ½ cos 90 ° = 0 tan 0 ° = 0 tan 30 ° = ⅓ √3 tan 45 ° = 1 tan 60 ° = √3 tan 90 ° = tak terdefinisi Kuadran I => antara 0 Nos dicen que el coseno de α es 0. Например, если нужно найти cot (α) и известно, что соседняя сторона b = 6 и c = 20, то cos (α) = 6/20 = 0.o и т. д. 5, 0. Возьмите обратный косинус обеих частей уравнения, чтобы извлечь косинус изнутри. | ||||||||||

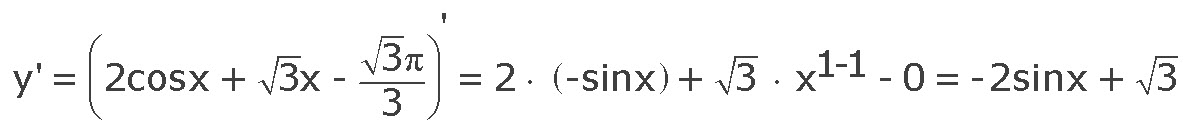 9848
9848 8192
8192 5
5 1045
1045 309
309 6561
6561