Диагонали в трапеции делятся в отношении: Если диагонали трапеции делятся точкой пересечения в отношении 1 : 3 — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Если диагонали трапеции делятся точкой пересечения в отношении 1 : 3

Решение:
Сначала вспомним теорию.

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Трапеция
Трапеция называется равнобедренной трапецией, если ее боковые стороны равны.
Равнобедренная трапеция
Трапеция, один из углов которой прямой, называется прямоугольной трапецией.
Прямоугольная трапеция

Также будет полезно вспомнить следующую теорему:

Трапеция разбивается диагоналями на два равновеликих треугольник (примыкающих к боковым сторонам) и два подобных треугольника (примыкающих к основаниям).

А также будет полезно вспомнить свойство трапеции:

Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в отношении:
Свойство трапеции
Это справедливо, в том числе , для самых диагоналей и высоты.

Снова обратимся к рисунку.

Так как треугольники AOD и BOC подобны, то справедливы следующие соотношения:

По условию диагонали трапеции делятся точкой пересечения в отношении 1 : 3, значит

Далее вспомним еще одно определение.

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме. На приведенном ниже рисунке это отрезок MN.
MN — средняя линия трапеции

Из соотношения:

следует, что 3BC = AD, значит:

MN = (AD + BC) : 2 = (3BC + BC): 2 = 4BC: 2 = 2BC

Таким образом, средняя линия трапеции в два раза больше меньшего основания. Утверждение верное.

Ответ: утверждение верно.

Отношение диагоналей трапеции в точке пересечения. Запоминаем и применяем свойства трапеции. Свойства трапеции, вписанной в окружность

Трапеция
— это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.

Также встречаются такие названия, как равнобокая
или равнобочная
.

— это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

a, b
— основания трапеции
(a
параллельно b
),

m, n
— боковые стороны
трапеции,

d 1 , d 2
— диагонали
трапеции,

h
— высота
трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),

MN
— средняя линия
(отрезок, соединяющий середины боковых сторон).

Площадь трапеции

Через полусумму оснований a, b
и высоту h
: S = \frac{a + b}{2}\cdot h
Через среднюю линию MN
и высоту h
: S = MN\cdot h
Через диагонали d 1 , d 2
и угол (\sin \varphi
) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}

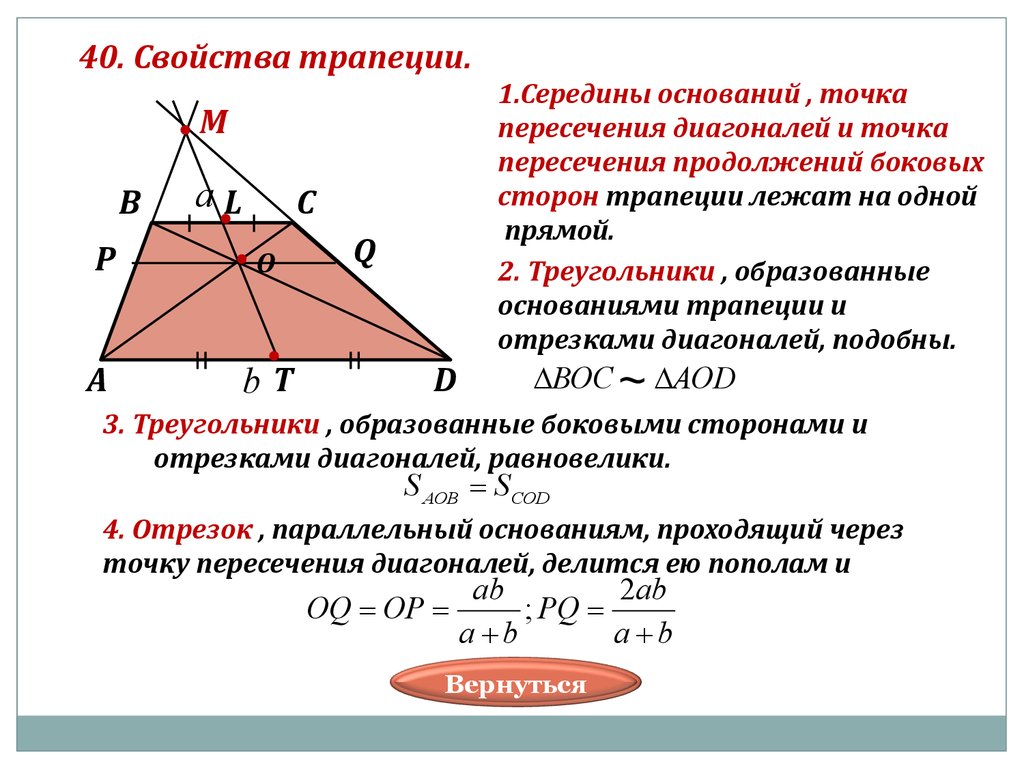
Свойства трапеции

Средняя линия трапеции

Средняя линия
параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:

MN || a, MN || b, MN = \frac{a + b}{2}

Сумма углов трапеции

Сумма углов трапеции
, прилежащих к каждой боковой стороне, равна 180^{\circ}
:

\alpha + \beta = 180^{\circ}

\gamma + \delta =180^{\circ}

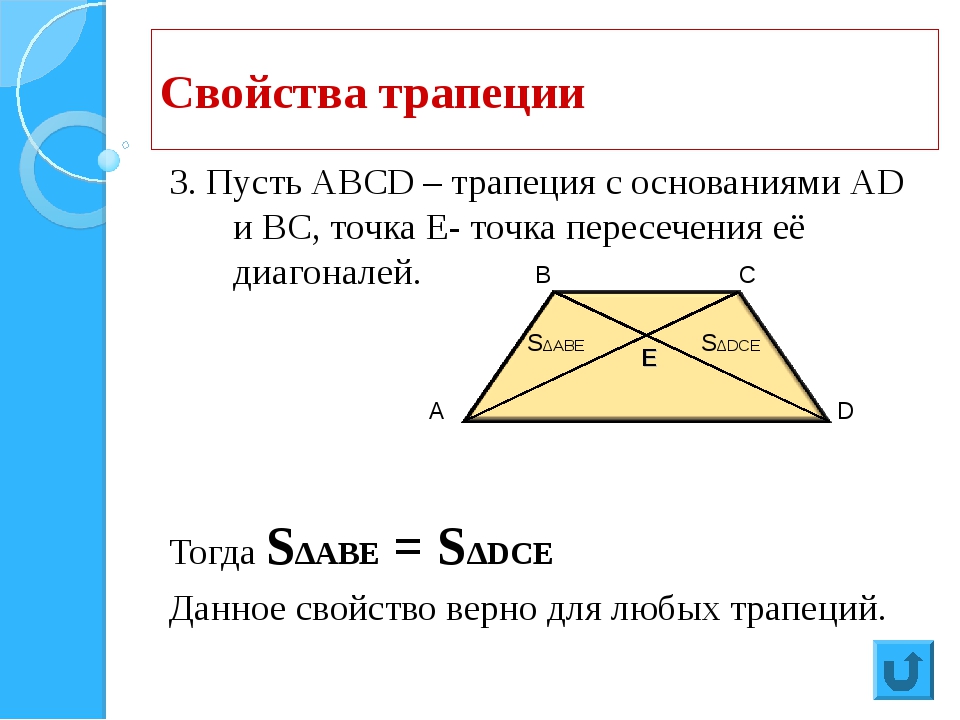
Равновеликие треугольники трапеции

Равновеликими
, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами. {2}
.

Отношение длин отрезков и оснований

Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:

\frac{OX}{OY} = \frac{BC}{AD}

Это будет являться справедливым и для высоты с самими диагоналями.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.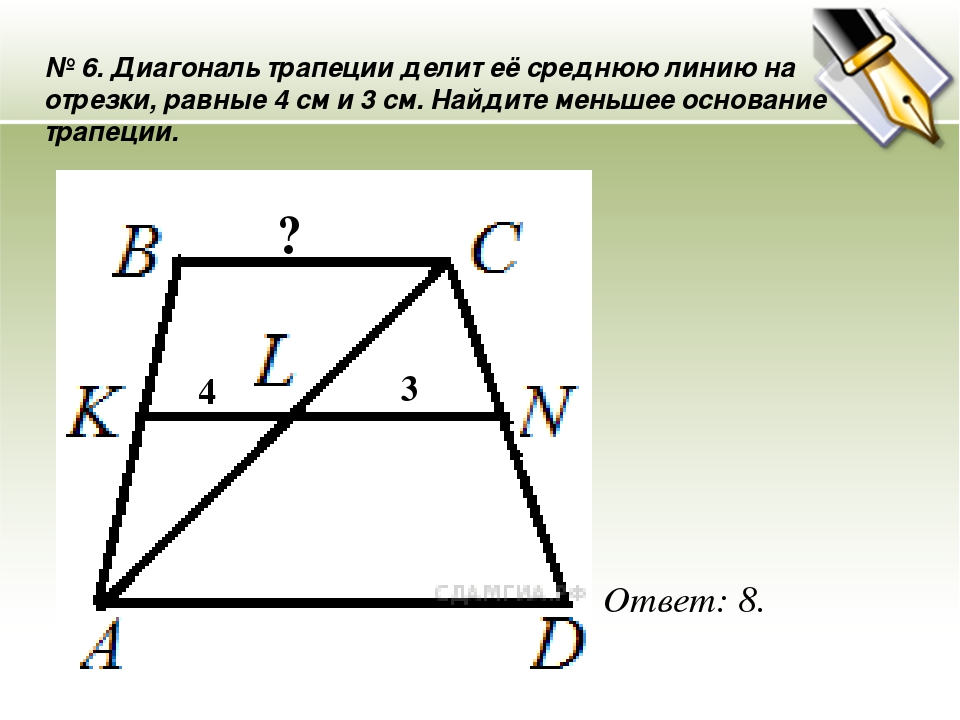

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
.
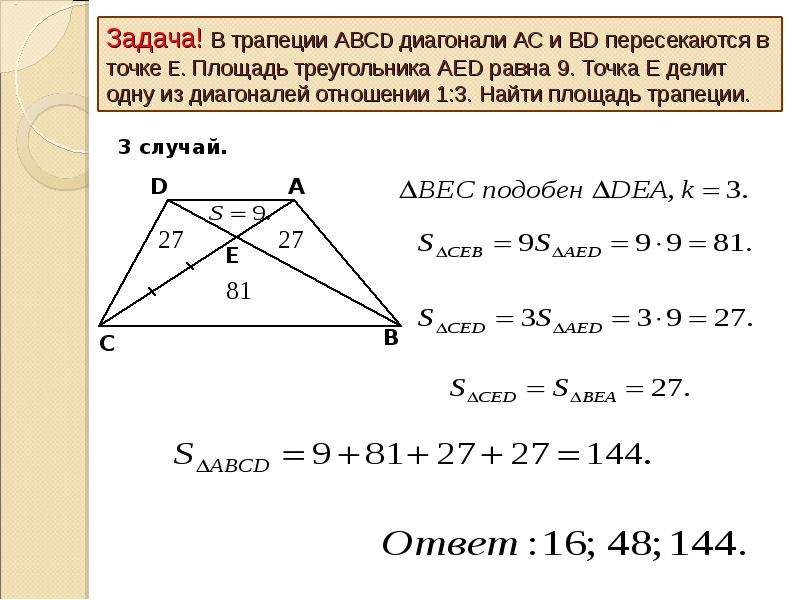
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 .
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием.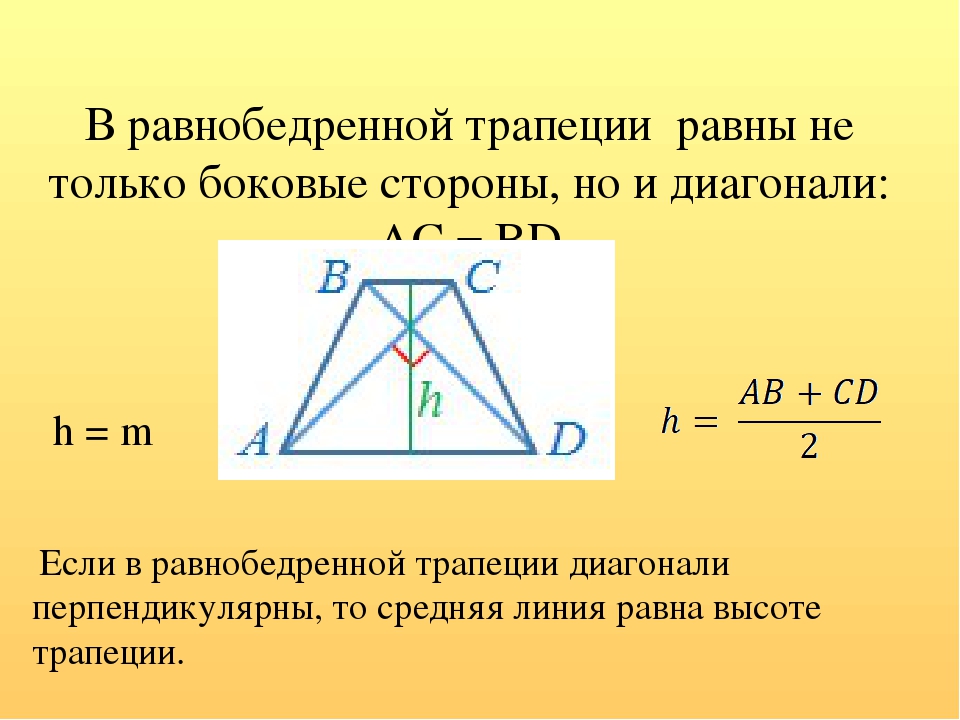 Требуется найти площадь трапеции.

Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.

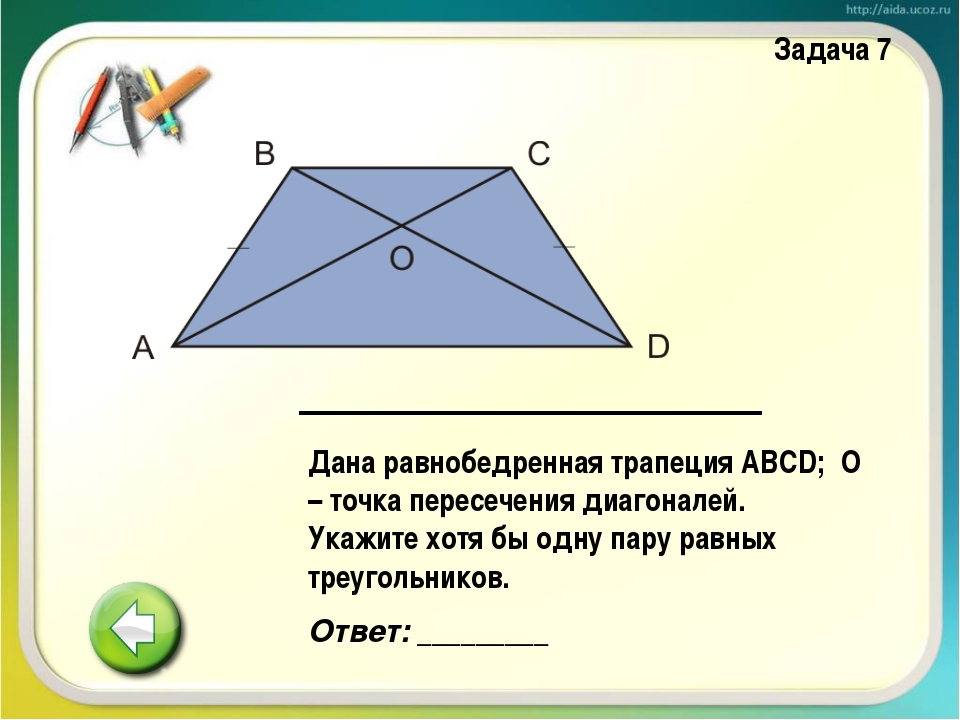
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.

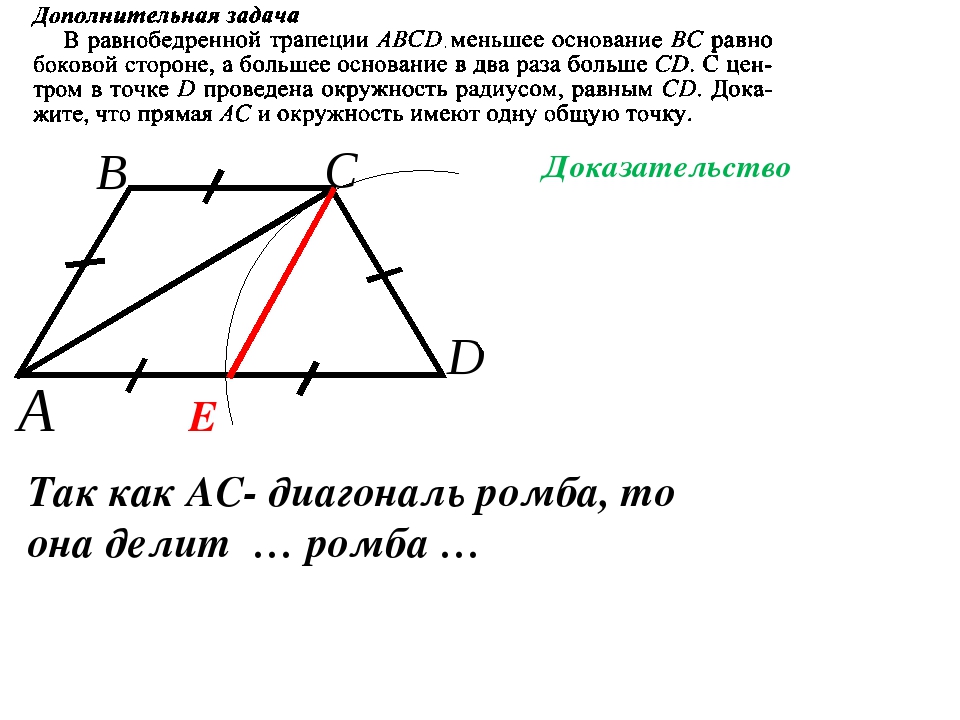
Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1.
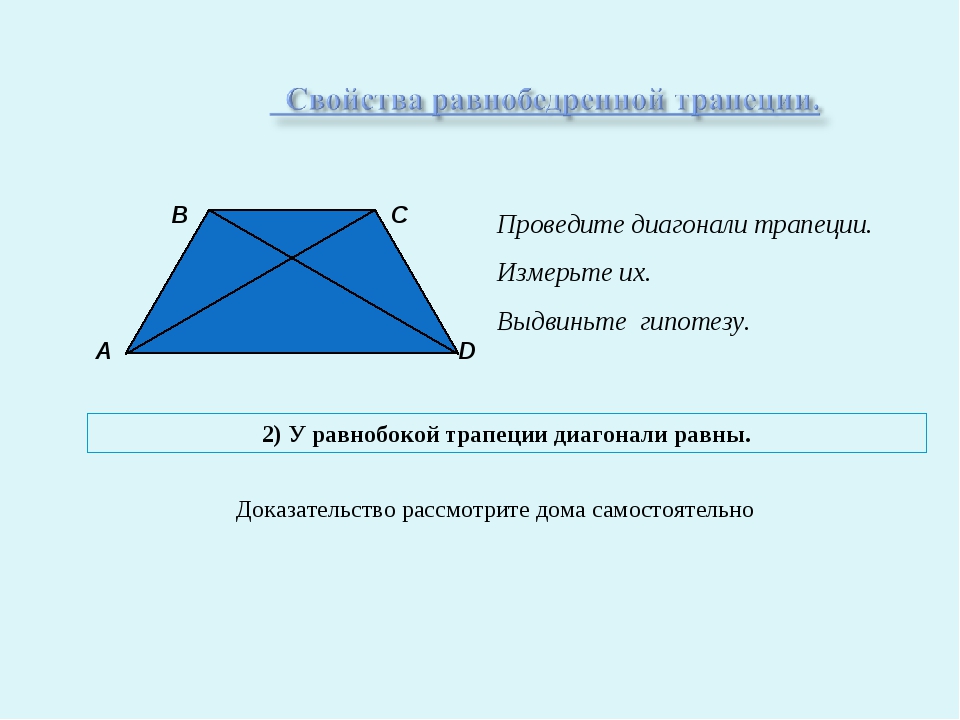
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.

Задача
.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение
.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 — (8 + b) 2 + (24 — b) 2 = 169

-(64 + 16b + b) 2 + (24 — b) 2 = -256

-64 — 16b — b 2 + 576 — 48b + b 2 = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

, где a b — основания трапеции, h — высота трапеции

S = (24 + 8) * 5 / 2 = 80 см 2

Ответ
: площадь трапеции равна 80 см 2 .

Трапеция сторона делится в отношении. Что такое Трапеция

ФГКОУ «МКК «Пансион воспитанниц МО РФ»

«УТВЕРЖДАЮ»

Руководитель отдельной дисциплины

(математика, информатика и ИКТ)

Ю. В. Крылова _____________

«___» _____________ 2015 г.

«Трапеция и ее свойства
»

Методическая разработка

преподавателя математики

Шаталиной Елены Дмитриевны

Рассмотрено и

на заседании ПМО от _______________

Протокол №______

Москва

2015 год

Оглавление

Введение 2

Определения 3

Свойства равнобедренной трапеции 4

Вписанные и описанные окружности 7

Свойства вписанных и описанных трапеций 8

Средние величины в трапеции 12

Свойства произвольной трапеции 15

Признаки трапеции 18

Дополнительные построения в трапеции 20

Площадь трапеции 25

10. Заключение

Список используемой литературы

Приложение

Доказательства некоторых свойств трапеции 27

Задачи для самостоятельных работ

Задачи по теме «Трапеция» повышенной сложности

Проверочный тест по теме «Трапеция»

Введение

Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.

Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.

В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.

Трапеция.

Определения

Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.

Трапеция, у которой есть прямые углы при боковой стороне, называется
прямоугольной
.

Отрезок, соединяющий середины боковых сторон, называется
средней линией трапеции
.

Расстояние между основаниями называется высотой
трапеции
.

. Свойства равнобедренной трапеции

3. Диагонали равнобедренной трапеции равны.

0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.

3. Вписанная и описанная окружность

Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.

Е
сли трапеция равнобедренная, то около неё можно описать окружность.

4
. Свойства вписанных и описанных трапеций

2.Если в равнобедренную
трапецию можно вписать окружность, то

сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.

.
Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.

Е
сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m
и n,
тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.

0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.

5.
Средние величины в трапеции

Среднее геометрическое

В любой трапеции с основаниями

a

для

справедливо неравенство

:

b
˂
h
˂
g
˂
m
˂
s
˂
a

6.
Свойства произвольной трапеции

. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.

2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.

3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.

Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.

5.
При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).

6.
Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.

1

2

+

d

2

2

=

c

2

+

d

2

+ 2

ab

В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований

d

—

–

8
. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.

7
. Признаки трапеции

8
. Дополнительные построения в трапеции

1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.

. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.

. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.

. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.

5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.

6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований

.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.

8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.

9. Биссектриса угла трапеции отсекает равнобедренный треугольник.

1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.

13.
Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.

9. Площадь трапеции

1

. Площадь трапеции равна произведению полусуммы оснований на высоту
S

= ½(a

+
b

)
h

или

лощадь трапеции равна произведению средней линии трапеции на высоту S

=
m

h

.

2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Площадь равнобедренной трапеции с радиусом вписанной окружности равным
r
и углом при основании
α:

10.
Заключение

ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?

Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.

Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.

Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.

Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.

Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.

Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн

В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.

Список используемой литературы

Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.

Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004

Гордин Р.К. Планиметрия. Задачник.

Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN
5-89155-188-3

Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).

Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.

Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.

Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.

Приложение

1.Доказательство некоторых свойств трапеции.

1.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках
K

Доказать, что если основания трапеции равны

а

, то

длина отрезка

KL

равна среднему геометрическому оснований трапеции.

Доказательство

Пусть

— точка пересечения диагоналей,
AD

а, ВС

Прямая

параллельна основанию
AD

, следовательно,

║

треугольники

BAD

подобны, поэтому

(1)

(2)

Подставим (2) в (1)
, получим KO =

Аналогично LO

= Тогда K

KO

+

LO

=

о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.

Доказательство: Пусть продолжения боковых сторон пересекаются в точке
К.

Через точку

и точку

пересечения диагоналей
проведём прямую

КО.

Окажем, что эта прямая делит основания пополам.

Обозначим
ВМ

х, МС

у,

и,

Имеем:

∆

ВКМ

∆AKN

→

∆
MК

∆NKD

→

∆BMO

∆DNO

∆CMO

∆
ANO

поэтому .

Перемножая полученные равенства, получим , откуда следует

x

=

y

,
но тогда и u

=
v

.

дачи для самостоятельных работ и их решения

3. Задачи по теме «Трапеция»
повышенной сложности.

Садовничий Ю.В. «Математика. Подготовка к ЕГЭ», Москва, ИЛЕКСА, 2011, стр. 252.

1 . В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции.

Ответ:
S
= 6.

2. Периметр равнобочной трапеции, описанной около круга, равен р.
Найти радиус этого круга, если известно, что острый угол при основании трапеции равен ɑ.

psina

3. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 5/11. Найти длины оснований трапеции.

Ответ: 1и 7.

Основание
АВ

трапеции
ABCD

вдвое длиннее основания
CD

и вдвое длиннее боковой стороны
AD.

Длина диагонали
АС

равна
а,

а длина боковой стороны
ВС

равна
b
.

Найти площадь трапеции.

Ответ:
S

= 3

ab

В трапеции PQRS
длина основания QR
равна 10, длина диагонали QS
равна 19, а величина угла QSP
равна 30°. Выяснить, что больше, длина основания QR
или длина стороны RS.

Ответ:
RS > QR.

В трапеции ABCD
сторона АВ
параллельна CD.
Диагонали BD
и АС
трапеции пересекаются в точке О,
причем треугольник ВОС
является равносторонним. Найти длину стороны ВС,
если АВ
= 5 и CD-
3.

В трапеции ABCD
основание AD
равно 16, сумма диагоналей АС
и BD
равна 36, угол CAD
равен 60°. Отношение площадей треугольников AOD
и ВОС,
где О
— точка пересечения диагоналей, равно 4. Найти площадь трапеции.

Ответ:
S=

90√3.

Иванов А.А., Иванов А.П., Математика: Пособие для подготовки к ЕГЭ и поступлению в вузы. – М.: Издательство МФТИ, 2003, стр. 238..

12. Площадь прямоугольной трапеции равна S, острый угол равен а. Найти высоту трапеции, если ее меньшая диагональ равна большему оснозанию. [√2
S
ctg а]

Около круга радиуса
R

описана равнобедренная трапеция с острым утлом а при основании. Найти периметр этой трапеции.

В равнобедренной трапеции, описанной около круга, отношение боковой стороны к меньшему основанию равно к.
Найти углы трапеции и допустимые значения к.

На меньшем основании равнобедренной трапеции построен правильный треугольник. Его высота равна высоте трапеции, а площадь в 5 раз меньше площади трапеции. Найти угол при большем основании трапеции.

Основания равнобедренной трапеции равны а и 6 (а > 6), угол при боольшем основании равен а. Найти радиус окружности, описанной около грапеции. [
(√/а
2
+Ь
2
+2а
b
cos2а
)
:(2sin2а)].

Площадь равнобедренной трапеции равна
S
, угол между ее диагонапями, противолежащий боковой стороне, равен ɑ. Найти высоту трапеции…

[√
Stg
(½ ɑ)]

4. Проверочный тест по теме «Трапеция»

В трапеции, имеющей прямой угол, основания равны 5 и 11, а большая диагональ √185. Площадь трапеции составляет

В трапеции боковые стороны и меньшее основание равны
Ь,

а острый угол вдвое меньше тупого. Площадь трапеции равна

51 в равнобедренной трапеции, описанной около окружности радиуса 5 м и имеющей основание 20 м, другое основание равно

Меньшее основание трапеции, вписанной в окружность, втрое меньше большего, которое является диаметром окружности. Синус угла трапеции равен

20] Основания равнобочной трапеции относятся как 3: 7, а диагональ делит острый угол пополам.25
j
В трапеции с диагональю 20, высотой 12 и площадью 150 вторая

диагональ равна

29
j
Равнобедренная трапеция с острым углом
а

описана около окруж- ности. Отношение ее большего основания к меньшему равно

Зо| В описанной около круга равнобочной трапеции расстояние от центра круга до дальней вершины трапеции втрое больше, чем до ближней. Тангенс острого угла трапецииравен

Четырёхугольник, у которого только две стороны параллельны называются трапецией
.

Параллельные стороны трапеции называются её основаниями
, а те стороны, которые не параллельны, называются боковыми сторонами
. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.

Средняя Линия Трапеции

Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.

Теорема:

Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин её оснований

MN || AB || DC
AM = MD; BN = NC

MN
средняя линия, AB
и CD

— основания, AD
и BC
— боковые стороны

MN = (AB + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин её оснований.

Основная задача
: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.

Средняя Линия Треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема
: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

AM = MC and BN = NC
=>

Применение свойств средней линии треугольника и трапеции

Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.

Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.

– это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD
и BC
), две другие – боковыми (на рисунке AB
и CD
).

Средняя линия трапеции
– это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL
).

Свойства средней линии трапеции

Доказательство теоремы о средней линии трапеции

Доказать
, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.

Дана трапеция ABCD
со средней линией KL
. Для доказательства рассматриваемых свойств требуется провести прямую через точки B
и L
. На рисунке 2 это прямая BQ
. А также продолжить основание AD
до пересечения с прямой BQ
.

Рассмотрим полученные треугольники LBC
и LQD
:

По определению средней линии KL
точка L
является серединой отрезка CD
. Отсюда следует, что отрезки CL
и LD
равны.
∠ BLC
= ∠ QLD
, так как эти углы вертикальные.
∠ BCL
= ∠ LDQ
, так как эти углы накрест лежащие при параллельных прямых AD
и BC
и секущей CD
.

Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC
и LQD
равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC
= ∠ LQD
, BC=DQ
и самое главное — BL=LQ
=> KL
, являющаяся средней линией трапеции ABCD
, также является и средней линией треугольника ABQ
. Согласно свойству средней линией треугольника ABQ
получаем:

KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
KL || AD
по свойству средней линии треугольника. А так как AD || BC
по определению трапеции, то KL || BC
.

Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — нет
.

Параллельные стороны трапеции называются основаниями
. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Отрезок, соединяющий середины оснований трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований:

Как видим, теория очень проста. А задачи, в которых применяются свойства трапеции, весьма разнообразны. В этой статье разобраны и стандартные задачи (номер 1 и 2), и более интересные.

1. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны .

Высота трапеции — это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины В.

2. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150. Найдите площадь трапеции.

Это стандартная задача. Углы АВН и ВАН — односторонние, значит, их сумма равна 180°, и тогда угол ВАН равен 30°. Из треугольника АВН найдем высоту ВН. Катет, лежащий напротив угла в 30, равен половине гипотенузы. Получаем, что ВН = 3,5 и площадь трапеции равна 42.

3. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Скажите, что вы видите на чертеже? Можно сказать, что изображена трапеция АВСD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, АВС и АСD, в которых проведены средние линии.

Мы помним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны.

Из треугольника АВD находим: х = 5.

В следующей задаче мы тоже воспользуемся свойством средней линии треугольника.

4. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции, PQ = 2,5. Легко доказать, что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии. Дальше все просто. Найдем отрезки РМ и NQ, являющиеся средними линиями треугольников ABC и BCD, а затем отрезок MN. Он равен 0,5.

5. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Периметр треугольника равен сумме его сторон, то есть a + b + c.
Периметр трапеции равен а + b + 4 + c + 4.
На сколько периметр трапеции больше периметра треугольника? Чему равен периметр трапеции?

Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.

Общие сведения

Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.

Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…

Виды трапеции

Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.

1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.

2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.

Главные принципы методики изучения свойств трапеции

К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.

Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.

Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.

Элементы и свойства равнобедренной трапеции

Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.

А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.

Решение

Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.

Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем тупой угол аналогично первому способу.

Свойство диагоналей равнобедренной трапеции

Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:

Высота фигуры будет равна сумме оснований, деленной на два;

Ее высота и средняя линия равны;

Центр окружности является точкой, в которой пересекаются ;

Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;

Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;

Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.

Подобные трапеции

Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.

Доказательство теоремы

Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.

Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.

Свойства подобия

Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.

Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.

Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.

Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).

Выводы подобия

Таким образом, мы доказали, что:

1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).

2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).

3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.

4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.

Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.

Отрезок, соединяющий середины диагоналей трапеции

Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.

Центр тяжести

Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.

Вписанные и описанные трапеции

Давайте перечислим особенности таких фигур:

1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.

2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.

Следствия вписанной окружности:

1. Высота описанной трапеции всегда равна двум радиусам.

2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.

Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.

Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.

Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).

Все формулы средней линии трапеции

Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):

1. Через основания: М = (А+Б)/2.

2. Через высоту, основание и углы:

М = А-Н*(ctgα+ctgβ)/2;

М = Б+Н*(ctgα+ctgβ)/2.

3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:

М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.

4. Через площадь и высоту: М = П/Н.

Трапеция. Свойства, признаки, площадь. Средняя линия трапеции

Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — нет.

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.

Если боковые стороны равны, трапеция называется равнобедренной.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований:

Как видим, теория очень проста. А задачи, в которых применяются свойства трапеции, весьма разнообразны. В этой статье разобраны и стандартные задачи (номер и ), и более интересные.

. Найдите высоту трапеции , опущенную из вершины , если стороны квадратных клеток равны .

Высота трапеции — это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины .

Ответ: .

. Основания трапеции равны и , боковая сторона, равная , образует с одним из оснований трапеции угол . Найдите площадь трапеции.

Это стандартная задача. Углы и — односторонние, значит, их сумма равна , и тогда угол равен . Из треугольника найдем высоту . Катет, лежащий напротив угла в , равен половине гипотенузы. Получаем, что и площадь трапеции равна .

. Основания трапеции равны и . Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Скажите, что вы видите на чертеже? Можно сказать, что изображена трапеция , и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, и , в которых проведены средние линии.

Из треугольника находим: .

Ты нашел то, что искал? Поделись с друзьями!

В следующей задаче мы тоже воспользуемся свойством средней линии треугольника.

. Основания трапеции равны и . Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем — среднюю линию трапеции, . Легко доказать, что отрезок , соединяющий середины диагоналей трапеции, лежит на средней линии. Дальше все просто. Найдем отрезки и , являющиеся средними линиями треугольников и , а затем отрезок . Он равен .

. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного , отсекает треугольник, периметр которого равен . Найдите периметр трапеции.

Периметр треугольника равен сумме его сторон, то есть .

Периметр трапеции равен .

Заметим, что периметр трапеции на 8 больше, чем периметр треугольника. Значит, он равен 15 + 8 = 23.

Ответ: .

Трапеция формулы основания. Трапеция. Свойства трапеции. III. Объяснение нового материала

Также встречаются такие названия, как равнобокая
или равнобочная
.

— это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

a, b
— основания трапеции
(a
параллельно b
),

m, n
— боковые стороны
трапеции,

d 1 , d 2
— диагонали
трапеции,

h
— высота
трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),

MN
— средняя линия
(отрезок, соединяющий середины боковых сторон).

Площадь трапеции

Через полусумму оснований a, b
и высоту h
: S = \frac{a + b}{2}\cdot h
Через среднюю линию MN
и высоту h
: S = MN\cdot h
Через диагонали d 1 , d 2
и угол (\sin \varphi
) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}

Свойства трапеции

Средняя линия трапеции

MN || a, MN || b, MN = \frac{a + b}{2}

Сумма углов трапеции

Сумма углов трапеции
, прилежащих к каждой боковой стороне, равна 180^{\circ}
:

\alpha + \beta = 180^{\circ}

\gamma + \delta =180^{\circ}

Равновеликие треугольники трапеции

Отношение длин отрезков и оснований

\frac{OX}{OY} = \frac{BC}{AD}

Это будет являться справедливым и для высоты с самими диагоналями.

ФГКОУ «МКК «Пансион воспитанниц МО РФ»

«УТВЕРЖДАЮ»

Руководитель отдельной дисциплины

(математика, информатика и ИКТ)

Ю. В. Крылова _____________

«___» _____________ 2015 г.

«Трапеция и ее свойства
»

Методическая разработка

преподавателя математики

Шаталиной Елены Дмитриевны

Рассмотрено и

на заседании ПМО от _______________

Протокол №______

Москва

2015 год

Оглавление

Введение 2

Определения 3

Свойства равнобедренной трапеции 4

Вписанные и описанные окружности 7

Свойства вписанных и описанных трапеций 8

Средние величины в трапеции 12

Свойства произвольной трапеции 15

Признаки трапеции 18

Дополнительные построения в трапеции 20

Площадь трапеции 25

10. Заключение

Список используемой литературы

Приложение

Доказательства некоторых свойств трапеции 27

Задачи для самостоятельных работ

Задачи по теме «Трапеция» повышенной сложности

Проверочный тест по теме «Трапеция»

Введение

Трапеция.

Определения

Трапеция, у которой есть прямые углы при боковой стороне, называется
прямоугольной
.

Отрезок, соединяющий середины боковых сторон, называется
средней линией трапеции
.

Расстояние между основаниями называется высотой
трапеции
.

. Свойства равнобедренной трапеции

3. Диагонали равнобедренной трапеции равны.

1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.

3. Вписанная и описанная окружность

Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.

Е
сли трапеция равнобедренная, то около неё можно описать окружность.

4
. Свойства вписанных и описанных трапеций

2.Если в равнобедренную
трапецию можно вписать окружность, то

.
Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.

1

0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.

5.
Средние величины в трапеции

Среднее геометрическое

В любой трапеции с основаниями

a

для

справедливо неравенство

:

b
˂
h
˂
g
˂
m
˂
s
˂
a

6.
Свойства произвольной трапеции

1

. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.

1

2

+

d

2

2

=

c

2

+

d

2

+ 2

ab

В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований

d

—

–

8
. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

7
. Признаки трапеции

8
. Дополнительные построения в трапеции

1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.

2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.

3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.

4

. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.

7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.

9. Биссектриса угла трапеции отсекает равнобедренный треугольник.

1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.

9. Площадь трапеции

1

. Площадь трапеции равна произведению полусуммы оснований на высоту
S

= ½(a

+
b

)
h

или

П

лощадь трапеции равна произведению средней линии трапеции на высоту S

=
m

h

.

Площадь равнобедренной трапеции с радиусом вписанной окружности равным
r
и углом при основании
α:

10.
Заключение

ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?

Список используемой литературы

Гордин Р.К. Планиметрия. Задачник.

Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.

Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.

Приложение

1.Доказательство некоторых свойств трапеции.

Доказать, что если основания трапеции равны

а

, то

длина отрезка

KL

равна среднему геометрическому оснований трапеции.

Доказательство

Пусть

— точка пересечения диагоналей,
AD

а, ВС

Прямая

параллельна основанию
AD

, следовательно,

║

треугольники

BAD

подобны, поэтому

(1)

(2)

Подставим (2) в (1)
, получим KO =

Аналогично LO

= Тогда K

KO

+

LO

=

Доказательство: Пусть продолжения боковых сторон пересекаются в точке
К.

Через точку

и точку

пересечения диагоналей
проведём прямую

КО.

Окажем, что эта прямая делит основания пополам.

Обозначим
ВМ

х, МС

у,

и,

Имеем:

∆

ВКМ

∆AKN

→

∆
MК

∆NKD

→

Сбор и использование персональной информации

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.

Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.

Свойства параллелограмма

1. Противолежащие стороны равны.
На рис. 11 AB
= CD
; BC
= AD
.

2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A
= ∠C
; ∠B
= ∠D
.

3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.

На рис. 11 отрезки AO
= OC
; BO
= OD
.

Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.

Параллельные стороны называются ее основаниями
, а две другие стороны — боковыми сторонами
.

Виды трапеций

1. Трапеция
, у которой боковые стороны не равны,
называется разносторонней
(рис. 12).

2. Трапеция, у которой боковые стороны равны, называется равнобокой
(рис. 13).

3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной
(рис. 14).

Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN
). Средняя линия трапеции параллельна основаниям и равна их полусумме.

Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).

Площадь параллелограмма и трапеции

Правило. Площадь параллелограмма
равна произведению его стороны на высоту, проведенную к этой стороне.

В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.

Определение и виды

В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.

Различные виды указаны на рисунке ниже
.

На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.

Важнейшие свойства и формулы

Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.

В её состав входят:

основания BC и AD — две стороны, параллельные по отношению друг к другу;
боковые стороны AB и CD — два непараллельных элемента;
диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
высота трапеции CH — перпендикулярный основаниям отрезок;
средняя линия EF — линия, соединяющая середины боковых сторон.

Основные свойства элементов

Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:

Кроме того, часто полезно знать и применять следующие утверждения:

Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.

Вычисление периметра и площади

Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):

P = AD + BC + AB + CD.

Вписанная и описанная окружность

Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.

Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p,
используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2
.

Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.

Частные случаи

Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения
, которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:

Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.

Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.

Задачи по школьной математике. Трапеция

Наибольший угол прямоугольной трапеции равен 120◦, а большая боковая сторона равна c. Найдите разность оснований.

Диагонали трапеции взаимно перпендикулярны, а средняя линия равна 5. Найдите отрезок, соединяющий середины оснований.

Высота равнобокой трапеции, проведенная из конца меньшего основания, делит ее большее основание на отрезки, равные 4 и 8. Найдите основания трапеции.

Найдите меньшее основание равнобокой трапеции, если высота, проведенная из конца меньшего основания, делит большее основание на отрезки, один из которых на 5 больше другого.

Боковая сторона равнобокой трапеции видна из точки пересечения диагоналей под углом, равным 60◦. Найдите диагонали трапеции, если ее высота равна h.

В равнобокой трапеции острый угол равен 60◦. Докажите, что меньшее основание равно разности большего основания и боковой стороны.

Меньшая боковая сторона прямоугольной трапеции равна 3, а большая образует угол, равный 30◦, с одним из оснований. Найдите это основание, если на нем лежит точка пересечения биссектрис углов при другом основании.

Докажите, что биссектрисы углов при боковой стороне трапеции пересекаются на ее средней линии.

Дана трапеция ABCD с основанием AD. Биссектрисы внешних углов при вершинах A и B пересекаются в точке P, а при вершинах C и D — в точке Q. Докажите, что отрезок PQ равен полупериметру трапеции.

Основания трапеции равны a и b (a > b). Найдите длину отрезка, соединяющего середины диагоналей трапеции.

Один из углов прямоугольной трапеции равен 120◦, большее основание равно 12. Найдите отрезок, соединяющий середины диагоналей, если известно, что меньшая диагональ трапеции равна ее большему основанию.

Найдите отношение оснований трапеции, если ее средняя линия делится диагоналями на три равные части.

Боковая сторона трапеции равна одному основанию и вдвое меньше другого. Докажите, что вторая боковая сторона перпендикулярна одной из диагоналей трапеции.

Диагонали трапеции взаимно перпендикулярны. Одна из них равна 6, а вторая образует с основанием угол, равный 30◦. Найдите среднюю линию трапеции.

Средняя линия трапеции равна 5, а отрезок, соединяющий середины оснований, равен 3. Углы при большем основании трапеции равны 30◦ и 60◦. Найдите основания и меньшую боковую сторону трапеции.

Одна из боковых сторон трапеции равна сумме оснований. Докажите, что биссектрисы углов при этой стороне пересекаются на другой боковой стороне.

Отрезок, соединяющий середины двух противоположных сторон четырехугольника, равен полусумме двух других сторон. Докажите, что этот четырехугольник — трапеция или параллелограмм.

Прямая, проведенная через вершину C трапеции ABCD параллельно диагонали BD, пересекает продолжение основания AD в точке M. Докажите, что треугольник ACM равновелик трапеции ABCD.

Боковые стороны трапеции лежат на перпендикулярных прямых. Найдите площадь четырехугольника с вершинами в серединах диагоналей и серединах оснований, если боковые стороны равны a и b.

Основания AD и BC трапеции ABCD равны соответственно a и b. Диагональ AC разделена на три равные части и через ближайшую к A точку деления M проведена прямая, параллельная основаниям. Найдите отрезок этой прямой, заключенный между диагоналями.

Площадь трапеции равна 27, основания 8 и 16. Найдите площади треугольников, на которые трапеция разделена диагоналями.

Большее основание равнобедренной трапеции равно 21, боковая сторона ее 10, а диагональ 17. Определите площадь трапеции.

Основания AD и BC трапеции ABCD равны a и b (a>b). Найдите длину отрезка, высекаемого диагоналями на средней линии трапеции. Найдите длину отрезка MN, концы которого делят стороны AB и CD в отношении AM : MB = DN : NC = p : q.

На стороне AD параллелограмма ABCD взята точка Р так, что АР : AD = 1 : n. Точка Q — точка пересечения прямых AC и BP. Найдите AQ : AC.

На диагонали BD параллелограмма ABCD взята точка K. Прямая АК пересекает прямые BC и CD в точках L и M. Докажите, что AK² = LK KM.

Найдите площадь равнобедренной трапеции, у которой боковая сторона, верхнее основание и средняя линия равны 13, 6 и 15 соответственно.

Периметр равнобедренной трапеции равен 36, а средняя линия — 10. Найдите боковую сторону.

Средняя линия равнобедренной трапеции ABCD с основаниями BC и AD равна 18. Найдите высоту трапеции, если BC : AD = 1 : 5, а боковая сторона равна 15.

В равнобедренной трапеции боковая сторона равна средней линии, а периметр равен 48. Определите боковую сторону трапеции.

Диагональ равнобедренной трапеции делит среднюю линию на две части, равные 2 и 5. Найдите площадь трапеции, если ее боковая сторона равна 5.

В равнобедренной трапеции основания равны 6 и 10. Диагональ равна 10. Найдите площадь трапеции.

В равнобедренной трапеции диагонали взаимно перпендикулярны. Найдите площадь трапеции, если ее основания равны 8 и 12.

Основания равнобедренной трапеции равны 6 и 10. Диагональ наклонена к основанию под углом 45^о. Найдите площадь трапеции.

Диагональ прямоугольной трапеции равна ее боковой стороне. Найдите среднюю линию трапеции, если ее высота равна 4, а боковая сторона равна 5.

В прямоугольной трапеции разность длин оснований равна 4, а большая боковая сторона равна 5. Найдите меньшую боковую сторону трапеции.

Меньшее основание трапеции равно 4. Большее основание больше средней линии на 4. Найдите среднюю линию.

В равнобедренной трапеции боковая сторона равна 52, высота равна 48, средняя линия равна 30. Найдите ее большее основание.

Прямая CF параллельна боковой стороне трапеции и делит основание AD на отрезки AF = 9 и FD = 5. Найдите среднюю линию трапеции.

В трапеции ABCD боковые стороны AB и CD продлены до пересечения в точке E. Найдите EC, если AB = 1, CD = 3 и BE = 2.

Углы при основании трапеции равны 90^о и 45^о. Одно основание в два раза больше другого и равно 24. Найдите меньшую боковую сторону трапеции.

Разность двух оснований равнобедренной трапеции равна 3. Синус угла при основании трапеции равен 0,8. Найдите боковую сторону трапеции.

Средняя линия равнобедренной трапеции равна 4. Площадь трапеции равна 8. Найдите тангенс угла между диагональю и основанием трапеции.

Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)

Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции.

Виды четырехугольников:

Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны

Ромб — это параллелограмм, у которого все стороны равны.

Прямоугольник — это параллелограмм, у которого все углы прямые.

Квадрат — это прямоугольник, у которого все стороны равны.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Свойства произвольных четырехугольников:

Сумма внутренних углов четырехугольника равна 360^o

Если соединить отрезками середины соседних сторон — получится параллелограмм:

Свойства параллелограмма:

Свойства ромба:

Диагонали ромба перпендикулярны, и делятся точкой пересечения пополам:

Диагонали ромба являются биссектрисами внутренних углов:

Если соединить отрезками середины соседних сторон любого ромба, получается прямоугольник:

Свойства прямоугольника:

Диагонали прямоугольника равны, и делятся точкой пересечения пополам:

Если соединить отрезками середины соседних сторон любого прямоугольника, то получится ромб:

Свойства квадрата:

Диагонали квадрата равны, перпендикулярны, и точкой делятся точкой пересечения пополам:

Свойства трапеции:

Средняя («серединная») линия трапеции параллельна основаниям, равна их полусумме, и делит любой отрезок с концами, лежащими на прямых, содержащих основания, пополам:

Сумма углов, прилежащих к боковой стороне трапеции, равна 180^о:

Треугольники, образованные боковыми сторонами и отрезками диагоналей трапеции — равновелики:

Треугольники, образованные боковыми сторонами и отрезками диагоналей трапеции — подобны:

Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции делится этой точкой в отношении:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.

Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator

Покажите, что диагонали трапеции делят ее на четыре треугольника, два из которых имеют одинаковую площадь? «Equi-extension»

Обычно трапеция определяется как четырехугольник с двумя параллельными сторонами. Равнобедренная трапеция — это особый случай трапеции, которая имеет боковую симметрию, что означает, что одна сторона будет зеркалом другой.

На изображении выше изображена равнобедренная трапеция, # «ABCD» #. Должно быть очевидно, что треугольники # «ABE» # и # «DCE» # имеют равные площади, поскольку они являются зеркальным отображением друг друга.Поэтому давайте сосредоточимся на попытке доказать, что эти два треугольника должны иметь одинаковую площадь для всех трапеций.

Площадь треугольника можно определить по тождеству:

#A = 1/2 (B xx H) #

Где # B # — основание треугольника, а # H # — высота. Треугольники # «ABE» # и # «DCE» # не имеют общих сторон, которые мы могли бы рассматривать как общую основу, однако треугольники # «ACD» # и # «DBA» # имеют общую сторону, основание трапеции. .

Если мы рассматриваем сторону # «AD» # как основание для обоих треугольников, то высота для обоих — это расстояние между линией # «AD» # и # «BC» #.Поскольку основание и высота у обоих треугольников равны, площадь обоих треугольников также должна быть одинаковой.

#A_ «ABD» = A_ «DCA» #

Теперь мы также можем видеть, что треугольник # «ABD» # состоит из треугольников # «ABE» # и # «AED» #. Кроме того, треугольник # «DCA» # состоит из треугольников # «DCE» # и # «AED» #.

#A_ «ABD» = A_ «ABE» + A_ «AED» #
#A_ «DCA» = A_ «DCE» + A_ «AED» #

Если мы вычтем площадь AED из ABD и DCA, мы увидим, что площади ABE и DCE действительно равны.

#A_ «ABD» = A_ «DCA» #
#A_ «ABE» + цвет (красный) отмена (цвет (черный) (A_ «AED»)) = A_ «DCE» + цвет (красный) отмена (цвет ( черный) (A_ «AED»)) #
#A_ «ABE» = A_ «DCE» #

Хотя я проиллюстрировал это доказательство с помощью равнобедренной трапеции, ни одна из работ не относилась конкретно к правильной трапеции. Следовательно, боковые треугольники любой трапеции можно показать равными, используя те же рассуждения.

Соотношение площадей треугольников в трапеции

В сегодняшнем уроке мы будем использовать аналогичные треугольники и треугольники одинаковой высоты, чтобы найти соотношение между площадями треугольников, образованных пересечением диагоналей трапеции.

Диагонали трапеции образуют 2 одинаковых треугольника. и два других набора треугольников с одинаковым основанием и высотой. Это свойство используется во многих геометрических задачах, которые требуют от вас определения соотношения площадей этих треугольников или соотношения сторон.

Вот один пример.

Задача

ABCD — это трапеция (AB || CD). Его диагонали AC и BD пересекаются в точке O. Отношение площадей треугольников △ ABO и △ CDO составляет 16:25. Найдите отношение площади △ AOD к площади трапеции.

Стратегия

Задачи, требующие определения соотношения площадей или соотношения отрезков линий, часто основываются на использовании похожих треугольников и того факта, что если ΔABC∼ ΔDEF, то AB / DE = BC / EF = AC / DF.

В других случаях, если мы просто сравниваем площади треугольников, они часто используют тот факт, что отношение площадей треугольников с одинаковым основанием равно отношению их высот, а отношение площадей треугольников с одинаковым основанием высота равна соотношению их оснований.Пример такой проблемы можно найти на этой странице.

Итак, в этой проблеме — у нас есть и то, и другое! Диагонали трапеции образуют два одинаковых треугольника (△ ABO и △ CDO) и несколько пар треугольников с одинаковым основанием (△ ACD и △ BDC; △ DBA и △ CAB) или одинаковой высоты (△ ABO и △ ADO; △ BAO и △ BOC).

И еще один намек в постановке задачи: соотношение между двумя треугольниками △ ABO и △ CDO составляет 16:25.

Это и подсказка, на которую похожи треугольники (△ ABO и △ CDO), и каков масштабный коэффициент — поскольку мы знаем, что отношение площадей подобных треугольников есть коэффициент масштабирования в квадрате, а 16 и 25 равны. квадраты целых чисел (4 и 5 соответственно).

Proof

(1) AB || CD // Учитывая
(2) ∠ACD≅ ∠CAB // Чередующиеся внутренние углы между двумя параллельными линиями
(3) ∠ABD ≅ ∠BDC // Чередующиеся внутренние углы между двумя параллельными линии
(4) ∠BOA ≅ ∠DOC // Вертикальные углы
(5) ΔABO∼ ΔCDO // (2), (3), (4), угол-угол-угол
(6) Площадь _ABO / Площадь _CDO = 16/25 // Дано
(7) AO / OC = BO / OD = √ (16/25) = & frac45; // Отношение площадей подобных треугольников — это квадрат масштабного коэффициента
(8) Площадь _ABO / Площадь _ADO = & frac45; // Соотношение площадей треугольников одинаковой высоты одинаково s отношение их оснований
(9) Площадь _ABO / Площадь _BOC = & frac45; // Соотношение площадей треугольников одинаковой высоты одинаковое s отношение их оснований

Установить площадь _ABO = 16k.Тогда Area _CDO = 25k, а Area _ADO = Area _BOC = 20k.

(10) Площадь _ABCD = Область _ABO + Область _ADO + Область _CDO + Область _BOC = 16k + 20k + 25k + 20k = 81k |
(11) Площадь _AOD / Площадь _ABCD = 20k / 81k = 20/81

Свойства промежуточного сегмента трапеции — Проблема 1

Промежуточный сегмент трапеции соединяет середины двух конгруэнтных сторон трапеции и параллелен паре параллельных сторон.

Длина среднего сегмента — это сумма двух оснований, деленная на 2. Помните, что основания трапеции — это две параллельные стороны.

Чтобы найти углы внутри трапеции, помните, что, поскольку две стороны параллельны, другие стороны можно рассматривать как поперечные, образуя соответствующие углы и те же внутренние боковые углы. Используя то, что известно о соответствующих и одинаковых внутренних углах, можно найти размеры недостающих углов трапеции.

В этой задаче нас просят найти длину этого сегмента и меру этих двух углов. Что ж, давайте начнем с того, что мы знаем об этой проблеме?

Хорошо, я вижу, что эта точка — середина этой стороны, а эта точка — середина этой другой стороны. Поскольку у меня две параллельные стороны, это будет трапеция, и, поскольку это средние точки, я создал промежуточный сегмент и две ключевые вещи, которые я знаю о средних сегментах, первое — это то, что они параллельны двух оснований, поэтому я вернусь сюда и отмечу этот средний сегмент как параллельный, и я также знаю, что длина моего среднего сегмента — это среднее значение двух оснований, поэтому, если вы сложите две базы и разделенные на 2, вы получите длину вашего среднего сегмента.

Итак, давайте найдем первый. ‘a’ — это расстояние до нашего среднего сегмента, поэтому я собираюсь сказать, что a равно среднему значению ваших двух оснований, которые равны 10 и 18. Итак, 10 и 18 равны 28, поэтому a равно 28, деленному на 2, поэтому a это 14, и наши единицы здесь — сантиметры, поэтому я собираюсь написать это 14 см.

Теперь найдем x. Что ж, поскольку эти две линии параллельны, я могу думать об этой стороне прямо здесь как о поперечине, создающей соответствующие углы, которые всегда совпадают. Итак, x конгруэнтен 55 градусам, потому что соответствующие углы должны быть конгруэнтными.Теперь, чтобы найти y, мне нужно будет смотреть на эту сторону как на поперечную.

Несколько способов выяснить это. Первый способ — сказать, что 120 градусов соответствует этому углу прямо здесь, поэтому этот угол должен быть 120 градусов. 120 градусов и y находятся на одной стороне поперечной, и они находятся между двумя параллельными линиями, поэтому это одна и та же сторона, что означает, что y плюс 120 градусов должны быть дополнительными, поэтому, если я вычитаю 120 градусов, я вижу, что y должен быть 60 градусов.

Итак, два ключевых момента в решении этой проблемы: один — помнить, что средний сегмент и трапеция параллельны двум основаниям, а их длина равна сумме двух оснований, деленных на 2.

Как найти углы в трапеции

В геометрии трапеция — это четырехугольник (четырехсторонняя фигура), в котором только одна пара противоположных сторон параллельна. Трапеции также известны как трапеции. Параллельные стороны трапеции называются основаниями. Непараллельные стороны называются ножками. Трапеция, как и круг, имеет 360 градусов. Поскольку у трапеции четыре стороны, у нее четыре угла. Трапеции названы по их четырем углам или вершинам, например, «ABCD».»

Определите, является ли трапеция равнобедренной трапецией. Равнобедренные трапеции имеют линию симметрии, разделяющую каждую половину. Ноги трапеции равны по длине, как и диагонали. В равнобедренной трапеции углы, имеющие общее основание, имеют одинаковую длину. та же мера. Дополнительные углы, которые являются углами, примыкающими к противоположным основаниям, имеют в сумме 180 градусов. Эти правила можно использовать для вычисления угла.

Перечислите данные измерения. Вам может быть предоставлено измерение угла или база.Или вам может быть дано измерение среднего сегмента, который параллелен обоим основаниям и имеет длину, равную среднему значению двух оснований. Используйте данные измерения, чтобы определить, какие измерения, если не угол, можно рассчитать. Эти рассчитанные измерения затем можно использовать для расчета угла.

Напомним соответствующие теоремы и формулы для решения измерений оснований, опор и диагоналей. Например, теорема 53 утверждает, что базовые углы равнобедренной трапеции равны.Теорема 54 утверждает, что диагонали равнобедренной трапеции равны. Площадь трапеции (независимо от того, является ли она равнобедренной) равна половине длины параллельных сторон, умноженной на высоту, которая представляет собой перпендикулярное расстояние между сторонами. Площадь трапеции также равна произведению среднего сегмента и высоты.

При необходимости нарисуйте прямоугольный треугольник внутри трапеции. Высота трапеции образует прямоугольный треугольник, который подразумевает угол трапеции.Используйте измерения, такие как площадь трапеции, чтобы вычислить высоту, опору или основание, которые разделяет треугольник. Затем найдите угол, используя правила измерения углов, применимые к треугольникам.

Иллюстративная математика

IM Комментарий

Цель этого задания — дать учащимся определение трапеции. Есть два конкурирующих определения слова «трапеция»:

Исключительное определение трапеции гласит, что трапеция имеет ровно одну пару параллельных противоположных сторон.
Включенное определение гласит, что трапеция имеет по крайней мере одну пару параллельных противоположных сторон.

Иногда люди говорят, что у трапеций «одна пара противоположных сторон параллельна», поэтому остается неясным, может быть их больше одной или нет. Вторая часть задания подталкивает учащихся к четкому пониманию того, какую версию они собираются. Из-за того, что учащиеся должны внимательно относиться к определениям, эта задача в значительной степени опирается на MP6, «Заботиться о точности».

После того, как учащиеся сформулируют определения для себя или с партнером, класс должен обсудить определение вместе. Класс должен выбрать одно определение, с которым все согласны, поскольку смысл четко сформулированных определений состоит в том, что мы все знаем, что говорим об одном и том же. Хотя оба определения правомерны, преимущество инклюзивного определения состоит в том, что любая теорема, верная для трапеции, верна и для параллелограмма. Кроме того, в своем исследовании Классификация четырехугольников (Information Age Publishing, 2008) Usiskin et al.заключить,

Преобладание преимуществ инклюзивного определения трапеции заставило все статьи, которые мы могли найти по этому предмету, и большинство книг по геометрии, выпускаемых колледжем, отдать предпочтение инклюзивному определению.

Инклюзивное определение устанавливает взаимосвязь между параллелограммами и трапециями, которая в точности аналогична взаимосвязи между квадратами и прямоугольниками; определение прямоугольников включает квадраты так же, как включающее определение трапеций включает параллелограммы.

Дополнительную информацию об этих проблемах см. В документе K-6 Geometry Progressions: http://commoncoretools.me/wp-content/uploads/2012/06/ccss_progression_g_k6_2012_06_27.pdf.

Решение

Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Он может иметь прямые углы (прямая трапеция) и равнобедренные стороны, но это не обязательно.
Иногда люди определяют трапеции, чтобы иметь по крайней мере одну пару противоположных сторон, параллельных, а иногда говорят, что есть одна и только одна пара противоположных сторон, параллельных.Параллелограмм соответствует «по крайней мере одному» варианту определения, потому что он имеет две пары противоположных сторон, параллельных друг другу, поэтому он попадает в категорию как трапеции, так и параллелограмма. Параллелограмм не подходит под «один-единственный» вариант определения. То, как студенты ответят на этот вопрос, зависит от их определения.

Примечание: если учащиеся дают разные определения, поначалу это нормально. Однако, чтобы иметь возможность обсуждать математические идеи в будущем, класс должен остановиться на одной из этих версий и двигаться дальше.См. Примечание в комментарии, поощряющее версию определения, включающую параллелограммы.

КАЛЬКУЛЯТОР ТРАПЕЗОИДА

3 калькулятора трапеций
Прокрутите вниз для получения инструкций и определений.
Щелкните здесь, чтобы просмотреть информацию обо всех четырехугольниках.
Чтобы получить калькулятор воздушных змеев, щелкните здесь.
Для калькулятора параллелограммов щелкните здесь параллелограммы.
Для калькулятора ромбов щелкните здесь ромбы.
Для калькулятора квадратов и прямоугольников щелкните здесь квадраты.
Площадь трапеции = ((сумма оснований) ÷ 2) • высота
Линии BC и AD параллельны и называются основаниями.
Линии AB и DC являются непараллельными сторонами и называются участками .
Линии AC (или q ) и BD (или p ) называются диагоналями
Линия, перпендикулярная линиям AD и BC, называется высотой или высотой.

Линия, параллельная линиям AD и BC, находится в середине линий AB и DC.
и называется средним сегментом или средним сегментом .
Длина медианы = (Линия AD + Линия BC) ÷ 2
Трапеции имеют 2 пары из смежных углов (A и B) и (B и C), которые являются дополнительными (добавить 180 °).

Для использования этого калькулятора вам потребуется
как базовой длины, так и площади.

Для использования этого калькулятора вам потребуется
как длины основания, так и высоты.

* * * * * * * * * E x a m p l e * * * * * * * * *
Трапеция имеет основания 30 и 55 сантиметров в длину, а непараллельные стороны (или ножки ) имеют длину 15 и 20 сантиметров.
Какова площадь трапеции?
Следуя диаграмме, мы обозначим 4 стороны как:
a = 55 b = 15 c = 30 d = 20
Прежде чем мы сможем использовать формулу площади, мы сначала должны определить высоту трапеции.
(высота) ² = (a + b-c + d) • (-a + b + c + d) • (ab-c + d) • (a + bcd) ÷ (4 • (a -c) ²)
(высота) ² = (55 + 15-30 + 20) • (-55 + 15 + 30 + 20) • (55-15-30 + 20) • (55 + 15-30-20) ÷ (4 • (55-30) ²)
(высота) ² = (60) • (10) • (30) • (20) ÷ (4 • (25) ²)
(высота) ² = 360,000 ÷ 2,500
(высота) ² = 144
высота = 12 см
Теперь воспользуемся формулой площади:
площадь трапеции
= ((сумма оснований) ÷ 2) • высота
площадь трапеции = ((55 + 30) ÷ 2) • 12
площадь трапеции = 510 см² Чтобы узнать, как рассчитать трапецию площадь без с использованием формул, нажмите здесь.
* * * * * * * * * Трапеции * * * * * * * * *
ВСЕ ТРАПЕЗОИДЫ имеют следующие
properties:
1) ОДНА пара противоположных сторон параллельна.
(BC и AD)
2) Сумма углов, прикрепленных к той же опоре = 180 °
∠ ‘A’ плюс ∠ ‘B’ = 180 °
∠ ‘C’ плюс ∠ ‘D’ = 180 °
Стоит упомянуть 4 особых случая трапеций.
Равнобедренная трапеция имеет
обе ноги одинаковой длины.AB = CD
Обе диагонали равны. AC = BD
Углы нижнего основания равны. ∠ A = ∠ D
Углы верхнего основания равны. ∠ B = ∠ C
Уголки, прикрепленные к той же опоре, являются дополнительными. ∠ A + ∠ B = 180 ° ∠ C + ∠ D = 180 °
Противоположные углы являются дополнительными. ∠ A + ∠ C = 180 ° ∠ B + ∠ D = 180 °
Правая трапеция имеет
два прямых угла.
Острая трапеция имеет два острых угла (A и D), расположенных на каждой стороне длинного основания (линия AD) и
, у него два тупых угла (B и C) на каждой стороне короткого основания . (линия BC).
Тупая трапеция имеет два тупых противоположных угла (A и C) и два острых противоположных угла (B и D).
ИЛИ (с использованием того же рисунка)
он имеет один острый угол и один тупой угол на на каждом основании : углы (B и C) и углы (A и D)
По умолчанию установлено 5 значащих цифр, но вы можете это изменить.
введя другое число в поле выше.
Ответы отображаются в экспоненциальном формате и для удобства чтения числами между
.001 и 1000 будут отображаться в стандартном формате (с одинаковым количеством
значащие цифры.)
Ответы должны отображаться правильно, но есть несколько браузеров, которые будут отображать
нет вывода вообще. Если да, введите ноль
в поле выше. Это устраняет всякое форматирование, но это лучше, чем не видеть
вывод вообще.
Указатель возврата к геометрии
_____________________
Вернуться на главную страницу
Авторские права © 1999 —
1728 Программные системы

Понимание иерархической классификации четырехугольников через упорядоченное отношение в соответствии с диагональными свойствами

Абстрактные

Цель этой статьи — предложить дополнительную среду обучения для понимания иерархической классификации четырехугольников для учащихся средней школы или учащихся с высшим образованием.Три диагональных свойства: «быть конгруэнтным, перпендикулярным» и «разделять друг друга в определенном соотношении» и все возможные комбинации этих свойств были использованы для построения четырехугольников в среде динамической геометрии. В соответствии с диагональными свойствами можно было построить 15 четырехугольников, а отношение порядка было построено на 16 четырехугольниках, включая четырехугольник, который не имел диагонального свойства. Определение отношения порядка таково: «любой четырехугольник Qi включен в другой четырехугольник Qj, если и только если Qi обладает всеми диагональными свойствами Qj.«В соответствии с этим соотношением была создана диаграмма упорядоченных отношений, и было обнаружено, что это отношение не было хорошо упорядоченным. После построения динамической геометрии каждого четырехугольника были отмечены наблюдения о диагональных свойствах специальных четырехугольников. Кроме того, условия при которые четырехугольник может быть вогнутым.Этот альтернативный подход к построению четырехугольника предоставил возможность определять четырехугольники более экономичным и менее запутанным способом, чем использование углов и свойств сторон.Например, «Воздушный змей — это четырехугольник, диагонали которого перпендикулярны и по крайней мере одна из диагоналей делит другую пополам» и «Трапеция — это четырехугольник, диагонали которого делят друг друга в одинаковом соотношении».

Цитата

Кабака, Т. (2017). Понимание иерархической классификации четырехугольников через упорядоченное отношение согласно диагональным свойствам. Международный журнал математического образования в науке и технологиях, 48 (8), 1240-1248.Получено 17 июля 2021 г. с сайта https://www.learntechlib.org/p/188557/.