|
Главная > Учебные материалы > Математика: Дифференциальные уравнения | ||||
|
| ||||
|
1.Понятие дифференциального уравнения. 2.Дифференциальное уравнение 1-го порядка. | ||||
|
16 17 18 19 20 21 22 23 24 | ||||
1.
| ||||
Дифференциальным уравнением называется уравнение, которое включает в себя функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Производные, которые содержатся в уравнении, могут быть различных порядков. Простейшее дифференциальное уравнение содержит функцию от одной переменной. | ||||
Дифференциальное уравнение в общем виде можно записать так: | ||||
|
Рассмотрим пример. Пусть задано уравнение x — y’ = 0
|
Рис.1 | |||
Если дифференциальное уравнение содержит функцию или вектор-функцию от одной переменной, то оно называется обыкновенным. Если неизвестная функция содержит две или большее число переменных, то дифференциальное уравнение называется уравнением в частных производных. Порядком дифференциального уравнения называется максимальный порядок входящей в него производной неизвестной функции. | ||||
2.Дифференциальное уравнение 1-го порядка. | ||||
Обыкновенное дифференциальное уравнение 1-го порядка можно записать в виде:
| ||||
Если уравнение можно представить в виде:
| ||||
Пример 1.
| ||||
| ||||
Пример 2. | ||||
Пример 3.
Яхта движется в спокойной воде со скоростью v = 45км/ч. На полном ходу ее двигатель был выключен. Через t = 60c. скорость яхты уменьшилась до v1 = 6 км/ч. Найти скорость яхты через 3 мин после остановки двигателя. Считать, что сопротивление воды пропорционально скорости движения яхты. | ||||
|
16 17 18 19 20 21 22 23 24 | ||||
Дифференциальные уравнения первого порядка
Далее в тексте – функции своих аргументов.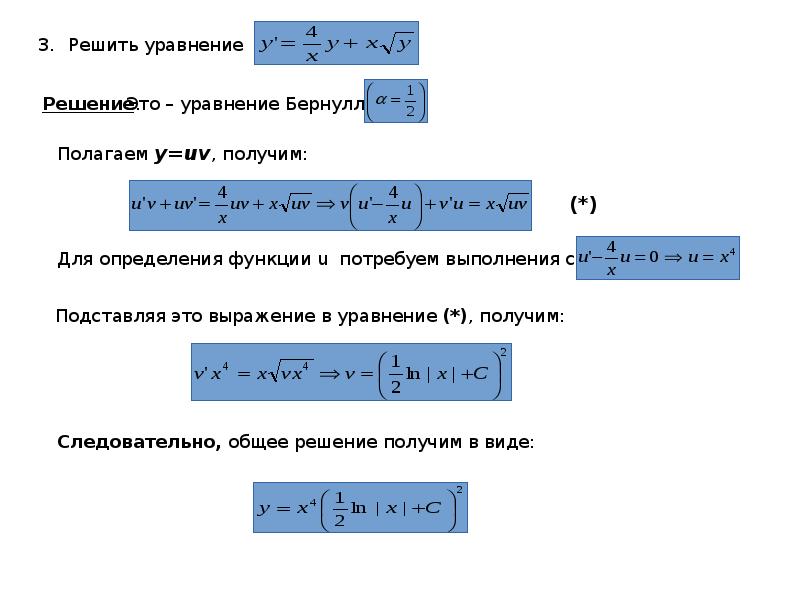 Штрих ′ означает производную по аргументу. – постоянные.
Штрих ′ означает производную по аргументу. – постоянные.
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Как решать дифференциальные уравнения первого порядка
Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .
Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.
Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.
Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.
Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.
Уравнения с разделяющимися переменными
;
.
Делим на и интегрируем. При получаем:
.
Подробнее >>>
Уравнения, приводящиеся к уравнениям с разделяющимися переменными
Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>
Однородные уравнения
Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>
Уравнения, приводящиеся к однородным
Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>
Обобщенные однородные уравнения
Делаем подстановку . Получаем однородное уравнение в переменных и .
Получаем однородное уравнение в переменных и .
Подробнее >>>
Линейные дифференциальные уравнения
Есть три метода решения линейных уравнений.
1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>
2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:
Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>
Уравнения Бернулли
Подстановкой уравнение Бернулли приводится к линейному уравнению.
Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
Уравнения Риккати
Оно не решается в общем виде. Подстановкой
уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:
оно приводится к виду:
,
где .
Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>
Уравнения Якоби
Решается подстановкой:
.
Подробнее >>>
Уравнения в полных дифференциалах
При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.
Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>
Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция, при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>
Уравнения, не решенные относительно производной y’
Уравнения, допускающие решение относительно производной y’
Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, допускающие разложение на множители
Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;
;
Подробнее >>>
Уравнения, не содержащие x и y
Здесь – постоянная:
,
где – корень уравнения
.
Подробнее >>>
Уравнения, не содержащие x или y
или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .
Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>
Уравнения, разрешенные относительно y
Уравнения Клеро
Такое уравнение имеет общее решение
Подробнее >>>
Уравнения Лагранжа
Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>
Уравнения, приводящиеся к уравнению Бернулли
Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
Дифференциальные уравнения I-го порядка
Как я и обещал в своей предыдущей статье, сегодня продолжим более детально изучать Дифференциальные уравнения.
§3. Однородные дифференциальные уравнения I-го порядка
Функцию f(x, y) называют однородной функцией порядка mотносительно своих аргументовxиy, если она выполняется тождество
f(tx, ty)= tmf(x, y) (3.1), где t – любой множитель.
Так, например, функции x2y– xy2, 2x2 – 3xy однородные: первая – третьего порядка, вторая – первого.
Определение 3.1. Дифференциальное уравнение y’ = f(x, y) (3.2) называется однородным, если его правая часть функция f(x, y) является однородной функцией нулевого порядка относительно своих аргументов x и y.
Интегрирование однородного уравнения с помощью специальной подстановки сводится к интегрированию уравнения с отделяемыми переменными.
Действительно, учитывая нулевой порядок однородности функции f(x, y), для любого t имеем f(tx, ty)= f(x, y).
В частности, если t = 1/x, получим:
Уравнение (3.2) запишется в виде
Введем вспомогательную неизвестную функцию с помощью подстановки: y = x· u, y’ = u + x· u’.
Уравнение (3.2) записывается в виде u + x· u’ = φ(u),
в котором переменные разделяются:
Отсюда находим общий интеграл уравнения:
где C=const.
Наконец, после вычисления интегралов и замены вспомогательной функции u ее выражением через x и y, найдем решение однородного уравнения.
Пример 3.1. Решить “дифур”
Решения. Это однородное Дифференциальное уравнение I-го порядка. Применим подстановку y = x· u, y’ = u + x· u’.
Применим подстановку y = x· u, y’ = u + x· u’.
Тогда получим уравнение с переменными, которые можно разделить, относительно вспомогательной функции u.
u +xu’ = u(ln u + 1)
xu’ = uln u
Решая его, получим
Это ОР уравнения.
Замечания. Уравнение вида P(x, y)dx + Q(x, y)dy = 0 (3.4), в котором функции P(x, y) и Q(x, y) – однородные, относительно своих аргументов x и y функции одного и того же измерения, является однородным и заменой y = ux сводится к уравнению с разделяемыми переменными.
Пример 3.2. Решить “дифур”
Решение. Это однородное уравнение, так как коэффициенты при dxи dy являются однородными функциями I-го порядка. Сделаем замену
y = ux, dy = xdu + udx
Получим “дифур” с переменными, которые можно разделить:
Заменив вспомогательную функцию u = y/x получаем, после преобразований, общий интеграл уравнения:
Пример 3.3. Решить “дифур”
Решения. Произведем следующюю замену
Получим
§4. Линейные дифференциальные уравнения I-го порядка. Уравнение Бернулли
Определение 4.1. Дифференциальное уравнение I-го порядка называется линейным, если и сама неизвестная функция и ее производная входят в это уравнение только в первой степени и не содержит их произведения.
В общем виде линейное дифференциальное уравнения I-го порядка:
y’ + P(x)y = Q(x) (4.1)
Используют несколько приемов решения дифференциального уравнений (4.1). Мы рассмотрим здесь метод Бернулли, согласно которому решение в следующем виде y(x) = u(x) · v(x) (4.3).
Тем самым искомыми становятся функции u(x) и v(x), одну из которых можно выбрать произвольно, а вторая – должна определяться уравнением.
Дифференцируем обе части равенства (4.3)
Подставим выражения для y(x) и y‘(x) в уравнение (4.1). Имеем
Подберем функцию v так, чтобы выполнялось равенство
Тогда функция u должна удовлетворять уравнению
Уравнение (4.4) является уравнением с переменными, которые можно разделить,
В результате интегрирования получим.
Если C = 0, получим
Подставляя значение v(x) в уравнение (4.5), получим относительно u(x) дифференциальное уравнение I-го порядка с переменными, которые можно разделить,
Окончательно по формуле (4.3) получим ОР уравнения (4.1) в виде
При решении конкретных линейных дифференциальных уравнений I-го порядка можно пользоваться готовыми формулами (4.6) или использовать прием Бернулли.
Пример 4.1. Решить “дифур”
Решения. Это линейное неоднородное уравнение I-го порядка, решаем методом Бернулли. Сведем его к виду (4.1.) (хотя это необязательно). Для чего обе части уравнения умножим на х. Получим:
y’ – 2xy = (x – x3)· ex2.
Произведем замену
y= u· v.
Дифференцируем это выражение по x:
Заменим в уравнении y’ и y выражениями через u и v, получим
Сгруппируем члены, содержащие функцию u, и вынесем эту функцию за скобки. Получим:
Найдем теперь такую функцию u, чтобы
При этом условии функция u(x) должна удовлетворять уравнению
Решим уравнение (1), разделив переменные:
По определению логарифма
Подставив найденное значение в уравнение ,получим следующий результат:
Это “дифур” с переменными, которые можно разделить,. Проинтегрировав его, получим следующее
ОР уравнения получим в виде
Пример 4.2. К линейному уравнению заменой z = y1-α сводят уравнения
y’ + P(x) · y = Q(x) · yα, α≠ 0, α≠ 1 (4.7), которое называется уравнением Бернулли.
Пример 4.3. Решить “дифур” со следующим начальным условием.
Имеем уравнение Бернулли. Разделив наш “дифур” на √y, получим
Сделаем замену
Получим линейное уравнение
Из предыдущего следует
Тогда, искомое ОР “дифура” имеет такой вид
Перейдем к поиску частного решения, удовлетворяющего начальному условию y(0)= 4, отсюда
Тогда частное решение первоначального “дифура” имеет такой вид
Уважаемые студенты, записывайтесь на мои занятия и я помогу Вам разобраться с «Дифурами» раз и навсегда!
Онлайн репетитор Андрей Зварыч.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Дифференциальные уравнения первого порядка
Уравнение
F(x,
y,
y
‘) = 0,
где
y
= y(x)
— неизвестная, непрерывно дифференцируема
на (a,b)
функция, называется обыкновенным
дифференциальным уравнением первого
порядка.
Функция
y
= y(x)
называется решением
дифференциального уравнения
F(x,
y,
y
‘) = 0, если она непрерывно дифференцируема
на (a,b)
и F(x,
y(x),
y
‘(x))
≡ 0 для всех x
из (a,b)
.
График
решения дифференциального уравнения
называют интегральной
кривой дифференциального уравнения.
Дифференциальное
уравнение 1–го порядка имеет бесконечно
много решений. Для того чтобы выделить
единственное решение, нужно задать
дополнительные (начальные) условия.
Задача
отыскания решения y
= y(x)
уравнения F(x,
y,
y
‘ ) = 0 , удовлетворяющего условию y(x0)
= y0,
называется задачей
Коши (или
начальной задачей).
Условие
y(x0)
= y0
— начальное условие.
Любое
конкретное решение y
= y(x)
(решение задачи Коши) уравнения 1–го
порядка, называется частным
решением уравнения.
Общее
решение уравнения, записанное в неявной
форме Φ(x,
y)
= C,
называется общим
интегралом уравнения.
Частное
решение уравнения, записанное в неявной
форме Φ(x,
y)
= 0, называется частным
интегралом уравнения.
Уравнение
1-го порядка, разрешенное относительно
производной, называют уравнением,
записанными в нормальной форме:
Уравнения
первого порядка часто записывают в
дифференциальной
форме:
M(x,
y)dx
+ N(x,
y)dy
= 0.
Решение
такого уравнения можно искать как в
виде y
=
y(x)
, так и в виде x
=
x(y)
.
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное
уравнение
вида
или
называется
дифференциальным
уравнением с разделяющимися переменными.
Заметим,
что в данных дифференциальных
уравнениях
каждая из функций зависит только от
одной переменной, т.е. происходит
разделение переменных.
Для
решения такого дифференциального
уравнения
необходимо домножить или разделить обе
части дифференциального
уравнения
на такое выражение, чтобы в одну часть
уравнения входили только функции от
и,
в другую часть уравнения — только функции
от,.
Затем в полученномдифференциальном
уравнении
надо проинтегрировать обе части:
Следует
заметить, что при делении обеих частей
дифференциального
уравнения
на выражение, содержащее неизвестные
и,
могут быть потеряны решения, обращающие
это выражение в ноль.
Обратим
внимание, что дифференциальные
уравнения с разделяющимися переменными
легко сводятся к интегрированию. В общем
случае получаем получаем два неопределенных
интеграла.
Пример
1 — решить дифференциальное уравнение
Заметим,
что в дифференциальном уравнении можно
разделить переменные, т.е. получаем,
дифференциальное
уравнение с разделяющимися переменными:
Пример
2 — решить дифференциальное уравнение
Заметим,
что в дифференциальном уравнении можно
разделить переменные, т.е. получаем,
дифференциальное
уравнение с разделяющимися переменными:
Пример
3 — решить дифференциальное уравнение
Заметим,
что в дифференциальном уравнении можно
разделить переменные, т.е. получаем,
дифференциальное
уравнение с разделяющимися переменными:
Линейные дифференциальные уравнения первого порядка.
Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. Научно-издательский центр «Регулярная и хаотическая динамика». 2000.
1. Линейные уравнения первого порядка.
Уравнение $$y’+P(x)y=Q(x)\qquad (1)$$ называется линейным. Чтобы его решить, надо сделать замену переменных $y=u(x)v(x),$ где $u(x) — $ решение однородного уравнения $u’+P(x)u=0.$ Это уравнение решается методом разделения переменных.
Далее, делаем обратную замену. $y’=(uv)’=u’v+uv’.$ Следовательно,
$$u’v+v’u+P(x)uv=Q(x)$$
$$v(u’+P(x)u)+v’u=Q(x).$$
Заметим, что $u’+P(x)u=0.$ Следовательно, получили уравнения с разделяющимися переменными $$v’u=Q(x)\\ v’=\frac{Q(x)}{u(x)}\Rightarrow v(x)=\int\frac{Q(x)}{u(x)}dx+C.2}$ те же рассуждения побуждают нас искать частное решение в виде $y=\frac{a}{x}.$ Подставляя $y=\frac{a}{x}$ в уравнение, найдем постоянную $a.$
Дифференциальные уравнения первого порядка с разделяющимися переменными
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения 1-го порядка с разделяющимися
переменными
Преподаватель естественнонаучных дисциплин Даниленко С.В.
Определение: Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х , искомую функцию у и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
F(x, y, y’)=0, F(x, y, y’’)=0, …, F(x, y, y (n) )=0.
Определение: Порядком дифференциального уравнения называется порядок старшей производной, входящей в данное уравнение.
Определение: Решением дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Определение: Общим решением дифференциального уравнения называется такое решение, в которое входят столько независимых произвольных постоянных, каков порядок уравнения.
Определение: Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных.
Определение: Дифференциальным уравнением 1–го порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Определение: Дифференциальным уравнением с разделяющимися переменными называется уравнение вида .
Для решения этого уравнения нужно сначала разделить переменные , а затем проинтегрировать обе части уравнения
Пример 1. Найти общее решение дифференциального уравнения
Решение. Интегрируем обе части уравнения:
Оба интеграла – табличные, следовательно
Пример 2. Найти общее решение дифференциального уравнения (1+y)dx=(x-1)dy
Решение . Разделив переменные, имеем
ln (x-1)=ln (1+y)+C → ln (x-1)=ln (1+y)+ln C
Общее решение: x-1=C (1+y)
Пример 3. Найти частное решение дифференциального уравнения y dу = x dх; удовлетворяющее начальным условиям у=4 при х = — 2
Решение. Интегрируем обе части уравнения:
16=4 +C C = 12
.
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С мы написали
Пример 4. Найти общее решение уравнения
Решение . Разделив переменные, имеем
Интегрируем обе части полученного уравнения:
Потенцируя последнее равенство, получим
х 2 =С(1+у 2 ).
Это и есть общее решение данного уравнения.
где f(x) и (х) – функции от х, называются линейными дифференциальными уравнениями 1-го порядка. В частном случае f(x) и (х) могут быть постоянными величинами.
Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки y=u z, где u и z – новые функции от х.
Линейные дифференциальные уравнения 1-го порядка
Определение. Уравнение вида или
ДОМАШНЕЕ ЗАДАНИЕ
1. Найти общее решение дифференциального уравнения:
а)
б)
2. Найти частное решение дифференциального уравнения (1+ y) dx = (1-x) dy; удовлетворяющее начальным условиям у=3 при х = — 2
Виды нелинейных дифференциальных уравнений 1-го порядка
ПГУ им. Т.Г. Шевченко
Курсовая работа
Виды нелинейных дифференциальных уравнений 1-го порядка
Выполнил:
студент 211 группы
специальности «ИКТиСС»
Бирт Игорь Андреевич
Проверил:
Тирасполь 2014 год
Содержание
1.Введение 3 стр.
2.Виды дифференциальных уравнений 4 стр.
3.Практическая часть 8 стр.
4.Литература 20 стр.
- ВВЕДЕНИЕ
Дифференциальное уравнение уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.
Порядок дифференциального уравнения наибольший порядок производных, входящих в него.
Процесс решения дифференциального уравнения называется интегрированием.
Все дифференциальные уравнения можно разделить на линейные и не линейные.
Нелинейное дифференциальное уравнение — дифференциальное уравнение (обыкновенное или с частными производными), в которое по крайней мере одна из производных неизвестной функции (включая и производную нулевого порядка — саму неизвестную функцию) входит нелинейно.
Иногда под Н.Д.У. понимается наиболее общее уравнение определенного вида. Напр., нелинейнымобыкновенным дифференциальным уравнением 1-го порядка наз. уравнение с произвольной
функцией при этом линейное обыкновенное дифференциальное уравнение 1-го порядка соответствует частному случаю
Н. д. у. с частными производными 1-го порядка для неизвестной функции z
от независимых переменных имеет вид:
где F- произвольная функция своих аргументов;
Виды нелинейных дифференциальных уравнений 1-го порядка:
Уравнения с разделенными переменными
П1.
Общий интеграл
П2.
Общий интеграл
Уравнение в полных дифференциалах
Где
Существует такая функция u(x, y), что
Общий интеграл уравнения в полных дифференциалах u(x, y) = C.
Функция u может быть представлена в виде
Однородное уравнение
где P(x, y), Q(x, y) — однородные функции одной и той же степени
.
Подстановка y = ux, dy = xdu + udx переводит однородное уравнение в линейное относительно функции u:
Уравнение вида
1. Если прямые и пересекаются в точке
(x0; y0), то замена приводит его к однородному уравнению
2. Если прямые и параллельны, то замена приводит к уравнению с разделяющимися переменными
Уравнение Бернулли
Подстановкой сводится к линейному
Уравнение Риккати
Если известно какое-либо из решений , то уравнение сводится к
линейному подстановкой .
Уравнение Лагранжа
Дифференцируя по x и полагая y’ = p, приходим к линейному уравнению относительно x как функции p:
Уравнение Клеро
— частный случай уравнения Лагранжа.
ПРАКТИЧЕСКАЯ ЧАСТЬ.
Уравнения Риккати
Решить дифференциальное уравнение
y’ = y + y2 + 1.
Решение.
Данное уравнение является простейшим уравнением Риккати с постоянными коэффициентами. Переменные x, y здесь легко разделяются, так что общее решение уравнения определяется в следующем виде:
Решить уравнение Риккати
Решение
Будем искать частное решение в форме:
Подставляя это в уравнение, находим:
Получаем квадратное уравнение для c:
Мы можем выбрать любое значение c. Например, пусть c = 2. Теперь, когда частное решение известно, сделаем замену:
Снова подставим это в исходное уравнение Риккати:
Как видно, мы получили уравнение Бернулли с параметром m = 2. Сделаем еще одну замену:
Разделим уравнение Бернулли на z2 (полагая, что z ≠ 0) и запишем его через переменную v:
Последнее уравнение является линейным и легко решается с помощью интегрирующего множителя:
Общее решение линейного уравнения определяется функцией
Теперь мы будем последовательно возвращаться к предыдущим переменным. Так как z = 1/v, то общее решение для z записывается следующим образом:
Следовательно,
Можно переименовать константу: 3C = C1 и записать ответ в виде
где C1 − произвольное действительное число.
Уравнения Бернули
Найти все решения дифференциального уравнения
Решение.
Данное уравнение является уравнением Бернулли с дробным параметром
m = 1/2. Его можно свести к линейному дифференциальному уравнению с помощью замены
Производная новой функции z(x) будет равна
Разделим исходное уравнение Бернулли на
Аналогично другим примерам на этой веб-странице, корень y = 0 также является тривиальным решением дифференциального уравнения. Поэтому можно записать:
Заменяя y на z, находим:
Итак, мы имеем линейное уравнение для функции z(x). Интегрирующий множитель здесь будет равен
Выберем в качестве интегрирующего множителя функцию u(x) = x. Можно проверить, что после умножения на u(x) левая часть уравнения будет представлять собой производную произведения z(x)u(x):
Тогда общее решение линейного дифференциального уравнения будет определяться выражением:
Возвращаясь к исходной функции y(x), записываем решение в неявной форме:
Итак, полный ответ имеет вид:
Уравнения с разделяющимися переменными
Найти все решения дифференциального уравнения
y’ = −xey.
Решение.
Преобразуем уравнение следующим образом:
Очевидно, что деление на ey не приводит к потере решения, поскольку ey > 0. После интегрирования получаем
Данный ответ можно выразить в явном виде:
В последнем выражении предполагается, что константа C > 0, чтобы удовлетворить области определения логарифмической функции.
Найти частное решение уравнения, при
y(0) = 0.
Решение.
Перепишем уравнение в следующем виде:
Разделим обе части на 1 + ex:
Поскольку 1 + ex > 0, то при делении мы не потеряли никаких решений. Интегрируем полученное уравнение:
Теперь найдем константу C из начального условия y(0) = 0.
Следовательно, окончательный ответ имеет вид:
Уравнение Клеро
Найти общее и особое решения дифференциального уравнения
y = xy’ + (y’)2
Решение
Полагая y’ = p, его можно записать в виде
Продифференцировав по переменной x, находим:
Заменим dy на pdx:
Приравнивая первый множитель к нулю, получаем:
Теперь подставим это во второе уравнение:
В результате получаем общее решение заданного уравнения Клеро. Графически, это решение представляется в виде однопараметрического семейства прямых. Приравнивая нулю второй сомножитель, находим еще одно решение:
Это уравнение соответствует особому решению дифференциального уравнения и в параметрической форме записывается как
Исключая p из системы, получаем следующее уравнение интегральной кривой:
С геометрической точки зрения, парабола
является огибающей семейства прямых, определяемых общим решением.
Найти общее и особое решения дифференциального уравнения
Решение.
Введем параметр y’ = p:
Дифференцируя обе части уравнения по переменной x, получаем:
Поскольку dy = pdx, то можно записать:
Рассмотрим случай dp = 0. Тогда p = C. Подставляя это в уравнение, находим общее решение:
Графически это решение соответствует однопараметрическому семейству прямых линий.
Второй случай описывается уравнением
Найдем соответствующее параметрическое выражение для y:
Параметр p можно исключить из формул для x и y. Возводя последние уравнения в квадрат и складывая их, получаем:
Полученное выражение является уравнением окружности радиусом 1, расположенным в начале координат. Таким образом, особое решение представляется единичной окружностью в плоскости xy, которая является огибающей для семейства прямых линий.
ЛИТЕРАТУРА
- Н.С. Пискунов «Дифференциальное и интегральное исчисление», том второй, издательство «Наука», Москва 1985
- В. Ф. Зайцев, А. Д. Полянин. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.
- К.Н. Лунгу, В.П. Норин и др. «Сборник задач по высшей математике», второй курс, Москва: Айрис-пресс, 2007
- Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.
- Источники информации в интернете.
PAGE \* MERGEFORMAT19
Дифференциальные уравнения — линейные уравнения
Показать общее уведомление
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Пол
6 мая 2021 г.
Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Линейные дифференциальные уравнения
Первым частным случаем дифференциальных уравнений первого порядка, который мы рассмотрим, является линейное дифференциальное уравнение первого порядка.В этом случае, в отличие от большинства случаев первого порядка, которые мы рассмотрим, мы действительно можем вывести формулу для общего решения. Общее решение выводится ниже. Однако мы рекомендуем вам не запоминать саму формулу. Вместо того, чтобы запоминать формулу, вы должны запомнить и понять процесс, который я собираюсь использовать для получения формулы. На самом деле с большинством проблем легче справиться, используя процесс, а не формулу.
Итак, давайте посмотрим, как решить линейное дифференциальное уравнение первого порядка.Помните, когда мы проходим этот процесс, цель состоит в том, чтобы прийти к решению в форме \ (y = y \ left (t \ right) \). Иногда легко упустить из виду цель, когда мы проходим через этот процесс впервые.
Чтобы решить линейное дифференциальное уравнение первого порядка, мы ДОЛЖНЫ начать с дифференциального уравнения в форме, показанной ниже. Если дифференциальное уравнение не в такой форме, то процесс, который мы собираемся использовать, не сработает.
\ [\ begin {уравнение} \ frac {{dy}} {{dt}} + p \ left (t \ right) y = g \ left (t \ right) \ label {eq: eq1} \ end {уравнение} \]
Где и \ (p (t) \), и \ (g (t) \) — непрерывные функции.Напомним, что быстрое и грязное определение непрерывной функции состоит в том, что функция будет непрерывной при условии, что вы можете рисовать график слева направо, даже не беря в руки карандаш / ручку. Другими словами, функция является непрерывной, если в ней нет дыр или разрывов.
Теперь мы собираемся предположить, что где-то в мире существует некоторая магическая функция, \ (\ mu \ left (t \ right) \), называемая интегрирующим коэффициентом . На этом этапе не беспокойтесь о том, что это за функция и откуда она взялась.Мы выясним, что такое \ (\ mu \ left (t \ right) \), когда у нас будет формула для общего решения.
Итак, теперь, когда мы предположили существование \ (\ mu \ left (t \ right) \), умножаем все в \ (\ eqref {eq: eq1} \) на \ (\ mu \ left (t \ right) \). Это даст.
\ [\ begin {уравнение} \ mu \ left (t \ right) \ frac {{dy}} {{dt}} + \ mu \ left (t \ right) p \ left (t \ right) y = \ mu \ left (t \ right) g \ left (t \ right) \ label {eq: eq2} \ end {уравнение} \]
Вот здесь и вступает в игру магия \ (\ mu \ left (t \ right) \).Мы собираемся предположить, что что бы ни было \ (\ mu \ left (t \ right) \), оно будет удовлетворять следующему.
\ [\ begin {уравнение} \ mu \ left (t \ right) p \ left (t \ right) = \ mu ‘\ left (t \ right) \ label {eq: eq3} \ end {уравнение} \]
Снова не беспокойтесь о том, как мы можем найти \ (\ mu \ left (t \ right) \), который будет удовлетворять \ (\ eqref {eq: eq3} \). Как мы увидим, при условии непрерывности \ (p (t) \) мы можем его найти. Итак, подставив \ (\ eqref {eq: eq3} \), мы приходим к.
\ [\ begin {уравнение} \ mu \ left (t \ right) \ frac {{dy}} {{dt}} + \ mu ‘\ left (t \ right) y = \ mu \ left (t \ right) g \ left (t \ right) \ label {eq: eq4} \ end {Equation} \]
На этом этапе мы должны признать, что левая часть \ (\ eqref {eq: eq4} \) — не что иное, как следующее правило продукта.\ prime} \, dt}} = \ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} \]
\ [\ begin {уравнение} \ mu \ left (t \ right) y \ left (t \ right) + c = \ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} \ label {eq: eq6} \ end {уравнение} \]
Обратите внимание, что сюда включена константа интегрирования \ (c \) из левой части интегрирования. Это жизненно важно. Если его не указывать, вы каждый раз будете получать неправильный ответ.
Последний шаг — это некоторая алгебра, которую нужно решить для решения, \ (y (t) \).
\ [\ begin {align *} \ mu \ left (t \ right) y \ left (t \ right) & = \ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} — c \\ y \ left (t \ right) & = \ frac {{\ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} — c} } {{\ mu \ left (t \ right)}} \ end {align *} \]
Теперь, с точки зрения обозначений, мы знаем, что постоянная интегрирования \ (c \) — это неизвестная константа, и поэтому, чтобы облегчить нашу жизнь, мы включим знак минус перед ней в константу и вместо этого будем использовать плюс. .Это НЕ повлияет на окончательный ответ решения. Итак, с этим изменением у нас есть.
\ [\ begin {уравнение} y \ left (t \ right) = \ frac {{\ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} + c}} {{\ mu \ left (t \ right)}} \ label {eq: eq7} \ end {уравнение} \]
Опять же, изменение знака константы не повлияет на наш ответ. Если вы решите сохранить знак минус, вы получите то же значение \ (c \), что и мы, за исключением того, что у него будет противоположный знак. Подключив \ (c \), мы получим точно такой же ответ.
С константами интеграции в этом разделе очень много шуток, так что вам нужно к этому привыкнуть. Когда мы делаем это, мы всегда будем стараться очень ясно дать понять, что происходит, и попытаться оправдать, почему мы сделали то, что мы сделали.
Итак, теперь, когда у нас есть общее решение для \ (\ eqref {eq: eq1} \), нам нужно вернуться и определить, что это за магическая функция \ (\ mu \ left (t \ right) \). . На самом деле это более простой процесс, чем вы думаете.\ prime} = p \ left (t \ right) \]
Как и в случае с процессом, прежде всего, нам нужно объединить обе стороны, чтобы получить.
\ [\ begin {align *} \ ln \ mu \ left (t \ right) + k & = \ int {{p \ left (t \ right) \, dt}} \\ \ ln \ mu \ left (t \ right) & = \ int {{p \ left (t \ right) \, dt}} + k \ end {align *} \]
Вы заметите, что константа интегрирования с левой стороны, \ (k \), была перемещена в правую часть и снова поглощена знаком минус, как мы это делали ранее.{\ int {{p \ left (t \ right) \, dt}}}} \ label {eq: eq8} \ end {уравнение} \]
Итак, теперь у нас есть формула для общего решения \ (\ eqref {eq: eq7} \) и формула для интегрирующего множителя \ (\ eqref {eq: eq8} \). Однако у нас есть проблема. У нас есть две неизвестные константы, и чем больше у нас неизвестных констант, тем больше у нас проблем в дальнейшем. Поэтому было бы неплохо, если бы мы смогли найти способ устранить одну из них (мы не будем
уметь устранить и то, и другое…. {\ int {{p \ left (t \ right) \, dt}}}} \ label {eq: eq10} \ end {формула} \]
Теперь реальность такова, что \ (\ eqref {eq: eq9} \) не так полезен, как может показаться.Часто проще просто выполнить процесс, который привел нас к \ (\ eqref {eq: eq9} \), чем использовать формулу. Мы не будем использовать эту формулу ни в одном из наших примеров. Нам нужно будет регулярно использовать \ (\ eqref {eq: eq10} \), поскольку эту формулу проще использовать, чем процесс ее получения.
Процесс решения
Процесс решения линейного дифференциального уравнения первого порядка выглядит следующим образом.
- Приведите дифференциальное уравнение в правильную начальную форму, \ (\ eqref {eq: eq1} \).
- Найдите интегрирующий коэффициент, \ (\ mu \ left (t \ right) \), используя \ (\ eqref {eq: eq10} \).
- Умножьте все в дифференциальном уравнении на \ (\ mu \ left (t \ right) \) и убедитесь, что левая часть становится правилом произведения \ (\ left ({\ mu \ left (t \ right) y \ left ( t \ right)} \ right) ‘\) и напишите это как таковое.
- Объедините обе стороны, убедитесь, что вы правильно справились с постоянной интеграции.
- Найдите решение \ (y (t) \).
Давайте поработаем пару примеров. Начнем с решения дифференциального уравнения, полученного нами в разделе «Поле направления».
Пример 1 Найдите решение следующего дифференциального уравнения.
\ [\ frac {{dv}} {{dt}} = 9,8–0,196 об. \]
Показать решение
Во-первых, нам нужно получить дифференциальное уравнение в правильной форме.
\ [\ frac {{dv}} {{dt}} + 0,196v = 9.{- 0,196т}} \]
Из решения этого примера мы теперь можем понять, почему постоянная интеграции так важна в этом процессе. Без него в этом случае мы получили бы одно постоянное решение \ (v (t) = 50 \). Используя постоянную интегрирования, мы получаем бесконечно много решений, по одному на каждое значение \ (c \).
Вернувшись в раздел поля направления, где мы впервые вывели дифференциальное уравнение, используемое в последнем примере, мы использовали поле направления, чтобы помочь нам наметить некоторые решения.Посмотрим, правильно ли мы их поняли. Чтобы набросать некоторые решения, все, что нам нужно сделать, это выбрать разные значения \ (c \), чтобы получить решение. Некоторые из них показаны на графике ниже.
Итак, похоже, мы неплохо сделали набросок графиков в секции поля направлений.
Теперь вспомните из раздела «Определения», что начальные условия позволят нам сосредоточиться на конкретном решении. В решениях дифференциальных уравнений первого порядка (не только линейных, как мы увидим) будет одна неизвестная константа, поэтому нам понадобится ровно одно начальное условие, чтобы найти значение этой константы и, следовательно, найти решение, к которому мы пришли.Начальное условие для дифференциальных уравнений первого порядка будет иметь вид
\ [y \ left ({{t_0}} \ right) = {y_0} \]
Напомним также, что дифференциальное уравнение с достаточным количеством начальных условий называется задачей начального значения (IVP). {- 0.{\ ln \, \, \ sec \ left (x \ right)}} = \ sec \ left (x \ right) \]
А интеграл сделать можно? Если нет, перепишите касательную обратно в синусы и косинусы, а затем используйте простую замену. Обратите внимание, что мы можем опустить столбцы абсолютного значения на секансе из-за ограничений на \ (x \). Фактически, это причина ограничений на \ (x \). Отметим также, что есть две формы ответа на этот интеграл. Они эквивалентны, как показано ниже. Что вы используете — это действительно вопрос предпочтений.{\ ln f \ left (x \ right)}} = f \ left (x \ right) \ label {eq: eq11} \ end {уравнение} \]
Это важный факт, о котором вы всегда должны помнить при возникновении подобных проблем. Мы захотим максимально упростить интегрирующий коэффициент во всех случаях, и этот факт поможет в этом упрощении.
Вернемся к примеру. Умножьте интегрирующий коэффициент на дифференциальное уравнение и убедитесь, что левая часть соответствует правилу произведения. Также обратите внимание, что мы умножаем интегрирующий коэффициент на переписанное дифференциальное уравнение, а НЕ на исходное дифференциальное уравнение.2} \ left (x \ right) \, dx}} \\ \ sec \ left (x \ right) y \ left (x \ right) & = — \ frac {1} {2} \ cos \ left ({ 2x} \ right) — \ tan \ left (x \ right) + c \ end {align *} \]
Обратите внимание на использование тригонометрической формулы \ (\ sin \ left ({2 \ theta} \ right) = 2 \ sin \ theta \ cos \ theta \), которая упростила интеграл. Затем найдите решение.
\ [\ begin {align *} y \ left (x \ right) & = — \ frac {1} {2} \ cos \ left (x \ right) \ cos \ left ({2x} \ right) — \ cos \ left (x \ right) \ tan \ left (x \ right) + c \ cos \ left (x \ right) \\ & = — \ frac {1} {2} \ cos \ left (x \ right) \ cos \ left ({2x} \ right) — \ sin \ left (x \ right) + c \ cos \ left (x \ right) \ end {align *} \]
Наконец, примените начальное условие, чтобы найти значение \ (c \).
\ [\ begin {align *} 3 \ sqrt 2 = y \ left ({\ frac {\ pi} {4}} \ right) & = — \ frac {1} {2} \ cos \ left ({\ frac {\ pi} {4}} \ right) \ cos \ left ({\ frac {\ pi} {2}} \ right) — \ sin \ left ({\ frac {\ pi} {4}} \ right) + c \ cos \ left ({\ frac {\ pi} {4}} \ right) \\ 3 \ sqrt 2 & = — \ frac {{\ sqrt 2}} {2} + c \ frac {{\ sqrt 2}} {2} \\ c & = 7 \ end {align *} \]
Тогда решение есть.
\ [y \ left (x \ right) = — \ frac {1} {2} \ cos \ left (x \ right) \ cos \ left ({2x} \ right) — \ sin \ left (x \ right) + 7 \ соз \ влево (х \ вправо) \]
Ниже представлен график решения.2} \]
Ниже представлен график решения.
Давайте рассмотрим последний пример, который больше рассматривает интерпретацию решения, а не поиск решения.
Пример 6 Найдите решение следующей IVP и определите все возможные варианты поведения решения как \ (t \ to \ infty \). {\ frac {t } {2}}} \]
Теперь, когда у нас есть решение, давайте посмотрим на долгосрочное поведение ( i.е. \ (t \ to \ infty \)) решения. Первые два члена решения останутся конечными при всех значениях \ (t \). Это последний член, который будет определять поведение решения. Экспонента всегда будет стремиться к бесконечности как \ (t \ to \ infty \), однако в зависимости от знака коэффициента \ (c \) (да, мы уже нашли его, но для простоты этого обсуждения мы продолжим называть это \ (c \)). В следующей таблице показано долгосрочное поведение решения для всех значений \ (c \).
| Диапазон \ (c \) | Поведение решения при \ (t \ to \ infty \) |
|---|---|
| \ (с \) <0 | \ (у \ влево (т \ вправо) \ к — \ infty \) |
| \ (с \) = 0 | \ (y \ left (t \ right) \) остается конечным |
| \ (с \)> 0 | \ (у \ влево (т \ вправо) \ в \ infty \) |
Это поведение также можно увидеть на следующем графике некоторых решений.
Теперь, поскольку мы знаем, как \ (c \) относится к \ (y_ {0} \), мы можем связать поведение решения с \ (y_ {0} \). В следующей таблице показано поведение решения в терминах \ (y_ {0} \) вместо \ (c \).
| Диапазон \ (y_ {0} \) | Поведение решения как \ (t \ to \ infty \) |
|---|---|
| \ ({y_0} <- \ frac {{24}} {{37}} \) | \ (у \ влево (т \ вправо) \ к — \ infty \) |
| \ ({y_0} = — \ frac {{24}} {{37}} \) | \ (y \ left (t \ right) \) остается конечным |
| \ ({y_0}> — \ frac {{24}} {{37}} \) | \ (у \ влево (т \ вправо) \ в \ infty \) |
Обратите внимание, что для \ ({y_0} = — \ frac {{24}} {{37}} \) решение останется конечным.Так бывает не всегда.
Исследование долгосрочного поведения решений иногда бывает важнее, чем само решение. Предположим, что указанный выше раствор дал температуру в металлическом бруске. В этом случае нам нужно решение (я), которое останется конечным в долгосрочной перспективе. Благодаря этому исследованию у нас теперь будет значение начального условия, которое даст нам это решение, и, что более важно, значения начального условия, которых нам нужно было бы избежать, чтобы мы не расплавили стержень.
Дифференциальные уравнения — разделяемые уравнения
Показать общее уведомление
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Пол
6 мая 2021 г.
Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-2: Разделимые уравнения
Теперь мы приступим к рассмотрению нелинейных дифференциальных уравнений первого порядка. Первый тип нелинейных дифференциальных уравнений первого порядка, который мы рассмотрим, — это сепарабельные дифференциальные уравнения.
Разделимое дифференциальное уравнение — это любое дифференциальное уравнение, которое мы можем записать в следующей форме.
\ [\ begin {уравнение} N \ left (y \ right) \ frac {{dy}} {{dx}} = M \ left (x \ right) \ label {eq: eq1} \ end {уравнение} \]
Обратите внимание, что для того, чтобы дифференциальное уравнение было разделимым, все \ (y \) в дифференциальном уравнении должны быть умножены на производную, а все \ (x \) в дифференциальном уравнении должны быть на другой стороне. сторона знака равенства.
Чтобы решить это дифференциальное уравнение, сначала проинтегрируем обе части относительно \ (x \), чтобы получить,
\ [\ int {{N \ left (y \ right) \ frac {{dy}} {{dx}} \, dx}} = \ int {{M \ left (x \ right) \, dx}} \ ]
Теперь помните, что \ (y \) на самом деле \ (y \ left (x \ right) \), поэтому мы можем использовать следующую замену:
\ [u = y \ left (x \ right) \ hspace {0,25 дюйма} du = y ‘\ left (x \ right) \, dx = \ frac {{dy}} {{dx}} \, dx \]
Применяя эту замену к интегралу, получаем
\ [\ begin {уравнение} \ int {{N \ left (u \ right) \, du}} = \ int {{M \ left (x \ right) \, dx}} \ label {eq: eq2} \ конец {уравнение} \]
На этом этапе мы можем (надеюсь) интегрировать обе стороны, а затем обратно подставить \ (u \) в левой части.Обратите внимание, что, как подразумевается в предыдущем предложении, на данный момент может оказаться невозможным вычислить один или оба интеграла. Если это так, то мы мало что можем сделать, чтобы использовать этот метод для решения дифференциального уравнения.
Итак, описанный выше процесс является математически правильным способом решения этого дифференциального уравнения. Однако обратите внимание, что если мы «отделим» производную, мы можем записать дифференциальное уравнение как,
\ [N \ left (y \ right) dy = M \ left (x \ right) dx \]
Очевидно, что мы не можем таким образом отделить производные, но давайте представим, что можем, и увидим, что приходим к ответу с меньшими усилиями.
Теперь мы объединяем обе стороны этого, чтобы получить,
\ [\ begin {уравнение} \ int {{N \ left (y \ right) dy}} = \ int {{M \ left (x \ right) dx}} \ label {eq: eq3} \ end {уравнение} \]
Итак, если мы сравним \ (\ eqref {eq: eq2} \) и \ (\ eqref {eq: eq3} \), мы увидим, что единственная разница находится слева, и даже тогда единственная реальная разница — \ (\ eqref {eq: eq2} \) имеет интеграл в терминах \ (u \), а \ (\ eqref {eq: eq3} \) имеет интеграл в терминах \ (y \). В остальном реальной разницы нет.Интеграл слева — это точно такой же интеграл в каждом уравнении. Единственное отличие — буква, используемая в интеграле. Если мы проинтегрируем \ (\ eqref {eq: eq2} \), а затем обратно подставим вместо \ (u \), мы получим то же самое, как если бы мы просто интегрировали \ (\ eqref {eq: eq3} \) от начала.
Поэтому, чтобы облегчить работу, мы просто воспользуемся \ (\ eqref {eq: eq3} \), чтобы найти решение дифференциального уравнения. Кроме того, после выполнения интеграций у нас будет неявное решение, которое мы, надеюсь, сможем найти для явного решения, \ (y (x) \).Обратите внимание, что не всегда можно найти явное решение.
Напомним из раздела «Определения», что неявное решение — это решение, которое не имеет формы \ (y = y \ left (x \ right) \), в то время как явное решение было записано в этой форме.
Нам также придется побеспокоиться о сроке действия многих из этих решений. Напомним, что интервал достоверности был диапазоном независимой переменной, \ (x \) в данном случае, на которой решение действительно.Другими словами, нам нужно избегать деления на ноль, комплексных чисел, логарифмов отрицательных чисел или нуля, и т. Д. Большинство решений, которые мы получим из разделяемых дифференциальных уравнений, не будут действительны для всех значений \ (x \ ).
Давайте начнем с довольно простого примера, чтобы мы могли увидеть процесс, не теряясь в деталях других проблем, которые часто возникают в связи с этими проблемами.
Пример 1 Решите следующее дифференциальное уравнение и определите интервал применимости решения.2} x \ hspace {0.25in} \, \, \, y \ left (1 \ right) = \ frac {1} {{25}} \]
Показать решение
Ясно, надеюсь, что это дифференциальное уравнение разделимо. Итак, давайте разделим дифференциальное уравнение и проинтегрируем обе части. Как и в случае с линейным первым порядком, официально мы возьмем константу интегрирования с обеих сторон из интегралов по обе стороны от знака равенства. Их можно переместить в одну сторону и впитать друг в друга. Мы будем использовать соглашение, которое помещает единственную константу на сторону с \ (x \), учитывая, что мы в конечном итоге будем решать для \ (y \), и поэтому константа все равно окажется на этой стороне.2}}} \ end {выровнять *} \]
Теперь, что касается решений, у нас есть решение. Однако нам нужно начать беспокоиться о сроках действия.
Напомним, что есть два условия, которые определяют срок действия. Во-первых, это должен быть непрерывный интервал без разрывов и отверстий. Во-вторых, он должен содержать значение независимой переменной в начальном условии, в данном случае x = 1.
Итак, в нашем случае нам нужно избежать двух значений \ (x \).А именно, \ (x \ ne \ pm \ sqrt {\ frac {{28}} {3}} \ приблизительно \ pm \, 3.05505 \), поскольку они дадут нам деление на ноль. Это дает нам три возможных интервала действия.
\ [- \ infty
Однако только один из них будет содержать значение \ (x \) из начального условия, поэтому мы можем видеть, что
\ [- \ sqrt {\ frac {{28}} {3}}
должен быть интервалом действия для этого решения.
Вот график решения.
Обратите внимание, что это не означает, что любой из двух других интервалов, перечисленных выше, не может быть интервалом применимости для любого решения дифференциального уравнения. При правильном начальном условии любое из этих условий могло быть периодом действия.
Мы предоставим вам возможность проверить детали следующих претензий. Если мы используем начальное условие
\ [y \ left ({- 4} \ right) = — \ frac {1} {{20}} \]
мы получим точно такое же решение, но в этом случае интервал действия будет первым.
\ [- \ infty
Аналогично, если мы используем
\ [y \ left (6 \ right) = — \ frac {1} {{80}} \]
в качестве начального условия мы снова получаем точно такое же решение, и в этом случае третий интервал становится интервалом действия.
\ [\ sqrt {\ frac {{28}} {3}}
Итак, простое изменение начального условия может дать любой из возможных интервалов. 2} — 4x — 2} \ right)}}} {2} \ end {align *} \]
Затем обратите внимание, что мы можем вынести 4 из квадратного корня (получится 2…), а затем немного упростить.2} — 4x + 2} \ end {align *} \]
Мы почти у цели. Обратите внимание, что на самом деле у нас здесь два решения («\ (\ pm \)»), и нам нужно только одно решение. На самом деле верным может быть только один из признаков. Итак, чтобы выяснить, какой из них правильный, мы можем повторно применить к нему начальное условие. Только один из знаков даст правильное значение, поэтому мы можем использовать его, чтобы выяснить, какой из знаков правильный. Включение \ (x \) = 1 в решение дает.
\ [3 = y \ left (1 \ right) = 2 \ pm \ sqrt {1 + 2 — 4 + 2} = 2 \ pm 1 = 3, \, 1 \]
В этом случае похоже, что «+» — правильный знак для нашего решения.2} — 4x + 2 \ ge 0 \]
Другими словами, нам нужно убедиться, что величина под радикалом остается положительной.
Используя систему компьютерной алгебры, такую как Maple или Mathematica, мы видим, что левая часть равна нулю при \ (x \) = –3,36523, а также два комплексных значения, но мы можем игнорировать комплексные значения для вычислений интервала достоверности. Наконец, ниже показан график количества под радикалом.
Итак, чтобы получить реальные решения, нам потребуется \ (x \ ge — 3.{\ mbox {36523}} \), потому что это диапазон значений \ (x \), для которых величина положительна. Также обратите внимание, что этот интервал также содержит значение \ (x \), которое находится в начальном состоянии, как и должно быть.
Следовательно, интервал действия решения равен \ (x \ ge — 3. {\ Mbox {36523}} \).
Вот график решения.
Пример 3 Решите следующую IVP и найдите интервал годности решения.2} \ end {align *} \]
Обратите внимание, что мы смогли возвести в квадрат обе стороны неравенства, потому что в этом случае обе стороны неравенства гарантированно будут положительными. Наконец, решая для \ (x \), мы видим, что единственный возможный диапазон \ (x \) ’, который не дает деления на ноль или квадратного корня из отрицательных чисел, будет
\ [- \ frac {{\ sqrt 5}} {2}
и, что довольно хорошо, это также содержит начальное условие \ (x = 0 \). Таким образом, этот интервал является нашим сроком действия.2} — 4x — 4> 0 \]
Квадратичная функция будет равна нулю в двух точках \ (x = 2 \ pm 2 \ sqrt 2 \). График квадратичной зависимости (показанный ниже) показывает, что на самом деле есть два интервала, в которых мы получим положительные значения многочлена и, следовательно, могут быть возможные интервалы достоверности.
Итак, возможные интервалы действия —
\ [\ begin {array} {c} — \ infty
Из квадратичного графика видно, что второй содержит \ (x \) = 5, значение независимой переменной из начального условия.2}}} dr}} & = \ int {{\ frac {1} {\ theta} d \ theta}} \\ — \ frac {1} {r} & = \ ln \ left | \ тета \ право | + c \ end {align *} \]
Теперь примените начальное условие, чтобы найти \ (c \).
\ [- \ frac {1} {2} = \ ln \ left (1 \ right) + c \ hspace {0,25 дюйма} c = — \ frac {1} {2} \]
Итак, неявное решение —
\ [- \ frac {1} {r} = \ ln \ left | \ тета \ право | — \ frac {1} {2} \]
Решение для \ (r \) дает нам явное решение.
\ [r = \ frac {1} {{\ frac {1} {2} — \ ln \ left | \ theta \ right |}} \]
Итак, есть две проблемы для нашего решения. Во-первых, нам нужно избегать \ (\ theta = 0 \) из-за натурального логарифма. Обратите внимание, что из-за абсолютного значения \ (\ theta \) нам не нужно беспокоиться о том, что \ (\ theta \) будет отрицательным. Нам также нужно будет избегать деления на ноль. Другими словами, нам нужно избегать следующих моментов.
\ [\ begin {align *} \ frac {1} {2} — \ ln \ left | \ тета \ право | & = 0 \\ \ ln \ left | \ тета \ право | & = \ frac {1} {2} \ hspace {0.{\ frac {1} {2}}} \\ \ theta & = \ pm \ sqrt {\ bf {e}} \ end {align *} \]
Итак, эти три точки разбивают числовую строку на четыре части, каждая из которых может быть периодом действия.
\ [\ begin {array} {c} — \ infty
Фактическим интервалом действия будет тот, который содержит \ (\ theta = 1 \). Следовательно, срок действия равен \ (0 <\ theta <\ sqrt {\ bf {e}} \).
Вот график решения.2} + 2t + 3} \ right) + \ frac {5} {2} \]
Невозможно найти явное решение этой проблемы, поэтому нам придется оставить решение в его неявной форме. Поиск интервалов достоверности из неявных решений часто может быть очень трудным, поэтому мы также не будем беспокоиться об этом для этой проблемы.
Как показал этот последний пример, не всегда можно найти явные решения, поэтому будьте начеку в таких случаях.
Дифференциальные уравнения — точные уравнения
Сначала определите \ (M \) и \ (N \) и убедитесь, что дифференциальное уравнение является точным.2} + 1 \ hspace {0,25 дюйма} {N_x} = 2x \ end {align *} \]
Итак, дифференциальное уравнение является точным согласно тесту. Однако мы уже знали это, поскольку дали вам \ (\ Psi \ left (x, y \ right) \). Однако неплохо проверить это и хотя бы один раз пройти тест.
Теперь, как нам найти \ (\ Psi \ left (x, y \ right) \)? Напомним, что
\ [\ begin {align *} {\ Psi _x} & = M \\ {\ Psi _y} & = N \ end {align *} \]
Мы можем использовать любой из них, чтобы начать поиск \ (\ Psi \ left (x, y \ right) \) путем интегрирования следующим образом.
\ [\ Psi = \ int {{M \, dx}} \ hspace {0,25 дюйма} {\ mbox {OR}} \ hspace {0,25 дюйма} \ Psi = \ int {{N \, dy}} \]
Однако нам нужно быть осторожными, поскольку это не даст нам точной функции, которая нам нужна. Часто не имеет значения, с какой из них вы работаете, в то время как в других задачах одна будет значительно проще, чем другая. В этом случае не имеет значения, какой из них мы используем, поскольку любой из них будет столь же простым.
Итак, воспользуемся первым.3} + h \ left (y \ right) \]
Обратите внимание, что в этом случае «константа» интегрирования на самом деле вообще не является константой, но вместо этого она будет функцией оставшейся переменной (переменных), в данном случае \ (y \).
Напомним, что при интеграции мы спрашиваем, какую функцию мы дифференцировали, чтобы получить функцию, которую мы интегрируем. Поскольку здесь мы работаем с двумя переменными и говорим о частичном дифференцировании по \ (x \), это означает, что любой член, содержащий только константы или \ (y \), отличался бы от нуля, поэтому нам нужно подтвердите этот факт, добавив функцию от \ (y \) вместо стандартной \ (c \).
Хорошо, у нас есть большая часть \ (\ Psi \ left (x, y \ right) \), нам просто нужно определить \ (h (y) \), и мы закончим. 2} + 1 = N \]
Отсюда видно, что
\ [h ‘\ left (y \ right) = 2y + 1 \]
Обратите внимание, что на этом этапе \ (h (y) \) должен быть только функцией \ (y \), и поэтому, если в уравнении на этом этапе есть какие-либо \ (x \), мы где-то ошиблись и пора его искать.2} + 25 = 0 \]
При решении этого уравнения равен нулю при \ (x \) = –11.81557624 и \ (x \) = –1.3963. Обратите внимание, что для решения этого уравнения вам потребуется некоторая вычислительная помощь. Вот график полинома под радикалом.
Итак, похоже, есть два интервала, где многочлен будет положительным.
\ [\ begin {array} {c} — \ infty
Однако напомним, что интервалы допустимости должны быть непрерывными интервалами и содержать значение \ (x \), которое используется в начальном условии.3} \]
Итак, как отмечалось выше, это линейное дифференциальное уравнение, которое мы знаем, как решить. 3} \ hspace {0.4} \ ln x \ end {выровнять *} \]
Обратите внимание, что мы опустили столбцы абсолютного значения на \ (x \) в логарифме из-за предположения, что \ (x> 0 \).
Теперь нам нужно определить постоянную интегрирования. Это можно сделать одним из двух способов. Мы можем преобразовать вышеприведенное решение в решение в терминах \ (y \), а затем использовать исходное начальное условие, или мы можем преобразовать начальное условие в начальное условие в терминах \ (v \) и использовать его.4} \ left ({1 + 16 \ ln \ frac {x} {2}} \ right)}} \]
Обратите внимание, что мы сделали небольшое упрощение в решении. Это поможет определить срок действия.
Однако, прежде чем найти интервал действия, мы упомянули выше, что можем преобразовать исходное начальное условие в начальное условие для \ (v \). Давайте вкратце поговорим о том, как это сделать. Для этого все, что нам нужно сделать, это вставить \ (x = 2 \) в подстановку, а затем использовать исходное начальное условие. {- \, \ frac {1} {{16}}}} \ hspace {0.{- \, \ frac {1} {{16}}}} Вот график решения. Возможно, вам сначала захочется прочитать о дифференциальных уравнениях и разделении переменных! Дифференциальное уравнение — это уравнение с функцией и одной или несколькими производными: Пример: уравнение с функцией y и ее производная Здесь мы рассмотрим решение специального класса дифференциальных уравнений, называемого линейными дифференциальными уравнениями первого порядка Они «Первого Ордена», когда их всего Дифференциальное уравнение первого порядка является линейным , когда его можно сделать так: dy Где P (x) и Q (x) — функции от x. Для ее решения есть специальный метод: И мы также используем производную от y = uv (см. Производные правила (правило продукта)): dy Вот пошаговый метод их решения: Давайте посмотрим на примере, чтобы увидеть: dy Во-первых, это линейно? Да, так как в форме dy Итак, давайте выполним шаги: Шаг 1: Так это: Становится этим: u Шаг 2: Факторизуйте детали, включающие v Фактор v : u Шаг 3. Положите член v равным нулю v член равен нулю: Итак: Шаг 4: Решите, используя разделение переменных, чтобы найти u Отдельные переменные: Поставьте знак интеграла: ∫ Интегрировать: ln (u) = ln (x) + C Сделайте C = ln (k): ln (u) = ln (x) + ln (k) Итак: u = kx Шаг 5: подставьте u обратно в уравнение на шаге 2 (помните, что термин v равен 0, поэтому его можно игнорировать): kx Шаг 6: Решите это, чтобы найти v Отдельные переменные: k dv = Поставить знак интеграла: ∫ k дв. Интегрировать: kv = ln (x) + C Сделайте C = ln (c): kv = ln (x) + ln (c) И так: kv = ln (cx) И так: v = Шаг 7: Подставляем в y = uv , чтобы найти решение исходного уравнения. y = uv: y = kx Упростить: y = x ln (cx) И получается это прекрасное семейство кривых: y = x ln (cx) для различных значений c Что означают эти кривые? Они являются решением уравнения Другими словами: В любом месте на любой из этих кривых Давайте проверим несколько точек на c = 0.6 кривая: Решение линейных дифференциальных уравнений первого порядка
dy
dx
Первый заказ
dy
dx
, а не
д 2 д
dx 2
или
д 3 л
dx 3
и т. Д. линейный
dx
+ Р (х) у = Q (х)
dx
= u
дв
dx
+ v
и
dx Ступеньки
Пример 1: Решите это:
dx
—
л
х
= 1
dx
+ P (x) y = Q (x)
, где P (x) = —
1
х
и Q (x) = 1
Подставляем y = uv и
dy
dx
= u
дв
dx
+ v
и
dx
dy
dx
—
л
х
= 1
дв
dx
+ v
и
dx
—
ув
х
= 1
дв
dx
+ v (
и
dx
—
u
х
) = 1
и
dx
—
u
х
= 0
и
dx
знак равно
u
х
и
u
знак равно
dx
х
и
u
= ∫
dx
х
дв
dx
= 1
dx
х
= ∫
dx
х
1
к
ln (сх)
1
к
ln (сх)
dy
dx
—
л
х
= 1
наклон минус
л
х
равно 1
Расчет по графику (до 1 знака после запятой):
| Точка | х | y | Уклон ( dy dx ) | dy dx — л х |
|---|---|---|---|---|
| А | 0,6 | -0,6 | 0 | 0 — −0.6 0,6 = 0 + 1 = 1 |
| B | 1,6 | 0 | 1 | 1 — 0 1,6 = 1 — 0 = 1 |
| С | 2,5 | 1 | 1,4 | 1,4 — 1 2,5 = 1,4 — 0,4 = 1 |
Почему бы не проверить несколько пунктов самостоятельно? Здесь вы можете построить кривую.
Может, вам поможет еще один пример? Может, посложнее?
Пример 2: Решите это:
dy
dx
—
3 года
х
= х
Во-первых, это линейно? Да, так как в форме
dy
dx
+ P (x) y = Q (x)
, где P (x) = —
3
х
и Q (x) = x
Итак, давайте выполним шаги:
Шаг 1:
Подставляем y = uv и
dy
dx
= u
дв
dx
+ v
и
dx
Так это:
dy
dx
—
3 года
х
= х
Становится этим: u
дв
dx
+ v
и
dx
—
3uv
х
= х
Шаг 2: Факторизуйте детали, включающие v
Фактор v : u
дв
dx
+ v (
и
dx
—
3u
х
) = х
Шаг 3. Положите член v равным нулю
v член = ноль:
и
dx
—
3u
х
= 0
Итак:
и
dx
знак равно
3u
х
Шаг 4: Решите, используя разделение переменных, чтобы найти u
Отдельные переменные:
и
u
= 3
dx
х
Поставьте знак интеграла: ∫
и
u
= 3 ∫
dx
х
Интегрировать: ln (u) = 3 ln (x) + C
Сделайте C = −ln (k): ln (u) + ln (k) = 3ln (x)
Тогда: uk = x 3
Итак: u =
х 3
к
Шаг 5: подставьте u обратно в уравнение на шаге 2
(помните, что термин v равен 0, поэтому его можно игнорировать) 🙁
х 3
к
)
дв
dx
= х
Шаг 6: Решите это, чтобы найти v
Отдельные переменные: dv = k x −2 dx
Поставьте знак интеграла: ∫ dv = ∫ k x −2 dx
Интегрировать: v = −k x −1 + D
Шаг 7: Подставляем в y = uv , чтобы найти решение исходного уравнения.
у = УФ: у =
х 3
к
(−k x −1 + D)
Упростить: y = −x 2 +
D
к
х 3
Заменить D / k одной константой c : y =
c
х 3 — х 2
И получается это прекрасное семейство кривых:
у = с
x 3 — x 2 для различных значений c
И еще пример, на этот раз еще на сложнее :
Пример 3: Решите это:
dy
dx
+ 2xy = −2x 3
Во-первых, это линейно? Да, так как в форме
dy
dx
+ P (x) y = Q (x)
, где P (x) = 2x и Q (x) = −2x 3
Итак, давайте выполним шаги:
Шаг 1:
Подставляем y = uv и
dy
dx
= u
дв
dx
+ v
и
dx
Так это:
dy
dx
+ 2xy = −2x 3
Становится этим: u
дв
dx
+ v
и
dx
+ 2xuv
= −2x 3
Шаг 2: Факторизуйте детали, включающие v
Фактор v : u
дв
dx
+ v (
и
dx
+ 2xu
) = −2x 3
Шаг 3. Положите член v равным нулю
v член = ноль:
и
dx
+ 2xu = 0
Шаг 4: Решите, используя разделение переменных, чтобы найти u
Отдельные переменные:
и
u
= −2x dx
Поставить знак интеграла: ∫
и
u
= −2 ∫ x dx
Интегрировать: ln (u) = −x 2 + C
Сделайте C = −ln (k): ln (u) + ln (k) = −x 2
Тогда: uk = e −x 2
Итак: u =
e −x 2
к
Шаг 5: подставьте u обратно в уравнение на шаге 2
(помните, что термин v равен 0, поэтому его можно игнорировать) 🙁
e −x 2
к
)
дв
dx
= −2x 3
Шаг 6: Решите это, чтобы найти v
Отдельные переменные: dv = −2k x 3 e x 2 dx
Поставьте знак интеграла: ∫ дв.
= ∫ −2k x 3 e x 2 dx
Интегрировать: v = о нет! это трудно!
Посмотрим… мы можем интегрировать по частям … где написано:
∫ RS dx = R ∫ S dx — ∫ R ‘(∫ S dx) dx
(Боковое примечание: здесь мы используем R и S, использование u и v может сбивать с толку, поскольку они уже означают что-то другое.)
Выбор R и S очень важен, это лучший выбор, который мы нашли:
Итак, вперед:
Первый вытащить k: v
= k ∫ −2x 3 e x 2 dx
R = −x 2 и S = 2x e x 2 : v
= k ∫ (−x 2 ) (2xe x 2 ) dx
Теперь интегрировать по частям: v
= kR ∫ S dx — k ∫ R ‘(∫ S dx) dx
Положим R = −x 2 и S = 2x e x 2
А также R ‘= −2x и ∫ S dx = e x 2
Таким образом, получается: v
= −kx 2 ∫ 2x e x 2 dx — k ∫ −2x (e x 2 ) dx
Теперь интегрируйте: v
= −kx 2 e x 2 + k e x 2 + D
Упростить: v
= ke x 2 (1 − x 2 ) + D
Шаг 7: Подставляем в y = uv , чтобы найти решение исходного уравнения.
у = УФ: у =
e −x 2
к
(ke x 2 (1 − x 2 ) + D)
Упростить: y = 1 — x 2 + (
D
к
) e — x 2
Заменить D / k одной константой c : y = 1 — x 2 +
c
э — x 2
И мы получаем красивое семейство кривых:
y = 1 — x 2 +
c
e — x 2 для различных значений c
Дифференциальные уравнения первого порядка
Вопросы по дифференциальным уравнениям в STEP и других экзаменах по продвинутой математике бывают нескольких форм.В первую очередь, это могут быть дифференциальные уравнения первого порядка, т. Е. Наивысшая существующая производная является первым или более высоким порядком, т. Е. Существует производная, превышающая первую. Иногда вопрос подводит вас к конкретному способу решения дифференциального уравнения.
Однако чаще вам потребуется применять стандартный метод решения, и в этой статье рассматриваются два основных метода для дифференциальных уравнений первого порядка. Тем не менее, стоит отметить, что, как и в случае с большинством экзаменов по STEP и другим экзаменам по продвинутой математике, вам следует убедиться, что вы очень хорошо знаете все дифференцирование и интеграцию на A-Level; что включает в себя важное неявное
дифференциация.Помня об этом заключительном моменте, давайте перейдем к нашему первому методу — разделению переменных.
Разделение переменных
Первый метод, используемый для «разделимых» дифференциальных уравнений первого порядка, — это разделение переменных. Дифференциальное уравнение первого порядка \ (dy / dt \) называется сепарабельным, если его можно записать в виде:
\ (\ hspace {3.25 in} \ frac {dy} {dt} = f (y) g ( t). \)
Тогда разделение переменных означает деление на \ (f (y) \), а затем интегрирование по \ (t \), i.д .:
\ (\ hspace {3 in} \ int \ frac {1} {f (y)} dy = \ int g (t) dt. \)
На самом деле ничего больше, кроме этого! Хотя, конечно, интегралы в левой и правой частях могут быть не очень простыми; они часто требуют от вас замены. Это одна из причин, почему знание интеграции A-Level наизнанку имеет ключевое значение; и вам следует рассмотреть возможность прохождения модуля 10, чтобы получить там несколько советов и подсказок.
Метод интегрирующих факторов
Наш второй метод использует правило произведения для дифференцирования для решения дифференциальных уравнений первого порядка, которые могут быть записаны в форме:
\ (\ hspace {3.{-3t}. \)
Итак, это два метода, с которыми вам нужно познакомиться, чтобы приступить к решению задач дифференциальных уравнений первого порядка STEP. Однако, чтобы по-настоящему все проверить, давайте перейдем к рассмотрению части прошлого вопроса STEP.
Пример
Этот отрывок взят из Вопроса 6 по STEP III 2008 и дает хорошее введение в дифференциальные уравнения первого порядка в STEP. Во-первых, нас сначала просят дифференцировать \ (y \) относительно \ (x \).2 + 2xp \ right) = 2p \ frac {dp} {dx} + 2x \ frac {dp} {dx} + 2p. \)
Тогда, реализуя LHS, \ (dy / dx \) можно заменить на \ (p \) и соответствующим образом переставив, находим:
\ (\ hspace {1,85 дюйма} \ frac {dp} {dx} = — \ frac {p} {2p + 2x} \ Rightarrow \ frac {dx} {dp} = — \ frac {(2p + 2x)} {p} = — 2-2 \ frac {x} {p}, \)
по мере необходимости.
Итак, теперь у нас есть дифференциальное уравнение для \ (x \), которое нам нужно решить. Во-первых, мы спрашиваем себя, разделимо ли оно, и мы надеемся, что ответ будет отрицательным.2. \)
Сводка
Вот и все! Мы рассмотрели два основных метода решения дифференциальных уравнений первого порядка в STEP и других экзаменах по продвинутой математике. Надеюсь, должно быть ясно, что вы должны быть счастливы легко дифференцировать и интегрировать стандартные выражения, и, кроме того, это просто вопрос практики с ключевыми методами. Однако для ШАГА III, в частности, более высокого порядка
возникают дифференциальные уравнения. Чтобы подготовиться к ним, перейдите к следующей статье в этом модуле.
Дифференциальные уравнения первого порядка | SpringerLink
Часть
Тексты для бакалавриата по математике
book series (UTM)
Abstract
Дифференциальные уравнения первого порядка представляют собой богатый пример дифференциальных уравнений многих форм, большинство из которых мы можем легко решить в формальном смысле, а многие из которых мы можем решить и фактически получить ответы. Из исчисления нам нужны правила дифференцирования, как формулы (для сумм, произведений, частных, цепных правил и т. Д.), Так и производные стандартных функций Mathematica ( x n , тригонометрические функции , логарифмы, экспоненты, гиперболические функции и т. д.), а также методы интегрирования.Скорее всего, мы увидим примеры большинства интегралов, которые вы когда-либо пробовали. Если это звучит как плохая новость, то хорошей новостью является то, что Mathematica может выполнить эти интеграции за вас. Вы будете вдохновителем, а Mathematica сделает всю работу. Вы обязаны обеспечить правильность работы, которую выполняет Mathematica , но Mathematica выполнит эти проверки правильности и согласованности за вас. Вы контролируете то, что делается; Mathematica выполняет тяжелую работу.Важно, чтобы вы вручную делали несколько примеров проблем каждого типа. Причина этого в том, что , если вы не знаете, как решить проблему самостоятельно, маловероятно, что вы будете знать, как вести Mathematica через процесс решения .
Ключевые слова
Дифференциальное уравнение с векторным полем Линейное дифференциальное уравнение Дифференциальное уравнение с константой включения
Эти ключевые слова были добавлены машиной, а не авторами.Это экспериментальный процесс, и ключевые слова могут обновляться по мере улучшения алгоритма обучения.

 Понятие дифференциального уравнения.
Понятие дифференциального уравнения. Другими словами это семейство интегральных кривых, т.к. постоянная С точно не определена. (Рис.1)
Другими словами это семейство интегральных кривых, т.к. постоянная С точно не определена. (Рис.1) В данном случае уравнение разрешено относительно производной.
В данном случае уравнение разрешено относительно производной.