Содержание
Как найти длину зная координаты точек. Нахождение координат середины отрезка: примеры, решения
Отрезком
называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов
(x1; y1)
и
(x2; y2)
. На оси
X
и
Y
из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций.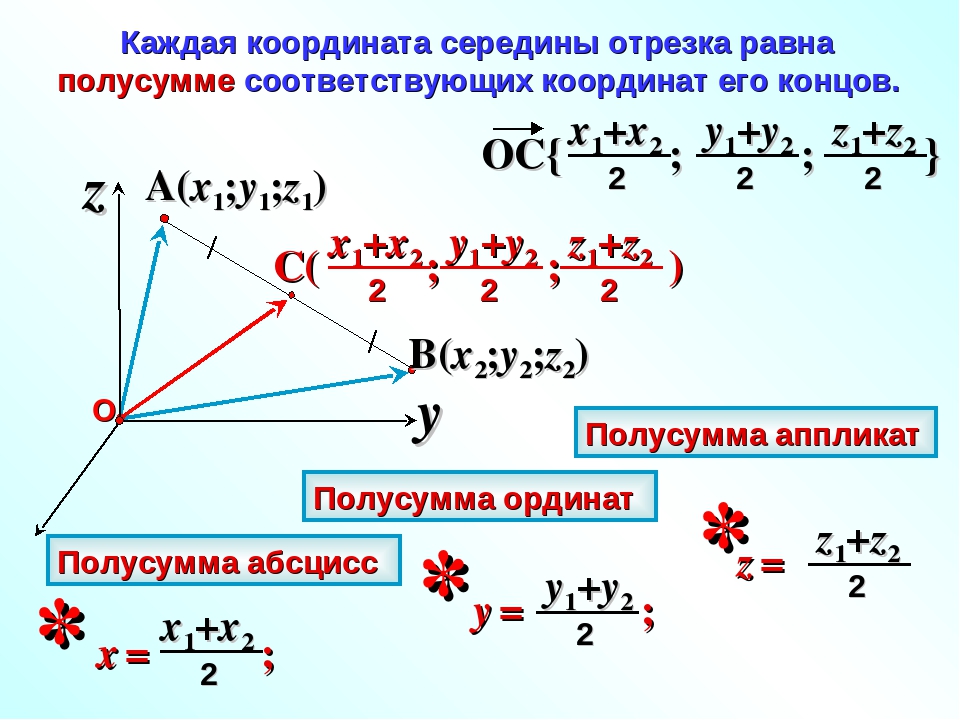 Итак, на ось Y
Итак, на ось Y
длина проекции равна y2-y1
, а на ось Х
длина проекции равна x2-x1
. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)²
. В данном случае |AB|
является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3)
и (2;5)
. Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5
. А это значит, что длина нашего отрезка равна 5:1/2
.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y)
исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1
.
Рассчитаем длину отрезка А
, для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²)
.
Если наш отрезок расположен между точками, координаты которых 2;4
и 4;1
, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61
.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1
Определение 1
Отрезок
– прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .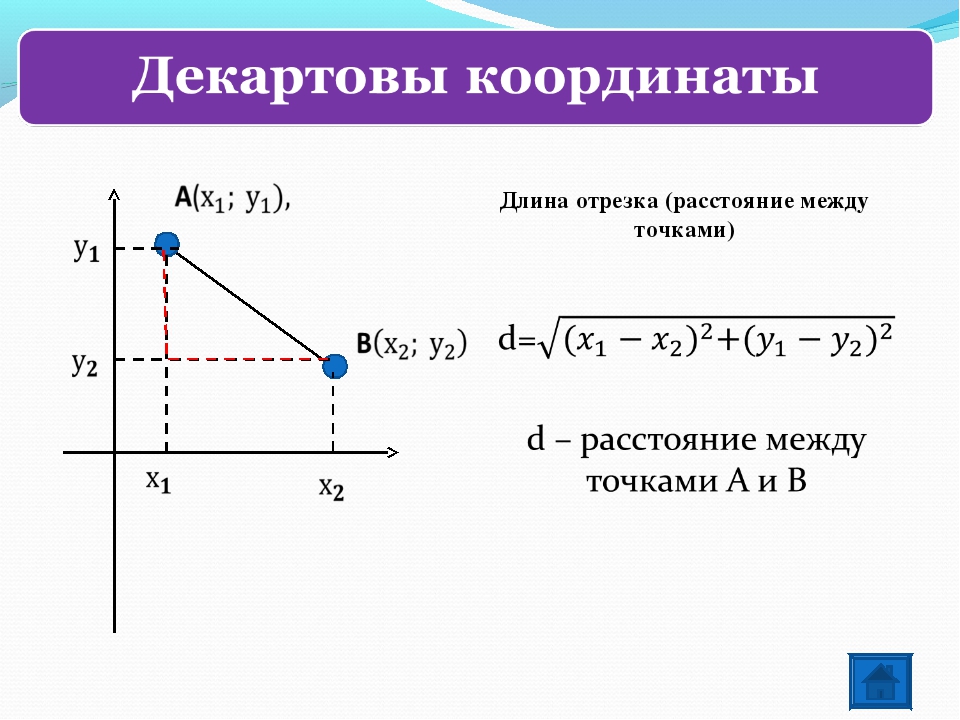
Определение 2
Длина отрезка
– расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка
– точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа
x A и
x B . Точка C – середина отрезка A B: необходимо определить координату
x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и
B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
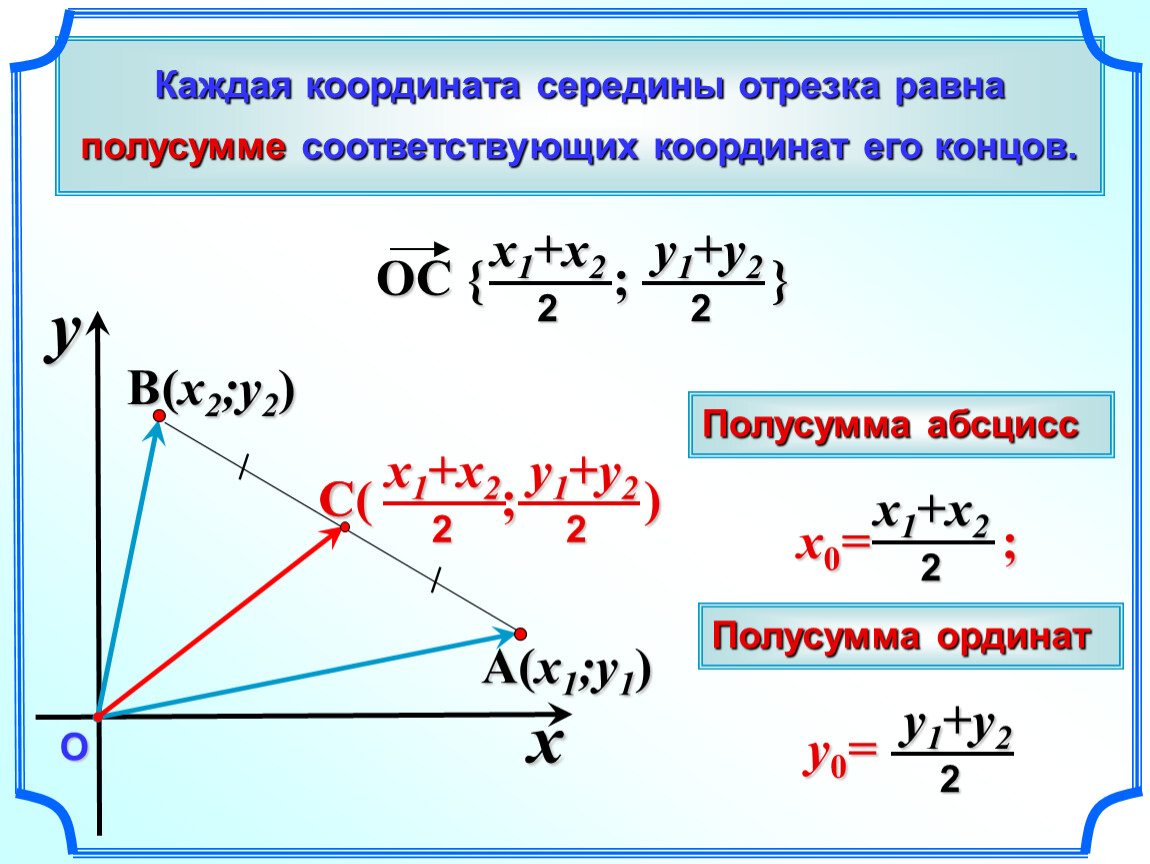
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов
A (x A , y A) и
B (x B , y B) определяются как
:
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные:
на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ
: координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные:
известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ:
58
Пример 3
Исходные данные:
в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ:
координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1.
Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами
x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами
этой точки.Пускай у вас сейчас есть две точки с координатами
x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность.Координаты вектора r, видимо, будут следующими: x1-x2, y1-y2, z1-z2. Тогда модуль вектора r либо расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)). 2))
2))
Видео по теме
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
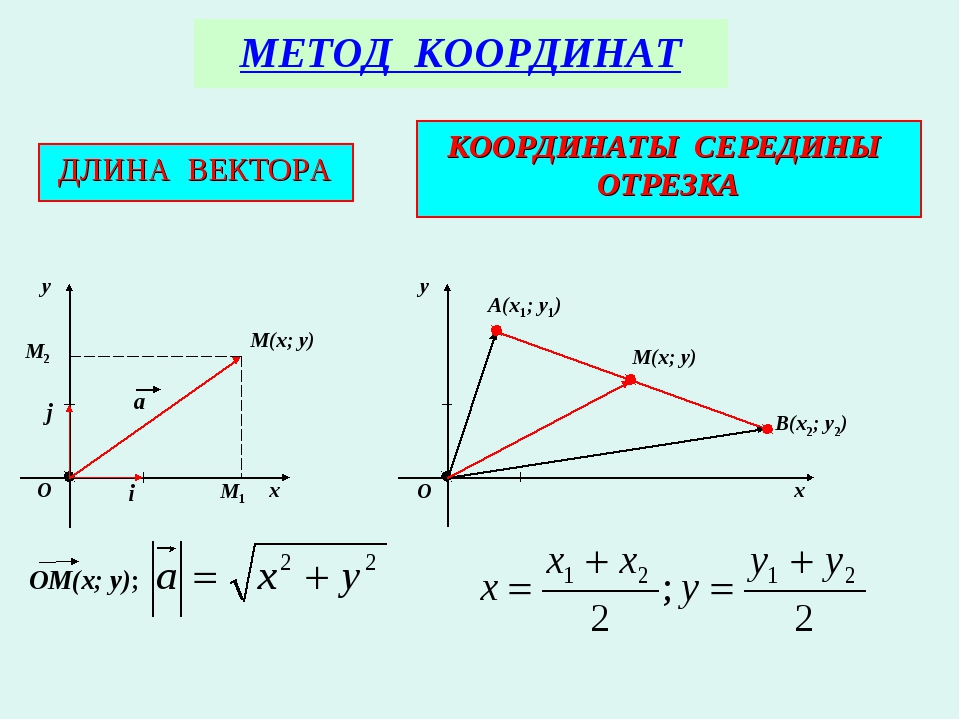
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Калькулятор онлайн — Длина отрезка. Расстояние между точками
Этот калькулятор онлайн вычисляет расстояние между двумя точками A и B (вычисляет длину отрезка AB).
Онлайн калькулятор для вычисления расстояния между двумя точками A и B (вычисления длины отрезка AB) не просто даёт ответ задачи, он приводит подробное
решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac{5}{7} \)
Как найти длину отрезка зная координаты точек.
 Нахождение координат середины отрезка: примеры, решения
Нахождение координат середины отрезка: примеры, решения
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
Отметим на листе бумаги две точки A
и B.
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком
.
Точка и отрезок − примеры геометрических фигур
.
Точки A
и B
называют концами отрезка
.
Существует единственный отрезок, концами которого являются точки A
и B.
Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5
обозначают одним из двух способов: AB
или BA.
Читают: «отрезок AB»
или «отрезок BA».
На рисунке 6
изображены три отрезка. Длина отрезка AB
равна 1
см. Он помещается в отрезке MN
ровно три раза, а в отрезке EF −
ровно 4
раза. Будем говорить, что длина отрезка
MN
равна 3
см, а длина отрезка EF −
4
см.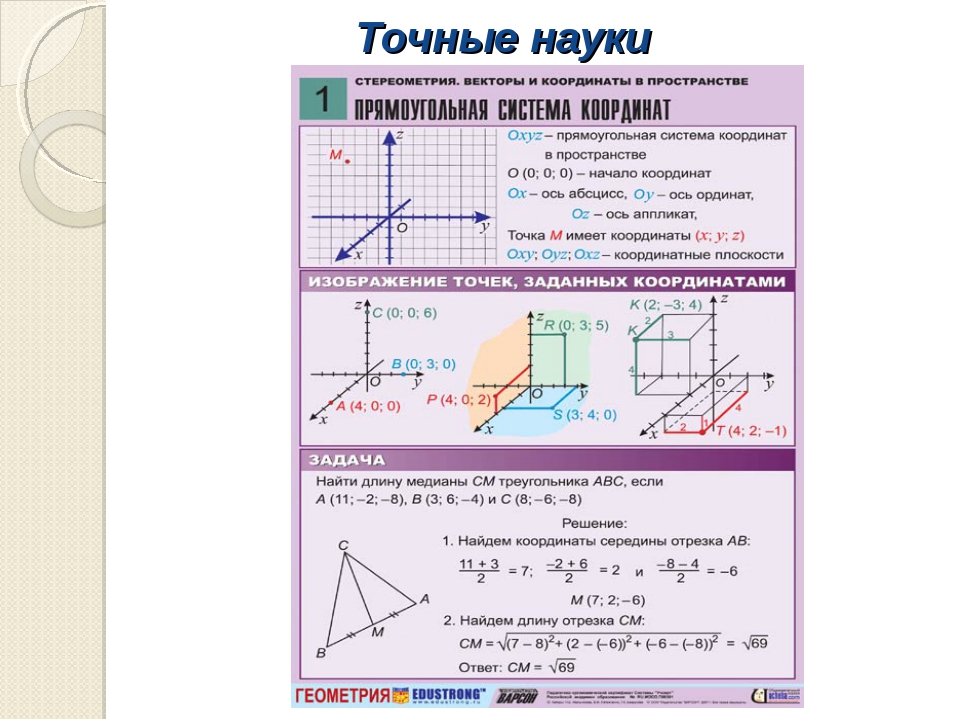
Также принято говорить: «отрезок MN
равен 3
см», «отрезок EF
равен 4
см». Пишут: MN =
3
см, EF =
4
см.
Длины отрезков MN
и EF
мы измерили единичным отрезком
, длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины
, например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
.
Длина отрезка обладает следующим свойством.
Если на отрезке AB
отметить точку C,
то длина отрезка AB
равна сумме длин отрезков AC
и CB
(рис. 8
).
Пишут: AB = AC + CB.
На рисунке 9
изображены два отрезка AB
и CD.
Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB
и CD
равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB
называют расстоянием
между точками A
и B.
Если несколько отрезков расположить так, как показано на рисунке 10,
то получится геометрическая фигура, которую называют ломаная
. Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E −
вершины ломаной
ABCDE,
точки A
и E −
концы ломаной
, а отрезки AB, BC, CD, DE −
ее звенья
(см. рис. 10
).
Длиной ломаной
называют сумму длин всех ее звеньев.
На рисунке 12
изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми
Такие ломаные называют замкнутыми
.
Пример 1
. Отрезок BC
на 3
см меньше отрезка AB,
длина которого равна 8
см (рис. 13
). Найдите длину отрезка AC.
Решение. Имеем: BC =
8
− 3
= 5
(см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC.
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13
см.
Пример 2
. Известно, что MK =
24
см, NP =
32
см, MP =
50
см (рис. 14
). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN =
50
− 32
= 18
(см).
Имеем: NK = MK − MN.
Отсюда NK =
24
− 18
= 6
(см).
Ответ: 6
см.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки.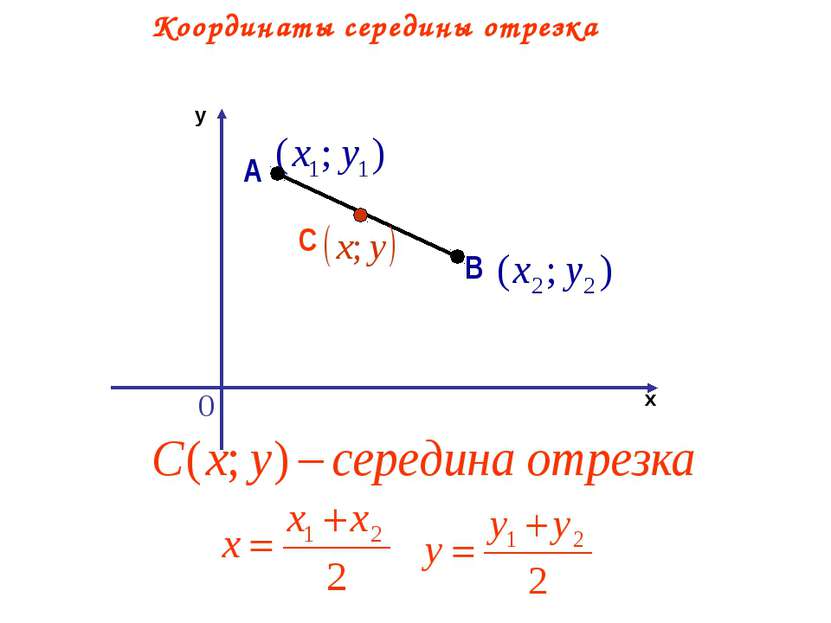 Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50.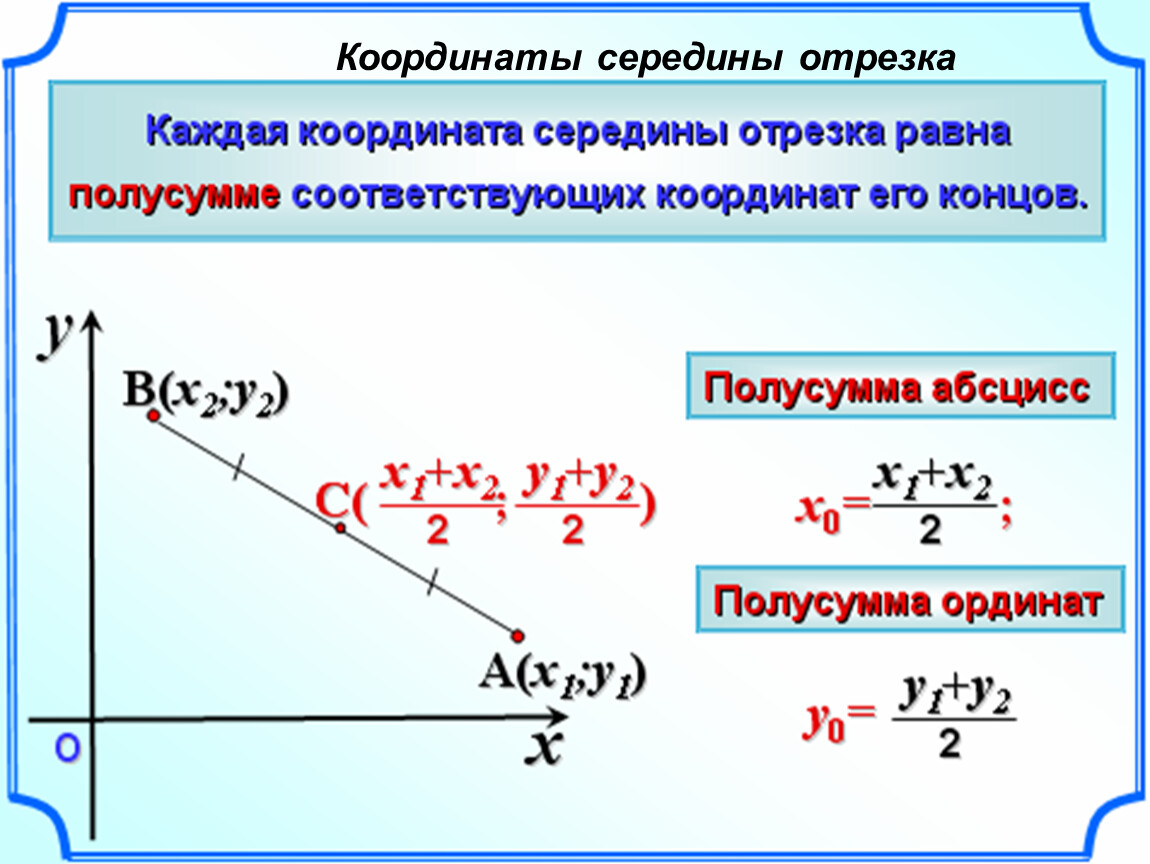 Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).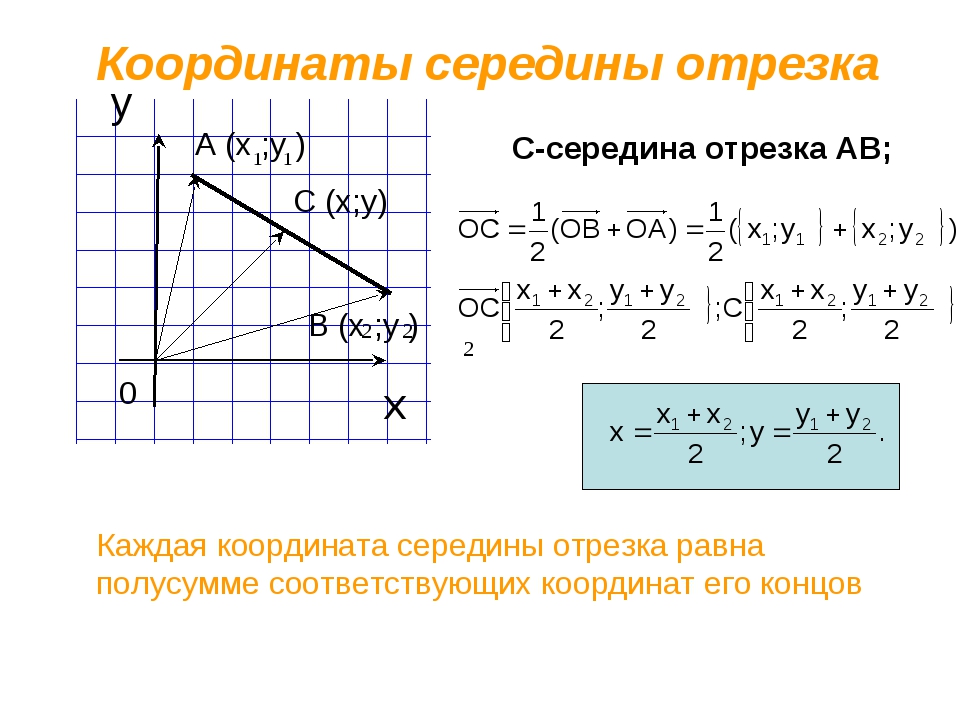
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных.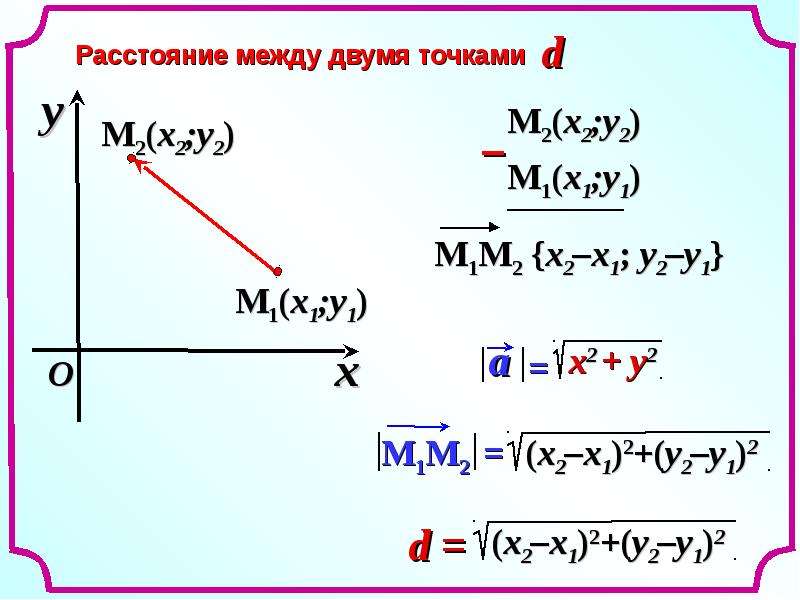 Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н
емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1
;у 1
) и (х 2
;у 2
) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b
, где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.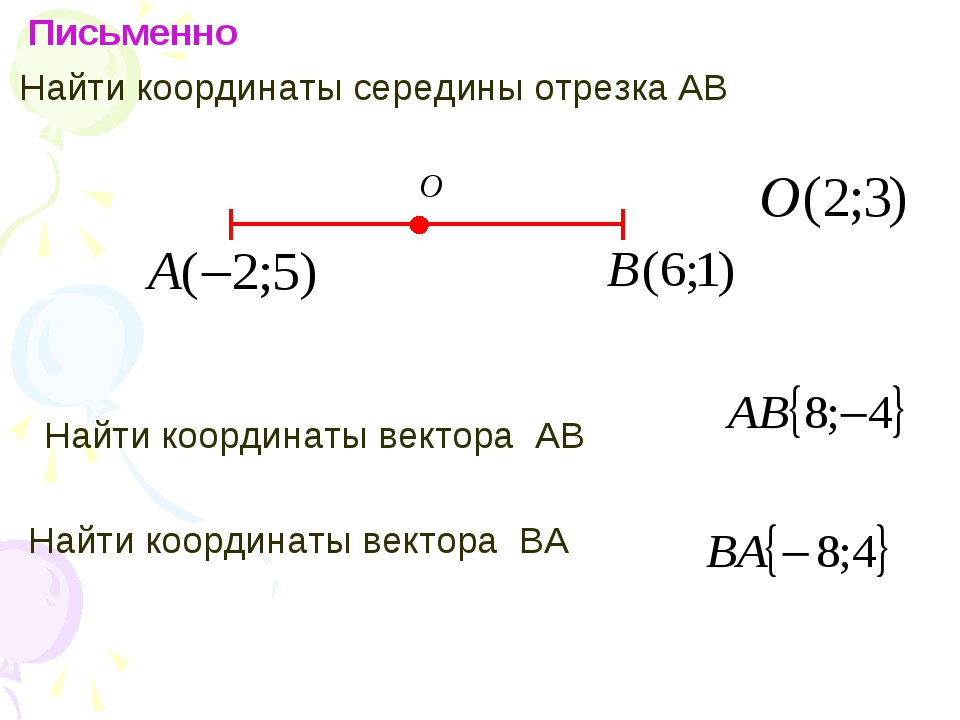
Ответ: 8
Найдите расстояние от точки A
с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A
(6;8) относительно оси Ox
.
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A
(6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки
O
(0;0) и
A
(6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.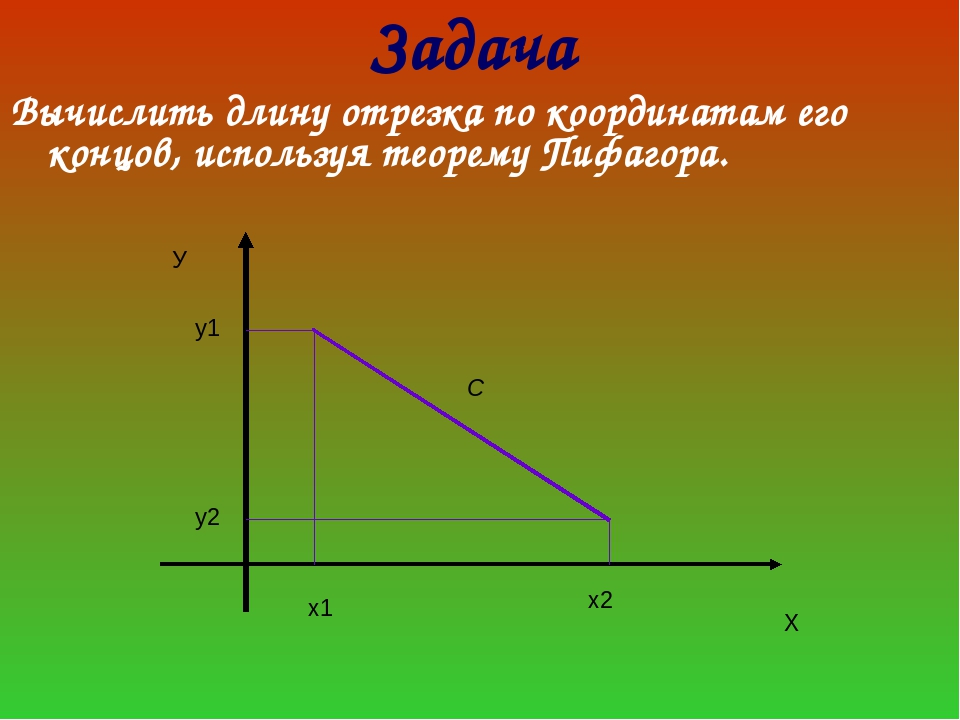 Середину отрезка несложно будет определить по клеткам.
Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A
(6;8) и B
(–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O
(0;0) и A
(6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол
ВОА
в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу
ОА.
По теореме Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ
.
Найдите расстояние от точки A
с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A
с координатами (6;8) до начала координат.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1
Определение 1
Отрезок
– прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка
– расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка
– точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа
x A и
x B . Точка C – середина отрезка A B: необходимо определить координату
x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и
B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.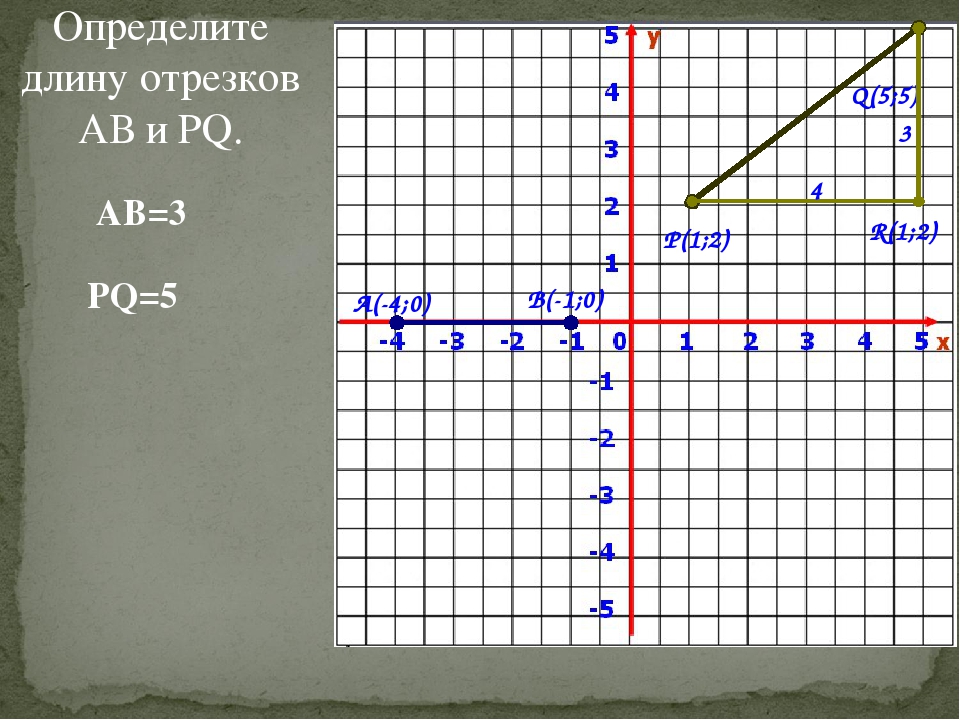
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов
A (x A , y A) и
B (x B , y B) определяются как
:
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные:
на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ
: координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные:
известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ:
58
Пример 3
Исходные данные:
в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ:
координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя.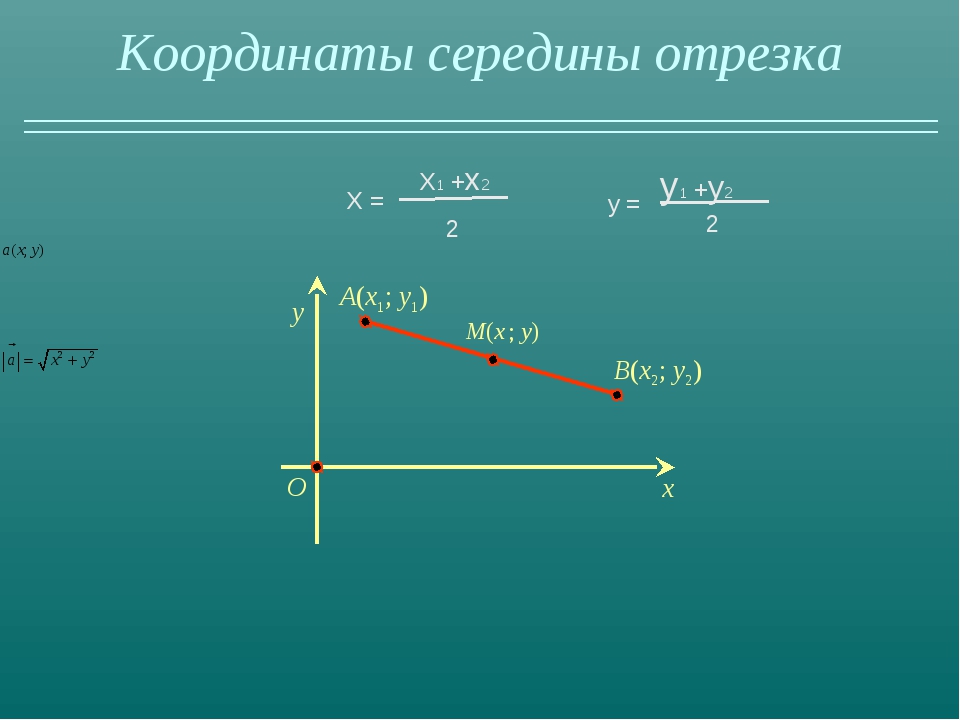 Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Расчет длины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1
Определение 1
Отрезок
– прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка
– расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка
– точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа
x A и
x B . Точка C – середина отрезка A B: необходимо определить координату
x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и
B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y .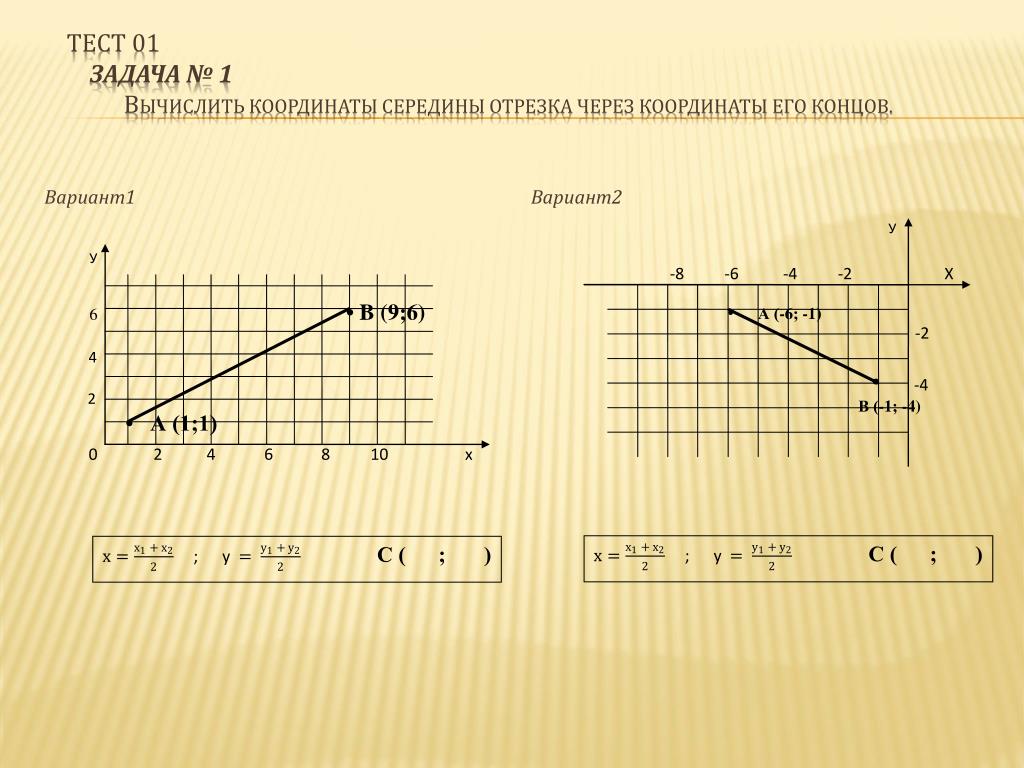 И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов
A (x A , y A) и
B (x B , y B) определяются как
:
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные:
на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ
: координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные:
известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ:
58
Пример 3
Исходные данные:
в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ:
координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н
емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1
;у 1
) и (х 2
;у 2
) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b
, где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A
с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A
(6;8) относительно оси Ox
.
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A
(6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки
O
(0;0) и
A
(6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A
(6;8) и B
(–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O
(0;0) и A
(6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол
ВОА
в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу
ОА.
По теореме Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ
.
Найдите расстояние от точки A
с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A
с координатами (6;8) до начала координат.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.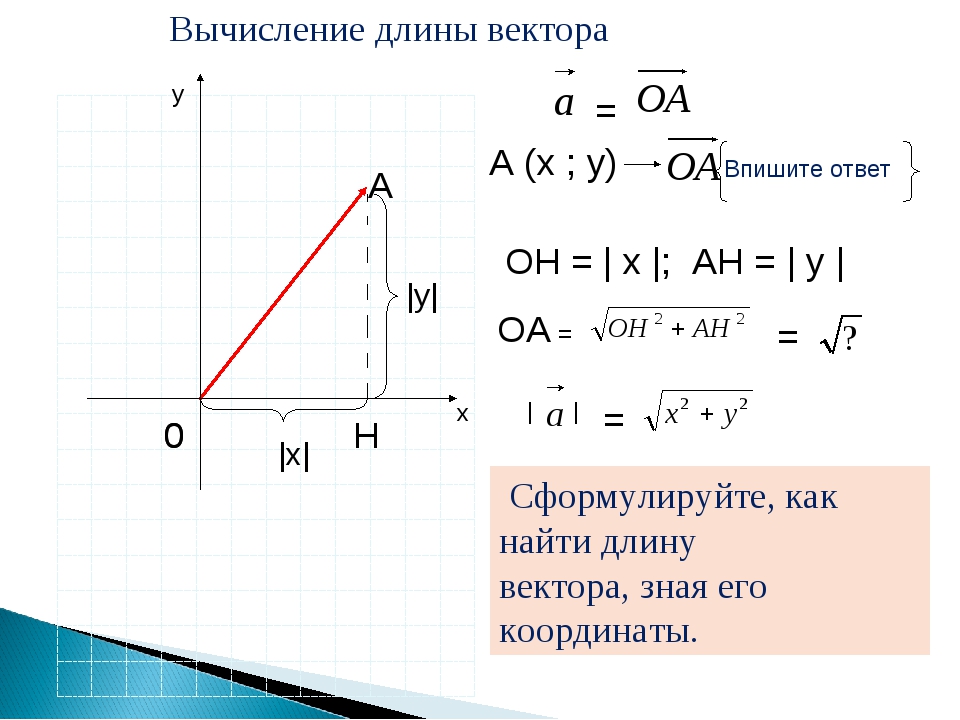
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Отрезком
называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов
(x1; y1)
и
(x2; y2)
. На оси
X
и
Y
из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y
длина проекции равна y2-y1
, а на ось Х
длина проекции равна x2-x1
. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)²
. В данном случае |AB|
является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3)
и (2;5)
. Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5
. А это значит, что длина нашего отрезка равна 5:1/2
.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник.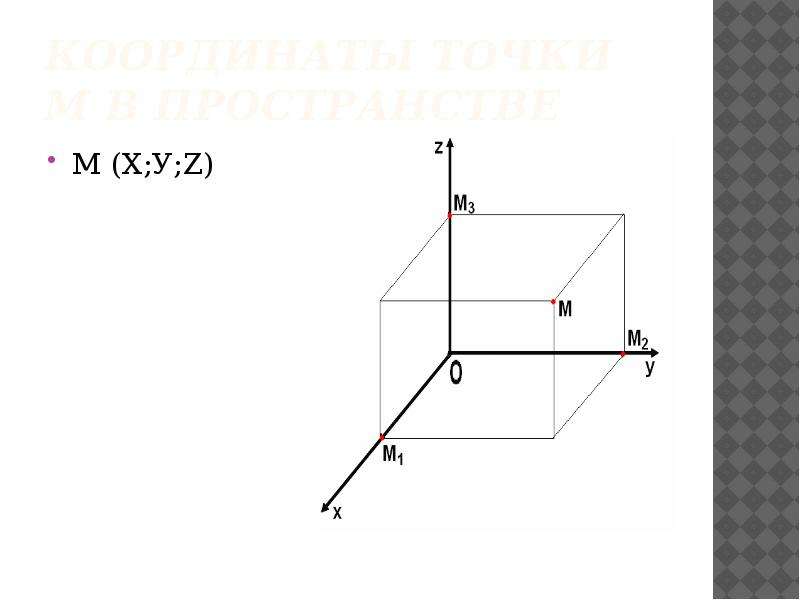 Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y)
исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1
.
Рассчитаем длину отрезка А
, для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²)
.
Если наш отрезок расположен между точками, координаты которых 2;4
и 4;1
, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61
.
Расстояние между двумя точками » Аналитическая геометрия f(x)dx.Ru
п.6. Расстояние между двумя точками на координатной оси и замечание о его обозначении.
Замечание . В геометрии и в школьной геометрии, в частности, принято обозначать одинаково и сам отрезок и его длину. Если имеется отрезок прямой, ограниченный точками А и В, то этот отрезок как геометрический объект обозначается АВ.
рис.15.
С другой стороны длина отрезка, т.е. расстояние между точками А и В обозначается точно также АВ.
Мы же, в нашем курсе, уже встретились с различными обозначениями длины отрезка:
.
Но и это еще не все. Если речь идет об отрезке на оси L, то есть, когда , то длину отрезка АВ мы можем обозначить и так:
.
А если ось мы обозначим другой буквой, например, Ох или Оу, то могут появиться и другие обозначения.
В дальнейшем мы будем стараться придерживаться традиционного обозначения и обозначать длину отрезка АВ также, как и сам отрезок: АВ.
Теорема. (О вычислении декартовой координаты вектора и расстоянии между точками числовой оси. )
)
Пусть Ох координатная ось, А, В – две её произвольные точки, – их координаты, – декартовая координата вектора . Тогда:
1) ; 2) .
Доказательство. По правилу треугольника сложения векторов имеем:
.
Применяя следствие о декартовых координатах векторов оси, получаем
.
2) Из определения декартовой координаты вектора оси следует, что . Подставляя сюда доказанное уже равенство , получаем .
Теорема доказана.
Замечание. Используя доказанную теорему, можно сформулировать два правила:
1) Для того, чтобы найти координату вектора на числовой оси, нужно из координаты его конца вычесть координату его начала.
2) Расстояние между двумя точками числовой оси равно модулю разности их координат.
Возможно найдутся ответы здесь:
Как найти длину стороны по координатам формула. Нахождение координат середины отрезка: примеры, решения
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
(рис. 3
).
Отметим на листе бумаги две точки A
и B.
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком
.
Точка и отрезок − примеры геометрических фигур
.
Точки A
и B
называют концами отрезка
.
Существует единственный отрезок, концами которого являются точки A
и B.
Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5
обозначают одним из двух способов: AB
или BA.
Читают: «отрезок AB»
или «отрезок BA».
На рисунке 6
изображены три отрезка. Длина отрезка AB
равна 1
см. Он помещается в отрезке MN
ровно три раза, а в отрезке EF −
ровно 4
раза. Будем говорить, что длина отрезка
MN
равна 3
см, а длина отрезка EF −
4
см.
Также принято говорить: «отрезок MN
равен 3
см», «отрезок EF
равен 4
см». Пишут: MN =
3
см, EF =
4
см.
Длины отрезков MN
и EF
мы измерили единичным отрезком
, длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины
, например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
.
Длина отрезка обладает следующим свойством.
Если на отрезке AB
отметить точку C,
то длина отрезка AB
равна сумме длин отрезков AC
и CB
(рис. 8
).
Пишут: AB = AC + CB.
На рисунке 9
изображены два отрезка AB
и CD.
Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB
и CD
равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB
называют расстоянием
между точками A
и B.
Если несколько отрезков расположить так, как показано на рисунке 10,
то получится геометрическая фигура, которую называют ломаная
. Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E −
вершины ломаной
ABCDE,
точки A
и E −
концы ломаной
, а отрезки AB, BC, CD, DE −
ее звенья
(см. рис. 10
).
Длиной ломаной
называют сумму длин всех ее звеньев.
На рисунке 12
изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми
.
Пример 1
. Отрезок BC
на 3
см меньше отрезка AB,
длина которого равна 8
см (рис. 13
). Найдите длину отрезка AC.
Решение. Имеем: BC =
Имеем: BC =
8
− 3
= 5
(см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC.
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13
см.
Пример 2
. Известно, что MK =
24
см, NP =
32
см, MP =
50
см (рис. 14
). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN =
50
− 32
= 18
(см).
Имеем: NK = MK − MN.
Отсюда NK =
24
− 18
= 6
(см).
Ответ: 6
см.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1.
Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами
x,y и z. 2))
2))
Видео по теме
Нахождение координат середины отрезка, примеры, решения. Нахождение координат середины отрезка, примеры, решения Как найти длину отрезка если известны координаты
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
Отметим на листе бумаги две точки A
и B.
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком
.
Точка и отрезок − примеры геометрических фигур
.
Точки A
и B
называют концами отрезка
.
Существует единственный отрезок, концами которого являются точки A
и B.
Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5
обозначают одним из двух способов: AB
или BA.
Читают: «отрезок AB»
или «отрезок BA».
На рисунке 6
изображены три отрезка. Длина отрезка AB
равна 1
см. Он помещается в отрезке MN
ровно три раза, а в отрезке EF −
ровно 4
раза. Будем говорить, что длина отрезка
MN
равна 3
см, а длина отрезка EF −
4
см.
Также принято говорить: «отрезок MN
равен 3
см», «отрезок EF
равен 4
см». Пишут: MN =
3
см, EF =
4
см.
Длины отрезков MN
и EF
мы измерили единичным отрезком
, длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины
, например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
.
Длина отрезка обладает следующим свойством.
Если на отрезке AB
отметить точку C,
то длина отрезка AB
равна сумме длин отрезков AC
и CB
(рис. 8
8
).
Пишут: AB = AC + CB.
На рисунке 9
изображены два отрезка AB
и CD.
Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB
и CD
равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB
называют расстоянием
между точками A
и B.
Если несколько отрезков расположить так, как показано на рисунке 10,
то получится геометрическая фигура, которую называют ломаная
. Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E −
вершины ломаной
ABCDE,
точки A
и E −
концы ломаной
, а отрезки AB, BC, CD, DE −
ее звенья
(см. рис. 10
рис. 10
).
Длиной ломаной
называют сумму длин всех ее звеньев.
На рисунке 12
изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми
.
Пример 1
. Отрезок BC
на 3
см меньше отрезка AB,
длина которого равна 8
см (рис. 13
). Найдите длину отрезка AC.
Решение. Имеем: BC =
8
− 3
= 5
(см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC.
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13
см.
Пример 2
. Известно, что MK =
24
см, NP =
32
см, MP =
50
см (рис. 14
). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN =
50
− 32
= 18
(см).
Имеем: NK = MK − MN.
Отсюда NK =
24
− 18
= 6
(см).
Ответ: 6
см.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. 2))
2))
Пусть отрезок задан двумя точками в плоскости координат, тогда можно найти его длину с помощью теоремы Пифагора.
Инструкция
Пусть заданы координаты концов отрезка (x1- y1) и (x2- y2). Начертите отрезок в системе координат.
Опустите перпендикуляры из концов отрезка на оси X и Y. Отрезки, отмеченные на рисунке красным, являются проекциями исходного отрезка на оси координат.
Если выполнить параллельный перенос, отрезков-проекций к концам отрезков, то получится прямоугольный треугольник. Катетами этого треугольника будут являться перенесенные проекции, а гипотенузой — сам отрезок AB.
Длины проекций легко вычисляются. Длина проекции на ось Y будет равна y2-y1, а длина проекции на ось X — x2-x1. Тогда по теореме Пифагора |AB|²- = (y2 — y1)²- + (x2 — x1)²-, где |AB| — длина отрезка.
Представив эту схему нахождения длины отрезка в общем случае, легко вычислять длину отрезка, не строя отрезок. Посчитаем длину отрезка, координаты концов которого (1-3) и (2-5).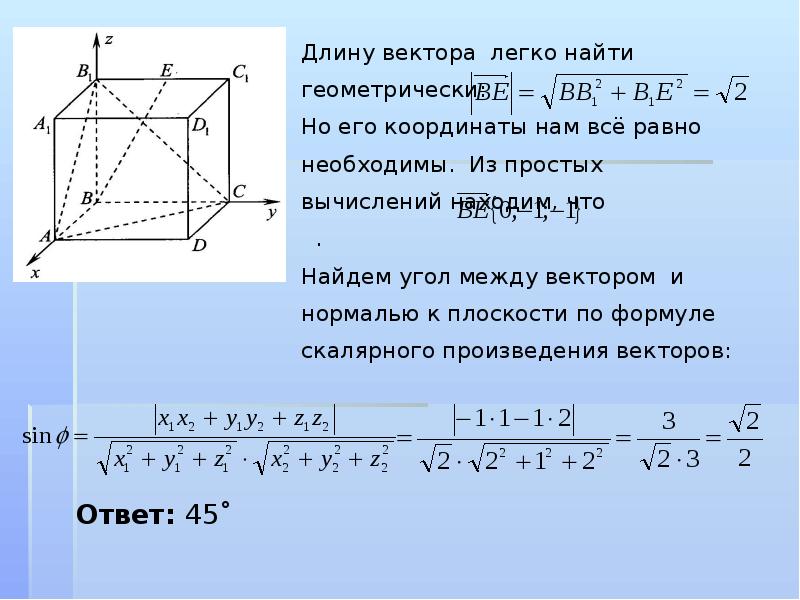 1/2.
1/2.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Трехмерная координатная геометрия — расстояние
В трехмерном пространстве точки представлены их положениями вдоль осей xxx, yyy и zzz, каждая из которых перпендикулярна друг другу; это аналогично интерпретации 2-х координатной геометрии, в которой каждая точка представлена только двумя координатами (по осям xxx и yyy).
dk
На рисунке выше цель состоит в том, чтобы найти расстояние от точки (x1, y1, z1) \ left (x_ {1}, y_ {1}, z_ {1} \ right) (x1, y1, z1) в точку (x2, y2, z2).2 \\ & = 64 \\
a & = \ pm2 \ sqrt {3}. \ _ \ квадрат
\ end {align} 52 + a2a = 82 = 64 = ± 23. □
Одномерная система координат
Координаты точки: \ ({x_0} \), \ ({x_1} \), \ ({x_2} \)
Расстояние между двумя точками: \ (d \)
Действительное число (отношение длины): \ (\ lambda \)
- Координаты точки — это набор чисел, которые определяют положение точки в наборе (на плоскости, в пространстве или на коллекторе). Система, в которой разные точки имеют уникальные координаты, называется системой координат или системой координат.
- В геометрии наиболее распространена декартова система координат.
Определяется своим происхождением и базисом (базисными векторами). Если базисные векторы (в \ (n \) -мерной системе координат) взаимно перпендикулярны друг другу, такая система координат называется прямоугольной декартовой системой. - Одномерная система координат определяется ее началом и единственным базисным вектором, который определяет положительное направление оси координат (\ (x \) — ось). Координаты любой точки в такой системе определяются одним действительным числом.
- Расстояние между двумя точками \ (A \ left ({{x_1}} \ right) \) и \ (B \ left ({{x_2}} \ right) \) на координатной линии равно абсолютному значению разность их координат:
\ (d = AB = \) \ (\ left | {{x_2} — {x_1}} \ right | = \) \ (\ left | {{x_1} — {x_2}} \ справа | \) - Деление отрезка прямой в соотношении \ (\ lambda \)
Пусть точка \ (C \ left ({{x_0}} \ right) \) делит отрезок прямой \ (AB \) в соотношении \ (\ lambda \). Тогда координата \ ({x_0} \) точки \ (C \) задается формулой
\ ({x_0} = {\ large \ frac {{{x_1} + \ lambda {x_2}}} {{ 1 + \ lambda}} \ normalsize}, \; \) \ (\ lambda = {\ large \ frac {{AC}} {{CB}} \ normalsize}, \; \) \ (\ lambda \ ne — 1 , \)
где \ ({x_1} \) — координата точки \ (A \), а \ ({x_2} \) — координата точки \ (B \). - В особом случае, когда \ (\ lambda = 1 \), предыдущая формула позволяет вычислить координату средней точки сегмента:
\ ({x_0} = {\ large \ frac {{{x_1} + {x_2 }}} {2} \ normalsize}, \; \) \ (\ lambda = 1. \)
% PDF-1.5
%
1 0 объект
>>>
эндобдж
2 0 obj
> поток
2014-11-25T02: 35: 55 + 05: 302014-11-25T02: 35: 58 + 05: 302014-11-25T02: 35: 58 + 05: 30Adobe InDesign CS5 (7.0)
AQBIAAAAAQAB / + 4AE0Fkb2JlAGSAAAAAAQUAAgAD / 9sAhAAMCAgICAgMCAgMEAsLCxAUDg0NDhQY
EhMTExIYFBIUFBQUEhQUGx4eHhsUJCcnJyckMjU1NTI7Ozs7Ozs7Ozs7AQ0LCxAOECIYGCIyKCEo
MjsyMjIyOzs7Ozs7Ozs7Ozs7Ozs7OztAQEBAQDtAQEBAQEBAQEBAQEBAQEBAQEBAQED / wAARCAEA
AMYDAREAAhEBAxEB / 8QBQgAAAQUBAQEBAQEAAAAAAAAAAwABAgQFBgcICQoLAQABBQEBAQEBAQAA
AAAAAAABAAIDBAUGBwgJCgsQAAEEAQMCBAIFBwYIBQMMMwEAAhEDBCESMQVBUWETInGBMgYUkaGx
QiMkFVLBYjM0coLRQwclklPw4fFjczUWorKDJkSTVGRFwqN0NhfSVeJl8rOEw9N14 / NGJ5SkhbSV
xNTk9KW1xdXl9VZmdoaWprbG1ub2N0dXZ3eHl6e3x9fn9xEAAgIBAgQEAwQFBgcHBgI7AQACEQMh
MRIEQVFhcSITBTKBkRShsUIjwVLR8DMkYuFygpJDUxVjczTxJQYWorKDByY1wtJEk1SjF2RFVTZ0
ZeLys4TD03Xj80aUpIW0lcTU5PSltcXV5fVWZnaGlqa2xtbm9ic3R1dnd4eXp7fh2 + f3 / 9oADAMB
AAIRAxEAPwD0Xp / T8A4GMTjUkmmuT6bf3R5JKbH7P6f / ANxqf + 22 / wBySlfs / p // AHGp / wC22 / 3J
KV + z + n / 9xqf + 22 / 3JKV + z + n / APcan / ttv9ySlfs / p / 8A3Gp / 7bb / AHJKV + z + n / 8Acan / ALbb / ckp
X7P6f / 3Gp / 7bb / ckpX7P6f8A9xqf + 22 / 3JKV + z + n / wDcan / ttv8AckpX7P6f / wBxqf8Attv9ySlf
s / p // can / ttv9ySlfs / p / wD3Gp / 7bb / ckpX7P6f / ANxqf + 22 / wBySlfs / p // AHGp / wC22 / 3JKV + z
+ n / 9xqf + 22 / 3JKV + z + n / APcan / ttv9ySlfs / p / 8A3Gp / 7bb / AHJKV + z + n / 8Acan / ALbb / ckpX7P6
f / 3Gp / 7bb / ckpX7P6f8A9xqf + 22 / 3JKV + z + n / wDcan / ttv8AckpX7P6f / wBxqf8Attv9ySlfs / p /
/ can / ttv9ySmvk9PwBdixjU63Gf0bf8ARW + SSmx0 / wD5Pxv + Jr / 6kJKQ9Qt6rW9g6fQ25pHvLnhs
H5pKbGP9ofQx2T + jtI97GkEA / GElJNp / eP4f3JKVtP7x / D + 5JStp / eP4f3JKVtP7x / D + 5JStp / eP
4f3JKVtP7x / D + 5JStp / eP4f3JKVtP7x / D + 5JStp / eP4f3JKVtP7x / D + 5JTQzbutV37cHHZbVAhzn
hpnvoUlNykXOpY64llhaC9oggOjUAx4pKZ7T + 8fw / uSUraf3j + H9ySlbT + 8fw / uSUraf3j + H9ySl
bT + 8fw / uSU0M67rNdwbg47Lqtolznhp3d9Ckpv7T + 8fw / uSUraf3j + H9ySlwIHMpKQZP89if8cf /
AD1ckpXT / wDk / G / 4mv8A6kJKbCSlmua5oc0hwOoI1BSUukpSSlJKUkpYOaXFoIkQSO4nhJS6Slmu
a4S0gjUSNeNElKJDQXOIAAkk6AAJKVykpdJSklKSUs1zXCWkEaiRrxokpdJSwc0uLQRIgkdxPCSl
0lKSUpJSklKSUpJTXyf57E / 44 / 8Anq5JSun / APJ + N / xNf / UhJTz / ANcegZHWsrBtotxqfs9eRX6t
7yyyl1zsdzL6AGOlzfRPdvPKSnGp + q3XGNxqbep476MavC / QDLuaw2Yr8d7 / AE211sbWHCt / uhzp
PZJSfG6J9a25FVt / W6WsryDcGsy73jYbMQ7XNsnf + jqt9rjtl + kDhKbHSOl / WTE6rgZOb1ah + Hj0
lmXV9puudbZtsBsAs2t97nh0R7Noa3SZSmvjdE + tbciq2 / rdLWV5BuDWZd7xsNmIdrm2Tv8A0dVv
tcdsv0gcJTTu + pvXMjp7aX9VxmZgyn5Tsk5FlpcX4 + NiOcTZXMuDLDt4bIA0SUyyPqh2l3THdPx +
pYrWuxMfDewXvrD20MzaxvfXXu2tN9btsQ7aQdElJW9M + tWcMm + nq / 2NtmZaWVW5Nu7Yy7Nay36P
sAa + otqb7HhgmJSUi / 5pdfP2qt / VaHY92VbfXjjLuZWGHJxsmpu1rIY72Wy5o5d37JTd + s / 1f691
jOyn9P64yjAyaSz7K + 97W73VbXCGhw2l9Veng5 / jDkphh / VjqWJnUZVfUKGCjJutJblWy + u / Lxch
zHN2xHo1vZt4mD3kJS / U / qk63Pzc7pORiYVmRkWZNNlNhosaTgvx2bnUsB / pLt7hMEE8kkJKVb0P
61m5llHX6qw5mX605Fr4suOR6BY1x2bQx9UjaNpZLeTKUwzPqz1fqGD0qrNzsO7Mw68qu3KddY51
Lr7abKrcd1jHve6tlW2XOaT3PKSlYP1a + sGNlutHWK21 / bbcplNWXcKxS7Ixrww1BoZ / Ni8OERLh
PiEpfD6F9bqraLczrlVrasg3ezKuaHs9TEJBa4PBmuu32mWgu004SmDPq59ZxU4M6zSMm1lVZsbk
2 + o41 / btrn3Bm9xYcit22A1 + 0thrUlNvF6P9ZKcgX29ZZaw5lV7pyrS01stynWM2bRoarKhsDg2W
6z3SnsWPZY3dW4OHi0yPwSUySUpJSklKSU18n + exP + OP / nq5JSun / wDJ + N / xNf8A1ISU5X1hobbd
SXdOszoafdW9zA3Xg7WuSU5P2Ov / AMocj / t5 / wD6TSUr7HX / AOUOR / 28 / wD9JpKV9jr / APKHI / 7e
f / 6TSUr7HX / 5Q5H / AG8 // wBJpKV9jr / 8ocj / ALef / wCk0lK + x1 / + UOR / 28 // ANJpKV9jr / 8AKHI /
7ef / AOk0lK + x1 / 8AlDkf9vP / APSaSlfY6 / 8AyhyP + 3n / APpNJSvsdf8A5Q5H / bz / AP0mkpX2Osa /
sHI / 7df / AOk0lK + x1 / 8AlDkf9uv / APSaSlfY6 / 8AyhyP + 3n / APpNJSjiFpBp6LkVngkWuMtOjm61
9wYSUoYhJIf0XIcwfQYbXDaO / FfcpKUcQt91HRciqxurLBa4lrhwYNcJKV9kMx + xcj0uRX6ro3fv
T6c8JKd7oDntosx / sL8GushzBY4v3F07o3NbxCSnVSUpJSklKSU18n + exP8Ajj / 56uSUrp // ACfj
f8TX / wBSElNfqfR2dTsZY6 + 2n0wRFZgGTOqSmkPqrUP + 1uT / AJw / uSUv / wA1qv8Aubk / 54 / uSUr /
AJrVf9zcn / PH9ySlf81qv + 5uT / nj + 5JTOj6t10X13jLyHGt7X7XOEHaZg6JKdlJSklKSUpJSklKS
UpJSklKSUpJSklKSUpJSklKSUpJSklNfJ / nsT / jj / wCerklK6f8A8n43 / E1 / 9SElIOov6yx7P2ZX
S9ke83TM + UOakpqet9bP9Bife7 / 0okpXrfWz / QYn3u / 9KJKV631s / wBBife7 / wBKJKU3J + s1TvWy
sel1FcusZSC6wtaJOxu8y49gkp0aqnw1t28v2y54e4NLhzoHaJKZGmTtG8a873kR / nJKUaiBJDzq
dBY86Tp3HZJS7qg3UB517WP4 + 9JSq23Mt26GogkkklwdLdo9zj2lJSZJSklKSUpJSklKSUpJSklK
SUpJSklKSUpJTXyf57E / 44 / + erklK6f / AMn43 / E1 / wDUhJTX6l1V / T3sY3FtyN4JmoSBHY6JKaf /
ADlt / wDK3J / zT / ckpX / OW3 / ytyf80 / 3JKV / zlt / 8rcn / ADT / AHJKWP1mu / 8AK3J + 4 / 8AkUlJ8Lrl
mZkNx3YV9AdP6R4IAj5JKbbc8aB1dgIME + jbBEcj9GkpTs1wp9QV2FwcAR6VmvcwC2f9qSlOzwJL
a7TB0AptkiPNg1lJTZaZnw8 / P4pKZJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKa + T / PYn / HH / z1
ckpXT / 8Ak / G / 4mv / AKkJKZX5mJjENyb66S7UCx7Wkjy3EJKR / tXpf / czH / 7dZ / 5JJSv2r0v / ALmY
/ wD26z / ySSlftXpf / czH / wC3Wf8AkklK / avS / wDuZj / 9us / 8kkpY9U6Wf + 1lH / brP / JJKUeqdLMT
mUaGf51n / kklL / tXpf8A3Mx / + 3Wf + SSUt + 1OlyT9sok / 8Kzt / aSUr9qdL / 7mUf8AbrP / ACSSl / 2r
0v8A7mY // brP / JJKV + 1el / 8AczH / AO3Wf + SSUr9q9L / 7mY // AG6z / wAkkpX7V6X / ANzMf / t1n / kk
lK / avS / + 5mP / ANus / wDJJKV + 1el / 9zMf / t1n / kklK / avS / 8AuZj / APbrP / JJKV + 1el / 9zMf / ALdZ
/ wCSSU2QQ4BzTIOoI4ISUukpSSlJKUkpr5P89if8cf8Az1ckpXT / APk / G / 4mv / qQkpz + uUX221Gr
p7M4BplzzG3XjkJKcz7Hmf8AlFT / AJ // AJmkpX2PM / 8AKKn / AD // ADNJSvseZ / 5RU / 5 // maSlfY8
z / yip / z / APzNJSvseZ / 5RU / 5 / wD5mkpX2PM / 8oqf8 / 8A8zSUr7Hmf + UVP + f / AOZpKV9jzP8Ayip /
z / 8AzNJSvseZ / wCUVP8An / 8AmaSlfY8z / wAoqf8AP / 8AM0lK + x5n / lFT / n / + ZpKV9jzP / KKn / P8A
/ M0lLfYsv / yiq / z / APzNJS / 2PM / 8oqf8 / wD8zSUr7Hmf + UVP + f8A + ZpKV9jzP / KKn / P / APM0lK + x
5n / lFT / n / wDmaSnc6Vf1C5r252KMUVhoqAdukaz3PEBJTfSUpJSklKSU18n + exP + OP8A56uSUrp /
/ J + N / wATX / 1ISU0Ot4XRsh9VnVsluMQC2vdY2sO7mN / PKIiTstnkhD5jTmfsz6nf + WVX / sTUj7cu
yz7xi / eh3q / Zn1O / 8sqv / YmpL25dlfeMX7w + 1NjfV / 6tZpc3DyvtBbq4VXMeQD47QUDEjcLoZIT +
Ugtj / mf0nxu / zh / 5FBer / mf0nxu / zh / 5FJSv + Z / SfG7 / ADh / 5FJSv + Z / SfG7 / OH / AJFJSbD + rXTs
HJZlUmzfWSW7nAjUR + 75pKdZJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklNfJ / nsT / AI4 / + erk
lK6f / wAn43 / E1 / 8AUhJTzn1q6NndY6pR9kY2xuNTNge4NH6Rzw2J / qKWExGB1amfCcmWJqwHL / 5m
9W / 7i0 / 57f7kuM / vJ9iP + bCv + ZvVv + 4tP + e3 + 5LjP7yvYj / mw6h2d + r / AFXpHVTm20NFTqjWW1Pa
TJLXcEt8EpzBjVqw4TDKZcNCuj1PrWf9x7Pvr / 8ASijps34K9az / ALj2ffX / AOlEqVfgr1rP + 49n
31 / + lEqVfgr1rP8AuPZ99f8A6USpV + CvWs / 7j2ffX / 6USpV + CvWs / wC49n31 / wDpRKlX4K9az / uP
Z99f / pRKlX4K9az / ALj2ffX / AOlEqVfgr1rP + 49n31 / + lEqVfgr1rP8AuPZ99f8A6USpV + CvWs / 7
j2ffX / 6USpV + CvWs / wC49n31 / wDpRKlX4K9az / uPZ99f / pRKlX4K9az / ALj2ffX / AOlEqVfgr1rP
+ 49n31 / + lEqVfgr1rP8AuPZ99f8A6USpV + CvWs / 7j2ffX / 6USpV + CvWs / wC49n31 / wDpRKlX4Mqr
haXiC11Z2ua6JBIDvzSRwUFAo8n + exP + OP8A56uSSrp // J + N / wATX / 1ISU1Or2PpqvsryBiODav0
xBcB7rNIAPKXRHVw / wBoZX / l4z / tt3 / pNJKv2hlf + Xlf / bbv / SaSlftDK / 8ALyv / ALbd / wCk0lK /
aGV / 5eV / 9tu / 9JpKV + 0Mr / y8r / 7bd / 6TSUr9oZX / AJeV / wDbbv8A0mkpX7Qyv / Lyv / tt3 / pNJSv2
hlf + Xlf / AG27 / wBJpKV + 0Mr / AMvK / wDtt3 / pNJSv2hlf + Xlf / bbv / SaSlftDK / 8ALyv / ALbd / wCk
0lK / aGV / 5eV / 9tu / 9JpKV + 0Mr / y8r / 7bd / 6TSUs7OynCD1xnyY8fkrSU7fQvtljH5F2YMyl + lZAI
gtJnlrSkp1UlKSUpJSklKSUpJTVxf6Vmf8az / wA9VpIDLJ / nsT / jj / 56uSSrp / 8Ayfjf8TX / ANSE
lNfqdWRcy6vGrqusLaoZcA5hh2kyCl0R1cj9m9b / AO4HT / 8AttiSVDA6s07H9Owi5 / 0C2phAjU7j
204SUr7J1Ejd + zMX3gMYPRZIsEbnO8Ge10h5JKV + zet / 9wOn / wDbbElLDG6gzabel4zgwxaGUMJd
Bk7PHRw + cpKbWB0 / Idktqz + n4jWAOc97KmRrAYGnXWQZ + SSnU / ZXS / 8AuHj / APbTP / IpKV + yul / 9
w8f / ALaZ / wCRSUr9ldL / AO4eP / 20z / yKSlfsrpf / AHDx / wDtpn / kUlK / ZXS / + 4eP / wBtM / 8AIpKV
+ yul / wDcPH / 7aZ / 5FJSv2V0v / uHj / wDbTP8AyKSlfsrpf / cPH / 7aZ / 5FJSeqmmhgroY2pg4awBo1
8gkpmkpSSlJKUkpSSlJKauL / AErM / wCNZ / 56rSQGWT / PYn / HH / z1cklXT / 8Ak / G / 4mv / AKkJKRZu
FX1D1cW1z2Ncysk1kB2jrD3BS6I6tD / mj0 // AE + T / nt / 9JpJcnJw + j4t78d46k91Z2lzNhafgYCS
kfpdF / c6p91aSlel0X9zqn3VpKV6XRf3OqfdWkpXpdF / c6p91aSlel0X9zqn3VpKV6XRf3OqfdWk
pXpdF / c6p91aSlel0X9zqn3VpKV6XRf3OqfdWkpXpdF / c6p91aSlel0X9zqn3VpKTYeB0fNyWYtf
7Rrc + YdZsDRALtTB8ElOp / zR6f8A6fJ / z2 / + k0lK / wCaPT / 9Pk / 57f8A0mkpX / NHp / 8Ap8n / AD2 /
+ k0lK / 5o9P8A9Pk / 57f / AEmkpX / NHp / + nyf89v8A6TSUr / mj0 / 8A0 + T / AJ7f / SaSk2H9W8PCyWZV
d17nVmQHuaWnSNYYElNzF / pWZ / xrP / PVaSAyyf57E / 44 / wDnq5JKun / 8n43 / ABNf / UhJSLNzqene
rlZAcWNZWDtEnV1g8Ql0R1aH / PDpP7t3 + AP / ACSSVH639LEQy4yY0a3v / bSU6TMo3Emt7Gs3BrSR
ukxrqHj86R8UlM3Ouby9nBP0COP7aSl9187S5swCRsPcxzvhJSwfaW7xYwtgmQx3b + 2kpRfcAXb2
7QJJDCflAfKSlb7dxZ6jNwExsMxxxvSUrddO0PYTMRsPhP8ApElJ0lKSUpJSklKSUpJSklKSUpJS
klKSUpJTVxf6Vmf8az / z1WkgMsn + exP + OP8A56uSSrp // J + N / wATX / 1ISUizb8jG9W3FpORaGVgV
gxMuslLojq5 / 7Z69 / wCVTv8AOP8AcklX7Z67 / wCVTv8AOP8Ackpi3qnWWN2s6PtaXF8AwNzjvJ + j
yXGUlMv2x13 / AMqnf5x / uSUr9sdd / wDKp3 + cf7klLftjrvH7Kd / nH + 5JS / 7Y66OOlO / zj / ckpb9s
ddmf2U6fHcf7klL / ALY67z + ynf5x / uSUr9s9d / 8AKp3 + cf7klK / bPXf / ACqd / nH + 5JSv2z13 / wAq
nf5x / uSUr9s9d / 8AKp3 + cf7klK / bPXf / ACqd / nH + 5JSw6x9YJ93SyR2gkf3pKX / bPXf / ACqd / nH +
5JSv2z13 / wAqnf5x / uSUr9s9d / 8AKp3 + cf7klMqur9bfaxlnTHMa5wDnbjoCdTwkp20lKSU1cX + l
Zn / GS / 8APVaSAyyf57E / 44 / + erkkq6f / AMn43 / E1 / wDUhJSLNZmv9VvT3srv2V7XWatjdZP5rkui
ИлиQ + zfW7 / uXjfd / 6hSSo4v1tMfrmONdYHb / tlJTo0UW2brcpjQ4ucNrtr9G + xrgQOHbd0eaSkn2W
rdOxkeG0eHwSUr7Kz2yys6e6Gga6doPmkpRxay4exkd4aP7ikpZ2K2BtZXPu / NA / q9nJKZfZqv8A
R1 / 5gSUhycXIND / sJrpyP8E8tECfh3HtKSmviUdYhtPU3sv1c / 1WbQ0QA1rHN9NszuJ4 / NSU3fst
Y4ZWRAiWidOZMfwSUxbj0j2kVk6ctbMzr / s0SU087E63vYOk300VgTY17RJeSf8AgnaQkptUMzXB
77dtbnOIDHfpI2kN3Ahw0e1sx2lJTP0sj1g / ez0u7C2T + dBDtPEJKXsryDVDHM9SB7ogTrrEOSU0
sPH6 + 1x + 3ZNVjC5p9jddoMuGjGcjRJTYyqeoHHcMK1jLzw5405 / qnt5JKc / 7N9bv + 5eN93 / qFJTs
UC5tFbcgh2oY0WObwXR7iNB3SUkSU1cX + lZn / Gs / 89VpIDLJ / nsT / jj / AOerkkq6f / yfjf8AE1 / 9
SElNXqgoeH05F78UWNr22MkGWueSAfmijYuX9h6b / wCW + R / nn + 5KlWr7D03 / AMt8j / PP9yVKtX2H
pv8A5b5H + ef7kqVavsPTf / LfI / zz / clSrV9h6b / 5b5H + ef7kqVavsPTf / LfI / wA8 / wByVKtX2Hpv
/ lvkf55 / uSpVq + w9N / 8ALfI / zz / clSrV9h6b / wCW + R / nn + 5KlWxPTuluIJ6teSOCXHT8EqVabHx +
n41zbm9VucWzAe7cJII1BCVKtvHL6aaDT9tIlgZvBM6Dbu45SpVub9h6b / 5b5Hyef7kqVbe6dd03
p7Hs + 3Ov3kGbSSRHholSrbn7X6b / AKdv4 / 3JUq1ftfpv + nb + P9yVKtX7X6b / AKdv4 / 3JUq1ftfpv
+ nb + P9yVKtX7X6b / AKdv4 / 3JUq1ftfpv + nb + P9yVKtX7X6b / AKdv4 / 3JUq1YFtd9uVdUdzh3N2uH
Bitg / KEioJMn + exP + OP / AJ6uQSrp / wDyfjf8TX / 1ISUyyHYrWh3UWNbMA2EAT / aSAtBIG6h2ukf6
TH / zmf3o8JRxx7q9bpH + kx / 85n96XCVcce7OpvT759D0rNvOza6J + CRBCRIHZJ9mx / 8ARM + 4IJV9
mx / 9Ez7gkpX2bH / 0TPuCSlfZsf8A0TPuCSlfZsf / AETPuCSlfZsf / RM + 4JKV9mx / 9Ez7gkpX2bH /
ANEz7gkpX2bH / wBEz7gkpX2bH / 0TPuCSlfZsf / RM + 4JKV9mx / wDRM + 4JKV9mx / 8ARM + 4JKV9mx / 9
Ez7gkpX2bH / 0TPuCSlfZsf8A0TPuCSlfZsf / AETPuCSlfZsf / RM + 4JKZsYysQxoaPAaJKQ5P89if
8cf / AD1ckpXT / wDk / G / 4mv8A6kJKea + tvSc / q / VMcYdPrtxqd1jS5rQPUc8N + mR + 4pscuGB1afMY
TkyxNWBu5P8AzR6v / wCV7f8Atyr / AMmlxn95PsQ / zf5K / wCaPV // ACvb / wBuVf8Ak0uM / vK9iH + b
/ J0fq30Hq3SurHLuxfTpdSayGvrJklp4D / JCc7jVqw4TDKZCNCnrfWs / 0Fn3s / 8AJqJtWr1rP9BZ
97P / ACaSrV61n + GS + 9n / AJNJVq9az / QWfez / AMmkq1etZ / oLPvZ / 5NJVq9az / QWfez / yaSrV61n +
GS + 9n / k0lWr1rP8AQWfez / yaSrV61n + GS + 9n / k0lWr1rP9BZ97P / ACaSrV61n + GS + 9n / AJNJVq9a
z / QWfez / AMmkq1etZ / oLPvZ / 5NJVq9az / QWfez / yaSrV61n + GS + 9n / k0lWr1rP8AQWfez / yaSrV6
1n + gs + 9n / k0lWr1rP9BZ97P / ACaSrXqubaXNALXVna5piQSA7sSOCkkFHk / z2J / xx / 8APVySldP /
AOT8b / ia / wDqQkpFmszXm1vT3srvLKtrrNWxusn81yXRHVofZvrd / wBy8b7v / UKSVfZvrd / 3Lxvu
/ wDUKSlfZvrd / wBy8b7v / UKSlfZvrd / 3Lxvu / wDUKSlfZvrd / wBy8b7v / UKSlfZvrd / 3Lxvu / wDU
KSlfZvrd / wBy8b7v / UKSlfZvrd / 3Lxvu / wDUKSlfZvrd / wBy8b7v / UKSlfZvrd / 3Lxvu / wDUKSlf
Zvrd / wBy8b7v / UKSlfZvrd / 3Lxvu / wDUKSlfZvrd / wBy8b7v / UKSlji / W4iBmYw8wP8A1CkptdOo
69XfPUsim2naRDBDt2mv821JTppKUkpSSlJKUkpSSmri / wBKzP8AjWf + eq0kBlk / z2J / xx / 89XJJ
V0 // AJPxv + Jr / wCpCSmv1GlmQ26qzIOK0tq / Sg7Yh2nckcpdEdXK / ZOJ / wCXb / 8At0f + TSSuOkYx
BI608gcn1Rp / 00lL / sajX / LNmg3H9INAY1 + n5pKY / snE / wDLt / 8A26P / ACaSlx0bHMR1mz3CR + кг
oHce / wAklMq + h2WkNq6xa8unaG2AkxzEPSUl / wCbNv8A5ZZP3n / ySSlf82bf / LLJ + 8 / + SSUr / mzb
/ wCWWT95 / wDJJKV / zZt / 8ssn7z / 5JJSv + bNv / llk / ef / ACSSlf8ANm3 / AMssn7z / AOSSUr / mzb / 5
ZZP3n / ySSm303o7 + n3uudl25Acws2WGQJIM8nwSU6SSlJKUkpSSlJKUkpSSmri / 0rM / 41n / nqtJA
ZZP89if8cf8Az1cklXT / APk / G / 4mv / qQkprdUdgMrud1IbsfbVuGvO58fR15S6I6uN9o + pf + iP3W
f3pJV9o + p4I2h7W / nNAfDvCZk6eSSlvth2TgDfb4OMOlzBxW7T6Igca6JKX9f6l / 6I / dZ / ekpb7R
9UgCGusB / MIDpY3u1sjjU8 + KSk2L1H6rYd4vxy9rm / QG15DJEOj4 + aSm7 / zq6N / pXf5jv7klK / 51
dG / 0rv8AMd / ckpX / ADq6N / pXf5jv7klK / wCdXRv9K7 / Md / ckpX / Oro3 + ld / mO / uSUr / nV0b / AErv
8x39ySlf86ujf6V3 + Y7 + 5JSv + dXRv9K7 / Md / ckpX / Oro3 + ld / mO / uSUr / nV0b / Su / wAx39ySlf8A
Oro3 + ld / mO / uSUr / AJ1dG / 0rv8x39ySlf86ujf6V3 + Y7 + 5JSv + dXRv8ASu / zHf3JKSUfWTpOTczH
qscX2ODWgscNT8klNrF / pWZ / xrP / AD1WkgMsn + exP + OP / nq5JKun / wDJ + N / xNf8A1ISUy2tdkWBw
BGxmh272JI6s / Qp / 0bfuCSXHt6f9YDY81ZGM1hcSwGsSGzoP5tJTH9n / AFj / AO5OL / 22P / SaSlfs
76yf9ycX / tsf + k0lK / Z31k / 7k4v / AG2P / SaSlfs76yf9ycX / ALbH / pNJSv2d9ZP + 5OL / ANtj / wBJ
pKWPT / rGBJycX / tsf + k0lL / s76yf9ycX / tsf + k0lK / Z31k / 7k4v / AG2P / SaSlfs76yf9ycX / ALbH
/ pNJSv2d9ZP + 5OL / ANtj / wBJpKV + zvrJ / wBycX / tsf8ApNJSv2d9ZP8AuTi / 9tj / ANJpKV + zvrJ /
3Jxf + 2x / 6TSU61GOG01tvax1oa0WODQAXR7iNB3SUk9Gn / Rt + 4JKV6NP + jb9wSUr0af9G37gkpXo
0 / 6Nv3BJShVUDIY0EcEAJKQYv9KzP + NZ / wCeq0kBlk / z2J / xx / 8APVySVdP / AOT8b / ia / wDqQkpF
m0ZGT6tWLcce0srIsAmIdZKXRHVz / wBjdd / 8tXf5p / vSSodG67OvVHH5H + 9JSbE6Z1Wm4Pyc / wBe
va4bHNMSQQJ9w7pKbfoZYhhurdo4a1u4P / XklM7KMl9Aq9VgeHTv2GNNRA9TsY7pKYmnMcT + mqBB
mfSdzH / HJKZW0ZD7C + uxjQ5mxwLHGfmLW + KSlmVZEm2yxjg5kFrWFpP7upsfwkptJKUkpSSlJKUk
pSSlJKUkpSSlJKUkpSSlJKauL / Ssz / jWf + eq0kBlk / z2J / xx / wDPVySVdP8A + T8b / ia / + pCSkWbj
WZnq0VXvxnFlZFlc7hDrD2IS6I6tD / m91D / y3yfvd / 6USSr / AJvdQ / 8ALfJ + 93 / pRJS3 / N7P / wDL
fJ + 93 / pRJS37BzY3ftjJj4u / 9KJKX / YGdJH7YydOdXf + lElLHoOaP + 9jJ0Mcu5 / 7cSUo9AzRz1jJ
/ wA53 / pRJSv2BnEx + 2MnmOXf + lPJJS / 7Azpj9r5MnjV3 / pRJS37BzoJ / bGTpzq7 / ANKJKXh2fzzx
1fJ + 93 / pRJS // N7qH / lvk / e7 / wBKJKV / ze6h / wCW + T97v / SiSlf83uof + W + T97v / AEokpi36t5rS
S3quQCeSNwn / AMESUy / 5vdQ / 8t8n73f + lElK / wCb3UP / AC3yfvd / 6USUr / m91D / y3yfvd / 6USU7V
bSytrHOLi0AFx5MDlJTJJSklNXF / pWZ / xrP / AD1WkgMsn + exP + OP / nq5JKun / wDJ + N / xNf8A1ISU
izKL8k21Y95xrCysi1o3EQ6ztIS6I6tL9i9X / wDLez / tv / 1IklX7F6v / AOW9n / bf / qRJTOjpHUqc
hl9vU7LWMILqy2A4A8H9IUlN37JZu / pFuognbV48fzXmkpe7Fc9znC17d8Ata2sjsD9Ktx7eKSlz
ik1ms3PMu3FxbXPER / Nx + CSlhi2h3mTaN2pIbVzoP9EkpHk4V9uMaKcp9T3O3C3a2W8kwGCvlJS2
DhZOKxjMjKfkva5x3uaBIcBod286R2KSkwoc0W / pHnfx7Wad9IYJ57ykppZnS + oZVwto6hZjNDWj
YGzJA1cYcwa / BJSL9i9X / wDLez / tv / 1IkpdnR + rNe1zurWOAIJb6fIHb + cSU7KSlJKUkpSSlJKUk
pSSlJKauL / Ssz / jWf + eq0kBlk / z2J / xx / wDPVySVdP8A + T8b / ia / + pCSkWbTl3 + rXhWii4sriwiY
AdZPil0R1c / 9mfWT / wAsm / 5v / mKSVfsz6yf + WTf83 / zFJSv2Z9ZP / LJv + b / 5ikpX7M + sn / lk3 / N /
8xSUr9mfWT / yyb / m / wDmKSlfsz6yf + WTf83 / AMxSUr9mfWT / AMsm / wCb / wCYpKV + zPrJ / wCWTf8A
N / 8AMUlK / Zn1k / 8ALJv + b / 5ikpX7M + sn / lk3 / N / 8xSUr9mfWT / yyb / m / + YpKV + zPrJ / 5ZN / zf / MU
lK / Zn1k / 8sm / 5v8A5ikpX7M + sn / lk3 / N / wDMUlLHpf1kIg9SHybH5GpKXHS / rIBA6k35tn / vqSlf
sz6yf + WTf83 / AMxSUyq6b9YW2sdZ1FrmBwLm7eQDqPopKdtJSklKSU1cX + lZn / Gs / wDPVaSAyyf5
7E / 44 / 8Anq5JKun / APJ + N / xNf / UhJTK / ExsmPtFTbNvG4TCSqRfsnpv / AHGq / wA0JWigr9k9N / 7j
Vf5oStVBX7J6b / 3Gq / zQlaqCv2T03 / uNV / mhK1UFfsnpv / car / NCVqoK / ZPTf + 41X + aErVQV + yem
/ wDcar / NCVqoK / ZPTf8AuNV / mhK1UFfsnpv / AHGq / wA0JWqgr9k9N / 7jVf5oStVBX7J6b / 3Gq / zQ
laqCv2T03 / uNV / mhK1UFfsnpv / car / NCVqoK / ZPTf + 41X + aErVQV + yem / wDcar / NCVqoK / ZPTf8A
uNV / mhK1UFfsnpv / AHGq / wA0JWqgr9k9N / 7jVf5oStVBX7J6b / 3Gq / zQlaqCv2T03 / uNV / mhK1UF
fsnpv / автомобиль / NCVqoJ6aKcdnp0MbW3mGiAklHk / wA9if8AHH / z1ckpXT / + T8b / AImv / qQkpjmM6k5z
fsNlVbY9wtaXEnyghJTX9L6wf6fF / wC23f8AkklK9L6wf6fF / wC23f8AkklK9L6wf6fF / wC23f8A
kklK9L6wf6fF / wC23f8AkklNjDZ1JrnfbrKrGx7RU0tIPnJKSm0kpSSlJKUkphc2x1T21O2WFpDH
HUBxGhSU5eFiW15hsDCxpc0tG3aamhrg9rn6epuPmfFJTrpKUkpSSlJKUkpz7a + uGx5puxxWXHYH
McSGzpPuSUx9L6wf6fF / 7bd / 5JJSvS + sH + nxf + 23f + SSUr0vrB / p8X / tt3 / kklK9L6wf6fF / 7bd /
5JJTdxhktpAy3MfbrJrBa3y0MpKYZP8APYn / ABx / 89XJKa / T + oYAwMYHJpBFNcj1G / ujzSU2P2h0
/ wD7k0 / 9uN / vSUr9odP / AO5NP / bjf70lK / aHT / 8AuTT / ANuN / vSUr9odP / 7k0 / 8Abjf70lK / aHT /
APuTT / 243 + 9JSv2h0 / 8A7k0 / 9uN / vSUr9odP / wC5NP8A243 + 9JSv2h0 // uTT / wBuN / vSUr9odP8A
+ 5NP / bjf70lK / aHT / wDuTT / 243 + 9JSv2h0 // ALk0 / wDbjf70lK / aHT / + 5NP / AG43 + 9JSv2h0 / wD7
k0 / 9uN / vSUr9odP / AO5NP / bjf70lK / aHT / 8AuTT / ANuN / vSUr9odP / 7k0 / 8Abjf70lK / aHT / APuT
T / 243 + 9JSv2h0 / 8A7k0 / 9uN / vSUr9odP / wC5NP8A243 + 9JSv2h0 // uTT / wBuN / vSUr9odP8A + 5NP
/ bjf70lK / aHT / wDuTT / 243 + 9JSv2h0 // ALk0 / wDbjf70lNfJ6hgG7FjJp0uM / pG / 6K3zSU // 2Q ==
AQBIAAAAAQAB / + 4AE0Fkb2JlAGSAAAAAAQUAAgAD / 9sAhAAMCAgICAgMCAgMEAsLCxAUDg0NDhQY
EhMTExIYFBIUFBQUEhQUGx4eHhsUJCcnJyckMjU1NTI7Ozs7Ozs7Ozs7AQ0LCxAOECIYGCIyKCEo
MjsyMjIyOzs7Ozs7Ozs7Ozs7Ozs7OztAQEBAQDtAQEBAQEBAQEBAQEBAQEBAQEBAQED / wAARCAEA
AMYDAREAAhEBAxEB / 8QBQgAAAQUBAQEBAQEAAAAAAAAAAwABAgQFBgcICQoLAQABBQEBAQEBAQAA
AAAAAAABAAIDBAUGBwgJCgsQAAEEAQMCBAIFBwYIBQMMMwEAAhEDBCESMQVBUWETInGBMgYUkaGx
QiMkFVLBYjM0coLRQwclklPw4fFjczUWorKDJkSTVGRFwqN0NhfSVeJl8rOEw9N14 / NGJ5SkhbSV
xNTk9KW1xdXl9VZmdoaWprbG1ub2N0dXZ3eHl6e3x9fn9xEAAgIBAgQEAwQFBgcHBgI7AQACEQMh
MRIEQVFhcSITBTKBkRShsUIjwVLR8DMkYuFygpJDUxVjczTxJQYWorKDByY1wtJEk1SjF2RFVTZ0
ZeLys4TD03Xj80aUpIW0lcTU5PSltcXV5fVWZnaGlqa2xtbm9ic3R1dnd4eXp7fh2 + f3 / 9oADAMB
AAIRAxEAPwD0Xp / T8A4GMTjUkmmuT6bf3R5JKbH7P6f / ANxqf + 22 / wBySlfs / p // AHGp / wC22 / 3J
KV + z + n / 9xqf + 22 / 3JKV + z + n / APcan / ttv9ySlfs / p / 8A3Gp / 7bb / AHJKV + z + n / 8Acan / ALbb / ckp
X7P6f / 3Gp / 7bb / ckpX7P6f8A9xqf + 22 / 3JKV + z + n / wDcan / ttv8AckpX7P6f / wBxqf8Attv9ySlf
s / p // can / ttv9ySlfs / p / wD3Gp / 7bb / ckpX7P6f / ANxqf + 22 / wBySlfs / p // AHGp / wC22 / 3JKV + z
+ n / 9xqf + 22 / 3JKV + z + n / APcan / ttv9ySlfs / p / 8A3Gp / 7bb / AHJKV + z + n / 8Acan / ALbb / ckpX7P6
f / 3Gp / 7bb / ckpX7P6f8A9xqf + 22 / 3JKV + z + n / wDcan / ttv8AckpX7P6f / wBxqf8Attv9ySlfs / p /
/ can / ttv9ySmvk9PwBdixjU63Gf0bf8ARW + SSmx0 / wD5Pxv + Jr / 6kJKaPWeqdT6fZWzA6e / Na9pL
nNJG0g8aNckpz / 8AnJ9Yv / KO373f + k0lK / 5yfWL / AMo7fvd / 6TSUr / nJ9Yv / ACjt + 93 / AKTSUr / n
J9Yv / KO373f + k0lK / wCcn1i / 8o7fvd / 6TSUr / nJ9Yv8Ayjt + 93 / pNJSv + cn1i / 8AKO373f8ApNJS
v + cn1i / 8o7fvd / 6TSUr / AJyfWL / yjt + 93 / pNJSv + cn1i / wDKO373f + k0lK / 5yfWL / wAo7fvd / wCk
0lOn0XqXUeoet9vwXYPp7dm4k7926eWt4gJKdNJSklKSUpJSklKSUpJSklKSUpJTXyf57E / 44 / 8A
nq5JSun / APJ + N / xNf / UhJTK7LxcchuRdXUXagPcGz95CSkf7T6b / ANy6P + 3Gf + SSUkpzMTIcWY99
drgJLWPa4x4wCkpMkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSmvk / z2J /
xx / 89XJKV0 // AJPxv + Jr / wCpCSnF + s7fq46 + j9uOsbZsPp7N30Z1 + iCkpxfT + oH + kv8Aus / 8ikpt
9L6j9S + j5DsnCttFjmGs7mvcNpLXfu / yUlOp / wA9fq9 / p3f9tv8A / IpKV / z1 + r3 + nd / 22 / 8A8ikp
X / PX6vf6d3 / bb / 8AyKSlf89fq9 / p3f8Abb // ACKSlf8APX6vf6d3 / bb / APyKSlf89fq9 / p3f9tv /
APIpKV / z1 + r3 + nd / 22 // AMikpX / PX6vf6d3 / AG2 // wAikpX / AD1 + r3 + nd / 22 / wD8ikpX / PX6vf6d
3 / BB / wDyKSlf89fq9 / p3f9tv / wDIpKV / z1 + r3 + nd / wBtv / 8AIpKV / wA9fq9 / p3f9tv8A / IpKZ0 / X
DoN9rKK73F9jgxo9N4kuMD81JTtJKUkpSSlJKUkpSSmvk / z2J / xx / wDPVySldP8A + T8b / ia / + pCS
mh2u7qVVtQwenV57S07nPLRtM8e5JTQGZ1yBP1eqnv76x / BJSvtnW / 8A53qv + 3K // IpKV9s63 / 8A
O9V / 25X / AORSUr7Z1v8A + d6r / tyv / wAikp1unVfacYW52BVi3EkGqGv0HBkBJTa + xYf + gq / zG / 3J
KV9iw / 8AQVf5jf7klK + xYf8AoKv8xv8AckpX2LD / ANBV / mN / uSUr7Fh / 6Cr / ADG / 3JKV9iw / 9BV /
mN / uSUr7Fh / 6Cr / Mb / ckpX2LD / 0FX + Y3 + 5JSvsWH / oKv8xv9ySlfYsP / AEFX + Y3 + 5JShiYjSHNpr
BGoIYNPwSUmSUpJSklKSUpJSklNfJ / nsT / jj / wCerklK6f8A8n43 / E1 / 9SElNhJTyvX83Iq6jZUz
rTMFoa2KCxxLTA1lrDz8UlNOjq17L632 / WGp9TXgvZ6TtWg6tn0 / BJTvN + t31dcSBmDTxZYPysSU
y / 51 / V7 / ALmM / wA1 / wD5FJTawOr9O6mXtwbxca4L4BETx9IDwSU3ElKSUpJSklKSUpJSklKSUpJS
klKSUpJSklKSUpJSklKSU18n + exP + OP / AJ6uSUrp / wDyfjf8TX / 1ISU0es9bv6VZXXVg3ZgsaXF1
Uw2DEGGuSU5NvW8TKf62T9XrbbXAAvspa46fynVykpGOqdOgF31ZcCewx2n / ANFBJSv2p0z / AOdp
/ wD7DM / 9JpKV + 1Omf / O0 / wD9hmf + k0lOh0XqeNZmDGxuj2dP9UHdb6Qrb7QSA4taElPQJKUkpSSl
JKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / AD1ckpXT / wDk / G / 4mv8A6kJKbCSn
nesdQ6vj576sTOwKKg1u2vIsa2wEgTuB1 + CSmzh9ZxzU0Z + fheoGtDjXeyC7XcfpDThHRbrbn5nW
OqevYMDqPSxQSPTNlzS8CBM6kcoLgh / a31hOg6n0n / t1qSndxOtdPGNUMzqGIb9o9UsuZt3d49yS
mxT1TpmRYKcfLotsdO1ldrHOMCTADieAkptJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJ
Ka + T / PYn / HH / AM9XJKV0 / wD5Pxv + Jr / 6kJKaPWfrJg9Dsrqy2WvNrS5vpBpEAxrue1JThZfXvqZ1
C45WZiW2WuADnObB0ED6NsJKQ / tH6h / 9wbPuP / pVJSv2j9Q / + 4Nv3O / 9KpKUOo / UMGRg26eTv / Sq
SnY6Z0f6rdWxRmYuFFZcWjeXAy3 + 2UlOhifV / o + DkNysXGbXbXO14LjEgtPLj2KSnRSUpJSklKSU
pJSklKSUpJSklKSUpJSklKSUpJSklKSU18n + exP + OP8A56uSUrp // J + N / wATX / 1ISU2ElOJ1Pqh2
ix8x9XT8Oi6gBpa + yxrXEkCdDa38iSm3h5WZbUx + a2umwhofWHgwYkkbXO8Y57I6LfVbmP6t9adf
T6fjmOCbme7 / AMGEILm30nqHWr7nt6vjU4tQbLHMsa4l0jTSx / ZJTrggiQZB4ISUukpSSlJKUkpS
SlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSmvk / wA9if8AHH / z1ckpXT / + T8b / AImv / qQkpB1HrfS +
lPZXn3ek6wFzRse6QNPzGuSU891DJ + o3U8p2Zl5Lza8AEtbcB7RA09NJTW9D / F7 / ANyLfuu / 9JpK
W9D / ABe / 9ybfuu / 9JpKX9D / F7 / 3It + 67 / wBJpKeh6T1zoFnodK6bkF7mt2VMLLASGNJ + k5gHDUlO
wkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSmvk / wA9if8AHH / z1ckpXT / + T8b / AImv
/ qQkpldiYuQQ7IprtLdAXtDo + 8FJTg9Tyhg5j8bG + r32utjWkXV1 + 10gaDbQ / ifFJTewqMbLpbdb
0uvHLmNca31skEzI9zG8eYCNLbNtLqOUzByX49P1fOW1olttdQ2u0n82l3wQXNL9r3 // ADqv / wC2
z / 7zJKd / pFdF + LVnO6ezAvdu / RlgD2QXM52MOo8klOikpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUk
pSSlJKUkpSSmvk / z2J / xx / 8APVySldP / AOT8b / ia / wDqQkpbK6lgYLmtzMiuhzxLRY4NkDwlJTz3
VMfovUcw5f7cFHqBoFddzdogAfvaJKav7G6NO3 / nC7iZ9ZkffvhJSh0bop0h2hPt5m5gH / VpKX / Y
vRv / AJ4v / B2f + TSUr9i9G / 8Ani / 8HZ / 5NJT0XSL + nVY9XT8bOrzLK2nUWNe9wkmSGuPikp0UlKSU
pJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklNfJ / nsT / jj / AOerklK6f / yfjf8AE1 / 9SElMMzpX
TuoOa / NoZc5ghpcOAUlPO9Tf9Vul5T8OzpT7bGAEmtgLSHAHQl89 / BJTewumdAz6G3VdPaxrmNcQ
9pkbpO36XkjS3i1prdQr + q / S7G05PTi5z2h59OuRrOh9 / KBSDbRPU / qeDB6Rfp4VN / 8ASqSXW6T0
/ wCrXWMZ2Tj9O9JrHmstubtdIDXTo52nuSU6eL0XpeDd6 + JjMqsAI3NGsHlJTdSUpJSklKSUpJSk
lKSUpJSklKSUpJSklKSUpJSklKSU18n + exP + OP8A56uSUrp // J + N / wATX / 1ISUksvopIFtjGE8Bz
gPypKcbqOD1PMynZGD1cY1Lg3bUAHAQNTO7ukprfsfr3 / l // ANAf + SSUxHROutO4dfM + YkfcXpKV
+ xuuhxeevnjWRp92 + ElL1dG668fouvF5J7Dd / wB / KSnoMKm + jFqpybfXtY2h3kRuPjCSk6SlJKUk
pSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSmvk / z2J / xx / 8APVySldP / AOT8b / ia / wDqQkpr9T6F
03q72WZ1Ze6sFrSHObAOv5pCSnneoYP1I6ZkOxcqu0WsALmtNhgOAI1mO6Sm3ifVz6rZ1TLcWlzg
9gfBseCA6YnXnRGlvELpz8qj6i4eQ7FyK7RZWYfBsIB + 9BcG10zpX1L6rc6rAZY99bd5l1rYEgfn
fFJTs4P1a6R03Jbl4lTmWsBDSXudAdIOhPmkp1ElKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUp
JSklKSU18n + exP8Ajj / 56uSUrp // ACfjf8TX / wBSElNhJTg9V6d9YMjNfb0 + zDbQQ3aL2Bz5A1k +
k / v5pKQMwPrtWIry8Fo8Gtjj / rCSmDuk / XB7i59 / T3OOpJrBJ / 8AZdJS9fTfrlUS6rJwGE6EtZH5
KElPQ4jcluNU3Mc1 + QGgWuZ9EujUjQJKTJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKU
kpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpo9Z + r1HWbK7bb7qTU0tAqIAMmdZBSU4mT0XoeDac
bJ6zk02MAlhsiARp + akpIfq / 0ptAyj1fKFJa1 / qeoNu1x2NP0e5SpF6013dP + rrTr12 / 4i0EfeGp
JbeH9WundQqN2F1XKura7YXNsEBwAMfR80lPTUVCimukEuFbQzc7k7RElJSRJSklKSUpJSklKSUp
JSklKSUpJSklKSUpJSklKSUpJSklNfJ / nsT / AI4 / + erklK6f / wAn43 / E1 / 8AUhJTYSU831rA6tf1
CyzE6Zg5VRDQLbxLzAEg / pG8fBJTWGP9ahQ7G / ZeB6L43Vydvtjbp6 / baEbQIgFD + y + vwB + xOmfD
aNP / AAZBLaxR9b8Ks1YnTcClhO4tZ7QSQBOl3kkp6PEdkuxqnZjWsyC0G1rPoh0agalJSZJSklKS
UpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklNfJ / nsT / jj / wCerklK6f8A8n43 / E1 / 9SElNPq /
SuodQsrfh9RswWsaQ5rGl24k86PYkpybekZ9DzXd9ZnVvHLXw0 / cb0lJG9A6u9rXV / WG57XCWlrC
4EeIi4pItG / o + czc276yvZt9rg72EE8T + nBHKSUbul3uAb / zpIAjh + v3 / aJSU2nfVnrLyHDr + RA1
ENdh5X6pKdvp2Nfh5dePk5Dsu1m7dc8QXS4uGm53AMcpKbKSlJKUkpSSlJKUkpSSlJKUkpSSlJKU
kpSSlJKUkpSSmvk / z2J / xx / 89XJKV0 // AJPxv + Jr / wCpCSmwkp5L6wYws6pa79hvz5awHIbZa0O0
GkM00SUxxup9Xw2CvH6Dc1ga1jWl7zDW8AbmE90bW8Iu2nk125l7snJ + rVtltkFzvVuEwI4EeCC5
F9ib / wDOxb / 29ekp7nCsstw6bLqjQ9zGl1R5YY + jr4JKTpKUkpSSlJKUkpSSlJKUkpSSlJKUkpSS
lJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKUkpSSlJKU
kpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKUkpSS
lJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT
8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5
P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKU
kpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKUkpSS
lJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKU
kpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP
/ wCT8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKU
kpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSS
lJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkpsJKUkpSSlJKUkpSSlJKU
kpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpSSlJKUkpr5P89if8cf / PVySldP / wCT8b / ia / 8AqQkp
FnV9We9v7OtoraB7xcxzyT5bXNSU1vR + s / 8A3Jw / + 2n / APk0lK9H6z / 9ycP / ALaf / wCTSUr0frP /
ANycP / tp / wD5NJSvR + s // cnD / wC2n / 8Ak0lNnBr6sx7v2jbRY0j2CljmEHz3OckpupKUkpSSlJKY
Wh7q3trO15aQ1x1gxoUlOZhYmTXm2WmRW4sNbNu01Na1wsa5 + nqb3HxPikp1klKSUpJSklKSU5l1
P1iNrzRkYrai4 + mHVPLg2faCQ / mElMPR + s // AHJw / wDtp / 8A5NJSvR + s / wD3Jw / + 2n / + TSUr0frP
/ wBycP8A7af / AOTSUr0frP8A9ycP / tp // k0lOhiNy20NGc9ll2u51QLW86QCSkpjk / z2J / xx / wDP
VySmv0 / qGAMDGByaQRTXI9Rv7o80lNj9odP / AO5NP / bjf70lK / aHT / 8AuTT / ANuN / vSUr9odP / 7k
0 / 8Abjf70lK / aHT / APuTT / 243 + 9JSv2h0 / 8A7k0 / 9uN / vSUr9odP / wC5NP8A243 + 9JSv2h0 // uTT
/ wBuN / vSUr9odP8A + 5NP / bjf70lK / aHT / wDuTT / 243 + 9JSv2h0 // ALk0 / wDbjf70lK / aHT / + 5NP /
AG43 + 9JSv2h0 / wD7k0 / 9uN / vSUr9odP / AO5NP / bjf70lK / aHT / 8AuTT / ANuN / vSUr9odP / 7k0 / 8A
bjf70lK / aHT / APuTT / 243 + 9JSv2h0 / 8A7k0 / 9uN / vSUr9odP / wC5NP8A243 + 9JSv2h0 // uTT / wBu
N / vSUr9odP8A + 5NP / bjf70lK / aHT / wDuTT / 243 + 9JSv2h0 // ALk0 / wDbjf70lK / aHT / + 5NP / AG43
+ 9JTXyeoYBuxYyadLjP6Rv8AorfNJT // 2Q ==
uuid: 40e6c2a1-8916-474b-ad14-d673162b620bxmp.сделал: FD0105EE1920681180838212EDF7EDC9xmp.did: FB7F11740720681188C68A053A992F47 Стойкость: pdf
0681188C68A053A992F472014-07-10T11: 36: 22 + 05: 30 Adobe InDesign 7.0 /; / метаданные
0681188C68A053A992F472014-07-10T13: 30: 53 + 05: 30 Adobe InDesign 7.0 /; / метаданные
068118083CFA8A33D2D302014-07-12T13: 29: 37 + 05: 30 Adobe InDesign 7.0 /; / метаданные
xmp.iid: 2D4276EB1920681180838212EDF7EDC9xmp.did: 360E29184620681180839D42260B0EA8xmp.сделал: FB7F11740720681188C68A053A992F47default3676application / pdf Adobe PDF Library 9.9 Ложь
конечный поток
эндобдж
3 0 obj
>
эндобдж
5 0 obj
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.0 0.0 612.0 792.0] / Type / Page >>
эндобдж
6 0 obj
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [0.0 0.0 612.0 792.0] / Type / Page >>
эндобдж
57 0 объект
> поток
BT
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_0 1 Тс
11 0 0 11 302.92 36.0389 тм
(2) Tj
ET
q
0 г
/ GS1 GS
/ Fm0 Do
Q
BT
/ T1_1 1 Тс
7 0 0 7 36 36,0472 тм
(\ 251 2015 College Board. Все права защищены.) Tj
59.015 0 Тд
(Мини-урок SpringBoard, блок геометрии 1) Tj
/ T1_0 1 Тс
-0.006 Tw 12 0 0 12 36 747.0601 Tm
(Расстояние и середина в трех измерениях \ (продолжение \)) Tj
/ CS1 CS 1 SCN
/ GS1 GS
0 Tw 13 0 0 13 36 710,3151 Tm
(ПРАКТИКА) Tj
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_2 1 Тс
11,5 0 0 11,5 36 691,8151 тм
[(F) 19 (o) 12 (re) -6 (a) 2 (c) 6 (hp) -5 (a) 9 (ir o) 12 (fp) -9 (o) 12 (in) 19 ( ts, f) -10 (дюйм) 4 (dt) -6 (h) 4 (e di) 3 (s) 5 (t) -6 (a) 9 (n) 4 (c) -1 (ea) 9 (n) 4 (dt) -6 (h) 4 (em) 2 (i) 1 (d) 12 (p) -9 (o) 12 (in) 19 (tb) -9 (et) -3 (w ) 8 (e) -5 (e) 1 (nt) -6 (h) 4 (et) -3 (w) 8 (og) -5 (i) 7 (v) 8 (e) 1 (np) — 9 (o) 12 (дюйм) 19 (ц.)] TJ
/ T1_3 1 Тс
0,279 Tw / Span >> BDC
0 -1,565 TD
() Tj
EMC
0,574 0 Тд
(1.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
EMC
1.339 0 Тд
[(\ (0, 0, 0 \) a) 9 (n) 4 (d \ (3, 4, 12 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
/ T1_5 1 Тс
-0,042 Tc 0,042 Tw [(1) -33 (3;) — 42 ()] ТДж
0 Tc 0 Tw () Tj
-0,003 Tc 0,003 Tw 0 -1,217 TD
[(mi) 3 (d) 5 (p) -10 (oi) 11 (n) -4 (t) -3 ()] TJ
/ T1_6 1 Тс
0 Tc 0 Tw (5) Tj
/ T1_5 1 Тс
-0,022 Tc 0,022 Tw [(\ () 36 (1,5) 10 (,) — 22 (2,) — 22 (6) 3 (\))] ТДж
/ CS0 cs 0.717 0,66 0,666 0,786 сбн
/ GS0 гс
/ T1_3 1 Тс
0 Tc 0,279 Tw / Span >> BDC
-1,826 -1,652 тд
() Tj
EMC
0,574 0 Тд
(2.) Tj
/ T1_2 1 Тс
0,26 Tw / Span >> BDC
() Tj
EMC
(\ (4,) Tj
/ T1_6 1 Тс
0 Tw 2.62 0 Td
(2) Tj
/ T1_2 1 Тс
[(3, 6 \) a) 9 (n) 4 (d \ (1, 0, 17 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-1,368 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
q 1 0 0 1 79.3097 605.3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,872 л
24,281 7,872 л
24,281 7,31 л
7,274 7,31 л
4.343 -3,878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_7 1 Тс
11,5 0 0 11,5 86,1534 602,5631 тм
(139) Tj
/ T1_5 1 Тс
1,652 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-9,686 -1,652 тд
() Tj
EMC
0,574 0 Тд
(3.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
EMC
1.339 0 Тд
[(\ (6, 5, 4 \) a) 9 (n) 4 (d \ (10, 9, 8 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
q 1 0 0 1 78,7897 554,0242 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6.84 7,872 л
19,469 7,872 л
19,469 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_9 1 Тс
11,5 0 0 11,5 86,3522 551,2717 тм
(48) Ти
/ T1_5 1 Тс
1,168 -0,04 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
EMC
0,574 0 Тд
(4.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
EMC
1.339 0 Тд
[(\ (1, 1, 1 \) a) 9 (n) 4 (d \ (10, 10, 10 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
К 1 0 0 1 79.1897 г. 501,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,5 7,873 л
24,5 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_10 1 Тс
11,5 0 0 11,5 86,2522 498,5631 тм
(243) Ти
/ T1_5 1 Тс
1,734 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
EMC
0,574 0 Тд
(5.) Tj
/ T1_2 1 Тс
0,26 Tw / Span >> BDC
() Tj
EMC
(\ () Tj
/ T1_6 1 Тс
0 Tw (2) Tj
/ T1_2 1 Тс
(4,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(5,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
[(19 \) a) 9 (n) 4 (d \ (8, 3, 12 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
1.252 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
q 1 0 0 1 79,1897 450,0243 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
30,031 7,873 л
30.031 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_11 1 Тс
11,5 0 0 11,5 86,0334 447,2718 тм
(1169) Tj
/ T1_5 1 Тс
2,028 -0,04 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-10,761 -1,652 тд
() Tj
EMC
0,574 0 Тд
(6.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
EMC
1.339 0 Тд
[(\ (5, 5, 18 \) a) 9 (n) 4 (d \ (5, 5,)] TJ
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(8 \)) Tj
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0.087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
q 1 0 0 1 79,0697 398,0243 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,5 7,873 л
24,5 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_12 1 Тс
11,5 0 0 11,5 86,1322 395,2718 тм
(676) Tj
/ T1_5 1 Тс
1,581 -0,04 тд
() Tj
/ T1_6 1 Тс
(5) Tj
/ T1_5 1 Тс
-0,039 Tc 0,039 Tw [(2) -17 (6;) — 39 ()] ТДж
0 Tc 0 Tw () Tj
-0,003 Tc 0,003 Tw -4,114 -1,217 Td
[(mi) 3 (d) 5 (p) -10 (oi) 11 (n) -4 (t) -3 ()] TJ
/ T1_6 1 Тс
0 Tc 0 Tw (5) Tj
/ T1_5 1 Тс
-0.032 Tc 0,032 Tw [(\ () 9 (5,) — 32 (5,) — 32 (5) 10 (\))] TJ
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_3 1 Тс
0 Tc 0,279 Tw / Span >> BDC
-1,826 -1,652 тд
() Tj
EMC
0,574 0 Тд
(7.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
EMC
1.339 0 Тд
[(\ (3, 6, 1 \) a) 9 (n) 4 (d \ (1, 6, 3 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
q 1 0 0 1 78,7897 345,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
13,469 7,873 л
13,469 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_13 1 Тс
11,5 0 0 11,5 86,1022 342,5631 тм
(8) Tj
/ T1_5 1 Тс
0,641 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
EMC
0,574 0 Тд
(8.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
EMC
1.339 0 Тд
[(\ (9, 6, 3 \) a) 9 (n) 4 (d \ ()] TJ
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(9,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(6,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(3 \)) Tj
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
EMC
К 1 0 0 1 79.0697 293,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,969 7,873 л
24,969 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_14 1 Тс
11,5 0 0 11,5 86,1322 290,5631 тм
(504) ТД
/ T1_5 1 Тс
1,622 0,022 тд
() Tj
/ T1_8 1 Тс
(> / ExtGState >>> / Subtype / Form >> stream
/ CS0 CS 0,717 0,66 0,666 0,786 SCN
1 Вт 4 М 0 Дж 0 Дж
/ GS0 гс
q 1 0 0 1 306 29,6339 см
0 0 мес.
5,412 0 9,8 4,388 9,8 9,8 в
9,8 15,212 5,412 19,6 0 19,6 в
-5,412 19,6 -9,8 15,212 -9.8 9,8 в
-9,8 4,388 -5,412 0 0 0 в
час
S
Q
конечный поток
эндобдж
12 0 объект
>
эндобдж
9 0 объект
[/ ICCBased 68 0 R]
эндобдж
68 0 объект
> поток
HuTK tKKJI, t (4 K% ҹh5J # Ғ (H
wqyy ~ 3̙g
Сегмент направленной линии — обзор
Основные идеи
Наше линейное уравнение основано на векторах (рисунок 5.1). Напомним, что мы рисуем вектор в виде направленного отрезка линии (с помощью стрелки), идущего от точки, называемой хвостом , до точки, называемой головой . Считается, что два таких сегмента представляют один и тот же вектор, если они имеют одинаковое направление и одинаковую длину. У них не обязательно должен быть один и тот же хвост. Когда мы смотрим на направленный линейный сегмент, мы на самом деле смотрим только на одного представителя вектора, хотя это различие часто теряется, когда мы свободно называем направленный линейный сегмент вектором.
Рисунок 5.1. Параметрический вид прямой.
Если вектор имеет хвост в точке A = ( x A , y A ) и его голову в точке B = ( x B , y B ), тогда вектор от A до B может быть представлен числовыми компонентами как 〈 x B s — x A , y B — y A 〉.Если A и B — трехмерные точки, то у нас будет 〈 x B — x A , y B — y A , z B — z A 〉. Векторы будут обозначаться строчными полужирными буквами, например a, p, u, x; например, p = 〈2, 3, 4〉. Полужирный шрифт неудобен для работы на классной доске или на бумаге, поэтому вы можете p → использовать вместо p, например, .
Векторы можно складывать, вычитать и умножать на скаляры. Например, если u = 〈1, 5, −3〉 и v = 〈−6, 2, −1〉, то u + v = 〈−5, 7, −4〉 и u — v = 〈7, 3, −2,〉 4 u = 〈4, 20, −12〉 и −2 u = 〈−2, −10, 6〉.
Здесь мы полагаемся на множество фактов о векторах, которые обычно вводятся при изучении многомерного исчисления. Три из этих фактов касаются геометрического смысла равенства, сложения и скалярного умножения векторов.
- 1.
Если u — вектор от B до A и v — вектор от D к C , то u и v имеют то же компоненты тогда и только тогда, когда направленный сегмент от B до A имеет ту же длину и направление, что и направленный сегмент от D до C .
- 2.
Если u и v — векторы, мы можем найти u + v следующим образом: Выберите направленный отрезок, представляющий u , а затем поместите представителя v так что его хвост находится во главе u. Вектор от хвоста u к голове v равен u + v.
- 3.
Если u вектор, а r скаляр (обычный число), то (a) если r> 0, r u указывает в том же направлении, что и u , и его длина в r в раза больше, и (b) если r <0, r u указывает в направлении, противоположном u , но это | r | раз дольше.
Вектор от начала координат до точки P называется вектором положения для P , и мы обозначаем его p. Обычно мы обозначаем вектор положения строчной полужирной версией заглавной буквы, используемой для точки. Если P имеет координаты ( x P , y P , z P ), то вектор положения p = 〈 x P , y P 9057 , z P 〉.Как видите, разница между точками и векторами положения очень мала, поэтому вы можете задаться вопросом, почему мы не используем одно и то же обозначение P для обозначения обоих или почему мы вообще вводим векторы. Одна из причин заключается в том, что вектор можно изменить так, чтобы он располагался хвостом в любой момент, когда мы захотим. Это важно при создании теории векторных вычислений и в некоторых приложениях. Однако в нашей работе, чтобы избежать путаницы, часто визуализируйте вектор положения как имеющий хвост в начале координат.
Предположим, нам даны координаты двух точек A, и B , а также дана третья точка X , и мы хотим знать, находится ли она на линии, определяемой точками A и B .Точки могут находиться в двухмерном или трехмерном пространстве — наш метод решения будет таким же. Для определенности предположим, что мы находимся в трех измерениях, поэтому A = ( x A , y A , z A ) и B = ( x B , y B , z B ), X = ( x , y , z ). X находится на линии AB↔ (Рисунок 5.1) тогда и только тогда, когда вектор x — a указывает в том же или противоположном направлении, что и b — a. Это означает
(5.1) x-a = t (b-a) для некоторого скаляра t.
(На рисунке 5.1 t = 1.5.) Уравнение (5.1) дает
(5.2) x = a + t (b-a).
Это можно представить как набор уравнений, по одному для каждой координаты пространства, в котором мы находимся. Например, в трех измерениях мы имеем
(5.3) x = xA + t (xB − xA), y = yA + t (yB − yA), z = zA + t (zB − zA).
В двумерном пространстве мы имеем только первые два из этих уравнений.
Уравнение (5.2), возможно, самый простой способ запомнить параметрические уравнения, но когда мы их используем, нам часто требуется (уравнение 5.3) или двумерная версия уравнения. (5.3).
ПРИМЕР 5.1
- (a)
Найдите параметрические уравнения линии, соединяющей точки A, (2, 1, −4) и B (5, 0, 2) в трехмерном пространстве. .
- (b)
Сделайте то же самое для точек A (0, a ) и B ( b , 0) в двухмерном пространстве.
РЕШЕНИЕ
- (a)
b — a = 〈5, 0, 2〉 — 〈2, 1, −4〉 = 〈3, −1, 6〉, поэтому мы имеем
x = 2 + 3t,
y = 1 — t ,
z = −4 + 6 t .
- (b)
b — a = 〈b, 0〉 — 〈0, a〉 = 〈b, −a〉, поэтому
x = 0 + bt
y = a — при .
Векторы a и b не входят в уравнение. (5.2) симметрично: a появляется дважды, а b только один раз. Учитывая две точки, такие как (2, 1) и (4, −1), как мы узнаем, какой из них использовать как a , а какой как b? Параметрические уравнения действительно будут различаться в зависимости от того, какой выбор вы сделаете, но когда мы используем параметрические уравнения для решения проблем, конечные результаты будут такими же.
ПРИМЕР 5.2 Точка на линии
Является ли X = (−3, 1) на прямой, определяемой выражениями (5, −2) и (1, 2)?
РЕШЕНИЕ
Возьмем a = 〈1, 2〉 и b = 〈5, — 2〉. Если X находится на линии, тогда должно быть значение t такое, что уравнение. (5.2) выполняется:
−3 = 1 + t (5-1) = 1 + 4 t ,
1 = 2 + t (−2-2) = 2-4 t .
Каждое из этих уравнений легко решается относительно t.Если мы получим то же значение t, то точка находится на линии. В этом случае мы получаем t = −1 и = 1/4, поэтому точка не лежит на прямой. Напротив, вы можете проверить, что (−3, 6) действительно лежит на прямой, поскольку оба уравнения имеют решение t = −1.
Как мы можем определить, находится ли (−3, 6) на отрезке отрезка AB ¯, соединяющем точки A и B из примера 5.2? Чтобы ответить на этот вопрос, мы анализируем три части, на которые A и B делят линию, которую они определяют.Части, естественно, соответствуют различным интервалам значений t . Вместо того чтобы думать о специальной точке (−3, 6), давайте рассмотрим произвольный вектор положения x , голова X которого лежит на линии AB↔, а значение параметра t соответствует x.
- 1.
Если t ≥ 1, то согласно уравнению. (5.1), x — a точки в том же направлении, что и b — a, и длина x — a , по крайней мере, равна длине b — а. Это означает, что X лежит на бесконечной части линии, начинающейся с B и отходящей от A .
- 2.
Если t ≤ 0, то x — a либо 0 (нулевой вектор), либо указывает в направлении, противоположном b — a. Это означает, что X лежит на бесконечной части линии, начинающейся с A и отходящей от B .
- 3.
Если 0 ≤ t ≤ 1, то x — a либо 0 , либо указывает в том же направлении, что и b — a, и длина x — a не больше длины b — a. Это означает, что X лежит на отрезке AB¯, определяемом линиями A и B .
Для точки на отрезке AB¯ соответствующее значение t говорит нам, как далеко на отрезке от A до B лежит точка.Например, если X — середина AB¯, то уравнение. (5.1) показывает, что должно быть t = 1/2. Аналогично, для точки 1/3 пути от A до B , t = 1/3 и так далее.
ПРИМЕР 5.3: Медианы треугольника
Медиана треугольника — это сегмент, соединяющий вершину с серединой противоположной стороны. На рисунке 5.2 AM¯1, BM¯2, CM¯3 — медианы. На медиане AM 1 найдите точку P 1 , которая составляет 2/3 пути от A до M 1 .Проделайте то же самое с каждой из двух других медиан, найдя «точки двух третей» P 2 и P 3 . Покажите, что все эти точки одинаковы: P 1 = P 2 = P 3 . Это показывает, что три медианы встречаются в одной точке, называемой центроидом треугольника.
Рисунок 5.2. Три середины и середина треугольника.
РЕШЕНИЕ
Поскольку M 1 является средней точкой BC ¯,
m1 = b + 12 (c − b) = 12 b +12 c.
Поскольку P 1 является «точкой двух третей» AM1¯,
p1 = a + 23 (m1 − a) = a + 23 (12b + 12c − a) = a + 13b + 13c −23a = 13 (a + b + c).
Когда мы вычисляем p 2 и p 3 с помощью того же метода, мы получаем ту же формулу. Попробуйте это как упражнение.
Формулы средней точки и расстояния в 3D — Концепция
Есть две формулы, которые важно помнить при рассмотрении векторов или положений в трехмерной системе координат.Формула средней точки и формула расстояния в 3D. Формула средней точки и расстояния в 3D может быть получена с использованием метода сложения геометрического представления векторов. Чтобы понять вывод формулы расстояния в трехмерном пространстве, мы должны понимать трехмерные векторные операции.
Я хочу вывести формулу средней точки для трех измерений, формула средней точки поможет мне найти среднюю точку между точками a, которые являются координатами x1, y1 и z1 и b, имеющими координаты x2, y2 и z2.Итак, у меня здесь нарисован отрезок ab, я пометил свою среднюю точку m и надеюсь найти формулу для его координат. Я также добавил вектор положения oa для точки a и вектор положения om для точки m. Теперь давайте найдем компоненты для вектора положения oa и напомним, что компоненты вектора положения — это в точности координаты конечной точки этого вектора, поэтому будут x1, y1, z1, и мне также понадобится вектор ab, чтобы найти m и каковы компоненты ab? Итак, поскольку вектор ab идет от точки a к точке b, а компоненты — x2-x1, y2-y1 и z2-z1, хорошо, как мы собираемся получить вектор положения om из oa и ab?
Что ж, давайте заметим, что вектор, который начинается в точке a и заканчивается в m, является половиной вектора, идущего от a до be, так что это вектор ab, этот вектор, начинающийся здесь и заканчивающийся здесь, является половиной ab скаляр несколько половин ab, поэтому мне нужно добавить это к oa, чтобы получить om.Итак, вектор om = oa плюс половина a b, так что он будет в компонентах x1, y1, z1 плюс половина этого, половина x2-x1, y2-y1 и z2-z1. Итак, давайте посмотрим, сможем ли мы объединить это за один шаг для первого компонента, который я собираюсь получить x1 плюс половина x2 минус половина x1, поэтому половина x1 плюс половина x2, теперь я получу y1 плюс половину y2 минус половина y1, это половина y1 плюс половина y2, и аналогично я получаю половину z1 плюс половину z2.
Каждая из них представляет собой точное среднее значение компонентов x и y этих двух точек, поэтому я могу записать это как x1 + x2 по 2, y1 + y2 по 2 и z1 + z2 по 2, это компоненты вектора om, которые идет из начала координат в точку m и, следовательно, координаты точки m таковы.Таким образом, средняя точка m сегмента, соединяющего x1, y1, z1 и x2, y2, z2, равна x1 + x2 на 2, y1 + y2 на 2 и z1 + z2 на 2, и это формула средней точки.
Как рассчитать расстояние между двумя координатами
Обновлено 15 декабря 2020 г.
Нукрейша Лэнгдон
Знание того, как рассчитать расстояние между двумя координатами, имеет множество практических применений в науке и строительстве. Чтобы найти расстояние между двумя точками на двумерной сетке, вам необходимо знать координаты x и y каждой точки.Чтобы найти расстояние между двумя точками в трехмерном пространстве, вам также необходимо знать z-координаты этих точек.
Формула расстояния используется для выполнения этой работы и проста: возьмите разницу между значениями X и разницу между значениями Y, сложите их квадраты и извлеките квадратный корень из суммы, чтобы найти прямую -линейное расстояние, то есть расстояние между двумя точками на картах Google над землей, а не на извилистой дороге или водном пути.
Расстояние в двух измерениях
Вычислите положительную разницу между координатами x и назовите это число X. Координаты x — это первые числа в каждом наборе координат. Например, если две точки имеют координаты (-3, 7) и (1, 2), то разница между -3 и 1 равна 4, и поэтому X = 4.
Вычислите положительную разницу между координатами y. и назовем это число Y. Координаты Y — вторые числа в каждом наборе координат.2 = 41
Таким образом, квадрат расстояния между координатами равен 41.
Извлеките квадратный корень из D 2 , чтобы найти D, фактическое расстояние между двумя точками. Например, если D 2 = 41, то D = 6,403, и поэтому расстояние между (-3, 7) и (1, 2) равно 6,403.
Расстояние в трех измерениях
Вычислите положительную разницу между координатами z и назовите это число Z. Координаты z — это третьи числа в каждом наборе координат.2 = 141
Таким образом, квадрат расстояния между координатами равен 141.
Извлеките квадратный корень из D 2 , чтобы найти D, фактическое расстояние между двумя точками. Например, если D 2 = 141, то D = 11,874, и поэтому расстояние между (-3, 7, 10) и (1, 2, 0) равно 11,87.
Строительные блоки — слова — подробно
Мир
сделано из многих вещей. Некоторых можно потрогать, сосчитать или увидеть. Есть и другие
вещи, которые существуют только в воображении, но эти воображаемые вещи могут
быть очень мощными инструментами! Вы можете видеть геометрию повсюду вокруг себя, созданную руками человека.
конструкции, в природе, в спорте, в производстве и в искусстве.В геометрии
есть только четыре воображаемых предмета — простые идеи — на которых все
остальное строится: точка, линия, плоскость и пространство.
Самое главное
о точке нужно помнить, что она не имеет абсолютно никаких размеров — нет
длина, без ширины, без глубины. Это просто место. Мы используем точку, например точку
N показано здесь, чтобы обозначить точку, но точка не является истинной точкой, потому что
любая написанная или напечатанная точка, независимо от ее размера, имеет размеры.
Линия — это
набор точек, который имеет только одно измерение, длину. Подумайте о множестве
точки, лежащие на единственном пути. Точки на одной линии называются коллинеарными.
точек. «Две точки необходимы для определения линии.
Обратите внимание, как
напишите символ для этой строки. Стрелки на линии DE показывают нам, что
Линия бесконечно тянется в обоих направлениях — у нее нет конечных точек. Когда два
линии пересекаются в точке, они называются «пересекающимися линиями».«
Набор точек
называется самолет лежит все на одной поверхности. В алгебре вы уже использовали
координатная плоскость для нанесения точек, поэтому вы знакомы хотя бы с одним
пример самолета. Поверхность стола — еще один пример плоскости, но
самолет на самом деле тянется бесконечно.
Также помните
что поверхность плоскости не имеет толщины. По крайней мере, три пункта не включены
такая же линия необходима для определения плоскости.
Наконец-то там
пространство, множество всех точек. Трудно проиллюстрировать идею
космос, так как он везде! Вы можете думать об этом как об открытой пустой комнате,
или внутри пустой коробки. Пространство не имеет границ и бесконечно простирается
во всех направлениях.
Конечно, эти
четыре срока — это только начало. Вы встретите еще много слов и их
значения, пока вы работаете над этим курсом геометрии.Прежде чем двигаться дальше, здесь
это еще три основных термина, с которыми необходимо ознакомиться. Вы будете их видеть
довольно часто.
Линейный сегмент
Отрезок линии
это просто часть линии, имеющая определенную длину и определенные конечные точки.
Обратите внимание на символ линейного сегмента. Чем он отличается от символа
за строчку?
Два линейных сегмента
имеющие одинаковую длину, называются конгруэнтными сегментами.Этот символ используется
чтобы показать соответствие.
Ray
Луч — это
часть линии, имеющая только одну конечную точку.

