Содержание
Первый признак подобия треугольников 8 класс онлайн-подготовка на Ростелеком Лицей
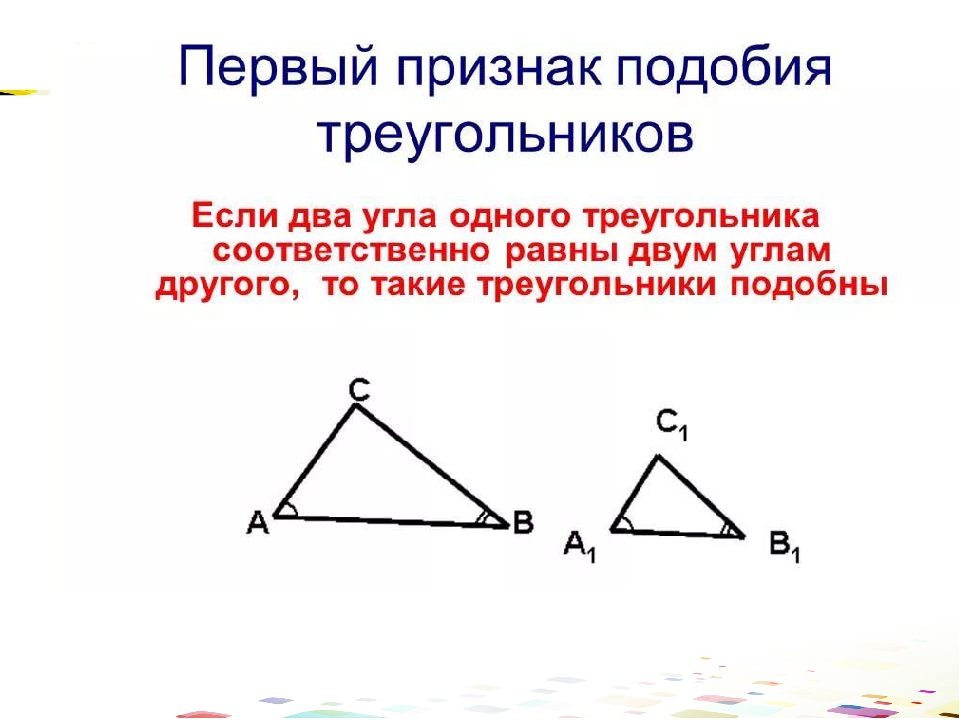
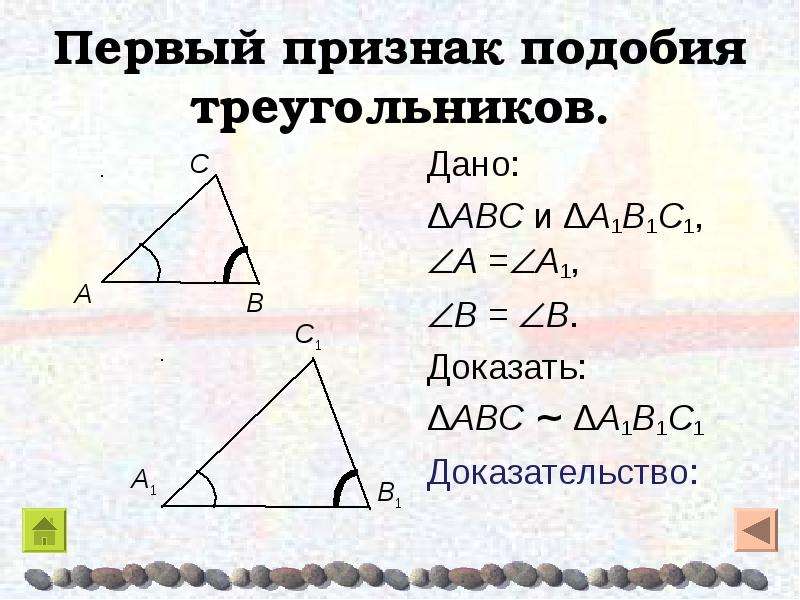
Первый признак подобия треугольников.
Докажем подобие треугольников по двум углам.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Дано: ΔABC, ΔA1B1C1,
∠A = ∠A1, ∠B = ∠B1,
Доказать: ΔABC∼ΔA1B1C1
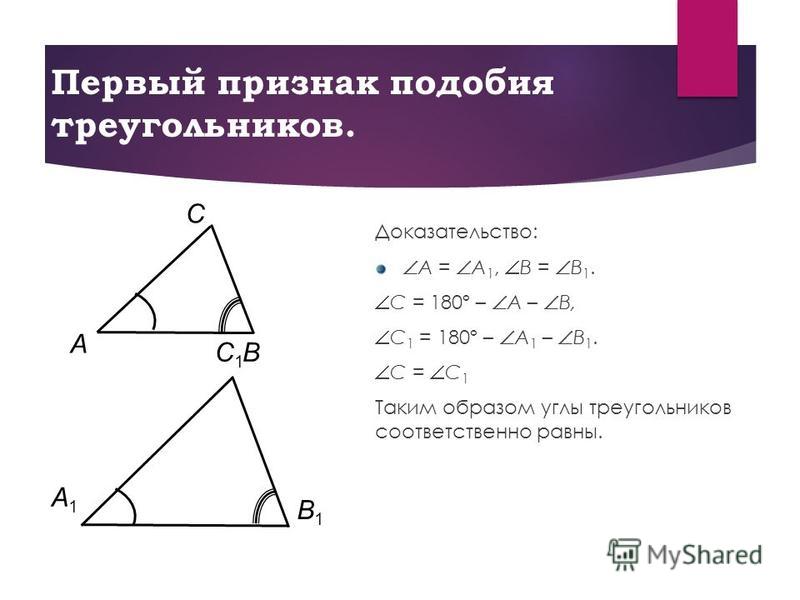
Доказательство:
-
По теореме о сумме углов треугольника
∠C = 180°-(∠A+∠B), ∠C1 = 180°-(∠A1+∠B1).
Так как ∠A = ∠A1и ∠B = ∠B1, то и ∠C = ∠C1.
-
Пусть AB<A1B1. На луче A1B1 отложим отрезок A1B2 такой, что A1B2 = AB.
-
Через точку B2 проведем прямую B2C2, параллельную прямой B1C1.
-
∠A1B2C2 = ∠A1B1C1 (как соответственные при B2C2∥ B1C1 и секущей A1B1).
Значит, ∠A1B2C2 = ∠B.
-
В треугольниках A1B2C2и ABC:
∠A1 = ∠A,
∠A1B2C2 = ∠B,
A1B2 = AB.
Значит, ΔA1B2C2= ΔABC (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: A1C2 = AC.
-
По теореме о пропорциональных отрезках А1С2:А1С1 = А1В2:А1В1.

Так как A1B2= AB и A1C2 = AC, то АС:А1С1 = АВ:А1В1.
-
Аналогично доказывается, что АВ:А1В1 = ВС:В1С1.
-
Таким образом, в треугольниках ABC и A1B1C1:
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1,
АВ:А1В1 = ВС:В1С1 = АС:А1С1.
Значит, ΔABC∼ΔA1B1C1 по определению подобных треугольников, что и требовалось доказать.
При решении задач чаще других используется именно 1-й признак подобия треугольников.
Задача 1. Доказать, что любые два равнобедренных треугольника, у которых углы между равными сторонами равны, являются подобными.
Решение. Пусть даны равнобедренные треугольники ABC и A1B1C1 с ∠A = ∠A1 (углы А и А1 лежат против оснований ВС и В1С1 соответственно). Так как треугольник ABC равнобедренный, то ∠B = ∠C = (180−∠A):2. Так как треугольник A1B1C1 равнобедренный, то ∠B1 = ∠C1 = (180−A1):2 = (180−∠A):2 = ∠B = ∠C.
То есть ∠B = ∠B1, ∠C = ∠C1. По первому признаку подобия получаем, что треугольники ABC и A1B1C1 подобны.
Задача 2.
Дано:
∠А = ∠В
СО:DO = 7:2
AC = 21 см
Найти: ВD
Решение: рассмотрим ∆АОС и ∆ВОD.
Так как ∠А = ∠В (по условию задачи), ∠АОС = ∠ВОD (как вертикальные углы), то по первому признаку подобия треугольников ∆АОС ~ ∆ВОD.
Следовательно, сходственные стороны треугольников пропорциональны:
АО:ВО = АС:BD = CO:DO
Подставив данные, получим 21:BD = 7:2
Ответ: BD = 6см.
Первый признак подобия | Треугольники
Теорема
(Первый признак подобия треугольников — подобие треугольников по двум углам)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Дано: ΔABC, ΔA1B1C1,
∠A=∠A1, ∠B=∠B1,
Доказать: ΔABC∼ ΔA1B1C1
Доказательство:
1) По теореме о сумме углов треугольника
∠C=180°-(∠A+∠B), ∠C1=180°-(∠A1+∠B1).
Так как ∠A=∠A1 и ∠B=∠B1, то и ∠C=∠C1.
2) На луче A1B1 отложим отрезок A1B2, A1B2=AB.
3) Через точку B2 проведем прямую B2C2, параллельную прямой B1C1.
4) ∠A1B2C2=∠A1B1C1 (как соответственные при B2C2 ∥ B1C1 и секущей A1B1).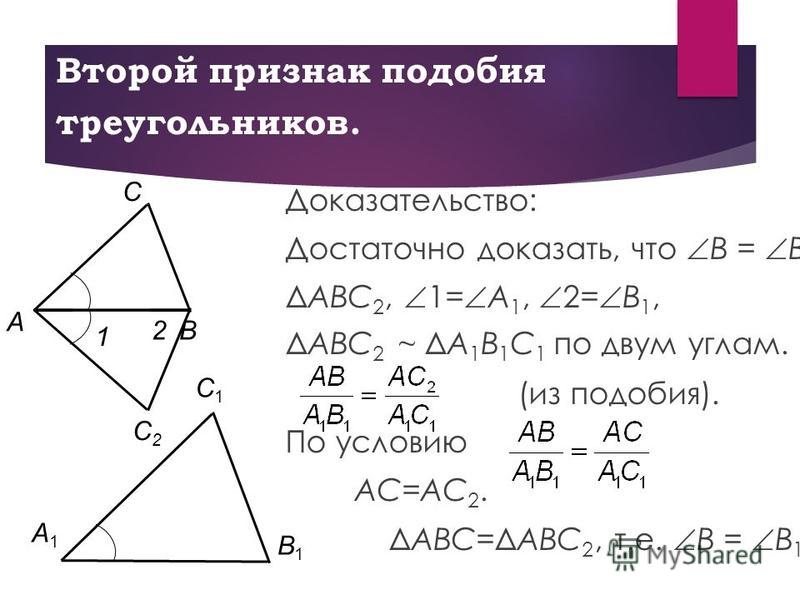
Значит, ∠A1B2C2=∠B.
5) В треугольниках A1B2C2 и ABC:
- ∠A1 =∠A,
- ∠A1B2C2=∠B,
- A1B2 =AB.
Значит, ΔA1B2C2 = ΔABC (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: A1C2=AC.
6) По теореме о пропорциональных отрезках,
Так как A1B2 =AB и A1C2=AC, то
7) Аналогично доказывается, что
8) Таким образом, в треугольниках ABC и A1B1C1:
∠A=∠A1, ∠B=∠B1, ∠C=∠C1,
Значит, ΔABC∼ ΔA1B1C1 (по определению подобных треугольников).
Что и требовалось доказать.
При решении задач чаще других используется именно 1-й признак подобия треугольников.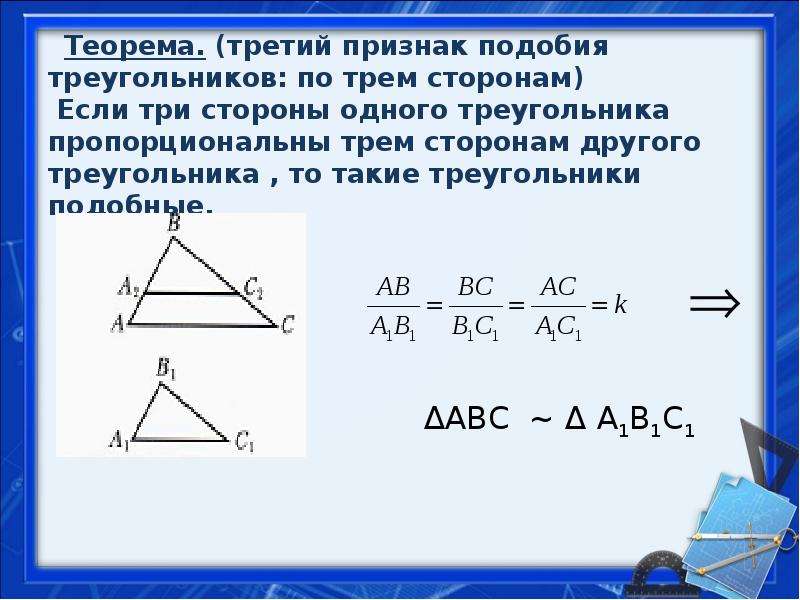
Подобные треугольники. Признаки подобия треугольников
Определение подобных треугольников
Определение 1. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Определение 2. Сходственными называются стороны подобных треугольников, лежащих напротив равных углов.
На рисунке 1 углы треугольников \( \small ABC \) и \( \small A_1B_1C_1 \) соответственно равны:
Тогда стороны \( \small AB \) и \( \small A_1B_1 \), \( \small BC \) и \( \small B_1C_1 \), \( \small AC \) и \( \small A_1C_1 \) называются сходственными.
Определение 1 можно понимать так: два треугольника подобны, если для них можно ввести обозначения и (Рис.1) так, что
Если два треугольника и подобны, то это обозначают так:
Коэффициент подобия треугольников
Коэффициентом подобия треугольников k − это число, равное отношению сходственных сторон (см. формулу (2)).
формулу (2)).
Перый признак подобия треугольников
Теорема 1. Если два угла одного треугольника соответсвенно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.2).
Поскольку сумма углов треугольника равна 180°, то можно записать:
и, так как , , получим:
Таким образом углы треугольника соответственно равны углам треугольника . Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).
Площади треугольников и по двум сторонам и углу между ними можно вычислить формулами:
Из (3) и (4), и из следует:
С другой стороны:
Из (6) и (7), и из следует:
Левые части уравнения (5) и (8) равны. Следовательно равны и правые части:
Умножая левую и правую части уравнения (9) на , получим:
Продолжая аналогичные рассуждения, получим:
Сравнивая (8) и (11), получим:
Умножая левую и правую части уравнения (12) на , получим:
Из (10) и (13), получим:
То есть стороны треугольника пропорциональны сходственным сторонам треугольника .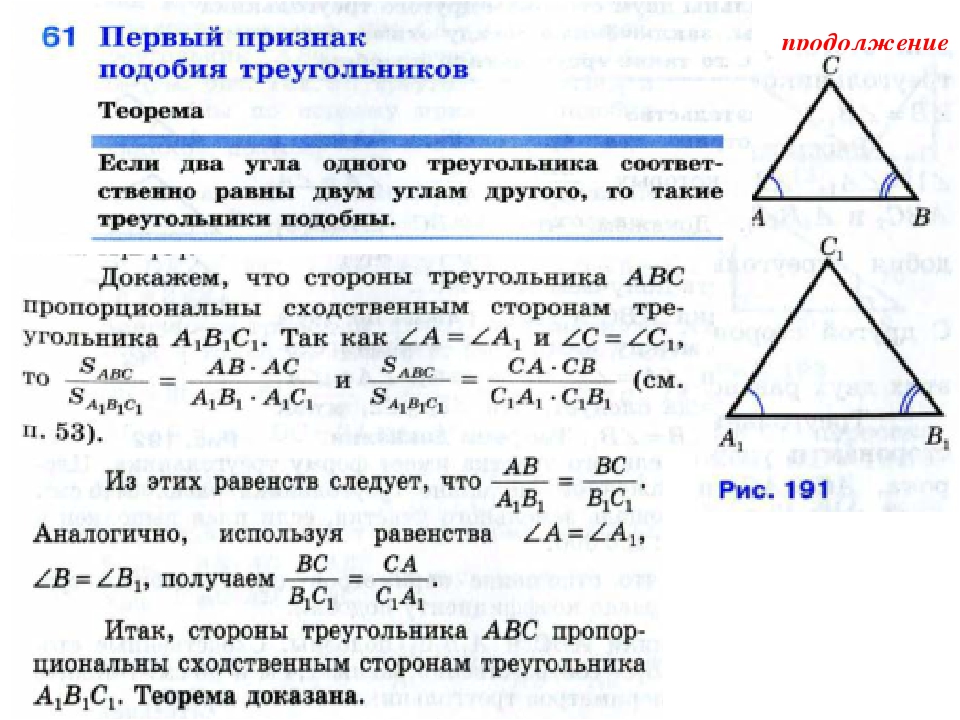 Что и требовалось доказать.
Что и требовалось доказать.
Второй признак подобия треугольников
Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.3).
Рассмотрим треугольник у которого
Из условия (15) следует, что треугольники и подобны (по первому признаку подобия треугольников). Следовательно:
Но по условию теоремы . Поэтому . Треугольники и равны по двум сторонам и углу между ними (сторона AB общая, , (поскольку и )). Следовательно и поскольку , то .
Получили, что и . Тогда по первому признаку подобия треугольников .
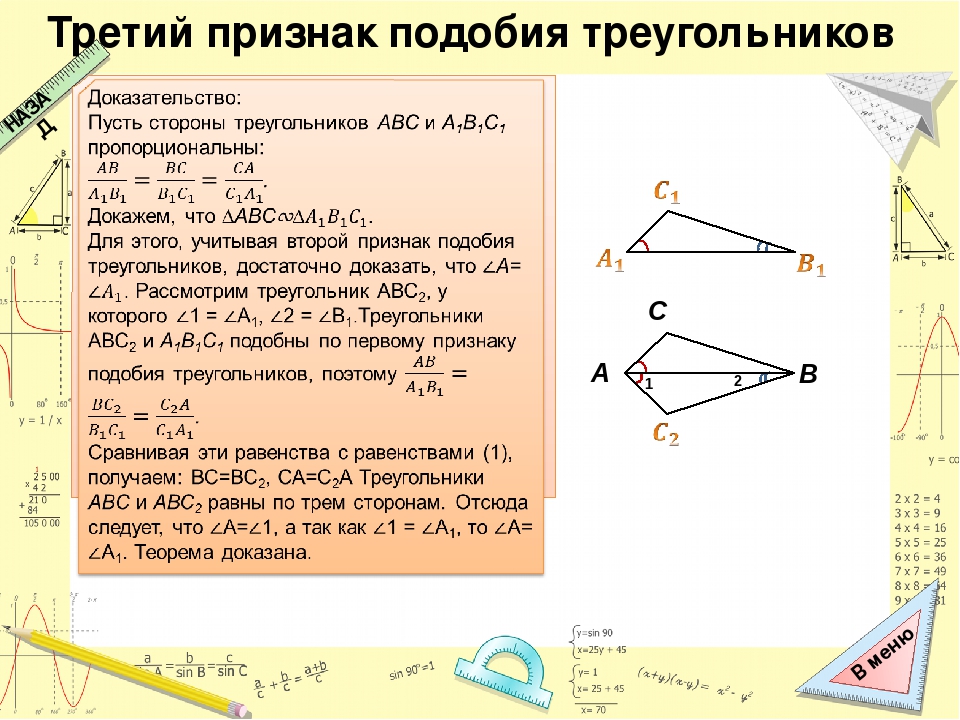
Третий признак подобия треугольников
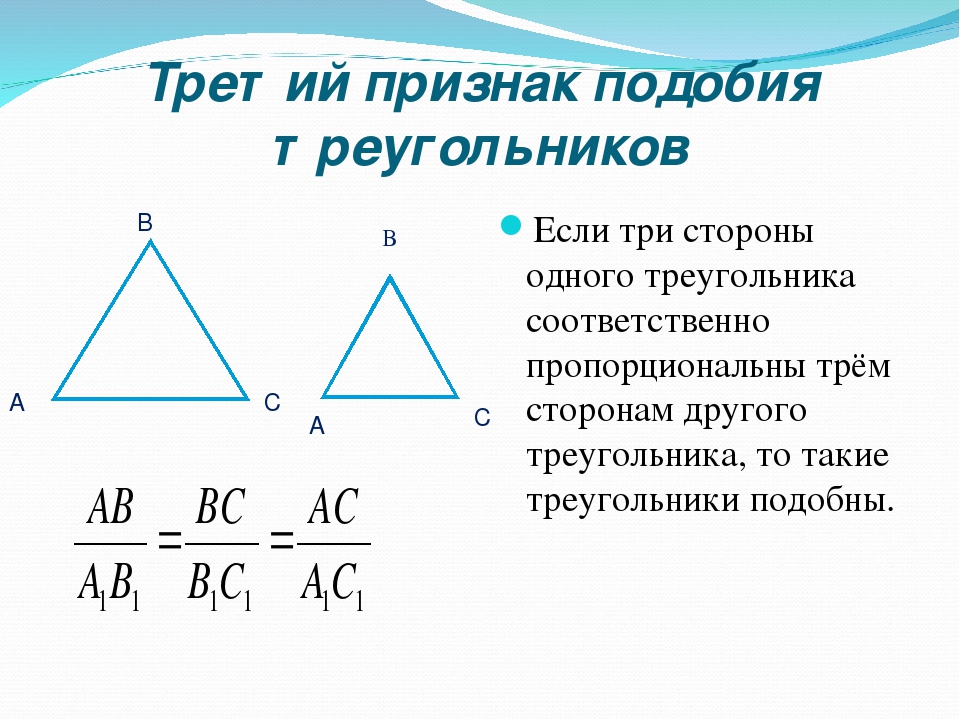
Теорема 3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть стороны треугольников пропорциональны:
Докажем, что .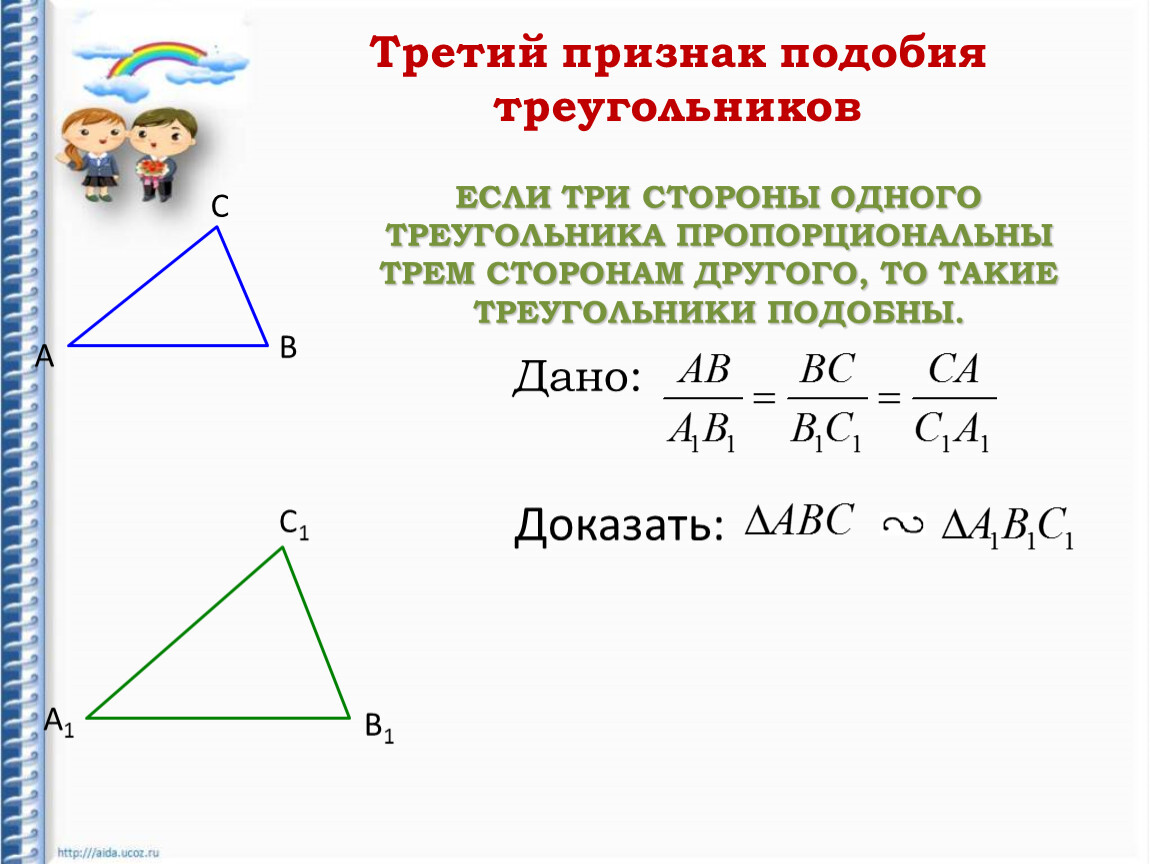 Рассотрим треугольник у которого , (Рис.3). Треугольники и подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:
Рассотрим треугольник у которого , (Рис.3). Треугольники и подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:
Сравнивая равенства (16) и (17) получаем: , .
Из этих рассуждений следует, что треугольники и равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда , а поскольку , то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .
Отношение площадей подобных треугольников
Теорема 4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Пусть треугольники и подобны. Тогда
и
где -коэффициент подобия.
Площади треугольников и по двум сторонам и углу между ними равны:
Тогда
Подобные треугольники | Математика
В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).
В треугольниках ABC и DEF (черт.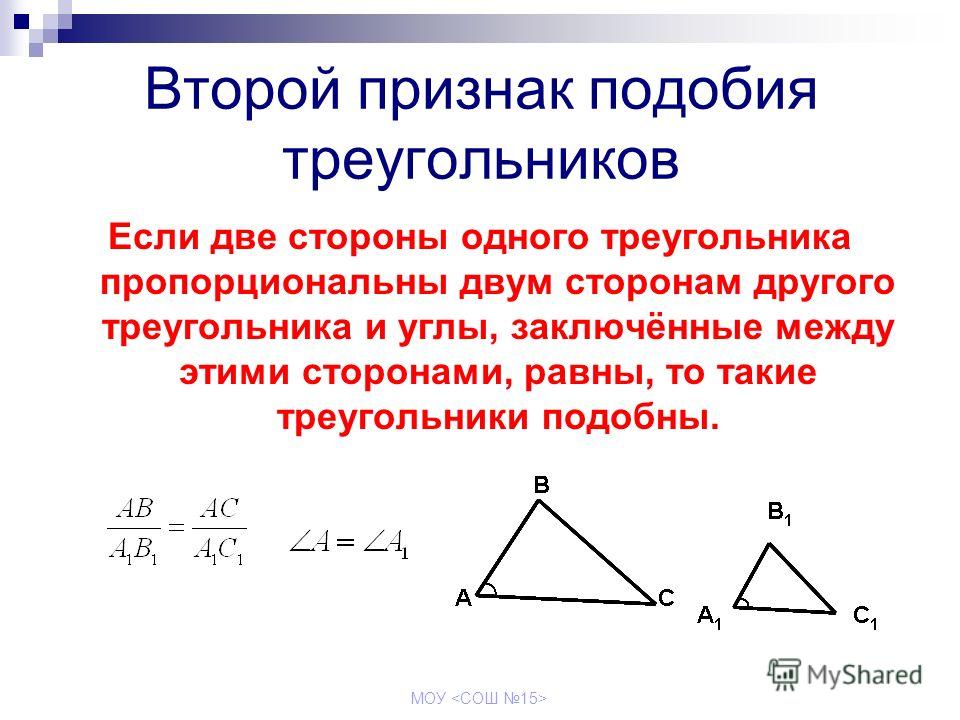 152), в которых
152), в которых
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.
Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.
Если в двух треугольниках (черт. 152) ABC и DEF углы равны
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
и соответственные стороны пропорциональны
AB/DE = AC/DF = BC/EF
то треугольники называются подобными.
Подобие обычно выражают знаком ∼.
Подобие двух треугольников изображают письменно:
ABC ∼ DEF.
Случаи подобия треугольников
Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.
Дано. В треугольниках ABC и DEF углы равны (черт. 153).
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:
AB/DE = AC/DF = BC/EF
Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,
∠D’ = ∠D, ∠D = ∠A
откуда
∠D’ = ∠A.
Если соответственные углы равны, то D’E || AC.
По теореме 86 имеют место равенства
AC/D’E’ = AB/BD’ = BC/BE’
Так как BD’ = ED, BE’ = EF, D’E’ = DF, то
AC/DF = AB/ED = BC/EF (ЧТД).
Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.
Доказательство.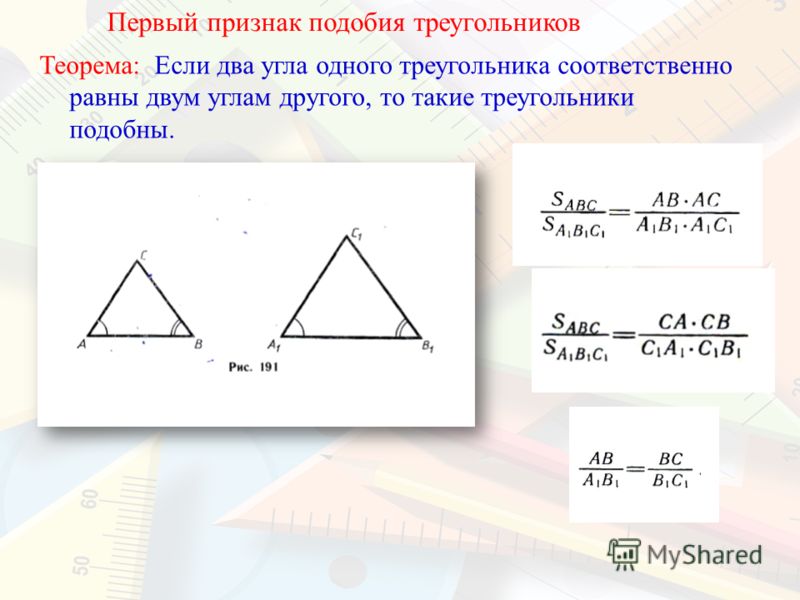 Если в двух треугольниках ABC и DEF два угла равны (черт. 153).
Если в двух треугольниках ABC и DEF два угла равны (черт. 153).
A = D, B = E
то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).
Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.
Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.
∠B = ∠E и AB/DE = BC/EF.
Требуется доказать, что треугольники подобны.
Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆BD’E’ = ∆DEF, следовательно,
∠D’ = ∠D, ∠E’ = ∠F.
Так как имеет место пропорция
AB/BD’ = BC/BE’
то сторона D’E’ || AC (теорема 87).
Поэтому ∠D’ = ∠A, ∠C = ∠E’.
Следовательно,
∠A = ∠D, ∠C = ∠F, ∠B = ∠E
т. е. три угла одного равны трем углам другого треугольника.
В этом же случае треугольники ABC и DEF подобны (ЧТД).
Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.
Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:
AB/ab = BC/bc = AC/ac (1)
Требуется доказать, что у них углы равны, т. е.
A = a, B = b, C = c.
Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:
AB/Ba’ = BC/Bc’ = AC/a’c’
Так как Ba’ = ba, то рядом с этими имеют место отношения:
AB/ab = BC/Bc’ = AC/a’c’ (2)
Сопоставляя отношения (1) и (2), заключаем, что
Bc’ = bc, a’c’ = ac,
следовательно, два треугольника a’Bc’ и abc равны, откуда
∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c
а так как
∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,
следовательно, углы двух треугольников ABC и abc равны (ЧТД).
Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.
Доказательство. Здесь могут быть два случая:
1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.
2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.
AB || a’b’, AC || a’c’, BC || b’c’.
Углы же между параллельными сторонами обращены в разные стороны.
В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.
Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,
∆ABC ~ a’b»c», следовательно, ∆ABC ~ a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’
Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.
Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.
Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:
ab ⊥ AB, ac ⊥ AC, bc ⊥ BC
Требуется доказать, что треугольники подобны.
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо
n = p как прямые
Углы при точке m равны как вертикальные,
а следовательно, и третьи углы равны ∠pCm = ∠mcn.
Так как
∠pCm = ∠ACB, ∠mcn = ∠acb
следовательно,
∠ACB = ∠acb
Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция
AB/ab = AC/ac = BC/bc
Подобие прямоугольных треугольников
Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.
Требуется доказать, что треугольники ABC и abc подобны.
Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).
Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.
Дано. В прямоугольных треугольниках ABC и abc (черт. 157)
AC/ac = AB/ab (a)
Требуется доказать, что ∠A = ∠a, ∠C = ∠c.
Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:
AC/mn = AB/Bm (b)
Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.
Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:
∠m = ∠a = ∠A и ∠n = ∠c = ∠C
следовательно, два треугольника ABC и abc подобны.
Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.
Даны два подобных треугольника ABC и FED (черт. 158), следовательно,
∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF
и проведены высоты BH и Eh.
Требуется доказать, что AB/FE = BH/Eh.
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,
AB/FE = BH/Eh (ЧТД).
Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.
Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).
∠ABD = ∠DBC или ∠α = ∠β
Требуется доказать, что AB/BC = AD/DC.
Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA
∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.
Так как ∠α = ∠β по условию, то
∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.
Из того, что AF || BD вытекает пропорция:
FB/BC = AD/DC
Заменяя FB равным отрезком AB, получим пропорцию:
AB/BC = AD/DC (ЧТД).
Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.
Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:
AB/BC = AD/DC (a)
Требуется доказать, что ∠α = ∠β.
Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:
FB/BC = AD/DC (b)
Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,
∠AFB = ∠FAB.
Так как ∠α = ∠FAB, ∠β = ∠AFB, то и
∠α = ∠β (ЧТД).
Отношения в прямоугольном треугольнике
Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.
Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.
Требуется доказать, что AD/BD = BD/DC.
Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает
A + α = α + β, или A = β, следовательно и C = α.
Из подобия треугольников ABD и BDC вытекает пропорция
AD/BD = BD/DC (ЧТД).
Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.
Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.
Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,
∠C = ∠α
Из подобия треугольников вытекает пропорция:
AD/AB = AB/AC (a)
b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,
∠A = ∠β, откуда
DC/BC = BC/AC (b)
Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.
Из предыдущих пропорций (a) и (b) вытекают равенства:
AB2 = AD · AC
BC2 = DC · AC
Складывая их, получим:
AB2 + BC2 = AD · AC + DC · AC или
AB2 + BC2 = AC (AD + DC) = AC · AC = AC2, т. е.
е.
AC2 = AB2 + BC2
откуда
a) Гипотенуза равна корню квадратному из суммы квадратов катетов.
b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.
Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.
Дано. В квадрате ABCD проведена диагональ AC (черт. 161).
Требуется доказать, что отношение AC/AD есть величина несоизмеримая.
Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.
a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо
AB + BC > AC.
Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.
b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.
c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами
∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF
На этом основании стороны EF и EC равны:
EF = EC (1)
Треугольники ABF и AEF равны, ибо они прямоугольны и у них
AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)
Таким образом из равенств (1) и (2) выходит, что
EC = EF = BF
Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз. Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.
d) Наложим второй остаток GC на первый EC.
В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.
Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.
Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d1, d2 и т. д., т. е. положив
AC = l, BC = a, CE = d1, GC = d2 и т. д.
имеем равенства:
l = a + d1, a = 2d1 + d2, d1 = 2d2 + d3 и т. д.
откуда
l/a = 1 + d1/a
a/d1 = 2 + d2/d1 или d1/a = ½ + d2/d1
d1/d2 = 2 + d3/d2 или d2/d1 = ½ + d3/d2
следовательно,
l/a = 1 + ½ + ½ + …
Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.
Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.
Действительно,
AC2 = AB2 + BC2.
Так как AB = BC, то AC2 = 2AB2, откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.
Соотношение между сторонами остроугольного и тупоугольного треугольника
Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.
Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.
Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.
Требуется доказать, что AB2 = BC2 + AC2 — 2AC · DC.
Доказательство. Для прямоугольного треугольника ABD имеем равенство:
Для прямоугольного треугольника ABD имеем равенство:
AB2 = BD2 + AD2 (a)
AD = AC — DC, AD2 = (AC — DC)2 = AC2 + DC2 — 2AC · DC
Из прямоугольного треугольника BDC имеем:
BD2 = BC2 — DC2
Вставляя величины BD2 и AD2 в равенство (a), получим:
AB2 = BC2 — DC2 + AC2 + DC2 — 2AC · DC, откуда
AB2 = BC2 + AC2 — 2AC · DC (ЧТД).
2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.
Доказательство. Из прямоугольного треугольника ABD имеем:
AB2 = BD2 + DA2
Из прямоугольного треугольника BCD имеем:
BD2 = BC2 — CD2
следовательно,
AB2 = BC2 — CD2 + DA2.
Так как
DA = CD — AC
DA2 = (CD — AC)2 = CD2 + AC2 — 2CD · AC, то
AB2 = BC2 — CD2 + CD2 + AC2 — 2CD · AC, откуда
AB2 = BC2 + AC2 — 2CD · AC (ЧТД).
Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.
Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.
Требуется доказать, что
AB2 = AC2 + BC2 + 2AC · CD
Доказательство. Из тупоугольного треугольника ABC имеем:
AB2 = BD2 + AD2 (a)
AD = AC + CD, AD2 = AC2 + CD2 + 2AC · CD
Из прямоугольного треугольника BCD вытекает, что
BD2 = BC2 — CD2
Заменяя AD2 и BD2 в равенстве (a), получим:
AB2 = BC2 — CD2 + AC2 + CD2 + 2AC · CD
откуда
AB2 = BC2 + AC2 + 2AC · CD (ЧТД).
Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.
Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.
Требуется доказать, что
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:
BD2 = AB2 + AD2 — 2AD · AE (1)
Из тупоугольного треугольника ACD равенство:
AC2 = CD2 + AD2 + 2AD · DF (2)
Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.
Сложив равенства (1) и (2), имеем:
BD2 + AC2 = AB2 + AD2 + CD2 + AD2
Так как AD = BC, то
BD2 + AC2 = AB2 + BC2 + CD2 + AD2 (ЧТД).
Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.
Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).
Требуется доказать, что
AB2 + BC2 = 2AD2 + 2BD2
Доказательство. Проведем высоту BE.
Из прямоугольных треугольников ABE и BCE вытекают равенства:
AB2 = BE2 + AE2
BC2 = BE2 + CE2
Сложив их, находим:
AB2 + BC2 = 2BE2 + AE2 + CE2 (a)
Так как AE = AD + DE = CD + DE, CE = CD — DE, то
AE2 = (CD + DE)2 = CD2 + DE2 + 2CD · DE
CE2 = (CD — DE)2 = CD2 + DE2 — 2CD · DE
откуда
AE2 + CE2 = 2CD2 + 2DE2 (b)
Заменяя в равенстве (a) сумму AE2 + CE2 из равенства (b), имеем:
AB2 + BC2 = 2BE2 + 2CD2 + 2DE2.
Из прямоугольного треугольника BDE видно, что
BE2 = BD2 — DE2
следовательно
AB2 + BC2 = 2BD2 — 2DE2 + 2CD2 + 2DE2
откуда
AB2 + BC2 = 2BD2 + 2CD2 (ЧТД).
Три признака подобия треугольников
Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).
Доказать, что \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С (рис. 367).
Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.
Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили \(\Delta\)MBN, который подобен \(\Delta\)ABC. Но \(\Delta\)MBN = \(\Delta\)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).
Из точки М проведём прямую MN || АС. Мы получили \(\Delta\)MBN, который подобен \(\Delta\)ABC. Но \(\Delta\)MBN = \(\Delta\)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).
Если \(\Delta\)MBN \(\sim\) \(\Delta\)AВС, то \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABC. Эта теорема выражает 1-й признак подобия треугольников.
Следствия. 1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Пусть в треугольниках ABC и А’В’С’ \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\) и ∠В = ∠В’
Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’ (рис.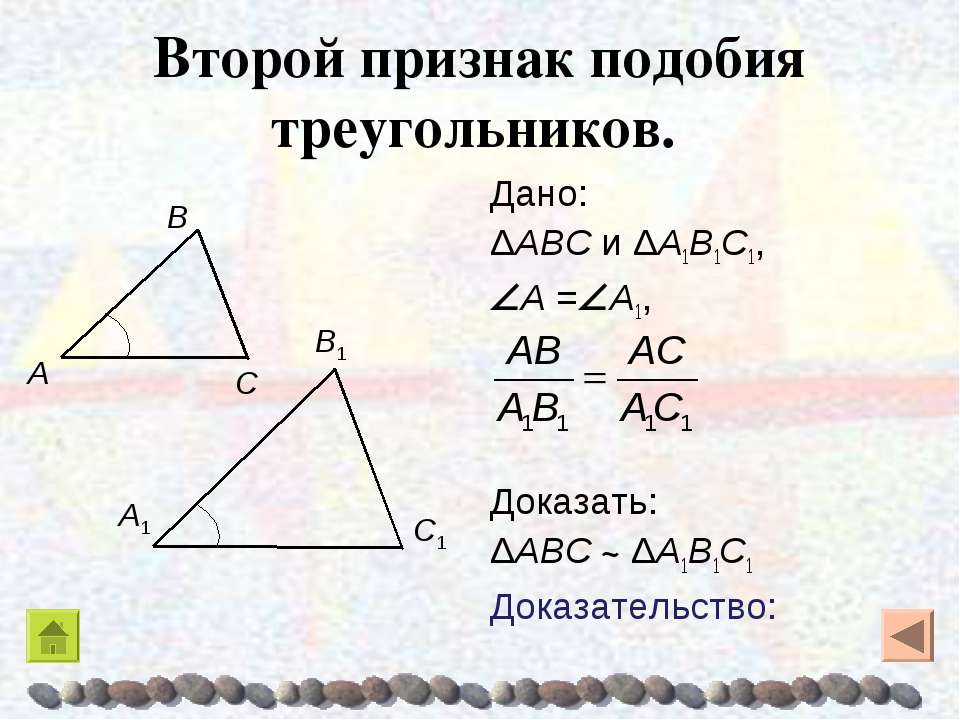 368).
368).
Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.
Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию AB/MB = BC/BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,
т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.
Так как \(\Delta\)MBN \(\sim\) \(\Delta\)А’В’С’, то, следовательно, и \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABС.
Эта теорема выражает 2-й признак подобия треугольников.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.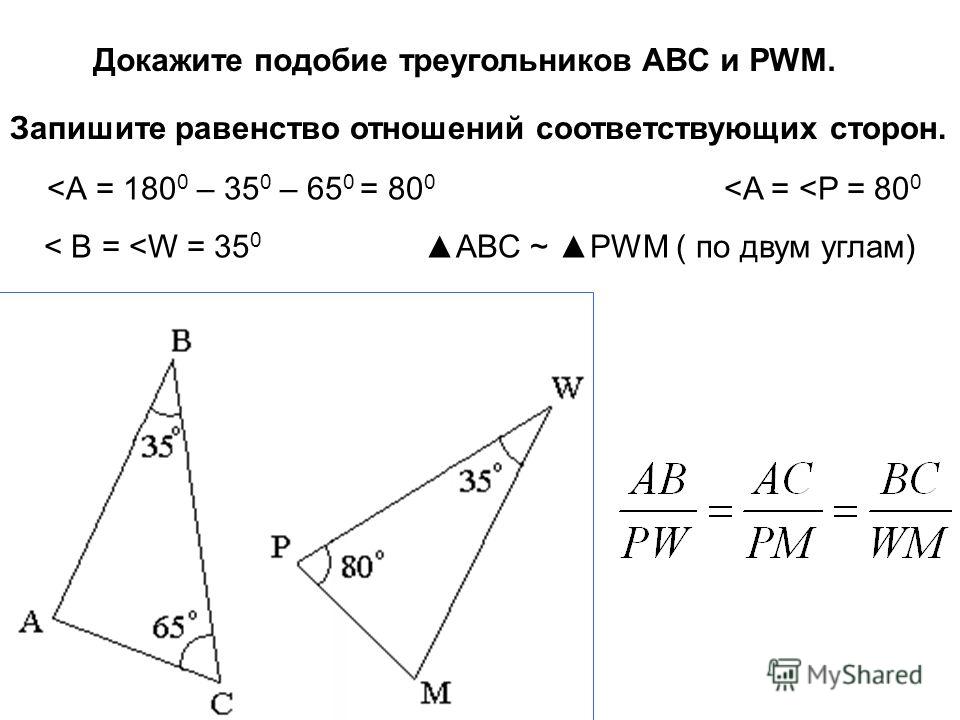
Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.
Пусть в треугольниках ABC и А’В’С’ \(\frac{AB}{A’B’} = \frac{BC}{B’C’} = \frac{AC}{A’C’}\) (рис. 369).
Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’
Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, \(\frac{AB}{MB} = \frac{BC}{BN} = \frac{AC}{MN}\).
Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. Для доказательства сравним две пропорции
\(\frac{AB}{MB} = \frac{BC}{NB}\) и \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\).
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.
Сравним ещё две пропорции: \(\frac{AB}{MB} = \frac{AC}{MN}\) и \(\frac{AB}{A’B’} = \frac{AC}{A’C’}\) . В этих пропорциях также имеется по три равных члена, следовательно, равны и четвёртые члены их, т. е. MN =А’С’.
В этих пропорциях также имеется по три равных члена, следовательно, равны и четвёртые члены их, т. е. MN =А’С’.
Оказалось, что три стороны \(\Delta\)BMN равны трём сторонам \(\Delta\)А’В’С’, а именно:
MB = А’В’, BN = В’С’ и MN = А’С’.
Следовательно, \(\Delta\)MBN = \(\Delta\)А’В’С’, а \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’.
Эта теорема выражает 3-й признак подобия треугольников.
Признаки подобия треугольников. Применение подобия к решению задач.
Признаки подобия треугольников
К учебнику Л.С.Атанасяна
Геометрия 7 — 9, Глава VII, 8 класс
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
Первый признак подобия треугольников
Теорема. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
В 1
В
С 1
С
А
А 1
Первый признак подобия треугольников
Теорема. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
В 1
В
С 1
С
А
А 1
Первый признак подобия треугольников
Теорема. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
В 1
В
С 1
С
А
А 1
Вывод: У треугольников АВС и А 1 В 1 С 1
Второй признак подобия треугольников
Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.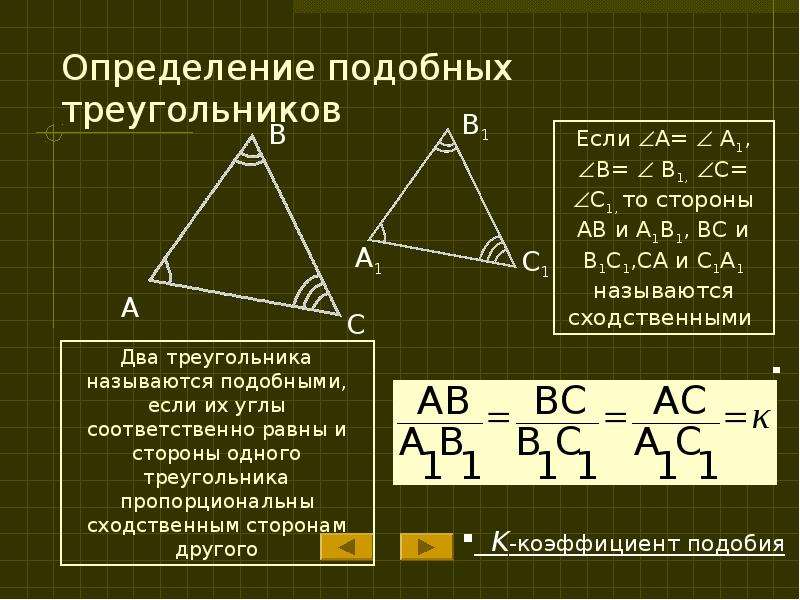
С 1
С
В 1
А 1
В
А
1
2
С 2
Второй признак подобия треугольников
Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
С
С 1
В 1
А 1
В
А
2
1
С 2
Третий признак подобия треугольников
Теорема. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
С 1
С
В 1
А 1
А
В
2
1
С 2
Третий признак подобия треугольников
Теорема. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
С 1
С
В 1
А 1
В
А
2
1
С 2
Применение подобия к доказательству теорем и решению задач
Средняя линия треугольника
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
В
M
2
N
1
С
А
Свойство медиан треугольника
Задача. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 :1, считая от вершины.
В
M
N
4
2
О
3
1
Аналогично, точка пересечения медиан СМ и ВК делит каждую из них в отношении 2 : 1. считая от вершины, и следовательно, совпадает с точкой О.
С
А
К
Вывод: Все три медианы треугольника АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины.
Свойство медиан треугольника
Задача. Доказать, что медианы треугольника делят его на 6 равновеликих треугольника
В
S 5
S 4
M
N
h
h
S 3
S 6
О
S 1
h
S 2
А
С
К
Свойство медиан треугольника
Задача.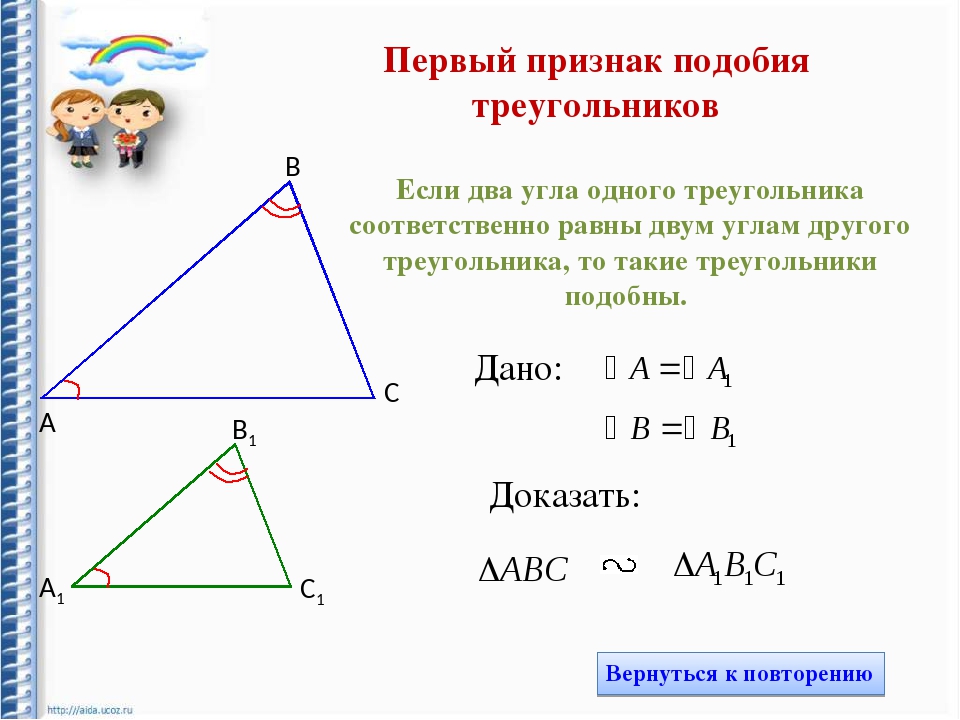 Доказать, что медианы треугольника делят его на 6 равновеликих треугольника
Доказать, что медианы треугольника делят его на 6 равновеликих треугольника
В
S 4
S 5
M
N
АО = 2х, ОN = x
BO = 2y, OK = y
CO = 2z, OM = z
S 3
S 6
О
S 1
S 2
С
А
К
Свойство медиан треугольника
№ 571 (Геометрия 7-9, автор Л.С. Атанасян) В треугольнике АВС медианы АА 1 и ВВ 1 пересекаются в точке О. Найдите площадь треугольника АВС, если площадь треугольника АВО равна S.
В
Проведем медиану СС1, Медианы разбили треугольник АВС на 6 равновеликих треугольников.
С 1
В 1
О
С
А
В 1
Свойство медиан треугольника
№ 569 (Геометрия 7-9, автор Л.С. Атанасян) Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен полуразности оснований.
В
С
Проведем среднюю линию МК.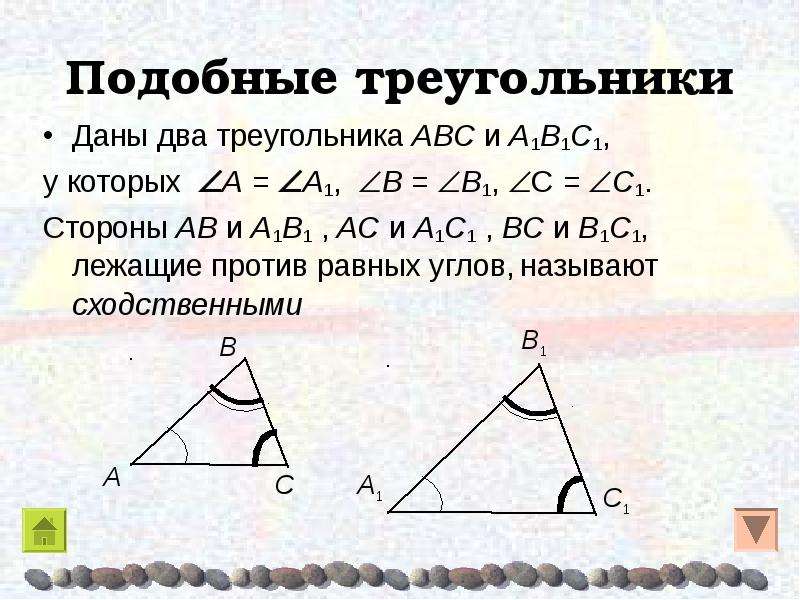
По теореме Фалеса МК пересечет отрезки АС и ВД в их серединах Р и Т.
Р
Т
М
К
Требуется доказать, что РТ параллелен основаниям АД и ВС и равен полуразности оснований.
Д
А
МК II ВС, МК II АД.
РТ- часть МК, поэтому РТ II АД и РТ II ВС.
Введем обозначения: BC = a, АД = b
Свойство медиан треугольника
№ 618 (Геометрия 7-9, автор Л.С. Атанасян) Точки М и N являются соответственно серединами сторон СД и ВС параллелограмма АВСД. Докажите, что прямые АМ и АN делят диагональ ВД на три равные части.
Доказать: ВК = КН = НД
М
В
С
Проведем диагональ АС,
К
Треугольник АВС: АМ – медиана, ВО – медиана, К – точка пересечения медиан, поэтому ВК : КО = 2 : 1, ВК = 2х, КО = х
О
N
Н
Д
А
Треугольник АСД: АN – медиана, ДО – медиана, Н – точка пересечения медиан, поэтому ДН : НО = 2 : 1, ДН = 2у, НО = у
ВО=2х+х=3х , ОД=2у+у= 3у
ВО = ОД, 3х = 3у, х = у
ВК=2х, КН=2х, НД=2х
Получили: ВК = КН = НД
Урок 17.
 признаки подобия треугольников — Геометрия — 8 класс
признаки подобия треугольников — Геометрия — 8 класс
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Процесс нахождения подобных треугольников можно упростить, зная признаки подобия треугольников.
Первый признак подобия треугольников:
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Дано: ∆ ABC и ∆A1B1C1
∠A = ∠A1, ∠B = ∠B1
Доказать:
∆ ABC ~ ∆ A1B1C1
Доказательство:
∠С = 180° — ∠A − ∠B
∠С1 = 180°- ∠A1 − ∠B1, но
∠A = ∠A1, ∠B = ∠B1
Следовательно ∠С = ∠С1
SABC/SA1B1C1 = (AB ∙ AC)/(A1B1 ∙ A1C1 ), т. к. ∠A = ∠A1
к. ∠A = ∠A1
SABC/SA1B1C1 = (CA ∙ CB)/(C1A1 ∙ C1B1), т.к. ∠С = ∠С1,
следовательно AB/(A1B1) = CB/(C1B1)
CB/(C1B1) = AC/(A1C1),
AB/(A1B1) = CB/(C1B1) = AC/(A1C1)
Второй признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Дано: ∆ ABC и ∆ A1B1C1
AB/(A1B1) = AC/(A1C1), ∠A = ∠A1
Доказать:
∆ ABC ~ ∆ A1B1C1
Доказательство:
1)∆ ABC2: ∠1 = ∠А, ∠2 = ∠В1
2)∆ ABC2 ~ ∆ A1B1C1, следовательно
AB/(A1B1) = (AC2)/(A1C1)
3) из условия известно, что AB/(A1B1) = AC/(A1C1), поэтому АС = АС2
4)∆ ABC = ∆ ABC2 (АВ – общая сторона, АС = АС2 и ∠1 = ∠А)
5)∠B = ∠2 = ∠В1, следовательно
∆ ABC ~ ∆ A1B1C1
Третий признак подобия треугольников.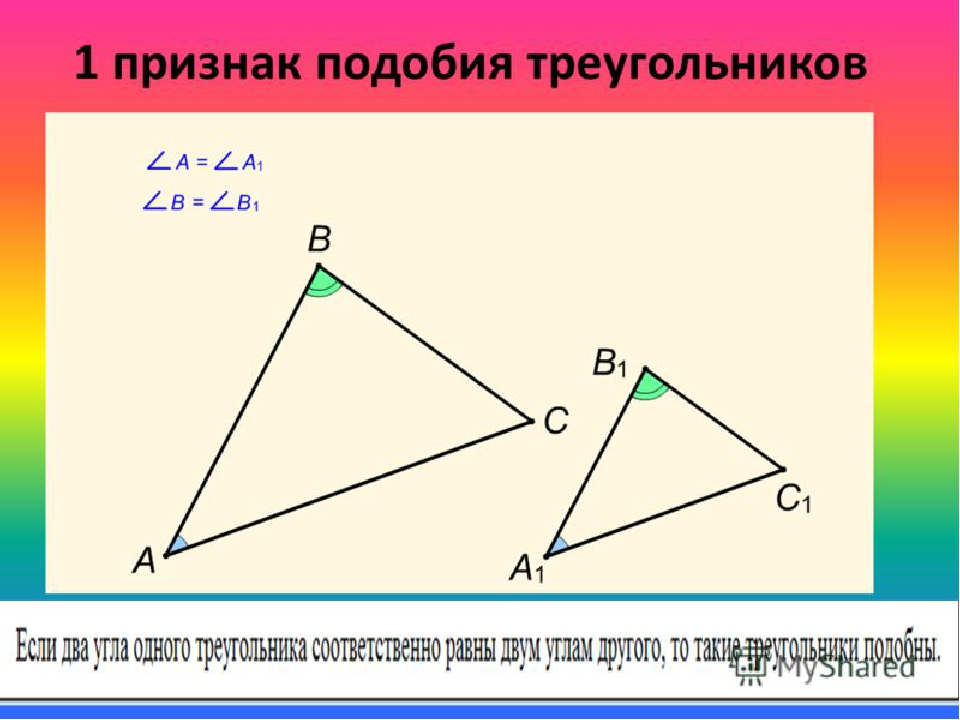
Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Рассмотрим трапецию ABCD (BC || AD)
Пусть диагонали AC и BD пересекаются в точке O.
Две пары накрест лежащих углов при параллельных прямых BС и АD равны, поэтому треугольники ВОС и DOA подобны по первому признаку.
Следовательно: стороны этих треугольников пропорциональны.
Диагонали трапеции точкой пересечения делятся на отрезки, пропорциональные основаниям трапеции.
Как определить, похожи ли треугольники
Два треугольника похожи, если имеют:
- все их углы равны
- соответствующих сторон в таком же соотношении
Но нам не нужно знать все три стороны и все три угла … обычно достаточно двух или трех из шести .
Есть три способа определить, похожи ли два треугольника: AA , SAS и SSS :
AA
AA означает «угол, угол» и означает, что два угла треугольников равны.
Если два треугольника имеют два равных угла, треугольники подобны.
Пример: эти два треугольника похожи:
Если два из их углов равны, то третий угол также должен быть равным, потому что углы треугольника всегда складываются и составляют 180 °.
В данном случае недостающий угол составляет 180 ° — (72 ° + 35 °) = 73 °
Таким образом, AA можно также назвать AAA (потому что, когда два угла равны, все три угла должны быть равны).
SAS
SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, где:
- соотношение между двумя сторонами такое же, как соотношение между двумя другими сторонами
- , и мы также знаем, что включенные углы равны.
Если два треугольника имеют две пары сторон с одинаковым соотношением, а входящие углы также равны, то треугольники подобны.
Пример:
В этом примере мы видим, что:
- одна пара сторон находится в соотношении 21: 14 = 3: 2
- другая пара сторон находится в соотношении 15: 10 = 3: 2
- между ними угол совпадения 75 °
Итак, информации достаточно, чтобы сказать нам, что два треугольника похожи на .
Использование тригонометрии
Мы также можем использовать тригонометрию для вычисления двух других сторон, используя закон косинусов:
Продолжение примера
В треугольнике ABC:
- a 2 = b 2 + c 2 — 2bc cos A
- a 2 = 21 2 + 15 2 — 2 × 21 × 15 × Cos 75 °
- а 2 = 441 + 225 — 630 × 0,2588 …
- a 2 = 666 — 163,055…
- а 2 = 502,944 …
- Итак, a = √502.94 = 22.426 …
В треугольнике XYZ:
- x 2 = y 2 + z 2 — 2yz cos X
- x 2 = 14 2 + 10 2 — 2 × 14 × 10 × Cos75 °
- x 2 = 196 + 100 — 280 × 0,2588 …
- x 2 = 296 — 72,469 …
- x 2 = 223,530 …
- Итак, x = √223.530 … = 14,950 …
Теперь давайте проверим соотношение этих двух сторон:
a: x = 22,426 .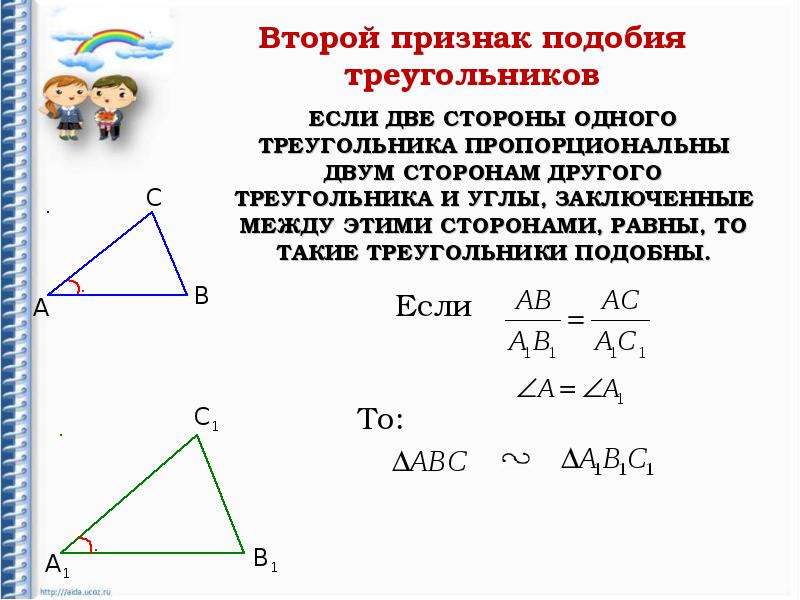 ..: 14,950 … = 3: 2
..: 14,950 … = 3: 2
то же соотношение, что и раньше!
Примечание: мы также можем использовать закон синусов, чтобы показать, что два других угла равны.
SSS
SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника со всеми тремя парами соответствующих сторон в одинаковом соотношении.
Если два треугольника имеют три пары сторон с одинаковым соотношением, то треугольники подобны.
Пример:
В этом примере соотношение сторон:
- a: x = 6: 7,5 = 12: 15 = 4: 5
- б: у = 8: 10 = 4: 5
- с: z = 4: 5
Все эти отношения равны, поэтому два треугольника подобны.
Использование тригонометрии
Используя тригонометрию, мы можем показать, что два треугольника имеют равные углы, используя закон косинусов в каждом треугольнике:
В треугольнике ABC:
- cos A = (b 2 + c 2 — a 2 ) / 2bc
- cos A = (8 2 + 4 2 — 6 2 ) / (2 × 8 × 4)
- cos A = (64 + 16 — 36) / 64
- cos A = 44/64
- cos A = 0.
 6875
6875 - Угол A = 46,6 °
В треугольнике XYZ:
- cos X = (y 2 + z 2 — x 2 ) / 2yz
- cos X = (10 2 + 5 2 — 7,5 2 ) / (2 × 10 × 5)
- cos X = (100 + 25 — 56,25) / 100
- cos X = 68,75 / 100
- cos X = 0,6875
- Угол X = 46,6 °
Значит, углы A и X равны!
Аналогичным образом мы можем показать, что углы B и Y равны, а углы C и Z равны.
Геометрия — похожие треугольники
Определение
Два треугольника подобны, если соответствующие углы совпадают и если отношение соответствующих сторон равно
постоянный. Если треугольники \ (\ bigtriangleup ABC \) и \ (\ bigtriangleup DEF \) равны
аналогично, мы можем записать это соотношение как
\ [\ bigtriangleup ABC∼ \ bigtriangleup DEF. \]
Разница между похожими и совпадающими треугольниками состоит в том, что похожие треугольники
не обязательно должны быть одинакового размера.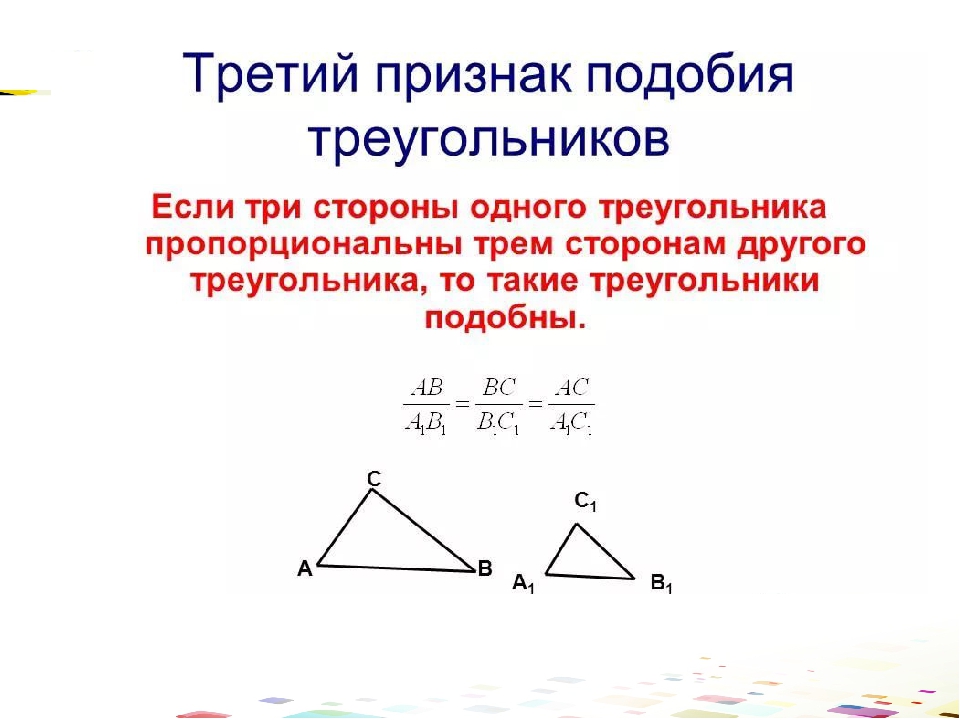
\ (\ cong \) congruence такая же форма и такой же размер
\ (\ sim \) подобие такая же форма
Теорема о пропорциональности треугольника
Интерактивная помощь в доказательстве теоремы о пропорциональности треугольника.
Поперечная линия — это линия, пересекающая две или несколько линий.
Теорема: Трансверсаль, параллельная одной из сторон
в треугольнике пропорционально делит две другие стороны.
Доказательство: Все, что вам нужно знать, чтобы доказать теорему
состоит в том, что площадь треугольника равна \ [A = \ frac {w \ cdot h} {2} \]
где \ (w \) — ширина, а \ (h \) — высота треугольника.
Сравните площади трижды!
Создайте треугольник \ (poly1 = \ bigtriangleup AED \) и треугольник \ (poly2 = \ bigtriangleup BED \).
Обозначим через \ (poly1 \) и \ (poly2 \) площади треугольников.
Каково соотношение \ (poly1 \) и \ (poly2 \)? Подтвердите свой ответ!Создайте треугольник \ (poly3 = \ bigtriangleup DEC \).
 Каково соотношение \ (poly3 \)
Каково соотношение \ (poly3 \)
и \ (poly1 \)? Подтвердите свой ответ!Каково соотношение \ (poly3 \) и \ (poly2 \)? Подтвердите свой ответ!
Покажите, что \ (\ dfrac {a} {b} = \ dfrac {c} {d} \)!
Следствие теоремы о пропорциональности
Следствие: Трансверсаль, параллельная стороне треугольника.
определяет новый меньший треугольник, похожий на исходный треугольник.
Проба:
Покажите, что соответствующие углы в двух треугольниках совпадают (равны).
Затем покажите, что \ [\ frac {a + b} {a} = \ frac {c + d} {c} \]
Нарисуйте еще одну поперечину параллельно другой стороне
и покажите, что \ [\ frac {a + b} {a} = \ frac {c + d} {c} = \ frac {AB} {DE} \]
Три случая, которые дают сходство
Сторона-угол-сторона (SAS) Если две стороны в треугольнике находятся в одном и том же
отношение к двум соответствующим сторонам другого треугольника, и если включенные углы
в обоих треугольниках одинаковые, значит, треугольники похожи.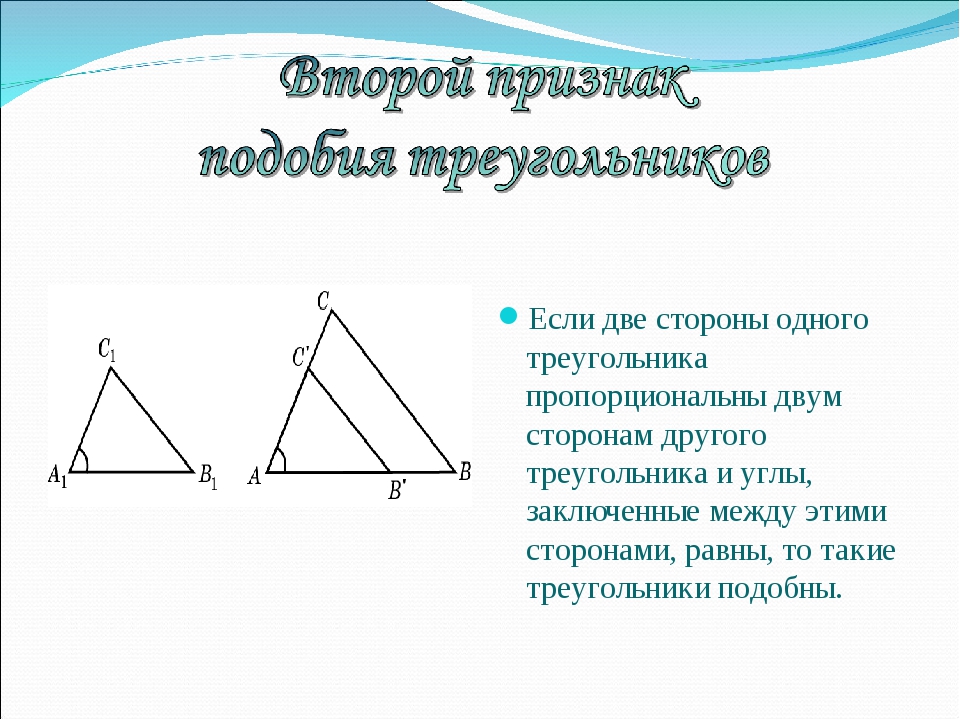
Доказательство
Поместите точку \ (G \) так, чтобы \ (AG = DE \).
Нарисуйте \ (GH \) так, чтобы \ (GH \) был параллелен \ (BC \).
Теперь \ (\ bigtriangleup AGH∼ \ bigtriangleup ABC \).
Покажите, что \ (AH = DF \)!
Тогда случай сравнения Side-Angle-Side дает \ (\ bigtriangleup AGH≅ \ bigtriangleup DEF \)
и доказательство сделано.
Доказательства двух других случаев аналогичны.
Сторона-сторона-сторона (SSS) Если три пары соответствующих сторон находятся в
такое же соотношение, тогда треугольники похожи.
Угол-угол-угол (AA) Если углы в треугольнике совпадают
(равны) соответствующим углам другого треугольника, то треугольники равны
похожий.
Также обратите внимание, что достаточно, чтобы два угла были равны (почему?).
Теорема о биссектрисе угла
Прямая, проходящая через C, параллельна AB.
Теорема: В треугольнике \ (\ bigtriangleup ABC \) проводится биссектриса угла в точке \ (B \). Биссектриса угла
пересекает \ (AC \) в точке \ (D \).Теорема биссектрисы угла утверждает, что:
\ [\ frac {AB} {AD} = \ frac {BC} {CD} \]
Проба: Проведите линию, параллельную от \ (AB \) до \ (C \). Пусть \ (E \) —
пересечение новой прямой и биссектрисы угла. Объясните почему:
\ (\ угол ABD = \ угол CED \)
треугольник \ (\ bigtriangleup BCE \) — равнобедренный треугольник, поэтому \ (BC = CE \).
\ (\ угол BDA = \ угол CDE \)
\ (\ bigtriangleup ABD \ sim \ bigtriangleup CED \)
\ (\ dfrac {AB} {AD} = \ dfrac {CE} {CD} \)
\ (\ dfrac {AB} {AD} = \ dfrac {BC} {CD} \)
Упражнения
Упражнение 1
Высоты в треугольниках
\ (AC \) параллельно \ (EF \).\ (AB \) параллельно \ (DF \). Высоты \ (h \), \ (h_1 \),
Высоты \ (h \), \ (h_1 \),
\ (h_2 \) и \ (h_3 \) перпендикулярны
высоты в треугольниках. Докажи то, что видишь!
Упражнение 2
Середины четырехугольника
Синие точки — это середины с каждой стороны. Докажи то, что видишь!
проб с похожими треугольниками — A Plus Topper
Определение:
Два треугольника похожи на тогда и только тогда, когда соответствующие стороны пропорциональны и соответствующие углы совпадают.
Существует три общепринятых метода доказательства сходства треугольников:
AA
Чтобы показать, что два треугольника подобны, достаточно показать, что два угла одного треугольника совпадают (равны) двум углам другого треугольника.
Теорема:
Если два угла одного треугольника совпадают с двумя углами другого треугольника, треугольники подобны.
SSS на сходство
SSS для подобных треугольников — это НЕ та же теорема, которую мы использовали для конгруэнтных треугольников. Чтобы показать, что треугольники подобны, достаточно показать, что три набора соответствующих сторон пропорциональны.
Чтобы показать, что треугольники подобны, достаточно показать, что три набора соответствующих сторон пропорциональны.
Теорема:
Если три набора соответствующих сторон двух треугольников пропорциональны, треугольники подобны.
SAS для подобия
SAS для подобных треугольников — это НЕ та же теорема, которую мы использовали для конгруэнтных треугольников. Чтобы показать, что треугольники подобны, достаточно показать, что два набора соответствующих сторон пропорциональны, а углы, которые они включают, совпадают.
Теорема:
Если угол одного треугольника конгруэнтен соответствующему углу другого треугольника и длины сторон, включая эти углы, пропорциональны, треугольники подобны.
Если треугольники похожи:
Теорема:
Соответствующие стороны подобных треугольников пропорциональны.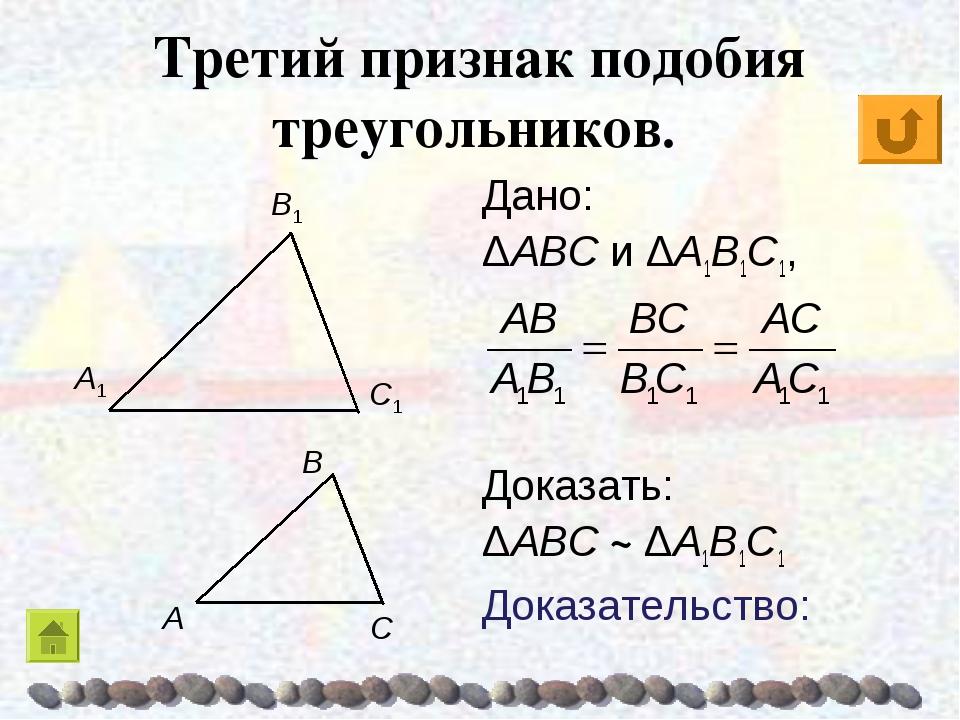
Работа с перекрывающимися треугольниками:
Во многих задачах, связанных с похожими треугольниками, один треугольник находится НА ВЕРХ (перекрытии) другого треугольника.
Поскольку \ (\ overline {DE} \) отмечен как параллельный \ (\ overline {AC} \), мы знаем, что у нас есть ∠BDE, конгруэнтное ∠DAC (по соответствующим углам). ∠B является общим для обоих треугольников, поэтому два треугольника похожи на AA.
Существует дополнительная теорема, которую можно использовать при работе с перекрывающимися треугольниками:
Дополнительная теорема: Если прямая параллельна одной стороне треугольника и пересекает две другие стороны треугольника, прямая делит эти две стороны пропорционально .
ярлыков подобия — Концепция — Геометрия Видео от Brightstorm
Существует четыре ярлыка конгруэнтности треугольника: SSS, SAS, ASA и AAS. У нас есть подобие треугольника, если (1) две пары углов конгруэнтны (AA) (2) две пары сторон пропорциональны, а включенные углы конгруэнтны (SAS), или (3) если три пары сторон пропорциональны (SSS) .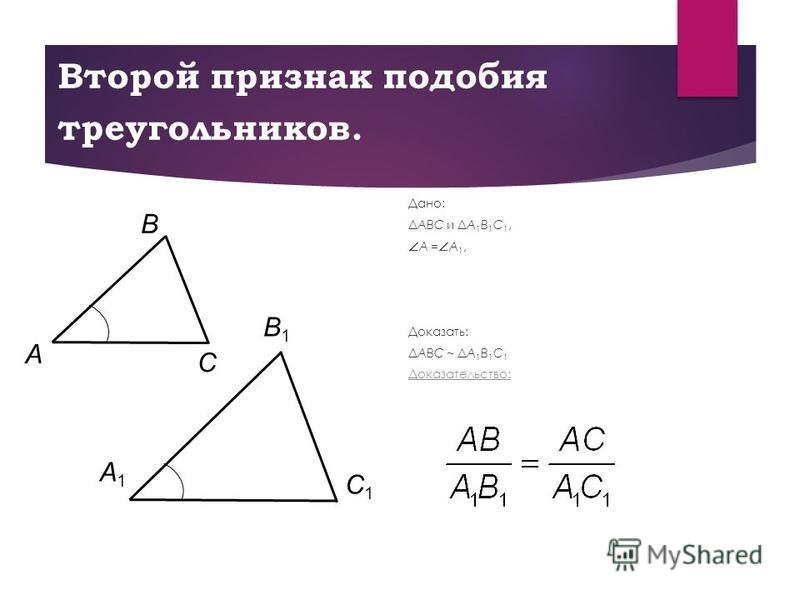 Обратите внимание, что AAA, AAS и ASA не указаны — их включение было бы излишним, поскольку все они имеют два совпадающих угла.
Обратите внимание, что AAA, AAS и ASA не указаны — их включение было бы излишним, поскольку все они имеют два совпадающих угла.
Если вам нужно доказать, что два треугольника похожи, мы проведем сравнение с конгруэнтностью, о чем мы говорили ранее. Мы сказали, что существует 4 простых способа доказать конгруэнтность двух треугольников. И эти 4 ярлыка были угловыми, боковыми, боковыми, боковыми и угловыми.
Итак, если бы вы знали только три вещи об этих двух треугольниках, если это один из этих ярлыков, то да, вы могли бы сказать, что эти треугольники должны быть конгруэнтными.Есть два, которые не сработали. И это были угловые и боковые углы. Таким образом, эти два ярлыка не дали вам достаточно информации, чтобы сказать, что эти два треугольника должны быть конгруэнтными, потому что, используя только три угла, вы можете построить два треугольника разных размеров.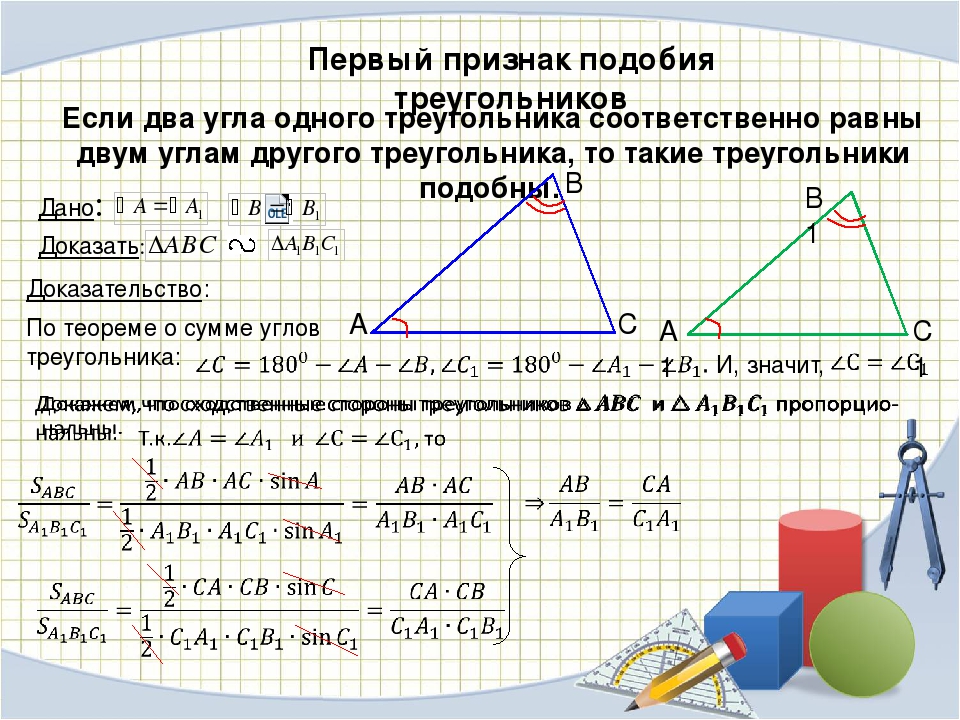
Мы собираемся провести сравнение со сходством. Давайте начнем с рассмотрения случая, когда все, что мы знаем о двух треугольниках, — это то, что два угла совпадают. Но сумма углов треугольника, если эти два угла конгруэнтны, то третий угол в каждом из этих треугольников должен быть конгруэнтным.И да, это был бы ярлык для того, чтобы сказать, что эти два треугольника должны быть похожими. Это означает, что соответствующие углы равны, а соответствующие стороны пропорциональны. Итак, под нашими ярлыками подобия я собираюсь использовать здесь другой маркер. Этот на исходе. Мы собираемся сказать, что угол — это сокращение.
Теперь обратите внимание, что я не записал угол, угол, угол. Причина в том, что если все, что вы знаете, это 2 угла, этого достаточно, потому что третий угол, который, я думаю, я мог бы записать, также должен быть конгруэнтным.Таким образом, угловой угол — это ярлык.
Рассмотрим второй случай. Допустим, все, что вы знали, — это сторона, включенный угол и другая сторона. И вы также знали, что соответствующие стороны пропорциональны. Что ж, этой информации было бы достаточно, чтобы сказать, что эти два треугольника похожи. Итак, мы собираемся включить сторону бокового угла в наш список ярлыков подобия. И последнее, допустим, если бы все, что мы знали, это то, что 3 стороны двух разных треугольников, которые соответствуют друг другу, пропорциональны. Таким образом, мы могли бы записать эту пропорцию, которая постоянна между соответствующими сторонами.Эти два треугольника также должны быть конгруэнтными. Итак, мы собираемся сказать, что эта боковая сторона также является ярлыком.
И вы также знали, что соответствующие стороны пропорциональны. Что ж, этой информации было бы достаточно, чтобы сказать, что эти два треугольника похожи. Итак, мы собираемся включить сторону бокового угла в наш список ярлыков подобия. И последнее, допустим, если бы все, что мы знали, это то, что 3 стороны двух разных треугольников, которые соответствуют друг другу, пропорциональны. Таким образом, мы могли бы записать эту пропорцию, которая постоянна между соответствующими сторонами.Эти два треугольника также должны быть конгруэнтными. Итак, мы собираемся сказать, что эта боковая сторона также является ярлыком.
Теперь, если я сравню эти два списка, вы заметите, что я пропустил угол стороны угла. И это я пропустил угловую сторону. Причина в том, что если вы знаете, что эти два угла совпадают, то это просто сокращение угла. То же самое и с ярлыком «угол угол». Пока вы знаете, что два угла совпадают, это все, что мне нужно знать для сходства.
Теперь вы заметите, что в этом списке нет бокового угла. Так что это что-то вроде странного человека, ищущего совпадения и сходства. Этой информации недостаточно, чтобы сказать, что 2 треугольника должны быть похожими. Таким образом, у вас есть только три ярлыка сходства, которые вам нужно запомнить. Угол, сторона, о нет, я как бы стер это там. Угловой угол, сторона бокового угла и боковая сторона стороны.
Так что это что-то вроде странного человека, ищущего совпадения и сходства. Этой информации недостаточно, чтобы сказать, что 2 треугольника должны быть похожими. Таким образом, у вас есть только три ярлыка сходства, которые вам нужно запомнить. Угол, сторона, о нет, я как бы стер это там. Угловой угол, сторона бокового угла и боковая сторона стороны.
% PDF-1.4
%
469 0 объект
>
эндобдж
xref
469 87
0000000016 00000 н.
0000003314 00000 н.
0000003399 00000 н.
0000003637 00000 н.
0000004083 00000 н.
0000004160 00000 н.
0000004235 00000 н.
0000004313 00000 н.
0000004573 00000 н.
0000007913 00000 п.
0000008309 00000 н.
0000008708 00000 н.
0000009587 00000 н.
0000009758 00000 н.
0000010098 00000 п.
0000010510 00000 п.
0000010898 00000 п.
0000016237 00000 п.
0000016499 00000 н.
0000016920 00000 н.
0000017403 00000 п.
0000017772 00000 п.
0000024388 00000 п.
0000024660 00000 п.
0000025017 00000 п.
0000025675 00000 п.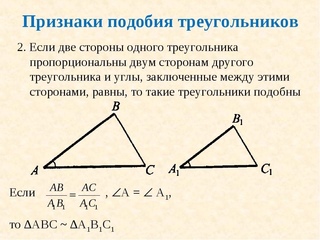
0000026113 00000 п.
0000026352 00000 п.
0000027094 00000 п.
0000027792 00000 п.
0000028218 00000 п.
0000028940 00000 п.
0000029362 00000 п.
0000029635 00000 п.
0000029683 00000 п.
0000029720 00000 н.
0000029773 00000 п.
0000030119 00000 п.
0000030427 00000 п.
0000030505 00000 п.
0000030581 00000 п.
0000032039 00000 п.
0000032542 00000 п.
0000032765 00000 п.
0000032831 00000 п.
0000033214 00000 п.
0000033412 00000 п.
0000033621 00000 п.
0000033912 00000 п.
0000034929 00000 п.
0000035215 00000 п.
0000035478 00000 п.
0000036732 00000 п.
0000037390 00000 п.
0000038137 00000 п.
0000038557 00000 п.
0000038953 00000 п.
0000042378 00000 п.
0000042653 00000 п.
0000043023 00000 п.
0000043334 00000 п.
0000046622 00000 н.
0000046799 00000 н.
0000046850 00000 п.
0000048075 00000 п.
0000048337 00000 п.
0000048714 00000 п.
0000049956 00000 н.
0000050484 00000 п.
0000062212 00000 п.
0000072985 00000 п.
0000074528 00000 п.
0000077220 00000 п.
0000078175 00000 п.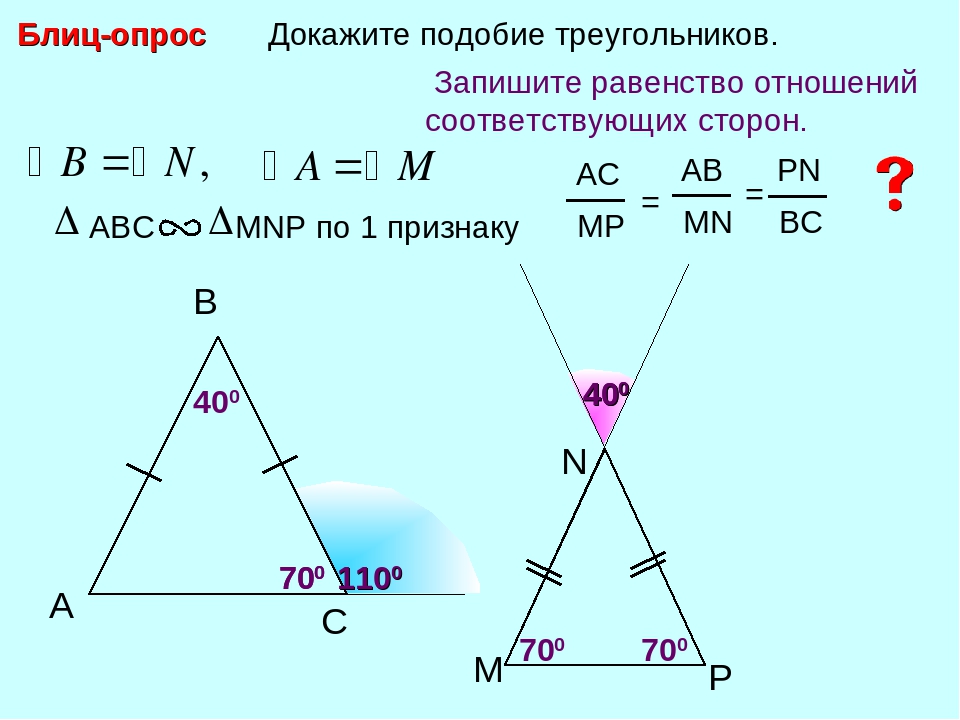
0000082924 00000 н.
0000086284 00000 п.
0000087632 00000 п.
0000088211 00000 п.
0000094756 00000 п.
0000095831 00000 п.
0000096958 00000 п.
0000114556 00000 н.
0000116288 00000 н.
0000117492 00000 н.
0000135090 00000 н.
0000136852 00000 н.
0000002036 00000 н.
трейлер
] / Назад 1085746 >>
startxref
0
%% EOF
555 0 объект
> поток
h ޤ iP [У {Y’aAaZ
BX23 $! EP
V-Ԥ5Uhmþ غ R ֵ RV.@ g3ww9-
|
Листы доказательства подобия треугольников
Как доказать подобие треугольников?
Подобные фигуры определяются как геометрические фигуры, которые имеют одинаковую форму, но разные размеры. Обычно мы используем три теоремы, чтобы установить подобие треугольников. Три задействованные теоремы: сторона-угол-сторона (SAS), угол-угол (AA) и сторона-сторона-сторона (SSS).
Угол-угол (AA) Теорема — Угол-угол (AA) теорема гласит, что два треугольника подобны, если две пары соответствующих им углов совпадают. Они могут казаться идентичными. Чтобы установить их конгруэнтность с помощью этой теоремы, вам нужно только сравнить две пары соответствующих углов.
Боковой угол-сторона (SAS) Теорема — В этой теореме следует порядок стороны, включенного угла и затем стороны. Теорема SAS гласит, что два треугольника подобны, если две стороны треугольника пропорциональны двум соответствующим сторонам второго треугольника, а включенные углы конгруэнтны. Теорема Сторона-Сторона-Сторона (SSS) — Последняя теорема, рассказывающая нам о конгруэнтности треугольника, утверждает, что если все три стороны одного треугольника пропорциональны всем трем соответствующим сторонам второго треугольника, то эти два треугольника равны конгруэнтный.
Теорема Сторона-Сторона-Сторона (SSS) — Последняя теорема, рассказывающая нам о конгруэнтности треугольника, утверждает, что если все три стороны одного треугольника пропорциональны всем трем соответствующим сторонам второго треугольника, то эти два треугольника равны конгруэнтный.
В геометрии треугольника мы часто пытаемся доказать, что два или более треугольника подобны. Если они похожи, они не одинаковы, но их соответствующие углы и стороны пропорциональны друг другу.Мы можем доказать сходство с помощью ряда различных методов, и все это основано на ситуации. Мы можем использовать постулат подобия угла-угла, если оба треугольника имеют две пары совпадающих углов. Если длины соответствующих сторон треугольников пропорциональны, мы можем использовать постулат углового подобия. Если они имеют одинаковый угол и соответствующие ветви этого угла равны по длине, мы можем использовать теорему подобия стороны-угла-стороны. Эти рабочие листы объясняют, как определить, есть ли треугольники и тому подобное, и как использовать сходство для решения проблем.

 Вот тот, в котором используются похожие треугольники.
Вот тот, в котором используются похожие треугольники.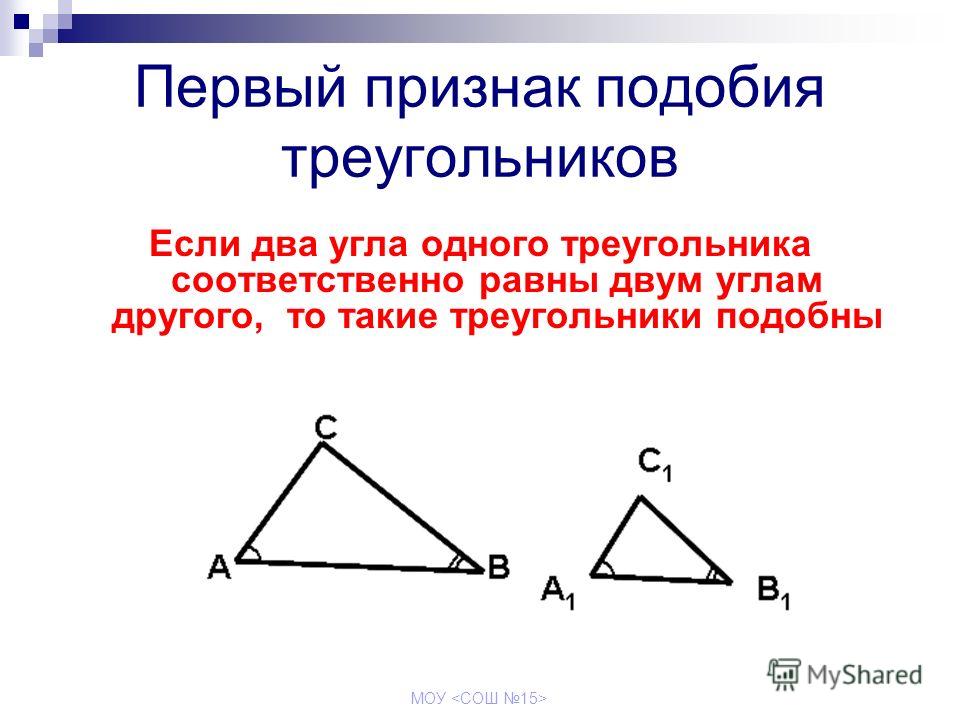 Оба имеют угол 90 °, и ∠CAB и .∠CAE имеют одинаковый угол. Если у них два равных угла, то по критерию сходства АА треугольники подобны. Убедившись, что вы записали заявление о подобии, можно сказать, что соответствующие углы конгруэнтны.
Оба имеют угол 90 °, и ∠CAB и .∠CAE имеют одинаковый угол. Если у них два равных угла, то по критерию сходства АА треугольники подобны. Убедившись, что вы записали заявление о подобии, можно сказать, что соответствующие углы конгруэнтны.